Сортировка слиянием (англ. Merge sort) — алгоритм сортировки, использующий дополнительной памяти и работающий за времени.
Содержание
- 1 Принцип работы
- 1.1 Слияние двух массивов
- 1.2 Рекурсивный алгоритм
- 1.3 Итеративный алгоритм
- 2 Время работы
- 3 Сравнение с другими алгоритмами
- 4 См. также
- 5 Примечания
- 6 Источники информации
Принцип работы
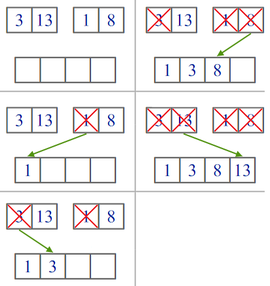
Пример работы процедуры слияния.
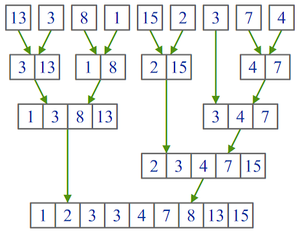
Пример работы рекурсивного алгоритма сортировки слиянием
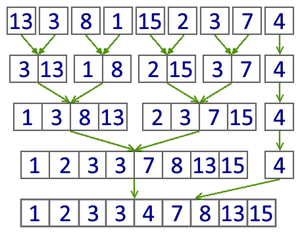
Пример работы итеративного алгоритма сортировки слиянием
Алгоритм использует принцип «разделяй и властвуй»: задача разбивается на подзадачи меньшего размера, которые решаются по отдельности, после чего их решения комбинируются для получения решения исходной задачи. Конкретно процедуру сортировки слиянием можно описать следующим образом:
- Если в рассматриваемом массиве один элемент, то он уже отсортирован — алгоритм завершает работу.
- Иначе массив разбивается на две части, которые сортируются рекурсивно.
- После сортировки двух частей массива к ним применяется процедура слияния, которая по двум отсортированным частям получает исходный отсортированный массив.
Слияние двух массивов
У нас есть два массива и (фактически это будут две части одного массива, но для удобства будем писать, что у нас просто два массива). Нам надо получить массив размером . Для этого можно применить процедуру слияния. Эта процедура заключается в том, что мы сравниваем элементы массивов (начиная с начала) и меньший из них записываем в финальный. И затем, в массиве у которого оказался меньший элемент, переходим к следующему элементу и сравниваем теперь его. В конце, если один из массивов закончился, мы просто дописываем в финальный другой массив. После мы наш финальный массив записываем заместо двух исходных и получаем отсортированный участок.
Множество отсортированных списков с операцией является моноидом, где нейтральным элементом будет пустой список.
Ниже приведён псевдокод процедуры слияния, который сливает две части массива — и
function merge(a : int[n]; left, mid, right : int):
it1 = 0
it2 = 0
result : int[right - left]
while left + it1 < mid and mid + it2 < right
if a[left + it1] < a[mid + it2]
result[it1 + it2] = a[left + it1]
it1 += 1
else
result[it1 + it2] = a[mid + it2]
it2 += 1
while left + it1 < mid
result[it1 + it2] = a[left + it1]
it1 += 1
while mid + it2 < right
result[it1 + it2] = a[mid + it2]
it2 += 1
for i = 0 to it1 + it2
a[left + i] = result[i]
Рекурсивный алгоритм
Функция сортирует подотрезок массива с индексами в полуинтервале .
function mergeSortRecursive(a : int[n]; left, right : int):
if left + 1 >= right
return
mid = (left + right) / 2
mergeSortRecursive(a, left, mid)
mergeSortRecursive(a, mid, right)
merge(a, left, mid, right)
Итеративный алгоритм
При итеративном алгоритме используется на меньше памяти, которая раньше тратилась на рекурсивные вызовы.
function mergeSortIterative(a : int[n]):
for i = 1 to n, i *= 2
for j = 0 to n - i, j += 2 * i
merge(a, j, j + i, min(j + 2 * i, n))
Время работы
Чтобы оценить время работы этого алгоритма, составим рекуррентное соотношение. Пускай — время сортировки массива длины , тогда для сортировки слиянием справедливо
— время, необходимое на то, чтобы слить два массива длины . Распишем это соотношение:
.
Сравнение с другими алгоритмами
Достоинства:
- устойчивая,
- можно написать эффективную многопоточную сортировку слиянием,
- сортировка данных, расположенных на периферийных устройствах и не вмещающихся в оперативную память[1].
Недостатки:
- требуется дополнительно памяти, но можно модифицировать до .
См. также
- Сортировка кучей
- Быстрая сортировка
- Timsort
- Cортировка слиянием с использованием O(1) дополнительной памяти
Примечания
- ↑ Wikipedia — External sorting
Источники информации
- Википедия — сортировка слиянием
- Визуализатор
- Викиучебник — Примеры реализации на различных языках программирования
Merge sort is a sorting algorithm that works by dividing an array into smaller subarrays, sorting each subarray, and then merging the sorted subarrays back together to form the final sorted array.
In simple terms, we can say that the process of merge sort is to divide the array into two halves, sort each half, and then merge the sorted halves back together. This process is repeated until the entire array is sorted.
One thing that you might wonder is what is the specialty of this algorithm. We already have a number of sorting algorithms then why do we need this algorithm? One of the main advantages of merge sort is that it has a time complexity of O(n log n), which means it can sort large arrays relatively quickly. It is also a stable sort, which means that the order of elements with equal values is preserved during the sort.
Merge sort is a popular choice for sorting large datasets because it is relatively efficient and easy to implement. It is often used in conjunction with other algorithms, such as quicksort, to improve the overall performance of a sorting routine.
Merge Sort Working Process:
Think of it as a recursive algorithm continuously splits the array in half until it cannot be further divided. This means that if the array becomes empty or has only one element left, the dividing will stop, i.e. it is the base case to stop the recursion. If the array has multiple elements, split the array into halves and recursively invoke the merge sort on each of the halves. Finally, when both halves are sorted, the merge operation is applied. Merge operation is the process of taking two smaller sorted arrays and combining them to eventually make a larger one.
Illustration:
To know the functioning of merge sort, lets consider an array arr[] = {38, 27, 43, 3, 9, 82, 10}
- At first, check if the left index of array is less than the right index, if yes then calculate its mid point
- Now, as we already know that merge sort first divides the whole array iteratively into equal halves, unless the atomic values are achieved.
- Here, we see that an array of 7 items is divided into two arrays of size 4 and 3 respectively.
- Now, again find that is left index is less than the right index for both arrays, if found yes, then again calculate mid points for both the arrays.
- Now, further divide these two arrays into further halves, until the atomic units of the array is reached and further division is not possible.
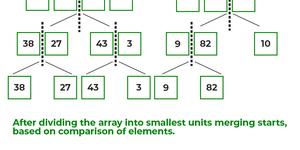
- After dividing the array into smallest units, start merging the elements again based on comparison of size of elements
- Firstly, compare the element for each list and then combine them into another list in a sorted manner.
- After the final merging, the list looks like this:
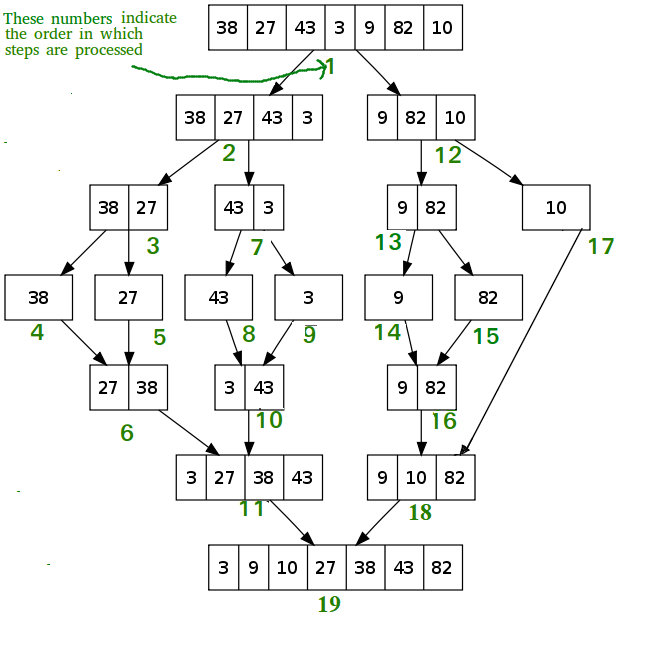
The following diagram shows the complete merge sort process for an example array {38, 27, 43, 3, 9, 82, 10}.
If we take a closer look at the diagram, we can see that the array is recursively divided into two halves till the size becomes 1. Once the size becomes 1, the merge processes come into action and start merging arrays back till the complete array is merged.
Recursive steps of merge sort
Algorithm:
step 1: start
step 2: declare array and left, right, mid variable
step 3: perform merge function.
if left > right
return
mid= (left+right)/2
mergesort(array, left, mid)
mergesort(array, mid+1, right)
merge(array, left, mid, right)step 4: Stop
Follow the steps below to solve the problem:
MergeSort(arr[], l, r)
If r > l
- Find the middle point to divide the array into two halves:
- middle m = l + (r – l)/2
- Call mergeSort for first half:
- Call mergeSort(arr, l, m)
- Call mergeSort for second half:
- Call mergeSort(arr, m + 1, r)
- Merge the two halves sorted in steps 2 and 3:
- Call merge(arr, l, m, r)
Below is the implementation of the above approach:
C++
#include <iostream>
using namespace std;
void merge(int array[], int const left, int const mid,
int const right)
{
auto const subArrayOne = mid - left + 1;
auto const subArrayTwo = right - mid;
auto *leftArray = new int[subArrayOne],
*rightArray = new int[subArrayTwo];
for (auto i = 0; i < subArrayOne; i++)
leftArray[i] = array[left + i];
for (auto j = 0; j < subArrayTwo; j++)
rightArray[j] = array[mid + 1 + j];
auto indexOfSubArrayOne
= 0,
indexOfSubArrayTwo
= 0;
int indexOfMergedArray
= left;
while (indexOfSubArrayOne < subArrayOne
&& indexOfSubArrayTwo < subArrayTwo) {
if (leftArray[indexOfSubArrayOne]
<= rightArray[indexOfSubArrayTwo]) {
array[indexOfMergedArray]
= leftArray[indexOfSubArrayOne];
indexOfSubArrayOne++;
}
else {
array[indexOfMergedArray]
= rightArray[indexOfSubArrayTwo];
indexOfSubArrayTwo++;
}
indexOfMergedArray++;
}
while (indexOfSubArrayOne < subArrayOne) {
array[indexOfMergedArray]
= leftArray[indexOfSubArrayOne];
indexOfSubArrayOne++;
indexOfMergedArray++;
}
while (indexOfSubArrayTwo < subArrayTwo) {
array[indexOfMergedArray]
= rightArray[indexOfSubArrayTwo];
indexOfSubArrayTwo++;
indexOfMergedArray++;
}
delete[] leftArray;
delete[] rightArray;
}
void mergeSort(int array[], int const begin, int const end)
{
if (begin >= end)
return;
auto mid = begin + (end - begin) / 2;
mergeSort(array, begin, mid);
mergeSort(array, mid + 1, end);
merge(array, begin, mid, end);
}
void printArray(int A[], int size)
{
for (auto i = 0; i < size; i++)
cout << A[i] << " ";
}
int main()
{
int arr[] = { 12, 11, 13, 5, 6, 7 };
auto arr_size = sizeof(arr) / sizeof(arr[0]);
cout << "Given array is n";
printArray(arr, arr_size);
mergeSort(arr, 0, arr_size - 1);
cout << "nSorted array is n";
printArray(arr, arr_size);
return 0;
}
C
#include <stdio.h>
#include <stdlib.h>
void merge(int arr[], int l, int m, int r)
{
int i, j, k;
int n1 = m - l + 1;
int n2 = r - m;
int L[n1], R[n2];
for (i = 0; i < n1; i++)
L[i] = arr[l + i];
for (j = 0; j < n2; j++)
R[j] = arr[m + 1 + j];
i = 0;
j = 0;
k = l;
while (i < n1 && j < n2) {
if (L[i] <= R[j]) {
arr[k] = L[i];
i++;
}
else {
arr[k] = R[j];
j++;
}
k++;
}
while (i < n1) {
arr[k] = L[i];
i++;
k++;
}
while (j < n2) {
arr[k] = R[j];
j++;
k++;
}
}
void mergeSort(int arr[], int l, int r)
{
if (l < r) {
int m = l + (r - l) / 2;
mergeSort(arr, l, m);
mergeSort(arr, m + 1, r);
merge(arr, l, m, r);
}
}
void printArray(int A[], int size)
{
int i;
for (i = 0; i < size; i++)
printf("%d ", A[i]);
printf("n");
}
int main()
{
int arr[] = { 12, 11, 13, 5, 6, 7 };
int arr_size = sizeof(arr) / sizeof(arr[0]);
printf("Given array is n");
printArray(arr, arr_size);
mergeSort(arr, 0, arr_size - 1);
printf("nSorted array is n");
printArray(arr, arr_size);
return 0;
}
Java
class MergeSort {
void merge(int arr[], int l, int m, int r)
{
int n1 = m - l + 1;
int n2 = r - m;
int L[] = new int[n1];
int R[] = new int[n2];
for (int i = 0; i < n1; ++i)
L[i] = arr[l + i];
for (int j = 0; j < n2; ++j)
R[j] = arr[m + 1 + j];
int i = 0, j = 0;
int k = l;
while (i < n1 && j < n2) {
if (L[i] <= R[j]) {
arr[k] = L[i];
i++;
}
else {
arr[k] = R[j];
j++;
}
k++;
}
while (i < n1) {
arr[k] = L[i];
i++;
k++;
}
while (j < n2) {
arr[k] = R[j];
j++;
k++;
}
}
void sort(int arr[], int l, int r)
{
if (l < r) {
int m = l + (r - l) / 2;
sort(arr, l, m);
sort(arr, m + 1, r);
merge(arr, l, m, r);
}
}
static void printArray(int arr[])
{
int n = arr.length;
for (int i = 0; i < n; ++i)
System.out.print(arr[i] + " ");
System.out.println();
}
public static void main(String args[])
{
int arr[] = { 12, 11, 13, 5, 6, 7 };
System.out.println("Given Array");
printArray(arr);
MergeSort ob = new MergeSort();
ob.sort(arr, 0, arr.length - 1);
System.out.println("nSorted array");
printArray(arr);
}
}
Python3
def mergeSort(arr):
if len(arr) > 1:
mid = len(arr)//2
L = arr[:mid]
R = arr[mid:]
mergeSort(L)
mergeSort(R)
i = j = k = 0
while i < len(L) and j < len(R):
if L[i] <= R[j]:
arr[k] = L[i]
i += 1
else:
arr[k] = R[j]
j += 1
k += 1
while i < len(L):
arr[k] = L[i]
i += 1
k += 1
while j < len(R):
arr[k] = R[j]
j += 1
k += 1
def printList(arr):
for i in range(len(arr)):
print(arr[i], end=" ")
print()
if __name__ == '__main__':
arr = [12, 11, 13, 5, 6, 7]
print("Given array is", end="n")
printList(arr)
mergeSort(arr)
print("Sorted array is: ", end="n")
printList(arr)
C#
using System;
class MergeSort {
void merge(int[] arr, int l, int m, int r)
{
int n1 = m - l + 1;
int n2 = r - m;
int[] L = new int[n1];
int[] R = new int[n2];
int i, j;
for (i = 0; i < n1; ++i)
L[i] = arr[l + i];
for (j = 0; j < n2; ++j)
R[j] = arr[m + 1 + j];
i = 0;
j = 0;
int k = l;
while (i < n1 && j < n2) {
if (L[i] <= R[j]) {
arr[k] = L[i];
i++;
}
else {
arr[k] = R[j];
j++;
}
k++;
}
while (i < n1) {
arr[k] = L[i];
i++;
k++;
}
while (j < n2) {
arr[k] = R[j];
j++;
k++;
}
}
void sort(int[] arr, int l, int r)
{
if (l < r) {
int m = l + (r - l) / 2;
sort(arr, l, m);
sort(arr, m + 1, r);
merge(arr, l, m, r);
}
}
static void printArray(int[] arr)
{
int n = arr.Length;
for (int i = 0; i < n; ++i)
Console.Write(arr[i] + " ");
Console.WriteLine();
}
public static void Main(String[] args)
{
int[] arr = { 12, 11, 13, 5, 6, 7 };
Console.WriteLine("Given Array");
printArray(arr);
MergeSort ob = new MergeSort();
ob.sort(arr, 0, arr.Length - 1);
Console.WriteLine("nSorted array");
printArray(arr);
}
}
Javascript
<script>
function merge(arr, l, m, r)
{
var n1 = m - l + 1;
var n2 = r - m;
var L = new Array(n1);
var R = new Array(n2);
for (var i = 0; i < n1; i++)
L[i] = arr[l + i];
for (var j = 0; j < n2; j++)
R[j] = arr[m + 1 + j];
var i = 0;
var j = 0;
var k = l;
while (i < n1 && j < n2) {
if (L[i] <= R[j]) {
arr[k] = L[i];
i++;
}
else {
arr[k] = R[j];
j++;
}
k++;
}
while (i < n1) {
arr[k] = L[i];
i++;
k++;
}
while (j < n2) {
arr[k] = R[j];
j++;
k++;
}
}
function mergeSort(arr,l, r){
if(l>=r){
return;
}
var m =l+ parseInt((r-l)/2);
mergeSort(arr,l,m);
mergeSort(arr,m+1,r);
merge(arr,l,m,r);
}
function printArray( A, size)
{
for (var i = 0; i < size; i++)
document.write( A[i] + " ");
}
var arr = [ 12, 11, 13, 5, 6, 7 ];
var arr_size = arr.length;
document.write( "Given array is <br>");
printArray(arr, arr_size);
mergeSort(arr, 0, arr_size - 1);
document.write( "<br>Sorted array is <br>");
printArray(arr, arr_size);
</script>
PHP
<?php
function merge(&$arr, $l, $m, $r)
{
$n1 = $m - $l + 1;
$n2 = $r - $m;
$L = array();
$R = array();
for ($i = 0; $i < $n1; $i++)
$L[$i] = $arr[$l + $i];
for ($j = 0; $j < $n2; $j++)
$R[$j] = $arr[$m + 1 + $j];
$i = 0;
$j = 0;
$k = $l;
while ($i < $n1 && $j < $n2) {
if ($L[$i] <= $R[$j]) {
$arr[$k] = $L[$i];
$i++;
}
else {
$arr[$k] = $R[$j];
$j++;
}
$k++;
}
while ($i < $n1) {
$arr[$k] = $L[$i];
$i++;
$k++;
}
while ($j < $n2) {
$arr[$k] = $R[$j];
$j++;
$k++;
}
}
function mergeSort(&$arr, $l, $r)
{
if ($l < $r) {
$m = $l + (int)(($r - $l) / 2);
mergeSort($arr, $l, $m);
mergeSort($arr, $m + 1, $r);
merge($arr, $l, $m, $r);
}
}
function printArray($A, $size)
{
for ($i = 0; $i < $size; $i++)
echo $A[$i]." ";
echo "n";
}
$arr = array(12, 11, 13, 5, 6, 7);
$arr_size = sizeof($arr);
echo "Given array is n";
printArray($arr, $arr_size);
mergeSort($arr, 0, $arr_size - 1);
echo "nSorted array is n";
printArray($arr, $arr_size);
return 0;
?>
Output
Given array is 12 11 13 5 6 7 Sorted array is 5 6 7 11 12 13
Time Complexity: O(N log(N)), Sorting arrays on different machines. Merge Sort is a recursive algorithm and time complexity can be expressed as following recurrence relation.
T(n) = 2T(n/2) + θ(n)
The above recurrence can be solved either using the Recurrence Tree method or the Master method. It falls in case II of the Master Method and the solution of the recurrence is θ(Nlog(N)). The time complexity of Merge Sort isθ(Nlog(N)) in all 3 cases (worst, average, and best) as merge sort always divides the array into two halves and takes linear time to merge two halves.
Auxiliary Space: O(n), In merge sort all elements are copied into an auxiliary array. So N auxiliary space is required for merge sort.
Is Merge sort In Place?
No, In merge sort the merging step requires extra space to store the elements.
Is Merge sort Stable?
Yes, merge sort is stable.
How can we make Merge sort more efficient?
Merge sort can be made more efficient by replacing recursive calls with Insertion sort for smaller array sizes, where the size of the remaining array is less or equal to 43 as the number of operations required to sort an array of max size 43 will be less in Insertion sort as compared to the number of operations required in Merge sort.
Analysis of Merge Sort:
A merge sort consists of several passes over the input. The first pass merges segments of size 1, the second merges segments of size 2, and the pass merges segments of size 2i-1. Thus, the total number of passes is [log2n]. As merge showed, we can merge two sorted segments in linear time, which means that each pass takes O(n) time. Since there are [log2n] passes, the total computing time is O(nlogn).
Applications of Merge Sort:
- Merge Sort is useful for sorting linked lists in O(N log N) time. In the case of linked lists, the case is different mainly due to the difference in memory allocation of arrays and linked lists. Unlike arrays, linked list nodes may not be adjacent in memory. Unlike an array, in the linked list, we can insert items in the middle in O(1) extra space and O(1) time. Therefore, the merge operation of merge sort can be implemented without extra space for linked lists.
In arrays, we can do random access as elements are contiguous in memory. Let us say we have an integer (4-byte) array A and let the address of A[0] be x then to access A[i], we can directly access the memory at (x + i*4). Unlike arrays, we can not do random access in the linked list. Quick Sort requires a lot of this kind of access. In a linked list to access i’th index, we have to travel each and every node from the head to i’th node as we don’t have a contiguous block of memory. Therefore, the overhead increases for quicksort. Merge sort accesses data sequentially and the need of random access is low. - Inversion Count Problem
- Used in External Sorting
Advantages of Merge Sort:
- Merge sort has a time complexity of O(n log n), which means it is relatively efficient for sorting large datasets.
- Merge sort is a stable sort, which means that the order of elements with equal values is preserved during the sort.
- It is easy to implement thus making it a good choice for many applications.
- It is useful for external sorting. This is because merge sort can handle large datasets, it is often used for external sorting, where the data being sorted does not fit in memory.
- The merge sort algorithm can be easily parallelized, which means it can take advantage of multiple processors or cores to sort the data more quickly.
- Merge sort requires relatively few additional resources (such as memory) to perform the sort. This makes it a good choice for systems with limited resources.
Drawbacks of Merge Sort:
- Slower compared to the other sort algorithms for smaller tasks. Although effecient for large datasets its not the best choice for small datasets.
- The merge sort algorithm requires an additional memory space of 0(n) for the temporary array. This is to store the subarrays that are used during the sorting process.
- It goes through the whole process even if the array is sorted.
- It requires more code to implement since we are dividing the array into smaller subarrays and then merging the sorted subarrays back together.
- Recent Articles on Merge Sort
- Coding practice for sorting.
- Quiz on Merge Sort
Solution of the drawback for additional storage:
Use linked list.
Other Sorting Algorithms on GeeksforGeeks:
3-way Merge Sort, Selection Sort, Bubble Sort, Insertion Sort, Merge Sort, Heap Sort, QuickSort, Radix Sort, Counting Sort, Bucket Sort, ShellSort, Comb Sort
Please write comments if you find anything incorrect, or if you want to share more information about the topic discussed above.
Сортировка — это процесс, который используют для упорядочивания элементов определенным образом. Алгоритм сортировки нужен для перегруппировки заданного массива в соответствии с определенным порядком. Он может сортировать массив в возрастающем или убывающем порядке. Используем алгоритм сортировки, потому что он помогает нам легко и быстро находить элементы в списке массивов. Основная цель алгоритмов сортировки — упростить поиск, добавление и удаление записей. Существуют разные типы алгоритмов сортировки, такие как:
-
Сортировка выбором.
-
Сортировка вставками.
-
Поразрядная сортировка.
-
Сортировка пузырьком.
-
Сортировка слиянием.
-
Пирамидальная сортировка.
-
Быстрая сортировка.
Сортировка слиянием — это алгоритм, который используется для сортировки последовательности элементов. Сначала массив разделяется на несколько подгрупп меньшего размера. Когда разделение завершилось, они снова объединяются. Во время этого процесса номера этих групп сортируются в возрастающем порядке. Когда были объединены группы с несколькими номерами, сравниваются по первому.
С этого момента список несортированных массивов делится на две части, это повторяется до тех пор, пока все элементы не будут разделены. Затем элементы сравниваются попарно, сортируются и объединяются. Этот процесс воспроизводиться до тех пор, пока список не будет перекомпилирован в один отсортированный список.
Сортировка слиянием работает, многократно разбивая данный массив на подмассив. А затем можно разбить их на дополнительные подмассивы. Когда размер подмассивов станет одним, мы объединим их, чтобы получить отсортированный массив. Сортировка слиянием выполняется рекурсивно.
Наибольшая временная сложность алгоритма равна O( nlog n ).
Принцип работы
Сортировка слиянием — это эффективный алгоритм сортировки. Он работает по технике «Разделяй и властвуй».
-
Разделяй: Это включает в себя разделение списка входных массивов на два списка одинакового размера.
-
Властвуй: То есть рекурсивная сортировка подсписоков.
-
Соединяй: Слияние обоих отсортированных подсписоков в один.
По этой технике большая задача делится на более мелкие части, а затем эти мелкие части которые легче будет решить, а затем их можно объединить, чтобы получить окончательный результат. В этом случае весь массив разделен на подсписок n. В каждом подсписке будет один элемент. И мы будем продолжать делить подсписок, пока не получим подсписок с одним элементом. Затем, наконец, мы объединяем каждый из подсписок, и этот процесс объединения подсписок продолжается до тех пор, пока мы не получим новый отсортированный подсписок. И мы продолжаем объединять подсписки, пока не получим окончательный полный отсортированный список.
Принцип работы включает следующие шаги:
-
Разделить заданный массив на подсписок;
-
Объединить подсписки для получения одного полного отсортированного списка.
Возьмем к примеру массив из пяти элементов от 0 до 4. Этот массив будет разделен на две (левую и правую) части. Левая часть массива содержит 2 элемента, а правая часть — 3 элемента. Левая часть также будет разделена на две части, и тогда мы получим два отдельных подсписка. Как только мы получим отсортированные подсписки для левой части, они будут объединены в один отсортированный левый массив.
Теперь отсортируем правую часть массива, сначала разделив его на две части. Правая часть теперь будет содержать еще две части, то есть левую и правую части. Левая часть содержит только один элемент, а правая часть содержит два элемента. Левая часть уже отсортирована. Итак, теперь мы отсортируем правую часть, разделив ее на две части. Теперь эти две отсортированные части правой части будут объединены. Затем отсортированные слева и справа части правой стороны будут объединены в один отсортированный правый массив. Наконец, мы получим единый отсортированный массив / список, объединив отсортированный слева и справа массив.
Пример
Чтобы понять эту концепцию, давайте рассмотрим массив «B», который приведен ниже. В этом массиве всего девять элементов.
Мы разделим этот массив на два подмассива. Для этого мы найдем его среднюю точку, а затем разделим этот массив от этой средней точки. Итак, находим средину:
Итак, этот массив разделен по индексу 4, подмассивы будут:
Теперь мы разделим эти два подсписка на дополнительные подсписки, чтобы в итоге получить подсписок только с одним элементом. Опять же, мы сначала будем ставить среднюю точку для каждого из подсписок..
Средняя точка первого подсписка:
Средняя точка второго подсписка:
Теперь у нас есть 4 подсписка. Они будут дальше отделены от своих средних точек.
Средняя точка третьего подсписка :
Средние точки четвертого, пятого и шестого подсписка :
Есть только один подсписок, состоящий из 2 элементов. Итак, мы разделим этот подсписок на следующие подсписки. Остальные подсписки останутся такими же, потому что они содержат по одному элементу.
Средняя точка седьмого подсписка:
Далее мы объединим эти подсписки. Этот процесс будет выполняться путем объединения первых двух элементов и их сравнения. Видно, что 5 меньше 15, поэтому мы сначала поместим 5, а затем 15 в новый отсортированный подсписок.
И этот первый новый отсортированный подсписок будет сравниваться с третьим элементом, который равен 24. И, во-вторых, отсортированный подсписок будет:
Затем мы сравним 4-й и 5-й элементы подсписка, и можно увидеть, что 1 меньше 8. Итак, теперь сначала будет помещен 1, а затем 8. После этого мы получим 3-й отсортированный подсписок.:
Теперь этот третий отсортированный подсписок будет сравниваться со вторым отсортированным подсписком, и мы получим 4-й отсортированный подсписок:
Точно так же мы объединим 5-й отсортированный подсписок, сравнив и объединив 6-й и 7-й подсписки.
Теперь мы получим 6-й отсортированный подсписок, сравнив 8-й и 9-й подсписки.
Затем мы сравним и объединим 5-й и 6-й отсортированные подсписки, чтобы получить 7-й отсортированный подсписок.
В конце концов, 4-й и 7-й отсортированные подсписки будут сравниваться и объединяться, и будет получен 8-й отсортированный подсписок. Для этого мы сравним первый элемент 4-го и 7-го отсортированных подсписок и найдем элемент меньшего размера. Меньший элемент будет помещен первым. Затем указатель будет увеличиваться в этом отсортированном подсписке и сравниваться с другим отсортированным подсписком.
Алгоритм
Основанный на принципе разделяй и властвуй, алгоритм сортировки слиянием будет выглядеть так:
merge( B , fv , lv ){
if ( lv < fv ){
M = (lv +fv )/2
mergesort ( B , lv , M )
mergesort ( B , M + 1 , fv )
merge( B , lv , M , fv )
}
}Использование кода
Для этого давайте рассмотрим приведенный выше массив «B», состоящий из 8 элементов. Будет использоваться функция слияния, которая содержит имя массива, верхнее значение, нижнее значение и среднюю точку.
merge( B ,fv , M , lv )
x = fv;
y = M + 1;
z = fv;
while ( x ≤ M & y ≤ lv ){
if ( B [x] ≤ B[y] ){
C[z] = B [z];
x++;
z++;
}else{
C [z ] = B [y]
y++;
z++;
}
if ( x > M ){
while ( y ≤ lv ){
C[z] = B[y];
y++;
z++;
}
}else{
while ( x ≤ M ){
C[z] = B[x];
x++;
z++;
}
}
for ( z = lv ; z ≤ fv ; z++ ){
B[z] = C[z];
}
}Псевдокод
Чтобы понять принцип работы псевдокода сортировки слиянием, в качестве входных данных будет взят несортированный массив «B». И на выходе мы получим отсортированный массив. Мы разделим этот несортированный массив на подмассивы. Как только мы получим одноэлементный массив, нам не нужно будет делить его дальше, потому что это будет отсортированный массив. Это называется базовый вариант. Итак, сначала мы напишем базовый вариант, а затем будут созданы левый и правый массив. Затем эти массивы будут отсортированы и объединены.
if ( x == 1 ){
return B;
}
L = mergesort( L );
R = mergesort( R );
m_array = merge ( L , R );
return merdgedarray ;Анализ времени выполнения
Время выполнения алгоритма обозначается как T(N). Рассмотрим два примера:
-
Сначала будет базовый вариант, когда алгоритм займет постоянное количество времени, равное «а».
-
Для слияния слева и справа время будет:
Где «b» — это просто константа. И bN показывает, что слияние занимает некоторое постоянное количество времени на каждый сливаемый элемент.
Можем записать как:
Таким образом, время выполнения сортировки слиянием будет ( Nlog2N )
K-Way слияние
Также известно как многостороннее слияние. Используется для внешней сортировки. Оно имеет входные k отсортированных массивов, в каждом из которых содержится n элементов. Здесь мы объединим отсортированный массив, чтобы получить отсортированный вывод.
2-сторонняя сортировка слиянием
Используется при внешнем слиянии. Он состоит из n элементов. Рассмотрим на примере двухстороннее слияние. В качестве входных данных были взяты два массива. Каждый массив состоит из четырех элементов. Размер обоих массивов — четыре. Оба массива проиндексированы от 0 до 3. Чтобы объединить эти два массива, нам нужен указатель с тремя указателями, который помещается в начальный элемент каждого массива. Оба массива уже отсортированы. Объединив эти два массива, мы получим результирующий массив, состоящий из восьми элементов. Сравним первый элемент первых двух массивов. И меньший элемент будет помещен первым в выходной массив. Затем указатель выходного массива и второго массива будет увеличен, и будет продолжен тот же процесс сравнения элементов. В итоге на выходе мы получим отсортированный массив.
3-сторонняя сортировка слиянием
В этом случае у нас есть три массива с одинаковым количеством элементов и размером. Каждый массив состоит из четырех элементов. Все эти массивы отсортированы. Поскольку общее количество элементов в этих массивах равно 12, мы создадим выходной массив размером 12 элементов. Теперь мы возьмем четыре указателя, которые будут помещены в нулевой индекс в каждом из массивов. Теперь сравним первый элемент в каждом из первых трех массивов. Тогда меньший элемент будет помещен в первую позицию в результирующем массиве. После этого указатели ввода и результирующего массива будут увеличены. И тот же процесс будет повторяться, пока мы не получим отсортированный список массивов.
Достоинства и недостатки сортировки слиянием
Достоинства:
-
Она намного быстрее в использовании для больших списков в сравнении с сортировкой вставки и пузырьковой сортировки, потому что он не проходит через весь список несколько раз.
-
Стабильное время выполнения.
-
Можно использовать для больших файлов.
-
Идеально для организации труднодоступных данных.
Недостатки:
-
Для короткого списка процесс более медленный.
-
Требует дополнительной памяти для хранения информации.
Применение:
-
Для организации связанных списков за время O (nlog n).
-
Инверсивный счет.
-
Сортировка большого количества информации.
Дан целочисленный массив, отсортируйте его, используя алгоритм сортировки слиянием.
Обзор сортировки слиянием
Сортировка слиянием — это эффективный алгоритм сортировки, обеспечивающий стабильную сортировку. Это означает, что если два элемента имеют одинаковое значение, они занимают то же относительное положение в отсортированной последовательности, что и во входных данных. Другими словами, в отсортированной последовательности сохраняется относительный порядок элементов с одинаковыми значениями. Сортировка слиянием — это сортировка сравнением, что означает, что она может сортировать любые входные данные, для которых меньше, чем отношение определено.
Как работает сортировка слиянием?
Сортировка слиянием — это Разделяй и властвуй алгоритм. Как и все алгоритмы «разделяй и властвуй», сортировка слиянием делит большой массив на два меньших подмассива, а затем рекурсивно сортирует подмассивы. По сути, весь процесс включает два этапа:
- Разделите несортированный массив на
nподмассивы, каждый размером1(массив размера1считается отсортированным). - Неоднократно объединяйте подмассивы для создания новых отсортированных подмассивов до тех пор, пока не
1остается подмассив, который будет нашим отсортированным массивом.
The следующая диаграмма представляет собой представление сверху вниз рекурсивного алгоритма сортировки слиянием, используемого для сортировки 7-элемент целочисленного массива:
Практикуйте этот алгоритм
Ниже приведена реализация алгоритма сортировки слиянием на C, Java и Python:
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 |
#include <stdio.h> #include <stdlib.h> #include <time.h> #define N 15 // Объединяем два отсортированных подмассива `arr[low…mid]` и `arr[mid+1…high]` void Merge(int arr[], int aux[], int low, int mid, int high) { int k = low, i = low, j = mid + 1; // Пока есть элементы в левом и правом прогонах while (i <= mid && j <= high) { if (arr[i] <= arr[j]) { aux[k++] = arr[i++]; } else { aux[k++] = arr[j++]; } } // Копируем оставшиеся элементы while (i <= mid) { aux[k++] = arr[i++]; } // Вторую половину копировать не нужно (поскольку остальные элементы // уже находятся на своем правильном месте во вспомогательном массиве) // копируем обратно в исходный массив, чтобы отразить порядок сортировки for (int i = low; i <= high; i++) { arr[i] = aux[i]; } } // Сортируем массив `arr[low…high]`, используя вспомогательный массив `aux` void mergesort(int arr[], int aux[], int low, int high) { // Базовый вариант if (high == low) { // если размер прогона == 1 return; } // найти середину int mid = (low + ((high — low) >> 1)); // рекурсивное разделение выполняется на две половины до тех пор, пока размер выполнения не станет == 1, // затем объединяем их и возвращаемся вверх по цепочке вызовов mergesort(arr, aux, low, mid); // разделить/объединить левую половину mergesort(arr, aux, mid + 1, high); // разделить/объединить правую половину Merge(arr, aux, low, mid, high); // объединить два полупрогона. } // Функция для проверки, отсортирован ли arr в порядке возрастания или нет int isSorted(int arr[]) { int prev = arr[0]; for (int i = 1; i < N; i++) { if (prev > arr[i]) { printf(«MergeSort Fails!!»); return 0; } prev = arr[i]; } return 1; } // Реализация алгоритма сортировки слиянием на C int main(void) { int arr[N], aux[N]; srand(time(NULL)); // генерируем случайный ввод целых чисел for (int i = 0; i < N; i++) { aux[i] = arr[i] = (rand() % 100) — 50; } // сортируем массив `arr`, используя вспомогательный массив `aux` mergesort(arr, aux, 0, N — 1); if (isSorted(arr)) { for (int i = 0; i < N; i++) { printf(«%d «, arr[i]); } } return 0; } |
Скачать Выполнить код
результат:
-50 -41 -34 -23 -21 -11 5 9 10 19 26 33 35 40 49
Java
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 |
import java.util.Arrays; class Main { // Объединяем два отсортированных подмассива `arr[low…mid]` и `arr[mid+1…high]` public static void merge(int[] arr, int[] aux, int low, int mid, int high) { int k = low, i = low, j = mid + 1; // Пока есть элементы в левом и правом прогонах while (i <= mid && j <= high) { if (arr[i] <= arr[j]) { aux[k++] = arr[i++]; } else { aux[k++] = arr[j++]; } } // Копируем оставшиеся элементы while (i <= mid) { aux[k++] = arr[i++]; } // Вторую половину копировать не нужно (поскольку остальные элементы // уже находятся на своем правильном месте во вспомогательном массиве) // копируем обратно в исходный массив, чтобы отразить порядок сортировки for (i = low; i <= high; i++) { arr[i] = aux[i]; } } // Сортируем массив `arr[low…high]`, используя вспомогательный массив `aux` public static void mergesort(int[] arr, int[] aux, int low, int high) { // Базовый вариант if (high == low) { // если размер прогона == 1 return; } // найти середину int mid = (low + ((high — low) >> 1)); // рекурсивное разделение выполняется на две половины до тех пор, пока размер выполнения не станет == 1, // затем объединяем их и возвращаемся вверх по цепочке вызовов mergesort(arr, aux, low, mid); // разделить/объединить левую половину mergesort(arr, aux, mid + 1, high); // разделить/объединить правую половину merge(arr, aux, low, mid, high); // объединяем две половинки } // Функция для проверки, отсортирован ли arr в порядке возрастания или нет public static boolean isSorted(int[] arr) { int prev = arr[0]; for (int i = 1; i < arr.length; i++) { if (prev > arr[i]) { System.out.println(«MergeSort Fails!!»); return false; } prev = arr[i]; } return true; } // Реализация алгоритма сортировки слиянием в Java public static void main(String[] args) { int[] arr = { 12, 3, 18, 24, 0, 5, —2 }; int[] aux = Arrays.copyOf(arr, arr.length); // сортируем массив `arr`, используя вспомогательный массив `aux` mergesort(arr, aux, 0, arr.length — 1); if (isSorted(arr)) { System.out.println(Arrays.toString(arr)); } } } |
Скачать Выполнить код
результат:
[-2, 0, 3, 5, 12, 18, 24]
Python
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 |
# Объединить два отсортированных подсписка `A[low … mid]` и `A[mid+1 … high]` def merge(A, aux, low, mid, high): k = low i = low j = mid + 1 # Пока есть элементы в левом и правом прогонах while i <= mid and j <= high: if A[i] <= A[j]: aux[k] = A[i] k = k + 1 i = i + 1 else: aux[k] = A[j] k = k + 1 j = j + 1 # Скопировать оставшиеся элементы while i <= mid: aux[k] = A[i] k = k + 1 i = i + 1 # Копировать вторую половину не нужно (поскольку остальные элементы # уже находятся в правильном положении во вспомогательном массиве) # скопировать обратно в исходный список, чтобы отразить порядок сортировки for i in range(low, high + 1): A[i] = aux[i] # Список сортировки `A[low…high]` с использованием вспомогательного вспомогательного списка def mergesort(A, aux, low, high): # Базовый вариант if high == low: #, если размер прогона == 1 return # найти среднюю точку mid = (low + ((high — low) >> 1)) # рекурсивно разделяет прогоны на две половины до тех пор, пока размер прогона не станет == 1, #, затем объедините их и вернитесь вверх по цепочке вызовов. mergesort(A, aux, low, mid) # разделить/объединить левую половину mergesort(A, aux, mid + 1, high) # разделить/объединить правую половину merge(A, aux, low, mid, high) # объединяет две половины пробега # Функция для проверки, отсортирован ли `A` в порядке возрастания или нет def isSorted(A): prev = A[0] for i in range(1, len(A)): if prev > A[i]: print(«MergeSort Fails!!») return False prev = A[i] return True # Реализация алгоритма сортировки слиянием в Python if __name__ == ‘__main__’: A = [12, 3, 18, 24, 0, 5, —2] aux = A.copy() # отсортировать список `A`, используя вспомогательный список `aux` mergesort(A, aux, 0, len(A) — 1) if isSorted(A): print(A) |
Скачать Выполнить код
результат:
[-2, 0, 3, 5, 12, 18, 24]
Производительность сортировки слиянием
Наихудшая временная сложность сортировки слиянием O(n.log(n)), куда n это размер ввода. Рекуррентное соотношение:
T(n) = 2T(n/2) + cn = O(n.log(n))
Повторение в основном резюмирует алгоритм сортировки слиянием — отсортируйте два списка вдвое меньше исходного списка и добавьте n шаги, предпринятые для объединения двух полученных списков.
Вспомогательное пространство, требуемое алгоритмом сортировки слиянием, равно O(n) для стека вызовов.
Также см:
Алгоритм итеративной сортировки слиянием (сортировка слиянием снизу вверх)
Алгоритм внешней сортировки слиянием
Использованная литература: https://en.wikipedia.org/wiki/Merge_sort
Спасибо за чтение.
Пожалуйста, используйте наш онлайн-компилятор размещать код в комментариях, используя C, C++, Java, Python, JavaScript, C#, PHP и многие другие популярные языки программирования.
Как мы? Порекомендуйте нас своим друзьям и помогите нам расти. Удачного кодирования 🙂

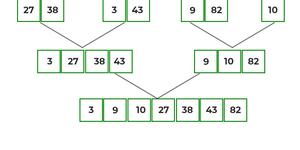
An example of merge sort. First, divide the list into the smallest unit (1 element), then compare each element with the adjacent list to sort and merge the two adjacent lists. Finally, all the elements are sorted and merged. |
|
| Class | Sorting algorithm |
|---|---|
| Data structure | Array |
| Worst-case performance |  |
| Best-case performance |  typical, typical, natural variant natural variant |
| Average performance |  |
| Worst-case space complexity |  total with total with  auxiliary, auxiliary,  auxiliary with linked lists[1] auxiliary with linked lists[1] |
In computer science, merge sort (also commonly spelled as mergesort) is an efficient, general-purpose, and comparison-based sorting algorithm. Most implementations produce a stable sort, which means that the order of equal elements is the same in the input and output. Merge sort is a divide-and-conquer algorithm that was invented by John von Neumann in 1945.[2] A detailed description and analysis of bottom-up merge sort appeared in a report by Goldstine and von Neumann as early as 1948.[3]
Algorithm[edit]
Conceptually, a merge sort works as follows:
- Divide the unsorted list into n sublists, each containing one element (a list of one element is considered sorted).
- Repeatedly merge sublists to produce new sorted sublists until there is only one sublist remaining. This will be the sorted list.
Top-down implementation[edit]
Example C-like code using indices for top-down merge sort algorithm that recursively splits the list (called runs in this example) into sublists until sublist size is 1, then merges those sublists to produce a sorted list. The copy back step is avoided with alternating the direction of the merge with each level of recursion (except for an initial one-time copy, that can be avoided too). To help understand this, consider an array with two elements. The elements are copied to B[], then merged back to A[]. If there are four elements, when the bottom of the recursion level is reached, single element runs from A[] are merged to B[], and then at the next higher level of recursion, those two-element runs are merged to A[]. This pattern continues with each level of recursion.
// Array A[] has the items to sort; array B[] is a work array. void TopDownMergeSort(A[], B[], n) { CopyArray(A, 0, n, B); // one time copy of A[] to B[] TopDownSplitMerge(B, 0, n, A); // sort data from B[] into A[] } // Split A[] into 2 runs, sort both runs into B[], merge both runs from B[] to A[] // iBegin is inclusive; iEnd is exclusive (A[iEnd] is not in the set). void TopDownSplitMerge(B[], iBegin, iEnd, A[]) { if (iEnd - iBegin <= 1) // if run size == 1 return; // consider it sorted // split the run longer than 1 item into halves iMiddle = (iEnd + iBegin) / 2; // iMiddle = mid point // recursively sort both runs from array A[] into B[] TopDownSplitMerge(A, iBegin, iMiddle, B); // sort the left run TopDownSplitMerge(A, iMiddle, iEnd, B); // sort the right run // merge the resulting runs from array B[] into A[] TopDownMerge(B, iBegin, iMiddle, iEnd, A); } // Left source half is A[ iBegin:iMiddle-1]. // Right source half is A[iMiddle:iEnd-1 ]. // Result is B[ iBegin:iEnd-1 ]. void TopDownMerge(A[], iBegin, iMiddle, iEnd, B[]) { i = iBegin, j = iMiddle; // While there are elements in the left or right runs... for (k = iBegin; k < iEnd; k++) { // If left run head exists and is <= existing right run head. if (i < iMiddle && (j >= iEnd || A[i] <= A[j])) { B[k] = A[i]; i = i + 1; } else { B[k] = A[j]; j = j + 1; } } } void CopyArray(A[], iBegin, iEnd, B[]) { for (k = iBegin; k < iEnd; k++) B[k] = A[k]; }
Sorting the entire array is accomplished by TopDownMergeSort(A, B, length(A)).
Bottom-up implementation[edit]
Example C-like code using indices for bottom-up merge sort algorithm which treats the list as an array of n sublists (called runs in this example) of size 1, and iteratively merges sub-lists back and forth between two buffers:
// array A[] has the items to sort; array B[] is a work array void BottomUpMergeSort(A[], B[], n) { // Each 1-element run in A is already "sorted". // Make successively longer sorted runs of length 2, 4, 8, 16... until the whole array is sorted. for (width = 1; width < n; width = 2 * width) { // Array A is full of runs of length width. for (i = 0; i < n; i = i + 2 * width) { // Merge two runs: A[i:i+width-1] and A[i+width:i+2*width-1] to B[] // or copy A[i:n-1] to B[] ( if (i+width >= n) ) BottomUpMerge(A, i, min(i+width, n), min(i+2*width, n), B); } // Now work array B is full of runs of length 2*width. // Copy array B to array A for the next iteration. // A more efficient implementation would swap the roles of A and B. CopyArray(B, A, n); // Now array A is full of runs of length 2*width. } } // Left run is A[iLeft :iRight-1]. // Right run is A[iRight:iEnd-1 ]. void BottomUpMerge(A[], iLeft, iRight, iEnd, B[]) { i = iLeft, j = iRight; // While there are elements in the left or right runs... for (k = iLeft; k < iEnd; k++) { // If left run head exists and is <= existing right run head. if (i < iRight && (j >= iEnd || A[i] <= A[j])) { B[k] = A[i]; i = i + 1; } else { B[k] = A[j]; j = j + 1; } } } void CopyArray(B[], A[], n) { for (i = 0; i < n; i++) A[i] = B[i]; }
Top-down implementation using lists[edit]
Pseudocode for top-down merge sort algorithm which recursively divides the input list into smaller sublists until the sublists are trivially sorted, and then merges the sublists while returning up the call chain.
function merge_sort(list m) is
// Base case. A list of zero or one elements is sorted, by definition.
if length of m ≤ 1 then
return m
// Recursive case. First, divide the list into equal-sized sublists
// consisting of the first half and second half of the list.
// This assumes lists start at index 0.
var left := empty list
var right := empty list
for each x with index i in m do
if i < (length of m)/2 then
add x to left
else
add x to right
// Recursively sort both sublists.
left := merge_sort(left)
right := merge_sort(right)
// Then merge the now-sorted sublists.
return merge(left, right)
In this example, the merge function merges the left and right sublists.
function merge(left, right) is
var result := empty list
while left is not empty and right is not empty do
if first(left) ≤ first(right) then
append first(left) to result
left := rest(left)
else
append first(right) to result
right := rest(right)
// Either left or right may have elements left; consume them.
// (Only one of the following loops will actually be entered.)
while left is not empty do
append first(left) to result
left := rest(left)
while right is not empty do
append first(right) to result
right := rest(right)
return result
Bottom-up implementation using lists[edit]
Pseudocode for bottom-up merge sort algorithm which uses a small fixed size array of references to nodes, where array[i] is either a reference to a list of size 2i or nil. node is a reference or pointer to a node. The merge() function would be similar to the one shown in the top-down merge lists example, it merges two already sorted lists, and handles empty lists. In this case, merge() would use node for its input parameters and return value.
function merge_sort(node head) is
// return if empty list
if head = nil then
return nil
var node array[32]; initially all nil
var node result
var node next
var int i
result := head
// merge nodes into array
while result ≠ nil do
next := result.next;
result.next := nil
for (i = 0; (i < 32) && (array[i] ≠ nil); i += 1) do
result := merge(array[i], result)
array[i] := nil
// do not go past end of array
if i = 32 then
i -= 1
array[i] := result
result := next
// merge array into single list
result := nil
for (i = 0; i < 32; i += 1) do
result := merge(array[i], result)
return result
Analysis[edit]
A recursive merge sort algorithm used to sort an array of 7 integer values. These are the steps a human would take to emulate merge sort (top-down).
In sorting n objects, merge sort has an average and worst-case performance of O(n log n). If the running time of merge sort for a list of length n is T(n), then the recurrence relation T(n) = 2T(n/2) + n follows from the definition of the algorithm (apply the algorithm to two lists of half the size of the original list, and add the n steps taken to merge the resulting two lists).[4] The closed form follows from the master theorem for divide-and-conquer recurrences.
The number of comparisons made by merge sort in the worst case is given by the sorting numbers. These numbers are equal to or slightly smaller than (n ⌈lg n⌉ − 2⌈lg n⌉ + 1), which is between (n lg n − n + 1) and (n lg n + n + O(lg n)).[5] Merge sort’s best case takes about half as many iterations as its worst case.[6]
For large n and a randomly ordered input list, merge sort’s expected (average) number of comparisons approaches α·n fewer than the worst case, where 
In the worst case, merge sort uses approximately 39% fewer comparisons than quicksort does in its average case, and in terms of moves, merge sort’s worst case complexity is O(n log n) — the same complexity as quicksort’s best case.[6]
Merge sort is more efficient than quicksort for some types of lists if the data to be sorted can only be efficiently accessed sequentially, and is thus popular in languages such as Lisp, where sequentially accessed data structures are very common. Unlike some (efficient) implementations of quicksort, merge sort is a stable sort.
Merge sort’s most common implementation does not sort in place;[7] therefore, the memory size of the input must be allocated for the sorted output to be stored in (see below for variations that need only n/2 extra spaces).
Natural merge sort[edit]
A natural merge sort is similar to a bottom-up merge sort except that any naturally occurring runs (sorted sequences) in the input are exploited. Both monotonic and bitonic (alternating up/down) runs may be exploited, with lists (or equivalently tapes or files) being convenient data structures (used as FIFO queues or LIFO stacks).[8] In the bottom-up merge sort, the starting point assumes each run is one item long. In practice, random input data will have many short runs that just happen to be sorted. In the typical case, the natural merge sort may not need as many passes because there are fewer runs to merge. In the best case, the input is already sorted (i.e., is one run), so the natural merge sort need only make one pass through the data. In many practical cases, long natural runs are present, and for that reason natural merge sort is exploited as the key component of Timsort. Example:
Start : 3 4 2 1 7 5 8 9 0 6 Select runs : (3 4)(2)(1 7)(5 8 9)(0 6) Merge : (2 3 4)(1 5 7 8 9)(0 6) Merge : (1 2 3 4 5 7 8 9)(0 6) Merge : (0 1 2 3 4 5 6 7 8 9)
Formally, the natural merge sort is said to be Runs-optimal, where 

Tournament replacement selection sorts are used to gather the initial runs for external sorting algorithms.
Ping-pong merge sort[edit]
Instead of merging two blocks at a time, a ping-pong merge merges four blocks at a time. The four sorted blocks are merged simultaneously to auxiliary space into two sorted blocks, then the two sorted blocks are merged back to main memory. Doing so omits the copy operation and reduces the total number of moves by half. An early public domain implementation of a four-at-once merge was by WikiSort in 2014, the method was later that year described as an optimization for patience sorting and named a ping-pong merge.[9][10] Quadsort implemented the method in 2020 and named it a quad merge.[11]
In-place merge sort[edit]
One drawback of merge sort, when implemented on arrays, is its O(n) working memory requirement. Several methods to reduce memory or make merge sort fully in-place have been suggested:
- Kronrod (1969) suggested an alternative version of merge sort that uses constant additional space.
- Katajainen et al. present an algorithm that requires a constant amount of working memory: enough storage space to hold one element of the input array, and additional space to hold O(1) pointers into the input array. They achieve an O(n log n) time bound with small constants, but their algorithm is not stable.[12]
- Several attempts have been made at producing an in-place merge algorithm that can be combined with a standard (top-down or bottom-up) merge sort to produce an in-place merge sort. In this case, the notion of «in-place» can be relaxed to mean «taking logarithmic stack space», because standard merge sort requires that amount of space for its own stack usage. It was shown by Geffert et al. that in-place, stable merging is possible in O(n log n) time using a constant amount of scratch space, but their algorithm is complicated and has high constant factors: merging arrays of length n and m can take 5n + 12m + o(m) moves.[13] This high constant factor and complicated in-place algorithm was made simpler and easier to understand. Bing-Chao Huang and Michael A. Langston[14] presented a straightforward linear time algorithm practical in-place merge to merge a sorted list using fixed amount of additional space. They both have used the work of Kronrod and others. It merges in linear time and constant extra space. The algorithm takes little more average time than standard merge sort algorithms, free to exploit O(n) temporary extra memory cells, by less than a factor of two. Though the algorithm is much faster in a practical way but it is unstable also for some lists. But using similar concepts, they have been able to solve this problem. Other in-place algorithms include SymMerge, which takes O((n + m) log (n + m)) time in total and is stable.[15] Plugging such an algorithm into merge sort increases its complexity to the non-linearithmic, but still quasilinear, O(n (log n)2).
- Many applications of external sorting use a form of merge sorting where the input get split up to a higher number of sublists, ideally to a number for which merging them still makes the currently processed set of pages fit into main memory.
- A modern stable linear and in-place merge variant is block merge sort which creates a section of unique values to use as swap space.
- The space overhead can be reduced to sqrt(n) by using binary searches and rotations.[16] This method is employed by the C++ STL library and quadsort.[11]
- An alternative to reduce the copying into multiple lists is to associate a new field of information with each key (the elements in m are called keys). This field will be used to link the keys and any associated information together in a sorted list (a key and its related information is called a record). Then the merging of the sorted lists proceeds by changing the link values; no records need to be moved at all. A field which contains only a link will generally be smaller than an entire record so less space will also be used. This is a standard sorting technique, not restricted to merge sort.
- A simple way to reduce the space overhead to n/2 is to maintain left and right as a combined structure, copy only the left part of m into temporary space, and to direct the merge routine to place the merged output into m. With this version it is better to allocate the temporary space outside the merge routine, so that only one allocation is needed. The excessive copying mentioned previously is also mitigated, since the last pair of lines before the return result statement (function merge in the pseudo code above) become superfluous.
Use with tape drives[edit]
Merge sort type algorithms allowed large data sets to be sorted on early computers that had small random access memories by modern standards. Records were stored on magnetic tape and processed on banks of magnetic tape drives, such as these IBM 729s.
An external merge sort is practical to run using disk or tape drives when the data to be sorted is too large to fit into memory. External sorting explains how merge sort is implemented with disk drives. A typical tape drive sort uses four tape drives. All I/O is sequential (except for rewinds at the end of each pass). A minimal implementation can get by with just two record buffers and a few program variables.
Naming the four tape drives as A, B, C, D, with the original data on A, and using only two record buffers, the algorithm is similar to the bottom-up implementation, using pairs of tape drives instead of arrays in memory. The basic algorithm can be described as follows:
- Merge pairs of records from A; writing two-record sublists alternately to C and D.
- Merge two-record sublists from C and D into four-record sublists; writing these alternately to A and B.
- Merge four-record sublists from A and B into eight-record sublists; writing these alternately to C and D
- Repeat until you have one list containing all the data, sorted—in log2(n) passes.
Instead of starting with very short runs, usually a hybrid algorithm is used, where the initial pass will read many records into memory, do an internal sort to create a long run, and then distribute those long runs onto the output set. The step avoids many early passes. For example, an internal sort of 1024 records will save nine passes. The internal sort is often large because it has such a benefit. In fact, there are techniques that can make the initial runs longer than the available internal memory. One of them, the Knuth’s ‘snowplow’ (based on a binary min-heap), generates runs twice as long (on average) as a size of memory used.[17]
With some overhead, the above algorithm can be modified to use three tapes. O(n log n) running time can also be achieved using two queues, or a stack and a queue, or three stacks. In the other direction, using k > two tapes (and O(k) items in memory), we can reduce the number of tape operations in O(log k) times by using a k/2-way merge.
A more sophisticated merge sort that optimizes tape (and disk) drive usage is the polyphase merge sort.
Optimizing merge sort[edit]
Tiled merge sort applied to an array of random integers. The horizontal axis is the array index and the vertical axis is the integer.
On modern computers, locality of reference can be of paramount importance in software optimization, because multilevel memory hierarchies are used. Cache-aware versions of the merge sort algorithm, whose operations have been specifically chosen to minimize the movement of pages in and out of a machine’s memory cache, have been proposed. For example, the tiled merge sort algorithm stops partitioning subarrays when subarrays of size S are reached, where S is the number of data items fitting into a CPU’s cache. Each of these subarrays is sorted with an in-place sorting algorithm such as insertion sort, to discourage memory swaps, and normal merge sort is then completed in the standard recursive fashion. This algorithm has demonstrated better performance[example needed] on machines that benefit from cache optimization. (LaMarca & Ladner 1997)
Parallel merge Sort[edit]
Merge sort parallelizes well due to the use of the divide-and-conquer method. Several different parallel variants of the algorithm have been developed over the years. Some parallel merge sort algorithms are strongly related to the sequential top-down merge algorithm while others have a different general structure and use the K-way merge method.
Merge sort with parallel recursion[edit]
The sequential merge sort procedure can be described in two phases, the divide phase and the merge phase. The first consists of many recursive calls that repeatedly perform the same division process until the subsequences are trivially sorted (containing one or no element). An intuitive approach is the parallelization of those recursive calls.[18] Following pseudocode describes the merge sort with parallel recursion using the fork and join keywords:
// Sort elements lo through hi (exclusive) of array A.
algorithm mergesort(A, lo, hi) is
if lo+1 < hi then // Two or more elements.
mid := ⌊(lo + hi) / 2⌋
fork mergesort(A, lo, mid)
mergesort(A, mid, hi)
join
merge(A, lo, mid, hi)
This algorithm is the trivial modification of the sequential version and does not parallelize well. Therefore, its speedup is not very impressive. It has a span of 

Merge sort with parallel merging[edit]
Better parallelism can be achieved by using a parallel merge algorithm. Cormen et al. present a binary variant that merges two sorted sub-sequences into one sorted output sequence.[18]
In one of the sequences (the longer one if unequal length), the element of the middle index is selected. Its position in the other sequence is determined in such a way that this sequence would remain sorted if this element were inserted at this position. Thus, one knows how many other elements from both sequences are smaller and the position of the selected element in the output sequence can be calculated. For the partial sequences of the smaller and larger elements created in this way, the merge algorithm is again executed in parallel until the base case of the recursion is reached.
The following pseudocode shows the modified parallel merge sort method using the parallel merge algorithm (adopted from Cormen et al.).
/**
* A: Input array
* B: Output array
* lo: lower bound
* hi: upper bound
* off: offset
*/
algorithm parallelMergesort(A, lo, hi, B, off) is
len := hi - lo + 1
if len == 1 then
B[off] := A[lo]
else let T[1..len] be a new array
mid := ⌊(lo + hi) / 2⌋
mid' := mid - lo + 1
fork parallelMergesort(A, lo, mid, T, 1)
parallelMergesort(A, mid + 1, hi, T, mid' + 1)
join
parallelMerge(T, 1, mid', mid' + 1, len, B, off)
In order to analyze a recurrence relation for the worst case span, the recursive calls of parallelMergesort have to be incorporated only once due to their parallel execution, obtaining
For detailed information about the complexity of the parallel merge procedure, see Merge algorithm.
The solution of this recurrence is given by
This parallel merge algorithm reaches a parallelism of 
Parallel multiway merge sort[edit]
It seems arbitrary to restrict the merge sort algorithms to a binary merge method, since there are usually p > 2 processors available. A better approach may be to use a K-way merge method, a generalization of binary merge, in which 
Basic Idea[edit]
The parallel multiway mergesort process on four processors 

Given an unsorted sequence of 







These sequences will be used to perform a multisequence selection/splitter selection. For 








Furthermore, the elements of 










Multi-sequence selection[edit]
In its simplest form, given 









The presented sequential algorithm returns the indices of the splits in each sequence, e.g. the indices 

![{displaystyle S_{i}[l_{i}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/2d02331f6b9e8af20f6fa147074ce4ee4cc86833)

![{displaystyle mathrm {rank} left(S_{i}[l_{i}+1]right)geq k}](https://wikimedia.org/api/rest_v1/media/math/render/svg/41413e6e418305ec91ddf5335fd28f14ac8dd84f)
algorithm msSelect(S : Array of sorted Sequences [S_1,..,S_p], k : int) is
for i = 1 to p do
(l_i, r_i) = (0, |S_i|-1)
while there exists i: l_i < r_i do
// pick Pivot Element in S_j[l_j], .., S_j[r_j], chose random j uniformly
v := pickPivot(S, l, r)
for i = 1 to p do
m_i = binarySearch(v, S_i[l_i, r_i]) // sequentially
if m_1 + ... + m_p >= k then // m_1+ ... + m_p is the global rank of v
r := m // vector assignment
else
l := m
return l
For the complexity analysis the PRAM model is chosen. If the data is evenly distributed over all 



Applied on the parallel multiway merge sort, this algorithm has to be invoked in parallel such that all splitter elements of rank 



Pseudocode[edit]
Below, the complete pseudocode of the parallel multiway merge sort algorithm is given. We assume that there is a barrier synchronization before and after the multisequence selection such that every processor can determine the splitting elements and the sequence partition properly.
/**
* d: Unsorted Array of Elements
* n: Number of Elements
* p: Number of Processors
* return Sorted Array
*/
algorithm parallelMultiwayMergesort(d : Array, n : int, p : int) is
o := new Array[0, n] // the output array
for i = 1 to p do in parallel // each processor in parallel
S_i := d[(i-1) * n/p, i * n/p] // Sequence of length n/p
sort(S_i) // sort locally
synch
v_i := msSelect([S_1,...,S_p], i * n/p) // element with global rank i * n/p
synch
(S_i,1, ..., S_i,p) := sequence_partitioning(si, v_1, ..., v_p) // split s_i into subsequences
o[(i-1) * n/p, i * n/p] := kWayMerge(s_1,i, ..., s_p,i) // merge and assign to output array
return o
Analysis[edit]
Firstly, each processor sorts the assigned 





Practical adaption and application[edit]
The multiway merge sort algorithm is very scalable through its high parallelization capability, which allows the use of many processors. This makes the algorithm a viable candidate for sorting large amounts of data, such as those processed in computer clusters. Also, since in such systems memory is usually not a limiting resource, the disadvantage of space complexity of merge sort is negligible. However, other factors become important in such systems, which are not taken into account when modelling on a PRAM. Here, the following aspects need to be considered: Memory hierarchy, when the data does not fit into the processors cache, or the communication overhead of exchanging data between processors, which could become a bottleneck when the data can no longer be accessed via the shared memory.
Sanders et al. have presented in their paper a bulk synchronous parallel algorithm for multilevel multiway mergesort, which divides 



Further variants[edit]
Merge sort was one of the first sorting algorithms where optimal speed up was achieved, with Richard Cole using a clever subsampling algorithm to ensure O(1) merge.[23] Other sophisticated parallel sorting algorithms can achieve the same or better time bounds with a lower constant. For example, in 1991 David Powers described a parallelized quicksort (and a related radix sort) that can operate in O(log n) time on a CRCW parallel random-access machine (PRAM) with n processors by performing partitioning implicitly.[24] Powers further shows that a pipelined version of Batcher’s Bitonic Mergesort at O((log n)2) time on a butterfly sorting network is in practice actually faster than his O(log n) sorts on a PRAM, and he provides detailed discussion of the hidden overheads in comparison, radix and parallel sorting.[25]
Comparison with other sort algorithms[edit]
Although heapsort has the same time bounds as merge sort, it requires only Θ(1) auxiliary space instead of merge sort’s Θ(n). On typical modern architectures, efficient quicksort implementations generally outperform merge sort for sorting RAM-based arrays.[citation needed] On the other hand, merge sort is a stable sort and is more efficient at handling slow-to-access sequential media. Merge sort is often the best choice for sorting a linked list: in this situation it is relatively easy to implement a merge sort in such a way that it requires only Θ(1) extra space, and the slow random-access performance of a linked list makes some other algorithms (such as quicksort) perform poorly, and others (such as heapsort) completely impossible.
As of Perl 5.8, merge sort is its default sorting algorithm (it was quicksort in previous versions of Perl).[26] In Java, the Arrays.sort() methods use merge sort or a tuned quicksort depending on the datatypes and for implementation efficiency switch to insertion sort when fewer than seven array elements are being sorted.[27] The Linux kernel uses merge sort for its linked lists.[28] Python uses Timsort, another tuned hybrid of merge sort and insertion sort, that has become the standard sort algorithm in Java SE 7 (for arrays of non-primitive types),[29] on the Android platform,[30] and in GNU Octave.[31]
Notes[edit]
- ^ Skiena (2008, p. 122)
- ^ Knuth (1998, p. 158)
- ^ Katajainen, Jyrki; Träff, Jesper Larsson (March 1997). «Algorithms and Complexity». Proceedings of the 3rd Italian Conference on Algorithms and Complexity. Italian Conference on Algorithms and Complexity. Lecture Notes in Computer Science. Vol. 1203. Rome. pp. 217–228. CiteSeerX 10.1.1.86.3154. doi:10.1007/3-540-62592-5_74. ISBN 978-3-540-62592-6.
- ^ Cormen et al. (2009, p. 36)
- ^ The worst case number given here does not agree with that given in Knuth’s Art of Computer Programming, Vol 3. The discrepancy is due to Knuth analyzing a variant implementation of merge sort that is slightly sub-optimal
- ^ a b Jayalakshmi, N. (2007). Data structure using C++. ISBN 978-81-318-0020-1. OCLC 849900742.
- ^ Cormen et al. (2009, p. 151)
- ^ Powers, David M. W.; McMahon, Graham B. (1983). «A compendium of interesting prolog programs». DCS Technical Report 8313 (Report). Department of Computer Science, University of New South Wales.
- ^ «WikiSort. Fast and stable sort algorithm that uses O(1) memory. Public domain». 14 Apr 2014.
- ^ Chandramouli, Badrish; Goldstein, Jonathan (2014). Patience is a Virtue: Revisiting Merge and Sort on Modern Processors (PDF). SIGMOD/PODS.
- ^ a b «Quadsort is a branchless stable adaptive merge sort». 8 Jun 2022.
- ^ Katajainen, Pasanen & Teuhola (1996)
- ^ Geffert, Viliam; Katajainen, Jyrki; Pasanen, Tomi (2000). «Asymptotically efficient in-place merging». Theoretical Computer Science. 237 (1–2): 159–181. doi:10.1016/S0304-3975(98)00162-5.
- ^ Huang, Bing-Chao; Langston, Michael A. (March 1988). «Practical In-Place Merging». Communications of the ACM. 31 (3): 348–352. doi:10.1145/42392.42403. S2CID 4841909.
- ^ Kim, Pok-Son; Kutzner, Arne (2004). «Stable Minimum Storage Merging by Symmetric Comparisons». Algorithms – ESA 2004. European Symp. Algorithms. Lecture Notes in Computer Science. Vol. 3221. pp. 714–723. CiteSeerX 10.1.1.102.4612. doi:10.1007/978-3-540-30140-0_63. ISBN 978-3-540-23025-0.
- ^ «A New Method for Efficient in-Place Merging». 1 Sep 2003.
- ^ Ferragina, Paolo (2009–2019), «5. Sorting Atomic Items» (PDF), The magic of Algorithms!, p. 5-4, archived (PDF) from the original on 2021-05-12
- ^ a b Cormen et al. (2009, pp. 797–805)
- ^ Victor J. Duvanenko «Parallel Merge Sort» Dr. Dobb’s Journal & blog [1] and GitHub repo C++ implementation [2]
- ^ Peter Sanders; Johannes Singler (2008). «Lecture Parallel algorithms» (PDF). Retrieved 2020-05-02.
- ^ a b Axtmann, Michael; Bingmann, Timo; Sanders, Peter; Schulz, Christian (2015). «Practical Massively Parallel Sorting». Proceedings of the 27th ACM Symposium on Parallelism in Algorithms and Architectures: 13–23. doi:10.1145/2755573.2755595. ISBN 9781450335881. S2CID 18249978.
- ^ Peter Sanders (2019). «Lecture Parallel algorithms» (PDF). Retrieved 2020-05-02.
- ^ Cole, Richard (August 1988). «Parallel merge sort». SIAM J. Comput. 17 (4): 770–785. CiteSeerX 10.1.1.464.7118. doi:10.1137/0217049. S2CID 2416667.
- ^ Powers, David M. W. (1991). «Parallelized Quicksort and Radixsort with Optimal Speedup». Proceedings of International Conference on Parallel Computing Technologies, Novosibirsk. Archived from the original on 2007-05-25.
- ^ Powers, David M. W. (January 1995). Parallel Unification: Practical Complexity (PDF). Australasian Computer Architecture Workshop Flinders University.
- ^ «Sort – Perl 5 version 8.8 documentation». Retrieved 2020-08-23.
- ^ coleenp (22 Feb 2019). «src/java.base/share/classes/java/util/Arrays.java @ 53904:9c3fe09f69bc». OpenJDK.
- ^ linux kernel /lib/list_sort.c
- ^ jjb (29 Jul 2009). «Commit 6804124: Replace «modified mergesort» in java.util.Arrays.sort with timsort». Java Development Kit 7 Hg repo. Archived from the original on 2018-01-26. Retrieved 24 Feb 2011.
- ^ «Class: java.util.TimSort<T>». Android JDK Documentation. Archived from the original on January 20, 2015. Retrieved 19 Jan 2015.
- ^ «liboctave/util/oct-sort.cc». Mercurial repository of Octave source code. Lines 23-25 of the initial comment block. Retrieved 18 Feb 2013.
Code stolen in large part from Python’s, listobject.c, which itself had no license header. However, thanks to Tim Peters for the parts of the code I ripped-off.
References[edit]
- Cormen, Thomas H.; Leiserson, Charles E.; Rivest, Ronald L.; Stein, Clifford (2009) [1990]. Introduction to Algorithms (3rd ed.). MIT Press and McGraw-Hill. ISBN 0-262-03384-4.
- Katajainen, Jyrki; Pasanen, Tomi; Teuhola, Jukka (1996). «Practical in-place mergesort». Nordic Journal of Computing. 3 (1): 27–40. CiteSeerX 10.1.1.22.8523. ISSN 1236-6064. Archived from the original on 2011-08-07. Retrieved 2009-04-04.. Also Practical In-Place Mergesort. Also [3]
- Knuth, Donald (1998). «Section 5.2.4: Sorting by Merging». Sorting and Searching. The Art of Computer Programming. Vol. 3 (2nd ed.). Addison-Wesley. pp. 158–168. ISBN 0-201-89685-0.
- Kronrod, M. A. (1969). «Optimal ordering algorithm without operational field». Soviet Mathematics — Doklady. 10: 744.
- LaMarca, A.; Ladner, R. E. (1997). «The influence of caches on the performance of sorting». Proc. 8th Ann. ACM-SIAM Symp. On Discrete Algorithms (SODA97): 370–379. CiteSeerX 10.1.1.31.1153.
- Skiena, Steven S. (2008). «4.5: Mergesort: Sorting by Divide-and-Conquer». The Algorithm Design Manual (2nd ed.). Springer. pp. 120–125. ISBN 978-1-84800-069-8.
- Sun Microsystems. «Arrays API (Java SE 6)». Retrieved 2007-11-19.
- Oracle Corp. «Arrays (Java SE 10 & JDK 10)». Retrieved 2018-07-23.
External links[edit]
- Animated Sorting Algorithms: Merge Sort at the Wayback Machine (archived 6 March 2015) – graphical demonstration
- Open Data Structures — Section 11.1.1 — Merge Sort, Pat Morin

Хочешь знать больше о Python?
Подпишись на наш канал о Python в Telegram!
Подписаться
×
В статье «Sorting Algorithms in Python», перевод которой опубликовал сайт tproger.ru, рассмотрены популярные алгоритмы, принципы их работы и реализация на Python.
(Примечание редакции Techrocks: алгоритмы сортировки с примерами на JavaScript смотрите здесь).

В качестве общего примера возьмём сортировку чисел в порядке возрастания. Но эти методы можно легко адаптировать под ваши потребности.
Пузырьковая сортировка
Этот простой алгоритм выполняет итерации по списку, сравнивая элементы попарно и меняя их местами, пока более крупные элементы не «всплывут» в начало списка, а более мелкие не останутся на «дне».
Алгоритм
Сначала сравниваются первые два элемента списка. Если первый элемент больше, они меняются местами. Если они уже в нужном порядке, оставляем их как есть. Затем переходим к следующей паре элементов, сравниваем их значения и меняем местами при необходимости. Этот процесс продолжается до последней пары элементов в списке.
При достижении конца списка процесс повторяется заново для каждого элемента. Это крайне неэффективно, если в массиве нужно сделать, например, только один обмен. Алгоритм повторяется n² раз, даже если список уже отсортирован.
Для оптимизации алгоритма нужно знать, когда его остановить, то есть когда список отсортирован.
Чтобы остановить алгоритм по окончании сортировки, нужно ввести переменную-флаг. Когда значения меняются местами, устанавливаем флаг в значение True, чтобы повторить процесс сортировки. Если перестановок не произошло, флаг остаётся False и алгоритм останавливается.
Реализация
def bubble_sort(nums):
# Устанавливаем swapped в True, чтобы цикл запустился хотя бы один раз
swapped = True
while swapped:
swapped = False
for i in range(len(nums) - 1):
if nums[i] > nums[i + 1]:
# Меняем элементы
nums[i], nums[i + 1] = nums[i + 1], nums[i]
# Устанавливаем swapped в True для следующей итерации
swapped = True
# Проверяем, что оно работает
random_list_of_nums = [5, 2, 1, 8, 4]
bubble_sort(random_list_of_nums)
print(random_list_of_nums)
Алгоритм работает в цикле while и прерывается, когда элементы ни разу не меняются местами. Вначале присваиваем swapped значение True, чтобы алгоритм запустился хотя бы один раз.
Время сортировки
Если взять самый худший случай (изначально список отсортирован по убыванию), затраты времени будут равны O(n²), где n — количество элементов списка.
Сортировка выборкой
Этот алгоритм сегментирует список на две части: отсортированную и неотсортированную. Наименьший элемент удаляется из второго списка и добавляется в первый.
Алгоритм
На практике не нужно создавать новый список для отсортированных элементов. В качестве него используется крайняя левая часть списка. Находится наименьший элемент и меняется с первым местами.
Теперь, когда нам известно, что первый элемент списка отсортирован, находим наименьший элемент из оставшихся и меняем местами со вторым. Повторяем это до тех пор, пока не останется последний элемент в списке.
Реализация
def selection_sort(nums):
# Значение i соответствует кол-ву отсортированных значений
for i in range(len(nums)):
# Исходно считаем наименьшим первый элемент
lowest_value_index = i
# Этот цикл перебирает несортированные элементы
for j in range(i + 1, len(nums)):
if nums[j] < nums[lowest_value_index]:
lowest_value_index = j
# Самый маленький элемент меняем с первым в списке
nums[i], nums[lowest_value_index] = nums[lowest_value_index], nums[i]
# Проверяем, что оно работает
random_list_of_nums = [12, 8, 3, 20, 11]
selection_sort(random_list_of_nums)
print(random_list_of_nums)
По мере увеличения значения i нужно проверять меньше элементов.
Время сортировки
Затраты времени на сортировку выборкой в среднем составляют O(n²), где n — количество элементов списка.
Сортировка вставками
Как и сортировка выборкой, этот алгоритм сегментирует список на две части: отсортированную и неотсортированную. Алгоритм перебирает второй сегмент и вставляет текущий элемент в правильную позицию первого сегмента.
Алгоритм
Предполагается, что первый элемент списка отсортирован. Переходим к следующему элементу, обозначим его х. Если х больше первого, оставляем его на своём месте. Если он меньше, копируем его на вторую позицию, а х устанавливаем как первый элемент.
Переходя к другим элементам несортированного сегмента, перемещаем более крупные элементы в отсортированном сегменте вверх по списку, пока не встретим элемент меньше x или не дойдём до конца списка. В первом случае x помещается на правильную позицию.
Реализация
def insertion_sort(nums):
# Сортировку начинаем со второго элемента, т.к. считается, что первый элемент уже отсортирован
for i in range(1, len(nums)):
item_to_insert = nums[i]
# Сохраняем ссылку на индекс предыдущего элемента
j = i - 1
# Элементы отсортированного сегмента перемещаем вперёд, если они больше
# элемента для вставки
while j >= 0 and nums[j] > item_to_insert:
nums[j + 1] = nums[j]
j -= 1
# Вставляем элемент
nums[j + 1] = item_to_insert
# Проверяем, что оно работает
random_list_of_nums = [9, 1, 15, 28, 6]
insertion_sort(random_list_of_nums)
print(random_list_of_nums)
Время сортировки
Время сортировки вставками в среднем равно O(n²), где n — количество элементов списка.
Пирамидальная сортировка
Также известна как сортировка кучей. Этот популярный алгоритм, как и сортировки вставками или выборкой, сегментирует список на две части: отсортированную и неотсортированную. Алгоритм преобразует второй сегмент списка в структуру данных «куча» (heap), чтобы можно было эффективно определить самый большой элемент.
Алгоритм
Сначала преобразуем список в Max Heap — бинарное дерево, где самый большой элемент является вершиной дерева. Затем помещаем этот элемент в конец списка. После перестраиваем Max Heap и снова помещаем новый наибольший элемент уже перед последним элементом в списке.
Этот процесс построения кучи повторяется, пока все вершины дерева не будут удалены.
Реализация
Создадим вспомогательную функцию heapify() для реализации этого алгоритма:
def heapify(nums, heap_size, root_index):
# Индекс наибольшего элемента считаем корневым индексом
largest = root_index
left_child = (2 * root_index) + 1
right_child = (2 * root_index) + 2
# Если левый потомок корня — допустимый индекс, а элемент больше,
# чем текущий наибольший, обновляем наибольший элемент
if left_child < heap_size and nums[left_child] > nums[largest]:
largest = left_child
# То же самое для правого потомка корня
if right_child < heap_size and nums[right_child] > nums[largest]:
largest = right_child
# Если наибольший элемент больше не корневой, они меняются местами
if largest != root_index:
nums[root_index], nums[largest] = nums[largest], nums[root_index]
# Heapify the new root element to ensure it's the largest
heapify(nums, heap_size, largest)
def heap_sort(nums):
n = len(nums)
# Создаём Max Heap из списка
# Второй аргумент означает остановку алгоритма перед элементом -1, т.е.
# перед первым элементом списка
# 3-й аргумент означает повторный проход по списку в обратном направлении,
# уменьшая счётчик i на 1
for i in range(n, -1, -1):
heapify(nums, n, i)
# Перемещаем корень Max Heap в конец списка
for i in range(n - 1, 0, -1):
nums[i], nums[0] = nums[0], nums[i]
heapify(nums, i, 0)
# Проверяем, что оно работает
random_list_of_nums = [35, 12, 43, 8, 51]
heap_sort(random_list_of_nums)
print(random_list_of_nums)
Время сортировки
В среднем время сортировки кучей составляет O(n log n), что уже значительно быстрее предыдущих алгоритмов.
Сортировка слиянием
Этот алгоритм относится к алгоритмам «разделяй и властвуй». Он разбивает список на две части, каждую из них он разбивает ещё на две и т. д. Список разбивается пополам, пока не останутся единичные элементы.
Соседние элементы становятся отсортированными парами. Затем эти пары объединяются и сортируются с другими парами. Этот процесс продолжается до тех пор, пока не отсортируются все элементы.
Алгоритм
Список рекурсивно разделяется пополам, пока в итоге не получатся списки размером в один элемент. Массив из одного элемента считается упорядоченным. Соседние элементы сравниваются и соединяются вместе. Это происходит до тех пор, пока не получится полный отсортированный список.
Сортировка осуществляется путём сравнения наименьших элементов каждого подмассива. Первые элементы каждого подмассива сравниваются первыми. Наименьший элемент перемещается в результирующий массив. Счётчики результирующего массива и подмассива, откуда был взят элемент, увеличиваются на 1.
Реализация
def merge(left_list, right_list):
sorted_list = []
left_list_index = right_list_index = 0
# Длина списков часто используется, поэтому создадим переменные для удобства
left_list_length, right_list_length = len(left_list), len(right_list)
for _ in range(left_list_length + right_list_length):
if left_list_index < left_list_length and right_list_index < right_list_length:
# Сравниваем первые элементы в начале каждого списка
# Если первый элемент левого подсписка меньше, добавляем его
# в отсортированный массив
if left_list[left_list_index] <= right_list[right_list_index]:
sorted_list.append(left_list[left_list_index])
left_list_index += 1
# Если первый элемент правого подсписка меньше, добавляем его
# в отсортированный массив
else:
sorted_list.append(right_list[right_list_index])
right_list_index += 1
# Если достигнут конец левого списка, элементы правого списка
# добавляем в конец результирующего списка
elif left_list_index == left_list_length:
sorted_list.append(right_list[right_list_index])
right_list_index += 1
# Если достигнут конец правого списка, элементы левого списка
# добавляем в отсортированный массив
elif right_list_index == right_list_length:
sorted_list.append(left_list[left_list_index])
left_list_index += 1
return sorted_list
def merge_sort(nums):
# Возвращаем список, если он состоит из одного элемента
if len(nums) <= 1:
return nums
# Для того чтобы найти середину списка, используем деление без остатка
# Индексы должны быть integer
mid = len(nums) // 2
# Сортируем и объединяем подсписки
left_list = merge_sort(nums[:mid])
right_list = merge_sort(nums[mid:])
# Объединяем отсортированные списки в результирующий
return merge(left_list, right_list)
# Проверяем, что оно работает
random_list_of_nums = [120, 45, 68, 250, 176]
random_list_of_nums = merge_sort(random_list_of_nums)
print(random_list_of_nums)
Обратите внимание, что функция merge_sort(), в отличие от предыдущих алгоритмов, возвращает новый список, а не сортирует существующий. Поэтому такая сортировка требует больше памяти для создания нового списка того же размера, что и входной список.
Время сортировки
В среднем время сортировки слиянием составляет O(n log n).
Быстрая сортировка
Этот алгоритм также относится к алгоритмам «разделяй и властвуй». Его используют чаще других алгоритмов, описанных в этой статье. При правильной конфигурации он чрезвычайно эффективен и не требует дополнительной памяти, в отличие от сортировки слиянием. Массив разделяется на две части по разные стороны от опорного элемента. В процессе сортировки элементы меньше опорного помещаются перед ним, а равные или большие —позади.
Алгоритм
Быстрая сортировка начинается с разбиения списка и выбора одного из элементов в качестве опорного. А всё остальное передвигаем так, чтобы этот элемент встал на своё место. Все элементы меньше него перемещаются влево, а равные и большие элементы перемещаются вправо.
Реализация
Существует много вариаций данного метода. Способ разбиения массива, рассмотренный здесь, соответствует схеме Хоара (создателя данного алгоритма).
def partition(nums, low, high):
# Выбираем средний элемент в качестве опорного
# Также возможен выбор первого, последнего
# или произвольного элементов в качестве опорного
pivot = nums[(low + high) // 2]
i = low - 1
j = high + 1
while True:
i += 1
while nums[i] < pivot:
i += 1
j -= 1
while nums[j] > pivot:
j -= 1
if i >= j:
return j
# Если элемент с индексом i (слева от опорного) больше, чем
# элемент с индексом j (справа от опорного), меняем их местами
nums[i], nums[j] = nums[j], nums[i]
def quick_sort(nums):
# Создадим вспомогательную функцию, которая вызывается рекурсивно
def _quick_sort(items, low, high):
if low < high:
# This is the index after the pivot, where our lists are split
split_index = partition(items, low, high)
_quick_sort(items, low, split_index)
_quick_sort(items, split_index + 1, high)
_quick_sort(nums, 0, len(nums) - 1)
# Проверяем, что оно работает
random_list_of_nums = [22, 5, 1, 18, 99]
quick_sort(random_list_of_nums)
print(random_list_of_nums)
Время выполнения
В среднем время выполнения быстрой сортировки составляет O(n log n).
Обратите внимание, что алгоритм быстрой сортировки будет работать медленно, если опорный элемент равен наименьшему или наибольшему элементам списка. При таких условиях, в отличие от сортировок кучей и слиянием, обе из которых имеют в худшем случае время сортировки O(n log n), быстрая сортировка в худшем случае будет выполняться O(n²).
Иногда полезно знать перечисленные выше алгоритмы, но в большинстве случаев разработчик, скорее всего, будет использовать функции сортировки, уже предоставленные в языке программирования.
Отсортировать содержимое списка можно с помощью стандартного метода sort():
>>> apples_eaten_a_day = [2, 1, 1, 3, 1, 2, 2] >>> apples_eaten_a_day.sort() >>> apples_eaten_a_day [1, 1, 1, 2, 2, 2, 3]
Или можно использовать функцию sorted() для создания нового отсортированного списка, оставив входной список нетронутым:
>>> apples_eaten_a_day_2 = [2, 1, 1, 3, 1, 2, 2] >>> sorted_apples = sorted(apples_eaten_a_day_2) >>> sorted_apples [1, 1, 1, 2, 2, 2, 3]
Оба эти метода сортируют в порядке возрастания, но можно изменить порядок, установив для флага reverse значение True:
# Обратная сортировка списка на месте >>> apples_eaten_a_day.sort(reverse=True) >>> apples_eaten_a_day [3, 2, 2, 2, 1, 1, 1] # Обратная сортировка, чтобы получить новый список >>> sorted_apples_desc = sorted(apples_eaten_a_day_2, reverse=True) >>> sorted_apples_desc [3, 2, 2, 2, 1, 1, 1]
В отличие от других алгоритмов, обе функции в Python могут сортировать также списки кортежей и классов. Функция sorted() может сортировать любую последовательность, которая включает списки, строки, кортежи, словари, наборы и пользовательские итераторы, которые вы можете создать.
Функции в Python реализуют алгоритм Tim Sort, основанный на сортировке слиянием и сортировке вставкой.
Сравнение скоростей сортировок
Для сравнения сгенерируем массив из 5000 чисел от 0 до 1000. Затем определим время, необходимое для завершения каждого алгоритма. Повторим каждый метод 10 раз, чтобы можно было более точно установить, насколько каждый из них производителен.

Пузырьковая сортировка — самый медленный из всех алгоритмов. Возможно, он будет полезен как введение в тему алгоритмов сортировки, но не подходит для практического использования.
Быстрая сортировка хорошо оправдывает своё название, почти в два раза быстрее, чем сортировка слиянием, и не требуется дополнительное место для результирующего массива.
Сортировка вставками выполняет меньше сравнений, чем сортировка выборкой и в реальности должна быть производительнее, но в данном эксперименте она выполняется немного медленней. Сортировка вставками делает гораздо больше обменов элементами. Если эти обмены занимают намного больше времени, чем сравнение самих элементов, то такой результат вполне закономерен.
Вы познакомились с шестью различными алгоритмами сортировок и их реализациями на Python. Масштаб сравнения и количество перестановок, которые выполняет алгоритм вместе со средой выполнения кода, будут определяющими факторами в производительности. В реальных приложениях Python рекомендуется использовать встроенные функции сортировки, поскольку они реализованы именно для удобства разработчика.

Автор: . Дата: 26-го октября 2008 г.
Сортировка слиянием — вероятно, один из самых простых алгоритмов сортировки (среди «быстрых» алгоритмов). Особенностью этого алгоритма является то, что он работает с элементами массива преимущественно последовательно, благодаря чему именно этот алгоритм используется при сортировке в системах с различными аппаратными ограничениями (например, при сортировке данных на жёстком диске, или даже на магнитной ленте). Кроме того, сортировка слиянием — чуть ли не единственный алгоритм, который может быть эффективно использован для сортировки таких структур данных, как связанные списки. Последовательная работа с элементами массива значительно увеличивает скорость сортировки в системах с кэшированием.
Сортировка слиянием — стабильный алгоритм сортировки. Это означает, что порядок «равных» элементов не изменяется в результате работы алгоритма. В некоторых задачах это свойство достаточно важно.
Этот алгоритм был предложен Джоном фон Нейманом в 1945 году
Везде в лекции элементы массивов нумеруются с нуля.
Процедура слияния
Допустим, у нас есть два отсортированных массива А и B размерами 


![$$begin{array}{l}aleftarrow0; bleftarrow0;\text{While }a<n_atext{ and }b<n_b\left|quadbegin{array}{l}text{If }A[a]leqslant B[b]\left|quadbegin{array}{l}C[a+b]leftarrow A[a];\aleftarrow a+1;end{array}right.\text{Else}\left|quadbegin{array}{l}C[a+b]leftarrow B[b];\bleftarrow b+1;end{array}right.\text{End;}end{array}right.\text{End;}\text{If }a<n_a\left|quadtext{Copy remain part of A}right.\text{Else}\left|quadtext{Copy remain part of B}right.\text{End;}end{array}$$ begin{array}{l}
a leftarrow 0; b leftarrow 0;\
text{While }a < n_atext{ and }b < n_b\
left|quadbegin{array}{l}
text{If }A[a]leqslant B[b]\
left|quadbegin{array}{l}
C[a+b] leftarrow A[a];\
a leftarrow a+1;
end{array}right.\
text{Else}\
left|quadbegin{array}{l}
C[a+b] leftarrow B[b];\
b leftarrow b+1;
end{array}right.\
text{End;}
end{array}right.\
text{End;}\
text{If }a<n_a\
left|quadtext{Copy remain part of A}right.\
text{Else}\
left|quadtext{Copy remain part of B}right.\
text{End;}
end{array}](https://web.archive.org/web/20090523191746im_/http://iproc.ru/wp-content/cache_tex/tex_cf350c12af27e88daef980b96c519a6c.png) |
(1) |
Для обеспечения стабильности алгоритма сортировки нужно, чтобы в случае равенства элементов тот элемент, что идёт раньше во входном массиве, попадал в результирующий массив в первую очередь. Мы увидим далее, что если два элемента попали в разные массивы (A и B), то тот элемент, что шёл раньше, попадёт в массив A. Следовательно, в случае равенства элемент из массива A должен иметь приоритет. Поэтому в алгоритме стои́т знак 

Недостатком представленного алгоритма является необходимость дописывать оставшийся кусок, из-за чего при дальнейших модификациях алгоритма нам придётся писать много повторяющегося кода. Чтобы этого избежать, будем использовать чуть менее эффективный, но более короткий алгоритм, в котором копирование «хвоста» встроено в основной цикл:
![$$begin{array}{l}aleftarrow0; bleftarrow0;\text{While }a+b<n_a+n_b\left|quadbegin{array}{l}text{If }bgeqslant n_btext{ or }left(a<n_atext{ and }A[a]leqslant B[b]right)\left|quadbegin{array}{l}C[a+b]leftarrow A[a];\aleftarrow a+1;end{array}right.\text{Else}\left|quadbegin{array}{l}C[a+b]leftarrow B[b];\bleftarrow b+1;end{array}right.\text{End;}end{array}right.\text{End;}end{array}$$ begin{array}{l}
a leftarrow 0; b leftarrow 0;\
text{While }a+b < n_a+n_b\
left|quadbegin{array}{l}
text{If }bgeqslant n_btext{ or }left(a<n_atext{ and }A[a]leqslant B[b]right)\
left|quadbegin{array}{l}
C[a+b] leftarrow A[a];\
a leftarrow a+1;
end{array}right.\
text{Else}\
left|quadbegin{array}{l}
C[a+b] leftarrow B[b];\
b leftarrow b+1;
end{array}right.\
text{End;}
end{array}right.\
text{End;}
end{array}](https://web.archive.org/web/20090523191746im_/http://iproc.ru/wp-content/cache_tex/tex_3b1896677eb39fb070eec37d83e1d8f5.png) |
(2) |
Очевидно, время работы процедуры слияния составляет 
Рис. 1. Пример работы процедуры слияния
Реализация процедуры слияния на языке программирования C++ представлена в листинге 1.
template<class T> void Merge(T const *const A, int const nA,
T const *const B, int const nB,
T *const C)
{ //Выполнить слияние массива A, содержащего nA элементов,
// и массива B, содержащего nB элементов.
// Результат записать в массив C.
int a(0), b(0); //Номера текущих элементов в массивах A и B
while( a+b < nA+nB ) //Пока остались элементы в массивах
{
if( (b>=nB) || ( (a<nA) && (A[a]<=B[b]) ) )
{ //Копирую элемент из массива A
C[a+b] = A[a];
++a;
} else { //Копирую элемент из массива B
C[a+b] = B[b];
++b;
}
}
}
Листинг 1. Реализация процедуры слияния
Сортировка слиянием
Процедура слияния требует два отсортированных массива. Заметив, что массив из одного элемента по определению является отсортированным, мы можем осуществить сортировку следующим образом:
- разбить имеющиеся элементы массива на пары и осуществить слияние элементов каждой пары, получив отсортированные цепочки длины 2 (кроме, быть может, одного элемента, для которого не нашлось пары);
- разбить имеющиеся отсортированные цепочки на пары, и осуществить слияние цепочек каждой пары;
- если число отсортированных цепочек больше единицы, перейти к шагу 2.
Проще всего формализовать этот алгоритм рекурсивным способом (в следующем разделе мы реализуем этот алгоритм итерационным способом). Функция 
 |
(3) |
Поскольку функция 
template<class T> void MergeSort(T *const A, int const n)
{ //Отсортировать массив A, содержащий n элементов
if( n < 2 ) return; //Сортировка не нужна
if( n == 2 ) //Два элемента проще поменять местами,
{ // если нужно, чем делать слияние
if( A[0] > A[1] ) { T const t(A[0]); A[0]=A[1]; A[1]=t; }
return;
}
T *const B( new T[n] ); //Сюда запишем результат
MergeSort(A , n/2 ); //Сортируем первую половину
MergeSort(A+n/2, n—n/2); //Сортируем вторую половину
Merge(A,n/2, A+n/2,n—n/2, B); //Слияние половин
//Копирование результата в исходный массив:
for(int i(0); i<n; ++i) A[i]=B[i];
delete[n] B; //Удаляем временный буфер
}
Листинг 2. Реализация сортировки слиянием
Время работы сортировки слиянием составляет 
Рис. 2. Пример работы рекурсивного алгоритма сортировки слиянием
Восходящая сортировка слиянием
Программа, представленная в листинге 2, имеет серьёзные недостатки: она выделяет и освобождает много буферов памяти, и делает копирование результатов слияния в исходный массив вместо того, чтобы вернуть новый массив в качестве результата (она не может вернуть новый массив в качестве результата, т.к. на входе получает зачастую лишь часть большого массива).
Чтобы избавиться от этих недостатков, откажемся от рекурсивной реализации, и сделаем сортировку следующим образом:
- выделим временный буфер памяти размером с исходный массив;
- выполним попарное слияние элементов, записывая результат во временный массив;
- поменяем местами указатели на временный массив и на исходный массив;
- выполним попарное слияние фрагментов длиной 2;
- аналогично продолжаем до тех пор, пока не останется один кусок;
- в конце работы алгоритма удаляем временный массив.
Такой алгоритм называется восходящей сортировкой слиянием. Реализация его на языке программирования C++ приведена в листинге 3.
template<class T> void MergeSortIterative(T *&A, int const n)
{ //Отсортировать массив A, содержащий n элементов.
// При работе указатель на A, возможно, меняется.
// (Функция получает ссылку на указатель на A)
T *B( new T[n] ); //Временный буфер памяти
for(int size(1); size<n; size*=2)
{ //Перебираем все размеры кусочков для слияния: 1,2,4,8…
int start(0); //Начало первого кусочка пары
for(; (start+size)<n; start+=size*2)
{ //Перебираем все пары кусочков, и выполняем попарное
// слияние. (start+size)<n означает, что начало
// следующего кусочка лежит внутри массива
Merge(A+start , size,
A+start+size, min(size,n—start—size),
B+start );
}
//Если последний кусочек остался без пары, просто копи-
// руем его из A в B:
for(; start<n; ++start) B[start]=A[start];
T *temp(B); B=A; A=temp; //Меняем местами указатели
}
delete[n] B; //Удаляем временный буфер
}
Листинг 3. Реализация восходящей сортировки слиянием
К сожалению, в этот алгоритм не так просто вписать оптимизацию для случая слияния двух элементов (если нужно, можно вписать эту оптимизацию в процедуру Merge).
Пример работы программы листинга 3 показан на рисунке:
Рис. 3. Пример работы восходящего алгоритма сортировки слиянием
Если требуется выполнять восходящую сортировку для части массива, или в других случаях, когда указатель на массив менять нельзя, то будет полезной модификация программы, которая, если нужно, копирует результат в исходный массив в конце работы:
template<class T> void MergeSortIter2(T *const A, int const n)
{ //Отсортировать массив A, содержащий n элементов.
T *B( A ); //Буфер памяти №1
T *C( new T[n] ); //Буфер памяти №2
for(int size(1); size<n; size*=2)
{ //Перебираем все размеры кусочков для слияния: 1,2,4,8…
int start(0); //Начало первого кусочка пары
for(; (start+size)<n; start+=size*2)
{ //Перебираем все пары кусочков, и выполняем попарное
// слияние. (start+size)<n означает, что начало
// следующего кусочка лежит внутри массива
Merge(B+start , size,
B+start+size, min(size,n—start—size),
C+start );
}
//Если последний кусочек остался без пары, просто копи-
// руем его из B в C:
for(; start<n; ++start) C[start]=B[start];
T *temp(B); B=C; C=temp; //Меняем местами указатели
}
//В данный момент результат работы находится в массиве B.
if( C == A )
{ // Если массив C является массивом A, то нужно
// скопировать результат работы из B в A.
for(int i(0); i<n; ++i) A[i]=B[i];
delete[n] B; //Удаляем временный буфер
} else {
delete[n] C; //Удаляем временный буфер
}
}
Листинг 4. Реализация восходящей сортировки слиянием
с сохранением результата работы в исходном массиве
Измерение быстродействия алгоритма
Измерим быстродействие программы из листинга 3. Условия измерения — те же, что для алгоритма пирамидальной сортировки (см. лекцию 5).
На рис. 4 показан график величины 
 |
(4) |
где n — количество сортируемых псевдослучайных четырёхбайтовых целых чисел, 
Рис. 4. Отношение времени сортировки к 
Красный цвет — сортировка слиянием,
серый цвет — пирамидальная сортировка
На графике проявляются две важные особенности алгоритма:
- Сортировка слиянием работает в полтора-два раза медленнее, чем пирамидальная сортировка, когда число сортируемых элементов меньше 500. Так как алгоритм сортировки слиянием рекурсивный, эта потеря быстродействия на сортировке малых массивов отражается на всём остальном графике. Если мы сможем ускорить алгоритм для сортировки малых объёмов данных — мы сможем ускорить его для сортировки любых объёмов данных.
- Скорость сортировки не падает, когда количество сортируемых данных становится больше размера кеша! Это означает, что именно сортировку слиянием следует использовать для сортировки больших объёмов данных.
Гибридная сортировка
Анализ быстродействия алгоритма наталкивает нас на мысль объединить преимущества алгоритмов пирамидальной сортировки и сортировки слиянием. К счастью, сделать это очень просто: нужно разбить массив сразу на большие кусочки (например, размером 512 элементов), и применить к ним алгоритм пирамидальной сортировки. Полученные отсортированные кусочки затем можно «досортировать» слиянием. Используя функции из лекции 5, требуемые изменения в алгоритме минимальны (за основу взята функция из листинга 3):
template<class T> void HybridSort(T *&A, int const n)
{ //Отсортировать массив A, содержащий n элементов.
// При работе указатель на A, возможно, меняется.
// (Функция получает ссылку на указатель на A)
//Размер кусочка для сортировки пирамидой:
// (нужно подбирать для максимального ускорения)
int const tileSize( 4096 );
for(int start(0); start<n; start+=tileSize)
HeapSort(A+start, min(tileSize,n—start) );
if( n <= tileSize ) return; //Больше сортировать не нужно
T *B( new T[n] ); //Временный буфер памяти
for(int size(tileSize); size<n; size*=2)
{ //Перебираем размеры кусочков для слияния,
// начиная с tileSize элементов
int start(0); //Начало первого кусочка пары
for(; (start+size)<n; start+=size*2)
{ //Перебираем все пары кусочков, и выполняем попарное
// слияние. (start+size)<n означает, что начало
// следующего кусочка лежит внутри массива
Merge(A+start , size,
A+start+size, min(size,n—start—size),
B+start );
}
//Если последний кусочек остался без пары, просто копи-
// руем его из A в B:
for(; start<n; ++start) B[start]=A[start];
T *temp(B); B=A; A=temp; //Меняем местами указатели
}
delete[n] B; //Удаляем временный буфер
}
Листинг 5. Реализация гибридной сортировки
Быстродействие гибридной сортировки показано на графике:
Рис. 5. Отношение времени сортировки к 
Красный цвет — гибридная сортировка,
синий цвет — сортировка слиянием,
серый цвет — пирамидальная сортировка
Из графика видно, что гибридная сортировка имеет время работы, как у пирамидальной сортировки при малом числе элементов, и незначительно быстрее сортировки слиянием при большом их числе.
Tiled-версия
Tile переводится, как «черепица», «плитка». Приём программирования, при котором большие объёмы данных разделяются для обработки и хранения на части меньшего размера («tiles»), называется «tiling». Вместо «tile» мы будем говорить «блок».
Основным недостатком представленных до сих пор реализаций сортировки слиянием является необходимость иметь 
Но связанные списки имеют большие накладные расходы по памяти и быстродействию: в каждом элементе требуется хранить указатель на следующий элемент, требуется время на создание и уничтожение элементов списка. Чтобы уменьшить накладные расходы, нужно хранить большое количество сортируемых данных в каждом элементе списка.
Связанные списки не позволяют быстро обращаться к произвольным элементам, поэтому мы пойдём немного другим путём: будем хранить массив указателей на блоки памяти большого размера (но умещающиеся в кэш процессора). Такая структура данных была описана в лекции 4 (раздел «Программная реализация алгоритма Гаусса»).
Процедура слияния будет освобождать обработанные блоки памяти, и выделять новые по мере записи результата. В этом случае максимальный дополнительный объём памяти, который понадобится, равен двукратному размеру блока памяти. Кроме того, указатели на результирующие блоки памяти после слияния можно легко перенести в исходный буфер. Для простоты будем считать, что все блоки, на которые разбит исходный массив имеют одинаковый размер: tileSize элементов.
template<class T> template<class T> void MergeTiled(T **const Array,
int const numTiles1, int const numTiles2, int const tileSize)
{ //Выполнить слияние двух цепочек из массива Array. Первая
// цепочка состоит из numTiles1 блоков, вторая цепочка
// состоит из numTiles2 блоков и идёт сразу за первой.
// Каждый блок имеет размер tileSize
//Массив для записи указателей на результирующие блоки:
T **Result = new T *[numTiles1+numTiles2];
Result[0] = new T[tileSize]; //Пока создаём один блок
//Номера текущих блоков в первой и второй исходных
// цепочках и в результирующей цепочке соответственно:
int tN1(0), tN2(0), tNR(0);
//Указатели на текущие блоки:
T *t1( Array[0] ), *t2( Array[numTiles1] ), *tR( Result[0] );
//Номера текущих элементов в соответствующих цепочках:
int n1(0), n2(0), nR(0);
while( true )
{
if( (tN2>=numTiles2) ||
( (tN1<numTiles1) && (t1[n1]<=t2[n2]) ) )
{
tR[nR] = t1[n1];
++n1; //Переходим к след. элементу в первой цепочке
if( n1>=tileSize )
{ //Текущий блок в первой цепочке закончился
//Удаляем текущий блок первой цепочки:
delete[tileSize] t1;
++tN1; //Увеличиваем номер текущего блока
//Переходим к следующему блоку первой цепочки:
if( tN1 < numTiles1 ) t1 = Array[tN1];
n1 = 0; //Перешли к началу следующего блока
}
} else {
tR[nR] = t2[n2];
++n2; //Переходим к след. элементу во второй цепочке
if( n2>=tileSize )
{ //Текущий блок во второй цепочке закончился
//Удаляем текущий блок второй цепочки:
delete[tileSize] t2;
++tN2; //Увеличиваем номер текущего блока
//Переходим к следующему блоку второй цепочки:
if( tN2 < numTiles2 ) t2 = Array[numTiles1+tN2];
n2 = 0; //Перешли к началу следующего блока
}
}
++nR;
if( nR>=tileSize )
{ //Текущий блок в результирующей цепочке закончился
//Увеличиваем номер текущего блока результата:
++tNR;
//Место для записи результата закончилось.
// Значит, закончились и исходные данные:
if( tNR >= numTiles1+numTiles2 ) break;
//Выделяем память под следующий блок результата:
Result[tNR] = tR = new T[tileSize];
nR = 0; //Перешли к началу следующего блока
}
}
//Исходные блоки удалены. Записываем указатели на результи-
// рующие блоки на место указателей на исходные блоки:
for(int tN(0); tN<numTiles1+numTiles2; ++tN)
Array[tN] = Result[tN];
//Удаляем массив указателей на результирующие блоки:
delete[numTiles1+numTiles2] Result;
}
Листинг 6. Tiled-версия процедуры слияния
Так как процедура слияния возвращает результат своей работы в исходный массив, нет необходимости заводить второй буфер в процедуре сортировки, которая благодаря этому упрощается. Данные внутри блока в данном примере сортируются пирамидальной сортировкой, поэтому этот алгоритм тоже можно назвать «гибридным»:
template<class T> void MergeSortTiled(T **const Array,
int const numTiles, int const tileSize)
{ //Отсортировать массив Array, содержащий numTiles блоков
// по tileSize элементов
//Вначале сортирую элементы каждого блока каким-нибудь из
// описанных ранее алгоритмов:
for(int tN(0); tN<numTiles; ++tN)
HeapSort(Array[tN], tileSize);
for(int size(1); size<numTiles; size*=2)
{ //Перебираем все размеры цепочек блоков
// для слияния: 1,2,4,8…
for(int start(0); (start+size)<numTiles; start+=size*2)
{ //Перебираем все пары цепочек, и выполняем попарное
// слияние. (start+size)<numTiles означает, что начало
// следующей цепочки лежит внутри массива
MergeTiled(Array+start,
size,
min(size,numTiles—start—size),
tileSize);
}
}
}
Листинг 7. Tiled-версия сортировки слиянием
Чем больше по размерам будет каждый блок памяти, тем меньше будут накладные расходы на работу с блоками. Однако, при большом размере блоков возрастают требования к дополнительному объёму памяти, требуемому программой. График скорости работы программы представлен на рисунке 6. Объём одного блока был выбран равным одному мегабайту, поэтому график начинается с 262144 элементов:
Рис. 6. Отношение времени сортировки к 
Красный цвет — tiled-версия сортировки слиянием,
серый цвет — гибридная сортировка
Из графика видно, что накладные расходы по работе с блоками совсем невелики, но они, к сожалению, растут по мере увеличения количества блоков. Зато у нас появляется возможность быстро сортировать данные, занимающие почти всю оперативную память компьютера.
Естественная сортировка
До сих пор мы рассматривали алгоритмы сортировки, которые никак не учитывают то, что данные (или их часть) могут быть уже отсортированы. Для алгоритма сортировки слиянием есть очень простая и эффективная модификация, которая называется «естественная сортировка» («Natural Sort»). Суть её в том, что нужно образовывать цепочки, и производить их слияние не в заранее определённом и фиксированном порядке, а анализировать имеющиеся в массиве данные. Алгоритм следующий:
- разбить массив на цепочки уже отсортированных элементов (в худшем случае, когда элементы в массиве идут по убыванию, все цепочки будут состоять из одного элемента);
- произвести слияние цепочек методом сдваивания.
Пример работы этого алгоритма показан на рисунке:
Рис. 7. Пример работы естественного алгоритма сортировки слиянием
В отличие от ранее рассмотренных вариантов алгоритма слияния, естественная сортировка справилась с задачей за 3, а не за 4 итерации.
Обратите внимание, что во время работы алгоритма не могут образоваться новые отсортированные цепочки кроме получившихся в результате слияний (докажите!), поэтому поиск отсортированных цепочек должен проводиться только на первом этапе. Но как хранить найденные цепочки? Выделять для них память — очень неэффективно. Самый простой способ — вообще их не хранить, а искать каждый раз заново. Это неэффективно, зато просто:
template<class T> void NaturalSort(T *&A, int const n)
{ //Отсортировать массив A, содержащий n элементов.
// При работе указатель на A, возможно, меняется.
// (Функция получает ссылку на указатель на A)
T *B( new T[n] ); //Временный буфер памяти
while(true) //Выполняем слияния, пока не останется один
{ // отсортированный участокк. Выход из цикла
// находится дальше
int start1 ,end1 ; //Первый отсортированный участок
int start2(—1),end2(—1); //Второй отсортированный участок
while(true)
{ //Цикл по всем парам отсортированных участков в массиве
//Начало первого участка для слияния находится после
// конца второго участка предыдущей пары:
start1 = end2+1; end1 = start1;
//Двигаемся вправо до нарушения сортировки:
while( (end1<n—1) && (A[end1]<=A[end1+1]) ) ++end1;
//Первый участок пары простирается до конца массива:
if( end1 == n—1 ) break;
//Начало второго участка для слияния находится после
// конца первого участка текущей пары:
start2 = end1+1, end2 = start2;
//Двигаемся вправо до нарушения сортировки:
while( (end2<n—1) && (A[end2]<=A[end2+1]) ) ++end2;
//Выполняем слияние двух отсортированных участков
Merge(A+start1, end1—start1+1,
A+start2, end2—start2+1,
B+start1 );
//Второй участок пары простирается до конца массива:
if( end2 == n—1 ) break;
}
//Данные полностью отсортированы и находятся в массиве A:
if( (start1==0) && (end1==n—1) ) break;
//Если последний кусочек остался без пары, просто копи-
// руем его из A в B:
if( end1 == n—1 )
{
for(; start1<n; ++start1) B[start1]=A[start1];
}
T *temp(B); B=A; A=temp; //Меняем местами указатели
}
delete[n] B; //Удаляем временный буфер
}
Листинг 8. Исходный код алгоритма естественной сортировки слиянием
Несмотря на то, что представленная реализация на каждой итерации примерно 25% времени проводит в поиске отсортированных фрагментов для слияния (хотя этот поиск достаточно произвести только в начале), она показывает неплохие результаты для случайного набора чисел:
Рис. 8. Отношение времени сортировки к 
Красный цвет — естественная сортировка,
серый цвет — восходящая сортировка слиянием
Если же исходные данные будут не случайны, а уже частично отсортированы, алгоритм естественной сортировки может ускориться в несколько раз!