

Подборка по базе: РГР_Основы расчета строительных конструкций.docx, Задание 3 Расчет трехфазных цепей.docx, Практическое занятие. План-факторный анализ показателей работы л, !ПЗ Расчет подстанции 29 вар 110-6.pdf, Методика расчета больших и малых потерь.pdf, ПР Расчет сопротивления заземления.pdf, Боевой расчет.docx, Совершенствование бухгалтерского учета расчетов с разными дебито, Указание Банка России от 9 декабря 2019 г N 5348 У О правилах на, МДК.03.01 Организация расчетов с бюджетом и внебюджетными фондам

Специальность/Направление
09.03.02Информационные системы и технологии
шифр название
Профиль подготовки _________________________________________________________
Практическая работа №1
вид работы (Курсовая работа, эссе, реферат, доклад и т.д.)
по дисциплине
Надежность информационных систем
на тему Расчет показателей надежности нерезервированных невосстанавливаемых систем
Выполнил: студент(ка) группы
ИС-182 Субботин Андрей Геннадьевич
Подпись студента: __________________________
Форма обучения
Очная
(очная, заочная)
Руководитель:
КТН Куралесин В.В.
Дата сдачи работы: ____.________.________
Дата защиты работы: ____.________.________
Оценка (зачёт):________________________ Подпись руководителя: ______________________
ВОРОНЕЖ 2020
Ход работы:
Задача 1. Аппаратура связи состоит из 2000 элементов, средняя интенсивность отказов которых λср= 0,33 ּ 10-5 1/час. Необходимо определить вероятность безотказной работы аппаратуры в течении t = 200 час и среднее время безотказной работы аппаратуры.
Решение: 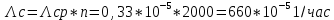
Задача 2. Невосстанавливаемая в процессе работы электронная машина состоит из 200000 элементов, средняя интенсивность отказов которых λср = 0,2 *10-6 1/час . Требуется определить вероятность безотказной работы электронной машины в течении t = 24 часа и среднее время безотказной работы электронной машины.
Решение: 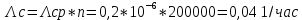
Задача 3. Система управления состоит из 6000 элементов, средняя
интенсивность отказов которых λср. = 0,16 * 10-6 1/час. Необходимо определить вероятность безотказной работы в течении t = 50 час и среднее время безотказной работы.
Решение: λс = λср * n = 0.16*10-6 *6000 = 960*10-6 1/час
Задача 4. Прибор состоит из n = 5 узлов. Надежность узлов характеризуется вероятностью безотказной работы в течение времени t, которая равна: P1(t)=0,98; P2(t)=0,99; P3(t)=0,998; P4(t)=0,975; P5(t)=0,985. Необходимо определить вероятность безотказной работы прибора.
Решение: При последовательном соединении:
Pс(t)=P1(t)*P2(t)*P3(t)*P4(t)*P5(t)
Pс(t)=0,98*0,99*0,998*0,975*0,985=0.9299
Задача 5. Система состоит из пяти приборов, среднее время безотказной работы которых равно: mt1=83 час; mt2=220 час; mt3=280 час; mt4=400 час; mt5=700 час. Для приборов справедлив экспоненциальный закон надежности. Требуется найти среднее время безотказной работы системы.
Решение: Экспоненциальный закон надежности: mср=1/λ
Среднее время безотказной работы системы: 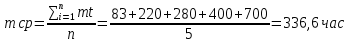
Задача 6. Прибор состоит из пяти блоков. Вероятность безотказной
работы каждого блока в течение времени t = 50 час равна: P1(50)=0,98;
P2(50)=0,99; P3(50)=0,998; P4(50)=0,975; P5(50)=0,985. Справедлив экспоненциальный закон надежности. Требуется найти среднее время безотказной работы прибора.
Решение: Найдем вероятность безотказной работы системы: 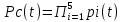
Pc(50)=0,98*0,99*0,998*0,975*0,985=0,929
Исходя из экспоненциального закона, найдем интенсивность отказов:
Найдем среднюю наработку до первого отказа:
Вывод: В данной практической работе были получены навыки расчета показателей невосстанавливаемых нерезервированных систем.
Предлагается несколько
простых примеров решения задач. Следует
помнить, что частота, интенсивность
отказов и параметр потока отказов,
вычисленные по формулам (1.35),
(1.6) и (1.13), являются
постоянными в диапазоне интервала
времени ∆t,
а функции
,
,
–
ступенчатыми кривыми или гистограммами.
Для удобства изложения в дальнейшем
при решении задач на определение частоты,
интенсивности и параметра потока отказов
по статистическим данным об отказах
изделий ответы относятся к середине
интервала ∆t.
При этом результаты вычислений
графически представляются не в виде
гистограмм, а в виде точек, отнесенных
к середине интервалов ∆ti
и соединенных плавной
кривой.
Пример 1
Допустим, что на испытание
поставлено 1000 однотипных электронных
ламп. За 3000 ч отказало 80 ламп, требуется
определить вероятность безотказной
работы P(t)
и вероятность отказа
Q(t)
в течение 3000 ч
|
Дано:
N
∆t
n |
Решение:
|
|
Найти:
P(t) Q(t) |
|
Пример 2
Допустим, что на испытание
поставлено 1000 однотипных электронных
ламп. За первые 3000 ч отказало 80 ламп, а
за интервал времени 3000–4000 ч
отказало еще 50 ламп.
Требуется определить частоту
f(∆t)
и интенсивность λ(∆t)
отказов электронных ламп в промежутке
времени ∆t
= 3000–4000 ч.
|
Дано:
N
∆t1
n1
∆t2
n2 |
Решение:
где
|
|
Найти:
a(∆t2) λ(∆t2) |
|
Пример 3
На испытание поставлено N0
= 400 изделий. За
время t
=
3000 ч отказало n(t)
= 200 изделий, за интервал
∆t
= 100 ч отказало n(∆t)
= 100
изделий. Требуется определить вероятность
безотказной работы за 3000 ч, вероятность
безотказной работы за 3100 ч, вероятность
безотказной работы за 3050 ч, частоту
отказов f(3050),
интенсивность отказов λ(3050).
t
= 0
t
= 3000 ч ∆t
= 100 ч
Рис.
1.3. Временной график
|
Дано:
N
t
n
∆t
n(∆t) |
Решение:
Вероятность безотказной работы
Для t
Для t
Среднее время исправно работающих
Число изделий, отказавших за время t
|
|
Найти: Р(3000) Р(3100) Р(3050)
f(3050) f(3100) λ(3000) λ(3050) λ(3100) |

Определяется частота отказа:

ч–1.
Так же определяется частота отказов за
интервалы 3000 и 3100 ч, причем началом
интервалов является t
= 0.
ч–1;
ч–1.
Определяется интенсивность отказов:
а) в интервале ∆t= 3050 ч,

б) в интервале
ч,
шт.;

в) в интервале
ч,
шт.;

Пример 4
В течение некоторого периода
времени производилось наблюдение за
работой одного объекта. За весь период
зарегистрировано n
= 15 отказов. До начала
наблюдений объект проработал 258 ч, к
концу наблюдения наработка составила
1233 ч. Определить среднюю наработку на
отказ tср.
|
Дано: n= 15 t1= 258 ч t2= 1233 ч |
Решение: Наработка за указанный период составила
∆t
Наработка на отказ по статистическим
|
|
Найти: tср |
где ti
– время исправной
работы между(i
– 1)иi
отказами;n
–число отказов за некоторое времяt.
Приняв
=
975 ч, можно определить среднюю наработку
на отказ
tср=
= 65 ч.
Пример 5
Производилось наблюдение
за работой трех однотипных объектов.
За период наблюдения было зафиксировано
по первому объекту 6 отказов, по второму
– 11 отказов, третьему – 8 отказов.
Наработка первого объекта t1
= 6181
ч, второго t2
=
329 ч,
третьего t3
=
245 ч. Определить наработку объектов на
отказ.
|
Дано:
N
n1
n2
n3
t1
t2
t3 |
Решение: 1-й вариант решения:
|
|
Найти: tср |
|
|
2-й вариант решения: |
,


ч;
ч;
ч;
ч.
Как видно, у задачи есть два варианта
решения. Первый основан на использовании
общей формулы вычисления средней
наработки; второй – более детальный:
сначала находится средняя наработка
для каждого элемента, а среднее значение
этих чисел и есть то, что определяется.
Пример 6
Система состоит из 5 приборов, причем
отказ любого одного из них ведет к отказу
системы. Известно, что первый отказал
34 раза в течение 952 ч работы, второй –
24 раза в течение 960 ч работы, а остальные
приборы в течение 210 ч работы отказали
4, 6 и 5 раз соответственно. Требуется
определить наработку на отказ системы
в целом, если справедлив экспоненциальный
закон надежности для каждого из пяти
приборов.
|
Дано: N= 5 шт. n1= 34 шт. n2= 24 шт. n3= 4 шт. n4= 6 шт. n5= 5 шт.
t1
t2 t3–5= 210 ч |
Решение: Используются следующие соотношения:
Определяется интенсивность отказов
где Nср
|
|
Найти: tср |
ч
–1;
ч–1;
или
ч–1;
тогда интенсивность отказов
системы будет
ч–1.
Средняя наработка на отказ системы
равна

Пример 7
За наблюдаемый период
эксплуатации в аппаратуре было
зафиксировано 8 отказов. Время
восстановления составило: t1
= 12 мин, t2
= 23 мин, t3
= 15 мин, t4
= 9 мин, t5
= 17 мин, t6
= 28 мин, t7
= 25 мин, t8
= 31 мин.
Требуется определить среднее время
восстановления аппаратуры.
|
Дано:
n
t1
t2
t3
t4
t5
t6
t7
t8 |
Решение:
|
|
Найти: tср.в |
Пример 8
Аппаратура имела среднюю
наработку на отказ tcp
= 65 ч и среднее время восстановления tв
= 1,25 ч. Требуется
определить коэффициент готовности
Кг.
|
Дано:
tcp
tв |
Решение:
|
|
Найти:
Кг |
Пример 9
Пусть
время работы элемента до отказа подчинено
экспоненциальному закону λ
=
2,5 · 10–5
ч–1.
Требуется определить вероятность
безотказной работы
P(t),
частоту отказов
f(t)
и среднюю наработку на отказ
tср,
если t
= 500, 1000, 2000 ч.
|
Дано:
λ
t1
t2
t3 |
Решение:
|
|
Найти: P(t) f(t) tср |
ч–1;
ч–1;
ч–1;
tср =;

Пример 10
Время работы изделия до
отказа подчиняется закону распределения
Рэлея. Требуется определить количественные
характеристики: P(t),
f(t),
λ(t),
tср
при t1
= 500 ч, t2
= 1000 ч, t3
= 2000 ч, если параметр распределения σ
= 1000 ч.
|
Дано:
t1
t2
t3
σ |
Решение:
Необходимо воспользоваться формулами,
|
|
Найти: P(t)
f(t) λ(t)
tср |






ч–1;






Пример 11
Время безотказной работы
гироскопического устройства с
шарикоподшипниками в осях ротора
гироскопа подчиняется закону Вейбулла
– Гнеденко с параметрами k
= 1,5, λо
= 10–4
ч–1,
а время его работы t
= 100 ч. Требуется
вычислить количественные характеристики
надежности такого устройства.
|
Дано: k = 1,5
λо
t |
Решение:
Используются формулы закона Вейбулла
Определяется вероятность безотказной
Частота отказов определяется по
|
|
Найти: P(t)
f(t) λ(t)
tср |
Тогда
ч–1
Интенсивность отказов
определяется по формуле


Вычисляется средняя наработка до первого
отказа

Сначала вычисляют значение гамма-функции,
воспользовавшись справочными данными
([8], табл. П.7.18):
.
Значения гамма-функции
|
х |
Г (х) |
|
1,67 |
0,90330 |
Полученные значения подставляют в
формулу [8, с. 38]:
ч.
Пример 12
Известно, что интенсивность
отказов λ
= 0,02 ч–1,
а среднее время восстановления tВ
= 10 ч. Требуется вычислить коэффициент
готовности и функцию готовности изделия.
|
Дано: tВ= 10 ч
λ= 0,02 |
Решение:
Коэффициент готовности изделия
Средняя наработка до первого отказа Тогда |
|
Найти:
КГ РГ |
Функция готовности изделия определяется
по формуле
,
где t
– любой момент времени,
при t
= 0 система находится
в исправном состоянии.
.
Пример 13
Система
состоит из 12 600 элементов, средняя
интенсивность отказов которых λср
= 0,32·10–6 ч–1.
Необходимо
определить вероятность безотказной
работы в течение t
= 50 ч.
|
Дано:
N
λср=
t |
Решение:
Интенсивность отказов
Вероятность безотказной
|
|
Найти: P(t) |
Пример 14
Система состоит из N
= 5 блоков. Надежность блоков характеризует-
ся вероятностью безотказной работы
в течение времени t,
которая равна:
p1(t)
= 0,98; p2(t)
= 0,99; p3(t)
= 0,97; p4(t)
= 0,985; p5(t)
= 0,975.
Требуется определить
вероятность безотказной работы системы.
|
Дано:
N
p1(t)
p3(t)
p4(t)
p5(t) |
Решение:
Необходимо воспользоваться
Вероятности
В данном случае q1 q5 |
|
Найти: Рс(t) |
Пример 15
Система состоит из трех
устройств. Интенсивность отказов
электронного устройства равна λ1
= 0,16·10–3
ч–1
= const.
Интенсивности отказов двух
электромеханических устройств линейно
зависят от времени и определяются
следующими формулами: λ2
= 0,23·10 –4t
ч–1,
λ3
= 0,06·10–6t2,6
ч–1.
Нужно рассчитать вероятность безотказной
работы изделия в течение 100 ч.
|
Дано: N= 3 λ1= 0,16 ·10–3 ч–1 λ2= 0,23 ·10–4t ч–1
λ3= 0,06 ·10–6t2,6 ч
t |
Решение:
Так как λ можно написать
|
|
Найти: Р(t) |
|
при t
= 100 ч
Пример 16
Система состоит из трех
блоков, средняя наработка до первого
отказа которых равна Т1
=160 ч, Т2
= 320 ч, Т3
= 600 ч. Для блоков
справедлив экспоненциальный закон
надежности.
Требуется определить среднюю наработку
до первого отказа системы.
|
Дано: N= 3
Т1
Т2
Т3 |
Решение:
Согласно экспоненциальному закону Интенсивность отказов системы:
Средняя наработка до первого отказа
|
|
Найти: tср.с |
|
следовательно,
Пример 17
Система состоит из двух
устройств. Вероятности безотказной
работы каждого из них в течение времени
t
= 100 ч равны: р1(100)
= 0,95; р2
(100) = 0,97. Справедлив
экспоненциальный закон надежности.
Необходимо найти среднюю наработку до
первого отказа системы
tср.с.
|
Дано:
N
t р1(100) = 0,95
р2 |
Решение:
Определяется вероятность безотказной
Определяется интенсивность отказов
|
|
Найти:
tcp.c |

П
ример 18
Вероятность безотказной
работы одного элемента в течение времени
t
равна p(t)
= 0,9997. Требуется определить вероятность
безотказной работы системы, состоящей
из N
= 100 таких же элементов.
|
Дано: p(t)= 0,9997
N |
Решение: 1-й вариант решения:
Если у всех элементов системы одинаковая
2-й вариант решения: |
|
Найти: Pc |
Так как вероятность
близка к единице, то можно воспользоваться
следующей формулой:
.
Для одного элемента системы:
т. е.
.
Из
следует
.
Получается, что первый вариант решения
более точен.
Пример 19
Вероятность безотказной
работы системы в течение времени t
равна
Рс(t)
= 0,95. Система состоит из N
= 120 равнонадежных элементов. Требуется
определить вероятность безотказной
работы элемента рi(t).
|
Дано: Рс(t)= 0,95
N |
Решение:
Очевидно, что вероятность безотказной
|
|
Найти: Рi(t) |
Тогда

Пример 20
В системе Nс
= 2500 элементов, вероятность безотказной
работы ее в течение одного часа Рс(1)
= 98 %. Предполагается, что все элементы
равнонадежны и интенсивность отказов
элементов λ
= 8,4·10–6
ч–1.
Требуется определить среднюю наработку
до первого отказа системы tср.с.
|
Дано:
Nс
Рс(1)
λ= |
Решение:
Интенсивность отказов системы
λс
средняя наработка до первого отказа
tср.с |
|
Найти: tср.с |
Пример 21
Система
состоит из пяти приборов, вероятности
исправной работы которых в течение
времени t
= 100 ч равны: p1(100)
= 0,9996; p2(100)
= 0,9998; p3(100)
= 0,9996; p4(100)
= 0,999; p5(100)
= 0,9998. Требуется определить частоту
отказов системы в момент времени t
= 100 ч.
Предполагается, что отказы
приборов независимы и для них справедлив
экспоненциальный закон надежности.
|
Дано:
t
p1(100)
p2(100)
p3(100)
p4(100) p5(100) = 0,9998 |
Решение:
По условиям задачи отказы приборов
|
|
Найти: fс |
|
Так как вероятность безотказной работы
системы близка к единице, то в соответствии
с формулой
интенсивность отказов можно вычислить
следующим образом:
ч–1,
тогда частоту отказов определим в
соответствии с формулой:
ас(t)
λс(1
– λсt)= 2,2·10–5(1 – 2,2·10–5·100) =
2,195·10–5ч–1.
Пример 22
Изделие состоит из 12
маломощных низкочастотных германиевых
транзисторов, 4 плоскостных кремниевых
выпрямителей, 50 керамических конденсаторов,
168 резисторов типа МЛТ, 1 силового
трансформатора, 2 накальных трансформаторов,
5 дросселей и 4 катушек индуктивности.
Необходимо найти вероятность безотказной
работы изделия в течение t
= 200 ч и среднюю наработку
до первого отказа.
|
Дано:
N1
N2
N3
N4 N5= 1 N6= 2
N7
N8 t= 200 ч |
Решение:
Для решения данной задачи вычисляются |
|
Найти: Рс(200) tср.с |
Таблица
1.2
|
Наименование и тип |
Количество элементов Ni |
Интенсивность
отказов, |
|
|
λi · |
Ni |
||
|
Транзистор маломощный низкочастотный германиевый |
12 |
0,3 |
3,6 |
|
Выпрямитель плоскостной кремниевый |
4 |
0,5 |
2 |
|
Конденсатор керамический |
50 |
0,14 |
7 |
|
Резистор типа МЛТ |
168 |
0,05 |
8,4 |
|
Трансформатор силовой |
1 |
0,3 |
0,3 |
|
Трансформатор накальный |
2 |
0,2 |
0,4 |
|
Дроссель |
5 |
0,1 |
0,5 |
|
Катушка индуктивности |
4 |
0,05 |
0,2 |
Интенсивность отказов
элементов
ч–1.
По данным табл. 1.2 и по формуле
для экспоненциального закона находится
вероятность безотказной работы изделия
в течение t
= 200 ч и средняя наработка до первого
отказа:
Соседние файлы в папке НАДЕЖНОСТЬ_1_ГРАДИРНИ
- #
21.03.201635.98 Mб60НАДЕЖНОСТЬ_Анцелиович_ГРАДИРНИ.djvu
- #
- #
- #
21.03.20163.52 Mб120НАДЕЖНОСТЬ_Герцбах_ГРАДИРНИ.pdf
- #
- #
|
2 / 2 / 1 Регистрация: 03.06.2021 Сообщений: 47 |
|
|
1 |
|
|
08.05.2022, 23:51. Показов 896. Ответов 8
Как тут использовать показательный закон? Блок прибора построен из трех независимых, параллельно действующих одинаковых элементов. Отказ блока происходит после отказа двух элементов. Случайное время исправной работы каждого из элементов распределено по показательному закону, а среднее значение этого времени — 100ч. Какова вероятность того, что блок безотказно проработает 200ч?
0 |
|
Programming Эксперт 94731 / 64177 / 26122 Регистрация: 12.04.2006 Сообщений: 116,782 |
08.05.2022, 23:51 |
|
8 |
|
1806 / 1143 / 223 Регистрация: 18.01.2021 Сообщений: 2,321 |
|
|
09.05.2022, 01:41 |
2 |
|
Как тут использовать показательный закон? Напрямую
0 |
|
2 / 2 / 1 Регистрация: 03.06.2021 Сообщений: 47 |
|
|
10.05.2022, 17:11 [ТС] |
3 |
|
Проверьте пожалуйста. Я не уверен с пределами интегрирования тк по условию именно 200ч, а не 200 и больше. Подскажите если что не так
0 |
|
1806 / 1143 / 223 Регистрация: 18.01.2021 Сообщений: 2,321 |
|
|
10.05.2022, 22:20 |
4 |
|
Последнюю строчку в топку
0 |
|
2 / 2 / 1 Регистрация: 03.06.2021 Сообщений: 47 |
|
|
11.05.2022, 00:05 [ТС] |
5 |
|
Последнюю строчку в топку Просто ошибся в ней или вообще все неправильно? Куда думать хоть
0 |
|
1806 / 1143 / 223 Регистрация: 18.01.2021 Сообщений: 2,321 |
|
|
11.05.2022, 07:44 |
6 |
|
Просто ошибся в ней или вообще все неправильно? Вычисления, наверное, правильные. Не проверял. Только отношения к задаче не имеют.
0 |
|
2 / 2 / 1 Регистрация: 03.06.2021 Сообщений: 47 |
|
|
11.05.2022, 19:23 [ТС] |
7 |
|
Red white socks, зачем я умножал… так по идее?
0 |
|
1806 / 1143 / 223 Регистрация: 18.01.2021 Сообщений: 2,321 |
|
|
11.05.2022, 21:58 |
8 |
|
Mist4ke, перечитайте схему Бернулли и исправьте свою формулу
0 |
|
2 / 2 / 1 Регистрация: 03.06.2021 Сообщений: 47 |
|
|
11.05.2022, 22:52 [ТС] |
9 |
|
?
0 |
|
IT_Exp Эксперт 87844 / 49110 / 22898 Регистрация: 17.06.2006 Сообщений: 92,604 |
11.05.2022, 22:52 |
|
Помогаю со студенческими работами здесь Найти вероятность того, что за время t безотказно будет работать только один элемент Вероятность того что данный прибор проработает 500 часов равна 0.8 Вероятность того что данный прибор проработает 500 часов равна… Определить вероятность того, что взятая наудачу деталь проработает положенное время Найти вероятность того, что в определенный момент времени окажется ровно 380 безотказно работающих автомобилей
Найти вероятность того, что взятый наугад диод проработает гарантийное число часов Искать еще темы с ответами Или воспользуйтесь поиском по форуму: 9 |

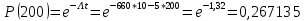
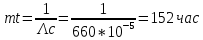
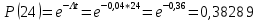
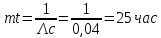
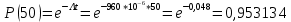
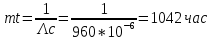
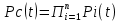
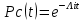
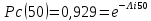
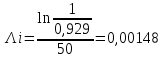
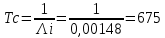
 ;
; ;
; .
. ;
; ч–1;
ч–1; ,
, ;
; шт.;
шт.; ч–1.
ч–1.
 .
. .
. .
. .
. ,
, ;
; .
. ,
, ;
; ;
; .
. ;
; ч–1;
ч–1; ч–1;
ч–1;






 .
.






 Найти вероятность того, что наудачу взятая лампа проработает заданное количество часов
Найти вероятность того, что наудачу взятая лампа проработает заданное количество часов