то приведенное определение корректно.
Функция распределения показательно распределенной случайной величины X имеет вид
|
x |
0 |
при x < 0; |
|||
|
F(x) = |
∫ |
||||
|
f (t)dt = |
−λt |
||||
|
−e |
при x ≥ 0. |
||||
|
−∞ |
1 |
Графики функций f(x) и F(x) при значениях параметра λ, равных 1 и 2, приведены на рисунках 14 и 15.
|
f (x) |
||||
|
2 |
||||
|
λ=2 |
||||
|
1 |
||||
|
λ=1 |
||||
|
0 |
1 |
2 |
3 |
x |
|
Рисунок 14 |
|
F(x) |
||||
|
1 |
||||
|
λ=2 |
||||
|
0,5 |
λ=1 |
|||
|
0 |
1 |
2 |
3 |
x |
Рисунок 15
Несложно доказать, что для случайной величины X, распределенной по показательному закону,
|
M [X ] = |
1 |
; |
D[X ] = |
1 |
; |
σ[X ] = |
1 |
. |
|
λ |
2 |
|||||||
|
λ |
λ |
Коэффициент асимметрии: A[X] = 2, как и следовало ожидать, асимметрия показательного распределения положительна. Коэффициент эксцесса случайной величины, распределенной по показательному закону положителен и равен 6: Ex[X] = 6.
В природе и технике существует множество явлений, которые могут быть, по крайней мере приближенно, описаны показательным законом распределения. Так, в общем случае, результаты измерений временных показателей хорошо аппроксимируются экспоненциальным распределением. В качестве примеров можно привести измерение продолжительности телефонных переговоров, периода атомного распада радиоактивных веществ, а также различные виды «задач обслуживания» (например, измерение времени безотказной работы оборудования, времени ремонта и т. п.). Доказано, что интервал времени T между двумя соседними событиями в простейшем потоке имеет показательное распределение с параметром, равным интенсивности потока.
Пример 21. Время безотказной работы радиоэлектронного оборудования является случайной величиной, распределенной по показательному закону. Определить вероятность безотказной работы оборудования в течение десяти часов эксплуатации,
если среднее время безотказной работы по статистическим данным составляет 200 часов.
Решение. Согласно условию, математическое ожидание случайной величины X, обозначающей время безотказной работы оборудования, равно 200. Учитывая, что для случайной величины, распределенной по показательному закону, M[X] = 1/λ, определяем значение параметра: λ = 1/M[X] = 1/200 = 0,005. Функция плотности распределения данной случайной величины X имеет вид
|
0 |
при x < 0; |
|
|
f (x) = |
−0,005x |
|
|
при x ≥ 0. |
||
|
0,005e |
Определим вероятность безотказной работы оборудования в течение десяти часов эксплуатации:
|
∞ |
∞ |
∞ |
|
|
P(X ≥10) = ∫ f (x)dx = ∫0,005e−0,005xdx = −e−0,005x |
= 0 + e−0,05 = 0,95123 . |
||
|
10 |
10 |
10 |
|
Пример 22. Случайная величина X распределена по экспоненциальному закону с параметром λ. Найти вероятность того, что эта случайная величина примет значение, удаленное от ее математического ожидания более чем на 3σ.
Решение. Как известно, математическое ожидание и среднее квадратическое отклонение случайной величины, распределенной по экспоненциальному закону с параметром λ, равны 1/λ. Тогда
P( X −M[X ] > 3σ) = P( X −1/ λ > 3/ λ) = P(X < −2 / λ) + P(X > 4 / λ).
Поскольку случайная величина, распределенная по показательному закону, может принимать только неотрицательные значения,
P( X − M[X ] > 3σ) = P(X > 4 / λ) = F(∞) − F(4 / λ) = =1 −e−λ ∞ −1 + e−λ(4 / λ) = e−4 = 0,0183.
То есть, примерно, только в 18 случаях из 1000 случайная величина, распределенная по показательному закону, может принимать значения, выходящие за рамки «трехсигмового интервала».
Нормальное распределение (иногда называемое законом Гаусса) играет исключительно важную роль в теории вероятностей и математической статистике и занимает среди других законов распределения особое положение. Это объясняется целым рядом причин:
1.Многие случайные величины имеют нормальное или близкое к нормальному распределение.
2.Нормальное распределение хорошо подходит в качестве аппроксимации других распределений (например, биномиального).
3.Нормальное распределение обладает рядом благоприятных математи-
ческих свойств, во многом обеспечивших его широкое применение в теории вероятностей и математической статистике.
Случайная величина X называется распределенной по нормальному закону, если ее плотность распределения вероятностей задается формулой
|
1 |
e− |
(x−m)2 |
||
|
f (x) = |
2σ2 , |
|||
|
σ 2π |
где σ> 0 и m – параметры распределения. Так как f(x) > 0 и
|
∞ |
1 |
e− |
(x−m)2 |
∞ |
1 |
1 |
∞ |
π |
|||
|
∫ |
2σ2 |
dx = ∫ |
e−t 2 |
2σdt = |
∫e−t 2 dt = |
=1, |
|||||
|
−∞ σ 2π |
−∞ σ 2π |
π −∞ |
π |
то приведенное выше определение корректно. (При проведении преобразований была сделана подстановка x − m = σ 

Основные свойства нормального распределения:
1. Нормальное распределение полностью определяется двумя параметрами: m и σ. Вероятностный смысл этих параметров таков: m – математиче-
ское ожидание, σ – среднее квадратическое отклонение рассматриваемой случайной величины. То есть для нормального распределения:
M[X] = m; D[X] = σ2; σ[X] = σ.
2. Кривая нормального распределения имеет колоколообразную форму, симметричную относительно прямой x = m, и при x →–∞ и x →∞ эта кривая асимптотически приближается к оси абсцисс.
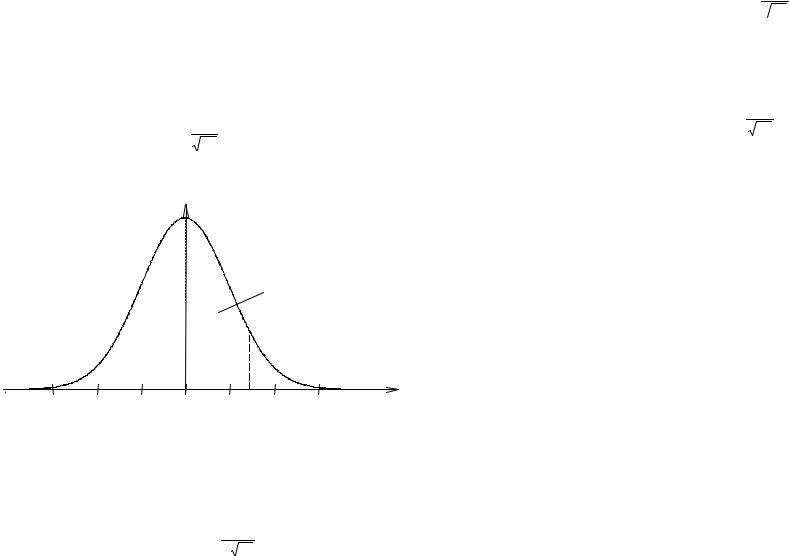
Общий вид графика функции плотности распределения вероятностей f(x) для произвольных значений параметров m и σ изображен на рисунке 16. Под
f(x)
m – 3σ m – 2 σ m – σ m m + σ m + 2σ m + 3σ x 0 ,683
0 ,954
0 ,997
Рисунок 16
45
графиком указаны вероятности попадания значений случайной величины на отрезки [m – iσ, m + iσ], i = 1, 2, 3 (см. пример 23).
3.Как видно из графика функции f(x), для нормально распределенной случайной величины вероятность получения значений, значительно удаленных от среднего значения m, быстро уменьшается с ростом величины отклонения.
4.Медиана и мода случайной величины, распределенной по нормальному закону, совпадают и равны математическому ожиданию m.
5.Коэффициенты асимметрии и эксцесса нормально распределенной случайной величины равны нулю: A[X] = 0; Eх[X] = 0.
Тот факт, что случайная величина X распределена по нормальному зако-
ну с параметрами m и σ, символически записывается: X N(m; σ). Этой случайной величине соответствует следующая функция распределения вероятностей:
|
x |
(t −m)2 |
|||||||
|
F(x) = |
1 |
∫e− |
2σ2 dt . |
|||||
|
σ |
2π −∞ |
|||||||
|
График функции распределения F(x) изображен на рисунке 17. |
||||||||
|
На рисунках 18 и 19 изображены графики функции f(x), соответствующие |
||||||||
|
различным значениям параметров m и σ. |
||||||||
|
F(x) |
||||||||
|
1 |
||||||||
|
0,5 |
||||||||
|
m– 3σ m– 2σ m– σ |
m m+ σ m+ 2σ m+ 3σ |
x |
||||||
|
Рисунок 17 |
||||||||
|
f(x) |
f(x) |
|||||||
|
m = 1, σ = 0,5 |
||||||||
|
m =1 |
||||||||
|
m =3 |
||||||||
|
σ=1 |
||||||||
|
σ=1 |
m = 1, σ = 1 |
|||||||
|
m = 1, σ = 2 |
||||||||
|
0 |
1 |
3 |
x |
m |
x |
|||
|
Рисунок 18 |
Рисунок 19 |
|||||||
|
46 |
Нормированное (стандартизованное) нормальное распределение.
Нормированным (или стандартизованным) нормальным распределением называется нормальное распределение с параметрами m = 0 и σ= 1.
Известно, что если случайная величина X распределена нормально с параметрами m и σ, то величина Z = (X – m)/σ также распределена нормально, но с параметрами m = 0, σ= 1 (то есть Z N(0; 1)). Нормирование распределения ведет просто к перенесению начала координат в центр распределения, то есть к «центрированию», и к масштабированию оси абсцисс в долях σ.
Функция плотности распределения вероятностей стандартного распределения имеет вид
|
1 |
e− |
x2 |
||
|
ϕ(x) = |
2 |
. |
||
|
2π |
В приложении A приведены значения этой функции для неотрицательных значений аргумента, график функции ϕ(x) изображен на рисунке 20.
ϕ(x)
Φ(х1)
|
–3 |
–2 |
–1 |
0 |
1 х1 2 |
3 |
x |
Рисунок 20
Вероятность попадания значения случайной величины на отрезок
[α, β].
Вычислим для нормально распределенной случайной величины X вероятность попадания на участок от α до β:
|
β |
1 β |
− |
(x−m)2 |
||
|
P(α < X < β) = ∫ f (x)dx = |
∫e |
2σ2 dx . |
|||
|
α |
σ |
2π α |
Сделав в интеграле замену переменной t = (x – a)/σ (то есть «нормируя» случайную величину) и соответственно изменяя пределы интегрирования,
47
получим
β−m
P(α < X < β) = 1 σ∫ e−t 2 / 2dt .

σ
Как известно, неопределенный интеграл ∫e−t2 / 2dt не выражается через элементарные функции, но его можно выразить через специальную функцию
|
1 |
x |
||
|
Φ(x) = |
∫e−t 2 / 2dt , |
(13) |
|
|
2π 0 |
называемую функцией Лапласа (или «интегралом вероятностей»), для которой составлены таблицы значений. В геометрической интерпретации, как следует из (13), Ф(x) равна площади фигуры под кривой ϕ(x), опирающейся на отрезок [0; x]. На рисунке 20 это фигура выделена штриховкой.
В приложении Б приведены значения функции Лапласа для положительных значений x. Функция Φ(x) – нечетная, то есть Φ(–x) = – Φ(x); при x > 5 можно принять Φ(x) = 0,5.
С помощью функции Лапласа вероятность попадания нормально распределенной случайной величины X на участок от α до β выражается формулой
|
β− m |
α − m |
(14) |
|||
|
P(α < X < β) = Φ |
σ |
−Φ |
σ |
. |
|
Примеры случайных величин, распределенных по нормальному закону.
Известно, что нормально распределенные случайные величины широко распространены на практике. Нормальное распределение возникает в тех случаях, когда складывается большое число независимых (или слабо зависимых) случайных величин X1, X2, …, Xn:
n
X= ∑Xi ,
i=1
причем эти величины сравнимы по порядку своего влияния на рассеивание суммы. Тогда, каковы бы ни были законы распределения отдельных величин Хi, закон распределения их суммы X будет близок к нормальному, причем тем ближе, чем больше число слагаемых n. На практике наиболее часто встречаются именно такие случайные величины.
Результаты измерения длины, массы, времени, ошибки измерения и многие другие случайные величины имеют нормальное или близкое к нормаль-
48

ному распределение.
Рассмотрим пример. Пусть производятся измерения некоторой физической величины. Любое измерение дает лишь приближенное значение измеряемой величины, так как на результат испытания оказывают влияние очень многие, не зависящие друг от друга случайные факторы: температурные колебания в помещении, воздействия окружающей среды, неточность измерительной шкалы, смена контрольного персонала и т. д.
В зависимости от источников появления ошибок различают систематические и случайные ошибки.
К систематическим ошибкам относятся, например, односторонние отклонения, вызванные, скажем, изменением настройки измерительного прибора или сменой контрольного персонала. Эти ошибки можно устранить путем систематического изучения причины их возникновения.
Случайные ошибки вызваны влиянием множества различных неконтролируемых причин: температурных колебаний, влажности, вибраций в окружающей среде и т. п. Каждый из этих факторов порождает ничтожную «частную ошибку». Но поскольку число этих факторов очень велико, совокупное их действие порождает уже заметную «суммарную ошибку». Полностью исключить воздействие этих факторов невозможно, так как нельзя заранее предусмотреть степень их влияния на результат конкретного измерения. Подобные случайные ошибки вызывают при измерениях отклонения в обе стороны от истинного значения.
Рассматривая общую ошибку как сумму очень большого числа взаимно независимых частных ошибок, мы вправе заключить, что суммарная ошибка имеет распределение, близкое к нормальному. Опыт подтверждает справедливость такого заключения.
Пример 23. Случайная величина X распределена по нормальному закону с параметрами M[X] = m, σ[X] = σ. Найти вероятность того, что случайная величина X будет принимать значения, удаленные от математического ожидания не более чем на: а) σ,
б) 2σ, в) 3σ.
Решение. Для вычисления искомых вероятностей воспользуемся формулой
(14):
|
m + σ− m |
m −σ− m |
= Φ(1) −Φ(−1) = |
|||
|
а) P(m −σ < X < m + σ) = Φ |
σ |
−Φ |
σ |
||
= 0,34134 −(−0,34134) = 0,68268;
|
m +2σ−m |
m −2σ−m |
= Φ(2) −Φ(−2) = |
|||||
|
б) P(m −2σ < X < m +2σ) = Φ |
σ |
−Φ |
σ |
||||
|
= 0,47725 −(−0,47725) = 0,9645; |
|||||||
|
m +3σ−m |
m −3σ−m |
= |
|||||
|
в) P(m −3σ < X < m +3σ) = Φ |
σ |
−Φ |
σ |
= Φ(3) −Φ(−3) |
|||
= 0.49865 −(−0.49865) = 0.9972.
На рисунке 16 под графиком кривой нормального распределения указаны площади фигур, ограниченных кривой f(x) и осью абсцисс, которые равны вероятностям попадания значения случайной величины на указанные отрезки.
Пример 24. Известно, что для некоторого измерительного устройства систематическая ошибка измерения дальности до объекта равна +20 м. Ошибки измерения распределены по нормальному закону со средним квадратическим отклонением, равным 75 м. Найти вероятность того, что полученное в результате измерения значение будет отличаться от истинного значения не более чем на 100 м.
Решение. Рассмотрим случайную величину X, характеризующую ошибку измерения дальности. Согласно условию, эта случайная величина распределена по нормальному закону с параметрами М[X] = 20, σ[X] = 75. Определим искомую вероятность с помощью формулы (14):
|
100 − 20 |
−100 − 20 |
|||||||||
|
P( |
X |
≤100) = P(−100 < X <100) = Φ |
−Φ |
= |
||||||
|
75 |
75 |
|||||||||
= Φ(1,071) − Φ(−1,6) = 0,3577 + 0,4452 = 0,8029.
Пример 25. Случайное отклонение размера детали от номинала при изготовлении ее на данном станке является случайной величиной, распределенной по нормальному закону со средним квадратическим отклонением, равным 5 мк. Систематические отклонения размера изготовленной детали от номинала отсутствуют. Сколько необходимо изготовить деталей, чтобы с вероятностью не менее 0,9 среди них была хотя бы одна годная, если для годной детали допустимо отклонение от номинала не более чем на 2 мк?
Решение. Рассмотрим случайную величину X – отклонение размера детали от номинала. Согласно условию, M[X] = 0 [мк], σ[X] = 5 [мк]. Найдем вероятность события A – {изготовление годной детали}:
|
2 −0 |
− 2 −0 |
|||||||
|
P(A) = P( |
X |
≤ 2) = P(−2 ≤ X ≤ 2) = Φ |
5 |
−Φ |
5 |
= |
||
= Φ(0,4) −Φ(−0,4) = 0,15542 + 0,15542 = 0,31084 ≈ 0,31.
Теперь условие задачи можно рассматривать как последовательность n независимых испытаний, в каждом из которых с вероятностью р= 0,31 происходит событие A, и с вероятностью q = 1 – p = 0,69 событие A не происходит. Вероятность того, что среди n изготовленных деталей будет хотя бы одна годная, представляет собой вероятность наступления события A хотя бы один раз в серии из n независимых испытаний:
1 − qn ≥ 0,9; qn ≤ 0,1; n ln q ≥ ln 0,1; n ≥ lnln0q,1 = lnln0,690,1 = 6,2.
Следовательно, n ≥7, то есть необходимо изготовить не менее 7 деталей, чтобы с вероятностью не менее 0,9 среди них была хотя бы одна годная.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Время — безотказная работа
Cтраница 1
Время безотказной работы, количество отказов в единицу времени и другие показатели надежности относятся к случайным величинам, поскольку они зависят от совокупности разнообразных факторов.
[1]
Время безотказной работы t — s — промежуток времени от момента окончания восстановления изделия после отказа до момента появления следующего отказа.
[2]
Время безотказной работы, или время возникновения отказа, представляет собой случайное явление, поэтому статистические характеристики надежности носят вероятностный характер и могут быть определены из опыта на основе статистических данных.
[3]
Время безотказной работы, наработка на отказ, время восстановления после отказа наиболее часто распределяются по следующим законам: экспоненциальному, нормальному, логарифмически-нормальному, гамма-распределению, Вейбулла, Рэлея. Использование нескольких законов распределений обусловлено большим различием условий связи элементов оборудования тепловозов ( механическое, электрическое и др.), физической природой отказов и неоднородностью ситуаций восстановления тепловозов после отказов.
[4]
Время безотказной работы всего изделия полностью зависит от надежности отдельных деталей.
[5]
Время безотказной работы линии будет равно наименьшей из этих величин.
[6]
Время безотказной работы радиоаппаратуры является случайной величиной X, распределенной по показательному закону с параметром / С.
[7]
Время X безотказной работы станка имеет экспоненциальное распределение.
[8]
Время безотказной работы электронной лампы распределено по закону р ( х) — Q Q3e — OSx, где х означает время в часах. Найти вероятность того, что лампа проработает безотказно не меньше 100 часов.
[9]
Время безотказной работы самолетного радиоэлектронного оборудования в полете является случайной величиной, распределенной по экспоненциальному закону.
[11]
Если время безотказной работы имеет нормальное распределение, то пользуясь понятием зоны практического рассеивания ( рис. 31) можно указать отрезок времени, а именно от 0 до Е ( т) — За.
[13]
Если время безотказной работы системы подчиняется экспоненциальному закону, то проведение плановых профилактик для данного случая нецелесообразно.
[14]
Дисперсия времени безотказной работы имеет размерность квадрата времени.
[15]
Страницы:
1
2
3
4
© Преподаватель Анна Евкова
При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org

























Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи
Сайт пишется, поддерживается и управляется коллективом преподавателей
Правовые документы
Telegram и логотип telegram являются товарными знаками корпорации Telegram FZ-LLC.
Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.
|
0 / 0 / 0 Регистрация: 22.10.2011 Сообщений: 4 |
|
|
1 |
|
безотказность работы радиоэлектронного устройства29.04.2013, 18:08. Показов 2444. Ответов 11
Товарищи, прошу у Вас помощи! За что Вам буду очень благодарна!)
0 |
|
7483 / 4147 / 474 Регистрация: 25.08.2012 Сообщений: 11,529 Записей в блоге: 11 |
|
|
29.04.2013, 18:39 |
2 |
|
Время безотказной работы радиоэлектронного… 1. Mx=1/мю = 500, мю = 0,002 Удачи.
0 |
|
0 / 0 / 0 Регистрация: 22.10.2011 Сообщений: 4 |
|
|
30.04.2013, 01:00 [ТС] |
3 |
|
Спасибо)
0 |
|
1943 / 1051 / 160 Регистрация: 06.12.2012 Сообщений: 4,604 |
|
|
30.04.2013, 01:43 |
4 |
|
1. Mx=1/мю = 500, мю = 0,002 «Центр тяжести» — это среднее значение. Медиана Ме это когда F(Me)=0,5.
1 |
|
7483 / 4147 / 474 Регистрация: 25.08.2012 Сообщений: 11,529 Записей в блоге: 11 |
|
|
30.04.2013, 09:50 |
5 |
|
Медиана Ме это когда F(Me)=0,5. Согласен, Таланов, сравнение не очень удачное.
0 |
|
1943 / 1051 / 160 Регистрация: 06.12.2012 Сообщений: 4,604 |
|
|
30.04.2013, 18:45 |
6 |
|
А «центр…» в смысле — и слева и справа — одна величина. В этом смысле, не более того. Я и то с большим трудом понял, куда там ТС. Слева случайных величин не меряно и справа, тоже. Какая там одна величина?
1 |
|
7483 / 4147 / 474 Регистрация: 25.08.2012 Сообщений: 11,529 Записей в блоге: 11 |
|
|
30.04.2013, 19:06 |
7 |
|
Какая там одна величина? Да вероятность слева и справа равны, как у Вас. сравнение , повторюсь.
0 |
|
1943 / 1051 / 160 Регистрация: 06.12.2012 Сообщений: 4,604 |
|
|
30.04.2013, 19:14 |
8 |
|
5. Медианой называется такое значение, относительно которого равновероятно Это не чёткое определение медианы.
0 |
|
7483 / 4147 / 474 Регистрация: 25.08.2012 Сообщений: 11,529 Записей в блоге: 11 |
|
|
01.05.2013, 14:35 |
9 |
|
Это не чёткое определение медианы. Вентцель Е. С.
0 |
|
rahim |
|
01.05.2013, 19:05
|
|
Не по теме: Для случая показательного закона (как и любого неперывного) вы оба даете одно и то же определение. А для произвольных распределений определение Е.С. не годится. Попробуйте им воспользоваться, например, для распределения P(X=0)=1/3, P(X=1)=2/3. В более позднем учебнике Е.С.Вентцель, Л.А.Овчаров «ТВ и ее инженерные приложения» это определение уже дано с оговорками, что оно касается только распределений с плотностями. Дискуссия реально ни о чем. Для показательного закона все равно, для произвольного все равно никто тут определения не знает. Вот на тему, зачем модератор форума решает студентке задачу, стоило бы подискутировать. Но и тут ответ ясен: наверное, дур мало на свете, еще одну хочет добавить.
0 |
|
7483 / 4147 / 474 Регистрация: 25.08.2012 Сообщений: 11,529 Записей в блоге: 11 |
|
|
01.05.2013, 19:23 |
11 |
|
что оно касается только распределений с плотностями. И в цитируемом мной учебнике есть оговорка что Ме — для непрерывных сл. величин, но формально ее можно Не по теме:
Вот на тему, зачем модератор форума решает студентке задачу, стоило бы подискутировать. Но и тут ответ ясен: наверное, дур мало на свете, еще одну хочет добавить. Многократно обсуждаемый вопрос.
0 |
|
618 / 281 / 10 Регистрация: 22.01.2013 Сообщений: 874 |
|
|
01.05.2013, 19:41 |
12 |
|
Обратил. Медиана определяется для любых величин, а не только для непрерывных. Только ее правильное определение определение не такое, как выше. А такое, как выше, совпадает с правильным только в случае непрерывной функции распределения.
0 |
18.274. Выразить начальный момент и-го порядка через центральные моменты и-го и меньших порядков и математическое ожидание, 18.275*. Случайная величина Х принимает только целые неотрицательные значения. Доказать, что т =~Р(Х>Ц. 18.276*. Случайная величина Х непрерывного типа неотрицательна, имеет конечное математическое ожидание и ее закон распределения задан функцией распределения гх(х). Показать, что математическое ожидание такой случайной величины может быть +00 ааписано в виде тх = (1 — Р„(х)] йх.
о 18.277. Пусть Х вЂ” С.В.Н.Т. с унимодальным законом распределения. Обозначим т~ ~= М ((Х вЂ” Их)~] (центральный момент втоРого поРЯдка относительно моды), т~э = М((Х вЂ” йх)э] (центральный момент второго порядка относительно медианы). Пусть, кроме того, д» ~ 5х.
Показать, что для равенства этих моментов ох + нх необходимо и достаточно, чтобы тх = 2 В задачах 18.278 — 18.311 изучаются некоторые классические распределения дискретного и непрерывного типов. 18.278. Из урны, содержащей 4 белых и 6 черных шаров, случайным образом и без возвращения извлекается 3 шара. Случайная величина Х вЂ” число белых шаров в выборке.
Описать закон распределения. Полученное распределение относится к семейству гиоергеометрических. 18.279 (продолжение). Для случайной величины из предыдущей задачи найти щ„и Вх. 18.280. Для сборки прибора требуется 4 однотипных детали. Всего имеется 10 деталей, из которых только 6 доброкачественные. Наудачу отбирают 5 деталей (одну деталь «про запасе). Найти вероятность того, что можно будет произвести сборку прибора. Гл.18.
Теория вероятностей 66 18.281. Производится тираж спортлото «6 из 45>. Некто купил одну карточку и заполнил ее. Какова вероятность того, что он правильно угадал Ь цифр (Ь = 6; 5)? Случайная величина Х непрерывного типа называется распределенной равномерно на отрезке [а, Ь] (при этом для краткости говорят: Х подчиняется закону >с (а, Ь)), если ее плотность распределения вероятностей постоянна на данном отрезке: О, если хф [а, Ь], Ух (х) — 1 — если х е [а, Ь]. Ь вЂ” а Равномерное распределение реализуется в экспериментах, в которых наудачу ставится точка на отрезке [а, Ь] (Х вЂ” координата поставленной точки), а также в экспериментах по измерению тех или иных физических величин с округлением (Х вЂ” ошибка округления).
18.282. Автобусы идут с интервалом 5 минут. Считая, что случайная величина Х вЂ” время ожидания автобуса на остановке— распределена равномерно на указанном интервале, найти среднее время ожидания и дисперсию времени ожидания. 18.283 (продолжение). В условиях предыдущей задачи найти функцию распределения случайной величины Х и вычислить вероятность того, что время ожидания превысит 3 мин. 18.284. Случайная величина Х распределена по закону >Ч (а, Ь). Найти выражения для т„и о„через параметры распределения а и Ь. 18.285.
Азимутальный лимб имеет цену делений один градус. Какова вероятность при считывании азимута угла сделать ошибку в пределах ж10 мин, если отсчет округляется до ближайшего целого числа градусов? 18.286. Шкала рычажных весов, установленных в лаборатории, имеет цену деления 1г. При измерении массы химических Л компонентов смеси отсчет делается с точностью до целого деления с округлением в ближайшую сторону. Какова вероятность, что абсолютная ошибка определения массы: а) не превысит величины среднеквадратичного отклонения возможных ошибок определения Рис.
7 массы; б) будет заключена между зна- чениями ох и 2ох? 18.287. Случайная величина Х распределена по закону равнобедренного треугольника в интервале ( — а, а) (закон Симпсона), если она непрерывного типа и ее плотность распределения вероятностей имеет вид, изображенный на рис. 7. Э 2. Случайные величины 67 Написать выражение для 7»(х), вычислить функцию распределения вероятностей.
18.288 (продолжение). Для случайной величины, распредеденной по закону Симпсона, найти математическое ожидание, дисперсию, моду, медиану и коэффициент эксцесса. Случайная величина Х называется распределенной по показательному (эксноненциальному) закону с параметром Л > 0 (при этом для краткости говорят: Х подчиняется закону Ех (Л)), если она непрерывного типа и ее плотность распределения вероятностей задается формулой О, если х(0, .у.
(*) = Ле»* если х > О. Показательное распределение часто встречается в теории массового обслуживания (например, Х вЂ” время ожидания при техническом обслуживании или Х вЂ” длительность телефонных разговоров, ежедневно регистрируемых на телефонной станции) и в теории надежности (например, Х вЂ” срок службы радиоэлектронной аппаратуры).
18.289. Время безотказной работы радиоаппаратуры является случайной величиной Х, распределенной по показательному закону с параметром Л. Вычислить математическое ожидание и дисперсию. 18.290 (продолжение). В условиях предыдущей задачи найти вероятность того, что радиоаппаратура не выйдет из строя в течение времени 1 = тя». Квантилью какого порядка для данного распределения является значение ти»7 18.291. Время ожидания у бензоколонки автозаправочной станции является случайной величиной Х, распределенной по показательному закону со средним временем ожидания, равным 1о.
Найти вероятности следующих событий: (ь з А = ~ — ( Х ( — ~о В = ~Х > 21о). ~2 2 18.292*. Пусть Х вЂ” время безотказной работы радиоэлектронной аппаратуры. Примем, что вероятность выхода из строя аппаратуры в течение времени Ьх с точностью до величины о (Ьх) Равна ЛЬх (Л > 0) независимо от времени х, в течение которого аппаратура уже проработала до рассматриваемого интервала времени Ьх. Вычислить функцию распределения случайной величины Х.
18.293. Случайная величина Х распределена по показательному закону с параметром Л. Вывести рекуррентную формулу, выражакяцую центральный момент (1+ 1)-го порядка через центральный момент Й-го порядка и математическое ожидание, и с ее помощью вычислить коэффициент асимметрии и коэффициент эксцесса показательного распределения. 68 Гл. 18. Теория вероятностей 18.294. Случайная величина Х распределена по закону Коши, определяемому функцией распределения вероятностей Рх (х) = б+ с агсь8 — при — оо < х < +оо.
а Выбрать коэффициенты а, б и с таким образом, чтобы данное распределение соответствовало случайной величине непрерывного типа. 18.295 (продолжение). Вычислить плотность вероятности рас- пределения Коши. Существуют ли математическое ожидание и моменты более высокого порядка у данного распределения? 18.298 (продолжение). Найти моду, медиану и квантиль ~р по- рядка р = 0,75 распределения Коши. 18.297.
Известно, что при стрельбе по плоской мишени в неиз- менных условиях случайная величина  — расстояние от точки попадания до центра мишени — подчиняется зикоку распределе- ния Рэлея с плотностью распределения вероятностей — е *~( ) при х>0, Л (х) = 0 при х <О, где о > 0 — параметр, характеризующий распределение. Постро- ить зскиз графика плотности вероятности уя(х), проверить усло- вие нормировки и вычислить характеристики тоя и Ря.
18.298 (продолжение). Для случайной величины В, распре- деленной по закону Рзлея, вычислить Ыя, бя и ая и выяснить взаимное расположение характеристик тя, Ия и Йя. 18.299. Скорость И молекул идеального газа, находящегося в равновесии при определенной температуре, является случайной величиной, подчиняюшейся закону распределения Максвелла с плотностью распределения вероятностей 0 при х<0, Л(х) = )2 — Д~? х е з? пи х>0 где параметр распределения,З > 0 определяется температурой и массой молекул. Выразить среднее значение и наиболее вероят- ное значение скорости молекул, а также дисперсию распределения через физический параметр,З. 18.300. Случайная величина Х подчиняется законй арксинрса с плотностью распределения вероятностей О, если (х! > а, Ух(х) = если (х! < а.
Д2 х2 Найти функцию распределения и вычислить т„, зз„. 3 2. Случайные величины 1 8.301 1продолжение). Для случайной величины, распределенной по закону арксинуса, вычислить с)», Ь» н йо 75. 18.302. Случайная величина Х непрерывного типа распределена по закону Лапласа с параметрами т Е ьь’ и сг > О, если ес пдотность распределения вероятностей задается формулой 1 ( (х — т~ь/21 У»1х) = — ехр — оо (х (+со. ьть/2 ~ и Выразить характеристики т» и а» через параметры распределения. 18.303.
|
15:11 найти вероятность безотказной работы |
|
Задача. Функция распределения случайной величины t – времени безотказной работы радиоаппаратуры имеет вид Найти: а) вероятность безотказной работы радиоаппаратуры в течение трех лет; б) плотность вероятности f (t); в) математическое ожидание и дисперсию. Решение.
События «элемент откажет» и «элемент не откажет»—противоположные, поэтому вероятность того, что элемент не oткaжeт
Вероятность безотказной работы радиоаппаратуры в течение трех лет — называется «функция надежности». Этот же результат можно получить непосредственно, пользуясь функцией надежности R(t), которая определяет вероятность безотказной работы элемента за время длительностью t. Если задана функция распределения
безотказной работы аппаратуры (или элемента), то вероятность отказа можно вычислить с помощью калькулятора. |
Категория: Теория вероятности | Просмотров: 5796 | | Теги: Функция надежности, вероятность безотказной работы, вероятность отказа | Рейтинг: 5.0/2 |



