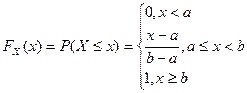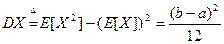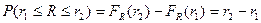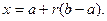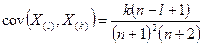Определение Непрерывная случайная величина Х имеет показательный закон распределения с параметром 

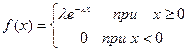
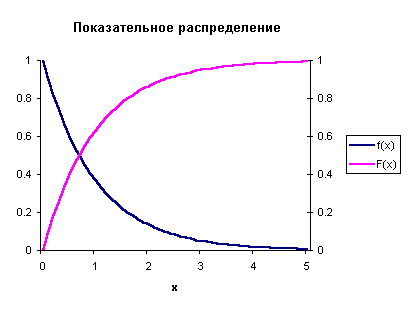
Кривая распределения 
Рис 2.
Получим выражение для функции распределения по формуле 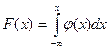
1) При 

2) При 
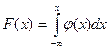

По соответствующим формулам получаем выражения для 

Задача. Среднее время безотказной работы прибора равно 80 ч. Полагая, что время безотказной работы прибора имеет показательный закон распределения, найти: а) выражение его плотности вероятности и функции распределения; б) вероятность того, что в течение 100 ч. прибор не выйдет из строя.
Решение. Х- время безотказной работы прибора, среднее время — 



Искомая вероятность
Замечание. Показательный закон распределения играет большую роль в теории массового обслуживания и теории надежности.
МОСКОВСКИЙ ГОСУДАРСТВЕННЫЙ ИНСТИТУТ ЭЛЕКТРОНИКИ И МАТЕМАТИКИ
Кафедра теории вероятностей и математической статистики
РЕФЕРАТ
По математической статистике
на тему:
«Равномерное распределение»
Выполнил: студенты группы М-65
Ражева А.А.
Кнутова А.С.
Проверил:Заведующий Кафедрой
Ивченко Г. И.
Москва 2012 г.
Непрерывное равномерное распределение — в теории вероятностей распределение, характеризующееся тем, что вероятность любого интервала зависит только от его длины.
Равномерное распределение полезно при описании переменных, у которых каждое значение равновероятно, иными словами, значения переменной равномерно распределены в некоторой области.
Определение
Говорят, что случайная величина имеет непрерывное равномерное распределение на отрезке [a,b], где 
Пишут: X ~ U (a,b) или
Иногда значения плотности в граничных точках x = a и x = b меняют на другие, например 0 или 
Если L (ξ) = U(a,b), то
Равномерное распределение U (a,b) описывает процесс «выбора точки наудачу» в интервале [a,b]. Так, если [a,b] – интервал между последовательными отправлениями автобуса от остановки, то время ожидания пассажира, не знающего расписания и пришедшего на остановку, есть случайная величина с распределением U (0,1). Распределение U (0,1) играет особую роль в методах моделирования с помощью компьютеров случайных величин с заранее заданными распределениями. Такие методы широко используют для приближенных вычислений интегралов, решений дифференциальных и интегральных уравнений и т.д.
Пример (Гипотеза случайности).
В некоторых случаях априори предполагается (постулируется), что исходные данные представляют собой случайную выборку из некоторого распределения, т.е. компоненты вектора данных X=(







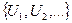
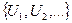

Функция распределения
Интегрируя определённую выше плотность, получаем:
Так как плотность равномерного распределения разрывна в граничных точках отрезка [a,b], то функция распределения в этих точках не является дифференцируемой. В остальных точках справедливо стандартное равенство:
Характеристическая функция случайной величины X ~ U(a,b):
Математическое ожидание и дисперсия по определению равны:
Вообще,
Стандартное равномерное распределение
Если a = 0, а b = 1, то есть X ~ U[0,1], то такое непрерывное равномерное распределение называют стандартным. Имеет место элементарное утверждение:
Если случайная величина X ~ U[0,1], и Y = a + (b − a)X, где a < b, тo Y ~ U[0,1].
Таким образом, имея генератор случайной выборки из стандартного непрерывного равномерного распределения, легко построить генератор выборки любого непрерывного равномерного распределения.
Более того, имея такой генератор и зная функцию обратную к функции распределения случайной величины, можно построить генератор выборки любого непрерывного распределения (не обязательно равномерного) с помощью метода обратного преобразования. Поэтому, стандартно равномерно распределённые случайные величины иногда называют базовыми случайными величинами.
Линейное преобразование
переводит СВ X ~ R(a,b) в СВ Y ~ R(0,1). Действительно,
Равномерное распределение является непрерывным аналогом дискретного распределения вероятностей для опытов с равновероятными исходами.
Значение
С помощью линейного преобразования приводится к равномерному распределению на отрезке [0,1]. Равномерное распределение является непрерывным аналогом распределений классической теории вероятностей, описывающих случайные эксперименты с равновероятными исходами.
Погрешность, происходящая от округления числа, удовлетворительно описывается равномерным распределением на отрезке [ − 1 / 2,1 / 2].
Если случайная величина ζ имеет непрерывную функцию распределения 
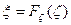
Моделирование
Обозначим буквой 
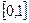
Если 

Моделировать случайную величину 
Мы рассмотрим метод псевдослучайных последовательностей, который наиболее просто реализуется в компьютере. Для получения псевдослучайной последовательности используем алгоритм, который называется методом середины квадратов. Поясним его на примере. Возьмем некоторое число 

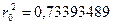







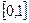

Метод обратных функций.
Пусть случайная величина 





Отсюда следует, что значение 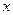




Последовательности значений 

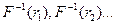


Моделирование случайной величины с равномерным распределением на отрезке
Пусть случайная величина 
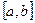
Составляем уравнение 
Последовательности значений 



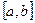
Порядковые статистики.
Случайная величина 

Для случая 
При этом:



А также:
Если же 



А также:

Отметим далее, что если 
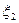


Оценивание параметров в равномерном распределении.
Введём статистический аналог теоретического математического ожидания случайной величины 

Введём статистический аналог теоретической дисперсии случайной величины 

Любая измеримая функция от выборки 
Статистика 

Статистика 

То есть для любого 
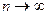

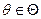
ü Возьмём выборку 

Оптимальной несмещённой оценкой θ в данном классе оценок является:
Её дисперсия:

ü Оценим теперь параметр θ равномерного распределения 

Статистики 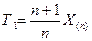

Кроме того, имеем: 

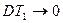



ü Пусть теперь 


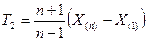
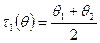

Достаточные статистики и оптимальные оценки.
Если для любой оценки 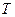


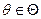
Итак, T* — оптимальная оценка для параметрической функции 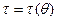



Статистика 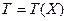



Теорема Рао-Блекуэлла-Колмогорова: Оптимальная оценка, если она существует, является функцией от достаточной статистики.
Теорема: Если существует полная достаточная статистика, то всякая функция от неё является оптимальной оценкой своего математического ожидания.
То есть оптимальная оценка однозначно определяется уравнением 
Функция 


Критерий факторизации.
Для того, чтобы статистика была достаточной для параметрического семейства распределений P, необходимо и достаточно, чтобы функция правдоподобия выборки 
Где множитель h(x) от 

ü Пусть 


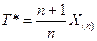
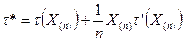
ü Пусть теперь 



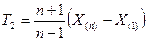

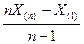


ü Статистика 


Если 
Аналогично, если 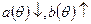
Этими двумя случаями исчерпываются ситуации, когда в модели 
Для модели 


|
Обзор компонентов Multisim Компоненты – это основа любой схемы, это все элементы, из которых она состоит. Multisim оперирует с двумя категориями… |
Композиция из абстрактных геометрических фигур Данная композиция состоит из линий, штриховки, абстрактных геометрических форм… |
Важнейшие способы обработки и анализа рядов динамики Не во всех случаях эмпирические данные рядов динамики позволяют определить тенденцию изменения явления во времени… |
ТЕОРЕТИЧЕСКАЯ МЕХАНИКА Статика является частью теоретической механики, изучающей условия, при которых тело находится под действием заданной системы сил… |
|
Этапы трансляции и их характеристика Трансляция (от лат. translatio — перевод) — процесс синтеза белка из аминокислот на матрице информационной (матричной) РНК (иРНК… Условия, необходимые для появления жизни История жизни и история Земли неотделимы друг от друга, так как именно в процессах развития нашей планеты как космического тела закладывались определенные физические и химические условия, необходимые для появления и развития жизни… Метод архитекторов Этот метод является наиболее часто используемым и может применяться в трех модификациях: способ с двумя точками схода, способ с одной точкой схода, способ вертикальной плоскости и опущенного плана… |
ние, дисперсию и моду.
|
ξ |
0 |
1 |
2 |
3 |
4 |
5 |
; Mξ = 3; Dξ = 1, 2; |
|
P |
0,01024 |
0,0768 |
0,2304 |
0,3456 |
0,2592 |
0,07776 |
мода 3.
14.7. Рабочий обслуживает четыре одинаковых станка. Вероятность того, что в течение часа станок потребует регулировки, равна 0,25. Приняв за случайную величину ξ число станков, которые рабочему придется регулировать в течение часа, составить ряд распределения этой величины, определить ее математическое ожидание, дисперсию и моду.
|
ξ |
0 |
1 |
2 |
3 |
4 |
; Mξ = 1; Dξ = 0, 75; мода 1. |
|
P |
81/256 |
108/256 |
54/256 |
12/256 |
1/256 |
14.8. В магазин зашли четыре покупателя. Вероятность того, что любой из них сделает покупку, равна 0,3. Приняв за случайную величину ξ число лиц, совершивших покупку, составить ряд распределения этой величины, определить ее математическое ожидание, дисперсию и моду
|
ξ |
0 |
1 |
2 |
3 |
4 |
; Mξ = 1, 2; Dξ = 0, 84; мода 1. |
|
P |
0,2401 |
0,4116 |
0,2646 |
0,0756 |
0,0081 |
14.9. В урне 20 белых и 10 черных шаров. Вынули подряд четыре шара, причем каждый вынутый шар возвращают в урну перед извлечением следующего и шары в урне перемешивают. Приняв за случайную величину ξ число извлеченных белых шаров, составить ряд распределения этой величины, определить ее математическое ожидание, дисперсию и моду.
|
ξ |
0 |
1 |
2 |
3 |
4 |
; Mξ = 8/3; Dξ = 8/9; мода 3. |
|
P |
1/81 |
8/81 |
24/81 |
32/81 |
16/81 |
14.10. Заявки на получение кредита, рассылаемые фирмой по банкам, удовлетворяются примерно в 30% случаев независимо друг от друга. Фирма разослала 12 заявок. Найти математическое ожидание и дисперсию числа удовлетворенных заявок ξ, а также P (ξ = [Mξ]), где [Mξ] — целая часть числа Mξ.
Mξ = 3, 6; Dξ = 2, 52; P(ξ = 3) = C123 · 0, 33 · 0, 79 0, 24.
14.11. Из перемешанной колоды в 36 карт выкладывают на стол в ряд карты лицом вверх. На карты этой колоды таким же образом кладут сверху карты второй такой же колоды. Найти среднее число пар одинаковых карт из верхней и нижней колоды. (Другими словами, найти математическое ожидание Mξ, где случайная величина ξ есть число пар одинаковых карт из верхней и нижней колоды.) 1.
§15. Геометрические распределение
Рассмотрим схему Бернулли с вероятностью «успеха» равной p. Это самое простое распределение (после детерминированного) имеет ряд распределения
41

|
ξ |
0 |
1 |
. |
|
|
P |
1 − p |
p |
||
Пусть эксперимент состоит в том, что испытания по схеме Бернулли проводятся неограниченное число раз. С таким экспериментом связаны две случайные величины: τ — номер первого «успеха» в последовательности испытаний и η — число «неудач», появившихся до первого успеха. Легко подсчитать, что случайные величины τ и η имеют следующие ряды распределения
|
τ |
1 |
2 |
. . . |
k |
. . . |
и |
η |
0 |
1 |
. . . |
k |
. . . |
. |
|
P |
p |
qp |
. . . |
qk−1p |
. . . |
P |
p |
qp |
. . . |
qkp |
. . . |
В строке вероятностей эти ряды содержат одну и ту же геометрическую прогрессию, поэтому они называются соответственно один- и нуль-геометрическим распределениями. 1- и 0-геометрические распределения связаны очевидной формулой η = τ − 1.
Формула вероятность для 1-геометрического распределения:
P(τ = k) = qk−1p,
где 0 < p < 1 и√q = p − 1. Основные числовые характеристики: Mτ = 1/p,
Dτ = q/p2, σ = pq .
Формула вероятность для 0-геометрического распределения определена по
формуле
P(η = k) = qkp,
где 0 < p < 1 и√q = p − 1. Основные числовые характеристики: Mη = q/p,
Dη = q/p2, σ = pq .
15.1. Стрелку выдаются патроны до тех пор, пока он не промахнется (т.е. до первого промаха). Вероятность его попадания в цель при каждом выстреле равна 0,9. Какова вероятность того, что он получит не менее трех патронов?
Случайная величина τ — число патронов, полученное до первого промаха.
|
Ряд распределения: |
τ |
1 |
2 |
3 |
. . . |
k |
. . . |
. То- |
|
P |
0, 1 |
0, 9 · 0, 1 |
0, 92 · 0, 1 |
. . . |
0, 9k−1 · 0, 1 |
. . . |
гда P(τ ≥ 3) = 1−P(τ < 3) = 1−P(τ = 1)−P(τ = 2) = 1−0, 1−0, 9·0, 1 = 0, 81.
15.2. Вероятность попадания баскетболистом в корзину при штрафном броске равна 1/3. На тренировке баскетболист выполняет штрафные броски до тех пор, пока не попадет в корзину, а затем передает мяч другому игроку. Пусть τ — количество бросков, сделанных баскетболистом. Составить формулу P(τ = k), найти Mτ и Dτ.
Случайная величина τ имеет 1-геометрическое распределение, в котором
|
p = 31 , q = 32 ; Тогда P(τ = k) = qk−1p = |
32 |
k−1 · 31 = |
2k |
1 |
; Mτ = 3; Dτ = 6. |
|
|
3k |
||||||
|
15.3. Вероятность изготовления |
бракованной детали на станке равна 0,05. |
|||||
|
( |
) |
Пусть η — число хороших деталей, изготовленных на станке с начала его работы до появления первой бракованной детали. Найти Mη и Fη(3).
42
Случайная величина η имеет 0-геометрическое распределение, в котором
|
p = 0, 05, q = 0, 95; |
Тогда P(η = k) = qkp = 0, 95k · 0, 05; Mη = q/p = |
|||||
|
19; |
F |
η |
≤ |
η |
+ P(η = 1) + P(η = 2) + P(η = 3) = |
|
|
η(3) = P( |
3) |
2= P( |
= 0) |
3 |
· 0, 05 0, 1875. |
|
|
0, 05 + 0, 95 · 0, 05 |
+ 0, 95 |
· 0, 05 |
+ 0, 95 |
15.4. Из колоды, состоящей из 36 карт, последовательно достают по одной карте, каждый раз возвращая её обратно. Найти среднее число извлеченных карт до появления туза пик и вероятность того, что до появления туза пик
|
придется извлекать не менее 3 карт. |
|||||||||||||||||||||||||||||||||||||
|
p = 1/36; |
35/36; |
η |
0 |
1 |
2 |
. . . |
k |
. . . |
; |
||||||||||||||||||||||||||||
|
q = |
1 |
1 |
( |
) |
2 · 361 |
( |
) |
k · |
1 |
||||||||||||||||||||||||||||
|
( |
) |
P |
36 |
3635 · |
36 |
3635 |
. . . |
3635 |
36 |
. . . |
|||||||||||||||||||||||||||
|
Mη = q/p = 35; |
≥ |
2 |
· |
( |
( |
) |
3 + . . . |
) |
( |
) |
3 |
0, 919. |
|||||||||||||||||||||||||
|
P(η |
3) = |
35 |
1 + 35 |
+ |
35 |
= |
35 |
||||||||||||||||||||||||||||||
|
36 |
36 |
36 |
36 |
36 |
15.5. При проведении операции срочно потребовался донор с редкой 33-й группой крови. По статистике такая группа крови встречается у 5% инопланетян. Сколько в среднем придется опросить инопланетян, чтобы найти персону с такой группой крови? Какова вероятность того, что из 10 сотрудников, работающих в операционной, найдется хотя бы один индивидуум с такой группой крови?
|
p = 0, 05; |
q = 0, 95; |
τ |
1 |
2 |
. . . |
k |
. . . |
; |
||
|
P |
0, 05 |
0, 95 · 0, 05 |
. . . |
0, 95k−1 · 0, 05 |
. . . |
|||||
|
Mτ = 1/p = 20; |
P(ξ10 ≥ 1) = 1 − P(ξ10 = 0) = 1 |
− C100 |
· 0, 050 · 0, 9510 0, 401. |
43

§16. Распределение Пуассона
Случайная величина ξ, имеющая счётное пространство элементарных событий
Ω = {0, 1, 2, . . . , k, . . . } = {0} N, подчиняется распределению Пуассона с
параметром λ > 0, если вероятность наступления события ξ = k определена по
формуле
P(ξ = k) = λk e−λ. k!
Это распределение зависит от одного параметра λ. Основные числовые харак-
√
теристики: Mξ = λ, Dξ = λ, σ = λ.
Теорема Пуассона. Если n → ∞ и p → 0 так, что np → λ, то для любого фиксированного значения k {0} N имеет место формула
|
λk |
||
|
P(ξ = k) = lim Ck pm qn−k = |
e−λ. |
|
|
n→∞ |
n |
k! |
Теорема Пуассона утверждает, что распределение Пуассона является предельным для биномиального распределения, когда число опытов n неограниченно увеличивается (n → ∞) и одновременно вероятность p «успеха»в одном опыте неограниченно уменьшается (p → 0), но так, что их произведение np в пределе стремится к постоянному значению λ, т.е. np → λ. На практике параметр λ удовлетворяет неравенству 0, 1 ≤ λ ≤ 10). Условие np → λ геометрически означает, что мода биномиального распределения, удовлетворяющая неравенству np − q ≤ m ≤ np + p, не убегает в бесконечность, а в пределе мода распределения Пуассона удовлетворяет неравенству λ − 1 ≤ m ≤ λ. Распределение Пуассона с параметром λ можно применять для приближенных вычислений вместо биномиального, когда число опытов n очень велико, а вероятность p «успеха»в отдельном опыте очень мала, т.е. в каждом отдельном опыте «успех»приходит редко. Поэтому закон Пуассона в литературе часто называют «законом редких явлений».
16.1. Завод отправил на базу 5000 доброкачественных изделий. Вероятность того, что в пути изделие повредится, равна 0,0002. Найти вероятность того, что по дороге на базу будут повреждены 3 изделия.
n = 5000, p = 0, 0002, k = 3. Тогда λ = np = 5000 · 0, 0002 = 1, следовательно P(ξ = 3) = 13!3 e−3 = 61e 0, 06.
16.2. В стае 1000 птиц, из которых 50 окольцованных. Орнитологи поймали 100 птиц. Каково среднее число окольцованных птиц среди пойманных? Какова вероятность того, что среди пойманных птиц нет окольцованных?
Произведено n = 100 независимых «опытов» , где «опыт»есть поимка одной птицы из стаи. Вероятностью «успеха» , т.е. поимки окольцованной птицы, при каждой поимке одинакова и равна p = 100050 = 0, 05. Поскольку n достаточно велико, p — мало, а λ = np = 100 · 0, 05 = 5 удовлетворяет условию 0, 1 ≤ λ ≤ 10, то можно считать, что случайная величина ξ — количество окольцованных
44

птиц среди пойманных — распределена по закону Пуассона. Тогда среднее число
окольцованных птиц среди пойманных, т.е. Mξ = λ = 5. Далее P(ξ = 0) =
50!0 e−5 = e15 0, 0067.
16.3. Семена ржи содержат 0,04% семян сорняков. Какова вероятность об-
наружить среди 5000 семян 5 семян сорняков?
n = 5000; p = 0, 0004; λ = 5000 · 0, 0004 = 2; P(ξ = 5) = 25!5 e−2 0, 0361.
16.4. Учебник издан тиражом 100 000 экземпляров. Вероятность того, что учебник сброшюрован неправильно, равна 0,00004. Найти вероятность того, что
тираж содержит ровно пять бракованных книг.
n = 100 000; p = 0, 00004; λ = 4; P(ξ = 5) = 45!5 e−4 0, 4248.
16.5. Супермаркет получил 10 000 бутылок минеральной воды. Вероятность того, что при перевозке бутылка окажется разбитой, равна 0,0003. Найти вероятность того, что супермаркет получит не менее двух разбитых бутылок.
|
n |
= 10 000; |
p |
= 0 |
, 0003 |
λ = 3 |
; |
P(ξ |
≥ |
2) = 1 |
− |
P(ξ < 2) = |
|
|
4; |
||||||||||||
|
1 − P(ξ = 0) − P(ξ = 1) = 1 |
− |
0, 801. |
||||||||||
|
e3 |
16.6. Вероятность изготовления бракованного сверла равна 0,02. Свёрла укладываются в коробки по 100 штук. Определить вероятность того, что количество бракованных свёрл в коробке не превышает двух.
n = 100; p = 0, 02; λ = 2; P(ξ ≤ 2) = P(ξ = 0) + P(ξ = 1) + P(ξ = 2) 0, 667.
§17. Простейший пуассоновский поток
Рассмотрим следующую задачу. Пусть с течением времени на оси Ot случайным образом возникают точки — моменты появления каких-то однотипных событий, например, появление вызовов на телефонной станции, приходы посетителей в магазин и т.п. Последовательность таких моментов появления событий назовем «потоком событий». Предположим, что поток обладает следующими свойствами.
1.Стационарность. Вероятность попадания фиксированного числа событий на интервале времени [t, t + τ] не зависит от начала t этого интервала, а зависит только от его длины τ. Это означает, что среднее число событий, появляющихся
вединицу времени (т.е. на любом интервале [t, t + 1]), постоянно. Обозначим это среднее через λ и будем называть интенсивностью потока.
2.Ординарность. Вероятность появления на малом интервале [t, t + ∆t] двух или более событий пренебрежимо мала по сравнению с вероятностью появления на нём одного события (т.е. при ∆t → 0 вероятность появления на этом интервале более одного события есть бесконечно малая величина более высокого порядка малости, чем вероятность появления на нём же ровно одного события).
3.Отсутствие последействия. Вероятность появления какого-нибудь числа событий на заданном интервале [t, t + τ] не зависит от того, сколько событий
45

появилось на любом другом не пересекающимся с ним участок (в частности, «будущее»потока не зависит от его «прошлого» , отсюда и термин — «отсутствие последействия»).
Случайная величина ξ, имеющая счётное пространство элементарных событий Ω = {0, 1, 2, . . . , k, . . . } = {0} N, называется простейшим пуассоновским потоком с интенсивностью λ > 0, если вероятность появления ξ = k событий за время τ определена по формуле
P(ξ = k) = (λτk!)k e−λτ .
√
Основные числовые характеристики: Mξ = λτ, Dξ = λτ, σ = λτ.
17.1. Станция скорой помощи получает телефонные звонки с интенсивностью λ = 0, 8 (зв./мин). Найти вероятность того, что за 2 минуты: а) никто не позво-
нит; б) будет принят ровно один вызов; в) будет принят хотя бы один вызов. Случайная величина ξ — число вызовов за 2 минуты — распределена по за-
кону Пуассона с параметром λτ = 0, 8 ·2 = 1, 6. Имеем: а) P(ξ = 0) = 10!,60 e−1,6
0, 202; б) P(ξ = 1) = 11!,61 e−1,6 0, 323; в) P(ξ ≥ 1) = 1−P(ξ < 1) = 1−0, 202 0, 798.
17.2. Сельская автоматическая телефонная станция соединяет в среднем за час 300 пар абонентов. Какова вероятность того, что за данную минуту она
соединит не более одной пары абонентов?
λ = 5 (пар/мин.); τ = 1; P(ξ ≤ 2) = P(ξ = 0) + P(ξ = 1) = e65 0, 0404.
17.3. В магазин приходят в среднем 30 покупателей в час. Какова вероятность, что в течение минуты в магазин не войдёт ни один покупатель?
|
1 |
||
|
λ = 0, 5 (пок./мин.); τ = 1; P(ξ = 0) = √ |
0, 606. |
|
|
e |
17.4. На регистрирующее устройство попадает в среднем 120 космических частиц в минуту. Какова вероятность, что за одну секунду будет зарегистрировано не менее двух частиц?
λ = 2 (ч./сек.); τ = 1; P(ξ ≥ 2) = 1 − P(ξ < 2) = 1 − P(ξ = 0) − P(ξ = 1) =
1 − e32 0, 594.
17.5. Коммутатор в течение часа получает в среднем 60 вызовов. Телефонистка отлучилась на 30 секунд. С какой вероятностью за это время на коммутатор придёт хотя бы один вызов?
λ = 1 (выз./мин.); τ = 0, 5; P(ξ ≥ 1) = 1 − P(ξ = 0) = 1 − 1 0, 394.
√
e
Основные непрерывные распределения
Случайная величина ξ, имеющая непрерывную функцию распределения Fξ(x), называется непрерывной.
46

Равномерное распределение
Случайная величина ξ имеет равномерное распределение на отрезке [a, b],
|
если её плотность вероятности определена по формуле |
|||||||||||||||
|
1 |
, a ≤ x ≤ b |
||||||||||||||
|
fξ(x) = |
b |
a |
. |
||||||||||||
|
{ |
−0 , x < a или x > b |
||||||||||||||
|
Её функция распределения |
|||||||||||||||
|
0 , |
x < a |
||||||||||||||
|
Fξ(x) = P(ξ |
x a |
||||||||||||||
|
≤ |
x) = b−a , a ≤ x ≤ b . |
||||||||||||||
|
1−, |
x > b |
||||||||||||||
|
a+b |
(b−a)2 |
b |
a |
||||||||||||
|
Mξ = |
Dξ = |
σ == |
− |
||||||||||||
|
Основные числовые характеристики: |
2 , |
12 , |
2√ |
3 |
, |
m = a+2 b, мод нет.
Пример. Известно, что случайная величина ξ, являющаяся погрешностью округления до ближайших целых чисел каких-либо величин, полученных в результате приближенных вычислений или приближенных измерений (с точностью до цены деления измерительного прибора), удовлетворительно описывается равномерным распределением с плотностью вероятностью
|
fξ(x) = |
1, |
−0, 5 ≤ x ≤ 0, 5 |
. |
|
{ |
0, |
x < −0, 5 или x > 0, 5 |
.
17.6. Если расписание движения трамваев соблюдается, то в среднем пассажир ожидает трамвай 3,5 минуты. Известно, что время ожидания имеет равномерное распределение. Минимальное время ожидания равно 0 (пришли на остановку, и трамвай подходит). Найти вероятность того, что пассажир будет
ожидать трамвай от 2 до 5 минут.
a = 0; Mξ = a+2 b = 3, 5; b = 7; P(2 ≤ ξ ≤ 5) = (5 − 2) · 17 = 37 .
17.7. Длина комнаты измеряется с помощью грубой рулетки с ценой деления 10 см. Округление производится до ближайшего деления. Случайная величина ξ — ошибка измерения. Найти и построить её плотности вероятности, найти математическое ожидание, дисперсию случайной величины и среднеквадратичное отклонение.
|
1 |
, |
−5 ≤ x ≤ 5 |
; Mξ = 0; Dξ = 25 |
; |
5 |
2, 9 см. |
||||
|
fξ(x) = |
10 |
σ = |
||||||||
|
√3 |
||||||||||
|
{ |
0, |
x < −5 или x > 5 |
3 |
17.8. Трамваи маршрута №2 ходят через каждые 5 минут. Пассажир подходит к трамвайной остановке в некоторый момент времени. Какова вероятность появления пассажира не ранее, чем через 1 минуту после ухода предыдущего трамвая, и не позднее, чем за 2 минуты до отхода следующего поезда?
|
fξ(x) = |
0, 2, |
0 ≤ x ≤ 5 |
; P(1 |
≤ |
ξ |
≤ |
3) = (3 |
− |
1) |
· |
0, 2; = 0, 4. |
|
{ |
0, |
x < 0 или x > 5 |
47
17.9. Случайная величина ξ равномерно распределена на отрезке [−a, b], где a > 0 и b > 0. Вероятность того, что эта случайная величина примет отрицательное значение, равна 0,75. Рассматривается другая случайная величина η, равномерно распределенная на отрезке [−3a, b]. Чему равна вероятность того,
|
что случайная величина η будет отрицательной? |
|||||
|
P(ξ < 0) = |
a |
= 0, 75, поэтому b = a. P(η < 0) = |
3a |
= 0, 9. |
|
|
a+b |
3a+b |
||||
|
3 |
Показательное (экспоненциальное) распределение
Случайная величина ξ имеет показательное (экспоненциальное) распределение с параметром λ > 0, если её плотность вероятности имеет вид
{
|
fξ(x) = |
0, |
x < 0 |
||||||||
|
λe−λx, x |
≥ |
0 . |
||||||||
|
Её функция распределения |
||||||||||
|
Fξ(x) = { |
0, |
x < 0 |
||||||||
|
1 − e−λx, x ≥ 0 . |
||||||||||
|
Основные числовые характеристики: Mξ = 1 , Dξ = |
1 |
, |
σ = 1 |
, |
Med ξ = ln 2 |
, |
||||
|
2 |
||||||||||
|
Mod ξ = 0. |
λ |
λ |
λ |
λ |
||||||
Показательное распределение играет большую роль в теории марковских случайных процессов, теории массового обслуживания и теории надежности
17.10. Показать, что случайная величина, равная интервалу времени T между двумя соседними событиями в простейшем пуассоновском потоке, имеет показательное распределение, параметр λ которого равен интенсивности потока,
|
т.е. |
||
|
fT (t) = { |
0, |
t < 0 |
|
λe−λt, t ≥ 0 . |
Найдем FT (t) = P(T ≤ t). Для этого на оси Ot отложим интервалы [0, T ] и [0, t]. Для того чтобы выполнялось неравенство T ≤ t, необходимо, чтобы хотя бы одно событие потока попало на интервал [0, t]. Поэтому FT (t) = P(T ≤ t) =
1 − P(ξ = 0) = 1 − e−λt при t ≥ 0. Отсюда fT (t) = FT′ (t) = λe−λt при t ≥ 0. Из условия нормировки следует, что fT (t) = 0 при t < 0.
17.11. Время безотказной работы персонального компьютера (ПК) — случайная величина , имеющая показательное распределение с параметром λ (физический смысл λ — среднее число отказов в единицу времени, если не учитывать простоев ПК). Известно, что ПК уже проработал без отказов время τ. Найти при этом условии плотность распределения fT (t) времени T , которое ПК проработает после момента τ до ближайшего отказа.
Так как простейший поток отказов не имеет последействия, то вероятность появления хотя бы одного отказа на интервале [τ, τ + t] не зависит от того, появлялись ли отказы ранее момента τ. Поэтому FT (t) = P(T ≤ t) = 1 − P(ξ =
48
0) = 1 − e−λt при t ≥ 0. Откуда fT (t) = 0 при t < 0. Заметим, что случайная величина — времени, оставшегося до следующего отказа, не зависит от того, сколько времени ПК уже проработал безотказно.
17.12. Случайная величина ξ распределена по показательному закону c па-
|
раметром λ = 10. Вычислить условную вероятность P {ξ > 100} |
{ξ > 90} . |
||||||||||||||||||||||||||
|
По |
определению условной |
вероятности |
P |
{ |
ξ( |
> 100 |
ξ |
> 90 |
) |
= |
|||||||||||||||||
|
P( ξ>100 |
} ∩ { |
ξ>90 |
} |
) |
P(ξ>100) |
1 |
− |
P(ξ |
≤ |
100) |
1 |
− |
(1 e 10 100) |
e |
1000 |
} |
{ |
} |
|||||||||
|
{ |
= |
= |
= |
− |
(= |
= |
e |
10 |
, 0000454 |
||||||||||||||||||
|
10 |
90 |
900 |
|||||||||||||||||||||||||
|
P(ξ>90) |
P(ξ>90) |
1−P(ξ≤90) |
1−(1−e |
) |
e |
− |
0 |
) |
. |
||||||||||||||||||
17.13. На профессиональной кольцевой гоночной трассе «Нижегородское кольцо» время T ремонта и обслуживания автомобиля после одного заезда является случайной величиной, удовлетворительно описывающейся экспоненциальным законом распределения. Было замечено, что в текущем сезоне на ремонт и обслуживание автомобиля после одного заезда тратилось в среднем 5 минут. Найти вероятность того, что при очередной поездке это время не превысит 30 минут.
|
По условию MT = 5. Поскольку MT = 1 , то λ = 0, 2. Плотность вероятности |
|||
|
λ |
|||
|
0, |
t < 0 |
||
|
имеет вид: fT (t) = { 0, 2e−0,2t, |
t ≥ 0 . Следовательно, получаем P (T ≤ 30) = |
||
|
30 |
0, 2 e−0,2tdt = −e−0,2t 030 = 1 − e−6 0, 998. |
||
|
∫0 |
|||
|
17.14. Опытами установлено, |
что в течение месяца выходит из строя 0,02% |
электрических лампочек определенного типа. Некто купил для своей новой трёхламповой люстры три лампочки этого типа. Какова вероятность того, что в течение 5 месяцев ни одна из лампочек в люстре не перегорит?
Случайная величина T — время от включения одной лампочки до того момента, когда она перегорит, подчиняется показательному закону распределения.
|
По условию задачи P (T < 1) |
= P (T ≤ 1) = FT (1) = 1 − e−λ·1 |
= 0, 0002, или |
|||||||||||
|
e−λ = 0, 9998 |
λ = |
− |
ln 0, 9998 |
||||||||||
|
. Отсюда |
. Тогда вероятность, что одна лампочка |
||||||||||||
|
не перегорит за 5 месяцев, равна P (T > 5) = 1 |
− |
P (T |
≤ |
5) = 1 |
− |
F |
T |
(5) = e−5λ = |
|||||
|
e |
5 ln 0,9998 |
= 0, 9998 |
5 |
||||||||||
|
0, 9990004. Поскольку время выхода из строя каждой из |
лампочек не зависит от времени выхода из строя других, то вероятность того, что ни одна из лампочек в люстре не перегорит в течение 5 месяцев, равна
0, 99900043 0, 997004 0, 997.
17.15.Время T безотказной работы станка является случайной величиной
споказательным распределением. Вероятность того, что станок не откажет за
5 часов работы, равна 0,60653. Найти MT , DT и σ.
По условию задачи P (T > 5) = 1 − P (T ≤ 5) = 1 − FT (5) = 1 − (1 − e−λ·5) =
|
e−5λ = 0, 60653 |
. Отсюда |
λ |
= |
− |
ln 0, 60653 = 0, 5000010… |
0, 5 |
. Плотность |
|||
|
вероятности имеет вид: fT (t) = { |
0, |
t < 0 |
||||||||
|
0, 5e−0,5t, |
t ≥ 0 . |
|||||||||
|
∞ |
∞ |
|||||||||
|
MT = 0, 5∫0 te−0,5tdt = 10, |
DT = 0, 5∫0 |
(t − 10)2e−0,5tdt = 100, σ = 10. |
17.16. Вероятность того, что некий прибор проработает 1 час, равна 0,9.
49
50
Какова вероятность того, что прибор безотказно проработает сутки?
Время T безотказной работы прибора является случайной величиной с показательным распределением. По условию задачи P (T > 1) = 1 − P (T ≤ 1) =
1 − FT (1) = 1 − (1 − e−λ·1) = e−λ = 0, 9. Отсюда λ = − ln 0, 9 0, 105.
P (T > 24) = 1 − P (T ≤ 24) = 1 − FT (24) = 1 − (1 − e−0,105·24) e−2,53 0, 0797.
17.17. 98% топливных насосов дизельных тракторов выходят из строя после работы 3000 часов. Какова вероятность того, что насос выйдет из строя в
|
интервале от 2000 до 2500 часов? |
|||||||||||||||||||
|
Время T безотказной работы прибора является случайной величиной с пока- |
|||||||||||||||||||
|
зательным |
распределением. |
По |
условию |
задачи P (T > 3000) |
= |
||||||||||||||
|
1 |
− |
P (T |
≤ |
3000) = 1 |
− |
FT (3000) = 1 |
− |
(1 |
− |
e−λ·3000) = e−3000λ = 0, 98. Отсюда λ = |
|||||||||
|
− |
ln 0,98 |
0, 0000067. |
Плотность |
вероятности |
имеет |
вид: |
|||||||||||||
|
3000 |
|||||||||||||||||||
|
0, |
t < 0 |
||||||||||||||||||
|
fT (t) |
= |
{ 0, 0000067e−0,0000067t, |
t ≥ 0 . |
P (2000 < T < 2500) |
= |
||||||||||||||
|
2500 |
−e−0,0000067t |
2500 |
= e−0,0134 |
− e−0,01675 |
|||||||||||||||
|
− |
= |
||||||||||||||||||
|
2000 |
|||||||||||||||||||
|
0, 0000067 |
e−0,0000067tdt = |
) |
|||||||||||||||||
|
2000 |
0, 0033. ( |
||||||||||||||||||
|
0, 986689 |
∫0, 983389 |
17.18. По данным страховых агентств некоторого государства вероятность того, что гражданин этой страны доживет до 70 лет, равна 0,87. Какова вероятность того, что случайный новорожденный этой страны доживет до свадьбы, если по статистике этот возраст составляет 22 года?
Время T жизни человека является случайной величиной с показательным
|
распределением. По условию задачи P ( |
T > |
70) = 1 −P ( |
≤ |
ln 0,87 |
− |
T |
|||||||
|
T |
70) = 1 |
F (70) = |
|||||||||||
|
1 − (1 − e−λ·70) |
= e−70λ |
= |
0, 87. |
Отсюда λ |
= |
− 70 |
0, 002. |
||||||
|
{ |
0, |
t < 0 |
|||||||||||
|
Плотность вероятности имеет |
вид: |
fT (t) = |
0, 002e−0,002t, |
t ≥ 0 . |
|||||||||
|
∞ |
|||||||||||||
|
P (T > 22) = 0, 002 |
e−0,002tdt |
0, 957 |
|||||||||||
|
22 |
. |
||||||||||||
|
17.19. |
Известно, что среднее время ожидания кассиром очередного поку- |
||||||||||||
|
∫ |
пателя, подошедшего к кассе, равно 0,2 минуты. Время ожидания T кассиром очередного покупателя можно считать случайной величиной, имеющей показательный закон распределения. Кассиру нужно сменить ленту кассового аппарата. На это ему требуется две минуты. Какова вероятность того, что за это время
не образуется очередь, т.е. к кассе не подойдет ни один покупатель?
MT = λ1 = 0, 2. Отсюда λ = 5. P (T > 2) = 1 − P (T ≤ 2) = 1 − FT (2) = 1 − (1 − e−5·2) = e−10 = 0, 0000454.
17.20. Блок прибора построен из трех независимых, параллельно действующих одинаковых элементов. Отказ блока происходит лишь в случае, когда отказывают все три элемента. Плотность распределения времени T исправной
|
работы каждого из элементов равна fT (t) = { |
0, |
t < 0 |
. Какова веро- |
|||
|
1 |
· e− |
t |
, |
t ≥ 0 |
||
|
300 |
||||||
|
300 |
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Показательное распределение
- Краткая теория
- Примеры решения задач
- Задачи контрольных и самостоятельных работ
Краткая теория
Показательным (экспоненциальным) называют распределение вероятностей непрерывной случайной величины
, которое описывается плотностью:
где
–
постоянная положительная величина.
Показательное
распределение определяется одним параметром
. Эта особенность распределения указывает на
его преимущество по сравнению с распределениями, зависящими от большего числа
параметров. Обычно параметры неизвестны и приходится находить их оценки
(приближенные значения); разумеется, проще оценить один параметр, чем два или три.
Примером непрерывной случайной величины, распределенной по показательному
закону, может служить время между появлениями двух последовательных событий
простейшего потока.
Функция распределения
показательного закона:
Графики плотности и
функции распределения показательного закона изображены на рисунке.
Вероятность попадания в
интервал
непрерывной
случайной величины
, распределенной по показательному закону:
Числовые характеристики показательного (экспоненциального) распределения
Математическое ожидание случайной величины, распределенной по показательному закону:
Дисперсия случайной величины, распределенной по показательному закону:
Среднее квадратическое отклонение случайной величины,
распределенной по показательному закону:
Коэффициенты асимметрии и эксцесса
для показательного распределения:
Таким
образом, математическое ожидание и среднее квадратическое
отклонение экспоненциального распределения равны между собой.
Показательный закон
распределения играет большую роль в теории массового обслуживания и теории
надежности. Так, например, интервал времени
между
двумя соседними событиями в простейшем потоке имеет показательное распределение
с параметром
–
интенсивностью потока.
При решении задач, которые выдвигает практика, приходится
сталкиваться с различными распределениями непрерывных случайных величин.
Смежные темы решебника:
- Непрерывная случайная величина
- Нормальный закон распределения случайной величины
- Равномерный закон распределения случайной величины
Примеры решения задач
Пример 1
Случайная величина
задана функцией распределения
Найдите математическое
ожидание и среднее квадратическое отклонение этого
распределения.
Найдите вероятность того,
что случайная величина примет значение от 0,2 до 1.
На сайте можно заказать решение контрольной или самостоятельной работы, домашнего задания, отдельных задач. Для этого вам нужно только связаться со мной:
ВКонтакте
WhatsApp
Telegram
Мгновенная связь в любое время и на любом этапе заказа. Общение без посредников. Удобная и быстрая оплата переводом на карту СберБанка. Опыт работы более 25 лет.
Подробное решение в электронном виде (docx, pdf) получите точно в срок или раньше.
Решение
Математическое
ожидание случайной величины, распределенной по показательному закону:
Среднее
квадратическое отлонение:
Вероятность того, что
случайная величина примет значение от 0,2 до 1
Ответ
.
Пример 2
На шоссе установлен контрольный пункт для
проверки технического состояния автомобилей. Найти математическое ожидание и
среднее квадратическое отклонение случайной величины T – время ожидания
очередной машины контролером, если поток машин простейший и время (в часах)
между прохождениями машин через контрольный пункт распределено по
показательному закону f(t)=5e-5t.
Указание: Время ожидания машины
контролером и время прохождения машин через контрольный пункт распределены
одинаково.
Решение
В нашем случае
параметр показательного распределения
Математическое
ожидание:
Дисперсия:
Среднее
квадратическое отклонение:
Ответ:
Пример 3
Постройте
интегральную и дифференциальную функции распределения случайной величины X.
Найдите математическое ожидание M(X), дисперсию D(X),
среднее квадратическое отклонение σ(X), моду xmod, медиану xmed , если известно, что
случайная величина X имеет показательное распределение с параметром λ=1.
На сайте можно заказать решение контрольной или самостоятельной работы, домашнего задания, отдельных задач. Для этого вам нужно только связаться со мной:
ВКонтакте
WhatsApp
Telegram
Мгновенная связь в любое время и на любом этапе заказа. Общение без посредников. Удобная и быстрая оплата переводом на карту СберБанка. Опыт работы более 25 лет.
Подробное решение в электронном виде (docx, pdf) получите точно в срок или раньше.
Решение
Плотность
распределения случайной величины
, распределенной по
показательному закону:
Функция
распределения:
Построим
графики дифференциальной и интегральной функций распределения:
График дифференциальной функции распределения
График интегральной функции распределения
Математическое
ожидание показательно распределенной случайной величины
:
Дисперсия:
Среднее
квадратическое отклонение:
найдем, исходя из условия:
Пример 4
Случайная
величина
распределена показательно с дисперсией 0,25.
Найти математическое ожидание и вероятность попадания
в интервал (0,5;1).
Решение
Дисперсия
случайной величины, распределенной по показательному закону:
Математическое
ожидание случайной величины, распределенной по показательному закону:
Вероятность
попадания в интервал
непрерывной случайной величины
, распределенной по
показательному закону:
В нашем
случае:
Ответ:
Задачи контрольных и самостоятельных работ
Задача 1
Время
безотказной работы двигателя автомобиля распределено по показательному закону.
Известно, что среднее время наработки двигателя на отказ между техническим
обслуживанием 100 ч. Определить вероятность безотказной работы двигателя за 80
ч.
На сайте можно заказать решение контрольной или самостоятельной работы, домашнего задания, отдельных задач. Для этого вам нужно только связаться со мной:
ВКонтакте
WhatsApp
Telegram
Мгновенная связь в любое время и на любом этапе заказа. Общение без посредников. Удобная и быстрая оплата переводом на карту СберБанка. Опыт работы более 25 лет.
Подробное решение в электронном виде (docx, pdf) получите точно в срок или раньше.
Задача 2
Среднее
время работы элемента, входящего в пожарно-техническое устройство, равно 1000
часов. Определить вероятность того, что элемент будет работать от 950 до 1150
часов, если время работы элемента распределено по показательному закону.
Задача 3
Вероятность
безотказной работы элемента распределена по экспоненциальному закону
f(t)=e-0.05t
Найти
вероятность того, что в результате испытания случайная величина попадет в
интервал (11;35). Найти характеристики данного распределения случайной
величины.
Задача 4
Непрерывная
случайная величина X задана интегральной функцией распределения
Найти
постоянную C, математическое ожидание случайной величины X,
вероятность попадания случайной величины в интервал [2;4].
Задача 5
Время
между отказами прибора распределено по показательному закону со средним
значением 25 часов. Определить математическое ожидание и дисперсию времени
безотказной работы автомобиля. Найти вероятность того, что очередной отказ
произойдет не позднее 15 часов.
Задача 6
Время
безотказной работы телевизора определенной модели описывается показательным (экспоненциальным)
законом распределения с постоянной λ. Что вероятнее, его безотказная работа в
промежутке времени [x1,x2]
или [x3,x4]? Записать
функции f(x),F(x) и построить их графики.
λ=1/10, x1=3, x2=5, x3=4, x4=8
На сайте можно заказать решение контрольной или самостоятельной работы, домашнего задания, отдельных задач. Для этого вам нужно только связаться со мной:
ВКонтакте
WhatsApp
Telegram
Мгновенная связь в любое время и на любом этапе заказа. Общение без посредников. Удобная и быстрая оплата переводом на карту СберБанка. Опыт работы более 25 лет.
Подробное решение в электронном виде (docx, pdf) получите точно в срок или раньше.
Задача 7
Испытывают
два независимо работающих элемента. Длительность времени t безотказной
работы первого элемента имеет показательное распределение с параметром 0,02,
второго -показательное распределение с параметром 0,06. Найдите вероятность
того, что за время длительностью t=6 ч откажет только один
элемент.
Задача 8
Среднее
время работы каждого из трех элементов, входящих в техническое устройство,
равно T=850 часов. Для безотказной работы устройства необходима безотказная
работа хотя бы одного из трех этих элементов. Определить вероятность, что
устройство будет работать от t1=750 до t2=820 часов, если время
работы каждого из трех элементов независимо и распределено по показательному
закону.
Задача 9
Время
устранения повреждения на канале связи T -случайная величина,
распределенная по закону f(t)=λe-λt (t≥0). Среднее время
восстановления канала — 10 минут. Определить вероятность того, что на
восстановление канала потребуется от 5 до 10 минут.
Задача 10
Дана плотность
распределения случайной величины X.
По какому
закону распределения случайная величина? Найти математическое ожидание,
дисперсию, функцию распределения?
Задача 11
Время
безотказной работы механизма подчинено показательному закону с плотностью
распределения вероятностей f(t)=0.04e-0.04t при t > 0 (t –
время в часах). Найти вероятность того, что механизм проработает безотказно не
менее 100 часов.
Задача 12
Длительность телефонного разговора
является случайной величиной, распределенной по показательному закону.
Известно, что средняя длительность телефонного разговора равна 9 минутам. Найти
вероятность того, что разговор будет длиться:
а) не более 5 минут.
б) более 5 минут.
На сайте можно заказать решение контрольной или самостоятельной работы, домашнего задания, отдельных задач. Для этого вам нужно только связаться со мной:
ВКонтакте
WhatsApp
Telegram
Мгновенная связь в любое время и на любом этапе заказа. Общение без посредников. Удобная и быстрая оплата переводом на карту СберБанка. Опыт работы более 25 лет.
Подробное решение в электронном виде (docx, pdf) получите точно в срок или раньше.
Задача 13
Случайная величина ξ подчинена
показательному закону с параметром λ=5:
Найдите вероятность того, что
случайная величина ξ примет значение меньшее, чем ее математическое ожидание.
Задача 14
Случайная
величина ξ имеет плотность вероятностей (показательное распределение)
Найдите
вероятность P{ξ>Mξ}
Задача 15
Время T
(минут), затрачиваемое клиентами парикмахерской в ожидании своей очереди,
удовлетворяет показательному распределению с параметром λ=0,05. Какова
вероятность того, что время ожидания превысит 25 минут и каково среднее время
ожидания.
Задача 16
Время T (час),
необходимое на ремонт легкового автомобиля удовлетворяет показательному
распределению с параметром λ=0,2. Какова вероятность того, что время ремонта
одного автомобиля не превысит 6 часов, и сколько часов в среднем затрачивается
на ремонт одного автомобиля.
Задача 17
Время
ожидания у бензоколонки автозаправочной станции является случайной величиной X,
распределенной по показательному закону, со средним временем ожидания, равным t0. Найти вероятности
следующих событий:
Задача 18
Случайная
величина X задана показательным законом распределения и
числовыми значениями параметров M(X)=3 и σx=3.
Требуется:
1) найти
функцию плотности f(x).
2) найти
вероятность попадания СВ X в указанный интервал [a,b]=[2,4].
Задача 19
Случайная
величина ξ задана функцией распределения
Найдите
математическое ожидание и среднее квадратическое отклонение этого
распределения.
Задача 20
Случайная величина ξ распределена по
показательному закону с параметром λ=0,3. Найдите математическое ожидание и
среднее квадратическое отклонение этой случайной величины.
- Краткая теория
- Примеры решения задач
- Задачи контрольных и самостоятельных работ
Задача 29119 4. Время безотказной работы элемента…
Условие
4. Время безотказной работы элемента распределено по показательному закону f(t) = 0,01e^(-0,01t) (t > 0), где t — время, ч. Найти
вероятность того, что элемент проработает безотказно 100 ч.
Отв. R (100) = 0,37.
математика ВУЗ
4562
Решение
★
Функция надежности в случае распределения случайной величины по показательному закону имеет вид:
R(t)=1- F(t)=1-(1-e^(-лямбдаt)= e^(-лямбда t)
По условию,
лямбда =0,01
t=100
R (100) = е^(-0,01*100)=е^(-1) = 1/e ≈ 0,37.
О т в е т.
Вероятность того, что элемент проработает безотказно 100 ч, приближенно равна 0,37.
Написать комментарий
Закажите у меня новую работу, просто написав мне в чат!
Среднее время безотказной работы прибора равно 80ч. Полагая, что время безотказной работы прибора имеет показательный закон распределения, найти: а) выражение его плотности вероятности и функции распределения; б) вероятность того, что в течение 100 ч прибор не выйдет из строя.
Решение По условию математическое ожидание случайной величины T равно 80 часов. Следовательно Откуда а) Тогда плотность распределения времени безотказной работы имеет вид: Функция распределения имеет вид: б) Вероятность попадания случайной величины в заданный интервал равна: Для данного случая Ответ: 𝑃(0<Х<100)=0,7135