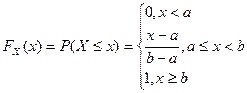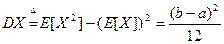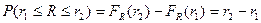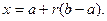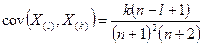выпадающих при однократном бросании игральной кости Г)Время безотказной работы прибора при контроле качества 2.Назови величины, которые являются случайными: А)Температура воздуха в течении суток Б)Вес пойманной рыбы В)Сумма выигрыша лотерейного билета Г)Количество часов в сутках в день солнечного затмения
Соня
02.03.20
Учеба и наука
1 ответ
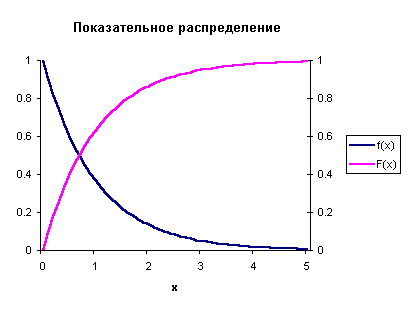
Определение Непрерывная случайная величина Х имеет показательный закон распределения с параметром 

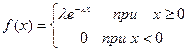
Кривая распределения 
Рис 2.
Получим выражение для функции распределения по формуле 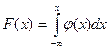
1) При 

2) При 
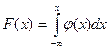

По соответствующим формулам получаем выражения для 

Задача. Среднее время безотказной работы прибора равно 80 ч. Полагая, что время безотказной работы прибора имеет показательный закон распределения, найти: а) выражение его плотности вероятности и функции распределения; б) вероятность того, что в течение 100 ч. прибор не выйдет из строя.
Решение. Х- время безотказной работы прибора, среднее время — 



Искомая вероятность
Замечание. Показательный закон распределения играет большую роль в теории массового обслуживания и теории надежности.
МОСКОВСКИЙ ГОСУДАРСТВЕННЫЙ ИНСТИТУТ ЭЛЕКТРОНИКИ И МАТЕМАТИКИ
Кафедра теории вероятностей и математической статистики
РЕФЕРАТ
По математической статистике
на тему:
«Равномерное распределение»
Выполнил: студенты группы М-65
Ражева А.А.
Кнутова А.С.
Проверил:Заведующий Кафедрой
Ивченко Г. И.
Москва 2012 г.
Непрерывное равномерное распределение — в теории вероятностей распределение, характеризующееся тем, что вероятность любого интервала зависит только от его длины.
Равномерное распределение полезно при описании переменных, у которых каждое значение равновероятно, иными словами, значения переменной равномерно распределены в некоторой области.
Определение
Говорят, что случайная величина имеет непрерывное равномерное распределение на отрезке [a,b], где 
Пишут: X ~ U (a,b) или
Иногда значения плотности в граничных точках x = a и x = b меняют на другие, например 0 или 
Если L (ξ) = U(a,b), то
Равномерное распределение U (a,b) описывает процесс «выбора точки наудачу» в интервале [a,b]. Так, если [a,b] – интервал между последовательными отправлениями автобуса от остановки, то время ожидания пассажира, не знающего расписания и пришедшего на остановку, есть случайная величина с распределением U (0,1). Распределение U (0,1) играет особую роль в методах моделирования с помощью компьютеров случайных величин с заранее заданными распределениями. Такие методы широко используют для приближенных вычислений интегралов, решений дифференциальных и интегральных уравнений и т.д.
Пример (Гипотеза случайности).
В некоторых случаях априори предполагается (постулируется), что исходные данные представляют собой случайную выборку из некоторого распределения, т.е. компоненты вектора данных X=(







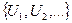
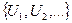

Функция распределения
Интегрируя определённую выше плотность, получаем:
Так как плотность равномерного распределения разрывна в граничных точках отрезка [a,b], то функция распределения в этих точках не является дифференцируемой. В остальных точках справедливо стандартное равенство:
Характеристическая функция случайной величины X ~ U(a,b):
Математическое ожидание и дисперсия по определению равны:
Вообще,
Стандартное равномерное распределение
Если a = 0, а b = 1, то есть X ~ U[0,1], то такое непрерывное равномерное распределение называют стандартным. Имеет место элементарное утверждение:
Если случайная величина X ~ U[0,1], и Y = a + (b − a)X, где a < b, тo Y ~ U[0,1].
Таким образом, имея генератор случайной выборки из стандартного непрерывного равномерного распределения, легко построить генератор выборки любого непрерывного равномерного распределения.
Более того, имея такой генератор и зная функцию обратную к функции распределения случайной величины, можно построить генератор выборки любого непрерывного распределения (не обязательно равномерного) с помощью метода обратного преобразования. Поэтому, стандартно равномерно распределённые случайные величины иногда называют базовыми случайными величинами.
Линейное преобразование
переводит СВ X ~ R(a,b) в СВ Y ~ R(0,1). Действительно,
Равномерное распределение является непрерывным аналогом дискретного распределения вероятностей для опытов с равновероятными исходами.
Значение
С помощью линейного преобразования приводится к равномерному распределению на отрезке [0,1]. Равномерное распределение является непрерывным аналогом распределений классической теории вероятностей, описывающих случайные эксперименты с равновероятными исходами.
Погрешность, происходящая от округления числа, удовлетворительно описывается равномерным распределением на отрезке [ − 1 / 2,1 / 2].
Если случайная величина ζ имеет непрерывную функцию распределения 
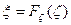
Моделирование
Обозначим буквой 
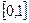
Если 

Моделировать случайную величину 
Мы рассмотрим метод псевдослучайных последовательностей, который наиболее просто реализуется в компьютере. Для получения псевдослучайной последовательности используем алгоритм, который называется методом середины квадратов. Поясним его на примере. Возьмем некоторое число 

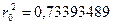







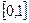

Метод обратных функций.
Пусть случайная величина 





Отсюда следует, что значение 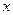




Последовательности значений 

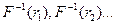


Моделирование случайной величины с равномерным распределением на отрезке
Пусть случайная величина 
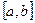
Составляем уравнение 
Последовательности значений 



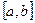
Порядковые статистики.
Случайная величина 

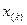
Для случая 
При этом:



А также:
Если же 



А также:

Отметим далее, что если 
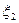


Оценивание параметров в равномерном распределении.
Введём статистический аналог теоретического математического ожидания случайной величины 

Введём статистический аналог теоретической дисперсии случайной величины 

Любая измеримая функция от выборки 
Статистика 

Статистика 

То есть для любого 
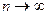

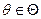
ü Возьмём выборку 

Оптимальной несмещённой оценкой θ в данном классе оценок является:
Её дисперсия:

ü Оценим теперь параметр θ равномерного распределения 

Статистики 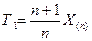

Кроме того, имеем: 

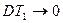



ü Пусть теперь 


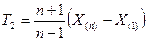
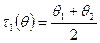

Достаточные статистики и оптимальные оценки.
Если для любой оценки 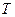


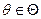
Итак, T* — оптимальная оценка для параметрической функции 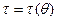



Статистика 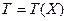



Теорема Рао-Блекуэлла-Колмогорова: Оптимальная оценка, если она существует, является функцией от достаточной статистики.
Теорема: Если существует полная достаточная статистика, то всякая функция от неё является оптимальной оценкой своего математического ожидания.
То есть оптимальная оценка однозначно определяется уравнением 
Функция 


Критерий факторизации.
Для того, чтобы статистика была достаточной для параметрического семейства распределений P, необходимо и достаточно, чтобы функция правдоподобия выборки 
Где множитель h(x) от 

ü Пусть 


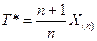
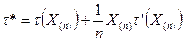
ü Пусть теперь 



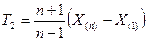

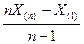


ü Статистика 


Если 
Аналогично, если 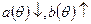
Этими двумя случаями исчерпываются ситуации, когда в модели 
Для модели 

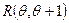

|
Вычисление основной дактилоскопической формулы Вычислением основной дактоформулы обычно занимается следователь. Для этого все десять пальцев разбиваются на пять пар… |
Расчетные и графические задания Равновесный объем — это объем, определяемый равенством спроса и предложения… |
Кардиналистский и ординалистский подходы Кардиналистский (количественный подход) к анализу полезности основан на представлении о возможности измерения различных благ в условных единицах полезности… |
Обзор компонентов Multisim Компоненты – это основа любой схемы, это все элементы, из которых она состоит. Multisim оперирует с двумя категориями… |

Дискретная СВ Х имеет геометрическое распределение, принимает значения 0, 1, … , ∞ с вероятностями
p( X = i) = pi = qi p ,
где p – параметр распределения (0 ≤ p ≤ 1), q = 1 – p.
Числовые характеристики геометрического распределения:
Дискретная значения 0, 1, … ,
m X = q / p , D X = q / p 2 .
СВ X имеет биномиальное распределение, если она принимает n со следующими вероятностями:
|
p(X =i) = p = |
n! |
piqn−i |
(7.2) |
|
i |
i!(n −i)! |
, |
|
где n, p – параметры распределения (0 ≤ p ≤1), q=1 – p. Числовые характеристики биномиального распределения:
m X = n p , D X = n q p .
Дискретная СВ Х имеет распределение Пуассона, если она принимает значения 0, 1, … , ∞ со следующими вероятностями:
|
p(X =i) = p = ai |
e−a |
(7.3) |
|
i |
i! |
, |
|
где a – параметр распределения (a > 0). |
||
|
Числовые характеристики пуассоновской СВ: |
||
|
m X = a , D X |
= a . |
Непрерывная СВ Х имеет равномерное распределение, если ее плотность вероятности в некотором интервале [а; b] постоянна, т.е. если все значения X в этом интервале равновероятны:
0, x <
f ( x ) = 1
b − a
0, x >
|
a , |
0 , x |
< a , |
||||||
|
− a |
||||||||
|
, a ≤ x ≤ b , F ( x ) = |
x |
, a |
≤ |
x ≤ |
b , |
|||
|
(7.4) |
||||||||
|
a |
||||||||
|
b. |
b |
− |
||||||
|
1, x |
> b . |
|||||||
Числовые характеристики равномерно распределенной СВ:
|
m X = |
a + b |
, D X |
= |
( b − a ) 2 |
. |
|
|
2 |
1 2 |
|||||
Непрерывная СВ T, принимающая только положительные значения, имеет экспоненциальное распределение, если ее плотность вероятности и функция распределения равны
|
λ e |
− λ t |
, t |
≥ 0 , |
− e |
−λt |
, t ≥ 0, |
||||
|
f (t ) = |
1 |
(7.5) |
||||||||
|
0 , t < 0 , |
F(t) = |
0, t < 0, |
||||||||
где λ – параметр распределения (λ > 0).

Числовые характеристики экспоненциальной СВ:
m T = 1 / λ , D T = 1 / λ 2 .
Непрерывная СВ Х имеет нормальное распределение, если ее плотность вероятности и функция распределения равны
|
f (x ) = |
1 |
exp − |
(x − m)2 |
F ( x ) = |
0 .5 + Φ |
x − m |
, |
||||||||
|
2 |
, |
(7.6) |
|||||||||||||
|
σ 2π |
2σ |
σ |
|||||||||||||
|
где m, σ – параметры распределения ( σ >0), |
|||||||||||||||
|
1 |
x |
t2 |
|||||||||||||
|
Φ(x) = |
∫e− |
dt — функция Лапласа. |
|||||||||||||
|
2 |
|||||||||||||||
|
2π |
|||||||||||||||
|
0 |
Значения функции Лапласа приведены в приложении. При использовании таблицы значений функции Лапласа следует учитывать, что Φ(–x) = –Φ(x),
Φ(0) = 0, Φ(∞) = 0,5.
Числовые характеристики нормальной СВ:
m X = m , D X = σ 2 ,
|
I [ k / 2 ] |
m |
k −2 i |
(σ |
/ 2) |
i |
|||||||
|
αk ( x) = k ! ∑ |
, |
|||||||||||
|
(k − 2i)!i ! |
||||||||||||
|
i =0 |
||||||||||||
|
0 , k − нечетное, |
||||||||||||
|
µ |
( x ) = |
2 k / 2 |
||||||||||
|
k |
k ! |
σ |
||||||||||
|
, k − четное. |
||||||||||||
|
( k / 2 ) ! |
2 |
Пример 7.1. Время безотказной работы аппаратуры является случайной величиной Х, распределенной по экспоненциальному закону. Среднее время безотказной работы 100 ч. Найти вероятность того, что аппаратура проработает больше среднего времени.
Решение. Так как среднее время безотказной работы, т.е. математическое ожидание, равно 100 ч, то параметр λ экспоненциального закона будет равен λ = 1 / m X = 1 / 100 = 0, 01 . Искомая вероятность
p(X > mX ) = p(100 < X < ∞) =1− F(100) = e−1 ≈ 0,368.
Пример 7.2. Для замера напряжения используются специальные датчики. Определить среднюю квадратическую ошибку датчика, если он не имеет систематических ошибок, а случайные распределены по нормальному закону и с вероятностью 0,8 не выходят за пределы ±0,2.
Решение. Из условия задачи следует, что p(-0,2<X<0,2) = 0,8. Так как распределение ошибок нормальное, а математическое ожидание m равно 0 (систематические ошибки отсутствуют), то
р{–0,2 < X < 0,2} = Ф(–0,2 / σ) – Ф(0,2 / σ) = 2Ф(0,2 / σ) = 0,8.
По таблице функции Лапласа находим аргумент 0,2/ σ =1,28, откуда
σ = 0,2 / 1,28 = 1,0156.

ЗАДАЧИ
7.1. По каналу связи пересылается пакет информации до тех пор, пока он не будет передан без ошибок. Вероятность искажения пакета равна 0,1, найти среднее количество попыток передать пакет.
Ответ: 1,11.
7.2. При работе прибора в случайные моменты времени возникают неисправности. Количество неисправностей, возникающих за определенный промежуток времени, подчиняется закону Пуассона. Среднее число неисправностей за сутки равно двум. Определить вероятность того, что: а) за двое суток не будет ни одной неисправности; б) в течение суток возникнет хотя бы одна неисправность; в) за неделю работы прибора возникнет не более трех неисправностей.
Ответ: а) 0,018; б) 0,865; в) 0,004.
7.3. Шкала рычажных весов имеет цену деления 1 г. При измерении массы отсчет делается с точностью до целого деления с округлением в ближайшую сторону. Какова вероятность того, что абсолютная ошибка определения массы: а) не превысит величины среднего квадратического отклонения возможных ошибок определения массы; б) будет заключена между
значениями σX и2σX .
|
Ответ: а) |
1 |
; б) 1 − |
1 |
. |
|
|
3 |
3 |
||||
7.4. Среднее время работы электронного модуля равно 700 ч. Определить время безотказной работы модуля с надежностью 0,8.
Ответ: 140 ч.
7.5. Сообщение передается последовательностью амплитудномодулированных импульсов с заданным шагом квантования ∆ (∆ – наименьшая разность амплитуд импульсов). На сообщение накладываются шумы, распределенные по нормальному закону N(0, σ). Если мгновенное значение шума превышает половину шага квантования, то при передаче сообщения возникает ошибка. Определить, при каком минимально допустимом шаге квантования ∆ вероятность ошибки из-за шумов не превысит 0,1.
Ответ: 3,4 σ.
7.6. СВ X – ошибка измерительного прибора – распределена нормально с дисперсией 16 мВ2. Систематическая ошибка прибора отсутствует. Вычислить вероятность того, что в пяти независимых измерениях ошибка: а) превысит по модулю 6 мВ не более трех раз; б) хотя бы один раз окажется в интервале
(0,5; 3,5) мВ.
Ответ: а) 0,999; б) 0,776.
8. ФУНКЦИИ ОДНОГО СЛУЧАЙНОГО АРГУМЕНТА
Рассмотрим функцию одного случайного аргумента Y = ϕ(X). Если X – непрерывная случайная величина, то плотность вероятности g(y) величины Y определяется по формуле
|
k |
|||||
|
g( y) = ∑ f (ψ j ( y)) |
ψ′j ( y) |
, |
(8.1) |
||
|
j=1 |
где f(х) – плотность вероятности величины X; ψj(y) – функции, обратные функции ϕ(x);
k – число обратных функций для данного y.
Весь диапазон значений Y необходимо разбить на интервалы, в которых число k обратных функций постоянно, и определить вид g(y) по формуле (8.1) для каждого интервала.
Если X – дискретная случайная величина, принимающая значения xi, то величина Y будет принимать дискретные значения yi = ϕ(xi) с вероятностями
p(yi) = p(xi).
Числовые характеристики функции Y = ϕ(X) одного случайного аргумента
Xопределяются по формулам:
–начальные моменты
|
∑n |
ϕ k ( xi ) pi |
для ДСВ |
|||
|
i =1 |
; |
(8.2) |
|||
|
α k ( y ) = M [Y k ] = M [ϕ k ( x)] = |
∞ |
||||
|
∫ ϕ k ( x) f ( x)dx для НСВ |
|||||
|
– математическое ожидание |
−∞ |
||||
|
m y = M [Y ] = M [ϕ (x )] = α1 ( x ) ; |
(8.3) |
||||
|
– центральные моменты |
|||||
|
n |
|||||
|
∑(ϕ( xi ) − m y )k pi |
для ДСВ |
||||
|
i=1 |
; |
(8.4) |
|||
|
µk ( y) = M[(Y − mY )k ] = |
∞ |
||||
|
∫ (ϕ( x) − my )k f ( x)dx для НСВ |
|||||
|
−∞ |
|||||
|
– дисперсия |
|||||
|
DY =µ2(y) =M[(Y −mY )2]=α2(y)−mY2 . |
(8.5) |
Пример 8.1. Определить плотность вероятности величины Y = X2, если X – случайная величина, равномерно распределенная на интервале [–1, 2].
Решение. Так как Х равномерно распределена в интервале [–1, 2], то ее
|
плотность вероятности равна (7.4): |
−1≤ x ≤ 2, |
|
1/3, |
|
|
f (x) = |
x < −1, x > 2. |
|
0, |

Построим график величины Y = X2 для x в интервале [–1, 2] и в зависимости от числа k обратных функций выделим следующие интервалы для
|
Y (рис. 8.1): |
k = 0, |
|||||||||||||||||||||||||||||
|
[–∞, 0[ |
||||||||||||||||||||||||||||||
|
[0, 1] |
k = 2, |
|||||||||||||||||||||||||||||
|
]1, 4] |
k = 1, |
|||||||||||||||||||||||||||||
|
]4, +∞] |
k = 0. |
|||||||||||||||||||||||||||||
|
Так как на интервалах [–∞, 0[ и ]4, +∞] |
||||||||||||||||||||||||||||||
|
обратная функция не существует, то для этих |
||||||||||||||||||||||||||||||
|
интервалов g(y) = 0. |
||||||||||||||||||||||||||||||
|
В интервале [0, 1] две обратные функции: |
||||||||||||||||||||||||||||||
|
ψ1(y) = + y и ψ2(y) = – y . |
||||||||||||||||||||||||||||||
|
По формуле (8.1) получим |
||||||||||||||||||||||||||||||
|
g( y) = fx (ψ1( y)) |
ψ1′( y) |
+ fx (ψ2( y)) |
ψ2′ ( y) |
= |
||||||||||||||||||||||||||
|
= fx ( y ) |
1 |
+ fx |
(− y ) |
1 |
= |
1 |
. |
|||||||||||||||||||||||
|
2 |
||||||||||||||||||||||||||||||
|
y |
2 |
y |
3 |
y |
||||||||||||||||||||||||||
|
В интервале ]1, 4] одна обратная функция |
||||||||||||||||||||||||||||||
|
ψ1(y) = + |
y , следовательно, |
|||||||||||||||||||||||||||||
|
g( y) = fx (ψ1( y)) |
ψ1′( y) |
= fx ( |
y ) |
1 |
= |
1 |
. |
Рис. 8.1 |
||||||||||||||||||||||
|
2 |
y |
6 |
y |
|||||||||||||||||||||||||||
|
Таким образом, плотность вероятности величины Y равна |
||||||||||||||||||||||||||||||
|
0, |
y < 0, |
|||||||||||||||||||||||||||||
|
1 |
||||||||||||||||||||||||||||||
|
0 ≤ y ≤1, |
||||||||||||||||||||||||||||||
|
y |
, |
|||||||||||||||||||||||||||||
|
3 |
||||||||||||||||||||||||||||||
|
g ( y) = |
1 |
|||||||||||||||||||||||||||||
|
, |
1 < y ≤ 4, |
|||||||||||||||||||||||||||||
|
6 |
y |
|||||||||||||||||||||||||||||
|
y > 4. |
||||||||||||||||||||||||||||||
|
0, |
||||||||||||||||||||||||||||||
Пример 8.2 Случайная величина X равномерно распределена от –1 до +1. Определить математическое ожидание и дисперсию величины Y = X2.
Решение. Плотность вероятности СВ X равна
0,5, −1 ≤ x ≤1, f (x) =
0 , x < −1, x >1.
Вычислим математическое ожидание Y по формуле (8.3):
|
m y = M [X 2 ] = ∫1 |
x 2 0, 5dx = |
1 . |
|
−1 |
3 |
Дисперсию Dy рассчитаем по формуле (8.5):
|
Dy = M[( X 2 )2 ] − mY2 = ∫1 |
(x2 )2 0,5dx − my2 = |
4 |
. |
|
|
45 |
||||
|
−1 |

ЗАДАЧИ
8.1. Определить плотность вероятности величины Y = lnX, если X – случайная величина, равномерно распределенная на интервале (1, 3).
|
0, 5e |
y |
, 0 |
≤ y < ln 3, |
||
|
Ответ: |
g ( y ) = |
||||
|
0 , y < 0, y > ln 3 . |
8.2. Определить плотность вероятности величины Y = |X|, если X – случайная равномерно распределенная величина со следующими характеристиками mx = 1, Dx = 1, и вычислить вероятность того, что р{1 ≤ Y < 2}.
|
0, y < 0, y > 2, 73, |
|||||
|
1 |
|||||
|
Ответ: g( y) = |
, 0 |
≤ y < 0, 73, |
|||
|
3 |
|||||
|
1 |
, 0, 73 ≤ y ≤ 2, 73. |
||||
|
2 3 |
|||||
р{1 ≤ Y < 2} = 0,445.
8.3. Случайная величина X равномерно распределена от 0 до 1. Определить математическое ожидание и дисперсию величины Y = X – 0,2 .
Ответ: mY = 0,34; DY = 0,0574.
8.4. Точка U, изображающая объект на круглом экране радиолокатора, распределена равномерно в пределах круга единичного радиуса. Найти дисперсию расстояния Y от точки U до центра экрана.
Ответ: DY = 1/18.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #