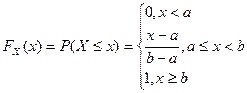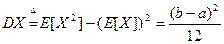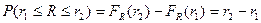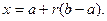|
09:54 вероятность безотказной работы |
|
Функция надежности Функцией надежности R (t) называют функцию, определяющую вероятность безотказной работы элемента за время длительностью t: P(T<t)= e—λt λ—интенсивность отказов (среднее число отказов в единицу времени).Пример решения задачи на вероятность безотказной работы элемента: Длительность времени безотказной работы элемента имеет показательное распределение F(t)= 1 -е-0,01t (t > 0). Найти вероятность того, что за время длительностью t=50 ч: а) элемент откажет; б) элемент не откажет, в)найти функцию надежности Решение задачи F(50) = 1 — е-0,01*50= 0,394;
б) события «элемент откажет» и «элемент не откажет»—противоположные, поэтому вероятность того, что элемент неoткaжeт Р = 1—0,394 = 0.606. R (50) =е-0,01*50 = 0,606. |
Категория: Теория вероятности | Просмотров: 10823 | | Теги: Функция надежности, функция распределения, длительность безотказной работы, вероятность безотказной работы | Рейтинг: 3.5/2 |
Определение Непрерывная случайная величина Х имеет показательный закон распределения с параметром 

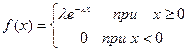
Кривая распределения 
Рис 2.
Получим выражение для функции распределения по формуле 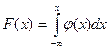
1) При 

2) При 
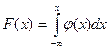

По соответствующим формулам получаем выражения для 

Задача. Среднее время безотказной работы прибора равно 80 ч. Полагая, что время безотказной работы прибора имеет показательный закон распределения, найти: а) выражение его плотности вероятности и функции распределения; б) вероятность того, что в течение 100 ч. прибор не выйдет из строя.
Решение. Х- время безотказной работы прибора, среднее время — 



Искомая вероятность
Замечание. Показательный закон распределения играет большую роль в теории массового обслуживания и теории надежности.
МОСКОВСКИЙ ГОСУДАРСТВЕННЫЙ ИНСТИТУТ ЭЛЕКТРОНИКИ И МАТЕМАТИКИ
Кафедра теории вероятностей и математической статистики
РЕФЕРАТ
По математической статистике
на тему:
«Равномерное распределение»
Выполнил: студенты группы М-65
Ражева А.А.
Кнутова А.С.
Проверил:Заведующий Кафедрой
Ивченко Г. И.
Москва 2012 г.
Непрерывное равномерное распределение — в теории вероятностей распределение, характеризующееся тем, что вероятность любого интервала зависит только от его длины.
Равномерное распределение полезно при описании переменных, у которых каждое значение равновероятно, иными словами, значения переменной равномерно распределены в некоторой области.
Определение
Говорят, что случайная величина имеет непрерывное равномерное распределение на отрезке [a,b], где 
Пишут: X ~ U (a,b) или
Иногда значения плотности в граничных точках x = a и x = b меняют на другие, например 0 или 
Если L (ξ) = U(a,b), то
Равномерное распределение U (a,b) описывает процесс «выбора точки наудачу» в интервале [a,b]. Так, если [a,b] – интервал между последовательными отправлениями автобуса от остановки, то время ожидания пассажира, не знающего расписания и пришедшего на остановку, есть случайная величина с распределением U (0,1). Распределение U (0,1) играет особую роль в методах моделирования с помощью компьютеров случайных величин с заранее заданными распределениями. Такие методы широко используют для приближенных вычислений интегралов, решений дифференциальных и интегральных уравнений и т.д.
Пример (Гипотеза случайности).
В некоторых случаях априори предполагается (постулируется), что исходные данные представляют собой случайную выборку из некоторого распределения, т.е. компоненты вектора данных X=(







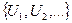
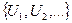

Функция распределения
Интегрируя определённую выше плотность, получаем:
Так как плотность равномерного распределения разрывна в граничных точках отрезка [a,b], то функция распределения в этих точках не является дифференцируемой. В остальных точках справедливо стандартное равенство:
Характеристическая функция случайной величины X ~ U(a,b):
Математическое ожидание и дисперсия по определению равны:
Вообще,
Стандартное равномерное распределение
Если a = 0, а b = 1, то есть X ~ U[0,1], то такое непрерывное равномерное распределение называют стандартным. Имеет место элементарное утверждение:
Если случайная величина X ~ U[0,1], и Y = a + (b − a)X, где a < b, тo Y ~ U[0,1].
Таким образом, имея генератор случайной выборки из стандартного непрерывного равномерного распределения, легко построить генератор выборки любого непрерывного равномерного распределения.
Более того, имея такой генератор и зная функцию обратную к функции распределения случайной величины, можно построить генератор выборки любого непрерывного распределения (не обязательно равномерного) с помощью метода обратного преобразования. Поэтому, стандартно равномерно распределённые случайные величины иногда называют базовыми случайными величинами.
Линейное преобразование
переводит СВ X ~ R(a,b) в СВ Y ~ R(0,1). Действительно,
Равномерное распределение является непрерывным аналогом дискретного распределения вероятностей для опытов с равновероятными исходами.
Значение
С помощью линейного преобразования приводится к равномерному распределению на отрезке [0,1]. Равномерное распределение является непрерывным аналогом распределений классической теории вероятностей, описывающих случайные эксперименты с равновероятными исходами.
Погрешность, происходящая от округления числа, удовлетворительно описывается равномерным распределением на отрезке [ − 1 / 2,1 / 2].
Если случайная величина ζ имеет непрерывную функцию распределения 
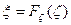
Моделирование
Обозначим буквой 
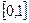
Если 

Моделировать случайную величину 
Мы рассмотрим метод псевдослучайных последовательностей, который наиболее просто реализуется в компьютере. Для получения псевдослучайной последовательности используем алгоритм, который называется методом середины квадратов. Поясним его на примере. Возьмем некоторое число 

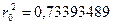







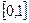

Метод обратных функций.
Пусть случайная величина 





Отсюда следует, что значение 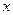




Последовательности значений 

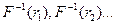


Моделирование случайной величины с равномерным распределением на отрезке
Пусть случайная величина 
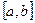
Составляем уравнение 
Последовательности значений 



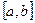
Порядковые статистики.
Случайная величина 

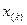
Для случая 
При этом:



А также:
Если же 



А также:

Отметим далее, что если 
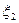


Оценивание параметров в равномерном распределении.
Введём статистический аналог теоретического математического ожидания случайной величины 

Введём статистический аналог теоретической дисперсии случайной величины 

Любая измеримая функция от выборки 
Статистика 

Статистика 

То есть для любого 
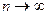

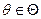
ü Возьмём выборку 

Оптимальной несмещённой оценкой θ в данном классе оценок является:
Её дисперсия:

ü Оценим теперь параметр θ равномерного распределения 

Статистики 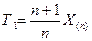

Кроме того, имеем: 

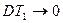



ü Пусть теперь 


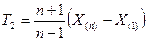
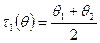

Достаточные статистики и оптимальные оценки.
Если для любой оценки 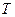


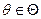
Итак, T* — оптимальная оценка для параметрической функции 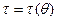



Статистика 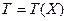



Теорема Рао-Блекуэлла-Колмогорова: Оптимальная оценка, если она существует, является функцией от достаточной статистики.
Теорема: Если существует полная достаточная статистика, то всякая функция от неё является оптимальной оценкой своего математического ожидания.
То есть оптимальная оценка однозначно определяется уравнением 
Функция 


Критерий факторизации.
Для того, чтобы статистика была достаточной для параметрического семейства распределений P, необходимо и достаточно, чтобы функция правдоподобия выборки 
Где множитель h(x) от 

ü Пусть 


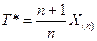
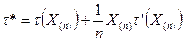
ü Пусть теперь 



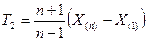

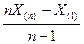


ü Статистика 


Если 
Аналогично, если 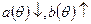
Этими двумя случаями исчерпываются ситуации, когда в модели 
Для модели 

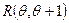

|
Аальтернативная стоимость. Кривая производственных возможностей В экономике Буридании есть 100 ед. труда с производительностью 4 м ткани или 2 кг мяса… |
Вычисление основной дактилоскопической формулы Вычислением основной дактоформулы обычно занимается следователь. Для этого все десять пальцев разбиваются на пять пар… |
Расчетные и графические задания Равновесный объем — это объем, определяемый равенством спроса и предложения… |
Кардиналистский и ординалистский подходы Кардиналистский (количественный подход) к анализу полезности основан на представлении о возможности измерения различных благ в условных единицах полезности… |
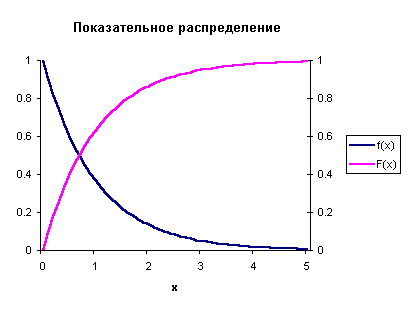
Показательное распределение
- Краткая теория
- Примеры решения задач
- Задачи контрольных и самостоятельных работ
Краткая теория
Показательным (экспоненциальным) называют распределение вероятностей непрерывной случайной величины
, которое описывается плотностью:
где
–
постоянная положительная величина.
Показательное
распределение определяется одним параметром
. Эта особенность распределения указывает на
его преимущество по сравнению с распределениями, зависящими от большего числа
параметров. Обычно параметры неизвестны и приходится находить их оценки
(приближенные значения); разумеется, проще оценить один параметр, чем два или три.
Примером непрерывной случайной величины, распределенной по показательному
закону, может служить время между появлениями двух последовательных событий
простейшего потока.
Функция распределения
показательного закона:
Графики плотности и
функции распределения показательного закона изображены на рисунке.
Вероятность попадания в
интервал
непрерывной
случайной величины
, распределенной по показательному закону:
Числовые характеристики показательного (экспоненциального) распределения
Математическое ожидание случайной величины, распределенной по показательному закону:
Дисперсия случайной величины, распределенной по показательному закону:
Среднее квадратическое отклонение случайной величины,
распределенной по показательному закону:
Коэффициенты асимметрии и эксцесса
для показательного распределения:
Таким
образом, математическое ожидание и среднее квадратическое
отклонение экспоненциального распределения равны между собой.
Показательный закон
распределения играет большую роль в теории массового обслуживания и теории
надежности. Так, например, интервал времени
между
двумя соседними событиями в простейшем потоке имеет показательное распределение
с параметром
–
интенсивностью потока.
При решении задач, которые выдвигает практика, приходится
сталкиваться с различными распределениями непрерывных случайных величин.
Смежные темы решебника:
- Непрерывная случайная величина
- Нормальный закон распределения случайной величины
- Равномерный закон распределения случайной величины
Примеры решения задач
Пример 1
Случайная величина
задана функцией распределения
Найдите математическое
ожидание и среднее квадратическое отклонение этого
распределения.
Найдите вероятность того,
что случайная величина примет значение от 0,2 до 1.
На сайте можно заказать решение контрольной или самостоятельной работы, домашнего задания, отдельных задач. Для этого вам нужно только связаться со мной:
ВКонтакте
WhatsApp
Telegram
Мгновенная связь в любое время и на любом этапе заказа. Общение без посредников. Удобная и быстрая оплата переводом на карту СберБанка. Опыт работы более 25 лет.
Подробное решение в электронном виде (docx, pdf) получите точно в срок или раньше.
Решение
Математическое
ожидание случайной величины, распределенной по показательному закону:
Среднее
квадратическое отлонение:
Вероятность того, что
случайная величина примет значение от 0,2 до 1
Ответ
.
Пример 2
На шоссе установлен контрольный пункт для
проверки технического состояния автомобилей. Найти математическое ожидание и
среднее квадратическое отклонение случайной величины T – время ожидания
очередной машины контролером, если поток машин простейший и время (в часах)
между прохождениями машин через контрольный пункт распределено по
показательному закону f(t)=5e-5t.
Указание: Время ожидания машины
контролером и время прохождения машин через контрольный пункт распределены
одинаково.
Решение
В нашем случае
параметр показательного распределения
Математическое
ожидание:
Дисперсия:
Среднее
квадратическое отклонение:
Ответ:
Пример 3
Постройте
интегральную и дифференциальную функции распределения случайной величины X.
Найдите математическое ожидание M(X), дисперсию D(X),
среднее квадратическое отклонение σ(X), моду xmod, медиану xmed , если известно, что
случайная величина X имеет показательное распределение с параметром λ=1.
На сайте можно заказать решение контрольной или самостоятельной работы, домашнего задания, отдельных задач. Для этого вам нужно только связаться со мной:
ВКонтакте
WhatsApp
Telegram
Мгновенная связь в любое время и на любом этапе заказа. Общение без посредников. Удобная и быстрая оплата переводом на карту СберБанка. Опыт работы более 25 лет.
Подробное решение в электронном виде (docx, pdf) получите точно в срок или раньше.
Решение
Плотность
распределения случайной величины
, распределенной по
показательному закону:
Функция
распределения:
Построим
графики дифференциальной и интегральной функций распределения:
График дифференциальной функции распределения
График интегральной функции распределения
Математическое
ожидание показательно распределенной случайной величины
:
Дисперсия:
Среднее
квадратическое отклонение:
найдем, исходя из условия:
Пример 4
Случайная
величина
распределена показательно с дисперсией 0,25.
Найти математическое ожидание и вероятность попадания
в интервал (0,5;1).
Решение
Дисперсия
случайной величины, распределенной по показательному закону:
Математическое
ожидание случайной величины, распределенной по показательному закону:
Вероятность
попадания в интервал
непрерывной случайной величины
, распределенной по
показательному закону:
В нашем
случае:
Ответ:
Задачи контрольных и самостоятельных работ
Задача 1
Время
безотказной работы двигателя автомобиля распределено по показательному закону.
Известно, что среднее время наработки двигателя на отказ между техническим
обслуживанием 100 ч. Определить вероятность безотказной работы двигателя за 80
ч.
На сайте можно заказать решение контрольной или самостоятельной работы, домашнего задания, отдельных задач. Для этого вам нужно только связаться со мной:
ВКонтакте
WhatsApp
Telegram
Мгновенная связь в любое время и на любом этапе заказа. Общение без посредников. Удобная и быстрая оплата переводом на карту СберБанка. Опыт работы более 25 лет.
Подробное решение в электронном виде (docx, pdf) получите точно в срок или раньше.
Задача 2
Среднее
время работы элемента, входящего в пожарно-техническое устройство, равно 1000
часов. Определить вероятность того, что элемент будет работать от 950 до 1150
часов, если время работы элемента распределено по показательному закону.
Задача 3
Вероятность
безотказной работы элемента распределена по экспоненциальному закону
f(t)=e-0.05t
Найти
вероятность того, что в результате испытания случайная величина попадет в
интервал (11;35). Найти характеристики данного распределения случайной
величины.
Задача 4
Непрерывная
случайная величина X задана интегральной функцией распределения
Найти
постоянную C, математическое ожидание случайной величины X,
вероятность попадания случайной величины в интервал [2;4].
Задача 5
Время
между отказами прибора распределено по показательному закону со средним
значением 25 часов. Определить математическое ожидание и дисперсию времени
безотказной работы автомобиля. Найти вероятность того, что очередной отказ
произойдет не позднее 15 часов.
Задача 6
Время
безотказной работы телевизора определенной модели описывается показательным (экспоненциальным)
законом распределения с постоянной λ. Что вероятнее, его безотказная работа в
промежутке времени [x1,x2]
или [x3,x4]? Записать
функции f(x),F(x) и построить их графики.
λ=1/10, x1=3, x2=5, x3=4, x4=8
На сайте можно заказать решение контрольной или самостоятельной работы, домашнего задания, отдельных задач. Для этого вам нужно только связаться со мной:
ВКонтакте
WhatsApp
Telegram
Мгновенная связь в любое время и на любом этапе заказа. Общение без посредников. Удобная и быстрая оплата переводом на карту СберБанка. Опыт работы более 25 лет.
Подробное решение в электронном виде (docx, pdf) получите точно в срок или раньше.
Задача 7
Испытывают
два независимо работающих элемента. Длительность времени t безотказной
работы первого элемента имеет показательное распределение с параметром 0,02,
второго -показательное распределение с параметром 0,06. Найдите вероятность
того, что за время длительностью t=6 ч откажет только один
элемент.
Задача 8
Среднее
время работы каждого из трех элементов, входящих в техническое устройство,
равно T=850 часов. Для безотказной работы устройства необходима безотказная
работа хотя бы одного из трех этих элементов. Определить вероятность, что
устройство будет работать от t1=750 до t2=820 часов, если время
работы каждого из трех элементов независимо и распределено по показательному
закону.
Задача 9
Время
устранения повреждения на канале связи T -случайная величина,
распределенная по закону f(t)=λe-λt (t≥0). Среднее время
восстановления канала — 10 минут. Определить вероятность того, что на
восстановление канала потребуется от 5 до 10 минут.
Задача 10
Дана плотность
распределения случайной величины X.
По какому
закону распределения случайная величина? Найти математическое ожидание,
дисперсию, функцию распределения?
Задача 11
Время
безотказной работы механизма подчинено показательному закону с плотностью
распределения вероятностей f(t)=0.04e-0.04t при t > 0 (t –
время в часах). Найти вероятность того, что механизм проработает безотказно не
менее 100 часов.
Задача 12
Длительность телефонного разговора
является случайной величиной, распределенной по показательному закону.
Известно, что средняя длительность телефонного разговора равна 9 минутам. Найти
вероятность того, что разговор будет длиться:
а) не более 5 минут.
б) более 5 минут.
На сайте можно заказать решение контрольной или самостоятельной работы, домашнего задания, отдельных задач. Для этого вам нужно только связаться со мной:
ВКонтакте
WhatsApp
Telegram
Мгновенная связь в любое время и на любом этапе заказа. Общение без посредников. Удобная и быстрая оплата переводом на карту СберБанка. Опыт работы более 25 лет.
Подробное решение в электронном виде (docx, pdf) получите точно в срок или раньше.
Задача 13
Случайная величина ξ подчинена
показательному закону с параметром λ=5:
Найдите вероятность того, что
случайная величина ξ примет значение меньшее, чем ее математическое ожидание.
Задача 14
Случайная
величина ξ имеет плотность вероятностей (показательное распределение)
Найдите
вероятность P{ξ>Mξ}
Задача 15
Время T
(минут), затрачиваемое клиентами парикмахерской в ожидании своей очереди,
удовлетворяет показательному распределению с параметром λ=0,05. Какова
вероятность того, что время ожидания превысит 25 минут и каково среднее время
ожидания.
Задача 16
Время T (час),
необходимое на ремонт легкового автомобиля удовлетворяет показательному
распределению с параметром λ=0,2. Какова вероятность того, что время ремонта
одного автомобиля не превысит 6 часов, и сколько часов в среднем затрачивается
на ремонт одного автомобиля.
Задача 17
Время
ожидания у бензоколонки автозаправочной станции является случайной величиной X,
распределенной по показательному закону, со средним временем ожидания, равным t0. Найти вероятности
следующих событий:
Задача 18
Случайная
величина X задана показательным законом распределения и
числовыми значениями параметров M(X)=3 и σx=3.
Требуется:
1) найти
функцию плотности f(x).
2) найти
вероятность попадания СВ X в указанный интервал [a,b]=[2,4].
Задача 19
Случайная
величина ξ задана функцией распределения
Найдите
математическое ожидание и среднее квадратическое отклонение этого
распределения.
Задача 20
Случайная величина ξ распределена по
показательному закону с параметром λ=0,3. Найдите математическое ожидание и
среднее квадратическое отклонение этой случайной величины.
- Краткая теория
- Примеры решения задач
- Задачи контрольных и самостоятельных работ
- Информация о материале
- Категория: Глава 13. Показательное распределение
-
Опубликовано: 14 сентября 2018
-
Просмотров: 9402
Глава 13. Задача 4. Время безотказной работы элемента распределено по показательному закону (f(x) = 0,01e^{-0,01t}) ((t > 0)), где (t) — время, ч. Найти вероятность того, что элемент проработает безотказно 100 ч.
Решение.
Показательным законом надежности называют функцию надежности, определяемую равенством
[R(t) = e^{-lambda t}, qquad (*)]
где (lambda) — интенсивность отказов.
Эта формула позволяет найти вероятность безотказной работы элемента на интервале времени длительностью (t), если время безотказной работы имеет, показательное распределение.
По условию задачи, постоянная интенсивность отказов (lambda = 0,01).
Воспользуемся формулой (*):
[R(100) = e^{-0,01cdot 100} = e^{-1} approx 0,37.]
Ответ. (R(100) = 0,37).
Закажите у меня новую работу, просто написав мне в чат!
Среднее время безотказной работы прибора равно 80 часов. Полагая, что время безотказной работы прибора имеет показательный закон распределения, найти: а) выражение его плотности вероятности и функции распределения, построить графики этих функций; б) вероятность того, что в течение 1000 часов прибор не выйдет из строя.
Решение а) Для показательного закона связь математического ожидания (среднего значения) и параметра распределения 𝜆 имеет вид: При 𝑀(𝑋)=80 получим параметр распределения 𝜆: Функция плотности распределения вероятности 𝑓(𝑥) и функция распределения 𝐹(𝑥) случайной величины 𝑋, имеющей показательное распределение, имеют вид: При 𝜆=180 получим: Построим графики функции распределения 𝐹(𝑥) и плотности распределения 𝑓(𝑥): б) Вероятность попадания случайной величины в заданный интервал (𝑎;𝑏)равна: Тогда вероятность того, что в течение 1000 часов прибор не выйдет из строя, равна:
Задача №3
Длительность времени
безотказной работы элемента имеет показательное распределение F(t)
= 1 — e0, 03 t.
Найти вероятность того, что за время длительностью t
= 100 ч: а)элемент откажет; б) элемент не откажет.
Решение
а) Так как функция
распределения F(t)
= 1 – e
—0,
03 t определяет
вероятность отказа элемента за время длительностью t, то, подставив t=100
в функцию распределения, получим вероятность отказа:
F(100) = 1 – e
—0, 03*100 =0.95
б) события «элемент откажет»
и «элемент не откажет» — противоположные, поэтому вероятность того, что элемент
не откажет:
P=1-0.95 = 0.05
Сообщения без ответов | Активные темы
| Автор | Сообщение | ||
|---|---|---|---|
|
Serge |
|
||
|
Время Т безотказной работы измерительного комплекса имеет показательное распределение с математическим ожиданием 1,5 тыс.ч. Какова вероятность того, что комплекс выйдет из строя не менее, чем после 500 часов работы?
|
||
| Вернуться к началу |
|
||
|
Serge |
|
||
|
Огромное человеческое спасибо
|
|||
| Вернуться к началу |
|
||
| Похожие темы | Автор | Ответы | Просмотры | Последнее сообщение |
|---|---|---|---|---|
|
Среднее время безотказной работы системы То вычислить ан-ким
в форуме MathCad |
Gluk62 |
0 |
207 |
20 дек 2020, 16:05 |
|
Вероятность безотказной работы
в форуме Теория вероятностей |
goshasit |
1 |
1884 |
19 мар 2015, 01:30 |
|
Вероятность безотказной работы схемы
в форуме Теория вероятностей |
MathematicHell |
1 |
697 |
06 дек 2015, 17:41 |
|
Вероятность безотказной работы системы
в форуме Комбинаторика и Теория вероятностей |
Baguvix |
0 |
524 |
23 ноя 2018, 17:19 |
|
Вероятность безотказной работы каждого
в форуме Теория вероятностей |
IVAN BATOV |
1 |
113 |
16 дек 2021, 11:46 |
|
Определение вероятности безотказной работы системы
в форуме Теория вероятностей |
UNIQUE |
5 |
522 |
14 апр 2016, 14:27 |
|
Вычислите вероятность безотказной работы системы
в форуме Теория вероятностей |
LikaLika |
1 |
450 |
22 май 2018, 15:57 |
|
Найти вероятность безотказной работы для элемента U(100,5000
в форуме Теория вероятностей |
plktre |
6 |
145 |
23 фев 2021, 15:58 |
|
Доказать время работы алгоритма
в форуме Дискретная математика, Теория множеств и Логика |
goos |
5 |
347 |
25 дек 2013, 16:20 |
|
Разберите строение комплекса
в форуме Химия и Биология |
Viktorya |
4 |
92 |
08 ноя 2022, 20:36 |
Кто сейчас на конференции |
|
Сейчас этот форум просматривают: нет зарегистрированных пользователей и гости: 14 |
| Вы не можете начинать темы Вы не можете отвечать на сообщения Вы не можете редактировать свои сообщения Вы не можете удалять свои сообщения Вы не можете добавлять вложения |
Powered by phpBB © 2000, 2002, 2005, 2007 phpBB Group
Вы можете создать форум бесплатно PHPBB3 на Getbb.Ru, Также возможно сделать готовый форум PHPBB2 на Mybb2.ru
Русская поддержка phpBB