Времени работы алгоритма tmax n соответствует

Сложность алгоритма и проблема распараллеливания

Ранее уже использовалось понятие сложности. Рассмотрим его полнее.

Пусть задан некоторый алгоритм A. Почти всегда существует
параметр n, характеризующий объем его данных. Пусть функция T(n) — время
выполнения A, а f —
некоторая функция от n. Говорят, что алгоритм A
имеет теоретическую (асимптотическую) сложность O(f(n)), если

,

где k — действительное.

Если алгоритм выполняется за фиксированное время, не зависящее от размера
задачи, говорят, что его сложность равна O (1).

Это определение обобщается в случае, если время выполнения существенно
зависит от нескольких параметров. Например, алгоритм, определяющий, входит ли множество m элементов в множество n элементов, может иметь, в
зависимости от используемых структур данных, сложность O (m n) или O (m+n).

Практически время выполнения алгоритма может зависеть от значений данных.
Так, время выполнения некоторых алгоритмов сортировки существенно сокращается, если
первоначально эти данные были частично упорядочены. Чтобы учитывать это,
сохраняя возможность анализировать алгоритм независимо от их данных, различают:

• максимальную
  сложность, определяемую значением T_max(n) — время
  выполнения алгоритма, когда выбранный набор n данных порождает наиболее
  долгое время выполнения алгоритма;
• среднюю сложность,
  определяемую значением T_ср(n) — средним временем
  выполнения алгоритма, примененного к n произвольным данным.

Эти понятия без труда распространяются на измерение сложности в единицах
объема памяти: можно говорить о средней и максимальной пространственной сложности.

Самыми лучшими являются линейные алгоритмы, имеющие сложность порядка an=b. Они называются также алгоритмами порядка O(n) где n
— размерность входных данных. Такие алгоритмы действительно существуют. Например, сложение двух чисел
столбиком в случае, если одно из них состоит из n, а другое — из m цифр, требует не более max(n, m) сложений и не более max(n, m) запоминаний.
Т.е. данный алгоритм имеет сложность порядка O(n+m). Разумеется, это выражение показывает
только порядок величины — постоянные факторы в нем не учитываются.

Обобщение линейности дает нам первый большой класс алгоритмов — полиномиальных.

Полиномиальным (или алгоритмом полиномиальной временной сложности)
называется алгоритм, у которого временная сложность есть O(p(n)), где p(n) — полином от n. Задачи, где для решения известен алгоритм, сложность которого составляет
полином заданной, постоянной и не зависящей от размерности входной величины n степени,
называют «хорошими» и относят их к классу P.

Экспоненциальной по природе считается задача сложностью не менее порядка xⁿ, где x — константа или полином от n. Например, это
задачи, в которых возможное число ответов уже экспоненциально. В частности, к ним относятся задачи, где
требуется построить все подмножества заданного множества или все поддеревья
заданного графа. Экспоненциальные задачи относят к классу E.

Соответственно, и алгоритмы, в оценку сложности которых n
входит в показатель степени, относятся к экспоненциальным.

Необходимо отметить, что при небольших значениях n
экспоненциальный алгоритм может быть даже менее сложным, чем полиномиальный. Тем не менее, различие между
этими типами алгоритмов весьма велико и проявляется при больших значениях n.

Особую группу по значениям сложности, близким к полиномиальным, составляют
алгоритмы, сложность которых является полиномиальной функцией от log n (поскольку log n растет медленнее, чем n ).

Для большей убедительности и сравнения полиномиальных и экспоненциальных
алгоритмов приведем таблицу, где единица времени — 1 мкс, а сложность
совпадает с необходимым количеством единиц времени для обработки набора n данных:

Таблица
3.1.
Сложность и время выполнения

Сложность	Размер задачи — n
	10	20	30	40	50	60
n	0.00001 с	0.00002 с	0.00003 с	0.00004 с	0.00005 с	0.00006 с
n	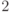0.0001 с	0.0004 с	0.0009 с	0.0016 с	0.0025 с	0.0036 с
n	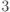0.001 с	0.008 с	0.027 с	0.064 с	0.125 с	0.216 с
n5	0.1 с	3.2 с	24.3 с	1.7 мин	5.2 мин	13.0 мин
2n	0.01 с	1.0 с	17.9 мин	12.7 дней	35.7 лет	366 веков
3n	0.59 с	58 мин	6.5 лет	3855 веков	2×108 веков	1.3×1013 веков

Приведенная таблица иллюстрирует причины, по которым полиномиальные
алгоритмы считаются более предпочтительными, чем экспоненциальные.

Уточним понятие сложности для итеративных и рекурсивных алгоритмов.

Отнесем к итеративным алгоритмам и те, к которым сводятся рекурсивные
алгоритмы (например, вычисление факториала n!). Тогда время их выполнения
(в случае сходящегося процесса) зависит от главного условия повторения итерации,
например, от требуемой точности. Если мы установим время или сложность одной итерации, то
сможем умножением на число итераций установить максимальную или среднюю
сложность. Число итераций устанавливается теоретически или экспериментально. Например, так
можно сделать при расчете значений функций по их разложению в ряд.

Однако иногда приходится решать оптимизационную задачу, выбирая между
сложностью одной итерации и количеством итераций.

Для большинства конечно-разностных схем решения дифференциальных уравнений
методом сеток можно считать, что сложность одной итерации составляет O(n²) или O(n x m), где n² — количество узлов при
равном разбиении по x и по y,
а nx m — то же
количество при различающемся разбиении по осям. Увеличение количества узлов,
покрывающих ту же область, т.е. уменьшение h_x и h_y, увеличивает скорость
сходимости — и, соответственно, уменьшает число итераций, но сложность каждой
итерации растет квадратично. Значит, необходим компромисс, который достигается
посредством изучения поведения процесса, как на теоретическом, так и на
экспериментальном уровне, вплоть до автоматической коррекции шагов в процессе
вычислений в зависимости от локального поведения аппроксимаций производных.
Т.е. шаги становятся непостоянными во всей области.

Однако по своей природе действительно рекурсивные алгоритмы по сложности
относятся к классу экспоненциальных алгоритмов. Как правило, это задачи
оптимизации, основанные на переборе (алгоритмы с возвратом, метод
«ветвей и границ»).

Имеется широко распространенное соглашение, по которому задача не считается
«хорошо решаемой», пока для нее не получен полиномиальный
алгоритм. Задача называется труднорешаемой,
если для ее решения не существует полиномиального алгоритма.

Эта градация относительна, ибо сложность определяется по наихудшему
варианту. Хотя реализация метода «ветвей и границ» — труднорешаемая задача
(при теоретической оценке по максимальной сложности), сейчас для многих задач
известны такие алгоритмы, которые практически очень быстро находят решение
именно методом ветвей и границ.

Однако есть понятие гарантированных и негарантированных оценок. Если сложность
задачи полиномиальная, мы можем уверенно предсказать оценку времени решения.
При решении задачи методом «ветвей и границ» незначительное
изменение начальных данных даже без изменения размерности задачи может непредсказуемо привести к
резкому скачку в увеличении времени решения. Т.е. существует большой разрыв
между значениями теоретической максимальной сложности и практической средней
сложности экспоненциальных алгоритмов. Постоянно ведутся поиски более
эффективных экспоненциальных алгоритмов.

Полиномиальные по сложности алгоритмы относят к классу P -сложных. Среди экспоненциальных выделяют алгоритмы, основанные на переборе, и их относят
в класс NP -сложных. Т.е. формально возможно существование
экспоненциальных алгоритмов, основанных не на переборе. Например, n!, растущий
быстрее, чем 2ⁿ.
К NP -сложным относятся, например, задачи линейного целочисленного
программирования, составление расписания, поиск кратчайшего пути в лабиринте и
т.д. Обратим внимание, что все это так называемые дискретные задачи — на
основе «неделимых» объектов.

В данном контексте мы и будем понимать термин «задача высокой
сложности», представляя важность применения методов распараллеливания.

Рассматривая
различные алгоритмы решения одной и
той же задачи, по­лезно проанализировать,
сколько вычислительных ресурсов они
требуют (время работы, память), и выбрать
наиболее эффективный. Конечно, надо
договориться о том, какая модель
вычислений используется. В данном
учебном пособии в качестве модели по
большей части используется обычная
однопроцессорная машина
с произвольным доступом
(random—access
machine,
RAM),
не предусматривающая параллельного
выполнения операций.

Под
временем
работы
(running
time)
алгоритма будем подразумевать число
элементар­ных шагов, которые он
выполняет. Положим, что одна строка
псевдокода требует не более чем
фиксированного числа операций (если
только это не словесное описание каких-то
сложных действий – типа «отсортировать
все точки по x-координате»).
Следует также различать вызов
(call)
процедуры (на который уходит фиксированное
число операций) и её исполнение
(execution),
которое может быть долгим.

Сложность
алгоритма – это величина, отражающая
порядок величины требуемого ресурса
(времени или дополнительной памяти) в
зависимости от размерности задачи.

Таким
образом, будем различать временную T(n)
и пространственную V(n)
сложности алгоритма. При рассмотрении
оценок сложности, будем использовать
только временную сложность. Пространственная
сложность оценивается аналогично. Самый
простой способ оценки – экспериментальный,
то есть запрограммировать алгоритм и
выполнить полученную программу на
нескольких задачах, оценивая время
выполнения программ. Однако, этот способ
имеет ряд недостатков. Во-первых,
экспериментальное программирование –
это, возможно, дорогостоящий процесс.
Во-вторых, необходимо учитывать, что на
время выполнения программ влияют
следующие факторы:

1. Временная
   сложность алгоритма программы;

2. Качество
   скомпилированного кода исполняемой
   программы;

3. Машинные
   инструкции, используемые для выполнения
   программы.

Наличие
второго и третьего факторов не позволяют
применять типовые единицы измерения
временной сложности алгоритма (секунды,
миллисекунды и т.п.), так как можно
получить самые различные оценки для
одного и того же алгоритма, если
использовать разных программистов
(которые программируют алгоритм каждый
по-своему), разные компиляторы и разные
вычислительные машины.

Часто,
временная сложность алгоритма зависит
от количества входных данных. Обычно
говорят, что временная сложность
алгоритма имеет порядок T(n)
от входных данных размера n.
Точно определить величину T(n)
на практике представляется довольно
трудно. Поэтому прибегают к асимптотическим
отношениям с использованием

O-символики.

Существует
метод, позволяющий теоретически оценить
время выполнения алгоритма, который
будет рассмотрен далее.

Листинг
1.3 – Псевдокод алгоритма сортировки
вставками с оценками времени выполнения

Для
вычисления суммарного времени выполнения
процедуры Insertion-Sort
отметим
около каждой стро­ки её стоимость
(число операций) и число раз, которое
эта строка исполняется. Для каждого j
от
2 до п
(здесь
п
=
length[A]
–
размер массива) требуется подсчитать,
сколько раз будет исполнена строка 5,
обозначим это число через t_j.
Строки
внутри цикла выполняются на один раз
меньше, чем проверка, поскольку последняя
проверка выводит из цикла. Строка
стоимостью c,
повторённая т
раз,
даёт вклад c
m
в
общее число операций (однако, это
выражение нельзя использовать для
оценки количества использованной
памяти). Сложив вклады всех строк, получим

Время
работы процедуры зависит не только от
п
но
и от того, какой именно массив размера
п
подан
ей на вход. Для процедуры Insertion-Sort
наиболее
благоприятен случай, когда массив уже
отсортиро­ван. Тогда цикл в строке 5
завершается после первой же проверки
(поскольку A[i]
≤
key
при
i
=
j
–
1), так что все t_j
равны
1, и общее время есть

Таким
образом, в наиболее благоприятном случае
время T(n),
необходимое для сортировки массива
размера п,
является
линейной функцией (linear
function)
от n,
т.е. имеет вид Т(п)
=
a  n + b
для некоторых констант a
и
b.
Эти константы определяются выбранными
значениями с₁,…,
с₈.

Если же массив
расположен в обратном (убывающем)
порядке, время работы

процедуры
будет максимальным: каждый элемент A[j]
придётся
сравнить со всеми элементами А[1],…,
A[j
–
1]. При этом t_j
= j.
Поскольку

получаем, что в
худшем случае время работы процедуры
равно

В
данном
случае
T(n)
– квадратичная
(quadratic
function),
т.е.
имеет
вид
Т(п) = an²
+ bn
+ с.
Константы
a, b и
с здесь
также определяются значениями с₁,…,с₈.

Обычно
говорят, что временная сложность
алгоритма имеет порядок T(n)
от входных данных размера n.
Точно определить величину T(n)
на практике представляется довольно
трудно. Поэтому прибегают к асимптотическим
отношениям с использованием O-символики.

Например,
если число тактов (действий), необходимое
для работы алгоритма, выражается как
16n² + 12n log n + 2n + 3,
то это алгоритм, для которого T(n)
имеет порядок O(n²).
При формировании асимптотической
O-оценки
из всех слагаемых исходного выражения
оставляется одно, вносящее наибольший
вклад при больших n
(остальными слагаемыми можно пренебречь)
и игнорируется коэффициент перед ним
(так как все асимптотические оценки
даются с точностью до константы).

Когда
используют обозначение O(),
имеют в виду не точное время исполнения,
а только его предел сверху, причем с
точностью до постоянного множителя.
Когда говорят, например, что алгоритму
требуется время порядка O(n²),
имеют в виду, что время исполнения задачи
растет не быстрее, чем квадрат количества
элементов.

Таблица 1.2
– Сравнительный анализ скорости роста
функций

Рисунок
1.1 – Примеры различных функциональных
зависимостей

Если
считать, что числа, приведенные в
таблице 1.2,
соответствуют микросекундам, то для
задачи с 1048476 элементами алгоритму со
временем работы T(log n)
потребуется 20 микросекунд, а алгоритму
со временем работы T(n²)
– более 12 дней.

Если
операция выполняется за фиксированное
число шагов, не зависящее от количества
данных, то принято писать O(1).

Следует
обратить внимание, что основание
логарифма в асимптотических оценках
не пишется. Причина этого весьма проста.
Пусть есть O(log₂ n).
Но log₂ n = log₃ n / log₃ 2,
а log₃ 2,
как и любую константу, символ О()
не учитывает. Таким образом, O(log₂ n)
= O(log₃ n).
К любому основанию можно перейти
аналогично, а, значит, и писать его не
имеет смысла.

Практически
время выполнения алгоритма зависит не
только от количества входных данных,
но и от их значений, например, время
работы некоторых алгоритмов сортировки
значительно сокращается, если первоначально
данные частично упорядочены, тогда как
другие методы оказываются нечувствительными
к этому свойству. Чтобы учитывать этот
факт, полностью сохраняя при этом
возможность анализировать алгоритмы
независимо от данных, различают:

• максимальную
  сложность T_max(n),
  или сложность наиболее неблагоприятного
  случая, когда алгоритм работает дольше
  всего;

• среднюю
  сложность T_mid(n)
  – сложность алгоритма в среднем;

• минимальную
  сложность T_min(n)
  – сложность в наиболее благоприятном
  случае, когда алгоритм справляется
  быстрее всего.

Теоретическая
оценка временной сложности алгоритма
осуществляется с использованием
следующих базовых принципов:

1. Время
   выполнения операций присваивания,
   чтения, записи обычно имеют порядок
   O(1).
   Исключением являются операторы
   присваивания, в которых операнды
   представляют собой массивы или вызовы
   функций;

2. Время
   выполнения последовательности операций
   совпадает с наибольшим временем
   выполнения операции в данной
   последовательности (правило сумм: если
   T₁(n)
   имеет порядок O(f(n)),
   а T₂(n)
   – порядок O(g(n)),
   то T₁(n)
   + T₂(n)
   имеет порядок O(max(f(n),
   g(n)));

3. Время
   выполнения конструкции ветвления
   (if-then-else)
   состоит из времени вычисления логического
   выражения (обычно имеет порядок O(1))
   и наибольшего из времени, необходимого
   для выполнения операций, исполняемых
   при истинном значении логического
   выражения и при ложном значении
   логического выражения;

4. Время
   выполнения цикла состоит из времени
   вычисления условия прекращения цикла
   (обычно имеет порядок O(1) )
   и произведения количества выполненных
   итераций цикла на наибольшее возможное
   время выполнения операций тела цикла.

5. Время
   выполнения операции вызова процедур
   определяется как время выполнения
   вызываемой процедуры;

6. При
   наличии в алгоритме операции безусловного
   перехода, необходимо учитывать изменения
   последовательности операций,
   осуществляемых с использованием этих
   операции безусловного перехода.

Итак,
время работы в худшем случае и в лучшем
случае могут
сильно
различаться. При анализе алгоритмов
наиболее часто используется время
работы в худшем случае
(worst—case
running
time),
которое определяется как максимальное
время работы для входов данного размера.
Почему? Вот несколько причин.

1. Зная
   время работы в худшем случае можно
   гарантировать, что выполнение
   алгоритма
   закончится за некоторое время при любом
   входе данного размера;

2. На
   практике «плохие» входы (для которых
   время работы близко к максимуму)
   встречаются наиболее часто. Например,
   для базы данных плохим запросом может
   быть поиск отсутствующего элемента
   (очень распространенная ситуация);

3. Время
   работы в среднем может быть до­вольно
   близко к времени работы в худшем случае.
   Пусть, например, сортируется массив
   из п
   случайных
   чисел
   с помощью процедуры Insertion-Sort.Сколько
   раз придётся выполнить цикл в строках
   5-8 (листинг 1.3)? В среднем около половины
   элементов массива A[1..j
   – 1]
   больше A[j],
   так
   что t_j
   в
   среднем можно считать равным j/2,
   и
   время Т(п)
   квадратично
   зависит от n.

В
некоторых случаях требуется также
среднее время
работы
(average—case
running
time,
expected
running
time)
алгоритма на входах данной длины.
Конечно, эта величина зависит от
выбранного распределения вероятно­стей,
и на практике реальное распределение
входов может отличаться от пред­полагаемого,
которое обычно считают равномерным.
Иногда можно добиться равномерности
распределения, используя датчик случайных
чисел.

Оценка времени, затраченного на выполнение алгоритма Графики функций, обычно используемых в анализе алгоритмов, показывающий количество операций N по сравнению с размером входных данных n для каждой функции

В информатике временная сложность — это вычислительная сложность, которая описывает время, необходимое для выполнения алгоритма . Временная сложность обычно оценивается путем подсчета числа элементарных операций, выполняемых алгоритмом, предполагая, что каждая элементарная операция требует фиксированного количества времени для выполнения. Таким образом, количество затраченного времени и количество элементарных операций, выполняемых алгоритмом, различаются не более чем на постоянный коэффициент.

Поскольку время работы алгоритма может варьироваться между разными входами одного и того же размера, обычно учитывает временную сложность наихудшего случая, которая представляет собой максимальное количество времени, требуемое для входных данных заданного размера. Менее распространенной и обычно указываемой явно является сложность среднего случая, которая представляет собой среднее время, затрачиваемое на входы заданного размера (это имеет смысл, потому что существует только конечное число возможных входов заданного размера). В обоих случаях временная сложность обычно выражается как функция размера ввода. Поскольку эту функцию, как правило, трудно вычислить точно, а время выполнения небольших входных данных обычно не имеет значения, обычно фокусируется на поведении сложности при увеличении размера входных данных, то есть на асимптотическом поведении функции сложность. Следовательно, временная сложность обычно выражается с использованием нотации большого O, обычно O (n), { displaystyle O (n),}O (n log ⁡ n), { displaystyle O (n log n),}O (n α), { displaystyle O (n ^ { alpha}),}O (2 n), { displaystyle O (2 ^ { n}),}и т. д., где n — размер ввода в единицах бит, необходимых для представления ввода.

Алгоритмические сложности классифицируются в соответствии с типом функции, указанной в нотации большой буквы O. Например, алгоритм с временной сложностью O (n) { displaystyle O (n)}представляет собой алгоритм с линейным временем и алгоритм с временной сложностью O (n α) { displaystyle O (n ^ { alpha})}для некоторой константы α>1 { displaystyle alpha>1}— алгоритм полиномиального времени.

Общее содержание

• 1 Таблица общего времени сложности
• 2 Постоянное время
• 3 Логарифмическое время
• 4 Полилогарифмическое время
• 5 Сублинейное время
• 6 Линейное время
• 7 Квазилинейное время
• 8 Субквадратичное время
• 9 Полиномиальное время
  • 9.1 Сильно и слабо полиномиальное время
  • 9.2 Классы сложности
• 10 Суперполиномиальное время
• 11 Квазиполиномиальное время
  • 11.1 Связь с NP-полными задачами
• 12 Субэкспоненциальное время
  • 12.1 Первое определение
  • 12.2 Второе определение
    • 12.2.1 Гипотеза экспоненциального времени
• 13 Экспоненциальное время e
• 14 Факториальное время
• 15 Двойное экспоненциальное время
• 16 См. также
• 17 Ссылки

Таблица общих временных сложностей

В следующей таблице приведены некоторые классы часто встречающихся временных сложностей. В таблице poly (x) = x, т. Е. Многочлен от x.

Постоянное время

Алгоритм называется постоянным временем (также записывается как O (1) время), если значение T (n) ограничено значением, которое не зависит от размера ввода. Например, доступ к любому отдельному элементу в массиве занимает постоянное время, так как для его обнаружения требуется выполнить только одну операцию . Аналогичным образом поиск минимального значения в массиве, отсортированном по возрастанию; это первый элемент. Однако нахождение минимального значения в неупорядоченном массиве не является операцией с постоянным временем, поскольку для определения минимального значения необходимо сканирование каждого элемента в массиве. Следовательно, это операция с линейным временем, занимающая время O (n). Однако, если количество элементов известно заранее и не меняется, можно сказать, что такой алгоритм работает в постоянное время.

Несмотря на название «постоянное время», время выполнения не обязательно должно зависеть от размера проблемы, но верхняя граница времени выполнения должна быть ограничена независимо от размера проблемы. Например, задача «обменять значения a и b при необходимости так, чтобы a≤b» называется постоянным временем, даже если время может зависеть от того, верно ли уже, что a ≤ b. Однако существует некоторая постоянная t такая, что необходимое время всегда не превышает t.

Вот несколько примеров фрагментов кода, которые выполняются в постоянное время:

int index = 5; int item = список [индекс]; если (условие истинно), то выполнить некоторую операцию, которая выполняется с постоянным временем else выполнить некоторую другую операцию, которая выполняется с постоянным временем для i = 1 до 100 для j = 1 до 200 выполнить некоторую операцию, которая выполняется с постоянным временем

Если T (n) равно O ( любое постоянное значение), это эквивалентно и указано в стандартных обозначениях как T (n), равное O (1).

Логарифмическое время

Говорят, что алгоритм принимает логарифмическое время, когда T (n) = O (log n) . Поскольку log a n и log b n связаны с помощью постоянного множителя, и такой множитель не имеет отношения к классификации большого O, стандартное использование алгоритмов логарифмического времени — O (log n), независимо от основания логарифма, фигурирующего в выражении T.

Алгоритмы, использующие логарифмическое время, обычно встречаются при операциях с двоичными деревьями или при использовании двоичного поиска.

Алгоритм O (log n) считается высокоэффективным, так как отношение количества операций к размеру ввода уменьшается и стремится к нулю при увеличении n. Алгоритм, который должен получить доступ ко всем элементам своего ввода, не может занимать логарифмическое время, поскольку время, необходимое для чтения ввода размера n, имеет порядок n.

Пример логарифмического времени дается поиском по словарю. Рассмотрим словарь D, который содержит n статей, отсортированных в алфавитном порядке. Мы предполагаем, что при 1 ≤ k ≤ n можно получить доступ к k-й записи словаря за постоянное время. Пусть D (k) обозначает эту k-ю запись. Согласно этим гипотезам, проверка того, есть ли слово w в словаре, может выполняться за логарифмическое время: рассмотрим D (⌊ n / 2 ⌋), { displaystyle D ( lfloor n / 2 rfloor),}где ⌊ ⌋ { displaystyle lfloor ; rfloor}обозначает функцию floor. Если w = D (⌊ n / 2 ⌋), { displaystyle w = D ( lfloor n / 2 rfloor),}, то все готово. Иначе, если w < D ( ⌊ n / 2 ⌋), {displaystyle wпродолжит поиск таким же образом в левой половине словаря, в противном случае продолжите аналогично с правой половиной словаря. Этот алгоритм похож на метод, который часто используется для поиска статьи в бумажном словаре.

Полилогарифмическое время

Алгоритм считается работающим за полилогарифмическое время, если его время T (n) равно O ((log n)) для некоторой постоянной k. Другой способ записать это — O (log n).

Например, упорядочение цепочки матриц может быть решено за полилогарифмическое время на параллельной машине с произвольным доступом, а граф может быть определяется как планарное полностью динамическим способом за время O (log n) на операцию вставки / удаления.

Сублинейное время

An Говорят, что алгоритм работает в сублинейном времени (часто пишется сублинейное время ), если T (n) = o (n). В частности, это включает алгоритмы с временной сложностью, определенной выше.

Типичные алгоритмы, которые являются точными, но работают в сублинейном времени, используют параллельную обработку (как и вычисление определителя матрицы NC 1) или, альтернативно, имеют гарантированные допущения на входной структуре (как логарифмическое время двоичный поиск и многие алгоритмы обслуживания дерева). Однако формальные языки, такие как набор всех строк, которые имеют 1-бит в позиции, указанной первыми log (n) битами строки, могут зависеть от каждого бита ввода и при этом быть вычислимыми. в сублинейное время.

Конкретный термин «алгоритм сублинейного времени» обычно зарезервирован для алгоритмов, которые отличаются от приведенных выше тем, что они выполняются на классических моделях последовательных машин и не допускают предварительных предположений на входе. Однако они могут быть рандомизированы и действительно должны быть рандомизированы для всех, кроме самых тривиальных задач.

Поскольку такой алгоритм должен давать ответ без чтения всего ввода, его особенности сильно зависят от доступа, разрешенного к вводу. Обычно для входа, представленного в виде двоичной строки b 1,…, b k, предполагается, что алгоритм может за время O (1) запросить и получить значение of b i для любого i.

Подлиннейные временные алгоритмы обычно рандомизированы и предоставляют только приблизительные решения. Фактически, свойство двоичной строки, имеющей только нули (и ни одной), можно легко доказать, что оно не разрешимо (не приближенным) сублинейным алгоритмом времени. Алгоритмы сублинейного времени возникают естественным образом при исследовании тестирования свойств.

Линейное время

Говорят, что алгоритм принимает линейное время или время O (n), если его временная сложность O (n). Неформально это означает, что время работы увеличивается не более чем линейно с размером входа. Точнее, это означает, что существует такая константа c, что время выполнения не превышает cn для каждого ввода размера n. Например, процедура, которая складывает все элементы списка, требует времени, пропорционального длине списка, если время добавления постоянное или, по крайней мере, ограничено константой.

Линейное время — это наилучшая временная сложность в ситуациях, когда алгоритм должен последовательно считывать все входные данные. Поэтому было вложено много исследований в открытие алгоритмов, показывающих линейное время или, по крайней мере, почти линейное время. Это исследование включает как программные, так и аппаратные методы. Для этого существует несколько аппаратных технологий, использующих параллелизм. Примером является память с адресацией по содержимому. Эта концепция линейного времени используется в алгоритмах сопоставления строк, таких как алгоритм Бойера – Мура и алгоритм Укконена.

Квазилинейное время

Считается, что алгоритм работает в квазилинейное время (также называемое логарифмическое время ), если T (n) = O (n log n) для некоторой положительной константы k; линейнофмический time — это случай k = 1. Используя мягкую нотацию O, эти алгоритмы равны Õ (n). Алгоритмы квазилинейного времени также имеют O (n) для любой константы ε>0 и, таким образом, работают быстрее, чем любой алгоритм с полиномиальным временем, временная граница которого включает член n для любого c>1.

Алгоритмы, работающие в квазилинейном времени, включают:

• Сортировка слиянием на месте, O (n log n)
• Quicksort, O (n log n), в его рандомизированном версия имеет время выполнения O (n log n) в ожидании наихудшего случая ввода. Его нерандомизированная версия имеет время работы O (n log n) только с учетом средней сложности случая.
• Heapsort, O (n log n), сортировка слиянием, внутренняя сортировка, сортировка двоичного дерева, гладкая сортировка, сортировка по терпению и т. Д. В худшем случае
• Быстрое преобразование Фурье, O (n log n)
• Массив Монжа вычисление, O (n log n)

Во многих случаях время выполнения n · log n является просто результатом выполнения операции Θ (log n) n раз (обозначения см. В Обозначение Big O § Семейство обозначений Бахмана – Ландау ). Например, сортировка двоичного дерева создает двоичное дерево, вставляя каждый элемент массива размера n один за другим. Поскольку операция вставки в самобалансирующееся двоичное дерево поиска занимает время O (log n), весь алгоритм занимает время O (n log n).

Сортировки сравнения требуют как минимум Ω (n log n) сравнений в худшем случае, потому что log (n!) = Θ (n log n) по приближению Стирлинга. Они также часто возникают из рекуррентного соотношения T (n) = 2T (n / 2) + O (n).

Субквадратичное время

Алгоритм называется субквадратичным временем, если T (n) = o (n).

Например, простые алгоритмы сортировки , основанные на сравнении, являются квадратичными (например, сортировка вставкой ), но можно найти более сложные алгоритмы, которые являются субквадратичными (например, сортировка по оболочке ). Никакие универсальные сортировки не выполняются за линейное время, но переход от квадратичной к субквадратичной имеет большое практическое значение.

Полиномиальное время

Алгоритм считается имеющим полиномиальное время, если его время работы ограничено сверху с помощью полиномиального выражения в размере входных данных для алгоритма, т. Е. T (n) = O (n) для некоторой положительной константы k. Проблемы, для которых существует детерминированный алгоритм полиномиального времени, относятся к класс сложности P, который является центральным в области теории сложности вычислений. В тезисе Кобхэма говорится, что полиномиальное время является синонимом слов «послушный», «выполнимый», «эффективный» или «быстрый».

Некоторые примеры алгоритмов полиномиального времени:

Сильно и слабо полиномиальное время

В некоторых контекстах, особенно в оптимизации, различают алгоритмы сильно полиномиального времени и слабо полиномиального времени . Эти две концепции актуальны только в том случае, если входные данные алгоритмов состоят из целых чисел.

В арифметической модели вычислений определено строго полиномиальное время. В этой модели вычислений основные арифметические операции (сложение, вычитание, умножение, деление и сравнение) выполняются за единичный временной шаг, независимо от размеров операндов. Алгоритм выполняется за строго полиномиальное время, если

1. количество операций в арифметической модели вычислений ограничено полиномом от количества целых чисел во входном экземпляре; и
2. пространство, используемое алгоритмом, ограничено полиномом от размера входных данных.

Любой алгоритм с этими двумя свойствами может быть преобразован в алгоритм с полиномиальным временем, заменив арифметические операции подходящими алгоритмами. для выполнения арифметических операций на машине Тьюринга. Если второе из вышеперечисленных требований не выполняется, то это уже неверно. Учитывая целое число 2 n { displaystyle 2 ^ {n}}(которое занимает пространство, пропорциональное n в модели машины Тьюринга), можно вычислить 2 2 n { displaystyle 2 ^ {2 ^ {n}}}с n умножениями с использованием повторного возведения в квадрат. Однако пространство, используемое для представления 2 2 n { displaystyle 2 ^ {2 ^ {n}}}, пропорционально 2 n { displaystyle 2 ^ {n}}, и поэтому экспоненциально, а не полиномиально в пространстве, используемом для представления входных данных. Следовательно, невозможно выполнить это вычисление за полиномиальное время на машине Тьюринга, но можно вычислить его полиномиальным числом арифметических операций.

И наоборот, есть алгоритмы, которые выполняются на нескольких шагах машины Тьюринга, ограниченных полиномом от длины двоично-закодированного ввода, но не выполняющих количество арифметических операций, ограниченных полиномом от количества вводить числа. Одним из примеров является алгоритм Евклида для вычисления наибольшего общего делителя двух целых чисел. Для двух целых чисел a { displaystyle a}и b { displaystyle b}алгоритм выполняет O (log ⁡ a + log ⁡ b) { displaystyle O ( log a + log b)}арифметические операции с числами, не более O (log ⁡ a + log ⁡ b) { displaystyle O ( log a + log b)}бит. В то же время количество арифметических операций не может быть ограничено количеством целых чисел во входных данных (которое в данном случае постоянно, во входных данных всегда только два целых числа). Из-за последнего наблюдения алгоритм не работает за строго полиномиальное время. Его реальное время работы зависит от величин a { displaystyle a}и b { displaystyle b}, а не только от количества целых чисел в ввод.

Алгоритм, который выполняется за полиномиальное время, но который не является строго полиномиальным, называется выполняющимся за слабо полиномиальное время . Хорошо известным примером проблемы, для которой известен алгоритм со слабо полиномиальным временем, но не известно, что он допускает алгоритм с сильно полиномиальным временем, является линейное программирование. Слабо-полиномиальное время не следует путать с псевдополиномиальным временем.

Классы сложности

Концепция полиномиального времени приводит к нескольким классам сложности в теории вычислительной сложности. Некоторые важные классы, определенные с использованием полиномиального времени, следующие.

P — это наименьший класс временной сложности на детерминированной машине, которая надежна с точки зрения изменений модели машины. (Например, переход от однопленочной машины Тьюринга к многоленточной машине может привести к квадратичному ускорению, но любой алгоритм, работающий за полиномиальное время в одной модели, также делает это и в другой.) Любое данное абстрактная машина будет иметь класс сложности, соответствующий задачам, которые могут быть решены на этой машине за полиномиальное время.

Суперполиномиальное время

Говорят, что алгоритм принимает суперполиномиальное время, если T (n) не ограничено сверху каким-либо полиномом. Используя маленькую омега-нотацию, это время ω (n) для всех констант c, где n — входной параметр, обычно количество битов во входных данных.

Например, алгоритм, который работает за 2 шага на входе размера n, требует суперполиномиального времени (точнее, экспоненциального времени).

Алгоритм, использующий экспоненциальные ресурсы, явно суперполиномиален, но некоторые алгоритмы лишь очень слабо суперполиномиальны. Например, тест простоты Адлемана – Померанса – Рамли выполняется в течение n раз на n-битовых входах; это растет быстрее, чем любой многочлен для достаточно большого n, но размер входных данных должен стать непрактично большим, прежде чем в нем не будет преобладать многочлен с малой степенью.

Алгоритм, требующий сверхполиномиального времени, лежит за пределами класса сложности P. Тезис Кобхэма утверждает, что эти алгоритмы непрактичны, и во многих случаях так и есть. Поскольку проблема P по сравнению с NP не решена, неизвестно, требует ли NP-полная проблема суперполиномиального времени.

Квазиполиномиальное время

Квазиполиномиальное время — это алгоритмы, которые работают дольше, чем полиномиальное время, но не настолько долго, чтобы быть экспоненциальным временем. Наихудшее время работы алгоритма квазиполиномиального времени составляет 2 O ((log ⁡ n) c) { displaystyle 2 ^ {O (( log n) ^ {c})}}для некоторого фиксированного c>0 { displaystyle c>0}. Для c = 1 { displaystyle c = 1}мы получаем алгоритм полиномиального времени, для c < 1 {displaystyle c<1}получаем алгоритм сублинейного времени.

Квазиполиномиальные алгоритмы времени обычно возникают в редукциях от NP-сложной проблемы к другой проблеме. Например, можно взять экземпляр сложной задачи NP, скажем 3SAT, и преобразовать его в экземпляр другой задачи B, но размер экземпляра станет 2 O ((log ⁡ n) c) { displaystyle 2 ^ {O (( log n) ^ {c})}}. В этом случае это сокращение не доказывает, что проблема B NP-трудна; это сокращение показывает только то, что нет алгоритм полиномиального времени для B unles s существует алгоритм квазиполиномиального времени для 3SAT (и, следовательно, для всего NP ). Точно так же есть некоторые проблемы, для которых мы знаем алгоритмы с квазиполиномиальным временем, но не известны алгоритмы с полиномиальным временем. Такие проблемы возникают в приближенных алгоритмах; Известным примером является направленная задача дерева Штейнера, для которой существует квазиполиномиальный алгоритм аппроксимации времени, обеспечивающий коэффициент аппроксимации O (log 3 ⁡ n) { displaystyle O ( log ^ {3} n)}(n — количество вершин), но показать существование такого алгоритма с полиномиальным временем — открытая проблема.

Другие вычислительные задачи с квазиполиномиальными временными решениями, но без известного полиномиального временного решения, включают проблему установленной клики, в которой цель — найти большую клику в объединение клики и случайного графа. Хотя квазиполиномиально разрешима, было высказано предположение, что проблема насаждаемой клики не имеет решения за полиномиальное время; эта насаждаемая клика гипотеза использовалась в качестве предположения о вычислительной сложности для доказательства сложности нескольких других задач в вычислительной теории игр, тестировании свойств и машинное обучение.

Класс сложности QP состоит из всех задач, которые имеют алгоритмы квазиполиномиального времени. Его можно определить в терминах DTIME следующим образом.

QP = ⋃ c ∈ N DTIME (2 (log ⁡ n) c) { displaystyle { mbox {QP}} = bigcup _ {c in mathbb {N}} { mbox {DTIME}} (2 ^ {( log n) ^ {c}})}

Отношение к NP-полным задачам

По сложности В теории нерешенная проблема P и NP спрашивает, все ли проблемы в NP имеют алгоритмы с полиномиальным временем. Все самые известные алгоритмы для NP-полных задач, таких как 3SAT и т. Д., Требуют экспоненциального времени. В самом деле, для многих естественных NP-полных задач предполагается, что они не имеют алгоритмов с субэкспоненциальным временем. Здесь «субэкспоненциальное время» означает второе определение, представленное ниже. (С другой стороны, многие задачи о графах, представленные естественным образом матрицами смежности, разрешимы за субэкспоненциальное время просто потому, что размер входных данных равен квадрату числа вершин.) Эта гипотеза (для задачи k-SAT) известна в качестве гипотезы экспоненциального времени. Поскольку предполагается, что NP-полные задачи не имеют алгоритмов квазиполиномиального времени, некоторые результаты неприемлемости в области алгоритмов аппроксимации делают предположение, что NP-полные задачи не имеют алгоритмов квазиполиномиального времени. Например, просмотрите известные результаты о несовместимости для задачи set cover.

Субэкспоненциальное время

Термин субэкспоненциальный время используется для выражения того, что время работы некоторого алгоритма может расти быстрее любого полином, но все же значительно меньше экспоненты. В этом смысле проблемы, которые имеют алгоритмы субэкспоненциального времени, несколько более разрешимы, чем те, которые имеют только экспоненциальные алгоритмы. Точное определение «субэкспоненциального» не является общепринятым, и мы перечисляем два наиболее широко используемых ниже.

Первое определение

Проблема называется субэкспоненциальной разрешимой во времени, если ее можно решить за время выполнения, логарифмы которого становятся меньше любого заданного полинома. Точнее, проблема находится в субэкспоненциальном времени, если для любого ε>0 существует алгоритм, который решает проблему за время O (2). Набор всех таких задач — это класс сложности SUBEXP, который можно определить в терминах DTIME следующим образом.

SUBEXP = ⋂ ε>0 DTIME (2 n ε) { displaystyle { text {SUBEXP}} = bigcap _ { varepsilon>0} { text {DTIME}} left (2 ^ {n ^ { varepsilon}} right)}

Это понятие субэкспоненты неоднородно с точки зрения ε в том смысле, что ε не является частью входных данных, и каждое ε может иметь свое собственное алгоритм решения проблемы.

Второе определение

Некоторые авторы определяют субэкспоненциальное время как время выполнения в 2. Это определение допускает большее время выполнения, чем первое определение субэкспоненциального времени. Пример такого субэкспоненциального временного алгоритма является наиболее известный классический алгоритм для целочисленной факторизации, решето общего числового поля, которое r не во времени около 2 O ~ (n 1/3) { displaystyle 2 ^ {{ tilde {O}} (n ^ {1/3})}}, где длина входа n. Другой пример — проблема изоморфизма графов, где алгоритм Люкса выполняется за время 2 O (n log ⁡ n) { displaystyle 2 ^ {O ({ sqrt {n log n}}) }}. (В 2015–2017 годах Бабай сократил сложность этой задачи до квазиполиномиального времени.)

Имеет значение, может ли алгоритм быть субэкспоненциальным по размеру экземпляра или количеству вершин или количество ребер. В параметризованной сложности это различие становится явным путем рассмотрения пар (L, k) { displaystyle (L, k)}из задач принятия решения и параметры k. SUBEPT — это класс всех параметризованных задач, которые выполняются во времени субэкспоненциально по k и полиномиально по входному размеру n:

SUBEPT = DTIME (2 o (k) ⋅ poly (n)). { displaystyle { text {SUBEPT}} = { text {DTIME}} left (2 ^ {o (k)} cdot { text {poly}} (n) right).}

Подробнее в точности, SUBEPT — это класс всех параметризованных задач (L, k) { displaystyle (L, k)}, для которых существует вычислимая функция f : N → N { displaystyle f: mathbb {N} to mathbb {N}}с f ∈ o (k) { displaystyle f in o (k)}и алгоритм, который определяет L во времени 2 f (k) ⋅ poly (n) { displaystyle 2 ^ {f (k)} cdot { text {poly}} (n)}.

Гипотеза экспоненциального времени

Гипотеза экспоненциального времени (ETH ) заключается в том, что 3SAT, проблема выполнимости булевых формул в конъюнктивная нормальная форма с не более чем тремя литералами на предложение и с n переменными не может быть решена за время 2. Точнее, гипотеза состоит в том, что существует некоторая абсолютная константа c>0, такая, что 3SAT не может быть определен в время 2 на любой детерминированной машине Тьюринга. С m, обозначающим количество пунктов, ETH эквивалентен гипотезе о том, что kSAT не может быть решен за время 2 для любого целого числа k ≥ 3. Гипотеза экспоненциального времени подразумевает P ≠ NP.

Экспоненциальное время

Алгоритм называется экспоненциальным временем, если T (n) ограничено сверху числом 2, где poly (n) — некоторый полином от n. Более формально алгоритм является экспоненциальным по времени, если T (n) ограничено O (2) для некоторой константы k. Задачи, допускающие алгоритмы экспоненциального времени на детерминированной машине Тьюринга, образуют класс сложности, известный как EXP.

EXP = ⋃ c ∈ N DTIME (2 nc) { displaystyle { text {EXP}} = bigcup _ {c in mathbb {N}} { text {DTIME}} left (2 ^ {n ^ {c}} right)}

Иногда экспоненциальное время используется для обозначения алгоритмов, которые T (n) = 2, где показатель степени не более чем линейная функция от n. Это приводит к классу сложности E.

E = ⋃ c ∈ N DTIME (2 cn) { displaystyle { text {E}} = bigcup _ {c in mathbb {N}} { text {DTIME }} left (2 ^ {cn} right)}

Факториальное время

Примером алгоритма, который работает во факториальном времени, является bogosort, заведомо неэффективный алгоритм сортировки, основанный на на метод проб и ошибок. Богосорт сортирует список из n элементов, неоднократно перетасовывая список, пока не будет обнаружено, что он отсортирован. В среднем случае каждый проход алгоритма богосорта будет проверять один из n! заказы n элементов. Если элементы отличаются друг от друга, сортируется только один такой порядок. Богосорт разделяет наследие с теоремой о бесконечной обезьяне.

Двойное экспоненциальное время

Алгоритм называется двойным экспоненциальным временем, если T (n) ограничено сверху числом 2, где poly (n) — некоторый многочлен от n. Такие алгоритмы относятся к классу сложности 2-EXPTIME.

2-EXPTIME = ⋃ c ∈ N DTIME (2 2 nc) { displaystyle { mbox {2-EXPTIME}} = bigcup _ {c in mathbb {N}} { mbox {DTIME}} left (2 ^ {2 ^ {n ^ {c}}} right)}

Хорошо известные алгоритмы двойной экспоненциальной зависимости времени включают:

• Процедуры принятия решений для арифметики Пресбургера
• Вычисление базиса Грёбнера (в худшем случае)
• Исключение квантора на реальных закрытых полях занимает как минимум удвоенное экспоненциальное время и может быть выполнено в это время.

См. также

• Алгоритмы замены блоков
• L-нотация
• Сложность пространства

Ссылки

В информатике временна́я сложность алгоритма определяет время работы, используемое алгоритмом, как функции от длины строки, представляющей входные данные ^[1]. Временная сложность алгоритма обычно выражается с использованием нотации «O» большое, которая исключает коэффициенты и члены меньшего порядка. Если сложность выражена таким способом, говорят об асимптотическом описании временной сложности, т.е. при стремлении размера входа к бесконечности. Например, если время, которое нужно алгоритму для выполнения работы, для всех входов длины n не превосходит 5n³ + 3n для некоторого n (большего некоторого n₀), асимптотическая временная сложность равна O (n³).

Временная сложность зачастую оценивается путём подсчёта числа элементарных операций, осуществляемых алгоритмом, где элементарная операция занимает для выполнения фиксированное время. Тогда полное время выполнения и число элементарных операций, выполненных алгоритмом, отличаются максимум на постоянный множитель.

Поскольку производительность алгоритма может отличаться при входах одного и того же размера, обычно используется временная сложность наихудшего случая^[en] поведения алгоритма, которая обозначается как T(n) и которая определяется как максимальное время, которое требуется для любого входа длины n. Реже, и это обычно оговаривается специально, время измеряется как средняя сложность^[en]. Сложность по времени классифицируется природой функции T(n). Например, алгоритм с T(n) = O(n) называется алгоритмом линейного времени, а об алгоритме с T(n) = O(Mⁿ) и mⁿ= O(T(n)) для некоторого M ≥ m > 1 говорят как об алгоритме с экспоненциальным временем.

Таблица сложностей по времени

Следующая таблица суммирует некоторые, обычно рассматриваемые, классы сложности. В таблице poly(x) = x^O(1), т.е. многочлен от x.

Постоянное время

Говорят, что алгоритм является алгоритмом постоянного времени (записывается как время O(1)), если значение T(n) ограничено значением, не зависящим от размера входа. Например, получение одного элемента в массиве занимает постоянное время, поскольку выполняется единственная команда для его обнаружения. Однако нахождение минимального значения в несортированном массиве не является операцией с постоянным временем, поскольку мы должны просмотреть каждый элемент массива. Таким образом, эта операция занимает линейное время, O(n). Если число элементов известно заранее и не меняется, о таком алгоритме можно говорить как об алгоритме постоянного времени.

Несмотря на название «постоянное время», время работы не обязательно должно быть независимым от размеров задачи, но верхняя граница времени работы не должна зависеть. Например, задача «обменять значения a и b, если необходимо, чтобы в результате получили a≤b«, считается задачей постоянного времени, хотя время работы алгоритма может зависеть от того, выполняется ли уже неравенство a ≤ b или нет. Однако существует некая константа t, для которой время выполнения задачи всегда не превосходит t.

Ниже приведены некоторые примеры кода, работающие за постоянное время:

int index = 5;
int item = list[index];
if (условие верно) then
   выполнить некоторые операции с постоянным временем работы
else
   выполнить некоторые операции с постоянным временем работы
for i = 1 to 100
   for j = 1 to 200
      выполнить некоторые операции с постоянным временем работы

Если T(n) равен O(некоторое постоянное значение), это эквивалентно T(n) равно O(1).

Логарифмическое время

Говорят, что алгоритм выполняется за логарифмическое время, если T(n) = O(log n). Поскольку в компьютерах принята двоичная система счисления, в качестве базы логарифма используется 2 (то есть, log₂ n). Однако при замене базы^[en] логарифмы log_a n и log_b n отличаются лишь на постоянный множитель, который в записи O-большое отбрасывается. Таким образом, O(log n) является стандартной записью для алгоритмов логарифмического времени независимо от базы логарифма.

Алгоритмы, работающие за логарифмическое время, обычно встречаются при операциях с двоичными деревьями или при использовании двоичного поиска.

O(log n) алгоритмы считаются высокоэффективными, поскольку время выполнения операции в пересчёте на один элемент уменьшается с увеличением числа элементов.

Очень простой пример такого алгоритма — деление строки пополам, вторая половина опять делится пополам, и так далее. Это занимает время O(log n) (где n — длина строки, мы здесь полагаем, что console.log и str.substring занимают постоянное время).
Это означает, что для увеличения числа печатей необходимо удвоить длину строки.

// Функция для рекурсивной печати правой половины строки
var right = function(str)
{
    var length = str.length;
    
    // вспомогательная функция
    var help = function(index)
    {
       // Рекурсия: печатаем правую половину
        if(index < length)
        {
          
            // Печатаем символы от index до конца строки
            console.log(str.substring(index, length));
            
            // рекурсивный вызов: вызываем вспомогательную функцию с правой частью
            help(Math.ceil((length + index)/2));
        }
    }
    help(0);
}

Полилогарифмическое время

Говорят, что алгоритм выполняется за полилогарифмическое время, если T(n) = O((log n)^k), для некоторого k. Например, задача о порядке перемножения матриц может быть решена за полилогарифмическое время на параллельной РАМ-машине^[en][4].

Сублинейное время

Говорят, что алгоритм выполняется за сублинейное время, если T(n) = o(n). В частности, сюда включаются алгоритмы с временной сложностью, перечисленные выше, как и другие, например, поиск Гровера со сложностью O(n^½).

Типичные алгоритмы, которые, являясь точными, всё же работают за сублинейное время, используют распараллеливание процессов (как это делают алгоритм NC₁ вычисления определителя матрицы), неклассические вычисления (как в поиске Гровера) или имеют гарантированное предположение о струтуре входа (как работающие за логарифмическое время, алгоритмы двоичного поиска и многие алгоритмы обработки деревьев). Однако формальные конструкции, такие как множество всех строк, имеющие бит 1 в позиции, определяемой первыми log(n) битами строки, могут зависеть от каждого бита входа, но, всё же, оставаться сублинейными по времени.

Термин алгоритм с сублинейным временем работы обычно используется для алгоритмов, которые, в отличие от приведённых выше примеров, работают на обычных последовательных моделях машин и не предполагают априорных знаний о структуре входа ^[5]. Однако для них допускается применение вероятностных методов и даже более того, алгоритмы должны быть вероятностными для большинства тривиальных задач.

Поскольку такой алгоритм обязан давать ответ без полного чтения входных данных, он в очень сильной степени зависит от способов доступа, разрешённых во входном потоке. Обычно для потока, представляющего собой битовую строку b₁,…,b_k, предполагается, что алгоритм может за время O(1) запросить значение b_i для любого i.

Алгоритмы сублинейного времени, как правило, вероятностны и дают лишь аппроксимированное решение. Алгоритмы сублинейного времени выполнения возникают естественным образом при исследовании проверки свойств^[en].

Линейное время

Говорят, что алгоритм работает за линейное время, или O(n), если его сложность равна O(n). Неформально, это означает, что для достаточно большого размера входных данных время работы увеличивается линейно от размера входа. Например, процедура, суммирующая все элементы списка, требует время, пропорциональное длине списка. Это описание не вполне точно, поскольку время работы может существенно отличаться от точной пропорциональности, особенно для малых значений n.

Линейное время часто рассматривается как желательный атрибут алгоритма^[6]. Было проведено много исследований для создания алгоритмов с (почти) линейным временем работы или лучшим. Эти исследования включали как программные, так и аппаратные подходы. В случае аппаратного исполнения некоторые алгоритмы, которые, с математической точки зрения, никогда не могут достичь линейного времени исполнения в стандартных моделях вычислений, могут работать за линейное время. Существуют некоторые аппаратные технологии, которые используют параллельность для достижения такой цели. Примером служит ассоциативная память. Эта концепция линейного времени используется в алгоритмах сравнения строк, таких как алгоритм Бойера — Мура и алгоритм Укконена.

Квазилинейное время

Говорят, что алгоритм работает за квазилинейное время, если T(n) = O(n log^k n) для некоторой константы k. Линейно-логарифмическое время является частным случаем с k = 1^[7]. При использовании обозначения слабое-O эти алгоритмы являются Õ(n). Алгоритмы квазилинейного времени являются также o(n^1+ε) для любого ε > 0 и работают быстрее любого полинома от n со степенью, строго большей 1.

Алгоритмы, работающие за квазилинейное время, вдобавок к линейно-логарифмическим алгоритмам, упомянутым выше, включают:

• Сортировка слиянием на месте, O(n log² n)
• Быстрая сортировка, O(n log n), в вероятностной версии имеет линейно-логарифмическое время выполнения в худшем случае. Невероятностная версия имеет линейно-логарифмическое время работы только для измерения сложности в среднем.
• Пирамидальная сортировка, O(n log n), сортировка слиянием, introsort, бинарная сортировка с помощью дерева, плавная сортировка, пасьянсная сортировка^[en], и т.д. в худшем случае
• Быстрые преобразования Фурье, O(n log n)
• Вычисление матриц Монжа, O(n log n)

Линейно-логарифмическое время

Линейно-логарифмическое является частным случаем квазилинейного времени с показателем k = 1 на логарифмическом члене.

Линейно-логарифмическая функция — это функция вида n • log n (т.е. произведение линейного^[en] и логарифмического членов). Говорят, что алгоритм работает за линейно-логарифмическое время, если T(n) = O(n log n).^[8] Таким образом, линейно-логарифмический элемент растёт быстрее, чем линейный член, но медленнее, чем любой многочлен от n со степенью, строго большей 1.

Во многих случаях время работы n • log n является просто результатом выполнения операции Θ(log n) n раз. Например, сортировка с помощью двоичного дерева создаёт двоичное дерево путём вставки каждого элемента в массив размером n один за другим. Поскольку операция вставки в сбалансированное бинарное дерево поиска^[en] занимает время O(log n), общее время выполнения алгоритма будет линейно-логарифмическим.

Сортировки сравнением^[en] требуют по меньшей мере линейно-логарифмического числа сравнений для наихудшего случая, поскольку log(n!) = Θ(n log n) по формуле Стирлинга. То же время выполнения зачастую возникает из рекуррентного уравнения T(n) = 2 T(n/2) + O(n).

Подквадратичное время

Говорят, что алгоритм выполняется за субквадратичное время, если T(n) = o(n²).

Например, простые, основанные на сравнении, алгоритмы сортировки квадратичны (например, сортировка вставками), но можно найти более продвинутые алгоритмы, которые имеют субквадратичное время выполнения (например, сортировка Шелла). Никакие сортировки общего вида не работают за линейное время, но переход от квадратичного к субквадратичному времени имеет большую практическую важность.

Полиномиальное время

Говорят, что алгоритм работает за полиномиальное время, если время работы ограничено сверху^[en] многочленом от размера входа для алгоритма, то есть T(n) = O(n^k) для некоторой константы k^[1][9]. Задачи, для которых алгоритмы с детерминированным полиномиальным временем существуют, принадлежат классу сложности P, который является центральным в теории вычислительной сложности. Тезис Кобэма^[en] утверждает, что полиномиальное время является синонимом понятий «легко поддающийся обработке», «выполнимый», «эффективный» или «быстрый»^[10].

Некоторые примеры алгоритмов полиномиального времени:

Строго и слабо полиномиальное время

В некоторых контекстах, особенно в оптимизации, различают алгоритмы со строгим полиномиальным временем и слабо полиномиальным временем. Эти две концепции относятся только ко входным данным, состоящим из целых чисел.

Строго полиномиальное время определяется в арифметической модели вычислений. В этой модели базовые арифметические операции (сложение, вычитание, умножение, деление и сравнение) берутся за единицы выполнения, независимо от длины операндов. Алгоритм работает в строго полиномиальное время, если^[11]

1. число операций в арифметической модели вычислений ограничено многочленом от числа целых во входном потоке, и
2. память, используемая алгоритмом, ограничена многочленом от размеров входа.

Любой алгоритм с этими двумя свойствами можно привести к алгоритму полиномиального времени путём замены арифметических операций на соответствующие алгоритмы выполнения арифметических операций на машине Тьюринга. Если второе из вышеприведённых требований не выполняется, это больше не будет верно. Если задано целое число (которое занимает память, пропорциональную n в машине Тьюринга), можно вычислить с помощью n операций, используя повторное возведение в степень. Однако память, используемая для представления , пропорциональна , и она скорее экспоненционально, чем полиномиально, зависит от памяти, используемой для входа. Отсюда — невозможно выполнить эти вычисления за полиномиальное время на машине Тьюринга, но можно выполнить за полиномиальное число арифметических операций.

Обратно — существуют алгоритмы, которые работают за число шагов машины Тьюринга, ограниченных полиномиальной длиной бинарно закодированного входа, но не работают за число арифметических операций, ограниченное многочленом от количества чисел на входе. Алгоритм Евклида для вычисления наибольшего общего делителя двух целых чисел является одним из примеров. Для двух целых чисел и время работы алгоритма ограничено шагам машины Тьюринга. Это число является многочленом от размера бинарного представления чисел и , что грубо можно представить как . В то же самое время число арифметических операций нельзя ограничить числом целых во входе (что в данном случае является константой — имеется только два числа во входе). Ввиду этого замечания алгоритм не работает в строго полиномиальное время. Реальное время работы алгоритма зависит от величин и , а не только от числа целых чисел во входе.

Если алгоритм работает за полиномиальное время, но не за строго полиномиальное время, говорят, что он работает за слабо полиномиальное время^[12].
Хорошо известным примером задачи, для которой известен слабо полиномиальный алгоритм, но не известен строго полиномиальный алгоритм, является линейное программирование. Слабо полиномиальное время не следует путать с псевдополиномиальным временем.

Классы сложности

Концепция полиномиального времени приводит к нескольким классам сложности в теории сложности вычислений. Некоторые важные классы, определяемые с помощью полиномиального времени, приведены ниже.

• P: Класс сложности задач разрешимости, которые могут быть решены в детерминированной машине Тьюринга за полиномиальное время.
• NP: Класс сложности задач разрешимости, которые могут быть решены в недетерминированной машине Тьюринга за полиномиальное время.
• ZPP: Класс сложности задач разрешимости, которые могут быть решены с нулевой ошибкой в вероятностной машине Тьюринга за полиномиальное время.
• RP: Класс сложности задач разрешимости, которые могут быть решены с односторонними ошибками в вероятностной машине Тьюринга за полиномиальное время.
• BPP: Класс сложности задач разрешимости, которые могут быть решены с двусторонними ошибками в вероятностной машине Тьюринга за полиномиальное время.
• BQP: Класс сложности задач разрешимости, которые могут быть решены с двусторонними ошибками в квантовой машине Тьюринга за полиномиальное время.

P является наименьшим классом временной сложности на детерминированной машине, которая является устойчивой^[en] в терминах изменения модели машины. (Например, переход от одноленточной машины Тьюринга к мультиленточной может привести к квадратичному ускорению, но любой алгоритм, работающий за полиномиальное время на одной модели, будет работать за полиномиальное время на другой.)

Суперполиномиальное время

Говорят, что алгоритм работает за суперполиномиальное время, если T(n) не ограничен сверху полиномом. Это время равно ω(n^c) для всех констант c, где n — входной параметр, обычно — число бит входа.

Например, алгоритм, осуществляющий 2ⁿ шагов, для входа размера n требует суперполиномиального времени (конкретнее, экспоненциального времени).

Ясно, что алгоритм, использующий экспоненциальные ресурсы, суперполиномиален, но некоторые алгоритмы очень слабо суперполиномиальны. Например, тест простоты Адлемана — Померанса — Румели^[en]* работает за время n^{O(log log n)} на n-битном входе. Это растёт быстрее, чем любой полином, для достаточно большого n, но размер входа должен стать очень большим, чтобы он не доминировался полиномом малой степени.

Алгоритм, требующий суперполиномиального времени, лежит вне класса сложности P. Тезис Кобэма^[en] утверждает, что эти алгоритмы непрактичны, и во многих случаях это так. Поскольку задача равенства классов P и NP не решена, никаких алгоритмов для решения NP-полных задач за полиномиальное время в настоящее время не известно.

Квазиполиномиальное время

Алгоритмы квазиполиномиального времени — это алгоритмы, работающие медленнее, чем за полиномиальное время, но не столь медленно, как алгоритмы экспоненциального времени. Время работы в худшем случае для квазиполиномиального алгоритма равно для некоторого фиксированного c. Хорошо известный классический алгоритм разложения целого числа на множители, общий метод решета числового поля, который работает за время около , не является квазиполиномиальным, поскольку время работы нельзя представить как для некоторого фиксированного c. Если константа «c» в определении алгоритма квазиполиномиального времени равна 1, мы получаем алгоритм полиномиального времени, а если она меньше 1, мы получаем алгоритм сублинейного времени.

Алгоритмы квазиполиномиального времени обычно возникают при сведении NP-трудной задачи к другой задаче. Например, можно взять NP-трудную задачу, скажем, 3SAT, и свести её к другой задаче B, но размер задачи станет равным . В этом случае сведение не доказывает, что задача B NP-трудна, такое сведение лишь показывает, что не существует полиномиального алгоритма для B, если только не существует квазиполиномиального алгоритма для 3SAT (а тогда и для всех NP-задач). Подобным образом — существуют некоторые задачи, для которых мы знаем алгоритмы с квазиполиномиальным временем, но для которых алгоритмы с полиномиальным временем неизвестны. Такие задачи появляются в аппроксимационых алгоритмах. Знаменитый пример — ориентированная задача Штайнера, для которой существует аппроксимационный квазиполиномиальный алгоритм с аппроксимационным коэффициентом (где n — число вершин), но существование алгоритма с полиномиальным временем является открытой проблемой.

Класс сложности QP состоит из всех задач, имеющих алгоритмы квазиполиномиального времени. Его можно определить в терминах DTIME следующим образом^[13]

Связь с NP-полными задачами

В теории сложности нерешённая проблема равенства классов P и NP спрашивает, не имеют ли все задачи из класса NP алгоритмы решения за полиномиальное время. Все хорошо известные алгоритмы для NP-полных задач, наподобие 3SAT, имеют экспоненциальное время. Более того, существует гипотеза, что для многих естественных NP-полных задач не существует алгоритмов с субэкспоненциальным временем выполнения. Здесь «субэкспоненциальное время » взято в смысле второго определения, приведённого ниже. (С другой стороны, многие задачи из теории графов, представленные естественным путём матрицами смежности, разрешимы за субэкспоненциальное время просто потому, что размер входа равен квадрату числа вершин.) Эта гипотеза (для задачи k-SAT) известна как гипотеза экспоненциального времени^[en][14]. Поскольку она предполагает, что NP-полные задачи не имеют алгоритмов квазиполиномиального времени, некоторые результаты неаппроксимируемости в области аппроксимационных алгоритмов исходят из того, что NP-полные задачи не имеют алгоритмов квазиполиномиального времени. Например, смотрите известные результаты по неаппроксимируемости задачи о покрытии множества.

Субэкспоненциальное время

Термин субэкспоненциальное^[en] время используется, чтобы выразить, что время выполнения некоторого алгоритма может расти быстрее любого полиномиального, но остаётся существенно меньше, чем экспоненциальное. В этом смысле задачи, имеющие алгоритмы субэкспоненциального времени, являются более податливыми, чем алгоритмы только с экспотенциальным временем. Точное определение «субэкспоненциальный» пока не является общепринятым^[15], и мы приводим ниже два наиболее распространённых определения.

Первое определение

Говорят, что задача решается за субэкспоненциальное время, если она решается алгоритмом, логарифм времени работы которого растёт меньше, чем любой заданный многочлен. Более точно — задача имеет субэкспоненциальное время, если для любого ε > 0 существует алгоритм, который решает задачу за время O(2^nε). Множество все таких задач составляет класс сложности SUBEXP, который в терминах DTIME можно выразить как^{[3][16][17][18]}.

Заметим, что здесь ε не является частью входных данных и для каждого ε может существовать свой собственный алгоритм решения задачи.

Второе определение

Некоторые авторы определяют субэкспоненциальное время как время работы 2^{o(n)[14][19][20]}. Это определение допускает большее время работы, чем первое определение. Примером такого алгоритма субэкспоненциального времени служит хорошо известный классический алгоритм разложения целых чисел на множители, общий метод решета числового поля, который работает за время около , где длина входа равна n. Другим примером служит хорошо известный алгоритм для задачи изоморфизма графов^[en], время работы которого равно .

Заметим, что есть разница, является ли алгоритм субэкспоненциальным по числу вершин или числу рёбер. В параметризованной сложности^[en] эта разница присутствует явно путём указания пары , задачи разрешимости и параметра k. SUBEPT является классом всех параметризованных задач, которые работают за субэкспоненциальное время по k и за полиномиальное по n^[21]:

Точнее, SUBEPT является классом всех параметризованных задач , для которых существует вычислимая функция с и алгоритм, который решает L за время .

Гипотеза об экспоненциональном времени

Гипотеза об экспоненциональном времени (‘ETH) утверждает, что 3SAT, задача выполнимости булевых формул в конъюнктивной нормальной форме с максимум тремя литералами на предложение и n переменными, не может быть решена за время 2^o(n). Точнее, гипотеза говорит, что существует некая константа c>0, такая, что 3SAT не может быть решена за время 2^cn на любой детерминированной машине Тьюринга. Если через m обозначить число предложений, ETH эквивалентна гипотезе, что k-SAT не может быть решена за время 2^o(m) для любого целого k ≥ 3^[22]. Из гипотезы об экспоненциальном времени следует, что P ≠ NP.

Экспоненциальное время

Говорят, что алгоритм работает за экспоненциальное время, если T(n) ограничено сверху значением 2^poly(n), где poly(n) — некий многочлен от n. Более формально, алгоритм работает за экспоненциальное время, если T(n) ограничено O(2^nk) с некоторой константой k. Задачи, которые выполняются за экспоненциальное время на детерминированных машинах Тьюринга, образуют класс сложности EXP.

Иногда термин экспоненциальное время используется для алгоритмов, для которых T(n) = 2^O(n), где показатель является не более чем линейной функцией от n. Это приводит к классу сложности E^[en].

Двойное экспоненциональное время

Говорят, что алгоритм выполняется за дважды экспоненциональное^[en] время, если T(n) ограничено сверху значением 2^2poly(n), где poly(n) — некоторый многочлен от n. Такие алгоритмы принадлежат классу сложности 2-EXPTIME^[en].

К хорошо известным дважды экспоненциальным алгоритмам принадлежат:

• Процедура вычисления для арифметики Пресбургера
• Вычисление базиса Грёбнера (в худшем случае^[23])
• Элиминация кванторов в вещественно замкнутых полях^[en] требует как минимум дважды экспоненциальное время выполнения ^[24] и может быть выполнена за это время^[25].

Смотрите также

• L-нотация
• Сложность по памяти^[en]

Примечания

In computer science, the time complexity is the computational complexity that describes the amount of computer time it takes to run an algorithm. Time complexity is commonly estimated by counting the number of elementary operations performed by the algorithm, supposing that each elementary operation takes a fixed amount of time to perform. Thus, the amount of time taken and the number of elementary operations performed by the algorithm are taken to be related by a constant factor.

Since an algorithm’s running time may vary among different inputs of the same size, one commonly considers the worst-case time complexity, which is the maximum amount of time required for inputs of a given size. Less common, and usually specified explicitly, is the average-case complexity, which is the average of the time taken on inputs of a given size (this makes sense because there are only a finite number of possible inputs of a given size). In both cases, the time complexity is generally expressed as a function of the size of the input.^[1]: 226 Since this function is generally difficult to compute exactly, and the running time for small inputs is usually not consequential, one commonly focuses on the behavior of the complexity when the input size increases—that is, the asymptotic behavior of the complexity. Therefore, the time complexity is commonly expressed using big O notation, typically , , , , etc., where n is the size in units of bits needed to represent the input.

Algorithmic complexities are classified according to the type of function appearing in the big O notation. For example, an algorithm with time complexity is a linear time algorithm and an algorithm with time complexity for some constant is a polynomial time algorithm.

Table of common time complexities[edit]

The following table summarizes some classes of commonly encountered time complexities. In the table, poly(x) = x^O(1), i.e., polynomial in x.

Name	Complexity class	Running time (T(n))	Examples of running times	Example algorithms
constant time			10	Finding the median value in a sorted array of numbers. Calculating (−1)n
inverse Ackermann time				Amortized time per operation using a disjoint set
iterated logarithmic time				Distributed coloring of cycles
log-logarithmic				Amortized time per operation using a bounded priority queue[2]
logarithmic time	DLOGTIME		,	Binary search
polylogarithmic time
fractional power		where	,	Searching in a kd-tree
linear time			n,	Finding the smallest or largest item in an unsorted array. Kadane’s algorithm. Linear search
«n log-star n» time				Seidel’s polygon triangulation algorithm.
linearithmic time			,	Fastest possible comparison sort Fast Fourier transform.
quasilinear time				Multipoint polynomial evaluation
quadratic time				Bubble sort, Insertion sort, Direct convolution
cubic time				Naive multiplication of two matrices Calculating partial correlation.
polynomial time	P		,	Karmarkar’s algorithm for linear programming AKS primality test[3][4]
quasi-polynomial time	QP		,	Best-known O(log2n)-approximation algorithm for the directed Steiner tree problem.
sub-exponential time (first definition)	SUBEXP	for all		Contains BPP unless EXPTIME (see below) equals MA.[5]
sub-exponential time (second definition)				Best classical algorithm for integer factorization formerly-best algorithm for graph isomorphism
exponential time (with linear exponent)	E		,	Solving the traveling salesman problem using dynamic programming
exponential time	EXPTIME		,	Solving matrix chain multiplication via brute-force search
factorial time				Solving the traveling salesman problem via brute-force search
double exponential time	2-EXPTIME			Deciding the truth of a given statement in Presburger arithmetic

Constant time[edit]

«Constant time» redirects here. For programming technique to avoid a timing attack, see Timing attack § Avoidance.

An algorithm is said to be constant time (also written as time) if the value of (the complexity of the algorithm) is bounded by a value that does not depend on the size of the input. For example, accessing any single element in an array takes constant time as only one operation has to be performed to locate it. In a similar manner, finding the minimal value in an array sorted in ascending order; it is the first element. However, finding the minimal value in an unordered array is not a constant time operation as scanning over each element in the array is needed in order to determine the minimal value. Hence it is a linear time operation, taking time. If the number of elements is known in advance and does not change, however, such an algorithm can still be said to run in constant time.

Despite the name «constant time», the running time does not have to be independent of the problem size, but an upper bound for the running time has to be independent of the problem size. For example, the task «exchange the values of a and b if necessary so that » is called constant time even though the time may depend on whether or not it is already true that . However, there is some constant t such that the time required is always at most t.

Here are some examples of code fragments that run in constant time:

int index = 5;
int item = list[index];
if (condition true) then
    perform some operation that runs in constant time
else
    perform some other operation that runs in constant time
for i = 1 to 100
    for j = 1 to 200
        perform some operation that runs in constant time

If is , where a is any constant value, this is equivalent to and stated in standard notation as being .

Logarithmic time[edit]

An algorithm is said to take logarithmic time when . Since and are related by a constant multiplier, and such a multiplier is irrelevant to big O classification, the standard usage for logarithmic-time algorithms is regardless of the base of the logarithm appearing in the expression of T.

Algorithms taking logarithmic time are commonly found in operations on binary trees or when using binary search.

An algorithm is considered highly efficient, as the ratio of the number of operations to the size of the input decreases and tends to zero when n increases. An algorithm that must access all elements of its input cannot take logarithmic time, as the time taken for reading an input of size n is of the order of n.

An example of logarithmic time is given by dictionary search. Consider a dictionary D which contains n entries, sorted by alphabetical order. We suppose that, for , one may access the kth entry of the dictionary in a constant time. Let denote this kth entry. Under these hypotheses, the test to see if a word w is in the dictionary may be done in logarithmic time: consider , where denotes the floor function. If , then we are done. Else, if , continue the search in the same way in the left half of the dictionary, otherwise continue similarly with the right half of the dictionary. This algorithm is similar to the method often used to find an entry in a paper dictionary.

Polylogarithmic time[edit]

An algorithm is said to run in polylogarithmic time if its time is for some constant k. Another way to write this is .

For example, matrix chain ordering can be solved in polylogarithmic time on a parallel random-access machine,^[6] and a graph can be determined to be planar in a fully dynamic way in time per insert/delete operation.^[7]

Sub-linear time[edit]

An algorithm is said to run in sub-linear time (often spelled sublinear time) if . In particular this includes algorithms with the time complexities defined above.

Typical algorithms that are exact and yet run in sub-linear time use parallel processing (as the NC¹ matrix determinant calculation does), or alternatively have guaranteed assumptions on the input structure (as the logarithmic time binary search and many tree maintenance algorithms do). However, formal languages such as the set of all strings that have a 1-bit in the position indicated by the first bits of the string may depend on every bit of the input and yet be computable in sub-linear time.

The specific term sublinear time algorithm is usually reserved to algorithms that are unlike the above in that they are run over classical serial machine models and are not allowed prior assumptions on the input.^[8] They are however allowed to be randomized, and indeed must be randomized for all but the most trivial of tasks.

As such an algorithm must provide an answer without reading the entire input, its particulars heavily depend on the access allowed to the input. Usually for an input that is represented as a binary string it is assumed that the algorithm can in time request and obtain the value of for any i.

Sub-linear time algorithms are typically randomized, and provide only approximate solutions. In fact, the property of a binary string having only zeros (and no ones) can be easily proved not to be decidable by a (non-approximate) sub-linear time algorithm. Sub-linear time algorithms arise naturally in the investigation of property testing.

Linear time[edit]

An algorithm is said to take linear time, or time, if its time complexity is . Informally, this means that the running time increases at most linearly with the size of the input. More precisely, this means that there is a constant c such that the running time is at most for every input of size n. For example, a procedure that adds up all elements of a list requires time proportional to the length of the list, if the adding time is constant, or, at least, bounded by a constant.

Linear time is the best possible time complexity in situations where the algorithm has to sequentially read its entire input. Therefore, much research has been invested into discovering algorithms exhibiting linear time or, at least, nearly linear time. This research includes both software and hardware methods. There are several hardware technologies which exploit parallelism to provide this. An example is content-addressable memory. This concept of linear time is used in string matching algorithms such as the Boyer–Moore string-search algorithm and Ukkonen’s algorithm.

Quasilinear time[edit]

An algorithm is said to run in quasilinear time (also referred to as log-linear time) if for some positive constant k;^[9] linearithmic time is the case .^[10] Using soft O notation these algorithms are . Quasilinear time algorithms are also for every constant and thus run faster than any polynomial time algorithm whose time bound includes a term for any .

Algorithms which run in quasilinear time include:

• In-place merge sort,
• Quicksort, , in its randomized version, has a running time that is in expectation on the worst-case input. Its non-randomized version has an running time only when considering average case complexity.
• Heapsort, , merge sort, introsort, binary tree sort, smoothsort, patience sorting, etc. in the worst case
• Fast Fourier transforms,
• Monge array calculation,

In many cases, the running time is simply the result of performing a operation n times (for the notation, see Big O notation § Family of Bachmann–Landau notations). For example, binary tree sort creates a binary tree by inserting each element of the n-sized array one by one. Since the insert operation on a self-balancing binary search tree takes time, the entire algorithm takes time.

Comparison sorts require at least comparisons in the worst case because , by Stirling’s approximation. They also frequently arise from the recurrence relation .

Sub-quadratic time[edit]

An algorithm is said to be subquadratic time if .

For example, simple, comparison-based sorting algorithms are quadratic (e.g. insertion sort), but more advanced algorithms can be found that are subquadratic (e.g. shell sort). No general-purpose sorts run in linear time, but the change from quadratic to sub-quadratic is of great practical importance.

Polynomial time[edit]

An algorithm is said to be of polynomial time if its running time is upper bounded by a polynomial expression in the size of the input for the algorithm, that is, T(n) = O(n^k) for some positive constant k.^[1][11] Problems for which a deterministic polynomial-time algorithm exists belong to the complexity class P, which is central in the field of computational complexity theory. Cobham’s thesis states that polynomial time is a synonym for «tractable», «feasible», «efficient», or «fast».^[12]

Some examples of polynomial-time algorithms:

Strongly and weakly polynomial time[edit]

In some contexts, especially in optimization, one differentiates between strongly polynomial time and weakly polynomial time algorithms. These two concepts are only relevant if the inputs to the algorithms consist of integers.

Strongly polynomial time is defined in the arithmetic model of computation. In this model of computation the basic arithmetic operations (addition, subtraction, multiplication, division, and comparison) take a unit time step to perform, regardless of the sizes of the operands. The algorithm runs in strongly polynomial time if:^[13]

1. the number of operations in the arithmetic model of computation is bounded by a polynomial in the number of integers in the input instance; and
2. the space used by the algorithm is bounded by a polynomial in the size of the input.

Any algorithm with these two properties can be converted to a polynomial time algorithm by replacing the arithmetic operations by suitable algorithms for performing the arithmetic operations on a Turing machine. The second condition is strictly necessary: given the integer (which takes up space proportional to n in the Turing machine model), it is possible to compute with n multiplications using repeated squaring. However, the space used to represent is proportional to , and thus exponential rather than polynomial in the space used to represent the input. Hence, it is not possible to carry out this computation in polynomial time on a Turing machine, but it is possible to compute it by polynomially many arithmetic operations.

However, for the first condition, there are algorithms that run in a number of Turing machine steps bounded by a polynomial in the length of binary-encoded input, but do not take a number of arithmetic operations bounded by a polynomial in the number of input numbers. The Euclidean algorithm for computing the greatest common divisor of two integers is one example. Given two integers and , the algorithm performs arithmetic operations on numbers with
at most bits. At the same time, the number of arithmetic operations cannot be bounded by the number of integers in the input (which is constant in this case, there are always only two integers in the input). Due to the latter observation, the algorithm does not run in strongly polynomial time. Its real running time depends logarithmically on the magnitudes of and (that is, on their length in bits) and not only on the number of integers in the input.

An algorithm that runs in polynomial time but that is not strongly polynomial is said to run in weakly polynomial time.^[14]
A well-known example of a problem for which a weakly polynomial-time algorithm is known, but is not known to admit a strongly polynomial-time algorithm, is linear programming. Weakly polynomial time should not be confused with pseudo-polynomial time, which depends linearly on the magnitude of values in the problem and is not truly polynomial time.

Complexity classes[edit]

The concept of polynomial time leads to several complexity classes in computational complexity theory. Some important classes defined using polynomial time are the following.

• P: The complexity class of decision problems that can be solved on a deterministic Turing machine in polynomial time
• NP: The complexity class of decision problems that can be solved on a non-deterministic Turing machine in polynomial time
• ZPP: The complexity class of decision problems that can be solved with zero error on a probabilistic Turing machine in polynomial time
• RP: The complexity class of decision problems that can be solved with 1-sided error on a probabilistic Turing machine in polynomial time.
• BPP: The complexity class of decision problems that can be solved with 2-sided error on a probabilistic Turing machine in polynomial time
• BQP: The complexity class of decision problems that can be solved with 2-sided error on a quantum Turing machine in polynomial time

P is the smallest time-complexity class on a deterministic machine which is robust in terms of machine model changes. (For example, a change from a single-tape Turing machine to a multi-tape machine can lead to a quadratic speedup, but any algorithm that runs in polynomial time under one model also does so on the other.) Any given abstract machine will have a complexity class corresponding to the problems which can be solved in polynomial time on that machine.

Superpolynomial time[edit]

An algorithm is defined to take superpolynomial time if T(n) is not bounded above by any polynomial. Using little omega notation, it is ω(n^c) time for all constants c, where n is the input parameter, typically the number of bits in the input.

For example, an algorithm that runs for 2ⁿ steps on an input of size n requires superpolynomial time (more specifically, exponential time).

An algorithm that uses exponential resources is clearly superpolynomial, but some algorithms are only very weakly superpolynomial. For example, the Adleman–Pomerance–Rumely primality test runs for n^{O(log log n)} time on n-bit inputs; this grows faster than any polynomial for large enough n, but the input size must become impractically large before it cannot be dominated by a polynomial with small degree.

An algorithm that requires superpolynomial time lies outside the complexity class P. Cobham’s thesis posits that these algorithms are impractical, and in many cases they are. Since the P versus NP problem is unresolved, it is unknown whether NP-complete problems require superpolynomial time.

Quasi-polynomial time[edit]

Quasi-polynomial time algorithms are algorithms that run longer than polynomial time, yet not so long as to be exponential time. The worst case running time of a quasi-polynomial time algorithm is for some fixed . For we get a polynomial time algorithm, for we get a sub-linear time algorithm.

Quasi-polynomial time algorithms typically arise in reductions from an NP-hard problem to another problem. For example, one can take an instance of an NP hard problem, say 3SAT, and convert it to an instance of another problem B, but the size of the instance becomes . In that case, this reduction does not prove that problem B is NP-hard; this reduction only shows that there is no polynomial time algorithm for B unless there is a quasi-polynomial time algorithm for 3SAT (and thus all of NP). Similarly, there are some problems for which we know quasi-polynomial time algorithms, but no polynomial time algorithm is known. Such problems arise in approximation algorithms; a famous example is the directed Steiner tree problem, for which there is a quasi-polynomial time approximation algorithm achieving an approximation factor of (n being the number of vertices), but showing the existence of such a polynomial time algorithm is an open problem.

Other computational problems with quasi-polynomial time solutions but no known polynomial time solution include the planted clique problem in which the goal is to find a large clique in the union of a clique and a random graph. Although quasi-polynomially solvable, it has been conjectured that the planted clique problem has no polynomial time solution; this planted clique conjecture has been used as a computational hardness assumption to prove the difficulty of several other problems in computational game theory, property testing, and machine learning.^[15]

The complexity class QP consists of all problems that have quasi-polynomial time algorithms. It can be defined in terms of DTIME as follows.^[16]

Relation to NP-complete problems[edit]

In complexity theory, the unsolved P versus NP problem asks if all problems in NP have polynomial-time algorithms. All the best-known algorithms for NP-complete problems like 3SAT etc. take exponential time. Indeed, it is conjectured for many natural NP-complete problems that they do not have sub-exponential time algorithms. Here «sub-exponential time» is taken to mean the second definition presented below. (On the other hand, many graph problems represented in the natural way by adjacency matrices are solvable in subexponential time simply because the size of the input is the square of the number of vertices.) This conjecture (for the k-SAT problem) is known as the exponential time hypothesis.^[17] Since it is conjectured that NP-complete problems do not have quasi-polynomial time algorithms, some inapproximability results in the field of approximation algorithms make the assumption that NP-complete problems do not have quasi-polynomial time algorithms. For example, see the known inapproximability results for the set cover problem.

Sub-exponential time[edit]

The term sub-exponential time is used to express that the running time of some algorithm may grow faster than any polynomial but is still significantly smaller than an exponential. In this sense, problems that have sub-exponential time algorithms are somewhat more tractable than those that only have exponential algorithms. The precise definition of «sub-exponential» is not generally agreed upon,^[18] and we list the two most widely used ones below.

First definition[edit]

A problem is said to be sub-exponential time solvable if it can be solved in running times whose logarithms grow smaller than any given polynomial. More precisely, a problem is in sub-exponential time if for every ε > 0 there exists an algorithm which solves the problem in time O(2^nε). The set of all such problems is the complexity class SUBEXP which can be defined in terms of DTIME as follows.^{[5][19][20][21]}

This notion of sub-exponential is non-uniform in terms of ε in the sense that ε is not part of the input and each ε may have its own algorithm for the problem.

Second definition[edit]

Some authors define sub-exponential time as running times in .^[17][22][23] This definition allows larger running times than the first definition of sub-exponential time. An example of such a sub-exponential time algorithm is the best-known classical algorithm for integer factorization, the general number field sieve, which runs in time about , where the length of the input is n. Another example was the graph isomorphism problem, which the best known algorithm from 1982 to 2016 solved in . However, at STOC 2016 a quasi-polynomial time algorithm was presented.^[24]

It makes a difference whether the algorithm is allowed to be sub-exponential in the size of the instance, the number of vertices, or the number of edges. In parameterized complexity, this difference is made explicit by considering pairs of decision problems and parameters k. SUBEPT is the class of all parameterized problems that run in time sub-exponential in k and polynomial in the input size n:^[25]

More precisely, SUBEPT is the class of all parameterized problems for which there is a computable function with and an algorithm that decides L in time .

Exponential time hypothesis[edit]

The exponential time hypothesis (ETH) is that 3SAT, the satisfiability problem of Boolean formulas in conjunctive normal form with at most three literals per clause and with n variables, cannot be solved in time 2^o(n). More precisely, the hypothesis is that there is some absolute constant c > 0 such that 3SAT cannot be decided in time 2^cn by any deterministic Turing machine. With m denoting the number of clauses, ETH is equivalent to the hypothesis that kSAT cannot be solved in time 2^o(m) for any integer k ≥ 3.^[26] The exponential time hypothesis implies P ≠ NP.

Exponential time[edit]

An algorithm is said to be exponential time, if T(n) is upper bounded by 2^poly(n), where poly(n) is some polynomial in n. More formally, an algorithm is exponential time if T(n) is bounded by O(2^nk) for some constant k. Problems which admit exponential time algorithms on a deterministic Turing machine form the complexity class known as EXP.

Sometimes, exponential time is used to refer to algorithms that have T(n) = 2^O(n), where the exponent is at most a linear function of n. This gives rise to the complexity class E.

Factorial time[edit]

An algorithm is said to be factorial time if T(n) is upper bounded by the factorial function n!. Factorial time is a subset of exponential time (EXP) because for all . However, it is not a subset of E.

An example of an algorithm that runs in factorial time is bogosort, a notoriously inefficient sorting algorithm based on trial and error. Bogosort sorts a list of n items by repeatedly shuffling the list until it is found to be sorted. In the average case, each pass through the bogosort algorithm will examine one of the n! orderings of the n items. If the items are distinct, only one such ordering is sorted. Bogosort shares patrimony with the infinite monkey theorem.

Double exponential time[edit]

An algorithm is said to be double exponential time if T(n) is upper bounded by 2^2poly(n), where poly(n) is some polynomial in n. Such algorithms belong to the complexity class 2-EXPTIME.

Well-known double exponential time algorithms include:

• Decision procedures for Presburger arithmetic
• Computing a Gröbner basis (in the worst case^[27])
• Quantifier elimination on real closed fields takes at least double exponential time,^[28] and can be done in this time.^[29]

See also[edit]

• L-notation
• Space complexity

References[edit]