Математика,
вопрос задал CoolNomy,
4 года назад
Ответы на вопрос
Ответил ksemkin09
1
Ответ:
если вся работа 30 мин нужно 30*3/5 и мы узнаем сколько длился эксперимент 30*3/5=18 мин
ответ 18 мин
ksemkin09:
воть
ksemkin09:
я чтарался
CoolNomy:
Спасибо
ksemkin09:
старался
ksemkin09:
пожалуйста
Аноним:
хорош
Предыдущий вопрос
Следующий вопрос
Новые вопросы
Окружающий мир,
7 месяцев назад
короткий рассказ о граните…
Математика,
7 месяцев назад
помогите пожалуйста 2,4,6 пожалуйста …
Русский язык,
4 года назад
Русский срочно 50 балов…
Физкультура и спорт,
4 года назад
Как правильно делать отжимания,подскажите пожалуйста…
Алгебра,
6 лет назад
На доске написаны числа 1, 4 и 5. За один ход разрешается выбрать любые два числа и прибавить к одному из них 1, а к другому 2. Можно ли через несколько ходов сделать все числа равными?
Биология,
6 лет назад
Каааакк ! Помогите срочно
Сколько семязачаток в завязи пестика вишни и огурца?
|
РАССМОТРЕНО |
СОГЛАСОВАНО |
УТВЕРЖДЕНО |
|
на заседании ПЦК протокол № 7 от 10.04.2021 руководитель ПЦК ______/Г.А.Шиховцова/ |
заместитель директора _______ /М.Л.Сафарова/ от 15.04.2021 |
Директор _______ /Г.В.Мисюля/ Приказ № ГС-13-227/1 от 05.04.2021 |
КОНТРОЛЬНО-ИЗМЕРИТЕЛЬНЫЙ МАТЕРИАЛ
по математике
для проведения итоговой контрольной работы
учащихся 6 классов
(базовый уровень)
2020 — 2021 учебный год
Учитель
Мингазова Вилия Ринатовна
СПЕЦИФИКАЦИЯ
итоговой контрольной работы по предмету «математика»
для 6-х классов
-
Назначение итоговой контрольной работы
Итоговая контрольная работа проводится с целью определения уровня усвоения учащимися контрольных элементов содержания и сформированности учебных действий, предусмотренных программой по математике для 6-х классов.
-
Документы, определяющие содержание и характеристики итоговой контрольной работы:
ФГОС основного общего образования (приказ Министерства образования и науки Российской Федерации от 17 декабря 2010 г. №1897 (с изменениями и дополнениями);
Основная образовательная программа основного общего образования МБОУ гимназии имени Ф.К.Салманова (приказ от 12.04.2018 №12/ГС/13-223/17).
-
Время выполнения итоговой контрольной работы
Итоговая контрольная работа рассчитана на 60 минут
-
Условия проведения итоговой контрольной работы
Выполняя итоговую контрольную работу, учащийся должен строго следовать инструкции к заданиям, представленной в КИМ. Ответы на задания вносятся учащимся непосредственно в КИМ, в поле, предусмотренное для внесения ответов, в том формате, какого требует инструкция к заданию.
При выполнении итоговой контрольной работы учащимся не разрешается пользоваться учебниками, рабочими тетрадями, справочными материалами. При необходимости ученик может использовать черновик. Записи в черновике учителем не проверяются и не оцениваются.
-
Структура и содержание итоговой контрольной работы
Итоговая контрольная работа состоит из 12 заданий, 10 из который базового уровня сложности, 2 — повышенного.
Типы заданий:
Содержание заданий соответствует основным требованиям примерной программы по математике для основного общего образования. Для разработки заданий использован Кодификатор элементов содержания и требований к уровню подготовки учащихся, освоивших основные общеобразовательные программы основного общего образования, по математике, в который включены планируемые образовательные результаты, которые относятся в блоку «Ученик научится».
-
План итоговой контрольной работы
Номер задания
Код КЭС
Тип задания
ВО (с выбором ответа)
КО (с кратким ответом)
РО (с развёрнутым ответом)
Уровень сложности
Б – базовый
П – повышенный
В — высокий
Примерное время на выполнения задания, мин
1.3.4
КО
Б
4
1.3.4
КО
Б
4
1.3.4
КО
Б
4
1.3.4
КО
Б
4
3.1.2
КО
Б
4
2.1.1
КО
Б
4
1.5.5
КО
Б
4
1.2.3
КО
Б
6
1.3.3
КО
Б
6
1.5.6
КО
Б
4
6.2.1
РО
П
8
3.3.2
РО
П
8
-
Распределение заданий итоговой контрольной работы по содержанию и проверяемым умениям
|
№ заданий |
КЭС |
Контролируемые элементы содержания |
КПУ |
Проверяемые требования к уровню подготовки |
Число заданий |
|
8 |
1.2.3 |
Нахождение части от целого и целого по его части |
1.3 |
Решать текстовые задачи, включая задачи, связанные с отношением, пропорциональностью величин, дробями, процентами |
1 |
|
9 |
1.3.3 |
Сравнение рациональных чисел |
1.4 |
Изображать числа точками на координатной прямой |
1 |
|
1, 2, 3, 4 |
1.3.4 |
Арифметические действия с рациональными числами |
1.1 |
Выполнять, сочетая устные и письменные приёмы, арифметические действия с рациональными числами |
4 |
|
7 |
1.5.5 |
Отношение, выражение отношения в процентах |
1.3 |
Решать текстовые задачи, включая задачи, связанные с отношением, пропорциональностью величин, дробями, процентами |
1 |
|
10 |
1.5.6 |
Пропорция. Пропорциональная и обратно пропорциональная зависимости |
1.3 |
Решать текстовые задачи, включая задачи, связанные с отношением, пропорциональностью величин, дробями, процентами |
1 |
|
6 |
2.1.1 |
Буквенные выражения. Числовое значение буквенного выражения |
2 |
Уметь выполнять преобразования алгебраических выражений |
1 |
|
5 |
3.1.2 |
Линейное уравнение |
3.1 |
Решать линейные, квадратные уравнения и рациональные уравнения, сводящиеся к ним, системы двух линейных уравнений и несложные нелинейные системы |
1 |
|
12 |
3.3.2 |
Решение текстовых задач алгебраическим способом |
3.4 |
Решать текстовые задачи алгебраическим методом, интерпретировать полученный результат, проводить отбор решений исходя из формулировки задачи |
1 |
|
11 |
6.2.1 |
Декартовы координаты на плоскости; координаты точки |
4.1 |
Определять координаты точки плоскости, строить точки с заданными координатами |
1 |
-
Ответы к заданиям итоговой контрольной работы
|
№ задания |
Правильные ответы |
Max балл |
Условия постановки балла |
|
|
Вариант 1 |
Вариант 2 |
|||
|
|
-9,5 |
1,5 |
1 |
Указан верный ответ |
|
|
-4,05 |
8,2 |
1 |
Указан верный ответ |
|
|
4,4 |
2,04 |
1 |
Указан верный ответ |
|
|
37,7 |
-32,3 |
1 |
Указан верный ответ |
|
|
5,7 |
-6,3 |
1 |
Указан верный ответ |
|
|
12,8 |
3 |
1 |
Указан верный ответ |
|
|
16 |
10 |
1 |
Указан верный ответ |
|
|
25 |
18 |
1 |
Указан верный ответ |
|
|
-5,2 |
-3,07 |
1 |
Указан верный ответ |
|
|
1,6 |
11,25 |
1 |
Указан верный ответ |
|
|
C(-7;4) |
Е(-2;2) |
2 |
Правильно отмечены на координатной плоскости точки и верно найдены координаты луча – 2 балла. Правильно отмечены на координатной плоскости точки – 1 балл. |
|
|
Решение: Пусть в ведре воды x л, тогда в баке 3х л. Составим и решим уравнение: х+3х=24 4х=24 х=6 Ответ: в ведре 6 л воды. |
Решение: Пусть одна часть отрезка x см, тогда вторая 2х см. Составим и решим уравнение: х+2х=36 3х=36 х=12 2х=24 Ответ: одна часть 12 см, вторая 24 см. |
2 |
Правильно составлено уравнение, получен верный ответ – 2 балла. Правильно составлено уравнение, но допущена одна арифметическая ошибка, с ее учетом решение доведено до конца – 1 балл. |
9. Система оценивания результатов выполнения итоговой контрольной работы
|
Первый тестовый балл, % |
90-100 |
70-89 |
50-69 |
25-49 |
Менее 25 |
|
Количество баллов |
13-14 |
10-12 |
7-9 |
4-6 |
0-3 |
|
Отметка |
5 |
4 |
3 |
2 |
1 |
План итоговой контрольной работы по математике для 6-х классов (60 минут)
|
Номер задания |
Код КЭС |
Расшифровка КЭС |
Проверяемое умение |
Тип задания* |
Уровень сложности** |
Примерное время на выполнения задания, мин |
|
|
1.3.4 |
Арифметические действия с рациональными числами |
Выполнять, сочетая устные и письменные приёмы, арифметические действия с рациональными числами. |
КО |
Б |
4 |
|
|
1.3.4 |
Арифметические действия с рациональными числами |
Выполнять, сочетая устные и письменные приёмы, арифметические действия с рациональными числами |
КО |
Б |
4 |
|
|
1.3.4 |
Арифметические действия с рациональными числами |
Выполнять, сочетая устные и письменные приёмы, арифметические действия с рациональными числами |
КО |
Б |
4 |
|
|
1.3.4 |
Арифметические действия с рациональными числами |
Выполнять, сочетая устные и письменные приёмы, арифметические действия с рациональными числами |
КО |
Б |
4 |
|
|
3.1.2 |
Линейное уравнение |
Решать линейные уравнения |
КО |
Б |
4 |
|
|
2.1.1 |
Буквенные выражения. Числовое значение буквенного выражения |
Уметь выполнять преобразования алгебраических выражений |
КО |
Б |
4 |
|
|
1.5.5 |
Отношение, выражение отношения в процентах |
Решать текстовые задачи, включая задачи, связанные с отношением, пропорциональностью величин, дробями, процентами |
КО |
Б |
4 |
|
|
1.2.3 |
Нахождение части от целого и целого по его части |
Решать текстовые задачи, включая задачи, связанные с отношением, пропорциональностью величин, дробями, процентами |
КО |
Б |
6 |
|
|
1.3.3 |
Сравнение рациональных чисел |
Изображать числа точками на координатной прямой |
КО |
Б |
6 |
|
|
1.5.6 |
Пропорция. Пропорциональная и обратно пропорциональная зависимости |
Решать текстовые задачи, включая задачи, связанные с отношением, пропорциональностью величин, дробями, процентами |
КО |
Б |
4 |
|
|
6.2.1 |
Декартовы координаты на плоскости; координаты точки |
Определять координаты точки плоскости, строить точки с заданными координатами |
РО |
П |
8 |
|
|
3.3.2 |
Решение текстовых задач алгебраическим способом |
Решать текстовые задачи алгебраическим методом, интерпретировать полученный результат, проводить отбор решений исходя из формулировки задачи |
РО |
П |
8 |
* Типы заданий — ВО (с выбором ответа), КО (с кратким ответом), РО (с развёрнутым ответом)
**Уровень сложности заданий — Б – базовый, П – повышенный, В — высокий
Итоговая контрольная работа по математике
6 класс 2020-2021 учебный год
1 вариант
ЧАСТЬ 1
Задания 1 – 10 решите на черновике, ответы занесите в таблицу бланка ответов.
№ 1. – 3,8 – 5,7. № 2. 37,26 : (– 9,2).
№ 3. – 2,9 + 7,3. № 4. – 5,8 ∙ (– 6,5).
№ 5. Решите уравнение: х + 6,4 = 12,1.
№ 6. Найдите значение выражения: m+2n при m=6,4, n=3,2
№ 7. В шестом классе 28 учащихся. Число мальчиков относиться к числу девочек как 3 : 4. Сколько в классе девочек?
№ 8. Сергей заполнил 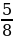
№ 9. Даны числа – 2,5; – 2,05; – 5,2; – 5. Какое из них наименьшее?
№ 10. Найдите неизвестный член пропорции 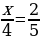
ЧАСТЬ 2
В заданиях 11 – 12 запишите полное решение и ответ.
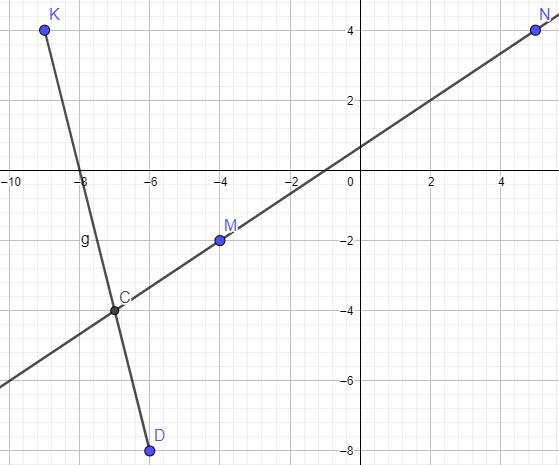
№ 11. На координатной плоскости проведите прямую MN через точки M(− 4; − 2) и N(5; 4) и отрезок KD, соединяющий точки K(− 9; 4) и D(− 6; − 8). Найдите координаты точки пересечения отрезка KD и прямой MN.
№ 12. В баке и ведре 24 литра воды. В ведре воды в 3 раза меньше, чем в баке. Сколько литров воды в ведре.
Итоговая контрольная работа по математике
6 класс 2020-2021 учебный год
2 вариант
ЧАСТЬ 1
Задания 1 – 10 решите на черновике, ответы занесите в таблицу бланка ответов.
№ 1. – 4,2 + 5,7. № 2. – 17,34 : (– 8,5).
№ 3. – 2,3 – 5,9. № 4. – 3,8 ∙ 8,5.
№ 5. Решите уравнение: 2,4 – х = 8,7.
№ 6. Найдите значение выражения: 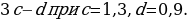
№ 7. В пятом классе 25 учащихся. Число девочек относиться к числу мальчиков как 3 : 2 Сколько в классе мальчиков?
№ 8. Во время лабораторной работы по физике эксперимент длился 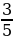
№ 9. Даны числа 7,3; 3,07; 3,7; 7. Какое из них наибольшее?
№ 10. Найдите неизвестный член пропорции 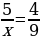
ЧАСТЬ 2
В заданиях 11 – 12 запишите полное решение и ответ.
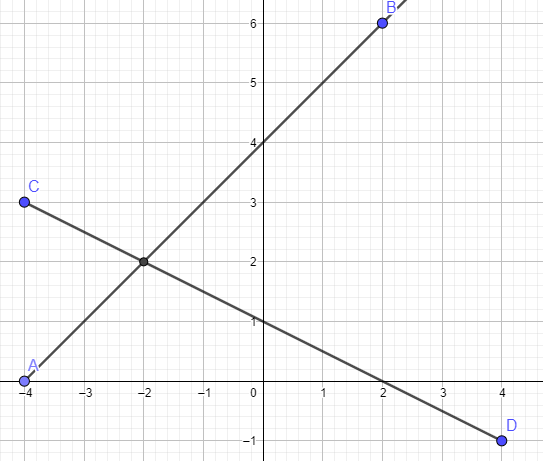
№ 11. Отметьте на координатной плоскости проведите точки А(− 4; 0), В(2; 6),С(− 4; 3) и D(4; − 1). Проведите луч АВ и отрезок СD. Найдите координаты точки пересечения луча АВ и отрезка СD.
№ 12. Отрезок длинной 36 см разрезали на две части так, что одна часть оказалась в 2 раза больше другой. Чему равна длина каждой части?
Итоговая контрольная работа по математике
учени ___ 6 ___ класса
____________________________________
Вариант ____
Ответы к заданиям 1 – 10 занесите в таблицу:
|
Номер задания |
1 |
2 |
3 |
4 |
5 |
|
Ответ |
|||||
|
Номер задания |
6 |
7 |
8 |
9 |
10 |
|
Ответ |
К заданиям 11 – 12 запишите полное решение и ответ:
Тип 5 № 1610
Тимур заметил, что если он погружается с головой в ванну, изначально заполненную водой на 0,7 объёма, то уровень воды доходит до края ванны. Найдите объём Тимура, если ванна вмещает 160 л. Ответ запишите в л.
Спрятать решение
Решение.
По закону Архимеда объём тела равен объёму вытесненной жидкости. Объём сосуда V, тогда объём жидкости вначале был 0,7V. Тогда объём вытесненной жидкости равен 0,3V. Получаем: — объём Тимура.
Ответ: 48.
Источник: ВПР 2020 год по физике 7 класс. Вариант 1.
Внимание! Администрация сайта rosuchebnik.ru не несет ответственности за содержание методических разработок, а также за соответствие разработки ФГОС.
- Участник: Мингалеев Артур Эдуардович
- Руководитель: Баскова Мария Аркадьевна
Цель настоящего исследования состояла в получении значения ускорения свободного падения при помощи математического маятника в условиях разного уровня высоты на уровнем моря.
1. Введение
Первым человеком, изучавшим природу падения тел, был греческий ученый Аристотель. Затем Галилео Галилей обобщил и не проанализировал опыт и эксперименты нескольких поколений исследователей. Он предположил, что в среде, свободной от воздуха, все тела будут падать с одинаковой скоростью. Также Галилей предположил, что во время падения скорость тел постоянно увеличивается. Экспериментировать со свободным падением тел продолжил Исаак Ньютон. В его выводах прослеживается мысль, что на Луне и на других планетах сила тяжести, воздействующая на одно и то же тело, будет неодинакова, зависит она напрямую от массы космического тела. Например, ускорение g на Луне в несколько раз меньше, чем на Земле. Таким образом, зная массу планеты, можно вычислить ускорение свободного падения тела на этой планете.
Цель настоящего исследования состояла в получении значения ускорения свободного падения при помощи математического маятника в условиях разного уровня высоты на уровнем моря. Для достижения поставленной цели были сформулированы следующие задачи исследования:
- Ознакомиться с историей открытия свободного падения тел;
- Изучить методы измерения ускорения свободного падения на поверхности Земли;
- Провести самостоятельные измерения ускорения свободного падения при помощи математического маятника;
- Провести измерения на различных высотах.
Гипотеза исследования: логично предположить, что ускорение свободного падения, полученные в разных экспериментах, должны быть близки к значению 9,8 м/с2 и отличаться на сотые или тысячные доли на глубине станции метро Кремлевская (–34 м) и на высоте небоскреба «Лазурные небеса» (+120 м). Также результаты измерений и вычислений могут отличаться погрешностью измерений.
Методы изучения: самостоятельная, индивидуальная работа в сочетании с теоретическими исследовательскими, проектными формами работы.
Читая много различной в том числе и технической литературы, я узнал о практическом применении различия ускорения свободного падения в разных точках на поверхности Земли. Я измерял g различными способами, рассчитывал погрешности измерений, опираясь на общепринятое значение g, учился грамотно проводить эксперимент. Выяснил, что свободное падение – движение равноускоренное. Ускорение свободного падения не зависит от массы тела. Гипотезу о том, что значения ускорения свободного падения должны быть близки к значению 9,8 м/с2 и отличаться только погрешностью измерений удалось подтвердить разными экспериментами. Наиболее точный результат ускорения свободного падения у меня получился с помощью математического маятника. Поэтому для исследования изменения значения ускорения свободного падения с высотой я выбрал именно этот способ измерения. Погрешность составила не более 10%.
В дальнейшем я хотел бы самостоятельно исследовать зависимость значения ускорения свободного падения от географического положения.
2. Основная часть
2.1. Исторические сведения об открытии свободного падения и методах его измерения
Еще тысячелетия назад люди замечали, что большая часть предметов падает все быстрее и быстрее, а некоторые падают равномерно. Но как именно падают эти предметы – этот вопрос первобытных людей не занимал. Тем не менее нашлись люди, которые по мере возможностей начали исследовать это явление. Сначала они проделывали опыты с двумя предметами. Например, брали два камня, и давали возможность им свободно падать, выпустив их из рук одновременно. Затем снова бросали два камня, но уже в стороны по горизонтали. Потом бросали один камень в сторону, и в тот же момент выпускали из рук второй, но так, чтобы он просто падал по вертикали. Люди извлекли из таких опытов много сведений о природе. Из опытов с падающими телами люди установили, что маленький и большой камни, выпущенные из рук одновременно, падают с одинаковой скоростью. То же самое можно сказать о кусках свинца, золота, железа, стекла, и т.д. самых разных размеров. Из подобных опытов выводиться простое общее правило: свободное падение всех тел происходит одинаково независимо от размера и материала, из которого тела сделаны. Между наблюдением за причинной связью явлений и тщательно выполненными экспериментами, вероятно, долго существовал разрыв. Две тысячи лет назад некоторые древние ученые, по-видимому, проводили вполне разумные опыты с падающими телами. Великий греческий философ и ученый Аристотель, по-видимому придерживался распространенного представления о том, что тяжелые тела падают быстрее, чем легкие. Аристотель и его последователи стремились объяснить, почему происходят те или иные явления, но не всегда заботились о том, чтобы пронаблюдать, что происходит и как происходит. Он говорил, что тела стремятся найти свое естественное место на поверхности Земли. В XIV столетии группа философов из Парижа восстала против теории Аристотеля и предложила значительно более разумную схему, которая передавалась из поколения в поколение и распространилась до Италии, оказав двумя столетиями позднее влияние на Галилея. Парижские философы говорили об ускоренном движении и даже о постоянном ускорении, объясняя эти понятия архаичным языком. Великий итальянский ученый Галилео Галилей обобщил имеющиеся сведения и представления и критически их проанализировал, а затем описал и начал распространять то, что считал верным. Галилей понимал, что последователей Аристотеля сбивало с толку сопротивление воздуха. Он указал, что плотные предметы, для которых сопротивление воздуха несущественно, падают почти с одинаковой скоростью.
Предположив, что произошло бы в случае свободного падения тел в вакууме, Галилей вывел следующие законы падения тел для идеального случая: все тела при падении движутся одинаково; начав падать одновременно, они движутся с одинаковой скоростью; движение происходит с «постоянным ускорением»; темп увеличения скорости тела не меняется, т.е. за каждую последующую секунду скорость тела возрастает на одну и ту же величину. Существует легенда, будто Галилей проделал большой демонстрационный опыт, бросая легкие и тяжелые предметы с вершины Пизанской падающей башни (одни говорят, что он бросал стальные и деревянные шары, а другие утверждают, будто это были железные шары весом 0,5 и 50 кг). Описаний такого публичного опыта нет, и Галилей, несомненно, не стал таким способом демонстрировать свое правило. Галилей знал, что деревянный шар намного отстал бы при падении от железного, но считал, что для демонстрации различной скорости падения двух неодинаковых железных шаров потребовалась бы более высокая башня. Итак, мелкие камни слегка отстают в падении от крупных, и разница становится тем более заметной, чем большее расстояние пролетают камни. И дело тут не просто в размере тел: деревянный и стальной шары одинакового размера падают не строго одинаково. Галилей знал, что простому описанию падения тел мешает сопротивление воздуха. Но он мог лишь уменьшить его и не мог устранить его полностью. Поэтому ему пришлось вести доказательство, переходя от реальных наблюдений к постоянно уменьшающимся сопротивлением воздуха к идеальному случаю, когда сопротивление воздуха отсутствует. Позже, оглядываясь назад, он смог объяснить различия в реальных экспериментах, приписав их сопротивлению воздуха.
Вскоре после Галилея были созданы воздушные насосы, которые позволили произвести эксперименты со свободным падением в вакууме. С этой целью Ньютон выкачал воздух из длинной стеклянной трубки и бросил сверху одновременно птичье перо и золотую монету. Даже столь сильно различающиеся по своей плотности тела падали с одинаковой скоростью. Именно этот опыт дал решающую проверку предположения Галилея. Опыты и рассуждения Галилея привели к простому правилу, точно справедливому в случае свободного падения тел в вакууме. Это правило в случае свободного падения тел в воздухе выполняется с ограниченной точностью. Поэтому верить в него, как в идеальный случай нельзя. Для полного изучения свободного падения тел необходимо знать, какие при падении происходят изменения температуры, давления, и др., то есть исследовать и другие стороны этого явления. Так Галилей установил признак равноускоренного движения:
S1 : S2 : S3 : … = 1 : 2 : 3 : … (при V0 = 0)
Таким образом, можно предположить, что свободное падение есть равноускоренное движение. Так как для равноускоренного движения перемещение рассчитывается по формуле, то если взять три некоторые точки 1,2,3 через которые проходит тело при падении и записать: (ускорение при свободном падении для всех тел одинаково), получится, что отношение перемещений при равноускоренном движении равно:
S1 : S2 : S3 = t12 : t22 : t32 (2)
Остается еще добавить небольшой комментарий относительно экспериментов со свободным падением тел Исаака Ньютона. В его выводах прослеживается мысль, что на Луне и на других планетах сила тяжести, воздействующая на одно и то же тело, будет неодинакова, зависит она напрямую от массы космического тела. Например, ускорение g на Луне в несколько раз меньше, чем на Земле. Таким образом, зная массу планеты, можно вычислить ускорение свободного падения тела на этой планете.
2.2. Практическая значимость нахождения значения ускорения свободного падения
Я много читаю и, как следствие склонен фантазировать. Для меня практическая значимость исследования заключается в возможности прогнозирования форм жизни на небесных телах, с которыми человечество столкнется при неизбежном освоении космоса. Ведь от значения g на другой планете зависит не только сила тяжести. Люди заранее смогут узнать, какие существа встретят их на той или иной планете, какими физическими характеристиками они будут обладать.
2.3. Методы измерения ускорения свободного падения
На самом деле методов по измерению ускорения свободного падения достаточно много. Приведу только те, которые сам испробовал.
1) Измерение ускорения свободного падения с помощью наклонной плоскости
Понадобится следующее оборудование:деревянный брусок, трибометр, штатив с муфтой и лапкой, электронный секундомер, динамометр, измерительная лента, линейка. Рассматривая движение бруска вниз по наклонной плоскости, можно записать второй закон Ньютона в векторном виде:
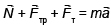
Записывая второй закон Ньютона в проекциях на оси координат:
Ох: – Fтр + mgsinα = ma
Oy: N – mgcosα = 0
и учитывая, что N = mgcosα; Fтр = μN; можно решить данную систему уравнений и получить ускорение свободного падения:
При этом ускорение a можно вычислить из формулы
так как начальная скорость бруска при скольжении по наклонной плоскости равна 0:
Видим, что для этого нужно измерить длину наклонной плоскости и время скольжения по ней бруска.
Для вычисления sinα и cosα нужно знать длину S и высоту h наклонной плоскости:
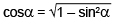
Для определения коэффициента трения скольжения положим трибометр на горизонтальную поверхность и с помощью динамометра равномерно протащим по нему брусок. В этом случае на брусок будут действовать 4 силы: сила тяжести, сила упругости пружины динамометра, сила трения, сила реакции опоры.
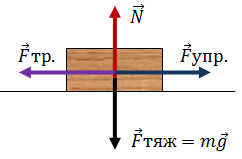
При равномерном движении бруска эти силы будут попарно равны: Fтр = Fупр, Fтяж = N, т. е. Fупр = μFтяж, тогда коэффициент трения равен
Для меня в этом методе оказалось слишком много математических действий, с которыми в курсе математики я еще не знаком. Поэтому даже не буду приводить результаты проделанных измерений и вычислений.
2) Определение g благодаря давлению жидкости
Как известно давление столба жидкости обусловлено следующими факторами: плотность жидкости, непосредственно высота столба жидкости и само значение ускорения свободного падения на данной планете.
Если преобразовать формулу P = ρgh, получится формула нахождения g. Эта формула выглядит так g = P / ρh, где Р – давление в жидкости на глубине h, которое можно узнать с помощью манометра, ρ – плотность воды равное 1000 кг/м3.
При подобных измерениях нужно учитывать погрешность измерительного прибора, манометра. Достаточно точного мне найти не удалось, поэтому для своих исследований я выбрал другой метод.
3) Измерение ускорения свободного падения с помощью математического маятника
Необходимое оборудование: секундомер, штатив с муфтой и лапкой, шарик на нерастяжимой нити, измерительная лента. При малых размерах шарика по сравнению с длиной нити и небольших отклонениях (до 10°) от положения равновесия период колебаний равен периоду колебаний математического маятника
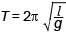
С другой стороны период колебаний маятника можно расчитать из определения, ведь период – это время одного полного колебания. Тогда период
и ускорения свободного падения может быть вычислено по формуле
Подготовка к проведению работы
В работе используется простейший маятник – шарик на нити. При малых размерах по сравнению с длиной нити и небольших отклонениях от положения равновесия период колебаний равен периоду колебаний математического маятника
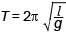
Тогда период
и ускорения свободного падения может быть вычислено по формуле
Результаты измерений и вычислений представлены в разделе 2.5
2.4. Теоретические расчеты по определению ускорения свободного падения различных высотах
Теоретически значение ускорения свободного падения на поверхности планеты Земля можно приблизительно подсчитать, представив планету точечной массой M, и вычислив гравитационное ускорение на расстоянии её радиуса R:
где G — гравитационная постоянная (G = 6,6743 · 10–11 (H ·м2)/кг2).
При вычислениях я применял такие значения:
R = 6370 · 103 м – радиус Земли на широте Казани;
M = 5,9722 · 1024 кг – масса Земли.
Таким образом теоретическое значение gт = 9,823386 м/с2.
Согласно формуле
естественно предположить, что ускорение свободного падения на разных высотах будет немного отличаться: на глубине будет больше, а на высоте меньше вычисленного выше.
Возможно эту небольшую разницу можно объяснить погрешностью измерений. Проверим.
Результаты вычислений значения ускорения свободного падения на различных высотах представлены в таблице:
|
В классе |
На станции метро Кремлевская |
На 36-м этаже небоскреба |
|
R = 6370 км, h = 0 |
R = 6370 км, h = –16 м |
R = 6370 км, h = +120 м |
|
9,8234 |
9,8231 |
9,8227 |
2.5. Экспериментальное определение ускорения свободного падения с помощью математического маятника
Как уже говорилось ранее, оборудование для проведения измерений требовалось весьма не замысловатое: секундомер, штатив с муфтой, шарик на нерастяжимой нити, измерительная лента. При малых размерах шарика по сравнению с длиной нити и небольших отклонениях (до 10°) от положения равновесия период колебаний равен периоду колебаний математического маятника
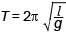
С другой стороны период колебаний маятника можно расчитать из определения, ведь период – это время одного полного колебания. Тогда период
и ускорения свободного падения может быть вычислено по формуле
Ход работы
Для начала я проделал все необходимые измерения в классе, в кабинете физики Лицея № 110. Кабинет находится на втором этаже. Учитывая высоту потолков (около 3 м), логично предположить, что вычисленные значения g должны быть близки к gт.
- Я установил на краю стола штатив. У его верхнего конца укрепил с помощью муфты кольцо и подвесил к нему шарик на нити. Шарик должен висеть и свободно совершать колебания.
- Нить я взял метровой длины для удобства вычислений.
- Отклонив шарик на небольшое расстояние (5-8 см), я возбудил колебания маятника.
- Измерил в пяти экспериментах время t 20 колебаний маятника и вычислил tср:
| tср = | t1 + t2 + t3 + t4 + t5 |
| 5 |
- Затем вычислил среднюю абсолютную погрешность измерения времени:
| ∆tср = | │t1 – tср│ + │t2 – tср│+ │t3– tср│ + │t4– tср│ + │t5– tср│ |
| 5 |
- Вычислил ускорение свободного падения по формуле:
Таблица результатов измерений в классе
| n |
N |
t, c |
tср, с |
Δtср, с |
g, м/с2 |
|
1 |
20 |
40,26 |
39,94 |
0,36 |
9,88924 |
|
2 |
20 |
39,20 |
|||
|
3 |
20 |
40,30 |
|||
|
4 |
20 |
40,18 |
|||
|
5 |
20 |
39,78 |
- Я определил относительную погрешность измерения времени εt.
| ε = | ∆t | = | ∆tи + ∆tотсчета | = | 1 с + 1 с | = | 2 c | = | 2 с | = 0,05 = 5% |
| t | t | t | tсредн | 39,94 с |
- Определил относительную погрешность измерения длины маятника:
| εl = | ∆l | = | ∆lи + ∆lотсчета | = | половина цены деления + цена деления | = |
| l | l | длина маятника |
| = | 0,0005 м + 0,001 м | = | 0,0015 м | = | 0,0015 м | = 0,0015 = 0,15% |
| l | l | 1 м |
- Вычислил относительную погрешность измерения g:
εg = εl+ 2εt = 0,05 + 2 · 0,0015 = 0,053 = 5,3%
- Определил абсолютную погрешность вычисления ускорения свободного падения:
∆g = εggсредняя = 0,053 · 9,73971 м/с2 = 0,5162 м/с2 ≈ 0,520
Итог моих измерений и вычислений:
9,37 ≤ g ≤ 10,41
Такие действия я проделал в казанском метрополитене, на станции метро Кремлевская и на 36-м этаже единственного в Казани небоскреба «Лазурные небеса».
Таблица результатов измерений на станции метро Кремлевская
|
n |
N |
t, c |
tср, с |
Δtср, с |
g, м/с2 |
|
1 |
20 |
31,80 |
31,71 |
0,042 |
9,96232 |
|
2 |
20 |
31,72 |
|||
|
3 |
20 |
31,62 |
|||
|
4 |
20 |
31,69 |
|||
|
5 |
20 |
31,71 |
При измерениях в метро пришлось использовать длину нити 63,5 см.
Относительная погрешность измерения времени εt = 0,063 = 6,3%.
Относительная погрешность измерения длины маятника: εl = 0,24%
Относительная погрешность измерения g: εg = 6,78%
Абсолютную погрешность вычисления ускорения свободного падения составила: 0,63 м/с2.
Итог моих измерений и вычислений:
9,33 ≤ g ≤ 10,59
Таблица результатов измерений на 36-м этаже небоскреба «Лазурные небеса»
| n |
N |
t, c |
tср, с |
Δtср, с |
g, м/с2 |
|
1 |
20 |
28,59 |
28,57 |
0,10 |
9,85664 |
|
2 |
20 |
28,56 |
|||
|
3 |
20 |
28,81 |
|||
|
4 |
20 |
28,52 |
|||
|
5 |
20 |
28,39 |
Здесь при измерениях пришлось длину нити еще сократить до 51 см.
Относительная погрешность измерения времени εt = 7%.
Относительная погрешность измерения длины маятника: εl = 0,29%
Относительная погрешность измерения g: εg = 7,58%
Абсолютную погрешность вычисления ускорения свободного падения составила: 0,75 м/с2.
Итог моих измерений и вычислений:
9,11 ≤ g ≤ 10,61
Таблица сравнения теоретически полученных значений g (м/с2) и полученных экспериментально
|
В классе |
На станции метро Кремлевская |
На 36-м этаже небоскреба |
|
|
R = 6370 км, h = 0 |
R = 6370 км, h = –16 м |
R = 6370 км, h = +120 м |
|
|
Теория |
9,8234 |
9,8231 |
9,8227 |
|
Эксперимент |
9,8892 |
9,9623 |
9,8566 |
3. Заключение
При подготовке к защите данной работы и в результате теоретического исследования, чтения разных книг и статей я узнал многое об ускорении свободного падения. Как уже упоминал, для меня практическая значимость исследования заключается в возможности прогнозирования форм жизни на небесных телах, с которыми человечество столкнется при неизбежном освоении космоса. Ведь люди заранее смогут узнать, какие существа встретят их на той или иной планете, какими физическими характеристиками они будут обладать.
Также я узнал, что расчеты различия ускорения свободного падения в разных точках на поверхности Земли могут указывать на гравитационные аномалии.
Самое главное, я научился измерять g, различными способами, рассчитывать погрешности измерений, грамотно проводить эксперимент.
Считаю цель исследования достигнута. Средние значение ускорения свободного падения на различных высотах отличаются в зависимости от высоты над уровнем моря: при увеличении высоты значение g уменьшается, при углублении в недра Земли – увеличивается. Экспериментально полученные значения хорошо это показывают.
Погрешность измерений достаточно велика, но не превышает 10%. Уменьшить погрешность возможно путем проведения большего числа измерений: ни 5, а 20; большего числа колебаний: не 20, а 100. Также при расчетах можно учесть, что Казань находится примерно на уровне 250-300 м над уровнем моря.
В дальнейшем хотелось бы усовершенствовать экспериментальные установки, чтобы измерять ускорение свободного падения с большей точностью.
Планирую самостоятельно исследовать значения ускорения свободного падения в различных уголках земного шара.