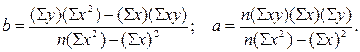Вероятность успеха по сравнению с вероятностью провала какого либо бизнеса это

Теория ожиданий основывается на предположении, что человек направляет свои усилия на достижение какой-либо цели только тогда, когда будет уверен в большой вероятности удовлетворения за этот счет своих потребностей или достижения цели. Мотивация является функцией фактора ожидания затраты труда — результаты , ожидания — результаты — вознаграждение и валентности (т.е. относительной степени удовлетворения). Наиболее эффективная мотивация достигается, когда люди верят, что их усилия обязательно позволят им достичь цели и приведут к получению особо ценного вознаграждения. Мотивация ослабевает, если вероятность успеха или ценность вознаграждения оценивается людьми невысоко.
[c.385]

В сравнении стратегий американских и японских корпораций полезно выделить два типа Ч — основанный на человеческих отношениях и С — стратегический. Два других типа стратегий — венчурный и бюрократический, которые следуют определенным устойчивым принципам,— существуют внутри типов Ч и С. Способ, каким менеджеры противостоят изменениям экономической конъюнктуры, обусловливает необходимость тех или иных незначительных усовершенствований стратегии, но основные черты ее остаются неизменными. Таким образом, стратегическое управление в Японии не предусматривает составления правил распределения капитала, как это делается в США. Напротив, правила распределения капитала естественным образом развиваются в самой организации, и компания лишь ждет более четкого развертывания тенденции. Тогда правило совершенствуется, и определяется его содержание. Тем самым для начала работы необходимы энергия и время, но вероятность успеха тогда высока.
[c.54]

Вероятность означает возможность получения определенного результата. В нашем примере вероятность успеха нефтяного проекта равна Д, а его неудача может составить 3/4. Вероятность представляет собой трудную для формулировки концепцию, так как она может зависеть от природы неопределенных событий и от надежд, которые люди возлагают на них. Объективный метод определения вероятности основан на вычислении частоты, с которой происходят некоторые события. Предположим, известно, что при разведке 100 морских нефтяных месторождений 25 были успешными, а 15 кончились неудачей. Тогда вероятность успеха в /4 считается объективной, потому что она непосредственно основана на частоте соответствующих событий, определенных на основе фактических данных.
[c.126]

Систематическое рассмотрение и оценка информации для получения достоверных выводов относительно прошлого состояния предприятия с целью оценки его жизнеспособности в будущем важны для анализа финансовых отчетов. Такой подход позволяет установить важнейшие характеристики, которые определяют вероятность успеха или банкротства предприятия, а именно [c.148]

Если организация обладает квалифицированными сотрудниками и руководителями с хорошо мотивированными целями, она в состоянии следовать различным альтернативным стратегиям. В противном случае вероятность успеха мала. Вначале следует изменить кадровую политику.
[c.183]

Будучи важнейшим элементом процесса предоставления ссуд, анализ финансовых отчетов помогает инвестору принять решение о выдаче ссуды и условиях этой выдачи. При анализе финансовых отчетов наиболее важным является финансовое положение компании в прошлом и в настоящее время и как оно отражено в финансовых отчетах, а не такие факторы, как стиль руководства компании и ее кредитная история. Но такие нефинансовые моменты помогают определить направление и глубину анализа финансовых отчетов. Анализ финансовых отчетов включает в себя систематическое рассмотрение и оценку информации для получения достоверных выводов относительно прошлого состояния компании с целью предвидения ее жизнеспособности в будущем. Такой анализ позволяет точно установить наиболее важные характеристики — производственные или финансовые, — которые определяют вероятность успеха или банкротства фирмы, а именно [c.175]

Но вероятность успеха любого общего утверждения, основанного на конечном числе наблюдений, должна стремиться к нулю независимо от числа наблюдений. Для преодоления этого затруднения стараются избегать прогнозов обобщенного характера и сосредоточиваются на вероятности осуществления частных прогнозов. Это ведет к распылению сферы изучения и к уменьшению получаемого общего знания. Кроме того, наблюдение связывают с развитием теорий частного, а не общего характера.
[c.75]

Мы имеем значения вероятности успеха при прохождении отдельных тестов В (сдал Математику) = 0.6, В (сдал Логику) = 0.8.
[c.59]

Проекты в сфере высоких технологий для них более привлекательны, чем в горнодобывающей промышленности. Все легко объяснимо в первом случае вероятность успеха и прибылей в дальнейшем заведомо больше. Теперь легко понять, почему столько венчурных фирм в Бостоне и Сан-Франциско, центрах деятельности фирм в сфере электроники. Кроме того, подобных фирм много и в Нью-Йорке, Чикаго, Далласе. Наверное, самым известным венчурным капиталистом в послевоенную эпоху был Лоуренс Рокфеллер, активно участвовавший в ряде начинающих и добившихся впоследствии успеха компаниях. Если же фирма не имеет отношения к «высоким технологиям», очень трудно убедить капиталиста в достоинствах начинания, ибо потенциальный рост и доходы недостаточно велики.
[c.768]

В обстановке риска (неопределенности) максимум, что может сделать менеджер, это определить вероятность успеха для каждой альтернативы.
[c.194]

Действительно, положительный результат можно увеличивать либо путем понижения плотности исследований и расширением территории поиска, либо за счет повышения вероятности успеха. Последнее возможно только путем выделения районов, перспективных на нефть и газ, и локализации поисков в них.
[c.151]

Анализ финансовых отчетов включает систематическое рассмотрение и оценку информации для получения достоверных выводов относительно прошлого состояния компании с целью предвидения ее жизнеспособности в будущем. Такой анализ позволяет точно установить наиболее важные характеристики — производственные или финансовые, — которые определяют вероятность успеха или банкротства фирмы, а именно [c.25]

Из каждых десяти венчурных инвестиций первого этапа, как правило, только две или три оказываются удачным вложением в самодостаточные предприятия и только одна способна принести такую большую прибыль, как «Марвин и компания»5. На этих статистических данных можно построить два правила успешного венчурного инвестирования. Первое — не бойтесь неопределенности, смиритесь с низкой вероятностью успеха. Но не входите в предприятие, если не видите для него шанса стать большой публичной компанией на прибыльном рынке. Нет смысла стрелять по далеким мишеням, если это не окупится с лихвой в случае вашей победы. Второе — уменьшайте потери сразу определяйте неудачников, и, если вы не в состоянии решить проблему — например, сменой руководства, — то, потеряв на этом деньги, не вкладывайте и не тратьте их снова.
[c.368]

Предположим, что у вас есть проект, который может привести вас либо к крупной победе, либо к крупному проигрышу. Вероятность успеха проекта перевешивает вероятность его неудачи, и если начать осуществление проекта сегодня, его чистая приведенная стоимость положительна. Однако этот проект не подпадает под принцип «сейчас или никогда». Должны ли вы инвестировать немедленно, или вам следует подождать Трудно сказать если проект действительно выигрышный, ожидание равнозначно потере или отсрочке его ближайших потоков денежных средств. Но если он окажется проигрышным, ожидание могло бы предотвратить большую ошибку.
[c.568]

Если позвать соседа, то в первой ситуации вероятность успеха равняется 0,1, а во второй — 0,9.
[c.223]

Вероятностная оценка успеха в ремонте для первого варианта действий равняется 0,1 х 0,5 + 0,9 х 0,3 = 0,32, для второго варианта действий — 0,1 х х 0,1 + 0,9 х 0,9 = 0,82. Предпочтительный вариант действий теперь очевиден —вероятность успеха во втором варианте больше.
[c.223]

Возможности компании классифицируются в соответствии с их привлекательностью и вероятностью успеха. Успех компании зависит не только от соответствия ее деловых возможностей основным требованиям целевого рынка, но и от того, превосходят ли они потенциал конкурентов. Сами по себе основные деловые способности компании не являются конкурентным преимуществом. Наиболее эффективно функционирует та компания, которая способна создать и постоянно воспроизводить максимальную ценность продукта для потребителя.
[c.133]

В матрице возможностей (рис. 3.8, а), в верхнем левом квадранте (1) представлены наиболее перспективные рыночные возможности компании, производящей осветительное оборудование для телестудий. Возможности, представленные в нижнем правом квадранте (4), незначительны и даже не рассматриваются. Возможности, представленные в верхнем правом (2) и нижнем левом квадрантах (3), должны быть тщательно проанализированы на случай, если через какое-то время их привлекательность и вероятность успеха увеличатся.
[c.133]

Вероятность успеха Высокая Низкая
[c.134]

Методику расчета общего рейтинга можно усовершенствовать и уточнить. Методика применяется с целью обеспечить систематический подход к обсуждению и оценке идей новинок — она не предназначена для того, чтобы играть решающую роль при принятии руководством окончательного решения. По мере того как идет процесс разработки идеи, компании необходимо постоянно пересматривать оценку общей вероятности успеха нового товара, используя следующую формулу [c.394]

Например, если оценочные значения вероятностей, стоящих в правой части формулы, равны 0,50, 0,65 и 0,74 соответственно, то компания может сделать вывод, что общая вероятность успеха равна 0,24. Затем компания должна принять решение о том, достаточно ли такого значения вероятности для продолжения разработки новинки.
[c.395]

Об уровне риска инновационной деятельности свидетельствует тот факт, что в среднем из каждых десяти венчурных фирм успеха добиваются лишь одно-два. Высокий риск, однако, сопровождается, как правило, и высокой его компенсацией возможная норма прибыли от внедрения инновационных проектов гораздо выше обычной, получаемой при осуществлении других видов предпринимательской деятельности. Именно это и позволяет инновационной сфере существовать и развиваться. Риск инновационной деятельности тем выше, чем более локализован инновационный проект если же таких проектов много и они в отраслевом плане рассредоточены, согласно закону больших чисел риск минимизируется и вероятность успеха инновационного предпринимательства возрастает. При этом прибыль от реализации успешных инновационных проектов настолько велика, что перекрывает затраты по всем остальным неудавшимся разработкам.
[c.207]

Управление процессом разработки нового продукта позволяет сократить затраты, время и риски. Исследования показали, что формализация процесса, предусматривающая регулярный контроль состояния дел, ясность целей разработки продукта и четкую ее рыночную направленность, увеличивает вероятность успеха независимо от того, является ли продуктом товар, услуга или технология.
[c.122]

Дальнейшее повышение вероятности успеха конверсии и реструктуризации ВПК напрямую зависит от активного участия правительства. К сожалению, на поворотном этапе после окончания «холодной войны» правительство США придерживалось в отношении ВПК политики сохранения существующего положения. Администрация Буша вообще отрицала возможность рыночных сил способствовать быстрой и эффективной перестройке оборонной промышленности. Основными аргументами являлись монопольный спрос на продукцию ВПК, строгое государственное регулирование, ограниченное количество поставщиков в каждой отрасли и отсутствие основных рыночных атрибутов. При таком подходе эффективное разукрупнение ВПК было невозможным. Конгресс и администрация США продолжали и продолжают по сей день финансирование расширения существующих мощностей и всемерно способствуют развитию экспорта вооружений. Их отказ от установления прозрачности будущей структуры ВПК, выработки целей и стратегии его развития приводил к тому, что все бюджетные решения в этой сфере носили бессистемный характер.
[c.283]

Предположим, что вероятность успеха для каждой компании равна 0,5 другими словами, компания либо получит одобрение FDA, либо нет, и решение об одобрении каждого из препаратов не зависит от решений по остальным препаратам.
[c.209]

Соотношение (71) означает, что если программа ГРР успешна, то ее можно повторить I/a раз и достигнуть при этом эффективности, равной 12%. Иначе говоря, можно рассчитывать на окупаемость вложенных средств, если вероятность успеха равна 12%. Производя такие расчеты для различных исходных данных, можно получить кривую зависимости требуемой вероятности успеха от величины запасов открываемых месторождений для заданного уровня эффективности. Задача
[c.177]

При анализе следует учитывать, что диверсификация имеет свои положительные и отрицательные стороны. Главная опасность диверсификации связана с распылением сил, а также с проблемами управления диверсифицированными предприятиями. Собственно, именно проблема управляемости крупных компании и привела к развитию методов портфельного анализа. Практика западного менеджмента свидетельствует, что вероятность успеха отдельных стратегий роста неодинакова вследствие уменьшения синергического эффекта для старого товара на старом рынке этот эффект составляет 50% для нового товара на старом рынке — 33 Для старого товара на новом рынке — 2О для нового товара на новом рынке — 5%5-
[c.88]

Важнейшее значение имеет этап выбора проектов проведения научных исследований для решения актуальных научно-технических проблем. Задачей этого этапа является отбор таких проектов, которые дали бы оптимальные результаты с точки зрения совокупности различных факторов значимости ожидаемых результатов, вероятности успеха в достижении цели, квалификации будущих исполнителей, стоимости работы и т.д. Решение подобных задач называют решением проблем выбора в уникальных ситуациях. В настоящее время имеются неплохие способы решения такого рода проблем. Наибольшую известность среди них получил так называемый системный подход.
[c.144]

В главе 10 мы познакомили вас с госпожой В. Хартией Вольнэсти, новатором в области воздушных сообщений, которая обдумывала покупку турбовинтового самолета для своей новой авиалинии «Вольный полет». На рисунке 21-1 представлены возможные результаты приобретения турбовинтового самолета. Если авиалиния начнет работать успешно и спрос на ее услуги будет высоким, то, по расчетам г-жи Хартии Вольнэсти, к концу первого года ее бизнес будет стоить 738 000 дол. В случае неудачи бизнес будет стоить только 415 000 дол. Г-жа Хартия Вольнэсти считает, что существует 60%-ная вероятность успеха для ее бизнеса, и потому она рассчитывает ожидаемую стоимость в 1-м году как (0,6 х 738) + (0,4 х 415) = 609, или 609 000 дол. Она дисконтирует по ставке 10%, равной затратам на капитал, и получает приведенную стоимость 609/1,1 = 553 000 дол.2 Отметим, что эти расчеты не допускают возможности отказа от бизнеса. Если бизнес не взлетит в первом же году3, г-же Хартии Вольнэсти будет лучше продать турбовинтовой самолет за 500 000 дол., нежели продолжать бизнес, стоимость которого составляет только 415 000 дол.
[c.562]

БЕНЧ-МАРКИНГ (англ, ben h-marking) — оценки вероятности успеха предпринимательской деятельности, разработка мероприятий для обеспечения превосходства над конкурентом за счет высокого качества товаров и сервиса.
[c.304]

Исследования, проводившиеся на базе данных, полученных от 120 американских корпораций, показали, что более 60% всех ОКР не превращаются в новую продукцию. Результаты опроса 50 американских компаний показали, что 50% их расходов на НИОКР были направлены на нововведения, которые оказались коммерчески неудачными, а 30% нововведений, получивших признание на рынке, вскоре перестали приносить прибыль. По оценкам американских экономистов, вероятность успеха нововведений, появившихся на рынке, не превышает 74%. Поэтому нововведения, требующие больших затрат, под силу лишь крупным компаниям, обеспеченным финансовыми средствами и ресурсами.
[c.390]

С точки зрения результатов, получаемых на начальном периоде функционирования t = 0, все фирмы могут быть разделены на успешные (сумевшие реализовать свой проект и получить доход) и неуспешные . Згметим, что вероятность успеха определяется как
[c.76]

Однако в отчетах о конечном «успехе» часто опущены подробности решения проблем, с которыми сталкивалась компания на, своем пути, и особенно тех, которые можно было избежать. Вероятность успеха предприятия существенно зависит от понимания возможных проблем и способности их предвидеть еще до заключения соглашения. Ниже обсуждаются требования, преоъявляемые к менеджерам трансфера технологиче-
[c.96]

Сколько будет стоить страхование портфеля акций, если он состоит из четырех инвестиций (по 25000 долл.) в акции разных фармацевтических компаний, вероятность успеха разработок каждой из которых составляет 0,5 и которые не зависят друг от друга [c.201]

Источник

ГЛОССАРИЙ

Адресная
социальная помощь
— вид государственной социальной помощи конкретной семье с учетом нуждаемости.

Аутсорсинг
— передача организацией определенных бизнес-процессов или

производственных функций на обслуживание другой компании,
специализирующейся в соответствующей области.

Бенчмаркинг—1)
сравнительный анализ эффективности компаний на основе системы взаимосвязанных
показателей, в том числе показателей бизнес-процессов; 2) процесс
систематизированного обмена информацией между организациями прежде всего по
вопросам совершенствования бизнес-процессов, направленный на взаимный обмен
опытом и знаниями в разных аспектах деятельности. Цель — стать более
конкурентоспособными, находясь как на одном и том же рынке, так и на совершенно
разных рынках (отраслях).

Бизнес-инкубатор
— организация, обеспечивающая малые предприятия физическим пространством для
работы, помещениями и сооружениями (на основе совместного использования),
доступом к техническим средствам и услугам в области ведения бизнеса.

Деятельность бизнес-инкубаторов способствует осуществлению начальной
стадии развития нового, как правило, малого предприятия, освоению новой
продукции и реализации инновационных проектов.

Бизнес-план
— программа деятельности организации (предприятия), план мер по достижению
конкретных целей, включающий оценку ожидаемых расходов и доходов.

Разрабатывается на основе маркетинговых исследований.

Благотворительная
деятельность
— социальное действие по реализации определенных общественных и частных усилий в
оказании помощи и поддержки нуждающимся лицам.

Она не регламентирована, что позволяет более гибко реагировать на
возникающие социальные проблемы.

Благотворительная
общественная организация
— общественное объединение, созданное на основе совместной деятельности для
защиты общественных интересов и достижения поставленных целей.

Благотворительный
общественный фонд
— один из видов некоммерческих фондов, не имеющих членства, общественное
объединение, цель которого — формирование имущества на основе добровольных
взносов, иных не запрещенных законом поступлений и его использование на полезные
цели. Учредители и управляющие имуществом фонда не вправе использовать указанное
имущество в собственных интересах.

Бюджет
проекта
— запланированные средства на проект, а также их распределение по статьям
затрат, исполнителям, структурным элементам проекта и т.п.; смета как
ограничение на величину затрат.

Внебюджетный
фонд
— фонд денежных средств, не включаемый в бюджетную систему.

К таким фондам относят фонды, которые создаются по решениям органов
государственной власти или органов местного самоуправления разного уровня.

Внебюджетный фонд должен иметь целевой характер. Источники его доходов в
основном формируются из платежей, имеющих целевое назначение, и иных платежей,
предусматриваемых к перечислению во внебюджетный фонд и в законодательном
порядке или вносимых в него в форме добровольных взносов.

Внедренческая
фирма
— посредническо-консультационная хозрасчетная организация (предприятие),
специализирующаяся на распространении инноваций.

Волонтерство
— добровольное принятие обязанностей по оказанию безвозмездной социальной
помощи, услуг, патронажа инвалидам, больным и престарелым, а также лицам и
социальным группам населения, находящимся в сложных жизненных условиях.
Волонтеры — люди, делающие что-либо по своей воли, а не по принуждению.

Волонтерская деятельность в социальной сфере рассматривается как
проявлениемилосердия и человеколюбия.

Государственная
социальная политика
— действия государства в социальной сфере, преследующие определенные цели,
соотнесенные с конкретно-историческими обстоятельствами, подкрепленные
финансовыми ресурсами и рассчитанные на определенные социальные результаты.

Государственный
социальный стандарт
— установленный законодательством Российской Федерации минимальный уровень
гарантий социальной защиты, обеспечивающий удовлетворение важнейших потребностей
человека, выражаемый в нормах и нормативах предоставления бесплатных и
общедоступных социальных услуг, социальных пособий и выплат.

Государство
социальное
— демократическое государство, опирающееся на широкую социальную основу и
проводящее социальную политику, направленную на повышение или обеспечение
определенного жизненного уровня населения, защиту и реализацию прав и свобод
граждан, на создание современных систем образования и социального обеспечения,
на поддержание неимущих и малообеспеченных слоев населения, на предотвращение и
успешное разрешение социальных конфликтов и т.д.

Гражданское
общество
— сфера общественной жизни, существующая одновременно и наряду с государством,
но независимо от его институтов; система самостоятельных, независимых от
государства общественных организаций, объединений, выражающих частные интересы
людей и создающих условия для их реализации.

Гражданское
общество —
сфера самоутверждения свободных граждан и создаваемых ими на добровольных
началах ассоциаций и организаций. В его пространстве реализуется все
многообразие социальных связей индивида и государства.

Демографическая
политика
— система общепринятых на уровне властных структур идей и концептуально
объединенных средств, с помощью которых государство, а также другие социальные
институты намереваются достичь определенных целей.

Демографическое
развитие
— совокупность взаимосвязанных изменений рождаемости, смертности, миграции и
определяемых ими численности и структуры населения.

Депопуляция
— устойчивое (не связанное с особенностями возрастной структуры и миграционными
процессами) превышение числа умерших над числом родившихся.

Жизненный
потенциал
— количество лет, которое может прожить человек, достигший определенного
возраста.

Жизненный
цикл инновации
— период времени, в течение которого инновации проходят стадии от зарождения до
внедрения и распространения.

Закономерности
— связи явлений, действие которых проявляется в виде тенденций, определяющих
основную линию развития той или иной сферы деятельности.

Здоровый
образ жизни
— категория общего понятия «образ жизни», включающая в себя благоприятные
условия жизнедеятельности человека, уровень его культуры и гигиенических
навыков, которые позволяют сохранять и укреплять здоровье, предупреждать
развитие его нарушений и поддерживать оптимальное качество жизни.

Здоровье
— состояние полного социально-биологического и психического благополучия,
отсутствие каких-либо болезненных состояний и физических дефектов.

Иерархия
потребностей
— порядок расположения человеческих потребностей по степени значимости от одного
до пяти: физиологические потребности, потребности самосохранения, социальные
потребности, потребности в уважении и потребности в самоуважении. Человек будет
стремиться удовлетворить в первую очередь самые важные из них. Как только ему
удается удовлетворить какую-то важную потребность, она на время перестает быть
движущим мотивом. Одновременно появляется побуждение к удовлетворению следующей
по важности потребности. Издержка — размер ресурсов (для упрощения измеренный в
денежной форме), использованных в процессе хозяйственной деятельности
предприятия на(за) определенный временной отрезок.

Изобретение
— техническое решение задачи, обладающее новизной, неочевидностью
(изобретательским уровнем) и пригодное к осуществлению промышленным путем.

Имитационная
модель
— модель, воспроизводящая реальную действительность для того, чтобы получать о
ней достоверные сведения.

Инвестиции
— долгосрочные вложения средств как внутри страны, так и за рубежом в целях
создания новых и модернизации действующих предприятий, освоения новейших
технологий и техники, увеличения производства и получения прибыли.

Инвестиционная
политика
— определение наиболее приоритетных направлений капитальных вложений, от которых
зависят повышение эффективности экономики, обеспечение наибольшего прироста
продукции и национального дохода на каждый рубль.

Инвестиционный
проект
— план вложения капитала в целях получения прибыли, система, включающая
определенный набор организационно-правовых и расчетно-финансовых документов,
необходимых для осуществления определенных целей, получения определенных
результатов.

Инвестиционный
процесс
— сложный комплекс работ, который включает следующие основные фазы: поиск и
изучение объекта инвестирования, его финансирование и контроль их исполнения.

Инвестор
— частный предприниматель, организация или государство, осуществляющие
долгосрочное вложение капитала в какое-либо дело, предприятие с целью получения
прибыли.

Инкубатор
(в социальной сфере)
— многофункциональный комплекс, предоставляющий разнообразные услуги новым
инновационным фирмам, находящимся на стадии возникновения и развития.

Инноватика
(теория инноваций)
— отрасль науки и практики, изучающая роль и место инноваций, творческий и
организующий потенциал их создателей в процессе управляемого развития,
особенности качественных изменений продуктов человеческой деятельности в ходе
реализации тех или иных полезных обществу новшеств.

Инновации
в социальной сфере
— инновации, оказывающие влияние на большие группы людей, как правило, имеющие
некоммерческий характер и направленные на улучшение качества жизни населения.

Инновации
социальные
— организуемое нововведение в социальной практике в ответ на изменение
социальных условий, потребностей общества, новые проблемы, не решаемые
традиционными способами.

Инновационная
деятельность
— качественная характеристика какой-либо деятельности (например, инновационная
социальная деятельность).

Инновационная
среда
— реальный жизненный фон, потенциально готовый к переменам и нуждающийся в
нововведениях, или же территория, сообщество, где целенаправленно происходят
управляемые человеком качественные изменения.

Инновационная
стратегия
— совокупность мер в среднесрочной и долгосрочной перспективе по разработке и
внедрению инноваций, воспроизводимых на производстве и востребованных рынком.

Инновационное
предпринимательство
— общественный технико-экономический процесс, направленный на создание лучших по
своим свойствам товаров, услуг, технологий путем практического использования
нововведений. Инновационный менеджмент — совокупность систематизированных знаний
по теории инноваций и современному менеджменту о методах создания наукоемких
инноваций и ихэффективности.

Инновационный
потенциал
— способность среды, коллектива, человека создавать и реализовывать возможности
своего развития.

Инновационный
поток
— динамическая совокупность нововведений, имеющих общую цель и предметно
связанных между собой в исходном или конечном пункте изменений.

Инновационный
процесс
— совокупность научно-технологических, технологических и организационных
изменений, происходящих в процессе реализации инноваций.

Инновационный
цикл
— период создания, распространения и использования нововведений.

Инновация
(нововведение)
— реализованная творческая идея, создавшая новую ценность.

Инновирование
— оптимизация инновационной деятельности с целью получения более высокого
социального результата.

Институционализация
— все многообразные процессы и структуры, посредством которых люди и группы
организуются в обществе.

Инфраструктура социальная — материально-вещественные элементы, обеспечивающие условия
жизнедеятельности человека в обществе (в производственной, политической и
духовной сферах, в семье и быту); совокупность таких отраслей, как наука,
образование, здравоохранение, торговля, общественное питание, бытовое
обслуживание, жилищно-коммунальное хозяйство, транспорт, связь и др. Степень
развития инфраструктуры социальной — важный показатель того, как человек живет,
в какой степени он социально защищен.

Качество
населения
— совокупность свойств населения: его образовательный уровень,
профессионально-квалификационная структура, состояние здоровья и т.д.

Кейс-метод
— деловая игра, сочетающая профессиональную и деловую игры. Учебный материал
подается учащимся в виде кейсов (проблем). Данный метод предполагает активное
участие в обсуждении деловой ситуации как студентов, так и преподавателей.

Конкурентоспособность
— способность определенного объекта превзойти конкурентов в заданных условиях.

Конкуренция
— соперничество нескольких субъектов в достижении схожей цели.

Консалтинг
— 1) консультирование производителей, продавцов и покупателей по широкому кругу
вопросов организационной, управленческой и экономической деятельности
предприятий, фирм и организаций; 2) деятельность специальных компаний по
консультированию производителей и покупателей в области техники, экономики и
экспертизы.

Критерии проекта — требования, предъявляемые к проекту на различных этапах проектирования
и используемые для оценивания проекта.

Макросоциальная
работа
— упорядочение деятельности населения отдельных территорий, формирование
территориальных сообществ и социальных групп исходя из интересов и возможностей
населения. Малообеспеченные граждане (семьи) — граждане (семьи), средний
совокупный доход которых (заработная плата, пенсии, пособия, другие виды
доходов) на одного человека (члена семьи) не превышает величины среднемесячного
прожиточного минимума на душу населения.

Маркетинг
— вид человеческой деятельности, направленный на удовлетворение нужд и
потребностей посредством обмена.

Маркетинговая стратегия — комплекс мероприятий по разработке, производству и сбыту товаров
(услуг) на основе запросов потребителей, направленный на максимизацию прибыли
предприятия.

Нововведение — результат научного труда, направленный на совершенствование
общественной практики и предназначенный для непосредственной реализации.
Нововведение (инновация) управленческое — процесс освоения новых организационных
форм, методов и техники в управлении.

Общественные
фонды
— структуры, объединяющие группы людей, материальные, финансовые, культурные и
иные ценности. Существуют за счет добровольных отчислений, взносов,
пожертвований государственных, общественных организаций, коммерческих,
финансовых структур и частных лиц. Эти средства направляются на различные
программы гуманитарной и благотворительной деятельности.

Организационные нововведения включают в себя три основных типа:
нововведения процедурного характера; нововведения, связанные со структурными
преобразованиями, и нововведения, связанные с изменением производственных
элементов, из которых состоит организация.

Охрана здоровья — совокупность мер политического, духовного, экономического, правового,
социального, культурного, научного, медицинского и санитарно-эпидемического
характера, направленных на оптимизацию условий для формирования, активного
сохранения, восстановления и укрепления здоровья и обеспечивающих снижение
уровня заболеваемости и увеличение популяции здоровых и практически здоровых
людей.

Поколение
— совокупность людей, родившихся в один и тот же год или несколько больший
промежуток времени (например, пятилетие).

Политика
предприятий в области человеческих ресурсов
— политика предприятий, включающая, наряду с неукоснительным соблюдением
действующего законодательства, ряд дополнительных мер, направленных на
облегчение совмещения их работниками родительских и профессиональных ролей. К
таким мерам относятся, например, введение гибкого графика рабочего времени,
оплата за счет предприятия части расходов работников, связанных с рождением и
воспитанием детей, планирование карьеры женщин с учетом необходимости выполнения
ими материнских обязанностей и т.д.

Потенциал
здоровья
— способность человека заботиться о своем собственном здоровье, принимать
решения и контролировать свою жизнь в целях обеспечения собственного здоровья.

Практика
социальной работы
— использование знаний и навыков социальной работы для предоставления социальных
услуг человеку, социальному слою, группе. Практика социальной работы включает в
себя социальную помощь, социальную терапию, социальную реабилитацию,
страхование, попечительство, посредничество и т.д.

Прогнозирование
— научно обоснованное предсказание вероятностного развития событий или явлений
на будущее на основе статистических, социальных, экономических и других
исследований.

Программа
социальная
— документ, определяющий содержание и последовательность действий, направленных
на решение конкретных социальных проблем.

Простое
воспроизводство населения
— воспроизводство населения, при котором численность поколений родителей равна
численности поколений детей, рожденных ими. Коэффициент естественного прироста
при этом стремится к нулю.

Профессиональное
выгорание
— психологическое состояние специалистов, интенсивно общающихся с клиентами в
эмоционально нагруженной атмосфере при оказании профессиональной помощи.

Профилактика
— система государственных, социальных, гигиенических и медицинских мер,
направленных на предупреждение социальных отклонений и обеспечение высокого
уровня социального и психологического здоровья населения в целом.

Профессионализм
в социальной работе
— определенный стандарт поведения, который характеризует социальную работу как
некое профессиональное сообщество людей, имеющих одни интересы, взгляды,
мировоззрение. Расселение населения — процесс распределения и перераспределения
населения натерритории. Включает в себя размещение населения, функциональные,
территориальные взаимосвязи населенных мест и миграции населения.

Региональная
социальная политика
— политика, направленная на снижение социально-экономического неравенства
территорий (регионов) в составе данного государства. Ее субъектами выступают
центральные и региональные власти. Региональная социальная политика ведется в
следующих направлениях: разработка региональных прогнозов, перспективных планов
и целевых программ развития, регулирование территориальных отношений
собственности и т.д.

Ресурс
— любой фактор (включая время), необходимый для выполнения работ проекта. Обычно
выделяют трудовые, финансовые и материальные ресурсы.

Реформа
социальная
— изменение какой-либо стороны общественной жизни при сохранении существующего
строя. Как правило, социальные реформы положительно влияют на общественные
процессы, однако это зависит от целей, задач, от того, в чьих интересах они
осуществляются.

Риск
— вероятность успеха по сравнению с вероятностью провала какого-либо бизнеса.

Оценить
риск
— значит попытаться количественно определить вероятность успеха или провала.

Рынок
инноваций
— сфера обмена между экономически свободными разработчиками и потребителями
инноваций, функционирующая благодаря структурам, реализующим рыночный обмен
инновациями, а также благодаря государственной и региональной поддержке в виде
определенных льготных условий и стимулов.

Социальная
защита
— система приоритетов и механизмов по реализации законодательно закрепленных
социальных, правовых и экономических гарантий граждан: органов управления всех
уровней, иных институтов: система социальных служб, обеспечивающих определенный
уровень социальной защищенности, достижение социально-приемлемого уровня жизни
населения в соответствии с конкретными условиями общественного развития.

Социальная
политика
— деятельность государства и других политических институтов по управлению
развитием социальной сферы общества. Социальная помощь — регулярные и
периодические мероприятия для наименее защищенных групп населения,
способствующие устранению или уменьшению социальной

недостаточности.

Социальная
профилактика
— комплекс мероприятий, применяемых в макросоциальной работе и направленных на
предупреждением аргинализации и перехода к асоциальному образу жизни социально
нестабильных категорий населения.

Социальная
сфера
— область жизнеобеспечения общества, в которой реализуется социальная политика
государства, направленная на поддержание благосостояния и дееспособности
граждан, удовлетворение насущных потребностей населения.

Социально
гигиенический мониторинг
— государственная система наблюдения, анализа, оценки и прогноза состояния
здоровья населения и среды обитания человека, а также определения
причинно-следственных связей между состоянием здоровья населения и воздействием
факторов среды обитания человека.

Социальное
консультирование
— предоставление специалистом социально-правовой и социально-психологической
информации, помогающей клиентам социальной службы налаживать связи с социальной
средой.

Социальное
обеспечение
— материальное обеспечение и социальное обслуживание пожилых и нетрудоспособных
граждан, а также семей с детьми, осуществляемые государством. Включает пенсии,
пособия, социальные выплаты и льготы.

Социальное
обслуживание
— деятельность социальных служб по социальной поддержке, оказанию
социально-бытовых, социально-медицинских, психолого-педагогических,
социально-правовых услуг и материальной помощи, проведению социальной адаптации
и реабилитации граждан, находящихся в трудной жизненнойситуации.

Социальное
партнерство
— идеология сотрудничества во всех сферах жизнедеятельности, представленных в
обществе; один из главных принципов демократического правового социального
государства. Способствует гармонизации отношений между различными слоями,
группами, взаимодействующими в обществе.

Социальное
пространство
— в широком смысле — все, что непосредственно обеспечивает защиту социальных
интересов человека, реализацию социальных потребностей граждан, мотивирует или
блокирует раскрытие сущностных сил человека, социума. В узком смысле —
характеристика социальных сред и возможностей социального развития индивидов,
групп, общностей.

Социальное
страхование (обязательное)
— часть государственной системы социальной защиты населения, спецификой которой
является осуществляемое в соответствии с федеральным законом страхование
работающих граждан от возможного изменения материального и (или) социального
положения, в том числе по независящим от них обстоятельствам.

Социальные
службы
— предприятия и учреждения, предоставляющие социальные услуги, а также граждане,
занимающиеся предпринимательской деятельностью по социальному обслуживанию без
образования юридического лица.

Социальные
услуги
— действия по социальному обслуживанию отдельных категорий граждан, клиентов
социальной службы.

Социальный
сервис
— социальное обслуживание, направленное на максимальный учет разнообразных
потребностей групп населения и их удовлетворение. Социальные службы предлагают
широкий спектр услуг на основе маркетинговой деятельности.

Стабилизация
численности населения
— достижение уровня простого воспроизводства при естественной убыли населения за
счет увеличения рождаемости, снижения смертности и иммиграции населения.

Страхование
— система социально-экономических отношений, при которых за счет взносов
предприятий, организаций и населения создаются страховые фонды, предназначенные
для возмещения ущерба от стихийных бедствий и других неблагоприятных случайных
явлений, а также для оказания гражданам или их семьям помощи при наступлении
определенных событий в их жизни, являющихся предметом страхового договора.

Территориальная
социальная работа
— одно из направлений макроссоциальной работы, работа с людьми на территории их
проживания.

Укрепление
здоровья
— процесс, позволяющий людям повысить контроль за своим
здоровьем, а также улучшить его.

Управление
персоналом
— деятельность, выполняемая в организации, которая способствует наиболее
эффективному использованию работников для достижения организационных и личных
целей.

Уровень
жизни
— обеспеченность населения необходимыми материальными благами, достигнутый
уровень их потребления и степень удовлетворения рациональных потребностей
различных социальных групп.

Услуга
— в маркетинге рассматривается как благо или вид деятельности, которые одна
сторона может предложить другой.

Участковая
социальная служба
— форма социальной работы по выявлению раннего неблагополучия семей, имеющих
детей, направленная на оказание всесторонней социальной помощи таким семьям, а
также на профилактику безнадзорности и беспризорности несовершеннолетних.

Учреждения
социального обслуживания
— учреждения, предназначенные для предоставления социальных услуг независимо от
формы собственности. Франчайзинг — вид отношений между рыночными субъектами,
когда одна сторона(франчайзер)
передает другой стороне (франчайзи) за плату (роялти) право наопределенный вид
бизнеса, используя разработанную систему его ведения.

Функция
системы качества
— относительно самостоятельный по своему характеру вид деятельности,
осуществляемый в системе качества.

Экспертиза
—
исследование, рассмотрение какого-либо вопроса, процесса, явления, требующее
специальных знаний для дачи мотивированного заключения специалистом (экспертом).

Эффективность
социальной работы
— максимально возможное удовлетворение социальных потребностей населения при
оптимальных затратах.

Источник

Теория вероятности и ее применение

Авторы
Руководители
Файлы работы
Наградные документы

Тюленева А.А. 1

1МБОУ СОШ 15

Саркисова Г.А. 1

1МБОУ СОШ 15

Текст работы размещён без изображений и формул.
Полная версия работы доступна во вкладке «Файлы работы» в формате PDF

ВВЕДЕНИЕ

Актуальность данного исследования связана с научными открытиями теории вероятности, с применением этих методов в практических задачах, которые могут встречаться в таких науках как экономика, физика, химия, генетика и другие технические науки.

Новизна работ в основном связана с применением методов теории вероятности в решении практических задач.

Цель исследования – познакомить учащегося с основами теории вероятности с теоретическими и практическими, в том числе и для решения сложных задач.

В соответствии с поставленной целью исследовательского проекта решаются следующие задачи:

Выяснить основные понятия теории вероятностей и формулы нахождения вероятности событий

Научиться рациональным способом решать задачи

Создать сборник задач по теории вероятностей для подготовки к ЕГЭ

Практическая значимость. Вероятностные схемы широко применяются в физике, химии, генетике, экономике и технических науках. Поэтому все эти задачи рассмотрены в данном сборнике задач по теории вероятности для ЕГЭ.

ИСТОРИЯ ВОЗНИКНОВЕНИЯ ТЕОРИИ ВЕРОЯТНОСТИ

Возникновение данной науки связано с желанием людей разбогатеть в игры в кости и казино. В данных играх возникло два основных вопроса, которыми и заинтересовались великие ученые — математики:

— Сколько раз надо бросать две игральные кости, чтобы случаев выпадения сразу двух шестерок было больше половины от общего числа бросаний?

— Как справедливо разделить поставленные на кон двумя игроками деньги, если они по каким-то причинам прекратили игру преждевременно?

Таким образом, азарт и жажда разбогатеть дали толчок возникновению новой чрезвычайно существенной математической дисциплины: теории вероятностей. В разработке ее основ принимали участие математики такого масштаба, как Паскаль и Ферма, Гюйгенс (1629—1695), который написал тракта «О расчетах при азартных играх», Яков Бернулли (1654—1705), Муавр (1667—1754), Лаплас (1749— 1827), Гаусс (1777—1855) и Пуассон (1781—1840). В наше время теория вероятности используется почти во всех отраслях знаний: в статистике, синоптике (прогноз погоды), биологии, экономике, технологии, строительстве и других научных направлениях. [1]

Первые задачи вероятностного характера возникли в различных азартных играх — костях, картах и других азартных играх (см. рисунок 1).

Рисунок 1 – Азартные игры и теория вероятности

Французский каноник XIII века Ришар де Фурниваль правильно подсчитал все возможные суммы очков после броска трёх костей и указал число способов, которыми может получиться каждая из этих сумм. Это число способов можно рассматривать как первую числовую меру ожидаемого события, аналогичную вероятности. [1]

В XVII веке начало формироваться отчётливое представление о проблематике теории вероятностей и появились первые математические (комбинаторные) методы решения вероятностных задач. Основателями математической теории вероятностей стали Блез Паскаль и Пьер Ферма (см. рисунок 2).

Рисунок 2 – Блез Паскаль и Пьер Ферма

Блез Паскаль в своих трудах далеко продвинул применение комбинаторных методов, которые систематизировал в своей книге «Трактат об арифметическом треугольнике» (1665). Опираясь на вероятностный подход, Паскаль даже доказывал (в посмертно опубликованных заметках), что быть верующим выгоднее, чем атеистом.

На книгу Гюйгенса опирались появившиеся в начале XVIII века трактаты Пьера де Монмора «Опыт исследования азартных игр» (опубликован в 1708 и переиздан с дополнениями в 1713 году) и Якоба Бернулли «Искусство предположений» (опубликован уже после смерти учёного, в том же 1713 году). Последний имел для теории вероятностей особенно большое значение.

В XIX веке число работ по теории вероятностей продолжало расти, были даже компрометирующие науку попытки распространить её методы далеко за разумные пределы — например, на область морали, психологии, юриспруденции и даже богословия. В частности, валлийский философ Ричард Прайс, а следом за ним и Лаплас, считали возможным рассчитать по формулам Байеса вероятность предстоящего восхода Солнца, Пуассон пытался провести вероятностный анализ справедливости судебных приговоров и достоверности показаний свидетелей. Философ Дж. С. Милль в 1843 году, указав на подобные спекулятивные применения, назвал исчисление вероятностей «позором математики». Эта и другие оценки свидетельствовали о недостаточной строгости обоснования теории вероятностей.

Математический аппарат теории вероятностей тем временем продолжал совершенствоваться. Основной сферой её применения в тот период была математическая обработка результатов наблюдений, содержащих случайные погрешности, а также расчёты рисков в страховом деле и других статистических параметров.[2]

В XIX, XX и XXI столетиях теория вероятностей проникает сначала в науку (астрономию, физику, биологию), потом в практику (сельское хозяйство, промышленность, медицину), и наконец, после изобретения компьютеров, в повседневную жизнь любого человека, пользующегося современными средствами получения и передачи информации.[2]

ТЕОРИЯ ВЕРОЯТНОСТИ: ТЕОРЕТИЧЕСКИЕ ВОПРОСЫ

Теория вероятностей — раздел математики, изучающий закономерности случайных явлений: случайные события, случайные величины, их свойства и операции над ними.

Теория вероятности появилась как наука из убеждения, что в основе массовых случайных событий лежат конкретные закономерности. Теория вероятности исследует данные закономерности.

Теория вероятностей занимается изучением событий, наступление которых достоверно неизвестно. Она позволяет судить о степени вероятности наступления одних событий по сравнению с другими.

Событием назовем всякий возможный факт, который

в результате опыта может произойти или не произойти.

Различают три вида событий:

1) невозможное – событие, которое в результате опыта

произойти не может;

2) достоверное – событие, которое в результате опыта

произойдет обязательно;

3) случайное – событие, которое в результате опыта

может произойти, а может не произойти.( Основное понятие теории вероятностей)

Вероятность события А равна отношению числа благоприятных исходов к числу всех равновозможных исходов:

P (A) = m/n, где n — общее число всех равновозможных исходов, а m — количество благоприятных исходов.

Равновозможными называются события, имеющие одинаковую возможность для их появления. Полная группа событий – это совокупность единственно возможных событий при данном испытании.

Пример:

Выпадение «орла» или «решки» при одном бросании монеты.

Два случайных события называются противоположными, если они несовместны и образуют полную группу событий. Событие, противоположное событию A, обозначают Ā. [3]

Пример № 1. Вероятность того, что новая шариковая ручка пишет плохо (или не пишет), равна 0,19. Покупатель в магазине выбирает одну такую ручку. Найдите вероятность того, что эта ручка пишет хорошо.

Решение: Вероятность того, что ручка пишет хорошо, равна 1 − 0,19 = 0,81.

Свойства:

Вероятность достоверного события равна единице

Вероятность невозможного события равна нулю

Вероятность случайного события есть положительное число, заключенное между нулем и единицей

Таким образом, вероятность любого события удовлетворяет двойному неравенству 0≤P(A)≤1

События называют независимыми, если вероятность наступления одного из них не зависит от появления или непоявления другого. В противном случае события называют зависимыми.

Пример №2. Вероятность того, что батарейка бракованная, равна 0,06. Покупатель в магазине выбирает случайную упаковку, в которой две таких батарейки. Найдите вероятность того, что обе батарейки окажутся исправными.

Решение: Вероятность того, что батарейка исправна, равна 0,94. Вероятность произведения независимых событий (обе батарейки окажутся исправными) равна произведению вероятностей этих событий: 0,94·0,94 = 0,8836.

События называют несовместными, если наступление одного из них исключает появление других событий в данном опыте. В противном случае события называют совместными.

Пример №3. На экзамене по геометрии школьнику достаётся один вопрос из списка экзаменационных вопросов. Вероятность того, что это вопрос на тему «Вписанная окружность», равна 0,2. Вероятность того, что это вопрос на тему «Параллелограм», равна 0,15. Вопросов, которые одновременно относятся к этим двум темам, нет. Найдите вероятность того, что на экзамене школьнику достанется вопрос по одной из этих двух тем.

Решение: Вероятность суммы двух несовместных событий равна сумме вероятностей этих событий: 0,2 + 0,15 = 0,35.

Суммой (объединением) двух событий А и В называют событие, заключающееся в том, что происходит по крайней мере одно из событий А и В.

Теорема о сложении вероятностей.

Вероятность суммы несовместных событий равна сумме их вероятностей: P(A + B) = P(A) + P(B)

Теорема о сложении вероятностей 2.

Вероятность суммы совместных событий вычисляется по формуле

P(A+B) = P(A) + P(B) – P(A*B)

Если случайные события A₁, A₂,…, A_n образуют полную группу несовместных событий, то справедливо равенство:

P(A₁) + P(A₂) + … + P(A_n) = 1. Такие события используются при решении задач на полную вероятность.

Произведением (пересечением) событий А и В называют событие, заключающееся в том, что происходят оба события и А, и В.

Теорема об умножении вероятностей.

Вероятность произведения независимых событий А и В вычисляется по формуле: P(A⋅B)=P(A)⋅P(B)

ПРАКТИЧЕСКИЕ ЗАДАЧИ ПО ТЕОРИИ ВЕРОЯТНОСТИ

Разберем подробно все виды задач по теории вероятности, которые могут встречаться в ЕГЭ.

Задача 1. На борту самолета 12 мест рядом с запасными выходами и 18 мест за перегородками, разделяющими салоны. Остальные места неудобны для пассажира высокого роста. Пассажир Волков высокого роста. Найдите вероятность того, что на регистрации при случайном выборе места пассажиру Волкову достанется удобное место, если всего в самолете 300 мест.

Решение:

В самолете 12 + 18 = 30 мест, удобных для Волкова. Всего в самолете 300 мест. Пример такого места представлен на рисунке 3.

Рисунок 3 – Место в самолете с запасным выходом

Поэтому нам необходимо количество удобных мест для Волкова и таких же высоких пассажиров разделить на общее количество мест в самолете. Поэтому вероятность того, что пассажир Волков получит удобное мест, равна 30 : 300 = 0,1.

Ответ: 0,1

Задача 2. Вероятность того, что новый электрический чайник прослужит больше года, равна 0,93. Вероятность того, что он прослужит больше двух лет, равна 0,87. Найдите вероятность того, что он прослужит меньше двух лет, но больше года.

Решение:

Проработав год, чайник может либо сломаться на второй год, либо благополучно служить и после 2 лет работы. Рассмотрим эти случайные события более подробно:

P(А) – чайник прослужит больше года, но меньше двух;

P(B) – чайник прослужит более двух лет;

P(C) – чайник прослужит ровно два года.

Так как эти три события несовместны (не могут произойти одновременно), то вероятность суммы этих событий равна сумме вероятностей каждого из них:

P(A+B+C)=P(A)+P(B)+P(C)

Вероятность события A требуется найти по условию задачи. Вероятность события B дана и равна P(B)=0,87. Вероятность события C равна нулю, так как связана с тем, что чайник должен выйти из строя точно в определенный час, минуту, секунду и т.д. (можно продолжать сколько угодно до долей секунды). Сумма всех трех вероятностей равна 0,93, так как P(A+B+C) – это вероятность возникновения или события А, или события B, или события C.

Представим решение данной задачи графически (см. рисунок 4)

Рисунок 4 – События поломки электрического чайника

Проведем расчёт вероятности поломки электрического чайника:

P(A)=P-P(B)=0,93-0,87=0,06.

Ответ: 0,06

Задача 3. Говорят, что в старину каждый десятый на Руси был Иван, в каждый двадцатый Петр. Если это верно, то кого было больше: Иванов Петровичей или Петров Ивановичей?

Решение:

Подсчитаем вероятности двух событий:

P(A) — случайно выбранного мужчину зовут Иван Петрович

P(B) — мужчину зовут Петр Иванович

Произведем расчет вероятности, что каждого мужчину зовут либо Иван, либо Петр – так как каждое случайное событие стремится к успешному выполнению, то числитель будет равен 1. Для этого:

P(A)=1/10=0.1 – это вероятность первого случайного события.

P(B)=1/20=0.05 – это вероятность второго случайного события.

Далее применяя теорему умножения вероятностей, произведем расчет. Вероятность быть Иваном Петровичем для жившего в старину россиянина равна: 0,1*0,05=0,005. Мы перемножили вероятности того, что наш древнерусский житель – Иван и что его отца зовут Петр. А вероятность оказаться Петром Ивановичем точно такая же: 0,05*0,1=0,005.

Ответ: 0,005 – это значит, что при смене комбинаций, количество мужчин с именами Иван и Петр одинаково.

Задача 4. Два грузовика, работая совместно, вывозят снег с улицы Нижняя Подгорная, причем первый грузовик должен сделать три рейса с грузом снега, а второй- два. Вероятность застрять с грузом снега при подъёме в горку равна 0,2 для первого грузовика и 0,25- для второго. С какой вероятностью грузовики вывезут снег с улицы Нижняя Подгорная, ни разу не застряв на горке?

Решение:

Вероятность для первого грузовика благополучно одолеть горку 1-0,2 = 0,8. Для второго 1-0,25 = 0,75.

Поскольку первый грузовик должен сделать 3 рейса, а второй – два, грузовики ни разу не застрянут на горке с вероятностью 0,8* 0,75* 0,8*0,75*0,8 = 0,36*0,8 = 0,288 – в данном случае опять применятся формула умножения вероятностей, но при этом учитывается, что грузовик первый едет три раза, а второй два раза.

Ответ: 0,288

Задача 5. Мини-пекарня продает пирожки с мясом, однако в среднем 2 пирожка из 10 оказываются без мяса. Покупатель купил 2 пирожка. Найдите вероятность того, что, хотя бы в одном из них найдется мясо.

Решение:

Для того, чтобы решить данную задачу необходимо нарисовать схему возможных исходов (см. рисунок 5):

Рисунок 5 – Возможные исходы при покупке двух пирожков

Благоприятные исходы в этой задаче – когда мясо будет только в первом пирожке, только во втором или в обоих. Не подходит только случай, когда оба пирожка окажутся без начинки – но для этого случая все равно вычисляем вероятность: 0,2*0,2 = 0,04.

После того, как вычислили случай без начинки, вычислим вероятность благоприятных исходов (что, хотя бы один из пирожков с мясом или в обоих случаях есть начинка): 1- 0,04 = 0,96.

Ответ: 0,96

Задача 6. Вероятность того, что клиент банка не вернет кредит, в период экономического роста равна 0,04, а в период экономического кризиса 0,2. Вероятность начала экономического кризиса оценивается в 0,45. Чему равна вероятность того, что клиент не вернет кредит?

Решение:

Для того, чтобы решить данную задачу необходимо нарисовать схему возможных исходов (см. рисунок 6).

Рисунок 6 – Возможные исходы для клиента банка

По условию задачи, экономический кризис начнется с вероятностью 0,45. С вероятностью 0,55 будет экономический рост – это первый исход, вторым исходом будет связана конкретно с клиентом банка.

Вероятность того, что клиент не вернет кредит, равна 0,55*0,04+0,45*0,2=0.112. Для решения данной задачи воспользовались формулой суммой вероятностей и перемножением. Однако следует учесть те исходы, когда клиент при любом раскладе возвращает кредит – при экономическом кризисе – 0,96; при экономическом кризисе – 0,8. Но по условию задачи эти исходы нам не интересны, поэтому их мы в расчете не учитываем.

Ответ: 0,112.

Задача 7. Склад оборудован двумя датчиками сигнализации различной конструкции, которые подают звуковой сигнал, если в помещение проникает посторонний. Вероятность выхода из строя в течение года для первого датчика равна 0,1 и второго 0,2. Найдите вероятность того, что в течение года хотя бы один датчик сигнализации останется исправным.

Решение:

Для того, чтобы решить данную задачу необходимо нарисовать схему возможных исходов (см. рисунок 7).

Рисунок 7 – Возможные неблагоприятные исходы для датчика

Нам подходят все исходы, кроме одного — когда в течение года сломались оба датчика. Вероятность этого неблагоприятного для нас исхода равна 0,1*0,2=0,02.

Вероятность благоприятного исхода (хотя бы один датчик сработал) равна 1-0,02=0,98 – для этого следует учитывать, что два датчика не работают вообще.

Ответ: 0,98

Задача 8. По статистике, только 10% из тех, кто создаёт свой первый бизнес, достигают успеха. Из тех, кто вторично открывает свое дело, успеха достигают 90%. При этом только 8% из тех, у кого первый бизнес оказался неудачным, готовы стартовать еще раз. Найдите вероятность сознания успешного бизнеса с первой или второй попытки.

Решение:

Для того, чтобы решить данную задачу необходимо нарисовать схему возможных исходов (см. рисунок 8).

Рисунок 8 – Благоприятные исходы

Проведем расчеты благоприятных исходов. Вероятность достичь успеха в бизнесе с первой попытки равна 0,1. Вероятность достижения успеха со второй попытки равна 90%(0,9). Но эту вторую попытку еще надо рискнуть сделать, и на это способны только 8%(0,08) из тех, у кого не получилось с первого раза – но как и для первого раза, во второй раз используем благоприятные исходы: 10% (0,1)- удачно; 90%(0,9) — неудачно.

. Получаем: P= 0,1+0,9*0,08*0,9=0,1648 — вероятность создания успешного бизнеса с первой или второй попытки. Для данного расчёта использовали формулу суммы вероятностей случайных событий.

Ответ:0,1648

Задача 9. В кармане у Пети было 2 монеты по 5 рублей и 4 монеты по 10 рублей. Петя, не глядя, переложил какие-то 3 монеты в другой карман. Найдите вероятность того, что пятирублевые монеты лежат теперь в разных карманах.

Решение:

Для решения данной задачи, необходимо помнить, что Петя мог переложить 3 монеты в другой карман так, чтобы пятирублевые монеты оказались в разных карманах, следующими вариантами, представленные в таблице 1.

Таблица 1 – Варианты вероятностей

1 вариант
5 рублей	10 рублей	10 рублей
2 вариант
10 рублей	5 рублей	10 рублей
3 вариант
10 рублей	10 рублей	5 рублей

2.Рассчитаем все три варианта вероятности. Для первой вероятности:

Данное выражение было получено так. Изначально всего 6 монет, две из них пятирублевые, следовательно, с вероятностью 2/6 выбирается первая пятирублевая монета. После этого в кармане остается 5 монет и вероятность выбора десятирублевой составляет 4/5. Затем, остается 4 монеты и 3 из них десятирублевые, поэтому последний множитель 3/4. По аналогии определяются вероятности для второго и третьего вариантов:

Искомая вероятность равна сумме вероятностей этих несовместных событий:

P=P₁+P₂+P₃

P= 0.2+0.2+0.2=0.6

Ответ: 0.6 – это вероятность того, что, хотя бы в разных карманах будут лежать пятирублевые монеты.

Задача 10. За круглый стол на 9 стульев в случайном порядке рассаживаются 7 мальчиков и 2 девочки. Найдите вероятность того, что обе девочки будут сидеть рядом.

Решение:

Решить данную задачу можно без применения формул комбинаторики.

Пусть одна из девочек заняла место за круглым столом. Тогда за столом остаётся 8 свободных мест. Вторая девочка может занять место слева или справа от первой, то есть благоприятных исходов два. Значит, вероятность того, что обе девочки сидят рядом, равна 2/8=1/4

Ответ: 0,25

Задача 11. В классе 26 человек, среди них два друга- Андрей и Сергей. Класс случайным образом разбивают на 2 группы по 13 человек. Найдите вероятность того, что Андрей и Сергей окажутся в одной группе.

Решение:

Пусть Андрей первым занял место в группе (неважно, в какой). И кроме него осталось еще 25 человек, среди которых его друг Сергей. Сколько у Сергея шансов оказаться в той же группе, что и Андрей?

В группе должно быть 13 человек, то есть Андрей и еще 12. Значит, вероятность того, что Сергей окажется в той же группе, что и Андрей, равна 12/25=0,48.

Ответ: 0,48

Задача 12. Монету бросают 10 раз. Во сколько раз событие «Орел выпадает ровно 8 раз» более вероятно, чем событие «Орел выпадет ровно 9 раз»?

Решение:

Начнем с числа возможных исходов. Если мы бросаем монету, возможных исходов два — орел или решка (см. рисунок 9).

Рисунок 9 – Орел и решка при первом броске

Бросим монету два раза. И вот уже 4 возможных исхода, которые представлены в таблице 2.


Решка-решка	Решка-орел	Орел-решка	Орел-орел

Это значит, что, каждый следующий бросок монеты увеличивает число возможных исходов в 2 раза (орел или решка). Для 10 бросков монеты количество возможных исходов, очевидно, равно 2¹⁰. По определению, вероятность равна отношению числа благоприятных исходов к общему числу исходов.

Каждый следующий бросок монеты увеличивает число возможных исходов в 2 раза (орел или решка). Для 10 бросков монеты количество возможных исходов, очевидно, равно 2¹⁰ . По определению, вероятность равна отношению числа благоприятных исходов к общему числу исходов. Рассмотрим случай, когда орел выпадет ровно 9 раз из 10 бросков монеты. Это значит, что решка выпала 1 раз. Это могло произойти при первом броске, при втором, при третьем… и, наконец, при десятом, всего 10 благоприятных исходов. Вероятность выпадения решки равно 1 раз из 10 бросков Р₁= 10/2¹⁰.

Теперь случай, когда орел выпал ровно 8 раз из 10 бросков монеты. Значит, решка выпала ровно 2 раза. Пронумеруем броски: 1, 2, 3…10. Решка могла выпасть ы первый и во второй раз. Обозначим эту комбинацию 12. Могла также выпасть в первый и третий раз, в первый и четвертый… Эти комбинации обозначаем как 13, 14… Пронумеруем таким образом все благоприятные исходы.

12, 13, 14, 15, 16, 17, 18, 19, 1 10

23, 24, 25, 26, 27, 28, 29, 2 10

34, 35, 36, 37, 38, 39, 3 10

45, 46, 47, 48, 49, 4 10

56, 57, 58, 69, 5 10

67, 68, 69, 6 10

78, 79, 7 10

89, 8 10

9 10

Количество благоприятных исходов равно 9+8+7+6+5+4+3+2+1=45.

Тогда Р₂=45/2¹⁰.

Поделив Р₂ на Р₁, получим, во сколько раз выпадение решки ровно 8 раз более вероятно, чем выпадение решки ровно 9 раз:

Р₂/Р₁=45/2¹⁰÷10/2¹⁰=4,5.

Ответ: 4,5.

Задача 13. Определите вероятность того, что в группе, состоящей из 23 человек, у двух людей будет совпадение дней рождения (число и месяц).

Решение:

Для решения данной задачи будем учитывать следующие условия:

В году 365 дней.

В группе нет людей, заведомо родившихся в один день (например, близнецов).

Рождаемость не зависит от дня недели или времени года.

Далее будем учитывать, что у людей в группе могут совпадать дни рождения.

Выберем наугад одного человека из группы и запомним его день рождения. Теперь выберем второго. Вероятность того, что его день рождения совпадает с днем рождения первого, равна 1/365, а вероятность несовпадения равна 1-1/365. Выбираем третьего. Вероятность того, что его день рождения совпадает с днем рождения первого или второго, равна 2/365, а вероятность противоположного события (несовпадения) равна 1-2/365.

Рассуждая аналогично, получим, что для 23-го человека в группе вероятность несовпадения его дня рождения со всеми предыдущими равна 1-22/365.

Тогда вероятность того, что все дни рождения различны:

Р=(1-1/365)*(1-2/365)*…*(1-22/365)=364*363*362*…*343/365²².

Подсчитаем вероятность того, что дни рождения совпадают:

Р1=1-Р=1-364/365*364/365*…*343/365=50,73%.

Вероятность того, что в группе из 23 человек хотя бы у двоих совпадут дни рождения, — больше половины.

Ответ: 50,73%

Задача 14. В случайном эксперименте симметричную монету бросают трижды. Найдите вероятность того, что орел выпадет все три раза.

Решение:

Вероятность, что выпадет орел или решка равна ½ или 0,5.

Равновозможны 8 исходов эксперимента: орел-орел-орел, орел-решка-орел, решка-орел-орел, решка-решка-орел, орел-орел-решка, орел-решка-решка, решка-орел-решка, решка-решка-решка.

Орел выпадает все три раза в одном случае: орел-орел-орел. Поэтому вероятность того, что орел выпадет все 3 раза, равна 1/8 =0,125. Данное значение получается при помощи умножению вероятностей появления орла в каждом эксперименте, получаем: .

Ответ: 0,125

Задача 15. Экзамен проходит по следующей схеме: если некоторый билет уже был вытянут, то после ответа экзаменатор откладывает его в сторону. Студент выучил 20 билетов из 30. Когда ему выгоднее идти- первым или вторым, — чтобы вероятность вынуть выученный билет была больше?

Решение:

Итак, для решения будем учитывать следующие условия:

— Назовем билеты, которые студент выучил, «счастливыми».

— Если студент пошел отвечать первым, вероятность вытянуть «счастливый» билет равна 20/30=2/3.

Если идти отвечать вторым, возможны два случая:

Первый билет, который вытянул кто-то другой, был «счастливым», и тогда «счастливых» билетов теперь 19.

Первый билет не был «счастливым», и «счастливых» билетов так и осталось 20.

Нарисуем схему возможных исходов, как всегда делаем в подобных задачах (см. рисунок 10).

Рисунок 10 – Схема возможных исходов счастливых билетов

Вот наш студент идет отвечать вторым. Вероятность вытянуть «счастливый» билет равна 2/3*19/29+1/3*20/29=2/3(формулы суммы вероятности). Удивительный ответ! Та же самая вероятность! Значит, неважно, первым или вторым идти отвечать, если ты выучил 20 билетов из 30.

Ответ: 2/3

ЗАКЛЮЧЕНИЕ

По результатам исследования можно сделать по трем вопросам следующие выводы.

В первом вопросе рассмотрен исторический процесс формирования теории вероятности как науки начиная от применения ее методов в азартных играх и заканчивая применением методов в научных сферах человеческой жизни.

Во втором вопросе представлены основные термины и понятия теории вероятности, представлены примеры решения задач.

В третьем вопросе более подробно рассмотрены практические задачи решения теории вероятности: начиная от простых задач и заканчивая задачами с применениями методов комбинаторики.

СПИСОК ИСПОЛЬЗОВАННОЙ ЛИТЕРАТУРЫ

История теории вероятности // URL: https://polit.ru/article/2014/02/07/ps_a_bufetov/

История теории вероятности // URL: https://online—matematika.ru/теория-вероятностей/история-предмета

Теория вероятности // URL: http://kvm.gubkin.ru/pub/inm/tv.pdf

Теория вероятности: базовые понятия // URL: http://www.mathprofi.ru/teorija_verojatnostei.html

Лекции по теории вероятности // https://mipt.ru/education/chair/mathematics/study/uchebniki/Л_ТВ_Горяйнов.pdf

ЕГЭ по математике // URL: https://ege—study.ru/ru/ege/materialy/matematika/

Просмотров работы: 2262

Источник

вероятность успеха | areliability.com

Про блондинку, динозавра, преподобного Томаса Байеса и вероятность успеха при малой выборке – нехватке статистической информации (например пусков новых ракет или удачных свиданий)

Часто можно услышать довольно известный анекдот, который в разных вариантах звучит следующим образом: Блондинка сдаёт экзамен по теории вероятностей и профессор, периодически поглядывая на её декольте, жадно вопрошает: «Скажите, голубушка, а вот какая вероятность того, что выйдя после экзамена из института на улицу вы встретите, ну, ну скажем динозавра?». Блондинка томно хлопает ресницами, поджимает сочные губки и тихо отвечает: «50/50».

Профессор закашливается:
— Что вы имеете в виду?
— Ну как что, или встречу или нет!

На этом месте полагается смеяться, радостно клеймя блондинок позором. Но так ли это?

Одна из хитростей и сложностей теории вероятностей — это вопрос, что нам делать и как определить вероятность успеха, когда размер выборки не очень велик или, иными словами, у нас крайне мало статистической информации. Предположим, у новой ракеты был только один пуск и этот пуск был успешный. Насколько безопасным будет следующий пуск? Какая вероятность успеха второго пуска?

Далёкий от теории вероятностей и наивный адепт частотного подхода скажет примерно так: «Был один пуск, был один успех, следовательно, разделив одно на другое мы получим вероятность успеха равную 1», полностью исключая возможность каких-либо отказов.

И умом, и чутьём мы понимаем, что рассуждать так полностью неверно. Предположим, у вас есть выбор: полететь на ракете, у которой было 99 успешных пусков и один сбой или на ракете, у который был всего 1 пуск, и он был успешный. Что бы вы выбрали? К гадалке не ходи (а обратись лучше ко мне за консультацией), скорее всего вы выберете ракету, которая уже слетала 100 раз, и ваша вера в неё основана на бо́льшем количестве информации.

Простая статистика не работает должным образом, когда мы имеем дело с небольшим объёмом выборки. Нам нужна формула, которая будет учитывать тот факт, что мы практически ничего не знаем. Нам поможет Байесовская статистика!

Удивительно, но сельский священник, преподобный Томас Байес в перерывах между литургией и булочками с маслом вывел в буквальном смысле душеспасительную формулу, которая помогает в XXI веке оценивать вероятность успеха космических пусков.

В отчёте о космических пусках я нашёл формулу Байеса для того, чтобы правильно оценить вероятность успеха при малой выборке:

P= (k+1)/(n+2)

Где P — вероятность успеха следующей попытки, k — количество успешных событий на данный момент, а n — общее количество событий на данный момент. Формула называется «Байесовская оценка первого уровня средней прогнозируемой вероятности успеха». Следовательно:

Для новой ракеты: k = 1, n = 1, поэтому P = 0.67
Для многократно слетавшей ракеты: k = 99, n = 100, поэтому P = 0.99

Для новой ракеты вероятность успеха составляет 2/3, что следующий полет будет удачным. Это более объективная оценка нашего недостатка информации относительно новой ракеты. Да, у нас был один успешный полёт, и это хорошо, но мы все ещё мало что знаем о новой ракете. Для многократно слетавшей ракеты формула предсказывает вероятность успеха в 0,98, что почти соответствует обычной оценке вероятности. Если мы разделим 99 успехов на 100 пусков мы получим 0,99.

А что, если пусков вообще ещё не было? Давайте воспользуемся формулой. Тогда k = 0 и n = 0. Байес говорит, что вероятность успеха составляет 0,5. Шанс пятьдесят на пятьдесят, в этом есть смысл. Мы ещё ничего не пробовали, и у нас нет никакой информации, так что ещё мы можем сказать?

Этот последний пункт поднимает сложную проблему с байесовскими рассуждениями. Мы должны сделать начальное предположение о вероятности. Шанс 50-50 звучит разумно, но это все ещё предположение.

Блондинка была права?

Конечно, формула относится не только к ракетам. Это формула позволяет оценить вероятность успеха для всего, что является успехом / неудачей, истиной / ложью.
С помощью формулы Байеса мы можем, например, оценить вероятность счастливого свидания, вероятность удачной доставки пиццы и многого другого.

Попробуйте посчитать на досуге Байесовскую вероятность успеха с помощью моего калькулятора:

Источник

Министерство образования Российской Федерации

_______________________________

САНКТ-ПЕТЕРБУРГСКИЙ

ГОСУДАРСТВЕННЫЙ ПОЛИТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ

В. М. МАКАРОВ

ПРОИЗВОДСТВЕННЫЙ
МЕНЕДЖМЕНТ

МОДЕЛИ И МЕТОДЫ ОБОСНОВАНИЯ

УПРАВЛЕНЧЕСКИХ РЕШЕНИЙ

Практикум

Санкт-Петербург

Издательство СПбГПУ

2003

УДК
658.512.6:621(075.8)

М
а к а р о в В.М.
Производственный менеджмент. Модели и
методы обоснования управленческих
решений: Практикум. СПб.: Изд-во СПбГПУ, 2003. с.

Пособие соответствует государственному
образовательному стандарту дисциплины «Менеджмент» подготовки
дипломированных специалистов по специальности 061100 «Менеджмент
организации» и 060800 «Экономика и управление на предприятии».

Рассмотрено управление как информационный процесс, описаны
содержание функции управления, требования к управленческим решениям. Из
множества методов обоснования управленческих решений приведены два основных:
прогнозирование и метод «платежной матрицы». При рассмотрении
прогнозирования кроме хорошо известных статистических методов подробно представлен
метод экспертной оценки. Материал изложен преимущественно в виде решения
типовых задач и снабжен контрольными заданиями.

Пособие содержит материал только одного раздела изучаемой
студентами дисциплины «Менеджмент» и продолжает серию изданий, где
излагаются специфические закономерности, модели и методы производственного
менеджмента.

Предназначено для студентов, получающих вторую
специальность в Высшей школе управления и финансов, а также для других студентов
факультета экономики и менеджмента (ФЭМ), изучающих дисциплины «Менеджмент»,
«Производственный менеджмент».

Табл. 4. Ил. 5.
Библиогр.: 4назв.

Печатается
по решению редакционно-издательского совета Санкт-Петербург-ского государственного
политехнического университета.

ã Санкт-Петербургский
государственный

политехнический университет, 2003

ПРЕДИСЛОВИЕ

Пособие предназначено для студентов Высшей школы
управления и финансов и студентов факультета экономики и менеджмента различных специальностей
направления 521500 «Менеджмент», изучающих дисциплины «Менеджмент»
или «Производственный менеджмент». Оно входит в серию практикумов, посвященных
решению задач производственного менеджмента, подготовленную к изданию
профессором В.М.
Макаровым. Это четвертое пособие в серии, издаваемой с 1997 года.

Цель пособия – систематизация и закрепление полученных
студентами знаний в области управления производством с использованием различных
моделей и методов.

В пособии кратко освещены два направления обоснования
принятия управленческих решений, имеющие на практике наибольшее применение:
прогнозирование и метод платежной матрицы. Издание содержит теоретический
материал по названным темам и большое число примеров и задач.

Отличительной особенностью серии является
использование автором несложного математического аппарата, что делает ее доступной
для студентов с различной степенью математической подготовки. В первую очередь

это
актуально для студентов Высшей школы управления и финансов, многие из которых
образование по первой специальности получали не в Политехническом университете.

Знакомства только с данным пособием недостаточно для
полного освоения материала. Оно дополняет лекции и может быть использовано для
аудиторных и самостоятельных практических занятий, а также для контроля
усвоения теоретического материала. Для более глубокого ознакомления с материалом
могут быть рекомендованы следующие издания:

1.
Карданская Н.Л. Принятие управленческого решения:
Учебник. М.: ЮНИТИ, 1999.

2. Козловский В.А., Маркина Т.В., Макаров В.М.
Производственный и операционный менеджмент: Учебник. СПб.: Спецлитература, 1998.

3. Козловский В.А., Маркина Т.В., Макаров В.М.
Производственный и операционный менеджмент: Практикум. СПб.: Спецлитература, 1998.

4. Льюис К.Д. Методы прогнозирования экономических
показателей. М.: ФиС, 1986.

ОСНОВЫ
ПРИНЯТИЯ УПРАВЛЕНЧЕСКИХ РЕШЕНИЙ

1.1. Управление как информационный процесс

Управление присутствует во всех сферах жизни. Оно
характерно для:

– технических систем (управление
машинами, оборудованием),

– биологических систем
(управление стаями птиц, стадами зверей),

– социально-экономических
систем (управление людьми).

Анализ процессов управления
в этих сферах показывает, что при всем различии им присущ ряд общих закономерностей.
Наука о наиболее общих законах управления
в технике, природе и обществе называется кибернетикой.

Кибернетика рассматривает
управление как информационный процесс,
осуществляемый в замкнутом контуре и
преследующий заданные цели (рис.
1.1). Процесс управления всегда предполагает наличие двух объектов: органа управления
(субъекта) и объекта управления. Субъект
управления преобразует по определенному закону информацию состояния в командную
информацию, подчиняющую поведение объекта управления определенной цели. Рассмотрим
этот процесс на примере предприятия — большой социально-экономической
системы. Социальной, потому что
предприятие – это организация, создаваемая людьми для достижения своих целей. Экономической, потому что эти цели имеют
экономический характер.

Вертикаль управления

Внешняя среда

Горизонтальные

УПРАВЛЯЮЩАЯ ПОДСИСТЕМА

(СУБЪЕКТ УПРАВЛЕНИЯ)

(партнерские) связи

Управленческие

УПРАВЛЯЕМАЯ ПОДСИСТЕМА

(ОБЪЕКТ
УПРАВЛЕНИЯ)

воздействия
Информация

(командная
обратной
связи

информация)

Рис. 1. 1. Замкнутый контур управления предприятием

В замкнутом
контуре происходит преобразование
информации, которое может быть формализовано следующим образом: y(t+Dt)=F(х(t)),
где

х(t) – информация состояния в текущий момент времени;

F – функция преобразования информации
состояния в командную информацию (принятие управленческих решений);

y(t+Dt) – командная информация на шаг вперед;

Dt – дискрета управления.

Вероятно, наибольшую сложность
и в то же время наибольший интерес представляет анализ содержания функции управления.
Концептуально её можно представить следующим образом:

Объективная составляющая – это такая часть работы по принятию решений,
которая поддается формализации, что позволяет передать ее помощникам руководителя
или автоматизировать

Субъективная составляющая – это неформализуемая часть работы менеджера,
позволяющая ему принимать окончательные решения на основе объективной
информации, но с использованием своих интуиции, знаний, опыта

на основе:	выбирает:
1) цели управления,	1) по определенным правилам,
2) имеющейся информации об объекте управления,	2) из множества возможных (альтернативных) вариантов,
3) имеющейся информации о состоянии окружающей среды	3) единственное лучшее на его взгляд управленческое решение

1.2. Решение — основа управления

Решение – один из необходимых
элементов волевого действия человека, предполагает осознание целей, средств их
достижения и ожидаемых результатов. Решения могут быть бытовыми, политическими,
конструкторскими, технологическими, управленческими. Именно управленческие
решения станут объектом нашего дальнейшего рассмотрения.

ПРОЦЕСС УПРАВЛЕНИЯ — ЭТО ПРОЦЕСС ВЫРАБОТКИ И
ОБЕСПЕЧЕНИЯ ИСПОЛНЕНИЯ УПРАВЛЕНЧЕСКИХ РЕШЕНИЙ.

Принятие решений является
важнейшей функцией управления, успешное осуществление которой обеспечивает
достижение организацией ее целей. Неумение качественно и рационально
осуществлять этот процесс, отсутствие в организации механизма его осуществления
характерно для большинства фирм и предприятий, государственных учреждений и
органов. Успех организации, в какой бы сфере она ни функционировала, во многом
зависит от умения принимать управленческие решения. Тем более это важно для
России, где большинство организаций проходят первые этапы своего развития в
рыночных условиях, и очень важно, какую технологию принятия решений они выбирают.

Известны различные подходы к
процессу подготовки и принятия решений. В рамках каждого подхода можно выделить
определенную совокупность последовательно применяемых приемов и методов, этапов
и процедур, имеющих прямые и обратные связи, которую называют технологией принятия решений.

Несмотря на многообразие методов
и способов принятия решений, нельзя выделить единственную, лучшую технологию.
Природа изучаемого процесса – это информационный
обмен. Именно его информационная природа (степень возможности получения
полной, достоверной и своевременной информации, степень риска и т. д.) и многие
другие факторы делают невозможным введение
этого процесса в четко формализованные рамки. Однако это не исключает возможности
создания более или менее универсальной технологии принятия управленческих
решений.

В условиях недостатка
информации по изучаемой проблеме, при невозможности все строго рассчитать и проанализировать,
при множественности мнений о целях, критериях и т.д. может не существовать
единственного, наилучшего решения. Трудно принять даже «хорошее»
решение. Принятие решения – процесс психологический, а поведение человека не
всегда логично. Иногда людьми движет логика, иногда – чувства. Поэтому способы
или методы (подходы), используемые руководителем, варьируются от спонтанных до
высоко логичных. Причем в любом случае может быть принято весьма рациональное решение.

Требования,
предъявляемые к управленческим решениям:

1) целенаправленность,

2) эффективность,

3) обоснованность,

4) адресность,

5) своевременность,

6) правомочность

6.1) решение не должно
противоречить правовым и нормативным актам,

6.2) решение должно соответствовать
уровню руководства,

7) непротиворечивость

7.1) решение не должно
противоречить предыдущим решениям,

7.2) решение не должно
противоречить решениям других руководителей,

осуществимость – решение
может быть выполнено в заданные сроки при имеющихся ресурсах,

9) четкость, т.е.
невозможность трактовать решение двусмысленно,

10) полнота,
т.е. предоставление всей информации,
необходимой для выполнения,

11)
краткость изложения,

12) ясность
и понятность, т.е. изложение решения доступными для исполнителей средствами,

13)
этичность.

Классификация принимаемых
управленческих решений:

а) По
уровню принятия решения:

высший уровень руко-водства (принимает стратегические решения,
относящиеся к предприятию в целом и определяющие линию его работы на долгосрочный
период)

средний уровень руко-водства (уровень цехов,
служб, отделов; принимает тактические решения на среднесрочную перспективу,
необходимые для следования общей стратегии фирмы)

руководители
первичных коллективов (принимают оперативные решения, обеспечивающие выполнение
тактических и стратегических разработок)

б) По
характеру решаемых задач

информационные (доводят до сведения подчиненных
что-либо)

организационные (меняют функции, организационную структуру или отношения)

оперативные
(обеспечивающие оперативное руководство коллективом)

в) По
методам принятия решений

эвристические
(основанные на опыте, интуиции руководителя)

алгоритмические
(обоснованные с помощью специальных методов)

г) В зависимости от характера исходной информации

принимаются
в условиях определенности (таких условий при принятии управленческих
решений подавляющее меньшинство)

принимаются в условиях риска (когда осуществимость
определенных событий в будущем имеет вероятностный характер)

принимаются
в условиях неопределенности (когда невозможно оценить вероятность свершения будущих
событий)

д) Как
принимаются решения

единолично коллегиально

Подготовка и принятие управленческих
решений представляют собой процесс
содержательного преобразования информации состояния в управленческую информацию. Будучи
по сути неформальным, творческим процессом, он включает ряд формализуемых моментов.

1.3. Процесс и методы
принятия управленческих решений

Процессы
принятия решений, понимаемые как выбор человеком одной из нескольких
альтернатив его дальнейшего поведения, сопровождает всю человеческую жизнь.
Большинство решений мы принимаем не задумываясь, так как существует автоматизм
поведения, выработанный практикой. Но возможны и ситуации, когда человек
испытывает мучительные раздумья. Это случается, когда он сталкивается либо с
новым объектом выбора, либо с новой обстановкой, в которой совершается выбор.

Принятие решений
представляет собой сознательный выбор одного из имеющихся вариантов (альтернатив)
действий, сокращающих разрыв между настоящим и будущим желательным состоянием — целью. Сам процесс принятия
решений включает множество различных элементов, но непременно в нем
присутствуют такие элементы, как цели,
средства, альтернативы. Принятие решений – это «центр», вокруг
которого вращается жизнь как отдельного человека, так и организации. Решение в
организации можно рассматривать как продукт управленческого труда, а его
принятие – как процесс, ведущий к появлению этого продукта.

Таким
образом, принятие управленческих решений отражается на всех аспектах
деятельности организации, и этот процесс является основной частью ежедневной
работы любого руководителя (менеджера).

Принятие решений в организации
это:

– сознательная и
целенаправленная деятельность, осуществляемая людьми — руководителями, менеджерами,

– поведение людей, основанное
как на фактах, так и на их ценностных ориентациях,

– процесс, базирующийся на
осознанном взаимодействии членов организации,

– выбор лучшей из ряда
альтернатив в рамках состояния внешней и внутренней организационной среды.

Принятие решений – это и
наука, и искусство.

Для принятия управленческих решений, таким
образом, должны быть определены:

– мотивирующие цели,

– допустимые альтернативные
способы достижения поставленных целей – стратегии,

– возможные состояния внешней
(неопределенной) среды,

– ожидаемые результаты
реализации стратегий при различных состояниях среды – исходы.

Затем альтернативы должны
быть оценены, согласно выбранному критерию решения, для выбора лучшей из них.
Хорошо, если этот выбор может быть каким-либо образом формализован. К этому
необходимо стремиться, однако в любом случае окончательное решение всегда
остается за руководителем.

Формализованные методы
обоснования принятия управленческих решений в мировой практике носят
название »исследование операций», где
под операцией понимают любой вид деятельности человека.

Далее будут подробно
рассмотрены два подхода к обоснованию принятия управленческих решений: это ряд
методов прогнозирования и метод платежной матрицы (дерева решений).

ПРОГНОЗИРОВАНИЕ

2.1. Роль планирования и прогнозирования в управлении производством

Ведущая роль в осуществлении
управления отводится:

1) постановке целей,

2) выбору лучшей стратегии
достижения целей,

3) увязке ресурсов, необходимых
для достижения выбранной стратегии.

Эти задачи решает ключевая
функция управления – планирование.

План – это совокупность
конкретных заданий, адресная директивная программа, содержащая все основные
параметры, необходимые для управления предприятием или любым его
подразделением.

Планированию в дореформенной
социалистической экономике отводилась важнейшая роль. Централизованное планирование являлось в нашей стране основой
командно-административной системы управления экономикой. В начальный период
перехода к рыночным отношениям наблюдались попытки вместе с
командно-административной системой отбросить и всю многоуровневую систему
планов, существовавшую в то время в народном хозяйстве, а заодно и весь опыт,
который был наработан в области планирования. Такой подход нельзя назвать
правильным. Вместе с разгосударствливанием экономики должно уйти из практики
лишь централизованное планирование, а
центр тяжести плановых работ должен переместиться на уровень предприятий и
организаций. Накопленный опыт «внутризаводского планирования», как
оно тогда называлось, может быть использован и сегодня, естественно, с
коррекцией ориентиров на рыночные отношения.

Прогноз в отличие от плана имеет предварительный вариантный характер, его
горизонт шире планового периода. Прогнозирование можно определить как преддирективный этап плановой работы.
Прогноз ограничивает области и возможности, в рамках которых ставятся реальные
цели и задачи, выявляет направления, которые должны стать объектом разработки и
принятия плановых решений.

Под прогнозированием понимаются
выявление качественных и количественных характеристик технических,
экономических, социальных и других систем или процессов в настоящем на основе
познания закономерностей их развития в прошлом и оценка будущих значений этих характеристик.

Любое управленческое
решение, последствия которого проявятся в будущем, основывается на том или ином способе предвидения, на
догадке о будущем, на прогностических оценках. Таким образом, прогноз по
существу является догадкой, но при использовании определенной методики в
прогнозе может содержаться нечто большее, чем догадка. Прогноз – это догадка, базирующаяся на знаниях.

Целью прогнозирования
является минимизация погрешности прогностических оценок. Очевидно, что научно
обоснованные и планомерно разрабатываемые прогнозы являются более точными и
эффективными (как основа принятия решений), чем случайные и интуитивные
прогнозы.

Прогнозы могут быть:

—
научно-технические;

—
демографические;

—
политические;

—
социальные;

—
экономические и т.п.

Для
предприятий, работающих в условиях рыночного хозяйствования, прогноз имеет
прежде всего коммерческое значение, а среди коммерческих прогнозов выделяется прогноз спроса на продукцию (услуги)
предприятия. Стоит отметить, что прогноз спроса должен учитывать и
научно-технические, и политические, и демографические, и социально-экономические
факторы.

Задачи коммерческого прогнозирования:

1)
выявление необходимости наращивания (свертывания)
производственных мощностей данного типа продукции в данном регионе и
определение темпов этого процесса;

2) формирование ориентировочных
планов производства с учетом имеющегося научно-технического потенциала;

3) оценка потребности в
ресурсах, необходимых для выполнения текущих планов.

Прогноз, ориентированный на
решение любой из этих задач, должен удовлетворять следующему условию: горизонт прогнозирования должен предусматривать
достаточно времени для принятия и эффективного выполнения соответствующих
управленческих решений.

Прогноз первого типа
называется долгосрочным, или стратегическим; второго типа – среднесрочным;
третьего типа – краткосрочным.

Очевидно, что чем шире
горизонт прогнозирования, тем более обобщенным и менее точным может быть
прогноз.

Известны различные методы прогнозирования:

1) экспертные методы;

2) метод анализа «индекса
деловой активности»;

3) статистические методы
прогнозирования на основе:

а) анализа временных рядов;

б) анализа факторных зависимостей.

Рассмотрим подробнее первый
и третий из этих методов.

2.2. Экспертные методы прогнозирования

Экспертные методы
применяются для оценки объектов и процессов, не поддающихся непосредственному
измерению, т. е. характеризующихся лишь качественно.
Это не обязательно прогнозирование; область применения экспертных методов
значительно шире, например, оценка знаний учащихся, качества товаров (вин,
парфюмерии, чая и др.), выступлений спортсменов. В конечном счете всенародное
голосование по выборам президента России – это тоже экспертная оценка, только
экспертами при этом выступаем все мы.

Экспертные методы — это совокупность специальных
методик обработки экспертных оценок, позволяющих свести ошибку прогнозирования
к минимуму.

Экспертные оценки –
это субъективные суждения специалистов в данной области, высказанные ими
открыто или скрыто, индивидуально, независимо от других, или коллективно.

Обычная форма представления
экспертных оценок — баллы. Наиболее близкий читателям пример — сдача плохим студентом экзамена комиссии из
трех преподавателей-экспертов. Принятая в наших школах и вузах система оценок также хорошо известна: знания
оцениваются по пятибалльной системе, лучшая оценка — 5; в Германии же, например, все наоборот — лучшая оценка единица. Однако привычная
пятибалльная шкала далеко не единственна. Так, мастерство спортсменов на
соревнованиях по фигурному катанию оценивается по шестибалльной системе, причем
используются целые и десятые доли баллов, гимнасты за свое выступление могут набрать
максимум десять баллов. Отсюда следует, что при проведении экспертизы в первую
очередь необходимо оговорить используемую систему балльной оценки.

Обоснование объективности
результатов экспертной оценки, кроме высокой квалификации экспертов, обусловлено
следующим предположением: неизвестная характеристика оцениваемого
(прогнозируемого) процесса трактуется как случайная
величина, а индивидуальные оценки экспертов — как множество ее реализаций, отражающее закон и параметры распределения
этой случайной величины. Предполагается, что истинное значение
прогнозируемой характеристики находится внутри диапазона оценок, полученных от
экспертов.

Недостатки экспертных
методов неизбежно связаны с их природой.

Для недостаточно
исследованных областей истинное значение прогнозируемой характеристики может
находиться вне диапазона данных экспертами оценок, т. е. один из экспертов,
давший крайнюю оценку, может оказаться наиболее близким к истине.

Даже для достаточно
исследованных областей экспертные оценки могут нести в себе не только
субъективные черты отдельных специалистов, но и коллективные субъективные черты,
рассматриваемые как «общественное мнение», «общественная точка
зрения», «научная школа» и т. п.
Они не исчезают при обработке результатов по специальным методикам, а
иногда могут даже усиливаться.

При коллективной экспертной
оценке, а иногда даже и при индивидуальной, на результат может заметно влиять
мнение одного человека: руководителя, самого авторитетного специалиста, «сильной
личности».

Наиболее известны следующие
экспертные методы.

1.
Метод «мозговой атаки», при котором все мнения, высказанные
экспертами, тотчас же обсуждаются до тех пор, пока все они не придут к общему
мнению. При этом приветствуется свободное высказывание самых необычных и оригинальных
мнений.

2.
Метод Дельфи — итеративный групповой метод
— самый старый из методов, пришедший к нам из
древней Греции.

3.
Метод индивидуальной разовой экспертной оценки — классический, хорошо формализованный метод.

2.3. Методика проведения индивидуальной разовой экспертной
оценки

Индивидуальная разовая экспертная
оценка проводится в четыре этапа:

1) подбор группы экспертов,
взаимная оценка их компетентности;

2) формирование списка
факторов, по которым будет оцениваться объект, и оценка их значимости;

3) оценка объектов анализа
(прогнозирования) с учетом значимости выделенных факторов и компетентности
экспертов;

4) ранжирование объектов с
учетом полученных ими обобщенных оценок; выводы.

Процедуру экспертизы
проводит группа менеджеров. Вначале они подбирают группу экспертов так, чтобы
минимизировать возможные недостатки метода, отмеченные ранее. Затем устанавливается
и доводится до экспертов шкала балльных оценок, которая будет использоваться в
дальнейшем. Экспертов собирают вместе фактически или виртуально, и первое, что
они делают, – оценивают компетентность друг друга. Результат – квадратная
матрица оценок К_ij, данных i-м
экспертом j-у (i = 1, 2,…, n, j = 1,
2,…, n), где n — общее количество экспертов.

Менеджеры обрабатывают
матрицу и рассчитывают коэффициенты компетентности экспертов: 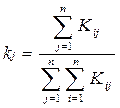, j = 1, 2, …, n.

Эксперты, получившие
минимальную оценку, могут быть исключены из группы.

На втором этапе эксперты
независимо друг от друга составляют перечни факторов оценки объектов. Все
факторы сводятся в единый список, который передается им для оценки. Результат
оценки – матрица размерности n´m,
где m – число
оцениваемых факторов, а F_ij – оценка, данная i-м
экспертом j-у фактору.

Менеджеры обрабатывают
матрицу и рассчитывают коэффициенты значимости факторов: 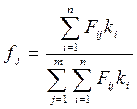, j = 1,
2, …, m.

Факторы ранжируются в порядке
убывания их значимости и наименее значимые по решению менеджеров могут быть
отброшены для сокращения объема работ на следующем этапе. После такого
отбрасывания расчет коэффициентов значимости должен быть повторен, но уже без
учета оценок, полученных исключенными из рассмотрения факторами. В любом случае
должно выполняться условие: 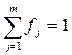. Аналогичное условие
выдвигается по отношению к коэффициентам компетентности экспертов.

На третьем, основном, этапе
эксперты оценивают объекты с учетом выделенных факторов. Результат оценки – Р матриц размерностью n´ m, где
Р – число оцениваемых объектов, а W_ij_р– оценка, данная i-м экспертом р-у объекту с учетом j-го фактора.

Менеджеры обрабатывают
информацию и рассчитывают обобщенные оценки всех объектов: 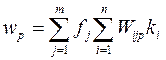, р = 1, 2, …, Р.

На четвертом этапе объекты
располагаются в порядке убывания (возрастания) значений обобщенной оценки,
таким образом из них отбираются лучшие. На любом этапе по результатам
выставления экспертами оценок можно определить коэффициент согласованности их
мнений: 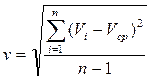. Здесь V – любая из выставляемых
экспертами оценок (K, F, W). В случае значительного
расхождения мнений группа может быть распущена.

Для целей разработки
простейшего прогноза может быть использована усеченная процедура, в которой
опущены выбор и оценка значимости факторов, прогнозируется состояние одного
объекта, балльная оценка может быть заменена оценкой процентной вероятности.
Так можно спрогнозировать вероятность успеха вывода товара на рынок,
вероятность успешного завершения научно-исследовательских работ и т. п. Полная
процедура используется для построения более сложных прогнозов, таких как оценка
выводимого на рынок товара по сравнению с товарами конкурирующих фирм, а также
для решения задач типа: выбор лучшего поставщика из нескольких возможных.

$ Пример.

Пусть четыре эксперта должны
спрогнозировать вероятность успеха продвижения товара на рынок. Результаты
взаимной балльной оценки их компетентности (из 6 баллов, высший – 6) и расчета
коэффициентов компетентности представлены в следующей таблице.

Эксперт, дающий оценку	Эксперт, получающий оценку	Итого
1	2	3	4
1	–	6	4	2	–
2	5	–	2	3	–
3	3	3	–	4	–
4	3	3	1	–	–

Итого	11	12	7	9	39
Коэффициент компетентности	0,282	0,308	0,179	0,231

Таблица оценки прогнозируемой
вероятности имеет следующий вид:

Эксперт	Оценка вероятности успеха, %	Коэффициент компетентности
1	35	0,282
2	20	0,308
3	45	0,179
4	40	0,231
Итого	33,325

Практически в этой ситуации
результат расчета 33,325 % — это средневзвешенное мнение экспертов. Если
и далее упрощать процедуру и исключить первый шаг, то придем к вырожденной
форме — к расчету простого усредненного
мнения экспертов.

$ Пример.

Те же независимые эксперты
должны дать прогноз успешного выхода на рынок новой фирмы, предлагающей услугу
– создание Web-страниц, на основе сравнения ее возможностей с
другими уже работающими на этом рынке фирмами. Здесь требуется сравнительная
оценка конкурентов по нескольким факторам, предварительный перечень которых
сформирован экспертами в следующем виде:

1) цена услуги создания Web-страницы,

2) «вес» программы
(т. е. объем памяти ПЭВМ, занимаемый программой),

3) сроки выполнения заказа,

4) качество и дизайн страниц,

5) условия оплаты.

Факторы получили у экспертов следующие оценки:

Эксперт	Оценка факторов	Коэффициент компетентности
1	2	3	4	5
1	1	6	2	5	2	0,282
2	1	5	5	6	2	0,308
3	3	6	3	6	1	0,179
4	2	4	2	5	2	0,231

Итого	1,589	5,230	3,103	5,487	1,821	17,230
Коэффициент значимости фактора	0,092	0,304	0,180	0,318	0,106	1,000

В результате проведенного
анализа было принято решение об исключении из рассмотрения 1-го и 5-го факторов
ввиду их низкой значимости. Это потребовало пересчета коэффициентов для
оставшихся в списке факторов. Пересчет выполнен в следующей таблице:

Итого	–	5,230	3,103	5,487	–	13,82
Коэффициент значимости фактора	–	0,378	0,225	0,397	–	1,000

Затем эксперты по оставшимся
трем факторам оценили восемь сторонних фирм и новую фирму (НФ). Результаты
оценки — девять таблиц и девять расчетов
по одной методике, представленной выше. Далее обработка экспертных оценок
показана на примере только одной новой фирмы.

Выставленные фирме баллы и
результаты их обработки представлены в следующей таблице.

Эксперт	Оценка объекта НФ по факторам	Коэффициент компетентности
1	2	3
1	4	5	5	0,282
2	2	6	4	0,308
3	3	5	6	0,179
4	3	6	6	0,231

Итого	2,974	5,539	5,102	4,396
Коэффициент значимости фактора	0,378	0,225	0,397

Для всех фирм результаты
обработки оценок в баллах сведены в таблицу:

Фактор оценки	Оцениваемая фирма	Коэффициент значимости фактора
НФ	1	2	3	4	5	6	7	8
«Вес» программы	*2,97*	5,13	3,02	3,25	2,03	5,11	2,47	4,51	3,72	0,378
Сроки исполнения	*5,54*	4,10	2,47	2,33	5,13	1,97	3,41	5,27	5,23	0,225
Качество и дизайн	*5,10*	4,39	5,66	3,08	2,64	2,78	2,53	5,33	4,98	0,397

Итого (обобщенная оценка)	*4,40*	4,61	3,94	2,97	2,97	3,48	2,70	5,01	4,56

Анализ результатов
показывает, что НФ занимает в рейтинге лишь четвертое место. Причина – высокий
«вес» программ. По этому фактору она занимает третье от конца место.
Вывод: следует обратить внимание на улучшение этой характеристики, может быть,
за счет увеличения сроков, которые не так значимы, по мнению экспертов, и по
которым НФ лидирует среди других фирм, сохраняя при этом неизменным качество
(3-е место).

Представлять результаты
экспертизы и выполнять их анализ удобно с помощью графиков, показанных на рис.
2.1.

2.4.
Статистический анализ временных рядов

Прогнозы на основе статистического
анализа ретроспективных рядов данных являются наиболее приемлемыми при условии,
что между прошлым и будущим имеется тесная причинно-следственная связь. При
этом прогноз следует корректировать всякий раз, когда заранее становятся известными
те или иные обстоятельства, влияющие на прогнозируемую величину, которые будут
иметь место в будущем. При прогнозировании спроса это:

—
появление новых рынков сбыта;

—
появление новых конкурентов;

—
проведение рекламных компаний;

—
появление новых научно-технических решений и т.п.

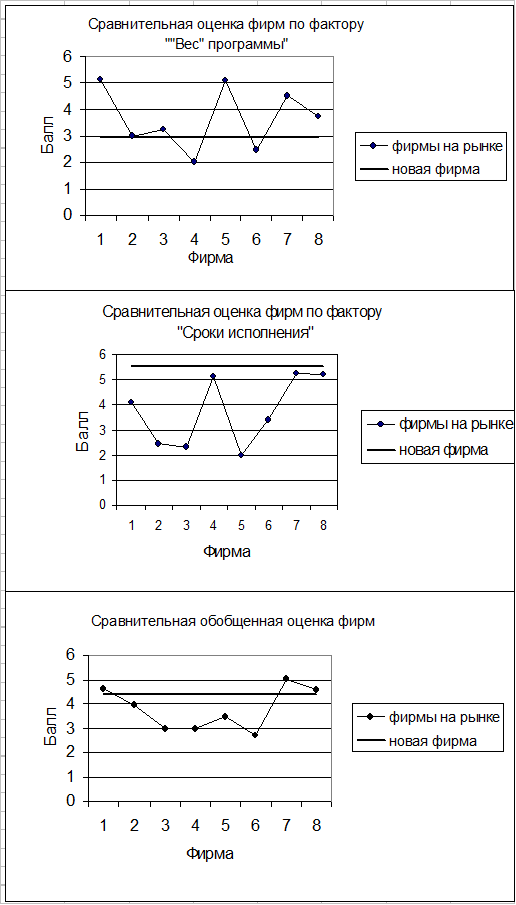Рис. 2.1. Графические результаты анализа
положения на рынке «новой фирмы»

Общий подход в этом способе
прогнозирования – попытка выявления трех типов зависимости прогнозируемого
параметра (l) от времени:

1) тренда (тенденции);

2) цикличности;

3) случайных отклонений (рис.
2.2).

Рис. 2.2. Иллюстрация действия на прогнозируемый
параметр трех типов зависимости от времени

l


                   t

Для их выявления:

1)
строится график зависимости прогнозируемого
параметра от времени по фактическим данным за отчетный период;

2)
выбирается прогностическая
функция и даются оценки на будущий период;

3)
рассчитывается погрешность этих оценок;

4)
принимается решение о принятии этой или о переходе
к другой прогностической функции.

Обычно прогностическая
функция подбирается методом наименьших
квадратов: требуется построить график функции по некоторой ограниченной
совокупности точек так, чтобы среднеквадратичное отклонение стремилось к минимуму:

s = ,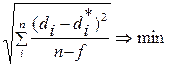

где   d – фактическое значение в i-й промежуток времени;

d_i* – значение прогностической функции в i-й
промежуток;

n – число промежутков;

f – число «степеней свободы».

В качестве прогностической может выступать любая
функция: константа, линейная, экспонента, парабола, синусоида и др.

Этот метод достаточно сложен для расчетов, но дает
хорошие результаты. Сегодня широко используются пакеты прикладных программ для
выполнения соответствующих расчетов, например, Statgraf. В ряде случаев можно пользоваться соответствующим
аппаратом из MS EXCEL.

Рассмотрим более простые методы, которые легко
применять без помощи ПЭВМ, однако они не обеспечивают такой точности.

Прогнозирование методом простого среднего

Рассчитывается среднее за отчетный период и
принимается в качестве прогностической оценки на будущее. Метод хорош, если
преобладающим является случайный тип зависимости прогнозируемого параметра от
времени.

Прогнозирование методом «скользящего»
среднего

где   m
– последний из моментов времени, для которого есть фактические данные;

к –
число моментов времени, учитываемых при прогнозе.

Метод простой, но
недостаточно точный, так как предполагает, что в следующем периоде значение
прогнозируемой функции будет средним за последние к интервалов.

Базу прогнозирования к
здесь нужно минимизировать.

Прогнозирование методом
«экспоненциального сглаживания»

Первая прогнозная оценка
здесь находится по формуле:

,

где   — коэффициент
сглаживания; 0 < < 1.

Вторая и последующие оценки
– по формуле:

.

$ Пример.

Известен спрос на товар
за первые 8 месяцев года. Требуется дать
прогноз относительно его реализации на 4 оставшихся месяца. Будем считать, что
по ходу дела нам становятся известны фактические данные за 8-й ¸ 12-й месяцы. Они также
указаны в таблице:

Месяц

1

2

3

4

5

6

7

8

9

10

11

12

Спрос

199

202

199

208

212

194

214

220

219

234

219

233

Спрогнозируем спрос на
основе данных последних месяцев, для которых спрос уже известен, т. е. базы
прогнозирования.

1.       Рассчитанный методом простого
среднего за 8 месяцев прогноз на 9-й, 10-й, 11-й, 12-й месяцы одинаков – 206.

Отклонение прогноза за 4
месяца от фактического спроса:

s = .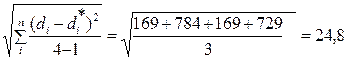

2.       Прогноз, рассчитанный методом
скользящего среднего (база – 5 месяцев):

на 9-й месяц:   ; факт – 219; Dd= 88;

на 10-й месяц: факт — 234; Dd²= 492;

на 11-й месяц:

на 12-й месяц:

Среднеквадратичное
отклонение за 4 месяца составило s = , что меньше, чем в первом случае.

3.       Прогноз, рассчитанный методом
экспоненциального сглаживания (база – 5 месяцев, = 0,2) на 9-й
месяц:

d₉ = (1 — 0,2) (220 + 0,2 ´ 214 + 0,2² ´194 + 0,2³ ´ 212 + 0,2⁴ ´208) = 218;

на 10-й месяц:   (1 — 0,2) 219 + 0,2 ´ 218 = 218,8;

на 11-й месяц:   (1 — 0,2) 234 + 0,2 ´ 218,8 = 231,0;

на 12-й месяц:   (1 — 0,2) 219 + 0,2 ´ 231 = 221,4.

Значение отклонения за 4
месяца: s =   т. е. меньше чем
ранее, следовательно, это лучший метод прогнозирования в данных условиях.

2.5. Факторный анализ статистик

Если значения
прогнозируемого параметра зависят не от времени, а от каких-либо других
факторов, то используется факторный статистический анализ. Обычно для этого с
помощью ПЭВМ по известной статистике подбирается аппроксимирующая функция одной
или многих переменных, которая и служит моделью для выработки прогноза.
Рассмотрим эту процедуру на примере.

$ Пример.

Предприниматель реализует
мороженое у станции метро. Он должен сделать заказ на следующую неделю с
разбивкой по дням. Каждое утро заказанное количество товара завозится на его
точки реализации. При неправильном заказе (прогнозе) в конце дня мороженого
может не хватить – тогда имеет место упущенная выгода, либо часть его останется
нереализованной; в таком случае возникнут проблемы с его хранением. Требуется
выявить факторы, определяющие объем продаж, собрать статистику продаж и
значений этих факторов, далее – разработать прогноз продаж мороженого на следующую
неделю. Предполагается, что дело происходит в разгар лета.

Среди факторов, влияющих на
объем продаж мороженого в это время, отобраны два наиболее существенных:
температура воздуха и день недели. Отметим, что второй фактор имеет логический
характер, что создает дополнительные трудности решения. Собранная за три недели
статистика представлена в табл. 2.1. Будем считать, что к моменту оценки объема
продаж известен прогноз погоды (температуры воздуха) на следующую неделю.

Подходов к решению этой
задачи несколько. Рассмотрим сначала наиболее распространенный классический
метод.

Для устранения
влияния на температурную функцию продаж логической переменной – дня недели — рассчитаем коэффициенты приведения для каждого
дня недели к среднедневной продаже (табл. 2.2). Затем с помощью этих коэффициентов
пересчитаем исходные данные о продажах (получим приведенные фактические
продажи, показанные в табл. 2.3 и на рис. 2.3). Аппроксимация этой зависимости
прямой, описываемой уравнением Q = 4,1t^o+ 23,76, дает очень хорошие результаты (коэффициент
корреляции 0,9). В табл. 2.3 даны также результаты расчетов продаж на основе
полученной трендовой линейной зависимости. С использованием этой же модели
можно спрогнозировать приведенные продажи на следующую неделю, а затем с
помощью коэффициентов приведения пересчитать их в индивидуальные прогнозы на каждый
день недели (табл. 2.4).

Значения
коэффициентов а и в при линейной аппроксимации могут быть рассчитаны как на ПЭВМ,
так и вручную по формулам:

Попытка
связать объемы продаж только с температурой, игнорируя влияние на них дня
недели, несостоятельна. Это наглядно подтверждает вид графика (см. рис. 2.2) и
значение коэффициента корреляции.

Другой, менее
точный подход к решению состоит в том, чтобы в единый статистический массив
свести данные с понедельника по четверг без разделения их на дни недели. То же следует
проделать с данными пятницы, субботы и воскресенья. Для каждого из массивов надо
подобрать аппроксимирующую кривую зависимости объемов продаж от температуры и
на ее основе делать прогноз.

При наличии
большей, чем сейчас, статистики эту процедуру можно осуществлять отдельно для
каждого дня недели, что упростит и сделает более точным решение этой задачи.

Таблица 2.1.                       Таблица 2.2

День недели

Первая неделя

Вторая неделя

Третья неделя

Среднее на день недели, кг

Коэффициент приведения

Продажа, кг

Темпера-тура воздуха, °С

Прода-жа, кг

Темпера-тура воздуха, °С

Продажа, кг

Темпера-тура воз-духа, °С

ПН

32,5

8

84,5

28

65

21

60,66

0,580

ВТ

35

10

84

26

77

23

65,33

0,624

СР

25

11

32,5

14

55

29

37,50

0,358

ЧТ

33,7

16

31,5

12

58,5

25

41,23

0,394

ПТ

95

17

66,5

15

114

27

91,83

0,878

СБ

216

22

171

18

216

24

201,00

1,922

ВС

277,5

30

166,5

20

259

19

234,33

2,241

ИТОГО:

714,7

636,5

844,5

104,55

Среднее

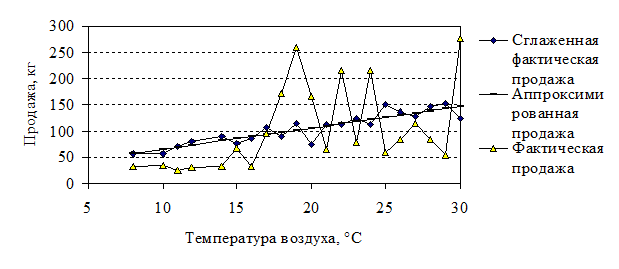Рис. 2.3. Графики зависимостей объема продаж от
температуры воздуха

Таблица 2.3

Температура воздуха, °С

Фактическая продажа, кг

Приведенная фактическая продажа,
кг

Трендовое значение продажи, кг

8

32,5

56

56,560413

10

35

56,4

64,760667

11

25

69,4

68,860793

12

31,5

80,8

72,960920

14

32,5

90,3

81,161174

15

66,5

75,6

85,261300

16

33,7

86,4

89,361427

17

95

108

93,461554

18

171

89,1

97,561681

19

259

115,6

101,66180

20

166,5

74,3

105,76193

21

65

112,1

109,86206

22

216

112,5

113,96218

23

77

124,2

118,06231

24

216

112,5

122,16244

25

58,5

150

126,26256

26

84

135,5

130,36269

27

114

129,5

134,46282

28

84,5

145,7

138,56294

29

55

152,8

142,66307

30

277,5

123,8

146,76320

Коэффициент корреляции

0,462

0,905

Значение коэффициента а

4,10

Значение коэффициента в

23,76

Таблица 2.4

День недели

Прогноз температуры воздуха, °С

Приведенный прогноз продажи,
кг

Прогноз продажи, кг

ПН

14

81,16

47,0

ВТ

11

68,86

43,0

СР

9

60,66

21,7

ЧТ

7

52,46

20,7

ПТ

8

56,56

49,7

СБ

13

77,06

148,1

ВС

15

85,26

191,1

ИТОГО:

521,3

Ошибка
прогноза определяется как среднеквадратическое отклонение фактических продаж от
величин, рассчитанных описанным выше способом для фактических значений
параметров (t, день недели). Особенность
этого расчета состоит в том, что здесь f = 2, так как прогноз продаж строится на прогнозе температуры воздуха.
Обычно f = 1. Полученное значение
ошибки s = 22,548.

@ Задачи.

1. Известна
статистика продаж товара за первые 6 месяцев года (см. табл. ниже). Сегодня 1
июля. Спрогнозируйте продажи на последующие 4 месяца методами простого и скользящего
среднего, методом экспоненциального сглаживания, если каждый месяц приносит
новые данные о продажах, также показанные в таблице. Оцените погрешность
прогноза каждым из методов. Постройте графики прогнозов всеми методами и график
фактических продаж.

Месяц

1

2

3

4

5

6

7

8

9

10

Продажа, шт.

476

458

439

460

462

444

430

421

450

412

2. Решите
задачу 1 с другими исходными данными (см. таблицы ниже). Дополнительно
попробуйте подобрать аппроксимирующую кривую на интервале в десять месяцев на
ПЭВМ с помощью пакета MS EXCEL. Сравните точность прогнозов
разными способами.

а)

Месяц

1

2

3

4

5

6

7

8

9

10

Продажа, шт.

2320

2335

2331

2370

2366

2357

2391

2388

2402

2412

б)

Месяц

1

2

3

4

5

6

7

8

9

10

Продажа, шт.

46

42

39

45

40

48

43

42

40

41

3. Дайте для
кафе обоснованный прогноз спроса на газированные напитки в бутылках на следующую
неделю, основываясь на статистике продаж за прошедшие три недели и на прогнозе
погоды на следующую неделю. Для расчета тенденции используйте пакет MS EXCEL. Постройте графики прогноза и фактических продаж.

Неделя

День недели

ПН

ВТ

СР

ЧТ

ПТ

СБ

ВС

1-я

Продажа, шт.

182

155

163

187

111

63

54

Температура воздуха, °С

26

24

27

23

24

19

18

2-я

Продажа, шт.

159

149

141

159

101

55

60

Температура воздуха, °С

19

23

18

16

15

15

15

3-я

Продажа, шт.

151

139

144

163

94

58

57

Температура воздуха, °С

16

19

21

18

14

15

12

4-я

Прогноз температуры, °С

13

13

13

20

23

23

23

Ответ. Уравнение аппроксимирующей прямой: Q = 97,8
+ 1,24 t°

Прогноз продаж
на будущую неделю:

154

139

140

172

106

61

59

ОБОСНОВАНИЕ ПРИНЯТИЯ РЕШЕНИЙ С ПОМОЩЬЮ МЕТОДА ПЛАТЕЖНОЙ МАТРИЦЫ

(ДЕРЕВА РЕШЕНИЙ)

3.1. Общая концепция решения задачи

Метод позволяет найти ответ
на вопрос: какая стратегия поведения в наибольшей степени соответствует
достижению поставленных целей в условиях неопределенности
внешней среды или риска. Он может
помочь менеджерам принимать управленческие решения в подавляющем большинстве случаев,
возникающих в их работе. Метод имеет три неоспоримых преимущества:

1)      заставляет менеджера ввести
в круг рассмотрения все возможные варианты,
в том числе и неблагоприятные (известно, что у менеджеров есть тенденция завышать
ожидаемые результаты или исключать из анализа неблагоприятные исходы; метод
позволяет избежать подобных ошибок, хотя они могут возникнуть при процедуре
прогнозирования вероятностей состояний внешней среды);

2)      формализует процесс оценки
вариантов и выбора лучшего из них даже при наличии очень скудной информации о
самих вариантах и об окружающей среде,

3)      используется на всех уровнях управления для решения
самых разнообразных задач.

Метод относится к
теоретико-игровым, но, несмотря на это, он предполагает и использование
аналитических зависимостей, и прогнозирование.

Платежная матрица – это запись в матричной форме денежных платежей.
Строки матрицы – альтернативные стратегии
поведения. Ее столбцы – возможные состояния
внешней среды. В клетках матрицы указываются платежи, или стоимостные
оценки ожидаемых исходов при принятии
данной управленческой альтернативы и возникновении определенного состояния
внешней среды. Подход к трактовке платежей может быть двояким: платежи могут
иметь смысл положительных результатов или доходов, а также — отрицательных результатов или расходов. В
первом случае целевой функцией задачи является максимизация доходов, во втором — минимизация расходов. Оба подхода к решению
симметричны, поэтому рассмотрение методов решения будем вести применительно к
первому из них, второй подход встретится в некоторых примерах.

$ Пример.

Компания по производству
легких быстромонтируемых складских помещений решает вопрос о строительстве
нового завода: построить большой завод, малый завод либо вообще отказаться от
строительства (пример принятия стратегического решения).

Внешняя рыночная среда
(спрос, конкуренты, распоряжения муниципальных властей и др.) может
благоприятствовать строительству, а может не благоприятствовать. Платеж –
совокупный доход компании (ден. ед.) от принятия того или иного решения — указан в следующей таблице:

Альтернативная

стратегия

Состояния среды

Благоприятное

Неблагоприятное

Строить
большой завод

200 000

–180 000

Строить маленький
завод

100 000

–20 000

Ничего
не строить

0

0

Возможные критерии для
принятия решения в условиях полной
неопределенности среды:

1.     МАХIMAX – ориентирован на
получение максимального ожидаемого результата (оптимистический подход). В
соответствии с ним в качестве оптимальной выбирается альтернатива, дающая максимум в клетках платежной
матрицы. Решение по этому критерию Þ строить большой завод.

2.     MAXIMIN – ориентирован на
получение гарантированного выигрыша при наихудшем состоянии внешней среды
(пессимистический подход, критерий Вальда). В соответствии с ним в качестве
оптимальной выбирается альтернатива,
имеющая максимальное для наименее благоприятных состояний среды значение
ожидаемого результата. Здесь решение Þ ничего не строить.

3.     Равновесный подход (критерий
Лапласа), при котором выбирается альтернатива с максимальным значением
усредненного по всем состояниям среды платежа. Здесь:

а) 200000 ´ 0,5 + (–180000) ´ 0,5 = 10000,

б) 100000 ´ 0,5 + (–20000)´0,5 = 40000 Þ оптимальная стратегия,

в) 0.

Если существует возможность задать оценки (спрогнозировать) вероятности
появления того или иного состояния окружающей среды, тогда решение будет
приниматься в условиях риска. Выбор
лучшего варианта в этом случае производится на основе расчета ожидаемой
денежной отдачи – Expected Monetary Value
(EMV). Значения EMV для каждой альтернативы рассчитываются как взвешенные по
вероятности суммы платежей (принцип Байеса):

EMV_i=P_ij p_j,

где P_ij
– платеж при выборе i-й альтернативы, и j-м состоянии среды;

р_j–
вероятность возникновения j – го
состояния внешней среды.

Критерий выбора лучшей
стратегии: EMV Þ max.

EMV – это ожидаемая средняя выгода от принятия решения при большом количестве
реализаций.

Обратите внимание: так как
возможные состояния среды взаимоисключают друг друга и в совокупности
исчерпывают все возможные варианты, сумма вероятностей их возникновения всегда
должна быть равна единице, т.е.:

.

Рассмотрим решение поставленной выше задачи в условиях риска. Для этого
зададим соотношение вероятностей двух состояний среды: 40 – 60%. Тогда:

EMV₁= 200000 ´ 0,4 + (–180000) 0,6 =
–28000,

EMV₂= 100000 ´ 0,4 + (–20000) 0,6 = 28000 Þ оптимальная
стратегия,

EMV₃= 0.

Рассмотрим
решение при другом соотношении вероятностей: 70–30 %.

EMV₁ = 200000 ´ 0,7 + (–180000) 0,3 = 86000 Þ оптимальная
стратегия,

EMV₂ = 100000 ´ 0,7 + (–20000) 0,3 = 64000,

EMV₃= 0.

Как видим, результат решения
задачи изменился, и нужно выбирать строительство большого завода.

Очевидно, что решение в
значительной степени зависит от заданного распределения вероятностей. Учитывая
то, что оценка (прогноз) вероятностей состояний среды может быть неточной,
определенный интерес представляет анализ
чувствительности решения к изменению распределения вероятностей.

3.2. Анализ чувствительности решения задачи

Анализ чувствительности — это определение такого
уровня вероятности, до которого данная альтернатива является лучшей. Анализ выполнúм только в случае двух
возможных состояний среды и любого числа альтернатив. В этом заключена его
ограниченность, так как на практике разнообразие состояний среды может быть
намного больше.

В целях выполнения анализа чувствительности строятся графики зависимости
значений EMV от распределения
вероятностей между состояниями среды. Построим такие графики для трех
альтернатив из рассмотренной выше задачи. Порядок их построения ясен из рис.
3.1. График для варианта «Ничего не предпринимать» совпадает с осью
вероятностей, так как значение его ординаты на всем интервале изменения
вероятностей равно нулю.

0

Платеж при неблагоприятном состоянии среды, тыс.
руб.

200

Платеж
при благо-

приятном
состоянии

среды,
тыс. руб.

Вероятность благоприятного состояния
среды

                                   100           2               1                                    0,83             100


А

                        1,0          3           0,75                                  В                    0

Вероятность
неблагоприятного состояния

                          0                        0,25            0,5                0,75                1,0


0,38

                     -100
-100

                    -200
-200

Рис. 3.1. Графики зависимости платежей от распределения
вероятностей состояния среды

График со всей очевидностью показывает, что при высокой вероятности
благоприятного состояния среды, лучше строить большой завод (первый вариант), при
ее уменьшении до определенного значения — маленький (второй вариант),
а при высокой вероятности неблагоприятного исхода лучше деньги в проект не
вкладывать (третий вариант).

Чтобы найти предельные точки (точки пересечения прямых) следует сначала
вывести уравнения прямых:

EMV₁ = 200 — 380 р₂,_.

EMV₂ = 100 — 120 р₂,

EMV₃ = 0,

а
затем приравнять их:

(·)А: EMV₁ = EMV₂ или 200 — 380 р₂= 100 — 120 р₂ Þ р₂= 0,38,

(·)В: EMV₂ = EMV₃ или 100 — 120 р₂ = 0 Þ р₂= 0,83.

В общем случае некоторые альтернативы при любом разложении вероятностей могут оказаться хуже других. Они
должны быть исключены из дальнейшего рассмотрения.

3.3.   Дерево решений задачи

Для решения данного типа задач можно использовать не только платежную
матрицу, но и строить дерево решений.
Например, для рассматриваемой задачи дерево имеет следующий вид:


благоприятная среда     40 %                   200000




неблагоприятная среда 60 %                –180000

            1                      благоприятная среда     40 %                   100000

            2                        неблагоприятная
среда 60 %                –20000

            3
0

                Узлы состояний
среды

При построении дерева узлы
принятия решения означают выбор альтернатив, который делает менеджер, а узлы
состояний среды — возможные ответы среды.
Сумма вероятностей для каждого узла среды, как уже указывалось, должна быть
равна единице. Узлы принятия решений и состояния среды должны чередоваться как
ходы в игре с противником.

Если построение дерева идет
слева направо, то расчет и принятие решений — справа налево: платежи
«сворачиваются» в значения EMV в узлах среды с соответствующими им
весами-вероятностями, а в узлах принятия решений происходит выбор лучших
альтернатив, например, по критерию EMV Þ max.

При решении простых задач
дерево не дает никаких преимуществ, но для решения многоуровневых задач его
преимущества неоспоримы. Дерево, как любое графическое изображение, более
наглядно, поэтому его построение предпочтительнее в более сложных ситуациях.

Построение дерева рассмотрим
еще на одном примере, в данном случае на решении задачи тактического планирования. Этот пример покажет также, что выделение
только двух состояний внешней среды — благоприятного и неблагоприятного
— далеко не единственный и не лучший способ ее
оценки, который применяется лишь в случаях, когда информация о среде очень
ограничена. Альтернативных вариантов стратегий в общем случае может быть много.

$ Пример.

Оптовый склад обслуживает
кино- и фотолаборатории, в том числе отпускает им проявитель. Статистика уровня
продаж: вероятность продажи        11
упаковок составляет 45 %, 12 упаковок – 35 %, 13 упаковок – 20 %. Прибыль от
реализации одной упаковки – 35 руб. Непроданные упаковки в конце недели
уничтожаются, при этом потери составляют 56 руб. с каждой упаковки. Какой
недельный запас проявителя оптимален?

Сначала следует обратить
внимание на то, что сумма вероятностей продажи 11, 12 и 13 упаковок равна 100
%. Это означает, что никаких других объемов недельных продаж не
зарегистрировано и в расчет они не могут быть включены.

Рассчитаем четыре варианта
платежей:

–     проданы все 11 упаковок: 35 ´ 11 = 385 руб., при
сделанном запасе в одиннадцать же упаковок никаких других вариантов не
существует;

–     проданы 11 при запасе 12, одна
уничтожена: 385 – 56 = 329 руб.;

–     проданы 12 т.е. весь запас:
35 ´ 12 = 420 руб., наличие
спроса – 13 упаковок здесь ничего не меняет;

–     при запасе 13 упаковок
возможны все три варианта: продажа 11 и уничтожение двух – 385 – 56 ´ 2 = 273 руб., 12 и уничтожение
одной – 420 –   – 56 = 364 руб., 13
упаковок – 35 ´ 13 = 455 руб.

Результаты
расчета (руб.) сведены в следующую таблицу:

Запас,

упаковки

Спрос, упаковки

EMV

11

12

13

11

385

385

385

385

12

329

420

420

379,05

13

273

364

455

341,25

Вероятность

0,45

0,35

0,20

Расчет EMV показывает, что
лучший вариант решения – запасать 11 упаковок.

Рассчитаем предельную цену полной информации о
продажах (алгоритм ее расчета представлен в следующем разделе):

EVPI = 385 ´ 0,45 + 420 ´ 0,35 + 455 ´ 0,20 – 385 = 26,25 руб.

Дерево решений этой задачи
имеет следующий вид:


11     100 %                             385

                 11


11       45 %                             329

                  12

                                                     12       55 %                             420


11       45 %                             273

                 13

                                                     12        35 %                           364


13        20 %                            455

             Узлы состояний среды

3.4. Предельная стоимость полной информации

Усложним решаемую задачу. Предположим, что на рынке есть фирмы,
специализирующиеся на сборе информации о внешней среде, необходимой менеджерам
для повышения степени обоснованности принимаемых решений.

Какова может быть предельная
цена при покупке данной информации?

Ответ на этот вопрос дает
показатель Expected Value of Perfect Information (EVPI), который
рассчитывается следующим образом:

EVPI = ожидаемый результат
при наличии полной информации о внешней среде — max EMV.

Ожидаемый результат при
наличии полной информации о внешней среде равен максимальной выгоде при одном
состоянии внешней среды, умноженной на вероятность этого состояния, плюс
максимальная выгода при другом состоянии, умноженная на вероятность этого
состояния, плюс … и т.д.

Так, за
полную информацию в первой из рассмотренной нами задач можно заплатить 52 тыс.
руб., так как max EMV = 28 тыс., а ожидаемый результат при наличии полной
информации равен   200 ´ 0,4 + 0 ´ 0,6 = 80 тыc. руб.

$ Пример.

Фирма рассматривает
возможность производства и реализации микросхем. Для этого либо требуется
создание системы комплексной автоматизации CAD/CAМ, которая стоит 500 тыс.
руб., либо можно нанять и обучить специалистов, что обойдется в 375 тыс. руб.
При благоприятном рынке микропроцессоры можно будет реализовать в количестве 25
тыс. шт., а при неблагоприятном – только 8 тыс. шт. Отпускная цена – 100 руб.
Себестоимость одной штуки в CAD/CAМ – 40 руб., при ручном производстве – 50
руб. Вероятность благоприятного варианта – 40 %. Требуется выбрать лучший
вариант по критерию EMV и определить величину EVPI.

Решение задачи представлено
в виде следующей платежной матрицы (руб.), расширенной на столбец EMV:

Стратегия

Состояния среды

EMV

Благоприятное

Неблагоприятное

1. CAD/CAМ

1 000 000

–20 000

388 000

2. Люди

875 000

25 000

365 000

3. Ничего не делать

0

0

0

Вероятность, %

40

60

В этой задаче наибольший
интерес представляет расчет платежей в матрице. Как получены их значения?

Ручная работа, благоприятная
среда:

25 000 (100 – 50) – 375 000
= 1 250 000 – 375 000 = 875 000 руб.;

неблагоприятная
среда:

8 000 (100 – 50) – 375 000 = 25 000 руб..

Автоматизация,
соответственно:

25 000 (100 – 40) – 500 000
= 1 000 000 руб.;

8 000 (100 – 40) – 500 000 =
–20 000 руб.

Расчет EMV показывает, что
лучшим вариантом является автоматизация. Предельная цена информации:

EVPI = (1 000 000 ´ 0,4 + 25 000 ´ 0,6) – 388 000 = 27 000
руб.

Строим
дерево:

                            благоприятное    40 %                  1 000 000



                             неблагоприятное 60
%                   –20 000

      1                     благоприятное     40 %                   875 000

      2                     неблагоприятное 60 %                     25 000


0

      3

        Узлы состояний среды

3.5. Многоуровневые задачи принятия решений

Проведем дальнейшее
усложнение задачи: рассмотрим принятие
решений на нескольких уровнях. Для этого вернемся к первому примеру и
дополним его.

$ Продолжение примера.

Предположим, что компания
может произвести дополнительные исследования стоимостью 10 000 ден. ед. в целях
повышения конкурентоспособности своей продукции. При этом вероятность удачного
исхода исследований по оценкам экспертов составляет 45 %; в этом случае
вероятность благоприятной для компании внешней среды увеличится до 78 %.
Вероятность отрицательных результатов исследования – 55 %; в этом случае
благоприятная для компании среда возникнет, по оценкам, только в 27 % случаев.
Требуется принять решение: проводить ли дополнительные исследования и строить
ли завод.

Отметим сразу, что здесь
решения должны приниматься дважды, причем решение о том или ином варианте
строительств должно быть принято на основе уже известных к тому времени
результатов дополнительных исследований. Это определяет последовательность
решения задачи, в частности, последовательность узлов принятия решений в дереве
для этой задачи.

Платежные матрицы для
решения многоуровневых задач, как правило, не строятся. Именно в этом случае
проявляются все преимущества графического метода – с помощью дерева решений.

Построим дерево решений и
рассчитаем на его основе значения EMV. Расчет ведем справа налево: от
известного к искомому.


благоприятн. 0,78   +190


большой завод

                                                                                      неблагопр.     0,22
–190


.                                                           маленький завод
  благоприятн.
0,78   +90

Проводятся доп.
  неблагопр.       0,22
–30

исследования 0,45
успех                       не
строить                                    –10


.
благоприятн. 0,27    190

                        0,55                  большой                     неблагопр.    0,73
–190

                    неудача


маленький                  благоприятн.   0,27
+90


неблагопр.       0,73
–30


не строить
   –10




благоприятн. 0,4   +200


большой завод

                                                                                       неблагопр.   0,6    –180

Не проводятся
благоприятн. 0,4   +100

доп. исследования                маленький завод


неблагопр.   0,6
–20


не строить
0

EMV₂= 190 ´ 0,78 – 190 ´ 0,22 = 106,4,

EMV₃= 90 ´ 0,78 – 30 ´ 0,22 = 63,6.

В этой ситуации лучшим было
бы строительство большого завода, так как
106,4 > 63,6 > — 10.

EMV₄= 190 ´ 0,27 – 190 ´ 0,73 = – 87,4,

EMV₅= 90 ´ 0,27 – 30 ´ 0,73 = 2,4.

В этой ситуации предпочтительнее строительство маленького
завода, так как     2,4 > — 10 > — 87,4.

EMV₆= 200 ´ 0,4 – 180 ´ 0,6 = – 28,

EMV₇= 100 ´ 0,4 – 20 ´ 0,6 = 28.

В этой ситуации также лучшим
вариантом является строительство маленького завода, так как   28 > — 28 > 0.

Надо ли проводить
исследование?

EMV₁= 0,45 ´ 106,4 + 0,55 ´ 2,4 = 49,2, что превышает
EMV₇ — лучшее для варианта «не проводить
исследования».

Вывод: исследование нужно
проводить, и при его положительном исходе нужно строить большой завод, ожидая
доход 106,4 тыс. руб., а при отрицательном – маленький, ожидая 2,4 тыс. руб.

Многоуровневые деревья
решений отнюдь не обязательно должны иметь такой симметричный вид, как в только
что рассмотренной задаче. В общем случае их «ветви» могут быть разной
длины и «кустистости», другими словами, разные альтернативы могут
иметь разное количество уровней принятия решений и число возможных ответов
среды. Рассмотрим пример решения такой задачи.

$ Пример.

Руководство фирмы решает
вопрос: производить или закупать новую микросхему для разрабатываемого
телевизора. По оценкам экспертов, в течение жизненного цикла этого телевизора
нужно будет произвести примерно 1 млн. таких микросхем.

Если микросхему производить
самим, то начальные затраты составят    0,5
млн. руб., а ее себестоимость будет равна 0,5 руб. Вероятность успеха в этом
случае – 60 %. В случае неудачи можно будет вложить еще 1 млн. руб. в доработку
проекта производства. Вероятность успеха доработки оценивается в 90 %. Однако,
и на этом этапе можно принять решение о покупке микросхем. Если доработка
окажется безуспешной, то необходимо будет производить закупку. Покупная
микросхема стоит 1,5 руб.

Необходимо выбрать лучший
вариант путем построения дерева решений.

Дерево
решений для этой задачи имеет вид:

                                     успех       р =
0,6                 0,5 млн.+ 1 млн.´ 0,5 = 1 млн.

                              1                            успешная      р = 0,9

Производить
0,5
млн.+ 1 млн.+ 0,5 ´ 1 млн.= 2 млн.

                        провал      доработка     2

                          р = 0,4                                 0,5 млн.+ 1 млн.+ 1,5 ´ 1 млн.= 3 млн.


неудачная   р = 0,1 и требуется закупка

     Закупать                            закупка              0,5 млн.+ 1,5 ´ 1 млн.= 2 млн.


                     1,5 ´ 1 млн.= 1,5 млн.

Рассчитаем ЕMV и будем
принимать решения на основе минимизации этого критерия, т.е. затрат:

ЕMV₂=
2 ´ 0,9 + 3 ´ 0,1 = 2,1 млн. руб. и
принимаем решение закупать, так как
2 < 2,1;

ЕMV₁=
1 ´ 0,6 + 2 ´ 0,4 = 1,4 млн. руб. –
решение производить, так как           1,4 < 1,5.

Ответ. Микросхемы следует попробовать производить, и в
случае успеха это потребует 1 млн. руб. затрат; в случае провала производства
их надо будет закупать, затратив на это 2 млн. руб.

Трудно
представить себе, как бы выглядели платежные матрицы решения этой задачи, если
бы не существовало решения с помощью построения дерева.

Метод
платежной матрицы помогает менеджерам принимать решения в самых разных
ситуациях, в частности, при решении задач снабжения, как в следующем примере.

$ Пример.

Фирма должна
выбрать одного из двух поставщиков микропереключателей. Объем закупок
планируется на уровне 10 000 шт. Известно, что у поставщика А в партии может
быть 2 % исправимого брака с вероятностью
80 % и     3 % брака с
вероятностью 20 %, а у поставщика В — 5 % брака с вероятностью 30
% и 6 % брака с вероятностью 70 %. Закупочные цены: у А – 40 коп., у В – 39
коп. Ремонт бракованного переключателя стоит 28 коп.

Для решения
задачи построим дерево:

                                 брак 2 %    р =
0,8   0,4 ´ 10000 + 0,28 ´ 0,02 ´ 10000 = 4056

                              1

                 А

                                   брак 3
%   р =
0,2   0,4 ´ 10000 + 0,28 ´ 0,03 ´ 10000 = 4084

                                   брак 5
%   р =
0,3 0,39 ´ 10000 + 0,28 ´ 0,05 ´ 10000 = 4040

                 В

                            2

                                   брак 6 %    р = 0,7 0,39 ´ 10000 + 0,28 ´ 0,06 ´ 10000 = 4068

Рассчитаем ЕMV:

ЕMV₁= 4056 ´ 0,8 + 4084 ´ 0,2 = 4061,6 руб.,

ЕMV₂= 4040 ´ 0,3 + 4068 ´ 0,7 = 4059,6 руб.

Выберем
поставщика В, минимизируя ожидаемые затраты.

@ Задачи.

1. Для перехода на производство новой продукции
предприятие может закупить оборудование трех различных отечественных
производителей. Все оборудование изготовлено на основе новых технологий,
поэтому качество его работы непредсказуемо (хорошая и плохая работа
равновероятны). Результаты работы (ден. ед.) представлены в следующей платежной
матрице:

Вариант приобретения оборудования

Качество работы
оборудования

Хорошее

Плохое

I

40 000

— 10 000

II

30 000

— 3 000

III

10 000

— 2 000

Не приобретать

0

0

Выберите лучший вариант по
критериям: МАХIMAX, MAXIMIN, равновесному, по критерию ЕMV, если
стало известно соотношение вероятностей хорошей и плохой работы — 25 к 75 %. Проведите анализ чувствительности
решения задачи. Определите предельную стоимость точной информации — EVPI.

2. Фирма решает, строить или нет новый цех на
основе новой рискованной технологии. Если новый цех будет работать хорошо,
фирма получит дополнительный доход 200 000 руб., если цех работать не будет, то
убыток составит 150 000 руб.; по оценкам, вероятность успеха составляет 40 %.

Фирма может произвести
дополнительные исследования,
направленные на совершенствование новой технологии, затратив на это 15 000
руб., причем успех и неудача этих исследований равновероятны. Если исследования
будут успешными, вероятность того, что цех заработает, возрастет до 90 %, если
нет – снизится до 20 %.

Помогите фирме принять
верное решение.

Ответ.
Надо проводить доработку и, если она успешна, – строить цех и ожидать результат
150 000 руб.; в противном случае – не строить, с потерей   15 000
руб.

3. Швейная фабрика г. Рязани
может закупить у одного из французских кутюрье его весенне-летнюю коллекцию
женской одежды за $20 000. По оценкам местных специалистов, постановка ее на
производство позволит фабрике получить дополнительную прибыль $25 000 с
вероятностью 50 % или $45 000 – с вероятностью 30 %. В случае, если местные
модницы не оценят французскую коллекцию по достоинству и фабрика не получит
прибыли от ее реализации, можно будет оперативно вернуться к коллекции,
разработанной своими силами, затратив на лишнюю перестройку производства с французской
коллекции на рязанскую $6 000. Вероятность успеха при этом оценивается в 50 %, а сам успех –
в $10 000 прибыли. Обратиться к собственным модельерам можно и сразу, не
поддаваясь французским соблазнам, потратив на это всего $500.

Помогите руководству фабрики
принять верное решение. Ответ обоснуйте путем построения дерева решений.

Ответ.
Фабрике следует попробовать купить французскую коллекцию, а в случае неудачи с
ее реализацией — деньги ни во что больше не
вкладывать, смирившись с потерей $20 000 и продолжая шить ватники.

4. Какой резервный запас готовой продукции
должен быть сделан на складе предприятия, если известно, что за время,
необходимое для его пополнения, покупателями может быть востребовано:

50 единиц продукции с
вероятностью 20 %,

    60              -«-                         -«-              50 %,

    70              -«-                         -«-              30 %.

Ответ следует обосновать с
точки зрения минимизации расходов предприятия. Известно, что хранение одной
единицы продукции в течение всего указанного времени обходится в 40 руб., а при
возникновении ее дефицита может быть принято решение либо о срочном
изготовлении недостающего количества продукции, либо о его закупке у стороннего
производителя с целью избежать потери имиджа надежного поставщика.

Срочное изготовление любого
количества продукции связано с дополнительными производственными издержками в
размере 500 руб., а срочная закупка ввиду нестабильности конъюнктуры рынка
может с равной вероятностью привести к потерям на каждой единице продукции от
35 до 55 руб.

Следует обратить внимание на
то, что ввиду постоянного расхода товара со склада затраты на его хранение
определяет не максимальный создаваемый запас, а средний запас за
рассматриваемый период.

Ответ. Необходимо сделать
запас 60 ед., а при спросе 70 ед. для избежания дефицита следует закупать
продукцию, ожидая затраты/потери на сумму 1650 руб.

5. Фирма
рассматривает возможность вложения свободных денежных средств в размере 10 млн.
руб. в строительство крупного сервисного центра в небольшом пригородном поселке
на трассе кольцевой автодороги, строящейся вокруг Санкт-Петербурга. Вложения
можно сделать немедленно, опередив всех потенциальных конкурентов, пользуясь
тем, что строительство дороги в этом районе еще не началось, а условия аренды
земли и найма подрядчиков самые выигрышные. В случае благоприятного стечения
обстоятельств (дорога построена, вероятность чего 50 %, бизнес удачен — 90 %) за два ближайших года предполагается
получить чистую прибыль в размере 160 % от вложенных средств. Во всех остальных
случаях ожидаются потери в размере 60 % от сделанных вложений.

Можно также
подождать год, конвертировав на это время деньги в валюту и положив ее в банк
под 12 % годовых, а через год снова вернуться к решению этого вопроса,
капитализировав полученные дивиденды. Вероятность того, что через год дорога
все-таки подойдет к поселку — 60 %. В этой ситуации вложенные
средства могут за следующий год дать прибыль 80 %, если бизнес будет удачен
(вероятность чего 70 % — конкуренты не дремлют), или
убыток составит 40 % в случае неудачи. Если через год дорога не будет построена,
то деньги все равно можно будет вложить в строительство центра, но вероятность
удачного бизнеса при этом снизится до 10 %. В любой ситуации можно ничего не
предпринимать, оставив деньги в банке.

Помогите
фирме принять решение. Исходите из того, что само строительство займет
незначительное время, а решение принимается на основе ожидаемых финансовых
результатов за первые два года ведения дел.

Ответ. Надо подождать год. Если к этому времени дорога
подойдет к поселку, то деньги в строительство центра надо вкладывать, ожидая
отдачи в сумме за два года 5408 тыс. руб. Если же строительство будет
тормозиться, то деньги следует оставить в банке, довольствуясь получением
процентов        2544 тыс. руб. (расчет
по формуле сложных процентов).

СОДЕРЖАНИЕ

Предисловие
……………………………………………………………………………………………….

3

Тема 1. Основы принятия управленческих решений
…………………………………….

4

1.1. Управление как информационный
процесс …………………………………….

4

1.2. Решение – основа управления
………………………………………………………..

5

1.3. Процесс и методы принятия
управленческих решений …………………..

8

Тема 2. Прогнозирование
…………………………………………………………………………….

9

2.1. Роль планирования и
прогнозирования в управлении производством

9

2.2. Экспертные методы
прогнозирования ……………………………………………

11

2.3. Методика проведения
индивидуальной разовой экспертной оценки

12

2.4. Статистический анализ временных
рядов ………………………………………

16

2.5. Факторный анализ статистик
…………………………………………………………

20

Тема 3. Обоснование
принятия решений с помощью метода платежной матрицы (дерева решений)
…………………………………………………………………….

24

3.1. Общая концепция решения задачи
…………………………………………………

24

3.2. Анализ чувствительности решения
задачи ……………………………………..

27

3.3. Дерево решений задачи …………………………………………………………………

28

3.4. Предельная стоимость полной
информации …………………………………..

30

3.5. Многоуровневые задачи принятия
решений …………………………………..

31

Макаров Василий Михайлович

ПРОИЗВОДСТВЕННЫЙ
МЕНЕДЖМЕНТ

МОДЕЛИ И МЕТОДЫ

ОБОСНОВАНИЯ
УПРАВЛЕНЧЕСКИХ РЕШЕНИЙ

Практикум

Редактор А.В. Явственная

Технический редактор А.И. Колодяжная

Оригинал-макет подготовлен
автором

Директор издательства А.В. Иванов

Свод. темплан 2003 г.

Лицензия ЛР № 020593 от
07.08.97.

Налоговая льгота –
Общероссийский классификатор продукции

ОК 005-93, т.2; 95 3005 –
учебная литература

Подписано в печать                        . Формат
60´84/16         Печать офсетная.

Усл. печ. л.          .
Уч.-изд. л.           .    Заказ             .    Тираж           .

_______________________________________________________________________________

Издательство СПбГПУ, член Издательско-полиграфической
ассоциации вузов

Санкт-Петербурга.

Адрес университета и
издательства: 195251, Санкт-Петербург,
Политехническая ул., 29

Источник

1. Занятие 3 Формула полной вероятности. Формулы Байеса Повторение испытаний в неизменных условиях и расчет вероятностей успеха

(неудачи)

2. Вопрос 1 Формула полной вероятности. Формулы Байеса

3. Формула полной вероятности

Пусть H 1 , H 2 ,…, H n – попарно несовместные события,
причем какое-то из них в результате опыта обязательно
произойдет, т.е. H i H j Ø i j и
n
Hi
— достоверное событие.
i 1
Известны априорные (доопытные) вероятности P ( H i ) 0 ,
i 1, n .
Пусть событие А может произойти совместно только с
одним из событий H 1 , H 2 ,…, H n , причем известны условные
вероятности события А: P ( А | H i ) 0 , i 1, n .
n
Тогда P( A) P( H i ) P( А | H i ).
i 1
События H 1 , H 2 ,…, H n называют гипотезами.
3

4. Пример на формулу полной вероятности

Три завода производят однотипные изделия, причем первый
завод производит 20% всей продукции, второй – 30%, третий – 50%.
Доля брака в продукции этих заводов составляет 5%, 2% и 1%
соответственно. Какова вероятность того, что наудачу взятое изделие
из продукции всех трех заводов окажется бракованным (событие A)?
Пусть H i — {выбранное изделие изготовлено на i-ом заводе}, i=1,
2, 3. События H i , i=1, 2, 3, попарно несовместные события, причем
какое-то из них в результате опыта обязательно произойдет. По
условию известны вероятности гипотез: P( H 1 ) 0,2 , P ( H 2 ) 0,3 ,
P ( H 3 ) 0,5 , а также условные вероятности события А:
P( А | H 1 ) 0,05 , P( А | H 2 ) 0,02 , P( А | H 3 ) 0,01 .
Тогда по формуле полной вероятности получаем:
3
P ( A) P ( H i ) P ( А | H i ) 0,2 0,05 0,3 0,02 0,5 0,01 0,021.
i 1
4

5. Формулы Байеса

Пусть после проведения эксперимента стало известно,
что событие А произошло. Необходимо вычислить
апостериорные
(послеопытные)
вероятности
гипотез
P( H i | A) . Это позволит ответить на вопрос, какая гипотеза
сопутствовала появлению события А? Формулы вычисления
этих вероятностей называются формулами Байеса:
P( H i ) P( A | H i )
,
P( H i | A)
P( A)
n
где P ( A) P ( H i ) P ( А | H i ).
i 1
5

6. Пример на формулы Байеса

Продолжая предыдущий пример, предположим, что
выбранное изделие оказалось бракованным. Определить
вероятности того, что оно произведено на первом, втором,
третьем заводе.
По формуле Байеса получаем:
P( H 1 ) P( A | H 1 ) 0,2 0,05
P( H 1 | A)
0,476 ;
P( A)
0,021
P( H 2 ) P( A | H 2 ) 0,3 0,02
P( H 2 | A)
0,286 ;
P( A)
0,021
P ( H 1 ) P ( A | H 3 ) 0,5 0,01
P ( H 3 | A)
0,238 .
P ( A)
0,021
6

7. Задача 1

Ковбой Джон попадает в муху на стене с вероятностью 0,9, если стреляет
из пристрелянного револьвера. Если Джон стреляет из непристрелянного
револьвера, то он попадает в муху с вероятностью 0,2. На столе лежит 10
револьверов, из них только 4 пристрелянные. Ковбой Джон видит на стене
муху, наудачу хватает первый попавшийся револьвер и стреляет в муху.
Найдите вероятность того, что Джон промахнётся.
Решение
Пусть событие А – Джон не попал в муху. Вероятность наступления
события А зависит от того, из какого револьвера стрелял Джон. Поэтому
выдвинем гипотезы:
H 1 — Джон для стрельбы выбрал пристрелянный револьвер;
H 2 — Джон для стрельбы выбрал непристрелянный револьвер.
Вероятности гипотез можно найти по определению, получаем:
4
6
P ( H 1 ) 0,4 , P( H 2 ) 0,6 . Условные вероятности промаха составляют:
10
10
P ( А | H 1 ) 1 0,9 0,1 , P( А | H 2 ) 1 0,2 0,8 . Тогда по формуле полной
вероятности получаем:
P ( A) P ( H 1 ) P ( А | H 1 ) P ( H 2 ) P ( А | H 2 ) 0,4 0,1 0,6 0,8 0,52.
7
Ответ: Джон промахнется с вероятностью 0,52.

8. Задача 2

Агрофирма закупает куриные яйца в двух домашних хозяйствах. 40% яиц
из первого хозяйства — яйца высшей категории, а из второго хозяйства — 20%
яиц высшей категории. Всего высшую категорию получает 35% яиц. Найдите
вероятность того, что яйцо, купленное у этой агрофирмы, окажется из первого
хозяйства.
Решение
Пусть событие А – куплено яйцо высшей категории. Вероятность
события А известна по условию P( A) 0,35 в тоже время она зависит от того, в
каком домашнем хозяйстве оно изготовлено. Поэтому выдвинем гипотезы:
H 1 — яйцо изготовлено первым хозяйством;
H 2 — яйцо изготовлено вторым хозяйством.
Вероятности гипотез не известны. Обозначим P( H 1 ) х , тогда
P( H 2 ) 1 х . Условные вероятности даны по условию: P ( А | H 1 ) 0,4 ,
P( А | H 2 ) 0,2 . Тогда по формуле полной вероятности получаем:
P ( A) P ( H 1 ) P ( А | H 1 ) P ( H 2 ) P ( А | H 2 ) х 0,4 (1 х) 0,2 0,35 ;
0,2 х 0,15 ;
х 0,75 .
Ответ: вероятность того, что яйцо, купленное у этой агрофирмы,
8
окажется из первого хозяйства, равна 0,75.

9. Вопрос 2 Повторение испытаний в неизменных условиях и расчет вероятностей успеха (неудачи)

10. Демонстрационный пример

Рассмотрим эксперимент: три стрелка независимо друг от друга
стреляют по мишени 1 раз. Вероятность попадания в мишень каждого из
них одинаковая и равна 0,7. Найдем вероятность того, что мишень будет
поражена ровно 2 раза.
ПЭС= , , , , , , , , где «+» на iом месте означает попадание i-го стрелка в цель; «–» — промах.
Так как стрелки стреляют независимо друг от друга, то события
«попадание в цель первого», «попадание в цель второго» и «попадание в
цель третьего стрелка» являются независимыми событиями. Тогда
Р( ) 0,7 0,7 0,7 0,343 . Вероятности остальных элементарных
событий рассчитываются аналогично:
Р ( ) 0,7 0,7 0,3 0,147 ; Р( ) 0,7 0,3 0,7 0,147 ;
Р( ) 0,7 0,7 0,3 0,147 ; Р( ) 0,7 0,3 0,3 0,063 ;
Р( ) 0,3 0,7 0,3 0,063 ; Р( ) 0,3 0,3 0,7 0,063 ;
Р ( ) 0,3 0,3 0,3 0,027 .
10

11. Продолжение демонстрационного примера

Событию А – «попадание двух стрелков из трех стрелявших»
благоприятствуют три исхода: А , , . Отметим, что этой
задаче исходы не являются равновозможными. Поэтому вероятность
события А найдем, используя формулу сложения вероятностей
несовместных событий:
Р( А) Р( ) Р( ) Р( ) 0,147 0,147 0,147 3 0,147 0,441.
Проанализируем эту формулу. Вероятность 0,147 получена по
формуле p k (1 p ) n k , где n – количество стрелков, p – вероятность
попадания одного стрелка, k – интересующее количество попаданий.
Множитель 3 – это количество способов, которыми можно расставить k
«плюсов» на n местах (порядок не имеет значение), в нашем случае это
3!
k
2
C n C3
3.
2!(3 2)!
Получили формулу Бернулли: P( А) C nk p k (1 p ) n k .
11

12. Повторные испытания. Схема Бернулли

Повторные испытания (последовательность испытаний) –
это последовательное проведение n раз одного и того же опыта
или одновременное проведение n одинаковых опытов.
Схемой
испытаний
Бернулли
называется
последовательность испытаний, обладающая тремя свойствами:
1) каждое испытание завершается одним из двух исходов,
условно называемых «успехом» (событие А) или «неудачей»
(событие А );
2) испытания независимы, т.е. вероятность исхода каждого из них
не зависит от того, какие исходы имели другие испытания;
3) вероятности «успеха» p и «неудачи» q=1-p одинаковы во всех
испытаниях.
12

13. Формула Бернулли

При рассмотрении схемы испытаний Бернулли
основной задачей является нахождение вероятности
события Ak , состоящего в том, что в n испытаниях
«успех» наступит ровно k раз, k 0, n . Вероятность
этого события определяется по формуле Бернулли:
Pn (k ) C nk p k q n k , k 0, n .
13

14. Задача 3

Что вероятнее выиграть у равносильного противника-шахматиста:
две партии из четырех или три из шести? Ничьи по внимание не
принимаются.
Решение
Имеем схему Бернулли. Повторные испытания – несколько партий в
шахматы с одним и тем же противником. Каждое партия заканчивается
либо выигрышем игрока («успех») или проигрышем («неудача»).
Испытания независимы. Вероятности «успеха» p 0,5 и «неудачи»
q 1 p 0,5 одинаковы во всех партиях.
Для ответа на вопрос необходимо сравнить две вероятности:
4!
P4 (2) C 42 0,5 2 0,5 2
0,5 4 0,375 ;
2! 2!
6!
3
3
3
P6 (3) C6 0,5 0,5
0,56 0,3125 .
3! 3!
Так как P4 (2) P6 (3) , то вероятность выиграть две партии из четырех
14
выше, чем три партии из шести.

15. Задача 4

Вероятность изготовления на автоматическом станке стандартной детали
равна 0,8. Найти вероятности возможного числа появления бракованных
деталей среди 5 отобранных. Каково наиболее вероятное число бракованных
деталей среди 5 отобранных.
Решение
Имеем схему Бернулли. Повторные испытания – изготовление 5 деталей
на одном и том же автоматическом станке (выбор 5 деталей их большой
партии). Каждая деталь может быть бракованной («успех») или годной
(«неудача»). Испытания независимы. Вероятности «успеха» p 0,2 и
«неудачи» q 0,8 одинаковы по всех деталей.
Среди выбранных 5 деталей бракованных может быть 0, 1, 2, 3, 4 или 5
деталей. Для нахождения вероятностей перечисленного количества «успехов» в
5 испытаниях воспользуемся формулой Бернулли:
P5 (0) C50 0,2 0 0,85 0,32768 ; P5 (1) C51 0,21 0,8 4 0,4096 ;
P5 (2) C52 0,2 2 0,83 0,2048 ; P5 (3) C53 0,2 3 0,8 2 0,0512 ;
P5 (4) C54 0,2 4 0,81 0,0064 ; P5 (5) C55 0,2 5 0,80 0,00032 .
Наиболее вероятное число бракованных деталей равно единице.
15

16. Наивероятнейшее число успехов

Выведем формулу для нахождения наивероятнейшего числа
успехов в n независимых испытаниях. Для нахождения k 0 составим
систему неравенств:
Pn (k 0 ) Pn (k 0 1);
Pn (k 0 ) Pn (k 0 1).
Решая первое неравенство системы, получаем:
n!
n!
p k0 q n k0
p k0 1q n k0 1 ;
k 0 !(n k 0 )!
(k 0 1)!(n k 0 1)!
1
1
q
p;
(n k 0 )
(k 0 1)
(k 0 1)q (n k 0 ) p ; k 0 ( p q ) np q ; k 0 np q .
Решая второе неравенство системы, получаем: k 0 np p .
Таким образом, np q k 0 np p .
16

17. Задача 5

Сколько раз необходимо подбросить игральную кость, чтобы
наивероятнейшее число выпадение тройки было равно 10?
Решение
Имеем схему Бернулли. Повторные испытания – подбрасывание
игральной кости n раз. Каждое подбрасывание может закончиться
«успехом» (выпала тройка) или «неудачей» (не выпала тройка).
1
Испытания независимы. Вероятности «успеха» p
и «неудачи»
6
5
q одинаковы во всех испытаниях.
6
Известно наивероятнейшее число успехов k 0 10 . Количество
испытаний n найдем из неравенства:
1 5
1 1
n 10 n или n 5 60 n 1 59 n 65 .
6 6
6 6
Таким образом, при количестве испытаний от 59 до 65
включительно, наивероятнейшее число выпадения тройки будет равно
17
10.

18.

Следующее занятие школы-семинара на
тему: «Решение оптимизационных задач»
Лектор: к.э.н.
Раменская Алина Владимировна
Дату и время можно уточнить по тел.
89128432428 или на нашей странице
https://vk.com/abiturient_fef_pm
18

Источник

Месяц	1	2	3	4	5	6	7	8	9	10	11	12
Спрос	199	202	199	208	212	194	214	*220*	*219*	*234*	*219*	*233*

День недели	Первая неделя	Вторая неделя	Третья неделя		Среднее на день недели, кг	Коэффициент приведения
Продажа, кг	Темпера-тура воздуха, °С	Прода-жа, кг	Темпера-тура воздуха, °С	Продажа, кг	Темпера-тура воз-духа, °С
ПН	32,5	8	84,5	28	65	21	60,66	0,580
ВТ	35	10	84	26	77	23	65,33	0,624
СР	25	11	32,5	14	55	29	37,50	0,358
ЧТ	33,7	16	31,5	12	58,5	25	41,23	0,394
ПТ	95	17	66,5	15	114	27	91,83	0,878
СБ	216	22	171	18	216	24	201,00	1,922
ВС	277,5	30	166,5	20	259	19	234,33	2,241
ИТОГО:	714,7		636,5		844,5		104,55	Среднее

Температура воздуха, °С	Фактическая продажа, кг	Приведенная фактическая продажа, кг	Трендовое значение продажи, кг
8	32,5	56	56,560413
10	35	56,4	64,760667
11	25	69,4	68,860793
12	31,5	80,8	72,960920
14	32,5	90,3	81,161174
15	66,5	75,6	85,261300
16	33,7	86,4	89,361427
17	95	108	93,461554
18	171	89,1	97,561681
19	259	115,6	101,66180
20	166,5	74,3	105,76193
21	65	112,1	109,86206
22	216	112,5	113,96218
23	77	124,2	118,06231
24	216	112,5	122,16244
25	58,5	150	126,26256
26	84	135,5	130,36269
27	114	129,5	134,46282
28	84,5	145,7	138,56294
29	55	152,8	142,66307
30	277,5	123,8	146,76320
Коэффициент корреляции	0,462	0,905
Значение коэффициента а	4,10
Значение коэффициента в	23,76

День недели	Прогноз температуры воздуха, °С	Приведенный прогноз продажи, кг	Прогноз продажи, кг
ПН	14	81,16	47,0
ВТ	11	68,86	43,0
СР	9	60,66	21,7
ЧТ	7	52,46	20,7
ПТ	8	56,56	49,7
СБ	13	77,06	148,1
ВС	15	85,26	191,1
		ИТОГО:	521,3

Месяц	1	2	3	4	5	6	7	8	9	10
Продажа, шт.	476	458	439	460	462	444	*430*	*421*	*450*	*412*

Месяц	1	2	3	4	5	6	7	8	9	10
Продажа, шт.	2320	2335	2331	2370	2366	2357	*2391*	*2388*	*2402*	*2412*

Неделя	День недели	ПН	ВТ	СР	ЧТ	ПТ	СБ	ВС
1-я	Продажа, шт.	182	155	163	187	111	63	54
Температура воздуха, °С	26	24	27	23	24	19	18
2-я	Продажа, шт.	159	149	141	159	101	55	60
Температура воздуха, °С	19	23	18	16	15	15	15
3-я	Продажа, шт.	151	139	144	163	94	58	57
Температура воздуха, °С	16	19	21	18	14	15	12
4-я	Прогноз температуры, °С	13	13	13	20	23	23	23

Альтернативная стратегия	Состояния среды
Благоприятное	Неблагоприятное
Строить большой завод	200 000	–180 000
Строить маленький завод	100 000	–20 000
Ничего не строить	0	0

Запас, упаковки	Спрос, упаковки	EMV
11	12	13
11	385	385	385	385
12	329	420	420	379,05
13	273	364	455	341,25
Вероятность	0,45	0,35	0,20

Стратегия	Состояния среды	EMV
Благоприятное	Неблагоприятное
1. CAD/CAМ	1 000 000	–20 000	388 000
2. Люди	875 000	25 000	365 000
3. Ничего не делать	0	0	0
Вероятность, %	40	60

Вариант приобретения оборудования	Качество работы оборудования
Хорошее	Плохое
I	40 000	— 10 000
II	30 000	— 3 000
III	10 000	— 2 000
Не приобретать	0	0

Предисловие ……………………………………………………………………………………………….	3
Тема 1. Основы принятия управленческих решений …………………………………….	4
1.1. Управление как информационный процесс …………………………………….	4
1.2. Решение – основа управления ………………………………………………………..	5
1.3. Процесс и методы принятия управленческих решений …………………..	8
Тема 2. Прогнозирование …………………………………………………………………………….	9
2.1. Роль планирования и прогнозирования в управлении производством	9
2.2. Экспертные методы прогнозирования ……………………………………………	11
2.3. Методика проведения индивидуальной разовой экспертной оценки	12
2.4. Статистический анализ временных рядов ………………………………………	16
2.5. Факторный анализ статистик …………………………………………………………	20
Тема 3. Обоснование принятия решений с помощью метода платежной матрицы (дерева решений) …………………………………………………………………….	24
3.1. Общая концепция решения задачи …………………………………………………	24
3.2. Анализ чувствительности решения задачи ……………………………………..	27
3.3. Дерево решений задачи …………………………………………………………………	28
3.4. Предельная стоимость полной информации …………………………………..	30
3.5. Многоуровневые задачи принятия решений …………………………………..	31

Теория вероятности и ее применение

ЗАКЛЮЧЕНИЕ

2.2. Экспертные методы прогнозирования

Представлять результаты экспертизы и выполнять их анализ удобно с помощью графиков, показанных на рис. 2.1.

2.4. Статистический анализ временных рядов

Прогнозирование методом «экспоненциального сглаживания»

$ Пример.

Месяц

1

2

3

4

5

6

7

8

9

10

11

12

Спрос

199

202

199

208

212

194

214

220

219

234

219

233

2.5. Факторный анализ статистик

1. Занятие 3 Формула полной вероятности. Формулы Байеса Повторение испытаний в неизменных условиях и расчет вероятностей успеха

2. Вопрос 1 Формула полной вероятности. Формулы Байеса

3. Формула полной вероятности

4. Пример на формулу полной вероятности

5. Формулы Байеса

6. Пример на формулы Байеса

7. Задача 1

8. Задача 2

9. Вопрос 2 Повторение испытаний в неизменных условиях и расчет вероятностей успеха (неудачи)

10. Демонстрационный пример

11. Продолжение демонстрационного примера

12. Повторные испытания. Схема Бернулли

13. Формула Бернулли

14. Задача 3

15. Задача 4

16. Наивероятнейшее число успехов

17. Задача 5

18.

Представлять результаты
экспертизы и выполнять их анализ удобно с помощью графиков, показанных на рис.
2.1.

2.4.
Статистический анализ временных рядов

Прогнозирование методом
«экспоненциального сглаживания»