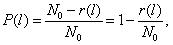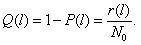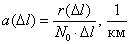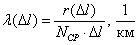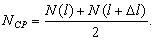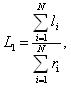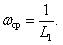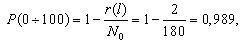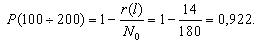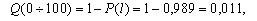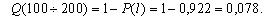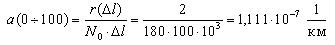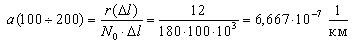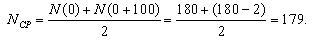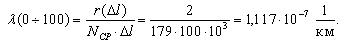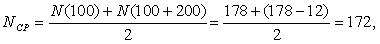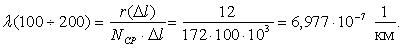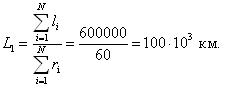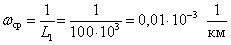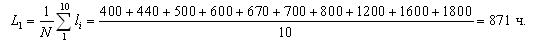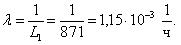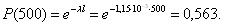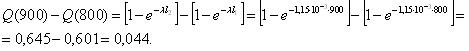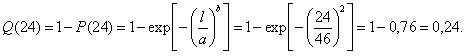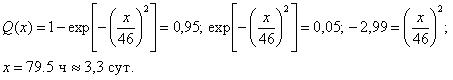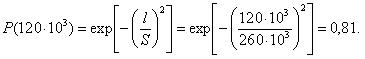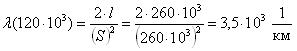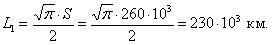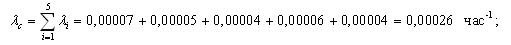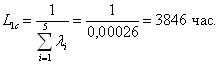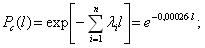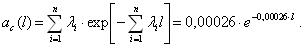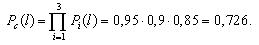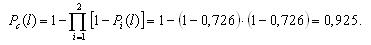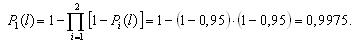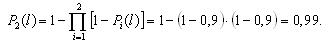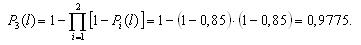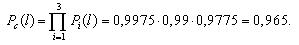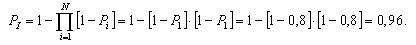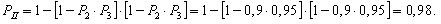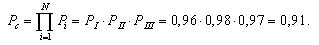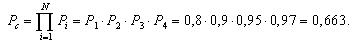Занятие № 5
Тема: Вероятность
безотказной работы и вероятность отказа.
Цель:
ü рассмотреть основные
показатели безотказной работы (вероятность безотказной работы и вероятность
отказа).
Основные понятия:
·
Показатели надежности
·
Вероятность безотказной
работы
·
Вероятность отказа
План занятия:
1. Организационный момент: приветствие, проверяется готовность к
занятию, отмечаются в журнале отсутствующие.
2. Проверка домашнего задания: фронтальный опрос.
3. Актуализация знаний: сообщение темы и цели занятия.
4. Изучение нового материала:
1.
Показатели надежности.
2.
Вероятность безотказной
работы.
3.
Вероятность отказа.
4.
Оценка вероятности
безотказной работы.
5. Закрепление
изученного материала:
ü Что называют
вероятностью безотказной работы?
ü Что называют вероятностью
отказа?
ü Дайте определение
понятия показатели надежности.
6. Домашнее
задание:
Яхъяев Н.Я. Основы теории надежности, стр. 39-41;
Задача:
На
испытание поставлено 1000 однотипных резисторов. За первые 10000 часов отказало
5, за последующие 5000 отказало еще 5. Определить вероятность безотказной
работы и вероятность отказа за 10000 часов, за 15000 часов и в промежутке между
10000 и 15000 часов.
7. Подведение
итогов занятия.
— Какое
состояние называется работоспособным? (Работоспособность – это состояние
изделия, при котором оно способно выполнять заданную функцию с параметрами,
установленными требованиями технической документации, в течение расчётного
срока службы).
Отказ –
это нарушение работоспособности. Свойство элемента или системы непрерывно
сохранять работоспособность при определённых условиях эксплуатации (до первого
отказа) называется безотказностью.
Безотказность
– свойство объекта сохранять работоспособное состояние в течение некоторого
времени или наработки.
И сегодня
на занятии мы рассмотрим показатели безотказности. Тема нашего занятия: «ВЕРОЯТНОСТЬ
БЕЗОТКАЗНОЙ РАБОТЫ И ВЕРОЯТНОСТЬ ОТКАЗА».
1. ПОКАЗАТЕЛИ
НАДЕЖНОСТИ.
Показатели
надежности – количественная характеристика одного или нескольких
свойств, составляющих надежность объекта.
Для
оценки, расчетов и исследования надежности технических устройств в процессе их
проектирования и эксплуатации используются количественные характеристики (критерии
надежности). Для показателей надежности используются две формы представления:
v Статистическая – при
эксперементальном исследовании надежности технических систем
v Вероятностная – при
априорных аналитических расчетах надежности.
В
соответствии с ГОСТ 27.002 – 89 показатели надежности подразделяются на:
Классификация
показателей надежности
|
Признак |
Показатель |
|
Число |
Единичный показатель |
|
Комплексный показатель |
|
|
Свойство |
Безотказность |
|
Долговечность |
|
|
Сохраняемость |
|
|
Ремонтопригодность |
|
|
Метод |
Расчетный показатель |
|
Экспериментальный показатель |
|
|
Эксплуатационный показатель |
|
|
Экстраполированный показатель |
|
|
Область |
Нормативный показатель, |
|
Оценочный показатель, |
|
|
Область |
Групповой показатель |
|
Индивидуальный показатель |
2. ВЕРОЯТНОСТЬ
БЕЗОТКАЗНОЙ РАБОТЫ.
Пусть
испытывается некоторое число изделий N0. По разным причинам они
будут выходить из строя, причем моменты отказов, т.е. время наработки каждого
изделия до отказов, является случайной величиной.
Вероятность
безотказной работы изделия есть вероятность того, что за
определенный рассматриваемый период времени работы (t) в заданных условиях
эксплуатации оно не откажет, т.е. вероятность того, что время наработки до
отказа (tотк) будет больше времени работы.
Р(t) = Вер (tотк>
t)
Если к
моменту t из поставленных на испытания N0 изделий останутся исправными N(t), то
статистическая вероятность безотказной работы изделия за время t, равно: , где N(t) – число работоспособных
изделий на момент t; N0 – общее число наблюдаемых изделий; n(t) –
число изделий, отказавших на момент t от начала испытаний.
При t = 0
все изделия исправны N(0) = N0 и P(0) = 1. Отказы изделия с течением
времени t приводят к монотонному убыванию функции Р(t). Практически для каждого
типа изделия существует наработка t*, больше которой ни одно изделие данного
типа проработать не может.
N(t) = 0,
при t ≥ t*соответственно Р(t) = 0, при t ≥ t*

образом, 0 ≤ P(t) ≤ 1.
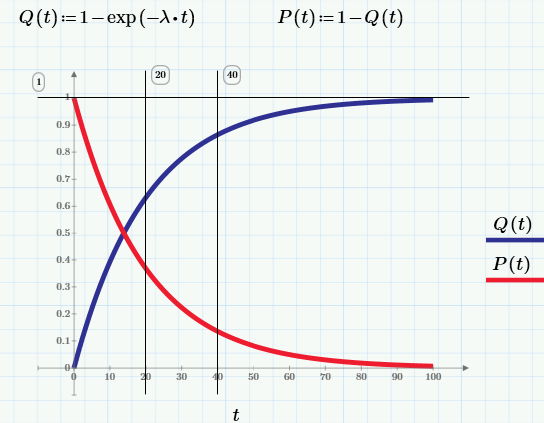
Вероятность
безотказной работы уменьшается с увеличением времени работы или наработки
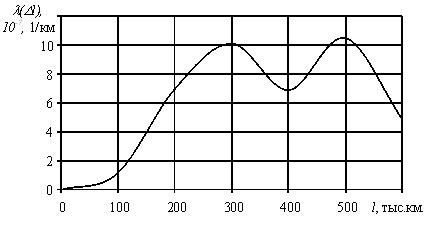
объекта. Зависимость вероятности безотказной работы от времени характеризуется
кривой убыли ресурса изделия, пример которой приведен на рисунке 1.
Рис. 1
В
начальный момент времени для работоспособного изделия вероятность его
безотказной работы равна единице (100%). По мере работы объекта эта вероятность
снижается и стремится к нулю.
Например: После
500 часов наработки из 56 агрегатов, поставленных на эксплуатацию, в работоспособном
состоянии оказалось 43 агрегата. Определить вероятность безотказной работы
агрегата в течение 500 час.
Решение:
Используем
формулу для определения вероятности безотказной работы объекта
Вероятность
безотказной работы агрегата в течение 500 часов составляет 76,8 %.
3. ВЕРОЯТНОСТЬ
ОТКАЗА.
Противоположным
событию безотказной работы является событие отказа
Вероятность
отказа
есть вероятность того, что время появления отказа будет меньше заданного
времени работы изделия, т.е. вероятность того, что время наработки до отказа (tотк)
будет меньше времени работы (t).
Q(t) = Вер (tотк<
t)
Статистическая
вероятность времени появления отказа равна: .
С течением
времени наработки число отказавших изделий непрерывно увеличивается.
Следовательно, вероятность отказов является монотонно возрастающей функцией.
Рис.2

зависимости вероятности возникновения отказа от времени показан на рисунке 2.
Для работоспособного объекта в начальный момент времени вероятность отказа
близка к нулю. Для того, чтобы отказ проявился, объекту необходимо начать
работать, при этом вероятность отказа увеличивается с увеличением времени и стремится
к единице. 0≤Q(t)≤1
Безотказная
работа изделия и его отказ являются двумя противоположными и несовместимыми
случайными величинами, поэтому их сумма всегда равна 1.
P(t)+Q(t)=1⟹P(t)=1-Q(t)
или Q(t)=1-P(t).
Например: Для
предыдущего примера определить вероятность отказа агрегатов за 500 часов
работы.
Решение:
Используем
формулу для вероятности отказа
или
Таким
образом, вероятность отказа агрегата за 500 часов составляет 23,2 %.
4. ОЦЕНКА
ВЕРОЯТНОСТИ БЕЗОТКАЗНОЙ РАБОТЫ.

за десятью однотипными изделиями в течение времени от 0 до t4. Здесь
сплошной прямой линией показана продолжительность безотказной работы изделия, а
крестиком – момент возникновения отказа.
Для наглядности
разместим наработки до отказов изделий последовательно по времени их появления.
Определение
технического состояния изделий в процессе испытаний производится в моменты
времени t1… t4. Оценки вероятностей безотказной работы за
соответствующие интервалы времени будут иметь вид:

полученным данным строится ступенчатый график – гистограмма, в конце каждого
интервала времени наблюдаемое значение вероятности в данном случае снижается на
долю изделий, отказавших на данном интервале.
Полученные
значения показывают приблизительно долю изделий, которые проработают безотказно
при испытаниях другой партии таких же изделий в аналогичных условиях.
Например:
Изготовив 20 новых изделий, можно утверждать, что в течение времени t3
приблизительно 12 изделий проработают безотказно (не проводя дополнительных
испытаний) 20*0,6=12. Это приближенная оценка будет тем точнее, чем больше
число испытанных изделий.
В качестве
показателя надежности может использоваться условная вероятность безотказной
работы на некотором интервале времени, которая вычисляется при условии, что
изделие было полностью исправно к началу этого времени.
Например: Условная
вероятность безотказной работы изделия на интервале времени от t2 до
t3 оценивается согласно выражению:
Как вычисляется среднее время до отказа и вероятность безотказной работы?
Время на прочтение
4 мин
Количество просмотров 116K
Понятиям MTTF (Mean Time To Failure — среднее время до отказа) и другим терминам теории надежности посвящено большое количество статей, в том числе на Хабре (см., например, тут). Вместе с тем, редкие публикации «для широкого круга читателей» затрагивают вопросы математической статистики, и уж тем более они не дают ответа на вопрос о принципах расчета надежности электронной аппаратуры по известным характеристикам ее составных элементов.
В последнее время мне довольно много приходится работать с расчетами надежности и рисков, и в этой статье я постараюсь восполнить этот пробел, отталкиваясь от своего предыдущего материала (из цикла о машинном обучении) о пуассоновском случайном процессе и подкрепляя текст вычислениями в Mathcad Express, повторить которые вы сможете скачав этот редактор (подробно о нем тут, обратите внимание, что нужна последняя версия 3.1, как и для цикла по machine learning). Сами маткадовские расчеты лежат здесь (вместе с XPS- копией).
1. Теория: основные характеристики отказоустойчивости
Вроде бы, из самого определения (Mean Time To Failure) понятен его смысл: сколько (конечно, в среднем, поскольку подход вероятностный) прослужит изделие. Но на практике такой параметр не очень полезен. Действительно, информация о том, что среднее время до отказа жесткого диска составляет полмиллиона часов, может поставить в тупик. Гораздо информативнее другой параметр: вероятность поломки или вероятность безотказной работы (ВБР) за определенный период (например, за год).
Для того чтобы разобраться в том, как связаны эти параметры, и как, зная MTTF, вычислить ВБР и вероятности отказа, вспомним некоторые сведения из математической статистики.
Ключевое понятие теории надежности — это понятие отказа, измеряемое, соответственно, интервальным показателем
Q(t) = вероятность того, что изделие откажет к моменту времени t.
Соотвественно, вероятность безотказной работы (ВБР, в английской терминологии «reliability»):
P(t) = вероятность того, что изделие проработает без отказа от момента t0=0 до момента времени t.
По определению, в момент t0=0 изделие находится в работоспособном состоянии, т.е. Q(0)=0, а P(0)=1.
Оба параметра — это интервальные характеристики отказоустойчивости, т.к. речь идет о вероятности отказа (или наоборот, безотказной работы) на интервале (0,t). Если отказ рассматривать, как случайное событие, то, очевидно, что Q(t) — это, по определению, его функция распределения. А точечную характеристику можно определить, как
p(t)=dQ(t)/dt = плотность вероятности, т.е. значение p(t)dt равно вероятности, что отказ произойдет в малой окрестности dt момента времени t.
И, наконец, самая важная (с практической точки зрения) характеристика: λ(t)=p(t)/P(t)=интенсивность отказов.
Это (внимание!) условная плотность вероятности, т.е. плотность вероятности возникновения отказа в момент времени t при условии, что до этого рассматриваемого момента времени t изделие работало безотказно.
Измерить параметр λ(t) экспериментально можно путём испытания партии изделий. Если к моменту времени t работоспособность сохранило N изделий, то за оценку λ(t) можно принять процент отказов в единицу времени, происходящих в окрестности t. Точнее, если в период от t до t+dt откажет n изделий, то интенсивность отказов будет примерно равна
λ(t)=n/(N*dt).
Именно эта λ-характеристика (в пренебрежении ее зависимостью от времени) и приводится чаще всего в паспортных данных различных электронных компонент и самых разных изделий. Только сразу возникает вопрос: а как вычислить вероятность безотказной работы и при чем здесь среднее время до отказа (MTTF).
А вот при чем.
2. Экспоненциальное распределение
В терминологии, которую мы только что использовали, пока не было никаких предположений о свойствах случайной величины — момента времени, в который происходит отказ изделия. Давайте теперь конкретизируем функцию распределения значения отказа, выбрав в качестве нее экспоненциальную функцию с единственным параметром λ=const (смысл которого будет ясен через несколько предложений).
Дифференцируя Q(t), получим выражение для плотности вероятности экспоненциального распределения:
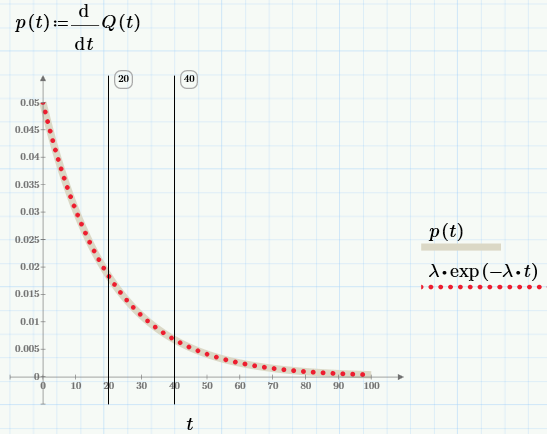
а из него – функцию интенсивности отказов: λ(t)=p(t)/P(t)=const=λ.
Что мы получили? Что для экспоненциального распределения интенсивность отказов – есть величина постоянная, причем совпадающая с параметром распределения. Этот параметр и является главным показателем отказоустойчивости и его часто так и называют λ-характеристикой.
Мало того, если теперь посчитать среднее время до первого отказа – тот самый параметр MTTF (Mean Time To Failure), то мы получим, что он равен MTTF=1/ λ.
Все это замечательные свойства экспоненциального распределения. Почему мы выбрали в качестве для описания отказов именно его? Да потому что это наиболее простая модель – модель пуассоновского потока событий, которая уже была нами рассмотрена в статье про анализ конверсии сайта. Поэтому-то в теории надежности наиболее часто используется показательное (экспоненциальное) распределение, для которого, как мы выяснили:
- надежность элементов можно оценить одним числом, т.к. λ=const;
- по известной λ довольно просто оценить остальные показатели надежности (например, ВБР для любого времени t);
- λ обладает хорошей наглядностью
- λ нетрудно измерить экспериментально
Но это еще не все, потому, что для экспоненциального распределения особенно легко делать расчет систем, состоящих из множества элементов. Но об этом – в следующей статье (продолжение следует).
Практика
1. Расчет показателей безотказности
1.1 Вероятность безотказной работы
1.2 Вероятность отказа
1.3 Частота отказа
1.4 Интенсивность отказа
1.5 Средняя наработка до отказа
1.6 Среднее значение параметра потока отказов
1.7 Пример расчета показателей безотказности
2. Примеры расчета показателей надежности для различных законов распределения случайных величин
2.1 Экспоненциальный закон распределения
2.2 Закон распределения Вейбулла-Гнеденко
2.3 Закон распределения Рэлея
3. Примеры расчета показателей надежности сложных систем
3.1 Основное соединение элементов
3.2 Резервное соединение
1.1 Вероятность безотказной работы
Вероятностью безотказной работы называется вероятность того, что при определенных условиях эксплуатации, в пределах заданной наработки не произойдет ни одного отказа.
Вероятность безотказной работы обозначается как P(l), которая определяется по формуле (1.1):
где N0 – число элементов в начале испытания; r(l) – число отказов элементов к моменту наработки.Следует отметить, что чем больше величина N0, тем с большей точностью можно рассчитать вероятность P(l).
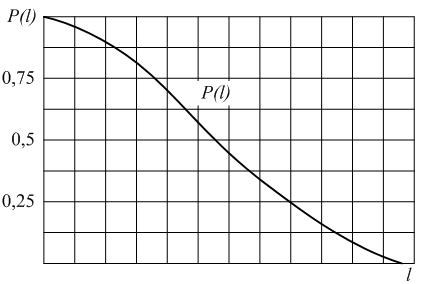
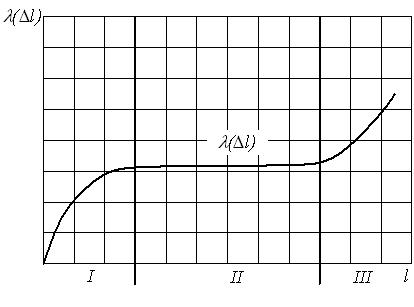
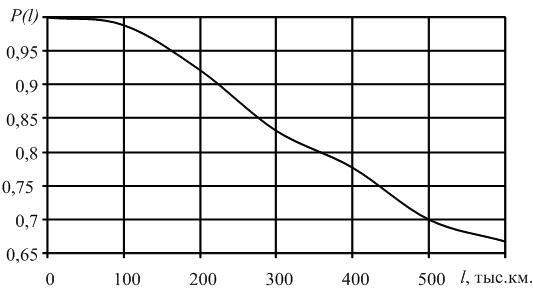
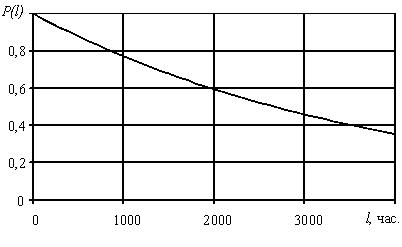
В начале эксплуатации исправного локомотива P(0) = 1, так как при пробеге l = 0 вероятность того, что ни один элемент не откажет, принимает максимальное значение – 1. С ростом пробега l вероятность P(l) будет уменьшаться. В процессе приближения срока эксплуатации к бесконечно большой величине вероятность безотказной работы будет стремиться к нулю P(l→∞) = 0. Таким образом в процессе наработки величина вероятности безотказной работы изменяется в пределах от 1 до 0. Характер изменения вероятности безотказной работы в функции пробега показан на рис. 1.1.
Рис.2.1. График изменения вероятности безотказной работы P(l)в зависимости от наработки
Основными достоинствами использования данного показателя при расчетах является два фактора: во-первых, вероятность безотказной работы охватывает все факторы, влияющие на надежность элементов, позволяя достаточно просто судить о его надежности, т.к. чем больше величина P(l), тем выше надежность; во-вторых, вероятность безотказной работы может быть использована в расчетах надежности сложных систем, состоящих из более чем одного элемента.
1.2 Вероятность отказа
Вероятностью отказа называют вероятность того, что при определенных условиях эксплуатации, в пределах заданной наработки произойдет хотя бы один отказ.
Вероятность отказа обозначается как Q(l), которая определяется по формуле (1.2):
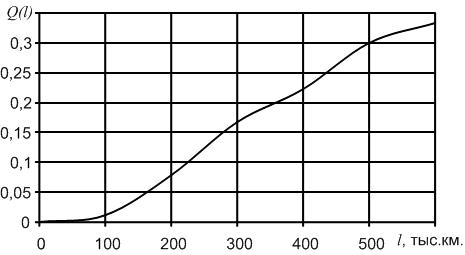
В начале эксплуатации исправного локомотива Q(0) = 0, так как при пробеге l = 0 вероятность того, что хотя бы один элемент откажет, принимает минимальное значение – 0. С ростом пробега l вероятность отказа Q(l) будет увеличиваться. В процессе приближения срока эксплуатации к бесконечно большой величине вероятность отказа будет стремиться к единице Q(l→∞) = 1. Таким образом в процессе наработки величина вероятности отказа изменяется в пределах от 0 до 1. Характер изменения вероятности отказа в функции пробега показан на рис. 1.2.Вероятность безотказной работы и вероятность отказа являются событиями противоположными и несовместимыми.
Рис.2.2. График изменения вероятности отказа Q(l) в зависимости от наработки
1.3 Частота отказов
Частота отказов – это отношение числа элементов в единицу времени или пробега отнесенного к первоначальному числу испытуемых элементов. Другими словами частота отказов является показателем, характеризующим скорость изменения вероятности отказов и вероятности безотказной работы по мере роста длительности работы.
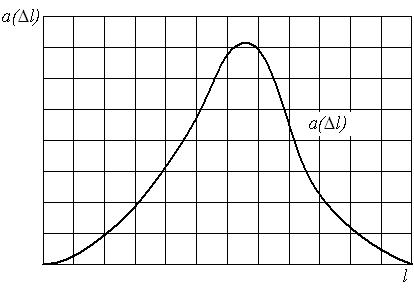
Частота отказов обозначается как 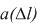
где – 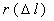
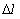
Данный показатель позволяет судить по его величине о числе элементов, которые откажут на каком-то промежутке времени или пробега, также по его величине можно рассчитать количество требуемых запасных частей.
Характер изменения частоты отказов в функции пробега показан на рис. 1.3.
Рис. 1.3. График изменения частоты отказов в зависимости от наработки
1.4 Интенсивность отказов
Интенсивность отказов представляет собой условную плотность возникновения отказа объекта, определяемую для рассматриваемого момента времени или наработки при условии, что до этого момента отказ не возник. Иначе интенсивность отказов – это отношение числа отказавших элементов в единицу времени или пробега к числу исправно работающих элементов в данный отрезок времени.
Интенсивность отказов обозначается как 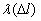
где
Как правило, интенсивность отказов 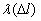
На рис. 1.4. представлен теоретический характер изменения интенсивности отказов в функции пробега.
Рис. 1.4. График изменения интенсивности отказов в зависимости от наработки
На графике изменения интенсивности отказов, изображенном на рис. 1.4. можно выделить три основных этапа отражающих процесс экс-плуатации элемента или объекта в целом.
Первый этап, который также называется этапом приработки, характеризуется увеличением интенсивности отказов в начальный период эксплуатации. Причиной роста интенсивности отказов на данном этапе являются скрытые дефекты производственного характера.
Второй этап, или период нормальной работы, характеризуется стремлением интенсивности отказов к постоянному значению. В течение этого периода могут возникать случайные отказы, в связи с появлением внезапной концентрации нагрузки, превышающей предел прочности элемента.
Третий этап, так называемый период форсированного старения. Характеризуется возникновением износовых отказов. Дальнейшая эксплуатация элемента без его замены становится экономически не рациональной.
1.5 Средняя наработка до отказа
Средняя наработка до отказа – это средний пробег безотказной работы элемента до отказа.
Средняя наработка до отказа обозначается как L1 и определяется по формуле (1.5):
где li – наработка до отказа элемента; ri – число отказов.
Средняя наработка до отказа может быть использована для предварительного определения сроков ремонта или замены элемента.
1.6 Среднее значение параметра потока отказов
Среднее значение параметра потока отказов характеризует среднюю плотность вероятности возникновения отказа объекта, определяемая для рассматриваемого момента времени.
Среднее значение параметра потока отказов обозначается как Wср и определяется по формуле (1.6):
1.7 Пример расчета показателей безотказности
Исходные данные.
В течение пробега от 0 до 600 тыс. км., в локомотивном депо произведен сбор информации по отказам ТЭД. При этом количество исправных ТЭД в начале периода эксплуатации составляло N0 = 180 шт. Суммарное количество отказавших ТЭД за анализируемый период составило ∑r(600000) = 60. Интервал пробега принять равным 100 тыс. км. При этом количество отказавших ТЭД по каждому участку составило: 2, 12, 16, 10, 14, 6.
Требуется.
Необходимо рассчитать показатели безотказности и построить их зависимости изменения во времени.
Сначала необходимо заполнить таблицу исходных данных так, как это показано в табл. 1.1.
Таблица 1.1.
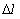 , тыс. км , тыс. км |
0 — 100 | 100 — 200 | 200 — 300 | 300 — 400 | 400 — 500 | 500 — 600 |
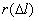 |
2 | 12 | 16 | 10 | 14 | 6 |
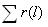 |
2 | 14 | 30 | 40 | 54 | 60 |
Первоначально по уравнению (1.1) определим для каждого участка пробега величину вероятности безотказной работы. Так, для участка от 0 до 100 и от 100 до 200 тыс. км. пробега вероятность безотказной работы составит:
Далее, используя зависимость (1.2) произведем расчет вероятности отказа ТЭД.
Произведем расчет частоты отказов по уравнению (1.3).
Далее по уравнению (1.4) произведем расчет интенсивности отказов ТЭД в зависимости от наработки.
Первоначально рассчитаем среднее количество работоспособных ТЭД на участке от 0 до 100 тыс. км. пробега:
Тогда интенсивность отказов на участке 0-100 тыс.км. будет равна:
Аналогичным образом определим величину интенсивности отказов для интервала 100-200 тыс. км.
По уравнениям (1.5 и 1.6) определим среднюю наработку до отказа и среднее значение параметра потока отказов.
Систематизируем полученные результаты расчета и представим их в виде таблицы (табл. 1.2.).
Таблица 1.2.
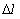 , тыс.км. , тыс.км. |
0 — 100 | 100 — 200 | 200 — 300 | 300 — 400 | 400 — 500 | 500 — 600 |
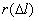 |
2 | 12 | 16 | 10 | 14 | 6 |
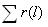 |
2 | 14 | 30 | 40 | 54 | 60 |
| P(l) | 0,989 | 0,922 | 0,833 | 0,778 | 0,7 | 0,667 |
| Q(l) | 0,011 | 0,078 | 0,167 | 0,222 | 0,3 | 0,333 |
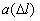 10-7, 1/км 10-7, 1/км |
1,111 | 6,667 | 8,889 | 5,556 | 7,778 | 3,333 |
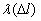 10-7, 1/км 10-7, 1/км |
1,117 | 6,977 | 10,127 | 6,897 | 10,526 | 4,878 |
Приведем характер изменения вероятности безотказной работы ТЭД в зависимости от пробега (рис. 1.5.). Необходимо отметить, что первой точкой на графике, т.е. при пробеге равном 0, величина вероятности безотказной работы примет максимальное значение – 1.
Рис. 1.5. График изменения вероятности безотказной работы в зависимости от наработки
Приведем характер изменения вероятности отказа ТЭД в зависимости от пробега (рис. 1.6.). Необходимо отметить, что первой точкой на графике, т.е. при пробеге равном 0, величина вероятности отказа примет минимальное значение – 0.
Рис. 1.6. График изменения вероятности отказа в зависимости от наработки
Приведем характер изменения частоты отказов ТЭД в зависимости от пробега (рис. 1.7.).
Рис. 1.7. График изменения частоты отказов в зависимости от наработки
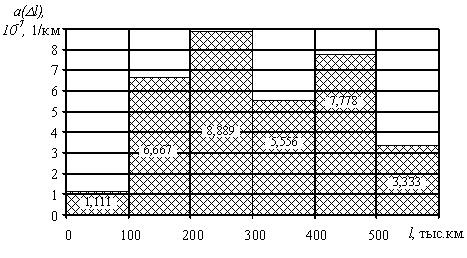
На рис. 1.8. представлена зависимость изменения интенсивности отказов от наработки.
Рис. 1.8. График изменения интенсивности отказов в зависимости от наработки
2.1 Экспоненциальный закон распределения случайных величин
Экспоненциальный закон достаточно точно описывает надежность узлов при внезапных отказах, имеющих случайный характер. Попытки применить его для других типов и случаев отказов, особенно постепенных, вызванных износом и изменением физико-химических свойств элементов показали его недостаточную приемлемость.
Исходные данные.
В результате испытания десяти топливных насосов высокого давления получены наработки их до отказа: 400, 440, 500, 600, 670, 700, 800, 1200, 1600, 1800 ч. Предполагая, что наработка до отказа топливных насосов подчиняется экспоненциальному закону распределения.
Требуется.
Оценить величину интенсивности отказов , а также рассчитать вероятность безотказной работы за первые 500 ч. и вероятность отказа в промежутке времени между 800 и 900 ч. работы дизеля.
Во-первых, определим величину средней наработки топливных насосов до отказа по уравнению:
Затем рассчитываем величину интенсивности отказов:
Величина вероятности безотказной работы топливных насосов при наработке 500 ч составит:
Вероятность отказа в промежутке между 800 и 900 ч. работы насосов составит:
2.2 Закон распределения Вэйбулла-Гнеденко
Закон распределения Вейбулла-Гнеденко получил широкое распространение и используется применительно к системам, состоящим из рядов элементов, соединенных последовательно с точки зрения обеспечения безотказности системы. Например, системы, обслуживающие дизель-генераторную установку: смазки, охлаждения, питания топливом, воздухом и т.д.
Исходные данные.
Время простоя тепловозов в неплановых ремонтах по вине вспомогательного оборудования подчиняется закону распределения Вейбулла-Гнеденко с параметрами b=2 и a=46.
Требуется.
Необходимо определить вероятность выхода тепловозов из неплановых ремонтов после 24 ч. простоя и время простоя, в течение которого работоспособность будет восстановлена с вероятностью 0,95.
Найдем вероятность восстановления работоспособности локомотива после простоя его в депо в течение суток по уравнению:
Для определения времени восстановления работоспособности локомотива с заданной величиной доверительной вероятности также используем выражение:
2.3 Закон распределения Рэлея
Закон распределения Рэлея используется в основном для анализа работы элементов, имеющих ярко выраженный эффект старения (элементы электрооборудования, различного рода уплотнения, шайбы, прокладки, изготовленные из резиновых или синтетических материалов).
Исходные данные.
Известно, что наработки контакторов до отказа по параметрам старения изоляции катушек можно описать функцией распределения Рэлея с параметром S = 260 тыс.км.
Требуется.
Для величины наработки 120 тыс.км. необходимо определить вероятность безотказной работы, интенсивность отказов и среднюю наработку до первого отказа катушки электромагнитного контактора.
3.1 Основное соединение элементов
Система, состоящая из нескольких независимых элементов, связанных функционально таким образом, что отказ любого из них вызывает отказ системы, отображается расчетной структурной схемой безотказной работы с последовательно соединенными событиями безотказной работы элементов.
Исходные данные.
Нерезервированная система состоит из 5 элементов. Интенсивности их отказов соответственно равны 0,00007; 0,00005; 0,00004; 0,00006; 0,00004 ч-1
Требуется.
Необходимо определить показатели надежности системы: интенсивность отказов, среднее время наработки до отказа, вероятность безотказной работы, частота отказов. Показатели надежности P(l) и a(l) получить в интервале от 0 до 1000 часов с шагом в 100 часов.
Вычислим интенсивность отказа и среднюю наработку до отказа по следующим уравнениям:
Значения вероятности безотказной работы и частоты отказов получим, используя уравнения приведенные к виду:
Результаты расчета P(l) и a(l) на интервале от 0 до 1000 часов работы представим в виде табл. 3.1.
Таблица 3.1.
| l, час | P(l) | a(l), час-1 |
| 0 | 1 | 0,00026 |
| 100 | 0,974355 | 0,000253 |
| 200 | 0,949329 | 0,000247 |
| 300 | 0,924964 | 0,00024 |
| 400 | 0,901225 | 0,000234 |
| 500 | 0,878095 | 0,000228 |
| 600 | 0,855559 | 0,000222 |
| 700 | 0,833601 | 0,000217 |
| 800 | 0,812207 | 0,000211 |
| 900 | 0,791362 | 0,000206 |
| 1000 | 0,771052 | 0,0002 |
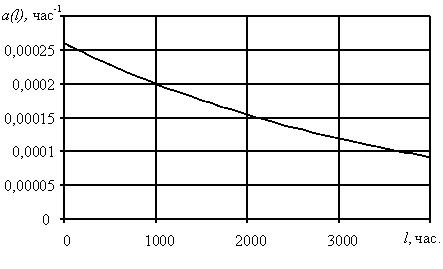
Графическая иллюстрация P(l) и a(l) на участке до средней наработки до отказа представлена на рис. 3.1, 3.2.
Рис. 3.1. Вероятность безотказной работы системы.
Рис. 3.2. Частота отказов системы.
3.2 Резервное соединение элементов
Исходные данные.
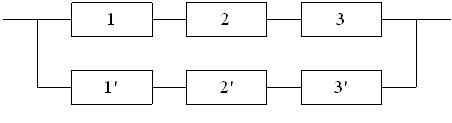
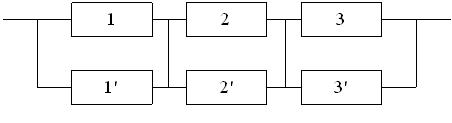
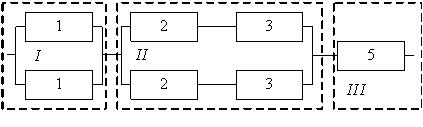
На рис. 3.3 и 3.4 показаны две структурные схемы соединения элементов: общего (рис. 3.3) и поэлементного резервирования (рис. 3.4). Вероятности безотказной работы элементов соответственно равны P1(l) = P ’1(l) = 0,95; P2(l) = P’2(l) = 0,9; P3(l) = P ’3(l) = 0,85.
Требуется.
Необходимо рассчитать надежность двух систем.
Рис. 3.3. Схема системы с общим резервированием.
Рис. 3.4. Схема системы с поэлементным резервированием.
Вероятность безотказной работы блока из трех элементов без резервирования рассчитаем по выражению:
Вероятность безотказной работы той же системы при общем резервировании (рис. 3.3) составит:
Вероятности безотказной работы каждого из трех блоков при поэлементном резервировании (рис. 3.4) будут равны:
Вероятность безотказной работы системы при поэлементном резервировании составит:
Таким образом, поэлементное резервирование дает более существенное увеличение надежности (вероятность безотказной работы возросла с 0,925 до 0,965, т.е. на 4%).
Исходные данные.
На рис. 3.5 представлена система с комбинированным соединением элементов. При этом вероятности безотказной работы элементов имеют следующие значения: P1=0,8; Р2=0,9; Р3=0,95; Р4=0,97.
Требуется.
Необходимо определить надежность системы. Также необходимо определить надежность этой же системы при условии, что резервные элементы отсутствуют.
Рис.3.5. Схема системы при комбинированном функционировании элементов.
Для расчета в исходной системе необходимо выделить основные блоки. В представленной системе их три (рис. 3.6). Далее рассчитаем надежность каждого блока в отдельности, а затем найдем надежность всей системы.
Рис. 3.6. Сблокированная схема.
Надежность системы без резервирования составит:
Таким образом, система без резервирования является на 28% менее надежной, чем система с резервированием.
Лекция №2.
Характеристики надёжности сложных
технических систем
Вопросы лекции:
Введение
2. Показатели
надёжности
Введение
При анализе
характеристик различных технических
устройств в литературе широко используют
понятие «система», под которым в самом
общем смысле понимают набор объектов
с определёнными свойствами, а также
набор связей между выделенными объектами1.
Границы системы определяет, как правило,
исследователь в соответствии с целью,
которая поставлена пред ним. Всё что
находится за пределами границ системы,
называется окружающей средой, которая
может оказывать непреднамеренно мешающее
воздействие на систему.
Отдельные объекты
системы называют также системными
элементами. В теории надёжности под
элементом обычно понимают такую часть
системы, надёжность которой в процессе
функционирования может быть рассмотрена
независимо от надёжности входящих в
эту часть более простых составляющих.
Так, например, котлоагрегат, турбина,
сетевой подогреватель могут
рассматриваться как элементы более
сложной системы ТЭЦ, а сама ТЭЦ является
элементом более сложной системы
теплоснабжения района. С другой стороны,
при анализе надёжности, например,
котлоагрегата его поверхности теплообмена,
коллекторы, арматура, устройства подачи
топлива выступают в роли элементов.
Учитывая условность деления системы
на элементы, часто в теории надёжности
используют обобщающие понятия
устройство,изделиеилиобъект,
которые относят к любой заранее
выделенной и функционально самостоятельной
части системы. Ниже чаще всего будет
использоваться понятиеобъект,
который может состоять из элементов.
Объекты и их
элементы в теории надёжности делят на
восстанавливаемыеиневосстанавливаемые.
Невосстанавливаемый объект работает
до первого отказа, а восстанавливаемый
после устранения последствий отказа
может использоваться по назначению.
Это деление также в определённой мере
условно так как, например, течь трубной
системы конденсатора является отказом,
в результате которого прекращается
работа турбины и проводятся восстановительные
работы (устранение отказа). Следовательно,
при таком отказе конденсатор и турбоагрегат
в целом выступают как восстанавливаемые
объекты. Но если исследовать безотказность
объекта только до наступления первого
отказа, то в таком случае течь трубной
системы может характеризовать надёжность
данного турбоагрегата как
невосстанавливаемого объекта.
В теории надёжности
при анализе свойств объектов считают,
что все показатели надёжности являются
функцией непрерывной величины – времени.
Допустим, что в момент времени t=0объект
находился в работоспособном состоянии,
а при наработкеt
= tот
наступил отказ. Это позволяет считатьtотнепрерывной случайной величиной,
удовлетворяющей неравенству.
Последнее неравенство даёт основание
получить функцию,
которая называетсявероятностью
отказа. Одновременно из теории
вероятностей известно, чтоявляется функцией распределения
случайной величиныtот.
Если рассмотреть
вероятность того, что время безотказной
работы объекта окажется больше заданного
времени t, то
получим выражение
,
(1)
которое определяет один
из основных показателей надёжности
вероятность безотказной работы.
При любом значении
наработки t объект
может быть только работоспособным или
потерявшим работоспособность.
Следовательно, вероятность того, что
он находится в одном из двух состояний,
равна вероятности достоверного события.
.
(2)
Как уже отмечалось,
вероятность отказа Q(t)(иначе функция ненадёжности) по
определению аналогична функции
распределения непрерывной случайной
величины, которая, как известно, есть
возрастающая функция. Тогда из (1.2)
следует, что вероятность безотказной
работы есть убывающая функция, т.е.
.
(3)
Примерный вид
функций P(t)иQ(t)показан на
рис.1. Как следует из рис.1, уменьшение
вероятности безотказной работыP(t)может рассматриваться как снижение с
увеличением наработки количества
работоспособных объектов. Соответственно,
величинаQ(t)
показывает рост с увеличением
наработки числа отказавших объектов.
Вероятность
безотказной работы P(t)может быть определена приближённо на
основе анализа эксплуатационных данных
или по результатам испытаний большого
количестваNоднотипных объектов. Если обозначитьNот(t)число отказавших в момент времениtобъектов, аNи(t)- число исправных в этот же момент
времени объектов, то приNотношениеNи(t)/N
P(t). Таким образом, при фиксированномN получим
Nи(t)/N
≈ P(t).
(4)

Функции P(t)иQ(t)
Непрерывная
случайная величина tот
характеризуется, кроме указанных
интегральных показателей, величиной
плотности распределения или плотностью
вероятности отказовf(t). Как известно
из теории вероятностей, плотность
распределения непрерывной случайной
величины есть функция, равная пределу
отношения вероятности того, что случайная
величина находится в каком-то малом
интервале, к ширине этого интервала
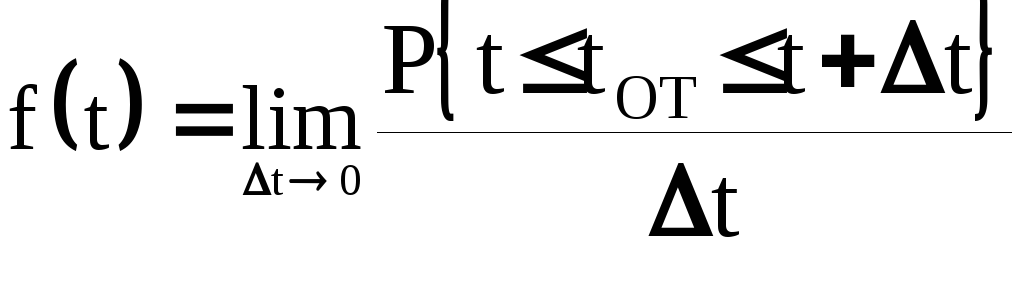
(5)
При t0
можно записать, что
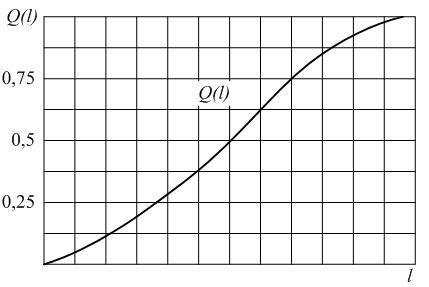
Примерное
положение кривой f(t)
в зависимости от наработки показано
на рис.2.
Как следует из
рис.2 площадка под кривой f(t), ограниченная снизу отрезкомtна оси абсцисс, численно равна вероятности
отказа в интервалеt.Точнее, приближается к ней приt→ 0.
Приближённо
определить значение функции f(t)можно опытным путём для отдельных
интервалов наработки (t,
t+t)
,
(6)

Плотность вероятности отказов
где Nот(t,
t+t
)/Nприближённая оценка вероятности
отказа за времяt, аNот(t,
t+t
)– число отказов в интервале (t,
t+t). Чем большеNи меньшеt,
тем точнее формула (6).
Вероятность отказа
за время tесть
интеграл отf(t), взятый для интервала от0доt:
.
(7)
Очевидно, что если
t=, то вероятность отказа равна единице.
Из этого следует, что вся площадь под
кривойf(t)всегда равна единице. Но раз,
то можно записать, что
. (8)
Из теории вероятностей
известно, что плотность распределения
есть производная от функции распределения
F(t).С учётом
этого из (5), (7) следует, что в теории
надёжности функция распределения
случайной величины имеет смысл вероятности
отказа, т.е.F(t) =
Q(t), и1-F(t)=P(t).
Одной из важнейших
характеристик надёжности является
интенсивность отказов. Эта
характеристика оценивает вероятность
отказа в интервале (t,
t+t) тех объектов, которые безотказно
проработали времяt, т.е. до начала данного интервала.
Функция интенсивности отказов может
быть определена следующим образом
,
(9)
где
— вероятность отказа в интервале (t,
t+t) для объектов безотказно проработавших
времяt.
На основе
эксплуатационных или опытных данных
можно приближённо оценить интенсивность
отказов следующим образом
,
(10)
где
— количество отказов в интервале(t,
t+t);
Nисп(t)
– число исправных объектов на начало
интервала;
— оценка вероятности
отказа в интервале (
t, t+t
)
тех объектов,
которые благополучно проработали время
t.
Интенсивность
отказов характеризует надёжность в
каждый данный момент времени. Поэтому
её иногда называют опасностью отказа.
Так как (t)определяет надёжность только тех
объектов, которые безотказно проработали
времяt, то
она имеет смысл условной (апостериорной)
вероятности. Если рассмотреть вероятность
отказа, определяемую площадью под кривой
плотности распределения (рис.2)f(t)·t,
то можно убедиться в том, что она
характеризует вероятность отказа любого
из множества рассматриваемых объектов
(априорная вероятность).
Между показателями
надёжности P(t),
f(t)и (t)
существует определённая связь.
Предположим, что испытываютсяNобъектов и в момент времениtчасть из нихNот(t)отказали, аNисп(t)остались работоспособными. Таким
образом, справедливо равенствоN
= Nисп(t)
+ Nот(t),с учётом которого можно записать
P(t)
= [N
– NOT(t)
] /N
= 1 — Nот(t)
/N, (11)
гдеNот(t)
/N
≈ Q(t).
Дифференцируя
уравнение (1.11) по времени можно получить
. (12)
Правая часть
уравнения (12) как это следует из (6) по
абсолютной величине есть предел выражения
для плотности распределения f(t).
.
(13)
Умножив и разделив
правую часть дифференциального уравнения
(12) на Nисп(t)получим
.
(14)
Произведение в
правой части состоит из двух сомножителей,
первый из которых есть приближённая
оценка вероятности безотказной работы
P(t)(см. (3)), а
второй есть оценка интенсивности
отказов(t)(см. (10)). Таким образом, на основании (14)
можно утверждать справедливость
равенства
=
-P(t)(t)(15)
или
(t)
= — P'(t)/P(t). (15а)
Формула (15а) даёт
наиболее общее выражение для вычисления
интенсивности отказов. Связь между
интенсивностью отказов и плотностью
распределения видна из сравнения
выражений (13) и (15), откуда следует
f(t)
=P(t)(t)
. (16)
Если в выражении
(15а) разделить переменные и проинтегрировать
(t)
в пределах от0доt и
соответственноdP(t)/P(t)
от1доP(t)
,то можно получить
.
Так как
, получаем
или

(17)
Формула (17) определяет
вероятность безотказной работы через
интенсивность отказов в общей форме.
При этом предполагается, что (t)
интегрируемая функция времени
наработки. Эта формула широко используется
в теории надёжности.
Среди показателей
надёжности, наиболее широко применяемых
на практике, выделяется среднее время
безотказной работы или наработка на
отказ Т. По
смыслуТ это
математическое ожидание непрерывной
случайной величины – наработки до
отказа. Из теории вероятностей известно,
что математическое ожидание определяется
интегралом
.
Так как случайная
величина tот
существует только на положительной
полуоси, то
.
После интегрирования
по частям получим
.
(18)
Первое слагаемое
в (18) при
равно нулю, так как функция
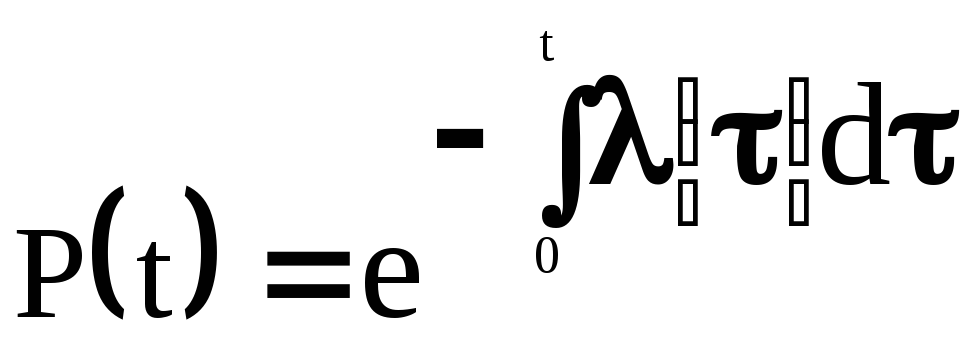
среднее время безотказной работы
определяется по формуле
.
(19)
Статистическая
оценка Т
при испытании всехNобъектов до отказа выполняется по
формуле
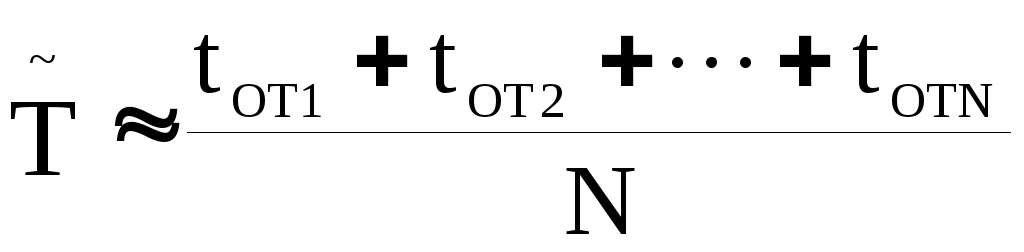
(20)
Чем больше N, тем точнее (20) приближается кТ.