Вероятность того что во время работы компьютера произойдет сбой

Условие

Решение

Написать комментарий

sasha255

Для сигнализации об аварии в двигателе установлены два независимо от работающих сигнализатора.Вероятность того что при аварии сигнализатор сработает равна0,95 для первого сигнализатора и 0,9 для второго.Найти вероятность того что при аварии а)сработает только один сигнализатор, б)сработают оба сигнализатора

2) Вероятность того что во время работы цифровой электронной машины произойдет сбой в арифметическом устройстве,в оперативной памяти,в остальных устройствах,относятся как 3:2:5.Вероятность обнаружения сбоя в арифметическом устройстве,в оперативной памяти и в остальных устройствах соответственно равны 0,8;0,9;0;9.Найти вероятность того что возникший сбой в машине будет найден.

3)Два равносильных противника играют в шахматы.Что вероятнее?
а)выиграть одну партию из двух или две партии из 4?
б)выиграть не менее 2х пртий из 4х или не менее 3х партий из 5?ничьи во внимание не принимаются

Источник

Брошены две игральные кости Найти вероятность того

Главная > Документ

Информация о документе
Дата добавления:
Размер:
Доступные форматы для скачивания:

Вероятности того, что во время работы цифровой электронной машины произойдет сбой в арифметическом устройстве, в оперативной памяти, в остальных устройствах,

относятся как 3:2:5. Вероятности обнаружения сбоя в арифметическом устройстве, в оперативной памяти и в остальных устройствах соответственно равны 0,8; 0,9; 0,9. Найти вероятность того, что возникший в машине сбой будет обнаружен.

Решение: Пусть А – событие того, что сбой будет обнаружен, тогда из формулы полной вероятности следует, что:

PA= PB1PB1A+PB2PB2A+PB3PB3A= 0,3*0,8+0,2*0,9+0,5*0,9=0,87.

Обозначим через А событие – деталь отличного качества

Можно сделать два предположения

-деталь произведена первым автоматом (так как производительность первого автомата вдвое больше второго автомата, то Р()=2/3)

-деталь произведена вторым автоматом (Р()=1/3)

Условная вероятность, что она будет отличного качества, если она произведена первым автоматом (A)=0,6

Условная вероятность, что она будет отличного качества, если она произведена первым автоматом (A)=0,84

Вероятность того, что наудачу взятая деталь окажется отличного качества, по формуле полной вероятности равна

P(A)=Р()*(A)+ Р()*(A)=2/3*0.6+1/3*0.84=0.68

Вероятность того, что взятая отличная деталь произведена первым автоматом, по формуле Бейеса равна

()===

Ответ:

Решение: Обозначим событие А – стрелок поразил мишень и гипотезы: B1 – стрелок выбрал винтовку с оптическим прицелом, B2 – без оптического прицела. Тогда . Условные вероятности попадания из винтовки с оптическим прицелом и без: . Вычислим вероятность попадания из наудачу взятой винтовки:

Теперь, воспользовавшись формулой Бейеса, получим ответ:

Число грузовых автомашин, проезжающих по шоссе, на котором стоит бензоколонка, относится к числу легковых машин, проезжающих по тому же шоссе как 3:2. Вероятность того, что будет заправляться грузовая машина, равна 0,1; для легковой машины эта вероятность равна 0,2. К бензоколонке подъехала для заправки машина. Найти вероятность того, что это грузовая машина.

Решение: Обозначим через А событие—подъезд автомобиля к заправке. Можно сделать два предположения: —проехал грузовой автомобиль, причем =3/5; — проехал легковой автомобиль, причем = 2/5.

Вероятность того, что проезжающий автомобиль подъедет на заправку, по формуле полной вероятности равна Р(А) = + = 3/5 0,1 + 2/5 0,2 = 0,14

Искомая вероятность того, что подъехавший к заправке автомобиль будет грузовым, по формуле Бейеса равна = = = 3/7

Две перфораторщицы набили на разных перфораторах по одинаковому комплекту перфокарт. Вероятность того, что первая перфораторщица допустит ошибку, равна 0,05; для второй перфораторщицы эта вероятность равна 0,1. При сверке перфокарт была обнаружена ошибка. Найти вероятность того, что ошиблась первая перфораторщица. (Предполагается, что оба перфоратора были исправны.)

Обозначим через событие А – ошибку перфораторщицы. Тогда, – ошибка сделана первой перфораторщицей, — ошибка сделана второй перфораторщицей. Причем P()=0,5 и P()=0,5, т.к. обе работали одинаково.

Условная вероятность того, что первая перфораторщица допустит ошибку, равна (A)=0,05;

Условная вероятность того, что вторая перфораторщица допустит ошибку, равна (A)=0,1.

Вероятность того, что наудачу взятая перфокарта, окажется с ошибкой равна, по формуле полной вероятности равна:

P(A)= P()*(A)+ P()*(A)=0,5*0,05+0,5*0,1=.

Искомая вероятность того, что взятая перфокарта произведена первой перфораторщицей, по формуле Бейеса равна:

===.

В специализированную больницу поступают

в среднем 50% больных с заболеванием К, 30%—с за-

заболеванием L, 20%—с заболеванием М- Вероятность

полного излечения болезни К равна 0,7; для болезней L

и М эти вероятности соответственно равны 0,8 и 0,9.

Больной, поступивший в больницу, был выписан здоро-

здоровым. Найти вероятность того, что этот больной страдал

P(A)= Pk(a)*P(k) + Pl(a)*P(l) + Pm(a)*P(m) = 0.7*0.5 + 0.8*0.3 + 0.9*0.2 = 0.77

А вероятность что больной страдал именно заболеванием К равно:

Pa(K) = (Pk(a)*P(k))/P(A)= (0.5*0.7)/0.77 = 5/11

Вероятность того, что изделие будет признано стандартным по формуле полной вероятности равна

P(A)= P() (A) + P() (A) = 0,55 * 0,9 + 0,45 * 0,98 = 0,936

Искомая вероятность того, что изделие проверил второй товаровед, по формуле Бейеса равна

()= P() * (A) / P(A)= 0,45*0,98 / 0,936 = 0,47.

Событие А может появится при условии появления одного из несовместимых событий В1, В2,…, Вn, образующих полную группу событий. После появления события А были переоценены вероятности гипотез, то есть были найдены условные вероятности РА(Вi) (i=1,2,…,n). Доказать, что сумма РА(Вi) (i=1,2,…,n) равна 1.

Что и требовалось доказать.

Событие может появиться при условии появления одного из несовместных событий (гипотез) , образующих полную группу событий. После появления события были переоценены вероятности этих гипотез, т.е. были найдены условные вероятности этих гипотез, причем оказалось, что . Чему равна условная вероятность гипотезы ?

Так как события образуют полную группу, и появится при условии появления лишь одного из них, то верно . Так как имеем , то:

Имеются три партии деталей по 20 деталей в каждой. Число стандартных деталей в первой, второй и третьей партиях соответственно равно 20, 15, 10. Из наудачу выбранной партии наудачу извлечена деталь, оказавшаяся стандартной. Деталь возвращают в партию

и вторично из той же партии наудачу извлекают деталь, которая также оказывается стандартной. Найти вероятность того, что детали были извлечены из третьей партии.

Обозначим через А событие – в каждом из двух испытаний была извлечена стандартная деталь. Можно предположить, что B1 – детали извлекались из первой партии; B2 – детали извлекались из второй партии; В3 – детали извлекались из третей партии.

Детали извлекались на удачу, поэтому вероятности предположений одинаковы:

P(B1) = P(B2) = P(B3) =

Вероятность того, что из первой партии будут последовательно извлечены две стандартные детали; поэтому

Условная вероятность т.е вероятность того, что из второй партии будут извлечены две стандартные детали:

Найдем условную вероятность т.е вероятность того, что из третей партии будут последовательно извлечены две стандартные детали:

Искомая вероятность того, что обе извлеченные детали стандартные взяты из третей партии, по формуле Бейеса равна

Ответ:

Батарея из трех орудий произвела залп, причем два снаряда попали в цель. Найти вероятность того, что первое орудие дало попадание, если вероятности попадания в цель первым, вторым и третьим орудиями соответственно равны , , .

Обозначим через A событие- два орудия попали в цель. Сделаем два предположения: — орудие не попало в цель.

По условию , следовательно

.

Найдем условную вероятность , т.е. вероятность того, что в цель попало два снаряда, причем первое орудие дало промах. Другими словами найдем вероятность того, что второе и третье орудие попали в цель. Эти два события независимы, поэтому применима теорема умножения:

Искомая вероятность того, что первое орудие дало попадание, по формуле Бейеса равна:

.

Ответ:

Три стрелка произвели залп, причем две пули поразили мишень. Найти вероятность того, что третий стрелок поразил мишень, если вероятности попадания в мишень первым, вторым и третьим стрелками соответственно равны 0,6, 0,5 и 0,4.

Решение. Обозначим через А событие – две пули поразили мишень. Сделаем два предположения (гипотезы): В1 – третий стрелок поразил мишень; В2 – третий стрелок не попал в мишень.

По условию, Р(В1) = 0,4; следовательно (событие В2 противоположно событию В1),

Найдем условную вероятность РВ1(А), т.е. вероятность того, что мишень поразили две пули, причем одна из них принадлежит третьему стрелку и, следовательно, вторая – либо первому стрелку (при этом второй не попал), либо второму стрелку (при этом первый не попал). Эти два события несовместны, поэтому применима теорема сложения:

РВ1(А) = p1∙q2 + p2∙q1 = 0,6∙0,5 + 0,5∙0,4 = 0,5.

Найдем условную вероятность РВ2(А), т.е. вероятность того, что мишень поразили две пули, причем третий стрелок промахнулся. Другими словами, найдем вероятность того, что первый и второй стрелки поразили мишень. Эти два события независимы, поэтому применима теорема умножения:

РВ2(А) = p1∙p2 = 0,6∙0,5 = 0,3.

Искомая вероятность того, что третий стрелок поразил мишень, по формуле Бейеса равна

РА(В1) = Р(В1)∙РВ1(А)/[ Р(В1)∙РВ1(А) + Р(В2)∙РВ2(А)] = 0,4∙0,5/( 0,4∙0,5 + 0,6∙0,3 ) = 10/19.

Два из трех независимо работающих элементов вычислительного устройства отказали. Найти вероятность того, что отказали первый и второй элементы, если вероятности отказа первого, второго и третьего элементов соответственно равны 0,2; 0,4 и 0,3.

Решение. Обозначим через А событие – отказали два элемента. Можно сделать следующие предположения (гипотезы):

Р(В1) = p1∙p2∙q3 = 0,2∙0,4∙0,7 = 0,056;

Р(В2) = p1∙p3∙q2 = 0,2∙0,3∙0,6 = 0,036;

Р(В3) = p2∙p3∙q1 = 0,4∙0,3∙0,8 = 0,096;

Вероятности последних трех гипотез не вычислены, так как при этих гипотезах событие А (отказали два элемента) невозможно и значит условные вероятности РВ4(А), РВ5(А) и РВ6(А) равны нулю, следовательно, равны нулю и произведения Р(В4)∙РВ4(А), Р(В5)∙РВ5(А) и Р(В6)∙РВ6(А) при любых значениях вероятностей гипотез В4, В5 и В6.

Поскольку при гипотезах В1, В2 и В3 событие А достоверно, то соответствующие условные вероятности равны единице:

РВ1(А) = РВ2(А) = РВ3(А) = 1.

По формуле полной вероятности, вероятность того, что отказали два элемента, равна

Р(А) = Р(В1)∙РВ1(А) + Р(В2)∙РВ2(А) + Р(В3)∙РВ3(А) + Р(В4)∙РВ4(А) + Р(В5)∙РВ5(А) + Р(В6)∙РВ6(А) = 0,056 + 0,036 + 0,096 = 0,188.

По формуле Бейеса, искомая вероятность того, что отказали первый и второй элементы,

РА(В1) = Р(В1)∙РВ1(А)/ Р(А) = 0,056/0,188 = 0,3.

Две из четырех независимо работающих ламп прибора отказали. Найти вероятность того, что отказали первая и вторая лампы, если вероятности отказа первой, второй, третьей и четвертой ламп соответственно равны 0,1, 0,2, 0,3 и 0,4.

Решение. Обозначим через А событие – отказали две лампы. Можно сделать следующие предположения (гипотезы):

Р(В1) = p1∙p2∙q3∙q4 = 0,1∙0,2∙0,7∙0,6 = 0,0084;

Р(В2) = p1∙q2∙p3 ∙q4 = 0,1∙0,8∙0,3∙0,6 = 0,0144;

Р(В3) = p1∙q2∙q3∙p4 = 0,1∙0,8∙0,7∙0,4 = 0,0224;

Р(В4) = q1∙p2∙p3∙q4 = 0,9∙0,2∙0,3∙0,6 = 0,0324;

Р(В5) = q1∙p2∙q3∙p4 = 0,9∙0,2∙0,7∙0,4 = 0,0504;

Р(В6) = q1∙q2∙p3∙p4 = 0,9∙0,8∙0,3∙0,4 = 0,0864;

Вероятности последних четырех гипотез не вычислены, так как при этих гипотезах событие А (отказали две лампы) невозможно и значит условные вероятности РВ7(А), РВ8(А), РВ9(А) и РВ10(А) равны нулю, следовательно, равны нулю и произведения Р(В7)∙РВ7(А), Р(В8)∙РВ8(А), Р(В9)∙РВ9(А) и Р(В10)∙РВ10(А) при любых значениях вероятностей гипотез В7, В8, В9 и В10.

Поскольку при гипотезах В1 – В6 событие А достоверно, то соответствующие условные вероятности равны единице:

РВ1(А) = РВ2(А) = РВ3(А) = РВ4(А) = РВ5(А) = РВ6(А) = 1.

По формуле полной вероятности, вероятность того, что отказали две лампы, равна

Р(А) = Р(В1)∙РВ1(А) + Р(В2)∙РВ2(А) + Р(В3)∙РВ3(А) + Р(В4)∙РВ4(А) + Р(В5)∙РВ5(А) + Р(В6)∙РВ6(А) + Р(В7)∙РВ7(А) + Р(В8)∙РВ8(А) + Р(В9)∙РВ9(А) + Р(В10)∙РВ10(А) = 0,0084 + 0,0144 + 0,0224 + 0,0324 + 0,0504 + 0,0864 = 0,2144.

По формуле Бейеса, искомая вероятность того, что отказали первая и вторая лампы, равна

РА(В1) = Р(В1)∙РВ1(А)/ Р(А) = 0,0084/0,2144

Два равносильных шахматиста играют в шахматы. Что вероятнее: выиграть две партии из четырех или три из шести (ничьи во внимание не принимаются)?

Играют равносильные шахматисты, поэтому вероятность выигрыша p=1/2; следовательно, вероятность проигрыша q также равна 1/2. Так как во всех партиях вероятность выигрыша постоянна и безразлично, в какой последовательности будут выиграны партии, то применима формула Бернулли.

Найдем вероятность того, что две партии из четырех будут выиграны:

Найдем вероятность того, что выиграны три партии из шести:

Так как P4(2)>P6(3), то вероятнее выиграть две партии из четырех, чем три из шести.

Два равносильных противника играют в шахматы. Что вероятнее: а) Выиграть одну партию из двух или две партии из четырех? б)выиграть не менее двух партий из четырех или не менее трех партий из пяти? Ничьи во внимание не принимаються.

Играют равносильные шахматисты, поэтому вероятность выигрыша ; следовательно, вероятность проигрыша . Так как во всех партиях вероятность выигрыша постоянна и безразлично, в какой последовательности будут выигранв партии, то применима формула Бернулли.

А) Найдем вероятность того, что две партии из четырех будут выиграны:

Найдем вероятность того, что одна партия из двух будет выиграна:

Б) Найдем вероятность выиграть не менее двух партий из четырех:

Найдем вероятность выиграть не менее трех партий из пяти:

Монету бросают пять раз. Найти вероятность того, что “герб” выпадет: а)мене двух раз; б)не менее двух раз.

При бросании монеты вероятность выпадения герба и решки, равновероятны, поэтому вероятность выпадения герба равна ; следовательно вероятность выпадения решки ; Так как при бросании вероятность постоянна, то применима формула Бернулли.

А) Найдем вероятность того, что герб выпадет менее двух раз:

;

.

.

Б) Найдем вероятность того, что герб выпадет не менее двух раз:

;

Ответ: a) ; б)

Источник

Пример 1

На фабрике
станки 1,2 и 3 производят соответственно 20%, 35% и 45% всех деталей. В их
продукции брак составляет соответственно 6%, 4%, 2%. Какова вероятность того,
что случайно выбранное изделие оказалось дефектным? Какова вероятность того,
что оно было произведено: а) станком 1; б) станком 2; в) станком 3?

Решение

Обозначим через

 событие, состоящее в том,
что стандартное изделие оказалось дефектным.

Событие

 может произойти только
при условии наступления одного из трех событий:

 -изделие произведено на
станке 1; 

 — изделие произведено на
станке 2; 

 — изделие произведено на
станке 3; 

Запишем условные вероятности:

По формуле полной вероятности
находим вероятность события

:

Вероятность того, что дефектное изделие
изготовлено на станке 1 найдем по формуле Бейеса:

Вероятность того, что дефектное изделие
изготовлено на станке 2:

Вероятность того, что дефектное изделие
изготовлено на станке 3:

Ответ: а)

; б)

; в)

.

Задача 1

На
отборочное предприятие поступили однотипные комплектующие с трех заводов в
количестве: 20 с первого завода; 50 со второго завода; 30 с третьего. Вероятность качественного
изготовления изделий на первом заводе 0,8, на втором 0,9
, на третьем 0,9. 1) Какова вероятность
того, что взятое случайным образом изделие будет качественным? 2) Взятое наугад
изделие оказалось качественным. Какова вероятность того, что это изделие завода
с номером N=1.

---

Задача 2

В
пирамиде 15 винтовок, 12 из которых снабжены оптическим прицелом. Вероятность
того, что стрелом поразит мишень при выстреле из винтовки с оптическим прицелом
равна 12/25; для винтовки без оптического прицела эта вероятность равна 2/25.
Найти вероятность того, что мишень будет поражена, если стрелок произведет один
выстрел из наудачу взятой винтовки.

---

Задача 3

На
предприятии работают две бригады рабочих: первая производит в среднем 3/4
продукции с процентом брака 4%, вторая – 1/4 продукции с процентом брака 6%.
Найти вероятность того, что взятое наугад изделие:

а)
окажется бракованным;

б)
изготовлено второй бригадой при условии, что изделие оказалось бракованным.

---

Задача 4

В одном
сосуде находятся 7 белых и 6
 черных шаров. Во втором – 5
 белых и 9
 черных. Бросают два кубика. Если сумма очков,
выпавших на верхних гранях, меньше 10, берут шар из первого сосуда, если больше
или равна 10 – из второго. Вынут белый шар. Какова вероятность того, что сумма
очков была не меньше 10?

---

Задача 5

Вероятность
того, что во время работы цифровой электронной машины произойдет сбой в
арифметическом устройстве, в оперативной памяти, в остальных устройствах,
относятся как 3:2:5. Вероятность обнаружения сбоя в арифметическом устройстве,
в оперативной памяти и в остальных устройствах соответственно равна 0,8; 0,9;
0,9. Найти вероятность того, что возникший в машине сбой будет обнаружен.

---

Задача 6

Имеется
пять урн. В первой, второй и третьей урнах находится по 2 белых и 3 черных
шара, в четвертой и пятой урнах — по 1 белому и 1 черному шару. Случайно
выбирается урна и из нее извлекается шар. Какова условная вероятность того, что
выбрана четвертая или пятая урна, если извлеченный шар оказался белым?

---

Задача 7

В двух
пакетах находятся конфеты. В первом пакете 16 штук сорта «Белочка» и 8 штук
сорта «Жар-птица», во втором 15 сорта «Белочка» и 5 сорта «Жар-птица». Из
первого пакета во второй переложили две конфеты, взятые случайным образом,
содержимое второго пакета перемешали и вытащили оттуда одну конфету, которая
оказалась «Жар-птицей».

Какова
вероятность, что из первого пакета во второй переложили одну «Белочку» и одну
«Жар-птицу»?

---

Задача 8

В городе N – 600
гостиничных номеров. Из них 100 номеров – в первой гостинице, 200 – во второй,
остальные – в третьей. В турфирме известно, что наличие свободного номера
нужного класса составляет вероятность 0,7; 0,5 и 0,8 соответственно в первой,
второй и третьей гостиницах. Определить вероятность того, что клиентов поселили
во вторую гостиницу.

---

Задача 9

Имеются
три партии радиоламп, насчитывающих соответственно 20,30 и 50 шт. Вероятности
того, что радиолампа проработает заданное время, равны 0,7; 0,8; 0,9. Какова
вероятность того, что наудачу выбранная лампа из 100 данных проработает
заданное время?

---

Задача 10

В первом
ящике 2 карандаша и 4 ручки, во втором — 3 карандаша и 1 ручка. Случайным
образом выбрали ящик и из него достали один предмет. Найти вероятность того,
что им оказался карандаш.

---

Задача 11

Для
участия в студенческих отборочных соревнованиях выделено из первой группы курса
4 студента, 6 из второй и 5 студентов из третьей. Вероятности того, что
отобранный студент из первой, второй, третьей группы попадает в сборную
института, соответственно равны 0.5, 0.4 и 0.2. Наудачу выбранный участник
соревнований попал в сборную. К какой из указанных групп он вероятнее всего
принадлежит?

---

Задача 12

Из 10
лотерейных билетов 3 выигрышных. При подготовке вечера 2 билета потеряли, и
было решено добавить один выигрышный. Какой стала вероятность того, что
случайно выбранным билет будет выигрышным?

---

Задача 13

В урне
находятся 5  шаров белого цвета и 4 шара
черного цвета. Три шара последовательно извлекаются из урны (без возвращения их
в урну). Найти вероятность того, что третий извлеченный шар будет белым.

---

Задача 14

Родион
Раскольников покупает себе топор. У первых трех торговцев по 15 топоров с
сосновыми топорищами и по 10 топоров с дубовыми.  Имеются еще два торговца, у каждого из
которых по 5 топоров с сосновыми топорищами и по 5 топоров с дубовыми. Раскольников
покупает первый попавшийся топор у наугад выбранного торговца. Какова
вероятность покупки топора с дубовым топорищем?

---

Задача 15

На базу
поступили одинаковые по объему партии холодильников с двух разных заводов.
Вероятность того, что холодильник проработает без поломок в течение гарантийного
срока, равна 0,85, если холодильник собран на 1-ом заводе, и 0,95, если на
втором. Найти вероятность того, что наугад взятый холодильник не сломается в
течение гарантийного срока.

---

Задача 16

Банки
закатывают два автомата с одинаковой производительностью. Доля банок с дефектом
укупорки для первого автомата составляет 1%, а для второго — 0,5%. Какова
вероятность того, что взятая наугад банка будет иметь дефект укупорки?

---

Задание 17

У рыбака
есть три излюбленных места рыбалки. Эти места он посещает с одинаковой
вероятностью. Вероятность того, что рыба клюнет в 1-м месте – 1/3, во втором –
1/2, в 3-м – 1/4. Известно, что рыбак забросил удочку 3 раза, а вытащил только
одну рыбу. Какова вероятность того, что рыбак рыбачил в первом месте?

---

Задача 18

В группе
из 20 пациентов имеются 4 человека с заболеванием A
, 10 — с заболеванием B
 и 6 с заболеванием C
. Вероятность аллергической
реакции при приеме витаминов для первой группы больных — 0,9, для второй — 0,7,
для третьей — 0,5. Найдите вероятность того, что: а) у наудачу выбранного
больного возникнет аллергическая реакция; б) у 2 наудачу выбранных больных
возникнет аллергическая реакция.

---

Задача 19

В
результате исследований, проведенных в хирургическом отделении одного лечебного
учреждения, установлено, что первая группа крови встречается у 40% больных,
вторая — у 30%, третья — у 20% , четвертая — у 10%. Во время операций
переливание крови требуется пациентам с первой группой — 2%, второй — 1%,
третьей -0,5% и четвертой -0,2%. Найдите вероятность того, что во время
операции пациенту не потребуется переливание крови.

---

Задача 20

Покупатель
пробует шестизарядный револьвер. Найти вероятность того, что при нажатии
покупателем на курок раздастся выстрел, если равновозможны все предположения о
количестве заряженных в револьвер патронов.

При вычислении
классической вероятности события A
делалось предположение, что все
элементарные исходы пространства
являются равновозможными. Но не всегда
это предположение имеет место. Часто
определить структуру пространства
элементарных исходов (ПЭИ) сложно, а
расчет их количества достаточно
громоздок. Рассмотрим далее схему, в
которой пространство элементарных
исходов образует некоторая полная
группа событий
,
попарно несовместных и единственно
возможных в данном опыте или эксперименте.
Эту совокупность событий мы назовем
гипотезами. Причем, известна
Р (Н_i)
− априорная вероятность каждой гипотезы
Н_i.
Из условия
полной группы следует, что
.
Это условие обязательно проверяется
при анализе правильности выбора системы
гипотез.

Если событие А
может появиться только при одной из
этих гипотез (то есть находится в одном
ПЭИ с системой гипотез), то вероятность
события
А
вычисляется по формуле
полной вероятности:

или Р
(А)
= Р
(Н₁)
Р
(А / Н₁)+
Р
(Н₂)
Р
(А / Н₂)+…
+ Р
(Н_n)
Р
(А / H_n),

где Р
(А/Н_i)
− условная вероятность события А
при гипотезе Н_i.

Таким образом,
зная вероятности гипотез и условные
вероятности события А
при каждой из гипотез, мы по формуле
полной вероятности можем найти вероятность
события А.

Примеры:

1. Из
   наблюдений установлено, что вероятность
   сбоя во время работы ЭВМ в процессоре,
   в оперативной памяти или в периферийных
   устройствах соотносятся между собой
   как 3:2:5. И пусть условные вероятности
   обнаружения сбоя в названных местах
   ЭВМ есть соответственно 0,8, 0,9 и 0,9.
   Найти вероятность того, что возникший
   где-то сбой будет обнаружен системой
   контроля.

Возможны три
гипотезы о месте сбоя:
— сбой в процессоре;— сбой в оперативной памяти;— сбой в периферийных устройствах.
Априорные вероятности этих гипотез
могут быть вычислены как

,
,.

Пусть событие
−
обнаружен сбой. Тогда его вероятность
вычисляется по формуле полной вероятности
через априорные вероятности гипотез и
условные вероятности событияпри гипотезах как.

1. Статистика запросов
   кредитов в банке такова: 10 % —
   государственные органы, 20 % —
   другие банки, остальные — физические
   лица. Вероятности того, что взятый
   кредит не будет возвращен, составляют
   0,01, 0,05 и 0,2 соответственно.
   Определить, какая доля кредитов в
   среднем не возвращается.

Пусть
событие

состоит в том, что взятый кредит не
возвращается, гипотеза Н₁
— в том, что запрос на этот кредит
поступил от государственного органа,
гипотеза Н₂ —
в том, что запрос на кредит поступил от
другого банка, гипотеза Н₃
— в том, что запрос на кредит поступил
от физического
лица. По условию вероятности гипотез
составляют Р (Н₁) ,Р (Н₂)
= 0,2, Р (Н₃)
=
1 – Р (Н₁)
– Р (Н₂)
= 0,7.
Апостериорные вероятности в свою очередь
по условию равны Р (А / Н₁)
= = 0,01, Р (А / Н₂)
= 0,05, Р (А / Н₃)
= 0,2.

По формуле полной
вероятности

Р (А)
=Р (А / Н₁)
Р (Н₁) +
Р (А / Н₂)
Р (Н₂)
+ Р (А / Н₃)
Р (Н₃)
= 0,01 · 0,1 +0,05 · 0,2 + 0,2 · 0,7
= 0,151.

1. Предприятие,
   производящее компьютеры, получает
   одинаковые комплектующие детали от
   трех поставщиков. Первый поставляет
   50 % всех комплектующих деталей, второй
   — 20 %, третий — 30 % деталей. Известно,
   что качество поставляемых деталей
   разное, и в продукции первого поставщика
   процент брака составляет 4 %, второго
   — 5 %, третьего — 2 %. Определите
   вероятность того, что деталь, выбранная
   наудачу из всех полученных, будет
   годной.

Пусть
событие

состоит в том, что выбранная деталь
годная, гипотеза Н₁
— в том, что выбран первый поставщик,
гипотеза Н₂ —
в том, что выбран второй поставщик,
гипотеза Н₃
— в том, что выбран третий поставщик.
По условию вероятности гипотез составляют
Р (Н₁) =0,5,
Р (Н₂)
= 0,2, Р (Н₃)
=
0,3. Апостериорные
вероятности в свою очередь по условию
равны Р (А / Н₁)
= 1- 0,04 = 0,96, Р (А / Н₂)
= 1- 0,05= 0,95, Р (А / Н₃)
= 1- 0,2 = 0,98.

По формуле полной
вероятности получим

Р (А)
=Р (А / Н₁)
Р (Н₁) +
Р (А / Н₂)
Р (Н₂)
+ Р (А / Н₃)
Р (Н₃)
= 0,5 · 0,96 +0,2 · 0,95 + 0,3 · 0,98
= 0,964.

То есть, вероятность
события составляет 96,4%.

Рассмотрим теперь
обратную задачу. Если до опыта вероятности
гипотез были равны Р
(Н₁),

Р
(Н₂),
…, Р
(Н_n),
а в результате опыта появилось событие
А,
то с учетом этого события «новые»,
т. е. условные, вероятности гипотез
вычисляются по формуле Байеса:

(i
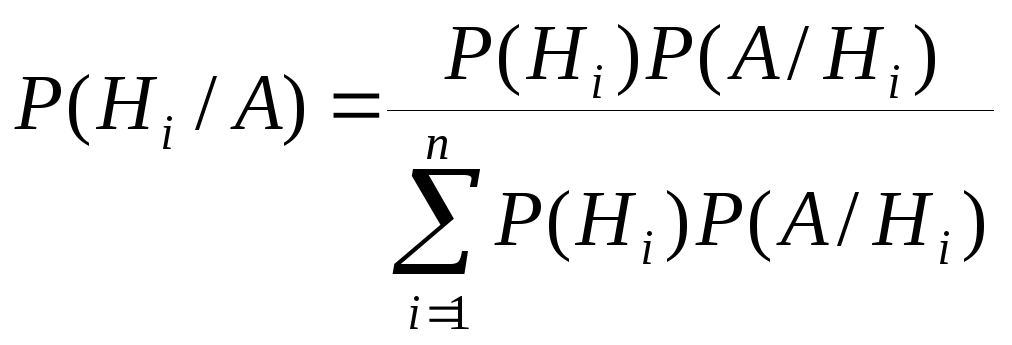
= 1, 2, …, n).

Формула
Байеса дает возможность «пересмотреть»
вероятности гипотез с учетом известного
результата опыта. Если после опыта,
закончившегося появлением события А,
производится еще один опыт, в котором
может появиться или не появиться событие
В,
то вероятность (условная) этого последнего
события вычисляется по формуле полной
вероятности, в которую подставлены не
прежние вероятности гипотез Р
(Н_i),
а новые Р
(Н_i / А)
(апостериорные вероятности):

Примеры:

1. 30 %
   пациентов, поступивших в больницу,
   принадлежат первой социальной группе,
   20 % — второй и 50 % — третьей.
   Вероятность заболевания туберкулезом
   для представителя каждой социальной
   группы соответственно равна 0,02, 0,03 и
   0,01. Проведенные анализы для случайно
   выбранного пациента показали наличие
   туберкулеза. Найти вероятность того,
   что это представитель третьей группы.

Обозначим через
Н₁,
Н₂,
Н₃
— гипотезы, заключающиеся в том, что
пациент принадлежит соответственно
первой, второй и третьей группам. Эти
гипотезы образуют полную группу событий,
причем Р
(Н₁)
= 0,3, Р
(Н₂)
= 0,2, Р
(Н₃)
= 0,5. По условию событие А
— обнаружение
туберкулеза
у больного — произошло, причем условные
вероятности равны Р
(А / Н₁)
= 0,02,
Р
(А / Н₂)
= 0,03, Р
(А / Н₃)
= 0,01. Апостериорную вероятность Р
(Н₃ / А)
вычислим по формуле Байеса:

1. Статистика
   запросов кредитов в банке такова: 10 % —
   государственные органы, 20 % —
   другие банки, остальные — физические
   лица. Вероятности того, что взятый
   кредит не будет возвращен, составляют
   0,01, 0,05 и 0,2 соответственно. Начальнику
   кредитного отдела доложили, что получено
   факсимильное сообщение о неисполнении
   обязательств по возврату кредита, в
   котором очень плохо пропечаталось имя
   клиента. Найти вероятность того, что
   кредит не возвращает какой-либо банк.

Пусть событие
состоит в том, что взятый кредит не
возвращается, гипотезаН₁—
в том, что запрос на этот кредит поступил
от государственного органа, гипотеза
Н₂ —
в том, что запрос на кредит поступил от
другого банка, гипотеза Н₃
— в том, что запрос на кредит поступил
от физического лица. По условию вероятности
гипотез составляют Р (Н₁) ,Р (Н₂)
= 0,2,
Р (Н₃)
=
0,7.
Условные вероятности, в свою очередь,
равны Р (А / Н₁)
=
= 0,01, Р (А / Н₂)
= 0,05, Р (А / Н₃)
= 0,2. По
формуле Байеса Р (Н₂ / А)

.

1. Известно,
   что 1 из 700 мальчиков рождается с
   лишней Y—хромосомой
   и у этих мальчиков наблюдается агрессивное
   поведение в 20 раз чаще, чем у обычных.
   У данного мальчика агрессивное поведение.
   Какова вероятность того, что у него
   лишняя Y—хромосома?

Пусть
означает наличие агрессивного поведения,—
наличие лишнейY—хромосомы,
а
− ее отсутствие. Тогда по условию.
По формуле полной вероятности.
По формуле Байеса находим искомую
вероятность.

Как видим, вероятность довольна мала.
Поэтому далеко не каждого мальчика с
агрессивным поведением надо зачислять
в отряд обладателей лишнейY-хромосомы.
Объясняется это тем, что хотя вклад
обладателей лишней хромосомы в агрессивное
поведение велик, но их доля среди
новорожденных очень мала.

1. Из
   10 студентов, которые пришли на экзамен
   по теории вероятностей, трое подготовились
   отлично, четверо — хорошо, двое —
   удовлетворительно, а один совсем не
   готовился — понадеялся на то, что все
   помнит. В билетах 20 вопросов. Отлично
   подготовившиеся могут ответить на все
   20 вопросов, хорошо — на 16 вопросов,
   удовлетворительно — на 10, не подготовившиеся
   — на 5 вопросов. Каждый студент
   получает наугад 3 вопроса из 20.
   Приглашенный первым студент ответил
   на все 3 вопроса. Какова вероятность
   того, что он отличник?

Обозначим
события:

=
{приглашен студент, подготовившийся
отлично},=
{приглашенстудент,
подготовившийся хорошо},
=
{приглашен студент, подготовившийся
удовлетворительно},
=
{приглашенныйстудент
к экзамену не готов} и событие
=
{приглашенный студент ответил на три
вопроса}. Согласно условию задачи
.По
формуле полной вероятности имеем

,
где

Тогда
.

По формуле Байеса
имеем
.

1. После
   осмотра больного врач считает, что
   равно возможно одно из двух заболеваний −
   C
   или D. Для
   уточнения диагноза больного направляют
   на анализ, исход которого дает
   положительную реакцию при заболевании
   С
   в 30 % случаев, а при заболевании D
   − в 20 % случаев. Анализ дал положительную
   реакцию. Какое заболевание становится
   более вероятным?

Сформулируем
систему гипотез следующим образом:
=
{пациент имеет заболеваниеС},
=
{пациент имеет заболеваниеD}.
Для ответа на поставленный вопрос нужно
найти апостериорные вероятности гипотез.
Априорные вероятности гипотез, согласно
условию задачи, равны:
.
Рассмотрим событие=
{анализ дал положительную реакцию}. Для
нахождения апостериорных вероятностей
гипотез, т. е.,
воспользуемся формулой Байеса. Для того
чтобы воспользоваться формулой Байеса,
необходимо найти условные вероятности
событияотносительно каждой из гипотез. Согласно
условию задачи они равны соответственно:.
По формуле полной вероятности найдем
вероятность события:.

Воспользуемся
формулой Байеса:

.

Так как
,
то заболеваниеС
становится более вероятным.

Задания для
самостоятельного решения:

1. У
   директора компании два списка с
   претендентами на работу. В первом
   списке — фамилии шести женщин и
   четырех мужчин. Во втором списке —
   фамилии четырех женщин и семи мужчин.
   Фамилия одного
   из претендентов случайно переносится
   из первого списка во второй. Затем
   фамилия одного из претендентов случайно
   выбирается из второго списка. Оказалось,
   что эта фамилия принадлежит мужчине.
   Какова вероятность того, что из первого
   списка была перенесена фамилия женщины?

2. Агент
   по недвижимости пытается продать
   участок земли под застройку. Он полагает,
   что участок будет продан в течение
   полугода с вероятностью 0,9, если
   экономическая ситуация в регионе не
   будет ухудшаться. Если же экономическая
   ситуация будет ухудшаться, то вероятность
   продать участок составит 0,5. Экономист,
   консультирующий агента, полагает, что
   с вероятностью, равной 0,7, экономическая
   ситуация в регионе в течение ближайшего
   полугода будет ухудшаться. Чему равна
   вероятность того, что участок будет
   продан в течение полугода?

3. Среди
   студентов академии 30 % первокурсников,
   35 % студентов учатся на втором курсе,
   остальные — старшекурсники. По данным
   деканатов известно, что на первом курсе
   20 % студентов сдали сессию только на
   отличные оценки, на втором — 30 %,
   среди старшекурсников 40 % отличников.
   Наудачу вызванный студент оказался
   отличником. Чему равна вероятность
   того, что он старшекурсник?

4. Нефтеразведочная
   экспедиция проводит исследования для
   определения вероятности наличия нефти
   на месте предполагаемого бурения
   скважины. Исходя из результатов
   предыдущих исследований, нефтеразведчики
   считают, что вероятность наличия нефти
   на проверяемом участке равна 0,4. На
   завершающем этапе разведки проводится
   сейсмический тест, который имеет
   определенную степень надежности: если
   на проверяемом участке есть нефть, то
   тест укажет на ее наличие в 85 % случаев;
   если нефти нет, то в 10 % случаев тест
   может ошибочно указать ее наличие.
   Сейсмический тест указал на присутствие
   нефти. Чему равна вероятность того, что
   запасы нефти на данном участке существуют
   в действительности?

5. При
   слиянии акционерного капитала двух
   фирм аналитики фирмы, получающей
   контрольный пакет акций, полагают, что
   сделка принесет успех с вероятностью
   0,65, если председатель совета директоров
   поглощаемой фирмы уйдет в отставку;
   если он откажется, то вероятность успеха
   будет равна 0,3. Предполагается, что
   вероятность ухода в отставку председателя
   составляет 0,7. Чему равна вероятность
   успеха сделки?

6. На
   химическом заводе установлена система
   аварийной сигнализации. Когда возникает
   аварийная ситуация, звуковой сигнал
   срабатывает с вероятностью 0,95. Звуковой
   сигнал может сработать случайно и без
   аварийной ситуации с вероятностью
   0,02. Вероятность случайной ситуации
   равна 0,04. Предположим, что звуковой
   сигнал сработал. Чему равна вероятность
   реальной аварийной ситуации?

7. Исследователями-психологами
   установлено, что мужчины и женщины
   по-разному реагируют на некоторые
   жизненные обстоятельства. Результаты
   исследований показали, что 70 % женщин
   позитивно реагируют на изучаемый круг
   ситуаций, в то время как 40 % мужчин
   реагируют на них негативно. Свое
   отношение к предполагаемым ситуациям
   отразили в анкете 15 женщин и 5 мужчин.
   Случайно извлеченная анкета содержит
   негативную реакцию. Чему равна вероятность
   того, что ее заполнял мужчина?

8. Двумя
   предприятиями выпускается однотипная
   продукция. Объем продукции, поставляемый
   в продажу вторым предприятием, в
   раз превышает соответствующий объем
   продукции первого предприятия. Доля
   брака в среднем составляет: на первом
   предприятии 10 %, а на втором — 5 %.
   Купленное изделие оказалось бракованным.
   Какова вероятность того, что оно было
   выпущено вторым предприятием?

9. В
   специализированную больницу поступают
   в среднем 70 % больных с заболеванием
   К,
   остальные — с заболеванием М. Вероятность
   полного излечения болезни К
   равна 0,8, а болезни М
   — 0,9. Больной, поступивший в больницу,
   был выписан здоровым. Какова вероятность
   того, что он болел болезнью K?

10. Один
    властелин, которому наскучил его
    звездочет со своими ложными предсказаниями,
    решил казнить его. Однако, будучи добрым
    повелителем, он решил дать звездочету
    последний шанс. Ему велено распределить
    по 2 урнам 4 шара: 2 черных и
    2 белых. Палач выберет наугад одну
    из урн и из нее вытащит один шар. Если
    шар будет черным, то звездочета казнят,
    в противном случае его жизнь будет
    спасена. Каким образом звездочет должен
    разместить шары в урнах, чтобы обеспечить
    себе максимальную вероятность быть
    спасенным?

Соседние файлы в папке Матан 2 семестр

• #
• #

 Готовое решение: Заказ №8391

 Тип работы: Задача

Статус:  Выполнен (Зачтена преподавателем ВУЗа)

 Предмет: Теория вероятности

 Дата выполнения: 16.09.2020

 Цена: 226 руб.

Чтобы получить решение, напишите мне в WhatsApp, оплатите, и я Вам вышлю файлы.

Кстати, если эта работа не по вашей теме или не по вашим данным, не расстраивайтесь, напишите мне в WhatsApp и закажите у меня новую работу, я смогу выполнить её в срок 1-3 дня!

Описание и исходные данные задания, 50% решения + фотография:

Вероятности того, что во время работы ЭВМ возникает сбой в арифметическом устройстве, в оперативной памяти и в остальных устройствах, относятся как 3 : 2 : 5. Вероятность обнаружения сбоя в арифметическом устройстве, в оперативной памяти и в остальных устройствах соответственно равны 0,8, 0,9 и 0,9. Найти вероятность того, что возникший в машине сбой будет обнаружен.

Решение.

Пусть событие A состоит в том, что возникший в машине сбой обнаружен.

Выдвинем следующие гипотезы:

H₁ – сбой возникнет в арифметическом устройстве;

H₂ – сбой возникнет в оперативной памяти;

H₃ – сбой возникнет в остальных устройствах.

Пусть за некоторый промежуток времени в оперативной памяти возникло 2k сбоев. Согласно пропорции, за это же время в арифметическом устройстве возникнет 3k сбоев, а в остальных устройствах – 5k сбоев. То есть всего возникнет 3k+2k+5k = 10k сбоев.