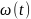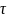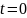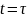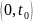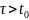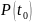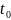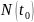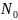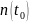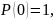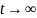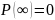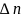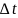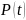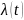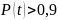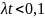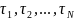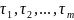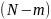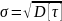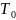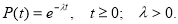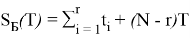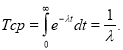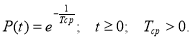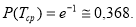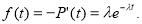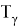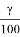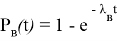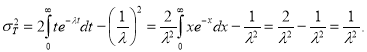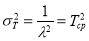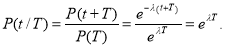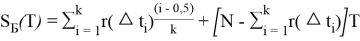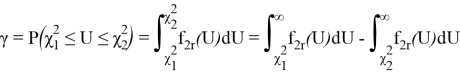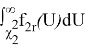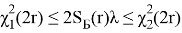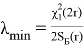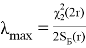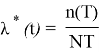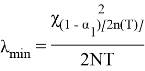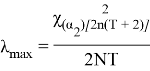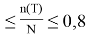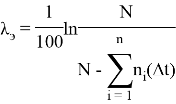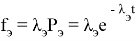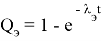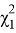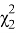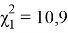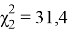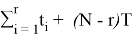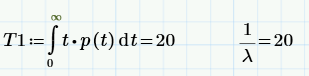Вероятность безотказной работы при экспоненциальном законе распределения времени безотказной работы

Макеты страниц

Зависимость
показателей безотказности от времени
и их взаимная связь определяются законами
распределения наработки на отказ. Для
анализа надежности гидропривода наиболее
часто используют три закона распределения:
экспоненциальный, нормальный,
логарифмически-нормальный, изредка –
распределение Вейбула.

Экспоненциальный
закон распределения
является параметрическим и характеризуется
постоянной интенсивностью отказов

.

Функция
распределения вероятности отказа имеет
вид:

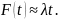
Вероятность
безотказной работы:

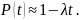
Достоинствами
экспоненциального закона являются
простота в практическом применении и
отсутствие громоздких вычислений. Он
нашел распространение в простых расчетах
надежности на стадиях разработки сложных
систем.

Рисунок
4 – Зависимость характеристик
экспоненциального закона распределения
от времени: а – зависимость плотности
распределения отказов от времени; б –
зависимость вероятности безотказной
работы от времени; в – зависимость
интенсивности отказов от времени

Распространение
также получила разновидность
экспоненциального закона распределения
– модель случайного выброса.

Модель
случайного выброса

Рисунок
5 – Модель случайного выброса

Если
принять, что допустимый уровень параметра

достаточно высоким и постоянным, а
также, что процесс изменения параметра

является стационарным, то время

до резкого достижения установленного
уровня подчиняется экспоненциальному
закону распределения.

Такая
модель применима для внезапных отказов
и случаев прочностных отказов.

Экспоненциальное
распределение целесообразно использовать
при сравнительной оценке надежности
нескольких вариантов схем проектируемых
гидроприводов, а также при предварительной
расчетной оценке безотказности
гидроприводов.

Остальные
законы распределения – нормальный,
логарифмически-нормальный и закон
Вейбула относят к так называемым
стареющим законам, у которых интенсивность
отказов монотонно возрастает с течением
времени. Это старение может быть связано
с накоплением повреждений, износом
трущихся пар, тепловым старением
материалов, накоплением усталостных
повреждений, коррозией и т.п. Все это
объясняется понятием постепенного
отказа.

Нормальный
закон распределения характерен
для постепенных отказов, имеющих место
при длительной эксплуатации или
длительных испытаниях. Время безотказной
работы вначале имеет низкую плотность
распределения, затем максимальную и
далее падающую.

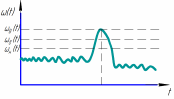
Рисунок
6 — Зависимость характеристик нормального
закона распределения от времени: а –
зависимость плотности распределения
отказов от времени; б – зависимость
вероятности безотказной работы от
времени; в – зависимость интенсивности
отказов от времени

Логарифмически-нормальный
закон распределения характерен
для таких постепенных отказов, у которых
средняя скорость процесса накопления
повреждений с некоторого момента
начинает убывать, т.е. происходит
«упрочнение» изделия.

1.6 Показатели надежности невосстанавливаемых приводов

Невосстанавливаемым
называют такой элемент, который работает
до первого отказа, после чего заменяется
таким же элементом, т.к. его восстановление
в условиях эксплуатации невозможно.

Основным
показателем надежности таких элементов
служит вероятность безотказной работы.

Пусть
время работы невосстанавливаемого
элемента представляет собой случайную
величину

.
В момент времени

элемент начинает работать, а в момент
времени

происходит отказ, следовательно,

— время жизни элемента. Тогда показателем
надежности будет вероятность безотказной
работы в интервале времени

при

.

В
вероятностной форме вероятность
безотказной работы примет вид:

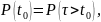
где

— вероятность того, что элемент, начав
работать в момент времени

,
не откажет в течение

;

—
случайная наработка элемента до первого
отказа.

В
статистической форме вероятность
безотказной работы примет вид:

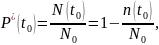
где

— число элементов, оставшихся
работоспособными к моменту времени

;

—
общее число элементов, поставленных на
испытания;

—
число отказавших элементов к моменту
времени

.

При

(начало работы)

при

.

Показателем,
противоположным вероятности безотказной
работы, является функция распределения
вероятности отказа при работе в интервале
времени

,
которая выражается как:

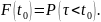
Вероятность
безотказной работы в интервале

в статистической оценке имеет вид:

Вероятность
безотказной работы в интервале

в вероятностной форме имеет вид:

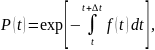
т.е.
это отношение числа отказавших элементов

в интервале времени

к произведению числа работоспособных
элементов

в момент времени

на
длительность интервала времени

.

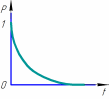
Рисунок
7 – Зависимость вероятности безотказной
работы от времени

Вероятность
отказа в интервале

в вероятностной форме:

Вероятность
отказа в интервале

в статистической форме:

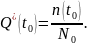
Плотность
распределения отказов в вероятностной
форме выражается как:

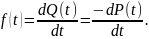
Плотность
распределения отказов в статистической
форме выражается как отношение числа
отказавших элементов

в интервале времени

к произведению числа работоспособных
элементов на интервале времени

:

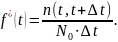
Частота
отказов
представляет собой плотность распределения
вероятностей наработки между отказами
и определяется статистически. Она
является отношением количества отказавших
однотипных невосстанавливаемых систем
(элементов)

в течение рассматриваемого интервала
времени

к произведению первоначального количества
рассматриваемых систем

и времени

:

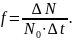
Интенсивностью
отказов
называется условная плотность вероятности
возникновения отказов невосстанавливаемого
элемента, определяемая для рассматриваемого
момента времени при условии, что до
этого времени отказа не было.

Интенсивность
отказов в вероятностной форме выражается
как:

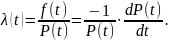
Отсюда

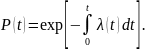
Интенсивность
отказов для некоторого момента времени
t
при статистической оценке выражается
как отношение числа отказавших элементов

в интервале времени

к произведению числа работоспособных
элементов

,
оставшихся работоспособными к моменту
времени t
для работы в интервале

на длительность интервала

:

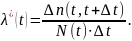
Интенсивность
отказов в отличие от плотности
распределения вероятностей отказов
относится к числу элементов

,
оставшихся работоспособными, а не к
общему числу элементов

.

Оценивая
только величину интенсивности отказов,
можно прийти к неправильному представлению
о надежности тех или иных элементов.
Может показаться, что с увеличением
частоты отказов уменьшается надежность
элементов системы и наоборот. Это
ошибочное представление, т.к. к концу
наблюдений число невосстанавливаемых
элементов в системе убывает.

Интенсивность
отказов характеризует надежность
изделий до их полного отказа. Все
отказавшие элементы в дальнейшем
испытании не участвуют, поэтому
интенсивность отказов можно использовать
лишь для оценки невосстанавливаемых
элементов (приводов).

Вероятность
безотказной работы

и интенсивность отказов

имеют однозначную связь. Функцию
распределения случайной величины
получить очень сложно, поэтому можно
получить сравнительно простые формулы
для вероятности безотказной работы и
вероятности отказов при некоторых видах
законов распределения. Для экспоненциального
закона распределения:

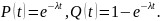
Для

или

экспоненциальная зависимость заменяется
первым членом разложения функции

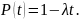
Средняя
наработка на отказ
(среднее время безотказной работы) –
математическое ожидание времени работы
привода до первого отказа. В вероятностной
форме выражается как:

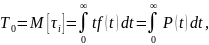
в
статистической форме:

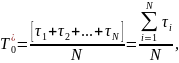
где

– время жизни каждого из элементов;

—
число элементов, поставленных на
испытания.

Так
как невозможно осуществить практические
испытания всех элементов до отказа, то
в первом приближении при большом числе

среднюю наработку до отказа можно
определить выражением:

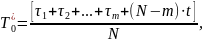
где

— время жизни каждого из отказавших
элементов;

—
время работы исправных

элементов к моменту последнего
наблюдаемого отказа или окончания
испытаний;

—
число элементов, поставленных на
испытания.

Наработка
на отказ
– отношение суммарной длительности
работы (наработки) изделия к числу
отказов, возникших за этот период, т.е.
средняя продолжительность безотказной
работы изделия.

Наработка
на отказ численно равна площади над
кривой

на участке времени

Для
экспоненциального закона надежности
наработка на отказ выражается как:

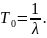
Дисперсия
времени безотказной работы
(время жизни) невосстанавливаемого
элемента в вероятностной форме выражается
как:

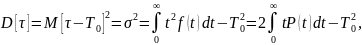
где

— среднее квадратичное отклонение
времени работы элемента до отказа от
среднего значения наработки до отказа

.

Дисперсия
времени безотказной работы в статистической
форме выражается как:

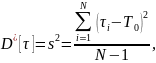
где

—
число элементов на испытаниях.

При
нормальном законе распределения
плотность распределения отказов
выражается как:

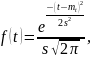
где

— оценка математического ожидания;

—
оценка среднего квадратичного отклонения.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

• #
• #
• #
• #
• #
• #
• #
• #
• #
• #
• #



В статье проведена оценка показателей надежности безотказной работы системы. На примере показан расчет основных показателей средствами VBA.

Ключевые слова:



безотказная работа, доверительный интервал, испытания, число отказов, экспоненциальный закон.

Проведение испытаний новых изделий или системы организуется в соответствии с планом, в котором указывается: количество испытуемых изделий (

N

), будут ли заменяться отказавшие изделия (

B

) и когда испытания необходимо прекратить (прекращение испытаний после истечения Т часов или прекращение испытаний при возникновении

r —

го отказа).

Экспоненциальный закон представляет собой постоянную интенсивность отказов, т. к. определяется параметром

λ- const

при

δ

=1

.

, интенсивность отказов

λ(t)

≡

λ

. (1)

Если указано время работы каждого изделия от начала работы до его отказа, расчет суммарной наработки всех элементов

S

Б(

r

) и

S

Б(

Т

) вычисляется с использованием выражения (2).

(2)

Среднее время безотказной работы —

T

_ср


при экспоненциальном законе распределения равно величине, обратной ИО — 1/

λ

, т. е.:

(3)

-плотность распределения наработки(4)

=

∙(-ln

).

Вероятность восстановления

P


_B

(

t

):

Дисперсия времени безотказной работы:

(5)

Условная вероятность безотказной работы устройства на интервале времени

t

, после того как оно безотказно проработало на интервале

τ

.

(6)

Под доверительным интервалом понимается диапазон значений параметра, в пределах которого с некоторой вероятностью γ может находиться его истинное значение. Вероятность γ называется доверительной вероятностью или коэффициентом доверия. Для экспоненциального закона распределения отказов при плане испытаний

N

, Б,

r

установлено, что величина

U

= 2

S


_Б

(

r

)λ подчиняется χ

²

— распределению с 2

r

степенями свободы, где

S


_Б

(

r

) — суммарная наработка изделий, установленных на испытание (может быть определена из выражения (7), λ — истинное значение интенсивности отказа,

r —

число отказов (или разрядов, если отказы сгруппированы по разрядам) [1].

(7)

Вероятность того, что величина

U

находится в пределах χ

²


₁

и χ

²


₂

, равна

Интеграл

табулирован. Поэтому, задавшись значениями λ

_min

и λ

_max

и зная из обработки результатов эксперимента суммарную наработку

S


_Б

(

r

), находим χ

²


₁

и χ

²


₂

и по таблице квантилей распределения χ

²

–квадрат находим коэффициент доверия γ.

Квантилем случайной величиныχ




называется такое значение случайной величины

х


_р

, для которого с вероятностью 1–

р

можно утверждать, что полученное значение этой случайной величины попадет в интервал (–∞,

х


_р

).

Однако чаще стоит обратная задача: по коэффициенту доверия γ и суммарной наработке изделий при испытании

S

Б(

r

) требуется найти λmin и λmax.

Установлено, что доверительный интервал будет минимальным, если площади под кривой плотности распределения

f


<sub>2



r</sub>


в


интервалах [0, χ

²


₁

] и [χ

²


₂

, ∞] равны.

Тогда значения χ

²


₁

и χ

²


₂

ограничивают соответственно площади 0,5(1+γ) и 0,5(1 — γ).

Последовательность определения доверительных интервалов сводится к следующему. Задавшись коэффициентом доверия γ, определяем 0,5(1+γ) и 0,5(1 — γ) и, зная число степеней свободы 2

r

, по таблице квантилей χ

²

– распределения находим значения χ

²


₁

и χ

²


₂

. Доверительные оценки λ

_min

и λ

_max

могут быть определены из неравенства

(8)

Отсюда найдем

(9)

(10)

Рассмотрим пример расчета показателей, полученных при испытании 100 изделий (из строя вышло 34). Испытания были прекращены после истечения 100 часов.

Для построения статистического ряда время испытаний разобьем на равные интервалы (разряды) продолжительностью 10 часов и для каждого разряда проведем расчет.

Поскольку за время испытания отказало 34 % изделий, оценка интенсивности отказов подсчитывалась с использованием выражений для плана

N

,

Б

,

Т.

Доверительные границы:

0,2

Частота отказов определялась для каждого разряда из выражения

.

f

э, λэ,

Q

э(

t

) — параметры потока отказов при экспоненциальном законе распределения [1, 2].

Вероятность отказа подсчитывалась по формуле

.

Листинг программы расчета показателей при экспоненциальном законе распределения:

‘Вычислим 1 строку таблицы(3)============================= t

Строка = 3

For СтолбецТаблицы = 4 To КоличествоСтолбцовТаблицы + 3

Sheets(«ОсновнаяТаблица»).Cells(Строка, СтолбецТаблицы).Value = Sheets(«ОсновнаяТаблица»).Cells(Строка — 1, СтолбецТаблицы).Value * ВременнойИнтервал

Next

‘Вычислим 2 строку таблицы(4)============================= n*

n = 0 ‘количество вышедших из строя элементов в периоде

СтрокаДанных = 4

СтрокаТаблицы = 4

СтолбецТаблицы = 4

КонтрольноеЗначениеВременногоИнтервала = ВременнойИнтервал

While Sheets(«Исходные данные»).Cells(СтрокаДанных, 1).Value <> «»

If КонтрольноеЗначениеВременногоИнтервала > ОбщееКоличествоЧасов Then GoTo конец

If Sheets(«Исходные данные»).Cells(СтрокаДанных, 1).Value <= КонтрольноеЗначениеВременногоИнтервала Then

n = n + 1

Else

Sheets(«ОсновнаяТаблица»).Cells(СтрокаТаблицы, СтолбецТаблицы).Value = n

КонтрольноеЗначениеВременногоИнтервала = КонтрольноеЗначениеВременногоИнтервала + ВременнойИнтервал

СтрокаДанных = СтрокаДанных — 1

СтолбецТаблицы = СтолбецТаблицы + 1

n = 0

End If

СтрокаДанных = СтрокаДанных + 1

Wend

If n <> 0 Then Sheets(«ОсновнаяТаблица»).Cells(СтрокаТаблицы, СтолбецТаблицы).Value = n

конец:

‘Вычислим 7 строку таблицы(9)=============================ЛямбдаЭ x 10^3

СтрокаТаблицы = 9

СтолбецТаблицы = 4

СуммаВышедшихЗаВсеВремя = 0

For n = СтолбецТаблицы To (КоличествоСтолбцовТаблицы + СтолбецТаблицы — 1)

СуммаВышедшихЗаВсеВремя = СуммаВышедшихЗаВсеВремя + Sheets(«ОсновнаяТаблица»).Cells(4, n).Value

Next

СтолбецТаблицы = 4

Sheets(«ОсновнаяТаблица»).Cells(СтрокаТаблицы, СтолбецТаблицы).Value = Round((1 / 100 * Log(КоличествоЭлементов / (КоличествоЭлементов — СуммаВышедшихЗаВсеВремя))) * 1000, 2)

Sheets(«ОсновнаяТаблица»).Range(Cells(СтрокаТаблицы, 4), Cells(СтрокаТаблицы, n — 1)).MergeCells = True

Sheets(«ОсновнаяТаблица»).Range(Cells(СтрокаТаблицы, 4), Cells(СтрокаТаблицы, n — 1)).HorizontalAlignment = xlCenter

‘Вычислим 8 строку таблицы(10)=============================fэ х 10^3

СтрокаТаблицы = 10

СтолбецТаблицы = 4

For n = СтолбецТаблицы To (КоличествоСтолбцовТаблицы + СтолбецТаблицы — 1)

Sheets(«ОсновнаяТаблица»).Cells(СтрокаТаблицы, n).Value = Round(((Sheets(«ОсновнаяТаблица»).Cells(9, СтолбецТаблицы).Value / 1000) * Exp(-Sheets(«ОсновнаяТаблица»).Cells(2, n).Value / 1000 * Sheets(«ОсновнаяТаблица»).Cells(9, СтолбецТаблицы).Value * ВременнойИнтервал) * 1000), 2)

Next

‘Вычислим 9 строку таблицы(11)=============================Рэ

СтрокаТаблицы = 11

СтолбецТаблицы = 4

For n = СтолбецТаблицы To (КоличествоСтолбцовТаблицы + СтолбецТаблицы — 1)

Sheets(«ОсновнаяТаблица»).Cells(СтрокаТаблицы, n).Value = Round(Exp(-Sheets(«ОсновнаяТаблица»).Cells(9, СтолбецТаблицы).Value * Sheets(«ОсновнаяТаблица»).Cells(3, n).Value / 1000), 2)

Next

‘Вычислим 10 строку таблицы(12)=============================Qэ(t)

СтрокаТаблицы = 12

СтолбецТаблицы = 4

For n = СтолбецТаблицы To (КоличествоСтолбцовТаблицы + СтолбецТаблицы — 1)

Sheets(«ОсновнаяТаблица»).Cells(СтрокаТаблицы, n).Value = 1 — Sheets(«ОсновнаяТаблица»).Cells(11, n).Value

Next

Результаты вычислений представлены в таблице Excel (Таблица 1).

Таблица 1

Результаты расчета основных показателей испытаний

Параметр	Разряды
1	2	3	4	5	6	7	8	9	10
t	10	20	30	40	50	60	70	80	90	100
n*	5	3	5	2	2	3	3	3	5	3
λэ	4,16
fэ	3,99	3,83	3,67	3,52	3,38	3,24	3,11	2,98	2,86	2,74
Рэ	0,96	0,92	0,88	0,85	0,81	0,78	0,75	0,72	0,69	0,66
Qэ	0,04	0,08	0,12	0,15	0,19	0,22	0,25	0,28	0,31	0,34

Для определения доверительных интервалов при экспоненциальном законе распределения по таблице квантилей χ

²

— квадрат распределений. найдем

(20) и

(20) [3]:

,

.

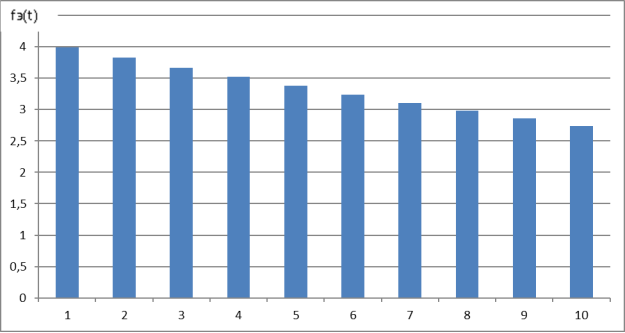
Результаты расчета fэ(t) представлены на рис 1.

Рис. 1. Гистограмма частоты отказов при экспоненциальном законе распределения

Поскольку в задаче задано время работы каждого изделия до отказа, суммарная наработка всех изделий

S


_Б

(

T

) подсчитывается по формуле (11)

S


_Б

(

T

) =

(11)

S


_Б

(

T

) = 8276 ч.

Литература:

1. Коваленко, В. Н., Новиков, А. А. Надежность устройств железнодорожной автоматики, телемеханики и связи. учеб. пособие. — Екатеринбург: УрГУПС, 1995. — с. 78.
2. Основы теории надежности автоматических систем управления: учеб. пособие для вузов / Л. П. Глазунов, В. П. Грабовецкий, О. В. Щербаков. — Л.: Энергоатомиздат, Ленинградское отд-ние, 1984. — 208 с.
3. Бронштейн И. Н., Семендяев К. А. Справочник по математике для инженеров и учащихся ВТУЗов. — М.: Наука, 1980. — 976 с.

Основные термины (генерируются автоматически): строка таблицы, коэффициент доверия, безотказная работа, доверительный интервал, распределение, суммарная наработка, VBA, время работы, случайная величина, суммарная наработка изделий.

Похожие статьи

Как вычисляется среднее время до отказа и вероятность безотказной работы?

Понятиям MTTF (Mean Time To Failure — среднее время до отказа) и другим терминам теории надежности посвящено большое количество статей, в том числе на Хабре (см., например, тут). Вместе с тем, редкие публикации «для широкого круга читателей» затрагивают вопросы математической статистики, и уж тем более они не дают ответа на вопрос о принципах расчета надежности электронной аппаратуры по известным характеристикам ее составных элементов.

В последнее время мне довольно много приходится работать с расчетами надежности и рисков, и в этой статье я постараюсь восполнить этот пробел, отталкиваясь от своего предыдущего материала (из цикла о машинном обучении) о пуассоновском случайном процессе и подкрепляя текст вычислениями в Mathcad Express, повторить которые вы сможете скачав этот редактор (подробно о нем тут, обратите внимание, что нужна последняя версия 3.1, как и для цикла по machine learning). Сами маткадовские расчеты лежат здесь (вместе с XPS- копией).

1. Теория: основные характеристики отказоустойчивости
Вроде бы, из самого определения (Mean Time To Failure) понятен его смысл: сколько (конечно, в среднем, поскольку подход вероятностный) прослужит изделие. Но на практике такой параметр не очень полезен. Действительно, информация о том, что среднее время до отказа жесткого диска составляет полмиллиона часов, может поставить в тупик. Гораздо информативнее другой параметр: вероятность поломки или вероятность безотказной работы (ВБР) за определенный период (например, за год).

Для того чтобы разобраться в том, как связаны эти параметры, и как, зная MTTF, вычислить ВБР и вероятности отказа, вспомним некоторые сведения из математической статистики.

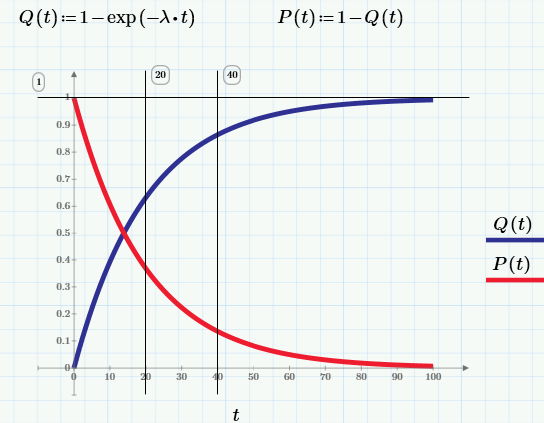
Ключевое понятие теории надежности — это понятие отказа, измеряемое, соответственно, интервальным показателем
Q(t) = вероятность того, что изделие откажет к моменту времени t.
Соотвественно, вероятность безотказной работы (ВБР, в английской терминологии «reliability»):
P(t) = вероятность того, что изделие проработает без отказа от момента t₀=0 до момента времени t.
По определению, в момент t₀=0 изделие находится в работоспособном состоянии, т.е. Q(0)=0, а P(0)=1.

Оба параметра — это интервальные характеристики отказоустойчивости, т.к. речь идет о вероятности отказа (или наоборот, безотказной работы) на интервале (0,t). Если отказ рассматривать, как случайное событие, то, очевидно, что Q(t) — это, по определению, его функция распределения. А точечную характеристику можно определить, как
p(t)=dQ(t)/dt = плотность вероятности, т.е. значение p(t)dt равно вероятности, что отказ произойдет в малой окрестности dt момента времени t.

И, наконец, самая важная (с практической точки зрения) характеристика: λ(t)=p(t)/P(t)=интенсивность отказов.
Это (внимание!) условная плотность вероятности, т.е. плотность вероятности возникновения отказа в момент времени t при условии, что до этого рассматриваемого момента времени t изделие работало безотказно.

Измерить параметр λ(t) экспериментально можно путём испытания партии изделий. Если к моменту времени t работоспособность сохранило N изделий, то за оценку λ(t) можно принять процент отказов в единицу времени, происходящих в окрестности t. Точнее, если в период от t до t+dt откажет n изделий, то интенсивность отказов будет примерно равна
λ(t)=n/(N*dt).

Именно эта λ-характеристика (в пренебрежении ее зависимостью от времени) и приводится чаще всего в паспортных данных различных электронных компонент и самых разных изделий. Только сразу возникает вопрос: а как вычислить вероятность безотказной работы и при чем здесь среднее время до отказа (MTTF).

А вот при чем.

2. Экспоненциальное распределение
В терминологии, которую мы только что использовали, пока не было никаких предположений о свойствах случайной величины — момента времени, в который происходит отказ изделия. Давайте теперь конкретизируем функцию распределения значения отказа, выбрав в качестве нее экспоненциальную функцию с единственным параметром λ=const (смысл которого будет ясен через несколько предложений).

Дифференцируя Q(t), получим выражение для плотности вероятности экспоненциального распределения:
,
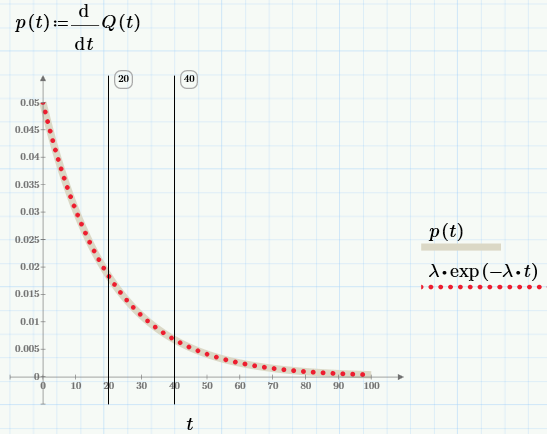
а из него – функцию интенсивности отказов: λ(t)=p(t)/P(t)=const=λ.

Что мы получили? Что для экспоненциального распределения интенсивность отказов – есть величина постоянная, причем совпадающая с параметром распределения. Этот параметр и является главным показателем отказоустойчивости и его часто так и называют λ-характеристикой.

Мало того, если теперь посчитать среднее время до первого отказа – тот самый параметр MTTF (Mean Time To Failure), то мы получим, что он равен MTTF=1/ λ.

Все это замечательные свойства экспоненциального распределения. Почему мы выбрали в качестве для описания отказов именно его? Да потому что это наиболее простая модель – модель пуассоновского потока событий, которая уже была нами рассмотрена в статье про анализ конверсии сайта. Поэтому-то в теории надежности наиболее часто используется показательное (экспоненциальное) распределение, для которого, как мы выяснили:

• надежность элементов можно оценить одним числом, т.к. λ=const;
• по известной λ довольно просто оценить остальные показатели надежности (например, ВБР для любого времени t);
• λ обладает хорошей наглядностью
• λ нетрудно измерить экспериментально

Но это еще не все, потому, что для экспоненциального распределения особенно легко делать расчет систем, состоящих из множества элементов. Но об этом – в следующей статье (продолжение следует).

Показательное распределение

• Краткая теория
• Примеры решения задач
• Задачи контрольных и самостоятельных работ

Краткая теория

---

Показательным (экспоненциальным) называют распределение вероятностей непрерывной случайной величины

, которое описывается плотностью:

где

 –
постоянная положительная величина.

Показательное
распределение определяется одним параметром

. Эта особенность распределения указывает на
его преимущество по сравнению с распределениями, зависящими от большего числа
параметров. Обычно параметры неизвестны и приходится находить их оценки
(приближенные значения); разумеется,  проще оценить один параметр, чем два или три.
Примером непрерывной случайной величины, распределенной по показательному
закону, может служить время между появлениями двух последовательных событий
простейшего потока.

Функция распределения
показательного закона:

Графики плотности и
функции распределения показательного закона изображены на рисунке.

Вероятность попадания в
интервал

 непрерывной
случайной величины

, распределенной по показательному закону:

Числовые характеристики показательного (экспоненциального) распределения

Математическое ожидание случайной величины, распределенной по показательному закону:

Дисперсия случайной величины, распределенной по показательному закону:

Среднее квадратическое отклонение случайной величины,
распределенной по показательному закону:

Коэффициенты асимметрии и эксцесса
для показательного распределения:

Таким
образом, математическое ожидание и среднее квадратическое
отклонение экспоненциального распределения равны между собой.

Показательный закон
распределения играет большую роль в теории массового обслуживания и теории
надежности. Так, например, интервал времени

 между
двумя соседними событиями в простейшем потоке имеет показательное распределение
с параметром

 –
интенсивностью потока.

При решении задач, которые выдвигает практика, приходится
сталкиваться с различными распределениями непрерывных случайных величин.

Смежные темы решебника:

• Непрерывная случайная величина
• Нормальный закон распределения случайной величины
• Равномерный закон распределения случайной величины

Примеры решения задач

---

Пример 1

Случайная величина

 задана функцией распределения

Найдите математическое
ожидание и среднее квадратическое отклонение этого
распределения.

Найдите вероятность того,
что случайная величина примет значение от 0,2 до 1.

На сайте можно заказать решение контрольной или самостоятельной работы, домашнего задания, отдельных задач. Для этого вам нужно только связаться со мной:

ВКонтакте
WhatsApp
Telegram

Мгновенная связь в любое время и на любом этапе заказа. Общение без посредников. Удобная и быстрая оплата переводом на карту СберБанка. Опыт работы более 25 лет.

Подробное решение в электронном виде (docx, pdf) получите точно в срок или раньше.

Решение

Математическое
ожидание случайной величины, распределенной по показательному закону:

Среднее
квадратическое отлонение:

Вероятность того, что
случайная величина примет значение от 0,2 до 1

Ответ

.

---

Пример 2

На шоссе установлен контрольный пункт для
проверки технического состояния автомобилей. Найти математическое ожидание и
среднее квадратическое отклонение случайной величины T – время ожидания
очередной машины контролером, если поток машин простейший и время (в часах)
между прохождениями машин через контрольный пункт распределено по
показательному закону f(t)=5e^-5t.

Указание: Время ожидания машины
контролером и время прохождения машин через контрольный пункт распределены
одинаково.

Решение

В нашем случае
параметр показательного распределения

Математическое
ожидание:

Дисперсия:

Среднее
квадратическое отклонение:

Ответ:

---

Пример 3

Постройте
интегральную и дифференциальную функции распределения случайной величины X.
Найдите математическое ожидание M(X), дисперсию D(X),
среднее квадратическое отклонение σ(X), моду x_mod, медиану x_med , если известно, что
случайная величина X имеет показательное распределение с параметром λ=1.

На сайте можно заказать решение контрольной или самостоятельной работы, домашнего задания, отдельных задач. Для этого вам нужно только связаться со мной:

ВКонтакте
WhatsApp
Telegram

Мгновенная связь в любое время и на любом этапе заказа. Общение без посредников. Удобная и быстрая оплата переводом на карту СберБанка. Опыт работы более 25 лет.

Подробное решение в электронном виде (docx, pdf) получите точно в срок или раньше.

Решение

Плотность
распределения случайной величины

, распределенной по
показательному закону:

Функция
распределения:

Построим
графики дифференциальной и интегральной функций распределения:

График дифференциальной функции распределения

График интегральной функции распределения

Математическое
ожидание показательно распределенной случайной величины

:

Дисперсия:

Среднее
квадратическое отклонение:

 найдем, исходя из условия: 

---

Пример 4

Случайная
величина

 распределена показательно с дисперсией 0,25.
Найти математическое ожидание и вероятность попадания

 в интервал (0,5;1).

Решение

Дисперсия
случайной величины, распределенной по показательному закону:

Математическое
ожидание случайной величины, распределенной по показательному закону:

Вероятность
попадания в интервал

 непрерывной случайной величины

, распределенной по
показательному закону:

В нашем
случае:

Ответ:

Задачи контрольных и самостоятельных работ

---

Задача 1

Время
безотказной работы двигателя автомобиля распределено по показательному закону.
Известно, что среднее время наработки двигателя на отказ между техническим
обслуживанием 100 ч. Определить вероятность безотказной работы двигателя за 80
ч.

На сайте можно заказать решение контрольной или самостоятельной работы, домашнего задания, отдельных задач. Для этого вам нужно только связаться со мной:

ВКонтакте
WhatsApp
Telegram

Мгновенная связь в любое время и на любом этапе заказа. Общение без посредников. Удобная и быстрая оплата переводом на карту СберБанка. Опыт работы более 25 лет.

Подробное решение в электронном виде (docx, pdf) получите точно в срок или раньше.

---

Задача 2

Среднее
время работы элемента, входящего в пожарно-техническое устройство, равно 1000
часов. Определить вероятность того, что элемент будет работать от 950 до 1150
часов, если время работы элемента распределено по показательному закону.

---

Задача 3

Вероятность
безотказной работы элемента распределена по экспоненциальному закону

f(t)=e^-0.05t

Найти
вероятность того, что в результате испытания случайная величина попадет в
интервал (11;35). Найти характеристики данного распределения случайной
величины.

---

Задача 4

Непрерывная
случайная величина X задана интегральной функцией распределения

Найти
постоянную C, математическое ожидание случайной величины X,
вероятность попадания случайной величины в интервал [2;4].

---

Задача 5

Время
между отказами прибора распределено по показательному закону со средним
значением 25 часов. Определить математическое ожидание и дисперсию времени
безотказной работы автомобиля. Найти вероятность того, что очередной отказ
произойдет не позднее 15 часов.

---

Задача 6

Время
безотказной работы телевизора определенной модели описывается показательным (экспоненциальным)
законом распределения с постоянной λ. Что вероятнее, его безотказная работа в
промежутке времени [x₁,x₂]

 или [x₃,x₄]? Записать
функции f(x),F(x) и построить их графики.

λ=1/10, x₁=3, x₂=5, x₃=4, x₄=8

На сайте можно заказать решение контрольной или самостоятельной работы, домашнего задания, отдельных задач. Для этого вам нужно только связаться со мной:

ВКонтакте
WhatsApp
Telegram

Мгновенная связь в любое время и на любом этапе заказа. Общение без посредников. Удобная и быстрая оплата переводом на карту СберБанка. Опыт работы более 25 лет.

Подробное решение в электронном виде (docx, pdf) получите точно в срок или раньше.

---

Задача 7

Испытывают
два независимо работающих элемента. Длительность времени t безотказной
работы первого элемента имеет показательное распределение с параметром 0,02,
второго -показательное распределение с параметром 0,06. Найдите вероятность
того, что за время длительностью t=6 ч откажет только один
элемент.

---

Задача 8

Среднее
время работы каждого из трех элементов, входящих в техническое устройство,
равно T=850 часов. Для безотказной работы устройства необходима безотказная
работа хотя бы одного из трех этих элементов. Определить вероятность, что
устройство будет работать от t₁=750 до t₂=820 часов, если время
работы каждого из трех элементов независимо и распределено по показательному
закону.

---

Задача 9

Время
устранения повреждения на канале связи T -случайная величина,
распределенная по закону f(t)=λe^-λt (t≥0). Среднее время
восстановления канала — 10 минут. Определить вероятность того, что на
восстановление канала потребуется от 5 до 10 минут.

---

Задача 10

Дана плотность
распределения случайной величины X.

По какому
закону распределения случайная величина? Найти математическое ожидание,
дисперсию, функцию распределения?

---

Задача 11

Время
безотказной работы механизма подчинено показательному закону с плотностью
распределения вероятностей f(t)=0.04e^-0.04t при t > 0 (t –
время в часах). Найти вероятность того, что механизм проработает безотказно не
менее 100 часов.

---

Задача 12

Длительность телефонного разговора
является случайной величиной, распределенной по показательному закону.
Известно, что средняя длительность телефонного разговора равна 9 минутам. Найти
вероятность того, что разговор будет длиться:

а) не более 5 минут.

б) более 5 минут.

На сайте можно заказать решение контрольной или самостоятельной работы, домашнего задания, отдельных задач. Для этого вам нужно только связаться со мной:

ВКонтакте
WhatsApp
Telegram

Мгновенная связь в любое время и на любом этапе заказа. Общение без посредников. Удобная и быстрая оплата переводом на карту СберБанка. Опыт работы более 25 лет.

Подробное решение в электронном виде (docx, pdf) получите точно в срок или раньше.

---

Задача 13

Случайная величина ξ подчинена
показательному закону с параметром λ=5:

Найдите вероятность того, что
случайная величина ξ примет значение меньшее, чем ее математическое ожидание.

---

Задача 14

Случайная
величина ξ имеет плотность вероятностей (показательное распределение)

Найдите
вероятность P{ξ>M_ξ}

---

Задача 15

Время T
(минут), затрачиваемое клиентами парикмахерской в ожидании своей очереди,
удовлетворяет показательному распределению с параметром λ=0,05. Какова
вероятность того, что время ожидания превысит 25 минут и каково среднее время
ожидания.

---

Задача 16

Время T (час),
необходимое на ремонт легкового автомобиля удовлетворяет показательному
распределению с параметром λ=0,2. Какова вероятность того, что время ремонта
одного автомобиля не превысит 6 часов, и сколько часов в среднем затрачивается
на ремонт одного автомобиля.

---

Задача 17

Время
ожидания у бензоколонки автозаправочной станции является случайной величиной X,
распределенной по показательному закону, со средним временем ожидания, равным t₀. Найти вероятности
следующих событий:

---

Задача 18

Случайная
величина X задана показательным законом распределения и
числовыми значениями параметров M(X)=3 и σ_x=3.

Требуется:

1) найти
функцию плотности f(x).

2) найти
вероятность попадания СВ X в указанный интервал [a,b]=[2,4].

---

Задача 19

Случайная
величина ξ задана функцией распределения

Найдите
математическое ожидание и среднее квадратическое отклонение этого
распределения.

---

Задача 20

Случайная величина ξ распределена по
показательному закону с параметром λ=0,3. Найдите математическое ожидание и
среднее квадратическое отклонение этой случайной величины.

• Краткая теория
• Примеры решения задач
• Задачи контрольных и самостоятельных работ