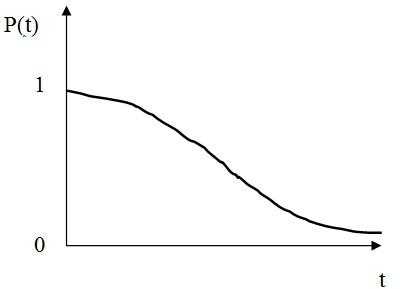
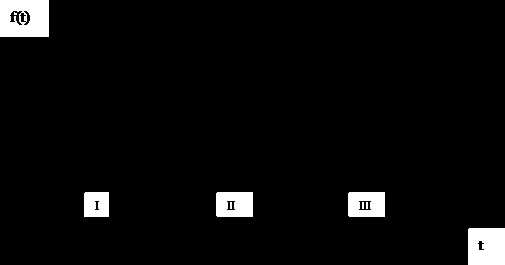
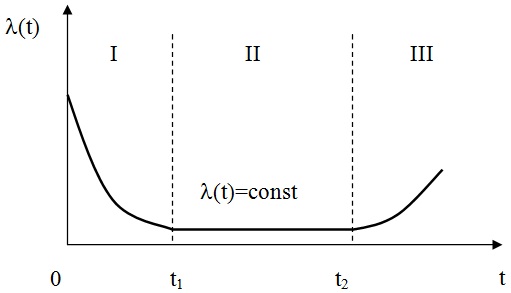
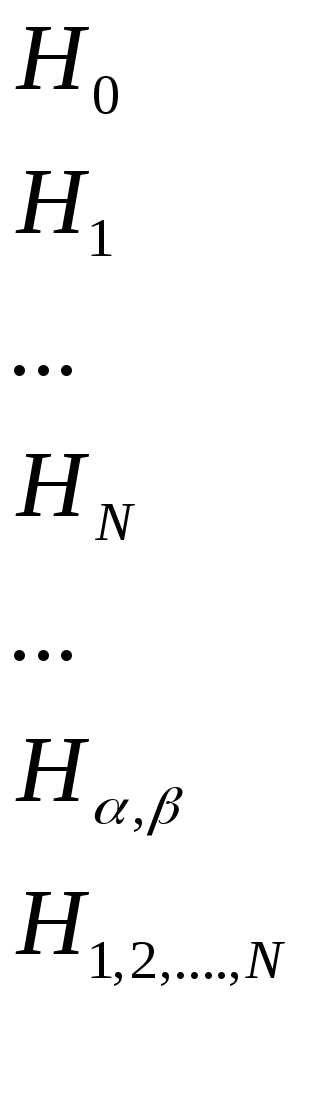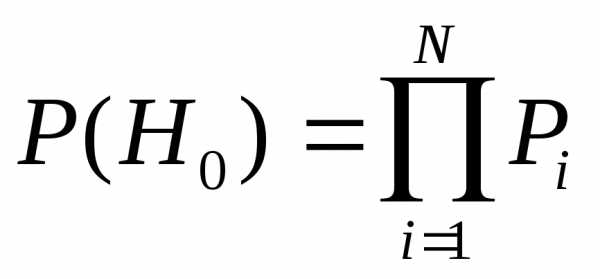Вероятность безотказной работы Р(t)
– вероятность того, что в заданном
интервале времени или заданной наработки
отказ изделия не произойдет. Эта функция
является убывающей. Р(О) = 1; Р()
= 0, следовательно О ≤ Р(t)
≤ 1. На рисунке 5 представлена графическая
интерпретация функции надежности.

5. Функции вероятности безотказной
работы Р(t) и вероятности
отказа Q(t)
Для невосстанавливаемых систем
вероятность безотказной работы
рассчитывается
,
где N(t) –
количество изделий, остающихся
работоспособными к моменту времени t;
No–
количество изделий, находившихся под
наблюдением.
Для восстанавливаемых систем
,
где n(t) –
количество изделий, в которых произошел
хотя бы один отказ к моменту времени t.
В некоторых случаях более удобной
характеристикой безотказности выступает
вероятность неисправной работы или
вероятность отказа Q(t).
Очевидно, что P(t) иQ(t)
события противоположные, несовместимые
и образуют полную группу событий.
Следовательно Q(t) = 1 –P(t);P(t)
= 1 –Q(t).
Использование показателя вероятности
безотказной работы несет в себе ряд
преимуществ:
-
применим для оценки простых и сложных
систем; -
применим для оценки на стадии
проектирования системы; -
является показателем изменения
надежности во времени; -
является достаточно полной характеристикой
надежности, поскольку учитывает большое
число факторов влияния.
Главным недостатком данного показателя
является то, что он может служить
достаточно полной характеристикой
только для невосстанавливаемых систем.
5.2. Наработка на отказ, до отказа, интенсивность и параметр потока отказов
Наработка на отказ T0есть среднее
время исправной работы между двумя
соседними отказами. Представляет собой
отношение наработки восстанавливаемой
системы к математическому ожиданию
числа отказов в течение этой наработки.
Величина случайная, точное значение
которой заранее предсказать невозможно.
Поэтому рассчитывается как среднее
статистическое значение

где m– число отказов за
время t,ti– время исправной работы между (i-1)
иi-mотказами,
ТМ– суммарное время безотказной
работы за время t.
Как видно этот показатель используется
для оценки безотказности восстанавливаемых
систем.
Для невосстанавливаемых систем
применяется показатель наработки до
отказа Тср(для восстанавливаемых
систем наработка до первого отказа).
Статистическое значение рассчитывается

где ti– время работыi-го изделия
до первого отказа.
Недостатки этих показателей сводятся
к следующему:
-
как математическое ожидание случайной
величины они не могут полностью
характеризовать время исправной работы,
поскольку неизвестна мера рассеяния
их величины; -
не позволяют оценить надежность изделий,
время работы которых меньше среднего
времени безотказной работы.
Интенсивность отказов
есть условная плотность вероятности
возникновения отказа невосстанавливаемой
системы. Статистическое значение
интенсивности отказов определяется
как отношение числа систем, отказавших
в единицу времени, к среднему числу
систем, остающихся исправными в данный
промежуток времени.
,
где
‑ количество изделий, отказавших за
время,
‑ количество изделий, оставшихся
исправными до конца наработкиt.
Параметр потока отказов
есть плотность вероятности возникновения
отказа восстанавливаемой системы.
Статистическое значение представляет
среднее число отказов в единицу времени
непрерывной работы
Как видно, параметр потока отказов
величина – обратная наработке на отказ,
следовательно
;
.
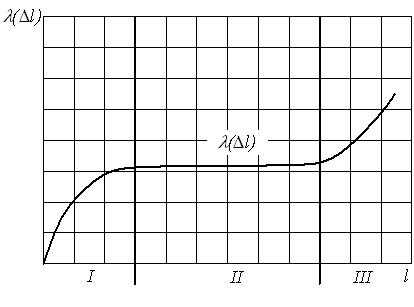
Закономерность изменения параметра
потока отказов во времени может носить
различный характер, как это показано
на рисунке 6.
Кривая 1 носит классический характер.
Стадия Iсоответствует
приработке, во время которой выявляются
скрытые дефекты и пропуски контроля.
Частота отказов уменьшается и
стабилизируется, что соответствует
переходу в стадию нормальной работы
(II). На этой стадии поток
отказов может рассматриваться как
стационарный ().

6. Варианты измененияво времени
Стадия III характеризуется лавинообразным
нарастанием отказов, когда проявляются
постепенные отказы, связанные с износом,
старением, усталостными явлениями.
Кривая 2 характеризует технические
системы, приработка которых проведена
до начала эксплуатации, например, в
условиях их производства. Кривая 3
характерна для технических систем,
элементы которых не испытывают старения
или износа и этап нормальной эксплуатации
отсутствует.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Вероятностью безотказной работы аппаратуры называется вероятность того, что она будет сохранять свои характеристики (параметры) в заданных пределах в течение определенного промежутка времени при определенных условиях эксплуатации, или, короче, – вероятностью безотказной работы аппаратуры называется вероятность того, что в определенных условиях эксплуатации в пределах заданной продолжительности работы отказ не возникает.
В дальнейшем эта характеристика обозначается P(t).
Пусть t – время, в течение которого необходимо определить вероятность безотказной работы, а Т1 – время работы аппаратуры от ее включения до первого отказа. Тогда, согласно определению вероятности безотказной работы, справедливо выражение:
, (1.1)
т.е. вероятность безотказной работы – это вероятность того, что время Т1 от момента включения аппаратуры до ее отказа будет больше или равно времени t, в течение которого определяется вероятность безотказной работы.
Из определения вероятности безотказной работы видно, что эта характеристика является функцией времени. Она имеет следующие очевидные свойства:
1) P(t) является убывающей функцией времени;
2) ;
3) Р(0) = 1, .
На практике для определения P(t) из статистических данных об отказах аппаратуры обычно используются методы непосредственного подсчета вероятностей. Вероятность безотказной работы определяется следующей статистической оценкой:
, (1.2)
где N0 – число образцов аппаратуры в начале испытания, n(t) – число отказавших образцов за время t.
При увеличении числа образцов N0 статистическая оценка вероятности обнаруживает устойчивость, т.е.
слабо отличается от вероятности безотказной работы:
. (1.3)
На практике иногда более удобной характеристикой является вероятность неисправной работы, или вероятность отказов. Эта характеристика может быть полезна, например, при сравнение надежности резервированной и не резервированной систем. Исправная работа и отказ являются событиями несовместными и противоположными. Поэтому вероятность безотказной работы и вероятность отказа Q(t) связаны зависимостью:
Q (t) = 1 – P (t), (1.4)
или с учетом выражения (1.1)
Q (t) = P (T1 t) (1.5)
Из выражения (1.5) видно, что вероятность отказа является интегральной функцией распределения времени работы (Т1) до отказа, т.е.
Q (t) = F (t) (1.6)
Производная от интегральной функции распределения есть дифференциальный закон (плотность) распределения:
. 1.7)
Тогда на основании выражений (1.6) и (1.7) получим:
, (1.8)
т.е.
производная от вероятности отказа подчиняется дифференциальному закону распределения времени работы (Т1) аппаратуры до ее отказа.
Для статистического определения вероятности отказа воспользуемся выражениями (1.4)и (1.3). Подставляя в выражение (1.4) вместо P(t) его выражение из формулы (1.3), получим:
. (1.9)
Вероятность безотказной работы P(t), как количественная характеристика надежности, обладает следующими достоинствами:
1) характеризует изменение надежности во времени;
2) входит во многие другие характеристики аппаратуры, а поэтому может быть полезна широкому кругу лиц, занимающихся вопросами проектирования, эксплуатации, ремонта и т.п. Например, вероятность безотказной работы наряду с точностью и живучестью определяет боевую эффективность оружия, а поэтому является необходимой для исследователя военных операций и полководца. Она определяет также стоимость изготовления и эксплуатации аппаратуры, а поэтому может быть полезной инженеру-экономисту;
3) охватывает большинство факторов, существенно влияющих на надежность аппаратуры, и поэтому достаточно полно характеризует надежность;
4) может быть сравнительно просто получена расчетным путем до изготовления системы. Это позволяет выбрать оптимальную в смысле надежности структуру системы и ее принципиальную схему;
5) является удобной характеристикой надежности, как простейших элементов, так и сложных систем и даже комплексов.
Указанные достоинства вероятности безотказной работы явились причиной наибольшего распространения этой характеристики.
Однако вероятность безотказной работы имеет также существенные недостатки:
1) характеризует надежность восстанавливаемых систем только до первого отказа, а поэтому является достаточно полной характеристикой надежности только систем разового использования;
2) не позволяет охарактеризовать зависимость между временными составляющими цикла эксплуатации; это не дает возможности установить, даже в вероятностном смысле, будет ли система готова к действию в данный момент времени или нет;
3) не всегда удобна для оценки надежности простых элементов, в особенности таких, у которых отсутствует старение;
4) по известной вероятности безотказной работы бывает трудно вычислить другие количественные характеристики надежности.
Эти недостатки позволяют сделать вывод, что вероятность безотказной работы, как, впрочем, и любая другая характеристика, не полностью характеризует такое свойство как надежность, и поэтому не может быть с ним отождествлена.
Практическая
работа №1.
Тема: Определение
показателей надёжности по статистическим
данным
Цель:определить показатели надёжности
и произвести расчеты на С++ партии изделий
при проведении испытаний в течение
заданного промежутка времени.
Теоретические
сведения
Показатели безотказности.
Вероятность безотказной работы
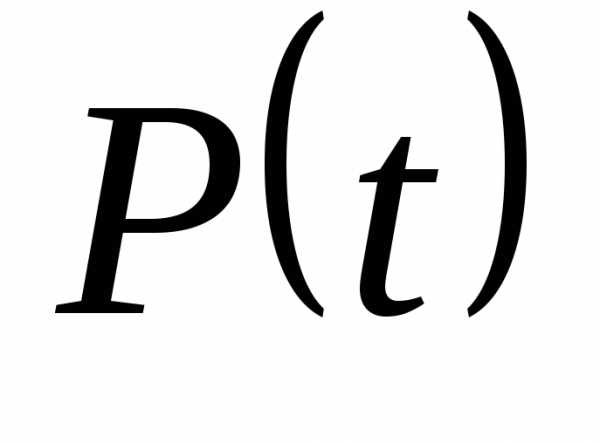
интервале времениtв
изделии не возникает отказа.;;
Для определения P(t)
используется следующая статическая
оценка:
где
– число изделий, поставленных на
испытание (эксплуатацию).

времениt.
Вероятность отказа— это величина, обратная вероятности
безотказной работы
Зависимость вероятности безотказной
работы от времени
Вероятность бессбойной работы
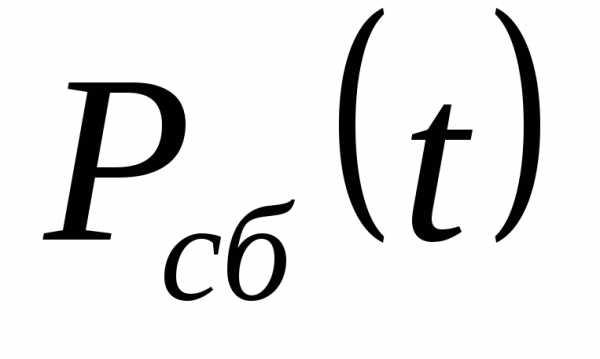
интервале времени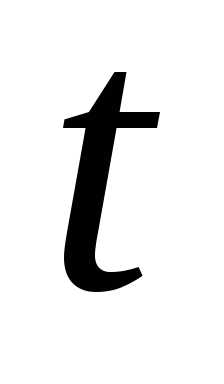
График зависимости от времени такой
же, как и для вероятности безотказной
работы
;
где —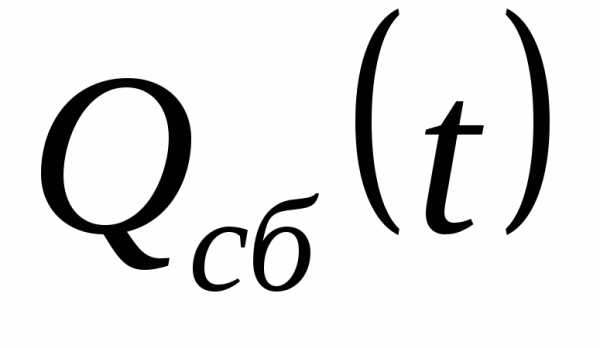
времени
.
Для определения стабильности оценки
мы имеем формулу:
где
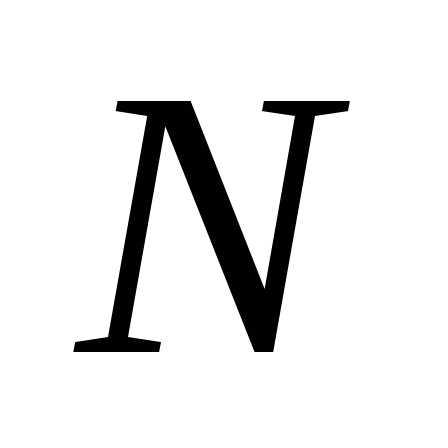
эксплуатацию.
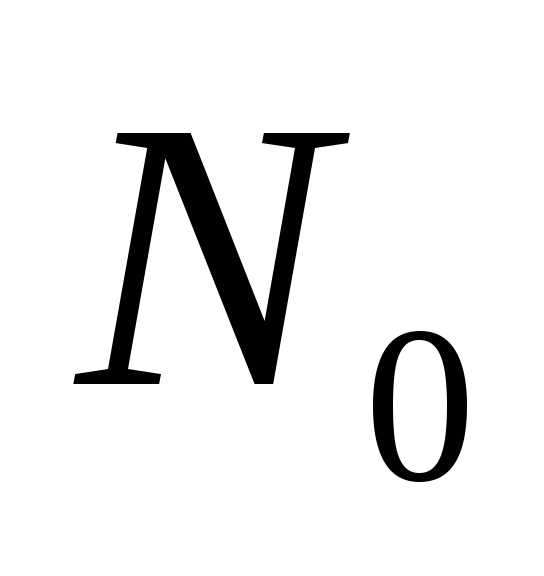
сбой в течение времениt.
Интенсивность отказа
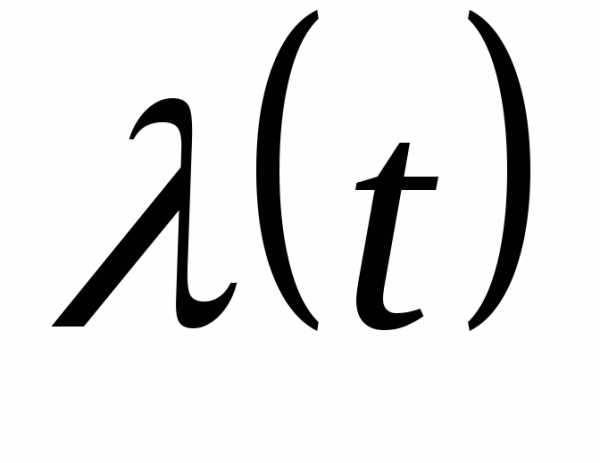
возникновения отказа не восстанавливаемого
объекта, определенного рассмотренного
момента времени, при условии, что до
этого момента отказ не возник.
Для определенно
используется следующая статистическая
оценка:
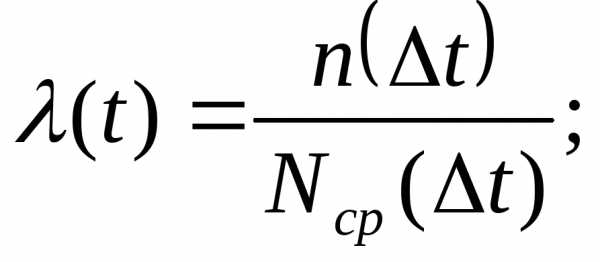
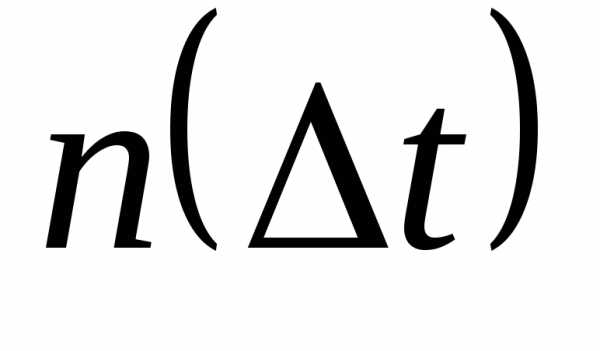
времени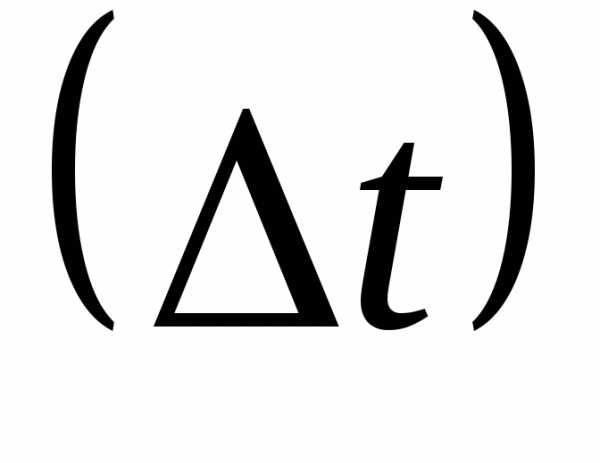
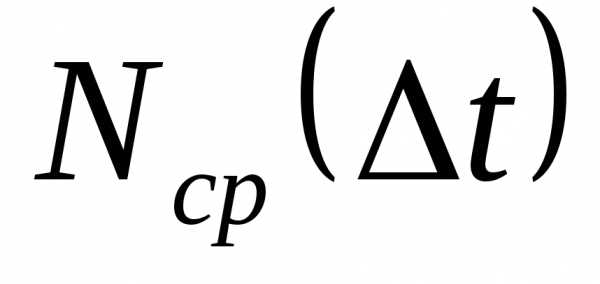
интервал времени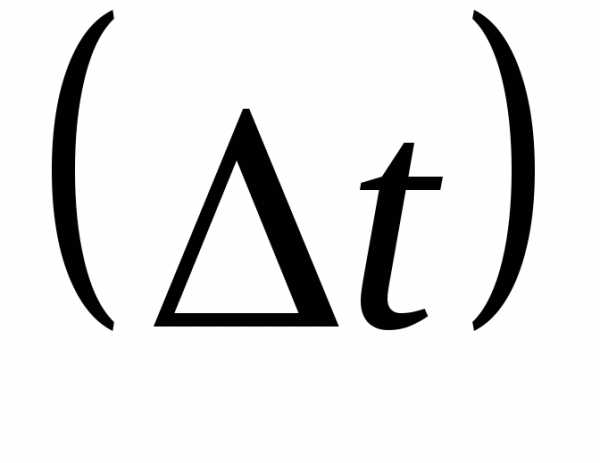
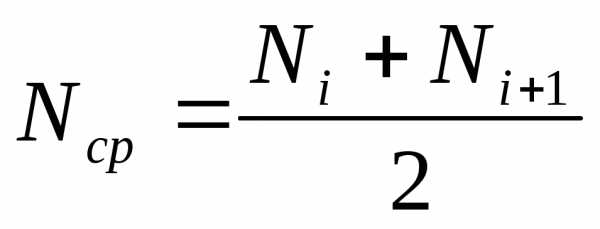
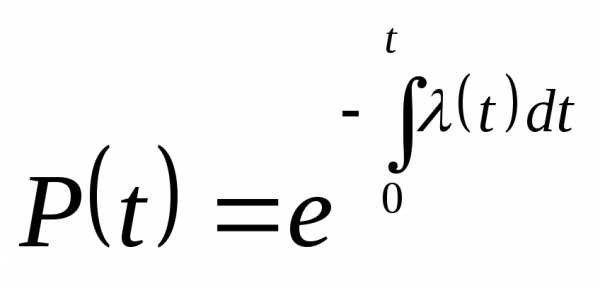
отказа и вероятностью безотказной
работы
Вероятность безотказной работы в
интервале времени
Средняя наработка до отказа (среднее
время безотказной работы) Т– это
математическое ожидание наработки до
первого отказа определяется так:
Частота отказов или плотность
распределения отказовравна
отношению числа отказавших объектов в
интервале времени
в начальный момент времени на ширину
интервала времени:
Постановка
задачи.
Проводится испытание объектов на
надёжность. Испытываемая партия

на интервале времени
часов, если за этот период отказало
первых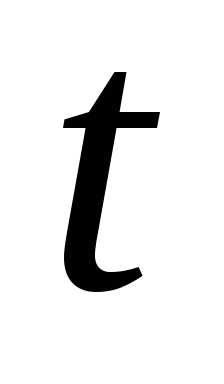
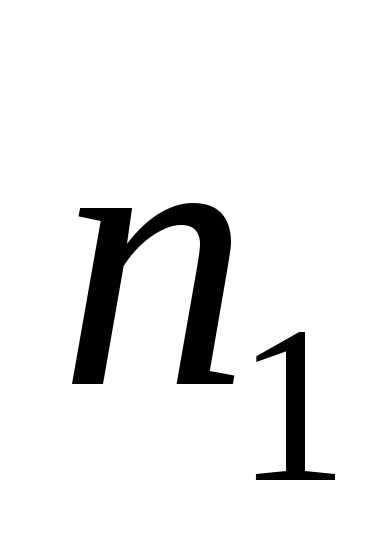
безотказной работы на интервале времени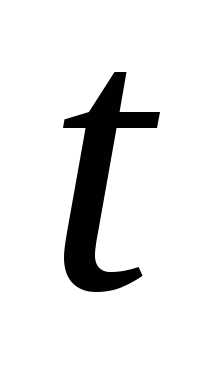

интенсивность отказов в моменты времени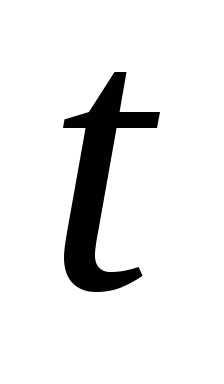
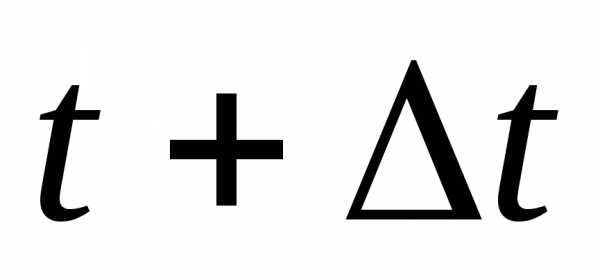
среднее время наработки на отказ,
учитывая интенсивность отказов в момент
времени
.
Варианты к
выполнению заданий.
|
№ варианта |
|
|
|
|
|
|
1 |
1000 |
5000 |
300 |
100 |
50 |
|
2 |
1500 |
6000 |
270 |
110 |
60 |
|
3 |
2000 |
7000 |
260 |
120 |
70 |
|
4 |
2500 |
8000 |
250 |
130 |
80 |
|
5 |
3000 |
9000 |
240 |
140 |
90 |
|
6 |
3500 |
11000 |
230 |
150 |
100 |
|
7 |
4000 |
5000 |
220 |
160 |
110 |
|
8 |
4500 |
6000 |
210 |
170 |
120 |
|
9 |
5000 |
7000 |
200 |
90 |
130 |
|
10 |
6000 |
8000 |
350 |
80 |
140 |
|
11 |
1000 |
9000 |
370 |
70 |
150 |
|
12 |
1500 |
10000 |
390 |
60 |
160 |
|
13 |
2000 |
5000 |
400 |
50 |
170 |
|
14 |
2500 |
6000 |
500 |
40 |
180 |
|
15 |
3000 |
7000 |
450 |
30 |
190 |
|
16 |
3500 |
8000 |
300 |
150 |
200 |
|
17 |
4000 |
9000 |
270 |
160 |
190 |
|
18 |
4500 |
10000 |
260 |
170 |
180 |
|
19 |
5000 |
5000 |
250 |
180 |
170 |
|
20 |
6000 |
6000 |
240 |
200 |
160 |
|
21 |
1000 |
7000 |
230 |
100 |
150 |
|
22 |
1500 |
8000 |
220 |
110 |
140 |
|
23 |
2000 |
9000 |
210 |
120 |
130 |
|
24 |
2500 |
10000 |
200 |
130 |
120 |
|
25 |
3000 |
5000 |
350 |
140 |
110 |
|
26 |
3500 |
6000 |
370 |
150 |
100 |
|
27 |
4000 |
7000 |
390 |
160 |
90 |
|
28 |
4500 |
8000 |
400 |
170 |
80 |
|
29 |
5000 |
9000 |
500 |
90 |
70 |
|
30 |
6000 |
10000 |
450 |
80 |
60 |
Пример выполнения
задания.
Проводится испытание объектов на
надёжность. Испытываемая партия
шт. Требуется определить частоту отказов
на интервале временичасов, если за этот период отказало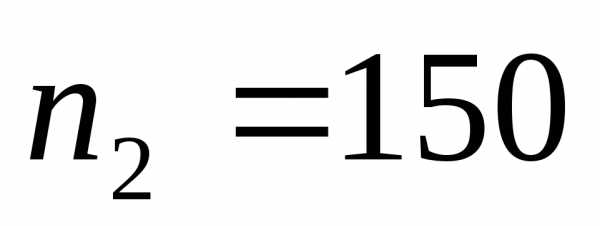
первыхчасов отказало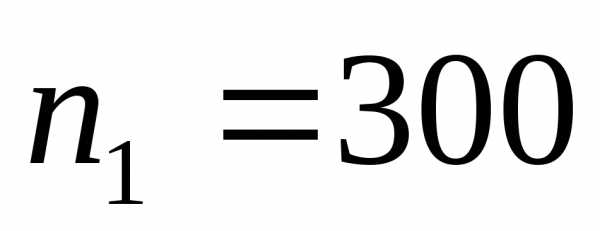
безотказной работы на интервале времени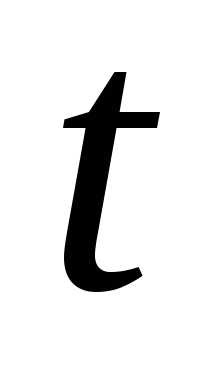

интенсивность отказов в моменты времени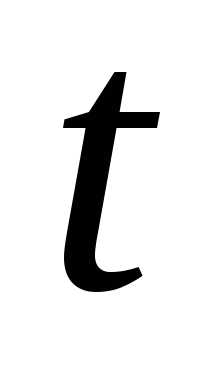
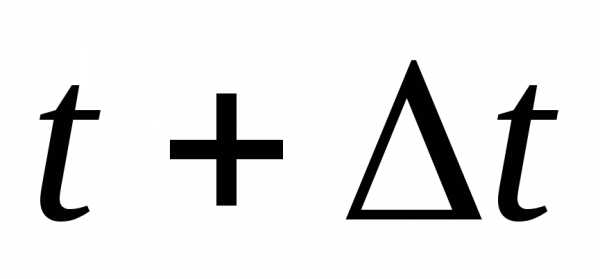
среднее время наработки на отказ,
учитывая интенсивность отказов в момент
времени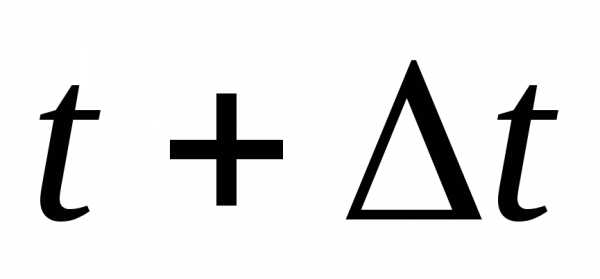
|
|
|
|
|
|
|
3000 |
2000 |
300 |
150 |
400 |
Решение.
-
Определяем частоту отказов
-
Определяем вероятность безотказной
работы за период времени t: -
Определяем вероятность безотказной
работы на интервале времени t+Δt: -
Определяем вероятность безотказной
работы на промежутке времени Δt: -
Определяем интенсивность отказов на
интервале времени t+ Δt:или -
Определяем интенсивность отказов на
интервале времени t:
Определяем среднее время наработки на
отказ:
Порядок выполнения
работы
-
Запускаем программу С++.
-
Создаем новый файл File→New…(<Ctrl>+<N>)
-
В диалоговом окне «New»
на вкладкеFilesвыбираемC++SourceFile,
задаем имя файлу и его расположение. -
Пишем код программы для расчета
вычислений:
Подключаем
необходимые заголовочные файлы
1. #include
«iostream.h»
Пишем
главную функцию программы
2. int
main()
3. {
Объявляем
переменные, которые нам даны по
заданию
4. int
N=3000;
5. int
t=2000;
6. int
n1=300;
7. int
n2=150;
8. int
delta_t=400;
Объявляем
переменные, которые нам понадобятся
для расчетов и присваиваем им начальные
нулевые
значения
9. double f_t=0,
10. P_t=0,
11. P_delta_t=0,
12. lyamb_delta_t=0,
13. lyamb_t=0,
14. T_M=0;
Зная
формулу вычисления частоты отказов,
запрограммируем расчеты
15. код
вычисления частоты отказов
Зная
формулу вычисления вероятности
безотказной работы за период времени
,
запрограммируем расчеты16. код
вычисления вероятности безотказной
работы времени t
Зная
формулу вычисления вероятности
безотказной работы на интервале времени
,
запрограммируем расчеты17. код
вычисления вероятности безотказной
работы на интервале времени
Определяем
вероятность безотказной работы на
промежутке времени,
зная формулу расчета18. код
вычисления вероятности безотказной
работы на промежутке времени
Определяем
интенсивность отказов на интервале
времени,
зная формулу вычисления. Интенсивность
отказов на интервале времениможно найти по одной из двух формул.
Рассчитаем, используя оба способа:I-й
способ —
или
II-й
способ —
19. код
вычисления интенсивность отказов на
интервале времени
(I-й
способ)
20. код
вычисления интенсивность отказов на
интервале времени
(II-й
способ)
Запрограммируем
расчеты интенсивности отказов на
интервале времени t, зная, что интенсивность
отказов на интервале времени t
рассчитывается по формуле:
21. код
вычисления интенсивность отказов на
интервале времени
Рассчитываем
среднее время наработки на отказ,
используя в формуле интенсивности
отказов на интервале времени t, полученные
двумя способам —
22. код
вычисления среднего времени наработки
на отказ (I-й
способ)
23. код
вычисления среднего времени наработки
на отказ (II-й
способ)
24. выводим
на экран результаты расчетов
Функция
main()
возвращает целочисленное значение:
25. return
0;
26. } -
Откомпилируйте проект, исправьте все
ошибки и предупреждения. -
Создайте исполнительный файл, с
возможностью ввода и вывода данных и
вывода ответов с различными способами
расчетов интенсивности отказов на
интервале времени
.
Содержание отчета
-
Содержание отчета должно быть оформлено
в тетради. -
Тема и цель работы.
-
Задание и данные, представленные в
табличном виде. -
Расчет показателей надежности.
-
Расчет показателей надежности с
вычислениями на компьютере. -
Сравнить данные, полученные вручную с
данными, получившимися в результате
расчетов на компьютере. -
Провести анализ: как изменяется результат
среднего времени наработки на отказ
при различных способах вычисления
интенсивности отказов на интервале
времени
.
studfiles.net
4.Вероятность безотказной работы
Вероятность
безотказной работы объекта называется
вероятность того, что он будет сохранять
свои параметры в заданных пределах в
течение определенного промежутка
времени при определенных условиях
эксплуатации.
В
дальнейшем полагаем, что эксплуатация
объекта происходит непрерывно,
продолжительность эксплуатации объекта
выражена в единицах времени t и эксплуатация
начата в момент времени t=0.
Обозначим
P(t) вероятность безотказной работы
объекта на отрезке времени [0,t]. Вероятность,
рассматриваемую как функцию верхней
границы отрезка времени, называют также
функцией надежности.
Вероятностная
оценка: P(t) = 1 – Q(t), где Q(t) — вероятность
отказа.
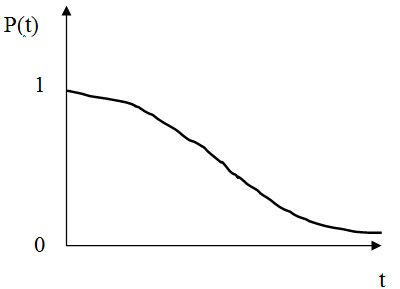
Рисунок
2. Типичная кривая вероятности безотказной
работы
Из
графика очевидно, что:
1.
P(t) – невозрастающая функция времени;
2.
0 ≤ P(t) ≤ 1;
3.
P(0)=1; P(∞)=0.
На
практике иногда более удобной
характеристикой является вероятность
неисправной работы объекта или вероятность
отказа:
Q(t)
= 1 – P(t).

характеристика вероятности отказов:
Q*(t) = n(t)/N.
5.Плотность вероятности отказа
Плотность
вероятности отказа — отношение числа
отказавших аппаратов в единицу времени
к числу аппаратов, первоначально
установленных на испытание, при условии,
что отказавшие аппараты не восстанавливаются
и не заменяются новыми.
a*(t)
= n(t)/(NΔt),
где
a*(t) — частота отказов;
n(t)
– число отказавших объектов в интервале
времени от t – t/2 до t+ t/2;
Δt
– интервал времени;
N
– число объектов, участвующих в испытании.
Между
плотностью вероятности отказа,
вероятностью безотказной работы и
вероятностью отказов при любом законе
распределения времени отказов существует
однозначная зависимость:
Q(t)
= ∫ a(t)dt.
6.Средняя наработка до отказа
Средняя
наработка до отказа — математическое
ожидание наработки объекта до первого
отказа.
Часто
этот показатель называют средним
временем безотказной работы и обозначают
Т0.

по двум формулам:
Для
наиболее часто используемого
экспоненциального распределения
tсредн.
= a , а экспоненциальное распределение
принимает вид:
7. Гамма-процентная наработка до отказа
Весьма
информативным показателем безотказности
невосстанавливаемых объектов является
гамма-процентная наработка до отказа,
понимаемая как наработка, в течение
которой отказ объекта не возникнет с
вероятностью γ, выраженной в процентах.
В
случае экспоненциального распределения
гамма-процентная наработка до отказа
определяется по формуле:
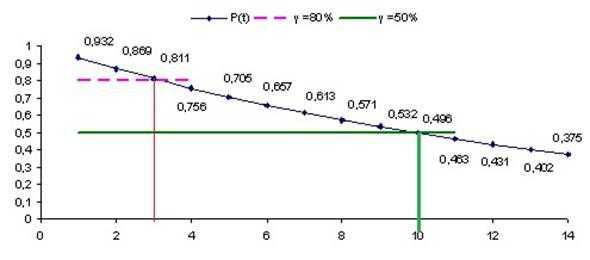
Рисунок
4
Наработку
до отказа обычно определяют для значений
γ > 80% (верхняя горизонтальная линия
на рис.4).
Для
прогнозирования потребности в запасных
частях определяют гамма-процентную
наработку и при меньших значениях,
например при γ = 50% (нижняя горизонтальная
линия на рис.4).
При
γ = 100% гамма-процентная наработка
называется установленной безотказной
наработкой, при γ = 50% гамма-процентная
наработка называется медианной
наработкой.

учитывать, что экстраполяция эмпирических
результатов за пределы продолжительности
испытаний может привести к значительным
ошибкам.
studfiles.net
Диагностика и надежность в технике
1. Расчет показателей безотказности
1.1 Вероятность безотказной работы
1.2 Вероятность отказа
1.3 Частота отказа
1.4 Интенсивность отказа
1.5 Средняя наработка до отказа
1.6 Среднее значение параметра потока отказов
1.7 Пример расчета показателей безотказности
2. Примеры расчета показателей надежности для различных законов распределения случайных величин
2.1 Экспоненциальный закон распределения
2.2 Закон распределения Вейбулла-Гнеденко
2.3 Закон распределения Рэлея
3. Примеры расчета показателей надежности сложных систем
3.1 Основное соединение элементов
3.2 Резервное соединение
1.1 Вероятность безотказной работы
Вероятностью безотказной работы называется вероятность того, что при определенных условиях эксплуатации, в пределах заданной наработки не произойдет ни одного отказа.
Вероятность безотказной работы обозначается как P(l), которая определяется по формуле (1.1):
где N0 – число элементов в начале испытания; r(l) – число отказов элементов к моменту наработки.Следует отметить, что чем больше величина N0, тем с большей точностью можно рассчитать вероятность P(l).
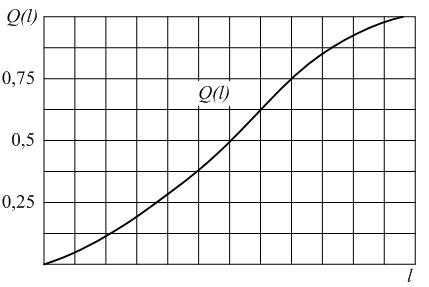
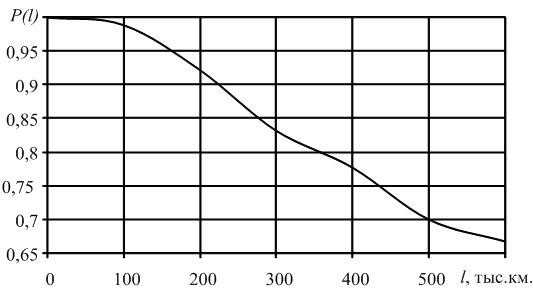
В начале эксплуатации исправного локомотива P(0) = 1, так как при пробеге l = 0 вероятность того, что ни один элемент не откажет, принимает максимальное значение – 1. С ростом пробега l вероятность P(l) будет уменьшаться. В процессе приближения срока эксплуатации к бесконечно большой величине вероятность безотказной работы будет стремиться к нулю P(l→∞) = 0. Таким образом в процессе наработки величина вероятности безотказной работы изменяется в пределах от 1 до 0. Характер изменения вероятности безотказной работы в функции пробега показан на рис. 1.1.
Рис.2.1. График изменения вероятности безотказной работы P(l)в зависимости от наработки
Основными достоинствами использования данного показателя при расчетах является два фактора: во-первых, вероятность безотказной работы охватывает все факторы, влияющие на надежность элементов, позволяя достаточно просто судить о его надежности, т.к. чем больше величина P(l), тем выше надежность; во-вторых, вероятность безотказной работы может быть использована в расчетах надежности сложных систем, состоящих из более чем одного элемента.
1.2 Вероятность отказа
Вероятностью отказа называют вероятность того, что при определенных условиях эксплуатации, в пределах заданной наработки произойдет хотя бы один отказ.
Вероятность отказа обозначается как Q(l), которая определяется по формуле (1.2):
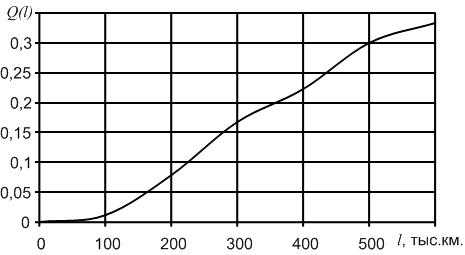
В начале эксплуатации исправного локомотива Q(0) = 0, так как при пробеге l = 0 вероятность того, что хотя бы один элемент откажет, принимает минимальное значение – 0. С ростом пробега l вероятность отказа Q(l) будет увеличиваться. В процессе приближения срока эксплуатации к бесконечно большой величине вероятность отказа будет стремиться к единице Q(l→∞) = 1. Таким образом в процессе наработки величина вероятности отказа изменяется в пределах от 0 до 1. Характер изменения вероятности отказа в функции пробега показан на рис. 1.2.Вероятность безотказной работы и вероятность отказа являются событиями противоположными и несовместимыми.
Рис.2.2. График изменения вероятности отказа Q(l) в зависимости от наработки
1.3 Частота отказов
Частота отказов – это отношение числа элементов в единицу времени или пробега отнесенного к первоначальному числу испытуемых элементов. Другими словами частота отказов является показателем, характеризующим скорость изменения вероятности отказов и вероятности безотказной работы по мере роста длительности работы.
Частота отказов обозначается как и определяется по формуле (1.3):
где – количество отказавших элементов за промежуток пробега .
Данный показатель позволяет судить по его величине о числе элементов, которые откажут на каком-то промежутке времени или пробега, также по его величине можно рассчитать количество требуемых запасных частей.
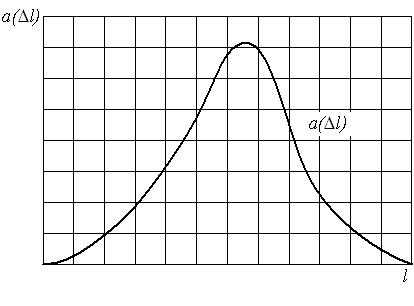
Характер изменения частоты отказов в функции пробега показан на рис. 1.3.
Рис. 1.3. График изменения частоты отказов в зависимости от наработки
1.4 Интенсивность отказов
Интенсивность отказов представляет собой условную плотность возникновения отказа объекта, определяемую для рассматриваемого момента времени или наработки при условии, что до этого момента отказ не возник. Иначе интенсивность отказов – это отношение числа отказавших элементов в единицу времени или пробега к числу исправно работающих элементов в данный отрезок времени.
Интенсивность отказов обозначается как и определяется по формуле (1.4):
где
Как правило, интенсивность отказов является неубывающей функцией времени. Интенсивность отказов обычно применяется для оценки склонности к отказам в различные моменты работы объектов.
На рис. 1.4. представлен теоретический характер изменения интенсивности отказов в функции пробега.
Рис. 1.4. График изменения интенсивности отказов в зависимости от наработки
На графике изменения интенсивности отказов, изображенном на рис. 1.4. можно выделить три основных этапа отражающих процесс экс-плуатации элемента или объекта в целом.
Первый этап, который также называется этапом приработки, характеризуется увеличением интенсивности отказов в начальный период эксплуатации. Причиной роста интенсивности отказов на данном этапе являются скрытые дефекты производственного характера.
Второй этап, или период нормальной работы, характеризуется стремлением интенсивности отказов к постоянному значению. В течение этого периода могут возникать случайные отказы, в связи с появлением внезапной концентрации нагрузки, превышающей предел прочности элемента.
Третий этап, так называемый период форсированного старения. Характеризуется возникновением износовых отказов. Дальнейшая эксплуатация элемента без его замены становится экономически не рациональной.
1.5 Средняя наработка до отказа
Средняя наработка до отказа – это средний пробег безотказной работы элемента до отказа.
Средняя наработка до отказа обозначается как L1 и определяется по формуле (1.5):
где li – наработка до отказа элемента; ri – число отказов.
Средняя наработка до отказа может быть использована для предварительного определения сроков ремонта или замены элемента.
1.6 Среднее значение параметра потока отказов
Среднее значение параметра потока отказов характеризует среднюю плотность вероятности возникновения отказа объекта, определяемая для рассматриваемого момента времени.
Среднее значение параметра потока отказов обозначается как Wср и определяется по формуле (1.6):
1.7 Пример расчета показателей безотказности
Исходные данные.
В течение пробега от 0 до 600 тыс. км., в локомотивном депо произведен сбор информации по отказам ТЭД. При этом количество исправных ТЭД в начале периода эксплуатации составляло N0 = 180 шт. Суммарное количество отказавших ТЭД за анализируемый период составило ∑r(600000) = 60. Интервал пробега принять равным 100 тыс. км. При этом количество отказавших ТЭД по каждому участку составило: 2, 12, 16, 10, 14, 6.
Требуется.
Необходимо рассчитать показатели безотказности и построить их зависимости изменения во времени.
Сначала необходимо заполнить таблицу исходных данных так, как это показано в табл. 1.1.
Таблица 1.1.
| , тыс. км | 0 — 100 | 100 — 200 | 200 — 300 | 300 — 400 | 400 — 500 | 500 — 600 |
| 2 | 12 | 16 | 10 | 14 | 6 | |
| 2 | 14 | 30 | 40 | 54 | 60 |
Первоначально по уравнению (1.1) определим для каждого участка пробега величину вероятности безотказной работы. Так, для участка от 0 до 100 и от 100 до 200 тыс. км. пробега вероятность безотказной работы составит:
Далее, используя зависимость (1.2) произведем расчет вероятности отказа ТЭД.
Произведем расчет частоты отказов по уравнению (1.3).
Далее по уравнению (1.4) произведем расчет интенсивности отказов ТЭД в зависимости от наработки.
Первоначально рассчитаем среднее количество работоспособных ТЭД на участке от 0 до 100 тыс. км. пробега:
Тогда интенсивность отказов на участке 0-100 тыс.км. будет равна:
Аналогичным образом определим величину интенсивности отказов для интервала 100-200 тыс. км.
По уравнениям (1.5 и 1.6) определим среднюю наработку до отказа и среднее значение параметра потока отказов.
Систематизируем полученные результаты расчета и представим их в виде таблицы (табл. 1.2.).
Таблица 1.2.
| , тыс.км. | 0 — 100 | 100 — 200 | 200 — 300 | 300 — 400 | 400 — 500 | 500 — 600 |
| 2 | 12 | 16 | 10 | 14 | 6 | |
| 2 | 14 | 30 | 40 | 54 | 60 | |
| P(l) | 0,989 | 0,922 | 0,833 | 0,778 | 0,7 | 0,667 |
| Q(l) | 0,011 | 0,078 | 0,167 | 0,222 | 0,3 | 0,333 |
| 10-7, 1/км | 1,111 | 6,667 | 8,889 | 5,556 | 7,778 | 3,333 |
| 10-7, 1/км | 1,117 | 6,977 | 10,127 | 6,897 | 10,526 | 4,878 |
Приведем характер изменения вероятности безотказной работы ТЭД в зависимости от пробега (рис. 1.5.). Необходимо отметить, что первой точкой на графике, т.е. при пробеге равном 0, величина вероятности безотказной работы примет максимальное значение – 1.
Рис. 1.5. График изменения вероятности безотказной работы в зависимости от наработки
Приведем характер изменения вероятности отказа ТЭД в зависимости от пробега (рис. 1.6.). Необходимо отметить, что первой точкой на графике, т.е. при пробеге равном 0, величина вероятности отказа примет минимальное значение – 0.
Рис. 1.6. График изменения вероятности отказа в зависимости от наработки
Приведем характер изменения частоты отказов ТЭД в зависимости от пробега (рис. 1.7.).
Рис. 1.7. График изменения частоты отказов в зависимости от наработки
На рис. 1.8. представлена зависимость изменения интенсивности отказов от наработки.
Рис. 1.8. График изменения интенсивности отказов в зависимости от наработки
2.1 Экспоненциальный закон распределения случайных величин
Экспоненциальный закон достаточно точно описывает надежность узлов при внезапных отказах, имеющих случайный характер. Попытки применить его для других типов и случаев отказов, особенно постепенных, вызванных износом и изменением физико-химических свойств элементов показали его недостаточную приемлемость.
Исходные данные.
В результате испытания десяти топливных насосов высокого давления получены наработки их до отказа: 400, 440, 500, 600, 670, 700, 800, 1200, 1600, 1800 ч. Предполагая, что наработка до отказа топливных насосов подчиняется экспоненциальному закону распределения.
Требуется.
Оценить величину интенсивности отказов , а также рассчитать вероятность безотказной работы за первые 500 ч. и вероятность отказа в промежутке времени между 800 и 900 ч. работы дизеля.
Во-первых, определим величину средней наработки топливных насосов до отказа по уравнению:
Затем рассчитываем величину интенсивности отказов:
Величина вероятности безотказной работы топливных насосов при наработке 500 ч составит:
Вероятность отказа в промежутке между 800 и 900 ч. работы насосов составит:
2.2 Закон распределения Вэйбулла-Гнеденко
Закон распределения Вейбулла-Гнеденко получил широкое распространение и используется применительно к системам, состоящим из рядов элементов, соединенных последовательно с точки зрения обеспечения безотказности системы. Например, системы, обслуживающие дизель-генераторную установку: смазки, охлаждения, питания топливом, воздухом и т.д.
Исходные данные.
Время простоя тепловозов в неплановых ремонтах по вине вспомогательного оборудования подчиняется закону распределения Вейбулла-Гнеденко с параметрами b=2 и a=46.
Требуется.
Необходимо определить вероятность выхода тепловозов из неплановых ремонтов после 24 ч. простоя и время простоя, в течение которого работоспособность будет восстановлена с вероятностью 0,95.
Найдем вероятность восстановления работоспособности локомотива после простоя его в депо в течение суток по уравнению:
Для определения времени восстановления работоспособности локомотива с заданной величиной доверительной вероятности также используем выражение:
2.3 Закон распределения Рэлея
Закон распределения Рэлея используется в основном для анализа работы элементов, имеющих ярко выраженный эффект старения (элементы электрооборудования, различного рода уплотнения, шайбы, прокладки, изготовленные из резиновых или синтетических материалов).
Исходные данные.
Известно, что наработки контакторов до отказа по параметрам старения изоляции катушек можно описать функцией распределения Рэлея с параметром S = 260 тыс.км.
Требуется.
Для величины наработки 120 тыс.км. необходимо определить вероятность безотказной работы, интенсивность отказов и среднюю наработку до первого отказа катушки электромагнитного контактора.
3.1 Основное соединение элементов
Система, состоящая из нескольких независимых элементов, связанных функционально таким образом, что отказ любого из них вызывает отказ системы, отображается расчетной структурной схемой безотказной работы с последовательно соединенными событиями безотказной работы элементов.
Исходные данные.
Нерезервированная система состоит из 5 элементов. Интенсивности их отказов соответственно равны 0,00007; 0,00005; 0,00004; 0,00006; 0,00004 ч-1
Требуется.
Необходимо определить показатели надежности системы: интенсивность отказов, среднее время наработки до отказа, вероятность безотказной работы, частота отказов. Показатели надежности P(l) и a(l) получить в интервале от 0 до 1000 часов с шагом в 100 часов.
Вычислим интенсивность отказа и среднюю наработку до отказа по следующим уравнениям:
Значения вероятности безотказной работы и частоты отказов получим, используя уравнения приведенные к виду:
Результаты расчета P(l) и a(l) на интервале от 0 до 1000 часов работы представим в виде табл. 3.1.
Таблица 3.1.
| l, час | P(l) | a(l), час-1 |
| 0 | 1 | 0,00026 |
| 100 | 0,974355 | 0,000253 |
| 200 | 0,949329 | 0,000247 |
| 300 | 0,924964 | 0,00024 |
| 400 | 0,901225 | 0,000234 |
| 500 | 0,878095 | 0,000228 |
| 600 | 0,855559 | 0,000222 |
| 700 | 0,833601 | 0,000217 |
| 800 | 0,812207 | 0,000211 |
| 900 | 0,791362 | 0,000206 |
| 1000 | 0,771052 | 0,0002 |
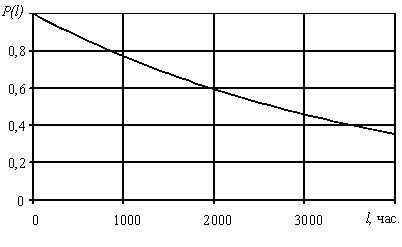
Графическая иллюстрация P(l) и a(l) на участке до средней наработки до отказа представлена на рис. 3.1, 3.2.
Рис. 3.1. Вероятность безотказной работы системы.
Рис. 3.2. Частота отказов системы.
3.2 Резервное соединение элементов
Исходные данные.
На рис. 3.3 и 3.4 показаны две структурные схемы соединения элементов: общего (рис. 3.3) и поэлементного резервирования (рис. 3.4). Вероятности безотказной работы элементов соответственно равны P1(l) = P ’1(l) = 0,95; P2(l) = P’2(l) = 0,9; P3(l) = P ’3(l) = 0,85.
Требуется.
Необходимо рассчитать надежность двух систем.
Рис. 3.3. Схема системы с общим резервированием.
Рис. 3.4. Схема системы с поэлементным резервированием.
Вероятность безотказной работы блока из трех элементов без резервирования рассчитаем по выражению:
Вероятность безотказной работы той же системы при общем резервировании (рис. 3.3) составит:
Вероятности безотказной работы каждого из трех блоков при поэлементном резервировании (рис. 3.4) будут равны:
Вероятность безотказной работы системы при поэлементном резервировании составит:
Таким образом, поэлементное резервирование дает более существенное увеличение надежности (вероятность безотказной работы возросла с 0,925 до 0,965, т.е. на 4%).
Исходные данные.
На рис. 3.5 представлена система с комбинированным соединением элементов. При этом вероятности безотказной работы элементов имеют следующие значения: P1=0,8; Р2=0,9; Р3=0,95; Р4=0,97.
Требуется.
Необходимо определить надежность системы. Также необходимо определить надежность этой же системы при условии, что резервные элементы отсутствуют.
Рис.3.5. Схема системы при комбинированном функционировании элементов.
Для расчета в исходной системе необходимо выделить основные блоки. В представленной системе их три (рис. 3.6). Далее рассчитаем надежность каждого блока в отдельности, а затем найдем надежность всей системы.
Рис. 3.6. Сблокированная схема.
Надежность системы без резервирования составит:
Таким образом, система без резервирования является на 28% менее надежной, чем система с резервированием.
diagnosticlab.ucoz.ru
Вероятность безотказной работы элемента p(t).
— вероятность того, что в заданном интервале времени t в элементе не возникнет отказ.
Если взять группу, состоящую из N одинаковых элементов, и поставить их на испытания то графически процесс испытания будет выглядеть так:
Так как отказ — случайная величина, то нельзя заранее сказать чему будет равно время работы i элемента, но можно определить вероятность того, что он не откажет в течении заданного времени t. Это может быть определено по данным испытания. Практически для вероятности безотказной работы p(t) используется следующая статистическая оценка p*(t)=[N-n(t)]/N, где N- число элементов на испытании, n(t)- число элементов отказавших в течение времени t. Точность оценки будет тем выше, чем больше N, в пределе статистическая оценка будет стремится к истинному значению при NÞ к бесконечности: p*(t)=Lim[N-n(t)]/NÞp(t).
Вероятность безотказной работы системы P(t).
— вероятность того, что в заданном интервале времени t в системе не возникнет отказ. Если элементы в системе соединены последовательно относительно надежности, то выход из строя хотя бы одного элемента приводит к отказу всей системы. Если вероятности безотказной работы элементов в системе будут p1(t), p2(t),.. pN(t) то в соответствии с теоремой умножения вероятности (вероятность произведения 2х событий равна произведению вероятности одного из них на условную вероятность другого, при условии что первая имело место) вероятность безотказной работы системы имеет вид: P(t)= p1(t) p2(t)… pN(t). Если p1(t)= p2(t)= pN(t), тогда P(t)=[p(t)]N. Так как вероятность безотказной работы элементов всегда меньше единицы, то из расчетов следует: 1) надежность системы уменьшается при увеличении числа элементов в ней; 2) вероятность безотказной работы системы всегда меньше вероятности безотказной работы самого ненадежного элемента.
Вероятность отказа системы Q(t).
Под вероятностью отказа системы понимают вероятность того, что за малый интервал времени t в системе произойдет отказ, т.е. время исправной работы системы будет меньше заданного. Так как безотказная работа и отказ- события противоположные, то Q(t)=1-P(t)
Q(t)=1-{[1- [1-q2(t)]… [1-qN(t)]} при q(t)- одинаковых Q(t)=1-[1-q(1)]N. Если надежность оценивается для малых промежутков времени, когда вероятность отказа много меньше 1, тогда Q(t)=1-{1-[q1(t)+ q2(t)+… qN(t)]}=Sqi(t)(от 1 до N). Если вероятность отказов элементов равны, то Q(t)=Nq(t).
Частота отказов f(t).
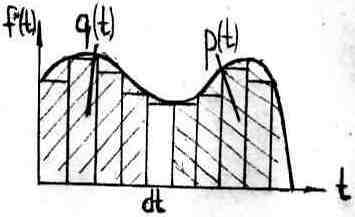
Достоинства этого критерия в том, что он позволяет судить о числе элементов которые откажут в течении определенного интервала времени. Понятие частоты отказов используется только для невосстанавливаемых изделий. Для восстанавливаемых изделий используется критерий средняя частота отказов (параметр потока отказов)- fср(t) – это отношение числа отказавших в единицу времени элементов к общему их числу, при условии что отказавшие элементы заменяются новыми: fср(t)= n(Dt)/(N*Dt). Если сравнить fср(t) и f(t) то мы увидим что fср(t)>f(t). Эти два критерия связаны между собой интегральным уравнением Вольтера второго рода. Достоинства этого критерия в том, что он отражает реальные условия эксплуатирования.
6. Средняя частота отказа — это отношения числа отказавших в единицу времени элементов к общему числу элементов при условии, что отказавшие элементы заменились новыми
Формула имеет вид
| f ср * (ti) = n(Δti)/NΔti; [1/r] | (1.19 ) |
где n(Δti) – число элементов отказавших в интервале Δti
N – число элементов поставленных на испытание
Δti– интервал времени для которого определяется средняя частота отказов.
fср(ti) = ω(t) = lim n(Δti)/NΔti
N→∞
F(t) = a(t) – частота отказов
Параметр потокоотказа и частота отказов для ординарных потоков с ограниченным последствием при мгновенном восстановлении связи интегрируемым уравнением Вольтера 2 рода
t
f ср (t) = f(t) + ∫ f ср (τ) f (t – τ) dτ
Данное уравнение в оперативной форме
fср (s) = f(s)/ 1-f(s)
f(s) = fср(s) / 1+ f ср(s)
∞ -sτ
f(s) = ∫f(t)e dt
Критерий этот используется для восстанавливающейся аппаратуры, а так как элементы которые вновь будут отказывать то всегда f ср(t) ≥ f(t)
Достоинство этого критерия в том ,что отражает реальны процесс эксплуатации аппаратуры.
Интенсивность отказов l(t).
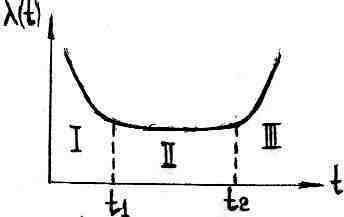
Интенсивность отказов для восстанавливаемых систем. Для этих систем под интенсивностью отказа системы понимают количество отказов в единицу времени. При этом после каждого отказа система восстанавливается, а отказавшие элементы заменяются новыми L(t)=1/mS[n(Dt)/Dt]( сумма от1 до m), где m- число интервалов наблюдения; n(Dt)- число элементов отказавших за Dt. Так как отказы любой системы слагаются из отказов входящих в нею элементов то при l(t)=const интенсивность отказов системы L(t) может быть определена: L(t)=Sfсрi(Dt)( сумма от i=1 до к), где к- число групп элементов с различной средней частотой отказов, т.е. интенсивность отказов равна сумме средних частот отказов всех элементов.
infopedia.su
Вероятность безотказной работы. — Мегаобучалка
Под вероятностью безотказной работы понимается вероятность того, что в заданном интервале времени или в пределах заданной наработки отказ не возникает.
Математически этот показатель можно определить как вероятность того, что время Т безотказной работы, являющегося случайной величиной, будет больше некоторого заданного времениt, т.е.
P*( t )=P{Т>t}
Согласно определению вероятность безотказной работы подсчитывается по формуле:
,
где : N0 – число образцов аппаратуры в начале испытаний;
n(t) –число отказавших образцов за время t.
На практике пользуются приближенной зависимостью:
.
Точность определения Р* (t) зависит от числа N0. Функция вероятности безотказной работы Р (t) является не возрастающей функцией времени и обладав следующими очевидными свойствами:
а) 0 < Р (t)< 1;
б) Р (0) = 1;
в) Р (¥) = 0.
График зависимости P(t) от времени представлен на рис. 2.1.
Рис. 2.1
На практике часто приходится пользоваться понятием вероятности отказа
Q* (t), т.е. события, противоположного событию безотказной работы.
Из определения Q* (t)= P*{T < t}=l — P (t) очевидно, что Р* (t) + Q* (t)= 1- как сумма противоположных событий. Вероятность безотказной работы является основным количественным показателем надежности, так как наиболее полно охватывает все многообразие факторов, влияющих на надежность. Чем больше P(t), тем выше ее надежность
Частота отказов
Частота отказов — число отказов в единицу времени, отнесенное к первоначальному числу элементов.
Прежде всего, определим статистически частоту отказов f * (t), которая имеет важное теоретическое значение, так как применяется в расчетах для связи с другими основными показателями надежности. В математическом смысле f * (t) есть безусловная плотность распределения наработки до отказа.
Из статистических данных, полученных в результате испытаний или опытной эксплуатации, частота отказов определяется по формуле:
,
где n(t) — число отказавших изделий в рассматриваемый интервал времени Dt, т.е.
в период от до ;
N0 — число изделии, первоначально взятых на испытание (поставленных на
эксплуатацию).
Считаем, что изделия при испытании (эксплуатации) не восстанавливаются и
не заменяются новыми.
Типичная кривая изменения частоты отказов изделий в соответствии с
зависимостью f * (t) показана на рис. 2.2. На этой кривой можно отметить три характерных участка.
Первый участок характеризуется большими значениями частоты отказов. Здесь проявляются отказы, обусловленные грубыми ошибками в принципиальной схеме или в конструкции изделия, технологии его изготовления, несоблюдением требований конструкторской и технологической документации, применением некондиционных материалов и элементов, слабым контролем качества изделий на всех этапах производства и ввода техники в эксплуатацию.
К этой группе отказов можно отнести также эксплуатационные отказы, вызванные слабым знанием правил эксплуатации (или отсутствием необходимого опыта). Поэтому первый период называется периодом приработки изделий (элементов).
Второй участок характерен сравнительно постоянным значением частоты отказов и называется периодом нормальной эксплуатации.
На третьем участке частота отказов вначале вновь возрастает за счет наступления старения и износа элементов или устройств, а затем падает до нуля. Этот период называется периодом старения.
Длительность вышерассмотренных участков различна: для первого она составляет величину порядка нескольких десятков, нескольких сотен часов в зависимости от сложности изделия; второй участок самый продолжительный и при расчетах принимается равным 2/3 технического ресурса; третий период зачастую не достигается, так как раньше наступает «моральное старение», при котором данный ТУ списывается.
Рисунок 2.2. Кривая изменения частоты отказов от наработки
Интенсивность отказов
Интенсивность отказов — вероятность отказов невосстанавливаемого изделия в единицу времени после данного момента времени при условии, что до этого момента отказ не возник. Интенсивность отказов определяется числом отказов в единицу времени, отнесенному к среднему числу элементов, исправно работающих в данный отрезок времени, т.е.
,
где — среднее число элементов, продолжающих исправно работать на интервале Dt.
Рисунок 2.3. Зависимость интенсивности отказов от наработки
Число определяют с помощью выражения:
Интенсивность отказов характеризует степень надежности элементов (изделий) в каждый момент времени, поэтому является более полной и качественной характеристикой надежности.
Зависимость l* от t представлена на рисунке 2.3.
Из сравнения данных по f * (t) и l* (t) следует, что l* (t) в начале испытаний (эксплуатации) несколько выше f * (t) , а в конце испытаний существенно отличается от частоты отказов (см. рис. 2.2).
Интенсивность отказов, являясь одним из основных количественных показателей надежности изделий, широко используется для определения других показателей свойств надежности.
megaobuchalka.ru
Оценка вероятности безотказной работы системы по результатам испытаний
Методика оценки результатов испытаний
систем, вероятность безотказной работы
которых подчиняется экспоненциальному
закону Р(t) = е—t/T,
может быть двоякой в зависимости от
характера системы.
По результатам испытаний оценивается
величина Т. Как известно из математической
статистики, по результатам испытаний
можно определить доверительный интервал
для Т с некоторой достоверностью
(вероятностью).
Если проведено испытание, в течение
которого система проработала tnчасов и при этом произошлоnотказов (последний отказ произошел в
моментtn),
то доверительный интервал для Т с
доверительной вероятностью 1 —αопределяется следующим образом:
(3.33)
где x2α/2(2n),x21-α/2(2n)
— значение функцииx2с 2nстепенями свободы дляα/2 и для 1-α/2
соответственно. Значение этой функции
находятno-известным
таблицам [3.1].
Пример 3.2. АСУ испытывалась в течение
140 ч. За это время произошло 10 отказов.
Необходимо по результатам испытаний
оценить среднее время наработки на
отказ с доверительной вероятностью
0,96=1—α.
По величинам α= 0,04 иn=10
определяемx2α/2(2n)
иx21-α/2(2n).
По таблицеx20,02=35,x20,98=9,2. Затем
вычисляем:Tmin= 2*140/35 = 8;Tmах =.2*140/9,2 = 31.
Следовательно, с доверительной
вероятностью 0,96 можно считать, что
истинная величина среднего времени
наработки на отказ заключена в пределах
8< Т < 31.
Описанная методика применима для
определения доверительного интервала
для Т по результатам законченного
испытания до отказа. Возникает вопрос
о продолжительности испытаний, так как
для Т .получается не одно значение,
а целый интервал значений. Если левая
доверительная граница доверительного
интервала стала больше Тзад, то испытания
можно прекратить и считать, что система
удовлетворяет заданному требованию.
Наоборот, если получилось, что правая
доверительная граница стала меньше,
то система не будет удовлетворять
поставленным требованиям.
Испытания могут быть прекращены, если
Тmах << Тзад. Если
Тmin<Тзад<Тmaxто нет оснований для принятия того или
иного решения; испытания необходимо
продолжать до тех пор, пока интервал
значений Т = Тmах—Tminне станет меньше некоторого значенияD. ВыборDи
принятие в этом случае решения зависят
от конкретных условий.
Матричный метод расчета надежности
В ряде случаев отказ элемента системы
приводит к изменению режимов работы
других связанных с ним элементов, что
может повлечь за собой изменение
характеристик надежности этих элементов.
Например, пробой конденсатора вызывает
изменение тока в цепях схемы, в результате
чего изменяются коэффициенты нагрузки
элементов, а следовательно, и их
надежность. В подобных случаях желательно
при расчете надежности учитывать
взаимозависимость отказов элементов
и перераспределение интенсивностей
отказов за счет изменения режимов
работы, вызванных отказами. Для решения
этой задачи может быть использован
матричный метод анализа и расчета
надежности (см. [4.5]), позволяющий учитывать
последствие отказов.
Сущность метода состоит в том, что для
определения вероятности безотказной
работы ВМ от внезапных отказов с учетом
последствия отказов составляется
матрица всевозможных несовместимых
событий x1,x2,…,xN,
вычисляются вероятности всех этих
событий, затем суммируются вероятности
благоприятных гипотез, при которых
система находится в работоспособном
состоянии.
В общем случае матрица несовместимых
событий для аппаратуры, состоящей
из N элементов, за период tимеет следующий вид:
В этой матрице хi—
состояниеi-гoэлемента;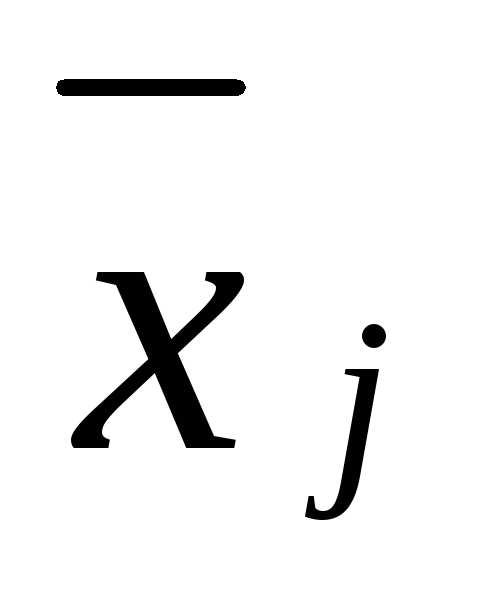
чтоiэлемент отказал;H0— гипотеза, заключающаяся в том, что ни
один из элементов не отказал; Нi— гипотеза, заключающаяся в том, чтоi-й элемент отказал; Нα,β— гипотеза отказа двух элементовαиβ, причем вначале
отказывает элементα, а
потомβ.
Так как матрица образует полную группу
несовместимых событий, то их можно
принять за соответствующие гипотезы.
Среди гипотез матрицы есть благоприятные
с точки зрения работоспособности
системы и неблагоприятные. Сумма
вероятностей всех гипотез равна единице.
Сумма вероятностей благоприятных
гипотез определяет надежность
системы, т. е. вероятность безотказной
работы за некоторое заданное время
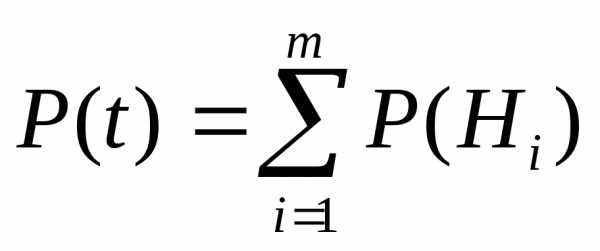
где m— число благоприятных
гипотез.
Наиболее трудоемкой частью расчета
является определение вероятностей
гипотез (состояний), особенно для сложных
устройств.
Вероятность отсутствия отказов элементов
определяется произведением вероятностей
безотказной работы всех элементов:
Вероятности остальных гипотез имеют
более сложные выражения и определяются
через условные вероятности частных
событий. Приведем без вывода формулу
для расчета вероятности отказа элемента
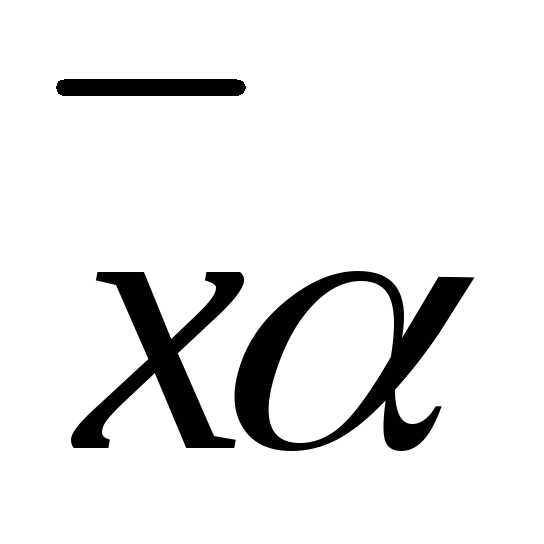
где υ≠α,λυα—изменение интенсивности отказовυ-roэлемента
вследствие отказаα-го
элемента.
Таким образом, для выполнения расчета
надежности с помощью данного метода
необходимо знать интенсивности отказов
элементов λпри
нормальных режимах работы устройства
и их изменения, вызванные сменой
режимов за счет отказов различных
элементов.
Пример 4.1. Узел аппаратуры состоит из
двух параллельно включенных блоков,
имеющих одинаковую интенсивность
отказов: λ1=λ2=
0,4*10-5. При отказе одного из блоков
узел еще продолжает функционировать,
но коэффициент электрической нагрузки
второго элемента увеличивается,
вследствие чего интенсивность отказов
возрастает до величиныλ1(2)=λ2(1)= 10-5. Требуется рассчитать
вероятность безотказной работы звена
на этих условиях за время 50000 ч.
Из общего числа состояний узла выбираем
следующие три благоприятные гипотезы:
оба элемента исправны (H0),
отказал 1-й элемент (Н1), отказал
2-й элемент (H2).
Остальные состояния, когда отказали
оба элемента в различной временной
последовательности, соответствуют
неблагоприятным гипотезам (отказ узла).
Вероятность первого состояния
Вероятность второго состояния
Вероятность третьего состояния
Вероятность безотказной работы узла
Если рассчитать надежность узла по
формуле для резервного соединения (без
учета последствия отказа), то вероятность
безотказной работы P(t)=1-(1—е—λt)2=1—(1—е-0,2)2 = =0.967, т. е. получаем
завышенный результат.
Матричный метод расчета надежности не
накладывает никаких ограничений на
структуру и способы соединения. В этом
его достоинство.
studfiles.net
Вероятность безотказной работы — это… Что такое Вероятность безотказной работы?
Вероятность безотказной работы — вероятность того, что в пределах заданной наработки не возникает отказ изделия (объекта). Источник: НП 068 05: Трубопроводная арматура для атомных станций. Общие технические требования 3.1.9 вероятность безотказной работы: Вероятность того, что в … Словарь-справочник терминов нормативно-технической документации
вероятность безотказной работы — Вероятность того, что в пределах заданной наработки отказ объекта не возникнет. [ГОСТ 27.002 89] [ОАО РАО «ЕЭС России» СТО 17330282.27.010.001 2008] Тематики надежность, основные понятия EN reliability functionsurvival function … Справочник технического переводчика
вероятность безотказной работы R ( t 1 , t 2 ) — 89 вероятность безотказной работы R ( t 1 , t 2 ): Вероятность выполнить требуемую функцию при данных условиях в интервале времени (t1, t2). Источник: ГОСТ Р 53480 2009: Надежность в технике. Термины и определения оригинал документа … Словарь-справочник терминов нормативно-технической документации
вероятность безотказной работы R(t1, t2) — 89 вероятность безотказной работы R(t1, t2): Вероятность выполнить требуемую функцию при данных условиях в интервале времени (t1, t2). Примечания 1 Обычно предполагают, что в начале интервала времени изделие находится в работоспособном состоянии … Словарь-справочник терминов нормативно-технической документации
вероятность безотказной работы — negendamumo tikimybė statusas T sritis Standartizacija ir metrologija apibrėžtis Tikimybė, kad per numatytą išdirbį objektas nesuges. atitikmenys: angl. reliability probability rus. вероятность безотказной работы, f pranc. probabilité de… … Penkiakalbis aiškinamasis metrologijos terminų žodynas
Вероятность безотказной работы — – вероятность того, что в пределах заданной наработки отказ объекта не возникнет. ГОСТ 27.002 89 … Коммерческая электроэнергетика. Словарь-справочник
вероятность безотказной работы — вероятность того, что в пределах заданной наработки отказ не возникнет … Политехнический терминологический толковый словарь
Вероятность безотказной работы — English: Reliability function Вероятность того, что в пределах заданной наработки отказ объекта не возникнет (по ГОСТ 27.002 89) Источник: Термины и определения в электроэнергетике. Справочник … Строительный словарь
Вероятность безотказной работы — показатель надёжности (См. Надёжность) устройства, схемы или отдельного элемента, который оценивает возможность сохранения изделием работоспособности (См. Работоспособность) в определённом интервале времени или при выполнении заданного… … Большая советская энциклопедия
Вероятность безотказной работы системы — [Р] способность системы не допускать отказов, приводящих к падению температуры в отапливаемых помещениях жилых и общественных зданий ниже +12 °С, в промышленных зданиях ниже +8 °С, более числа раз, установленного нормативами. Источник: СНиП 41 02 … Словарь-справочник терминов нормативно-технической документации
dic.academic.ru
Различают вероятностные (математические) и статистические показатели надежности. Математические показатели надежности выводятся из теоретических функций распределения вероятностей отказов. Статистические показатели надежности определяются опытным путем при испытаниях объектов на базе статистических данных эксплуатации оборудования.
Надежность является функцией многих факторов, большинство из которых случайны. Отсюда ясно, что для оценки надежности объекта необходимо большое количество критериев.
Критерий надежности – это признак, по которому оценивается надежность объекта.
Критерии и характеристики надежности носят вероятностный характер, поскольку факторы, влияющие на объект, носят случайный характер и требуют статистической оценки.
Количественными характеристиками надежности могут быть:
• вероятность безотказной работы;
• среднее время безотказной работы;
• интенсивность отказов;
• частота отказов;
• различные коэффициенты надежности.
1. Вероятность безотказной работы
Служит одним из основных показателей при расчетах на надежность.
Вероятность безотказной работы объекта называется вероятность того, что он будет сохранять свои параметры в заданных пределах в течение определенного промежутка времени при определенных условиях эксплуатации.
В дальнейшем полагаем, что эксплуатация объекта происходит непрерывно, продолжительность эксплуатации объекта выражена в единицах времени t и эксплуатация начата в момент времени t=0.
Обозначим P(t) вероятность безотказной работы объекта на отрезке времени [0,t]. Вероятность, рассматриваемую как функцию верхней границы отрезка времени, называют также функцией надежности.
Вероятностная оценка: P(t) = 1 – Q(t), где Q(t) — вероятность отказа.
Типичная кривая вероятности безотказной работы
Из графика очевидно, что:
1. P(t) – невозрастающая функция времени;
2. 0 ≤ P(t) ≤ 1;
3. P(0)=1; P(∞)=0.
На практике иногда более удобной характеристикой является вероятность неисправной работы объекта или вероятность отказа:
Q(t) = 1 – P(t).
Статистическая характеристика вероятности отказов: Q*(t) = n(t)/N
2. Частота отказов
Частотой отказов называется отношение числа отказавших объектов к их общему числу перед началом испытания при условии что отказавшие объекты не ремонтируются и не заменяются новыми, т.е
a*(t) = n(t)/(NΔt)
где a*(t) — частота отказов;
n(t) – число отказавших объектов в интервале времени от t – t/2 до t+ t/2;
Δt – интервал времени;
N – число объектов, участвующих в испытании.
Частота отказов есть плотность распределения времени работы изделия до его отказа. Вероятностное определение частоты отказов a(t) = -P(t) или a(t) = Q(t).
Таким образом, между частотой отказов, вероятностью безотказной работы и вероятностью отказов при любом законе распределения времени отказов существует однозначная зависимость: Q(t) = ∫ a(t)dt.
Отказ трактуют в теории надежности как случайное событие. В основе теории лежит статистическое истолкование вероятности. Элементы и образованные из них системы рассматривают как массовые объекты, принадлежащие одной генеральной совокупности и работающие в статистически однородных условиях. Когда говорят об объекте, то в сущности имеют в виду наугад взятый объект из генеральной совокупности, представительную выборку из этой совокупности, а часто и всю генеральную совокупность.
Для массовых объектов статистическую оценку вероятности безотказной работы P(t) можно получить, обработав результаты испытаний на надежность достаточно больших выборок. Способ вычисления оценки зависит от плана испытаний.
Пусть испытания выборки из N объектов проведены без замен и восстановлений до отказа последнего объекта. Обозначим продолжительности времени до отказа каждого из объектов t1, …, tN. Тогда статистическая оценка:
P*(t) = 1 — 1/N ∑η(t-tk)
где η — единичная функция Хевисайда.
Для вероятности безотказной работы на определенном отрезке [0, t] удобна оценка P*(t) = [N — n(t)]/N,
где n(t) – число объектов, отказавших к моменту времени t.
Частота отказов, определяемая при условии замены отказавших изделий исправными, иногда называется средней частотой отказов и обозначается ω(t).
3. Интенсивность отказов
Интенсивностью отказов λ(t) называется отношение числа отказавших объектов в единицу времени к среднему числу объектов, работающих в данный отрезок времени, при условии, что отказавшие объекты не восстанавливаются и не заменяются исправными: λ(t) = n(t)/[NсрΔt]
где Nср = [Ni + Ni+1]/2 — среднее число объектов, исправно работавших в интервале времени Δt;
Ni – число изделий, работавших в начале интервала Δt;
Ni+1 – число объектов, исправно работавших в конце интервала времени Δt.
Ресурсные испытания и наблюдения над большими выборками объектов показывают, что в большинстве случаев интенсивность отказов изменяется во времени немонотонно.
Типичная кривая изменения интенсивности отказов объекта
Из кривой зависимости отказов от времени видно, что весь период работы объекта можно условно поделить на 3 периода.
I — й период – приработка.
Приработочные отказы являются, как правило, результатом наличия у объекта дефектов и дефектных элементов, надежность которых значительно ниже требуемого уровня. При увеличении числа элементов в изделии даже при самом строгом контроле не удается полностью исключить возможность попадания в сборку элементов, имеющих те или иные скрытые дефекты. Кроме того, к отказам в этот период могут приводить и ошибки при сборке и монтаже, а также недостаточная освоенность объекта обслуживающим персоналом.
Физическая природа таких отказов носит случайный характер и отличается от внезапных отказов нормального периода эксплуатации тем, что здесь отказы могут иметь место не при повышенных, а и при незначительных нагрузках («выжигание дефектных элементов»).
Снижение величины интенсивности отказов объекта в целом, при постоянном значении этого параметра для каждого из элементов в отдельности, как раз и объясняется «выжиганием» слабых звеньев и их заменой наиболее надежными. Чем круче кривая на этом участке, тем лучше: меньше дефектных элементов останется в изделии за короткий срок.
Чтобы повысить надежность объекта, учитывая возможность приработочных отказов, нужно:
• проводить более строгую отбраковку элементов;
• проводить испытания объекта на режимах близких к эксплуатационным и использовать при сборке только элементы, прошедшие испытания;
• повысить качество сборки и монтажа.
Среднее время приработки определяют при испытаниях. Для особо важных случаев необходимо увеличить срок приработки в несколько раз по сравнению со средним.
II — й период – нормальная эксплуатация
Этот период характеризуется тем, что приработочные отказы уже закончились, а отказы, связанные с износом, еще не наступили. Этот период характеризуется исключительно внезапными отказами нормальных элементов, наработка на отказ которых очень велика.
Сохранение уровня интенсивности отказов на этом этапе характеризуется тем, что отказавший элемент заменяется таким же, с той же вероятностью отказа, а не лучшим, как это происходило на этапе приработки.
Отбраковка и предварительная обкатка элементов, идущих на замену отказавших, имеет для этого этапа еще большее значение.
Наибольшими возможностями в решении этой задачи обладает конструктор. Нередко изменение конструкции или облегчение режимов работы всего одного-двух элементов обеспечивает резкое повышение надежности всего объекта. Второй путь – повышение качества производства и даже чистоты производства и эксплуатации.
III – й период – износ
Период нормальной эксплуатации заканчивается, когда начинают возникать износовые отказы. Наступает третий период в жизни изделия – период износа.
Вероятность возникновения отказов из-за износов с приближением к сроку службы возрастает.
С вероятностной точки зрения отказ системы в данном промежутке времени Δt = t2 – t1 определяется как вероятность отказа:
∫a(t) = Q2(t) — Q1(t)
Интенсивность отказов есть условная вероятность того, что в промежуток времени Δt произойдет отказ при условии, что до этого он не произошел λ(t) = [Q2 — Q1]/[ΔtP(t)]
λ(t) = lim [Q2 — Q1]/[ΔtP(t)] = [dQ(t)]/[P(t)dt] = Q'(t)/P(t) = -P'(t)/P(t)
так как a(t) = -P'(t), то λ(t) = a(t)/P(t).
Эти выражения устанавливают зависимость между вероятностью безотказной работы, частотой и интенсивностью отказов. Если a(t) – невозрастающая функция, то справедливо соотношение:
ω(t) ≥ λ(t) ≥ a(t).
4. Среднее время безотказной работы
Средним временем безотказной работы называется математическое ожидание времени безотказной работы.
Вероятностное определение: среднее время безотказной работы равно площади под кривой вероятности безотказной работы.
T = ∫P(t)dt
Статистическое определение: T* = ∑θi/N0
где θI – время работы i-го объекта до отказа;
N0 – начальное число объектов.
Очевидно, что параметр Т* не может полностью и удовлетворительно характеризовать надежность систем длительного пользования, так как является характеристикой надежности только до первого отказа. Поэтому надежность систем длительного использования характеризуют средним временем между двумя соседними отказами или наработкой на отказ tср:
tср = ∑θi/n = 1/ω(t),
где n – число отказов за время t;
θi – время работы объекта между (i-1)-м и i-м отказами.
Наработка на отказ – среднее значение времени между соседними отказами при условии восстановления отказавшего элемента.


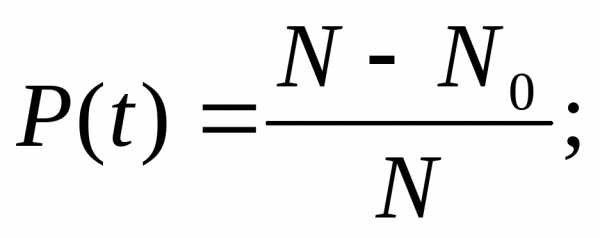
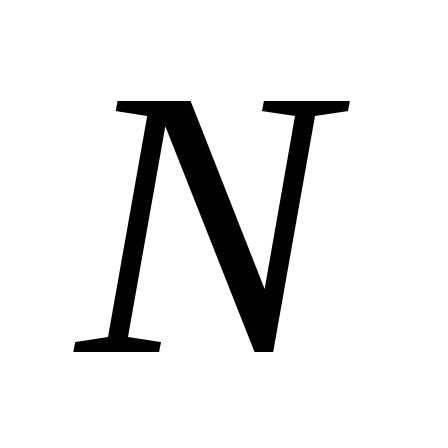
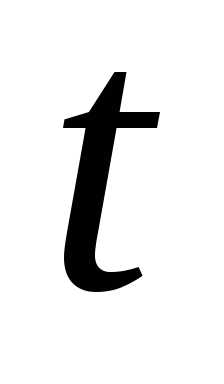
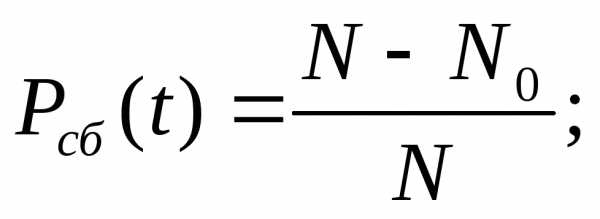
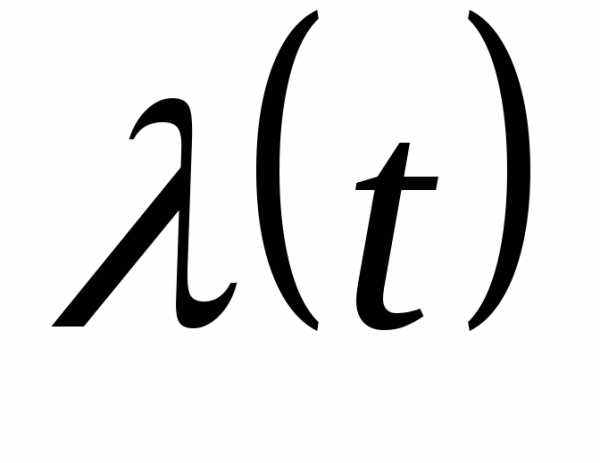


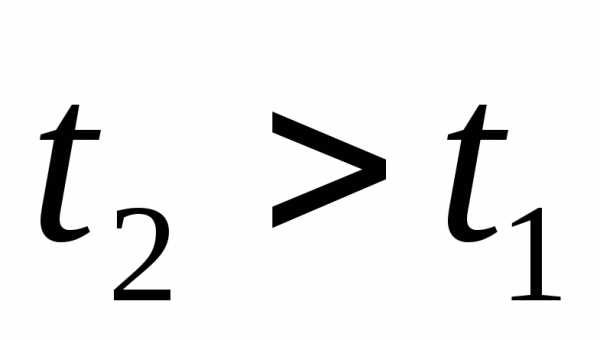
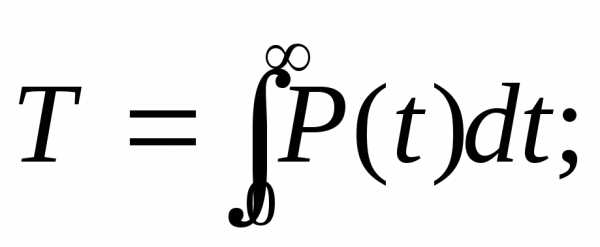

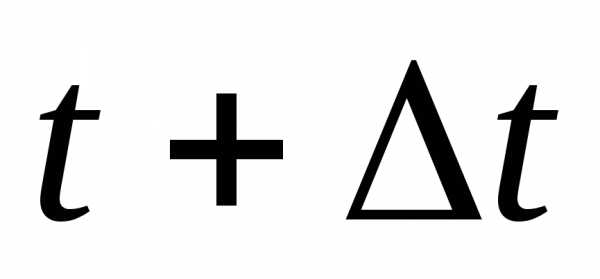
 ,
, ,
,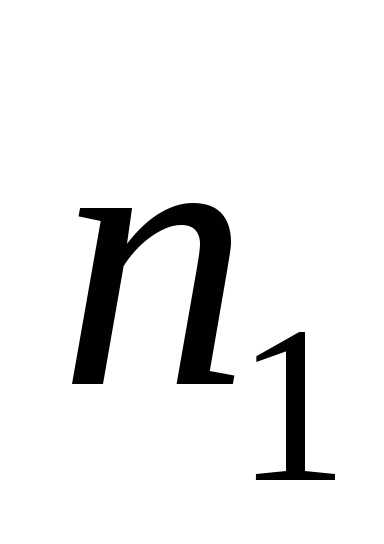 ,
,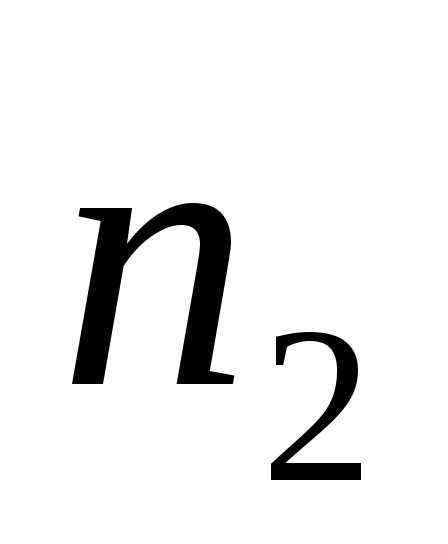 ,
, ,
,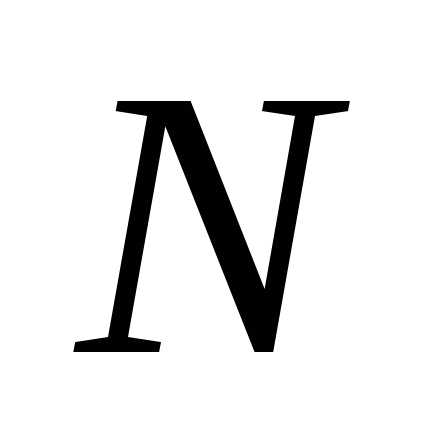 ,
, ,
,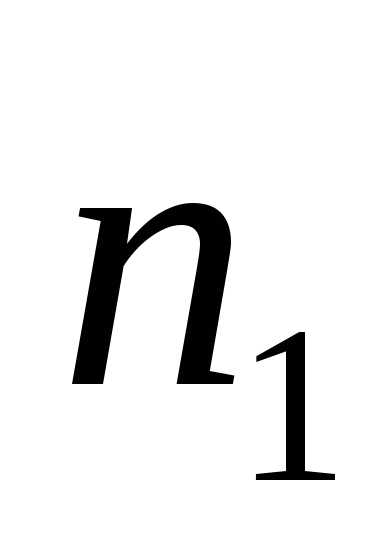 ,
,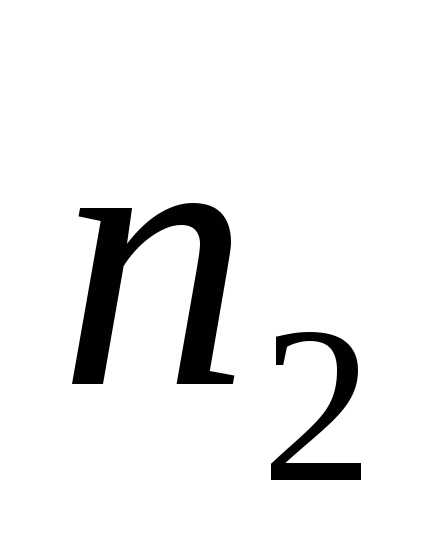 ,
, ,
,
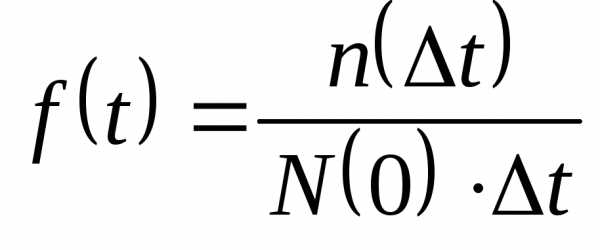 15. код
15. код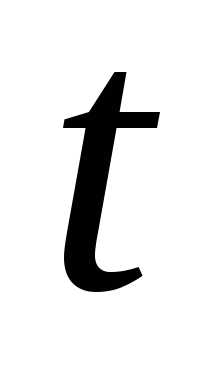 ,
, 16. код
16. код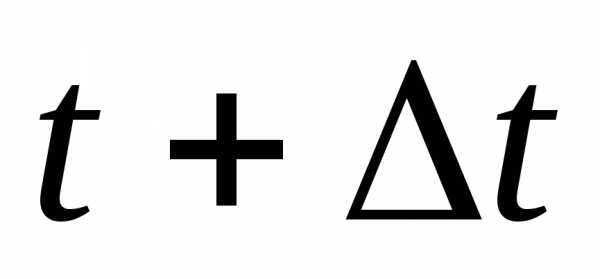 ,
,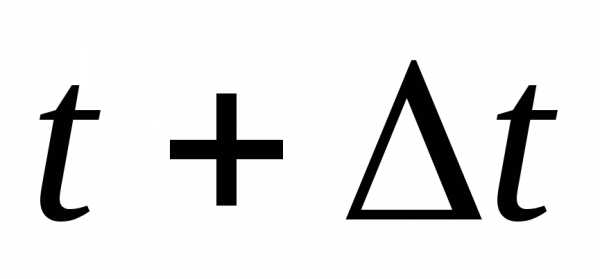 Определяем
Определяем ,
,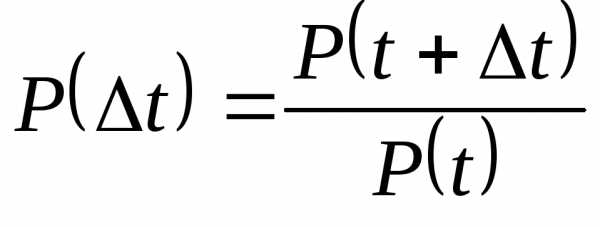 18. код
18. код Определяем
Определяем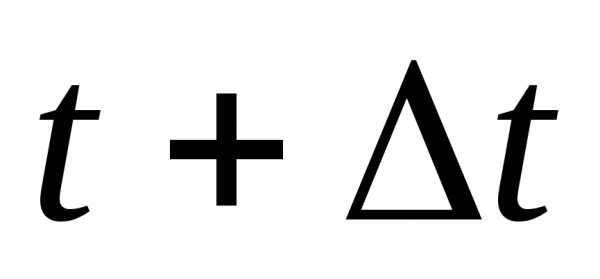 ,
,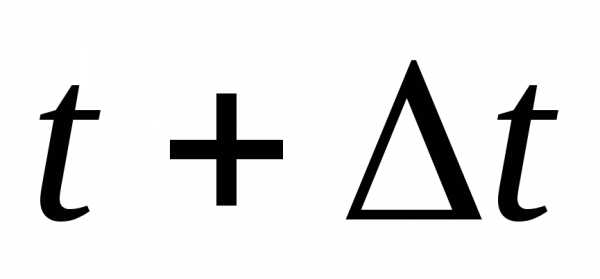 можно найти по одной из двух формул.
можно найти по одной из двух формул. или
или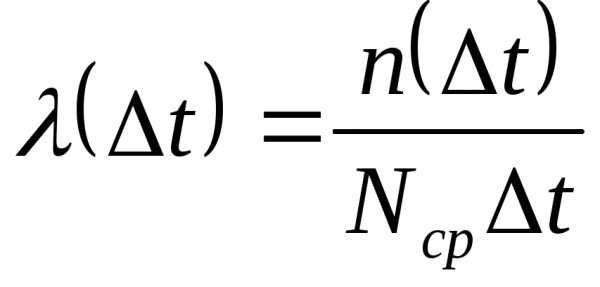
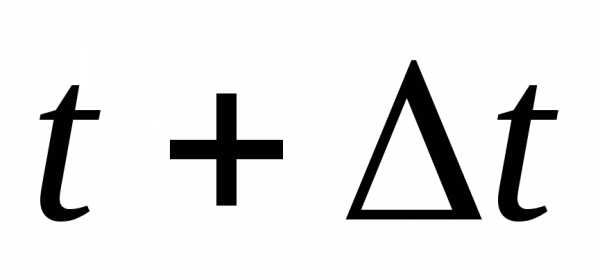 (I-й
(I-й (II-й
(II-й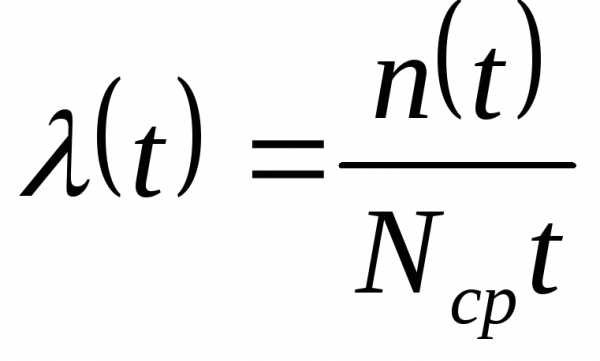 21. код
21. код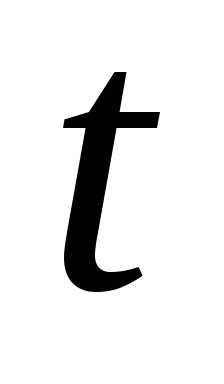 Рассчитываем
Рассчитываем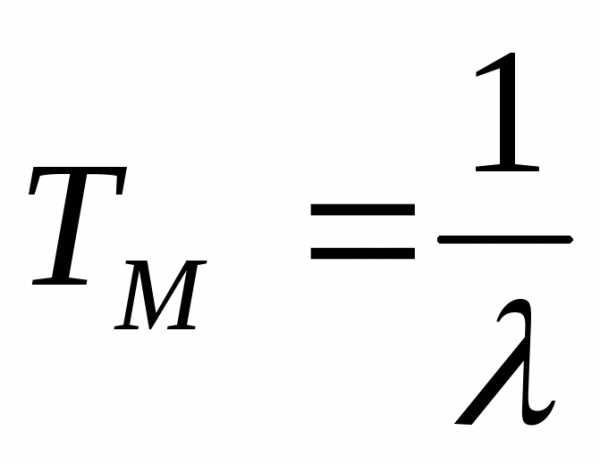 22. код
22. код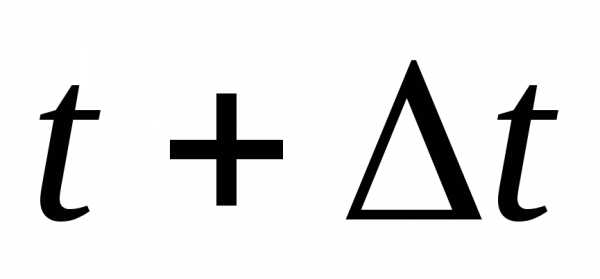 .
.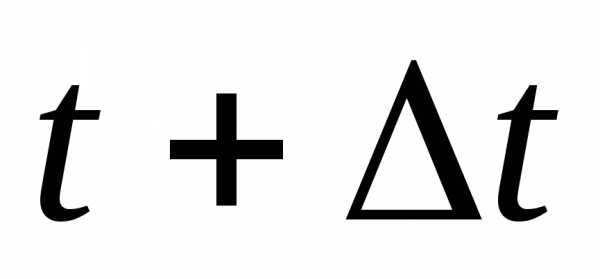 .
.