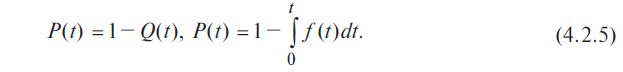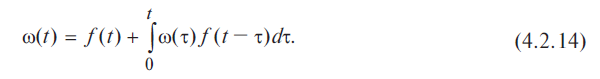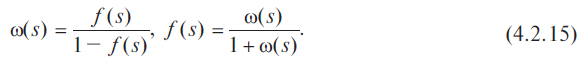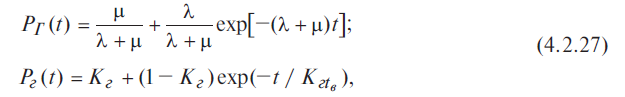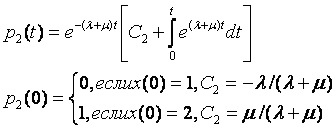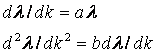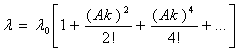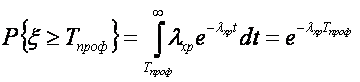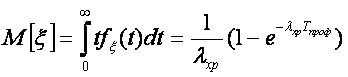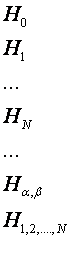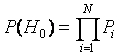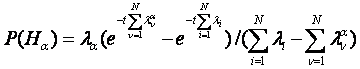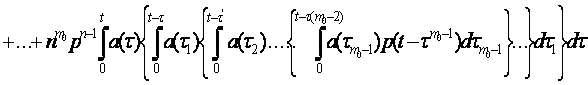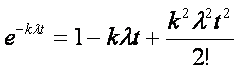Занятие № 5
Тема: Вероятность
безотказной работы и вероятность отказа.
Цель:
ü рассмотреть основные
показатели безотказной работы (вероятность безотказной работы и вероятность
отказа).
Основные понятия:
·
Показатели надежности
·
Вероятность безотказной
работы
·
Вероятность отказа
План занятия:
1. Организационный момент: приветствие, проверяется готовность к
занятию, отмечаются в журнале отсутствующие.
2. Проверка домашнего задания: фронтальный опрос.
3. Актуализация знаний: сообщение темы и цели занятия.
4. Изучение нового материала:
1.
Показатели надежности.
2.
Вероятность безотказной
работы.
3.
Вероятность отказа.
4.
Оценка вероятности
безотказной работы.
5. Закрепление
изученного материала:
ü Что называют
вероятностью безотказной работы?
ü Что называют вероятностью
отказа?
ü Дайте определение
понятия показатели надежности.
6. Домашнее
задание:
Яхъяев Н.Я. Основы теории надежности, стр. 39-41;
Задача:
На
испытание поставлено 1000 однотипных резисторов. За первые 10000 часов отказало
5, за последующие 5000 отказало еще 5. Определить вероятность безотказной
работы и вероятность отказа за 10000 часов, за 15000 часов и в промежутке между
10000 и 15000 часов.
7. Подведение
итогов занятия.
— Какое
состояние называется работоспособным? (Работоспособность – это состояние
изделия, при котором оно способно выполнять заданную функцию с параметрами,
установленными требованиями технической документации, в течение расчётного
срока службы).
Отказ –
это нарушение работоспособности. Свойство элемента или системы непрерывно
сохранять работоспособность при определённых условиях эксплуатации (до первого
отказа) называется безотказностью.
Безотказность
– свойство объекта сохранять работоспособное состояние в течение некоторого
времени или наработки.
И сегодня
на занятии мы рассмотрим показатели безотказности. Тема нашего занятия: «ВЕРОЯТНОСТЬ
БЕЗОТКАЗНОЙ РАБОТЫ И ВЕРОЯТНОСТЬ ОТКАЗА».
1. ПОКАЗАТЕЛИ
НАДЕЖНОСТИ.
Показатели
надежности – количественная характеристика одного или нескольких
свойств, составляющих надежность объекта.
Для
оценки, расчетов и исследования надежности технических устройств в процессе их
проектирования и эксплуатации используются количественные характеристики (критерии
надежности). Для показателей надежности используются две формы представления:
v Статистическая – при
эксперементальном исследовании надежности технических систем
v Вероятностная – при
априорных аналитических расчетах надежности.
В
соответствии с ГОСТ 27.002 – 89 показатели надежности подразделяются на:
Классификация
показателей надежности
|
Признак |
Показатель |
|
Число |
Единичный показатель |
|
Комплексный показатель |
|
|
Свойство |
Безотказность |
|
Долговечность |
|
|
Сохраняемость |
|
|
Ремонтопригодность |
|
|
Метод |
Расчетный показатель |
|
Экспериментальный показатель |
|
|
Эксплуатационный показатель |
|
|
Экстраполированный показатель |
|
|
Область |
Нормативный показатель, |
|
Оценочный показатель, |
|
|
Область |
Групповой показатель |
|
Индивидуальный показатель |
2. ВЕРОЯТНОСТЬ
БЕЗОТКАЗНОЙ РАБОТЫ.
Пусть
испытывается некоторое число изделий N0. По разным причинам они
будут выходить из строя, причем моменты отказов, т.е. время наработки каждого
изделия до отказов, является случайной величиной.
Вероятность
безотказной работы изделия есть вероятность того, что за
определенный рассматриваемый период времени работы (t) в заданных условиях
эксплуатации оно не откажет, т.е. вероятность того, что время наработки до
отказа (tотк) будет больше времени работы.
Р(t) = Вер (tотк>
t)
Если к
моменту t из поставленных на испытания N0 изделий останутся исправными N(t), то
статистическая вероятность безотказной работы изделия за время t, равно: , где N(t) – число работоспособных
изделий на момент t; N0 – общее число наблюдаемых изделий; n(t) –
число изделий, отказавших на момент t от начала испытаний.
При t = 0
все изделия исправны N(0) = N0 и P(0) = 1. Отказы изделия с течением
времени t приводят к монотонному убыванию функции Р(t). Практически для каждого
типа изделия существует наработка t*, больше которой ни одно изделие данного
типа проработать не может.
N(t) = 0,
при t ≥ t*соответственно Р(t) = 0, при t ≥ t*

образом, 0 ≤ P(t) ≤ 1.
Вероятность
безотказной работы уменьшается с увеличением времени работы или наработки
объекта. Зависимость вероятности безотказной работы от времени характеризуется
кривой убыли ресурса изделия, пример которой приведен на рисунке 1.
Рис. 1
В
начальный момент времени для работоспособного изделия вероятность его
безотказной работы равна единице (100%). По мере работы объекта эта вероятность
снижается и стремится к нулю.
Например: После
500 часов наработки из 56 агрегатов, поставленных на эксплуатацию, в работоспособном
состоянии оказалось 43 агрегата. Определить вероятность безотказной работы
агрегата в течение 500 час.
Решение:
Используем
формулу для определения вероятности безотказной работы объекта
Вероятность
безотказной работы агрегата в течение 500 часов составляет 76,8 %.
3. ВЕРОЯТНОСТЬ
ОТКАЗА.
Противоположным
событию безотказной работы является событие отказа
Вероятность
отказа
есть вероятность того, что время появления отказа будет меньше заданного
времени работы изделия, т.е. вероятность того, что время наработки до отказа (tотк)
будет меньше времени работы (t).
Q(t) = Вер (tотк<
t)
Статистическая
вероятность времени появления отказа равна: .
С течением
времени наработки число отказавших изделий непрерывно увеличивается.
Следовательно, вероятность отказов является монотонно возрастающей функцией.
Рис.2

зависимости вероятности возникновения отказа от времени показан на рисунке 2.
Для работоспособного объекта в начальный момент времени вероятность отказа
близка к нулю. Для того, чтобы отказ проявился, объекту необходимо начать
работать, при этом вероятность отказа увеличивается с увеличением времени и стремится
к единице. 0≤Q(t)≤1
Безотказная
работа изделия и его отказ являются двумя противоположными и несовместимыми
случайными величинами, поэтому их сумма всегда равна 1.
P(t)+Q(t)=1⟹P(t)=1-Q(t)
или Q(t)=1-P(t).
Например: Для
предыдущего примера определить вероятность отказа агрегатов за 500 часов
работы.
Решение:
Используем
формулу для вероятности отказа
или
Таким
образом, вероятность отказа агрегата за 500 часов составляет 23,2 %.
4. ОЦЕНКА
ВЕРОЯТНОСТИ БЕЗОТКАЗНОЙ РАБОТЫ.

за десятью однотипными изделиями в течение времени от 0 до t4. Здесь
сплошной прямой линией показана продолжительность безотказной работы изделия, а
крестиком – момент возникновения отказа.
Для наглядности
разместим наработки до отказов изделий последовательно по времени их появления.
Определение
технического состояния изделий в процессе испытаний производится в моменты
времени t1… t4. Оценки вероятностей безотказной работы за
соответствующие интервалы времени будут иметь вид:

полученным данным строится ступенчатый график – гистограмма, в конце каждого
интервала времени наблюдаемое значение вероятности в данном случае снижается на
долю изделий, отказавших на данном интервале.
Полученные
значения показывают приблизительно долю изделий, которые проработают безотказно
при испытаниях другой партии таких же изделий в аналогичных условиях.
Например:
Изготовив 20 новых изделий, можно утверждать, что в течение времени t3
приблизительно 12 изделий проработают безотказно (не проводя дополнительных
испытаний) 20*0,6=12. Это приближенная оценка будет тем точнее, чем больше
число испытанных изделий.
В качестве
показателя надежности может использоваться условная вероятность безотказной
работы на некотором интервале времени, которая вычисляется при условии, что
изделие было полностью исправно к началу этого времени.
Например: Условная
вероятность безотказной работы изделия на интервале времени от t2 до
t3 оценивается согласно выражению:
2.1. Критерии и количественные характеристики надежности
Критерием
надежности называется
признак, по которому можно количественно
оценить надежность различных устройств.
К числу наиболее широко применяемых
критериев надежности относятся:
— вероятность
безотказной работы в течение определенного
времени P(t);
— средняя
наработка до первого отказа Tср;
— наработка
на отказ tср;
— частота
отказов f(t)
или а(t);
— интенсивность
отказов λ(t);
— параметр
потока отказов ω(t);
— функция
готовности Kг(t);
— коэффициент
готовности Kг.
Характеристикой
надежности следует
называть количественное значение
критерия надежности конкретного
устройства. Выбор количественных
характеристик надежности зависит от
вида объекта.
2.1.2.
Критерии надежности невосстанавливаемых
объектов
Рассмотрим
следующую модель работы устройства.
Пусть в работе (на испытании) находится
N0
элементов и работа считается законченной,
если все они отказали. Причем вместо
отказавших элементов отремонтированные
не ставятся. Тогда критериями надежности
данных изделий являются:
— вероятность
безотказной работы P(t);
— частота
отказов f(t)
или a(t);
— интенсивность
отказов λ(t);
— средняя
наработка до первого отказа Tср.
Вероятностью
безотказной работы называется
вероятность того, что при определенных
условиях эксплуатации в заданном
интервале времени или в пределах заданной
наработки не произойдет ни одного
отказа.
Согласно
определению:
P(t
)
= P(T
>
t
),
(4.2.1)
где:
T
—
время работы элемента от его включения
до первого отказа;
t
—
время, в течение которого определяется
вероятность безотказной работы.
Вероятность
безотказной работы по
статистическим данным об
отказах оценивается выражением:
(4.2.2)
где:
N0
— число элементов в начале работы
(испытаний);
n(t)
— число отказавших элементов за время
t;
—
статистическая
оценка вероятности безотказной работы.
При большом числе элементов (изделий)
N0
статистическая оценка P
(t)
практически совпадает с вероятностью
безотказной работы P(t).
На практике иногда более удобной
характеристикой является вероятность
отказа Q(t).
Вероятностью
отказа называется
вероятность того, что при определенных
условиях эксплуатации в заданном
интервале времени возникает хотя бы
один отказ. Отказ и безотказная работа
являются событиями несовместными и
противоположными, поэтому:
Частотой
отказов по
статистическим
данным называется
отношение числа отказавших элементов
в единицу времени к первоначальному
числу работающих (испытываемых) при
условии, что все вышедшие из строя
изделия не восстанавливаются. Согласно
определению:
где:
n(Δt)
— число отказавших элементов в интервале
времени от (t
–
Δt)
/ 2 до (t
+
Δt)
/ 2.
Частота
отказов есть
плотность вероятности (или закон
распределения) времени работы изделия
до первого отказа. Поэтому:
Интенсивностью
отказов по
статистическим
данным называется
отношение числа отказавших изделий в
единицу времени к среднему числу изделий,
исправно работающих в данный отрезок
времени. Согласно определению
где:
— среднее число исправно работающих
элементов в интервале Δt;
Ni
—
число изделий, исправно работающих в
начале интервала Δt;
Ni+1
— число элементов, исправно работающих
в конце интервала Δt.
Вероятностная
оценка характеристики λ(t)
находится из выражения:
λ(t
)
=
f
(t
)
/ P(t
).
(4.2.7)
Интенсивность
отказов и вероятность безотказной
работы связаны между
собой
зависимостью:
Средней
наработкой до первого отказа называется
математическое ожидание времени работы
элемента до отказа. Как математическое
ожидание, Tср
вычисляется
через частоту отказов (плотность
распределения времени безотказной
работы):
Так
как t
положительно
и P(0)=1,
а P(∞)
=
0,
то:
По
статистическим
данным об
отказах средняя наработка до первого
отказа вычисляется по формуле
где:
ti
— время безотказной работы i-го
элемента;
N0
— число исследуемых элементов.
Как
видно из формулы (4.2.11), для определения
средней наработки до первого отказа
необходимо знать моменты выхода из
строя всех испытуемых элементов. Поэтому
для вычисления средней наработки на
отказ пользоваться указанной формулой
неудобно. Имея данные о количестве
вышедших из строя элементов ni
в
каждом i-м
интервале времени, среднюю наработку
до первого отказа лучше определять из
уравнения:
В
выражении (4.2.12) tсрi
и
m
находятся
по следующим формулам:
tcpi
=
(ti–1
+
ti
)
/ 2, m
=
tk
/
Δt,
где:
ti–1
—
время начала i-го
интервала;
ti
—
время конца i-го
интервала;
tk
—
время, в течение которого вышли из строя
все элементы;
Δt
=
(ti–1
–
t1
)
— интервал времени.
Из
выражений для оценки количественных
характеристик надежности видно, что
все характеристики, кроме средней
наработки до первого отказа, являются
функциями времени. Конкретные выражения
для практической оценки количественных
характеристик надежности устройств
рассмотрены в разделе «Законы распределения
отказов».
Рассмотренные
критерии надежности позволяют достаточно
полно оценить надежность невосстанавливаемых
изделий. Они также позволяют оценить
надежность
восстанавливаемых изделий до первого
отказа.
Наличие нескольких критериев вовсе не
означает, что всегда нужно оценивать
надежность элементов по всем критериям.
Наиболее
полно надежность изделий характеризуется
частотой
отказов f(t)
или a(t).
Это объясняется тем, что частота отказов
является плотностью распределения, а
поэтому несет в себе всю информацию о
случайном явлении — времени безотказной
работы.
Средняя
наработка до первого отказа является
достаточно наглядной характеристикой
надежности. Однако применение этого
критерия для оценки надежности сложной
системы ограничено в тех случаях, когда:
— время
работы системы гораздо меньше среднего
времени безотказной работы;
— закон
распределения времени безотказной
работы не однопараметрический и для
достаточно полной оценки требуются
моменты высших порядков;
— система
резервированная;
— интенсивность
отказов не постоянная;
— время
работы отдельных частей сложной системы
разное.
Интенсивность
отказов —
наиболее удобная характеристика
надежности простейших элементов, так
как она позволяет более просто вычислять
количественные характеристики надежности
сложной системы.
Наиболее
целесообразным критерием надежности
сложной системы является
вероятность
безотказной работы.
Это объясняется следующими особенностями
вероятности безотказной работы:
— она
входит в качестве сомножителя в другие,
более общие характеристики системы,
например, в эффективность и стоимость;
— характеризует
изменение надежности во времени;
— может
быть получена сравнительно просто
расчетным путем в процессе проектирования
системы и оценена в процессе ее испытания.
2.1.3.
Критерии надежности восстанавливаемых
объектов
Рассмотрим
следующую модель работы. Пусть в работе
находится N
элементов
и отказавшие элементы немедленно
заменяются исправными (новыми или
отремонтированными). Если не учитывать
времени, потребного на восстановление
системы, то количественными характеристиками
надежности могут быть параметр потока
отказов ω(t)
и
наработка на отказ tср.
Параметром
потока отказов называется
отношение числа отказавших изделий в
единицу времени к числу испытываемых
при условии, что все вышедшие из строя
изделия заменяются исправными (новыми
или отремонтированными). Статистическим
определением служит
выражение:
где:
n(Δt)
— число отказавших образцов в интервале
времени от t
–
Δt/2
до
t
+Δt/2;
N
—
число испытываемых элементов;
Δt
—
интервал времени.
Параметр
потока отказов и частота отказов для
ординарных потоков с ограниченным
последействием связаны интегральным
уравнением Вольтера второго рода:
По
известной f
(t)
можно найти все количественные
характеристики надежности невосстанавливаемых
изделий. Поэтому (4.2.14) является основным
уравнением, связывающим количественные
характеристики надежности невосстанавливаемых
и восстанавливаемых элементов при
мгновенном восстановлении.
Уравнение
(4.2.14) можно записать в операторной форме:
Соотношения
(4.2.15) позволяют найти одну характеристику
через другую, если существуют преобразования
Лапласа функций f(s)
и ω(s)
и обратные преобразования выражений
(4.2.15).
Параметр
потока отказов обладает следующими
важными свойствами:
1)
для любого момента времени, независимо
от закона распределения времени
безотказной работы, параметр потока
отказов больше, чем частота отказов, т.
е. ω(t)
> f(t);
2)
независимо от вида функций f(t)
параметр потока отказов ω(t)
при t
→
∞ стремится
к 1/Tср.
Это важное свойство параметра потока
отказов означает, что при длительной
эксплуатации ремонтируемого изделия
поток его отказов, независимо от закона
распределения времени безотказной
работы, становится стационарным. Однако
это вовсе не означает, что интенсивность
отказов есть величина постоянная;
3)
если λ(t)
— возрастающая функция времени, то λ(t)
> ω(t)
> f(t),
если λ(t)
— убывающая функция, то ω(t)
> λ(t)
> f(t);
4)
при λ(t
)
≠
const
параметр потока отказов системы не
равен сумме параметров потока отказов
элементов, т. е.:
Это
свойство параметра потока отказов
позволяет утверждать, что при вычислении
количественных характеристик надежности
сложной системы нельзя суммировать
имеющиеся в настоящее время значения
интенсивности отказов элементов,
полученных по статистическим данным
об отказах изделий в условиях эксплуатации,
так как указанные величины являются
фактически параметрами потока отказов;
5)
при λ(t)
= λ= const параметр потока отказов равен
интенсивности отказов
ω(t)
= λ(t)
= λ.
Из
рассмотрения свойств интенсивности и
параметра потока отказов видно, что эти
характеристики различны.
В
настоящее время широко используются
статистические данные об отказах,
полученные в условиях эксплуатации
оборудования. При этом они часто
обрабатываются таким образом, что
приводимые характеристики надежности
являются не интенсивностью отказов, а
параметром потока отказов ω(t).
Это вносит ошибки при расчетах надежности.
В ряде случаев они могут быть значительными.
Для
получения интенсивности отказов
элементов из статистических данных об
отказах ремонтируемых систем необходимо
воспользоваться формулой (4.2.6), для чего
необходимо знать предысторию каждого
элемента технологической схемы. Это
может существенно усложнить методику
сбора статистических данных об отказах.
Поэтому целесообразно определять λ(t)
по параметру потока отказов ω(t).
Методика расчета сводится
к
следующим вычислительным операциям:
— по
статистическим данным об отказах
элементов ремонтируемых изделий и по
формуле (4.2.13) вычисляется параметр
потока отказов и строится гистограмма
ωi(t);
— гистограмма
заменяется кривой, которая аппроксимируется
уравнением;
— находится
преобразование Лапласа ωi(s)
функции ωi(t);
— по
известной
ωi(s)
на основании (4.2.15) записывается
преобразование Лапласа fi
(s)
частоты отказов;
— по
известной fi(s)
находится обратное преобразование
частоты отказов fi(t);
— находится
аналитическое выражение для интенсивности
отказов по формуле:
— строится
график λi(t).
Если
имеется участок, где λi(t)
= λi
=
const, то постоянное значение интенсивности
отказов принимается для оценки вероятности
безотказной работы. При этом считается
справедливым экспоненциальный закон
надежности.
Приведенная
методика не может быть применена, если
не удается найти по f(s)
обратное преобразование частоты отказов
f(t).
В этом случае приходится применять
приближенные методы решения интегрального
уравнения (4.2.14).
Наработкой
на отказ называется
среднее значение времени между соседними
отказами. Эта характеристика определяется
по статистическим
данным об
отказах по формуле:
где:
ti
—
время исправной работы элемента между
(i
–
1)-м и i-м
отказами;
n
—
число отказов за некоторое время t.
Из
формулы (4.2.18) видно, что в данном случае
наработка на отказ определяется по
данным испытания одного образца изделия.
Если на испытании находится N
образцов
в течение времени t,
то наработка на отказ вычисляется по
формуле:
где:
tij
—
время исправной работы j-го
образца изделия между (i
–
1)-м и i-м
отказом;
nj
—
число отказов за время tj-го
образца.
Наработка
на отказ является достаточно наглядной
характеристикой надежности, поэтому
она получила широкое распространение
на практике. Параметр потока отказов
и наработка на отказ характеризуют
надежность восстанавливаемого изделия
и не учитывают времени, необходимого
на его восстановление. Поэтому они не
характеризуют готовности устройства
к выполнению своих функций в нужное
время. Для этой цели вводятся такие
критерии, как коэффициент готовности
и коэффициент вынужденного простоя.
Коэффициентом
готовности называется
отношение времени исправной работы к
сумме времен исправной работы и
вынужденных простоев устройства, взятых
за один и тот же календарный срок. Эта
характеристика по статистическим
данным определяется:
где:
tр
—
суммарное время исправной работы
изделия;
tп
—
суммарное время вынужденного простоя.
Времена
tр
и
tп
вычисляются
по формулам:
где:
tрi
—
время работы изделия между (i
–
1)-м и i-м
отказом;
tпi
—
время вынужденного простоя после i-го
отказа;
n
—
число отказов (ремонтов) изделия.
Для
перехода к вероятностной трактовке
величины tр
и
tп
заменяются
математическими ожиданиями времени
между соседними отказами и времени
восстановления соответственно. Тогда:
Kr
=
tcp
/
(tcp
+
tв
),
(4.2.22)
где:
tср
—
наработка на отказ;
tв
—
среднее время восстановления.
Коэффициентом
вынужденного простоя называется
отношение времени вынужденного простоя
к сумме времен исправной работы и
вынужденных простоев изделия, взятых
за один и тот же календарный срок.
Согласно
определению:
K
п
=
t
p
/
(t
p
+
tп
),
(4.2.23)
или,
переходя к средним величинам:
Kп
=
tв
/
(tcp
+
tв
).
(4.2.24)
Коэффициент
готовности и коэффициент вынужденного
простоя связаны между собой зависимостью:
Kп
=
1–
Kг
.
(4.2.25)
При
анализе надежности восстанавливаемых
систем обычно коэффициент готовности
вычисляют по формуле:
Kг
=Tcp
/
(Tcp
+
tв
).
(4.2.26)
Формула
(4.2.26) верна только в том случае, если
поток отказов простейший, и тогда tср
=
Tср.
Часто
коэффициент готовности, вычисленный
по формуле (4.2.26), отождествляют с
вероятностью того, что в любой момент
времени восстанавливаемая система
исправна. На самом деле указанные
характеристики неравноценны и могут
быть отождествлены при определенных
допущениях.
Действительно,
вероятность возникновения отказа
ремонтируемой системы в начале
эксплуатации мала. С ростом времени t
эта
вероятность возрастает. Это означает,
что вероятность застать систему в
исправном состоянии в начале эксплуатации
будет выше, чем после истечения некоторого
времени. Между тем на основании формулы
(4.2.26) коэффициент готовности не зависит
от времени работы.
Для
выяснения физического смысла коэффициента
готовности Kг
запишем
формулу для вероятности застать систему
в исправном состоянии. При этом рассмотрим
наиболее простой случай, когда
интенсивность отказов λ и интенсивность
восстановления μ есть величины постоянные.
Предполагая,
что при t
=
0
система находится в исправном состоянии
(P(0)
= 1), вероятность застать систему в
исправном состоянии определяется из
выражений:
где
λ
= 1
/Tcp
;
μ
= 1
/ tв
;
Kг
=Tcp
/
(Tcp
+
tв
).
Это
выражение устанавливает зависимость
между коэффициентом готовности системы
и вероятностью застать ее в исправном
состоянии в любой момент времени t.
Из
(4.2.27) видно, что
приt
→
∞,
т. е. практически коэффициент готовности
имеет смысл вероятности застать изделие
в исправном состоянии при установившемся
процессе эксплуатации.
В
некоторых случаях критериями
надежности восстанавливаемых систем
могут быть критерии невосстанавливаемых
систем,
например: вероятность
работы, частота отказов, средняя наработка
до первого отказа, интенсивность отказов.
Такая необходимость
возникает:
— когда
имеет смысл оценивать надежность
восстанавливаемой системы до первого
отказа;
— в
случае, когда применяется резервирование
с восстановлением отказавших резервных
устройств в процессе работы системы,
причем отказ всей резервированной
системы не допускается.
Вероятностью безотказной работы аппаратуры называется вероятность того, что она будет сохранять свои характеристики (параметры) в заданных пределах в течение определенного промежутка времени при определенных условиях эксплуатации, или, короче, – вероятностью безотказной работы аппаратуры называется вероятность того, что в определенных условиях эксплуатации в пределах заданной продолжительности работы отказ не возникает.
В дальнейшем эта характеристика обозначается P(t).
Пусть t – время, в течение которого необходимо определить вероятность безотказной работы, а Т1 – время работы аппаратуры от ее включения до первого отказа. Тогда, согласно определению вероятности безотказной работы, справедливо выражение:
, (1.1)
т.е. вероятность безотказной работы – это вероятность того, что время Т1 от момента включения аппаратуры до ее отказа будет больше или равно времени t, в течение которого определяется вероятность безотказной работы.
Из определения вероятности безотказной работы видно, что эта характеристика является функцией времени. Она имеет следующие очевидные свойства:
1) P(t) является убывающей функцией времени;
2) ;
3) Р(0) = 1, .
На практике для определения P(t) из статистических данных об отказах аппаратуры обычно используются методы непосредственного подсчета вероятностей. Вероятность безотказной работы определяется следующей статистической оценкой:
, (1.2)
где N0 – число образцов аппаратуры в начале испытания, n(t) – число отказавших образцов за время t.
При увеличении числа образцов N0 статистическая оценка вероятности обнаруживает устойчивость, т.е.
слабо отличается от вероятности безотказной работы:
. (1.3)
На практике иногда более удобной характеристикой является вероятность неисправной работы, или вероятность отказов. Эта характеристика может быть полезна, например, при сравнение надежности резервированной и не резервированной систем. Исправная работа и отказ являются событиями несовместными и противоположными. Поэтому вероятность безотказной работы и вероятность отказа Q(t) связаны зависимостью:
Q (t) = 1 – P (t), (1.4)
или с учетом выражения (1.1)
Q (t) = P (T1 t) (1.5)
Из выражения (1.5) видно, что вероятность отказа является интегральной функцией распределения времени работы (Т1) до отказа, т.е.
Q (t) = F (t) (1.6)
Производная от интегральной функции распределения есть дифференциальный закон (плотность) распределения:
. 1.7)
Тогда на основании выражений (1.6) и (1.7) получим:
, (1.8)
т.е.
производная от вероятности отказа подчиняется дифференциальному закону распределения времени работы (Т1) аппаратуры до ее отказа.
Для статистического определения вероятности отказа воспользуемся выражениями (1.4)и (1.3). Подставляя в выражение (1.4) вместо P(t) его выражение из формулы (1.3), получим:
. (1.9)
Вероятность безотказной работы P(t), как количественная характеристика надежности, обладает следующими достоинствами:
1) характеризует изменение надежности во времени;
2) входит во многие другие характеристики аппаратуры, а поэтому может быть полезна широкому кругу лиц, занимающихся вопросами проектирования, эксплуатации, ремонта и т.п. Например, вероятность безотказной работы наряду с точностью и живучестью определяет боевую эффективность оружия, а поэтому является необходимой для исследователя военных операций и полководца. Она определяет также стоимость изготовления и эксплуатации аппаратуры, а поэтому может быть полезной инженеру-экономисту;
3) охватывает большинство факторов, существенно влияющих на надежность аппаратуры, и поэтому достаточно полно характеризует надежность;
4) может быть сравнительно просто получена расчетным путем до изготовления системы. Это позволяет выбрать оптимальную в смысле надежности структуру системы и ее принципиальную схему;
5) является удобной характеристикой надежности, как простейших элементов, так и сложных систем и даже комплексов.
Указанные достоинства вероятности безотказной работы явились причиной наибольшего распространения этой характеристики.
Однако вероятность безотказной работы имеет также существенные недостатки:
1) характеризует надежность восстанавливаемых систем только до первого отказа, а поэтому является достаточно полной характеристикой надежности только систем разового использования;
2) не позволяет охарактеризовать зависимость между временными составляющими цикла эксплуатации; это не дает возможности установить, даже в вероятностном смысле, будет ли система готова к действию в данный момент времени или нет;
3) не всегда удобна для оценки надежности простых элементов, в особенности таких, у которых отсутствует старение;
4) по известной вероятности безотказной работы бывает трудно вычислить другие количественные характеристики надежности.
Эти недостатки позволяют сделать вывод, что вероятность безотказной работы, как, впрочем, и любая другая характеристика, не полностью характеризует такое свойство как надежность, и поэтому не может быть с ним отождествлена.
1. Основные понятия и определения надежности.
Надежность – свойство объекта выполнять заданные функции, сохраняя во времени и в заданных пределах значения, установленных эксплуатационных показателей.
Элемент— один или несколько однотипных устройств, предметов, имеющих количественные характеристики надежности, учитываемые при расчете надежности всего соединения.
Ячейка — отдельная механическая конструкция, не имеющая самостоятельного функционального назначения.
Узел (блок)— несколько деталей, ячеек, объединенных для выполнения определенной функции, но не имеющих как целое самостоятельного эксплуатационного назначения. ( регистр команд, счетчик циклов, дешифратор операций).
Устройство—соединение деталей, узлов, имеющее самостоятельное эксплуатационное назначение блок питания, арифметическое устройство (АУ) и т. д.
Прибор — группа блоков, имеющая конструктивно самостоятельное назначение.
Установка — группа приборов.
Система—устройство, состоящее из нескольких установок. Надежность его имеет самостоятельное значение.
Различают системы восстанавливаемые (после отказов их можно ремонтировать) и невосстанавливаемые
Отказ—это частичная или полная утрата свойств элемента, которая существенным образом снижает или приводит к полной потере работоспособности. Отказ наступает всякий раз, когда устройство не сохраняет своих параметров в заданных пределах.
По характеру возникновения отказы могут быть разделены на внезапные и постепенные. Внезапные отказы определяются резким изменением параметров, определяющих качество изделия -предвидеть невозможно. Постепенные отказы возникают при постепенном изменении параметров, определяющих качество изделия в результате старения или износа, когда эти параметры выходят за установленные пределы.
По признакам проявления: явные, неявные. По взаимосвязи между собой: зависимые и независимые. По степени взаимодействия: полные и частичные. По хар-ру воздействия: самовостанавлив, временные, перемежающиеся. По хар-ру устранения: расстройки, повреждения, аварии.
Неисправность — изменение характеристик системы без изменения качества функционирования всей аппаратуры.
Система исправна, если она соответствует всем предъявляемым требованиям, т. е. все ее параметры, как основные, так и второстепенные, находятся в заданных пределах. Выход любого параметра из этих пределов означает неисправность. Система работоспособна, если она нормально выполняет заданные функции и ее основные параметры находятся в пределах нормы. Утрата работоспособности означает отказ.
Простые системы. Они при отказе элементов либо полностью теряют работоспособность, либо продолжают свои функции в полном объеме, если отказавший элемент зарезервирован. Такие системы могут находиться только в двух состояниях: рабочем и нерабочем.
Сложные системы. Они обладают способностью при отказе элементов продолжать выполнение своих функций, но с пониженной эффективностью, т. е. могут находиться в нескольких рабочих состояниях. К сложным системам обычно относят многоканальные комплексы с разветвленной структурой, состоящие из нескольких самостоятельных, но взаимосвязанных устройств, например автоматизированные системы управления ПВО, предприятиями и др.
2. Вероятность исправной работы. Среднее время безотказной работы. Среднее время между отказами.
Вероятность исправной (безотказной) работы. Пусть имеется совокупность элементов, каждый из которых характеризуется неотрицательной случайной величиной Т, называемой длительностью его безотказной работы. Длительность безотказной работы будет «возрастом» элемента к моменту, когда произойдет отказ. Случайная величина Т является неотрицательной и имеет дискретное или непрерывное распределение.
Практический интерес представляет второй случай, когда время безотказной работы имеет непрерывное распределение. По определению, функцией распределения (интегральным законом распределения) случайной величины Т называется функция F (t) =Р {Т<=t}, определяемая как вероятность того, что элемент отказал до момента t. Для целей расчета надежности удобнее пользоваться функцией, дополнительной к F (t) и называемой вероятностью безотказной работы P(t). Эта функция задает вероятность того, что элемент не откажет до момента времени t. Очевидно, что Р (t) = = Р {Т > t}, Р(0)=1, Р(оо)=0 и является невозрастающей функцией времени.
При испытании партии изделий вероятность исправной работы

где N0—число изделий в начале испытаний; пk—число изделий, которые вышли из строя в интервале времени ?tk; t—время, для которого определяется вероятность исправной работы; ?tk—принятая продолжительность интервала времени наблюдения; N (t) — число изделий, исправно работающих в интервале [0, t]. Вероятность отказа
(1.2)
Согласно (1.2),
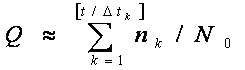
Среднее время безотказной работы. Под этим термином в теории надежности понимается математическое ожидание времени исправной работы:
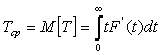
Практически среднее время исправной работы однотипных элементов
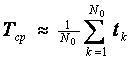
где N0—число элементов, над которыми проводятся испытания; tk—время исправной работы
k-го элемента. Так как трудно определить tk, удобнее пользоваться другим выражением:
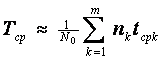
где 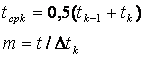
t—время, в течение которого вышли из строя все элементы; ?tk—величина интервала времени.
Величина Tср позволяет определить количество запасных элементов за время работы, но полностью не характеризует надежность элементов. При равенстве Тср у двух каких-либо групп элементов, имеющих разное распределение отказов, надежность может быть неодинаковая. Среднее время Тср до ремонта отличается от Т’ср после ремонта. Они равны, если элементы не изнашиваются, т. е. не зависят от времени.
Q(t)=F(t). (1.8)
Вероятность того, что за время t не произойдет отказа,
P(t)=1-Q(t)=1-F(t), (1.9)
Q‘(t)=dF(t)/dt. (1.10)
Следовательно, среднее время работы есть математическое ожидание случайной величины:
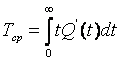
тогда из (1.9) получаем
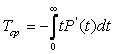
Интегрирование по частям
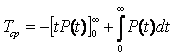
с учетом—[tP(t)]?0=0, дает выражение
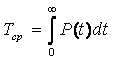
Число элементов, которые будут работать непрерывно к моменту t, определяется из (1.1):
N(t)=N0P(t). (1.15)
За интервал ?t число отказавших элементов
п (t) = N (t)-N(t + ?t) = N0 [Р (t)-Р (t +?t)]. (1.16)
Среднее время между отказами. Это математическое ожидание исправной работы между соседними отказами:
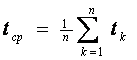
где п—число отказавших элементов; tk—время исправной работы между (k—1)-м и k-м отказом аппаратуры.
3. Интенсивность отказов. Частота отказов. Средняя и суммарная частота отказов. Среднее время восстановления.
Интенсивность отказов. Отношение числа отказавших изделий в единицу времени к среднему числу изделий, продолжающих исправно работать, есть интенсивность отказов (ч-1)
(1.19)
где п(t)—число отказавших элементов в отрезке времени от t—?t/2 до t+?t/2; ; Nk-i(t)— число исправных элементов в начале интервала времени ?t; Nk(t)—число исправно работающих элементов в конце интервала ?t.
Интенсивность отказов называют ?-характеристикой. Таким образом, интенсивность отказов показывает, какая часть элементов выходит из строя в единицу времени по отношению к среднему числу исправно работающих элементов.
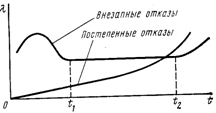
Как видно из рис. 1.1, работа элементов и систем характеризуется тремя этапами. Первый этап ([0, t1]—период доводки)—начальный, отличается небольшим количеством отказов. Здесь выходят из строя элементы с малым запасом прочности. Тренировка деталей повышает эксплуатационную надежность. Второй этап ([t1, t2] — период нормальной эксплуатации) характеризуется пониженным уровнем и примерным постоянством интенсивности отказов. Здесь отказы в основном носят внезапный характер. Продолжительность этого периода зависит от среднего срока службы элементов и от условий эксплуатации. Третий этап (от t2 и далее—период старения) обусловлен износом и старением элементов и характерен значительным ростом числа отказов. С наступлением этого периода дальнейшая эксплуатация системы нецелесообразна.
Частота отказов. Отношение числа отказавших изделий в единицу времени к первоначальному числу испытываемых изделий при условии, что число испытываемых изделий во время испытания уменьшается, есть частота отказов (ч-1)
(1.20)
где п (t)—число отказавших изделий в интервале времени от t—?t/2 до t+?t/2; N0—первоначальное число испытываемых изделий.
По величине частоты отказов рассчитывают число запасных изделий:
(1.21)
Рис. 1.2. Частота отказов а (t)

Подставляя в (1.20) значение п(t) из (1.16), получаем а(t)={N0[P(t)—P(t+?t)]}/(N0?t). Если ?t?0, то
a(t)=-P‘(t)=Q‘(t), (1.22)
т. е. частота отказов есть плотность распределения времени выхода элементов из строя.
Тогда
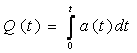

Подставляя в (1.19) значение п(t) из (1.16), получаем выражение интенсивности отказов в следующем виде:
?(t)=-dP/[P(t)dt]. (1.25)
Интегрируя обе части (1.25) в интервале от 0 до t, получаем, т.е.
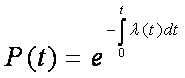
Рис. 1.3. Экспоненциальный закон надежности
Если ?(t)= const. то (1.26) представляет собой экспоненциальный закон надежности. По этому закону вероятность исправной работы элементов, обладающих интенсивностью отказов ?, убывает со временем по экспоненциальной кривой (рис. 1.3). Это справедливо на нормальном участке работы системы, когда эффект старения неощутим. Такую кривую называют функцией надежности. Она имеет большое значение для практического использования, когда необходимо знать, с какой вероятностью АСУ способна выполнить задание, требующее определенной продолжительности безотказной работы. Подставив значение Р (t) в (1.14), получим
Если ?(t) равна постоянной величине ,то
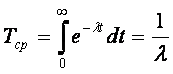
где ? = 1/Тcр—среднее число отказов в единицу времени.
Тогда (1.26) принимает вид
(1.28)
Важное характеристическое свойство показательного закона надежности, которое состоит в том, что вероятность безотказной работы P[t, t+?] в некотором интервале [t, t+?] не зависит от времени предшествующей работы t, а определяется только интенсивностью отказов и длиной интервала ?? Другими словами, будущее поведение элемента в смысле безотказного функционирования не зависит от прошлого, если нам известно, что до момента t элемент не отказал. Действительно, по формуле для полной вероятности имеем
4. Критерии надежности для восстанавливаемых систем.
Во введении было дано качественное определение надежности АСУ. Это определение должно быть дополнено количественными характеристиками. На их основании сравниваются между собой различные системы с точки зрения их надежности, кроме того, и технические условия включаются вполне определенные требования, что важно при разработке новых систем.
Количественные критерии применяют в зависимости от назначения систем или ее фактического использования. В связи с этим различают три класса систем.
К I классу относятся системы, которые по условиям не могут ремонтироваться во время работы. От этих систем требуется безотказная работа в течение заданного времени:
(1.35)
Системы II класса должны в произвольный момент времени быть готовыми к работе и не иметь неисправностей в течение заданного времени. Обычно этот класс систем длительно находится в состоянии готовности, а используется кратковременно, в случае необходимости. Аппаратура II класса ремонтируется во время эксплуатации. Характеристикой таких восстанавливаемых систем является вероятность успешного использования
(1.36)

К III классу относится аппаратура, использующаяся непрерывно, т. е. наибольшую часть времени работает безотказно. Так, при использовании машин для решения математических задач в вычислительных центрах желательно получить наибольший процент полезного рабочего времени в пределах каждого рабочего
цикла. В этом случае важной характеристикой, учитывающей возможность восстановления аппаратуры после появления отказов, является коэффициент готовности
(1.37)
Эта вероятность зависит от того, насколько быстро достигается восстановление рабочего состояния системы после отказа, поэтому данная характеристика для систем многоразового действия является важным параметром наряду с вероятностью безотказной работы. Современным требованиям отвечают те устройства, которые имеют высокую степень ремонтопригодности.
Дадим вывод коэффициента готовности при следующих предположениях: 1) поток отказов системы носит пуассоновский характер и интенсивность отказов равна ?; 2) время восстановления системы является случайной величиной, распределенной по экспоненциальному закону F(х)= 1-е?x, где ?— интенсивность восстановления; 3) система может находиться в двух состояниях: состоянии х(t)=1 (работоспособности) и состоянии x(t) = 2 (ремонта). Диаграмма состояний системы изображена на рис. 1.6.
Здесь tpi— интервал времени, в течение которого система работоспособна; tbi — интервал времени, в течение которого система ремонтируется. Это случайные величины, распределенные по показательному закону с параметрами ?и ? соответственно.
Поведение системы с точки зрения работоспособности опишем графом переходов (рис. 1.7). На этом рисунке кружки с номером обозначают состояние системы, а стрелки (дуги) — направление переходов системы и вероятности этих переходов за бесконечно малый интервал времени.
Вероятности переходов в силу сделанных предположений и свойства показательного закона надежности не зависят от времени t. Введем вероятности нахождения системы в состояниях 1 и 2 как p1(t) и p2(t). Очевидно, что pl(t) +p2(t) = 1 для любого момента времени.
Рассмотрим поведение системы в интервале времени [0, t+?t]. Тогда система в момент t+?t будет находиться в состоянии 1, если она в момент tнаходилась в этом состоянии и за время ?t не наблюдалось отказов, а также, если система в момент времени tнаходилась в состоянии 2 и завремя ?t был закончен ее ремонт.
Следовательно, р1(t+?t) = (1-??t)pl(t) + ?p2(t)?t +0(?t). Аналогичные рассуждения приводят к уравнению для р2(t+?t) = (1-??t)p2(t) + ?p1(t)?t +0(?t). Предельный переход ?t—>0 дает дифференциальные уравнения, описывающие поведение системы во времени:
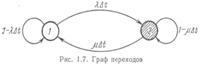
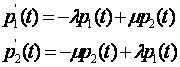
Решая (1.38), получаем дифференциальное уравнение для искомых вероятностей
(1.39)
Общий интеграл уравнения (1.39)
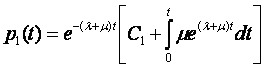
позволяет оценить вероятности состояния в зависимости от начального состояния:
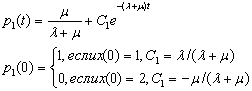
(1.42)
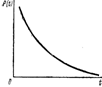
(1.43)
Таким же образом определяют вероятности нахождения системы в состоянии ремонта при условии, что в начальный момент система была или работоспособна [р21(t)] или неработоспособна [р22(t)]:
(1.44)
(1.45)
При t>? выражения (1.42) и (1.43) приобретают вид
(1.46)
При сравнении разных систем по коэффициенту готовности необходимо учитывать также и некоторые другие показатели рассматриваемой системы, в том числе стоимость, габариты, вес, эксплутационные расходы и др.
Проведем анализ работы АСУ на примере вычислительной системы, выполняющей случайные задания. Если заявка на решение задачи придет в момент, когда машина находится в ремонте, то задание не будет выполнено. Это может привести к нежелательным результатам. Аналогичная ситуация возникает, если во время решения задачи происходит отказ. Пусть нас интересует момент первого несвоевременного выполнения задания или невыполнение задания вообще. Назовем это событие отказом на выполнение. Оценим вероятность этого события в следующих предположениях:
1) закон отказов вычислительной машины (ВМ) носит пуассоновский характер, интенсивность отказов ?;
2) время восстановления подчинено показательному закону с интенсивностью ?;
- вероятность поступления задания стационарна и для бесконечно малого промежутка времени ?t определяется как ??t;
- время решения задачи имеет экспоненциальное распределение
с параметром ?;
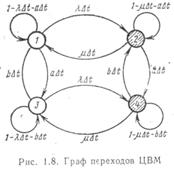
Возможны четыре состояния с точки зрения надежного функционирования системы: x=1 (BM исправна и простаивает из-за отсутствия задания); х = 2(ВМ в ремонте и задание на вычисления не поступало); х = 3 (ВМ исправна и решает задачу); х = 4 (ВМ в ремонте, заявка на решение поступила в систему).
Граф состояний с указанными вероятностями переходов для рассматриваемого случая изображен на рис. 1.8. Используя метод, примененный при выводе коэффициента готовности, получаем уравнения относительно вероятностей нахождения системы во всех состояниях:

Решая систему (1.47) и переходя к пределу, получаем стационарные вероятности нахождения системы во всех четырех состояниях:
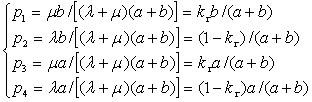
Тогда вероятность невыполнения задания определяется как
(1.49)
5. Количественные характеристики надежности при постепенных отказах.
Для аппаратуры, в которой имеют место постепенные отказы, обусловленные старением и износом, часто пользуются нормальным законом распределения. Поскольку значение времени безотказной работы — положительная величина, частота отказов
(1.50)
где С — постоянная усеченного нормального распределения, которую определяют из нормирующего условия 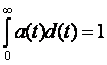
Если среднее квадратическое отклонение а невелико по сравнению с Т, то можно приближенно для расчетов пользоваться неусеченным нормальным распределением при С ?1/(?v2?). Тогда за время t исходное выражение количественного определения вероятности отказа элемента
a(t)= —P‘(t)=Q‘ (t)
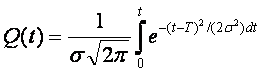
Здесь математическое ожидание времени исправной работы элемента, приближенно равное среднему времени исправной работы элемента, определяется экспериментально по результатам испытания партии однотипных элементов (испытания проводятся до выхода из строя всех элементов партии):
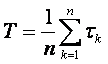
где tk —время работы k—гoэлемента до выхода его из строя; п — число испытываемых элементов партии (вместо Т может быть любой контролируемый параметр);
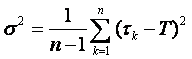
— дисперсия значений времени исправной работы различных элементов в испытуемой партии. Если п > 20, то можно заменить п-1 значением п. Если сделать замену вида
х = (1 — T)/?, то
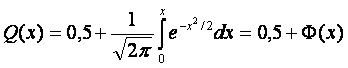
где первый член представляет половину площади, ограниченной кривой Гаусса, второй член Ф(х) — интеграл вероятности (значение этой функции см. в табл. П2).
Если (1.51) нормировано относительно х = (1 — T)/?, то
(1.55)
Вероятность исправной работы группы элементов, подверженных постепенным отказам,
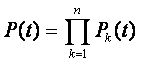
где n — число подгрупп с однотипными элементами.
6. Соотношение для определения надежности с учетом условий эксплуатации.
Формулы для вычисления надежности ЭВМ справедливы, если условия эксплуатации строго определены и соответствуют условиям, в которых получены характеристики ? и ?.
Условия эксплуатации в общем виде определяются комплексом интенсивностей внешних воздействий, климатических факторов (влажность, давление, температура), механических нагрузок (вибрации, ускорение, удары), эксплуатационных факторов (время работы, режим схемы, отклонения питающих напряжений). Если имеется п внешних факторов, то через ?1,?2,…,?n обозначим соответствующие интенсивности внешних воздействий. Обычно условия эксплуатации изменяются случайно в некоторых пределах, так что интенсивности внешних воздействий можно рассматривать как случайные величины со своими законами распределения вероятностей.
Пусть ?(?1,?2,…,?n,t) представляет собой многомерный закон распределения плотности вероятностей интенсивностей внешних воздействий в предполагаемых условиях эксплуатации.
Частота, и интенсивность отказов в функции интенсивностей внешних воздействий ?1,?2,…,?n будут
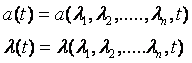
При этом надежность систем определяется как математическое ожидание функций интенсивностей:
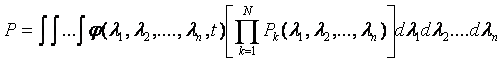
(1.58)
Таким образом, надежность основного устройства может быть определена при использовании соотношения .(1.58), если известны условные вероятности безотказной работы его узлов, функции интенсивностей внешних факторов Pk(?1,?2,…,?n) и плотность вероятностей ?(?1,?2,…,?n) интенсивностей внешних воздействий в предполагаемых условиях эксплуатации. Приближенная оценка надежности
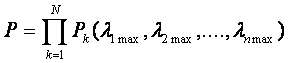
но величина надежности здесь существенно занижена.
Определить опытным путем переходные коэффициенты для самых разнообразных условий эксплуатации и для различных комбинаций воздействующих факторов и их величины практически почти невозможно. Поэтому возникает вопрос о получении математических зависимостей, позволяющих рассчитывать интенсивность отказов для различных условий эксплуатации и нагрузок. Для общности изложения в дальнейшем все внешние воздействия (в том числе и электрическая нагрузка) назовем термином «нагрузка».
Под коэффициентом нагрузки, который может изменяться от 0 до 1, понимается отношение ее рабочей величины к исходной номинальной нагрузке. Равенство коэффициента нагрузки нулю в некоторых случаях означает отсутствие нагрузки (электрической, вибрационной), в других условиях соответствует некоторому нормальному значению (тепловой). Итак, необходимо определить зависимость интенсивности отказов в виде ?=f(k), где k— обобщенное значение коэффициента нагрузки.
Из опыта эксплуатации ЭВМ известны следующие зависимости интенсивности отказов от коэффициента нагрузки:
а) при коэффициенте нагрузки, равном нулю, интенсивность отказов имеет некоторое значение ?0. Это объясняется тем, что даже при самых благоприятных условиях в радиодеталях протекают физико-химические процессы, приводящие к отказам;
б) функция ?1=f1(k) является монотонно возрастающей. С увеличением коэффициента нагрузки количество радиодеталей, выходящих из строя в единицу времени, возрастает;
в) функция ?‘=f2(k) является монотонно возрастающей. С увеличением коэффициента нагрузки на одну и ту же величину относительное изменение величины ? прямо пропорционально абсолютному значению коэффициента нагрузки;
г) при значениях коэффициента нагрузки, близких к нулю ?‘0=f2(k)=0. В этом случае незначительное изменение коэффициента не приводит к изменению величины ?.
Рассмотрим приращение функций ? и ?‘. В случае малых изменений коэффициента нагрузки ?k в первом приближении можно принять, что функции ?1 и ?2 линейно зависят от ?k и пропорциональны значению функции в начале интервала ?k. Таким образом, можно записать следующие выражения:
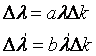
где а и b— некоторые коэффициенты.
При ?t>0 получим следующую систему уравнений:
произведя замену, получим d2?/dk2 — ab? = 0.
Решение этого дифференциального уравнения имеет вид
(1.61)
где А = vаb.
Так как f1(0) = ?0, f2(0) = 0, то, используя начальные условия, получаем
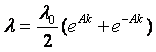
Данная функция удовлетворяет перечисленным выше условиям и свойствам.
Выражение (1.62) можно представить в следующем виде:
или
где ?0 — номинальная интенсивность отказов при воздействии нескольких видов нагрузок.
При малых значениях коэффициента нагрузки можно пренебречь слагаемыми начиная со второго члена. Тогда ? = ?0. Зная величину A для конкретного типа радиодеталей, можно установить диапазон вариации коэффициента нагрузки, при котором величина интенсивности отказов изменится незначительно. Это требование и следует соблюдать при проектировании ЭВМ. Используя (1.62), необходимо определить коэффициент нагрузки, в качестве которого можно принять: при электрической нагрузке — отношение рабочего значения некоторого электрического параметра (мощность, напряжение, ток) к его номинальному значению; при тепловой нагрузке — отношение абсолютной разности между рабочей температурой окружающей среды и номинальной температурой к номинальному значению температуры (20±5°С); при вибрационной нагрузке — отношение величины действующего ускорения к величине g0 = 9,81 м/с2, при влажности — отношение абсолютной разности между рабочим значением относительной влажности и его номинальным значением к номинальному значению влажности. За номинальное значение влажности принимают величину 65±15%. Аналогично определяют коэффициенты нагрузок для других случаев.
Если на некоторую радиодеталь действует несколько нагрузок k1,k2,…km, то при небольших их значениях можно считать воздействия независимыми. Тогда
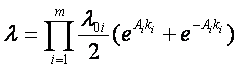
Подобный подход — приближенный и оказывается верным только при малых значениях коэффициентов нагрузок, так как между нагрузками существует корреляционная связь. Например, тепловой пробой совместно с электрическим вызывает выход триода из строя.
7. Параметры надежности при хранении систем.
Отказы аппаратуры и входящих в нее элементов наблюдаются не только .в процессе работы, но и в процессе хранения. Поэтому необходимо ввести параметры, характеризующие надежность системы при хранении.
Сохраняемость a(t) — вероятность того, что система (прибор, узел, деталь) сохраняет работоспособность в течение заданного срока хранения в определенных условиях и является аналогом вероятности безотказной работы при хранении. Понятие «работа» здесь используется условно лишь для удобства, так как речь идет на самом деле о неработающих элементах. Следовательно, сохраняемость характеризует те же параметры, что и вероятность безотказной работы, а именно ?хр и Tхр, связанные между собой зависимостью
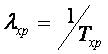
где Tхр—средняя «наработка» на отказ при хранении, равная математическому ожиданию времени между двумя последующими отказами; ?хр—интенсивность отказов элемента при хранении. Сохраняемость элемента
(1.65)
Так как сохраняемость принципиально ничем не отличается от работы (при условии справедливости экспоненциального закона), то определение параметров сохраняемости по данным эксперимента производится так же, как параметров безотказной работы.
Оценка
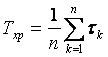
в случае испытания системы с заменой элементов и
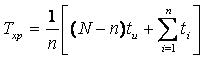
в случае испытания элементов без замены. Здесь п — число отказов; ?k — время между последовательными отказами; N—число элементов в партии, поставленной на испытание; tи — время испытания партии изделий; ti.— время работы 1-го изделия до отказа.
Готовность характеризуется коэффициентом готовности, который при работе и хранении различен. Это обусловлено тем, что отказ работающей системы устраняется сразу же после ее возникновения, а отказ хранящейся системы обнаруживается и устраняется лишь спустя некоторое время, при профилактике. От момента возникновения отказа до момента начала профилактики система неисправна. Коэффициент готовности kгпри хранении выводится следующим образом. Система не готова к работе в некоторый момент времени, если в ней имеется неустранимый отказ. В этом случае для некоторого интервала времени длительностью Тпроф (интервал времени между двумя последовательными профилактиками) kгесть отношение среднего времени, в течение которого в системе не было повреждений, к выражению (Тпроф + ?проф). Если повреждение устраняют через промежуток времени длины Тпроф, то в системе не будет повреждения от начала этого интервала до первого повреждения. Этот промежуток времени есть случайная величина ? с плотностью распределения вероятности
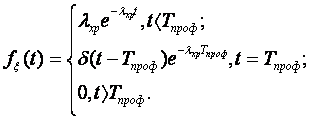
Случайная величина принимает значение в интервале [0, Tпроф], причем для значений, меньших Тпроф, функция плотности вероятности равна ?хре-?xpt. Вероятность того, что ? > Tпроф, будет
математическое ожидание случайной величины ?
тогда коэффициент готовности при хранении
(1.69)
где ?рем—среднее время ремонта.
Учитывая значения (1.68), получаем окончательное выражение для коэффициента готовности при хранении
8. Характеристики надежности сложных систем.
Отличительными чертами сложных систем, к которым относятся современные АСУ, являются: многоканальность, т. е. наличие нескольких каналов, каждый из которых выполняет определенную функцию, частную по отношению к общей задаче системы; многосвязность, т. е. большое количество функциональных связей между элементами системы; наличие вспомогательных и дублирующих устройств.
Благодаря перечисленным особенностям сложная система может находиться в нескольких рабочих состояниях, так как выход из строя некоторых ее элементов не вызывает полного отказа системы, т.е. прекращения выполнения ею заданных функций, но ухудшает в той или иной степени качество функционирования. Следовательно, отказ элемента переводит систему из состояния с полной работоспособностью в состояние с частичной работоспособностью.
ЛСУ можно характеризовать функциональной и эффективной надежностью.
Функциональная надежность РФ — вероятность того, что данная система будет удовлетворительно выполнять свои функции в течение заданного времени. Функциональная надежность отличается от определения надежности, данной в гл. 1, тем, что учитывает наличие схемы контроля в системе. В дальнейшем под функциональной надежностью понимается надежность, рассматриваемая в предыдущих главах.
Эффективная надежность РЭ — среднее значение (математическое ожидание) величины, характеризующей относительный объем и полезность выполняемых системой функций в течение заданного времени по сравнению с ее предельными возможностями. Введение критерия эффективной надежности объясняется тем, что одними показателями надежности, взятыми отдельно, не удается оценить функционирование сложной системы. Сложная система кроме надежности каждого блока и всей системы характеризуется еще относительной важностью потери системой тех или иных качеств поэтому под РЭ понимается некоторая количественная мера, оценивающая качество выполнения системой своих функций. В ряде случаев выполнение конкретной частной задачи с некоторой эффективностью требует работоспособности лишь части аппаратуры. С другой стороны, даже при полной работоспособности всех элементов системы нельзя говорить о выполнении некоторой задачи как о достоверном событии. Основная идея метода определения эффективной надежности заключается в том, что учитывают не только внутренние свойства самой системы, но и качество функционирования и выполнения задачи и выходной эффект.
Пусть система находится в каком-либо состоянии j. Эффективную надежность этой системы в данном состоянии называют частной (условной) эффективностью. Это может быть вероятность того, что система, находясь в состоянии j, способна решить задачу, выбранную случайным образом (независимо от состояния j) в соответствии с некоторым вероятностным законом из определенного множества задач. Тогда под эффективностью можно понимать количество задач, решенных системой в том пли ином состоянии.
Частная эффективность системы характеризуется вероятностью получения этой эффективности. В общем случае эффективная надежность системы со счетным множеством дискретных состояний определяется как математическое ожидание выходного эффекта
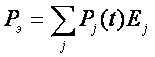
9. Матричный метод расчета надежности.
В ряде случаев отказ элемента системы приводит к изменению режимов работы других связанных с ним элементов, что может повлечь за собой изменение характеристик надежности этих элементов. Например, пробой конденсатора вызывает изменение тока в цепях схемы, в результате чего изменяются коэффициенты нагрузки элементов, а следовательно, и их надежность. В подобных случаях желательно при расчете надежности учитывать взаимозависимость отказов элементов и перераспределение интенсивностей отказов за счет изменения режимов работы, вызванных отказами. Для решения этой задачи может быть использован матричный метод анализа и расчета надежности (см. [4.5]), позволяющий учитывать последствие отказов.
Сущность метода состоит в том, что для определения вероятности безотказной работы ВМ от внезапных отказов с учетом последствия отказов составляется матрица всевозможных несовместимых событий x1, x2,…, xN, вычисляются вероятности всех этих событий, затем суммируются вероятности благоприятных гипотез, при которых система находится в работоспособном состоянии.
В общем случае матрица несовместимых событий для аппаратуры, состоящей из N элементов, за период t имеет следующий вид:
В этой матрице хi— состояние i-гo элемента; означает, что i элемент отказал; H0 — гипотеза, заключающаяся в том, что ни один из элементов не отказал; Нi — гипотеза, заключающаяся в том, что i-й элемент отказал; Н?,? — гипотеза отказа двух элементов ? и ?, причем вначале отказывает элемент ?, а потом ?.
Так как матрица образует полную группу несовместимых событий, то их можно принять за соответствующие гипотезы. Среди гипотез матрицы есть благоприятные с точки зрения работоспособности системы и неблагоприятные. Сумма вероятностей всех гипотез равна единице.
Сумма вероятностей благоприятных гипотез определяет надежность системы, т. е. вероятность безотказной работы за некоторое заданное время
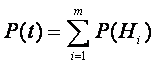
где m — число благоприятных гипотез.
Наиболее трудоемкой частью расчета является определение вероятностей гипотез (состояний), особенно для сложных устройств.
Вероятность отсутствия отказов элементов определяется произведением вероятностей безотказной работы всех элементов:
Вероятности остальных гипотез имеют более сложные выражения и определяются через условные вероятности частных событий. Приведем без вывода формулу для расчета вероятности отказа элемента :
где ???, ??? —изменение интенсивности отказов ?-ro элемента вследствие отказа ?-го элемента.
Таким образом, для выполнения расчета надежности с помощью данного метода необходимо знать интенсивности отказов элементов ? при нормальных режимах работы устройства и их изменения, вызванные сменой режимов за счет отказов различных элементов.
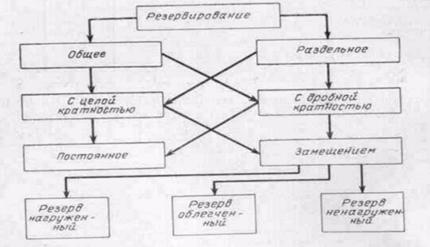
10. Повышение надежности автоматизированных систем управления путем резервировании. Методы резервирования. Общее постоянное резервирование с целой кратностью.
Резервированным соединением изделий называется такое соединение, при котором отказ наступает только после отказа основного изделия и всех резервных изделий.
На практике применяются способы резервирования, приведенные на рис. 3.1. Схемные обозначения различных способов резервирования приведены на рис. 3.2. Общим резервированием называется метод повышения надежности, три котором резервируется изделие в целом (рис. 3.2,д). Раздельным резервированием называется
Рис. 3.1. Способы резервирования.
Рис. 3.2. Схемные обозначения различных способов резервирования: а — общее постоянное с целое кратностью: б — раздельное постоянное с целой кратностью, в — общее замещением с целой кратностью; г —раздельное замещением с целой кратностью; д — общее постоянное с дробной кратностью. е?раздельное замещением с дробной кратностью.
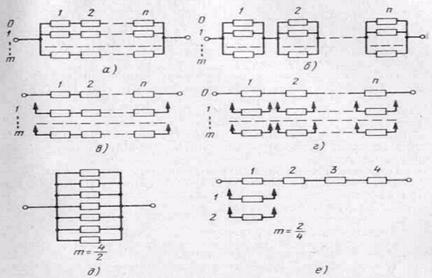
Различают резервирование с целой и дробной кратностью. Схемные обозначения обоих видов резервирования при постоянном включении резерва одинаковы. Для их различия на схеме указывается кратность резервирования m.
При резервировании с целой кратностью величина m есть целое число, при резервировании с дробной кратностью величина m есть дробное несокращаемое число. Например, m = 4/2 означает наличие резервирования с дробной кратностью, при котором число резервных элементов равно четырем, число основных — двум, а общее число элементов равно шести. Сокращать дробь нельзя, так как если m = 4/2=2, то это означает, что имеет место резервирование с целой кратностью, мри котором число резервных элементов равно двум, а общее число элементов равно трем.
По способу включения резервирование разделяется на постоянное и резервирование замещением. Постоянное резервирование — резервирование, при котором резервные изделия подключены к основным в течение всего времени работы и находятся в одинаковом с ними режиме. Резервирование замещением — резервирование, при котором резервные изделия замещают основные после их отказа.
При включении резерва по способу замещения резервные элементы до момента включения в работу могут находиться в трех состояниях:
— нагруженном резерве;
— облегченном резерве;
— ненагруженном резерве.
Приведем основные расчетные формулы для указанных выше видов резервирования.
1. Общее резервирование с постоянно включенным резервом с целой кратностью (рис. 3.2,а):

где pi(t) —вероятность безотказной работы i-го элемента в течение времени t; n — число элементов основной или любой резервной цепи; m — число резервных цепей (кратность резервирования).
При экспоненциальном законе надежности, когда pi(t)=e-?it

где 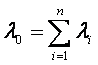
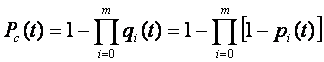
где qi(t), pi(t) — вероятность отказов и вероятность безотказной работы в течение времени t i-го изделия соответственно.
11. Раздельное постоянное резервирование с целой кратностью. Общее резервирование замещением с целой кратностью.
Раздельное резервирование с постоянно включенным резервом и с целой кратностью (рис. 3.2,6):
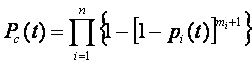
где pi(t) — вероятность безотказной работы i-гo элемента; mi—кратность резервирования i-гo элемента; n — число элементов основной системы.
При экспоненциальном законе надежности, когда pi(t)=e-?it
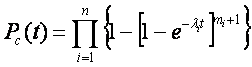
При равнонадежных элементах и одинаковой кратности их резервирования
(3.6)
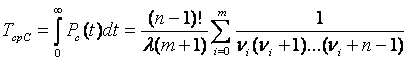
где ?i=(i+1)/(m+1)
.
12. Раздельное резервирование замещением с целой кратностью. Общее постоянное резервирование с дробной кратностью.
Раздельное резервирование замещением с целой кратностью (рис. 3.2,г):
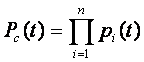
где pi(t) —вероятность безотказной работы системы из-за отказов элементов i-гo типа, резервированных по способу замещения. Вычисляется Pi(t) по формулам общего резервирования замещением (формулы (3.8), (3.9), (3.11).
Общее резервирование с дробной кратностью и постоянно включенным резервом (рис. 3.2,6):
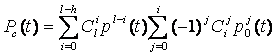
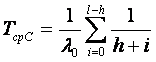
где ро(t) —вероятность безотказной работы основного или любого резервного элемента; l—общее число основных и резервных систем; h —число систем, необходимых для нормальной работы резервированной системы.
В данном случае кратность резервирования
m=(l—h)/h.
13. Скользящее резервирование. Вероятность безотказной работы резервированной системы в случае «обрыва» и «короткого замыкания».
. Скользяще резервирование.
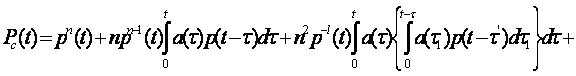
где ?’ = ?+?1; ?» = ? +?1+?2+…; ?m0-1=?+ ?1+…+?m0-1; n — число элементов основной системы; m0—число резервных элементов; p(t — ti) — вероятность безотказной работы одного элемента в течение времени t — ti; ti= t, t-?, t-?m0-1; а(?i) — частота отказов одного из основных элементов в момент времени ?i, ?i=?, ?1, ?2, …, ?m0-1.
При экспоненциальном законе надежности
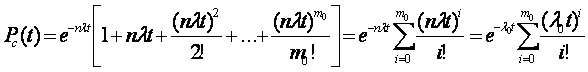
где ?0=n? — интенсивность отказов нерезервированной системы; ? — интенсивность отказов элемента; n — число элементов основной системы; Tcpo — среднее время безотказной работы нерезервированной системы; m0 — число резервных элементов.
В этом случае кратность резервирования
m=m0/n (3.19)
Приведенные выше формулы [кроме выражений (3.8), (3.11), (3.12)] могут быть использованы только в тех случаях, когда справедливо допущение об отсутствии последействия отказов.
Последействие отказов имеет место практически всегда при постоянном включении резерва, а также в случае резервирования замещением при недогруженном состоянии резерва.
Выражение (3.8) является основным при получении расчетных формул в случае учета влияния последействия отказов. При этом члены p(t—?) и am(?) должны быть записаны с учетом последействия отказав, вида резервирования и его кратности.
Элементы (резервированных устройств в ряде случаев могут иметь два вида отказов — «обрыв» и «короткое замыкание». В этом случае вычислять вероятность безотказной работы следует, суммируя вероятности всех благоприятных (не приводящих к отказу) гипотез, т. е.
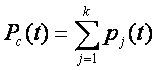
где pj(t) —.вероятность j-й благоприятной гипотезы, вычисленной с учетом двух видов отказов; k — число благоприятных гипотез.
При вычислениях рj(t) следует иметь виду, что для элементов сложной системы справедливы выражения
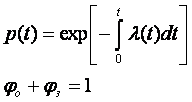
где ?(t) — интенсивность отказов элемента; ?0, ?З — вероятность возникновения «обрыва» и «короткого замыкания» соответственно.
При экспоненциальном законе надежности
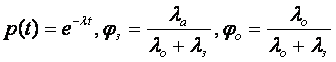
где ?0, ?З — интенсивность отказов элемента по «обрыву» и «короткому замыканию» соответственно.
14. Расчет надежности резервированных систем по схеме «гибели» («чистого размножения»). Выигрыш надежности.
Расчет надежности резервированных систем иногда полезно выполнять, используя схему «гибели» («чистого размножения»). В соответствии с этой схемой преобразование Лапласа вероятности возникновения n отказов вычисляется по формуле
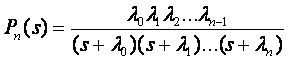
При неравных корнях знаменателя обратное преобразование Лапласа P»(s) будет
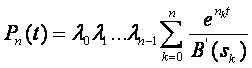
В формулах (3.23) и (3.24) приняты обозначения: ?0 — интенсивность отказов системы до выхода из строя первого элемента; ?1 — интенсивность отказов системы в промежутке времени от момента отказа первого элемента до второго; ?2 — интенсивность отказов системы в промежутке времени от момента отказа второго элемента до третьего и т.д.; n — число отказавших элементов; sk= -?k—k-й корень знаменателя выражения (3.23); B'(sk)—производная знаменателя в точке sk.
При одинаковых опасностях отказов ?i, т.е. ?0=?1=…=?n, расчетные формулы имеют вид
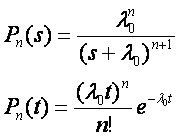
При расчетах надежности по формулам (3.23) — (3.25) следует помнить, что они не определяют вероятности безотказной работы (или вероятности отказа) резервированной системы, а определяют лишь вероятность n-го состояния системы, т.е. вероятность того, что в системе откажут n элементов. Для вычисления вероятности безотказной работы необходимо находить вероятности 0, 1, …, n отказов, когда система еще находится в работоспособном состоянии (исправна), и суммировать полученные вероятности.
Среднее время безотказной работы системы при использовании схемы «гибели» вычисляется по формуле
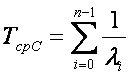
где ?i— интенсивность отказов системы до выхода из строя i-го элемента.
При схемной реализации резервирования в ряде случаев конкретные технические решения не приводятся к логическим схемам расчета надежности (рис. 3.2).
В этих случаях следует для получения аналитических выражений для количественных характеристик надежности использовать метод перебора благоприятных гипотез. Вероятность безотказной работы в этом случае вычисляется по выражению (3.20).
При анализе надежности резервированных устройств на этапе проектирования приходится сравнивать различные схемные решения. В этом случае за критерий качества резервирования принимается выигрыш надежности. Выигрышем надежности называется отношение количественной характеристики надежности резервированного устройства к той же количественной характеристике нерезервированного устройства или устройства с другим видом резервирования.
Наиболее часто используются следующие критерии качества резервированных устройств: Gq(t) — выигрыш надежности в течение времени t по вероятности отказов; Gp(t) — выигрыш надежности в течение времени t по вероятности безотказной работы; GT — выигрыш надежности ;по среднему времени безотказной работы.
При резервировании элементов электроники (резисторов, конденсаторов, контактов реле, диодов и т.п.) всегда произведение интенсивности отказов элемента на время его работы значительно меньше единицы, т.е. ?t<<1. Поэтому при вычислении Gg(t) и Gp(t) целесообразно функции вида е-k?t (экспоненциальный случай) разложить в ряд при небольшом k:
Если система исправна при отказе m элементов, то необходимо брать не менее чем m+2 членов разложения.
Как вычисляется среднее время до отказа и вероятность безотказной работы?
Время на прочтение
4 мин
Количество просмотров 116K
Понятиям MTTF (Mean Time To Failure — среднее время до отказа) и другим терминам теории надежности посвящено большое количество статей, в том числе на Хабре (см., например, тут). Вместе с тем, редкие публикации «для широкого круга читателей» затрагивают вопросы математической статистики, и уж тем более они не дают ответа на вопрос о принципах расчета надежности электронной аппаратуры по известным характеристикам ее составных элементов.
В последнее время мне довольно много приходится работать с расчетами надежности и рисков, и в этой статье я постараюсь восполнить этот пробел, отталкиваясь от своего предыдущего материала (из цикла о машинном обучении) о пуассоновском случайном процессе и подкрепляя текст вычислениями в Mathcad Express, повторить которые вы сможете скачав этот редактор (подробно о нем тут, обратите внимание, что нужна последняя версия 3.1, как и для цикла по machine learning). Сами маткадовские расчеты лежат здесь (вместе с XPS- копией).
1. Теория: основные характеристики отказоустойчивости
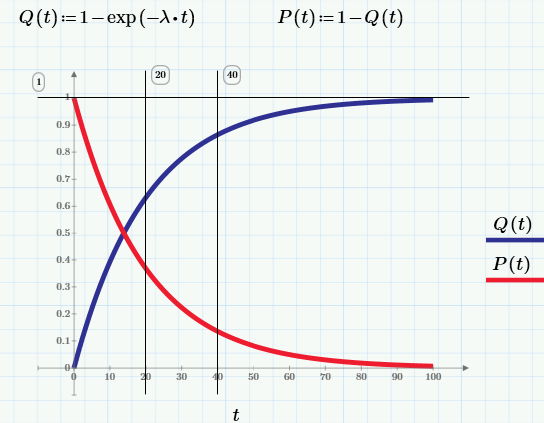
Вроде бы, из самого определения (Mean Time To Failure) понятен его смысл: сколько (конечно, в среднем, поскольку подход вероятностный) прослужит изделие. Но на практике такой параметр не очень полезен. Действительно, информация о том, что среднее время до отказа жесткого диска составляет полмиллиона часов, может поставить в тупик. Гораздо информативнее другой параметр: вероятность поломки или вероятность безотказной работы (ВБР) за определенный период (например, за год).
Для того чтобы разобраться в том, как связаны эти параметры, и как, зная MTTF, вычислить ВБР и вероятности отказа, вспомним некоторые сведения из математической статистики.
Ключевое понятие теории надежности — это понятие отказа, измеряемое, соответственно, интервальным показателем
Q(t) = вероятность того, что изделие откажет к моменту времени t.
Соотвественно, вероятность безотказной работы (ВБР, в английской терминологии «reliability»):
P(t) = вероятность того, что изделие проработает без отказа от момента t0=0 до момента времени t.
По определению, в момент t0=0 изделие находится в работоспособном состоянии, т.е. Q(0)=0, а P(0)=1.
Оба параметра — это интервальные характеристики отказоустойчивости, т.к. речь идет о вероятности отказа (или наоборот, безотказной работы) на интервале (0,t). Если отказ рассматривать, как случайное событие, то, очевидно, что Q(t) — это, по определению, его функция распределения. А точечную характеристику можно определить, как
p(t)=dQ(t)/dt = плотность вероятности, т.е. значение p(t)dt равно вероятности, что отказ произойдет в малой окрестности dt момента времени t.
И, наконец, самая важная (с практической точки зрения) характеристика: λ(t)=p(t)/P(t)=интенсивность отказов.
Это (внимание!) условная плотность вероятности, т.е. плотность вероятности возникновения отказа в момент времени t при условии, что до этого рассматриваемого момента времени t изделие работало безотказно.
Измерить параметр λ(t) экспериментально можно путём испытания партии изделий. Если к моменту времени t работоспособность сохранило N изделий, то за оценку λ(t) можно принять процент отказов в единицу времени, происходящих в окрестности t. Точнее, если в период от t до t+dt откажет n изделий, то интенсивность отказов будет примерно равна
λ(t)=n/(N*dt).
Именно эта λ-характеристика (в пренебрежении ее зависимостью от времени) и приводится чаще всего в паспортных данных различных электронных компонент и самых разных изделий. Только сразу возникает вопрос: а как вычислить вероятность безотказной работы и при чем здесь среднее время до отказа (MTTF).
А вот при чем.
2. Экспоненциальное распределение
В терминологии, которую мы только что использовали, пока не было никаких предположений о свойствах случайной величины — момента времени, в который происходит отказ изделия. Давайте теперь конкретизируем функцию распределения значения отказа, выбрав в качестве нее экспоненциальную функцию с единственным параметром λ=const (смысл которого будет ясен через несколько предложений).
Дифференцируя Q(t), получим выражение для плотности вероятности экспоненциального распределения:
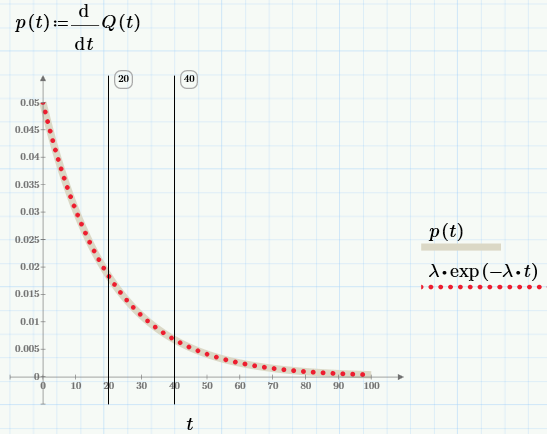
а из него – функцию интенсивности отказов: λ(t)=p(t)/P(t)=const=λ.
Что мы получили? Что для экспоненциального распределения интенсивность отказов – есть величина постоянная, причем совпадающая с параметром распределения. Этот параметр и является главным показателем отказоустойчивости и его часто так и называют λ-характеристикой.
Мало того, если теперь посчитать среднее время до первого отказа – тот самый параметр MTTF (Mean Time To Failure), то мы получим, что он равен MTTF=1/ λ.
Все это замечательные свойства экспоненциального распределения. Почему мы выбрали в качестве для описания отказов именно его? Да потому что это наиболее простая модель – модель пуассоновского потока событий, которая уже была нами рассмотрена в статье про анализ конверсии сайта. Поэтому-то в теории надежности наиболее часто используется показательное (экспоненциальное) распределение, для которого, как мы выяснили:
- надежность элементов можно оценить одним числом, т.к. λ=const;
- по известной λ довольно просто оценить остальные показатели надежности (например, ВБР для любого времени t);
- λ обладает хорошей наглядностью
- λ нетрудно измерить экспериментально
Но это еще не все, потому, что для экспоненциального распределения особенно легко делать расчет систем, состоящих из множества элементов. Но об этом – в следующей статье (продолжение следует).