Вероятность безотказной работы экспоненциального закона за время определяется по формуле

Макеты страниц

ЭКСПОНЕНЦИАЛЬНЫЙ ЗАКОН НАДЕЖНОСТИ

Основной период эксплуатации обычно характеризуется почти постоянной интенсивностью отказов. В этом периоде отказы происходят от случайных факторов (попадание посторонних предметов, неблагоприятное сочетание внешних факторов, усталостные разрушения и др и носят внезапный характер. Время появления отказа не связано с предыдущей наработкой изделия.

При экспоненциальном законе надежности предполагается, что интенсивность отказов является величиной постоянной (рис. 2):

Вероятность безотказной работы по уравнению (17)

Плотность распределения отказов

Среднее время безотказной работы

Вероятность безотказной работы можно теперь записать в такой форме:

Экспоненциальный закон распределения справедлив для описания потока отказов с постоянной интенсивностью.

Рис. 2. Экспоненциальное распределение времени безотказной работы

Понятие потока отказов вводится для восстанавливаемых в процессе эксплуатации изделий.

Для потока отказов величина представляет собой среднюю наработку на один отказ.

Важным свойством экспоненциального закона надежности является то, что он относится к «нестареющим» системам. Для такого закона (и только для него!) прогнозируемая вероятность безотказной работы не зависит от предыдущей наработки

Пример 1. Изделие имеет ресурс и интенсивность отказов (среднее время наработки на отказ

Определить вероятность безотказной работы первые и за весь ресурс, считая справедливым экспоненциальный закон надежности.

Решение. Вероятность безотказной работы за первые работы

за весь ресурс

но если известно, что изделие отработало исправно то вероятность отсутствия отказов за последние снова будет 0,999.

Рассмотрим определение интеисивности отказов (или средней наработки на отказ) при экспоненциальном распределении. Если известно, что для

испытуемых изделий время работы до отказа составило то следует принять

Однако на практике информация о работоспособности изделий относится к определенному времени эксплуатации, а течение которого часть изделий получила отказы, а остальные отработали его исправно Тогда следует принять для данного времени испытаний

Пример 2. Определить среди наработку до отказа для экспоненциаль ного закона надежности, если за время эксплуатации имеются следующие данные — 30 изделий отработали исправно изделий по изделий по сняты три изделия после наработки соответственно 500, 2000 и 2500 ч.

Решение. Суммарное время наработки

Средняя наработка на отказ

Источник

Расчет показателей надежности с помощью методов теории вероятности

При
анализе и расчете показателей надежности
математическим методом необходимо
знать функцию распределения и функцию
плотности распределения вероятности
оцениваемого параметра. На практике
используются типовые законы распределения
случайной величины, к которым весьма
близки реальные распределения показателей
надежности во времени.

Нормальное
распределение.Является основным
в математической статистике. Оно
образуется, когда на случайную величину
действует большое количество факторов.
В теории надежности нормальным
распределением описывают наработки
на отказ объектов вследствие их износа
и старения.

Нормальный
закон распределения характеризуется
двумя статистическими параметрами:
математическим ожиданием µ и стандартным
отклонением σ. Для оценки математического
ожидания можно использовать среднее
арифметическое значение случайной
величины. Статистические параметры
нормального распределения

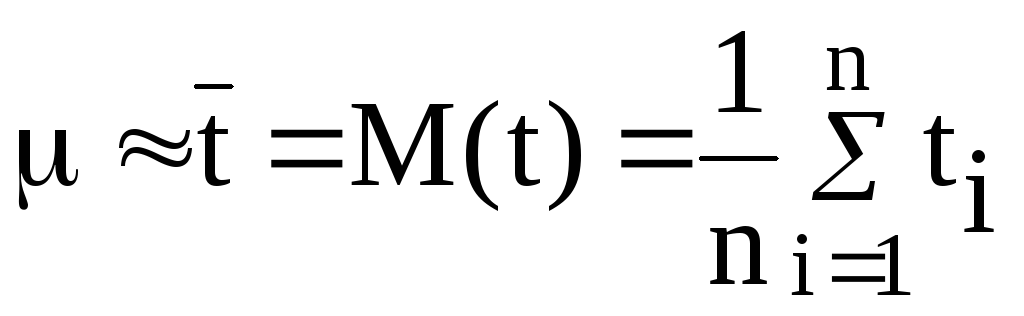
где
— среднее арифметическое значение
параметра (временной параметр),t_i– выборочные значения случайной величины

σ – стандартное отклонение случайной
величины,

D(t) — дисперсия случайной величины.

Характер
нормального распределения определяется
функциями распределения и вероятности
плотности случайной величины. Функция
распределения случайной величины при
нормальном законе распределения
(рассматриваем временной параметр,
поскольку показатели надежности являются
временными характеристиками)

плотность вероятности нормального
закона распределения

С помощью нормального распределения
можно описать вероятность отказа объекта
вследствие его старения или износа Q
(t) = F(t) в
зависимости от наработки объекта t.
Вероятность безотказной работы в этом
случае

ЗависимостьP(t) называют
также кривой (функцией) убыли ресурсов.

На рис.
14 a) показаны графики
функции нормального распределения и
соответствующей ей кривой убыли ресурсов.
Математическому ожиданию μ соответствует
уровень вероятности 0,5.

Общий
вид графика плотности вероятности при
нормальном распределении показан на
рис. 14 b). В границах ±
3относительно
среднего значения укладывается 99,73 %
значений случайной величины. Эти границы
часто используются для оценки пределов
изменения значений случайной величины
при нормальном ее распределении.

Для
выполнения расчетов с использованием
нормального распределения применяют
нормированное нормальное распределение
(табулированную функцию Лапласа для
вероятности попадания нормированной
нормальной величины Х в интервал
(0, x):

где
— квантиль нормированного нормального
распределения.

На
рис. 15 показан график нормированного
нормального распределения. В таблицах
приводятся значения Ф(х) для положительных
квантили х. Для отрицательных значений
квантили вероятность равна

Нормированное
нормальное распределение удобно
использовать при расчетах как вероятности
случайной величины, так и для расчета
значения случайной величины по ее
вероятности.

Для
вычисления вероятности
попадания
случайной величиныtв
интервал t1 ÷ t2 c использованием функции
Лапласа необходимо найти

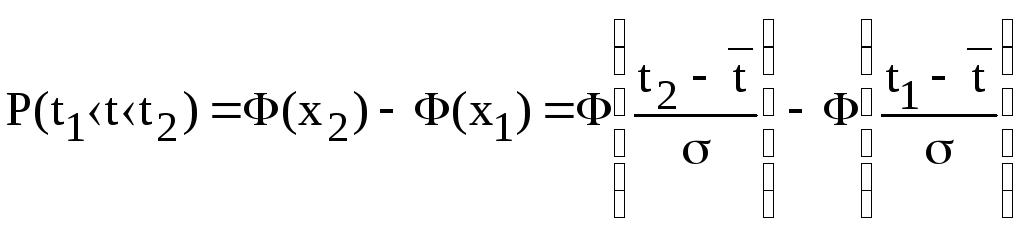
Если
необходимо решить обратную задачу:
определить наработку, соответствующую
заданной вероятности безотказной
работы, то используют квантили нормального
распределения

где x- квантиль нормированного
нормального распределения, которая
зависит от требуемой вероятности и
приводится в таблицах.

Нормальному
распределению подчиняется наработка
на отказ многих восстанавливаемых и
невосстанавливаемых объектов.

Пример
1.Наработка объекта до отказа
имеет нормальное распределение с
математическим ожиданием μ = 1000 час и
стандартным отклонением σ = 200 час.
Определить вероятность безотказной
работы объекта в течение 400 час.

Решение:

Вероятность
безотказной работы может быть вычислена
через функцию распределения

Для
расчета используем табулированное
нормированное нормальное распределение
Ф(х). Определим квантиль распределения

Для
отрицательного значения квантили
.
Вероятность безотказной работы равна

Вычисляем значение вероятности, используя
табулированную функцию Ф(х)

Вероятность
безотказной работы объекта в течение
400 час составляет 99,865%.

Пример
2. Определить вероятность
безотказной работы подшипника качения
в течение 1500 час, если его ресурс по
износу подчиняется нормальному закону
распределения с математическим ожиданием
3500 час и стандартным отклонением 1000
час.

Решение:

Вычисляем
квантиль нормированного нормального
распределения

Вероятность
безотказной работы

Вероятность
безотказной работы подшипника в течение
1500 час составляет 97,72%.

Пример
3. Наработка объекта до отказа
подчиняется нормальному закону
распределения с параметрами µ = 1000 час
и σ = 200 час. Определить гамма-процентный
ресурс объекта при вероятности 90%.

Решение:

Определим
вероятность отказа
По таблице нормированного нормального
распределения находим квантиль,
соответствующую вероятности 0,1: х =
-1,281. Используем выражение для значения
случайной величины

,
следовательно,
90% ресурс изделия равенчас.

Экспоненциальное
распределение.Этот закон описывает надежность работы
изделия в период его нормальной
эксплуатации, когда постепенные отказы
вследствие износа и старения еще не
проявляются и надежность характеризуется
внезапными отказами. Эти отказы вызываются
неблагоприятным сочетанием различных
факторов и имеют постоянную интенсивность. Экспоненциальное
распределение часто называют основным
законом надежности. Экспоненциальное
распределение наиболее применимо для
оценки безотказности объектов в период
после приработки и до проявления
постепенных отказов. Этот закон
используется также при решении задач
об обслуживании сложных систем.

Экспоненциальное
распределение имеет только один параметр
λ и является частным случаем распределения
Вейбулла и гамма — распределения. Функция
распределения случайной величины при
экспоненциальном законе распределения

плотность вероятности экспоненциального
распределения

Функция
распределения описывает вероятность
возникновения отказов объекта. Вероятность
безотказной работы может быть определена
как

где - интенсивность
отказов. Приможно
принять

Экспоненциальное
распределение иллюстрируется графиками
функции распределения F(t)
и вероятности безотказной работыP(t),
показанными на рис. 16. Это распределение
справедливо для положительных значений
случайной величины.

Графики
плотности вероятности случайной величины
при экспоненциальном распределении
приведены на рис. 17. График 1 построен
для параметра λ = 0,0015, а график 2 – для λ
= 0,001. Начальное значение на графике
равно λ.

Математическое
ожидание и среднее квадратическое
отклонение для экспоненциального закона
равны между собой

Равенствоявляется существенным признаком для
отнесения экспериментального распределения
к теоретическому экспоненциальному
распределению.

Рассмотрим
примеры использования закона
экспоненциального распределения для
расчетов надежности.

Пример
1. Наработка на отказ сложной
технической системы подчиняется
экспоненциальному закону распределения
с параметром λ = 15*10^-5час^-1.
Определить вероятность безотказной
работы системы в течение 100 час и найти
среднее значение наработки на отказ.

Решение:

Определим вероятность безотказной
работы при наработке Tчерез функцию распределения
экспоненциального закона

после подстановки конкретных значений
получим

.
Следовательно,
вероятность наработки 100 час составляет
98,5 %. Среднее значение наработки может
быть определено через параметр
распределения λ

час.

Пример
2. Интенсивность отказов
электрического элемента равна λ=10^-61/час. Отказы подчиняются экспоненциальному
закону распределения случайной величины.
Найти вероятность безотказной работы
элемента в течение 10000 час.

Решение:

Используем
формулу для вероятности безотказной
работы при экспоненциальном распределении

,
следовательно,
вероятность безотказной работы элементаP(10000) = 99 %.

Распределение
Вейбулла.Вейбулл описал с его
помощью разброс усталостной прочности
стали, предела ее упругости, размер
частиц копоти и др. Это распределение
применяют также при описании надежности
сложных технических систем.

Распределение
Вейбулла является двухпараметрическим
универсальным законом, так как при
изменении параметров оно в пределе
может описывать нормальное распределение,
логарифмически нормальное распределение,
экспоненциальное и др. Распределение
Вейбулла характеризуется параметром
масштаба λ и параметром формы α.

Функция
распределения для закона Вейбулла имеет
вид

функция надежности

где - параметр формы
кривой распределения,- параметр масштаба.

Плотность
вероятности распределения Вейбулла
выражается зависимостью

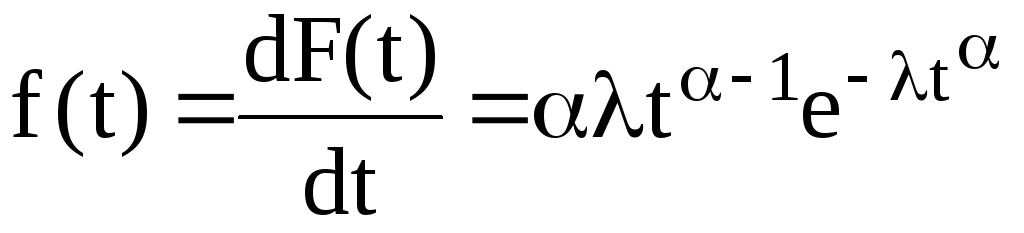
Если
для закона Вейбулла принят α = 1, то
получим экспоненциальное распределение,
которое является частным случаем
распределения Вейбулла.

Графики
функций распределения F(t)
и вероятности безотказной работыP(t)
показаны на рис. 18. При увеличении
параметра формы α кривая приближается
к нормальному распределению.

Графики
плотности вероятности распределения
Вейбулла приведены на рис. 19. Влияние
параметра формы на вид кривой в этом
случае выражены еще резче. При увеличении
параметра форма кривой от экспоненциальной
зависимости стремится к характерной
для нормального распределения
колоколообразной кривой.

Выбором
параметров масштаба λ и формы α можно
в широких пределах изменять форму
кривой, что позволяет использовать
закон Вейбулла для самых разных случаев
математического описания надежности
многих объектов.

Статистические
параметры распределения Вейбулла
вычисляются через параметры α и λ.
Математическое ожидание для закона
Вейбулла

,
стандартное
отклонение

где
— гамма функция параметра α. Для непрерывной
величины гамма-функция

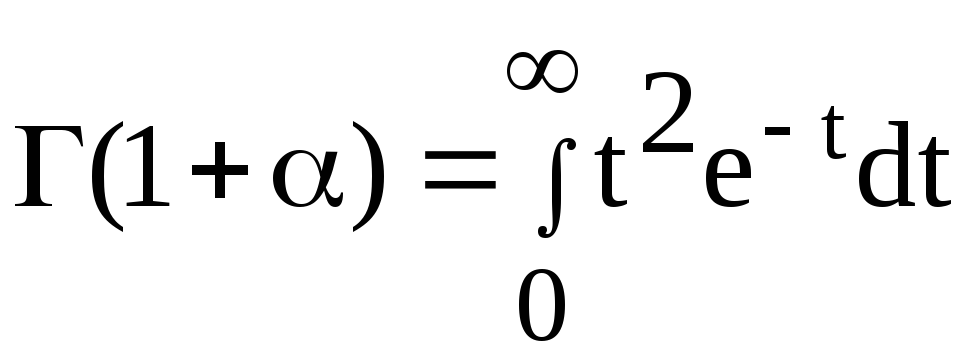
Для
вычисления значения гамма-функции Г(n
+ ), где n — целое
число,- дробное
число при 2 ≤n≤ 6 можно
использовать более простую формулу

При n 6 значения
Г(n+) можно находить
по формуле

Г(n+1)
= n!

Рассмотрим
пример использования распределения
Вейбулла для расчета надежности.

Пример
1. Определить вероятность
безотказной работы генератора в течение
1000 час, если его наработка на отказ
описывается распределением Вейбулла
с параметрами α = 2 и λ = 6,667*10^-7.

Решение:

Вероятность
безотказной работы равна

.
Следовательно,
вероятность безотказной работы генератора
в течение 1000 час составляет 51,3 %.

Пример
2. Случайная наработка изделия
до отказа распределена по закону Вейбулла
с параметрами,.
Найти вероятность безотказной работы
изделия при заданной наработкечас.

Решение:

Используем
формулу для расчета вероятности
безотказной работы при распределении
Вейбулла

Следовательно,
вероятность безотказной работы в течение
300 час составляет 91,39 %.

Пример
3. Для предыдущего примера найти
наработку до отказа при вероятности
безотказной работы 99 %.

Решение:

Используем
уравнение вероятности безотказной
работы

откуда,

следовательно,

час.

Гамма
– распределение.Распределение
характеризуется двумя параметрами: λ
– параметр масштаба и α – параметр
формы. Оно имеет ограничение с одной
стороны (0t). Если параметр
формы кривой- целое
число, то гамма-распределение списывает
время, необходимые для появления событий
(например, отказов) при условии, что они
независимы и появляются с постоянной
интенсивностью.
Это распределение описывает наработку
системы с резервированием, время
восстановления, а также распределение
постепенных отказов вследствие износа.

Кривые
распределения изменяют свою форму в
широких пределах при изменении параметров
λ и α. Функция гамма-распределения

,
F(t) ≡ 0 при t ‹ 0.

Плотность
вероятности гамма-распределения (0,0)

приt≥ 0,приt< 0,
где— гамма-функция.

Вероятность
безотказной работы

Графики
для функций распределенияF(t)
и вероятности безотказной работыP(t)
приведены на рис. 20. Характер зависимостей
изменяется в широких пределах при
изменении параметров распределения.

Графики
для плотности вероятности гамма-распределения
показаны на рис. 21. При 1 характер зависимости
для плотности распределения убывающий.
При= 1 иполучается экспоненциальное распределение,
при3 кривая распределения приближается к
нормальному закону распределения.

Математическое
ожидание и дисперсия для гамма-распределения
соответственно равны

Пример.
Определить вероятность безотказной
работы изделия в течение 1000 час, если
наработка до отказа этого изделия
подчиняется гамма-распределению с
параметрами α = 4 и λ = 10^-3.

Решение:

Используем
выражение для вероятности безотказной
работы

=.
Для
вычисления выражения можно использовать
таблицы гамма-распределения или
компьютерные программы. Ниже показанMathcad-документ для вычисления
вероятности

В результате вычисления получим P(1000)
= 0,981= 98,1 %.

Распределение
Пуассона.Распределение
используется для дискретных случайных
величин. Описывает появление внезапных
отказов в сложных системах и распределение
времени восстановления, число отказов
однотипного оборудования за определенный
интервал времени и т.п.

Функция
распределения Пуассонадля
целочисленного аргумента m = 0,1,2 …

приt0..

Плотность
вероятности дискретного распределения

где
t — фиксированный интервал времени,0. Чем меньше значение, тем ассиметричнее
распределение. Пример графика для
распределения Пуассона показан на рис.
22. График построен для λ = 0,5.

Сумма
вероятностей

Математическое
ожидание и дисперсия распределения
Пуассона

Источник

Показательное распределение

Краткая теория
Примеры решения задач
Задачи контрольных и самостоятельных работ

Краткая теория

Показательным (экспоненциальным) называют распределение вероятностей непрерывной случайной величины

, которое описывается плотностью:

где

–
постоянная положительная величина.

Показательное
распределение определяется одним параметром

. Эта особенность распределения указывает на
его преимущество по сравнению с распределениями, зависящими от большего числа
параметров. Обычно параметры неизвестны и приходится находить их оценки
(приближенные значения); разумеется, проще оценить один параметр, чем два или три.
Примером непрерывной случайной величины, распределенной по показательному
закону, может служить время между появлениями двух последовательных событий
простейшего потока.

Функция распределения
показательного закона:

Графики плотности и
функции распределения показательного закона изображены на рисунке.

Вероятность попадания в
интервал

непрерывной
случайной величины

, распределенной по показательному закону:

Числовые характеристики показательного (экспоненциального) распределения

Математическое ожидание случайной величины, распределенной по показательному закону:

Дисперсия случайной величины, распределенной по показательному закону:

Среднее квадратическое отклонение случайной величины,
распределенной по показательному закону:

Коэффициенты асимметрии и эксцесса
для показательного распределения:

Таким
образом, математическое ожидание и среднее квадратическое
отклонение экспоненциального распределения равны между собой.

Показательный закон
распределения играет большую роль в теории массового обслуживания и теории
надежности. Так, например, интервал времени

между
двумя соседними событиями в простейшем потоке имеет показательное распределение
с параметром

–
интенсивностью потока.

При решении задач, которые выдвигает практика, приходится
сталкиваться с различными распределениями непрерывных случайных величин.

Смежные темы решебника:

Непрерывная случайная величина
Нормальный закон распределения случайной величины
Равномерный закон распределения случайной величины

Примеры решения задач

Пример 1

Случайная величина

задана функцией распределения

Найдите математическое
ожидание и среднее квадратическое отклонение этого
распределения.

Найдите вероятность того,
что случайная величина примет значение от 0,2 до 1.

На сайте можно заказать решение контрольной или самостоятельной работы, домашнего задания, отдельных задач. Для этого вам нужно только связаться со мной:

ВКонтакте
WhatsApp
Telegram

Мгновенная связь в любое время и на любом этапе заказа. Общение без посредников. Удобная и быстрая оплата переводом на карту СберБанка. Опыт работы более 25 лет.

Подробное решение в электронном виде (docx, pdf) получите точно в срок или раньше.

Решение

Математическое
ожидание случайной величины, распределенной по показательному закону:

Среднее
квадратическое отлонение:

Вероятность того, что
случайная величина примет значение от 0,2 до 1

Ответ

Пример 2

На шоссе установлен контрольный пункт для
проверки технического состояния автомобилей. Найти математическое ожидание и
среднее квадратическое отклонение случайной величины T – время ожидания
очередной машины контролером, если поток машин простейший и время (в часах)
между прохождениями машин через контрольный пункт распределено по
показательному закону f(t)=5e^-5^t.

Указание: Время ожидания машины
контролером и время прохождения машин через контрольный пункт распределены
одинаково.

Решение

В нашем случае
параметр показательного распределения

Математическое
ожидание:

Дисперсия:

Среднее
квадратическое отклонение:

Ответ:

Пример 3

Постройте
интегральную и дифференциальную функции распределения случайной величины X.
Найдите математическое ожидание M(X), дисперсию D(X),
среднее квадратическое отклонение σ(X), моду x_mod, медиану x_med, если известно, что
случайная величина X имеет показательное распределение с параметром λ=1.

ВКонтакте
WhatsApp
Telegram

Подробное решение в электронном виде (docx, pdf) получите точно в срок или раньше.

Решение

Плотность
распределения случайной величины

, распределенной по
показательному закону:

Функция
распределения:

Построим
графики дифференциальной и интегральной функций распределения:

График дифференциальной функции распределения

График интегральной функции распределения

Математическое
ожидание показательно распределенной случайной величины

Дисперсия:

Среднее
квадратическое отклонение:

найдем, исходя из условия:

Пример 4

Случайная
величина

распределена показательно с дисперсией 0,25.
Найти математическое ожидание и вероятность попадания

в интервал (0,5;1).

Решение

Дисперсия
случайной величины, распределенной по показательному закону:

Математическое
ожидание случайной величины, распределенной по показательному закону:

Вероятность
попадания в интервал

непрерывной случайной величины

, распределенной по
показательному закону:

В нашем
случае:

Ответ:

Задачи контрольных и самостоятельных работ

Задача 1

Время
безотказной работы двигателя автомобиля распределено по показательному закону.
Известно, что среднее время наработки двигателя на отказ между техническим
обслуживанием 100 ч. Определить вероятность безотказной работы двигателя за 80
ч.

ВКонтакте
WhatsApp
Telegram

Подробное решение в электронном виде (docx, pdf) получите точно в срок или раньше.

Задача 2

Среднее
время работы элемента, входящего в пожарно-техническое устройство, равно 1000
часов. Определить вероятность того, что элемент будет работать от 950 до 1150
часов, если время работы элемента распределено по показательному закону.

Задача 3

Вероятность
безотказной работы элемента распределена по экспоненциальному закону

f(t)=e^-0.05t

Найти
вероятность того, что в результате испытания случайная величина попадет в
интервал (11;35). Найти характеристики данного распределения случайной
величины.

Задача 4

Непрерывная
случайная величина X задана интегральной функцией распределения

Найти
постоянную C, математическое ожидание случайной величины X,
вероятность попадания случайной величины в интервал [2;4].

Задача 5

Время
между отказами прибора распределено по показательному закону со средним
значением 25 часов. Определить математическое ожидание и дисперсию времени
безотказной работы автомобиля. Найти вероятность того, что очередной отказ
произойдет не позднее 15 часов.

Задача 6

Время
безотказной работы телевизора определенной модели описывается показательным (экспоненциальным)
законом распределения с постоянной λ. Что вероятнее, его безотказная работа в
промежутке времени [x₁,x₂]

или [x₃,x₄]? Записать
функции f(x),F(x) и построить их графики.

λ=1/10, x₁=3, x₂=5, x₃=4, x₄=8

ВКонтакте
WhatsApp
Telegram

Подробное решение в электронном виде (docx, pdf) получите точно в срок или раньше.

Задача 7

Испытывают
два независимо работающих элемента. Длительность времени t безотказной
работы первого элемента имеет показательное распределение с параметром 0,02,
второго -показательное распределение с параметром 0,06. Найдите вероятность
того, что за время длительностью t=6 ч откажет только один
элемент.

Задача 8

Среднее
время работы каждого из трех элементов, входящих в техническое устройство,
равно T=850 часов. Для безотказной работы устройства необходима безотказная
работа хотя бы одного из трех этих элементов. Определить вероятность, что
устройство будет работать от t₁=750 до t₂=820 часов, если время
работы каждого из трех элементов независимо и распределено по показательному
закону.

Задача 9

Время
устранения повреждения на канале связи T -случайная величина,
распределенная по закону f(t)=λe^-λt (t≥0). Среднее время
восстановления канала — 10 минут. Определить вероятность того, что на
восстановление канала потребуется от 5 до 10 минут.

Задача 10

Дана плотность
распределения случайной величины X.

По какому
закону распределения случайная величина? Найти математическое ожидание,
дисперсию, функцию распределения?

Задача 11

Время
безотказной работы механизма подчинено показательному закону с плотностью
распределения вероятностей f(t)=0.04e^-0.04t при t > 0 (t –
время в часах). Найти вероятность того, что механизм проработает безотказно не
менее 100 часов.

Задача 12

Длительность телефонного разговора
является случайной величиной, распределенной по показательному закону.
Известно, что средняя длительность телефонного разговора равна 9 минутам. Найти
вероятность того, что разговор будет длиться:

а) не более 5 минут.

б) более 5 минут.

ВКонтакте
WhatsApp
Telegram

Подробное решение в электронном виде (docx, pdf) получите точно в срок или раньше.

Задача 13

Случайная величина ξ подчинена
показательному закону с параметром λ=5:

Найдите вероятность того, что
случайная величина ξ примет значение меньшее, чем ее математическое ожидание.

Задача 14

Случайная
величина ξ имеет плотность вероятностей (показательное распределение)

Найдите
вероятность P{ξ>M_ξ}

Задача 15

Время T
(минут), затрачиваемое клиентами парикмахерской в ожидании своей очереди,
удовлетворяет показательному распределению с параметром λ=0,05. Какова
вероятность того, что время ожидания превысит 25 минут и каково среднее время
ожидания.

Задача 16

Время T (час),
необходимое на ремонт легкового автомобиля удовлетворяет показательному
распределению с параметром λ=0,2. Какова вероятность того, что время ремонта
одного автомобиля не превысит 6 часов, и сколько часов в среднем затрачивается
на ремонт одного автомобиля.

Задача 17

Время
ожидания у бензоколонки автозаправочной станции является случайной величиной X,
распределенной по показательному закону, со средним временем ожидания, равным t₀. Найти вероятности
следующих событий:

Задача 18

Случайная
величина X задана показательным законом распределения и
числовыми значениями параметров M(X)=3 и σ_x=3.

Требуется:

1) найти
функцию плотности f(x).

2) найти
вероятность попадания СВ X в указанный интервал [a,b]=[2,4].

Задача 19

Случайная
величина ξ задана функцией распределения

Найдите
математическое ожидание и среднее квадратическое отклонение этого
распределения.

Задача 20

Случайная величина ξ распределена по
показательному закону с параметром λ=0,3. Найдите математическое ожидание и
среднее квадратическое отклонение этой случайной величины.

Краткая теория
Примеры решения задач
Задачи контрольных и самостоятельных работ

Источник