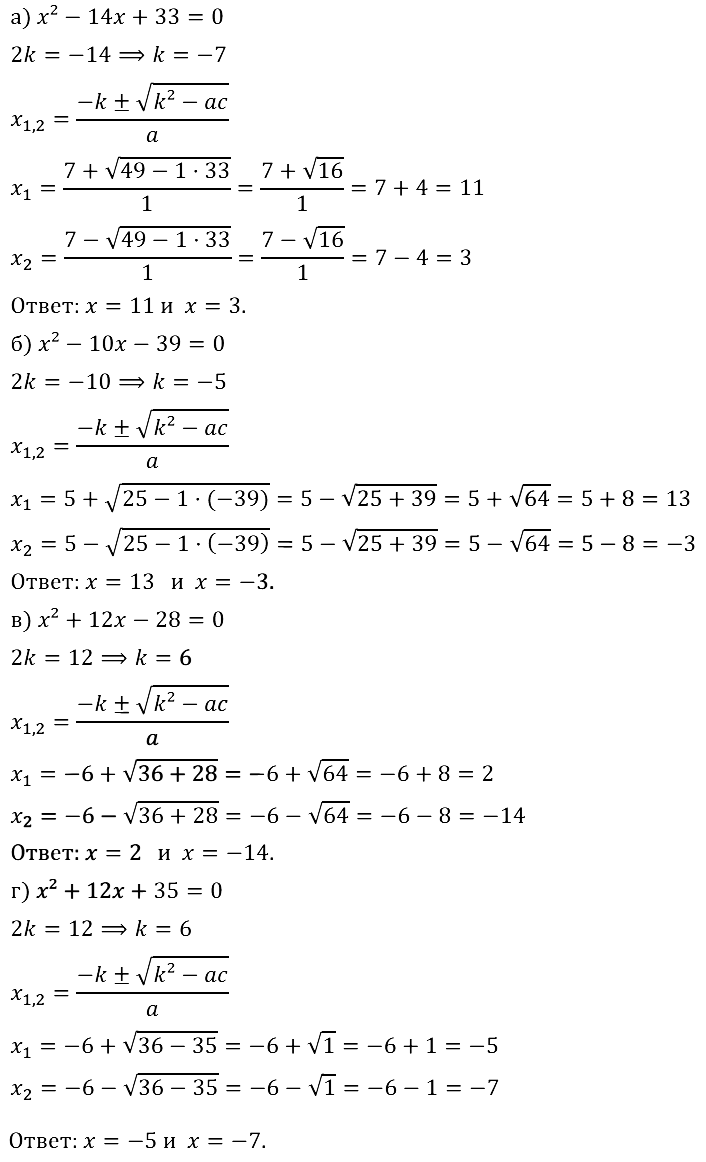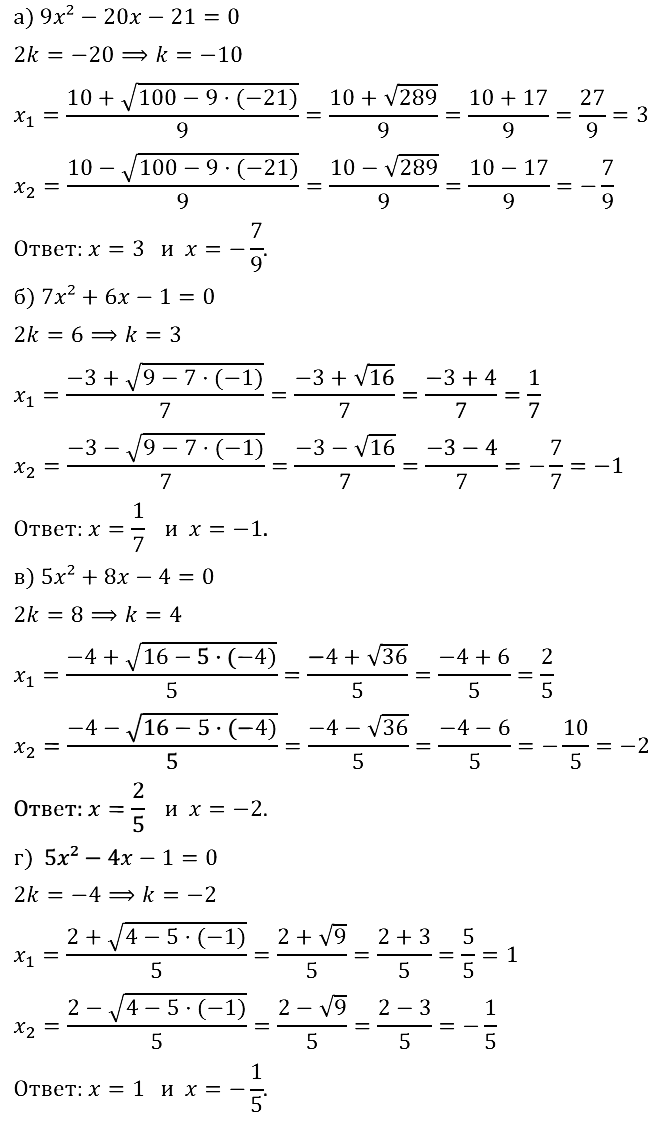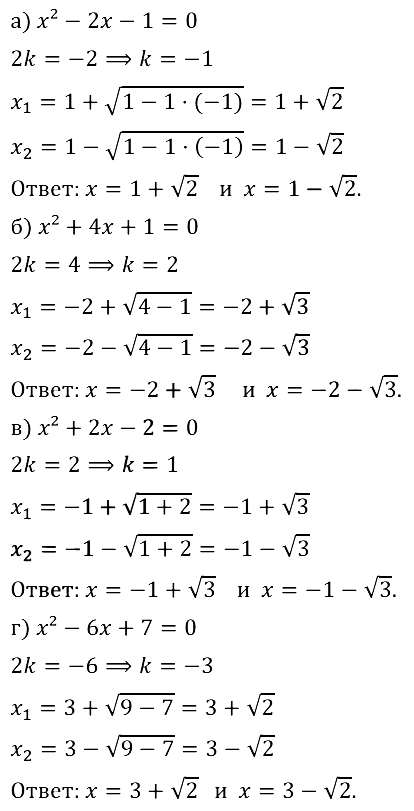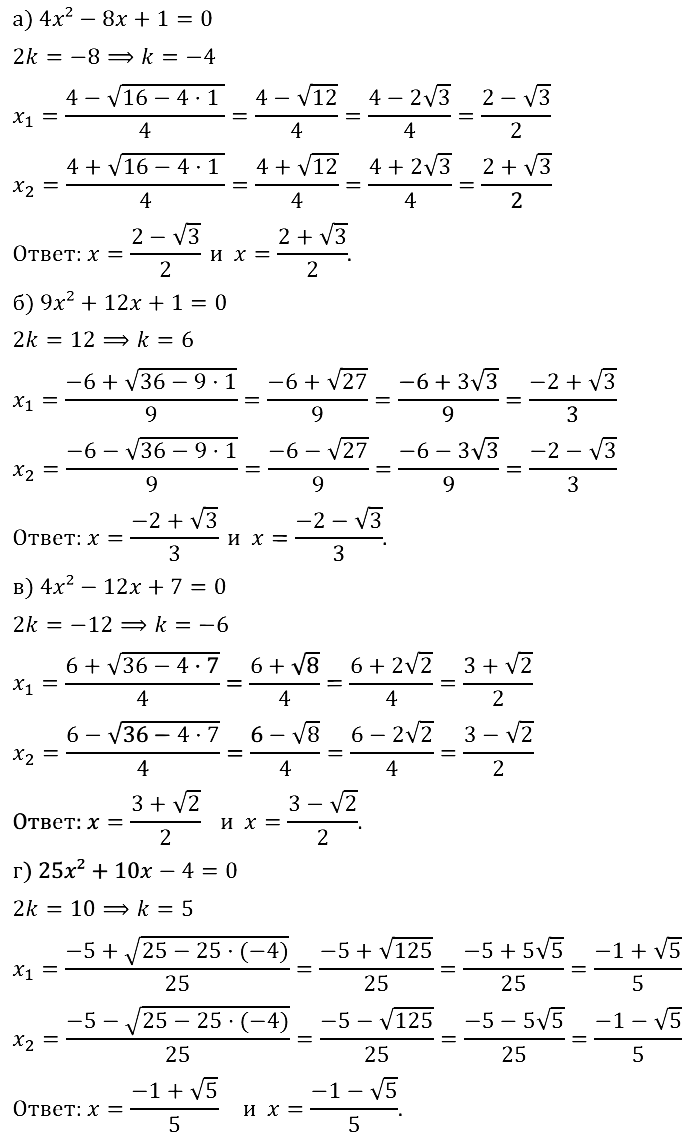Алгебра 8 класс. Часть 2 (Задачник) УМК Мордкович (2018-2020). § 31. Ещё одна формула корней квадратного уравнения. ОТВЕТЫ на упражнения 31.1 — 31.28. ГЛАВА 4. КВАДРАТНЫЕ УРАВНЕНИЯ. Нажмите на спойлер, чтобы посмотреть ответ на задание.
Вернуться в ОГЛАВЛЕНИЕ.
§ 31. Ещё одна формула корней квадратного уравнения
№ 31.1. Решите уравнение:
а) х^2 – 14х + 33 = 0; б) х^2 – 10х – 39 = 0; в) х^2 + 12x – 28 = 0; г) х^2 + 12x + 35 = 0.
Смотреть ответы на № 31.01
№ 31.2. а) х^2 + 34х + 280 = 0; б) х^2 – 16х – 132 = 0;
в) х^2 – 24х + 108 = 0; г) х^2 + 26х – 120 = 0.
Смотреть ответы на № 31.02
№ 31.3. а) 9х^2 – 20х – 21 = 0; б) 7х^2 + 6х – 1 = 0;
в) 5х^2 + 8х – 4 = 0; г) 5х^2 – 4х – 1 = 0.
Смотреть ответы на № 31.03
№ 31.4. а) х^2 – 2х – 1 = 0; б) х^2 + 4х + 1 = 0;
в) х^2 + 2х – 2 = 0; г) х^2 – 6х + 7 = 0.
Смотреть ответы на № 31.04
№ 31.5. а) 4х^2 – 8х + 1 = 0; б) 9х^2 + 12x + 1 = 0;
в) 4х^2 – 12x +7 = 0; г) 25х^2 + 10х – 4 = 0.
Смотреть ответы на № 31.05
№ 31.6.
Смотреть ответы на № 31.06
№ 31.7. Площадь прямоугольника равна 675 см2. Найдите стороны прямоугольника, если одна из них на 30 см меньше другой.
Смотреть ответы на № 31.07
№ 31.8. От квадратного листа отрезали полосу шириной 6 см. Площадь оставшейся части равна 135 см2. Определите первоначальные размеры листа.
Смотреть ответы на № 31.08
№ 31.9. Произведение двух натуральных чисел, одно из которых на 6 больше другого, равно 187. Найдите эти числа.
Смотреть ответы на № 31.09
№ 31.10. Найдите площадь прямоугольника, если известно, что одна сторона прямоугольника на 14 см больше другой, а диагональ прямоугольника равна 34 см.
Смотреть ответы на № 31.10
№ 31.11. Мотоциклист задержался с выездом на 6 мин. Чтобы наверстать потерянное время, он увеличил намеченную скорость на 10 км/ч. С какой скоростью ехал мотоциклист, если весь путь равен 30 км?
Смотреть ответы на № 31.11
№ 31.12. Катер должен был пройти 36 км за определенное время, но был задержан с отправлением на 12 мин и поэтому, чтобы прийти вовремя, шел со скоростью на 6 км/ч большей, чем предполагалось по расписанию. С какой скоростью шел катер?
Смотреть ответы на № 31.12
№ 31.13. Два автобуса выехали одновременно из пункта А в пункт В, расстояние между которыми 48 км. Один из автобусов, двигаясь на 4 км/ч быстрее другого, прибыл в В на 10 мин раньше, чем другой. Найдите скорости автобусов.
Смотреть ответы на № 31.13
№ 31.14. Поезд был задержан у семафора на 24 мин и, чтобы прибыть на станцию назначения по расписанию, должен был оставшиеся 195 км пройти со скоростью, на 10 км/ч превышающей первоначальную. Найдите первоначальную скорость поезда.
Смотреть ответы на № 31.14
№ 31.15. Расстояние 400 км скорый поезд прошел на 1 ч быстрее товарного. Какова скорость каждого поезда, если скорость движения товарного поезда на 20 км/ч меньше, чем скорого?
Смотреть ответы на № 31.15
№ 31.16. На середине пути между станциями А и В поезд был задержан на 10 мин. Чтобы прибыть в B по расписанию, машинисту пришлось увеличить первоначальную скорость поезда на 12 км/ч. Найдите первоначальную скорость поезда, если известно, что расстояние между станциями равно 120 км.
Смотреть ответы на № 31.16
№ 31.17. Катер прошел 8 км по течению реки и 16 км против течения, затратив на весь путь 4/3 ч. Какова скорость движения катера по течению, если собственная скорость катера равна 20 км/ч?
Смотреть ответы на № 31.17
№ 31.18. Моторная лодка прошла 7 км по течению реки и 10 км против течения, затратив на путь по течению на 0,5 ч меньше, чем на путь против течения. Собственная скорость лодки равна 12 км/ч. Найдите скорость хода лодки против течения.
Смотреть ответы на № 31.18
№ 31.19.
Смотреть ответы на № 31.19
№ 31.20.
Смотреть ответы на № 31.20
№ 31.21.
Смотреть ответы на № 31.21
№ 31.22.
Смотреть ответы на № 31.22
№ 31.23.
Смотреть ответы на № 31.23
№ 31.24. Расстояние между городами А и В равно 120 км. Через 2 ч после отправления из А мотоциклист был задержан у шлагбаума на 6 мин. Чтобы прибыть в В в намеченный срок, он увеличил скорость на 12 км/ч. С какой скоростью стал двигаться мотоциклист?
Смотреть ответы на № 31.24
№ 31.25. Велосипедист проехал 40 км от города до фермы. Возвращаясь, он сначала 2 ч ехал с той же скоростью, а затем сделал остановку на 20 мин. После остановки велосипедист увеличил скорость на 4 км/ч и затратил на обратный путь столько же времени, сколько на путь от города до фермы. С какой скоростью двигался велосипедист после остановки?
Смотреть ответы на № 31.25
№ 31.26. В начале года завод выпускал 800 изделий в месяц. В течение года завод дважды увеличивал выпуск продукции на одно и то же число процентов. На сколько процентов завод увеличивал выпуск продукции каждый раз, если в конце года он выпускал уже 1152 изделия в месяц?
Смотреть ответы на № 31.26
№ 31.27. Университет в течение двух лет увеличивал количество принятых студентов на один и тот же процент. На сколько процентов увеличивался прием студентов ежегодно, если количество поступивших возросло с 2000 человек до 2880?
Смотреть ответы на № 31.27
№ 31.28. Для очистки пруда, содержащего 2800 м3 воды, предполагалось к определенному сроку выкачать всю воду с помощью насосов. Так как насосов было прислано меньше, чем ожидалось, то ежедневно выкачивали на 20 м3 меньше предполагаемой нормы. Через день после истечения намеченного срока оставалось выкачать еще 100 м3 воды. За сколько дней предполагалось выкачать воду первоначально?
Смотреть ответы на № 31.28
Вы смотрели: Алгебра 8 класс. Часть 2 (Задачник) УМК Мордкович (2018-2020). ГЛАВА 4. КВАДРАТНЫЕ УРАВНЕНИЯ. § 31. Ещё одна формула корней квадратного уравнения. ОТВЕТЫ на упражнения 31.1 — 31.28. Вернуться в ОГЛАВЛЕНИЕ.
Просмотров: 34 209
— ответы

ГДЗ #1

28.25. Велосипедист проехал 40 км от города до фермы. Возвращаясь, он сначала 2 ч ехал с той же скоростью, а затем сделал остановку на 20 мин. После остановки велосипедист увеличил скорость на 4 км/ч и затратил на обратный путь столько же времени, сколько на путь от города до фермы. С какой скоростью двигался велосипедист после остановки?
На этой странице вы сможете найти и списать готовое домешнее задание (ГДЗ) для школьников по предмету Алгебра, которые посещают 8 класс из книги или рабочей тетради под названием/издательством «Часть 2», которая была написана автором/авторами: Мордкович. ГДЗ представлено для списывания совершенно бесплатно и в открытом доступе.
№2593
Экзамены с этой задачей: Задачи на движение по прямой Задачи на движение по прямой
Предмет и тема: Математика, Арифметика и начала Алгебры, Текстовые задачи, Задачи на движение, Движение вдогонку и движение с отставанием, Основы элементарной алгебры, Многочлены, квадратный трехчлен, Квадратные уравнения, Рациональные уравнения как математические модели реальных ситуаций,
Задача в следующих классах: 8 класс
Сложность задачи : 1
Задача встречается в следующей книге: Мордкович
Условие
Велосипедист проехал 40 км от города до фермы. Возвращаясь, он сначала 2 ч ехал с той же скоростью, а затем сделал остановку на 20 мин. После остановки велосипедист увеличил скорость на 4 км/ч и затратил на обратный путь столько же времени, сколько на путь от города до фермы. С какой скоростью двигался велосипедист после остановки?
Ответ
16 км/ч
Решение № 2593:
Пусть первоначальная скорость была ( x ) км/ч, обратно он проехал 2ч и проехал ( 2x ) км, осталось (40-2x ) км. После остановки на 20 минут, он скорость увеличил и ехал ( x+4 ) км/ч, отсюда: (frac{40}{x}=frac{40-2x}{x+4}+2+frac{1}{3}
frac{40}{x}=frac{40-2x}{x+4}+frac{7}{3};
frac{40}{x}=frac{120-6x+7x+28}{3(x+4)}
frac{40}{x}=frac{x+148}{3x+12}; 40(3x+2)=x(x+148)
x^{2}+148x-120x-480=0
x^{2}+28x-480=0
x^{2}+28x-480=0
k=14
x_{1}=-kpm sqrt{k^{2}-c}=-14pm sqrt{196+480}=-14pm sqrt{676}=-14pm 2b
x_{1}=-14-2b=-40
x_{2}=-14+2b=12
x=12, 12+4=16 ).

Велосипедист проехал от города А до города В 40км. Возвращаясь обратно, он 2ч ехал с той же скоростью,а за тем сделал остановку на 20 мин. Начав движение после остановки, он увеличил скорость на 4 км/ч поэтому затратил на путь от В до А столько же времени,что и на путь из А до В. Сколько времени затратил велосипедист от Адо В?
Светило науки — 988 ответов — 0 раз оказано помощи
путь=скорость*время
время=путь/скорость
его скорость х
путь 40 км
время затраченное на дорогу 40/х
20 мин=1/3 часа
за 2 часа он проехал 2*х
оставшееся время он ехал со скоростью х+4
затратил время (40-2х)/(х+4)
всего на обратный путь 2+1/3 + (40-2х)/(х+4)
40/x=2+1/3+(40-2x)/(x+4)
40/x=7/3 +(40-2x)/(х+4)
40/х=(7(х+4)+3(40-2х))/(3(х+4)
40/х=(7х+28+120-6х)/(3х+12)
40/х=(х+148)/(3х+12)
х(х+148)=40(3х+12)
х²+148х-120х-480=0
х²+28х-480=0
х=12 км/ч
время=40/12
время=3 1/3 часа= 3 часа 20 минут