Величина значение которой можно изменять во время работы алгоритма называется

Основано на учебнике Босовой Людмилы Леонидовны, code-live.ru, cppstudio.com

Алгоритмы  описывают последовательность действий, производи­мых над некоторыми объектами, стол, стул, число (сложить два числа например). Или например сохранении данных в электронном журнале такими объектами могут быть СНИЛС ученика, его фамилия, имя, отчество, класс,  и т. д.

В информатике отдельный информационный объект (число, символ, строка, таблица и др.) называется величиной или переменной.

Из школьного курса математики мы все знаем, что такое переменные.

А если очень сильно утрировать, и говорить еще проще — то переменная  это ящик, содержи­мым которого является некоторое значение (число). В программировании принципы довольно схожи. Переменная — это «ячейка» оперативной памяти компьютера, в которой может храниться какая-либо информация. Или как в нашем случае мы будем говорить о величине.

Величины (переменные) делятся на постоянные (константы) и изменяемые. По­стоянной (константой) называется величина, значение которой ука­зывается в тексте алгоритма и не меняется в процессе его исполне­ния. Изменяемой называется величина, значение которой меняется в процессе исполнения алгоритма. При исполнении алгоритма в каж­дый момент времени изменяемая величина обычно имеет значение, называе­мое текущим значением.

В математике и физике оперируют числовыми величинами — на­туральными, целыми, действительными числами. При составлении алгоритмов чаще всего используют величины целого и ве­щественного типов (числа с дробной частью: иррациональные и рациональные)

Имя величины (переменной) может состоять из одной или нескольких латин­ских букв, из латинских букв и цифр: А1, М, АР.

Рекомендуется выбирать мнемонические имена, т. е. имена, отражающие суть объектов решаемой задачи, например SUMMA, PLAN, СЕNА и т. д.

Если величину (переменную) представить как ящик, содержи­мым которого является некоторое значение, то имя величины — это ярлык, повешенный на ящик.

• Коменты VK
• Анонимные коменты, G+ или Facebook

§ 2.3. Объекты алгоритмов

Информатика. 8 класса. Босова Л.Л. Оглавление

---

Ключевые слова:

• величина
• константа
• переменная
• тип
• имя
• присваивание
• выражение
• таблица

2.3.1. Величины. Объекты алгоритмов

Алгоритмы описывают последовательность действий, производимых над некоторыми объектами, определёнными условием задачи. Например, при решении задачи о начислении зарплаты сотрудникам предприятия такими объектами могут быть табельный номер сотрудника, его фамилия, имя, отчество, оклад, отработанное время и т. д.

В информатике отдельный информационный объект (число, символ, строка, таблица и др.) называется величиной.

Величины делятся на постоянные (константы) и переменные. Постоянной (константой) называется величина, значение которой указывается в тексте алгоритма и не меняется в процессе его исполнения. Переменной называется величина, значение которой меняется в процессе исполнения алгоритма. При исполнении алгоритма в каждый момент времени переменная обычно имеет значение, называемое текущим значением.

Пример 1. Величины, выражающие количество дней в неделе, ускорение свободного падения, количество дней в первой декаде месяца, являются константами. Величины, выражающие количество дней в месяце, пульс человека, количество дней в третьей декаде месяца, являются переменными.

В алгоритмах над величинами выполняются некоторые операции. Например:

• арифметические операции +, -, * (умножение), / (деление);
• операции отношения <, >, <=, >=, =, ;
• логические операции И, ИЛИ, НЕ.

Объекты, над которыми выполняются операции, называются операндами. Не всякий объект может быть операндом для выполнения любой операции. Например, текст не может быть объектом для выполнения арифметических операций; отрицательное число не может быть операндом для извлечения квадратного корня и т. д.

Множество величин, объединённых определённой совокупностью допустимых операций, называют величинами определённого типа. При составлении алгоритмов используют величины числового (целого и вещественного), символьного, литерного и логического типов.

В математике и физике оперируют числовыми величинами — натуральными, целыми, действительными числами. При составлении алгоритмов чаще всего используют числовые величины целого и вещественного¹ типов, которые в алгоритмическом языке обозначаются цел и вещ соответственно.

• ¹ Термин «вещественный» принято использовать наряду с термином «действительный».

В задачах, возникающих в повседневной жизни, встречаются и нечисловые величины, значениями которых являются символы, слова, тексты и др. При составлении алгоритмов обработки текстовой информации используют величины символьного (сим) и литерного (лит) типов. Значением символьной величины является один символ: русская или латинская буква, цифра, знак препинания или другой символ. Значением литерной величины является последовательность символов. Иногда эту последовательность называют строкой или цепочкой. Литерные значения в алгоритме записывают в кавычках, например: ‘алгоритм’, ‘литерная величина’, ‘2011’.

Величины логического (лог) типа могут принимать всего два значения:

• ДА (ИСТИНА, TRUE, 1);
• НЕТ (ЛОЖЬ, FALSE, 0).

Для ссылок на величины используют их имена (идентификаторы). Имя величины может состоять из одной или нескольких латинских букв, из латинских букв и цифр: Al, М, АР.

Рекомендуется выбирать мнемонические имена, т. е. имена, отражающие суть объектов решаемой задачи, например, SUMMA, PLAN, CENA и т. д.

Если величину представить как ящик, содержимым которого является некоторое значение, то имя величины — это ярлык, повешенный на ящик.

2.3.2. Выражения. Объекты алгоритмов

Выражение — языковая конструкция для вычисления значения с помощью одного или нескольких операндов.

Выражения состоят из операндов (констант, переменных, функций), объединённых знаками операций. Выражения записываются в виде линейных последовательностей символов (без подстрочных и надстрочных символов, обыкновенных дробей и т. д.); знаки операций пропускать нельзя. Порядок выполнения операций определяется скобками и приоритетом (старшинством) операций; операции одинакового приоритета выполняются слева направо.

Различают арифметические, логические и строковые выражения.

Арифметические выражения служат для определения числового значения. Например, 2*х+3 — арифметическое выражение, значение которого при х — 1 равно пяти, а при х = -1 — единице. Выражение sqrt(x) служит для обозначения операции извлечения квадратного корня из x (?x).

Логические выражения описывают некоторые условия, которые могут удовлетворяться или не удовлетворяться. Логическое выражение может принимать одно из двух значений — ИСТИНА или ЛОЖЬ. Например, логическое выражение (х > 5) и (х < 10) определяет принадлежность точки х интервалу (5; 10):

При х = 6 значение этого выражения — ИСТИНА, а при х = 12 — ЛОЖЬ.

Строковые выражения состоят из величин (констант, переменных) символьного и литерного типов, соответствующих функций и операций сцепления (присоединения). Операция сцепления обозначается знаком « + » и позволяет соединить в одну последовательность несколько последовательностей символов. Значениями строковых выражений являются последовательности символов. Например, если А = ‘том’, то значение строкового выражения ‘а’+А есть ‘атом’.

2.3.3. Команда присваивания. Объекты алгоритмов

Задать конкретное значение величины можно с помощью операции присваивания, которая записывается так:

• <имя переменной>:= <выражение>

Знак «:=» читается: «присвоить». Например, запись А := В + 5 читается так: «переменной А присвоить значение выражения В плюс 5».

Знаки присваивания «:=» и равенства «=» — разные знаки:

• знак «=» означает равенство двух величин, записанных по обе стороны от этого знака;
• знак «:=» предписывает выполнение операции присваивания.

Например, запись А : = А + 1 выражает не равенство значений А и A + 1, а указание увеличить значение переменной А на единицу.

При выполнении команды присваивания сначала вычисляется значение выражения, стоящего справа от знака «:=», затем результат присваивается переменной, стоящей слева от знака «:=». При этом тип выражения должен быть совместим с типом соответствующей переменной.

Свойства присваивания:

• 1) пока переменной не присвоено значение, она остаётся неопределённой;
• 2) значение, присвоенное переменной, сохраняется в ней вплоть до выполнения следующего присваивания этой переменной нового значения;
• 3) если мы присваиваем некоторой переменной очередное значение, то предыдущее её значение теряется безвозвратно.

Пример 2. Составим алгоритм, в результате которого переменные А и В литерного типа обменяются своими значениями.

Решение вида

• А: =В
• В: =А

неверно, так как после выполнения первой команды присваивания первоначальное значение переменной А будет безвозвратно утеряно. Вторая команда присвоит переменной В текущее значение переменной А. В результате обе переменные получат одно и то же значение.

Для поиска правильного решения воспользуемся аналогией. Если требуется перелить жидкость из сосуда 1 в сосуд 2, а из сосуда 2 — в сосуд 1, то без дополнительного сосуда 3 здесь не обойтись. Алгоритм переливаний представлен на рис. 2.4.

Для решения исходной задачи введём промежуточную переменную М. Алгоритм обмена значениями переменных А я В запишем так:

• алг обмен значениями (лит А, В)

арг А, В
рез А, В

нач лит М

М:=А
А: =В
В:=М

кон

Если А и В — числовые величины, то обмен их значениями можно организовать и без промежуточной переменной, например так:

• А:=А+В
• В:=А-В
• А:=А-В

2.3.4.Табличные величины. Объекты алгоритмов

В практической деятельности человек часто использует всевозможные таблицы. Это, например, список учащихся в классном журнале, табель успеваемости, таблица результатов спортивных соревнований и т. д. Чаще всего встречаются линейные и прямоугольные таблицы.

Линейная таблица

Линейная таблица (одномерный массив) представляет собой набор однотипных данных, записанных в одну строку или один столбец. Элементы строки (столбца) всегда нумеруются. Например, с помощью линейной таблицы могут быть представлены дни недели (рис. 2.5, а) или количество уроков, пропущенных учеником в течение 5-дневной учебной недели (рис. 2.5, б).

Прямоугольная таблица

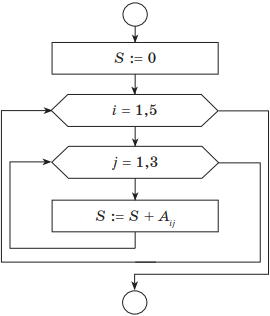
Прямоугольная таблица (двумерный массив) — это упорядоченный некоторым образом набор строк (столбцов), содержащих одинаковое количество элементов. Строки прямоугольных таблиц имеют свою нумерацию, столбцы — свою. Например, с помощью прямоугольной таблицы можно представить количество уроков, пропущенных всеми учениками 8 класса в течение 5-дневной учебной недели (рис. 2.6).

Всей совокупности элементов табличной величины даётся одно имя. Элементы различают по их номерам, называемым индексами. Индекс записывается в квадратных скобках сразу за именем таблицы.

Если первую из рассмотренных нами таблиц (см. рис. 2.5, а) назвать WEEK, то WEEK[1] = ‘понедельник’, WEEK[6] = ‘суббота’.

Назовём третью из рассмотренных таблиц LES. Тогда LES[1,1] = 6, LES[2,5] = 6, LES[3,4] = 0.

Образно линейная и прямоугольная таблицы показаны на рис. 2.7.

Объекты алгоритмов. Самое главное

В информатике отдельный информационный объект (число, символ, строка, таблица и др.) называется величиной.

Величины делятся на постоянные (их значения указываются в тексте алгоритма и не меняются в процессе его исполнения) и переменные (их значения меняются в процессе исполнения алгоритма). При составлении алгоритмов используют величины целого, вещественного, логического, символьного и литерного типов.

Для ссылок на величины используют их имена (идентификаторы). Имя величины может состоять из одной или нескольких латинских букв, из латинских букв и цифр.

Таблица (массив) — набор некоторого числа однотипных элеменЧ^ тов, которым присвоено одно имя. Положение элемента в таблице однозначно определяется его индексами.

---

Объекты алгоритмов. Вопросы и задания

2. Каковы основные способы записи алгоритмов?

3. Чем вызвано существование многих способов записи алгоритмов?

4. Дайте словесное описание алгоритма сложения двух обыкновенных дробей а/b и c/d.

5. Представьте в виде построчной записи алгоритм решения следующей задачи: «Имеются четыре арбуза различной массы. Как, пользуясь чашечными весами без гирь, путём не более пяти взвешиваний расположить их по возрастанию веса?».

6. Представьте с помощью блок-схемы алгоритм решения следующей задачи: «Из трёх монет одинакового достоинства одна фальшивая (более лёгкая). Как её найти с помощью одного взвешивания на чашечных весах без гирь?».

7. Запишите на алгоритмическом языке алгоритм построения окружности заданного радиуса r, проходящей через заданные точки А и В.

8. В среде КуМир запишите и выполните алгоритм переливаний (пример 4) для исполнителя Водолей.

9. Подготовьте краткую биографическую справку о Маркове А. А. (младшем).

---

§ 2.2. Способы записи алгоритмов

§ 2.3. Объекты алгоритмов

§ 2.4. Основные алгоритмические конструкции

---

Всякий алгоритм
составляется для конкретного исполнителя.
 

Компьютер
работает с информацией.
Информация, обрабатываемая компьютерной программой, называется данными.

Величина — это отдельный информационный объект, отдельная еденица данных.

Команды в компьютерной программе определяют действия,выполняемые над величинами.
Существует три основных типа величин, с которыми

работает
компьютер: числовой, символьный и логический.

Основными
характеристиками величин являются имя, значение, вид и
тип.

Конкретное обозначение величины
называют ИМЕНЕМ.

ИМЯ величины
состоит из одной или нескольких латинских букв, цифр, других знаков.
Заглавные и строчные буквы в именах величин считаются  одинаковыми, вначале всегда пишется буква.

Например: А,
DR, t45, q1$, massa1.

Конкретное данное, которому
равна величина в каждый момент времени,
называют значением.

ЗНАЧЕНИЕ
величины может
быть представлено числом, каким-либо текстом или арифметическим выражением.

Например: 5,
-12.89,»новость», «**,**», 5+45*a-b/3

Запятая в
десятичных дробях заменяется точкой. Текст — это любой набор знаков, взятый в кавычки.
Можно использовать скобки. Количество открытых и закрытых скобок должно быть одинаково.

Знаки арифметического действия в значениях величин заменяются:

Математика	Информатика	Пример
cложение	+	a+ b => a + b
вычитание	—	a — b => a — b
умножение	*	a . b => a * b
деление	/	a : b => a / b
возведение в степен ь	^	a 4   => a ^ 4

ВИДЫ    ВЕЛИЧИН

ПОСТОЯННЫЕ	ПЕРЕМЕННЫЕ
значения таких величин не меняются   в процессе исполнения  алгоритма	значения таких величин могут изменяться при выполнении    алгоритма
21.5 ; -1000 ; «ОИиВТ«	a, b14 , summa8 , d$

Типы величин

ТИП	Значения величин	ПРИМЕРЫ
целый	Значения целых величин — целые числа	5; -100 ; 32
вещественный	значения вещественных величин — действительные числа	2.5 ; -31.78 ; a ;  b ;  21+32*a
символьный (литерный или строковый)	значения символьных величин — набор символов (текст), взятый в кавычки.       После   имен   символьных   величин ставится знак $ ( символьное).	«ШКОЛА» ; «*!*» ; A$
логический	значений таких величин всего два:	true ( истинно ) false ( ложно )
другие

Главными элементами любой программы являются переменные, константы (постоянные) и операторы.
    Переменная — это одна или несколько
ячеек оперативной памяти. Переменной сопоставляется целый набор характеристик. Одним из основных атрибутов является имя переменной. Но для имени имеются специальные условия: в имени нужно
использовать только буквы латинского алфавита, имеется максимальная длина имени. Второй характеристикой переменной является ее значение. Но содержимое ячейки может
меняться во время работы, поэтому переменная и называется переменной, множество допустимых значений определяют тип переменной.
    Константа отличается от переменной тем,
что ее значение не может быть изменено.
  Система команд. Всякий алгоритм строится исходя из
системы команд исполнителя, для которого он предназначен. Независимо от того, на каком языке программирования будет написана программа, алгоритм работы с величинами составляется из следующих
команд: присваивание, ввод, обращение к вспомогательному алгоритму, цикл, ветвление.

Tags: 5Б

• Взрослым: Skillbox, Geekbrains, Хекслет, Eduson, XYZ, Яндекс.
• 8-11 класс: Умскул, Лектариум, Годограф, Знанио.
• До 7 класса: Алгоритмика, Кодланд, Реботика.
• Английский: Инглекс, Puzzle, Novakid.

Величины

Алгоритмы представляют последовательность операций, которые производились над предметами, описанными условием задачи. К примеру, при разрешении задачи о расчёте заработной платы работникам компании такими предметами могут стать табельный номер работника, его фамилия, имя, отчество, оклад, выработанное время и другое.

В информатике самостоятельный информационный предмет именуется величиной.

Величины разделяются на постоянные и переменные. Постоянной именуется величина, значение которой описывается в формулировке алгоритма и не изменяется в ходе его выполнения. Переменной именуется величина, значение которой изменяется в ходе осуществления алгоритма. При выполнении алгоритма в любой период времени переменная обычно имеет значение, которое именуется текущим значением.

Пример

Величины, которые характеризуют число дней в неделе, ускорение свободного падения, число дней в первой декаде месяца — константы. Величины, которые определяют число дней в месяце, человеческий пульс, число дней в третьей декаде месяца — переменные.

В алгоритмах над величинами осуществляются определённые манипуляции. К примеру:

• арифметические процедуры +, -, *, /;
• процедуры отношения <, >, <=, >=, =;
• логические процедуры И, ИЛИ, НЕ.

Предметы, над которыми осуществляются процедуры, именуют операндами. Не любой предмет считается операндом для осуществления всякой процедуры. К примеру, текст не считается объектом для осуществления арифметических процедур, отрицательное число не является операндом для извлечения квадратного корня и так далее.

Огромное число величин, которые объединены некоторым набором допустимых процедур, именуют величинами конкретного вида. При определении алгоритмов применяют величины числового, символьного, литерного и логического видов.

В математике и физике применяют числовые величины. При определении алгоритмов в основном применяют числовые величины целого и вещественного типов, которые в алгоритмическом языке обозначают цел и вещ.

Текстовые и логические величины

В задачах, которые появляются в бытовой жизни, наблюдаются и нечисловые величины, значениями которых считаются знаки, слова, тексты и другие. При формулировке алгоритмов обработки текстовых данных применяют величины символьного и литерного видов. Значением символьной величины считается единственный символ: русская или латинская буква, цифра, знак препинания или прочий символ. Значением литерной величины считается последовательность знаков. Порой эту последовательность именуют строкой или цепочкой. Литерные значения в алгоритме пишут в кавычках.

Величины логического типа могут принимать лишь такие значения:

• ДА (Истина, True, 1);
• НЕТ (Ложь, False, 0).

Для ссылок на величины применяют их наименования или идентификаторы. Наименование величины может содержать одну или множество латинских букв, латинские буквы и цифры.

Стоит подбирать мнемонические наименования, другими словами, наименования, отображающие смысл объектов разрешаемой задачи.

Если величину изобразить как ящик, содержимым которого является какое-то значение, тогда наименование величины — ярлык, навешанный на ящик.

Посмотрите видео

Теория:

Алгоритмы описывают последовательность действий, производимых над некоторыми объектами, определёнными условием задачи.

Например, при решении задачи о начислении зарплаты сотрудникам предприятия такими объектами могут быть табельный номер сотрудника, его фамилия, имя, отчество, оклад, отработанное время и т.д.

В информатике отдельный информационный объект (число, символ, строка, таблица и др.) называется величиной.

Величины делятся на постоянные (константы) и переменные.

Постоянной (константой) называется величина, значение которой указывается в тексте алгоритма и не меняется в процессе его исполнения.
Переменной называется величина, значение которой меняется в процессе исполнения алгоритма.

При исполнении алгоритма в каждый момент времени переменная обычно имеет значение, называемое текущим значением.

Пример:

Величины, выражающие количество дней в неделе, ускорение свободного падения, количество дней в первой декаде месяца, являются константами.Величины, выражающие количество дней в месяце, пульс человека, количество дней в третьей декаде месяца, являются переменными.

В алгоритмах над величинами выполняются некоторые операции. Например:

• арифметические операции +,−,⋅,÷ ;
• операции отношения >,<,≥,≤,= ;
• логические операции И, ИЛИ, НЕ.

Объекты, над которыми выполняются операции, называются операндами.

Не всякий объект может быть операндом для выполнения любой операции. Например, текст не может быть объектом для выполнения арифметических операций; отрицательное число не может быть операндом для извлечения квадратного корня и т.д.

Множество величин, объединённых определённой совокупностью допустимых операций, называют величинами определённого типа.

При составлении алгоритмов используют величины числового (целого и вещественного), символьного, литерного и логического типов.

В математике и физике оперируют числовыми величинами: натуральными, целыми, действительными числами. При составлении алгоритмов чаще всего используют числовые величины целого и вещественного типов, которые в алгоритмическом языке обозначаются цел и вещ соответственно.

В задачах, возникающих в повседневной жизни, встречаются и нечисловые величины, значениями которых являются символы, слова, тексты и др. При составлении алгоритмов обработки текстовой информации используют величины символьного (сим) и литерного (лит) типом. Значением символьной величины является один символ: русская или латинская буква, цифра, знак препинания или другой символ. Значением литерной величины является последовательность символов. Иногда эту последовательность называют строкой или цепочкой. Литерные значения в алгоритме записывают в кавычках, например: ‘алгоритм’, ‘литерная величина’ , ‘2011’.

Величины логического (лог) типа могут принимать всего два значения:

• ДА (ИСТИНА, TRUE, 1 );
• НЕТ (ЛОЖЬ, FALSE, 0 ).

Для ссылок на величины используют их имена (идентификаторы). Имя величины может состоять из одной или нескольких латинских букв, из латинских букв и цифр: А1, М, АР.

Рекомендуется выбирать мнемонические имена, т.е. имена, отражающие суть объектов решаемой задачи, например, SUMMA, PLAN, CENA и т.д. Если величину представить как ящик, содержимым которого является некоторое значение, то имя величины — это ярлык, повешенный на ящик.

Задание к уроку:

1. Запишите в тетради определения, выделенные рамкой.
2. Установите соответствия между типами величин и из значениями. Схему зарисовываем в тетради и устанавливаем соответствия стрелочками.

Скриншот или фотографию выполненного задания отправляем через форму внизу страницы или в сообщении в Дневник.ru

Алгоритмизация и программирование

Алгоритмы, виды алгоритмов, описание алгоритмов. Формальное исполнение алгоритмов

Термин «алгоритм», впервые употребленный в современном значении. Лейбницем (1646–1716), является латинизированной формой имени великого персидского математика Мухаммеда бен Муссы аль-Хорезми (ок. 783 – ок. 850). Его книга «Об индийском счете» в XII в. была переведена на латинский язык и пользовалась широкой популярностью не одно столетие. Имя автора европейцы произносили как Алгоритми (Algorithmi), и со временем так стали называть в Европе всю систему десятичной арифметики.

Научное определение алгоритма дал А. Чёрч в 1930 году. В наше время понятие алгоритма является одним из основополагающих понятий вычислительной математики и информатики.

Алгоритм — это точное и полное описание последовательности действий над заданными объектами, позволяющее получить конечный результат.

Можно сказать, что алгоритм решения какой-либо задачи — это последовательность шагов реализации (или нахождения) этого решения, а процесс построения алгоритма (алгоритмизация) — разложение задачи на элементарные действия или операции.

Область математики, известная как теория алгоритмов, посвящена исследованию свойств, способов записи, области применения различных алгоритмов, а также созданию новых алгоритмов. Теория алгоритмов находит широкое применение в различных областях деятельности человека — в технике, производстве, медицине, образовании и т. д. Появление компьютера позволило решать чрезвычайно сложные, трудоемкие задачи.

Определение алгоритма для применения в области информатики нуждается в некотором уточнении. Во-первых, решение задач в информатике всегда связано с преобразованием информации, а значит, исходными данными и результатом работы алгоритма должна быть информация. Это может быть представлено в виде схемы.

Во-вторых, алгоритмы в информатике предназначены для реализации в виде компьютерных программ или для создания некоторой компьютерной технологии. Для выполнения алгоритма требуется конечный объем оперативной памяти и конечное время.

Основные требования, предъявляемые к алгоритмам:

Дискретность (прерывность): алгоритм должен представлять решение задачи в виде последовательности простых (или ранее определенных) этапов (шагов). Каждый шаг алгоритма формулируется в виде инструкций (команд).

Определенность (детерминированность; лат. determinate — определенность, точность): шаги (операции) алгоритма должны допускать однозначную трактовку и быть понятными для исполнителя алгоритма. Это свойство указывает на то, что любое действие в алгоритме должно быть строго определено и описано для каждого случая.

Массовость: алгоритм должен давать решение не только для конкретного набора значений, а для целого класса задач, который определяется диапазоном возможных исходных данных (область применимости алгоритма). Свойство массовости подразумевает использование переменных в качестве исходных данных алгоритма.

Результативность: алгоритм должен давать конкретный результат, т. е. должны быть рассмотрены все возможные ситуации и для каждой из них получен результат. Под результатом может пониматься и сообщение о том, что задача решения не имеет.

Конечность: количество шагов алгоритма должно быть конечным.

Эффективность: количество шагов и сами шаги алгоритма должны быть такими, чтобы решение могло быть найдено за конечное и, более того, приемлемое время.

Для оценки и сравнения алгоритмов существует много критериев. Чаще всего анализ алгоритма (или, как говорят, анализ сложности алгоритма) состоит в оценке временных затрат на решение задачи в зависимости от объема исходных данных. Используются также термины «временная сложность», «трудоемкость» алгоритма. Фактически эта оценка сводится к подсчету количества основных операций в алгоритме, поскольку каждая из них выполняется за заранее известное конечное время. Кроме временной сложности, должна оцениваться также емкостная сложность, т. е. увеличение затрат памяти в зависимости от размера исходных данных. Оценка сложности дает количественный критерий для сравнения алгоритмов, предназначенных для решения одной и той же задачи. Оптимальным (наилучшим) считается алгоритм, который невозможно значительно улучшить в плане временных и емкостных затрат.

Анализом сложности алгоритмов, исследованием классов задач, решаемых с помощью алгоритмов той или иной сложности, и многими другими теоретическими вопросами занимается специальная область информатики.

Алгоритмы можно представлять как некоторые структуры, состоящие из отдельных базовых элементов.

Логическая структура любого алгоритма может быть представлена комбинацией трех базовых структур:

1. следование — образуется из последовательности действий, следующих одно за другим;
2. ветвление (развилка) — обеспечивает в зависимости от результатов проверки условия (ДА или НЕТ) выбор одного из альтернативных путей алгоритма;
3. цикл — обеспечивает многократное выполнение некоторой совокупности действий, которая называется телом цикла.

Для описания алгоритмов наиболее распространены следующие методы (языки):

Обычный язык. Изложение алгоритма ведется на обычном языке с разделением на последовательные шаги.

Блок-схемы. Графическое изображение алгоритма с помощью специальных значков-блоков.

Формальные алгоритмические языки (языки программирования). При записи алгоритмов используют строго определенный набор символов и составленных из них специальных зарезервированных слов. Имеют строгие правила построения языковых конструкций.

Псевдокод. Синтез алгоритмического и обычного языков. Элементы некоторого базового алгоритмического языка используются для строгой записи базовых структур алгоритма.

Словесный способ (запись на обычном языке) не имеет широкого распространения, т. к. таких описаний есть ряд недостатков:

• строго не формализуемы;
• достаточно многословны;
• могут допускать неоднозначность толкования отдельных предписаний;
• сложные задачи с анализом условий, с повторяющимися действиями трудно представляются в словесной или словесно-формульной форме.

Графический способ представления информации является более наглядным и компактным по сравнению со словесным. При графическом представлении алгоритм изображается в виде последовательности связанных между собой функциональных блоков, каждый из которых соответствует выполнению одного или нескольких действий. Такое графическое представление алгоритма называется блок-схемой. Определенному типу действия (ввод/вывод данных, проверка условия, вычисление выражения, начало и конец алгоритма и т. п.) соответствует определенная геометрическая фигура — блочный символ. Блоки соединяются между собой линиями переходов, которые определяют очередность выполнения действий.

Название символа	Графическое изображение	Комментарии
Пуск/Останов (блоки начала и конца алгоритма)		Указание на начало или конец алгоритма
Ввод/Вывод данных (блоки ввода, вывода		Организация ввода/вывода в общем виде
Процесс (операторные блоки)		Выполнение вычислительного действия или последовательности действий (можно объединять в один блок), которые изменяют значение, форму представления или размещение данных
Условие (условный блок)		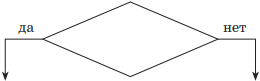Выбор направления выполнения алгоритма. Если условие, записанное внутри ромба, выполняется, то управление передается по стрелке «да», в противном случае — по стрелке «нет». Таким образом, реализуется процесс изменения последовательности вычислений в зависимости от выполнения условия
Начало цикла с параметром		Используется для организации циклических конструкций с известным количеством итераций (повторений) и известным шагом изменения параметра цикла. Внутри блока для параметра цикла указываются через запятую его начальное значение, конечное значение и шаг изменения. Цикл, для которого неизвестно количество повторений, записывается с помощью условного и операторных блоков
Предопределенный процесс		Используется для указания обращений к вспомогательным алгоритмам, существующим автономно в виде некоторых самостоятельных модулей, и для обращения к библиотечным подпрограммам
Печать сообщений (документ)		Вывод результатов на печать

При составлении блок-схемы необходимо проверять выполнение следующих условий:

1. из каждого прямоугольника и параллелограмма (кроме конца алгоритма) должна выходить только одна стрелка;
2. в каждый прямоугольник и параллелограмм (кроме начала алгоритма) должна входить хотя бы одна стрелка;
3. в каждый ромб должна входить хотя бы одна стрелка, а выходить из него — две стрелки, помеченные словами «ДА» и «НЕТ».

Псевдокод занимает промежуточное положение между естественным языком и языками программирования. В псевдокоде не приняты строгие синтаксические правила для записи команд, что отличает формальные языки программирования. Однако в псевдокоде есть некоторые конструкции, которые присущи формальным языкам, что облегчает переход от записи алгоритма на псевдокоде к записи алгоритма на языке программирования. Псевдокоды бывают разные. Рассмотрим учебный (школьный) алгоритмический язык АЯ.

Алфавит учебного алгоритмического языка является открытым. В него могут быть введены любые понятные всем символы: русские и латинские буквы, знаки математических операций, знаки отношений, специальные знаки и т. д. Кроме алфавита, в алгоритмической нотации определяются служебные слова, которые являются неделимыми. Служебные слова обычно выделяются жирным шрифтом или подчеркиванием. К служебным словам относятся:

алг — заголовок алгоритма	нц — начало цикла	знач
нач — начало алгоритма	кц — конец цикла	и
кон — конец алгоритма	дано	или
арг — аргумент	надо	не
рез — результат	если	да
цел — целый	то	нет
сим — символьный	иначе	при
лит — литерный	всё	выбор
лог — логический	пока	утв
вещ — вещественный	для	ввод
таб — таблица	от	вывод
длин — длина	до

Общий вид записи алгоритма на псевдокоде:

алг — название алгоритма (аргументы и результаты)

дано — условие применимости алгоритма

надо — цель выполнения алгоритма

нач — описание промежуточных величин

последовательность команд (тело алгоритма)

кон

Часть алгоритма от слова алг до слова нач называется заголовком, а часть, заключенная между словами нач и кон, — телом алгоритма (исполняемой частью алгоритма).

В предложении алг после названия алгоритма в круглых скобках указываются характеристики (арг, рез) и тип значения (цел, вещ, сим, лит или лог) всех входных (аргументы) и выходных (результаты) переменных. При описании массивов (таблиц) используется служебное слово таб, дополненное именем массива и граничными парами по каждому индексу элементов массива.

Команды учебного языка:

1. Оператор присваивания, который обозначается «:=» и служит для вычисления выражений, стоящих справа, и присваивания их значений переменным, указанным в левой части. Например, если переменная а имела значение 5, то после выполнения оператора присваивания а := а + 1, значение переменной а изменится на 6.

2. Операторы ввода/вывода:

ввод (список имен переменных)

вывод (список вывода)

Список вывода может содержать комментарии, которые заключаются в кавычки.

3. Оператор ветвления (с использованием команды если…то… иначе…всё; выбор);

4. Операторы цикла (с использованием команд для, пока, до).

Запись алгоритма на псевдокоде:

Здесь в предложениях дано и надо после знака «|» записаны комментарии. Комментарии можно помещать в конце любой строки, они существенно облегчают понимание алгоритма.

При записи алгоритма в словесной форме, в виде блок-схемы или на псевдокоде допускается произвольное изображение команд. Вместе с тем такая запись позволяет понять человеку суть дела и исполнить алгоритм. Однако алгоритм, предназначенный для исполнения на компьютере, должен быть записан на строго формализованном языке. Такой язык называется языком программирования, а запись алгоритма на этом языке — компьютерной программой.

Для решения одной и той же задачи можно предложить несколько алгоритмов. Алгоритмы составляются с ориентацией на определенного исполнителя алгоритма. У каждого исполнителя имеется свой конечный набор команд, которые для него понятны и исполняемы. Этот набор называется системой команд исполнителя. Пользуясь системой команд, исполнитель может выполнить алгоритм формально, не вникая в содержание поставленной задачи. От исполнителя требуется только строгое выполнение последовательности действий, предусмотренной алгоритмом. Таким образом, в общем случае алгоритм претерпевает изменения по стадиям:

• первая стадия — алгоритм должен быть представлен в форме, понятной человеку, который его разрабатывает;
• вторая стадия — алгоритм должен быть представлен в форме, понятной исполнителю алгоритма (вторая стадия может отсутствовать, если исполнять алгоритм будет сам разработчик).

Примеры решения задач

Пример 1. Исполнитель Утроитель может выполнить только две команды, которым присвоены номера:

1 — вычти 1;

3 — умножь на 3.

Первая команда уменьшает число на 1, вторая — увеличивает его втрое.

Написать набор команд (не более пяти) получения из числа 3 числа 16. В ответе указать только номера команд.

Решение.

1 (3 – 1 = 2)

3 (2 * 3 = 6)

3 (6 * 3 = 18)

1 (18 – 1 = 17)

1 (17 – 1 = 16)

Ответ: 13311

Пример 2. Имеется Исполнитель алгоритма, который может передвигаться по числовой оси.

Система команд Исполнителя алгоритма:

1. «Вперед N» (Исполнитель алгоритма делает шаг вперед на N единиц).

2. «Назад M» (Исполнитель алгоритма делает шаг назад на M единиц).

Переменные N и M могут принимать любые целые положительные значения. Известно, что Исполнитель алгоритма выполнил программу из 50 команд, в которой команд «Назад 2» на 12 больше, чем команд «Вперед 3». Других команд в программе не было. Какой одной командой можно заменить эту программу, чтобы Исполнитель алгоритма оказался в той же точке, что и после выполнения программы?

Решение.

1. Найдем, сколько было команд «Вперед», а сколько «Назад». Учитывая, что общее количество команд равно 50 и что команд «Назад» на 12 больше, чем команд «Вперед». Получим уравнение: x + (x + 12) = 50, где x — количество команд «Вперед». Тогда общее количество команд «Вперед»: x = 19, а количество команд «Назад»: 19 + 12 = 31.

2. Будем вести отсчет от начала числовой оси. Выполнив 19 раз команду «Вперед 3», Исполнитель алгоритма оказался бы на отметке числовой оси 57 (19 * 3 = 57). После выполнения 31 раз команды «Назад 2» (31 * 2 = 62) он оказался бы на отметке –5 (57 – 62 = –5).

3. Все эти команды можно заменить одной — «Назад 5».

Ответ: команда«Назад 5».

Пример 3. Черепашка является исполнителем для создания графических объектов на рабочем поле. При движении Черепашка оставляет след в виде линии. Черепашка может исполнять следующие команды:

Название команды	Параметр	Действия исполнителя
вп	Число шагов	Продвигается в направлении головы на указанное число шагов
нд	Число шагов	Продвигается в направлении, противоположном направлению головы на указанное число шагов
пр	Число градусов	Поворачивается направо относительно направления, заданного головой черепашки
лв	Число градусов	Поворачивается налево относительно направления, заданного головой черепашки

Для записи повторяющихся действий (цикла) используется команда Повтори. В этой команде два параметра: первый задает количество повторений (итераций), а второй — список команд которые должны повторяться (тело цикла); список заключается в квадратные скобки.

Записать для исполнителя Черепашка алгоритмы:

а) построения квадрата со стороной 100;

б) построения правильного шестиугольника со стороной 50.

в) построения изображения цифры 4, если голова Черепашки смотрит на север.

Ответ: а) Повтори 4 [вп 100 пр 90]; б) Повтори 6 [вп 50 пр 360/6]; в) вп 100; повтори [лв 135 вп 50].

Пример 4. Два игрока играют в следующую игру (это вариант восточной игры). Перед ними лежат три кучки камней, в первой из которых 2, во второй — 3, в третьей — 4 камня. У каждого игрока неограниченно много камней. Игроки ходят по очереди. Ход состоит в том, что игрок или удваивает число камней в одной из кучек, или добавляет по два камня в каждую из них. Выигрывает игрок, после хода которого либо в одной из кучек становится не менее 15 камней, либо общее число камней в трех кучках становится не менее 25. Кто выиграет при безошибочной игре обоих игроков — игрок, делающий первый ход, или игрок, делающий второй ход? Каким должен быть первый ход выигрывающего игрока? Ответ следует обосновать.

Решение. Удобнее всего составить таблицу возможных ходов обоих игроков. Заметим, что в каждом случае возможны всего четыре варианта хода. В таблице курсивом выделены случаи, которые сразу же приносят поражение игроку, делающему этот ход (например, когда камней в какой-либо кучке становится больше или равно 8, другой игрок непременно выигрывает следующим ходом, удваивая количество камней в этой кучке). Из таблицы видно, что при безошибочной игре обоих игроков первый всегда выиграет, если первым ходом сделает 4, 5, 6. У второго игрока в этом случае все ходы проигрышные.

	1-й ход	2-й ход
Начало	1-й игрок	2-й игрок	1-й игрок	2-й игрок
2,3,4	4,3,4	8,3,4	выигрыш
4,6,4	8,6,4	выигрыш
4,12,4	выигрыш
4,6,8	выигрыш
6,8,6	выигрыш
4,3,8	выигрыш
6,5,6	12,5,6	выигрыш
6,10,6	выигрыш
6,5,12	выигрыш
8,7,8	выигрыш
	2,6,4	4,6,4	8,6,4	выигрыш
4,12,4	выигрыш
4,6,8	выигрыш
6,8,6	выигрыш
2,12,4	выигрыш
2,6,8	выигрыш
4,8,6	выигрыш
2,3,8	выигрыш
4,5,6	8,5,6	выигрыш
4,10,6	выигрыш
4,5,12	выигрыш
6,7,8	выигрыш

Пример 5. Записано 7 строк, каждая из которых имеет свой номер. В нулевой строке после номера записана цифра 001. Каждая последующая строка содержит два повторения предыдущей строки и добавленной в конец большой буквы латинского алфавита (первая строка — A, вторая строка — B и т. д.). Ниже приведены первые три строкиєтой записи (в скобках указан номер строки):

(0) 001

(1) 001001A

(2) 001001A001001AB

Какой символ находится в последней строке на 250-м месте (считая слева направо)?

Примечание. Первые семь букв латинского алфавита: A, B, C, D, E, F, G.

Решение. Найдем длину каждой строки. Длина каждой следующей строки в два раза больше длины предыдущей плюс один символ, длина строк составит:

(0) 3 символа;

(1) 32+1=7;

(2) 72+1=15;

(3) 152+1=31;

(4) 312+1=63;

(5) 632+1=127;

(6) 1272+1=255 символов.

Так как задано 7 строк, а нумерация начинается с нулевой строки, последняя строка имеет номер 6 и содержит 255 символов. Последний символ в строке — F. Предпоследний элемент — E, далее идут символы D, C, B, A, 1 (по правилу формирования строк). Таким образом, 250-й символ — это 1.

Ответ: 1.

Пример 6. Имеется фрагмент алгоритма, записанный на учебном алгоритмическом языке:

n := Длина(а)

k = 2

b := Извлечь(а, k)

нц для i от 7 до n – 1

с := Извлечь(а, i)

b := Склеить(b, с)

кц

Здесь переменные а, b, с — строкового типа; переменные n, i — целые.

В алгоритме используются следующие функции:

Длина(х) — возвращает количество символов в строке х. Имеет тип «целое».

Извлечь(х, i) — возвращает i-й символ слева в строке х. Имеет строковый тип.

Склеить(х, у) — возвращает строку, в которой находятся все символы строки х, а затем все символы строки у. Имеет строковый тип.

Какое значение примет переменная b после выполнения этого фрагмента алгоритма, если переменная а имела значение «ВОСКРЕСЕНЬЕ»?

Решение. Находим общее число символов в строке а, получим, что n = 11.

Выполняя команду b := Извлечь(а, k) при k = 2, получим, что b примет значение «О«.

В цикле последовательно, начиная с 7-го символа строки а и заканчивая предпоследним (n – 1), извлекаем символ из строки а и присоединяем к строке b.

В результате получим слово «ОСЕНЬ» (символы с номерами 2 + 7 + 8 + 9 + 10).

Ответ: «ОСЕНЬ«

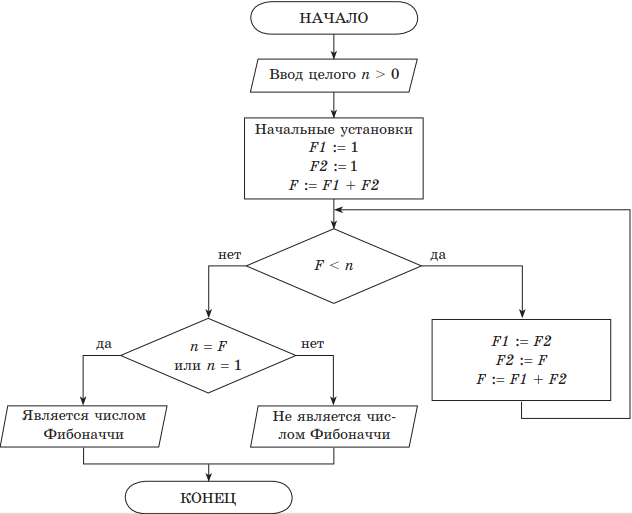
Пример 7. Леонардо из Пизы, известный как Фибоначчи, был первым из великих математиков Европы позднего Средневековья. Числовой ряд, который называется его именем, получился в результате решения задачи о кроликах, которую Фибоначчи изложил в своей «Книге Абака», написанной в 1202 году. Он выглядит так:

1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144,…

В этом ряду каждое следующее число, начиная с третьего, равно сумме двух предыдущих. Составить словесный алгоритм и блок-схему проверки принадлежности введенного числа n ряду Фибоначчи.

Решение. Словесный алгоритм:

1. Ввести число n.
2. Установить значение первых трех чисел Фибоначчи: 1, 1, 2 (сумма двух предыдущих чисел).
3. Пока введенное число n больше очередного числа Фибоначчи, взять два последних числа Фибоначчи и получить из них новое число Фибоначчи.
4. Если число Фибоначчи равно введенному n или было введено число n = 1, значит, что было введено число Фибоначчи, в противном случае — введенное число не является числом Фибоначчи.

Приведенный словесный алгоритм в пункте 1, 2 содержит начальные установки, в пункте 3 — цикл с условием, а пункт 4 — это вывод результата работы алгоритма.

Блок-схема алгоритма:

Обозначения:

F — текущее число ряда Фибоначчи;

F1 и F2 — два предыдущих числа ряда Фибоначчи для числа F;

n — число, для которого требуется определить, является ли оно числом из ряда Фибоначчи.

Использование основных алгоритмических конструкций: следование, ветвление, цикл

Логическая структура любого алгоритма может быть представлена комбинацией трех базовых структур: следование, ветвление, цикл.

Базовая структура СЛЕДОВАНИЕ указывает на то, что управление передается последовательно от одного действия к другому.

Учебный алгоритмический язык	Язык блок-схем
действие 1 действие 2 … действие n

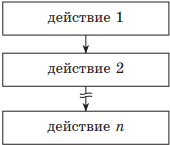Использование исключительно этой структуры возможно лишь для достаточно простых задач, ход решения которых не меняется в зависимости от конкретных исходных данных и состоит в последовательном выполнении определенных операций.

В качестве примера рассмотрим решение простой задачи.

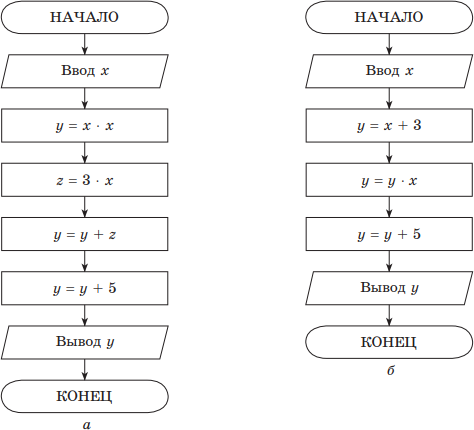
Пример. Найти y(x) = x2 + 3x + 5, используя только операции умножения и сложения.

Решение. На рис. приводятся два алгоритма, реализующие решение поставленной задачи.

Порядок вычисления y(x) в первом случае — обычный, а во втором — (x + 3) x + 5. Обе формулы эквивалентны, но в первом случае для вычисления необходимо 2 умножения, 2 сложения и 3 переменных (x, y, z), а во втором используются 1 умножение, 2 сложения и 2 переменные (x, y).

Приведенный пример показывает, что даже простые задачи могут решаться с помощью различных вариантов алгоритмов.

Обратите внимание, как в блоке следования используется оператор присваивания.

Операция присваивания — важнейшая операция во всех языках программирования. С помощью присваивания переменные получают новые значения: в левой части инструкции ставится идентификатор величины, а в правой части — выражение, значение которого можно определить.

В операторах присваивания используется либо привычный знак равенства, либо сочетание двоеточия и знака равенства «:=». Поскольку знак присваивания — это не знак равенства, возможны записи вида Х := Х + 1 или А := А – В. Нужно учитывать, что оператор присваивания будет выполняться только в том случае, если значения всех переменных правой части уже определены.

Базовая структура ВЕТВЛЕНИЕ (РАЗВИЛКА) используется в случае, когда выполнение программы может измениться в зависимости от результата проверки условия и пойти двумя разными (альтернативными) путями. Другими словами, условие является некоторым высказыванием (предикатом) и может быть истинным или ложным (принимать значение TRUE или FALSE). Каждый из путей ведет к общему выходу, так что работа алгоритма будет продолжаться независимо от того, какой путь будет выбран.

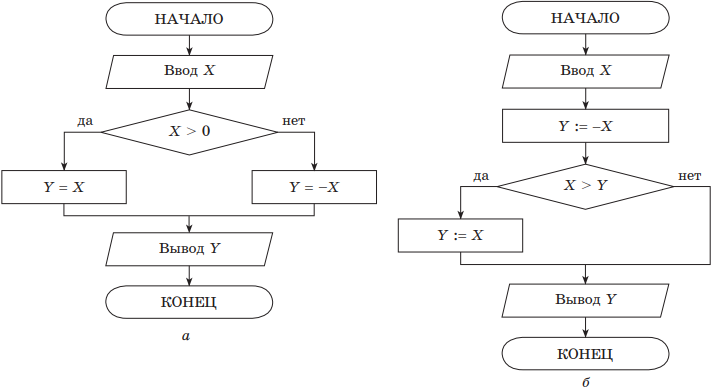
Различают две структуры этого типа — полную и неполную. В случае полной структуры, если условие выполняется (является истинным), вслед за ним выполняется действие 1, иначе — действие 2. В случае неполной структуры, если условие выполняется (является истинным), то вслед за ним выполняется действие 1, иначе ничего не происходит.

Важную роль в операторах ветвления играют содержащиеся в них условия. В простейшем случае условиями служат отношения между величинами. Условия с одним отношением называют простыми условными выражениями, или простыми условиями. В некоторых задачах необходимы более сложные условия, состоящие из нескольких простых, например условие А < X < С, т. е. Х < А и (Х > C) (возможна запись (Х < А) and (Х > C)). Объединение нескольких простых условий в одно образует составное условное выражение, или составное условие. Составные условия образуются с помощью логических операторов not (отрицание), and (логическое И), or (логическое ИЛИ), хоr (исключающее ИЛИ).

Структура ВЕТВЛЕНИЕ существует в четырех основных вариантах:

если — то (неполная структура);

если — то — иначе (полная структура);

выбор (неполный);

выбор — иначе (полный).

Учебный алгоритмический язык	Язык блок-схем
1) если — то
если условие то действие 1 всё
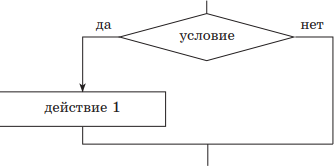2) если — то — иначе
если условие то действие 1 иначедействие 2 всё
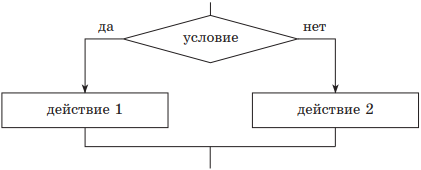3) выбор
выбор при условие 1: действие 1 при условии 2: действие 2 … при условие N: действие N всё
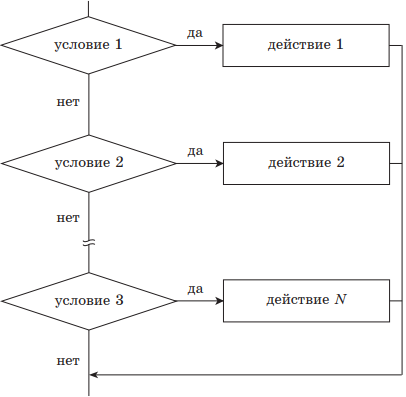4) выбор — иначе
выбор при условие 1: действие 1 при условие 2: действие 2 … при условие N: действие N + 1 иначе действия N + 1 всё

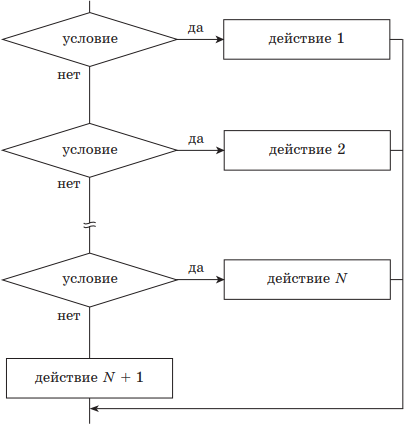В качестве простого примера рассмотрим нахождение модуля числа y(x) = |x|. Решение приведено на рис. для случаев полной (а) и неполной (б) структур ветвления.

Базовая структура ЦИКЛ служит для записи алгоритмов, в которых некоторая часть алгоритма (тело цикла) должна повторяться несколько раз. Количество повторений цикла может определяться разными способами, в зависимости от которых различают три вида циклов.

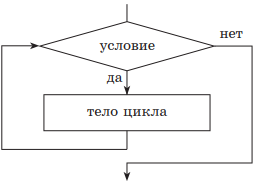
1. Цикл с предусловием, или цикл «пока». При реализации этого цикла сначала проверяется условие его выполнения. Пока оно выполняется, будут происходить повторения тела цикла. Отсюда и другое его название — цикл «пока». Если условие не выполняется при первой проверке, то тело цикла не будет выполняться вообще. После выхода из цикла управление передается следующей структуре. Для того чтобы избежать зацикливания, т. е. бесконечного цикла, в теле цикла обязательно должны изменяться параметры, записанные в условии.

Учебный алгоритмический язык	Язык блок-схем
нц пока условие тело цикла (последовательность действий) кц

2. Цикл с параметром. Этот вид цикла удобно использовать в тех случаях, когда заранее извесно количество повторений цикла. Вводится понятие счетчика цикла, который по умолчанию считается равным либо 1, либо –1. В некоторых случаях изменение счетчика цикла (приращение) указывают явно. Для организации цикла необходимо задать верхнюю и нижнюю границы изменения счетчика цикла. В зависимости от значения верхней и нижней границы определяется шаг цикла (1 или −1), т. е. значение счетчика цикла.

Учебный алгоритмический язык	Язык блок-схем
нц для i от i1 до i2 тело цикла (последовательность действий) кц

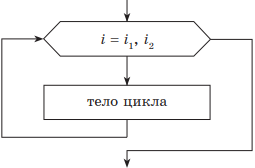3. Цикл с постусловием, или цикл «до». При реализации этого цикла условие завершение цикла проверяется после тела цикла. В этом случае тело цикла всегда выполняется хотя бы один раз. Цикл будет выполняться до выполнения условия, отсюда и другое название — цикл «до». А пока условие не выполнено, будет повторяться тело цикла (выполнение условия, таким образом, является условием окончания цикла). В этом случае, как и в цикле «пока», необходимо предусмотреть в теле цикла изменение параметров условия цикла.

Учебный алгоритмический язык	Язык блок-схем
нц тело цикла (последовательность действий) до условие кц

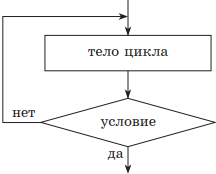Для всех видов цикла предусмотрена возможность досрочного выхода, т. е. прерывание работы цикла.

Помимо трех рассмотренных видов цикла существует и так называемый интерационные циклы. Особенностью итерационного цикла является то, что число повторений операторов тела цикла заранее неизвестно. Для его организации используется цикл типа пока. Выход из итерационного цикла осуществляется в случае выполнения заданного условия. На каждом шаге вычислений происходит последовательное приближение и проверка условия достижения искомого результата. Классический пример — вычисление суммы ряда с заданной точностью.

Алгоритм, в состав которого входит итерационный цикл, называется итерационным алгоритмом. Итерационные алгоритмы используются при реализации итерационных численных методов. В итерационных алгоритмах необходимо обеспечить обязательное условие выхода из цикла (сходимость итерационного процесса). В противном случае произойдет зацикливание алгоритма, т. е. не будет выполняться основное свойство алгоритма — результативность.

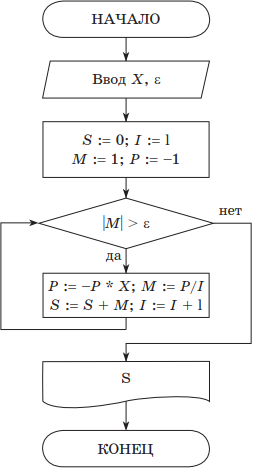
Пример. Вычислить сумму знакопеременного ряда $S=x-{x^2}/{2}+{x^3}/{3}-{x^4}/{4}+…$ с заданной точностью $ε$.

Для данной знакочередующейся бесконечной суммы требуемая точность будет достигнута, когда очередное слагаемое станет по абсолютной величине меньше $ε$.

Решение. Запишем блок-схему алгоритма, где будем использовать следующие обозначения:

$S$ — частичная сумма ряда (стартовое значение равно 0);

$ε$ — точность вычисления;

$i$ — номер очередного слагаемого;

$m$ — значение очередного слагаемого;

$p$ — числитель очередного слагаемого.

На псевдокоде алгоритм можно записать следующим образом:

Примечание. Следует отметить, что ряд будет сходящимся только при выполнении условия 0 < х < 1.

Возможны случаи, когда внутри тела цикла необходимо повторить некоторую последовательность операторов, т. е. организовать внутренний цикл. Такая структура получила название цикла в цикле, или вложенного цикла. Глубина вложения циклов (количество вложенных друг в друга циклов) может быть различной.

При использовании такой структуры для экономии времени выполнения необходимо выносить из внутреннего цикла во внешний все действия, результаты которых не зависят от параметра внутреннего цикла.

Пример. Вычислить сумму элементов для заданной матрицы (таблицы из 5 строк и 3 столбцов) А(5,3).

Решение. Алгоритм решения задачи на псевдокоде:

Основная часть блок-схемы нахождения суммы элементов матрицы будет иметь следующий вид:

Здесь порядок выполнения вложенных циклов следующий: счетчик внутреннего цикла изменяется быстрее, т. е. для i = 1(внешний цикл), j пробегает значения 1, 2, 3 (внутренний цикл); далее i = 2, j опять пробегает значения 1, 2, 3 и т. д.

Примеры решения задач

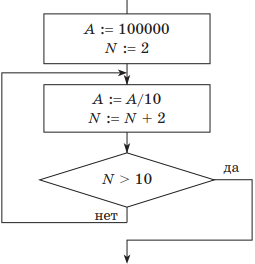
Пример 1. Дан фрагмент блок-схемы некоторого алгоритма.

Определить значение переменной А после выполнения фрагмента алгоритма.

Какие исправления нужно внести, чтобы изменение значения переменной А происходило в обратном порядке?

Как записать исходный алгоритм с помощью двух других видов цикла?

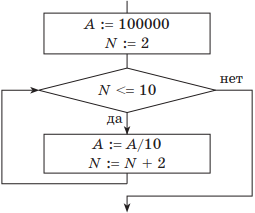
Решение. Если представить пошаговое выполнение алгоритма в виде таблицы, получим:

Начальные установки:	A = 100000; N = 2
1-я итерация	A = 10000; N = 4
2-я итерация	A = 1000; N = 6
3-я итерация	A = 100; N = 8
4-я итерация	A = 10; N = 10
5-я итерация, выполнилось условие выхода: N > 10	Ответ: А = 1; N = 12

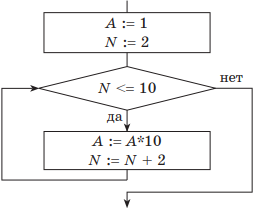
Таблица обратного хода изменения значения А будет иметь такой вид:

Начальные установки:	A = 1; N = 2
1-я итерация	A = 10; N = 4
2-я итерация	A = 100; N = 6
3-я итерация	A = 1000; N = 8
4-я итерация	A = 10000; N = 10
5-я итерация, выполнилось условие выхода: N > 10	А = 100000; N = 12

Блок-схема алгоритма примет такой вид:

В алгоритме нужно изменить начальное значение А и операцию деления заменить операцией умножения. Счетчик N в данном случае изменять не нужно.

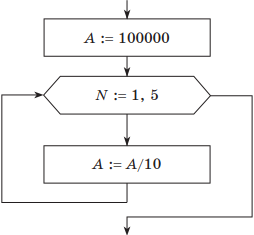
В приведенной в условии блок-схеме используется цикл с предусловием. Для цикла с параметром блок-схема алгоритма будет иметь такой вид:

Понятно, что цикл должен выполниться пять раз. В заголовке цикла необходимо указать начальное и конечное значение счетчика цикла N (приращение по умолчанию равно 1).

Для цикла с постусловием блок-схема исходного алгоритма имеет такой вид:

В данной схеме условие завершения цикла находится после тела цикла. Цикл, в отличие от цикла с предусловием, выполняется, пока значение условия ложно.

Пример 2. Сколько раз выполнится тело цикла в программе?

Q := 27; P := 36

нц пока (div(Q, 5) = div(P, 7))

Q := Q + 2

P := P + 3

кц

Примечание. Результат функции div(X, Y) — целая часть от деления X на Y.

Решение. Рассмотрим пошаговое выполнение алгоритма, оформив его в виде таблицы.

Начальные установки	Q := 27; P := 36
Проверка выполнения условия	div(27, 5) = 5; div(36, 7) = 5; 5 = 5
1-я итерация; выполнение тела цикла	Q := 29; P := 39
Проверка выполнения условия	div(29, 5) = 5; div(39, 7) = 5; 5 = 5
2-я итерация; выполнение тела цикла	Q := 31; P := 42
Проверка выполнения условия	div(31, 5) = 6; div(42, 7) = 6; 6 = 6
3-я итерация; выполнение тела цикла	Q := 33; P := 45
Проверка выполнения условия	div(33, 5) = 6; div(45, 7) = 6 6 = 6
4-я итерация; выполнение тела цикла	Q := 35; P := 48
Проверка выполнения условия. Условие не выполняется, цикл завершает работу	div(35, 5) = 7; div(48, 7) = 6; 7 ≠ 6

Ответ: цикл выполнится 4 раза.

Использование переменных. Объявление переменной (тип, имя, значение).
Локальные и глобальные переменные

Величины служат для описания объектов и процессов в материальном мире. Каждая величина имеет некоторые характеристики. В программировании понятие величины несколько отличается от понятия величины в естественных науках — оно является более формальным. Величиной называют объект — переменную, с которым связывается определенное множество значений. Такому объекту присваивается имя — идентификатор. Понятие переменной в программировании сходно с понятием переменной в математике. Например, в алгебраическом равенстве C = F + 2B – 5 значение переменной С зависит от значений переменных F и B, указанных в правой части равенства. Например, при F = 2 и B = 6, С = 9. Такое же равенство можно записать в программе, например на языке программирования Бейсик: C = F + 2B – 5. В терминах языка программирования C, F и B — это идентификаторы (имена) переменных.

Переменная — это объект программы, имеющий имя и изменяемое значение. Для хранения переменной в памяти компьютера выделено определенное место.

Переменные величины в отличие от постоянных величин (констант) могут со временем менять свое значение. Константой называется величина, которая в ходе выполнения программы не меняет своего значения.

Назначение программы состоит в обработке информации, при этом, конечно, основную роль играют переменные.

Переменная характеризуется:

• идентификатором;
• типом;
• значением.

Каждая переменная имеет свой идентификатор, т. е. свое уникальное имя. Имя переменной показывает, в каком месте памяти компьютера она хранится, значение переменной считывается из указанного ее именем места в памяти. Двух переменных с одним именем в одном программном модуле (блоке) быть не должно. Примерами идентификаторов величин могут быть, например, следующие последовательности символов: a1, SUMMA, X_1, Y_1, My_program.

Во многих языках программирования существуют некоторые ограничения на задания имен переменных. Имена составляются из букв и цифр; первой литерой должна быть буква. Знак подчеркивания «_» считается буквой, его удобно использовать, чтобы улучшить восприятие длинных имен переменных. Разумно давать переменным логически осмысленные имена, в соответствии с их назначением. Нельзя использовать в качестве имен зарезервированные (служебные) слова языка программирования.

Тип переменной — это диапазон (набор) всех значений, которые может принимать данная переменная. Тип переменной определяет, какие операции для нее допустимы. Другими словами, тип переменной — это характеристика, которая для величины определяет:

• необходимый размер памяти;
• диапазон значений, которые может принимать величина;
• возможные операции над величиной (подразумеваются действия относительно использования величин в выражениях);
• формы представления величин (или формат представления величин).

Стандартные типы — это числовые, литерные и логические типы.

Числовой тип, к которому относятся целые и вещественные величины, позволяет оперировать с числами. Целые числа, которые в учебном алгоритмическом языке составляют тип цел, сверху ограничены положительным числом N_max, а снизу — отрицательным числом N_min. Значения N_max и N_min определяются объемом ячеек памяти, в которые записываются целые числа. Обычно для целых чисел выделяется два байта памяти, соответственно границы диапазона равны [N_min = –32768 и N_max = 32767]. Считается, что все операции с величинами типа цел выполняются по обычным правилам арифметики, за одним исключением: возможны две операции деления div и mod.

Операция div обозначает целочисленное деление. При делении с точностью до целых чисел получается два результата — частное и остаток. Знак результата берется по обычным правилам, а полученный остаток игнорируется. Например:

23 div 5 = 4;

2 div 6 = 0;

(–13) div 5 = –2;

(–13) div (–5) = 2.

Операция mod определяет остаток при делении двух целых чисел.

Например:

23 mod 5 = 3;

2 mod 6 = 2;

(–13) mod 5 = –3;

(–13) mod (–5) = 3;

8 mod 2 = 0.

Целые числа чаще всего используются в простых арифметических выражениях и выступают в программах в качестве различных счетчиков и значений индексов.

К другому числовому типу относятся вещественные (вещ) величины. Значения вещественных величин могут изображаться в форме с фиксированной запятой (например, 0,3333; 2,0; –4,567 и т. д.) и с плавающей запятой (например, 7,010², 5,173*10^–3 и т. д.).

В отличие от целых чисел, действия с вещественными числами могут быть неточными — это связано с ошибками округлений. Объем памяти, который предоставляется для хранения значений вещественной переменной, — от 4 до 10 байтов (в зависимости от выбранного формата числа). Над числовыми величинами можно выполнять как арифметические операции, так и операции сравнения (>, <, >=, <=, =, ).

Литерный тип, включающий символы и строки, дает возможность работать с текстом. Литерные величины — это произвольные последовательности символов: букв, цифр, знаков препинания, пробела и других специальных знаков (возможными символами могут быть символы таблицы ASCII). Литерные величины обычно заключаются в кавычки: «а», «В», «СТРОКА», «1_2_3». В учебном алгоритмическом языке литерные величины обозначаются как лит. В других языках программирования (например, в Паскале) различают символьный (char) и строковый (string) типы. Величины символьного типа состоят из одного символа и занимают в памяти всего 1 байт. Величины строкового типа представляют собой различные последовательности символов, которые предусмотрены кодовой страницей, установленной в компьютере. Длина строки может составлять от 0 до 255 символов. Над всеми литерными величинами возможны операции сравнения. С помощью отношений типа «a» < «b», «b» < «c», «c» < «d»,… выполняется упорядочение литерных величин (сортировка по возрастанию или убыванию).

Еще одной операцией, характерной для символьных и строковых величин, является операция конкатенации (слияния): «a» + «b» = «ab».

Логический тип позволяет определять логические переменные, которые могут принимать только два значения: истина (true) или ложь (false). Для представления логической величины достаточно одного бита, однако, поскольку место в памяти выделяется по байтам, логической величине отводится минимальная «порция» памяти — один байт. Над логическими величинами можно выполнять все стандартные логические операции.

Значение — это непосредственно то, чему равна переменная в конкретный момент времени. Это может быть число, символ, текст и т. д. Значение переменной в программе можно задать двумя способами: присваиванием и с помощью процедуры ввода.

Оператор присваивания

Во всех языках программирования оператор присваивания является одним из важнейших. С помощью присваивания переменные получают новые значения, например:

Д := 13;

D1 := C;

Х := Х + 1.

В операторах присваивания используется либо обычный знак равенства, либо сочетание двоеточия и знака равенства «:=». Поскольку знак присваивания — это не знак равенства, возможны записи вида Х := Х + 1 или А := А – В. Нужно учитывать, что оператор присваивания будет выполняться только в том случае, если значения всех переменных в правой части уже определены и выполняется соответствие типов для правой и левой части оператора присваивания. Например, С := А > B выполнится только в том случае, если для переменной С определен булевский (логический) тип. Операция присваивания может быть применена к большинству типов величин. Однако для каждого из типов предусмотрен свой набор операций.

Локальные, глобальные и общие переменные

Каждая переменная характеризуется областью действия или областью видимости. По зоне видимости в языках программирования различают локальные и глобальные переменные. Первые доступны только конкретному подалгоритму (вспомогательному алгоритму, подпрограмме, модулю), вторые — всему алгоритму (программе). С распространением модульного и объектного программирования появились еще и общие переменные, доступные для определенных уровней иерархии подпрограмм.

Ограничение зоны видимости придумали как для возможности использовать одинаковые имена переменных, так и для защиты от ошибок, связанных с неправомерным использованием переменных.

Имена локальных и глобальных переменных могут совпадать. При этом действует правило: локальные переменные на время работы подпрограмм, в которых они объявлены, экранируют, т. е. перекрывают глобальные переменные. Например, если в основной программе переменная с именем с определена как логическая, а в подпрограмме идентификатор с используется для задания вещественной переменной, то только на время работы подпрограммы с можно использовать как число — в остальных случаях идентификатор с определяет логическую переменную.

Примеры решения задач

Пример 1. Значения заданных переменных А, В перераспределить таким образом, чтобы А и В поменялись значениями.

Решение. Возможны два варианта решения:

С использованием промежуточной переменной С	Без использования дополнительной переменной
C := A; A := B; B := C	A := A + B; B := A – B; A := A – B

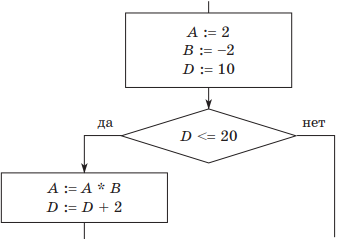
Пример 2. Определить значение переменной A после выполнения фрагмента алгоритма:

Решение. Оформим решение в виде таблицы.

A	B	D	Условие
2	–2	10	да
–4	–2	12	да
8	–2	14	да
–16	–2	16	да
32	–2	18	да
–64	–2	20	да
128	–2	22	нет — окончание цикла

Ответ: А = 128.

Пример 3. Определить значение переменной S:

A := –1; B := 1

нц пока A + B < 10

A := A + 1; B := B + A

кц

S := A * B

Решение. Оформим решение в виде таблицы.

A	B	A + B	S
–1	1	0
0	1	1
1	2	3
2	4	6
3	7	10 — условие выхода из цикла	21

Ответ: S = 21.

Пример 4. Записать последовательность операций присваивания (:=), которая позволит определить номера подъезда и этажа по номеру N квартиры девятиэтажного дома, считая, что на каждом этаже по 4 квартиры, а нумерация квартир начинается с первого подъезда.

Решение.

4 * 9 = 36 {количество квартир в подъезде}

Х := (N – 1) div 36 + 1 {номер подъезда}

N := N – (X – 1) * 36 { N ∊[1, 36] }

Y := (N – 1) div 4 + 1 {номер этажа}

Например, для квартиры с номером 150 получим:

Х = (150 – 1) div 36 + 1 = 4 + 1 = 5;

N = 150 – (5 – 1) * 36 = 6;

Y = (6 – 1) div 4 + 1 = 2.

Ответ: квартира с номером 150 находится в пятом подъезде, на втором этаже.