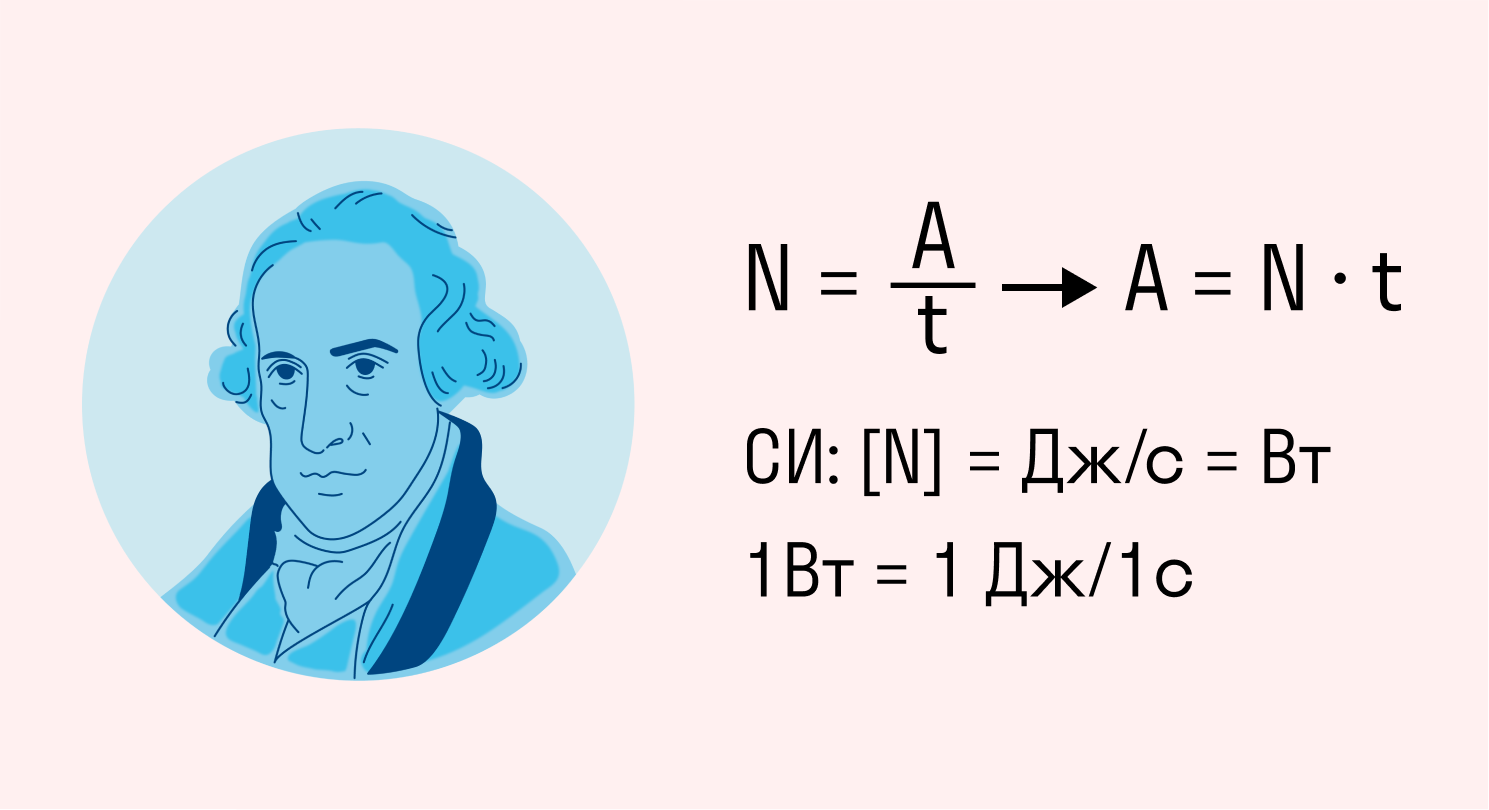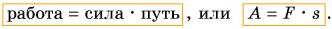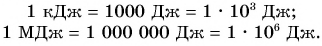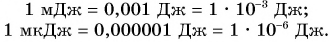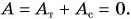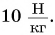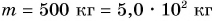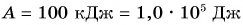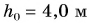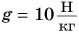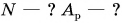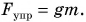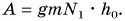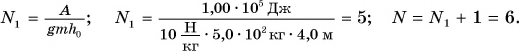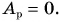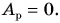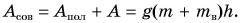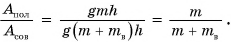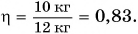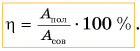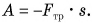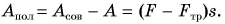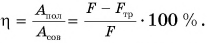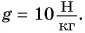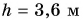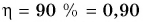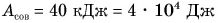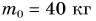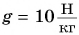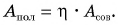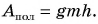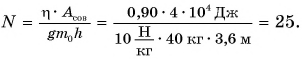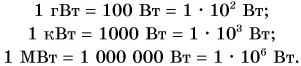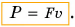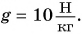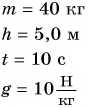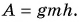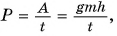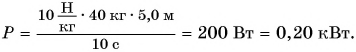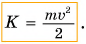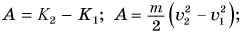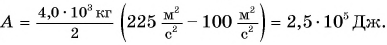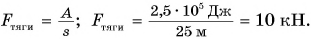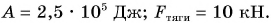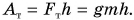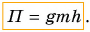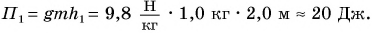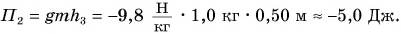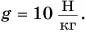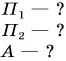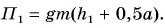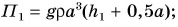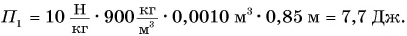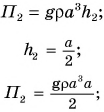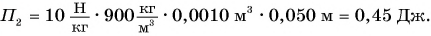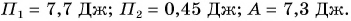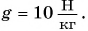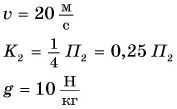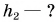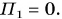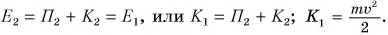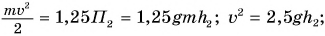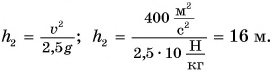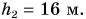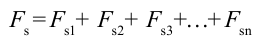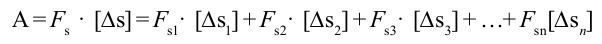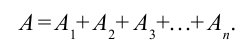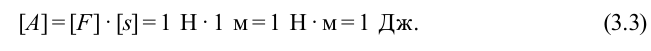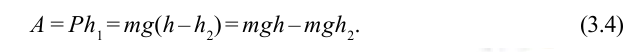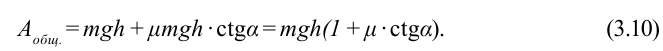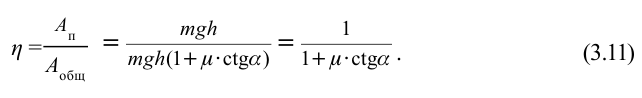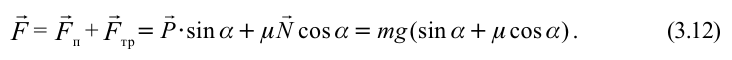Определение мощности
Допустим, нам необходимо убрать урожай пшеницы с поля площадью 100 га. Это можно сделать вручную или с помощью комбайна. Очевидно, что пока человек обработает 1 га площади, комбайн успеет сделать намного больше. В данном случае разница между человеком и техникой — именно то, что называют мощностью. Отсюда вытекает первое определение.
Мощность в физике — это количество работы, которая совершается за единицу времени.
Рассмотрим другой пример: между точкой А и точкой Б расстояние 15 км, которое человек проходит за 3 часа, а автомобиль может проехать всего за 10 минут. Понятно, что одно и то же количество работы они сделают за разное время. Что показывает мощность в данном случае? Как быстро или с какой скоростью выполняется некая работа.
В электромеханике эта величина имеет еще одно определение.
Мощность — это скалярная физическая величина, которая характеризует мгновенную скорость передачи энергии от системы к системе или скорость преобразования, изменения, потребления энергии.
Напомним, что скалярными величинами называются те, значение которых выражается только числом (без вектора направления).
Мощность человека в зависимости от деятельности
|
Вид деятельности |
Мощность, Вт |
|---|---|
|
Неспешная ходьба |
60–65 |
|
Бег со скоростью 9 км/ч |
750 |
|
Плавание со скоростью 50 м/мин |
850 |
|
Игра в футбол |
930 |
Получай лайфхаки, статьи, видео и чек-листы по обучению на почту
Полезные подарки для родителей
В колесе фортуны — гарантированные призы, которые помогут наладить учебный процесс и выстроить отношения с ребёнком!
Как обозначается мощность: единицы измерения
В таблице выше вы увидели обозначение в ваттах, и читая инструкции к бытовой технике, можно заметить, что среди характеристик прибора обязательно указано количество ватт. Это единица измерения механической мощности, используемая в международной системе СИ. Она обозначается буквой W или Вт.
Измерение мощности в ваттах было принято в честь шотландского ученого Джеймса Уатта — изобретателя паровой машины. Он стал одним из родоначальников английской промышленной революции.
В физике принято следующее обозначение мощности: 1 Вт = 1 Дж / 1с.
Это значит, что за 1 ватт принята мощность, необходимая для совершения работы в 1 джоуль за 1 секунду.
В каких единицах еще измеряется мощность? Ученые-астрофизики измеряют ее в эргах в секунду (эрг/сек), а в автомобилестроении до сих пор можно услышать о лошадиных силах.
Интересно, что автором этой последней единицы измерения стал все тот же шотландец Джеймс Уатт. На одной из пивоварен, где он проводил свои исследования, хозяин накачивал воду для производства с помощью лошадей. И Уатт выяснил, что 1 лошадь за секунду поднимает около 75 кг воды на высоту 1 метр. Вот так и появилось измерение в лошадиных силах. Правда, сегодня такое обозначение мощности в физике считается устаревшим.
Одна лошадиная сила — это мощность, необходимая для поднятия груза в 75 кг за 1 секунду на 1 метр. 🐴
|
Единицы измерения |
Вт |
|---|---|
|
1 ватт |
1 |
|
1 киловатт |
103 |
|
1 мегаватт |
106 |
|
1 эрг в секунду |
10-7 |
|
1 метрическая лошадиная сила |
735,5 |
Подготовка к ОГЭ по физике онлайн поможет снять стресс перед экзаменом и получить высокий балл.
Все формулы мощности
Зная определения, несложно понять формулы мощности, используемые в разных разделах физики — в механике и электротехнике.
В механике
Механическая мощность (N) равна отношению работы ко времени, за которое она была выполнена.
Основная формула:
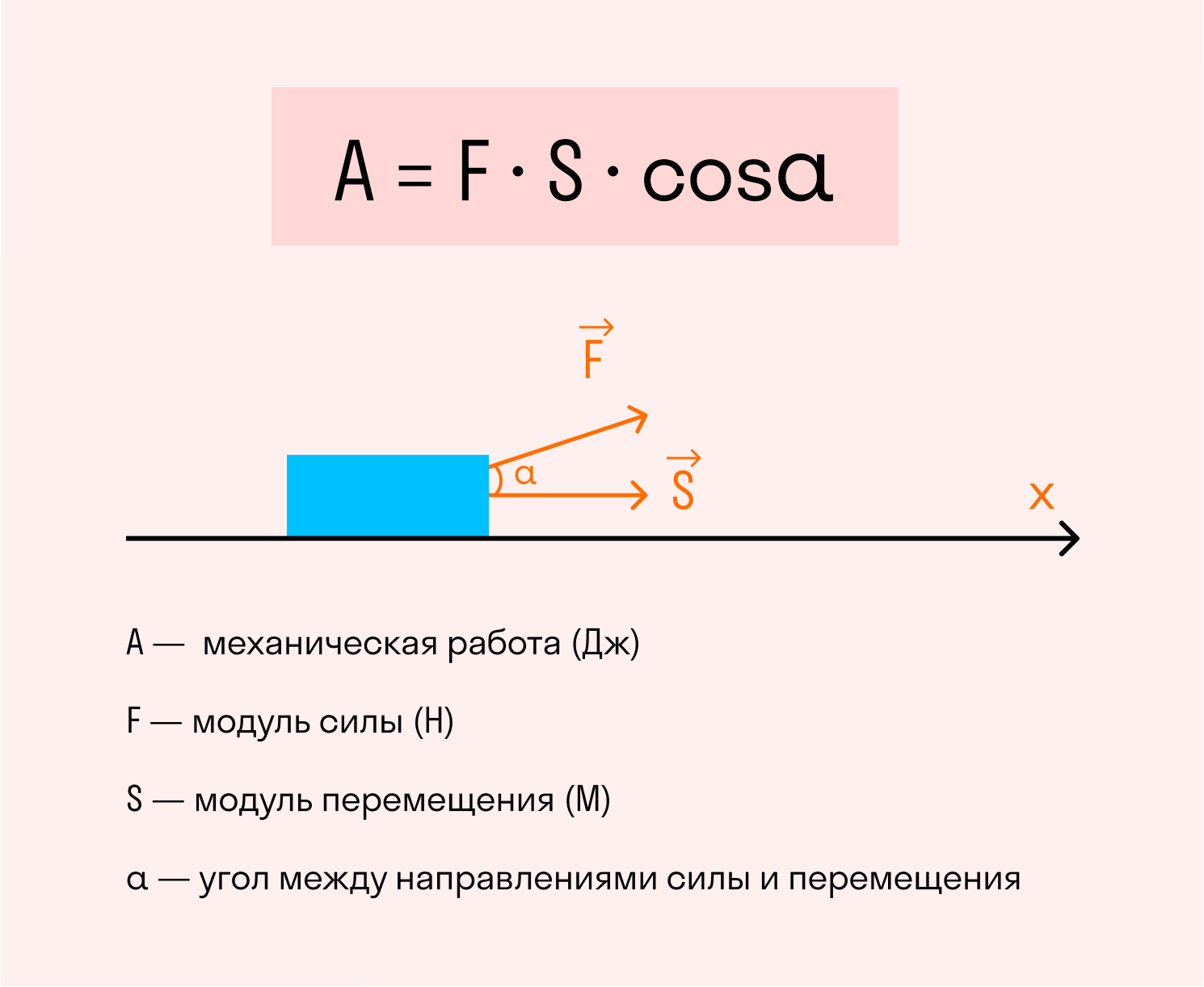
N = A / t, где A — работа, t — время ее выполнения.
Если вспомнить, что работой называется произведение модуля силы, модуля перемещения и косинуса угла между ними, мы получим формулу измерения работы.
Если направления модуля приложения силы и модуля перемещения объекта совпадают, угол будет равен 0 градусов, а его косинус равен 1. В таком случае формулу можно упростить:
A = F × S
Используем эту формулу для вычисления мощности:
N = A / t = F × S / t = F × V
В последнем выражении мы исходим из того, что скорость (V) равна отношению перемещения объекта на время, за которое это перемещение произошло.
В электротехнике
В общем случае электрическая мощность (P) говорит о скорости передачи энергии. Она равна произведению напряжения на участке цепи на величину тока, проходящего по этому участку.
P = I × U, где I — сила тока, U — напряжение.
В электротехнике существует несколько видов мощности: активная, реактивная, полная, пиковая и т. д. Но это тема отдельного материала, сейчас же мы потренируемся решать задачи на основе общего понимания этой величины. Посмотрим, как найти мощность, используя вышеуказанные формулы по физике.
Задача 1
Допустим, человек поднимает ведро воды из колодца, прикладывая силу 60 Н. Глубина колодца составляет 10 м, а время, необходимое для поднятия — 30 сек. Какова будет мощность человека в этом случае?
Решение:
Найдем вначале величину работы, используя тот факт, что мы знаем расстояние перемещения (глубину колодца 10 м) и приложенную силу 60 Н.
A = F × S = 60 Н × 10 м = 600 Дж
Когда известно значение работы и времени, найти мощность несложно:
N = A / t = 600 Дж / 30 сек = 20 Вт
Ответ: мощность человека при поднятии ведра — 20 ватт.
Задача 2
В комнате включена лампа мощностью 100 Вт. Напряжение домашней электросети — 220 В. Какая сила тока проходит через эту лампу?
Решение:
Мы знаем, что Р = 100 Вт, а U = 220 В.
Поскольку P = I × U, следовательно I = P / U.
I = 100 / 220 = 0,45 А.
Ответ: через лампу пройдет сила тока 0,45 А.
Вопросы для самопроверки
-
Что характеризует механическая мощность?
-
Какие существуют единицы измерения мощности в физике?
-
Какая из единиц измерения считается устаревшей?
-
Мощность можно назвать скалярной величиной? Что это означает?
-
Как из формулы нахождения мощности получить работу?
-
Какой буквой обозначается мощность в механике, а какой — в электротехнике?
-
Какую работу производит за 30 минут устройство мощностью 600 Вт?
-
Как узнать напряжение в сети, если мы знаем мощность подключенного к ней прибора и силу тока, проходящую через прибор?
-
Если в течение 1 часа автомобиль №1 едет со скоростью 60 км/ч, а автомобиль №2 — со скоростью 90 км/ч, одинаковую ли мощность они развивают в это время?
-
Допустим, автобус отвез пассажиров из города А в город В за 1 час. Если он планирует вернуться в город А пустым по той же трассе и потратить на это 1 час, ему понадобится развить такую же мощность или меньшую?
Содержание:
Работа, мощность и энергия:
Мы часто слышим от друзей: «Я сегодня выполнил большую работу: выучил наизусть стихотворение и решил пять задач по математике». Но с точки зрения физики никакой работы не совершено, даже если выучить наизусть целую поэму. Что же такое работа в физике?
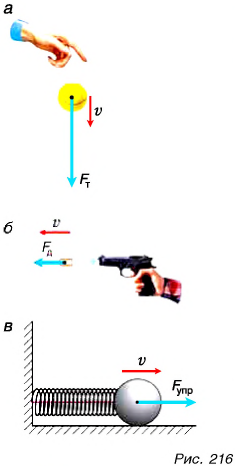
В физике работа оценивает то, что вызвала сила, действуя на движущееся тело. Покажем это на примерах. Рассмотрите внимательно рисунок 216. Что общего в результатах действия силы тяжести на мяч (рис. 216, а), силы давления газа на пулю в пистолете (рис. 216, б) и силы упругости сжатой пружины на шарик (рис. 216, в) после пережигания нити? Все перечисленные силы вызывают разгон тел (мяча, пули, шарика), т. е. увеличение скорости движения.
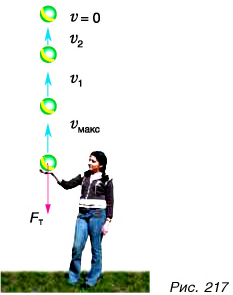
Л может ли сила, действующая на движущееся тело, уменьшать его скорость? Подбросьте мяч и наблюдайте за его движением вверх (рис. 217). Теперь сила тяжести уменьшает скорость его движения. Во всех случаях, когда сила изменяет скорость движения (увеличивает или уменьшает), говорят, что сила совершает механическую работу.
Механическая работа является физической величиной. Ее значение можно рассчитать. Рассмотрим самый простой случай: направление силы совпадает с направлением движения. Например, идет разгон спортивных саней (рис. 218). Изменение скорости саней, а значит, и работа по их разгону зависят от значения действующей силы (силы спортсменов, разгоняющих сани) и от пройденного санями пути. Чем больше сила и путь, тем большая совершается работа. Этот вывод справедлив для всех движущихся под действием силы тел.
Таким образом, механическая работа — физическая величина, пропорциональная действующей на тело силе и пройденному пути.
Обозначим работу буквой А. Тогда, если направление силы совпадает с направлением движения тела,
Единицей работы в СИ является 1 джоуль (1 Дж). Названа она в честь известного английского физика Дж. П. Джоуля. Один джоуль — это работа, совершаемая силой 1 Н на пути 1 м.
1 джоуль = 1 ньютон • 1 метр.
Для измерения большой работы используют кратные джоулю единицы:
В случае малой работы применяются дольные единицы:
Из формулы работы следует, что если есть силы, но нет движения, то нет и работы. Например, сила тяжести, действующая на лежащий на столе мяч (рис. 219, а), работы не совершает, а в случае падающего мяча (рис. 219, б) — совершает.
Сила не всегда увеличивает скорость движения тела. Так, при движении мяча вверх (см. рис. 217) сила тяжести замедляет его движение. Аналогично при скольжении шайбы по льду сила трения уменьшает скорость движения шайбы. Работу силы (тяжести, трения) в подобных случаях считают отрицательной.
Но положительная и отрицательная работы могут совершаться одновременно и даже быть равными по абсолютной величине. В этом случае скорость движения постоянна. Например, электропоезд на данном участке пути движется равномерно. Это значит, что равнодействующая сил (тяги двигателя и сопротивления движению) равна нулю. По и сила тяги, и сила сопротивления совершают работу. Только работа силы тяги 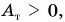
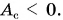
Главные выводы:
- Механическая работа характеризует результат действия силы на движущееся тело и пропорциональна действующей на тело силе и пройденному телом пути.
- Силы, ускоряющие движение тела; совершают положительную работу.
- Силы, замедляющие движение тела, совершают отрицательную работу.
- Единица работы в СИ — 1 джоуль (1 Дж).
Пример решения задачи:
Подъемный кран равномерно поднимает с земли бетонную плиту массой m = 500 кг на один из этажей строящегося дома. Сила упругости троса при этом совершает работу А = 100 кДж. Определите, на какой этаж была поднята плита, если высота одного этажа 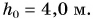
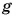
Дано:
Решение:
При равномерном подъеме сила упругости троса равна силе тяжести, действующей на плиту:
Работа силы упругости 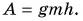
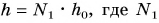
Отсюда
Так как движение плиты равномерное, то равнодействующая сил, приложенных к ней, 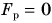
Ответ: плита поднята на 6-й этаж; работа равнодействующей сил
Полезная и совершённая работа
Оценивая работу машины, механизма и др., говорят об их коэффициенте полезного действия (КПД). Но что такое КПД? Что означают слова «полезного действия»? А что такое неполезное действие?
Рассмотрим ситуацию: идет уборка картофеля на поле. Фермер поднимает картофель в ведре в кузов автомашины (рис. 221), выгружает, а ведро опускает на землю. Механическую работу совершает мускульная сила фермера, поднявшего ведро массой, например, 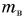
Цель фермера — погрузить в кузов картофель. Исходя из этого, полезной работой является работа по подъему картофеля: 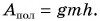
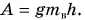
Какую долю составляет полезная работа от совершенной?
Обозначим отношение 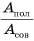
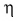
КПД, как правило, выражают в процентах.
Таким образом, КПД (эффективность работы) в данном случае равен 83 %.
Рассмотрим еще один пример. Дети разгоняют санки, действуя силой F в направлении их движения (рис. 222). Совершенная (полная) работа здесь 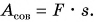
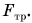
Полезной же работой была
Тогда доля полезной работы (КПД)
Физическая величина, равная отношению полезной работы к совершенной (полной), называется коэффициентом полезного действия.
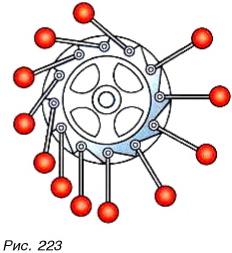
А могут ли механизм, машина, человек работать так, чтобы КПД = 100 %, т. е. чтобы вся совершенная работа была полезной?
Ученые неоднократно пытались создать такую машину (рис. 223), но все попытки оказались безуспешными. (Самостоятельно познакомьтесь в Интернете или справочной литературе с информацией о вечном двигателе.) В работе любой машины, механизма всегда есть неполезная работа, идущая на преодоление трения, сопротивления. А значит, КПД всегда меньше 100 %. А вот сделать неполезную работу минимальной означает повысить КПД.
Главные выводы:
- Совершенная (т. е. полная) механическая работа всегда больше полезной.
- КПД показывает, какую долю составляет полезная работа от всей совершенной.
- Чем больше полезная работа, тем выше КПД.
- КПД всегда меньше 100 %.
Пример решения задачи:
При подъеме картофеля из хранилища глубиной h = 3,6 м подъемным устройством с КПД 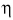
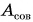
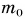
Дано:
Решение:
Зная совершенную работу и КПД, можно найти полезную работу по подъему мешков картофеля:
Полезная работа — это работа подъемного устройства по преодолению силы тяжести, действующей на картофель:
Масса 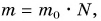
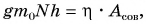
Ответ: N = 25 мешков.
Мощность и единицы мощности
Приобретая автомобиль (рис. 226), газонокосилку, микроволновую печь (рис. 227) и др., человек интересуется их мощностью. Именно мощность является паспортной характеристикой машин и механизмов. Что же такое мощность? Почему так важно ее знать?
Рассмотрим пример. Человек лопатой копает яму для погреба в течение нескольких дней. Такую же яму экскаватор (рис. 228) выкопает за несколько минут. Работа выполняется одинаковая. Одинаковая масса грунта поднимается на одну и ту же высоту. Но быстрота совершения работы человеком и экскаватором разная. За единицу времени экскаватор выполняет во много раз большую работу, чем человек. Для описания быстроты совершения работы вводится мощность.
Физическая величина, равная отношению работы к промежутку времени, за который эта работа совершена, называется мощностью. Обозначается мощность буквой Р.
За единицу мощности в СИ принимается мощность, при которой действующая на тело сила за время t = 1 с совершает работу А = 1 Дж. Эта единица мощности называется ватт (Вт) в честь английского изобретателя Дж. Уатта. Для измерения больших мощностей используют кратные единицы: гектоватт (гВт), киловатт (кВт), мегаватт (МВт). Обратите внимание:
Для малых мощностей употребляются дольные единицы — милливатт (мВт), микроватт (мкВт):
В быту часто необдуманно единицу мощности киловатт принимают за единицу работы. Но работа 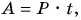
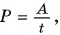
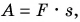
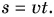
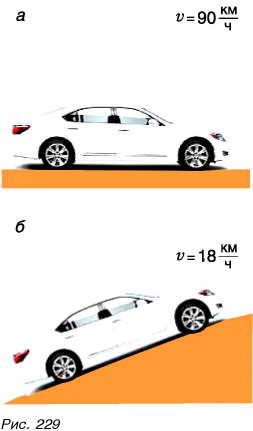
Мощность пропорциональна силе, совершающей работу, и скорости движения. Тогда при постоянной мощности чем меньше скорость, тем больше сила. Вот почему водитель, трогаясь с места или поднимаясь в гору (рис. 229), когда требуется большая сила, едет на малой скорости. Тем самым он увеличивает силу тяги двигателя автомобиля.
Главные выводы
- Мощность — физическая величина, характеризующая быстроту совершения работы.
- Единицей мощности в СИ является 1 ватт.
- Одинаковую мощность можно получить либо при большой скорости и небольшой силе, либо при малой скорости и большой силе.
Для любознательных
В автомобилестроении по традиции используют старинную единицу мощности — лошадиную силу (л. с.). С помощью рисунка сформулируйте самостоятельно определение мощности в 1 лошадиную силу.
Запишем связь 1 л. с. и ватта: 1 л. с. = 736 Вт.
В этих внесистемных единицах мощность первого белорусского трактора МТЗ-2 (1953 г.) была равна 37 л. с. Освоенный в 2010 г. трактор «Беларус-3023» имеет двигатель мощностью 300 л. с. Переведите эти знамения мощности в единицы СИ самостоятельно и сравните их.
Пример решения задачи:
На уроке физкультуры мальчик массой m = 40 кг поднялся по канату на высоту h = 5,0 м за промежуток времени t = 10 с. Определите среднюю мощность, развиваемую мальчиком при подъеме. Коэффициент
Дано:
Решение:
При подъеме по канату работа мускульной силы рук идет на преодоление силы тяжести.
Тогда
Ответ: P = 0, 20 кВт.
Кинетическая энергия
Энергия — одно из наиболее важных и сложных понятий. Причем не только в физике, но и в других науках. А что же такое кинетическая энергия?
Рассмотрим два примера. Шайба, попадая в сетку ворот (рис. 230), прогибает ее. Молот для забивания свай (рис. 231), падая на сваю, загоняет ее в землю на некоторую глубину. Чтобы сильнее прогнуть сетку или глубже забить сваю, шайба и молот должны иметь большую скорость. И шайба, и молот совершили работу. При этом скорость их движения изменилась (уменьшилась до нуля). Совершенные ими работы были разными, даже если предположить, что скорости движения были одинаковыми. Но массы молота и шайбы не равны.
Если тело способно совершить работу, то оно обладает энергией. В физике энергию движущегося тела называют кинетической (от греч. kinetikos — приводящий в движение). Кинетическая энергия обозначается буквой К (или 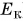
Большая кинетическая энергия движущихся тел — камня, автомобиля, железнодорожного состава (рис. 232), метеорита и др. — означает, во-первых, что при разгоне их до данной скорости разгоняющей силой была совершена большая работа и, во-вторых, при их остановке тормозящей силой будет совершена такая же большая работа.
Из примеров следует, что кинетическая энергия зависит от массы тела и скорости его движения. Какой является эта зависимость?
Опыты показывают, что кинетическая энергия прямо пропорциональна массе тела и квадрату скорости его движения:
Увеличение скорости движения тела, например в 4 раза, приводит к возрастанию кинети- Обратите внимание! ческой энергии в 16 раз. Об этом должны всегда помнить водители и пешеходы.
Главные выводы:
- Кинетическая энергия выражает способность движущихся тел совершать работу.
- Кинетическая энергия, как и работа, измеряется в джоулях.
- Кинетическая энергия тела зависит от его массы и скорости.
- Изменить (увеличить или уменьшить) кинетическую энергию тела можно только путем совершения работы (положительной или отрицательной).
Пример решения задачи:
Скорость движения груженого автомобиля массой m = 4,0 т увеличилась от 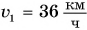
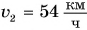
Дано:
Решение:
Чтобы увеличить кинетическую энергию от 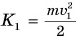
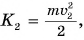
Но работа 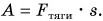
Ответ:
Потенциальная энергия
При разгоне любого тела (санок, автомобиля и др.) у него возникает способность совершить механическую работу — у движущегося тела появляется кинетическая энергия. А если тело неподвижно? Обладает ли оно способностью совершить работу?
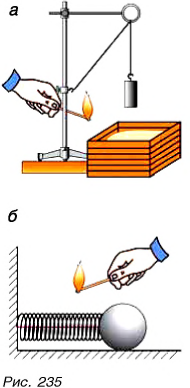
Проведем два опыта. В первом поднимем и укрепим на нити над ящиком с песком гирю (рис. 235, а). Во втором между упором и шариком поместим предварительно сжатую и связанную ниткой пружину (рис. 235, б). Оба тела (гиря и пружина) неподвижны 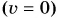
Важно понимать, что потенциальная энергия не появляется сама по себе. В этих опытах гиря была поднята над столом, пружина была сжата какой-то силой. Значит, чтобы тело запасло потенциальную энергию, необходимо совершить работу. Чем сильнее будет сжата пружина, чем выше будет поднято тело, тем больше у них будет запас потенциальной энергии. Тела, представленные на рисунке 236, уже обладают потенциальной энергией. У трамплина она вызвана прогибом (деформацией) доски, у мышеловки — закручиванием пружины, у лука — изменением расположения древка и тетивы. Из этих и других примеров следует, что потенциальная энергия — это энергия, обусловленная взаимным расположением взаимодействующих тел или частей тела (гири и Земли, стрелы и тетивы, звеньев пружины). Обозначается потенциальная энергия буквой П (или 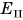
Именно благодаря потенциальной энергии сжатой (закрученной) пружины работают механические часы, реле времени микроволновых печей, стиральных машин, движутся некоторые детские игрушки. Потенциальная энергия поднятой с помощью плотины воды заставляет работать гидроэлектростанции (рис. 237).
Главные выводы:
- Неподвижные взаимодействующие тела (система тел) могут обладать способностью совершать механическую работу, а значит, потенциальной энергией.
- Значение потенциальной энергии зависит от взаимного расположения взаимодействующих тел (частей тела).
- Потенциальная энергия изменяется только при совершении работы.
Расчет потенциальной энергии
Кинетическая энергия тела, зависящая от его массы и скорости, выражается формулой 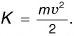
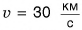
Рассмотрим отдельно два случая: потенциальную энергию притяжения поднятого над поверхностью Земли тела и потенциальную энергию деформированного тела.
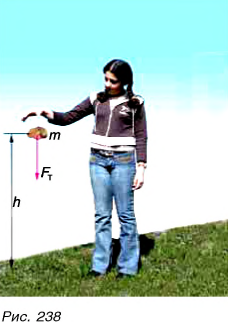
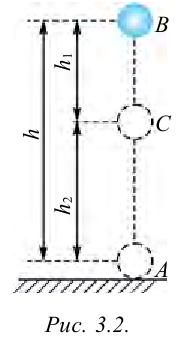
В первом случае формулу для расчета потенциальной энергии легко вывести. Если тело массой m поднято относительно поверхности Земли на высоту h (рис. 238), то при его падении сила тяжести 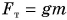
Это и есть потенциальная энергия поднятого тела:
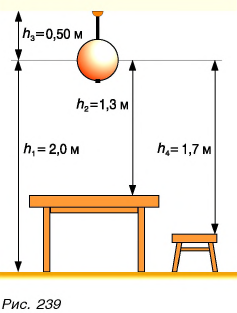
Значение потенциальной энергии относительно. Так, относительно пола потенциальная энергия светильника (рис. 239) массой m = 1,0 кг, центр тяжести которого расположен на высоте 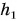
Относительно потолка 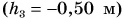
Поэтому, приводя значение потенциальной энергии, необходимо указывать уровень, относительно которого она задана, — нулевой уровень потенциальной энергии (это может быть, к примеру, поверхность пола, потолка, стола и т. д.).
Гораздо сложнее дело обстоит с расчетом потенциальной энергии деформированного тела. Мы можем растянуть или сжать пружину, изогнуть или закрутить ее (рис. 240). Потенциальная энергия у пружины будет в каждом из этих случаев. И чем больше упругая деформация, тем больше потенциальная энергия пружины. В данном примере расчет потенциальной энергии придется вести по различным формулам. Более детально с этим вы будете знакомиться в 9-м классе.
Главные выводы:
- Потенциальная энергия притяжения тела к Земле зависит от массы тела и высоты его подъема над нулевым уровнем энергии.
- Значение потенциальной энергии тела зависит от выбора нулевого уровня энергии.
- Потенциальная энергия деформированного тела зависит от величины деформации.
Пример решения задачи:
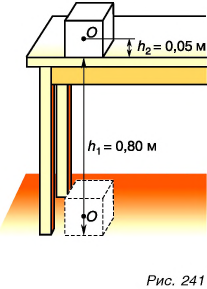
Парафиновый однородный кубик с длиной ребра а = 10 см лежит на столе на высоте 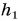
Дано:
Решение:
Потенциальная энергия кубика относительно поверхности пола (рис. 241) определяется положением его центра (точки O):
Масса кубика 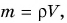
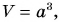
Потенциальная энергия кубика относительно поверхности стола:
Работа по подъему кубика на высоту 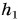
Ответ:
Закон сохранения механической энергии
Кинетическая и потенциальная энергии — это два вида механической энергии. Связаны ли они друг с другом? И если да, то в чем выражается эта связь?
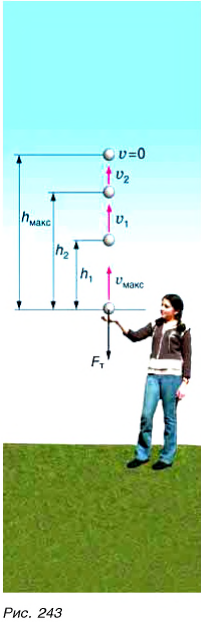
Проследим за движением брошенного вверх металлического шарика (рис. 243). В нижней точке траектории сила действия руки на шарик сообщает ему кинетическую энергию. Шарик движется вверх. Скорость его движения, а значит, и кинетическая энергия уменьшаются. Но исчезает ли кинетическая энергия бесследно? Поднимаясь выше, шарик приобретает все большую потенциальную энергию (вспомните: 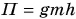
Если сопротивление воздуха мало (и им можно пренебречь), брошенный вверх шарик возвращается назад практически с такой же, как в момент бросания, скоростью и кинетической энергией.
А каким будет значение механической энергии шарика в промежуточных точках? Например, на высоте 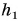
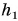
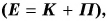
Если силами трения или сопротивления движению нельзя пренебречь, этот закон не выполняется. Заменим в опыте металлический шарик на пенопластовый брусок такой же массы (рис. 244). Мы увидим, что даже при большей, чем у металлического шарика, начальной скорости он не поднимется на такую же высоту и вернется назад с заметно меньшей скоростью. Убывает кинетическая энергия движущейся по горизонтальной поверхности льда шайбы, но потенциальная энергия взамен не появляется. За счет кинетической энергии шайбы совершается работа против сил трения.
В заключение заметим, что явление превращения энергии из одного вида в другой человек научился использовать в практических целях. Энергия падающей воды приводит в действие водяные мельницы и гидроэлектростанции. В Республике Беларусь успешно реализуется государственная программа использования энергии рек. Важная роль в ней отводится таким рекам, как Неман и Западная Двина. Па Немане работает Гродненская ГЭС мощностью 17 МВт. Установленная мощность Витебской ГЭС на Западной Двине — 40 МВт.
Кинетическую энергию ветра человек с давних времен начал использовать с помощью паруса (рис. 245), затем стал применять в ветряных мельницах. В последние годы в нашей стране начато сооружение ветроэлектростанций (рис. 246). Они уникальны тем, что не оказывают вредного воздействия на окружающую среду. Во многих странах успешно используют энергию приливов и отливов вод морей и океанов. Там созданы приливные электростанции.
Главные выводы:
- Кинетическая и потенциальная энергии взаимо-превращаемы.
- При отсутствии сил трения и сопротивления движению полная механическая энергия тела (системы тел) сохраняется.
- Закон сохранения механической энергии не выполняется, если силами трения (сопротивления) нельзя пренебречь.
- Заказать решение задач по физике
Пример решения задачи:
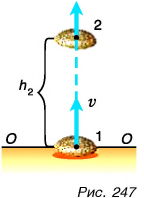
Камень бросили вертикально вверх со скоростью 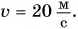
Дано:
Решение:
За нулевой уровень потенциальной энергии примем уровень O — O, проходящий через точку бросания камня (рис. 247). Значит,
Полная механическая энергия камня в точке бросания 1:
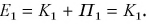
Полная механическая энергия камня в точке 2:
По условию 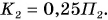
Ответ:
Энергия и работа
Энергия – эта количественная мера различных форм движения и взаимодействия (по гречески слово «энергия» означает действие). Энергия в зависимости от вида движения в природе проявляется по-разному. Например, механическая, тепловая, электромагнитная, ядерная энергия и другие. В результате взаимодействия энергия одного вида превращается в энергию другого вида. Однако во всех этих процессах энергия, переданная от одного тела второму (независимо от ее вида), будет равна энергии, полученной вторым телом от первого.
Как известно из второго закона Ньютона, чтобы изменить механическое движение тела на него должны подействовать другие тела. Иначе говоря, среди этих тел происходит обмен энергиями. Для описания такого обмена энергии в механике введено понятие механическая работа, которую принято обозначать буквой 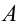
Механическая работа. Величина, равная скалярному произведению силы на перемещение в направлении действия силы, называется механической работой, т.е.
Здесь: 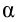
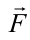
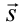
Если учитывать, что 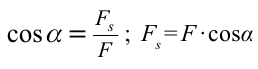
Здесь 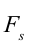
Основываясь на выражении (3.2), можно сделать следующий вывод:
если 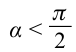
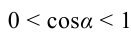
если 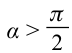
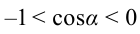
если 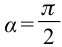
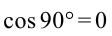
Работа считается аддитивной (аддитив – по-латински означает суммарный) величиной (в физике аддитивность величины означает, что величина, относящаяся к системе в целом, равна сумме величины, относящихся к ее составным частям).
Если на тело действует несколько сил, то будет:
тогда полная работа равна работе, выполненной равнодействующей сил.
или
Единица работы. Единица измерения работы в системе СИ – Джоуль (Дж):
В качестве единицы работы в СИ принята работа выполненная силой 1Н при смещении тела на 1 м.
Работа силы тяжести. На поверхности Земли на тело действует сила тяжести со стороны Земли, равная 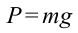
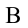
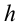
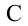
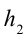
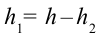
Здесь выполненная силой тяжести работа выражается следующей формулой:
Здесь: 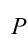
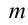
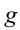
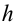
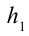
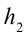
Работа, выполненная силой тяжести, не зависит от формы пути, зависит только от высоты спуска. Поэтому работа, выполненная под действием силы тяжести, зависит не от формы траектории, а от начального и конечного состояний. Такая сила называются потенциальной или консервативной. Поле такой силы называется потенциальным полем.
При движении тела вниз из-за соответствия направления силы тяжести и смещения выполненная работа будет положительной, при движении вверх из-за противоположности направлений работа будет отрицательной. Поэтому в случае, когда тело под воздействием силы тяжести смещено и вернулось обратно, выполненная общая работа равняется нулю.
Полной механической энергией системы называется сумма кинетической и потенциальной энергии системы. Например, полная механическая энергия тела массой 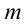
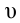
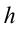
Полная механическая энергия системы остается неизменной с течением времени:
Возможны лишь превращения потенциальной энергии и кинетическую и обратно. Выражение (3.5) представляет собой закон сохранения механической энергии.
Проведенные многочисленные эксперименты, теоретические выводы подтвердили строгое соблюдение закона сохранения энергии.
В природе постоянно происходят превращения одного вида энергии в другой (например, механическая энергия переходит в тепловую энергию). Поэтому этот закон также называют законом сохранения и превращения энергии. Этот закон является основным законом природы и действителен не только для макроскопических, но и микроскопических систем.
Энергия никогда не исчезает, ниоткуда не появляется, она может только преобразовываться из одного вида в другой.
В закрытых системах полная энергия сохраняется.
Например, потенциальная энергия тела, падающего с высоты 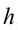
Коэффициент полезного действия. Введена величина, показывающая, какая часть израсходованной энергии машин и двигателей превращается в полезную работу.
Отношение полезной работы к полной работе называется коэффициентом полезного действия (КПД) и обозначается буквой 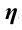
Если полезную работу обозначить 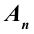
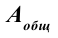
КПД не может быть больше единицы (100%). В машинах и двигателях в результате работы силы трения часть полной энергии расходуется и поэтому КПД всегда меньше единицы.
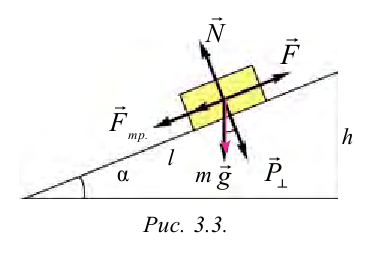
Рассмотрим наклонную плоскость и выполненную работу при подъеме тела вверх. По «золотому правилу» механики, во сколько раз выигрываем в силе, во столько раз проиграем в расстоянии. Но из-за увеличения расстояния смещения не меняется выполненная работа.
Рассмотрим груз с весом 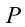
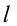
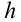
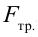
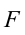
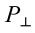
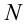
Если не учитывать силу трения, получим уравнение:
Однако с учетом силы трения,
Тогда 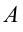
Коэффициент полезного действия:
Сила притяжения, действующая на груз, равна:
- Движение и силы
- Давление в физике
- Строение вещества в физике
- Физическое тело и вещество в физике
- Золотое правило механики
- Потенциальная энергия
- Кинетическая энергия
- Закон сохранения и превращения механической энергии
Если на тело действует сила и оно движется, то совершается механическая работа. Мы знаем, что эта физическая величина зависит от приложенной силы и пройденного пути ($A = Fs$) и измеряется в джоулях.
Очевидно, что на совершение одной и той же работы в разных случаях уходит разное количество времени. Например, на девятый этаж дома нужно поднять шкаф. Если его загрузят в лифт, то работа будет выполнена за несколько секунд. А если грузчик будет поднимать шкаф пешком по лестнице? На выполнение такой работы уйдет гораздо больше времени.
Таким же образом грузовой автомобиль способен переместить груз большой массы за один раз, тогда как легковому автомобилю придется съездить несколько раз до пункта назначения и обратно, чтобы доставить весь груз.
Так появляется новая физическая величина, позволяющая описать насколько быстро может быть выполнена та или иная работа, — мощность. О ней вы и узнаете на данном уроке.
Определение мощности
Что показывает мощность?
Эта величина позволяет нам характеризовать быстроту выполнения работы.
Мощность — это физическая величина, равная отношению работы ко времени, за которое она была совершена.
Как вычислить мощность, зная работу и время?
Чтобы вычислить мощность, нужно работу разделить на время, в течение которого совершена эта работа:
$мощность = frac{работа}{время}$
или
$N = frac{A}{t}$,
где $N$ — мощность, $A$ — работа, $t$ — время выполнения работы.
Мощность может быть:
- Постоянной, если за каждую секунду совершается одинаковая работа
- Непостоянной, если за каждую секунду совершается разная работа. В таком случае говорят о средней мощности: $N_{ср} = frac{A}{t}$
Единица измерения мощности
За единицу мощности принимают такую мощность, при которой за $1 space с$ совершается работа в $1 space Дж$.
Как называется единица мощности?
Эта единица называется ваттом ($Вт$) в честь ученого Джеймса Уатта (рисунок 1).
Чему равен $1 space Вт$? Из формулы мощности ($N = frac{A}{t}$) следует:
$1 space ватт = frac{1 space джоуль}{1 space секунда} = 1 frac{Дж}{с}$.
Какие единицы мощности используют в технике?
Часто используются другие единицы мощности — киловатт ($кВт$), мегаватт ($МВт$) и милливатт ($мВт$):
$1 space МВт = 1 000 000 space Вт$,
$1 space Вт = 0.000001 space МВт$,
$1 space кВт = 1000 space Вт$,
$1 space Вт = 0.001 space кВт$,
$1 space мВт = 0.001 space Вт$,
$1 space Вт = 1000 space мВт$.
Также мощность иногда измеряют в лошадиных силах ($л. с.$):
$1 space л. с. = 735.5 space Вт$
$1 space Вт = 0.00013596 space л. с.$
Эта единица измерения не так популярна как ватт, но до сих пор используется, например, в автомобильной индустрии.
Определение механической работы при известной мощности
Обычно мощность указывают в паспорте технического устройства. В таблице 1 приведены значения мощностей двигателей некоторой техники и др.
| Устройство | $N$, $кВт$ | Устройство | $N$, $кВт$ |
| Телевизор | $0.3$ | Кондиционер | $2.6$ |
| Холодильник | $0.6$ | Дизель тепловоза ТЭ10Л | $2200$ |
| Фен для волос | $1.2$ | Ракета-носитель космического корабля «Восток» | $15 space 000 space 000$ |
| Стиральная машина | $2.5$ | Ракета-носитель космического корабля «Энергия» | $125 space 000 space 000$ |
Мощность человека при нормальных условиях работы в среднем составляет $70–80 space Вт$. При больших физических нагрузках человек способен развить мощность до $730 space Вт$ и более.
Вычисление работы при известной мощности
Как, зная мощность и время работы, рассчитать работу?
Если нам известна мощность, то мы можем рассчитать работу, совершенную в течение определенного промежутка времени. Для этого из формулы мощности ($N = frac{A}{t}$) выразим работу.
Чтобы вычислить работу, нужно мощность умножить на время, в течение которого совершалась эта работа:
$A = Nt$.
Примеры задач
Задача №1
С плотины высотой $30 space м$ каждую минуту падает $150 space м^3$ воды. Найдите мощность потока воды.
Дано:
$h = 30 space м$
$V = 150 space м^3$
$rho = 1000 frac{кг}{м^3}$
$t = 60 space с$
$g = 9.8 frac{Н}{кг}$
$N — ?$
Посмотреть решение и ответ
Скрыть
Решение:
Мощность определяется по формуле:
$N = frac{A}{t}$.
А работу можно рассчитать по формуле:
$A = Fs$.
В нашем случае пройденный водой путь $s$ — это и есть высота плотины $h$, с которой падает вода. Вода падает под силой действия силы тяжести:
$F = gm$.
Рассчитаем массу падающей воды:
$m = rho V$,
$m = 1000 frac{кг}{м^3} cdot 150 м^3 = 150space 000 space кг$.
Теперь можем рассчитать силу тяжести:
$F = gm$
$F = 9,8 frac{Н}{кг} cdot 150 space 000 space кг = 1 space 470 space 000 space Н$.
Работа, совершаемая потоком воды в минуту:
$A = Fh$,
$A = 1 space 470 space 000 space Н cdot 30 space м = 44 space 100 space 000 space Дж$.
Вычислим мощность потока:
$N = frac{A}{t}$,
$N = frac{44 space 100 space 000 space Дж}{60 space с} = 735 space 000 space Вт = 735 space кВт$.
Ответ: $N = 735 space кВт$.
Задача №2
Мощность кондиционера составляет $2.6 space кВт$. Какую работу он совершает за $20 space мин$?
Дано:
$N = 2.6 space кВт$
$t = 20 space мин$
СИ:
$N = 2600 space Вт$
$t = 1200 space с$
$A — ?$
Посмотреть решение и ответ
Скрыть
Решение:
Рассчитаем работу по формуле:
$A = Nt$.
$A = 2600 space Вт cdot 1200 space с = 3 space 120 space 000 space Вт cdot с = 3 space 120 space 000 space Дж = 3120 space кДж approx 3 space МДж$.
Ответ: $A approx 3 space МДж$.
Задача №3
Подъемный кран мощностью $12 space кВт$ может равномерно поднять груз массой $2.5 space т$ за $30 space c$. Какую работу произведет кран? Рассчитайте высоту, на которую он поднимет груз.
Дано:
$N = 12 space кВт$
$m = 2.5 space т$
$t = 30 space с$
$g = 9.8 frac{Н}{кг}$
СИ:
$N = 12 space 000 space Вт$
$m = 2500 space кг$
$A — ?$
$h — ?$
Посмотреть решение и ответ
Скрыть
Решение:
Рассчитаем работу, которую произведет подъемный кран по формуле:
$A = Nt$,
$A = 12 space 000 space Вт cdot 30 space с = 360 space 000 space Дж = 360 space кДж$.
Из определения работы мы знаем, что: $A = Fs$. В нашем случае пройденный путь $s$ будет высотой $h$, на которую кран поднимает груз. На груз действует сила тяжести: $F = F_{тяж} = gm$.
Выразим высоту:
$h = s = frac{A}{F} = frac{A}{F_{тяж}} = frac{A}{gm}$.
Рассчитаем ее:
$h = frac{360 space 000 space Дж}{9.8 frac{Н}{кг} cdot 2500 space кг} approx 14.7 cdot frac{Н cdot м}{Н} = 14.7 space м$.
Ответ: $A = 360 space кДж$, $h = 14.7 space м$.
Упражнения
Упражнение №1
Выразите в киловаттах и мегаваттах мощность: $2500 space Вт$; $100 space Вт$.
Выразите в ваттах мощность: $5 space кВт$; $2.3 space кВт$; $0.3 space кВт$; $0.05 space МВт$; $0.001 space МВт$.
Посмотреть ответ
Скрыть
Ответ:
$N_1 = 2500 space Вт = 2.5 space кВт = 0.0025 space МВт = 2.5 cdot 10^{-3} space МВт$,
$N_2 = 100 space Вт = 0.1 space кВт = 0.0001 space МВт = 10^{-4} space МВт$.
$N_3 = 5 space кВт = 5000 space Вт$,
$N_4 = 2.3 space кВт = 2300 space Вт$,
$N_5 = 0.3 space кВт = 300 space Вт$,
$N_6 = 0.05 space МВт = 50 space 000 space Вт$,
$N_7 = 0.001 space МВт = 1000 space Вт$.
Упражнение №2
С плотины высотой $22 space м$ за $10 space мин$ падает $500 space т$ воды. Какая мощность развивается при этом?
Дано:
$t = 10 space мин$
$m = 500 space т$
$h = 22 space м$
$g = 9.8 frac{Н}{кг}$
СИ:
$t = 600 space с$
$m = 5 cdot 10^5 space кг$
$N — ?$
Посмотреть решение и ответ
Скрыть
Решение:
Мощность мы можем рассчитать по формуле:
$N = frac{A}{t}$.
А работу можно рассчитать по формуле:
$A = Fs$.
Пройденный водой путь $s$ — это и есть высота плотины $h$, с которой падает вода под силой действия силы тяжести:
$F = F_{тяж} = gm$.
Подставим эти выражения в формулу для мощности и рассчитаем ее:
$N = frac{A}{t} = frac{gmh}{t}$,
$N = frac{9.8 frac{Н}{кг} cdot 5 cdot 10^5 space кг cdot 22 space м}{600 space с} = frac{1078 cdot 10^5 space Дж}{600 space с} approx 1.8 cdot 10^5 space Вт approx 180 space кДж$.
Ответ: $N approx 180 space кДж$.
Упражнение №3
Какова мощность человека при ходьбе, если за $2 space ч$ он делает 10 000 шагов и за каждый шаг совершает $40 space Дж$ работы?
Дано:
$t = 2 space ч$
$n = 10 space 000$
$A_1 = 40 space Дж$
СИ:
$t = 7200 space с$
$N — ?$
Посмотреть решение и ответ
Скрыть
Решение:
Чтобы вычислить мощность, нам нужно знать общую работу, которая будет совершена за все сделанные человеком шаги:
$A = A_1n$.
Рассчитаем мощность:
$N = frac{A}{t} = frac{A_1n}{t}$,
$N = frac{40 space Дж cdot 10 space 000}{7200 space с} approx 55.6 space Вт$.
Ответ: $N approx 55.6 space Вт$.
Упражнение №4
Какую работу совершает двигатель мощностью $100 space кВт$ за $20 space мин$?
Дано:
$N = 100 space кВт$
$t = 20 space мин$
СИ:
$N = 10^5 space Вт$
$t = 1200 space с$
$A — ?$
Посмотреть решение и ответ
Скрыть
Решение:
Выразим работу из определения мощности:
$N = frac{A}{t}$,
$A = Nt$.
Рассчитаем ее:
$A = 10^5 space Вт cdot 1200 space с = 120 cdot 10^6 space Дж = 120 space МДж$.
Ответ: $A = 120 space МДж$.
Упражнение №5
Транспортер за $1 space ч$ поднимает $30 space м^3$ песка на высоту $6 space м$. Вычислите необходимую для этой работы мощность двигателя. Плотность песка равна $1500 frac{кг}{м^3}$.
Дано:
$t = 1 space ч$
$V = 30 space м^3$
$h = 6 space м$
$rho = 1500 frac{кг}{м^3}$
$g = 9.8 frac{Н}{кг}$
СИ:
$t = 3600 space с$
$N — ?$
Посмотреть решение и ответ
Скрыть
Решение:
Мощность рассчитывается по формуле:
$N = frac{A}{t}$.
Работа, которую совершает при подъеме песка транспортер:
$A = Fs = F_{тяж} h = gmh = g rho Vh$.
Подставим полученное выражение в формулу мощности и рассчитаем ее:
$N = frac{g rho Vh}{t}$,
$N = frac{9.8 frac{Н}{кг} cdot 1500 frac{кг}{м^3} cdot 30 space м^3 cdot 6 space м}{3600 space с} = frac{2 space 646 space 000 space Дж}{3600 space с} = 735 space Вт$.
Ответ: $N = 735 space Вт$.
Упражнение №6
Штангист поднял штангу массой $125 space кг$ на высоту $70 space см$ за $0.3 space с$. Какую среднюю мощность развил спортсмен при этом?
Дано:
$h = 70 space см$
$m = 125 space кг$
$t = 0.3 space с$
$g = 9.8 frac{Н}{кг}$
СИ:
$h = 0.7 space м$
$N — ?$
Посмотреть решение и ответ
Скрыть
Решение:
Чтобы вычислить мощность, которую развил спортсмен, нам нужно знать, какую работу он совершил при подъеме штанги. Чтобы ее поднять, спортсмен преодолел силу тяжести, действующую на штангу:
$A = Fs = F_{тяж}h = gmh$.
Подставим полученное выражение в формулу мощности и рассчитаем ее:
$N = frac{A}{t} = frac{gmh}{t}$,
$N = frac{9.8 frac{Н}{кг} cdot 125 space кг cdot 0.7 space м}{0.3 space с} = frac{857.5 space Дж}{0.3 space с} approx 2860 space Дж$.
Ответ: $N approx 2860 space Дж$.
Задания
Задание №1
Рассчитайте мощность, которую вы развиваете, поднимаясь равномерно вначале медленно, а затем быстро с первого на второй этаж школы. Все необходимые данные получите сами.
Для того, чтобы рассчитать механическую работу, вам понадобится узнать высоту между этажами школы (высоту потолка) и свою собственную массу. Также необходимо измерить с помощью секундомера время, которое у вас занимает медленный и быстрый подъемы на второй этаж. Для примера возьмем высоту потолков, равную $4 space м$, массу, равную $50 space кг$, время быстрого подъема $5 space с$ и медленного подъема $20 space с$.
Дано:
$h = 4 space м$
$m = 50 space кг$
$t_1 = 5 space с$
$t_2 = 20 space с$
$g = 9.8 frac{Н}{кг}$
$N_1 — ?$
$N_2 — ?$
Посмотреть решение и ответ
Скрыть
Решение:
Мощность характеризует быстроту выполнения механической работы, которую мы совершаем, поднимаясь на второй этаж. Работа же будет определяться силой, по модулю равной силе тяжести, и расстоянием между этажами школы:
$N = frac{A}{t} = frac{F_{тяж}h}{t} = frac{gmh}{t}$.
Рассчитаем мощность, которую мы развиваем при быстром подъеме:
$N_1 = frac{gmh}{t_1}$,
$N_1 = frac{9.8 frac{Н}{кг} cdot 50 space кг cdot 4 space м}{5 space с} = frac{1960 space Дж}{5 space с} = 392 space Вт$.
Рассчитаем мощность, которую мы развиваем при медленном подъеме:
$N_2 = frac{gmh}{t_2}$,
$N_2 = frac{9.8 frac{Н}{кг} cdot 50 space кг cdot 4 space м}{5 space с} = frac{1960 space Дж}{20 space с} = 98 space Вт$.
Получается, что при быстром подъеме мы развиваем мощность, в 4 раза большую, чем при медленном подъеме.
Ответ: $N_1 = 392 space Вт$, $N_2 = 98 space Вт$.
Задание №2
Установите по паспорту прибора мощность электродвигателей пылесоса, мясорубки, кофемолки.
Посмотреть ответ
Скрыть
Ответ:
Мощность электроприборов указывается в их технический паспортах. Если вы не смогли найти документы домашней техники или у вас дома нет чего-то из перечисленного, то ниже указаны средние мощности данных приборов.
$N_{пылесоса} = 2000 space Вт$,
$N_{мясорубки} = 1300 space Вт$,
$N_{кофемолки} = 180 space Вт$.
Конспект по физике для 7 класса «Мощность». ВЫ УЗНАЕТЕ: Что такое мощность. Как рассчитать мощность. Единицы мощности. ВСПОМНИТЕ: Что такое механическая работа? Как рассчитать механическую работу?
Конспекты по физике Учебник физики Тесты по физике
Мощность
Слово «мощность» всем нам хорошо знакомо и употребляется достаточно часто. Мы говорим, что один автомобиль мощнее другого, и, как нам кажется, хорошо понимаем, что означают эти слова.
ОПРЕДЕЛЕНИЕ МОЩНОСТИ
В физике существует физическая величина «мощность», которая напрямую связана с понятием работы.
Нам всем хорошо известно, что одна и та же работа может быть совершена за разное время. Например, лошадь, везущая груженые сани, может в одном случае двигаться медленно и перевезти их на определённое расстояние за полчаса. В другом случае та же лошадь, двигаясь быстрее, перевезёт эти же сани на то же самое расстояние за меньшее время. В этом примере одна и та же механическая работа совершается за разное время.
Физическую величину, характеризующую быстроту выполнения работы, называют мощностью. Мощность показывает, какая работа совершается за единицу времени. Таким образом, чтобы найти мощность, надо механическую работу разделить на время, за которое она совершена.
Мощность равна отношению работы ко времени, за которое она была совершена.
ЕДИНИЦЫ МОЩНОСТИ
За единицу мощности принимают такую мощность, при которой за 1 с совершается работа в 1 Дж. Эту единицу называют ваттом (Вт) в честь английского учёного Джеймса Уатта.
1 Вт = 1 Дж/с.
В технике широко используют более крупные единицы мощности — киловатт (кВт) и мегаватт (МВт), а также более мелкую единицу милливатт (мВт): 1 МВт = 1000 000 Вт, 1 кВт = 1000 Вт, 1 мВт = 0,001 Вт. Также применяется внесистемная единица мощности лошадиная сила (1л.с.): 1 л.с. = 735,5 Вт.
Джеймс Уатт — английский изобретатель, первым построивший паровую машину, в качестве единицы мощности использовал лошадиную силу. С её помощью он сравнивал работоспособность лошади и своей паровой машины. Эту единицу часто используют и в наши дни для характеристики мощности двигателей автомобиля. Однако мощность, равная одной «лошадиной силе» (735,5 Вт) на самом деле значительно больше той, которую средняя лошадь способна развивать сколько-нибудь долгое время.
РЕШЕНИЕ ЗАДАЧ
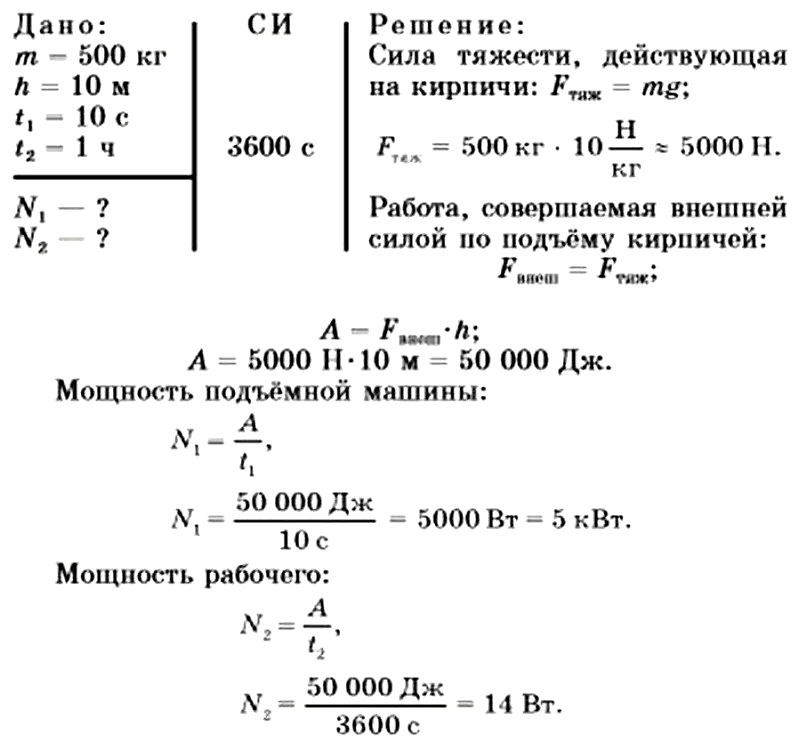
Рассчитаем мощность двигателя подъёмной машины, если она может поднять кирпичи массой 500 кг на высоту 10 м за 10 с. Сравним полученную мощность с мощностью, которую развил бы рабочий, поднимая эти же кирпичи на ту же высоту, если ему потребуется для этого 1 ч. Запишем условие задачи и решим её.
Ответ: N1 = 5 кВт, N2 = 14 Вт.
Мощность является важной характеристикой любого двигателя. Различные двигатели имеют мощности от сотых и десятых долей киловатта (двигатель электрической бритвы, швейной машины) до миллионов киловатт (двигатели ракет носителей космических кораблей). Например, мощность двигателя автомобиля «Жигули» равна 75 кВт, мощность электрической плиты — 8 кBт, а мощность двигателя космического корабля составляет 20 000 000 кВт. Можно также оценить мощность человека при ходьбе, она в среднем равна 60 Вт. А мощность бегущего гепарда достигает 1 кВт.
ДЛЯ СПРАВКИ:
Джеймс Уатт (1736—1819). Английский изобретатель, создатель универсальной паровой машины, член Лондонского королевского общества.
Вы смотрели Конспект по физике для 7 класса «Мощность»: Что такое мощность. Как рассчитать мощность. Единицы мощности.
Вернуться к Списку конспектов по физике (В оглавление).
Пройти онлайн-тест «»