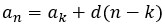В течение 25 банковских дней акции компании дорожали ежедневно 888 948

В течение 25 банковских дней акции компании дорожали ежедневно на одну и ту же сумму. Сколько стоила акция компании в последний день этого периода, если в 7-й день акция стоила 888 рублей, а в 12-й день — 948 рублей.

Источник

Ответ:

1104 рубля

Объяснение:

Так как цена увеличивалась на одну и ту же сумму, имеем арифметическую прогрессию, в которой

а₇ = 888

а₁₂ = 948

найти надо а₂₅.

Формула n-го члена арифметической прогрессии:

$a_{12}=a_1+11d=948$

Получили систему уравнений:

$left{ begin{array}{ll}a_1+6d=888\a_1+11d=948end{array}$

Домножим первое уравнение на (- 1) и сложим уравнения:

$left{ begin{array}{ll}-a_1-6d=-888\a_1+11d=948end{array}$

$left{ begin{array}{ll}5d=60\a_1+6d=888end{array}$

$left{ begin{array}{ll}d=12\a_1+6cdot 12=888end{array}$

$left{ begin{array}{ll}d=12\a_1=888-72end{array}$

$left{ begin{array}{ll}d=12\a_1=816end{array}$

Найдем а₂₅:

$a_{25}=a_1+24d$

$a_{25}=816+24cdot 12=816+288=1104$

Значит, в 25-ый день акция стоила 1104 рубля.

Источник

В течение 25 банковских дней акции компании дорожали ежедневно на одну и ту же сумму. Сколько стоила акция компании в последний день этого периода, если в 7-й день акция стоила 999 рублей, а в 12-й день — 1064 рубля.

Решение:

Если в задаче сказано, что что-то там меняется на одно и то же число, то решать мы эту задачу будем с помощью формул арифметической прогрессии.

Конкретно для этой задачи нам потребуется формула, на которую в школьном курсе алгебры не обращают внимания. А ведь она иногда очень полезна.

Вот и она!

Обрати внимание, что k < n.

Итак, что же нам дано:

а₇ = 999 — стоимость акции в 7-й день;

а₁₂ = 1064 — стоимость акции в 12-й день.

Наша задача с помощью той формулы найти разность прогрессии d. Подставляем данные в формулу:

а₁₂ = а₇ + d(12 — 7);

1064 = 999 + 5d;

d = 13 — на столько рублей акции дорожали ежедневно.

Теперь, зная а₇ (можно и а₁₂, кстати, взять) и применяя всё ту же формулу, найдем а₂₅.

а₂₅ = а₇ + d(25 — 7);

a₂₅ = 999 + 13 · 18 = 1233 (руб.) — стоимость акции в последний, двадцать пятый, день.

Ответ: 1233.

Не можешь найти нужную задачу? Предложи свою! Наша группа в VK.

#838

Источник

Задание 10974

В течение 20 банковских дней акции компании дорожали ежедневно на одну и ту же сумму. Сколько стоила акция компании в последний день этого периода, если в 9-й день акция стоила 888 рублей, а в 13-й день — 940 рублей?

Ответ: 1031

Видео-решение
Решение 1

Предложить свое решение / сообщить об ошибке

Скрыть

Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!

Скрыть
$$a_9=888; a_{13}=940.$$ $$d=frac{a_m-a_n}{m-n}=frac{940-888}{13-9}=13.$$ $$a_{20}=a_{13}+13(20-13)=940+91=1031.$$

Источник

В течение 25 банковских дней акции компании дорожали ежедневно на одну и ту же сумму. Сколько стоила акция компании в последний день этого периода, если в 7-й день акция стоила 777 рублей, а в 12-й день – 852 рубля?

📜Теория для решения:
Арифметическая прогрессия и сумма ее членов

Посмотреть решение

В содержании задачи есть фраза, что акции дорожали ежедневно на одну и ту же сумму, следовательно, имеем арифметическую прогрессию. Итак, определяем, что известно: в 7-й день акция стоила 777 рублей, это а₇=777; в 12-й день – 852 рубля, это а₁₂=852. Известно, что акции дорожали 25 дней, а найти надо стоимость акции в последний, т.е. в 25-ый день, значит, будем искать а₂₅.

1 способ:

В данной арифметической прогрессии нет первого члена, не идет речь про сумму, поэтому воспользуемся формулой а_n=a_k+d(n – k), где n>k. Числа n и k – это порядковые номера. Составим формулу для наших данных и подставим в неё значения: а₁₂=а₇+d(12-7); 852=777+d(12 – 7). Упростим выражение и найдем разность d, 852–777= d(12 – 7); 75= d∙5; отсюда d=75:5=15. Итак, мы нашли, что акции ежедневно дорожали на 15 рублей.

Теперь, зная число d, мы можем найти а₂₅ через, например, а₁₂, используя всё ту же формулу. Получаем: а₂₅=а₁₂+d(25-12); а₂₅=852+15(25-12)=852+15∙13= 852+195=1047. Значит, 1047 рублей стоила акция в последний день.

2 способ:

Можно решить данную задачу другим способом по формуле связи между любыми двумя членами арифметической прогрессии: d=an−akk−n , где k>n. Составим формулу для наших а₁₂ и а₇, а затем подставим в нее данные: d=a12−a712−7; d=852−77712−7=15. Теперь по этой же формуле найдем а₂₅, связывая его с а₁₂: d=a25−a1225−12; 15=a25−85213; найдем отсюда а₂₅, а₂₅=15∙13+852=1047.

Ответ: 1047

Даниил Романович | Просмотров: 5.3k

Источник

В течение 20 банковских дней акции компании дорожали ежедневно на одну и ту же сумму. Сколько стоила акция компании в последний день этого периода, если в 9-й день акция стоила 555 рублей, а в 13-й день – 631 рублей?

Источник: ОГЭ Ященко 2023 (36 вар)

Решение:

Каждый день акции дорожают на одну и ту же сумму. В промежуток с 9-го по 13-й день акции выросли в цене:

13 – 9 = 4 раза

За эти 4 дня дня акции подорожали на:

631 – 555 = 76 рубля

Значит, каждый день они дорожают на:

76/4 = 19 рублей

С 13-го по 20-й день акции вырастут:

20 – 13 = 7 раз

На 20-й день они будут стоить:

13-й день + 7·19 = 631 + 7·19 = 764

Ответ: 764.

Есть три секунды времени? Для меня важно твоё мнение!

Насколько понятно решение?

Средняя оценка: 4 / 5. Количество оценок: 34

Оценок пока нет. Поставь оценку первым.

Новости о решённых вариантах ЕГЭ и ОГЭ на сайте ↙️

Вступай в группу vk.com 😉

Расскажи, что не так? Я исправлю в ближайшее время!

В отзыве оставь любой контакт для связи, если хочешь, что бы я тебе ответил.

Источник