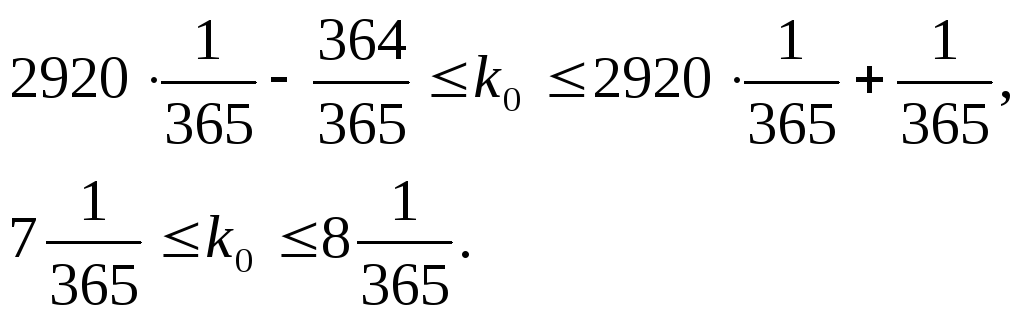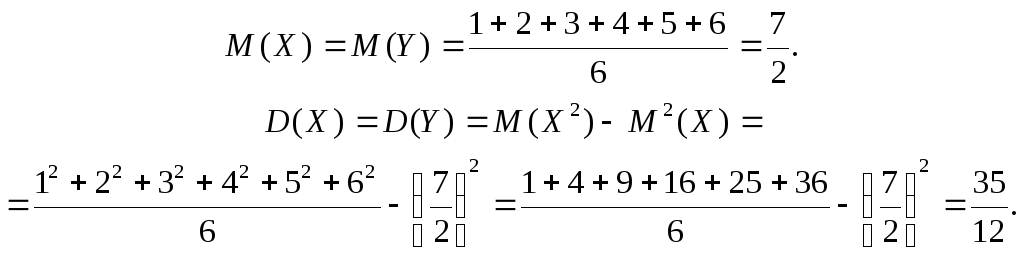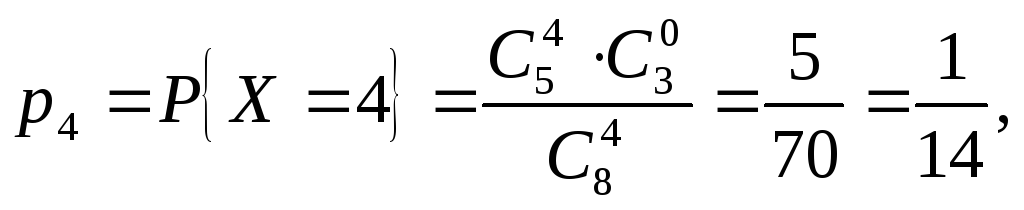В среднем по 10 договоров страховая компания выплачивает страховые суммы в связи с наступлением

Формула Бернулли

Формулы теории вероятностей имеют смысл
только в случае, когда возможно повторение
испытаний достаточно большое число
раз. Пусть производится пнезависимых
испытаний и вероятность появления
некоторого событияАв каждом из
испытаний равнар = р (А) и не зависит
от номера испытания. Пустьq
= 1 – p, тогда
вероятность того, что в п независимых
испытаниях событиеАпроизойдет
ровнотраз вычисляется по формуле
Бернулли:

Р_п(т) =

р^т 
q^п-т.

(14)

Пример
13.Играется матч между шахматистамиXиY.
Вероятность того, чтоX
выиграет каждую отдельную партию
равна,
вероятность выигрыша партииYравна.
Ничьих партий не бывает (т.е., если они
происходят, то они не учитываются). Матч
состоит из 6 партий. Найти вероятность
выигрыша матчаX,
вероятность выигрыша матчаYи вероятность ничейного исхода.

Решение.Здесь число испытанийп = 6; р =
,q =
.
Введем обозначения:А_i(I
= 0,1,…, 6)– событие, заключающееся в
том, чтоXвыигралi
партий из 6. По условию задачи требуется
найтир(А₄ + А₅
+ А₆) = р(А₄) +
р(А₅) + р(А₆) –Xвыиграл не менее
четырех партий (здесь вероятность суммы
равна сумме вероятностей, т.к. слагаемые
в скобках – несовместимые события).
Далее,

р(А₄) = р₆(4)
=


= 15
=,

р(А₅) = р₆(5)
=


= 6
=,

р(А₆) = р₆(6)
=


= 1
=.

Тогда вероятность того, что Xвыиграет матч равна

Р(А₄ + А₅ +
А₆) =
=0.68.

Ничья происходит при счете ”3 -3”, т.е.

Р(А₃) = р₆(3)
=


= 20
==0.22.

Вероятность выигрыша матча Y
равна

Р(А₀ + А₁ +
А₂) =1 – р(А₃
+ А₄ + А₅ + А₆)
= 1 – 0.68 – 0.22 = 0.1.

Интересно заметить, что вероятность
того, что наиболее искусный игрок не
будет выявлен после шести партий не
мала (0.32).

Наивероятнейшее число
появления события в серии изn
испытаний определяется неравенством

(15)

где p– вероятность
появления события в одном испытании,q— вероятность не появления события в
одном испытании.

Пример 14. В одном из учебных заведений
обучается 2920 студентов. Вероятность
того, что день рождения наудачу взятого
по списку студента приходится на
определенный день года равнаНайти наивероятнейшее число студентов,
родившихся 1 января.

Решение. Имеем

следовательно,

Поскольку
— целое число, то= 8.

Случайные величины Математическое ожидание и дисперсия

Случайное событие, заключающееся в
появлении того или иного числа, называется
случайной величиной. Различают два
вида случайных величин (с.в.):дискретные
и непрерывные. Случайная величина,
принимающая отдельные изолированные
значения, называетсядискретной.

Законом распределения (или просто
распределением) называется соответствие
между возможными значениями с.в. и
вероятностями, с которыми она принимает
эти значения.Законы распределения
задают различными способами: при помощи
формул, в виде таблиц и т.д. случайные
величины обозначаются большими буквами
латинского алфавитаX,
Yи т.д.

Рассмотрим закон распределения
дискретной случайной величины:

Таблица 2

X	x₁	x₂	…	x_k	…	x_n
Y	p₁	p₂	…	p_k	…	p_n

Здесь
р_k=
Вер=Р(читается: вероятность того, что случайная
величина примет значение равноеx_k).
Так как в законе распределения перечислены
все возможные значения случайной
величины, то следует предполагать, чтоx_kx_iприkj,р₁ + р₂ +…+
р_п= 1, и очевидно.

Пример18. В среднем по 10% договоров
страховая компания выплачивает страховые
суммы в связи с наступлением страхового
случая. Составить закон распределения
числа таких договоров среди наудачу
выбранных четырех.

Решение. Вероятностьpтого, что по договору будет выплачена
страховая сумма равнаследовательно,Пусть случайная величинаX—
число договоров, по которым выплачивается
страховая сумма среди наудачу выбранных
четырех. ТогдаX
принимает значения 0, 1, 2, 3, 4. Найдем
вероятности, соответствующие указанным
значениямX:

Таким
образом, получим закон распределения
случайной величины

X	0	1	2	3	4
p	0.6561	0.2916	0.0486	0.0036	0.0001

Проверка:
следовательно, закон распределения
составлен правильно.

Математическим
ожиданием случайной величины называется
сумма произведений возможных значений
случайной величины на вероятности, с
которыми она принимает свои возможные
значения.

(18)

Вероятностный смысл математического
ожидания заключается в том, что
математическое ожидание примерно равно
среднему арифметическому значений,
которые принимает случайная величина
в результате проведения достаточно
большого числа испытаний, т.е., если
проведено Nиспытаний
и с.в. значениеx₁принялаN₁
раз,x₂
– N₂ раз,
и т.д.x_n
–N_nраз, то величинас очень большой вероятностью будет мало
отличаться отM(X).(Подробнее об этом смотрите в теме
«интервальные оценки параметров
распределения», а также [1,2].)

Пример19. В тесто для калорийных
булочек добавляют изюм. Определить
сколько изюминок попадает в каждую
булочку.

Решение. Пусть для изготовления
булочек замешиваютVкгтеста, а на одну булочку используютv кг(например, 0.1кг). Тогда из одного замеса можно
испечьN=V/vбулочек. Допустим, что в
каждую булочку необходимо положитьизюминок (например,=10).
Справедливо предположение, что в каждую
булочку изюминка может попасть независимо
от других. Введем случайную величинуX— число изюминок в булочке. Случайная
величинаXраспределена
по биноминальному закону (14):

Вер{X=m}=P_n(m)=,

где p = 1/N
= v/V,q =1-p,n =N,m=0,1,…,n,

где
=np.

Предположим, что N большое число,
тогда вероятностьpмала..

При больших значениях nпользоваться формулой (14) затруднительно.
Например, приN=200, вероятность того,
что в данную булочку попадет ровно 9
изюминок равна

P₂₀₀(9)==.

Расчеты существенно упрощаются, если
рассмотреть предельный случай, когда
n,
а
=np остается постоянным числом (на
практике это соответствует тому, что
вероятность появления случайного
события мала, а число испытаний велико).
В этом предельном случае распределение
вероятностей подчиняетсяформуле
Пуассона (16).

Используя формулу (14), получим
P₂₀₀(9)=0.12768; по формуле
(16) находимP₂₀₀(9)
=0.12511.
Таким образом, ошибка при использовании
формулы Пуассона в данном случае равна
0.002.

Закон распределения Пуассона имеет
вид:

X	0	1	…	m	…
P	.	.		.

Дисперсией
называется математическое ожидание от
квадрата отклонения случайной величины
от ее математического ожидания:

(19)

Справедлива формула для вычисления
дисперсии:

(20)

где
Дисперсия случайной величины характеризует
рассеяние случайной величины относительно
ее среднего значения (математического
ожидания).

Свойства
математического ожидания и дисперсии:

Математическое
ожидание постоянной величины есть сама
постоянная:

М(С) =
С.

Константу
можно выносить за знак математического
ожидания:

М(СХ)
= С М(Х).

Здесь закон распределения с.в. СХполучается из закона распределения
с.в.Хумножением ее возможных
значений на постояннуюС, т.е. если
с.в. определена законом распределения,
представленном в таблице 1., тоСХопределяется следующей таблицей:

Таблица 3

X	Cx₁	Cx₂	…	Cx_k	…	Cx_n
P	p₁	p₂	…	p_k	…	p_n

Математическое
ожидание суммы двух случайных величин
равно сумме их математических ожиданий:

М(Х + Y) = М(Х) +
М(Y).

Свойства дисперсиинепосредственно
следуют из соответствующих свойств
математического ожидания:

Дисперсия
постоянной величины равна нулю:

D(C) = 0.

Постоянную
можно выносить за знак дисперсии,
возведя ее в квадрат:

D(C
X) = C²D(X).

Дисперсия
суммы независимых случайных величин
равна сумме дисперсий:

D(X
+Y) = D(X)
+ D(Y),

где X иY
независимы(случайные величины
называютсянезависимыми, если закон
распределения каждой из них не зависит
от того, какие возможные значения приняла
другая с.в.).

Важным примером распределения дискретной
случайной величины является биноминальное
распределение. Пусть имеется некоторое
случайное событиеА, вероятность
появления которого в каждом из испытаний
постоянна и равнаp.
Производитсяnнезависимых испытаний. Случайная
величинаХ– число появлений событияАвnнезависимых
испытаниях. Возможными значениями с.в.Х, распределенной по биноминальному
закону, являются все целые числа от 0 доn. ВеличинаВер{Х
= k} – вероятность
того, что вnиспытаниях
событиеАпроизойдет ровноkраз – вычисляется поформуле Бернулли.

(21)

где q
= 1 – р.

Введем в рассмотрение случайные величины
Х_i,i
= 1,2,… n-число
появлений событияАвi—испытании.
ТогдаХ = Х₁ + Х₂
+ …+ Х_n –
общее число появлений событияАвnнезависимых
испытаниях – равно сумме числа появления
событияАв каждом изnиспытаний. Случайные величиныХ_i,
i = 1,2,…, nпринимают только два значения: 0 – с
вероятностьюqи 1 –
с вероятностьюp.

Следовательно,

Далее,

(22)

а так
как случайные величины X_iнезависимы, то

(23)

Таким образом, математическое ожидание
числа появлений события Авnнезависимых испытаниях равно произведению
числа испытаний на вероятность появления
событияА, а дисперсия равна
произведению числа испытаний на
вероятность появления событияАи
на вероятность его не появления.

Найдем
математическое ожидание и дисперсию
случайной, имеющей распределение
Пуассона:

M(X)=m
=,D(X)=m²
—=.

Пример19.
Пусть некоторая случайная величина
распределена по закону Пуассона. По
результатам наблюдаемых значений 2; 1;
1; 3; 1; 4; 2; 5; 1; 7 найти неизвестный параметрслучайной величины.

Решение. Математическое ожиданиеM(X)случайной величины есть ее среднее
значение. Для случайной величины,
распределенной по закону Пуассона

Пример
20.Бросаются две игральные кости.
Случайная величинаХ– число очков,
выпавших на первой игральной кости;Y– на второй;Z–
суммарное число очков, выпавших на двух
игральных костях. Вычислить математическое
ожидание и дисперсию случайных величинХ,Y,Z.

Решение.Закон распределения с.в.Хзадается
таблицей:

Таблица 4

X	1	2	3	4	5	6
Р

Законы распределения с.в. XиYсовпадают, т.е.X
= Y, аZ
= X + Y.
Заметим, чтоZ = X
+ Y 
2·X (!!) .

Вычислим математическое ожидание и
дисперсию с.в. Z,
пользуясь законом распределения,
заданным в таблице 1:

Пример
21.Из ящика, содержащего 3 черных и 5
белых шаров, наудачу извлекается 4 шара.
Случайная величинаХ– число
вытащенных белых шаров. Найти математическое
ожидание и дисперсию с.в.Х.

Решение.
Построим закон распределения с.в.Х.
Она может принимать любое значение от
1 до 4.

Таблица 5

X	1	2	3	4
P	p₁	p₂	р₃	р₄

Для того, чтобы понять, что представляет
собой сумма случайных величин, рассмотрим
следующий пример.

Пример 22. Производится стрельба из
трех орудий. Первое попадает при каждом
выстреле с вероятностью 0.8, второе —
0.5, третье — 0.6. Все орудия выстрелили по
одному разу. Случайная величина X — число
снарядов, попавших в цель. Требуется
построить закон распределения, найти
математическое ожидание и дисперсию
случайной величины X.

Решение.Введем обозначения:A-cобытие, заключающееся
в том, что первое орудие попало в цель,
B — второе орудие попало в цель, C — третье.
Далее находимP(X=0)=P

P(X=1)=P

P(X=2)=P

P(X=3)=P

Закон распределения нашей случайной
величины имеет вид:

X	0	1	2	3
P	0.04	0.26	0.46	0.24

Вычислим математическое ожидание и
дисперсию:

M(X)=

D(X)=M()-=

Введем в рассмотрение следующие случайные
величины: X₁— число снарядов,
попавших в цель из первого орудия,X₂— число снарядов, попавших в цель
из первого орудия,

X₃— число снарядов, попавших
в цель из первого орудия. Законы
распределения этих случайных величин
имеют вид:

X₁	0	1		X₂	0	1		X₃	0	1
P	0.2	0.8		P	0.5	0.5		P	0.4	0.6

M(X₁)=

D(X₁)=M()-M²(X₁)=

Аналогично находим M(X₂)
= 0.5; M(X₃)
= 0.6; D(X₂)
= 0.25; D(X₃)
= 0.24.

Нетрудно видеть, что X=X₁+X₂+X₃,следовательно

М(X)= M(X₁)+
M(X₂)+
M(X₃)=0.8+0.5+0.6=1.9.

Так как случайные величины X₁,
X₂, X₃независимы,
то

D(X)= D(X₁)+
D(X₂)+
D(X₃)=0.16+0.25+0.24=0.65.

Предположим, что из первого орудия
выстрелили 100 раз, из второго -200, из
третьего-250 раз, случайная величина X
число попаданий в цель. Построить закон
распределения такой случайной величины
сложно, так как она может принимать
очень много значений. возможные значения-
любое число от 0 до 550. Однако M(X)=D(X)=среднее квадратичное отклонение
Полученный результат можно интерпретировать
следующим образом (приближенно)- в цель
попадет 550 снарядов ‘плюс минус’ 11.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

Источник

В первой задаче используйте биномиальное распределение.

Во второй задаче из имеющихся данных находится средняя доля деталей, обладающих одноврменно двумя дефектами, после чего вопросы сводятся просто к определению условной вероятности.

Третья несколько странная по постановке. Вообще-то стандартная математическая модель для числа клиентов, обслуженных системой за определенный промежуток времени — распределение Пуассона. Параметр распределения равен , так как он совпадает со средним значением. Но решить задачи непосредственно с помощью этого распределения не получится, так как там большие числа.

Думаю, что подразумевается использовать нормальное приближение. Так как величина, распределенная по Пуассону с параметром 200, имеет то же распределение, что и сумма двухсот независимых величин с параметром 1, то можно применять ЦПТ. Нормируйте данную величину и замените на стандартное нормальное распределение.

В справочнике написано, что если $xi$ имеет распределение Пуассона с большим параметром , то величина имеет распределение, близкое к нормальному, с параметрами $(sqrt{lambda},frac{1}{4})$ . Но не думаю, что от Вас требуют применения этого факта, если только его явно не было в курсе. Скорее все-таки такое нормальное приближение, как я написал выше, хотя оно и отличается от данного.

Источник

dypemounov536

Вопрос по математике:

В среднем по 15% договоров страховая компания выплачивает страховую сумму. Найти вероятность того, что из десяти договоров с наступлением страхового случая будет связано с выплатой страховой суммы: а) три договора; б) менее двух договоров

Трудности с пониманием предмета? Готовишься к экзаменам, ОГЭ или ЕГЭ?

Воспользуйся формой подбора репетитора и занимайся онлайн. Пробный урок — бесплатно!

Ответы и объяснения 1

yanshes

Формула Бернулли: Вероятность того, что при n испытаниях событие А наступит k раз с вероятностью успеха p :

где и

A) Вероятность того, что в n=10 договорах, событие наступит ровно k=3 раза, равна

Б) Обозначим событие А — «выплата страховой суммы менее двух договоров».
Вероятность события А нужно найти как сумма вероятностей в n=10 договорах, события которых наступят ровно k=1 и k=0 раз.

Знаете ответ? Поделитесь им!

Гость

Гость ?

Как написать хороший ответ?

Чтобы добавить хороший ответ необходимо:

Отвечать достоверно на те вопросы, на которые знаете
правильный ответ;
Писать подробно, чтобы ответ был исчерпывающий и не
побуждал на дополнительные вопросы к нему;
Писать без грамматических, орфографических и
пунктуационных ошибок.

Этого делать не стоит:

Копировать ответы со сторонних ресурсов. Хорошо ценятся
уникальные и личные объяснения;
Отвечать не по сути: «Подумай сам(а)», «Легкотня», «Не
знаю» и так далее;
Использовать мат — это неуважительно по отношению к
пользователям;
Писать в ВЕРХНЕМ РЕГИСТРЕ.

Есть сомнения?

Не нашли подходящего ответа на вопрос или ответ отсутствует?
Воспользуйтесь поиском по сайту, чтобы найти все ответы на похожие
вопросы в разделе Математика.

Трудности с домашними заданиями? Не стесняйтесь попросить о помощи —
смело задавайте вопросы!

Математика — наука о структурах, порядке и отношениях, исторически сложившаяся на основе операций подсчёта, измерения и описания формы объектов.

Источник

Помогаю со студенческими работами здесь

Составить закон распределения случайной величины, равной числу стандартных деталей среди отобранных
В партии из 8 деталей 6 деталей – стандартные. Наугад отбираются
две детали.
Составить закон…

Составить закон распределения числа
один из пяти гаечных ключей подходит к гайке .
Составить закон распределения числа экспериментов…

Составить закон распределения числа
В партии из 8 деталий имеется 3 стандартных. Наугад отобраны 4 деталию СВ Х- число стандартных…

Искать еще темы с ответами

Или воспользуйтесь поиском по форуму:

Источник

В среднем по 10% договоров страховая компания выплачивает страховые суммы в связи с наступлением страхового случая. Составить закон распределения числа таких договоров среди наудачу выбранных четырех. Вычислить математическое ожидание и дисперсию этой случайной величины.

Скачать решение бесплатно

Купить решение

* Оплата через сервис ЮMoney.

Другие задачи по теории вероятности

В билете три задачи. Вероятность правильного решения первой задачи равна 0,9, второй – 0,8, третьей – 0,7. Составить закон распределения числа правильно решенных задач в билете и вычислить математическое ожидание и дисперсию этой случайной величины.

Вероятность попадания в цель при одном выстреле равна 0,8 и уменьшается с каждым выстрелом на 0,1. Составить закон распределения числа попаданий в цель, если сделано три выстрела. Найти математическое ожидание, дисперсию и среднеквадратичное отклонение этой случайной величины.

Произведено два выстрела в мишень. Вероятность попадания в мишень первым стрелком равна 0,8, вторым – 0,7. Составить закон распределения числа попаданий в мишень. Найти математическое ожидание, дисперсию и функцию распределения этой случайной величины и построить её график. (Каждый стрелок делает по одному выстрелу.)

Найти закон распределения числа пакетов трех акций, по которым владельцем будет получен доход, если вероятность получения дохода по каждому из них равна соответственно 0,5, 0,6, 0,7. Найти математическое ожидание и дисперсию данной случайной величины, построить функцию распределения.

Дан ряд распределения случайной величины X:

Найти функцию распределения этой случайной величины, если её математическое ожидание равно 3,4, а дисперсия равна 0,84.

Из пяти гвоздик две белые. Составить закон распределения и найти функцию распределения случайной величины, выражающей число белых гвоздик среди двух одновременно взятых.

Из десяти телевизоров на выставке 4 оказались фирмы «Сони». Наудачу для осмотра выбрано 3. Составить закон распределения числа телевизоров фирмы «Сони» среди 3 отобранных.

Источник

Пример 1:

В среднем по 8% договоров страховая компания выплачивает страховую сумму. Найти вероятность того, что из n = 13 договоров с наступлением страхового случая будет связано с выплатой страховой суммы три договора.