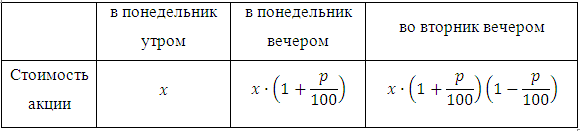В понедельник акции компании подорожали на некоторое число процентов а во вторник еще раз подорожали

в понедельник акции строительной компании подорожали на некоторое число процентов, а во вторник – ещё раз подорожали на то же самое число процентов. в результате они стали стоить на 10,25% дороже, чем при открытии в понедельник. на сколько процентов подорожали акции компании в понедельник?

Источник

В понедельник акции компании подорожали на некоторое количество процентов, а во вторник подешевели на то же самое количество процентов. В результате они стали стоить на 4 % дешевле, чем при открытии торгов в понедельник. На сколько процентов подорожали акции компании в понедельник?

Спрятать решение

Решение.

Обозначим первоначальную стоимость акций за 1. Пусть в понедельник акции компании подорожали на и их стоимость стала составлять Во вторник акции подешевели на и их стоимость стала составлять В результате они стали стоить на 4 % дешевле, чем при открытии торгов в понедельник, то есть 0,96. Таким образом,

Ответ: 20.

Источник: Яндекс: Тренировочная работа ЕГЭ по математике. Вариант 1.

Источник

В понедельник акции компании подорожали

Дата: 2018-02-05

6575

Категория: Проценты

Метка: ЕГЭ-№9

99566. В понедельник акции компании подорожали на некоторое количество процентов, а во вторник подешевели на то же самое количество процентов. В результате они стали стоить на 4% дешевле, чем при открытии торгов в понедельник. На сколько процентов подорожали акции компании в понедельник?

Пусть при открытии торгов в понедельник акции стоили рублей. К вечеру понедельника они подорожали на р% и стали стоить

Теперь уже эта величина принимается за 100%, и к вечеру вторника акции подешевели на р% по сравнению этой величиной. Запишем данные в таблицу:

По условию, акции в итоге подешевели на 4%, значит стали стоить

Получаем

Поделим обе части уравнения на и применим в левой части формулу сокращенного умножения:

По смыслу задачи р>0. Получаем, что р=20.

Акции кампании в понедельник подорожали на 20%.

Ответ: 20

Используя этот сайт, Вы соглашаетесь с тем, что мы сохраняем и используем файлы cookies, а также используем похожие технологии для улучшения работы сайта.

Источник

Решение:

Пусть х десятичная запись количества процентов на которые дорожали и дешевели акции.
100% = 1 – первоначальная стоимость акций;
100 – 4 = 96% = 0,96 – конечная стоимость акций;
Составим уравнение по условию задачи:

1·(1 + х)·(1 – х) = 0,96
1 – х² = 0,96
–х² = 0,96 – 1
–х² = –0,04
х² = 0,04
х = ±√0,04
х = ±0,2

Количество процентов должно быть положительным, значит акции дорожали и дешевели на 0,2 = 20%.

Ответ: 20.

Источник

Обозначим через с стоимость акций при открытии торгов в понедельник, а через х число процентов, на которые акции подорожали в понедельник.

Тогда в понедельник акции стали стоить:

с + (х/100)с = с * (1 + х/100).

Согласно условию задачи, во вторник акции подешевели на то же самое число процентов, следовательно, во вторник акции стали стоить:

с * (1 + х/100) — с * (1 + х/100) * (х/100) = с * (1 + х/100) * (1 — х/100).

Известно, что в результате акции стали стоить на 4% дешевле, чем при открытии торгов в понедельник, следовательно, можем составить следующее уравнение:

с * (1 + х/100) * (1 — х/100) = с — (4/100)с.

Решаем полученное уравнение:

с * (1 — х^2/10000) = c * 0.96;

1 — х^2/10000 = 0.96;

х^2/10000 = 1 — 0.96;

х^2/10000 = 0.04;

х^2 = 10000 * 0.04;

х^2 = 400;

х^2 = 20^2;

х = 20%.

Ответ: в понедельник акции подорожали на 20%.

Источник