Главная / Алгоритмы и дискретные структуры /
Алгоритмы и структуры данных поиска / Тест 2
Алгоритмы и структуры данных поиска — тест 2
Упражнение 1:
Номер 1
Какие существуют метрики, отображающие эффективность алгоритма?
Ответ:
(1) процессорное время, память
(2) надежность, масштабируемость
(3) адаптивность, простота реализации
Номер 2
В функциональной парадигме при проектировании алгоритма, какой оценкой на время работы интересуются?
Ответ:
(1) оценкой в худшем случае
(2) оценкой в среднем
(3) оценкой в лучшем случае
Номер 3
При размере входных данных N, как рассчитывается время работы алгоритма?
Ответ:
(1) не зависимо от N
(2) в сравнении с N
(3) как функция от параметра N
Упражнение 2:
Номер 1
Считается ли компьютерная память важным ресурсом, учитывающимся при разработке эффективного алгоритма?
Ответ:
(1) да
(2) нет
Номер 2
Считается ли процессорное время важным ресурсом, учитывающимся при разработке эффективного алгоритма?
Ответ:
(1) да
(2) нет
Номер 3
Возможна ли такая ситуация при проектировании алгоритма, когда можно сэкономить на одном ресурсе в ущерб другому (процессорное время / память)?
Ответ:
(1) нет
(2) да
Номер 4
Зависит ли время работы алгоритма от размера входных данных N?
Ответ:
(1) нет
(2) да
Упражнение 3:
Номер 1
Если T - время работы алгоритма, N - размер входных данных, что отображает функция max T(I) для N(I) = N?
Ответ:
(1) время работы алгоритма в худшем случае для конкретного входа I
(2) время работы алгоритма в лучшем случае при рассмотрении всех входов (I) размера N
(3) время работы алгоритма в худшем случае при рассмотрении всех входов (I) размера N
Номер 2
При рассмотрении времени работы T(M) и памяти M(N) что нас интересует?
Ответ:
(1) точный вид функций T(N) и M(N)
(2) приближенный до константы вид функций. Используется O-символика
(3) приближенный вид функций. Используется o-символика
Номер 3
При оценивании функций какая оценка соответствует символике f = O(g)?
Ответ:
(1) оценка снизу
(2) оценка сверху
(3) асимптотическое равенство
Номер 4
При оценивании функций символике f = Θ(g) соответствует:
Ответ:
(1) оценка снизу
(2) оценка сверху
(3) асимптотическое равенство
Упражнение 4:
Номер 1
Если при оценивании фиксированного алгоритма оценки сверху и снизу совпали, то какие действия предпринимаются?
Ответ:
(1) время оценивается как Θ(N) и оценивание сводится к придумыванию наихудшего случая для алгоритма
(2) берется сумма оценок сверху и снизу и делится на 2
(3) это означает что оценка произведена неверно
Номер 2
O-символика датет приближенную оценку. Что нужно сделать, чтобы найти оценку точнее?
Ответ:
(1) выполнить болшее количество тестов
(2) нужно для начала определиться, нас интересует оценка на фиксированный алгоритм или на задачу и выполнять оценку исходя из этого
(3) изменить входные данные
Номер 3
Что означает найти оценку для фиксированного алгоритма?
Ответ:
(1) нужно указать такую оценку, которая справедлива для всех мысленных алгоритмов
(2) нужно найти оценку снизу, сверху. Если оценки совпали, то оценка равна Θ(N). И как правило оценка сводится к наихудшиму случаю
(3) означает что нужно найти среднюю оценку для алгоритма
Номер 4
Что означает найти оценку снизу на задачу?
Ответ:
(1) нужно указать такую оценку, которая справедлива для всех мысленных алгоритмов. То есть понять какие время и память точно понадобятся
(2) нужно найти оценки снизу, сверху. Если оценки совпали, то оценка равна Θ(N). И как правило оценка сводится к наихудшиму случаю
(3) означает что нужно найти среднюю оценку для алгоритма
Упражнение 5:
Номер 1
Чем такая схема <CPU - Память> отличается от реальной жизни?
Ответ:
(1) может быть несколько CPU в одном модуле
(2) может быть неопределенное количество промежуточных элементов, например кэш
(3) CPU может отсутствовать
(4) память устроена гораздо сложнее
(5) не учтена внешняя память
(6) память может отсутствовать
Номер 2
Какие из перечисленных ниже утверждений относятся к параметру машинное слово w в стандартной модели оперативной памяти (RAM - model)?
Ответ:
(1) w это количество ячеек в памяти
(2) w это число бит в одной ячейке памяти
(3) w это максимально допустимый размер переменной
(4) w хранит числа ограниченной битности
(5) w это число бит, необходимых для представления одной буквы или цифры
Номер 3
Какие характеристики относятся к стандартной модели оперативной памяти (RAM - model)?
Ответ:
(1) каждая ячейка памяти имеет динамический размер
(2) память это набор ячеек
(3) каждая ячейка это число ограниченной битности
(4) манипуляции с числами, хранящимися в ячейке, выполняются за константое время
(5) ячеек в теоретической модели памяти бесконечно много, как в машине Тьюринга
Упражнение 6:
Номер 1
В чем состоит отличие в работе алгоритма для модели "разрешающие деревья" от RAM - модели и модели машины Тьюринга?
Ответ:
(1) алгоритм неограничен в своих дейстиях
(2) разрешено действие только одного типа
(3) в такой модели можно программировать
Номер 2
Что представляе собой программа для модели "разрешающие деревья"?
Ответ:
(1) программа на языке, похожем на Assembler, C
(2) структура в виде дерева
(3) это некоторая таблица, в которой записано, что нужно делать в зависимости от состояния
Номер 3
Какая нижняя оценка справедлива для задачи сортировки?
Ответ:
(1) O(log N)
(2) Ω(N*log N)
(3) O(N2)
Упражнение 7:
Номер 1
В алгоритмической модели "разрешающее дерево" в каком случае работа алгоритма завершается?
Ответ:
(1) если алгоритм дошел до корня
(2) если алгоритм дошел до листа
(3) если алгоритм перебрал все листья
(4) если алгоритм перебрал все ключи
Номер 2
С какого элемента начинается работа в разрешающем дереве в стандартном случае?
Ответ:
(1) с листьев
(2) с корня
(3) с любого возможного ключа
Номер 3
Что называется бинарным деревом?
Ответ:
(1) у которго ключи представлены в двоичном виде
(2) у каждой вершины которого, кроме листьев, есть ровно два сына
(3) в вершинах которого хранятся двоичные значения
Номер 4
Что нзывается правильным разрешающим деревом?
Ответ:
(1) так еще называют бинарное дерево, то есть имеющее для каждого родителя не более двух потомков
(2) которое приводит к требуемому результату, если идти по алгоритму вниз
(3) на предпоследнем уровне которого у всех родителей есть по два сына
(4) которое приводит к какому-либо результату, если идти по алгоритму вниз
Упражнение 8:
Номер 1
Что назыавется сложностью для алгоритма, заданного разрешающим деревом?
Ответ:
(1) это количество всех возможныз путей в дереве
(2) это высота дерева, то есть максимальная длина пути от корня дерева до вершины
(3) это количество листьев в дереве, то есть элементов на нижних уровнях
Номер 2
Как оценивается сложность правильного дерева сортировки (в худшем случае)?
Ответ:
(1) T = Ω(log N)
(2) T = Ω(N*log N)
(3) T = Ω(N2)
(4) T = O(N)
Номер 3
Можно ли сортировать быстрее чем за T = Ω(N*log N), если разрешить дополнительные операции с ключами?
Ответ:
(1) нет
(2) да, за T = Ω(N*log(log N)), но это нереализуемо на практике
(3) да, за T = Ω(N*log(log N)) и это реализуемо на практике
Номер 4
Сколько листьев должно быть в правильном дереве для множества из N элементов?
Ответ:
(1) N2
(2) N!
(3) N*log N
(4) 2N
Номер 5
Какое из перечисленных ниже высказываний не характеризует разрешающие деревья?
Ответ:
(1) разрешающее дерево не является алгоритмом в общем понимании этого слова
(2) для решения алгоритмической задачи всегда строится одно разрешающее дерево
(3) модель не строит единую инструкцию для всевозможных входов в задаче
Номер 6
Почему модель алгоритма "разрешающее дерево" не очень типична для практики?
Ответ:
(1) дерево не всегда решает задачу корректно
(2) конкретное дерево годится для данного конкретного числа элементов
(3) задача выполняется гораздо дольше, чем на других алгоритмических моделях
Упражнение 9:
Номер 1
Пусть имеется двоичный счетчик, то есть вектор, состоящий из битов, представляющий двоичное число. Изначально все биты равны 0. Пусть есть операция Increment, какова ее сложность в худшем случае?
Ответ:
(1) O(1)
(2) Θ(N)
(3) O(N2)
(4) O(log N)
Номер 2
Пусть имеется двоичный счетчик, то есть вектор, состоящий из битов, представляющий двоичное число. Изначально все биты равны 0. Для M операций Increment, какова их сложность в худшем случае?
Ответ:
(1) O(M + N)
(2) O(M*N)
(3) O(N)
(4) O(M)
Номер 3
Пусть имеется двоичный счетчик, то есть вектор, состоящий из битов, представляющий двоичное число. Изначально все биты равны 0. Для M операций Increment в каком случае справедлива оценка O(M*N)?
Ответ:
(1) в лучшем случае
(2) в худшем случае
(3) в среднем
Упражнение 10:
Номер 1
По какому принципу выбирается размер reallocation для аддитивного метода? Если C - старый размер массива.
Ответ:
(1) C’ = C*d, d — константа > 1
(2) C’ = C + d, d — число добавляемых элементов
(3) C’ = C2/d, d — константа > 1
Номер 2
По какому принципу выбирается размер reallocation для мультипликативного метода? Если C - старый размер массива.
Ответ:
(1) C’ = C*d, d — константа > 1
(2) C’ = C + d, d — число добавляемых элементов
(3) C’ = C2/d, d — константа > 1
Номер 3
Какое время будет затрачено на выполнение последовательности из M операций для аддитивного метода увеличения рамера массива?
Ответ:
(1) O(M * log M)
(2) O(M2)
(3) O(M)
Номер 4
Какое время будет затрачено на выполнение последовательности из M операций для мультипликативного метода увеличения рамера массива?
Ответ:
(1) O(M * log M)
(2) O(M)
(3) O(M2)
Упражнение 11:
Номер 1
Для оценки сложности цепочки инкрементов, пусть 1 у.е. компьютер требует за 1 элементарную операцию. Пусть записано некоторое двоичное число 010111, над каждой 1 лежит по 1 у.е., сколько потребуется элементарных действий для операции Increment?
Ответ:
4
Номер 2
Пусть 1 у.е. компьютер требует за 1 элементарную операцию. Пусть записано некоторое двоичное число, начиная справа имеем k единиц до 0. При текущем балансе -(k+1) (credit: k, debit: 1), если k единиц снять со структуры, 1 положить, сколько нужно попросить у клиента, чтобы выйти в 0?
Ответ:
2
Номер 3
Пусть 1 у.е. компьютер требует за 1 элементарную операцию. Пусть записано некоторое двоичное число, начиная справа имеем k единиц до 0. При текущем балансе -(k+1) (credit: k, debit: 1), если k единиц снять со структуры, 1 положить, сколько нужно попросить у клиента, чтобы выйти в 0 для 5 запросов?
Ответ:
10
Номер 4
Пусть 1 у.е. компьютер требует за 1 элементарную операцию. Пусть записано некоторое двоичное число, начиная справа имеем k единиц до 0. При текущем балансе -(k+1) (credit: k, debit: 1), чему равна учетная стоимость?
Ответ:
2
Упражнение 12:
Номер 1
Для библиотеки std::vector, реализующей массив на C++, что происходит, когда нужно добавить еще один элемент в конец массива, если массив полностью заполнен?
Ответ:
(1) происходит ошибка
(2) переопределение размера(realocatioon), все элементы копируются в новый массив увеличенного размера, элемент добавляется в конец
(3) последний элемент массива заменяется на новый
(4) размер массива увеличивается на единицу, новый элемент добавляется в конец массива
(5) для добавляемого элемента создается дополнительный пустой массив, который затем прибавляется к заполненному
Номер 2
При анализе учетных стоимостей операций C(ai) с каждым из состояний Si связано некоторое вещественное значение ϕi, называемое потенциалом. Тогда чему равняется приведенная стоимоть C'(ai)?
Ответ:
(1) C'(ai) = C(ai) + ϕi — ϕi-1
(2) C'(ai) = C(ai) — C(ai-1)
(3) C'(ai) = C(ai) + ϕi-1 + ϕi
Номер 3
Для задачи о бинарном поиске, какую нужно использовать функцию потенциала, чтобы получить приведенную стоимость C'(ai) = 2
Ответ:
(1) ϕ(S) = #(1 in S) — количество единиц в состоянии S
(2) ϕ(S) = -#(1 in S) — количество единиц в состоянии S
(3) ϕ(S) = k + 1 — количество единиц справа до 0 в состоянии S
(4) ϕ(S) = k — количество единиц слева до 0 в состоянии S
Номер 4
Если подобрать такую функцию потенциала ϕ, что приведенная стоимость будет ограничена каким-то числом M: C'(ai) <= M. Тогда какая будет линейная оценка для суммы стоимостей?
Ответ:
(1) Σ(i..n)C(ai) = ΣC'(ai) — ϕ(Sn)
(2) Σ(i..n)C(ai) = ΣC'(ai) — ϕ(S1) + ϕ(Sn)
(3) Σ(i..n)C(ai) = ΣC'(ai) + ϕ(Sn)
Упражнение 13:
Номер 1
Какие две операции должен выполнять хороший стэк?
Ответ:
(1) push, get
(2) push, pop
(3) insert, get
(4) enqueue, decueue
Номер 2
Какова учетная стоимость операций в стэке, реализованном с помощью вектора?
Ответ:
(1) O(N)
(2) O(1)
(3) O(log N)
Номер 3
Что называется гистерезисом с точки зрения структур данных?
Ответ:
(1) если в структуре данных реализованы дополнительные свойства (поддержка минимума, максимума, сортировка)
(2) если структура данных может не только увеличивать свой размер, но и уменьшать его в зависимости от заполненности
(3) если в структуре данных хранятся все предыдущие ее модификации
(4) если структура данных может только увеличивать свой размер, но не уменьшать
Номер 4
Как будет называться свойство структуры данных, для которой выполняется следующее: если коэффициент заполнения становится больше 1, тогда размер структуры увеличивается (например в 2 раза), если коэффициент заполнения падает до 1/4 раза, тогда размер структуры уменьшается в два раза.
Ответ:
(1) амортизация
(2) гистерезис
(3) persistant (версионирование)
Упражнение 14:
Номер 1
Какие минусы есть у структуры данных Linked lists при использовании ее для реализации стэка?
Ответ:
(1) локальность с точки зрения кэшироваия
(2) много мелких аллокаций (переопределений памяти)
(3) memory overhead (много дополнительного места для поддержания структуры)
(4) нельзя хранить разные типы даных
Номер 2
Какие плюсы есть у структуры данных Chunked vector по сравнению с Linked lists, при использовании в качестве стэка?
Ответ:
(1) доступ к элементу по индексу происходит быстрее
(2) меньше overhead (дополнительного места для поддержания структуры)
(3) лучше локальность с точки зрения кэширования
(4) лучше с точки зрения аллокаций
Номер 3
Какие высказывания относятся к структуре данных chunked vector?
Ответ:
(1) в каждом узле содержатся указатель на следующий узел и данные
(2) выделение памяти происходит значительного размера, а сами блоки соединены между собой указателями
(3) эта структура используется для реализации стэка
(4) в конце структуры указатель нулевой, указатель на верний элемент хранится отдельно
(5) время доступа к элементу константное
Номер 4
Какие высказывания относятся к структуре данных linked lists?
Ответ:
(1) в каждом узле содержатся указатель на следующий узел и данные
(2) выделение памяти происходит значительного размера, а сами блоки соединены между собой указателями
(3) эта структура используется для реализации стэка
(4) в конце структуры указатель нулевой, указатель на верний элемент хранится отдельно
(5) время доступа к элементу константное
Упражнение 15:
Номер 1
Как эффективно реализовать стэк с поддержкой минимума?
Ответ:
(1) использовать один стэк и переменную для хранения текущего минимума, которую нужно обновлять
(2) использовать два стэка: один основной для значений, второй для хранения ответов для текущего минимума
(3) использовать один стэк и функцию для вычисления минимума
Номер 2
Как (с помощью каких структур данных) можно эффективно реализовать очередь с поддержкой минимума?
Ответ:
(1) с помощью очереди и стэка
(2) с помощью двух стэков
(3) очередь с дополнительной переменной
(4) с помощью очереди и функции для вычисления минимума
Номер 3
Какая будет стоимость операций enqueue и dequeue в учетном смысле, если очередь реализована с помощью двух стэков?
Ответ:
(1) O(N)
(2) O(1)
(3) O(log N)
(4) O(N * log N)
Номер 4
С помощью каких структур данных, перечисленных ниже, нельзя реализовать очередь?
Ответ:
(1) linked lists
(2) один стэк
(3) chunked vector
(4) два стэка
Номер 5
Что такое циклическая очередь?
Ответ:
(1) очередь, реализованная с помощью структуры данных linked lists
(2) очередь, в которой элементы хранятся по индексам, вычисляемым по некоторому модулю
(3) очередь, реализованная с помощью структуры данных chunked vector
(4) очередь, динамически изменяющая свой размер
Упражнение 16:
Номер 1
Что означает свойство persistent (версионирование) для структуры данных?
Ответ:
(1) структура данных изменяет свои свойства в зависимости от текущей задачи
(2) структура данных хранит историю своего развития и модификаций
(3) структура данных динамически изменяет свой размер в зависимости от заполненности
Номер 2
Какая существует главная проблема, мешающая реализации immutable очереди с помощью двух стэков?
Ответ:
(1) большой объем памяти для хранения структуры
(2) трудность анализа учетных стоимостей
(3) сложность реализации
(4) низкая производительность
Номер 3
Какое время выполнения операции Push у persistent стэка? Если N - длина стэка
Ответ:
(1) O(log N)
(2) O(1)
(3) O(N)
Номер 4
Существует подход для освобождения памяти для persistent stack, называемый подсчет ссылок (ref-counting). Как его можно описать?
Ответ:
(1) для каждой вершины (узла) мы храним указатели на все ссылающиеся вершины
(2) для каждой вершины (узла) мы помним сколько стрелок на нее ссылается (число)
(3) помечаются все элементы, достижимые из корней
Упражнение 17:
Номер 1
Выберите, чем характеризуется подход для освобождения памяти для persistent stack, называемый подсчет ссылок (ref-counting)?
Ответ:
(1) он корректен
(2) необходимо хранить счетчик на каждую вершину
(3) структура при этом не является неизменияемой (immutable)
(4) помечаются все элементы, достижимые из корней
(5) структура эффективна в многопоточном режиме
Номер 2
Чем характеризуется подход с использованием сборщика мусора для эффективной работы с памятью в peristent-стэке?
Ответ:
(1) для каждой вершины (узла) мы помним сколько стрелок на нее ссылается (число)
(2) помечаются элементы, достижимые из корней
(3) структура при этом по настоящему неизменяема
(4) такая структура эффективна в многопоточном режиме
Номер 3
Каких двух строк не хватает в приведенном псевдокоде операции Push persistent-стэка? S - ссылка на стэк, v - данные для новой вершины. Push(S, v) w = new Node() ... ... return w
Ответ:
(1) w.data = v
(2) w.next = S
(3) w = S
(4) S.data = v
(5) S.next = w
Номер 4
Какие строки лишние в приведенном псевдокоде операции Pop для persistent-стэка? S - ссылка на стэк. Pop(S) w = new Node() w.next = S return S.next
Ответ:
(1) w = new Node()
(2) w.next = S
(3) return S.next
Правильные ответы выделены зелёным цветом.
Все ответы: В курсе рассматриваются базовые алгоритмы и структуры данных, включая хешировани, сложность и модели вычислений, деревья поиска, B-деревья, задачи геометрического поиска, динамическую связность в графах и другое.
Для направленного леса, в операции addEdge(x, y) при каких условиях можно добавлять ребро из x в y?
(1) если x — корень поддерева, если ребро не приводит к возникновению цикла
(2) если y — корень поддерева, если ребро не приводит к возникновению цикла
(3) если y — не корень поддерева, ребро может приводить к возникновению цикла
(4) если x — не корень поддерева, ребро может приводить к возникновению цикла
Какая структура данных используется для решения задач, связанных с интервалами?
(1) интервальный массив
(2) интервальное дерево
(3) интервальная хэш-таблица
(4) дерево сегментов
Какие существуют метрики, отображающие эффективность алгоритма?
(1) процессорное время, память
(2) надежность, масштабируемость
(3) адаптивность, простота реализации
Какова типичная оценка по времени для наивного алгоритма сортировки?
(1) O(N * log N)
(2) O(N2)
(3) O(N)
(4) O(N3)
Пусть известна последовательность из n ключей, представленная массивом A. Что называется k-ой порядковой статистикой?
(1) k-ый элемент в массиве A
(2) элемент в массиве A, встречающийся k раз
(3) k-ый в порядке возрастания ключ в массиве A
(4) частота встречаемости k-го элемента в массиве A
Какие существуют основные операции для отображений Map/Dictionary?
(1) Insert(v) — вставить значение v в конец словаря
(2) Set(k, v) — назначить ключу k значение v
(3) Get(k) — получить по ключу k значение v
(4) Extract-min — получить ключ для минимального значения
Какие свойства должны быть выполнены для любой вершины v, чтобы дерево являлось бинарным деревом поиска?
(1) для любой вершины x все вершины в ее поддереве имеют ключи меньшие, чем ключ x
(2) для любой вершины x в левом поддереве вершины v справедливо неравенство key(x) <= key(v)
(3) для любой вершины x все вершины в ее поддереве имеют ключи большие, чем ключ x
(4) для любой вершины y в правом поддереве вершины v справедливо неравенство key(v) <= key(y)
Какую структуру данных нужно использовать, чтобы свести задачу RMQ к LCA?
(1) кучу
(2) декартово дерево
(3) дерево поиска
(4) B-дерево
Какую глубину имеет дерево интервалов? Если N — количество интервалов
(1) O(N)
(2) O(log N)
(3) O(N2)
(4) O(N * log N)
Считается ли компьютерная память важным ресурсом, учитывающимся при разработке эффективного алгоритма?
Что означает стабильность алгоритма сортировки?
(1) процент ошибок при сортировке меньше
1
(2) если при работе алгоритма относительный порядок пар с равными ключами не меняется
(3) время работы алгоритма относительно стабильно при различной величине входных данных
В представленном ниже псевдокоде алгоритма поиска порядковой статистики что находится на пропущенном месте?
Random-select(A, k)
задать λ
…
если k <= |A1|:
вернуть Random-select(A1, k)
иначе:
вернуть Random-select(A2, k — |A1|)
(1) пустая строка, ничего не пропущено
(2) разделить (A, λ) -> (A1, A2)
(3) разделить (A, k) -> (A1, A2)
(4) разделить (A, |A| — k) -> (A1, A2)
Какая скорость чтения и записи для отображения, реализованного с помощью прямой адресации?
(1) O(log N)
(2) O(1)
(3) O(N)
Для n-арного дерева поиска каждой вершине соответствует:
(1) 1 ключ
(2) (n-1) ключей
(3) n ключей
В какой позиции достигается минимум на отрезке [i, j] в последовательности A (декартово дерево с индексами i = 1,…,n)?
(1) k = min(i..j)
(2) k = (j — i)/2
(3) k = lca(i, j)
(4) k = lca(A)
Если откладывать одномерные интервалы [l, r] на двумерной плоскости, то в какой области будут находиться интервалы, пересекаемые с точкой x?
(1) если от точки (x, x) провести лучи вверх и вправо, то справа сверху будет находиться искомая область
(2) если от точки (x, x) провести лучи вверх и влево, то слева сверху будет находиться искомая область
(3) если от точки (x, x) провести лучи вниз и влево, то слева внизу будет находиться искомая область
(4) если от точки (x, x) провести лучи вниз и вправо, то справа внизу будет находиться искомая область
Если T — время работы алгоритма, N — размер входных данных, что отображает функция max T(I) для N(I) = N?
(1) время работы алгоритма в худшем случае для конкретного входа I
(2) время работы алгоритма в лучшем случае при рассмотрении всех входов (I) размера N
(3) время работы алгоритма в худшем случае при рассмотрении всех входов (I) размера N
Как можно описать алгоритм сортировки выбором?
(1) для нового неупорядоченного элемента в правой части множества итеративно выбирается место среди уже упорядоченных ключей
(2) итеративно выбирается место среди оставшихся неупорядоченных ключей, найденный минимум или максимум вынимается из текущего множества в ответ
(3) исходная пследовательность A делится на две части A1 и A2, которые рекурсивно сортируются
Какие существуют особенности для алгоритма, который ищет k-ую порядковую статистику за линейное время в худшем случае?
(1) используется рандомизированный выбор разделителя
(2) используется приближенная медиана в качестве разделителя
(3) используется точная медиана в качестве разделителя
(4) поиск разделителя производится с помощью рекурсивного вызова
Для метода цепочек, использующегося при разрешении коллизий в чем заключается основная идея?
(1) все ключи, имеющие разный хэш-код образуют одну ячейку-список хэш-таблицы
(2) все ключи, имеющие одинаковый хэш-код, попадают в одну ячейку-список хэш-таблицы
(3) если ячейка с вставляемым хэш-ключем уже занята, то пробуют вставить в следующую, пока не найдут для нее место
(4) для поиска места для вставляемого ключа ячейки таблицы просматриваются последовательно, но с некоторым шагом k
Какое дерево называется разбалансированным?
(1) размеры левых и правых поддеревьев в нем сильно различаются
(2) если в нем нарушен порядок неубывания ключей
(3) если значения ключей в левом поддереве намного меньше значений ключей в правом поддереве
(4) если существуют вершины-потомки, ключи которых больше ключей родителей, если в остальных вершинах это свойство не нарушено
Какой способ обхода дерева используется для предобработки в задаче offline LCA?
(1) In-order обход
(2) Post-order обход
(3) Pre-order обход
По каким критериям выбирается разделитель, делящий на левые и правые поддеревья в приоритетном дереве поиска (priority search tree)?
(1) случайным образом
(2) делит отрезки примерно поровну
(3) по среднему значению отсортированных левых концов отрезков
(4) по среднему значению отсортированных правых концов отрезков
Если при оценивании фиксированного алгоритма оценки сверху и снизу совпали, то какие действия предпринимаются?
(1) время оценивается как Θ(N) и оценивание сводится к придумыванию наихудшего случая для алгоритма
(2) берется сумма оценок сверху и снизу и делится на 2
(3) это означает что оценка произведена неверно
Какая сложность у процедуры слияния для алгоритма сортировки слияием (MergeSort) для массива длины L?
(1) O(L2)
(2) O(L1 + L2), L1 и L2 — длины двух частей массива
(3) O(L12 + L22), L1 и L2 — длины двух частей массива
(4) O(L12 * L22), L1 и L2 — длины двух частей массива
Что такое куча, каково ее назначение?
(1) хранит упорядоченный по неубыванию или невозрастанию набор ключей и связанных с ними значений
(2) структура данных, которая хранит в себе ключи-приоритеты и связные с ними значения
(3) так называют любое, неупорядоченное ни по каким параметрам множество значений
(4) любая структура данных, представленная в виде дерева, хранящая в себе ключи и связанные с ними значения
Какая формула задает линейный способ просматривания ячеек хэш-таблицы?
(1) h(k,j) = (h0(k) + j * h1(k)) mod m
(2) h(k,j) = (h0(k) + j) mod m
(3) h(k,j) = (h0(k) + j * h0(k)) mod m
Какие действия предпринимают для сохранения свойств красного черного дерева, если при операции вставки вершины x, x и y оказались красными, если y — родитель x, y — корень?
(1) x — становится черным
(2) y — становится черным
(3) ничего не предпринимают
(4) x и y — становятся черными
Какие операции из структуры disjoin set union используются в предобработке для задачи offline LCA?
(1) Unite
(2) Create
(3) Remove
(4) Get-min
Какой размер имеет структура данных приоритетное дерево поиска?
(1) O(N2)
(2) O(N * log N)
(3) O(log N)
(4) O(N)
Чем такая схема <CPU — Память> отличается от реальной жизни?
(1) может быть несколько CPU в одном модуле
(2) может быть неопределенное количество промежуточных элементов, например кэш
(3) CPU может отсутствовать
(4) память устроена гораздо сложнее
(5) не учтена внешняя память
(6) память может отсутствовать
При использовании подхода Bottom-up для алгоритма сортировки слиянием, на блоки какого размера разбивается массив размера n на k-ом шаге?
(1) n/2k
(2) 2k
(3) n/k
(4) k
Какие операции есть в структуре данных куча?
(1) Insert(k)
(2) Remove(k)
(3) Get-min()
(4) Extract(k)
(5) Extract-min()
(6) Decrease-key(k)
Какое предположение должно быть выполнено, чтобы была справедлива гипотеза простого равномерного хэширования?
(1) значение хеш-функции от ключа k является случайной величиной, равномерно распределенной на множестве {0, …, M1}
(2) для различных ключей k1 и k2 хеш-коды h(k1) и h(k2) зависят друг от друга
(3) вероятность появления коллизий<= 0.01
(4) количество значений не должно превышать 264 — 1
Отметьте верные утверждения, характеризующие операцию splay(x) в splay-дереве
(1) при поднятии x вращения не совершаются
(2) x становится корнем
(3) T(время работы операции) = Θ(глубина x)
(4) учетная стоимость любой операции splay O(log N)
Как происходит оптимизация в алгоритме поиска LCA для дерева T?
(1) вычисляются все наименьшие общие предки для всех пар вершин дерева T во время предобработки, чтобы потом бытро выводить ответ на запрос
(2) во время предобработки анализируется структура дерева T, а затем быстро вычисляются наименьшие общие предки для заданных пар вершин
(3) наименьшие общие предки вычисляются для каждого запроса без предобработки
В чём состоит идея оптимизации в структуре двумерное дерево отрезков для задачи поиска в квадратичной области, позволяющая достичь времени работы O(log N)?
(1) на всех уровнях дерева запоминаются пезультаты работы алгоритма для всех запросов
(2) пересчет результатов бинарного поиска для списков нижнего уровня с помощью сохранения позиций, в которые перемещаются точки со списков верхнего уровня
(3) в каждой вершине запоминаются результаты работы для наиболее часто встречающихся запросов
В чем состоит отличие в работе алгоритма для модели «разрешающие деревья» от RAM — модели и модели машины Тьюринга?
(1) алгоритм неограничен в своих дейстиях
(2) разрешено действие только одного типа
(3) в такой модели можно программировать
Как описывается алгоритм быстрой сортировки (quick-sort)?
(1) для нового неупорядоченного элемента в правой части множества итеративно выбирается место среди уже упорядоченных ключей
(2) массив делится рекурсивно на две части, элементы массива переставляются так, чтобы в левой части оказались элементы, которые не больше чем элементы в правой части
(3) итеративно выбирается место среди оставшихся неупорядоченных ключей, найденный минимум или максимум вынимается из текущего множества в ответ
(4) исходная пследовательность A делится на две одинаковые по размеру части A1 и A2, которые рекурсивно сортируются
Что делает операция Decrease-key для кучи?
(1) извлекает минимальное значение и возвращает его
(2) возвращает миниальное значение без извлечения
(3) удаляет значение по итератору
(4) по итератору и новому значению ключа обновляет этот ключ в структуре данных
Как вычисляется коэффициент заполнения для равномерно распределенной хэш-функции H: k -> {0,…, N-1}?
(1) α = N/M
(2) α = M/N
(3) α = 1 + M/N
(4) α = 1 + N/M
Какой тип вращения сплэй-дерева изображен на рисунке?
(1) zig-zig
(2) zig
(3) zig-zag
У структуры данных дерево отрезков рассмотрим произвольную вершину v и относящийся к ней отрезок [l, r]. Если l ≠ r, каких сыновей имеет эта вершина?
(1) [l, l+1], [l+1, l+2],…, [r-1, r]
(2) [l, m] и [m+1, r], m = (l + r)/2
(3) l и r
(4) [l, m] и [m+1, r], m — любое число меньшее l и большее r
Какая память необходима для двумерного дерева отрезков?
(1) O(N)
(2) O(N * log N)
(3) O(N2)
(4) O(log2 N)
В алгоритмической модели «разрешающее дерево» в каком случае работа алгоритма завершается?
(1) если алгоритм дошел до корня
(2) если алгоритм дошел до листа
(3) если алгоритм перебрал все листья
(4) если алгоритм перебрал все ключи
Как можно добиться, чтобы логарифмическая оценка для алгоритма быстрой сортировки была справедлива не в среднем, а в худшем случае?
(1) элиминация хвостовой рекурсии
(2) рекурсивный вызов для меньшего подотрезка делать последним
(3) в качестве разделителя использовать медиану из трех элементов последовательности: левой границы, правой границы и середины
(4) если глубина рекурсии превышает определенное критичное значение, то использовать другой алгоритм
Какое дерево можно назвать полным бинарным?
(1) каждая вершина является листом или имеет одного или двух сыновей
(2) каждая вершина является листом или имеет ровно два сына, все листья находятся на одной глубине
(3) каждая вершина является листом или имеет ровно два сына, листья могут находиться на соседних уровнях
В случае универсального хэширования чему равно среднее время успешного поиска ключа для хэш-функции H: k -> {0,…, N-1}, если k1, …, kn — все ключи, присутствующие в хеш-таблице?
(1) Θ(1)
(2) Θ(M/N + 1)
(3) Θ(M)
(4) Θ(N)
Если в splay-дереве есть операция, работающая за O(глубина вершины), можно ли ее ускорить до учетного логарифма, если да то как это сделать?
(1) этого сделать нельзя
(2) исключить операцию splay
(3) в конце операции вызывать процедуру splay от той вершины, до которой дошли
(4) в начале операции вызывать процедуру splay для текущей вершины
Сколько памяти потребуется для предварительного построения таблицы минимумов (RMQ) для отрезков [i, j], где j это степень двойки, какое время будет для запроса после такой предобработки?
(1) O(N * log N), O(1)
(2) O(N2), O(log N)
(3) O(N2), O(1)
(4) O(N), O(1)
Какие указатели должны быть в дереве отрезков, работающим за O(log N) по принципу Fractional cascading?
(1) указатель на место, откуда точка переместилась и указатель на предыдущий элемент
(2) первые указатели показывают куда точки перемещаются при распределении между списками, вторые указатели показывают следующую точку другого типа в верхнем списке
(3) указатель на ответ для следующего уровня и точный указатель на предыдущий ответ в текущем отрезке
Что назыавется сложностью для алгоритма, заданного разрешающим деревом?
(1) это количество всех возможныз путей в дереве
(2) это высота дерева, то есть максимальная длина пути от корня дерева до вершины
(3) это количество листьев в дереве, то есть элементов на нижних уровнях
Пусть на вход алгоритма быстрой сортировки поступает N различных ключей. Тогда каким будет матожидание времени его работы при случайном равномерном и независимом выборе разделителяя?
(1) O(N2)
(2) O(N * log N)
(3) непределенное
(4) O(N)
(5) O(log N)
Как можно построить кучу из N элементов за время O(N)?
(1) создать пустую кучу, применить операцию Insert для каждого элемента
(2) это невозможно, потому что все операции в куче работают за O(log N)
(3) применить операцию MakeHeap для второй половины элементов, затем восстановить свойства кучи только для этой половины элементов
При каких условия можно получить свободную от коллизий хэш-функцию?
(1) использовать метод открытой адресации
(2) если неизвестно с какими ключами предстоит иметь дело
(3) выбрать размер хэш-таблицы квадратичным по количеству ключей
(4) выбирать хэш-функции из универсального семейства
Какой будет учетная стоимость zig-шага для операции splay? Если r — ранг, r' — новый ранг, v — вращаемая вершина, u — корень в начале операции
(1) ≤ r'(v) - r(v)
(2) ≤ 1 + 3(r'(v) - r(v))
(3) ≤ 1 + 3(r'(u) - r(u))
(4) ≤ 4
В алгоритме ±1-RMQ на блоки с минимумами какого размера разбивается исходная последовательность?
(1) на блоки одинакового размера, кроме последнего. Для каждого блока ищется минимум
(2) на блоки единичного размера
(3) на три блока
(4) на два блока
Какие действия должна уметь выполнять структура данных для задачи о динамической связности в графах? Для полностью динамического случая
(1) ChangeEdge
(2) AddEdge
(3) RemoveEdge
(4) Connected
(5) FindEdge
Пусть имеется двоичный счетчик, то есть вектор, состоящий из битов, представляющий двоичное число. Изначально все биты равны 0. Пусть есть операция Increment, какова ее сложность в худшем случае?
(1) O(1)
(2) Θ(N)
(3) O(N2)
(4) O(log N)
Какие из перечисленных высказываний относятся к внутреннему типу случайности (internal randomness)?
(1) алгоритм сам генерирует значения, использует их для принятия решений
(2) на вход приходят случайные данные. Тогда на множестве входов есть некоторое распределение
(3) анализ происходит по внутреннему датчику случайности
(4) сложность изучается в среднем относительно меры на множестве входов
Какие операции включает в себя процедура вставки (Insert(k)) для кучи?
(1) приписывание ключа в конец кучи
(2) Sift-up()
(3) Sift-down()
(4) приписывание ключа в начало (корень) кучи
Как зависит размер памяти, необходимый для реализании метода совершенного хэширования от количества ключей n?
(1) квадратично
(2) линейно
(3) константно
(4) логарифмически
Какими свойствами обладают декартовы деревья?
(1) деревья поиска и хэш-функции
(2) деревья поиска и кучи
(3) кучи и хэш-функции
(4) деревья поиска с вершинами-массивами
Для алгоритма ±1-RMQ сколько существуют типов приведенных блоков размера k?
(1) 2 * k — 1
(2) 2k-1
(3) 2k+1
(4) k2 — 1
Какой тип имеет задача о динамической связности в графе, если ответы на все запросы про связность будут получены после обработки всех операций, а не по мере их поступления?
(1) динамический
(2) оффлайн
(3) онлайн
(4) инкрементальный
По какому принципу выбирается размер reallocation для аддитивного метода? Если C — старый размер массива.
(1) C’ = C*d, d — константа > 1
(2) C’ = C + d, d — число добавляемых элементов
(3) C’ = C2/d, d — константа > 1
Отметьте высказывания, характерные для алгоритма слияния, работающего с диском
(1) входной массив считывается блоками одной длины M (в байтах)
(2) все блоки входного массива считываются в оперативную память одновременно и каждый блок сортируется с помощью merge-sort, затем происходит слияние по одному блоку
(3) при слиянии данные считываются параллельно в двух местах, параллельно вычисляется минимум
(4) последовательное чтение с диска работает эффективнее, чем случайное, поэтому Merge-sort хорошо подходит для работы с диском
(5) алгоритм сортировки слиянием эффективен при работе с данными на диске
(6) оперативная память экономится, чтобы считываемые данные не были равны размеру входа
Как можно реализовать биномиальную кучу размерности
T3?
(1) построить троичную бинарную кучу из бинарных куч размерности T1
(2) объединить корни куч размерностей T1 и T2
(3) построить кучу из трех элементов
Что означает ложно-положительное срабатывание для интерфейса множества с ошибками фильтр Блюма?
(1) ключ в множестве есть, а операция Contains(k) выдает False
(2) операция Contains(k) выдала True, а ключа в множестве нет
(3) при попытке удаления ключа (Remove(k)) создается его резервная копия
(4) если выполняется не тот запрос к множеству, который был отправлен
Отметьте верные утверждения, характеризующие декартовы деревья.
(1) сложность рекурсивного построения дерева в худшем случае O(log N)
(2) декартово дерево можно построить для всякого набора пар и ключей
(3) структура дуча имеет логарифмическое матожидание высоты в худшем случае
(4) может поддерживать операции split, merge
(5) дерево можно построить рекурсивно
(6) быстрее чем за O(N2) построить декартово дерево нельзя
Как длина Эйлерова обхода зависит от числа вершин в дереве?
(1) квадратично
(2) линейно
(3) экспоненциально
(4) логарифмически
Если задача такова, что в графе нет и не может быть циклов, то что можно сказать о ней?
(1) значит задача не может быть решена быстро, за время O(log N)
(2) задача сводится к задаче связности в деревьях Эйлерова обхода. Время O(log N)
(3) задача может быть решена быстро, за время O(N)
Для оценки сложности цепочки инкрементов, пусть 1 у.е. компьютер требует за 1 элементарную операцию. Пусть записано некоторое двоичное число 010111, над каждой 1 лежит по 1 у.е., сколько потребуется элементарных действий для операции Increment?
Для системы кодирования по Хаффману, что означает безпрефиксный код?
(1) любой из кодов символа алфавита является префиксом для любого другого символа
(2) любой из кодов символа алфавита не является префиксом для любого другого символа
(3) любой из кодов символа алфавита не состоит из кода другого символа
Как склеить 2 бинарных дерева T1(с корнем α) и T2(с корнем β), если α <= β?
(1) соеденить α с β, α — родитель
(2) это невозможно
(3) соеденить β с α, β — родитель
Какие существуют стандартные операции для интерфейса множества с ошибками, например для фильтра Блюма?
(1) Remove(k)
(2) Insert(k)
(3) Contains(k)
(4) Get(k)
Как происходит удаление ключа x из декартового дерева T?
(1) вершина удаляется аналогично удалению из кучи
(2) вызыватся split(T, x), получаются деревья T1, T2. Если x∈T, удалить вершину с ключем x из T1, выполнить Merge(T1, T2)
(3) вершина удаляется аналогично удалению из дерева поиска
(4) вершина удаляется без дополнительных операций
Какую асимптотику по памяти имеет сведение задачи RMQ к ±1-RMQ?
(1) квадратичную
(2) линейную
(3) логарифмическую
(4) не использует дополнительную память
Какой обход является конкатенацией двух исходных обходов в операциях со списками для структуры Rope, реализующей динамически связный граф?
(1) Pre-order
(2) In-order
(3) Post-order
Для библиотеки std::vector, реализующей массив на C++, что происходит, когда нужно добавить еще один элемент в конец массива, если массив полностью заполнен?
(1) происходит ошибка
(2) переопределение размера(realocatioon), все элементы копируются в новый массив увеличенного размера, элемент добавляется в конец
(3) последний элемент массива заменяется на новый
(4) размер массива увеличивается на единицу, новый элемент добавляется в конец массива
(5) для добавляемого элемента создается дополнительный пустой массив, который затем прибавляется к заполненному
В каком месте дереве Хаффмана будут находиться два символа с наименьшими частотами?
(1) в соседних листьях на верхнем уровне
(2) в соседних листьях на нижнем уровне
(3) на разных уровнях дерева
За какое время работает операция Insert в бинарном дереве?
(1) O(1)
(2) O(N)
(3) O(log N)
(4) O(N * log N)
Как можно проверить, попадает ли ключ k в хэш-таблицу T фильтра Блюма, заданного хэш-функциями h1,…,hs: k -> [0, m-1] или нет?
(1) вычислить логическое ИЛИ по всем значениям T[hi(k)]. Если оно равно 0 то не попадает, если 1, то попадает
(2) вычислить логическое И по всем значениям T[hi(k)]. Если оно равно 0 то не попадает, если 1, то попадает
(3) вычислить T[∑ hi(k)]. 0 — не попадает, 1 — попадает
Отметьте верные утверждения, относящиеся к B-деревьям
(1) степень вершины не может быть больше 2
(2) ключи, вставленные операцией Insert, хранятся в листьях
(3) в нелистовых вершинах хранятся копии ключей, находящихся в листьях ниже по дереву
(4) в каждой вершине содержатся максимальные ключи из всех поддеревьев с d-сыновьями
(5) данные находятся во всех вершинах
(6) B-дерево всегда полностью сбалансированно
Какими свойствами должны обладать леса в остовном лесе?
(1) первый граф в цепочке остовных лесов это граф без ребер
(2) остовные леса вложены друг в друга
(3) последний граф в цепочке остовных лесов это граф без ребер
(4) связные компоненты для графа Gi с n вершинами в цепочке имеют размер не более n/(2i)
Какие две операции должен выполнять хороший стэк?
(1) push, get
(2) push, pop
(3) insert, get
(4) enqueue, decueue
Чему равен ранг вершины v = Null левацкого дерева?
(1) 1
(2) 0
(3) Null
(4) может принимать любое значение
При реализации структуры приближенного множества (Lossy Map) с помощью более блюмового фильтра, как будет работать операция Get(k)?
(1) выдает по некоторому ключу значение и с большой вероятностью это значение удовлетворяет нашим требованиям
(2) может выдать правильное значение, если функция определена в этой точке или если функция неопределена в этой точке, то выдать случайное значение. Или выдает Null, если функция неопределена в этой точке
(3) выдает значение, если функция определена в этой точке, либо выдает Null, если функция неопределена в этой точке
Сколько ключей у вершины B-дерева с d сыновьями?
(1) d
(2) d-1
(3) d+1
(4) 2*d
(5) 1
Если до вставки нового ребра E его вершины u и v находились в разных компонентах связности, какие действия предпринимают, чтобы сохранить структуру динамически связного графа?
(1) добавляем в остовный лес на любом уровне ребро E
(2) добавляем в остовный лес на нулевом уровне ребро E
(3) добавлять ребро E в граф нельзя
(4) добавляем в остовный лес на всех уровнях ребро E
Какие минусы есть у структуры данных Linked lists при использовании ее для реализации стэка?
(1) локальность с точки зрения кэшироваия
(2) много мелких аллокаций (переопределений памяти)
(3) memory overhead (много дополнительного места для поддержания структуры)
(4) нельзя хранить разные типы даных
При выполнении какого свойства куча будет называться левацкой?
(1) rank(left(v)) >= rank(right(v)) для любой вершины v
(2) rank(left(v)) <= rank(right(v)) для любой вершины v
(3) rank(v) <= rank(parent(v)) для любой вершины v
(4) rank(v) >= rank(parent(v)) для любой вершины v
(5) rank(left(v)) = rank(right(v)) для любой вершины v
Что делает операция Unite(x, y) в системе непересекающихся множеств?
(1) объединяет множества, содержащие x, y в одно
(2) отображает, в одном или в разных множествах содержатся x, y
(3) объединяет два элемента x, y в один элемент по заранее определенной функции
(4) объединяет одноэлементные множества x, y в одно множество
Если удаляемое ребро имеет уровень i = l(u, v) то на каких уровнях леса оно лежит?
(1) от Fi до последнего
(2) от F0 до Fi
(3) только Fi
(4) на всех уровнях
Как эффективно реализовать стэк с поддержкой минимума?
(1) использовать один стэк и переменную для хранения текущего минимума, которую нужно обновлять
(2) использовать два стэка: один основной для значений, второй для хранения ответов для текущего минимума
(3) использовать один стэк и функцию для вычисления минимума
Отметьте какие утверждения относятся к левацким кучам
(1) ранг правого сына всегда на 1 меньше чем ранг родителя
(2) ранг растет линейно по числу элементов
(3) Операция Insert сводится к созданию кучи из одного элемента, а затем к слиянию
(4) левацкая куча хранит в каждой вершине помимо ее приоритета также ранг
(5) если у кучи есть правый сын, но нет левого, то она может быть левацкой
Какое время работы у операций Unite, Equivalent для ранговой эвристики?
(1) O(N)
(2) O(log N)
(3) O(N * log N)
(4) O(1)
Что означает свойство persistent (версионирование) для структуры данных?
(1) структура данных изменяет свои свойства в зависимости от текущей задачи
(2) структура данных хранит историю своего развития и модификаций
(3) структура данных динамически изменяет свой размер в зависимости от заполненности
В каком случае вершина v(отличная от корня) называется тяжелой для косой кучи?
(1) weight(v) >= 1/2weight(parent(v))
(2) weight(v) > 1/2weight(parent(v))
(3) weight(v) > weight(parent(v))
(4) weight(v) <= 1/2weight(parent(v))
Выберите, чем характеризуется подход для освобождения памяти для persistent stack, называемый подсчет ссылок (ref-counting)?
(1) он корректен
(2) необходимо хранить счетчик на каждую вершину
(3) структура при этом не является неизменияемой (immutable)
(4) помечаются все элементы, достижимые из корней
(5) структура эффективна в многопоточном режиме
Что называется потенциалом косой кучи?
(1) количество хороших вершин в ней
(2) количество плохих вершин в ней
(3) общее количество вершин в ней
(4) количество тяжелых вершин в ней
В чем заключается задача RMQ для массива чисел?
(1) для пары индексов i, j вывести минимум на отрезке [i, j] для массива, скорость не важна
(2) для пары индексов i, j вывести минимум на отрезке [i, j] для массива, с наилучшей скоростью
(3) для пары индексов i, j вывести количество ключей, попавших в отрезок [i, j]
(4) для пары индексов i, j вывести ключи, попавшие в отрезок [i, j]
(5) для пары индексов i, j вывести сумму значений, попавших в отрезок [i, j]
Какая основная идея применяется для решения задач, связанных с интервалами, с помощью статической структуры данных?
(1) Линейное программирование
(2) Разделяй и властвуй
(3) Жадные алгоритмы
(4) Динамическое программирование
В функциональной парадигме при проектировании алгоритма, какой оценкой на время работы интересуются?
(1) оценкой в худшем случае
(2) оценкой в среднем
(3) оценкой в лучшем случае
Какова оценка по времени для продвинутых алгоритмов сортировки (в худшем или среднем случае)?
(1) O(N2)
(2) O(N * log N)
(3) O(N)
(4) O(log N)
Какое математическое ожидание времени работы у алгоритма поиска k-ой порядковой статистики (Random-варианта)?
(1) O(log N)
(2) O(N)
(3) O(N * log N)
(4) O(N2)
С помощью каких структур данных можно реализовать Map/Dictionary?
(1) простого массива
(2) хэш-таблиц
(3) односвязного или двусвязного списка
(4) деревьев поиска
Какие действия включает в себя операция вставки (Insert(x)) в двоичном дереве поиска?
(1) поиск ключа x в дереве
(2) если поиск завершился неудачей, создадим новую вершину w с ключем x
(3) если поиск завершился удачей, создадим новую вершину w с ключем x
(4) вершину w объявим левым сыном v, если key(v) > key(w)
(5) вершину w объявим правым сыном v, если key(v) < key(w)
Для декартова дерева с вершинами (key = N, prior = aN), если k = lca(i, j), то чем будет являться вершина ak?
(1) минимум на отрезке [i, j]
(2) любая вершина из отрезка [i, j]
(3) первая вершина из отрезка [i, j]
(4) средняя вершина из отрезка [i, j]
(5) вершина с медианой по значению из отрезка [i, j]
Какой прием можнно использовать, чтобы эффективнее искать интервалы, пересекающие заданную точку с помощью статической структуры данных?
(1) Эффективные прямого перебора ничего не придумано
(2) Вести поиск только по правым или по левым концам интервалов
(3) Разделить интервалы на дерево групп, для более быстрого доступа к соответствующей группе или интервалу
Считается ли процессорное время важным ресурсом, учитывающимся при разработке эффективного алгоритма?
Всегда ли свойство стабильности является важным для алгоритма сортировки?
(1) да, так как оно напрямую влияет на качетсво сортировки
(2) нет
(3) да, так как от стабильности зависит скорость работы алгоритма
В представленном ниже псевдокоде алгоритма поиска порядковой статистики что находится на пропущенном месте?
Random-select(A, k)
задать λ
разделить (A, λ) -> (A1, A2)
…
вернуть Random-select(A1, k)
иначе:
вернуть Random-select(A2, k — |A1|)
(1) если k > |A1|:
(2) если k <= |A1|:
(3) если k > |A2|:
(4) если k == λ
Что такое хэш-коллизия?
(1) совпадение хэш-кодов различных ключей
(2) совпадение хэш-кодов для одинаковых значений из множества
(3) совпадение хэш-кодов одинаковых ключей
Какой обход дерева нужно использовать, чтобы ключи двоичного дерева поиска были выведены в порядке неубывания?
(1) Pre-order обход
(2) In-order обход
(3) Post-order обход
За какое время строится декартово дерево для набора {(1, a1),…,(n, an)}
(1) O(log N)
(2) O(n)
(3) O(N * log N)
(4) O(N2)
Какая структура данных может искать точки в «колодце»(двустороннее ограничение по одной координате и одностороннее ограничение по другой координате)?
(1) очередь с приоритетами
(2) приоритетное дерево поиска (priority search tree)
(3) декартово дерево
(4) куча
При рассмотрении времени работы T(M) и памяти M(N) что нас интересует?
(1) точный вид функций T(N) и M(N)
(2) приближенный до константы вид функций. Используется O-символика
(3) приближенный вид функций. Используется o-символика
Какая сложность у алгоритма сортировки выбором?
(1) O(N * log N)
(2) Θ(N2)
(3) Θ(N3)
Для приведенного псевдокода поиска k-ой порядковой статистики, выберите строки, которых не хватает для корректной работы алгоритма:
Select (A, k)
…
partition(A, λ) -> (A1, A2)
if k <= |A1| then:
return Select(A1, k)
else:
return Select(A2, k — |A1|)
(1) group by 5 elements
(2) group by k elements
(3) sort groups
(4) λ = median of medians
(5) λ = random of medians
Какие сложности у операций добавления и извлечения для метода цепочек?
(1) O(L), O(L), L — длина цепочки для текущей хэш-функции
(2) O(L), O(L * N), L — длина цепочки для текущей хэш-функции
(3) O(L), O(L), L — длина цепочки для текущей хэш-функции
(4) O(1), O(L), L — длина цепочки для текущей хэш-функции
Какую высоту имеет красно-черное дерево с n внутреннеми вершинами (не считая Nil-листьев)?
(1) не менее 2 * lg(n+1)
(2) не больше 2 * lg(n+1)
(3) не менее n/2
(4) не менее n
Какая структура данных используется дополнительно в предобработке для offline LCA?
(1) куча
(2) красно-черное дерево
(3) система непересекающихся множеств
(4) хэш-таблица
(5) B-дерево
Какое время поиска у приоритетного дерева поиска (priority search tree)?
(1) O(log N)
(2) O(log N + k)
(3) O(log N * k)
(4) O(N + k)
O-символика датет приближенную оценку. Что нужно сделать, чтобы найти оценку точнее?
(1) выполнить болшее количество тестов
(2) нужно для начала определиться, нас интересует оценка на фиксированный алгоритм или на задачу и выполнять оценку исходя из этого
(3) изменить входные данные
Для алгоритма сортировки слиянием merge-sort при каком количестве элементов в последовательности рекурсивное деление должно прерываться, в стандартном виде?
Как можно удалить элемент из кучи?
(1) по переданному значению
(2) по переданному ключу или итератору
(3) по ключу или значению
Какая формула задает метод двойного хэширования для просматривания ячеек хэш-таблицы?
(1) h(k,j) = (h0(k) + j * h1(k)) mod m
(2) h(k,j) = (h0(k) + j) mod m
(3) h(k,j) = (h0(k) + j * h0(k)) mod m
Какие действия предпринимают для сохранения свойств красного черного дерева после операции вставки вершины x в следующей ситуации. Если A — родитель x, B — родитель A; B — черная вершина; A, C — красные; C — дядя x
(1) ничего делать не нужно
(2) A и C сделать черными, B — красным
(3) A сделать черными, x — красным
(4) x сделать черными
Отметьте верные свойства функции LCA
(1) очевидное решение, не использующее предобработку, имеет сложность O(log N) для ответа на запрос
(2) симметричность, то есть lca(u, v) = lca(v, u)
(3) если u является потомком v или совпадает с ней, то lca(u,v) = v
Если корень приоритетного дерева поиска выбирается по минимальной r координате отрезка [l, r], то по каким параметрам происходит деление на левые и правые поддеревья?
(1) по r координате
(2) по l координате
(3) по l и r координатам
(4) по другим параметрам
Какие из перечисленных ниже утверждений относятся к параметру машинное слово w в стандартной модели оперативной памяти (RAM — model)?
(1) w это количество ячеек в памяти
(2) w это число бит в одной ячейке памяти
(3) w это максимально допустимый размер переменной
(4) w хранит числа ограниченной битности
(5) w это число бит, необходимых для представления одной буквы или цифры
Какая сложность у алгоритма сортировки слиянием?
(1) O(N)
(2) O(N * log N)
(3) O(N2)
(4) O(log N)
Для кучи, реализованной поверх массива, у каких операций время работы будет O(1)?
(1) Get-min()
(2) Extract-min()
(3) Insert(k)
(4) Remove(k)
(5) Decrease-key(k)
Пусть мы выполняем запрос Get для некоторого ключа k и пусть перед этим в структуру были вставлены некоторые ключи k1,…,kn. Для каждого ключа ki обозначим через Xi,j случайную величину, равную 1, если h(ki)=h(kj), и 0 в противном случае. Какая будет длина цепочки с индексом i?
(1) Σ(i=1..n)1/Xi,j
(2) Σ(i=1..n)Xi,j
(3) Σ(i=1..n)(Xi,j * h(ki))
Отметьте верные утверждения, относящиеся к splay-деревьям
(1) время работы операции splay может быть больше чем O(log N)
(2) операция Find включает операцию splay
(3) сплэй-деревья не поддерживают баланс постоянно, вместо этого они остаются сбалансированными в среднем
(4) дерево самобалансируется за счет вызовов операции splay
(5) splay-деревья не поддерживают объединения
Какая вершина называется наименьшим общим предком для вершин u, v?
(1) любая вершина, находящаяся на пересечении путей от вершин u и v вверх по дереву до корня
(2) первая, максимально удаленная от корня точка пересечения путей от вершин u и v вверх по дереву до корня
(3) минимально удаленная от корня точка пересечения путей от вершин u и v вверх по дереву до корня
(4) наименьшая по значению ключа из вершин u и v
Что такое каскады в структуре Fractional cascading?
(1) нижние поддеревья в дереве поиска
(2) вспомогательные структуры, которые позволяют получить ответ для части, когда известен ответ для целого
(3) части, на которые разбиваются исходные списки
(4) ответы на запросы для каждого списка
Что представляе собой программа для модели «разрешающие деревья»?
(1) программа на языке, похожем на Assembler, C
(2) структура в виде дерева
(3) это некоторая таблица, в которой записано, что нужно делать в зависимости от состояния
По какому признаку отрезок разбивается на две части в алгоритме быстрой сортировки (quick-sort)?
(1) разбивается поровну
(2) в левую часть помещаются ключи <=λ, в правую часть помещаются ключи >=λ, λ выбирается определенным образом(часто случайно)
(3) в левую часть помещаются ключи, делящиеся на цело на λ, в правую часть помещаются ключи, не делящиеся на цело на λ
(4) в левую часть помещаются ключи <=λ, в правую часть помещаются ключи >=λ, λ является медианой отрезка на каждой итерации
Что делает операция Extract-min для кучи?
(1) извлекает минимальное значение и возвращает его
(2) возвращает миниальное значение без извлечения
(3) удаляет значение по итератору
(4) по итератору и новому значению ключа обновляет этот ключ в структуре данных
В предположении гипотезы простого равномерного хэширования, чему равно среднее время безуспешного поиска ключа для хэш-функции H: k -> {0,…, N-1}?
(1) Θ(M/N)
(2) Θ(log M/N)
(3) Θ(M * N)
(4) Θ(M/N + 1)
Какой тип вращения сплэй-дерева изображен на рисунке?
(1) zig-zig
(2) zig
(3) zig-zag
Для динамической задачи RMQ, не использующей предобработку, какое время используется на запрос?
(1) O(N)
(2) O(log N)
(3) O(1)
(4) O(N2)
Какое время поиска у структуры данных двумерное дерево отрезков, работающей с квадратной области поиска [x1, x2] x [y1, y2]?
(1) O(N)
(2) O(log2 N)
(3) O(N2)
(4) O(log N)
С какого элемента начинается работа в разрешающем дереве в стандартном случае?
(1) с листьев
(2) с корня
(3) с любого возможного ключа
Выберите утверждения, характерные для алгоритма быстрой сортировки (quick-sort).
(1) на каждой итерации массив делится на две части: больше и меньше разделителя λ
(2) алгоритм использует top-down подход
(3) на каждой итерации массив делится на две равные части
(4) алгоритм использует bottom-up подход
(5) сложность алгоритма O(N * log N)
Какое дерево можно назвать почти полным бинарным?
(1) каждая вершина либо лист, либо имеет двух или одного сына: левого или правого
(2) каждая вершина либо лист, либо имеет ровно два сына, все листья находятся на одной глубине
(3) если взять полное бинарное дерево и убрать на последнем уровне часть сыновей, начиная справа, то получится почти полное бинарное дерево
Если использовать универсальное семейство хэш-функций для хранения n ключей, то при размере хэш-таблицы M = n2, какова будет вероятность получить хотя бы одну коллизию?
(1) не больше 2/3
(2) не больше 1/2
(3) меньше 1/M
(4) меньше 1/N
В каком случае можно выполить zig-шаг для splay-дерева?
(1) если рассматриваемая вершина находится на глубине 0
(2) если рассматриваемая вершина находится на глубине 1
(3) если рассматриваемая вершина находится на глубине 2
(4) если рассматриваемая вершина находится на любой глубине
Каким должен быть размер блока для алгоритма ±1-RMQ, чтобы сократить сложность предобработки?
(1) log N
(2) (log N)/2
(3) √N
(4) N/2
Пусть есть k списков: L1,...,Lk. В чем заключается задача fractional cascading?
(1) нужно предобработать списки с помощью указателей за разумное время, так, чтобы быстро выводить минимальный элемент для каждого списка
(2) нужно предобработать списки с помощью указателей за разумное время, так, чтобы быстро выводить первый минимальный элемент, больше или равный X для каждого списка
(3) нужно предобработать списки с помощью указателей за разумное время, так, чтобы быстро выводить первый максимальный элемент, больше или равный X для каждого списка
(4) нужно предобработать списки с помощью указателей за разумное время, так, чтобы быстро выводить сумму элементов каждого списка
Как оценивается сложность правильного дерева сортировки (в худшем случае)?
(1) T = Ω(log N)
(2) T = Ω(N*log N)
(3) T = Ω(N2)
(4) T = O(N)
Пусть на вход алгоритма быстрой сортировки поступает N различных ключей. Тогда каким будет матожидание глубины рекурсии?
(1) O(N * log N)
(2) O(N2)
(3) O(N)
(4) O(log N)
За какое время выполняется операция MakeHeap, то есть построение кучи из набора размером N?
(1) O(N * log N)
(2) O(N)
(3) O(N2)
(4) O(N2 * log N)
Какие характеристики имеет совершенная хэш-функция?
(1) имеет вероятность получения коллизий <= 1/m2, m — количество ключей
(2) просто вычислима, за O(1) в худшем случае
(3) линейное в среднем время построения
(4) не дает коллизий на ограниченном множестве {k1,…,kn}
Какой будет учетная стоимость zigzig-шага для операции splay? Если r — ранг, r' — новый ранг, v — вращаемая вершина, u — корень в начале операции
(1) ≤ r'(v) - r(v)
(2) ≤ 1 + 3(r'(v) - r(v))
(3) ≤ 1 + 3(r'(u) - r(u))
(4) ≤ 3(r'(v) - r(v))
В алгоритме ±1-RMQ после разделения исходной последовательности на блоки, на какие части разделяется отрезок запроса?
(1) на три части: конечный отрезок некоторого блока; второй составлен из целого числа подряд идущих блоков; начальный отрезок некоторого блока
(2) на целое число подряд идущих блоков, крайние точки попадают в крайние блоки
(3) на две части: одна содержит первую точку, вторая содержит вторую точку
Какие действия должна уметь выполнять структура данных для задачи о динамической связности в графах? Для инкрементальной связности
(1) ChangeEdge
(2) AddEdge
(3) RemoveEdge
(4) Connected
(5) FindEdge
Пусть имеется двоичный счетчик, то есть вектор, состоящий из битов, представляющий двоичное число. Изначально все биты равны 0. Для M операций Increment, какова их сложность в худшем случае?
(1) O(M + N)
(2) O(M*N)
(3) O(N)
(4) O(M)
Какие из перечисленных высказываний относятся к внешнему типу случайности (external randomness)?
(1) алгоритм сам генерирует значения, использует их для принятия решений
(2) на вход приходят случайные данные. Тогда на множестве входов есть некоторое распределение
(3) анализ происходит по внутреннему датчику случайности
(4) сложность изучается в среднем относительно меры на множестве входов
Какие операции включает в себя процедура извлечения минимума (Extract-min()) для кучи?
(1) Sift-up()
(2) Sift-down()
(3) приписывание ключа в конец кучи
(4) перемещение конечного элемента кучи в начало(корень) кучи
За какое в среднем количество проб можно обнаружить хэш-функцию, не дающую коллизий для второго уровня схемы совершенного хэширования?
(1) O(N)
(2) O(1)
(3) O(N2)
(4) O(log N)
Алгоритм рекурсивного построения декартвого дерева аналогичен алгоритму:
(1) сортировка слиянием
(2) быстрая сортировка
(3) двоичный поиск
(4) сортировка кучей
На сколько различаются глубины соседних вершин в Эйлеровом обходе?
(1) на 2
(2) на 1
(3) на разное число
Какой тип имеет задача о динамической связности в графе, если ответы выдаются сразу после выполнения различных действий с графом и поступления запроса о связности?
(1) динамический
(2) оффлайн
(3) онлайн
(4) инкрементальный
По какому принципу выбирается размер reallocation для мультипликативного метода? Если C — старый размер массива.
(1) C’ = C*d, d — константа > 1
(2) C’ = C + d, d — число добавляемых элементов
(3) C’ = C2/d, d — константа > 1
Отметьте утверждения, характерные для алгоритма сортировки слиянием (Merge-sort), работающего с памятью на диске
(1) область сортировки разбивается на части размера M, где M — размер оперативной памяти
(2) запись на диск происходит поэлементно, то есть блоками минимального размера
(3) блоки сливаются не парами, а на большее число потоков, чтобы умеьшить высоту дерева рекурсии
(4) считываемые в оперативную память блоки нужно брать как можно меньшего размера, лучше поэлементно
Сколько узлов имеет биномиальное дерево Ti?
(1) i
(2) 2i
(3) 2i+1
(4) i2
Для фильтра Блюма как изменяется вероятность ложного срабатывания с увеличением размера хранимого множества (числа вставленных элементов)?
(1) уменьшается
(2) увеличивается
(3) не изменяется
Отметить верные утверждения для операции Merge декартового дерева
(1) Merge(T, Null) = T, Merge(Null, t) ≠ T
(2) для деревьев T1 с корнем u, T2 с корнем v, p(u) < p(v), при их слиянии корнем будет v
(3) сложность O(log N)
(4) для T1(α — левое поддерево, β — правое поддерево) с корнем u, T2(γ — левое поддерево, δ — правое поддерево) с корнем v, p(u) < p(v), то при слиянии корнем нового дерева будет u, левым поддеревом α, правым результат Merge(β, T2)
Если построить Эйлеров обход дерева и для каждой вершины отложить ее глубину, то чему будет равен LCA двух вершин?
(1) вершина с наибольшей глубиной между исходными двумя вершинами
(2) вершина с наименьшей глубиной между исходными двумя вершинами
(3) вершина с наименьшей глубиной, ближайшая к одной из двух вершин
(4) вершина с наименьшей глубиной среди всех отложенных вершин
Если исходное дерево без выделенного корня, то можно ли его сделать Эйлеровым графом?
(1) нет
(2) да, если его удвоить, обойдя Эйлеровым обходом
(3) оно и так уже является Эйлеровым графом
(4) да, если добавить к нему корень
Пусть 1 у.е. компьютер требует за 1 элементарную операцию. Пусть записано некоторое двоичное число, начиная справа имеем k единиц до 0. При текущем балансе -(k+1) (credit: k, debit: 1), если k единиц снять со структуры, 1 положить, сколько нужно попросить у клиента, чтобы выйти в 0?
Каким будет оптимальный порядок бинарного слияния всех отрезков L1,…,Ln различной длины в алгоритме сортировки слиянием?
(1) сначала нужно сливать отрезки наименьшей длины, затем прибавлять к полученному отрезку следующий по длине отрезок и так далее
(2) использовать n-ичное дерево Хаффмана для определения порядка слияния для каждого Li, n зависит от количества отрезков и разброса их длин
(3) использовать бинарное дерево кодирования Хаффмана для определения порядка слияния для каждого Li, на нижнем уровне дерева будут находиться отрезки наименьшей длины, на верхнем уровне — отрезки наибольшей длины
(4) использовать бинарное дерево кодирования Хаффмана для определения порядка слияния для каждого Li, на верхнем уровне дерева будут находиться отрезки наименьшей длины, на нижнем — уровне отрезки наибольшей длины
За какое время выполняется слияние двух деревьев?
(1) O(N)
(2) O(log N)
(3) O(1)
(4) O(N * log N)
Какие допустимы ситуации для односторонней ошибки в интерфейсе множества с ошибками?
(1) разрешается ложноотрицательное срабатывание, когда ключ в множестве есть, а операция Contains(k) выдает False
(2) разрешается ложноположительное срабатывание, при котором операция Contains(k) выдалет True, а ключа в множестве нет
(3) запрещается ложноположительное срабатывание
(4) запрещается ложноотрицательное срабатывание
Как происходит добавление ключа x к декартовому дереву T?
(1) выполняется Split(T, x), получаем T1, T2, вершину (x, p), p — приоритет, x — ключ. Выполняется Merge(T1, (x, p)) = T1x. Выполняется Merge(T1x, T2)
(2) выполняется Merge(T, x)
(3) вершина добавляется аналогично операции добавления для кучи
(4) вершина добавляется аналогично операции добавления для дерева поиска
Если в алгоритме ±1-RMQ для каждого типа приведенного блока, а также для каждого его начального и конечного отрезка вычислить минимум по данному отрезку, тогда сколько значений всего нужно предпосчитать?
(1) 2 * k — 1
(2) 2k-1
(3) k * 2k
(4) k2 — 1
Что такое остовный лес в графе?
(1) лес в графе, минимальный с точки зрения связности
(2) лес в графе, максимальный с точки зрения связности
(3) граф с полным набором всех его ребер
(4) граф с дополнительным набором ребер, обеспечивающих полную связность
При анализе учетных стоимостей операций C(ai) с каждым из состояний Si связано некоторое вещественное значение ϕi, называемое потенциалом. Тогда чему равняется приведенная стоимоть C'(ai)?
(1) C'(ai) = C(ai) + ϕi — ϕi-1
(2) C'(ai) = C(ai) — C(ai-1)
(3) C'(ai) = C(ai) + ϕi-1 + ϕi
Какую сумму нужно оптимизировать в задаче оптимизации порядка бинарного слияния всех отрезков L1,…,Ln различной длины? Если pi — глубина i-го листа в дереве слияния
(1) Φ = Σ li / pi
(2) Φ = Σ li pi
(3) Φ = Σ li + pi
За какое время работает операция Extract-min в бинарном дереве?
(1) O(1)
(2) O(N)
(3) O(log N)
(4) O(N * log N)
Как происходит вставка (Insert(k)) ключа k в таблицу T, реализованную фильтром Блюма?
(1) вычислить хэш-коды h1(k),…,hs(k), после чего в получившиеся индексы ячеек булева массива T записать значение True
(2) вычислить сумму ∑ hi(k) и записать в таблицу T, в ячейку с получившимся индексом значение True
(3) по хэш-функции h(k) определяется булево значение и вставляется в индекс таблицы T
(4) вычислить хэш-коды h1(k),…,hs(k), после чего в соответствующие значения записать ключ k
Какие операции есть у B-дерева?
(1) Get(x)
(2) Insert(x)
(3) Remove(x)
(4) Find(x)
(5) Get-min/Get-max
Каким образом нужно преобразовать граф, чтобы получить лес?
(1) для графа строится Эйлеров обход
(2) ребрам приписываются уровни E -> {0, 1, ..., log N}
(3) пребразование происходит без добавления новых ребер
(4) в каждом из графов на всех уровнях поддерживается остовный лес
(5) остовные леса на каждом уровне должны быть вложены друг в друга
Какова учетная стоимость операций в стэке, реализованном с помощью вектора?
(1) O(N)
(2) O(1)
(3) O(log N)
Если у левацкого дерева вершина v не равна Null, то чему равен ранг этой вершины?
(1) 1 + min(left(v), right(v))
(2) min(left(v), right(v))
(3) 1 + max(left(v), right(v))
Предположим, что при реализации структуры приближенное множество (Lossy Map) с помощью более блюмового фильтра функция отображает из ключей в один бит. Как можно реализовать такую структуру?
(1) Такую структуру реализовать нельзя
(2) с помощью одного Блюм-фильтра для области определения функции, значению 0 будет выдаваться если функция неопределена в этой точке, 1 если функция определена или неопределена для случая ложноположительного срабатывания
(3) С помощью двух множеств: прообраз всех значений 0 и прообраз всех значений 1. Построить два Блюм-фильтра для этих двух множеств
Какие значения может принимать α (коэффициент заполнения дерева)?
(1) от 1/2 до 1
(2) от 1 до d/2(количество вершин на нижнем уровне)
(3) от 0 до d(количество вершин на нижнем уровне)
(4) от 0 до 1/2
Если ребро, которое мы хотим удалить, не принадлежит остовному лесу, то что это значит для структуры динамически связного графа?
(1) связность между вершинами может нарушиться
(2) связность между любой парой вершин сохранится
(3) придется перестраивать лес и пересчитывать связность
(4) необходимо выяснить является ли данное ребро мостом в графе
Какие плюсы есть у структуры данных Chunked vector по сравнению с Linked lists, при использовании в качестве стэка?
(1) доступ к элементу по индексу происходит быстрее
(2) меньше overhead (дополнительного места для поддержания структуры)
(3) лучше локальность с точки зрения кэширования
(4) лучше с точки зрения аллокаций
Можно ли любую кучу превратить в левацкую, если да, то как?
(1) нельзя
(2) если обменять левого и правого сына в тех вершинах v, для которых свойство левацкости (rank(left(v)) >= rank(right(v))) нарушается
(3) если выполнить процедуру просеивания (вверх или вниз) для тех вершин, у которых свойство левацкости нарушается
(4) если удалить те вершины, у которых свойство левацкости нарушается
Как работает операция Equivalent(x, y)?
(1) сравниваются ключи x, y
(2) сравниваются корни деревьев, содержащих элементы x и y
(3) сравниваются хэш-функции от x, y, заранее определенные для данного типа множества
(4) определяется соответствие x, y какому-то заданному свойству или условию
Если при удалении ребра оказалось что оно находилось в остовном лесе, то что это значит?
(1) связность не пострадает и ничего дополнительно делать не нужно
(2) необходимо выяснить является ли данное ребро мостом в графе и выполнить соответствующие действия
(3) связность графа точно нарушится
Как (с помощью каких структур данных) можно эффективно реализовать очередь с поддержкой минимума?
(1) с помощью очереди и стэка
(2) с помощью двух стэков
(3) очередь с дополнительной переменной
(4) с помощью очереди и функции для вычисления минимума
Отметьте, какие утверждения относятся к операции слияния (Meld) двух левацких куч
(1) при слиянии двух левацких куч получается куча со свойствами левацкости без совершения дополнительных действий
(2) операция слияния выполняется рекурсивно
(3) если одна из двух сливаемых куч пустая, то результат их слияния равен другой куче
(4) время выполнения операции слияния двух левацких куч O(log N)
(5) если для приоритетов корней (u и v) двух куч выполняется u < v, то u ставится корнем результата слияния
Для эвристики сжатия путей в чем заключается оптимизация дерева?
(1) для всех листьев дополнительно делается ссылка на корень дерева
(2) для каждой вершины на пути операции Get-root перебросить ее родителя так, чтобы родителем стал корень дерева
(3) дерево поддерживается сбалансированным всегда
(4) за счет увеличения степени вершин высота дерева уменьшается
Какая существует главная проблема, мешающая реализации immutable очереди с помощью двух стэков?
(1) большой объем памяти для хранения структуры
(2) трудность анализа учетных стоимостей
(3) сложность реализации
(4) низкая производительность
Чему равен вес для вершины v w(v) для косой кучи?
(1) рангу вершины v
(2) количеству вершин в поддереве с корнем v (считая и саму вершину)
(3) количеству вершин в правом поддереве
(4) приоритету вершины, умноженному на ее ранг
Чем характеризуется подход с использованием сборщика мусора для эффективной работы с памятью в peristent-стэке?
(1) для каждой вершины (узла) мы помним сколько стрелок на нее ссылается (число)
(2) помечаются элементы, достижимые из корней
(3) структура при этом по настоящему неизменяема
(4) такая структура эффективна в многопоточном режиме
Для косой кучи выполняется следующее свойство. В дереве из N вершин на любом пути, идущем вниз, содержится:
(1) не более log N тяжелых вершин
(2) не более log N легких вершин
(3) не более log N плохих вершин
В чем заключается задача LCA для заданного дерева?
(1) для пары индексов вершин i, j вывести количество ключей, попавших в отрезок [i, j]
(2) для пары индексов вершин i, j вывести значения, попавшие в отрезок [i, j]
(3) для пары индексов вершин i, j вывести всех общих предков
(4) для пары индексов вершин i, j вывести наименьшего общего предка
При построении дерева интервалов какие интервалы попадут в корень дерева?
(1) Находящиеся с левого края на интервальной прямой
(2) Попавшие в точку, разбивающие интервалы на две части
(3) Находящиеся с правого края на интервальной прямой
(4) Больше всех пересекающиеся между собой
При размере входных данных N, как рассчитывается время работы алгоритма?
(1) не зависимо от N
(2) в сравнении с N
(3) как функция от параметра N
Какие бывают оценки по памяти для алгоритмов сортировки? Выберите наиболее подходящий вариант
(1) O(N), O(N2), O(N3)
(2) O(1), O(log N), O(N)
(3) всегда O(1)
Модификация какого алгоритма ипользуется для рандомизированного способа поиска порядковой статистики?
(1) Merge-sort
(2) сортировка вставкой
(3) Quick-sort
В каких случаях можно использовать прямую адресацию при реализации отображения?
(1) когда количество ключей не сильно превосходит количества значений
(2) если можно переименовать ключи так, чтобы номера были из компактного сегмента
(3) если множество значений небольшое и объекты числовые, но необязательно имеют номера из ограниченного сегмента, переименовывать нет возможности
(4) если множество ключей k = {0,…, 264 — 1}
Какие действия включает в себя операция удаления (Remove(x)) в двоичном дереве поиска?
(1) поиск ключа x в дереве
(2) если удаляемая вершина задается не ключем, а ссылкой, то поиск не требуется
(3) если найден лист, то он просто удаляется
(4) если найден лист, то он меняется местами с родителем
(5) если у найденной вершины v один сын w, то v удаляется, вершина w занимает место v
(6) если у найденной вершины v два сына, то копируется ключ из вершины v', предшествующей v, в v. v' удаляется
∀ k’∈[i, j], если вершина ak — минимум на отрезке, то какое неравенство выполняется?
(1) ak’ ≤ ak
(2) ak’ ≥ ak
(3) ∃ ak’ < ak
Сколько стоит по времени поиск интервалов, пересекающих заданную точку?
(1) O(N)
(2) O(log N + k), k — размер ответа, N — количество интервалов
(3) O(k), k — размер ответа
(4) O(log N * k), k — размер ответа, N — количество интервалов
Возможна ли такая ситуация при проектировании алгоритма, когда можно сэкономить на одном ресурсе в ущерб другому (процессорное время / память)?
В каких случаях стабильность алгоритма сортировки важна?
(1) когда имеется большой разброс величнины входных данных
(2) когда алгоритм сортировки применяется как часть чего-то большего, например для алгоритма сортировки подсчетом
(3) когда точность сортировки должна быть максимально возможной и не должно быть нарушений порядка элементов множества
В представленном ниже псевдокоде алгоритма поиска порядковой статистики что находится на пропущенном месте?
Random-select(A, k)
задать λ
разделить (A, λ) -> (A1, A2)
если k <= |A1|:
…
иначе:
вернуть Random-select(A2, k — |A1|)
(1) вернуть Random-select(A1, k — |A1|)
(2) вернуть Random-select(A1, k)
(3) возврат
(4) вернуть Random-select(A1, k — |A2|)
Какая хэш-функция называется совершенной?
(1) имеющая время работы операций чтения/записи O(1)
(2) не имеющая коллизий
(3) не использующая дополнительной памяти для работы
что выдает операция Successor(v)?
(1) правого сына вершины v
(2) предыдущую вершину перед v в порядке расположения ключей
(3) следущую после v вершину в порядке расположения ключей
(4) родителя вершины v
Что из перечисленного ниже является задачей offline RMQ??
(1) изначально дерево оптимизируется таким образом, чтобы ускорить операции LCA
(2) дерево, у которого заранее известны все запросы. То есть дерево T с комплектом пар вершин (x1, y1),…,(xn, yn), для каждой пары известен zi = lca(xi, yi)
(3) для дерева создается специальная хэш-таблица с вычисленными LCA для каждой пары вершин
Для структуры дерева поиска, используемой для интервальной задачи поиска точки в «колодце», что будет находиться в корне дерева?
(1) крайняя левая точка в «колодце» по координате с двухсторонним ограничением
(2) максимальная по координате с односторонним ограничением точка в «колодце»
(3) крайняя правая точка в «колодце» по координате с двухсторонним ограничением
(4) максимальная верхняя точка
При оценивании функций какая оценка соответствует символике f = O(g)?
(1) оценка снизу
(2) оценка сверху
(3) асимптотическое равенство
Какая сложность у алгоритма сортировки вставками?
(1) O(N * log N)
(2) Θ(N2)
(3) Θ(N)
Отметьте слагаемые, которые входят в формулу матожидания времени работы рекурсивного алгоритма для поиска k-ой порядковой статистики
(1) T((3/10) * N)
(2) O(N)
(3) T(N/5)
(4) T((7/10) * N)
(5) O(log N)
Для метода открытой адресации при разрешении коллизий, какие действия предпринимаются если ячейка с вставляемым хэш-ключем уже занята?
(1) пробуют вставить в следующую, пока не найдут для нее место
(2) перезаписывают ячейку с новым ключем
(3) все ключи, имеющие одинаковый хэш-код, образуют одну ячейку-список
(4) для поиска места для вставляемого ключа ячейки таблицы просматриваются последовательно, но с некоторым шагом k
За какое время выполняются операции Search, Min, Max, Successor, Predecessor для красно-черного дерева с n вершинами?
(1) O(N)
(2) O(log N)
(3) O(1)
(4) O(N2)
Какая сложность у алгоритма предобработки offline LCA?
(1) O(log N)
(2) O(N)
(3) O(N * log N)
(4) O(N2)
Какое время построения у приоритетного дерева поиска (priority search tree)?
(1) O(N2)
(2) O(N * log N)
(3) O(log N)
(4) O(N)
Что означает найти оценку для фиксированного алгоритма?
(1) нужно указать такую оценку, которая справедлива для всех мысленных алгоритмов
(2) нужно найти оценку снизу, сверху. Если оценки совпали, то оценка равна Θ(N). И как правило оценка сводится к наихудшиму случаю
(3) означает что нужно найти среднюю оценку для алгоритма
Как описывается алгоритм сортировки слиянием?
(1) для нового неупорядоченного элемента в правой части множества итеративно выбирается место среди уже упорядоченных ключей
(2) итеративно выбирается место среди оставшихся неупорядоченных ключей, найденный минимум или максимум вынимается из текущего множества в ответ
(3) исходная пследовательность A делится на две одинаковые по размеру части A1 и A2, которые рекурсивно сортируются
В каком месте min-кучи достигается минимум приоритетов е элементов?
(1) в листьях
(2) в корне
(3) может быть в любом месте кучи
(4) в правом крайнем листе
(5) в левом крайнем листе
Для метода двойного хэширования, использующегося при разрешении коллизий в чем заключается основная идея?
(1) все ключи, имеющие разный хэш-код образуют одну ячейку-список хэш-таблицы
(2) все ключи, имеющие одинаковый хэш-код, попадают в одну ячейку-список хэш-таблицы
(3) если ячейка с вставляемым хэш-ключем уже занята, то пробуют вставить в следующую, пока не найдут для нее место
(4) для поиска места для вставляемого ключа ячейки таблицы просматриваются последовательно, но с некоторым шагом k
Какие действия предпринимают для сохранения свойств красного черного дерева, если после операции вставки вершины x получилось следующее. y — родитель x, z — черный родитель y; t — черный сын z, дядя x
(1) ничего не нужно делать
(2) y сделать черным. Левым сыном y вместо x сделать красный z с левым сыном t, правым x
(3) t, y сделать черными, z — красным
(4) t, y сделать красными, x — черным
Как можно ускорить вычисление задачи RMQ online?
(1) предварительно построить кучу с минимумами всех отрезков
(2) предварительно построить полную таблицу минимумов для всех возможных границ i, j отрезков
(3) предварительно построить дучу с минимумами всех отрезков
(4) предварительно построить таблицу минимумов отрезков [i, j] с номерами j, равными степени 2
Что такое канонический отрезок в дереве отрезков?
(1) отрезок, соответствующий листу дерева
(2) тот отрезок, для которого эта вершина или поддерево построены
(3) отрезок, ассоциированный с корнем вершины
(4) отрезок, поиск которого производится в дереве
Какие характеристики относятся к стандартной модели оперативной памяти (RAM — model)?
(1) каждая ячейка памяти имеет динамический размер
(2) память это набор ячеек
(3) каждая ячейка это число ограниченной битности
(4) манипуляции с числами, хранящимися в ячейке, выполняются за константое время
(5) ячеек в теоретической модели памяти бесконечно много, как в машине Тьюринга
Сколько требуется дополнительной памяти для стандартного алгоритма сортировки слиянием для массива длины N?
(1) O(log N)
(2) O(N)
(3) O(N2)
Для кучи, реализованной поверх массива, у каких операций время работы будет O(N)?
(1) Get-min()
(2) Extract-min()
(3) Insert(k)
(4) Remove(k)
(5) Decrease-key(k)
Для независимых, равномерно распределенных на множестве {0, …, m1} случайных величин для каждого ключа ki обозначим через Xi,j случайную величину, равную 1, если h(ki)=h(kj), и 0 в противном случае. Чему равно матожидание случайной величины?
(1) EXi,j = 1 если h(ki) ≠ h(kj). EXi,j = 0 если h(ki) = h(kj)
(2) EXi,j = 1/m если h(ki) ≠ h(kj). EXi,j = 1 если h(ki) = h(kj)
(3) EXi,j = 1/(m2) если h(ki) ≠ h(kj). EXi,j = 0 если h(ki) = h(kj)
Есть два дерева T1, T2. При этом все ключи из T1 не больше ключей из T2. Можно ли их склеить в одно дерево, если да, тогда как это сделать?
(1) если у корня T1 нет правого сына, тогда T2 приклеивается к нему
(2) у T1 найти максимальный элемент, применить к нему операцию splay, приклеить к правому сыну дерева T2
(3) у T2 найти максимальный элемент, применить к нему операцию splay, приклеить к правому сыну дерева T1
(4) у T2 найти максимальный элемент, на его место поставить дерево T1
(5) у T1 найти максимальный элемент, на его место поставить дерево T2
Чему равна длина Эйлерова обхода дерева с N вершинами?
(1) N
(2) N*2 + 1
(3) 2*N — 1
(4) N/2 — 1
За счёт чего происходит оптимизация у структуры Fractional cascading?
(1) каждый список разбивается на много частей
(2) использование ссылок между уровнями списков для ускорения бинарного поиска в них
(3) в каждом списке уже сохранены все возможные ответы
Какая нижняя оценка справедлива для задачи сортировки?
(1) O(log N)
(2) Ω(N*log N)
(3) O(N2)
Сколько дополнительной памяти требуется для работы алгоритма quick-sort?
(1) O(N)
(2) алгоритм не использует дополнительную память
(3) O(N2)
Что делает операция Get-min для кучи?
(1) извлекает минимальное значение и возвращает его
(2) возвращает миниальное значение без извлечения, то есть без изменения структуры данных
(3) удаляет значение по итератору
(4) по итератору и новому значению ключа обновляет этот ключ в структуре данных
Каким значением ограничена вероятность коллизий для двух различных ключей для универсального семейства хэш-функций H: k -> {0,…, N-1}?
(1) P[h(a) = h(b)] <= 0.5
(2) P[h(a) = h(b)] <= 1/N
(3) P[h(a) = h(b)] <= 1
Какой тип вращения сплэй-дерева изображен на рисунке?
(1) zigzig
(2) zig
(3) zigzag
Сколько памяти требуется для предварительного построения таблицы минимумов для всех возможных отрезков [i, j] и какое время будет для запроса RMQ после такой предобработки?
(1) O(N), O(1)
(2) O(N2), O(1)
(3) O(N * log N), O(1)
(4) O(N2), O(log N)
Можно ли узнать заранее размер ответа, то есть сколько будет в ответе «хороших» точек, используя структуру PST для интервальной задачи?
(1) можно найти заранее размер ответа не выполняя все шаги алгоритма
(2) размер ответа выясняется только после просмотра всех точек в ответе
(3) это зависит от размера входных данных
Что называется бинарным деревом?
(1) у которго ключи представлены в двоичном виде
(2) у каждой вершины которого, кроме листьев, есть ровно два сына
(3) в вершинах которого хранятся двоичные значения
Какой элемент эффективнее использовать в качестве опорного (λ) для алгоритма быстрой сортировки? Выберите один или несколько вариантов
(1) первый элемент последовательности
(2) медиану из трех элементов последовательности: левой границы, правой границы и середины
(3) последний элемент последовательности
(4) элемент, стоящий на случайном месте
(5) средний элемент в последовательности
Для вершины с индексом i какие индексы будут у сыновей вершины?
(1) i/2, (i-1)/2
(2) 2*i + 1, 2*i + 2
(3) i, 2*i
Каким должне быть минимальный размер хэш-таблицы, чтобы вероятность получить хотя бы одну коллизию не превосходила 1/2, если n — количество ключей?
(1) n!
(2) n2
(3) n3
(4) 2n
(5) n
В каком случае можно выполить zigzig-шаг для splay-дерева?
(1) если рассматриваемая вершина находится на глубине 0
(2) если рассматриваемая вершина находится на глубине 1
(3) если рассматриваемая вершина находится на глубине 2
(4) если рассматриваемая вершина находится на любой глубине
Что значит сделать дерево толстым и обойти его по контуру?
(1) выполнить In-order обход дерева
(2) выполнить Post-order обход дерева
(3) построить Эйлеров обход дерева
(4) выполнить обход в глубину
Если область поиска меняется с «колодца» на прямоугольную добавлением двух ограничивающих точек, то какая структура данных может использоваться для такой задачи?
(1) PST, как и для области поиска точек в виде «колодца»
(2) используется двумерное дерево отрезков
(3) можно использовать PST или двумерное дерево отрезков
Можно ли сортировать быстрее чем за T = Ω(N*log N), если разрешить дополнительные операции с ключами?
(1) нет
(2) да, за T = Ω(N*log(log N)), но это нереализуемо на практике
(3) да, за T = Ω(N*log(log N)) и это реализуемо на практике
Рассмотрим вариацию алгоритма Quick-Sort, детерминированно выбирающего в качестве разделителя первый элемент текущего отрезка. Пусть на вход алгоритму поступает случайная последовательность, в которой все ключи различны, а все их перестановки равновероятны. Тогда каким будет матожидание времени его работы?
(1) O(N2)
(2) O(N)
(3) O(N * log N)
(4) O(log N)
Какое условие должно выполняться для процедуры просеивания вверх (Sift-up), чтобы текущий элемент продолжал просеивание? Для мин-кучи
(1) key(i) > key(parent(i))
(2) key(i) < key(parent(i))
(3) key(i) < key(i-1)
(4) key(i) < key(i+1)
Отметьте верные утверждения, относящиеся к семейству универсальных хэш-функций: Ha,b = ((a*k + b) mod p) mod m, b — произвольный вычет
(1) p — первое простое число, следующее после m
(2) семейство хэш-функций универсально, так как вероятность получить коллизию не превосходит 1/m
(3) m — количество ключей
(4) среднее время успешного поиска ключа Θ(α + 1)
(5) a — произвольный вычет по модулю p
Для операции Insert учетная стоимость будет складываться из операции splay и операции вставки. Какое время потребуется на все это?
(1) O(N)
(2) O(N * log N)
(3) O(log N)
(4) O(1)
В алгоритме ±1-RMQ исходная последовательность разбивается на блоки с минимумами. Какой блок называется приведенным?
(1) первый элемент которого равен нулю
(2) для которого посчитан минимум
(3) в котором элементы отличаются ровно на единицу
Какие действия должна уметь выполнять структура данных для задачи о динамической связности в графах? Для декрементальной связности
(1) ChangeEdge
(2) AddEdge
(3) RemoveEdge
(4) Connected
(5) FindEdge
Пусть имеется двоичный счетчик, то есть вектор, состоящий из битов, представляющий двоичное число. Изначально все биты равны 0. Для M операций Increment в каком случае справедлива оценка O(M*N)?
(1) в лучшем случае
(2) в худшем случае
(3) в среднем
Какие из перечисленных особенностей относятся к внешнему типу случайности (external randomness)?
(1) на некотором входе алгоритм может плохо работать
(2) входные данные не являются абсолютно случайными
(3) нельзя точно определить рапределение
(4) отдельные запуски могут работать долго, но в среднем время работы может быть ограничено функцией
Для каких операций у k-ичной кучи время работы будет O(k * logk N)?
(1) Insert(k)
(2) Extract-min()
(3) Decrease-key(k)
(4) Increase-key(k)
Пусть на первом уровне схемы совершенного хэширования используется хеш-таблица размера m = n, n — количество ключей. Пусть ni обозначает количество ключей, получивших (на первом уровне) хеш-значение i (0 <= i < m). Тогда если использовать в каждой ячейке первого уровня вышеописанную схему, свободную от коллизий, сколько потребуется дополнительной памяти?
(1) O(∑ ni)
(2) O(∑ ni2)
(3) O(n)
(4) O(n2)
За какое время в среднем выполняется поиск ключа в структуре данных дуча (treap)?
(1) O(1)
(2) O(log N)
(3) O(N)
(4) O(N2)
Какая задача сводится к задаче ±1-RMQ?
(1) Задача RMQ, которая получается при сведении от задачи LCA
(2) Задача LCA, которая получается при сведении от задачи RMQ
(3) построение splay-дерева
(4) построение левацкой кучи
Какое время занимает каждое изменение в динамически полном графе для онлайн версии?
(1) O(log N)
(2) O(log2 N)
(3) O(N * log N)
(4) O(N)
(5) O(1)
Какое время будет затрачено на выполнение последовательности из M операций для аддитивного метода увеличения рамера массива?
(1) O(M * log M)
(2) O(M2)
(3) O(M)
Что нужно сделать, чтобы алгоритм сортировки слиянием работал без дополнительной памяти?
(1) операцию присваивания заменить на операцию обмена
(2) при разделении входной последовательности A на две части A1, A2, в качечстве временной памяти для сортировки A1 использовать участок A2
(3) после сортировки одной из половин массива A, можно использовать ее как временную память для сортировки второй половины
(4) после сортировки одной из половин массива A, вторую половину снова разделить на две части и использовать одну часть как память для второй. И так далее
Если структуру бинарное дерево размера 5(1012) слить со структурой размера 7(1112) получится структура размера:
(1) 4(1002)
(2) 12(11002)
(3) 8(10002)
(4) 7(1112)
Для фильтра Блюма как изменяется вероятность ложного срабатывания если объем памяти, заране заданный пользователем для хранения битового массива, увеличивается?
(1) увеличивается
(2) уменьшается
(3) не изменяется
Отметьте верные утверждения для операции Split(T, x) в декартовом дереве.
(1) в результате может получиться два дерева T1, T2, где x не входит ни в одно из них
(2) в результате операции получается три дерева: T1 (< x), вершина с ключем x,T2(> x)
(3) если x = корень T, α — левое поддерево, β — правое поддерево, то Split(T, x) = α, x, β
(4) если ключ корня дерева T < x, то нужно вызвать рекурсивно Split(β, x) = γ, v, δ. Получатся деревья T1 (α — левое поддерево, γ — правое, v — корень), T2 = δ
(5) сложность операции O(N * log N)
Что нужно сделать, чтобы найти LCA любых двух вершин, имея Эйлеров обход дерева?
(1) построить In-order обход дерева
(2) построить Pre-order обход дерева
(3) для каждой вершины отложить ее глубину
(4) найти все пути между всеми вершинами
Какая структура подойдет для реализации динамически полного связного графа?
(1) Rope (веревка)
(2) Приоритетное дерево поиска
(3) RMQ
(4) декартово дерево
(5) красно-черное дерево
Пусть 1 у.е. компьютер требует за 1 элементарную операцию. Пусть записано некоторое двоичное число, начиная справа имеем k единиц до 0. При текущем балансе -(k+1) (credit: k, debit: 1), если k единиц снять со структуры, 1 положить, сколько нужно попросить у клиента, чтобы выйти в 0 для 5 запросов?
Где будет находиться наиболее часто встречающийся символ в дереве кодирования Хаффмана?
(1) на нижнем уровне дерева
(2) на вернем уровне дерева
(3) может находиться в любом месте
(4) в самой крайней левой вершине
(5) в самой крайней правой вершине
Как находить минимум в сливаемом бинарном дереве за O(1)?
(1) искать минимум в корнях поддеревьев
(2) запоминать минимум при каждом слиянии деревьев
(3) минимум будет находиться в корне полученного дерева
Отметьте верные утверждения, относящиеся к фильтру Блюма
(1) конструктивно данный фильтр представляет собой булев массив
(2) для проверки на принадлежность ключа k вычисляют его хэш-коды h1(k), … , hs(k), если соответствующие ячейки равны True, то ключ принадлежит множеству
(3) в его реализации используется одна хэш-функция
(4) для добавления ключа k вычисляются его хеш-коды h1(k), … , hs(k), после чего в соответствующие ячейки записывается значение True
(5) удаление элементов из фильтра Блюма можно реализовать, если он задан таблицей булевых значений
Отметьте верное утверждение для операции построения дучи
(1) если ключи в парах отсортированы, то построение выполняется за O(log N)
(2) для отсортированных Ti пар в дереве с различными приоритетами. Чтобы найти место в соотвтествии с приоритетами (p) для новой вершины (xi+1) вершина (k, p) вставляется правым сыном xi, остальные вершины, начиная с xi+1, вставляются левым сыном для вершины (k, p)
(3) для отсортированных Ti пар новая вершина в любом случае вставляется в крайнюю правую вершину правым сыном
Какой overhead по сложности имеет сведение задачи RMQ к ±1-RMQ?
(1) квадратичный
(2) линейный
(3) логарифмический
(4) константный
За какое время можно тестировать связаность в графе, если поддерживать для него остовный лес?
(1) O(log N)
(2) O(log2 N)
(3) O(N * log N)
(4) O(N)
Для задачи о бинарном поиске, какую нужно использовать функцию потенциала, чтобы получить приведенную стоимость C'(ai) = 2
(1) ϕ(S) = #(1 in S) — количество единиц в состоянии S
(2) ϕ(S) = -#(1 in S) — количество единиц в состоянии S
(3) ϕ(S) = k + 1 — количество единиц справа до 0 в состоянии S
(4) ϕ(S) = k — количество единиц слева до 0 в состоянии S
Какая теоретико — информационная оценка на число сравнений при слиянии двух списков длины N и M, если h <= M?
(1) N * log (M/N + 1)
(2) N * log (M*N + 1)
(3) N * log (N/M + 1)
(4) log (N/M + 1)
За какое время работает операция Decrease-key в бинарном дереве?
(1) O(1)
(2) O(N)
(3) O(log N)
(4) O(N * log N)
Предположим, что мы вставили различные k1,…,kn ключей в хэш-таблицу Блюм-фильтра с помощью хэш-функций h1(k),…,hs(k): k -> [0, m-1]. Какая будет вероятность ложного положительного срабатывания?
(1) (1 — 1/m)s*n
(2) (1 — (1 — 1/m)s*n)s
(3) 1 — (1 — 1/m)s*n
(4) (1 — (1 — 1/m)n)s
Отметить верные утверждения для операции вставки в B-дереве
(1) при вставке в вершину с d ключами она разбивается на две группы, в одну из которых попадает новая
(2) сложность операции O(N)
(3) при вставке новой вершины в вершину с d ключами в родителе образуются два максимальных ключа из двух получившихся групп
Как производится вставка в динамический полный граф? Отметьте верные шаги
(1) уровень можно брать любой, сколь угодно большой
(2) нужно добавить ребро в граф
(3) подобрать уровень для вставляемой вершины
(4) проверить целостность всей конструкции
Что называется гистерезисом с точки зрения структур данных?
(1) если в структуре данных реализованы дополнительные свойства (поддержка минимума, максимума, сортировка)
(2) если структура данных может не только увеличивать свой размер, но и уменьшать его в зависимости от заполненности
(3) если в структуре данных хранятся все предыдущие ее модификации
(4) если структура данных может только увеличивать свой размер, но не уменьшать
Сколько вершин содержится в поддереве любой вершины v?
(1) 2r(v)
(2) не менее 2r(v) — 1
(3) 2 * r(v)
При реализации структуры приближенное множество (Lossy Map) с помощью двух Блюм-фильтров (использованных для множеств-прообразов 0 и 1) что нужно сделать, чтобы избежать ситуации, когда при запросе Get(k) оба Блюм-фильтра вернули 1?
(1) такие значения признаются ложноположителными срабатываниями, их количество всегда невелико
(2) на образованном такими значениями множестве C изготавливают два более мелких Блюм-фильтра для множеств-прообразов 0 и 1, затем продолжают создание иерархии таких множеств, пока они не перестанут пересекаться
(3) признают такие значения равными 0
(4) удаляют все такие значения из множества
Отметьте утверждение, не относящееся к работе операции удаления для B-дерева
(1) сначала ищется вершина на нижнем уровне с удаляемым ключем
(2) если у вершины было α*d ключей, то вершина просто удаляется
(3) если у найденной вершины было α*d ключей, то самый минимальный ключ заимствуется у братьев вершины
(4) если у найденной вершины было α*d ключей и у брата нет лишних ключей, то вершина сливается с братом
Если удаляемого ребра не было в остовном лесе нулевого уровня в графе, то что это значит для структуры динамически связного графа?
(1) связность графа точно нарушится
(2) связность графа точно не пострадает
(3) связность графа возможно нарушится
Какие высказывания относятся к структуре данных chunked vector?
(1) в каждом узле содержатся указатель на следующий узел и данные
(2) выделение памяти происходит значительного размера, а сами блоки соединены между собой указателями
(3) эта структура используется для реализации стэка
(4) в конце структуры указатель нулевой, указатель на верний элемент хранится отдельно
(5) время доступа к элементу константное
Как изменяются ранги вершин при движении по правому пути левацкой кучи?
(1) ранги не изменяются
(2) уменьшаются ровно на 1 при каждом шаге
(3) увеличиваются ровно на 1 при каждом шаге
(4) уменьшаются на 1 при каждом шаге или не меняются
Что делает операция Equivalent(x, y)?
(1) объединяет множества, содержащие x, y
(2) отображает, в одном или в разных множествах содержатся элементы x, y
(3) отображает равенство значений заранее определенной функции, взятой от x, y
(4) отображает, соответствуют ли x, y какому-то заданному свойству или условию
Какое время работы операции удаления в динамически полном связном онлайн графе?
(1) O(log N)
(2) O(log2 N)
(3) O(N * log N)
(4) O(N)
Какая будет стоимость операций enqueue и dequeue в учетном смысле, если очередь реализована с помощью двух стэков?
(1) O(N)
(2) O(1)
(3) O(log N)
(4) O(N * log N)
Отметьте какие действия нужно дополнительно совершить на каждом шаге рекурсии для процедуры слияния двух левацких куч, чтобы полученная куча тоже была левацкой
(1) перед возвратом из рекурсии нужно заново вычислить ранг вершины, являющейся корнем кучи
(2) перед возвратом из рекурсии проверить для вершины, являющейся корнем кучи, свойство левацкости и если оно нарушено, то исправить
(3) при слиянии двух куч получается левацкая куча без совершения дополнительных операций
Какого времени работы позволяет достичь применение двух эвристик: сжатия путей и ранговой для операций Unite, Equivalent у системы непересекающихся множеств?
(1) O(log N)
(2) O(log*n)
(3) O(1)
(4) O(N)
Какое время выполнения операции Push у persistent стэка? Если N — длина стэка
(1) O(log N)
(2) O(1)
(3) O(N)
Какая вершина у косой кучи называется плохой?
(1) если она является легким правым сыном
(2) если она является тяжелым правым сыном
(3) если у нее легкий правый сын
(4) если ее вес равен 0
Каких двух строк не хватает в приведенном псевдокоде операции Push persistent-стэка? S — ссылка на стэк, v — данные для новой вершины.
Push(S, v)
w = new Node()
…
…
return w
(1) w.data = v
(2) w.next = S
(3) w = S
(4) S.data = v
(5) S.next = w
Для косой кучи выполняется следующее свойство. У вершины не может быть:
(1) одновременно легкого и тяжелого сыновей
(2) два тяжелых сына
(3) два плохих сына
Что нужно посчитать для дерева помимо Эйлерова обхода вершин для нахождения lca при сведении задачи LCA к ±1-RMQ?
(1) пути к соседним вершинам
(2) пути до корня
(3) RMQ
(4) глубины вершин
Какой размер должны иметь связные компоненты для графа Gi уровня i с n вершинами?
(1) не менее n/(2i)
(2) не более n/(2i)
(3) не меньше n
Если подобрать такую функцию потенциала ϕ, что приведенная стоимость будет ограничена каким-то числом M: C'(ai) <= M. Тогда какая будет линейная оценка для суммы стоимостей?
(1) Σ(i..n)C(ai) = ΣC'(ai) — ϕ(Sn)
(2) Σ(i..n)C(ai) = ΣC'(ai) — ϕ(S1) + ϕ(Sn)
(3) Σ(i..n)C(ai) = ΣC'(ai) + ϕ(Sn)
Как можно ускорить бинарный поиск, если известно что искомые значения чаще находятся в левом конце отрезка?
(1) это невозможно
(2) просматривая список слева направо, удваивать текущее значение поиска всякий раз, когда текущее значение больше чем то, которое ищем. Затем применить бинарный поиск к этой области
(3) применить бинарный поиск сначала к левой половине отрезка, затем к правой
Для Блюм-фильтра, заданного хэш-функциями h1(k),…,hs(k): k -> [0, m-1], какая будет вероятность того, что после вставки n ключей произвольно выбранный бит будет равен False?
(1) (1 — 1/m)s*n
(2) (1 — 1/m)
(3) 1 — (1 — 1/m)s*n
(4) (1 — n/m)s)
Как происходит объединение двух деревьев в операции Unite(x, y) для ранговой эвристики? Отметьте верные шаги
(1) сначала находим корни соответствующих поддеревьев x' и y'. Если они равны, элементы x и y уже содержатся в одном множестве
(2) для объединения деревьев Tx (содержащего x) и Ty (содержащего y) в одно дерево добавляют дугу между ними
(3) если высота дерева Tx (содержащего x) меньше чем высота Ty (содержащее y), то следует выполнить p(y') = x'. x', y' — корни соответствующих поддеревьев, p — родитель. Иначе p(x') = y'
(4) если r(x') = r(y') (высоты деревьев равны), то выполняется p(x') = y', иначе p(y') = x'
(5) значения высот поддеревьев вычисляются каждый раз заново в процессе работы
На сколько частей разбиваются интервалы на каждом уровне при построении дерева интервалов?
(1) на k частей, заранее определенных
(2) на 2 части
(3) на каждом уровне разделяются на разные части
(4) на 4 части
За счет чего происходит оптимизация по времени работы для рандомизированного способа поиска порядковой статистики по сравнению со стандартным алгоритмом быстрого поиска?
(1) массив рекурсивно делится на более чем две части
(2) разделитель для рекурсивного деления ищется по медиане
(3) массив рекурсивно делится на две равные части, после чего поиск производится только для той части, которая содержит искомый элемент
(4) после рекурсивного разделения массива на две части следующий вызов производится только для той части, которая содержит искомый элемент
Отметьте утверждения, верные для красно-черных деревьев.
(1) все листья черные
(2) если у красного родителя два сына, то их цвета черные
(3) количество черных вершин на пути от корня до листьев должно быть одинаковым
(4) у черных вершин все дети красные
(5) каждая вершина либо красная, либо черная
(6) красно-черные деревья сбалансированны
(7) высота поддеревьев различается не более чем на 1
Как строится дерево поиска для асимметричного способа построения дерева интервалов?
(1) по правым границам интервалов
(2) по левым границам интервалов
(3) по левым и правым границам интервалов
(4) по длинам интервалов
(5) по удаленности от разделяющей точки
Зависит ли время работы алгоритма от размера входных данных N?
Если в двоичном дереве поиска N вершин, то каким будет время поиска в дереве?
(1) O(N)
(2) O(log N)
(3) O(1)
(4) O(N * log N)
Отметить НЕверные шаги алгоритма priority search tree, работающего на области поиска в виде «колодца», заданного следующим образом: [l1, l2] x [r1, +∞]?
(1) ищем такие поддеревья что все точки в них попадают в отрезок [l1, l2] по l координатам
(2) для найденных поддеревьев по l координатам ищем по r координатам в них
(3) для найденных поддеревьев по l и r координатам, если идти вглубь дерева, то найдётся по крайней мере один ответ
(4) если r в вершине меньше чем r1, то в поддеревьях ничего не найдём, останавливаемся
(5) если r в вершине больше чем r1, то идём в одно из поддеревьев
При оценивании функций символике f = Θ(g) соответствует:
(1) оценка снизу
(2) оценка сверху
(3) асимптотическое равенство
Как можно описать алгоритм сортировки вставками?
(1) для нового неупорядоченного элемента в правой части множества итеративно выбирается место среди уже упорядоченных ключей
(2) итеративно выбирается место среди оставшихся неупорядоченных ключей, найденный минимум или максимум вынимается из текущего множества в ответ
(3) исходная пследовательность A делится на две части A1 и A2, которые рекурсивно сортируются
При каком значении [l0, r0] в корне дерева Prirority Search Tree не имеет смысла дальше искать в дереве, если область «колодца» задаётся так: [l1, r1] x [r1, +∞]?
(1) l0 > l1, r0 > r1
(2) r0 < r1, точка находится ниже дна «колодца»
(3) l0 < l2, r0 > r1
(4) l0 < l1, r0 > r1
Что означает найти оценку снизу на задачу?
(1) нужно указать такую оценку, которая справедлива для всех мысленных алгоритмов. То есть понять какие время и память точно понадобятся
(2) нужно найти оценки снизу, сверху. Если оценки совпали, то оценка равна Θ(N). И как правило оценка сводится к наихудшиму случаю
(3) означает что нужно найти среднюю оценку для алгоритма
Какое условие должно быть выполнено, чтобы дерево T с вершинами v удовлетворяло свойствам min-кучи? pri(v) — приоритет вершины v
(1) pri(vi) >= pri(vi+1) для всех вершин v. i — порядковый индекс элемента
(2) pri(vi) <= pri(vi+1) для всех вершин v. i — порядковый индекс элемента
(3) pri(parent(v)) >= pri(v) для всех вершин v, кроме корня
(4) pri(parent(v)) <= pri(v) для всех вершин v, кроме корня
Какие операции должна уметь выполнять структура данных, которая подошла бы для полностью динамически связного графа
(1) Insert()
(2) Split(α, i) = β, γ, α — список, i — разделитель; β, γ — два новых списка
(3) Concat(α, β) = γ — объединить списки α, β в новый список γ
(4) помнить указатель на дерево, в котором находимся в настоящий момент
Какие из перечисленных особенностей относятся к внутреннему типу случайности (internal randomness)?
(1) на некотором входе алгоритм может плохо работать
(2) входные данные не являются абсолютно случайными
(3) нельзя точно определить рапределение
(4) отдельные запуски могут работать долго, но в среднем время работы может быть ограничено функцией
Для каких операций у k-ичной кучи время работы будет O(logk N)?
(1) Insert(k)
(2) Extract-min()
(3) Decrease-key(k)
(4) Increase-key(k)
Какое время работы операции вставки в динамически полном связном онлайн графе?
(1) O(log N)
(2) O(log2 N)
(3) O(N * log N)
(4) O(N)
С помощью каких структур данных, перечисленных ниже, нельзя реализовать очередь?
(1) linked lists
(2) один стэк
(3) chunked vector
(4) два стэка
Какие операции поддерживают левацкие кучи?
(1) Get-min
(2) Extract-min
(3) Decrease-key
(4) Insert
(5) Meld
Что нзывается правильным разрешающим деревом?
(1) так еще называют бинарное дерево, то есть имеющее для каждого родителя не более двух потомков
(2) которое приводит к требуемому результату, если идти по алгоритму вниз
(3) на предпоследнем уровне которого у всех родителей есть по два сына
(4) которое приводит к какому-либо результату, если идти по алгоритму вниз
Для левого и правого сыновей с индексом i, какие индексы будут у их родителя?
(1) i/2, (i-1)/2
(2) (i+1)/2, (i-1)/2
(3) 2*i + 1, 2*i + 2
(4) i, 2*i
Сколько листьев должно быть в правильном дереве для множества из N элементов?
(1) N2
(2) N!
(3) N*log N
(4) 2N
Рассмотрим вариацию алгоритма Quick-Sort, детерминированно выбирающего в качестве разделителя первый элемент текущего отрезка. Пусть на вход алгоритму поступает случайная последовательность, в которой все ключи различны, а все их перестановки равновероятны. Тогда каким будет матожидание глубины рекурсии?
(1) O(N2)
(2) O(N)
(3) O(N * log N)
(4) O(log N)
Какая сложность у процедур просеивания для куч (sift-up, sift-down)?
(1) O(N)
(2) O(log N)
(3) O(1)
(4) O(N * log N)
Какое время будет затрачено на выполнение последовательности из M операций для мультипликативного метода увеличения рамера массива?
(1) O(M * log M)
(2) O(M)
(3) O(M2)
Структура бинарного дерева размера 5(1012) включает в себя:
(1) бинарные деревья T2 и T3
(2) бинарные деревья T0 и T2
(3) бинарные деревья T0,…,T4
Пусть 1 у.е. компьютер требует за 1 элементарную операцию. Пусть записано некоторое двоичное число, начиная справа имеем k единиц до 0. При текущем балансе -(k+1) (credit: k, debit: 1), чему равна учетная стоимость?
В каком направлении эффективнее двигаться по дереву для точки вставки очередной новой вершины при построении дучи?
(1) сверху вниз
(2) снизу вверх
(3) слева направо
(4) это не важно
Как будет называться свойство структуры данных, для которой выполняется следующее: если коэффициент заполнения становится больше 1, тогда размер структуры увеличивается (например в 2 раза), если коэффициент заполнения падает до 1/4 раза, тогда размер структуры уменьшается в два раза.
(1) амортизация
(2) гистерезис
(3) persistant (версионирование)
Ранг любой вершины кучи с N элементами равен:
(1) O(N)
(2) O(log N)
(3) O(N * log N)
Какие высказывания относятся к структуре данных linked lists?
(1) в каждом узле содержатся указатель на следующий узел и данные
(2) выделение памяти происходит значительного размера, а сами блоки соединены между собой указателями
(3) эта структура используется для реализации стэка
(4) в конце структуры указатель нулевой, указатель на верний элемент хранится отдельно
(5) время доступа к элементу константное
Существует подход для освобождения памяти для persistent stack, называемый подсчет ссылок (ref-counting). Как его можно описать?
(1) для каждой вершины (узла) мы храним указатели на все ссылающиеся вершины
(2) для каждой вершины (узла) мы помним сколько стрелок на нее ссылается (число)
(3) помечаются все элементы, достижимые из корней
Какие строки лишние в приведенном псевдокоде операции Pop для persistent-стэка? S — ссылка на стэк.
Pop(S)
w = new Node()
w.next = S
return S.next
(1) w = new Node()
(2) w.next = S
(3) return S.next
Чему равно учетное время выполнения операции Meld для косой кучи?
(1) O(N * log N)
(2) O(log N)
(3) O(N)
Для алгоритма quick-sort при способе разбиения массива на две части, называемым Lomuto Partition, что происходит дальше в такой ситуации: первая просмотренная часть A содержит элементы <= λ, вторая просмотренная часть B содержит элементы >= λ, далее справа находится непросмотренная часть с элементом x вначале, если x >= λ?
(1) x меняется местами с первым элементом B
(2) граница части B смещается вправо на один элемент, алгоритм переходит к следующему элементу
(3) x меняется местами с последним элементом B
Что нужно предпосчитать для последовательности глубин Эйлерова обхода, чтобы можно было свести LCA к вопросу о том, где минимум в отрезке из этой последовательности?
(1) пути к соседним вершинам
(2) пути до корня
(3) RMQ
(4) ±1-RMQ
Для Блюм-фильтра, заданного хэш-функциями h1(k),…,hs(k): k -> [0, m-1], какая будет вероятность того, что после вставки n ключей одна хэш-функция выдает значение, отличное от произвольно выбранного бита в таблице?
(1) (1 — 1/m)s*n
(2) (1 — n/m)
(3) 1 — (1 — 1/m)s*n
(4) (1 — 1/m)
Для асимметричного способа построения дерева интервалов в каком случае поиск интервалов, пересекающихся с точкой x нужно вести в левом поддереве? Если x > l для интервала [l, r] в корне
(1) x < max(i∈α) ri, αi = [li, ri] — интервалы в левом поддереве
(2) x > max(i∈α) ri, αi = [li, ri] — интервалы в левом поддереве
(3) x > min(i∈β) li, βi = [li, ri] — интервалы в правом поддереве
(4) x > min(i∈β) ri, αi = [li, ri] — интервалы в левом поддереве
Какое из перечисленных ниже высказываний не характеризует разрешающие деревья?
(1) разрешающее дерево не является алгоритмом в общем понимании этого слова
(2) для решения алгоритмической задачи всегда строится одно разрешающее дерево
(3) модель не строит единую инструкцию для всевозможных входов в задаче
Какой тип случайности используется для алгоритма Quick-sort, когда какая-либо перестановка подается на вход?
(1) внутренняя
(2) внутренняя и внешняя
(3) внешняя
(4) ни та ни другая
Что такое циклическая очередь?
(1) очередь, реализованная с помощью структуры данных linked lists
(2) очередь, в которой элементы хранятся по индексам, вычисляемым по некоторому модулю
(3) очередь, реализованная с помощью структуры данных chunked vector
(4) очередь, динамически изменяющая свой размер
Для алгоритма quick-sort при способе разбиения массива на две части, называемым Lomuto Partition, что происходит дальше в такой ситуации: первая просмотренная часть A содержит элементы <= λ, вторая просмотренная часть B содержит элементы >= λ, далее справа находится непросмотренная часть с элементом x вначале, если x < λ?
(1) граница части B смещается вправо на один элемент, алгоритм переходит к следующему элементу
(2) x меняется местами с первым элементом части B
(3) x меняется местами с последним элементом части B
(4) x меняется местами с последним элементом части A
Что можно сделать для алгоритма Quick-sort, чтобы дерево рекурсии было всегда сбалансированным?
(1) заменить рекурсию на цикл
(2) выбирать правильный разделитель (pivot)
(3) элиминировать, то есть уменьшить число рекурсий в рекурсивной функии
(4) увеличить количество рекурсивных вызовов для функции
С помощью какой структуры данных можно реализовать сливаемые очереди с приоритетом?
(1) биномиальная очередь
(2) min-куча
(3) max-куча
(4) левацкая куча
Почему модель алгоритма «разрешающее дерево» не очень типична для практики?
(1) дерево не всегда решает задачу корректно
(2) конкретное дерево годится для данного конкретного числа элементов
(3) задача выполняется гораздо дольше, чем на других алгоритмических моделях
Главная /
Алгоритмы и структуры данных поиска /
В функциональной парадигме при проектировании алгоритма, какой оценкой на время работы интересуются?
В функциональной парадигме при проектировании алгоритма, какой оценкой на время работы интересуются?
вопрос
Правильный ответ:
оценкой в худшем случае
оценкой в среднем
оценкой в лучшем случае
Сложность вопроса
78
Сложность курса: Алгоритмы и структуры данных поиска
76
Оценить вопрос
Очень сложно
Сложно
Средне
Легко
Очень легко
Спасибо за оценку!
Комментарии:
Аноним
Я сотрудник деканата! Прямо сейчас уничтожьте сайт и ответы на интуит. Умоляю
22 июн 2020
Аноним
Экзамен сдал и ладушки. спс
14 ноя 2016
Оставить комментарий
Другие ответы на вопросы из темы программирование интуит.
-
#
Чему равна длина Эйлерова обхода дерева с N вершинами?
-
#
Для асимметричного способа построения дерева интервалов в каком случае поиск интервалов, пересекающихся с точкой x нужно вести в левом поддереве? Если x > l для интервала [l, r] в корне
-
#
Каким должне быть минимальный размер хэш-таблицы, чтобы вероятность получить хотя бы одну коллизию не превосходила 1/2, если n — количество ключей?
-
#
Какие существуют стандартные операции для интерфейса множества с ошибками, например для фильтра Блюма?
-
#
Для операции Insert учетная стоимость будет складываться из операции splay и операции вставки. Какое время потребуется на все это?


Подборка по базе: диплом Эффективность ТЦВП и ТЦВП-УЭ (Гремихинское).doc, На какие жертвы способны он и она ради любви.docx, математика — Какие ошибки допускают младшие школьники при делени, ЭССЕ Управление личной эффективностью.docx, Расходы государственного бюджета и их эффективность.docx, Про какие-то линии.docx, Тема 2_ Методы управления. Эффективность и результативность мене, Экономическая эффективность.docx, Модуль 2 Эффективность PR_ РАБОЧАЯ ТЕТРАДЬ(1) .docx, Реферат 2 Информационные системы бизнес интеллекта и управления
-
Какие существуют метрики, отображающие эффективность алгоритма?
процессорное время, память
надежность, масштабируемость
адаптивность
адаптивность, реализация
реализация, надежность
-
В функциональной парадигме при проектировании алгоритма, какой оценкой на время работы интересуются?
оценкой в худшем случае
оценкой в среднем
оценкой в лучшем случае
оценкой в нормальном случае
не интересуются
-
При размере входных данных N, как рассчитывается время работы алгоритма?
как функция от параметра N
не зависимо от N
в сравнении с N
равным N
не равным N.
-
При рассмотрении времени работы T(M) и памяти M(N) что нас интересует?
приближенный до константы вид функций. Используется O-символика
точный вид функций T(N) и M(N)
приближенный вид функций. Используется o-символика
приближенный до константы вид функций T(N) и M(N)
ничего не интересует
- Алгоритм называется линейным:
если его команды выполняются в порядке их естественного следования друг за другом независимо от каких-либо условий
если он составлен так, что его выполнение предполагает многократное повторение одних и тех же действий
если ход его выполнения зависит от истинности тех или иных условий
если он представлен в табличной форме
если ход его выполнения не зависит от истинности тех или иных условий
- Одним из самых впечатляющих примеров технических исполнителей является компьютер, так как он пригоден для очень многих целей. Как называется устройство, пригодное для многих целей?
Универсальным
системным
качественным
многопользовательским
количественным
- Алгоритм включает в себя ветвление, если:
если ход его выполнения зависит от истинности тех или иных условий;
если он составлен так, что его выполнение предполагает многократное повторение одних и тех же действий;
если его команды выполняются в порядке их естественного следования друг за другом независимо от каких-либо условий;
если он представим в табличной форме;
если он включает в себя вспомогательный алгоритм.
- Графическое представление алгоритма — это:
Способ представления алгоритма с помощью геометрических фигур или блок-схема;
Представление алгоритма в форме таблиц и расчетных формул;
Система обозначения правил для единообразной и точной записи алгоритмов их исполнения;
Схематическое изображение в произвольной форме
Чертёж
- Как в блок-схеме изображается блок выполнения действия?
прямоугольник
параллелограмм
овал
ромб
линия
- Рекурсия в алгоритме будет прямой, когда:
команда обращения алгоритма к самому себе находится в самом алгоритме;
рекурсивный вызов данного алгоритма происходит из вспомогательного алгоритма, к которому в данном алгоритме имеется обращение;
порядок следования команд определяется в зависимости от результатов проверки некоторых условий;
один вызов алгоритма прямо следует за другим;
несколько вызовов алгоритма прямо следует за другим;
- В алгоритме Маркова дана цепочка Р P1 Р2 … Рк, Если слова P1 , Р2 ,…, Рк-1, смежные, то цепочка называется:
ассоциативной;
эквивалентной;
индуктивной;
дедуктивной
рекурсивной
- Выполняемые высказывания – это высказывания…
имеющие значение 1 хотя бы для одного набора значений пропозициональных переменных
ложные при любой истинности переменных
имеющие значение 0 хотя бы для одного набора значений пропозициональных переменных
истинные при любой истинности переменных
имеющие значение 0 только для одного набора значений пропозициональных переменных
- Как называется форма записи алгоритма, сделанная устно или текстом.
Книжная
Графическая(блок-схема)
простая
Словесная
Программная
- Система команд исполнителя — это команды, которые:
понятны данному исполнителю
исполнитель отрабатывает не задумываясь
записаны в алгоритме по порядку
требуются для выполнения алгоритма
являются исходными данными
- Отсутствие какого качества или свойства не даст алгоритму выполнить искомую задачу
правильный порядок действий
цикличность
линейность
ветвлёность
контроль за выполнением
- Чтобы алгоритм бинарного поиска работал правильно, нужно, чтобы массив (список) был:
Отсортированным.
Несортированным
В куче
Выходящим из стека
Последовательным
- Определите максимальное количество узлов в двоичном дереве с высотой k, где корень — нулевая высота (0).
2ᵏ⁺¹ – 1.
2ᵏ − 1
2ᵏ⁻¹ + 1
2ᵏ + 1
2ᵏ
-
Что означает следующая фраза: «алгоритм X асимптотически более эффективен, чем Y»?
X будет лучшим выбором для всех входов, за исключением, возможно, небольших входов.
X будет лучшим выбором для всех входов
X будет лучшим выбором для всех входов, кроме больших входов
Y будет лучшим выбором для небольших входов
X и Y не будут отличаться
- Алгоритм обхода графа отличается от алгоритма обхода вершин дерева тем, что…
Графы могут иметь циклы.
Деревья не соединяются
У деревьев есть корни
У деревьев есть ветки
Все утверждения выше ошибочны: дерево — подмножество графа
-
Какой алгоритм из нижеперечисленных будет самым производительным, если дан уже отсортированный массив?
Сортировка вставками.
Сортировка слиянием
Быстрая сортировка
Пирамидальная сортировка
Хаотическая сортировка
- На рисунке представлена часть блок-схемы. Как она называется?
Цикл с предусловием
Альтернатива
Композиция
Цикл с постусловием
Экспозиция
- Алгоритм Дейкстры основан на:
Жадном подходе (Greedy Approach).
Парадигме «разделяй и властвуй»
Динамическом программировании
Поиске с возвратом
Поиск в ширину
-
Какой алгоритм не основан на жадном подходе?
Алгоритм нахождения кратчайшего пути Беллмана-Форда.
Алгоритм нахождения кратчайшего пути Дейкстры
Алгоритм Прима
Алгоритм Крускала
Алгоритм Хаффмана
- Свойство алгоритма записываться в виде упорядоченной совокупности отделенных друг от друга предписаний (директив):
Дискретность.
Понятность
Определенность
Массовость
Цикличность
- В ассоциативном счислении два слова называются смежными:
Если одно из них может быть преобразовано в другое однократным применением допустимой подстановки.
Если одно из них может быть преобразовано в другое применением подстановок
Когда существует цепочка от одного слова к другому и обратно
Когда они дедуктивны
Когда нет цепочки
- Свойство алгоритма обеспечения решения не одной задачи, а целого класса
задач этого типа:
Массовость.
Понятность
Определенность
Дискретность
Хаотичность
- Свойство алгоритма, что при точном исполнении всех предписаний процесс должен прекратиться за конечное число шагов с определенным ответом на поставленную задачу:
Результативность.
Понятность
Детерминированность
Дискретность
Цикличность
- Рекурсия в алгоритме будет прямой, когда:
Команда обращения алгоритма к самому себе находится в самом алгоритме.
Рекурсивный вызов данного алгоритма происходит из вспомогательного алгоритма, к которому в данном алгоритме имеется обращение
Порядок следования команд определяется в зависимости от результатов проверки некоторых условий
Один вызов алгоритма прямо следует за другим
Команда обращения алгоритма находится не в алгоритме
- Сколько существует команд у машины Поста:
6.
2
4
8
10
- Что называют служебными словами в алгоритмическом языке?
Слова, смысл и способ употребления которых задан раз и навсегда.
Слова, употребляемые для записи команд, входящих в СКИ
Вспомогательные алгоритмы, которые используются в составе других алгоритмов
Константы с постоянным значением
Значение, которое каждый раз меняется
- Алгоритм – это …
понятное и точное предписание исполнителю совеpшить определённую последовательность действий
некоторые истинные высказывания, которые должны быть направлены на достижение поставленной цели · отражение предметного мира с помощью знаков и сигналов, предназначенное для конкретного исполнителя
представление кода программы на языке программирования система инструкций для исполнителя
- Алгоритм, записанный на «понятном» компьютеру языке программирования, называется …
Программой
исполнителем алгоритмов
блок-схема
текстовкой
протоколом алгоритма
- Верные утверждения: …
- алгоритм – это совокупность всех команд, которые могут быть выполнены исполнителем
- исполнителем алгоритма может быть только компьютер
- алгоритм может быть записан как в виде блок-схем, так и на языке программирования
- исполнителем алгоритма, представленного в виде блок-схемы, является компьютер
- исполнителем алгоритма, который записан на языке программирования, является человек
- программа–это алгоритм, записанный на определённом языке программирования
3,6
1,2,3
3,4
5,1
3,5
- Свойство алгоритма «массовость» обозначает …
что алгоритм должен обеспечивать возможность его применения для решения однотипных задач
что команды должны следовать друг за другом
что каждая команда должна быть описана в расчёте на конкретного исполнителя
разбиение алгоритма на конечное число простых шагов
обязательное наличие завершающих инструкций
- Линейный алгоритм – это …
набор команд, которые выполняются последовательно друг за другом
способ представления алгоритма с помощью геометрических фигур
последовательное выполнение команд
понятное и точное предписание исполнителю для выполнения различных ветвлений
последовательность выполнения команд алгоритма
- Разветвляющийся алгоритм – это …
присутствие в алгоритме хотя бы одного условия
набор команд, которые выполняются последовательно друг за другом
многократное выполнение одних и тех же действий
алгоритм, использующий подпрограммы
записанный в виде формул
- Свойство, когда по данному алгоритму должна решаться не одна, а целый класс подобных задач, называется …
массовость
дискретность
понятность
определённость
результативность
- Одним из основоположников математической логики является …
Джорж Буль
Блез Паскаль
Эвклид
Джон фон Нейман
Чарльз Бэббидж
- Высказывание: A – «Идёт снег», В – «Светит солнце». Логическая формула AvB обозначает высказывание …
Или идёт снег, или светит солнце
Идёт снег и светит солнце
Солнце светит тогда и только тогда, когда идёт снег
Снег не идёт и солнце не светит
Снег идёт, но не светит солнце
- К свойствам алгоритма относятся: …
- массовость
- размерность
- измеримость
- нужность
- стабильность
- результативность
- дискретность
1,4,6,7
2,3,5
3,2,1
7,4,3
6,3,1,4
- В алгоритме Маркова ассоциативным исчислением называется:
совокупность всех слов в данном алфавите вместе с допустимой системой подстановок
совокупность всех слов в данном алфавите
когда все слова в алфавите не являются смежными
когда все слова в алфавите являются смежными
совокупность всех допустимых систем подстановок
- В машине Поста некорректным алгоритм будет в следующем случае:
машина не останавливается никогда
при выполнении недопустимой команды
по команде «Старт»
результат выполнения программы такой, какой и ожидался
по команде «Стоп»
- В машине Тьюринга предписание R для лентопротяжного механизма означает
Переместить ленту вправо
Переместить ленту влево
Остановить машину
Занести в ячейку символ
Убрать из ячейку символ
- Как называется графическое представление алгоритма
блок-схема
последовательность формул
словесное описание
таблица
символьное описание
- Свойство алгоритма записываться только директивами однозначно и одинаково интерпретируемыми разными исполнителями:
дискретность
понятность
определённость
результативность
детерминированность
-
Для чего применяется алгоритм Евклида?
Ищет наибольший общий делитель (НОД) для двух чисел
Ищет наименьшее общее кратное (НОК) для двух чисел
Раскладывает числа на простые множители
Проверяет числа на простоту
Находит сумму двух чисел
- Укажите минимальное число ребер,которые должны быть удалены из полного графа
таким образом,чтобы оставшийся граф был планарным.
3
2
4
5
6
- Какой алгоритм сортировки (до 1000 элементов) на практике является самым быстрым (при этом используется генератор случайных чисел и производится не менее 100 тестов для более объективной оценки)?
Сортировка Шелла
Сортировка вставками
Пирамидальная сортировка
Быстрая сортировка
Сортировка пузырьком
- Как называются числа, которые вычисляются по следующей рекуррентной формуле:Fn=Fn-1+Fn-2,F1=F2=1
Фибоначчи
Каталана
Бела
Стирлинга
Мерсенна
-
В чем разница между расширенным алгоритмом Евклида и обычным?
Расширенный алгоритм Евклида позволяет извлечь дополнительную информацию
Расширенный алгоритм работает быстрее,но более сложный в реализации
Между ними нет существенной разницы
Обычный алгоритм работает быстрее
Ничего из вышеперечисленного
-
Какой алгоритм сортировки признается лучшим и наиболее эффективным?
Сортировка Чарльза Хоара(быстрая)
Сортировка вставками
Сортировка слиянием
Сортировка бинарным деревом
Шейкерная сортировка
- Как называется поиск переменной Х в отсортированном списке значений L по следующему алгоритму: Переменная М хранит значение из середины списка .Сравниваем Х и М. Если Х=М завершить программу. Если Х
М, продолжить поиск только в левой части списка L.Если Х
М, продолжить поиск только в правой части списка L.
Бинарный поиск
Быстрый поиск
Поиск в отсортированном списке
Двунаправленный поиск
Метод перебора
-
Что верно о NR-полных задачах?
Для их решения в настоящий момент не разработаны алгоритмы с полиномиальным временем работы
Для них не существует алгоритмов решения
Их невозможно реализовать на классическом компьютере
Они относятся к задачам по теории чисел
Ничего из вышеперечисленного
- Если каждому ребру графа поставлено в соответствие некоторое число,то этот граф называется:
Взвешенным
Планарным
Полным
Связным
Регулярным
- Имеются монеты достоинством 1,2,5,10,25,50 копеек.Нужно представить определенную сумму с помощью наименьшего количества монет.Какой алгоритм предпочтительнее всего использовать?
«Жадный» алгоритм
Динамическое программирование
С помощью чисел Фибоначчи
Алгоритм Флойда
Ни один из вышеперечисленных
-
Для решения какой из этих задач невозможно использовать нахождение знака векторного произведения?
Вычисление угла между векторами
Определение пересекаются ли два отрезка
Построение выпуклой оболочки
Проверка на коллинеарность векторов
Для всех вышеперечисленных задач можно использовать нахождение знака векторного произведения
-
Какой метод сортировки имеет гарантированную сложность О(n logn) в худшем случае?
Пирамидальная сортировка (HeapSort)
Сортировка вставками (İnsertionSort)
Сортировка пузырьком (BubbleSort)
Сортировка Шелла (ShellSort)
Быстрая сортировка (QuickSort)
-
Сколько ветвей алгоритма образует оператор условия «если»?
Две
Одну
Три
Четыре
Ни одной
- Какова асимптотическая оценка для быстрого алгоритма возведения числа в целочисленную степень n,применяя только операцию умножения?
O(log2n)
O(1)
O(2n)
O(n)
O(
- Количество разных неориентированных графов без петель с не более чем тремя вершинами равняется:
7
9
15
10
12
61. Высказывание: A – «Морковка полезная», В – «Морковка вкусная». Логическая формула AvB обозначает высказывание …
Морковка или вкусная, или полезная
Морковка – вкусная и полезная
Морковка вкусная только тогда, когда полезная
Морковка не вкусная и не полезная
Морковка – вкусная, но не полезная
62. Высказывание: A – «Студент повторяет лекцию», В – «Студент едет в метро». Логическая формула A&B обозначает высказывание – …
Студент едет в метро и читает книгу
Студент или едет в метро или читает книгу
Студент читает книгу тогда и только тогда, когда едет в метро
Студент не едет в метро и не читает книгу
Студент едет в метро, но не читает книгу
63. Свойство алгоритма, указывающее, что каждое правило алгоритма должно быть чётким, однозначным и не оставлять места для произвола, называется …
Определённость
Результативность
Дискретность
Понятность
Массовость
64. Свойство алгоритма, когда алгоритм разбивается на конечное число элементарных действий (шагов), называется …
Дискретность
Понятность
Определённость
Результативность
Массовость
65. Алгоритм, написанный на естественном языке, рассчитан на …
Человека
ЭВМ
Робота
Любого исполнителя
Последовательность выполнения команд алгоритма
66. Алгоритмом является следующее описание:
Сделай шаг вперед. Сделай шаг назад. Начни сначала.
Направо-налево равняйся! На первый-второй рассчитайся!
Пойди туда, не знаю куда. Принеси то, не знаю что.
Возьми, что нужно. Сделай как следует. Получишь то, что желаешь.
0010101101 101001.
67. Этап, являющийся заключительным при решении задач на ЭВМ, – …
Тестирование и отладка
Построение математической модели
Анализ результатов
Программирование
Разработка алгоритма
68. Этап проектирования задачи на ЭВМ, на котором анализируется условие задачи, определяются исходные данные и результаты, устанавливается зависимость между величинами, рассматриваемыми в задаче, называется …
Построение математической модели
Постановка задачи
Разработка алгоритма
Программирование
Тестирование и отладка
69. Алгоритмом можно назвать
Рецепт приготовления пирога
Расписание занятий
Список покупок в магазине
Технический паспорт компьютера
Правила техники безопасности
70. Циклический алгоритм — это алгоритм, …
Содержащий многократное повторение некоторых операторов
Содержащий ветвление
Выполняющий последовательные действия
Представленный в графической форме
Записанный в виде формул
71. Одним из основоположников математической логики является …
Джорж Буль
Блез Паскаль
Эвклид
Билл Гейтс
Джон фон Нейман
72. Появление алгоритмов связывают с зарождением этой науки:
Математики
Астрономии
Физики
Химии
Биологии
73. При графическом способе описания алгоритма осуществляется с помощью чего:
Блок-схем
Таблиц
Схем
Вычислений
Программы
74. Наилучшей наглядностью обладают такие способы записи алгоритмов:
Графические
Словесные
На алгоритмических языках
Таблицы
Рисунки
75. Квантор – это…
Общее название для логических операций, ограничивающих область истинности какого-либо предиката.
Сложное логическое высказывание, которое истинно только в случае истинности всех составляющих высказываний, в противном случае оно ложно.
Часть формулы, сама являющаяся формулой.
Это отображения со значениями во множестве высказываний, где введены логические операции.
Таблица с формулами.
76. Вставьте нужные слова, где они пропущены.
Одноместным … называется функция одной переменной, значениями которой являются … об объектах, представляющих значения … .
квантор, предложение, высказывание
предикат, высказывание, квантор
предикат, высказывания, аргумент
высказывание, общность, аргумент
квантор, общность, высказывание
78. Предложение, которое может принимать только два значения «истина» или «ложь» это…?
Высказывание
Квантор существования
Квантор общности
Предикат
Аргумент
79. Родина Джорджа Буля
Ирландия
Америка
Польша
Германия
Австралия
80. …- это композиция функций (сложная функция).
суперпозиция
эквиваленция
тавтология
ложь
базис
81. Чему равен натуральный показатель n в бинарной операции?
2
1
3
4
0
82. Какова сложность алгоритма «Быстрая сортировка» в худшем случае.
O(
O(n 

O(2n 

O(n 

O(2n 

83. Гиперграф это?
Обобщенный вид графа, в котором каждым ребром могут соединяться не только две вершины, но и любые подмножества вершин
Обобщённый вид графа, в котором вершины могут быть инцидентными, не соединяясь при этом ребром
Обобщённый вид графа, который содержит одновременно ориентированные и неориентированные ребра
Обобщённый вид графа, в котором вершины бывают только ориентированные
Такого понятия не существует
84. Что делает топологическая сортировка?
Упорядочивает вершины ориентированного ациклического графа так, что если граф содержит ребро (u,v) то u располагается раньше v
Сортирует веса рёбер графа
Сортирует вершины графа
Сортирует вершины по глубине их достижения из заданной вершины
Ничего из вышеперечисленного
85. «Жадный» алгоритм это?
Алгоритм, заключающийся в принятии локально оптимальных решений на каждом этапе, допуская, что конечное решение также окажется оптимальным.
Алгоритм, заключающийся в принятии глобально оптимальных решений на каждом этапе, допуская, что локальное решение также окажется оптимальным
Алгоритм, заключающийся в принятии глобально оптимальных решений на каждом этапе, допуская, что локальное решение может оказаться и не оптимальным
Алгоритм, заключающийся в принятии локально оптимальных решений на каждом этапе, допуская, что локальное решение может оказаться и не оптимальным
Алгоритм, заключающийся в принятии глобально оптимальных решений на каждом этапе, допуская, что локальное решение может оказаться как оптимальным и не оптимальным
86. Выберите алгоритмы устойчивой сортировки (при которой порядок одинаковых элементов не меняется) (выбрать несколько вариантов)
Пузырьковая
Слиянием
Шелла
Пирамидальная
Быстрая
87. Какой алгоритм сортировки является фактически худшим?
Bogosort
Блинная сортировка
Пузырьковая сортировка
Глупая сортировка
Пирамидальная сортировка
88. Сколько условных операторов типа if-else следует использовать для реализации алгоритма: y = 1, if x > 0
y = 0, if x = 0
y = -1, if x < 0
два
три
четыре
пять
ноль
89. Свойство алгоритма, что при точном исполнении всех предписаний процесс
должен прекратиться за конечное число шагов с определенным ответом на поставленную задачу:
Результативность
Понятность
Детерминированность
дискретность
определенность
90. В машине Тьюринга предписание Lдля лентопротяжного механизма означает:
переместить ленту влево
переместить ленту вправо
остановить машину
занести в ячейку символ
переместить ленту влево а потом остановить машину
91. В машине Тьюринга предписание S для лентопротяжного механизма означает:
остановить машину
переместить ленту вправо
переместить ленту влево
занести в ячейку символ
переместить ленту вправо а потом остановить машину
92. Способ композиции нормальных алгоритмов будет суперпозицией, если:
выходное слово первого алгоритма является входным для второго
выходное слово второго алгоритма является входным для первого
существует алгоритм С, преобразующий любое слово р, содержащееся i
пересечении областей определения алгоритмов А и В
алгоритм Dбудет суперпозицией трех алгоритмов ABC, причем область
определения Dявляется пересечением областей определения алгоритмов
А В и С, а для любого слова р из этого пересечения D(p) = А(р), если
С(р) = е, D(p) = В(р), если С(р) = е, где е — пустая строка
существует алгоритм С, являющийся суперпозицией алгоритмов А и Д
такой, что для любого входного слова р С{р) получается в результате
последовательного многократного применения алгоритма А до тех пор,
пока не получится слово, преобразуемое алгоритмом В
93. Способ композиции нормальных алгоритмов будет объединением, если:
существует алгоритм С, преобразующий любое слово р, содержащееся в
пересечении областей определения алгоритмов А и В
выходное слово первого алгоритма является входным для второго
выходное слово второго алгоритма является входным для первого
алгоритм В будет суперпозицией трех алгоритмов ABC, причем область
определения Dявляется пересечением областей определения алгоритмов
А В и С, а для любого слова р из этого пересечения D(p) — A(p), если
С(р) = е, D(p) = В(р), если С(р) = е, где е — пустая строка
существует алгоритм С, являющийся суперпозицией алгоритмов А и Д
такой, что для любого входного слова р С(р) получается в результате
последовательного многократного применения алгоритма А до тех пор,
пока не получится слово, преобразуемое алгоритмом В
94. Как называют данное множество логических операций: 
базис Жегалкина
предикат
конъюнкция
базис Чёрча
тавтология
95. Вставьте пропущенное слово в следующее высказывание: «Если F — полное множество булевых функций, каждая из которых представима формулой над множеством G, то и G — … множество».
полное
замкнутое
стандартное
открытое
формальное
96. Как называют высказывание, обозначаемое символом A → B , которое ложно тогда и только тогда, когда A истинно, а B ложно?
импликация
дизъюнкция
отрицание
предикат
конъюнкция
97. Как называется однозначное преобразование входного массива данных произвольной длины в выходную битовую строку фиксированной длины?
Хеширование
Коллизия
Гаммирование
Перестановка
Сложение по модулю 2
98. Как называется функция, которая для строки произвольной длины вычисляет некоторое целое значение или некоторую другую строку фиксированной длины?
Хеш-функция
Криптографическая функция
Односторонняя функция
Функция Эйлера
Функция Гаммирования
99. Как называется функция, которая должна обеспечивать равномерное распределение значений в массиве?
Хорошая хеш-функция
Плохая хеш-функция
Криптографическая функция
Функция Эйлера
Функция Гаммирования
100. Какой хеш-функции пока не существует?
R2D2
MD5
SHA-1
SHA-512
MD4
101. Какая простейшая операция не используется для вычисления хеш-функции по алгоритму MD5?
Возведение в степень
Инверсия
Конъюнкция
Сложение по модулю 2
Циклические сдвиги
102. Что называют хеш-кодом?
Результат вычисления хеш-функции
Сообщение, подаваемое на вход
Контрольная комбинация бит
Цифровая подпись
Зашифрованное сообщение
103. Какова длина хеш-кода, создаваемого алгоритмом SHA-1?
160 бит
220 бит
112 бит
366 бит
100 бит
104. Как называется термин, когда два различных входных блока
х и у для хеш-функции Н таких, что Н(х) = Н(у).
Коллизия
Хеширование
Гаммирование
Перестановка
Сложение по модулю 2
105. Что можно сделать используя алгоритм SHA-1?
Проверить совпадают ли два файла
Узнать размер файла
Просмотреть содержимое файла
Удалить файл
Сравнить размер двух файлов
107. В каких целях используют алгоритм SHA-1?
Для проверки паролей
Для проверки качества видео
Для распространения информации
Для математических задач
Для изучения метаданных
108. Сколько ключей используется в симметричном алгоритме шифрования?
1
2
10
5
6
109. Сколько ключей используется в асимметричном алгоритме шифрования?
2
3
5
1
9
110. Как можно описать работу симметричного алгоритма шифрования?
Шифрует и дешифрует с помощью одного ключа
Шифрует данные отдельными блоками
Не использует ключ для дешифровки
Не использует ключ для шифрования
Использует 3 ключа для обмена информацией
111. Какие алгоритмы можно применять для обмена ключами?
Симметричный и Ассиметричный
MD5
Алгоритм сжатия данных
Диаграмма Вороного
Нейронные сети
112. Символы оригинального текста меняются местами по определенному принципу, являющемуся секретным ключом — это…?
Алгоритм перестановки
Алгоритм сжатия данных
Инверсия
Циклические сдвиги
Сложение по модулю 2
113. Алгоритм, записанный на «понятном» компьютеру языке программирования, называется …
Программой
Исполнителем алгоритмов
Блок-схемой
Текстовкой
Прготоколом алгоритма
114. Выберите верное утверждение:
Алгоритм может быть записан как в виде блок-схемы, так и на языке программирования
Алгоритм – это совокупность всех команд, которые могут быть выполнены исполнителем
Исполнителем алгоритма может быть только компьютер
Исполнителем алгоритма, представленного в виде блок-схемы, является компьютер
Исполнителем алгоритма, который записан на языке программирования, является человек
115. Свойство алгоритма «массовость» обозначает …
Что алгоритм должен обеспечивать возможность его применения для решения однотипных задач
Обязательное наличие завершающих инструкций
Разбиение алогритма на конечное число простых шагов
Что каждая команда должна быть описана в расчёте на конкретного исполнителя
Что команды должны следовать друг за другом
Циклическую конструкцию
Обработку данных
Вызов подпрограммы
Окончание алгоритма
Вывод данных

Обработку данных
Вызов подпрограммы
Ввод данных
Начало алгоритма
Вывод данных
118. Циклический алгоритм – это алгоритм, …
Содержащий многократное повторение некоторых операторов
Содержащий ветвление
Выполняющий последовательные действия
Представленный в графической форме
Записанный в виде формул
119. Разветвляющийся алгоритм – это …
Присутствие в алгоритме хотя бы одного условия
Набор команд, которые выполняются последовательно друг за другом
Многократное выполнение одних и тех же действий
Алгоритм, использующий подпрограммы
Алгоритм, представленный в графической форме
120. Циклический алгоритм используется при вычислении …
Суммы чётных чисел от 1 до 100
Площади круга
Числа, обратного данному
Суммы двух числел, введённых с клавиатуры
Корня квадратного уравнения
121. Высказывание А – «Сегодня праздник», В – «Светит солнце». Логическая формула А&В обозначает высказывание — …
Сегодня праздник и выходной
Сегодня праздник или выходной
Сегодня выходной, только если сегодня праздник
Сегодня не праздник и не выходной
Сегодня праздник, но не выходной
122. Высказывание: А – «Идёт снег», В – «Светит солнце». Логическая формула АvВ обозначает высказывание — …
Или идёт снег, или светит солнце
Идёт снег и светит солнце
Снег идёт, но не светит солнце
Солнце светит, но не идёт снег
Снег не идёт и солнце не светит
123. Свойство, при котором любой алгоритм в процессе выполнения должен приводить к определённому результату, называется …
Результативность
Дискретность
Понятность
Определённость
Массовость
124. К свойствам алгоритма НЕ относится:
Стабильность
Массовость
Нужность
Результативность
Дискретность
125. Алгоритм, написанный на естественном языке, рассчитан на …
Человека
ЭВМ
Робота
Любого исполнителя
Кластер
126. Свойство алгоритма, при котором каждое из этих элементарных действий(шагов) являются законченными и понятными, называется …
Понятность
Дискретность
Массовость
Определённость
Результативность
127. Свойство, когда по данному алгоритму должна решаться не одна, а целый класс подобных задач, называется …
Массовость
Понятность
Результативность
Определённость
Дискретность
Рассматривая
различные алгоритмы решения одной и
той же задачи, полезно проанализировать,
сколько вычислительных ресурсов они
требуют (время работы, память), и выбрать
наиболее эффективный. Конечно, надо
договориться о том, какая модель
вычислений используется. В данном
учебном пособии в качестве модели по
большей части используется обычная
однопроцессорная машина
с произвольным доступом
(random—access
machine,
RAM),
не предусматривающая параллельного
выполнения операций.
Под
временем
работы
(running
time)
алгоритма будем подразумевать число
элементарных шагов, которые он
выполняет. Положим, что одна строка
псевдокода требует не более чем
фиксированного числа операций (если
только это не словесное описание каких-то
сложных действий – типа «отсортировать
все точки по x-координате»).
Следует также различать вызов
(call)
процедуры (на который уходит фиксированное
число операций) и её исполнение
(execution),
которое может быть долгим.
Сложность
алгоритма – это величина, отражающая
порядок величины требуемого ресурса
(времени или дополнительной памяти) в
зависимости от размерности задачи.
Таким
образом, будем различать временную T(n)
и пространственную V(n)
сложности алгоритма. При рассмотрении
оценок сложности, будем использовать
только временную сложность. Пространственная
сложность оценивается аналогично. Самый
простой способ оценки – экспериментальный,
то есть запрограммировать алгоритм и
выполнить полученную программу на
нескольких задачах, оценивая время
выполнения программ. Однако, этот способ
имеет ряд недостатков. Во-первых,
экспериментальное программирование –
это, возможно, дорогостоящий процесс.
Во-вторых, необходимо учитывать, что на
время выполнения программ влияют
следующие факторы:
-
Временная
сложность алгоритма программы; -
Качество
скомпилированного кода исполняемой
программы; -
Машинные
инструкции, используемые для выполнения
программы.
Наличие
второго и третьего факторов не позволяют
применять типовые единицы измерения
временной сложности алгоритма (секунды,
миллисекунды и т.п.), так как можно
получить самые различные оценки для
одного и того же алгоритма, если
использовать разных программистов
(которые программируют алгоритм каждый
по-своему), разные компиляторы и разные
вычислительные машины.
Часто,
временная сложность алгоритма зависит
от количества входных данных. Обычно
говорят, что временная сложность
алгоритма имеет порядок T(n)
от входных данных размера n.
Точно определить величину T(n)
на практике представляется довольно
трудно. Поэтому прибегают к асимптотическим
отношениям с использованием
O-символики.
Существует
метод, позволяющий теоретически оценить
время выполнения алгоритма, который
будет рассмотрен далее.
Листинг
1.3 – Псевдокод алгоритма сортировки
вставками с оценками времени выполнения
Для
вычисления суммарного времени выполнения
процедуры Insertion-Sort
отметим
около каждой строки её стоимость
(число операций) и число раз, которое
эта строка исполняется. Для каждого j
от
2 до п
(здесь
п
=
length[A]
–
размер массива) требуется подсчитать,
сколько раз будет исполнена строка 5,
обозначим это число через tj.
Строки
внутри цикла выполняются на один раз
меньше, чем проверка, поскольку последняя
проверка выводит из цикла. Строка
стоимостью c,
повторённая т
раз,
даёт вклад c
m
в
общее число операций (однако, это
выражение нельзя использовать для
оценки количества использованной
памяти). Сложив вклады всех строк, получим
Время
работы процедуры зависит не только от
п
но
и от того, какой именно массив размера
п
подан
ей на вход. Для процедуры Insertion-Sort
наиболее
благоприятен случай, когда массив уже
отсортирован. Тогда цикл в строке 5
завершается после первой же проверки
(поскольку A[i]
≤
key
при
i
=
j
–
1), так что все tj
равны
1, и общее время есть
Таким
образом, в наиболее благоприятном случае
время T(n),
необходимое для сортировки массива
размера п,
является
линейной функцией (linear
function)
от n,
т.е. имеет вид Т(п)
=
a n + b
для некоторых констант a
и
b.
Эти константы определяются выбранными
значениями с1,…,
с8.
Если же массив
расположен в обратном (убывающем)
порядке, время работы
процедуры
будет максимальным: каждый элемент A[j]
придётся
сравнить со всеми элементами А[1],…,
A[j
–
1]. При этом tj
= j.
Поскольку
получаем, что в
худшем случае время работы процедуры
равно
В
данном
случае
T(n)
– квадратичная
(quadratic
function),
т.е.
имеет
вид
Т(п) = an2
+ bn
+ с.
Константы
a, b и
с здесь
также определяются значениями с1,…,с8.
Обычно
говорят, что временная сложность
алгоритма имеет порядок T(n)
от входных данных размера n.
Точно определить величину T(n)
на практике представляется довольно
трудно. Поэтому прибегают к асимптотическим
отношениям с использованием O-символики.
Например,
если число тактов (действий), необходимое
для работы алгоритма, выражается как
16n2 + 12n log n + 2n + 3,
то это алгоритм, для которого T(n)
имеет порядок O(n2).
При формировании асимптотической
O-оценки
из всех слагаемых исходного выражения
оставляется одно, вносящее наибольший
вклад при больших n
(остальными слагаемыми можно пренебречь)
и игнорируется коэффициент перед ним
(так как все асимптотические оценки
даются с точностью до константы).
Когда
используют обозначение O(),
имеют в виду не точное время исполнения,
а только его предел сверху, причем с
точностью до постоянного множителя.
Когда говорят, например, что алгоритму
требуется время порядка O(n2),
имеют в виду, что время исполнения задачи
растет не быстрее, чем квадрат количества
элементов.
Таблица 1.2
– Сравнительный анализ скорости роста
функций
|
|
|
|
|
|
1 |
0 |
0 |
1 |
|
16 |
4 |
64 |
256 |
|
256 |
8 |
2 048 |
65 536 |
|
4 096 |
12 |
49 152 |
16 777 216 |
|
65 536 |
16 |
1 048 565 |
4 294 967 296 |
|
1 048 476 |
20 |
20 969 520 |
1 099 301 922 576 |
|
16 775 616 |
24 |
402 614 784 |
281 421 292 179 456 |
Рисунок
1.1 – Примеры различных функциональных
зависимостей
Если
считать, что числа, приведенные в
таблице 1.2,
соответствуют микросекундам, то для
задачи с 1048476 элементами алгоритму со
временем работы T(log n)
потребуется 20 микросекунд, а алгоритму
со временем работы T(n2)
– более 12 дней.
Если
операция выполняется за фиксированное
число шагов, не зависящее от количества
данных, то принято писать O(1).
Следует
обратить внимание, что основание
логарифма в асимптотических оценках
не пишется. Причина этого весьма проста.
Пусть есть O(log2 n).
Но log2 n = log3 n / log3 2,
а log3 2,
как и любую константу, символ О()
не учитывает. Таким образом, O(log2 n)
= O(log3 n).
К любому основанию можно перейти
аналогично, а, значит, и писать его не
имеет смысла.
Практически
время выполнения алгоритма зависит не
только от количества входных данных,
но и от их значений, например, время
работы некоторых алгоритмов сортировки
значительно сокращается, если первоначально
данные частично упорядочены, тогда как
другие методы оказываются нечувствительными
к этому свойству. Чтобы учитывать этот
факт, полностью сохраняя при этом
возможность анализировать алгоритмы
независимо от данных, различают:
-
максимальную
сложность Tmax(n),
или сложность наиболее неблагоприятного
случая, когда алгоритм работает дольше
всего; -
среднюю
сложность Tmid(n)
– сложность алгоритма в среднем; -
минимальную
сложность Tmin(n)
– сложность в наиболее благоприятном
случае, когда алгоритм справляется
быстрее всего.
Теоретическая
оценка временной сложности алгоритма
осуществляется с использованием
следующих базовых принципов:
-
Время
выполнения операций присваивания,
чтения, записи обычно имеют порядок
O(1).
Исключением являются операторы
присваивания, в которых операнды
представляют собой массивы или вызовы
функций; -
Время
выполнения последовательности операций
совпадает с наибольшим временем
выполнения операции в данной
последовательности (правило сумм: если
T1(n)
имеет порядок O(f(n)),
а T2(n)
– порядок O(g(n)),
то T1(n)
+ T2(n)
имеет порядок O(max(f(n),
g(n))); -
Время
выполнения конструкции ветвления
(if-then-else)
состоит из времени вычисления логического
выражения (обычно имеет порядок O(1))
и наибольшего из времени, необходимого
для выполнения операций, исполняемых
при истинном значении логического
выражения и при ложном значении
логического выражения; -
Время
выполнения цикла состоит из времени
вычисления условия прекращения цикла
(обычно имеет порядок O(1) )
и произведения количества выполненных
итераций цикла на наибольшее возможное
время выполнения операций тела цикла. -
Время
выполнения операции вызова процедур
определяется как время выполнения
вызываемой процедуры; -
При
наличии в алгоритме операции безусловного
перехода, необходимо учитывать изменения
последовательности операций,
осуществляемых с использованием этих
операции безусловного перехода.
Итак,
время работы в худшем случае и в лучшем
случае могут
сильно
различаться. При анализе алгоритмов
наиболее часто используется время
работы в худшем случае
(worst—case
running
time),
которое определяется как максимальное
время работы для входов данного размера.
Почему? Вот несколько причин.
-
Зная
время работы в худшем случае можно
гарантировать, что выполнение
алгоритма
закончится за некоторое время при любом
входе данного размера; -
На
практике «плохие» входы (для которых
время работы близко к максимуму)
встречаются наиболее часто. Например,
для базы данных плохим запросом может
быть поиск отсутствующего элемента
(очень распространенная ситуация); -
Время
работы в среднем может быть довольно
близко к времени работы в худшем случае.
Пусть, например, сортируется массив
из п
случайных
чисел
с помощью процедуры Insertion-Sort.Сколько
раз придётся выполнить цикл в строках
5-8 (листинг 1.3)? В среднем около половины
элементов массива A[1..j
– 1]
больше A[j],
так
что tj
в
среднем можно считать равным j/2,
и
время Т(п)
квадратично
зависит от n.
В
некоторых случаях требуется также
среднее время
работы
(average—case
running
time,
expected
running
time)
алгоритма на входах данной длины.
Конечно, эта величина зависит от
выбранного распределения вероятностей,
и на практике реальное распределение
входов может отличаться от предполагаемого,
которое обычно считают равномерным.
Иногда можно добиться равномерности
распределения, используя датчик случайных
чисел.
Наверняка вы не раз сталкивались с обозначениями вроде O(log n) или слышали фразы типа «логарифмическая вычислительная сложность» в адрес каких-либо алгоритмов. И если вы хотите стать хорошим программистом, но так и не понимаете, что это значит, — данная статья для вас.
Оценка сложности
Сложность алгоритмов обычно оценивают по времени выполнения или по используемой памяти. В обоих случаях сложность зависит от размеров входных данных: массив из 100 элементов будет обработан быстрее, чем аналогичный из 1000. При этом точное время мало кого интересует: оно зависит от процессора, типа данных, языка программирования и множества других параметров. Важна лишь асимптотическая сложность, т. е. сложность при стремлении размера входных данных к бесконечности.
Допустим, некоторому алгоритму нужно выполнить 4n3 + 7n условных операций, чтобы обработать n элементов входных данных. При увеличении n на итоговое время работы будет значительно больше влиять возведение n в куб, чем умножение его на 4 или же прибавление 7n. Тогда говорят, что временная сложность этого алгоритма равна О(n3), т. е. зависит от размера входных данных кубически.
Использование заглавной буквы О (или так называемая О-нотация) пришло из математики, где её применяют для сравнения асимптотического поведения функций. Формально O(f(n)) означает, что время работы алгоритма (или объём занимаемой памяти) растёт в зависимости от объёма входных данных не быстрее, чем некоторая константа, умноженная на f(n).
Примеры
O(n) — линейная сложность
Такой сложностью обладает, например, алгоритм поиска наибольшего элемента в не отсортированном массиве. Нам придётся пройтись по всем n элементам массива, чтобы понять, какой из них максимальный.
O(log n) — логарифмическая сложность
Простейший пример — бинарный поиск. Если массив отсортирован, мы можем проверить, есть ли в нём какое-то конкретное значение, методом деления пополам. Проверим средний элемент, если он больше искомого, то отбросим вторую половину массива — там его точно нет. Если же меньше, то наоборот — отбросим начальную половину. И так будем продолжать делить пополам, в итоге проверим log n элементов.
O(n2) — квадратичная сложность
Такую сложность имеет, например, алгоритм сортировки вставками. В канонической реализации он представляет из себя два вложенных цикла: один, чтобы проходить по всему массиву, а второй, чтобы находить место очередному элементу в уже отсортированной части. Таким образом, количество операций будет зависеть от размера массива как n * n, т. е. n2.
Бывают и другие оценки по сложности, но все они основаны на том же принципе.
Также случается, что время работы алгоритма вообще не зависит от размера входных данных. Тогда сложность обозначают как O(1). Например, для определения значения третьего элемента массива не нужно ни запоминать элементы, ни проходить по ним сколько-то раз. Всегда нужно просто дождаться в потоке входных данных третий элемент и это будет результатом, на вычисление которого для любого количества данных нужно одно и то же время.
Аналогично проводят оценку и по памяти, когда это важно. Однако алгоритмы могут использовать значительно больше памяти при увеличении размера входных данных, чем другие, но зато работать быстрее. И наоборот. Это помогает выбирать оптимальные пути решения задач исходя из текущих условий и требований.
Наглядно
Время выполнения алгоритма с определённой сложностью в зависимости от размера входных данных при скорости 106 операций в секунду:
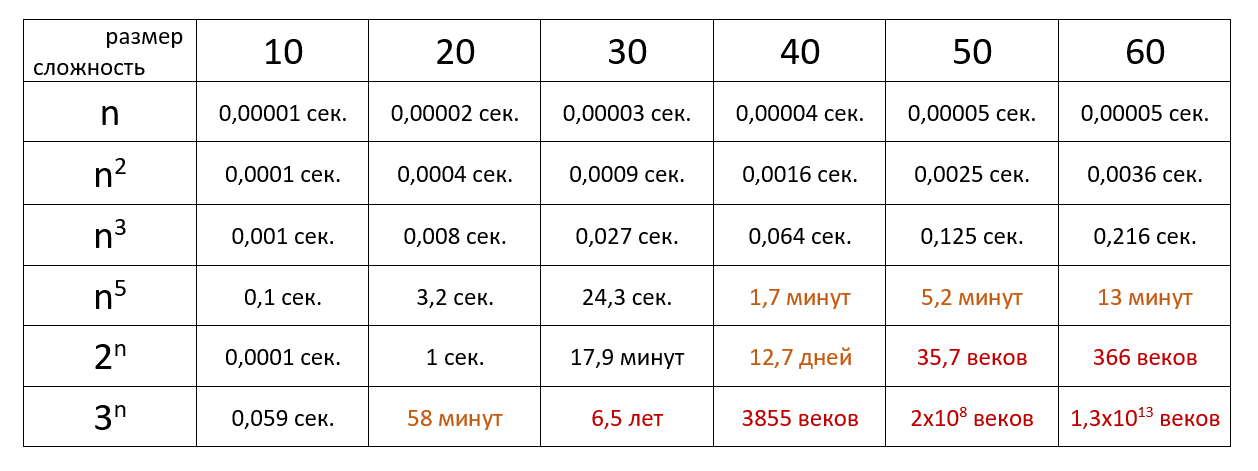
Если хочется подробнее и сложнее, заглядывайте в нашу статью из серии «Алгоритмы и структуры данных для начинающих».



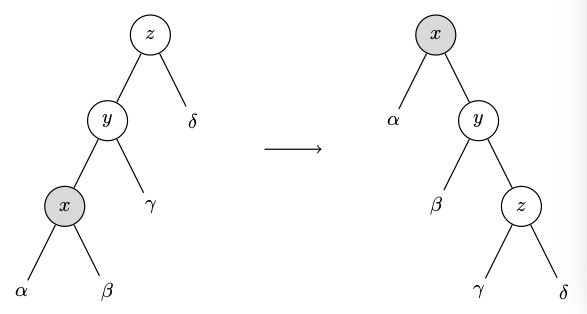


 таким образом,чтобы оставшийся граф был планарным.
таким образом,чтобы оставшийся граф был планарным. М, продолжить поиск только в левой части списка L.Если Х
М, продолжить поиск только в левой части списка L.Если Х
