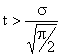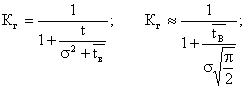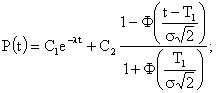У каких изделий можно аппроксимировать время безотказной работы нормальным законом распределения

В этот
период постепенные отказы еще не
проявляются и надежность характеризуется
внезапными отказами. Эти отказы вызываются
неблагоприятным стечением многих
обстоятельств и поэтому имеют постоянную
интенсивность, которая не зависит от
возраста изделия:

λ(t)
=
λ = const,

где
λ=1/m_t
;
m_t
—
средняя наработка до отказа (обычно в
часах). Тогда λ
выражается
числом отказов в час и, как правило,
составляет малую дробь.

Вероятность
безотказной работы

Она
подчиняется экспоненциальному закону
распределения времени безотказной
работы и одинакова за любой одинаковый
промежуток времени в период нормальной
эксплуатации.

Вероятность
возникновения отказа

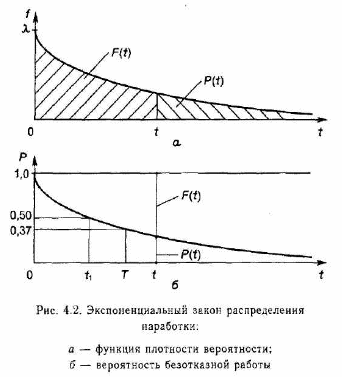
Плотность
вероятности отказов определяется (рис.
4.2, а)

Средняя наработка
до отказа

Дисперсия наработки
до отказа

При
экспоненциальном законе интенсивность
отказов является величиной постоянной,
обратно пропорциональной наработке до
отказа или среднему времени безотказной
работы. Это означает, что предшествующее
использование объекта до некото­рого
момента времени t
не
влияет на остаточное время безотказной
работы. Значит, в процессе эксплуатации
объект не испытывает влияния износа,
то есть не стареет. Следовательно, для
отказов износового характера этот закон
неприменим. Закон характерен для
внезапных, аварийных отказов (например
в период приработки), связанных с
по­ломками и разрушениями объекта.
Особенно важно, что с экспонен­циальным
законом хорошо согласуются распределения
наработки до отказа сложных восстанавливаемых
систем, состоящих из многих элементов.

Экспоненциальным
законом распределения можно аппроксимировать
время безотказной работы широкого круга
объектов (изделии):

— особо
ответственных машин, эксплуатируемых
в период после окончания приработки и
до существенного проявления постепенных
отказов;

— элементов
радиоэлектронной аппаратуры;

— машин
с последовательной заменой отказавших
деталей;

— машин вместе с
электро- и гидрооборудованием и системами
управления и др;

—сложных объектов, состоящих из многих
элементов (при этом время безотказной
работы каждого может не быть распределено
по экспоненциальному закону; нужно
только, чтобы отказы одного элемента,
не подчиняющегося этому закону, не
доминировали над другими).

П

а –
функция плотности вероятности

б –
вероятность безотказной работы

Рисунок
4.3. Экспоненциальный закон распределения

риведем примеры неблагоприятного
сочетания условий работы деталей машин,
вызывающих их внезапный отказ (поломку).
Для зубчатой передачи это может быть
действием максимальной пиковой нагрузки
на наиболее слабый зуб при его зацеплении
в вершине и при взаимодействии с зубом
сопряженного колеса, при котором
погрешности шагов сводят к минимуму
или исключают участие в работе второй
пары зубьев. Такой случай может встретиться
только через много лет эксплуатации
или не встретиться совсем.

Примером
неблагоприятного сочетания условий,
вызывающего поломку вала, может явиться
действие максимальной пиковой нагрузки
при положении наиболее ослабленных
предельных волокон вала в плоскости
нагрузки.

Существенное
достоинство экспоненциального
распределения — его простота: оно
имеет только один параметр.

Если,
как обычно, λt
≤
0,1, то формула для вероятности безотказной
работы упрощается в результате разложения
в ряд и отбрасывания малых членов:

Плотность
распределения (в общем случае)

Значения
вероятности безотказной работы в
зависимости от λ(t)
t≈
t
/ m_t
(рис.1.3):

λ(t)
t
. 1
0,1 0,01 0,001 0,0001

P{t) 0,368
0,9 0,99 0,999 0,9999

Так
как при tlm_t
= 1
вероятность
P(t)
≈
0,37,
то
63% отказов возникает за время t
< m_t
и
только 37% позднее. Из приведенных значений
следует, что для обеспечения требуемой
вероятности безотказной работы 0,9 или
0,99 можно использовать только малую долю
среднего срока службы (соответственно
0,1 и 0,01).

Если
работа изделия происходит при разных
режимах, а следовательно, и интенсивностях
отказов λ₁
(за время t₁)
и λ
₂
(за время t₂),
то

Эта
зависимость следует из теоремы умножения
вероятностей

Для
определения на основании опытов
интенсивности отказов оценивают
среднюю наработку до отказа

где N
— общее число наблюдений. Тогда λ=
1
/ m_t.

Для
системы
.
Если
λ₁=
λ₂.
.
.=
λ_n,
то

.
Таким
образом, вероятность безотказной работы
системы, состоящей из элементов с
вероятностью безотказной работы по
экспоненциальному закону, также
подчиняется экспоненциальному закону,
причем интенсивности отказов отдельных
элементов складываются.

Используя
экспоненциальный закон распределения,
несложно определить среднее число
изделий п,
которые
выйдут из строя к заданному моменту
времени, и среднее число изделий N_р,
которые останутся работоспособными.
При λt
≤
0,1

n
≈ N
λt
N_p
≈ N(1—
λt)

Пример.
Оценить
вероятность Р
(t)
отсутствия внезапных отказов меха­низма
в течение t
= 10000 ч, если интенсивность отказов
составляет λ
= 1
/ m_t
= 10^-81/ч.

Решение.
Так как λt
=
10^-8∙10⁴=
10^-4
< 0,1, то пользуемся прибли­женной
зависимостью

Р
(t)=
1 — λt
=
1 — 10^-4
= 0,9999.

Расчет
по точной зависимости Р(t)
= e^-λt
в
пределах четырех знаков после запятой
дает точное совпадение.

К 1.6. НАДЕЖНОСТЬ
В ПЕРИОД ПОСТЕПЕННЫХ ОТКАЗОВ

Для
постепенных отказов нужны законы
распределения времени безотказной
работы, которые дают вначале низкую
плотность распределения, затем максимум
и далее падение, связанное с уменьшением
числа работоспособных элементов.

В связи
с многообразием причин и условий
возникновения отказов в этот период
для описания надежности применяют
несколько законов распределений, которые
устанавливают путем аппроксимации
результатов испытаний или наблюдений
в эксплуатации.

Нормальное
распределение хорошо описывает
распределение вероятностей
наработки до отказа, ресурса элементов
и других показателей надежности,
когда они зависят от большого числа
однородных по своему влиянию случайных
факторов, влияние каждого из которых
по сравнению
с совокупностью всех остальных
незначительно. Этот закон
характерен для постепенных отказов,
вызванных износом и старением. Нормальному
распределению «подчиняется» наработка
до отказа многих
восстанавливаемых и невосстанавливаемых
объектов, размеры и ошибки измерений
деталей и др. Нормальное распределение
является
наиболее универсальным,
удобным
и широко применяемым для практических
расчетов
(рис.
1.5, 1.6).

Плотность
распределения

Распределение
имеет два независимых параметра:
математическое ожидание m_t
и
среднее квадратическое отклонение S_t.
Значения параметров m_t
и
S_t
оценивают по результатам испытаний по
формулам (4.5) и (4.7).

Математическое
ожидание определяет на графике (см. рис.
1.5) положение петли, а среднее квадратическое
отклонение — ширину петли.

Кривая
плотности распределения тем острее и
выше, чем меньшеS_t.
Она начинается от t
= –
∞
и распространяется до t
= + ∞.
Это не является существенным недостатком,
особенно если m_t≤
3S_t,
так
как площадь, очерченная уходящими в
бесконечность ветвями кривой плотности,
выражающая соответствующую вероятность
отказов, очень мала. Так, вероятность
отказа за период времени до m_t–3S_t
составляет всего 0,135% и обычно не
учитывается в расче­тах. Вероятность
отказа до m_t–2S_t
равна 2,175%. Наибольшая ордината кривой
плотности распределения равна 0,399/S_t.

И

а –
функция плотности вероятности

б –
вероятность безотказной работы

Рисунок
4.3. Нормальный закон

распределения

нтегральная функция распределения.

Вероятность
отказа и вероятность безотказной работы
соответственно Q(t)=F(t);
P(f)=1–F(t).

Вычисление
интегралов заменяют использованием
таблиц. Таблицы для нормального
распределения в функции (t–m_t)
и
S_t
были бы громоздкими, так как имели бы
два независимых параметра. Можно обойтись
небольшими таблицами для нормального
распределения, у которого m_x
=0 и S_x=1.
Для
этого распределения функция плотности

имеет одну переменную х.
Величина
х
является
центрированной, так как т_х
=
0,
и
нормированной, так как S_x=1.
Функция
плотности распределения записывается
в относительных координатах с началом
на оси симметрии петли.

Функция
распределения – интеграл от плотности
распределения

.

Из
этого уравнения следует, F₀(x)
+
F₀(–x)
= 1, отсюда F₀(–x)
= 1–
F₀(x)

Для
использования таблиц следует применять
подстановку x
=
(t—m_t)/S_t;
при
этом х
называется
квантилью
нормированного нормального распределения
и
обычно обозначается u_р.

Плотность
распределения и вероятность безотказной
работы соответственно f(t)=f_o(x)/S_t
Q(t)=F₀(x);
P(t)
=1–F₀(x),
где
f_o(x)
и F₀(x)
берут
по таблицам [5, 50]. Например:

x …………………………	0	1	2	3	4
fo(x) ………………………	0,3989	0,2420	0,0540	0,0044	0,0001
F0(x) ……………………..	0,5	0,8413	0,9772	0,9986	0,9999

Втабл. 1.1 приведены непосредственно
значенияP(t)
в
зависимости от x=u_p=(t–m_t)/S_t
в
употребительном диапазоне. В литературе
по надежности часто вместо интегральной
функции распределения F₀(x)
пользуются
функцией Лапласа:

Очевидно, что

Вероятность
отказа и вероятность безотказной работы,
выраженные через функции Лапласа,
отличающиеся пределами интегриро­вания,
имеют вид:

;

.

С

а –
плотность вероятности f(t)

б – вероятность
безотказной работы

в – интенсивность
отказов

Рисунок
4.3. Основные характеристики нормального
распределения при разных значениях
среднего квадратического отклонения

равнивая изделия с одинаковой
средней наработкой до отказа и разным
средним квадратическим отклонениемS,
нужно
подчеркнуть, что хотя при больших S_t
и имеются экземпляры с большой
долговечностью, но чем меньше S_t,
тем много лучше изделия.

Помимо
задачи оценки вероятности безотказной
работы за данное
время
или за данную наработку встречается
обратная задача – определение времени
или наработки, соответствующих заданной
вероятности безотказной работы.

Значения
этой наработки (времени) определяют с
помощью квантилей нормированного
нормального распределения t=m_t
+ u_p
S_t.
Значения
квантилей даются в таблицах в зависимости
от требуемой вероятности, в частности
от вероятности безотказной работы.

Операции
с нормальным распределением проще, чем
с другими, поэтому им часто заменяют
другие распределения. При малых
коэффициентах вариации S_t/m_t
нормальное
распределение хорошо заменяет
биномиальное, пуассоново и логарифмически
нормальное.

Распределение
суммы независимых случайных величин
U=X+Y+Z,
называемое
композицией
распределений, при
нормальном распределении слагаемых
также является нормальным распределением.

Математическое
ожидание и дисперсия композиции
соответственно равны

;

,

где
т_х,
т_у,
m_z
–
математические ожидания случайных
величин X,
Y,
Z;
S_x,
S_y,
S_z
–
дисперсия тех же величин.

Пример.
Оценить
вероятность Р
(t)
безотказной
работы в течение t
=1,5-10⁴
ч изнашиваемого подвижного сопряжения,
если ресурс по износу подчиняется
нормальному распределению с параметрами
m_t
=4-10⁴
ч,
S_t
=10⁴
ч.

Решение.
Находим квантиль
;
по табл. 1.1

определяем,
что Р
(t)
=0,9938.

Таблица 1.1

Нормальное распределение
Квантиль up	Вероятность безотказной работы P(t)	Квантиль up	Вероятность безотказной работы P(t)	Квантиль up	Вероятность безотказной работы P(t)
0,000 –0,1 –0,126 –0,2 –0,253 –0,3 –0,385 –0,4 –0,5 –0,524 –0,6 –0,674 –0,7 –0,8 –0,842 –0,9 –1,0 –1,036	0,5 0,5398 0,55 0,5793 0,6 0,6179 0,65 0,6554 0,6915 0,7 0,7257 0,75 0,7580 0,7881 0,8 0,8159 0,8413 0,85	–1,1 –1,2 –1,282 –1,3 –1,4 –1,5 –1,6 –1,645 –1,7 –1,751 –1,8 –1,881 –2,0 –2,054 –2,1 –2,170 –2,2 –2,3	0,8643 0,8849 0,9 0,9032 0,9192 0,9332 0,9452 0,95 0,9554 0,96 0,9641 0,97 0,9772 0,98 0,9821 0,985 0,9861 0,9893	–2,326 –2,4 –2,409 –2,5 –2,576 –2,6 –2,652 –2,7 –2,748 –2,8 –2,878 –2,9 –3,0 –3,09 –3,291 –3,5 –3,719 –4,0	0,99 0,9918 0,992 0,9938 0,995 0,9953 0,996 0,9965 0,997 0,9974 0,998 0,9981 0,9986 0,999 0,9995 0,9998 0,9999 0,99997

Поскольку
длительность безотказной работы объекта
не может быть отрицательной, нормальное
распределение в общем виде к задачам
надежности может применяться только
при S
<< m_t.
Если
условие не выполняется, то применяется
усеченный нормальный закон. Сущ­ность
усечения заключается в том, что из
совокупности значений случайной величины
исключаются все значения t<0
и f(t)=0
при
t<0.

Функция плотности
усеченного нормального закона
распределения

,

где А
—
нормирующий постоянный множитель.
Значения А
вычисляют
по формуле

,

где
Ф(m_t
/ S_t
) —
функция Лапласа.

Усеченное
нормальное распределение с хорошей
точностью описывает результаты анализа
надежности сложных систем с учетом
ухода параметров элементов в процессе
эксплуатации (точности, прочности,
вибраций, температуры и др.) за допустимые
пределы. Тем не менее при m_t
/ S_t
>2, что
имеет место в большинстве случаев при
расчетах надежности рассматриваемых
машин с нормальным распределением
времени безотказной работы, множитель
А
мало
отличается от единицы, и усеченное
нормальное распределение достаточно
точно описывается обычным нормальным
законом.

Распределение
Вейбулладовольно
универсально, охватывает путем
варьирования параметров широкий диапазон
случаев изменения вероятности. Оно
хорошо описывает отказы усталостные,
возникающие в результате совместного
воздействия износа и ударных нагрузок,
например, отказы подшипников качения;
объектов, состоящих из последовательно
соединенных дублированных элементов,
и других. Используется для оценки
надежности деталей и узлов машин, в
частности, автомобилей, подъемно-транспортных
и других машин. Применяется также для
оценки надежности по приработочным
отказам.

Плотность вероятности
наработки до отказа для распределения
Вейбулла

,

где
a
—
параметр масштаба (задает масштаб кривой
распределения по оси абсцисс);

b
—
параметр формы (определяет остроту и
асимметрию кривой плотности распределения).

Вероятность
безотказной работы

.

Вероятность
возникновения отказа

а –
плотность вероятности f(t)

б –
вероятность безотказной работы

в –
интенсивность отказов λ(t)

Рисунок
4.5.
Основные характеристики распределения
Вейбулла при разных

значениях
b
и a

Интенсивность
отказов
.

Кривые
изменения плотности вероятности и
вероятности безотказ­ной работы
представлены на рис. 4.4, а,
б.

Величины
a
и b
всегда
положительны. При b
= 1
распределение
Вейбулла переходит в экспоненциальное,
которое, таким образом, является частным
случаем распределения Вейбулла. При b
< 1
интенсивность отказов f(t)
становится
убывающей функцией времени, поэтому
закон Вейбулла с параметром b
< 1
можно использовать для оценки надежности
объектов в период их приработки. При b
> 1
распределение Вейбулла характеризуется
возрастающей функцией интенсивности
отказов, и его удобно использовать для
оценки надежности износовых отказов.
При b
=
3,5…4,0 распределение Вейбулла близко к
нормальному, и функция плотности
вероятности приобретает колоколообразную
форму.

Распределение
Вейбулла получило широкое распространение
при расчетах надежности, поскольку
подбором параметров а
и
b
можно
добиться более полного соответствия
теоретического закона распределения
опытным данным.

Для
расчета параметров a
и
b
по
опытным данным удобно пользо­ваться
методом наименьших квадратов.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

• #
• #
• #
• #
• #
• #
• #
• #
• #
• #
• #

НОРМАЛЬНОЕ РАСПРЕДЕЛЕНИЕ ВРЕМЕНИ БЕЗОТКАЗНОЙ РАБОТЫ

Нормальное распределение применяют в теории надежности для описания отказов, вызванных изнашиванием детали.

Рис. 3. Нормальное распределение времени безотказной работы

Плотность распределения времени безотказной работы при нормальном законе распределения (рис. 3)

где параметры распределения — среднее значение времени и среднее квадратическое отклонение.

При нррмальиом распределении время может быть отрицательным, что противоречит физическому смыслу. Однако если среднее время значительно превышает а отрицательная часть распределения не имеет практического значения.

Функция распределения

где Ф — функция Лапласа.

Вероятность безотказной работы при нормальном законе распределения

Приведем еще значение интенсивности отказов

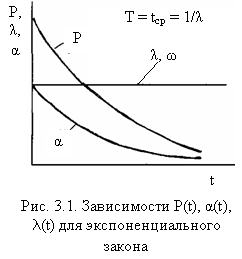
Экспоненциальный закон

При экспоненциальном законе распреде­ления времени возникновения отказов интенсивность отказов является ве­личиной постоянной. Зависимости между основными количественными характери­стиками надежности будут выражены формулами:

                                                                   ^(3.1)

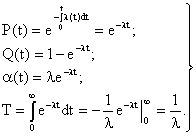
Основные количественные характеристики надежности для экспонен­циального закона приведены на рис. 3.1. Условие λ(f) = const означат, что средняя частота отказов и среднее время между соседними отказами соответственно равны интенсивности отказов и среднему времени безотказной работы аппаратуры, т.е.:

              (3.2)

Для экспоненциального закона распределения времени возникновения отказов средняя частота отказов превращается в интенсивность отказов, а среднее время между соседними отказами  –  в среднее время безотказной ра­боты. Основными же характеристиками надежности являются:

1) вероятность безотказной работы P(t);

2) интенсивность отказов l(t);

3) частота отказов α(t);

4) среднее время безотказной работы Т.

В случае экспоненциального закона эти характеристики пригодны для оценки надежности как аппаратуры разового использования, так и аппара­туры длительного использования, работающей в режиме смены отказавших элементов.

Из выражения для вероятности безотказной работы (3.1) видно, что она уменьшается с течением времени по экспоненциальному закону. Выражение

 

часто называют экспоненциальным законом надежности.

Выясним смысл среднего времени безотказной работы. Очевидно, что при t = Т вероятность безотказной работы будет иметь значение:

.

Из этого выражения видно, что при экспоненциальном законе надеж­ности среднее время безотказной работы – это время, в течение которого ве­роятность безотказной работы уменьшается в е раз.

Коэффициенты надежности для экспоненциального закона распреде­ления выражаются следующими формулами:

коэффициент готовности

;

коэффициент вынужденного простоя

;

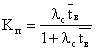
коэффициент профилактики

;

частота профилактики

;

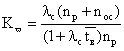
коэффициент отказов элементов

;

относительный коэффициент отказов элементов

;

коэффициент расхода элементов

.

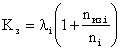
Здесь l_c – интенсивность отказов системы, а l_i – интенсив­ность отказов элементов. Эти выражения становятся очевидными, если учесть, что в данном случае средняя частота отказов равна интенсивности отказов и        .

Выясним физический смысл коэффициентов, учитывающих вынуж­денный простой аппаратуры, для чего вычислим вероятность того, что в любой момент времени аппаратура будет исправна, если потоки отказов и восстановления простейшие.

Рассмотрим вначале промежуток времени от t до t + Dt, и вычислим вероятность того, что в конце этого промежутка аппаратура будет исправна.

Обозначим:

P(t + Dt) – вероятность того, что в конце промежутка t + Dt аппаратура будет исправна;

P(t) – вероятность того, что в момент времени t аппаратура будет исправна;

P₁(t) – вероятность того, что в момент времени t аппаратура находится в состоянии ремонта;

l – интенсивность отказов;

m_в – интенсивность восстановления.

Очевидно, что в конце промежутка Δt в силу ординарности потока отказов система будет исправна при следующих условиях:

а) в момент времени t аппаратура будет исправна и за промежуток Dt отказов не возникло;

б) в момент времени t аппаратура находилась в ремонте, но в течение Dt была восстановлена.

Предполагая, что промежуток времени Δt мал и ограничиваясь первыми двумя членами разложения показательной функции в ряд, можно для вероятностей событий а и б записать:

                               (3.3)

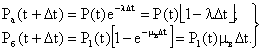
Тогда вероятность безотказной работы аппаратуры на основании теоремы о полной вероятности будет:

или после очевидных преобразований

.

Устремляя Δt к нулю и переходя к пределу, получим:

.                                                  (3.4)

Так как состояния а и б образуют полную группу несовместимых событий, то

P_i(t) = l – P(t).

Подставляя это значение в формулу (3.4), получим:

                                             (3.5)

Предполагая, что при t = 0 система исправна, будем иметь Р(0) = 1, P₁(0) = 0. При этих начальных условиях решение дифференциального уравнения (3.5) имеет вид:

                                                  (3.6)

Учитывая, что

,

получим

.                                       (3.7)

Выражение (3.7) позволяет уяснить физический смысл коэффициентов К_г, К_п, К_пр.

Из выражения (3.7) видно, что при t = 0     P(t) = l, а при t = ∞   P(t) = K_г. Отсюда следует, что коэффициент готовности показывает вероятность исправного состояния системы в любой момент времени t при установившихся условиях эксплуатации. В начале же эксплуатации P(t) < K_r даже при простейших потоках отказов и восстановления.

Закон Рэлея

При распределении времени возникновения отказов по закону Рэлея частота отказов определяется из выражения:

                                                      (3.8)

где а – параметр распределения Рэлея.

Тогда вероятность безотказной работы, опасность отказов и среднее время безотказной работы будут выражаться следующими формулами:

;                             (3.9)

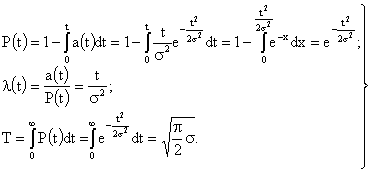
Зависимости основных количественных характеристик надежности для закона Рэлея приведены на рис. 3.2.

Из формул (3.9) видно, что интенсивность отказов растет линейно с течением времени. Это означает, что при распределении времени возникновения отказов по закону Рэлея происходит интенсивное старение аппаратуры, и количество отказов не удовлетворяет условиям стационарного случайного процесса. При этом с течением времени вероятность безотказной работы уменьшается значительно интенсивнее, чем при экспоненциальном законе.

Из выражения (3.9) для P(t) и рис. 3.2. также видно, что в области малых t  интенсивность безотказной работы системы уменьшается с течением времени медленнее, чем при экспоненциальном законе. Это означает, что сложные автоматические системы, предназначенные для малого времени непрерывной работы, целесообразно строить на элементах, имеющих рэлеевский закон распределения между отказами. Условие целесообразности применения таких элементов по сравнению с элементами, поток отказов которых подчиняется экспоненциальному распределению, аналитически можно записать в виде следующего неравенства:

.                                                     (3.10)

Это условие вытекает из сравнения выражений для вероятности безотказной работы при указанных законах распределения времени возникновения отказов.

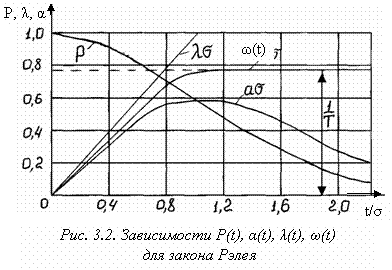
В области больших значений t вероятность безотказной работы систе­мы с рэлеевским законом распределения уменьшается с течением времени значительно быстрее, чем при экспоненциальном. Это означает, что сконст­руировать на данных элементах высоконадежную систему, предназначен­ную для длительной непрерывной работы, затруднительно.

Найти аналитическое выражение для средней частоты отказов при распределении времени возникновения отказов по закону Рэлея весьма сложно. Поэтому оценим α(t) приближенно.

Так как Р(t) является возрастающей функцией, то средняя частота от­казов располагается между интенсивностью отказов l(t) и частотой отказов α(t). Кроме того,

l(0) = α(0) = w(0) =0.

В области больших значений t средняя частота отказов асимптотиче­ски стремится к среднему времени безотказной работы, т.е.:

                                              (3.11)

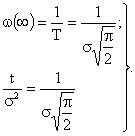
Тогда значение t, при котором происходит излом, будет равно:

.

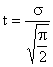
Предполагая, что средняя частота представляет собой ломаную, сов­падающую в области малых значений t с интенсивностью отказов, а в облас­ти больших значений t с прямой α(t), можно записать:

 

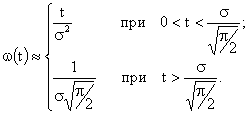
Зависимость  w(t) приведена на рис. 3.2. Коэффициенты надежности для случаев:

              и                    

приближенно могут быть выражены соответственно формулами:

коэффициент готовности

коэффициент вынужденного простоя

;

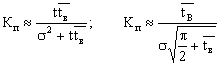
коэффициент профилактики

;

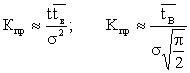
частота профилактики

коэффициент отказов элементов

;

относительный коэффициент отказов элементов

;

коэффициент расхода элементов

.

Здесь s_с – параметр распределения отказов системы, s_i – параметр распределения отказов элементов.

Из выражений для коэффициентов надежности видно, что в данном случае они являются функциями времени.

Исключение составляют лишь ко­эффициенты отказов элементов.

Нормальное распределение

Длительность безотказной работы аппа­ратуры не может быть отрицательной. Поэтому количественные характери­стики надежности имеет смысл рассматривать только при усеченном нор­мальном законе распределения времени между отказами.

Частота отказов в этом случае определяется из выражения:

.                                                (3.12)

Здесь T₁, s² – среднее значение и дисперсия времени между отказами в нормальном законе соответственно, С  –  постоянная усеченного нормального распределения, которая выбирается из условия:

,

и равна

.

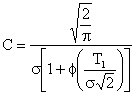
Тогда вероятность безотказной работы можно представить в виде:

                                         (3.13)

где 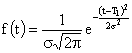 – нормальный закон распределения времени между отказами.

Подставляя в выражение (3.13) значение постоянной С и вычисленный интеграл, получим следующую формулу для вероятности безотказной ра­боты:

.

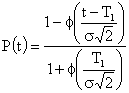
Интенсивность отказов в данном случае будет равна:

                                       (3.15)

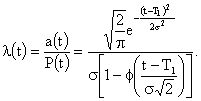
Вычислим среднее время безотказной работы. Для рассматриваемого случая:

.

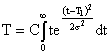
Обозначим:

,

тогда

.

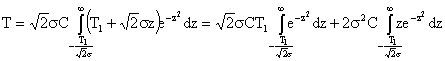
Вычислим первый интеграл вероятности, пользуясь известным соотношением:

,

тогда получим:

.

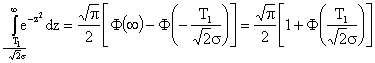
Второй интеграл будет иметь вид:

.

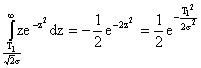
Подставляя вычисленные интегралы в выражение для Т и делая элементарные преобразования, получим выражение среднего времени безотказной работы в виде:

.

Основные характеристики надежности для нормального закона распределения между отказами имеют вид (рис. 3.3).

Из рисунка 3.3 видно, что интенсивность отказов начинается с нуля и с течением времени сильно растет. Это означает, что поток отказов не является стационарным и происходит старение элементов. В области малых значений t старение элементов оказывает несущественное влияние на надежность, и поэтому вероятность безотказной работы системы уменьшается незначительно. При длительной эксплуатации системы, отказы элементов которой имеют нормальное распределение, ее надежность быстро снижается, и поэтому вероятность безотказной работы быстро падает.

Гамма-распределение

При этом распределении частота отказов выражается формулой:

,                                                (3.16)

где l₀ – параметр гамма-распределения.

Тогда при целом и положи­тельном k вероятность безотказной работы, опасность отказов и среднее время безотказной работы выражается следующими формулами:

                  (3.17)

Параметр гамма-распределения характеризует асимметрию и эксцесс гамма-распределе­ния. В зависимости от его значения существенно изменится вид основных количественных характеристик надёжности. Зависимости a(t), l(t) и P(t) приведены на рис. 3.4. Из рисунка и выражения (3.16) видно, что при k = l гамма-распределение превращается в экспоненциальное. При k > l интенсивность отказов возрастает, а при k < l убывает.

Гамма-распределению удовлетворяет время возникновения отказов резервированных систем с включением резерва по способу замещения и при условии, что потоки отказов основной системы и всех резервных являются простейшими. В этом случае параметр распределения k равен числу всех систем (основной и резервных), т.е.

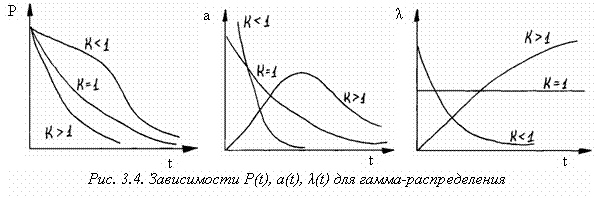
k = m + l.

Гамма-распределение также может быть характеристикой времени возникновения отказов сложных электромеханических систем, если имеют место мгновенные отказы элементов на начальной стадии эксплуатации или в процессе обработки системы, т.е. при k < l гамма-распределение является удобной характеристикой времени возникновения отказов аппаратуры в течение времени её приработки.

Распределение Вейбулла

При распределении Вейбулла частота отказов задается выражением:

.                                              (3.18)

Параметр l₀ определяет масштаб, а параметр k – асимметрию и эксцесс распределения. Для распределения Вейбулла основные количественные характеристики надёжности выражаются следующими формулами:

;

;

.

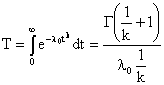
Зависимости основных количественных характеристик надёж­ности от времени приведены на рис. 3.5. Из рисунков и выражения (3.18) видно, что при k = l распределение Вейбулла превращается в экспо­ненциальное распределение. При k > l интенсивность отказов начина­ется с нуля и с течением времени возрастает. При k < l интенсивность отказов начинается с +∞ и в области больших t стремится к нулю.

Это означает, что распределение Вейбулла так же, как и гамма-распределение, по-видимому, может быть использовано в качестве характеристики надёжности ап­паратуры в течение времени её приработки. Это распределение на­блюдается для некоторых механических деталей и, в частности, при­меняется при изучении надёжности шарикоподшипников. Распределение Вейбулла с параметром k = 1,4 – 1,9 наблюдается у неко­торых типов электронных ламп. Оно также может быть использовано при ускоренных испытаниях элементов в форсированных режимах.

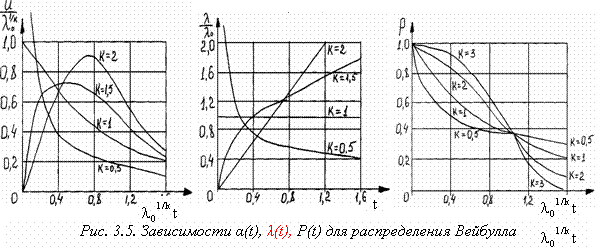
Для распределения Вейбулла так же, как и для гамма-распределения, не удаётся в общем виде найти выражение для средней частоты отказов, что затрудняет анализ системы по коэффициентам надёжности, так как приходится решать интегральное уравнение Вольтерра приближенными способами.

Суперпозиция распределений

Рассмотренные законы распределения времени возникновения отказов могут в большинстве случаев характеризовать надёжность сложной системы лишь на ограниченных участках времени её работы. Так, например, на участке приработки время возникновения отказов может подчиняться гамма-распределению или распределению Вейбулла, на участке нормальной работы – экспоненциальному, а на участке старения – нормальному распределению. В связи с этим для оценки надёжности сложной систе­мы на длительном участке её эксплуатации целесообразно использо­вать суперпозицию рассмотренных законов распределения времени между отказами.

В качестве примера рассмотрим суперпозицию двух экспонен­циальных законов.

Пусть

,

где l₁ < l₂, C₁, C₂ – постоянные, определяемые из условия С₁ + С₂ = 1 и зависящие от соотношения между l₁ и l₂.

Для этого случая основные количественные характеристики надежности будут иметь вид:

;

;

.

Так как l₂ > l₁, то в области больших значений t члены в выраже­нии для интенсивности отказов, имеющие множителем е^—l2t, близки к нулю и тогда l(t) » l₁. При малых значениях t            e^—l1t        и         е^—l2t близки к единице, и

l(t) = C₁l₁ + C₂l₂ > l₁.

Таким образом, интенсивность отказов с течением времени уменьшается:

от          l(t) =C₁l₁ + C₂l₂       при t = 0

до          l₁                                при t ® ∞.

Зависимость l(t) для суперпозиции двух экспоненциальных за­конов при l₂ < l₁ показана на рисунке (3.6.). На рисунке видно, что за­кон распределения, представляющий собой суперпозицию двух экспоненциальных законов, может характеризовать на

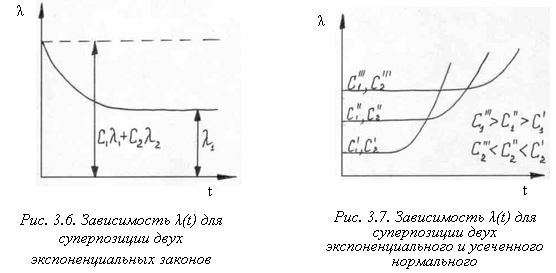
дёжность сложной системы с учётом периода приработки. Такой же вывод можно было бы получить при суперпозиции экспоненциального закона с гамма-распределением и распределением Вейбулла при k < l .

Влияние постепенных отказов может быть уточнено при суперпозиции экспоненциального и усеченного нормального законов распределения. В этом случае частота отказов представляется в следующем виде:

,

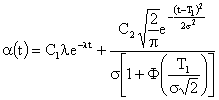
где С₁ и С₂ – коэффициенты, учитывающие степень влияния внезапных и постепенных отказов.

Тогда основные количественные характеристики надёжности можно представить в виде следующих соотношений:

;

.

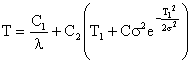
Зависимость λ(t) для различных С₁и С₂ показаны на рис. (3.7.). Из рисунка видно, что в области малых значений t интенсивность от­казов – величина постоянная, а в области больших t она возрастает, что свидетельствует о появлении старения аппаратуры и, как следст­вие, возникновении постепенных отказов.