Страховая компания делит водителей на три группы - Контакты компаний и предприятий

Задача 2.

Электролампы изготавливаются на трех заводах. Первый завод производит 45% общего количества электроламп, второй – 40%, третий – 15%. Продукция первого завода содержит 70% стандартных ламп, второго – 80%, третьего – 81%. В магазин поступает продукция всех трех заводов. Какова вероятность того, что купленная в магазине лампа стандартная.

Решение.

А = {купленная в магазине лампа стандартная}, Н1 = {лампа с первого завода}, Н2 = {лампа со второго завода}, Н3 = {лампа с третьего завода}.

Р(Н1) = 0,45; Р(Н2) = 0,4; Р(Н3) = 0,15.

Р(А/Н1) = 0,7; Р(А/Н2) = 0,8; Р(А/Н3) = 0,81.

P( A) = 0,45× 0,7 + 0,4× 0,8 + 0,15× 0,81 = 0,7565.

Задача 3.

Агентство по страхованию автомобилей разделяет водителей по трем классам: 1 класс – мало рискуют, 2 класс – рискуют средне, 3 класс – сильно рискуют. Из всех водителей, застраховавших автомобили, 30% принадлежат к классу 1, 50% — к классу 2 и 20% — к классу 3. Вероятность того, что в течение года водитель класса 1 попадет хотя бы в одну аварию, равна 0,01; для водителя класса 2 вероятность равна 0,02; для водителя третьего класса – 0,08. Водитель страхует свою машину и в течение года попадает в аварию. Какова вероятность того, что он относится к классу 1? К классу 2? К классу 3?

Решение.

А = {водитель попадает в аварию}. Н1 = {водитель относится к 1 классу}, Н2 = {водитель относится к 2 классу}, Н3 = {водитель относится к 3 классу}. Р(Н1) = 0,3; Р(Н2) = 0,5; Р(Н3) = 0,2;

Р(А/Н1) = 0,01; Р(А/Н2) = 0,02; Р(А/Н3) = 0,08;

P( A) = 0,3× 0,01+ 0,5× 0,02 + 0,2× 0,08 = 0,029 .

По формуле Байеса пересчитаем вероятности гипотез, после того, как событие А произошло:

P(H1 \| A) =	0,3× 0,01	» 0,1035 ;
		0,029
P(H 2	\| A) =	0,5× 0,02	» 0,3448 ;
		0,029
P(H3	\| A) =	0,2× 0,08	» 0,5517 .
		0,029

6. Формула Бернулли.

Рассматривается последовательность независимых испытаний, в каждом из которых вероятность наступления события А одинакова и равна р (условно это событие

рассматривается как успех, а его ненаступления ( A ) как неудача, причем p( A) = 1— p = q ).

Вероятность того, что в n испытаниях успех наступит ровно m раз, обозначим через

Pn(m).

Имеет место формула Бернулли:

Pn (m) = Cnm p m q n− m .

Задача 1.

Что вероятнее выиграть у равносильного противника а) три партии из четырех или пять партий из восьми? б) не менее трех партий из четырех или не менее пяти партий из восьми?

Решение.

Так как противники равносильные, то вероятности выигрыша и проигрыша каждой партии одинаковы и равны p = q = ½.

а) Найдем вероятность выигрыша трех партий из четырех:

P (3) = C 3

1 ö

3 ×

æ 1

ö 1

= 1 .

2 ø

è 2

Аналогично, P (5) =

C 5

ö 5

ö 3

Так как

, то вероятнее выиграть три партии из четырех.

б) Вероятность выиграть не менее 3-хпартий их четырех (обозначим ее R4 (3) ). R4 (3) = P4 (3) + P4 (4) = 14 + 161 = 165 ;

Вероятность выиграть не менее пяти партий из восьми ( R8 (5) ):

R8 (5) = P8 (5) + P8 (6) + P8 (7) + P8 (8) = 25693 .

Так как 25693 > 165 , то вероятнее выиграть не менее пяти партий из восьми.

Задача 2.

Всхожесть семян ржи составляет 90%. Чему равна вероятность того, что из семи посеянных семян взойдут пять?

Решение.

Вероятность всхожести отдельно взятого семени р=0,9; q=1-0,9=0,1. По формуле Бернулли:

P7 (5) = C75 p5 q 2 = C75 × (0,9)5 × (0,1)2 = 0,124 .

Таким образом, в среднем в 124 случаях из 1000 из 7 посеянных семян взойдут 5.

7. Дискретные и непрерывные случайные величины.

Величина, которая в зависимости от случай принимает различные числовые значения, называется случайной. Обозначаются они буквами Х, У и т.п.

Вероятность того, что случайная величина Х примет значение, меньшее х, называется функцией распределения случайной величины Х:

F(x)=P(X<x).

Основные свойства функции распределения: 1. Если a<b, то P(a ≤ X < b) = F(b) − F(a) .

2.Функция распределения – неубывающая функция.

3.Функция распределения непрерывна слева, то есть

			lim F( x) = F(a) .
			x→ a−	0
4.	lim F( x) = 1	;	lim F( x) = 0.
	x→ + ∞		x→ − ∞

7.1. Дискретная случайная величина.

Случайная величина называется дискретной, если ее значения можно перенумеровать.

Функция распределения дискретной случайной величины определяется посредством

равенства: F( x) = å pi , где суммирование распространяется на все индексы, для которых

xi<x.

Дискретная случайная величина может быть задана: 1) рядом распределения, 2) многоугольником распределения, 3) функцией распределения.

Рядом распределения называется совокупность всех частных значений, которые принимает случайная величина xi, и соответствующих им вероятностей pi = P{X = xi } . Ряд распределения обычно задается в виде таблицы:

Х		х1	x2	…	xn	…
Р		Р1	р2	…	pn	…
å	pi = 1.
i
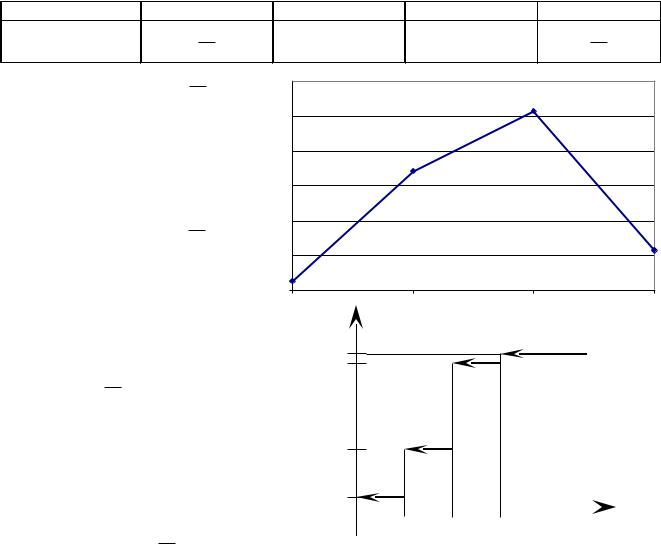
Многоугольником распределения называется графическое изображение ряда.
Откладываются точки Ai ( xi , pi )	и соединяются ломанной.

Напоминаем схему решения задач на построение законов распределения.

1)Необходимо обозначить и описать случайную величину, о которой идет речь в задаче.

2)Описать множество ее возможных значений xi.

3)Рассмотреть каждое из событий {X=xi}, i=1,2,…, n.

4)Вычислить вероятность каждого из событий {X=xi} с помощью основных теорем и формул.

5) Проверить правильность составленного распределения с помощью равенства

ån pi = 1. i= 1

Задача 1.

В урне 7 шаров, из которых 4 белых, а остальные черные. Из урны наудачу извлекаются 3 шара. Х – число извлеченных белых шаров. Найти а) закон распределения;

б) построить многоугольник распределения; в) найти и F(x); г)Найти вероятность

события X ³ 2 .

Решение.

Возможные значения случайной величины Х: 0, 1, 2, 3. Заполняем таблицу:

Х						0		1			2	3
Р						1		12			18	4
		C40 × C33			35		35			35	35
P{X = 0} =		=	1	,		3/5
C73		35		1/2				18/35
P{X = 1} =	C41 × C32			12
=	,
C73	35		2/5
P{X = 2} =	C42 × C31		=	18	,	P	3/10		12/35
C73		35
P{X = 3} =	C43 × C30		=	4			1/5
C 3		35 .						4/35
		7						1/10

									1/35
									0
									0	1		2	3
Найдем F(x).							F(x)			X
						1
ì	0, x £	0;
ï	1	,0 <	x £	1;				31/35
ï	35
ï
F( x) = íï	13	,1 < x £ 2;
ï	35								13/35
ï	31	,2 <	x £		3;
ï	35
ï	1, x >	3.						1/35
î
P{ X ³ 2} =	18 +	4			22 .		0	1	2	3	x
	=
		35	35		35

Задача 2.

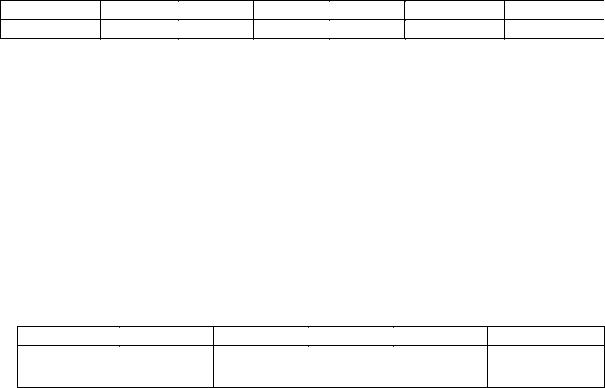
Пусть ведется стрельба по цели до первого попадания с конечным запасом «k». Пусть Х – число израсходованных патронов до первого попадания. Составить закон распределения случайной величины Х.

Решение.

X		1	2	3	…	k-1	k
P		p	qp	q2p		qk-2p	qk-1p+qk
P{ X = 1} =	p;
P{ X = 2} = q × p;
P{ X = 3} = q2 × p;
…
P{ X = k — 1} = qk − 2 × p.
Событие { X = k}	означает, что израсходован весь запас патронов.

P{ X = k} = qk − 1 × p + q k .

Задача 3.

Имеется 5 ключей, из которых только один подходит к замку. Найти закон распределения случайной величины Х – числа проб при открывании замка, если испробованный ключ в следующих опробываниях не участвует.

Решение.

Х					1					2	3	4	5
Р					1					1	1	1	1
					5					5	5	5	5
P{ X = 1} =	1	;
	5
P{ X = 2} =	4	×	1	= 1	;
	5		4		5
P{ X = 3} =	4	×	3	×	1	=	1 ;
	5		4		3		5
P{ X = 4} =	4	×	3	×	2	×	1	=	1	;
	5		4		3		2		5
P{ X = 5} =	4	×	3	×	2	×	1	×1 =	1 .
	5		4		3		2			5

7.2. Непрерывная случайная величина.

Непрерывной случайной величиной называется такая величина, которая может принимать любые числовые значения из некоторого интервала (конечного и бесконечного). Задать ее можно с помощью функции распределения F(x) или плотности распределения f(x) (дифференциальной функции распределения). Дифференциальной

функцией распределения f(x) называется функция	f ( x) = lim	P( x <	X < x + x)	.

	x→ 0	D x

График функции f(x) называется кривой распределения.

Свойства дифференциальной функции распределения.

1. f ( x) ³ 0 для любого х.

2. P(α < X < β ) = ò f ( x)dx (см. рис.).

f(x)

				x

	+ò∞	α	β

3.	f ( x)dx = 1.

−∞

4.Связь между дифференциальной и интегральной функциями распределения:

F( x) = òx f (t)dt ,

− ∞

F ′( x) = f ( x) , если в точке х функция f(x) непрерывна.

Пример непрерывного распределения.

Равномерное распределение.

Непрерывная случайная величина Х имеет равномерное распределение на отрезке [a, b], если на этом отрезке плотность вероятности случайной величины постоянна, то есть

ì	0, x <	a;
f ( x) = íï c, a £ x £ b;
ï	0, x >	b.
î

Найдем параметр с. Так как +ò∞ f ( x)dx = 1, то имеем:

	− ∞
òa 0× dx + òb c × dx +	+ò∞ 0× dx = 1;
− ∞	a	b

Следовательно, c = Таким образом,

с(b-a)=1,

1 . b — a

ì		0, x
f ( x) = íï	1		, a
	a
ï b —
î		0, x

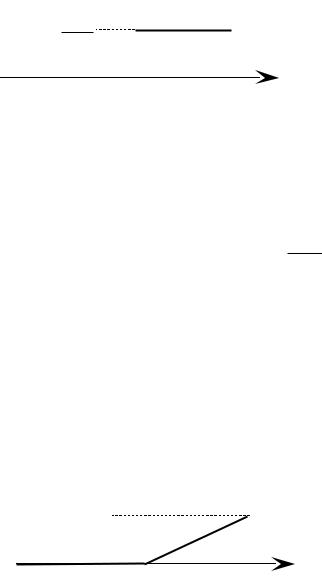
Построим график f(x).

f(x)

b − a

		a	b	x
Найдем функцию распределения F(x):

F( x) = òx f ( x)dx .

− ∞

Если x<a, то F( x)

òx

0 × dx =

0 .

− ∞

Если a £ x £ b , то F( x) = ò 0 × dx +

× dx =

b —

b — a

Если x>b, то F( x)

− ∞

0× dx +

× dx +

0× dx = 1.

b —

Таким образом,

− ∞

0, x <

F( x) = íï

x — a

, a £ x £ b;

ï b —

1, x >

График F(x) представим на рисунке:

=x — a . b — a

F(x)

		1		x

		a	b
Задача 1.	f ( x) = íì	0, x < 0;
Дана функция
	î	Cxe− x , x ³ 0.

При каком С она является плотностью вероятности?

Решение.

Во-первых, f ( x) ³ 0 , если f(x) – плотность вероятности, то есть C ³ 0 . Во-вторых, +ò∞ f ( x)dx = 1.

− ∞

+ ∞

× dx +

Cxe− x dx = C

xe− x dx = C lim

—

— e− A + 1ö

C = 1

− ∞

→ ∞

Ответ: С=1.

8. Числовые характеристики случайной величины.

Пусть Х – случайная дискретная величина, закон распределения которой имеет вид:

X	x1	x2	…	xk	…	xn
P	p1	p2	…	pk	…	pn
Математическим	ожиданием	МХ случайной	величины	Х	называется сумма

произведений значений случайной величины на вероятности, с которыми она принимает эти значения:

MX = ån xi pi .

i= 1

Математическим ожиданием непрерывной случайной величины с плотностью f(x) называется

MX = +ò∞ x × f ( x) × dx ,

− ∞

при условии, что интеграл сходится.

Свойства математического ожидания.

1.M[C]=C, где С – постоянная.

2.M[CX]=CM[X], где С – постоянная.

3.M[X1+X2+…+Xn]=M[X1]+M[X2]+…+M[Xn].

4.Если — независимы, то M[X1×X2×…×Xn]=M[X1] ×M[X2] ×…×M[Xn]. Дисперсией случайной величины Х называется число DX

DX=M[(X—MX)2].

Число σ ( x) = DX называется средним квадратическим отклонением случайной

величины Х.

Справедлива формула

DX=M[X2]-(M[X])2 (*), Этой формулой удобно пользоваться на практике.

Формула нахождения дисперсии для дискретной случайной величины

DX = å (xi — MX )2 pi ,

или с учетом формулы (*):

DX = å xi2 pi — (MX ) 2 .

Формула нахождения дисперсии непрерывной случайной величины:

DX = +ò∞ ( x — MX ) 2 f ( x) × dx , или

− ∞

DX = +ò∞ x 2 f ( x) × dx — (MX ) 2 .

− ∞

Свойства дисперсии.

1.D[C]=0, где С – постоянная.

2.D[CX]=C2D[X], где С – постоянная.

3.D[X ± Y]=D[X] + D[Y], где X, Y – независимые случайные величины.

Задача 1.

Случайная величина Х задана плотностью f(x):

													ì	0, x £ 0;
												f ( x) = íï	2x,0 < x < 1;
													ï	0, x ³ 1.
													î
Найти MX, DX, σX.
Решение.													1
MX =	+ò∞ x × f ( x) × dx = ò1	x × 2x × dx =	2x3		=	2 ,

	− ∞								0		3		0	3

DX = M [X 2 ]— (M [X ])2 ,
M [X 2 ] = ò1 x2 × 2x × dx =	x4		1	=	1	,

2			2
	0									0

DX =	1 —	4	=	9 − 8 =		1	,
9	18
	2			18
σ X =		1		=			1	.
18
3	2

Задача 2.

Пусть задан закон распределения некоторой случайной величины Х:

Х		2	4
Р		0,6	0,4
Найти МХ и DX.
Решение.
MX = å xi	pi = 2× 0,6 + 4× 0,4 = 2,8.
i

DX = M [X 2 ]— (M [X ])2

Напишем закон распределения случайной величины Х2:

М[X2]=4×0,6+16×0,4=8,8; DX=8,8-(2,8)2=0,96.

Задача 3.

Согласно таблицам смертности, вероятность того, что 25-летний человек проживет еще один год равна 0,992; а вероятность того, что он умрет в течение года равна 0,008. Страховая компания предлагает застраховать жизнь на 10000 рублей. Какова должна быть величина годового взноса, чтобы подобная страховка не была для страховых органов убыточной?

Решение.

Пусть Х – случайная величина, равная выплате застрахованному лицу страховой суммы (за вычетом страхового взноса а). Тогда закон распределения случайной величины Х будет таким:

Х	а-10000	а
Р	0,008	0,992

х1=а-10000, если застрахованный умрет и х2=а, если застрахованный проживет еще

год.

МХ=(а-10000)×0,008+а×0,992=(а-80).

Чтобы страховые органы в среднем не терпели убытка, необходимо, чтобы МХ³0, следовательно, а³80 рублей.

Задача 4

Дискретная случайная величина X может принимать только два значения x1 и x2 , причем x1 < x2 . Известна вероятность p1 = P{ X = x1} = 0,1, MX = 3,9, DX = 0,09 . Написать закон распределения дискретной случайной величины.

Решение.

Составим таблицу: в первом ряду возможные значения случайной величины, во втором – вероятности, с которыми она эти значения принимает:

Х	x1	x2
Р	p1 = 0,1	p
		2
Т.к. p1 + p2 = 1, то	p2 = 1− 0,1 = 0,9 .

Запишем MX :

MX = x1 Ч0,1+ x2 Ч0,9 = 3,9 . Найдем DX :

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

Источник

Вопросы »

Комбинаторика,вероятность » Страховая компания делит , водителей, заключивших договор авто каско на следующие группы риска

Страховая компания делит , водителей, заключивших договор авто каско на следующие группы риска

создана: 08.10.2013 в 21:02
…………………………………………

irinff :

19. Страховая компания делит , водителей, заключивших договор авто каско на следующие группы риска: 1 группа – низкий риск; 2 группа — средний; 3 группа – высокий риск. Среди клиентов страховой компании 25% — первой группы; 65% — второй группы; 10% — третьей группы. Вероятность того, что страховое событие произойдет и страховая компания будет вынуждена выплатить страховое возмещение для первой группы риска оценивается как 0,1; для второй группы – 0,2; для третьей – 0,3. Какова вероятность того, что случайно выбранный клиент, получивший страховое возмещение, относится к группе среднего риска? 20. Работа сотрудников торгового зала супермаркета организована в две смены. В первой смене работают 5 мужчин и 7 женщин, во второй смене – 9 мужчин и 10 женщин. Из второй смены в первую был переведен один сотрудник. Клиент супермаркета пригласил сотрудника торгового зала для консультации. Консультировал клиента сотрудник – мужчина. Какова вероятность того, что из второй смены в первую была переведена женщина?

Хочу написать ответ

Источник

Составитель преподаватель кафедры высшей математики Ищанов Т.Р. Занятие №4. Формула полной вероятности. Вероятность гипотез. Формулы Байеса.

Теоретический материал

Доказательство. По условию, событие А может наступить, если наступит одно из несовместных событий .

Другими словами, появление события А означает осуществление одного, безразлично какого, из несовместных событий . Пользуясь для вычисления вероятности события А теоремой сложения, получим

Остается вычислить каждое из слагаемых. По теореме умножения вероятностей зависимых событий имеем

$[P(B_1A)=P(B1)cdot P_{B_1}(A);]$

$[P(B_2A)=P(B_2)cdot P_{B_2}(A);ldots; P(B_nA)=P(B_n)P_{B_n}(A).]$

Подставив правые части этих равенств в соотношение (*), получим формулу полной вероятности

$[P(A)=P(B_1)P_{B_1}(A)+P(B_2)P_{B_2}(A)+cdots+P(B_n)P_{B_n}(A).]$

Пример 1. Имеется два набора деталей. Вероятность того, что деталь первого набора стандартна, равна 0,8, а второго—0,9. Найти вероятность того, что взятая наудачу деталь (из наудачу взятого набора) — стандартная.
Решение. Обозначим через А событие «извлеченная деталь стандартна».
Деталь может быть извлечена либо из первого набора (событие B₁), либо из второго (событие B₂).
Вероятность того, что деталь вынута из первого набора, .
Вероятность того, что деталь вынута из второго набора, .
Условная вероятность того, что из первого набора будет извлечена стандартная деталь, $P_{B_1}(A)= 0,8$ .
Условная вероятность того, что из второго набора будет извлечена стандартная деталь $P_{B_2}(A)=0,9$ .
Искомая вероятность того, что извлеченная наудачу деталь — стандартная, по формуле полной вероятности равна

$[P(A)=P(B_1)P_{B_1}(A)+P_{B_2}P_{B_2}(A)=0,5cdot 0,8+0,5cdot 0,9=0,85.]$

Пример 2. В первой коробке содержится 20 радиоламп, из них 18 стандартных; во второй коробке—10 ламп, из них 9 стандартных. Из второй коробки наудачу взята лампа и переложена в первую. Найти вероятность того, что лампа, наудачу извлеченная из первой коробки, будет стандартной.
Решение. Обозначим через А событие «из первой коробки извлечена стандартная лампа».
Из второй коробки могла быть извлечена либо стандартная лампа (событие B₁), либо нестандартная (событие B₂).
Вероятность того, что из второй коробки извлечена стандартная лампа,
Вероятность того, что из второй коробки извлечена нестандартная лампа,
Условная вероятность того, что из первой коробки извлечена стандартная лампа, при условии, что из второй коробки в первую была переложена стандартная лампа, равна $P_{B_1}(A)= 19/21.$
Условная вероятность того, что из первой коробки извлечена стандартная лампа, при условии, что из второй коробки в первую была переложена нестандартная лампа, равна $P_{B_2}(A) = 18/21.$
Искомая вероятность того, что из первой коробки будет извлечена стандартная лампа, по формуле полной вероятности равна

$[P(A)=P(B_1)P_{B_1}(A)+P(B_2)P_{B_2}(A)=frac{9}{10}cdotfrac{19}{21}+frac{1}{10}cdotfrac{18}{21}=0,9.]$

Вероятность гипотез. Формулы Байеса

Пусть событие A может наступить при условии появления одного из несовместных событий , образующих полную группу. Поскольку заранее не известно, какое из этих событий наступит, их называют гипотезами. Вероятность появления события A определяется по формуле полной вероятности:

$[P(A)=P(B_1)P_{B_1}(A)+P(B_2)P_{B_2}(A)+cdots+P(B_n)P_{B_n}(A). quad (*)]$

Допустим, что произведено испытание, в результате которого появилось событие А. Поставим своей задачей определить, как изменились (в связи с тем, что событие А уже наступило) вероятности гипотез. Другими словами, будем искать условные вероятности

$[P_{A}(B_1),P_{A}(B_2),cdots,P_{A}(B_n).]$

Найдем сначала условную вероятность $P_{A}(B_1)$ . ПО теореме умножения имеем

$[P(AB_1)=P(A)P_{A}(B_1)=P(B_1)P_{B_1}(A).]$

Отсюда

$[P_{A}(B_1)=frac{P(B_1)P_{B_1}(A)}{P(A)}.]$

Заменив здесь Р (А) по формуле (*), получим

$[P_{A}(B_1)=frac{P(B_1)P_{B_1}(A)}{P(B_1)P_{B_1}(A)+P(B_2)P_{B_2}(A)+cdots+P(B_n)P_{B_n}(A)}]$

Аналогично выводятся формулы, определяющие условные вероятности остальных гипотез, т. е. условная вероятность любой гипотезы может быть вычислена по формуле

$[P_{A}(B_i)=frac{P(B_i)P_{B_i}(A)}{P(B_1)P_{B_1}(A)+P(B_2)P_{B_2}(A)+cdots+P(B_n)P_{B_n}(A)}.]$

Полученные формулы называют формулами Байеса (по имени английского математика, который их вывел; опубликованы в 1764 г.). Формулы Бейеса позволяют переоценить вероятности гипотез после того, как становится известным результат испытания, в итоге которого появилось событие А.

Пример. Детали, изготовляемые цехом завода, попадают для проверки их на стандартность к одному из двух контролеров. Вероятность того, что деталь попадает к первому контролеру, равна 0,6, а ко второму — 0,4. Вероятность того, что годная деталь будет признана стандартной первым контролером, равна 0,94, а вторым—0,98. Годная деталь при проверке была признана стандартной. Найти вероятность того, что эту деталь проверил первый контролер.
Решение. Обозначим через А событие, состоящее в том, что годная деталь признана стандартной. Можно сделать два предположения:
1)деталь проверил первый контролер (гипотеза );
2)деталь проверил второй контролер (гипотеза ). Искомую вероятность того, что деталь проверил первый контролер, найдем по формуле Байеса:

$[P_{A}(B_1)=frac{P(B_1)P_{B_1}(A)}{P(B_1)P_{B_1}(A)+P(B_2)P_{B_2}(A)}.]$

По условию задачи имеем:
(вероятность того, что деталь попадает к первому контролеру);
(вероятность того, что деталь попадет ко второму контролеру);
$P_{B_1}(A)=0,94$ (вероятность того, что годная деталь будет признана первым контролером стандартной);
$P_{B_2}(A)= 0,98$ (вероятность того, что годная деталь будет признана вторым контролером стандартной).
Искомая вероятность

$[P_A(B_1)=frac{0,6cdot 0,94}{0,6cdot 0,94+0,4cdot 0,98}approx 0,59.]$

Как видно, до испытания вероятность гипотезы равнялась 0,6, после того, как стал известен результат испытания, вероятность этой гипотезы (точнее, условная вероятность) изменилась и стала равной 0,59. Таким образом, использование формулы Байеса позволило переоценить вероятность рассматриваемой гипотезы.

Практический материал.
1. (4) Сборщик получил 3 коробки деталей, изготовленных заводом № 1, и 2 коробки деталей, изготовленных заводом № 2. Вероятность того, что деталь завода № 1 стандартна, равна 0,8, а завода № 2 — 0,9, Сборщик наудачу извлек деталь из наудачу взятой коробки. Найти вероятность того, что извлечена стандартная деталь.
Отв. 0,84.
2. (5) В первом ящике содержится 20 деталей, из них 15 стандартных; во втором—30 деталей, из них 24 стандартных; в третьем — 10 деталей, из них 6 стандартных. Найти вероятность того, что наудачу извлеченная деталь из наудачу взятого ящика—стандартная.
Отв. 43/60.
3. (6) В телевизионном ателье имеется 4 кинескопа. Вероятности того, что кинескоп выдержит гарантийный срок службы, соответственно равны 0,8; 0,85; 0,9; 0,95. Найти вероятность того, что взятый наудачу кинескоп выдержит гарантийный срок службы.
Отв. 0,875.
4. (3) В группе спортсменов 20 лыжников, 6 велосипедистов и 4 бегуна. Вероятность выполнить квалификационную норму такова: для лыжника—0,9, для велосипедиста—0,8. и для бегуна—0,75. Найти вероятность того, что спортсмен, выбранный наудачу, выполнит норму.
Отв. 0,86.
5. © В белом ящике 12 красных и 6 синих шаров. В черном – 15 красных и 10 синих шаров. Бросают игральный кубик. Если выпадет количество очков, кратное 3, то наугад берут шар из белого ящика. Если выпадет любое другое количество очков, то наугад берут шар из черного ящика. Какова вероятность появления красного шара?

Показать решение

Решение:
Возможны две гипотезы:
– при бросании кубика выпадет количество очков, кратное 3, т.е. или 3 или 6;
– при бросании кубика выпадет другое количество очков, т.е. 1, 2, 4 или 5.
По классическому определению вероятности гипотез равны:

$[P(H_1) = frac26 = frac13;qquad P(H_2) = frac46 = frac23.]$

Поскольку гипотезы составляют полную группу событий, то должно выполняться равенство

$[P(H_1)+P(H_2)=frac13+frac23=1.]$

Пусть событие А состоит в появлении красного шара. Условные вероятности этого события зависят от того, какая именно гипотеза реализовалась, и составляют соответственно:

$[P_{H_1}(A)=frac{12}{18}=frac23;qquad P_{H_2}(A)=frac{15}{25}=frac35]$

Тогда по формуле полной вероятности вероятность события А будет равна:

$[P(A)=frac13cdotfrac23+frac23cdotfrac35=frac{10+18}{9cdot5}=frac{28}{45}=0,62.]$

6. (7) В двух ящиках имеются радиолампы. В первом ящике содержится 12 ламп, из них 1 нестандартная; во втором 10 ламп, из них 1 нестандартная. Из первого ящика наудачу взята лампа и переложена во второй. Найти вероятность того, что наудачу извлеченная из второго ящика лампа будет нестандартной.
Отв. 13/132.

7. (89 Г) В урну, содержащую два шара, опущен белый шар, после чего из нее наудачу извлечен один шар. Найти вероятность того, что извлеченный шар окажется белым, если равновозможны все возможные предположения о первоначальном составе шаров (по цвету).

Показать решение

Решение. Обозначим через А событие – извлечен белый шар. Возможны следующие предположения (гипотезы) о первоначальном составе шаров:

— белых шаров нет,

— один белый шар,

— два белых шара.
Поскольку всего имеется три гипотезы, причем по условию они равновероятны, и сумма вероятностей гипотез равна единице (так как они образуют полную группу событий), то вероятность каждой из гипотез равна 1/3, т.е. .
Условная вероятность того, что будет извлечен белый шар, при условии, что первоначально в урне не было белых шаров, $P_{B_1 } (A)=1/3$ .
Условная вероятность того, что будет извлечен белый шар, при условии, что первоначально в урне был один белый шар, $P_{B_2} (A)=2/3$ .
Условная вероятность того, что будет извлечен белый шар, при условии, что первоначально в урне было два белых шара $P_{B_3} (A)=3/3=1$ .
Искомую вероятность того, что будет извлечен белый шар, находим по формуле полной вероятности:

$[P(A)=P(B_1)P_{B_1}(A)+P(B_2)P_{B_2}(A)+P(B_3)P_{B_3} (A)=frac13cdotfrac13+frac13cdotfrac23+frac13cdot 1=frac23.]$

8. (10) В ящик, содержащий 3 одинаковых детали, брошена стандартная деталь, а затем наудачу извлечена одна деталь. Найти вероятность того, что извлечена стандартная деталь, если равновероятны все возможные предположения о числе стандартных деталей, первоначально находящихся в ящике.
Отв. 0,625.

9. (6.5.2Л) Для улучшения качества радиосвязи используются два радиоприемника. Вероятность приема сигнала каждым приемником равна 0,8, и эти события (прием сигнала приемником) независимы. Определить вероятность приема сигнала, если вероятность безотказной работы за время сеанса радиосвязи для каждого приемника равна 0,9.

Показать решение

Решение.
Пусть событие А={сигнал будет принят}. Рассмотрим четыре гипотезы:

={первый приемник работает, второй — нет};

={второй работает, первый — нет};

={оба приемника работают};

={оба приемника не работают}.

Событие А может произойти только с одной из этих гипотез. Найдем вероятность этих гипотез, рассматривая следующие события:

={первый приемник работает},

={второй приемник работает}.

Тогда:

$[P(H_1 )=P(C_1cdotbar{C_2})=P(C_1 )cdot P(bar{C_2})=0,9cdot 0,1=0,09;]$

$[P(H_2)=P(bar{C_1}cdot C_2)=P(bar{C_1}cdot P(C_2)=0,1cdot 0,9=0,09;]$

$[P(H_4 )=P(bar{C_1}cdot bar{C_2})=P(bar{C_1} )cdot P(bar{C_2})=0,1cdot 0,1=0,01.]$

Контроль:

$[sum_{i=1}^4 P(H_i )=0,09+0,09+0,81+0,01=1.]$

Условные вероятности $P_{H_i}(A)$ соответственно равны:

$P_{H_1}(A)=0,8;$

$P_{H_2}(A)=0,8;$

$P_{H_3}(A)=0,8+0,8-0,8cdot 0,8=0,96;$

$P_{H_4}(A)=0.$

Теперь по формуле полной вероятности находим искомую вероятность

10. (11) При отклонении от нормального режима работы автомата срабатывает сигнализатор С-1 с вероятностью 0,8, а сигнализатор С-11 срабатывает с вероятностью 1. Вероятности того, что автомат снабжен сигнализатором С-1 или С-11, соответственно равны 0,6 и 0,4. Получен сигнал о разделке автомата. Что вероятнее: автомат снабжен сигнализатором С-1 или С-11?
Отв. Вероятность того, что автомат снабжен сигнализатором С-1, равна 6/11, а С- 11— 5/11

11. (12) Для участия в студенческих отборочных спортивных соревнованиях выделено из первой группы курса 4, из второй — 6, из третьей группы — 5 студентов. Вероятности того, что студент первой, второй и третьей группы попадает в сборную института, соответственно равны 0,9; 0,7 и 0,8. Наудачу выбранный студент в итоге соревнования попал в сборную. К какой из групп вероятнее всего принадлежал этот студент?
Отв. Вероятности того, что выбран студент первой, второй, третьей групп, соответственно равны: 18/59, 21/59, 20/59.

12. (1.34К) В торговую фирму поступили телевизоры от трех поставщиков в отношении 1:4:5. Практика показала, что телевизоры, поступающие от 1-го, 2-го и 3-го поставщиков, не потребуют ремонта в течении гарантийного срока соответственно в 98, 88 и 92% случаев.
1) Найти вероятность того, что поступивший в торговую фирму телевизор не потребует ремонта в течение гарантийного срока.
2) Проданный телевизор потребовал ремонта в течение гарантийного срока. От какого поставщика вероятнее всего поступил этот телевизор?

Показать решение

Решение.
Обозначим события: — телевизор поступил в торговую фирму от i-го поставщика (i=1,2,3);
A – телевизор не потребует ремонта в течение гарантийного срока.
По условию

$[P(H_1)=frac{1}{1+4+5}=0,1;qquad P_{H_1} (A)=0,98;]$

$[P(H_2)=frac{4}{1+4+5}=0,4;qquad P_{H_2} (A)=0,88;]$

$[P(H_3)=frac{5}{1+4+5}=0,5;qquad P_{H_3} (A)=0,92.]$

По формуле полной вероятности

Событие телевизор потребует ремонта в течение гарантийного срока:

По условию

$[P_{H_1} (bar{A})=1-0,98=0,02;]$

$[P_{H_2} (bar{A})=1-0,88=0,12;]$

$[P_{H_3} (bar{A})=1-0,92=0,08.]$

По формуле Байеса

$[P_{overline{A}} (H_1)=frac {0,1cdot 0,02}{0,09}=0,022;qquad P_{overline{A}} (H_2)=frac {0,4cdot 0,12}{0,09}=0,533;]$

$[P_{overline{A}} (H_3)=frac {0,5cdot 0,08}{0,09}=0,444.]$

Таким образом, после наступления события вероятность гипотезы H₂ увеличилась с P (H₂)=0,4 до максимальной

$P_{bar{A}}(H_2)=0,533$ ,

а гипотезы H₃ — уменьшилась от максимальной P (H₃)=0,5 до $P_{bar{A}} (H_3 )=0,444$ ; если ранее (до наступления события А) наиболее вероятной была гипотеза H₃, то теперь, в свете новой информации (наступления события А), наиболее вероятна гипотеза H₂ -поступление данного телевизора от 2-го поставщика.

13. (1.35К) Известно, что в среднем 95% выпускаемой продукции удовлетворяют стандарту. Упрощенная схема контроля признает пригодной продукцию с вероятностью 0,98, если она стандартна, и с вероятностью 0,06, если она нестандартна. Определить вероятность того, что:
1) взятое наудачу изделие пройдет упрощенный контроль;
2) изделие стандартное, если оно: а) прошло упрощенный контроль; б) дважды прошло упрощенный контроль.

Показать решение

Решение.
1). Обозначим события:
— взятое наудачу изделие соответственно стандартное или нестандартное;
— изделие прошло упрощенный контроль.

По условию

$[P(H_1)=0,95,qquad P(H_2)=0,05,qquad P_{H_1}(A)=0,98,qquad P_{H_2}(A)=0,06.]$

Вероятность того, что взятое наудачу изделие пройдет упрощенный контроль, по формуле полной вероятности:

2. а). Вероятность того, что изделие, прошедшее упрощенный контроль, стандартное, по формуле Байеса:

$[P_{A}(H_1)=frac{0,95cdot 0,98}{0,934}=0,997.]$

2. б). Пусть событие — изделие дважды прошло упрощенный контроль. Тогда по теореме умножения вероятностей:

$[P_{H_1}(A^*)=0,98cdot 0,98=0,9604, qquad P_{H_2}(A^*)=0,06cdot 0,06=0,0036.]$

По формуле Байеса

$[P_{A^*}(H_1)=frac{0,95cdot 0,9604}{0,95cdot 0,9604+0,05cdot 0,0036}=0,9998.]$

Так как

$[P_{A^*}(H_2)=1-P_{A^*}(H_1)=1-0,9998=0,0002]$

очень мала, то гипотезу о том, что изделие, дважды прошедшее упрощенный контроль, нестандартное, следует отбросить как практически невозможное событие.

14. (1.36К) Два стрелка независимо друг от друга стреляют по мишени, делая каждый по одному выстрелу. Вероятность попадания в мишень для первого стрелка равна 0,8; для второго – 0,4. После стрельбы в мишени обнаружена одна пробоина. Какова вероятность того, что она принадлежит:
а) 1-му стрелку;
б) 2-му стрелку?

Показать решение

Решение.
Обозначим события:

— оба стрелка не попали в мишень;

— оба стрелка попали в мишень;

— 1-й стрелок попал в мишень, 2-й нет;

— 1-й стрелок не попал в мишень, 2-й попал;

— в мишени одна пробоина (одно попадание).

Найдем вероятности гипотез и условные вероятности события для этих гипотез:

$[P(H_1)=0,2cdot 0,6=0,12,qquad P_{H_1}(A)=0;]$

$[P(H_2)=0,8cdot 0,4=0,32,qquad P_{H_2}(A)=0;]$

$[P(H_3)=0,8cdot 0,6=0,48,qquad P_{H_3}(A)=1;]$

$[P(H_4)=0,2cdot 0,4=0,08,qquad P_{H_4}(A)=1.]$

Теперь по формуле Байеса

$[P_{A}(H_3)=frac{0,48cdot 1}{0,12cdot 0+0,32cdot 0+0,48cdot 1+0,08cdot 1}=frac{6}{7}=0,857;]$

$[P_{A}(H_4)=frac{0,08cdot 1}{0,12cdot 0+0,32cdot 0+0,48cdot 1+0,08cdot 1}=frac{1}{7}=0,143,]$

т.е. вероятность того, что попал в цель 1-й стрелок при наличии одной пробоины, в 6 шесть раз выше, чем для второго стрелка.

15. (6.5.8Л) Техническое устройство выйдет из строя, если откажут не менее двух из трех независимо работающих элементов. Вероятности отказов 1-го, 2-го, 3-го элементов соответственно равны 0,2; 0,4; 0,3. Известно, что устройство отказало. Найти вероятность того, что отказали 1-й и 2-й элементы.

Показать решение

Решение.
Пусть событие А={устройство отказало}. До опыта, т.е. до отказа устройства, можно сделать следующие предположения-гипотезы:

={откажут все три элемента};

={откажут два элемента: 1-й и 2-й, 3-й — не откажет};

={откажут два элемента: 1-й и 3-й, 2-й — не откажет};

={откажут два элемента: 2-й и 3-й, 1-й — не откажет};

={откажет один элемент: 1-й, не откажут 2-й и 3-й};

={откажет один элемент: 2-й, не откажут 1-й и 3-й};

={откажет один элемент: 3-й, не откажут 1-й и 2-й};

={все элементы, будут работать}.

Пользуясь правилом умножения вероятностей для независимых событий, найдем вероятности этих гипотез:

Контроль:

$[sum_{i=0}^7 P(H_i)=0,024+0,056+cdots+0,336=1.]$

Учитывая, что в результате опыта произошло событие А, которое невозможно при гипотезах H₄, H₅, H₆, H₇ и достоверно при гипотезах H₀, H₁, H₂, H₃, найдем условные вероятности событий $P_{H_i}(A)$ :

$[P_{H_0}(A)=1;qquad P_{H_1}(A)=1;]$

$[P_{H_2}(A)=1;qquad P_{H_3}(A)=1;]$

$[P_{H_4}(A)=0;qquad P_{H_5}(A)=0;]$

$[P_{H_6}(A)=0;qquad P_{H_7}(A)=0.]$

Найдем вероятность гипотезы при условии, что событие А произошло по формуле Байеса. Для этого предварительно найдем вероятность события А по формуле:

$[P(A)=sum_{i=0}^7 P(H_i)cdot P_{H_i}(A)=0,024cdot 1+0,056cdot 1+0,096cdot 1+0+0+0+0=0,212.]$

Отсюда

$[P_{A}(H_1)=frac{P(H_1)cdot P_{H_1}(A)}{P(A)}=frac{0,056cdot 1}{0,212}=frac{56}{212}=frac{14}{53}approx 0,264.]$

16.(1.36аК) Компания по страхованию автомобилей разделяет водителей на три класса, которые включают 20%, 50% и 30% водителей соответственно. Вероятности того, что в течение года водитель попадет в аварию, равны 0,01, 0,03 и 0,1 соответственно для каждого класса. Наугад выбранный водитель два года подряд из пяти лет срока страховки попал в аварию. Какова вероятность того, что он относится:
а) к первому классу;
б) к третьему классу?

Показать решение

Решение.
Обозначим события:

— водитель соответственно первого, второго и третьего класса;

— водитель два года подряд из пяти лет срока страховки попадал в аварию.

По условию

Найдем условные вероятности события (учитываем, что из пяти лет водитель три года не попадал в аварию, два года — попадал, причем попадал два года подряд, что дает четыре варианта (по годам 1-2, 2-3, 3-4, 4-5)):

$[P_{H_1}(A)=4cdot 0,01^2cdot 0,99^3=0,00039;]$

$[P_{H_2}(A)=4cdot 0,03^2cdot 0,97^3=0,00329;]$

$[P_{H_3}(A)=4cdot 0,1^2cdot 0,9^3=0,02916.]$

По формуле Байеса:

$[P_{A}(H_1)=frac{0,2cdot 0,00039}{0,2cdot 0,00039+0,5cdot 0,00329+0,3cdot 0,02916}=0,007;]$

$[P_{A}(H_3)=frac{0,3cdot 0,02916}{0,2cdot 0,00039+0,5cdot 0,00329+0,3cdot 0,02916}=0,835,]$

т.е. после наступления события A гипотеза практически невозможна и должна быть отвергнута.

Источник

Вопросы » Комбинаторика,вероятность » Страховая компания делит , водителей, заключивших договор авто каско на следующие группы риска

Вопросы »

Комбинаторика,вероятность » Страховая компания делит , водителей, заключивших договор авто каско на следующие группы риска