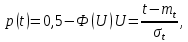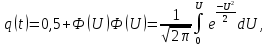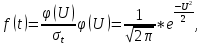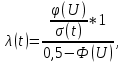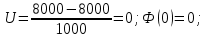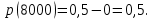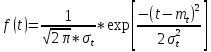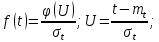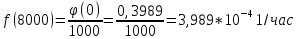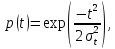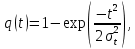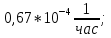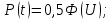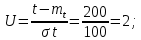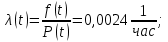Среднее время исправной работы изделия равно 1260 час время исправной работы подчинено закону релея

---

С этим файлом связано 11 файл(ов). Среди них: Яицкая Отчёт..docx, documents_prik111_2022.shtml.pdf, fff.docx, Лабораторная работа № 4.docx, Лабораторная работа Кривко_Сурин.docx, манин.docx, Лаба Кривко_Сурин.docx, ПР№4 (2).doc, лабораторка 0.docx, Письмо-запрос.docx, Саши (1).docx и ещё 1 файл(а).
Показать все связанные файлы

---

Подборка по базе: ильдар отчет.docx, Отчет по работе.docx, Вывод отчета на печать — Антиплагиат.pdf, Статья. Основные направления деятельности классного руководителя, 1111 мой отчет.docx, Финансовая отчетность по МСФО за 2020 год.pdf, Отчёт о работе библиотеки за 2021-2022уч г.docx, Тема 1. Общие сведения о работе личного состава ГДЗС в изолирующ, Отчет по лабораторной работе. МЕХАНИКА. 4.docx, Типовой план проведения занятий с машинистами имеющими стаж в ра

---

В ОРОНЕЖСКИЙ ИНСТИТУТ ВЫСОКИХ ТЕХНОЛОГИЙ – АНОО ВО

Специальность/Направление

09.03.01 Информатика и вычислительная техника

шифр название

Отчет по лабораторной работе №2

вид работы (Курсовая работа, эссе, реферат, доклад и т.д.)

по дисциплине Надежность автоматизированных систем

Расчет показателей надежности резервированных не восстанавливаемых систем
Выполнил: студентка группы ИВТ-202

название группы

Рязанова Алина Альбертовна

ФИО студента

Форма обучения ____

очная_____

(очная, заочная)

Руководитель:

Куралесин Вячеслав Викторович

ФИО руководителя
Воронеж 2022

Цель работы: рассчитать показатели надежности резервированных не восстанавливаемых систем.
Решение задач:

Задача 2.6. Вероятность безотказной работы автоматической линии изготовления цилиндров автомобильного двигателя в течении 120 час равна 0.9. Предполагается, что справедлив экспоненциальный закон надежности. Требуется рассчитать интенсивность отказов и частоту отказов линии для момента времени t =120 час., а также среднее время безотказной работы.

Решение:

Если P = 0,9; t = 120, то

P(t) = e^-λ*t

P(120) = e^-λ*120

λ = 8,8*10^-4 1/час

f(t) = λ(t)*P(t)

f(t) = 8,8*10^-4*0,9=7,92*10^-4

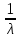
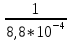
m_t = = = 1136 час.

Задача 2.7. Среднее время безотказной работы автоматической системы управления равно 640 час. Предполагается, что справедлив экспоненциальный закон надежности. Необходимо определить вероятность безотказной работы в течение 120 час., частоту отказов для момента времени t=120 час и интенсивность отказов.

Решение:

Если m(t) = 640 час, t = 120 час, то

m_t =

λ = 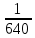= 1,56 *10^-3 1/час.

P(t) = e^-λ*t

P(120)= 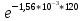= 0,83

f(120) = λ(120)*P(120)

f(120) = 1,56*10^-3*0,83 = 1,29*10^-3 1/час

Задача 2.8. Время работы изделия подчинено нормальному закону с параметрами m_t = 8000 час., 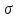_t =1000 час. Требуется вычислить количественные характеристики надежности p(t), q(t), f(t), m_t для t=8000 час.

Решение:

Воспользуемся формулами

для p(t), q(t), f(t), m_t.

1. Вычислим вероятность безотказной работы:

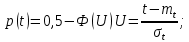
1. Определим частоту отказа f(t):

Введем обозначение

Тогда

1. Рассчитаем интенсивность отказов q(t):

1/час

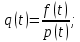
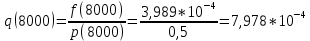
1. Среднее время безотказной работы элемента:

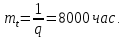
Задача 2.9. Время безотказной работы прибора подчинено закону Релея с параметром t= 1860 час. Требуется вычислить Р(t), f(t), 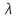(t) для t = 1000 час и среднее время безотказной работы прибора.

Решение:

),

,

;

;

;

;

;

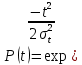
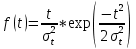
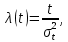
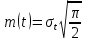
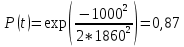
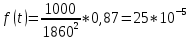
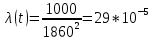
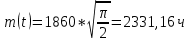
Задача 2.10. Время исправной работы скоростных шарикоподшипников подчинено закону Вейбулла с параметрами к=2,6 ; а= 1,65*10^-7 1/час. Требуется вычислить количественные характеристики надежности p(t), q(t), f(t), m_t для t=150 час. и среднее время безотказной работы шарикоподшипников.

Решение:

𝑝(𝑡) = 𝑒^{−𝑎𝑡𝑘},

q(𝑡) = 1 − 𝑒^{−𝑎𝑡𝑘},

𝑓(𝑡) = 𝑎𝑘𝑡^𝑘-1 * p(t);

𝑚(𝑡) = ;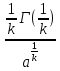

;

;

;

;

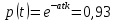
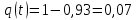
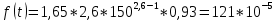
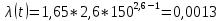
𝑚(𝑡) = ;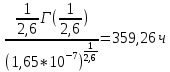

Задача 2.11. Вероятность безотказной работы изделия в течение t=1000 час. Р(1000)=0,95. Время исправной работы подчинено закону Релея. Требуется определить количественные характеристики надежности p(t), q(t), f(t), m_t.

Решение:

;

;

;

= 3122,16 ч;

;

;

;

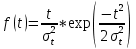
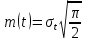
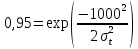
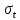
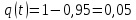
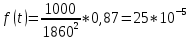
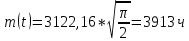
Задача 2.12. Среднее время исправной работы изделия равно 1260 час. Время исправной работы подчинено закону Релея. Необходимо найти его количественные характеристики надежности p(t), q(t), f(t), m_t для t=1000 час.

Решение:

;

;

;

;

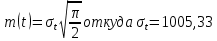
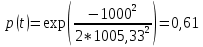
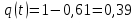
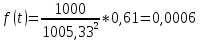
Задача 2.13. В результате анализа данных об отказах изделия установлено, что частота отказов имеет вид f(t)=2e^-t (1-e^-t ) . Необходимо найти количественные характеристики надежности p(t), q(t), f(t), m_t.

Решение:

;

;

;

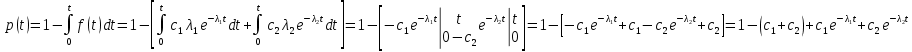
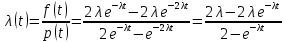
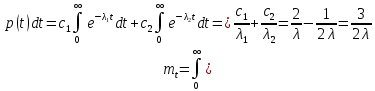
Задача 2.14. В результате анализа данных об отказах изделий установлено, что вероятность безотказной работы выражается формулой P(t)=3e^-t-3e^-2t+e^-3t. Требуется найти количественные характеристики надежности p(t), q(t), f(t), m_t.

Решение:

;

;

;

;

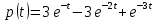
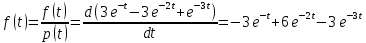
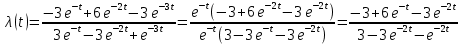
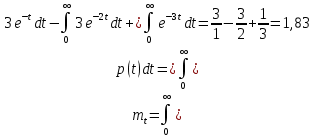
Задача 2.15. Определить вероятность безотказной работы и интенсивность отказов прибора при t = 1300 часов работы, если при испытаниях получено значение среднего времени безотказной работы mt=1500 час. и среднее квадратическое отклонение σ_t= 100 час.

Решение:

Дано:

t = 1300; m_t = 1500 час; σ_t = 100 час;

P-?; λ-?

По эксп. Закону:

;

= =

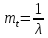
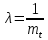
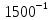
По нормальному закону:

;

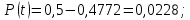
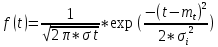
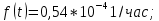
Вывод: в ходе выполнения лабораторной работы мы рассчитали показатели надежности резервированных не восстанавливаемых систем.

Сообщения без ответов | Активные темы

Похожие темы	Автор	Ответы	Просмотры	Последнее сообщение
Прикладная задачка в форуме Механика	Mihel	1	263	12 фев 2018, 05:40
Прикладная задача в форуме Интегральное исчисление	Alatte	5	445	30 апр 2016, 22:58
Прикладная геометрическая задача в форуме Геометрия	eugend1980	1	87	11 сен 2022, 10:28
Прикладная задача для программиста в форуме Функциональный анализ, Топология и Дифференциальная геометрия	new118	4	470	13 авг 2013, 17:05
Прикладная задача расчёта З/П в форуме Исследование операций и Задачи оптимизации	Creator87	0	490	30 май 2013, 15:18
Прикладная задача из биологии в форуме Теория вероятностей	mad_math	2	206	21 май 2018, 15:55
Задача про систему надежности в форуме Теория вероятностей	Mary111	11	1684	17 ноя 2015, 10:03
Показательный закон надежности в форуме Теория вероятностей	Goodwin90	1	461	21 май 2014, 22:09
Задача по теории надёжности в форуме Теория вероятностей	xzibitcar	0	340	30 мар 2018, 18:47
Прикладная задача по лучистому теплообмену в форуме Интегральное исчисление	Rzhevskiy	29	647	15 апр 2019, 16:55

Кто сейчас на конференции

Сейчас этот форум просматривают: нет зарегистрированных пользователей и гости: 19

Вы не можете начинать темы Вы не можете отвечать на сообщения Вы не можете редактировать свои сообщения Вы не можете удалять свои сообщения Вы не можете добавлять вложения

Среднее время исправной работы изделия равно 1260 час. Время исправной работы подчинено закону Релея. Необходимо найти его количественные характеристики надежности P(t), f(t), l(t)для t = 1000 час.

66. Время работы изделия подчинено нормальному закону с параметрами m_t = 8000 час., σ_t =1000 час. Требуется вычислить количественные характеристики надежности p(t) , f(t) , λ(t) для t=8000 час.

67. Время исправной работы скоростных шарикоподшипников подчинено закону Вейбулла с параметрами α=2,6 ; λ= 1,65*10^-7 1/час.

Требуется вычислить количественные характеристики надежности Р(t), f(t), λ(t) для t=150 час. и среднее время безотказной работы шарикоподшипников.

68. Вероятность безотказной работы изделия в течение t=1000 час. Р(1000)=0,95. Время исправной работы подчинено экспоненциальному закону. Требуется определить количественные характеристики надежности f(t), λ (t), m_t.

69. Среднее время исправной работы изделия равно 1260 час. Время исправной работы подчинено экспоненциальному закону. Необходимо найти его количественные характеристики надежности P(t), f(t), λ (t) для t=1000 час.

Дано:

T=1260ч

t=1000ч

p(t)-?

λ(t)-?

f(t)-?

Решение:

1) -интенсивность отказа

2)Варианты безотказной работы

3) Частота отказов

70. В результате анализа данных об отказах изделия установлено, что частота отказов имеет вид f(t)=2e^-t (1-e^-t) . Необходимо найти количественные характеристики надежности P(t), λ (t), m_t.

Дано:

f(t)=2e^-t (1-e^-t)

p(t)-?

λ(t)-?

m_t-?

Решение:

1)

=1-2 – вероятность безотказной работы на интенсивность времени от 0 до t

2) интенсивность отказов изделия

= среднее время безотказной работы изделия

Достарыңызбен бөлісу: