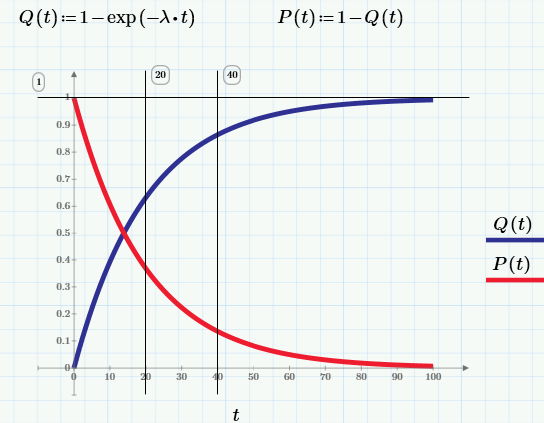
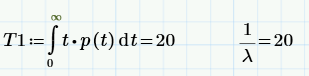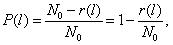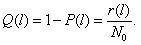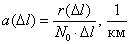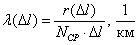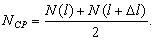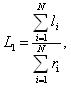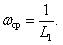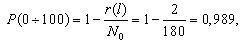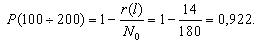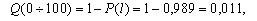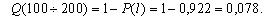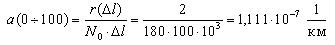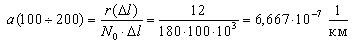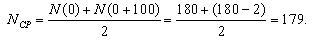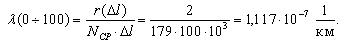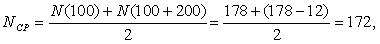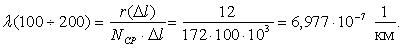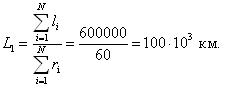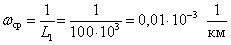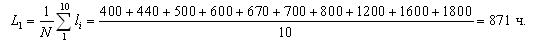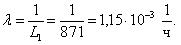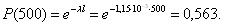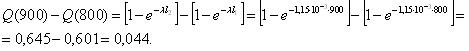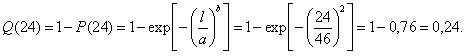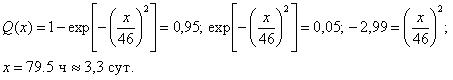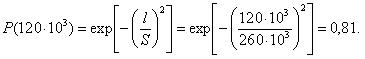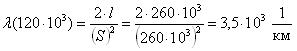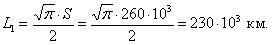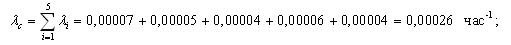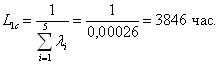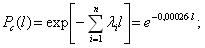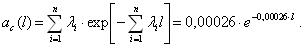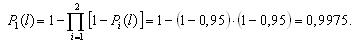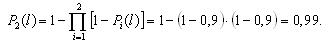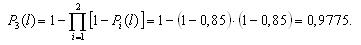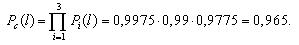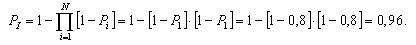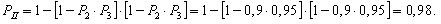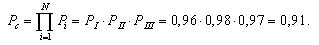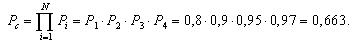Как вычисляется среднее время до отказа и вероятность безотказной работы?
Время на прочтение
4 мин
Количество просмотров 116K
Понятиям MTTF (Mean Time To Failure — среднее время до отказа) и другим терминам теории надежности посвящено большое количество статей, в том числе на Хабре (см., например, тут). Вместе с тем, редкие публикации «для широкого круга читателей» затрагивают вопросы математической статистики, и уж тем более они не дают ответа на вопрос о принципах расчета надежности электронной аппаратуры по известным характеристикам ее составных элементов.
В последнее время мне довольно много приходится работать с расчетами надежности и рисков, и в этой статье я постараюсь восполнить этот пробел, отталкиваясь от своего предыдущего материала (из цикла о машинном обучении) о пуассоновском случайном процессе и подкрепляя текст вычислениями в Mathcad Express, повторить которые вы сможете скачав этот редактор (подробно о нем тут, обратите внимание, что нужна последняя версия 3.1, как и для цикла по machine learning). Сами маткадовские расчеты лежат здесь (вместе с XPS- копией).
1. Теория: основные характеристики отказоустойчивости
Вроде бы, из самого определения (Mean Time To Failure) понятен его смысл: сколько (конечно, в среднем, поскольку подход вероятностный) прослужит изделие. Но на практике такой параметр не очень полезен. Действительно, информация о том, что среднее время до отказа жесткого диска составляет полмиллиона часов, может поставить в тупик. Гораздо информативнее другой параметр: вероятность поломки или вероятность безотказной работы (ВБР) за определенный период (например, за год).
Для того чтобы разобраться в том, как связаны эти параметры, и как, зная MTTF, вычислить ВБР и вероятности отказа, вспомним некоторые сведения из математической статистики.
Ключевое понятие теории надежности — это понятие отказа, измеряемое, соответственно, интервальным показателем
Q(t) = вероятность того, что изделие откажет к моменту времени t.
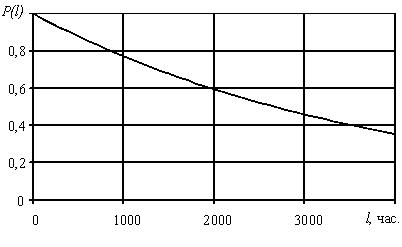
Соотвественно, вероятность безотказной работы (ВБР, в английской терминологии «reliability»):
P(t) = вероятность того, что изделие проработает без отказа от момента t0=0 до момента времени t.
По определению, в момент t0=0 изделие находится в работоспособном состоянии, т.е. Q(0)=0, а P(0)=1.
Оба параметра — это интервальные характеристики отказоустойчивости, т.к. речь идет о вероятности отказа (или наоборот, безотказной работы) на интервале (0,t). Если отказ рассматривать, как случайное событие, то, очевидно, что Q(t) — это, по определению, его функция распределения. А точечную характеристику можно определить, как
p(t)=dQ(t)/dt = плотность вероятности, т.е. значение p(t)dt равно вероятности, что отказ произойдет в малой окрестности dt момента времени t.
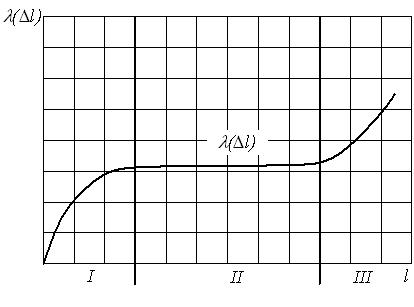
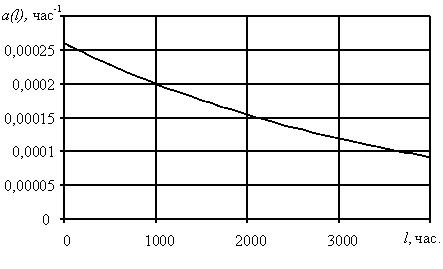
И, наконец, самая важная (с практической точки зрения) характеристика: λ(t)=p(t)/P(t)=интенсивность отказов.
Это (внимание!) условная плотность вероятности, т.е. плотность вероятности возникновения отказа в момент времени t при условии, что до этого рассматриваемого момента времени t изделие работало безотказно.
Измерить параметр λ(t) экспериментально можно путём испытания партии изделий. Если к моменту времени t работоспособность сохранило N изделий, то за оценку λ(t) можно принять процент отказов в единицу времени, происходящих в окрестности t. Точнее, если в период от t до t+dt откажет n изделий, то интенсивность отказов будет примерно равна
λ(t)=n/(N*dt).
Именно эта λ-характеристика (в пренебрежении ее зависимостью от времени) и приводится чаще всего в паспортных данных различных электронных компонент и самых разных изделий. Только сразу возникает вопрос: а как вычислить вероятность безотказной работы и при чем здесь среднее время до отказа (MTTF).
А вот при чем.
2. Экспоненциальное распределение
В терминологии, которую мы только что использовали, пока не было никаких предположений о свойствах случайной величины — момента времени, в который происходит отказ изделия. Давайте теперь конкретизируем функцию распределения значения отказа, выбрав в качестве нее экспоненциальную функцию с единственным параметром λ=const (смысл которого будет ясен через несколько предложений).
Дифференцируя Q(t), получим выражение для плотности вероятности экспоненциального распределения:
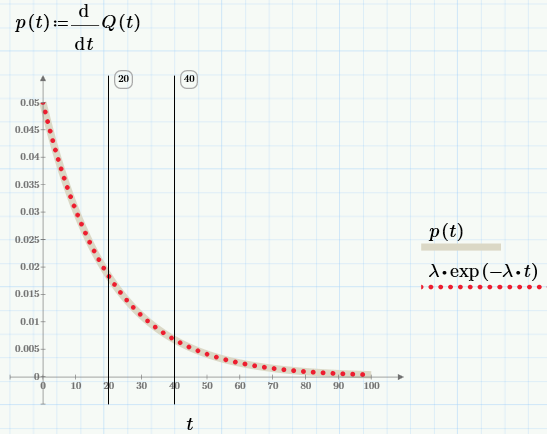
а из него – функцию интенсивности отказов: λ(t)=p(t)/P(t)=const=λ.
Что мы получили? Что для экспоненциального распределения интенсивность отказов – есть величина постоянная, причем совпадающая с параметром распределения. Этот параметр и является главным показателем отказоустойчивости и его часто так и называют λ-характеристикой.
Мало того, если теперь посчитать среднее время до первого отказа – тот самый параметр MTTF (Mean Time To Failure), то мы получим, что он равен MTTF=1/ λ.
Все это замечательные свойства экспоненциального распределения. Почему мы выбрали в качестве для описания отказов именно его? Да потому что это наиболее простая модель – модель пуассоновского потока событий, которая уже была нами рассмотрена в статье про анализ конверсии сайта. Поэтому-то в теории надежности наиболее часто используется показательное (экспоненциальное) распределение, для которого, как мы выяснили:
- надежность элементов можно оценить одним числом, т.к. λ=const;
- по известной λ довольно просто оценить остальные показатели надежности (например, ВБР для любого времени t);
- λ обладает хорошей наглядностью
- λ нетрудно измерить экспериментально
Но это еще не все, потому, что для экспоненциального распределения особенно легко делать расчет систем, состоящих из множества элементов. Но об этом – в следующей статье (продолжение следует).
Средним временем безотказной работы называется математическое ожидание времени безотказной работы.
Эта характеристика надежности обозначается T. Как всякое математическое ожидание случайной величины среднее время безотказной работы определяется из выражения:
. (1.25)
Приведенное определение является вероятностным. Для определения среднего времени безотказной работы из статистических данных пользуются формулой:
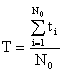
где ti— время безотказной работы i-го образца, N0— число образцов, над которыми проводится испытание.
Из выражения (1.26) видно, что для определения T необходимо знать моменты отказов всех образцов аппаратуры, над которыми проводится эксперимент. При большом числе образцов N0 это может сильно усложнить эксперимент.
Выражение (1.26) является статистическим определением среднего времени безотказной работы.
Среднее время безотказной работы является одной из наиболее наглядных количественных характеристик надежности. Однако этой характеристике надежности свойственны существенные недостатки. Как математическое ожидание случайной величины, она не может полностью характеризовать время работы аппаратуры. Необходимо еще знать, по меньшей мере, дисперсию времени отказов аппаратуры. Кроме того, T фактически не позволяет оценить надежность аппаратуры, время работы которой во много раз меньше среднего времени безотказной работы.
Из выражения (1.26) видно, что для вычисления T определяются времена отказов каждого из N0 образцов. В дальнейшем они в эксперименте не участвуют. Таким образом, среднее время безотказной работы характеризует надежность аппаратуры до первого отказа. Это означает, что T хорошо характеризует надежность аппаратуры разового использования, например, простейших элементов, которые после отказа не ремонтируются.
Величину T можно использовать и для оценки надежности сложных устройств. Однако в этом случае T характеризует надежность до первого их отказа.
У аппаратуры длительного использования, работающей в режиме смены отказавших элементов, среднее время безотказной работы до первого отказа может существенно отличаться от среднего времени между первым и вторым отказами, вторым и третьим и т.д. Это означает, что среднее время безотказной работы может характеризовать надежность такой аппаратуры только до первого отказа.
Поэтому надежность аппаратуры длительного использования оценивают, в отличие от среднего времени безотказной работы, так называемой наработкой на отказ.
Этой характеристике дают следующее определение: наработкой на отказ называется среднее значение времени между соседними отказами, при условии восстановления каждого отказавшего элемента.
Эта характеристика обозначается tср и определяется из статистических данных об отказах по формуле:
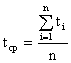
где ti – время исправной работы аппаратуры между (i – 1)-м и i-м отказами; n – число отказов аппаратуры за время t.
Из определения и формулы (1.27) видно, что наработка на отказ является средним временем между соседними отказами. Формулой (1.27) удобно пользоваться, если tср определяется по данным об отказах лишь одного образца аппаратуры. Если испытание проводится с несколькими образцами, то tср вычисляется по формуле:
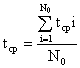
где tср.i — среднее время между соседними отказами i-го образца, вычисленное по формуле (1.27), N0 – число испытываемых образцов.
Найти связь среднего времени между соседними отказами с другими количественными характеристиками надежности проще всего через среднюю частоту отказов. Действительно, если известны средние частоты отказов элементов сложной системы, то среднее число отказов системы в любом промежутке времени определяется ее суммарной частотой отказов. Тогда среднее время между соседними отказами будет равно величие, обратной суммарной частоте отказов, т.е.
(1.29)
или
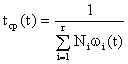
где r – число типов элементов.
Вероятность безотказной работы P(t), частота отказов α(t) (средняя частота отказов ), интенсивность отказов
и среднее время безотказной работы T (среднее время между соседними отказами tср) являются основными количественными характеристиками надежности. Каждая из них имеет свои достоинства и недостатки. Ни одна из них не является исчерпывающей характеристикой надежности. Только все они в совокупности во многих случаях могут характеризовать достаточно полно надежность аппаратуры в течение времени ее работы.

31
2.1. Основные теоретические сведения
Критерии надежности резервированных невосстанавливаемых систем те же, что и нерезервированных невосстанавливаемых систем.
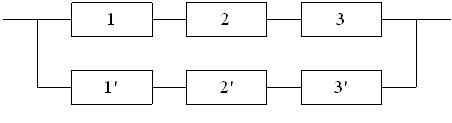
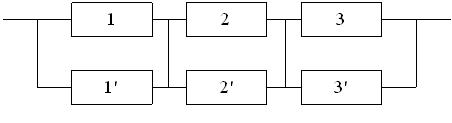
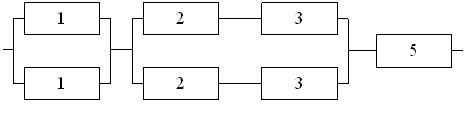
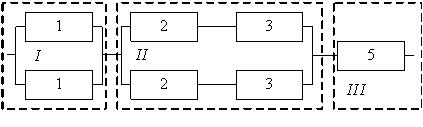
Основными видами резервирования являются: общее постоянное, общее замещением, раздельное постоянное, раздельное замещением. Структурные схемы резервированных систем приведены на рис. 2.1.
Рис. 2.1. Структурные схемы резервированных систем: общее резервирование с постоянно включенным резервом (а), раздельное резервирование с постоянно включенным резервом (б), общее резервирование замещением (в), раздельное резервирование замещением (г)
32
Приведем основные соотношения для показателей надежности резервированных сис-
тем.
2.1.1. Общее резервирование с постоянно включенным резервом
Пусть Pi(t) – вероятность безотказной работы i-го элемента за время t; Qi(t) – вероятность отказа i-го элемента за время t; f(t) – плотность распределения времени до отказа i-го элемента в момент времени t. Тогда вероятность безотказной работы, плотность распределения времени безотказной работы и интенсивность отказов системы с кратностью резервирования m определяется соотношениями:
|
T |
|||||||
|
Pc (t) =1−∏(1− Pi (t)), |
(2.1) |
||||||
|
i=0 |
|||||||
|
m |
|||||||
|
fc (t) = ∑(1− P0 (t))… fi (t)…(1− Pm (t)), |
(2.2) |
||||||
|
i=0 |
|||||||
|
m |
m |
||||||
|
∑ f j (t)∏Qi (t) |
|||||||
|
λ |
(t) |
= |
j=0 |
i≠ j |
. |
(2.3) |
|
|
c |
m |
||||||
|
1− |
∏Qi (t) |
i=0
В частности, для экспоненциальных распределений времени до отказа элементов с одинаковыми параметрами λ имеют место равенства:
|
P (t) =1−(1−e−λt )m+1 , |
|||||
|
c |
|||||
|
fc (t) = (m +1)λe−λt (1−e−λt )m , |
|||||
|
λc (t) = |
(m + |
1)λe−λt (1−e−λt )m |
. |
||
|
1 |
−(1−e−λt )m+1 |
||||
Среднее время безотказной работы системы определяется выражением:
|
1 |
m+1 |
1 |
|||
|
T1 = |
∑ |
. |
|||
|
λ k =1 |
k |
Формулы справедливы для случая, когда нерезервированная система рассматривается как один элемент, показатели надежности которого известны. В действительности любая система состоит из большого числа элементов, каждый из которых имеет показатель надежности, самостоятельно учитываемый при расчете. В таком случае формула для вероятности безотказной работы имеет вид:
|
m |
n |
|
|
Pc (t) =1−∏(1−∏Pij (t)) , |
(2.8) |
|
|
i=0 |
j=1 |
где n – число элементов нерезервированной системы, Pij(t) – вероятность безотказной работы элемента с номером (i,j).
2.1.2. Общее резервирование замещением
Вероятность безотказной работы, плотность распределения времени до отказа и среднее время безотказной работы системы определяются выражениями:
|
m |
|||
|
Pc (t) = P0 (t) + ∑ f0 f1 … fi−1 Pi (t), |
(2.9) |
||
|
i=1 |
|||
|
fc (t) = f0 |
f1 … fm (t). |
(2.10) |
|
|
Если все элементы равнонадежны, то: |
|||
|
m |
1 |
||
|
Pc (t) = ∑ f *(i ) P(t) =1− ∫ f *(m+1)(x)dx. |
(2.11) |
||
|
i=0 |
0 |
Формулы содержат свертки функций, обозначенные символом (*). Свертка функций f(t) и g(t), заданных при t ≥ 0, определяется соотношением:
33
|
f g(t) = ∫1 |
f (t − x)g(x)dx = ∫1 |
f (x)g(t − x)dx. |
(2.12) |
|
0 |
0 |
Выражение fc (t) = f0 f1 … fm (t).представляет собой i-кратную свертку функции f(t).
1442443
i
Если интенсивность отказов элементов постоянна и равна λ , то формулы для вероятности и среднего времени безотказной работы системы имеют вид:
|
m |
(λt) |
j |
|||
|
Pc (t) = ∑ |
e−λt , |
(2.13) |
|||
|
j! |
|||||
|
j=0 |
|||||
|
T = |
1 |
(m +1). |
(2.14) |
||
|
λ |
|||||
|
c |
2.1.3. Раздельное резервирование
Пусть исходная система состоит из т элементов. Тогда казной работы безотказной системы при раздельном резервировании выражаются следующими формулами:
– раздельное резервирование с постоянно включенным резервом:
|
n |
m |
||
|
Pc (t) = ∏(1−∏(1− Pij (t))), |
(2.15) |
||
|
j=1 |
i=0 |
||
|
– раздельное резервирование замещением: |
|||
|
n |
m |
||
|
Pc (t) = ∏∑ f0 j |
f1 j … fi−1, j Pij (t). |
(2.16) |
|
|
j=1 |
i=0 |
В формулах приняты следующие обозначения: Pij(t) – вероятность безотказной работы элемента с номером (i,j), fij(t) – плотность распределения времени до отказа элемента, i = 0,1, 2,…, m; j = 1, 2,…, n .
2.1.4. Резервирование с дробной кратностью
Приведем формулы для показателей надежности мажоритарных систем (систем с дробной кратностью резервирования), в которых n – общее число элементов, (n – m) основных и m резервных элементов. Отказ такой системы наступает при отказе (m + 1)-го элемента.
Показатели надежности мажоритарной системы при условии, что все элементы имеют одинаковую надежность, вычисляются по формулам:
|
m |
|||
|
Pc (t) = ∑Cni Qi (t)Pn−i (t), |
(2.17) |
||
|
i=0 |
|||
|
fc (t) = (n − m)CnmQm (t)Pn−m (t) f (t), |
(2.18) |
||
|
λc (t) = |
(n − m)CnmQm (t)Pn−m (t) |
λ(t). |
(2.19) |
|
m |
|||
|
∑Cni Qi (t)Pn−i (t) |
i=0
2.1.5. Скользящее резервирование
Скользящее резервирование представляет собой резервирование замещением с кратностью m/(n – m), где n – общее число элементов, m – число резервных элементов, (n – m) – число основных резервируемых элементов.
Вероятность безотказной работы системы со скользящим резервом при условии, что все элементы системы имеют одинаковую надежность, равна
|
m |
m |
|
|
Pc (t) = ∑ |
∑ f *(k1 ) P(t) f *(k2 ) P(t)… f *(kn−m ) P(t). |
(2.20) |
k =0 k1 +k2 +…+kn−m =k
Если элементы системы имеют экспоненциальное распределение вероятности времени до отказа с параметром λ , то вероятность безотказной работы, интенсивность отказов и среднее время безотказной работы системы соответственно равны:

Pc (t)
λc (t)
2.2. Примеры решения задач
34
|
m |
((n |
− m)λt) |
k |
|||||||
|
= ∑ |
e−(n−m)λt , |
|||||||||
|
k! |
||||||||||
|
k =0 |
||||||||||
|
((n − m)λt)m |
||||||||||
|
= (n − m)λ |
m! |
, |
||||||||
|
m |
k |
|||||||||
|
∑ |
((n − m)λt) |
|||||||||
|
k =0 |
k! |
|||||||||
|
T |
= |
m +1 |
T . |
|||||||
|
1c |
n − m |
1 |
Примеры и задачи для самостоятельного решения требуют использования компьютерных технологий. Применение универсальных математических программных средств позволит получить решение в короткое время без особого труда. В некоторых случаях решение удается получить в аналитическом виде. В примерах приводятся компьютерные технологии решения задач с применением систем Derive 5 и Excel. Отметим, что систему Derive 5 необходимо использовать всегда, где требуется получить решение в аналитическом виде.
Пример 2.1. Дана резервированная система с постоянным резервом кратности m = 2. Элементы системы имеют постоянную интенсивность отказа λ = 0,05 час-1. Найти показатели надежности системы: вероятность безотказной работы, плотность распределения времени до отказа, интенсивность отказа, среднее время безотказной работы.
Решение. Воспользуемся формулами (2.4)–(2.6). Тогда получим:
|
P (t) =1 |
−(1 |
−e−λt )m+1 =1−(1 |
−e−0.05t )3 , |
|||||||
|
c |
||||||||||
|
fc (t) = (m +1)λe−λt (1−e−λt )m |
= 3* 0.05λe−0.05t (1−e−0.05t )2 , |
|||||||||
|
λc (t) = |
(m +1)λe−λt (1−e−λt )m |
= |
1.15λe−0.05t (1−e−0.05t )2 |
= |
0.15(1−e−0.05t )2 |
. |
||||
|
1 |
−(1−e−λt )m+1 |
1−(1−e−0.05t )3 |
3 |
−3e−0.05t + e−0.1t |
||||||
Табулируя функции, найдем искомые показатели надежности, представленные в табл.
2.1.
Наиболее просто табулирование выполнить с помощью функции VECTOR системы Derive. Технология табулирования на экране монитора имеет вид:

f (t)
35
Пользователь вводит выражение вероятности безотказной работы (строка #1). Функции f(t) и λ (t) получены в соответствии с формулами:
f (t) = −P(t), λ(t) = P(t) .
Производная получена с помощью кнопки Find Derivative панели инструментов (строки #2 и #3). Интенсивность отказа (строка #4) получена в результате выполнения операции #3/#1. Функция табуляции представляется в следующем виде:
VECTOR([t,#1,#3,#4],t,0,100,5)
С помощью кнопки Sub панели инструментов вводятся исходные данные задачи. После щелчка мыши по кнопке Approximate на экране появиться решение в виде табл. 2.1.
Таблица 2.1
Показатели надежности резервированной системы с постоянно подключенным резервом и кратностью резервирования m = 2
|
t, час |
Рс(t) |
Fc(t) |
λ c(t) |
|
0 |
1 |
0 |
0 |
|
5 |
0,989177 |
0,005716 |
0,005778 |
|
10 |
0,939084 |
0,014085 |
0,014499 |
|
15 |
0,853108 |
0,19726 |
0,023122 |
|
20 |
0,747420 |
0,022049 |
0,029501 |
|
25 |
0,636777 |
0,021878 |
0,034357 |
|
30 |
0,531138 |
0,020200 |
0,038031 |
|
35 |
0,435977 |
0,017794 |
0,040814 |
|
40 |
0,353538 |
0,015177 |
0,042930 |
|
45 |
0,284042 |
0,012653 |
0,044546 |
|
50 |
0,226594 |
0,010374 |
0,045784 |
|
55 |
0,179785 |
0,008402 |
0,046736 |
|
60 |
0,142048 |
0,006743 |
0,047469 |
|
65 |
0,111871 |
0,005374 |
0,048036 |
|
70 |
0,087884 |
0,004260 |
0,048475 |
|
75 |
0,068907 |
0,003364 |
0,048815 |
|
80 |
0,053947 |
0,002648 |
0,049079 |
|
85 |
0,042185 |
0.002079 |
0,049283 |
|
90 |
0,032958 |
0.001630 |
0,049442 |
|
95 |
0,025731 |
0,001275 |
0,049566 |
|
100 |
0,020078 |
0,000997 |
0,049662 |
Графическая иллюстрация результатов дана на рис. 2.3. Согласно (2.7), среднее время безотказной работы системы будет равно:
|
1 |
m+1 |
1 |
1 |
1 |
|||||
|
T1c = |
∑ |
= 20(1+ |
+ |
) = 36,7 час. |
|||||
|
k |
2 |
3 |
|||||||
|
λ k =1 |
Пример 2.2. Требуется определить кратность резервирования системы с постоянным резервом, обеспечивающим вероятность безотказной работы 0,96 в течение времени t = 150 час. Элементы системы равнонадежны и имеют экспоненциальное распределение со средним временем безотказной работы T = 300 час. Найти также кратность резервирования для системы, элементы которой имеют распределение Рэлея с тем же средним.
Решение. Кратность резервирования может быть определена по формуле:
m= ln(1− Pc (t)) −1, ln(1− P (t))

36
где Р(t) – вероятность безотказной работы элемента в течение времени t, Pc(t) = 0,96 – вероятность безотказной работы системы в течение времени t.
Рис. 2.2. Вероятность безотказной работы
Рис. 2.3. Интенсивность и плотность распределения до отказа
Для экспоненциального распределения P1 (t) = e−λ1t ,
элемента.
Для распределения Рэлея P2 (t) = e−λ2t 2 , где λ2 = 4πT 2
В течение времени t = 150 час получим:
– для экспоненциального закона:
где λ1 = T1 – интенсивность отказа
– параметр распределения.
−1
P1 (t) = e−λ1t = e T = e0.5 = 0,606531;
– для закона Рэлея:
37
|
πt2 |
||||||||||
|
P (t) = e−λ2t 2 |
= e− |
= e |
π1502 |
= 0,821725. |
||||||
|
4T 2 |
||||||||||
|
e |
4 3002 |
|||||||||
|
Подставляя значения и P1(t), и Р2(t) в формулу для кратности резервирования т, полу- |
||||||||||
|
чим: |
||||||||||
|
– для экспоненциального распределения: |
||||||||||
|
m = |
ln(1−0,966) |
−1 = 2,45; |
||||||||
|
1 |
ln(1−0,606531) |
|||||||||
|
– для распределения Рэлея: |
ln(1−0,966) |
|||||||||
|
m2 |
= |
−1 = 0,87. |
||||||||
|
ln(1−0,821725) |
||||||||||
Округляя до целых чисел в большую сторону, получим m1 = 3, m2 = 1. Таким образом, для достижения заданной надежности в первом случае потребуется 3 резервных элемента, а во втором случае – только один.
Из примера видно, что надежность системы определяется не только ее структурой и временем работы, но также законом распределения времени до отказа элементов.
Пример 2.3. В условиях предыдущего примера необходимо обеспечить заданную надежность системы в течение времени t = 450 час. Решение.
Решение. Определим вероятность безотказной работы элемента в течение времени t = 450 час для экспоненциального распределения и распределения Рэлея:
|
−1 |
450 |
||||||||
|
P (t) = e−λ1t = e T |
= e |
300 |
= 0,22313; |
||||||
|
1 |
|||||||||
|
P (t) = e−λ2t2 = e− |
πt 2 |
π 4502 |
|||||||
|
4T 2 |
= e |
4*3002 |
= 0,17082. |
||||||
|
e |
|||||||||
|
Найдем кратность резервирования: |
|||||||||
|
– для экспоненциального распределения: |
|||||||||
|
m = |
ln(1−0,966) |
−1 =11,7; |
|||||||
|
1 |
ln(1−0,22313) |
||||||||
|
– для распределения Рэлея: |
ln(1−0,966) |
||||||||
|
m2 = |
−1 =16,2. |
||||||||
|
ln(1−0,17082) |
|||||||||
Округление до целых чисел дает требуемую кратность m1 = 12, m2 = 17. Если система работает время t = 450 час, то для достижения заданной надежности необходимо иметь 12 резервных элементов в первом случае и 17 резервных элементов во втором случае.
Из расчета следует, что структурное резервирование не может обеспечить вероятность безотказной работы системы 0,96 в течение 450 часов. Кратность резервирования настолько высока, что ее практическая реализуемость вряд ли возможна.
Пример 2.4. Структурная схема системы представляет собой дублированную систему с постоянно включенным резервом. Элементы системы имеют разные законы распределения времени до отказа: экспоненциальный с интенсивностью отказа λ = 2·10-3 час-1 и Вейбулла с параметрами α = 4, β = 500 час. Необходимо определить: вероятность безотказной работы
системы Pc(t), среднее время безотказной работы T1с, интенсивность отказов λ c(t). Решение получить в виде формул, таблиц и графиков.
Решение. В строках #1 и #2 представлены выражения вероятности безотказной работы системы при экспоненциальном законе распределения времени до отказа, а в строках #3 и #4
– при распределении Вейбулла (графическая интерпретация приведена на рис. 2.4). В строках #5 и #6 находятся выражения вероятности отказа и вероятности безотказной работы системы при общем резервировании с постоянно включенным резервом в виде следующих фор-
мул: Qc(t) = (1 – Pl(t))(1 – P2(t)), Pc(t) = l – Qc(t).

38
Встроке #7 находится производная от вероятности отказа системы, а в строке #8 – плотность распределения времени до отказа, полученная по формуле f(t) = Q′(t).
Врезультате интегрирования вероятности безотказной работы (строка #9) получено среднее время безотказной работы системы (строка #10), которое равно примерно 662 часам.
В строке #11 находится выражение для интенсивности отказа системы, полученное по формуле:
f (t)
λc (t) = Pc (t) .
c
Табулирование функции Pc(t) осуществлено в строке #12, а его результаты сведены в таблицу (строка #13).

39
На рис. 2.5 приведены зависимости от времени вероятностей безотказной работы элементов. Из графиков видно, что вероятность безотказной работы системы с законом распределения времени до отказа Вейбулла больше в области малых значений t и меньше при больших t.
Рис. 2.4. Вероятность безотказной работы элементов системы с законом распределения времени до отказа: экспоненциальным (кривая I ) и Вейбулла (кривая 2 )
Интересным, с точки зрения теории надежности, является график интенсивности отказов резервированной системы, построенный системой Derive по выражению #13 (рис. 2.5). Согласно теории интенсивность отказа резервированной системы при t = 0 равна нулю и с ростом t приближается к интенсивности отказа наиболее надежного элемента резервированной системы.
В нашем случае при больших t более надежной является система с экспоненциальным законом распределения времени до отказа, имеющей интенсивность отказа λ = 0,002 час-1. Из рис. 2.5 видно, что это условие идеально выполняется.
Рис. 2.5. Интенсивность отказа системы

40
Рис. 2.6. Вероятность безотказной работы при различной кратности резервирования
Пример 2.5. Дана резервированная система с постоянным резервом кратности m, все элементы которой равнонадежны и имеют усеченный нормальный закон распределения времени до отказа с параметрами m0 = 400 час и δ = 200 час. Определить все показатели надежности системы. Результаты представить в виде таблиц и графиков. Принять m = 0, 1, 2.
Решение. Для равнонадежных элементов формулы (2.1)–(2.3) показателей надежности принимают вид:
|
P (t) =1 |
−(1 |
−e−λt )m+1 , |
|||
|
c |
|||||
|
fc (t) = (m +1)λe−λt (1−e−λt )m , |
|||||
|
λc (t) = |
(m + |
1)λe−λt (1−e−λt )m |
. |
||
|
1 |
−(1−e−λt )m+1 |
||||
Плотность распределения времени до отказа и вероятность безотказной работы для усеченного нормального распределения равны соответственно:
|
(t −m |
)2 |
0.5 −Φ |
0 |
( |
t − m0 |
) |
||||||||||||||||
|
1 |
e− |
0 |
δ0 |
|||||||||||||||||||
|
f (t) = |
2δ0 |
, P(t) = |
, |
|||||||||||||||||||
|
δ |
0 |
2π (0.5 |
+ Φ |
0 |
( |
m0 |
)) |
0.5 + Φ |
0 |
( |
m0 |
) |
||||||||||
|
δ |
0 |
δ |
0 |
|||||||||||||||||||
где Ф0(t) – функция Лапласа. Для исходных данных задачи получим:
|
f (t) = |
1 |
e− |
2*200 |
2 |
, P(t) = |
0.5 −Φ0 ( |
t − 400 |
) . |
||
|
200 |
||||||||||
|
(t −400) |
||||||||||
|
200 |
2π (0.5 + Φ0 (2)) |
0.5 + Φ0 (2) |
Значения вероятности безотказной работы системы Pc(t) для кратности резервирования m = 0, 1, 2 содержатся в табл. 2.2. Соответствующие графики приведены на рис. 2.6.
Следует иметь в виду, что при больших значениях t вероятность безотказной работы настолько мала, что нет смысла эксплуатировать систему. Таблица необходима только для иллюстрации результатов решения задачи, представления решения в графическом виде и вычисления среднего времени безотказной работы системы методом Симпсона.
Из графиков следует, что Pc(t) возрастает при увеличении кратности резервирования, причем этот эффект тем сильнее, чем меньше m.
На основе данных табл. 2.2 приближенно вычислим среднее время безотказной работы системы для значений m = 0, 1, 2. Воспользуемся формулой Симпсона:

|
41 |
||||
|
h |
n−1 |
|||
|
T1 |
= |
(1+ ∑(3 + (−1)k )Pc (kh)), |
||
|
3 |
k =1 |
в которой шаг интегрирования примем равным h = 50 час, n = 20. Расчеты показывают, что
|
при m = 0 T1 ≈ 411час, при m = 1 T1 ≈ 518 час, при m = 2 |
T1 ≈ 573 час. |
|||||
|
Таблица 2.2 |
||||||
|
Вероятность безотказной работы резервированной системы |
||||||
|
t, час |
m = 0 |
m = 1 |
m = 2 |
|||
|
0 |
1,00000 |
1,00000 |
1,00000 |
|||
|
50 |
0,98229 |
0,99969 |
0.99999 |
|||
|
100 |
0,95492 |
0,99797 |
0,99991 |
|||
|
150 |
0,91517 |
0,99280 |
0,99939 |
|||
|
200 |
0,86093 |
0,98066 |
0,99731 |
|||
|
250 |
0,79138 |
0,95648 |
0,99092 |
|||
|
300 |
0.70756 |
0,91448 |
0,97499 |
|||
|
350 |
0,61264 |
0,84996 |
0,94188 |
|||
|
400 |
0,51164 |
0,76150 |
0,88353 |
|||
|
450 |
0,41064 |
0,65265 |
0,79528 |
|||
|
500 |
0,31572 |
0,53176 |
0.67959 |
|||
|
550 |
0,23190 |
0,41003 |
0,54684 |
|||
|
600 |
0,16235 |
0,29834 |
0,41225 |
|||
|
650 |
0,10811 |
0,20453 |
0,29053 |
|||
|
700 |
0,06836 |
0,13205 |
0,19139 |
|||
|
750 |
0,04099 |
0,08030 |
0,11800 |
|||
|
800 |
0,02328 |
0,04602 |
0,06823 |
|||
|
850 |
0,01251 |
0,02486 |
0,03706 |
|||
|
900 |
0,00635 |
0,01267 |
0,01894 |
|||
|
950 |
0,00305 |
0,00609 |
0,00912 |
|||
|
1000 |
0,00138 |
0,00276 |
0,00414 |
В табл. 2.3 содержатся значения плотности распределения вероятностей fс(t) для той же кратности резервирования. Графики fc(t) приведены на рис. 2.7.
Рис. 2.7. Плотность распределения времени до отказа при различной кратности резервирования

42
|
Таблица 2.3 |
|||
|
Плотность распределения времени до отказа |
|||
|
t, час |
m = 0 |
m = 1 |
m = 2 |
|
0 |
0,00028 |
0,00000 |
0,00000 |
|
50 |
0,00044 |
0,00002 |
0,00000 |
|
100 |
0,00066 |
0,00006 |
0,00000 |
|
150 |
0,00093 |
0,00016 |
0,00002 |
|
200 |
0,00154 |
0,00034 |
0,00007 |
|
250 |
0,00180 |
0,00064 |
0,00020 |
|
300 |
0,00198 |
0,00105 |
0,00046 |
|
350 |
0,00204 |
0,00153 |
0,00089 |
|
400 |
0,00198 |
0,00199 |
0,00146 |
|
450 |
0,00180 |
0.00233 |
0,00206 |
|
500 |
0,00154 |
0,00247 |
0,00253 |
|
550 |
0,00124 |
0,00237 |
0,00273 |
|
600 |
0,00093 |
0,00207 |
0,00261 |
|
650 |
0,00066 |
0,00167 |
0,00223 |
|
700 |
0,00044 |
0,00123 |
0,00173 |
|
750 |
0,00028 |
0,00085 |
0,00122 |
|
800 |
0,00016 |
0,00054 |
0,00079 |
|
850 |
0,00009 |
0,00032 |
0,00048 |
|
900 |
0,00005 |
0,00018 |
0,00027 |
|
950 |
0,00002 |
0,00009 |
0,00014 |
|
1000 |
0,00154 |
0,00005 |
0,00007 |
При m = 0 имеем график плотности усеченного нормального распределения времени до отказа основной системы. С увеличением кратности резервирования увеличивается среднее время безотказной работы и уменьшается дисперсия. Указанные факторы более ощутимы для системы с меньшей кратностью резервирования.
Интенсивности отказа системы для различных кратностей т имеют значения, приведенные в табл. 2.4. Соответствующие графики показаны на рис. 2.8.
Рис. 2.8. Интенсивность отказа системы при различной кратности резервирования
Из графиков следует, что большей кратности резервирования соответствует меньшая интенсивность отказов.

43
Таблица 2.4 Интенсивность отказа резервированной системы
|
t, час |
m = 0 |
m = 1 |
m = 2 |
|
0 |
0,00028 |
0,00002 |
0,00000 |
|
50 |
0,00045 |
0,00006 |
0,00000 |
|
100 |
0,00069 |
0,00016 |
0,00000 |
|
150 |
0,00102 |
0,00035 |
0,00000 |
|
200 |
0,00144 |
0,00067 |
0,00002 |
|
250 |
0,00195 |
0,00115 |
0,00007 |
|
300 |
0,00255 |
0,00180 |
0,00020 |
|
350 |
0,00323 |
0,00262 |
0,00047 |
|
400 |
0,00399 |
0,00357 |
0,00095 |
|
450 |
0,00482 |
0,00464 |
0,00165 |
|
500 |
0,00571 |
0,00577 |
0,00259 |
|
550 |
0,00664 |
0,00695 |
0,00372 |
|
600 |
0,00763 |
0,00815 |
0,00499 |
|
650 |
0,00864 |
0,00935 |
0,00632 |
|
700 |
0,00969 |
0,01054 |
0,00768 |
|
750 |
0,01077 |
0,01173 |
0,00902 |
|
800 |
0,01187 |
0,01290 |
0,01032 |
|
850 |
0.01298 |
0,01407 |
0,01159 |
|
900 |
0,01411 |
0,01524 |
0,01282 |
|
950 |
0,01526 |
0,01640 |
0,01402 |
|
1000 |
0,01641 |
0,00000 |
0,01521 |
Пример 2.6. Определить вероятность безотказной работы и плотность распределения времени до отказа мажоритарной системы, состоящей из n = 5 элементов с постоянной интенсивностью отказа λ = 0,004 час-1 при числе резервных элементов m = 1, 2, 3.
Решение. Для постоянной интенсивности отказов элементов P(t) = e−λt и Q(t) = 1 – e−λt . В соответствии с формулами (2.16) и (2.17) получим
m
Pc (t) = ∑Cn1 (1−e−λt )i e−λ(n−i)t , fc (t) = (n − m)λCn!m (1−e−λt )m e−λ(n−m)t . i=0n
Формула для Pc(t) представляет собой накопленные суммы биномиального распределе-
ния вероятностей с параметрами n = 5 и p = 1 – e−λt .
Вычисления по этим формулам в системе Derive настолько просто, что нет необходимости приводить здесь решение. Такие формулы также удобно программируются в Excel. В колонку А запишем значения t от 0 до 500 часов с шагом 20 часов. В ячейки В1 : F1 поместим кратность резервирования m. В ячейку В2 запишем формулу:
В2 = БИНОМРАСП(В$1;5;1–ЕХР(–0,004*$А2);1),
которую скопируем на остальные ячейки блока В2 : F27. В результате получим табл. 2.5. Таблица составлена при m = 0, 1, 2, 3, 4. Следует при этом иметь в виду, что при m = 0 и
m = 4 схема не является мажоритарной.
Графики Pc(t) при различном числе резервных элементов приведены на рис. 2.9 (номера кривых соответствуют числу резервных элементов). Из рисунка следует, что с ростом кратности резервирования надежность системы существенно увеличивается.
Плотность fс(t) без постоянного коэффициента (n – m) λ есть формула Бернулли для вычисления вероятностей биномиального распределения в зависимости от кратности резер-
вирования с параметрами n = 5 и р = 1 – e−λt . Поместим в колонку G время, а кратность резервирования в ячейки H1 : L1. В ячейку Н2 запишем формулу:
Н2 = (5–Н$1)*0,004*БИНОМРАСП(Н$1; 5; 1–ЕХР(–0,004*$А2); 0),

44
Таблица 2.5 Вероятность безотказной работы системы с дробной кратностью резервирования
|
A |
B |
C |
D |
E |
F |
|
|
1 |
t, час |
1 |
1 |
2 |
3 |
4 |
|
2 |
0 |
0,6703 |
1 |
1 |
1 |
1 |
|
3 |
20 |
0,4493 |
0,9495 |
0,9960 |
0,9998 |
1,0000 |
|
4 |
40 |
0,3012 |
0,8391 |
0,9744 |
0,9979 |
0,9999 |
|
5 |
60 |
0,2019 |
0,7097 |
0,9313 |
0,9914 |
0.9996 |
|
6 |
80 |
0,1353 |
0,5826 |
0,8697 |
0,9780 |
0,9985 |
|
7 |
100 |
0,0907 |
0,4681 |
0,7955 |
0,9565 |
0,9961 |
|
8 |
120 |
0,0608 |
0,3702 |
0,7145 |
0,9266 |
0,9919 |
|
9 |
140 |
0,0408 |
0,2891 |
0,6317 |
0,8890 |
0,9855 |
|
10 |
160 |
0,0273 |
0,2235 |
0,5511 |
0,8448 |
0,9764 |
|
11 |
180 |
0,0183 |
0,1714 |
0,4752 |
0,7955 |
0,9644 |
|
12 |
200 |
0,0123 |
0,1305 |
0,4056 |
0,7428 |
0,9494 |
|
13 |
220 |
0.0082 |
0,0989 |
0,3433 |
0,6881 |
0,9314 |
|
14 |
240 |
0.0055 |
0,0745 |
0,2883 |
0,6329 |
0,9105 |
|
15 |
260 |
0,0037 |
0,0560 |
0,2406 |
0,5782 |
0,8870 |
|
16 |
280 |
0,0025 |
0,0419 |
0,1995 |
0,5251 |
0,8612 |
|
17 |
300 |
0,0017 |
0,0312 |
0,1647 |
0,4742 |
0,8334 |
|
18 |
320 |
0,0011 |
0,0232 |
0,1353 |
0,4262 |
0,8039 |
|
19 |
340 |
0,0007 |
0,0172 |
0,1107 |
0,3812 |
0,7730 |
|
20 |
360 |
0,0005 |
0,0128 |
0,0902 |
0,3396 |
0,7413 |
|
21 |
380 |
0,0003 |
0,0094 |
0,0733 |
0,3014 |
0,7089 |
|
22 |
400 |
0,0002 |
0,0070 |
0,0594 |
0,2666 |
0,6762 |
|
23 |
420 |
0,0002 |
0,0051 |
0,0480 |
0,2351 |
0,6434 |
|
24 |
440 |
0,0001 |
0,0038 |
0,0387 |
0,2067 |
0,6109 |
|
25 |
460 |
0,0001 |
0,0028 |
0,0311 |
0,1813 |
0,5788 |
|
26 |
480 |
0,0000 |
0,0020 |
0,0250 |
0,1586 |
0,5474 |
|
27 |
500 |
1 |
0,0015 |
0,0200 |
0,1384 |
0,5167 |
Рис. 2.9. Вероятность безотказной работы мажоритарной системы

45
которую скопируем на остальные ячейки блока Н2 : L27. В результате получим табл. 2.6, которая содержит значения плотности fс(t) при различных m и t.
Табулирование функции fс(t) в системе Derive осуществляется с помощью Функции VECTOR, которая представляется в следующем виде:
VECTOR([t,fl(t),f2(t),f3(t),f4(t)],t,0,500,20).
Это наиболее простой способ представления решения в табличном виде. Графики плотностей изображены на рис. 2.10.
|
Таблица 2.6 |
||||||
|
Плотность распределения времени безотказной работы системы |
||||||
|
G |
H |
I |
J |
K |
L |
|
|
1 |
t, час |
0 |
1 |
2 |
3 |
4 |
|
2 |
0 |
0,02000 |
0,00000 |
0,00000 |
0,00000 |
0,00000 |
|
3 |
20 |
0,01341 |
0,00447 |
0,00056 |
0,00003 |
0,00000 |
|
4 |
40 |
0,00899 |
0,00624 |
0,00162 |
0,00019 |
0,00001 |
|
5 |
60 |
0,00602 |
0,00654 |
0,00266 |
0,00048 |
0,00003 |
|
6 |
80 |
0,00404 |
0,00609 |
0,00345 |
0,00087 |
0,00008 |
|
7 |
100 |
0,00271 |
0,00532 |
0,00393 |
0,00129 |
0,00016 |
|
8 |
120 |
0,00181 |
0,00447 |
0,00413 |
0,00170 |
0,00026 |
|
9 |
140 |
0.00122 |
0,00365 |
0,00411 |
0,00206 |
0,00039 |
|
10 |
160 |
0,00082 |
0,00292 |
0,00393 |
0,00235 |
0,00053 |
|
11 |
180 |
0,00055 |
0,00230 |
0,00365 |
0,00256 |
0,00068 |
|
12 |
200 |
0,00037 |
0,00180 |
0,00330 |
0,00270 |
0,00083 |
|
13 |
220 |
0,00025 |
0,00139 |
0,00293 |
0,00276 |
0,00097 |
|
14 |
240 |
0,00016 |
0,00106 |
0,00257 |
0,00276 |
0,00111 |
|
15 |
260 |
0,00011 |
0,00081 |
0,00222 |
0,00270 |
0,00124 |
|
16 |
280 |
0,00007 |
0,00061 |
0,00189 |
0,00260 |
0,00134 |
|
17 |
300 |
0,00005 |
0,00046 |
0,00160 |
0,00248 |
0,00144 |
|
18 |
320 |
0,00003 |
0,00035 |
0,00134 |
0,00233 |
0,00151 |
|
19 |
340 |
0,00002 |
0,00026 |
0.00112 |
0,00216 |
0,00157 |
|
20 |
360 |
0,00001 |
0,00019 |
0,00093 |
0,00200 |
0,00161 |
|
21 |
380 |
0,00001 |
0,00014 |
0,00077 |
0,00183 |
0,00163 |
|
22 |
400 |
0,00001 |
0,00011 |
0,00063 |
0,00166 |
0,00164 |
|
23 |
420 |
0,00000 |
0,00008 |
0,00051 |
0,00150 |
0,00163 |
|
24 |
440 |
0,00000 |
0,00006 |
0,00042 |
0,00134 |
0,00162 |
|
25 |
460 |
0,00000 |
0,00004 |
0,00034 |
0,00120 |
0,00159 |
|
26 |
480 |
0,00000 |
0,00003 |
0,00028 |
0,00107 |
0,00156 |
|
27 |
500 |
0,00000 |
0,00002 |
0,00022 |
0,00095 |
0,00151 |
Кривая 0 соответствует плотности распределения времени до отказа нерезервированной системы, состоящей из 5 элементов. Кривая 4 представляет собой плотность распределения времени до отказа резервированной системы с одним основным и четырьмя резервными элементами.
Пример 2.7. Дана резервированная система с резервом замещением кратности m = 2. Элементы системы имеют постоянную интенсивность отказа , λ = 0,05 час-1. Определить вероятность безотказной работы и среднее время безотказной работы системы. Сравнить Pc(t) с постоянно включенным резервом.
Решение. По формуле (2.13) получим:
Pc (t) = (λtj!) j e−λt = (1+ λt + (λ2t)2 )e−λt .

46
Рис. 2.10. Плотность распределения времени безотказной работы мажоритарной системы
Рассчитанные Pc(t) при различных значениях t сведены в табл. 2.7. Для сравнения в таблицу помещены также значения Pc(t) для постоянно включенного резерва.
График вероятности безотказной работы для обоих видов резервирования оказан на рис. 2.11.
Среднее время безотказной работы для резерва замещением по формуле (2.11) равно T1c = 3T1c = 3·20 = 60 час. Для постоянного резерва, как было показано в примере 2.1, это время составляет 36,7 часа.
Таблица 2.7 Вероятность безотказной работы системы при различных видах резервирования
|
t, час |
Резерв замещением |
Постоянный резерв |
|
0 |
1 |
1 |
|
10 |
0,985612 |
0,939084 |
|
20 |
0.919699 |
0,74742 |
|
30 |
0,808847 |
0,531138 |
|
40 |
0,676676 |
0,353538 |
|
50 |
0,543813 |
0,226594 |
|
60 |
0,42319 |
0,142048 |
|
70 |
0,320847 |
0,087884 |
|
80 |
0,238103 |
0,053947 |
|
90 |
0,173578 |
0,032958 |
|
100 |
0,124652 |
0,020078 |
|
110 |
0,088376 |
0,01221 |
|
120 |
0,061969 |
0,007418 |
|
130 |
0,043036 |
0,004504 |
|
140 |
0,029636 |
0,002733 |
|
150 |
0,020257 |
0.001658 |
|
160 |
0,013754 |
0,001006 |
|
170 |
0,009283 |
0,00061 |
|
180 |
0,006232 |
0,00037 |

47
Рис. 2.11. Вероятность безотказной работы для резерва замещением (кривая 1) и для постоянно включенного резерва (кривая 2)
Пример 2.8. Даны 3 системы с кратностями резервирования m = 0, 2, 4 (резерв замещением). Элементы системы равнонадежны и имеют гаммараспределение времени до отказа с параметрами α = 3, β =100 часам. Определить показатели надежности систем: вероятность
безотказной работы, плотность и среднее время безотказной работы. Привести таблицы и графики.
Общее число элементов в системах равно n = 1, 3, 5 соответственно.
Решение. Воспользуемся формулами (2.10)–(2.12). Если f(t) – плотность гаммараспределения с параметрами α и β , то n-кратная свертка f*(n)(t) также имеет гамма-
распределение с параметрами nα и β . Поэтому плотность распределения времени до отказа и вероятность безотказной работы выражаются равенствами:
|
t nαa−1 |
e− |
1 |
, |
||||||
|
fc (t) = f *(n) (t) = |
β |
||||||||
|
β nα Γ(nα) |
|||||||||
|
− t |
t nαa−1 |
e− |
x |
||||||
|
P (t) =1 |
β |
dx. |
|||||||
|
c |
∫0 |
β nα Γ(nα) |
|||||||
Плотность и функция гамма-распределения легко вычисляются в Excel. Для этого на листе Excel в графе А поместим время t, изменяющееся от О До 2000 часов с шагом 100 часов. Вторую строку таблицы заполним формулами:
В2 = ГАММАРАСП(А2;1*3;100;0), С2 = ГАММАРАСП(А2;3*3;100;0), 02 = ГАММАРАСП(А2;5*3;100;0),
Е2 = 1 – ГАММАРАСП($А2;1*3;100;1), F2 = 1 – ГАММАРАСП($А2;3*3;100;1), G2 = 1 – ГАММАРАСП($А2;5*3;100;1).
В ячейках В2 : D2 содержатся значения плотности гамма-распределения (последний аргумент равен 0) с параметром формы, соответствующим числу элементов 1, 3, 5. В ячейках Е2: G2 содержатся значения функции гаммараспределения (последний аргумент равен 1) с такими же параметрами формы.
Копируя эти формулы на блок ячеек ВЗ : G22, получим табл. 2.8.

48
Таблица 2.8 Плотность и вероятность безотказной работы для различной кратности резервирования
|
A |
B |
C |
D |
E |
F |
G |
|
|
1 |
t |
f(t), m = 0 |
f(t), m = 2 |
f(t), m = 4 |
P(t), m = 0 |
P(t), m = 2 |
P(t), m = 4 |
|
2 |
0 |
0 |
0 |
0 |
1 |
1 |
I |
|
3 |
100 |
0,00184 |
0,00000 |
0,00000 |
0,9197 |
1,0000 |
1,0000 |
|
4 |
200 |
0,00271 |
0,00001 |
0,00000 |
0,6767 |
0,9998 |
1,0000 |
|
5 |
300 |
0,00224 |
0,00008 |
0,00000 |
0,4232 |
0,9962 |
1,0000 |
|
6 |
400 |
0,00147 |
0,00030 |
0,00000 |
0,2381 |
0,9786 |
1,0000 |
|
7 |
500 |
0,00084 |
0,00065 |
0,00000 |
0,1247 |
0,9319 |
0,9998 |
|
8 |
600 |
0,00045 |
0,00103 |
0,00002 |
0,0620 |
0,8472 |
0,9986 |
|
9 |
700 |
0,00022 |
0,00130 |
0,00007 |
0,0296 |
0,7291 |
0,9943 |
|
10 |
800 |
0,00011 |
0,00140 |
0,00017 |
0,0138 |
0,5925 |
0,9827 |
|
11 |
900 |
0,00005 |
0,00132 |
0,00032 |
0,0062 |
0,4557 |
0,9585 |
|
12 |
1000 |
0,00002 |
0,00113 |
0,00052 |
0,0028 |
0,3328 |
0,9165 |
|
13 |
1100 |
0,00001 |
0,00089 |
0,00073 |
0,0012 |
0,2320 |
0,8540 |
|
14 |
1200 |
0,00000 |
0,00066 |
0,00090 |
0,0005 |
0,1550 |
0,7720 |
|
15 |
1300 |
0,00000 |
0,00046 |
0,00102 |
0,0002 |
0,0998 |
0,6751 |
|
16 |
1400 |
0.00000 |
0,00030 |
0,00106 |
0,0001 |
0,0621 |
0,5704 |
|
17 |
1500 |
0,00000 |
0,00019 |
0,00102 |
0.0000 |
0,0374 |
0,4657 |
|
18 |
1600 |
0,00000 |
0,00012 |
0,00093 |
0,0000 |
0,0220 |
0,3675 |
|
19 |
1700 |
0,00000 |
0,00007 |
0,00080 |
0,0000 |
0,0126 |
0,2808 |
|
20 |
1800 |
0,00000 |
0,00004 |
0,00065 |
0,0000 |
0,0071 |
0,2081 |
|
21 |
1900 |
0,00000 |
0,00002 |
0,00051 |
0,0000 |
0,0039 |
0,1497 |
|
22 |
2000 |
0,00000 |
0,00001 |
0,00039 |
0,0000 |
0,0021 |
0,1049 |
По колонкам Е, F, G таблицы можно построить графики вероятности безотказной работы для кратностей резервирования m = 0, 2, 4 (рис. 2.12).
Рис. 2.12. Вероятность безотказной работы системы с резервом замещением
По колонкам В, С, D можно построить графики плотности распределения времени безотказной работы для тех же кратностей резервирования (рис. 2.13).
Среднее время безотказной работы резервированной системы вычислим по формуле (2.11): T1c = nT1, где T1 = αβ = 300 час – среднее время безотказной работы одного элемента.

49
Для системы с заданными кратностями резервирования соответственно получим T1c = T1 = 300 час, T1с = 3T1 = 900 час, T1c = 5T1 = 1500 час.
Рис. 2.13. Плотность распределения времени до отказа системы с резервом замещением
Пример 2.9. Вычислить среднее время безотказной работы системы при общем резервировании с постоянно включенным резервом и нормальном законе распределения времени до отказа нерезервированной системы.
Решение получить в аналитическом виде и в виде таблицы при следующих значениях исходных данных: кратность резервирования k = 1…10, параметры нормального закона распределения m = 100, δ = 20.
Решение. Далее приведена технология решения задачи в системе Derive (см. ниже).

50
В строках #1 и #2 определены области изменения переменных. В строке #3 приводится выражение плотности нормального закона распределения времени до отказа. Интеграл (строка #4) от плотности является вероятностью отказа системы (строка #5). В строке #6 определяется выражение вероятности безотказной работы резервированной системы с кратностью k. В строках #7 и #8 находятся выражения среднего времени безотказной работы резервированной системы. Табулирование функции осуществлено с помощью функции VECTOR (строка #9), а ее результаты приведены в строке #10.
Пример 2.10. Дана резервированная система со скользящим резервом, состоящая из 4-х элементов: два основных и два резервных (n = 4, m = 2). Время безотказной работы каждого элемента имеет нормальное распределение с математическим ожиданием Т = 500 час и средним квадратическим отклонением δ = 100 час. Найти вероятность безотказной работы, аналогичным показателем для экспоненциального распределения.
Решение. Раскрывая формулу (2.19) при n = 4, m = 2, получим
Рс(е) = Р2(t) + 2f *P(t)P(t) + 2f*(2)*Р(t)P(t)+ (f*P(t))2 ,
где P(t) – вероятность безотказной работы, а f(t) – плотность распределения времени до отказа одного элемента. Поскольку сумма к независимых нормально величин имеет нор-
мальное распределение с параметрами kT и 
|
f *(k ) P(t) = Φ0 (t − kT ) −Φ0 (t −(k +1)T ), |
|||||||||||||||
|
где Ф0(t) – функция Лепласа. Тогда: |
kδ |
k +1δ |
|||||||||||||
|
при k = 0: |
t −T |
||||||||||||||
|
P(t) = 0.5 + Φ |
0 |
( |
); |
||||||||||||
|
при k = 1: |
δ |
||||||||||||||
|
t −T |
t − 2T |
||||||||||||||
|
f |
* P(t) = Φ |
0 |
( |
) −Φ |
0 |
( |
); |
||||||||
|
при k = 2: |
δ |
2δ |
|||||||||||||
|
t − 2T |
t −3T |
||||||||||||||
|
f *2 * P(t) = Φ0 ( |
) −Φ0 ( |
). |
|||||||||||||
|
2δ |
3δ |
Функция Лапласа просто вычисляется в Excel. Оформим рабочий лист, как показано в табл. 2.9. В колонку А запишем значения t от 0 до 1800 часов с шагом 100 часов. Значения Т
δи поместим в ячейки G1 и H1 соответственно.
Вячейки В2 : Е2 запишем формулы, соответствующие вычислению функций P(t), f*P(t), f*(2)*Р(t) и Pc(t):

51
Из (2.20) получим вероятность безотказной работы с элементами, имеющими экспоненциальное время до отказа:
Pc, э (t) = (1+ 2λt) + 2(λt)2 e−2λt ,
где λ = T1 . В ячейку F2 поместим соответствующую формулу:
F2 = (1 + 2*А2/$М$1 + 2*(А2/$М$1)^2) * EXP(-2*A2/$M$1).
В результате копирования формул на ячейки ВЗ:F20 получим табл. 2.9.
Таблица 2.9
Расчеты вероятности безотказной работы для нормального и экспоненциального распределений
|
А |
В |
С |
D |
Е |
F |
|
|
1 |
t |
P(t) |
f*P(t) |
f(2)*P(t) |
Pc,n (t) |
Pc,n (t) |
|
2 |
0 |
1 |
2.87104Е-07 |
8J4349E-13 |
1,0000 |
1,0000 |
|
3 |
100 |
0,999968 |
3,16859Е-05 |
8J4349E-13 |
1,0000 |
0,9921 |
|
4 |
200 |
0.99865 |
0,001349959 |
8J4238E-13 |
1,0000 |
0,9526 |
|
5 |
300 |
0,97725 |
0,02274969 |
8,13349Е-13 |
1,0000 |
0,8795 |
|
6 |
400 |
0,841345 |
0,158644207 |
8.07798Е-13 |
1,0000 |
0,7834 |
|
7 |
500 |
0,5 |
0,499796482 |
7,93920Е-13 |
0,9996 |
0,6767 |
|
8 |
600 |
0,158655 |
0,839005810 |
7,80154Е-13 |
0,9953 |
0,5697 |
|
9 |
700 |
0,02275 |
0,960302572 |
7,74825Е-13 |
0,9664 |
0,4695 |
|
10 |
800 |
0,00135 |
0,920000380 |
7,73936Е-13 |
0,8489 |
0,3799 |
|
11 |
900 |
3,17Е-05 |
0,760218327 |
7J3936E-13 |
0,5780 |
0,3027 |
|
12 |
1000 |
2,87Е-07 |
0,499999713 |
7.73936Е-13 |
0,2500 |
0,2381 |
|
13 |
1100 |
9,9Е-10 |
0,239749986 |
7J3936E-13 |
0,0575 |
0,1851 |
|
14 |
1200 |
1Д9Е-12 |
0,078649653 |
7,73936Е-13 |
0,0062 |
0,1425 |
|
15 |
1300 |
0 |
0,016947366 |
7.73936Е-13 |
0,0003 |
0,1088 |
|
16 |
1400 |
0 |
0,002338930 |
7J3936E-13 |
0,0000 |
0,0824 |
|
17 |
1500 |
0 |
0,000203518 |
7,73936Е-13 |
0,0000 |
0,0620 |
|
18 |
1600 |
0 |
1.10526Е-05 |
7.73936Е-13 |
0,0000 |
0,0463 |
|
19 |
1700 |
0 |
3,72109Е-07 |
7J3936E-13 |
0,0000 |
0,0344 |
|
20 |
1800 |
0 |
7,73015Е-09 |
7,73936Е-13 |
0,0000 |
0,0255 |
Из таблицы видно, что функция f*(2)*P(t) практически не влияет на надежность всей системы. На основе колонок Е и F построены графики вероятностей безотказной работы Pc,н(t) и Pc,э(t) для нормального и экспоненциального случаев. Они представлены на рис. 2.14.
Графики вероятностей безотказной работы системы со скользящим резервом для рассмотренных законов распределения очень сильно отличаются друг от друга. В случае нормального распределения (с малой дисперсией) в течение отельного времени работы система практически абсолютно надежна, но в течение короткого времени она теряет ресурс и быстро становится ненадёжной.

52
Рис. 2.14. Вероятность безотказной работы системы при нормальном (кривая 1) и экспоненциальном (кривая 2) распределениях
2.3. Задачи для самостоятельного решения
2.1. Техническая система представляет собой дублированную систему с постоянно включенным резервом. Вероятность безотказной работы основной и резервной подсистем в течение t = 200 час равна 0,8. Найти вероятность безотказной работы и вероятность отказа системы в течение времени t. Найти среднее время безотказной работы системы при условии, что ее подсистемы имеют постоянную интенсивность отказа.
Ответ: Pc(t) = 0,96, Qс(t) = 0,04, T1c = 1344 час.
2.2. Интенсивность отказа элементов системы λ = 0,0025 час-1. Требуется определить кратность резервирования системы с постоянно включенным резервом, построенную из этих элементов, которая обеспечивает среднее время безотказной работы системы T1c = 800 час.
Ответ: m = 3 .
2.3. Найти показатели надежности резервированной системы с постоянным резервом кратности m = 3, элементы которой имеют интенсивности отказа λ 0 = 0,004 час-1, λ 1 = 0,007 час-1, λ 2 = 0,002 час-1, λ 3 = 0,001 час-1. Время непрерывной работы системы t = 120 час.
2.4.Определить показатели надежности мажоритарной системы, состоящей из 6 равнонадежных элементов, время до отказа которых равномерно распределено на интервале от 0 до 1000 часов. Количество резервных элементов равно 2. Получить аналитическое и графическое представления показателей надежности системы.
2.5.Получить формулу для вероятности безотказной работы мажоритарной системы, состоящей из элементов разной надежности при n = 4, m = 2.
2.6. Интенсивность отказа одного элемента λ = 0,0035 час-1. Требуется определить кратность резервирования системы (резерв замещением), построенную из этих элементов, которая обеспечивает среднее время безотказной работы системы Т1с = 800 час.
Ответ: m = 2.
2.7. Найти показатели надежности Pc(t), Tс, λ c(t) резервированной системы (резерв замещением) кратности m = 3, элементы которой имеют интенсивности отказа λ 0 = 0,04 час-1, λ 1 = 0,07 час-1, λ 2 = 0,02 час-1 , λ 3 = 0,1 час-1. Решение получить в виде формул, таблиц и графиков.
53
2.8.Для резерва замещением кратности m получить формулу вероятности безотказной работы, если элементы системы равнонадежны и имеют гамма-распределение времени до отказа с параметрами α иβ .
2.9.Для резерва замещением кратности m получить формулу плотности распределения времени безотказной работы при условии, что элементы системы равнонадежны и имеют нормальное распределение с параметрами m и β (δ < m / 3) .
2.10.Даны две системы со скользящим резервом. Первая система состоит из n = 7 элементов, из которых m = 3 резервных. Вторая система состоит из n = 5 элементов с m = 2 ре-
зервными. Определить более надежную систему по критерию вероятности безотказной работы. Элементы обеих систем имеют постоянную интенсивность отказа λ = 0,01 час-1.
2.11.Дана последовательно-параллельная система размером 3х5 (5 элементов нерезервированной системы, 3 резервных подсистемы) с постоянно включенным резервом. Все элементы имеют одинаковую надежность, время до отказа элементов имеет распределение Рэлея с математическим ожиданием Т = 50 час. Требуется определить вероятность безотказной работы системы при общем и раздельном резервировании. Провести сравнение по критерию
Рс(t).
Указание: воспользоваться формулами (2.8) и (2.14).
2.12.Дана последовательно-параллельная система размером 3×5 (5 элементов нерезер-
вированной системы, 3 резервных подсистемы), резервированная методом замещения. Все элементы имеют одинаковую интенсивность отказа λ = 0,02 час-1. Требуется определить вероятность безотказной работы системы при общем и раздельном резервировании. Провести
сравнение по критерию Pc(t).
Указание: воспользоваться формулами (2.9) и (2.15).
2.13.Элементы резервированной системы с постоянно включенным резервом имеют распределение Вейбулла времени работы до отказа. Найти выражение для среднего времени безотказной работы системы при кратности резервирования m = 0, 1, 2, 3, 4, 5 . Вычислить среднее время безотказной работы при параметрах закона распределения α = 2,5, β = 20.
Решение представить в виде таблицы.
2.14. Элементы резервированной системы с постоянно включенным резервом имеют усеченно-нормальное распределение времени до отказа. Найти выражение для среднего времени безотказной работы системы при кратности резервирования m = 0, 1, 2, 3, 4, 5. Вычислить значение среднего времени безотказной работы при параметрах закона распределения m0 = 380, δ 0 = 200. Решение представить в виде таблицы.
Указание: воспользоваться программными средствами символьной математики, напри-
мер Derive 5.
2.15. Даны две системы с постоянно включенным резервом с дробной кратностью резервирования m = 1/2 и m = 2/3 соответственно. Определить показатели надежности систем Pc(t), Tc, λ с(t). Решение представить в виде формул, графиков и таблиц. Известны следующие исходные данные для числового анализа: время работы системы t = 0…500 час, среднее время безотказной работы нерезервированной системы T = 550 час, основная и все резервные системы равнонадежны и имеют экспоненциальное распределение времени до отказа. Определить, какая из систем имеет более высокие показатели надежности.
2.16. Даны две системы, описанные в задаче 2.15. Определить критическое время tкр, свыше которого резервирование с дробной кратностью не целесообразно. Определить значение вероятности P(tкр). Решение получить в аналитическом и численном виде.
2.17. Даны две системы, описанные в задаче 2.15. Определить аналитические выражения интенсивностей отказов резервированных систем и найти предел lim λ c(t). Представить функцию λ c(t) в виде графика и объяснить полученный результат.
54
Ответ: 2 λ и 3 λ .
2.18. Резервированная система с постоянно включенным резервом состоит из двух подсистем, имеющих различные законы распределения времени до отказа. Необходимо вычислить Рс(t), Т1с, λ с(t). Решение получить в аналитическом виде, в виде графиков и таблиц. Графики представить в диапазоне t = 0..500 час. Исходные данные содержатся в табл. 2.10.
|
Законы распределения времени до отказа |
Таблица 2.10 |
|||||
|
Вариант |
Закон |
Вариант |
Закон |
Вариант |
Закон |
|
|
распределения |
распределения |
распределения |
||||
|
1 |
Ехр(0,005) |
6 |
W(1,2; 200) |
11 |
Ехр(0,0015) |
|
|
R(0,0002) |
TN(400; 180) |
TN(350; 180) |
||||
|
2 |
Ехр(0,004) |
7 |
N(360; 110) |
12 |
R(0,0001) |
|
|
N(400; 120) |
Г(4;95) |
TN(390; 190) |
||||
|
3 |
Ехр(0,007) |
8 |
N(410; 130) |
13 |
W(2; 100) |
|
|
Г(4; 120) |
R(0,0006) |
N(360; 100) |
||||
|
4 |
W(3; 50) |
9 |
R(0,0004) |
14 |
N(420; 140) |
|
|
R(0,0005) |
Г(3,2; 220) |
TN(380; 200) |
||||
|
5 |
W(l,5; 150) |
10 |
Ехр(0,001) |
15 |
TN(400;215) |
|
|
Г(2,5; 145) |
W(l,l; 160) |
Exp(0,002) |
||||
Указание: решение целесообразно получить с помощью систем символьной Математики, например Derive 5.
Практика
1. Расчет показателей безотказности
1.1 Вероятность безотказной работы
1.2 Вероятность отказа
1.3 Частота отказа
1.4 Интенсивность отказа
1.5 Средняя наработка до отказа
1.6 Среднее значение параметра потока отказов
1.7 Пример расчета показателей безотказности
2. Примеры расчета показателей надежности для различных законов распределения случайных величин
2.1 Экспоненциальный закон распределения
2.2 Закон распределения Вейбулла-Гнеденко
2.3 Закон распределения Рэлея
3. Примеры расчета показателей надежности сложных систем
3.1 Основное соединение элементов
3.2 Резервное соединение
1.1 Вероятность безотказной работы
Вероятностью безотказной работы называется вероятность того, что при определенных условиях эксплуатации, в пределах заданной наработки не произойдет ни одного отказа.
Вероятность безотказной работы обозначается как P(l), которая определяется по формуле (1.1):
где N0 – число элементов в начале испытания; r(l) – число отказов элементов к моменту наработки.Следует отметить, что чем больше величина N0, тем с большей точностью можно рассчитать вероятность P(l).
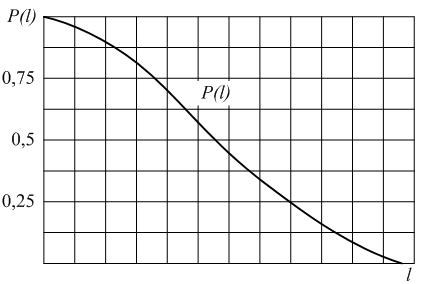
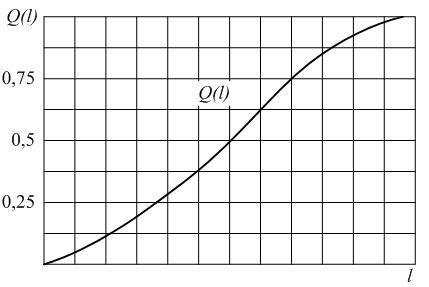
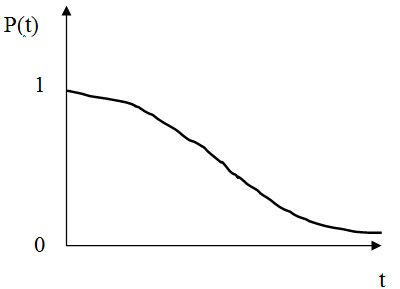
В начале эксплуатации исправного локомотива P(0) = 1, так как при пробеге l = 0 вероятность того, что ни один элемент не откажет, принимает максимальное значение – 1. С ростом пробега l вероятность P(l) будет уменьшаться. В процессе приближения срока эксплуатации к бесконечно большой величине вероятность безотказной работы будет стремиться к нулю P(l→∞) = 0. Таким образом в процессе наработки величина вероятности безотказной работы изменяется в пределах от 1 до 0. Характер изменения вероятности безотказной работы в функции пробега показан на рис. 1.1.
Рис.2.1. График изменения вероятности безотказной работы P(l)в зависимости от наработки
Основными достоинствами использования данного показателя при расчетах является два фактора: во-первых, вероятность безотказной работы охватывает все факторы, влияющие на надежность элементов, позволяя достаточно просто судить о его надежности, т.к. чем больше величина P(l), тем выше надежность; во-вторых, вероятность безотказной работы может быть использована в расчетах надежности сложных систем, состоящих из более чем одного элемента.
1.2 Вероятность отказа
Вероятностью отказа называют вероятность того, что при определенных условиях эксплуатации, в пределах заданной наработки произойдет хотя бы один отказ.
Вероятность отказа обозначается как Q(l), которая определяется по формуле (1.2):
В начале эксплуатации исправного локомотива Q(0) = 0, так как при пробеге l = 0 вероятность того, что хотя бы один элемент откажет, принимает минимальное значение – 0. С ростом пробега l вероятность отказа Q(l) будет увеличиваться. В процессе приближения срока эксплуатации к бесконечно большой величине вероятность отказа будет стремиться к единице Q(l→∞) = 1. Таким образом в процессе наработки величина вероятности отказа изменяется в пределах от 0 до 1. Характер изменения вероятности отказа в функции пробега показан на рис. 1.2.Вероятность безотказной работы и вероятность отказа являются событиями противоположными и несовместимыми.
Рис.2.2. График изменения вероятности отказа Q(l) в зависимости от наработки
1.3 Частота отказов
Частота отказов – это отношение числа элементов в единицу времени или пробега отнесенного к первоначальному числу испытуемых элементов. Другими словами частота отказов является показателем, характеризующим скорость изменения вероятности отказов и вероятности безотказной работы по мере роста длительности работы.
Частота отказов обозначается как 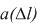
где – 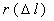
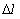
Данный показатель позволяет судить по его величине о числе элементов, которые откажут на каком-то промежутке времени или пробега, также по его величине можно рассчитать количество требуемых запасных частей.
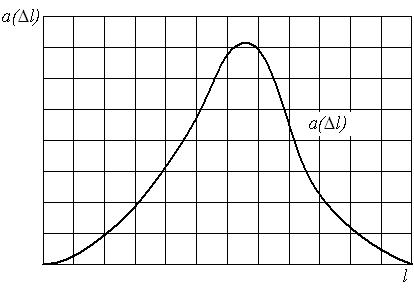
Характер изменения частоты отказов в функции пробега показан на рис. 1.3.
Рис. 1.3. График изменения частоты отказов в зависимости от наработки
1.4 Интенсивность отказов
Интенсивность отказов представляет собой условную плотность возникновения отказа объекта, определяемую для рассматриваемого момента времени или наработки при условии, что до этого момента отказ не возник. Иначе интенсивность отказов – это отношение числа отказавших элементов в единицу времени или пробега к числу исправно работающих элементов в данный отрезок времени.
Интенсивность отказов обозначается как 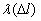
где
Как правило, интенсивность отказов 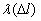
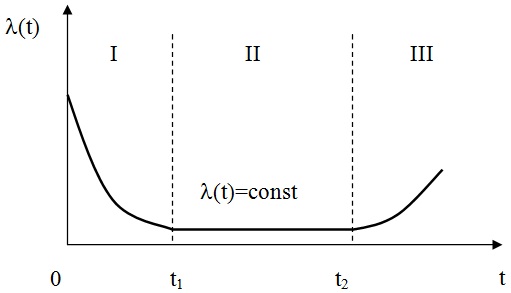
На рис. 1.4. представлен теоретический характер изменения интенсивности отказов в функции пробега.
Рис. 1.4. График изменения интенсивности отказов в зависимости от наработки
На графике изменения интенсивности отказов, изображенном на рис. 1.4. можно выделить три основных этапа отражающих процесс экс-плуатации элемента или объекта в целом.
Первый этап, который также называется этапом приработки, характеризуется увеличением интенсивности отказов в начальный период эксплуатации. Причиной роста интенсивности отказов на данном этапе являются скрытые дефекты производственного характера.
Второй этап, или период нормальной работы, характеризуется стремлением интенсивности отказов к постоянному значению. В течение этого периода могут возникать случайные отказы, в связи с появлением внезапной концентрации нагрузки, превышающей предел прочности элемента.
Третий этап, так называемый период форсированного старения. Характеризуется возникновением износовых отказов. Дальнейшая эксплуатация элемента без его замены становится экономически не рациональной.
1.5 Средняя наработка до отказа
Средняя наработка до отказа – это средний пробег безотказной работы элемента до отказа.
Средняя наработка до отказа обозначается как L1 и определяется по формуле (1.5):
где li – наработка до отказа элемента; ri – число отказов.
Средняя наработка до отказа может быть использована для предварительного определения сроков ремонта или замены элемента.
1.6 Среднее значение параметра потока отказов
Среднее значение параметра потока отказов характеризует среднюю плотность вероятности возникновения отказа объекта, определяемая для рассматриваемого момента времени.
Среднее значение параметра потока отказов обозначается как Wср и определяется по формуле (1.6):
1.7 Пример расчета показателей безотказности
Исходные данные.
В течение пробега от 0 до 600 тыс. км., в локомотивном депо произведен сбор информации по отказам ТЭД. При этом количество исправных ТЭД в начале периода эксплуатации составляло N0 = 180 шт. Суммарное количество отказавших ТЭД за анализируемый период составило ∑r(600000) = 60. Интервал пробега принять равным 100 тыс. км. При этом количество отказавших ТЭД по каждому участку составило: 2, 12, 16, 10, 14, 6.
Требуется.
Необходимо рассчитать показатели безотказности и построить их зависимости изменения во времени.
Сначала необходимо заполнить таблицу исходных данных так, как это показано в табл. 1.1.
Таблица 1.1.
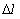 , тыс. км , тыс. км |
0 — 100 | 100 — 200 | 200 — 300 | 300 — 400 | 400 — 500 | 500 — 600 |
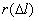 |
2 | 12 | 16 | 10 | 14 | 6 |
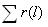 |
2 | 14 | 30 | 40 | 54 | 60 |
Первоначально по уравнению (1.1) определим для каждого участка пробега величину вероятности безотказной работы. Так, для участка от 0 до 100 и от 100 до 200 тыс. км. пробега вероятность безотказной работы составит:
Далее, используя зависимость (1.2) произведем расчет вероятности отказа ТЭД.
Произведем расчет частоты отказов по уравнению (1.3).
Далее по уравнению (1.4) произведем расчет интенсивности отказов ТЭД в зависимости от наработки.
Первоначально рассчитаем среднее количество работоспособных ТЭД на участке от 0 до 100 тыс. км. пробега:
Тогда интенсивность отказов на участке 0-100 тыс.км. будет равна:
Аналогичным образом определим величину интенсивности отказов для интервала 100-200 тыс. км.
По уравнениям (1.5 и 1.6) определим среднюю наработку до отказа и среднее значение параметра потока отказов.
Систематизируем полученные результаты расчета и представим их в виде таблицы (табл. 1.2.).
Таблица 1.2.
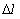 , тыс.км. , тыс.км. |
0 — 100 | 100 — 200 | 200 — 300 | 300 — 400 | 400 — 500 | 500 — 600 |
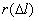 |
2 | 12 | 16 | 10 | 14 | 6 |
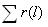 |
2 | 14 | 30 | 40 | 54 | 60 |
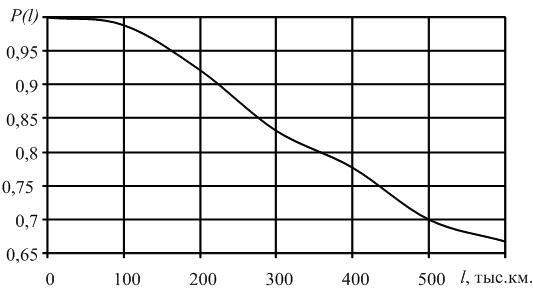
| P(l) | 0,989 | 0,922 | 0,833 | 0,778 | 0,7 | 0,667 |
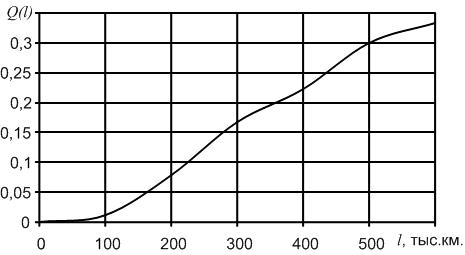
| Q(l) | 0,011 | 0,078 | 0,167 | 0,222 | 0,3 | 0,333 |
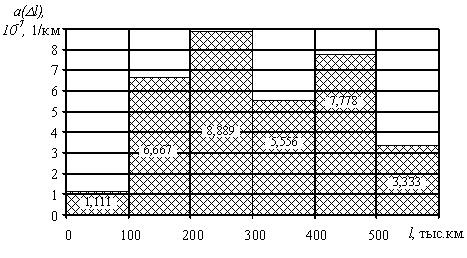
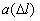 10-7, 1/км 10-7, 1/км |
1,111 | 6,667 | 8,889 | 5,556 | 7,778 | 3,333 |
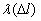 10-7, 1/км 10-7, 1/км |
1,117 | 6,977 | 10,127 | 6,897 | 10,526 | 4,878 |
Приведем характер изменения вероятности безотказной работы ТЭД в зависимости от пробега (рис. 1.5.). Необходимо отметить, что первой точкой на графике, т.е. при пробеге равном 0, величина вероятности безотказной работы примет максимальное значение – 1.
Рис. 1.5. График изменения вероятности безотказной работы в зависимости от наработки
Приведем характер изменения вероятности отказа ТЭД в зависимости от пробега (рис. 1.6.). Необходимо отметить, что первой точкой на графике, т.е. при пробеге равном 0, величина вероятности отказа примет минимальное значение – 0.
Рис. 1.6. График изменения вероятности отказа в зависимости от наработки
Приведем характер изменения частоты отказов ТЭД в зависимости от пробега (рис. 1.7.).
Рис. 1.7. График изменения частоты отказов в зависимости от наработки
На рис. 1.8. представлена зависимость изменения интенсивности отказов от наработки.
Рис. 1.8. График изменения интенсивности отказов в зависимости от наработки
2.1 Экспоненциальный закон распределения случайных величин
Экспоненциальный закон достаточно точно описывает надежность узлов при внезапных отказах, имеющих случайный характер. Попытки применить его для других типов и случаев отказов, особенно постепенных, вызванных износом и изменением физико-химических свойств элементов показали его недостаточную приемлемость.
Исходные данные.
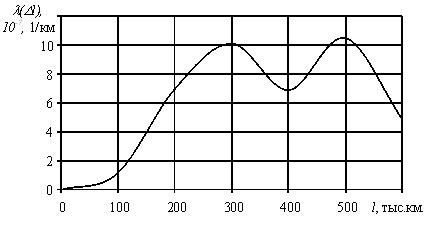
В результате испытания десяти топливных насосов высокого давления получены наработки их до отказа: 400, 440, 500, 600, 670, 700, 800, 1200, 1600, 1800 ч. Предполагая, что наработка до отказа топливных насосов подчиняется экспоненциальному закону распределения.
Требуется.
Оценить величину интенсивности отказов , а также рассчитать вероятность безотказной работы за первые 500 ч. и вероятность отказа в промежутке времени между 800 и 900 ч. работы дизеля.
Во-первых, определим величину средней наработки топливных насосов до отказа по уравнению:
Затем рассчитываем величину интенсивности отказов:
Величина вероятности безотказной работы топливных насосов при наработке 500 ч составит:
Вероятность отказа в промежутке между 800 и 900 ч. работы насосов составит:
2.2 Закон распределения Вэйбулла-Гнеденко
Закон распределения Вейбулла-Гнеденко получил широкое распространение и используется применительно к системам, состоящим из рядов элементов, соединенных последовательно с точки зрения обеспечения безотказности системы. Например, системы, обслуживающие дизель-генераторную установку: смазки, охлаждения, питания топливом, воздухом и т.д.
Исходные данные.
Время простоя тепловозов в неплановых ремонтах по вине вспомогательного оборудования подчиняется закону распределения Вейбулла-Гнеденко с параметрами b=2 и a=46.
Требуется.
Необходимо определить вероятность выхода тепловозов из неплановых ремонтов после 24 ч. простоя и время простоя, в течение которого работоспособность будет восстановлена с вероятностью 0,95.
Найдем вероятность восстановления работоспособности локомотива после простоя его в депо в течение суток по уравнению:
Для определения времени восстановления работоспособности локомотива с заданной величиной доверительной вероятности также используем выражение:
2.3 Закон распределения Рэлея
Закон распределения Рэлея используется в основном для анализа работы элементов, имеющих ярко выраженный эффект старения (элементы электрооборудования, различного рода уплотнения, шайбы, прокладки, изготовленные из резиновых или синтетических материалов).
Исходные данные.
Известно, что наработки контакторов до отказа по параметрам старения изоляции катушек можно описать функцией распределения Рэлея с параметром S = 260 тыс.км.
Требуется.
Для величины наработки 120 тыс.км. необходимо определить вероятность безотказной работы, интенсивность отказов и среднюю наработку до первого отказа катушки электромагнитного контактора.
3.1 Основное соединение элементов
Система, состоящая из нескольких независимых элементов, связанных функционально таким образом, что отказ любого из них вызывает отказ системы, отображается расчетной структурной схемой безотказной работы с последовательно соединенными событиями безотказной работы элементов.
Исходные данные.
Нерезервированная система состоит из 5 элементов. Интенсивности их отказов соответственно равны 0,00007; 0,00005; 0,00004; 0,00006; 0,00004 ч-1
Требуется.
Необходимо определить показатели надежности системы: интенсивность отказов, среднее время наработки до отказа, вероятность безотказной работы, частота отказов. Показатели надежности P(l) и a(l) получить в интервале от 0 до 1000 часов с шагом в 100 часов.
Вычислим интенсивность отказа и среднюю наработку до отказа по следующим уравнениям:
Значения вероятности безотказной работы и частоты отказов получим, используя уравнения приведенные к виду:
Результаты расчета P(l) и a(l) на интервале от 0 до 1000 часов работы представим в виде табл. 3.1.
Таблица 3.1.
| l, час | P(l) | a(l), час-1 |
| 0 | 1 | 0,00026 |
| 100 | 0,974355 | 0,000253 |
| 200 | 0,949329 | 0,000247 |
| 300 | 0,924964 | 0,00024 |
| 400 | 0,901225 | 0,000234 |
| 500 | 0,878095 | 0,000228 |
| 600 | 0,855559 | 0,000222 |
| 700 | 0,833601 | 0,000217 |
| 800 | 0,812207 | 0,000211 |
| 900 | 0,791362 | 0,000206 |
| 1000 | 0,771052 | 0,0002 |
Графическая иллюстрация P(l) и a(l) на участке до средней наработки до отказа представлена на рис. 3.1, 3.2.
Рис. 3.1. Вероятность безотказной работы системы.
Рис. 3.2. Частота отказов системы.
3.2 Резервное соединение элементов
Исходные данные.
На рис. 3.3 и 3.4 показаны две структурные схемы соединения элементов: общего (рис. 3.3) и поэлементного резервирования (рис. 3.4). Вероятности безотказной работы элементов соответственно равны P1(l) = P ’1(l) = 0,95; P2(l) = P’2(l) = 0,9; P3(l) = P ’3(l) = 0,85.
Требуется.
Необходимо рассчитать надежность двух систем.
Рис. 3.3. Схема системы с общим резервированием.
Рис. 3.4. Схема системы с поэлементным резервированием.
Вероятность безотказной работы блока из трех элементов без резервирования рассчитаем по выражению:
Вероятность безотказной работы той же системы при общем резервировании (рис. 3.3) составит:
Вероятности безотказной работы каждого из трех блоков при поэлементном резервировании (рис. 3.4) будут равны:
Вероятность безотказной работы системы при поэлементном резервировании составит:
Таким образом, поэлементное резервирование дает более существенное увеличение надежности (вероятность безотказной работы возросла с 0,925 до 0,965, т.е. на 4%).
Исходные данные.
На рис. 3.5 представлена система с комбинированным соединением элементов. При этом вероятности безотказной работы элементов имеют следующие значения: P1=0,8; Р2=0,9; Р3=0,95; Р4=0,97.
Требуется.
Необходимо определить надежность системы. Также необходимо определить надежность этой же системы при условии, что резервные элементы отсутствуют.
Рис.3.5. Схема системы при комбинированном функционировании элементов.
Для расчета в исходной системе необходимо выделить основные блоки. В представленной системе их три (рис. 3.6). Далее рассчитаем надежность каждого блока в отдельности, а затем найдем надежность всей системы.
Рис. 3.6. Сблокированная схема.
Надежность системы без резервирования составит:
Таким образом, система без резервирования является на 28% менее надежной, чем система с резервированием.
Различают вероятностные (математические) и статистические показатели надежности. Математические показатели надежности выводятся из теоретических функций распределения вероятностей отказов. Статистические показатели надежности определяются опытным путем при испытаниях объектов на базе статистических данных эксплуатации оборудования.
Надежность является функцией многих факторов, большинство из которых случайны. Отсюда ясно, что для оценки надежности объекта необходимо большое количество критериев.
Критерий надежности – это признак, по которому оценивается надежность объекта.
Критерии и характеристики надежности носят вероятностный характер, поскольку факторы, влияющие на объект, носят случайный характер и требуют статистической оценки.
Количественными характеристиками надежности могут быть:
• вероятность безотказной работы;
• среднее время безотказной работы;
• интенсивность отказов;
• частота отказов;
• различные коэффициенты надежности.
1. Вероятность безотказной работы
Служит одним из основных показателей при расчетах на надежность.
Вероятность безотказной работы объекта называется вероятность того, что он будет сохранять свои параметры в заданных пределах в течение определенного промежутка времени при определенных условиях эксплуатации.
В дальнейшем полагаем, что эксплуатация объекта происходит непрерывно, продолжительность эксплуатации объекта выражена в единицах времени t и эксплуатация начата в момент времени t=0.
Обозначим P(t) вероятность безотказной работы объекта на отрезке времени [0,t]. Вероятность, рассматриваемую как функцию верхней границы отрезка времени, называют также функцией надежности.
Вероятностная оценка: P(t) = 1 – Q(t), где Q(t) — вероятность отказа.
Типичная кривая вероятности безотказной работы
Из графика очевидно, что:
1. P(t) – невозрастающая функция времени;
2. 0 ≤ P(t) ≤ 1;
3. P(0)=1; P(∞)=0.
На практике иногда более удобной характеристикой является вероятность неисправной работы объекта или вероятность отказа:
Q(t) = 1 – P(t).
Статистическая характеристика вероятности отказов: Q*(t) = n(t)/N
2. Частота отказов
Частотой отказов называется отношение числа отказавших объектов к их общему числу перед началом испытания при условии что отказавшие объекты не ремонтируются и не заменяются новыми, т.е
a*(t) = n(t)/(NΔt)
где a*(t) — частота отказов;
n(t) – число отказавших объектов в интервале времени от t – t/2 до t+ t/2;
Δt – интервал времени;
N – число объектов, участвующих в испытании.
Частота отказов есть плотность распределения времени работы изделия до его отказа. Вероятностное определение частоты отказов a(t) = -P(t) или a(t) = Q(t).
Таким образом, между частотой отказов, вероятностью безотказной работы и вероятностью отказов при любом законе распределения времени отказов существует однозначная зависимость: Q(t) = ∫ a(t)dt.
Отказ трактуют в теории надежности как случайное событие. В основе теории лежит статистическое истолкование вероятности. Элементы и образованные из них системы рассматривают как массовые объекты, принадлежащие одной генеральной совокупности и работающие в статистически однородных условиях. Когда говорят об объекте, то в сущности имеют в виду наугад взятый объект из генеральной совокупности, представительную выборку из этой совокупности, а часто и всю генеральную совокупность.
Для массовых объектов статистическую оценку вероятности безотказной работы P(t) можно получить, обработав результаты испытаний на надежность достаточно больших выборок. Способ вычисления оценки зависит от плана испытаний.
Пусть испытания выборки из N объектов проведены без замен и восстановлений до отказа последнего объекта. Обозначим продолжительности времени до отказа каждого из объектов t1, …, tN. Тогда статистическая оценка:
P*(t) = 1 — 1/N ∑η(t-tk)
где η — единичная функция Хевисайда.
Для вероятности безотказной работы на определенном отрезке [0, t] удобна оценка P*(t) = [N — n(t)]/N,
где n(t) – число объектов, отказавших к моменту времени t.
Частота отказов, определяемая при условии замены отказавших изделий исправными, иногда называется средней частотой отказов и обозначается ω(t).
3. Интенсивность отказов
Интенсивностью отказов λ(t) называется отношение числа отказавших объектов в единицу времени к среднему числу объектов, работающих в данный отрезок времени, при условии, что отказавшие объекты не восстанавливаются и не заменяются исправными: λ(t) = n(t)/[NсрΔt]
где Nср = [Ni + Ni+1]/2 — среднее число объектов, исправно работавших в интервале времени Δt;
Ni – число изделий, работавших в начале интервала Δt;
Ni+1 – число объектов, исправно работавших в конце интервала времени Δt.
Ресурсные испытания и наблюдения над большими выборками объектов показывают, что в большинстве случаев интенсивность отказов изменяется во времени немонотонно.
Типичная кривая изменения интенсивности отказов объекта
Из кривой зависимости отказов от времени видно, что весь период работы объекта можно условно поделить на 3 периода.
I — й период – приработка.
Приработочные отказы являются, как правило, результатом наличия у объекта дефектов и дефектных элементов, надежность которых значительно ниже требуемого уровня. При увеличении числа элементов в изделии даже при самом строгом контроле не удается полностью исключить возможность попадания в сборку элементов, имеющих те или иные скрытые дефекты. Кроме того, к отказам в этот период могут приводить и ошибки при сборке и монтаже, а также недостаточная освоенность объекта обслуживающим персоналом.
Физическая природа таких отказов носит случайный характер и отличается от внезапных отказов нормального периода эксплуатации тем, что здесь отказы могут иметь место не при повышенных, а и при незначительных нагрузках («выжигание дефектных элементов»).
Снижение величины интенсивности отказов объекта в целом, при постоянном значении этого параметра для каждого из элементов в отдельности, как раз и объясняется «выжиганием» слабых звеньев и их заменой наиболее надежными. Чем круче кривая на этом участке, тем лучше: меньше дефектных элементов останется в изделии за короткий срок.
Чтобы повысить надежность объекта, учитывая возможность приработочных отказов, нужно:
• проводить более строгую отбраковку элементов;
• проводить испытания объекта на режимах близких к эксплуатационным и использовать при сборке только элементы, прошедшие испытания;
• повысить качество сборки и монтажа.
Среднее время приработки определяют при испытаниях. Для особо важных случаев необходимо увеличить срок приработки в несколько раз по сравнению со средним.
II — й период – нормальная эксплуатация
Этот период характеризуется тем, что приработочные отказы уже закончились, а отказы, связанные с износом, еще не наступили. Этот период характеризуется исключительно внезапными отказами нормальных элементов, наработка на отказ которых очень велика.
Сохранение уровня интенсивности отказов на этом этапе характеризуется тем, что отказавший элемент заменяется таким же, с той же вероятностью отказа, а не лучшим, как это происходило на этапе приработки.
Отбраковка и предварительная обкатка элементов, идущих на замену отказавших, имеет для этого этапа еще большее значение.
Наибольшими возможностями в решении этой задачи обладает конструктор. Нередко изменение конструкции или облегчение режимов работы всего одного-двух элементов обеспечивает резкое повышение надежности всего объекта. Второй путь – повышение качества производства и даже чистоты производства и эксплуатации.
III – й период – износ
Период нормальной эксплуатации заканчивается, когда начинают возникать износовые отказы. Наступает третий период в жизни изделия – период износа.
Вероятность возникновения отказов из-за износов с приближением к сроку службы возрастает.
С вероятностной точки зрения отказ системы в данном промежутке времени Δt = t2 – t1 определяется как вероятность отказа:
∫a(t) = Q2(t) — Q1(t)
Интенсивность отказов есть условная вероятность того, что в промежуток времени Δt произойдет отказ при условии, что до этого он не произошел λ(t) = [Q2 — Q1]/[ΔtP(t)]
λ(t) = lim [Q2 — Q1]/[ΔtP(t)] = [dQ(t)]/[P(t)dt] = Q'(t)/P(t) = -P'(t)/P(t)
так как a(t) = -P'(t), то λ(t) = a(t)/P(t).
Эти выражения устанавливают зависимость между вероятностью безотказной работы, частотой и интенсивностью отказов. Если a(t) – невозрастающая функция, то справедливо соотношение:
ω(t) ≥ λ(t) ≥ a(t).
4. Среднее время безотказной работы
Средним временем безотказной работы называется математическое ожидание времени безотказной работы.
Вероятностное определение: среднее время безотказной работы равно площади под кривой вероятности безотказной работы.
T = ∫P(t)dt
Статистическое определение: T* = ∑θi/N0
где θI – время работы i-го объекта до отказа;
N0 – начальное число объектов.
Очевидно, что параметр Т* не может полностью и удовлетворительно характеризовать надежность систем длительного пользования, так как является характеристикой надежности только до первого отказа. Поэтому надежность систем длительного использования характеризуют средним временем между двумя соседними отказами или наработкой на отказ tср:
tср = ∑θi/n = 1/ω(t),
где n – число отказов за время t;
θi – время работы объекта между (i-1)-м и i-м отказами.
Наработка на отказ – среднее значение времени между соседними отказами при условии восстановления отказавшего элемента.