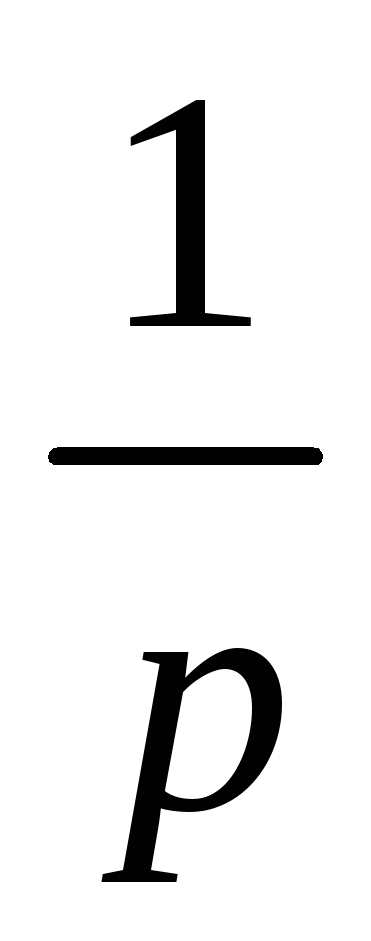
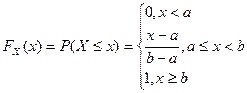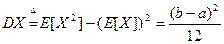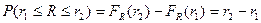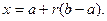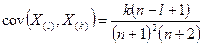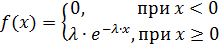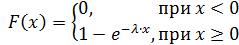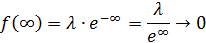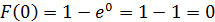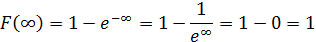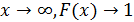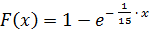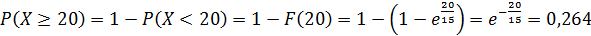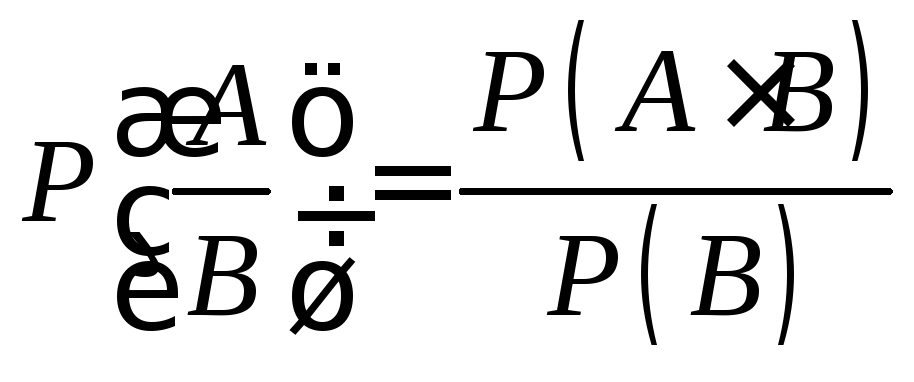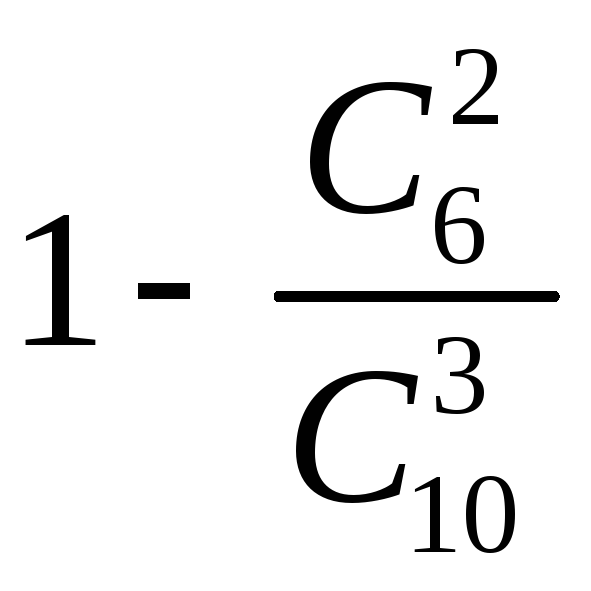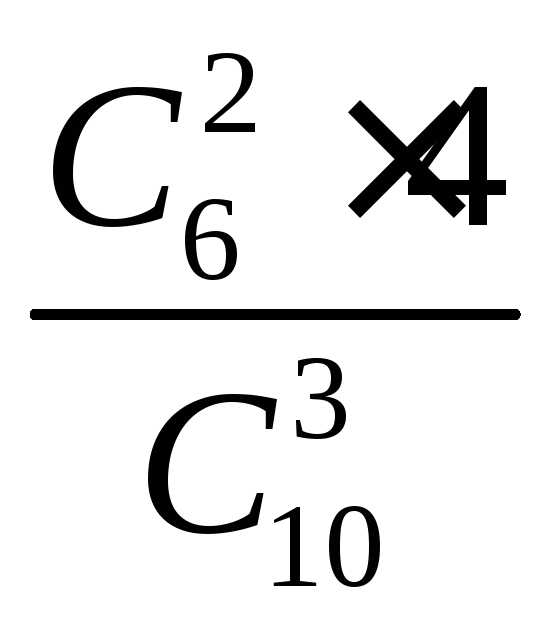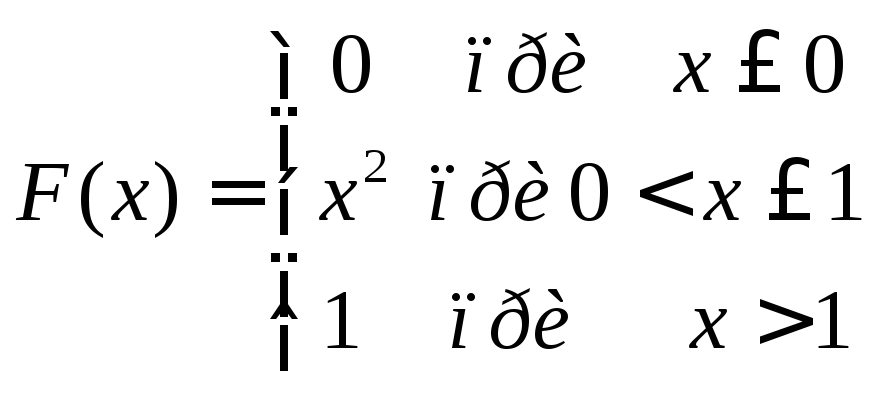Определение Непрерывная случайная величина Х имеет показательный закон распределения с параметром 

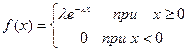
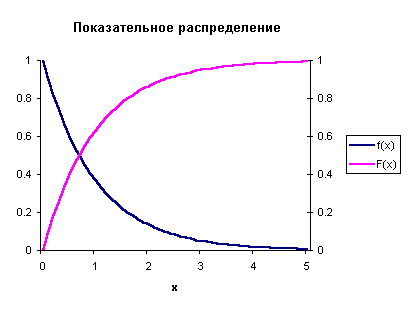
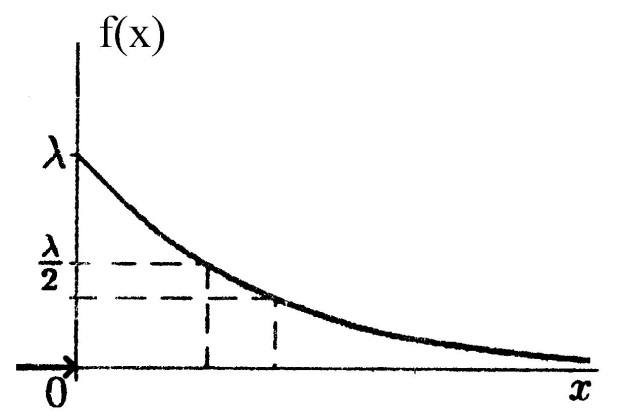
Кривая распределения 
Рис 2.
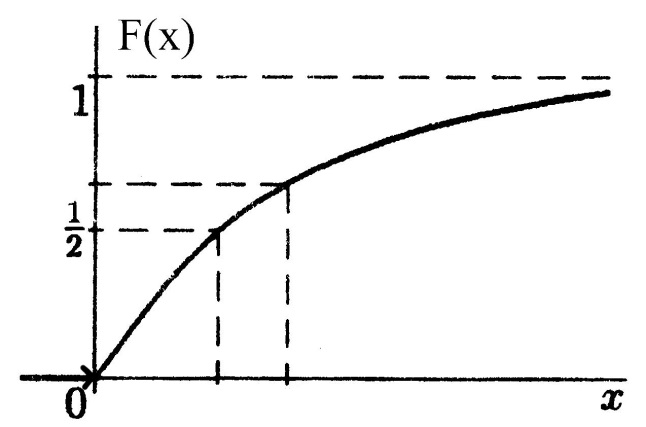
Получим выражение для функции распределения по формуле 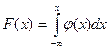
1) При 

2) При 
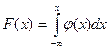

По соответствующим формулам получаем выражения для 

Задача. Среднее время безотказной работы прибора равно 80 ч. Полагая, что время безотказной работы прибора имеет показательный закон распределения, найти: а) выражение его плотности вероятности и функции распределения; б) вероятность того, что в течение 100 ч. прибор не выйдет из строя.
Решение. Х- время безотказной работы прибора, среднее время — 



Искомая вероятность
Замечание. Показательный закон распределения играет большую роль в теории массового обслуживания и теории надежности.
МОСКОВСКИЙ ГОСУДАРСТВЕННЫЙ ИНСТИТУТ ЭЛЕКТРОНИКИ И МАТЕМАТИКИ
Кафедра теории вероятностей и математической статистики
РЕФЕРАТ
По математической статистике
на тему:
«Равномерное распределение»
Выполнил: студенты группы М-65
Ражева А.А.
Кнутова А.С.
Проверил:Заведующий Кафедрой
Ивченко Г. И.
Москва 2012 г.
Непрерывное равномерное распределение — в теории вероятностей распределение, характеризующееся тем, что вероятность любого интервала зависит только от его длины.
Равномерное распределение полезно при описании переменных, у которых каждое значение равновероятно, иными словами, значения переменной равномерно распределены в некоторой области.
Определение
Говорят, что случайная величина имеет непрерывное равномерное распределение на отрезке [a,b], где 
Пишут: X ~ U (a,b) или
Иногда значения плотности в граничных точках x = a и x = b меняют на другие, например 0 или 
Если L (ξ) = U(a,b), то
Равномерное распределение U (a,b) описывает процесс «выбора точки наудачу» в интервале [a,b]. Так, если [a,b] – интервал между последовательными отправлениями автобуса от остановки, то время ожидания пассажира, не знающего расписания и пришедшего на остановку, есть случайная величина с распределением U (0,1). Распределение U (0,1) играет особую роль в методах моделирования с помощью компьютеров случайных величин с заранее заданными распределениями. Такие методы широко используют для приближенных вычислений интегралов, решений дифференциальных и интегральных уравнений и т.д.
Пример (Гипотеза случайности).
В некоторых случаях априори предполагается (постулируется), что исходные данные представляют собой случайную выборку из некоторого распределения, т.е. компоненты вектора данных X=(







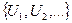
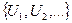

Функция распределения
Интегрируя определённую выше плотность, получаем:
Так как плотность равномерного распределения разрывна в граничных точках отрезка [a,b], то функция распределения в этих точках не является дифференцируемой. В остальных точках справедливо стандартное равенство:
Характеристическая функция случайной величины X ~ U(a,b):
Математическое ожидание и дисперсия по определению равны:
Вообще,
Стандартное равномерное распределение
Если a = 0, а b = 1, то есть X ~ U[0,1], то такое непрерывное равномерное распределение называют стандартным. Имеет место элементарное утверждение:
Если случайная величина X ~ U[0,1], и Y = a + (b − a)X, где a < b, тo Y ~ U[0,1].
Таким образом, имея генератор случайной выборки из стандартного непрерывного равномерного распределения, легко построить генератор выборки любого непрерывного равномерного распределения.
Более того, имея такой генератор и зная функцию обратную к функции распределения случайной величины, можно построить генератор выборки любого непрерывного распределения (не обязательно равномерного) с помощью метода обратного преобразования. Поэтому, стандартно равномерно распределённые случайные величины иногда называют базовыми случайными величинами.
Линейное преобразование
переводит СВ X ~ R(a,b) в СВ Y ~ R(0,1). Действительно,
Равномерное распределение является непрерывным аналогом дискретного распределения вероятностей для опытов с равновероятными исходами.
Значение
С помощью линейного преобразования приводится к равномерному распределению на отрезке [0,1]. Равномерное распределение является непрерывным аналогом распределений классической теории вероятностей, описывающих случайные эксперименты с равновероятными исходами.
Погрешность, происходящая от округления числа, удовлетворительно описывается равномерным распределением на отрезке [ − 1 / 2,1 / 2].
Если случайная величина ζ имеет непрерывную функцию распределения 
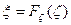
Моделирование
Обозначим буквой 
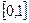
Если 

Моделировать случайную величину 
Мы рассмотрим метод псевдослучайных последовательностей, который наиболее просто реализуется в компьютере. Для получения псевдослучайной последовательности используем алгоритм, который называется методом середины квадратов. Поясним его на примере. Возьмем некоторое число 

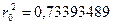







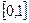

Метод обратных функций.
Пусть случайная величина 





Отсюда следует, что значение 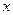




Последовательности значений 

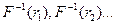


Моделирование случайной величины с равномерным распределением на отрезке
Пусть случайная величина 
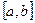
Составляем уравнение 
Последовательности значений 



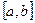
Порядковые статистики.
Случайная величина 

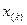
Для случая 
При этом:



А также:
Если же 



А также:

Отметим далее, что если 
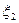


Оценивание параметров в равномерном распределении.
Введём статистический аналог теоретического математического ожидания случайной величины 

Введём статистический аналог теоретической дисперсии случайной величины 

Любая измеримая функция от выборки 
Статистика 

Статистика 

То есть для любого 
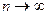

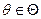
ü Возьмём выборку 

Оптимальной несмещённой оценкой θ в данном классе оценок является:
Её дисперсия:

ü Оценим теперь параметр θ равномерного распределения 

Статистики 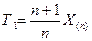

Кроме того, имеем: 

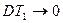



ü Пусть теперь 


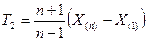
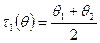

Достаточные статистики и оптимальные оценки.
Если для любой оценки 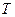


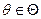
Итак, T* — оптимальная оценка для параметрической функции 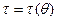



Статистика 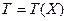



Теорема Рао-Блекуэлла-Колмогорова: Оптимальная оценка, если она существует, является функцией от достаточной статистики.
Теорема: Если существует полная достаточная статистика, то всякая функция от неё является оптимальной оценкой своего математического ожидания.
То есть оптимальная оценка однозначно определяется уравнением 
Функция 


Критерий факторизации.
Для того, чтобы статистика была достаточной для параметрического семейства распределений P, необходимо и достаточно, чтобы функция правдоподобия выборки 
Где множитель h(x) от 

ü Пусть 


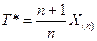
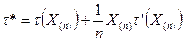
ü Пусть теперь 



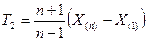

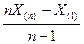


ü Статистика 


Если 
Аналогично, если 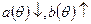
Этими двумя случаями исчерпываются ситуации, когда в модели 
Для модели 

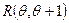

|
Практические расчеты на срез и смятие При изучении темы обратите внимание на основные расчетные предпосылки и условности расчета… |
Функция спроса населения на данный товар Функция спроса населения на данный товар: Qd=7-Р. Функция предложения: Qs= -5+2Р,где… |
Аальтернативная стоимость. Кривая производственных возможностей В экономике Буридании есть 100 ед. труда с производительностью 4 м ткани или 2 кг мяса… |
Вычисление основной дактилоскопической формулы Вычислением основной дактоформулы обычно занимается следователь. Для этого все десять пальцев разбиваются на пять пар… |
|
Неисправности автосцепки, с которыми запрещается постановка вагонов в поезд. Причины саморасцепов ЗАПРЕЩАЕТСЯ: постановка в поезда и следование в них вагонов, у которых автосцепное устройство имеет хотя бы одну из следующих неисправностей: Понятие метода в психологии. Классификация методов психологии и их характеристика Метод – это путь, способ познания, посредством которого познается предмет науки (С… ЛЕКАРСТВЕННЫЕ ФОРМЫ ДЛЯ ИНЪЕКЦИЙ К лекарственным формам для инъекций относятся водные, спиртовые и масляные растворы, суспензии, эмульсии, новогаленовые препараты, жидкие органопрепараты и жидкие экстракты, а также порошки и таблетки для имплантации… |
Закажите у меня новую работу, просто написав мне в чат!
Среднее время безотказной работы прибора равно 80ч. Полагая, что время безотказной работы прибора имеет показательный закон распределения, найти: а) выражение его плотности вероятности и функции распределения; б) вероятность того, что в течение 100 ч прибор не выйдет из строя.
Решение По условию математическое ожидание случайной величины T равно 80 часов. Следовательно Откуда а) Тогда плотность распределения времени безотказной работы имеет вид: Функция распределения имеет вид: б) Вероятность попадания случайной величины в заданный интервал равна: Для данного случая Ответ: 𝑃(0<Х<100)=0,7135

131. Случайная величина X задана плотностью распределения вероятностей
|
0, |
если x ≤ −π 2, |
|
f (x)= A(1 +cos 2x), |
если −π 2 < x ≤π 2, |
|
если x >π 2. |
|
|
0, |
Найти параметр A и вычислить математическое ожидание случайной величины X .
132.Минутная стрелка электрических часов перемещается скачком в конце каждой минуты. Найти вероятность того, что в данное мгновение часы покажут время, которое отличается от истинного не более чем на 20 секунд.
133.Цена деления амперметра равна 0,1 А. Показания округляют до ближайшего целого деления. Найти вероятность того, что при отсчете будет сделана ошибка, превышаю-
щая 0,02 А.
134.Среднее время безотказной работы прибора равно 80 ч. Полагая, что время безотказной работы прибора имеет показательный закон распределения, найти: а) плотность распределения и функцию распределения; б) вероятность того, что в течение 100 ч прибор не выйдет из строя.
135.Полагая, что рост мужчин определенной возрастной группы есть нормально распределенная случайная величина X с параметрами a =173 см и σ =6 см, найти: а) долю костюмов третьего роста (170-176 см), которую нужно предусмотреть в общем объеме производства для данной возрастной группы; б) долю костюмов четвертого роста (176-
|
182 см); |
в) квантиль уровня α =0,1; г) правостороннюю критическую границу уровня |
|
α =0,1; |
д) двусторонние критические границы уровня α =0,1. Сформулировать для слу- |
чайной величины X правило «трех сигма».
136. Коробки с конфетами упаковываются автоматически. Их средняя масса равна 540 г. Известно, что 5% коробок имеют массу, меньшую 500 г. Каков процент коробок, масса которых: а) менее 470 г; б) находится в пределах от 500 до 550 г; в) более 550 г;
|
г) отличается от средней по абсолютной величине не более, чем на 30 г? |
||||||||
|
137. |
Текущая цена акции распределена нормально с параметрами a =15 |
$ и σ =0,2 |
$ . |
|||||
|
Найти |
вероятность |
того, что |
цена акции: а) не выше |
15,3 $ ; б) не |
ниже |
15,4 |
$ ; |
|
|
в) находится в пределах от 14,9 |
$ до 15,3 $ . С помощью правила «трех сигма» найти гра- |
|||||||
|
ницы, в которых будет находиться цена акции. |
||||||||
|
138. |
Цена ценной бумаги распределена нормально. В течение последнего года 20% ра- |
|||||||
|
бочих дней она была ниже 88 |
$ , а 75% рабочих дней она была выше |
90 $ . Найти: |
||||||
|
а) математическое |
ожидание |
и |
среднее квадратическое |
отклонение цены |
бумаги; |
б) вероятность того, что в день покупки цена бумаги будет заключена в пределах от 83 $ до 96 $ . С надежностью 0,95 определить максимальное отклонение цены бумаги от ее среднего значения по абсолютной величине.
139. Квантиль уровня α =0,15 нормально распределенной случайной величины X ра-
|
вен 12, а квантиль уровня β =0,6 |
равен 16. Найти математическое ожидание и среднее |
|||||||||||
|
квадратическое отклонение случайной величины X . |
||||||||||||
Ответы |
||||||||||||
|
1. 151200. 2. 5040. |
3. 100000. 4. 13800. |
5. 81. |
6. nk . |
7. 15600. 8. 40320. |
9. 2mn . |
|||||||
|
10. |
2n ! |
. 11. 18 19! . |
12. (n −2)!. 14. 792. |
15. |
C5226 |
. 16. |
52! |
. 17. C486 . 18. 32. |
19. 26. |
|||
|
(2n − m)! |
(13!)4 |
|||||||||||
|
2 |
||||||||||||
|
20. 165. 21. а) 84; б) 286. |
22. 495. |
23. а) 210; |
б) 420; |
в) 151200. |
24. а) 20; б) 288; |
в) 504; |
||||||
|
г) 5120; д) 17856; е) 193536. |
||||||||||||
|
10 |

|
25. |
= {либо |
, |
ничьявыиграллибовторойигрок}; |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
A |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
A + B ={выигралодинизигроков( |
ничья)}; |
событие); |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
неA + B = Ω (достоверное |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
− B = {ничья}. |
26. |
A − B ={ровноодноизчетырехизделий |
бракованныявляетсям}; |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
A |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
= A − B . |
27. а) |
A = , |
B = Ω; |
б) A = Ω, |
B = ; |
в) A = B . |
28. Нет. |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
AB |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
29. |
AB ={наоднойизкостейвыпало1очко, а на другой- 4 очка}; |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
A |
= {на одной изкостей выпало 2 очка, а на другой- 3 очка}. |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
B |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
30. |
ABC ={обапрыгнулидальшечемна6 м, ноюношапрыгнулдальшедевушки}; |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
A − AB ={юношапрыгнулдальшечемна6 м, нонедальшедевушки}; |
A |
C = A − AB . |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
B |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
31. а) A |
; б) |
AB |
; в) |
ABC ; |
г) |
A + B +C ; д) |
AB + BC + AC ; е) |
A |
+ |
B |
+ |
C ; |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
B |
C |
B |
C |
A |
C |
A |
B |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
C |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
ж) |
AB |
+ A |
C + |
BC ; |
з) |
; |
и) |
. |
32. |
A1 A2 (A3 + A4 ). |
34. а) |
A ; |
б) |
A |
; |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
C |
B |
A |
A |
B |
C |
ABC |
B |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
в) B + AC ; г) A + B +C . |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
35. |
17 |
. |
36. |
2 |
. |
37. а) |
C63 C433 |
≈ 0,01765 ; |
б) |
C64 C432 |
≈ 0,00097 ; |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
19 |
7 |
C496 |
C496 |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
в) |
C65 C431 |
≈ 0,000018 ; |
г) |
1 |
≈ 0,000000071 . 38. |
349 |
. 39. 0,1512 . |
40. 0,297 . |
41. а) |
2 |
; |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
C496 |
C496 |
595 |
91 |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
б) |
24 |
; |
в) |
67 |
. |
42. |
2 |
. |
43. |
68 |
. |
44. |
3 |
. |
45. а) |
32 |
; |
б) |
1 |
; |
в) |
8 |
. 46. |
3 |
. |
47. |
1 |
. |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
91 |
91 |
95 |
38 |
33 |
33 |
33 |
5 |
20 |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
3 |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
48. |
12! |
≈ 0,0000054 . 49. |
1 |
. 50. |
5 |
. |
51. |
2 |
. 52. |
1 |
. |
53. |
1 |
. |
54. |
105 |
. 55. |
(k −1)(n − k ). |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
1212 |
216 |
18 |
9 |
60 |
210 |
256 |
Cn2 |
56.а) 4; б) 13.
57.1 . 58. 1 . 59. 2 . 60. 3 . 61. 251 . 62. 2 . 63. 1 . 64. 3 +ln 4 .
4 4 π 4 800 3 2 9
|
65. |
1 |
. 66. |
1 |
. 67. |
65 − |
2 55 |
= |
1526 |
. 68. |
1 |
. 70. События зависимы. 73. а) 0,855 ; |
|||||||||||||||||||||||||||||||||||||||||||||||||
|
n |
−1 |
8 |
65 −55 |
4651 |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
756 |
13 |
228 |
1081 |
125 |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
б) 0,14 ; в) 0,995 . 74. а) 0,188 ; б) 0,024 ; в) 0,788 . |
75. а) |
; |
б) |
; в) |
. |
76. |
. |
|||||||||||||||||||||||||||||||||||||||||||||||||||||
|
1 |
2 |
1 |
187 |
1309 |
1309 |
1296 |
||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
77. |
а) |
; |
б) |
; |
в) |
. 78. |
0,166 . |
79. 0,568 . |
80. а) 0,0404 ; |
б) 0,3024 ; |
в) 0,4404 . |
|||||||||||||||||||||||||||||||||||||||||||||||||
|
3 |
3 |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
32 |
2 |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
81. |
Вероятность выигрыша для игрока, бросающего монету первым, равна |
; для второго |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
3 |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
1 |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
игрока |
она |
равна |
. |
82. 0,5 . |
83. 0,42504 . |
84. 5. |
85. |
p p |
2 |
(p |
3 |
+ p |
4 |
− p |
3 |
p |
4 |
). |
||||||||||||||||||||||||||||||||||||||||||
|
3 |
1 |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
86. |
p1 (p2 + p3 − p2 p3 )p4 (1 − p5 )+ p5 . |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
2 |
n + 2 |
2 |
3 |
3 |
11 |
23 |
19 |
|||||||||||||||||||||||||||||||||||||||||||||||||||||
|
87. |
. 88. |
. 89. |
. 90. |
. 91. |
. 92. |
. 93. |
. 94. |
. 95. На машине A . |
||||||||||||||||||||||||||||||||||||||||||||||||||||
|
3 |
2(n +1) |
5 |
10 |
10 |
25 |
45 |
40 |
|||||||||||||||||||||||||||||||||||||||||||||||||||||
|
96. |
1 |
. 97. |
8 |
. |
98. |
8 |
. |
99. Вероятность того, |
что кабан убит первым охотником, в 6 |
раз |
||||||||||||||||||||||||||||||||||||||||||||||||||
|
3 |
11 |
23 |
больше, чем вероятность того, что он убит вторым охотником; следовательно, кабана надо разделить в отношении 6:1.
|
100. а) 0,01536 ; б) 0,9984 . 101. а) Так как |
P4 (2)= 0,375 > P6 (3)= 0,3125 , то вероят- |
|
|
нее выиграть две |
партии из четырех, |
чем три из шести; б) так как |
|
P4 |
(m ≥ 2)= 0,6875 > P6 |
(m ≥ 3)= 0,65625 , то вероятнее выиграть не менее двух партий из |
11
четырех, чем не менее трех из шести. 102. 0,2 . 103. 55. 104. 8. 105. а) 0,3125 ; б) 0,78125 .
|
106. |
2 |
. 107. 0,4096 ; 3 и 4. 108. Не менее 299. 109. 0,54432 . 110. 0,25625 . 111. а) 0,0532 ; |
|||||||||||||||||||||||||||||||||||||||||||||
|
27 |
|||||||||||||||||||||||||||||||||||||||||||||||
|
б) 0,4772 . 112. 0,99698 . |
113. 0,9772 . |
114. а) 0,0031; |
б) 0,9197 . |
115. а) 0,005399 ; |
|||||||||||||||||||||||||||||||||||||||||||
|
б) 0,9772 . 116. 0,3734 . 117. 0,981 . |
|||||||||||||||||||||||||||||||||||||||||||||||
|
118. |
|||||||||||||||||||||||||||||||||||||||||||||||
|
X |
3 |
4 |
; |
||||||||||||||||||||||||||||||||||||||||||||
|
P |
0,8 |
0,2 |
|||||||||||||||||||||||||||||||||||||||||||||
|
0, |
если x ≤ 3, |
||||||||||||||||||||||||||||||||||||||||||||||
|
F(x)= |
0,8, |
если 3 < x ≤ 4, |
|||||||||||||||||||||||||||||||||||||||||||||
|
если x > 4. |
|||||||||||||||||||||||||||||||||||||||||||||||
|
1, |
|||||||||||||||||||||||||||||||||||||||||||||||
|
119. |
|||||||||||||||||||||||||||||||||||||||||||||||
|
X |
0 |
1 |
2 |
3 |
|||||||||||||||||||||||||||||||||||||||||||
|
P |
5 |
15 |
9 |
1 |
; |
||||||||||||||||||||||||||||||||||||||||||
|
30 |
30 |
30 |
30 |
||||||||||||||||||||||||||||||||||||||||||||
|
0, |
если x ≤ 0, |
||||||||||||||||||||||||||||||||||||||||||||||
|
5 |
|||||||||||||||||||||||||||||||||||||||||||||||
|
, |
если 0 < x ≤1, |
||||||||||||||||||||||||||||||||||||||||||||||
|
30 |
|||||||||||||||||||||||||||||||||||||||||||||||
|
F(x)= |
20 |
, |
если 1 < x ≤ 2, |
||||||||||||||||||||||||||||||||||||||||||||
|
30 |
|||||||||||||||||||||||||||||||||||||||||||||||
|
29 |
, |
если 2 < x ≤ 3, |
|||||||||||||||||||||||||||||||||||||||||||||
|
30 |
|||||||||||||||||||||||||||||||||||||||||||||||
|
если x > 4; |
|||||||||||||||||||||||||||||||||||||||||||||||
|
1, |
|||||||||||||||||||||||||||||||||||||||||||||||
|
M (X )=1,2 ; D(X )= 0,56 ; σ(X )≈ 0,7483 ; Mo(X )=1. |
|||||||||||||||||||||||||||||||||||||||||||||||
|
120. |
|||||||||||||||||||||||||||||||||||||||||||||||
|
X |
0 |
1 |
2 |
3 |
4 |
; |
|||||||||||||||||||||||||||||||||||||||||
|
P |
0,0024 |
0,0404 |
0,2144 |
0,4404 |
0,3024 |
||||||||||||||||||||||||||||||||||||||||||
|
M (X )= 3; D(X )= 0,7 ; σ(X )≈ 0,8367 ; Mo(X )= 3 . |
|||||||||||||||||||||||||||||||||||||||||||||||
|
121. |
|||||||||||||||||||||||||||||||||||||||||||||||
|
X |
1 |
2 |
3 |
4 |
; |
||||||||||||||||||||||||||||||||||||||||||
|
P |
0,6 |
0,24 |
0,096 |
0,064 |
|||||||||||||||||||||||||||||||||||||||||||
|
M (X )=1,624 ; D(X )= 0,810624 ; σ(X )≈ 0,9003; Mo(X )=1. |
|||||||||||||||||||||||||||||||||||||||||||||||
|
122. |
|||||||||||||||||||||||||||||||||||||||||||||||
|
X |
0 |
1 |
2 |
3 |
4 |
; |
|||||||||||||||||||||||||||||||||||||||||
|
P |
0,6561 |
0,2916 |
0,0486 |
0,0036 |
0,0001 |
||||||||||||||||||||||||||||||||||||||||||
|
M (X )= 0,4 ; D(X )= 0,36 ; σ(X )= 0,6 ; Mo(X )= 0 . |
|||||||||||||||||||||||||||||||||||||||||||||||
|
123. |
|||||||||||||||||||||||||||||||||||||||||||||||
|
Y = 5X |
–10 |
5 |
10 |
; |
|||||||||||||||||||||||||||||||||||||||||||
|
P |
0,4 |
0,3 |
0,3 |
||||||||||||||||||||||||||||||||||||||||||||
|
Z = X 2 |
1 |
4 |
. |
||||||||||||||||||||||||||||||||||||||||||||
|
124. |
P |
0,3 |
0,7 |
||||||||||||||||||||||||||||||||||||||||||||
|
; |
|||||||||||||||||||||||||||||||||||||||||||||||
|
Z = X +Y |
–2 |
0 |
2 |
4 |
6 |
12

|
P |
0,05 |
0,32 |
0,3 |
0,24 |
0,09 |
|||||||||||||||||||||
|
U = X −Y |
–2 |
0 |
2 |
4 |
6 |
; |
||||||||||||||||||||
|
P |
0,15 |
0,36 |
0,26 |
0,2 |
0,03 |
|||||||||||||||||||||
|
V = XY |
–8 |
–4 |
0 |
4 |
8 |
; |
||||||||||||||||||||
|
P |
0,03 |
0,02 |
0,8 |
0,06 |
0,09 |
|||||||||||||||||||||
|
M (X )=1,6 ; |
M (Y )= 0,4 ; |
M (X +Y )= 2 ; |
M (X −Y )=1,2 ; M (XY )= 0,64 ; D(X )= 3,04 ; |
|||||||||||||||||||||||
|
D(Y )=1,44 ; |
D(X +Y )= 4,48 ; D(X −Y )= 4,48 . |
|||||||||||||||||||||||||
|
125. |
||||||||||||||||||||||||||
|
Z = X +Y |
0 |
1 |
2 |
3 |
4 |
; |
||||||||||||||||||||
|
P |
0,0144 |
0,1104 |
0,3124 |
0,3864 |
0,1764 |
|||||||||||||||||||||
|
M (Z )= 2,6 ; D(Z )= 0,9 ; σ(Z )≈ 0,9487 ; Mo(Z )= 3. |
||||||||||||||||||||||||||
|
126. |
||||||||||||||||||||||||||
|
Z = X +Y |
0 |
1 |
2 |
3 |
4 |
; |
||||||||||||||||||||
|
P |
0,05 |
0,3 |
0,2 |
0,3 |
0,15 |
|||||||||||||||||||||
|
M (Z )= 2,2 ; |
D(Z )=1,36 ; σ(Z )≈1,1662 ; Mo(Z )=1 и Mo(Z )= 3. |
0,
127. а) f (x)= 2x,
1,
P(0,5 ≤ X ≤1)= 0,75 ;
|
π |
1 |
|||||||
|
P |
≤ X ≤π |
= |
. |
|||||
|
3 |
2 |
|||||||
|
F(x)= 0, |
1)e−2 x , |
|||||||
|
1 −(2x + |
||||||||
|
M (X )= 0 . |
132. |
|
если x ≤ 0, |
б) M (X )= |
2 |
D(X )= |
1 |
в) P(X = 0,5)= 0 , |
||||||||||||
|
если 0 < x ≤1, |
, |
; |
|||||||||||||||
|
если x >1; |
3 |
18 |
|||||||||||||||
|
0, |
если x ≤ 0, |
||||||||||||||||
|
P(X < 0,5)= 0,25 . |
128. F(x)= |
1 −cos x, |
если 0 < x ≤π 2, |
||||||||||||||
|
если x >π 2; |
|||||||||||||||||
|
1, |
|||||||||||||||||
|
129. P (2) |
= |
3(π + 2)2 (3π − 2) |
≈ 0,2967 . |
130. A = 4 ; |
|||||||||||||
|
3 |
64π 3 |
||||||||||||||||
|
если x < 0, |
P(−1 ≤ X ≤1)=1 |
−3e−2 ≈ 0,594. |
131. A = |
1 |
; |
||||||||||||
|
если x ≥ 0; |
|||||||||||||||||
|
π |
|||||||||||||||||
|
1 |
0, |
если x < 0, |
|||||||||||||||
|
. |
133. |
0,6 . |
134. а) |
f (x)= |
1 |
− |
x |
||||||||||
|
3 |
|||||||||||||||||
|
80 , если x ≥ 0, |
|||||||||||||||||
|
e |
|||||||||||||||||
|
80 |
|
0, |
если x < 0, |
5 |
|||||||||||||||||||
|
F(x)= |
б) e− |
135. а) P(170 ≤ X ≤176)≈ 0,383 ; |
|||||||||||||||||||
|
− |
x |
4 ≈ 0,2865 . |
|||||||||||||||||||
|
80 , если x ≥ 0; |
|||||||||||||||||||||
|
1 |
−e |
||||||||||||||||||||
|
б) |
P(176 ≤ X ≤182)≈ 0,2417 ; |
в) K0,1 |
≈165,32 ; |
г) B0,1 ≈180,68 ; |
д) B0,1 ≈163,13 , |
||||||||||||||||
|
≈182,87 ; |
правило |
«трех |
сигма»: |
P(155 ≤ X ≤191)≈ 0,9973 . |
|||||||||||||||||
|
B0,1 |
|||||||||||||||||||||
|
136. а) P(X < 470)≈ 0,002 ; |
б) P(500 ≤ X ≤ 550)≈ 0,6096 ; |
в) P(X > 550)≈ 0,3409 ; |
|||||||||||||||||||
|
г) |
P( |
X −540 |
≤ 30)≈ 0,7814 . |
137. а) P(X ≤15,3)≈ 0,9332 ; |
б) P(X ≥15,4)≈ 0,0228 ; |
||||||||||||||||
|
в) |
P( |
14,9 ≤ X ≤15,3)≈ 0,6247 . |
С вероятностью 0,9973 , т.е. практически достоверно, что |
||||||||||||||||||
|
цена акции будет находиться в границах от 14,4 |
$ до 15,6 $ . |
138. а) a ≈ 98,09, σ ≈11,98 ; |
|||||||||||||||||||
|
б) |
P(83 ≤ X ≤ 96)≈ 0,3287 . С вероятностью 0,95 |
отклонение цены бумаги от ее среднего |
|||||||||||||||||||
|
значения по абсолютной величине не превысит 23,48 |
$ . 139. a ≈15,21, |
σ ≈ 3,1. |
13
Содержание
- Показательный (экспоненциальный закон распределения).
- Экспоненциально распределенная случайная величина
- Примеры решений
- Решебник по теории вероятности онлайн
- Показательный (экспоненциальный закон распределения)
- Примерные варианты тестов
Показательный (экспоненциальный закон распределения).
Случайная величина Х распределена по показательному закону распределения с параметром λ, если её плотность вероятности имеет вид:
Функция распределения имеет вид:
Математическое ожидание и дисперсия для случайной величины, распределенной по показательному закону, находятся по формулам:
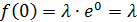
То есть при
Пример.
Установлено, что время ремонта телевизоров есть случайная величина X, распределенная по показательному закону.
Определить вероятность того, что на ремонт телевизора потребуется не менее 20дней, если среднее время ремонта телевизоров составляет 15 дней. Найти плотность вероятности, функцию распределения и среднее квадратическое отклонение случайной величины X.
Решение:
По условию математическое ожидание M(х)=1/λ = 15, откуда параметр λ = 1/15. Тогда плотность вероятности и функция распределения примут вид:
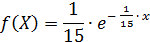
Искомую вероятность P(Х ≥20) можно было найти по формуле, интегрируя плотность вероятности, то есть
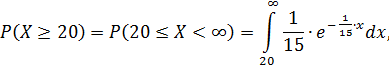
Найдем среднее квадратическое отклонение: σ(X) = М(Х) = 15 дней.
Экспоненциально распределенная случайная величина
На странице Непрерывная случайная величина мы разобрали примеры решений для произвольно заданных законов распределения (многочлены, логарифмы и т.п.). Здесь же мы разберем примеры только для одного типа СВ — распределенных по показательному (или экспоненциальному) закону.
Плотность распределения величины $X$ с экспоненциальным законом распределения задается формулой:
Функция распределения величины $X$:
Здесь $lambda$ — единственный параметр данного распределения, полностью определяющий его свойства. В частности, числовые характеристики выражаются через этот параметр: $M(X)=1/lambda$, $D(X)=1/lambda^2$.
Экспоненциальное распределение моделирует время между двумя последовательными свершениями события, а параметр $lambda$ описываетс среднее число наступлений события в единицу времени. Обычно с помощью этого закона описывают: продолжительность обслуживания покупателя, время жизни оборудования до отказа, промежуток времени между поломками и т.п.
В этом разделе мы приведем разные примеры задач с полным решением, где используются показательно распределенные случайные величины.
Примеры решений
Задача 1. Среднее время безотказной работы прибора равно 80 часов. Полагая, что время безотказной работы прибора имеет показательный закон распределения, найти:
а) выражение его плотности вероятности и функции распределения;
б) вероятность того, что в течение 100 часов прибор не выйдет из строя.
Задача 2. Известно, что время работы прибора до первого отказа подчиняется показательному распределению со средним значением 1 год. Какова вероятность, что до первого отказа пройдет не менее 2 лет?
Задача 3. Установлено, что время ремонта телевизоров есть случайная величина $X$, распределенная по показательному закону с параметром $lambda=1/3$ (1/день). Определить вероятность того, что на ремонт телевизора потребуется не менее 5 дней.
Задача 4. Время в годах безотказной работы прибора подчинено показательному закону, т.е. плотность распределения этой случайной величины такова: $f(t)=2e^<-2t>$ при $tge 0$ и $f(t)=0$ при $tlt 0$.
1) Найти формулу функции распределения этой случайной величины.
2) Определить вероятность того, что прибор проработает не более года.
3) Определить вероятность того, что прибор безотказно проработает 3 года.
4) Определить среднее ожидаемое время безотказной работы прибора.
Задача 5. Предполагая, что случайное время обслуживания абонента службой «09» распределено по показательному закону и средняя продолжительность обслуживания составляет 1,5 минуты, найдите вероятность того, что абонент будет обслужен более, чем за 2 минуты.
Задача 6. Длительность телефонного разговора подчиняется показательному закону. Найти среднюю длительность разговора, если вероятность того, что разговор продлится более 5 минут, равна 0,4.
Задача 7. Случайная величина задана плотностью распределения $p(x)=ce^<-3x>$ при $x gt 0$, и ноль в остальных случаях. Найти постоянную $c$, математическое ожидание, дисперсию и среднее квадратическое отклонение.
Задача 8. Непрерывная случайная величина $xi$ распределена по показательному закону с параметром $lambda$, равному номеру варианта 9. Найти плотность распределения случайной величины $xi$, функцию распределения, построить графики этих функций. Найти математическое ожидание, дисперсию, среднее квадратическое отклонение случайной величины $xi$ и вероятность того, что $xi$ принимает значения, меньшие своего математического ожидания.
Задача 9. Случайная величина $xi$ распределена по показательному закону с параметром 2. Найти $M_<xi>$, $D_<xi>$ вероятность попадания $xi$ в интервал $(-1;2)$. Нарисовать графики плотности распределения и функции распределения $xi$.
Задача 10. Известно, что $Х$ распределено по экспоненциальному закону $Exp(lambda)$. Найдите вероятность события $|Х — МХ | lt 3sigma$ («правило $3sigma$» для показательного распределения).
Решебник по теории вероятности онлайн
Больше 11000 решенных и оформленных задач по теории вероятности:
Показательный (экспоненциальный закон распределения)
Случайная величина Х распределена по показательному закону распределения с параметром λ, если её плотность вероятности имеет вид:
Функция распределения имеет вид:
Математическое ожидание и дисперсия для случайной величины, распределенной по показательному закону, находятся по формулам:
То есть при
Пример.
Установлено, что время ремонта телевизоров есть случайная величина X, распределенная по показательному закону.
Определить вероятность того, что на ремонт телевизора потребуется не менее 20 дней, если среднее время ремонта телевизоров составляет 15 дней. Найти плотность вероятности, функцию распределения и среднее квадратическое отклонение случайной величины X.
Решение:
По условию математическое ожидание M(х)=1/λ = 15, откуда параметр λ = 1/15. Тогда плотность вероятности и функция распределения примут вид:

Искомую вероятность P(Х ≥20) можно было найти по формуле, интегрируя плотность вероятности, то есть

Найдем среднее квадратическое отклонение: σ(X) = М(Х) = 15 дней.
Равномерный закон распределения.
Непрерывная случайная величина Х имеет равномерный закон распределения (закон постоянной плотности) на отрезке [a; b], если на этом отрезке функция плотности вероятности случайной величины постоянна, то есть
Следовательно, математическое ожидание случайной величины, равномерно распределенной на отрезке (a, b), равняется середине этого отрезка.
Дисперсия имеет вид:
Найдем вероятность попадания значения случайной величины, имеющей равномерное распределение, на интервал 
Функция распределения примет вид:
Пример.
Поезда метрополитена идут регулярно с интервалом 2 мин. Пассажир выходит на платформу в случайный момент времени. Какова вероятность того, что ждать пассажиру придется не больше полминуты.
Найти математическое ожидание и среднее квадратическое отклонение случайной величины X – времени ожидания поезда.
Решение:
Случайная величина X – время ожидания поезда на временном (в минутах) отрезке [0;2] имеет равномерный закон распределения f (x)=1/2.
Поэтому вероятность того, что пассажиру придется ждать не более полминуты, равна 1/4 от равной единице площади прямоугольника, т.е.
Найдем математическое ожидание, дисперсию и среднее квадратическое отклонение:
Примерные варианты тестов
Ниже приведено несколько примеров компьютерных тестов с указанием правильных ответов.
Как называется число m0 (наступления
события в n независимых испытаниях, в каждом из которых вероятность появления события равна p), определяемое из
Потребитель может увидеть рекламу определенного товара по телевидению (событие А), на рекламном стенде (событие В) и прочесть в газете (событие С). Что означает событие А + В + С :
а) потребитель увидел все три вида рекламы;
б) потребитель не увидел ни одного вида рекламы;
в) потребитель увидел хотя бы один вид рекламы;
г) потребитель увидел ровно один вид рекламы;
д) потребитель увидел рекламу по телевидению.
На пяти одинаковых карточках написаны буквы И, Л, О, С, Ч. Если перемешать их, и разложить наудачу в ряд две карточки, то вероятность р получить слово ИЛ равна …. В ответе запишите число
Если A и B — независимые события, то вероятность наступления хотя бы одного из двух событий A и B вычисляется по формуле
г) 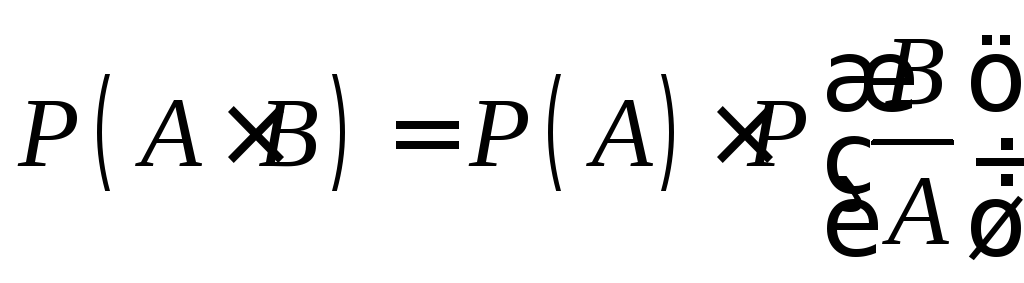
Из 10 коммерческих банков 4 находятся за чертой города. Налоговый инспектор выбирает наугад для проверки 3 банка. Какова вероятность того, что хотя бы 2 из них — в черте города?
а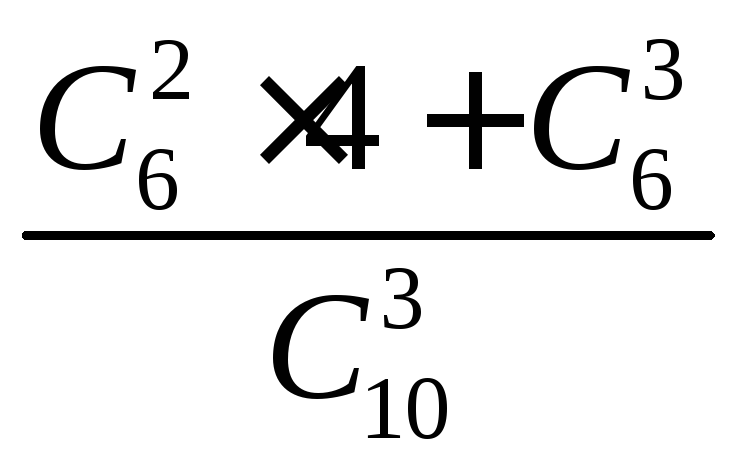
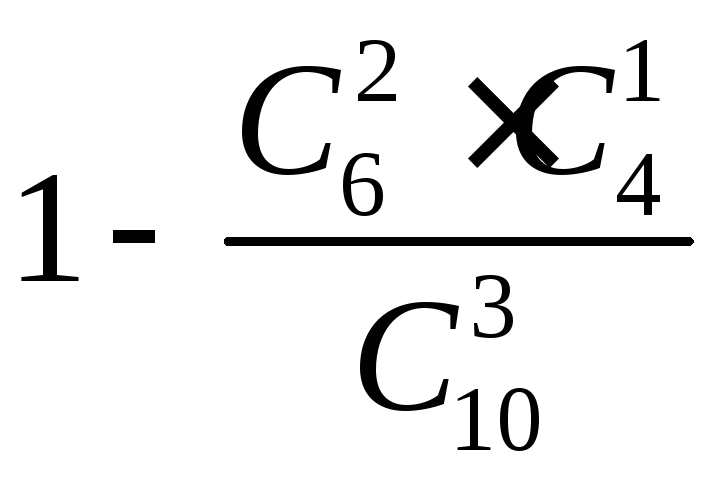
г) 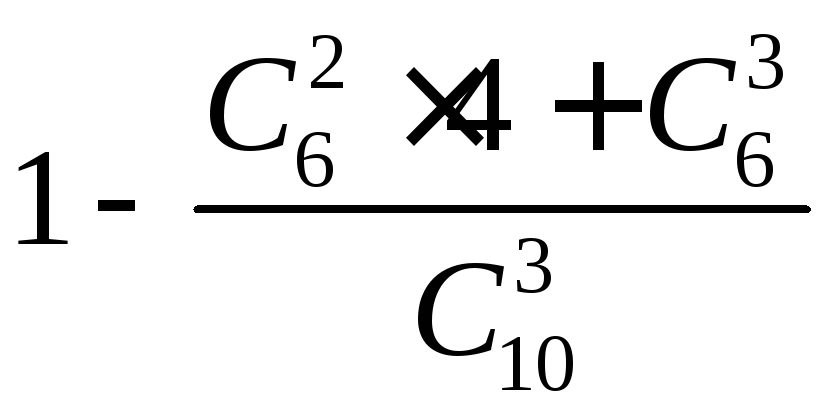
Сколькими способами можно составить список из пяти студентов? В ответ записать полученное число.
Подбрасываются две игральные кости. Найти вероятность Р того, что сумма выпавших очков равна четырем. В ответ записать число 24 Р.
Партия из 10 телевизоров содержит 3 неисправных телевизора. Из этой партии выбираются наугад 2 телевизора. Найти вероятность Р того, что оба они будут неисправными. В ответ записать число 45 Р.
Данное предприятие в среднем выпускает 20 % продукции высшего сорта и 70 % продукции первого сорта. Найти вероятность Р того, что случайно взятое изделие этого предприятия будет высшего или первого сорта. В ответ записать число 30 Р.
Случайная величина Х задана функцией распределения
Найти вероятность Р того, что в результате испытания случайная величина Х примет значение, принадлежащее интервалу (0,1; 0,6). В ответ записать число 20 Р.
Случайная величина Х распределена равномерно на интервале (2; 6) и р (х) – ее плотность вероятности. Найти р (3). В ответ записать число 40 р (3).
Задан статистический ряд распределения
Подборка по базе: Вычислить площадь фигуры ПРИМЕРЫ.docx, Сборник задач по высшей математике.pdf, Практические задачи к теме 5.docx, ситуационные задачи Физкульутра.docx, 8 класс задачи.docx, Тесты, кейсы и задачи.docx, Тема 2.2 Педагогическая деятельность и педагогическое взаимоде, Решение педагогической задачи.docx, Решение педагогической задачи.docx, Урок 2. Решение задач с помощью систем уравнений второй степени.
Решение
1. а) По формулам (4.26) и (4.30) запишем
,
б) Доля костюмов 4-го роста (176 – 182 см.) в общем объеме производства определится по формуле (4.32) как вероятность
(рис. 4.13), так как по (4.33)
,
Долю костюмов 3-го роста (170–176 см) можно было определить аналогично по формуле (4.32), но проще это сделать по формуле (4.34), если учесть, что данный интервал симметричен относительно математического ожидания а= М(Х)=173, т.е. не равенство
170 < X<176 равносильно неравенству |Х— 173| ≤3:
,
(рис. 4.13).
в) Квантиль X0,7 случайной величины Xнайдем из уравнения (3.29) с учетом (4.30):
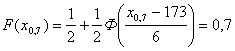
откуда
.
По табл. II приложений находим t = 0,524 и
Х0,7 = 6*t + 173 = 6*0,524 + 173 ≈ 176 (см).
Это означает, что 70% мужчин данной возрастной группы имеют рост до 176 см.
10%-ная точка – это квантиль X0,9 = 181 см (находится аналогично), т.е. 10% мужчин имеют рост не менее 181 см.
2. Практически достоверно, что рост мужчин данной возрастной группы заключен в границах от a-3σ = 173-3*6 = 155 до a + 3σ = 173 + 3*6 = 191 (см), т.е. 155 ≤ Х ≤ 191 (см).
Задания
4.1. Вероятность выигрыша по облигации займа за все время его действия равна 0,1. Составить закон распределения числа выигравших облигаций среди приобретенных 19. Найти математическое ожидание, дисперсию, среднее квадратическое отклонение и моду этой случайной величины.
4.2. По данным примера 4.11 найти математическое ожидание, дисперсию и среднее квадратическое отклонение доли (частости) выигравших облигаций среди приобретенных. Составить функцию распределения случайной величины, имеющей биномиальный закон распределения с параметрами n и р.
4.3. Устройство состоит из 1000 элементов, работающих независимо один от другого. Вероятность отказа любого элемента в течение времени tравна 0,002. Необходимо:
а) составить закон распределения отказавших за время tэлементов;
б) найти математическое ожидание и дисперсию этой случайной величины;
в) определить вероятность того, что за время t откажет хотя бы один элемент.
4.4. Вероятность поражения цели равна 0,05. Производится стрельба по цели до первого попадания. Необходимо:
а) составить закон распределения числа сделанных выстрелов;
б) найти математическое ожидание и дисперсию этой случайной величины;
в) определить вероятность того, что для поражения цели потребуется не менее 5 выстрелов.
4.5. В магазине имеются 20 телевизоров, из них 7 имеют дефекты. Необходимо:
а) составить закон распределения числа телевизоров с дефектами среди выбранных наудачу пяти;
б) найти математическое ожидание и дисперсию этой случайной величины;
в) определить вероятность того, что среди выбранных нет телевизоров с дефектами.
4.6. Цена деления шкалы измерительного прибора равна 0,2. Показания прибора округляют до ближайшего целого числа. Полагая, что при отсчете ошибка округления распределена по равномерному закону, найти:
1) математическое ожидание, дисперсию и среднее квадратическое отклонение этой случайной величины;
2) вероятность того, что ошибка округления:
а) меньше 0,04;
б) больше 0,05.
4.7. Среднее время безотказной работы прибора равно 80 ч. Полагая, что время безотказной работы прибора имеет показательный закон распределения, найти:
а) выражение его плотности вероятности и функции распределения;
б) вероятность того, что в течение 100 ч прибор не выйдет из строя.
4.8. Текущая цена акции может быть смоделирована с помощью нормального закона распределения с математическим ожиданием 15 ден. ед. и средним квадратическим отклонением 0,2 ден. ед.
1. Найти вероятность того, что цена акции:
а) не выше 15,3 ден. ед.;
б) не ниже 15,4 ден. ед.;
в) от 14,9 до 15,3 ден. ед.
2. С помощью правила трех сигм найти границы, в которых будет находиться текущая цена акции.
4.9. Цена некой ценной бумаги нормально распределена. В течение последнего года 20% рабочих дней она была ниже 88 ден. ед., а 75% – выше 90 ден. ед. Найти:
а) математическое ожидание и среднее квадратическое отклонение цены ценной бумаги;
б) вероятность того, что в день покупки цена будет заключена в пределах от 83 до 96 ден. ед.;
в) с надежностью 0,95 определить максимальное отклонение цены ценной бумаги от среднего (прогнозного) значения (по абсолютной величине).
4.10. Коробки с конфетами упаковываются автоматически. Их средняя масса равна 540 г. Известно, что масса коробок с конфетами имеет нормальное распределение, а 5% коробок имеют массу, меньшую 500 г. Каков процент коробок, масса которых:
а) менее 470 г;
б) от 500 до 550 г;
в) более 550 г;
г) отличается от средней не более, чем на 30 г (по абсолютной величине)?
4.11. Случайная величина Xимеет нормальное распределение с математическим ожиданием а= 25. Вероятность попадания Хвинтервал (10; 15) равна 0,09. Чему равна вероятность попадания Xв интервал:
а) (35;40);
б) (30;35)?
4.12. Нормально распределенная случайная величина имеет следующую функцию распределения: F(x) = 0,5 + 0,5Ф(x-1). Из какого интервала (1;2) или (2;6) она примет значение с большей вероятностью?
4.13. Квантиль уровня 0,15 нормально распределенной случайной величины Xравен 12, а квантиль уровня 0,6 равен 16. Найти математическое ожидание и среднее квадратическое отклонение случайной величины.
4.14. 20%-ная точка нормально распределенной случайной величины равна 50, а 40%-ная точка равна 35. Найти вероятность того, что случайная величина примет значение в интервале (25;45).
4.15. Месячный доход семей можно рассматривать как случайную величину, распределенную по логнормальному закону. Полагая, что математическое ожидание этой случайной величины равно 1000 ден. ед., а среднее квадратическое отклонение 800 ден. ед., найти долю семей, имеющих доход:
а) не менее 1000 ден. ед.;
б) менее 500 ден. ед.
4.16. Известно, что нормально распределенная случайная величина принимает значение:
а) меньшее 248 с вероятностью 0,975;
б) большее 279 с вероятностью 0,005.
Найти функцию распределения случайной величины X.
4.17. Случайная величина Xраспределена по нормальному закону с нулевым математическим ожиданием. Вероятность попадания этой случайной величины на отрезок от –1 до +1 равна 0,5. Найти выражения плотности вероятности и функции распределения случайной величины X.
4.18. Имеется случайная величина X,распределенная по нормальному закону с математическим ожиданием аи дисперсией σ2. Требуется приближенно заменить нормальный закон распределения равномерным законом в интервале (а; р); границы а, р подобрать так, чтобы сохранить неизменными математическое ожидание и дисперсию случайной величины X.
4.19. Случайная величина Xраспределена по нормальному закону с математическим ожиданием а= 0. При каком значении среднего квадратического отклонения овероятность попадания случайной величины Xв интервал (1;2) достигает максимума?
4.20. Время ремонта телевизора распределено по показательному закону с математическим ожиданием, равным 0,5 ч. Некто сдает в ремонт два телевизора, которые одновременно начинают ремонтировать, и ждет, когда будет отремонтирован один из них. После этого с готовым телевизором он уходит. Найти закон распределения времени:
а) потраченного клиентом;
б) которое должен потратить клиент, если он хочет забрать сразу два телевизора.
5 ГЛАВА
Многомерные случайные величины
В главе рассматриваются:
— понятие многомерной случайной величины и ее закон распределения;
— функция распределения многомерной случайной величины;
— плотность вероятности двумерной случайной величины;
— ковариация и коэффициент корреляции.
Типовые задачи
Пример 5.1
Закон распределения дискретной двумерной случайной величины (Х, Y) задан в табл. 5.2.
Таблица 5.2
|
xi |
-1 |
0 |
1 |
2 |
|
1 |
0,10 |
0,25 |
0,30 |
0,15 |
|
2 |
0,10 |
0,05 |
0,00 |
0,05 |
Найти:
а) законы распределения одномерных случайных величин Xи Y;
б) условные законы распределения случайной величины Xпри условии Y = 2 и случайной величины Yпри условии X= 1;
в) вычислить P(
Y<
X).
Решение
а) Случайная величина Xможет принимать значения:
Х =1 с вероятностью P1= 0,10 + 0,25 + 0,30 + 0,15 = 0,8;
X= 2с вероятностью P2
=
0,10 + 0,05 + 0,00 + 0,05 = 0,2,
т.е. ее закон распределения
|
X: |
xi |
1 |
2 |
|
pi |
0,8 |
0,2 |
Аналогично закон распределения
|
Y: |
yj |
-1 |
0 |
1 |
2 |
|
pj |
0,2 |
0,3 |
0,3 |
0,2 |
б) Условный закон распределения Х при условии, что Y = 2. получим, если вероятность pij
, стоящие в последнем столбце табл.5.2, разделим на их сумму, т.е. p(Y= 2) = 0,2. Получим
|
Х |
х |
1 |
2 |
|
pj(х |
0,75 |
0,25 |
Аналогично для получения условного закона распределения Y при условии Х = 1 вероятности pij, стоящие в первой строке табл. 5.2, делим на их сумму, т.е. на p(X = 1) = 0,8. Получим
|
YХ=1 |
yj |
-1 |
0 |
1 |
2 |
|
pi(yj) |
0,125 |
0,3125 |
0,375 |
0,1875 |
в) Для нахождения вероятностей Р(Y< Х) складываем вероятности событий pij из табл. 5.2, для которых yj< х
i.
Получим
Р(Y< Х) = 0,10 + 0,25 + 0,10 + 0,05 + 0,00 = 0,5
Среднее время безотказной работы прибора равно 80ч. Полагая, что время безотказной работы имеет показательный закон распределения, найти: а) выражение его плотности вероятности и функции распределения; б) вероятность того, что в течение 100ч прибор не выйдет из строя.
Скачать решение бесплатно
Купить решение
* Оплата через сервис ЮMoney.
Другие задачи по теории вероятности
Текущая цена акции может быть смоделирована с помощью нормального закона распределения с математическим ожиданием 15 ден.ед. и средним квадратичным отклонением 0,2 ден.ед. Найти вероятность того, что цена акции а) не выше 15,3 ден.ед.; б) не ниже 15,4 ден.ед.; в) от 14,9 до 15,3 ден.ед. С помощью правила трёх сигм найти границы, в которых будет находиться текущая цена акции.
Цена некой ценной бумаги нормально распределена. В течение последнего года 20% рабочих дней она была ниже 88 ден.ед., а 75% — выше 90 ден.ед. Найти: а) математическое ожидание и среднее квадратичное отклонение цены ценной бумаги; б) вероятность того, что в день покупки цена будет заключена в пределах от 83 до 96 ден.ед.; в) с надежностью 0,95 определить максимальное отклонение цены ценной бумаги от среднего (прогнозного) значения (по абсолютной величине).
Коробки с конфетами упаковываются автоматически. Их средняя масса равна 540г. Известно, что масса коробок с конфетами имеет нормальное распределение, а 5% коробок имеют массу, меньшую 500г. Каков процент коробок, масса которых: а) менее 470г.; б) от 500 до 550г.; в) более 550г.; г) отличается от средней не более, чем на 30г. (по абсолютной величине).
Случайная величина имеет нормальное распределение с математическим ожиданием a=25. Вероятность попадания X в интервал (10;15) равна 0,09. Чему равна вероятность попадания X в интервал: а) (35;40); б) (30;35)?
Нормально распределенная случайная величина имеет следующую функцию распределения: F(x)=0,5+0,5Ф(x-1). Из какого интервала (1;2) или (2;6) она примет значение с большей вероятностью?
Квантиль уровня 0,15 нормально распределенной случайной величины X равен 12, а квантиль уровня 0,6 равен 16. Найти математическое ожидание и среднее квадратичное отклонение случайной величиной.
20%-ная точка нормально распределенной случайной величины равна 50, а 40%-ная точка равна 35. Найти вероятность того, что случайная величина примет значение в интервале (25;45)