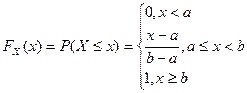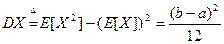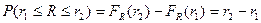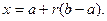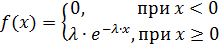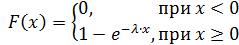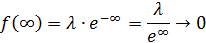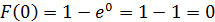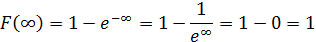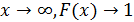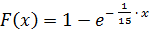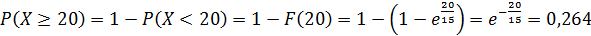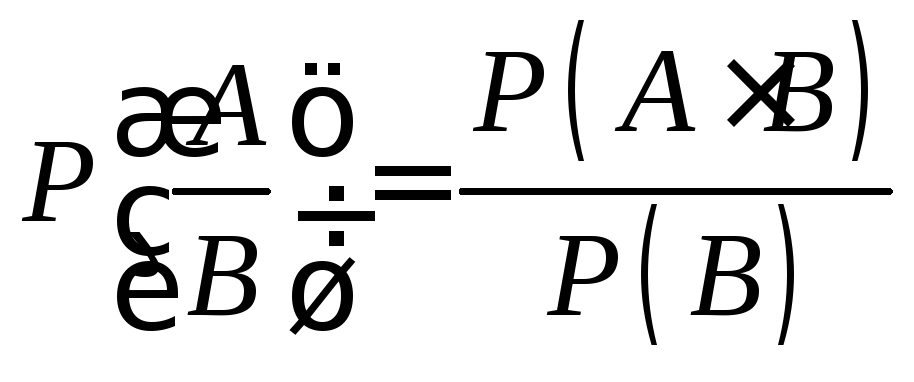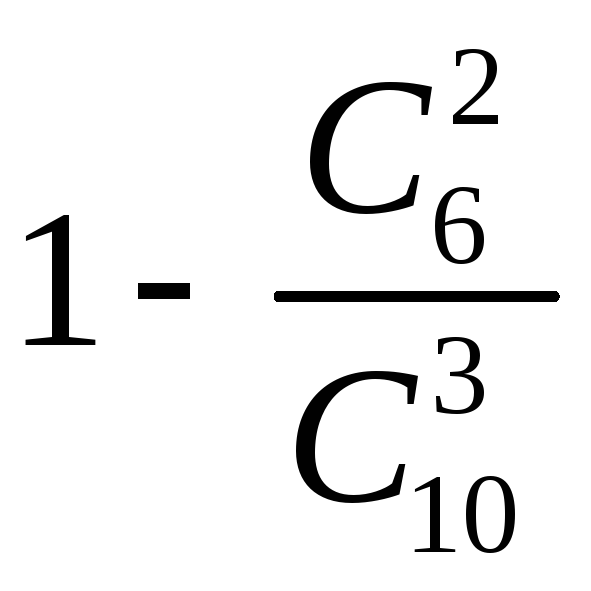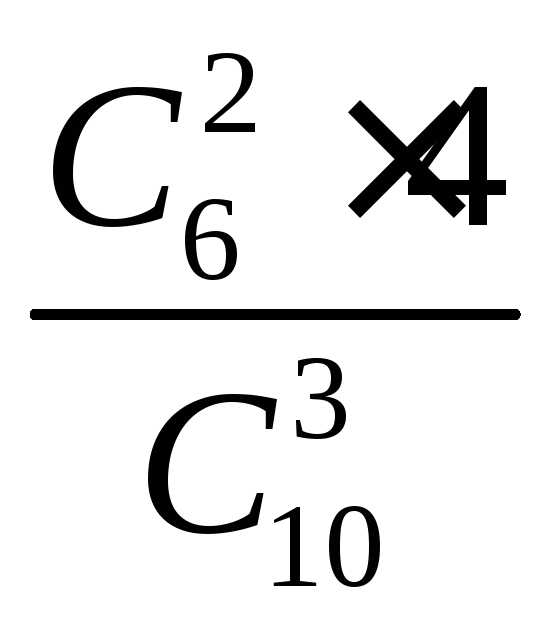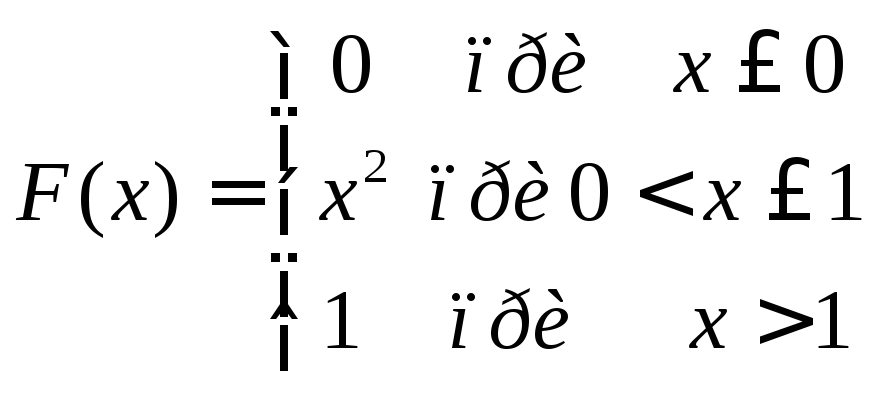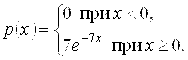Определение Непрерывная случайная величина Х имеет показательный закон распределения с параметром 

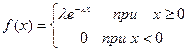
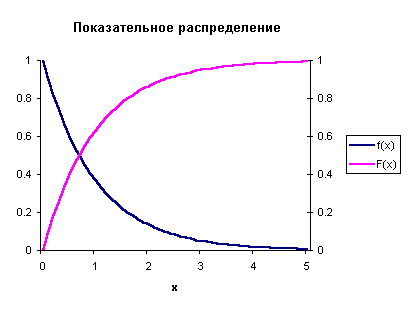
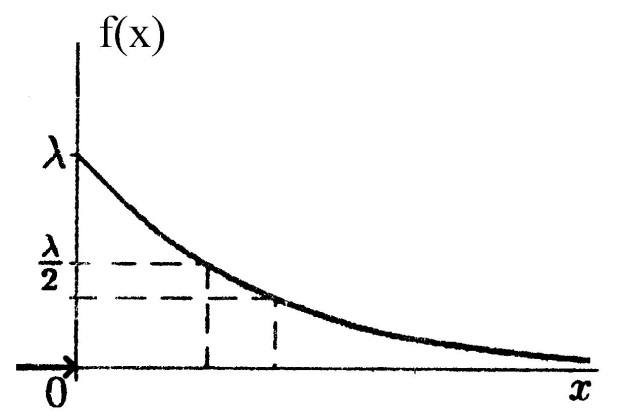
Кривая распределения 
Рис 2.
Получим выражение для функции распределения по формуле 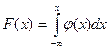
1) При 

2) При 
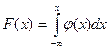

По соответствующим формулам получаем выражения для 

Задача. Среднее время безотказной работы прибора равно 80 ч. Полагая, что время безотказной работы прибора имеет показательный закон распределения, найти: а) выражение его плотности вероятности и функции распределения; б) вероятность того, что в течение 100 ч. прибор не выйдет из строя.
Решение. Х- время безотказной работы прибора, среднее время — 



Искомая вероятность
Замечание. Показательный закон распределения играет большую роль в теории массового обслуживания и теории надежности.
МОСКОВСКИЙ ГОСУДАРСТВЕННЫЙ ИНСТИТУТ ЭЛЕКТРОНИКИ И МАТЕМАТИКИ
Кафедра теории вероятностей и математической статистики
РЕФЕРАТ
По математической статистике
на тему:
«Равномерное распределение»
Выполнил: студенты группы М-65
Ражева А.А.
Кнутова А.С.
Проверил:Заведующий Кафедрой
Ивченко Г. И.
Москва 2012 г.
Непрерывное равномерное распределение — в теории вероятностей распределение, характеризующееся тем, что вероятность любого интервала зависит только от его длины.
Равномерное распределение полезно при описании переменных, у которых каждое значение равновероятно, иными словами, значения переменной равномерно распределены в некоторой области.
Определение
Говорят, что случайная величина имеет непрерывное равномерное распределение на отрезке [a,b], где 
Пишут: X ~ U (a,b) или
Иногда значения плотности в граничных точках x = a и x = b меняют на другие, например 0 или 
Если L (ξ) = U(a,b), то
Равномерное распределение U (a,b) описывает процесс «выбора точки наудачу» в интервале [a,b]. Так, если [a,b] – интервал между последовательными отправлениями автобуса от остановки, то время ожидания пассажира, не знающего расписания и пришедшего на остановку, есть случайная величина с распределением U (0,1). Распределение U (0,1) играет особую роль в методах моделирования с помощью компьютеров случайных величин с заранее заданными распределениями. Такие методы широко используют для приближенных вычислений интегралов, решений дифференциальных и интегральных уравнений и т.д.
Пример (Гипотеза случайности).
В некоторых случаях априори предполагается (постулируется), что исходные данные представляют собой случайную выборку из некоторого распределения, т.е. компоненты вектора данных X=(







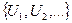
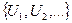

Функция распределения
Интегрируя определённую выше плотность, получаем:
Так как плотность равномерного распределения разрывна в граничных точках отрезка [a,b], то функция распределения в этих точках не является дифференцируемой. В остальных точках справедливо стандартное равенство:
Характеристическая функция случайной величины X ~ U(a,b):
Математическое ожидание и дисперсия по определению равны:
Вообще,
Стандартное равномерное распределение
Если a = 0, а b = 1, то есть X ~ U[0,1], то такое непрерывное равномерное распределение называют стандартным. Имеет место элементарное утверждение:
Если случайная величина X ~ U[0,1], и Y = a + (b − a)X, где a < b, тo Y ~ U[0,1].
Таким образом, имея генератор случайной выборки из стандартного непрерывного равномерного распределения, легко построить генератор выборки любого непрерывного равномерного распределения.
Более того, имея такой генератор и зная функцию обратную к функции распределения случайной величины, можно построить генератор выборки любого непрерывного распределения (не обязательно равномерного) с помощью метода обратного преобразования. Поэтому, стандартно равномерно распределённые случайные величины иногда называют базовыми случайными величинами.
Линейное преобразование
переводит СВ X ~ R(a,b) в СВ Y ~ R(0,1). Действительно,
Равномерное распределение является непрерывным аналогом дискретного распределения вероятностей для опытов с равновероятными исходами.
Значение
С помощью линейного преобразования приводится к равномерному распределению на отрезке [0,1]. Равномерное распределение является непрерывным аналогом распределений классической теории вероятностей, описывающих случайные эксперименты с равновероятными исходами.
Погрешность, происходящая от округления числа, удовлетворительно описывается равномерным распределением на отрезке [ − 1 / 2,1 / 2].
Если случайная величина ζ имеет непрерывную функцию распределения 
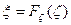
Моделирование
Обозначим буквой 
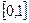
Если 

Моделировать случайную величину 
Мы рассмотрим метод псевдослучайных последовательностей, который наиболее просто реализуется в компьютере. Для получения псевдослучайной последовательности используем алгоритм, который называется методом середины квадратов. Поясним его на примере. Возьмем некоторое число 

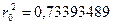







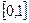

Метод обратных функций.
Пусть случайная величина 





Отсюда следует, что значение 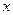




Последовательности значений 

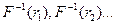


Моделирование случайной величины с равномерным распределением на отрезке
Пусть случайная величина 
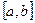
Составляем уравнение 
Последовательности значений 



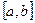
Порядковые статистики.
Случайная величина 

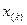
Для случая 
При этом:



А также:
Если же 



А также:

Отметим далее, что если 
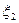


Оценивание параметров в равномерном распределении.
Введём статистический аналог теоретического математического ожидания случайной величины 

Введём статистический аналог теоретической дисперсии случайной величины 

Любая измеримая функция от выборки 
Статистика 

Статистика 

То есть для любого 
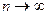

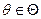
ü Возьмём выборку 

Оптимальной несмещённой оценкой θ в данном классе оценок является:
Её дисперсия:

ü Оценим теперь параметр θ равномерного распределения 

Статистики 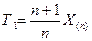

Кроме того, имеем: 

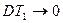



ü Пусть теперь 


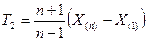
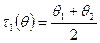

Достаточные статистики и оптимальные оценки.
Если для любой оценки 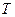


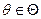
Итак, T* — оптимальная оценка для параметрической функции 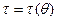



Статистика 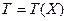



Теорема Рао-Блекуэлла-Колмогорова: Оптимальная оценка, если она существует, является функцией от достаточной статистики.
Теорема: Если существует полная достаточная статистика, то всякая функция от неё является оптимальной оценкой своего математического ожидания.
То есть оптимальная оценка однозначно определяется уравнением 
Функция 


Критерий факторизации.
Для того, чтобы статистика была достаточной для параметрического семейства распределений P, необходимо и достаточно, чтобы функция правдоподобия выборки 
Где множитель h(x) от 

ü Пусть 


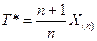
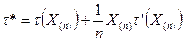
ü Пусть теперь 



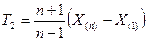

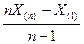


ü Статистика 


Если 
Аналогично, если 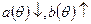
Этими двумя случаями исчерпываются ситуации, когда в модели 
Для модели 


|
Расчетные и графические задания Равновесный объем — это объем, определяемый равенством спроса и предложения… |
Кардиналистский и ординалистский подходы Кардиналистский (количественный подход) к анализу полезности основан на представлении о возможности измерения различных благ в условных единицах полезности… |
Обзор компонентов Multisim Компоненты – это основа любой схемы, это все элементы, из которых она состоит. Multisim оперирует с двумя категориями… |
Композиция из абстрактных геометрических фигур Данная композиция состоит из линий, штриховки, абстрактных геометрических форм… |

Полученный результат позволяет сформулировать правило «трех сигм»: если случайная величина распределена нормально, то модуль ее отклонения от х = а не превосходит 3σ.
Числовые характеристики
Для вычисления математического ожидания нормально распределенной случайной величины воспользуемся тем, что интеграл Пуассона
|
z2 |
|||||||||||||||||||||||||||||||
|
e 2 dz |
2 . |
||||||||||||||||||||||||||||||
|
1 |
( x a )2 |
x a |
1 |
z2 |
|||||||||||||||||||||||||||
|
) |
|||||||||||||||||||||||||||||||
|
M(X) |
xe 2 2 dx (z |
( z a)e 2 dz |
|||||||||||||||||||||||||||||
|
2 |
2 |
||||||||||||||||||||||||||||||
|
1 |
z2 |
a |
z2 |
a |
|||||||||||||||||||||||||||
|
ze |
2 dz |
e 2 dz |
0 |
2 |
a |
||||||||||||||||||||||||||
|
2 |
2 |
2 |
|||||||||||||||||||||||||||||
(первое слагаемое равно 0, так как подынтегральная функция нечетна, а пределы интегрирования симметричны относительно нуля).
|
1 |
( x a )2 |
||||||||||||||||||||||
|
D(X) |
(x a)2 e 2 2 dx |
||||||||||||||||||||||
|
2 |
|||||||||||||||||||||||
|
2 |
z2 |
z2 |
|||||||||||||||||||||
|
z |
ze 2 |
dz (u |
z, dv ze |
2 ) |
|||||||||||||||||||
|
2 |
|||||||||||||||||||||||
|
2 |
z2 |
z2 |
2 |
||||||||||||||||||||
|
z |
e 2 |
e 2 dz |
0 |
2 |
2 . |
||||||||||||||||||
|
2 |
2 |
||||||||||||||||||||||
.
Следовательно, параметры нормального распределения (а и σ) равны соответственно математическому ожиданию и среднему квадратическому отклонению исследуемой случайной величины.
|
Замечание. Можно показать, что для нормального распределения |
4 |
3 |
, и, |
|
4 |
соответственно, эксцесс Ех = 0. Для кривых с более острой вершиной Ех >0, в случае более плоской вершины Ех < 0.
Показательное распределение
Показательным (экспоненциальным) называют распределение вероятностей непрерывной случайной величины Х, которое описывается плотностью
63

|
f (x) |
0, |
x |
0 |
(8) |
|||
|
e |
x , x |
0. |
|||||
В отличие от нормального распределения, показательный закон определяется только одним параметром λ. В этом его преимущество, так как обычно параметры распределения заранее не известны и их приходится оценивать приближенно. Понятно, что оценить один параметр проще, чем несколько.
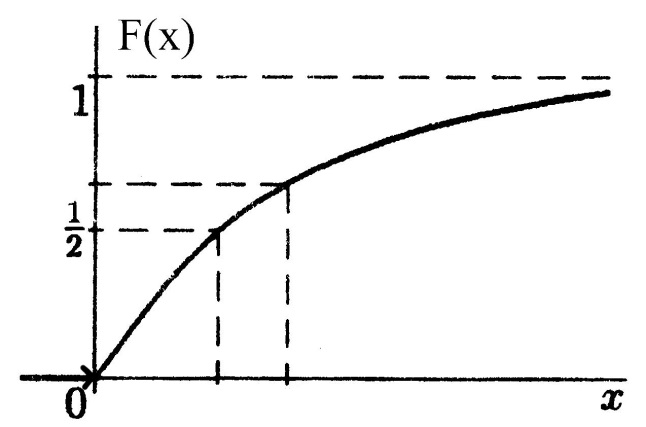
Найдем функцию распределения показательного закона:
|
x |
0 |
x |
||
|
F(x) |
f (t)dt |
0 dt |
e t dt 1 e x . |
|
|
0 |
||||
|
Следовательно, |
||||
|
F(x) |
0, |
x |
0 |
|
|
1 e |
x , |
x 0. |
||
Теперь можно найти вероятность попадания показательно распределенной случайной величины в интервал (а, b):
p(a X b) e a e b .
Значения функции е-х можно найти из таблиц.
Функция надежности
Пусть элемент (то есть некоторое устройство) начинает работать в момент времени t0 = 0 и должен проработать в течение периода времени t. Обозначим за Т непрерывную случайную величину – время безотказной работы элемента, тогда функция F(t) = p(T > t) определяет вероятность отказа за время t. Следовательно, вероятность безотказной работы за это же время равна
R(t) = p(T > t) = 1 – F(t).
Эта функция называется функцией надежности.
Показательный закон надежности
Часто длительность безотказной работы элемента имеет показательное распределение, то есть
F(t) = 1 – e— t .
Следовательно, функция надежности в этом случае имеет вид:
R(t) = 1 – F(t) = 1 – (1 – e— t) = e— t .
Определение. Показательным законом надежности называют функцию надежности, определяемую равенством
R(t) = e— t ,
где – интенсивность отказов.
64

Пример 4.
Пусть время безотказной работы элемента распределено по показательному закону с плотностью распределения f(t) = 0,1 e—0,1t при t ≥ 0. Найти вероятность того, что элемент проработает безотказно в течение 10 часов.
Решение.
Так как = 0,1, R(10) = e-0,1·10 = e-1 = 0,368.
Числовые характеристики
Для показательного распределения
|
M(X) |
xe |
xdx |
xe |
x |
e |
xdx |
||||||||||||||
|
0 |
0 |
0 |
||||||||||||||||||
|
1 |
1 |
|||||||||||||||||||
|
e |
x |
; |
||||||||||||||||||
|
0 |
||||||||||||||||||||
|
1 |
1 |
|||||||||||||||||||
|
D(X) |
x2 e xdx |
x2 e x |
2 xe |
xdx |
||||||||||||||||
|
2 |
2 |
|||||||||||||||||||
|
0 |
0 |
0 |
||||||||||||||||||
|
2 |
1 |
1 |
; |
1 |
. |
|||||||||||||||
|
2 |
2 |
2 |
||||||||||||||||||
ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ
Задача 1.
Стрелок делает 6 выстрелов по мишени. Вероятность попадания при каждом выстреле равна 0,7. Для случайной величины Х – числа попаданий – найти вероятность того, что Х < 3.
Указание
Случайная величина Х распределена по биномиальному закону. Найдите вероятности того, что Х равна 0, 1 и 2.
Решение
Случайная величина Х распределена по биномиальному закону, поэтому
|
p(X k) |
C6k 0, 7k 0, 36 k |
|||||
|
p(0) |
0, 36 |
0, 000729; |
||||
|
p(1) |
6 |
0, 7 |
0, 35 |
0, 010206; |
||
|
p(2) |
C62 |
0, 49 0, 34 |
0, 059535; |
|||
|
p(X 3) |
p(0) |
p(1) |
p(2) 0, 07047. |
Ответ: 0,07047.
65

Задача 2.
Стрелок делает 6 выстрелов по мишени. Вероятность попадания при каждом выстреле равна 0,7. Для случайной величины Х – числа попаданий – найти дисперсию.
Указание
Случайная величина Х распределена по биномиальному закону, поэтому D(X) = npq.
Решение
D(X) npq 6 0,7 0, 3 1, 26.
Ответ: 1,26.
Задача 3.
Вероятность повреждения изделия при перевозке составляет 2%. Случайная величина Х – число изделий из партии в 100 штук, поврежденных при перевозке. Найти вероятность того, что X < 2 (ответ округлить до третьего знака после запятой).
Указание
Можно считать, что Х распределена по закону Пуассона, то есть
|
p(X k) |
k e |
, |
np |
|
|
k ! |
||||
(здесь п – число изделий, р – вероятность повреждения одного изделия).
Решение
Воспользуемся формулой Пуассона:
|
p(X |
k) |
k e |
, |
np |
|
|
k ! |
|||||
|
2k e 2 |
|||||
|
2, |
p(X |
k) |
k ! . |
||
|
p(X 0) e 2 , p(X 1) 2e 2 , p(X 2) 2e 2 , |
|||||
|
p(X 2) p(X |
0) p(X 1) |
p(X |
2) 5e 2 0, 677. |
Ответ: 0,677.
Задача 4.
Цена деления шкалы измерительного прибора равна 0,2. Показания прибора округляют до ближайшего числа на шкале. Полагая, что ошибка измерения Х распределена по равномерному закону, найти дисперсию D(X).
Указание
Воспользуйтесь формулой для вычисления дисперсии равномерно распределенной случайной величины:
66

|
D(X) |
(b a)2 |
. |
|||
|
12 |
|||||
|
Решение |
|||||
|
a 0, b 0, 2, D(X) |
(b a)2 |
0,04 |
1 |
. |
|
|
12 |
12 |
300 |
|||
Ответ: 3001 .
Задача 5.
Измерительный прибор имеет систематическую ошибку 5 м, а случайные ошибки распределены по нормальному закону со средним квадратическим отклонением 75 м. Найти вероятность того, что ошибка измерения не превысит по модулю 5 м.
Указание
Из условия задачи следует, что параметры нормального закона а = 5, = 75. Для определения искомой вероятности воспользуйтесь формулой
|
p( |
X |
) |
a |
a |
. |
|||||
|
Решение |
||||||||||
|
Параметры нормального закона а = 5, |
= 75. Тогда |
|||||||||
|
p( 5 |
X |
5) |
5 |
5 |
5 |
5 |
||||
|
75 |
75 |
|||||||||
|
(0) |
( 0, 133) |
0 0, 053 |
0, 053. |
Ответ: 0,053.
Задача 6.
Какой наименьшей ширины должно быть поле допуска, чтобы с вероятностью не более 0,0027 получалась деталь с контролируемым размером вне поля допуска, если случайные отклонения размера от середины поля допуска распределены по нормальному закону с параметрами а = 0, = 5?
Указание
Используйте «правило трех сигм».
Решение
Если вероятность выхода размера детали из поля допуска равна 0,0027, то вероятность того, что размер попадает в поле допуска, равна 1 – 0,0027 = 0,9973. Именно такова вероятность попадания нормально распределенной случайной величины в интервал (а — 3 , а + 3 ). Следовательно, размеры
67

поля допуска: (0 – 15, 0 + 15) = (-15, 15), а ширина поля допуска – не менее
30.
Ответ: 30.
Задача 7.
Среднее время безотказной работы прибора равно 80 часам. Полагая, что время безотказной работы распределено по показательному закону, найти вероятность того, что в течение 100 часов прибор не выйдет из строя.
|
Указание |
||||
|
Найдите значение параметра |
из условия, что М(Х) = 1/ , и воспользуйтесь |
|||
|
формулой |
||||
|
R(t) |
e |
t . |
||
|
Решение |
||||
|
1 |
1 |
0, 0125; |
||
|
M(X) |
80 |
|||
|
R(100) |
e 0,0125 100 |
e 1,25 0, 286. |
||
|
Ответ: 0,286. |
1.2.4. Двумерные случайные величины. Коррелированность случайных величин
Наряду с одномерными случайными величинами, возможные значения которых определяются одним числом, теория вероятностей рассматривает и многомерные случайные величины. Каждое возможное значение такой величины представляет собой упорядоченный набор нескольких чисел. Геометрической иллюстрацией этого понятия служат точки п-мерного пространства, каждая координата которых является случайной величиной (дискретной или непрерывной), или п-мерные векторы. Поэтому многомерные случайные величины называют еще случайными векторами.
Дискретные двумерные случайные величины
Закон распределения дискретной двумерной случайной величины (Х, Y) имеет вид таблицы с двойным входом, задающей перечень возможных значений каждой компоненты и вероятности p(xi, yj), с которыми величина принимает значение (xi, yj):
68

|
Y |
Х |
||||||
|
x1 |
x2 |
… |
xi |
… |
xn |
||
|
y1 |
p(x1, y1) |
p(x2, y1) |
… |
p(xi, y1) |
… |
p(xn, y1) |
|
|
… |
… |
… |
… |
… |
… |
… |
|
|
yj |
p(x1, yj) |
p(x2, yj) |
… |
p(xi, yj) |
… |
p(xn, yj) |
|
|
… |
… |
… |
… |
… |
… |
… |
|
|
ym |
p(x1, ym) |
p(x2, ym) |
… |
p(xi, ym) |
… |
p(xn, ym) |
При этом сумма вероятностей, стоящих во всех клетках таблицы, равна 1. Зная закон распределения двумерной случайной величины, можно найти законы распределения ее составляющих. Действительно, событие Х = х1 представляется собой сумму несовместных событий (X = x1, Y = y1), (X = x1, Y = y2),…, (X = x1, Y = ym), поэтому
р(Х = х1) = p(x1, y1) + p(x1, y2) +…+ p(x1, ym)
(в правой части находится сумма вероятностей, стоящих в столбце, соответствующем Х = х1). Так же можно найти вероятности остальных возможных значений Х. Для определения вероятностей возможных значений Y нужно сложить вероятности, стоящие в строке таблицы, соответствующей
Y = yj.
Пример 1.
Дан закон распределения двумерной случайной величины:
|
Y |
X |
||
|
-2 |
3 |
6 |
|
|
-0,8 |
0,1 |
0,3 |
0,1 |
|
-0,5 |
0,15 |
0,25 |
0,1 |
Найти законы распределения составляющих.
Решение. Складывая стоящие в таблице вероятности «по столбцам», получим ряд распределения для Х:
Складывая те же вероятности «по строкам», найдем ряд распределения для Y:
Непрерывные двумерные случайные величины
Функцией распределения F(x, y) двумерной случайной величины (X, Y) называется вероятность того, что X < x, a Y < y:
F(x, y) p(X x,Y y). (1)
69

Это означает, что точка (X, Y) попадет в область, заштрихованную на рис. 1, если вершина прямого угла располагается в точке (х, у).
Замечание. Определение функции распределения справедливо как для непрерывной, так и для дискретной двумерной случайной величины.
Свойства функции распределения:
1)0 ≤ F(x, y) ≤ 1 (так как F(x, y) является вероятностью).
2)F(x, y) есть неубывающая функция по каждому аргументу:
F(x2, y) ≥ F(x1, y), если x2 > x1; F(x, y2) ≥ F(x, y1), если y2 > y1.
Доказательство.
F(x2, y) = p(X < x2, Y < y) = p(X < x1, Y < y) + p(x1 ≤ X < x2, Y < y) ≥ ≥ p(X < x1, Y < y) = F(x1, y).
Аналогично доказывается и второе утверждение.
3)Имеют место предельные соотношения:
|
a) |
F( |
, y) |
0; |
|
b) |
F(x, |
) |
0; |
|
c) |
F( |
, |
) 0; |
d)F( , ) 1.
Доказательство.
События а), b) и с) невозможны ( так как невозможно событие
X или Y ),
а событие d) достоверно, откуда следует справедливость приведенных
|
равенств. |
||
|
4) |
При у = |
функция распределения двумерной случайной величины |
|
становится функцией распределения составляющей Х: |
||
|
F(x, ) F1(x). |
||
|
При |
х = |
функция распределения двумерной случайной величины |
становится функцией распределения составляющей Y :
F( , y) F2(y).
70

Доказательство.
Так как событие Y < достоверно, то
F(x, ) p(X x) F1(x).
Аналогично доказывается второе утверждение.
Плотностью совместного распределения вероятностей (двумерной плотностью вероятности) непрерывной двумерной случайной величины называется смешанная частная производная 2-го порядка от функции распределения:
|
f (x, y) |
2F(x, y) |
. |
(2) |
|
|
x y |
||||
Замечание. Двумерная плотность вероятности представляет собой предел отношения вероятности попадания случайной точки в прямоугольник со сторонами х и у к площади этого прямоугольника при х 0, у 0.
Свойства двумерной плотности вероятности:
1) f(x, y) ≥ 0 (см. предыдущее замечание: вероятность попадания точки в прямоугольник неотрицательна, площадь этого прямоугольника положительна, следовательно, предел их отношения неотрицателен).
yx
2)F(x, y) f (x, y)dxdy
(cледует из определения двумерной плотности вероятности).
yx
3)F(x, y) f (x, y)dxdy
(поскольку это вероятность того, что точка попадет на плоскость Оху, то есть достоверного события).
Вероятность попадания случайной точки в произвольную область
Пусть в плоскости Оху задана произвольная область D. Найдем вероятность того, что точка, координаты которой представляют собой систему двух случайных величин (двумерную случайную величину) с плотностью распределения f(x, y), попадет в область D. Разобьем эту область прямыми, параллельными осям координат, на прямоугольники со сторонами х и у. Вероятность попадания в каждый такой прямоугольник равна f ( i , i ) x y,
где ( i , i ) — координаты точки, принадлежащей прямоугольнику. Тогда вероятность попадания точки в область D есть предел интегральной суммы
|
n |
||
|
f ( |
i , i ) x y, , |
|
|
i 1 |
||
|
то есть |
||
|
p((X,Y) D) |
f (x, y)dxdy. |
(3) |
|
D |
71

Отыскание плотностей вероятности составляющих двумерной случайной величины
Выше было сказано, как найти функцию распределения каждой составляющей, зная двумерную функцию распределения. Тогда по определению плотности распределения
|
x |
||||||||
|
d |
f (x, y) |
|||||||
|
f1 |
(x) |
dF1(x) |
dF(x, ) |
f (x, y)dy. (4) |
||||
|
dx |
dx |
dx |
||||||
Аналогично находится
Условные законы распределения составляющих дискретной двумерной случайной величины
Рассмотрим дискретную двумерную случайную величину и найдем закон распределения составляющей Х при условии, что Y примет определенное значение (например, Y = у1). Для этого воспользуемся формулой Байеса, считая гипотезами события Х = х1, Х = х2,…, Х = хп, а событием А – событие Y = у1. При такой постановке задачи нам требуется найти условные вероятности гипотез при условии, что А произошло. Следовательно,
|
р |
(x |
) |
p(xi , y1 ) |
. |
|
y1 i |
p(y1 ) |
|||
Таким же образом можно найти вероятности возможных значений Х при условии, что Y принимает любое другое свое возможное значение:
|
р |
(x ) |
p(xi , y j ) |
. |
(5) |
|
|
y j |
|||||
|
i |
p(y j ) |
||||
Аналогично находят условные законы распределения составляющей Y:
px (y j ) p(xi , y j ) . (5 ) i p(xi )
Пример 2.
Найдем закон распределения Х при условии Y = -0,8 и закон распределения Y при условии Х = 3 для случайной величины, рассмотренной в примере 1.
|
р(x1 /y1 ) |
0, 1 |
1 |
0, 2; р(x2 |
/y1 ) |
0, 3 |
3 |
0, 6; |
||||||
|
0, 5 |
5 |
0, 5 |
5 |
||||||||||
|
р(x3 /y1 ) |
0, 1 |
1 |
0, 2. |
||||||||||
|
0, 5 |
5 |
||||||||||||
|
р(у1 |
/х2 ) |
0, 3 |
6 |
; р(у2 |
/х2 ) |
0, 25 |
5 |
. |
|||||
|
0, 55 |
11 |
0, 55 |
11 |
||||||||||
72
Соседние файлы в папке ТВиМС
- #
- #
- #
- #
Закажите у меня новую работу, просто написав мне в чат!
Среднее время безотказной работы прибора равно 80 часов. Полагая, что время безотказной работы прибора имеет показательный закон распределения, найти: а) выражение его плотности вероятности и функции распределения, построить графики этих функций; б) вероятность того, что в течение 1000 часов прибор не выйдет из строя.
Решение а) Для показательного закона связь математического ожидания (среднего значения) и параметра распределения 𝜆 имеет вид: При 𝑀(𝑋)=80 получим параметр распределения 𝜆: Функция плотности распределения вероятности 𝑓(𝑥) и функция распределения 𝐹(𝑥) случайной величины 𝑋, имеющей показательное распределение, имеют вид: При 𝜆=180 получим: Построим графики функции распределения 𝐹(𝑥) и плотности распределения 𝑓(𝑥): б) Вероятность попадания случайной величины в заданный интервал (𝑎;𝑏)равна: Тогда вероятность того, что в течение 1000 часов прибор не выйдет из строя, равна:
Содержание
- Показательный (экспоненциальный закон распределения).
- Экспоненциально распределенная случайная величина
- Примеры решений
- Решебник по теории вероятности онлайн
- Показательный (экспоненциальный закон распределения)
- Примерные варианты тестов
Показательный (экспоненциальный закон распределения).
Случайная величина Х распределена по показательному закону распределения с параметром λ, если её плотность вероятности имеет вид:
Функция распределения имеет вид:
Математическое ожидание и дисперсия для случайной величины, распределенной по показательному закону, находятся по формулам:
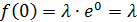
То есть при
Пример.
Установлено, что время ремонта телевизоров есть случайная величина X, распределенная по показательному закону.
Определить вероятность того, что на ремонт телевизора потребуется не менее 20дней, если среднее время ремонта телевизоров составляет 15 дней. Найти плотность вероятности, функцию распределения и среднее квадратическое отклонение случайной величины X.
Решение:
По условию математическое ожидание M(х)=1/λ = 15, откуда параметр λ = 1/15. Тогда плотность вероятности и функция распределения примут вид:
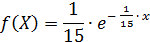
Искомую вероятность P(Х ≥20) можно было найти по формуле, интегрируя плотность вероятности, то есть
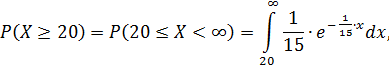
Найдем среднее квадратическое отклонение: σ(X) = М(Х) = 15 дней.
Экспоненциально распределенная случайная величина
На странице Непрерывная случайная величина мы разобрали примеры решений для произвольно заданных законов распределения (многочлены, логарифмы и т.п.). Здесь же мы разберем примеры только для одного типа СВ — распределенных по показательному (или экспоненциальному) закону.
Плотность распределения величины $X$ с экспоненциальным законом распределения задается формулой:
Функция распределения величины $X$:
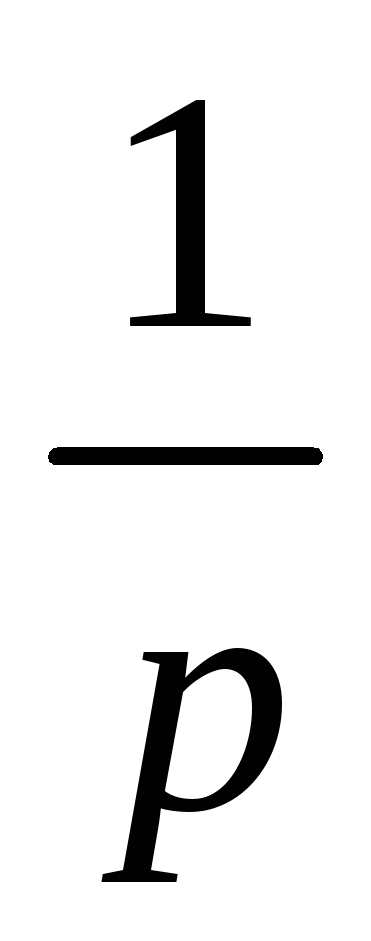
Здесь $lambda$ — единственный параметр данного распределения, полностью определяющий его свойства. В частности, числовые характеристики выражаются через этот параметр: $M(X)=1/lambda$, $D(X)=1/lambda^2$.
Экспоненциальное распределение моделирует время между двумя последовательными свершениями события, а параметр $lambda$ описываетс среднее число наступлений события в единицу времени. Обычно с помощью этого закона описывают: продолжительность обслуживания покупателя, время жизни оборудования до отказа, промежуток времени между поломками и т.п.
В этом разделе мы приведем разные примеры задач с полным решением, где используются показательно распределенные случайные величины.
Примеры решений
Задача 1. Среднее время безотказной работы прибора равно 80 часов. Полагая, что время безотказной работы прибора имеет показательный закон распределения, найти:
а) выражение его плотности вероятности и функции распределения;
б) вероятность того, что в течение 100 часов прибор не выйдет из строя.
Задача 2. Известно, что время работы прибора до первого отказа подчиняется показательному распределению со средним значением 1 год. Какова вероятность, что до первого отказа пройдет не менее 2 лет?
Задача 3. Установлено, что время ремонта телевизоров есть случайная величина $X$, распределенная по показательному закону с параметром $lambda=1/3$ (1/день). Определить вероятность того, что на ремонт телевизора потребуется не менее 5 дней.
Задача 4. Время в годах безотказной работы прибора подчинено показательному закону, т.е. плотность распределения этой случайной величины такова: $f(t)=2e^<-2t>$ при $tge 0$ и $f(t)=0$ при $tlt 0$.
1) Найти формулу функции распределения этой случайной величины.
2) Определить вероятность того, что прибор проработает не более года.
3) Определить вероятность того, что прибор безотказно проработает 3 года.
4) Определить среднее ожидаемое время безотказной работы прибора.
Задача 5. Предполагая, что случайное время обслуживания абонента службой «09» распределено по показательному закону и средняя продолжительность обслуживания составляет 1,5 минуты, найдите вероятность того, что абонент будет обслужен более, чем за 2 минуты.
Задача 6. Длительность телефонного разговора подчиняется показательному закону. Найти среднюю длительность разговора, если вероятность того, что разговор продлится более 5 минут, равна 0,4.
Задача 7. Случайная величина задана плотностью распределения $p(x)=ce^<-3x>$ при $x gt 0$, и ноль в остальных случаях. Найти постоянную $c$, математическое ожидание, дисперсию и среднее квадратическое отклонение.
Задача 8. Непрерывная случайная величина $xi$ распределена по показательному закону с параметром $lambda$, равному номеру варианта 9. Найти плотность распределения случайной величины $xi$, функцию распределения, построить графики этих функций. Найти математическое ожидание, дисперсию, среднее квадратическое отклонение случайной величины $xi$ и вероятность того, что $xi$ принимает значения, меньшие своего математического ожидания.
Задача 9. Случайная величина $xi$ распределена по показательному закону с параметром 2. Найти $M_<xi>$, $D_<xi>$ вероятность попадания $xi$ в интервал $(-1;2)$. Нарисовать графики плотности распределения и функции распределения $xi$.
Задача 10. Известно, что $Х$ распределено по экспоненциальному закону $Exp(lambda)$. Найдите вероятность события $|Х — МХ | lt 3sigma$ («правило $3sigma$» для показательного распределения).
Решебник по теории вероятности онлайн
Больше 11000 решенных и оформленных задач по теории вероятности:
Показательный (экспоненциальный закон распределения)
Случайная величина Х распределена по показательному закону распределения с параметром λ, если её плотность вероятности имеет вид:
Функция распределения имеет вид:
Математическое ожидание и дисперсия для случайной величины, распределенной по показательному закону, находятся по формулам:
То есть при
Пример.
Установлено, что время ремонта телевизоров есть случайная величина X, распределенная по показательному закону.
Определить вероятность того, что на ремонт телевизора потребуется не менее 20 дней, если среднее время ремонта телевизоров составляет 15 дней. Найти плотность вероятности, функцию распределения и среднее квадратическое отклонение случайной величины X.
Решение:
По условию математическое ожидание M(х)=1/λ = 15, откуда параметр λ = 1/15. Тогда плотность вероятности и функция распределения примут вид:

Искомую вероятность P(Х ≥20) можно было найти по формуле, интегрируя плотность вероятности, то есть

Найдем среднее квадратическое отклонение: σ(X) = М(Х) = 15 дней.
Равномерный закон распределения.
Непрерывная случайная величина Х имеет равномерный закон распределения (закон постоянной плотности) на отрезке [a; b], если на этом отрезке функция плотности вероятности случайной величины постоянна, то есть
Следовательно, математическое ожидание случайной величины, равномерно распределенной на отрезке (a, b), равняется середине этого отрезка.
Дисперсия имеет вид:
Найдем вероятность попадания значения случайной величины, имеющей равномерное распределение, на интервал 
Функция распределения примет вид:
Пример.
Поезда метрополитена идут регулярно с интервалом 2 мин. Пассажир выходит на платформу в случайный момент времени. Какова вероятность того, что ждать пассажиру придется не больше полминуты.
Найти математическое ожидание и среднее квадратическое отклонение случайной величины X – времени ожидания поезда.
Решение:
Случайная величина X – время ожидания поезда на временном (в минутах) отрезке [0;2] имеет равномерный закон распределения f (x)=1/2.
Поэтому вероятность того, что пассажиру придется ждать не более полминуты, равна 1/4 от равной единице площади прямоугольника, т.е.
Найдем математическое ожидание, дисперсию и среднее квадратическое отклонение:
Примерные варианты тестов
Ниже приведено несколько примеров компьютерных тестов с указанием правильных ответов.
Как называется число m0 (наступления
события в n независимых испытаниях, в каждом из которых вероятность появления события равна p), определяемое из
Потребитель может увидеть рекламу определенного товара по телевидению (событие А), на рекламном стенде (событие В) и прочесть в газете (событие С). Что означает событие А + В + С :
а) потребитель увидел все три вида рекламы;
б) потребитель не увидел ни одного вида рекламы;
в) потребитель увидел хотя бы один вид рекламы;
г) потребитель увидел ровно один вид рекламы;
д) потребитель увидел рекламу по телевидению.
На пяти одинаковых карточках написаны буквы И, Л, О, С, Ч. Если перемешать их, и разложить наудачу в ряд две карточки, то вероятность р получить слово ИЛ равна …. В ответе запишите число
Если A и B — независимые события, то вероятность наступления хотя бы одного из двух событий A и B вычисляется по формуле
г) 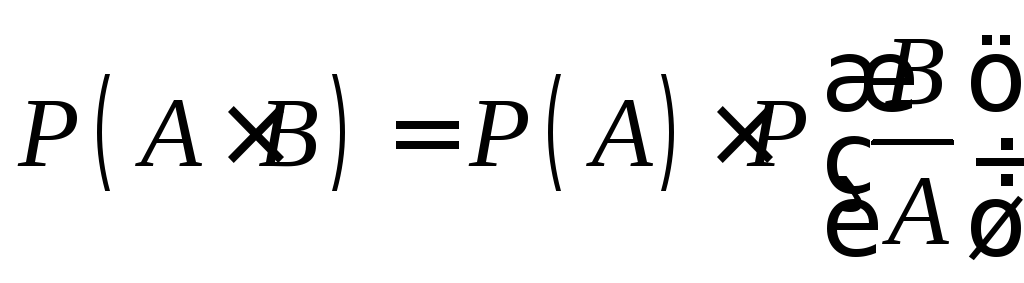
Из 10 коммерческих банков 4 находятся за чертой города. Налоговый инспектор выбирает наугад для проверки 3 банка. Какова вероятность того, что хотя бы 2 из них — в черте города?
а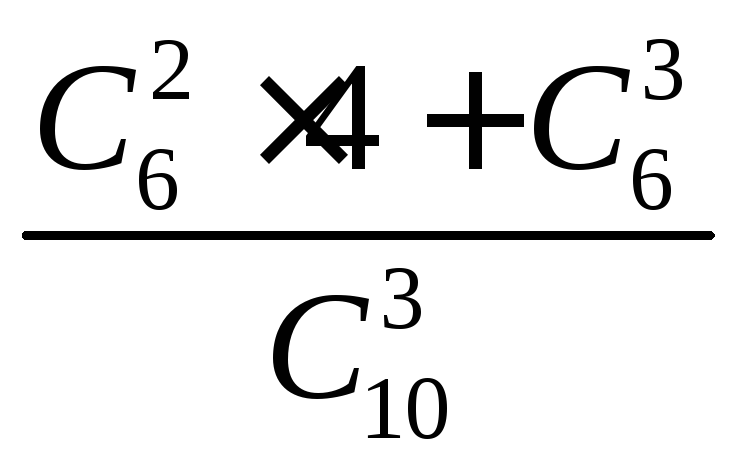
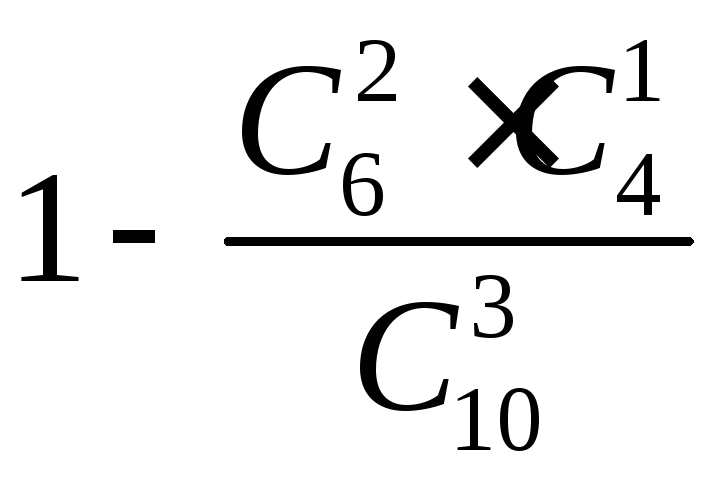
г) 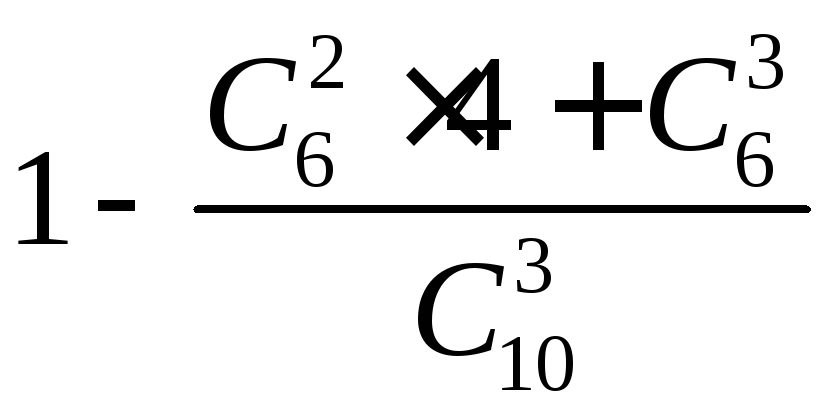
Сколькими способами можно составить список из пяти студентов? В ответ записать полученное число.
Подбрасываются две игральные кости. Найти вероятность Р того, что сумма выпавших очков равна четырем. В ответ записать число 24 Р.
Партия из 10 телевизоров содержит 3 неисправных телевизора. Из этой партии выбираются наугад 2 телевизора. Найти вероятность Р того, что оба они будут неисправными. В ответ записать число 45 Р.
Данное предприятие в среднем выпускает 20 % продукции высшего сорта и 70 % продукции первого сорта. Найти вероятность Р того, что случайно взятое изделие этого предприятия будет высшего или первого сорта. В ответ записать число 30 Р.
Случайная величина Х задана функцией распределения
Найти вероятность Р того, что в результате испытания случайная величина Х примет значение, принадлежащее интервалу (0,1; 0,6). В ответ записать число 20 Р.
Случайная величина Х распределена равномерно на интервале (2; 6) и р (х) – ее плотность вероятности. Найти р (3). В ответ записать число 40 р (3).
Задан статистический ряд распределения
8.44. Случайная величина Х распределена по показательному закону
Найти математическое ожидание, дисперсию, среднее квадратическое отклонение и функцию распределения этой случайной величины. Найти вероятность попадания значений случайной величины Х в интервал .
Ответ: ;
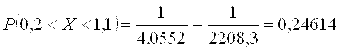
8.45. Среднее время безотказной работы прибора равно 85 ч. Полагая, что время безотказной работы прибора имеет показательный закон распределения, найти: а) выражение его плотности вероятности и функции распределения; б) вероятность того, что в течение 100 ч прибор не выйдет из строя.
Ответ: а) 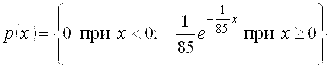
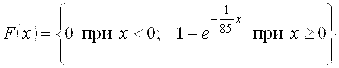
Б) .
8.46. Найти эксцесс показательного распределения.
Ответ: .
8.47. Производится испытание трех элементов, работающих независимо один от другого. Длительность времени безотказной работы элементов распределена по показательному закону: для первого элемента ; для второго —
для третьего элемента
Найти вероятности того, что в интервале времени
часов откажут: а) только один элемент; б) только два элемента; в) хотя бы один элемент; г) все три элемента; д) не менее двух элементов.
Ответ: а) 0,069; б) 0,4172; в) 0,9975; г) 0,511; д) 0,928.
8.48. Р %-м ресурсом элемента называется такое число T, что за время T элемент не выходит из строя с вероятностью Р. Считается, что время T непрерывной работы электрической лампочки распределено по показательному закону. Найти вероятность того, что лампочка будет гореть в течение 2 лет, если ее 90 %-й ресурс составляет 6 мес.
Ответ: .
8.49. Срок службы жесткого диска компьютера – случайная величина, подчиняющаяся экспоненциальному распределению со средней в 12 000 часов. Найти долю жестких дисков, срок службы которых превысит 20 000 часов.
Ответ: .
8.50. Срок службы батареек для слуховых аппаратов приблизительно подчиняется экспоненциальному закону с . Какова доля батареек со сроком службы больше чем 9 дней?
Ответ: .
8.51. Служащий рекламного агентства утверждает, что время, в течение которого телезрители помнят содержание коммерческого рекламного ролика, подчиняется экспоненциальному закону с Дня. Найти долю зрителей, способных вспомнить рекламу спустя 7 дней.
Ответ: .
8.52. Компьютерный программист использует экспоненциальное распределение для оценки надежности своих программ. После того, как он нашел 10 ошибок, он убедился, что время (в днях) до нахождения следующей ошибки подчиняется экспоненциальному распределению с . Найти среднее время, потраченное для нахождения первой ошибки; определить вероятность того, что для нахождения первой ошибки понадобится более 5 дней; найти вероятность того, что на нахождение одиннадцатой ошибки потребуется от 3 до 10 дней.
Ответ: М (Х) = 4; ;
.
8.53. Случайная величина Х распределена по показательному закону: Р(Х) = = 0 при Х < 0, При
. Найти математическое ожидание, дисперсию, среднее квадратическое отклонение и функцию распределения этой случайной величины. Найти вероятность попадания случайной величины Х в интервал (0,2; 1,1).
Ответ: М (Х) = 1/6; ;
;
;
.
| < Предыдущая | Следующая > |
|---|