Среднее изменение курса акции компании в течение одних биржевых торгов составляет 0,3%. Оценить вероятность того, что на ближайших торгах курс изменится более чем на 3%.
Скачать решение бесплатно
Купить решение
* Оплата через сервис ЮMoney.
Другие задачи по теории вероятности
Электростанция обслуживает сеть на 1600 электроламп, вероятность включения каждой из которых вечером равна 0,9. Оценить с помощью неравенства Чебышева вероятность того, что число ламп, включенных в сеть вечером, отличается от своего математического ожидания не более чем на 100 (по абсолютной величине). Найти вероятность того же события, используя следствие из интегральной теоремы Муавра—Лапласа.
Вероятность того, что акции, переданные на депозит, будут востребованы, равна 0,08. Оценить с помощью неравенства Чебышева вероятность того, что среди 1000 клиентов от 70 до 90 востребуют свои акции.
Среднее значение длины детали 50см, а дисперсия — 0,1. Используя неравенство Чебышева, оценить вероятность того, что случайно взятая деталь окажется по длине не менее 49,5 и не более 50,5см. Уточнить вероятность того же события, если известно, что длина случайно взятой детали имеет нормальный закон распределения.
Оценить вероятность того, что отклонение любой случайной величины от ее математического ожидания будет не более двух средних квадратических отклонений (по абсолютной величине).
В течение времени t эксплуатируются 500 приборов. Каждый прибор имеет надежность 0,98 и выходит из строя независимо от других. Оценить с помощью неравенства Чебышева вероятность того, что доля надежных приборов отличается от 0,98 не более чем на 0,1 (по абсолютной величине).
Вероятность сдачи в срок всех экзаменов студентом факультета равна 0,7. С помощью неравенства Чебышева оценить вероятность того, что доля сдавших в срок все экзамены из 2000 студентов заключена в границах от 0,66 до 0,74.
Бензоколонка N заправляет легковые и грузовые автомобили. Вероятность того, что проезжающий легковой автомобиль подъедет на заправку, равна 0,3. С помощью неравенства Чебышева найти границы, в которых с вероятностью, не меньшей 0,79, находится доля заправившихся в течение 2ч легковых автомобилей, если за это время всего заправилось 100 автомобилей.
Глава 7. Закон больших чисел. Центральная предельная теорема.
§ 1. Неравенство Чебышева
Пусть случайная величина имеет математическое ожидание М и дисперсию D. Тогда для любого 0 справедливо неравенство Чебышева:
.
Это неравенство часто используют в виде:
Доказательство этих неравенств основывается на неравенстве Маркова: для любой случайной величины вероятность события не превосходит произведения частного 1 на математическое ожидание модуля случайной величины, то есть Р() . Справедливо и неравенство Колмогорова: если 1,2,…,n независимые случайные величины имеют конечные дисперсии Di, то для любого 0 справедливо неравенство
.
Задача 1. В 400 испытаниях Бернулли вероятность успеха в каждом испытании равна 0,8. С помощью неравенства Чебышева оценить вероятность того, что разница между числом успехов в этих испытаниях и средним числом успехов не превысит 20.
Решение. Число успехов в этих испытаниях распределено по закону Бернулли, поэтому среднее число успехов равно М=np=400×0,8=320, а D=npq=400×0,8×0,2=64. Тогда в силу неравенства Чебышева имеем:
Вычислим эту же вероятность с помощью приближенной (интегральной) формулы Муавра-Лапласа (см. главу 4):

Последнее вычисление показывает, что неравенство Чебышева дает довольно грубые оценки вероятностей.
§ 2. Закон больших чисел
Пусть задана бесконечная последовательность независимых одинаково распределенных случайных величин , для которых существуют математическое ожидание
и дисперсия
. Тогда для любого >0

Суть закона больших чисел состоит в том, что при возрастании числа слагаемых (т.е. одинаково распределенных случайных величин) среднее арифметическое этих слагаемых мало отличается от математического ожидания . Любое отклонение среднего арифметического случайных величин от числа
при достаточно большом числе слагаемых – маловероятно.
Например. Пусть – последовательность случайных величин, каждая из которых равна числу успехов в одном испытании Бернулли (т.е. 1 в случае успеха и 0 – в случае неудачи). Закон распределения каждой такой случайной величины имеет вид:
Здесь и
. Тогда среднее арифметическое
равно частоте успехов в n испытаниях, и закон больших чисел утверждает, что эта частота успехов стремится к вероятности успеха p, если число слагаемых (т.е. число испытаний) стремится к бесконечности.
§ 3. Центральная предельная теорема (ЦПТ)
Если — независимые одинаково распределенные случайные величины, такие, что
и
, i = 1, 2, …, то для любого вещественного х
,
Смысл центральной предельной теоремы заключается в том, что сумма случайных величин при надлежащем «центрировании» и «нормировании» и при увеличении числа слагаемых (
) ведет себя почти как стандартно распределенная случайная величина. (Напомним, что называется стандартно распределенной, если
.)
Например. Пусть – последовательность случайных величин, удовлетворяющая условиям предыдущего примера. В этом случае сумма
есть число успехов в
испытаниях Бернулли. Из ЦПТ следует, что

где 
Тогда вероятность того, что число успехов будет заключено между и
равна
Этот результат называется интегральной теоремой Муавра–Лапласа и используется при npq<9. Если р1 и npq 9 , для биномиального распределения используют пуассоновское приближение , основанное на формуле Пуассона при р0, n, np.
Задача 2. В продукции цеха детали отличного качества составляют 50. Детали укладываются в коробки по 200 шт. в каждой. Какова вероятность того, что число деталей отличного качества в коробке отличаться от 100 не более, чем на 5?
Решение. Пусть n — случайное число деталей отличного качества в коробке, тогда при n=200, получим:
Задача 3. Используя условия предыдущей задачи, указать в каких границах с вероятностью 0,997 находится число деталей отличного качества в коробке.
Решение. По таблицам при условии находим t и следовательно, Sn лежит в пределах
, т.е. число деталей отличного качества в коробке с вероятностью 0,997 находится в пределах 100 21.
Задача 4. Используя условия примера 1, определить, сколько деталей надо положить в коробку, чтобы с вероятностью, не меньшей 0,99, можно было утверждать, что число деталей отличного качества в коробке не меньше 100.
Решение. Необходимо найти n из условия Р (Sn 100) 0,99. Используя нормальное приближение, получаем
,
и из таблиц получаем неравенство откуда, полагая
, при
имеем х2-2,3х-2000, откуда получаем n240.
Задача 5. Известно, что процент брака для некоторой детали равен 0,5%. Контролер проверяет 1000 деталей. Какова вероятность обнаружить ровно 3 бракованных детали? Какова вероятность обнаружить не меньше 3-х бракованных деталей?
Решение. Имеем 1000 испытаний Бернулли с вероятностью р=0,005 «успеха», здесь npq5. Применяя пуассоновское приближение с = np = 5, получаем

и по таблицам находим: P(m1000 =3) 0,14, Р(m10003) 0,875.
Задача 8. Телефонная станция обслуживает 2000 абонентов, в час пик каждый абонент использует связь в среднем в течение 2 минут, т.е. мы считаем, что абонент с вероятностью использует связь. Какое наименьшее число линий необходимо, чтобы только один из 100 вызовов получал отказ?
Решение. Считая вызовы абонентов независимым, имеем 2000 испытаний Бернулли с вероятностью «успеха» р= . Надо найти число линий N из условия
Р(m2000N) 0,01. Применяя приближение Пуассона с , по таблицам находим N87. При использовании нормального приближения получается, что достаточно 86 линий.
Задачи для самостоятельного решения
Теоретические задачи.
-
Пусть задана последовательность независимых случайных величин
, имеющих следующий закон распределения:
Применим ли к этой последовательности закон больших чисел?
-
Пусть задана последовательность независимых случайных величин
, имеющих следующий закон распределения:
|
n |
|
|
|
P |
1/2 |
1/2 |
Применим ли к этой последовательности закон больших чисел?
-
Доказать закон больших чисел в «обобщенной форме»: пусть
– последовательность случайных величин, у которых существуют математические ожидания
и дисперсии
, причем все дисперсии ограничены одной константой C>0. Тогда для любого >0
.
-
Пусть случайная величина имеет нормальное распределение с параметрами М=а, D=2. Найти вероятности
и
, пользуясь таблицами функции Лапласа, оцените те же вероятности с помощью неравенства Чебышева.
-
Пусть случайная величина имеет распределение Лапласа, т.е. ее плотность равна
. Найти М и D. Найти вероятности
и
и сравнить их с оценками, получаемыми с помощью неравенства Чебышева.
-
Будет ли выполнен закон больших чисел для последовательности независимых случайных величин 1, 2, … n , … если
1).
2). Р( .
-
Пусть некоторая величина а измеряется прибором без систематической ошибки, но со средним квадратическим отклонением . Это означает, что результат измерения можно считать случайной величиной с М=а, D=2. Какова вероятность при 100 измерениях получить для среднего арифметического (из этих 100 измерений) отклонение от величины а более, чем на
? Дать оценки этой вероятности с помощью неравенства Чебышева и с помощью ЦПТ.
-
Пусть 1, 2, … i, … — независимые, одинаково распределенные случайные величины с функцией распределения F(x). Пусть задана случайная величина
.
Выполняется ли для последовательности 1,2, … i, … закон больших чисел?
-
Пусть для последовательностей
и
случайных величин существуют числа а и b такие, что
, для любого 0. Доказать, что
а)
б) если f(x, у) непрерывна в точке (а, b), то для любого 0
.
-
Последовательности 1, , … и 1, 2, … случайных величин таковы, что
и существует функция распределения F(x), для каждой точки непрерывности которой выполняется соотношения
. Доказать, что для каждой точки непрерывности F(x) справедливо равенство
.
Вычислительные задачи.
-
Средний размер вклада в отделении банка равен 6000руб. Оценить вероятность, что случайно взятый вклад не превысит 10000 руб.
-
Среднее количество вызовов, поступающих на АТС завода в течение часа, равно 300. Оценить вероятность того, что в течении следующего часа число вызовов на коммутатор: а) превысит 400; б) будет не более 300.
-
По статистическим данным в среднем 87% новорожденных доживают до 50 лет. С помощью неравенства Чебышева оценить вероятность того, что из 1000 новорожденных доля доживших до 50 лет будет отличаться от вероятности этого события не более, чем на 0,04 (по абсолютной величине).
-
Среднее изменение курса акции компании в течении биржевых торгов составляет 0,3%. Оценить вероятность того, что на ближайших торгах курс изменится более, чем на 3%.
-
Отделение банка обслуживает в среднем 100 клиентов в день. Оценить вероятность того, что сегодня в отделении банка будет обслужено: а) не более 200 клиентов; б) более 150 клиентов.
-
Вероятность сдачи в срок всех экзаменов студентом факультета равна 0,7. С помощью неравенства Чебышева оценить вероятность того, что доля сдавших в срок все экзамены из 2000 студентов заключена в границах от 0,66 до 0,74.
-
В среднем 10% работоспособного населения некоторого региона – безработные. Оценить с помощью неравенства Чебышева вероятность того, что уровень безработицы среди обследованных 10000 работоспособных жителей города будет в пределах от 9% до 11% (включительно).
-
Опыт страховой кампании показывает, что страховой случай приходится примерно на каждый пятый договор. Оценить с помощью неравенства Чебышева необходимое количество договоров, которые следует заключить, чтобы с вероятностью 0,9 можно было утверждать, что доля страховых случаев отклонится от 0,1 не более чем на 0,01 (по абсолютной величине). Уточните ответ с помощью следствия из интегральной теоремы Муавра-Лапласа.
-
Дисперсия каждой из 3500 независимых случайных величин равна 5. Оценить вероятность того, что отклонение средней арифметической этих случайных величин от средней математической их математических ожиданий не превысит 0,25.
-
Ежедневно новая сделка заключается с вероятностью 0,2 (но не более одной в день). За сколько дней с вероятностью 0,9 можно ожидать заключения не менее 50 сделок?
-
. В продукции цеха детали отличного качества составляют 80%. В каких пределах будет находиться с вероятностью 0,99 число деталей отличного качества, если взять 10000 деталей. Сделать оценку с помощью неравенства Чебышева и с помощью теоремы Муавра-Лапласа.
-
Театр, вмещающий 1000 человек, имеет два разных входа. Около каждого из входов имеется свой гардероб. Сколько мест должно быть в каждом из гардеробов для того, чтобы среднем в 99 случаях из 100 все эти зрители могли раздеться в гардеробе того входа, через который они вошли? Предполагается, что зрители приходят парами и каждая пара независимо от других выбирает с вероятностью 0,5 любой из входов. На сколько можно будет сократить число мест в гардеробе, если зрители будут приходить поодиночке и также независимо друг от друга с равной вероятностью выбирать любой из входов?
-
Аппаратура состоит из 100 одинаково надежных и независимо работающих элементов, каждый из которых может отказать в течение суток с вероятностью 0,01. На обнаружение отказавшего элемента и его замену требуется 20 минут, в течение которых аппаратура простаивает. а) Найти вероятность того, что время простоя в сутки будет не более 40 минут. б) Найти среднее время простоя аппаратуры в сутки.
-
В поселке 2500 жителей. Каждый из них примерно 6 раз в месяц ездит на поезде в город, выбирая дни поездок по случайным мотивам независимо от остальных. Какой наименьшей вместимостью должен обладать поезд, чтобы он переполнялся в среднем не чаще одного раза в 100 дней (поезд ходит раз в сутки)?
-
На заводе 1000 станков, каждый из которых в среднем в течение 24 дней в месяц потребляет электроэнергию независимо от других станков с некоторой постоянной интенсивностью единиц в день. Какое количество электроэнергии необходимо заводу ежедневно, чтобы не чаще 2 раза в 100 дней он испытывал недостаток электроэнергии?
-
Предприятие выпускает 30% изделий — стоимостью 1 руб., 30% изделий — стоимостью 2 руб. и 40% изделий — стоимостью 3 руб. Какова вероятность получить за 1000 случайно отобранных изделий не менее 2150 руб.?
-
Известно, что 1/3 всех деталей, сходящих с конвейера, подвергается выборочному контролю на основании некоторого случайного признака. Пусть через контроль прошло 100 деталей. В каких пределах с вероятностью 0,99 лежит общее число деталей, сошедших с конвейера?
-
Известно, что вес некоторой детали является случайной величиной , имеющей равномерное распределение на отрезке от 1 до 2г. В каких пределах с вероятностью 0,99 будет находиться суммарный вес 10000 деталей?
-
Для проверки эффективности новый метод стимулирования роста производительности труда был введен на 100 предприятиях. При этом на 32 предприятиях введение нового метода вызвало снижение производительности труда, а на 68 — повышение производительности труда. Какова вероятность того, что чисто случайные колебания вызовут не меньшее отклонение от числа 50 — половины общего числа предприятий?
7
|
X: |
xi |
1 |
2 |
|
pi |
0,8 |
0,2 |
и
|
Y: |
yj |
-1 |
0 |
1 |
2 |
|
pj |
0,2 |
0,3 |
0,3 |
0,2 |
Найдем
математические ожидания и средние
квадратические отклонения этих случайных
величин:
,
,
Для
нахождения математического
ожидания M(
XY) произведения
случайных величин X и Y можно
было составить закон распределения
произведения двух дискретных случайных
величин (с вероятностями его значений
из табл. 5.2), а затем по нему найти M(
XY)
Закон
распределения (XY) имеет
вид:
|
(х |
-2 |
-1 |
0 |
1 |
2 |
4 |
|
pk |
0,1 |
0,1 |
0,3 |
0,3 |
0,15 |
0,05 |
Но
делать это вовсе не обязательно. M(
XY) Можно
найти непосредственно по табл. 5.2
распределения двумерной случайной
величины (
X,
Y) по
формуле:
,
где
двойная сумма означает суммирование
по всем nm клеткам
таблицы (n –
число строк, m –
число столбцов):
Вычислим
ковариациюKxy по
формуле:
Kxy = – axay =
0,5-1,2*0,5 = -0,1.
Вычислим
коэффициент корреляции ρ по формуле:
т.е.
между случайными величинами X и Y существует
отрицательная линейная зависимость;
следовательно, при увеличении (уменьшении)
одной из случайных величин другая имеет
некоторую тенденцию уменьшаться
(увеличиваться).
Пример
5.5
По
данным примера 5.3 определить:
а)
ковариацию и коэффициент корреляции
случайных величин X и Y;
б)
коррелированы или некоррелированы эти
случайные величины.
Решение
а)
Вначале найдем математические ожидания ах=
М{Х) и ay=
M(
Y) по
формулам:
Аналогично ау =
0 (то, что ах = ау = 0,
очевидно из соображения симметрии
распределения в круге, из которой
следует, что центр его массы лежит в
начале координат).
По
формуле (5.34) ковариация:
Соответственно
коэффициент корреляции .
б)
Так как р = 0, то случайные
величины X и
Y некоррелированы.
Убеждаемся в том, что из некоррелированности
величин еще не вытекает их
независимость.
Пример
5.6
Найти
плотность вероятности случайной
величины Y =
1-X3,
где случайная величина X распределена
по закону Коши с плотностью
вероятности
.
Решение
По
условию y = f(x)
= 1-x3,
откуда .
Производная (по абсолютной
величине):
.
Плотность
вероятности:
Пример
5.7
Найти
математическое ожидание и дисперсию
случайной величины Y =
2-3sinX,
если плотность вероятности случайной
величины X естьφ(х)
= cosX на
отрезке [-π/2, π/2].
Решение
По
формуле (5.57)
Дисперсия D(Y)
= M(Y2)
– :
.
Пример
5.8
Найти
закон распределения суммы двух случайных
величин, распределенных равномерно на
отрезке [0; 1].
Решение
Пусть Z =
X+
Y, где φ1(x)=
1 при 0 ≤ х ≤ 1
и
φ2(у) =
1 при 0 ≤ у ≤ 1.
По
формуле (5.49) плотность
вероятности:
Если z <
0, то для 0 ≤ x ≤
1 z—x <
0; если z >
2, то для 0 ≤ x ≤
1 z—x >
1, следовательно, в этих случаях φ2(z—x)
= 0 и φ(z)
= 0.
Пусть
0 ≤ z ≤
2. Подынтегральная функция φ2(z—x)
будет отлична от нуля только для
значений х,
при которых 0 ≤ z —
x ≤
1 или, что то же самое, при z -1
≤ x ≤ z.
Если
0 ≤ z ≤
1, то .
Если
1 ≤ z ≤
2, то .
Объединяя
все случаи,
получим:
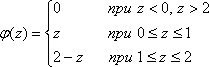
Закон
распределения (5.60) называется законом
распределения Симпсона или законом
равнобедренного треугольника (рис.
5.16).
Вычисление
φ(z) можно было провести и иначе: вначале
найти функцию распределения F(
z), а
затем – ее производную, т.е. φ(z) = F’(z).
Преимущество такого подхода состоит в
возможности использования геометрической
интерпретации функции F(z)
как площади SD области D –
части квадрата (со стороной, равной 1),
лежащей левее и ниже прямой у
= z —
х(рис.
5.17).
|
|
Действительно
(см. рис. 5.17), при 0 ≤ z ≤ 1 SD = z2/2 (площадь
заштрихованного треугольника со
стороной z),
а при 1 ≤ z ≤
2 SD =
1 — (2 -z)2/2
(площадь квадрата без площади
незаштрихованного треугольника, сторона
которого, как нетрудно показать, равна
(2 – z).Следовательно,
и
выражение (5.60) для φ(
z) получается
дифференцированием F(z).
Задания
5.1. Закон
распределения двумерной дискретной
случайной величины (
X,
Y) задан
в табл. 5.3.
Таблица
5.3
|
xi |
0 |
1 |
2 |
3 |
|
-1 |
0,02 |
0,03 |
0,09 |
0,01 |
|
0 |
0,04 |
0,20 |
0,16 |
0,10 |
|
1 |
0,05 |
0,10 |
0,15 |
0,05 |
Найти:
а)
законы распределения одномерных
случайных величин Х
и
Y;
б)
условные законы распределения случайной
величины X при
условии Y = 2
и случайной величины Y при
условии Х
= 1;
в)
вероятность P(Y > X).
5.2. Рассматривается
двумерная случайная
величина (
X,
Y), где X – поставка
сырья, Y – поступление
требования на него. Известно, что
поступление сырья и поступление
требования на него могут произойти в
любой день месяца (30 дней) с равной
вероятностью. Определить:
а)
выражение совместной плотности и функции
распределения двумерной случайной
величины (Х,У),
б)
плотности вероятности и функции
распределения одномерных
составляющих X и Y;
в)
зависимы или независимы X и Y;
г)
вероятности того, что поставка сырья
произойдет до и после поступления
требования.
5.3. Двумерная
случайная величина (
X,
Y) распределена
равномерно внутри квадрата R с
центром в начале координат. Стороны
квадрата равны корень2 и
составляют углы 45° с осями координат.
Определить:
а)
выражение совместной плотности двумерной
случайной величины (
X,
Y);
б)
плотности вероятности одномерных
составляющих X и Y;
в)
их условные плотности;
г)
зависимыили независимы Х
и
Y.
5.4. Даны
плотности вероятности независимых
составляющих двумерной случайной
величины (
X,
Y):
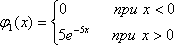
Найти
выражение совместной плотности и функции
распределения двумерной случайной
величины.
В
примерах 5.14–5.16 определить:
а)
ковариацию и коэффициент корреляции
случайных величин X и Y,
б)
коррелированы или некоррелированы эти
случайные величины.
5.5. Использовать
данные примера 5.10.
5.6. Использовать
данные примера 5.11.
5.7. Использовать
данные примера 5.12.
5.8. Случайная
величина X распределена
на всей числовой оси с плотностью
вероятности φ(х)
= 0,5е-│Х│.
Найти плотность вероятности случайной
величины Y =
X2 и
ее математическое ожидание.
5.9. Найти
закон распределения суммы двух независимых
случайных величин, каждая из которых
распределена по стандартному нормальному
закону, т.е. N(0,1).
5.10. Двумерная
случайная величина определяется
следующим образом. Если при подбрасывании
игральной кости выпадает четное число
очков, то Х
= 1,
в противном случае X =
0;
Y = 1,
когда число очков кратно трем, в противном
случае Y=0.
Найти:
а)
законы распределения двумерной случайной
величины (
X,
Y) и
ее одномерных составляющих;
б)
условные законы распределения
Х и
Y.
5.11. Двумерная
случайная величина (
X,
Y) распределена
с постоянной совместной плотностью
внутри квадрата ОАВС, где O(0;0), A(0;1), B(1;1),
С(1;0). Найти выражение совместной плотности
и функции распределения двумерной
случайной величины (
X,
Y).
5.12. Поверхность
распределения двумерной случайной
величины (
X,
Y) представляет
прямой круговой конус, основанием
которого служит круг с центром в начале
координат и с радиусом 1. Вне этого круга
совместная плотность двумерной случайной
величины (
X,
Y) равна
нулю. Найти выражения совместной
плотности φ(х, у), плотностей
вероятностей одномерных
составляющих φ1(x), φ2 (y),
условных плотностей φ
x(y),
φ
y(x).
Выяснить, являются ли случайные
величины X и Y. зависимыми;
коррелированными.
5.13. Двумерная
случайная величина (
X,
Y) распределена
по закону
Найти:
а)
коэффициент А;
б)
вероятность попадания случайной
величины (
X,
Y) в
пределы квадрата, центр которого
совпадает с началом координат, а стороны
параллельны осям координат и имеют
длину 2.
Установить,
являются ли величины X и Y зависимыми;
найти φ1(х),
φ2(
y).
5.14. Совместная
плотность двумерной случайной
величины (
X,
У) имеет
вид
Найти:
а)
постоянную С;
б)
плотности вероятности одномерных
составляющих;
в)
их условные плотности;
г)
числовые характеристики ах,
ау,
D(Х),
D(
Y),
ρ.
5.15. Найти
совместную плотность двумерной случайной
величины (
X,
Y) и
вероятность ее попадания в
область D – прямоугольник,
ограниченный прямыми х
= 1, х
= 2,у
= 3, у
= 5, если
известна ее функция
распределения (
X,
Y):
5.16. Задана
совместная плотность двумерной случайной
величины (X,
Y):
.
Найти
функцию распределения F(x,y).
5.17. Имеются
независимые случайные величины X и Y. Случайная
величина X распределена
по нормальному закону с параметрами
ах =
0, .
Случайная величина Y распределена
равномерно на интервале (0;1). Найти
выражения совместной плотности и функции
распределения двумерной случайной
величины (X,
Y).
5.18. Совместная
плотность двумерной случайной
величины (X,
Y) задана
формулой:
Найти ax, ay, ,
, ρ.
5.19. Независимые
случайные величины X,
Y распределены
по нормальным законам с параметрами ax =
2, ay =
-3, =
1, =
4. Найти вероятности событий:
а)
(X < ax)(Y < ay);
б) Y < X-5;
в)(│X│<
1)(│Y│<
2).
5.20. Задана
плотность вероятности φ(х)
случайной величины Х,
принимающей только положительные
значения. Найти плотность вероятности
случайной величины Y,
если:
а) Y = e—
x;
б) Y = lnX;
в) Y = X3;
г) Y =
1/X2;
д) Y = .
5.21. Случайная
величина Х равномерно
распределена в интервале (-π/2; π/2). Найти
плотность вероятности случайной
величины Y =sinX.
5.22. Случайная
величина распределена по закону Релея
с плотностью вероятности
Найти
закон распределения случайной
величины Y = .
5.23. Случайная
величина Х распределена
по закону Коши с плотностью
вероятности
.
Найти
плотность вероятности обратной
величины Y =
1/X.
5.24. Дискретная
случайная величина Х имеет
ряд распределения
|
xi |
-1 |
0 |
1 |
2 |
|
pi |
0,2 |
0,1 |
0,3 |
0,4 |
Найти
математическое ожидание и дисперсию
случайной величины
Y=
2х
5.25. Имеются
две случайные величины X и Y, связанные
соотношением Y =
2 – ЗХ. Числовые
характеристики случайной величины Xзаданы ах=
—1; D(
X)
= 4.
Найти:
а)
математическое ожидание и дисперсию
случайной величины Y;
б)
ковариацию и коэффициент корреляции
случайной величин Х
и
Y.
5.26. Случайная
величина X задана
плотностью вероятности φ(x) = cosx в
интервале (0, π/2); вне этого интервала
φ(x) = 0. Найти математическое ожидание
случайной величины Y=
X2.
5.27. Случайная
величина X распределена
с постоянной плотностью вероятности в
интервале (1;2) и нулевой плотностью вне
этого интервала. Найти математическое
ожидание и дисперсию случайной
величины Y = 1/x
5.28. Непрерывная
случайная величина X распределена
в интервале (0;1) по закону с плотностью
вероятности
Найти
математическое ожидание и дисперсию
случайной величины Y=
X2.
5.29. Непрерывная
случайная величина распределена по
показательному закону с параметром Х
= 2. Найти
математическое ожидание и дисперсию
случайной величины Y=
e—
X.
5.30. Случайная
величина X распределена
по нормальному закону с параметрами а =
0, σ2 =
5. Найти математическое ожидание случайной
величины Y=1
— ЗХ2 +
4Х3.
5.31. Имеются
две независимые случайные
величины X и
Y. Величина X распределена
по нормальному закону с параметрами ах= 1, =
4. Величина Y распределена
равномерно в интервале (0;2). Найти:
а) М(Х
— У),
D(Х
—
Y);
б) M(
X2),
M(
Y2).
6
ГЛАВА
Закон
больших чисел и предельные теоремы
В
главе рассматриваются:
— неравенство
Маркова;
— неравенство
Чебышева;
— теоремы
Чебышева и Бернулли;
— центральная
предельная теорема.
Типовые
задачи
Пример
6.1
Среднее
количество вызовов, поступающих на
коммутатор завода в течении часа, равно
300. Оценить вероятность того, что в
течение следующего часа число вызовов
на коммутатор:
а)
превысит 400;
б)
будет не более 500.
Решение
а)
По условию М(Х)
= 300. По формуле (6.1.) Р(Х >
400) ≤ ,
т.е. вероятность того, что число вызовов
превысит 400, будет не более 0,75.
б)
По формуле (6.3) Р(Х ≤
500) ≥ =
0,4, т.е. вероятность того, что число
вызовов не более 500, будет не менее
0,4.
Пример
6.2
Сумма
всех вкладов в отделение банка составляет
2 млн.руб., а вероятность того, что случайно
взятый вклад не превысит 10 тыс.руб.,
равна 0,6. Что можно сказать о числе
вкладчиков?
Решение
Пусть Х –
размер случайно взятого вклада, а n –
число всех вкладов. Тогда из условия
задачи следует, что средний размер
вклада М(Х)
= тыс.руб.
Согласно неравенству Маркова
(6.3):
или
Учитывая,
что Р(Х ≤
10) = 0,6, получим ,
откуда n ≤
500, т.е. число вкладчиков не более
500.
Пример
6.3
Средний
расход воды на животноводческой ферме
составляет 1000 л в
день, а среднее квадратичное отклонение
этой случайной величины не превышает
200 л. Оценить
вероятность того, что расход воды на
ферме в любой выбранный день не превзойдет
2000 л,используя:
а)
неравенство Маркова;
б)
неравенство Чебышева.
Решение
а)
Пусть X –
расход воды на животноводческой ферме
(л). По условию М(Х)
= 1000.
Используя неравенство Маркова (6.3),
получим Р(Х < 2000) > 1*1000/2000 = 0,5, т.е. не
менее, чем 0,5.
б)
Дисперсия D(
X)
= а2 < 2002.
Так как границы интервала 0 < X < 2000
симметричны относительно математического
ожидания М(Х)
= 1000,
то для оценки вероятности искомого
события можно применить неравенство
Чебышева (6.6):
т.е.
не менее, чем 0,96. В данной задаче оценку
вероятности события, найденную с помощью
неравенства Маркова (р
≥ 0,5),
удалось уточнить с помощью неравенства
Чебышева (Р > 0,96).
Пример
6.4
Вероятность
выхода с автомата стандартной детали
равна 0,96. Оценить с помощью неравенства
Чебышева вероятность того, что число
бракованных среди 2000 деталей находится
в границах от 60 до 100 (включительно).
Уточнить вероятность того же события
с помощью интегральной теоремы
Муавра-Лапласа. Объяснить различие
полученных результатов.
Решение
По
условию вероятность того, что деталь
бракованная, равна Р =
1 – 0,96 = 0,04. Число бракованных деталей X —
т имеет
биномиальный закон распределения, а
его границы 60 и 100 симметричны относительно
математического ожидания а
= М(Х) = пр = 2000*0,04
= 80.
Следовательно,
оценку вероятности искомого
события
можно
найти по формуле (6.6):
,
т.е.
не менее чем 0,808.
Применяя
следствие (2.13) интегральной теоремы
Муавра-Лапласа, получим
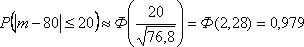
т.е.
вероятность искомого события приближенно
равна 0,979.
Полученный
результат Р
≈ 0,979
не противоречит оценке, найденной с
помощью неравенства Чебышева – Р
> 0,808.
Различие результатов объясняется тем,
что неравенство Чебышева дает лишь
нижнюю границу оценки вероятности
искомого события для любой случайной
величины, а интегральная теорема
Муавра–Лапласа дает достаточно точное
значение самой вероятности Р (тем
точнее, чем больше п), так
как она применима лишь для случайной
величины, имеющей определенный, а именно
– биномиальный закон распределения.
Пример
6.5
Оценить
вероятность того, что отклонение любой
случайной величины от ее математического
ожидания будет не более трех средних
квадратических отклонений (по абсолютной
величине) – (правило
трех сигм).
Решение
По
формуле (6.6), учитывая, что D(
X)
=
σ2, получим:
,
т.е.
не менее, чем 0,889. Напомним, что для
нормального закона правило трех сигм
выполняется с вероятностью Р, равной
0,9973, т.е. Р =
0,9973. Можно показать, что для равномерного
закона распределения Р =
1, для показательного – Р =
0,9827 и т.д. Таким образом, правило трех
сигм (с достаточно большой вероятностью
его выполнения) применимо для большинства
случайных величин, встречающихся на
практике.
Пример
6.6
По
данным примера 2.8 с помощью неравенства
Чебышева оценить вероятность того, что
из 1000 новорожденных доля доживших до
50 лет будет отличаться от вероятности
этого события не более, чем на 0,04 (по
абсолютной величине).
Решение
Полагая п =
1000, р =
0,87, q =
0,13, по формуле (6.7):
т.е.
не менее, чем 0,929.
Замечание
Если
математическое ожидание М(Х)
> А или
дисперсия случайной величины D(
X) >
е2,
то правые части неравенств Маркова и
Чебышева в форме соответственно (6.3) и
(6.6) будут отрицательными, а в форме (6.1)
и (6.4) будут больше 1. Это означает, что
применение указанных неравенств в этих
случаях приведет к тривиальному
результату: вероятность события больше
отрицательного числа либо меньше числа,
превосходящего 1. Но такой вывод очевиден
и без использования данных.
Пример
6.7
Для
определения средней продолжительности
горения электроламп в партии из 200
одинаковых ящиков было взято на выборку
по одной лампе из каждого ящика. Оценить
вероятность того, что средняя
продолжительность горения отобранных
200 электроламп отличается от средней
продолжительности горения ламп во всей
партии не более чем на 5 ч (по абсолютной
величине), если известно, что среднее
квадратическое отклонение продолжительности
горения ламп в каждом ящике меньше 7
ч.
Решение
Пусть Xi – продолжительность
горения электролампы, взятой из i-го
ящика (ч). По условию дисперсия D(
Xi)<
72 =
49. Очевидно, что средняя продолжительность
горения отобранных ламп равна
(X1+X2+…+X200)/200,
а средняя продолжительность горения
ламп во всей партии (М(Х1)
+
M(
X2)
+…+M(X200))/200=(a1+a2+…+a200)/200.
Тогда
вероятность искомого события по
формуле (6.12):
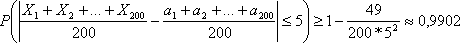
т.е.
не менее, чем 0,9902.
Пример
6.8
Сколько
надо провести измерений данной величины,
чтобы с вероятностью не менее 0,95
гарантировать отклонение средней
арифметической этих измерений от
истинного значения величины не более,
чем на 1 (по абсолютной величине), если
среднее квадратическое отклонение
каждого из измерений не превосходит
5?
Решение
Пусть Xi –
результат i-го
измерения (i =
1,2,…,n); а
– истинное
значение величины, т.е. M(
Xj) = a при
любом i.
Необходимо найти п, при
котором
В
соответствии с (6.12) данное
неравенство будет выполняться, если
,
откуда и
,
т.е.
потребуется не менее 500
измерений.
Задания
6.1. Среднее
изменение курса акции компании в течение
одних биржевых торгов составляет 0,3%.
Оценить вероятность того, что на ближайших
торгах курс изменится более, чем на
3%.
6.2. Отделение
банка обслуживает в среднем 100 клиентов
день. Оценить вероятность того, что
сегодня в отделении банка будет
обслужено:
а)
не более 200 клиентов,
б)
более 150 клиентов.
6.3. Электростанция
обслуживает сеть на 1600 электроламп,
вероятность включения каждой из которых
вечером равна 0,9. Оценить с помощью
неравенства Чебышева вероятность того,
что число ламп, включенных в сеть вечером,
отличается от своего математического
ожидания не более чем на 100 (по абсолютной
величине). Найти вероятность того же
события, используя следствие из
интегральной теоремы
Муавра-Лапласа.
6.4. Вероятность
того, что акции, переданные на депозит,
будут востребованы, равна 0,08. Оценить
с помощью неравенства Чебышева вероятность
того, что среди 1000 клиентов от 70 до 90
востребуют свои акции.
6.5. Среднее
значение длины детали 50 см, а дисперсия
– 0,1. Используя неравенство Чебышева,
оценить вероятность того, что случайно
взятая деталь окажется по длине не менее
49,5 и не более 50,5 см. Уточнить вероятность
того же события, если известно, что длина
случайно взятой детали имеет нормальный
закон распределения.
6.6. Оценить
вероятность того, что отклонение любой
случайной величины от ее математического
ожидания будет не более двух средних
квадратических отклонений (по абсолютной
величине).
6.7. В
течение времени t эксплуатируются
500 приборов. Каждый прибор имеет надежность
0,98 и выходит из строя независимо от
других. Оценить с помощью неравенства
Чебышева вероятность того, что доля
надежных приборов отличается от 0,98 не
более чем на 0,1 (по абсолютной
величине).
6.8. Вероятность
сдачи в срок всех экзаменов студентом
факультета равна 0,7. С помощью неравенства
Чебышева оценить вероятность того, что
доля сдавших в срок все экзамены из 2000
студентов заключена в границах от 0,66
до 0,74.
6.9. Бензоколонка N заправляет
легковые и грузовые автомобили.
Вероятность того, что проезжающий
легковой автомобиль подъедет на заправку,
равна 0,3. С помощью неравенства Чебышева
найти границы, в которых с вероятностью,
не меньшей 0,79, находится доля заправившихся
в течение 2 ч легковых автомобилей, если
за это время всего заправилось 100
автомобилей.
6.10. В
среднем 10% работоспособного населения
некоторого региона – безработные.
Оценить с помощью неравенства Чебышева
вероятность того, что уровень безработицы
среди обследованных 10 000 работоспособных
жителей города будет в пределах от 9 до
11% (включительно).
6.11. Выход
цыплят в инкубаторе составляет в среднем
70% числа заложенных яиц. Сколько нужно
заложить яиц, чтобы с вероятностью, не
меньшей 0,95, ожидать, что отклонение
числа вылупившихся цыплят от математического
ожидания их не превышало 50 (по абсолютной
величине)? Решить задачу с помощью:
а)
неравенства Чебышева;
б)
интегральной теоремы Муавра-Лапласа.
6.12. Опыт
работы страховой компании показывает,
что страховой случай приходится примерно
на каждый пятый договор. Оценить с
помощью неравенства Чебышева необходимое
количество договоров, которые следует
заключить, чтобы с вероятностью 0,9 можно
было утверждать, что доля страховых
случаев отклонится от 0,1 не более чем
на 0,01 (по абсолютной величине). Уточнить
ответ с помощью следствия из интегральной
теоремы Муавра – Лапласа.
6.13. В
целях контроля из партии в 100 ящиков
взяли по одной детали из каждого ящика
и измерили их длину. Требуется оценить
вероятность того, что вычисленная по
данным выборки средняя длина детали
отличается от средней длины детали во
всей партии не более чем на 0,3 мм, если
известно, что среднее квадратическое
отклонение не превышает 0,8 мм.
6.14. Сколько
нужно произвести измерений, чтобы с
вероятностью, равной 0,9973, утверждать,
что погрешность средней арифметической
результатов этих измерений не превысит
0,01, если измерение характеризуется
средним квадратическим отклонением,
равным 0,03?
7
ГЛАВА
Элементы
теории случайных процессов и теории
массового обслуживания
В
главе рассматриваются:
— определение
случайного процесса и его характеристики,
понятие марковского случайного
процесса;
— основные
понятия теории массового
обслуживания;
— потоки
событий;
— уравнение
Колмогорова;
— СМО
с отказами;
— метод
Монте-Карло.
Типовые
задачи
Пример
7.1
Случайный
процесс определяется формулой X(
t)
=
Xcoswt, где X – случайная
величина. Найти основные характеристики
этого процесса, если М(Х)
= а,
D(
X)
= а2.
Решение
На
основании свойств математического
ожидания и дисперсии имеем:
Корреляционную
функцию найдем по формуле
(7.1):
Нормированную
корреляционную функцию найдем по формуле
(7.2):
Пример
7.2
Построить
граф состояний следующего случайного
процесса: устройство S состоит
из двух узлов, каждый из которых в
случайный момент времени может выйти
из строя, после чего мгновенно начинается
ремонт узла, продолжающийся заранее
неизвестное случайное время.
Решение
Возможные
состояния системы: S0 –
оба узла исправны; S1 –
первый узел ремонтируется, второй
исправен; S2 –
второй узел ремонтируется, первый
исправен; S3 —
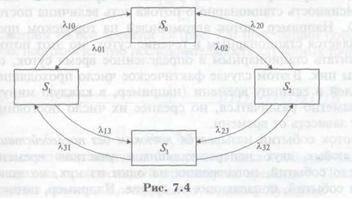
оба узла ремонтируются. Граф системы
приведен на рис. 7.4.
Стрелка,
направленная, например, из S0 в
S1, означает
переход системы в момент отказа первого
узла, из S1 в S0 –
переход в момент окончания ремонта
этого узла.
На
графе отсутствуют стрелки из S0 в S3 и
из S1 в S2.
Это объясняется тем, что выходы узлов
из строя предполагаются независимыми
друг от друга и, например, вероятностью
одновременного выхода из строя двух
узлов (переход из S0 в S3) или одновременного
окончания ремонтов двух узлов (переход
из S3 в S0) можно
пренебречь.
Пример
7.3
На
автоматическую телефонную станцию
поступает простейший поток вызовов с
интенсивностью альфа = 1,2 вызовов в
минуту. Найти вероятность того, что за
две минуты:
а)
не придет ни одного вызова;
б)
придет ровно один вызов;
в)
придет хотя бы один вызов.
Решение
а)
Случайная величина X –
число вызовов за две минуты – распределена
по закону Пуассона с параметром λτ =
1,2*2 = 2,4. Вероятность того, что вызовов
не будет (m =
0), по формуле (7.5):
.
б)
Вероятность одного вызова (m =
1):
.
в)
Вероятность хотя бы одного вызова:
.
Пример
7.4
Найти
предельные вероятности для системы S из
примера 7.2, граф состояний которой
приведен на рис. 7.4, при λ01 =
1, λ02 =
2, λ10 =
2, λ13 =
2, λ20 =
3, λ23 =
1, λ31 =
3, λ32 =
2.
Решение
Система
алгебраических уравнений, описывающих
стационарный режим для данной системы,
имеет вид (7.14)
или
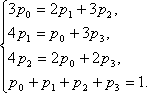
(Здесь
вместо одного «лишнего»уравнения
системы (7.14) записали нормировочное
условие(7.12).)
Решив
систему (7.15), получим p0 =
0,40, p1 =
0,20, p2 =
0,27, p3 =
0,13, т.е. в предельном стационарном режиме
системе S в
среднем 40% времени будет находиться в
состоянии S0 (оба
узла исправны), 20% — в состоянии S1 (первый
узел ремонтируется, второй работает),
27% — в состоянии S2 (второй
узел ремонтируется, первый работает) и
13% времени – в состоянии S3 (оба
узла ремонтируются).
Пример
7.5
Найти
средний чистый доход от эксплуатации
в стационарном режиме системы S в
условиях примеров 7.2 и
7.4, если известно, что в единицу времени
исправная работа первого и второго
узлов приносит доход соответственно в
10 и 6 ден. ед., а их ремонт требует затрат
соответственно в 4 и 2 ден. ед. Оценить
экономическую эффективность имеющейся
возможности уменьшения вдвое среднего
времени ремонта каждого из двух узлов,
если при этом придется вдвое увеличить
затраты на ремонт каждого узла (в единицу
времени).
Решение
Из
примера 7.4 следует, что в среднем первый
узел исправно работает долю времени,
равную p0+
р2 =
0,40 + 0,27
= 0,67, а второй узел –p0 +
р1 =
0,40 +
0,20 = 0,60. в то же время первый узел находится
в ремонте в среднем долю времени,
равную р1 +
р3 = 0,20
+ 0,13 = 0,33, а второй узел
– р2+р3= =0,27+0,13=0,40. Поэтому
средний чистый доход в единицу времени
от эксплуатации системы, т.е. разность
между доходами и затратами, равен
D =
0,67*10+0,60*6-0,33*4-0,40*2 = 8,18 ден. ед.
Уменьшение
вдвое среднего времени ремонта каждого
из узлов в соответствии с (7.10) будет
означать увеличение вдвое интенсивностей
потока «окончаний ремонтов» каждого
узла, т.е. теперь λ10 =
4, λ20 =
6, λ31 =
6, λ32 =
4 и система линейных алгебраических
уравнений (7.14), описывающая стационарный
режим системы S, вместе
с нормировочным условием (7.12) примет
вид:
Решив
систему,
получим р0 = 0,60, р1 = 0,15, р2 =0,20, р3 = 0,05.
Учитывая,
что р0 +
р2 =0,60
+ 0,20 = 0,80, р0 +
р1 =
0,60 + 0,15 = 0,75, р1 +
р3 = 0,15
+ 0,05 = 0,20, р2 +
р3 = 0,20
+ 0,05 = 0,25, а затраты на ремонт первого и
второго узлов составляют теперь
соответственно 8 и 4 ден. ед., вычислим
средний чистый доход в единицу
времени:
D1 =
0,80*10+0,75*6-0,20*8-0,25*4 = 9,9 ден. ед.
Так
как D1 больше D (примерно
на 20%), то экономическая целесообразность
ускорения ремонтов узлов очевидна.
|
|
Простая задача из теории вероятностей
|
|
28/12/18 |
Среднее изменение курса акций компании в течение одних биржевых торгов составило 1%, а среднеквадратическое отклонение оценивается как 0,5%. Оценить вероятность p того, что на ближайших торгах курс изменится менее, чем на 2%.
Для оценки вероятности неравенством Чебышёва данных многовато, а если сослаться на ЦПТ и посчитать по нормальному распределению, то это уже и не оценка получается. Что-то у меня ум за разум зашёл. ))
|
|
|
|
|
Cash |
Re: Простая задача из теории вероятностей
|
||
12/09/10 |
Почему для Чебышёва данных многовато? В самый раз, на мой взгляд.
|
||
|
|
|||
|
Cryohron |
Re: Простая задача из теории вероятностей
|
|
28/12/18 |
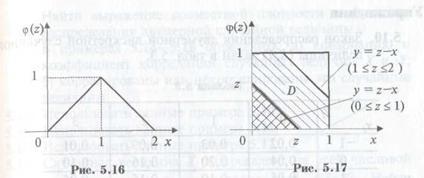
X — изменение курса акций компании в течение одних биржевых торгов Значение 2. Оценим вероятность того, что «изменение изменения» курса (случайной величины X) относительно среднего значения не превысит 2%. Значение Что, вообще, происходит?
|
|
|
|
|
mihaild |
Re: Простая задача из теории вероятностей
|
||
16/07/14 |
Это не неравенство Чебышева. И вообще неправда. Значение Ну так у вас и получилась оценка на
|
||
|
|
|||
|
Cryohron |
Re: Простая задача из теории вероятностей
|
|
28/12/18 |
|
|
|
|
|
mihaild |
Re: Простая задача из теории вероятностей
|
||
16/07/14 |
В неравенстве Маркова говорится о положительных величинах (а для них не нужен модуль).
|
||
|
|
|||
|
Cryohron |
Re: Простая задача из теории вероятностей
|
|
28/12/18 |
Читал форум. Много думал. Неравенство Чебышёва: Чтобы выполнялось условие Ответ справедлив, если
|
|
|
|
|
—mS— |
Re: Простая задача из теории вероятностей
|
||
23/11/06 |
Ответ справедлив, если Конечно, нет. Всегда
|
||
|
|
|||
|
Cryohron |
Re: Простая задача из теории вероятностей
|
|
28/12/18 |
Ответ справедлив, если Конечно, нет. Всегда Да, конечно! Спасибо!
|
|
|
|
Модераторы: Модераторы Математики, Супермодераторы

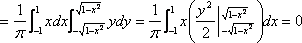
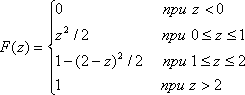
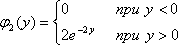
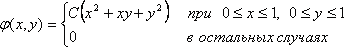
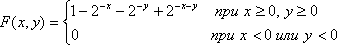
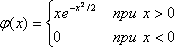
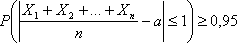
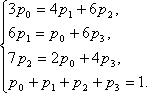
 0,6094
0,6094 .
. 



 не использовалось.
не использовалось.



 не использовалось.
не использовалось.
 . А надо было получить оценку на
. А надо было получить оценку на  .
.



 выберем
выберем 



 , т.е берется модуль изменения курса акций в течение одних биржевых торгов. Если же это не так, то для оценки вероятности не обойтись без предположения о виде распределения. Я так думаю.
, т.е берется модуль изменения курса акций в течение одних биржевых торгов. Если же это не так, то для оценки вероятности не обойтись без предположения о виде распределения. Я так думаю.