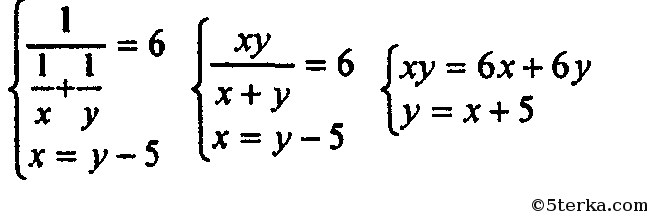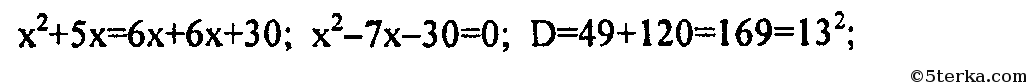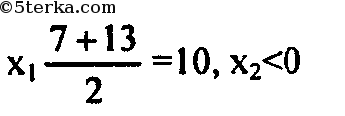Алгебра,
вопрос задал myhamsters12,
5 лет назад
au456:
Я изначально условие понял так что два обычных комбайна было. Думал все — перегрелся ))) это ж надо так условие составлять …
au456:
Только прочитав решение понял о другом толковании задачи )))
Ответы на вопрос
Ответ:
за 10 часов.
Объяснение:
Пусть модернизированный комбайн может выполнить задание за х часов, тогда обычный комбайн это же задание может выполнить за х+5 часов.
За 1 час модернизированный комбайн выполнит 1/х часть задания.
За 1 час обычный комбайн может выполнить 1(х+5) часть задания.
Вместе за 1 час они могут выполнить 1/6 часть задания.
1/х + 1/(х+5) = 1/6
6х+30+6х-х²-5х=0
х²-7х-30=0
По теореме Виета х=-3 (не подходит) х=10.
Решение в приложении.
Приложения:

Новые вопросы
Решение:
Если размер работы не указан, то принимаем работу за 1.
Пусть х ч время работы первого комбайна, тогда (х + 12) — время работы второго (он выполняет работу на 12 часов дольше первого).
Выразим производительность первого комбайна. Для этого работу разделим на время.
То же самое с производительностью второго комбайна.
Запишем формулу для нахождения их совместной производительности.
В то же время, работая вместе, они управляется за 8 часов, значит, можно записать, что их производительность равна 1/8.
Составим и решим уравнение:
Приведем дроби к общему знаменателю и сразу домножим на него, чтобы от него же и избавиться.
Раскрываем скобки, приводим подобные слагаемые и получаем квадратное уравнение.
По теореме Виета находим корни.
Время работы не может быть отрицательным, значит, корень х = -8 не подходит.
Ответ: 12 часов.
Не можешь найти нужную задачу? Предложи свою! Наша группа в VK.
#719
7.21. Два комбайна, работая совместно, могут выполнить задание за 6 ч. Первый комбайн, работая один, может выполнить это задание на 5 ч скорее, чем второй комбайн. За сколько времени может выполнить задание первый комбайн, работая один?
7.21.
Пусть 1-й комбайн работая один может выполнить задание за х часов, а второй за у, примем объем всей работы за 1, тогда получим систему:
Ответ: за 10 часов.
Источник:
Решебник
по
алгебре
за 9 класс (А.Г. Мордкович, Л.А. Александрова, Т.Н. Мишустина и др., 2010 год),
задача №7.21.
к главе «§7. Системы уравнений как математические модели реальных ситуаций».
Все задачи
← 7.20. В колледже для проведения письменного экзамена по математике было заготовлено 400 листов бумаги. Но на экзаменах по предыдущим предметам отсеялось 20 человек, поэтому каждому абитуриенту смогли дать на 1 лист бумаги больше, чем предполагалось. Сколь
7.22. Две бригады, работая вместе, могут выполнить задание за 8 ч. Первая бригада, работая одна, могла бы выполнить задание на 12 ч быстрее, чем вторая бригада. За сколько часов могла бы выполнить задание первая бригада, если бы она работала одна? →
Комментарии
Пусть х ч — время работы первого комбайна, тогда (х + 5) ч — время работы второго комбайна. Совместная работа 6 ч.
Работу по выполнению задания примем за единицу (целое), тогда
1/х — часть работы, которую выполнит первый комбайн за 1 час;
1/(х+5) — часть работы, которую выполнит второй комбайн за 1 час;
1/6 — часть работы, которую они выполнят вместе за 1 час.
Уравнение:
1/х + 1/(х+5) = 1/6
Домножим обе части уравнения на 6
6/х + 6/(х+5) = 1
6 · (х + 5) + 6х = 1 · х · (х + 5)
6х + 30 + 6х = х² + 5х
12х + 30 = х² + 5х
х² + 5х — 12х — 30 = 0
х² — 7х — 30 = 0
D = b² — 4ac = (-7)² — 4 · 1 · (-30) = 49 + 120 = 169
√D = √169 = 13
х₁ = (7-13)/(2·1) = (-6)/2 = -3 (не подходит, так как < 0)
х₂ = (7+13)/(2·1) = 20/2 = 10
Ответ: за 10 часов.