Вопрос
48. Модель оценки доходности финансовых
активов (CAPM)
Модель
оценки доходности финансовых активов
(Capital Asset Pricing Model, САРМ), увязывающая
систематический риск и доходность
актива. Как и любая теория финансов,
модель САРМ сопровождается рядом
предпосылок, которые в акцентированном
виде были сформулированы М. Дженсеном
и опубликованы им в 1972 г. Эти предпосылки
таковы:
1.
Основной целью каждого инвестора
является максимизация возможного
прироста своего богатства на конец
планируемого периода путем оценки
ожидаемых доходностей и среднеквадратических
отклонений альтернативных инвестиционных
портфелей.
2.
Все инвесторы могут брать и давать ссуды
неограниченного размера по некоторой
безрисковой процентной ставке Cf при
этом не существует ограничений на
«короткие» продажи любых активов.
3.
Все инвесторы одинаково оценивают
величину ожидаемых значений доходности,
дисперсии и ковариации всех активов;
это означает, что инвесторы находятся
в равных условиях в отношении
прогнозирования показателей.
4.
Все активы абсолютно делимы и совершенно
ликвидны (т. е. всегда могут быть проданы
на рынке по существующей цене).
5.
Не существует трансакционных расходов.
6.
Не принимаются во внимание налоги.
7.
Все инвесторы принимают цену как
экзогенно заданную величину (т. е. они
полагают, что их деятельность по покупке
и продаже ценных бумаг не оказывает
влияния на уровень цен на рынке этих
бумаг).
8.
Количество всех финансовых активов
заранее определено и фиксировано.
Как
легко заметить, многие из сформулированных
предпосылок носят исключительно
теоретический характер и не могут быть
выполнены на практике.
Модель
оценки доходности финансовых активов
(САРМ) предполагает, что цена собственного
капитала Се равна безрисковой доходности
плюс премия за систематический риск:
Се
= Cf + β (Ст – Cf),
где
Cf – доходность безрисковых
вложений;
β
– коэффициент, рассчитываемый для
каждой акции;
Cm
– средняя ставка доходности,
сложившаяся на рынке ценных бумаг.
Основа
вычисления стоимости капитала по САРМ
– безрисковая доходность, Cf .
В
качестве безрисковой ставки дохода в
мировой практике используют обычно
ставку дохода по долгосрочным
государственным долговым обязательствам
(облигациям или векселям); считают, что
государство – самый надежный гарант
по своим обязательствам (вероятность
его банкротства практически исключаема).
Однако,
как показывает практика, государственные
ценные бумаги в России не воспринимают
как безрисковые. Для определения ставки
дисконта в качестве безрисковой может
быть принята ставка по вложениям,
характеризующимся наименьшим уровнем
риска (ставка по валютным депозитам в
Сбербанке или других наиболее надежных
банках). Можно также основываться на
безрисковой ставке для западных компаний,
но в этом случае обязательно прибавление
странового риска с целью учета реальных
условий инвестирования, существующих
в России. Для инвестора она представляет
собой альтерна-тивную ставку дохода,
которую характеризуют практическим
отсутствием риска и высокой степенью
ликвидности. Безрисковую ставку
используют как точку отсчета для оценки
различных видов риска, характеризующих
вложения в данное предприятие, на основе
чего и выстраивают требуемую ставку
дохода.
Таким
образом, показатель (Cm – Cf) –
имеет вполне наглядную интерпретацию,
представляя собой рыночную (т.е. в
среднем) премию за риск вложения своего
капитала не в безрисковые государственные
ценные бумаги, а в рисковые ценные бумаги
(акции, облигации корпораций и пр.).
Аналогично показатель (Се – Cf)
представляет собой премию за риск
вложения капитала в ценные бумаги именно
данной компании. Модель САРМ означает,
что премия за риск вложения в ценные
бумаги данной компании прямо пропорциональна
рыночной премии за риск.
Модель
позволяет спрогнозировать доходность
финансового актива; в свою очередь, зная
этот показатель и имея данные об ожидаемых
доходах по этому активу, можно рассчитать
его теоретическую стоимость. Не случайно
поэтому модель называют еще моделью
ценообразования финансовых активов.
Систематический
риск в рамках модели САРМ измеряется с
помощью β-коэффициентов (бета-коэффициентов).
Каждый вид ценной бумаги имеет собственный
β-коэффициент, представляющий собой
индекс доходности данного актива по
отношению к доходности в среднем на
рынке ценных бумаг. Значение показателя
β рассчитывается по статистическим
данным для каждой компании, котирующей
свои ценные бумаги на бирже, и периодически
публикуется в специальных справочниках.
Для каждой компании β меняется с течением
времени и зависит от многих факторов,
в частности имеющих отношение к
характеристике деятельности компании
с позиции долгосрочной перспективы.
Очевидно, что сюда относится, прежде
всего, показатель уровня финансового
левериджа, отражающего структуру
источников средств: при прочих равных
условиях чем выше доля заемного капитала,
тем более рисковая компания и тем выше
ее β.
В
целом по рынку Ценных бумаг β-коэффициент
равен единице; для отдельных компаний
он колеблется около единицы, причем
большинство β-коэффициентов находится
в интервале от 0,5 до 2,0. Интерпретация
β-коэффициента для акций конкретной
компании заключается в следующем31:
-
β
= 1 означает, что акция данной компании
имеют среднюю степень риска, сложившуюся
на рынке в целом; -
β
< 1 означает, что ценные бумаги данной
компании менее рискованны, чем в среднем
на рынке (так, β =0,5 означает, что данная
ценная бумага в два раза менее рискованна,
чем в среднем на рынке); -
β
> 1 означает, что ценные бумаги данной
компании более рискованны, чем в среднем
на рынке; -
увеличение
β-коэффициента в динамике означает,
что вложения в ценные бумаги данной
компании становятся более рискованными; -
снижение
β-коэффициента в динамике означает,
что вложения ценные бумаги данной
компании становятся менее рискованными.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Модель оценки доходности финансовых активов
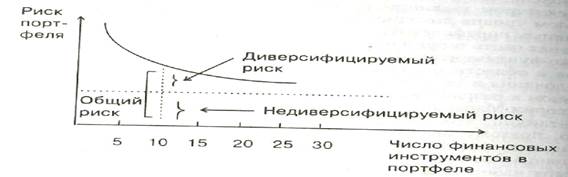
Любое предприятие может рассматриваться как совокупность некоторых активов (материальных и финансовых), находящихся в определенном сочетании. Владение любым из этих активов связано с определенным риском в плане воздействия этого актива на величину общего дохода предприятия. То же самое в полном объеме относится к портфелям ценных бумаг, причем, как было отмечено выше, степень риска изменяется обратно пропорционально количеству включенных в портфель случайным образом видов ценных бумаг (рисунок 1). Общий риск портфеля состоит из двух частей:
• диверсифицируемый (несистематический) риск, т.е. риск, который может быть элиминирован за счет диверсификации (инвестирование 1 млн. руб. в акции десяти компаний менее рискованно, нежели инвестирование той же суммы в акции одной компании);
• недиверсифицируемый (систематический, или рыночный) риск, т.е. риск, который нельзя уменьшить путем изменения структуры портфеля.
Рисунок 1- Зависимость степени риска от диверсификации портфеля
Исследования показали, что если портфель состоит из 10—20 различных видов ценных бумаг, включенных в портфель с помощью случайной выборки из имеющегося на рынке ценных бумаг набора, то несистематический риск может быть сведен к минимуму (рисунок 1). Таким образом, этот риск поддается элиминированию довольно несложными методами, поэтому основное внимание следует уделять возможному уменьшению систематического риска.
Существует «теория портфеля» — теория финансовых инвестиций, в рамках которой с помощью статистических методов и осуществляются наиболее выгодное распределение риска портфеля ценных бумаг и оценка прибыли. Эта теория состоит из четырех основных элементов:
• оценка активов;
• инвестиционные решения;
• оптимизация портфеля;
• оценка результатов.
В процессе управления инвестиционным портфелем менеджер постоянно сталкивается с задачей отбора новых инструментов и анализа возможности их включения в портфель. Какими же методами можно это делать? Существует несколько способов, однако наибольшую известность получила модель оценки доходности финансовых активов (Capital Asset Pricing Model, САРМ), увязывающая систематический риск и доходность портфеля.
Как и любая теория финансов, модель САРМ сопровождается рядом предпосылок, которые в акцентированном виде были сформулированы М. Дженсеном и опубликованы им в 1972 г. Эти предпосылки таковы:
1. Основной целью каждого инвестора является максимизация возможного прироста своего богатства на конец планируемого периода путем оценки ожидаемых доходностей и среднеквадратических отклонений альтернативных инвестиционных портфелей.
2. Все инвесторы могут брать и давать ссуды неограниченного размера по некоторой безрисковой процентной ставке kгf, при этом не существует ограничений на «короткие» продажи любых активов.
3. Все инвесторы одинаково оценивают величину ожидаемых значений доходности, дисперсии и ковариации всех активов; это означает, что инвесторы находятся в равных условиях в отношении прогнозирования показателей.
4. Все активы абсолютно делимы и совершенно ликвидны (т. е. всегда могут быть проданы на рынке по существующей цене).
5. Не существует трансакционных расходов.
6. Не принимаются во внимание налоги.
7. Все инвесторы принимают цену как экзогенно заданную величину (т. е. они полагают, что их деятельность по покупке и продаже ценных бумаг не оказывает влияния на уровень цен на рынке этих бумаг).
8. Количество всех финансовых активов заранее определено и фиксировано.
Как легко заметить, многие из сформулированных предпосылок носят исключительно теоретический характер и не могут быть выполнены на практике.
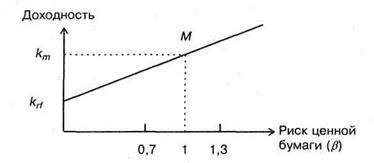
Для понимания логики модели легче всего воспользоваться графическим представлением (рисунок 2). Ставится задача найти взаимосвязь между ожидаемой доходностью (у) и риском ценной бумаги (х), т.е. построить функцию у = f(x}. Построение основывается на следующих очевидных рассуждениях: а) доходность ценной бумаги связана с присущим ей риском прямой связью; б) риск характеризуется некоторым показателем β; в) «средней» ценной бумаге, т.е. бумаге, имеющей средние значения риска и доходности, соответствуют B = 1 и доходность km;r) имеются безрисковые ценные бумаги со ставкой kгf и β = 0.
Исходя из приведенных выше предпосылок доказывается, что искомая зависимость y =f(х) представляет собой прямую линию. Итак, мы имеем две точки с координатами (0, krf) и (1, km). Из курса геометрии известно, что уравнение прямой, проходящей через точки (х1,у1) и (х2,у2), задается формулой:

Подставляя в формулу исходные данные, получим:
y = krf + (km — krf) • x. (14)
Рисунок 2 — Логика представления модели САРМ
Имея в виду, что переменная х представляет собой риск, характеризуемый показателем β, а у — ожидаемую доходность ke, получим следующую формулу, которая и представляет собой модель САРМ:
ke= krf + β • (km-krf) (15)
где ke — ожидаемая доходность акций данной компании;
krf — доходность безрисковых ценных бумаг (в частности, в США берут за основу государственные казначейские векселя, используемые для краткосрочного (до 1 года) регулирования денежного рынка);
km — ожидаемая доходность в среднем на рынке ценных бумаг;
β — бета-коэффициент данной компании.
Показатель (km — krf) имеет вполне наглядную интерпретацию, представляя собой рыночную (т.е. в среднем) премию за риск вложения своего капитала не в безрисковые государственные ценные бумаги, а в рисковые ценные бумаги (акции, облигации корпораций и пр.). Аналогично показатель (ke — krf) представляет собой премию за риск вложения капитала в ценные бумаги именно данной компании. Модель САРМ означает, что премия за риск вложения в ценные бумаги данной компании прямо пропорциональна рыночной премии за риск.
Модель САРМ позволяет спрогнозировать доходность финансового актива; в свою очередь, зная этот показатель и имея данные об ожидаемых доходах по этому активу, можно рассчитать его теоретическую стоимость. Не случайно поэтому модель САРМ называют еще моделью ценообразования финансовых активов.
Систематический риск в рамках модели САРМ измеряется с помощью β -коэффициентов (бета-коэффициентов). Каждый вид ценной бумаги имеет собственный β -коэффициент, представляющий собой индекс доходности данного актива по отношению к доходности в среднем на рынке ценных бумаг. Значение показателя β рассчитывается по статистическим данным для каждой компании, котирующей свои ценные бумаги на бирже, и периодически публикуется в специальных справочниках. Для каждой компании βменяется с течением времени и зависит от многих факторов, в частности имеющих отношение к характеристике деятельности компании с позиции долгосрочной перспективы. Очевидно, что сюда относится прежде всего показатель уровня финансового левериджа, отражающего структуру источников средств: при прочих равных условиях чем выше доля заемного капитала, тем более рисковая компания и тем выше ее β.
В целом по рынку ценных бумаг β -коэффициент равен единице; для отдельных компаний он колеблется около единицы, причем большинство β-коэффициентов находится в интервале от 0,5 до 2,0. Интерпретация β-коэффициента для акций конкретной компании заключается в следующем:
β = 1 означает, что акции данной компании имеют среднюю степень риска, сложившуюся на рынке в целом;
β < 1 означает, что ценные бумаги данной компании менее рискованны, чем в среднем на рынке (так, β = 0,5 означает, что данная ценная бумага в два раза менее рискованна, чем в среднем на рынке);
β > 1 означает, что ценные бумаги данной компании более рискованны, чем в среднем на рынке;
увеличение β-коэффициента в динамике означает, что вложения в ценные бумаги данной компании становятся более рискованными;
снижение β-коэффициента в динамике означает, что вложения в ценные бумаги данной компании становятся менее рискованными.
Важным свойством модели САРМ является ее линейность относительно степени риска. Это дает возможность определять β-коэффициент портфеля как средневзвешенную β-коэффициентов, входящих в портфель финансовых активов:
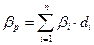
где
βi – значение β-коэффициента i-го актива в портфеле;
βр – значение β-коэффициента портфеля;
di – значение i-го актива в портфеле;
n – число различных финансовых активов в портфеле.
Модель САРМ не идеальна и неоднократно подвергалась критике и имперической проверке.
Три основные подхода, альтернативные модели САРМ: теория арбитражного ценообразования, теория ценообразования опционов, теория преференций состояний в условиях неопределенности.
|
Расчетные и графические задания Равновесный объем — это объем, определяемый равенством спроса и предложения… |
Кардиналистский и ординалистский подходы Кардиналистский (количественный подход) к анализу полезности основан на представлении о возможности измерения различных благ в условных единицах полезности… |
Обзор компонентов Multisim Компоненты – это основа любой схемы, это все элементы, из которых она состоит. Multisim оперирует с двумя категориями… |
Композиция из абстрактных геометрических фигур Данная композиция состоит из линий, штриховки, абстрактных геометрических форм… |
|
Потенциометрия. Потенциометрическое определение рН растворов Потенциометрия — это электрохимический метод исследования и анализа веществ, основанный на зависимости равновесного электродного потенциала Е от активности (концентрации) определяемого вещества в исследуемом растворе… Гальванического элемента При контакте двух любых фаз на границе их раздела возникает двойной электрический слой (ДЭС), состоящий из равных по величине, но противоположных по знаку электрических зарядов… Сущность, виды и функции маркетинга персонала Перснал-маркетинг является новым понятием. В мировой практике маркетинга и управления персоналом он выделился в отдельное направление лишь в начале 90-х гг.XX века… |
1. РИСК И ДОХОДНОСТЬ ФИНАНСОВЫХ АКТИВОВ
2.
Риск и доходность
менеджменте
в финансовом
рассматриваются
как
две
взаимосвязанные категории. Они могут быть
ассоциированы как с каким-либо отдельным
видом финансовых активов, так и с их
комбинацией.
3.
В приложении к финансовым активам используют следующую
интерпретацию риска и его меры:
рисковость актива характеризуется степенью вариабельности
дохода (или доходности), который может быть получен благодаря
владению данным активом.
Так, государственные ценные бумаги обладают относительно
небольшим риском, поскольку вариация дохода по ним в стабильной,
не подверженной кризисам экономике практически равна 0. Напротив,
обыкновенная акция любой компании представляет собой значительно
более рисковый актив, поскольку доход по такого рода акциям может
ощутимо варьировать.
4.
полученных дивидендов
Доход, обеспечиваемый
каким-либо активом, состоит
из двух компонентов
дохода от изменения
стоимости актива
5.
Доход, исчисленный в процентах к первоначальной
стоимости актива, называется доходностью данного актива,
или нормой прибыли.
Доходность актива k =
Дивиденды + (Текущая рыночная цена акции – Цена приобретения)
Цена приобретения
Доход — это абсолютный показатель, его можно
суммировать в пространстве и времени; доходность показатель относительный и такого суммирования делать уже
нельзя.
6.
Размахом вариации называется разность между
максимальным и минимальным значениями признака ряда
х1, х2, х3, … , хn:
R = xmax – xmin.
Недостатки данного показателя:
1) дает грубую оценку степени вариации значений признака;
2) является абсолютным показателем и потому его применение
в сравнительном анализе весьма ограничено;
3) его величина слишком зависит от крайних значений
ранжирования ряда.
7.
Дисперсия является средним квадратом отклонений значений
признака от его средней и рассчитывается по формуле
n
1
2
2
∑
(x
–
x)
Var = σ = n
j
j=1
Среднее квадратическое отклонение
показывает среднее
отклонение значений варьирующего признака относительно центра
распределения, в данном случае средней арифметической. Этот показатель
рассчитывается по формуле
σ = √Var
Все вышеприведенные показатели обладают одним общим
недостатком — это абсолютные показатели, значение которых существенно
зависит от абсолютных значений исходного признака ряда. Поэтому большее
применение имеет коэффициент вариации, рассчитываемый по формуле
CV =
σ
x
100%
8.
Принимая
решение
о
целесообразности
инвестирования денежных средств в финансовые
активы, инвестор должен прежде всего оценить
риск, присущий этим активам, затем ожидаемую их
доходность и далее определить, достаточна ли эта
доходность для компенсации ожидаемого риска.
9.
При
оценке
портфеля
и
целесообразности
операций с входящими в него активами необходимо
оперировать показателями доходности портфеля в
целом:
n
kp = ∑ kj dj ,
j=1
где kp – доходность j-го актива;
dj – доля j-го актива в портфеле;
n – число активов в портфеле.
10.
Теория инвестиционного портфеля
Уильяма Шарпа и Гарри Марковица:
1.
Успех инвестиций в основном зависит от правильного
распределения средств по типам активов.
2. Риск инвестиций в определенный тип ценных бумаг
определяется
вероятностью
отклонения
прибыли
от
ожидаемого значения.
3. Общая доходность и риск инвестиционного портфеля могут
меняться путем варьирования его структурой.
4. Все оценки, используемые при составлении инвестиционного
портфеля, носят вероятностный характер.
11.
Этапы формирования
инвестиционного портфеля:
1) формулирование целей его создания и
определение их приоритетности в частности;
2) выбор финансовой компании;
3) выбор банка, который будет вести
инвестиционный счет.
12.
Общий риск инвестиционного портфеля
Диверсифицируемый
(несистематический)
Недиверсифицируемый
(систематический, рыночный)
Риск, который может
быть элиминирован
за счет
диверсификации
Риск, который нельзя
уменьшить путем
изменения структуры
портфеля
13.
Зависимость степени риска от
диверсификации портфеля
14.
Модель оценки доходности финансовых активов
CAMP (Capital Asset Pricing Model)
Модель САРМ увязывает систематический риск и
доходность портфеля.
Модель САРМ означает, что премия за риск вложения
в ценные бумаги данной компании прямо пропорциональна
рыночной премии за риск.
Модель САРМ позволяет спрогнозировать доходность
финансового актива; в свою очередь, зная этот показатель и
имея данные об ожидаемых доходах по этому активу, можно
рассчитать его теоретическую стоимость. Поэтому модель
САРМ называют еще моделью ценообразования финансовых
активов.
15.
Логика представления модели САРМ
y = krf + (km – krf)∙x
16.
Модель САРМ
ke = krf + β∙(km – krf),
где ke – ожидаемая доходность акций данной компании;
krf – доходность безрисковых ценных бумаг;
km – ожидаемая доходность в среднем на рынке ценных бумаг;
β – бета-коэффициент данной компании.
17.
В
процессе
управления
инвестиционным
портфелем менеджер постоянно сталкивается с задачей
отбора новых инструментов и анализа возможности их
включения в портфель.
В целом по рынку ценных бумаг β-коэффициент
равен единице; для отдельных компаний он колеблется
около единицы, причем большинство β-коэффициентов
находится в интервале от 0,5 до 2,0.
18.
Интерпретация β-коэффициента для акций конкретной
компании заключается в следующем:
β = 1 означает, что акции данной компании имеют среднюю
степень риска, сложившуюся на рынке в целом;
β < 1 означает, что акции данной компании менее рискованны, чем
в среднем на рынке;
β > 1 означает, что акции данной компании более рискованны, чем
в среднем на рынке;
увеличение β-коэффициента в динамике означает, что вложения в
ценные бумаги данной компании становятся более рискованными;
снижение β-коэффициента в динамике означает, что вложения в
ценные бумаги данной компании становятся менее рискованными.
Страница 406 из 552
Моделью оценки капитальных финансовых активов
(Capital Asset Pricing Model, САРМ) называется модель, описывающая зависимость между показателями доходности и риска индивидуального финансового актива и рынка в целом. Синоним: модель ценообразования на рынке капитальных финансовых активов. Являясь рыночным товаром, торгуемая ценная бумага подвержена действию законов этого рынка, в том числе в отношении логики и закономерностей ценообразования. В числе этих закономерностей — взаимное влияние основных характеристик (т. е. цены, стоимости, риска, доходности) торгуемых товаров друг на друга и возможность управления значениями этих характеристик путем формирования комбинаций товаров. Эта закономерность была подмечена американским исследователем Г. Марковицем, создавшим теорию портфеля.
Представленные Марковицем идеи и математический аппарат носили в значительной степени теоретический характер, однако для реализации предложенной им теории необходимы были хотя и однотипные, но множественные расчеты в ходе перебора различных комбинаций торгуемых на рынке финансовых активов. При этом требовалось не только оценить ожидаемую доходность каждой акции, но и рассчитать парные ковариации доходностей разных комбинаций. Компьютеры в те годы были малопроизводительными, а потому любая оптимизационная задача оказывалась исключительно дорогостоящей.
Поэтому настоящим прорывом в области управления финансовыми инвестициями стал предложенный в 1964 г. У. Шарпом упрощенный и более практичный вариант математического аппарата, получивший название однофакторной модели, Идея Шарпа заключалась в формулировании и обосновании утверждения о том, что доходность любого капитального финансового актива, обращающегося на фондовом рынке, тесно коррелирует с некоторым фактором, присущим данному рынку и являющимся одной из ключевых его характеристик. По мнению Шарпа, в качестве такого фактора мог выступать уровень цен на рынке, валовый национальный продукт или некий индекс цен. Главное, чтобы при обособлении этого фактора действительно можно было утверждать, что он в значительной степени предопределяет значение ожидаемой доходности любого актива, торгуемого на данном рынке [Sharpe, 1964].
Предложенная Шарпом техника уже позволяла эффективно управлять крупными портфелями, включающими сотни капитальных финансовых активов. Исследования в этом направлении проводили также Дж. Трейнор, Дж. Линтнер, Я. Моссин, Ф. Блэк и другие ученые. В результате совместных усилий была разработана модель САРМ, объясняющая, в частности, поведение доходности любой ценной бумаги, обращающейся на рынке1.
1 Считается, что модель САРМ была независимо получена У. Шарпом, Дж. Линтнером и Дж. Моссином (см.: [Sharpe, 1963, 1964; Lintner, 1965; Mossin. 19661), а потому ее нередко называют SLM-моделъю (по первым буквам фамилии авторов).
Логика модели такова. Основными индикаторами на рынке капитальных финансовых активов, используемыми инвесторами, являются средняя рыночная доходность km, безрисковая доходность krf под которой обычно понимают доходность долгосрочных государственных ценных бумаг; ожидаемая доходность ценной бумаги ke, целесообразность операции с которой анализируется; коэффициент « β, характеризующий предельный вклад данной акции в риск рыночного портфеля, под которым понимается портфель, состоящий из инвестиций во все котируемые на рынке ценные бумаги; причем пропорция вложения в конкретную бумагу равна ее доле в обшей капитализации рынка. В среднем для рынка β = 1 для ценной бумаги, более рисковой по сравнению с рынком, β > 1; для ценной бумаги, менее рисковой по сравнению с рынком, β < 1
Очевидно, что разность (km — krf) представляет собой рыночную премию за риск вложения средств не в безрисковые, а в рыночные активы1; разность (ke — krf) — это ожидаемая премия за риск вложения в данную ценную бумагу. Эти показатели связаны пропорциональной зависимостью через бета-коэффициент (линейность представления будет доказана ниже).
ke-krf = β(km-krf). (20.17)
Представление (20.17) удобно для понимания сути взаимосвязи между премиями и риском ценных бумаг фирмы (напомним, что для рынка β = 1). Поскольку на практике речь идет об оценке ожидаемой доходности конкретной ценной бумаги (или портфеля), то представление (20.17) преобразуется следующим образом:
ke = krf+β(km-krf) (20.18)
Обе формулы выражают модель оценки финансовых активов (САРМ), применяемую, в частности, для прогнозирования доходности любой ценной бумаги, обращающейся на рынке. Модель имеет очень простую интерпретацию: чем выше риск, олицетворяемый с данной фирмой, по сравнению со среднерыночным (а рынок рисков но определению), тем больше премия, получаемая от инвестирования в ее ценные бумаги. Как известно, на основе прогнозной доходности и данных об ожидаемых доходах, генерируемых некоторой ценной бумагой, можно рассчитать ее теоретическую стоимость; поэтому модель САРМ часто называют моделью ценообразования на рынке капитальных финансовых активов. Заметим, что известны разные представления САРМ — в терминах доходности (наиболее распространено) и в терминах стоимостных оценок (подробнее см.: (Крушвиц, 2000]).
Как видно из модели (20.18), ожидаемая доходность (ke) акций некоей фирмы АЛ является функцией трех взаимосвязанных и взаимообусловленных параметров: среднерыночной доходности, безрисковой доходности и присущего данной фирме β-коэффициента.
1 Смысл премии заключается в том, что инвестор стоит перед выбором; (а) вложить свои средства в государственные ценные бумаги, которые обещают небольшой доход, но доход и собственно инвестированную в активы сумму можно будет наверняка получить; (б) вложить в рыночные ценные бумаги, которые рисковы сами по себе, поскольку никто не гарантирует возврата вложенных в них средств. Инвестор выберет второй вариант лишь в том случае, если ему предложат дополнительное вознаграждение в виде надбавки к доходности, предлагаемой по безрисковым ценным бумагам, Этим объясняется тот факт, что kт всегда больше krf, иначе никто не будет покупать корпоративные ценные бумаги.
Среднерыночная доходность (Market Rate of Return) в общем случае представляет собой доходность рыночного портфеля. В качестве km берут, например, среднюю доходность по акциям, включенным в рыночный портфель, используемый для расчета какого-либо общеизвестного индекса (упомянем, в частности, о «Dow Jones 30 Industrials» и «Standard & Poor’s 500-Stock Index»). Значения Km МОЖНО найти в файлах ведущих информационно-аналитических агентств и бирж.
Безрисковая доходность (Risk-free Rate of Return) представляет собой ожидаемый среднегодовой темп прироста экономики в долгосрочной перспективе, но с поправкой на текущую флуктуацию, обусловленную изменением краткосрочной ликвидности и инфляцией. Единого мнения в отношении значения krf нет. Так, американские финансовые аналитики согласны с тем, что в качестве krf следует брать доходность по казначейским обязательствам, но вот какие обязательства использовать — долго- или краткосрочные, единства нет.
Бета-коэффициент (Beta-coefficient) являет собой основной фактор, отражающий взаимные корреляции доходности данной фирмы с доходностями ценных бумаг, обращающихся на данном рынке. Он представляет собой меру систематического риска акций данной компании, характеризующую вариабельность ее доходности по отношению к среднерыночной доходности (т. е. к доходности рыночного портфеля). Можно еще сказать, что β выражает чувствительность доходности акций данного эмитента по отношению к среднерыночной доходности. Значение β колеблется около 1 (для рынка в среднем β = 1), поэтому для фирмы с высокими его значениями любое изменение на рынке в среднем может приводить к еще большей колеблемости ее показателей доходности. Коротко говоря, β — показатель рисковости ценных бумаг фирмы.
Модель САРМ является основным инструментом для оценки целесообразности операций с финансовыми активами на рынке капитала. В отличие от модели Гордона, она уже не предполагает необходимости оценки возможных к получению дивидендов. Решающую роль имеет точность оценки соответствующих параметров САРМ. Эти показатели инерционны, а их значения оцениваются, периодически корректируются и публикуются агентствами по фирмам, ценные бумаги которых котируются на рынке, т. е. уровень профессионализма в оценке krf, β и km гораздо выше, нежели при индивидуальной оценке рядовым инвестором перспектив фирмы в отношении ее ожидаемых доходов.
Как и любая теория финансов, модель САРМ сопровождается рядом предпосылок, которые в акцентированном виде были сформулированы М. Дженсеном (Michael C.Jensen) и опубликованы им в 1972 г. [Jensen, p. 357—398]. Эти предпосылки таковы.
• Основной целью каждого инвестора является максимизация возможного прироста своего богатства на конец планируемого периода путем оценки ожидаемых доходностей и средних квадратических отклонений альтернативных инвестиционных портфелей.
• Все инвесторы могут получать и предоставлять кредиты в неограниченном объеме по некоторой безрисковой процентной ставке krf при этом не существует ограничений на короткие продажи 1 любых активов.
1 Термин «короткая продажа» означает продажу ценных бумаг, которыми инвестор не владеет. Эта операция делается им в надежде, что цена этих активов в ближайшее время будет падать и можно будет прикупить недостающие бумаги. Подобные операции делаются, как правило, в спекулятивных целях.
• Все инвесторы одинаково оценивают величину ожидаемых значений доходности, дисперсии и ковариации всех активов. Это означает, что инвесторы находятся в равных условиях в отношении прогнозирования показателей.
• Все активы абсолютно делимы и совершенно ликвидны (т. е. всегда могут быть проданы на рынке но существующей цене).
• Не существует трансакционных расходов.
• Не принимаются во внимание налоги.
• Все инвесторы принимают цену как экзогенно заданную величину (т.е. полагают, что их деятельность но покупке и продаже ценных бумаг не оказывает влияния на уровень цен на рынке этих бумаг).
• Количество всех финансовых активов заранее определено и фиксировано.
Как легко заметить, многие из сформулированных предпосылок носят исключительно теоретический характер. Но даже если абстрагироваться от условностей этих ограничений, возможность практического применения САРМ зависит от развития финансового рынка, наличия надлежащей статистики и системности в ее обновлении; в частности, предсказательная сила модели в значительной степени определяется адекватностью значений β-коэффициентов. Каждый вид ценной бумаги имеет собственный β-коэффициент, представляющий собой индекс доходности данного актива по отношению к доходности в среднем на рынке ценных бумаг. Значение показателя р рассчитывается по статистическим данным для каждой компании, котирующей свои ценные бумаги на бирже, и периодически публикуется в специальных справочниках. Для каждой компании β меняется с течением времени и зависит от факторов, имеющих отношение к характеристике деятельности компании с позиции долгосрочной перспективы. Очевидно, что сюда относится прежде всего уровень финансового левериджа, отражающего структуру источников средств: при прочих равных условиях чем выше доля заемного капитала, тем более рискова компания и тем выше ее β1.
Логика расчета β-коэффициента такова.
Пусть имеется совокупность показателей доходности но группе компаний за ряд периодов {kij}, где кij — показатель доходности i-й компании (i= 1, 2 …,t) в j-м периоде ( j = 1,2..,п). Тогда общая формула расчета β-коэффициента для произвольной i-й компании имеет вид
где
(20.19)
ночном доходностью;
— вариация среднерыночной доходности;
— доходность в среднем на рынке ценных бумаг в j-м периоде;
1 Известный специалист в области бухгалтерского учета и финансового анализа Б. Лев (Baruch Lev) показал, что значение β зависит также от уровня операционного левериджа, т.е. чем больше доля постоянных расходов в обшей их сумме, тем выше β (Lev. 1974(b)].
— доходность в среднем на рынке ценных бумаг за все периоды;
— доходность ценных бумаг i-й компании в среднем за все периоды.
Из приведенных формул можно сделать выводы. Во-первых, показатель β действительно можно рассматривать как характеристику рисковости финансового актива, поскольку он отражает связь между вариациями доходности актива и рынка в среднем. Во-вторых, поскольку доходность безрискового актива не зависит от рынка, т.е. не колеблется в динамике, числитель в (20.19) равен 0, а потому для этого актива β = 0. В-третьих, для среднерыночного финансового актива (или рыночного портфеля) числитель и знаменатель в (20.19) совпадают, т. е. для такого актива (портфеля) β = 1
Приведенный алгоритм расчета по формуле (20.19) трудоемок, а потому можно воспользоваться более простым алгоритмом, дающим приблизительное значение β-коэффициента.
Пусть kij) — доходность акций i-й компании в j-м году, a kmj — доходность на рынке в среднем (j = 1, 2, …,п) за все анализируемые периоды. Если к рынку применима модель САРМ, то, как следует из модели, β-коэффициент представляет собой коэффициент эластичности, а его значение можно рассчитать как отношение приращения доходности акций i-й компании к приращению среднерыночной доходности.
(20.20)
Подчеркнем, что алгоритм, задаваемый формулой (20.20), весьма приблизителен, поскольку приращения можно считать разными способами. Приемлемый вариант может быть таким: (1) рассчитывают средние {например, по годам) значения доходности акций данной компании и по рынку в целом; (2) строят уравнение линейной регрессии, отражающее зависимость средней доходности акций данной компании от доходности на рынке в среднем; (3) коэффициент регрессии (т. е. коэффициент при параметре km) и будет β-коэффициентом.
Пример
В табл. 20.2 приведена динамика показателей доходности компании NN по годам.
Таблица 20.2 Динамика показателей доходности
|
Год |
Доходность компании NN, % |
Среднерыночная доходность, % |
|
1 |
12 |
10 |
|
2 |
18 |
12 |
|
4 |
4 |
8 |
|
5 |
9 |
10 |
|
6 |
18 |
13 |
|
7 |
16 |
14 |
Рассчитать значение β-коэффициента.
Решение
За исследуемый период доходность акций компании NN менялась от 4% до 18%, в то время как среднерыночная доходность изменилась с 8 до 14%. Поэтому из (20.20) следует
Таким образом, акции компании NN примерно в 2.3 раза более рисковы, нежели среднерыночный портфель. Иными словами, доходность акций компании в большей степени варьирует по сравнению с рынком. Отсюда вывод: отдавая предпочтение акциям компании NN, можно больше выиграть, но можно и больше проиграть.
Можно сделать более точный расчет, построив уравнение регрессии и найдя коэффициент регрессии.
ke =-12,4+ 2,6km.
При таком расчете получаем, что β = 2,6, т.е. акции компании примерно в 2,6 раза более рисковы по сравнению с рынком.
В целом по рынку ценных бумаг β = 1; для отдельных компаний он колеблется около 1, причем большинство β-коэффициентов находится в интервале от 0,5 до 2,0. Интерпретация β-коэффициента для акций конкретной компании заключается в следующем:
• β = 1; акции данной компании имеют среднюю степень риска, сложившуюся на рынке в целом;
• β < 1; ценные бумаги данной компании менее рисковы, чем в среднем на рынке (так, р = 0,5 означает, что данная ценная бумага вдвое менее рискова, чем в среднем по рынку);
• β > 1; ценные бумаги данной компании более рисковы, чем в среднем на рынке;
• увеличение β-коэффициента в динамике означает, что вложения в ценные бумаги данной компании становятся более рисковыми;
• снижение β-коэффициента в динамике означает, что вложения в ценные бумаги данной компании становятся менее рисковыми.
В качестве примера можно привести усредненные данные о β-коэффициентах ряда американских компаний в 1987—1991 гг. [Ross, Westerfield, Jaffe, p. 264];
наивысшие значения β имели компании «American Express» — 1,5; «Bank America» — 1,4; «Chrysler» — 1,4;
средние значения β имели компании «Digital Equipment Co» — 1,1; «Walt Disney» — 0,9; «Du Pont» — 1,0;
наименьшие значения β имели компании «General Mills» — 0,5; «Gillette» — 0,6; «Southern California Edison» — 0,5.
Следует отметить, что единого подхода к исчислению β-коэффициентов (в частности, в отношении количества и вида исходных наблюдений) не существует. Так, известный американский банкирский дом «Merrill Lynch», занимающийся публикацией рыночных индикаторов, при расчете β-коэффициентов компаний в качестве km использует индекс «S&P 500» и месячные данные о доходности компаний за 5 лет, т.е. 60 наблюдений; компания «Value Line» ориентируется на индекс курсов акций Нью-Йоркской фондовой биржи (NYSE Composite Index), включающий данные о доходности обыкновенных акций более чем 1800 компаний, и использует 260 недельных наблюдений.
В 1995 г. β-коэффициенты появились на отечественном рынке ценных бумаг. Расчеты выполнялись информационно-аналитическим агентством «Анализ, консультация и маркетинг» (АК&М), однако список компаний, как правило, не превышал полутора десятков, охватывая, в основном, предприятия энергетики и нефтегазового комплекса. Значения β-коэффициентов ощутимо варьировали. Так, в январе 1997 г. нефтедобывающая отрасль имела β = 0,9313, а нефтехимическая — 0,1844. Бета-коэффициенты периодически публикуются в прессе.
Пример
Оценить целесообразность инвестирования в акции компании АА с β = 1,6 или компании ВВ с β = 0,9, если klf = 6%: km = 12%. Инвестиция делается в том случае, если доходность составляет не менее 15%.
Решение
Необходимые для принятия решения оценки можно рассчитать с помощью модели САРМ. По формуле (20.18) находим:
для компании АА: ke = 6%+ 1,6 * (12% — 6%) = 15,6%;
для компании ВВ: ke = 6%+ 0,9*(12%- 6%) = 11,4%.
Таким образом, инвестиция целесообразна лишь в акции компании АА.
Как видно из (20.18), САРМ линейна относительно уровня риска р. Это важнейшее свойство модели дает возможность определять β-коэффициент портфеля как средневзвешенную β-коэффициентов входящих в него финансовых активов.
(20.21)
где βk — значение β-коэффициента k-гo актива в портфеле; βp — значение β-коэффициента портфеля; dk — доля 6-го актива в портфеле; n — число различных финансовых активов в портфеле.
Пример
Портфель включает следующие активы: 12% акции компании А, имеющие β = 1; 18% акции компании В, имеющие β = 1,2; 25% акции компании С, имеющие β = 1,8; 45% акции компании D, имеющие β = 0,7. Рассчитать значение β-коэффи-циента портфеля. Решение По формуле (20.20)
βр = 0.12*1+0,18*1,2+ 0,25*1,8+ 0,45*0,7 = 1,1. Риск портфеля несколько выше среднерыночного риска.