Случайный эксперимент определение времени работы определенного мобильного телефона от батареи какие

В статье рассказывается о методах, позволяющих проанализировать время работы мобильных устройств от батареи, что необходимо иметь в виду на этапе проектирования.

Время работы от батареи является важнейшим параметром, который нужно учитывать при проектировании мобильных устройств. Многие мобильные устройства характеризуются расширенной функциональностью, существенно сокращающей время их работы. Для максимального продления времени работы от батареи инженеры должны применять сложные схемы управления питанием.
Для оценки времени работы инженеры применяют анализ разряда батареи, включающий измерение параметров питаемого устройства, его программного и аппаратного обеспечения и отдельных узлов. Методы анализа включают измерение разрядной характеристики и изучение влияния разряда на разные режимы работы и используемые профили. По результатам анализа инженер может выбрать компромиссную схему управления питанием, максимально продлевающую срок службы батареи.
Большинство систем управления питанием экономит энергию батареи, переводя неиспользуемые в тот или иной момент подсистемы в спящий режим, причем зачастую на доли миллисекунд. В результате ток потребления устройства приобретает импульсный характер с длительностью событий менее секунды. Например, сотовый телефон GSM во время передачи может потреблять ток 2-А импульсами, длительностью примерно 500 мкс, в промежутке между которыми ток потребления спадает до миллиамперного уровня на оставшиеся 4,5 мс кадра GSM.

Два метода измерения времени работы от батареи

Один метод измерения времени работы от батареи заключается в тесте снижения напряжения, в ходе которого тестируемое устройство включается при полностью заряженной батарее, а затем измеряется время работы до минимального ее заряда. Этот тест может быть достаточно длительным, поскольку время работы определяется по снижению напряжения до такого значения, когда устройство отключается. Кроме того, результат такого теста зависит от начального состояния батареи, которое может существенно изменяться.
Альтернативный подход заключается в измерении потребляемого тока, который позволяет достаточно точно оценить время работы. Для этого тестируемое устройство на короткое время переводится в рабочий режим, и в этом режиме выполняется измерение потребляемого тока. Затем время работы рассчитывается путем деления номинальной емкости батареи на измеренное значение тока. При использовании этого метода не приходится ждать полного разряда батареи.

Идеальная система

Давайте рассмотрим элементы идеальной системы для анализа разряда батарей, показанной на рисунке 1. Во-первых, система должна включать средства для перевода тестируемого устройства в нужное рабочее состояние (генератор входных воздействий). Для мобильных телефонов в этой роли обычно выступает эмулятор базовой станции. Во-вторых, нужны средства для подачи на тестируемое устройство соответствующего питания, для чего используется либо аккумуляторная батарея, либо источник питания. Источник питания более предпочтителен для тестирования, т.к. обеспечивает согласованность теста и позволяет быстро воспроизводить разные состояния батареи, не ожидая, пока батарея достигнет этих состояний (полностью заряжена, частично разряжена, полностью разряжена). Другими важными элементами системы являются датчик для измерения тока, дигитайзер для регистрации сигналов тока и напряжения, а также программное обеспечение для анализа и сохранения данных, объем которых может быть достаточно большим (до нескольких гигабайт) в случае долговременного тестирования.

Рис. 1. Идеальная система для измерения и анализа тока разряда батарей

Выбор источника питания

Анализ разряда батареи с помощью источника питания позволяет измерять характеристики тестируемого устройства, независимо от его батареи. Источник питания должен характеризоваться быстрым откликом, чтобы минимизировать падение напряжения во время переходных процессов, порождаемых импульсным характером потребления при переключении режимов работы тестируемого устройства или во время импульсной передачи. Многие источники питания общего назначения демонстрируют в таких условиях падение напряжения до 1 В, поэтому следует использовать специальные источники питания (называемые иногда эмуляторами батареи), способные работать в таких условиях без падения напряжения.

Выбор датчика тока и дигитайзера

Быстро изменяющийся ток потребления мобильного устройства порождает две метрологические проблемы, связанные с диапазоном и скоростью измерения. Во-первых, динамический диапазон тока может превышать значение 1000:1 или даже 1 000 000:1. Если максимальный потребляемый ток в активном режиме достигает 1…3 А, то в спящем режиме он падает до десятых долей мкА. Такой диапазон измеряемых значений существенно затрудняет выбор датчика тока.
Можно, конечно, использовать для измерений тока последовательно включенный резистор или токовый шунт, но выбор токового шунта соответствующей величины может оказаться весьма непростой задачей. Если сопротивление шунта оптимально для измерения самого малого тока, то при больших потребляемых токах на нем будет падать большое напряжение, оказывая значительное влияние на измерительную цепь. Если же шунт оптимизирован для измерения большого тока, то, скорее всего напряжение на нем окажется недостаточным для измерения микроамперных токов. Проблему измерения токов разного уровня можно решить, применив несколько шунтов для разных диапазонов, но при этом придется прерывать измерения на время переключения шунтов.
Что касается скорости, то дигитайзер, измеряющий напряжение на токовом шунте и напряжение питания мобильного устройства, должен иметь частоту дискретизации не менее 50 кГц, чтобы захватывать субмиллисекундные токовые импульсы, характерные для сложных схем управления питанием.

Упрощение анализа с помощью комплементарной интегральной функции распределения

Для коммуникационных систем, таких как системы третьего поколения, характерны высокие уровни амплитудной модуляции, необходимые для передачи данных на высоких скоростях. Это порождает сложные формы потребляемого тока случайного характера при рассмотрении его во временной области.
На рисунке 2 показана зависимость потребляемого тока от времени для ВЧ-усилителя телефона cdma2000 в режиме передачи данных по трем каналам. Если рассматривать длительные периоды времени с частой сменой режимов работы, то потребляемый ток становится еще более сложным и непредсказуемым, затрудняя анализ влияния изменений конструкции на потребляемый ток.
Лучший способ визуализации и анализа сложных по форме потребляемых токов заключается в исследовании их статистических характеристик с помощью комплементарной интегральной функции распределения (CCDF). График CCDF показывает зависимость тока, откладываемого по оси X, от интегрального процента появления, откладываемого по оси Y (см. рис. 3). Рассматривая статистическое распределение потребляемого тока, можно быстро увидеть, как часто устройство работает в том или ином режиме потребления. Сравнивая графики CCDF разных схем, можно увидеть, когда устройство потребляет большую мощность (т.е., проводит большую часть времени в состоянии большого потребления), а когда меньшую (т.е., проводит большую часть времени в состоянии малого потребления). Таким образом, можно увидеть, какая схема работает лучше (потребляет меньше мощности), или выявить недостатки конструкции (неожиданные всплески потребления).

Рис. 2. Форма потребляемого ВЧ-усилителем телефона cdma2000 тока, представленная во временной области

Рис. 3. Кривая того же потребляемого тока, что и на рисунке 2, но на графике CCDF

Серийно выпускаемые решения для анализа разряда батарей

Многие изготовители контрольно-измерительного оборудования выпускают продукты, которые можно использовать в разных частях описанной испытательной системы. Некоторые из них предлагают источники питания, обеспечивающие стабильное выходное напряжение в импульсном режиме потребления, близкое по характеру к напряжению батареи. Компания Agilent предлагает всевозможные приборы, позволяющие построить полное решение для анализа разряда батарей с несколькими вариантами соотношения цены и качества.
Решения начального уровня состоят из источников постоянного напряжения для мобильных устройств серии Agilent Technologies 66300. Источник питания Agilent 66300 предназначен специально для питания мобильных устройств и одновременного измерения потребляемого тока. В состав системы для измерения и анализа тока входит имитирующий работу батареи источник питания с высокоскоростным измерительным дигитайзером (подобным тому, что применяется в осциллографах), способным выполнять точные измерения тока в активном состоянии устройства, в режиме ожидания и в отключенном режиме. Этот источник постоянного напряжения и прилагаемое к нему программное обеспечение позволяют наблюдать формы потребляемого тока так, как это делается на осциллографе, и просматривать зарегистрированные данные и графики CCDF без какого-либо программирования. Если же требуется большая точность и скорость регистрации, то можно воспользоваться другими решениями компании Agilent.

Измеряем потребление батарейки на мобильных устройствах. Эксперимент в Яндексе

В наши дни можно утверждать, что телефон перестал быть устройством только для звонков. Он позволяет нам оплачивать покупки, находить правильную дорогу, вызывать такси. Ситуация, в которой у вас садится батарейка, становится одной из самых стрессовых. Остаться ночью на незнакомой улице без телефона довольно неприятно. При этом расход батарейки растет во многом как следствие расширения возможностей.

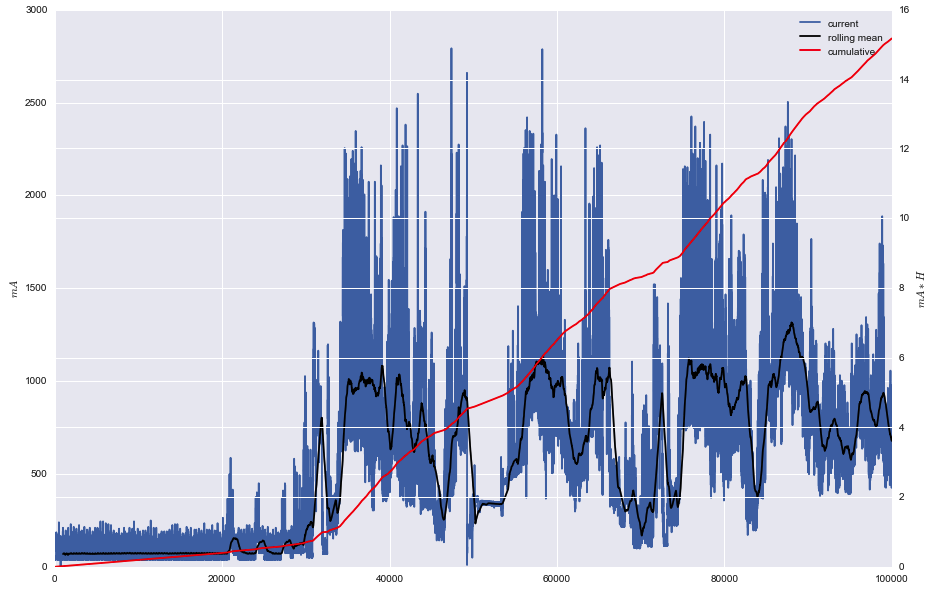
Производители как железа, так и софта, стараются решить эту проблему. Для Яндекса она тоже актуальна, потому что наши сервисы — это то, что должно быть под рукой у человека в любой момент. Мы по-разному над этим работаем и в рамках эксперимента создали устройство для измерения тока, который потребляется телефоном с батарейки. Теперь мы умеем мерить мгновенные значения тока с батарейки телефона (Nexus, iPhone и др.) в миллиамперах 500 раз в секунду, сохранять эту метрику на диск и считать по ней среднее потребление.

Под катом я расскажу, как у нас это получилось. Будет много фото железок, но заранее прошу прощения за качество — снимки сделаны в боевых условиях.

С самого начала у нас была какая-то тактика

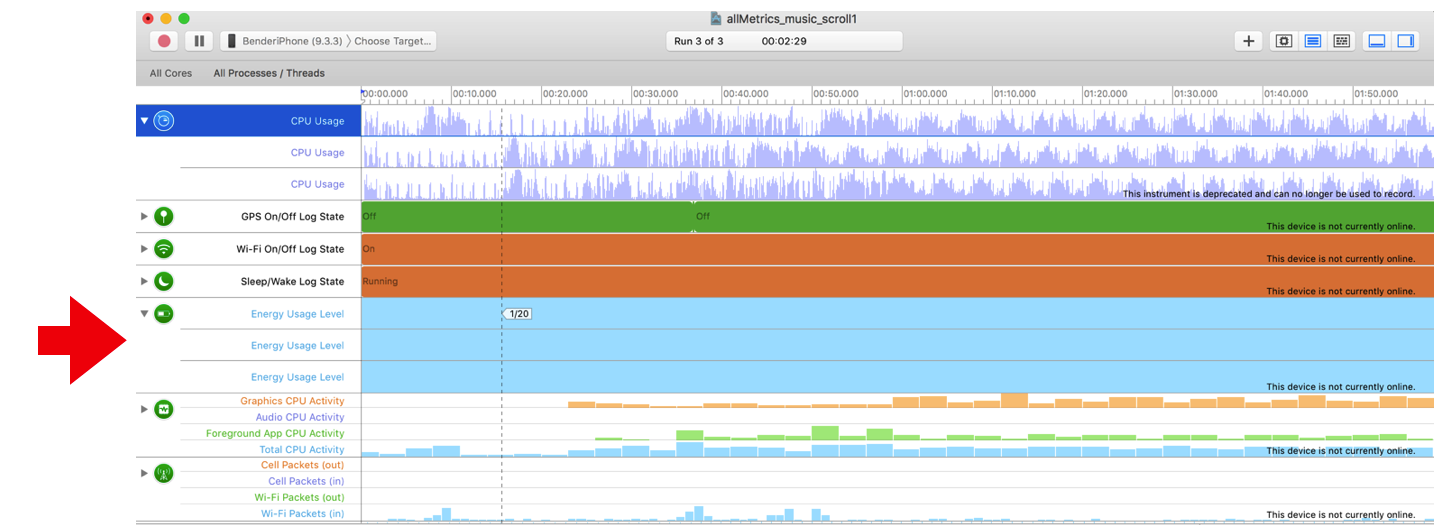
Несколько месяцев назад, когда мы начинали прикручивать нагрузочное тестирование телефонов к Яндекс.Танку (это наш opensource инструмент для тестирования производительности), мы столкнулись с тем, что одну из самых важных метрик — потребление тока с батарейки — мы не можем замерить достоверно, а на некоторых телефонах не можем замерить вообще. Например, вот как выглядит график потребления тока на iPhone, полученный стандартными средствами от Apple:

Все три запуска теста значение потребления вообще не изменялось и было равно 1/20. Удивляет использованная единица измерения — 1/20 означает, что если телефон дальше будет работать с тем же энергопотреблением, то сядет он за 20 часов. То есть, метрика получается очень неточная и не очень интерпретируемая. Кроме того, цифры в сыром виде получить нельзя, только разве что скриншот сделать и приложить его к тикету.

С Android девайсами ситуация выглядит лучше, но все равно далека от идеала. Ток замерять можно, читая из /proc/… циферку, но лучше не делать это слишком часто — опросом значения можно просадить производительность телефона и испортить тесты. На разных девайсах циферка находится в разных местах файловой системы. На части Android телефонов вообще отсутствует железка, измеряющая ток, поэтому на них не получится программными средствами снимать потребление. На Nexus, которые мы взяли как reference, значение в /proc меняется раз в 20 секунд.

В общем, мы решили попробовать измерять потребление хардверно и таким образом убить всех зайцев разом: так можно мерить вообще на всех девайсах, включая ноутбуки и холодильники. Мы знали о существовании Power Monitor, но цена устройства (примерно $800 за штуку, а на каждый телефон потребуется свой девайс), и его несовместимость с Linux (а значит, и сложности с автоматизацией), заставили задуматься о своем велосипеде. Аналогичная ситуация наблюдается с осциллографами и другими измерительными устройствами общего назначения на рынке — покупать дорого, автоматизировать сложно.

Существует еще проект BattOr, по описанию это примерно то, что мы хотим. Сам я не пробовал связаться с авторами, но коллеги говорят, что команду купил Google и с тех пор от них ничего не слышно и на почту они не отвечают. Совпадение? =)

Для начала, в качестве proof-of-concept, мы собрали схему с шунтом, аналогичную представленной в этой статье. Ток мы измеряли в разрыве провода USB. Поскольку значение силы тока ожидалось небольшое, до 500 мА, пришлось усиливать напряжение с помощью инструментального усилителя, а не снимать его напрямую с шунта ардуинкой.

После еще некоторых танцев с бубном нам удалось получить на экране ноутбука график потребления телефоном тока с USB. Тут мы поняли, что таких измерений нам не хватает — мы мерим не ток с батарейки, а ток с USB, телефон запасает энергию в батарейке, и мы не можем сопоставить график потребления тока с тем, что происходит на телефоне. Решили, что нужно вытаскивать батарейку из телефона и использовать вместо нее внешнее питание, а USB во время тестов вообще не втыкать.

Электроника работает на белом дыме

Как известно, все, чему нас учили на уроках физики и электротехники, — ложь, никаких электронов не существует, а устройства работают на белом дыме. И если этот белый дым выходит, то устройство работать перестает. В очередном эксперименте белый дым вышел из Arduino и мы ее потеряли. Оказалось, что между “0” на входе нашего блока питания и “-“ на его выходе — 88 вольт переменного напряжения. После еще нескольких экспериментов с разными БП мы поняли, что не все они одинаково хороши, но есть такие, которые нам подходят. И мы стали использовать эти подходящие. Также мы решили больше не использовать схему с шунтом и инструментальным усилителем и вместо этого взять готовый модуль измерения тока к Arduino на базе MAX471, которая по сути то же самое, только в виде микросхемы. Еще мы рассматривали вариант на базе датчика Холла (ACS712), но, изучив документацию на этот чип, увидели, что он сильно шумит и решили даже не пробовать.

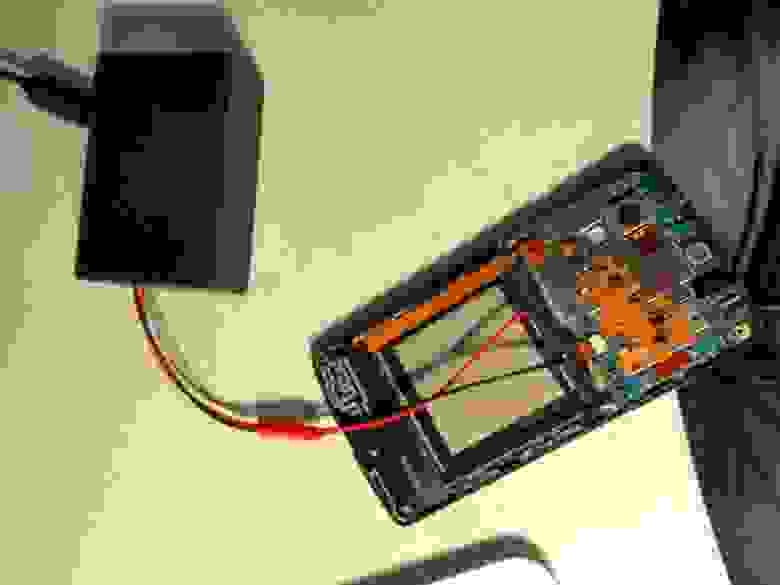
Для того, чтобы питать современный телефон не от встроенной батареи, а от внешнего источника, мало его разобрать и вытащить батарею — уж слишком умны современные батареи. Поэтому мы вытаскиваем из батареи контроллер и подключаемся уже к нему.

Чтобы вернуть модифицированный таким образом iPhone (или другое устройство) в собранное состояние, мы сверлим корпус и выводим два проводка.

Вот такая коробочка у нас получилась в результате. Правда, в метро ее лучше не возить, телефон, провода, вот это все… могут не понять =)

Что нам это дает

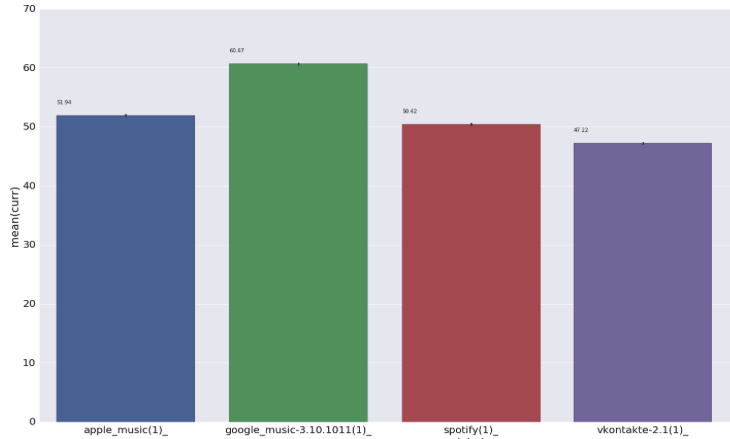
Мы уже начали внедрять тестирование наших приложений на энергопотребление, так что ждите улучшений в этой области. Процитирую коллег, которые пользуются нашей коробочкой.

Для получения релевантного результата теста при прямых замерах батарейки этим устройством достаточно пяти минут. Если же замерять «как раньше», то есть смотреть на скорость уменьшения % заряда батареи — то требуется 6-8 часов, плюс не забывайте про человеческий фактор. То есть, время теста сократили с 8 часов до 5 минут: почти в 100 раз.

Текущий разброс результатов замера ± 15%. Это не идеал и надо погрешность уменьшать. Однако, теперь доверие к результату повысилось за счёт исключения человеческого фактора и существенно меньшего времени на 1 замер. Достаточно выполнить за полдня много-много замеров и отсечь результаты, пострадавшие от внезапных всплесков непонятной активности на телефоне.

Стало возможным кросс-платформенное, и кросс-девайсное сравнение значений. Единица измерения — mA, а не «скорость уменьшения процентов заряда», которая зависит от платформы, объёма батареи, «свежести» батареи, не говоря уже про запущенные процессы… Сравнить только mA при одном и том же запущенном Я.Сервисе на Andoird и на iOS — нельзя. Надо добавить поправочный коэффициент — сколько жрёт каждая платформа, без Я.Сервиса. Но, это опять-таки вопрос на пол дня замеров (и это с кофе-поболтать).

Пара слов про софт

Чтобы собирать данные от Arduino (а она просто 500 раз в секунду шлет их по USB), мы написали простенькую читалку. На Python возникли проблемы с повторным открытием устройства на чтение — во второй раз данные уже не читались. Мы не стали разбираться и просто переписали то же самое на Golang — после этого все заработало.

Тут нас ждали еще небольшие грабли: в буфере устройства с предыдущего запуска остаются старые данные. Поэтому сейчас мы просто отбрасываем первые 500 измерений (1 секунда). Затем собранные в .csv данные обрабатываем скриптом на Python (в котором используются Pandas и Seaborn) и получаем графики, которые вы видели в начале статьи.

Если вам интересны исходники читалки, прошивка и код для обработки данных — могу поделиться, пишите в личку.

Цели урока:

• раскрыть значение теории вероятностей в
  развитии математико-статистического
  мировоззрения;
• рассмотреть понятия: случайный опыт, случайное
  событие, элементарный исход;
• рассмотреть различные способы кодирования
  элементарных исходов;
• показать взаимосвязь теории вероятности и
  информации;
• рассмотреть роль теории вероятностей в
  обработке статистических данных;
• научить выполнять переход от словесного
  описания событий и экспериментов к
  теоретико-множественному;
• рассмотреть различные подходы к введению
  понятия вероятность;
• показать роль компьютера в обработке
  экспериментальных данных.

Оборудование: компьютер, видеопроектор,
экран.

План занятия

1. История развития «науки о случае».
2. Случайные события. Случайный эксперимент.
   Элементарные исходы.
3. Классическое определение вероятности. Примеры.
4. Вероятность и информация.

История развития «науки о случае» [4]

Вопрос к классу: приходилось ли вам встречаться
со словом «вероятно»? Где, при каких
обстоятельствах? Вероятность относится к числу
понятий, которыми мы охотно пользуемся в
повседневной жизни, совсем не задумываясь об
этом. Например, на вопрос «Завтра пойдем на
хоккей?» мы отвечаем «Вероятно, да». В этой
короткой реплике имеется попытка оценить
возможность появления данного события.

Если сравнивать с тысячелетней историей
математики, теория вероятностей — наука совсем
молодая, первые научные трактаты появляются
только в XVI в. Но то, что случайность подчиняется
каким-то своим законам, люди заметили еще в
глубокой древности. Можно считать установленным,
что во время игры или гадания кости животных
подбрасывали и следили за тем, как они упадут.
Было хорошо известно, что некоторые грани кости
выпадают чаще, но никаких количественных оценок
случайности люди не знали. Игры, основанные на
случайности, вызывали огромное возбуждение,
азарт у всех участников. Игроки старались как-то
обобщить накопленный опыт и найти надежные
правила, увеличивающие шансы в игре. Как вы
считаете, подчиняется ли вероятность некоторым
законам? Оказывается, да.

<Презентация (слайды 1 — 4)>

Давайте и мы попробуем посмотреть, как
проявляются законы, которым подчиняется случай.
Проведем такой эксперимент. Возьмите любую
монету и подбросьте ее 10 раз. Подсчитайте,
сколько раз она упадет на «орла» и сколько раз
на «решку»? При единичном подбрасывании
выпадение «орла» и «решки» происходит
совершенно случайно. Но если подбросить монету 100
раз, то почти наверняка можно утверждать, что
примерно половину раз она упадет на «орла».
Знаменитый французский естествоиспытатель
Бюффон (1707 — 1788) проделал этот опыт 4040 раз, при
этом выпадение «орла» равнялось 2048. Английский
математик Пирсон (1857 — 1936) повторил опыт 12 тысяч
раз, число выпадений герба составило 6019. Из этих
опытов видно, что доля появления герба явно
стремится к 0,5.

Как вы думаете, с какой частотой будет выпадать
шестерка при подбрасывании игрального кубика? А
если подбрасывать канцелярскую кнопку, то как
чаще всего она будет падать? Почему? (Кнопка
несимметрична, поэтому нельзя считать
равновозможными исходы двух событий — кнопка
падает или острием, или шляпкой).

Начиная со второй половины ХХ века
количественное измерение явлений,
математическое моделирование различных
процессов стали непременным условием научного
творчества. Особое значение приобрели
вероятностно-статистические методы. Во всем мире
настолько усилился интерес к «науке о случае»,
что теория вероятностей стала модной в самом
лучшем смысле этого слова.

В России первые исследования по теории
вероятностей были выполнены к середине XIX
столетия. Они связаны с именами замечательных
ученых-математиков Н.И.Лобачевского,
М.В.Остроградского, В.Я.Буняковского.
В.Я.Буняковский впервые дал на русском языке
терминологию новой науки, которая не изменялась
до сих пор. Во второй половине XIX века блестящие
открытия были сделаны П.Л.Чебышевым,
А.М.Ляпуновым и А.А.Марковым, с тех пор теорию
вероятностей стали называть «русской наукой».
С.Н.Бернштейн, А.Я.Хинчин, А.Н Колмогоров
продолжили традиции своих учителей.

Сейчас нет области знания, в которой бы не
использовались методы теории вероятностей. Это
физика, геодезия, теория измерений, медицина,
биология, космонавтика, теория стихосложения,
лингвистика, психология, теория информации,
теория надежности, статистический контроль
качества, планирование эксперимента и другие.

Нельзя не отметить, что теория вероятностей
является математической основой одной из новых
наук ХХ века — кибернетики. Существенный
отпечаток на развитие теории вероятностей
наложило еще одно детище научно-технической
революции — компьютеры, возможности которых,
образно говоря, открыли шлюзы, сквозь которые
вероятностно-статистические методы хлынули в
практику.

<Презентация (слайды 5 — 7)>

Случайные события. Случайный эксперимент.
Элементарные исходы. [6]

Рассмотрим еще раз пример с подбрасыванием
монеты. Этот эксперимент можно считать
простейшим случайным опытом. В результате такого
опыта монета может с равными шансами упасть на
одну из двух своих сторон.

Определение. Событие называется случайным,
если при одних и тех же условиях оно может как
произойти, так и не произойти.

Говоря о случайном событии, мы всегда имеем в
виду наличие определенных условий, без которых
об этом событии не имеет смысла говорить (в
примере с монетой есть возможность неоднократно
воспроизводить одни и те же условия, в которых
наблюдается данное событие). Этот комплекс
условий называется случайным опытом или
случайным экспериментом. До эксперимента, как
правило, невозможно сказать, произойдет данное
событие или нет, — это выясняется лишь после его
завершения. Но в теории вероятностей принято
считать случайными и события невозможные
(которые никогда не могут произойти), и события
достоверные (которые происходят при каждом таком
эксперименте). Например, при подбрасывании
игрального кубика появление 7 очков —
невозможное событие. Кроме случайного события, с
опытом связано еще одно важное понятие —
элементарного исхода.

Определение. Элементарным исходом называется
один из взаимоисключающих друг друга вариантов,
которыми может завершиться случайный
эксперимент.

Определение. Элементарным событием называется
исход, неделимый на более мелкие исходы.

А любое неэлементарное событие будет состоять
из некоторого множества исходов, которые
называются благоприятными для этого события.
Благоприятны они в том смысле, что приводят к
наступлению данного события. Если обозначить
множество всех возможных исходов опыта буквой А,
то каждый исход есть элемент а этого множества, а
любое случайное событие В — это подмножество А.

Невозможному событию соответствует пустое
множество благоприятных исходов, а достоверному
— множество всех исходов В.

Мы ввели три важнейших понятия, лежащие в
основе теории вероятностей: случайный
эксперимент, случайное событие, элементарный
исход.

Определения вероятности

Как видно из примеров, многие явления нам
кажутся случайными только при первом
(поверхностном) взгляде на них. При более
углубленном изучении обнаруживается, что сквозь
нагромождение случайностей пробивает себе
дорогу закономерность. Так, в первом примере доля
выпадения «решки» колеблется вокруг числа 0,5; во
втором примере (игральный кубик) выпадение
любого числа от 1 до 6 приблизительно равняется 1/6.
Закономерности такого рода привлекли внимание
ученых. Для того чтобы численно выразить эту
закономерность, были введены различные
определения понятия вероятности. Рассмотрим те
из них, которые получили наибольшую известность.

<Презентация (слайд 8)>

Классическое определение вероятности

Исторически первым определением понятия
вероятности является классическое определение
(начало XIX века). Всякое событие мы будем
рассматривать как исход некоторого испытания.
Например, событие «цель поражена» является
случайным исходом испытания, состоящего в том,
что по цели был выпущен снаряд. Классическое
определение вероятности тесно связано с
некоторыми свойствами событий. Во-первых,
события должны быть несовместными, т.е. появление
одного из событий в единичном испытании
исключает появление другого события в этом же
испытании. Во-вторых, при рассмотрении группы
этих событий не может произойти никакое другое
событие, не входящее в эту группу (события
единственно возможные). В-третьих, события должны
быть равновозможными, т.е. ни у одного из событий
нет каких-либо преимуществ перед другими.

Определение. Вероятностью случайного события А
называется отношение числа благоприятных
исходов к общему числу несовместных единственно
возможных и равновозможных исходов.

Используя математические символы, данное
определение можно записать так: Р(А) = , где Р(А) —
вероятность события А, m — число исходов,
благоприятных для события А, n — общее число
несовместных единственно возможных и
равновозможных исходов.

Используя это определение, можно вывести, что
вероятность достоверного события равна 1,
вероятность невозможного события равна 0,
вероятность случайного события заключена между 0
и 1.

<Презентация (слайд 9)>

Пример 1. Одной из первых задач, для решения
которых были использованы методы классической
теории вероятностей, является следующей:
вычислить вероятности всех возможных значений
суммы очков, выпадающих при подбрасывании двух
игральных костей. Очевидно, самым маленьким
значением суммы является число 2, самым большим —
число 12. Будем последовательно вычислять
вероятности всех значений от 2 до 12. Сначала
вычислим общее число возможных исходов. Их будет
36 (каждая цифра, выпадающая на первой игральной
кости, может складываться с шестью различными
цифрами, выпадающими на второй игральной кости).
Эти исходы отвечают трем требованиям,
предъявляемым классической вероятности. Они
несовместны, т.к. появление одного исхода
исключает появление других в единичном
испытании. Они единственно возможны, т.к. при
одном подбрасывании двух игральных костей
возможен один и только один из этих исходов. Они
равновозможны, т.к. в силу случайного падения
игральных костей нет никаких оснований считать
какой-либо исход более возможным, чем другие.
Выполнение трех перечисленных требований
позволяет использовать классическое
определение для подсчета вероятности. Появлению
числа 2 (как и числа 12) благоприятствует всего
один исход, появлению числа 3 благоприятствуют
уже два исхода (1+2, 2+1). Продолжая вычисления
аналогичным образом, все полученные результаты
представим в следующем виде:

Пример 2. Подбрасываем две одинаковые монеты.
Какова вероятность того, что она упадут на одну и
ту же сторону?

Опыт имеет четыре равновозможных исхода: обе
монеты упадут на «орла», обе монеты упадут на
«решку», первая монета упадет на «орла», вторая
— на «решку», вторая монета упадет на «орла»,
первая — на «решку». Благоприятных для нашего
события будут два исхода, поэтому искомая
вероятность равна ?.

Пример 3. Из коробки, в которой 2 белых и два
черных шара, вытаскивают два шара. Какова
вероятность того, что они окажутся одного цвета?
Ответ: Р(А) = 2/3.

Пример 4. Брошены две игральные кости. Найти
вероятность того, что сумма очков на выпавших
гранях равна семи. Ответ: Р = 1/6.

Пример 5. Монета брошена два раза. Найти
вероятность того, что хотя бы один раз появится
«герб». Ответ: Р = ?.

Вероятность и информация.

Выясним, какая связь существует между теорией
информации и теорией вероятностей.

К числу основных понятий теории вероятностей
относится понятие информации. В последние годы
на границе между точными и гуманитарными науками
создан целый ряд новых дисциплин,
синтезировавших абстрактно-математический
метод точных наук и описательный метод наук
гуманитарных. К числу этих наук относится и
теория информации. Первые работы по
статистической теории информации опубликовал
американский математик и инженер К.Шеннон в 1948
году. Как вы уже знаете, понятие информации тесно
связано с понятием неопределенности. Информация
о состоянии системы имеет смысл только при
наличии некоторой неопределенности (энтропии)
относительно состояния этой системы (если
состояние системы заранее известно, то
информативность сообщения равна нулю).

Можно ли измерить степень неопределенности
системы? Чтобы ответить на этот вопрос,
рассмотрим три примера: А — подбрасывание
монеты, В — подбрасывание игральной кости, С —
изготовление детали. В третьем примере
предположим, что брак составляет 1% всех деталей.
Будем называть каждый из этих примеров системой.
Система характеризуется двумя параметрами:
количеством возможных состояний и вероятностями
этих состояний. Выясним, как зависит
неопределенность системы от этих двух
параметров. Первая система (монета) может
принимать всего два возможных состояния —
выпадение «орла» (событие А1) или выпадение
«решки» (событие А2). Вторая система (игральная
кость) может принимать шесть возможных состояний
— выпадение одного очка (событие В1), двух очков
(событие В2) и т.д., значит, неопределенность какой
системы больше? (второй). Какой вывод вы можете
сделать? (Из этого можно сделать первый вывод:
неопределенность системы зависит от числа
возможных состояний системы).

Но если сравнивать между собой первую и третью
системы, то для третьей системы почти наверняка
можно предсказать, что (?): (изготовленная деталь
окажется годной). Рассмотрим вероятности всех
этих событий: Р(А1) = 0,5 и Р(А2) = 0,5; Р(В1), Р(В2) и т.д.
приблизительно равны 0,167. Вероятность того, что
изготовленная деталь окажется годной составит
0,99. Напрашивается второй вывод (какой?):
неопределенность системы зависит от вероятности
возможных состояний системы.

Формула, в которой учитываются оба параметра
системы, была открыта К. Шенноном и записывается
таким образом: энтропией системы Х называется
величина

Н(Х) = — , в
качестве основания логарифма удобнее принять
число 2. В качестве единицы измерения энтропии
Шеннон предложил принять энтропию, заключенную в
системе, находящейся в двух равновозможных
состояниях (пример с монетой), эта единица
измерения получила название «бит», что означает
двоичный знак.

Вероятностные исследования, какими бы
абстрактными они не показались, всегда нацелены
на практику. Проведем эксперимент. Выберите
любую страницу текста в ваших конспектах,
подсчитайте общее количество символов на ней
(знаки препинания не учитывайте, а пробелы между
словами надо учитывать), а затем подсчитайте
количество букв «а», разделите второе число на
первое и запишите ответ в тетрадях. Какие у вас
получились числа? (Близкие к 0,06). А если проделать
те же вычисления для буквы «о», то получится
примерно 0,09. Это значит, что частота буквы
обладает статистической устойчивостью, эти
частоты приняты за приближенные значения
вероятностей, например, частота появления буквы
«а» равна 0,062; буквы «ф» — 0,002; знака «пробел» —
0,175.

Учитываются частоты букв при изготовлении
клавиатур компьютеров: часто встречающиеся
буквы расположены на самых удобных местах,
встречающиеся редко — на менее удобных. В 1963 году
в науке появилось понятие речевой вероятности
(математическая лингвистика). Получение
статистических характеристик речи необходимо
для развития техники телефонной связи. Работа
современных технических устройств в той или иной
мере связана с переработкой и передачей
информации. Расшифровывая символы, всегда
используют частоту появления букв в том или ином
языке. При передаче информации коды шифруются
различными способами, возникает задача
отыскания оптимального способа кодирования.

Домашнее задание

Задача 1. В ящике имеется 15 деталей, среди
которых 10 окрашенных. Сборщик наудачу извлекают 3
детали. Найти вероятность того, что извлеченные
детали окажутся окрашенными. (Отв. 24/91)

Задача 2. В ящике 100 деталей, из них 10
бракованных. Наудачу извлечены 4 детали. Найти
вероятность того, что среди извлеченных деталей
нет бракованных. (Отв.0,65)

Список литературы

1. Коваленко И.Н., Филиппова А.А. Теория
   вероятностей и математическая статистика.
   Учебное пособие для втузов. М., Высшая школа, 1973, 368
   с.
2. Гмурман В.Е. Теория вероятностей и
   математическая статистика. Учебное пособие для
   вузов. Изд.6-е, стер. — М., Высшая школа, 1998. — 479 с.
3. Гмурман В.Е. Руководство к решению задач по
   теории вероятностей и математическая
   статистике. Учебное пособие для втузов. Изд.2-е,
   доп. — М., Высшая школа, 1975. — 333 с.
4. Гнеденко Б.В., Хинчин А.Я. Элементарное введение
   в теорию вероятностей. Изд.8-е, испр. — М., Наука,
   1976. — 168 с.
5. Чубарев А.М., Холодный В.С. Невероятная
   вероятность. М., Знание, 1976. — 128 с.
6. Бунимович Е., Булычев В. Вероятность и
   статистика в курсе математики основной школы.
   Учебно-методическая газета Математика №№ 17 —
   24.2007

Приложение.

Пользуюсь iPhone 13 Pro Max полтора года, и последние месяца два начал замечать заметно ускорившуюся разрядку аккумулятора. Раньше так не было.

Я давно не из тех, кто заморачивается по этому поводу — главное, что работает, и на этом спасибо. Списал момент на установку бета-прошивок и подуставший аккумулятор.

В выходные случайно, в Настройках, обратил внимание на функцию, про которую уже совсем забыл. Выключил. iPhone теперь работает дольше чуть ли не на треть.

Выключите режим модема

Да, всё настолько просто, что даже немного глупо. Настройки -> Режим модема.

Когда Режим модема включён, смартфон в постоянном режиме «раздаёт» сигнал Wi-Fi и Bluetooth близлежащим девайсам. Это ускоряет разрядку аккумулятора на любом устройстве.

Если вы пользуетесь только девайсами Apple и активируете этот режим с другого своего «яблочного» гаджета, то он выключится автоматически при отсоединении устройства. Но если активировать настройку вручную, режим будет работать всегда, пока не отключите. Многие это забывают, и я в их числе.

На некоторых устройствах активный Режим модема может даже замедлять скорость зарядки от сети — например, iPhone 12 mini и iPhone SE последних двух поколений. Так что загляните и выключите, не пожалеете.

Также, в том же меню, советую выключить и Семейный доступ к точке. Если понадобится, всегда сможете зайти в Настройки и включить функцию вручную. Нечего ей 99% времени впустую тратить заряд аккумулятора.

После этих процедур заметил замедление разрядки моего iPhone — минимум на четверть за день. Может, эта простейшая инструкция и вам поможет.

(45 голосов, общий рейтинг: 4.40 из 5)

Что влияет на время работы смартфона

Помните старые добрые времена, когда вы заряжали аккумулятор мобильного телефона всего лишь один раз в три дня? Сегодня такого не бывает. Газета The Washington Post изучила 13 смартфонов и протестировала качество их батарей, чтобы ответить на главный вопрос — соответствуют ли они обещаниям производителей.

Было установлено, что гарантии производителей относительно целого дня работы на одной зарядке для таких смартфонов, как iPhone XR и Samsung Note 9, не выполняются — батареи смогли продержаться только 12 часов в режиме воспроизведения видео.

Размер дисплея существенно влияет на время работы аккумуляторов. Из-за большой площади дисплея смартфон требует больше энергии, особенно при высокой яркости.    Дополнительно есть миллионы приложений, которые могут потреблять много энергии батареи, даже если вы этого не замечаете. Кроме того, на энергопотребление сильно влияет начинка смартфона — наиболее энергоэффективными считаются процессоры Snapdragon из средней и топовой линеек.

iPhone и Android: отличия аккумуляторов

Разные производители используют в смартфонах разные батареи. В то время, как все Android-бренды указывают, какой емкостью обладает аккумулятор смартфона, Apple описывает характеристики батареи в продолжительности работы в режиме разговора. На самом деле аккумулятор новых iPhone относительно небольшой — до 3500 мАч в топовой версии iPhone 11 Pro Max.

Хорошо быть уверенным, что твой телефон будет работать в то время, когда он нужен. Ведь внезапное окончание заряда аккумулятора может привести к отсутствию связи именно тогда, когда должен произойти важный звонок. Чтобы свести вероятность данной проблемы к минимуму неплохо бы знать какое количество электрической энергии потребляет телефон в том или ином режиме своей работы. Допустим вы зарядили телефон на 100% и планируете обходится без подзарядки продолжительное время. Но при этом есть нужда в использовании различных приложений, которые установлены на телефоне. Дело в том, что при работе разных приложение потребление тока также разное. Давайте с вами разберемся, как можно измерить количество потребляемой энергии телефоном, чтобы для себя знать, какими функциями можно больше пользоваться, а какие лучше запускать только при необходимости. Чтобы продлить время работы телефона, когда он используется в отсутствии доступа к подзарядке.

Итак, нам понадобится обычный амперметр постоянного тока. Простой электронный мультиметр для этих целей как раз подойдет. Если у вас его еще нет, то желательно приобрести хотя бы самую дешевую его модель. Так как в личном инструменте домашнего мастера он должен быть у каждого. Берем мультиметр, выставляем на нем режим измерения постоянного тока на пределе до 10 ампер. Но перед этим нужно подготовить для измерения сам телефон. Для этого снимаем заднюю крышку телефона, чтобы добраться до аккумулятора. Выключаем телефон и вынимает аккумулятор.

Как известно, чтобы измерить ток, нужно щупы мультиметра подключить в разрыв цепи, а именно. Эти щупы мультиметра должны быть между плюсовым выводом аккумулятора и плюсовым контактом самого телефона. Хотя можно измерительные щупы подключить и между минусами тех же контактов. То есть, если мы будем использовать плюсовые контакты, то минус аккумулятора и минус питания телефона должны быть соединены. Ну, а если используются минусовые контакты, то соединены должны быть плюсовые контакты.

Теперь как можно сделать выводы, к которым и будем подсоединять свой амперметр, своими руками (это нужно для удобства измерения). Берем два куска изолированного многожильного провода, небольшого сечения. Подойдут любые провода диаметром где-то 0,3-0,5 мм. Слишком толстые будет не совсем удобно использовать, а слишком тонкие будет являться дополнительным сопротивлением для прохождения тока. Длина проводов где-то 20 см. Хотя она особо роли не играет. Лишь бы не были слишком длинные или слишком короткие. Ведь это просто не совсем удобно. С концов этих проводов снимаем изоляцию на расстоянии где-то 3 мм.

Еще нам понадобится кусочек обычного скотча, который будет служить изолятором между ранее заготовленными проводами, а точнее между их оголенными частями. Смысл заключается в том, чтобы аккуратно соединить концы этих проводов, ровно зафиксировав между ними этот кусочек скотча. Размеры куска скотча должны быть такими, чтобы полностью покрывать один контактный вывод на аккумуляторе (плюса или минуса). После этого эту проволочную конструкцию нужно также аккуратно зажать между аккумулятором и контактами питания самого телефона. В итоге мы получим как бы разрыв одного из полюсов питания телефона. Если соединить эти провода другими концами, то телефон включится, нажав предварительно кнопку включения.

Итак, теперь можно приступать к самому измерению тока потребления. Мы измерительные щупы мультиметра подсоединяем к нашим проводам, идущим от телефона. Включаем мультиметр  и телефон, после чего пристально смотрим на экран амперметра. Уже при запуске амперметр покажет определенные значения тока. Дожидаемся пока телефон полностью загрузит свою операционную систему и войдет в нормальный режим своей работы. Ну, а теперь уже можно и тестировать величину потребления тока в различных режимах работы устройства связи и развлечения.

Начинаем по очереди запускать различные приложения на телефоне, и при этом наблюдаем за изменением потребляемого тока.

Лично у меня получилось так:

» больше всего тока потребляется при записи видео с камеры, около 700 мА;
» при работе самого экрана на средней яркости ток около 200 мА;
» в режиме ожидания с погасшим экраном ток практически не потребляется;
» при воспроизведении видео на плеере ток где-то около 250 мА;
» при прослушивании музыки с погасшим экраном ток около 30 мА;
» просмотр фотографий приравнивается к рабочему экрану – 200 мА;
» в режиме телефонного разговора ток потребления около 300 мА.

Теперь как можно исходя их увиденных величин тока понять, на сколько именно хватит заряда аккумулятора смартфона. Тут все просто. Нужно имеющуюся емкость остаточного заряда аккумулятора разделить на имеющиеся значения тока. Допустим мы полностью зарядили свой смартфон. Реальная емкость аккумулятора в этом телефоне равна 3000 ампер. Значит нужно 3000 разделить, к примеру на 300 мА (средне потребляемый ток при разговоре по телефону). В итоге мы получим 10 часов беспрерывных разговоров на полном заряде аккумулятора. Если же наш аккумулятор разрядился на половину и имеет заряд на 50%, то значит его емкость уже равна где-то 1500 мА. Значит при половинном заряде мы будет разговаривать без перерыва около 5 часов (1500 делим на 300). Вряд ли вы будете без перерыва столько говорить, хотя у некоторых так и бывает.

В результате наших действий мы имеем. Допустим батарея разрядилась уже до 20%. При этом мы сразу же в голове подсчитываем, что примерная остаточная емкость заряда аккумулятора равна где-то 600 мА. И зная какие функции телефона сколько потребляют тока мы начинаем экономить. То есть, можно слушать музыку без включенного экрана, либо разговаривать непродолжительное время. Примерно прикидывая остаточное время. В итоге мы можем обезопасить себя от нежданного полного разряда своего телефона и его внезапного отключения.

P.S. Как по мне, так знать сколько именно потребляет телефон электроэнергии просто необходимо. Ведь в этом случае вы защитите самого себя от проблемы неожиданного отключения своего устройства связи в самый неподходящий момент. Причем, что процедура измерения силы тока на телефоне достаточно проста, и ее может сделать даже школьник.