Задание 5
Определите, на какой маршрут до станции потребуется меньше всего времени. В ответе укажите, сколько минут потратят на дорогу Ваня с дедушкой, если поедут этим маршрутом.
Решение:
1-й маршрут по шоссе по шоссе состоит из Николаевка – Сосновка и Сосновка – Игнатьево, на него потратят t1 = 117 минут (см. задание 4).
2-й маршрут Николаевка – Дачный по тропинке 17 км со скоростью 15 км/ч и Дачный – Игнатьево по шоссе 16 км со скоростью 20 км/ч:
t_{2}=frac{17}{15}+frac{16}{20}=frac{17}{15}+frac{4}{5}=frac{17cdot 1+4cdot 3}{15}=frac{17+12}{15}=frac{29}{15} часа
Найдём сколько это в минутах:
frac{29}{15}cdot 60=29cdot 4=116 минут
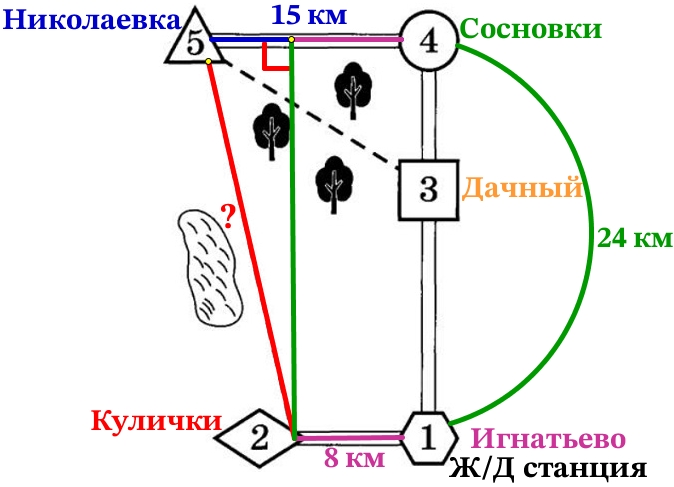
Найдём расстояние Николаевка – Куличи из прямоугольного треугольника.
В нём меньший катет равен разнице между расстояниями Николаевка – Сосновки и Куличи – Игнатьево:
15 – 8 = 7 км
Больший катет равен расстоянию между Сосновки – Игнатьево т.е. 24 км.
Гипотенуза это искомое расстояние Николаевка – Куличи (х), найдём по теореме Пифагора:
х2 = 72 + 242
х2 = 49 + 576
х2 = 625
х = √625 = 25 км
3-й маршрут Николаевка – Куличи по тропинке 25 км со скоростью 15 км/ч и Куличи – Игнатьево по шоссе 8 км со скоростью 20 км/ч:
t_{2}=frac{25}{15}+frac{8}{20}=frac{5}{3}+frac{2}{5}=frac{5cdot 5+2cdot 3}{15}=frac{25+6}{15}=frac{31}{15} часа
Найдём сколько это в минутах:
frac{31}{15}cdot 60=31cdot 4=124 минут
Меньше всего времени Ваня с дедушкой потратят на 2-й маршрут – 116 минут.
Ответ: 116.
Тренировочный вариант №298 Алекса Ларина ОГЭ 2022 по математике 9 класс с ответами и решением по новой демоверсии ОГЭ 2022 года для подготовки к экзамену, дата выхода варианта на сайте: 03.11.2021 (3 ноября 2021 года)
Тренировочный вариант №298: вариант | ответы
Усложненная версия варианта: вариант | ответы
Вариант Алекса Ларина №298 ОГЭ 2022 по математике:
Усложненная версия варианта:
Интересные задания и ответы с 1 варианта
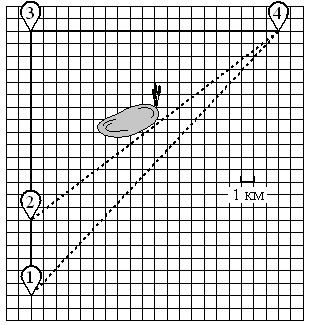
Ваня летом отдыхает у дедушки с бабушкой в деревне Николаевке. Ваня с дедушкой собираются съездить на велосипедах в село Игнатьево на железнодорожную станцию. Из Николаевки в Игнатьево можно проехать по шоссе до деревни Сосновка, где нужно свернуть под прямым углом направо на другое шоссе, ведущее в Игнатьево через посёлок Дачный. Из Николаевки в Игнатьево можно проехать через посёлок Дачный и не заезжая в Сосновку, но тогда первую часть пути надо будет ехать по прямой лесной дорожке. Есть и третий маршрут: доехать по прямой тропинке мимо озера до деревни Кулички и там, повернув налево, по шоссе добраться до Игнатьево. Дороги из Кулички в Игнатьево и из Дачного в Игнатьево образуют прямой угол. По шоссе Ваня с дедушкой едут со скоростью 20 км/ч, а по лесной дорожке и тропинке – 15 км/ч. Расстояние по шоссе от Николаевки до Сосновки равно 15 км, от Игнатьево до Сосновки – 24 км, от Игнатьево до Дачного – 16 км, а от Игнатьево до Куличек – 8 км.
1)Пользуясь описанием, определите, какими цифрами на плане обозначены населённые пункты. В ответе запишите последовательность пяти цифр без пробелов, запятых и других разделительных символов.
Ответ: 51432
2)Сколько километров проедут Ваня с дедушкой, если они поедут на станцию по шоссе через Сосновку?
Ответ: 39
3)Найдите расстояние (в км) от д. Николаевка до п. Дачный по лесной дорожке.
Ответ: 17
4)Сколько минут затратят на дорогу Ваня с дедушкой, если поедут на станцию через Сосновку?
Ответ: 117
5)Определите, на какой маршрут до станции потребуется меньше всего времени. В ответе укажите, сколько минут потратят на дорогу Ваня с дедушкой, если поедут этим маршрутом.
Ответ: 116
10)В коробке 14 пакетиков с чёрным чаем и 6 пакетиков с зелёным чаем. Павел наугад вынимает один пакетик. Какова вероятность того, что это пакетик с зелёным чаем?
Ответ: 0,3
14)Ваня, Миша, Алик и Вадим ловили рыбу. Оказалось, что количества рыб, пойманных каждым из них, образуют в указанном порядке арифметическую прогрессию. Если бы Алик поймал столько же рыб, сколько Вадим, а Вадим поймал бы на 12 рыб больше, то количества рыб, пойманных юношами, образовали бы в том же порядке геометрическую прогрессию. Сколько рыб поймал Миша?
Ответ: 6
16)В параллелограмм вписана окружность. Найдите периметр параллелограмма, если одна из его сторон равна 12.
Ответ: 48
17)Найдите площадь треугольника с длинами сторон 86, 122 и 136.
Ответ: 5160
19)Какие из следующих утверждений верны? Если верных утверждений несколько, запишите их номера в порядке возрастания без пробелов, запятых и других символов между ними. 1) Основания любой трапеции параллельны. 2) Тангенс любого острого угла меньше единицы. 3) Сумма углов любого треугольника равна 360 градусам.
Ответ: 1
21)Смешав 60%‐ый и 30%‐ый растворы кислоты и добавив 5 кг чистой воды, получили 20%‐ый раствор кислоты. Если бы вместо 5 кг воды добавили 5 кг 90%‐го раствора той же кислоты, то получили бы 70%‐ый раствор кислоты. Сколько килограммов 60%‐го раствора использовали для получения смеси?
Ответ: 2
Интересные задания и ответы с 2 варианта
На рисунке (см. выше) изображена схема метро в городе N. Станция Листопадная расположена на кольцевой ветке между Мечтательной и Тихим садом. Кольцевая ветка имеет форму окружности, на ней находятся ещё Корабликовая и Космическая станции. Возвышенная станция – соседняя с Мечтательной. Между Возвышенной и Апрельской расположена станция Роста. Несколько станций в метрополитене, а именно: Апрельская, Лирическая и Ностальгическая, являются конечными, от них поезда идут только в одну сторону. Рядом с Ностальгической находится Задумчивая станция. Петя живёт рядом со станцией Новаторской.
1)Для станций, указанных в таблице, определите, какими цифрами они обозначены на плане. Заполните таблицу. В ответе запишите последовательность четырёх цифр без пробелов, запятых и других разделительных символов.
Ответ: 2476
2)Бригада меняет рельсы на участке между станциями Ностальгическая и Задумчивая протяжённостью 3,2 км. Работы начались в понедельник. Каждый рабочий день бригада меняла по 400 метров. По субботам и воскресеньям замена рельсов не осуществлялась, но проезд был закрыт до конца всего ремонта. Сколько дней был закрыт проезд между указанными станциями?
Ответ: 10
4)Найдите расстояние (по железной дороге) между станциями Роста и Возвышенной, если расстояние между Мечтательной и Апрельской равно 9 км, расстояние от станции Мечтательной до станции Роста равно 5,5 км, а от Возвышенной до Апрельской – 6,2 км. Все расстояния даны по железной дороге. Ответ выразите в км.
Ответ: 2,7
5)Школьник Петя в среднем за месяц совершает 55 поездок на метро. Для оплаты поездок можно покупать различные карточки. Стоимость одной поездки для разных видов карточек различна (см. таблицу ниже). По истечении месяца Петя уедет из города к бабушке в деревню и неиспользованные карточки обнулятся. Во сколько рублей обойдётся самый дешёвый вариант?
Ответ: 2400
10)В сериале «Тайна Санта‐Барбары» участвует 20 героев. Каждую серию происходит одно из событий: некоторый герой узнаёт Тайну, некоторый герой узнаёт, что кто‐то знает Тайну, некоторый герой узнаёт, что кто‐то не знает Тайну. Какое наибольшее число серий может продолжаться сериал?
Ответ: 780
14)В ходе распада радиоактивного изотопа его масса уменьшается вдвое каждые 9 минут. В начальный момент масса изотопа составляла 640 мг. Найдите массу изотопа через 45 минут. Ответ дайте в миллиграммах.
Ответ: 20
17)Дан четырёхугольник, сумма диагоналей которого равна 18. Найдите периметр четырёхугольника с вершинами в серединах сторон данного.
Ответ: 18
19)Какие из следующих утверждений верны? Если верных утверждений несколько, запишите их номера в порядке возрастания без пробелов, запятых и других символов между ними. 1) Смежные углы всегда равны. 2) Каждая из биссектрис равнобедренного треугольника является его высотой. 3) Существует прямоугольник, диагонали которого взаимно перпендикулярны.
Ответ: 3
21)Дано трёхзначное число (число не может начинаться с нуля), не кратное 100. Какое наибольшее натуральное значение может иметь частное данного числа и суммы его цифр?
Ответ: 91
23)Продолжение биссектрисы AD остроугольного треугольника ABC пересекает описанную окружность в точке E . Из точки D на стороны AB и AC опущены перпендикуляры DP и DQ соответственно. площадь Найдите четырёхугольника APEQ , если известно, что площадь треугольника ABC равна 7.
Ответ: 7
24)Многоугольник можно разрезать на две равные части тремя различными способами. Докажите, что этот многоугольник может не иметь ни центра симметрии, ни оси симметрии.
Другие тренировочные варианты ОГЭ 2022 по математике:
Вариант Алекса Ларина №297 ОГЭ 2022 по математике 9 класс с ответами
Вариант Алекса Ларина №296 ОГЭ 2022 по математике 9 класс с ответами
ПОДЕЛИТЬСЯ МАТЕРИАЛОМ
1. Пользуясь описанием, определите, какими цифрами на плане обозначены населённые пункты. В ответ запишите полученную последовательность четырёх цифр.
| Населенные пункты | д. Березовка | с. Игнатьево | д. Николаевка | д. Свистуха |
| Цифры | 1 | 2 | 4 | 3 |
Ответ: 1243.
Немного дополню картинку.
2. Сколько километров проедут Миша с дедушкой, если они поедут по шоссе через Берёзовку?
Миша с дедушкой выезжают из Николаевки. Если ехать по шоссе, то им надо проехать до Березовки 36 км, а затем до Игннатьево еще 15 км. Итого 36 + 15 = 51 км.
Ответ: 51.
3. Найдите расстояние от д. Николаевка до с. Игнатьево по прямой. Ответ дайте в километрах.
Дорога по лесной дорожке ни что иное, как гипотенуза C прямоугольного треугольника с катетами 36 км и 15 км.
Найдем ее по теореме Пифагора.
С2 = 362 + 152 = 1 296 + 225 = 1 521;
С = √1521 = 39.
Ответ: 39.
4. Сколько минут затратят на дорогу Миша с дедушкой, если поедут на станцию через Берёзовку?
Чтобы найти время надо расстояние поделить на скорость.
Расстояние равно 51 км (задача 2), скорость по шоссе равна 20 км/ч (из условия задачи).
Находим время:
51 : 20 = 2,55 ч = 2,55 · 60 = 153 минуты.
Ответ: 153.
5. Определите, на какой маршрут до станции потребуется меньше всего времени. В ответ укажите сколько минут потратят на дорогу Миша с дедушкой, если проедут этим маршрутом.
Время пути Миши и дедушки по шоссе мы нашли — 153 минуты.
Найдем время пути по лесной дороге.
Длина дороги равна 39 км (задача 3), а скорость путешественников равна 15 км/ч (условие задачи).
Находим время по лесной дорожке.
39 : 15 = 2,6 ч = 2,6 · 60 = 156 минут.
Но еще есть и третий маршрут — это путь от Николаевки до Свистухи по шоссе, а затем от Свистухи до Игнатьево по лесной дороге.
Найдем время пути от Николаевки до Свистухи: 16 : 20 = 0,8 ч = 0,8 · 60 = 48 минут.
И найдем время пути от Свистухи до Игнатьево.
Здесь не все так просто, т.к. длина лесной дороги нам не известна. Найдем ее по теореме Пифагора.
с2 = 152 + (36 — 16)2 = 225 + 400 = 625;
с = √625 = 25.
Время по лесной дороге: 25 : 15 = 5/3 ч = 5/3 · 60 = 100 минут.
Подведем итог. Время, которое затратят Миша с дедушкой, поехав через Свистуху и лесную дорогу, равно 48 + 100 = 148 минутам. Этот путь менее затратный по времени.
Ответ: 148.
Не можешь найти нужную задачу? Предложи свою! Наша группа в VK.
Сколько километров проедут Володя с дедушкой от деревни Сосенки до села Кленовое, если они поедут по шоссе через деревню Жуки?
2. Сколько километров проедут Володя с дедушкой от деревни Сосенки до села Кленовое, если они поедут по шоссе через деревню Жуки?
Решение:
Ответ: 56
Ответ:
1. 51 км проедет Миша с дедушкой,если они поедут по шоссе через Берёзовку.
2. 153 минуты затратят на дорогу Миша с дедушкой, если поедут на станцию через Берёзовку
Пошаговое объяснение:
Номера деревень и расстояние между ними:
д.Игнатьево №2 Расстояние от д.Игнатьево до д.Березовка — 15 км
д.Березовка №1 Расстояние от д.Березовка до д.Свистуха 36 — 16 = 20 км
д.Свистуха №3 Расстояние от д.Свистуха до д.Николаевка 16 км
д.Николаевка №4 Расстояние от д.Николаевка до д.Березовка — 36 км
1. 36 км + 15 км = 51 км проедет Миша с дедушкой,если они поедут по шоссе через Берёзовку. (51 км = 36 км от д.Николаевка до д. Березовка + 15 км от д.Березовка до д.Игнатьево)
2. Расстояние от д.Николаевка до д.Игнатьево — 51 км, скорость по шоссе 20 км/час
51 км : 20 км/час = 2,55 час * 60 мин = 153 минуты затратят на дорогу Миша с дедушкой, если поедут на станцию через Берёзовку
Страница 1 из 7
Типы заданий, которые будут на реальном ОГЭ: план местности, участок, квартира, тарифы, листы бумаги, шины, печи для бани.
Практические задачи №1-5 к ОГЭ по математике
Прочитайте внимательно текст и выполните задания 1–5.
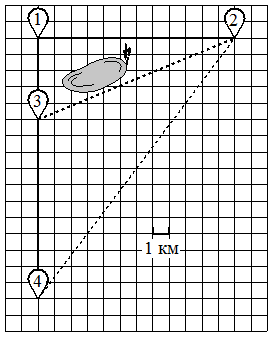
Никита и папа летом живут в деревне Лягушкино. В субботу они собираются съездить на велосипедах в село Вятское в спортивный магазин. Из деревни Лягушкино в село Вятское можно проехать по прямой лесной дорожке. Есть более длинный путь: по прямолинейному шоссе через деревню Куровка до деревни Марусино, где нужно повернуть под прямым углом налево на другое шоссе, ведущее в село Вятское. Есть и третий маршрут: в деревне Куровка можно свернуть на прямую тропинку в село Вятское, которая идёт мимо пруда.
Лесная дорожка и тропинка образуют с шоссе прямоугольные треугольники.
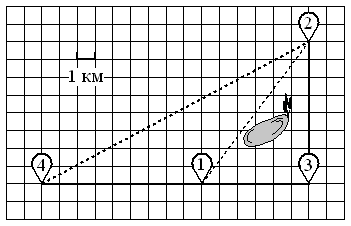
По шоссе Никита с папой едут со скоростью 25 км/ч, а по лесной дорожке и тропинке — со скоростью 15 км/ч. На плане изображено взаимное расположение населённых пунктов, длина стороны каждой клетки равна 1 км.
Анализ:
1 — Куровка, 2 — Вятское, 3 — Марусино, 4 — Лягушкино
Задание 1.
Пользуясь описанием, определите, какими цифрами на плане обозначены населённые пункты.
Заполните таблицу, в бланк ответов перенесите последовательность трёх цифр без пробелов, запятых и других дополнительных символов.
|
Насел. пункты |
д. Лягушкино |
с. Вятское |
д. Куровка |
|
Цифры |
Ответ:
421
Задание 1.
Пользуясь описанием, определите, какими цифрами на плане обозначены населённые пункты.
Заполните таблицу, в бланк ответов перенесите последовательность трёх цифр без пробелов, запятых и других дополнительных символов.
|
Насел. пункты |
д. Марусино |
с. Вятское |
д. Куровка |
|
Цифры |
Ответ:
321
Задание 1.
Пользуясь описанием, определите, какими цифрами на плане обозначены населённые пункты.
Заполните таблицу, в бланк ответов перенесите последовательность трёх цифр без пробелов, запятых и других дополнительных символов.
|
Насел. пункты |
д. Лягушкино |
д. Марусино |
д. Куровка |
|
Цифры |
Ответ:
431
Задание 1.
Пользуясь описанием, определите, какими цифрами на плане обозначены населённые пункты.
Заполните таблицу, в бланк ответов перенесите последовательность трёх цифр без пробелов, запятых и других дополнительных символов.
|
Насел. пункты |
д. Лягушкино |
с. Вятское |
д. Марусино |
|
Цифры |
Ответ:
423
Задание 2.
Сколько километров проедут Никита с папой от деревни Лягушкино до села Вятское, если они поедут по шоссе через деревню Марусино?
Решение:
8+15=23 км
Ответ: 23
Задание 2.
Сколько километров проедут Никита с папой от деревни Куровка до села Вятское, если они поедут по шоссе через деревню Марусино?
Решение:
8+6=14 км
Ответ: 14
Задание 3.
Найдите расстояние от деревни Лягушкино до села Вятское по прямой. Ответ дайте в километрах.
Решение:
$sqrt{8^2+15^2}=sqrt{289}=17$
Ответ: 17
Задание 3.
Найдите расстояние от деревни Куровка до села Вятское по прямой. Ответ дайте в километрах.
Решение:
$sqrt{8^2+6^2}=sqrt{100}=10$
Ответ: 10
Задание 4.
Сколько минут затратят на дорогу из деревни Лягушкино в село Вятское Никита с папой, если поедут через деревню Марусино?
Решение:
Формула пути S=vt; t=S/v
S=23 км; v=25 км/ч
23 км : 25 км/ч = 0,92 ч
0,92 * 60 = 55,2 мин
Ответ: 55,2
Задание 4.
Сколько минут затратят на дорогу из деревни Лягушкино в село Вятское Никита с папой, если они поедут по прямой лесной дорожке?
Решение:
$sqrt{8^2+15^2}=sqrt{289}=17$ км
15 км/ч = 15 : 60 = 0,25 км/мин
t=S/v
17/0,25 = 68 мин
Ответ: 68
Задание 4.
Сколько минут затратят на дорогу из деревни Лягушкино в село Вятское Никита с папой, если они поедут сначала по шоссе, а затем свернут в деревне Куровка на прямую тропинку, которая проходит мимо пруда?
Решение:
$sqrt{8^2+6^2}=sqrt{100}=10$ км от Куровки до Вятского
9 км по шоссе
10*60/15=40 мин от Куровки до Вятского
9*60/25=21,6 мин по шоссе
40+21,6=61,6 мин на всю дорогу
Ответ: 61,6
Задание 5.
В таблице указана стоимость (в рублях) некоторых продуктов в четырёх магазинах, расположенных в деревне Лягушкино, селе Вятское, деревне Куровка и деревне Марусино.
|
Наименование продукта |
д. Лягушкино |
с. Вятское |
д. Куровка |
д. Марусино |
|
Молоко (1 л) |
32 |
38 |
31 |
44 |
|
Хлеб (1 батон) |
26 |
28 |
35 |
25 |
|
Сыр «Российский» (1 кг) |
220 |
260 |
230 |
240 |
|
Говядина (1 кг) |
360 |
350 |
330 |
400 |
|
Картофель (1 кг) |
16 |
15 |
22 |
17 |
Никита с папой хотят купить 3 батона хлеба, 2 кг говядины и 3 кг картофеля. В каком магазине такой набор продуктов будет стоить дешевле всего?
В ответ запишите стоимость данного набора в этом магазине.
Решение:
Лягушкино 3*26+2*360+3*16 = 78+720+48=846
Вятское 3*28+2*350+3*15 = 84+700+45=829
Куровка 3*35+2*330 +3*22 = 115+660+66=841
Марусино 3*25+2*400+3*17 = 75+800+51=926
Ответ: 829
Задание 5.
В таблице указана стоимость (в рублях) некоторых продуктов в четырёх магазинах, расположенных в деревне Лягушкино, селе Вятское, деревне Куровка и деревне Марусино.
|
Наименование продукта |
д. Лягушкино |
с. Вятское |
д. Куровка |
д. Марусино |
|
Молоко (1 л) |
32 |
38 |
31 |
44 |
|
Хлеб (1 батон) |
26 |
28 |
35 |
25 |
|
Сыр «Российский» (1 кг) |
220 |
260 |
230 |
240 |
|
Говядина (1 кг) |
360 |
350 |
330 |
400 |
|
Картофель (1 кг) |
16 |
15 |
22 |
17 |
Никита с папой хотят купить 6 л молока, 4 батона хлеба и 3 кг говядины. В каком магазине такой набор продуктов будет стоить дешевле всего? В ответ запишите стоимость данного набора в этом магазине.
Решение:
Лягушкино 6*32+4*26+3*360=192+104+1080=1376
Вятское 6*38+4*28+3*350=228+112+1050=1390
Куровка 6*31+4*35+3*330=186+140+990=1316
Марусино 6*44+4*25+3*400=264+100+1200=1564
Ответ: 1316
79233F
Прочитайте внимательно текст и выполните задания 1–5.
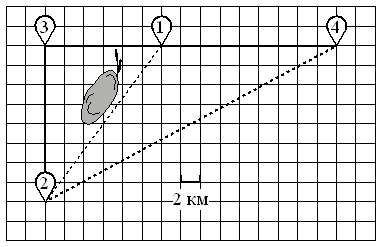
Полина летом отдыхает у дедушки в деревне Ясная. В четверг они собираются съездить на велосипедах в село Майское в магазин. Из деревни Ясная в село Майское можно проехать по прямой лесной дорожке. Есть более длинный путь: по прямолинейному шоссе через деревню Камышёвка до деревни Хомяково, где нужно повернуть под прямым углом налево
на другое шоссе, ведущее в село Майское. Есть и третий маршрут: в деревне Камышёвка можно свернуть на прямую тропинку в село Майское, которая идёт мимо пруда.
Лесная дорожка и тропинка образуют с шоссе прямоугольные треугольники.
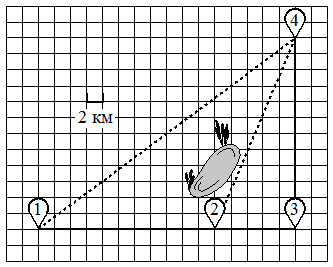
По шоссе Полина с дедушкой едут со скоростью 20 км/ч, а по лесной дорожке и тропинке — со скоростью 15 км/ч. На плане изображено взаимное расположение населённых пунктов, длина стороны каждой клетки равна 2 км.
Задание 1.
Пользуясь описанием, определите, какими цифрами на плане обозначены населённые пункты.
Заполните таблицу, в бланк ответов перенесите последовательность трёх цифр без пробелов, запятых и других дополнительных символов.
|
Насел. пункты |
д. Камышёвка |
д. Ясная |
д. Хомяково |
|
Цифры |
Ответ:
213
Задание 1.
Пользуясь описанием, определите, какими цифрами на плане обозначены населённые пункты.
Заполните таблицу, в бланк ответов перенесите последовательность трёх цифр без пробелов, запятых и других дополнительных символов.
|
Насел. пункты |
с. Майское |
д. Хомяково |
д. Ясная |
|
Цифры |
Ответ:
432
Задание 1.
Пользуясь описанием, определите, какими цифрами на плане обозначены населённые пункты.
Заполните таблицу, в бланк ответов перенесите последовательность трёх цифр без пробелов, запятых и других дополнительных символов.
|
Насел. пункты |
д. Камышёвка |
с. Майское |
д. Хомяково |
|
Цифры |
Решение:
Ответ: 243
Задание 1.
Пользуясь описанием, определите, какими цифрами на плане обозначены населённые пункты.
Заполните таблицу, в бланк ответов перенесите последовательность трёх цифр без пробелов, запятых и других дополнительных символов.
|
Насел. пункты |
д. Ясная |
д. Камышёвка |
с. Майское |
|
Цифры |
Ответ:
123
Задание 2.
Сколько километров проедут Полина с дедушкой от деревни Ясная до села Майское, если они поедут по шоссе через деревню Хомяково?
Решение:
Расстояние, которое проедут Полина с дедушкой, проезжая через Хомяково, равно сумме длин катетов прямоугольного треугольника с катетами 32 км и 24 км.
Таким образом, имеем, что искомое расстояние равно 32 + 24 = 56 км.
Ответ: 56
Задание 2.
Сколько километров проедут Полина с дедушкой от деревни Камышёвка до села Майское, если они поедут по шоссе через деревню Хомяково?
Решение:
Расстояние, которое проедут Полина с дедушкой, проезжая через Хомяково, равно сумме длин катетов прямоугольного треугольника с катетами 10 км (5 клеток) и 24 км (12 клеток).
Таким образом, имеем, что искомое расстояние равно 10 + 24 = 34 км.
Ответ: 34
Задание 3.
Найдите расстояние от деревни Ясная до села Майское по прямой. Ответ дайте в километрах.
Решение:
Расстояние от деревни Ясная до села Майское соответствует длине гипотенузы прямоугольного треугольника с катетами 32 км и 24 км. По теореме Пифагора имеем:
√322 + 242 = √1024 + 576 = 40 км.
Ответ: 40
Задание 3.
Найдите расстояние от деревни Камышёвка до села Майское по прямой. Ответ дайте в километрах.
Решение:
Расстояние от деревни Камышёвка до села Майское соответствует длине гипотенузы прямоугольного треугольника с катетами 10 км и 24 км. По теореме Пифагора имеем:
√102 + 242 = √100 + 576 = 26 км.
Ответ: 26
Задание 4.
Сколько минут затратят на дорогу из деревни Ясная в село Майское Полина с дедушкой, если поедут через деревню Хомяково?
Решение:
По шоссе из деревни Ясное до деревни Хомяково Полина с дедушкой проедут 32 километра со скоростью 20 км/ч.
Следовательно, они затратят
32 : 20 = 1,6 часа или 96 минут.
Далее из деревни Хомякова до села Майское они проедут еще 24 км также по шоссе с такой же скоростью, значит, им понадобится еще
24 : 20 = 1,2 часа или 72 минуты.
Таким образом, Полина с дедушкой на весь путь затратят
96 + 72 = 168 минут.Ответ: 168
Задание 4.
Сколько минут затратят на дорогу из деревни Ясная в село Майское Полина с дедушкой, если они поедут по прямой лесной дорожке?
Решение:
Расстояние от деревни Ясная до села Майское соответствует длине гипотенузы прямоугольного треугольника с катетами 32 км и 24 км. По теореме Пифагора имеем:
√322 + 242 = √1024 + 576 = 40 км.
при скорости по лесной тропинке 15 км/ч получается
40:15=2 10/15 = 2 2/3. 2/3 часа это 60*2:3=40 минут
2*60=120 минут — 2 часа
120+40=160 минут
Ответ: 160
Задание 4.
Сколько минут затратят на дорогу из деревни Ясная в село Майское Полина с дедушкой, если они поедут сначала по шоссе, а затем свернут в Камышёвке на прямую тропинку, которая проходит мимо пруда?
Решение:
По шоссе из деревни Ясное до деревни Камышёвка Полина с дедушкой проедут 22 километра со скоростью 20 км/ч. Следовательно, на этот путь затратят
22 : 20 = 1,1 часа или 1,1 * 60 = 66 минут.
Далее, по условию задачи, они свернут на лесную тропинку, расстояние по которой можно найти как длину гипотенузы прямоугольного треугольника с катетами 10 км и 24 км.
По теореме Пифагора найдем путь по лесной тропинке
√102 + 242 = √100 + 576 = 26 км.
По лесной тропинке Полина с дедушкой едут со скоростью 15 км/ч, следовательно, они затратят
26 : 15 = 1 11/15 часа или 1 11/15 * 60 = 104 минуты.
Таким образом, Полина с дедушкой на весь путь затратят
66 + 104 = 170 минут.Ответ: 170
Задание 5.
В таблице указана стоимость (в рублях) некоторых продуктов в четырёх магазинах, расположенных в деревне Ясная, селе Майское, деревне Камышёвка и деревне Хомяково.
|
Наименование продукта |
д. Ясная |
с. Майское |
д. Камышёвка |
д. Хомяково |
|
Молоко (1 л) |
42 |
38 |
41 |
33 |
|
Хлеб (1 батон) |
25 |
21 |
29 |
30 |
|
Сыр «Российский» (1 кг) |
310 |
320 |
290 |
280 |
|
Говядина (1 кг) |
340 |
380 |
410 |
390 |
|
Картофель (1 кг) |
15 |
20 |
17 |
18 |
Полина с дедушкой хотят купить 2 л молока, 3 кг говядины и 2 кг картофеля. В каком магазине такой набор продуктов будет стоить дешевле всего? В ответ запишите стоимость данного набора в этом магазине.
Решение:
В деревне Ясная стоимость набора составит 2*42 + 3*340 + 2*15 = 1134 руб.
В селе Майское стоимость набора составит 2*38 + 3*380 + 2*20 = 1256 руб.
В деревне Камышёвка стоимость набора составит 2*41 + 3*410 + 2*17 = 1346 руб.
В деревне Хомяково стоимость набора составит 2*33 + 3*390 + 2*18 = 1272 руб.Самый дешёвый набор продуктов можно купить в деревне Ясная по цене 1134 руб.
Ответ: 1134
Задание 5.
В таблице указана стоимость (в рублях) некоторых продуктов в четырёх магазинах, расположенных в деревне Ясная, селе Майское, деревне Камышёвка и деревне Хомяково.
|
Наименование продукта |
д. Ясная |
с. Майское |
д. Камышёвка |
д. Хомяково |
|
Молоко (1 л) |
42 |
38 |
41 |
33 |
|
Хлеб (1 батон) |
25 |
21 |
29 |
30 |
|
Сыр «Российский» (1 кг) |
310 |
320 |
290 |
280 |
|
Говядина (1 кг) |
340 |
380 |
410 |
390 |
|
Картофель (1 кг) |
15 |
20 |
17 |
18 |
Полина с дедушкой хотят купить 3 л молока, 1 кг сыра «Российский» и 3 кг картофеля. В каком магазине такой набор продуктов будет стоить дешевле всего? В ответ запишите стоимость данного набора в этом магазине.
Решение:
В деревне Ясная стоимость набора составит 3*42+1*310+3*15 = 126+310+45=481 руб.
В селе Майское стоимость набора составит 3*38+1*320+3*20 = 114+320+60=494 руб.
В деревне Камышёвка стоимость набора составит 3*41+1*290+3*17 = 123+290+51=464 руб.
В деревне Хомяково стоимость набора составит 3*33+1*280+3*18 =99+280+54=433 руб.
Ответ: 433
F6B6DD
Прочитайте внимательно текст и выполните задания 1–5.
Дима летом отдыхает у дедушки в деревне Васильевка. Во вторник они собираются съездить на велосипедах в село Плодородное на ярмарку.
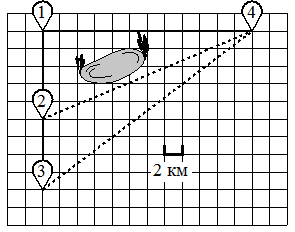
Из деревни Васильевка в село Плодородное можно проехать по прямой лесной дорожке. Есть более длинный путь: по прямолинейному шоссе через деревню Шарковка до деревни Рассвет, где нужно повернуть под прямым углом направо на другое шоссе, ведущее в село Плодородное. Есть и третий маршрут: в деревне Шарковка можно свернуть на прямую тропинку в село Плодородное, которая идёт мимо пруда.
Лесная дорожка и тропинка образуют с шоссе прямоугольные треугольники.
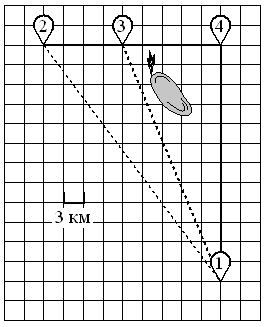
По шоссе Дима с дедушкой едут со скоростью 25 км/ч, а по лесной дорожке и тропинке — со скоростью 18 км/ч. На плане изображено взаимное расположение населённых пунктов, длина стороны каждой клетки равна 3 км.
Задание 1.
Пользуясь описанием, определите, какими цифрами на плане обозначены населённые пункты.
Заполните таблицу, в бланк ответов перенесите последовательность трёх цифр без пробелов, запятых и других дополнительных символов.
|
Насел. пункты |
д. Рассвет |
с. Плодородное |
д. Васильевка |
|
Цифры |
Ответ:
412
Задание 1.
Пользуясь описанием, определите, какими цифрами на плане обозначены населённые пункты.
Заполните таблицу, в бланк ответов перенесите последовательность трёх цифр без пробелов, запятых и других дополнительных символов.
|
Насел. пункты |
д. Рассвет |
с. Плодородное |
д. Шарковка |
|
Цифры |
Ответ:
413
Задание 1.
Пользуясь описанием, определите, какими цифрами на плане обозначены населённые пункты.
Заполните таблицу, в бланк ответов перенесите последовательность трёх цифр без пробелов, запятых и других дополнительных символов.
|
Насел. пункты |
д. Васильевка |
д. Шарковка |
д. Рассвет |
|
Цифры |
Ответ:
234
Задание 1.
Пользуясь описанием, определите, какими цифрами на плане обозначены населённые пункты.
Заполните таблицу, в бланк ответов перенесите последовательность трёх цифр без пробелов, запятых и других дополнительных символов.
|
Насел. пункты |
д. Шарковка |
с. Плодородное |
д. Васильевка |
|
Цифры |
Ответ:
312
Задание 2.
Сколько километров проедут Дима с дедушкой от деревни Васильевка до села Плодородное, если они поедут по шоссе через деревню Рассвет?
Решение:
(4+5+12)*3=63 км
Ответ: 63
Задание 2.
Сколько километров проедут Дима с дедушкой от деревни Шарковка до села Плодородное, если они поедут по шоссе через деревню Рассвет?
Решение:
(5+12)*3=51 км
Ответ: 51
Задание 3.
Найдите расстояние от деревни Васильевка до села Плодородное по прямой. Ответ дайте в километрах.
Решение:
По теореме Пифагора
√(4+5)2+122 = √81+144 = √225 = 15 клеток
15*3 = 45 км
Ответ: 45
Задание 3.
Найдите расстояние от деревни Шарковка до села Плодородное по прямой. Ответ дайте в километрах.
Решение:
√52+122 = √25+144 = √169 = 13 клеток
13*3 = 39 км
Ответ: 39
Задание 4.
Сколько минут затратят на дорогу из деревни Васильевка в село Плодородное Дима с дедушкой, если поедут через деревню Рассвет?
Решение:
(4+5+12)*3=63 км нужно проехать по шоссе
63 * 60 = 151,2 мин
25Ответ: 151,2
Задание 4.
Сколько минут затратят на дорогу из деревни Васильевка в село Плодородное Дима с дедушкой, если они поедут по прямой лесной дорожке?
Решение:
По теореме Пифагора
√(4+5)2+122 = √81+144 = √225 = 15 клеток
15*3 = 45 км по прямой
45 * 60 = 150 минут
18
Ответ: 150
Задание 4.
Сколько минут затратят на дорогу из деревни Васильевка в село Плодородное Дима с дедушкой, если они поедут сначала по шоссе, а затем свернут в Шарковке на прямую тропинку, которая проходит мимо пруда?
Решение:
4*3 = 12 км от Васильевки до Шарковки по шоссе
12 * 60 = 28,8 мин от Васильевки до Шарковки по шоссе
25
√52+122 = √25+144 = √169 = 13 клеток
13*3 = 39 км от Шарковки до Плодородное по прямой
39 * 60 = 130 мин от Шарковки до Плодородное по прямой
18
130 + 28,8 = 158,8 минОтвет: 158,8
Задание 5.
В таблице указана стоимость (в рублях) некоторых продуктов в четырёх магазинах, расположенных в деревне Васильевка, селе Плодородное, деревне Шарковка и деревне Рассвет.
|
Наименование продукта |
д. Васильевка |
с. Плодородное |
д. Шарковка |
д. Рассвет |
|
Молоко (1 л) |
37 |
38 |
36 |
39 |
|
Хлеб (1 батон) |
16 |
18 |
22 |
21 |
|
Сыр «Российский» (1 кг) |
240 |
280 |
250 |
260 |
|
Говядина (1 кг) |
420 |
430 |
415 |
410 |
|
Картофель (1 кг) |
30 |
28 |
35 |
25 |
Дима с дедушкой хотят купить 2 л молока, 3 кг говядины и 2 кг картофеля. В каком магазине такой набор продуктов будет стоить дешевле всего? В ответ запишите стоимость данного набора в этом магазине.
Решение:
Васильевка 2*37 + 3*420 + 2*30 = 1394
Плодородное 2*38 + 3*430 + 2*28 = 1422
Шарковка 2*36 + 3*415 + 2*35 = 1387
Рассвет 2*39 + 3*410 + 2*25 = 1358Ответ: 1358
Задание 5.
В таблице указана стоимость (в рублях) некоторых продуктов в четырёх магазинах, расположенных в деревне Васильевка, селе Плодородное, деревне Шарковка и деревне Рассвет.
|
Наименование продукта |
д. Васильевка |
с. Плодородное |
д. Шарковка |
д. Рассвет |
|
Молоко (1 л) |
37 |
38 |
36 |
39 |
|
Хлеб (1 батон) |
16 |
18 |
22 |
21 |
|
Сыр «Российский» (1 кг) |
240 |
280 |
250 |
260 |
|
Говядина (1 кг) |
420 |
430 |
415 |
410 |
|
Картофель (1 кг) |
30 |
28 |
35 |
25 |
Дима с дедушкой хотят купить 4 кг сыра «Российский», 5 кг говядины, 6 кг картофеля. В каком магазине такой набор продуктов будет стоить дешевле всего? В ответ запишите стоимость данного набора в этом магазине.
Решение:
Васильевка 4*240 + 5*420 + 6*30 = 3240
Плодородное 4*280 + 5*430 + 6*28 = 3438
Шарковка 4*250 + 5*415 + 6*35 = 3285
Рассвет 4*260 + 5*410 + 6*25 = 3240Ответ: 3240
EAE764
Прочитайте внимательно текст и выполните задания 1–5.
Саша летом отдыхает у дедушки в деревне Масловка. В субботу они собираются съездить на велосипедах в село Захарово в магазин. Из деревни Масловка в село Захарово можно проехать по прямой лесной дорожке. Есть более длинный путь: по прямолинейному шоссе через деревню Вёсенка до деревни Полянка, где нужно повернуть под прямым углом направо на другое шоссе, ведущее в село Захарово. Есть и третий маршрут: в деревне Вёсенка можно свернуть на прямую тропинку в село Захарово, которая идёт мимо пруда.
Лесная дорожка и тропинка образуют с шоссе прямоугольные треугольники.
По шоссе Саша с дедушкой едут со скоростью 20 км/ч, а по лесной дорожке и тропинке — со скоростью 15 км/ч. На плане изображено взаимное расположение населённых пунктов, сторона каждой клетки равна 1 км.
Анализ:
1 — Масловка, 2 — Вёсенка, 3 — Полянка, 4 — Захарово
1-2 — 6 км, 2-3 — 15 км, 3-4 — 20 км
Задание 1.
Пользуясь описанием, определите, какими цифрами на плане обозначены населённые пункты.
Заполните таблицу, в бланк ответов перенесите последовательность трёх цифр без пробелов, запятых и других дополнительных символов.
|
Насел. пункты |
д. Масловка |
с. Захарово |
д. Вёсенка |
|
Цифры |
Ответ:
142
Задание 1.
Пользуясь описанием, определите, какими цифрами на плане обозначены населённые пункты.
Заполните таблицу, в бланк ответов перенесите последовательность трёх цифр без пробелов, запятых и других дополнительных символов.
|
Насел. пункты |
д. Полянка |
с. Захарово |
д. Вёсенка |
|
Цифры |
Ответ:
342
Задание 1.
Пользуясь описанием, определите, какими цифрами на плане обозначены населённые пункты.
Заполните таблицу, в бланк ответов перенесите последовательность трёх цифр без пробелов, запятых и других дополнительных символов.
|
Насел. пункты |
д. Масловка |
д. Полянка |
д. Вёсенка |
|
Цифры |
Ответ:
132
Задание 1.
Пользуясь описанием, определите, какими цифрами на плане обозначены населённые пункты.
Заполните таблицу, в бланк ответов перенесите последовательность трёх цифр без пробелов, запятых и других дополнительных символов.
|
Насел. пункты |
д. Масловка |
с. Захарово |
д. Полянка |
|
Цифры |
Ответ:
143
Задание 2.
Сколько километров проедут Саша с дедушкой от деревни Масловка до села Захарово, если они поедут по шоссе через деревню Полянка?
Решение:
6 + 15 + 20 = 41 км
Ответ: 41
Задание 2.
Сколько километров проедут Саша с дедушкой от деревни Вёсенка до села Захарово, если они поедут по шоссе через деревню Полянка?
Решение:
15 + 20 = 35 км
Ответ: 35
Задание 3.
Найдите расстояние от деревни Масловка до села Захарово по прямой. Ответ дайте в километрах.
Решение:
По теореме Пифагора вначале узнаем катеты, а потом вычислим гипотенузу.
6+15=21 км от Масловки до Полянки
20 км от Полянки до Захарово
По теореме Пифагора
√(20)2+212 = √400+441 = √841 = 29 кмОтвет: 29
Задание 3.
Найдите расстояние от деревни Вёсенка до села Захарово по прямой. Ответ дайте в километрах.
Решение:
По теореме Пифагора вначале узнаем катеты, а потом вычислим гипотенузу.
15 км от Вёсенки до Полянки
20 км от Полянки до Захарово
По теореме Пифагора
√(15)2+202 = √225+400 = √625 = 25 км
Ответ: 25
Задание 4.
Сколько минут затратят на дорогу из деревни Масловка в село Захарово Саша с дедушкой, если поедут через деревню Полянка?
Решение:
15 + 20 = 35 км расстояние из деревни Масловка в село Захарово
35:20=1 15/20 = 1 3/4
1*60=60 минут
3/4 = 60*3/4= 45 минут
60+45=105 минут
Ответ: 105
Задание 4.
Сколько минут затратят на дорогу из деревни Масловка в село Захарово Саша с дедушкой, если они поедут по прямой лесной дорожке?
Решение:
По теореме Пифагора вначале узнаем катеты, а потом вычислим гипотенузу.
6+15=21 км от Масловки до Полянки
20 км от Полянки до Захарово
По теореме Пифагора
√(20)2+212 = √400+441 = √841 = 29 км от Масловки до Захарово
29:15=1 14/15
1*60=60 минут
60*14/15= 56 минут
60+56=116 минут
Ответ: 116
Задание 4.
Сколько минут затратят на дорогу из деревни Масловка в село Захарово Саша с дедушкой, если они поедут сначала по шоссе, а затем свернут
в деревне Вёсенка на прямую тропинку, которая проходит мимо пруда?
Решение:
По теореме Пифагора вначале узнаем катеты, а потом вычислим гипотенузу.
15 км от Весенки до Полянки
20 км от Полянки до Захарово
По теореме Пифагора
√(20)2+152 = √400+225 = √625 = 25 км от Весенки до Захарово
6 км от Масловки до Весенки
Теперь считаем для шоссе:
60*6:20=360:20=18 минут
25:15=1 10/15= 1 2/3
1*60=60 минут
60*2:3=120:3=40 минут
60+40=100 минут
100+18=118 минут
Ответ: 118
Задание 5.
В таблице указана стоимость (в рублях) некоторых продуктов в четырёх магазинах, расположенных в деревне Масловка, селе Захарово, деревне Вёсенка и деревне Полянка.
|
Наименование продукта |
д. Масловка |
с. Захарово |
д. Вёсенка |
д. Полянка |
|
Молоко (1 л) |
45 |
40 |
42 |
52 |
|
Хлеб (1 батон) |
29 |
28 |
31 |
22 |
|
Сыр «Российский» (1 кг) |
250 |
270 |
290 |
280 |
|
Говядина (1 кг) |
350 |
380 |
360 |
390 |
|
Картофель (1 кг) |
35 |
25 |
32 |
24 |
Саша с дедушкой хотят купить 2 л молока, 2 кг говядины
и 4 кг картофеля. В каком магазине такой набор продуктов будет стоить дешевле всего? В ответ запишите стоимость данного набора в этом магазине.
Решение:
Масловка 2*45+2*350+4*35=90+700+140=930 руб.
Захарово 2*40+2*380+4*25=80+760+100=940 руб.
Вёсенка 2*42+2*360+4*32=84+720+128=932 руб.
Полянка 2*52+2*390+4*24= 104+780+96=980 руб.
Ответ: 930
Задание 5.
В таблице указана стоимость (в рублях) некоторых продуктов в четырёх магазинах, расположенных в деревне Масловка, селе Захарово, деревне Вёсенка и деревне Полянка.
|
Наименование продукта |
д. Масловка |
с. Захарово |
д. Вёсенка |
д. Полянка |
|
Молоко (1 л) |
45 |
40 |
42 |
52 |
|
Хлеб (1 батон) |
29 |
28 |
31 |
22 |
|
Сыр «Российский» (1 кг) |
250 |
270 |
290 |
280 |
|
Говядина (1 кг) |
350 |
380 |
360 |
390 |
|
Картофель (1 кг) |
35 |
25 |
32 |
24 |
Саша с дедушкой хотят купить 3 батона хлеба, 2 кг сыра «Российский» и 5 кг картофеля. В каком магазине такой набор продуктов будет стоить дешевле всего? В ответ запишите стоимость данного набора в этом магазине.
Решение:
Масловка 3*29+2*250+5*35= 87+500+175=762руб.
Захарово 3*28+2*270+5*25= 84+540+125=749 руб.
Вёсенка 3*31+2*290+5*32= 93+580+160= 833 руб.
Полянка 3*22+2*280+5*24= 66+560+120= 746 руб.
Ответ: 746
650747
Прочитайте внимательно текст и выполните задания 1–5.
Саша летом отдыхает у дедушки в деревне Васильково. В субботу они собираются съездить на велосипедах в село Иваново в магазин.
Из деревни Васильково в село Иваново можно проехать по прямой лесной дорожке. Есть более длинный путь: по прямолинейному шоссе через деревню Камышино до деревни Журавушка, где нужно повернуть
под прямым углом направо на другое шоссе, ведущее в село Иваново. Есть
и третий маршрут: в деревне Камышино можно свернуть на прямую тропинку в село Иваново, которая идёт мимо пруда.
Лесная дорожка и тропинка образуют с шоссе прямоугольные треугольники.
По шоссе Саша с дедушкой едут со скоростью 20 км/ч, а по лесной дорожке и тропинке — со скоростью 15 км/ч. На плане изображено взаимное расположение населённых пунктов, длина стороны каждой клетки равна 1 км.
Анализ:
1 — Журавушка 2 — Иваново 3 — Камышино 4 — Васильково
Задание 1.
Пользуясь описанием, определите, какими цифрами на плане обозначены населённые пункты.
Заполните таблицу, в бланк ответов перенесите последовательность трёх цифр без пробелов, запятых и других дополнительных символов.
|
Насел. пункты |
д. Васильково |
с. Иваново |
д. Камышино |
|
Цифры |
Ответ:
423
Задание 1.
Пользуясь описанием, определите, какими цифрами на плане обозначены населённые пункты.
Заполните таблицу, в бланк ответов перенесите последовательность трёх цифр без пробелов, запятых и других дополнительных символов.
|
Насел. пункты |
д. Журавушка |
д. Камышино |
с. Иваново |
|
Цифры |
Ответ:
132
Задание 1.
Пользуясь описанием, определите, какими цифрами на плане обозначены населённые пункты.
Заполните таблицу, в бланк ответов перенесите последовательность трёх цифр без пробелов, запятых и других дополнительных символов.
|
Насел. пункты |
д. Васильково |
д. Журавушка |
д. Камышино |
|
Цифры |
Ответ:
413
Задание 1.
Пользуясь описанием, определите, какими цифрами на плане обозначены населённые пункты.
Заполните таблицу, в бланк ответов перенесите последовательность трёх цифр без пробелов, запятых и других дополнительных символов.
|
Насел. Пункты |
д. Васильково |
с. Иваново |
д. Журавушка |
|
Цифры |
Ответ:
421
Задание 2.
Сколько километров проедут Саша с дедушкой от деревни Васильково до села Иваново, если они поедут по шоссе через деревню Журавушка?
Решение:
1км=1клетка
11 + 5 + 12 = 29 км
Ответ: 29
Задание 2.
Сколько километров проедут Саша с дедушкой от деревни Камышино до села Иваново, если они поедут по шоссе через деревню Журавушка?
Решение:
1км=1клетка
5+12= 17 км
Ответ: 17
Задание 3.
Найдите расстояние от деревни Васильково до села Иваново по прямой. Ответ дайте в километрах.
Решение:
1км=1клетка
Используем теорему Пифагора
(5+11)2 + 122= x2√(5+11)2+122=√(16)2+122 = √256+144= √400 = 20 км
Ответ: 20
Задание 3.
Найдите расстояние от деревни Камышино до села Иваново по прямой. Ответ дайте в километрах.
Решение:
Решение:
1км=1клетка
Используем теорему Пифагора
52 + 122= x2√52+122 =√25+144 = √169= 13
Ответ: 13
Задание 4.
Сколько минут затратят на дорогу из деревни Васильково в село Иваново Саша с дедушкой, если поедут через деревню Журавушка?
Решение:
Решение:
1км=1клетка
s=v*t формула скорости
20 км/ч скорость по шоссеИспользуем теорему Пифагора
11+5+12=29 (км) надо проехать
29/20 = 1 9/20 (ч)
60 *1 9/20 = 60/1 +60* 9/20 = 60 + 540/20 = 60 + 27 = 87 минОтвет: 87
Задание 4.
Сколько минут затратят на дорогу из деревни Васильково в село Иваново Саша с дедушкой, если они поедут по прямой лесной дорожке?
Решение:
1км=1клетка
s=v*t формула скорости
15 км/ч скорость по лесной дорожке
Используем теорему Пифагора
(5+11)2 + 122= x2√(5+11)2+122=√(16)2+122 = √256+144= √400 = 20 км по лесной дорожке
20/15 = 1 5/15 (ч)
60*1 5/15 = 60/1 + 60*1/3 = 60 + 20 = 80 мин
Ответ: 80
Задание 4.
Сколько минут затратят на дорогу из деревни Васильково в село Иваново Саша с дедушкой, если они поедут сначала по шоссе, а затем свернут
в Камышино на прямую тропинку, которая проходит мимо пруда?
Решение:
Решение:
1км=1клетка
Используем теорему Пифагора
52 + 122= x2√52+122 =√25+144 = √169= 13 км по тропинке
60 * 13/15 = 52 мин займет время по тропинке
60 * 11/20 = 660/20 = 33 мин займет время по шоссе
52+33 = 85 мин займет время из деревни Васильково в село Иваново Саша с дедушкой, если они поедут сначала по шоссе, а затем свернут
в Камышино на прямую тропинку, которая проходит мимо прудаОтвет: 85
Задание 5.
В таблице указана стоимость (в рублях) некоторых продуктов в четырёх магазинах, расположенных в деревне Васильково, селе Иваново, деревне Камышино и деревне Журавушка.
|
Наименование продукта |
д. Васильково |
с. Иваново |
д. Камышино |
д. Журавушка |
|
Молоко (1 л) |
35 |
34 |
33 |
31 |
|
Хлеб (1 батон) |
28 |
25 |
30 |
24 |
|
Сыр «Российский» (1 кг) |
270 |
260 |
310 |
220 |
|
Говядина (1 кг) |
390 |
420 |
400 |
380 |
|
Картофель (1 кг) |
16 |
24 |
20 |
22 |
Саша с дедушкой хотят купить 2 л молока, 3 кг говядины и 2 кг картофеля.
В каком магазине такой набор продуктов будет стоить дешевле всего?
В ответ запишите стоимость данного набора в этом магазине.
Решение:
Васильково 2*35+ 3*390+ 2*16= 70+1170+32=1272
Иваново 2*34+ 3*420+ 2*24=64+1260+48=1372
Камышино 2*33+ 3*400+ 2*20=66+1200+40=1306
Журавушка 2*31+ 3*380+ 2*22=62+1140+44=1246
Ответ: 1246
Задание 5.
В таблице указана стоимость (в рублях) некоторых продуктов в четырёх магазинах, расположенных в деревне Васильково, селе Иваново, деревне Камышино и деревне Журавушка.
|
Наименование продукта |
д. Васильково |
с. Иваново |
д. Камышино |
д. Журавушка |
|
Молоко (1 л) |
35 |
34 |
33 |
31 |
|
Хлеб (1 батон) |
28 |
25 |
30 |
24 |
|
Сыр «Российский» (1 кг) |
270 |
260 |
310 |
220 |
|
Говядина (1 кг) |
390 |
420 |
400 |
380 |
|
Картофель (1 кг) |
16 |
24 |
20 |
22 |
Саша с дедушкой хотят купить 3 батона хлеба, 2 кг сыра «Российский» и 2 кг говядины. В каком магазине такой набор продуктов будет стоить дешевле всего? В ответ запишите стоимость данного набора в этом магазине.
Решение:
Васильково 3*28+2*270+2*390=84+540+780=1404
Иваново 3*25+2*260+2*420=75+520+840=1435
Камышино 3*30+2*310+2*400=90+620+800=1510
Журавушка 3*24+2*220+2*380=72+440+760=1272
Ответ: 1272
E4DF9C
Прочитайте внимательно текст и выполните задания 1–5.
Серёжа летом отдыхает с папой в деревне Пирожки. В среду они собираются съездить на машине в село Княжеское. Из деревни Пирожки в село Княжеское можно проехать по прямой грунтовой дороге. Есть более длинный путь: по прямолинейному шоссе через деревню Васильево
до деревни Рябиновка, где нужно повернуть под прямым углом налево
на другое шоссе, ведущее в село Княжеское. Есть и третий маршрут:
в деревне Васильево можно свернуть на прямую грунтовую дорогу в село Княжеское, которая идёт мимо пруда.
Шоссе и грунтовые дороги образуют прямоугольные треугольники.
Анализ:
Пирожки 4
Васильево 1
Рябиновка 3
Княжеское 2
По шоссе Серёжа с папой едут со скоростью 60 км/ч, а по грунтовой дороге — со скоростью 40 км/ч. На плане изображено взаимное расположение населённых пунктов, длина стороны каждой клетки равна 2 км.
Задание 1.
Пользуясь описанием, определите, какими цифрами на плане обозначены населённые пункты.
Заполните таблицу, в бланк ответов перенесите последовательность трёх цифр без пробелов, запятых и других дополнительных символов.
|
Насел. пункты |
д. Пирожки |
с. Княжеское |
д. Рябиновка |
|
Цифры |
Ответ:
423
Задание 1.
Пользуясь описанием, определите, какими цифрами на плане обозначены населённые пункты.
Заполните таблицу, в бланк ответов перенесите последовательность трёх цифр без пробелов, запятых и других дополнительных символов.
|
Насел. пункты |
д. Васильево |
с. Княжеское |
д. Рябиновка |
|
Цифры |
Ответ:
123
Задание 1.
Пользуясь описанием, определите, какими цифрами на плане обозначены населённые пункты.
Заполните таблицу, в бланк ответов перенесите последовательность трёх цифр без пробелов, запятых и других дополнительных символов.
|
Насел. пункты |
д. Пирожки |
д. Васильево |
д. Рябиновка |
|
Цифры |
Ответ:
413
Задание 1.
Пользуясь описанием, определите, какими цифрами на плане обозначены населённые пункты.
Заполните таблицу, в бланк ответов перенесите последовательность трёх цифр без пробелов, запятых и других дополнительных символов.
|
Насел. пункты |
д. Пирожки |
с. Княжеское |
д. Васильево |
|
Цифры |
Ответ:
421
Задание 2.
Сколько километров проедут Серёжа с папой от деревни Пирожки до села Княжеское, если они поедут по шоссе через деревню Рябиновка?
Решение:
6+9+8=23 клетки
23*2=46 км
Ответ: 46
Задание 2.
Сколько километров проедут Серёжа с папой от деревни Васильево до села Княжеское, если они поедут по шоссе через деревню Рябиновка?
Решение:
6+8=14 клеток
14*2=28 км
Ответ: 28
Задание 3.
Найдите расстояние от деревни Пирожки до села Княжеское по прямой. Ответ дайте в километрах.
Решение:
2км=1клетка
Используем теорему Пифагора
(6+9)2 + 82= x2√ (6+9)2 + 82 = √152+82 = √225+64= √289 = 17 клеток
2*17=34 кмОтвет: 34
Задание 3.
Найдите расстояние от деревни Васильево до села Княжеское по прямой. Ответ дайте в километрах.
Решение:
2км=1клетка
Используем теорему Пифагора
62 + 82= x2√62 + 82 = √36+64= √100 = 10 клеток
2*10=20 км
Ответ: 20
Задание 4.
Сколько минут затратят на дорогу из деревни Пирожки в село Княжеское Серёжа с папой, если поедут через деревню Рябиновка?
Решение:
6+9+8=23 клетки
2*23=46 км60*46/60=46 мин
Ответ: 46
Задание 4.
Сколько минут затратят на дорогу из деревни Пирожки в село Княжеское Серёжа с папой, если они поедут по прямой грунтовой дороге?
Решение:
2км=1клетка
Используем теорему Пифагора
(6+9)2 + 82= x2√ (6+9)2 + 82 = √ 152+82 = √ 225+64= √ 289 = 17 клеток
2*17=34 км из деревни Пирожки в село Княжеское по прямой грунтовой дороге60*34/40 = 51 минута
Ответ: 51
Задание 4.
Сколько минут затратят на дорогу из деревни Пирожки в село Княжеское Серёжа с папой, если они поедут сначала по шоссе, а затем свернут в деревне Васильево на прямую грунтовую дорогу, которая проходит мимо пруда?
Решение:
9 клеток из Пирожки до Васильева
9*2=18 км60*18/60=18 минут
√ 62 + 82 = √ 36+64= √ 100 = 10 клеток
2*10=20 км от Васильева до Княжеское60*20/40= 30 минут
Ответ: 30
Задание 5.
В таблице указана стоимость (в рублях) некоторых продуктов в четырёх магазинах, расположенных в деревне Пирожки, селе Княжеское, деревне Васильево и деревне Рябиновка.
|
Наименование продукта |
д. Пирожки |
с. Княжеское |
д. Васильево |
д. Рябиновка |
|
Молоко (1 л) |
48 |
45 |
50 |
52 |
|
Хлеб (1 батон) |
34 |
32 |
33 |
28 |
|
Сыр «Российский» (1 кг) |
240 |
280 |
270 |
260 |
|
Говядина (1 кг) |
370 |
400 |
380 |
420 |
|
Картофель (1 кг) |
22 |
16 |
28 |
30 |
Серёжа с папой хотят купить 2 л молока, 3 батона хлеба и 1 кг сыра «Российский». В каком магазине такой набор продуктов будет стоить дешевле всего? В ответ запишите стоимость данного набора в этом магазине.
Решение:
Пирожки 2*48+3*34+1*240=96+102+240=438
Княжеское 2*45+3*32+1*280=90+96+280=466
Васильево 2*50+3*33+1*270=100+99+270=469
Рябиновка 2*52+3*28+1*260=104+84+260=448Ответ: 438
Задание 5.
В таблице указана стоимость (в рублях) некоторых продуктов в четырёх магазинах, расположенных в деревне Пирожки, селе Княжеское, деревне Васильево и деревне Рябиновка.
|
Наименование продукта |
д. Пирожки |
с. Княжеское |
д. Васильево |
д. Рябиновка |
|
Молоко (1 л) |
48 |
45 |
50 |
52 |
|
Хлеб (1 батон) |
34 |
32 |
33 |
28 |
|
Сыр «Российский» (1 кг) |
240 |
280 |
270 |
260 |
|
Говядина (1 кг) |
370 |
400 |
380 |
420 |
|
Картофель (1 кг) |
22 |
16 |
28 |
30 |
Серёжа с папой хотят купить 3 л молока, 1 кг говядины и 4 кг картофеля.
В каком магазине такой набор продуктов будет стоить дешевле всего?
В ответ запишите стоимость данного набора в этом магазине.
Решение:
Пирожки 3*48+1*370+4*22=144+370+88=602
Княжеское 3*45+1*400+4*16=135+400+64=599
Васильево 3*50+1*380+4*28=150+380+112=642
Рябиновка 3*52+1*420+4*30=156+420+120=696
Ответ: 599
8C173F
Прочитайте внимательно текст и выполните задания 1–5.
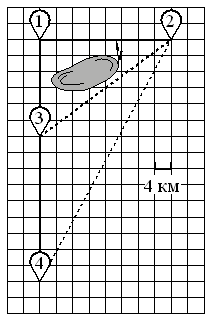
Гриша летом отдыхает у дедушки в деревне Грушёвка. В понедельник они собираются съездить на велосипедах в село Абрамово на ярмарку.
Из деревни Грушёвка в село Абрамово можно проехать по прямой лесной дорожке. Есть более длинный путь: по прямолинейному шоссе через деревню Таловка до деревни Новая, где нужно повернуть
под прямым углом направо на другое шоссе, ведущее в село Абрамово. Есть и третий маршрут: в деревне Таловка можно свернуть на прямую тропинку
в село Абрамово, которая идёт мимо пруда.
Лесная дорожка и тропинка образуют с шоссе прямоугольные треугольники.
По шоссе Гриша с дедушкой едут со скоростью 15 км/ч, а по лесной дорожке и тропинке — со скоростью 12 км/ч. На плане изображено взаимное расположение населённых пунктов, длина стороны каждой клетки равна 2 км.
Анализ:
Грушёвка 3
Таловка 2
Новая 1
Абрамово 4
Задание 1.
Пользуясь описанием, определите, какими цифрами на плане обозначены населённые пункты.
Заполните таблицу, в бланк ответов перенесите последовательность трёх цифр без пробелов, запятых и других дополнительных символов.
|
Насел. пункты |
д. Новая |
с. Абрамово |
д. Грушёвка |
|
Цифры |
Ответ:
143
Задание 1.
Пользуясь описанием, определите, какими цифрами на плане обозначены населённые пункты.
Заполните таблицу, в бланк ответов перенесите последовательность трёх цифр без пробелов, запятых и других дополнительных символов.
|
Насел. пункты |
д. Таловка |
д. Грушёвка |
с. Абрамово |
|
Цифры |
Ответ:
234
Задание 1.
Пользуясь описанием, определите, какими цифрами на плане обозначены населённые пункты.
Заполните таблицу, в бланк ответов перенесите последовательность трёх цифр без пробелов, запятых и других дополнительных символов.
|
Насел. пункты |
д. Грушёвка |
д. Таловка |
д. Новая |
|
Цифры |
Ответ:
321
Задание 1.
Пользуясь описанием, определите, какими цифрами на плане обозначены населённые пункты.
Заполните таблицу, в бланк ответов перенесите последовательность трёх цифр без пробелов, запятых и других дополнительных символов.
|
Насел. пункты |
д. Новая |
с. Абрамово |
д. Таловка |
|
Цифры |
Ответ:
142
Задание 2.
Сколько километров проедут Гриша с дедушкой от деревни Грушёвка до села Абрамово, если они поедут по шоссе через деревню Новая?
Решение:
1клетка = 2 км
4+5+12=9+12=21 клетка
21*2=42 км
Ответ: 42
Задание 3.
Найдите расстояние от деревни Грушёвка до села Абрамово по прямой. Ответ дайте в километрах.
Решение:
2км = 1 клетка
Используем теорему Пифагора
(5+4)2 + 122= x2√ (5+4)2+122=√ 92+122 = √ 81+144= √ 225 = 15 клеток
15*2=30 км
Ответ:30
Задание 3.
Найдите расстояние от деревни Таловка до села Абрамово по прямой. Ответ дайте в километрах.
Решение:
2км = 1 клетка
Используем теорему Пифагора
52 + 122= x2
√ 52+122 = √ 25+144 = √ 169 = 13 клеток
13*2=26 кмОтвет: 26
Задание 4.
Сколько минут затратят на дорогу из деревни Грушёвка в село Абрамово Гриша с дедушкой, если поедут через деревню Новая?
Решение:
2км = 1 клетка
По шоссе Гриша с дедушкой едут со скоростью 15 км/ч
4+5+12=21 клетка
2*21=42 км60*42/15=168 минут
Ответ: 168
Задание 4.
Сколько минут затратят на дорогу из деревни Грушёвка в село Абрамово Гриша с дедушкой, если они поедут по прямой лесной дорожке?
Решение:
2км = 1 клетка
по лесной дорожке и тропинке — со скоростью 12 км/ч
Используем теорему Пифагора
(5+4)2 + 122= x2
√ (5+4)2+122 = √ 92+122 = √ 81+144= √ 225 = 15 клеток
15*2=30 км
60*30/12=1800/12=150 минОтвет: 150
Задание 4.
Сколько минут затратят на дорогу из деревни Грушёвка в село Абрамово Гриша с дедушкой, если они поедут сначала по шоссе, а затем свернут
в Таловке на прямую тропинку, которая проходит мимо пруда?
Решение:
2км=1клетка
4*2=8 км
60*8/15=32 мин потратят на дорогу по шоссе от Грушевки до Таловки√ 52+122 = √ 25+144 = √ 169 = 13 клеток
13*2=26 км от Таловки до Абрамово
60*13/12=65 минут32+65=97 минут
Ответ: 97
Задание 5.
В таблице указана стоимость (в рублях) некоторых продуктов в четырёх магазинах, расположенных в деревне Грушёвка, селе Абрамово, деревне Таловка и деревне Новая.
|
Наименование продукта |
д. Грушёвка |
с. Абрамово |
д. Таловка |
д. Новая |
|
Молоко (1 л) |
32 |
33 |
31 |
34 |
|
Хлеб (1 батон) |
24 |
21 |
26 |
20 |
|
Сыр «Российский» (1 кг) |
320 |
310 |
330 |
300 |
|
Говядина (1 кг) |
390 |
360 |
370 |
420 |
|
Картофель (1 кг) |
10 |
18 |
15 |
12 |
Гриша с дедушкой хотят купить 3 батона хлеба, 1,5 кг сыра «Российский» и 5 кг картофеля. В каком магазине такой набор продуктов будет стоить дешевле всего? В ответ запишите стоимость данного набора в этом магазине.
Решение:
Грушевка 3*24+1,5*320+5*10=72+480+50=602
Абрамово 3*21+1,5*310+5*18=63+465+90=618
Таловка 3*26+1,5*330+5*15=78+495+75=648
Новая 3*20+1,5*300+5*12=60+450+60=570
Ответ: 570
Задание 5.
В таблице указана стоимость (в рублях) некоторых продуктов в четырёх магазинах, расположенных в деревне Грушёвка, селе Абрамово, деревне Таловка и деревне Новая.
|
Наименование продукта |
д. Грушёвка |
с. Абрамово |
д. Таловка |
д. Новая |
|
Молоко (1 л) |
32 |
33 |
31 |
34 |
|
Хлеб (1 батон) |
24 |
21 |
26 |
20 |
|
Сыр «Российский» (1 кг) |
320 |
310 |
330 |
300 |
|
Говядина (1 кг) |
390 |
360 |
370 |
420 |
|
Картофель (1 кг) |
10 |
18 |
15 |
12 |
Гриша с дедушкой хотят купить 4 л молока, 5 батонов хлеба и 2 кг говядины. В каком магазине такой набор продуктов будет стоить дешевле всего? В ответ запишите стоимость данного набора в этом магазине.
Решение:
Грушевка 4*32+5*24+2*390=128+120+780=1028
Абрамово 4*33+5*21+2*360=132+105+720=957
Таловка 4*31+5*26+2*370=124+130+740=994
Новая 4*34+5*20+2*420=136+100+840=1076
Ответ: 957
C09A0A
Прочитайте внимательно текст и выполните задания 1–5.
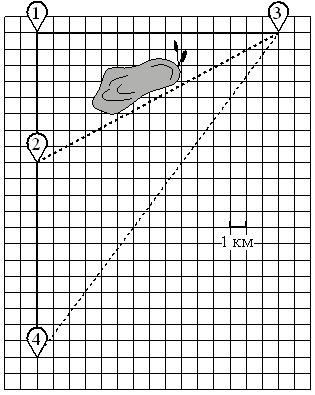
Ваня летом отдыхает у дедушки в деревне Дивная. В пятницу они собираются съездить на велосипедах в село Ольгино в библиотеку.
Из деревни Дивная в село Ольгино можно проехать по прямой лесной дорожке. Есть более длинный путь: по прямолинейному шоссе до села Ровное через деревню Калиновка, где нужно повернуть под прямым углом направо на другое шоссе, ведущее в село Ольгино. Есть и третий маршрут:
в деревне Калиновка можно свернуть на прямую тропинку в село Ольгино, которая идёт мимо пруда.
Лесная дорожка и тропинка образуют с шоссе прямоугольные треугольники.
По шоссе Ваня с дедушкой едут со скоростью 15 км/ч, а по лесной дорожке и тропинке — со скоростью 10 км/ч. На плане изображено взаимное расположение населённых пунктов, длина стороны каждой клетки равна 1 км.
Анализ:
Сначала нужно разобраться, какими буквами на плане обозначены деревни и сёла. Шоссе показано сплошной линией, а тропинки — пунктиром.
Значит, цифрами 1 и 4 обозначены д. Дивная, где отдыхает Ваня, и с. Ольгино.
Можно предположить, что д. Дивная отмечена цифрой 4. Но тогда д. Калиновка окажется не между д. Дивной и с. Ровное, а между с. Ровное и с. Ольгино. Это противоречит условию. Остаётся единственный вариант:
1 — д. Дивная, 2 — д. Калиновка, 3 — с. Ровное, 4 — с. Ольгино.
Для удобства подпишите названия населённых пунктов на рисунке.
По условию, шоссе поворачивает в с. Ровное под прямым углом, а тропинки тоже прямые. Таким образом, получаются прямоугольные треугольники и при решении задач на расстояния по этому плану потребуется теорема Пифагора (она есть в бланке ОГЭ). Самое главное при этом — не ошибиться в подсчёте клеточек.
Задание 1.
Пользуясь описанием, определите, какими цифрами на плане обозначены населённые пункты.
Заполните таблицу, в бланк ответов перенесите последовательность трёх цифр без пробелов, запятых и других дополнительных символов.
|
Насел. пункты |
с. Ольгино |
д. Дивная |
с. Ровное |
|
Цифры |
Решение:
Рассуждение уже приведено в обсуждении сюжета. Деревня Калиновка расположена между д. Дивная и с. Ровное, поэтому единственный подходящий
вариант: 1 — д. Дивная, 2 — д. Калиновка, 3 — с. Ровное и 4 — с. Ольгино.Ответ: 413
Задание 1.
Пользуясь описанием, определите, какими цифрами на плане обозначены населённые пункты.
Заполните таблицу, в бланк ответов перенесите последовательность трёх цифр без пробелов, запятых и других дополнительных символов.
|
Насел. пункты |
д. Калиновка |
с. Ровное |
с. Ольгино |
|
Цифры |
Ответ:
234
Задание 1.
Пользуясь описанием, определите, какими цифрами на плане обозначены населённые пункты.
Заполните таблицу, в бланк ответов перенесите последовательность трёх цифр без пробелов, запятых и других дополнительных символов.
|
Насел. пункты |
с. Ровное |
д. Калиновка |
д. Дивная |
|
Цифры |
Ответ:
321
Задание 1.
Пользуясь описанием, определите, какими цифрами на плане обозначены населённые пункты.
Заполните таблицу, в бланк ответов перенесите последовательность трёх цифр без пробелов, запятых и других дополнительных символов.
|
Насел. пункты |
д. Калиновка |
с. Ольгино |
д. Дивная |
|
Цифры |
Ответ:
241
Задание 2.
Сколько километров проедут Ваня с дедушкой от деревни Дивная до села Ольгино, если они поедут по шоссе через село Ровное?
Решение:
От д. Дивная до с. Ровное по шоссе 28 км, а от с. Ровное до с. Ольгино — ещё 21 км. Всего 49 км.
Ответ: 49.
Задание 2.
Сколько километров проедут Ваня с дедушкой от деревни Калиновка до села Ольгино, если они поедут по шоссе через село Ровное?
Решение:
От д. Калиновка до с. Ровное по шоссе 20 км, а от с. Ровное до с. Ольгино — ещё 21 км. Всего 41 км.
Ответ: 41
Задание 3.
Найдите расстояние от деревни Дивная до села Ольгино по прямой. Ответ дайте в километрах.
Решение:
1км = 1 клетка
Используем теорему Пифагора
282 + 212= x2
√ 282+212 = √ 784+441= √ 1225 = 35 кмОтвет: 35
Задание 3.
Найдите расстояние от деревни Калиновка до села Ольгино по прямой. Ответ дайте в километрах.
Решение:
Протяжённость тропинки найдем с помощью теоремы Пифагора.
Расстояние от Калиновки до с. Ровное 20 км, а от с. Ровное до с. Ольгино — 21 км. При этом шоссе поворачивает в с. Ровное под прямым углом.
Из прямоугольного треугольника Калиновка — Ровное — Ольгино по тереме Пифагора находим протяжённость тропинки:
202 + 212 = 841 = 292.
Значит, протяжённость тропинки Калиновка — Ольгино равна 29 км.Ответ: 29
Задание 4.
Сколько минут затратят на дорогу из деревни Дивная в село Ольгино Ваня с дедушкой, если они поедут через село Ровное?
Решение:
От д. Калиновка до с. Ровное по шоссе 20 км, а от с. Ровное до с. Ольгино — ещё 21 км. Всего 41 км.
Скорость по шоссе 15 км/ч
60*41/15=164 минуты
Ответ: 164
Задание 4.
Сколько минут затратят на дорогу из деревни Дивная в село Ольгино Ваня с дедушкой, если они поедут по прямой лесной дорожке?
Решение:
1км = 1 клетка
Используем теорему Пифагора
282 + 212= x2
√ 282+212 = √ 784+441= √ 1225 = 35 км
10 км/ч скорость по лесной дорожке
60*35/10=210 мин
Ответ: 210
Задание 4.
Сколько минут затратят на дорогу из деревни Дивная в село Ольгино Ваня с дедушкой, если они поедут сначала по шоссе, а затем свернут в Калиновке на прямую тропинку, которая проходит мимо пруда?
Решение:
От д. Дивная до д. Калиновка 8 км по шоссе, и Ваня с дедушкой проедут это расстояние за 8/15 часа, то есть за 8/15 · 60 = 32 минуты.
Затем они свернут на тропинку, протяжённость которой мы нашли в предыдущей задаче: 29 км. Это расстояние со скоростью 10 км/ч Ваня с дедушкой проедут за 2,9 ч, то есть за 174 минуты.
Следовательно, на весь путь они затратят 174 + 32 = 206 (мин.).Ответ: 206.
Задание 5.
В таблице указана стоимость (в рублях) некоторых продуктов в четырёх магазинах, расположенных в селе Ольгино, деревне Дивная, селе Ровное
и деревне Калиновка.
|
Наименование продукта |
с. Ольгино |
д. Дивная |
с. Ровное |
д. Калиновка |
|
Молоко (1 л) |
35 |
32 |
38 |
36 |
|
Хлеб (1 батон) |
25 |
22 |
19 |
20 |
|
Сыр «Российский» (1 кг) |
240 |
280 |
260 |
300 |
|
Говядина (1 кг) |
370 |
420 |
380 |
350 |
|
Картофель (1 кг) |
17 |
18 |
19 |
22 |
Ваня с дедушкой хотят купить 3 л молока, 0,5 кг сыра «Российский» и 2 кг картофеля. В каком магазине такой набор продуктов будет стоить дешевле всего? В ответ запишите стоимость данного набора в этом магазине.
Решение:
Эту и похожие задачи лучше всего решать прямо в таблице, дополнив её строкой «Всего». Разумеется, нужно оставить строки только с теми продуктами, которые нужны.
Можно сократить вычисления, заметив, что в с. Ровное и в д. Калиновка цены на все три нужных товара выше, чем в д. Дивная. Поэтому можно сравнить стоимость набора только в д. Дивная и в с. Ольгино.
Ольгино:
Молоко (1 л) 35 · 3 = 105
Сыр «Российский» (1кг) 240 · 0,5 = 120
Картофель (1 кг) 17 · 2 = 34
Всего: 105 + 120 + 34 =259Дивная:
Молоко (1 л) 32 · 3 = 96
Сыр «Российский» (1кг) 280 · 0,5 = 140
Картофель (1 кг) 18 · 2 = 36
Всего: 96 + 140 + 36 =272Дешевле всего нужный набор продуктов обойдётся в с. Ольгино: 259 р.
Ответ: 259.
Задание 5.
В таблице указана стоимость (в рублях) некоторых продуктов в четырёх магазинах, расположенных в селе Ольгино, деревне Дивная, селе Ровное
и деревне Калиновка.
|
Наименование продукта |
с. Ольгино |
д. Дивная |
с. Ровное |
д. Калиновка |
|
Молоко (1 л) |
35 |
32 |
38 |
36 |
|
Хлеб (1 батон) |
25 |
22 |
19 |
20 |
|
Сыр «Российский» (1 кг) |
230 |
270 |
250 |
300 |
|
Говядина (1 кг) |
370 |
420 |
380 |
350 |
|
Картофель (1 кг) |
17 |
18 |
19 |
22 |
Ваня с дедушкой хотят купить батон хлеба, 2 кг говядины и 3 кг картофеля. В каком магазине такой набор продуктов будет стоить дешевле всего? В ответ запишите стоимость этого набора в этом магазине.
Решение:
Ольгино 1*25+ 2*370+3*17=25+740+51=816
Дивная 1*22+ 2*420+3*18=22+840+54=916
Ровное 1*19+ 2*380+3*19=19+760+57=836
Калиновка 1*20+ 2*350+3*22=20+700+66=786
Ответ: 786
Задание 5.
В таблице указана стоимость (в рублях) некоторых продуктов в четырёх магазинах, расположенных в селе Ольгино, деревне Дивная, селе Ровное
и деревне Калиновка.
|
Наименование продукта |
с. Ольгино |
д. Дивная |
с. Ровное |
д. Калиновка |
|
Молоко (1 л) |
35 |
32 |
38 |
36 |
|
Хлеб (1 батон) |
25 |
22 |
19 |
20 |
|
Сыр «Российский» (1 кг) |
230 |
270 |
250 |
300 |
|
Говядина (1 кг) |
370 |
420 |
380 |
350 |
|
Картофель (1 кг) |
17 |
18 |
19 |
22 |
Ваня с дедушкой хотят купить 4 л молока, 2 батона хлеба и 1 кг сыра «Российский». В каком магазине такой набор продуктов будет стоить дешевле всего? В ответ запишите стоимость этого набора в этом магазине.
Решение:
Ольгино 4*35+2*25+1*230=140+50+230=420
Дивная 4*32+2*22+1*270=128+44+270=442
Ровное 4*38+2*19+1*250=152+38+250=440
Калиновка 4*36+2*20+1*300=144+40+300=484
Ответ: 420
Задание 5.
В таблице указана стоимость (в рублях) некоторых продуктов в четырёх магазинах, расположенных в селе Ольгино, деревне Дивная, селе Ровное
и деревне Калиновка.
|
Наименование продукта |
с. Ольгино |
д. Дивная |
с. Ровное |
д. Калиновка |
|
Молоко (1 л) |
35 |
32 |
38 |
36 |
|
Хлеб (1 батон) |
25 |
22 |
19 |
20 |
|
Сыр «Российский» (1 кг) |
230 |
270 |
250 |
300 |
|
Говядина (1 кг) |
370 |
420 |
380 |
350 |
|
Картофель (1 кг) |
17 |
18 |
19 |
22 |
Ваня с дедушкой хотят купить 3 кг картофеля, 1,5 кг говядины и батон хлеба. В каком магазине такой набор продуктов будет стоить дешевле всего?
В ответ запишите стоимость этого набора в этом магазине.
Решение:
Ольгино 3*17+1,5*370+1*25=51+555+25=631
Дивная 3*18+1,5*420+1*22=54+630+22=706
Ровное 3*19+1,5*380+1*19=57+570+19=646
Калиновка 3*22+1,5*350+1*20=66+525+20=611
Ответ: 611
34E199
Прочитайте внимательно текст и выполните задания 1–5.
На рисунке изображён план сельской местности.
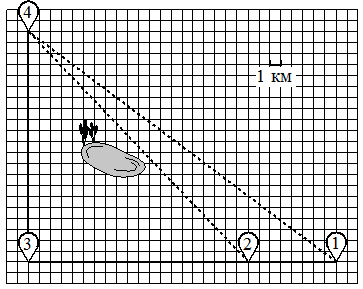
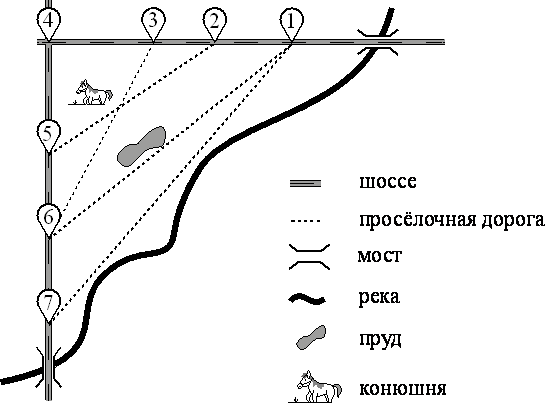
Таня на летних каникулах приезжает в гости к дедушке в деревню Антоновка (на плане обозначена цифрой 1). В конце каникул дедушка на машине собирается отвезти Таню на автобусную станцию, которая находится в деревне Богданово. Из Антоновки в Богданово можно проехать по просёлочной дороге мимо реки. Есть другой путь — по шоссе до деревни Ванютино, где нужно повернуть под прямым углом налево на другое шоссе, ведущее в Богданово. Третий маршрут проходит по просёлочной дороге мимо пруда до деревни Горюново, где можно свернуть на шоссе до Богданово. Четвёртый маршрут пролегает по шоссе до деревни Доломино, от Доломино до Горюново по просёлочной дороге мимо конюшни и от Горюново до Богданово по шоссе. Ещё один маршрут проходит по шоссе до деревни Егорка, по просёлочной дороге мимо конюшни от Егорки до Жилино и по шоссе от Жилино до Богданово.
Шоссе и просёлочные дороги образуют прямоугольные треугольники.
По шоссе Таня с дедушкой едут со скоростью 50 км/ч, а по просёлочным дорогам — со скоростью 30 км/ч. Расстояние от Антоновки до Доломино равно 12 км, от Доломино до Егорки — 4 км, от Егорки до Ванютино — 12 км, от Горюново до Ванютино — 15 км, от Ванютино до Жилино — 9 км, а от Жилино до Богданово — 12 км.
Анализ:
1 — Антоновка, 2 — Егорка, 3 — Доломино, 4 — Ванютино, 5 — Жилино, 6 — Горюново, 7 — Богданово
Задание 1.
Пользуясь описанием, определите, какими цифрами на плане обозначены деревни.
Заполните таблицу, в бланк ответов перенесите последовательность четырёх цифр без пробелов, запятых и других дополнительных символов.
|
Деревни |
Ванютино |
Горюново |
Егорка |
Жилино |
|
Цифры |
Ответ:
4625
Задание 1.
Пользуясь описанием, определите, какими цифрами на плане обозначены деревни.
Заполните таблицу, в бланк ответов перенесите последовательность четырёх цифр без пробелов, запятых и других дополнительных символов.
|
Деревни |
Егорка |
Ванютино |
Доломино |
Жилино |
|
Цифры |
Ответ:
2435
Задание 1.
Пользуясь описанием, определите, какими цифрами на плане обозначены деревни.
Заполните таблицу, в бланк ответов перенесите последовательность четырёх цифр без пробелов, запятых и других дополнительных символов.
|
Деревни |
Богданово |
Горюново |
Доломино |
Егорка |
|
Цифры |
Ответ:
7632
Задание 1.
Пользуясь описанием, определите, какими цифрами на плане обозначены деревни.
Заполните таблицу, в бланк ответов перенесите последовательность четырёх цифр без пробелов, запятых и других дополнительных символов.
|
Деревни |
Богданово |
Ванютино |
Егорка |
Жилино |
|
Цифры |
Ответ:
7425
Задание 2.
Найдите расстояние от Антоновки до Егорки по шоссе. Ответ дайте в километрах.
Решение:
Расстояние от Антоновки до Доломино состоит из расстояний от Антоновки до Егорки и от Егорки до Доломино, следовательно, расстояние от Антоновки до Егорки равно 12 — 4=8 км.
Ответ: 8
Задание 2.
Найдите расстояние от Доломино до Ванютино по шоссе. Ответ дайте в километрах.
Решение:
12-4=8км
Ответ: 8
Задание 2.
Найдите расстояние от Горюново до Жилино по шоссе. Ответ дайте в километрах.
Решение:
15-9=6 км
Ответ: 6
Задание 2.
Найдите расстояние от Ванютино до Богданово по шоссе. Ответ дайте
в километрах.
Решение:
9+12=21 км
Ответ: 21
Задание 3.
Найдите расстояние от Егорки до Жилино по прямой. Ответ дайте в километрах.
Решение:
Расстояние от Егорки до Жилино соответствует гипотенузе прямоугольного треугольника с катетами 12 км и 9 км. По теореме Пифагора $sqrt{144+81}=15$
Ответ: 15.
Задание 3.
Найдите расстояние от Доломино до Горюново по прямой. Ответ дайте в километрах.
Решение:
Катеты прямоугольного треугольника:
1) 12-4=8 км
2) 15 км
По теореме Пифагора $sqrt{64+225}=17$ кмОтвет: 17
Задание 3.
Найдите расстояние от Антоновки до Горюново по прямой. Ответ дайте в километрах.
Решение:
1) (12-4)+12=8+12=20 км
2) 15 км
По теореме Пифагора $sqrt{400+225}=25$ км
Ответ: 25
Задание 3.
Найдите расстояние от Антоновки до Богданово по прямой. Ответ дайте в километрах.
Решение:
1) (12-4)+12=8+12=20 км
2) 9+12=21 км
По теореме Пифагора $sqrt{400+441}=29$ км
Ответ: 29
Задание 4.
Сколько минут затратят на дорогу Таня с дедушкой из Антоновки в Богданово, если поедут мимо пруда через Горюново?
Решение:
Расстояние от Антоновки до Горюнова соответствует гипотенузе треугольника с катетами 20 км и 15 км. Найдем ее по теореме Пифагора: $sqrt{400+225}=25$ км.
По проселочной дороге Таня с дедушкой едут со скоростью 30 км/ч. Следовательно, на путь от Антоновки до Горюново они затратят 25 : 30 = 5/6 часа или 5/6*60=50 минут.
Расстояние от Горюново до Богданово 6 км, скорость по шоссе Тани с дедушкой составляет 50 км/ч. Следовательно, на путь от Горюново до Богданово они затратят 6 : 50 = 0,12 часа или 7,2 минуты.
Таким образом, на весь путь Таня с дедушкой затратят 50 + 7,2=57,2 минуты.
Ответ: 57,2.
Задание 4.
Сколько минут затратят на дорогу Таня с дедушкой из Антоновки в Богданово, если поедут через Доломино и Горюново мимо конюшни?
Решение:
Найдем расстояние по шоссе от Антоновки, до Доломино и от Горюново до Богданово
12 км + 12-(15-9)=12+6=18 км
При этом скорость составляет 50 км/ч
60*18/50=21.6 мин
теперь найдем врем по проселочной дороге
Катеты для вычисления гипотенузы:
1) 12-4 = 8 км
2) 15 км
По теореме Пифагора $sqrt{64+225}=17$ км
60*17/30=34 мин
21.6+34=55,6 минОтвет: 55,6
Задание 4.
Сколько минут затратят на дорогу Таня с дедушкой из Антоновки в Богданово, если поедут через Егорку и Жилино мимо конюшни?
Решение:
По шоссе они будут ехать от Антоновки до Егорки расстояние:
12 – 4 = 8 км
Далее по просёлочной дороге от Егорки до Жилино, найдём расстояние как гипотенузу по теореме Пифагора:
По теореме Пифагора $sqrt{144+81}=15$ км
Далее по шоссе из Жилино до Богданово 12 км.
Всего по шоссе: 8 + 12 = 20 км.
Всего по просёлочной дороге: 15 км.
По шоссе Таня с дедушкой едут со скоростью 50 км/ч, а по просёлочным дорогам – со скоростью 30 км/ч.
Найдём их время в пути:60*20/50=24 мин по шоссе
60*15/30=30 мин по проселочной дороге
30+24=54 минутыОтвет: 54
Задание 4.
Сколько минут затратят на дорогу Таня с дедушкой из Антоновки в Богданово, если поедут напрямик?
Решение:
Найдем расстояние.
катеты прямоугольного треугольника:
1) (12-4)+12=8+12=20 км
2) 9+12=21 км
По теореме Пифагора $sqrt{400+441}=29$ км
найдем время перемещения для расстояния 29 км при скорости 30 км/ч
60*29/30=58 мин
Ответ: 58
Задание 4.
За какое наименьшее количество минут Таня с дедушкой могут добраться из Егорки в Жилино?
Решение:
Из Егорки в Жилино можно проехать по шоссе, а можно по проселочной дороге.
Рассчитаем время маршрута по прямой из деревни Егорки в деревню Жилино по проселочной местности и время маршрута из деревни Егорки в деревню Жилино по шоссе через деревню Ванютино. Расстояние от Егорки до Жилино соответствует гипотенузе треугольника с катетами 12 км и 9 км. По теореме Пифагора имеем: корень из 144 плюс 81=15 км. Следовательно, этот путь Таня с дедушкой проедут за:
60*15/30 = 30 минут.
Расстояние от Егорки до Ванютино 12 км, от Ванютино до Жилино 9 км. Следовательно, этот путь 12 + 9 = 21 км. 60*21/50= 25,2 минуты. Таким образом, наименьшее количество времени Таня с дедушкой затратят на путь из деревни Егорки в деревню Жилино по шоссе через деревню Ванютино — 25,2 минуты.
Ответ: 25,2
Задание 4.
За какое наименьшее количество минут Таня с дедушкой могут добраться из Доломино в Горюново?
Решение:
Из Доломино в Горюново существует два маршрута.
1-й маршрут по шоссе, расстояние:12 – 4 + 15 = 23 км
Скорость 50 км/ч, найдём время в пути:
60*23/50=27,6 минут
2-й маршрут на прямую по просёлочной дороге, расстояние находим по теореме Пифагора:
$sqrt{64+225}=17$ км
Скорость 30 км/ч, найдём время в пути:
60*17/30=34 минуты
Наименьшее количество минут 27,6.
Ответ: 27,6
Задание 4.
За какое наименьшее количество минут Таня с дедушкой могут добраться из Антоновки в Горюново?
Решение:
Рассмотрим вариант по шоссе и по пересеченной местности.
1)По шоссе:
12-4+12=8+12 +15 =35 км
Найдем время:
60*35/50=42 мин2) напрямую:
Найдем катеты прямоугольного треугольника.
1) 15 км
2) 12-4+12=20 км
$sqrt{400+225}=25$ км
Найдем время:
60*25/30=50 мин3) еще один вариант по шоссе до Егорки, потом до Жилино напрямую, а потом снова по шоссе, а потом по пересеченной местности
(12-4)+(15-9)=8+6=14 км
60*14/50=16.8 минКатеты
12 и 9 км
$sqrt{144+81}=15$ км
60*15/30=30 мин
30+16.8 = 46.8 минОтвет: 42
Задание 4.
За какое наименьшее количество минут Таня с дедушкой могут добраться из Антоновки в Богданово?
Решение:
Рассмотрим вариант по шоссе и по пересеченной местности.
1) по шоссе
12-4+12=8+12=20+9+12=41км
найдем время
60*41/50=49,2 мин2) напрямую
катеты:
1) 12-4+12=20 км
2) 9+12=21 км
$sqrt{400+441}=29$ км
найдем время
60*29/30=58 минОтвет: 49,2
Задание 5.
На просёлочных дорогах машина дедушки расходует 9,2 литра бензина на 100 км. Известно, что на путь из Антоновки до Богданово через Ванютино и путь через Доломино и Горюново мимо конюшни ей необходим один и тот же объём бензина. Сколько литров бензина на 100 км машина дедушки расходует на шоссе?
Решение:
Получается, что на расстояние по шоссе от Ванютино до Горюново напрямую, потрачено столько же как между этими пунктами по шоссе. Значит надо найти сколько потрачено бензина напрямую, так как расход напрямую нам известен и произвести корректировку исходя из соотношения расстояний напрямую и по шоссе.
Итак. Напрямую проехали:
катеты прямоугольника:
1) 12-4=8 км
2) 15 км
$sqrt{64+225}=17$ км
Значит потратили бензина:
17*9,2/100=1,564 литратеперь найдем это расстояние по шоссе:
12-4+15=8+15=23 км
на них потратили также 1,564 литра
1,564/23=0,068 л тратится на 1 км
0,068*100 = 6,8 л тратится на 100 км.Ответ: 6,8.
Задание 5.
На просёлочных дорогах машина дедушки расходует 8,2 литра бензина на 100 км. Известно, что на путь из Антоновки до Богданово через Ванютино и путь напрямик ей необходим один и тот же объём бензина. Сколько
литров бензина на 100 км машина дедушки расходует на шоссе?
Решение:
Получается, что на расстояние по шоссе от Антоновки через Ванютино до Багданово по шоссе и напрямую потрачено одинаковое количество. Значит надо найти сколько потрачено бензина напрямую всего, так как расход напрямую нам известен и произвести корректировку исходя из соотношения расстояний напрямую и по шоссе.
Итак. Напрямую проехали:
катеты прямоугольника:
1) 12-4+12=8+12=20 км
2) 9+12=21 км
$sqrt{400+441}=29$ км
Значит потратили бензина:
29*8,2/100=2,378 литра потратили напрямуютеперь найдем это расстояние по шоссе:
12-4+12+9+12=20+21=41 км
на них потратили также 2,378 литра
2,378/41=0,058 л тратится на 1 км
0,058*100 = 5,8 л тратится на 100 км.
Ответ: 5,8
Задание 5.
На просёлочных дорогах машина дедушки расходует 9,1 литра бензина на 100 км. Известно, что на путь из Антоновки до Богданово через Ванютино и путь через Горюново мимо пруда ей необходим один и тот же объём бензина. Сколько литров бензина на 100 км машина дедушки расходует на шоссе?
Решение:
Получается, что на путь напрямую от Антоновки до Горюново, потрачено столько же бензина как по шоссе от Антоновки до Горюново через Ванютино. Значит находим расход бензина напрямую, так как известен расход на 100 км, и потом найдем рассход по шоссе.
Итак. Напрямую проехали до Горюново:
катеты прямоугольника:
1) 12-4+12=8+12=20 км
2) 15 км
$sqrt{400+225}=25$ км
расход составил:
25*9,1/100=2,275 литрапроехали по шоссе до Горюново
12-4+12 + 15= 35 км
2,275/35=0,065 литра тратили на км
0,,065*100 = 6,5 л н 100 кмОтвет: 6,5
Задание 5.
На просёлочных дорогах машина дедушки расходует 7,7 литра бензина на 100 км. Известно, что на путь из Антоновки до Богданово через Ванютино и путь через Егорку и Жилино мимо конюшни ей необходим один и тот же объём бензина. Сколько литров бензина на 100 км машина дедушки расходует на шоссе?
Решение:
Получается, что с Егорки до Жилино по прямой, потрачено столько же бензина, сколько С Егорки до Жилино по шоссе. Значит находим сколько потратили бензина по прямой, и возьмем этот объем бензина для расхода по шоссе, в сооответствии с пройденным расстоянием.
Итак. Напрямую проехали:
катеты прямоугольника:
1) 12 км
2) 9 км
$sqrt{144+81}=15$ км
расход составил:
15*7,7/100=1,155 литраТеперь найдем пробег по шоссе от Егорки до Жилино
12+9=21 км
1,155/21=0,055 л на километр
0,055*100=5,5 литра на 100 кмОтвет: 5,5
Задание 5.
На шоссе машина дедушки расходует 6,8 литра бензина на 100 км. Известно, что на путь из Антоновки до Богданово через Ванютино и путь через Доломино и Горюново мимо конюшни ей необходим один и тот же объём бензина. Сколько литров бензина на 100 км машина дедушки расходует на просёлочных дорогах?
Решение:
получается, что от Доломино до Горюново потрачено одинаково бензина, что по прямой, что по шоссе
найдем это расстояние по шоссе:
12-4+15=8+15=23 км
на них потратили
23*6,8/100= 1,564л потратил бензина на 23 км по шоссеНапрямую проехали:
катеты прямоугольника:
1) 12-4=8 км
2) 15 км
$sqrt{64+225}=17$ км
потратили бензина 1,564:
1,564/17=0,092 литра потратили на каждый км
0,092*100=9,2 литра расход на 100 кмОтвет: 9,2
Задание 5.
На шоссе машина дедушки расходует 5,8 литра бензина на 100 км. Известно, что на путь из Антоновки до Богданово через Ванютино и путь напрямик ей необходим один и тот же объём бензина. Сколько литров бензина на 100 км машина дедушки расходует на просёлочных дорогах?
Решение:
Получается, что на расстояние по шоссе от Антоновки через Ванютино до Багданово по шоссе и напрямую потрачено одинаковое количество. Значит надо найти сколько потрачено бензина по шоссе всего, так как расход по шоссе нам известен и произвести корректировку исходя из соотношения расстояний напрямую и по шоссе.
найдем расстояние по шоссе:
12-4+12+9+12=20+21=41 км
41*5,8/100=2,378 л потраченоНапрямую проехали:
катеты прямоугольника:
1) 12-4+12=8+12=20 км
2) 9+12=21 км
$sqrt{400+441}=29$ км
2,378/29=0,082 л потрачено на 1 км пути напрямую
0,082 *100 = 8,2 литра расход напрямуюОтвет: 8,2
Задание 5.
На шоссе машина дедушки расходует 6,5 литра бензина на 100 км. Известно, что на путь из Антоновки до Богданово через Ванютино и путь через Горюново мимо пруда ей необходим один и тот же объём бензина. Сколько литров бензина на 100 км машина дедушки расходует на просёлочных дорогах?
Решение:
Получается, что на путь напрямую от Антоновки до Горюново, потрачено столько же бензина как по шоссе от Антоновки до Горюново через Ванютино. Значит находим расход бензина по шоссе, так как известен расход на 100 км, и потом найдем расход напрямую.
проехали по шоссе до Горюново
12-4+12 + 15= 35 км
35*6,5/100 = 2,275 л потратилиНапрямую проехали до Горюново:
катеты прямоугольника:
1) 12-4+12=8+12=20 км
2) 15 км
$sqrt{400+225}=25$ км
расход составил:
2,275/25=0,091 л на км тратится напрямую
0,091*100=9,1 л на 100 км
Ответ: 9.1
Задание 5.
На шоссе машина дедушки расходует 5,5 литра бензина на 100 км. Известно, что на путь из Антоновки до Богданово через Ванютино и путь через Егорку и Жилино мимо конюшни ей необходим один и тот же объём бензина. Сколько литров бензина на 100 км машина дедушки расходует на просёлочных дорогах?
Решение:
Получается, что с Егорки до Жилино по прямой, потрачено столько же бензина, сколько С Егорки до Жилино по шоссе. Значит находим сколько потратили бензина по шоссе, и возьмем этот объем бензина для расхода по прямой, в соответствии с пройденным расстоянием.
найдем пробег по шоссе от Егорки до Жилино
12+9=21 км
21*5,5/100=1,155 л потраченоИтак. Напрямую проехали:
катеты прямоугольника:
1) 12 км
2) 9 км
$sqrt{144+81}=15$ км
1,155/15=0,077 л на 1 км
0,077 *100 = 7,7 л на 100 кмОтвет: 7.7
B64540
Прочитайте внимательно текст и выполните задания 1–5.
Гриша летом отдыхает у дедушки в деревне Осиновка. В субботу они собираются съездить на велосипедах в село Николаево в магазин. Из деревни Осиновка в село Николаево можно проехать по прямой лесной дорожке. Есть более длинный путь: по прямолинейному шоссе через деревню Зябликово до деревни Старая, где нужно повернуть под прямым углом направо
на другое шоссе, ведущее в село Николаево. Есть и третий маршрут:
в деревне Зябликово можно свернуть на прямую тропинку в село Николаево, которая идёт мимо пруда. Лесная дорожка и тропинка образуют с шоссе прямоугольные треугольники.
По шоссе Гриша с дедушкой едут со скоростью 15 км/ч, а по лесной дорожке и тропинке — со скоростью 10 км/ч. На плане изображено взаимное расположение населённых пунктов, длина стороны каждой клетки равна 1 км.
Анализ:
1 Старая
2 Зябликово
3 Николаево
4 Осиновка
Задание 1.
Пользуясь описанием, определите, какими цифрами на плане обозначены населённые пункты.
Заполните таблицу, в бланк ответов перенесите последовательность трёх цифр без пробелов, запятых и других дополнительных символов.
|
Насел. пункты |
д. Осиновка |
с. Николаево |
д. Зябликово |
|
Цифры |
Ответ:
432
Задание 1.
Пользуясь описанием, определите, какими цифрами на плане обозначены населённые пункты.
Заполните таблицу, в бланк ответов перенесите последовательность трёх цифр без пробелов, запятых и других дополнительных символов.
|
Насел. пункты |
д. Старая |
с. Николаево |
д. Зябликово |
|
Цифры |
Ответ:
132
Задание 1.
Пользуясь описанием, определите, какими цифрами на плане обозначены населённые пункты.
Заполните таблицу, в бланк ответов перенесите последовательность трёх цифр без пробелов, запятых и других дополнительных символов.
|
Насел. пункты |
д. Осиновка |
д. Старая |
д. Зябликово |
|
Цифры |
Ответ:
412
Задание 1.
Пользуясь описанием, определите, какими цифрами на плане обозначены населённые пункты.
Заполните таблицу, в бланк ответов перенесите последовательность трёх цифр без пробелов, запятых и других дополнительных символов.
|
Насел. пункты |
д. Осиновка |
с. Николаево |
д. Старая |
|
Цифры |
Ответ:
431
Задание 2.
Сколько километров проедут Гриша с дедушкой от деревни Осиновка до села Николаево, если они поедут по шоссе через деревню Старая?
Решение:
15+8+12=35 км
Ответ: 35
Задание 2.
Сколько километров проедут Гриша с дедушкой от деревни Зябликово до села Николаево, если они поедут по шоссе через деревню Старая?
Решение:
8+15=23 км
Ответ: 23
Задание 3.
Найдите расстояние от деревни Осиновка до села Николаево по прямой. Ответ дайте в километрах.
Решение:
по теореме Пифагора
катеты прямоугольника:
1) 8+12=20 км
2) 15 км
$sqrt{400+225}=25$ км
Ответ: 25
Задание 3.
Найдите расстояние от деревни Зябликово до села Николаево по прямой. Ответ дайте в километрах.
Решение:
по теореме Пифагора
катеты прямоугольника:
1) 8 км
2) 15 км
$sqrt{64+225}=17$ км
Ответ: 17
Задание 4.
Сколько минут затратят на дорогу из деревни Осиновка в село Николаево Гриша с дедушкой, если поедут через деревню Старая?
Решение:
8+12+15=35км
60*35/15=140 мин
Ответ: 140
Задание 4.
Сколько минут затратят на дорогу из деревни Осиновка в село Николаево Гриша с дедушкой, если они поедут по прямой лесной дорожке?
Решение:
по теореме Пифагора
катеты прямоугольника:
1) 8+12=20 км
2) 15 км
$sqrt{400+225}=25$ км
60*25/10=150 мин
Ответ: 150
Задание 4.
Сколько минут затратят на дорогу из деревни Осиновка в село Николаево Гриша с дедушкой, если они поедут сначала по шоссе, а затем свернут
в деревне Зябликово на прямую тропинку, которая проходит мимо пруда?
Решение:
по шоссе
12 км
60*12/15=48 минпо теореме Пифагора
катеты прямоугольника:
1) 8 км
2) 15 км
$sqrt{64+225}=17$ км
60*17/10=102 мин102+48=150мин
Ответ: 150
Задание 5.
В таблице указана стоимость (в рублях) некоторых продуктов в четырёх магазинах, расположенных в деревне Осиновка, селе Николаево, деревне Зябликово и деревне Старая.
|
Наименование продукта |
д. Осиновка |
с. Николаево |
д. Зябликово |
д. Старая |
|
Молоко (1 л) |
44 |
48 |
54 |
60 |
|
Хлеб (1 батон) |
26 |
19 |
23 |
18 |
|
Сыр «Российский» (1 кг) |
310 |
330 |
340 |
290 |
|
Говядина (1 кг) |
370 |
320 |
330 |
360 |
|
Картофель (1 кг) |
24 |
26 |
25 |
27 |
Гриша с дедушкой хотят купить 3 л молока, 2 батона хлеба и 3 кг картофеля. В каком магазине такой набор продуктов будет стоить дешевле всего? В ответ запишите стоимость данного набора в этом магазине.
Решение:
Осиновка 3*44+2*26+3*24=132+52+72=256
Николаево 3*48+2*19+3*26=144+38+78=260
Зябликово 3*54+2*23+3*25=162+46+75=283
Старая 3*60+2*18+3*27=180+36+81=297
Ответ: 260
Задание 5.
В таблице указана стоимость (в рублях) некоторых продуктов в четырёх магазинах, расположенных в деревне Осиновка, селе Николаево, деревне Зябликово и деревне Старая.
|
Наименование продукта |
д. Осиновка |
с. Николаево |
д. Зябликово |
д. Старая |
|
Молоко (1 л) |
44 |
48 |
54 |
60 |
|
Хлеб (1 батон) |
26 |
19 |
23 |
18 |
|
Сыр «Российский» (1 кг) |
310 |
330 |
340 |
290 |
|
Говядина (1 кг) |
370 |
320 |
330 |
360 |
|
Картофель (1 кг) |
24 |
26 |
25 |
27 |
Гриша с дедушкой хотят купить 5 л молока, 2 кг сыра «Российский» и 2 кг говядины. В каком магазине такой набор продуктов будет стоить дешевле всего? В ответ запишите стоимость данного набора в этом магазине.
Решение:
Осиновка 5*44+2*310+2*370=220+620+740=1580
Николаево 5*48+2*330+2*320=240+660+640=1540
Зябликово 5*54+2*340+2*330=270+680+660=1610
Старая 5*60+2*290+2*360=300+580+720=1600
Ответ: 1540
BA66FC
Прочитайте внимательно текст и выполните задания 1–5.
Володя летом отдыхает у дедушки в деревне Ёлочки. В воскресенье они собираются съездить на машине в село Кленовое. Из деревни Ёлочки в село Кленовое можно проехать по прямой грунтовой дороге. Есть более длинный путь: по прямолинейному шоссе через деревню Сосенки до деревни Жуки, где нужно повернуть под прямым углом направо на другое шоссе, ведущее
в село Кленовое. Есть и третий маршрут: в деревне Сосенки можно свернуть на прямую грунтовую дорогу в село Кленовое, которая идёт мимо пруда.
Шоссе и грунтовые дороги образуют прямоугольные треугольники.
По шоссе Володя с дедушкой едут со скоростью 80 км/ч, а по грунтовой дороге — со скоростью 40 км/ч. На плане изображено взаимное расположение населённых пунктов, длина стороны каждой клетки равна 4 км.
Анализ:
1 Жуки 2 Кленовое 3 Сосенки 4 Елочки
Задание 1.
Пользуясь описанием, определите, какими цифрами на плане обозначены населённые пункты.
Заполните таблицу, в бланк ответов перенесите последовательность трёх цифр без пробелов, запятых и других дополнительных символов.
|
Насел. пункты |
д. Ёлочки |
с. Кленовое |
д. Жуки |
|
Цифры |
Ответ:
421
Задание 1.
Пользуясь описанием, определите, какими цифрами на плане обозначены населённые пункты.
Заполните таблицу, в бланк ответов перенесите последовательность трёх цифр без пробелов, запятых и других дополнительных символов.
|
Насел. пункты |
с. Кленовое |
д. Ёлочки |
д. Сосенки |
|
Цифры |
Ответ:
243
Задание 1.
Пользуясь описанием, определите, какими цифрами на плане обозначены населённые пункты.
Заполните таблицу, в бланк ответов перенесите последовательность трёх цифр без пробелов, запятых и других дополнительных символов.
|
Насел. пункты |
д. Ёлочки |
д. Сосенки |
д. Жуки |
|
Цифры |
Ответ:
431
Задание 1.
Пользуясь описанием, определите, какими цифрами на плане обозначены населённые пункты.
Заполните таблицу, в бланк ответов перенесите последовательность трёх цифр без пробелов, запятых и других дополнительных символов.
|
Насел. пункты |
д. Сосенки |
с. Кленовое |
д. Жуки |
|
Цифры |
Ответ:
321
Задание 2.
Сколько километров проедут Володя с дедушкой от деревни Ёлочки до села Кленовое, если они поедут по шоссе через деревню Жуки?
Решение:
1 клетка — 4 км
36+24+32=92км
Ответ: 92
Задание 2.
Сколько километров проедут Володя с дедушкой от деревни Сосенки до села Кленовое, если они поедут по шоссе через деревню Жуки?
Решение:
1 клетка — 4 км
24+32=56 км
Ответ: 56
Задание 3.
Найдите расстояние от деревни Ёлочки до села Кленовое по прямой. Ответ дайте в километрах.
Решение:
1 клетка — 4 км
по теореме Пифагора
катеты прямоугольника:
1) 36+24=60 км
2) 32 км
$sqrt{3600+1024}=68$ км
Ответ: 68
Задание 3.
Найдите расстояние от деревни Сосенки до села Кленовое по прямой. Ответ дайте в километрах.
Решение:
1 клетка — 4 км
по теореме Пифагора
катеты прямоугольника:
1) 24 км
2) 32 км
$sqrt{576+1024}=40$ км
Ответ: 40
Задание 4.
Сколько минут затратят на дорогу из деревни Ёлочки в село Кленовое Володя с дедушкой, если поедут через деревню Жуки?
Решение:
1 клетка — 4 км
36+24+32=92км
по шоссе 80 км/ч
92/80=1,15 часа
60*1,15=69 мин
Ответ: 69
Задание 4.
Сколько минут затратят на дорогу из деревни Ёлочки в село Кленовое Володя с дедушкой, если они поедут по прямой грунтовой дороге?
Решение:
по грунтовой дороге скорость 40 км/ч
1 клетка — 4 км
по теореме Пифагора
катеты прямоугольника:
1) 36+24=60 км
2) 32 км
$sqrt{3600+1024}=68$ км
68/40=1,7
60*1,7=102 мин
Ответ: 102
Задание 4.
Сколько минут затратят на дорогу из деревни Ёлочки в село Кленовое Володя с дедушкой, если они поедут сначала по шоссе, а затем свернут в деревне Сосенки на грунтовую дорогу, которая проходит мимо пруда?
Решение:
по грунтовой дороге скорость 40 км/ч
по шоссе 80 км/ч
1 клетка — 4 км
по теореме Пифагора
катеты прямоугольника:
1) 24 км
2) 32 км
$sqrt{576+1024}=40$ км
40/40=1 час
1*60=60 мин36/60=0,6 часа
0,6*60=36 мин60+36=96 мин
Ответ: 96
Задание 5.
В таблице указана стоимость (в рублях) некоторых продуктов в четырёх магазинах, расположенных в деревне Ёлочки, селе Кленовое, деревне Сосенки и деревне Жуки.
|
Наименование продукта |
д. Ёлочки |
с. Кленовое |
д. Сосенки |
д. Жуки |
|
Молоко (1 л) |
42 |
45 |
38 |
43 |
|
Хлеб (1 батон) |
22 |
25 |
23 |
27 |
|
Сыр «Российский» (1 кг) |
320 |
290 |
270 |
280 |
|
Говядина (1 кг) |
410 |
420 |
450 |
430 |
|
Картофель (1 кг) |
26 |
18 |
24 |
16 |
Володя с дедушкой хотят купить 5 л молока, 3 кг сыра «Российский» и 4 кг картофеля. В каком магазине такой набор продуктов будет стоить дешевле всего? В ответ запишите стоимость данного набора в этом магазине.
Решение:
Ёлочки 5*42+3*320+4*26=210+960+104=1274
Кленовое 5*45+3*290+4*18=225+870+72=1167
Сосенки 5*38+3*270+4*24=190+810+96=1096
Жуки 5*43+3*280+4*16=215+840+64=1119
Ответ: 1096
Задание 5.
В таблице указана стоимость (в рублях) некоторых продуктов в четырёх магазинах, расположенных в деревне Ёлочки, селе Кленовое, деревне Сосенки и деревне Жуки.
|
Наименование продукта |
д. Ёлочки |
с. Кленовое |
д. Сосенки |
д. Жуки |
|
Молоко (1 л) |
42 |
45 |
38 |
43 |
|
Хлеб (1 батон) |
22 |
25 |
23 |
27 |
|
Сыр «Российский» (1 кг) |
320 |
290 |
270 |
280 |
|
Говядина (1 кг) |
410 |
420 |
450 |
430 |
|
Картофель (1 кг) |
26 |
18 |
24 |
16 |
Володя с дедушкой хотят купить 3 батона хлеба, 2 кг сыра «Российский» и 3 кг говядины. В каком магазине такой набор продуктов будет стоить дешевле всего? В ответ запишите стоимость данного набора в этом магазине.
Решение:
Ёлочки 3*22+2*320+3*410=66+640+1230=1936
Кленовое 3*25+2*290+3*420=75+580+1260=1915
Сосенки 3*23+2*270+3*450=69+540+1350=1959
Жуки 3*27+2*280+3*430=81+560+1290=1931
Ответ: 1915
35C016
ОГЭ математика
141 вариант
1. Пользуясь описанием, определите, какими цифрами на плане
обозначены населённые пункты. В ответе запишите полученную последовательность
четырёх цифр.
|
Населённые |
Дубёнки |
Бережки |
Ушаково |
Афонино |
|
Цифры |
Гриша летом отдыхает у дедушки в деревне Ушаково. В субботу они
собираются съездить на машине в село Бережки. Из Ушакова в Бережки можно
проехать по прямой грунтовой дороге. Есть более длинный путь по шоссе — через
деревню Дубёнки до деревни Афонино, где нужно повернуть под прямым углом налево
на другое шоссе, ведущее в Бережки. Есть и третий маршрут: в деревне Дубёнки
можно свернуть на прямую грунтовую дорогу, которая идёт мимо озера прямо в село
Бережки.
По шоссе Гриша с дедушкой едут со скоростью 60 км/ч, а по
грунтовой дороге —50 км/ч. На плане изображено взаимное расположение населённых
пунктов, сторона каждой клетки равна 2 км.
2. Найдите расстояние от деревни Ушаково до села Бережки по прямой.
Ответ выразите в километрах.
3. Сколько километров проедут Гриша с дедушкой, если они поедут по
шоссе через Афонино?
4. Сколько времени затратят на дорогу Гриша с дедушкой, если они
поедут сначала до деревни Дубёнки, а затем свернут на грунтовую дорогу, идущую
мимо озера? Ответ выразите в минутах.
5. Определите, на какой маршрут потребуется меньше всего времени. В
ответе укажите, сколько минут потратят на дорогу Гриша с дедушкой, если поедут
этим маршрутом.
6.
Найдите значение выражения 3,8 + 2,9.
7. На координатной прямой отмечены числа .
Какое из следующих утверждений неверно?
1)
2)
3)
4)
8. Найдите значение выражения при
9. Найдите корень уравнения −5 + 9x = 10x +
4.
10. В таблице представлены результаты четырёх стрелков, показанные ими
на тренировке.
|
Номер стрелка |
Число выстрелов |
Число попаданий |
|
1 |
42 |
28 |
|
2 |
70 |
20 |
|
3 |
54 |
45 |
|
4 |
46 |
42 |
Тренер решил послать на соревнования того стрелка, у которого
относительная частота попаданий выше. Кого из стрелков выберет тренер? Укажите
в ответе его номер.
11. Установите соответствие между графиками функций и формулами,
которые их задают.
ГРАФИКИ ФУНКЦИЙ
ФОРМУЛЫ
1)
2)
3)
В таблице под каждой буквой укажите соответствующий номер.
12. Период колебания математического маятника (в
секундах) приближенно можно вычислить по формуле , где
—
длина нити (в метрах). Пользуясь этой формулой, найдите длину нити маятника (в
метрах), период колебаний которого составляет 3 секунды.
13. Решите неравенство
1) [-8;8]
2)
3) нет решений
4)
14. Бригада рабочих могла выполнить всю работу за 24 ч, если бы
работали одновременно все рабочие. однако по плану в первый час работал один
рабочий, во второй час — 2 рабочих, в третий — 3 и т. д. до тех пор, пока в
работу не включились все рабочие. И только несколько часов перед завершением
работала вся бригада. Время работы, предусмотренное планом, было бы сокращено
на 6 часов, если бы с самого начала работы работала бы вся бригада, за
исключением пяти рабочих. Найдите количество рабочих.
15.
Найдите больший угол равнобедренной трапеции , если
диагональ образует с основанием
и
боковой стороной углы, равные 17° и 23°
соответственно. Ответ дайте в градусах.
16.
Касательные в точках A и B к
окружности с центром O пересекаются под углом 12°. Найдите
угол ABO. Ответ дайте в градусах.
17. 
квадрата равен 24. Найдите площадь квадрата.
18. 
бумаге с размером клетки 1х1 изображён треугольник. Найдите его площадь.
19. Укажите номера верных утверждений.
1) Любые три прямые имеют не более одной общей точки.
2) Если угол равен 120°, то смежный с ним равен 120°.
3) Если расстояние от точки до прямой больше 3, то и длина любой
наклонной, проведённой из данной точки к прямой, больше 3.
Если
утверждений несколько, запишите их номера в порядке возрастания.
20. Решите уравнение
21. Моторная лодка прошла против течения реки 77 км и вернулась в
пункт отправления, затратив на обратный путь на 2 часа меньше, чем на путь
против течения. Найдите скорость лодки в неподвижной воде, если скорость течения
реки равна 4 км/ч.
22. Постройте график функции
и
определите, при каких значениях прямая
будет иметь с
графиком единственную общую точку.
23. В прямоугольном треугольнике с прямым
углом известны катеты:
,
. Найдите
медиану этого треугольника.
24. В окружности через середину O хорды BD проведена
хорда AC так, что дуги AB и CD равны.
Докажите, что O — середина хорды AC.
25. Медиана BM и биссектриса AP треугольника ABC пересекаются
в точке K, длина стороны AC втрое больше длины стороны AB.
Найдите отношение площади треугольника AKM к площади
четырёхугольника KPCM.
Решение
1. Пользуясь описанием, определите, какими цифрами на плане
обозначены населённые пункты. В ответе запишите полученную последовательность
четырёх цифр.
|
Населённые |
Дубёнки |
Бережки |
Ушаково |
Афонино |
|
Цифры |
Гриша летом отдыхает у дедушки в деревне Ушаково. В субботу они
собираются съездить на машине в село Бережки. Из Ушакова в Бережки можно
проехать по прямой грунтовой дороге. Есть более длинный путь по шоссе — через
деревню Дубёнки до деревни Афонино, где нужно повернуть под прямым углом налево
на другое шоссе, ведущее в Бережки. Есть и третий маршрут: в деревне Дубёнки
можно свернуть на прямую грунтовую дорогу, которая идёт мимо озера прямо в село
Бережки.
По шоссе Гриша с дедушкой едут со скоростью 60 км/ч, а по
грунтовой дороге —50 км/ч. На плане изображено взаимное расположение населённых
пунктов, сторона каждой клетки равна 2 км.
Решение.
Пользуясь описанием и рисунком можно заметить, что деревня Дубенки
соответствует цифре 2, деревня Бережки — цифре 4, деревня Ушаково — цифре 3 и
деревня Афонино —цифре 1.
Ответ: 2431.
2. Найдите расстояние от деревни Ушаково до села Бережки по прямой.
Ответ выразите в километрах.
Решение.
Расстояние от деревни Ушаково до села Бережки соответствует длине
гипотенузы прямоугольного треугольника с катетами 30 и 16. По теореме Пифагора
имеем:
Ответ: 34.
3. Сколько километров проедут Гриша с дедушкой, если они поедут по
шоссе через Афонино?
Решение.
Расстояние, которое проедут Гриша с дедушкой, проезжая через
Афонино, равно сумме длин катетов прямоугольного треугольника с катетами 30 и
16. Таким образом, имеем, что искомое расстояние равно 30 + 16 = 46.
Ответ: 46.
4. Сколько времени затратят на дорогу Гриша с дедушкой, если они
поедут сначала до деревни Дубёнки, а затем свернут на грунтовую дорогу, идущую
мимо озера? Ответ выразите в минутах.
Решение.
По шоссе Гриша с дедушкой проедут 18 километров со скоростью 60
км/ч. Следовательно, они затратят 18 : 60 = 0,3 часа или 18 минут. Дальше по
условию задачи они свернут на грунтовую дорогу длина которой равна длине
гипотенузы прямоугольного треугольника с катетами 12 и 16. Таким образом, по
теореме Пифагора длина составит:
По грунтовой дороге Гриша с дедушкой едут со скоростью 50 км/ч,
следовательно они затратят 20 : 50 = 0,4 часа или 24 минуты.
Таким образом, Гриша с дедушкой на весь путь затратят 24 + 18 = 42
минуты.
Ответ: 42.
5. Определите, на какой маршрут потребуется меньше всего времени. В
ответе укажите, сколько минут потратят на дорогу Гриша с дедушкой, если поедут
этим маршрутом.
Решение.
Гриша с дедушкой могут поехать тремя разными маршрутами.
Рассмотрим каждый из них.
1) По грунтовой дороге напрямую. Длина такого пути равна длине
гипотенузы прямоугольного треугольника с катетами 30 и 16. По теореме Пифагора
имеем:
Двигаясь по грунтовой дороге со скоростью 50 км/ч дедушка с Гришой
потратят 34 : 50 = 0,68 часа или 40,8 минут.
2) Сначала по шоссе, а затем по грунтовой дороге вдоль озера. По
шоссе Гриша с дедушкой проедут 18 километров со скоростью 60 км/ч.
Следовательно, они затратят 18 : 60 = 0,3 часа или 18 минут. Дальше по условию
задачи они свернут на грунтовую дорогу длина которой равна длине гипотенузы
прямоугольного треугольника с катетами 12 и 16. Таким образом, по теореме
Пифагора длина составит:
По грунтовой дороге Гриша с дедушкой едут со скоростью 50 км/ч,
следовательно они затратят 20 : 50 = 0,4 часа или 24 минуты.
Таким образом, Гриша с дедушкой на весь путь затратят 24 + 18 = 42
минуты.
3) По шоссе через Афонино. Расстояние, которое проедут Гриша с
дедушкой, проезжая через Афонино, равно сумме длин катетов прямоугольного
треугольника с катетами 30 и 16. Таким образом, имеем, что искомое расстояние
равно 30 + 16 = 46.
Двигаясь по шоссе со скоростью 60 км/ч Гриша с дедушкой потратят
46 : 60 часа или 46 минут.
Таким образом, самый быстрый путь составит 40,8 минут.
Ответ: 40,8.
6.
Найдите значение выражения 3,8 + 2,9.
Решение.
Найдем значение выражения: 3,8 + 2,9 = 6,7.
Ответ: 6,7.
7. На координатной прямой отмечены числа .
Какое из следующих утверждений неверно?
1)
2)
3)
4)
Решение.
Заметим, что
и
Проверим все варианты ответа:
1) — верно, так
как , а
2) — неверно: так
как и
, имеем:
3) — верно, так как
а
4) — верно, так
как а
Ответ указан под номером 2.
8. Найдите значение выражения при
Решение.
Преобразуем выражение:
Подставим значение
Ответ: −0,2.
9. Найдите корень уравнения −5 + 9x = 10x +
4.
Решение.
Последовательно получаем:
Ответ: −9.
10. В таблице представлены результаты четырёх стрелков, показанные ими
на тренировке.
|
Номер стрелка |
Число выстрелов |
Число попаданий |
|
1 |
42 |
28 |
|
2 |
70 |
20 |
|
3 |
54 |
45 |
|
4 |
46 |
42 |
Тренер решил послать на соревнования того стрелка, у которого
относительная частота попаданий выше. Кого из стрелков выберет тренер? Укажите
в ответе его номер.
Решение.
Найдём относительную частоту попаданий каждого из стрелков:
Заметим, что Приведём
и
к общему знаменателю и
сравним: Таким
образом, наибольшая относительная частота попаданий у четвёртого стрелка.
Ответ: 4.
11. Установите соответствие между графиками функций и формулами,
которые их задают.
ГРАФИКИ ФУНКЦИЙ
ФОРМУЛЫ
1)
2)
3)
В таблице под каждой буквой укажите соответствующий номер.
Решение.
Напомним, что если прямая задана уравнением ,
то: при тангенс угла наклона
прямой к оси абсцисс положителен.
Уравнение задает прямую,
которая пересекает ось ординат в точке 3. Ее график изображен на рисунке Б).
Уравнение задает прямую, которая
пересекает ось ординат в точке 0. Ее график изображен на рисунке A).
Уравнение задает прямую, которая
пересекает ось ординат в точке -3. Ее график изображен на рисунке B).
Тем самым, искомое соответствие: А — 2, Б — 1, В — 3.
Ответ: 213.
12. Период колебания математического маятника (в
секундах) приближенно можно вычислить по формуле ,
где — длина нити (в метрах). Пользуясь этой формулой, найдите длину
нити маятника (в метрах), период колебаний которого составляет 3 секунды.
Решение.
Подставим в формулу значение :
Ответ: 2,25.
13. Решите неравенство
1) [-8;8]
2)
3) нет решений
4)
Решение.
Решим неравенство: Корнями уравнения
являются числа -8 и 8. Поэтому
Ответ: 2
14. Бригада рабочих могла выполнить всю работу за 24 ч, если бы
работали одновременно все рабочие. однако по плану в первый час работал один
рабочий, во второй час — 2 рабочих, в третий — 3 и т. д. до тех пор, пока в
работу не включились все рабочие. И только несколько часов перед завершением
работала вся бригада. Время работы, предусмотренное планом, было бы сокращено
на 6 часов, если бы с самого начала работы работала бы вся бригада, за
исключением пяти рабочих. Найдите количество рабочих.
Решение.
Пусть всего было n рабочих, тогда объем работы
составляет 24n (считаем, что за 1 час один рабочий выполняет
единицу объема работы). Пусть также время работы по плану составляло x часов.
Тогда:
Найдем количество рабочих из уравнения Получаем:
Ответ: 25 рабочих.
15.
Найдите больший угол равнобедренной трапеции , если
диагональ образует с основанием
и
боковой стороной углы, равные 17° и 23°
соответственно. Ответ дайте в градусах.
Решение.
В равнобедренной трапеции углы при основаниях равны. Угол ABC —
тупой, а угол BAD — острый, значит, ∠ABC — больший угол
равнобедренной трапеции. Углы CAD и BCA равны
как накрест лежащие. Тогда:
Ответ: 140
16.
Касательные в точках A и B к
окружности с центром O пересекаются под углом 12°. Найдите
угол ABO. Ответ дайте в градусах.
Решение.
Введём обозначение, как показано на рисунке. Касательные,
проведённые к окружности из одной точки равны, поэтому следовательно,
треугольник — равнобедренный. Откуда
Угол
между касательной и хордой равен половине дуги, которую он заключает, значит,
дуга равна 168°. Угол AOB — центральный, поэтому он
равен дуге, на которую опирается, следовательно, равен 168°. Рассмотрим
треугольник AOB, он равнобедренный, следовательно,
Ответ: 6.
17. 
квадрата равен 24. Найдите площадь квадрата.
Решение.
Периметр квадрата равен сумме длин всех его сторон. Таким образом,
сторона квадрата равна 6. Площадь квадрата равна квадрату его стороны, поэтому
она равна 36.
Ответ: 36.
18. 
бумаге с размером клетки 1х1 изображён треугольник. Найдите его площадь.
Решение.

треугольника равна половине произведения основания на высоту, проведенную к
данному основанию. Таким образом:
Ответ: 15
19. Укажите номера верных утверждений.
1) Любые три прямые имеют не более одной общей точки.
2) Если угол равен 120°, то смежный с ним равен 120°.
3) Если расстояние от точки до прямой больше 3, то и длина любой
наклонной, проведённой из данной точки к прямой, больше 3.
Если
утверждений несколько, запишите их номера в порядке возрастания.
Решение.
Проверим каждое из утверждений.
1) «Любые три прямые имеют не более одной общей точки» — верно.
Если прямые имеют две и более общих точек, то они совпадают. (См. комментарии к
задаче.)
2) «Если угол равен 120°, то смежный с ним равен 120°» — неверно.
Сумма смежных углов равна 180°.
3) «Если расстояние от точки до прямой больше 3, то и длина любой
наклонной, проведённой из данной точки к прямой, больше 3» — верно.
Т. к. расстояние — длина кратчайшего отрезка до прямой, а все наклонные —
длиннее.
Ответ: 13.
20. Решите уравнение
Решение.
Последовательно получаем:
Ответ: −8; −5.
21. Моторная лодка прошла против течения реки 77 км и вернулась в
пункт отправления, затратив на обратный путь на 2 часа меньше, чем на путь против
течения. Найдите скорость лодки в неподвижной воде, если скорость течения реки
равна 4 км/ч.
Решение.
Пусть км/ч — скорость лодки в неподвижной
воде, тогда км/ч — скорость лодки
против течения реки, а км/ч — скорость лодки
по течению. Лодка затратила на путь по течению реки на 2 часа меньше, чем
против течения, составим уравнение:
Корень −18 не подходит по условию задачи, следовательно, скорость
моторной лодки в стоячей воде равна 18 км/ч.
Ответ: 18.
22. Постройте график функции
и
определите, при каких значениях прямая
будет иметь с
графиком единственную общую точку.
Решение.
Построим график функции (см. рисунок).
Из графика видно, что прямая будет иметь с
графиком функции единственную точку пересечения при принадлежащем
множеству (−1; 0].
Ответ: (−1; 0].
23. В прямоугольном треугольнике с прямым
углом известны катеты:
,
.
Найдите медиану этого треугольника.
Решение.
Медиана, проведенная к гипотенузе, равна её половине:
Ответ: 5.
24. В окружности через середину O хорды BD проведена
хорда AC так, что дуги AB и CD равны.
Докажите, что O — середина хорды AC.
Решение.
Вписанные углы ADB, CBD , ACB и DAC опираются
на равные дуги, значит, они равны.
Получаем, что треугольники СOВ и AOD подобны
по двум углам; их коэффициент подобия равен BO:OD. Поскольку BO
= OD , эти треугольники равны, следовательно, AO = OC.
25. Медиана BM и биссектриса AP треугольника ABC пересекаются
в точке K, длина стороны AC втрое больше длины
стороны AB. Найдите отношение площади треугольника AKM к
площади четырёхугольника KPCM.
Решение.
Пусть площадь треугольника равна
Медиана
делит треугольник на два равновеликих треугольника, поэтому Биссектриса
делит площадь треугольника пропорционально прилежащим сторонам, то есть:
Откуда
Рассмотрим
треугольник
— биссектриса,
следовательно:
Откуда
Выразим
площадь треугольника
Найдём отношение площади треугольника к
площади четырёхугольника
Ответ: