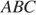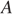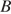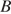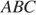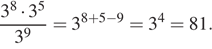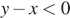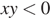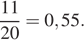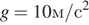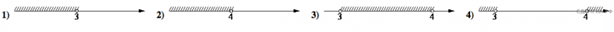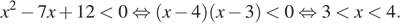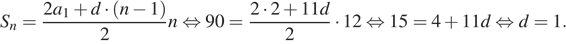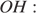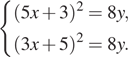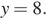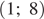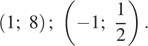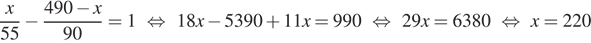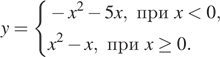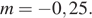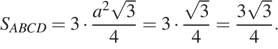Версия для печати и копирования в MS Word
Сколько времени затратят на дорогу Гриша с дедушкой, если они поедут сначала до деревни Дубёнки, а затем свернут на грунтовую дорогу, идущую мимо озера? Ответ выразите в минутах.
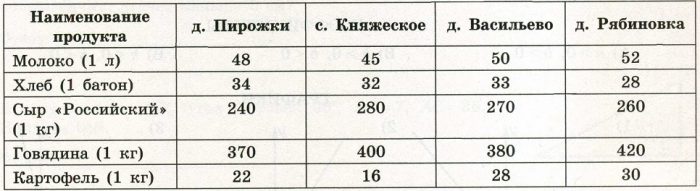
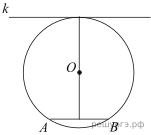
Гриша летом отдыхает у дедушки в деревне Ушаково. В субботу они собираются съездить на машине в село Бережки. Из Ушакова в Бережки можно проехать по прямой грунтовой дороге. Есть более длинный путь по шоссе — через деревню Дубёнки до деревни Афонино, где нужно повернуть под прямым углом налево на другое шоссе, ведущее в Бережки. Есть и третий маршрут: в деревне Дубёнки можно свернуть на прямую грунтовую дорогу, которая идёт мимо озера прямо в село Бережки.
По шоссе Гриша с дедушкой едут со скоростью 60 км/ч, а по грунтовой дороге —50 км/ч. На плане изображено взаимное расположение населённых пунктов, сторона каждой клетки равна 2 км.
1
Пользуясь описанием, определите, какими цифрами на плане обозначены населённые пункты. В ответе запишите полученную последовательность четырёх цифр.
| Населённые пункты | Дубёнки | Бережки | Ушаково | Афонино |
|---|---|---|---|---|
| Цифры |
2
Найдите расстояние от деревни Ушаково до села Бережки по прямой. Ответ выразите в километрах.
3
Сколько километров проедут Гриша с дедушкой, если они поедут по шоссе через Афонино?
4
Определите, на какой маршрут потребуется меньше всего времени. В ответе укажите, сколько минут потратят на дорогу Гриша с дедушкой, если поедут этим маршрутом.
Спрятать решение
Решение.
По шоссе Гриша с дедушкой проедут 18 километров со скоростью 60 км/ч. Следовательно, они затратят 18 : 60 = 0,3 часа или 18 минут. Дальше по условию задачи они свернут на грунтовую дорогу длина которой равна длине гипотенузы прямоугольного треугольника с катетами 12 и 16. Таким образом, по теореме Пифагора длина составит:
По грунтовой дороге Гриша с дедушкой едут со скоростью 50 км/ч, следовательно, они затратят 20 : 50 = 0,4 часа или 24 минуты.
Таким образом, Гриша с дедушкой на весь путь затратят 24 + 18 = 42 минуты.
Ответ: 42.
Предмет: Математика,
автор: abdhulikova
Приложения:

Ответы
Автор ответа: vapor17
0
Ответ:
46
Пошаговое объяснение:
Пирожки — Рябиновка
15 клеток
Рябиновка — Княжеское
8 клеток
15+8 = 23 клеток
23 * 2 = 46 км
abdhulikova:
что то не правильно, 4-Пирожки; 3-Рябиновка; 1-Васильево; 2-Княжеское.
Предыдущий вопрос
Следующий вопрос
Интересные вопросы
Предмет: Математика,
автор: gryshabakumenko
45:(21.5/7-3.5/7) +(6.2/5-3.3/5) :7
3 года назад
Предмет: Математика,
автор: tarartem2011
НАПИШИТЕ РЕШЕНИЕ
1) Для приготовления раствора для укладки кирпича требуется 80 кг песка, а цемента – на 40 кг меньше. Во сколько раз меньше требуется цемента, чем песка?
2) В класс привезли 20 новых парт, а стульев — в два раза больше. На сколько меньше привезли парт, чем стульев?
3) В магазине игрушек на 4 полках 28 кукол, а на 6 полках 48 машинок. На сколько на каждой полке машинок больше, чем кукол?
4) В саду 5 рядов яблонь по 8 деревьев и 4 ряда груш по 5 деревьев. Во сколько раз яблонь больше, чем груш?
3 года назад
Предмет: Русский язык,
автор: Arinabocharova321
Помогите пожалуйста кому не лень!!
3 года назад
Предмет: Математика,
автор: msSamigatovamailru
помогите решить : 30целых — 15целых 9/10 — 12 целых 3/10
5 лет назад
Предмет: Биология,
автор: ul73arcad
Помогите пж срочно!!!Тип побега:Прямостоячий, Лежачий, Ползучий, Вьющийся,
Цепляющийся, Лазающий. Его стрение, примеры!!!
5 лет назад
1. Пользуясь описанием, определите, какими цифрами на плане обозначены населённые пункты. В ответ запишите полученную последовательность четырёх цифр.
| Населенные пункты | д. Березовка | с. Игнатьево | д. Николаевка | д. Свистуха |
| Цифры | 1 | 2 | 4 | 3 |
Ответ: 1243.
Немного дополню картинку.
2. Сколько километров проедут Миша с дедушкой, если они поедут по шоссе через Берёзовку?
Миша с дедушкой выезжают из Николаевки. Если ехать по шоссе, то им надо проехать до Березовки 36 км, а затем до Игннатьево еще 15 км. Итого 36 + 15 = 51 км.
Ответ: 51.
3. Найдите расстояние от д. Николаевка до с. Игнатьево по прямой. Ответ дайте в километрах.
Дорога по лесной дорожке ни что иное, как гипотенуза C прямоугольного треугольника с катетами 36 км и 15 км.
Найдем ее по теореме Пифагора.
С2 = 362 + 152 = 1 296 + 225 = 1 521;
С = √1521 = 39.
Ответ: 39.
4. Сколько минут затратят на дорогу Миша с дедушкой, если поедут на станцию через Берёзовку?
Чтобы найти время надо расстояние поделить на скорость.
Расстояние равно 51 км (задача 2), скорость по шоссе равна 20 км/ч (из условия задачи).
Находим время:
51 : 20 = 2,55 ч = 2,55 · 60 = 153 минуты.
Ответ: 153.
5. Определите, на какой маршрут до станции потребуется меньше всего времени. В ответ укажите сколько минут потратят на дорогу Миша с дедушкой, если проедут этим маршрутом.
Время пути Миши и дедушки по шоссе мы нашли — 153 минуты.
Найдем время пути по лесной дороге.
Длина дороги равна 39 км (задача 3), а скорость путешественников равна 15 км/ч (условие задачи).
Находим время по лесной дорожке.
39 : 15 = 2,6 ч = 2,6 · 60 = 156 минут.
Но еще есть и третий маршрут — это путь от Николаевки до Свистухи по шоссе, а затем от Свистухи до Игнатьево по лесной дороге.
Найдем время пути от Николаевки до Свистухи: 16 : 20 = 0,8 ч = 0,8 · 60 = 48 минут.
И найдем время пути от Свистухи до Игнатьево.
Здесь не все так просто, т.к. длина лесной дороги нам не известна. Найдем ее по теореме Пифагора.
с2 = 152 + (36 — 16)2 = 225 + 400 = 625;
с = √625 = 25.
Время по лесной дороге: 25 : 15 = 5/3 ч = 5/3 · 60 = 100 минут.
Подведем итог. Время, которое затратят Миша с дедушкой, поехав через Свистуху и лесную дорогу, равно 48 + 100 = 148 минутам. Этот путь менее затратный по времени.
Ответ: 148.
Не можешь найти нужную задачу? Предложи свою! Наша группа в VK.
ОГЭ математика
141 вариант
1. Пользуясь описанием, определите, какими цифрами на плане
обозначены населённые пункты. В ответе запишите полученную последовательность
четырёх цифр.
|
Населённые |
Дубёнки |
Бережки |
Ушаково |
Афонино |
|
Цифры |
Гриша летом отдыхает у дедушки в деревне Ушаково. В субботу они
собираются съездить на машине в село Бережки. Из Ушакова в Бережки можно
проехать по прямой грунтовой дороге. Есть более длинный путь по шоссе — через
деревню Дубёнки до деревни Афонино, где нужно повернуть под прямым углом налево
на другое шоссе, ведущее в Бережки. Есть и третий маршрут: в деревне Дубёнки
можно свернуть на прямую грунтовую дорогу, которая идёт мимо озера прямо в село
Бережки.
По шоссе Гриша с дедушкой едут со скоростью 60 км/ч, а по
грунтовой дороге —50 км/ч. На плане изображено взаимное расположение населённых
пунктов, сторона каждой клетки равна 2 км.
2. Найдите расстояние от деревни Ушаково до села Бережки по прямой.
Ответ выразите в километрах.
3. Сколько километров проедут Гриша с дедушкой, если они поедут по
шоссе через Афонино?
4. Сколько времени затратят на дорогу Гриша с дедушкой, если они
поедут сначала до деревни Дубёнки, а затем свернут на грунтовую дорогу, идущую
мимо озера? Ответ выразите в минутах.
5. Определите, на какой маршрут потребуется меньше всего времени. В
ответе укажите, сколько минут потратят на дорогу Гриша с дедушкой, если поедут
этим маршрутом.
6.
Найдите значение выражения 3,8 + 2,9.
7. На координатной прямой отмечены числа .
Какое из следующих утверждений неверно?
1)
2)
3)
4)
8. Найдите значение выражения при
9. Найдите корень уравнения −5 + 9x = 10x +
4.
10. В таблице представлены результаты четырёх стрелков, показанные ими
на тренировке.
|
Номер стрелка |
Число выстрелов |
Число попаданий |
|
1 |
42 |
28 |
|
2 |
70 |
20 |
|
3 |
54 |
45 |
|
4 |
46 |
42 |
Тренер решил послать на соревнования того стрелка, у которого
относительная частота попаданий выше. Кого из стрелков выберет тренер? Укажите
в ответе его номер.
11. Установите соответствие между графиками функций и формулами,
которые их задают.
ГРАФИКИ ФУНКЦИЙ
ФОРМУЛЫ
1)
2)
3)
В таблице под каждой буквой укажите соответствующий номер.
12. Период колебания математического маятника (в
секундах) приближенно можно вычислить по формуле , где
—
длина нити (в метрах). Пользуясь этой формулой, найдите длину нити маятника (в
метрах), период колебаний которого составляет 3 секунды.
13. Решите неравенство
1) [-8;8]
2)
3) нет решений
4)
14. Бригада рабочих могла выполнить всю работу за 24 ч, если бы
работали одновременно все рабочие. однако по плану в первый час работал один
рабочий, во второй час — 2 рабочих, в третий — 3 и т. д. до тех пор, пока в
работу не включились все рабочие. И только несколько часов перед завершением
работала вся бригада. Время работы, предусмотренное планом, было бы сокращено
на 6 часов, если бы с самого начала работы работала бы вся бригада, за
исключением пяти рабочих. Найдите количество рабочих.
15.
Найдите больший угол равнобедренной трапеции , если
диагональ образует с основанием
и
боковой стороной углы, равные 17° и 23°
соответственно. Ответ дайте в градусах.
16.
Касательные в точках A и B к
окружности с центром O пересекаются под углом 12°. Найдите
угол ABO. Ответ дайте в градусах.
17. 
квадрата равен 24. Найдите площадь квадрата.
18. 
бумаге с размером клетки 1х1 изображён треугольник. Найдите его площадь.
19. Укажите номера верных утверждений.
1) Любые три прямые имеют не более одной общей точки.
2) Если угол равен 120°, то смежный с ним равен 120°.
3) Если расстояние от точки до прямой больше 3, то и длина любой
наклонной, проведённой из данной точки к прямой, больше 3.
Если
утверждений несколько, запишите их номера в порядке возрастания.
20. Решите уравнение
21. Моторная лодка прошла против течения реки 77 км и вернулась в
пункт отправления, затратив на обратный путь на 2 часа меньше, чем на путь
против течения. Найдите скорость лодки в неподвижной воде, если скорость течения
реки равна 4 км/ч.
22. Постройте график функции
и
определите, при каких значениях прямая
будет иметь с
графиком единственную общую точку.
23. В прямоугольном треугольнике с прямым
углом известны катеты:
,
. Найдите
медиану этого треугольника.
24. В окружности через середину O хорды BD проведена
хорда AC так, что дуги AB и CD равны.
Докажите, что O — середина хорды AC.
25. Медиана BM и биссектриса AP треугольника ABC пересекаются
в точке K, длина стороны AC втрое больше длины стороны AB.
Найдите отношение площади треугольника AKM к площади
четырёхугольника KPCM.
Решение
1. Пользуясь описанием, определите, какими цифрами на плане
обозначены населённые пункты. В ответе запишите полученную последовательность
четырёх цифр.
|
Населённые |
Дубёнки |
Бережки |
Ушаково |
Афонино |
|
Цифры |
Гриша летом отдыхает у дедушки в деревне Ушаково. В субботу они
собираются съездить на машине в село Бережки. Из Ушакова в Бережки можно
проехать по прямой грунтовой дороге. Есть более длинный путь по шоссе — через
деревню Дубёнки до деревни Афонино, где нужно повернуть под прямым углом налево
на другое шоссе, ведущее в Бережки. Есть и третий маршрут: в деревне Дубёнки
можно свернуть на прямую грунтовую дорогу, которая идёт мимо озера прямо в село
Бережки.
По шоссе Гриша с дедушкой едут со скоростью 60 км/ч, а по
грунтовой дороге —50 км/ч. На плане изображено взаимное расположение населённых
пунктов, сторона каждой клетки равна 2 км.
Решение.
Пользуясь описанием и рисунком можно заметить, что деревня Дубенки
соответствует цифре 2, деревня Бережки — цифре 4, деревня Ушаково — цифре 3 и
деревня Афонино —цифре 1.
Ответ: 2431.
2. Найдите расстояние от деревни Ушаково до села Бережки по прямой.
Ответ выразите в километрах.
Решение.
Расстояние от деревни Ушаково до села Бережки соответствует длине
гипотенузы прямоугольного треугольника с катетами 30 и 16. По теореме Пифагора
имеем:
Ответ: 34.
3. Сколько километров проедут Гриша с дедушкой, если они поедут по
шоссе через Афонино?
Решение.
Расстояние, которое проедут Гриша с дедушкой, проезжая через
Афонино, равно сумме длин катетов прямоугольного треугольника с катетами 30 и
16. Таким образом, имеем, что искомое расстояние равно 30 + 16 = 46.
Ответ: 46.
4. Сколько времени затратят на дорогу Гриша с дедушкой, если они
поедут сначала до деревни Дубёнки, а затем свернут на грунтовую дорогу, идущую
мимо озера? Ответ выразите в минутах.
Решение.
По шоссе Гриша с дедушкой проедут 18 километров со скоростью 60
км/ч. Следовательно, они затратят 18 : 60 = 0,3 часа или 18 минут. Дальше по
условию задачи они свернут на грунтовую дорогу длина которой равна длине
гипотенузы прямоугольного треугольника с катетами 12 и 16. Таким образом, по
теореме Пифагора длина составит:
По грунтовой дороге Гриша с дедушкой едут со скоростью 50 км/ч,
следовательно они затратят 20 : 50 = 0,4 часа или 24 минуты.
Таким образом, Гриша с дедушкой на весь путь затратят 24 + 18 = 42
минуты.
Ответ: 42.
5. Определите, на какой маршрут потребуется меньше всего времени. В
ответе укажите, сколько минут потратят на дорогу Гриша с дедушкой, если поедут
этим маршрутом.
Решение.
Гриша с дедушкой могут поехать тремя разными маршрутами.
Рассмотрим каждый из них.
1) По грунтовой дороге напрямую. Длина такого пути равна длине
гипотенузы прямоугольного треугольника с катетами 30 и 16. По теореме Пифагора
имеем:
Двигаясь по грунтовой дороге со скоростью 50 км/ч дедушка с Гришой
потратят 34 : 50 = 0,68 часа или 40,8 минут.
2) Сначала по шоссе, а затем по грунтовой дороге вдоль озера. По
шоссе Гриша с дедушкой проедут 18 километров со скоростью 60 км/ч.
Следовательно, они затратят 18 : 60 = 0,3 часа или 18 минут. Дальше по условию
задачи они свернут на грунтовую дорогу длина которой равна длине гипотенузы
прямоугольного треугольника с катетами 12 и 16. Таким образом, по теореме
Пифагора длина составит:
По грунтовой дороге Гриша с дедушкой едут со скоростью 50 км/ч,
следовательно они затратят 20 : 50 = 0,4 часа или 24 минуты.
Таким образом, Гриша с дедушкой на весь путь затратят 24 + 18 = 42
минуты.
3) По шоссе через Афонино. Расстояние, которое проедут Гриша с
дедушкой, проезжая через Афонино, равно сумме длин катетов прямоугольного
треугольника с катетами 30 и 16. Таким образом, имеем, что искомое расстояние
равно 30 + 16 = 46.
Двигаясь по шоссе со скоростью 60 км/ч Гриша с дедушкой потратят
46 : 60 часа или 46 минут.
Таким образом, самый быстрый путь составит 40,8 минут.
Ответ: 40,8.
6.
Найдите значение выражения 3,8 + 2,9.
Решение.
Найдем значение выражения: 3,8 + 2,9 = 6,7.
Ответ: 6,7.
7. На координатной прямой отмечены числа .
Какое из следующих утверждений неверно?
1)
2)
3)
4)
Решение.
Заметим, что
и
Проверим все варианты ответа:
1) — верно, так
как , а
2) — неверно: так
как и
, имеем:
3) — верно, так как
а
4) — верно, так
как а
Ответ указан под номером 2.
8. Найдите значение выражения при
Решение.
Преобразуем выражение:
Подставим значение
Ответ: −0,2.
9. Найдите корень уравнения −5 + 9x = 10x +
4.
Решение.
Последовательно получаем:
Ответ: −9.
10. В таблице представлены результаты четырёх стрелков, показанные ими
на тренировке.
|
Номер стрелка |
Число выстрелов |
Число попаданий |
|
1 |
42 |
28 |
|
2 |
70 |
20 |
|
3 |
54 |
45 |
|
4 |
46 |
42 |
Тренер решил послать на соревнования того стрелка, у которого
относительная частота попаданий выше. Кого из стрелков выберет тренер? Укажите
в ответе его номер.
Решение.
Найдём относительную частоту попаданий каждого из стрелков:
Заметим, что Приведём
и
к общему знаменателю и
сравним: Таким
образом, наибольшая относительная частота попаданий у четвёртого стрелка.
Ответ: 4.
11. Установите соответствие между графиками функций и формулами,
которые их задают.
ГРАФИКИ ФУНКЦИЙ
ФОРМУЛЫ
1)
2)
3)
В таблице под каждой буквой укажите соответствующий номер.
Решение.
Напомним, что если прямая задана уравнением ,
то: при тангенс угла наклона
прямой к оси абсцисс положителен.
Уравнение задает прямую,
которая пересекает ось ординат в точке 3. Ее график изображен на рисунке Б).
Уравнение задает прямую, которая
пересекает ось ординат в точке 0. Ее график изображен на рисунке A).
Уравнение задает прямую, которая
пересекает ось ординат в точке -3. Ее график изображен на рисунке B).
Тем самым, искомое соответствие: А — 2, Б — 1, В — 3.
Ответ: 213.
12. Период колебания математического маятника (в
секундах) приближенно можно вычислить по формуле ,
где — длина нити (в метрах). Пользуясь этой формулой, найдите длину
нити маятника (в метрах), период колебаний которого составляет 3 секунды.
Решение.
Подставим в формулу значение :
Ответ: 2,25.
13. Решите неравенство
1) [-8;8]
2)
3) нет решений
4)
Решение.
Решим неравенство: Корнями уравнения
являются числа -8 и 8. Поэтому
Ответ: 2
14. Бригада рабочих могла выполнить всю работу за 24 ч, если бы
работали одновременно все рабочие. однако по плану в первый час работал один
рабочий, во второй час — 2 рабочих, в третий — 3 и т. д. до тех пор, пока в
работу не включились все рабочие. И только несколько часов перед завершением
работала вся бригада. Время работы, предусмотренное планом, было бы сокращено
на 6 часов, если бы с самого начала работы работала бы вся бригада, за
исключением пяти рабочих. Найдите количество рабочих.
Решение.
Пусть всего было n рабочих, тогда объем работы
составляет 24n (считаем, что за 1 час один рабочий выполняет
единицу объема работы). Пусть также время работы по плану составляло x часов.
Тогда:
Найдем количество рабочих из уравнения Получаем:
Ответ: 25 рабочих.
15.
Найдите больший угол равнобедренной трапеции , если
диагональ образует с основанием
и
боковой стороной углы, равные 17° и 23°
соответственно. Ответ дайте в градусах.
Решение.
В равнобедренной трапеции углы при основаниях равны. Угол ABC —
тупой, а угол BAD — острый, значит, ∠ABC — больший угол
равнобедренной трапеции. Углы CAD и BCA равны
как накрест лежащие. Тогда:
Ответ: 140
16.
Касательные в точках A и B к
окружности с центром O пересекаются под углом 12°. Найдите
угол ABO. Ответ дайте в градусах.
Решение.
Введём обозначение, как показано на рисунке. Касательные,
проведённые к окружности из одной точки равны, поэтому следовательно,
треугольник — равнобедренный. Откуда
Угол
между касательной и хордой равен половине дуги, которую он заключает, значит,
дуга равна 168°. Угол AOB — центральный, поэтому он
равен дуге, на которую опирается, следовательно, равен 168°. Рассмотрим
треугольник AOB, он равнобедренный, следовательно,
Ответ: 6.
17. 
квадрата равен 24. Найдите площадь квадрата.
Решение.
Периметр квадрата равен сумме длин всех его сторон. Таким образом,
сторона квадрата равна 6. Площадь квадрата равна квадрату его стороны, поэтому
она равна 36.
Ответ: 36.
18. 
бумаге с размером клетки 1х1 изображён треугольник. Найдите его площадь.
Решение.

треугольника равна половине произведения основания на высоту, проведенную к
данному основанию. Таким образом:
Ответ: 15
19. Укажите номера верных утверждений.
1) Любые три прямые имеют не более одной общей точки.
2) Если угол равен 120°, то смежный с ним равен 120°.
3) Если расстояние от точки до прямой больше 3, то и длина любой
наклонной, проведённой из данной точки к прямой, больше 3.
Если
утверждений несколько, запишите их номера в порядке возрастания.
Решение.
Проверим каждое из утверждений.
1) «Любые три прямые имеют не более одной общей точки» — верно.
Если прямые имеют две и более общих точек, то они совпадают. (См. комментарии к
задаче.)
2) «Если угол равен 120°, то смежный с ним равен 120°» — неверно.
Сумма смежных углов равна 180°.
3) «Если расстояние от точки до прямой больше 3, то и длина любой
наклонной, проведённой из данной точки к прямой, больше 3» — верно.
Т. к. расстояние — длина кратчайшего отрезка до прямой, а все наклонные —
длиннее.
Ответ: 13.
20. Решите уравнение
Решение.
Последовательно получаем:
Ответ: −8; −5.
21. Моторная лодка прошла против течения реки 77 км и вернулась в
пункт отправления, затратив на обратный путь на 2 часа меньше, чем на путь против
течения. Найдите скорость лодки в неподвижной воде, если скорость течения реки
равна 4 км/ч.
Решение.
Пусть км/ч — скорость лодки в неподвижной
воде, тогда км/ч — скорость лодки
против течения реки, а км/ч — скорость лодки
по течению. Лодка затратила на путь по течению реки на 2 часа меньше, чем
против течения, составим уравнение:
Корень −18 не подходит по условию задачи, следовательно, скорость
моторной лодки в стоячей воде равна 18 км/ч.
Ответ: 18.
22. Постройте график функции
и
определите, при каких значениях прямая
будет иметь с
графиком единственную общую точку.
Решение.
Построим график функции (см. рисунок).
Из графика видно, что прямая будет иметь с
графиком функции единственную точку пересечения при принадлежащем
множеству (−1; 0].
Ответ: (−1; 0].
23. В прямоугольном треугольнике с прямым
углом известны катеты:
,
.
Найдите медиану этого треугольника.
Решение.
Медиана, проведенная к гипотенузе, равна её половине:
Ответ: 5.
24. В окружности через середину O хорды BD проведена
хорда AC так, что дуги AB и CD равны.
Докажите, что O — середина хорды AC.
Решение.
Вписанные углы ADB, CBD , ACB и DAC опираются
на равные дуги, значит, они равны.
Получаем, что треугольники СOВ и AOD подобны
по двум углам; их коэффициент подобия равен BO:OD. Поскольку BO
= OD , эти треугольники равны, следовательно, AO = OC.
25. Медиана BM и биссектриса AP треугольника ABC пересекаются
в точке K, длина стороны AC втрое больше длины
стороны AB. Найдите отношение площади треугольника AKM к
площади четырёхугольника KPCM.
Решение.
Пусть площадь треугольника равна
Медиана
делит треугольник на два равновеликих треугольника, поэтому Биссектриса
делит площадь треугольника пропорционально прилежащим сторонам, то есть:
Откуда
Рассмотрим
треугольник
— биссектриса,
следовательно:
Откуда
Выразим
площадь треугольника
Найдём отношение площади треугольника к
площади четырёхугольника
Ответ:
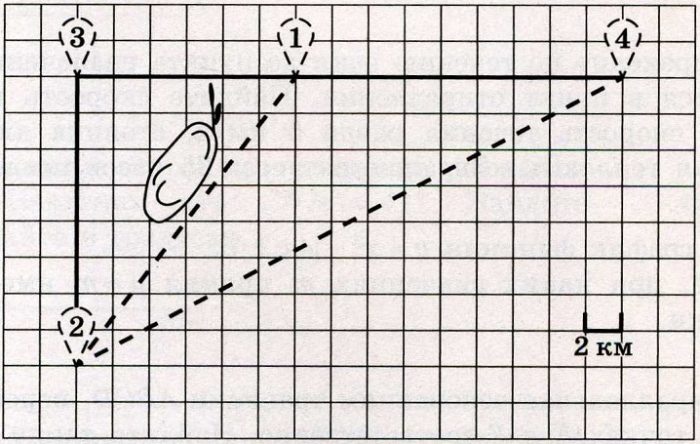
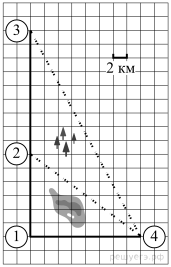
Серёжа летом отдыхает с папой в деревне Пирожки. В среду они собираются съездить на машине в село Княжеское. Из деревни Пирожки в село Княжеское можно проехать по прямой грунтовой дороге. Есть более длинный путь: по прямолинейному шоссе через деревню Васильево до деревни Рябиновки, где нужно повернуть под прямым углом налево на другое шоссе, ведущее в село Княжеское. Есть и третий маршрут: в деревне Васильево можно свернуть на прямую грунтовую дорогу в село Княжеское, которая идёт мимо пруда.
Шоссе и грунтовые дороги образуют прямоугольные треугольники.
По шоссе Серёжа с папой едут со скоростью 60 км/ч, а по грунтовой дороге – со скоростью 40 км/ч. На плане изображено взаимное расположение населённых пунктов, длина стороны каждой клетки равна 2 км.
Источник: ОГЭ Ященко 2022 (36 вар).
Задание 1
Пользуясь описанием, определите, какими цифрами на плане обозначены населённые пункты.
Заполните таблицу, в бланк ответов перенесите последовательность трёх цифр без пробелов, запятых и других дополнительных символов.
Решение
Из деревни Пирожки (4) в село Княжеское (2) можно проехать по прямой грунтовой дороге.
… более длинный путь: по прямолинейному шоссе через деревню Васильево (1) до деревни Рябиновки (3), где нужно повернуть под прямым углом налево на другое шоссе, ведущее в село Княжеское (2).
… третий маршрут: в деревне Васильево (1) можно свернуть на прямую грунтовую дорогу в село Княжеское (2), которая идёт мимо пруда.
Ответ: 423.
Задание 2
Сколько километров проедут Серёжа с папой от деревни Пирожки до села Княжеское, если они поедут по шоссе через деревню Рябиновку?
Решение
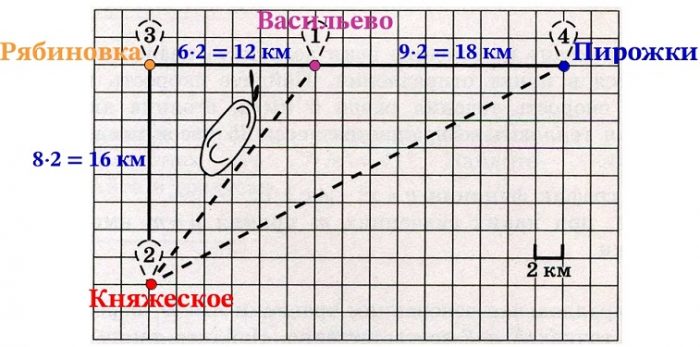
По плану одна клетка равна 2 км, считаем клетки и умножаем на 2. Расстояние от Пирожки до Княжеское равно (посчитал всё на рисунке):
18 + 12 + 16 = 46 км
Ответ: 46
Задание 3
Найдите расстояние от деревни Васильево до села Княжеское по прямой. Ответ дайте в километрах.
Решение
Дорога по прямой (х) из Васильево в Княжеское является гипотенузой (рисунок из задания 2) прямоугольного треугольника, найдём её по теореме Пифагора:
х2 = 122 + 162 = 144 + 256 = 400
х = √400 = 20 км
Ответ: 20
Задание 4
Сколько минут затратит на дорогу из деревни Пирожки в село Княжеское Серёжа с папой, если они поедут по прямой грунтовой дороге?
Решение
Грунтовая дорога по прямой (y) из Пирожки в Княжеское является гипотенузой (рисунок из задания 2) прямоугольного треугольника, найдём её по теореме Пифагора:
y2 = (12 + 18)2 + 162 = 302 + 162 = 900 + 256 = 1156
y = √1156 = 34 км
По грунтовой дороге они едут со скоростью 40 км/ч. Найдём время пути:
frac{34}{40}=frac{17}{20} часа
Переведём в минуты (1 час = 60 мин):
frac{17}{20}cdot 60=17cdot 3=51 мин
Ответ: 51
Задание 5
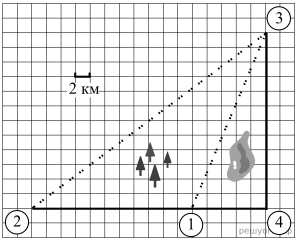
В таблице указана стоимость (в рублях) некоторых продуктов в четырёх магазинах, расположенных в деревне Пирожки, селе Княжеском, деревне Васильево и деревне Рябиновке.
Серёжа с папой хотят купить 2 л молока, 3 батона хлеба и 1 кг сыра «Российский». В каком магазине такой набор продуктов будет стоить дешевле всего? В ответ запишите стоимость данного набора в этом магазине.
Решение:
Смотрим по таблице цену продуктов и находим стоимость покупки в каждом магазине.
Пирожки:
2·48 + 3·34 + 1·240 = 96 + 102 + 240 = 438 рублей
Княжеское:
2·45 + 3·32 + 1·280 = 90 + 96 + 280 = 466 рублей
Васильево:
2·50 + 3·33 + 1·270 = 100 + 99 + 270 = 469 рублей
Рябиновка:
2·52 + 3·28 + 1·260 = 104 + 84 + 260 = 448 рублей
Наименьшая стоимость 438 рублей.
Ответ: 438
Есть три секунды времени? Для меня важно твоё мнение!
Насколько понятно решение?
Средняя оценка: 4.8 / 5. Количество оценок: 248
Оценок пока нет. Поставь оценку первым.
Новости о решённых вариантах ЕГЭ и ОГЭ на сайте ↙️
Вступай в группу vk.com 😉
Расскажи, что не так? Я исправлю в ближайшее время!
В отзыве оставь любой контакт для связи, если хочешь, что бы я тебе ответил.
Сколько километров проедут Гриша с дедушкой, если они поедут по шоссе через Афонино?
Гриша летом отдыхает у дедушки в деревне Ушаково. В субботу они собираются съездить на машине в село Бережки. Из Ушакова в Бережки можно проехать по прямой грунтовой дороге. Есть более длинный путь по шоссе — через деревню Дубёнки до деревни Афонино, где нужно повернуть под прямым углом налево на другое шоссе, ведущее в Бережки. Есть и третий маршрут: в деревне Дубёнки можно свернуть на прямую грунтовую дорогу, которая идёт мимо озера прямо в село Бережки.
По шоссе Гриша с дедушкой едут со скоростью 60 км/ч, а по грунтовой дороге —50 км/ч. На плане изображено взаимное расположение населённых пунктов, сторона каждой клетки равна 2 км.
Решение.
Расстояние, которое проедут Гриша с дедушкой, проезжая через Афонино, равно сумме длин катетов прямоугольного треугольника с катетами 30 и 16. Таким образом, имеем, что искомое расстояние равно 30 + 16 = 46.
Ответ: 46.
Домашнее задание по алгебре на 17.05.2021
1. Задание 1
Пользуясь описанием, определите, какими цифрами на плане обозначены населённые пункты. В ответе запишите полученную последовательность четырёх цифр.
| Населённые пункты | Кулаки | Илькино | Осинки | Кудрино |
| Цифры |
Гена летом отдыхает у дедушки в деревне Осинки. В воскресенье они собираются съездить на машине в село Кудрино. Из деревни Осинки в Кудрино можно проехать по прямой грунтовой дороге. Есть более длинный путь по шоссе — через деревню Илькино до деревни Кулаки, где нужно повернуть под прямым углом налево на другое шоссе, ведущее в Кудрино. Есть и третий маршрут: в Илькине можно свернуть на прямую грунтовую дорогу, которая идёт мимо озера прямо в Кудрино.
По шоссе Гена с дедушкой едут со скоростью 60 км/ч, а по грунтовой дороге — 40 км/ч. На плане изображено взаимное расположение населённых пунктов, сторона каждой клетки равна 2 км.
Решение.
Пользуясь описанием и рисунком можно заметить, что деревня Кулаки соответствует цифре 4, деревня Илькино — цифре 1, деревня Осинки — цифре 2 и деревня Кудрино —цифре 3.
Ответ: 4123.
Ответ: 4123
2. Задание 2
Найдите расстояние от деревни Осинки до села Кудрино по прямой. Ответ выразите в километрах.
Гена летом отдыхает у дедушки в деревне Осинки. В воскресенье они собираются съездить на машине в село Кудрино. Из деревни Осинки в Кудрино можно проехать по прямой грунтовой дороге. Есть более длинный путь по шоссе — через деревню Илькино до деревни Кулаки, где нужно повернуть под прямым углом налево на другое шоссе, ведущее в Кудрино. Есть и третий маршрут: в Илькине можно свернуть на прямую грунтовую дорогу, которая идёт мимо озера прямо в Кудрино.
По шоссе Гена с дедушкой едут со скоростью 60 км/ч, а по грунтовой дороге — 40 км/ч. На плане изображено взаимное расположение населённых пунктов, сторона каждой клетки равна 2 км.
Решение.
Расстояние от деревни Осинки до села Кудрино соответствует длине гипотенузы прямоугольного треугольника с катетами 32 и 24. По теореме Пифагора имеем:
Ответ: 40.
Ответ: 40
3. Задание 3
Сколько километров проедут Гена с дедушкой, если они поедут по шоссе через деревню Кулаки?
Гена летом отдыхает у дедушки в деревне Осинки. В воскресенье они собираются съездить на машине в село Кудрино. Из деревни Осинки в Кудрино можно проехать по прямой грунтовой дороге. Есть более длинный путь по шоссе — через деревню Илькино до деревни Кулаки, где нужно повернуть под прямым углом налево на другое шоссе, ведущее в Кудрино. Есть и третий маршрут: в Илькине можно свернуть на прямую грунтовую дорогу, которая идёт мимо озера прямо в Кудрино.
По шоссе Гена с дедушкой едут со скоростью 60 км/ч, а по грунтовой дороге — 40 км/ч. На плане изображено взаимное расположение населённых пунктов, сторона каждой клетки равна 2 км.
Решение.
Расстояние, которое проедут Гена с дедушкой, проезжая через Кулаки, равно сумме длин катетов прямоугольного треугольника с катетами 32 и 24. Таким образом, имеем, что искомое расстояние равно 32 + 24 = 56.
Ответ: 56.
Ответ: 56
4. Задание 4
Сколько времени затратят на дорогу Гена с дедушкой, если они поедут сначала до Илькино, а затем свернут на грунтовую дорогу, идущую мимо озера? Ответ выразите в минутах.
Гена летом отдыхает у дедушки в деревне Осинки. В воскресенье они собираются съездить на машине в село Кудрино. Из деревни Осинки в Кудрино можно проехать по прямой грунтовой дороге. Есть более длинный путь по шоссе — через деревню Илькино до деревни Кулаки, где нужно повернуть под прямым углом налево на другое шоссе, ведущее в Кудрино. Есть и третий маршрут: в Илькине можно свернуть на прямую грунтовую дорогу, которая идёт мимо озера прямо в Кудрино.
По шоссе Гена с дедушкой едут со скоростью 60 км/ч, а по грунтовой дороге — 40 км/ч. На плане изображено взаимное расположение населённых пунктов, сторона каждой клетки равна 2 км.
Решение.
По шоссе Гена с дедушкой проедут 22 километра со скоростью 60 км/ч. Следовательно, они затратят 22 : 60 = 0,37 часа или 22 минуты. Дальше по условию задачи они свернут на грунтовую дорогу длина которой равна длине гипотенузы прямоугольного треугольника с катетами 24 и 10. Таким образом, по теореме Пифагора длина составит:
По грунтовой дороге Гена с дедушкой едут со скоростью 40 км/ч, следовательно они затратят 26 : 40 = 0,65 часа или 39 минут.
Таким образом, Гена с дедушкой на весь путь затратят 22 + 39 = 61 минута.
Ответ: 61.
Ответ: 61
5. Задание 5
Определите, на какой маршрут потребуется меньше всего времени. В ответе укажите, сколько минут потратят на дорогу Гена с дедушкой, если поедут этим маршрутом.
Гена летом отдыхает у дедушки в деревне Осинки. В воскресенье они собираются съездить на машине в село Кудрино. Из деревни Осинки в Кудрино можно проехать по прямой грунтовой дороге. Есть более длинный путь по шоссе — через деревню Илькино до деревни Кулаки, где нужно повернуть под прямым углом налево на другое шоссе, ведущее в Кудрино. Есть и третий маршрут: в Илькине можно свернуть на прямую грунтовую дорогу, которая идёт мимо озера прямо в Кудрино.
По шоссе Гена с дедушкой едут со скоростью 60 км/ч, а по грунтовой дороге — 40 км/ч. На плане изображено взаимное расположение населённых пунктов, сторона каждой клетки равна 2 км.
Решение.
Гена с дедушкой могут поехать тремя разными маршрутами. Рассмотрим каждый из них.
1) По грунтовой дороге напрямую. Длина такого пути соответствует длине гипотенузы прямоугольного треугольника с катетами 32 и 24. По теореме Пифагора имеем:
Двигаясь по грунтовой дороге со скоростью 40 км/ч дедушка с Геной потратят 40 : 40 = 1 час или 60 минут.
2) Сначала по шоссе, а затем по грунтовой дороге вдоль озера. По шоссе Гена с дедушкой проедут 22 километра со скоростью 60 км/ч. Следовательно, они затратят 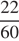
По грунтовой дороге Гена с дедушкой едут со скоростью 40 км/ч, следовательно они затратят 26 : 40 = 0,65 часа или 39 минут.
Таким образом, Гена с дедушкой на весь путь затратят 22 + 39 = 61 минута.
3) По шоссе через Кулаки. Расстояние, которое проедут Гена с дедушкой, проезжая через Кулаки, равно сумме длин катетов прямоугольного треугольника с катетами 32 и 24. Таким образом, имеем, что искомое расстояние равно 32 + 24 = 56.
Двигаясь по шоссе со скоростью 60 км/ч, Гена с дедушкой потратят 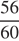
Таким образом, самый быстрый путь составит 56 минут.
Ответ: 56.
Ответ: 56
6. Задание 6
Найдите значение выражения 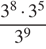
Решение.
Найдем значение выражения:
Ответ: 81.
Ответ: 81
7. Задание 7
На координатной прямой отмечены числа x и y.
Какое из приведённых утверждений неверно?
В ответе укажите номер правильного варианта.
1)
2)
3)
4)
Решение.
Заметим, что 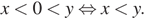
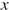
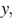
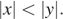
1) 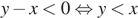
2) 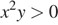
3) 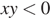
4) 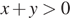
Ответ указан под номером: 1.
Ответ: 1
8. Задание 8
Упростите выражение 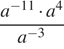

Решение.
Упростим выражение:
При 
Ответ: 16.
Ответ: 16
9. Задание 9
Решите уравнение 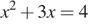
Если корней несколько, запишите их в ответ без пробелов в порядке возрастания.
Решение.
Запишем уравнение в виде 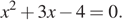
Тем самым это числа −4 и 1.
Ответ: −41.
Ответ: -41
-41
10. Задание 10
Родительский комитет закупил 20 пазлов для подарков детям в связи с окончанием учебного года, из них 11 с машинами и 9 с видами городов. Подарки распределяются случайным образом между 20 детьми, среди которых есть Илюша. Найдите вероятность того, что Илюше достанется пазл с машиной.
Решение.
Вероятность того, что Коле достанется пазл с машиной равна
Ответ: 0,55.
Ответ: 0,55
0,55
11. Задание 11
На рисунке изображён график квадратичной функции y=f(x).
Какие из следующих утверждений о данной функции неверны? Запишите их номера.
1) Функция возрастает на промежутке [2; +∞)
2) f( −1 ) < f( 5 )
3) Наименьшее значение функции равно −9
Решение.
Проверим каждое утверждение.
1) На луче [2; +∞) большему значению аргумента сответствует большее значение функции. Следовательно, функция возрастает на этом луче; первое утверждение верно.
2) Значения фунцкии в точках −1 и 5 равны нулю, поэтому f(−1) = f(5). Второе утверждение неверно.
3) Наименьшее значение функции равно −9. Третье утверждение верно.
Ответ: 2.
Ответ: 2
12. Задание 12
Полную механическую энергию тела (в джоулях) можно вычислить по формуле 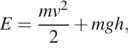
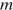
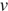
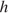
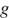
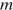

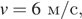
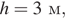
Решение.
Выразим массу: 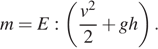
Ответ: 7.
Ответ: 7
13. Задание 13
На каком рисунке изображено множество решений неравенства 
Решение.
Решим неравенство:
Ответ: 3.
Ответ: 3
14. Задание 14
Грузовик перевозит партию щебня массой 90 тонн, ежедневно увеличивая норму перевозки на одно и то же число тонн. Известно, что за первый день было перевезено 2 тонны щебня. Определите, сколько тонн щебня было перевезено за десятый день, если вся работа была выполнена за 12 дней.
Решение.
Пусть в первый день грузовик перевез 
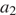
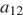

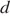
Имеем:
Следовательно, за десятый день было перевезено 11 тонн щебня.
Ответ: 11.
Ответ: 11
15. Задание 15
Сумма двух углов равнобедренной трапеции равна 220°. Найдите меньший угол трапеции. Ответ дайте в градусах.
Решение.
Так как сумма односторонних углов трапеции равна 180°, в условии говорится о сумме углов при основании. Поскольку трапеция является равнобедренной, углы при основании равны. Значит, каждый из них равен 110°. Сумма односторонних углов трапеции равна 180°, поэтому меньший угол равен 180° − 110° = 70°.
Ответ: 70.
Ответ: 70
16. Задание 16
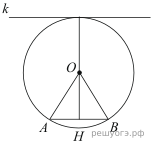
Радиус окружности с центром в точке O равен 65, длина хорды AB равна 66 (см. рисунок). Найдите расстояние от хорды AB до параллельной ей касательной k.
Решение.
Проведём построение и введём обозначения, как показано на рисунке. Рассмотрим треугольники 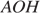
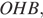
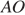
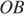
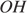

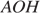
Следовательно, расстояние от хорды до параллельной ей касательной равно 56 + 65 = 121.
Ответ: 121.
Ответ: 121
17. Задание 17
В ромбе сторона равна 10, одна из диагоналей — 10, а угол, лежащий напротив этой диагонали, равен 60°. Найдите площадь ромба, деленную на 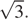
Решение.
Площадь ромба равна произведению сторон на синус угла между ними:
Ответ: 50.
Ответ: 50
18. Задание 18
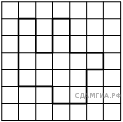
На клетчатой бумаге с размером клетки 1х1 изображена фигура. Найдите её площадь.
Решение.
Площадь данной фигуры равна выделенным клеткам. Посчитаем клетки — их 15. Таким образом, площадь равна 15.
Ответ: 15.
Ответ: 15
19. Задание 19
Укажите номера верных утверждений.
1) Если угол острый, то смежный с ним угол также является острым.
2) Диагонали квадрата взаимно перпендикулярны.
3) В плоскости все точки, равноудалённые от заданной точки, лежат на одной окружности.
Если утверждений несколько, запишите их номера в порядке возрастания.
Решение.
Проверим каждое из утверждений.
1) «Если угол острый, то смежный с ним угол также является острым» — неверно, т. к. смежные углы в сумме составляют 180°.
2) «Диагонали квадрата взаимно перпендикулярны» — верно, т. к. квадрат — частный случай ромба.
3) «В плоскости все точки, равноудалённые от заданной точки, лежат на одной окружности» — верно, т. к. окружность — это множество точек, находящихся на заданном расстоянии от данной точки.
Ответ: 23.
Ответ: 23
20. Задание 20
Решите систему уравнений
Решение.
Правые части уравнений системы равны, значит,
откуда 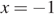
При 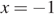
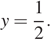

Решения системы уравнений: 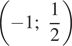
Ответ:
Критерии проверки:
21. Задание 21
Расстояние между городами А и В равно 490 км. Из города А в город В со скоростью 55 км/ч выехал первый автомобиль, а через час после этого навстречу ему из города В выехал со скоростью 90 км/ч второй автомобиль. На каком расстоянии от города А автомобили встретятся?
Решение.
Пусть 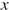

Составим таблицу по данным задачи:
Так как второй автомобиль вышел на 1 ч. позже первого, составим уравнение:
Ответ: 220 км.
Другое решение:
За первый час пути автомобиль, выехавший из города А, проехал 55 километров и расстояние от него до города В стало равным 435 км. Далее, скорость сближения двух автомобилей равна 145 км/ч, значит, они встретятся через 3 часа после выезда второго автомобиля. Таким образом, первый автомобиль до встречи находился в пути 4 часа, и проехал за это время 220 километров.
Ответ: 220 км.
Критерии проверки:
220 км.
22. Задание 22
Постройте график функции 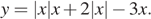
Решение.
Раскрывая модуль, получим, что функцию можно представить следующим образом:
Этот график изображён на рисунке:
Из графика видно, что прямая 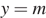
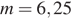
Ответ: −0,25; 6,25.
Критерии проверки:
−0,25; 6,25.
23. Задание 23
В трапеции ABCD основание AD вдвое больше основания ВС и вдвое больше боковой стороны CD. Угол ADC равен 60°, сторона AB равна 1. Найдите площадь трапеции.
Решение.
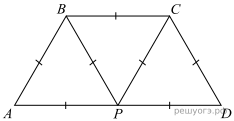
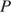
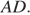
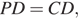
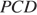
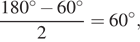

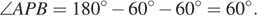
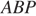
Ответ:
Критерии проверки:
24. Задание 24
В окружности с центром 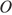

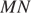
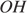
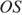
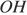
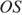
Решение.
Проведем ОK, ON, OL, OM — радиусы. Треугольники KOL и MON равны по трем сторонам, тогда высоты OH и OS также равны как элементы равных треугольников. Что и требовалось доказать.
Критерии проверки:
25. Задание 25
В треугольнике