Решето эратосфена с линейным временем работы

vector<bool> sieve(int n) {
    vector<bool> is_prime(n+1, true);
    for (int i = 2; i <= n; i++)
        if (is_prime[i])
            for (int j = 2*i; j <= n; j += i)
                prime[j] = false;
    return is_prime;            
}

const int n = 1e6;

int d[n+1];
vector<int> p;
 
for (int k = 2; k <= n; k++) {
    if (p[k] == 0) {
        d[k] = k;
        p.push_back(k);
    }
    for (int x : p) {
        if (x > d[k] || x * d[k] > n)
            break;
        d[k * x] = x;
    }
}

Решето Эратосфена

Определение. Целое положительное число называется простым, если оно имеет ровно два различных натуральных делителя — единицу и самого себя. Единица простым числом не считается.

Решето Эратосфена (англ. sieve of Eratosthenes) — алгоритм нахождения всех простых чисел от $1$ до $n$.

Основная идея соответствует названию алгоритма: запишем ряд чисел $1, 2,ldots, n$, а затем будем вычеркивать

• сначала числа, делящиеся на $2$, кроме самого числа $2$,

• потом числа, делящиеся на $3$, кроме самого числа $3$,

• с числами, делящимися на $4$, ничего делать не будем — мы их уже вычёркивали,

• потом продолжим вычеркивать числа, делящиеся на $5$, кроме самого числа $5$,

…и так далее.

Самая простая реализация может выглядеть так:

vector<bool> sieve(int n) {
    vector<bool> is_prime(n+1, true);
    for (int i = 2; i <= n; i++)
        if (is_prime[i])
            for (int j = 2*i; j <= n; j += i)
                prime[j] = false;
    return is_prime;            
}

Этот код сначала помечает все числа, кроме нуля и единицы, как простые, а затем начинает процесс отсеивания составных чисел. Для этого мы перебираем в цикле все числа от $2$ до $n$, и, если текущее число простое, то помечаем все числа, кратные ему, как составные.

Если память позволяет, то для оптимизации скорости лучше использовать не вектор bool, а вектор char — но он займёт в 8 раз больше места. Компьютер не умеет напрямую оперировать с битами, и поэтому при индексации к vector<bool> он сначала достаёт нужный байт, а затем битовыми операциями получает нужное значение, что занимает приличное количество времени.

Время работы

Довольно легко показать, что асимптотическое время работы алгоритма хотя бы не хуже, чем $O(n log n)$: даже если бы мы входили в цикл вычёркиваний для каждого числа, не проверяя его сначала на простоту, суммарно итераций было бы

$$
sum_k frac{n}{k} = frac{n}{2} + frac{n}{3} + frac{n}{4} + ldots + frac{n}{n} = O(n log n)
$$

Здесь мы воспользовались асимптотикой гармонического ряда.

У исходного алгоритма асимптотика должна быть ещё лучше. Чтобы найти её точнее, нам понадобятся два факта про простые числа:

1. Простых чисел от $1$ до $n$ примерно $frac{n}{ln n}$ .

2. Простые числа распределены без больших «разрывов» и «скоплений», то есть $k$-тое простое число примерно равно $k ln k$.

Мы можем упрощённо считать, что число $k$ является простым с «вероятностью» $frac{1}{ln n}$. Тогда, время работы алгоритма можно более точнее оценить как

$$
sum_k frac{1}{ln k} frac{n}{k}
approx n int frac{1}{k ln k}
= n ln ln k Big |_2^n
= O(n log log n)
$$

Асимптотику алгоритма можно улучшить и дальше, до $O(n)$.

Линейное решето

Основная проблема решета Эратосфена состоит в том, что некоторые числа мы будем помечать как составные несколько раз — а именно столько раз, сколько у них различных простых делителей. Чтобы достичь линейного времени работы, нам нужно придумать способ, как рассматривать все составные числа ровно один раз.

Обозначим за $d(k)$ минимальный простой делитель числа $k$ и заметим следующий факт: у составного числа $k$ есть единственное представление $k = d(k) cdot r$, и при этом у числа $r$ нет простых делителей меньше $d(k)$.

Идея оптимизации состоит в том, чтобы перебирать этот $r$, и для каждого перебирать только нужные множители — а именно все от $2$ до $d(r)$ включительно.

Алгоритм

Немного обобщим задачу — теперь мы хотим посчитать для каждого числа $k$ на отрезке $[2, n]$ его минимальный простой делитель $d_k$, а не только определить его простоту.

Изначально массив $d$ заполним нулями, что означает, что все числа предполагаются простыми. В ходе работы алгортима этот массив будет постепенно заполняться. Помимо этого, будем поддерживать список $p$ всех найденных на текущий момент простых чисел.

Теперь будем перебирать число $k$ от $2$ до $n$. Если это число простое, то есть $d_k = 0$, то присвоим $d_k = k$ и добавим $k$ в список $p$.

Дальше, вне зависимости от простоты $k$, начнём процесс расстановки значений в массиве $d$ — переберем найденные простые числа $p_i$, не превосходящие $d_k$, и сделаем присвоение $d_{p_i k} = p_i$.

const int n = 1e6;

int d[n+1];
vector<int> p;
 
for (int k = 2; k <= n; k++) {
	if (p[k] == 0) {
		d[k] = k;
		p.push_back(k);
	}
	for (int x : p) {
	    if (x > d[k] || x * d[k] > n)
            break;
	    d[k * x] = x;
	}
}

Алгоритм требует как минимум в 32 раза больше памяти, чем обычное решето, потому что требуется хранить делитель (int, 4 байта) вместо одного бита на каждое число. Линейное решето хоть и имеет лучшую асимптотику, но на практике проигрывает также и по скорости оптимизированному варианту решета Эратосфена.

Применения

Массив $d$ он позволяет искать факторизацию любого числа $k$ за время порядка размера этой факторизации:

$$
factor(k) = {d(k)} cup factor(k / d(k))
$$

Знание факторизации всех чисел — очень полезная информация для некоторых задач. Ленейное решето интересно не своим временем работы, а именно этим массивом минимальных простых делителей.

Время на прочтение
4 мин

Количество просмотров 16K

В комментариях к одному из прошлых постов о решете Эратосфена был упомянут этот короткий алгоритм из Википедии:

Алгоритм 1:

1: для i := 2, 3, 4, ..., до n: 
2:  если lp[i] = 0:
3:       lp[i] := i
4:       pr[] += {i}
5:   для p из pr пока p ≤ lp[i] и p*i ≤ n:
6:       lp[p*i] := p
Результат:
 lp - минимальный простой делитель для кажого числа до n
 pr - список всех простых до n.

Алгоритм простой, но не всем он показался очевидным. Главная же проблема в том, что на Википедии нет доказательства, а ссылка на первоисточник (pdf) содержит довольно сильно отличающийся от приведенного выше алгоритм.

В этом посте я попытаюсь, надеюсь, доступно доказать, что этот алгоритм не только работает, но и делает это за линейную сложность.

Определения

— множество простых чисел.
— минимальный простой делитель числа:
— остальные множители:

Обратите внимание, все определения выше даны для .

Некоторые очевидные свойства введенных выше функций, которые будут использоваться дальше:

Доказательство

Лемма 1:
Доказательство: Т.к. любой делитель также является делителем , а не превосходит любой делитель , то не превосходит и любой делитель , включая наименьший из них. Единственная проблема в этом утверждении, если не имеет простых делителей, но это возможно только в случае , который исключен в условии леммы.

Пусть

Т.к. (по определению ), если бы нам было дано множество , то мы смогли бы вычислить для всех составных чисел до n. Это делает, например, следующий алгоритм:

Алгоритм 2:

1: Для всех (l,r) из E:
2:    lp[l*r] := l;

Заметим, что , поэтому алгоритм 2 выше работает за линейную сложность.

Далее я докажу, что алгоритм 1 из Википедии на самом деле просто перебирает все элементы этого множества, ведь его можно параметризовать и по-другому.

Пусть

Лемма 2:
Доказательство:

Пусть => .

По определению : , . По лемме 1, .
т.к. , то .
Поскольку , .
Так же, по определению , , следовательно, .
Все 4 условия выполнены, значит, => .

Пусть . Пусть .
По определению , . Значит, — простой делитеть .

Т.к , то Значит,
По определению, Также, очевидно,
Все условия для выполнены =>

Следовательно,

Теперь осталось перебрать правильные и из определения множества и применить алгоритм 2. Именно это и делает Алгоритм 1 (только вместо r используется переменная i). Но есть проблема! Что бы перебрать все элементы множества для вычисления нам надо знать ведь в определении есть условие .

К счастью, эта проблема обходится правильным порядком перебора. Надо перебирать во внешнем цикле, а — во внутреннем. Тогда уже будет вычислено. Этот факт доказывает следующая теорема.

Теорема 1:
Алгоритм 1 поддерживает следующий инвариант: После выполнения итерации внешнего цикла при i=k, все простые числа до k включительно будут выделены в список pr. Также будет подсчитано для всех в массиве lp.

Доказательство:
Докажем по индукции. Для k=2 инвариант проверяется вручную. Единственное простое число 2 будет добавлено в список pr, потому что массив lp[] изначально заполнен нулями. Также, единственное составное число у которого — это 4. Несложно убедиться, что внутренний цикл выполнится ровно один раз (при n>3) и правильно выполнит lp[4] := 2.

Теперь допустим, что инвариант выполняется для итерации i=k-1. Докажем, что он будет выполнятся и для итерации i=k.

Для этого достаточно проверить что число i, если оно простое, будет добавлено в список pr и что будет подсчитано для всех составных чисел т.ч. Именно эти числа из инварианта для k не покрыты уже инвариантом для k-1.

Если i простое, то lp[i] будет равно 0, ведь единственная операция записи в массив lp, которая теоретически могла бы подсчитать lp[i] (в строке 6), всегда пишет в составные индексы, ведь p*i (для i > 1) — всегда составное. Поэтому число i будет добавлено в список простых. Также, в строке 3 будет подсчитано lp[i].

Если же i составное, то на начало итерации lp[i] уже будет подсчитано по инварианту для i=k-1, ведь или следовательно i попадает под условие инварианта в предыдущей итерации. Поэтому составное число i не будет добавлено в список простых чисел.

Далее, имея корректное lp[i] и все простые числа до i включительно цикл в строках 5-6 переберет все элементы , у которых вторая часть равна i:

Все нужные простые числа в списке pr есть, т.к. нужны только числа до . Поэтому будут подсчитаны значения lp[] для всех составных чисел , у которых . Это ровно все те числа, которых не хватало при переходе от инварианта для k-1 к инварианту для k.

Следовательно, инавриант выполняется для любых i = 2..n.

По инварианту из Теоремы 1 для i=n получается, что все простые числа до n и все lp[] будут подсчитаны алгоритмом 1.

Более того, поскольку в строках 5-6 перебираются различные элементы множества , то суммарно внутренний цикл выполнит не более операций. Операция проверки в цикле выполнится ровно раз ( раз вернет true и n-1 раз, для каждого i, вернет false). Все оставшиеся операции вложены в один цикл по i от 2 до n.
Отсюда следует, что сложность алгоритма 1 — O(n).

Привет, сегодня поговорим про решето эратосфена, обещаю рассказать все что знаю. Для того чтобы лучше понимать что такое
решето эратосфена , настоятельно рекомендую прочитать все из категории Алгоритмы и теория алгоритмов.

решето эратосфена — алгоритм нахождения всех простых чисел до некоторого целого числа n, который приписывают древнегреческому математику Эратосфену Киренскому . Как и во многих случаях, здесь название алгоритма говорит о принципе его работы, то есть решето подразумевает фильтрацию, в данном случае фильтрацию всех чисел за исключением простых. По мере прохождения списка нужные числа остаются, а ненужные (они называются составными) исключаются.

Вполне вероятно, что алгоритм, придуманный более 2000 лет назад греческим математиком Эратосфеном Киренским, был первым в своем роде. Его единственная задача – нахождение всех простых чисел до некоторого заданного числа N. Термин «решето» подразумевает фильтрацию, а именно фильтрацию всех чисел за исключением простых. Так, обработка алгоритмом числовой последовательности оставит лишь простые числа, все составные же отсеются.

Рассмотрим в общих чертах работу метода. Дана упорядоченная по возрастанию последовательность натуральных чисел. Следуя методу Эратосфена, возьмем некоторое число P изначально равное 2 – первому простому числу, и вычеркнем из последовательности все числа кратные P: 2P, 3P, 4P, …, iP (iP≤N). Далее, из получившегося списка в качестве P берется следующее за двойкой число – тройка, вычеркиваются все кратные ей числа (6, 9, 12, …). По такому принципу алгоритм продолжает выполняться для оставшейся части последовательности, отсеивая все составные числа в заданном диапазоне.

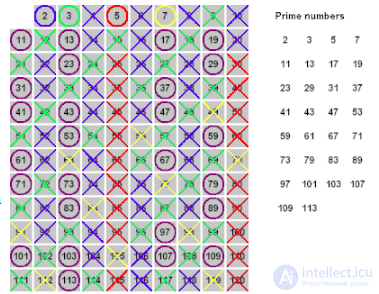
В приведенной таблице записаны натуральные числа от 2 до 100. Красным помечены те, которые удаляются в процессе выполнения алгоритма «Решето Эратосфена».

Программная реализация алгоритма Эратосфена потребует:

1. организовать логический массив и присвоить его элементам из диапазона от 2 до N логическую единицу;
2. в свободную переменную P записать число 2, являющееся первым простым числом;
3. исключить из массива все числа кратные P², ступая с шагом по P;
4. записать в P следующее за ним не зачеркнутое число;
5. повторять действия, описанные в двух предыдущих пунктах, пока это возможно.

Обратите внимание: на третьем шаге мы исключаем числа, начиная сразу с P², это связано с тем, что все составные числа меньшие P будут уже зачеркнуты. Поэтому процесс фильтрации следует остановить, когда P² станет превышать N. Это важное замечание позволяет улучшить алгоритм, уменьшив число выполняемых операций.

Так будет выглядеть псевдокод алгоритма:

Оптимизированная реализация (начинающаяся с квадратов) на псевдокоде

Он состоит из двух циклов: внешнего и внутреннего. Внешний цикл выполняется до тех пор, пока P² не превысит N. Само же P изменяется с шагом P+1. Внутренний цикл выполняется лишь в том случае, если на очередном шаге внешнего цикла окажется, что элемент с индексом P не зачеркнут. Именно во внутреннем цикле происходит отсеивание всех составных чисел.

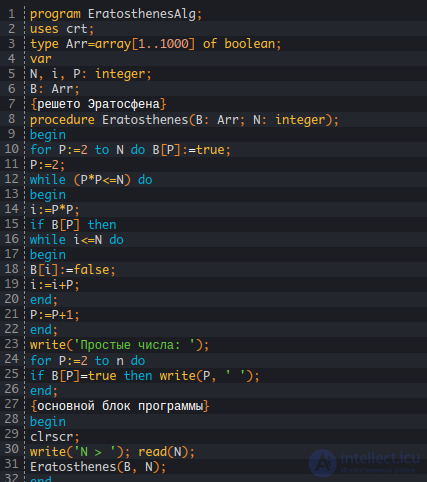
Код программы на C++:

Код программы на Pascal:

Решето Эратосфена для выявления всех простых чисел в заданной последовательности ограниченной некоторым N потребует O(Nlog (log N)) операций. Поэтому уместнее использовать данный метод чем, например, наиболее тривиальный и затратный перебор делителей.

Сложность алгоритма

Сложность алгоритма составляет операций при составлении таблицы простых чисел до .

Доказательство сложности

При выбранном для каждого простого будет выполняться внутренний цикл, который совершит действий. Сложность алгоритма можно получить из оценки следующей величины:

Так как количество простых чисел, меньших либо равных , оценивается как , и, как следствие, {displaystyle k}-е простое число примерно равно , то сумму можно преобразовать:

Здесь из суммы выделено слагаемое для первого простого числа, чтобы избежать деления на нуль. Данную сумму можно оценить интегралом

В итоге получается для изначальной суммы:

{displaystyle sum limits _{pin mathbb {P} colon pleq n}{frac {n}{p}}approx nln ln n+o(n)}

Более строгое доказательство (и дающее более точную оценку с точностью до константных множителей) можно найти в книге Hardy и Wright «An Introduction to the Theory of Numbers» .

Модификации метода

Неограниченный, постепенный вариант

В этом варианте простые числа вычисляются последовательно, без ограничения сверху, как числа находящиеся в промежутках между составными числами, которые вычисляются для каждого простого числа p, начиная с его квадрата, с шагом в p (или для нечетных простых чисел 2p) . Может быть представлен символически в парадигме потоков данных как

используя нотацию абстракции списков, где обозначает разницу между арифметическими прогрессиями.

Первое простое число 2 (среди возрастающих положительных целых чисел) заранее известно, поэтому в этом самореферентном определении нет порочного круга.

Псевдокод поэтапного отсеивания, в неэффективной, для простоты, реализации (ср. с нижеследующими вариантами):

Перебор делителей

Решето Эратосфена часто путают с алгоритмами, которые поэтапно отфильтровывают^[en] составные числа, тестируя каждое из чисел-кандидатов на делимость используя по одному простому числу на каждом этапе.

Широко известный функциональный код Дэвида Тернера 1975 г.^[10] часто принимают за решето Эратосфена, но на самом деле это неоптимальный вариант с перебором делителей (в оптимальном варианте не используются делители, большие квадратного корня тестируемого числа) . Об этом говорит сайт https://intellect.icu . В псевдокоде,

Сегментированное решето

Как замечает Соренсон, главной проблемой реализации решета Эратосфена на вычислительных машинах является не количество выполняемых операций, а требования по объему занимаемой памяти (впрочем, его замечание относится к неактуальному сейчас компьютеру DEC VAXstation 3200, выпущенному в 1989 году). При больших значениях n, диапазон простых чисел может превысить доступную память; хуже того, даже при сравнительно небольших n использование кэша памяти далеко от оптимального, так как алгоритм, проходя по всему массиву, нарушает принцип локализованности ссылок^[en].

Для решения представленной проблемы используется сегментированное решето, в котором за итерацию просеивается только часть диапазона простых чисел.^[11] Данный метод известен с 1970-х годов и работает следующим образом: ^[12]

1. Разделяем диапазон от 2 до n на отрезки (сегменты) некоторой длины Δ ≤ √n.
2. Находим все простые числа в первом отрезке, используя обычное решето.
3. Каждый из последующих отрезков оканчивается на некотором числе m. Находим все простые числа в отрезке следующим образом:
   1. Создаем булевый массив размера Δ
   2. Для каждого простого числа p ≤ √m из уже найденных, отмечаем в массиве как «непростые» все числа кратные p, перебирая числа с шагом в p, начиная с наименьшего кратного p числа в данном отрезке.

Если число Δ выбрано равным √n, то сложность алгоритма по памяти оценивается как O(√n), а операционная сложность остается такой же, что и у обычного решета Эратосфена.^[12]

Для случаев, когда n настолько велико, что все просеиваемые простые числа меньшие √n не могут уместиться в памяти, как того требует алгоритм сегментированного сита, используют более медленные, но с гораздо меньшими требованиями по памяти алгоритмы, например решето Соренсона.^[13]

Решето Эйлера[

Доказательство тождества Эйлера для дзета-функции Римана содержит механизм отсеивания составных чисел подобный решету Эратосфена, но так, что каждое составное число удаляется из списка только один раз. Схожее решето описано в Gries & Misra 1978 г. как решето с линейным временем работы (см. ниже).

Составляется исходный список начиная с числа 2. На каждом этапе алгоритма первый номер в списке берется как следующее простое число, результаты произведения которого на каждое число в списке помечаются для последующего удаления. После этого из списка убирают первое число и все помеченные числа, и процесс повторяется вновь:

Здесь показан пример начиная с нечетных чисел, после первого этапа алгоритма. Таким образом, после k-го этапа рабочий список содержит только числа взаимно простые с первыми k простыми числами (то есть числа не кратные ни одному из первых k простых чисел), и начинается с (k+1)-го простого числа. Все числа в списке, меньшие квадрата его первого числа, являются простыми.

В псевдокоде,

Решето только по нечетным числам[

Поскольку все четные числа, кроме 2, — составные, то можно вообще не обрабатывать никак четные числа, а оперировать только нечетными числами. Во-первых, это позволит вдвое сократить объем требуемой памяти. Во-вторых, это уменьшит количество выполняемых алгоритмом операций (примерно вдвое).

Это можно обобщить на числа взаимно простые не только с 2 (то есть нечетные числа), но и с 3, 5, и т. д.

Уменьшение объема потребляемой памяти

Алгоритм Эратосфена фактически оперирует с битами памяти. Следовательно, можно существенно сэкономить потребление памяти, храня {displaystyle n} переменных булевского типа не ка байт, а как бит, то есть байт памяти.

Такой подход — «битовое сжатие» — усложняет оперирование этими битами. Любое чтение или запись бита будут представлять собой несколько арифметических операций. Но с другой стороны существенно улучшается компактность в памяти. Бо́льшие интервалы умещаются в кэш-память которая работает гораздо быстрее обычной так что при работе по-сегментно общая скорость увеличивается.

Решето Эратосфена с линейным временем работы

Этот алгоритм обнаруживает для каждого числа i в отрезке [2…n] его минимальный простой делитель lp[i] (lp от англ. least prime).

Также поддерживается список всех простых чисел — массив pr[], поначалу пустой. В ходе работы алгоритма этот массив будет постепенно заполняться.

Изначально все величины lp[i] заполним нулями.

Дальше следует перебрать текущее число i от 2 до n. Здесь может быть два случая:

• lp[i] = 0: это означает, что число i — простое, так как для него так и не обнаружилось других делителей.

Следовательно, надо присвоить lp[i] = i и добавить i в конец списка pr[].

• lp[i] ≠ 0: это означает, что текущее число i — составное, и его минимальным простым делителем является lp[i].

В обоих случаях дальше начинается процесс расстановки значений в массиве lp[i]: следует брать числа, кратные i, и обновлять у них значение lp[]. Однако основная цель — научиться делать это таким образом, чтобы в итоге у каждого числа значение lp[] было бы установлено не более одного раза.

Утверждается, что для этого можно поступить таким образом. Рассматриваются числа вида x = p ⋅ i, где p последовательно равно всем простым числам не превосходящим lp[i] (как раз для этого понадобилось хранить список всех простых чисел).

У всех чисел такого вида проставим новое значение lp[x] — оно должно быть равно p^[14].

Псевдокод

Сложность алгоритма на практике

Решето Эратосфена является популярным способом оценки производительности компьютера.^[15] Как видно из вышеизложенного доказательства сложности алгоритма, избавившись от константы и слагаемого очень близкого к нулю (ln (ln n — ln ln n) — ln ln 2 ≈ ln ln n), временная сложность вычисления всех простых чисел меньше n аппроксимируется следующим соотношением O(n ln ln n). Однако алгоритм имеет экспоненциальную временную сложность в отношении размера входных данных, что делает его псевдополиномиальным алгоритмом. Памяти же для базового алгоритма требуется O(n).^[16]

Сегментированная версия имеет ту же операционную сложность O(n ln ln n), . что и несегментированная версия, но уменьшает потребность в используемой памяти до размера сегмента (размер сегмента значительно меньше размера всего массива простых чисел), который равен O(√n/ln n).^[17] Также существует очень редко встречающееся на практике оптимизированное сегментированное решето Эратосфена. Оно строится за O(n) операций и занимает O(√n ln ln n/ln n) бит в памяти.^[16][18][17]

На практике оказывается, что оценка ln ln n не очень точна даже для максимальных практических диапазонов таких как 10¹⁶.^[18] Ознакомившись с вышеописанным доказательством сложности, нетрудно понять откуда взялась неточность оценки. Расхождение с оценкой можно объяснить следующим образом: в пределах данного практического диапазона просеивания существенное влияние оказывают постоянные смещения. Таким образом очень медленно растущий член ln ln n не становится достаточно большим, чтобы константами можно было справедливо пренебречь, до тех пор пока n не приблизится к бесконечности, что естественно выходит за границы любого прикладного диапазона просеивания. Данный факт показывает, что для актуальных на сегодняшний день входных данных производительность решета Эратосфена намного лучше, чем следовало ожидать, используя только асимптотические оценки временной сложности.^[18]

Следует также отметить, что решето Эратосфена работает быстрее, чем часто сравниваемое с ним решето Аткина только для значений n меньших 10 ¹⁰ .^[19] Сказанное справедливо при условии, что операции занимают примерно одно и то же время в циклах центрального процессора, а это является разумным предположением для одного алгоритма, работающего с огромным битовым массивом.^[20] С учетом этого предположения получается, что сито Аткина быстрее чем максимально факторизованное решето Эратосфена для n свыше 10 ¹³ , но при таких диапазонах просеивания потребуется занять огромное пространство в оперативной памяти, даже если была использована «битовая упаковка».^[21] Однако раздел о сегментированной версии решета Эратосфена показывает, что предположение о сохранении равенства во времени, затрачиваемом на одну операцию, между двумя алгоритмами не выполняется при сегментации.^[12][19] В свою очередь это приводит к тому, что решето Аткина (несегментированное) работает медленнее, чем сегментированное решето Эратосфена с увеличением диапазона просеивания, за счет уменьшения времени на операцию для второго.

Использование нотации O большого также не является правильным способом сравнения практических характеристик даже для вариаций решета Эратосфена, поскольку данная нотация игнорирует константы и смещения, которые могут быть очень значительными для прикладных диапазонов. Например, одна из вариаций решета Эратосфена известная как решето Притчарда^[16] имеет производительность O(n),^[18] но ее базовая реализация требует либо алгоритма «одного большого массива»^[17] (то есть использования обычного массива, в котором хранятся все числа до n), который ограничивает его диапазон использования до объема доступной памяти, либо он должен быть сегментирован для уменьшения использования памяти. Работа Притчарда уменьшила требования к памяти до предела, но платой за данное улучшение по памяти является усложнение вычислений, что приводит увеличению операционной сложности алгоритмов.^[18]

Популярным способом ускорения алгоритмов, работающих с большими массивами чисел, является разного рода факторизация.^[22] Применение методов факторизации дает значительное уменьшение операционной сложности за счет оптимизации входного массива данных.^[23][24] Для индексных алгоритмов часто используют кольцевую факторизацию.^[23][25] Рассматриваемые в данной статье алгоритмы нахождения всех простых чисел до заданного n подобные решету Эратосфена относятся к индексным, что позволяет применять к ним метод кольцевой факторизации.^[26]

Несмотря на теоретическое ускорение, получаемое с помощью кольцевой факторизации, на практике существуют факторы, которые не учитываются при расчетах, но способны оказать существенное влияние на поведение алгоритма, что в результате может не дать ожидаемого прироста в быстродействии.^[27] Рассмотрим наиболее существенные из них:

• Умножение и деление. При аналитических расчетах предполагается, что скорость выполнения арифметических операций равноценна. Но на самом деле это не так, и умножение, и деление выполняются гораздо медленнее, чем сложение и вычитание. Таким образом данный фактор никак не влияет на решето Эратосфена, поскольку оно использует только сложение и вычитание, но является весьма существенным для решета Питчарда (один из результатов усложнения вычислений упомянутого выше).^[28]
• Оптимизация компилятора. Компилятор оптимизирует на стадии компиляции все программы для более корректного исполнения машиной. Но часто бывает очень сложно сказать, какой вклад дает данная оптимизация, и будет ли этот вклад одинаковым для двух различных алгоритмов.^[29]
• Кэш. Процессор использует кэш, чтобы ускорить извлечение инструкций и данных из памяти. Наличие кэша приводит к тому, что программы, использующие локализованные ссылки, будут работать быстрее. Но алгоритмы просеивания простых чисел, которые используют факторизацию высокой степени, часто генерируют случайные ссылки в память, что снижает их производительность.^[29]

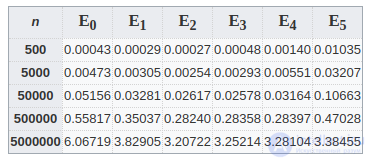
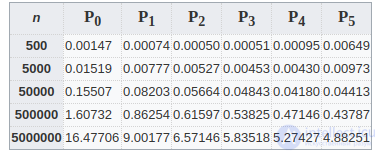
Для наглядности представления вклада факторизации в производительность алгоритмов просеивания ниже приведены две таблицы. В таблицах приведены результаты измерения реального времени исполнения решета Эратосфена и решета Питчарда в секундах для разных диапазонов n и разных степеней кольцевой факторизации. E_i и P_i обозначения для решета Эратосфена и Питчарда соответственно, где индекс i означает степень кольцевой факторизации. Стоит отметить, что E₀ и P₀ означают отсутствие факторизации.^[29]

Из таблицы видно, что лучшую производительность имеет решето Эратосфена со средней степенью факторизации E₂. Данный факт можно объяснить влиянием кэш-фактора, рассмотренного выше, на алгоритмы с высокой степенью факторизации.

В заключение стоит отметить, что с увеличением n соотношение времен становится все больше в пользу решета Эратосфена, а на диапазоне n = 5000000 оно стабильно быстрее при любых факторизациях. Данный факт еще раз подтверждает проигрыш в быстродействии решета Питчарда из-за сложных вычислений.

См также

• простое число , простые числа ,
• решето сундарама ,
• решето аткина ,
• Корекурсия

Напиши свое отношение про решето эратосфена. Это меня вдохновит писать для тебя всё больше и больше интересного. Спасибо Надеюсь, что теперь ты понял что такое решето эратосфена
и для чего все это нужно, а если не понял, или есть замечания,
то нестесняся пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории
Алгоритмы и теория алгоритмов

Решето́ Эратосфе́на — алгоритм нахождения всех простых чисел до некоторого целого числа n, который приписывают древнегреческому математику Эратосфену Киренскому^[1]. Как и во многих случаях, здесь название алгоритма говорит о принципе его работы, то есть решето подразумевает фильтрацию, в данном случае фильтрацию всех чисел за исключением простых. По мере прохождения списка нужные числа остаются, а ненужные (они называются составными) исключаются.

История[править | править вики-текст]

Название «решето» метод получил потому, что, согласно легенде, Эратосфен писал числа на дощечке, покрытой воском, и прокалывал дырочки в тех местах, где были написаны составные числа. Поэтому дощечка являлась неким подобием решета, через которое «просеивались» все составные числа, а оставались только числа простые. Эратосфен дал таблицу простых чисел до 1000.

Алгоритм[править | править вики-текст]

Для нахождения всех простых чисел не больше заданного числа n, следуя методу Эратосфена, нужно выполнить следующие шаги:

1. Выписать подряд все целые числа от двух до n (2, 3, 4, …, n).
2. Пусть переменная p изначально равна двум — первому простому числу.
3. Зачеркнуть в списке числа от 2p до n считая шагами по p (это будут числа кратные p: 2p, 3p, 4p, …).
4. Найти первое незачёркнутое число в списке, большее чем p, и присвоить значению переменной p это число.
5. Повторять шаги 3 и 4, пока возможно.

Теперь все незачёркнутые числа в списке — это все простые числа от 2 до n.

На практике, алгоритм можно улучшить следующим образом. На шаге № 3 числа можно зачеркивать начиная сразу с числа p², потому что все составные числа меньше него уже будут зачеркнуты к этому времени. И, соответственно, останавливать алгоритм можно, когда p² станет больше, чем n.^[2] Также, все p большие чем 2 — нечётные числа, и поэтому для них можно считать шагами по 2p, начиная с p².

Сложность алгоритма[править | править вики-текст]

Сложность алгоритма составляет операций при составлении таблицы простых чисел до ^[3].

Доказательство сложности[править | править вики-текст]

При выбранном для каждого простого будет выполняться внутренний цикл, который совершит действий. Следовательно, нужно оценить следующую величину:

Так как количество простых чисел, меньших либо равных , оценивается как , и, как следствие, -е простое число примерно равно , то сумму можно преобразовать:

Здесь из суммы выделено слагаемое для первого простого числа, чтобы избежать деления на нуль. Теперь следует оценить эту сумму интегралом:

В итоге получается для изначальной суммы:

Более строгое доказательство (и дающее более точную оценку с точностью до константных множителей) можно найти в книге Hardy и Wright «An Introduction to the Theory of Numbers»^[4].

Псевдокод[править | править вики-текст]

Оптимизированная реализация (начинающаяся с квадратов) на псевдокоде^[5][6]:

Вход: натуральное число n

Пусть A — булевый массив, индексируемый числами от 2 до n, 
изначально заполненный значениями true.

 для i := 2, 3, 4, ..., пока i2  n:
  если A[i] = true:
    для j := i2, i2 + i, i2 + 2i, ..., пока j  n:
      A[j] := false

Выход: числа i, для которых A[i] = true - это все простые числа от 2 до n.

Пример для n = 30[править | править вики-текст]

Запишем натуральные числа начиная от 2 до 30 в ряд:

2  3  4  5  6  7  8  9  10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30

Первое число в списке, 2 — простое. Пройдём по ряду чисел, зачёркивая все числа кратные 2 (то есть каждое второе, начиная с 2² = 4):

2  3  4  5  6  7  8  9  10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30

Следующее незачеркнутое число, 3 — простое. Пройдём по ряду чисел, зачёркивая все числа кратные 3 (то есть каждое третье, начиная с 3² = 9):

2  3  4  5  6  7  8  9  10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30

Следующее незачеркнутое число, 5 — простое. Пройдём по ряду чисел, зачёркивая все числа кратные 5 (то есть каждое пятое, начиная с 5² = 25). И т. д.

2  3  4  5  6  7  8  9  10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30

Необходимо провести зачёркивание кратных для всех простых чисел p, для которых p² ≤ n. В результате все составные числа будут зачеркнуты, а незачеркнутыми останутся все простые числа.

Для n = 30 уже после зачёркивания кратных числу 5 все составные числа получаются зачеркнутыми:

2  3     5     7           11    13          17    19          23                29

Модификации метода[править | править вики-текст]

Неограниченный, постепенный вариант[править | править вики-текст]

В этом варианте простые числа вычисляются последовательно, без ограничения сверху, как числа находящиеся в промежутках между составными числами, которые вычисляются для каждого простого числа p, начиная с его квадрата, с шагом в p (или для нечетных простых чисел 2p)^[2]. Первое простое число 2 (среди возрастающих положительных целых чисел) заранее известно, поэтому в этом самореферентном определении нет порочного круга.

Перебор делителей[править | править вики-текст]

Решето Эратосфена часто путают с алгоритмами, которые отфильтровывают из заданного интервала составные числа, тестируя каждое из чисел-кандидатов с помощью перебора делителей.^[7]

Широко известный функциональный код Дэвида Тёрнера 1975 года^[8] часто принимают за решето Эратосфена,^[7] но на самом деле это далёкий от оптимального вариант с перебором делителей.

Решето Эйлера[править | править вики-текст]

Решето Эйлера^{[источник не указан 129 дней]} это вариант решета Эратосфена, в котором каждое составное число удаляется из списка только один раз.

Составляется исходный список начиная с числа 2. На каждом этапе алгоритма первый номер в списке берется как следующее простое число, и определяются его произведения на каждое число в списке которые маркируются для последуюшего удаления. После этого из списка убирают первое число и все помеченные числа, и процесс повторяется вновь:

[2] (3) 5  7  9 11  13 15 17 19 21 23 25 27 29 31 33 35 37 39 41 43 45 47 49 51 53 55 57 59 61 63 65 67 69 71 73 75 77 79  ...
[3]    (5) 7    11  13    17 19    23 25    29 31    35 37    41 43    47 49    53 55    59 61    65 67    71 73    77 79  ...
[4]       (7)   11  13    17 19    23       29 31       37    41 43    47 49    53       59 61       67    71 73    77 79  ...
[5]            (11) 13    17 19    23       29 31       37    41 43    47       53       59 61       67    71 73       79  ...
[...]

Здесь показан пример начиная с нечетных чисел, после первого этапа алгоритма. Таким образом, после k-го этапа рабочий список содержит только числа взаимно простые с первыми k простыми числами (то есть числа не кратные ни одному из первых k простых чисел), и начинается с (k+1)-го простого числа. Все числа в списке, меньшие квадрата его первого числа, являются простыми.

Решето только по нечётным числам[править | править вики-текст]

Поскольку все чётные числа, кроме 2, — составные, то можно вообще не обрабатывать никак чётные числа, а оперировать только нечётными числами. Во-первых, это позволит вдвое сократить объём требуемой памяти. Во-вторых, это уменьшит количество выполняемых алгоритмом операций (примерно вдвое).

Это можно обобщить на числа взаимно простые не только с 2 (то есть нечетные числа), но и с 3, 5, и т. д.

Уменьшение объёма потребляемой памяти[править | править вики-текст]

Алгоритм Эратосфена фактически оперирует с битами памяти. Следовательно, можно существенно сэкономить потребление памяти, храня переменных булевского типа не как байт, а как бит, то есть байт памяти.

Такой подход — «битовое сжатие» — усложняет оперирование этими битами. Любое чтение или запись бита будут представлять из себя несколько арифметических операций. Но с другой стороны существенно улучшается компактность в памяти. Бо’льшие интервалы умещаются в кэш-память которая работает гораздо быстрее обычной так что при работе по-сегментно общая скорость увеличивается.

Решето Эратосфена с линейным временем работы[править | править вики-текст]

Описание алгоритма: обнаружить для каждого числа от в отрезке его минимальный простой делитель .

Кроме того, потребуется хранить список всех найденных простых чисел — для этого будет использоваться массив , поначалу пустой. В ходе работы алгоритма этот массив будет постепенно заполняться.

Изначально все величины заполним нулями.

Дальше следует перебрать текущее число от 2 до . Здесь может быть два случая:

Следовательно, надо присвоить и добавить в конец списка .

В обоих случаях дальше начинается процесс расстановки значений в массиве : следует брать числа, кратные , и обновлять у них значение . Однако основная цель — научиться делать это таким образом, чтобы в итоге у каждого числа значение было бы установлено не более одного раза.

Утверждается, что для этого можно поступить таким образом. Рассмотриваются числа вида:

где последовательность  — это все простые, не превосходящие (как раз для этого понадобилось хранить список всех простых чисел).

У всех чисел такого вида проставим новое значение  — очевидно, оно будет равно ^[9].

Псевдокод[править | править вики-текст]

 Вход: натуральное число n

Пусть pr - целочисленный массив, поначалу пустой;
      lp - целочисленный массив, индексируемый от 2 до n, заполненный нулями

 для i := 2, 3, 4, ..., до n: 
   если lp[i] = 0:
       lp[i] := i
       pr[] += {i}
   для pj из pr пока pj  lp[i]:
       lp[i*pj] := pj

Выход: все числа в массиве pr - это все простые числа от 2 до n.

См. также[править | править вики-текст]

• Решето Сундарама
• Решето Аткина
• Корекурсия

Примечания[править | править вики-текст]

Литература[править | править вики-текст]

• Гальперин Г. «Просто о простых числах» // Квант. — № 4.
• Под. ред. Невская И.И. Неопубликованные материалы Л.Эйлера по теории чисел. — «Наука», 1997.
• Проф. Д.Ф.Егоров. Элементы теории чисел. — Государственное издательство Москва, 1923.
• Кордемский Б. А. Математическая смекалка. — М.: ГИФМЛ, 1958. — 576 с.

Ссылки[править | править вики-текст]

• Решето Эратосфена от М. Гарднера
• Алгоритм составления таблицы простых чисел от заданного до другого числа
• Реализация алгоритма поиска простых чисел на Java
• Доказательство сложности алгоритма
• Еще раз о поиске простых чисел

Обновлено: 22.03.2023

Определение. Целое положительное число называется простым, если оно имеет ровно два различных натуральных делителя — единицу и самого себя. Единица простым числом не считается.

Решето Эратосфена (англ. sieve of Eratosthenes) — алгоритм нахождения всех простых чисел от (1) до (n) .

Основная идея соответствует названию алгоритма: запишем ряд чисел (1, 2,ldots, n) , а затем будем вычеркивать

сначала числа, делящиеся на (2) , кроме самого числа (2) ,

потом числа, делящиеся на (3) , кроме самого числа (3) ,

с числами, делящимися на (4) , ничего делать не будем — мы их уже вычёркивали,

потом продолжим вычеркивать числа, делящиеся на (5) , кроме самого числа (5) ,

Самая простая реализация может выглядеть так:

Этот код сначала помечает все числа, кроме нуля и единицы, как простые, а затем начинает процесс отсеивания составных чисел. Для этого мы перебираем в цикле все числа от (2) до (n) , и, если текущее число простое, то помечаем все числа, кратные ему, как составные.

Если память позволяет, то для оптимизации скорости лучше использовать не вектор bool , а вектор char — но он займёт в 8 раз больше места. Компьютер не умеет напрямую оперировать с битами, и поэтому при индексации к vector он сначала достаёт нужный байт, а затем битовыми операциями получает нужное значение, что занимает приличное количество времени.

Время работы

Довольно легко показать, что асимптотическое время работы алгоритма хотя бы не хуже, чем (O(n log n)) : даже если бы мы входили в цикл вычёркиваний для каждого числа, не проверяя его сначала на простоту, суммарно итераций было бы

[ sum_k frac = frac + frac + frac + ldots + frac = O(n log n) ]

Здесь мы воспользовались асимптотикой гармонического ряда.

У исходного алгоритма асимптотика должна быть ещё лучше. Чтобы найти её точнее, нам понадобятся два факта про простые числа:

Простых чисел от (1) до (n) примерно (frac<ln n>) .

[ sum_k frac <ln k>frac approx n int frac = n ln ln k Big |_2^n = O(n log log n) ]

Асимптотику алгоритма можно улучшить и дальше, до (O(n)) .

Линейное решето

Основная проблема решета Эратосфена состоит в том, что некоторые числа мы будем помечать как составные несколько раз — а именно столько раз, сколько у них различных простых делителей. Чтобы достичь линейного времени работы, нам нужно придумать способ, как рассматривать все составные числа ровно один раз.

Обозначим за (d(k)) минимальный простой делитель числа (k) и заметим следующий факт: у составного числа (k) есть единственное представление (k = d(k) cdot r) , и при этом у числа (r) нет простых делителей меньше (d(k)) .

Идея оптимизации состоит в том, чтобы перебирать этот (r) , и для каждого перебирать только нужные множители — а именно все от (2) до (d(r)) включительно.

Алгоритм

Немного обобщим задачу — теперь мы хотим посчитать для каждого числа (k) на отрезке ([2, n]) его минимальный простой делитель (d_k) , а не только определить его простоту.

Изначально массив (d) заполним нулями, что означает, что все числа предполагаются простыми. В ходе работы алгортима этот массив будет постепенно заполняться. Помимо этого, будем поддерживать список (p) всех найденных на текущий момент простых чисел.

Теперь будем перебирать число (k) от (2) до (n) . Если это число простое, то есть (d_k = 0) , то присвоим (d_k = k) и добавим (k) в список (p) .

Дальше, вне зависимости от простоты (k) , начнём процесс расстановки значений в массиве (d) — переберем найденные простые числа (p_i) , не превосходящие (d_k) , и сделаем присвоение (d_ = p_i) .

Алгоритм требует как минимум в 32 раза больше памяти, чем обычное решето, потому что требуется хранить делитель ( int , 4 байта) вместо одного бита на каждое число. Линейное решето хоть и имеет лучшую асимптотику, но на практике проигрывает также и по скорости оптимизированному варианту решета Эратосфена.

Применения

Массив (d) он позволяет искать факторизацию любого числа (k) за время порядка размера этой факторизации:

[ factor(k) = cup factor(k / d(k)) ]

Знание факторизации всех чисел — очень полезная информация для некоторых задач. Ленейное решето интересно не своим временем работы, а именно этим массивом минимальных простых делителей.

Удивительно, но этот алгоритм популярен до сих пор. И сегодня, мы разберемся, как пользоваться тем, что называется решетом Эратосфена.

Занимательно, что поисковик так и норовит подсунуть портрет Евклида, вместо портрета Эратосфена. Хотя, про Евклида и его алгоритм, я уже написала две статьи. Ну, раз великий интернет настаивает, то в конце этой публикации прикреплю ссылку на статью про алгоритм Евклида. Там можно полюбоваться его портретом

Решето Эратосфена

Название, на самом деле, говорящее. Эратосфен, действительно, отбирал простые числа при помощи своеобразного решета.

Натуральное число, большее единицы, называют простым, если оно имеет всего два натуральных делителя: единицу и само это число

Чтобы выделять простые числа, не превосходящие число n , Эратосфен предложил такой алгоритм:

При таком подходе, те числа, которые останутся не вычеркнутыми и будут являться простыми.

На самом деле, им можно пользоваться и для выделения простых чисел из какого-то отрезка натурального ряда, начинающегося не с единицы.

Ну что ж, посмотрим это на примере и вместе ответим на вопросы, которые я задала Вам в начале статьи.

Решето Эратосфена в современной жизни

Автор работы награжден дипломом победителя III степени

Текст работы размещён без изображений и формул.
Полная версия работы доступна во вкладке «Файлы работы» в формате PDF

На этот вопрос можно дать два ответа. Первый из них имеет теоретическое значение. Попытки генерации простых чисел ведут к появлению новых интересных инструментов для расчетов, особенно для компьютерных вычислений. Кроме того, наличие большого списка простых чисел позволяет проверять теоремы, которые еще не доказаны. Если кто-то выдвигает гипотезу относительно простых чисел, но оказывается, что одно из миллионов чисел нарушает ее, то вопрос снимается. Это стимулирует поиск простых чисел различных видов: простых чисел Мерсенна, чисел-близнецов и так далее. Иногда такой поиск превращается в соревнование, в котором устанавливаются мировые рекорды и за победы присуждаются большие призы.

Но есть и другая, более практическая причина, связанная с так называемым шифрованием. Электронная почта, банковские операции, кредитные карты и мобильная телефонная связь — все это защищено секретными кодами, непосредственно основанными на свойствах простых чисел.

Исходя из этих рассуждений, считаю, что данная тема представляет и сейчас огромный интерес ученых, поэтому актуальность ее очевидна.

Целью моей работы является исследование применения решета Эратосфена в современной жизни.

Исходя из этой цели, в своем исследовании мне предстоит решить следующие задачи:

выяснить актуальность этой темы;

дать определение понятиям, используемым при изучении данной темы;

изучить биографию и труды Эратосфена;

Для достижения поставленной цели нами использовались следующие методы исследования:

методы экспериментально-теоретического уровня: анализ и синтез, теоретический анализ литературных источников;

методы эмпирического уровня: анкетирование, сравнение.

Этапы проекта: теоретический и практический.

2.1. Используемые понятия, актуальные проблемы в исследовании простых чисел

Для изучения данной темы дадим определение основным понятиям, необходимым для ее исследования.

Натуральные числа – это числа, которые используются при счёте предметов: 1,2,3,4,5,……… Все натуральные числа, записанные в порядке возрастания, образуют ряд натуральных чисел. В натуральном ряду за каждым числом следует еще одно число, большее предыдущего на единицу. Как известно, натуральных чисел – бесконечно много.

Простое число — натуральное число, имеющее ровно два различных натуральных делителя — единицу и самого себя. Пр имеры простых чисел: 2,3,5,7,11,13,17,19. Простые числа поставили перед математиками немало сложных вопросов, на многие из которых ответ до сих пор не найден.

Из первой тысячи натуральных чисел 168 чисел являются простыми. Есть простые числа и во второй, третьей, четвертой тысячах. Можно предположить, что среди любых тысячи натуральных чисел, идущих подряд, встречаются простые. Но это не так.

Исследуя таблицы простых чисел, французский математик Жозеф Луи Франсуа Бертран(1822-1900) выдвинул предположение, что при n 1 между числами n и 2 n содержится хотя бы одно простое число. Данный факт смог доказать выдающийся русский математик и механик Пафнутий Львович Чебышёв (1821-1894).

В мире простых чисел существует множество нерешенных задач. Если мы обратимся к учебнику Математика: 6 автора Мерзляка А.Г, то увидим на форзаце таблицу простых чисел, в которой выделены красным цветом простые числа, отличающиеся на 2. Такие пары простых чисел называются близнецами. Но вычислить, сколько пар таких близнецов, конечно это количество или бесконечно, пока не удалось никому.

Также неизвестно, сколько на данный момент существует простых чисел, состоящих только из единиц, и конечно или бесконечно множество простых чисел, в записи которых нет ни одного нуля.

Составным числом называется натуральное число , большее, чем единица, которое не является простым . Каждое составное число является произведением двух или более натуральных чисел, больших 1. Перечислим подряд несколько составных чисел: 4, 6, 8, 9, 10, 12, 14, 15, 16, 18, 20, 21, 22, 24, 25.

А число 1 имеет только один делитель — само это число, поэтому оно не относится ни к простым, ни к составным числам. Таким образом, множество натуральных чисел состоит из простых чисел, составных чисел и единицы. [3]

Разберем, что же такое решето, и почему данное слово используется в математике. Когда в каком-то веществе или продукте необходимо отделить мелкие частички от более крупных, то используют решето. Например, после помола зерна с помощью решета отделяют муку от отрубей.

2.2 История жизни и деятельность великого Эратосфена

Рис. 1 Эратосфен

Эратосфен — древний математик, живший в 276-194 годах до нашей эры. Он является одним из самых разносторонних ученых античности. История сохранила краткие сведения из биографии Эратосфена, однако на него очень часто ссылались авторитетные и знаменитые мудрецы, философы античности: Архимед, Страбон и другие. Родился Эратосфен в Африке, в Кирене, поэтому нет ничего удивительного в том, что своё образование он начал в Александрии. Живой ум Эратосфена пытался постичь практически все известные на тот момент науки. И как все учёные, он наблюдал за природой. [2]

Эратосфен заложил основы математической географии, вычислив с большой точностью величину земного шара, изобрел широту и долготу, а так же придумал високосный день.

Математиков и после смерти Эратосфена волновала проблема нахождения простых чисел. В 1909 году американский математик Деррик Норман Лемер опубликовал таблицы простых чисел в промежутке от 1 до 10.017.000. Книга таблиц имеется в Российской государственной библиотеке в Москве. [1]

Запишем первые сто натуральных чисел в виде таблицы.

Зачеркнём в этой таблице число 1, которое не является простым. Далее обведём число 2, а остальные чётные числа таблицы зачеркнём. (Приложение II )

Первым из оставшихся чисел будет число 3, которое мы тоже обведём. Далее вычеркнем из таблицы все числа, кратные трём, кроме самого числа 3. (Приложение III )

Первым из оставшихся чисел будет число 5. Далее проделаем такую же операцию с числами 5 и 7. (Приложение IV )

На этом этапе просеивание завершено. Все оставшиеся числа в таблице являются простыми. Действительно, числа 4,6,8,9,10 оказались вычеркнутыми. Если составное число больше 10, но меньше 100, то его можно представить в виде произведения двух множителей, один из которых меньше 10. Составное число с таким множителем кратно одному из чисел 2,3,5,7, а значит, будет вычеркнуто.

Посмотрев интернет источники, я обнаружила сайт, на котором говорилось, что решето используется не только в математике, но и в информатике. Технологии, компьютеры и информатика позволили математикам, изучающим алгебраические теории, выйти на новый этап развития науки. Первым делом, воспользовавшись уникальной возможностью, они стали интегрировать известные арифметические и геометрические исследования в программирование.

На данный момент проведение соревнований для школьников по различным предметам снова набирают популярность. Лауреаты и победители таких мероприятий выходят на новый уровень обучения и могут получить неплохие перспективы в дальнейшей деятельности, в том числе материальные гранды.

Олимпиады по информатике включают в себя не только сложные задачи, но и нахождение таких известных понятий, как простые числа. Решето Эратосфена при этом используется в качестве наиболее актуального способа вычисления последовательностей, путем интегрирования аксиомы в программный код. Несмотря на древность открытия, данная теория помогает быстро и эффективно освоиться в труднодоступных расчетах.

Новый вариант в компьютерной реализации требует меньше оперативной памяти, что означает меньший объём подкачки страниц из виртуальной памяти — следовательно, процесс существенно ускоряется.

2.4 Практическая часть

Я провела анкетирование в двух классах шестой параллели МАОУ СОШ № 73 г. Челябинска, чтобы узнать, насколько актуальна данная тема, и что учащиеся вообще об этом знают. В анкетировании приняли участие 43 человека. Учащимся было задано три вопроса, на которые было предложено дать краткий ответ: да или нет. Результаты анкетирования следующие:

Знаете ли Вы, что представляет собой решето, для чего оно используется?

Да: 5 человек, нет: 38 человек.

Знаете ли Вы, что такое простые числа, составные числа?

Да: 21 человек, нет: 22 человека.

Да: 9 человек, нет: 34 человека.

Рис.2 Доска для просеивания простых чисел

Математика – наука, которая появилась несколько тысяч лет и активно использовалась уже в Древней Греции. При этом многие ученые-теоретики, жившие в то время, делали открытия, ставшие великими и гениальными, но настоящее признание получили несколько веков спустя, когда технологии позволили понять весь потенциал исследований античных арифметиков.

Я считаю, что сформулированные цели в моей исследовательской работе выполнены, а гипотеза исследования подтверждена.

Список используемой литературы:

Мерзляк А.Г. Математика: 6 класс: учебник / А.Г. Мерзляк, В.Б. Полонский, М.С. Якир; под ред. В.Е. Подольского. — М. : Вентана — Граф, 2019. – 334 с.

Простое число // Математическая энциклопедия (в 5 томах) . — М. : Советская Энциклопедия, 1977. — Т. 4.

Толково-образовательный. Новый словарь русского языка Ефремова Т.Ф. — М.: Рус. яз., 2000.- 1209 с.

Ушаков Д.Н Толковый словарь / Д.Н. Ушаков. — М.: Славянский Дом Книги , 2014 г. – 960с.

Об античном ученом Эратосфене Киренском, которому приписывают наш метод, википедия говорит следующее [1]:

Обычно метод Эратосфена описывают при помощи картинки, где изображено некоторое количество первых чисел натурального ряда (единицу, как и договорились, мы сразу выбросим из рассмотрения):

Первые 50 натуральных чисел

Идея в том, что мы берем подряд числа из натурального ряда. Для каждого взятого числа k добавляем это же число k и полученный результат вычеркиваем. Потом снова добавляем и снова вычеркиваем. Делаем так, пока не дойдем до конца интервала. Почему мы вычеркиваем эти числа? Потому что это каждое такое число кратно k, оно заведомо составное, а не простое.

Но мы идем дальше. К двойке прибавляем само это число 2+2. Получилось 4. Надо ли здесь задавать себе вопрос: в первый раз или не в первый мы встретили это число? Нет, не надо. Потому что мы работаем с двойкой! Получившееся число 4 вычеркиваем.

Кстати, как долго нам надо идти вперед? Это зависит от точной постановки задачи, а мы пока этого не сделали, и подходили к задаче по-простецки — находили простые числа. Но мы не уточняли, сколько именно простых чисел мы хотим найти. В самом деле – сколько?

Поиск простых чисел на заданном интервале

Наверное, имеет смысл искать N первых простых чисел. Но это не очень простая постановка задачи – вы это скоро увидите. Давайте для начала рассмотрим более простую задачу: найти все простые числа, меньше или равные заданного числа M.

Пусть это M равно 50. Значит, надо добавлять нашу двойку, пока не дойдем до 50.

Начав с 2, и добавляя по 2, мы получим следующую картину (красным выделены вычеркнутые числа):

Вычеркнули от 2 по +2

Вычеркнули от 3 по +3

Нетрудно видеть, что какие-то числа нам пришлось вычеркивать по второму разу, начиная с той же шестерки – ведь мы уже вычеркнули 6, когда работали с числом 2. Есть ли в этом что-то нехорошее? Если рассматривать эту работу с вычислительной точки зрения, то как будто бы это нехорошо. Вообще любая повторная работа, которую можно избежать – это нехорошо. Потому что мы тратим вычислительное время. Но в данном случае лучше все же закрыть глаза на эту избыточность. Потому что иначе нам пришлось бы как-то проверять, а не вычеркивали ли мы это число раньше? А это, само по себе, тоже лишняя вычислительная работа.

Вычеркнули от 5 по +5

Как долго следует продолжать этот процесс? В самом начале мы сказали, что надо перебирать все числа в заданном интервале [2; M]. Но нетрудно догадаться, что на самом деле достаточно остановиться на числе M/2 (или его целой части для нечетных M). Ведь когда мы перейдем к следующему за ним числу K = [M/2] + 1, то число K + K заведомо окажется вне диапазона [2; M].

В любом случае, когда мы закончим перебирать все числа в интервале [2; M] (или только первую половину этого интервала), мы получим, что больше нам вычеркивать нечего. Это значит, что числа, оставшиеся незакчеркнуыми – и есть простые:

Всего мы нашли 16 простых чисел на нашем интервале, причем заранее мы не могли знать, сколько именно мы найдем. В этом и состоит главная прелесть и загадка простых чисел: не существует простого понимания того, насколько плотно простые числа расположены на числовой оси. Вспомним, какую постановку задачи мы сами для себя выбрали – найти все простые числа на заданном отрезке, – то есть, не превосходящие некоторого числа M.

Давайте для начала запрограммируем на Python первую задачу – для заданного интервала, а потом станем думать, как это трансформировать в решение второй задачи.

nums = list(range(maxNum + 1))

for j in range(i + i, len(nums), i):

В результате чего убедимся, что на отрезке [1; 100] всего 25 простых чисел. А теперь представим, что нашему заказчику совершенно все равно, какой интервал мы рассматриваем. Ему важно, чтобы мы нашли ему 100 первых простых чисел. А уж на каком интервале они лежат – как получится. Как нам нужно действовать?

Поиск заданного количества простых чисел

Кстати, почему это так? Это очень интересный вопрос, но им надо подробно заниматься не здесь, а в теории чисел. Но на самом деле, интуитивно, это и так ясно. Ведь чем больше число, тем больше шансов, что у него окажутся делители, большие единицы, но меньшие его самого.

Можем ли мы хотя бы оценить, насколько реже – в каком-то количественном исчислении — будут попадаться простые числа по мере продвижения по числовой оси? Наверное, можно. Но, опять же, сейчас это не наша тема. Пусть этим занимаются числовые теоретики.

В каком-то смысле, на этом месте можно было бы остановиться и считать задачу решенной. Мы нашли принципиальный способ находить требуемое количество первых простых чисел. Но, к сожалению, с практической точки зрения, этот способ очень плохой. Все дело в том, что нам придется многократно повторять одну и ту же работу. Представьте, что мы уже проделали все нужные вычисления на отрезке [1; M] и не нашли требуемое количество N простых чисел. Мы говорим: не беда! – и начинаем работу заново на отрезке [1; 2M]. И нам неизбежно придется пройти сначала по отрезку [1; M], но ведь мы это уже делали! Получается, мы сделаем эту работу повторно.

Вообще, такие оценки далеко не всегда легко выполнять, но программист постепенно должен этому учиться. Кроме этого, как и почти все в программировании, такие оценки можно делать по-разному. Конечно – при правильно проведенной оценке конечный результат не должен изменяться. Поэтому автор сделает так, как нравится ему. Изобразим наши поисковые интервалы геометрически:

Удвоили поисковый интервал

Мы видим казалось бы — простую вещь: при увеличении поискового интервала в 2 раза объем вычислений увеличился в 2 раза. Однако – не совсем так. Ведь мы уже один раз проделали кусок работы на начальном интервале [1; M], а потом мы еще дважды ее выполнили. Всего получается уже
m + 2m = 3m.

Пусть нам снова не хватило простых чисел, найденных на интервале [1; 2M]. Тогда мы переходим к интервалу [1; 4M]. И мы видим, что полное количество проделанных нами вычислений от самого начала работы равно m + 2m +4m = 7m.

Еще раз удвоили поисковый интервал

Теперь мы уже можем разглядеть, по какому закону нарастает объем вычислений – это закон геометрической прогрессии. Поскольку знаменатель этой прогрессии равен 2, сумма k членов прогрессии равна m * (2^k – 1) / (2 -1), то есть – m * (2^k — 1). Напомним: k слагаемых в нашей сумме означает, что мы k-1 раз удваивали размер поискового интервала.

Это не просто очень сильный рост, это самый плохой рост, какой только можно вообразить, и любой ИТ-специалист сразу схватится за голову: такой алгоритм просто никуда не годится. Надо искать какой-то другой метод.

Нам снова поможет довольно простая идея: давайте, вместо того, чтобы все время начинать работу заново, попробуем просто продолжать эту работу. Легко сказать, а как сделать?

Если бы мы проверяли только деление, скажем на 2 или 3, или любое другое, но одно конкретное число, мы бы шли и шли вдоль первого интервала, потом увидели бы, что одного этого интервала нам не хватае, и пошли бы дальше, и нет проблем. Но проблема в том, что проработав число 2, мы его бросаем, и работаем с числом 3, и так далее. А когда приходит время расширить интервал – мы уже ничего не помним, и поэтому не знаем, за что хвататься.

Какое число не возьми – ту же двойку – мы не знаем, откуда надо начинать новый отсчет.

Хорошая формулировка проблемы часто содержит, частично или даже полностью, путь к ее решению, и это именно наш случай. Если мы не знаем, откуда нам начинать прыгать через 2 (3, 5, 7 — и так далее) – давайте просто будем это записывать, чтобы не забыть.

Запоминать лучше в виде словаря. Словарь – это простейший объект в языках Python и JavaScript. Возможно, и в каких-то других языках тоже, но кругозор автора не бесконечен. А в этих двух языках словарь представляет собой перечень пар : , заключенный в фигурные скобки <>:

В качестве ключа могут применяться разные типы данных, но мы для простоты будем считать, что у нас ключами будут числа (чаще всего применяют строки). Значение может быть вообще любое: число, строка, список, или любой другой объект (не обязательно словарь – есть еще экземпляры классов, но мы в эту область не заглядываем).

В языках Си и С++ существует похожий тип данных, называемый структурой (struct), но это менее гибкий тип данных, чем словарь Python. Любопытно, что в JavaScript вообще все объекты, включая очень сложные, строятся на основе словарей, а классов, как в С++, Java или Python, нет вообще, но можно наследовать объекты. В этом отношении, JavaScript – самый необычный объектно-ориентированный язык.

Мы немного отклонились от нашей основной задачи, но только для того, чтобы подсветитить, насколько словарь – действительно важнейший тип данных, и далеко не в одном только Python, на котором мы решаем нашу задачу.

Возможно, это не самая простая и понятная формулировка, поэтому давайте повторим ее другими словами. Допустим, мы нашли простое число 2. Мы последовательно вычеркивали, в нашем текущем интервале, числа: 4, 6, 8, … и остановились, например, на числе 240. А наш интервал поиска заканчивался, например, на числе 241. Дальше нам идти некуда – в рамках данного интервала.

Запоминать эту пару чисел мы будем в виде одной записи в словаре:

Вообще, всегда надо стремиться к тому, чтобы имена переменных максимально отражали содержательный смысл тех данных, которые эта переменная описывает. Это не всегда удается в полной мере, но стараться все равно надо.

Дополним наш предыдущий код заполнением словаря pev_primes по мере того, как мы проходим по начальному поисковому диапазону [1; maxNum]:

nums = list(range(maxNum + 1))

for j in range(i + i, len(nums), i):

Последнее значение j и есть то число, последнее для i, которое мы вычеркнули в текущем интервале, поэтому его надо запомнить.

Давайте посмотрим, что мы сохранили:

Что-то пошло не так

Это только первый вопрос, но есть еще и другой: почему значение 94 у ключа 53 такое же, как у ключа 47. Есть и третий вопрос: почему значение 94 так и повторяется до самого конца словаря pev_primes.

Обнаружить причину произошедшего на самом деле несложно. Число 53 – первое, большее половины нашего диапазона. Если мы добавим 53 к 53, мы сразу выходим за пределы поискового диапазона. Это значит, что цикл

for j in range(i + i, len(nums), i):

— даже не начнет выполняться. Тогда, что же мы будем записывать в наш словарь в инструкции prev_primes[i] = j ? Это будет то значение j, которое осталось от предыдущего i, при котором цикл for еще выполнялся – как раз 94.

to_remove = range(i + i, len(nums)+1,

for j in to_remove :

if len(to_remove) > 0:

Теперь стало лучше

def add_primes(minNum, maxNum, prev_primes) :

nums = list(range(minNum, maxNum+1))

for prime, last_removed in prev_primes.items():

to_remove = range(last_removed + prime, maxNum+1, prime)

И удалять числа придется тоже чуть похитрее, чем раньше: чтобы получить индекс нужного числа в списке nums, нужно из этого числа вычесть начало диапазона:

for num in to_remove :

nums[num — minNum] = 0

Итак, что мы сделали. Мы продолжили вычеркивание чисел, кратным тем простым, которые мы нашли на предыдущем интервале, точнее – на всех предыдущих интервалах. Мы же будем продолжать расширять поисковый интервал неопределенно долго. Но на текущем интервале должны найтись какие-то новые простые числа в списке nums!

def add_primes(minNum, maxNum, prev_primes) :

nums = list(range(minNum, maxNum+1))

for num in nums :

Первое же встречное, но обязательно ненулевое – т.е. не вычеркнутое число, и есть простое, как и раньше.

Как и раньше, удалять надо с числа next_prime + next_prime, с шагом next_prime.

to_remove = range(next_prime * 2, maxNum+1, next_prime)

for num1 in to_remove:

nums[num1 — minNum] = 0

Как и раньше, к данному простому числу next_prime привязываем то число, которое мы вычеркнули последним:

if len(to_remove) > 0:

add_primes(minNum, maxNum, prev_primes)

minNum = maxNum + 1

Наконец, выполняем все вместе:

Выше уже говорилось, что мы не можем так подгадать, чтобы найти ровно требуемое (например, 100) количество простых чисел. Но мы можем проверить, что нашли не меньше, и в этом месте прекращаем развдигать наше раздвижное сито. И, чтобы вывести ровно 100 чисел, просто возьмем срез от найденного списка:

[2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47, 53, 59, 61, 67, 71, 73, 79, 83, 89, 97]

[2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47, 53, 59, 61, 67, 71, 73, 79, 83, 89, 97]

[2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47, 53, 59, 61, 67, 71, 73, 79, 83, 89, 97]

for num in nums :

if len(to_remove) > 0:

Получаем такую трассировку нашей программы:

101 : 103 : 107 : 109 : 113 : …

Точнее говоря – работа идет, но недостаточная: мы вычеркиваем числа, кратные только ранее найденным простым, а новые простые мы не находим и не и не используем.

Это окажется последней настройкой нашей задумки, программа заработает уже полностью правильно, в чем легко может убедиться любой начинающий кибернетик – программист галактических искусственных разумов. Последние добавления в программу выделены отдельно.

def add_primes(minNum, maxNum, prev_primes):

»’добавляем простые числа и последние вычеркнутые числа»’

nums = list(range(minNum, maxNum+1)

for prime, last_removed in prev_primes.items():

to_remove = range(last_removed + prime, maxNum+1, prime)

to_remove = range(last_removed, maxNum+1, prime)

for num in to_remove :

nums[num — minNum] = 0

for num in nums :

to_remove = range(next_prime * 2, maxNum+1, next_prime)

for num1 in to_remove:

nums[num1 — minNum] = 0

if len(to_remove) > 0:

prev_primes[next_prime] = 2 * next_prime

add_primes(minNum, maxNum, prev_primes)

minNum = maxNum + 1

Проверяем результат: (можете сравнить с готовыми таблицами простых чисел):.

[2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47, 53, 59, 61, 67, 71, 73, 79, 83, 89, 97, 101, 103, 107, 109, 113, 127, 131, 137, 139, 149, 151, 157, 163, 167, 173, 179, 181, 191, 193, 197, 199, 211, 223, 227, 229, 233, 239, 241, 251, 257, 263, 269, 271, 277, 281, 283, 293, 307, 311, 313, 317, 331, 337, 347, 349, 353, 359, 367, 373, 379, 383, 389, 397, 401, 409, 419, 421, 431, 433, 439, 443, 449, 457, 461, 463, 467, 479, 487, 491, 499, 503, 509, 521, 523, 541]

Читайте также:

  

• Экспертиза ценности электронных документов кратко

  

• Кормление рабочих лошадей кратко

  

• История тгу кызыл кратко

  

• Наукоемкое трудоемкое и металлоемкое машиностроение это в географии кратко

  

• Антропософия кратко и понятно