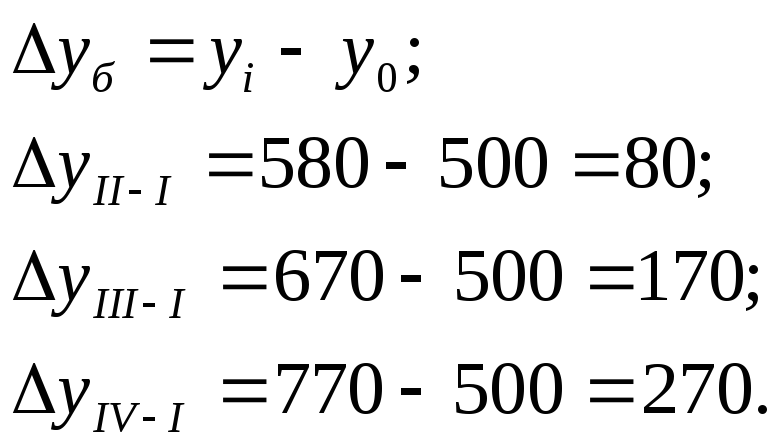Методы прогнозирования продаж
Качественное и точное прогнозирование продаж – одно из главных и неотъемлемых условий эффективного развития каждого предприятия, не зависимо будто фармацевтическая, кондитерская, ликеро-водочная, строительная отрасль.
- Аналитика бизнеса
- Методы анализа данных Data Mining
- Методы прогнозирования продаж
Оглавление

Качественное и точное прогнозирование продаж – одно из главных и неотъемлемых условий эффективного развития каждого предприятия, не зависимо будто фармацевтическая, кондитерская, ликеро-водочная, строительная отрасль.
Существует очень огромное количество разнообразных методов составления прогноза, из которых каждый отдельно взятый специалист в той или иной отрасли, занимающийся прогнозированием на базе исторических данных, может выбрать наиболее подходящий метод для конкретной. Правильный выбор метода составления прогноза – залог получения полноценной информации для принятия управленческих решений. Предлагаем вашему вниманию некоторые наиболее известные методы прогнозирования продаж.
1. Экстраполяция по скользящей средней.
Как правило применяется при краткосрочном прогнозировании (прогноз на месяц, квартал, год), используется в том случае, когда имеющиеся данные не позволяют выявить тренд изменения спроса.
Метод скользящей средней состоит в замене фактических уровней динамического ряда расчетными, имеющими значительно меньшие колебания, чем исходные данные. При этом средняя рассчитывается по группам данных за определенный интервал времени, причем каждая последующая группа образуется со сдвигом на один период (год, месяц). В результате первоначальные колебания динамического ряда сглаживаются, поэтому и операция называется сглаживанием рядов динамики (основная тенденция развития выражается при этом уже в виде некоторой плавной линии). Таким образом, при прогнозировании исходят из простого предположения, что следующий во времени показатель по своей величине будет равен средней, рассчитанной за последний интервал времени.
Пример расчета 3-месячной и 9-месячной скользящей средней. период продажи 3 недельная 9 недельная
Недостаток метода заключается в том, что требуется много данных для расчета прогнозного значения показателя.
2. Экспоненциальная средняя.
При составлении отчетов влияние на прошлые данные должны затухать по мере удаления от момента, на который составляется прогноз. Одним из простейших приемов сглаживания динамического ряда с учетом «устаревания» данных является расчет коэффициентов, получивших название экспоненциальных средних, которые широко применяются в краткосрочном прогнозировании. Основная идея метода состоит в использовании в качестве прогноза линейной комбинации прошлых и текущих периодов.
Экспоненциальная средняя рассчитывается по формуле:
Qt = a * yt + (1 – a)* Qt -1
где Qt – экспоненциальная средняя (сглаженное значение уровня ряда) на момент t; a – коэффициент, характеризующий вес текущего наблюдения при расчете экспоненциальной средней (параметр сглаживания), причем 0 < a ≤ 1. При прогнозировании продаж эта формула приобретает вид: новый прогноз продаж = a * последняя продажа + (1 – a) * предыдущий прогноз Применение скользящей и экспоненциальных средних в качестве основы для прогностической оценки имеет смысл лишь при относительно небольшой волатильности данных. Данные методы прогнозирования относятся к числу наиболее распространенных методов экстраполяции трендов.
3. Прогнозирование на основе сезонных колебаний.
Широкое распространение в разных видах деятельности получил метод основанный на базе сезонных колебаний уровней динамического ряда. При этом под сезонными колебаниями понимаются такие изменения уровня динамического ряда, которые вызываются влияниями времени года. Сезонные колебания строго цикличны – повторяются через каждый год, хотя сама длительность времен года имеет колебания. Для изучения сезонных колебаний необходимо иметь данные за каждый квартал, а лучше за каждый месяц, иногда даже за декады, хотя декадные уровни могут уже сильно исказиться мелкомасштабными случайными колебаниями. Методика статистического прогноза по сезонным колебаниям основана на их экстраполяции, т.е. на предположении, что параметры сезонных колебаний сохраняются до прогнозируемого периода. Для измерения сезонных колебаний исчисляются индексы сезонности Is. Индексы сезонности определяются отношением исходных (эмпирических) уровней ряда динамики yi, к теоретическим (расчетным) уровням yti, выступающим в качестве базы сравнения:
Именно в результате того, что в приведенной выше формуле измерение сезонных колебаний производится на базе соответствующих теоретических уровней тренда yti, в исчисляемых при этом индивидуальных индексах сезонности влияние основной тенденции развития элиминируется (устраняется). Поскольку на сезонные колебания могут накладываться случайные отклонения, для их устранения производится усреднение индивидуальных индексов одноименных внутригодовых периодов анализируемого ряда динамики. Поэтому для каждого периода годового цикла определяются обобщенные показатели в виде средних индексов сезонности (Is): ∑Isi. Рассчитанные таким образом средние индексы сезонности свободны от влияния основной тенденции развития и случайных отклонений.
В зависимости от характера тренда выделяют два способа измерения сезонных колебаний:
– способ переменной средней (для рядов внутригодовой динамики с ярко выраженной основной тенденцией развития): выступающие при этом в качестве переменной базы сравнения теоретические уровни yti представляют своего рода «среднюю ось кривой», т.к. их расчет основан на положениях метода наименьших квадратов;
– способ постоянной средней (для рядов внутригодовой динамики, в которых повышающийся (снижающийся) тренд отсутствует, или он незначителен):
В этой формуле базой сравнения является общий для анализируемого ряда динамики средний уровень y. Вышеизложенные методы прогноза сезонных колебаний не являются единственными. Так, для выявления сезонности можно использовать и рассмотренный выше метод скользящей средней, и другие методы.
4. Прогнозирование методом линейной регрессии.
Метод базируется на анализе взаимосвязи двух переменных (метод парной корреляции) – оценке влияния вариации факторного показателя Х (например, расходов на рекламу) на результативный показатель У (например, на объем продаж):
с использованием метода наименьших квадратов. В основу данного метода положено требование минимальности сумм квадратов отклонений эмпирических данных уi от выровненных ухi:
Для определения параметров а и b исходного уравнения на основе требований метода наименьших квадратов при помощи дифференциальных исчислений составляется система нормальных уравнений:

Почитать еще
Машинное обучение
Глубокое обучение – это продвинутая форма машинного обучения. Глубокое обучение относится к способности компьютерных систем, известных
Выборка. Типы выборок
Суммарная численность объектов наблюдения (люди, домохозяйства, предприятия, населенные пункты и т.д.), обладающих определенным набором признаков
Обзор основных видов сегментации
Загрузить программу ВІ Демонстрации решений Аналитика бизнеса Оглавление Сегментация бренда Сегментация помогает принимать более эффективные
Несколько видео о наших продуктах
Проиграть видео
Презентация аналитической платформы Tibco Spotfire
Проиграть видео
Отличительные особенности Tibco Spotfire 10X
Проиграть видео
Как аналитика данных помогает менеджерам компании
Экстраполяция
— нахождение неизвестного значения
динамического ряда за его пределами
путем механического переноса тенденций
прошлого на будущее. Экстраполяция —
наиболее часто используемый и сравнительно
простой метод прогнозирования. Для ее
применения нужен минимум информации:
всего один динамический ряд прогнозируемого
показателя, как правило, за 5—7 лет
(периодов). Для прогнозирования может
быть использована одна из трех
разновидностей экстраполяции, причем
выбор конкретного способа из этих трех
зависит от характера имеющегося
динамического ряда. Рассмотрим подробнее
применение этих способов на конкретных
примерах.
Расчет
прогноза по среднему уровню ряда
применяется тогда, когда динамический
ряд не имеет тенденции роста или снижения
и его колебания относительно невелики.
В этом случае в качестве прогноза может
быть использована средняя арифметическая
показателей этого ряда.
Пример
10. Нужно
спрогнозировать возможную продажу
хлеба в торговой палатке на 7-й день,
если его продажа в предыдущие шесть
дней характеризуется следующими данными
(табл. 8.24):
Таблица
8.24
|
Дни |
1-й |
2-й |
3-й |
4-й |
5-й |
6-й |
|
Продажа |
1220 |
1275 |
1235 |
1265 |
1217 |
1270 |
Решение.
Нетрудно заметить, что данный динамический
ряд относительно стабилен и колеблется
около средней величины. Расчет проводится
по формуле простой средней арифметической:
кг.
Полученную
величину (1247 кг) можно прогнозировать
как объем возможной продажи хлеба на
7-й день. Разумеется, фактическая продажа
может несколько отличаться от нашего
прогноза, но возможную среднюю ошибку
прогноза рассчитывают по формуле
кг,
где
— средняя ошибка прогноза;
— дисперсия (
);
n
— число показателей в динамическом
ряду. Такое значение вполне приемлемо,
поскольку при краткосрочном прогнозировании
допускается средняя ошибка прогноза
до 5%, а в нашем случае она составляет
лишь 1,6% (20,45:
1247 ∙ 100).
Пример
11.
Экспертам
было предложено спрогнозировать объемы
продаж зубной щетки «Colgate
360 Супер чистота» в следующем году. В
распоряжении экспертов были данные о
продажах всех зубных щеток «Колгейт-Палмолив»
и условия поставок, а также щеток
конкурентов. По данным проведенного
экспертного опроса о перспективах
продаж зубной щетки «Colgate
360 Супер чистота», составлена таблица
8.25.
Таблица
8.25
Данные
экспертного опроса о перспективности
объема продаж зубной щетки «Colgate
360 Супер чистота» в городе
|
Эксперт |
Прогноз объема |
Эксперт |
Прогноз объема |
Эксперт |
Прогноз объема |
|
1 |
22 |
11 |
17 |
21 |
23 |
|
2 |
31 |
12 |
23 |
22 |
17 |
|
3 |
18 |
13 |
28 |
23 |
27 |
|
4 |
22 |
14 |
22 |
24 |
28 |
|
5 |
16 |
15 |
31 |
25 |
23 |
|
6 |
32 |
16 |
25 |
26 |
18 |
|
7 |
23 |
17 |
18 |
27 |
29 |
|
8 |
27 |
18 |
19 |
28 |
30 |
|
9 |
19 |
19 |
20 |
29 |
27 |
|
10 |
20 |
20 |
20 |
30 |
30 |
Для
определения оптимального количества
групп с равными интервалами – m
, воспользуемся формулой Стэрджесса:
,
где
N
– число экспертов (30).
Ширина
интервала l
равна:
Результаты
расчетов представлены в таблице 8.26.
Таблица
8.26
Данные упорядоченного
вариационного ряда
|
Величина |
16-19,2 |
19,2-22,4 |
22,4-25,6 |
25,6-28,8 |
28,8-32 |
|
Среднее |
17,7 |
20,8 |
24 |
27,2 |
30,4 |
|
Количество |
8 |
6 |
5 |
5 |
6 |
Средняя
величина прогнозируемого объема продаж
определится по данным табл. 8.26:
тыс.
руб.
Рассчитываем
характеристику ряда распределения
прогнозов экспертов по объему продаж,
для этого составим расчетную таблицу
8.27.
Таблица
8.27
Расчетная таблица
|
Величина |
Количество |
Середина |
|
|
|
|
16-19,2 |
8 |
17,7 |
141,6 |
2506,32 |
49,12 |
|
19,2-22,4 |
6 |
20,8 |
124,8 |
2595,84 |
13,74 |
|
22,4-25,6 |
5 |
24 |
120 |
2880 |
1,25 |
|
25,6-28,8 |
5 |
27,2 |
136 |
3699,2 |
68,45 |
|
28,8-32 |
6 |
30,4 |
182,2 |
5544,96 |
75,66 |
|
∑ |
30 |
——— |
704,8 |
17226,32 |
256,22 |
Дисперсия
признака представляет собой средний
квадрат отклонений вариантов от их
средней величины, она исчисляется по
формуле:
.
Среднее
квадратическое отклонение равно корню
квадратному из дисперсии. Для вариационного
ряда:
В
соответствии с теоремой Чебышева 75%
значений признака попадут в интервал
17,7-29,3 тыс. руб., а 89% всех значений попадут
в интервал 14,8-32,2 тыс. руб.
2.
Прогнозирование
по средним темпам роста (снижения)
имеет смысл тогда, когда ряду динамики
свойственна устойчивая тенденция к
повышению или снижению. В этом случае
предполагается, что каждый последующий
член динамического ряда равен предыдущему,
умноженному на средний коэффициент
темпов роста (снижения) Iср
.Коэффициент
исчисляется по формуле
Затем
на основе этого коэффициента можно
вычислить прогноз по формуле
где
у1—
начальный показатель ряда; уn
— конечный показатель ряда; уt
— прогнозируемый показатель; n
— количество членов динамического
ряда; k
— время упреждения прогноза (число
прогнозируемых интервалов).
Пример
12. Торговая
организация обслуживает 100 тыс. жителей.
Требуется рассчитать прогноз возможного
объема продажи картофеля в 7-м году, если
его продажа в расчете на одного человека
за предыдущие пять лет характеризуется
данными из таблицы 8.28.
Таблица
8.28
Динамика продаж
|
Год |
1-й |
2-й |
3-й |
4-й |
5-й |
|
Продажа |
97 |
96 |
94 |
92 |
90 |
Решение:
;
кг;
т.
Таким
образом, прогноз возможной продажи
картофеля в 7-м году в расчете на одного
человека составляет 86,44 кг, а в целом по
торговой организации Yt
— 8644 т.
Пример
13. Фирма
продает чемоданы на роликах. Данные
годового объема продаж чемоданов в тыс.
руб. представлены в табл. 8.29. Найти
средний объем продаж методом скользящей
средней и оценить перепады в продажах
через индекс сезонности. Составить
график маркетинговых мероприятий по
стимулированию продаж.
Сущность
метода заключается в том, что исчисляется
средний уровень из определенного числа,
обычно нечетного (3,5,7 и т.д.), первых по
счету уровней ряда, затем – из такого
же числа уровней, но начиная со второго
по счету, далее – начиная с третьего и
т.д. Скользящие средние находим по
формуле

когда
m=(2p-1)
– нечетное число; при m=3
,p=1,
т.е. при t=2
y2=(y1+y2+y3)/3,
при t=3
y3=(y2+y3+y4)/3
и т.д. Значение общего среднего уровня
можно получить по формуле
,
где
n
– количество
значений выборки.
Таким
образом, средняя как бы «скользит» по
ряду динамики, передвигаясь на один
срок. Скользящая
средняя представляет собой сглаженный
ряд и усредненную закономерность
прогнозирования будущей деятельности.
Недостатком
сглаживания ряда является «укорачивание»
сглаженного ряда по сравнению с
фактическим. Индексы
сезонности определяются по формуле

Таблица
8.29
Исходные
данные и результаты расчета продаж по
скользящей средней
|
Месяцы |
Объем |
Темп |
Трехмесячная средняя |
Индексы |
|
январь февраль март апрель май июнь июль август сентябрь октябрь ноябрь декабрь |
45 50 73 80 91 130 155 100 78 60 58 80 |
— 111,11 146,0 109,58 113,75 142,85 119,23 64,51 78,0 76,92 96,66 138,93 |
— (45+50+73)/3=56 (50+73+80)/3=67,67 (73+80+91)/3=81,34 (80+91+130)/=100,3 (91+130+155)/3=125,34 (130+155+100)/3=128,34 (155+100+78)/3=111 (100+78+60)/3=79,34 (78+60+58)/3=65,34 (60+58+80)/3=66 — |
— 56/88,07=64 77 93 114 100,65 143 127 91 75 75 |
|
|
|
95,9 |
Прогноз объема продаж на январь месяц
следующего года =
88,07∙108,86/100
= 95,87 тыс. руб.
Совокупность
исчисленных для каждого интервала
времени индексов сезонности характеризует
сезонную волну развития изучения явления
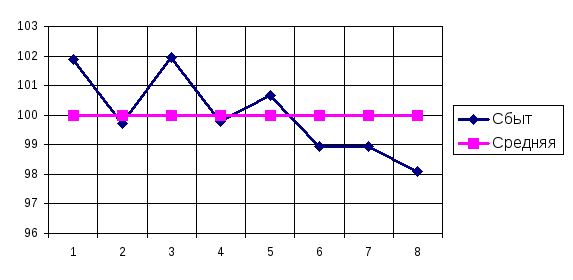
в динамике. На рис. 8.8 показан график
сезонности (по месяцам) продаж чемоданов
для примера из табл. 8.29.
Рис.
8.8. Характеристика сезонной волны продаж
на примере роликовых чемоданов
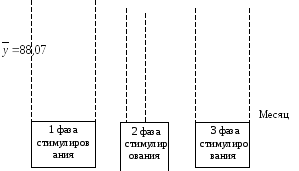
Характеристика
функции сбыта объясняется сезоном
отдыха и путешествий. Исходя из графика
продаж (рис. 8.8) фирма выделяет 3 фазы
проведения кампании по стимулированию
(табл. 8.30).
Таблица
8.30
План-график
проведения мероприятий по стимулированию
|
Фаза |
Фаза |
Фаза |
|
С |
С |
С |
Пример
14.
Необходимо
осуществить прогнозирование объема
продаж товаров и услуг компьютерного
магазина «Железо» методом экстраполяции.
На основании анализа бухгалтерской
отчетности составим таблицу 8.31 объема
продаж.
Таблица
8.31
Исходные данные
по динамике продаж
|
Кварталы года |
I |
II |
III |
IV |
|
Выручка тыс. руб. |
500 |
580 |
670 |
770 |
1). Определим среднегодовой объем выручки
за отчетный период:
тыс.
руб.
2). Найдем абсолютное изменение объема
выручки, тыс. руб. Абсолютный прирост
рассчитывается как разность между двумя
уровнями ряда. В зависимости от базы
сравнения абсолютные приросты могут
рассчитываться как цепные и как базисные.
Цепные показатели, то есть по отношению
к предыдущему кварталу:
Базисные, то есть по отношению к отчетному
кварталу:
3). Вычислим темпы роста, в %. Темп роста
показывает, во сколько раз сравниваемый
уровень больше уровня, с которым
производится сравнение.
а) цепные по формуле
КII—I= 580 /500*100 = 116; КIII—II= 670 /580*100 = 115; КIV—III= 770 /670 *100 = 115.
б) базисные по формуле
KII—I= 580 / 500 *100 = 116;KIII—I= 670 / 500*100 = 134;KIV= 770 / 500*100 = 154.
4). Вычислим темпы прироста (сокращения),
в %. Темп прироста показывает на сколько
процентов сравниваемый уровень больше
или меньше уровня, принятого за базу
сравнения: Тпр= Тр–100;
а) цепные: TII-I
= 116 – 100 = 16; TIII-II
= 115 – 100 = 15; TIV-III
= 115 – 100 = 15.
б) базисные:
TII-I
= 116 – 100 = 16; TIII-I
= 134 – 100 = 34; TIV-I
= 154 – 100 = 54.
Произведенные математические расчеты
по динамике вариационных рядов сведем
в таблицу 8.32.
5). Средний абсолютный прирост составит
в тыс. руб.:
,
то есть
в среднем за период времени с 1гопо 4ыйкварталы объем выручки
увеличился на 90 тыс. руб.
6). Средний темп роста, в %
.
Таким образом, за период времени с 1гопо 4ыйкварталы года объем выручки
ежеквартально увеличивался на 115,3%.
Таблица 8.32
Исходные
данные и математические расчеты по
динамике вариационных рядов
|
Квартал |
Выручка тыс. руб. |
Абсолютные изменения тыс. руб. |
Темпы роста, в % |
Темпы прироста, в % |
|||
|
цепные |
базисные |
цепные |
базисные |
цепные |
базисные |
||
|
I |
500 |
— |
— |
— |
— |
— |
— |
|
II |
580 |
80 |
80 |
116 |
116 |
16 |
16 |
|
III |
670 |
90 |
170 |
115 |
134 |
15 |
34 |
|
IV |
770 |
100 |
270 |
115 |
154 |
15 |
54 |
7). Прогноз выручки на I-й
иII-й кварталыследующего
года:
На основе среднего абсолютного прироста:
YI=
770 + 90 = 860 тыс. руб.;YII= 860 + 90 = 950 тыс. руб.
На основе среднего темпа роста:
YI=
770*1,153 = 887,81 тыс. руб.;YII= 887,81*1,153 = 1023,6 тыс. руб.
8). Прогноз на IIиIIIкварталы будущего года по методу
скользящей средней:
3.
Выравнивание
(сглаживание) динамического ряда.
Этот
способ экстраполяции также применяется
при наличии устойчивой тенденции роста
или снижения. Тенденция развития
прогнозируемого явления приблизительно
описывается графиком какого-либо
математического уравнения, а затем на
основе подобранного уравнения
рассчитывается прогноз.
В
схематическом виде данный метод
представлен на рис. 8.9. В зависимости от
характера динамического ряда на практике
для прогнозных расчетов применяются
различные математические функции.
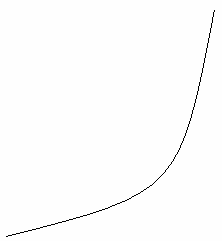
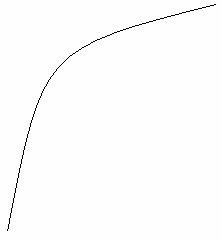
Наиболее часто используемые функции и
соответствующие им графики показаны
на рис. 8.10.
Рис.
8.9. Прогнозирование развития рынка
методом экстраполяции
y y

t
t
y y

t
t
Рис.
8.10. Графики
математических функций, описывающих
тенденции развития спроса
Выравнивание
по скользящей средней. Сущность
метода заключается в том, что исчисляется
средний уровень из определенного числа,
обычно нечетного (3,5,7 и т.д.), первых по
счету уровней ряда, затем – из такого
же числа уровней, но начиная со второго
по счету, далее – начиная с третьего и
т.д.
Скользящие средние
находим по формуле

когда
m=(2p-1)
– нечетное число; при m=3
,p=1,
т.е. при t=2
y2=(y1+y2+y3)/3,
при t=3
y3=(y2+y3+y4)/3
и т.д. Значение общего среднего уровня
можно получить по формуле
,
где
n
– количество значений выборки.
Таким
образом, средняя как бы «скользит» по
ряду динамики, передвигаясь на один
срок. Недостатком сглаживания ряда
является «укорачивание» сглаженного
ряда по сравнению с фактическим.
Пример
15.
Необходимо
рассчитать средний темп роста регионального
рынка рекламы и прогноз его линейного
роста на следующий год исходя из таблицы
8.33.
Таблица
8.33
Исходные данные
рекламного рынка
|
Годы |
Объем |
Темп |
Средний |
|
2007 2008 2009 2010 2011 |
175 190 210 240 280 |
— 108,57 110,52 114,28 116,66 |
112,51 |
Прогноз объема рекламного рынка (2012 г.)
= Объем рекламы (2010 г.)*(средний темп роста
/ 100) = 280(112,51/100)=. 315,03 млн. руб.
Вместе с тем, с помощью этого метода
трудно прогнозировать период менее 3-5
лет, поскольку слишком мала выборка,
массив обрабатываемой статистической
информации, а также период проявления
действия циклических колебаний.
Пример
16.
Рассмотрим
тенденцию сбытовой деятельности
предприятия по данным табл. 8.34.
Таблица
8.34
Исходные данные
и результаты расчета скользящей-средней
|
Месяцы |
Объем |
Трехмесячная |
Индексы |
|
1 2 3 4 5 6 7 8 9 10 |
85 70 83 80 75 78 82 71 78 80 |
— (85+70+83)/3=79,3 (70+83+80)/3=77,6 (83+80+75)/3=79,33 (80+75+78)/=77,66 (75+78+82)/3=78,33 (78+82+71)/3=77 (82+71+78)/3=77 (71+78+80)/3=76,33 — |
— 79,3/77,82=101,90 99,71 101,94 99,79 100,65 98,94 98,94 98,08 |
|
|
99,99 |
Таким образом,
скользящая средняя представляет собой
сглаженный ряд и усредненную закономерность
прогнозирования будущей деятельности.
Индексы сезонности
определяются по формуле
Iс
=
100%.
Совокупность
исчисленных для каждого интервала
времени индексов сезонности характеризует
сезонную волну развития изучения явления
в динамике. На рис. 8.11 показан график
сезонности для примера из табл. 8.34.
Рис.
8.11. Сезонная волна сбытовой деятельности
Выравнивание
по прямой
используется, как правило, в тех случаях,
когда абсолютные приросты практически
постоянны, т.е. когда уровни изменяются
в арифметической прогрессии или близко
к ней.
Простейшей моделью, выражающей тенденции
развития является линейная функция
тренда. Рассмотрим построение линии
тренда по прямой
y
= a0
+ a1t,
где
t
– порядковый
номер периода или момента времени; а1
– коэффициент регрессии, определяющий
направление развития тренда. Если а0,
то уровни ряда динамики равномерно
возрастают, а при а0
происходит их равномерное снижение.
Этому типу динамики присущи постоянные
приросты:
Рассмотрим линейный прогноз развития
на основании данных табл. 8.35 .
Таблица
8.35
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- Выдержка
- Другие работы
- Помощь в написании
Метод экстраполяции тренда (реферат, курсовая, диплом, контрольная)
В логистике, так же как и в других сферах экономической деятельности, широко распространен метод экстраполяции тренда, предполагающий, что закономерность, действующая внутри анализируемого временного ряда, выступающего в качестве базы прогнозирования, сохраняется и на период прогноза. Прогнозирование в этом случае можно свести к подбору аналитически выраженных моделей трендов типа у = f (t) по данным предпрогнозного периода и экстраполяции полученных трендов на интервале прогноза.
Формально исследуемый процесс может быть записан в аддитивном или мультипликативном виде. Аддитивная модель имеет вид:
где у — расчетные значения временного ряда;
yt — тренд или детерминированная составляющая; st — сезонная составляющая, отражающая периодические колебания, которые повторяются через примерно одинаковые промежутки в течение небольшого промежутка времени;
vt — циклическая составляющая, отражающая периодические колебания, повторяющиеся в течение длительного промежутка времени;
dt — составляющая, позволяющая учесть другие важные факторы, такие как фаза жизненного цикла, эффект от маркетинговых мероприятий и др.;
ег — случайная составляющая, обусловленная стохастическим характером социально-экономических процессов (случайные колебания, характеризующиеся абсолютной нерегулярностью величины, частоты, направления возникновения, поэтому их предсказание на основе анализа временного ряда оказывается невозможным).
Мультипликативная модель имеет вид:
где Is — коэффициент (индекс), учитывающий сезонные колебания; Iv — коэффициент (индекс), учитывающий циклические колебания; Id— коэффициент (индекс), учитывающий другие важные факторы (фаза жизненного цикла, эффект от маркетинговых мероприятий и др.); Et — случайная составляющая.
Модели (8.1) и (8.2) практически приближают прогноз к плану.
В частных случаях количество составляющих моделей (8.1) и (8.2) может быть меньше, например только yt и в, или больше, если необходимо выделить «сезонные» составляющие применительно к часам суток, к дням недели, месяцам. В этом случае модели (8.1) и (8.2) могут включать несколько сезонных компонент. Чем меньше составляющих модели удается описать, тем больше будет случайная составляющая, которая и характеризует неопределенность.
В простом варианте, когда модели (8.1) и (8.2) содержат только yt и е, процедуру прогнозирования в этом случае можно представить в виде следующей последовательности.
Первый этап — подбор зависимости для описания уравнения тренда. Вид функции обычно задают, используя полиномы различных порядков, экспоненциальные, степенные функции и т. п. Параметры модели прогнозирования определяются методом наименьших квадратов (МНК), при этом модель тренда должна быть такой, чтобы сумма квадратов отклонений расчетных значений от фактических была наименьшей.
Если модель тренда является линейной, у* = а0 + axt, то расчет коэффициентов уравнения а0 и ах производится по формулам:
Второй этап — продолжение полученного тренда за интервал значений, но которым строилась зависимость, или определение точечного прогноза. Для получения значения прогноза на t-й год в уравнение тренда подставляются конкретные значения t.
Важно запомнить
Соотношение длины предпрогнозного периода и периода прогноза должно быть не менее, чем 3:1.
Третий этап — расчет ошибки прогноза. Тренд характеризует лишь средний уровень ряда на каждый момент времени, в том числе и на прогнозный период. Отдельные наблюдения в прошлом (на интервале наблюдения) отклоняются от линии тренда — это дает право предполагать, что и в будущем следует ожидать таких отклонений. Значит, прогноз имеет погрешность, которая помимо колебаний значений от среднего уровня объясняется еще и наличием неопределенности при определении параметров модели тренда, поскольку их оценивание производится на основе ограниченной совокупности данных.
Погрешность прогноза можно оценить по среднему квадратическому отклонению.
где у* — расчетные (теоретические) значения; ух — фактические значения; к — число степеней свободы, определяемое в зависимости от числа наблюдений (N) и числа оцениваемых параметров (z), к = N ~ z; для линейного тренда 2 = 2, для параболы второй степени z = 3 и т. д.
Погрешность прогноза отражается в виде доверительного интервала, с помощью которого точечный прогноз преобразуется в интервальный.
Четвертый этап — определение интервала прогноза. При использовании трендовых моделей прогнозов следует иметь в виду, что погрешность прогноза растет при увеличении периода упреждения, так как тренд выявлен на основе данных, охваченных периодом наблюдения, и чем дальше от этого периода, тем выше вероятность ошибочного суждения. Поэтому при определении интервального прогноза следует учесть корректировочный коэффициент[1]:
где N — продолжительность наблюдения; L — период упреждения.
Доверительный интервал прогноза при небольшом числе наблюдений и при предположении о нормальном распределении прогнозных оценок определяется следующим образом:
где ta — табличное значение-критерия Стьюдента с k степенями свободы и уровнем значимости a; ot/ — ошибка модели прогноза, рассчитанная как среднее квадратическое отклонение.
Метод экстраполяции тренда достаточно прост и легко реализуется на компьютерах. К недостаткам метода можно отнести следующее. Во-первых, модель тренда жестко фиксируется, и с помощью МНК можно получить достоверный прогноз лишь на небольшой период упреждения. Во-вторых, МНК очень просто реализуется только для линейных зависимостей и нелинейных функций, приводимых к линейному виду.
Рассмотренный способ прогнозирования позволяет уменьшить неопределенность спроса, расхода материальных ресурсов, например в управлении запасами: изменить параметры поставки или размер страхового запаса.
Рассмотрим ситуацию, в которой может использоваться трендовая модель прогноза для решения типичных задач управления запасами. Сразу же следует предупредить читателя, что данный разбор ситуации — не просто рассмотрение возможностей прогнозирования на основе каких-либо данных. Мы попытаемся последовательно показать на примере конкретных данных, как можно корректно использовать трендовое прогнозирование именно в целях решения задач управления запасами. Для этого практика и теория в данной ситуации тесно и неразделимо переплелись.
? Разбор ситуации Напомним, что трендовая модель позволяет дать прогноз как на один, так и на несколько периодов, если мы хотим быстро реагировать и вносить изменения в систему поставки. Рассмотрим ситуацию, в которой известны значения расхода деталей со склада за пять дней работы (табл. 8.2). Начальный запас равен 50 ед.
1. Для начала подберем уравнение тренда yt в виде линейной зависимости yt = а0 + а{ t. Расчет коэффициентов уравнения а0 и ах производится по формулам (8.3) и (8.4), которые получены на основе метода наименьших квадратов. Результаты представлены в табл. 8.3.
Данные о спросе и остатках
|
День. |
Спрос, ед. |
Остаток, ед. |
Таблица 8.3
Исходные данные и результаты расчета коэффициентов линейной зависимости при N=5
|
б> дн. |
У г ел. |
б2 |
yfi |
Прогноз[2] у) |
(У, ~ Уд2 |
|
Суммы. 16 = 15. |
м. II. |
1‘? = 55. |
X </, 6=513. |
; |
Х (</,-</;)2 = 13. |
Подставляя значения сумм из табл. 8.3 в формулы (8.3) и (8.4), находим а0 = 45,2; аЛ = -3,0. Таким образом, уравнение прогноза запишется в виде.
Для оценки границ интервального прогноза необходимо по (8.5) рассчитать среднее квадратичное отклонение:
На основании полученных зависимостей yt и ст можно определить прогнозные оценки:
- • среднего времени расхода текущего запаса Т;
- • страхового запаса QcTp с заданной доверительной вероятностью Р для отдельной реализации;
- • страхового запаса с заданной доверительной вероятностью отсутствия дефицита при t = T.
Приняв yt = 0, находим прогнозную величину среднего времени расхода Т:
т.е. текущий запас закончится в среднем за 15 дн.
Рассчитываем страховой запас. В ряде работ по управлению запасами для расчета страхового запаса предлагается использовать формулу.
где — параметр нормального закона распределения, соответствующий доверительной вероятности (3.
Параметр ?р определяет для нормального закона число средних квадратических отклонений, которые нужно отложить от центра рассеивания (влево и вправо) для того, чтобы вероятность попадания в полученный участок была равна (3. В нашем случае доверительные интервалы откладывают вверх и вниз от среднего значения г/г. Значения коэффициента fp можно посмотреть в прил. 1.
Таким образом, страховой запас рассчитывается практически так же, как и границы интервального прогноза, т. е. формула для расчета страхового запаса аналогична формуле (8.7).
Для рассматриваемой ситуации для доверительной вероятности Э = = 0,9 находим tр = 1,643 и по (8.8) величину страхового запаса.
Примем Q. = 3,0 ед.
На рис. 8.3 приведены нижняя и верхняя границы, определенные по формуле (8.8), при (3 = 0,9.
Рис. 8.3. Прогноз текущего расхода деталей на складе (N = 5):
- ——прогноз; —•—фактические данные; —*—нижняя граница;
- —*—верхняя граница
Важно запомнить По одной реализации невозможно оценить вероятностный характер длительности функциональных циклов поставки.
Это означает, что по одной реализации делать оценки, лежащие в основе принятия решений по управлению запасами, не вполне корректно. Однако можно предположить, что выявленная тенденция расхода запаса сохранится. В этом случае для оценки прогнозной величины страхового запаса можно воспользоваться формулой.
где т — параметр, характеризующий количество дней задержки поставки заказа.
Рассчитаем величину страхового запаса_при условии задержки на один день по сравнению с прогнозной оценкой Т = 15 дн., т. е. на 16-й день.
По формуле (8.9) находим.
Аналогично при т = 2 (17-й день) = 9,0 ед.
2. Другой подход к оценке страхового запаса Q(.Tp(P) на основе прогнозной модели заключается в том, что величина страхового запаса выбирается с учетом вероятности отсутствия дефицита F (y). Допустим, что случайная величина расхода запаса при Т — 15 распределена по нормальному закону с параметрами yt _ 15 = 0, ат= о{/ (см. формулу (8.5)). Тогда, воспользовавшись уравнением функции нормального закона, определим вероятность отсутствия дефицита при величине страхового запаса Q{/
где yt — уравнение тренда; а — среднее квадратическое отклонение, формула (8.5).
Сделаем в интеграле замену переменной.
и приведем его к виду.
Интеграл (8.12) не выражается через элементарные функции, поэтому для расчетов можно воспользоваться численными методами и компьютером или специальными таблицами для нормальной функции распределения с параметрами: среднее значение тх = 0 и ах = 1.
(уу.
Очевидно, что F{y) = Ф :-— .
I )
В нрил. 1 приведен ряд значений функции Ф (х) и Р (х).
Между параметрами (3 и х, а также (3 и Ф (х) существует соотношение.
На рис. 8.4 приведены графики нормальной функции распределения и плотности нормального распределения.
Рис. 8.4. Нормальный закон распределения:
а — плотность распределения; 6 — функция распределения Появление дефицита означает, что текущая величина запаса на складе равна нулю, т. е. у = 0.
Следовательно, для определения вероятности отсутствия дефицита.
—Ti
необходимо по формуле (8.11) рассчитать х — —1— и по таблице прил. 1.
о с помощью х найти Р (х).
Для рассматриваемого примера рассчитаем вероятности отсутствия дефицита деталей на складе на 13-й, 14-й и 15-й дни. Так, для t= 13 получаем.
и.
По таблице прил. 1 находим Р (Т = 13) > 0,999, т. е. вероятность дефицита ничтожно мала.
Аналогично для t = 14 получим уг_ 14 = 3,2; х = 1,6, и вероятность отсутствия дефицита Рт= 14 = 0,95.
Наконец, для t = 15 вероятность отсутствия дефицита Р = 0,5.
Важно запомнить Так же, как при оценке прогнозной величины страхового запаса, определение вероятности отсутствия дефицита по одной реализации справедливо только при строгом соблюдении сроков поставки. Если они не соблюдаются, то расчет должен проводиться с учетом рассеивания длительности функциональных циклов поставки.
3. Определим ошибку прогноза среднего времени 7 при условии, ч то поставки планируются через 10 дн.:
где Гф, 7П — соответственно фактическая и прогнозная продолжительность цикла, дн.
Подставив значения в (8.15), находим.
Ошибка прогноза велика, но это закономерно, так как нарушено одно из эмпирических правил экстраполяционного прогнозирования: между предпрогнозным периодом t и периодом упреждения (прогноза) т — Т — t должно соблюдаться соотношение:
Если следовать соотношению (8.16), то при t = 5 допустимая величина времени прогноза.
Следовательно, величина надежного прогноза соответствует 7=7 дн. и период упреждения составляет т = 2 дн.
При средней длине функционального цикла расхода запасов, равной 7 = = 10 дн., находим по формуле (8.17) допустимую величину времени прогноза t = 7,5 дн.
Увеличим длину динамического ряда до N= 7 (рис. 8.5).
Рис. 8.5. Прогноз текущего расхода деталей на складе (IV = 7):
- ——прогноз; —»—фактические данные; —*—нижняя граница;
- —х— — верхняя граница
Выполнив аналогичные расчеты (табл. 8.4), получим уравнение тренда 
Соответственно, ст(у = 2,3.
Рассчитаем среднее прогнозное время расхода запаса со склада 
Таблица 8.4
Исходные данные и результаты расчета коэффициентов линейной модели при N=7
|
и |
У; |
tf |
Ук |
у’, |
(у-Vi)2 |
|
43,1. |
4,41. |
||||
|
39,2. |
0,04. |
||||
|
35,3. |
7,29. |
||||
|
31,4. |
12,96. |
||||
|
27,6. |
0,25. |
||||
|
23,6. |
0,36. |
||||
|
19,7. |
0,49. |
||||
|
М. — Г*. II ю. |
ХУ,-=223. |
Хб- =140. |
Хм = 784 |
; |
Х (1/-*/.)2 = 25,8. |
Рассчитаем величину страхового запаса для 12-го, 13-го и 14-го дн. по формуле (8.9). Примем (3 = 0,95, т. е. ?» = 1,96. Тогда.
Определим вероятность дефицита на складе на 10-й день.
гг J. /0(1Ч -(47,3−3,9 10).
По формуле (8.11) находим х =-—-1 = -3,61; по таблице прил. 1 Рт= к) * 1,0, т. е. наличие дефицита маловероятно. Аналогично для Рт-п = 0,98, для Рг_12— 0,6.
Сравнение результатов прогнозирования с разным количеством исходных данных показывает, что увеличение длины предпрогнозного периода позволяет повысить точность прогноза и вероятность отсутствия дефицита в случае увеличения длины функционального цикла.
4. Выше говорилось, что доверительные границы прогноза могут быть определенны по формуле (8.7), которая включает табличное значение-критерия Стьюдента с k степенями свободы и уровнем значимости р и учитывает расхождение границ.
Определим страховой запас по формуле.
Число степеней свободы при N = 7 и линейной зависимости расхода равно k = 7 — 2 = 5. Предыдущий расчет страхового запаса выполнялся при доверительной вероятности 0,95, поэтому мы также выберем уровень значимости 0,05. По табл. 8.5 находим для k = 5 значение критерия Стьюдента t005 = 2,571.
Таблица 8.5
Значения критерия Стыодента.
|
к |
*0,1. |
*0.05. |
*0.01. |
к |
*0,1. |
*0.05. |
*0,01. |
|
2,920. |
4,303. |
9,925. |
1,729. |
2,093. |
2,861. |
||
|
2,353. |
3,182. |
5,841. |
1,725. |
2,086. |
2,845. |
||
|
2,132. |
2,776. |
4,604. |
1,721. |
2,080. |
2,831. |
||
|
2,015. |
2,571. |
4,032. |
7,717. |
2,074. |
2,819. |
||
|
1,953. |
2,447. |
3,707. |
1,714. |
2,069. |
2,807. |
||
|
1,895. |
2,365. |
3,499. |
1,711. |
2,064. |
2,797. |
||
|
1,860. |
2,306. |
3,355. |
1,708. |
2,060. |
2,787. |
||
|
1,833. |
2,262. |
3,250. |
1,706. |
2,056. |
2,779. |
||
|
1,812. |
2,228. |
3,169. |
1,703. |
2,052. |
2,771. |
||
|
1,796. |
2,201. |
3,106. |
1,701. |
2,048. |
2,763. |
||
|
1,782. |
2,179. |
3,055. |
1,699. |
2,045. |
2,756. |
||
|
1,771. |
2,160. |
3,012. |
1,697. |
2,042. |
2,750. |
||
|
1,761. |
2,145. |
2,977. |
1,684. |
2,021. |
2,704. |
||
|
1,753. |
2,131. |
2,947. |
1,671. |
2,000. |
2,660. |
||
|
1,746. |
2,120. |
2,921. |
1,658. |
1,980. |
2,617. |
||
|
1,740. |
2,110. |
2,898. |
оо. |
1,645. |
1,960. |
2,576. |
|
|
1,734. |
2,101. |
2,878. |
—. |
—. |
—. |
—. |
Страховой запас равен
На рис. 8.6 показаны нижняя и верхняя границы, определенные, но формуле (8.7), при уровне значимости а = 0,05 и К= 1, а также границы интервального прогноза при коэффициенте К, учитывающем расхождение границ прогноза.
Рис. 8.6. Прогноз текущего расхода деталей на складе (N = 7) с учетом объема данных и расхождения границ интервального прогноза:
—Ф—фактические данные;——прогноз; —*—нижняя граница при К = 1; —х—верхняя граница при К = 1; —*—нижняя граница с учетом расхождения границ интервала прогноза; —•— — верхняя граница с учетом расхождения границ интервала прогноза Рассмотрим определение нижней границы доверительного интервала прогноза по формуле (8.7). Для t = 8 рассчитаем множитель К по формуле (8.6).
Нижняя граница прогноза для t — 8 равна.
Для ?=12
нижняя граница прогноза для t = 12 равна.
Формула (8.18) для расчета страхового запаса учитывает повышенную неопределенность оценки из-за малого объема данных. Выбор нормального распределения при малом N вместо распределения Стыодепта приводит к существенному расхождению прогнозных оценок и к неоправданному сужению доверительного интервала. Подставим в формулу (8.9) вместо параметра нормального распределения значение критерия Стыодента и рассчитаем величину страхового запаса при условии задержки на один день по сравнению с прогнозной оценкой, т.с. на 13-й день:
Аналогично, при т = 2 (14-й день) ус — 13,71 = 14 ед.
Расчеты показывают, что страховой запас должен быть увеличен примерно на две единицы в день по сравнению с расчетами по формуле (8.8).
5. Рассмотрим ансамбль из четырех реализаций расхода деталей на складе. Допустим, что информация ограничена 7 днями.
Рассчитаем средние значения и дисперсии для каждого дня прогнозного периода по формулам:
Например, для l-ro дня найдем.
Результаты расчетов приведены в табл. 8.6.
Расчет параметров для ансамбля реализаций.
Таблица 8.6
|
б. |
Уи |
Уъ |
Ум |
Ум |
Оу «- Уи)2 |
(>»» ~ ~ Уъ)2 |
~ Ум)2 |
|
^Лт, гУ»)2 п-1. |
||
|
15,33. |
3,92. |
||||||||||
|
4,67. |
2,16. |
||||||||||
|
37,5. |
0,25. |
2,25. |
2,25. |
0,25. |
1,67. |
1,29. |
|||||
|
33,75. |
1,56. |
3,06. |
0,56. |
1,56. |
2,25. |
1,50. |
|||||
|
27,75. |
0,06. |
33,06. |
1,56. |
18,06. |
17,58. |
4,19. |
|||||
|
32,67. |
5,72. |
||||||||||
|
19,5. |
0,25. |
110,25. |
42,25. |
20,25. |
57,67. |
7,59. |
|||||
|
Сумма. |
131,83. |
; |
Для аппроксимации средних значений m (t) выберем линейную зависимость.
Воспользовавшись методом наименьших квадратов, найдем коэффициенты й0 и Ьх. Спрогнозируем среднюю величину времени расхода запаса:
Зависимости D (t) и а (?) носят явно нелинейный характер, и для точных прогнозов они могут быть аппроксимированы полиномами различных порядков, например в виде параболы:
В первом приближении ограничимся средними значениями дисперсии и среднего квадратического отклонения а, которое рассчитывается по формуле.
При подстановке значений из табл. 8.5 находим.
Рассчитаем величину страхового запаса.
В первом случае расчет производится по формуле (8.8). Например, при (3 = 0,95 находим.
Во втором случае расчет QcT|) производится по формуле (8.9).
Особенность расчета для ансамбля реализаций состоит в том, что имеется возможность оценки величины т — среднего количества дней, в которые наблюдается дефицит деталей. В общем случае т можно рассчитать по формуле.
где t{ — число дней дефицита в г-й реализации; t = 0, 1,2,…; я, — количество.
i-x реализаций.
Пусть в рассматриваемом примере в первой реализации (/ = 1) не наблюдается дефицита, т. е. = 0; у второй (i = 2) — два дня дефицита, ti = 2; а у третьей (i = 3) и четвертой (i = 4) нет дефицита.
Тогда по формуле (8.24).
При подстановке в (8.9) находим.
В заключение к вопросу прогнозирования по трендовым моделям следует сделать следующие замечания.
- 1. Рассчитанные величины среднего запаса получены при условии, что наблюдающая величина дефицита и вариация ежедневного расхода — независимые величины. Несомненно, это допущение требует проверки.
- 2. При наличии большого количества реализаций расчет величины т должен быть выполнен до проведения прогнозных расчетов.
- 3. Проверка формул (8.9) и (8.24) может быть осуществлена с использованием имитационного моделирования. <
- [1] Четыркин Е. М. Статистические методы прогнозирования. М.: Статистика, 1975.
- [2] Значения округлены.
Показать весь текст
Заполнить форму текущей работой