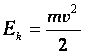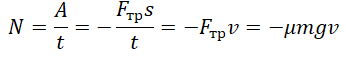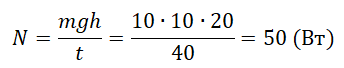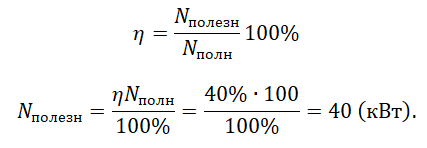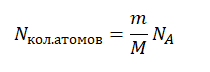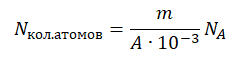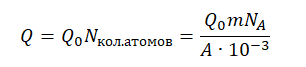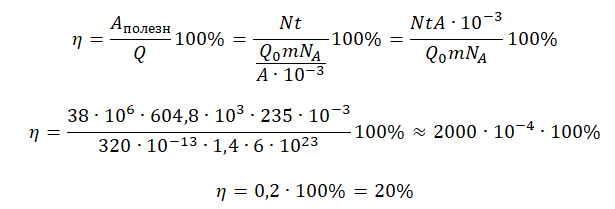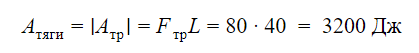Когда под действием
некоторой силы тело совершает перемещение,
то действие силы характеризуется
величиной, которая называется механической
работой.
Механическая
работа
— мера действия силы, в результате
которого тела совершают перемещение.
Р
постоянной силы.
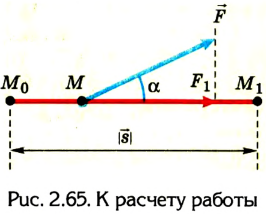
Если тело движется прямолинейно под
действием постоянной силы
,
составляющей некоторый угол
с направлением перемещения
(рис.1), работа равна произведению этой
силы на перемещение точки приложения
силы и на косинус угла
между векторами
и
;
или работа равна скалярному произведению
вектора силы на вектор перемещения:
.
1 Дж — работа,
совершаемая силой в 1Н при перемещении
на 1м в направлении действия силы.
-
если
— острый угол,
,
;
-
если
— тупой угол,
,
;
-
если
,
.
Работа
переменной силы.
Чтобы найти работу переменной силы,
пройденный путь разбивают на большое
число малых участков так, чтобы их можно
было считать прямолинейными, а действующую
в любой точке данного участка силу —
постоянной.
Элементарная
работа (т.е. работа на элементарном
участке
)
равна
,
а вся работа переменной силы на всем
пути S
находится интегрированием:
.
Для характеристики
быстроты совершения работы вводят
понятие мощности.
Мощность
постоянной силы
численно равна работе, совершаемой этой
силой за единицу времени.
.
1 Вт- это мощность
силы, которая за 1 с совершает 1 Дж работы.
В случае переменной
мощности (за малые одинаковые промежутки
времени совершается различная работа)
вводится понятие мгновенной мощности:
,
где
скорость
точки приложения силы.
Т.о.
мощность равна скалярному произведению
силы
на
скорость
точки её приложения.
-
Кинетическая и
потенциальная энергии. Законы сохранения
энергии и импульса.
Все введенные
ранее величины характеризовали только
механическое движение. Однако форм
движения материи много, постоянно
происходит переход от одной формы
движения к другой. Необходимо ввести
физическую величину, характеризующую
движение материи во всех формах её
существования, с помощью которой можно
было бы количественно сравнивать
различные формы движения материи.
Энергия численно
равна максимальной работе, которую тело
может совершить, и измеряется в тех же
единицах, что и работа. При переходе
энергии из одного вида в другой нужно
подсчитать энергию тела или системы до
и после перехода и взять их разность.
Эту разность принято называть работой:
.
Т. о., физическая
величина, характеризующая способность
тела совершать работу, называется
энергией.
Механическая
энергия тела может быть обусловлена
либо движением тела с некоторой скоростью,
либо нахождением тела в потенциальном
поле сил.
Кинетическая
энергия.
Энергия,
которой обладает тело вследствие своего
движения, называется кинетической.
Работа, совершенная
над телом, равна приращению его
кинетической энергии.
Найдем
эту работу для случая, когда равнодействующая
всех приложенных к телу сил равна
.
,
Работа, совершенная
телом за счет кинетической энергии,
равна убыли этой энергии.
Потенциальная
энергия.
Если в каждой точке
пространства на тело воздействуют
другие тела с силой, величина которой
может быть различна в разных точках,
говорят, что тело находится в поле сил
или силовом поле.
Все силы в механике
подразделяются на консервативные и
неконсервативные (или диссипативные).
Силы,
работа которых не зависит от формы
траектории, а определяется только
начальным и конечным положением тела
в пространстве, называются консервативными.
Силы,
работа которых зависит от формы пути,
называются неконсервативными
(силы трения).
Потенциальной
энергией называют часть общей механической
энергии системы, которая определяется
только взаимным расположением тел,
составляющих систему, и характером сил
взаимодействия между ними. Потенциальная
энергия
— это энергия, которой обладают тела или
части тела вследствие их взаимного
расположения.
В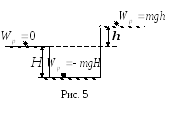
считать потенциальную энергию какого-то
определенного положения тела равной
нулю, а энергию других положений брать
по отношению к нулевому уровню. Конкретный
вид функции
зависит от характера силового поля и
выбора нулевого уровня. Поскольку
нулевой уровень выбирается произвольно,
может иметь отрицательные значения.
Например, если принять за нуль потенциальную
энергию тела, находящегося на поверхности
Земли, то в поле сил тяжести вблизи
земной поверхности потенциальная
энергия тела массой m,
поднятого на высоту h
над поверхностью, равна
(рис. 5).
Потенциальная
энергия этого же тела, лежащего на дне
ямы глубиной H,
равна
.
В рассмотренном
примере речь шла о потенциальной энергии
системы Земля-тело.
Потенциальной
энергией может обладать не только
система взаимодействующих тел, но
отдельно взятое тело. В этом случае
потенциальная энергия зависит от
взаимного расположения частей тела.
—
потенциальная энергия упругой деформации,
если принять, что потенциальная энергия
недеформированного тела равна нулю;
где
k
— коэффициент упругости, x
— деформация тела.
В общем случае
тело одновременно может обладать и
кинетической и потенциальной энергиями.
Сумма этих энергий называется полной
механической энергией тела:
Полная механическая
энергия системы равна сумме её кинетической
и потенциальной энергий. Полная энергия
системы равна сумме всех видов энергии,
которыми обладает система.
Механической
системой называется совокупность тел,
выделенная для рассмотрения. Тела,
образующие механическую систему, могут
взаимодействовать, как между собой, так
и с телами, не принадлежащими данной
системе. В соответствие с этим силы,
действующие на тела системы, подразделяют
на внутренние и внешние.
Внутренними
называются силы, с которыми тела системы
взаимодействуют между собой
Внешними называются
силы, обусловленные воздействием тел,
не принадлежащих данной системе.
Замкнутой
(или изолированной) называется система
тел, на которую не действуют внешние
силы.
Для
замкнутых систем оказываются неизменными
(сохраняются) три физических величины:
энергия, импульс и момент импульса. В
соответствии с этим имеют место три
закона сохранения: энергии, импульса,
момента импульса.
Закон сохранения
энергии — результат обобщения многих
экспериментальных данных. Идея этого
закона принадлежит Ломоносову, изложившему
закон сохранения материи и движения, а
количественная формулировка дана
немецким врачом Майером и естествоиспытателем
Гельмгольцем.
Закон
сохранения механической энергии:
в поле только консервативных сил полная
механическая энергия остается постоянной
в изолированной системе тел. Наличие
диссипативных сил (сил трения) приводит
к диссипации (рассеянию) энергии, т.е.
превращению её в другие виды энергии и
нарушению закона сохранения механической
энергии.
Закон
сохранения и превращения полной энергии:
полная энергия изолированной системы
есть величина постоянная.
Сумма
импульсов тел, составляющих механическую
систему, называется импульсом системы:
Для системы тел
внутренние силы, согласно третьему
закону Ньютона, попарно равны и
противоположно направлены, т.е. их
геометрическая сумма равна нулю.
Т.о.,
производная по времени импульса
механической системы равна геометрической
сумме внешних сил, действующих на
систему,
Для
замкнутой системы
.
Закон
сохранения импульса:
импульс замкнутой системы материальных
точек остается постоянным.
Из этого закона
следует неизбежность отдачи при стрельбе
из любого орудия. Пуля или снаряд в
момент выстрела получают импульс,
направленный в одну сторону, а винтовка
или орудие получают импульс, направленный
противоположно. Для уменьшения этого
эффекта применяют специальные
противооткатные устройства, в которых
кинетическая энергия орудия превращается
в потенциальную энергию упругой
деформации и во внутреннюю энергию
противооткатного устройства.
Закон сохранения
импульса лежит в основе движения судов
(подводных лодок) при помощи гребных
колес и винтов, и водометных судовых
двигателей (насос всасывает забортную
воду и отбрасывает ее за корму). При этом
некоторое количество воды отбрасывается
назад, унося с собой определенный
импульс, а судно приобретает такой же
импульс, направленный вперед. Этот же
закон лежит в основе реактивного
движения.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Содержание:
Мощность:
Одинаковую работу можно совершить за разные промежутки времени. Например, можно поднять груз за минуту, а можно поднимать этот же груз в течение часа.
Физическую величину, равную отношению совершенной работы
Единицей мощности в SI является джоуль в секунду (Дж/с), или ватт (Вт), названный так в честь английского изобретателя Дж. Уатта. Один ватт — это такая мощность, при которой работу в 1 Дж совершают за 1 с. Итак,
Человек может развивать мощность в сотни ватт. Чтобы оценить, насколько могущество человеческого разума, создавшего двигатели, больше «могущества» человеческих мускулов, приведем такие сравнения:
- мощность легкового автомобиля примерно в тысячу раз больше средней мощности человека;
- мощность авиалайнера примерно в тысячу раз больше мощности автомобиля;
- мощность космического корабля примерно в тысячу раз больше мощности самолета.
Мощность
Механическая работа всегда связана с движением тел. А движение происходит во времени. Поэтому и выполнение работы, как и превращение механической энергии, всегда происходит на протяжении определенного времени.
Работа выполняемая на протяжении определенного времени:
Простейшие наблюдения показывают, что время выполнения работы может быть разным. Так, школьник может подняться по лестнице на пятый этаж за 1-2 мин, а пожилой человек — не меньше чем за 5 мин. Грузовой автомобиль КрАЗ может перевезти определенный груз на расстояние 50 км за 1 ч. Но если этот груз частями начнет перевозить легковой автомобиль с прицепом, то потратит на это не меньше 12 ч.
Для описания процесса выполнения работы, учитывая его скорость, используют физическую величину, которая называется мощностью.
Что такое мощность
Мощность — это физическая величина, которая показывает скорость выполнения работы и равна отношению работы ко времени, за которое эта работа выполняется.
Так как при выполнении работы происходит превращение энергии, то можно считать, что мощность характеризует скорость превращения энергии.
Как рассчитать мощность
Для расчета мощности нужно значение работы разделить на время, за которое эта работа была выполнена:
Если мощность обозначить латинской буквой 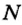
Единицы мощности
Для измерения мощности используется единица ватт (Вт). При мощности 1 Вт работа 1 Дж выполняется за 1 с:
Единица мощности названа в честь английского механика Джеймса Уатта, который внес значительный вклад в теорию и практику построения тепловых двигателей.

Главная заслуга Уатта в том, что он отделил водяной конденсатор от нагревателя и сконструировал насос для охлаждения конденсатора. Фактически он увеличил разность температур между нагревателем и конденсатором (холодильником), благодаря чему увеличил экономичность паровой машины. Позже теоретически это обоснует Сади Карно.
Он один из первых высказал предположение, что вода — это сложное вещество, состоящее из водорода и кислорода.
Как и для других физических величин, для единицы мощности существуют производные единицы:
Пример №1
Определить мощность подъемного крана, если работу 9 МДж он выполняет за 5 мин.
Дано:
Решение
По определению 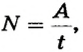
Ответ. Мощность крана 30 кВт.
Пример №2
Человек массой 60 кг поднимается на пятый этаж дома за 1 мин. Высота пяти этажей дома равна 16 м. Какую мощность развивает человек?
Дано:
Решение
По определению
Работа определяется
Тогда
Ответ. Человек развивает мощность 160 Вт.
Зная мощность и время, можно рассчитать работу:
Скорость движения зависит от мощности
Мощность связана со скоростью соотношением:
где 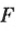
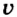
Если известны мощность двигателя и значения сил сопротивления, то можно рассчитать возможную скорость автомобиля или другой машины, которая выполняет работу:
Таким образом, из двух автомобилей при равных силах сопротивления большую скорость будет иметь тот, у которого мощность двигателя больше.
Каждый конструктор знает, что для увеличения скорости движения автомобиля, самолета или морского корабля нужно или увеличивать мощность двигателя, или уменьшать силы сопротивления. Поскольку увеличение мощности связано с увеличением потребления топлива, то средствам современного транспорта, как правило, придают специфическую обтекаемую форму, при которой сопротивление воздуха будет наименьшим, а все подвижные части изготавливают так, чтобы сила трения была минимальной.
Итоги:
- Существуют два вида механической энергии: кинетическая и потенциальная.
- Если тело перемещается или деформируется под действием силы, то выполняется механическая работа.
- Простыми механизмами являются рычаги и блоки.
- Ни один простой механизм не дает выигрыша в работе.
- Качество механизма определяется коэффициентом полезного действия, который определяет часть полезной работы в общей выполненной работе.
- Тело, при перемещении которого может быть выполнена работа, обладает энергией.
- Взаимодействующие тела обладают потенциальной энергией.
- Движущееся тело обладает кинетической энергией, которая зависит от скорости и массы тела.
- Потенциальная и кинетическая энергии могут превращаться друг в друга. Такие превращения происходят в равной мере, если отсутствуют силы трения.
- Сумму кинетической и потенциальной энергий называют полной механической энергией системы.
- В замкнутой системе при отсутствии сил трения сумма кинетической и потенциальной энергий остается постоянной.
- Закон сохранения и превращения энергии подтверждает невозможность существования вечного двигателя (perpetuum mobile).
- Мощность характеризует скорость превращения одного вида энергии в другой.
Механическая работа и мощность
С помощью импульса невозможно описать все случаи взаимодействия. Поэтому в физике применяют еще и понятие механической работы.
В механике работа зависит от значения и направления силы, а также перемещения точки ее приложения. Из курса физики 8 класса вам известно, что
A = Fs,
где F — значение силы, действующей на тело; s — модуль перемещения тела.
Если сила F постоянна, а перемещение 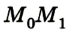
где s = 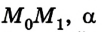
Робота является величиной скалярной. Произведение 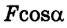
Легко заметить, что если 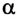
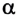
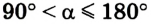
Пример №3
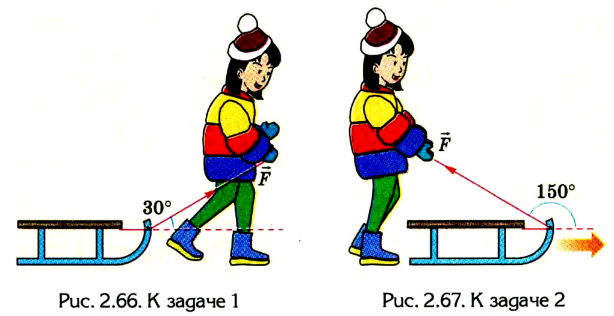
Девочка тянет санки равномерно, прикладывая к веревке силу 50 Н. Веревка натягивается под углом 30° к горизонту (рис. 2.66). Какую работу выполнит девочка, переместив санки на 20 м?
Дано:
F = 50 Н,
s = 20 м, 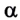
А-?
Решение
По определению
Соответственно
Ответ: А = 870 Дж (работа силы положительная, поскольку cos 30° > 0).
- Заказать решение задач по физике
Пример №4
Решим предыдущую задачу для случая, когда девочка удерживает санки, съехавшие с горки (рис. 2.67). В данном случае 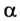
Дано:
F = 50 Н, s = 20 м,
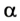
А — ?
Решение
А = Fscosa;
А = 50 Н • 20 м • (-0,87) 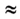
Ответ: А = -870 Дж (работа силы отрицательная, поскольку cos 150° < 0).
Таким образом, в зависимости от направления действия силы по отношению к перемещению работа может иметь положительные и отрицательные значения.
Например, работа, которую выполняет двигатель автомобиля, будет положительной, поскольку направление силы тяги автомобиля совпадает с направлением его движения. Положительной будет и работа человека, поднимающего какой-либо груз с земли на определенную высоту. Силы трения, действующие на автомобиль, выполняют отрицательную работу, поскольку направлены в противоположном направлении к перемещению.
Возможны случаи, когда работа равна нулю, хотя перемещение тела происходит. Например, если 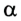
Мощность — это физическая величина, характеризующая скорость совершения работы. Поскольку во время выполнения работы происходит превращение энергии, можно сделать вывод, что мощность показывает скорость превращения одного вида энергии в другой.
В механике мощность обозначают буквой N и рассчитывают по формуле
N= — =—,
t t
где 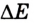
Если известны мощность и время, за которое совершена работа, то можно рассчитать и саму работу:
A = Nt.
Основная единица измерения мощности — ватт (Вт):
Всё о мощности
Одна и та же работа в разных случаях может быть выполнена за различные промежутки времени, т. е. она может совершаться неодинаково быстро. Например, при подъеме груза на определенную высоту подъемным краном (рис. 148) будет затрачено гораздо меньше времени, чем при использовании лебедки.
Для характеристики процесса выполнения работы важно знать не только ее численное значение, но и время, за которое она выполняется. Очевидно, что чем меньшее время требуется для выполнения данной работы, тем эффективнее работает машина, механизм и др.
Величина, характеризующая быстроту совершения работы, называется мощностью. Ее обычно обозначают буквой Р.
Если в течение промежутка времени Δt была совершена работа А, то средняя мощность равна отношению работы к этому промежутку времени:
Из определения видно, что мощность численно равна работе, совершаемой в единицу времени. Таким образом, единицей мощности является джоуль в секунду 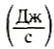
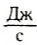
Понятно, что во времена Уатта на заре технической революции мощность построенной паровой машины было естественно сравнить с мощностью лошади — единственным в то время «двигателем».
Может ли человек развивать мощность, равную 1 л. с.? Ответ на этот вопрос положительный. Рассмотрим разбег спортсмена на короткие дистанции. Хорошие спортсмены дистанцию в 100 м пробегают за 10 с, т. е. их средняя скорость 10 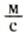
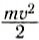
Если предположить, что масса спортсмена т = 80 кг, то
Разумеется, развивать такую мощность длительное время не сможет даже очень тренированный человек.Если известна мощность, то работа выражается равенством:
A = P∆t. (2)
Это позволяет ввести еще одну единицу работы (а значит, и энергии) следующим путем. За единицу работы можно принять работу, которая совершается некоторой силой в течение 1 с при мощности в 1 Вт. Она называется ватт-секундой. Понятно, что 1 Вт.c = 1 Дж. Часто используются более крупные внесистемные единицы работы и энергии: киловатт-час (кВт.ч) и мегаватт-час (МВт . ч):
1 кВт .ч= 1000кВт.3600 с = 3,6∙ 106 Дж;
1 МВт.ч= 1000кВт.3600 с = 3,6∙ 109 Дж.
При движении любого тела на него в общем случае действует несколько сил. Каждая сила совершает работу, и, следовательно, для каждой силы мы можем вычислить мощность.
Наиболее общее выражение для работы постоянной силы, направленной под углом 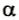
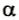
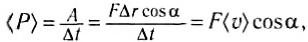
так как 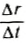
Ясно, что если модуль силы в некоторой момент времени равен F и модуль мгновенной скорости υ, а угол между ними 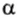
P = Fυcos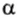
Как следует из формулы (4), при заданной мощности мотора сила тяги тем меньше, чем больше скорость движения автомобиля. Вот почему водители при подъеме в гору, когда нужна наибольшая сила тяги, переключают двигатель на пониженную передачу. Для движения по горизонтальному участку с постоянной скоростью достаточно, чтобы сила тяги преодолевала силу сопротивления движению. Формула (4) позволяет объяснить, что быстроходные поезда, автомобили, корабли, самолеты нуждаются в двигателях большой мощности и конструкции, обеспечивающей как можно меньшую силу сопротивления.
Любой двигатель или механическое устройство предназначены для выполнения определенной механической работы. Эта работа называется полезной работой. Для двигателя автомобиля — это работа по его перемещению, для токарного станка — работа по вытачиванию детали и т. п.
В любой машине, в любом двигателе полезная работа всегда меньше той энергии, которая затрачивается для приведения их в действие, потому что всегда существуют силы трения, работа которых приводит к нагреванию каких-либо частей устройства. А нагревание нельзя считать полезным результатом действия машины.
Поэтому каждое устройство характеризуется особой величиной, которая показывает, насколько эффективно используется подводимая к нему энергия. Эта величина называется коэффициентом полезного действия (КПД) и обычно обозначается греческой буквой η (эта).
Коэффициентом полезного действия называется отношение полезной )аботы, совершенной машиной за некоторый промежуток времени, ко всей утраченной работе (подведенной энергии) за тот же промежуток времени:
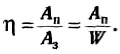
Коэффициент полезного действия обычно выражается в процентах, поскольку и полезную, и затраченную работы можно представить как произведение мощности на промежуток времени, в течение которого работала машина, то коэффициент полезного действия можно определить следующим образом:
где Pn и Р3 — полезная мощность и затраченная мощность соответственно.
Главные выводы:
- Мощность численно равна работе, которую совершает сила в единицу времени.
- Мощность силы равна произведению силы на скорость тела и косинус угла между направлением силы и скорости в данный момент времени.
- Коэффициентом полезного действия называется отношение полезной работы, совершенной машиной за некоторый промежуток времени, ко всей затраченной работе (подведенной энергии) за тот же промежуток времени.
- Взаимодействие тел
- Механическая энергия и работа
- Золотое правило механики
- Потенциальная энергия
- Криволинейное движение
- Ускорение точки при ее движении по окружности
- Инерциальные системы отсчета
- Энергия в физике

Главная
Контакты
Случайная статья
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Единицы работы.
В международной системе единиц (СИ):
[А] = Дж = Н • м
Механическая работа равна одному джоулю, если под действием силы в 1 Н оно перемещается на 1 м в направлении действия этой силы.
Мощность
Мощность — физическая величина, характеризующая скорость совершения работы и численно равная отношению работы к интервалу времени, за который эта работа совершена.
Мощность показывает, какая работа совершается за единицу времени.
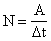
Единицы мощности
В международной системе единиц (СИ):
Мощность равна одному ватту, если за 1 с совершается работа 1 Дж.
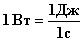
1 л.с. (лошадиная сила) ≈ 735 Вт
Энергия. Виды механической энергии. Работа и энергия.
кинетическую энергию и потенциальную энергию.
Кинетическая энергия — энергия движущегося тела.(От греческого слова kinema — движение). По определению кинетическая энергия покоящегося в данной системе отсчета тела обращается в ноль.
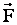 в направлении действия силы.
в направлении действия силы.Тогда:
 .
.Т.к.
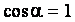 .
.Т.к. движение равноускоренное, то:
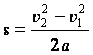 .
.
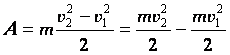 .
.
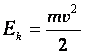 — кинетической энергией называется величина, равная половине произведения массы тела на квадрат его скорости.
— кинетической энергией называется величина, равная половине произведения массы тела на квадрат его скорости.[Ek]=Дж.
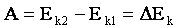 — эта формула выражает теорему о кинетической энергии: изменение кинетической энергии тела (материальной точки)за некоторый промежуток времени равно работе, совершенной силой, действующей на тело, за этот же промежуток времени
— эта формула выражает теорему о кинетической энергии: изменение кинетической энергии тела (материальной точки)за некоторый промежуток времени равно работе, совершенной силой, действующей на тело, за этот же промежуток времени
A = ΔEk
|
Энергия. Виды механической энергии. Работа и энергия. |
|
|
Энергия — физическая величина, характеризующая состояние тела или системы тел по их движению и взаимодействию. В механике энергия тела или системы тел определяется взаимным положением тел или системы тел и их скоростями. При изменении состояния тела (изменении энергии) совершается механическая работа. Т.о. изменение энергии при переходе системы из одного состояния в другое равно работе внешних сил. Механическая работа — мера изменения энергии тела. |
|
|
В механике выделяют два вида энергии: кинетическую энергию и потенциальную энергию. |
|
|
Кинетическая энергия. Кинетическая энергия — энергия движущегося тела.(От греческого слова kinema — движение). По определению кинетическая энергия покоящегося в данной системе отсчета тела обращается в ноль. |
|
|
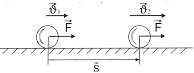
Пусть тело движется под действием постоянной силы Тогда: Т.к. Т.к. движение равноускоренное, то: |
|
|
Следовательно: |
|
|
|
[Ek]=Дж. |
|
Кинетическая энергия — величина относительная, зависящая от выбора СО, т.к. скорость тела зависит от выбора СО. |
|
|
Т.о. |
|
|
Эта теорема справедлива для любого движения и для сил любой природы. Если тело разгоняется из состояния покоя, то Ek1=0. Тогда A = Ek2. Следовательно, кинетическая энергия численно равна работе, которую необходимо совершить, чтобы разогнать тело из состояния покоя до данной скорости. |
|
|
Вывод: Работа силы равна изменению кинетической энергии тела, т.е. A = ΔEk. Причем, A>0, если Ekувеличивается, и А<0, если Ek<0. |
A = ΔEk |
Второй закон Ньютона в импульсной форме позволяет определить, как меняется скорость тела по модулю и направлению, если в течение некоторого времени на него действует определенная сила:
Работа силы
В механике также важно уметь вычислять изменение скорости по модулю, если при перемещении тела на некоторый отрезок на него действует некоторая сила. Воздействия на тела сил, приводящих к изменению модуля их скорости, характеризуется величиной, зависящей как от сил, так и от перемещений. Эту величину в механике называют работой силы.
Работа силы обозначается буквой А. Это скалярная физическая величина. Единица измерения — Джоуль (Дж).
Работа силы равна произведению модуля силы, модуля перемещения и косинусу угла между ними:
Важно!
Механическая работа совершается, если:
- На тело действует сила.
- Под действием этой силы тело перемещается.
- Угол между вектором силы и вектором перемещения не равен 90 градусам (потому что косинус прямого угла равен нулю).
Внимание! Если к телу приложена сила, но под ее действием тело не начинает движение, механическая работа равна нулю.
Пример №1. Груз массой 1 кг под действием силы 30 Н, направленной вертикально вверх, поднимается на высоту 2 м. Определить работу, совершенной этой силой.
Так как перемещение и вектор силы имеют одно направление, косинус угла между ними равен единице. Отсюда:
Работа различных сил
Любая сила, под действием которой перемещается тело, совершает работу. Рассмотрим работу основных сил в таблице.
| Работа силы тяжести |
Модуль силы тяжести: Fтяж = mg Работа силы тяжести: A = mgs cosα |
| Работа силы трения скольжения |
Модуль силы трения скольжения: Fтр = μN = μmg Работа силы трения скольжения: A = μmgs cosα |
| Работа силы упругости |
Модуль силы упругости: Fупр = kx Работа силы упругости: |
Работа силы упругости
Работа силы упругости не может быть определена стандартной формулой, так как она может применяться только для постоянной по модулю силы. Сила же упругости меняется по мере сжатия или растяжения пружины. Поэтому берется среднее значение, равное половине суммы сил упругости в начале и в конце сжатия (растяжения):
Нужно также учесть, что перемещение тела под действием силы упругости равно разности удлинения пружины в начале и конце:
s = x1 – x2
Перемещение и направление силы упругости всегда сонаправлены, поэтому угол между ними нулевой. А косинус нулевого угла равен 1. Отсюда работа силы упругости равна:
Работы силы трения покоя
Работы силы трения покоя всегда равна 0, так как под действием этой силы тело не сдвигается с места. Исключение составляет случай, когда покоящееся тело лежит на подвижном предмете, на который действует некоторая сила. Относительно системы координат, связанной с подвижным предметом, работа силы трения покоя будет нулевой. Но относительно системы отсчета, связанной с Землей, эта сила будет совершать работу, так как тело будет двигаться, оставаясь на поверхности движущегося предмета.
Пример №2. Груз массой 100 кг волоком перетащили на 10 м по плоскости, поверхность которой имеет коэффициент трения 0,4. Найти работу, совершенной силой трения скольжения.
A = μmgs cosα = 0,4∙100∙10∙10∙(–1) = –4000 (Дж) = –4 (кДж)
Знак работы силы
Знак работы силы определяется только косинусом угла между вектором силы и вектором перемещения:
- Если α = 0о, то cosα = 1.
- Если 0о < α < 90o, то cosα > 0.
- Если α = 90о, то cosα = 0.
- Если 90о < α < 180o, то cosα < 0.
- Если α = 180о, то cosα = –1.
Работа силы трения скольжения всегда отрицательна, так как сила трения скольжения направлена противоположно перемещению тела (угол равен 180о). Но в геоцентрической системе отсчета работа силы трения покоя будет отличной от нуля и выше нуля, если оно будет покоиться на движущемся предмете (см. рис. выше). В таком случае сила трения покоя будет направлена с перемещением относительно Земли в одну сторону (угол равен 0о). Это объясняется тем, что тело по инерции будет пытаться сохранить покой относительно Земли. Это значит, что направление возможного движения противоположно движению предмета, на котором лежит это тело. А сила трения покоя направлена противоположно направлению возможного движения.
Геометрический смысл работы
Графическое определение
Механическая работа численно равна площади фигуры, ограниченной графиком с осями OF и OX.
A = Sфиг
Мощность
Определение
Мощность — физическая величина, показывающая, какую работу совершает тело в единицу времени. Мощность обозначается буквой N. Единица измерения: Ватт (Вт). Численно мощность равна отношению работы A, совершенной телом за время t:
Рассмотрим частные случаи определения мощности в таблице.
Мощность при равномерном прямолинейном движении тела |
Работа при равномерном прямолинейном движении определяется формулой: A = Fтs Fт — сила тяги, s — перемещение тела под действием этой силы. Отсюда мощность равна: |
Мощность при равномерном подъеме груза |
Когда груз поднимается, совершается работа, по модулю равная работе силе тяжести. За перемещение в этом случае можно взять высоту. Поэтому: |
Мгновенная мощность при неравномерном движении |
Выше мы уже получили, что мощность при постоянной скорости равна произведению этой скорости на силу тяги. Но если скорость постоянно меняется, можно вычислить мгновенную мощность. Она равна произведению силы тяги на мгновенную скорость: |
Мощность силы трения при равномерном движении по горизонтали |
Мощность силы трения отрицательна так же, как и работа. Это связано с тем, что угол между векторами силы трения и перемещения равен 180о (косинус равен –1). Учтем, что сила трения скольжения равна произведению силы нормальной реакции опоры на коэффициент трения: |
Пример №3. Машина равномерно поднимает груз массой 10 кг на высоту 20 м за 40 с. Чему равна ее мощность?
Коэффициент полезного действия
Не вся работа, совершаемая телами, может быть полезной. В реальном мире на тела действует несколько сил, препятствующих совершению работы другой силой. К примеру, чтобы переместить груз на некоторое расстояние, нужно совершить работу гораздо большую, чем можно получить при расчете по формулам выше.
Определения:
- Работа затраченная — полная работа силы, совершенной над телом (или телом).
- Работа полезная — часть полной работы силы, которая вызывает непосредственно перемещение тела.
- Коэффициент полезного действия (КПД) — процентное отношение полезной работы к работе затраченной. КПД обозначается буквой «эта» — η. Единицы измерения эта величина не имеет. Она показывает эффективность работы механизма или другой системы, совершающей работу, в процентах.
КПД определяется формулой:
Работа может определяться как произведение мощности на время, в течение которого совершалась работа:
A = Nt
Поэтому формулу для вычисления КПД можно записать в следующем виде:
Частые случаи определения КПД рассмотрим в таблице ниже:
Устройство |
Работа полезная и полная |
КПД |
| Неподвижный блок, рычаг |
Aполезн = mgh Асоверш. |
 |
| Наклонная плоскость |
Aполезн = mgh Асоверш. = Fl l — совершенный путь (длина наклонной плоскости). |
 |
Пример №4. Определите полезную мощность двигателя, если его КПД равен 40%, а его мощность по паспорту равна 100 кВт.
В данном случае необязательно переводить единицы измерения в СИ. Но в таком случае ответ мы тоже получим в кВт. Из этой формулы выразим полезную мощность:
Задание EF17557
Какую мощность развивает сила тяги трактора, перемещая прицеп со скоростью 18 км/ч, если она составляет 16,5 кН?
Ответ:
а) 916 Вт
б) 3300 Вт
в) 82500 Вт
г) 297000 Вт
Алгоритм решения
1.Записать исходные данные и перевести единицы измерения в СИ.
2.Записать формулу для расчета мощности.
3.Выполнить общее решение задачи.
4.Подставить известные данные и выполнить вычисления.
Решение
Запишем исходные данные:
• Сила тяги, перемещающая прицеп, равна: Fт = 16,5 кН.
• Скорость перемещения прицепа под действием силы тяги: v = 18 км/ч.
Переведем единицы измерения в СИ:
16,5 кН = 16,5∙103 Н
18 км/ч = 18000/3600 м/с = 5 м/с
Мощность равна отношению работы ко времени, в течение которого эта работа совершалась:
N=At
Но работа равна произведению силы, перемещения и косинуса угла между векторами силы и перемещения. В данном случае будем считать, что угол равен нулю, следовательно косинус — единице. Тогда работа равна:
A = Fs
Тогда мощность равна:
N=Fst=Fv=16,5·103·5=82500 (Вт)
Ответ: в
pазбирался: Алиса Никитина | обсудить разбор | оценить
Задание EF17574
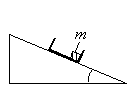
1) увеличится
2) уменьшится
3) не изменится
Запишите в таблицу выбранные цифры для каждой физической величины. Цифры в ответе могут повторяться.
|
Время движения |
Ускорение |
Модуль работы силы трения |
Алгоритм решения
1.Установить наличие и характер зависимости кинематических характеристик движения от массы тела.
2.Вывести формулу для модуля работы силы трения.
3.Установить, как изменится модуль работы силы трения при уменьшении массы тела вдвое.
Решение
При скольжении с наклонной плоскости происходит равноускоренное движение. Положение тела в любой момент времени при таком движении можно определить с помощью кинематических уравнений:
x=xo+v0xt+axt22
y=yo+v0yt+ayt22
Из этих уравнений видно, что ускорение и время никак не зависят от массы тела. Следовательно, при уменьшении массы тела в 2 раза его время движения и ускорение не изменятся.
Чтобы выразить модуль работы силы трения, выберем такую систему отсчета, чтобы вектор силы трения был расположен вдоль оси Ox.Тогда сила трения будет равна:
Fтр = μmg
Известно, что работа определяется формулой:
A = Fs cosα
Тогда работа силы трения равна:
A = μmgs cosα
Вектор силы трения всегда направлен противоположно вектору перемещения. Поэтому косинус угла между ними равен –1. Но нас интересует только модуль работы. Поэтому будем считать, что он равен:
A = μmgs
Модуль работы силы трения и масса тела зависят прямо пропорционально. Следовательно, если массу тела уменьшить вдвое, то и модуль работы силы трения уменьшится вдвое.
Поэтому правильная последовательность цифр в ответе: 332.
Ответ: 332
pазбирался: Алиса Никитина | обсудить разбор | оценить
Задание EF18646
В первой серии опытов брусок перемещают при помощи нити равномерно и прямолинейно вверх по наклонной плоскости. Во второй серии опытов на бруске закрепили груз, не меняя прочих условий.
Как изменятся при переходе от первой серии опытов ко второй сила натяжения нити и коэффициент трения между бруском и плоскостью?
Для каждой величины определите соответствующий характер её изменения:
1) увеличится
2) уменьшится
3) не изменится
Запишите в таблицу выбранные цифры для каждого ответа. Цифры в ответе могут повторяться.
| Сила натяжения нити | Коэффициент трения |
Алгоритм решения
- Определить, какая величина изменилась во второй серии опытов.
- Определить, как зависит от этой величины сила натяжения нити.
- Определить, как зависит от этой величины коэффициент трения.
Решение
Когда к бруску подвесили груз, увеличилась масса. Когда тело на нити перемещается вверх прямолинейно и равномерно, сила натяжения нити определяется модулем силы тяжести:
T = mg
Эта формула показывает, что сила натяжения нити и масса тела зависят прямо пропорционально. Если, добавив к бруску груз, масса увеличится, то сила натяжения нити тоже увеличится.
Коэффициент трения — это величина, которая зависит только от материалов и типа поверхности. Поэтому увеличение массы тела на него никак не повлияют.
Верная последовательность цифр в ответе: 13.
Ответ: 13
pазбирался: Алиса Никитина | обсудить разбор | оценить
Задание EF18271
Определите коэффициент полезного действия атомной электростанции, расходующей за неделю уран-235 23592U массой 1,4 кг, если её мощность равна 38 МВт. При делении одного ядра урана-235 выделяется энергия 200 МэВ.
Алгоритм решения
1.Записать исходные данные и перевести их в СИ.
2.Записать формулу для определения КПД атомной электростанции.
3.Решить задачу в общем виде.
4.Подставить известные данные и вычислить искомую величину.
5.Массовое число: A = 235.
6.Зарядовое число: Z = 92.
Решение
Запишем исходные данные:
• Энергия, выделяемая при делении одного ядра урана-235: Q0 = 200 МэВ.
• Масса урана-235: m = 1,4 кг.
• Время, в течение которого происходит деление: t = 1 неделя.
• Мощность атомной электростанции: N = 38 МВт.
Переведем все единицы измерения в СИ:
1 эВ = 1,6∙10–19 Дж
200 МэВ = 200∙106∙1,6∙10–19 Дж = 320∙10–13 Дж
1 неделя = 7∙24∙60∙60 с = 604,8∙103 с
38 МВт = 38∙106 Вт
КПД атомной электростанции есть отношение полезной работы к выделенной за это же время энергии:
η=AполезнQ100%
Полезную работу мы можем вычислить по формуле:
A=Nt
Выделенное количество теплоты мы можем рассчитать, вычислив количество атомов, содержащихся в 1,4 кг урана-235 и умножив их на энергию, выделяемую при делении одного такого атома.
Количество атомов равно произведению количество молей на постоянную Авогадро:
Nкол.атомов = νNA
Количество молей равно отношения массы вещества к его молярной массе, следовательно:
Молярная масса численно равна массовому числу в граммах на моль. Следовательно:
M = A (г/моль) = A∙10–3 (кг/моль)
Отсюда количество атомов равно:
Энергия, выделенная всеми атомами, равна:
Теперь можем вычислить КПД:
pазбирался: Алиса Никитина | обсудить разбор | оценить
Алиса Никитина | Просмотров: 11k
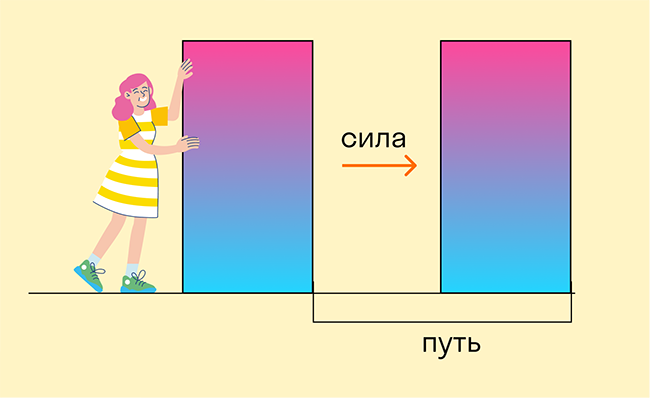
Для нас привычно понятие «работа» в бытовом смысле. Работая, мы совершаем какое-либо действие, чаще всего полезное. В физике (если точнее, то в механике) термин «работа» показывает, какую силу в результате действия приложили, и на какое расстояние тело в результате действия этой силы переместилось.
Например, нам нужно поднять велосипед по лестнице в квартиру. Тогда работа будет определяться тем, сколько весит велосипед и на каком этаже (на какой высоте) находится квартира.
Механическая работа — это физическая величина, прямо пропорциональная приложенной к телу силе и пройденному телом пути.
Чтобы рассчитать работу, нам необходимо умножить численное значение приложенной к телу силы F на путь, пройденный телом в направлении действия силы S. Работа обозначается латинской буквой А.
Механическая работа
А = FS
A — механическая работа [Дж]
F — приложенная сила [Н]
S — путь [м]
Если под действием силы в 1 ньютон тело переместилось на 1 метр, то данной силой совершена работа в 1 джоуль.
Поскольку сила и путь — векторные величины, в случае наличия между ними угла формула принимает вид.
Механическая работа
А = FScosα
A — механическая работа [Дж]
F — приложенная сила [Н]
S — путь [м]
α — угол между векторами силы и перемещения [°]
Числовое значение работы может становиться отрицательным, если вектор силы противоположен вектору скорости. Иными словами, сила может не только придавать телу скорость для совершения движения, но и препятствовать уже совершаемому перемещению. В таком случае сила называется противодействующей.
Для совершения работы необходимы два условия:
- чтобы на тело действовала сила,
- чтобы происходило перемещение тела.
Сила, действующая на тело, может и не совершать работу. Например, если кто-то безуспешно пытается сдвинуть с места тяжелый шкаф. Сила, с которой человек действует на шкаф, не совершает работу, поскольку перемещение шкафа равно нулю.
Запомнить!
Работа равна нулю, если:
- при приложенной силе перемещение отсутствует;
- сила не приложена и тело перемещается по инерции;
- угол между векторами силы и перемещения равен 90°.
Полезная и затраченная работа
Был такой мифологический персонаж у древних греков — Сизиф. За то, что он обманул богов, те приговорили его после смерти вечно таскать огромный булыжник вверх по горе, откуда этот булыжник скатывался — и так без конца. В общем, Сизиф делал совершенно бесполезное дело с нулевым КПД. Поэтому бесполезную работу и называют «сизифов труд».
Чтобы разобраться в понятиях полезной и затраченной работы, давайте пофантазируем и представим, что Сизифа помиловали и камень больше не скатывается с горы, а КПД перестал быть нулевым.
Полезная работа в этом случае равна потенциальной энергии, приобретенной булыжником. Потенциальная энергия, в свою очередь, прямо пропорциональна высоте: чем выше расположено тело, тем больше его потенциальная энергия. Выходит, чем выше Сизиф прикатил камень, тем больше полезная работа.
Потенциальная энергия
Еп = mgh
m — масса тела [кг]
g — ускорение свободного падения [м/с2]
h — высота [м]
На планете Земля g ≈ 9,8 м/с2
Затраченная работа в нашем примере — это механическая работа Сизифа. Механическая работа зависит от приложенной силы и пути, на протяжении которого эта сила была приложена.
Механическая работа
А = FS
A — механическая работа [Дж]
F — приложенная сила [Н]
S — путь [м]
И как же достоверно определить, какая работа полезная, а какая затраченная?
Все очень просто! Задаем два вопроса:
-
За счет чего происходит процесс?
-
Ради какого результата?
В примере выше процесс происходит ради того, чтобы тело поднялось на какую-то высоту, а значит — приобрело потенциальную энергию (для физики это синонимы).
Происходит процесс за счет энергии, затраченной Сизифом — вот и затраченная работа.
Мощность
На заводах по всему миру большинство задач выполняют машины. Например, если нам нужно закрыть крышечками тысячу банок колы, аппарат сделает это в считанные минуты. У человека эта задача заняла бы намного больше времени. Получается, что машина и человек выполняют одинаковую работу за разные промежутки времени. Для того, чтобы описать скорость выполнения работы, нам потребуется понятие мощности.
Мощностью называется физическая величина, равная отношению работы ко времени ее выполнения.
Мощность
N = A/t
N — мощность [Вт]
A — механическая работа [Дж]
t — время [с]
Один ватт — это мощность, при которой работа в один джоуль совершается за одну секунду.
Также для мощности справедлива другая формула:
Мощность
N = Fv
N — мощность [Вт]
F — приложенная сила [Н]
v — скорость [м/с]
Как и для работы, для мощности справедливо правило знаков: если векторы направлены противоположно, значение мощности будет отрицательным.
Поскольку сила и скорость — векторные величины, в случае наличия между ними угла формула принимает следующий вид:
Мощность
N = Fvcosα
N — мощность [Вт]
F — приложенная сила [Н]
v — скорость [м/с]
α — угол между векторами силы и скорости [°]
Получай лайфхаки, статьи, видео и чек-листы по обучению на почту
Полезные подарки для родителей
В колесе фортуны — гарантированные призы, которые помогут наладить учебный процесс и выстроить отношения с ребёнком!
Примеры решения задач
Задача 1
Ложка медленно тонет в большой банке меда. На нее действуют сила тяжести, сила вязкого трения и выталкивающая сила. Какая из этих сил при движении тела совершает положительную работу? Выберите правильный ответ:
-
Выталкивающая сила.
-
Сила вязкого трения.
-
Сила тяжести.
-
Ни одна из перечисленных сил.
Решение
Поскольку ложка падает вниз, перемещение направлено вниз. В ту же сторону, что и перемещение, направлена только сила тяжести. Это значит, что она совершает положительную работу.
Ответ: 3.
Задача 2
Ящик тянут по земле за веревку по горизонтальной окружности длиной L = 40 м с постоянной по модулю скоростью. Модуль силы трения, действующей на ящик со стороны земли, равен 80 H. Чему равна работа силы тяги за один оборот?
Решение
Поскольку ящик тянут с постоянной по модулю скоростью, его кинетическая энергия не меняется. Вся энергия, которая расходуется на работу силы трения, должна поступать в систему за счет работы силы тяги. Отсюда находим работу силы тяги за один оборот:
Ответ: 3200 Дж.
Задача 3
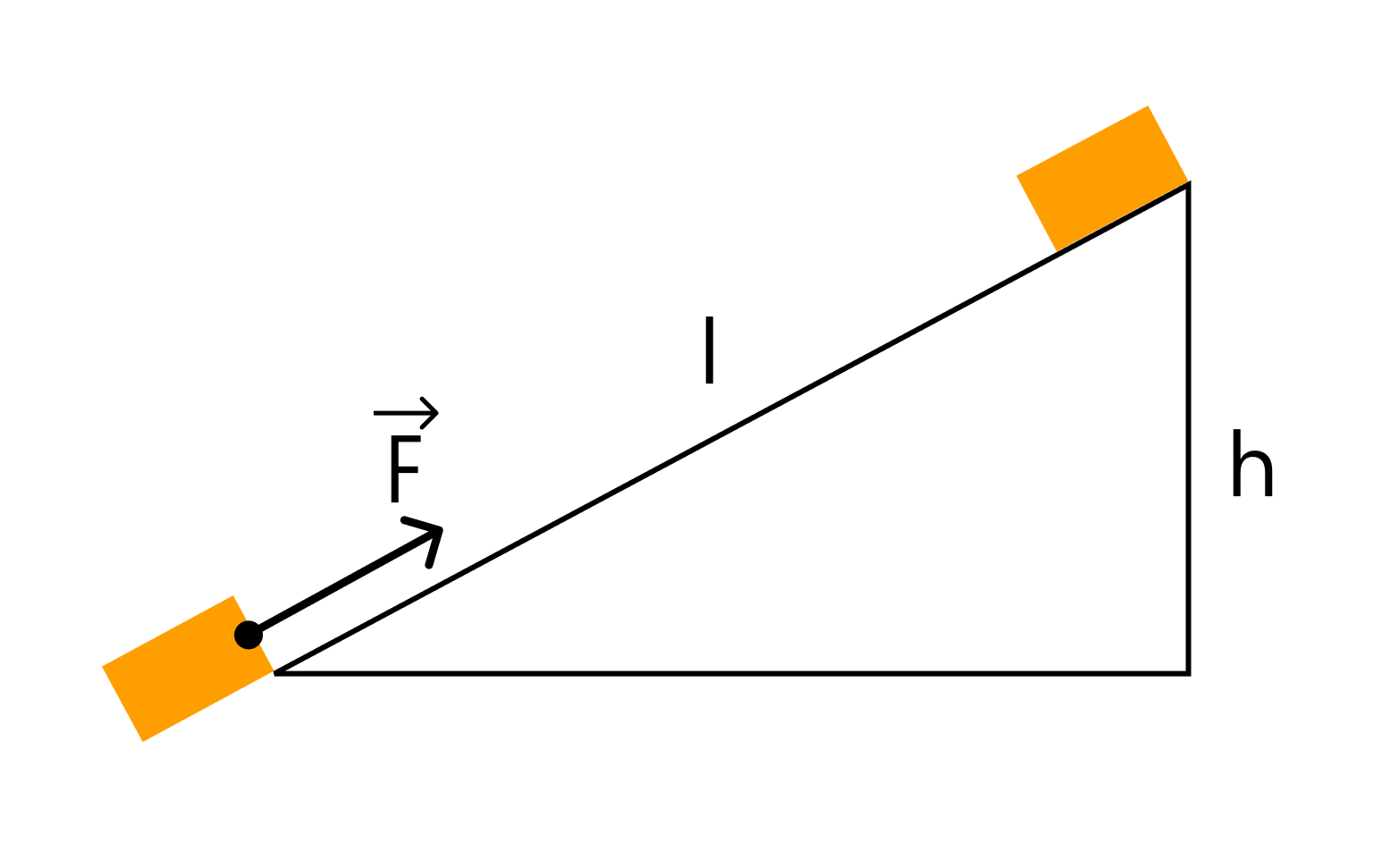
Тело массой 2 кг под действием силы F перемещается вверх по наклонной плоскости на расстояние l = 5 м. Расстояние тела от поверхности Земли при этом увеличивается на 3 метра. Вектор силы F направлен параллельно наклонной плоскости, модуль силы F равен 30 Н. Какую работу при этом перемещении в системе отсчета, связанной с наклонной плоскостью, совершила сила F?
Решение
В данном случае нас просят найти работу силы F, совершенную при перемещении тела по наклонной плоскости. Это значит, что нас интересуют сила F и пройденный путь. Если бы нас спрашивали про работу силы тяжести, мы бы считали через силу тяжести и высоту.
Работа силы определяется как скалярное произведение вектора силы и вектора перемещения тела. Следовательно:
A = Fl = 30 * 5 = 150 Дж
Ответ: 150 Дж.
Задача 4
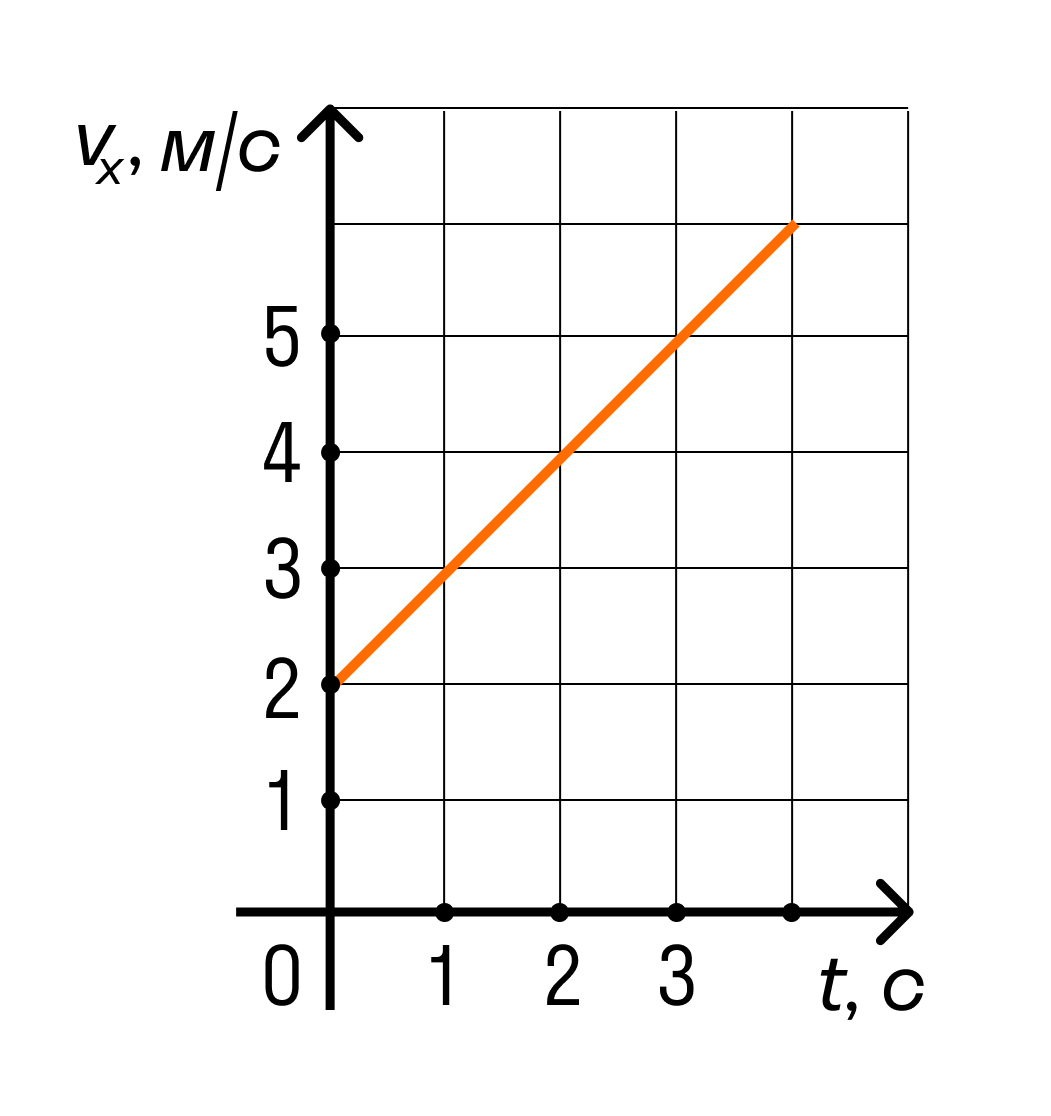
Тело движется вдоль оси ОХ под действием силы F = 2 Н, направленной вдоль этой оси. На рисунке приведен график зависимости проекции скорости vx тела на эту ось от времени t. Какую мощность развивает эта сила в момент времени t = 3 с?
Решение
На графике видно, что проекция скорости тела в момент времени 3 секунды равна 5 м/с.
Мощность можно найти по формуле N = Fv.
N = FV = 2×5 = 10 Вт
Ответ: 10 Вт.
Попробуйте онлайн-курс подготовки к ЕГЭ по физике с опытным преподавателем в Skysmart!




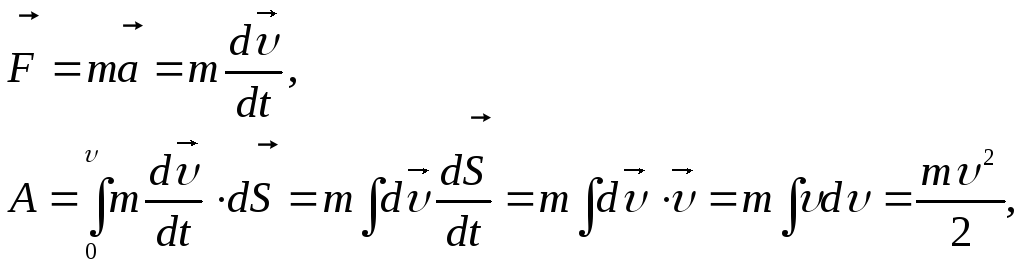
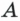
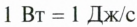



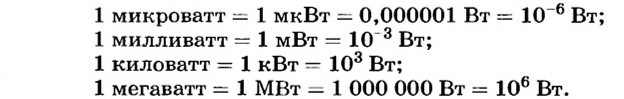
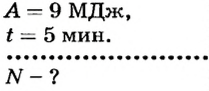
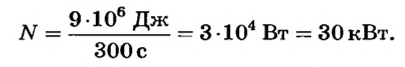
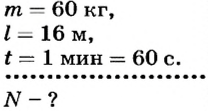
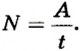
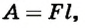
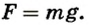
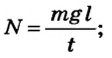
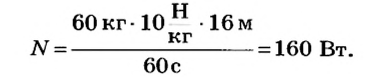

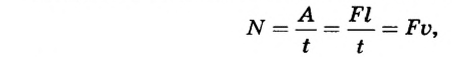

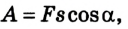
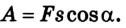
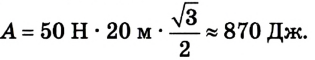
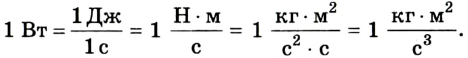
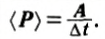
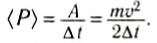
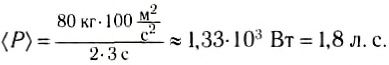
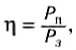
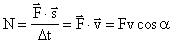
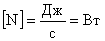
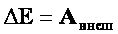

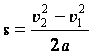 .
.
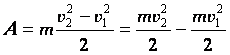 .
.