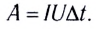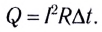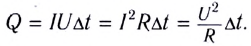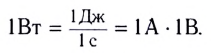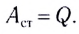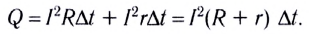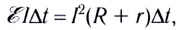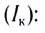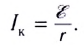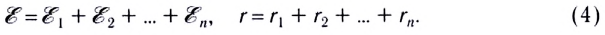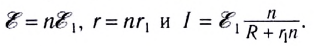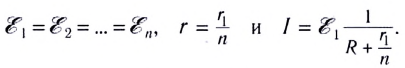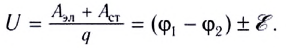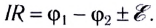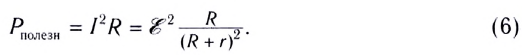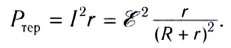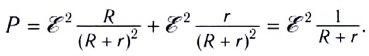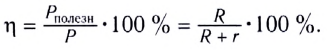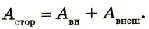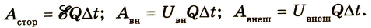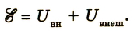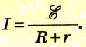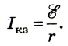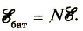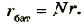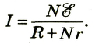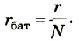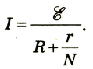Работа совершаемая эдс за любое время вычисляется по формуле

ЭДС. Закон Ома для полной цепи

Темы кодификатора ЕГЭ: электродвижущая сила, внутреннее сопротивление источника тока, закон Ома для полной электрической цепи.
Сторонняя сила
Закон Ома для полной цепи
КПД электрической цепи
Закон Ома для неоднородного участка

Автор статьи — профессиональный репетитор, автор учебных пособий для подготовки к ЕГЭ Игорь Вячеславович Яковлев

Темы кодификатора ЕГЭ: электродвижущая сила, внутреннее сопротивление источника тока, закон Ома для полной электрической цепи.

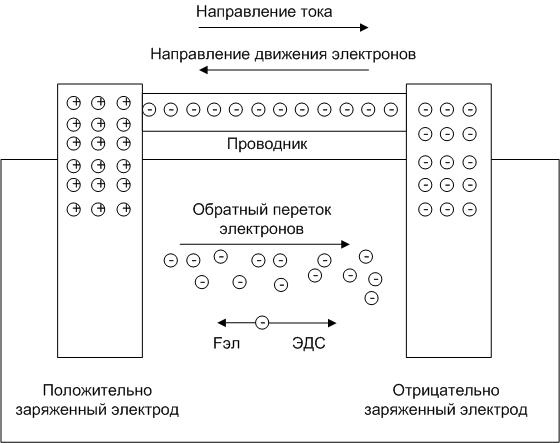
До сих пор при изучении электрического тока мы рассматривали направленное движение свободных зарядов во внешней цепи, то есть в проводниках, подсоединённых к клеммам источника тока.

Как мы знаем, положительный заряд :

• уходит во внешнюю цепь с положительной клеммы источника;

• перемещается во внешней цепи под действием стационарного электрического поля, создаваемого другими движущимися зарядами;

• приходит на отрицательную клемму источника, завершая свой путь во внешней цепи.

Теперь нашему положительному заряду нужно замкнуть свою траекторию и вернуться на положительную клемму. Для этого ему требуется преодолеть заключительный отрезок пути — внутри источника тока от отрицательной клеммы к положительной. Но вдумайтесь: идти туда ему совсем не хочется! Отрицательная клемма притягивает его к себе, положительная клемма его от себя отталкивает, и в результате на наш заряд внутри источника действует электрическая сила $vec{F_E}$ , направленная против движения заряда (т.е. против направления тока).

к оглавлению ▴

Сторонняя сила

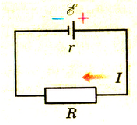
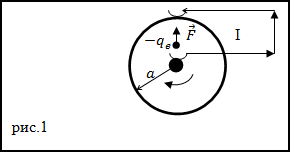
Тем не менее, ток по цепи идёт; стало быть, имеется сила, «протаскивающая» заряд сквозь источник вопреки противодействию электрического поля клемм (рис. 1).

Рис. 1. Сторонняя сила

Эта сила называется сторонней силой; именно благодаря ей и функционирует источник тока. Сторонняя сила $vec{F_{CT}}$ не имеет отношения к стационарному электрическому полю — у неё, как говорят, неэлектрическое происхождение; в батарейках, например, она возникает благодаря протеканию соответствующих химических реакций.

Обозначим через $A_{CT}$ работу сторонней силы по перемещению положительного заряда q внутри источника тока от отрицательной клеммы к положительной. Эта работа положительна, так как направление сторонней силы совпадает с направлением перемещения заряда. Работа сторонней силы $A_{CT}$ называется также работой источника тока.

Во внешней цепи сторонняя сила отсутствует, так что работа сторонней силы по перемещению заряда во внешней цепи равна нулю. Поэтому работа сторонней силы по перемещению заряда вокруг всей цепи сводится к работе по перемещению этого заряда только лишь внутри источника тока. Таким образом, $A_{CT}$ — это также работа сторонней силы по перемещению заряда по всей цепи.

Мы видим, что сторонняя сила является непотенциальной — её работа при перемещении заряда по замкнутому пути не равна нулю. Именно эта непотенциальность и обеспечивает циркулирование электрического тока; потенциальное электрическое поле, как мы уже говорили ранее, не может поддерживать постоянный ток.

Опыт показывает, что работа $A_{CT}$ прямо пропорциональна перемещаемому заряду . Поэтому отношение $A_{CT}/q$ уже не зависит от заряда и является количественной характеристикой источника тока. Это отношение обозначается :

$mathcal E = frac{displaystyle A_{CT}}{displaystyle q vphantom{1^a}}.$ (1)

Данная величина называется электродвижущей силой (ЭДС) источника тока. Как видим, ЭДС измеряется в вольтах (В), поэтому название «электродвижущая сила» является крайне неудачным. Но оно давно укоренилось, так что приходится смириться.

Когда вы видите надпись на батарейке: «1,5 В», то знайте, что это именно ЭДС. Равна ли эта величина напряжению, которое создаёт батарейка во внешней цепи? Оказывается, нет! Сейчас мы поймём, почему.

к оглавлению ▴

Закон Ома для полной цепи

Любой источник тока обладает своим сопротивлением , которое называется внутренним сопротивлением этого источника. Таким образом, источник тока имеет две важных характеристики: ЭДС и внутреннее сопротивление.

Пусть источник тока с ЭДС, равной , и внутренним сопротивлением подключён к резистору (который в данном случае называется внешним резистором, или внешней нагрузкой, или полезной нагрузкой). Всё это вместе называется полной цепью (рис. 2).

Рис. 2. Полная цепь

Наша задача — найти силу тока в цепи и напряжение на резисторе .

За время по цепи проходит заряд q = It . Согласно формуле (1) источник тока совершает при этом работу:

$A_{CT} = Eq = EIt.$ (2)

Так как сила тока постоянна, работа источника целиком превращается в теплоту, которая выделяется на сопротивлениях и . Данное количество теплоты определяется законом Джоуля–Ленца:

(3)

Итак, $A_{CT} = Q$ , и мы приравниваем правые части формул (2) и (3):

После сокращения на получаем:

Вот мы и нашли ток в цепи:

$I = frac{displaystyle mathcal E}{displaystyle R + r vphantom{1^a}}.$ (4)

Формула (4) называется законом Ома для полной цепи.

Если соединить клеммы источника проводом пренебрежимо малого сопротивления (R = 0) , то получится короткое замыкание. Через источник при этом потечёт максимальный ток — ток короткого замыкания:

$I_{K3} = frac{displaystyle mathcal E}{displaystyle r vphantom{1^a}}.$

Из-за малости внутреннего сопротивления ток короткого замыкания может быть весьма большим. Например, пальчиковая батарейка разогревается при этом так, что обжигает руки.

Зная силу тока (формула (4)), мы можем найти напряжение на резисторе с помощью закона Ома для участка цепи:

$U = IR = frac{displaystyle mathcal E R}{displaystyle R + r vphantom{1^a}}.$ (5)

Это напряжение является разностью потенциалов между точками и (рис. 2). Потенциал точки равен потенциалу положительной клеммы источника; потенциал точки равен потенциалу отрицательной клеммы. Поэтому напряжение (5) называется также напряжением на клеммах источника.

Мы видим из формулы (5), что в реальной цепи будет — ведь умножается на дробь, меньшую единицы. Но есть два случая, когда .

1. Идеальный источник тока. Так называется источник с нулевым внутренним сопротивлением. При r = 0 формула (5) даёт .

2. Разомкнутая цепь. Рассмотрим источник тока сам по себе, вне электрической цепи. В этом случае можно считать, что внешнее сопротивление бесконечно велико: . Тогда величина R + r неотличима от , и формула (5) снова даёт нам .

Смысл этого результата прост: если источник не подключён к цепи, то вольтметр, подсоединённый к полюсам источника, покажет его ЭДС.

к оглавлению ▴

КПД электрической цепи

Нетрудно понять, почему резистор называется полезной нагрузкой. Представьте себе, что это лампочка. Теплота, выделяющаяся на лампочке, является полезной, так как благодаря этой теплоте лампочка выполняет своё предназначение — даёт свет.

Количество теплоты, выделяющееся на полезной нагрузке за время , обозначим $Q_{polezn}$ .

Если сила тока в цепи равна , то

$Q_{polezn} = I^2Rt.$

Некоторое количество теплоты выделяется также на источнике тока:

$Q_{ist} = I^2rt.$

Полное количество теплоты, которое выделяется в цепи, равно:

$Q_{poln} = Q_{polezn} + Q_{ist} = I^2Rt + I^2rt = I^2(R + r)t.$

КПД электрической цепи — это отношение полезного тепла к полному:

$eta = frac{displaystyle Q_{polezn}}{displaystyle Q_{poln} vphantom{1^a}} = frac{displaystyle I^2Rt}{displaystyle I^2(R+r)t vphantom{1^a}} = frac{displaystyle R}{displaystyle R+r vphantom{1^a}}.$

КПД цепи равен единице лишь в том случае, если источник тока идеальный (r = 0) .

к оглавлению ▴

Закон Ома для неоднородного участка

Простой закон Ома U = IR справедлив для так называемого однородного участка цепи — то есть участка, на котором нет источников тока. Сейчас мы получим более общие соотношения, из которых следует как закон Ома для однородного участка, так и полученный выше закон Ома для полной цепи.

Участок цепи называется неоднородным, если на нём имеется источник тока. Иными словами, неоднородный участок — это участок с ЭДС.

На рис. 3 показан неоднородный участок, содержащий резистор и источник тока. ЭДС источника равна , его внутреннее сопротивление считаем равным нулю (если внутреннее сопротивление источника равно , можно просто заменить резистор на резистор R + r ).

Рис. 3. ЭДС «помогает» току:

Сила тока на участке равна , ток течёт от точки к точке . Этот ток не обязательно вызван одним лишь источником . Рассматриваемый участок, как правило, входит в состав некоторой цепи (не изображённой на рисунке), а в этой цепи могут присутствовать и другие источники тока. Поэтому ток является результатом совокупного действия всех источников, имеющихся в цепи.

Пусть потенциалы точек и равны соответственно и . Подчеркнём ещё раз, что речь идёт о потенциале стационарного электрического поля, порождённого действием всех источников цепи — не только источника, принадлежащего данному участку, но и, возможно, имеющихся вне этого участка.

Напряжение на нашем участке равно: . За время через участок проходит заряд q = It , при этом стационарное электрическое поле совершает работу:

$A_{POL} = Uq = UIt.$

Кроме того, положительную работу совершает источник тока (ведь заряд прошёл сквозь него!):

$A_{CT} = mathcal Eq = mathcal EIt.$

Сила тока постоянна, поэтому суммарная работа по продвижению заряда , совершаемая на участке стационарным электрическим полем и сторонними силами источника, целиком превращается в тепло: $A_{POL} + A_{CT} = Q$ .

Подставляем сюда выражения для $A_{POL}$ , $A_{CT}$ и закон Джоуля–Ленца:

Сокращая на , получаем закон Ома для неоднородного участка цепи:

(6)

или, что то же самое:

(7)

Обратите внимание: перед стоит знак «плюс». Причину этого мы уже указывали — источник тока в данном случае совершает положительную работу, «протаскивая» внутри себя заряд от отрицательной клеммы к положительной. Попросту говоря, источник «помогает» току протекать от точки к точке .

Отметим два следствия выведенных формул (6) и (7).

1. Если участок однородный, то . Тогда из формулы (6) получаем U = IR — закон Ома для однородного участка цепи.

2. Предположим, что источник тока обладает внутренним сопротивлением . Это, как мы уже упоминали, равносильно замене на R + r :

Теперь замкнём наш участок, соединив точки и . Получим рассмотренную выше полную цепь. При этом окажется, что и предыдущая формула превратится в закон Ома для полной цепи:

Таким образом, закон Ома для однородного участка и закон Ома для полной цепи оба вытекают из закона Ома для неоднородного участка.

Может быть и другой случай подключения, когда источник «мешает» току идти по участку. Такая ситуация изображена на рис. 4. Здесь ток, идущий от к , направлен против действия сторонних сил источника.

Рис. 4. ЭДС «мешает» току:

Как такое возможно? Очень просто: другие источники, имеющиеся в цепи вне рассматриваемого участка, «пересиливают» источник на участке и вынуждают ток течь против . Именно так происходит, когда вы ставите телефон на зарядку: подключённый к розетке адаптер вызывает движение зарядов против действия сторонних сил аккумулятора телефона, и аккумулятор тем самым заряжается!

Что изменится теперь в выводе наших формул? Только одно — работа сторонних сил станет отрицательной:

$A_{CT} = mathcal E q = mathcal EIt.$

Тогда закон Ома для неоднородного участка примет вид:

(8)

или:

где по-прежнему — напряжение на участке.

Давайте соберём вместе формулы (7) и (8) и запишем закон Ома для участка с ЭДС следующим образом:

Ток при этом течёт от точки к точке . Если направление тока совпадает с направлением сторонних сил, то перед ставится «плюс»; если же эти направления противоположны, то ставится «минус».

Повторим основные понятия и определения по теме «Закон Ома».

Напомним, что напряжение измеряется в вольтах.

Сила тока измеряется в амперах.

Сопротивление измеряется в омах. Эта единица измерения названа в честь Георга Симона Ома, открывшего взаимосвязь между напряжением, сопротивлением цепи и силой тока в этой цепи.

Основные определения, которые мы используем в решении задач:

Источник тока – это устройство, способное создавать необходимую для существования тока разность потенциалов.

Можно сказать, что источник тока действует, как насос. Он «качает» электроны по проводникам, как водяной насос воду по трубам. Эту аналогию можно продолжить. При этом источник тока совершает работу, за счёт химических реакций, происходящих внутри него.

Если эту работу разделить на переносимый источником заряд q (суммарный заряд всех проходящих через источник электронов), то мы получим величину, которую называют электродвижущей силой или сокращённо ЭДС.

Измеряется эта ЭДС, как и разность потенциалов, в вольтах и имеет примерно тот же смысл.

По определению, сила тока равна отношению суммарного заряда электронов, проходящих через сечение проводника, ко времени прохождения. Измеряется сила тока в амперах (А).

Свойство проводника препятствовать прохождению по нему тока характеризуется величиной, которую назвали электрическим сопротивлением – R. Проходя через проводник, электрический ток нагревает его.

Сопротивление измеряют в омах (Ом).

Сам источник тока тоже обладает сопротивлением. Такое сопротивление принято называть внутренним сопротивлением источника r (Ом).

Именно немецкому учёному Георгу Ому удалось установить, от чего может зависеть электрическое сопротивление проводника. Проведя многочисленные эксперименты, Ом сделал следующие выводы:

Сопротивление проводника тем больше, чем больше его длина.
Сопротивление проводника тем больше, чем меньше его толщина или площадь поперечного сечения.

Кроме того, Ом выяснил, что каждый материал обладает своим электрическим сопротивлением. Величина, которая показывает, каким сопротивлением будет обладать проводник единичной длины и единичной площади сечения из данного материала, называется удельным электрическим сопротивлением: (Ом*мм²/м). Эта величина справочная. Таким образом, получается, что электрическое сопротивление проводника равно:

Рассмотрим задачи ЕГЭ по теме «Закон Ома» для полной цепи.

Задача 1. На рисунке приведён график зависимости напряжения на концах железного провода площадью поперечного сечения 0,05 мм² от силы тока в нём. Чему равна длина провода? Ответ дайте в метрах. Удельное сопротивление железа 0,1 Ом*мм²/м.

Решение:

Из закона Ома для проводника или участка цепи без источника следует:

$displaystyle I=frac{U}{R};$

$displaystyle R=frac{U}{I}.$

По графику: при

Из формулы сопротивления выражаем и находим длину проводника:

Ответ: 10.

Задача 2. Через поперечное сечение проводников за 8 с прошло 10²⁰ электронов. Какова сила тока в проводнике? Ответ дайте в амперах.

Решение:

По определению силы тока:

$displaystyle I=frac{q}{t}.$

Заряд всех электронов: где е — модуль заряда электрона, $e=1,6cdot 10^{-19}$ Кл.

Тогда $displaystyle I=frac{Ncdot e}{t}=frac{10^{20}cdot 1,6cdot 10^{-19}}{8}=2 A.$

Ответ: 2.

Задача 3. Идеальный амперметр и три резистора общим сопротивлением 66 Ом включены последовательно в электрическую цепь, содержащую источник с ЭДС равной 5 В, и внутренним сопротивлением r=4 Ом. Каковы показания амперметра? (Ответ дайте в амперах, округлив до сотых.)

Решение:

По закону Ома для полной цепи:

Тогда $displaystyle I=frac{5}{66+4}=0,07 A.$

Ответ: 0,07.

Задача 4. ЭДС источника тока равна 1,5 В. Определите сопротивление внешней цепи, при котором сила тока будет равна 0,6 А, если сила тока при коротком замыкании равна 2,5 А. Ответ дайте в Ом, округлив до десятых.

Решение:

Сила тока короткого замыкания определяется следующим образом:

Отсюда выражаем и находим внутреннее сопротивление источника:

При внешнем сопротивлении, не равном нулю, сила тока в цепи определяется законом Ома для полной цепи:

Отсюда выражаем сопротивление резистора и находим его:

Ответ: 1,9.

Задача 5. На рисунке изображена схема электрической цепи, состоящей из источника постоянного напряжения с ЭДС 5 В и пренебрежимо малым внутренним сопротивлением, ключа, резистора с сопротивлением 2 Ом и соединительных проводов. Ключ замыкают. Какой заряд протечет через резистор за 10 минут? Ответ дайте в кулонах.

Решение:

Выражаем время в секундах: t = 10 минут = 600 с.

Определяем силу тока по закону Ома для полной цепи:

Внутреннее сопротивление пренебрежимо мало, поэтому r = 0.

По определению силы тока:

$displaystyle I=frac{q}{t}.$

Отсюда Кл.

Ответ: 1500.

Если вам нравятся наши материалы — записывайтесь на курсы подготовки к ЕГЭ по физике онлайн

Спасибо за то, что пользуйтесь нашими публикациями.
Информация на странице «ЭДС. Закон Ома для полной цепи» подготовлена нашими редакторами специально, чтобы помочь вам в освоении предмета и подготовке к ЕГЭ и ОГЭ.
Чтобы успешно сдать нужные и поступить в ВУЗ или техникум нужно использовать все инструменты: учеба, контрольные, олимпиады, онлайн-лекции, видеоуроки, сборники заданий.
Также вы можете воспользоваться другими статьями из разделов нашего сайта.

Публикация обновлена:
09.03.2023

Источник

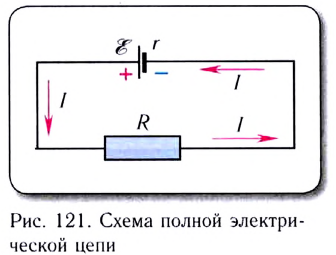
Закон Ома для полной цепи:

Работа тока на участке цепи равна произведению силы тока, напряжения па этом участке и промежутка времени, в течение которого совершалась работа:

Закон Джоуля — Ленца:

количество теплоты, выделяемое проводником с током, равно произведению квадрата силы тока, сопротивления и времени прохождения тока по проводнику:

Для однородного участка цепи количество выделившейся теплоты можно вычислить по любой из трех эквивалентных формул:

Мощность, идущая на нагревание проводника, равна работе, которая совершается током за единицу времени:

Единицей мощности электрического тока, так же как и механической мощности, является ватт (1 Вт):

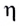
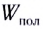
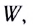
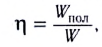
Коэффициент полезного действия (КПД) определяется отношением полезно использованной энергии к полной энергии полученной системой: и является характеристикой эффективности работы системы.

Рассмотрим полную электрическую цепь, содержащую источник ЭДС 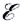с внутренним сопротивлением r и подключенный к ним резистор сопротивлением R (рис. 121).

Из определения ЭДС источника тока следует, что совершаемая источником работа

Из закона сохранения энергии следует, что в такой цепи происходит превращение энергии, запасенной источником тока, только в теплоту. При этом работа сторонних сил за промежуток времени 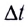равна выделившемуся в цепи количеству теплоты:

По закону Джоуля — Ленца

Таким образом,

откуда

Полученное выражение представляет собой закон Ома для полной цепи:
сила тока в полной цепи прямо пропорциональна электродвижущей силе источника тока и обратно пропорциональна полному сопротивлению цепи.
Заметим, что максимально возможный ток в цепи с данным источником тока возникает в том случае, если сопротивление внешней части цепи стремится к нулю.

Максимально возможный ток через источник называют также током короткого замыкания

Короткое замыкание представляет серьезную опасность для мощных источников тока, поскольку может вывести их из строя.

У гальванических элементов (батареек) сила тока короткого замыкания небольшая, поэтому оно для них не очень опасно.

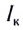
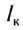
Внутреннее сопротивление свинцовых аккумуляторов имеет значение от r = 0,1 Ом до r = 0,01 Ом, и сила тока короткого замыкания в них может быть от = 20 А до = 200 А. А поскольку при этом возможно разрушение пластин аккумуляторов, то следует соблюдать меры безопасности при работе с ними.
В быту, в осветительных сетях, на распределительных станциях ЭДС имеет величины свыше 100 В, а внутреннее сопротивление цепи очень мало, и согласно закону Ома для замкнутой цепи сила тока короткого замыкания может доходить до 1000 А. Вследствие этого короткое замыкание может привести к пожару. Для зашиты от пожаров в электрические цепи включаются плавкие предохранители, которые плавятся при определенной силе тока и размыкают цепь.

Короткое замыкание может возникнуть из-за плохой изоляции, когда два токоведущих провода соединяются между собой (закорачиваются). Внешнее сопротивление цепи в этом случае стремится к нулю, и сила тока резко возрастает.

Короткое замыкание электропроводки в быту может стать причиной пожара, поэтому ни в коем случае не занимайтесь ремонтом электрических сетей самостоятельно!

Закон Ома для полной цепи можно записать в следующем виде:

Таким образом, ЭДС источника равна сумме падений напряжений на внешнем и внутреннем участках замкнутой цепи.

Закон Ома для полной цепи наглядно можно показать с помощью рисунка 122, где в качестве источника тока взят гальванический элемент Вольта (Сu—Zn).
Потенциал клеммы у цинковой пластины условно принят за нуль. Длина перпендикуляра к проводнику АВС в данной точке цепи пропорциональна ее потенциалу.

Падение напряжения на внешнем участке цепи равно IR, внутри источника — Ir.
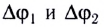
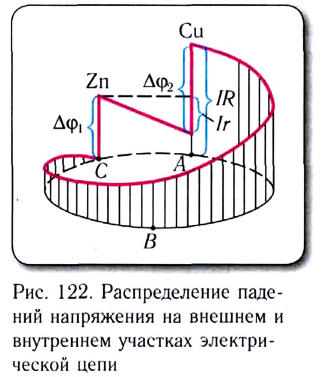
Скачки потенциалов на цинковой и медной пластинах соответственно обусловлены химическими процессами.
Для лучшего понимания процессов, происходящих в замкнутой электрической цепи рассмотрим аналогичную механическую модель (рис. 123).

Подобно тому как шарик скатывается по винтовой наклонной плоскости под действием силы тяжести из положения 2 в положение 3, так электроны движутся на внешнем участке цепи под действием сил электрического поля.
Для того чтобы поднять шарик в исходное положение 2, необходимо совершить работу против силы тяжести, которая в случае электрической цепи аналогична работе сторонних сил внутри источника тока.

В данном случае пружинное устройство 1, совершающее работу за счет энергии упругой деформации, является механическим аналогом источника ЭДС в замкнутой цепи.

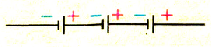
Для работы различных устройств мы используем батарейки (гальванические элементы), которые включаем последовательно с соблюдением полярности.
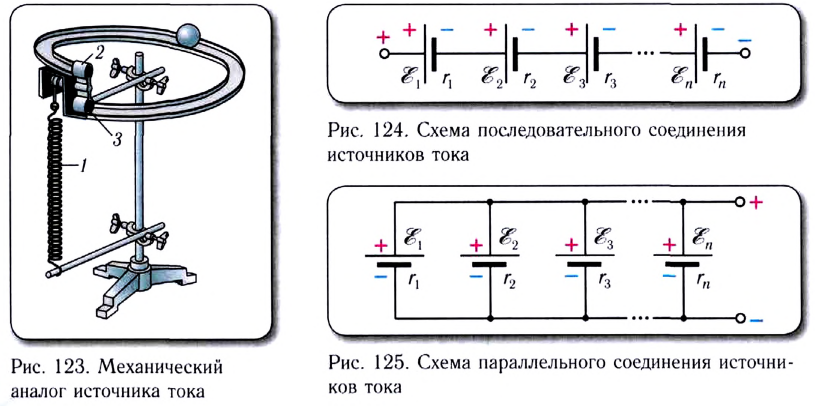
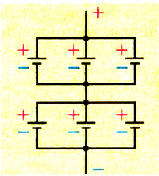
При последовательном соединении n источников тока, когда «минус» первого источника соединяется с «плюсом» второго и т. д. (рис. 124), их ЭДС и внутренние сопротивления суммируются:

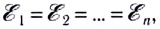
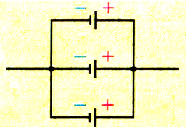
В частном случае, если то

Параллельное соединение источников тока, когда «плюсы» всех источников соединяются в один узел, а «минусы» — в другой (рис. 125), используется значительно реже для повышения надежности электропитания. Можно показать, что при параллельном соединении п одинаковых источников тока суммарная ЭДС батареи равна ЭДС одного источника, а внутреннее сопротивление рассчитывается по законам параллельного соединения:

Работа по перемещению зарядов на неоднородном участке цепи равна сумме работ, совершаемых сторонними силами источника тока и силами электрического поля.

Поскольку напряжение на участке цепи равно отношению работы к перенесенному заряду 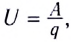то

Знак перед 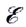берется положительный, если ЭДС увеличивает потенциал в цепи в направлении прохождения тока, и отрицательный — если уменьшает.

С учетом того, что U = IR (R — полное сопротивление резисторов и источников ЭДС на участке цепи), находим силу тока на участке цепи:

Эта формула выражает закон Ома для неоднородного участка цепи: падение напряжения на неоднородном участке цепи — произведение силы тока I и сопротивления участка цепи R:

Отметим, что падение напряжения пропорционально суммарной работе всех сил, в то время как напряжение U пропорционально работе только электростатических сил.

Мощность, выделяемая на внешнем участке цепи, в которую включены тепловые потребители энергии, называется полезной мощностью. Для ее вычисления используются формулы:

Мощность, выделяемая на внутреннем сопротивлении источника тока, называется теряемой мощностью и вычисляется по формулам:

Сумма полезной и теряемой мощностей равна полной мощности источника тока, которая учитывает выделение энергии как на внешнем, так и на внутреннем участках цепи:

Коэффициент полезного действия источника тока, определяемый как отношение полезной мощности к полной, зависит от сопротивления нагрузки и внутреннего сопротивления источника тока:

Наибольшую полезную мощность от данного источника можно получить тогда, когда внешнее сопротивление равно внутреннему (R = r), и в этом случае максимальный КПД 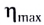= 50 % (докажите это).

Заказать решение задач по физике

Закон Ома для полной цепи

Открытый Г. Омом закон для участка цени в общем случае справедлив и для полной цепи, если принимать во внимание как внешнюю, так и внутреннюю части цепи. Математическую запись закона Ома для этого случая можно получить на основании закона сохранения энергии, универсального для всех процессов в природе.

Пусть электрическая цепь состоит из источника тока, имеющего ЭДС и внутреннее сопротивление г, и проводника сопротивлением R (рис. 1.51).

Pиc. 151. Замкнутая электрическая цепь

Согласно закону сохранения энергии работа сторонних сил равна сумме работ электрического тока во внешней и внутренней частях цепи:

По определению

Отсюда

Если учесть, что по закону Ома для участка цепи U =IR, то получим формулу этого закона для полной цепи:

Таким образом, сила тока в полной цепи пропорциональна электроднижущей силе источника и обратно пропорциональна полному сопротивлению цепи.

Сила тока в полной цепи пропорциональна электродвижущей силе источника и обратно пропорциональна полному сопротивлению цепи:

Пользуясь законом Ома для полной цепи, можно рассчитать два экстремальных случая н электрической цепи — короткое замыкание и разомкнутую цепь. Если сопротивление внешней цепи стремится к нулю (короткое замыкание), то сила тока в цепи

Это будет максимальное значение силы тока для данной цепи.
Если цепь разорвана (R→∞ ), то ток в цени прекращается при любых значениях ЭДС и внутреннего сопротивления. В последнем случае напряжение нм полюсах источника тока будет равно электродвижущей силе. Поэтому иногда дают упрощенное определение ЭДС: это величина, равная напряжению на клеммах источника при разомкнутой цепи.

Источники тока могут соединяться в батареи. Существуют несколько способов соединения источников тока.

Последовательным называют соединение, при котором соединяются друг с другом разноименные полюса источников: положительный предыдущего с отрицательным следующего и т. д. (рис. 1.52). Чаще всего соединяют источники с одинаковыми характеристиками, поэтому при последовательном соединении N источников ЭДС батареи будет в N раз больше, чем ЭДС одного источника:

Внутреннее сопротивление такой батареи будет также в N раз больше:

Рис. 152. Схема последовательного соединения источников тока

Для последовательного соединения источников тока закон Ома для полной цепи будет записываться:

Последовательное соединение источников τoιca удобно в том случае, когда сопротивление потребителя значительно больше внутреннего сопротивления одного источника тока.
Параллельным является соединение, при котором все одноименные полюса соединяется в один узел (рис. 1.53).

Pиc. 153. Схема параллельного соединения источников тока

Параллельное соединение применяют тогда, когда в цепи необходимо получить большое значение силы тока при небольшом напряжении.

Электродвижущая сила батареи параллельно соединенных одинаковых источников равна ЭДС одного источника:

Формула закона Ома для параллельного соединения источников имеет вид:

Параллельное соединения удобно тогда» когда сопротивление внешней части цепи значительно меньше внутреннего сопротивления одного источника.

При смешанном соединении батареи источников тока (параллельно или последовательно) в свою очередь соединяют последовательно или параллельно (рис. 1.54).

Pиc. 1.54. Смешанное соединение источников тoκa

Закон Ома для цепи переменного тока с последовательным соединением сопротивлений
Сила и закон Ампера
Закон взаимодействия прямолинейных параллельных проводников с током
Сила Лоренца
Звуковые волны в физике
Электрическое поле в физике
Работа по перемещению заряда в электростатическом поле
Закон Ома для однородного участка электрической цепи

Источник

Определение 1

Во время протекания тока по однородному участку цепи электрическое поле совершает работу. За пройденное время Δt по цепи имеется заряд Δq=IΔt.

Электрическое поле выделенного участка выполняет работу, формулу которой мы запишем так: ΔA=(φ1–φ2) Δq=Δφ12IΔt=UIΔt, где U=Δφ12 – напряжение. Такая величина называется работой электрического тока.

Обе части формулы RI=U выражают закон Ома для однородного участка цепи с сопротивлением R, умноженным на IΔt. В итоге получим соотношение RI2Δt=UIΔt=ΔA, выражающее закон сохранения энергии для однородного участка цепи. Работа ΔA электрического тока I, протекающего по неподвижному проводнику с сопротивлением R, преобразуется в тепло ΔQ, выделяющееся на проводнике. ΔQ=ΔA=RI2Δt.

Закон Джоуля-Ленца

Дж. Джоуль и Э. Ленц установили закон преобразования работы тока в тепло.

Определение 2

Формула мощности электрического тока (измеряется в амперах) записывается в виде отношения изменения работы тока ΔA за определенный промежуток времени Δt:

P=∆A∆t=UI=I2R=U2R.

Работа и мощность электрического тока обратно пропорциональны.

По таблице СИ понятно, в чем измеряется мощность: в ваттах (ВТ), а работа в Джоулях (Дж).

Перейдем к рассмотрению полной цепи постоянного тока, которая состоит из источника с электродвижущей силой ε и внутренним сопротивлением r на участке R. Запись основного закона Ома для полной цепи имеет вид (R + r)I=ε. При умножении обеих частей на Δq=IΔt получаем, что соотношение для выражения сохранения энергии полной цепи постоянного тока запишется: R I2Δt+r I2Δt=ε IΔt=ΔAст. Из левой части видно, что ΔQ=R I2Δt обозначает выделяющееся тепло на внешнем участке за промежуток времени Δt, а ΔQист=rI2Δt – внутри источника за тот же время.

εIΔt – это обозначение работы сторонних сил ΔAст,действующих внутри. Если имеется замкнутая цепь, тогда ΔAстпереходит в тепло, которое выделяется во внешней цепи (ΔQ) и внутри источника (ΔQист).

ΔQ+ΔQист=ΔAст=εIΔt.

Работа сторонних сил

Работа электрического поля не входит в данное соотношение, так как в замкнутой цепи работа не совершается, следовательно, тепло идет только от внутренних сторонних сил. В данном случае электрическое поле перераспределяет тепло по всем участкам цепи.

Внешняя цепь может иметь не только проводник с R сопротивлением, но и механизм, потребляющий мощность. Такой случай говорит о том, что R эквивалентно сопротивлению нагрузки. Энергия, которая выделяется по внешней цепи, преобразуется в тепло и другие виды энергии.

Определение 3

Работа, совершаемая сторонними силами за единицу времени, равняется Pист=εI=ε2R+r. Внешняя цепь характеризуется мощностью P=RI2=εI-rI2=ε2R(R+r)2.

Коэффициентом полезного источника называют отношение η=PPист, записываемое как η=PPист=1-rεI=RR+r.

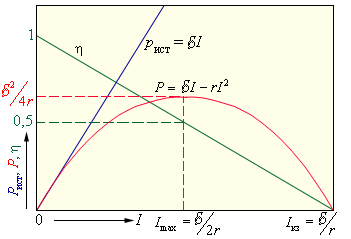
Рисунок 1.11.1 показывает зависимость Pист, полезной Р, выделяемой во внешней цепи, кпд η от тока I для источника с ЭДС, равной ε, и внутренним сопротивлением r. Изменение тока в цепи происходит в пределах от I=0( при R=∞) до I=Iкз=εr( при R=0).

Рисунок 1.11.1. Зависимость мощности источника Pист, мощности во внешней цепи Р и КПД источника η от силы тока.

Приведенные графики показывают, что максимальная мощность во внешней цепи может быть достигнута при R=r и запишется Pmax=ε24r. Формула тока в цепи будет иметь вид Imax=12Iкз=ε2r, где КПД источника не превышает 50%. При I→0 может достигаться максимальное значение КПД, тогда сопротивление R→∞. При коротком замыкании значение мощности Р=0. Тогда она только выделяется внутри источника, что грозит перегревом, причем КПД обращается в ноль.

Источник

§ 09-г. Работа электрического тока

Изучая применение электрического тока, нужно уметь вычислять количество электроэнергии, которое расходуется на то или иное действие тока. Например, подъём лифта, нагревание чайника и тому подобное. Поэтому выведем формулу для подсчёта работы тока.

В предыдущем параграфе
мы узнали формулу:

P = I · U

Однако из 7-го класса мы знаем
другую формулу для мощности:

N = A / t

В левых частях этих равенств стоят разные символы, но они обозначают одну и ту же физическую величину – мощность. Следовательно, правые части формул можно приравнять: I · U = A / t . Выразим работу:

Формула для вычисления работы электрического тока или, что то же самое, для расчета потреблённой электроэнергии.

A = I · U · t

A – работа электрического тока, Дж
I – сила электрического тока, А
U – электрическое напряжение, В
t – время наблюдения, с

По этой формуле вычисляется работа тока или, что то же самое, израсходованная электроэнергия. Поясним, что выделенные нами термины – синонимы.

В момент замыкания цепи электрическое поле источника энергии приводит в движение заряженные частицы в проводнике (электроны и/или ионы), и их энергия возрастает. Сумма энергий всех частиц тела является внутренней энергией тела (см. § 7-д), значит, внутренняя энергия проводника в момент возникновения в нём тока возрастает. Согласно первому закону термодинамики, внутренняя энергия может расходоваться на теплопередачу или совершение работы (см. § 6-з). Но, расходуясь, она постоянно пополняется от источника энергии.

Вспомним, что прохождение тока по проводнику всегда сопровождается действиями тока (см. § 8-з). При этом обязательно происходит превращение электроэнергии в другие виды энергии. Например, внутреннюю (утюг или чайник), механическую (пылесос или вентилятор) и так далее. Поэтому под выражением «ток совершает работу» мы будем понимать превращение электроэнергии в другие виды энергии. В таком смысле работа тока и израсходованная электроэнергия – выражения-синонимы.

Для измерения потреблённой электроэнергии служат специальные измерительные приборы – счётчики электроэнергии.

Для учёта электроэнергии вместо джоуля используется более крупная единица – киловатт-час (обозначение: 1 кВт·ч). Например, счётчик на рисунке показывает значение 254,7 кВт·ч. Это может означать, что за всё время учёта потребитель мощностью 254,7 кВт работал 1 час или что потребитель мощностью 2547 Вт работал 100 часов (и так далее, соблюдая пропорцию).

Найдём связь киловатт-часа с более привычной нам единицей для измерения работы – джоулем.

1 кВт · ч = 1000 Вт · 60 мин =
= 1000 Дж/с · 3600 с = 3 600 000 (Дж/с)·с =
= 3 600 000 Дж = 3,6 МДж

Итак, 1 кВт·ч = 3,6 МДж.

Примечание. Формула для работы тока A = I·U·t поможет выяснить физический смысл электрического напряжения. Выразим его:

	U =	A		Следовательно,	1 В = 1	Дж
I·t	А·с

Отсюда видно, что 1 вольт – это такое напряжение, при котором ток силой 1 ампер способен за 1 секунду производить 1 джоуль работы. Другими словами, электрическое напряжение показывает работу, которую ежесекундно совершают силы электрического поля для поддержания в цепи тока силой 1 ампер.

Кроме того, из формулы I = q / t (см. § 9-б) следует: q = I · t. Тогда:

	U =	A		Следовательно,	1 В = 1	Дж
q	Кл

Исходя из этой формулы, 1 вольт может рассматриваться и как такое напряжение, при котором работа сил электрического поля при перемещении заряда в 1 Кл будет равна 1 Дж. Обобщённо мы скажем: электрическое напряжение является одной из характеристик электрического поля, перемещающего заряды по проводнику.

Источник

Если материал понравился Вам и оказался для Вас полезным, поделитесь им со своими друзьями!

Источник

Содержание:

Определение и формула ЭДС
Закон Ома для произвольного участка цепи
Единицы измерения
Примеры решения задач

Для поддержания электрического тока в проводнике длительное время, необходимо чтобы от конца проводника, имеющего меньший потенциал
(учтем, что носители тока предполагаются положительными зарядами) постоянно убирались доставляемые током заряды, при этом к концу с
большим потенциалом заряды постоянно подводились. То есть следует обеспечить круговорот зарядов. В этом круговороте заряды должны
перемещаться по замкнутому пути. Движение носителей тока при этом реализуется при помощи сил неэлектростатического происхождения.
Такие силы именуются сторонними. Получается, что для поддержания тока нужны сторонние силы, которые действуют на всем протяжении цепи
или на отдельных участках цепи.

Определение и формула ЭДС

Определение

Скалярная физическая величина, которая равна работе сторонних сил по перемещению единичного положительного заряда, называется
электродвижущей силой (ЭДС), действующей в цепи или на участке цепи. ЭДС обозначается
$varepsilon$ . Математически определение ЭДС запишем как:

$$varepsilon=frac{A}{q}(1)$$

где A – работа сторонних сил, q – заряд, над которым производится работа.

Электродвижущая сила источника численно равна разности потенциалов на концах элемента, если он разомкнут, что дает возможность измерить ЭДС по напряжению.

ЭДС, которая действует в замкнутой цепи, может бытьопределена как циркуляция вектора напряжённости сторонних сил:

$$varepsilon=oint_{L} bar{E}^{*} d bar{l}(2)$$

где $bar{E}^{*}$ — напряженность поля сторонних сил. Если напряженность поля сторонних
сил не равна нулю только в части цепи, например, на отрезке 1-2, тогда интегрирование в выражении (2) можно вести только по
данному участку. Соответственно, ЭДС, действующая на участке цепи 1-2 определяется как:

$$varepsilon=int_{1}^{2} bar{E}^{*} d bar{l}(3)$$

Формула (2) дает самое общее определение ЭДС, которое можно использовать для любых случаев.

Закон Ома для произвольного участка цепи

Участок цепи, на котором действуют сторонние силы, называют неоднородным. Для него выполняется равенство:

$$U_{12}=varphi_{1}-varphi_{2}+varepsilon_{12}(4)$$

где U₁₂=IR₂₁ – падение напряжения (или напряжение) на участке цепи 1-2 (I-сила тока);
$varphi_{1}-varphi_{2}$ – разность потенциалов концов участка;
$varepsilon_12$ – электродвижущая сила, которую содержит участок цепи.
$varepsilon_12$ равна алгебраической сумме ЭДС всех источников, которые находятся на данном участке.

Следует учитывать, что ЭДС может быть положительной и отрицательной. ЭДС называют положительной, если она увеличивает потенциал в
направлении тока (ток течет от минуса к плюсу источника).

Единицы измерения

Размерность ЭДС совпадает с размерностью потенциала. Основной единицей измерения ЭДС в системе СИ является: [$varepsilon$]=В

1В=1Дж/1Кл

Примеры решения задач

Пример

Задание. Электродвижущая сила элемента равна 10 В. Он создает в цепи силу тока равную 0,4 А.
Какова работа, которую совершают сторонние силы за 1 мин?

Решение. В качество основы для решения задачи используем формулу для вычисления ЭДС:

$$varepsilon=frac{A}{q}(1.1)$$

Заряд, который проходит в рассматриваемой цепи за 1 мин. можно найти как:

$$q=I Delta t(1.2)$$

Выразим из (1.1) работу, используем (1.2) для вычисления заряда, получим:

$$A=varepsilon I Delta t$$

Переведем время, данной в условиях задачи в секунды ($Delta t$ мин=60 с), проведем вычисления:

$A=10 cdot 0,4 cdot 60=240$ (Дж)

Ответ. A=240 Дж

236

проверенных автора готовы помочь в написании работы любой сложности

Мы помогли уже 4 396 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!

Пример

Задание. Металлический диск, имеющий радиус a, вращается с угловой скоростью
$omega$, включен в электрическую цепь при
помощи скользящих контактов, которые касаются оси диска и его окружности (рис.1). Какой будет ЭДС, которая появится между осью
диска и его наружным краем?

Решение. В условиях, которые описаны в задаче, на каждый электрон проводника действует центробежная сила (F)
которая является сторонней. Вследствие ее действия, в диске возникает ЭДС и между осью диска и его наружным краем появляется напряжение.
Формулу для вычисления центробежной силы запишем как:

$$F=m r omega^{2}(2.1)$$

где m – масса электрона, r – расстояние от оси диска.Fдействует на заряженную частицу (электрон), следовательноучитывая (2.1), имеем:

$$E^{*}=frac{F}{q}=frac{m r omega^{2}}{q}$$

где q – заряд электрона.

В соответствии с формулой, определяющей ЭДС участка цепи, получаем:

$$varepsilon=int_{1}^{2} bar{E} d bar{l}=int_{0}^{a} E^{*} d r=int_{0}^{a} frac{m r omega^{2}}{q} d r=frac{m r omega^{2} a^{2}}{2 q}$$

Ответ. $varepsilon=frac{m r omega^{2} a^{2}}{2 q}$

Читать дальше: Формулы по физике.

Источник

При прохождении тока в цепи электрическое поле совершает работу по перемещению заряда. В этом случае работу электрического поля называют работой электрического тока.

При прохождении заряда (q) по участку цепи электрическое поле будет совершать работу: (A=qcdot U), где (U) — напряжение электрического поля, (A) — работа, совершаемая силами электрического поля по перемещению заряда (q) из одной точки в другую.

Для выражения любой из этих величин можно использовать приведённый ниже рисунок.

Рис. (1). Зависимость между работой, напряжением и зарядом

Количество заряда, прошедшее по участку цепи, пропорционально силе тока и времени прохождения заряда:

q=I⋅t

Работа электрического тока на участке цепи пропорциональна напряжению на её концах и количеству заряда, проходящего по этому участку:

A=U⋅q

Работа электрического тока на участке цепи пропорциональна силе тока, времени прохождения заряда и напряжению на концах участка цепи:

A=U⋅I⋅t

Чтобы выразить любую из величин из данной формулы, можно воспользоваться рисунком.

Рис. (2). Зависимость между работой, силой тока и временем прохождения заряда

Единицы измерения величин:

работа электрического тока ([A]=1) Дж;

напряжение на участке цепи ([U]=1) В;

сила тока, проходящего по участку ([I]=1) А;

время прохождения заряда (тока) ([t]=1) с.

Для измерения работы электрического тока нужны вольтметр, амперметр и часы. Например, для определения работы, которую совершает электрический ток, проходя по спирали лампы накаливания, необходимо собрать цепь, изображённую на рисунке. Вольтметром измеряется напряжение на лампе, амперметром — сила тока в ней. А при помощи часов (секундомера) засекается время горения лампы.

Рис. (3). Схема и часы для измерения

Например:

I = 1,2 АU = 5 Вt = 1,5 мин = 90 сА = U⋅I⋅t = 5⋅1,2⋅90 = 540 Дж

Обрати внимание!

Работа чаще всего выражается в килоджоулях или мегаджоулях.

(1) кДж = 1000 Дж или (1) Дж = (0,001) кДж;
(1) МДж = 1000000 Дж или (1) Дж = (0,000001) МДж.

Для потребителей электрической энергии существуют приборы, позволяющие в пределах ошибки измерения получать числовые данные о ее расходе в единицу времени.

Рис. (4). Электросчетчик

Механическая мощность численно равна работе, совершённой телом в единицу времени:

N = Аt

. Чтобы найти мощность электрического тока, надо поступить точно также, т.е. работу тока,

A=U⋅I⋅t

, разделить на время.

Мощность электрического тока обозначают буквой (Р):

P=At=U⋅I⋅tt=U⋅I

. Таким образом:

Мощность электрического тока равна произведению напряжения на силу тока:

P=U⋅I

Из этой формулы можно определить и другие физические величины.
Для удобства можно использовать приведённый ниже рисунок.

Рис. (5). Зависимость между мощностью, напряжением и силой тока

За единицу мощности принят ватт: (1) Вт = (1) Дж/с.

Из формулы

P=U⋅I

следует, что

(1) ватт = (1) вольт ∙ (1) ампер, или (1) Вт = (1) В ∙ А.

Обрати внимание!

Используют также единицы мощности, кратные ватту: гектоватт (гВт), киловатт (кВт), мегаватт (МВт).
(1) гВт = (100) Вт или (1) Вт = (0,01) гВт;
(1) кВт = (1000) Вт или (1) Вт = (0,001) кВт;
(1) МВт = (1 000 000) Вт или (1) Вт = (0,000001) МВт.

Пример:

Измерим силу тока в цепи с помощью амперметра, а напряжение на участке — с помощью вольтметра.

Рис. (6). Схема

Так как мощность тока прямо пропорциональна напряжению и силе тока, протекающего через лампочку, то перемножим их значения:

I=1,2АU=5ВP =U⋅I=5⋅1,2=6Вт

Ваттметры измеряют мощность электрического тока, протекающего через прибор. По своему назначению и техническим характеристикам ваттметры разнообразны.

В зависимости от сферы применения у них различаются пределы измерения.

Аналоговый ваттметр	Аналоговый ваттметр	Аналоговый ваттметр	Цифровой ваттметр

Рис. (7). Приборы для измерения

Подключим к цепи по очереди две лампочки накаливания, сначала одну, затем другую и измерим силу тока в каждой из них. Она будет разной.

Рис. (8). Лампы различной мощности в цепи

Сила тока в лампочке мощностью (25) ватт будет составлять (0,1) А. Лампочка мощностью (100) ватт потребляет ток в четыре раза больше — (0,4) А. Напряжение в этом эксперименте неизменно и равно (220) В. Легко можно заметить, что лампочка в (100) ватт светится гораздо ярче, чем (25)-ваттовая лампочка. Это происходит оттого, что её мощность больше. Лампочка, мощность которой в (4) раза больше, потребляет в (4) раза больше тока. Значит:

Обрати внимание!

Мощность прямо пропорциональна силе тока.

Что произойдёт, если одну и ту же лампочку подсоединить к источникам различного напряжения? В данном случае используется напряжение (110) В и (220) В.

Рис. (8). Лампа, подключенная к источнику тока с различным напряжением

Можно заметить, что при большем напряжении лампочка светится ярче, значит, в этом случае её мощность будет больше. Следовательно:

Обрати внимание!

Мощность зависит от напряжения.

Рассчитаем мощность лампочки в каждом случае:

I=0,2АU=110ВP=U⋅I=110⋅0,2=22Вт

I=0,4АU=220ВP=U⋅I=220⋅0,4=88Вт.

Можно сделать вывод о том, что при увеличении напряжения в (2) раза мощность увеличивается в (4) раза.
Не следует путать эту мощность с номинальной мощностью лампы (мощность, на которую рассчитана лампа). Номинальная мощность лампы (а соответственно, ток через нить накала и её расчётное сопротивление) указывается только для номинального напряжения лампы (указано на баллоне, цоколе или упаковке).

Рис. (9). Маркировка

В таблице дана мощность, потребляемая различными приборами и устройствами:

Таблица (1). Мощность различных приборов

Название	Рисунок	Мощность
Калькулятор		(0,001) Вт
Лампы дневного света		(15 — 80) Вт
Лампы накаливания		(25 — 5000) Вт
Компьютер		(200 — 450) Вт
Электрический чайник		(650 — 3100) Вт
Пылесос		(1500 — 3000) Вт
Стиральная машина		(2000 — 4000) Вт
Трамвай		(150 000 — 240000) Вт

Источники:

Рис. 1. Зависимость между работой, напряжением и зарядом. © ЯКласс.
Рис. 3. Схема и часы для измерения. © ЯКласс.
Рис. 5. Зависимость между мощностью, напряжением и силой тока. © ЯКласс.
Рис. 6. Схема. © ЯКласс.
Таблица 1. Мощность различных приборов. Компьютер. Указание авторства не требуется, 2021-08-14, Pixabay License, https://pixabay.com/ru/photos/яблоко-стул-компьютер-1834328/.

Источник

На чтение 9 мин Просмотров 1.1к. Опубликовано 11.09.2022 Обновлено 11.09.2022

Содержание

Понятие ЭДС и единица измерения
Где и как образуется электродвижущая сила
Виды ЭДС
Законы и формулы
ЭДС аккумуляторной батареи
ЭДС индукции
Внутреннее сопротивление источника ЭДС
Закон Ома для полной цепи
Как найти мощность ЭДС

Чтобы в какой-либо среде (металле, растворе, ионизированном газе и т.п.) протекал электрический ток в течение продолжительного времени, недостаточно наличия свободных носителей заряда и электрического поля. Еще потребуется сила, которая будет разделять заряды в направлении, противоположном направлению электрического поля.

Понятие ЭДС и единица измерения

Если имеется заряженный предмет и соединить его с электрически нейтральным (или противоположно заряженным предметом), некоторое время в цепи будет существовать ток. Как только все свободные электроны перейдут от одного тела к другому, и заряды уравняются, ток прекратится.

Опыт с двумя электроскопами

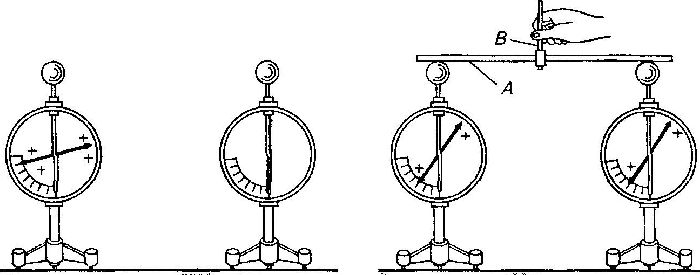
Это можно увидеть на примере школьного опыта с двумя электроскопами. Один из них заряжен (например, положительно), а другой заряда не имеет. Если их соединить металлическим стержнем, то заряды перейдут от одного прибора к другому. Количество зарядов уравновесится, потенциалы электроскопов станут равными, электрическое поле прекратит действие на электроны, и ток перестанет течь.

Чтобы ток продолжался, надо носители зарядов из второго электроскопа перенести обратно в первый. Для этого нужна сторонняя сила, действующая против направления электрического поля. Такая сила называется ЭДС. Расшифровка этого сокращения – электродвижущая сила.

Перенос зарядов посредством ЭДС

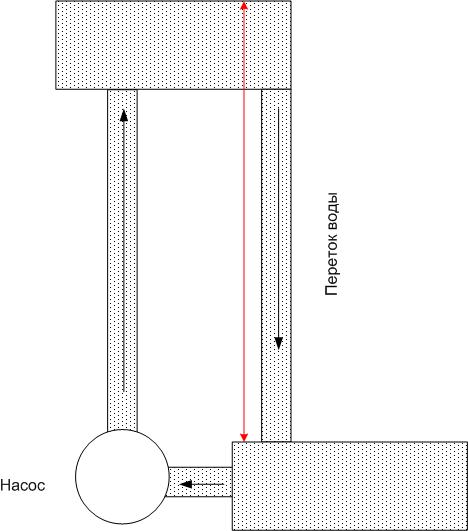
Можно провести аналогию с водой. Если есть два бассейна, один из которых находится выше другого, то вода может перетекать из верхнего водоема в нижний. Но как только запас воды закончится, переток прекратится. Чтобы он продолжался, надо воду из нижнего бассейна перекачивать обратно в верхний (например, с помощью насоса).

Необходимость наличия ЭДС на примере перетока воды

ЭДС обозначается греческой буквой ε (эпсилон), а иногда E. Измеряется ЭДС, как и напряжение, в вольтах (1 В). Понятие электродвижущей силы является не очень удачным – сила не измеряется в вольтах. Но этот термин укоренился и широко применяется.

Из-за сходства единиц измерения часто происходит путаница ЭДС и напряжения. Эти термины регулярно подменяются друг с другом. В некоторых случаях действительно принципиальной разницы нет, но в целом эти понятия различны.

В видео простыми словами объясняется чем отличаются ЭДС и напряжение

Где и как образуется электродвижущая сила

Электродвижущая сила образуется в источнике питания. Это необходимое условие существования разности потенциалов на выходных клеммах такого источника. Образовываться ЭДС может по-разному, в зависимости от устройства источника.

Виды ЭДС

Электродвижущая сила может быть различной природы (но всегда неэлектрической). В зависимости от типа источника питания ЭДС может быть:

фотоэлектрического характера – возникает в полупроводниковых переходах при облучении видимым светом или ультрафиолетом (на этом эффекте основана работа солнечных батарей);
электрохимической природы – всем известные гальванические элементы и аккумуляторы;
термоэлектрической ЭДС – возникает при разности температур между холодным и горячим спаем металлов (термопары для генерации электроэнергии и измерения температуры);
пьезоэлектрической природы (возникает при деформации некоторых материалов) – применяется в пьезозажигалках;
ЭДС электромагнитного характера – генераторы электростанций, автомобилей и т.п.

В технике встречаются и некоторые другие виды ЭДС, но реже.

Законы и формулы

Электродвижущая сила совершает работу по переносу заряда, а движущийся заряд представляет собой электрический ток/ Этот ток равен I=qt, где q – заряд, перенесенный полем за время t. За это время поле совершает работу A=ε*q= ε*I*t.

Можно определить ЭДС, как отношение работы по переносу заряда к величине этого заряда:

ε=A/q=A/(I*t)

ЭДС аккумуляторной батареи

ЭДС аккумуляторной батареи определяется типом электрохимических реакций, протекающих внутри элемента. Для различных технологий батарей наибольшая электродвижущая сила составит:

Свинцово-кислотные элементы – 2,17 вольта.
Никель-кадмиевые батареи – 1,37 вольта.
Никель-металлогидридные элементы – 1,37 вольта.
Щелочные аккумуляторы – 1,45 вольта.
Литий-ионные элементы – 4,2 вольта.

Электродвижущая сила химических источников тока не зависит от размеров и площади пластин. Чтобы повысить выходное напряжение, единичные аккумуляторы соединяют в батареи последовательно.

Последовательно соединенные элементы автомобильной батареи

ЭДС индукции

Основной источник получения электроэнергии на Земле – генераторы постоянного и переменного тока. Их принцип действия основан на создании ЭДС индукции.

Если замкнутый контур находится в магнитном поле, и его пронизывает магнитный поток Ф, и этот поток изменяется во времени (по направлению или по величине), то в контуре возникает ЭДС. Ее величина равна:

ε=∆Ф/∆t, где Ф – магнитный поток, а t – время его изменения.

Ток в замкнутом контуре, вызываемый ЭДС индукции под действием внешнего магнитного поля

В свою очередь магнитный поток зависит от величины магнитной индукции и площади поверхности, охватываемой контуром. Следовательно, чтобы увеличить ЭДС, надо усиливать магнитное поле (повышением тока возбуждения), или увеличивать площадь витка (при разработке или изготовлении генератора), или заставить магнитный поток изменяться быстрее (например, увеличивая скорость вращения ротора генератора). Каждый путь имеет определенные технические ограничения, поэтому в генераторах делают большое количество витков, соединяя их последовательно. При этом электродвижущие силы всех контуров складываются.

Статор автомобильного генератора – витки соединяются последовательно

Внутреннее сопротивление источника ЭДС

Пусть имеется источник тока — например, аккумулятор — с напряжением на разомкнутых клеммах (в отсутствие нагрузки) 12 вольт. Если его нагрузить на сопротивление в 5 Ом, напряжение на клеммах упадет (например, до 11,5 вольт). Если нагрузить аккумулятор на сопротивление 1 Ом, на его выходных терминалах напряжение снизится до 9,86 вольт.

Снижение выходного напряжения аккумулятора при уменьшении сопротивления нагрузки

Это явление легко объяснить, если ввести понятие внутреннего сопротивления источника питания. При разделении зарядов они движутся к соответствующим полюсам, но при этом взаимодействуют с кристаллической решеткой вещества, с ионами электролитов и отдают часть своей энергии. Движение носителей заряда замедляется, ток уменьшается, его ограничивает внутреннее сопротивление источника.

Это сопротивление включается последовательно с нагрузкой, и часть выходного напряжения падает на нем. Чем меньше сопротивление нагрузки, тем больше ток, тем больше потеря напряжения на внутреннем сопротивлении источника.

Внутреннее сопротивление определяется его конструкцией и типом ЭДС. Например, в аккумуляторе внутреннее сопротивление зависит от электрохимических реакций, протекающих в источнике тока.

Внутреннее сопротивление в виде резистора внутри источника тока

Для анализа электрических цепей внутреннее сопротивление рисуется на схеме в виде резистора, подключенного внутри источника параллельно его выходным клеммам. На самом деле, конечно, никакого резистора там нет, но это удобно для рассмотрения процессов, протекающих в цепи.

Для наглядности рекомендуем видео-урок.

Закон Ома для полной цепи

Один из фундаментальных законов электротехники – закон Ома для участка цепи. Согласно ему, ток на участке цепи прямо пропорционален напряжению и обратно пропорционален сопротивлению.

Ток в полной цепи, в которую кроме нагрузки входит еще и источник, определяется величиной ЭДС, приложенной к внутреннему сопротивлению r и сопротивлению внешней нагрузки R, включенными последовательно. Общее значение сопротивления равно r+R. Следовательно, ток определяется соотношением I=ε/(R+r).

Как найти мощность ЭДС

Идеальный источник имеет нулевое внутреннее сопротивление. В нем напряжение под нагрузкой не уменьшается и всегда равно ЭДС. На практике таких источников не бывает.

Согласно закону Ома для полной цепи, формула ЭДС источника выглядит, как ε=I*R+I*r (в таком виде формулируется второй закон Кирхгофа). В этом выражении:

I*R=Uвнеш – напряжение на внешней нагрузке;
i*r=Uвнутр – падение напряжения на внутреннем сопротивлении источника.

Если источник идеален, то r=0 и вся ЭДС прикладывается к нагрузке. Чем выше r и выше ток, тем меньше напряжения достается потребителю, тем меньшая мощность выделяется на нем. Отсюда очевидно, что с ростом внутреннего сопротивления r, при равном токе, снижается напряжение на внешней нагрузке.

Внутреннее сопротивление источника можно рассчитать по результатам измерений напряжения на терминалах источника ЭДС по итогам двух замеров. Для этого надо воспользоваться законом Ома для полной цепи. Так, в рассмотренном примере, в первом случае падение напряжения на резисторе в 5 Ом составляет 11,5 вольт. Тогда можно найти ток в цепи по формуле:

I=U/R=11,5/5=2,3 А.

Выражение для ЭДС примет вид:

ε= 2,3*5+2,3*r=11,5+2,3*r.

Для второго замера на сопротивлении 1 Ом ток составит:

I=U/R=9,86/1=9,86 ампер

Следовательно,

ε= 9,86 *1+9,86 *r=9,86 +9,86 *r.

Левые части уравнений равны, тогда можно приравнять правые:

11,5+2,3*r=9,86 +9,86 *r

Путем несложных вычислений получается, что r=0,217 Ом. Если источник имеет меньшее внутреннее сопротивление, то при подключении той же нагрузки на ней будет большее напряжение. Напряжение на разомкнутых клеммах (на холостом ходу) в отсутствие ток будет примерно равно значению величины ЭДС. Таким образом, чем меньше внутреннее сопротивление, тем большее напряжение способен выдавать источник в нагрузку и тем больше мощность ЭДС.

Если же идеальный источник тока замкнуть накоротко, ток короткого замыкания будет бесконечным, так как R=r=0. На самом деле этого не происходит – в реальном источнике ток КЗ при R=0 ограничивается внутренним сопротивлением r.

Электродвижущая сила является одним из основополагающих понятий в физике. Ее суть и значение надо четко осознавать, в противном случае дальнейшее освоение электротехники будет затруднено.

Источник