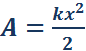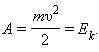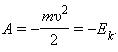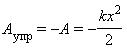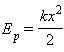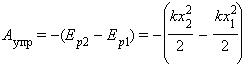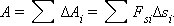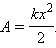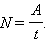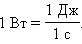Работа силы совершаемая в единицу времени называется

Энергетические характеристики движения вводятся на основе понятия механической работы или работы силы.

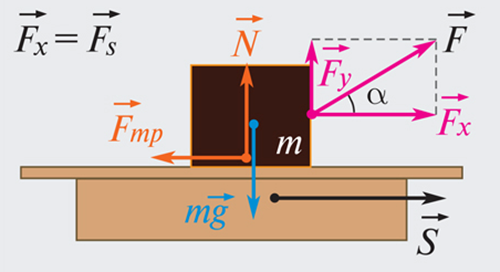
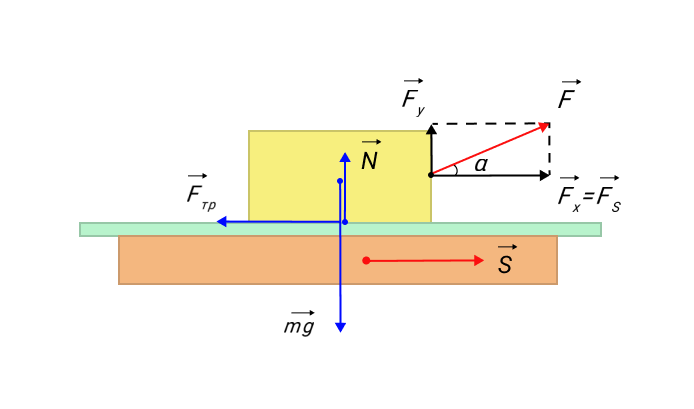
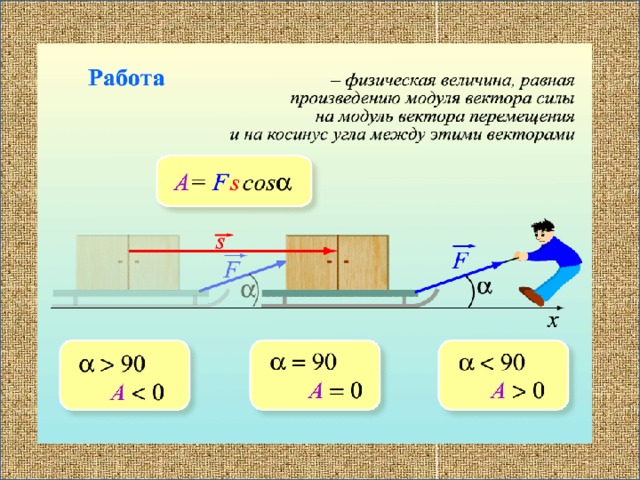
Если действующая на тело сила  вызывает его перемещение s, то действие этой силы характеризуется величиной, называемой механической работой (или, сокращенно, просто работой).

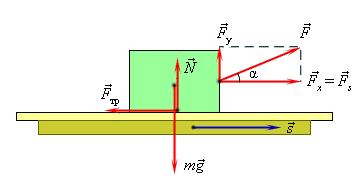
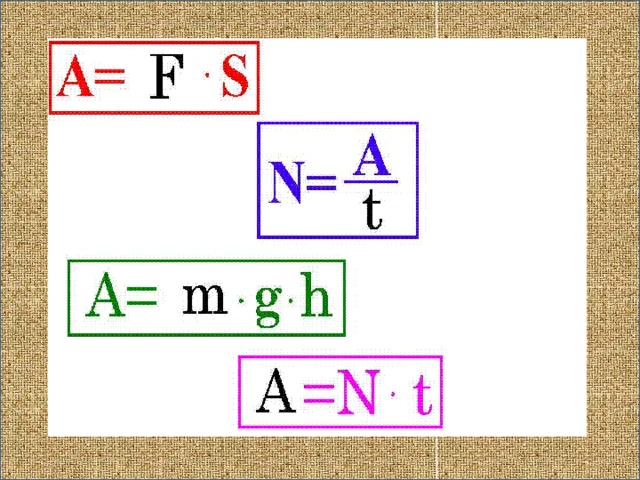
Механическая работа А — скалярная величина, равная произведению модуля силы F, действующей на тело, и модуля перемещения s, совершаемого телом в направлении действия этой силы.

Если направления перемещения тела и приложенный силы не совпадают, то работу можно вычислить как произведение модулей силы и перемещения, умноженному на косинус угла α между векторами силы   и перемещения  (рис. 1.18.1):

Работа является скалярной величиной. Она может быть как положительной (0° ≤ α < 90°), так и отрицательной (90° < α ≤ 180°). При α = 90° работа, совершаемая силой, равна нулю. В системе СИ работа измеряется в джоулях (Дж).

Джоуль равен работе, совершаемой силой в 1 Н на перемещении 1 м в направлении действия силы.

Рисунок 1.18.1. Работа силы :

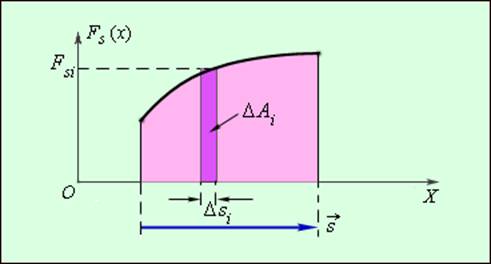
Если проекция  силы  на направление перемещения  не остается постоянной, работу следует вычислять для малых перемещений Δsi и суммировать результаты:

Это сумма в пределе (Δsi → 0) переходит в интеграл.

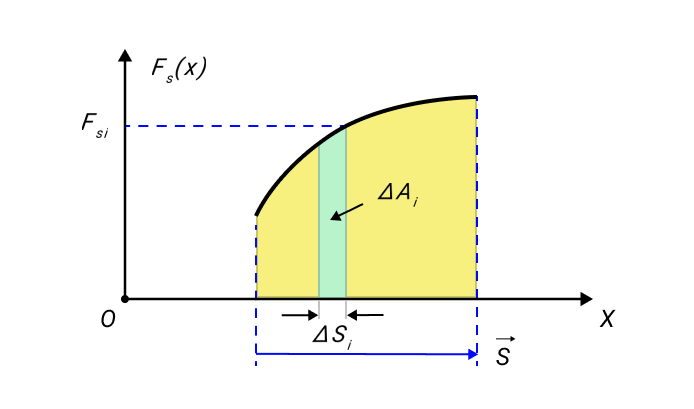
Графически работа определяется по площади криволинейной фигуры под графиком Fs(x) (рис. 1.18.2).

Рисунок 1.18.2. Графическое определение работы. ΔAi = FsiΔsi

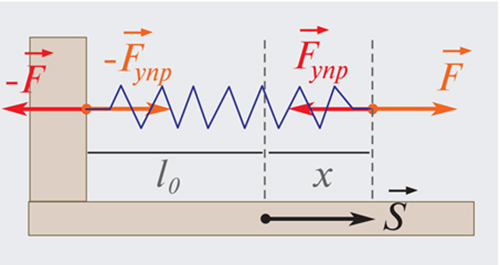
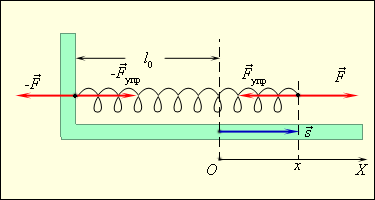
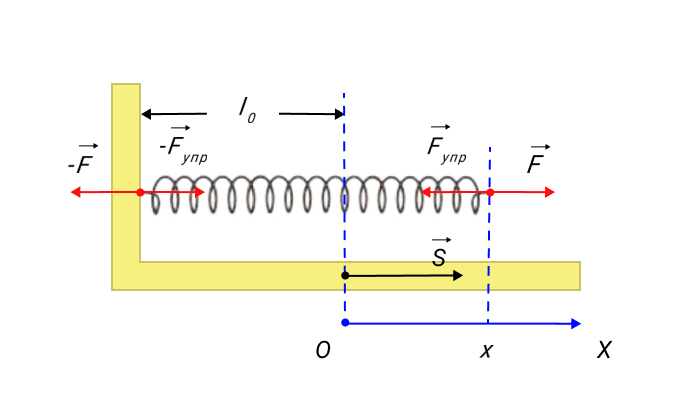
Примером силы, модуль которой зависит от координаты, может служить сила упругости пружины, подчиняющаяся закону Гука. Для того, чтобы растянуть пружину, к ней нужно приложить внешнюю силу  модуль которой пропорционален удлинению пружины (рис. 1.18.3).

Рисунок 1.18.3. Растянутая пружина. Направление внешней силы  совпадает с направлением перемещения  :    k – жесткость пружины.

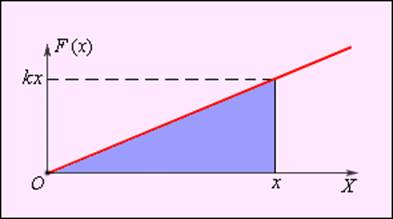
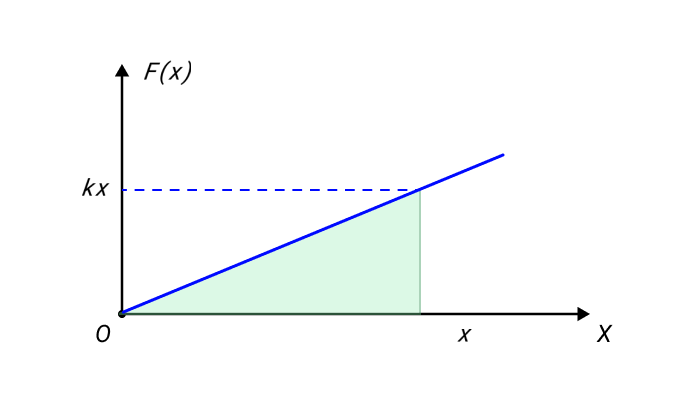
Зависимость модуля внешней силы от координаты x изображается на графике прямой линией (рис. 1.18.4).

Рисунок 1.18.4. Зависимость модуля внешней силы от координаты при растяжении пружины

По площади треугольника на рис. 1.18.4 можно определить работу, совершенную внешней силой, приложенной к правому свободному концу пружины:

Этой же формулой выражается работа, совершенная внешней силой при сжатии пружины. В обоих случаях работа упругой силы  равна по модулю работе внешней силы  и противоположна ей по знаку.

Если к телу приложено несколько сил, то общая работа всех сил равна алгебраической сумме работ, совершаемых отдельными силами. При поступательном движении тела, когда точки приложения всех сил совершают одинаковое перемещение, общая работа всех сил равна работе равнодействующей приложенных сил.

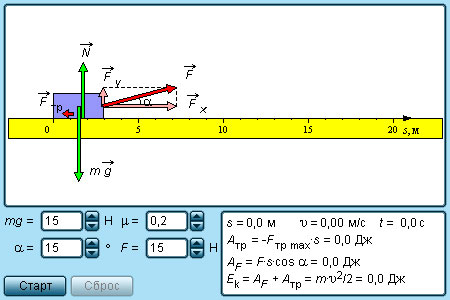Модель. Механическая работа.

Мощность

Работа силы, совершаемая в единицу времени, называется мощностью. Мощность N это физическая величина, равная отношению работы A к промежутку времени t, в течение которого совершена эта работа:

В Международной системе (СИ) единица мощности называется ватт (Вт). Ватт равен мощности силы, совершающей работу в 1 Дж за время 1 с.

Энергетические характеристики движения вводятся на основе понятия механической работы или работы силы.

Если на тело действует сила и тело под действием этой силы перемещается, то говорят, что сила совершает работу.

Механическая работа – это скалярная величина, равная произведению модуля силы, действующей на тело, на модуль перемещения и на косинус угла между вектором силы  и вектором перемещения (или скорости).

A = Fs cos α

Работа является скалярной величиной. Она может быть как положительна (0° ≤ α < 90°), так и отрицательна (90° < α ≤ 180°). При α = 90° работа, совершаемая силой, равна нулю.

В системе СИ работа измеряется в джоулях (Дж). Джоуль равен работе, совершаемой силой в 1 Н на перемещении 1 м в направлении действия силы.

[1 Дж=1 Н·м]

Работа силы, совершаемая в единицу времени, называется мощностью.

Мощность N – физическая величина, равная отношению работы A к промежутку времени t, в течение которого совершена эта работа:

 N=A/t

В Международной системе (СИ) единица мощности называется ватт (Вт). Ватт равен мощности силы, совершающей работу в 1 Дж за время 1 с.

Внесистемная единица мощности 1 л.с.=735 Вт

Связь между мощностью и скоростью при равномерном движении:

N=A/t  так как   A=FScosα      тогда   N=(FScosα)/t, но S/t = v   следовательно

N=Fvcos α

В технике используются единицы работы и мощности:

1 Вт·с = 1 Дж;     1Вт·ч = 3,6·10³ Дж;      1кВт·ч = 3,6·10⁶ Дж

Если тело способно совершить работу, то говорят, что оно обладает энергией.

 Механическая энергия тела – это скалярная величина, равная максимальной работе, которая может быть совершена в данных условиях.

Обозначается  Е Единица энергии в СИ  [1Дж = 1Н*м]

Механическая работа есть мера изменения энергии в различных процессах А = ΔЕ.

Различают два вида механической энергии – кинетическая Ек и потенциальная Еp энергия.

Полная механическая энергия тела равна сумме его кинетической и потенциальной энергий

Е = Ек + Еp

Кинетическая энергия – это энергия тела, обусловленная его движением.

Физическая величина, равная половине произведения массы тела на квадрат его скорости, называется кинетической энергией тела:

Кинетическая энергия – это энергия движения. Кинетическая энергия тела массой m, движущегося со скоростью  равна работе, которую должна совершить сила, приложенная к покоящемуся телу, чтобы сообщить ему эту скорость:

Если тело движется со скоростью , то для его полной остановки необходимо совершить работу

Наряду с кинетической энергией или энергией движения в физике важную роль играет понятиепотенциальной энергии или энергии взаимодействия тел.

Потенциальная энергия – энергия тела, обусловленная взаимным расположением взаимодействующих между собой тел или частей одного тела. 

Понятие потенциальной энергии можно ввести только для сил, работа которых не зависит от траектории движения тела и определяется только начальным и конечным положениями. Такие силы называются консервативными. Работа консервативных сил на замкнутой траектории равна нулю.

Свойством консервативности обладают сила тяжести и сила упругости. Для этих сил можно ввести понятие потенциальной энергии.

Потенциальная энергия тела в поле силы тяжести (потенциальная энергия тела, поднятого над землёй):

Ep = mgh

Она равна работе, которую совершает сила тяжести при опускании тела на нулевой уровень.

Понятие потенциальной энергии можно ввести и для упругой силы. Эта сила также обладает свойством консервативности. Растягивая (или сжимая) пружину, мы можем делать это различными способами.

Можно просто удлинить пружину на величину x, или сначала удлинить ее на 2x, а затем уменьшить удлинение до значения x и т. д. Во всех этих случаях упругая сила совершает одну и ту же работу, которая зависит только от удлинения пружины x в конечном состоянии, если первоначально пружина была недеформирована. Эта работа равна работе внешней силы A, взятой с противоположным знаком :

где k – жесткость пружины.

Растянутая (или сжатая) пружина способна привести в движение прикрепленное к ней тело, то есть сообщить этому телу кинетическую энергию. Следовательно, такая пружина обладает запасом энергии. Потенциальной энергией пружины (или любого упруго деформированного тела) называют величину

Потенциальная энергия упруго деформированного тела равна работе силы упругости при переходе из данного состояния в состояние с нулевой деформацией.

Если в начальном состоянии пружина уже была деформирована, а ее удлинение было равно x1, тогда при переходе в новое состояние с удлинением x2 сила упругости совершит работу, равную изменению потенциальной энергии, взятому с противоположным знаком:

Потенциальная энергия при упругой деформации – это энергия взаимодействия отдельных частей тела между собой силами упругости.

Если тела, составляющие замкнутую механическую систему, взаимодействуют между собой только силами тяготения и упругости, то работа этих сил равна изменению потенциальной энергии тел, взятому с противоположным знаком:

A = –(Ep2 – Ep1).

По теореме о кинетической энергии эта работа равна изменению кинетической энергии тел:

A = Ek2 – Ek1

Следовательно   Ek2 – Ek1 = –(Ep2 – Ep1)      или        Ek1 + Ep1 = Ek2 + Ep2.

Сумма кинетической и потенциальной энергии тел, составляющих замкнутую систему и взаимодействующих между собой силами тяготения и силами упругости, остается неизменной.

Это утверждение выражает закон сохранения энергии в механических процессах. Он является следствием законов Ньютона.

Сумму E = Ek + Ep называют полной механической энергией.

Полная механическая энергия замкнутой системы тел, взаимодействующих между собой только консервативными силами, при любых движениях этих тел не изменяется. Происходят лишь взаимные превращения потенциальной энергии тел в их кинетическую энергию, и наоборот, или переход энергии от одного тела к другому.

Е = Ек + Еp = const

Закон сохранения механической энергии выполняется только тогда, когда тела в замкнутой системе взаимодействуют между собой консервативными силами, то есть силами, для которых можно ввести понятие потенциальной энергии.

В реальных условиях практически всегда на движущиеся тела наряду с силами тяготения, силами упругости и другими консервативными силами действуют силы трения или силы сопротивления среды.

Сила трения не является консервативной. Работа силы трения зависит от длины пути.

Если между телами, составляющими замкнутую систему, действуют силы трения, то механическая энергия не сохраняется. Часть механической энергии превращается во внутреннюю энергию тел (нагревание).

Энергетические характеристики движения
вводятся на основе понятия механической
работы или работы силы.

Работой A, совершаемой постоянной
силой
называется
физическая величина, равная произведению
модулей силы и перемещения, умноженному
на косинус угла α между векторами силы
и
перемещения
(рис. 1.18.1):

A = Fs cos α.

Работа является скалярной величиной.
Она может быть как положительна
(0° ≤ α < 90°), так и отрицательна
(90° < α ≤ 180°). При α = 90°
работа, совершаемая силой, равна нулю.
В системе СИ работа измеряется в джоулях
(Дж).

Джоуль равен работе, совершаемой силой
в 1 Н на перемещении 1 м в направлении
действия силы.

1

Рисунок 1.18.1. Работа силы :

Если проекция
силы
на
направление перемещения
не
остается постоянной, работу следует
вычислять для малых перемещений
и
суммировать результаты:

Это сумма в пределе (Δs_i → 0)
переходит в интеграл.

Графически работа определяется по
площади криволинейной фигуры под
графиком F_s(x) (рис. 1.18.2).

2

Рисунок 1.18.2. Графическое определение работы. ΔAi = FsiΔsi.

Примером силы, модуль которой зависит
от координаты, может служить упругая
сила пружины, подчиняющаяся закону
Гука. Для того, чтобы растянуть пружину,
к ней нужно приложить внешнюю силу
модуль
которой пропорционален удлинению
пружины (рис. 1.18.3).

3

Рисунок 1.18.3. Растянутая пружина. Направление внешней силы совпадает с направлением перемещения .   k – жесткость пружины.

Зависимость модуля внешней силы от
координаты x изображается на графике
прямой линией (рис. 1.18.4).

4

Рисунок 1.18.4. Зависимость модуля внешней силы от координаты при растяжении пружины.

По площади треугольника на рис. 1.18.4
можно определить работу, совершенную
внешней силой, приложенной к правому
свободному концу пружины:

Этой же формулой выражается работа,
совершенная внешней силой при сжатии
пружины. В обоих случаях работа упругой
силы
равна
по модулю работе внешней силы
и
противоположна ей по знаку.

Если к телу приложено несколько сил, то
общая работа всех сил равна алгебраической
сумме работ, совершаемых отдельными
силами, и равна работе равнодействующей
приложенных сил.

Работа силы, совершаемая в единицу
времени, называется мощностью.
Мощность N – физическая величина,
равная отношению работы A к промежутку
времени t, в течение которого совершена
эта работа:

В Международной системе (СИ) единица
мощности называется ватт (Вт). Ватт
равен мощности силы, совершающей работу
в 1 Дж за время 1 с.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

• #
• #
• #
• #
• #
• #
• #
• #
• #
• #
• #

Энергетические характеристики движения вводятся на основе понятия механической работы или работы силы. Другими словами, работа — мера воздействия силы.

Определение механической работы

Работа А, совершаемая постоянной силой F→, — это физическая скалярная величина, равная произведению модулей силы и перемещения, умноженному на косинус угла α между векторами силы F→ и перемещением s→.

Данное определение рассматривается на рисунке 1.

Формула работы записывается как,

A=Fs cos α.

Работа – это скалярная величина. Единица измерения работы по системе СИ — Джоуль (Дж).

Джоуль равняется работе, совершаемой силой в 1 Н на перемещение 1 м по направлению действия силы.

Рисунок 1. Работа силы F→: A=Fs cos α=Fss

При проекции Fs→ силы F→ на направление перемещения s→ сила не остается постоянной, а вычисление работы для малых перемещений Δsi суммируется и производится по формуле:

A=∑∆Ai=∑Fsi∆si.

Данная сумма работы вычисляется из предела (Δsi→0), после чего переходит в интеграл.

Графическое изображение работы определяют из площади криволинейной фигуры, располагаемой под графиком Fs(x)рисунка 2.

Рисунок 2. Графическое определение работы ΔAi=FsiΔsi.

Примером силы, зависящей от координаты, считается сила упругости пружины, которая подчиняется закону Гука. Чтобы произвести растяжение пружины, необходимо приложить силу F→, модуль которой пропорционален удлинению пружины. Это видно на рисунке 3.

Рисунок 3. Растянутая пружина. Направление внешней силы F→ совпадает с направлением перемещения s→. Fs=kx, где k обозначает жесткость пружины.

F→упр=-F→

Зависимость модуля внешней силы от координат x можно изобразить на графике с помощью прямой линии.

Рисунок 4. Зависимость модуля внешней силы от координаты при растяжении пружины.

Из выше указанного рисунка возможно нахождение работы над внешней силой правого свободного конца пружины, задействовав площадь треугольника. Формула примет вид

A=kx22.

Данная формула применима для выражения работы, совершаемой внешней силой при сжатии пружины. Оба случая показывают, что сила упругости F→упр равняется работе внешней силы F→, но с противоположным знаком.

Если на тело действует несколько сил, то их общая работа равняется сумме всех работ, совершаемых над телом. Когда тело движется поступательно, точки приложения сил перемещаются одинаково, то есть общая работа всех сил будет равна работе равнодействующей приложенных сил.

Мощность

Мощностью называют работу силы, совершаемую в единицу времени.

Запись физической величины мощности, обозначаемой N, принимает вид отношения работы А к промежутку времени t совершаемой работы, то есть:

N=At.

Система СИ использует в качестве единицы мощности ватт (Вт). 1 Ватт — это мощность, которую совершает работу в 1 Дж за время 1 с.

Помимо Ватта, существуют и внесистемные единицы измерения мощности. Например, 1 лошадиная сила примерна равна 745 Ваттам.  

Механическая работа

и

мощность.

Митрофанова Н. А. — учитель физики

7 класс

Механическая

работа.

Я работаю!

Механическая работа — физическая величина, характеризующая результат действия силы и численно равная скалярному произведению вектора силы и вектора перемещения, совершенного под действием этой силы .

A = Fs cos α.

В системе СИ работа измеряется в джоулях (Дж).

1 джоуль равен работе, совершаемой силой в 1 Н

при перемещении на 1 м в направлении действия силы.

Ответы: 1 – б, 2 – в, 3 – а, 4 – г, 5 – б, 6 – б, в 7 – б,в, 8 – б, 9 – а, 10 – б,в

Мощность.

Работа силы, совершаемая в единицу времени,

называется мощностью.

Мощность N это физическая величина, равная отношению

работы A к промежутку времени t, в течение которого

совершена эта работа:

В Международной системе (СИ) единица мощности называется ватт (Вт).

Ватт равен мощности силы, совершающей работу в 1 Дж

за время 1 с.

Джеймс Уатт ( 1736 — 1819 ) пользовался другой единицей мощности — лошадиной силой

( 1 л.с. ), которую он ввел с целью возможности сравнения работоспособности паровой машины и лошади. 1л.с. = 735Вт

Джеймс Уатт

(1736-1819 гг.)

Однако, мощность одной средней лошади — около 1/2 л.с., хотя лошади бывают разные.

Лошадь может доводить свою мощность при беге и прыжках до десятикратной и более величины.

Делая прыжок на высоту в 1м, лошадь весом 500кг развивает мощность равную

5 000 Вт = 6,8 л.с.

В среднем мощность человека при спокойной ходьбе равна приблизительно 0,1л.с. т.е 70 — 90Вт.

Оказывается, самым мощным источником механической энергии является огнестрельное оружие

С помощью пушки можно бросить ядро массой 900кг со скоростью 500м/с, развивая за 0,01 секунды около 110 000 000 Дж работы. Эта работа равнозначна работе по подъему 75 т груза на вершину пирамиды Хеопса ( высота 150м ).

Мощность выстрела пушки будет составлять

11 000 000 000Вт = 15 000 000 л.с.

1 вариант

2 вариант

1. Определите работу, совершаемую при поднятии груза весом 4 Н на высоту 4 м

• Укажите, в каком из перечисленных

случаев совершает­ся механическая работа.

А. 16 Дж

Б. 1 Дж

В. 8 Дж

А. На столе стоит гиря.

Б. На пружине висит груз.

В. Трактор тянет прицеп

2. На какую высоту надо поднять гирю весом 100 Н, чтобы совершить работу 200 Дж?

2. Велосипедист за 10 с совершил работу 800 Дж. Чему равна мощность велосипедиста?

А. 8000 Вт

Б. 40 Вт

В. 80 Вт

А. 1м

Б. 2 м

В. 1,5 м

3. Какую работу может совершить двигатель мощностью 600 Вт за 5 мин?  

3. Определите работу, совершаемую двигателем мощностью 400 Вт за 30 с.

А. 1 200 Дж

Б. 15 000 Дж

В. 12 000 Дж

А. 180 кДж

Б. 250 кДж

В. 18 кДж

4. В каком из перечисленных случаев совершается механическая работа?

4. За какое время двигатель мощностью

4 кВт совершит ра­боту в 30 000 Дж?

А. 7,5 с

А. Вода давит на стенку сосуда.

Б. 8 с

В. 20 с

Б. Мальчик поднимается вверх по лестнице.

В. Кирпич лежит на земле..

5. Какого веса груз можно поднять на высоту 2 м, совершив работу 10 Дж?

5. Вычислите работу, произведенную силой 0,02 кН, если расстояние, пройденное телом по направлению действия этой силы, равно 20 м.

А. 2 Н

Б. 5 Н

В. 10 Н

А. 20 Дж

Б. 10 Дж

В. 400 Дж

Ответы:

1 вариант — В, Б, В, А, В

2 вариант — А, В, А, Б, Б.

Главная

»

Самолетостроение

»

Физика

»

Работа и мощность.

Работа и мощность.

Энергетические характеристики движения вводятся на основе понятия механической работы или работы силы.

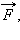
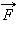
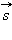
Работой A, совершаемой постоянной силой  называется физическая величина, равная произведению модулей силы и перемещения, умноженному на косинус угла α между векторами силы  и перемещения  (рис. 1.18.1): 

Работа является скалярной величиной. Она может быть как положительной (0° ≤ α < 90°), так и отрицательной (90° < α ≤ 180°). При α = 90° работа, совершаемая силой, равна нулю. В системе СИ работа измеряется в джоулях (Дж).

Джоуль равен работе, совершаемой силой в 1 Н на перемещении 1 м в направлении действия силы.

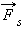
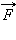
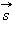
Если проекция  силы  на направление перемещения  не остается постоянной, работу следует вычислять для малых перемещений Δs_i и суммировать результаты: 

Это сумма в пределе (Δs_i → 0) переходит в интеграл.

Графически работа определяется по площади криволинейной фигуры под графиком F_s(x) (рис. 1.18.2).

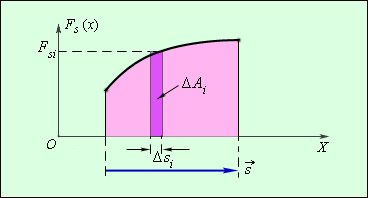Рисунок 1.18.2. Графическое определение работы. ΔAi = FsiΔsi

Примером силы, модуль которой зависит от координаты, может служить сила упругости пружины, подчиняющаяся закону Гука. Для того, чтобы растянуть пружину, к ней нужно приложить внешнюю силу  модуль которой пропорционален удлинению пружины (рис. 1.18.3).

Зависимость модуля внешней силы от координаты x изображается на графике прямой линией (рис. 1.18.4).

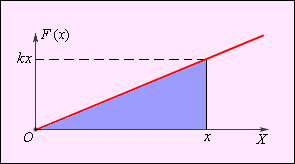Рисунок 1.18.4. Зависимость модуля внешней силы от координаты при растяжении пружины

По площади треугольника на рис. 1.18.4 можно определить работу, совершенную внешней силой, приложенной к правому свободному концу пружины: 

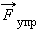
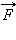
Этой же формулой выражается работа, совершенная внешней силой при сжатии пружины. В обоих случаях работа упругой силы  равна по модулю работе внешней силы  и противоположна ей по знаку.

Если к телу приложено несколько сил, то общая работа всех сил равна алгебраической сумме работ, совершаемых отдельными силами. При поступательном движении тела, когда точки приложения всех сил совершают одинаковое перемещение, общая работа всех сил равна работе равнодействующей приложенных сил.

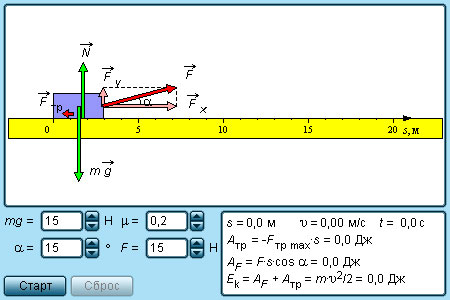Модель. Механическая работа

Работа силы, совершаемая в единицу времени, называется мощностью. Мощность N это физическая величина, равная отношению работы A к промежутку времени t, в течение которого совершена эта работа: 

В Международной системе (СИ) единица мощности называется ватт (Вт). Ватт равен мощности силы, совершающей работу в 1 Дж за время 1 с. 

---

Друзья! Приглашаем вас к обсуждению. Если у вас есть своё мнение, напишите нам в комментарии.