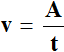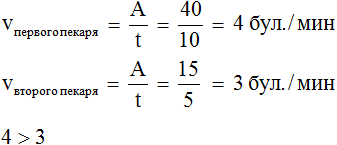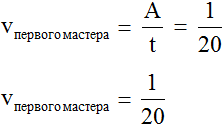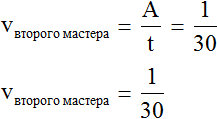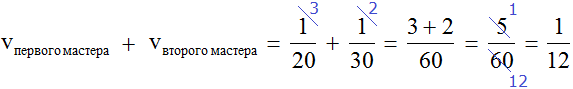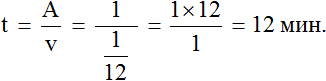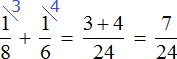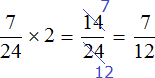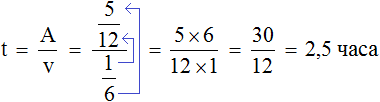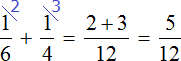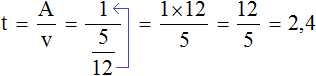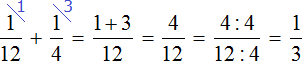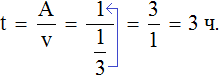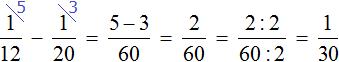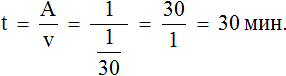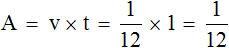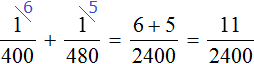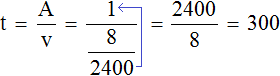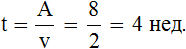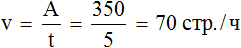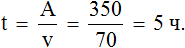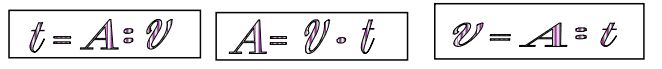Продолжаем изучать элементарные задачи по математике. Сегодня мы рассмотрим очень интересную физическую величину — производительность.
Что такое сила?
Сила — это физическое явление, способное изменять форму материальных тел, вызывать их движение, менять направление и скорость движения этих тел или приводить тело в состояние покоя.
Примеры сил:
- ребята слепили снеговика, а хулиганы его разрушили. Получается, что хулиганы приложили к снеговику свою силу, тем самым вызвали изменение формы снеговика;
- на дворе стояла тележка. Прохожий случайно задел её и тележка сдвинулась с места. Получается, что прохожий применил силу к тележке и вызвал её движение;
- далее тот же прохожий остановил тележку, чтобы она далеко не уехала. Получается, что прохожий применил силу, тем самым привел тележку в состояние покоя.
Сила является физической величиной — мерой воздействия на тело других тел. Сила обозначается заглавной латинской буквой F.
Что такое работа?
Работа — это количественная мера действия силы на тело. Работа зависит от количества силы, приложенной на тело и от направления этой силы, а также от перемещения данного тела.
Например, если мы попробуем сдвинуть шкаф с места и он сдвинется, то можно сказать, что мы совершили работу, поскольку сила, которую мы приложили, привела к тому, что шкаф совершил перемещение на некоторое расстояние.
Если же мы, к примеру, попробуем толкнуть стену, то стена с места не сдвинется, а значит и работа не будет совершена, поскольку сила была приложена, но эта сила не вызвала никакого перемещения стены.
Работа обозначается заглавной латинской буквой A.
Производительность
Производительностью называют работу, выполненную за единицу времени. Под единицей подразумевается 1 час, 1 минута или 1 секунда. Производительность обозначается латинской буквой v
Рассмотрим следующий пример. Два пекаря пекли булочки. Первый пекарь испёк 40 булочек за 10 минут, а второй 15 булочек за 5 минут. Как узнать, кто из пекарей работал быстрее, первый или второй?
Работал быстрее тот, кто за одну минуту выпекает больше булочек. Говорят, что у него производительность больше. Для нахождения производительности предусмотрено следующее правило:
Чтобы найти производительность, надо выполненную работу разделить на время работы.
Также, можно воспользоваться формулой:
где v — производительность, A — выполненная работа, t — время работы.
Вернемся к нашей задаче. Зная правило или формулу нахождения производительности, можно определить сколько булочек приходится на одну минуту.
Найдём производительность первого пекаря. Разделим работу, которую он выполнил, на время которое он на нее затратил. Выполненная работа это количество испеченных им булочек, то есть 40, а время — 10 минут
40 : 10 = 4 булочки в минуту
Аналогично найдём производительность второго пекаря. Разделим 15 на 5
15 : 5 = 3 булочки в минуту
4 > 3
Первый пекарь в минуту выпекает больше булочек чем второй, значит его производительность выше. Отсюда делаем вывод, что работает он быстрее второго пекаря.
Также можно воспользоваться формулой нахождения производительности. В этом случае решение принимает следующий вид:
Под буквой v можно делать метки, указывающие для кого/чего мы находим производительность.
Задача 2. Тому нужно за 2 дня прочитать книгу, в которой 100 страниц. В первый день он читал 4 часа со скоростью 12 страниц в час. С какой скоростью ему надо читать оставшуюся часть книги, если у него есть на это 4 часа?
Узнаем сколько страниц Том прочитал в первый день. Он читал 12 страниц в час. Чтению в первый день он посвятил 4 часа, поэтому для нахождения количества прочитанных страниц в первый день, нужно 12 умножить на 4
12 × 4 = 48 страниц прочитано в первый день
Узнаем сколько страниц осталось прочесть. Вычтем из общего количества страниц (100) количество прочитанных страниц (48)
100 − 48 = 52 страницы осталось прочесть
Осталось прочесть 52 страницы. Теперь найдем такую производительность, при которой Том сможет прочесть 52 страницы за 4 часа. Раскидаем 52 страницы на 4 часа поровну
52 : 4 = 13 страниц в час
Ответ: чтобы прочитать оставшуюся часть книги за 4 часа, Том должен читать ее со скоростью 13 страниц в час.
Замечание. В некоторых источниках слово «производительность» может быть заменено на слова «скорость», «эффективность», «продуктивность», «плодотворность».
Задача 3. Один насос работал 4 часа, выкачивая 158 вёдер воды в час, а другой — 3 часа, выкачивая 169 вёдер воды в час. Определить какой из насосов выкачал больше вёдер.
Решение
Определим сколько всего вёдер выкачал каждый насос по отдельности. Для этого умножим их производительность на время их работы:
158 в/ч × 4 = 632 вёдер выкачал первый насос
169 в/ч × 3 = 507 вёдер выкачал второй насос
632 > 507
Ответ: первый насос выкачала больше вёдер, чем второй.
Задача 4. За 2 часа насос выкачал 80 литров воды. Определить сколько литров он выкачает за 5 часов.
Решение
Сначала нужно определить сколько литров воды насос выкачивает за час. Для этого 80 литров разделим на 2 часа — получим 40 литров
80 : 2 = 40 литров в час
За один час насос выкачивает 40 литров воды. За 5 часов выкачает в пять раз больше
40 × 5 = 200 литров
Ответ: за 5 часов насос выкачает 200 литров воды.
Если известны производительность и время работы, то можно найти выполненную работу. Выполненная работа равна производительности умноженной на время работы:
A = v × t
Например, если производительность пекаря составляет 50 булочек в час, и он проработал 4 часа, то можно найти всю выполненную работу за эти четыре часа. Для этого производительность (50 бул/ч) нужно умножить на время его работы (4ч)
50 × 4 = 200 булочек
Если известны работа и производительность, то можно найти время работы. Время работы равно отношению выполненной работы к производительности:
Например, если в неделю бригада отстраивает 2 этажа, то можно узнать сколько недель потребуется для отстройки 8 этажей. Чтобы определить время отстройки восьми этажей, нужно выполненную работу (8 этажей) разделить на производительность (2 эт./нед):
8 : 2 = 4 нед.
Либо с помощью формулы, приведенной выше:
Если в неделю строится 2 этажа, то 8 этажей будет отстроено за четыре недели. В данном случае вся работа была равна восьми. Производительность была равна двум, поскольку по определению производительность есть работа, выполненная за единицу времени – в нашем случае два этажа за неделю.
Задача 6. Принтер работает с производительностью 70 стр./ч. Сколько страниц он напечатает за 5 часов?
Решение
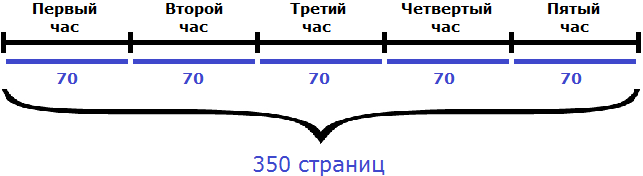
Если в час принтер печатает 70 страниц, то за 5 часов он напечатает в 5 раз больше:
70 × 5 = 350 страниц
Также, решение можно записать с помощью формулы нахождения работы. В данном случае, количество напечатанных страниц являются выполненной работой:
A = v × t = 70 × 5 = 350 страниц
A = 350 страниц
Задача 7. Принтер напечатал 350 страниц за 5 часов. С какой производительностью он работал?
Решение
Если в течении пяти часов принтер напечатал 350 страниц, то в течении часа он печатал . То есть работал с производительностью 70 страниц в час:
350 : 5 = 70 стр./ч.
Либо с помощью формулы нахождения производительности:
Задача 8. Принтер работал с производительностью 70 страниц в час и напечатал 350 страниц. Определить время работы принтера.
Решение
Выражение «работал с производительностью 70 страниц в час» означает, что в каждом часе принтер печатал по 70 страниц. И это продолжалось до тех пор, пока он не напечатал 350 страниц. Очевидно, что разделив 350 страниц по 70, мы определим время работы принтера, то есть узнаем сколько часов он работал
350 : 70 = 5 ч.
Либо с помощью формулы нахождения времени:
Задача 9. Машинистка в первый день напечатала 48 страниц рукописи, а во второй день — на 12 страниц больше, чем в первый. На всю работу в эти 2 дня она затратила 9 часов. Сколько часов работала она в каждый из этих дней, если производительность её не менялась ?
Решение
Определим сколько страниц напечатала машинистка во второй день. В условии сказано, что напечатала она на 12 страниц больше, чем в первый:
48 + 12 = 60 страниц во второй день.
Определим сколько страниц машинистка напечатала за два дня:
48 + 60 = 108 страниц за два дня.
На эту работу машинистка затратила 9 часов. Также сказано, что производительность её не менялась. Если мы разделим выполненную работу (108) на время выполнения (9), то определим производительность машинистки:
108 : 9 = 12 страниц в час.
Теперь мы можем определить сколько часов работала машинистка в каждый из двух дней. Для этого поочередно разделим выполненные работы в каждом из двух дней на производительность:
48 : 12 = 4 часа работала машинистка в первый день
60 : 12 = 5 часов работала машинистка во второй день.
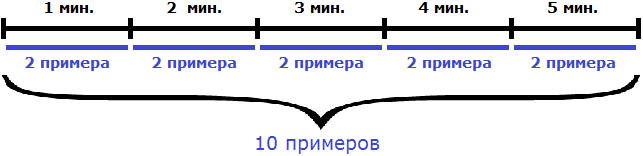
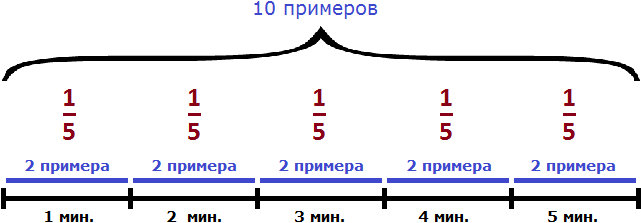
Задача 10. Джон решил 10 примеров за 5 минут. С какой производительностью он решал эти примеры?
10 примеров это выполненная Джоном работа. 5 минут — время работы. Разделим выполненную работу на время работы и определим производительность Джона:
10 : 5 = 2 примера в минуту.
Производительность Джона равна двум примерам в минуту.
Задача 11. Джон решил несколько примеров за 5 минут. С какой производительностью он решил эти примеры?
Это та же самая задача, что и предыдущая, но в ней работа не выражена каким-либо числом. Сказано лишь то, что Джон выполнил эту работу за 5 минут. Поэтому, конкретную производительность в такой задаче узнать нельзя. Но можно воспользоваться дробями. Обозначим выполненную работу через единицу. Тогда производительность работы Джона будет выражаться дробью – частью примеров, решенных за единицу времени. Если вы изучили задачи на дроби, то должны понимать о чем идёт речь.
Итак, обозначим выполненную работу через единицу:
A = 1
Мы знаем, что для нахождения производительности, выполненную работу нужно разделить на время. Время работы у нас равно пяти минутам. Поэтому, единицу делим на пять минут:
Дробь выражает часть работы, выполненную Джоном за единицу времени. Если мы вернемся к предыдущей задаче, где выполненная работа была равна десяти примерам и найдем одну пятую от этой работы, то получим 2
Выражать выполненную работу через единицу часто приходится при решении задач на совместную работу.
Задачи на совместную работу
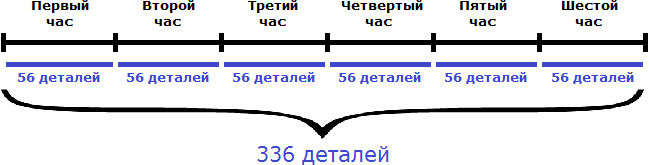
Задача 1. Первый мастер за 2 часа изготавливает 64 детали, а второй за 3 часа – 72 детали. За сколько часов они изготовят 336 деталей?
В данной задаче речь идет о совместной работе. Необходимо определить производительность обоих мастеров и найти время за которое они изготовят 336 деталей.
Для начала определим производительность первого мастера:
64 : 2 = 32 дет./час
Определим производительность второго мастера:
72 : 3 = 24 дет./час
Определим совместную производительность мастеров. Для этого сложим количество деталей, которые они изготавливают по отдельности за единицу времени. То есть сложим их производительности:
32 дет./час + 24 дет./час = 56 дет./час
Вместе за один час мастера изготавливают 56 деталей. Чтобы узнать за сколько часов они изготовят 336 деталей, нужно определить сколько раз 336 содержит по 56
336 : 56 = 6 часов
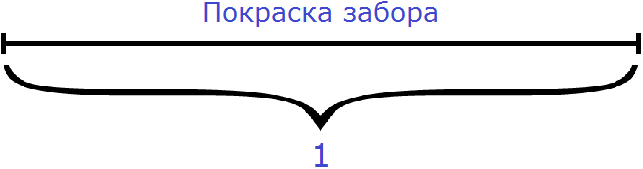
Задача 2. Первый мастер может покрасить забор за 20 минут, а второй мастер – за 30 минут. За сколько минут, работая вместе, они могут покрасить забор?
Решение
В данной задаче, в отличие от предыдущей, работа не выражена каким-либо числом. Сказано лишь то, что эту работу первый мастер может выполнить за 20 минут, а второй за 30 минут.
В такой ситуации можно воспользоваться дробями. Мы можем обозначить всю работу (покраску забора) через единицу.
Итак, обозначим работу (покраску забора) через единицу:
A = 1
Производительность первого мастера будет выражáться дробью . То есть за одну минуту он покрасит одну двадцатую часть забора. Единица это вся работа, а двадцать минут это время работы. Запишем производительность первого мастера с помощью формулы нахождения производительности:
А производительность второго мастера будет выражáться дробью . То есть за одну минуту он покрасит одну тридцатую часть забора:
Определим общую производительность мастеров. Для этого сложим дроби, выражающие производительность первого и второго мастеров:
это дробь, выражающая общую производительность обоих мастеров. То есть за одну минуту мастера вместе покрасят
часть забора.
Определим время за которое мастера покрасят забор вместе. Для этого воспользуемся формулой нахождения времени: разделим выполненную работу на общую производительность мастеров. Выполненная работа у нас выражена единицей, а производительность — дробью
Ответ: работая вместе, мастера покрасят забор за 12 минут.
Задача 3. Первый рабочий может выполнить заказ за 8 часов, а второй за 6 часов. Два часа они работали вместе, а заканчивал работу один второй рабочий. Сколько времени потребовалось для выполнения этого заказа?
Решение
Обозначим всю работу через единицу
A = 1
Тогда первый рабочий за один час может выполнить часть работы, а второй рабочий
часть работы. А вместе за один час они могут выполнить
часть работы
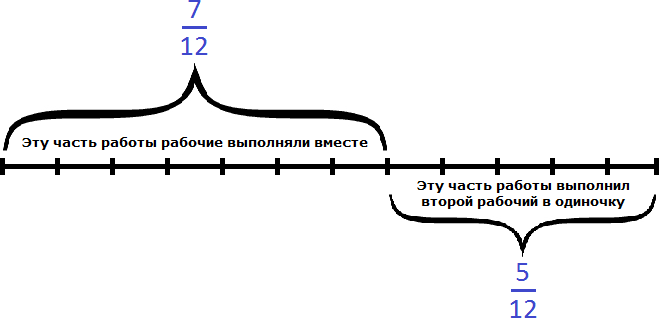
Рабочие работали вместе два часа, поэтому умножим часть работы, выполняемую ими за один час на 2:
Остальную часть работы, а именно работы заканчивал один второй рабочий:
Второй рабочий за один час мог выполнить часть работы. Чтобы определить время за которое он завершил оставшуюся
часть работы, воспользуемся формулой нахождения времени.
Переменная A теперь равна , переменная v —
Теперь определим общее время заказа. Первые два часа рабочие работали вместе, остальную часть работы второй рабочий выполнил за два с половиной часа, отсюда имеем 4,5 ч.
2 + 2,5 = 4,5 ч.
Ответ: для выполнения заказа потребовалось 4,5 ч.
Задача 4. Одна труба наполняет бассейн за 6 ч, а другая – за 4 ч. За
сколько часов наполняют бассейн обе трубы, работая вместе?
Решение
Обозначим работу (наполнение бассейна) через единицу
A = 1
Тогда первая труба за один час выполнит часть работы, а вторая труба —
часть работы. Работая вместе за один час они выполнят
часть работы:
Определим время за которое обе трубы наполняют бассейн, работая вместе:
2,4 это два целых часа и четыре десятых часа
2,4 = 2 ч + 0,4 ч
А четыре десятых часа это 24 минуты
60 мин. × 0,4 = 24 мин.
Ответ: работая вместе обе трубы наполнят бассейн за 2 ч 24 мин.
Задачи для самостоятельного решения
Задача 1. Первая бригада может выполнить некоторое задание за 12 часов, вторая – за 4 часа. За сколько часов они выполнят задание, если будут работать вместе?
Решение
Обозначим работу через единицу:
A = 1
Тогда первая бригада за один час выполнит 



Определим время за которое обе бригады выполнят задание, работая вместе:
Ответ: обе бригады выполнят задание за 3 часа.
Задача 2. Лошадь съедает копну сена за 1 сутки, корова может съесть такую же копну за 3 суток, а овца за 6 суток. За какое время съедят эту копну лошадь, корова и овца вместе.
Решение
Работа в данном случае это съедание копны сена. Обозначим её через единицу:
A = 1
Тогда производительность лошади будет выражáться единицей, производительность коровы — дробью 
. Их совместная производительность равна следующей сумме:
Определим время, за которое лошадь, корова и овца съедят 1 копну сена:
Ответ: лошадь, корова и овца съедят 1 копну сена за суток или 16 часов.
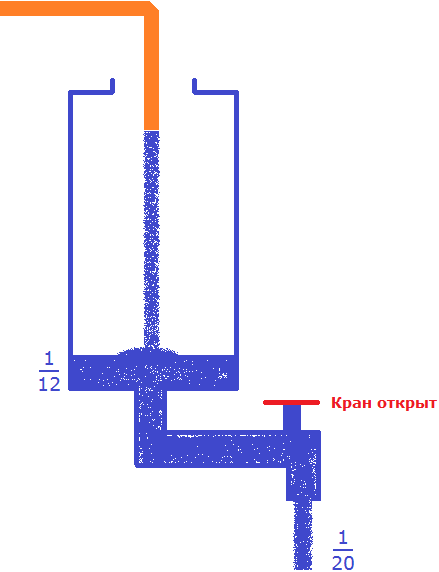
Задача 3. Сосуд наполняется шлангом за 12 мин, а полный сосуд опорожняется при открытии крана за 20 мин. За какое время наполнится пустой сосуд, если одновременно открыть кран и вливать в него воду через шланг?
Решение
Работа в данном случае это наполнение сосуда. Обозначим эту работу через единицу:
A = 1
В условии сказано, что сосуд наполняется шлангом за 12 минут. Значит в минуту будет наполняться 

В сосуд поступает воды больше, чем вытекает. Дробь 

Несмотря на то, что часть поступающей в сосуд воды будет вытекать, с каждой минутой сосуд будет пополняться на определенную часть. Узнаем, что эта за часть. Для этого из поступающей 
Каждую минуту сосуд будет наполняться на 
Определим время за которое наполнится пустой сосуд, если одновременно открыть кран и вливать в него воду через шланг:
Ответ: если одновременно открыть кран и вливать в пустой сосуд воду через шланг, то он наполнится за 30 минут.
Задача 4. Через первую трубу бассейн можно заполнить за 20 ч, через вторую за 30 ч. Какая часть бассейна заполнится через обе трубы за 1 ч?
Решение
Работа в данном случае это заполнение бассейна. Обозначим эту работу через единицу:
A = 1
Производительность заполнения бассейна через первую трубу будет выражáться дробью 

Производительность по определению есть работа, выполненная за единицу времени. Значит дробь 

Ответ: за один час заполнится 
Задача 5. На прокладку траншеи требуется затратить 10 ч. Экскаватор проработал 8 ч, после чего ему осталось пройти 50 м. Найти общую длину траншеи.
Решение
В задаче подразумевается, что экскаватор работал с одинаковой производительностью на протяжении всей работы. На работу требовалось затратить 10 ч. Проработано было 8 ч. Значит осталось еще 2 часа. На 2 часа приходятся оставшиеся 50 метров траншеи. Если разделить 50 метров на 2, то можно определить сколько метров экскаватор прокладывает за один час:
50 : 2 = 25 м./ч
В час экскаватор прокладывал 25 метров. Работал он 10 часов. Умножим 25 на 10, мы определим общую длину траншеи:
25 × 10 = 250 м
Ответ: общая длина траншеи составляет 250 м.
Задача 6. Ванна заполняется холодной водой за 6 мин 40 с, горячей – за 8 мин. Кроме того, если из полной ванны вынуть пробку, вода вытечет за 13 мин 20 с. Сколько времени понадобится, чтобы наполнить ванну полностью, при условии, что открыты оба крана, но ванна не заткнута пробкой?.
Решение
Для удобства переведем время данное в задаче в секунды
6 мин 40 с = 400 с
8 мин = 480 с
13 мин 20 с = 800 с
Обозначим заполнение ванны через единицу:
A = 1
Производительность первого крана будет выражáться дробью 


Одновременно с открытыми двумя кранами, вынута пробка из ванны. Поэтому часть поступающей в ванну воды сразу выходит через слив. Эта часть будет выражáться дробью 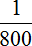
С каждой секундой ванна будет пополняться на определенную часть воды. Узнаем какая это часть. Для этого из поступающей части воды вычтем ту часть, которая вытекает через слив.
Определим сколько времени понадобится, чтобы наполнить ванну:
Ванна наполнится за 300 секунд. Поскольку задача завершена, секунды можно обратно перевести в минуты. Триста секунд это пять минут:
300 : 60 = 5 мин
Ответ: ванна заполнится за 5 мин.
Понравился урок?
Вступай в нашу новую группу Вконтакте и начни получать уведомления о новых уроках
Возникло желание поддержать проект?
Используй кнопку ниже

|
Урок математики |
Дата |
Класс 4 |
|||||||||||||||||||||||
|
Тема занятия: |
Зависимости между величинами: производительность, время, затраченное на работу, выполненная |
||||||||||||||||||||||||
|
Общие цели: |
В течение урока, основываясь на понятии «производительность», «время работы», «работа» установить взаимосвязь между этими величинами и вывести формулу работы А= v · t (v = А : t t = А : v) |
||||||||||||||||||||||||
|
Результаты обучения: |
Учащиеся смогут: 1. Владеть понятиями «производительность», «время работы», «работа». 2. Самостоятельно выявить зависимость между величинами: объёмом выполненной работы (А), производительностью (V) и временем (t), построить формулу работы А= v · t. 3. Установить взаимосвязь между этими величинами. 4. Находить и использовать формулы для решения задач А= v · t, v = А : t, t = А : v 5. Развивать навыки устного и письменного счета, внимание, логическое мышление. |
||||||||||||||||||||||||
|
Материалы и оборудование |
Карточки с текстами заданий, самостоятельной работы. |
||||||||||||||||||||||||
|
Ход урока |
|||||||||||||||||||||||||
|
Этапы проведения урока |
Действия преподавателя и действия участников |
Модули, формы работы |
|||||||||||||||||||||||
|
Повторение изученного материала |
1. Устный счет 1. Вычисли сумму чисел 2 478 и 3 000. 4. 90725= 90000+700+20+5 5. 282 6. 560000 7. 450:3= 150 8. 4400 9. 4 ) |
Индивидуально, парная работа |
|||||||||||||||||||||||
|
I этап – Вызов |
|||||||||||||||||||||||||
|
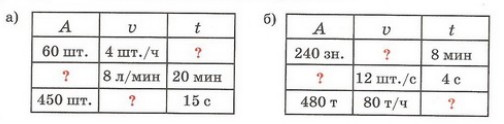
Целеполагание «Вкусная задача» На масленицу я напекла гору вкусных блинов. Я их выпекала в несколько приёмов. В начале, я выпекала 3 блина в минуту. Сколько блинов приготовила я, работая 20 минут. – Чем эта задача отличается от тех, которые мы решали. (Задачи были с известными величинами: стороны и площадь; время, скорость и путь; стоимость, количество и цена. А в этой задаче не все величины знакомы, знаем только время). – Почему возникли затруднения? (Новые величины, нет формул). – Что мы называем формулой? (Формулой мы называем равенство, которое помогает нам установить зависимость между величинами). — Что нужно найти в задаче? (Сколько всего блинов испекла я, т.е. мою работу). Эта формула называется «ФОРМУЛА РАБОТЫ» А= v · t – О каких величинах ещё идет речь? (Выпекала 3 блина в минуту, т.е. скорость работы). – Что такое производительность труда? (В толковом словаре: способность выпускать определённое количество продукции). Скорость работы называют «ПРОИЗВОДИТЕЛЬНОСТЬЮ». Обозначим эту величину буквой «V». Что будет являться производительностью труда? (Количество заданий, которые выполнили за 1 мин). Что при этом важно учитывать? (Время работы). — Какие единицы времени чаще всего используют? (Час, день, ночь, сутки, минуты) Как по-другому можно определить, что такое производительность? На доске: производительность труда — это работа, выполненная за единицу времени. – Что ещё известно в задаче? (Время работы). О какой величине идёт речь? (О времени). Какой буквой обозначается эта величина? (t). Запишите в таблицу величины.
– Что нужно узнать в задаче? (Количество всех блинов, т.е. какую работу выполнила я) – Как найти количество блинов, которые испекла я за 20 минут, если известно, что за 1 минуту я выпекаю 3 блина. (Надо 3 блина умножить на 20 минут: 3×20=60 блинов испекла я). А= v · t — это равенство называется формулой работы. Оно означает, что работа равна производительности, умноженной на время работы. — А теперь составим обратные формулы v = А : t, t = А : v Памятка Производительность – v Работа — А Время — t v = А : t А= v · t t = А : v — Как вы думаете, над чем нам сегодня предстоит работать? Чему будем учиться? Какие задачи будем решать? 2. Знать зависимость между величинами: объёмом выполненной работы (А), производительностью (V) и временем (t), формулу работы А= v · t. 3. Установить взаимосвязь между этими величинами. 4. Находить и использовать формулы для решения задач А= v · t, v = А : t, t = А : v 5. Развивать навыки устного и письменного счета, внимание, логическое мышление. |
КО КМ ДО |
||||||||||||||||||||||||
|
II стадия – Осмысление |
|||||||||||||||||||||||||
|
1. Стратегия «Интервью». Работа с учебником: стр. 77 – 78, чтение правила, запись формулы, выполнение № 2.
2. № 6, стр. 78 3. 1 уровень Вале и Гале было поручено сделать флажки для ёлки. Валя сделала за 2 часа 40 флажков, а Галя за 3 часа — 45 флажков. Кто из них работает быстрее? За 5 мин обёрточный автомат заворачивает 725 конфет, а рабочий вручную за 9 мин 162 конфеты. На сколько меньше производительность труда рабочего по сравнению с производительностью автомата? Решение: 725 : 5 = 145 (к.) 162 : 9 = 18 (к) 145 – 18 = на 127 (к) 3 уровень а) Один экскаватор за 7 часов выкапывает 133 м канавы, а другой экскаватор за 19 часов выкапывает 342 метра канавы. Какой экскаватор выгоднее приобрести, если цена на них одинаковая? Решение: 133 : 7 = 19 (м) 342 : 19 = 18 (м) Выгоднее приобрести экскаватор, который выкапывает за час 19 м. б) В квартире неисправны два крана холодной воды. На кухне за час набегает 1 литр воды. В ванной вода бежит тонкой струйкой, за сутки может уйти в канализацию 18 литров. Сколько всего литров питьевой воды уйдет за 1 сутки из двух кранов? Сколько стоит эта вода, если 1л стоит 13 тенге? Решение: 24 + 18 = 42 (л) 42 х 13 = 546 (тг) за сутки Валеологическая музыкальная пауза |
Парная работа Воз. особ Групповая работа ДО Возр особ ОиТД |
||||||||||||||||||||||||
|
Карточка
_____________________________________________________________________ Ответ:______________________________________________________________
______________________________________________________________________ Ответ: _______________________________________________________________
_____________________________________________________________________ Ответ:______________________________________________________________ |
Инд работа |
||||||||||||||||||||||||
|
Рефлексия Работа с оценочным листом
— Закончите предложения: Сегодня на уроке я запомнил… Мне понравилось выполнять… Мне было сложно… Я хочу похвалить… Я хочу пожелать…. — Урок я хочу закончить пословицей о труде. Всегда помните: «Всякое умение трудом дается». |
|||||||||||||||||||||||||
|
Домашнее задание Ученик А: № 7, стр. 78 Ученик В: Придумать, записать и решить 3 задачи на нахождение производительности, выполненной работы, времени. |
Задачи на работу и производительность уравнения
Два оператора, работая вместе, могут набрать текст газеты объявлений за 8 ч. Если первый оператор будет работать 3 ч, а второй 12 ч, то они выполнят только 75% всей работы. За какое время может набрать весь текст каждый оператор, работая отдельно?
Пусть первый оператор может выполнить данную работу за x часов, а второй за y часов. За один час первый оператор выполняет часть всей работы, а второй
. Составим систему уравнений:
Ответ: первый оператор за 12 ч, второй оператор за 24 ч.
На изготовление 231 детали ученик тратит на 11 часов больше, чем мастер на изготовление 462 таких же деталей. Известно, что ученик за час делает на 4 детали меньше, чем мастер. Сколько деталей в час делает ученик?
Предположим, что ученик делает x деталей в час, . Тогда мастер делает
детали в час.
Составим таблицу по данным задачи:
| Производительность (дет/ч) |
Время (ч) | Объём работ (дет) | |
|---|---|---|---|
| Ученик | x | 231 | |
| Мастер | 462 |
Так как ученик потратил на работу на 11 часов больше, можно составить уравнение:
.
Решим уравнение, предварительно разделив обе части на 11:
.
Корни полученного квадратного уравнения: −28 и 3. Отбрасывая отрицательный корень, находим, что ученик делает в час 3 детали.
Производительность
Продолжаем изучать элементарные задачи по математике. Сегодня мы рассмотрим очень интересную физическую величину — производительность.
Что такое сила?
Сила — это физическое явление, способное изменять форму материальных тел , вызывать их движение , менять направление и скорость движения этих тел или приводить тело в состояние покоя.
- ребята слепили снеговика, а хулиганы его разрушили. Получается, что хулиганы приложили к снеговику свою силу, тем самым вызвали изменение формы снеговика;
- на дворе стояла тележка. Прохожий случайно задел её и тележка сдвинулась с места. Получается, что прохожий применил силу к тележке и вызвал её движение;
- далее тот же прохожий остановил тележку, чтобы она далеко не уехала. Получается, что прохожий применил силу, тем самым привел тележку в состояние покоя.
Сила является физической величиной — мерой воздействия на тело других тел. Сила обозначается заглавной латинской буквой F.
Что такое работа?
Работа — это количественная мера действия силы на тело. Работа зависит от количества силы, приложенной на тело и от направления этой силы, а также от перемещения данного тела.
Например, если мы попробуем сдвинуть шкаф с места и он сдвинется, то можно сказать, что мы совершили работу, поскольку сила, которую мы приложили, привела к тому, что шкаф совершил перемещение на некоторое расстояние.
Если же мы, к примеру, попробуем толкнуть стену, то стена с места не сдвинется, а значит и работа не будет совершена, поскольку сила была приложена, но эта сила не вызвала никакого перемещения стены.
Работа обозначается заглавной латинской буквой A.
Производительность
Производительностью называют работу, выполненную за единицу времени. Под единицей подразумевается 1 час, 1 минута или 1 секунда. Производительность обозначается латинской буквой v
Рассмотрим следующий пример. Два пекаря пекли булочки. Первый пекарь испёк 40 булочек за 10 минут, а второй 15 булочек за 5 минут. Как узнать, кто из пекарей работал быстрее, первый или второй?
Работал быстрее тот, кто за одну минуту выпекает больше булочек. Говорят, что у него производительность больше. Для нахождения производительности предусмотрено следующее правило:
Чтобы найти производительность, надо выполненную работу разделить на время работы.
Также, можно воспользоваться формулой:
где v — производительность, A — выполненная работа, t — время работы.
Вернемся к нашей задаче. Зная правило или формулу нахождения производительности, можно определить сколько булочек приходится на одну минуту.
Найдём производительность первого пекаря. Разделим работу, которую он выполнил, на время которое он на нее затратил. Выполненная работа это количество испеченных им булочек, то есть 40, а время — 10 минут
40 : 10 = 4 булочки в минуту
Аналогично найдём производительность второго пекаря. Разделим 15 на 5
15 : 5 = 3 булочки в минуту
Первый пекарь в минуту выпекает больше булочек чем второй, значит его производительность выше. Отсюда делаем вывод, что работает он быстрее второго пекаря.
Также можно воспользоваться формулой нахождения производительности. В этом случае решение принимает следующий вид:
Под буквой v можно делать метки, указывающие для кого/чего мы находим производительность.
Задача 2. Тому нужно за 2 дня прочитать книгу, в которой 100 страниц. В первый день он читал 4 часа со скоростью 12 страниц в час. С какой скоростью ему надо читать оставшуюся часть книги, если у него есть на это 4 часа?
Узнаем сколько страниц Том прочитал в первый день. Он читал 12 страниц в час. Чтению в первый день он посвятил 4 часа, поэтому для нахождения количества прочитанных страниц в первый день, нужно 12 умножить на 4
12 × 4 = 48 страниц прочитано в первый день
Узнаем сколько страниц осталось прочесть. Вычтем из общего количества страниц ( 100 ) количество прочитанных страниц ( 48 )
100 − 48 = 52 страницы осталось прочесть
Осталось прочесть 52 страницы. Теперь найдем такую производительность, при которой Том сможет прочесть 52 страницы за 4 часа. Раскидаем 52 страницы на 4 часа поровну
52 : 4 = 13 страниц в час
Ответ: чтобы прочитать оставшуюся часть книги за 4 часа, Том должен читать ее со скоростью 13 страниц в час.
Замечание. В некоторых источниках слово «производительность» может быть заменено на слова «скорость», «эффективность», «продуктивность», «плодотворность».
Задача 3. Один насос работал 4 часа, выкачивая 158 вёдер воды в час, а другой — 3 часа, выкачивая 169 вёдер воды в час. Определить какой из насосов выкачал больше вёдер.
Решение
Определим сколько всего вёдер выкачал каждый насос по отдельности. Для этого умножим их производительность на время их работы:
158 в/ч × 4 = 632 вёдер выкачал первый насос
169 в/ч × 3 = 507 вёдер выкачал второй насос
Ответ: первый насос выкачала больше вёдер, чем второй.
Задача 4. За 2 часа насос выкачал 80 литров воды. Определить сколько литров он выкачает за 5 часов.
Решение
Сначала нужно определить сколько литров воды насос выкачивает за час. Для этого 80 литров разделим на 2 часа — получим 40 литров
80 : 2 = 40 литров в час
За один час насос выкачивает 40 литров воды. За 5 часов выкачает в пять раз больше
40 × 5 = 200 литров
Ответ: за 5 часов насос выкачает 200 литров воды.
Если известны производительность и время работы, то можно найти выполненную работу. Выполненная работа равна производительности умноженной на время работы:
A = v × t
Например, если производительность пекаря составляет 50 булочек в час, и он проработал 4 часа, то можно найти всю выполненную работу за эти четыре часа. Для этого производительность (50 бул/ч) нужно умножить на время его работы (4ч)
50 × 4 = 200 булочек
Если известны работа и производительность, то можно найти время работы. Время работы равно отношению выполненной работы к производительности:
Например, если в неделю бригада отстраивает 2 этажа, то можно узнать сколько недель потребуется для отстройки 8 этажей. Чтобы определить время отстройки восьми этажей, нужно выполненную работу (8 этажей) разделить на производительность (2 эт./нед):
Либо с помощью формулы, приведенной выше:
Если в неделю строится 2 этажа, то 8 этажей будет отстроено за четыре недели. В данном случае вся работа была равна восьми. Производительность была равна двум, поскольку по определению производительность есть работа, выполненная за единицу времени – в нашем случае два этажа за неделю.
Задача 6. Принтер работает с производительностью 70 стр./ч. Сколько страниц он напечатает за 5 часов?
Решение
Если в час принтер печатает 70 страниц, то за 5 часов он напечатает в 5 раз больше:
70 × 5 = 350 страниц
Также, решение можно записать с помощью формулы нахождения работы. В данном случае, количество напечатанных страниц являются выполненной работой:
A = v × t = 70 × 5 = 350 страниц
Задача 7. Принтер напечатал 350 страниц за 5 часов. С какой производительностью он работал?
Решение
Если в течении пяти часов принтер напечатал 350 страниц, то в течении часа он печатал 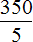
350 : 5 = 70 стр./ч.
Либо с помощью формулы нахождения производительности:
Задача 8. Принтер работал с производительностью 70 страниц в час и напечатал 350 страниц. Определить время работы принтера.
Решение
Выражение «работал с производительностью 70 страниц в час» означает, что в каждом часе принтер печатал по 70 страниц. И это продолжалось до тех пор, пока он не напечатал 350 страниц. Очевидно, что разделив 350 страниц по 70, мы определим время работы принтера, то есть узнаем сколько часов он работал
Либо с помощью формулы нахождения времени:
Задача 9. Машинистка в первый день напечатала 48 страниц рукописи, а во второй день — на 12 страниц больше, чем в первый. На всю работу в эти 2 дня она затратила 9 часов. Сколько часов работала она в каждый из этих дней, если производительность её не менялась ?
Решение
Определим сколько страниц напечатала машинистка во второй день. В условии сказано, что напечатала она на 12 страниц больше, чем в первый:
48 + 12 = 60 страниц во второй день.
Определим сколько страниц машинистка напечатала за два дня:
48 + 60 = 108 страниц за два дня.
На эту работу машинистка затратила 9 часов. Также сказано, что производительность её не менялась. Если мы разделим выполненную работу (108) на время выполнения (9), то определим производительность машинистки:
108 : 9 = 12 страниц в час.
Теперь мы можем определить сколько часов работала машинистка в каждый из двух дней. Для этого поочередно разделим выполненные работы в каждом из двух дней на производительность:
48 : 12 = 4 часа работала машинистка в первый день
60 : 12 = 5 часов работала машинистка во второй день.
Задача 10. Джон решил 10 примеров за 5 минут. С какой производительностью он решал эти примеры?
10 примеров это выполненная Джоном работа. 5 минут — время работы. Разделим выполненную работу на время работы и определим производительность Джона:
10 : 5 = 2 примера в минуту.
Производительность Джона равна двум примерам в минуту.
Задача 11. Джон решил несколько примеров за 5 минут. С какой производительностью он решил эти примеры?
Это та же самая задача, что и предыдущая, но в ней работа не выражена каким-либо числом. Сказано лишь то, что Джон выполнил эту работу за 5 минут. Поэтому, конкретную производительность в такой задаче узнать нельзя. Но можно воспользоваться дробями. Обозначим выполненную работу через единицу. Тогда производительность работы Джона будет выражаться дробью – частью примеров, решенных за единицу времени. Если вы изучили задачи на дроби, то должны понимать о чем идёт речь.
Итак, обозначим выполненную работу через единицу:
Мы знаем, что для нахождения производительности, выполненную работу нужно разделить на время. Время работы у нас равно пяти минутам. Поэтому, единицу делим на пять минут:
Дробь 
Выражать выполненную работу через единицу часто приходится при решении задач на совместную работу.
Задачи на совместную работу
Задача 1. Первый мастер за 2 часа изготавливает 64 детали, а второй за 3 часа – 72 детали. За сколько часов они изготовят 336 деталей?
В данной задаче речь идет о совместной работе. Необходимо определить производительность обоих мастеров и найти время за которое они изготовят 336 деталей.
Для начала определим производительность первого мастера:
64 : 2 = 32 дет./час
Определим производительность второго мастера:
72 : 3 = 24 дет./час
Определим совместную производительность мастеров. Для этого сложим количество деталей, которые они изготавливают по отдельности за единицу времени. То есть сложим их производительности:
32 дет./час + 24 дет./час = 56 дет./час
Вместе за один час мастера изготавливают 56 деталей. Чтобы узнать за сколько часов они изготовят 336 деталей, нужно определить сколько раз 336 содержит по 56
336 : 56 = 6 часов
Задача 2. Первый мастер может покрасить забор за 20 минут, а второй мастер – за 30 минут. За сколько минут, работая вместе, они могут покрасить забор?
Решение
В данной задаче, в отличие от предыдущей, работа не выражена каким-либо числом. Сказано лишь то, что эту работу первый мастер может выполнить за 20 минут, а второй за 30 минут.
В такой ситуации можно воспользоваться дробями. Мы можем обозначить всю работу (покраску забора) через единицу.
Итак, обозначим работу (покраску забора) через единицу:
Производительность первого мастера будет выражáться дробью 
А производительность второго мастера будет выражáться дробью 
Определим общую производительность мастеров. Для этого сложим дроби, выражающие производительность первого и второго мастеров:


Определим время за которое мастера покрасят забор вместе. Для этого воспользуемся формулой нахождения времени: разделим выполненную работу на общую производительность мастеров. Выполненная работа у нас выражена единицей, а производительность — дробью
Ответ: работая вместе, мастера покрасят забор за 12 минут.
Задача 3. Первый рабочий может выполнить заказ за 8 часов, а второй за 6 часов. Два часа они работали вместе, а заканчивал работу один второй рабочий. Сколько времени потребовалось для выполнения этого заказа?
Решение
Обозначим всю работу через единицу
Тогда первый рабочий за один час может выполнить 
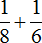
Рабочие работали вместе два часа, поэтому умножим часть работы, выполняемую ими за один час на 2:
Остальную часть работы, а именно 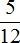
Второй рабочий за один час мог выполнить часть работы. Чтобы определить время за которое он завершил оставшуюся 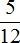
Переменная A теперь равна 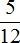
Теперь определим общее время заказа. Первые два часа рабочие работали вместе, остальную часть работы второй рабочий выполнил за два с половиной часа, отсюда имеем 4,5 ч.
Ответ: для выполнения заказа потребовалось 4,5 ч.
Задача 4. Одна труба наполняет бассейн за 6 ч, а другая – за 4 ч. За
сколько часов наполняют бассейн обе трубы, работая вместе?
Решение
Обозначим работу (наполнение бассейна) через единицу
Тогда первая труба за один час выполнит часть работы, а вторая труба — 
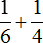
Определим время за которое обе трубы наполняют бассейн, работая вместе:
2,4 это два целых часа и четыре десятых часа
А четыре десятых часа это 24 минуты
60 мин. × 0,4 = 24 мин.
Ответ: работая вместе обе трубы наполнят бассейн за 2 ч 24 мин.
Задачи для самостоятельного решения
Решение
Обозначим работу через единицу:
Тогда первая бригада за один час выполнит 



Определим время за которое обе бригады выполнят задание, работая вместе:
Ответ: обе бригады выполнят задание за 3 часа.
Решение
Работа в данном случае это съедание копны сена. Обозначим её через единицу:
Тогда производительность лошади будет выражáться единицей, производительность коровы — дробью 
Определим время, за которое лошадь, корова и овца съедят 1 копну сена:
Ответ: лошадь, корова и овца съедят 1 копну сена за суток или 16 часов.
Решение
Работа в данном случае это наполнение сосуда. Обозначим эту работу через единицу:
В условии сказано, что сосуд наполняется шлангом за 12 минут. Значит в минуту будет наполняться 

В сосуд поступает воды больше, чем вытекает. Дробь 

Несмотря на то, что часть поступающей в сосуд воды будет вытекать, с каждой минутой сосуд будет пополняться на определенную часть. Узнаем, что эта за часть. Для этого из поступающей 
Каждую минуту сосуд будет наполняться на 
Определим время за которое наполнится пустой сосуд, если одновременно открыть кран и вливать в него воду через шланг:
Ответ: если одновременно открыть кран и вливать в пустой сосуд воду через шланг, то он наполнится за 30 минут.
Решение
Работа в данном случае это заполнение бассейна. Обозначим эту работу через единицу:
Производительность заполнения бассейна через первую трубу будет выражáться дробью 

Производительность по определению есть работа, выполненная за единицу времени. Значит дробь 

Ответ: за один час заполнится 
Решение
В задаче подразумевается, что экскаватор работал с одинаковой производительностью на протяжении всей работы. На работу требовалось затратить 10 ч. Проработано было 8 ч. Значит осталось еще 2 часа. На 2 часа приходятся оставшиеся 50 метров траншеи. Если разделить 50 метров на 2, то можно определить сколько метров экскаватор прокладывает за один час:
В час экскаватор прокладывал 25 метров. Работал он 10 часов. Умножим 25 на 10, мы определим общую длину траншеи:
Ответ: общая длина траншеи составляет 250 м.
Решение
Для удобства переведем время данное в задаче в секунды
6 мин 40 с = 400 с
8 мин = 480 с
13 мин 20 с = 800 с
Обозначим заполнение ванны через единицу:
Производительность первого крана будет выражáться дробью 


Одновременно с открытыми двумя кранами, вынута пробка из ванны. Поэтому часть поступающей в ванну воды сразу выходит через слив. Эта часть будет выражáться дробью 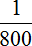
С каждой секундой ванна будет пополняться на определенную часть воды. Узнаем какая это часть. Для этого из поступающей части воды вычтем ту часть, которая вытекает через слив.
Определим сколько времени понадобится, чтобы наполнить ванну:
Ванна наполнится за 300 секунд. Поскольку задача завершена, секунды можно обратно перевести в минуты. Триста секунд это пять минут:
Ответ: ванна заполнится за 5 мин.
Понравился урок?
Вступай в нашу новую группу Вконтакте и начни получать уведомления о новых уроках
Возникло желание поддержать проект?
Используй кнопку ниже
16 thoughts on “Производительность”
Спасибо за прекрасные уроки. Жду с нетерпением уроки на уравнениe. Знаю,знаю у вас пока времени нет =)
Одно замечание- некоторые действительно сложные примеры Вы недостаточно разъясняете…простое разжёвываете слишком, а сложное недостаточно…
А в целом большое спасибо.
Спасибо за урок!
Производительность и задачи на движение очень схожи между собой.
я, в общем-то, всё! остался урок по элементам статистики и перехожу на алгебру =) жаль здесь её нет(
Согласен. В будущем хотелось бы увидеть разделы по алгебре и геометрии
здраствуйте ! спасибо вам ! продолжение будет
Задачи на работу в ЕГЭ 2019. Примеры с решением
Еще одним классическим примером текстовых задач, которые могут встретиться в 11 задании профильного ЕГЭ, — это задачи на работу. Это всевозможные задачи про рабочих, которые делают детали, про трубы, которые наполняют бассейны, а также про совместную работу.
Научиться решать такие задачи довольно просто, главное – выучить одну единственную формулу, знать основные правила решения задач этого типа и следовать трем простым шагам.
Формула, которую обязан знать каждый
Формула, без которой не получится решить не одну задачу на работу:
Время – это время, за которое выполняется заданный объем работы.
Производительность – это, по сути, скорость выполнения заданного объема работы за определенное время. Например, рабочий делает 10 деталей в час – это и есть его производительность.
Из данной формулы нужно уметь выражать производительность и время:
Как решать задачи на работу: основные правила
При решении задач на работу нужно знать следующие правила:
- Если работу выполняют двое рабочих, то их производительности складываются
- Если объем работы в задаче не задан и нет данных, позволяющих его найти, и при этом объем работы не важен для решения задачи, то работа принимается за единицу.
- За переменную Х, как правило, удобнее всего брать производительность
Решение задачи на работу: 3 простых шага
Решение задачи на работу сводится к трем шагам:
- Задаем переменную Х и составляем таблицу
- Составляем уравнение на основании таблицы и условий задачи, решаем его
- Возвращаемся к условиям задачи, вспоминаем, что требовалось найти и находим ответ
Не забывайте про третий шаг, так как часто ученики, верно решив уравнение, сразу записывают ответ к задаче, забывая о том, что требовалось найти по условиям задачи. И по сути правильная решенная задача не получает заслуженного балла.
Примеры решения задач на работу: от простого к сложному
Задача 1
Первый рабочий выполняет заказ из 120 деталей на 2 часа быстрее, чем второй. Также известно, что первый рабочий делает на 3 детали в час больше, чем второй. Сколько деталей в час изготавливает первый рабочий?
1. Составим таблицу на основании условий задачи. Производительность первого рабочего примем за Х. Тогда производительность второго рабочего будет х — 3, так как второй рабочий делает на 3 детали в час меньше первого. Время выполнения всей работы получаем путем деления всей работы на производительность.

120 (х- 3) + 2х (х-3) = 120х
120х – 360 + 2х 2 – 6х – 120х =0
2х 2 – 6х – 360 = 0
Делим обе части уравнения на 2:
х 2 – 3х – 180 = 0
3. Возвращаемся к условиям задачи. Нам нужно было найти, сколько деталей изготавливает первый рабочий. Именно эту величину мы обозначали за Х. Х2 нам не подходит по смыслу задачи. Следовательно, первый рабочий изготавливает 15 деталей в час.
Ответ: 15 деталей в час
Задача 2
Первая труба наполняет резервуар объемом 180 литров, а вторая труба наполняет резервуар объемом 120 литра. При этом известно, что одна из труб пропускает на 1 литр воды в минуту меньше, чем другая. Необходимо определить, сколько литров в минуту пропускает первая труба, если резервуары наполняются одновременно.
1. На основании условия задачи составляем таблицу. Производительность первой трубы, то есть сколько воды она пропускает в минуту, обозначим за Х. Тогда производительность второй трубы будет либо на 1 литр в минуту больше, либо на 1 литр в минуту меньше. Это мы можем обозначить, как х ± 1. Время рассчитываем по формуле и заносим в таблицу:



180х – 120х = 180
Решаем второе уравнение:
180х – 120х = -180
3. Возвращаемся к условиям задачи. Нам необходимо было определить, сколько литров в минуту пропускает первая труба. Именно это – производительность первой трубы мы и обозначали за Х. Х2 нам не подходит по смыслу задачи. Следовательно, первая труба пропускает 3 литра в минуту.
Ответ: 3 литра в минуту
Задача 3
Первая труба пропускает на 5 литров воды в минуту меньше, чем вторая. Определить сколько литров воды в минуту пропускает первая труба, если известно, что бассейн объемом 300 литров она заполняет на 3 минуты дольше, чем вторая.
1. На основании условий задачи составляем таблицу. Производительность второй трубы обозначим за Х. Тогда производительность первой трубы Х – 5, так как она пропускает на 5 литров воды в минуту меньше. Объем бассейна (это объем работы труб) равен 300 литрам. Время работы труб определяем по формуле и заносим в таблицу:


300х – 3х (х-5) = 300 (х — 5)
300х – 3х 2 + 15х – 300х + 1500 = 0
-3х 2 + 15х + 1500 = 0
Делим обе части уравнения на -3:
х 2 — 5х — 500 = 0
3. Возвращаемся к условиям задачи. Нам необходимо было найти производительность первой трубы, которую мы обозначили, как (х – 5).
Подставляем полученное значение Х:
Подставляем х1: 25 – 5 = 20
Подставляем х2: -20 – 5 = -25
Второй результат нам не подходит по смыслу задачи. Следовательно, производительность первой трубы равна 20 литров в минуту.
Ответ: 20 литров в минуту.
Примеры решения задачи на совместную работу
Задача 4
Двое рабочих, работая вместе, могут выполнить работу за 15 часов. За сколько часов, работая отдельно, выполнит эту работу первый рабочий, если он за 4 часа выполняет такую же часть работы, какую второй — за 5 часов.
Решение. Способ 1:
1. Составим таблицу на основании условий задачи. Так как общий объем работы нам не дан в задачи, то принимаем его за единицу. Этот объем работы двое рабочих выполняют за 15 часов, следовательно, их производительность труда равна 1/15. Обозначим за Х время, которое потребуется первому рабочему для выполнения всей работы. Тогда его производительность будет равна 1/х. Следовательно, за 4 часа первый рабочий выполнит 4 * 1/х= 4/х части работы. Эту же часть работы 4/х второй рабочий может выполнить за 5 часов, следовательно, его производительность труда равна 4/х / 5 =4/5х. Заносим полученные данные в таблицу:


3. Возвращаемся к условиям задачи. Нам нужно определить, за какое время выполнит всю работу первый рабочий. Именно это мы и обозначали за Х. Следовательно, первый рабочий выполнит всю работу, работая один, за 27 часов.
Теперь разберем, как эту же задачу можно решить с помощью системы уравнений.
Решение. Способ 2:
1. Составим таблицу на основании условий задачи. Обозначим производительность труда первого рабочего за х1, а производительность второго рабочего – за х2. Следовательно, их общая производительность равна х1 + х2. А их общая работа, выполненная за 15 часов, равна 15 (х1 + х2) = 1.
Также по условию задачи известно, что одинаковое количество работы первый работник выполняет за 4 часа (т.е. его работа равна 4х1), а второй работник за 5 часов (т.е. его работа равна 5х2). Таким образом:
4х1 = 5х2
2. Сведем в систему уравнений, полученные в первом пункте уравнения:
Умножаем обе части уравнения на 4:


Таким образом, мы решили задачу на совместную работу двумя способами: с помощью уравнения и с помощью системы уравнений. Выбирайте тот, который вам понятнее.
Надеюсь, мы достаточно подробно разобрали, как решать задачи на работу и теперь вы легко с ними справитесь.
источники:
http://spacemath.xyz/proizvoditelnost/
http://yourrepetitor.ru/zadachi-na-rabotu-v-ege-2019-primery-s-resheniem/
Тема: Работа, производительность,
время.
Цель:
ввести понятия «производительность», «выполненная работа», «время,
затраченное на работу»
Задачи:
v
установить связь между
величинами «производительность», «выполненная работа», «время, затраченное на
работу» в ходе исследовательской работы учащихся;
v
Познакомить с новым видом
задач на производительность;
v
Развивать навыки умножения
и деления многозначного числа на однозначное;
v
Формировать навыки устных
и письменных вычислений;
v
Воспитывать позитивное
отношение к труду.
Оборудование: учебник, карточки для индивидуальной работы, табличка с пословицей –
эпиграфом урока, карточки для введения в новую тему, песочные часы, таблица,
стикеры — цветочки.
Ход урока
I. Организационный момент.
У.- Начинается урок,
Он пойдёт ребятам впрок,
Постарайтесь всё понять,
Учитесь тайны открывать,
Ответы полные давать,
Чтоб за работу получать
Только лишь отметку «пять»!
Слово учителя: Какую работу мы можем выполнить на
сегодняшнем уроке математики? Решать задачи, думать над примерами, считать,
записывать условие задачи и т.д.
— Надо нам сегодня поработать!
— А какие пословицы о труде вы знаете?
· Не спеши языком, торопись делом.
· Дело мастера боится.
· Без труда не вытащишь рыбку из пруда.
· Рабочие руки не знают скуки.
— Эпиграфом нашего урока будет пословица. Прочитайте:
|
ВСЯКОЕ УМЕНИЕ ТРУДОМ ДАЁТСЯ
|
.
— Объясните значение
пословицы.
II. Актуализация опорных знаний.
1.Индивидуальная работа. Умножение и деление многозначного числа на
однозначное. Решение примеров на карточках.
Учащиеся решают примеры и делают проверку. (Взаимопроверка)
Вопросы после проверки:
— Какую работу выполняли? Кто быстрее справился? Почему?
2.Работа с классом. «Математическая разминка»
— Сколько богатырей у дядьки Черномора?
— Сколько месяцев в году, кроме летних?
— Сколько граммов в 4,5 килограммах?
— Количество букв в названии нашей страны увеличить в 400 раз.
— Мальчик лёг спать в 9 часов вечера, а смог заснуть только через три
часа. Который час показывали часы?
— Количество месяцев зимы увеличьте в 320 раз.
— Умножьте количество букв в детском имени Александра на число слогов в
нём же.
3. Повторение устных приёмов умножения и деления чисел, оканчивающихся
нулями. Игра «Кто быстрей?» (Ответы спрятаны под звездой)
140 · 5 = 700 45 000 · 2 = 90 000
700 · 6 = 4200
800 · 9 = 7200 8 000 : 4 = 2 000
6 300 : 7 = 900
— Как решали данные примеры?
4. Математический диктант.
Чему равна сумма 120 и произведения чисел 30 и 5?
Найдите частное чисел 250 и 2.
Увеличьте 460 в 2 раза.
Увеличьте 380 на 200.
Сумма чисел 800, первое слагаемое 320. Найдите второе слагаемое.
Найдите произведение чисел 320 и 3.
Запишите частное чисел 4 800 и 4.
Запишите число, меньшее 1 800 в два раза.
При проверке объяснить способ вычисления.
III. Объяснение нового материала
1. Подготовка к восприятию нового материала
— Вот песочные часы, песок высыпается в нижнюю часть за 1 минуту.
Перед вами карточки с заданиями. Сколько заданий вы успеете выполнить за одну
минуту?
- Вычисли, чему равен периметр квадрата со
стороной 60 см. - Чему равен периметр прямоугольника со
сторонами 8 см и 7 см? - Вычисли периметр треугольника со
сторонами 30 см, 45 см, 57 см. - Вычисли длину стороны квадрата, периметр
которого равен 48 см. - Найди длину прямоугольника, периметр
которого равен 30 см и ширина равна 5 см. - Вычисли площадь прямоугольника со
сторонами 7 см и 4 см. - Чему равна ширина прямоугольника, если
площадь его 45 кв. см, а длина равна 5 см? - Длина прямоугольника – 54 мм, а ширина –
на 24 мм меньше. Вычисли периметр и площадь прямоугольника.
— Минута закончилась. Переверните листок, проверьте правильность
решения. Поставьте + или – за решение.
— Сколько заданий за 1 минуту выполнили?
— А сколько бы вы выполнили за 40 минут, если бы решали весь урок
аналогичные задания? (3 · 40 = 120 з., 4 · 40 = 160 з. и т.д.)
— Что такое 40 минут? (Время выполнения задания)
— Что обозначает число 3? (Количество заданий, выполняемых за
1 минуту)
— А что обозначает число 120? ( Количество заданий, которое можно
выполнить за урок)
2. «Открытие» детьми нового знания
— Как вы думаете, над чем сегодня предстоит работать? ( Будем
учиться находить время работы, количество заданий, и всю работу)
Учитель:
— В математике существуют понятия: (карточки)
|
|
Время, затраченное на работу
|
|
|||
— А как вы понимаете слово «производительность»? (это объём работы,
выполненный за единицу времени)
— В
случае с заданиями на карточках, что будет являться производительностью труда?
(количество заданий, которые выполнили за 1 мин.)

каждого из вас? (Разная)
— Когда
умножали производительность своего труда на время 40 мин, что вы получили? (Количество
заданий, которое можем выполнить за весь урок, объём всей работы)
— Почему объём работы оказался разным у разных учеников? (Потому что
разная производительность труда)
3. Сообщение темы и цели урока. Работа по таблице.
4. Знакомство с единицами измерения производительности.
— Производительность ткацкого станка 9м/ч. — «Девять метров в час». Это
значит, что за час можно изготовить 9 метров ковра.
ΙV. Первичное закрепление.
1.
Нахождение
производительности. Задачи
Учащиеся чертят таблицу в тетрадях
А) Бригада посадила 1200 деревьев за 20 дней.
Б) Бассейн вместимостью 18 000 л наполнился через трубу за 6 ч.
В) 360 т кирпича машина перевезла за 60 рейсов.
Г) Мастерская переплела 600 книг за 10 дней.
Д) Комбайн собрал 8000 ц зерна за 10 дней.
|
Производительность |
Время, затраченное на работу |
Выполненная работа |
|
|
1) |
60 деревьев в день |
20 дней |
1200 деревьев |
|
2) |
3 000 л/ч |
6 часов |
18 000 л |
|
3) |
6 т за рейс |
60 рейсов |
360 т |
|
4) |
6 книг в день |
10 дней |
600 книг |
|
5) |
800 ц за день |
10 дней |
8 000 ц |
Вывод:
Чтобы найти производительность, надо выполненную работу разделить на время,
затраченное на работу
— Глядя в таблицу, скажите, в каких единицах измеряется
производительность?
2. Работа с правилом и формулой нахождения производительности.
Установка на запоминание правила и формулы.
Физминутка
Мы сейчас бревно распилим.
Пилим, пилим, пилим, пилим.
Мы сейчас дрова расколем.
Колем, колем, колем, колем.
Раз-два. Раз-два!
Будут на зиму дрова.
3. Сравнение задач. Задача «Рабочий в час изготавливает 20
деталей. Сколько деталей он сделает за 6 часов?»
Анализ задачи 1):
— Что нужно узнать в задаче? Сколько деталей изготовит рабочий за 6
часов, т.е. объём выполненной работы
— Что для этого надо знать? Сколько деталей он делает за час и время
работы
— Известно, сколько деталей он делает за час? (производительность 20
деталей в час)
— Известно время, затраченное на работу? 6 часов
— Как найти объём выполненной работы? 
Решение: 20 · 6 = 120 деталей
Ответ: 120 деталей изготовят за 6 часов.
Анализ задачи 2): «Рабочий за 7 часов изготавливает 175 деталей.
Сколько деталей рабочий делает за час?»
— Что известно в задаче? объём выполненной работы – 175 деталей и
время работы – 7 ч
— Что нужно узнать? Производительность

Решение: 175 : 7 = 25деталей в час
Ответ: 25 деталей в час изготавливал рабочий.
Анализ задачи 3): «Рабочий за час изготавливает 23 детали.
Сколько времени он потратил, чтобы изготовить 184 детали?»
— Что нужно узнать в задаче? Время, затраченное на работу
— Что для этого надо знать? Выполненную работу и производительность
— Известен объём работы? Известна производительность?
— Как найти время, затраченное на работу? Выполненную работу
разделить на производительность
Решение: 184 : 23 = 8 ч
Ответ: за 8 часов
— Сравнить задачи.
— Повторить, как найти производительность? Объём выполненной работы?
Время, затраченное на работу?
V. Закрепление пройденного материала.
Задание повышенной сложности.
— решить задачу при помощи графа.
«Слесарь, штукатур, водитель, маляр, крановщик, токарь и плотник были в
отпуске в разное время. Отпуск маляра был позже отпуска слесаря, отпуск
которого был позже отпуска плотника. Отпуск токаря был раньше отпуска
крановщика, но позже отпуска штукатура. Отпуск водителя был раньше отпуска
плотника, но позже отпуска крановщика. Кто из рабочих был в отпуске раньше, кто
позже?»
Рекомендации к решению.
Изображаем точками названия профессий людей. Учащиеся
анализируют условие задачи. Далее
нужно выбрать одно из отношений «раньше» или «позже». Например,
выбрали отношение «раньше». Это слово записываем около
рисунка. Читаем задачу снова, заменяя предложение со словом «позже»
предложением со словом «раньше» и показываем это на рисунке с помощью
стрелки: ведем стрелку от одного рабочего к другому, который ушёл в отпуск
раньше.

раньше
Ответ: Раньше всех пошёл в отпуск штукатур, позже всех – маляр.
VI. Рефлексия.
— С какими новыми понятиями познакомились на уроке?
— Какая производительность была у нас на уроке? Скажите одним словом.
— Можете теперь сказать, что всякое умение трудом даётся?
Урок 15. Формула работы
Гипермаркет знаний>>Математика>>Математика 3 класс>> Урок 15. Формула работы
Содержание
- 1 Что такое формула работы?
- 2 Практические задания
- 3 Подведение итогов
- 4 Вопросы на закрепление изученного материала
- 5 Домашнее задание
Что такое формула работы?

Решение:
Валя сделала меньше флажков, но она и работала меньше. Чтобы сравнить, кто из них работал быстрее, а кто медленнее, надо вычислить, сколько флажков сделала каждая из девочек за 1 час:
40: 2 = 20 (фл.) 45 : 3 = 15 (фл.)
Теперь видно, что Валя работала быстрее, так как она делала в час 20 флажков, а Галя только 15.
Скорость работы называют иначе производительностью. В нашем примере производительность Вали — 20 флажков в час, а производительность Гали — 15 флажков в час.
Итак, производительность — это работа, выполненная за единицу времени. Если обозначить всю выполненную работу буквой А, производительность — буквой V, а время работы — буквой I, то можно записать равенство:
Это равенство называется формулой работы. Оно означает, что работа равна производительности, умноженной на время работы.
Из формулы работы по правилу нахождения неизвестного множителя легко найти величины и t:
— Производительность равна работе, делённой на время работы.
— Время равно работе, делённой на производительность.
Практические задания
1. Объясни смысл предложений:
а) Вася ест мороженое с производительностью 3 мороженых в час.
б) Оля лепит пельмени с производительностью 2 штуки в минуту.
в) Денис делает табуретки с производительностью 4 табуретки в день.
г) Лёня читает книги с производительностью 5 книг в год.
д) Гена копает картошку с производительностью 3 ведра в час.
е) Ира печатает на машинке с производительностью 120 знаков в минуту.
2. Мастер вытачивает 8 деталей в час. Сколько деталей он сделает за 2 ч, 4 ч, 6 ч, 7 ч, 9 ч, t ч? Заполни таблицу и запиши формулу зависимости работы А, выполненной мастером, от времени работы t.
3. Тане надо вымыть 36 тарелок. Сколько времени она затратит на эту работу, если будет мыть в минуту 2 тарелки, 3 тарелки, 4 тарелки, 6 тарелок, 9 тарелок, тарелок? Заполни таблицу и запиши формулу зависимости времени работы t от производительности
4. По данным таблицы составь задачи и реши их:
5. Завод выпускает 208 автомобилей в день. Сколько автомобилей выпустит завод в год? (Считать, что в году 365 дней.)
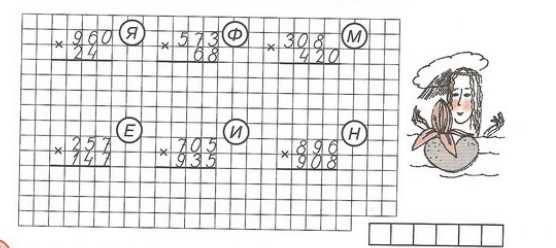
6. Расшифруй название цветка, расположив ответы примеров в порядке убывания. Почему цветок так называется?
7. Выполни действия:
152 • 387 492 • 604 999 • 555 333 • 707
8. Сравни:
7 дм 5 мм … 75 мм 6 т 8 ц … 6 800 кг
9 м 2 дм … 920 дм 6 кг 8 г … 6 800 г
2 км 32 м … 203 200 см 6 ч 8 мин … 68 мин
9. Реши уравнения с комментированием и сделай проверку:
а) (700 : х + 20): 4 — 40; б) 2 • (500-у :3) = 820.
10. Составь программу действий и вычисли:
а) 234 240 : 6 • 9 — (20 030 — 7358): 4;
б) 834 024 + 7900 ¦ 25 — (483 • 504): 8 • 10.
11. Запиши множество делителей и множество кратных числа 26.
12*. у Пусть А — множество чисел, меньших 5, а В — множество чисел, больших, чем 2, но меньших 7. Запиши множества А и В с помощью фигурных скобок. Найди их объединение и пересечение и нарисуй диаграмму Венна.
Подведение итогов
Каждый из вас, наверное, понимает, что люди трудятся для того, чтобы создавать разные полезные вещи, услуги, продукты и так далее. И важным в труде каждого человека является его производительность. А теперь давайте попробуем ответить, зачем необходимо увеличивать производительность труда? Оказывается, это делается по одной простой причине, ведь чем выше производительность труда, тем меньше затрат и времени уходит на производство какого-то одного товара.
А теперь давайте попробуем подвести итог нашего урока и выяснить, все ли нам понятно в этой теме? На этом уроке мы с вами ставили такие цели, как найти формулу работы, научиться ее пользоваться и попробовать решать задачи с помощью формулы работы. Как мне кажется, с этими задачами мы с вами справились.
На сегодняшнем уроке вы узнали, что такое формула работы и выглядит она вот так:
Также вы уже знаете, что обозначает каждая из букв в этой формуле:
Также, на сегодняшнем уроке вы при решении задач пробовали установить взаимосвязь между величинами, которые имеются в формуле работы:
Вопросы на закрепление изученного материала
1. А теперь давайте вспоминать, как нужно пользоваться формулой работы?
2. А теперь внимательно подумайте и вспомните, каким другим словом можно заменить скорость, с которой была выполнена работа?
3. Что нам необходимо сделать, что узнать производительность работы?
4. Какой буквой в формуле работы принято обозначать время?
5. Какой буквой принято в формуле работы обозначать выполненную работу?
6. Как мы можем найти время работы, если нам известна производительность и выполненная работа?
Домашнее задание
1. Решите задачи и узнайте, чему равна производительность, если:
а) Наталья съедает за 1 час 3 яблока.
б) Женя помогает маме готовить обед. Она за 2 минуты лепит 4 вареника.
в) За 1 год Таня прочитывает 8 книг.
г) Строитель кладет 60 кирпичей за 20 минут.
д) Миша моет 5 тарелок за 10 минут.
2. С помощью формулы работы составьте задачи, решите их и недостающие значения запишите в таблицу:
3. Подумайте, какую работу вы выполняете ежедневно дома, и составьте задачи, рассчитывающие вашу производительность в течение дня. Например, домашнее задание по математике вы делаете 30 минут, по природоведению – 10 минут, а по чтению – 20 минут, значит на выполнение домашних заданий по 3м предметам, вы тратите 60 минут. Так какая же ваша производительность при выполнении работы «домашнее задание»? Сравните свои результаты со своими одноклассниками.
Петерсон Людмила Георгиевна. Математика. 3 класс. Часть 3. — М.: Издательство «Ювента», 2005, — 64 с.: ил.
Авторські права | Privacy Policy |FAQ | Партнери | Контакти | Кейс-уроки
© Автор системы образования 7W и Гипермаркета Знаний — Владимир Спиваковский
При использовании материалов ресурса
ссылка на edufuture.biz обязательна (для интернет ресурсов —
гиперссылка).
edufuture.biz 2008-© Все права защищены.
Сайт edufuture.biz является порталом, в котором не предусмотрены темы политики, наркомании, алкоголизма, курения и других «взрослых» тем.
Разработка — Гипермаркет знаний 2008-
Ждем Ваши замечания и предложения на email: 
По вопросам рекламы и спонсорства пишите на email: 
гречиху фасуют два дозатора. В один дозатор засыпают (200) кг гречихи, и он расфасовывает крупу в пакеты за (20) мин. В другой засыпают (330) кг, и он расфасовывает крупу за (30) мин. Какой из дозаторов работает быстрее?
Сначала найдём, скорость каждого дозатора.
Эту задачу можно представить в виде таблицы:
— килограммов гречихи расфасовывает первый дозатор за (1) мин.
— килограммов гречихи расфасовывает второй дозатор за (1) мин.
Значит, работает быстрее второй дозатор.