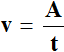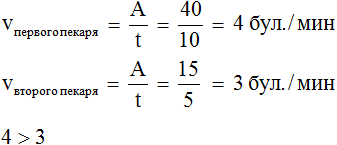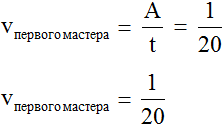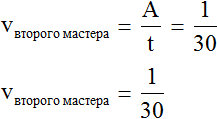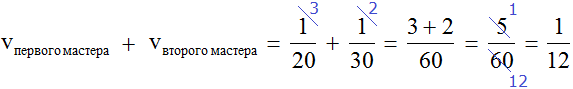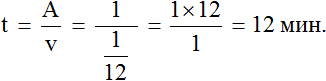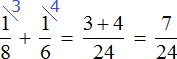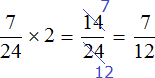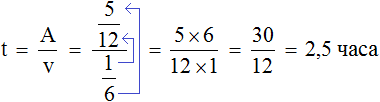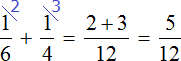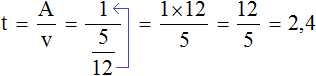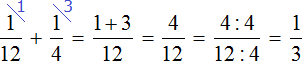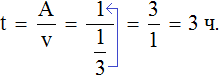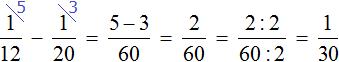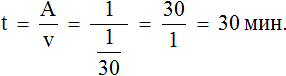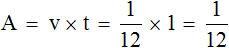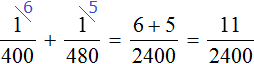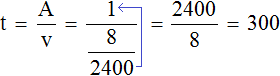Технологическая
карта по математики
Тема: Задачи
на работу: производительность труда, время, объем работы.
Тип урока: изучение нового
Цель:
создать условия для знания понятия «производительность»,
«выполненная работа», «время, затраченное на работу»; умение решать задачи с
этими величинами.
Планируемые
результаты:
Личностные: формирование
психологических условий развития общения, кооперации сотрудничества; доброжелательность,
доверие и внимание к людям, готовность к сотрудничеству и дружбе, оказанию
помощи тем, кто в ней нуждается;
Предметные: знают: формулы
решения задачи; умеют: применять формулы для решения задачи.
Метапредметные:
Коммуникативные:
уважение к окружающим – умение слушать и слышать, умение с достаточной полнотой
и точностью выражать свои мысли в соответствии с задачами и условиями
коммуникации;
Регулятивные:
целеполагание как постановка учебной задачи на основе соотнесения того, что уже
известно и усвоено учащимися, оценка — выделение и осознание обучающимся того,
что уже усвоено и что ещё нужно усвоить, осознание качества и уровня усвоения;
оценка результатов работы;
Ход урока
|
Деятельность |
Деятельность |
УУД |
||||||||||||||||||||||
|
Организационный |
||||||||||||||||||||||||
|
-Школьный Сегодня мы совершим путешествие в космос. Будем все — А какие это люди? И мы с вами будем учиться быть такими. |
Приветствие смелые, сильные, умные, дружные |
Коммуникативные: |
||||||||||||||||||||||
|
Актуализация |
||||||||||||||||||||||||
|
— Чтобы путешествие было удачным, необходимо соблюдать правила: — Итак, в путь! Правильные ответы позволят вам занять место в Высказывания великих людей о математике. — Ну, раз мы с вами на космическом корабле, то ваши тетради это -Откройте их и запишите число классная работа. Записи должны вестись четко, аккуратно. — Мы в школе подготовки космонавтов. — Чтобы отправится в путь, вы должны выполнить математический Проверка • • • 6 • 6 • 54 • 72 • • • 3 • 3 Проверка выполненного домашнего задания. Рабочая тетрадь Ст.18 №3
140*6=840(р)заплатили за все костюмы 840:420=2(п)детских сапог купили Ответ: купили 2 пары детских сапог. |
— — — + — + + — + +
140*6=840(р)заплатили за все костюмы 840:420=2(п)детских сапог купили Ответ: купили 2 пары детских сапог. |
Коммуникативные: Личностные: |
||||||||||||||||||||||
|
Формулирование |
||||||||||||||||||||||||
|
Внимание! Обратите Кощей С такими Вторая Дима и С таким Давайте На Чем эта Почему возникли Что О каких Скорость Что еще Как вы думайте, Правило. Вы Тема Какую -Инопланетяне Следующая |
Эта Известно Да Эта Известно Известно Затрудняемся Задачи Новые Сколько Выпекала Время Задачи Задачи Сегодня Сегодня |
Предметные: Регулятивные: Коммуникативные: Личностные: |
||||||||||||||||||||||
|
Усвоение |
||||||||||||||||||||||||
|
Запишите и запомним формулы что бы решать подобные задачи. Производительность V Время t Объём работы А А= V * t Решите задачу по этой формуле Рабочий в час Анализ задачи Что нужно узнать в Что для этого надо Известно, сколько Известно время, Как найти объём Заполните таблицу и V= A : t Самостоятельно решите Рабочий за 7 часов изготавливает Заполните таблицу и Фронтальная проверка Что известно в задаче? Что нужно узнать? Как нашли? Запишите формулу на t= A : V Рабочий за час Анализ задачи — Что нужно узнать в — Что для этого надо — Известен объём — Как найти время, Заполните таблицу и Повторить, как найти |
Сколько деталей изготовит рабочий за 6 часов, т.е. объём Сколько деталей он делает за час и время работы производительность 20 деталей в час 6 Решение: Ответ: объём Производительность Решение: Ответ: Время, Выполненную Да Выполненную Ответ: А= V * t V= A : t t= A : V |
Предметные: Коммуникативные: Личностные: |
||||||||||||||||||||||
|
Физминутка |
||||||||||||||||||||||||
|
Крош |
||||||||||||||||||||||||
|
Закрепление |
||||||||||||||||||||||||
|
Следующая наша планета юпитер Решение задачи (работа в паре) Два автомата упаковывают учебники в пачки. В Что известно в задаче? Что нужно найти? Чему равен объём работы первого автомата, второго? Чему равно время первого автомата, второго? Заполним таблицу Решение задачи Проверка на слайде 120:20=6 — столько книг упаковывает первый 210:30=7 — столько книг упаковывает второй 7-6=1 на Ответ: второй автомат работает быстрее. Самостоятельная работа, определите и запишите в а) производительность кондитера, если он за 3 Заполните карточки, которые я раздала A = V×… V= … : t t=A : … |
Объём Производительность 120, 210 20, 30 120:20=6 210:30=7 7-6=1 на 150:3=50(К)в 180:2=90(П)за А= V * t V= A t= A : V |
Предметные: Коммуникативные: Личностные: |
||||||||||||||||||||||
|
Итог. |
||||||||||||||||||||||||
|
— Молодцы вы С какими Повторить, Рефлексия На ваших столах В желтый, если В красный, если Корабли |
Задачи А= V * t V= A : t t= A : V |
Предметные: Коммуникативные: Личностные: |
Задачи на производительность 4 класс
1.Человек расходует 150 л воды в сутки. Сколько воды он израсходует за неделю?
2. Бабушка вяжет внуку свитер. За 3 часа бабушка связала 114 рядов. С какой скоростью вяжет бабушка?
3. За 15 дней корректор прочитал рукопись в 960 страниц. Сколько страниц в день читал корректор?
4. Ваня съел за месяц (30 дней) 180 кусков сахара. Сколько кусков сахара он съедал каждый день?
5. Катя платит за проезд 80 рублей в день. Сколько дней она сможет оплачивать проезд, если у нее 400 рублей?
6. Бетономешалка замешивает 24 л бетона в час. Сколько бетона получится, ели она будет работать 6 часов?
7. Ксерокс делает 8 копий в минуту. За сколько времени будет сделано 288 копий?
8. В пекарне выпекают ежедневно 500 батонов. Сколько батонов будет изготовлено за 2 недели?
9. Завод выпускает 250 автомобилей в месяц. Сколько автомобилей будет произведено за полгода?
10. Комбайн за 12 дней убрал картофель с поля площадью 36 га. Какова производительность комбайна?
11. Один мастер ремонтирует 20 пар обуви в день. Другой – 18 пар обуви в день. Сколько пар обуви отремонтируют оба мастера за 4 дня?
12. На первой скорости станок изготавливает 200 деталей в час. На второй скорости 260 деталей в час. Станок работал 2 часа на первой скорости и 3 часа на второй. Сколько деталей было изготовлено за это время?
13. Строитель выкладывает 120 кирпичей в час. Сколько кирпичей он положит за 5 дней, работая по 8 часов в день?
14. Девочка прочитывает 25 страниц в день. Сколько страниц останется ей прочитать через 5 дней, если в книге 160 страниц?
15. Первые полгода завод выпускал 800 телевизоров в месяц. Затем начал выпускать на 150 телевизоров в месяц больше. Сколько телевизоров завод выпустил за год?
16.Мастер и ученик получили заказ на изготовление 72 табуреток. Мастер может сделать эту работу за 6 дней, а ученик за 12 дней. За сколько дней они выполнят эту работу вместе?
17.Фабрика получила заказ на пошив 168 платьев. Одна бригада может выполнить его за 28 дней, а другая – за 21 день. За сколько дней обе бригады выполнят заказ, если будут работать вместе?
18.Через один кран в цистерну поступает 15 л молока в минуту. Через другой кран – 17 л в минуту. Сколько литров молока будет в цистерне через 45 минут, если открыты оба крана?
19.Один трубоукладчик прокладывает 24 м труб в час. Другой 32 м труб в час. Сколько метров труб уложат обе машины за 6 часов, работая одновременно?
20. Станок штампует 1000 пластиковых тарелок в час. На новом станке стали выпускать на 600 тарелок в час больше. Сколько тарелок выпустят на новом станке за 8-часовой рабочий день?
21. Два корректора должны прочесть 720 страниц рукописи за 5 дней. Один корректор прочитывает 64 страницы в день. Сколько страниц в день должен читать второй корректор, чтобы закончить рукописи в срок?
22. Через кран с горячей водой наливается 10 л в минуту, а через кран с холодной водой – 8 л в минуту. Сколько нужно времени, чтобы наполнить ванну, которая вмещает 360 литров?
23. На лодочной станции надо покрасить 168 лодок. Один мастер может выполнить эту работу за 28 дней, а другой – за 21 день. За сколько дней они могут выполнить эту работу, работая вместе?
24. Одна бригада рабочих может построить 15 км шоссейной дороги за 30 дней, а другая – за 60 дней. За сколько дней могут построить эту дорогу обе бригады, работая вместе?
25. Одна бригада рабочих может посадить 600 плодовых деревьев за 10 дней, а другая — за 15 дней. За сколько дней могут посадить эти деревья две бригады, работая вместе?
26. На швейной фабрике два одинаковых автомата пришивают пуговицы к пальто. Один автомат работал 50 минут, другой 40 минут. Сколько пуговиц пришил каждый автомат, если вместе они пришили 1.350 пуговиц?
27. Библиотеке нужно переплести 4500 книг. Одна мастерская может переплести эти книги за 30 дней, а другая – за 45. За сколько дней могут выполнить заказ обе эти мастерские, работая одновременно?
28. Один трубоукладчик прокладывает 24 м труб в час. Другой 32 м труб в час. Сколько метров труб уложат обе машины за 6 часов, работая одновременно?
29.Один мастер ремонтирует 20 пар обуви в день. Другой – 18 пар обуви в день. Сколько пар обуви отремонтируют оба мастера за 4 дня?
30.Производительность первого насоса 180 л/ч, второго – 140 л/ч. Сколько воды перекачают два насоса за 3 часа, работая одновременно?
31.На первой скорости станок изготавливает 200 деталей в час. На второй скорости 260 деталей в час. Станок работал 2 ч на первой скорости и 3 ч на второй. Сколько деталей было изготовлено за это время?
32.Станок штампует 1000 пластиковых тарелок в час. На новом станке стали выпускать на 600 тарелок в час больше. Сколько тарелок выпустят на новом станке за 8-часовой рабочий день?
33.Два корректора должны прочесть 720 страниц рукописи за 5 дней. Один корректор прочитывает 64 страницы в день. Сколько страниц в день должен читать второй корректор, чтобы закончить рукописи в срок?
34.Мастер и ученик получили заказ на изготовление 72 табуреток. Мастер может сделать эту работу за 6 дней, а ученик за 12 дней. За сколько дней они выполнят эту работу вместе?
35.Через кран с горячей водой наливается 10 л в минуту, а через кран с холодной водой – 8 л в минуту. Сколько нужно времени, чтобы наполнить ванну, которая вмещает 360 литров?
36.Фабрика получила заказ на пошив 168 платьев. Одна бригада может выполнить его за 28 дней, а другая – за 21 день. За сколько дней обе бригады выполнят заказ, если будут работать вместе?
37.Мастер производил на 5 изделий в час больше, чем его ученик. За 2 часа совместной работы они произвели 58 изделий. Сколько изделий за семичасовую смену произведет каждый из них?
38. Двумя автомобилями необходимо вывезти из леса на станцию 420 бревен. Первый автомобиль за 5 рейсов перевез третью часть всех бревен. Остальные бревна перевез второй автомобиль, который вывозил на 42 бревна больше за 1 рейс. Какое число рейсов совершил второй автомобиль?
39.По плану слесарю необходимо сделать 120 гаек за 5 часов. Но он в час делал на 8 деталей больше нормы. Сколько гаек слесарь изготовил за это время?
40.Группа электриков в новом доме, состоящего из 21 этажа, устанавливает розетки и выключатели. Группа подключает к электросети каждый день по 3 этажа. Сколько дней потребуется, чтобы подключить к электросети весь дом?
Продолжаем изучать элементарные задачи по математике. Сегодня мы рассмотрим очень интересную физическую величину — производительность.
Что такое сила?
Сила — это физическое явление, способное изменять форму материальных тел, вызывать их движение, менять направление и скорость движения этих тел или приводить тело в состояние покоя.
Примеры сил:
- ребята слепили снеговика, а хулиганы его разрушили. Получается, что хулиганы приложили к снеговику свою силу, тем самым вызвали изменение формы снеговика;
- на дворе стояла тележка. Прохожий случайно задел её и тележка сдвинулась с места. Получается, что прохожий применил силу к тележке и вызвал её движение;
- далее тот же прохожий остановил тележку, чтобы она далеко не уехала. Получается, что прохожий применил силу, тем самым привел тележку в состояние покоя.
Сила является физической величиной — мерой воздействия на тело других тел. Сила обозначается заглавной латинской буквой F.
Что такое работа?
Работа — это количественная мера действия силы на тело. Работа зависит от количества силы, приложенной на тело и от направления этой силы, а также от перемещения данного тела.
Например, если мы попробуем сдвинуть шкаф с места и он сдвинется, то можно сказать, что мы совершили работу, поскольку сила, которую мы приложили, привела к тому, что шкаф совершил перемещение на некоторое расстояние.
Если же мы, к примеру, попробуем толкнуть стену, то стена с места не сдвинется, а значит и работа не будет совершена, поскольку сила была приложена, но эта сила не вызвала никакого перемещения стены.
Работа обозначается заглавной латинской буквой A.
Производительность
Производительностью называют работу, выполненную за единицу времени. Под единицей подразумевается 1 час, 1 минута или 1 секунда. Производительность обозначается латинской буквой v
Рассмотрим следующий пример. Два пекаря пекли булочки. Первый пекарь испёк 40 булочек за 10 минут, а второй 15 булочек за 5 минут. Как узнать, кто из пекарей работал быстрее, первый или второй?
Работал быстрее тот, кто за одну минуту выпекает больше булочек. Говорят, что у него производительность больше. Для нахождения производительности предусмотрено следующее правило:
Чтобы найти производительность, надо выполненную работу разделить на время работы.
Также, можно воспользоваться формулой:
где v — производительность, A — выполненная работа, t — время работы.
Вернемся к нашей задаче. Зная правило или формулу нахождения производительности, можно определить сколько булочек приходится на одну минуту.
Найдём производительность первого пекаря. Разделим работу, которую он выполнил, на время которое он на нее затратил. Выполненная работа это количество испеченных им булочек, то есть 40, а время — 10 минут
40 : 10 = 4 булочки в минуту
Аналогично найдём производительность второго пекаря. Разделим 15 на 5
15 : 5 = 3 булочки в минуту
4 > 3
Первый пекарь в минуту выпекает больше булочек чем второй, значит его производительность выше. Отсюда делаем вывод, что работает он быстрее второго пекаря.
Также можно воспользоваться формулой нахождения производительности. В этом случае решение принимает следующий вид:
Под буквой v можно делать метки, указывающие для кого/чего мы находим производительность.
Задача 2. Тому нужно за 2 дня прочитать книгу, в которой 100 страниц. В первый день он читал 4 часа со скоростью 12 страниц в час. С какой скоростью ему надо читать оставшуюся часть книги, если у него есть на это 4 часа?
Узнаем сколько страниц Том прочитал в первый день. Он читал 12 страниц в час. Чтению в первый день он посвятил 4 часа, поэтому для нахождения количества прочитанных страниц в первый день, нужно 12 умножить на 4
12 × 4 = 48 страниц прочитано в первый день
Узнаем сколько страниц осталось прочесть. Вычтем из общего количества страниц (100) количество прочитанных страниц (48)
100 − 48 = 52 страницы осталось прочесть
Осталось прочесть 52 страницы. Теперь найдем такую производительность, при которой Том сможет прочесть 52 страницы за 4 часа. Раскидаем 52 страницы на 4 часа поровну
52 : 4 = 13 страниц в час
Ответ: чтобы прочитать оставшуюся часть книги за 4 часа, Том должен читать ее со скоростью 13 страниц в час.
Замечание. В некоторых источниках слово «производительность» может быть заменено на слова «скорость», «эффективность», «продуктивность», «плодотворность».
Задача 3. Один насос работал 4 часа, выкачивая 158 вёдер воды в час, а другой — 3 часа, выкачивая 169 вёдер воды в час. Определить какой из насосов выкачал больше вёдер.
Решение
Определим сколько всего вёдер выкачал каждый насос по отдельности. Для этого умножим их производительность на время их работы:
158 в/ч × 4 = 632 вёдер выкачал первый насос
169 в/ч × 3 = 507 вёдер выкачал второй насос
632 > 507
Ответ: первый насос выкачала больше вёдер, чем второй.
Задача 4. За 2 часа насос выкачал 80 литров воды. Определить сколько литров он выкачает за 5 часов.
Решение
Сначала нужно определить сколько литров воды насос выкачивает за час. Для этого 80 литров разделим на 2 часа — получим 40 литров
80 : 2 = 40 литров в час
За один час насос выкачивает 40 литров воды. За 5 часов выкачает в пять раз больше
40 × 5 = 200 литров
Ответ: за 5 часов насос выкачает 200 литров воды.
Если известны производительность и время работы, то можно найти выполненную работу. Выполненная работа равна производительности умноженной на время работы:
A = v × t
Например, если производительность пекаря составляет 50 булочек в час, и он проработал 4 часа, то можно найти всю выполненную работу за эти четыре часа. Для этого производительность (50 бул/ч) нужно умножить на время его работы (4ч)
50 × 4 = 200 булочек
Если известны работа и производительность, то можно найти время работы. Время работы равно отношению выполненной работы к производительности:
Например, если в неделю бригада отстраивает 2 этажа, то можно узнать сколько недель потребуется для отстройки 8 этажей. Чтобы определить время отстройки восьми этажей, нужно выполненную работу (8 этажей) разделить на производительность (2 эт./нед):
8 : 2 = 4 нед.
Либо с помощью формулы, приведенной выше:
Если в неделю строится 2 этажа, то 8 этажей будет отстроено за четыре недели. В данном случае вся работа была равна восьми. Производительность была равна двум, поскольку по определению производительность есть работа, выполненная за единицу времени – в нашем случае два этажа за неделю.
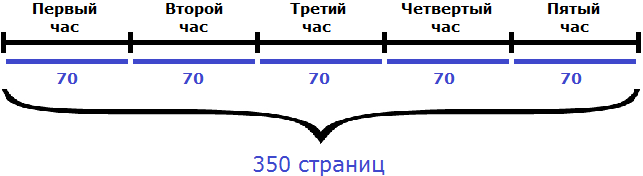
Задача 6. Принтер работает с производительностью 70 стр./ч. Сколько страниц он напечатает за 5 часов?
Решение
Если в час принтер печатает 70 страниц, то за 5 часов он напечатает в 5 раз больше:
70 × 5 = 350 страниц
Также, решение можно записать с помощью формулы нахождения работы. В данном случае, количество напечатанных страниц являются выполненной работой:
A = v × t = 70 × 5 = 350 страниц
A = 350 страниц
Задача 7. Принтер напечатал 350 страниц за 5 часов. С какой производительностью он работал?
Решение
Если в течении пяти часов принтер напечатал 350 страниц, то в течении часа он печатал 
. То есть работал с производительностью 70 страниц в час:
350 : 5 = 70 стр./ч.
Либо с помощью формулы нахождения производительности:
Задача 8. Принтер работал с производительностью 70 страниц в час и напечатал 350 страниц. Определить время работы принтера.
Решение
Выражение «работал с производительностью 70 страниц в час» означает, что в каждом часе принтер печатал по 70 страниц. И это продолжалось до тех пор, пока он не напечатал 350 страниц. Очевидно, что разделив 350 страниц по 70, мы определим время работы принтера, то есть узнаем сколько часов он работал
350 : 70 = 5 ч.
Либо с помощью формулы нахождения времени:
Задача 9. Машинистка в первый день напечатала 48 страниц рукописи, а во второй день — на 12 страниц больше, чем в первый. На всю работу в эти 2 дня она затратила 9 часов. Сколько часов работала она в каждый из этих дней, если производительность её не менялась ?
Решение
Определим сколько страниц напечатала машинистка во второй день. В условии сказано, что напечатала она на 12 страниц больше, чем в первый:
48 + 12 = 60 страниц во второй день.
Определим сколько страниц машинистка напечатала за два дня:
48 + 60 = 108 страниц за два дня.
На эту работу машинистка затратила 9 часов. Также сказано, что производительность её не менялась. Если мы разделим выполненную работу (108) на время выполнения (9), то определим производительность машинистки:
108 : 9 = 12 страниц в час.
Теперь мы можем определить сколько часов работала машинистка в каждый из двух дней. Для этого поочередно разделим выполненные работы в каждом из двух дней на производительность:
48 : 12 = 4 часа работала машинистка в первый день
60 : 12 = 5 часов работала машинистка во второй день.
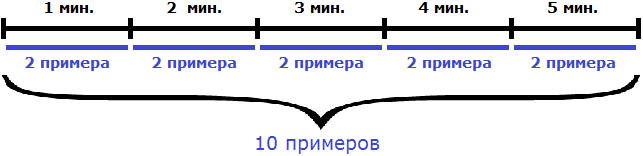
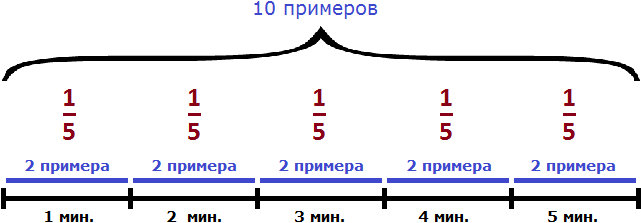
Задача 10. Джон решил 10 примеров за 5 минут. С какой производительностью он решал эти примеры?
10 примеров это выполненная Джоном работа. 5 минут — время работы. Разделим выполненную работу на время работы и определим производительность Джона:
10 : 5 = 2 примера в минуту.
Производительность Джона равна двум примерам в минуту.
Задача 11. Джон решил несколько примеров за 5 минут. С какой производительностью он решил эти примеры?
Это та же самая задача, что и предыдущая, но в ней работа не выражена каким-либо числом. Сказано лишь то, что Джон выполнил эту работу за 5 минут. Поэтому, конкретную производительность в такой задаче узнать нельзя. Но можно воспользоваться дробями. Обозначим выполненную работу через единицу. Тогда производительность работы Джона будет выражаться дробью – частью примеров, решенных за единицу времени. Если вы изучили задачи на дроби, то должны понимать о чем идёт речь.
Итак, обозначим выполненную работу через единицу:
A = 1
Мы знаем, что для нахождения производительности, выполненную работу нужно разделить на время. Время работы у нас равно пяти минутам. Поэтому, единицу делим на пять минут:
Дробь выражает часть работы, выполненную Джоном за единицу времени. Если мы вернемся к предыдущей задаче, где выполненная работа была равна десяти примерам и найдем одну пятую от этой работы, то получим 2
Выражать выполненную работу через единицу часто приходится при решении задач на совместную работу.
Задачи на совместную работу
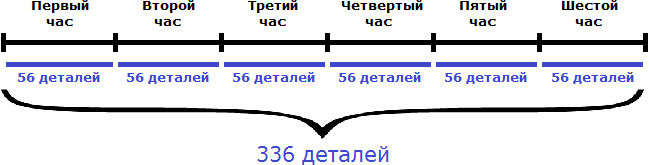
Задача 1. Первый мастер за 2 часа изготавливает 64 детали, а второй за 3 часа – 72 детали. За сколько часов они изготовят 336 деталей?
В данной задаче речь идет о совместной работе. Необходимо определить производительность обоих мастеров и найти время за которое они изготовят 336 деталей.
Для начала определим производительность первого мастера:
64 : 2 = 32 дет./час
Определим производительность второго мастера:
72 : 3 = 24 дет./час
Определим совместную производительность мастеров. Для этого сложим количество деталей, которые они изготавливают по отдельности за единицу времени. То есть сложим их производительности:
32 дет./час + 24 дет./час = 56 дет./час
Вместе за один час мастера изготавливают 56 деталей. Чтобы узнать за сколько часов они изготовят 336 деталей, нужно определить сколько раз 336 содержит по 56
336 : 56 = 6 часов
Задача 2. Первый мастер может покрасить забор за 20 минут, а второй мастер – за 30 минут. За сколько минут, работая вместе, они могут покрасить забор?
Решение
В данной задаче, в отличие от предыдущей, работа не выражена каким-либо числом. Сказано лишь то, что эту работу первый мастер может выполнить за 20 минут, а второй за 30 минут.
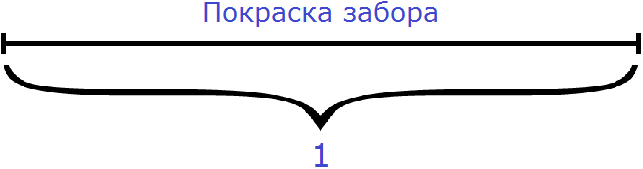
В такой ситуации можно воспользоваться дробями. Мы можем обозначить всю работу (покраску забора) через единицу.
Итак, обозначим работу (покраску забора) через единицу:
A = 1
Производительность первого мастера будет выражáться дробью 
. То есть за одну минуту он покрасит одну двадцатую часть забора. Единица это вся работа, а двадцать минут это время работы. Запишем производительность первого мастера с помощью формулы нахождения производительности:
А производительность второго мастера будет выражáться дробью 
. То есть за одну минуту он покрасит одну тридцатую часть забора:
Определим общую производительность мастеров. Для этого сложим дроби, выражающие производительность первого и второго мастеров:
это дробь, выражающая общую производительность обоих мастеров. То есть за одну минуту мастера вместе покрасят часть забора.
Определим время за которое мастера покрасят забор вместе. Для этого воспользуемся формулой нахождения времени: разделим выполненную работу на общую производительность мастеров. Выполненная работа у нас выражена единицей, а производительность — дробью
Ответ: работая вместе, мастера покрасят забор за 12 минут.
Задача 3. Первый рабочий может выполнить заказ за 8 часов, а второй за 6 часов. Два часа они работали вместе, а заканчивал работу один второй рабочий. Сколько времени потребовалось для выполнения этого заказа?
Решение
Обозначим всю работу через единицу
A = 1
Тогда первый рабочий за один час может выполнить 
часть работы, а второй рабочий 
часть работы. А вместе за один час они могут выполнить 
часть работы
Рабочие работали вместе два часа, поэтому умножим часть работы, выполняемую ими за один час на 2:
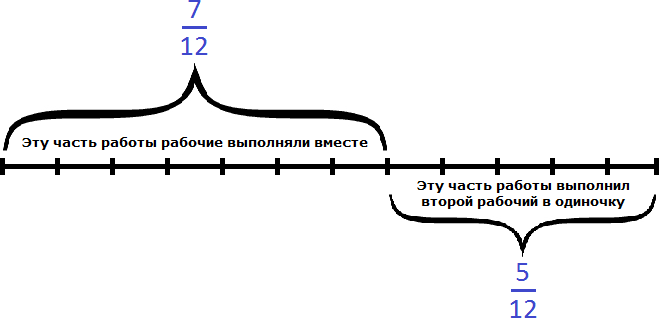
Остальную часть работы, а именно 
работы заканчивал один второй рабочий:
Второй рабочий за один час мог выполнить часть работы. Чтобы определить время за которое он завершил оставшуюся часть работы, воспользуемся формулой нахождения времени.
Переменная A теперь равна , переменная v —
Теперь определим общее время заказа. Первые два часа рабочие работали вместе, остальную часть работы второй рабочий выполнил за два с половиной часа, отсюда имеем 4,5 ч.
2 + 2,5 = 4,5 ч.
Ответ: для выполнения заказа потребовалось 4,5 ч.
Задача 4. Одна труба наполняет бассейн за 6 ч, а другая – за 4 ч. За
сколько часов наполняют бассейн обе трубы, работая вместе?
Решение
Обозначим работу (наполнение бассейна) через единицу
A = 1
Тогда первая труба за один час выполнит часть работы, а вторая труба — 
часть работы. Работая вместе за один час они выполнят 
часть работы:
Определим время за которое обе трубы наполняют бассейн, работая вместе:
2,4 это два целых часа и четыре десятых часа
2,4 = 2 ч + 0,4 ч
А четыре десятых часа это 24 минуты
60 мин. × 0,4 = 24 мин.
Ответ: работая вместе обе трубы наполнят бассейн за 2 ч 24 мин.
Задачи для самостоятельного решения
Задача 1. Первая бригада может выполнить некоторое задание за 12 часов, вторая – за 4 часа. За сколько часов они выполнят задание, если будут работать вместе?
Решение
Обозначим работу через единицу:
A = 1
Тогда первая бригада за один час выполнит часть работы, а вторая за один час часть работы. Их общая производительность равна сумме дробей и :
Определим время за которое обе бригады выполнят задание, работая вместе:
Ответ: обе бригады выполнят задание за 3 часа.
Задача 2. Лошадь съедает копну сена за 1 сутки, корова может съесть такую же копну за 3 суток, а овца за 6 суток. За какое время съедят эту копну лошадь, корова и овца вместе.
Решение
Работа в данном случае это съедание копны сена. Обозначим её через единицу:
A = 1
Тогда производительность лошади будет выражáться единицей, производительность коровы — дробью 
, производительность овцы — дробью . Их совместная производительность равна следующей сумме:
Определим время, за которое лошадь, корова и овца съедят 1 копну сена:
Ответ: лошадь, корова и овца съедят 1 копну сена за 
суток или 16 часов.
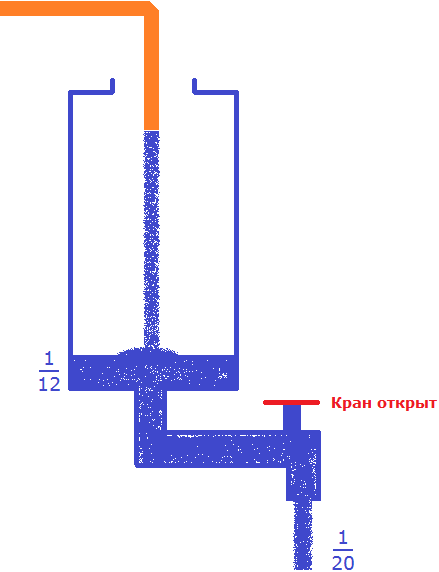
Задача 3. Сосуд наполняется шлангом за 12 мин, а полный сосуд опорожняется при открытии крана за 20 мин. За какое время наполнится пустой сосуд, если одновременно открыть кран и вливать в него воду через шланг?
Решение
Работа в данном случае это наполнение сосуда. Обозначим эту работу через единицу:
A = 1
В условии сказано, что сосуд наполняется шлангом за 12 минут. Значит в минуту будет наполняться часть сосуда. При этом сказано, что одновременно открыт кран сосуда и из него вытекает вода, которой наполняется сосуд. Вода, которая вытекает равна части сосуда, поскольку в условии сказано, что полный сосуд опорожняется за 20 минут.
В сосуд поступает воды больше, чем вытекает. Дробь больше, чем .
Несмотря на то, что часть поступающей в сосуд воды будет вытекать, с каждой минутой сосуд будет пополняться на определенную часть. Узнаем, что эта за часть. Для этого из поступающей части вычтем ту часть, которая вытекает:
Каждую минуту сосуд будет наполняться на .
Определим время за которое наполнится пустой сосуд, если одновременно открыть кран и вливать в него воду через шланг:
Ответ: если одновременно открыть кран и вливать в пустой сосуд воду через шланг, то он наполнится за 30 минут.
Задача 4. Через первую трубу бассейн можно заполнить за 20 ч, через вторую за 30 ч. Какая часть бассейна заполнится через обе трубы за 1 ч?
Решение
Работа в данном случае это заполнение бассейна. Обозначим эту работу через единицу:
A = 1
Производительность заполнения бассейна через первую трубу будет выражáться дробью , через вторую трубу — дробью . Совместная производительность будет выражáться дробью
Производительность по определению есть работа, выполненная за единицу времени. Значит дробь является ответом к задаче, поскольку нас интересовало какая часть бассейна заполнится через обе трубы за 1 час. Это можно проверить, воспользовавшись формулой нахождения работы. Переменная v у нас имеет значение , а переменная t равна единице (одному часу). Формула нахождения работы позволит нам определить какая часть работы будет выполнена за 1 час:
Ответ: за один час заполнится часть бассейна.
Задача 5. На прокладку траншеи требуется затратить 10 ч. Экскаватор проработал 8 ч, после чего ему осталось пройти 50 м. Найти общую длину траншеи.
Решение
В задаче подразумевается, что экскаватор работал с одинаковой производительностью на протяжении всей работы. На работу требовалось затратить 10 ч. Проработано было 8 ч. Значит осталось еще 2 часа. На 2 часа приходятся оставшиеся 50 метров траншеи. Если разделить 50 метров на 2, то можно определить сколько метров экскаватор прокладывает за один час:
50 : 2 = 25 м./ч
В час экскаватор прокладывал 25 метров. Работал он 10 часов. Умножим 25 на 10, мы определим общую длину траншеи:
25 × 10 = 250 м
Ответ: общая длина траншеи составляет 250 м.
Задача 6. Ванна заполняется холодной водой за 6 мин 40 с, горячей – за 8 мин. Кроме того, если из полной ванны вынуть пробку, вода вытечет за 13 мин 20 с. Сколько времени понадобится, чтобы наполнить ванну полностью, при условии, что открыты оба крана, но ванна не заткнута пробкой?.
Решение
Для удобства переведем время данное в задаче в секунды
6 мин 40 с = 400 с
8 мин = 480 с
13 мин 20 с = 800 с
Обозначим заполнение ванны через единицу:
A = 1
Производительность первого крана будет выражáться дробью 
, производительность второго крана — дробью 
. Совместная производительность обоих кранов равна сумме дробей и
Одновременно с открытыми двумя кранами, вынута пробка из ванны. Поэтому часть поступающей в ванну воды сразу выходит через слив. Эта часть будет выражáться дробью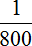 
.
С каждой секундой ванна будет пополняться на определенную часть воды. Узнаем какая это часть. Для этого из поступающей части воды вычтем ту часть, которая вытекает через слив.
Определим сколько времени понадобится, чтобы наполнить ванну:
Ванна наполнится за 300 секунд. Поскольку задача завершена, секунды можно обратно перевести в минуты. Триста секунд это пять минут:
300 : 60 = 5 мин
Ответ: ванна заполнится за 5 мин.
Понравился урок?
Вступай в нашу новую группу Вконтакте и начни получать уведомления о новых уроках
Возникло желание поддержать проект?
Используй кнопку ниже
Деятельность учителя
Деятельность учеников
УУД
Организационный момент
-Школьный звонок нас позвал на урок математики – интересный и важный. Здравствуйте ребята! Садитесь!
Сегодня мы совершим путешествие в космос. Будем все космонавтами. А каких космонавтов вы знаете? (показ портретов)
— А какие это люди?
И мы с вами будем учиться быть такими.
Приветствие
смелые, сильные, умные, дружные
Коммуникативные: уважение к окружающим – умение слушать и слышать
Актуализация знаний
— Чтобы путешествие было удачным, необходимо соблюдать правила: быть внимательными, активными, правильно выполнять задания, не допускать ошибок, иначе можем потерпеть кораблекрушение.
— Итак, в путь! Правильные ответы позволят вам занять место в ракете.
Высказывания великих людей о математике.
— Ну, раз мы с вами на космическом корабле, то ваши тетради это – бортовые журналы.
-Откройте их и запишите число классная работа. Записи должны вестись четко, аккуратно.
— Мы в школе подготовки космонавтов.
— Чтобы отправится в путь, вы должны выполнить математический диктант.(работа по карточкам)
Проверка выполненного математического диктанта
• Произведение чисел 6 и 8 равно 56.
• Частное чисел 81 и 9 равно 8.
• 6 увеличить в 9 раз. Получится 34.
• 6 увеличили на 9. Получили 15.
• 54 разделить на 9, получится 7.
• 72 уменьшить в 8 раз, получится 9.
• 36:6 = 6
• 72:9 = 9
• 3 увеличить на 7, равно 10.
• 3 увеличить в 3 раза, равно 9.
Проверка выполненного домашнего задания.
Рабочая тетрадь
Ст.18 №3
|
Цена |
Кол-во |
Стоим. |
|
|
Костюм |
140 |
6 |
одинакого |
|
сапог |
420 |
? |
140*6=840(р)заплатили за все костюмы
840:420=2(п)детских сапог купили
Ответ: купили 2 пары детских сапог.
—
—
—
+
—
+
+
—
+
+
|
Цена |
Кол-во |
Стоим. |
|
|
Костюм |
140 |
6 |
одинакого |
|
сапог |
420 |
? |
140*6=840(р)заплатили за все костюмы
840:420=2(п)детских сапог купили
Ответ: купили 2 пары детских сапог.
Коммуникативные: уважение к окружающим – умение слушать и слышать, умение с достаточной полнотой и точностью выражать свои мысли в соответствии с задачами и условиями коммуникации;
Личностные: формирование психологических условий развития общения, кооперации сотрудничества; доброжелательность, доверие и внимание к людям, готовность к сотрудничеству и дружбе, оказанию помощи тем, кто в ней нуждается;
Формулирование темы и задачи урока
Внимание! В космосе появился неопознанный летающий объект в виде тарелки (показ картинки). Это инопланетяне. Они хотят захватить наш корабль. Приготовьтесь к космическому бою.
Обратите внимание на задачи, что скажете про первую задачу, что в ней известно, какие величины?
Кощей Бессмертный проехал на Змее Горыныче 180 км. Сколько часов они были в пути, если средняя скорость Змея Горыныча 90 км/ч?
С такими видами задач знакомы, умеете их решать?
Вторая задача, что можете сказать о ней, что известно, что нужно узнать?
Дима и Настя купили для украшения елки игрушки по одинаковой цене, уплатив за них 48 рублей. Дима купил 5 игрушек, а Настя 7 игрушек. Сколько денег уплатил за игрушки каждый ребенок?
С таким типом задач вы знакомы?
Давайте посмотрим на третью задачу. Что скажете о ней, о чем она и какие величины присутствуют?
На масленицу Ксюша напекла гору вкусных блинов. Ксюша выпекала их в несколько приемов. В начале, она выпекала 3 блина в минуту. Сколько блинов приготовила Ксюша, работая 20 минут?
Чем эта задача отличается от тех, которые мы решали сейчас?
Почему возникли затруднения?
Что нужно найти в задаче?
О каких величинах ещё идет речь?
Скорость работы называют «ПРОИЗВОДИТЕЛЬНОСТЬЮ».
Что еще известно в задаче?
Как вы думайте, как называются эти задачи?
Правило.
Вы догадались какая тема нашего урока?
Тема нашего урока
Какую цель поставите перед собой?
-Инопланетяне побеждены. Мы летим дальше.
Следующая планета, на которую мы отправимся- Сатурн, посмотрим какие задания ждут нас на ней.
Эта задача на скорость, время, расстояние.
Известно расстояние и скорость, нужно найти время
Да
Эта задача на количество, цена, стоимость.
Известно количество игрушек, что они стоят одинаково 48 рублей, нужно найти сколько заплатил каждый ребёнок. Да
Известно сколько блинов выпекла Ксюша за 1 минуту
Затрудняемся ответить
Задачи были с известными величинами: время, скорость и путь. А в этой задаче не все величины знакомы, знаем только время.
Новые величины, нет формул.
Сколько всего блинов испекла Маша т.е. её работу
Выпекала 3 блина в минуту, т.е. обьём работы
Время работы.
Задачи на работу, производительность и время
Задачи на работу: производительность труда, время, объем работы.
Сегодня мы узнаем, что такое производительность, объем работы и время
Сегодня мы будем учиться устанавливать взаимосвязь между работой, временем и производительностью.
Предметные: знают: формулы решения задачи; умеют: применять формулы для решения задачи.
Регулятивные: целеполагание как постановка учебной задачи на основе соотнесения того, что уже известно и усвоено учащимися, оценка — выделение и осознание обучающимся того, что уже усвоено и что ещё нужно усвоить, осознание качества и уровня усвоения; оценка результатов работы;
Коммуникативные: уважение к окружающим – умение слушать и слышать, умение с достаточной полнотой и точностью выражать свои мысли в соответствии с задачами и условиями коммуникации;
Личностные: формирование психологических условий развития общения, кооперации сотрудничества; доброжелательность, доверие и внимание к людям, готовность к сотрудничеству и дружбе, оказанию помощи тем, кто в ней нуждается;
Усвоение материала
Запишите и запомним формулы что бы решать подобные задачи.
Производительность V
Время t
Объём работы А
А= V * t
Решите задачу по этой формуле
Рабочий в час изготавливает 20 деталей. Сколько деталей он сделает за 6 часов?
Анализ задачи
Что нужно узнать в задаче?
Что для этого надо знать?
Известно, сколько деталей он делает за час?
Известно время, затраченное на работу?
Как найти объём выполненной работы?
Заполните таблицу и запишите решение с пояснением.
V= A : t
Самостоятельно решите задачу по этой формуле
Рабочий за 7 часов изготавливает 175 деталей. Сколько деталей рабочий делает за час?
Заполните таблицу и запишите решение с пояснением
Фронтальная проверка решения
Что известно в задаче?
Что нужно узнать?
Как нашли?
Запишите формулу на нахождение времени
t= A : V
Рабочий за час изготавливает 23 детали. Сколько времени он потратил, чтобы изготовить 184 детали?
Анализ задачи
— Что нужно узнать в задаче?
— Что для этого надо знать?
— Известен объём работы? Известна производительность?
— Как найти время, затраченное на работу?
Заполните таблицу и запишите решение задачи с пояснением
Повторить, как найти объём выполненной работы? производительность? время, затраченное на работу?
Сколько деталей изготовит рабочий за 6 часов, т.е. объём выполненной работы
Сколько деталей он делает за час и время работы
производительность 20 деталей в час
6 часов
Решение: 20 · 6 = 120 деталей
Ответ: 120 деталей изготовят за 6 часов.
объём выполненной работы – 175 деталей и время работы – 7 ч
Производительность
Решение: 175 : 7 = 25деталей в час
Ответ: 25 деталей в час изготавливал рабочий.
Время, затраченное на работу
Выполненную работу и производительность
Да
Выполненную работу разделить на производительность Решение: 184 : 23 = 8 ч
Ответ: за 8 часов
А= V * t
V= A : t
t= A : V
Предметные: знают: формулы решения задачи; умеют: применять формулы для решения задачи.
Коммуникативные: уважение к окружающим – умение слушать и слышать, умение с достаточной полнотой и точностью выражать свои мысли в соответствии с задачами и условиями коммуникации;
Личностные: формирование психологических условий развития общения, кооперации сотрудничества; доброжелательность, доверие и внимание к людям, готовность к сотрудничеству и дружбе, оказанию помощи тем, кто в ней нуждается;
Физминутка
Крош
Закрепление
Следующая наша планета юпитер
Решение задачи (работа в паре)
Два автомата упаковывают учебники в пачки. В один автомат загружают 120 книг, и он упаковывает их в течение 20 мин. В другой загружают 210 книг, и он упаковывает их в течение 30 мин. Какой из автоматов работает быстрее?
Что известно в задаче?
Что нужно найти?
Чему равен объём работы первого автомата, второго?
Чему равно время первого автомата, второго?
Заполним таблицу
Решение задачи
Проверка на слайде
120:20=6 — столько книг упаковывает первый автомат за 1 мин.
210:30=7 — столько книг упаковывает второй автомат за 1 мин.
7-6=1 на столько книг больше упаковывает 2 автомат чем первый, следовательно, 2 автомат работает быстрее.
Ответ: второй автомат работает быстрее.
Самостоятельная работа, определите и запишите в таблице с пояснением и ответом:
а) производительность кондитера, если он за 3 часа сделал 150 кг конфет; б) производительность фасовщика, если он за 2 дня сделал 180 подарков;
Заполните карточки, которые я раздала
A = V×…
V= … : t
t=A : …
Объём работы и время работы.
Производительность
120, 210 книг
20, 30 минут
120:20=6 — столько книг упаковывает первый автомат за 1 мин.
210:30=7 — столько книг упаковывает второй автомат за 1 мин.
7-6=1 на столько книг больше упаковывает 2 автомат чем первый, следовательно, 2 автомат работает быстрее.
150:3=50(К)в час
180:2=90(П)за 1 день
А= V * t
V= A : t
t= A : V
Предметные: знают: формулы решения задачи; умеют: применять формулы для решения задачи.
Коммуникативные: уважение к окружающим – умение слушать и слышать, умение с достаточной полнотой и точностью выражать свои мысли в соответствии с задачами и условиями коммуникации;
Личностные: формирование психологических условий развития общения, кооперации сотрудничества; доброжелательность, доверие и внимание к людям, готовность к сотрудничеству и дружбе, оказанию помощи тем, кто в ней нуждается;
Итог. Рефлексия
— Молодцы вы справились со всеми заданиями, наше путешествие подошло к концу. Осталось ответить на вопросы.
С какими задачами сегодня познакомились?
Повторить, как найти объём выполненной работы? производительность? время, затраченное на работу?
Рефлексия
На ваших столах лежат космические корабли, раскрасьте их в зелёный если, вы справлялись с заданиями.
В желтый, если были затруднения.
В красный, если на этом уроке вы не справлялись с заданиями.
Корабли выставляем на «лесенку успеха»
Задачи на работу: производительность труда, время, объем работы.
А= V * t
V= A : t
t= A : V
Предметные: знают: формулы решения задачи; умеют: применять формулы для решения задачи.
Коммуникативные: уважение к окружающим – умение слушать и слышать, умение с достаточной полнотой и точностью выражать свои мысли в соответствии с задачами и условиями коммуникации;
Личностные: формирование психологических условий развития общения, кооперации сотрудничества; доброжелательность, доверие и внимание к людям, готовность к сотрудничеству и дружбе, оказанию помощи тем, кто в ней нуждается;
11. Сюжетные текстовые задачи
1. Вспоминай формулы по каждой теме
2. Решай новые задачи каждый день
3. Вдумчиво разбирай решения
Задачи на производительность труда
(blacktriangleright) Задачи из данной подтемы в определенном смысле схожи с задачами на прямолинейное движение: роль скорости здесь играет производительность труда (p) , роль расстояния — объем работы (A). Формула: [{large{A=pcdot t}}]
(blacktriangleright) Значит, например, если два рабочих работают одновременно, то производительность их общей работы (p) равна сумме производительностей каждого: (p=p_1+p_2).
Задание
1
#2823
Уровень задания: Легче ЕГЭ
Четыре одинаковых кота съедают четыре пачки корма “Корм 1” за четыре дня. Пять таких же котов съедают пять пачек корма “Корм 2” за пять дней. Во сколько раз больше период, на который одному такому коту хватит одной пачки корма “Корм 2”, чем период, на который одному такому коту хватит одной пачки корма “Корм 1”?
По условию четыре кота съедают четыре пачки корма “Корм 1” за четыре дня, тогда каждый кот ест свою пачку корма “Корм 1” четыре дня. Аналогично каждый кот ест свою пачку корма “Корм 2” пять дней, следовательно, искомая величина равна (5 : 4 = 1,25).
Ответ: 1,25
Задание
2
#855
Уровень задания: Равен ЕГЭ
Один маляр может покрасить забор за 2 часа, а второй маляр тот же забор – за 3 часа. За сколько часов маляры покрасят такой же забор, работая вместе?
За час первый маляр красит (dfrac{1}{2}) забора, а второй (dfrac{1}{3}) забора.
Вместе за час они красят (dfrac{1}{2} + dfrac{1}{3} = dfrac{5}{6}) забора.
Таким образом, малярам понадобится (1 : dfrac{5}{6} = 1,2) часа.
Ответ: 1,2
Задание
3
#2139
Уровень задания: Равен ЕГЭ
Один гигантский комар может выпить литр крови за полчаса, а второй гигантский комар – за четверть часа. За сколько минут гигантские комары выпьют литр крови на двоих?
За час первый комар выпивает (2) литра, а второй (4) литра.
Вместе за час они выпьют (2 + 4 = 6) литров.
Таким образом, комарам на распитие литра крови понадобится (dfrac{1}{6}) часа, то есть (10) минут.
Ответ: 10
Задание
4
#851
Уровень задания: Равен ЕГЭ
Таня может перемыть гору посуды за 20 минут, а Настя за 60 минут. За сколько минут девочки перемоют две горы посуды, работая вместе?
За минуту Таня моет (dfrac{1}{20}) часть одной горы посуды, а Настя (dfrac{1}{60}) часть горы посуды.
Вместе за минуту они моют (dfrac{1}{20} + dfrac{1}{60} = dfrac{1}{15}) горы посуды.
Таким образом, на две горы посуды девочкам понадобится (2 : dfrac{1}{15} = 30) минут.
Ответ: 30
Задание
5
#850
Уровень задания: Равен ЕГЭ
Боря может поклеить обои в комнате общежития за 10 часов, а его сосед Савва – за 6 часов. За сколько часов ребята поклеят обои в комнате, работая вместе?
За час Боря клеит (dfrac{1}{10}) часть комнаты, а Савва (dfrac{1}{6}) часть комнаты.
Вместе за час они клеят (dfrac{1}{10} + dfrac{1}{6} = dfrac{8}{30}) комнаты.
Таким образом, ребятам понадобится (1 : dfrac{8}{30} = 3,75) часа.
Ответ: 3,75
Задание
6
#849
Уровень задания: Равен ЕГЭ
Отличник Илья решает все 300 уравнений из учебника за 2 часа, а двоечница Уля решает все 300 уравнений из учебника за 30 часов. Уля решала уравнения из учебника 10 часов, после чего на помощь пришёл Илья. Сколько времени в итоге Уля потратила на получение всех решений всех уравнений (в том числе с помощью Ильи)? Ответ дайте в часах.
За час Уля решает (dfrac{1}{30}) всех уравнений, а Илья (dfrac{1}{2}) всех уравнений.
За первые 10 часов Уля решила (10cdotdfrac{1}{30} = dfrac{1}{3}) всех уравнений, после чего ей оставалось ещё (1 — dfrac{1}{3} = dfrac{2}{3}) всех уравнений.
За час совместной работы Уля и Илья решали (dfrac{1}{30} + dfrac{1}{2} = dfrac{8}{15}) от всех уравнений, тогда (dfrac{2}{3}) от всех уравнений они решили за (dfrac{2}{3} : dfrac{8}{15} = 1,25) часа.
В итоге Уля потратила (10 + 1,25 = 11,25) часа.
Ответ: 11,25
Задание
7
#848
Уровень задания: Равен ЕГЭ
Лев съедает антилопу за 20 минут, а львица съедает такую же антилопу за 30 минут. Спустя 10 минут после того, как лев приступил к поеданию антилопы, к нему присоединилась львица, и они доели антилопу вместе. Сколько минут в такой ситуации потребовалось на поедание антилопы льву и львице?
В минуту лев съедает (dfrac{1}{20}) антилопы, а львица (dfrac{1}{30}) антилопы.
За 10 минут лев съел (dfrac{1}{20} cdot 10 = dfrac{1}{2}) антилопы, после чего осталось (1 — dfrac{1}{2} = 0,5) антилопы.
Поедая вместе, лев и львица в минуту съедают (dfrac{1}{20} + dfrac{1}{30} = dfrac{1}{12}) антилопы, тогда
с начала совместного поедания до конца прошло (0,5 : dfrac{1}{12} = 6) минут.
Всего на антилопу льву и львице потребовалось (10 + 6 = 16) минут.
Ответ: 16
Курс Глицин. Любовь, друзья, спорт и подготовка к ЕГЭ
Курс Глицин. Любовь, друзья, спорт и подготовка к ЕГЭ
2-й способ решения – без таблицы
Как обойтись без составления таблицы?
Сразу составить уравнение.
Для этого определим, какая величина нам не нужна в уравнении, чтобы затем приравнять.
Производительность? Ее и надо найти. Работа? Она нам дана по условию, поэтому глупо от нее избавляться. Остается время: оно нам и неизвестно, и не нужно.
Слева от знака равно будем писать формулу времени для первого рабочего, а справа – для второго.
Напомню, что первый работал на ( displaystyle 2) часа дольше, поэтому к времени второго надо будет прибавить ( displaystyle 2):
( displaystyle frac{112}{x}=frac{112}{x+1}+2)
То же самое уравнение, что и в первом способе, только без таблицы и системы уравнений.
А теперь вспомним, что я говорил в сааамом начале: задачи на работу и на движение – это то же самое. Спорное заявление, да? Ну, давай проверим, есть ли аналогия.
Во-первых, сравним формулы:
| Движение | Работа |
| ( displaystyle v=frac{S}{t}) | ( displaystyle P=frac{A}{t}) |
| Скорость движения | Скорость выполнения работы, т.е. производительность |
| Пройденный путь | Выполненная работа |
| Потраченное на движение время | Потраченное на работу время |
Теперь рассмотрим задачу:
Пример №1
Расстояние ( displaystyle 112) км первый велосипедист проезжает на ( displaystyle 2) часа дольше, чем второй.
Сколько км в час проезжает первый велосипедист, если известно, что второй за час проезжает на один километр больше, чем первый?
Ничего не напоминает? Да я же просто заменил слова: «Заказ» на «расстояние», «деталь» на «километр», «рабочий» на «велосипедист», «выполняет» на «проезжает». Суть осталась той же. Даже решение будет точно таким же (разберу здесь только II способ – без таблицы).
Пусть скорость первого ( displaystyle x), тогда второго ( displaystyle x+1). Сколько времени едет первый? ( displaystyle frac{112}{x}). Сколько времени едет второй? ( displaystyle frac{112}{x+1}). На сколько время первого больше, чем второго? На ( displaystyle 2) часа:
( displaystyle frac{112}{x}=frac{112}{x+1}+2).
То же самое уравнение! Вот и получается, что работа и движение – одно и то же.
Как решать задачи на совместную работу
Задачи на совместную работу отличаются от обычных, представленных выше, тем, что в них работа выполняется одновременно (совместно) несколькими рабочими (трубами и т.д.).
Пример №2
Первая труба заполняет бассейн за ( displaystyle 6) часов, а вторая – за ( displaystyle 4).
За какое время они заполнят бассейн, работая вместе?
Решение
Во-первых, давай придумаем аналогию с движением.
Придумал?
Бассейн – это путь. Допустим, из ( displaystyle A) в ( displaystyle B). Итак, первый автомобиль проезжает путь ( displaystyle AB) за ( displaystyle 6) часов, второй – за ( displaystyle 4).
А теперь как сформулировать вопрос? За какое время они проедут весь путь, двигаясь вместе? Бред.
Если двигаться параллельно, то каждый проходит весь путь самостоятельно. А в какой ситуации нам важно, какой путь автомобили проходят в сумме? Все гениальное просто: если они движутся навстречу друг другу!
Тогда что нас просят найти? Время, через которое они встретятся.
Поразмысли немного над этой аналогией. Все понял? Тогда идем дальше.
Какова «скорость» (а по-настоящему, производительность) первого? Путь (работа) деленный на время: ( displaystyle {{P}_{1}}=frac{A}{{{t}_{1}}}=frac{A}{6}). А второго? ( displaystyle {{P}_{2}}=frac{A}{{{t}_{2}}}=frac{A}{4}).
С какой производительностью работают две трубы вместе (не забывай, это задачи на совместную работу)? Берем количество литров, которое налила в бассейн первая труба за один час, прибавляем количество литров, которое налила в бассейн вторая труба за один час, – именно столько наливают в бассейн обе трубы за один час. То есть производительности складываются:
( displaystyle P={{P}_{1}}+{{P}_{2}})
То же самое, что и относительная скорость: с какой скоростью второй автомобиль приближается к первому? Со скоростью, равной сумме скоростей: ( displaystyle v={{v}_{1}}+{{v}_{2}}).
Итак,
( displaystyle P={{P}_{1}}+{{P}_{2}}=frac{A}{6}+frac{A}{4}=frac{5A}{12}).
Тогда время, за которое с такой производительностью будет выполнена работа ( A):
( displaystyle t=frac{A}{P}=frac{A}{frac{5A}{12}}=frac{12}{5}=2,4) (ч)
Итак, правило:
При совместной работе производительности складываются
А теперь давай рассмотрим самый сложный пример, научившись решать который, ты сможешь с легкостью справится с любой задачей на ЕГЭ.
Пример 8
На изготовление ( displaystyle 600) деталей первый рабочий тратит на ( displaystyle 10) часов меньше, чем второй рабочий на изготовление ( displaystyle 500) таких же деталей. За какое время, работая совместно, они изготовят партию в ( displaystyle 1000) деталей, если известно, что за час первый рабочий делает на ( displaystyle 5) деталей больше?
Решение:
Давай определимся, что нам нужно найти? Нам нужно найти время, за которое рабочие изготовят ( displaystyle 1000) деталей, то есть: ( displaystyle frac{1000}{{{P}_{1}}+{{P}_{2}}}).
Значит, нужно найти ( displaystyle {{P}_{1}}) и ( displaystyle {{P}_{2}}).
Первый рабочий за час делает на ( displaystyle 5) деталей больше. Обозначим производительность первого рабочего за х, тогда производительность второго – ( displaystyle x-5).
( displaystyle 600) деталей первый рабочий делает за ( displaystyle {{t}_{1}}) часов, а ( displaystyle 500) таких же деталей второй рабочий делает за ( displaystyle {{t}_{2}}={{t}_{1}}+10) часов.
То есть: ( displaystyle {{t}_{1}}=frac{600}{x}, a {{t}_{2}}={{t}_{1}}+10=frac{500}{x-5}).
Приравняв ( displaystyle {{t}_{1}}), получаем уравнение: