Задание 2.2.1.
Пути,
связывающие исходное и завершающее
событие сетевой модели называют:
—
замкнутые
+
полные
—
главные
Задание 2.2.2.
Самый
… из всех полных путей называется
критическим путем:
—
короткий
+
продолжительный
—
средний
Задание 2.2.3.
К
временным параметрам относят:
+
продолжительность работ
—
критические работы
—
критические события
Задание 2.2.4.
Позднее
время окончания работы минус ее
продолжительность равно позднему
времени:
—
наступления работы
+
начало работы
—
окончания события
Задание 2.2.5.
Разница
между поздним и ранним сроками наступления
события — это:
—
полный резерв
—
независимый резерв времени
+
резерв времени наступления события
Задание 2.2.6.
В
левом сегменте сетевого графика
указывается раннее время:
—
окончания события
+
наступления события
—
наступления работы
—
окончания работы
Задание 2.2.7.
Максимально
возможный запас времени для выполнения
данной работы сверх продолжительности
самой работы при условии, что в результате
такой задержки конечное для данной
работы событие наступит не позднее, чем
в свой поздний срок.:
+
Полный
резерв времени выполнения работы
—
Свободный
резерв времени выполнения работы
—
Независимый
резерв времени выполнения работы
Задание 2.2.8.
Запас
времени, которым можно располагать при
выполнении данной работы в предположении,
что предшествующее и последующее события
этой работы наступают в свои самые
ранние сроки:
—
Полный
резерв времени выполнения работы
+
Свободный
резерв времени выполнения работы
—
Независимый
резерв времени выполнения работы
Задание 2.2.9.
Запас
времени, на который можно отложить
начало выполнения работы без риска
повлиять на какие бы то ни было сроки
наступления каких-либо событий в модели
вообще:
—
Полный
резерв времени выполнения работы
—
Свободный
резерв времени выполнения работы
+
Независимый
резерв времени выполнения работы
Задание 2.2.10
В
правом сегменте сетевого графика
указывается позднее время:
—
окончания события
+
наступления события
—
наступления работы
—
окончания работы
Тема 2.3. «Методы расчета временных параметров и критического пути»
Задание 2.3.1.
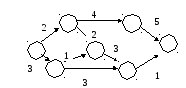
Определите
критический путь:
— 8
+ 11
— 12
Задание 2.3.2.
Определите
раннее время наступления второго
события:
|
1 |
2 |
|
|
1 |
0 |
2 2 |
|
2 |
2 |
+ 2
— 4
— 6
Задание
2.3.3.
Раннее
время окончания работы 1-2 равно:
|
1 |
2 |
|
|
1 |
0 |
4 |
|
2 |
4 |
4 |
— 2
+ 4
— 6
Задание
2.3.4.
Позднее
время наступления третьего события
равно:
|
1 |
2 |
3 |
|
|
1 |
0 |
2 2 |
|
|
2 |
2 |
7 9 |
|
|
3 |
9 |
— 7
+ 9
— 16
Задание
2.3.5.
Позднее
время начала работы 3-2 равно:
|
1 |
2 |
3 |
|
|
1 |
0 |
3 3 |
|
|
2 |
3 |
1 4 |
|
|
3 |
1 |
4 4 |
+ 3
— 4
— 5
Задание
2.3.6.
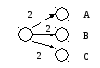
Раннее
время начала работы А, В и С равно:
+ 0
— 2
— 6
Задание 2.3.7.
Определите
позднее время начала работы В:
— 4
+ 7
— 10
Задание 2.3.8.
Определите
табличным методом позднее время начала
работы М:
|
Работа |
Непосредственно |
Непосредственно следующая |
Продолжительность |
Раннее время начала |
Позднее время начала |
Позднее время |
|
М |
D,H |
— |
10 |
26 |
36 |
|
|
N |
G,L |
— |
5 |
19 |
31 |
36 |
+ 26
— 31
— 36
Задание
2.3.9.
Полный
резерв времени работы М равен:
|
Работа |
Продолжительность |
Время окончания |
|
|
Раннее |
Позднее |
||
|
M |
10 |
26 |
36 |
|
N |
5 |
24 |
36 |
— 26
— 16
+ 10
Задание
2.3.10.
Раннее
время непосредственно следующее
за работой А работы В равно 14.
Продолжительность и раннее время начала
работы А равно 7 и 1 соответственно.
Определите свободный резерв времени
работы А:
+
6
—
8
—
22
В конце 50-х годов в США для осуществления программы исследовательских и конструкторских работ по созданию ракеты «Поларис» впервые был использован метод планирования и управления, основанный на идее определения, оценки вероятных сроков и контроля так называемого «критического пути» всего комплекса работ. Результаты превзошли все ожидания: во-первых, заметно уменьшилось число сбоев в работе из-за несогласованности используемых ресурсов, резко сократилась общая продолжительность выполнения всего комплекса работ, получен огромный эффект из-за снижения суммарной потребности в ресурсах и, соответственно, уменьшения общей стоимости программы. Вскоре после того, как результаты выполнения программы «Поларис» стали достоянием общественности, весь мир заговорил о методе PERT (Project Evaluation and Review Technique) как о новом подходе к организации управления.
За прошедшее с тех пор время метод «критического пути» не только получил широкое применение в повседневной практике управления, но и обусловил появление специальной научно-прикладной дисциплины – управление проектами. В центре внимания этой дисциплины находятся вопросы планирования, организации, контроля и регулирования хода выполнения проектов, организации материально-технического, финансового и кадрового обеспечения проектов, оценки инвестиционной привлекательности различных вариантов реализации проектов.
В современной деловой среде актуальность проектного управления как метода организации и управления производством значительно возросла. Это обусловлено объективными тенденциями в глобальной реструктуризации бизнеса. Принцип концентрации производственно-экономического потенциала уступил место принципу сосредоточения на развитии собственного потенциала организации. Крупные производственно-хозяйственные комплексы конгломеративного типа быстро замещаются гибкими сетевыми структурами, среди участников которых доминирует принцип предпочтения использования внешних ресурсов внутренним (outsourcing). Поэтому производственная деятельность всё больше превращается в комплекс работ со сложной структурой используемых ресурсов, сложной организационной топологией, сильной функциональной зависимостью от времени и огромной стоимостью.
Объект проектного управления
Термин проект, как известно, происходит от латинского слова projectus, что в буквальном переводе означает «брошенный вперед». Таким образом, сразу становится ясно, объект управления, который можно представить в виде проекта, отличает возможность его перспективного развертывания, т.е. возможность предусмотреть его состояния в будущем. Хотя различные официальные источники трактуют понятие проекта по-разному2 , во всех определениях четко просматриваются особенности проекта как объекта управления, обусловленные комплексностью задач и работ, четкой ориентацией этого комплекса на достижение определенных целей и ограничениями по времени, бюджету, материальным и трудовым ресурсам.
Однако, любая деятельность, в том числе и та, которую никто не собирается называть проектом, выполняется в течение определенного периода времени и связана с затратами определенных финансовых, материальных и трудовых ресурсов. Кроме того, любая разумная деятельность, как правило, целесообразна, т.е. направлена на достижение определенного результата. И, тем не менее, в одних случаях к управлению деятельностью подходят как к управлению проектом, а в других случаях – нет.
Деятельность как объект управления рассматривается в виде проекта тогда, когда
- она объективно имеет комплексных характер и для ее эффективного управления важное значение имеет анализ внутренней структуры всего комплекса работ (операций, процедур и т.п.);
- переходы от одной работы к другой определяют основное содержание всей деятельности;
- достижение целей деятельности связано с последовательно-параллельным выполнением всех элементов этой деятельности;
- ограничения по времени, финансовым, материальным и трудовым ресурсам имеют особое значение в процессе выполнения комплекса работ;
- продолжительность и стоимость деятельности явно зависит от организации всего комплекса работ.
Поэтому, объектом проектного управления принято считать особым образом организованный комплекс работ, направленный на решение определенной задачи или достижение определенной цели, выполнение которого ограничено во времени, а также связано с потреблением конкретных финансовых, материальных и трудовых ресурсов. При этом под «работой» понимается элементарная, неделимая часть данного комплекса действий.
Элементарность работы – понятие условное и относительное. То, что нецелесообразно делить в одной системе действий, полезно разукрупнять в другой. Например, если за элемент комплекса работ по сборке автомобиля принимается технологическая операция, то одной из «работ» может считаться установка сборщиком фары. Эта «работа» в данном случае неделима, так как остаются неизменными ее факторы – исполнитель, предмет и объект действия. Но, как только мы начинаем рассматривать исполнение этой работы как отдельную задачу, она сама превращается в комплекс.
Однако если задача возникает регулярно, а ее решение превращается в рутинную деятельность, доведенную до автоматизма, то нет никакого особого смысла каждый раз, приступая к ее решению, рассматривать и моделировать ее сложную структуру. Результат известен заранее и время, потраченное на планирование, будет просто потеряно. Поэтому объектом проектного управления является, как правило, комплекс взаимосвязанных работ, направленных на решение некоторой оригинальнойзадачи. Но, в том то и дело, что в современной деловой среде, при стремительном развитии техники, технологии и организации производства, при стремительной смене видов и разновидностей товаров и услуг на рынках, появление перед менеджером оригинальных задач стало фактически обычной ситуацией. Если в конце пятидесятых годов, на заре зарождения проектного управления, в качестве объектов такого управления выступали исключительно научно-исследовательские и опытно-конструкторские программы, то в наши дни уже мало кого можно удивить техническими, организационными, экономическими и даже социальными проектами. Уже в самом определении типа проекта заложена характеристика области его приложения.
Теоретические основы проектного управления
Для описания, анализа и оптимизации проектов наиболее подходящими оказались сетевые модели, представляющие из себя разновидность ориентированных графов.
В сетевой модели роль вершин графа могут играть события, определяющие начало и окончание отдельных работ, а дуги в этом случае будут соответствовать работам. Такую сетевую модель принято называть сетевой моделью с работами на дугах (Activities on Arrows, AoA). В то же время, возможно, что в сетевой модели роль вершин графа играют работы, а дуги отображают соответствие между окончанием одной работы и началом другой. Такую сетевую модель принято называть сетевой моделью с работами в узлах (Activities on Nodes, AoN).
Пусть множество A={a1, a2, a3, … an} – комплекс работ, выполнение которых требуется для решения определенной задачи, например, строительства дома. Тогда, если множество V={v1, v2, v3, …, vm} будет представлять комплекс событий, возникающих в процессе выполнения комплекса работ, то сетевая модель будет задаваться ориентированным графом G=(V, A), в котором элементы множества V играют роль вершин, а элементы множества A – роль дуг, соединяющих вершины, причем каждой дуге ai можно поставить в однозначное соответствие пару вершин (vsi, vfi), первая из которых будет определять момент начала работы аi, а вторая – момент окончания этой работы. Такая сетевая модель будет сетевой моделью с работами на дугах.
Теперь пусть множество A={a1, a2, a3, … an} – по-прежнему будет рассматриваться как комплекс работ, выполнение которых требуется для решения определенной задачи, например, строительства дома. Тогда, если множество V={v1, v2, v3, …, vm} будет представлять комплекс отношений предшествования-следования работ в процессе их выполнения, то сетевая модель будет задаваться ориентированным графом G=(A, V), в котором элементы множества A играют роль вершин, а элементы множества V – роль дуг, соединяющих вершины, причем каждой дуге vi можно поставить в однозначное соответствие пару вершин (asi, afi), первая из которых будет непосредственно предшествующей работой в данной паре, а вторая – непосредственно следующей. Такая сетевая модель будет сетевой моделью с работами в узлах.
Сетевая модель может быть представлена: 1) сетевым графиком, 2) в табличной форме, 3) в матричной форме, 4) в форме диаграммы на шкале времени. Как будет показано ниже, переход от одной формы представления к другой не составляет большого труда.
Преимущество сетевых графиков и временных диаграмм перед табличной и матричной формами представления состоит в их наглядности. Однако это преимущество исчезает прямо пропорционально тому, как увеличиваются размеры сетевой модели. Для реальных задач сетевого моделирования, в которых речь идет о тысячах работ и событий, вычерчивание сетевых графиков и диаграмм теряет всякий смысл.
Преимущество табличной и матричной формы перед графическими представлениями состоит в том, что с их помощью удобно осуществлять анализ параметров сетевых моделей; в этих формах применимы алгоритмические процедуры анализа, выполнение которых не требует наглядного отображения модели на плоскости.
Сетевым графикомназывается полное графическое отображение структуры сетевой модели на плоскости.
Если сетевым графиком на плоскости отображается сетевая модель типа АоА, то однозначное представление должны получить все работы и все события модели. Однако структура сетевого графика модели АоА может быть более избыточна, чем структура самой отображаемой сетевой модели. Дело в том, что по правилам построения сетевого графика для удобства его анализа необходимо, чтобы два события были соединены только единственной работой, что в принципе не соответствует реальным обстоятельствам в окружающей нас действительности. Поэтому принято вводить в структуру сетевого графика элемент, которого нет ни в действительности, ни в сетевой модели. Этот элемент называется фиктивной работой. Таким образом, структура сетевого графика образуется из трех типов элементов (в отличие от структуры сетевой модели, где только два типа элементов):
- событий – моментов времени, когда происходит начало или окончание выполнения какой-либо работы (работ);
- работ – неделимых частей комплекса действий, необходимых для решения некоторой задачи;
- фиктивных работ – условных элементов структуры сетевого графика, используемых исключительно для указания логической связи отдельных событий.
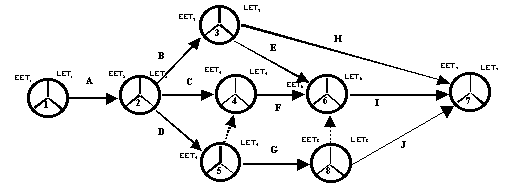
Графически события изображаются кружками, разделенными на три равных сегмента (радиусами под углом в 120°); работы изображаются сплошными линиями со стрелками на конце, ориентированными слева направо; фиктивные работы изображаются пунктирными линиями со стрелками на конце, ориентированными слева направо. Пример сетевого графика модели АоА представлен ниже на рис. 1.
Отметим, что индексация работ производится рядом с соответствующими стрелками; фиктивные работы не индексируются; индексы событий проставляются в нижнем сегменте соответствующего кружка. Заполнение остальных сегментов рассматривается ниже.
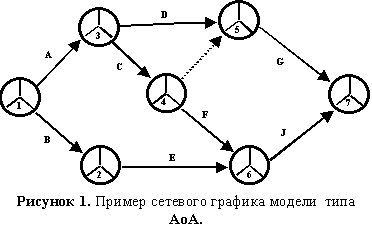
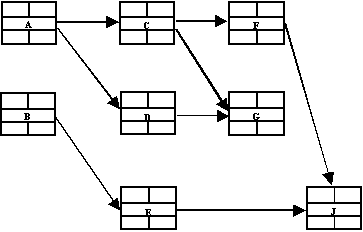
Если сетевым графиком отображается модель типа AoN, то избыточности структуры удается избежать. Здесь нет необходимости вводить в качестве дополнительного структурного элемента фиктивные работы, поскольку отсутствуют те структурные элементы, которые они призваны обслуживать, а именно – события. В сетевом графике модели типа AoN есть только узлы (или вершины), которые обозначают работы и дуги (сплошные линии со стрелками, ориентированными слева направо), которые обозначают отношения предшествования-следования работ. Никаких событий и никаких фиктивных работ! Заметим, что в наиболее известной программе по проектному управлению Microsoft Project реализуется именно этот тип модели.
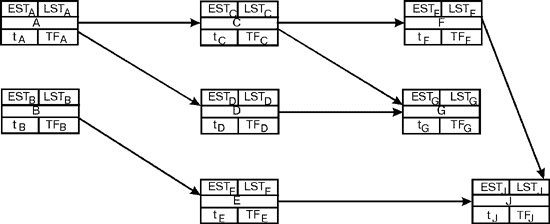
Здесь узлы сети, соответствующие работам, принято изображать прямоугольниками, поделенными на 5 секторов. В центральном секторе проставляется индекс (или записывается наименование работы). Заполнение остальных секторов рассматривается ниже. Пример сетевого графика для модели типа AoN представлен ниже на рис. 2.
Рисунок 2. Пример сетевого графика модели типа АоN.
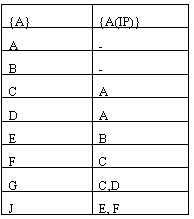
В табличной форме сетевая модель задается множеством {A, A(IP)}, где А – это множество индексов работ, а A(IP) множество комбинаций работ, непосредственно предшествующих работе А. Для рассматриваемого выше примера табличная форма сетевой модели будет такой, которая представлена в табл. 1.
Таблица 1.Табличная форма сетевой модели.
Матричная форма описания сетевой модели задается в виде отношения между событиями (ei, ej), которое равно 1, если между этими событиями есть работа (либо реальная, либо фиктивная) и 0 – в противном случае. Матричная форма для описания сетевой модели из рассматриваемого выше примера приведена ниже в табл. 2:
Таблица 2
|
События |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
|
1 |
1 |
1 |
|||||
|
2 |
1 |
1 |
|||||
|
3 |
1 |
1 |
1 |
||||
|
4 |
1 |
1 |
1 |
||||
|
5 |
1 |
1 |
1 |
||||
|
6 |
1 |
1 |
1 |
||||
|
7 |
1 |
1 |
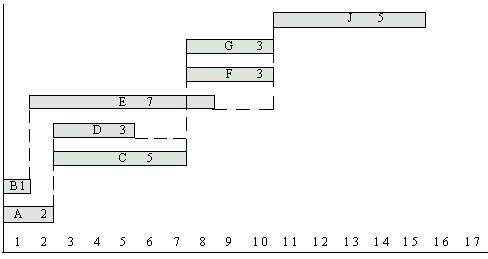
Описание сетевой модели в форме временной диаграммы (или графика Ганта) предполагает размещение работ в координатной системе, где по оси абсцисс (X) откладывается время (t), а по оси ординат (Y) – работы. Точкой начала отсчета любой из работ будет момент окончания всех ее предшествующих работ. Если работе не предшествует ничто, то она откладывается от начала временной шкалы, т.е. с самого левого края диаграммы. На рис. 3 представлен график Ганта для сетевой модели по данным табл. 1 с добавлением информации о продолжительности выполнения работ.
Поскольку в сетевых графиках моделей типа АоА вершины соответствуют событиям, постольку эти элементы структуры обладают свойством «сшивания» предыдущих работ с последующими. Иными словами, любое событие наступает только тогда, когда закончены все предшествующие ему работы. С другой стороны, оно является предпосылкой для начала следующих за ним работ. Событие не имеет продолжительности и наступает мгновенно. В связи с этим предъявляются особые требования к его определению.
Так, каждое событие, включаемое в сетевой график, должно быть полно, четко и всесторонне определено, его формулировка должна включать результат всех непосредственно предшествующих ему работ. И пока не выполнены все работы, непосредственно предшествующие данному событию, не может наступить и само событие, а, следовательно, не может быть начата ни одна из работ, непосредственно следующих за ним. Более того, если то или иное событие наступило, то это означает, что могут быть немедленно и реально начаты работы, следующие за ним. Если же по какой-либо причине хотя бы одна из таких работ не может быть начата, следовательно, нельзя считать данное событие наступившим.
Рисунок 3
Различаются следующие разновидности событий сетевого графика модели АоА:
- исходное событие – результат, в отношении которого условно предполагается, что он не имеет предшествующих работ;
- завершающее событие – результат, в отношении которого предполагается, что за ним не следует ни одна работа; это и является конечной целью выполнения всего комплекса работ или решением задачи;
- промежуточное событие или просто событие. Это любой достигаемый результат в выполнении одной или нескольких работ, дающий возможность начать последующие работы;
- начальное событие – событие, непосредственно предшествующее данной конкретной работе;
- конечное событие – событие, непосредственно следующее за данной работой.
Временные параметры (или временные характеристики) сетевой модели являются главными элементами аналитической системы проектного управления. Именно для их определения и последующего улучшения выполняется вся подготовительная, вспомогательная работа по составлению сетевой модели проекта и ее последующей оптимизации.
Различают следующие временные параметры:
- продолжительность работ;
- раннее время начала работы;
- раннее время окончания работы;
- позднее время начала работы;
- позднее время окончания работы;
- раннее время наступления события;
- позднее время наступления события;
- продолжительность критического пути;
- резерв времени наступления события;
- полный резерв времени выполнения работы;
- свободный резерв времени выполнения работы;
- независимый резерв времени выполнения работы.
Продолжительность работы (ti) – календарное время, которое занимает выполнение работы.
Раннее время начала работы (ESTi) – наиболее ранний из возможных сроков начала выполнения работы.
Раннее время окончания работы (EFTi) – равно раннему времени начала работы плюс ее продолжительность.
Позднее время окончания работы (LFTi) – наиболее поздний из допустимых сроков окончания работы.
Позднее время начала работы (LSTi) – равно позднему времени окончания работы минус ее продолжительность.
Раннее время наступления события (EETj) – характеризует наиболее ранний из возможных сроков свершения того или иного события. Поскольку каждое событие является результатом свершения одной или нескольких работ, а те в свою очередь следуют за какими-либо предшествующими событиями, то срок его наступления определяется величиной наиболее длительного отрезка пути от исходного события до рассматриваемого.
Позднее время наступления события (LETj) – характеризует наиболее поздний из допустимых сроков совершения того или иного события. Если установлен срок наступления завершающего события, являющегося результатом всего комплекса проводимых работ, то каждое промежуточное событие должно наступить не позже определенного срока. Этот срок и является предельно допускаемым сроком наступления события.
Любая последовательность непосредственно следующих друг за другом работ в сетевой модели называется путем. Путей в сетевой модели может быть очень много, но при этом пути, связывающие исходное и завершающее события сетевой модели, называются полными, а все остальные – неполными. Сумма продолжительностей выполнения работ, составляющих тот или иной путь, называется продолжительностью этого пути.
Самый продолжительный из всех полных путей называется критическим путем сетевой модели. Таким образом, продолжительность критического пути равна сумме продолжительностей всех работ, составляющих этот путь.
Работы, лежащие на критическом пути, называются критическими работами, а события – критическими событиями.
Уже одного определения критического пути сетевой модели проекта достаточно для организации управления всем комплексом работ. Жестко контролируя календарные сроки выполнения критических работ, можно в итоге избежать потерь. У работ, не находящихся на критическом пути, как правило, имеются резервы времени, позволяющие на некоторое время откладывать их выполнение, если это необходимо.
Резерв времени наступления события – это разница между поздним и ранним сроками наступления этого события.
Полный резерв времени выполнения работы (TFi) – это максимально возможный запас времени для выполнения данной работы сверх продолжительности самой работы при условии, что в результате такой задержки конечное для данной работы событие наступит не позднее, чем в свой поздний срок.
Свободный резерв времени выполнения работы (FFi) – это запас времени, которым можно располагать при выполнении данной работы в предположении, что предшествующее и последующее события этой работы наступают в свои самые ранние сроки.
Независимый резерв времени выполнения работы (IFi) – это запас времени, на который можно отложить начало выполнения работы без риска повлиять на какие бы то ни было сроки наступления каких-либо событий в модели вообще.
Параметры раннего и позднего времени наступления события используются в маркировке вершин сетевого графика модели типа АоА. В левый сегмент записывается раннее время наступления соответствующего события (ЕETj), а в правый – позднее (LETj), что показано на рис 4.
Рисунок 4. Пример маркировки времени наступления событий
В маркировке вершин сетевого графика модели типа AoN помимо индекса работ используются параметры (см. Рис. 5):
- раннего времени начала выполнения работы (ESTj), которое записывается в левый верхний сектор прямоугольника, маркирующего вершину работы;
- позднего времени начала выполнения работы (LSTj), которое записывается в правый верхний сектор прямоугольника, маркирующего вершину работы;
- продолжительность выполнения работы (tj), которая записывается в левый нижний сектор прямоугольника, маркирующего вершину работы;
- полный резерв времени выполнения работы (TFi) – который записывается в правый нижний сектор прямоугольника, маркирующего вершину работы.
Рисунок 5. Пример маркировки вершин сетевого графика модели типа АоN
Методы расчета временных параметров и критического пути сетевой модели проекта
Если размеры сетевого графика невелики, то его временные параметры и критический путь могут быть найдены путем непосредственного рассмотрения графика вершина за вершиной, работа за работой. Но, естественно, по мере увеличения масштабов модели вероятность появления ошибки в расчетах будет возрастать в геометрической прогрессии. Поэтому, даже при небольших размерах модели целесообразно воспользоваться одним из наиболее подходящих алгоритмических методов расчета, позволяющих подойти к этой задаче формально.
Самыми распространенными методами расчета временных параметров сетевой модели являются табличный и матричный. Поэтому, даже если исходная информация по сетевой модели представлена в виде сетевого графика или временной диаграммы, приступая к анализу, ее следует привести к табличной либо матричной форме.
В качестве примера будем рассматривать модель, заданную изначально сетевым графиком, приведенным на рис. 6.
Рисунок 6. Пример сетевого графика для иллюстрации методов расчета временных параметров
Как табличный, так и матричный метод расчета временных параметров сетевой модели основывается на следующих соотношениях, вытекающих из определений временных параметров. Для удобства понимания индекс работы, как правило, состоит из двух букв, например, [ij], первая из которых соответствует индексу начального события работы, а вторая – индексу конечного события работы. С учетом этого замечания:
- Раннее время начала работы [ij] совпадает с ранним временем наступления события [i], т.е.
ESTij = EET [i]. - Позднее время окончания работы [ij] совпадает с поздним временем наступления события [j], т.е.
LFTij = LET [j]. - Раннее время окончания работы [ij]:
EFTij = ESTij + tij.
- Позднее время начала работы [ij]:
LSTij = LFTij – tij. - Раннее время наступления события [j] совпадает с самым поздним (максимальным) ранним временем окончания из всех тех работ, для которых данное событие является конечным, т.е.
EET[j] = max { EFTrj, EFTnj, …, EFTmj}, где [rj], [nj], …, [mj] – индексы работ, для которых событие [j] является конечным. - Позднее время наступления события [j] совпадает с самым ранним (минимальным) поздним временем начала из всех тех работ, для которых данное событие является начальным, т.е.
LET[j] = min { LSTjr, LSTjn, …, LSTjm}, где [jr], [jn], …, [jm] – индексы работ, для которых событие [j] является начальным. - Для исходного и заключительного события сетевой модели справедливо:
EET[s] = LET[s] - Но если для исходного события принимается, как правило, момент времени, равный 0, то для заключительного события он появляется в результате расчетов и по нему можно судить о продолжительности критического пути. Итак, для заключительного события справедливо:
EET[f] = LET[f] = TK, где TK – продолжительность критического пути. - Полный резерв времени выполнения работы [ij]:
TFij = LЕT[j] – EET[i] – tij. - Свободный резерв времени выполнения работы [ij]:
FFij = EЕT[j] – EET[i] – tij. - Независимый резерв времени выполнения работы [i]:
IFi = EЕT[j] – LET[i] – tij.
Рассмотрим сначала матричный метод определения временных параметров.
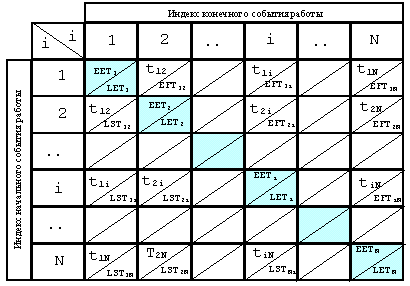
Прежде всего, необходимо составить квадратную матрицу (см. Рис. 7), число столбцов и строк, в которой равно числу событий сетевой модели. Строки и столбы индексируются в одинаковом порядке индексами события. Полученные на пересечении строк и столбцов клетки разбиваются на две части по диагонали снизу слева вверх вправо. Левая верхняя часть клетки называется ее числителем, правая нижняя – знаменателем.
Первый шаг заполнения матрицы заключается в следующем. Если события [i] и [j] соединяются какой-то работой, то продолжительность этой работы tij заносится в числители двух клеток: клетки, лежащей на пересечении i-й строки и j-го столбца, и клетки лежащей на пересечении j-й строки и i-го столбца. Эти действия выполняются для всех работ сетевой модели, а числители всех остальных клеток, кроме клеток, лежащих на главной (слева сверху вправо вниз) диагонали матрицы, заполняются нулями или вообще не заполняются.
Следующий шаг заполнения матрицы первоначально предполагает занесение в числитель первой клетки главной диагонали значения 0. Это равносильно тому, что мы полагаем, что раннее время наступления исходного события сетевой модели равно 0. Затем осуществляем заполнение знаменателей тех клеток первой строки, лежащих справа от (или над) главной диагонали, чьи числители содержат значения больше 0. При этом значения, которые проставляются в знаменатели, вычисляются как сумма числителя клетки данной строки, лежащей на главной диагонали, и числителя заполняемой клетки. Таким образом, мы подсчитываем раннее время окончания соответствующей работы. Результат выполнения этих действий приведен на рис. 8.
Рисунок 7. Разметка матрицы при определении временных параметров сетевой модели матричным методом
Рисунок 8.
Нетрудно проверить по формулам, что раннее время окончания работы 1-2 равно 4, а работы 1-4 равно 7.
Следующий шаг заполнения матрицы начинается с того, что мы должны решить, какое значение должно стоять в числителе диагональной клетки второй строки. По определению это должно быть значение, соответствующее раннему началу события 2. Раннее начало некоторого события, являющегося конечным для нескольких работ, равно моменту раннего окончания самой поздней из работ, которые заканчиваются данным событием. Значит, просто необходимо просмотреть знаменатели клеток столбца 2 сверху вниз до главной диагонали и выбрать максимальное значение, после чего записать его в числитель диагональной клетки 2. В нашем примере это будет знаменатель клетки 1-2, который равен 4.
После этого также, как были подсчитаны знаменатели в первой строке выше диагонали, подсчитываются знаменатели клеток второй строки выше диагонали.
Процедуры, описанные выше, повторяются до тех пор, пока не будет найден числитель последней диагональной клетки.
Дойдя до последней диагональной клетки (см. Рис. 9), мы получили значение раннего времени наступления завершающего события сетевой модели (36), которое и определяет продолжительность критического пути. Вместе с тем, для завершающего события, как известно, раннее время равно позднему времени его наступления, следовательно, знаменатель этой клетки будет равен ее числителю. Запишем это.
Рисунок 9
Получив значение знаменателя последней диагональной клетки, можно вычислить значения знаменателей клеток (чьи числители больше 0), находящихся в той же строке слева (ниже) от главной диагонали. Они будут равны разнице значения знаменателя соответствующей диагональной клетки и значения числителя клетки, для которой производится расчет. Так, например, значение знаменателя клетки 8-7 будет равно 36-5=31, а клетки 8-4 будет равно 36-6=30.
После подсчета всех знаменателей в последней строке можно найти значение знаменателя в диагональной клетке на предпоследней строке. Оно будет равно минимальному значению из знаменателей всех клеток, лежащих в данном столбце ниже главной диагонали, т.е. 31.
Затем аналогичным образом обсчитываем предпоследнюю строку и находим знаменатель третьей от конца диагональной клетки.
Из заполненной матрицы нетрудно увидеть не только продолжительность критического пути (числитель или знаменатель последней диагональной клетки), но также сам критический путь. Он проходит через события, у которых раннее и позднее время наступления равны, т.е. через события, у которых в соответствующих диагональных клетках совпадают числители и знаменатели. В нашем примере это будут события 1, 2, 4, 6, 8 (см. Рис. 9).
В соответствии с расчетными формулами резервов времени, которые были приведены выше, полный резерв времени выполнения работы, находящейся между событиями i и j, определяется разностью значений знаменателя диагональной клетки j-j и знаменателя клетки j в строке i выше главной диагонали. Чтобы найти свободный резерв времени выполнения работы, находящейся между событиями i и j, необходимо из числителя диагональной клетки j-j вычесть числитель диагональной клетки i-i и числитель клетки i-j. Чтобы найти независимый резерв времени выполнения работы, находящейся между событиями i и j, необходимо из числителя диагональной клетки j-j вычесть знаменатель диагональной клетки i-i и числитель клетки i-j.
Так, для работы 3-5 полный резерв будет равен 29-9=20, свободный – 17-2-7=8, а независимый – 17-22-7=-12 (принимается равным 0). Для работы 2-6 полный резерв будет равен 26-12=14, свободный – 26-4-8=14 и независимый – 26-4-8=14.
На рис. 10 приведены результаты расчетов всех резервов времени на основании данных из таблицы на рис. 9.
Табличный метод. Составляется таблица, число строк в которой равно числу работ, включающая в себя следующие столбцы (в порядке их следования слева направо):
- индекс работы;
- индексы непосредственно предшествующих работ;
- индексы непосредственно следующих работ;
- продолжительность выполнения работы;
- раннее время начала выполнения работы;
- позднее время начала выполнения работы;
- раннее время окончания выполнения работы;
- позднее время окончания выполнения работы;
- полный резерв времени работы;
- свободный резерв времени работы;
- независимый резерв времени работы.
Исходная информация, связанная с описанием топологии сетевой модели, содержится в столбцах (1), (2) и (4). Суть табличного метода расчета временных параметров сетевой модели состоит в последовательном заполнении остальных столбцов данной таблицы.
Алгоритм табличного метода предусматривает выполнение следующих последовательных шагов.
Рисунок 10
ШАГ 1. Определение индексов непосредственно следующих работ.
Рассматриваем работу с индексом [i]. Непосредственно следующие за ней работы – это те работы, для которых работа [i] является непосредственно предшествующей. Следовательно, индексы непосредственно следующих работ – это индексы тех работ, у которых в столбце (2) содержится индекс работы [i].
ШАГ 2. Определение раннего времени начала и раннего времени окончания работ.
Определение раннего времени начала и раннего окончания работ, т.е. заполнение столбцов (5) и (7) таблицы должно осуществляться одновременно, т.к. время начала одних работ зависит от времени окончания других.
Заполнение указанных столбцов осуществляется последовательно от начала сетевой модели к ее концу, т.е. сверху вниз. При этом действуют следующие правила:
- Раннее время окончания рассматриваемой работы равно раннему времени ее начала (из столбца (5)) плюс продолжительность работы (из столбца (4)).
- Раннее время начала выполнения работы равно 0, если данной работе непосредственно не предшествует ни одна из работ сетевой модели, или равно максимальному раннему времени окончания среди всех непосредственно предшествующих ей работ (из столбца (7)).
Продолжительность критического пути равна максимальному значению в столбце (7).
ШАГ 3. Определение позднего времени окончания и позднего времени начала работ.
Определение позднего времени окончания и позднего начала работ, т.е. заполнение столбцов (6) и (8) таблицы должно осуществляться также одновременно, т.к. время начала одних работ зависит от времени окончания других.
Заполнение указанных столбцов осуществляется последовательно от конца сетевой модели к ее началу, т.е. снизу вверх. При этом действуют следующие правила:
- Позднее время начала рассматриваемой работы равно позднему времени ее окончания (из столбца (8)) минус продолжительность работы (из столбца (4)).
- Позднее время окончания выполнения работы равно продолжительности критического пути, если за данной работой нет ни одной непосредственно следующей работы (из столбца (3)) сетевой модели, или равно минимальному позднему времени начала среди всех непосредственно следующих за данной работой работ (из столбца (6)).
Шаг 4. Определение полного резерва времени выполнения работы.
Полный резерв времени работы [i] находится как разность значений ее позднего и раннего времени окончания (соответственно, столбцы (8) и (7)), либо как разность значений ее позднего и раннего начала выполнения (соответственно, столбцы (6) и (5)).
Шаг 5. Определение свободного резерва времени выполнения работы.
Свободный резерв времени работы [i] определяется как разность между значением раннего времени начала любой из непосредственно следующих за ней работ и суммой раннего времени начала работы [i] и ее продолжительности.
Шаг 6. Определение независимого резерва времени выполнения работы.
Независимый резерв времени работы [i] определяется как разность между значением раннего времени начала любой из непосредственно следующих за ней работ и суммой позднего времени наступления начального события работы [i] и ее продолжительности. Позднее время наступления начального события работы [i] табличным путем определяется как минимальное позднее время начала тех работ, у которых с работой [i] одинаковый состав непосредственно предшествующих работ.
По приведенным выше правилам заполнена следующая табл. 3.
Таблица 3.
| Работа | Непосредс. Предшеств. |
Непосредств Следующая. |
t | EST | LST | EFT | LFT | TF | FF | IF |
| A | ? | D, E | 4 | 0 |
Источник: Журнал “МЕНЕДЖМЕНТ В РОССИИ И ЗА РУБЕЖОМ” №6 1998
Автор: В.С.Ефремов
Позднее время окончания работы (LFTi) – наиболее поздний из допустимых сроков окончания работы.
Позднее время начала работы (LSTi) – равно позднему времени окончания работы минус ее продолжительность.
Раннее время наступления события (EETj) – характеризует наиболее ранний из возможных сроков свершения того или иного события. Поскольку каждое событие является результатом свершения одной или нескольких работ, а те в свою очередь следуют за какими-либо предшествующими событиями, то срок его наступления определяется величиной наиболее длительного отрезка пути от исходного события до рассматриваемого.
Позднее время наступления события (LETj) – характеризует наиболее поздний из допустимых сроков совершения того или иного события. Если установлен срок наступления завершающего события, являющегося результатом всего комплекса проводимых работ, то каждое промежуточное событие должно наступить не позже определенного срока. Этот срок и является предельно допускаемым сроком наступления события.
Любая последовательность непосредственно следующих друг за другом работ в сетевой модели называется путем. Путей в сетевой модели может быть очень много, но при этом пути, связывающие исходное и завершающее события сетевой модели, называются полными, а все остальные – неполными. Сумма продолжительностей выполнения работ, составляющих путь, называется продолжительностью этого пути.
Самый продолжительный из всех полных путей называется критическим путем сетевой модели. Таким образом, продолжительность критического пути равна сумме продолжительностей всех работ, составляющих этот путь.
Работы, лежащие на критическом пути, называются критическими работами, а события – критическими событиями.
Уже одного определения критического пути сетевой модели проекта достаточно для организации управления всем комплексом работ. Жестко контролируя календарные сроки выполнения критических работ, можно в итоге избежать потерь. У работ, не находящихся на критическом пути, как правило, имеются резервы времени, позволяющие на некоторое время откладывать их выполнение, если это необходимо.
Резерв времени наступления события – это разница между поздним и ранним сроками наступления этого события.
Полный резерв времени выполнения работы (TFi) – это максимально возможный запас времени для выполнения данной работы сверх продолжительности самой работы при условии, что в результате такой задержки конечное для данной работы событие наступит не позднее, чем в свой поздний срок.
Свободный резерв времени выполнения работы (FFi) – это запас времени, которым можно располагать при выполнении данной работы в предположении, что предшествующее и последующее события этой работы наступают в свои самые ранние сроки.
Независимый резерв времени выполнения работы (IFi) – это запас времени, на который можно отложить начало выполнения работы без риска повлиять на какие бы то ни было сроки наступления каких-либо событий в модели вообще.
Параметры раннего и позднего времени наступления события используются в маркировке вершин сетевого графика модели типа АоА. В левый сегмент записывается раннее время наступления соответствующего события (ЕETj), а в правый – позднее (LETj), что показано на рис 1.2.4.
Рис. 1.2.4.Пример маркировки времени наступления событий
В маркировке вершин сетевого графика модели типа AoN помимо индекса работ используются параметры (см. Рис. 1.2.5):
• раннего времени начала выполнения работы (ESTj), которое записывается в левый верхний сектор прямоугольника, маркирующего вершину работы;
• позднего времени начала выполнения работы (LSTj), которое записывается в правый верхний сектор прямоугольника, маркирующего вершину работы;
• продолжительность выполнения работы (tj), которая записывается в левый нижний сектор прямоугольника, маркирующего вершину работы;
• полный резерв времени выполнения работы (TFi) – который записывается в правый нижний сектор прямоугольника, маркирующего вершину работы.
Рис.1.2.5. Пример маркировки вершин сетевого графика модели типа АоN
1.2.3. Методы расчета временных параметров и критического пути сетевой модели проекта
Если размеры сетевого графика невелики, то его временные параметры и критический путь могут быть найдены путем непосредственного рассмотрения графика вершина за вершиной, работа за работой. Но, естественно, по мере увеличения масштабов модели вероятность появления ошибки в расчетах будет возрастать в геометрической прогрессии. Поэтому, даже при небольших размерах модели целесообразно воспользоваться одним из наиболее подходящих алгоритмических методов расчета, позволяющих подойти к этой задаче формально.
Самыми распространенными методами расчета временных параметров сетевой модели являются табличный и матричный. Поэтому, даже если исходная информация по сетевой модели представлена в виде сетевого графика или временной диаграммы, приступая к анализу, ее следует привести к табличной либо матричной форме.
В качестве примера будем рассматривать модель, заданную изначально сетевым графиком, приведенным на рис. 1.2.6.
Рис. 1.2.6. Пример сетевого графика для иллюстрации методов расчета временных параметров


Подборка по базе: Экономика 1 Задание 3 не проверено преподавателем.docx, Практическое задание 1.docx, Практическое задание 2.docx, Практическое задание 1.docx, История России Задание 1.docx, Практическое задание_Коучинг глубинных изменений.docx, Практическое задание_Лайф-коучинг.docx, Грамматическое задание.docx, ТК задание 19.doc, Практическое задание 1.docx
Практическое задание 2. Организация сетевого планирования проекта
Как уже говорилось в лекционном материале, для описания, анализа и оптимизации проектов очень удобным инструментом являются сетевые модели и в выполняемых лабораторных работах будут рассматриваться два основных представления сетевых моделей: сетевой график и временная диаграмма.
Рассмотрим практические примеры.
Напомним, что иногда роль вершин графа могут играть события, определяющие начало и окончание отдельных работ, а дуги в этом случае соответствуют работам. Графы такого типа называют “работа-дуга”, а соответствующую сетевую модель — сетевой моделью с работами на дугах (Activities on Arrows, AoA). Этот тип модели является устаревшим, часто обладает избыточностью (фиктивные работы) и в программных продуктах фактически не используется (хотя иногда еще встречается в отечественной литературе).
Когда в сетевой модели вершинами графа являются работы, а дуги отображают соответствие между окончанием одной работы и началом следующей, то графы такого типа называют “работа-вершина”, а соответствующую сетевую модель называют сетевой моделью с работами в узлах (Activities on Nodes, AoN). В Microsoft Project реализуется только этот тип модели, его и рассмотрим в практическом примере.
Выделяются следующие виды работ:
- простая
- событие (работа с нулевой длительностью, работа — веха)
- суммарная (состоящая из множества вложенных в нее работ любого вида)
Различают достаточно много временных параметров, но в примере будем рассматривать лишь те, которые непосредственно будут вычисляться в Microsoft Project.
Это:
- продолжительность работы;
- раннее время начала работы;
- раннее время окончания работы;
- позднее время начала работы;
- позднее время окончания работы;
- общий резерв времени выполнения работы
Продолжительность работы – это календарное время, которое занимает выполнение работы.
Любая последовательность непосредственно следующих друг за другом работ в сетевой модели называется путем. Путей в сетевой модели может быть много. Пути, связывающие исходное и завершающее события сетевой модели, называются полными, а все остальные – неполными. Сумма продолжительностей выполнения работ, составляющих тот или иной путь, называется продолжительностью этого пути.
Самый продолжительный из всех полных путей называется критическим путем и, соответственно, продолжительность критического пути равна сумме продолжительностей всех работ, составляющих этот путь.
Работы, критического пути, называются критическими работами, а события – критическими событиями.
Понятие критического пути сетевой модели проекта является очень важным, так как на его основе строится метод организации управления всем комплексом работ – метод критического пути (Critical Path Method, CPM). Суть метода состоит в том, что именно продолжительность критического пути определяет длительность проекта, и, соответственно для сокращения длительности выполнения проекта необходимо сокращать длительность задач, лежащих на критическом пути (обычно распараллеливанием работ или назначением дополнительных трудовых ресурсов). Работы, лежащие на критическом пути не имеют резервов времени, у работ же, не находящихся на критическом пути, как правило, имеются резервы времени, позволяющие на некоторое время откладывать их выполнение, если это необходимо.
Через понятие критического пути можно дать определения оставшихся временных параметров:
Раннее время начала работы Tрн – это самая ранняя дата, с которой возможно начать работу с учетом необходимости выполнения всех предыдущих работ с имеющимися у них временными ограничениями
Раннее время окончания работы Тро – это самая ранняя дата, с которой возможно окончание работы с учетом ее длительности и с учетом необходимости выполнения всех предыдущих работ с имеющимися у них временными ограничениями
Позднее время начала работы Тпн – это самая поздняя дата, с которой можно начать работу без изменения продолжительности критического пути и даты окончания проекта
Позднее время окончания работы Тпо – это самая поздняя дата, с которой можно завершить работу без изменения продолжительности критического пути и даты окончания проекта
Полный (общий) резерв времени выполнения работы Tпр – это интервал времени, в пределах которого приращение длительности рассматриваемой работы, не изменит даты окончания реализации проекта
Рассмотрим пример расчета сетевой модели.
Исходная информация для построения топологии сетевой модели и продолжительности работ дана в таблице ниже.
Таблица 1. Исходная информация.
| Код работы | Наименование работы | Продолжительность
Работы, дней |
| 1-2 A
1-4 B 2-4 C 4-6 D 5-4 F 5-7 G 3-6 I 7-6 J 3-8 K 6-8 L 7-8 M |
Исследование внутреннего рынка
Исследование зарубежного рынка Определение сегмента внутреннего рынка Определение политики освоения сегментов внутреннего и зарубежного рынков Исследование качества выпускаемого товара Разработка программы по адаптации товара на рынке Разработка рекламной политики по продвижению товара на рынке Разработка программы услуг по передвижению товара Выбор посредников Разработка политики оптовой и розничной торговли Разработка торговой марки и упаковки Определение ценовой политики Разработка программы сервисного обслуживания |
3
7 4 2 8 6 2 10 4 7 8 |
Данная сетевая модель отображает процесс маркетингового исследования фирмы, желающей выйти со своим товаром на рынок.
Цель расчета – определить окончательный срок исследования и календарные даты наступления событий и сроков начала и окончания работ.
Если рассматривать сетевую модель типа “работа-дуга”, она будет выглядеть следующим образом
Рисунок 1. Сетевая модель типа «работа-дуга».
Перерисуем сетевую модель в представлении “работы — вершины”, указывая рядом с обозначением ее длительность.
Рисунок 2. Сетевая модель типа «работа-вершина».
Ручной расчет временных параметров реализуется по шагам, а получаемые результаты удобно заносить в таблицу 1:
ШАГ 1. Определение последовательности выполнения работ
В первый столбец таблицы занесем перечень работ с указанием длительности каждой из них. Непосредственно предшествующие работы занесем во второй столбец, а непосредственно следующие работы – в третий столбец.
ШАГ 2. Определение раннего времени начала и раннего времени окончания работ.
Определение раннего времени начала и раннего окончания работ, т.е. заполнение столбцов (4) и (5) таблицы 1 должно осуществляться одновременно, т.к. время начала одних работ зависит от времени окончания других.
Заполнение указанных столбцов осуществляется последовательно от начала сетевой модели к ее концу. При этом действуют следующие правила:
- Раннее время начала выполнения работы равно 0, если данной работе непосредственно не предшествует ни одна из работ сетевой модели, или равно максимальному раннему времени окончания среди всех непосредственно предшествующих ей работ
- Раннее время окончания рассматриваемой работы равно раннему времени ее начала (из столбца (4)) плюс продолжительность работы (из столбца (5)).
Продолжительность критического пути равна максимальному значению в столбце (5).
Исходя из вышесказанного, первыми будут рассматриваться работы A, B, E, как не имеющие предшественников (заполняем для них соответствующие ячейки столбцов 4 и 5).
За работой A идут работы C, H, для которых также заполняем соответствующие им ячейки столбцов 4 и 5, исходя из рассчитанного раннего времени окончания работы А и продолжительностей работ C, H
За работой E идут работы F, G, для которых также заполняем соответствующие им ячейки столбцов 4 и 5, исходя из рассчитанного раннего времени окончания работы E и продолжительностей работ F, G
Далее по сформулированным правилам рассчитываем последовательно параметры работ в следующей последовательности D, I, J, K, L, M, N и заполняем все ячейки столбцов 4 и 5
Продолжительность критического пути составляет
(СЛЕДУЕТ РАССЧИТАТЬ) дней. Очевидно, что он состоит из работ E, G, J, L. Это означает, что все работы сетевой модели по маркетинговому исследованию могут быть выполнены не менее чем за следует рассчитать дней.
ШАГ 3. Определение позднего времени окончания и позднего времени начала работ.
Определение позднего времени окончания и позднего начала работ, т.е. заполнение столбцов (6) и (7) таблицы 1 должно осуществляться также одновременно, т.к. время начала одних работ зависит от времени окончания других.
Заполнение указанных столбцов осуществляется последовательно от конца сетевой модели к ее началу. При этом действуют следующие правила:
- Позднее время окончания выполнения работы равно продолжительности критического пути, если за данной работой нет ни одной непосредственно следующей работы (из столбца (5)) сетевой модели, или равно минимальному позднему времени начала среди всех непосредственно следующих за данной работой работ
- Позднее время начала рассматриваемой работы равно позднему времени ее окончания (из столбца (7)) минус продолжительность работы (из столбца (1)).
Исходя из вышесказанного, первыми будут рассматриваться работы K, L, M, как не имеющие следующих за ними работ (заполняем для них соответствующие ячейки столбцов 6 и 7).
Перед работой L идут работы I, D, J, для которых также заполняем соответствующие им ячейки столбцов 6 и 7, исходя из рассчитанного позднего времени начала работы L и продолжительностей работ I, D, J
Перед работой K и работой I идет работа H, для которой также заполняем соответствующие ей ячейки столбцов 6 и 7, исходя из рассчитанного позднего времени начала работы K и работы I и продолжительности работы H,
Перед работой M и работой J идет работа G, для которой также заполняем соответствующие ей ячейки столбцов 6 и 7, исходя из рассчитанного позднего времени начала работы M и работы J и продолжительности работы G,
Далее по сформулированным правилам рассчитываем последовательно параметры работ в следующей последовательности C, B, F, A, E и заполняем все ячейки столбцов 6 и 7
Шаг 4. Определение полного резерва времени выполнения работы.
Полный резерв времени работы находится как разность значений ее позднего и раннего времени окончания (соответственно, столбцы (7) и (5)), либо как разность значений ее позднего и раннего начала выполнения (соответственно, столбцы (6) и (4)). Значения полного резерва заносим в соответствующие ячейки столбца 8.
ПЕРВЫЕ 6 СТРОК ТАБЛИЦЫ ПРЕДСТАВЛЯЮТ СОБОЙ ПРИМЕР РАСЧЕТ ПО МЕТОДИКЕ, ПРИВЕДЕННОЙ ВЫШЕ. ОСТАЛЬНЫЕ ЗНАЧЕНИЯ (СТРОКИ 7-13) СЛЕДУЕТ РАССЧИТАТЬ САМОСТОЯТЕЛЬНО.
Таблица 2. Расчет параметров.
| 1
Работа, длительность |
2
Непосредс. Предшеств. |
3
Непосредств Следующая. |
4
Tрн |
5
Тро |
6
Тпн |
7
Тпо |
8
Tпр |
| A 3 | – | C, H | 0 | 3 | 7 | 10 | |
| B 7 | – | D | 0 | 7 | 9 | 16 | |
| C 4 | A | D | 3 | 7 | 12 | 16 | |
| D 2 | B, C, F | L | 13 | 15 | 16 | 18 | |
| E 5 | — | F, G | 0 | 5 | 0 | 5 | |
| F 8 | E | D | 5 | 13 | 8 | 16 | |
| G 3 | E | J, M | |||||
| H 6 | A | I, K | |||||
| I 2 | H | L | |||||
| J 10 | G | L | |||||
| K 4 | H | – | |||||
| L 7 | D, I, J | — | |||||
| M 8 | G | – |
В целях единообразия с выполняемой лабораторной работой введем две вехи, означающие начало и окончание процесса маркетингового исследования и отобразим это на рисунке
Рисунок 3. Сетевая модель типа «работа-вершина».