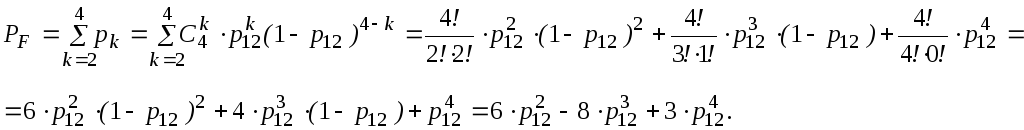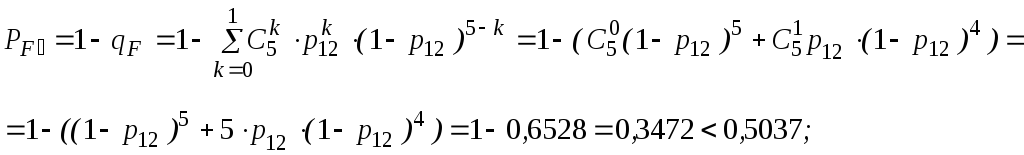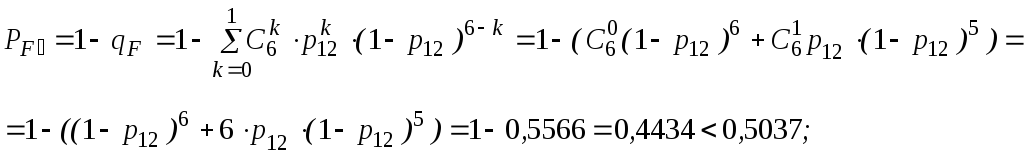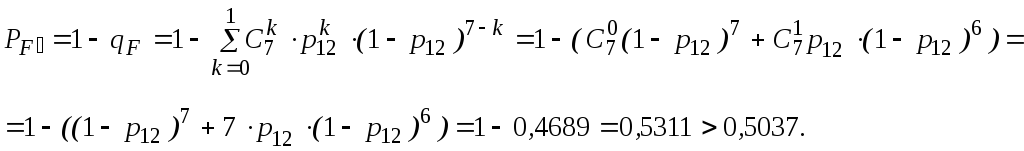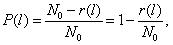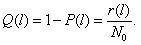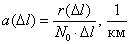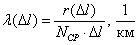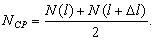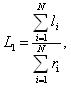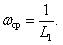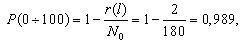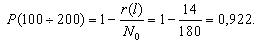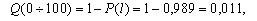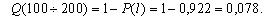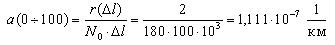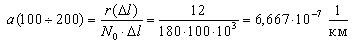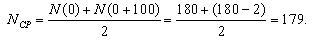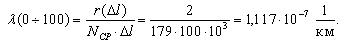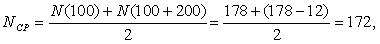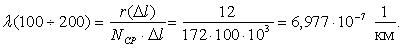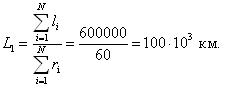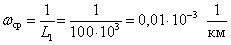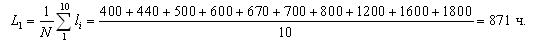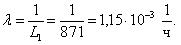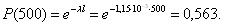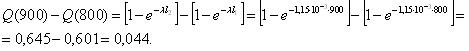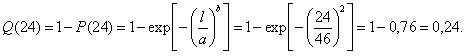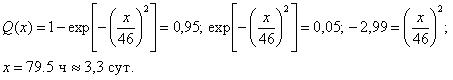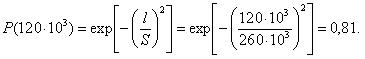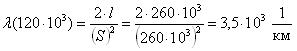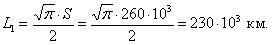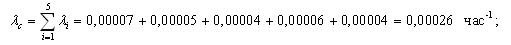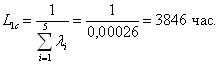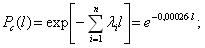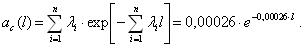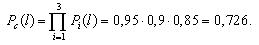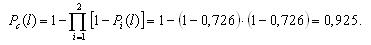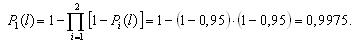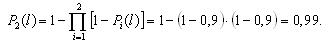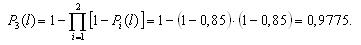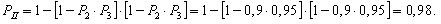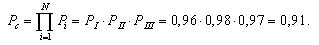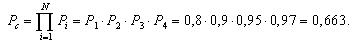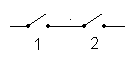РАСЧЕТ
НАДЕЖНОСТИ ИНФОРМАЦИОННОЙ СИСТЕМЫ
Задание
По структурной
схеме надежности информационной системы
и заданным значениям интенсивности
отказов ее элементов:
1) построить график
изменения вероятности безотказной
работы системы от времени наработки в
диапазоне снижения вероятности до
уровня 0,1 – 0,2;
2) определить время
наработки системы соответствующее
заданному γ (гамма-процентному ресурсу
системы);
3) обеспечить при
заданном γ (гамма-процентном ресурсе)
увеличение времени наработки системы
не менее чем в 1,5 раза за счет структурного
резервирования элементов системы.
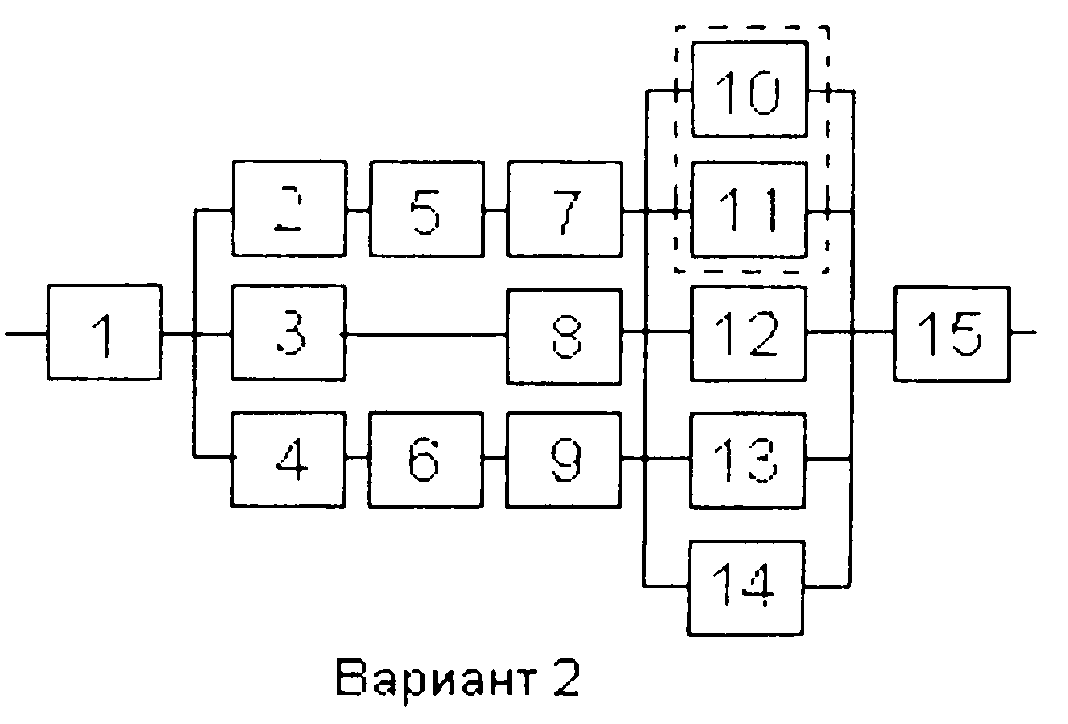
Варианты структурных схем и значения
интенсивностей отказов приведены на
рис. 7 и в табл. 2, соответственно.
Пример расчета
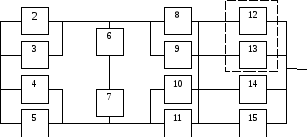
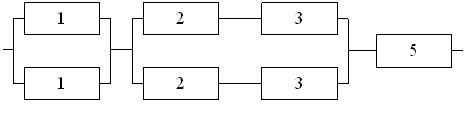
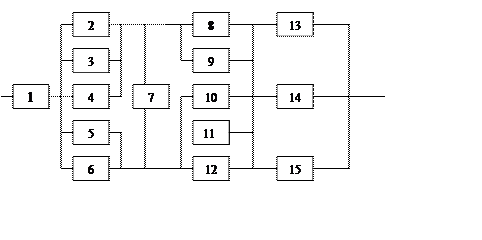
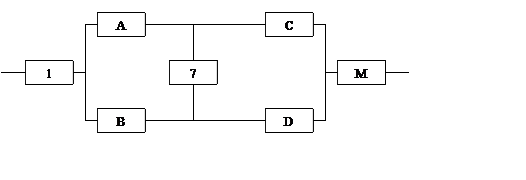
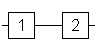
Структурная схема
надежности приведена на рис. 1.
Рис. 1
Значения интенсивности
отказов элементов составляют:
где γ –
(гамма-процентный ресурс системы) –
вероятность безотказной работы системы,
выраженный в процентах, по истечении
определенного времени непрерывной
работы (наработки) системы.
Все элементы
системы работают в режиме нормальной
эксплуатации. Резервирование отдельных
элементов или групп элементов должно
осуществляться идентичными по надежности
резервными элементами или группами
элементов. Переключатели при резервировании
считаются идеальными. На схемах обведенные
пунктиром m
элементов являются функционально
необходимыми.
Расчет
1. В исходной схеме
элементы
2 и
3 образуют
параллельное соединение. Заменяем их
квазиэлементом А. Учитывая, что p2
= p3,
получим:
(1)
2. Элементы 4 и 5
также образуют параллельное соединение,
заменив которое элементом В и учитывая,
что p4
= p5,
получим:
(2)
3. Элементы 6 и 7 в
исходной схеме соединены последовательно.
Заменяем их элементом С, для которого
при p6
= p7:
(3)
4. Элементы
8 и
9 образуют
параллельное соединение. Заменяем их
элементом D,
для которого при p8
= p9
, получим:
(4)
5.
Элементы
10 и
11 образуют
параллельное соединение. Заменяем их
элементом Е,
причем,
так как p10
= p11
= p8,
то
(5)
6.
Элементы
12, 13, 14 и
15 образуют
соединение
«2 из 4»,
которое заменяем элементом F.
Так как p12
= p13
= p14
= p15,
то для определения вероятности безотказной
работы элемента
F можно
воспользоваться выражением, в основе
которого лежит формула биноминального
распределения (биноминальному
распределению подчиняется дискретная
случайная величина k
– число появлений некоторого события
в серии из n
опытов, если в отдельном опыте вероятность
появления события составляет p).
где
–
биноминальный
коэффициент, называемый «числом сочетаний
по k
из n»
(т. е. сколькими разными способами
можно реализовать ситуацию k
из n).
.
Поскольку для
отказа системы «m
из n»
достаточно, чтобы количество исправных
элементов было меньше m,
вероятность отказа может быть найдена
по теореме сложения вероятностей для
k
= 0, 1, …, (m
– 1):
Аналогичным образом
можно найти вероятность безотказной
работы как сумму для k
= m,
m
+ 1, …, n:
.
В данном конкретном
случае, при n
= 4 и m
= 2, вероятность безотказной работы
элемента F
определится выражением:
(6)
7.
Преобразованная схема изображена на
рис. 2.
Рис. 2
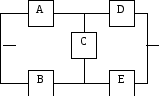
8.
Элементы А, В, С, D
и Е (рис. 2)
образуют мостиковую систему, которую
можно заменить квазиэлементом G.
Для расчета вероятности безотказной
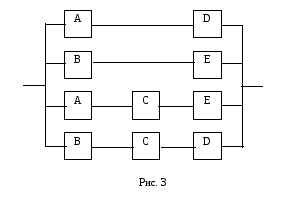
работы воспользуемся методом минимальных
путей. Логическая схема мостиковой
системы по методу минимальных путей
приведена на рис. 3
Система, изображенная
на рис. 3 работоспособна до тех пор, пока
работоспособны элементы А и D
или – B
и E,
или – A,
C
и E,
или – B,
C
и D.
Таким образом, вероятность работы
квазиэлемента G
можно определить по формуле:
(7)
9. После преобразования
схема примет вид, изображенный на рис.
4.
Рис. 4
10. В преобразованной
схеме (рис. 4) элементы 1, G,
и F
образуют последовательное соединение.
Тогда вероятность безотказной работы
всей системы определяется выражением:
(8)
11.
Так как по условию все элементы системы
работают в периоде нормальной эксплуатации,
то вероятность безотказной работы
элементов с
1 по
15 (рис.
1) подчиняются
экспоненциальному закону:
(9)
12.
Результаты расчетов вероятностей
безотказной работы элементов
1 –
15
исходной схемы по формуле
(9) для
наработки до 3·106
часов представлены в табл.
1.
Таблица 1
|
Наработка, |
|||||||||
|
Элемент |
|
0,5 |
1 |
1,5 |
2 |
2,5 |
3 |
1,9 |
2,85 |
|
1 |
0,001 |
0,9990 |
0,9985 |
0,9985 |
0,9980 |
0,9975 |
0,9970 |
0,9981 |
0,9972 |
|
2 |
0,1 |
0,9512 |
0,9048 |
0,8607 |
0,8187 |
0,7788 |
0,7408 |
0,8270 |
0,7520 |
|
6,7 |
0,01 |
0,9950 |
0,9900 |
0,9851 |
0,9802 |
0,9753 |
0,9704 |
0,9812 |
0,9719 |
|
8 |
0,2 |
0,9048 |
0,8187 |
0,7408 |
0,6703 |
0,6065 |
0,5488 |
0,6839 |
0,5655 |
|
12 |
0,5 |
0,7788 |
0,6065 |
0,4724 |
0,3679 |
0,2865 |
0,2231 |
0,3867 |
0,2405 |
|
A, |
— |
0,9976 |
0,9909 |
0,9806 |
0,9671 |
0,9511 |
0,9328 |
0,9701 |
0,9385 |
|
C |
— |
0,9900 |
0,9802 |
0,9704 |
0,9608 |
0,9512 |
0,9418 |
0,9627 |
0,9446 |
|
D, |
— |
0,9909 |
0,9671 |
0,9328 |
0,8913 |
0,8452 |
0,7964 |
0,9001 |
0,8112 |
|
F |
— |
0,9639 |
0,8282 |
0,6449 |
0,4687 |
0,3246 |
0,2173 |
0,5018 |
0,2458 |
|
G |
— |
1,0000 |
1,0000 |
0,9999 |
0,9994 |
0,9979 |
0,9940 |
0,9996 |
0,9955 |
|
P |
— |
0,9629 |
0,8270 |
0,6439 |
0,4675 |
0,3231 |
0,2153 |
0,5006 |
0,2440 |
|
F’ |
— |
0,9993 |
0,9828 |
0,9173 |
0,7954 |
0,6413 |
0,4859 |
0,8234 |
0,5311 |
|
P’ |
— |
0,9983 |
0,9813 |
0,9158 |
0,7934 |
0,6383 |
0,4815 |
0,8215 |
0,5272 |
13.
Результаты расчетов вероятностей
безотказной работы квазиэлементов А,
В, С, D,
Е,
F и
G по формулам
(1) –
(7) и
также
представлены в табл.
1.
14.
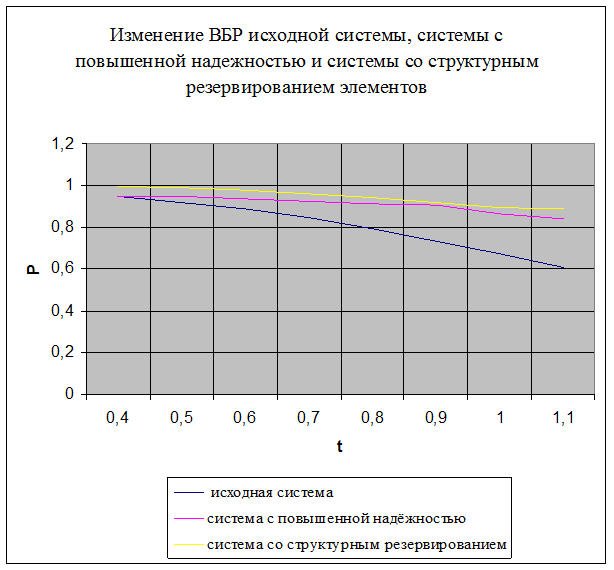
На рис.
5 представлен
график зависимости вероятности
безотказной работы системы Р
от времени (наработки) t.
Рис. 5
15.
По графику (рис.
5,
кривая Р)
находим для
γ = 50%
(Р
= 0.5)
γ-процентную
наработку системы t
=
1,9·106
ч.
16. Проверочный
расчет при
t
=
1,9·106
ч показывает (табл.
1),
что
Pγ
=
0,5006 ~ 0,5.
17.
По условиям задания находим время,
превышающее в 1,5 раза время, соответствующее
вероятности безотказной работы, равное
0,5 (Pγ
= 0,5):
.
(10)
= 1,5·1,9·106
= 2,85·106
ч.
18. Расчет
показывает (табл.
1), что при
=
2,85·106
ч для элементов преобразованной схемы
(рис.
4) p1
()
= 0,9972, pG
()
= 0,9955 и pF
()
= 0,2458.
Следовательно, из трех последовательно
соединенных элементов минимальное
значение вероятности безотказной работы
имеет элемент F
(система
«2 из
4»
в
исходной схеме (рис.
1)),
и именно увеличение его надежности даст
максимальное
увеличение надежности системы в целом.
19.
Для того чтобы при
= 2.85
106
ч система в целом имела вероятность
безотказной работы P’
= 0,5, надо
найти необходимую вероятность безотказной
работы элемента F.
Так как
где
– необходимая
вероятность безотказной работы элемента
F,
то
(11)
20.
Для элемента
F системы
«2 из
4» резервирование
означает увеличение общего числа
элементов. Аналитически определить
минимально необходимое количество
элементов достаточно сложно, так как
число элементов должно быть целым и
функция
=
f(n)
дискретна.
21.
Для повышения надежности системы
«2 из
4» добавляем
к ней элементы, идентичные по надежности
исходным элементам
12 –
15, до тех
пор, пока вероятность безотказной работы
квазиэлемента
F
не достигнет заданного значения:
— добавляем элемент
16, получаем
систему
«2 из 5»:
(12)
— добавляем элемент
17, получаем
систему
«2 из 6»:
(13)
— добавляем элемент
18, получаем
систему
«2 из 7»:
(14)
2
Таким образом,
для повышения надежности до требуемого
уровня, необходимо в исходной схеме
(рис.
1) систему
«2 из
4» достроить
элементами
16, 17 и
18 до системы
«2 из
7» (рис.
6).
23.
Результаты расчетов вероятностей
безотказной работы квазиэлемента
«F»
(«2
из 7»)
и системы в целом Р’
представлены в табл.
1.
24.
Расчеты показывают, что при t’
= 2,85106
ч, Р’
= 0,5272 >
0,5, что
соответствует условию задания.
ВЫВОД
1. По данным расчета
вероятности безотказной работы системы
от времени построен график P(t).
2. По графику найдено
время, соответствующее 50% -процентному
ресурсу системы (t
= 1,9
106 ч).
3. Для увеличения
наработки системы в 1,5 раза при 50%
-процентном ресурсе
системы предложено нагруженное
резервирование основных элементов 12,
13, 14 и 15
идентичными по надежности резервными
элементами 16, 17 и 18.
4. Рассчитана
вероятность безотказной работы системы
с повышенной надежностью от времени,
построен график P’(t)
системы с
повышенной надежностью,
на графике
(рис. 7) показано время (t’
= 2,85
106 ч)
соответствующее 50%
-процентному ресурсу.
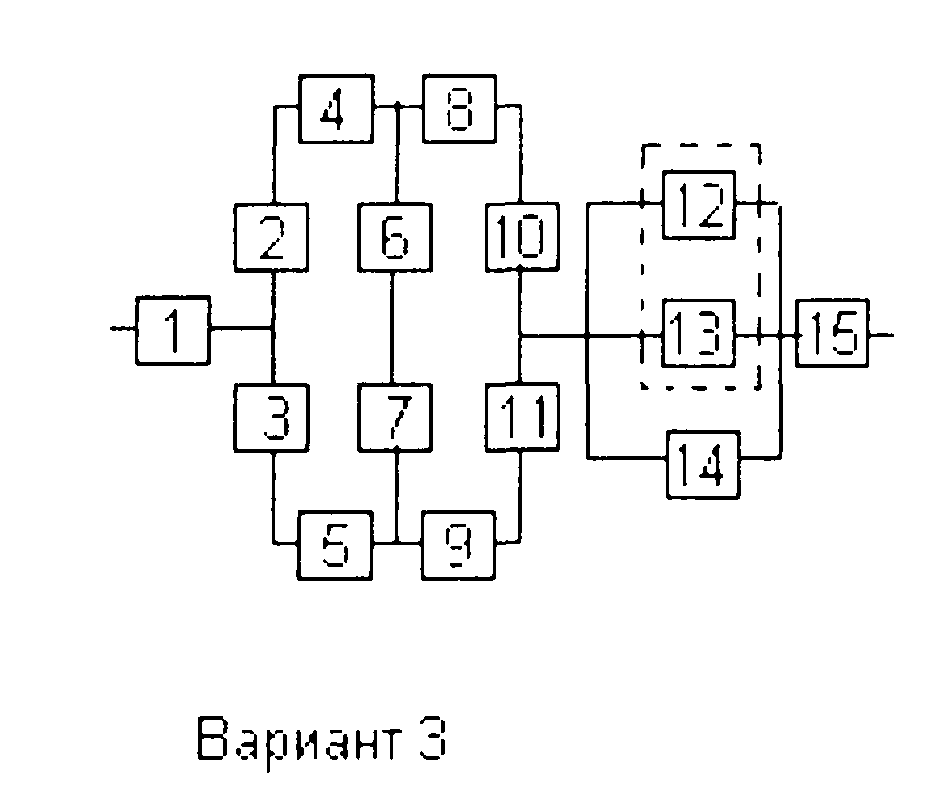
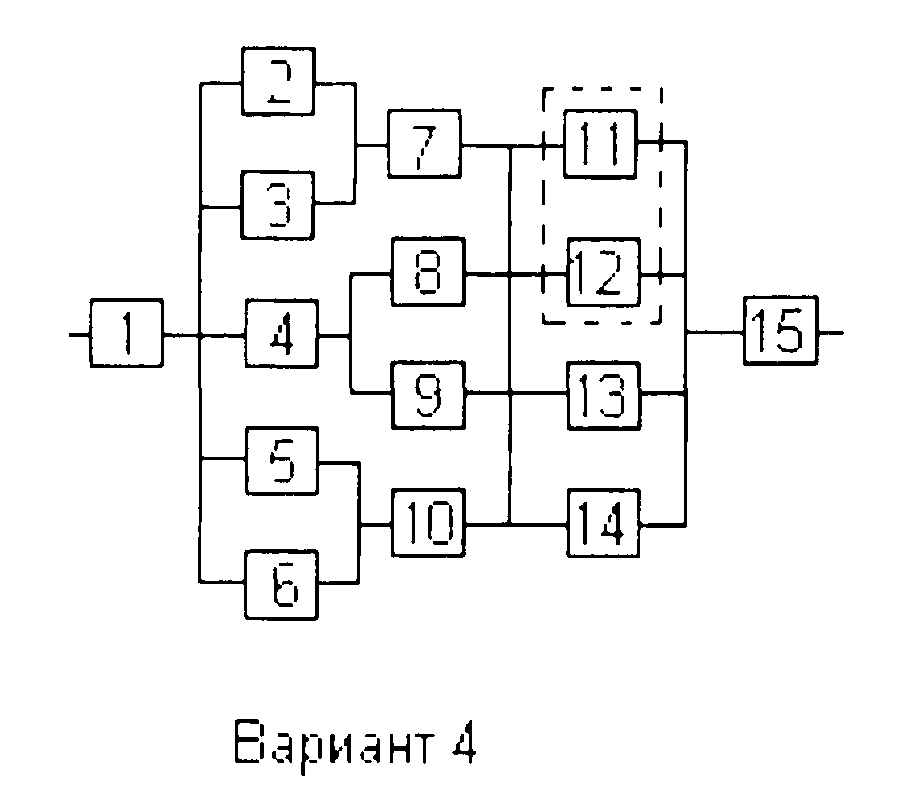
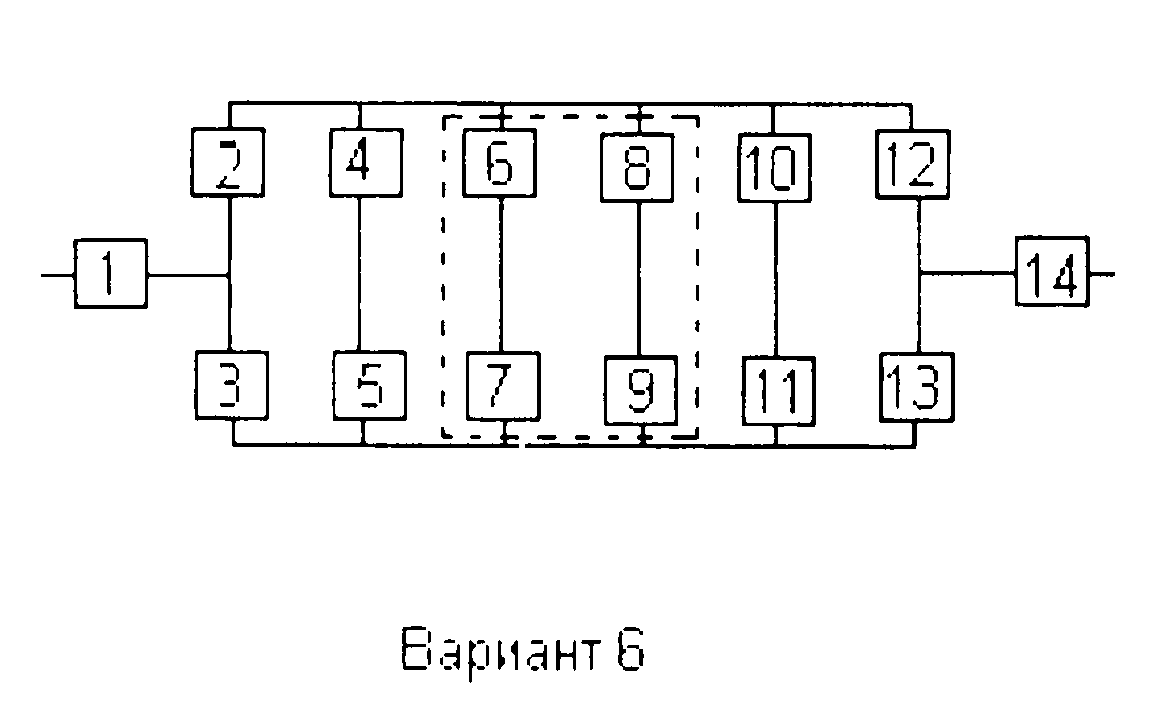
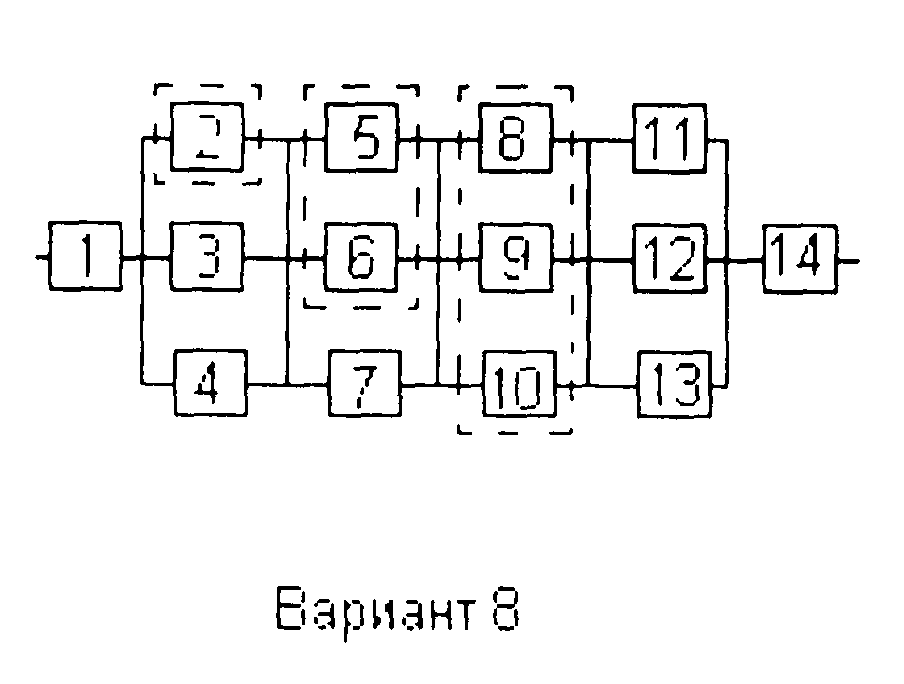
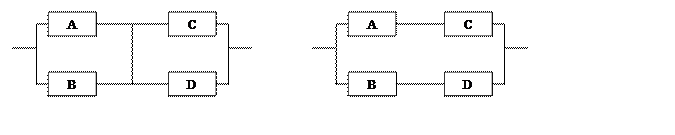
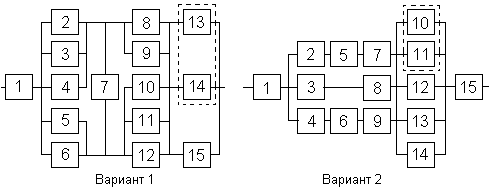
Вариант 1
Вариант 2
Вариант 3
Вариант 4
Вариант 5
Вариант 6
Вариант 7
Вариант 8
Вариант 9
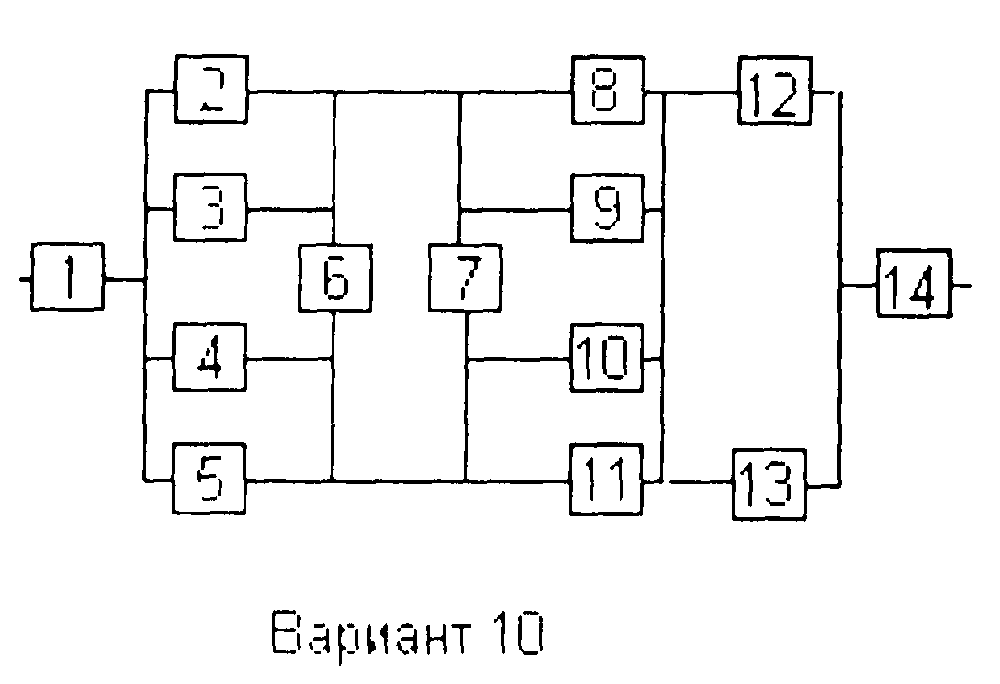
Вариант 10
Вариант 11
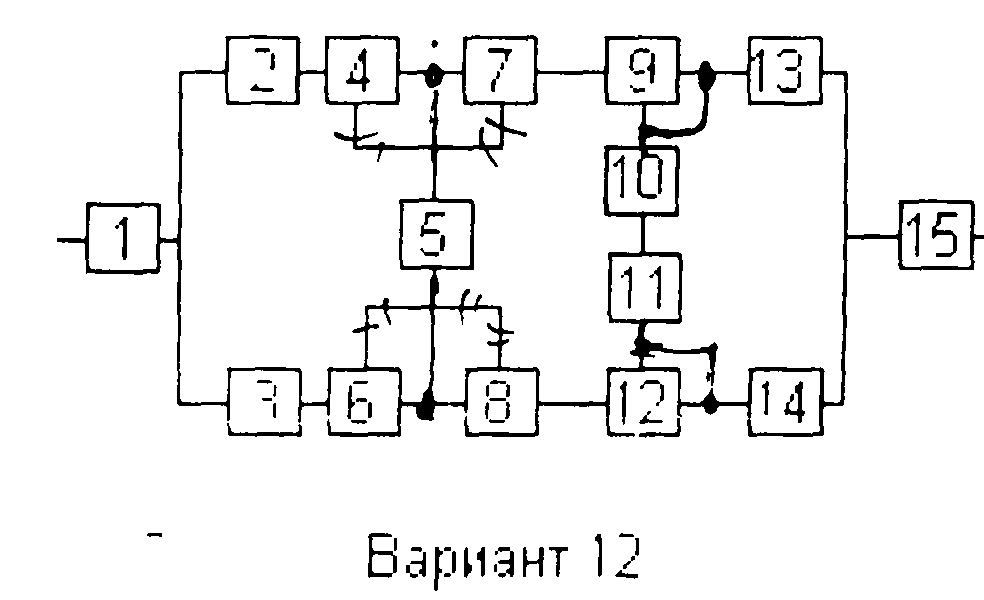
Вариант 12
Вариант 13
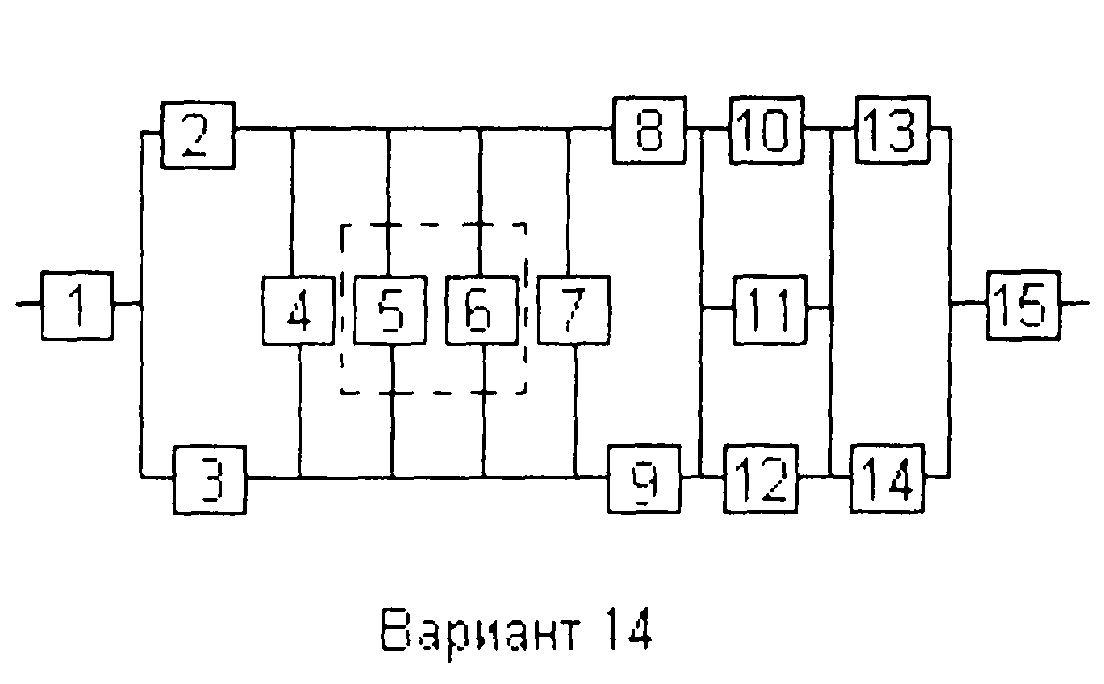
Вариант 14
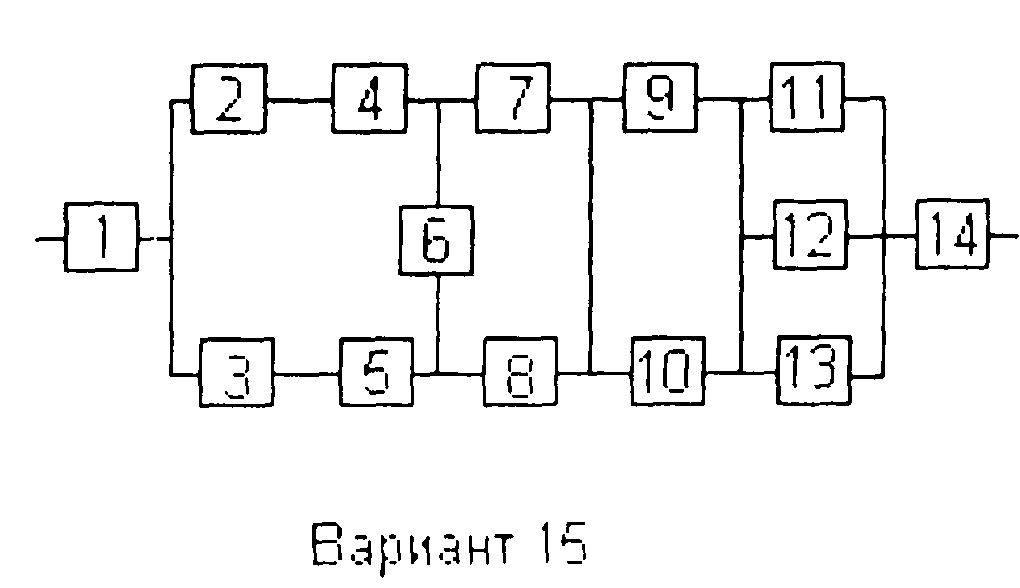
Вариант 15
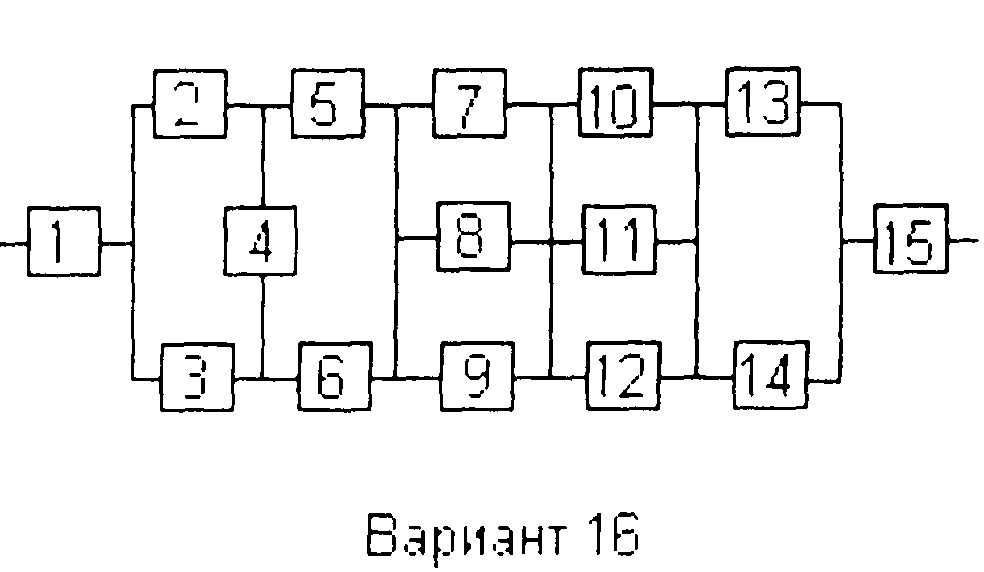
Вариант 16
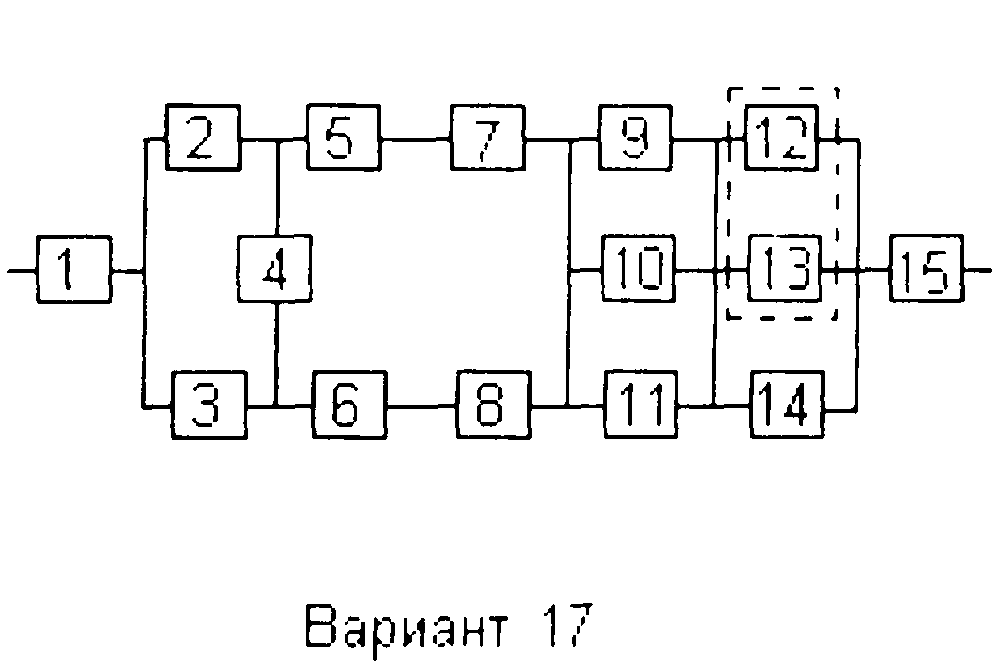
Вариант 17
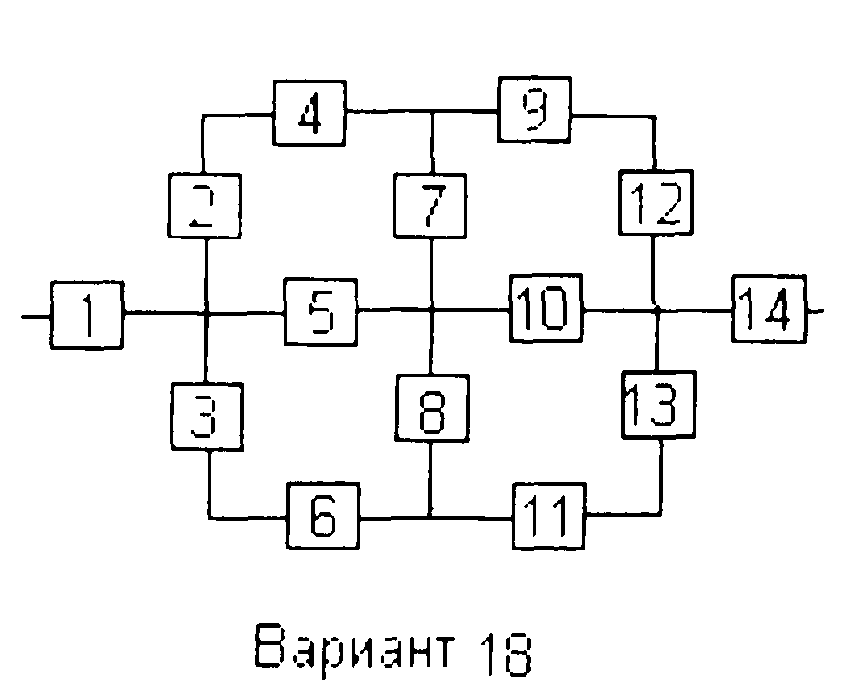
Вариант 18
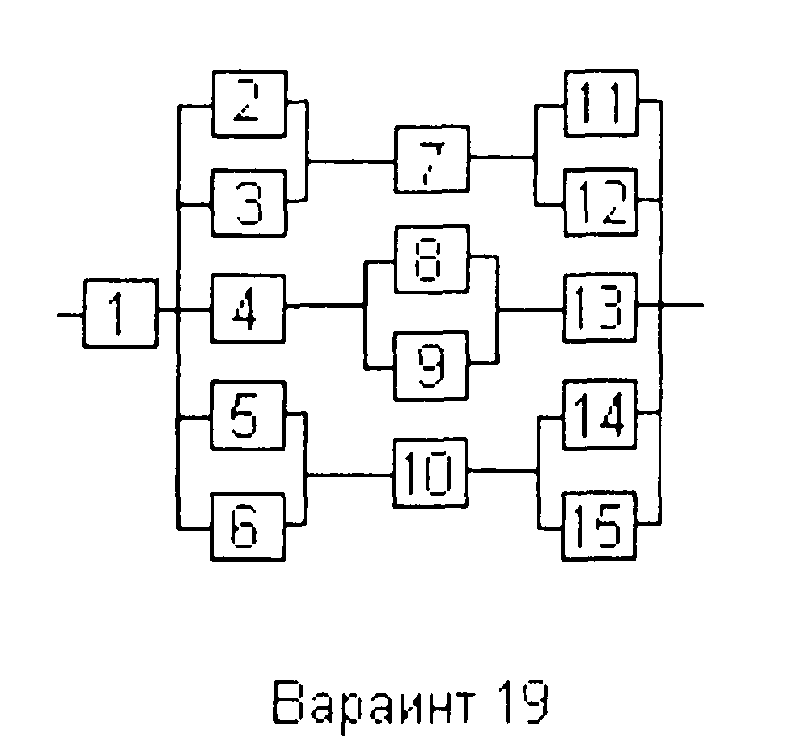
Вариант 19
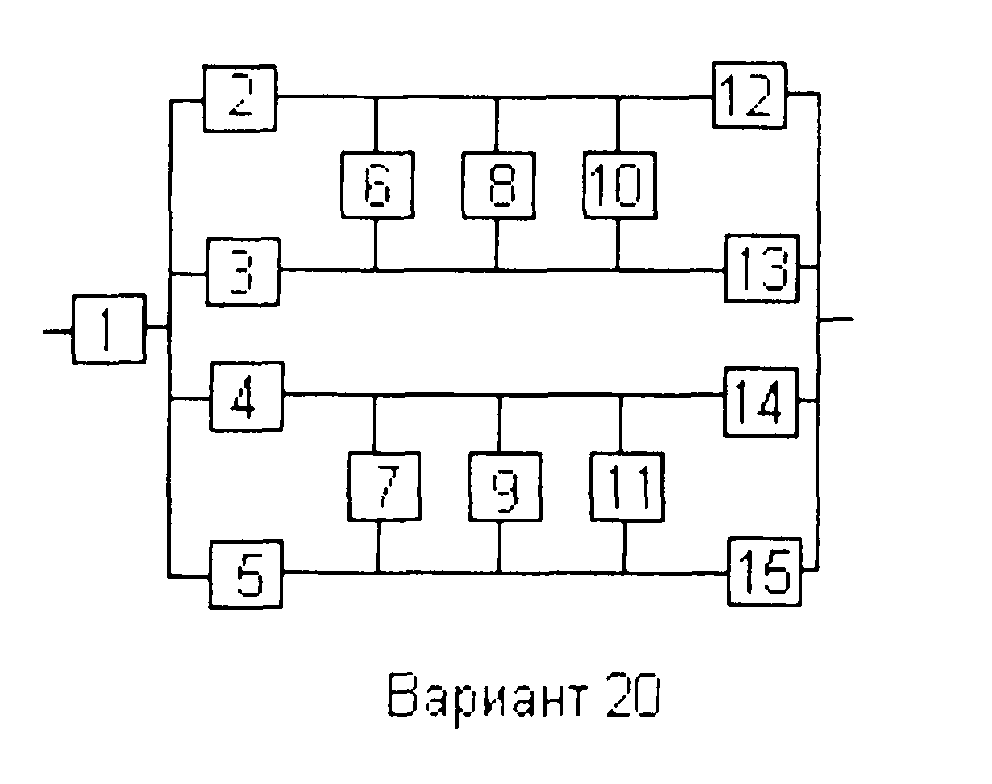
Вариант 20
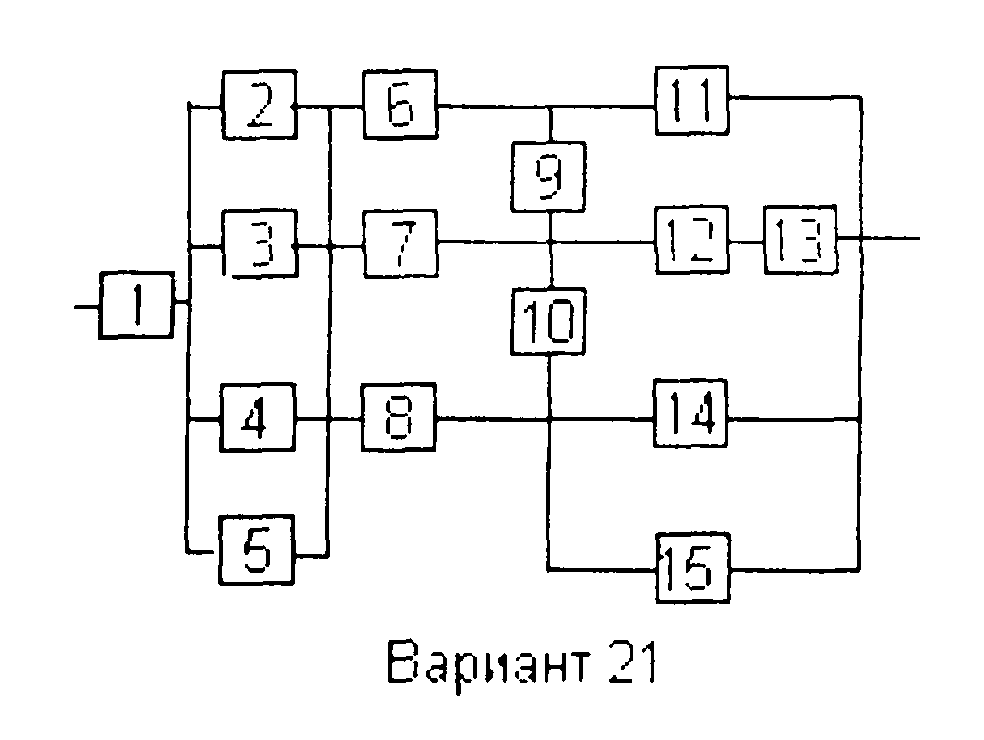
Вариант 21
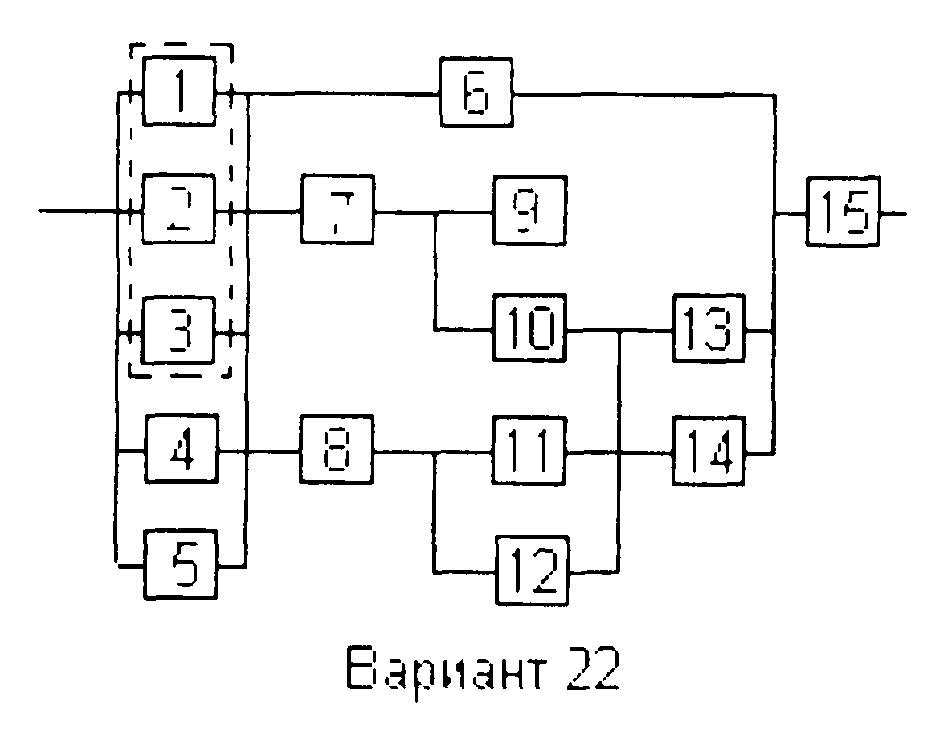
Вариант 22
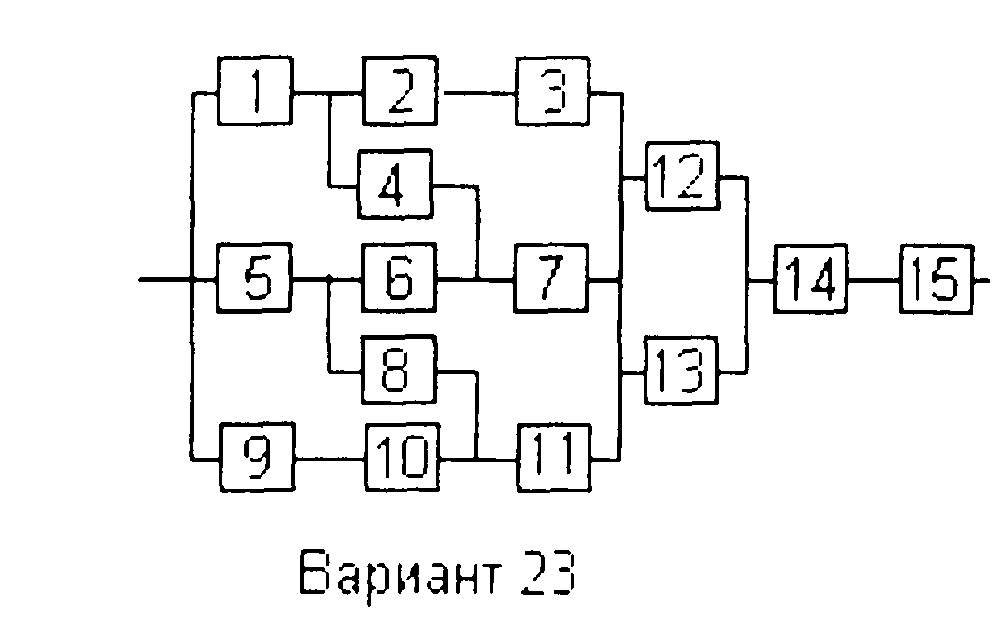
Вариант 23
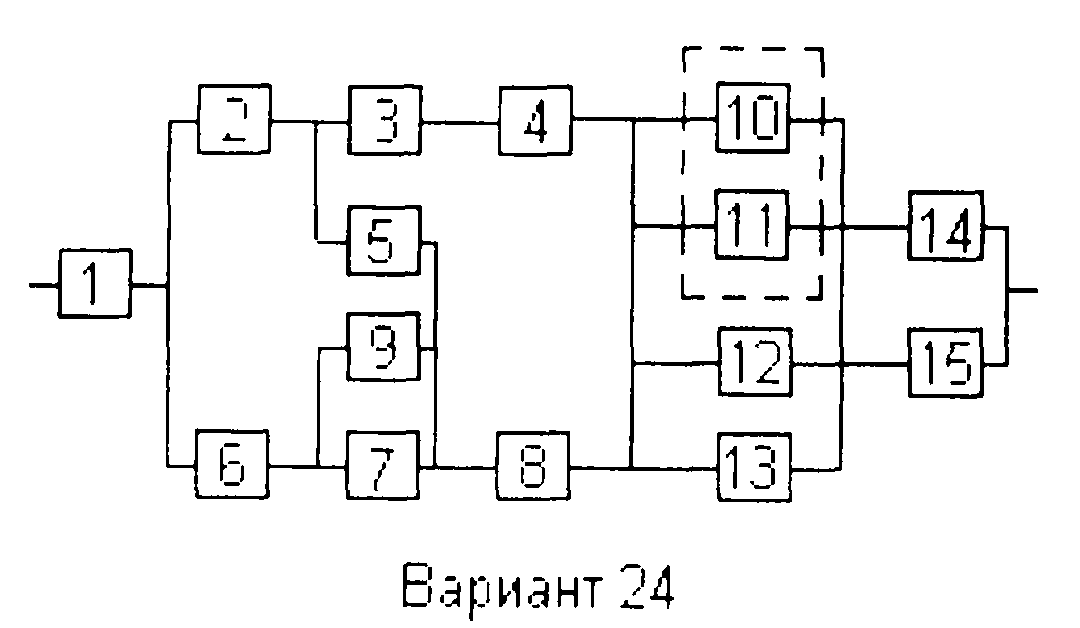
Вариант 24
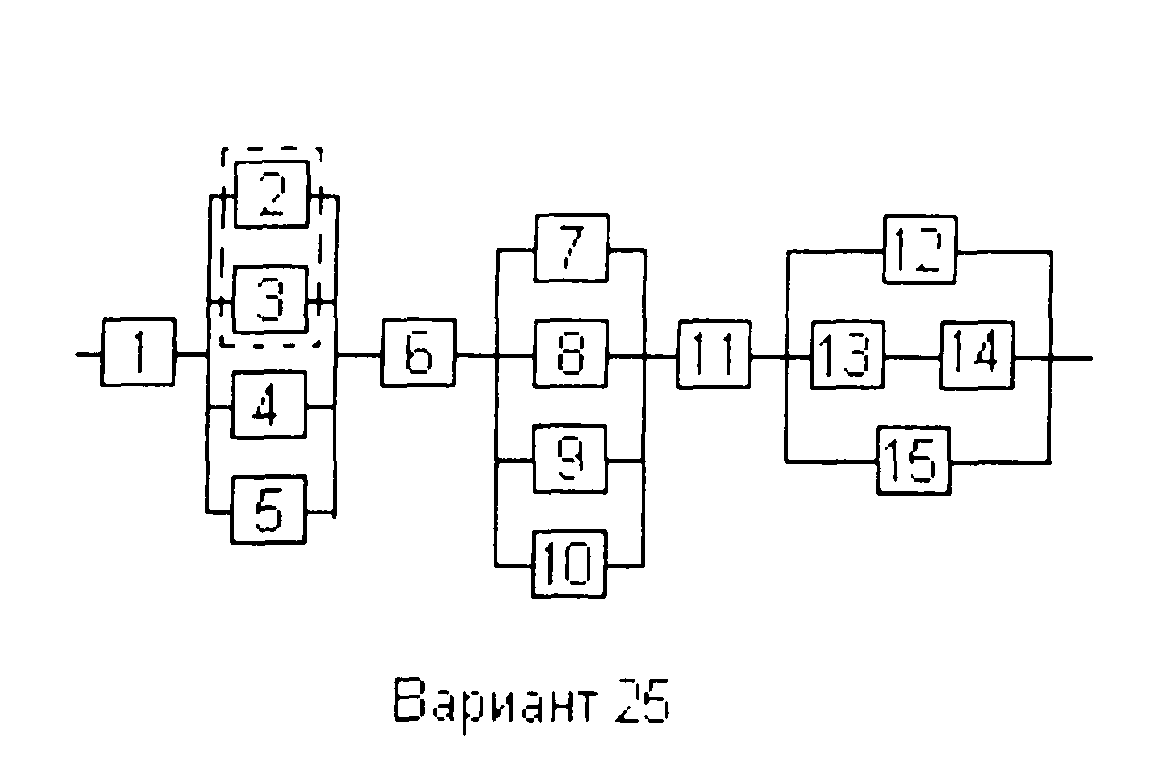
Вариант 25
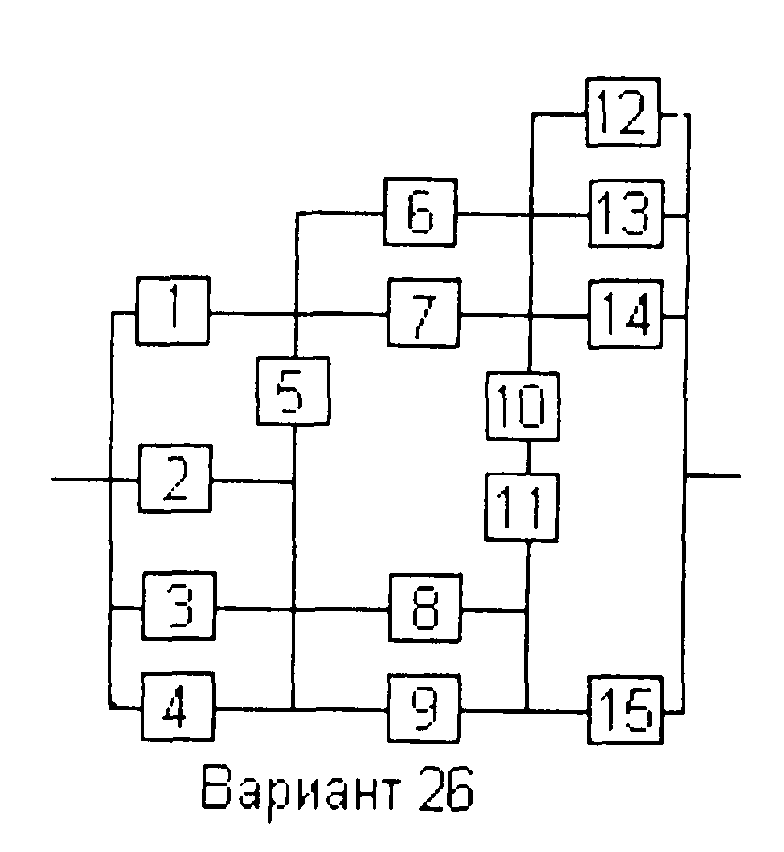
Вариант 26
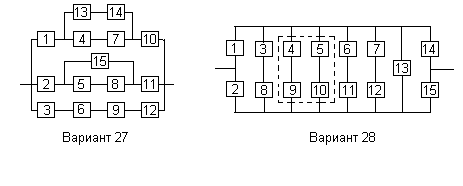
Вариант 27
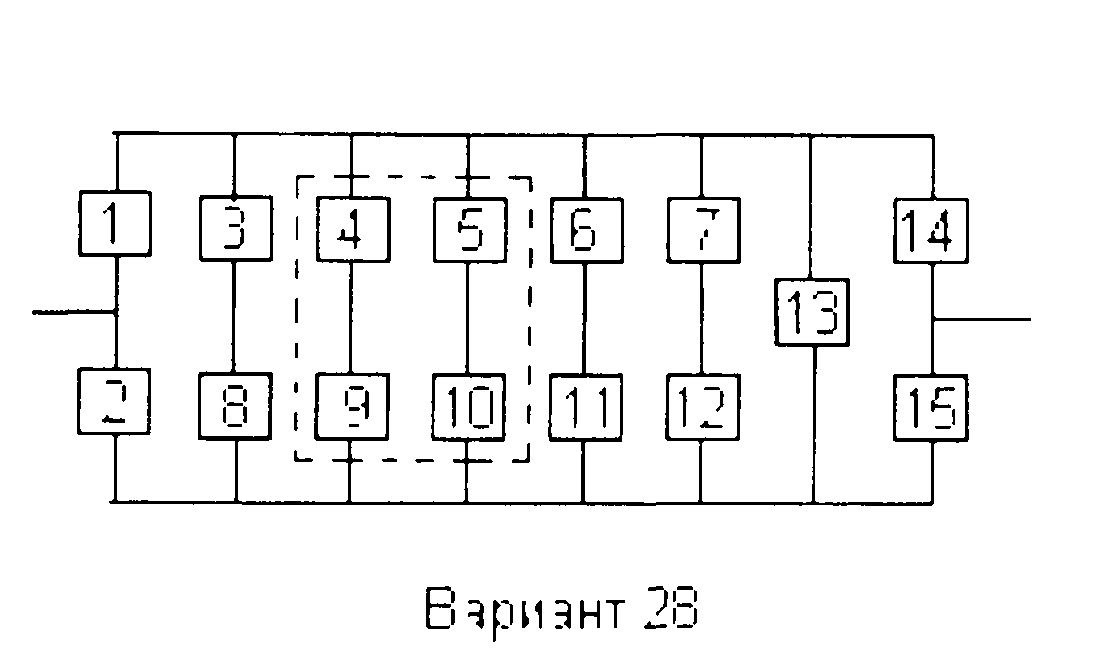
Вариант 28
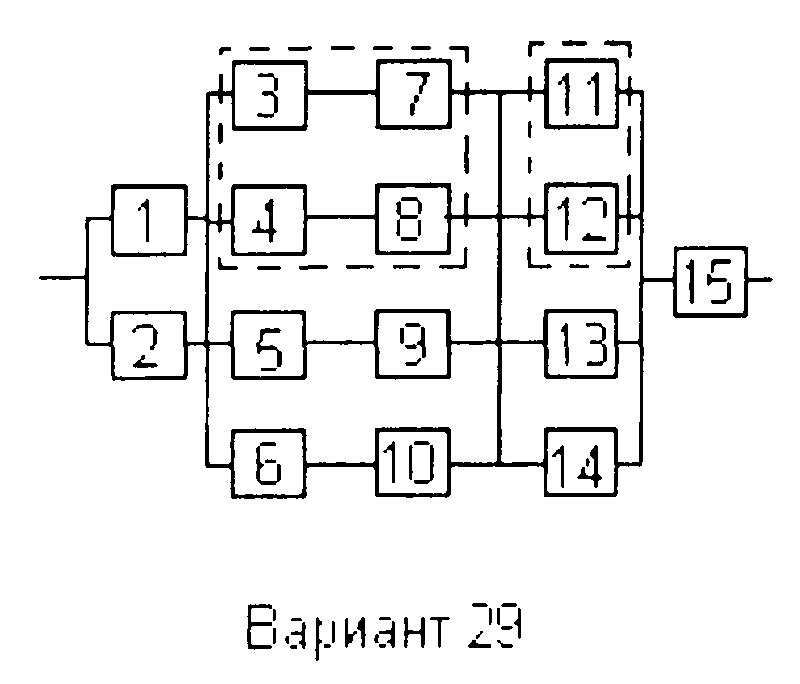
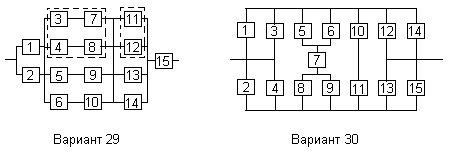
Вариант 29
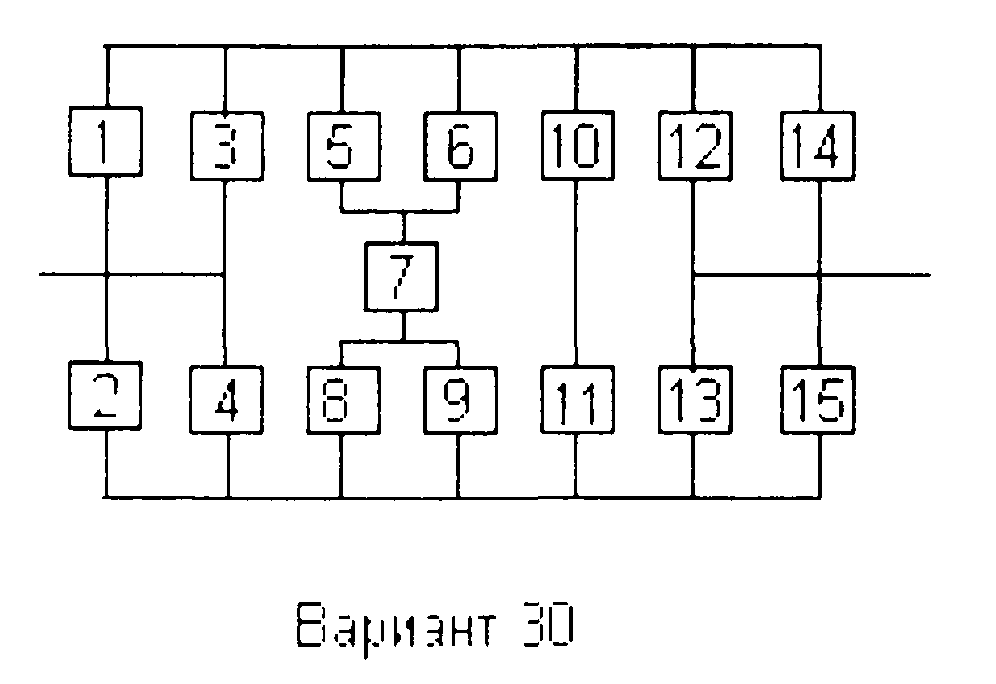
Вариант 30
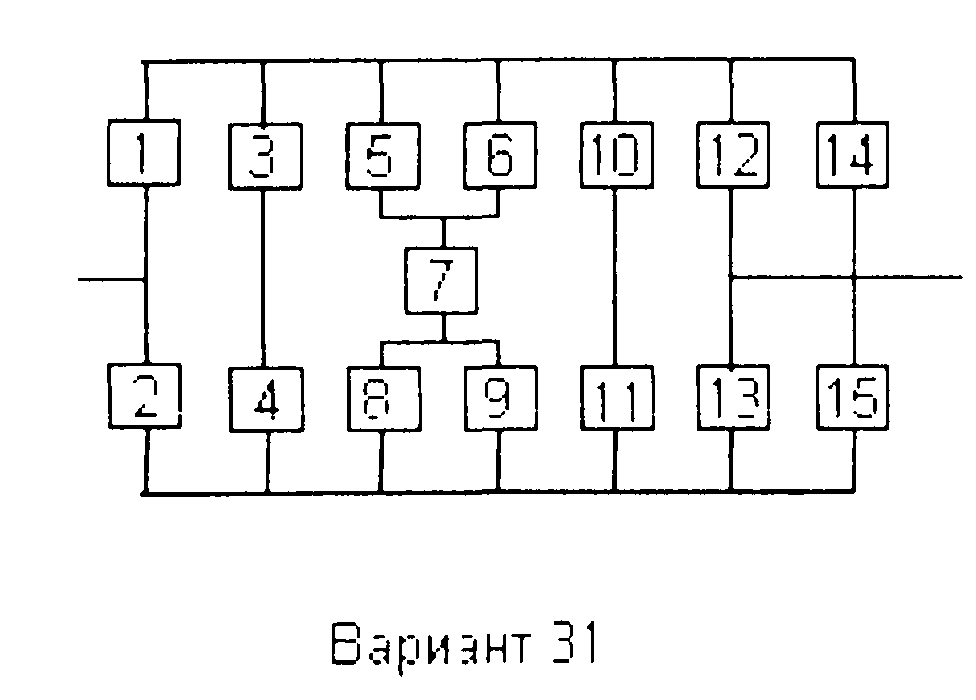
Вариант 31
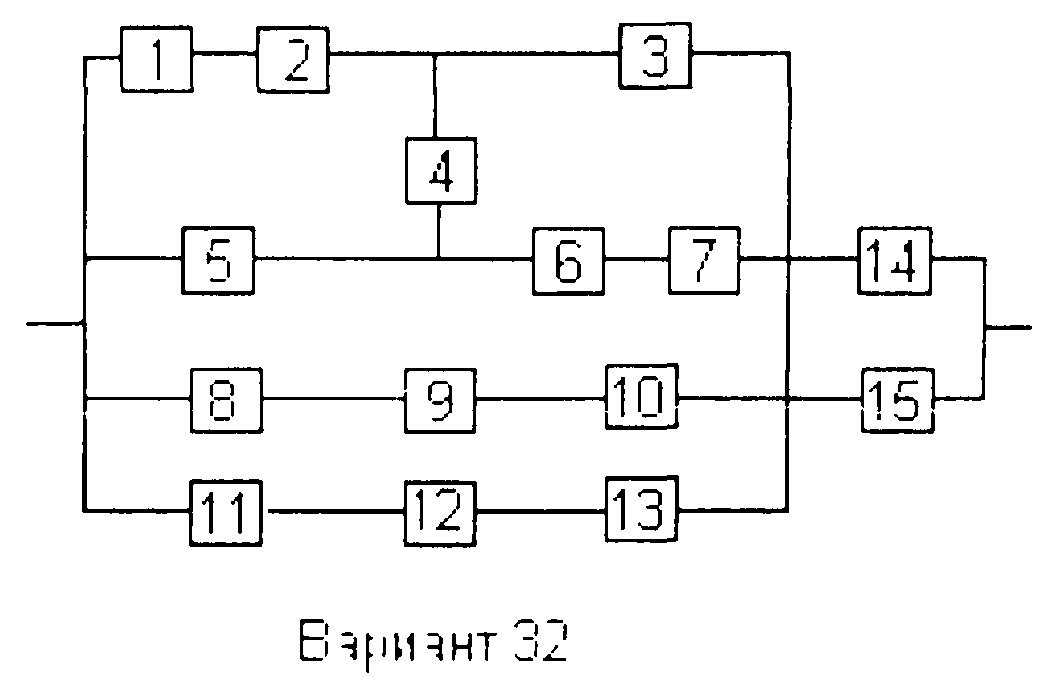
Вариант 32
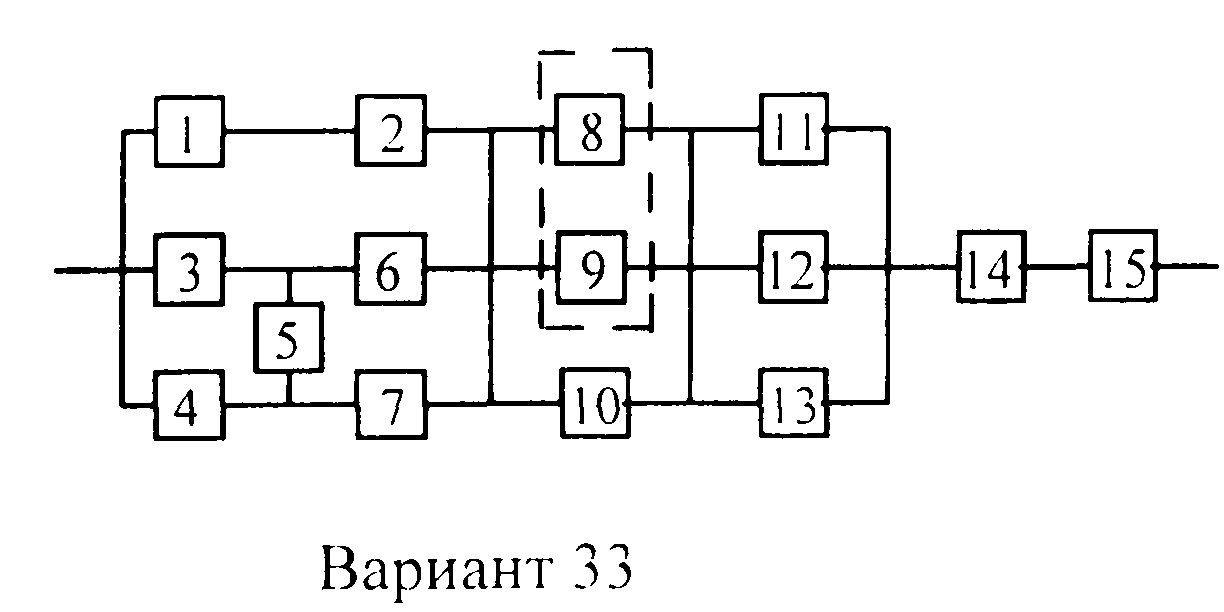
Вариант 33
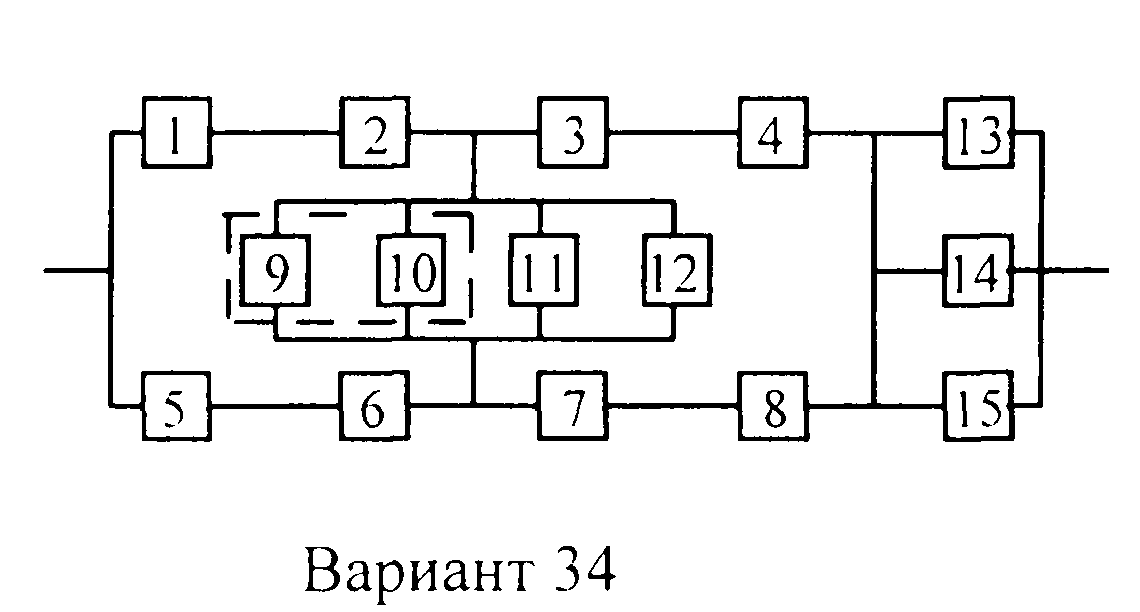
Вариант 34
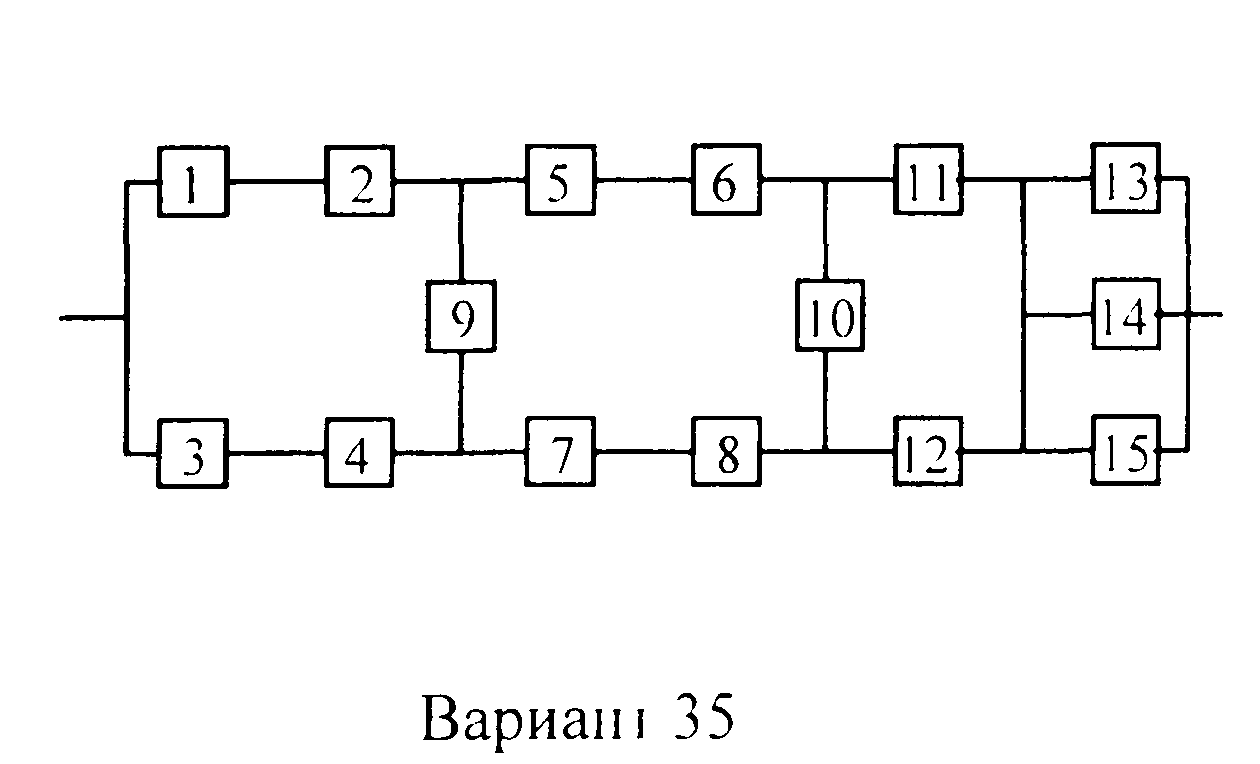
Вариант 35
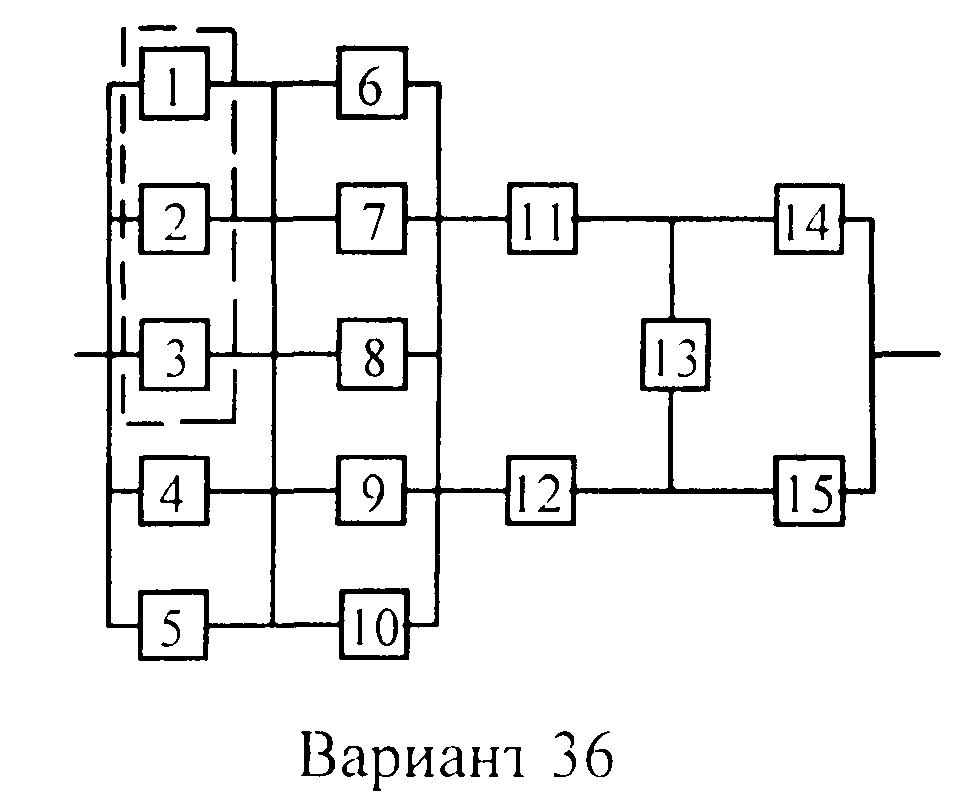
Вариант 36
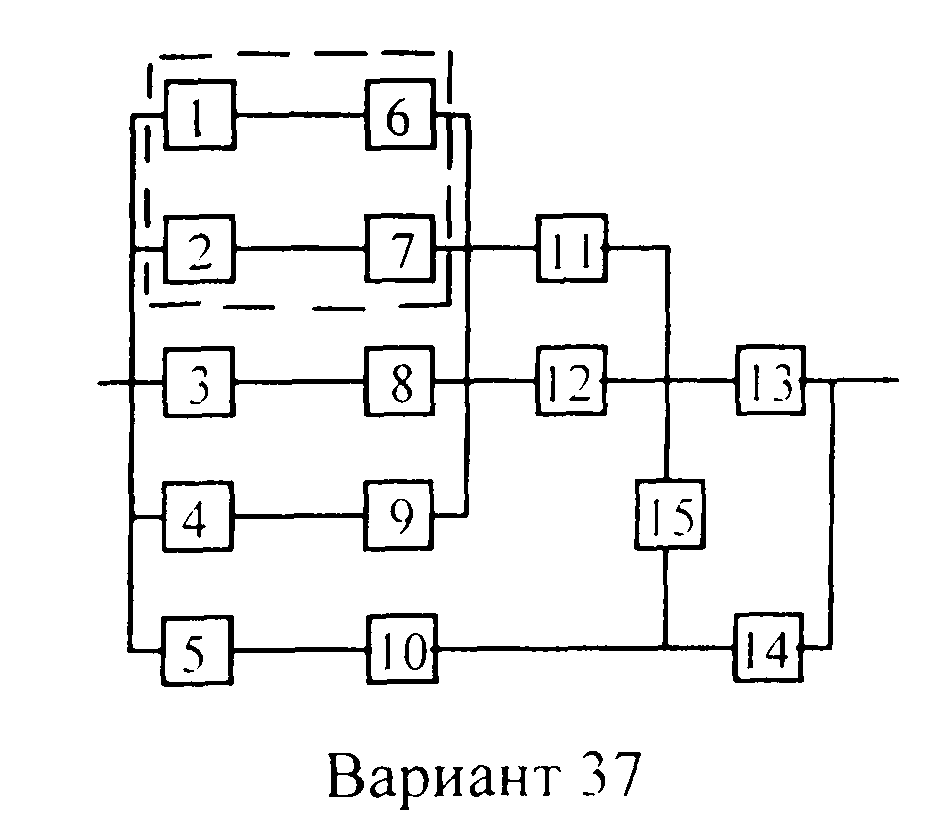
Вариант 37
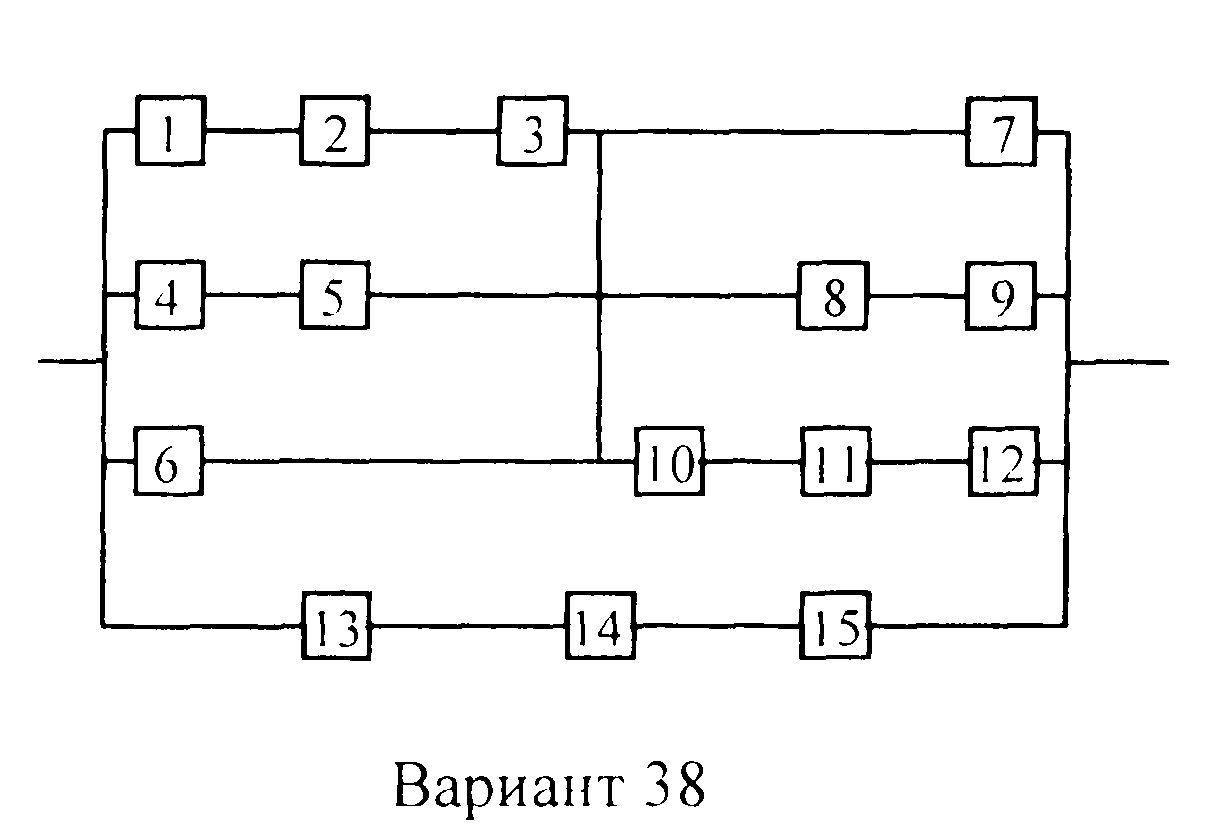
Вариант 38
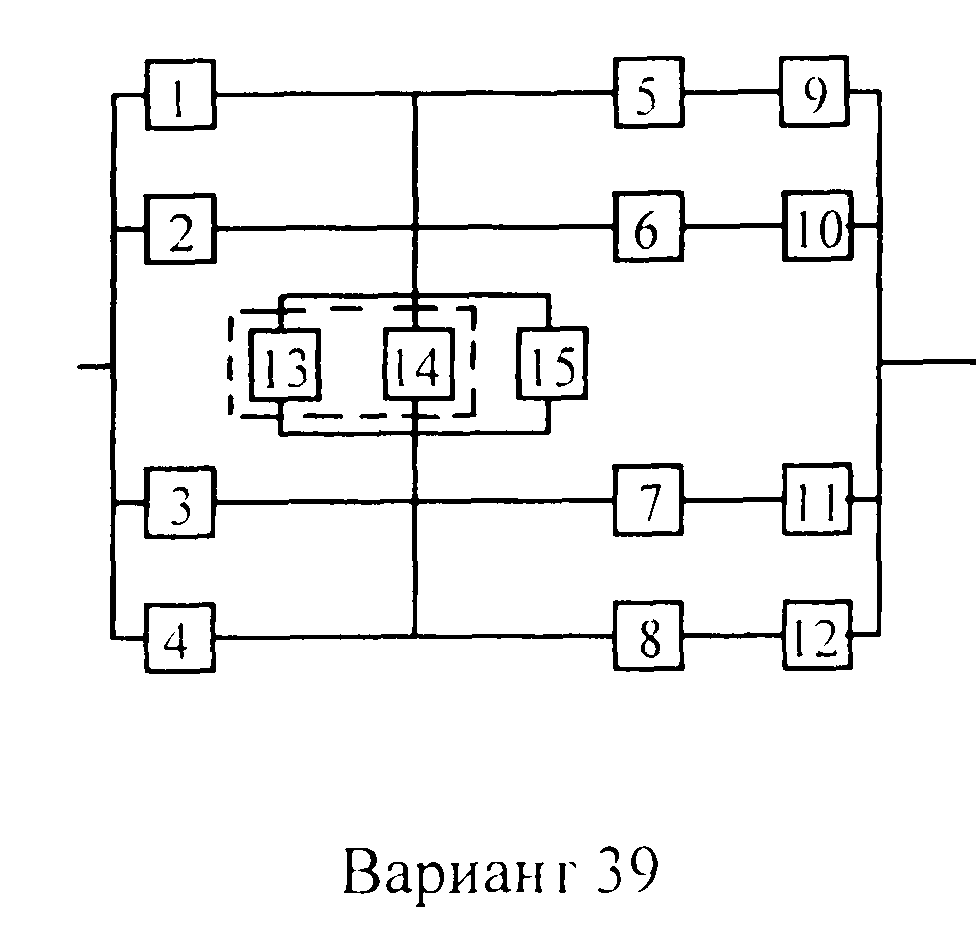
Вариант 39
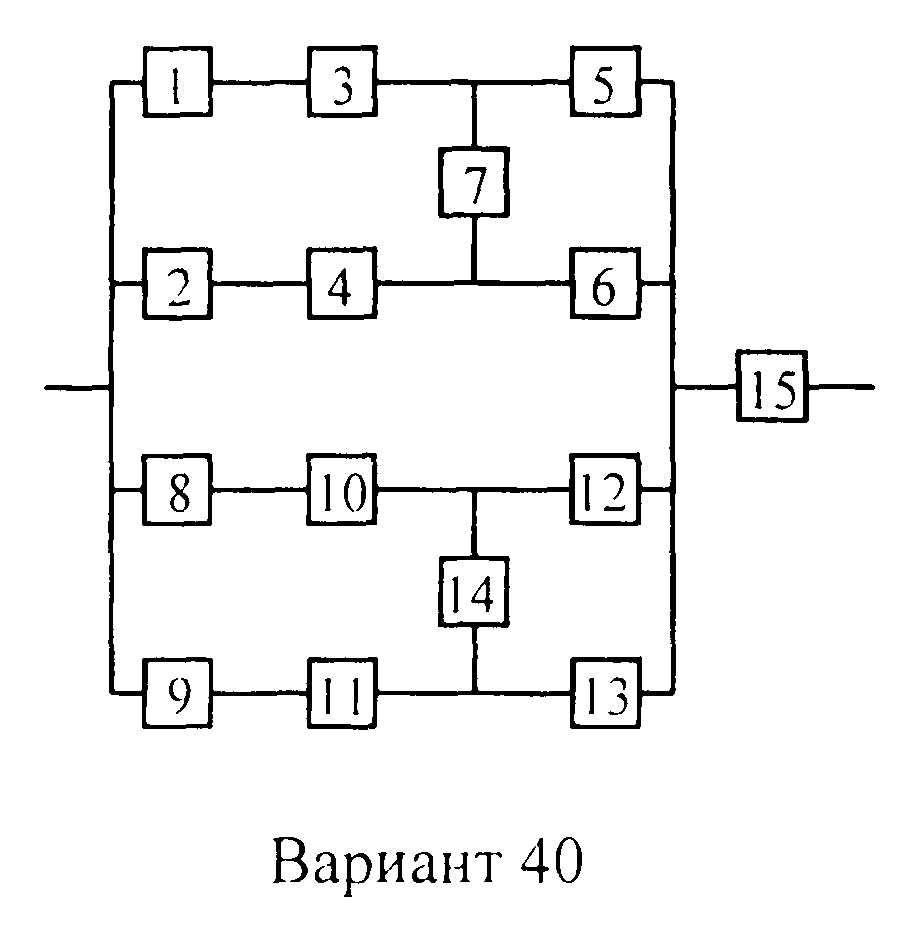
Вариант 40
Таблица 2
Численные значения
параметров к заданию
|
№ вар. |
γ% |
И |
||||||||||||||
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
13 |
14 |
15 |
||
|
1 |
90 |
0.1 |
1.0 |
0.5 |
1.0 |
0.1 |
||||||||||
|
2 |
95 |
0.2 |
0.5 |
1.0 |
0.1 |
|||||||||||
|
3 |
80 |
0.1 |
1.0 |
2.0 |
1.0 |
5.0 |
0.2 |
|||||||||
|
4 |
70 |
0.05 |
1.0 |
0.5 |
0.2 |
0.02 |
||||||||||
|
5 |
50 |
0.01 |
0.05 |
0.1 |
0.5 |
1.0 |
||||||||||
|
6 |
75 |
0.01 |
0.05 |
1.0 |
0.05 |
0.1 |
— |
|||||||||
|
7 |
65 |
0.05 |
0.5 |
0.05 |
0.005 |
0.1 |
0.2 |
0.1 |
— |
|||||||
|
8 |
85 |
0.1 |
0.5 |
0.01 |
0.5 |
0.1 |
— |
|||||||||
|
9 |
60 |
0.03 |
0.5 |
1.0 |
0.03 |
0.1 |
— |
|||||||||
|
10 |
50 |
0.1 |
0.5 |
1.0 |
0.5 |
1.0 |
0.1 |
— |
||||||||
|
11 |
75 |
0.05 |
0.2 |
0.5 |
0.2 |
0.1 |
||||||||||
|
12 |
65 |
0.02 |
0.1 |
1.0 |
2.0 |
0.1 |
0.05 |
|||||||||
|
13 |
70 |
0.01 |
0.2 |
0.1 |
1.0 |
0.5 |
0.1 |
— |
||||||||
|
14 |
50 |
0.01 |
0.1 |
10.0 |
0.2 |
10.0 |
0.5 |
0,3 |
||||||||
|
15 |
85 |
0.01 |
1.0 |
5.0 |
0.2 |
5.0 |
0.1 |
— |
||||||||
|
16 |
80 |
0.1 |
1.0 |
2.0 |
1.0 |
5.0 |
3.0 |
1.0 |
0.05 |
|||||||
|
17 |
95 |
0.1 |
5.0 |
1.0 |
5.0 |
10.0 |
5.0 |
1.0 |
0.2 |
|||||||
|
18 |
60 |
0.01 |
1.0 |
0.1 |
— |
|||||||||||
|
19 |
75 |
0.1 |
5.0 |
0.5 |
5.0 |
1.0 |
3.0 |
1.0 |
5.0 |
0.5 |
5.0 |
|||||
|
20 |
90 |
0.1 |
10.0 |
20.0 |
10.0 |
|||||||||||
|
21 |
90 |
0.1 |
1.0 |
0.5 |
2.0 |
0.5 |
0.2 |
1.0 |
||||||||
|
22 |
80 |
1.0 |
0.2 |
0.5 |
1.0 |
0.5 |
1.0 |
1.0 |
0.1 |
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Практика
1. Расчет показателей безотказности
1.1 Вероятность безотказной работы
1.2 Вероятность отказа
1.3 Частота отказа
1.4 Интенсивность отказа
1.5 Средняя наработка до отказа
1.6 Среднее значение параметра потока отказов
1.7 Пример расчета показателей безотказности
2. Примеры расчета показателей надежности для различных законов распределения случайных величин
2.1 Экспоненциальный закон распределения
2.2 Закон распределения Вейбулла-Гнеденко
2.3 Закон распределения Рэлея
3. Примеры расчета показателей надежности сложных систем
3.1 Основное соединение элементов
3.2 Резервное соединение
1.1 Вероятность безотказной работы
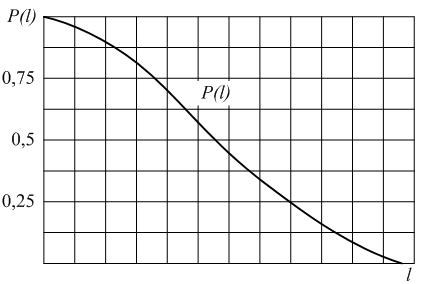
Вероятностью безотказной работы называется вероятность того, что при определенных условиях эксплуатации, в пределах заданной наработки не произойдет ни одного отказа.
Вероятность безотказной работы обозначается как P(l), которая определяется по формуле (1.1):
где N0 – число элементов в начале испытания; r(l) – число отказов элементов к моменту наработки.Следует отметить, что чем больше величина N0, тем с большей точностью можно рассчитать вероятность P(l).
В начале эксплуатации исправного локомотива P(0) = 1, так как при пробеге l = 0 вероятность того, что ни один элемент не откажет, принимает максимальное значение – 1. С ростом пробега l вероятность P(l) будет уменьшаться. В процессе приближения срока эксплуатации к бесконечно большой величине вероятность безотказной работы будет стремиться к нулю P(l→∞) = 0. Таким образом в процессе наработки величина вероятности безотказной работы изменяется в пределах от 1 до 0. Характер изменения вероятности безотказной работы в функции пробега показан на рис. 1.1.
Рис.2.1. График изменения вероятности безотказной работы P(l)в зависимости от наработки
Основными достоинствами использования данного показателя при расчетах является два фактора: во-первых, вероятность безотказной работы охватывает все факторы, влияющие на надежность элементов, позволяя достаточно просто судить о его надежности, т.к. чем больше величина P(l), тем выше надежность; во-вторых, вероятность безотказной работы может быть использована в расчетах надежности сложных систем, состоящих из более чем одного элемента.
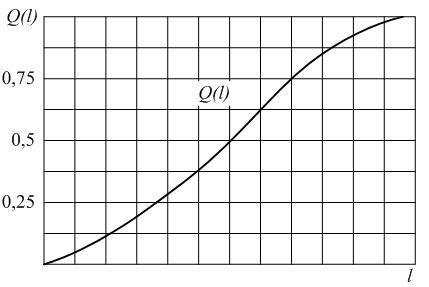
1.2 Вероятность отказа
Вероятностью отказа называют вероятность того, что при определенных условиях эксплуатации, в пределах заданной наработки произойдет хотя бы один отказ.
Вероятность отказа обозначается как Q(l), которая определяется по формуле (1.2):
В начале эксплуатации исправного локомотива Q(0) = 0, так как при пробеге l = 0 вероятность того, что хотя бы один элемент откажет, принимает минимальное значение – 0. С ростом пробега l вероятность отказа Q(l) будет увеличиваться. В процессе приближения срока эксплуатации к бесконечно большой величине вероятность отказа будет стремиться к единице Q(l→∞) = 1. Таким образом в процессе наработки величина вероятности отказа изменяется в пределах от 0 до 1. Характер изменения вероятности отказа в функции пробега показан на рис. 1.2.Вероятность безотказной работы и вероятность отказа являются событиями противоположными и несовместимыми.
Рис.2.2. График изменения вероятности отказа Q(l) в зависимости от наработки
1.3 Частота отказов
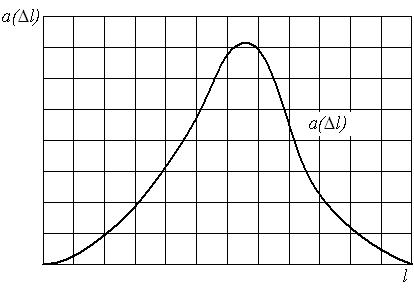
Частота отказов – это отношение числа элементов в единицу времени или пробега отнесенного к первоначальному числу испытуемых элементов. Другими словами частота отказов является показателем, характеризующим скорость изменения вероятности отказов и вероятности безотказной работы по мере роста длительности работы.
Частота отказов обозначается как 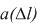
где – 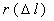
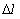
Данный показатель позволяет судить по его величине о числе элементов, которые откажут на каком-то промежутке времени или пробега, также по его величине можно рассчитать количество требуемых запасных частей.
Характер изменения частоты отказов в функции пробега показан на рис. 1.3.
Рис. 1.3. График изменения частоты отказов в зависимости от наработки
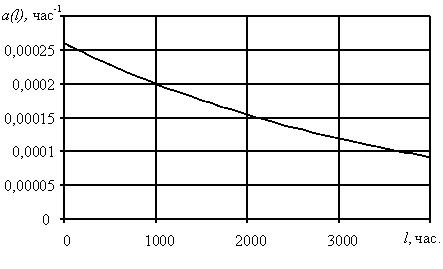
1.4 Интенсивность отказов
Интенсивность отказов представляет собой условную плотность возникновения отказа объекта, определяемую для рассматриваемого момента времени или наработки при условии, что до этого момента отказ не возник. Иначе интенсивность отказов – это отношение числа отказавших элементов в единицу времени или пробега к числу исправно работающих элементов в данный отрезок времени.
Интенсивность отказов обозначается как 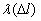
где
Как правило, интенсивность отказов 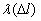
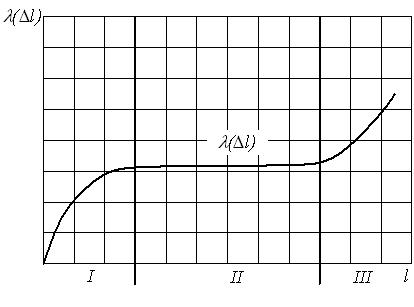
На рис. 1.4. представлен теоретический характер изменения интенсивности отказов в функции пробега.
Рис. 1.4. График изменения интенсивности отказов в зависимости от наработки
На графике изменения интенсивности отказов, изображенном на рис. 1.4. можно выделить три основных этапа отражающих процесс экс-плуатации элемента или объекта в целом.
Первый этап, который также называется этапом приработки, характеризуется увеличением интенсивности отказов в начальный период эксплуатации. Причиной роста интенсивности отказов на данном этапе являются скрытые дефекты производственного характера.
Второй этап, или период нормальной работы, характеризуется стремлением интенсивности отказов к постоянному значению. В течение этого периода могут возникать случайные отказы, в связи с появлением внезапной концентрации нагрузки, превышающей предел прочности элемента.
Третий этап, так называемый период форсированного старения. Характеризуется возникновением износовых отказов. Дальнейшая эксплуатация элемента без его замены становится экономически не рациональной.
1.5 Средняя наработка до отказа
Средняя наработка до отказа – это средний пробег безотказной работы элемента до отказа.
Средняя наработка до отказа обозначается как L1 и определяется по формуле (1.5):
где li – наработка до отказа элемента; ri – число отказов.
Средняя наработка до отказа может быть использована для предварительного определения сроков ремонта или замены элемента.
1.6 Среднее значение параметра потока отказов
Среднее значение параметра потока отказов характеризует среднюю плотность вероятности возникновения отказа объекта, определяемая для рассматриваемого момента времени.
Среднее значение параметра потока отказов обозначается как Wср и определяется по формуле (1.6):
1.7 Пример расчета показателей безотказности
Исходные данные.
В течение пробега от 0 до 600 тыс. км., в локомотивном депо произведен сбор информации по отказам ТЭД. При этом количество исправных ТЭД в начале периода эксплуатации составляло N0 = 180 шт. Суммарное количество отказавших ТЭД за анализируемый период составило ∑r(600000) = 60. Интервал пробега принять равным 100 тыс. км. При этом количество отказавших ТЭД по каждому участку составило: 2, 12, 16, 10, 14, 6.
Требуется.
Необходимо рассчитать показатели безотказности и построить их зависимости изменения во времени.
Сначала необходимо заполнить таблицу исходных данных так, как это показано в табл. 1.1.
Таблица 1.1.
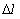 , тыс. км , тыс. км |
0 — 100 | 100 — 200 | 200 — 300 | 300 — 400 | 400 — 500 | 500 — 600 |
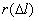 |
2 | 12 | 16 | 10 | 14 | 6 |
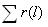 |
2 | 14 | 30 | 40 | 54 | 60 |
Первоначально по уравнению (1.1) определим для каждого участка пробега величину вероятности безотказной работы. Так, для участка от 0 до 100 и от 100 до 200 тыс. км. пробега вероятность безотказной работы составит:
Далее, используя зависимость (1.2) произведем расчет вероятности отказа ТЭД.
Произведем расчет частоты отказов по уравнению (1.3).
Далее по уравнению (1.4) произведем расчет интенсивности отказов ТЭД в зависимости от наработки.
Первоначально рассчитаем среднее количество работоспособных ТЭД на участке от 0 до 100 тыс. км. пробега:
Тогда интенсивность отказов на участке 0-100 тыс.км. будет равна:
Аналогичным образом определим величину интенсивности отказов для интервала 100-200 тыс. км.
По уравнениям (1.5 и 1.6) определим среднюю наработку до отказа и среднее значение параметра потока отказов.
Систематизируем полученные результаты расчета и представим их в виде таблицы (табл. 1.2.).
Таблица 1.2.
 , тыс.км. , тыс.км. |
0 — 100 | 100 — 200 | 200 — 300 | 300 — 400 | 400 — 500 | 500 — 600 |
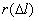 |
2 | 12 | 16 | 10 | 14 | 6 |
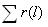 |
2 | 14 | 30 | 40 | 54 | 60 |
| P(l) | 0,989 | 0,922 | 0,833 | 0,778 | 0,7 | 0,667 |
| Q(l) | 0,011 | 0,078 | 0,167 | 0,222 | 0,3 | 0,333 |
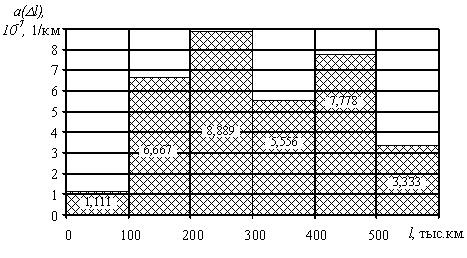
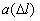 10-7, 1/км 10-7, 1/км |
1,111 | 6,667 | 8,889 | 5,556 | 7,778 | 3,333 |
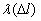 10-7, 1/км 10-7, 1/км |
1,117 | 6,977 | 10,127 | 6,897 | 10,526 | 4,878 |
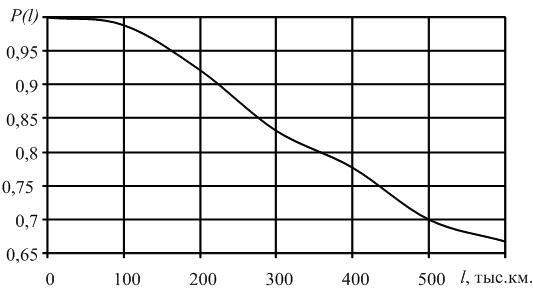
Приведем характер изменения вероятности безотказной работы ТЭД в зависимости от пробега (рис. 1.5.). Необходимо отметить, что первой точкой на графике, т.е. при пробеге равном 0, величина вероятности безотказной работы примет максимальное значение – 1.
Рис. 1.5. График изменения вероятности безотказной работы в зависимости от наработки
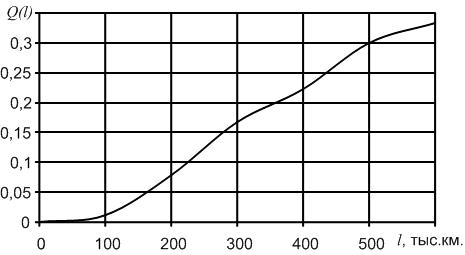
Приведем характер изменения вероятности отказа ТЭД в зависимости от пробега (рис. 1.6.). Необходимо отметить, что первой точкой на графике, т.е. при пробеге равном 0, величина вероятности отказа примет минимальное значение – 0.
Рис. 1.6. График изменения вероятности отказа в зависимости от наработки
Приведем характер изменения частоты отказов ТЭД в зависимости от пробега (рис. 1.7.).
Рис. 1.7. График изменения частоты отказов в зависимости от наработки
На рис. 1.8. представлена зависимость изменения интенсивности отказов от наработки.
Рис. 1.8. График изменения интенсивности отказов в зависимости от наработки
2.1 Экспоненциальный закон распределения случайных величин
Экспоненциальный закон достаточно точно описывает надежность узлов при внезапных отказах, имеющих случайный характер. Попытки применить его для других типов и случаев отказов, особенно постепенных, вызванных износом и изменением физико-химических свойств элементов показали его недостаточную приемлемость.
Исходные данные.
В результате испытания десяти топливных насосов высокого давления получены наработки их до отказа: 400, 440, 500, 600, 670, 700, 800, 1200, 1600, 1800 ч. Предполагая, что наработка до отказа топливных насосов подчиняется экспоненциальному закону распределения.
Требуется.
Оценить величину интенсивности отказов , а также рассчитать вероятность безотказной работы за первые 500 ч. и вероятность отказа в промежутке времени между 800 и 900 ч. работы дизеля.
Во-первых, определим величину средней наработки топливных насосов до отказа по уравнению:
Затем рассчитываем величину интенсивности отказов:
Величина вероятности безотказной работы топливных насосов при наработке 500 ч составит:
Вероятность отказа в промежутке между 800 и 900 ч. работы насосов составит:
2.2 Закон распределения Вэйбулла-Гнеденко
Закон распределения Вейбулла-Гнеденко получил широкое распространение и используется применительно к системам, состоящим из рядов элементов, соединенных последовательно с точки зрения обеспечения безотказности системы. Например, системы, обслуживающие дизель-генераторную установку: смазки, охлаждения, питания топливом, воздухом и т.д.
Исходные данные.
Время простоя тепловозов в неплановых ремонтах по вине вспомогательного оборудования подчиняется закону распределения Вейбулла-Гнеденко с параметрами b=2 и a=46.
Требуется.
Необходимо определить вероятность выхода тепловозов из неплановых ремонтов после 24 ч. простоя и время простоя, в течение которого работоспособность будет восстановлена с вероятностью 0,95.
Найдем вероятность восстановления работоспособности локомотива после простоя его в депо в течение суток по уравнению:
Для определения времени восстановления работоспособности локомотива с заданной величиной доверительной вероятности также используем выражение:
2.3 Закон распределения Рэлея
Закон распределения Рэлея используется в основном для анализа работы элементов, имеющих ярко выраженный эффект старения (элементы электрооборудования, различного рода уплотнения, шайбы, прокладки, изготовленные из резиновых или синтетических материалов).
Исходные данные.
Известно, что наработки контакторов до отказа по параметрам старения изоляции катушек можно описать функцией распределения Рэлея с параметром S = 260 тыс.км.
Требуется.
Для величины наработки 120 тыс.км. необходимо определить вероятность безотказной работы, интенсивность отказов и среднюю наработку до первого отказа катушки электромагнитного контактора.
3.1 Основное соединение элементов
Система, состоящая из нескольких независимых элементов, связанных функционально таким образом, что отказ любого из них вызывает отказ системы, отображается расчетной структурной схемой безотказной работы с последовательно соединенными событиями безотказной работы элементов.
Исходные данные.
Нерезервированная система состоит из 5 элементов. Интенсивности их отказов соответственно равны 0,00007; 0,00005; 0,00004; 0,00006; 0,00004 ч-1
Требуется.
Необходимо определить показатели надежности системы: интенсивность отказов, среднее время наработки до отказа, вероятность безотказной работы, частота отказов. Показатели надежности P(l) и a(l) получить в интервале от 0 до 1000 часов с шагом в 100 часов.
Вычислим интенсивность отказа и среднюю наработку до отказа по следующим уравнениям:
Значения вероятности безотказной работы и частоты отказов получим, используя уравнения приведенные к виду:
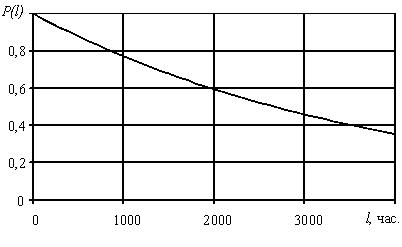
Результаты расчета P(l) и a(l) на интервале от 0 до 1000 часов работы представим в виде табл. 3.1.
Таблица 3.1.
| l, час | P(l) | a(l), час-1 |
| 0 | 1 | 0,00026 |
| 100 | 0,974355 | 0,000253 |
| 200 | 0,949329 | 0,000247 |
| 300 | 0,924964 | 0,00024 |
| 400 | 0,901225 | 0,000234 |
| 500 | 0,878095 | 0,000228 |
| 600 | 0,855559 | 0,000222 |
| 700 | 0,833601 | 0,000217 |
| 800 | 0,812207 | 0,000211 |
| 900 | 0,791362 | 0,000206 |
| 1000 | 0,771052 | 0,0002 |
Графическая иллюстрация P(l) и a(l) на участке до средней наработки до отказа представлена на рис. 3.1, 3.2.
Рис. 3.1. Вероятность безотказной работы системы.
Рис. 3.2. Частота отказов системы.
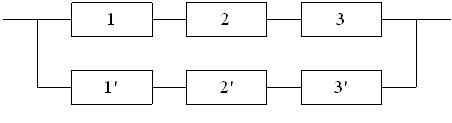
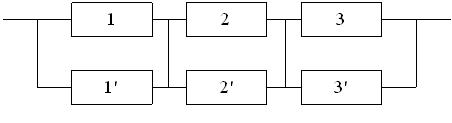
3.2 Резервное соединение элементов
Исходные данные.
На рис. 3.3 и 3.4 показаны две структурные схемы соединения элементов: общего (рис. 3.3) и поэлементного резервирования (рис. 3.4). Вероятности безотказной работы элементов соответственно равны P1(l) = P ’1(l) = 0,95; P2(l) = P’2(l) = 0,9; P3(l) = P ’3(l) = 0,85.
Требуется.
Необходимо рассчитать надежность двух систем.
Рис. 3.3. Схема системы с общим резервированием.
Рис. 3.4. Схема системы с поэлементным резервированием.
Вероятность безотказной работы блока из трех элементов без резервирования рассчитаем по выражению:
Вероятность безотказной работы той же системы при общем резервировании (рис. 3.3) составит:
Вероятности безотказной работы каждого из трех блоков при поэлементном резервировании (рис. 3.4) будут равны:
Вероятность безотказной работы системы при поэлементном резервировании составит:
Таким образом, поэлементное резервирование дает более существенное увеличение надежности (вероятность безотказной работы возросла с 0,925 до 0,965, т.е. на 4%).
Исходные данные.
На рис. 3.5 представлена система с комбинированным соединением элементов. При этом вероятности безотказной работы элементов имеют следующие значения: P1=0,8; Р2=0,9; Р3=0,95; Р4=0,97.
Требуется.
Необходимо определить надежность системы. Также необходимо определить надежность этой же системы при условии, что резервные элементы отсутствуют.
Рис.3.5. Схема системы при комбинированном функционировании элементов.
Для расчета в исходной системе необходимо выделить основные блоки. В представленной системе их три (рис. 3.6). Далее рассчитаем надежность каждого блока в отдельности, а затем найдем надежность всей системы.
Рис. 3.6. Сблокированная схема.
Надежность системы без резервирования составит:
Таким образом, система без резервирования является на 28% менее надежной, чем система с резервированием.
Страницы работы
Фрагмент текста работы
Цель работы: получение навыков преобразования сложных
технических систем и расчета сложных систем с комбинированным соединением
элементов, овладение методами повышения надежности систем.
ИСХОДНЫЕ
ДАННЫЕ К РАБОТЕ
По структурной схеме надежности системы в соответствии
с вариантом задания и по требуемому значению вероятности безотказной работы
системы ρ и значениям интенсивности её отказов λί требуется:
1. построить график изменения вероятности безотказной
работы системы от времени наработки в диапазоне снижения вероятности до уровня
0,1-0,2;
2. определить ρ-процентную наработку системы;
3. обеспечить увеличение ρ-процентной наработки не
менее чем в 1,5 раза за счет:
— повышения надежности элементов;
— структурного резервирования элементов системы.
Численные значения
параметров
|
Номер варианта |
γ, % |
Интенсивность отказов элементов λί · 10-6, |
||||||||||||
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
13 |
14 |
15 |
|
1 |
90 |
0,1 |
1,0 |
0,5 |
1,0 |
0,1 |
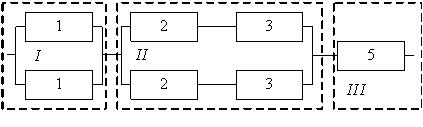
Рисунок 1 – Структурная
схема надежности
ХОД РАБОТЫ
1. В исходной схеме элементы 2,3 и 4 образуют
параллельное соединение. Заменяем их квазиэлементом А, учитывая, что p2=p3=p4, получим
pA = 1-q2q3q4=1-q23=1-(1-p2)3
2. Элементы 5 и 6 образуют параллельное соединение ,
заменив которое квазиэлементом В и учитывая, что р5=р6=р2,
получим
РВ= 1-q5q6=1-q22=1-(1-p2)2
3.Элементы 8,9 образуют параллельное соединение,
заменив которое квазиэлементом С, учитывая, что р8=р9=р2,
получим
рС= 1-q8q9=1-q22=pВ
4. Элементы 10,11,12 также образуют параллельное
соединение, заменив которое квазиэлементом D, учитывая, что
р10=р11=р12=р2, получим
рD= 1-q13q14q15=1-q23=1-(1-p2)3=pA
5. Элементы 13,14 и 15 образуют соединение «2 из 3».
Так как р13=р14=р15, то для определения ВБР
элемента М воспользуемся комбинаторным методом:
Рm= ∑3k=2 pk= ∑3k=2 Ck3 pk13 (1- p13)3-k= C23 p213 (1- p13)3-2 + C33 p313 (1- p13)3-3= = 3!/2!(3-2)! · p213 (1- p13) + 3!/3!(3-3)! · p313 (1- p13) — p313= (3·2·1)/(3·2·1) · p213 (1- p13)0· p313= 3 p213 -2p313 =
Преобразованная схема
изображена на рисунке 1.1
6. Элементы А, В, 7, С, D образуют мостиковую систему, которую
можно заменить квазиэлементом N. Для
расчета ВБР воспользуемся методом разложения относительно особого элемента, в
качестве которого выберем элемент 7. Тогда:
Рn= p 7 Рn
( p 7=1)+ p
7 Рn ( p
7=0), где
Рn ( p 7=1)-ВБР
мостиковой схемы при абсолютно надежном элементе 7
Рn ( p 7=0)- ВБР
мостиковой схемы при отказавшем элементе 7
Преобразование мостиковой схемы при абсолютно надежном
и отказавшем элементе 7 изображено на рисунке 1.2.
Рисунок 1.2 Преобразование мостиковой схемы
7. Учитывая, что рВ=рС, рА=рD
получим:
Рn= p 7 [1-(1-pА)(1-pВ)] ·
[1-(1-pС)(1-pD)] + (1+p7) [1-(1-pА pВ)(1-pС pD)]
8. После преобразований схема изображена на рисунке
1.3
9. В преобразованной схеме элементы 1, M, N образуют последовательное соединение. Тогда ВБР всей
системы
р= р1 рN рM
10. Так как по условию все элементы системы работают в
периоде нормальной эксплуатации, то ВБР элементов 1-15 подчиняются
экспоненциальному закону:
Рi =
exp(-λί t)
11. Результаты расчетов ВБР элементов 1-15 исходной
схемы по формуле Рi =
exp(-λί t) для наработки
до 3·106 часов представлены в виде таблицы 1.
Таблица 1 – Расчет безотказной работы системы
|
Элемент |
λί · 10-6, 1/ч |
Наработка t, 106 ч |
|||||||
|
0,4 |
0,5 |
0,6 |
0,7 |
0,8 |
0,9 |
1 |
1,1 |
||
|
1 |
0,1 |
0,960789 |
0,951229 |
0,941765 |
0,932394 |
0,923116 |
0,913931 |
0,90483 |
0,895834 |
|
2,6 |
1 |
0,67032 |
0,606531 |
0,548812 |
0,496585 |
0,449329 |
0,40657 |
0,367879 |
0,332871 |
|
7 |
0,5 |
0,818731 |
0,778801 |
0,740818 |
0,704688 |
0,67032 |
0,637628 |
0,606531 |
0,57695 |
|
8,12 |
1 |
0,67032 |
0,606531 |
0,548812 |
0,496585 |
0,449329 |
0,40657 |
0,367879 |
0,332871 |
|
13,15 |
0,1 |
0,960789 |
0,951229 |
0,941765 |
0,932394 |
0,923116 |
0,913931 |
0,904484 |
0,895834 |
|
A,D |
— |
0,9642 |
0,9391 |
0,9081 |
0,8724 |
0,833 |
0,791 |
0,7474 |
0,7031 |
|
B,C |
— |
0,8913 |
0,8452 |
0,7964 |
0,7466 |
0,6967 |
0,6479 |
0,6004 |
0,555 |
|
N |
— |
0,99 |
0,9219 |
0,9527 |
0,9193 |
0,8758 |
0,823465 |
0,7642 |
0,7003 |
|
M |
— |
0,9955 |
0,9931 |
0,9902 |
0,9869 |
0,9832 |
0,999362 |
0,9745 |
0,9697 |
|
P |
— |
0,9468 |
0,9219 |
0,8884 |
0,8459 |
0,7948 |
0,7368 |
0,6739 |
0,6083 |
|
2′ |
0,66 |
0,767974 |
0,718924 |
0,673007 |
0,630022 |
0,589783 |
0,552114 |
0,516851 |
0,48384 |
|
В′, С′ |
— |
0,9729 |
0,9512 |
0,944 |
0,9204 |
0,9086 |
0,9024 |
0,8687 |
0,8459 |
|
N′ |
— |
0,9977 |
0,9801 |
0,9871 |
0,9768 |
0,9602 |
0,9539 |
0,912 |
0,8729 |
|
Р′ |
— |
0,9502 |
0,9489 |
0,9401 |
0,9257 |
0,9144 |
0,908 |
0,8686 |
0,8438 |
|
2′′ |
— |
0,6703 |
0,6134 |
0,5488 |
0,4947 |
0,4493 |
0,3894 |
0,3679 |
0,3125 |
|
С′′, В′′ |
— |
0,9998 |
0,9901 |
0,9813 |
0,9386 |
0,8724 |
0,8869 |
0,8991 |
0,8831 |
|
1′′ |
— |
0,9996 |
0,9972 |
0,9966 |
0,9953 |
0,9941 |
0,9929 |
0,9909 |
0,9868 |
|
N′′ |
— |
0,9999 |
0,9968 |
0,9944 |
0,9602 |
0,9323 |
0,9301 |
0,9271 |
0,9206 |
|
P′′ |
— |
0,9984 |
0,9897 |
0,9813 |
0,9638 |
0,9411 |
0,9206 |
0,8954 |
0,8879 |
12. На рисунке 1.4 представлен график зависимости
вероятности безотказной работы системы Р от времени наработки t.
Рисунок 1.4
13. По графику находим для γ=90% (Рγ =0,9)
γ- процентную наработку системы Тγ = 0,6·106 ч.
14. проверочный расчет при t = 0,6·106 ч показывает, что Рγ=0,89705≈0,9.
15. По условиям задания повышенная γ- процентная
наработка системы Тγ′ = 1,5 Тγ =1,5· 0,6·106 =
0,9·106 ч.
16. Расчет показывает, что при t =
0,9·106 ч для элементов преобразованной схемы р1=
0,913931, рN =
0,8235, рМ = 0,9993. Следовательно, из трех последовательно
соединенных элементов минимальное значение ВБР имеет элемент N.
Следовательно увеличение его надежности даст максимальное увеличение надежности
системы в целом.
17. Для того, чтобы при Тγ′
= 0,9·106 ч система в целом имела ВБР Рγ=0,9, необходимо,
чтобы элемент N имел
ВБР:
рN =рγ
/ р1рМ=0,9/0,913931*0,9993=0,9854.
При данном значении ВБР элемент N
надежен, однако, чтобы повысить надежность системы необходимо увеличить
надежность двух элементов: 1 и N.
18. Для определения
минимально необходимой вероятности безотказной работы элементов необходимо
решить уравнение из седьмого пункта относительно р2 при рN=0,9854.
Поскольку аналитический метод является более сложным, то целесообразнее
воспользоваться графическим методом. Для этого по данным таблицы строим график
зависимости
Похожие материалы
- Изучение методов расчета функции надежности системы с учетом разнообразных связей её элементов
- Расчет сложных систем с комбинированным соединением элементов. Критерии надежности восстанавливаемых изделий. Расчет характеристик надежности невосстанавливаемых резервированных изделий
- Расчет структурной надежности системы (наработка исходной системы составляет 75%)
Информация о работе
Тип:
Отчеты по лабораторным работам
Структурная надежность систем
РАСЧЕТЫ СТРУКТУРНОЙ НАДЕЖНОСТИ СИСТЕМ
ВВЕДЕНИЕ
Надежностью называют свойство объекта сохранять во времени в установленных пределах значения всех параметров, характеризующих способность выполнять требуемые функции в заданных режимах и условиях применения, технического обслуживания, ремонтов, хранения и транспортировки. Расширение условий эксплуатации, повышение ответственности выполняемых радиоэлектронными средствами (РЭС) функций, их усложнение приводит к повышению требований к надежности изделий.
Надежность является сложным свойством, и формируется такими составляющими, как безотказность, долговечность, восстанавливаемость и сохраняемость. Основным здесь является свойство безотказности — способность изделия непрерывно сохранять работоспособное состояние в течение времени. Потому наиболее важным в обеспечении надежности РЭС является повышение их безотказности.
Особенностью проблемы надежности является ее связь со всеми этапами “жизненного цикла” РЭС от зарождения идеи создания до списания: при расчете и проектировании изделия его надежность закладывается в проект, при изготовлении надежность обеспечивается, при эксплуатации — реализуется. Поэтому проблема надежности — комплексная проблема и решать ее необходимо на всех этапах и разными средствами. На этапе проектирования изделия определяется его структура, производится выбор или разработка элементной базы, поэтому здесь имеются наибольшие возможности обеспечения требуемого уровня надежности РЭС. Основным методом решения этой задачи являются расчеты надежности (в первую очередь — безотказности), в зависимости от структуры объекта и характеристик его составляющих частей, с последующей необходимой коррекцией проекта. Некоторые способы расчета структурной надежности рассматриваются в данном пособии .
1. КОЛИЧЕСТВЕННЫЕ ХАРАКТЕРИСТИКИ БЕЗОТКАЗНОСТИ
Безотказность (и другие составляющие свойства надежности) РЭС проявляется через случайные величины: наработку до очередного отказа и количество отказов за заданное время. Поэтому количественными характеристиками свойства здесь выступают вероятностные переменные.
Наработка есть продолжительность или объем работы объекта. Для РЭС естественно исчисление наработки в единицах времени, тогда как для других технических средств могут быть удобнее иные средства измерения (например, наработка автомобиля — в километрах пробега). Для невосстанавливаемых и восстанавливаемых изделий понятие наработки различается: в первом случае подразумевается наработка до первого отказа (он же является и последним отказом), во втором — между двумя соседними во времени отказами (после каждого отказа производится восстановление работоспособного состояния). Математическое ожидание случайной наработки Т
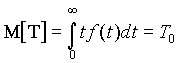
является характеристикой безотказности и называется средней наработкой на отказ (между отказами). В (1.1) через t обозначено текущее значение наработки, а f(t) — плотность вероятности ее распределения.
Вероятность безотказной работы — вероятность того, что в пределах заданной наработки t отказ объекта не возникнет:
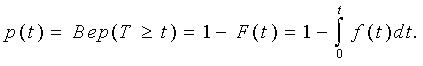
Вероятность противоположного события называется вероятностью отказа и дополняет вероятность безотказной работы до единицы:
(1.3)
В (1.2) и (1.3) F(t) есть интегральная функция распределение случайной наработки t. Плотность вероятности f(t) также является показателем надежности, называемым частотой отказов:
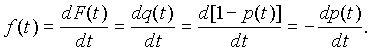
Из (1.4) очевидно, что она характеризует скорость уменьшения вероятности безотказной работы во времени.
Интенсивностью отказов называют условную плотность вероятности возникновения отказа изделия при условии, что к моменту t отказ не возник:
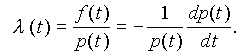
Функции f(t) и (t) измеряются в ч
.
Интегрируя (1.5), легко получить:

Это выражение, называемое основным законом надежности, позволяет установить временное изменение вероятности безотказной работы при любом характере изменения интенсивности отказов во времени. В частном случае постоянства интенсивности отказов(t) =
= const (1.6) переходит в известное в теории вероятностей экспоненциальное распределение:
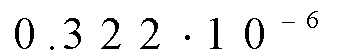
Поток отказов при(t)=const называется простейшим и именно он реализуется для большинства РЭС в течении периода нормальной эксплуатации от окончания приработки до начала старения и износа.
Подставив выражение плотности вероятности f(t) экспоненциального распределения (1.7) в (1.1), получим:
(1.8)
т.е. при простейшем потоке отказов средняя наработка Т0 обратна интен-сивности отказов . С помощью (1.7) можно показать, что за время средней наработки, t=T0, вероятность безотказной работы изделия составляет 1/е. Часто используют характеристику, называемую
— процентной наработкой — время, в течении которого отказ не наступит с вероятностью
(%):
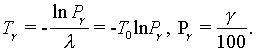
Выбор параметра для количественной оценки надежности определяется назначением, режимами работы изделия, удобством применения в расчетах на стадии проектирования.
2. СТРУКТУРНО — ЛОГИЧЕСКИЙ АНАЛИЗ ТЕХНИЧЕСКИХ СИСТЕМ
Конечной целью расчета надежности технических устройств является оптимизация конструктивных решений и параметров, режимов эксплуатации, организация технического обслуживания и ремонтов. Поэтому уже на ранних стадиях проектирования важно оценить надежность объекта, выявить наиболее ненадежные узлы и детали, определить наиболее эффективные меры повышения показателей надежности. Решение этих задач возможно после пред- варительного структурно — логического анализа системы.
Большинство технических объектов, в том числе РЭС, являются сложными системами, состоящими из отдельных узлов, деталей, агрегатов, устройств контроля, управления и т.д.. Техническая система (ТС) — совокупность технических устройств (элементов), предназначенных для выполнения определенной функции или функций. Соответственно, элемент — составная часть системы.
Расчленение ТС на элементы достаточно условно и зависит от постановки задачи расчета надежности. Например при анализе работоспособности технологической линии ее элементами могут считаться отдельные установки и станки, транспортные и загрузочные устройства и т.д.. В свою очередь станки и устройства также могут считаться техническими системами и при оценке их надежности должны быть разделены на элементы — узлы, блоки, которые, в свою очередь — на детали и т.д..
При определении структуры ТС в первую очередь необходимо оценить влияние каждого элемента и его работоспособности на работоспособность системы в целом. С этой точки зрения целесообразно разделить все элементы на четыре группы:
1. Элементы, отказ которых практически не влияет на работоспособность системы (например, деформация кожуха, изменение окраски поверхности и т.п.).
2. Элементы, работоспособность которых за время эксплуатации практически не изменяется и вероятность безотказной работы близка к единице (корпусные детали, малонагруженные элементы с большим запасом прочности).
3. Элементы, ремонт или регулировка которых возможна при работе изделия или во время планового технического обслуживания (наладка или замена технологического инструмента оборудования, настройка частоты селек-тивных цепей РЭС и т.д.).
4. Элементы, отказ которых сам по себе или в сочетании с отказами других элементов приводит к отказу системы.
Очевидно, при анализе надежности ТС имеет смысл включать в рас-смотрение только элементы последней группы.
Для расчетов параметров надежности удобно использовать структурно — логические схемы надежности ТС, которые графически отображают взаимосвязь элементов и их влияние на работоспособность системы в целом. Структурно — логическая схема представляет собой совокупность ранее выделенных элементов, соединенных друг с другом последовательно или параллельно. Критерием для определения вида соединения элементов (последовательного или параллельного) при построении схемы является влияние их отказа на работоспособность ТС.
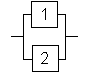
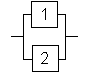
Последовательным (с точки зрения надежности) считается соединение, при котором отказ любого элемента приводит к отказу всей системы (рис. 2.1).
Параллельным (с точки зрения надежности) считается соединение, при котором отказ любого элемента не приводит к отказу системы, пока не откажут все соединенные элементы (рис. 2.2).
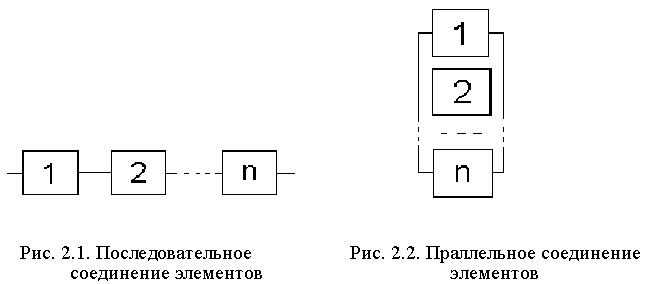
Определенная аналогия здесь прослеживается с цепью, составленной из проводящих элементов (исправный элемент пропускает ток, отказавший не пропускает): работоспособному состоянию ТС соответствует возможность протекания тока от входа до выхода цепи .
Примером последовательного соединения элементов структурно — логической схемы может быть технологическая линия, в которой происходит переработка сырья в готовый продукт, или РЭС, в котором последовательно осуществляется преобразование входного сигнала. Если же на некоторых участках линии, или пути сигнала, предусмотрена одновременная обработка на нескольких единицах оборудования, то такие элементы (единицы оборудова-ния) могут считаться соединенными параллельно.
Однако не всегда структурная схема надежности аналогична конструктив-ной или электрической схеме расположения элементов. Например, подшипники на валу редуктора работают конструктивно параллельно друг с другом, однако выход из строя любого из них приводит к отказу системы. Аналогично дейст-вие индуктивности и емкости параллельного колебательного контура в селективных каскадах РЭС. Указанные элементы с точки зрения надежности образуют последовательное соединение.
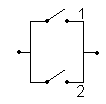
Кроме того, на структуру схемы надежности может оказывать влияние и вид возникающих отказов. Например, в электрических системах для повыше-ния надежности в ряде случаев применяют параллельное или последовательное соединение коммутирующих элементов (рис. 2.3). Отказ таких изделий может происходить по двум причинам: обрыва (т.е. невозможности замыкания цепи) и замыкания (т.е. невозможности разрыва соединения). В случае отказа типа “обрыв” схема надежности соответствует электрической схеме системы (при “обрыве” любого коммутатора при последовательном их соединении возникает отказ, при параллельном — все функции управления будет выполнять исправный коммутатор). В случае отказа типа “замыкание” схема надежности противоположна электрической (в параллельном включении утратится возможность отк-лючения тока, а в последовательном общего отказа не происходит).
|
Электрическая схема |
Структурная схема надежности при отказе типа |
|
|
обрыв |
замыкание |
|
|
|
|
|
|
|
|
|
Рис. 2.3. Электрические и структурные схемы соединения коммутационных элементов при различных видах отказов
В целом анализ структурной надежности ТС, как правило, включает следующие операции:
1. Анализируются устройства и выполняемые системой и ее составными частями функции , а также взаимосвязь составных частей.
2. Формируется содержание понятия “безотказной работы” для данной конкретной системы.
3. Определяются возможные отказы составных частей и системы, их причины и возможные последствия.
4. Оценивается влияние отказов составных частей системы на ее работоспособность.
5. Система разделяется на элементы, показатели надежности которых известны.
6. Составляется структурно — логическая схема надежности технической системы, которая является моделью ее безотказной работы.
7. Составляются расчётные зависимости для определения показателей надёжности ТС с использованием данных по надежности её элементов и с учётом структурной схемы.
В зависимости от поставленной задачи на основании результатов расчета характеристик надежности ТС делаются выводы и принимаются решения о необходимости изменения или доработки элементной базы, резервировании отдельных элементов или узлов, об установлении определенного режима профилактического обслуживания, о номенклатуре и количестве запасных элементов для ремонта и т.д..
3. РАСЧЕТЫ СТРУКТУРНОЙ НАДЕЖНОСТИ СИСТЕМ
Расчеты показателей безотказности ТС обычно проводятся в предпо-ложении, что как вся система, так и любой ее элемент могут находиться только в одном из двух возможных состояний — работоспособном и неработоспособном и отказы элементов независимы друг от друга. Состояние системы (рабо-тоспособное или неработоспособное) определяется состоянием элементов и их сочетанием. Поэтому теоретически возможно расчет безотказности любой ТС свести к перебору всех возможных комбинаций состояний элементов, определению вероятности каждого из них и сложению вероятностей рабо-тоспособных состояний системы.
Такой метод (метод прямого перебора — см. п. 3.3) практически универсален и может использоваться при расчете любых ТС. Однако при большом количестве элементов системы n такой путь становится нереальным из-за большого объема вычислений (например, при n=10 число возможных состояний системы составляет, = 1024, при n=20 превышает
, при n=30 -более
). Поэтому на практике используют более эффективные и экономичные методы расчета, не связанные с большим объемом вычислений. Возможность применения таких методов связана со структурой ТС.
3.1. Системы с последовательным соединением элементов
Системой с последовательным соединением элементов называется система, в которой отказ любого элемента приводит к отказу всей системы (см. п. 2, рис 2.1). Такое соединение элементов в технике встречается наиболее часто, поэтому его называют основным соединением.
В системе с последовательным соединением для безотказной работы в течении некоторой наработки t необходимо и достаточно, чтобы каждый из ее n элементов работал безотказно в течении этой наработки. Считая отказы элементов независимыми, вероятность одновременной безотказной работы n элементов определяется по теореме умножения вероятностей: вероятность совместного появления независимых событий равна произведению вероятностей этих событий:
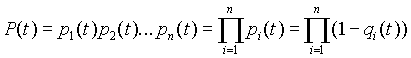
(далее аргумент t в скобках , показывающий зависимость показателей надежности от времени, опускаем для сокращения записей формул). Соответственно, вероятность отказа такой ТС
Если система состоит из равнонадёжных элементов (), то
(3.3)
Из формул (3.1) — (3.3) очевидно, что даже при высокой надежности элементов надежность системы при последовательном соединении оказывается тем более низкой, чем больше число элементов (например, при и
имеем
, при
, а при
). Кроме того, поскольку все сомножители в правой части выражения (3.1) не превышают единицы, вероятность безотказной работы ТС при последовательном соединении не может быть выше вероятности безотказной работы самого ненадежного из ее элементов (принцип “хуже худшего”) и из малонадежных элементов нельзя создать высоконадежной ТС с последовательным соединением.
Если все элементы системы работают в периоде нормальной эксплуа-тации и имеет место простейший поток отказов (см. п. 1), наработки элементов и системы подчиняются экспоненциальному распределению (1.7) и на основании (3.1) можно записать
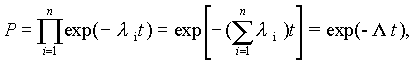
где
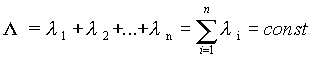
есть интенсивность отказов системы. Таким образом, интенсивность отказов системы при последовательном соединении элементов и простейшем потоке отказов равна сумме интенсивностей отказов элементов. С помощью выраже-ний (1.8) и (1.9) могут быть определены средняя и — процентная наработки.
Из (3.4) — (3.5) следует, что для системы из n равнонадёжных элементов ()
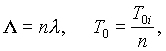
т.е. интенсивность отказов в n раз больше, а средняя наработка в n раз меньше, чем у отдельного элемента.
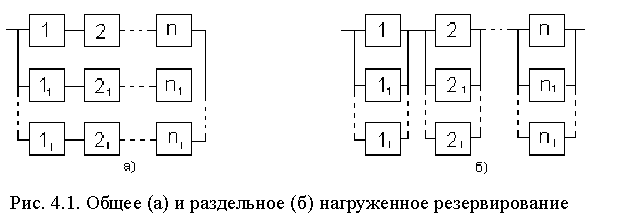
3.2. Системы с параллельным соединением элементов
Системой с параллельным соединением элементов называется система, отказ которой происходит только в случае отказа всех ее элементов (см. п. 2, рис. 2.2). Такие схемы надежности характерны для ТС, в которых элементы дублируются или резервируются, т.е. параллельное соединение используется как метод повышения надежности (см. п. 4.2). Однако такие системы встречаются и самостоятельно (например, системы двигателей четырехмоторного самолета или параллельное включение диодов в мощных выпрямителях).
Для отказа системы с параллельным соединением элементов в течение наработки t необходимо и достаточно, чтобы все ее элементы отказали в течение этой наработки. Так что отказ системы заключается в совместном отказе всех элементов, вероятность чего (при допущении независимости отказов) может быть найдена по теореме умножения вероятностей как произведение вероятностей отказа элементов:
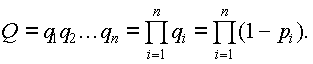
Соответственно, вероятность безотказной работы
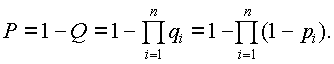
Для систем из равнонадежных элементов ()
(3.9)
т.е. надежность системы с параллельным соединением повышается при увеличении числа элементов (например, при и
, а при
).
Поскольку , произведение в правой части (3.7) всегда меньше любого из сомножителей, т.е. вероятность отказа системы не может быть выше вероятности самого надежного ее элемента (“лучше лучшего”) и даже из сравнительно ненадежных элементов возможно построение вполне надежной системы.
При экспоненциальном распределении наработки (1.7) выражение (3.9) принимает вид
(3.10)
откуда с помощью (1.1) после интегрирования и преобразований средняя наработка системы определяется
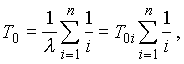
где — средняя наработка элемента. При больших значениях n справедлива приближенная формула

Таким образом, средняя наработка системы с параллельным соединением больше средней наработки ее элементов (например, при
, при
).
3.3. Системы типа “m из n”
Систему типа “m из n” можно рассматривать как вариант системы с параллельным соединением элементов, отказ которой произойдет, если из n элементов, соединенных параллельно, работоспособными окажутся менее m элементов (m < n).
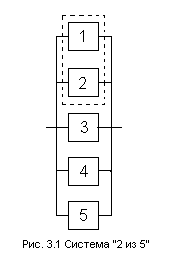
На рис. 3.1 представлена система “2 из 5”, которая работоспособна, если из пяти её элементов работают любые два, три, четыре или все пять (на схеме пунктиром обведены функционально необходимые два элемента, причем выделение элементов 1 и 2 произведено условно, в действительности все пять элементов равнозначны). Системы типа “m из n” наиболее часто встречаются в электрических и связных системах (при этом элементами выступают связую-щие каналы), технологических линий, а также при структурном резервировании (см. п. 4.1, 4.2).
Для расчета надежности систем типа “m из n“ при сравнительно небольшом количестве элементов можно воспользоваться методом прямого перебора. Он заключается в определении работоспособности каждого из возможных состояний системы, которые определяются различными сочета-ниями работоспособных и неработоспособных состояний элементов.
Все состояния системы “2 из 5“ занесены в табл. 3.1. (в таблице работоспособные состояния элементов и системы отмечены знаком “+“, неработоспособные — знаком “-“). Для данной системы работоспособность определяется лишь количеством работоспособных элементов. По теореме умножения вероятностей вероятность любого состояния определяется как произведение вероятностей состояний, в которых пребывают элементы . Например, в строке 9 описано состояние системы, в которой отказали элементы 2 и 5, а остальные работоспособны. При этом условие “2 из 5“ выполняется, так что система в целом работоспособна. Вероятность такого состояния
(предполагается, что все элементы равнонадежны). С учетом всех возможных состояний вероятность безотказной работы системы может быть найдена по теореме сложения вероятностей всех работоспособных сочетаний. Поскольку в табл. 3.1 количество неработоспособных состояний меньше, чем работоспособных (соответственно 6 и 26), проще вычислить вероятность отказа системы. Для этого суммируются вероятности неработоспособных состояний (где не выполняется условие “ 2 из 5 “)
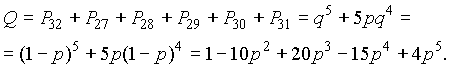
Тогда вероятность безотказной работы системы
(3.14)
Расчет надежности системы “m из n“ может производиться комбинаторным методом, в основе которого лежит формула биномиального распределения. Биномиальному распределению подчиняется дискретная случайная величина k — число появлений некоторого события в серии из n опытов, если в отдельном опыте вероятность появления события составляет p. При этом вероятность появления события ровно k раз определяется
(3.15)
где — биномиальный коэффициент, называемый “числом сочетаний по k из n“ (т.е. сколькими разными способами можно реализовать ситуацию “k из n“):
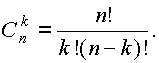
Значения биномиальных коэффициентов приведены в приложении.
Поскольку для отказа системы “m из n“ достаточно, чтобы количество исправных элементов было меньше m, вероятность отказа может быть найдена по теореме сложения вероятностей для k = 0, 1, … (m-1):
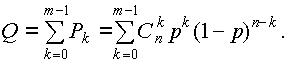
Аналогичным образом можно найти вероятность безотказной работы как сумму (3.15) для k=m, m+1, … , n:
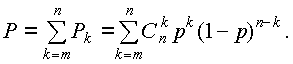
Таблица 3.1
Таблица состояний системы “2 из 5”
|
|
Состояние элементов |
Состояние |
Вероятность |
||||
|
состояния |
1 |
2 |
3 |
4 |
5 |
системы |
состояния системы |
|
1 |
+ |
+ |
+ |
+ |
+ |
+ |
|
|
2 |
+ |
+ |
+ |
+ |
— |
+ |
|
|
3 |
+ |
+ |
+ |
— |
+ |
+ |
|
|
4 |
+ |
+ |
— |
+ |
+ |
+ |
|
|
5 |
+ |
— |
+ |
+ |
+ |
+ |
|
|
6 |
— |
+ |
+ |
+ |
+ |
+ |
|
|
7 |
+ |
+ |
+ |
— |
— |
+ |
|
|
8 |
+ |
+ |
— |
+ |
— |
+ |
|
|
9 |
+ |
— |
+ |
+ |
— |
+ |
|
|
10 |
— |
+ |
+ |
+ |
— |
+ |
|
|
11 |
+ |
+ |
— |
— |
+ |
+ |
|
|
12 |
+ |
— |
+ |
— |
+ |
+ |
|
|
13 |
— |
+ |
+ |
— |
+ |
+ |
|
|
14 |
+ |
— |
— |
+ |
+ |
+ |
|
|
15 |
— |
+ |
— |
+ |
+ |
+ |
|
|
16 |
— |
— |
+ |
+ |
+ |
+ |
|
|
17 |
+ |
+ |
— |
— |
— |
+ |
|
|
18 |
+ |
— |
+ |
— |
— |
+ |
|
|
19 |
— |
+ |
+ |
— |
— |
+ |
|
|
20 |
+ |
— |
— |
— |
+ |
+ |
|
|
21 |
— |
+ |
— |
— |
+ |
+ |
|
|
22 |
— |
— |
— |
+ |
+ |
+ |
|
|
23 |
+ |
— |
— |
+ |
— |
+ |
|
|
24 |
— |
+ |
— |
+ |
— |
+ |
|
|
25 |
— |
— |
+ |
— |
+ |
+ |
|
|
26 |
— |
— |
+ |
+ |
— |
+ |
|
|
27 |
+ |
— |
— |
— |
— |
— |
|
|
28 |
— |
+ |
— |
— |
— |
— |
|
|
29 |
— |
— |
+ |
— |
— |
— |
|
|
30 |
— |
— |
— |
+ |
— |
— |
|
|
31 |
— |
— |
— |
— |
+ |
— |
|
|
32 |
— |
— |
— |
— |
— |
— |
|
Очевидно, что Q+P=1, поэтому в расчетах следует выбирать ту из формул (3.17), (3.18), которая в данном конкретном случае содержит меньшее число слагаемых.
Для системы “2 из 5“ (рис. 3.1) по формуле (3.18) получим:
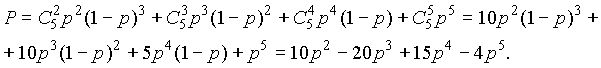
Вероятность отказа той же системы по (3.17):
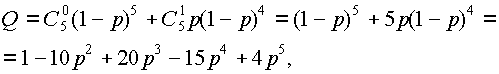
что, как видно, дает тот же результат для вероятности безотказной работы.
В табл. 3.2 приведены формулы для расчета вероятности безотказной работы систем типа “m из n“ при m<=n<=5. Очевидно, при m=1 система превращается в обычную систему с параллельным соединением элементов, а при m = n — с последовательным соединением.
Таблица 3.2
|
Общее число элементов , n |
|||||
|
m |
1 |
2 |
3 |
4 |
5 |
|
1 |
|
|
|
|
|
|
2 |
— |
|
|
|
|
|
3 |
— |
— |
|
|
|
|
4 |
— |
— |
— |
|
|
|
5 |
— |
— |
— |
— |
|
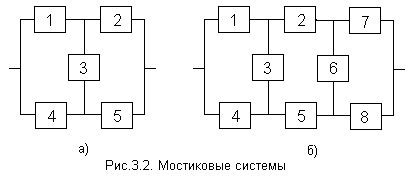
3.4. Мостиковые схемы
Мостиковая структура (рис. 3.2, а, б) не сводится к параллельному или последовательному типу соединения элементов, а представляет собой параллельное соединение последовательных цепочек элементов с диагональными элементами, включенными между узлами различных параллельных ветвей (элемент 3 на рис. 3.2, а, элементы 3 и 6 на рис. 3.2, б). Работоспособность такой системы определяется не только количеством отказавших элементов, но и их положением в структурной схеме. Например, работоспособность ТС, схема которой приведена на рис. 3.2, а, будет утрачена при одновременном отказе элементов 1 и 2, или 4 и 5, или 2, 3 и 4 и т.д.. В то же время отказ элементов 1 и 5, или 2 и 4, или 1, 3 и 4, или 2, 3 и 5 к отказу системы не приводит.
Таблица 3.3
Таблица состояний мостиковой системы
|
|
Состояние |
Вероятность состояния |
||||||
|
сост. |
1 |
2 |
3 |
4 |
5 |
системы |
в общем случае |
при равнонадежных элементах |
|
1 |
+ |
+ |
+ |
+ |
+ |
+ |
|
|
|
2 |
+ |
+ |
+ |
+ |
— |
+ |
|
|
|
3 |
+ |
+ |
+ |
— |
+ |
+ |
|
|
|
4 |
+ |
+ |
— |
+ |
+ |
+ |
|
|
|
5 |
+ |
— |
+ |
+ |
+ |
+ |
|
|
|
6 |
— |
+ |
+ |
+ |
+ |
+ |
|
|
|
7 |
+ |
+ |
+ |
— |
— |
— |
|
|
|
8 |
+ |
+ |
— |
+ |
— |
+ |
|
|
|
9 |
+ |
— |
+ |
+ |
— |
+ |
|
|
|
10 |
— |
+ |
+ |
+ |
— |
+ |
|
|
|
11 |
+ |
+ |
— |
— |
+ |
+ |
|
|
|
12 |
+ |
— |
+ |
— |
+ |
+ |
|
|
|
13 |
— |
+ |
+ |
— |
+ |
+ |
|
|
|
14 |
+ |
— |
— |
+ |
+ |
+ |
|
|
|
15 |
— |
+ |
— |
+ |
+ |
+ |
|
|
|
16 |
— |
— |
+ |
+ |
+ |
— |
|
|
|
17 |
+ |
+ |
— |
— |
— |
— |
|
|
|
18 |
+ |
— |
+ |
— |
— |
— |
|
|
|
19 |
— |
+ |
+ |
— |
— |
— |
|
|
|
20 |
+ |
— |
— |
— |
+ |
— |
|
|
|
21 |
— |
+ |
— |
— |
+ |
+ |
|
|
|
22 |
— |
— |
— |
+ |
+ |
— |
|
|
|
23 |
+ |
— |
— |
+ |
— |
+ |
|
|
|
24 |
— |
+ |
— |
+ |
— |
— |
|
|
|
25 |
— |
— |
+ |
— |
+ |
— |
|
|
|
26 |
— |
— |
+ |
+ |
— |
— |
|
|
|
27 |
+ |
— |
— |
— |
— |
— |
|
|
|
28 |
— |
+ |
— |
— |
— |
— |
|
|
|
29 |
— |
— |
+ |
— |
— |
— |
|
|
|
30 |
— |
— |
— |
+ |
— |
— |
|
|
|
31 |
— |
— |
— |
— |
+ |
— |
|
|
|
32 |
— |
— |
— |
— |
— |
— |
|
|
Для расчета надежности мостиковых систем можно воспользоваться методом прямого перебора, как это было сделано для систем “m из n“ (п. 3.3), но при анализе работоспособности каждого состояния системы необходимо учитывать не только число отказавших элементов, но и их положение в схеме (табл. 3.3). Вероятность безотказной работы системы определяется как сумма вероятностей всех работоспособных состояний:
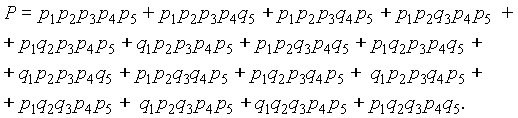
В случае равнонадёжных элементов
(3.22)
Метод прямого перебора эффективен только при малом количестве элементов n, о чем говорилось в начале разд. 3, поскольку число состояний системы составляет . Например, для схемы на рис. 3.2,б их количество составит уже 256. Некоторое упрощение достигается, если в таблицу состояний включать только сочетания, отвечающие работоспособному (или только неработоспособному) состоянию системы в целом.
Для анализа надежности ТС, структурные схемы которых не сводятся к параллельному или последовательному типу, можно воспользоваться также методом логических схем с применением алгебры логики (булевой алгебры). Применение этого метода сводится к составлению для ТС формулы алгебры логики, которая определяет условие работоспособности системы. При этом для каждого элемента и системы в целом рассматриваются два противоположных события — отказ и сохранение работоспособности.
Для составления логической схемы можно воспользоваться двумя методами — минимальных путей и минимальных сечений.
Рассмотрим метод минимальных путей для расчета вероятности безотказной работы на примере мостиковой схемы (рис. 3.2,а).
Минимальным путем называется последовательный набор работоспо-собных элементов системы, который обеспечивает ее работоспособность, а отказ любого из них приводит к ее отказу.
Минимальных путей в системе может быть один или несколько. Очевидно, система с последовательным соединением элементов (рис. 2.1) имеет только один минимальный путь, включающий все элементы. В системе с параллельным соединением (рис. 2.2) число минимальных путей совпадает с числом элементов и каждый путь включает один из них.
Для мостиковой системы из пяти элементов (рис. 3.2,а) минимальных путей четыре: (элементы 1 и 4), (2 и 5), (1, 3 и 5), (2, 3 и 5). Логическая схема такой системы (рис. 3.3) составляется таким образом, чтобы все элементы каждого минимального пути были соединены друг с другом последовательно, а все минимальные пути параллельно.
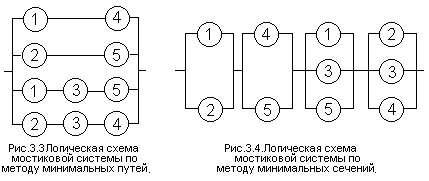
Затем для логической схемы составляется функция алгебры логики А по общим правилам расчета вероятности безотказной работы , но вместо символов вероятностей безотказной работы элементов и системы Р используются символы события (сохранения работоспособности элемента ai и системы А). Так, “отказ“ логической схемы рис. 3.3 состоит в одновременном отказе всех четырех параллельных ветвей, а “безотказная работа” каждой ветви — в одновременной безотказной работе ее элементов. Последовательное соединение элементов логической схемы соответствует логическому умножению (“И”), параллельное — логическому сложению (“ИЛИ”). Следовательно, схема рис. 3.3 соответствует утверждению: система работоспособна, если работоспособны элементы 1 и 4, или 2 и 5, или 1,3 и 5, или 2,3 и 4. Функция алгебры логики запишется:
(3.23)
В выражении (3.23) переменные а рассматриваются как булевы, т.е. могут приниматься только два значения: 0 или 1. Тогда при возведении в любую степень k любая переменная a сохраняет свое значение: . На основе этого свойства функция алгебры логики (3.23) может быть преобразована к виду
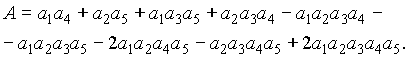
Заменив в выражении (3.24) символы событий их вероятностями
, получим уравнение для определения вероятности безотказной работы системы
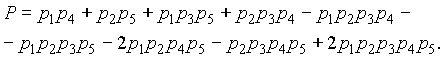
Для системы равнонадёжных элементов () выражение (3.25) легко преобразуется в формулу (3.22).
Метод минимальных путей дает точное значение только для сравнительно простых систем с небольшим числом элементов. Для более сложных систем результат расчета является нижней границей вероятности безотказной работы.
Для расчета верхней границы вероятности безотказной работы системы служит метод минимальных сечений.
Минимальным сечением называется набор неработоспособных элементов, отказ которых приводит к отказу системы, а восстановление работоспособности любого из них — к восстановлению работоспособности системы. Как и минимальных путей, минимальных сечений может быть несколько. Очевидно, система с параллельным соединением элементов имеет только одно минимальное сечение, включающее все ее элементы (восстановление любого восстановит работоспособность системы). В системе с последовательным соединением элементов число минимальных путей совпадает с числом элементов, и каждое сечение включает один из них .
В мостиковой системе (рис. 3.2, а) минимальных сечений четыре (элементы 1 и 2), (4 и 5), (1, 3 и 5) , (2, 3 и 4). Логическая схема системы (рис.3.4) составляется таким образом, чтобы все элементы каждого мини-мального сечения были соединены друг с другом параллельно, а все мини-мальные сечения — последовательно. Аналогично методу минимальных путей, составляется функция алгебры логики. “Безотказная работа” логической системы рис. 3.4 заключается в “безотказной работе” всех последовательных участков, а “отказ” каждого из них — в одновременном “отказе” всех парал-лельно включенных элементов. Как видно, поскольку схема метода минимальных сечений формулирует условия отказа системы, в ней последо-вательное соединение соответствует логическому “ИЛИ”, а параллельное — логическому “И”. Схема рис. 3.4 соответствует формулировке: система отка-жет, если откажут элементы 1 и 2, или 4 и 5, или 1, 3 и 5, или 2, 3 и 4. Функция алгебры логики запишется
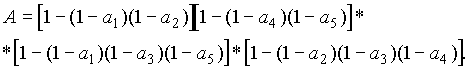
После преобразований с использованием свойств булевых переменных (3.26) приобретает форму (3.24), после замены событий их вероятностями переходит в выражение (3.25).
Таким образом, для мостиковой системы из пяти элементов верхняя и нижняя границы вероятности безотказной работы, полученные методами минимальных сечений и минимальных путей, совпали с точными значениями (3.22), полученными методом прямого перебора. Для сложных систем это может не произойти, поэтому методы минимальных путей и минимальных сечений следует применять совместно.
В ряде случаев анализа надежности ТС удается воспользоваться методом разложения относительно особого элемента, основанными на известной в математической логике теореме о разложении функции логики по любому аргументу. Согласно ей, можно записать:
(3.27)
где и
— вероятности безотказной работы и отказа i — го элемента,
и
-вероятности работоспособного состояния системы при условии, что i — й элемент абсолютно надежен и что i — й элемент отказал.
Для мостиковой схемы (рис. 3.2, а) в качестве особого элемента целесообразно выбрать диагональный элемент 3. При мостиковая схема превращается в параллельно — последовательное соединение (рис. 3.5, а), а при
— в последовательно — параллельное (рис. 3.5, б).
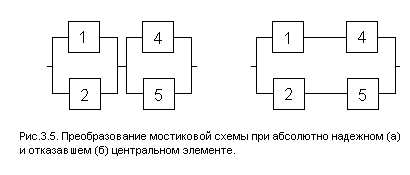
Для преобразованных схем можно записать:
(3.28)
(3.29)
Тогда на основании формулы (3.27) получим:
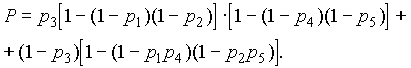
Легко убедиться, что для равнонадёжных элементов формула (3.30) об-ращается в (3.22).
Этим методом можно воспользоваться и при разложении относительно нескольких “особых” элементов. Например, для двух элементов (i, j) выражение (3.27) примет вид:
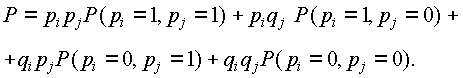
Вероятность безотказной работы мостиковой схемы (рис. 3.2, б) при разложении относительно диагональных элементов 3 и 6 по (3.31) определится:
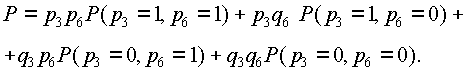
Вероятности легко ставить, выполнив предварительно преобразованные схемы, подобно рис. 3.5, а, б.
3.5. Комбинированные системы
Большинство реальных ТС имеет сложную комбинированную структуру, часть элементов которой образует последовательное соединение, другая часть — параллельное, отдельные ветви элементы или ветви структуры образуют мостиковые схемы или типа “m из n”.
Метод прямого перебора для таких систем оказывается практически не реализуем. Более целесообразно в этих случаях предварительно произвести декомпозицию системы, разбив ее на простые подсистемы — группы элементов, методика расчета надежности которых известна. Затем эти подсистемы в структурной схеме надежности заменяются квазиэлементами с вероятностями безотказной работы, равными вычисленным вероятностям безотказной работы этих подсистем. При необходимости такую процедуру можно выполнить несколько раз, до тех пор, пока оставшиеся квазиэлементы не образуют структуру, методика расчета надежности которой также известна.
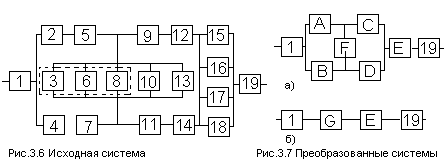
В качестве примера рассмотрим комбинированную систему, представленную на рис. 3.6. Здесь элементы 2 и 5, 4 и 7, 9 и 12, 11 и 14 попарно образуют друг с другом последовательные соединения. Заменим их соответственно квазиэлементами А, В, С, Д, для которых расчет надежности элементарно выполняется по формулам п. 3.1. Элементы 15, 16, 17 и 18 образуют параллельное соединение (п. 3.2), а элементы 3, 6, 8, 10 и 13 — систему “3 из 5” (п. 3.2). Соответствующие квазиэлементы обозначим E и F. В результате преобразованная схема примет вид, показанный на рис. 3.7, а. В ней в свою очередь элементы А, В, С, Д, F образуют мостиковую схему (п. 3.4), которую заменяем квазиэлементом 6. Схема, полученная после таких преобразований (рис.3.7,б), образует последовательное соединение элементов 1, G, E, 19, для которых справедливы соотношения п. 3.1. Отметим, что метод прямого перебора для исходной системы потребовал бы рассмотреть возможных состояний.
4. ПОВЫШЕНИЕ НАДЕЖНОСТИ ТЕХНИЧЕСКИХ СИСТЕМ
4.1. Методы повышения надежности
es New Roman»>
Расчетные зависимости для определения основных характеристик надежности ТС показывают, что надежность системы зависит от ее структуры (структурно — логической схемы) и надежности элементов. Поэтому для сложных систем возможны два пути повышения надежности: повышение надежности элементов и изменение структурной схемы.
Повышение надежности элементов на первый взгляд представляется наиболее простым приемом повышения надежности системы. Действительно, теоретически всегда можно указать такие характеристики надежности элемен-тов, чтобы вероятность безотказной работы системы удовлетворяла заданным требованиям. Однако практическая реализация такой высокой надежности элементов может оказаться невозможной. Рассмотрение методов обеспечения надежности элементов ТС является предметом специальных технологических и физико-химических дисциплин и выходит за рамки теории надежности. Однако, в любом случае, высоконадежные элементы, как правило, имеют большие габариты, массу и стоимость. Исключение составляет использование более совершенной элементной базы, реализуемой на принципиально новых физических и технологических принципах (например, в РЭС — переход от дискретных элементов на интегральные схемы).
Изменение структуры системы с целью повышения надежности подразумевает два аспекта.
С одной стороны, это означает перестройку конструктивной или функциональной схемы ТС (структуры связей между составными элементами), изменение принципов функционирования отдельных частей системы (например, переход от аналоговой обработки сигналов к цифровой). Такого рода преобразования ТС возможны исключительно редко, так что этот прием, в общем, не решает проблемы надежности.
С другой стороны, изменение структуры понимается как введение в ТС дополнительных, избыточных элементов, включающихся в работу при отказе основных. Применение дополнительных средств и возможностей с целью сохранения работоспособного состояния объекта при отказе одного или нескольких его элементов называется резервированием.
Принцип резервирования подобен рассмотренному ранее параллельному соединению элементов (п. 3.2) и соединению типа “n из m” (п. 3.3), где за счет избыточности возможно обеспечение более высокой надежности системы, чем ее элементов.
Выделяют несколько видов резервирования (временное, информацион-ное, функциональное и др.). Для анализа структурной надежности ТС интерес представляет структурное резервирование — введение в структуру объекта дополнительных элементов, выполняющих функции основных элементов в случае их отказа.
Классификация различных способов структурного резервирования осуществляется по следующим признакам:
1) по схеме включения резерва:
— общее резервирование, при котором резервируется объект в целом;
— раздельное резервирование, при котором резервируются отдельные элементы или их группы;
— смешанное резервирование, при котором различные виды резервирования сочетаются в одном объекте;
2) по способу включения резерва:
— постоянное резервирование, без перестройки структуры объекта при возникновении отказа его элемента;
— динамическое резервирование, при котором при отказе элемента происходит перестройка структуры схемы. В свою очередь подразделяется на:
а) резервирование замещением, при котором функции основного элемента передаются резервному только после отказа основного;
б) скользящее резервирование, при котором несколько основных элементов резервируется одним или несколькими резервными, каждый из которых может заменить любой основной (т.е. группы основных и резервных элементов идентичны).
3) по состоянию резерва:
— нагруженное резервирование, при котором резервные элементы (или один из них) находятся в режиме основного элемента;
— облегченное резервирование, при котором резервные элементы (по крайней мере один из них) находятся в менее нагруженном режиме по сравнению с основными;
— ненагруженное резервирование, при котором резервные элементы до начала выполнения ими функций находятся в ненагруженном режиме.
Основной характеристикой структурного резервирования является кратность резервирования — отношение числа резервных элементов к числу резервируемых ими основных элементов, выраженное несокращаемой дробью (типа 2:3; 4:2 и т.д.). Резервирование одного основного элемента одним резервным (т.е. с кратностью 1:1) называется дублированием.
Количественно повышение надежности системы в результате резервирования или применения высоконадежных элементов можно оценить по коэффициенту выигрыша надежности, определяемому как отношение показателя надежности до и после преобразования системы. Например, для системы из n последовательно соединенных элементов после резервирования одного из элементов (k-го) аналогичным по надежности элементом коэффициент выигрыша надежности по вероятности безотказной работы составит
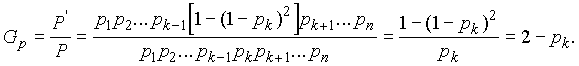
Из формулы (4.1) следует, что эффективность резервирования (или другого приема повышения надежности) тем больше, чем меньше надежность резервируемого элемента (при , при
). Следова-тельно, при структурном резервировании максимального эффекта можно до-биться при резервировании самых ненадежных элементов ( или групп элемен-тов).
В общем случае при выборе элемента (или группы элементов) для повышения надежности или резервирования необходимо исходить из условия обеспечения при этом максимального эффекта. Например, для мостиковой схемы (рис. 3.2,а) из формулы (3.21) можно получить выражение для частных производных вероятности безотказной работы системы по вероятности безотказной работы каждого из элементов, которые для идентичных по надежности элементов принимают следующий вид:
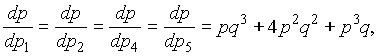
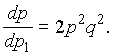
Очевидно, максимальное увеличение надежности системы обеспечит увеличение надежности или резервирование того элемента, частная производная для которого при данных условиях принимает максимально положительное значение. Сравнение выражений (4.2) и (4.3) показывает, что при любых положительных значениях p и q выражение (4.2) больше выражения (4.3) и, следовательно, в мостиковой схеме с идентичными элементами эффективность повышения надежности или резервирования “периферийных” элементов 1, 2, 4 и 5 (см. рис. 3.2, а) выше, чем диагонального элемента 3, если в качестве критерия эффективности взять вероятность безотказной работы.
Таким образом, наибольшее влияние на надежность системы оказывают элементы, обладающие высоким значением производной , а при последова-тельном соединении — наименее надежные.
В более сложных случаях для выбора элементов, подлежащих изменению, используются как аналитические, так и численные методы оптимизации надежности.
4.2. Расчет надежности систем с резервированием
Расчет количественных характеристик надежности систем с резервированием отдельных элементов или групп элементов во многом определяется видом резервирования. Ниже рассматриваются схемы расчетов для самых распространенных случаев простого резервирования, к которым путем преобразований может быть приведена и структура смешенного резервирования. При этом расчетные зависимости получены без учета надежности переключающих устройств, обеспечивающих перераспределение нагрузки между основными и резервными элементами (т.е. для “идеальных” переключателей). В реальных условиях введение переключателей в структурную схему необходимо учитывать и в расчете надежности систем.
Расчет систем с нагруженным резервированием осуществляется по формулам последовательного и параллельного соединения элементов аналогично расчету комбинированных систем (п. 3.5). При этом считается, что резервные элементы работают в режиме основных как до, так и после их отказа, поэтому надежность резервных элементов не зависит от момента их перехода из резервного состояния в основное и равна надежности основных элементов.
Для системы с последовательным соединением n элементов (рис. 2.1) при общем резервировании с кратностью l (рис. 4.1, а)
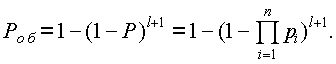
В частности , при дублировании (l=1)
(4.5)
При раздельном резервировании (рис. 4.1,б)
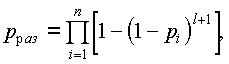
а при раздельном дублировании (l=1)
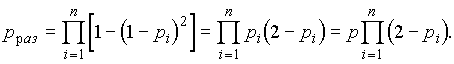
Тогда коэффициенты выигрыша надежности по вероятности безотказной работы при дублировании
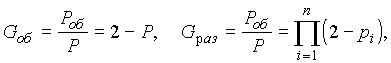
откуда следует, что раздельное резервирование эффективнее общего (например, для системы из трех одинаковых элементов при ,
.
При ненагруженном резервировании резервные элементы последовательно включаются в работу при отказе основного, затем первого резервного и т.д. (рис. 4.2), поэтому надежность резервных элементов зависит от момента их перехода в основное состояние. Такое резервирование в различных ТС встречается наиболее часто, т.к. оно по сути аналогично замене отказавших элементов и узлов на запасные.
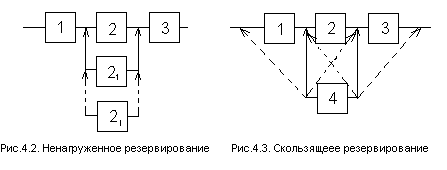
Если резервные элементы до их включения абсолютно надежны, то для системы с ненагруженным резервированием кратности l (всего элементов l+1)
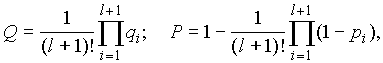
т.е. вероятность отказа в (l+1)! раз меньше, чем при нагруженном (параллельном соединении, см. формулу (3.7)).
Для идентичных по надежности основного и резервного элементов
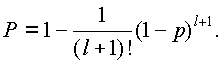
При экспоненциальном распределении наработки (простейшем потоке отказов, см. 1.7) в случае можно воспользоваться приближенной формулой
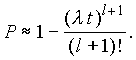
При ненагруженном резервировании средняя наработка на отказ
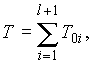
а для идентичных элементов
Облегченное резервирование используется при большой инерционности переходных процессов, происходящих в элементе при его переходе из резервного в основной режим, и нецелесообразности применения нагруженного резервирования из — за недостаточного выигрыша в надежности (в РЭС это характерно для устройств на электровакуумных приборах). Очевидно, облегченный резерв занимает промежуточное положение между нагруженным и ненагруженным.
Точные выражения для расчета надежности систем при облегченном резервировании весьма громоздки и неоднозначны, однако при экспонен-циальном распределении наработки справедлива приближенная формула
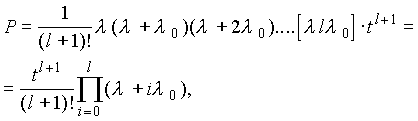
где — интенсивность отказов элементов в облегченном режиме, l — кратность резервирования.
Скользящее резервирование используется для резервирования нескольких одинаковых элементов системы одним или несколькими одинаковыми резервными (рис. 4.3, здесь все элементы идентичны, а элемент 4 — избыточный). Очевидно, отказ системы произойдет, если из общего количества идентичных элементов (основных и резервных) число отказавших превышает число резервных. Расчет вероятности безотказной работы систем со скользящим резервированием аналогичен расчету систем типа “m из n”, см. п. 3.3.
5. МЕТОДИЧЕСКИЕ РЕКОМЕНДАЦИИ
Задание на курсовую работу (КР) содержит в качестве исходных данных структурную схему надежности технической системы (ТС) и интенсивность отказов ее элементов (см. п. 7). То есть студент оказывается в ситуации, когда выполнены п. 1 — 6 анализа структурной надежности ТС (см. разд. 2), и ему надлежит в первую очередь выполнить п. 7 — составить расчетные зависимости для определения показателей надежности системы для различных значений наработки t, чтобы графически изобразить вероятность безотказной работы P(t) как функцию наработки.
Поскольку заданная схема надежности является комбинированной, ее следует подвергнуть декомпозиции, как это описано в п. 3.5. Далее, вводя соответствующие квазиэлементы, преобразовать исходную схему к простейшему виду и , используя соответствующие формулы п. 3.1 — 3.4, для ряда значений наработки t в предположении простейшего потока отказов формулы (1.7) вычислить значения вероятностей безотказной работы элементов, квазиэлементов и всей системы. В пояснительной записке следует привести все промежуточные преобразования исходной схемы, конкретные рабочие расчетные формулы с их обоснованием, а результаты расчета представить в виде таблицы, в которой по столбцам изменяется значение наработки t, а по строкам в столбцах приводятся вычисленные значения вероятностей безотказной работы элементов, квазиэлементов и всей системы, полученные по рабочим формулам. При этом диапазон измерения наработки t должен обеспечить снижение вероятности безотказной работы системы до уровня 0.1 — 0.2 и содержать не менее 8-10 значений аргумента.
После этого строится график зависимости P(t) по результатам расчета. И него графически по заданному значению определяется
— процентная наработка системы (см. (1.9)),
.
По заданию требуется предложить способы увеличения — процентной наработки в 1.5 раза за счет повышения надежности элементов и за счет структурного резервирования.
Предварительно следует определить элемент или квазиэлемент окончательно преобразованной схемы, повышение надежности которого даст максимальный эффект в отношении надежности всей системы. Критерии выбора приведены в п. 4.1. Поскольку аналитически определить производные вида (4.2), (4.3) обычно не удается, выбор элемента может быть осуществлен по величине вероятности безотказной работы.
Для дальнейших действий необходимо вычислить требуемое улучшенное значение — процентной наработки
элементарным умножением
на 1.5. Следовательно, чтобы удовлетворить заданию в отношении повышения надежности системы, необходимо обеспечить вероятность безотказной работы
за время
. Теперь следует повторить расчет надежности элементов, квазиэлементов и всей системы за время
и дополнить этим столбцом предыдущую таблицу . Зная вероятности безотказной работы всех элементов преобразованной схемы и требуемое значение
, легко определить, какую вероятность безотказной работы
за время
должен иметь квазиэлемент, избранный для модернизации.
По первому варианту модернизации необходимо определить интенсивности отказов элементов, входящих в данный квазиэлемент, при которых при неизменной структуре квазиэлемента обеспечивалось бы необходимое значение . Проще это осуществить графоаналитическим методом, задавая ряд пропорционально уменьшенных (по сравнению с исходной) интенсивностей отказов для составляющих квазиэлемента и просчитывая каждый раз величину
. Из построенного по этим данным графика можно определить необходимую кратность снижения интенсивности отказов элементов и сами значения интенсивности. Для найденного решения следует выполнить проверочный расчет вероятности безотказной работы системы за время
.
По второму методу надежность выбранного квазиэлемента можно повысить за счет резервирования без изменения надежности составляющих элементов. При этом, основываясь на рекомендациях и соображениях, изложенных в п. 4.1, 4.2, учитывая структуру модернизируемого квазиэлемента, нужно выбрать, какие его составляющие элементы и как следует резервировать для достижения наибольшего эффекта. Далее остается определить необходимую кратность резервирования . Поскольку
есть величина дискретная, аналитически ее определить невозможно. Для решения задачи нужно последовательно увеличивать кратность резервирования, начиная с единицы, каждый раз по соответствующим формулам из п. 4.2 определять величину вероятности безотказной работы квазиэлемента в течении времени
. Как только необходимое значение
будет обеспечено, окажется реализованным второй метод повышения надежности системы. Для найденного решения также необходимо провести проверку вероятности безотказной работы системы за время
. Модернизированную структуру с резервированием следует привести в пояснительной записке.
Для построения зависимостей вероятностей безотказной работы от времени для модернизированной системы по первому и второму методу удобно дополнить ранее составленную таблицу соответствующими строками. Графики этих зависимостей следует изобразить совместно с кривой P(t) исходной системы.
Полученное семейство кривых позволяет провести сравнение двух вариантов модернизации, которое следует привести в качестве вывода к работе.
Пояснительная записка должна быть оформлена в соответствии с СТП КрПИ 3.1 — 92 “Текстовые документы. Требования к оформлению”. Все действия и использование расчетных сотношений должны быть объяснены и обоснованы. Для заимствуемой информации (формулы, численные значения констант) необходимо указать источник заимствования.
Задания на курсовую работу приведены в разд. 6, а в разд. 7 — пример расчета надежности.
6. ИСХОДНЫЕ ДАННЫЕ К РАБОТЕ
По структурной схеме надежности технической системы в соответствии с вариантом задания, требуемому значению вероятности безотказной работы системы и значениям интенсивностей отказов ее элементов
(табл. 6.1) требуется:
1. Построить график изменения вероятности безотказной работы системы от времени наработки в диапазоне снижения вероятности до уровня 0.1 — 0.2.
2. Определить — процентную наработку технической системы.
3. Обеспечить увеличение — процентной наработки не менее, чем в 1.5 раза за счет:
а) повышения надежности элементов;
б) структурного резервирования элементов системы.
Все элементы системы работают в режиме нормальной эксплуатации (простейший поток отказов). Резервирование отдельных элементов или групп элементов осуществляется идентичными по надежности резервными элементами или группами элементов. Переключатели при резервировании считаются идеальными.
На схемах обведенные пунктиром m элементов являются функционально необходимыми из n параллельных ветвей.
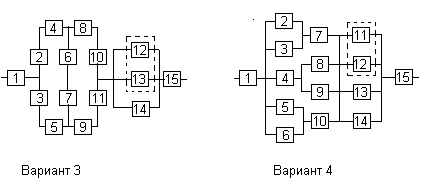
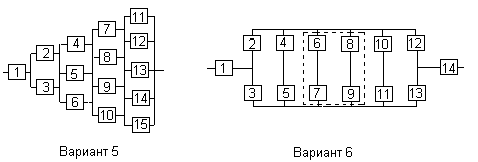
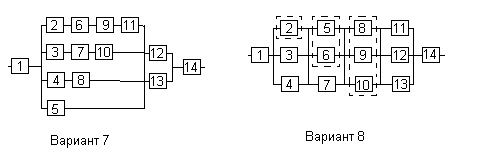
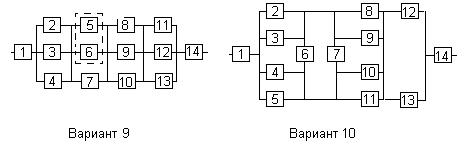
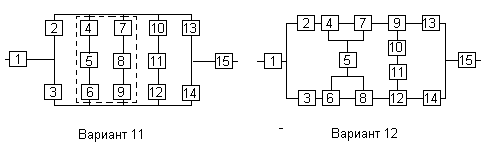
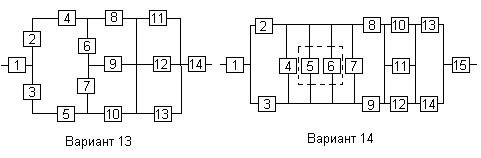
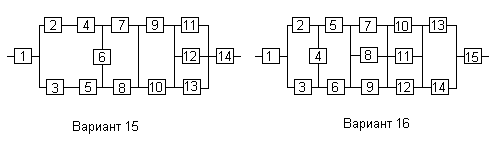
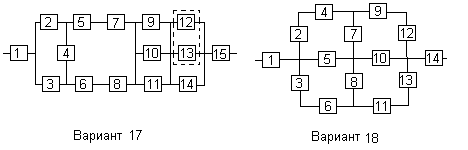
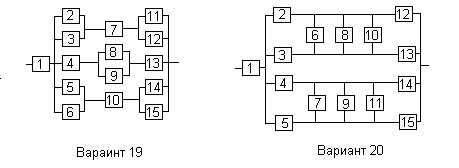
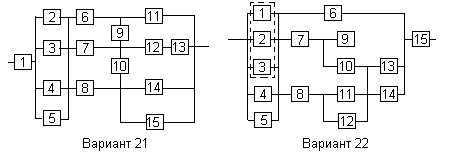
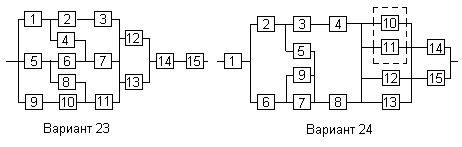
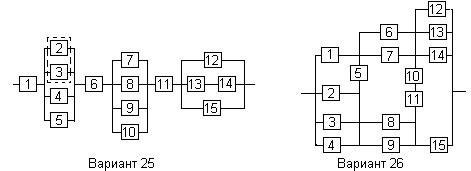
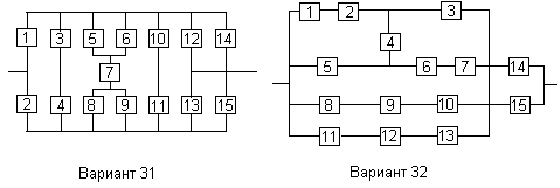
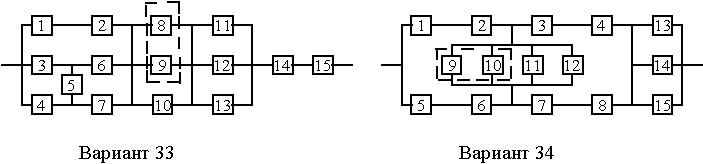
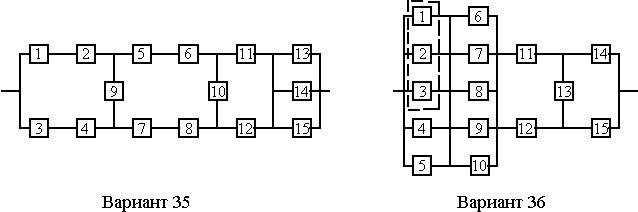
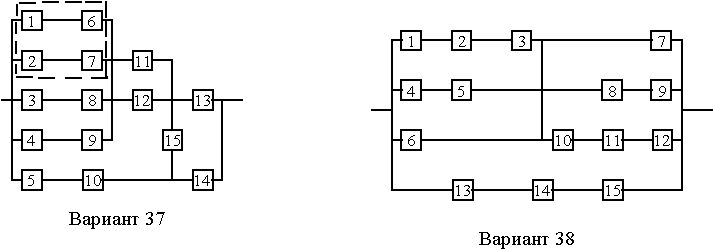
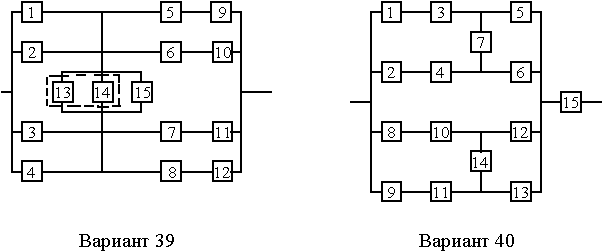
7. ПРИМЕР РАСЧЕТА НАДЕЖНОСТИ
Структурная схема надежности приведена на рис 7.1. Значения интенсивности отказов элементов даны в 1/ч.
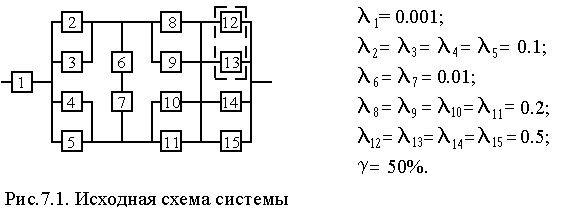
1. В исходной схеме элементы 2 и 3 образуют параллельное соединение. Заменяем их квазиэлементом А. Учитывая, что , получим
. (7.1)
2. Элементы 4 и 5 также образуют параллельное соединение, заменив которое элементом В и учитывая, что , получим
. (7.2)
3. Элементы 6 и 7 в исходной схеме соединены последовательно. Заменяем их элементом С, для которого при
. (7.3)
4. Элементы 8 и 9 образуют параллельное соединение. Заменяем их элементом D, для которого при , получим
. (7.4)
5. Элементы 10 и 11 с параллельным соединением заменяем элементом Е , причем, так как , то
(7.5)
6. Элементы 12 , 13 , 14 и 15 образуют соединение “2 из 4”, которое заменяем элементом F. Так как, то для определения вероятности безотказной работы элемента F можно воспользоваться комбинаторным методом (см. раздел 3.3):
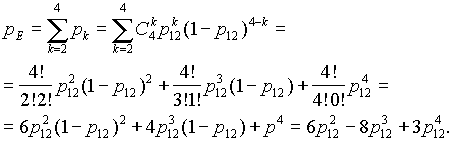
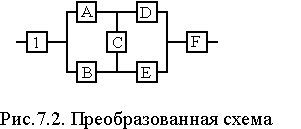
7. Преобразованная схема изображена на рис. 7.2.
8. Элементы A, B, C, D и Е образуют (рис. 7.2) мостиковую систему, которую можно заменить квазиэлементом G. Для расчета вероятности безотказной работы воспользуемся методом разложения относительно особого элемента (см. раздел 3.4), в качестве которого выберем элемент С. Тогда
(7.7)
где — вероятность безотказной работы мостиковой схемы при абсолютно надежном элементе С (рис. 7.3, а),
— вероятность безотказной работы мостиковой схемы при отказавшем элементе С (рис. 7.3, б).
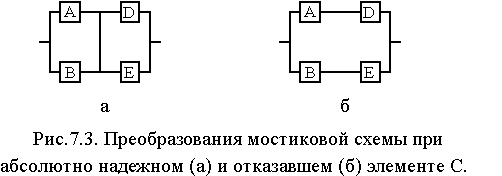
Учитывая, что , получим
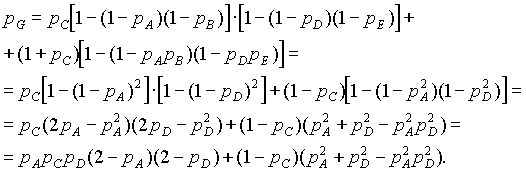
9. После преобразований схема изображена на рис. 7.4.
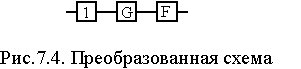
10. В преобразованной схеме (рис. 7.4) элементы 1, G и F образуют последовательное соединение. Тогда вероятность безотказной работы всей системы
(7.9)
11. Так как по условию все элементы системы работают в периоде нормальной эксплуатации, то вероятность безотказной работы элементов с 1 по 15 (рис. 7.1) подчиняются экспоненциальному закону:
(7.10)
12. Результаты расчетов вероятностей безотказной работы элементов 1 — 15 исходной схемы по формуле (7.10) для наработки до часов представлены в таблице 7.1.
13. Результаты расчетов вероятностей безотказной работы квазиэле-ментов A, B, C, D, E, F и G по формулам (7.1) — (7.6) и (7.8) также представлены в таблице 7.1.
14. На рис. 7.5 представлен график зависимости вероятности безотказной работы системы P от времени (наработки) t.
15. По графику (рис. 7.5, кривая P) находим для
— процентную наработку системы
ч.
16. Проверочный расчет при ч показывает (таблица 7.1), что
.
17. По условиям задания повышенная — процентная наработка сис-темы
ч.
Таблица 7.1
Расчет вероятности безотказной работы системы
|
Элемент |
l i, |
Наработка t, x 106 ч |
|||||||
|
x10-6 ч-1 |
0,5 |
1,0 |
1,5 |
2,0 |
2,5 |
3,0 |
1,9 |
2,85 |
|
|
1 |
0,001 |
0,9995 |
0,9990 |
0,9985 |
0,9980 |
0,9975 |
0,9970 |
0,9981 |
0,9972 |
|
2 — 5 |
0,1 |
0,9512 |
0,9048 |
0,8607 |
0,8187 |
0,7788 |
0,7408 |
0,8270 |
0,7520 |
|
6,7 |
0,01 |
0,9950 |
0,9900 |
0,9851 |
0,9802 |
0,9753 |
0,9704 |
0,9812 |
0,9719 |
|
8 — 11 |
0,2 |
0,9048 |
0,8187 |
0,7408 |
0,6703 |
0,6065 |
0,5488 |
0,6839 |
0,5655 |
|
12 — 15 |
0,5 |
0,7788 |
0,6065 |
0,4724 |
0,3679 |
0,2865 |
0,2231 |
0,3867 |
0,2405 |
|
A, B |
— |
0,9976 |
0,9909 |
0,9806 |
0,9671 |
0,9511 |
0,9328 |
0,9701 |
0,9385 |
|
C |
— |
0,9900 |
0,9801 |
0,9704 |
0,9608 |
0,9512 |
0,9417 |
0,9628 |
0,9446 |
|
D, E |
— |
0,9909 |
0,9671 |
0,9328 |
0,8913 |
0,8452 |
0,7964 |
0,9001 |
0,8112 |
|
F |
— |
0,9639 |
0,8282 |
0,6450 |
0,4687 |
0,3245 |
0,2172 |
0,5017 |
0,2458 |
|
G |
— |
0,9924 |
0,9888 |
0,9863 |
0,9820 |
0,9732 |
0,9583 |
0,9832 |
0,9594 |
|
P |
— |
0,9561 |
0,8181 |
0,6352 |
0,4593 |
0,3150 |
0,2075 |
0,4923 |
0,2352 |
|
12` — 15` |
0,322 |
0,8513 |
0,7143 |
0,6169 |
0,5252 |
0,4471 |
0,3806 |
0,5424 |
0,3994 |
|
F` |
— |
0,9883 |
0,9270 |
0,8397 |
0,7243 |
0,6043 |
0,4910 |
0,7483 |
0,5238 |
|
P` |
— |
0,9803 |
0,9157 |
0,8270 |
0,7098 |
0,5866 |
0,4691 |
0,7343 |
0,5011 |
|
16 — 18 |
0,5 |
0,7788 |
0,6065 |
0,4724 |
0,3679 |
0,2865 |
0,2231 |
0,3867 |
0,2405 |
|
F« |
— |
0,9993 |
0,9828 |
0,9173 |
0,7954 |
0,6413 |
0,4858 |
0,8233 |
0,5311 |
|
P« |
— |
0,9912 |
0,9708 |
0,9034 |
0,7795 |
0,6226 |
0,4641 |
0,8079 |
0,5081 |
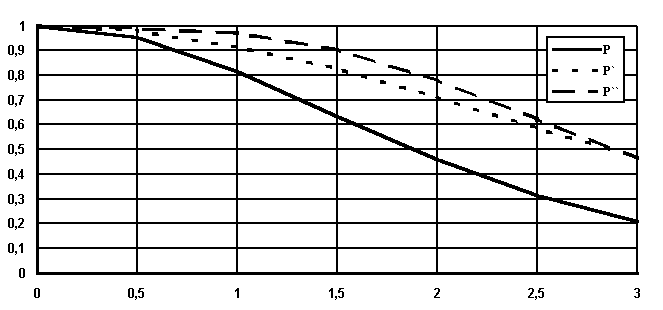
Рис 7.5. Изменение вероятности безотказной работы исходной системы (Р), системы с повышенной надежностью (Р`) и системы со структурным резервированием элементов (Р«).
18. Расчет показывает (таблица 7.1), что при ч для элементов преобразованной схемы (рис. 7.4)
,
и
. Следовательно, из трех последовательно соединенных элементов минимальное значение вероятности безотказной работы имеет элемент F (система “2 из 4” в исходной схеме (рис. 7.1)) и именно увеличение его надежности даст максимальное увеличение надежности системы в целом .
19. Для того, чтобы при ч система в целом имела вероятность безотказной работы
, необходимо, чтобы элемент F имел вероятность безотказной работы (см. формулу (7.9))
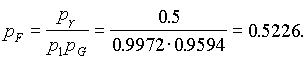
При этом значении элемент F останется самым ненадежным в схеме (рис. 7.4) и рассуждения в п.18 останутся верными.
Очевидно, значение , полученное по формуле (7.11), является мини-мальным для выполнения условия увеличения наработки не менее, чем в 1.5 раза, при более высоких значениях
увеличение надежности системы будет большим.
20. Для определения минимально необходимой вероятности безотказной работы элементов 12 — 15 (рис. 7.1) необходимо решить уравнение (7.6) относительно при
. Однако, т.к. аналитическое выражение этого уравнения связано с определенными трудностями , более целесообразно использовать графо-аналитический метод. Для этого по данным табл. 7.1 строим график зависимости
. График представлен на рис. 7.6.
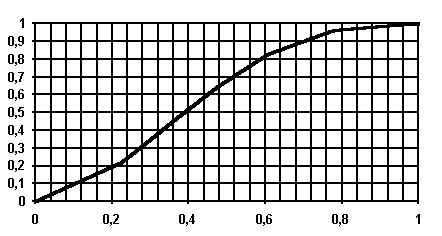
Рис. 7.6. Зависимость вероятности безотказной работы системы “2 из 4” от вероятности безотказной работы ее элементов.
21. По графику при находим
.
22. Так как по условиям задания все элементы работают в периоде нормальной эксплуатации и подчиняются экспоненциальному закону (7.10), то для элементов 12 — 15 при находим
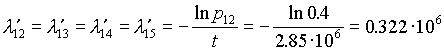
. (7.12)
23. Таким образом, для увеличения — процентной наработки ситемы необходимо увеличить надежность элементов 12, 13, 14 и 15 и снизить интенсивность их отказов с
до
ч
, т.е. в 1.55 раза.
24. Результаты расчетов для системы с увеличенной надежностью элементов 12, 13, 14 и 15 приведены в таблице 7.1. Там же приведены расчетные значения вероятности безотказной работы системы “2 из 4” F` и системы в целом P`. При ч вероятность безотказной работы системы
, что соответствует условиям задания. График приведен на рис 7.5.
25. Для второго способа увеличения вероятности безотказной работы системы — структурного резервирования — по тем же соображениям (см. п. 18) также выбираем элемент F, вероятность безотказной работы которого после резервирования должна быть не ниже (см. формулу ( 7.11 )).
26. Для элемента F — системы “2 из 4” — резервирование означает увеличение общего числа элементов. Аналитически определить минимально необходимое количество элементов невозможно, т.к. число элементов должно быть целым и функция дискретна.
27. Для повышения надежности системы “2 из 4” добавляем к ней элементы, идентичные по надежности исходным элементам 12 — 15, до тех пор, пока вероятность безотказной работы квазиэлемента F не достигнет заданного значения.
Для расчета воспользуемся комбинаторным методом (см. раздел 3.3) :
— добавляем элемент 16, получаем систему “2 из 5”:
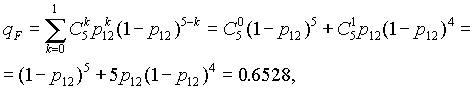
(7.14)
— добавляем элемент 17, получаем систему “2 из 6”:
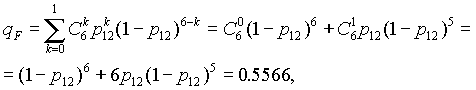
(7.16)
— добавляем элемент 18, получаем систему “2 из 7”:
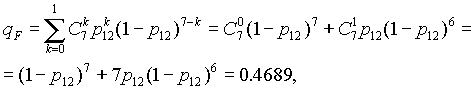
(7.18)
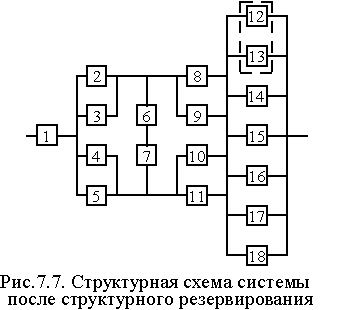
28. Таким образом, для повышения надежности до требуемого уровня необходимо в исходной схеме (рис. 7.1) систему “2 из 4” достроить элементами 16, 17 и 18 до системы “2 из 7” (рис. 7.7).
29. Результаты расчетов вероятностей безотказной работы системы “2 из 7” F« и системы в целом P« представлены в таблице 7.1.
30. Расчеты показывают, что при ч
, что соот-ветствует условию задания.
31. На рис. 7.5 нанесены кривые зависимостей вероятности безотказной работы системы после повышения надежности элементов 12 — 15 (кривая ) и после структурного резервирования (кривая
).
Выводы:
1. На рис. 7.5 представлена зависимость вероятности безотказной работы системы (кривая ). Из графика видно, что 50% — наработка исходной системы составляет
часов.
2. Для повышения надежности и увеличения 50% — наработки системы в 1.5 раза (до часов) предложены два способа:
а) повышение надежности элементов 12, 13, 14 и 15 и уменьшение их отказов с до
ч
;
б) нагруженное резервирование основных элементов 12, 13, 14 и 15 идентичными по надежности резервными элементами 16, 17 и 18 (рис. 7.7).
3. Анализ зависимостей вероятности безотказной работы системы от времени (наработки) (рис. 7.5) показывает, что второй способ повышения надежности системы (структурное резервирование) предпочтительнее первого, так как в период наработки до часов вероятность безотказной работы системы при структурном резервировании (кривая
) выше, чем при увеличе-нии надежности элементов (кривая
).
Таблица 6.1
Численные значения параметров к заданию
|
№ |
g, |
Интенсивности отказов элементов, l i , x10-6 1/ч |
||||||||||||||
|
вар. |
% |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
13 |
14 |
15 |
|
1 |
90 |
0.1 |
1.0 |
0.5 |
1.0 |
0.1 |
||||||||||
|
2 |
95 |
0.2 |
0.5 |
1.0 |
0.1 |
|||||||||||
|
3 |
80 |
0.1 |
1.0 |
2.0 |
1.0 |
5.0 |
0.2 |
|||||||||
|
4 |
70 |
0.05 |
1.0 |
0.5 |
0.2 |
0.02 |
||||||||||
|
5 |
50 |
0.01 |
0.05 |
0.1 |
0.5 |
1.0 |
||||||||||
|
6 |
75 |
0.01 |
0.05 |
1.0 |
0.05 |
0.1 |
— |
|||||||||
|
7 |
65 |
0.05 |
0.5 |
0.05 |
0.005 |
0.1 |
0.2 |
0.1 |
— |
|||||||
|
8 |
85 |
0.1 |
0.5 |
0.2 |
0.01 |
0.5 |
0.1 |
— |
||||||||
|
9 |
60 |
0.03 |
0.5 |
0.2 |
1.0 |
0.03 |
0.1 |
— |
||||||||
|
10 |
50 |
0.1 |
0.5 |
1.0 |
0.5 |
1.0 |
0.1 |
— |
||||||||
|
11 |
75 |
0.05 |
0.2 |
0.5 |
0.2 |
0.1 |
||||||||||
|
12 |
65 |
0.02 |
0.1 |
1.0 |
2.0 |
0.1 |
0.05 |
|||||||||
|
13 |
70 |
0.01 |
0.2 |
0.1 |
1.0 |
0.5 |
0.1 |
— |
||||||||
|
14 |
50 |
0.01 |
0.1 |
10.0 |
0.2 |
10.0 |
0.5 |
— |
||||||||
|
15 |
85 |
0.01 |
1.0 |
5.0 |
0.2 |
5.0 |
0.1 |
— |
||||||||
|
16 |
80 |
0.1 |
1.0 |
2.0 |
1.0 |
5.0 |
3.0 |
1.0 |
0.05 |
|||||||
|
17 |
95 |
0.1 |
5.0 |
1.0 |
5.0 |
10.0 |
5.0 |
1.0 |
0.2 |
|||||||
|
18 |
60 |
0.01 |
1.0 |
0.1 |
— |
|||||||||||
|
19 |
75 |
0.1 |
5.0 |
0.5 |
5.0 |
1.0 |
3.0 |
1.0 |
5.0 |
0.5 |
5.0 |
|||||
|
20 |
90 |
0.1 |
10.0 |
20.0 |
10.0 |
|||||||||||
|
21 |
90 |
0.1 |
1.0 |
0.5 |
2.0 |
0.5 |
0.2 |
1.0 |
||||||||
|
22 |
80 |
1.0 |
0.2 |
0.5 |
1.0 |
0.5 |
1.0 |
1.0 |
0.1 |
|||||||
|
23 |
70 |
0.5 |
0.2 |
1.0 |
0.5 |
1.0 |
0.5 |
1.0 |
0.2 |
0.5 |
1.0 |
0.2 |
||||
|
24 |
60 |
1.0 |
2.0 |
4.0 |
2.0 |
4.0 |
5.0 |
1.0 |
||||||||
|
25 |
50 |
0.5 |
10.0 |
0.5 |
5.0 |
0.8 |
5.0 |
1.0 |
5.0 |
|||||||
|
26 |
60 |
1.0 |
2.0 |
3.0 |
5.0 |
2.0 |
5.0 |
1.0 |
||||||||
|
27 |
70 |
5.0 |
10.0 |
15.0 |
10.0 |
10.0 |
15.0 |
10.0 |
||||||||
|
28 |
80 |
1.0 |
2.0 |
5.0 |
2.0 |
1.0 |
||||||||||
|
29 |
90 |
5.0 |
20.0 |
50.0 |
30.0 |
1.0 |
||||||||||
|
30 |
80 |
2.0 |
1.0 |
2.0 |
1.0 |
5.0 |
2.0 |
5.0 |
2.0 |
1.0 |
2.0 |
1.0 |
2.0 |
1.0 |
||
|
31 |
70 |
2.0 |
1.0 |
2.0 |
1.0 |
5.0 |
2.0 |
5.0 |
2.0 |
1.0 |
2.0 |
1.0 |
2.0 |
1.0 |
||
|
32 |
60 |
5.0 |
2.0 |
5.0 |
1.0 |
2.0 |
3.0 |
1.0 |
||||||||
|
33 |
60 |
1.0 |
2.0 |
3.0 |
4.0 |
2.0 |
3.0 |
5.5 |
0.2 |
0.5 |
||||||
|
34 |
90 |
6.0 |
3.0 |
6.0 |
3.0 |
6.0 |
20.0 |
10.0 |
||||||||
|
35 |
95 |
1.0 |
2.0 |
1.0 |
2.0 |
1.0 |
5.0 |
|||||||||
|
36 |
80 |
2.0 |
1.0 |
0.6 |
||||||||||||
|
37 |
70 |
10.0 |
30.0 |
5.0 |
2.0 |
|||||||||||
|
38 |
90 |
3.0 |
2.0 |
1.0 |
2.0 |
3.0 |
2.0 |
|||||||||
|
39 |
90 |
8.0 |
3.0 |
5.0 |
2.0 |
|||||||||||
|
40 |
80 |
2.0 |
5.0 |
8.0 |
2.0 |
5.0 |
8.0 |
|||||||||
|
№ |
g, |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
13 |
14 |
15 |
|
вар. |
% |
Интенсивности отказов элементов, l i , x10-6 1/ч |
ПРИЛОЖЕНИЕ
Биномиальные коэффициенты 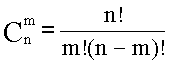
|
n |
m |
||||||||||
|
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
|
|
0 |
1 |
||||||||||
|
1 |
1 |
1 |
|||||||||
|
2 |
1 |
2 |
1 |
||||||||
|
3 |
1 |
3 |
3 |
1 |
|||||||
|
4 |
1 |
4 |
6 |
4 |
1 |
||||||
|
5 |
1 |
5 |
10 |
10 |
5 |
1 |
|||||
|
6 |
1 |
6 |
15 |
20 |
15 |
6 |
1 |
||||
|
7 |
1 |
7 |
21 |
35 |
35 |
21 |
7 |
1 |
|||
|
8 |
1 |
8 |
28 |
56 |
70 |
56 |
28 |
8 |
1 |
||
|
9 |
1 |
9 |
36 |
84 |
126 |
126 |
84 |
36 |
9 |
1 |
|
|
10 |
1 |
10 |
45 |
120 |
210 |
252 |
210 |
120 |
45 |
10 |
1 |
|
11 |
1 |
11 |
55 |
165 |
330 |
462 |
462 |
330 |
165 |
55 |
11 |
|
12 |
1 |
12 |
66 |
220 |
495 |
792 |
924 |
792 |
495 |
220 |
66 |
|
13 |
1 |
13 |
78 |
286 |
715 |
1287 |
1716 |
1716 |
1287 |
715 |
286 |
|
14 |
1 |
14 |
91 |
364 |
1001 |
2002 |
3003 |
3432 |
3003 |
2002 |
1001 |
|
15 |
1 |
15 |
105 |
455 |
1365 |
3003 |
5005 |
6435 |
6435 |
5005 |
3003 |
|
16 |
1 |
16 |
120 |
560 |
1820 |
4368 |
8008 |
11440 |
12870 |
11440 |
8008 |
|
17 |
1 |
17 |
136 |
680 |
2380 |
6188 |
12376 |
19448 |
24310 |
24310 |
19448 |
|
18 |
1 |
18 |
153 |
816 |
3060 |
8568 |
18564 |
31824 |
43758 |
48620 |
43758 |
|
19 |
1 |
19 |
171 |
969 |
3876 |
11628 |
27132 |
50388 |
75582 |
92378 |
92378 |
|
20 |
1 |
20 |
190 |
1140 |
4845 |
15504 |
38760 |
77520 |
125970 |
167960 |
184756 |
Примечание: Для m>10 можно воспользоваться свойством симметрии:
Дата добавления: 23.01.2001