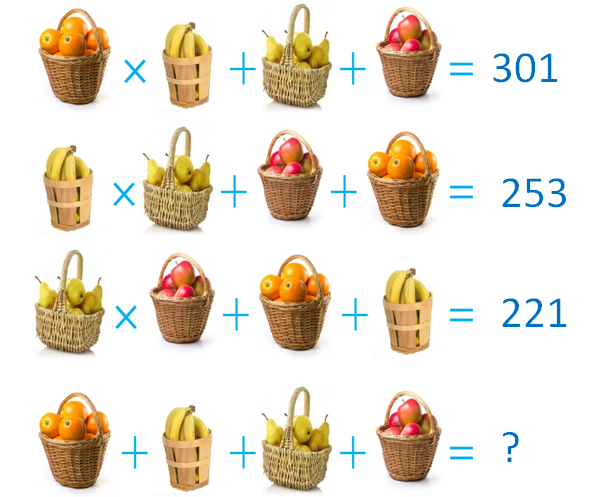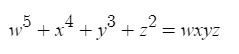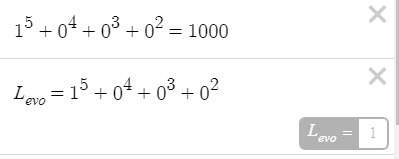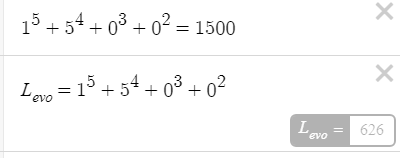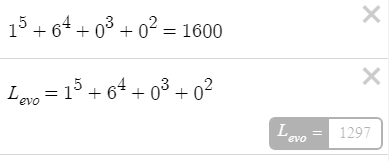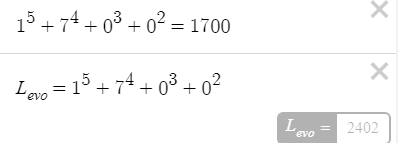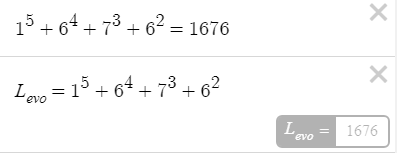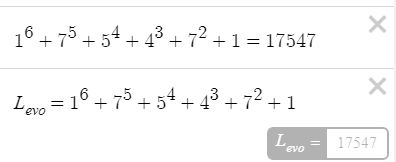Итак, вот решение, казалось бы, на первый взгляд, легкой задачи про яблоки и грузовик.
Очевидно, что вы не можете загрузить в грузовик 1000 яблок, и проехав 1000 км до Лунограда, привезти в город все 1000 яблок. Все ваши яблоки в кузове в этом случае уйдут на оплату проезда по платной трассе. Естественно, вы должны придумать способ поэтапной перевозки яблок до определенного отрезка пути, где вы, сгрузив первую партию яблок, вернетесь назад и снова загрузите полную машину. И т.д. Для тех, кто попал на эту страницу и не знает, о чем идет речь, будет интересно узнать суть самой загадки. Это можно сделать здесь.
Для тех же кто пришел сюда за правильным ответом, то ниже публикуем обещанное решение.
Решение

Правильный ответ: в Луноград вы можете максимально доставить 833 яблока. Как? Вот схема.
Итак, для того чтобы суметь перевезти 833 яблок по платной трассе на расстояние 1000 км, вам сначала необходимо загрузить в грузовик 1000 яблок и проехать от Новоколоменска 333 км. Это почти треть пути до Лунограда.
На расстоянии 333 км вы должны сгрузить на обочину 667 яблок. Остальные вы, естественно, отдадите за проезд по платной автомагистрали.
Далее, вы должны вернуться и снова загрузить 1000 яблок и привезти на 333-й километр еще 667 яблок. Затем вернитесь и заберите оставшиеся 1000 яблок и отвезите груз снова на 333-й километр трассы.
В итоге после трех рейсов у вас на обочине должно быть 2001 яблоко. Остальные 999 яблок вы отдадите за оплату проезда.
Теперь перейдем ко второму этапу нашей хитрой перевозки яблок. Загрузите 1000 яблок и проедьте еще 500 км, остановившись на 833-м километре платной трассы. Сгрузите оставшиеся яблоки на обочину и вернитесь, забрав еще 1000 яблок, чтобы отвезти груз на 833-й километр. Увы, одно яблоко вы при последней поездке будете вынуждены оставить на обочине, поскольку оно не влезет в ваш грузовик.
Итак, что мы имеем перед последним этапом перевозки? 1000 яблок на расстоянии 167 км от Лунограда. Наверное, вы уже поняли, что все, загадка решена, поскольку, загрузив 1000 яблок и проехав оставшиеся 167 км за проезд, мы отдадим 167 яблока. В итоге в Луноград мы доставим 833 яблока.
Надеемся наша загадка была нетрудная. Хотя признаем, что она не из легких. Для многих из вас, возможно, для решения нужно было время. Надеемся вы нашли решение, как за минимальную плату доставить из одного города в другой максимальное количество яблок.
Удачи! Ждите очередных загадок.
Получи верный ответ на вопрос 🏆 «На складе хранилось 7 т фруктов. В первый день со склада вывезли 1236 кг фруктов, во второй день в 2 раза больше, чем в первый день, а в …» по предмету 📕 Математика, используя встроенную систему поиска. Наша обширная база готовых ответов поможет тебе получить необходимые сведения!
Найти готовые ответы
Главная » ⭐️ Математика » На складе хранилось 7 т фруктов. В первый день со склада вывезли 1236 кг фруктов, во второй день в 2 раза больше, чем в первый день, а в третий остальные фрукты. Сколько кг фруктов вывезли в третий день?
4
Задача. Сколько фруктов в четырех корзинах?
3 ответа:
7
0
Наверное, это не самый лучший способ, но другого у меня все равно нет.
<hr />
Имеем систему из трех ур-й с четырьмя неизвестными.
{ab + c + d = 301;
{bc + d + a = 253;
{cd + a + b = 221.
Вычтем из первого ур-я второе, в результате чего получим
a — c = 48/(b-1), откуда
a = с + 48/(b-1).
Вычтем из второго ур-я третье и получим
b — d = 32/(c-1).
Поскольку числа у нас натуральные, (с — 1) является делителем числа 32, а значит с может принимать только следующие значения: 33, 17, 9, 5, 3, 2.
При с = 33, d = b — 1, a = (15 + 33b)/(b-1).
Подставим данные значения во второе уравнение.
33b + b — 1 + (15 + 33b)/(b-1) = 253 или
34b² — 255b + 269 = 0.
Однако данное уравнение имеет только иррациональные корни, стало быть, с не равно 33.
При с = 17, d = b — 2, a = (31 + 17b)/(b-1).
И вновь подставляем полученные значения во второе ур-е.
17b + b — 2 + (31 + 17b)/(b-1) = 253 или
9b² — 128b + 143 = 0.
Единственным натуральным корнем данного ур-я является b = 13.
Тогда d = 13 — 2 = 11, a = 17 + 48/12 = 21.
Таким образом, общее количество фруктов в четырех корзинах (21 + 13 + 17 + 11) = 62.
<hr />
P.S. Все три равенства при этих значениях выполняются, я проверила.
0
0
В корзину столько фруктов не в лезет 1550
0
0
Есть два пути решения таких задачь: написать программу на компьюторе и своей головой. Программа (я использовала питон) пишется буквально в несколько строчек и считает за несколько секудн. Можно перебирать “ручками” или составить систему уравнений. Но “питонистый” способ мне нравится больше: он пороще и быстрее. В корзинах соответственно 21, 13, 17, 11, всего как несложно посчитать 62 фрукта.
Читайте также
Попробую посчитать.
От 1 до 9 — 9 раз по 0,4 = 3,6 с. И таких групп будет
1…9, 21…29, …, 91…99 — 9
101…109, 121…129, …, 191…199 — 9
901…909, 921…929, …, 991…999 — 9
10*9 = 90 групп по 3,6 с = 324 с, это мы досчитали до 1000
1000 таких групп по 324 с = 324000 с, это мы досчитали до миллиона.
И это только однозначные числа!
10, 20, …, 90 — 9 раз по 0,5 с = 4,5 с
Таких групп будет по одной в каждой сотне, то есть 10000 групп, 10000*4,5 = 45000 с
11, 12, …, 19 — 9 раз по 0,7 с = 6,3 с
Таких групп будет по одной в каждой сотне, то есть 10000 групп, 10000*6,3 = 63000 с
100, 200, …, 900 — 9 раз по 0,8 с = 7,2 с
Таких групп будет по одной в каждой тысяче, то есть 1000 групп, 1000*7,2 = 7200 с
Тысячи тут счет особый. Одна тысяча произносится как просто «тысяча», то есть за 1 с.
Но чисел, начинающихся на одну тысячу, всего 1000 — от 1000 до 1999, это 1000 с.
Потом идут 10 тыс, их и есть 10000 по 1,5 с, то есть 15000 с
Потом 11 тыс, 12 тыс, …, 19 тыс, по 9000 раз в каждой сотне тысяч, 90000 групп по 1,7 с, всего 90000*1,7 = 153000 с.
Во всех остальных случаях (21000, 181000, 301000 и т.д.) слово «одна» произносится, то есть за 1,4 с.
Таких групп будет 8000 в первых 100000, 8000*1,4 = 11200 с, и по 9000 в каждых следующих, 9*9000*1,4 = 113400 с.
Всего 113400 + 11200 = 124600 с
Дальше, 2000, 3000, …, 9000 произносится за 1,4 с. Таких групп будет по 9000 из каждых 10000, то есть 9000*100 = 900000.
Это займет 900000*1,4 = 1260000 с.
Затем 20 тыс, …, 90 тыс, по 80000 раз в каждой сотне тысяч, по 1,5 с, всего 80000*1,5 = 120000 с.
И, наконец, сотни тысяч.
100 тыс, 200 тыс, …, 900 тыс — это 900000 раз по 1,8 с, то есть 1620000 с.
Осталось добавить промежутки между словами и числами, но как их считать, я так сразу не соображу.
В конце надо будет сложить жирные числа, но у меня уже сил нет. Закончи сам!
Следует знать о скрупулезности и щепетильности автора при составлении своих задач. Поэтому условие задачи следует читать, ну ОЧЕНЬ внимательно.
Во первых, в условии не сказано, что эти уравнения представляют систему.
Во вторых, не сказано, что каждой цифре соответствует буква. Сказано «а буквы — цифры». То есть, разным буквам могут соответствовать одинаковые цифры.
Это принципиально все меняет.
Не думаю что существуют методики решения таких уравнений аналитически, поэтому остается только метод подбора. Но 90000+9000 вариантов это очень круто и не реально даже для взрослого человека не говоря уже о школьниках и 45 минутах урока.
Попробуем избавиться от этого огромного числа вариантов.
Рассмотрим первое уравнение.
Очевидно , что w не равно нулю. А также, максимально число справа может равняться w999
Допустим
w=5
5^5=3125 это меньше 5999
w=6
6^5=7776 это уже больше чем 6999
Следовательно w может колебаться в диапазоне от 1 до 5
Будем надеяться, что данные уравнения имеют по одному решению и удача не всегда поворачивается к нам спиной. Решение может быть найдено вначале пути, что сократит число вариантов.
Примем w=1
Необходимо очень сильно увеличить левую часть записи. Правая при этом тоже будет увеличиваться, но меньше. Берем значение «х» на вскидку 5
626 значительно меньше 1500. Попробуем увеличить «х»
Дистанция сокращается. Еще раз увеличим.
А это явно перебор. Значит «х» равен 6, а недостающее значение доберем младшими разрядами.
По этой же схеме, методом последовательных приближений пробуем найти значение «у» и z.
Учитывая тот факт, что при изменении значения переменных правую часть легко представить зрительно,то можно примерно оценить недостающую величину левой части.
В любом самом простом калькуляторе если набрать например 7*7 и последовательно нажимать кнопку равно, то всякий раз число 7 будет возводиться в следующую степень. Возвести в пятую степень это четыре раза ударить по кнопке равно. Поэтому очень легко найти те числа при которых значение меньше необходимого и уже больше. После чего взять меньшее.
Поскольку все должно быть понятно, избавлю свой ответ от большого числа ненужных фотографий.
Окончательно.
Нам повезло, решение нашлось при v=1, что избавило от ряда ненужных вычислений. Но даже если бы это было не так, то все равно не очень проблемно, чуть чуть больше времени.
Аналогично находим решение для второго уравнения.
Для решения этих уравнений времени потребовалось не так много. В принципе, несколько десятков вычислений. Сорока пяти минут на это хватает с лихвой.
Возможно существует более рациональное решение, но мне оно неизвестно.
Для начала можно найти сумму чисел и букв на всех шариках, висящих на ёлке:
5Х + 3У + 3Z + 7 + 28 + 24 = 2X + 3( X + У + Z ) = 2Х + 3 × 36 + 59 = 2Х + 167
С другой стороны площадь всей «ёлки» можно найти из площади маленького самого верхнего треугольника, умножив её на 9 ( это видно из подобия большого и малого треугольников: их основания и высоты относятся, как 1 к 3 ):
9 * ( 2Х + 7 ) = 18Х + 63
Приравниваем оба найденные значения площади ёлки:
2Х + 167 = 18Х + 63
16Х = 104
Х = 6,5
В принципе, теперь можно найти значения площадей маленького треугольника и средней и нижний трапеций и всей «ёлки», при желании.
Площадь маленького верхнего треугольника будет равна 7 + 6,5 + 6,5 = 20
Площадь средней трапеции равна утроенной площади маленького треугольника:
3 × 20 = 60
С другой стороны площадь средней трапеции равна 3Х + У + 28.
Приравниваем оба найденные значения площади средней трапеции и находим значение У:
3Х + У + 28 = 60
У = 60 — 28 — 3Х = 32 — 3 × 6,5 = 32 — 19,5 = 12,5
Значение Z проще будет найти из выражения Х + У + Z = 36:
Z = 36 — Х — У = 36 — 6,5 — 12,5 = 17
Впрочем, для проверки можно найти значение Z и через площадь нижней трапеции, которая с одной стороны равна 2У + 3Z + 24,
а с другой стороны она же равна пятикратному значению площади маленького треугольника 5 × 20 = 100
По традиции, приравниваем найденные значения:
2У + 3Z + 24 = 100
2 × 12,5 + 3Z + 24 = 100
25 + 3Z + 24 = 100
3Z = 100 — 49
3Z = 51
Z = 17
В общем, вот такие у меня получились значения:
Х = 6,5
У = 12,5
Z = 17
Просматривается следующая логика:
Первое число-77
Второе число-7*7=49
Третье число-4*9=36
Четвертое число-3*6=18
Пятое( и в данном случае последнее) число-1*8=8.
Ответ: следующее число-8.Вот как- то так!
Я что то не понял к чему тут такие большие вычисления.
Угловая скорость это угол пройденный телом по окружности за единицу времени.
У 2R она равна W, а у R она равна 3W.
Если взять W=360 градусов то есть полный оборот то получится что 2R сделает один оборот, а R сделает 3 оборота. И никаких формул тут не надо.
Спасибо за внимание.
Найди верный ответ на вопрос ✅ «Грузовик в первый день проехал 600 км, а во второй день 200 км. Весь путь занял 8 часов. Сколько часов в день проезжал грузовик, если он …» по предмету 📙 Математика, а если ответа нет или никто не дал верного ответа, то воспользуйся поиском и попробуй найти ответ среди похожих вопросов.
Искать другие ответы
Главная » ⭐️ Математика » Грузовик в первый день проехал 600 км, а во второй день 200 км. Весь путь занял 8 часов. Сколько часов в день проезжал грузовик, если он ехал всё время с одинаковой скоростью.
Никому не хочется заказать для своей дачи грузовик дров и остаться с носом, выяснив по итогу, что топлива привезли меньше, чем обещали. Еще хуже, когда обманутый хозяин и вовсе не догадывается о том, что его обвели вокруг пальца. Для того, чтобы подобного не случалось, необходимо уметь рассчитывать, сколько именно кубов дров было привезено еще до того момента, как они будут выгружены из кузова.
Дрова привозят вот так. |Фото: vsevolozhsk.blizko.ru.
Кто-то заказывает дрова для дачи, кто-то для бани. Ситуация, когда за небольшие деньги обещали привезти 5 кубов, а по итогу привезли всего 3 куба, увы, не является какой-то редкостью. Недобросовестные продавцы рассчитывают на невнимательность или неграмотность людей в данном вопросе. Чаще всего обманывают неместных или когда поставщик сам не является местным, ведь новый клиент всегда найдется. Поэтому очень важно иметь представление о том, как именно кубы дров подсчитываются.
Можно посчитать прямо в кузове. |Фото: drova-sdk.ru.
Хуже всего, когда дрова привозят не аккуратной кладкой, а насыпью. Посчитать объем таких дров намного сложнее. При этом важно помнить следующее: если заказали 5 кубов дров, а вам привезли их насыпью, да еще и в какой-нибудь «ГАЗели» — точно обманывают. Прежде всего нужно пересчитать насыпь в кладку. Для этого сначала придется померять длину нескольких привезённых поленьев и высчитать объем кузова грузовика (V). Для этого умножаем высоту кузова на длину и на ширину в метрах.
Лучше рубить самому. |Фото: ktozvonil.me.
Померяв среднюю длину поленьев, выводим коэффициент перерасчета в складометры (k1): для поленьев длиной 0.25 м – 0.8, для 0.33 м – 0.78, для 0.5 м – 0.75 и для 0.75 м – 0.73. Зная все это, можно высчитать насыпной объем дров. Для этого используется следующая формула Vдров = V * k1. После этого следует еще раз пересчитать объем, переведя дрова в цельное дерево. Для этого используется статичный коэффициент перерасчета в цельное дерево (k2) и формула: Vцельный = Vдров * k2, где k2 всегда равно 0.7. По итогу, получаем более-менее реальный объем привезенного дерева.
Россыпь посчитать сложнее. ¦Фото: chel.pulscen.ru.
Видео с нашего канала расскажет про cкрытые возможности индикаторной отвертки, о которых не помешало бы знать домашним мастерам:
Если хочется узнать еще больше интересного, то стоит почитать про газ, дрова, электричество: что выгоднее выбрать для отопления собственного дома.
— простые задачи на скорость, время и расстояние;
— задачи на встречное и противоположное движение;
— задачи на движение в одном направлении (на сближение и удаление);
— решение задач на движение по реке.
Скорость, время и расстояние: определения, обозначения, формулы
скорость = расстояние: время — формула нахождения скорости;
время = расстояние: скорость — формула нахождения времени;
расстояние = скорость · время — формула нахождения расстояния.
Скорость – это расстояние, пройденное за единицу времени: за 1 секунду, за 1 минуту, за 1 час и так далее.
Пример обозначения: 7 км/ч (читается: семь километров в час).
Если весь путь проходится с одинаковой скоростью, то такое движение называется равномерным.
На сайте представлены калькуляторы онлайн, с помощью которых можно перевести скорость, время и расстояние в другие единицы измерения:
1.Конвертер единиц измерения скорости
2.Конвертер единиц измерения времени
3.Конвертер единиц измерения расстояния (длины)
Примеры простых задач.
Задача 1.
Автомобиль проехал 180 км за 2 часа. Чему равна скорость автомобиля?
Решение: 180:2=90 (км/ч.)
Ответ: Скорость автомобиля равна 90 км/ч.
Задача 2.
Автобус проехал путь в 240 км со скоростью 80 км/ч. Сколько времени ехал автобус?
Решение: 240:80=3 (ч.)
Ответ: Автобус проехал 3 часа.
Задача 3.
Грузовик ехал 5 часов со скоростью 70 км/ч. Какое расстояние проехал грузовик за это время?
Решение: 70 · 3 = 350 (км)
Ответ: Грузовик за 5 часов проехал 350 км.
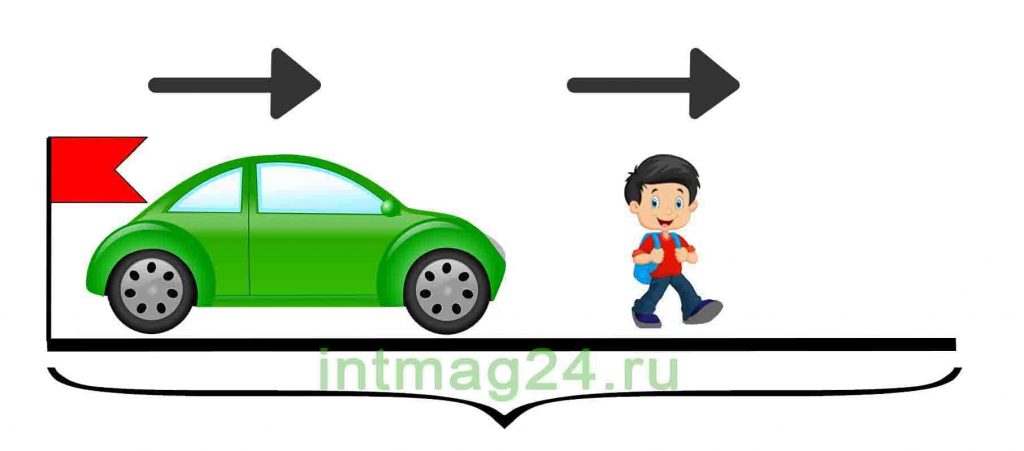
Задачи на встречное движение
В таких задачах два объекта движутся навстречу друг другу.
Задачи на встречное движение можно решать двумя способами:
1. Найти значения скорости, времени и расстояния для каждого объекта.
2. Найти скорость сближения объектов (как сумму их скоростей), общие время и расстояние. Скорость сближения — это расстояние, пройденное двумя объектами навстречу друг другу за единицу времени.
Задача 4.
Из двух пунктов навстречу друг другу одновременно выехали два поезда и встретились через 3 часа. Первый поезд ехал со скоростью 80 км/ч, а второй – со скоростью 70 км/ч. На каком расстоянии друг от друга находятся пункты?
Решение:
Первый способ. Найти расстояние, которое проехал каждый автобус, и сложить полученные данные:
80*3=240 (км) – проехал 1й автобус, 70*3=210 (км) – проехал 2й поезд,
240+210=450 (км) – проехали два поезда.
Второй способ. Найти скорость сближения поездов, то есть на сколько сокращалось расстояние между ними каждый час; а затем найти расстояние:
80+70=150 (км/ч), 150*3=450 (км).
Ответ: города находятся на расстоянии 450 км.
Задача 5.
Из двух городов навстречу друг другу одновременно выехали два автобуса. Первый автобус ехал со скоростью 80 км/ч, а второй – со скоростью 70 км/ч. Какое расстояние будет между ними через 2 часа, если расстояние между городами 450 км?
Решение:
Первый способ. Определить, сколько километров проехал каждый автобус и найти расстояние, которое осталось проехать:
80*2=160 (км)-проехал 1й автобус, 70*2=140 (км)-проехал 2й автобус,
160+140=300 (км)-проехали два автобуса, 450-300=150 (км)-осталось проехать.
Второй способ. Найти скорость сближения автобусов и умножить ее на время в пути.
80*70=150 (км/ч) – скорость сближения; 150*2=300 (км) – проехали два автобуса; 450-300=150 (км) – осталось проехать.
Ответ: Через 2часа расстояние между автобусами будет 150 км.
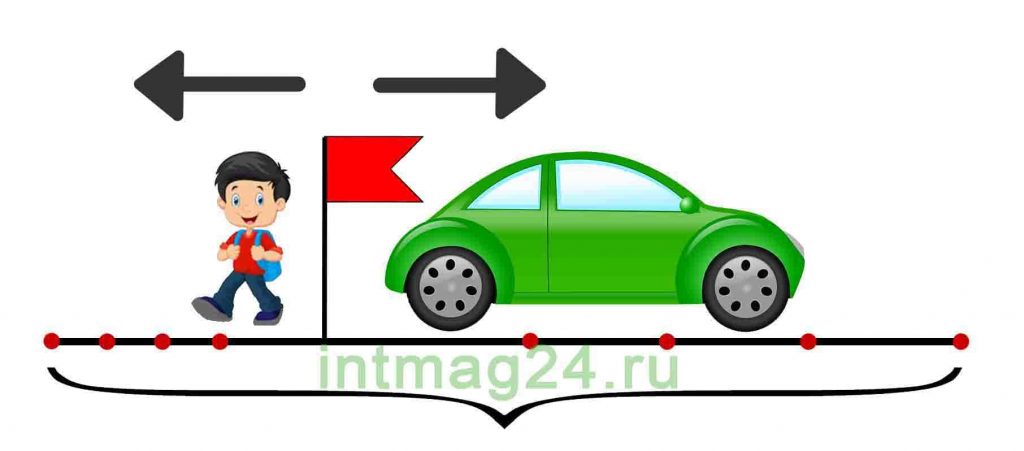
Задачи на движение в противоположных направлениях
В таких задачах два объекта движутся в противоположных направлениях, отдаляясь друг от друга. В таком типе задачи используется скорость удаления. Задачи на движение в противоположных направлениях также можно решить двумя способами:
1. Найти значения скорости, времени и расстояния для каждого объекта.
2. Найти скорость удаления объектов (как сумму их скоростей), общие время и расстояние. Скорость удаления — это расстояние, которое увеличивается за единицу времени между двумя объектами, двигающимися в противоположных направлениях.
Задача 6.
Два автомобиля выехали одновременно из одного и того же пункта в противоположных направлениях. Скорость первого автомобиля 100 км/ч, скорость второго – 70 км/ч. Какое расстояние будет между автомобилями через 4 часа?
Решение:
Первый способ. Определить расстояние, которое проехал каждый автомобиль и найти сумму полученных результатов:
1) 100 · 4 = 400 (км) – проехал первый автомобиль
2) 70 · 4 = 280 (км) – проехал второй автомобиль
400 + 280 = 680 (км)
Второй способ. Найти скорость удаления, то есть значение увеличения расстояния между автомобилями за каждый час, а затем скорость удаления умножить на время в пути.
100 + 70= 170 км/ч – это скорость удаления автомобилей.
170 · 4 = 680 (км)
Ответ: Через 4 часа между автомобилями будет 680 км.
Задача 7.
Из двух населённых пунктов, расстояние между которыми 40 км, вышли в противоположных направлениях два туриста. Первый турист шёл со скоростью 4 км/ч, а второй — 5 км/ч. Какое расстояние между туристами будет через 5 часов?
Решение:
Первый способ. Определить сколько километров прошёл каждый из туристов за 5 часов, сложить полученные результаты, а затем к полученному расстоянию прибавить расстояние между населенными пунктами.
1) 4 · 5 = 20 (км) – прошёл первый турист;
2) 5 · 5 = 25 (км) – прошёл второй турист;
3) 20 + 25 = 45 (км);
4) 45 + 40 = 85 (км).
Второй способ. Найти скорость удаления пешеходов, затем найти пройденное расстояние, к полученному результату прибавить расстоянием между населёнными пунктами.
4 + 5 = 9 (км/ч);
9 · 5 = 45 (км);
45 + 40 = 85 (км);
Ответ: Через 5 часов расстояние между пешеходами будет 85 км.
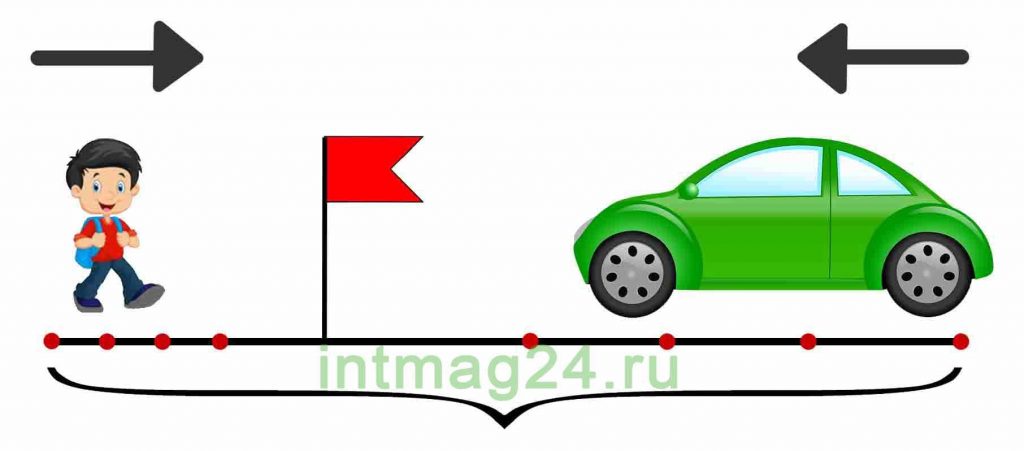
Задачи на движение в одном направлении
В таких задачах два объекта движутся в одном направлении с разной скоростью, при этом они сближаются друг с другом или отдаляются друг от друга. Соответственно находится скорость сближения или скорость удаления объектов.
Формула нахождения скорости сближения или удаления двух объектов, которые движутся в одном направлении: из большей скорости вычесть меньшую.
Задача 8.
Из города выехал автомобиль со скоростью 40 км/ч. Через 4 часа вслед за ним выехал второй автомобиль со скоростью 60 км/ч. Через сколько часов второй автомобиль догонит первый?,
Решение:
Задачу можно решить с помощью уравнения.
В этом случае скорость первого автомобиля 40 км/час, время в пути на 4 часа больше, чем время второго автомобиля (или t+4). Скорость второго автомобиля 60 км/час, время в пути – t. Расстояние оба автомобиля проехали одинаковое. Поэтому можно составить уравнение: 40*(t+4)=60*t. Отсюда получаем t=8 (часов) – время в пути второго автомобиля, за которое он догонит первый.
Решение задачи без использования уравнения.
Так как на момент выезда второго автомобиля из города первый уже был в пути 4 часа, то за это время он успел удалиться от города на: 40 · 4 = 160 (км).
Второй автомобиль движется быстрее первого, значит, каждый час расстояние между автомобилями будет сокращаться на разность их скоростей: 60 — 40 = 20 (км/ч) – это скорость сближения.
Разделив расстояние между автомобилями на скорость их сближения, можно узнать, через сколько часов они встретятся: 160 : 20 = 8 (ч)
Ответ: Второй автомобиль догонит первый через 8 часов.
Задача 9.
Из двух посёлков между которыми 5 км, одновременно в одном направлении вышли два пешехода. Скорость пешехода, идущего впереди, 4 км/ч, а скорость пешехода, идущего позади 5 км/ч. Через сколько часов после выхода второй пешеход догонит первого?
Решение: Так как второй пешеход движется быстрее первого, то каждый час расстояние между ними будет сокращаться. Значит можно определить скорость сближения пешеходов: 5 — 4 = 1 (км/ч).
Оба пешехода вышли одновременно, значит расстояние между ними равно расстоянию между посёлками (5 км). Разделив расстояние между пешеходами на скорость их сближения, узнаем через сколько второй пешеход догонит первого: 5 : 1 = 5 (ч)
Ответ: Через 5 часов второй пешеход догонит первого.
Задача 10.
Два автомобиля выехали одновременно из одного и того же пункта в одном направлении. Скорость первого автомобиля 80 км/ч, а скорость второго – 40 км/ч.
1) Чему равна скорость удаления между автомобилями?
2) Какое расстояние будет между автомобилями через 3 часа?
3) Через сколько часов расстояние между ними будет 200 км?
Решение:
1) 80 — 40 = 40 (км/ч) — скорость удаления автомобилей друг от друга.
2) 40 · 3 = 120 (км) – расстояние между ними через 3 часа./
3) 200 : 40 = 5 (ч) – время, через которое расстояние между автомобилями станет 200 км.
Ответ:
1) Скорость удаления между автомобилями равна 40 км/ч.
2) Через 3 часа между автомобилями будет 120 км.
3) Через 5 часов между автомобилями будет расстояние в 200 км.
Задачи на движение по реке
Рассмотрим задачи, в которых речь идёт о движении объекта по реке. Скорость любого объекта в стоячей воде называют собственной скоростью этого объекта.
Чтобы узнать скорость объекта, который движется по течению реки, надо к собственной скорости объекта прибавить скорость течения реки. Чтобы узнать скорость объекта, который движется против течения реки, надо из собственной скорости объекта вычесть скорость течения реки.
Задача 11.
Лодка движется по реке. За сколько часов она преодолеет расстояние 120 км, если ее собственная скорость 27 км/ч, а скорость течения реки 3 км/ч?
Решение:
1) лодка движется по течению реки.
27 + 3 = 30 (км/ч) – скорость лодки по течению реки.
120 : 30 = 4 (ч) – проплывет путь.
2) лодка движется против течения реки.
27 — 3 = 24 (км/ч) — скорость лодки против течения реки
120 : 24 = 5 (ч) – проплывет путь.
Ответ:
1) При движении по течению реки лодка потратит 4 часа на путь.
2) При движении против течения реки лодка потратит 5 часов на путь.
Итак, для решения задач на движение:
- Основная формула:S=ν*t;
- Нужно сделать чертеж, который поможет определить тип задачи.
- Все цифры нужно привести в единые единицы измерения: длина и время
Заключение.
Решая много задач по данной теме, ученик обязательно научится быстро ориентироваться в понятиях «скорость», «время» и «расстояние» и быстро решать задачи всех типов.
Весь курс начальной школы (за 1-4 классы) в краткой форме на сайте edu.intmag24.ru. С помощью курса можно быстро повторить основные моменты и правила по предметам: русский язык, математика, окружающий мир.
Для решения более сложных задач на движение посмотрите, как составлять схемы и таблицы данных для наглядного представления и структурирования данных.

Страница 6
Ответы к странице 6
Раздел 1. Натуральные числа и действия над ними. Глава 1. Натуральные числа. Параграф 1. Ряд натуральных чисел
Задание 1. Назовите 14 первых натуральных чисел.
Ответ:
1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14.
Задание 2. Какого числа не хватает в записи натурального ряда чисел: 1,2,3,4,5,6,7,9,10,11,…?
Ответ:
не хватает числа 8.
7
Ответы к странице 7
Задание 3. Из чисел 5,1/6,8,129,0,3/7,4128,1/5 выберите натуральные.
Решение
5; 8; 129; 4128.
Задание 4. Запишите число, которое в натурально ряду следует за числом:
1) 34;
2) 246;
3) 8297.
Решение
35
247
8289
Задание 5. Запишите число, которое в натуральном ряду следует за числом:
1) 72;
2) 121;
3) 6459.
Решение
1) 73
2) 122
3) 6459
Задание 6. Запишите число, которое в натуральном ряду является предыдущим числу:
1) 58;
2) 631;
3) 4500.
Решение
1) 57
2) 630
3) 4499
Задание 7. Запишите число, которое в натуральном ряду является предыдущим числу:
1) 42;
2) 215;
3) 3240.
Решение
1) 42
2) 215
3) 3240
Задание 8. Сколько чисел стоит в натуральном ряду между числами:
1) 6 и 24;
2) 18 и 81?
Решение
1) 17 чисел
2) 62 числа
Задание 9. Сколько чисел стоит в натуральном ряду между числами:
1) 13 и 28;
2) 29 и 111?
Решение
1) 15 чисел
2) 81 число
Задание 10. Некоторое натуральное число, большее 3, обозначили буквой a. Запишите для числа a два предыдущих и три последующих натуральных числа.
Решение
Предыдущие числа: a − 1; a − 2.
Последующие числа: a + 1; a + 2; a + 3.
Упражнения для повторения
Задание 11. Вычислите:
1) 238 + 435;
2) 4385 + 2697;
3) 843 − 457;
4) 2000 − 546;
5) 3400 − 896
6) 23 * 46;
7) 98 * 34;

Решение
+238
435
673+4385
2697
7082−843
457
386−2000
546
1454−3400
896
2504× 23
46
138
92
1058× 98
34
392
294
3332× 645
36
3870
1935
23220
Задание 12. Первое летописное упоминание о Москве встречается в Ипатьевской летописи в 1147 г. Сколько лет прошло от первого летописного упоминания Москвы?
Решение
Решение будет зависеть от года, в котором вы выполняете домашнее задание. Пример для 2021 года:
2021 − 1187 = 834 (г.)
Ответ: 834 года прошло.
Задание 13. Выполните действия:
1435 1392
1) 43 + 24 * 58 − 39 = 1396
67 3886
2) (43 + 24) * 58 − 39 = 3847
456 19
3) 43 + 24 * (58 − 39) = 499
67 19
4) (43 + 24) * (58 − 39) = 1273
Задание 14
Собираясь в гости к своей бабушке, Карлсон решил подкрепиться. Для этого на завтрак он съел 26 банок варенья, а на обед − на 16 банок больше. Сколько банок варенья съел Карлсон?
Решение
1) 26 + 16 = 42 (б.) — съел Карлсон на обед.
2) 26 + 42 = 68 (б.) — съел Карлсон всего.
Ответ: 68 банок варенья.
Задание 15
На одном участке растут 34 куста смородины, а на другом − на 18 кустов меньше. Сколько всего кустов смородины растёт на двух участках?
Решение
1) 34 − 18 = 16 (к.) — растет на втором участке.
2) 34 + 16 = 50 (к.) — растет всего.
Ответ: 50 кустов.
8
Ответы к странице 8
Ответы к задаче от мудрой совы
Задание 16. В квадрате (рис.1) суммы чисел в каждом столбце, в каждой строке и диагоналях должны быть одинаковыми. Найдите число, которое должно быть записано вместо звездочки.
Решение
В первом столбце сумма чисел 33, значит и в остальных строках, столбцах и диагоналях будет по 33.
10 15 8
9 11 13
14 7 12
10
Ответы к странице 10
Параграф 2. Цифры. Десятичная запись натуральных чисел
Задание 17. Назовите разряд, в котором стоит цифра 4 в записи числа:
1) 34;
2) 246;
3) 473;
4) 24569.
Решение
1) разряд единиц
2) разряд десятков
3) разряд сотен
4) разряд тысяч
Задание 18. Прочитайте число:
1) 234642;
2) 502013;
3) 9145679;
4) 105289001;
5) 6704917320;
6) 72016050400;
7) 491872653000;

Решение
Двести тридцать четыре тысячи шестьсот сорок два.
Пятьсот две тысячи тринадцать.
Девять миллионов сто сорок пять тысяч шестьсот семьдесят девять.
Сто пять миллионов двести восемьдесят девять тысяч один.
Шесть миллиардов семьсот четыре миллиона девятьсот семнадцать тысяч триста двадцать.
Семьдесят два миллиарда шестнадцать миллионов пятьдесят тысяч четыреста.
Четыреста девяносто один миллиард восемьсот семьдесят два миллиона шесть пятьдесят три тысячи.
Триста пять миллиардов два миллиона восемьсот тысяч семьсот сорок восемь.
Задание 19. Запишите десятичной записью число:
1) 34 миллиона 384 тысячи 523;
2) 85 миллионов 128 тысяч 23;
3) 16 миллионов 26 тысяч 4;
4) 6 миллионов 60 тысяч 17;
5) 8 миллиардов 801 миллион 30 тысяч 5;
6) 22 миллиарда 33 миллиона 418;
7) 251 миллиард 538;

9) 607 миллиардов 3.
Решение
34384523
85128023
160026004
6060017
8801030005
22033000418
251000000538
46000000854
607000000003
Задание 20. Запишите десятичной записью число:
1) 23 миллиона 275 тысяч 649;
2) 56 миллионов 319 тысяч 48;
3) 12 миллионов 20 тысяч 21;
4) 8 миллионов 7 тысяч 3;
5) 6 миллиардов 325 миллионов 800 тысяч 954;
6) 14 миллиардов 52 миллиона 819;
7) 368 миллиардов 742 тысячи;

Решение
23275649
56319048
12020021
8007003
6325800954
14052819
368000742000
92000000029
11
Ответы к странице 11
Задание 21. Запишите десятичной записью число:
1) Сорок шесть миллиардов четыреста пятьдесят семь миллионов семьсот двадцать семь тысяч триста восемьдесят восемь;
2) Шестьсот тридцать два миллиарда двести четыре миллиона тридцать пять тысяч сорок семь;
3) Сто пять миллиардов пятьсот тридцать девять тысяч сто;
4) Тридцать миллиардов двадцать тысяч девяносто;
5) Восемь миллиардов семь миллионов пятнадцать тысяч четырнадцать;
6) один миллиард две тысячи два.
Ответ
46457727388
632204035047
150000539100
30000020090
8007015014
1000002002
Задание 22. Запишите десятичной записью число:
1) три миллиона триста тридцать три тысячи триста тридцать три;
2) три миллиона триста тысяч;
3) три миллиона три тысячи;
4) три миллиона тридцать;
5) три миллиона тридцать тысяч триста;
6) три миллиона три тысячи три;
7) три миллиона три.
Ответ
1) 3333333
2) 3300000
3) 3003000
4) 3000030
5) 3030300
6) 3003003
7) 3000003
Задание 23. Запишите десятичной записью число:
1) шестьдесят восемь миллиардов двести сорок девять миллионов девятьсот пятьдесят четыре тысячи семьсот двадцать три;
2) восемьсот четырнадцать миллиардов сто девять миллионов две тысячи тридцать два;
3) триста семь миллиардов шестьсот двадцать одна тысяча четыреста;
4) девяносто миллиардов десять тысяч двадцать;
5) два миллиарда три миллиона четыре тысячи пять;
6) один миллиард одна тысяча один.
Ответ
68249954723
814109002032
307000621400
90000010020
2003004005
1000001001
Задание 24. Запишите и прочитайте число, которое образуется, если записать число 514 подряд:
1) два раза;
2) три раза;
3) четыре раза.
Ответ
514514 − пятьсот четырнадцать тысяч пятьсот четырнадцать
514514514 − пятьсот четырнадцать миллионов пятьсот четырнадцать тысяч пятьсот четырнадцать
514514514514 − пятьсот четырнадцать миллиардов пятьсот четырнадцать миллионов пятьсот четырнадцать тысяч пятьсот четырнадцать
Задание 25. Запишите и прочитайте число, которое образуется, если записать число 48 подряд:
1) два раза;
2) три раза;
3) четыре раза;
4) пять раз.
Ответ
4848 − четыре тысячи восемьсот сорок восемь
484848 − четыреста восемьдесят четыре тысячи восемьсот сорок восемь
48484848 − сорок восемь миллионов четыреста восемьдесят четыре тысячи восемьсот сорок восемь
4848484848 − четыре миллиарда восемьсот сорок восемь миллионов четыреста восемьдесят четыре тысячи восемьсот сорок восемь
Задание 26. Запишите в виде суммы разрядных слагаемых число:
1) 846;
2) 2375;
3) 12619;
4) 791105;
5) 32598009;
6) 540007020.
Ответ 7 гуру
1) 846 = 8 * 100 + 4 * 10 + 6 * 1
2) 2375 = 2 * 1000 + 3 * 100 + 7 * 10 + 5 * 1
3) 12619 = 10000 + 2000 + 600 + 10 + 9
4) 791105 = 7 * 100000 + 9 * 10000 + 1 * 1000 + 1 * 100 + 0 * 10 + 5 * 1
5) 32598009 = 3 * 10000000 + 2 * 1000000 + 5 * 100000 + 9 * 10000 + 8 * 1000 + 0 * 100 + 0 * 10 + 9 * 1
6) 540007020 = 5 * 100000000 + 4 * 10000000 + 0 * 1000000 + 0 * 100000 + 0 * 10000 + 7 * 1000 + 0 * 100 + 2 * 10 + 0 * 1
12
Ответы к странице 12
Задание 27. Запишите в виде суммы разрядных слагаемых число:
1) 34729;
2) 75194;
3) 478254;
4) 189390;
5) 23487901;
6) 140028045.
Решение
1) 34729 = 3 * 10000 + 4 * 1000 + 7 * 100 + 2 * 10 + 9 * 1
2) 75194 = 7 * 10000 + 5 * 1000 + 1 * 100 + 9 * 10 + 4 * 1
3) 478254 = 4 * 100000 + 7 * 10000 + 8 * 1000 + 2 * 100 + 5 * 10 + 4 * 1
4) 189390 = 1 * 100000 + 8 * 10000 + 9 * 1000 + 3 * 100 + 9 * 10 + 0 * 1
5) 23487901 = 2 * 10000000 + 3 * 1000000 + 4 * 100000 + 8 * 10000 + 7 * 1000 + 9 * 100 + 0 * 10 + 1 * 1
6) 140028045 = 1 * 100000000 + 4 * 10000000 + 0 * 1000000 + 0 * 100000 + 2 * 10000 + 8 * 1000 + 0 * 100 + 4 * 10 + 5 * 1
Задание 28. Запишите число, которое:
1) на 1 меньше наименьшего трёхзначного числа:
2) на 4 больше наибольшего трёхзначного числа;
3) на 5 меньше наименьшего пятизначного числа;
4) на 6 больше наибольшего шестизначного числа;
5) на 7 больше наименьшего восьмизначного числа.
Решение
1) 100 − 1 = 99
2) 999 + 4 = 1003
3) 10000 − 5 = 9995
4) 999999 + 6 = 1000005
5) 10000000 + 7 = 10000007
Задание 29. Запишите наибольшее восьмизначное число, а также следующее и предыдущие числа.
Ответ 7 гуру
Наибольшее восьмизначное число: 99999999
Следующее: 99999999 + 1 = 100000000
Предыдущее: 99999999 − 1 = 99999998
Задание 30. Запишите наименьшее семизначное число, а также следующее и предыдущее числа.
Ответ
Наименьшее семизначное число: 1000000
Следующее: 1000000 + 1 = 1000001
Предыдущее: 1000000 − 1 = 999999
Задание 31. Двузначное число записали подряд два раза. Во сколько раз полученное четырехзначное число больше данного двузначного числа?
Решение
Можно взять любое двузначное число. Пусть двузначное число 12, тогда четырехзначное число 1212.
_1212|12
12 |101
_1
0
_12
12
0
В 101 раз четырехзначное число больше двузначного числа.
Задание 32. Трёхзначное число записали подряд два раза. Во сколько раз полученное шестизначное число больше данного трёхзначного числа?
Решение
Пусть трёхзначное число 121, тогда шестизначное 121121.
_121121 |121
121 |1001
_1
0
_12
0
_121
121
0
В 1001 раз шестизначное число больше данного трёхзначного числа.
Задание 33. В книге пронумерованы страницы с первой по сто семьдесят вторую. Сколько цифр напечатано при нумерации страниц?
Решение
С 1 по 9 страницы напечатали 9 цифр.
2 * 90 = 180 (ц.) — напечатали с 10 по 99 страницы
3 * 73 = 219 (ц.) — напечатали с 100 по 172 страницы
9 + 180 + 219 = 408 (ц.) — напечатано при нумерации страниц.
Ответ: 408 цифр.
Задание 34. Для нумерации страниц книги напечатано 2004 цифры. Сколько страниц в этой книге.
Решение
С 1 по 9 страницы напечатали 9 цифр.
С 10 по 99 страницы напечатали
2 * 90 = 180 (ц.) — напечатали с 10 по 99 страницы
С 100 по 199 напечатали
3 * 100 = 300 (ц.) — напечатали с 100 по 199 страницы
следовательно в каждых последующих 100 страниц печатали по 300 цифр.
2004 − 9 − 180 = 1815 (ц.) — было написано на трехзначных номерах страниц.
_1815 |300
1800 |6
151800 цифр было напечатано с 100 по 699 страницу.
15 : 3 = 5, то есть еще на 5 страницах были напечатаны оставшиеся 15 цифр.
699 + 5 = 704 (стр.) — в книге.
Ответ: 104 страницы.
Задание 35. Каких трёхзначных чисел больше: все цифры которых чётные или все цифры которых нечетные?
Решение
Все цифры чётные:
2, 4, 6, 8 − эти 4 цифры мы можем взять для первой цифры трехзначного числа;
2, 4, 6, 8, 0 − эти 5 цифр мы можем взять для второй цифры трехзначного числа;
2, 4, 6, 8, 0 − эти 5 цифр мы можем взять для третей цифры трехзначного числа.
4 * 5 * 5 = 100, то есть всего существует 100 трёхзначных чисел, все цифры которых четные.
Все цифры нечётные:
1, 3, 5, 7, 9 − эти 5 цифр мы можем взять для первой цифры трехзначного числа;
1, 3, 5, 7, 9 − эти 5 цифр мы можем взять для второй цифры трехзначного числа;
1, 3, 5, 7, 9 − эти 5 цифр мы можем взять для третей цифры трехзначного числа.
5 * 5 * 5 = 125, то есть всего существует 125 трёхзначных чисел, все цифры которых нечетные.
125 > 100, следовательно трёхзначных чисел, все цифры которых нечетные больше, чем трёхзначных чисел, все цифры которых четные.
Ответы к упражнениям для повторения
!Задание 36. Вычислите:
1) 24 * 564 = 13536
2) 754 * 60 = 45240
3) 2504 * 82 = 205328
4) 364 * 276 = 100464
5) 407 * 306 = 124542
6) 852 : 6 = 142
7) 67216 : 8 = 8402
782 : 34 = 8402
9) 1134 : 42 = 27
10) 3198 : 26 = 723
11) 4532 : 22 = 206
12) 14210 : 35 = 406
!Задание 37. Вычислите действия:
1) 49 + 26 * (54 − 27) = 49 + 26 * 27 = 49 + 702 = 751
2) 36 : 9 + 18 * 5 = 4 + 90 = 94
3) (801 − 316) * 29 = 485 * 29 = 14065
4) (488 + 808) : 18 = 1296 : 18 = 72
Задание 38. Первый полет в космос совершил в 1961 г. гражданин Советского Союза Юрий Гагарин. Через восемь лет после этого на Луну ступил первый человек − гражданин США Нейл Армстронг. Еще через 31 год на Международной космической станции (МКС) начал работать первый экипаж. Сколько лет работают космонавты на МКС?
Решение
Если год сейчас не 2021-й, замените это число и проведите вычисления самостоятельно
1961 + 8 = 1969 (г.) − высадка человека на Луне.
1696 + 31 = 2000 (г.) − начало работы на МКС.
2021 − 2000 = 21 (г.) — работают космонавты на МКС.
Ответ: 21 год.
13
Ответы к странице 13
Задание 39. Масса булавы Ильи Муромца равна 60 пудов, а его меча − в 12 раз меньше. Какова общая масса булавы и меча Ильи Муромца?
Решение
60 : 12 = 5 (п.) — масса меча.
60 + 5 = 65 (п.) — общая масса оружия.
Ответ: 65 пудов.
Задание 40. Чтобы помочь заболевшему Карабасу−Барабасу, Дуремар решил поставить ему пиявки. Для первой процедуры он использовал 24 пиявки, а для второй − в 3 раза больше. Сколько всего пиявок понадобилось Дуремару, чтобы вылечить Карабаса−Барабаса?
Решение
24 * 3 = 72 (п.) — потребовалось для первой процедуры.
24 + 72 = 96 (п.) — понадобилось Дуремару, чтобы вылечить Карабаса−Барабаса.
Ответ: 96 пиявок.
Задание 41. Вертолет за 4 ч может пролететь 720 км. Какое расстояние он пролетит за 6 ч с той же скоростью?
Решение
720 : 4 = 180 (км/ч) — скорость самолета.
180 * 6 = 1080 (км) — пролетит самолет за 6 часов.
Ответ: 1080 км.
Задание 42. За три дня кузнец Вакула изготовил 432 подковы. Сколько подков он изготовит за пять дней, работая с той же производительностью?
Решение
432 : 3 = 144 (п.) — изготавливает Вакула в 1 день.
144 * 5 = 720 (п.) — изготовит Вакула за 5 дней.
Ответ: 720 подков.
Задача от мудрой совы
Задание 43. В этом году день рождения отца был в воскресенье. В какой день недели праздновала свой день рождения мать, если она на 62 дня моложе отца?
Решение задачи
В одной неделе 7 дней, тогда:
62 : 7 = 8 (ост.6)
8 недель + 6 дней составил промежуток времени от день рождения отца до день рождения матери. Так как до полной недели не хватает одного дня, значит день рождения матери был в субботу.
20
Ответы к странице 20
Параграф 3. Отрезок. Длина отрезка
Задание 44. Запишите все отрезки, изображенные на рисунке 15.
Ответ
а) AB; BC; AC; BK.
б) OP; OT; OR; RT; PR; PT.
в) AE; AC; AD; EC; ED; CD.
г) MN; ME; MQ; NE; NP; EP; EQ; PQ.
Задание 45. Запишите все отрезки, изображенные на рисунке 16.
Ответ 7 гуру
а) AC; AD; BD; AO; BO; OD; OC.
б) FE; FK; KE; SE; SN; NE; MP; MK; MN; KN; KP; NP.
Задание 46. Отметьте в тетради точки A, B, C, D и соедините их попарно отрезками. Сколько отрезков
образовалось? Сколько образовалось отрезков с концом в точке А?
Решение
6 отрезков, 3 отрезка с концом в точке A: AD, AC, AB.
Задание 47. Начертите отрезки MN и AC так, чтобы MN = 6 см 3 мм, AC = 5 см 3 мм.
Задание 48. Начертите отрезки EF и BK так, чтобы EF = 9 см 2 мм, BK = 7 см 6 мм.
21
Ответы к странице 21
Задание 49. Начертите отрезок AB, длина которого равна 8 см 9 мм. Отметьте на нём точку C так, чтобы CB = 3 см 4 мм. Какова длина отрезка AC?
Решение
AC = AB − CB = 8 см 9 мм − 3 см 4 мм = 5 см 5 мм
Задание 50. Начертите отрезок TP, длина которого равна 7 см 8 мм. Отметьте на нём точку E так, чтобы TE = 2 см 6 мм. Какова длина отрезка EP?
Решение
EP = TP − TE = 7 см 8 мм − 2 см 6 мм = 5 см 2 мм
Задание 51. Сравните на глаз отрезки AB и CD (рис. 17). Проверьте свой вывод измерением.
Решение
AB = CD = 22 мм
Задание 52. Назовите все ломанные, изображенные на рисунке 11. Какая из них имеет наибольшее количество звеньев?
Решение
Ломанные: BAC, ADE, BADE, CADE.
Наибольшее количество звеньев у ломанных BADE, CADE.
Задание 53. Назовите звенья ломанной, изображенной на рисунке 18, и измерьте их длины (в миллиметрах). Вычислите длину ломаной.
Решение
Звенья ломаной: AB; BE; EK; KP; PR.
AB = 21 мм
BE = 20 мм
EK = 18 мм
KP = 13 мм
PR = 13 мм
ABEKPR = AB + BE + EK + KP + PR = 21 + 20 + 18 + 13 + 13 = 85 (мм)
Задание 54. Запишите звенья ломанной, изображенной на рисунке 19, и измерьте их длины (в миллиметрах). Вычислите длину ломанной.
Решение
Звенья ломаной: ST, TK, KM, MD, DO, OF.
ST = 30 мм
TK = 14 мм
KM = 13 мм
MD = 12 мм
DO = 13 мм
OF = 14 мм
STKMDOF = ST + TK + KM + MD + DO + OF = 30 + 14 + 13 + 12 + 13 + 14 = 96 (мм)
Задание 55. Отметьте в узле клеток тетради точку A; точку B разместите на 4 клетки левее и на 5 клеток выше точки A; точку C − на 3 клетки правее и на 1 клетку выше точки B; точку D − на 3 клетки правее и на 3 клетки ниже точки C; точку E − на 1 клетку правее и на 2 клетки ниже точки D. Соедините последовательно отрезками точки A, B, C, D и E. Какая фигура образовалась? Запишите её название и укажите количество звеньев.
Решение
Образовалась ломанная, состоящая из 4 звеньев.
Задание 56. Вычислите длину ломанной ABCDE, если AB = 8 см, BC = 14 см, CD = 23 см, DE = 10 см.
Решение
ABCDE = AB + BC + CD + DE = 8 + 14 + 23 + 10 = 55 (см)
Задание 57. Вычислите длину MNKPEF, если MN = 42 мм, NK = 38 мм, KP = 19 мм, PE = 12 мм, EF = 29 (мм).
Решение
MNKPEF = MN + NK + KP + PE + EF = 42 + 38 + 19 + 12 + 29 = 140 мм
22
Ответы к странице 22
Задание 58. Начертите в тетради ломаную, изображенную на рисунке 20. Измерьте длины звеньев (в миллиметрах) и найдите длину ломаной.
Решение
AB = 18 мм
BC = 30 мм
CD = 36 мм
ABCD = AB + BC + CD = 18 + 30 + 36 = 84 (мм)
Задание 59. Известно, что отрезок SK в 3 раза больше отрезка RS (рис.21). Найдите длину отрезка RK, если RS = 34 см.
Решение
SK = 3 * RS = 3 * 34 = 102 см
RK = RS + SK = 34 + 102 = 136 см
Задание 60. Известно, что отрезок DB в 5 раз меньше отрезка AD (рис.22). Найдите длину отрезка AB, если AD = 135 см.
Решение
DB = AD : 5 = 135 : 5 = 27 (см)
AB = AD + DB = 135 + 27 = 162 (см)
Задание 61. Известно, что AC = 32 см, BC = 9 см, CD = 12 см (рис.23). Найдите длины отрезков AB и BD.
Решение
AB = AC − BC = 32 − 9 = 23 см
BD = BC + CD = 9 + 12 = 21 см
Задание 62. Известно, что MF = 43 см, ME = 26 см, KE = 18 см (рис.24). Найдите длины отрезков MK и EF.
Решение
MK = ME − KE = 26 − 18 = 8 см
EF = MF — ME = 43 — 26 = 17 см
Задание 63. Даны две точки A и B. Сколько можно провести отрезков, соединяющих эти точи? Сколько можно провести ломаных, соединяющих эти точки?
Решение
Существует единственный отрезок, концами которого являются точки A и B.
Ломанных соединяющих точки A и B можно провести бесконечно много.
Задание 64. Начертите отрезок MK и отметьте на нем точки A и C. Запишите все образовавшиеся отрезки.
Решение
М А С К
.__.__.__.MA, MC, MK, AC, AK, CK.
Задание 65. Длина отрезка AB = 28 см. Точки M и K принадлежат этому отрезку, причём точка K лежит между точками M и B, AM = 12 см, BK = 9 см. Найдите длину отрезка MK.
Решение
MK = AB − AM − KB = 28 − 12 − 9 = 7 см
Задание 66. Точка C принадлежит отрезку AB, длина отрезка AC равна 15 см, а отрезок AB на 5 см больше отрезка AC. Чему равна длина отрезка BC? Есть ли в условии задачи лишние данные?
Решение
BC = 5 см.
Длина отрезка AC лишние данные.
23
Ответы к странице 23
Задание 67. Отрезки MT и FK равны (рис.25). Сравните отрезки MF и TK.
Решение
MF = TK
Задание 68. Постройте ломанную ACDM так, чтобы AC = 15 мм, CD = 24 мм, DM = 32 мм. Вычислите длину ломаной.
Решение
ACDM = AC + CD + DM = 15 + 24 + 32 = 71 мм
Задание 69. Постройте ломаную CEFK так, чтобы звено CE было равно 8 мм, звено EF было на 14 мм больше звена CE, а звено FK − на 7 мм меньше звена EF. Вычислите длину ломаной.
Решение
EF = CE + 14 мм = 8 + 14 = 22 мм
FK = EF − 7 мм = 22 − 7 = 15 мм
CEFK = CE + EF + FK = 8 + 22 + 15 = 45 мм
Задание 70. Вычислите длину ломаной, изображенной на рисунке 26.
Решение
а) Чтобы вычислить длину ломанной нужно посчитать сколько единичных отрезков длиной 5 мм в ней содержится, а затем количество найденных отрезков умножить на длину единичного.
Длина ломанной = 25 отрезков * 5 мм = 125 ммб) Чтобы вычислить длину ломанной нужно посчитать сколько единичных отрезков длиной 4 мм в ней содержится, а затем количество найденных отрезков умножить на длину единичного.
Длина ломанной = 21 отрезок * 4 мм = 84 ммв) Чтобы вычислить длину ломанной нужно посчитать сколько единичных отрезков длиной 8 мм в ней содержится, а затем количество найденных отрезков умножить на длину единичного.
Длина ломанной = 31 отрезок * 8 мм = 248 мм
Задание 71. Известно, что AC = 8 см, BD = 6 см, BC = 2 см (рис. 27). Найдите длину отрезка AD.
Решение
AB = AC − BC = 8 − 2 = 6 см
AD = AB + BD = 6 + 6 = 12 см
Задание 72. Известно, что MF = 30 см, ME = 18 см, KF = 22 см (рис.28). Найдите длину отрезка KE.
Решение
MK = MF − KF = 30 − 22 = 8 см
KE = ME − MK = 18 − 8 = 10 см
24
Ответы к странице 24
Задание 73. Известно, что KP = PE = EF = FT = 2 см (рис.29). Какие еще равные отрезки есть на этом рисунке? Найдите их длины.
Решение
KE = ET = PF = 4 см
KF = PT = 6 см
Задание 74. На первом отрезке отметили семь точек так, что расстояние между любыми соседними точками равно 3 см, а на втором − десять точек так, что расстояние между любыми соседними точками равно 2 см. Расстояние между какими крайними точками больше: лежащими на первом отрезке или лежащими на втором отрезке?
Решение
Первый отрезок состоит из 6 равных частей по 3 см, значит расстояние между крайними точками (длина отрезка) будет равна 6 * 3 = 18 см.
Второй отрезок состоит из 9 равных частей по 2 см, значит расстояние между крайними точками (длина отрезка) будет равна 9 * 2 = 18 см.
18 см = 18 см, следовательно отрезки равны.
Задание 75. Известно, что AE = 12 см, AQ = QB, BM = MC, CK = KD, DR = RE, MK = 4 см (рис. 30). Найдите длину отрезка QR.
Решение
Так как BM = MC, а CK = KD, то BD = 4 см * 2 = 8 (см)
(AE − BD) = (AQ + QB + DR + RE) = 12 − 8 = 4 (см)
Так как AQ = QB, DR = RE, то (AQ + RE) = 4 : 2 = 2 (см)
QR = AE − (AQ + RE) = 12 − 2 = 10 (см)
Задание 76. Какое наименьшее количество точек надо отметить на отрезках, изображенных на рисунке 31, чтобы на каждом из них были две отмеченные точки, не считая концов отрезков?
Задание 77. У Маши есть линейка, на которой отмечены только 0 см, 5 см и 13 см (рис.32). Как, пользуясь этой линейкой, он может построить отрезок длиной:
1) 3 см;
2) 2 см;
3) 1 см.
Решение
1) 13 − 5 − 5 = 3 (см)
2) (5 + 5 + 5) − 13 = 2 (см)
3) (13 + 13) − (5 + 5 + 5 + 5 + 5) = 26 − 25 = 1 (см)
25
Ответы к странице 25
Упражнения для повторения
!Задание 78. Вычислите:
1) 258 * 75 = 19350
2) 280 * 70 = 19600
3) 6409 * 48 = 307632
4) 685 * 293 = 200705
5) 104 * 904 = 94016
6) 868 : 7 = 124
7) 81225 : 9 = 9025
896 : 28 = 32
9) 3328 : 52 = 64
10) 9044 : 38 = 238
11) 14496 : 48 = 302
12) 37592 : 74 = 508
!Задание 79. Выполните действия:
1) 38 * 17 − 4832 : 16 = 646 − 302 = 344
2) 3596 − 3596 : (2314 − 2256) = 3596 − 3596 : 58 = 3596 − 62 = 3534
Задание 80. Детскому саду подарили четыре ящика конфет по 5 кг в каждом и шесть ящиков печенья по 3 кг в каждом. На сколько килограммов больше подарили конфет, чем печенья?
Решение
4 * 5 = 20 (кг) — конфет подарили всего.
6 * 3 = 18 (кг) печенья подарили всего.
20 − 18 = на 2 (кг) конфет подарили больше, чем печенья.
Ответ: на 2 кг.
Задание 81. Медведица Настасия Петровна заготовила на зиму 7 бочонков мёда по 12 кг в каждом и 8 бочонков мёда по 10 кг в каждом. Сколько всего килограммов мёда заготовила Настасия Петровна?
Решение задачи
7 * 12 + 8 * 10 = 84 + 80 = 164 (кг) — меда было всего заготовлено.
Ответ: 164 кг.
Задание 82. В магазин привезли 240 кг бананов и 156 кг апельсинов. Треть привезенных фруктов продали в первый день, а остальные − во второй день. Сколько килограммов фруктов продали во второй день?
Решение
240 + 156 = 396 (кг) — фруктов было привезено всего.
396 : 3 = 132 (кг) — фруктов продали в 1 день.
396 − 132 = 264 (кг) — фруктов продали во второй день.
Ответ: 264 кг.
Задание 83. Кот Матроскин вырастил в своем саду 246 кг яблок и 354 кг груш. Шестую часть всех фруктов он отдал своим друзьям из детского сада, пятую часть всех фруктов − друзьям из школы, а остальное − в больницу. Сколько килограммов фруктов Матроскин отдал в больницу?
Решение задачи
246 + 354 = 600 (кг) — фруктов всего вырастил Матроскин.
600 : 6 = 100 (кг) — фруктов Матроскин отдал друзьям из детского сада.
600 : 5 = 120 (кг) — фруктов Матроскин отдал друзьям из школы.
600 − 100 − 120 = 380 (кг) — Матроскин отдал в больницу.
Ответ: 380 кг.
Задача от мудрой совы
Задание 84. Укажите наименьшее число, сумма цифр которого равна 101.
Ответ 7 гуру
299999999999
11 * 9 + 2 = 101
29
Ответы к странице 29
Параграф 4. Плоскость. Прямая. Луч
Задание 85. Отметьте в тетради точки M и K и проведите через них прямую. Отметьте на отрезке MK точку N. Принадлежит ли точка N прямой MK? Отметьте на прямой MK точку P, лежащую вне отрезка MK. Запишите все возможные обозначения этой прямой.
Решение
M N K P
__.___.___.___._Точка N принадлежит прямой MK.
Прямые: MN; MK; MP; NK; NP; KP; PK; KN; PN; PM; KM; NM.
Задание 86. Проведите произвольную прямую и отметьте на ней точки A, B и C. Запишите все возможные обозначения этой прямой.
Решение
А В С
__.______.___.__Прямые: AB; AC; BC; CB; CA.
30
Ответы к странице 30
Задание 87. Рассмотрите рисунок 38. Верно ли утверждение:
1) точка Q принадлежит отрезку ME — верно
2) точка Q принадлежит лучу EF — не верно
3) точка Q принадлежит лучу FE — верно
4) точка E принадлежит лучу MF и лучу FM — верно
5) точка M принадлежит отрезку QE — не верно
6) точка M принадлежит прямой QE — верно
Задание 88. Пересекаются ли изображенные на рисунке 39:
1) прямая CE и отрезок AB;
2) луч OK и прямая CE;
3) луч OK и отрезок AB?
Решение
1) прямая CE и отрезок AB пересекаются, так как прямая бесконечна
2) луч OK и прямая CE пересекаются, так как у луча нет конца
3) луч OK и отрезок AB не пересекаются
Задание 89. Пересекаются ли изображенные на рисунке 40:
1) прямая MP и отрезок EF;
2) луч ST и прямая MP;
3) отрезок EF и луч ST?
Решение
1) прямая MP и отрезок EF не пересекаются
2) луч ST и прямая MP пересекаются, так как у луча нет конца
3) отрезок EF и луч ST пересекаются, так как у луча нет конца
Задание 90. Отметьте в тетради:
1) четыре точки, из которых никакие три не лежат на одной прямой;
2) пять точек, из которых никакие три не лежат на одной прямой.
Задание 91. На прямой AB отмечены две точки M и N. Назовите фигуры, которые при этом образовались.
Ответ
A M N B
__.___.___.___.__Отрезок MN.
Лучи: MA; MB; MN; NA; NM; NB.
Прямые: AB; BA; AM; MA; AN; NA; MN; MB; NB; BN; BM.
Задание 92. Запишите все отрезки, прямые и лучи, изображенные на рисунке 41.
Ответ 7 гуру
а) Отрезки: AK; AM; MK.
Прямые: NC; CN; NA; KN; AK; AC; CK.
Лучи: MB; MD; AC; KN; KC; AN; AB; KD.б) Отрезки: BC; BF; AB.
Прямые: EK; KE; EF; KF.
Лучи: BT; AD; AC; AB; FE; FK.
Задание 93. Запишите все отрезки, прямые и лучи, изображенные на рисунке 42.
Ответ
Отрезки: AB; AD; AC; DC; CB.
Прямые: EF; ED; EB; FB; FD.
Лучи: AK; DF; DE; BE; BF.
31
Ответы к странице 31
Задание 94. Начертите два луча так, чтобы их общая часть была:
1) точкой;
2) отрезком;
3) лучом.
Задание 95. Отметьте на плоскости M, K, T и F так, чтобы луч MK пересекал прямую TF, а луч TF не пересекал прямую MK.
Задание 96. Начертите прямую АС, отрезки KE и BD, луч ST так, чтобы отрезок KE пересекал прямую АС и не пересекал луч ST, отрезок BD не пересекал прямую AC и луч ST пересекались.
Задание 97. Начертите луч CD, прямую AB и отрезки MK и OP так, чтобы отрезок MK лежал на прямой AB, отрезок OP − на луче CD и чтобы прямая AB пересекала отрезок OP, а луч CD − отрезок MK.
Задание 98. Сколько лучей образуется, если на прямой отметить:
1) четыре точки;
2) 100 точек.
Ответ 7 гуру
1) Из каждой точки на прямой образуется 2 луча, следовательно 4 * 2 = 8 (лучей)
2) Из каждой точки на прямой образуется 2 луча, следовательно 100 * 2 = 200 (лучей)
Задание 99. Точки A, B и C лежат на одной прямой. Найдите длину отрезка BC, если AB = 24 см, AC = 32 см. Сколько решений имеет задача?
Ответ
Задача имеет два решения:
1) BC = AC − AB = 32 − 24 = 8 (см) ___.А___.В___.С___
2) BC = AB + AC = 32 + 24 = 56 (см) ___.В___.А___.С___
Задание 100. Точки M, K и N лежат на одной прямой. Найдите длину отрезка KN, если MK = 15 см, MN = 6 см.
Решение
Задача имеет два решения:
1) KN = MK − MN = 15 − 6 = 9 (см) ___.M___.N___.K___
2) KN = MK + MN = 15 + 6 = 21 (см) ___.N___.M___.K___
Задание 101. На плоскости проведено пять попарно пересекающихся прямых. Каким может оказаться наименьшее количество точек пересечения этих прямых?
Наибольшее количество?
Решение
Наименьшее количество 1.
Наибольшее количество 10.
Задание 102. На плоскости проведены три прямые. Каким может оказаться наибольшее количество частей, на которые эти прямые разбили плоскость, и каким − наименьшее?
Наибольшее: 7 частей,
наименьшее: 4 части.
Задание 103. Проведите шесть прямых и отметьте на них 11 точек, так, чтобы на каждой прямой было отмечено ровно 4 точки.
Задание 104. На плоскости проведены три прямые. На одной прямой отмечено пять точек, на второй − семь точек, а на третьей − три точки. Какое наименьшее количество различных точек может оказаться отмеченным?
Решение
12 точек
Ответы к упражнениям для повторения
Задание 105. В парке растет 168 дубов, берез − в 4 раза меньше, чем дубов, а кленов − на 37 деревьев, больше чем берез. Сколько всего дубов, берез и кленов растет в парке?
Решение
168 : 4 = 42 (д.) — берез растет в парке.
42 + 37 = 79 (д.) — кленов растет в парке.
168 + 42 + 79 = 289 (д.) — всего растет в парке.
Ответ: 289 деревьев.
Задание 106. Группа туристов прошла пешком 72 км, проехала на поезде расстояние в 5 раз большее, чем прошла пешком, а на автобусе проехала на 128 км меньше, чем на поезде. Сколько всего километров прошли и проехали туристы?
Решение
72 * 5 = 360 (км) — проехали туристы на поезде.
360 − 128 = 232 (км) — проехали туристы на автобусе.
72 + 360 + 232 = 664 (км) — всего преодолели туристы.
Ответ: 664 км.
32
Ответы к странице 32
Задание 107. Отправившись в гости к Змею Горынычу, Баба−яга пролетела в своей ступе 276 км за 4 часа, а остальные 156 км прошла за 6 ч в сапогах−скороходах. На сколько скорость движения ступы больше, чем скорость движения сапог−скороходов?
Решение задачи
276 : 4 = 69 (км/ч) — пролетела Баба−яга в ступе.
156 : 6 = 26 (км/ч) — прошла Баба−яга в сапогах−скороходах.
69 − 26 = на 43 (км/ч) — скорость движения ступы больше, чем скорость движения сапог−скороходов.
Ответ: на 43 км/ч.
Задание 108. По течению реки лодка проплывает 95 км за 5 ч, а против течения − 119 км за 7 ч. На сколько скорость движения лодки против течения меньше ее скорости движения по течению?
Решение задачи
95 : 5 = 19 (км/ч) — скорость лодки по течению.
119 : 7 = 17 (км/ч) — скорость лодки против течения.
19 − 17 = на 2 (км/ч) — скорость движения лодки против течения меньше ее скорости движения по течению.
Ответ: на 2 км/ч.
Задание 109. На прямой отметили 20 точек так, что расстояние между любыми двумя соседними точками равно 4 см. Найдите расстояние между крайними точками.
Решение задачи
Известно, что точек 20, значит промежутков между точками 19.
19 * 4 = 76 см расстояние между крайними точками.
Задание 110. На прямой отметили точки так, что расстояние между любыми двумя соседними точками равно 5 см, а между крайними точками − 45 см. Сколько точек отмечено на прямой?
Решение задачи
45 : 5 = 9 (отрезков)
9 + 1 = 10 (точек) отмечено на прямой.
Ответ: 10 точек.
Задача от мудрой совы
Задание 111. Как расставить 16 учеников в три ряда, чтобы в каждом ряду их было поровну?
36
Ответы к странице 36
Параграф 5. Шкала. Координатный луч
Задание 112. Запишите показания термометров, изображенных на рисунке 54.
Ответ
10°С 25°С 18°С 21°С
Задание 113. Какую температуру будет показывать термометр, изображенный на рисунке 54, в, если его столбик:
1) опустится на шесть делений;
2) поднимается на четыре деления?
Ответ
18°С − 6°С = 12°С
18°С + 4°С = 22°С
37
Ответы к странице 37
Задание 114. Какую температуру будет показывать термометр, изображенный на рисунке 54, г, если его столбик:
1) поднимется на три деления;
2) опустится на пять делений?
Решение
21°С + 3°С = 24°С
21°С − 5°С = 16°С
Задание 115. Найдите координаты точек A, B, C, D, E на рисунке 55.
Ответ
A(1), B(3), C(7), D(8), E(10).
Задание 116. Найдите координаты точек P, K, S, T, F на рисунке 56.
Ответ
P(2), K(3), S(6), T(7), F(11).
Задание 117. Отметьте на координатном луче точки, соответствующие числам 1, 3, 5, если единичный отрезок равен 1 см. Начертите еще два координатных луча и отметьте на них эти же числа, выбрав за длину единичного отрезка:
1) 2 см;
2) 5 мм.
Задание 118. Начертите координатный луч и отметьте на нем точки, изображающие числа: 2, 3, 4, 8, 9.
Задание 119. Начертите координатный луч и отметьте на нем точки, изображающие числа:
5, 6, 7, 10.
Задание 120. Запишите все натуральные числа, расположенные на координатном луче:
1) левее числа 12;
2) левее числа 18, но правее числа 8.
Ответ
1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11.
9, 10, 11, 12, 13, 14, 15, 16, 17.
Задание 121. Начертите координатный луч и отметьте на нем все натуральные числа, которые больше 3 и меньше 7.
Задание 122. Начертите координатный луч и отметьте на нем все натуральные числа, которые больше 5 и меньше 10.
Задание 123. Сколько натуральных чисел расположено на координатном луче между числами:
1) 132 и 140;
2) 487 и 492;
3) 2126 и 2128;
4) 3714 и 3715?
Решение
140 − 132 − 1 = 7 чисел
492 − 487 − 1 = 4 числа
2128 − 2126 − 1 = 1 число
3715 − 3714 − 1 = 0 чисел
Задание 124. Запишите натуральные числа, расположенные на координатном луче между числами:
1) 234 и 239;
2) 1518 и 1524;
3) 7564 и 7566;
4) 32025 и 32030.
Ответ
1) 235, 236, 237, 238.
2) 1519, 1520, 1521, 1522, 1523.
3) 7565
4) 32026, 32027, 32028, 32029.
38
Ответы к странице 38
Задание 125. Начертите отрезок длиной 8 см. Над одним концом отрезка напишите число 0, а над другим − 16. Разделите отрезок на четыре равные части. Назовите числа, которые соответствуют каждому штриху деления. Отметьте на полученной шкале числа 3, 7, 9, 10, 13, 14, 15.
Задание 126. Начертите отрезок длиной 9 см. Над одним концом отрезка напишите число 0, а над другим − 18. Разделите отрезок на шесть равных частей. Назовите числа, которые соответствуют каждому штриху деления. Отметьте на полученной шкале числа 4, 7, 8, 10, 11, 16, 17.
Задание 127. Найдите координаты точек A, B, C, D, E, F на рисунке 57.
Ответ
A(10), B(90), C(50), D(140), E(190), F(125).
Задание 128. Найдите координаты точек M, N, P, T, K, S на рисунке 58.
Ответ
M(10), N(80), P(70), T(130), K(180), S(155).
Задание 129. Перенесите в тетрадь рисунок 59. Отметьте на координатном луче точки B(12), C(2), D(8).
Задание 130. Перенесите в тетрадь рисунок 60. Отметьте на координатном луче точки E(27), F(6), K(15), P(21).
Задание 131. Начертите координатный луч и отметьте на нем точку, удаленную от точки B(5) на:
1) шесть единичных отрезков;
2) три единичных отрезка.
39
Ответы к странице 39
Задание 132. Начертите координатный луч и отметьте на нем точку, удаленную от точки A(7) на:
1) десять единичных отрезков;
2) четыре единичных отрезка;
3) семь единичных отрезка;
4) пять единичных отрезка.
Задание 133. Какое число на координатном луче соответствует точке, в которую указывает стрелка (рис.61)?
Решение
а) 55 = 46 + 9
б) 268 = 293 − 25
Задание 134. Какое число на координатном луче соответствует точке, в которой начинается стрелка (рис.62)?
Решение
а) 74 = 82 − 8
б) 424 = 408 + 16
Задание 135. Кузнечик за один прыжок перемещается вдоль координатного луча вправо на пять единичных отрезков или влево − на три единичных отрезка. Первый прыжок кузнечик совершает вправо на пять единичных отрезков. Сможет ли он за несколько прыжков из точки О(0) попасть:
1) в точку A(7);
2) в точку B(8)?
Решение
1) Сможет: 5 + 5 − 3 = 7
2) Сможет: 5 + 5 + 5 + 5 − 3 − 3 − 3 − 3 = 8
Ответы к упражнениям для повторения
!Задание 136. Выполните действия:
1) 265 + 35 * 16 = 265 + 560 = 825
2) (265 + 35) * 16 = 300 * 16 = 4800
3) 336 − 192 : 12 = 336 − 16 = 320
4) (336 − 192) : 12 = 144 : 12 = 12
40
Ответы к странице 40
Задание 137. Высота Исаакиевского собора (г.Санкт−Петербург) равна 102 м, что на 21 м больше высоты колокольни Ивана Великого на территории Московского Кремля. Высота Колокольни Ивана Великого на 24 м меньше высоты храма Христа Спасителя в Москве. Какова высота храма Христа Спасителя?
Решение задачи
102 − 21 = 81 (м) — высота Колокольни Ивана Великого.
81 + 24 = 105 (м) — высота храма Христа Спасителя.
Ответ: 105 м.
Задание 138. Из двух городов, расстояние между которыми равно 1008 км, выехали одновременно навстречу друг другу два автомобиля и встретились через 8 ч после начала движения. Скорость одного автомобиля 70 км/ч. Найдите скорость другого автомобиля.
Решение
70 * 8 = 560 (км) — проехал первый автомобиль.
1008 − 560 = 448 (км) — проехал второй автомобиль.
448 : 8 = 56 (км/ч) — скорость второго автомобиля.
Ответ: 56 км/ч.
Задание 139. Из двух городов отправились одновременно навстречу друг другу два поезда со скоростями 48 км/ч и 54 км/ч. Найдите расстояние между городами, если поезда встретились через 4 ч после начала движения.
Решение
48 * 4 = 192 (км) — проехал первый поезд.
54 * 4 = 216 (км) — проехал второй поезд.
192 + 216 = 408 (км) — расстояние между городами.
Ответ: 408 км.
Задание 140. Стоимость 7 кг яблок такая же, как 4 кг груш. Сколько килограммов груш можно купить на ту же сумму, что и 42 кг яблок?
Решение
42 : 7 = в 6 (раз) — увеличилось количество яблок.
4 * 6 = 24 (кг) груш можно купить на ту же сумму, что и 42 кг яблок.
Ответ: 24 кг.
Задача от мудрой совы
Задание 141. Вдоль забора растут восемь кустов малины. Количество ягод на соседних кустах отличается на одну. Может ли на всех кустах вместе расти 225 ягод?
Решение задачи
Количество ягод на соседних кустах отличается на одну. Значит число ягод на одном кусте четное, на другом нечетное, на следующем четное и так далее. Так как кустов 8, то значит на 4 кустах четное количество ягод, а на 4 кустах нечетное.
Сумма ягод на четырех четных кустах будет четным числом, так как сумма четных чисел равно четное число.
Сумма ягод на четырех нечетных кустах будет также четным, так как сумма двух нечетных чисел равно четному числу.
Получается что 225 ягод не может расти на 8 кустах, так как сумма ягод на четных кустах + сумма ягод на нечетных кустах будет четным числом, а число 225 − нечетное.
42-43
Ответы к странице 42-43
Параграф 6. Сравнение натуральных чисел
Задание 142. Прочитайте неравенство:
1) 4 < 9;
2) 18 > 10;
3) 257 < 263;
4) 132 > 95;
5) 8 < 12 < 20;
6) 29 < 30 < 31.
Ответ
4 < 9 число 4 меньше числа 9
18 > 10 число 18 больше числа 10
257 < 263 число 257 меньше числа 263
132 > 95 число 132 больше числа 95
8 < 12 < 20 число 12 больше числа 8, но меньше числа 20
29 < 30 < 31 число 30 больше числа 29 но меньше числа 31
Задание 143. Запишите в виде неравенства утверждение:
1) 7 меньше 12;
2) 16 больше 13;
3) 92 больше 43;
4) 2516 меньше 3939;
5) 5 больше 4, но меньше 6;
6) 40 больше 30, но меньше 50.
Ответ
7 < 12
16 > 13
92 > 43
2516 < 3939
4 < 5 < 6
30 < 40 <50
Задание 144. Сравните числа:
1) 326 и 362;
2) 483 и 480;
3) 1999 и 2002;
4) 6235 и 6196;
5) 21396 и 21298;
6) 72168 и 72170;
7) 5716007 и 5715465;

9) 4398657436 и 4398659322;
10) 16000023009 и 16000032000.
Ответ
326 < 362
483 > 480
1999 < 2002
6235 > 6196
21396 > 21298
72168 < 72170
5716007 > 5715465
3654987 < 3654991
4398657436 < 4398659322
16000023009 < 16000032000
Задание 145. Сравните числа:
1) 642 и 624;
2) 786 и 779;
3) 4897 и 5010;
4) 4455 и 5444;
5) 1400140 и 1401400;
6) 224978 и 224988;
7) 6130852 и 6130941;

Ответ
642 > 624
786 > 779
4897 < 5010
4455 < 5444
1400140 < 1401400
224978 < 224988
6130852 < 6130941
5287746525 > 52877363638
Задание 146. Расположите в порядке возрастания числа: 894, 479, 846, 591, 701.
Ответ
479, 591, 701, 846, 894.
Задание 147. Расположите в порядке убывания числа: 639, 724, 731, 658, 693.
Ответ
731, 724, 693, 658, 639.
Задание 148. Назовите все натуральные числа, которые:
1) больше 678, но меньше 684;
2) больше 935, но меньше 940;
3) больше 2934450, но меньше 2934454;
4) больше 12706, но меньше 12708;
5) больше 24315, но меньше 24316.
Ответ
1) 679, 680, 681, 682, 683.
2) 936, 937, 938, 939.
3) 2934451, 2934452, 2934453.
4) 12707
5) нет таких чисел
Задание 149. Запишите все натуральные числа, которые:
1) больше 549, но меньше 556;
2) больше 1823236, но меньше 1823240;
3) больше 47246, но меньше 47248.
Ответ
1) 550, 551, 552, 553, 554, 555.
2) 1823237, 1823238, 1823239.
3) 47247
Задание 150. Отметьте на координатном луче все натуральные числа, которые:
1) меньше 12;
2) больше 4, но меньше 10.
Задание 151. Запишите цифру, которую можно поставить вместо звездочки, чтобы получилось верное неравенство (рассмотрите все возможные случаи):
1) 526* < 5261;
2) 4345 > 438;
3) 7286 < 728;
4) 2*09 > 2710.
Ответ
1) 5260 < 5261
2) 4345 > 4338
4345 > 4328
4345 > 4318
4345 > 4308
3) 7286 < 7288
7286 < 7298
4) 2809 > 2710
2909 > 2710
Задание 152. Запишите цифру, которую можно поставить вместо звездочки, чтобы получилось верное неравенство (рассмотрите все возможные случаи):
1) 321* > 3217;
2) 93*0 < 9332.
Ответ 7 гуру
1) 3218 > 3217
3219 > 3217
2) 9330 < 9332
9320 < 9332
9310 < 9332
9300 < 9332
Задание 153. 1) Запишите какое−либо натуральное число, которое больше 473 и меньше 664, содержащее цифру 5 в разряде десятков. Сколько таких чисел можно написать?
2) Запишите какое−либо натуральное число, которое больше 578, но меньше 638, содержащее цифру 6 в разряде сотен. Сколько таких чисел можно написать? Запишите наименьшее и наибольшее из таких чисел?
Ответ
1) 473 < 652 < 664
Таких чисел можно записать 20, 549> 10 чисел < 560 и 649> 10 чисел < 660.
2) 578 < 600 < 638, таких числе можно записать 38, наименьшее из которых равно 600, а наибольшее равно 637.
44
Ответы к странице 44
Задание 154
Запишите какое−либо натуральное число, которое больше 2364 и меньше 2432, содержащее цифру 8 в разряде единиц. Сколько таких чисел можно написать? Запишите наименьшее и наибольшее из таких чисел?
Ответ
2364 < 2378 < 2432
можно записать 7 таких чисел, наименьшее из которых равно 2368, а наибольшее 2428.
Задание 155
На координатном луче отметили числа 5, 12, a, b и c (рис. 64).
Сравните:
1) a и 5;
2) 12 и b;
3) a и 12;
4) c и a.
Решение
1) a < 5
2) 12 > b
3) a < 12
4) c > a
Задание 156
Маша, Катя, Петя и Дима собирали каждый в свою корзинку грибы. В одной корзинке оказалось 34 гриба, во второй — 58 грибов, в третьей — 76 грибов, в четвертой — 82 гриба. Сколько грибов собрал каждый из них, если Петя собрал больше грибов, чем Дима, но меньше, чем Катя, а Маша меньше, чем Дима?
Решение
Маша собрала меньшее число грибов — 34.
Дима занял третье место собрав 58 грибов, т.к Петя собрал больше, но меньше, чем Маша.
Петя на втором месте, у него 76 грибов.
Катя на первом месте — 82 гриба.
Задание 156 из старой редакции учебника. Кощей Бессмертный, Баба−яга, Леший и Соловей−разбойник собирали каждый в свою корзину мухоморы. В одной корзинке оказалось 134 гриба, во второй − 158, в третей − 176, в четвертой − 182. Сколько мухоморов собрал каждый из членов веселой компании, если известно, что Леший собрал больше мухоморов, чем Кощей, но меньше, чем Соловей−разбойник, а Баба−яга меньше, чем Кощей?
Решение задачи
По условию задачи собрали грибов:
Баба − яга < Кощей Бессмертный < Леший < Соловей−разбойник, следовательно:
Баба − яга собрала 134 мухомора;
Кощей Бессмертный собрал 158 мухомора;
Леший собрал 176 мухомора;
Соловей−разбойник собрал 182 мухомора.
Задание 157
Запишите в виде двойного неравенства утверждения:
1) число 7 больше 5 и меньше 10;
2) число 62 меньше 70 и больше 60;
3) число 54 меньше 94 и больше 44;
4) число 128 больше 127 и меньше 129.
Ответ
1) 5 < 7 < 10
2) 60 < 62 < 70
3) 44 < 54 < 94
4) 127 < 128 < 129
Задание 158
Запишите в виде двойного неравенства утверждения:
1) число 56 больше 52 и меньше 58;
2) число 258 больше 250 и меньше 261;
3) число 4325 меньше 4400 и больше 4300;
4) число 999999 меньше 1000000 и больше 555558.
Ответ
1) 52 < 56 < 58
2) 250 < 258 < 261
3) 4300 < 4325 < 4400
4) 555558 < 999999 < 1000000
Задание 159 с ответами
В записи чисел вместо нескольких цифр поставили звездочки.
Сравните эти числа:
43*** < 48***
38* < 1***
9*4 < 9**3
6*9 < 96*
Задание 160 с ответами
В записи чисел вместо нескольких цифр поставили звездочки.
Сравните эти числа:
35**** > 32****
**68 > 86*
45
Ответы к странице 45
Задание 158 старый учебник. Между какими двумя ближайшими натуральными числами находится число;
1) 24;
2) 56;
3) 258;
4) 4325;
5) 999999;
6) 1300000?
Ответ запишите в виде двойного неравенства.
Ответ
1) 23 < 24 < 25
2) 55 < 56 < 57
3) 257 < 258 < 259
4) 4324 < 4325 < 4326
5) 999998 < 999999 < 1000000
6) 1299999 < 1300000 < 1300001
Задание 159 старый учебник. В записи чисел вместо нескольких цифр поставили звездочки.
Сравните эти числа:
43*** < 48***
38* < 1***
9*4 < 9**3
6*9 < 96*
Задание 160 старый учебник. В записи чисел вместо нескольких цифр поставили звездочки.
Сравните эти числа:
35**** > 32****
**68 > 86*
Задание 161
Сравните:
1) 2 км и 1968 м;
2) 4 дм и 4 м;
3) 3 км 94 м и 3126 м;
4) 712 кг и 8 ц;
5) 15 т и 35 ц;
6) 6 ц 23 кг и 658 кг;
7) 4 т 275 кг и 42 ц 75 кг;

9) 8 т и 81 ц;
10) 83 дм 7 см и 8 м 30 см.
Ответ
2 км > 1968 м
4 дм < 4 м
3 км 94 м < 3126 м
712 кг < 8 ц
15 т > 35 ц
6 ц 23 кг < 658 кг
4 т 275 кг = 42 ц 75 кг
5 т 7 ц 36 кг < 5 т 863 кг
8 т < 81 ц
83 дм 7 см > 8 м 30 см
Задание 162
Сравните:
1) 6892 м и 7 км;
2) 8 см и 8 дм;
3) 4 км 43 м и 4210 м;
4) 27 дм 3 см и 270 см;
5) 9 ц и 892 кг;
6) 2 ц 86 кг и 264 кг;
7) 3 т 248 кг и 32 ц 84 кг;

Решение
6892 м < 7 км
8 см < 8 дм
4 км 43 м < 4210 м
27 дм 3 см > 270 см
9 ц > 892 кг
2 ц 86 кг > 264 кг
3 т 248 кг < 32 ц 84 кг
12 т 2 кг = 120 ц 2 кг
Ответы к упражнениям для повторения
!Задание 163
Вычислите:
1) 936 : 24 − 2204 : 58 = 39 − 38 = 1
2) 5481 : 27 + 23 * 27 = 203 + 621 = 824
3) 3000 − (1085 − 833) : 42 = 3000 − 252 : 42 = 3000 − 6 = 2994
4) (1248 + 652) * (1423 − 1373) = 1900 * 50 = 95000
Задание 164
Из 24 м ткани можно сшить семь одинаковых платьев. Сколько таких платьев можно сшить из 48 м этой ткани?
Решение
48 : 24 = в 2 (раза) — стало больше ткани.
7 * 2 = 14 (п.) — можно сшить из 48 м ткани.
Ответ: = 14 платьев.
Задание 165
Знаменитый университет Сорбонна, находящийся в Париже (Франция), основан в 1215 г. Он основан на 6 лет позже Кембриджского университета (Великобритания) и на 540 раньше Московского государственного университета имени М.В.Ломоносова. Определите год основания:
1) Кембриджского университета;
2) Московского государственного университета имени М.В.Ломоносова.
Сколько лет исполняется в этом году Новосибирскому государственному Университету, если Кембриджский университет основан раньше него на 750 лет?
Решение задачи
Если год сейчас не 2021-й, замените это число и проведите вычисления самостоятельно
1215 − 6 = 1209 (год) основания Кембриджского университета.
1215 + 540 = 1755 (год) основания Московского государственного университета имени М.В.Ломоносова.
1209 + 750 = 1959 (год) основания Новосибирского государственного Университета.
2021 − 1959 = 62 (года) Новосибирскому государственному Университету исполняется в 2021 году.
Ответ: 62 года.
46
Ответы к странице 46
Задача от мудрой совы
Задание 166. Семь гномов собрали вместе 28 грибов. Все они собрали разное количество грибов, и ни у кого не оказалось пустой корзинки. Сколько грибов собрал каждый гном?
Решение
Предположим, что:
первый гном собрал 1 гриб;
второй − 2 гриба;
третий − 3 гриба;
четвертый − 4 гриба;
пятый − 5 грибов;
шестой − 6 грибов;
седьмой − 7 грибов,
Проверка:
1 + 2 + 3 + 4 + 5 + 6 + 7 = 28 (грибов) — собрали гномы вместе.
51
Ответы к странице 51
Глава 2. Сложение и вычитание натуральных чисел.
Параграф 7. Сложение натуральных чисел. Свойства сложения.
Задание 167
Найдите сумму:
1) +14238
18345
325832) +25726
46177
719033) +32662
4879
375414) +7892
34608
425005) +295361
475829
7711906) +28177246
42989511
711667577) +2713486
733982
3447468
+75392867428
9671635803
85064503231
Задание 168
Выполните сложение:
1) +47586
4705
522912) +68638
54382
1230203) +114931
209596
3245274) +228637
5428735
56573725) +59462181428
4740582804
642027642326) 12814
+1256064
9787
1278665
Задание 169
Аня и Коля решали задачи. Коля решил 26 задач, а Аня − на 16 задач больше. Сколько задач решили Коля и Аня вместе?
Решение задачи
26 + 16 = 42 (з.) — решила Аня.
26 + 42 = 68 (з.) решили дети вместе.
Ответ: 68 задач.
Задание 170
Миша купил книгу за 170 р., что на 12 р. меньше, чем заплатил Петя за свою новую книгу. Сколько рублей заплатили за книги Миша и Петя вместе?
Решение
170 + 12 = 182 (р.) — заплатил Петя.
170 + 182 = 352 (р.) — заплатили за книги Миша и Петя вместе.
Ответ: 352 рубля.
Задание 171
Выполните сложение, выбирая удобный порядок вычислений:
1) (42 + 37) + 58 = (42 + 58) + 37 = 100 + 37 = 137
2) 29 + (98 + 71) = (29 + 71) + 98 = 100 + 98 = 198
3) (215 + 818) + 785 = (215 + 785) + 818 = 1000 + 818 = 1818
4) 634 + (458 + 166) = (634 + 166) = 800 + 458 = 1258
5) 183 + 732 + 268 + 317 = (183 + 317) + (732 + 268) = 500 + 1000 = 1500
6) 339 + 584 + 416 + 661 = (339 + 661) + (584 + 416) = 1000 + 1000 = 2000
7) (15083 + 1458) + (4917 + 6542) = (15083 + 4917) + (1458 + 6542) = 20000 + 8000 = 28000
(1654 + 18135) + (7346 + 11865) = (1654 + 7346) + (18135 + 11865) = 9000 + 30000 = 39000
Задание 172
Используйте свойства сложения при вычислении суммы:
(146 + 322) + 178 = (322 + 178) + 146 = 500 + 146 = 646
784 + (179 + 116) = (784 + 116) + 179 = 900 + 179 = 1079
625 + 481 + 75 + 219 = (625 + 75) + (481 + 219) = 700 + 700 = 1400
427 + 88 + 273 + 112 = (427 + 273) + (88 + 112) = 700 + 200 = 900
Задание 173 старого учебника. Три бельчонка Рыжик, Пушистик и Ушастик собирали орехи. Рыжик собрал 38 орехов, что на 16 меньше, чем Пушистик, а Ушастик на 23 ореха больше, чем Рыжик. Сколько всего орехов они собрали?
Решение задачи
38 + 16 = 54 (ор.) — собрал Пушистик.
38 + 23 = 61 (ор.) — собрал Ушастик.
38 + 54 + 61 = 153 (ор.) — собрали бельчата вместе.
Ответ: 153 ореха.
Задание 173
Стена Московского Кремля состоит из трех участков: южного, восточного и западного. Длина южного участка составляет 685 м, что на 45 м меньше длины восточного. Длина западного участка на 135 м больше длины южного. Сколько метров составляет общая длина стен Московского Кремля?
1) 685 — 45 = 640 (м) — длина восточного участка
2) 685 + 135 = 820 (м) — длина западного участка
3) 685 + 640 + 820 = 2145 (м) — общая длина стен Московского Кремля
Ответ: 2145 м.
52
Ответы к странице 52
Задание 174. У Иры в коллекции есть 26 марок, посвященных историческим событиям, а также марки, посвященные архитектуре и спорту. Марок по архитектуре у нее на 15 больше, чем по истории, и на 14 меньше, чем на спортивную тему. Сколько марок в коллекции у Иры?
Решение задачи
26 + 15 = 41 (м.) — по архитектуре.
41 + 14 = 55 (м.) — по спорту.
26 + 41 + 55 = 122 (м.) — всего в коллекции у Иры.
Ответ: 122 марки.
Задание 175. На одной полке было 17 книг, на второй − на 18 книг больше, чем на первой, а на третьей − на 6 книг больше, чем на первой и второй вместе. Сколько всего книг было на трех полках?
Решение задачи
17 + 18 = 35 (к.) — было на 2 полке.
17 + 35 = 52 (к.) — было на первой и второй полке вместе.
52 + 6 = 58 (к.) — было на 3 полке.
52 + 58 = 110 (к.) — было на трех полках.
Ответ: 110 книг.
Задание 176. Отправившись в велосипедный поход, группа туристов в первый день проехала 42 км, что на 12 км меньше, чем во второй, а в третий − на 4 км больше, чем в первый и второй вместе. Сколько километров проехали туристы за три дня?
Решение задачи
42 + 12 = 54 (км) — проехали туристы во второй день.
42 + 54 = 96 (км) — проехали туристы за два дня.
96 + 4 = 100 (км) — проехали в третий день.
96 + 100 = 196 (км) — проехали туристы за три дня.
Ответ: 196 км.
Задание 177. Упростите выражение:
1) (74 + x) + 38 = (74 + 38) + x = 112 + x
2) 238 + (a + 416) = (238 + 416) + a = 654 + a
3) y + 324 + 546 = y + (324 + 546) = y 870
4) 2753 + m + 4199 = (2753 + 4199) + m = 6952 + m
5) (b + 457) + (143 + 872) = (b + 872) + (457 + 143) = b + (872 + 600) = b + 1472
6) (2235 + c) + (4671 + 1765) = (4671 + c) + (2235 + 1765) = (4671 + 4000) + c = 8671 + c
7) (1696 + 3593) + (p + 1304) = (1696 + 1304) + (3593 + p) = (3000 + 3593) + p = 6593 + p
(542 + 8951) + (4568 + a + 1049) = (542 + 4568) + (8951 + 1049) + a = (10000 + 10000) + a = 20000 + a
Задание 178. Упростите выражение:
1) (56 + a) + 14 = (56 + 14) + a = 70 + a
2) 342 + (b + 58) = (342 + 58) + b = 400 + b
3) 805 + x + 195 = (805 + 195) + x = 1000 + x
4) m + 4563 + 1837 = m + (4563 + 1837) = m + 6400
Задание 179. Дядя Федор выехал из города в Простоквашино в 15 ч 40 мин и потратил на дорогу 3 ч 50 мин. В котором часу дядя Федор приехал в Простоквашино?
Решение задачи
15 ч 40 мин + 3 ч 50 мин = (15 ч + 3ч) + (40 мин + 50 мин) = 18 ч + 90 мин = 18 ч + 60 мин + 30 мин = 19 ч 30 мин — время прибытия Федора в Простоквашино.
Ответ: 19 ч 30 мин.
Задание 180. Поезд отправляется от станции A в 9 ч 57 мин и прибывает на станцию B через 2 ч 36 мин. В котором часу поезд прибывает на станцию B?
Решение задачи
9 ч 57 мин + 2 ч 36 мин = (9 ч + 2 ч) + (57 мин + 36 мин) = 11 ч + 93 мин = 11 ч + 60 мин + 33 мин = 12 ч 33 мин — время прибытия поезда на станцию B.
Ответ: 12 ч 33 мин.
53
Ответы к странице 53
Задание 181. 1) Как изменится сумма, если одно из слагаемых увеличить на 12?
увеличится на 12.
2) Как изменится сумма, если одно из слагаемых увеличить на 23, а второе − на 17?
23 + 17 = 40, увеличится на 40
3) Как изменится сумма, если одно из слагаемых уменьшить на 34?
уменьшится на 34
4) Как изменится сумма, если одно из слагаемых уменьшить на 16, а второе на 9?
16 + 9 = 25, уменьшится на 25
5) Как изменится сумма, если одно из слагаемых увеличить на 28, а второе уменьшить на 15?
28 − 15 = 13, увеличится на 13
6) Одно из слагаемых увеличили на 3. На сколько надо увеличить второе слагаемое, чтобы сумма увеличилась на 14?
14 − 3 = 11, второе слагаемое необходимо увеличить на 11
7) Одно из слагаемых увеличили на 8. Как надо изменить второе слагаемое, чтобы сумма:
а) увеличилась на 3:
8 − 3 = 5, второе слагаемое необходимо уменьшить на 5;
б) уменьшилась на 5:
8 + 5 = 13, второе слагаемое необходимо уменьшить на 13.
Задание 182. Найдите сумму:
1) 76 м 39 см + 41 м 58 см;
2) 4 км 238 м + 3 км 474 м;
3) 64 м 86 см + 27 м 45 см;
4) 16 м 527 м + 37 км 783 м;
5) 12 ч 24 мин + 9 ч 18 мин;
6) 35 мин 17 с + 16 мин 35 с;
7) 18 ч 42 мин + 14 ч 29 мин;

Решение
1) 76 м 39 см + 41 м 58 см = (76 м + 41 м) + (39 см + 58 см) = 117 м 97 см
2) 4 км 238 м + 3 км 474 м = (4 км + 3 км) + (238 м + 474 м) = 7 км 712 м
3) 64 м 86 см + 27 м 45 см = (64 м + 27 м) + (86 см + 45 см) = 91 м + 131 см = 91 м + 100 см + 31 см = 92 м 31 см
4) 16 км 527 м + 37 км 783 м = (16 км + 37 км) + (527 м + 783 м) = 53 км + 1310 м = 53 км + 1000 м + 310 м = 54 км 310 м
5) 12 ч 24 мин + 9 ч 18 мин = (12 ч + 9 ч) + (24 мин + 18 мин) = 21 ч 42 мин
6) 35 мин 17 с + 16 мин 35 с = (35 мин + 16 мин) + (17 с + 35 с) = 51 мин 52 с
7) 18 ч 42 мин + 14 ч 29 мин = (18 ч + 14 ч) + (42 мин + 29 мин) = 32 ч + 71 мин = 32 ч + 60 мин + 11 мин = 33 ч 11 мин
53 мин 32 с + 44 мин 56 с = (53 мин + 44 мин) + (32 с + 56 с) = 97 мин + 88 с = 60 мин + 37 мин + 60 с + 28 с = 1 ч 38 мин 28 с
Задание 183. Найдите сумму:
1) 4 дм 6 см + 5 дм 8 см;
2) 8 м 5 см + 6 м 96 см;
3) 12 км 29 м + 24 км 92 м;
4) 2 т 4 ц 56 кг + 9 т 6 ц 48 кг;
5) 3 ч 48 мин + 2 ч 26 мин;
6) 25 мин 17 с + 7 мин 54 с.
Решение
1) 4 дм 6 см + 5 дм 8 см = (4 дм + 5 дм) + (6 см + 8 см) = 9 дм + 10 см + 4 см = 10 дм 4 см
2) 8 м 5 см + 6 м 96 см = (8 м + 6 м) + (5 см + 96 см) = 14 м + 100 см + 1 см = 15 м 1 см
3) 12 км 29 м + 24 км 92 м = (12 км + 24 км) + (29 м + 92 м) = 36 км + 100 м + 21 м = 36 км 121 м
4) 2 т 4 ц 56 кг + 9 т 6 ц 48 кг = (2 т + 9 т) + (4 ц + 6 ц) + (56 кг + 48 кг) = 11 т + 10 ц + 100 кг + 4 кг = 12 т 1 ц 4 кг
5) 3 ч 48 мин + 2 ч 26 мин = (3 ч + 2 ч) + (48 мин + 26 мин) = 5 ч + 60 мин + 14 мин = 6 ч 14 мин
6) 25 мин 17 с + 7 мин 54 с = (25 мин + 7 мин) + (17 с + 54 с) = 32 мин + 60 с + 11 с = 33 мин 11 с
Задание 184. Вместо звездочек поставьте цифры так, чтобы сложение было выполнено верно.
Решение
+1726
4356
6082+2539
37958
404978256
+53647
2190
64093+99
98
197
Задание 185. Вместо звездочек поставьте цифры так, чтобы сложение было выполнено верно.
Решение
+ 3625
8437
12062+2943
57681
60624
Задание 186. Не выполнения вычислений, расположите данные суммы в порядке возрастания:
782 + 659;
943 + 1105;
782 + 943;
129 + 288;
288 + 659;
1105 + 2563.
Решение
129 + 288; 288 + 659; 782 + 659; 782 + 943; 943 + 1105; 1105 + 2563.
Задание 187. Найдите сумму наиболее удобным способом:
1) 1 + 2 + 3 + …+ 9 + 10;
2) 1 + 2 + 3 + … + 99 + 100.
Решение
1 + 2 + 3 + 4 + 5 + 6 + 7 + 8 + 9 + 10 = (1 + 9) + (2 +
+ (3 + 7) + (4 + 6) + 5 + 10 = 10 + 10 + 10 + 10 + 5 + 10 = 55
1 + 2 + 3 + … + 99 + 100 = (1 + 100) + (2 + 99) + (3 + 98) + … + (50 + 51) = 101 * 50 = 5050, так как число слагаемых сто, то пар слагаемых − 50
54
Ответы к странице 54
Задание 188. 1) На сколько сумма 1 + 3 + 5 + … + 99 меньше, чем сумма 2 + 4 + 6 + … + 100?
2) Какая из сумм 1 + 3 + 5 + … + 2001 и 2 + 4 + 6 + … + 2000 больше и на сколько?
Решение
1) 1 + 3 + 5 + … + 99 = (1 + 99) + (3 + 97) + (5 + 95) + … + (49 + 51) = 100 * 25 = 2500
т.к. берутся только нечетные числа, то слагаемых 50, значит число пар слагаемых равно 25.
2 + 4 + 6 + … + 100 = (2 + 100) + (4 + 98) + (6 + 96) + … + (50 + 52) = 101 * 25 = 2550
2550 − 2500 = 50, то есть на 50 первая сумма меньше второй.2) 1 + 3 + 5 + … + 2001 = (1 + 2001) + (3 + 1999) + … + (999 + 1003) + 1001 = 2002 * 500 + 1001
т.к. суммируются только нечетные числа, то слагаемых 1001, значит число пар слагаемых 500 и число 1001 не вошло в пару.
2 + 4 + 6 + … + 2000 = (2 + 2000) + (4 + 1998) + … + (1000 + 1002) = 2002 * 50
2002 * 500 + 1001 − 2002 * 50 = 1001, то есть на 1001 первая сумма больше второй.
Задание 189. В записи 4 4 4 4 4 4 4 4 поставьте между некоторыми цифрами знак «+» так, чтобы получилось выражение, значение которого равно 500.
Ответ 7 гуру
444 + 44 + 4 + 4 + 4 = 444 + 56 = 500
Задание 190. Замените звездочки числами так, чтобы сумма любых трех соседних чисел равна 20; 7, *, *, *, *, *, *, 9.
Ответ
7, 9, 4, 7, 9, 4, 7, 9.
Задание 191. Слава разрезал проволоку на кусочки и составил фигуру, изображенную на рисунке 65. Мог ли Слава разрезать эту же проволоку так, чтобы составить фигуру, изображенную на рисунке 66?
Решение
На фигуру изображенную на рисунке 65 потребовалось 15 кусочков по 1 см и 12 кусочков по 2 см, то есть потребовалось: 15 * 1 + 12 * 2 = 15 + 24 = 39 см проволоки;
На фигуру изображенную на рисунке 66 потребуется 12 кусочков по 1 см и 12 кусочков по 3 см, то есть потребуется: 12 * 1 + 12 * 3 = 12 + 36 = 48 см проволоки.
Получается, что Слава не мог разрезать эту же проволоку так, чтобы составить фигуру, изображенную на рисунке 66, так как ему не хватило бы проволоки.
Ответы к упражнениям для повторения
Задание 192. Отметьте на координатном луче натуральные числа, которые больше 6, но меньше 12.
Задание 193. Запишите все шестизначные числа, которые больше 999 888 и оканчиваются цифрой 5.
Ответ
999895, 999905, 999915, 999925, 999935, 999945, 999955, 999965, 999975, 999985, 999995.
Задание 194. Скороход прошел 24 км за 4 ч. На обратном пути он увеличил скорость на 2 км/ч. Сколько времени он потратил на обратный путь?
Решение задачи
24 : 4 = 6 (км/ч) — скорость скорохода.
6 + 2 = 8 (км/ч) — скорость скорохода при возвращении обратно.
24 : 8 = 3 (ч) — потратил скороход на обратный путь.
Ответ: 3 часа.
Задание 195. Вася старше сестры Светы на 5 лет. На сколько лет он будет старше Светы через 7 лет?
Решение
Через 7 лет брат останется старше своей сестры на 5 лет, так как и брат и сестра повзрослеют на одинаковое количество лет.
Задача от мудрой совы
Задание 196. Можно ли таблицу из пяти строк и шести столбцов заполнить натуральными числами, так чтобы сумма чисел каждой строки была равна 30, а сумма чисел каждого столбца − 20?
Решение
Нельзя, так как сумма чисел в каждом столбце равна 20, столбцов 6, значит сумма всех чисел таблицы 20 * 6 = 120.
Сумма чисел каждой строки равно 30, строк 5, значит сумма всех чисел 30 * 5 = 150
120 ≠ 150
57
Ответы к странице 57
Параграф 8. Вычитание натуральных чисел
Задание 197
Найдите разность:
1) _27146
24317
28292) _12030
11164
8663) _82314
78425
38894) _56789
9876
469135) _524278
344929
17933496) _46000185
8123456
378767297) _72430034
23082408
49347626
_1000000000
637891452
362108548
Задание 198
Найдите разность:
1) _35476
24839
106372) _46002
28396
176063) _60015
7428
525874) _372894
216156
1567385) _38020301
18479563
195407386) _537866285
496707539
41158746
Задание 199
На сколько:
1) число 4328 меньше, чем число 21514;
2) число 258143 больше, чем число 164 275?
Решение
_21514
4328
17186_258143
164275
93868
Задание 200
На сколько:
1) число 34725 больше, чем число 28816;
2) число 16546 меньше, чем число 56289?
Решение
_34725
28816
5909_56289
16546
39743
Задание 201
В таблице приведены максимальные расстояния от Солнца до некоторых планет Солнечной системы:
Найдите, на сколько километров:
1) Земля расположена ближе к Солнцу, чем Сатурн;
2) Уран расположен дальше от Солнца, чем Меркурий.
Решение
1) _1506750000
149600000
1357150000
Земля расположена ближе к Солнцу, чем Сатурн на 1 357 150 000 км2) _3007665000
57910000
2949755000
Уран расположен дальше от Солнца, чем Меркурий на 2 949 755 000 км
Задание 202 старый учебник. В Российской Федерации 1295 поселков городского типа, а городов − на 196 меньше. Сколько всего городов и поселков городского типа в Российской Федерации?
Решение задачи
1) 1295 − 196 = 1099 (шт.) — городов в РФ.
2) 1295 + 1099 = 2394 (шт.) — всего городов и поселков городского типа в Российской Федерации.
Ответ: 2394 городов и поселков городского типа.
Задание 202
В Российской Федерации 1209 поселков городского типа, а городов − на 96 меньше. Сколько всего городов и поселков городского типа в Российской Федерации?
Решение задачи
1) 1209 − 96 = 1113 (шт.) — городов в РФ.
2) 1209 + 1113 = 2322 (шт.) — всего городов и поселков городского типа в Российской Федерации.
Ответ: 2322 городов и поселков городского типа.
58
Ответы к странице 58
Задание 203
Увлекшись грибной охотой, пес Шарик в первый день собрал 73 гриба, что на 16 грибов больше, чем во второй день. Сколько всего грибов Шарик за два дня?
Решение
73 − 16 = 57 (г.) — собрал Шарик во второй день.
73 + 57 = 130 (г.) — собрал Шарик за два дня.
Ответ: 130 грибов.
Задание 204
В августе корова Звездочка дала 278 и молока, а в сентябре − на 26 л меньше. Сколько всего литров молока дала корова Звёздочка за эти два месяца?
Решение
278 − 26 = 252 (л) — молока дала Звездочка в сентябре.
278 + 252 = 530 (л) — молока дала корова Звёздочка за эти два месяца.
Ответ: 530 л.
Задание 205
Площадь Швеции равна 450000 км2, что на 242000 км2 больше площади Белоруссии, которая на 130000 км2 меньше площади Финляндии. Сколько квадратных километров составляет площадь Финляндии?
Решение
450000 − 242000 = 208000 (км2) — площадь Белоруссии.
208000 + 130000 = 338000 (км2) — площадь Финляндии.
Ответ: 338000 км2.
!Задание 206
Вычислите:
1) 25375 + 16686 − 21239 = 42061 − 20822 = 20822
2) (7829 − 5878) − (20000 − 18453) = 1951 − 1547 = 404
3) (5689 − 3458 + 1723) − (25002 − 24848) + 2967 = (2231 + 1723) − 154 + 2967 = 3954 − 154 + 2967 = 3800 + 2967 = 6767
!Задание 207
Вычислите:
1) 84218 − 57134 + 34615 = 27084 + 34615 = 61699
2) (44516 − 17398) − (14259 + 12262) = 27118 − 26521 = 597
3) (6754 + 2853 − 1508) − (29006 − 27999) + 5818 = (9607 − 1508) − 1007 + 5818 = 8099 − 1007 + 5818 = 7092 + 5818 = 12910
Задание 208
Дорогу из Орла в Дубки построили за три месяца. За первый месяц построили часть дороги длиной 21 км, за второй − на 8 км меньше, чем за первый. Всего за первые два месяца было построено на 13 км больше, чем за третий. Какова длина дороги из Орла в Дубки?
Решение
1) 21 − 8 = 13 (км) — дороги построили за 2 месяц.
2) 21 + 13 = 34 (км) — дороги построили за два месяца.
3) 34 − 13 = 21 (км) — дороги построили за третий месяц.
4) 21 + 13 + 21 = 55 (км) — длина дороги из Орла в Дубки.
Ответ: 55 км.
Задание 209
Денис, Дмитрий и Николай сдали на завод сахарную свеклу. Денис сдал 56 ц свеклы, что на 18 ц больше, чем Дмитрий. Вместе они сдали на 28 ц свеклы больше, чем Николай. Сколько всего центнеров сахарной свеклы они сдали?
Решение
1) 56 − 18 = 38 (ц) — сдал Дмитрий.
2) 56 + 38 = 94 (ц) — сдали Дмитрий и Денис вместе.
3) 94 − 28 = 66 (ц) — сдал Николай.
4) 94 + 66 = 160 (ц) — сдали все вместе.
Ответ: 160 ц.
Задание 210 старый учебник. За три дня Рокфор съел 230 головок сыра. За первый день он съел 74 головки, что на 16 головок больше, чем за второй. Сколько головок сыра съел Рокфор за третий день?
Решение
1) 74 − 16 = 58 (г.) — съел во второй день.
2) 74 + 58 = 132 (г.) — за два дня.
3) 230 − 132 = 98 (г.) — съел Рокфор за третий день.
Ответ: 98 головок сыра.
Задание 210
Во время Великой Отечественной войны за 1942, 1943 и 1944 годы было произведено 84800 боевых самолетов. В 1943 году было произведено 29900 самолетов, что на 8200 самолетов больше, чем в 1942 году. Сколько самолетов было произведено в 1944 году?
Решение
1) 29900 — 8200 = 21700 (с.) — произведено в 1942 г.
51600
2) 84800 — (21700 + 29900) = 33200 (с.) — произведено в 1944 г.
Ответ: 33200 самолетов.
Задание 211
Щукин, Карпов и Сомов отправились на рыбалку. Вместе они поймали 192 карася, причем Щукин поймал 53 карася, что на 15 больше, чем поймал Карпов. Сколько карасей поймал Сомов?
Решение
1) 53 − 15 = 38 (к.) — поймал Карпов.
2) 53 + 38 = 91 (к.) — поймал Щукин и Карпов вместе.
3) 192 − 91 = 101 (к.) — поймал Сомов.
Ответ: 101 карася.
Задание 212
Царевны Елена, Катерина и Марья пряли пряжу. У Елены и Катерины получилось вместе 112 м пряжи, а у Катерины и Марьи − 193 м. Сколько метров пряжи спряла каждая царевна, если всего ее получилось 240 м?
Решение
1) 240 − 193 = 47 (м) — спряла Елена.
2) 240 − 112 = 128 (м) — спряла Марья.
3) 193 − 128 = 65 (м) — спряла Екатерина.
Ответ: 47 м, 128 м, 65 м.
Задание 213
Расстояние между Тридевятым царством и Тридесятым государством, которое составляет 365 верст, Емеля преодолел на своей печи за три дня. (Верста − старинная русская мера длины, равная приблизительно 1067 м.) За первые два дня он проехал 246 верст, а за первый и третий − 268 верст. Сколько верст проезжала печь каждый день?
Решение задачи
1) 365 − 246 = 119 (верст) — проехала печь в третий день.
2) 268 − 119 = 149 (верст) — проехала печь в первый день.
3) 246 − 149 = 97 (верст) — проехала печь во второй день.
Ответ: 149 верст, 97 верст, 119 верст.
59
Ответы к странице 59
Задание 214. Маша посчитала выращенные ею цветы. Георгинов и роз оказалось 78, а остальные цветы составляли гладиолусы, причем гладиолусов было на 9 меньше, чем роз. Сколько цветов каждого вида вырастила Маша, если всего их было 124?
Решение
124 − 78 = 46 (цв.) — гладиолусов.
46 + 9 = 55 (цв.) — роз.
78 − 55 = 23 (цв.) — георгины.
Ответ: 46 гладиолусов, 55 роз, 23 георгины.
Задание 215. Коля собрал модели автомобилей, самолетов и пароходов, причем автомобилей и самолетов у него было 56 моделей, а самолетов − на 12 моделей больше, чем пароходов. Сколько моделей каждого вида было у Коли, если всего его коллекция насчитывала 82 модели?
Решение
82 − 56 = 26 (м.) — пароходов
26 + 12 = 38 (м.) — самолетов
56 − 38 = 18 (м.) — автомобилей
Ответ: 26 пароходов, 38 самолетов, 18 автомобилей.
Задание 216. Проверьте, верно ли неравенство:
1) 24017 − 15035 < 12386 − 2987;
2) 1674 − (673 + 437) > 1885 − (648 + 664).
Решение
24017 − 15035 < 12386 − 2987
_24017
15035
8982_12386
2987
93998982 < 9399 верно
1674 − (673 + 437) > 1885 − (648 + 664)
+673
437
1110_1674
1110
564+648
664
1312_1885
1312
573564 < 573 неверно
Задание 217. Проверьте, верно ли равенство:
6011 − (1539 − 438) < 5791 − (2418 − 1336)
Решение
6011 − (1539 − 438) < 5791 − (2418 − 1336)
_1539
438
1101_6011
1101
4910_2418
1336
1082_5791
1082
47094910 > 4709 неверно
Задание 218. Поезд отправляется от станции A в 7 ч 37 мин и в тот же день прибывает на станцию B в 9 ч 12 мин. Сколько времени поезд едет от станции A до станции B?
Решение
9 ч 12 мин − 7 ч 37 мин = 8 ч 72 мин − 7 ч 37 мин = (8 ч − 7 ч) + (72 мин − 37 мин) = 1 ч 35 мин время время поезда в пути
Ответ: 1 ч 35 мин.
Задание 219. Поезд отправляется от станции A и в тот же день прибывает на станцию B в 15 ч 20 мин. В котором часу поезд отправляется от станции A, если путь от A до B занимает 6 ч 48 мин?
Решение
15 ч 20 мин − 6 ч 48 мин = 14 ч 80 мин − 6 ч 48 мин = (14 − 6) + (80 − 48) = 8 ч 32 мин
Ответ: в 8 ч 32 мин.
Задание 220. Найдите разность:
1) 76 м 39 см − 41 м 24 см = (76 м − 41 м) + (39 см − 24 см) = 35 м 15 см
2) 64 м 45 см − 27 м 86 см = 63 м 145 см − 27 м 86 см = (63 м − 27 м) + (145 см − 86 см) = 36 м 59 см
3) 22 км 527 м − 17 км 783 м = 21 км 1527 м − 17 км 783 м = (21 км − 17 км) + (1527 м − 783 м) = 14 км 744 м
4) 4 км 238 м − 3 км 474 м = 3 км 1238 м − 3 км 474 м = (3 км − 3 км) + (1238 м − 474 м) = 764 м
5) 12 ч 24 мин − 9 ч 18 мин = (12 ч − 9 ч) + (24 мин − 18 мин) = 3 ч 6 мин
6) 18 мин 42 с − 14 мин 29 с = (18 мин − 14 мин) + (42 с − 29 с) = 4 мин 13 с
7) 35 мин 17 с − 15 мин 35 с = 34 мин 77 с − 15 мин 35 с = (34 мин − 15 мин) + (77 с − 35 с) = 19 мин 42 с
53 ч 32 мин − 44 ч 56 мин = 52 ч 92 мин − 44 ч 56 мин = (52 ч − 44 ч) + (92 мин − 56 мин) = 8 ч 36 мин
60
Ответы к странице 60
Задание № 221
Найдите разность:
1) 3 дм 2 см − 2 дм 6 см = 2 дм 12 см − 2 дм 6 см = (2 дм − 2 дм) + (12 см − 6 см) = 6 см
2) 54 м 18 см − 27 м 35 см = 53 м 118 см − 27 м 35 см = (53 м − 27 м) + (118 см − 35 см) = 26 м 83 см
3) 3 кг 26 г — 1 кг 920 г = 2 кг 1026 г — 1 кг 920 г = 1 кг 106 г
4) 4 км 8 м − 1 км 19 м = 3 км 1008 м − 1 км 19 м = (3 км − 1 км) + (1008 м − 19 м) = 2 км 989 м
5) 8 т 6 ц 25 кг − 4 т 8 ц 74 кг = 7 т 15 ц 125 кг − 4 т 8 ц 74 кг = (7 т − 4 т) + (15 ц − 8 ц) + (125 кг − 74 кг) = 3 т 7 ц 51 кг
6) 16 ч 26 мин − 9 ч 52 мин = 15 ч 86 мин − 9 ч 52 мин = (15 ч − 9 ч) + (86 мин − 52 мин) = 6 ч 34 мин
7) 10 мин 4 с − 5 мин 40 с = 9 мин 64 с − 5 мин 40 с = (9 мин − 4 мин) + (64 с − 40 с) = 5 мин 24 с
2 ч 36 мин 16 с — 5 мин 35 с = 2 ч 35 мин 76 с — 5 мин 35 с = 2 ч 30 мин 41 с
Задание № 221 старый учебник. Найдите разность:
1) 3 дм 2 см − 2 дм 6 см = 2 дм 12 см − 2 дм 6 см = (2 дм − 2 дм) + (12 см − 6 см) = 6 см
2) 54 м 18 см − 27 м 35 см = 53 м 118 см − 27 м 35 см = (53 м − 27 м) + (118 см − 35 см) = 26 м 83 см
3) 4 км 8 м − 1 км 19 м = 3 км 1008 м − 1 км 19 м = (3 км − 1 км) + (1008 м − 19 м) = 2 км 989 м
4) 8 т 6 ц 25 кг − 4 т 8 ц 74 кг = 7 т 15 ц 125 кг − 4 т 8 ц 74 кг = (7 т − 4 т) + (15 ц − 8 ц) + (125 кг − 74 кг) = 3 т 7 ц 51 кг
5) 16 ч 26 мин − 9 ч 52 мин = 15 ч 86 мин − 9 ч 52 мин = (15 ч − 9 ч) + (86 мин − 52 мин) = 6 ч 34 мин
6) 10 мин 4 с − 5 мин 40 с = 9 мин 64 с − 5 мин 40 с = (9 мин − 4 мин) + (64 с − 40 с) = 5 мин 24 с
Задание № 222
1) Как изменится разность, если уменьшаемое увеличить на 8?
Разность увеличится на 8
2) Как изменится разность, если уменьшаемое уменьшить на 4?
Разность уменьшится на 4
3) Как изменится разность, если вычитаемое увеличить на 7?
Разность уменьшится на 7
4) Как изменится разность, если вычитаемое уменьшить на 5?
Разность увеличится на 5
5) Как изменится разность, если уменьшаемое увеличить на 10, а вычитаемое − на 6?
Разность увеличится на 4
6) Как изменится разность, если уменьшаемое увеличить на 9, а вычитаемое − на 12?
Разность увеличится на 21
7) Как изменится разность, если уменьшаемое уменьшить на 14, а вычитаемое − на 9?
Разность уменьшится на 5

Разность увеличится на 4
9) Как изменится разность, если уменьшаемое увеличить на 16, а вычитаемое уменьшить на 8?
Разность увеличится на 24
10) Как изменится разность, если уменьшаемое увеличить на 3, а вычитаемое уменьшить на 6?
Разность увеличится на 9
11) Как изменится разность, если уменьшаемое уменьшить на 20, а вычитаемое увеличить на 15?
Разность уменьшится на 35
12) Как изменится разность, если уменьшаемое уменьшить на 10, а вычитаемое увеличить на 30?
Разность уменьшится на 40
Задание № 223
1) Уменьшаемое увеличили на 2. Как надо изменить вычитаемое, чтобы разность:
а) уменьшилась на 12;
б) увеличилась на 6;
в) уменьшилась на 2;
г) увеличилась на 2;
д) не изменилась;
е) увеличилась на 1?
2) Вычитаемое уменьшили на 8. Как надо изменить уменьшаемое, чтобы разность:
а) увеличилась на 3;
б) уменьшилась на 5;
в) увеличилась на 4;
г) уменьшилась на 10;
д) увеличилась на 8;
е) не изменилась?
Ответы
1) а) увеличить на 14;
б) уменьшить на 6;
в) увеличить на 2;
г) менять не надо;
д) увеличить на 2;
е) увеличить на 1?2) а) уменьшить на 5;
б) уменьшить на 13;
в) уменьшить на 4;
г) уменьшить на 18;
д) менять не надо;
е) уменьшить на 8?
Задание № 224
Вместо звездочек поставьте цифры так, чтобы вычитание было выполнено верно.
Решение
1)
_1000
999
12)
_86541
9172
773693)
_7278
4359
29194)
_294676
157869
1368075) _100900
42757
581436) В учебнике опечатка, забыли одну звездочку в разности.
_5353535
484848
4868687
61
Ответы к странице 61
Задание № 225. Вместо звездочек поставьте цифры так, чтобы вычитание было выполнено верно.
Решение
_95673
8927
86746_84562
7816
76746
Задание № 226. На остановке из троллейбуса вышло 15 пассажиров, а вошло − 8.
На следующей остановке вышло 6 пассажиров и вошло 12.
Сколько пассажиров было в троллейбусе до первой остановки, если после второй их стало 31?
Решение
1) 31 − 12 + 6 = 25 (п.) — было после первой остановки.
2) 25 + 15 − 8 = 32 (п.) — было до первой остановки.
Ответ: 32 пассажира.
Задание № 227. Между завтраком и обедом Женя Съел 7 слив, которые лежали в тарелке. После обеда мама положила туда еще 14 слив. Между обедом и ужином Женя съел 9 слив. После ужина мама положила в тарелку еще 5 слив, и в ней стало 20 слив. Сколько слив было в тарелке сначала?
Решение задачи
20 − 5 + 9 − 14 + 7 = 17 (с.)
Ответ: 17 слив.
Задание № 228. В первый день Василий собрал в своем саду 26 ящиков яблок, а во второй − 14 таких же ящиков яблок. Сколько килограммов яблок собрал Василий в первый день и сколько − во второй, если во второй день он собрал на 192 кг меньше, чем в первый?
Решение задачи
1) 26 − 14 = 12 (ящ.)
2) 192 : 12 = 16 (кг) — яблок в одном ящике.
3) 26 * 16 = 416 (кг) — яблок собрал Василий в первый день.
4) 14 * 16 = 221 (кг) — собрал Василий во второй день.
Ответ: 416 кг, 221 кг.
Задание № 229. Один поезд находился в пути 7 ч, а второй − 13 ч. Второй поезд проехал на 360 км больше, чем первый. Сколько километров проехал каждый поезд, если они двигались с одинаковой скоростью?
Решение
1) 13 − 7 = на 6 (ч) — второй поезд ехал дольше первого.
2) 360 : 6 = 60 (км/ч) — скорость и первого и второго поезда.
3) 7 * 60 = 420 (км) — проехал первый поезд.
4) 420 + 360 = 780 (км) — проехал второй поезд.
Ответ: 420 км, 780 км.
Задание № 230. Найдите значение выражения, выбирая удобный порядок вычислений:
1) (412 + 116) − 112 = (412 − 112) + 116 = 300 + 116 = 416
2) (593 + 675) − 275 = (675 − 275) + 593 = 400 + 593 = 993
3) (792 + 301) − 201 = (301 − 201) + 792 = 100 + 792 = 892
4) (987 + 614) − 187 = (987 − 187) + 614 = 800 + 614 = 1414
5) 844 − (244 + 318) = (844 − 244) − 318 = 600 − 318 = 282
6) 729 − (396 + 229) = (729 − 229) − 396 = 500 − 396 = 104
7) 393 − (193 + 155) = (393 − 193) − 155 = 200 − 155 = 45
672 − (202 + 172) = (672 − 172) − 202 = 500 − 202 = 298
Задание № 231. Найдите значение выражения, выбирая удобный порядок вычислений:
1) (176 + 343) − 243 = (343 − 243) + 176 = 100 + 176 = 276
2) (684 + 915) − 484 = (684 − 484) + 915 = 200 + 915 = 1115
3) (259 + 101) − 59 = (259 − 59) + 101 = 200 + 101 = 301
4) 1287 − (487 + 164) = (1287 − 487) + 164 = 800 − 164 = 636
5) 971 − (235 + 371) = (971 − 371) − 235 = 600 − 235 = 365
6) 5393 − (1393 + 158) = (5393 − 1393) − 158 = 4000 − 158 = 3842
Задание № 232. Упростите выражение:
1) (35 + х) − 15;
2) (432 + b) − 265;
3) (a + 636) − 129;
4) 96 − (m + 48);
5) 516 − (216 + x);
6) 444 − (y + 58).
Решение
1) (35 + х) − 15 = (35 − 15) + х = 20 + х
2) (432 + b) − 265 = (432 − 265) + b = 167 + b
3) (a + 636) − 129 = (636 − 129) + a = 507 + a
4) 96 − (m + 48) = (96 − 48) − m = 48 − m
5) 516 − (216 + x) = (516 − 216) − x = 300 − x
6) 444 − (y + 58) = (444 − 58) − y = 386 − y
Задание № 233. Упростите выражение:
1) (a + 546) − 328 = (546 − 328) + a = 218 + a
2) (с + 961) − 592 = (961 − 592) + c = 369 + c
3) (151 + b) − 109 = (151 − 109) + b = 42 + b
4) 272 − (125 + y) = (272 − 125) − y = 147 − y
5) 925 − (p + 735) = (925 − 735) − p = 190 − p
6) 707 − (n + 534) = (707 − 534) − n = 173 − n
62
Ответы к странице 62
Задание № 234 старый учебник. Заполните имеющиеся пропуски в таблице, в которой приведены данные о выступлениях российских школьников на международных олимпиадах в 2001 − 2010 гг.
Задание № 234
Заполните имеющиеся пропуски в таблице, в которой приведены данные о выступлениях российских школьников на международных математических олимпиадах в 2006 − 2015 гг.
Заполняем пропуски цифрами:
3
6
6
0
2
2 0
6
2
3
6 0Последняя цифра 6 следует из итогового количества медалей (36) с учетом, что бронзовых 0.
Задание № 235
В двузначном числе 6 десятков. Между цифрами этого числа вписали цифру 0. На сколько полученное трехзначное число больше, чем данное двузначное?
Решение
Пусть дано число 65 и если вписать между числами 0, то получится 605.
605 − 65 = 540
Рассмотрим другое число, например 69, вписав 0 получим 609, тогда:
609 − 69 = 540 , следовательно на 540 трехзначное число больше, чем данное двузначное.
Задание № 236
В записи 1 2 3 4 5 6 7 8 9 поставьте между некоторыми цифрами знак «+» или «−» так, чтобы в результате арифметических действия получилось число 100.
Решение
123 − 45 − 67 + 89 = 100
Ответы к упражнениям для повторения
!Задание № 237
Выполните действия:
1) 25 * (63 − 741 : 19) = 25 * (63 − 39) = 25 * 24 = 600
2) (900 − 7218 : 9) * 12 = (900 − 802) * 12 = 98 * 12 = 1176
3) 3926 : 13 * 8 + 2584 = 302 * 8 + 2584 = 2416 + 2584 = 5000
4) 690 − 2944 : 64 * 15 = 690 − 46 * 15 = 690 − 690 = 0
63
Ответы к странице 63
Задание № 238. На отрезке AB отметили точку C. Расстояние между серединами отрезков AC и AB составляет 12 см. Какова длина отрезка AB?
Ответ
А.____.Е____.С__.D__.В
ED = 12 см
Так как AE = EC, CD = DB, то весь отрезок AB = 2 * 12 = 24 см.
Задание № 239. Начертите координатный луч и отметьте на нем точки A(1), B(7), C(3), D(9). На этом же луче отметьте точки, которые удалены от точки B:
1) на три единичных отрезка;
2) на восемь единичных отрезков.
Найдите координаты Этих точек.
Ответ
Задача от мудрой совы
Задание № 240. Во сколько раз путь по лестнице с первого этажа на десятый длиннее, чем путь с первого этажа на второй?
Решение задачи
С первого этажа на второй − два лестничных марша (один этаж);
с первого этажа на десятый − 18 лестничных маршей (9 этажей).
18 : 2 = 9 : 1 = в 9 раз путь по лестнице с первого этажа на десятый длиннее, чем путь с первого этажа на второй.
65
Ответы к странице 65
Параграф 9. Числовые и буквенные выражения. Формулы
Задание № 241. Прочитайте числовые выражения, используя термины «сумма», «разность», «произведение», «частное»:
1) 12 + 16 сумма чисел 12 и 16
2) 39 − 24 разность чисел 39 и 24
3) 18 * 19 произведение чисел 18 и 19
4) 98 : 14 частное чисел 98 и 14
5) (238 + 124) − 95 разность суммы чисел 238 и 124 и числа 95
6) 39 * 16 + 48 * 2 сумма произведения чисел 39 и 16 и произведения чисел 48 и 2
7) 204 : 6 − 10 : 3 разность частного чисел 204 и 6 и частного чисел 102 и 3
(53 + 38) * (53 − 38) произведение суммы чисел 53 и 38 и их разности
Задание № 242. Найдите значение выражения:
1) 56 + 42 : 14 − 7;
2) (56 + 42) : (14 − 7);
3) (56 + 42) : 14 − 7;
4) 56 + 42 : (14 − 7).
Решение
1) 56 + 42 : 14 − 7 = 56 + 3 − 7 = 59 − 7 = 52
2) (56 + 42) : (14 − 7) = 98 : 2 = 49
3)(56 + 42) : 14 − 7 = 98 : 14 − 7 = 7 − 7 = 0
4) 56 + 42 : (14 − 7) = 56 + 42 : 7 = 56 + 6 = 62
66
Ответы к странице 66
Задание № 243. Найдите значение выражения:
1) 374 + x, если х = 268;
2) 374 − x, если х = 268;
3) a + b + 988, если a = 836, b = 442;
4) a − 314 + 625 − с, если a = 836, c = 442.
Решение
1) 374 + 268 = 642
2) 374 − 268 = 106
3) 714 + 569 + 988 = 2271
4) 836 − 314 + 625 − 442 = 836 − (314 + 442) + 625 = 836 − 756 + 625 = 80 + 625 = 705
Задание № 244. Найдите значение выражения:
1) y + 653, если y = 894;
2) y − 653, если y = 894;
3) a − b − 569, если a = 2316, b = 1495.
Решение
y + 653, при y = 894: 894 + 653 = 1547
y − 653, при y = 894: 894 − 653 = 241
a − b − 569, при a = 2316, b = 1495:
2316 − 1495 − 569 = 252
Задание № 245. В классе учатся a мальчиков и 14 девочек. Сколько всего учащихся в этом классе?
Ответ
a + 14 учащихся в этом классе.
Задание № 246. В саду растет 158 деревьев, из них a деревьев составляют яблони, а остальные − вишни. Сколько вишневых деревьев растет в саду?
Ответ:
158 − a вишневых деревьев.
Задание № 247. За 8 ч самолет пролетел s км. С какой скоростью летел самолет?
Решение
V=s/t
При t = 8 V=s/8 (км/ч)
Ответ: s/8 км/ч скорость самолёта.
Задание № 248. Автомобиль проехал s км со скоростью 65 км/ч. Сколько времени автомобиль был в пути?
Решение
t=s/V
При V = 65 км/ч t=s/65 (ч)
Ответ: s/65 ч автомобиль бы в пути.
Задание № 249. Найдите по формуле пути расстояние, которое пройдет поезд за 6 ч, двигаясь со скоростью 67 км/ч.
Решение
S = V * t
S = 67 * 6 = 402 (км)
Ответ: 402 км пройдет поезд за 6 ч.
Задание № 250. Найдите по формуле пути расстояние, которое проплывет моторная лодка за 7 ч, двигаясь со скоростью 32 км/ч.
Решение
S = V * t
S = 32 * 7 = 224 (км)
Ответ: 224 км проплывет моторная лодка за 7 ч.
Задание № 251. Вычислите значение y по формуле y = 4x − 7, если:
1) x = 26;
y = 4 * 26 − 7 = 104 − 7 = 97
2) х = 15.
y = 4 * 15 − 7 = 60 − 7 = 53
Задание № 252. Вычислите значение a по формуле a = 86 − 5b, если:
1) b = 17
a = 86 − 5b = 86 − 5 * 17 = 86 − 85 = 1
2) b = 9.
a = 86 − 5b = 86 − 5 * 9 = 86 − 45 = 41
Задание № 253. Составьте числовое выражение и найдите его значение:
1) разность суммы чисел 238 и 416 и числа 519;
2) сумма разности чисел 823 и 374 и разности чисел 3477 и 3086;
3) произведение суммы и разности чисел 15 и 12;
4) частное суммы чисел 209 и 193 и разности чисел 42930 и 42924.
Ответы
1) (238 + 416) − 519 = 654 − 519 = 135
2) (823 − 374) + (3477 − 3086) = 840
3) (15 + 12) * (15 − 12) = 27 * 3 = 81
4) (209 + 193) : (42930 − 42924) = 67
Задание № 254. Составьте числовое выражение и найдите его значение:
1) сумма разности чисел 238 и 149 и числа 506;
2) частное суммы и разности чисел 48 и 16;
3) произведение суммы чисел 124 и 126 и разности чисел 313 и 307;
4) разность произведения чисел 32 и 15 и частного чисел 896 и 28.
Ответы 7 гуру
1) (238 − 149) + 506 = 595
2) (48 + 16) : (48 − 16) = 64 : 32 = 2
3) (124 + 126) * (313 − 307) = 250 * 6 = 1500
4) 32 * 15 − 896 : 28 = 448
Задание № 255. Упростите выражение и найдите его значение:
1) 476 + a + 224, если a = 221;
2) x + 246 − 46, если x = 137;
3) 973 − 243 − y, если y = 258.
Решение
476 + a + 224 = (476 + 224) + a = 700 + a = 700 + 221 = 921
x + 246 − 46 = (246 − 46) + x = 200 + x = 200 + 137 = 337
973 − 243 − y = (973 − 243) − y = 730 − y = 730 − 258 = 472
Задание № 256. Упростите выражение и найдите его значение:
1) 2318 + b + 6682, если b = 5195;
2) 829 − 329 + m, если m = 700.
Решение
2318 + b + 6682 = (2318 + 6682) + b = 9000 + b = 9000 + 5195 = 14195
829 − 329 + m = (829 − 329) + m = 500 + m = 500 + 700 = 1200
67
Ответы к странице 67
Задание № 257. На первом участке росло 67 кустов смородины. Потом x кустов пересадили на второй участок, а на первый посадили y новых кустов. Сколько кустов стало на первом участке? Вычислите значение полученного выражения, если х = 18, y = 25.
Решение задачи
На первом участке стало (67 − х + y) кустов.
Если х = 18, y = 25, то 67 − х + y = 67 − 18 + 25 = 74 (к.)
Ответ: (67 − х + y) кустов, 74 куста.
Задание № 258. У Винни−Пуха было m горшочков меда. Пятачок подарил ему еще 24 горшочка, и они вместе съели n горшочков меда. Сколько горшочков меда осталось после этого у Винни−Пуха? Вычислите значение полученного выражения, если m = 56, n = 12.
Решение
Количество горшочков меда (m + 24 − n) шт.
Если m = 56, n = 12, то m + 24 − n = 56 + 24 − 12 = 80 − 12 = 68 (шт.)
Ответ: (m + 24 − n) горшочков, 68 горшочков.
Задание № 259. Пьеро купил m карандашей по 24 сольдо и пять тетрадей по n сольдо, заплатив за тетради больше, чем за карандаши. На сколько больше заплатил Пьеро за тетради, чем за карандаши? Вычислите значение полученного выражения при m = 6, n = 32.
Решение
Пьеро заплатил больше на (5n − 24m) сольдо.
Если m = 6, n = 32, то 5n − 24m = 5 * 32 − 24 * 6 = 160 − 144 = 16 (c.)
Ответ: на (5n − 24m) сольдо, на 16 cольдо.
Задание № 260. Мальвина Купила 8 конфет по a сольдо и b пирожных по 65 сольдо, заплатив за конфеты меньше, чем за пирожные. На сколько меньше заплатила Мальвина за конфеты, чем за пирожные? Вычислите значение полученного выражения при a = 14, b = 4.
Решение
Разница между стоимостью пирожных и стоимостью конфет (65b − 8a) сольдо
Если a = 14, b = 4, то 65b − 8a = 65 * 4 − 8 * 14 = 250 − 112 = на 148 (с.)
Ответ: на (65b − 8a) сольдо, на 148 сольдо.
Задание № 261. В цистерне было 712 л воды. Каждый час из нее вытекает 18 л. Составьте формулу для вычисления объема воды, которая осталась в цистерне через t ч, и вычислите этот объем, если:
1) t = 4;
2) t = 12.
Решение
Пусть V − объем воды, которая осталась в цистерне
V = 712 − 18t
1) Если t = 4, то V = 712 − 18 * 4 = 712 − 72 = 640
2) Если t = 4, то V = 712 − 18 * 12 = 712 − 216 = 496
Ответ: V = 712 − 18t, 640 л, 496 л.
Задание № 262. Илья разложил по m марок из шести альбомов, и еще 12 марок у него осталось. Составьте формулу для вычисления количества марок, которые есть у Ильи, и вычислите это количество, если:
1) m = 18;
2) m = 36.
Пусть k − количество марок, которые есть у Ильи, тогда:
k = 6m + 12
1) Если m = 18, то k = 6 * 18 + 12 = 108 + 12 = 120
2) Если m = 36, то k = 6 * 36 + 12 = 216 + 12 = 228
Ответ: 120 марок, 228 марок.
Задание № 263. Точки A, B и C лежат на одной прямой. Расстояние между A и B равно 30 см, а между точками B и C − 10 см. Найдите расстояние между точками A и C.
1)AB = 30 см, BC = 10 см.
AC = AB + BC = 30 + 10 = 40 см
2)AB = 30 см, BC = 10 см.
AC = AB − BC = 30 − 10 = 20 см
68
Ответы к странице 68
Задание № 264. Наташа купила художественный альбом за 630 р. и несколько сборников стихов по 60 р. каждый. Сколько сборников купила Наташа, если за всю покупку она заплатила 990 р.?
Решение
1) 990 − 630 = 360 (руб.) — потратила Наташа на сборники стихов
2) 360 : 60 = 6 (сб.) — стихов купила Наташа
Ответ: 6 сборников стихов.
Задание № 265. Масса полного ящика с яблоками составляет 25 кг. После того, как продали половину яблок, масса ящика с оставшимися яблоками оказалась равной 15 кг. Какова масса пустого ящика?
Решение
1) 25 − 15 = 10 (кг) — яблок продали
2) 10 * 2 = 20 (кг) — яблок было всего в ящике
3) 25 − 20 = 5 (кг) — масса пустого ящика.
Ответ: 5 кг.
Задание № 266. Кабинки развлекательного аттракциона «Колесо обозрения» (рис. 68) последовательно пронумерованы числами 1, 2, 3, и т.д. Сколько всего кабинок, если известно, что когда кабинка с номером 24 занимает самую высокую позицию, то кабинка с номером 10 − самую низкую?
Решение
Колесо имеет форму круга.
Посчитаем количество кабинок половины круга:
когда кабинка № 24 наверху, а кабинка № 10 внизу, то между ними находится 13 кабинок с правой стороны и столько же с левой стороны, следовательно:
13 * 2 = 26 кабинок находится между кабинками № 24 и № 10.
26 + 2 = 28 кабинок всего на аттракционе.
71-72
Ответы к странице 71-72
Параграф 10. ГДЗ к теме учебника математики Уравнения 5 класс, Мерзляк
Страница 71
Задание № 267. Какое из чисел 3, 12, 14 является корнем уравнения: 1) х + 16 = 28; 2) 4х − 5 = 7?
Ответ
х + 16 = 28
х = 28 − 16
х = 124х − 5 = 7
4х = 7 + 5
х = 12 : 4
х = 3
Страница 72
Задание № 268. Какое из чисел 3, 12, 14 является корнем уравнения: 1) 234 − y = 220; 2) 72 : b + 13 = 19?
Ответ
234 − y = 220
y = 234 − 220
y = 14
234 − 14 = 220
220 = 220
Ответ: у=1472 : b + 13 = 19
72 : b = 19 − 13
b = 72 : 6
b = 12
72 : 12 + 13 = 19
19 = 19
Ответ: b =12
Задание № 269. Решите уравнение:
1) x + 34 = 76;
2) 238 + y = 416;
3) a + 157 = 324;
4) 356 + b = 782;
5) x − 546 = 216;
6) 206 − y = 139;
7) 895 − a = 513;

Ответ
x + 34 = 76
х = 76 − 34
х = 42
Ответ: 42.238 + y = 416
y = 416 − 238
y = 178
Ответ: 178a + 157 = 324
a = 324 − 157
a = 167
Ответ: 167356 + b = 782
b = 782 − 356
b = 426
Ответ: 426x − 546 = 216
x = 216 + 546
x = 762
Ответ: 762206 − y = 139
y = 206 − 139
y = 67
Ответ: 67895 − a = 513
a = 895 − 513
a = 382
Ответ: 382m − 2092 = 1067
m = 1067 + 2092
m = 3159
Ответ: 3159
Задание № 270. Решите уравнение:
1) x + 48 = 94;
2) 234 + y = 452;
3) x − 174 = 206;
4) 378 − b = 165.
Решение
x + 48 = 94
x = 94 − 48
x = 46
Ответ: 46234 + y = 452
y = 452 − 234
у = 218
Ответ: 218x − 174 = 206
x = 206 + 174
x = 380
Ответ: 380378 − b = 165
b = 378 − 165
b = 213
Ответ: 213
Задание № 271. Решите уравнение:
1) (134 + x) − 583 = 426;
2) (208 + x) − 416 = 137;
3) (x − 506) + 215 = 429;
4) (y − 164) + 308 = 500;
5) (942 − a) − 126 = 254;
6) (801 − b) − 224 = 368;
7) 475 − (x − 671) = 325;

9) 403 − (634 − a) = 366;
10) 643 − (581 − b) = 292;
11) 987 − (x + 364) = 519;
12) 3128 − (m + 425) = 1509.
Решение
(134 + x) − 583 = 426
x = 426 − 134 + 583
x = 292 + 583
x = 875
Ответ: 875(208 + x) − 416 = 137
x = 137 − 208 + 416
x = 135 + 210
x = 345
Ответ: 345(x − 506) + 215 = 429
x = 429 + 506 − 215
x = 429 + 291
x = 720
Ответ: 720(y − 164) + 308 = 500
y = 500 + 164 − 308
y = 664 − 308
y = 356
Ответ: 356(942 − a) − 126 = 254
a = 942 − 254 − 126
a = 688 − 126
a = 562
Ответ: 562(801 − b) − 224 = 368
b = 801 − 224 − 368
b = 801 − 592
b = 209
Ответ: 209475 − (x − 671) = 325
475 − x + 671 = 325
x = 475 + 671 − 325
x = 150 + 671
x = 821
Ответ: 821972 − (y − 504) = 284
y = 972 + 504 − 284
y = 1476 − 284
y = 1192
Ответ: 1192403 − (634 − a) = 366
a = 366 − 403 + 634
a = 1000 − 403
a = 597
Ответ: 597643 − (581 − b) = 292
b = 292 + 581 − 643
b = 873 − 643
b = 230
Ответ: 230987 − (x + 364) = 519
x = 987 − 364 − 519
x = 623 − 519
x = 104
Ответ: 1043128 − (m + 425) = 1509
m = 3128 − 425 − 1509
m = 2703 − 1509
m = 1194
Ответ: 1194
Задание № 272. Решите уравнение:
1) (39 + x) − 84 = 78;
2) (x − 83) + 316 = 425;
3) (600 − x) − 92 = 126;
4) 253 − (x − 459) = 138;
5) 502 − (217 − x) = 421;
6) 871 − (x + 157) = 385.
Решение
(39 + x) − 84 = 78
x = 78 + 84 − 39
x = 162 − 39
x = 123
Ответ: 123(x − 83) + 316 = 425
x − 83 = 425 − 316
x = 109 + 83
x = 192
Ответ: 192(600 − x) − 92 = 126
600 − x = 126 + 92
x = 600 − 218
x = 382
Ответ: 382253 − (x − 459) = 138
x − 459 = 253 − 138
x = 115 + 459
x = 574
Ответ: 574502 − (217 − x) = 421
217 − x = 502 − 421
217 − x = 81
x = 217 − 81
x = 136
Ответ: 136871 − (x + 157) = 385
x + 157 = 875 − 385
x = 486 − 157
x = 329
Ответ: 329
Задание № 273. Решите с помощью уравнения задачу.
1) Оксана задумала число. Если к этому числу прибавить 43 и полученную сумму вычесть из числа 96, то получим число 25. Какое число задумала Оксана?
Решение
Пусть задуманное число x, тогда:
96 − (x + 43) = 25
x + 43 = 96 − 25
x + 43 = 71
x = 71 − 43
x = 28
Ответ: Оксана задумала число 28.
2) У Буратино было 74 сольдо. После того как он купил себе учебники для школы , папа Карло дал ему 25 сольдо. Тогда у Буратино стало 68 сольдо. Сколько сольдо потратил Буратино на учебники?
Решение
Пусть x − количество сольдо, потраченное Буратино на учебники, тогда:
(74 − x) + 25 = 68
74 − х = 68 − 25
74 − x = 43
x = 74 − 43
x = 31
Ответ: 31 сольдо потратил Буратино на учебники.
73
Ответы к странице 73
Задание № 274
Решите с помощью уравнения задачу. Ваня задумал число. Если к этому числу прибавить 27 и из полученного суммы вычесть 14, то получим 36. Какое число задумал Ваня?
Решение
Пусть х − число, задуманное Ваней, тогда:
(x + 27) − 14 = 36
x + 27 = 36 + 14
x = 50 − 27
x = 23
Ответ: 23 — число, задуманное Ваней.
Задание № 275
Какое число надо подставить вместо a, чтобы корнем уравнения:
1) (x + a) − 7 = 42 было число 22;
(x + a) − 7 = 42, при x = 22 равно:
(22 + a) − 7 = 42
22 + a = 42 + 7
a = 49 − 22
a = 27
Ответ: 27.
2) (a − x) + 4 = 15 было число 3?
(a − x) + 4 = 15, при x = 3 равно:
(a − 3) + 4 = 15
a − 3 = 15 − 4
a = 11 + 3
a = 14
Ответ: 14.
Задание № 276
Какое число надо подставить вместо a, чтобы корнем уравнения:
1) (x − 7) + a = 23 было число 9;
(x − 7) + a = 23, при x = 9 равно:
(9 − 7) + a = 23
2 + a = 23
a = 23 − 2
a = 21
Ответ: 21.
2) (11 + x) + 101 = a было число 5?
(11 + x) + 101 = a, при x = 5 равно:
(11 + 5) + 101 = a
a = 16 + 101
a = 117
Ответ: 117.
Задание № 277
Лиза была в школе с 8 ч 15 мин до 15 ч 20 мин. Вечером она пошла на тренировку. Там она провела на 5 ч 40 мин меньше времени, чем в школе. Сколько времени Лиза была на тренировке?
Решение
1) 15 ч 20 мин − 8 ч 15 мин = 7 ч 5 мин
2) 7 ч 5 мин − 5 ч 40 мин = 6 ч 65 мин − 5 ч 40 мин = 1 ч 25 мин
Ответ: 1 ч 25 мин Лиза была на тренировке.
Задание 278
Начертите отрезок длиной 12 см. Над одним концом отрезка напишите число 0, а над другим − 480. Поделите отрезок на шесть равных частей. Отметьте на полученной шкале числа 40, 100, 280, 360, 420.
Ответ
Задание № 279 старый учебник. Можно ли, имея 450 р., купить 3 кг бананов по 42 р. за 1 кг, 2 кг мандаринов по 50 р. за 1 кг и 4 кг апельсинов по 48 р. за 1 кг?
Решение
3 * 42 + 2 * 50 + 4 * 48 = 126 + 100 + 192 = 418 (р.) потребуется на покупку всех фруктов, а так как 418 < 450, т осуществить покупку можно.
Задание № 279
Можно ли, имея 900 р., купить 3 кг бананов по 65 р. за 1 кг, 2 кг мандаринов по 130 р. за 1 кг и 4 кг апельсинов по 95 р. за 1 кг?
Решение
3 * 65 + 2 * 130 + 4 * 95 = 195 + 260 + 380 = 835 (р.) — потребуется на покупку всех фруктов, а так как 835 < 900, то осуществить покупку можно.
Задание № 280
В трёх ящичках лежат шары: в первом ящичке − два белых; во втором ящичке − два черных; в третьем − белый и черный. На ящички наклеены этикетки ББ, ЧЧ, БЧ так, что содержимое каждого из них не соответствует этикетке. Как вынув один шар, узнать, что в каком ящичке лежит?
Решение
По условию несоответствия этикеток:
в ящичке ББ будут либо черные, либо белый и черный шарики;
в ящичке ЧЧ будут либо белые, либо белый и черный шарики;
Нужно взять один шар из ящичка с надписью БЧ:
если шарик в БЧ черный, значит и второй шарик в БЧ черный, а это означает что в ББ черный и белый шарики, а в ЧЧ оба белых шарика;
если шарик в БЧ белый, значит и второй шарик в БЧ белый, а это означает что в ЧЧ черный и белый шарики, а в ББ оба черных шарика.
75
Ответы к странице 75
Параграф 11. Угол. Обозначение углов
Задание № 281. Как можно обозначить угол, изображенный на рисунке 73?
∠MKN, ∠NKM, ∠K.
Задание № 282. На каком из рисунков 74, а, б, в луч OK является биссектрисой угла AOB?
На рисунке в.
Задание № 283. Назовите все углы, изображенные на рисунке 75.
∠BAM, ∠BAE, ∠EAM.
Задание № 284. Запишите все углы, изображенные на рисунке 76.
∠OTF, ∠OTC, ∠CTF.
76
Ответы к странице 76
Задание № 285. Какие из лучей, изображенных на рисунке 77, пересекают сторону угла BOC?
Ответ
Лучи: AK, ST.
Задание № 286. Какие из лучей, изображенных на рисунке 78, пересекают сторону угла BOC?
Ответ
Лучи: RP, FE.
Задание № 287. Начертите ∠MNE и проведите лучи NA и NC между его сторонами. Запишите все образовавшиеся углы.
Ответ
∠MNE, ∠MNA, ∠ANC, ∠CNE, ∠MNC, ∠ANE.
Задание № 288. На рисунке 79 ∠ABE = ∠CBF. Есть ли еще на этом рисунке равные углы?
Ответ
∠ABF = ∠CBE
Задание № 289. На рисунке 80 ∠AOB = ∠DOE, ∠BOC = ∠COD. Есть ли еще на этом рисунке равные углы?
Ответ
∠AOC = ∠EOC, ∠AOD = ∠EOB.
Задание № 290. На рисунке 81 углы FOK и MOE равны. Какие еще углы, изображенные на этом рисунке, равны?
Ответ
∠FOM = ∠EOK
Задание № 291. Составьте числовое выражение и найдите его значение:
1) произведение суммы чисел 18 и 20 и числа 8;
(18 + 20) * 8 = 38 * 8 = 304
2) частное от деления разности чисел 128 и 29 на число 11;
(128 − 29) : 11 = 99 : 11 = 9
3) частное от деления произведения чисел 15 и 6 на их разность.
15 * 6 : (15 − 6) = 90 : 9 = 10
77
Ответы к странице 77
Задание № 292
Решите уравнение: 1) x + 504968 = 1017216; 2) 120340526 − x = 7908049.
Решение уравнения
x + 504968 = 1017216
х = 1017216 − 504968
х = 512248
512248 + 504968 = 1017216
1017216 = 1017216
Ответ: х = 512248._1017216
504968
512248
120340526 − x = 7908049
х = 120340526 − 7908049
х = 112432477
120340526 − 112432477 = 7908049
7908049 = 7908049
Ответ: х = 112432477_120340526
7908049
112432477
Задание № 293 старый учебник. На XXIX Олимпийских играх, состоявшихся в 2008 г. в Пекине (Китай), олимпийская сборная России завоевала 73 медали. Наши спортсмены получили 44 золотых и серебряных медали, а золотых и бронзовых − 52. Сколько медалей каждого вида завоевала на этой олимпиаде наша сборная?
Решение
1) 73 − 52 = 21 (м.) — серебряную
2) 44 − 21 = 23 (м.) — золотых
3) 52 − 23 = 29 (м.) — бронзовых
Ответ: 21,23 и 29 медалей.
Задание № 293
На XXII зимних Олимпийских играх, состоявшихся в 2014 г. в в городе Сочи, олимпийская сборная России завоевала 33 медали. Наши спортсмены получили 24 золотых и серебряных медали, а золотых и бронзовых − 22. Сколько медалей каждого вида завоевала на этой олимпиаде наша сборная?
Решение
1) 33 − 22 = 11 (м.) — серебряных
2) 24 − 11 = 13 (м.) — золотых
3) 22 − 13 = 9 (м.) — бронзовых
Ответ: 11, 13 и 9 медалей.
Задание № 294
Учащиеся пятых классов ехали на двух автобусах на экскурсию. Когда из одного автобуса, в котором было 42 учащихся, восемь учащихся перешли во второй автобус, то в обоих автобусах учащихся стало поровну. Сколько учащихся было сначала?
Решение
1) 42 − 8 = 34 (уч.) — стало во втором автобусе
2) 34 − 8 = 26 (уч.) — было во втором автобусе
Ответ: 26 учащихся.
Задание № 295
На озере начали распускаться кувшинки. Каждый день количество кувшинок возрастало вдвое. На двадцатый день кувшинками заросла вся поверхность озера. На какой день половина озера была покрыта кувшинками?
Ответ
Половина озера была покрыта кувшинками на 19−й день (на 20−й день число удвоилось и озеро заросло полностью).
81
Ответы к странице 81
Параграф 12. ГДЗ к теме учебника математики Виды углов. Измерение углов 5 класс, Мерзляк
Задание № 296. Начертите:
1) острый угол EFC;
2) прямой угол ORT;
3) тупой угол D;
4) развернутый угол KAP.
Решение
Задание № 297. Найдите на рисунке 93 острые, тупые и прямые углы.
Решение
Острые углы: ∠ACM, ∠CMK, ∠TPO;
Тупые углы: ∠AKM, ∠PTQ, ∠TQO;
Прямые углы: ∠CAK, ∠POQ.
Задание № 298. Какие из данных углов острые, тупые, прямые, развернутые:
∠A = 96°; ∠B = 84°; ∠S = 180°; ∠D = 90°; ∠R = 162°; ∠E = 60°; ∠Q = 100°; ∠M = 72°?
Решение
Острые углы: ∠B = 84°; ∠E = 60°; ∠M = 72°;
Тупые углы: ∠A = 96°; ∠R = 162°; ∠Q = 100°;
Прямые углы: ∠D = 90°;
Развернутый углы: ∠S = 180°.
82
Ответы к странице 82
Задание № 299. Найдите, пользуясь транспортиром, градусные меры углов, изображенных на рисунке 94. Определите вид каждого угла.
Ответ
∠AMK = 28° − острый;
∠CTF = 33° − острый;
∠POB = 120° − тупой;
∠SNE = 125° − тупой.
Задание № 300. Найдите, пользуясь транспортиром, градусные меры углов, изображенных на рисунке 95. Определите вид каждого угла.
Ответ
∠PRT = 133° − тупой;
∠EFM = 40° − острый;
∠BCQ = 110° − тупой;
∠AKS = 67° − острый.
Задание № 301. Начертите угол градусная мера которого равна:
1) 38°; 2) 124°; 3) 92°; 4) 90°; 5) 87°; 6) 54°; 7) 170°; 
Определите вид каждого угла.
Ответ
Проводим луч ОА. Откладываем углы АОВ, отмеряя по транспортиру с вершиной в точке О.
∠AOB = 124° − тупой
∠AOB = 92° − тупой
∠AOB = 90° − прямой
∠AOB = 87° − острый
∠AOB = 54° − острый
∠AOB = 170° − тупой
∠AOB = 65° − острый
Задание № 302. Проведите луч. Отложите от этого луча угол, градусная мера которого равна:
1) 40°; 2) 130°; 3) 68°; 4) 164°.
Определите вид каждого из построенных углов.
Ответ
∠AOB = 40° − острый
∠COB = 130° − тупой
∠DOB = 68° − острый
∠EOB = 164° − тупой
Задание № 303. На рисунке 96 ∠CMK = 132°, а угол AMK − развернутый. Вычислите величину угла AMC.
Ответ
∠AMC = ∠AMK − ∠CMK = 180° − 132° = 48°
Задание № 304. На рисунке 97 угол AOK − прямой, ∠POC = 54°, а угол COK − развернутый. Вычислите величину угла AOP.
Ответ
∠AOP = ∠COK − ∠AOK − ∠POC = 180° − 90° − 54° = 36°
83
Ответы к странице 83
Задание № 305. Какой из углов, изображенных на рисунке 98, наибольший? Наименьший?
Ответ
∠C − наибольший;
∠D − наименьший.
Задание № 306. Начертите угол CDE, равный 152°. Лучом DA разделите этот угол на два угла так, чтобы ∠CDA = 98°. Вычислите величину угла ADE.
Ответ
∠ADE = ∠CDE − ∠CDA
∠ADE = 152° − 98° = 54°
Задание № 307. Начертите угол ABC, равный 106°. Лучом BD разделите этот угол на два угла так, чтобы ∠ABD = 34°. Вычислите величину угла DBC.
Ответ
∠DBC = ∠ABC − ∠ABD
∠DBC = 106° − 34° = 72°
Задание № 308. Из вершины прямого угла BOM (рис.99) проведены два луча OA и OC так, что ∠BOC = 74°, ∠AOM = 62°. Вычислите величину угла AOC.
Ответ
∠AOB = ∠BOM − ∠AOM = 90° − 62° = 28°;
∠COM = ∠BOM − ∠COB = 90° − 74° = 16°;
∠AOC = ∠BOM − ∠AOB − ∠COM = 90° − 28° − 16° = 46°.
Задание № 309. Из вершины развернутого угла ACP (рис.100) проведены два луча CT и CF так, что ∠ACF = 158°; ∠TCP = 134°. Вычислите величину угла TCF.
Ответ
∠ACT = ∠ACP − ∠TCP = 180° − 134° = 46°;
∠FCP = ∠ACP − ∠ACF = 180° − 158° = 22°;
∠TCF = ∠ACP − ∠ACT − ∠FCP = 180° − 46° − 22° = 112°.
Задание № 310. Верно ли утверждение:
1) угол, который меньше тупого, − острый; Не верно, так как прямой угол тоже меньше тупого, как и острый.
2) угол, который меньше развернутого, − тупой; Не верно, так как меньше развернутого может быть и тупой, и острый, и прямые углы.
3) половина тупого угла − острый угол; Верно.
4) сумма градусных мер двух острых углов больше 90°; Не верно, может быть и меньше 90°.
5) угол, который больше прямого, − тупой? Не верно: больше прямого может быть тупой и развернутой угол.
Задание № 311. Найдите градусную меру угла между стрелками часов, если они показывают:
1) 3 ч — 90°
2) 6 ч — 180°
3) 4 ч — 120°
4) 11 ч — 30°
5) 7 ч — 150°
84-85
Ответы к странице 84-85
Задание № 312. Луч BK является биссектрисой угла CBD, ∠ABK = 146° (рис.101,а). Вычислите градусную меру угла CBD.
Ответ
∠KBC = ∠ABC − ∠ABK = 180° − 146° = 34°
∠CBD = 2 * ∠KBC = 2 * 34° = 68°
Задание № 313. Луч OA является биссектрисой угла COM, ∠COM = 54° (рис.101,б). Вычислите градусную меру угла BOA.
Ответ
∠MOA = ∠COM : 2 = 54° : 2 = 27°
∠BOM = ∠BOC − ∠COM = 180° − 54° = 126°
∠BOA = ∠MOA − ∠BOM = 27° + 126° = 153°
Задание № 314. Проведите три прямые, пересекающиеся в одной точке. Запишите все развернутые углы, образовавшиеся при этом.
Ответ
Развернутые углы: ∠AOD, ∠BON, ∠MOC.
Задание № 315. Проведите шесть прямых, пересекающихся в одной точке. Верно ли, что среди образовавшихся при этом углов есть угол, градусная мера которого меньше 31°?
Ответ
Верно, так как 360° : 12 = 30°
Задание № 316. Заполните цепочку вычислений:
4 см -> 1200см -> 1080 см -> 120 см -> 420 см.
120 мин -> 4 ч -> 40 мин -> 39 мин 6 с.
Задание № 317. Верно ли неравенство (a + 253) * 7 < (9864 − a) : 4 при a = 124?
Ответ
(124 + 253) * 7 < (9864 − 124) : 4
377 * 7 < 9740 : 4
2639 < 2325 неверно
неравенство при a = 124 неверно.
Задание № 318. В четыре стакана помещается столько же молока, сколько и в банку. В стакан и банку помещается 1 кг 200 г молока. Сколько грамм молока помещается в стакан?
Решение
4 стакана = 1 банка, следовательно банка + стакан = 4 + 1 = 5 стаканов.
1 кг 200 г = 1200 г : 5 = 240 (г) умещается в один стакан.
Ответ: 240 г.
Задание № 319. Длина сухопутной границы России с Китаем, Монголией и Казахстаном составляет 15 293 км. Найдите длину границы России с каждым из этих государств, если длина границы с Китаем и Монголией равна 7694 км, а с Китаем и Казахстаном − 11808 км.
Решение
15293 − 7964 = 7599 (км) длина границы с Казахстаном
_15293
7964
7599
15293 − 11808 = 3485 (км) длина границы с Монголией
_15293
11808
3485
7599 + 3485 = 11084 (км) длина границы с Казахстаном и Монголией вместе
+7599
3485
11084
15293 − 11084 = 4209 (км) длина границы с Китаем
_15293
11084
4209
Ответ: 7599 км, 3485 км, 11084 км, 4209 км.
Задание № 320. Улитка за день поднимается вверх по столбу на 3 м, а за ночь съезжает на 2 м вниз. На какой день она доберется до вершины столба, высота которого равна 20 м?
Решение
3 − 2 = 1 (м) — высота подъема улитки в сутки.
За 17 суток улитка поднимется на 17 метров.
На 18 день улитка поднимется на 3 метра и достигнет 17 + 3 = 20 м, то есть вершины столба.
Ответ: на 18-й день.
87
Ответы к странице 87
Параграф 13. ГДЗ к теме учебника Многоугольники. Равные фигуры
Задание № 321. Назовите вершины и стороны пятиугольника, изображенного на рисунке 109.
Ответ
Вершины: M, N, K, P, E.
Стороны: MN, NK, KP, PE, EM.
Задание № 322. Начертите:
1) четырехугольник; 2) пятиугольник; 3) шестиугольник; 4) семиугольник.
Ответ
Задание № 323. Вычислите периметр пятиугольника, стороны которого равны 2 см, 4 см, 5 см 5 мм, 6 см, 7 см.
Ответ
Р = 2 см + 4 см + 5 см 5 мм + 6 см + 7 см = 24 см 5 мм
Задание № 324. Вычислите периметр шестиугольника, три стороны которого равны по 8 см, а три другие − по 10 см.
Ответ
Р = 3 * 8 + 3 * 10 = 24 + 30 = 54 см
Задание № 325. Нарисуйте в тетради фигуру, равную той, которая изображена на рисунке 110.
Ответ
Перечерчиваем фигуры в тетрадь.
88
Ответы к странице 88
Задание № 326. Нарисуйте в тетради фигуру, равную той, которая изображена на рисунке 111.
Ответ
Перечерчиваем фигуры в тетрадь.
Задание № 327. Одна из сторон четырех угольника равна 8 см, вторая сторона в 3 раза больше первой, а третья − на 7 см меньше второй и на 9 см больше четвертой. Вычислите периметр четырехугольника.
Решение
1) 8 * 3 = 24 (см) — длина второй стороны
2) 24 − 7 = 17 (см) — длина третьей стороны
3) 17 − 9 = 8 (см) — длина четвертой стороны
4) 8 + 24 + 17 + 8 = 57 (см) — Р
Ответ: 57 см.
Задание № 328. Стороны пятиугольника пронумеровали. Первая сторона равна 4 см, а каждая следующая сторона на 2 см длиннее предыдущей. Вычислите периметр пятиугольника.
Решение
1) 4 + 2 = 6 (см) — длина второй стороны
2) 6 + 2 = 8 (см) — длина третьей стороны
3) 8 + 2 = 10 (см) — длина четвертой стороны
4) 10 + 2 = 12 (см) — длина пятой стороны
5) 4 + 6 + 8 + 10 + 12 = 40 (см) — Р
Ответ: 40 см.
Задание № 329. 1) Сколько диагоналей можно провести из одной вершины: а) пятиугольника; б) девятиугольника; в) n − угольника, где n > 3?
2) Сколько всего диагоналей можно провести: а) в пятиугольнике; б) в девятиугольнике: в) n − угольнике, где n > 3?
Ответ
1)
а) Всего вершин 5 − (исходная вершина) − (2 вершины, лежащие с исходной на одной стороне) = 2, то есть в пятиугольнике из одной вершины можно провести только две диагонали;
б) Всего вершин 9 − (исходная вершина) − (2 вершины, лежащие с исходной на одной стороне) = 6, то есть в девятиугольнике из одной вершины можно провести только 6 диагоналей;
в) Всего вершин n − (исходная вершина) − (2 вершины, лежащие с исходной на одной стороне) = n − 3, то есть в n − угольнике из одной вершины можно провести только n − 3 диагоналей.2)
а) Из каждой вершины пятиугольника можно провести по 2 диагонали, одна (половина) из которых будет совпадать с диагональю от другой вершины, следовательно: (5 * 2) : 2 = 5 диагоналей можно провести в пятиугольнике;
б) Из каждой вершины девятиугольника можно провести по 6 диагоналей, половина из которых будет совпадать с диагоналями от другой вершины, следовательно: (9 * 6) : 2 = 27 диагоналей можно провести в девятиугольнике;
в) Из каждой вершины n − угольника можно провести по n − 3 диагоналей, половина из которых будет совпадать с диагоналями от другой вершины, следовательно: ( n * ( n − 3 ) ) : 2 = ( n*n − 3 n ) : 2 диагоналей можно провести в n − угольнике.
Задание № 330. Как используя шаблон угла, градусная мера которого равна 13°, построить угол, градусная мера которого равна 2°?
Ответ
Отложим от производного луча шаблоном угла последовательно угол 14 раз: 14 * 13° = 182°
Полученный таким образом угол больше развернутого на 2°.
Задание № 331. Как построить угол, градусная мера которого равна 1°, используя шаблон угла, градусная мера которого равна:
а) 19°;
Отложим от производного луча шаблоном угла последовательно угол 19 раз: 19 * 19° = 361°.
Полученный угол больше угла 360° на 1°.
б) 7°?
Отложим от производного луча шаблоном угла последовательно угол 13 раз: 13 * 7° = 91°.
Полученный угол больше прямого угла на 1°.
Задание № 332. Существует ли многоугольник с периметром, равным 1000000 см, который можно целиком расположить в квадрате со стороной 1см?
Ответ
Существует. Это многоугольник в виде звезды с очень большим количеством лучей.
Задание № 333. Сравните: 1) 3986 г и 4 кг; 2) 6 м и 712 см; 3) 60 см и 602 мм; 4) 999 кг и 10 ц.
Ответ
4000 г
1) 3986 г < 4 кг600 см
2) 6 м < 712 см600 мм
3) 60 см < 602 мм1000 кг
4) 999 кг < 10 ц
89
Ответы к странице 89
Задание № 334
Выполните сложение, выбирая удобный порядок вычислений:
1) (636 + 927) + 364 = (636 + 364) + 927 = 1000 + 927 = 1927
2) (425 + 798) + 675 = (425 + 675) + 798 = 1100 + 798 = 1898
3) 212 + 493 + 788 + 807 = (212 + 788) + (493 + 807) = 1000 + 1300 = 2300
4) 161 + 455 + 839 + 945 = (161 + 839) + (455 + 945) = 1000 + 1400 = 2400
Задание № 335
Известно, что ∠ABC = 74°, а луч BD − его биссектриса. Вычислите величину угла DBC.
Биссектриса делит угол пополам, следовательно:
∠DBC = ∠ABC : 2 = 74° : 2 = 37°
Задание № 336 старый учебник. Высота самой высокой горы Европы Монблан равна 4807 м. Она на 2153 м ниже самой высокой горы Южной Америки Аконкагуа, которая на 767 м выше самой высокой горы Северной Мак−Кинли. Какова высота самой высокой горы Африки Килиманджаро, если она на 298 м ниже горы Мак−Кинли? Какова высота самой высокой горы мира Эверест (рис.112), если она на 2953 м выше горы Килиминджаро?
Решение
1) 4807 + 2153 = 6960 (м) — высота горы Аконкагуа
2) 6960 − 767 = 6193 (м) — высота горы Мак−Кинли
3) 6193 − 298 = 5895 (м) — высота горы Килиманджаро
4) 5895 + 2953 = 8848 (м) — высота Эвереста
Ответ: 8848 м.
Задание № 336
Высота самой высокой горы Европы Монблан равна 4809 м. Она на 2151 м ниже самой высокой горы Южной Америки Аконкагуа, которая на 770 м выше самой высокой горы Северной Америки Денали. Какова высота самой высокой горы Африки Килиманджаро, если она на 295 м ниже горы Денали? Какова высота самой высокой горы мира Джомолунгмы (Эверест) (рис.112), если она на 2953 м выше горы Килиминджаро?
Решение
1) 4809 + 2151 = 6960 (м) — высота горы Аконкагуа
2) 6960 − 770 = 6190 (м) — высота горы Денали
3) 6190 − 295 = 5895 (м) — высота горы Килиманджаро
4) 5895 + 2953 = 8848 (м) — высота Эвереста
Ответ: 5895 м, 8848 м.
Задание № 337
Лимоны одинаковой массы продают поштучно. Масса каждого лимона составляет целое количество граммов. Купили больше двух, но меньше семи лимонов. Масса всей покупки составляет 850 г. Какова масса одного лимона?
Решение
850 без остатка делится только на 5, поэтому купили 5 лимонов.
850 : 5 = 170 (г.) масса одного лимона
Ответ: 170 г.
92
Ответы к странице 92
Параграф 14. Треугольник и его виды
Задание № 338. Определите вид треугольника, изображенного на рисунке 121, в зависимости от вида его углов и количества равных сторон.
Ответ
а. Остроугольный разносторонний
б. Прямоугольный разносторонний
в. Остроугольный равнобедренный
г. Тупоугольный равнобедренный
д. Тупоугольный разносторонний
е. Прямоугольный равнобедренный
Задание № 339. Начертите:
1) разносторонний остроугольный треугольник;
2) равнобедренный прямоугольный треугольник;
3) равнобедренный тупоугольный треугольник.
Ответ
93
Ответы к странице 93
Задание № 340. Начертите:
1) разносторонний прямоугольный треугольник;
2) разносторонний тупоугольный треугольник;
3) равнобедренный остроугольный треугольник.
Ответ
Задание № 341. Найдите периметр треугольника со сторонами 16 см, 22 см и 28 см.
Ответ
Р = 16 + 22 + 28 = 66 см
Задание № 342. Найдите периметр треугольника со сторонами 14 см, 17 см и 17 см.
Ответ
Р = 14 + 17 + 17 = 48 см
Задание № 343. Начертите произвольный треугольник, измерьте его стороны и углы, найдите периметр и сумму углов этого треугольника.
Ответ
∠ABC = 90°
∠BCA = 45°
∠CAB = 45°
AB = 3 см
BC = 3 см
AC = 4 см 24 мм
Р = 3 + 3 + 4,24 = 10,24 (см)
Задание № 344. Одна сторона треугольника равна 24 см, вторая − на 18 см больше первой, а третья сторона − в два раза меньше второй. Найдите периметр треугольника.
Решение
1) 24 + 18 = 42 (см) — длина второй стороны треугольника
2) 42 : 2 = 21 (см) — длина третьей стороны треугольника
3) 24 + 42 + 21 = 87 (см) — периметр треугольника
Ответ: 87 см.
Задание № 345. Одна сторона треугольника равна 12 см, вторая сторона в 3 раза больше первой, а третья − на 8 см меньше второй. Найдите периметр треугольника.
Решение
1) 12 * 3 = 36 (см) — длина второй стороны треугольника
2) 36 − 8 = 28 (см) — длина третьей стороны треугольника
3) 12 + 36 + 28 = 76 (см) — периметр треугольника
Ответ: 76 см.
Задание № 346. 1) Найдите периметр равнобедренного треугольника, основание которого равно 13 см, а боковая сторона − 8 см.
Так как треугольник равнобедренный, то и вторая боковая сторона равна 8 см, следовательно:
Р = 13 + 8 + 8 = 29 (см)
Ответ: 29 см.
2) Периметр равнобедренного треугольника равен 39 см, а основание − 15 см. Найдите боковые стороны треугольника.
Так как треугольник равнобедренный, то его боковые стороны равны:
1) 39 − 15 = 24 (см) — длина двух боковых сторон треугольника
2) 24 : 2 = 12 (см) — длина каждой боковой стороны треугольника
Ответ: 24 см и 12 см.
Задание № 347. Периметр равнобедренного треугольника равен 28 см, а боковая сторона − 10 см. Найдите основание треугольника.
Решение
Так как треугольник равнобедренный, то его боковые стороны равны, тогда:
28 − (10 * 2) = 28 − 20 = 8 (см) — длина основания треугольника
Ответ: 8 см.
94
Ответы к странице 94
Задание № 348
Периметр треугольника равен p см, одна сторона − 22 см, вторая сторона − b см. Составьте выражение для нахождения третьей стороны. Вычислите длину третьей стороны, если p = 72, b = 26.
Решение
Третья сторона равна p − 22 − b
Если p = 72, b = 26, то 72 − 22 − 26 = 24
Ответ: (p − 22 − b ) см, длина третьей стороны треугольника 24 см .
Задание № 349
Периметр треугольника равен 97 см, одна сторона − а см, вторая − b см. Составьте выражение для нахождения третьей стороны. Вычислите длину третьей стороны, если а = 32, b = 26.
Решение
Третья сторона равна 97 − а − b
Если а = 32, b = 26, то 97 − 32 − 26 = 39 (см) — длина третьей стороны
Ответ: (97 − а − b) см, длина третьей стороны треугольника 39 см.
Задание № 350
С помощью линейки и транспортира постройте треугольник ABC и укажите его вид, если:
1) две стороны равны 3 см и 6 см, а угол между ними − 40°; Разносторонний тупоугольный
2) две стороны равны 2 см 5 мм и 5 см, а угол между ними − 130°; Разносторонний тупоугольный
3) две стороны равны по 3 см 5 мм, а угол между ними − 54°; Равнобедренный остроугольный
4) сторона AB равна 4 см, а углы CAB и CBA соответственно равны 30° и 70°; Разносторонний остроугольный
5) сторона AB равна 2 см 5 мм, а углы CAB и CBA соответственно равны 100° и 20°; Разносторонний тупоугольный
6) сторона BC равна 5 см, а углы ABC и BCA соответственно равны 30° и 60°; Разносторонний прямоугольный
7) сторона BC равна 5 см 5 мм, а углы ABC и BCA равны по 45°; Равнобедренный прямоугольный

Задание № 351
С помощью линейки и транспортира постройте треугольник и укажите его вид, если:
1) две стороны равны 3 см и 4 см, а угол между ними − 90°; Разносторонний прямоугольный
2) две стороны равны 4 см 5 мм, а угол между ними − 60°; Остроугольный равносторонний
3) одна сторона равна 6 см, а углы, прилежащие к этой стороне, − 90° и 45°; Равнобедренный прямоугольный
4) одна сторона равна 4 см 5 мм, а углы, прилежащие к этой стороне, − по 35°. Равнобедренный тупоугольный
Задание № 352
Постройте треугольник, стороны которого содержат четыре точки, изображенные на рисунке 122.
Ответ
Задание № 353
Сколько треугольников изображено на рисунке 123?
Ответ
а) 7 треугольников.
б) 18 треугольников.
95
Ответы к странице 95
Задание № 353 старый учебник. Сколько треугольников изображено на рисунке 123?
Ответ
а) 7 треугольников.
б) 18 треугольников.
Задание № 354
Запишите все углы, изображенные на рисунке 124, и укажите вид каждого угла.
Ответ
Острые углы: ∠ABM; ∠KBC.
Тупы углы: ∠ABK; ∠MBK; ∠MBC.
Развернутый угол: ∠ABC.
Задание № 355
Миша делал домашнее задание по математике с 16 ч 48 мин до 17 ч 16 мин, а Дима − с 17 ч 53 мин до 18 ч 20 мин. Кто из мальчиков дольше делал задание и на сколько минут?
Решение
17 ч 16 мин − 16 ч 48 мин = 16 ч 76 мин − 16 ч 48 мин = 28 мин делал домашнее задание Миша
18 ч 20 мин − 17 ч 53 мин = 17 ч 80 мин − 17 ч 53 мин = 27 мин делал домашнее задание Дима
28 − 27 = 1
Ответ: на 1 минуту Миша делал домашнее задание дольше, чем Дима.
Задание № 356
Решите уравнение:
1) 429 + m = 2106;
2) 348 − k = 154;
3) (m + 326) − 569 = 674;
4) 5084 − (k − 299) = 568.
Ответ
1) 429 + m = 2106,
m = 2106 − 429,
m = 1677.
429 + 1677 = 2106
2106 = 2106
Ответ: m = 1677.2) 348 − k = 154,
k = 348 − 154,
k = 194.
348 − 194 = 154
154 = 154
Ответ: k = 194.3) (m + 326) − 569 = 674,
m + 326 = 674 + 569,
m + 326 = 1243,
m = 1243 − 326,
m = 917.
(917 + 326) − 569 = 674
674 = 674
Ответ: m = 917.4) 5084 − (k − 299) = 568,
k − 299 = 5084 − 568,
k − 299 = 4516,
k = 4516 + 299,
k = 4815.
5084 − (4815 − 299) = 568
568 = 568
Ответ: k = 4815.
Задание № 357
Вместо звездочек поставьте цифры так, чтобы действие было выполнено правильно.
Ответ
+74768
25232
100000
_101230
45675
55555
Задание № 358
Каждый учащийся гимназии изучает по крайней мере один из двух иностранных языков. Английский язык изучают 328 учеников, французский язык − 246 учеников, а английский и французский одновременно − 109 учеников. Сколько всего учеников учится в гимназии?
Пояснение от 7 гуру: эта задача требует знания диаграмм Эйлера — Венна, тогда ее решить проще простого. Если не учили, пытаемся мыслить логически.
Решение
1) 328 − 109 = 219 (уч.) — изучают только английский язык
2) 246 − 109 = 137 (уч.) — изучают только французский язык
3) 219 + 137 + 109 = 465 (уч.) — учится в гимназии всего
Ответ: 465 учеников.
98
Ответы к странице 98
Параграф 15. ГДЗ к разделу учебника математики Прямоугольник. Ось симметрии фигуры 5 класс, автор Мерзляк
Задание № 359. Постройте:
1) Прямоугольник, соседние стороны которого равны 4 см и 2 см;
2) квадрат со стороной 3 см.
Ответ
Задание № 360. Постройте прямоугольник, соседние стороны которого равны 25 мм и 35 мм.
Ответ
AB = CD = 2 см 5 мм
BC = AD = 3 см 5 мм
99
Ответы к странице 99
Задание № 361. Вычислите периметр:
1) прямоугольника, соседние стороны которого равны 42 см и 23 см;
2) квадрата со стороной 8 дм.
Ответ
1) Р = 2 * 42 + 2 * 23 = 84 + 46 = 130 (см)
2) Р = 4 * 8 = 32 (дм)
Задание № 362. Найдите периметр прямоугольника, соседние стороны которого равны 13 мм и 17 мм.
Ответ
Р = 2 * 13 + 2 * 17 = 26 + 34 = 60 (мм) = 6 (см)
Задание № 363. Какие из букв, изображенных на рисунке 135, имеют ось симметрии?
Ответ
А, В, Е, Т.
Задание № 364. Сколько осей симметрии имеет многоугольник изображенный на рисунке 136?
Ответ
а) — 2, б) — 1, в) — 6
Задание № 365. 1) Длина одной из сторон прямоугольника равна 14 см, что на 5 см больше длины соседней стороны. Найдите периметр прямоугольника.
2) Периметр прямоугольника равен 34 см, а одна из его сторон − 12 см. Найдите длину соседней стороны прямоугольника.
Ответ
1) 14 − 5 = 9 (см) — длина соседней стороны прямоугольника
Р = 14 * 2 + 9 * 2 = 28 + 18 = 46 (см)
Ответ: 46 см.2) 12 * 2 = 24 (см) — длина двух известных сторон прямоугольника;
34 − 24 = 10 (см) — длина двух соседних сторон прямоугольника;
10 : 2 = 5 (см) — длина соседней стороны.
Ответ: 12 см.
Задание № 366. Одна сторона прямоугольника равна 8 см, а соседняя − в 4 раза больше. Найдите периметр прямоугольника.
Решение
1) 8 * 4 = 32 (см) — соседняя сторона
2) 2 * 8 + 2 * 32 = 16 + 64 = 80 (см) — Р
Ответ: 80 см.
Задание № 367. Квадрат со стороной 12 см и прямоугольник, одна из сторон которого равна 8 см, имеют равные периметры. Найдите неизвестную сторону прямоугольника.
Решение
1) 4 * 12 = 48 (см) — периметр квадрата
2) 8 * 2 = 16 (см) — длина двух известных сторон прямоугольника
3) 48 − 16 = 32 (см) — длина двух неизвестных сторон прямоугольника
4) 32 : 2 = 16 (см) — длина неизвестной стороны прямоугольника
Ответ: 16 см.
Задание № 368. Прямоугольник, соседние стороны которого равны 42 см и 14 см, и квадрат имеют равные периметры. Найдите длину стороны квадрата.
Решение
1) 2 * 42 + 2 * 14 = 84 + 28 = 112 (см) — периметр прямоугольника
2) 112 : 4 = 28 (см) — длина стороны квадрата
Ответ: 28 см.
Задание № 369. Сколько квадратов изображено на рисунке 137?
а) 14 б) 13
Задание № 370. Из куска проволоки сделали модель пятиугольника (рис.138). Какие из моделей перечисленных фигур, длины сторон которых выражаются натуральным числом сантиметров, можно сделать из этого куска проволоки:
1) квадрат;
2) пятиугольник, все стороны которого равны;
3) равносторонний треугольник?
Решение
Узнаем длину проволоки из которой сделан пятиугольник, найдя его периметр:
P = 6 + 5 + 3 + 2 + 4 = 20 (см)1) 20 : 4 = 5 (см)
Из этой проволоки можно сделать квадрат со стороной 5 см.2) 20 : 5 = 4 (см)
Из этой проволоки можно сделать пятиугольник, каждая сторона которого равна 4 см.3) Равносторонний треугольник сделать не получится, так как 20 см не делится на 3 без остатка.
100
Ответы к странице 100
Задание № 371
Прямоугольник ABCD разрезали на квадраты так, как показано на рисунке 139. Сторона наименьшего из квадратов равна 4 см. Найдите длины сторон прямоугольника ABCD.
Решение
Сторона наименьшего квадрата 4 см,
4 * 3 = 12 (см) — сторона наибольшего квадрата
AD = BC = 12 + 12 + 4 = 28 (см)
Стороны AD и BC состоят из 4 средних квадратов
28 : 4 = 7 (см) — сторона среднего квадрата
CD = AB = 7 + 4 * 3 = 19 (см)
Ответ: 28 см и 19 см.
Задание № 372
Начертите прямоугольник, соседние стороны которого равны 3 см и 6 см. Разделите его на три равных прямоугольника. Вычислите периметр каждого из полученных прямоугольников. Сколько решений имеет задача.
Ответ
Задача имеет 2 решения:
1) AK = KM = MD = BN = NP = PC = 6 : 3 = 2 (см)
P ABNK = P KNPM = P MPCD = 2 * 2 + 2 * 3 = 10 (см)2) AK = KM = MD = BN = NP = PC = 3 : 3 = 1 (см)
P ABNK = P KNPM = P MPCD = 2 * 1 + 2 * 6 = 14 (см)Ответ: 10 см или 14 см.
Задание № 373
Существует ли среди прямоугольников с периметром 12 см такой, который можно разделить на два равных квадрата? В случае положительного ответа выполните рисунок и вычислите периметр каждого из полученных квадратов.
Решение
Прямоугольник ABCD со сторонами 4 см и 2 см.
Р ABCD = 2 * 2 + 2 * 4 = 4 + 8 = 12 (см)
Разделив прямоугольник пополам получим квадрат со стороной 2 см, периметр которого равен:
Р ABEF = Р FECD = 2 * 4 = 8 (см)
Ответ: 8 см — периметр каждого из квадратов.
Задание № 374
Как надо разделить квадрат на четыре равные части, чтобы из них можно было сложить два квадрата?
Ответ
Затем из каждой пары треугольников складываем квадрат.
Задание № 375
Как надо разрезать равнобедренный прямоугольный треугольник на четыре равные части, чтобы из них можно было сложить квадрат?
Ответ
Задание № 376
Как надо разрезать прямоугольник со сторонами 8 см и 4 см на четыре части, чтобы из них можно было сложить квадрат?
Ответ
Задание № 377
Как надо разрезать квадрат на треугольник и четырехугольник, чтобы из них можно было сложить треугольник?
Ответ
Треугольник ставим поверх четырехугольника и получается большой треугольник.
Задание № 378
Как надо разрезать квадрат со стороной 6 см на две части по ломанной, состоящей из трех звеньев, чтобы из полученных частей можно было сложить прямоугольник?
Ответ
Задание № 379
Проведите прямую MK, луч PS и отрезок AB так, чтобы луч пересекал отрезок AB и прямую MK, а прямая MK не пересекала отрезок AB.
Задание № 380
В магазине имеются лимоны, апельсины и мандарины, всего 740 кг. Если бы продали 55 кг лимонов, 36 кг апельсинов и 34 кг мандаринов, то оставшиеся массы лимонов, апельсинов и мандаринов оказались бы равными. Сколько килограммов фруктов каждого вида имеется в магазине?
Поделить нацело не получится, так как в задаче опечатка. В принципе, можно решить эту задачу, используя дроби:
Решение
1) 55 + 36 + 34 = 125 (кг) — фруктов всего бы продали
2) 740 − 126 = 615 (кг) — фруктов осталось бы в магазине
3) 615 : 3 = 205 (кг) — масса каждого из оставшихся бы видов фруктов
4) 205 + 55 = 260 (кг) — лимонов имеется в магазине
5) 205 + 36 = 241 (кг) — апельсинов имеется в магазине
6) 205 + 34 = 239 (кг) — мандаринов имеется в магазине
Ответ: 260 кг лимонов, 241 кг апельсинов, 239 кг мандаринов.
101
Ответы к странице 101
Задание № 381
От дома до дачи можно доехать на автобусе, или на электропоезде, или на маршрутном такси. В таблице указано время, которое надо затратить на каждый участок пути. Какое наименьшее время потребуется на дорогу? Каким видом транспорта при этом надо воспользоваться?
10 мин + 1 ч 15 мин + 5 мин = 1 ч 30 мин — время на автобусе
8 мин + 56 мин + 10 мин = 1 ч 14 мин — время на электропоезде
7 мин + 1 ч 5 мин + 8 мин = 1 ч 20 мин — время на маршрутном такси
Ответ: 1 ч 14 мин, электропоездом.
Задание № 381 старый учебник. 1) Одно из слагаемых увеличили на 19. Как следует изменить второе слагаемое, чтобы сумма не изменилась?
Уменьшить второе слагаемое на 19.
2) Вычитаемое уменьшили на 47. Как следует изменить уменьшаемое, чтобы разность не изменилась?
Уменьшить уменьшаемое на 47.
3) Уменьшаемое увеличили на 26. Как следует изменить вычитаемое, чтобы разность не изменилась?
Увеличить вычитаемое на 26.
Задание № 382
Найдите сумму корней уравнений:
1) (x − 18) − 73 = 39 и 24 + (y − 52) = 81;
2) (65 − x) + 14 = 51 и (y + 16) + 37 = 284.
Решение
1) (x − 18) − 73 = 39
x − 18 = 39 + 73
x = 112 + 18
x = 130
24 + (y − 52) = 81
y − 52 = 81 − 24
y = 57 + 52
y = 109
x + y = 130 + 109 = 2392) (65 − x) + 14 = 51
65 − x = 51 − 14
x = 65 − 37
x = 28
(y + 16) + 37 = 284
y + 16 = 284 − 37
y = 247 − 16
y = 231
x + y = 28 + 231 = 259
Задание № 383
Как с помощью пятилитрового бидона и трехлитровой банки набрать на берегу реки 4 л воды?
Решение
Шаг 1.
Налить воды в банку и вылить в бидон.
Шаг 2.
Снова набрать воды в банку и вылит в бидон. В бидон поместится только 2 литра, а 1 литр воды останется в банке.
Шаг 3.
Выливаем воду из бидона в реку и наливаем в бидон 1 литр, оставшейся воды в банке.
Шаг 4.
Набираем из реки полную банку (3 литра) и выливаем в бидон в котором уже есть 1 литр.
102-103
Задание № 2 Проверьте себя в тестовой форме
1 — А
2 — В
3 — Б
4 — А
5 — В
6 — В
7 — Б
8 — Г
9 — Г
10 — Г
11 — В
12 — Б
110
Ответы к странице 110
Глава 3. Умножение и деление натуральных чисел
Параграф 16. Умножение. Переместительное свойство умножения
Задание № 384 с ответами
Запишите сумму в виде произведения:
1) 6 + 6 + 6 + 6 + 6 + 6 + 6 + 6;
6 * 8 = 48
2) 9 + 9 + 9 + 9 + 9;
9 * 5 = 45
3) n + n + n + n + n + n + n;
n * 7 = 7n
4) 2 + 2 + . . . + 2 101 слагаемое;
2 * 101 = 202
5) 5 + 5 + . . . + 5 m слагаемых;
5m
6) m + m + . . . + m k слагаемых.
mk
Задание № 385
Выполните умножение:
1) 516 * 32;
2) 418 * 46;
3) 4519 * 52;
4) 314 * 258;
5) 133 * 908;
6) 215 * 204;
7) 626 * 480;

9) 2984 * 4006.
Решение
516 * 32 = 16512
418 * 46 = 19228
4519 * 52 = 234988
314 * 258 = 81012
133 * 908 = 120764
215 * 204 = 43860
626 * 480 = 300480
1234 * 567 = 699678
2984 * 4006 = 11953904
Задание № 386
Выполните умножение:
1) 706 * 53;
2) 304 * 29;
3) 5245 * 67;
4) 591 * 289;
5) 465 * 506;
6) 328 * 406;
7) 934 * 260;

9) 1234 * 2007.
Решение
Задание № 387
Вычислите:
1) 704 * 69 + 1424;
704 * 69 + 1424 = 48576 + 1424 = 50000
2) 412 * 42 − 7304;
412 * 42 − 7304 = 17304 − 7304 = 10000
3) (938 − 543) * 34;
(938 − 543) * 34 = 395 * 34 = 13430
4) 85 * (870 − 567);
85 * (870 − 567) = 85 * 303 = 25755
5) (294 + 16) * (348 − 279);
(294 + 16) * (348 − 279) = 310 * 69 = 21390
6) 294 + 16 * 348 − 279;
294 + 16 * 348 − 279 = 294 + 5568 − 279 = 5862 − 279 = 5583
7) (294 + 16) * 348 − 279;
(294 + 16) * 348 − 279 = 310 * 348 − 279 = 107880 − 279 = 107601

294 + 16 * (348 − 279) = 294 + 16 * 69 = 294 + 1104 = 1398
Решение
Задание № 388
Вычислите:
1) 603 * 84 + 2536;
603 * 84 + 2536 = 50652 + 2536 = 53188
2) 318 * 56 − 5967;
318 * 56 − 5967 = 17808 − 5967 = 11841
3) 64 * 96 − 77;
64 * 96 − 77 = 6144 − 77 = 6067
4) 64 * (96 − 77).
64 * (96 − 77) = 64 * 19 = 1216
Решение
Задание № 389
Вычислите значение выражения:
1) 17x + 432, если x = 58;
2) (739 − x) * y, если x = 554, y = 4900.
Решение
Задание № 390
Вычислите значение выражения:
1) 976 − 24x, если x = 36;
2) x * 63 − y, если x = 367, y = 19742.
Решение
Задание № 391
Выполните умножение:
1) 693 * 100;
2) 974 * 1000;
3) 540 * 20;
4) 120 * 400;
5) 760 * 350;
6) 460 * 1800.
Решение
693 * 100 = 69300
974 * 1000 = 974000
540 * 20 = 10800
120 * 400 = 48000
760 * 350 = 266000
460 * 1800 = 828000
Задание № 392
Выполните умножение:
1) 214 * 10;
2) 100 * 328;
3) 10000 * 546;
4) 140 * 80;
5) 580 * 240;
6) 270 * 3000.
Решение
214 * 10 = 2140
100 * 328 = 32800
10000 * 546 = 5460000
140 * 80 = 11200
580 * 240 = 139200
270 * 3000 = 810000
Задание № 393
Готовясь к школе, Буратино купил 34 тетради по 12 сольдо и 18 тетрадей по 16 сольдо. Сколько сольдо заплатил Буратино за все тетради?
Решение
1) 34 * 12 = 408 (с.) — заплатил Буратино за 34 тетради
2) 18 * 16 = 288 (с.) — заплатил Буратино за 18 тетрадей
3) 408 + 288 = 696 (с.) — заплатил Буратино за все тетради
Ответ: 696 сольдо.
111
Ответы к странице 111
Задание № 394
Кот Матроскин продал 42 л молока по 64 р. за 1 литр и 16 кг творога по 320 р. за килограмм. Сколько денег выручил Матроскин за свой товар?
Решение
1) 42 * 64 = 2688 (руб.) — выручил Матроскин за молоко
2) 16 * 320 = 5120 (руб.) — выручил Матроскин за творог
3) 2688 + 5120 = 7808 (руб.) — выручил Матроскин за весь товар
Ответ: 7808 рублей.
Задание № 395
В походе, длившемся несколько дней, турист 14 ч плыл по реке на лодке со скоростью 8 км/ч и шел пешком 23 ч со скоростью 4 км/ч. Какой путь, по реке или по суше, был длиннее и на сколько километров?
Решение
1) 14 * 8 = 112 (км) — турист плыл по реке
2) 23 * 4 = 92 (км) — турист шел пешком
3) 112 − 92 = 20 (км) — разница
Ответ: на 20 км путь по реке был длиннее, чем по суше.
Задание № 396
Путешественник плыл на моторной лодке 5 ч по реке со скоростью 27 км/ч и 7 ч по озеру со скоростью 21 км/ч. Какой путь, по реке или по озеру, был длиннее и на сколько километров?
Решение
1) 5 * 27 = 135 (км) — плыл путешественник по реке
2) 7 * 21 = 147 (км) — плыл путешественник по озеру
3) 147 − 135 = 12 (км) — разница
Ответ: на 12 км путь по озеру был длиннее, чем по реке.
Задание № 397
В школу завезли апельсины, мандарины и лимоны. Апельсинов было 94 кг, что в 7 раз меньше, чем мандаринов, и на 16 кг больше, чем лимонов. Сколько всего килограммов фруктов завезли в школу?
Решение
1) 94 * 7 = 658 (кг) — мандаринов завезли в школу
2) 94 − 16 = 78 (кг) — лимонов завезли в школу
3) 94 + 658 + 78 = 830 (кг) фруктов завезли в школу всего
Ответ: 830 кг.
Задание № 398
Школе для кабинет музыки выделили 50 000 р. на покупку компьютера, музыкального центра и мультимедиапроектора. Музыкальный центр стоит 3 600 р., что в 4 раза меньше стоимости компьютера и на 28 200 р. меньше стоимости мультимедиапроектора. Хватит ли выделенных денег на покупку?
Решение
1) 3600 * 4 = 14400 (р.) — стоит компьютер
2) 3600 + 28200 = 31800 (р.) — стоит мультимедиапроектор
3) 3600 + 14400 + 31800 = 49800 (р.) — нужно на всю покупку
49800 < 50000
Ответ: выделенных денег хватит.
Задание № 399
Найдите значение выражения:
1) (318 * 207 − 64934) * 276 + 604 * 88;
2) 869 * (61124 − 488 * 125) − 509 * 74.
Решение
Задание № 400
Найдите значение выражения:
1) (214 * 104 + 7544) * 35 − 508 * 722;
2) 647 * (36900 − 255 * 144) − 318 * 92.
Решение
Задание № 401
Из одного порта в другой одновременно отправились теплоход и катер. Скорость теплохода составляет 28 км/ч, а скорость катера − 36 км/ч. Какое расстояние будет между ними через 5 ч после начала движения?
Решение
1) 28 * 5 = 140 (км) — прошел теплоход
2) 36 * 5 = 180 (км) — проплыл катер
3) 180 − 140 = 40 (км) — будет между теплоходом и катером через 5 ч после начала движения
Ответ: 40 км.
Задание № 402
Из одного села в одном направлении одновременно выехали два велосипедиста. Один из них ехал со скоростью 12 км/ч, а второй − 9 км/ч. Какое расстояние будет между ними через 6 ч после начала движения?
Решение
1) 12 * 6 = 72 (км) — проехал первый велосипедист
2) 9 * 6 = 54 (км) — проехал второй велосипедист
3) 72 − 54 = 18 (км) — будет между ними через 6 ч после начала движения
Ответ: 18 км.
Задание № 403
С одной станции в противоположных направлениях одновременно отправились два поезда. Один из них двигался со скоростью 64 км/ч, а второй − 57 км/ч. Какое расстояние будет между ними через 9 ч после начала движения?
Решение
1) 64 * 9 = 576 (км) — проехал первый поезд
2) 57 * 9 = 513 (км) — проехал второй поезд
3) 576 + 513 = 1089 (км) — будет между ними через 9 ч после начала движения
Ответ: 1089 км.
Задание № 404
Из одного города в противоположных направлениях одновременно выехали два автомобиля. Скорость одного из них была 74 км/ч, что на 8 км/ч больше, чем скорость другого. Какое расстояние будет между ними через 7 ч после начала движения?
Решение
1) 74 * 7 = 518 (км) — проехал первый автомобиль
2) 74 − 8 = 66 (км/ч) — скорость второго автомобиля
3) 66 * 7 = 462 (км) — проехал второй автомобиль
4) 518 + 462 = 980 (км) — будет между автомобилями через 7 ч после начала движения
Ответ: 980 км.
112
Ответы к странице 112
Задание № 405
Из двух городов одновременно навстречу друг другу выехали велосипедист и легковой автомобиль. Велосипедист ехал со скоростью 11 км/ч, а автомобиль − в 7 раз быстрее. Найдите расстояние между городами, если велосипедист и автомобиль встретились через 4 ч после начала движения.
Решение
1) 11 * 4 = 44 (км) — проехал велосипедист
2) 11 * 7 = 77 (км/ч) — скорость автомобиля
3) 77 * 4 = 308 (км) — проехал автомобиль
4) 44 + 308 = 352 (км) — расстояние между городами
Ответ: 352 км.
Задание № 406
Из двух сел одновременно навстречу друг другу отправились велосипедист и пешеход. Пешеход шел со скоростью 3 км/ч, что в 4 раза меньше скорости велосипедиста. Найдите расстояние между селами, если велосипедист и пешеход встретились через 3 ч после начала движения.
Решение
1) 3 * 3 = 9 (км) — прошел пешеход
2) 3 * 4 = 12 (км/ч) — скорость велосипедиста
3) 12 * 3 = 36 (км) — проехал велосипедист
4) 9 + 36 = 45 (км) — расстояние между селами
Ответ: 45 км.
Задание № 407
Всегда ли произведение двух натуральных чисел больше, чем их сумма?
Ответ
Нет, например:
1 * 2 < 1 + 2;
1 * 13 < 1 + 13.
Задание № 408 с ответами
Как изменится произведение двух натуральных чисел, если:
1) один из множителей увеличить в 8 раз;
произведение увеличится в 8 раз
2) один из множителей уменьшить в 5 раз;
произведение уменьшится в 5 раз
3) каждый множителей увеличить в 6 раз;
произведение увеличится в 6 * 6 = 36 раз
4) один множитель увеличить в 13 раз, а другой − в 40 раз;
произведение увеличится в 13 * 40 = 520 раз
5) один множитель увеличить в 12 раз, а другой уменьшить в 3 раза?
произведение увеличится в 4 раза 12 : 3 = 4
Задание № 409
Из двух поселков, расстояние между которыми равно 3 км, одновременно навстречу друг другу вышли два пешехода. Один из них двигался со скоростью 5 км/, а второй − 4 км/ч. Какое расстояние будет между пешеходами через 2 ч после начала движения?
Решение
1) 5 * 2 = 10 (км) — пройдет первый пешеход за 2 часа
2) 4 * 2 = 8 (км) — пройдет второй пешеход за 2 часа
3) (10 − 3) + (8 − 3) + 3 = 15 (км) будет между пешеходами через 2 ч после начала движения
Ответ: 15 км.
Задание № 410
Вместо звёздочек поставьте цифры так, чтобы умножение было выполнено верно.
Ответ
Задание № 411
Вместо звёздочек поставьте цифры так, чтобы умножение было выполнено верно.
Решение
113
Ответы к странице 113
Задание № 412. При каких значениях a верно равенство:
1) a * 5 = 5;
2) a * 5 = 0;
3) a * 5 = a;
4) a * 1 = 1;
5) a * 1 = a;
6) a * a = a;
7) 0 * a = a;

9) a * 1 = 0?
Ответы
1) a * 5 = 5
a = 12) a * 5 = 0
a = 03) a * 5 = a
a = 04) a * 1 = 1
a = 15) a * 1 = a
при любом a6) a * a = a
a = 0; 1.7) 0 * a = a
a = 0
0 * a = 0
при любом a9) a * 1 = 0
при a = 0
Задание № 413. Сумма и произведение четырех натуральных чисел равны 8. Найдите эти числа.
Решение
1 + 1 + 2 + 4 = 8
1 * 1 * 2 * 4 = 8
Задание № 414. В записи 1 * 2 * 3 * 4 * 5 замените звездочки знаками «+» или «*» и расставьте скобки так, чтобы значение полученного выражения равнялось 100.
Решение
(1 * 2 + 3) * 4 * 5 = 5 * 4 * 5 = 100
Задание № 415. Найдите величину угла ABM (рис.141), если ∠MBK − прямой и ∠ABM = ∠CBK.
Ответ
∠MBK = 90°, так как прямой;
∠ABM = ∠CBK;
∠ABC = 180°, так как развернутый;
∠ABM = (∠ABC − ∠MBK) : 2 = (180° − 90°) : 2 = 90° : 2 = 45°
Задание № 416. Угол ABC равен 72°, луч BD − биссектриса угла ABC, луч BE − биссектриса угла ABD. Вычислите величину угла CBE.
Так как луч BD − биссектриса угла ABC, то:
∠ABD = ∠DBC = 72° : 2 = 36°.
Так как луч BE − биссектриса угла ABD, то:
∠EBD = ∠ABE = 36° : 2 = 18°.
∠CBE = ∠EBD + ∠DBC = 18° + 36° = 54°
Задание № 417. По формуле a = b : 4 − 6 найдите значение a, если:
1) b = 600;
2) b = 64;
3) b = 24;
4) b = 100.
Решение
1) a = 600 : 4 − 6 = 150 − 6 = 144
2) a = 64 : 4 − 6 = 16 − 6 = 10
3) a = 24 : 4 − 6 = 6 − 6 = 0
4) a = 100 : 4 − 6 = 25 − 6 = 19
Задание № 418. Сумма длин первой и второй стороны треугольника равна 33 см, первой и третьей − 39 см, второй и третьей 42 см. Найдите периметр треугольника.
Решение
Так как каждая сторона в суммах длин указана по два раза, то:
33 + 39 + 42 = 114 (см) — удвоенный периметр треугольника
Р = 114 : 2 = 57 (см)
Ответ: 57 см.
Задание № 419. Задача от мудрой совы
1) Сложите из десяти спичек три квадрата.
2) Сложите из 19 спичек шесть квадратов. (складываем как а рисунке 142)
3) Какие четыре спички надо убрать (рис.142), чтобы остались четыре маленьких квадрата и один большой?
Ответ
117
Ответы к странице 117
Параграф 17. Сочетательное и распределительное свойства умножения
Задание № 420 с ответами
Вычислите удобным способом:
1) 2 * 328 * 5 = (2 * 5) * 328 = 10 * 328 = 3280
2) 125 * 43 * 8 = (125 ** 43 = 1000 * 43 = 43000
3) 25 * 243 * 4 = (25 * 4) * 243 = 100 * 243
4) 4 * 36 * 5 = (4 * 5) * 36 = 20 * 36 = 720
5) 50 * 236 * 2 = (50 * 2) * 236 = 100 * 236 = 23600
6) 250 * 3 * 4 = (250 * 4) * 3 = 1000 * 3 = 3000
Задание № 421 с ответами
Вычислите удобным способом:
1) 4 * 17 * 25 = (4 * 25) * 17 = 100 * 17 = 1700
2) 5 * 673 * 2 = (5 * 2) * 673 = 10 * 673 = 6730
3) 8 * 475 * 125 = (8 * 125) * 475 = 1000 * 475
4) 73 * 5 * 4 = (5 * 4) * 73 = 20 * 73 = 1460
5) 2 * 916 * 50 = (2 * 50) * 916 = 100 * 916 = 91600
6) 5 * 9 * 200 = (5 * 200) * 9 = 1000 * 9 = 9000
Задание № 422 с ответами
Упростите выражение:
1) 13 * 2a = 26a
2) 9x * 8 = 72x
3) 23 * 4b = 92b
4) 28 * y * 5 = 140y
5) 6a * 8b = 48ab
6) 11x * 14y = 154xy
7) 27m * 3n = 81mn
4a * 8 * b * 3 * c = 96abc
9) 12x * 3y * 5z = 180xyz
Задание № 423 с ответами
Упростите выражение:
1) 12 * 3x = 36x
2) 10x * 6 = 60x
3) 5a * 7b = 35ab
4) 8m * 12n = 96mn
5) 2a * 3b * 4c = 24abc
6) 5x * 2y * 10z = 100xyz
Задание № 424 с ответами
Вычислите значение выражения наиболее удобным способом:
1) 318 * 78 + 318 * 22 = 318 * (78 + 22) = 318 * 100 = 31800
2) 856 * 92 − 853 * 92 = 92 * (856 − 853) = 92 * 3 = 276
3) 943 * 268 + 943 * 232 = 943 * (268 + 232) = 943 * 500 = 471500
4) 65 * 246 − 65 * 229 − 65 * 17 = 65 * (246 − 229 − 17) = 65 * 10 = 650
Задание № 425 с ответами
Вычислите значение выражения наиболее удобным способом:
1) 47 * 632 + 632 * 53 = 632 * (47 + 53) = 632 * 100 = 63200
2) 598 * 49 − 597 * 49 = 49 * (598 − 597) = 49 * 1 = 49
3) 754 * 324 − 754 * 314 = 754 * (324 − 314) = 754 * 10 = 7540
4) 37 * 46 − 18 * 37 + 37 * 72 = 37 * (46 − 18 + 72) = 37 * 100 = 3700
Задание № 426 с ответами
Раскройте скобки:
1) 2(a + 5) = 2a + 10
2) 8(7 − x) = 8 * 7 − 8x = 56 − 8x
3) 12(x + y) = 12x + 12y
4) (c − 9) * 11 = 11c − 9 * 11 = 11c − 99
5) (8 + y) * 16 = 8 * 16 + 16y = 128 + 16y
6) 15(4a − 3) = 15 * 4a − 15 * 3 = 60a − 45
7) 7(6a + 8b) = 7 * 6a + 7 * 8b = 42a + 56b
10(2m − 3n + 4k) = 10 * 2m − 10 * 3n + 10 * 4k = 20m − 30n + 40k
9) (24x + 17y − 36z) * 4 = 24x * 4 + 17y * 4 − 36z * 4 = 96x + 68y − 144z
Задание № 427 с ответами
Раскройте скобки:
1) 4(a + 2) = 4a + 8
2) 3(m − 5) = 3m − 15
3) (p − q) * 9 = 9p − 9q
4) 12(a + b) = 12a + 12b
5) 5(2m − 1) = 10m − 5
6) (3c + 5d) * 14 = 42c + 70d
Задание № 428 с ответами
Упростите выражение:
1) 6a + 8a = 14a
2) 28c − 15c = 13c
3) 13y − 2y = 11y
4) m + 29m = 30m
5) 98p − p = 97p
6) 17k + k = 18k
7) 4x + 13x + 15x = 32x
67z − 18z + 37 = 49z + 37
9) 35x + x − 6 = 36x − 6 = 6(6x − 1)
118
Ответы к странице 118
Задание № 429 с ответами
Упростите выражение:
1) 13b + 19b = 32b
2) 44d − 37d = 7d
3) 34n + n = 35n
4) 127q − q = 126q
5) 36y − 19y + 23y = 40y
6) 49a + 21a + 30 = 70a + 30 = 10 * (7a + 3)
Задание № 430
Упростите выражение и найдите его значение:
1) 25x * 4y, если x = 12, y = 11;
2) 8k * 125c, если k = 58, c = 8.
Решение
1) 25x * 4y = 100xy,
если x = 12, y = 11, то 100 * 12 * 11 = 13200
2) 8k * 125c = 1000kc,
если k = 58, c = 8, то 1000 * 58 * 8 = 464000
Задание № 431
Упростите выражение и найдите его значение:
1) 5a * 20b, если a = 4, b = 68;
2) 4m * 50n, если m = 22, n = 34.
Решение
1) 5a * 20b = 100ab
если a = 4, b = 68, то 100 * 4 * 68 = 27200
2) 4m * 50n = 200mn,
если m = 22, n = 34, то 200 * 22 * 34 = 149600
Задание № 432
Вычислите наиболее удобным способом значение выражения:
1) 398 * 36 + 36b, если b = 602;
2) 986b − 86 * 83, если b = 83.
Решение
1) 398 * 36 + 36b = 36 * (398 + b) = 36 * (398 + 602) = 36 * 1000 = 36000
2) 986b − 86 * 83 = 986 * 83 − 86 * 83 = 83 * (986 − 86) = 83 * 900 = 74700
Задание № 433
Вычислите наиболее удобным способом значение выражения:
1) 631 * 18 + x * 369, если x = 18;
2) 58a − 58 * 824, если a = 1024.
Решение
1) при x = 18
631 * 18 + x * 369 = 631 * 18 + 18 * 369 = 18 * (631 + 369) = 18 * 1000 = 18000
2) при a = 1024
58a − 58 * 824 = 58 * (a − 824) = 58 * (1024 − 824) = 58 * 200 = 11600
Задание № 434
Упростите выражение и найдите его значение::
1) 13p + 37p, если p = 14;
2) 72b − 43b, если b = 54;
3) 38x + 17x − 54x + x, если x = 678;
4) 86c − 35c − c + 296, если c = 47.
Решение
1) 13p + 37p = p * (13 + 37) = p * 50,
если p = 14, то 14 * 50 = 7002) 72b − 43b = b * (72 − 43) = b * 29,
если b = 54, то 54 * 29 = 15663) 38x + 17x − 54x + x = x * (38 + 17 − 54 + 1) = x * 2,
если x = 678, то 678 * 2 = 13564) 86c − 35c − c + 296 = c * (86 − 35 − 1) + 296 = c * 50 + 296,
если c = 47, то 47 * 50 + 296 = 2350 + 296 = 2646
Задание № 435
Упростите выражение и найдите его значение:
1) 34x + 66x, если x = 8;
2) 54a − 39a, если a = 26;
3) 18m − 5m + 7m, если m = 394;
4) 19z − 12z + 33z − 192, если z = 82.
Решение
1) 34x + 66x = x * (34 + 66) = 100x ,
если х = 8, то 100 * 8 = 8002) 54a − 39a = a * (54 − 39) = 15a ,
если a = 26, то 15 * 26 = 3903) 18m − 5m + 7m = 20m,
если m = 394, то 20 * 394 = 78804) 19z − 12z + 33z − 192 = z * (19 − 12 + 33) − 192 = 40z − 192 ,
если z = 82, то 40 * 82 − 192 = 3280 − 192 = 3088
Задание № 436 с ответами
Вычислите удобным способом:
1) 16 * 25 = (4 * 4) * 25 = 4 * (4 * 25) = 4 * 100 = 400
2) 25 * 8 * 5 = (25 * 4) * (4 * 5) = (25 * 4) * (2 * 5) = 100 * 10 = 1000
3) 15 * 12 = 15 * (6 * 2) = (15 * 2) * 6 = 30 * 6 = 180
4) 375 * 24 = 375 * (4 * 6) = (375 * 4) * 6 = 1500 * 6 = 9000
Задание № 437 с ответами
Вычислите удобным способом:
1) 25 * 14 * 6 = 25 * (2 * 7) * 6 = (25 * 2) * (7 * 6) = 2100
2) 125 * 25 * 32 = 125 * 25 * (4 *= (125 *
* (25 * 4) = 1000 * 100 = 100 000
3) 75 * 36 = 75 * (4 * 9) = (75 * 4) * 9 = 300 * 9 = 2700
4) 96 * 50 = (48 * 2) * 50 = 48 * (2 * 50) = 48 * 100 = 4800
Задание № 438 с ответами
Вычислите значение выражения, используя распределительное свойство умножения:
1) 43 * 64 + 43 * 23 − 87 * 33 = 43 * (64 + 23) − 87 * 33 = 43 * 87 − 87 * 33 = 87 * (43 − 33) = 87 * 10 = 870
2) 84 * 53 − 84 * 28 + 16 * 61 − 16 * 36 = 84 * (53 − 28) + 16 * (61 − 36) = 84 * 25 + 16 * 25 = 25 * (84 + 16) = 25 * 100 = 2500
Задание № 439 с ответами
Вычислите значение выражения, используя распределительное свойство умножения:
1) 93 * 24 − 27 * 24 + 66 * 76 = 24 * (93 − 27) + 66 * 76 = 24 * 66 + 66 * 76 = 66 * (24 + 76) = 66 * 100 = 6600
2) 82 * 46 + 82 * 54 + 135 * 18 − 18 * 35 = 82 * (46 + 54) + 18 * (135 − 35) = 82 * 100 + 18 * 100 = 100 *(82 + 18) = 100 * 100 = 10000
Задание № 440
Выполните умножение:
1) 2 км 56 м * 68;
2) 7 р. 9 к. * 54;
3) 4 км 90 м * 43;
4) 3 т 5 ц 65 кг * 8;
5) 3 ч 48 мин * 25;
6) 5 ч 12 мин 36 с * 15.
Решение
1) 2 км 56 м * 68 = 68 * (2 км + 56 м) = 68 * 2 км + 68 * 56м = 136 км + 3808 м = 136 + 3000 м + 808 м = 139 км 808 м
2) 7 р. 9 к. * 54 = 54 * (7 р. + 9 к.) = 54 * 7 р. + 54 * 9 к. = 378 р. + 486 к. = 378 р. + 400 к. + 86 к. = 382 р. 86 к.
3) 4 км 90 м * 43 = 43 * (4 км + 90 м) = 43 * 4 км + 43 * 90 м = 172 км + 3870 м = 172 км + 3000 м + 870 м = 175 км 870 м
4) 3 т 5 ц 65 кг * 8 = 8 * (3 т 5 ц 65 кг) = 8 * 3 т + 8 * 5 ц + 8 * 65 кг = 24 т 40 ц 520 кг = 24 т + 45 ц + 20 кг = 28 т 5 ц 20 кг
5) 3 ч 48 мин * 25 = 25 * (3 ч + 48 мин) = 75 ч + 1200 мин = 75 ч + 20 ч = 95 ч
6) 5 ч 12 мин 36 с * 15 = 15 * (5 ч + 12 мин + 36 с) = 75 ч + 180 мин + 540 с = 75 ч + 3 ч + 9 мин = 78 ч 9 мин
119
Ответы к странице 119
Задание № 441
Выполните умножение:
1) 8 ц 26 кг * 27;
2) 14 р. 80 к. * 406;
3) 6 т 45 кг * 82;
4) 5 м * 8 см * 42;
5) 7 мин 5 с * 24;
6) 4 сут 6 ч * 12.
Решение
1) 8 ц 26 кг * 27 = 27 * (8 ц + 26 кг) = 27 * 8 ц + 27 * 26 кг = 216 ц 702 кг = 216 ц + 700 кг + 2 кг = 223 ц 2 кг
2) 14 р. 80 к. * 406 = 406 * (14 р. + 80 к.) = 406 * 14 р. + 406 * 80 к. = 5684 р. + 32480 к. = 5684 р. + 32400 к. + 80 к. = 6008 р. 80 к.
3) 6 т 45 кг * 82 = 82 * (6 т + 45 кг) = 82 * 6 т + 82 * 45 кг = 492 т + 3690 кг = 492 т + 3600 кг + 92 кг = 492 т + 36 ц + 92 кг = 495 т 6 ц 92 кг
4) 5 м * 8 см * 42 = 42 * (5 м + 8 см) = 42 * 5 м + 42 * 8 см = 210 м + 336 см = 210 м + 300 см + 36 см = 213 см + 36 см
5) 7 мин 5 с * 24 = 24 * (7 мин + 5 с) = 24 * 7 мин + 24 * 5 с = 168 мин + 120 с = 120 мин + 48 мин + 2 мин = 2 ч 50 мин
6) 4 сут 6 ч * 12 = 12 * (4 сут + 6 ч) = 48 сут + 72 ч = 48 сут + 3 сут = 51 сут
Задание № 442
Сколькими нулями оканчивается произведение всех натуральных чисел:
1) от 1 до 10 включительно;
2) от 15 до 24 включительно;
3) от 10 до 30 включительно;
4) от 1 до 100 включительно?
Решение
Ноль в конце дают круглые десятки, 2*5, 4*5, 6*5 или 8*5. Чтобы узнать, сколькими нулями оканчивается произведение натуральных чисел, считаем сначала круглые десятки. Сколько их, столько нулей. Затем ищем сочетания с пятерками. Как правило, требуется найти произведение натуральных чисел, данных по порядку, поэтому ищем пары чисел, оканчивающиеся на 2 и 5, они будут давать по 1 нулю.
1) Двумя нулями. Один даст множитель 10, а второй получится при умножении 2 на 5.
2) Двумя нулями. Один — от числа 20, второй — произведение 15 и любого чётного числа.
3) Пятью нулями. Нули на конце произведения дадут 10, 20, 30 и произведения чисел, оканчивающихся на 5 (т. е. 15 и 25) с чётными, получим 5 нулей.
4) 21 ноль. От 1 до 100 есть 10 чисел, оканчивающихся на 5, 9 чисел на 0, и одно, оканчивается на два нуля (100). Итого 21 нулём будет оканчиваться произведение.
Ответы к упражнениям для повторения
Задание № 443
Угол ABC − прямой, луч BP − биссектриса угла ABK, луч BM − биссектриса угла CBK (рис.145). Какова градусная мера угла MBP?
Решение
∠АВР = ∠РВК, примем его за х
∠КВМ = ∠MBC, примем за у, тогда
2х + 2у = 90 градусов
∠МВР = х+у,
2(х+у) = 90°
х + у = 90° : 2
х + у = 45°
∠MBP = 45°
Ответ: 45°.
Задание № 444
По двору бегали котята и цыплята. Вместе у них было 14 голов и 38 ног. Сколько котят и сколько цыплят бегало по двору?
Решение
1) 38 : 2 = 19 (шт.) — котят и цыплят бегало бы по двору, если бы у каждого из них было бы по 2 ноги, но так как у котят по 4 ноги и голов всего 14, то:
2) 19 − 14 = 5 (шт.) — котят бегало по двору
3) 14 − 5 = 9 (шт.) — цыплят бегало по двору
Ответ: 5 котят и 9 цыплят.
Задание № 445
Семья из двух взрослых и ребенка может поехать на отдых поездом или на автомобиле. Билет на поезд на одного взрослого стоит 1440 р., а для ребенка в 2 раза меньше. Автомобиль расходует 12 л бензина на 100 км, а цена одного литра бензина составляет 40 р. Расстояние до места отдыха равно 600 км. Каким видом транспорта этой семье дешевле доехать до места отдыха.
1) 1440 : 2 = 720 (р.) — стоит детский билет.
2) 1440 * 2 + 720 = 3600 (р.) — потратят на билеты на поезде
3) 12 * 40 = 480 (л) — бензина тратится на 100 км.
4) 600 : 100 = 6 (раз) — больше, чем 100 км, нужно проехать
5) 480 * 6 = 2880 (р.) — стоит весь бензин
3600 > 2880
Ответ: на автомобиле поехать дешевле.
Задание № 445 из старой редакции
В первом ящике на 14 кг апельсинов меньше, чем во втором, и на 18 кг больше, чем в третьем. Сколько килограммов апельсинов во всех трех ящиках вместе, если во втором ящике их 44 кг?
Решение задачи
1) 44 − 14 = 30 (кг) — апельсинов было в первом ящике
2) 30 − 18 = 12 (кг) — апельсинов было во втором ящике
3) 30 + 44 + 12 = 86 (кг) апельсинов было во всех трех ящиках вместе
Ответ: 86 кг.
Задание № 446
В 5 классе учатся трое друзей: Миша, Дима и Саша. Один из них занимается футболом, второй − плаванием, а третий − боксом. У футболиста нет ни брата, ни сестры, он самый младший из друзей. Миша старше боксера и дружит с сестрой Димы. Каким видом спорта занимается каждый из друзей?
Решение
Узнаем кто из друзей футболист:
Это не Миша, так как он не самый младший, и это не Дима, так как у него есть сестра. Получается что футболист − Саша.
Узнаем кто из друзей боксер:
По условию Миша старше боксера, значит он не боксер, получается что боксер Дима.
Следовательно Миша занимается плаванием.Решение становится наглядным, если построить и заполнить таблицу
М. Д. С.
ф. — — +
п. + — —
б. — + —
123
Ответы к странице 123
Параграф 18. Деление
Задание № 447. Известно, что 243 * 425 = 103275. Чему равно значение выражения: 1) 103275 : 243; 2) 103275 : 425?
Ответ
1) 103275 : 243 = 425
2) 103275 : 425 = 243
Задание № 448. Известно, что 4608 : 48 = 96. Чему равно значение выражения: 1) 96 * 48; 2) 4608 : 96?
Ответ
1) 96 * 48 = 4608
2) 4608 : 96 = 48
Задание № 449. Заполните таблицу
Ответ
Делимое 320 96 84 0 0 945 637 3232
Делитель 40 12 6 264 128 1 637 16
Частное 8 8 14 0 0 945 1 202
124
Ответы к странице 124
Задание № 450. Выполните деление:
1) 1548 : 36;
2) 2668 : 58;
3) 5562 : 18;
4) 3672 : 34;
5) 15552 : 72;
6) 16728 : 68;
7) 16320 : 48;

9) 942866 : 178.
Решение
Задание № 451. Выполните деление:
1) 2812 : 74;
2) 1248 : 24;
3) 6565 : 13;
4) 9384 : 46;
5) 18526 : 59;
6) 15652 : 26;
7) 63378 : 63;

9) 1334504 : 214.
Решение
Задание № 452. Выполните деление:
1) 34250000 : 10 = 3425000
2) 34250000 : 1000 = 34250
3) 34250000 : 10000 = 3425
4) 25600 : 80 = 320
5) 25600 : 800 = 32
6) 2430000 : 180 = 13500
7) 2430000 : 1800 = 1350
2430000 : 18000 = 135
Задание № 453. Выполните деление:
1) 32596800 : 10 = 3259680
2) 876900 : 100 = 8769
3) 240000 : 10000 = 24
4) 450000 : 150 = 3000
5) 36000 : 12000 = 3
6) 124360000 : 40000 = 3109
Задание № 454. Выполните действия:
1) 256 + 144 : 16 − 8;
2) (256 + 144) : (16 − 8);
3) (256 + 144) : 16 − 8;
4) 256 + 144 : (16 − 8).
Решение
256 + 144 : 16 − 8 = 256 + 9 − 8 = 257
1) 144 : 16 = 9
2) 256 + 9 = 265
3) 265 − 8 = 257(256 + 144) : (16 −
= 400 : 8 = 50
1) 256 + 144 = 400
2) 16 − 8 = 8
3) 400 : 8 = 50(256 + 144) : 16 − 8 = 400 : 16 − 8 = 25 − 8 = 17
1) 256 + 144 = 400
2) 400 : 16 = 25
3) 25 − 8 = 17256 + 144 : (16 −
= 256 + 144 : 8 = 256 + 18 = 274
1) 16 − 8 = 8
2) 144 : 8 = 18
3) 256 + 18 = 274
Задание № 455. Найдите значение выражения:
1) 4704 − 4704 : (46 + 38);
2) 2808 : 72 + 15808 : 52.
Решение
Задание № 456. Найдите значение выражения:
1) 3264 − 3264 : (92 − 44);
2) 18144 : 84 − 2924 : 68.
Решение
Задание № 457. Решите уравнение:
1) 13x = 195;
2) x * 18 = 468;
3) 11x + 6x = 408;
4) 33m − m = 1024;
5) x : 19 = 26;
6) 476 : x = 14.
Ответы
13x = 195
x = 195 : 13
x = 15
Ответ: 15x * 18 = 468
x = 468 : 18
x = 26
Ответ: 2611x + 6x = 408
17x = 408
x = 408 : 17
x = 24
Ответ: 2433m − m = 1024
32m = 1024
m = 1024 : 32
m = 32
Ответ: 32x : 19 = 26
x = 26 * 19
x = 494
Ответ: 494476 : x = 14
x = 476 : 14
x = 34
Ответ: 34
Задание № 458. Решите уравнение:
1) 19x = 95;
2) x * 22 = 132;
3) 38x − 16x = 1474;
4) y + 27y = 952;
5) x : 25 = 16;
6) 324 : x = 27.
Ответы
19x = 95
x = 95 : 19
x = 5
Ответ: 5x * 22 = 132
x = 132 : 22
x = 6
Ответ: 638x − 16x = 1474
22x = 1474
x = 1474 : 22
x = 67
Ответ: 67y + 27y = 952
28y = 952
y = 952 : 28
y = 34
Ответ: 34x : 25 = 16
x = 16 * 25
x = 400
Ответ: 400324 : x = 27
x = 324 : 27
x = 12
Ответ: 12
Задание № 459. Всадник преодолевает расстояние между двумя селами за 5 ч, если двигается со скоростью 12 км/ч. С какой скоростью он должен двигаться, чтобы преодолеть это расстояние за 4 ч?
Решение задачи
1) 12 * 5 = 60 (км) — расстояние между двумя селами
2) 60 : 4 = 15 (км/ч) — скорость, с которой должен двигаться всадник, чтобы преодолеть это расстояние за 4 ч
Ответ: 15 км/ч.
Задание № 460. Вика купила 8 кг конфет по 90 р. за килограмм. Сколько килограммов конфет по 60 р. за килограмм она сможет купить за эти же деньги?
Решение задачи
1) 8 * 90 = 720 (руб.) — потратила Вика
2) 720 : 60 = 12 (кг) — конфет по 60 р. за килограмм Вика сможет купить за эти же деньги
Ответ: 12 кг конфет.
125
Ответы к странице 125
Задание № 461. Найдите значение выражения:
1) 82275 − 64 * 56 + 9680 : 16 − 23637;
2) (204 * 402 − 30456 : 423) : 36 − 1388;
3) 1376 : (621 − 589) + (138 − 69) * 29.
Решение
Задание № 462. Найдите значение выражения:
1) 49184 + 4575 : 15 − 62 * 93 − 33999;
2) (306 * 307 − 187 * 36) : 45 + 5780;
3) 1885 : (542 − 477) + 48 * (134 − 92).
Решение
Задание № 463. Малыш купил для Карлсона 8 пирожных и 12 булочек с повидлом, заплатив за всю покупку 408 крон. Одно пирожное стоит 24 кроны. Какова цена одной булочки?
Решение задачи
1) 8 * 24 = 192 (крон) — стоят пирожные
2) 408 − 192 = 216 (крон) — стоят булочки
3) 216 : 12 = 18 (крон) — цена одной булочки
Ответ: 18 крон.
Задание № 464. Дед Афанасий заготовил на зиму 6 бочек квашеной капусты и 14 бочонков соленых огурцов. В одной бочке вмещается 26 кг капусты. Сколько килограммов огурцов в одном бочонке, если всего дед Афанасий заготовил 324 кг овощей?
Решение
1) 6 * 26 = 156 (кг) — капусты было заготовлено
2) 324 − 156 = 168 (кг) — огурцов было заготовлено
3) 168 : 14 = 12 (кг) — огурцов в одном бочонке
Ответ: 12 кг.
Задание № 465. Сколько килограммов масла можно изготовить из 261 кг сливок, если из 9 кг сливок получается 2 кг масла?
Решение
1) 261 : 9 = 29 (раз) — во столько больше можно приготовить масла из 261 кг сливок, чем из 9 кг
2) 29 * 2 = 58 (кг) масла можно изготовить из 261 кг сливок
Ответ: 58 кг.
Задание № 466. Автомобиль расходует 8 л бензина на 100 км пути. Хватит ли 20 л бензина, чтобы доехать из Рязани до Владимира, расстояние между которыми 233 км?
Решение
1) 8 * 2 = 16 (л) — бензина расходуется на 200 км пути
2) 8 : 2 = 4 (л) — бензина расходуется на 50 км пути
3) 16 + 4 = 20 (л) — бензина хватит на 200 + 50 = 250 км пути.
250 > 233
Ответ: 20 л бензина хватит чтобы доехать из Рязани до Владимира
Задание № 467. Было собрано 328 кг проса. Сколько из этого проса можно получить пшена, если из 4 кг проса получается 3 кг пшена?
Решение
1) 328 : 4 = 82 (раза) — во столько больше можно получить пшена из 328 кг проса, чем из 4 кг проса
2) 82 * 3 = 246 (кг) — пшена получится из 328 кг проса
Ответ: 246 кг.
Задание № 468. Расстояние между двумя пристанями равно 476 км. Двигаясь по течению реки, катер проходит это расстояние за 14 ч. За сколько часов он пройдет это расстояние против течения реки, если скорость течения равна 3 км/ч?
Решение
1) 476 : 14 = 34 (км/ч) — скорость катера по течению реки
2) 34 − 3 = 31 (км/ч) — скорость катера
3) 31 − 3 = 28 (км/ч) — скорость катера против течения
4) 476 : 28 = 17 (ч) — потребуется катеру, чтобы пройти 476 км против течения реки
Ответ: 17 часов
Задание № 469. Расстояние между двумя портами равно 504 км. Двигаясь против течения реки, теплоход проходит это расстояние за 21 ч. За сколько часов он пройдет это расстояние по течению реки, если скорость течения равна 2 км/ч?
Решение
1) 504 : 21 = 24 (км/ч) — скорость теплохода против течения
2) 24 + 2 = 26 (км/ч) — скорость теплохода
3) 26 + 2 = 28 (км/ч) — скорость теплохода по течению
4) 504 : 28 = 18 (ч) — потребуется теплоходу, чтобы пройти 504 км по течению реки
Ответ: 18 ч.
126
Ответы к странице 126
Задание № 470. Из Цветочного и Солнечного городов, расстояние между которыми равно 136 км, выехали одновременно навстречу друг другу Винтик и Шпунтик. Винтик двигался со скоростью 16 км/ч. С какой скоростью ехал Шпунтик, если они встретились через 14 ч после выезда?
Решение задачи
1) 16 * 4 = 64 (км) — проехал до встречи Винтик
2) 136 − 64 = 72 (км) — проехал до встречи Шпунтик
3) 72 : 4 = 18 (км/ч) — скорость с которой ехал Шпунтик
Ответ: 18 км/ч
Задание № 471. Расстояние между двумя городами равно 1264 мили (1 сухопутная миля = 1609 м). Из них одновременно вылетели навстречу друг другу два вертолета и встретились через 8 ч после вылета. Скорость одного из вертолетов 82 миль/ч. С какой скоростью летел второй вертолет?
Решение от 7 гуру
1) 8 * 82 = 656 (миль) — пролетел до встречи первый вертолет
2) 1264 − 656 = 608 (миль) — пролетел до встречи второй вертолет
3) 608 : 8 = 76 (миль/ч) — скорость второго вертолета
Ответ: 76 миль/ч.
Задание № 472. В 6 ч утра из Мурома в Киев выехал со скоростью 9 км/ч Илья Муромец.В 8 ч утра из Мурома в Киев выехал Алеша Попович и догнал Илью Муромца в 2 ч дня. С какой скоростью ехал Алеша Попович?
Решение
2 часа дня = 14 часов дня
1) 14 − 6 = 8 (ч) — потратил до встречи Илья Муромец
2) 8 * 9 = 72 (км) — проехал до встречи Илья Муромец
3) 14 − 8 = 6 (ч) — потратил до встречи Алеша Попович
4) 72 : 6 = 12 (км/ч) — скорость Алеши Поповича
Ответ: 12 км/ч.
Задание № 473. В 8 ч 57 мин черепаха Катрина отправилась в путешествие из своего пруда в соседний. В 9 ч 5 мин из этого же пруда в том же направлении отправилась черепаха Виктория и догнала Катрину в 9 ч 29 мин. Найдите, с какой скоростью двигалась Катрина, если известно, что Виктория двигалась со скорость 8 м/мин.
Решение задачи
1) 9 ч 29 мин − 9 ч 5 мин = 24 минуты двигалась до встречи черепаха Виктория
2) 24 * 8 = 192 м преодолела до встречи черепаха Виктория
3) 9 ч 29 мин − 8 ч 57 мин = 8 ч 89 мин − 8 ч 57 мин = 32 минуты двигалась до встречи черепаха Катрина
4) 192 : 32 = 6 (м/мин) — скорость черепахи Катрины
Ответ: 6 м/мин.
Задание № 474. С двух станций, расстояние между которыми равно 24 км, одновременно в одном направлении отправились два поезда. Впереди двигался поезд со скоростью 58 км/ч. Через 4 ч после начала движения его догнал второй поезд. Найдите скорость второго поезда.
Решение
1) 58 * 4 = 232 (км) — проехал до встречи первый поезд
2) 232 + 24 = 256 (км) — проехал до встречи второй поезд
3) 256 : 4 = 64 (км/ч) скорость второго поезда
Ответ: 64 км/ч.
Задание № 475. Расстояние между селами Грушевое и Яблоневое равно 30 км. Из этих сел одновременно в одном направлении отправились казаки Серошапка и Черноус. Черноус скакал на коне со скоростью 9 км/ч и через 6 ч после начала движения догнал Серошапку, который шел пешком. С какой скоростью шел Серошапка?
Решение
1) 9 * 6 = 54 (км) — проехал до встречи Черноус
2) 54 − 30 = 24 (км) — проехал до встречи Серошапка
3) 24 : 6 = 4 (км/ч) — скорость Серошапки
Ответ: 4 км/ч.
Задание № 476. Расстояние между городами Сен−Жермен и Сен−Антуан равно 12 лье (старинная французская единица длины, 1 лье приблизительно равно 4444 м). Из этих городков одновременно в одном направлении выехали Портос со скоростью 1 лье/ч и дАртаньян со скоростью 3 лье/ч, причем Портос скакал впереди. Через сколько часов после выезда дАртаньян догонит Портоса?
Решение
1) 3 − 1 = 2 (лье/ч) — разница между скоростями дАртаньяна и Портоса
2) 12 : 2 = 6 (ч) — потребуется дАртаньяну, чтобы догнать Портоса
Ответ: через 6 часов.
Задание № 477. Расстояние между островами Акулий и Китовый равно 48 морским милям (1 морская миля = 1852 м). От этих островов одновременно в одном направлении отчалили фрегаты «Отважный» и «Стремительный», причем «Отважный» плыл впереди «Стремительного». Скорость «Отважного» равна 12 миль/ч, а «Стремительного» − 18 миль/ч. Через сколько часов «Стремительный» догонит фрегат «Отважный»?
Решение
1) 18 − 12 = 6 (миль/ч) — разница скоростей «Стремительного» и «Отважного»,
то есть один корабль догоняет другой со скоростью 6 миль/ч. При старте расстояние между ними было 48 миль, каждый час это расстояние сокращается на 6 миль, значит можно найти время:
2) 48 : 6 = 8 (ч) потребуется «Стремительному», чтобы догнать «Отважный»
Ответ: через 8 часов.
127
Ответы к странице 127
Задание № 478. Школьники Василий, Андрей, Дмитрий и Сергей собрали 326 кг яблок. Василий собрал 37 кг яблок, что в 3 раза меньше, чем Андрей, а Дмитрий и Сергей собрали яблок поровну. Кто из школьников собрал больше килограммов яблок?
Решение
1) 37 * 3 = 111 (кг) — яблок собрал Андрей
2) 37 + 111 = 148 (кг) — собрали Андрей и Василий вместе
3) 326 − 148 = 178 (кг) — собрали Дмитрий и Сергей вместе
4) 178 : 2 = 89 (кг) — собрали и Дмитрий, и Сергей
111 > 89 > 37
Ответ: больше всего яблок собрал Андрей.
Задание № 479. Рабочие Иван, Петр, Степан и Павел изготовили 160 деталей. Иван изготовил 81 деталь, что в 3 раза больше, чем Петр, а Степан и Павел изготовили деталей поровну. Кто из рабочих изготовил меньше всех деталей?
Решение
1) 81 : 3 = 27 (д.) — изготовил Петр
2) 81 + 27 = 108 (д.) — изготовили Петр и Иван вместе
3) 160 − 108 = 52 (д.) — изготовили Степан и Павел вместе
4) 52 : 2 = 26 (д.) — изготовил и Степан, и Павел
81 > 27 > 26
Ответ: Степан и Павел изготовили меньше всех деталей.
Задание № 480. Буратино живет на расстоянии 1 км 200 м от школы. Уроки в школе начинаются в 8 ч 30 мин. Буратино делает за минуту 120 шагов, длина шага − 40 см. В котором часу Буратино должен выходить из дома, чтобы приходить в школу за 10 мин до начала занятий?
Решение
1 км 200 м = 1200 м = 120000 см.
1) 120 * 40 = 4800 (см) — проходит Буратино за 1 минуту
2) 120000 : 4800 = 25 (мин.) — идет Буратино до школы
3) 25 + 10 = 35 мин, то есть за 35 минут до начала занятий должен выходить Буратино из дома
4) 8 ч 30 мин − 35 мин = 7 ч 90 мин − 35 мин = 7 ч 55 мин − время в которое Буратино должен выходить из дома
Ответ: в 7 ч 55 мин.
Задание № 481. Дежурные первого отряда за 6 мин чистят 24 картофелины, а дежурные второго отряда за 9 мин − 45 картофелин. За сколько минут совместной работы они почистят 198 картофелин?
Решение
1) 24 : 6 = 4 (к.) — в минуту чистят дежурные первого отряда
2) 45 : 9 = 5 (к.) — в минуту чистят дежурные второго отряда
3) 4 + 5 = 9 (к.) — в минуту чистят совместно дежурные первого и второго отрядов
4) 198 : 9 = 22 (мин) — потребуется дежурным двух отрядов, чтобы почистить 198 картофелин
Ответ: за 22 минуты.
Задание № 482. На сколько дней школьной столовой хватит 800 л сока, если мальчики за 8 дней выпивают 960 л сока, а девочки за 6 дней − 480 л?
Решение
1) 960 : 8 = 120 (л) — сока в день выпивают мальчики
2) 480 : 6 = 80 (л) — сока в день выпивают девочки
3) 120 + 80 = 200 (л) — сока в день выпивают мальчики и девочки совместно
4) 800 : 200 = 4 (дня) — в столовой смогут поить детей соком
Ответ: на 4 дня.
Задание № 483. За четыре дня работы три оператора набрали на компьютере вместе 288 страниц. Сколько страниц наберет один оператор за 7 дней, если у них одинаковая производительность труда?
Решение
1) 288 : 4 = 72 (стр.) — в день набирают совместно три оператора
2) 72 : 3 = 24 (стр.) — в день набирает один оператор
3) 24 * 7 = 168 (стр.) — наберет один оператор за 7 дней
Ответ: 168 страниц.
Задание № 484. Для работы шести одинаковых двигателей в течении 8 ч требуется 672 л топлива. На сколько часов работы хватит 98 л топлива одному такому двигателю?
Решение
1) 672 : 8 = 84 (л) — расходуют 6 двигателей за 1 час
2) 84 : 6 = 14 (л) — расходует за час один двигатель
3) 98 : 14 = 7 (ч) — проработает один двигатель на 98 литрах топлива
Ответ: 7 ч.
Задание № 485. Белочки Рыженькая и Жёлтенькая собирали орехи. Рыженькая собрала 6 мешочков орехов, а Желтенькая − 7 таких же мешочков. Вместе они собрали 52 кг орехов. Сколько килограммов орехов собрала Рыженькая и сколько − Желтенькая?
Решение
1) 6 + 7 = 13 (м.) — орехов собрали обе белочки
2) 52 : 13 = 4 (кг) — орехов в одном мешочке
3) 6 * 4 = 24 (кг) — собрала Рыженькая
4) 7 * 4 = 28 (кг) — собрала Желтенькая
Ответ: 24 кг и 28 кг.
Задание № 486. Двигаясь по пустыне в течении трех дней, караван преодолел 63 км. В первый день караван двигался 6 ч, во второй − 8 ч, а в третий − 7 ч. Сколько километров проходил караван каждый день, если известно, что он двигался все дни с постоянной скоростью?
Решение
1) 6 + 8 + 7 = 21 (ч) — двигался караван в течении трех дней
2) 63 : 21 = 3 (км/ч) — скорость каравана
3) 6 * 3 = 18 (км) — прошел караван в первый день
4) 8 * 3 = 24 (км) — прошел караван во второй день
5) 7 * 3 = 21 (км) — прошел караван в третий день
Ответ: 18 км, 24 км, 21 км.
Задание № 487. Фермер привез на рынок 420 кг яблок и 180 кг груш в 50 одинаковых ящиках. Сколько ящиков было с яблоками и сколько − с грушами?
Решение
1) 420 + 180 = 600 (кг) — масса всех фруктов
2) 600 : 50 = 12 (кг) — масса фруктов в одном ящике
3) 420 : 12 = 35 (ящ.) — с яблоками
4) 180 : 12 = 15 (ящ.) — с грушами
Ответ: 35 ящиков и 15 ящиков.
Задание № 488. Али−Баба перевозил найденное в пещере разбойников золото на четырех ослах в 22 одинаковых мешках. На первого осла он погрузил 80 кг золота, на второго − 100 кг, на третьего − 120 кг, на четвертого − 140 кг. Сколько мешков золота было нагружено на каждого осла?
Решение
1) 80 + 100 + 120 + 140 = 440 (кг) — суммарная масса золота
2) 440 : 22 = 20 (кг) — масса золота в одном ящике
3) 80 : 20 = 4 (м.) — золота погрузили на первого осла
4) 100 : 20 = 5 (м.) — золота на второго осла
5) 120 : 20 = 6 (м.) — золота на третьего осла
5) 140 : 20 = 7 (м.) — золота на четвертого осла
Ответ: 4, 5 , 6 и 7 мешков.
128
Ответы к странице 128
Задание № 489. Решите уравнение:
1) 21(18 + x) = 714;
2) 16(4x − 34) = 608;
3) 12(152 + 19x) = 2052;
4) (152x + 32) * 6 = 192.
Решение
21(18 + x) = 714
18 + x = 714 : 21
x = 34 − 18
x = 16
Ответ: 1616(4x − 34) = 608
4x − 34 = 608 : 16
4x = 38 + 34
x = 72 : 4
x = 18
Ответ: 1812(152 + 19x) = 2052
152 + 19x = 2052 : 12
19x = 171 − 152
x = 19 : 19
x = 1
Ответ: 1(152x + 32) * 6 = 192
152x + 32 = 192 : 6
152x = 32 − 32
152x = 0
x = 0
Ответ: 0
Задание № 490. Решите уравнение:
1) 8(x − 14) = 56;
2) (46 − x) * 19 = 418;
3) 9(143 − 13x) = 234;
4) 17(5x − 16) = 238.
Решение
8(x − 14) = 56
x − 14 = 56 : 8
x − 14 = 7
x = 7 + 14
x = 21
Ответ: 21(46 − x) * 19 = 418
46 − x = 418 : 19
x = 46 − 22
x = 24
Ответ: 249(143 − 13x) = 234
143 − 13x = 234 : 9
13x = 143 − 26
x = 117 : 13
x = 9
Ответ: 917(5x − 16) = 238
5x − 16 = 238 : 17
5x = 14 + 16
x = 30 : 5
x = 6
Ответ: 6
Задание № 491. Решите уравнение:
1) 14x + 4x − 48 = 240;
2) 25b − 7b − 9 = 279;
3) 16a − 7a + 96 = 222;
4) 20y + 5y + y + 19 = 227.
Решение
14x + 4x − 48 = 240
18x = 240 + 48
x = 288 : 18
x = 16
Ответ: 1625b − 7b − 9 = 279
18b = 279 + 9
b = 288 : 18
b = 16
Ответ: 1616a − 7a + 96 = 222
9a = 222 − 96
a = 126 : 9
a = 14
Ответ: 1420y + 5y + y + 19 = 227
26y = 227 − 19
y = 208 : 26
y = 8
Ответ: 8
Задание № 492. Решите уравнение:
1) 9b + 6b − 15 = 615;
2) 2a + 123a + 97 = 472;
3) 17x − x + 5x − 19 = 170;
4) 73y − y − 22y + 40 = 190.
Решение
9b + 6b − 15 = 615
15b = 615 + 15
b = 630 : 15
b = 42
Ответ: 422a + 123a + 97 = 472
125a = 472 − 97
a = 375 : 125
a = 3
Ответ: 317x − x + 5x − 19 = 170
21x = 170 + 19
x = 189 : 21
x = 9
Ответ: 973y − y − 22y + 40 = 190
50y = 190 − 40
y = 150 : 50
y = 3
Ответ: 3
Задание № 493. Решите уравнение:
1) (x + 14) : 9 = 13;
2) 966 : (x + 17) = 23;
3) x : 8 − 6 = 49;
4) 52 + 72 : х = 56;
5) 56 : (x − 6) = 8;
6) 56 : x − 6 = 8.
Решение
(x + 14) : 9 = 13
x + 14 = 13 * 9
x = 117 − 14
x = 103
Ответ: 103966 : (x + 17) = 23
x + 17 = 966 : 23
x = 42 − 17
x = 25
Ответ: 25x : 8 − 6 = 49
x : 8 = 49 + 6
x = 55 * 8
x = 440
Ответ: 44052 + 72 : x = 56
72 : x = 56 − 52
x = 72 : 4
x = 18
Ответ: 1856 : (x − 6) = 8
x − 6 = 56 : 8
x = 7 + 6
x = 13
Ответ: 1356 : x − 6 = 8
56 : x = 8 + 6
56 : x = 14
x = 56 : 14
x = 4
Ответ: 4
Задание № 494. Решите уравнение:
1) (x − 23) : 26 = 8;
2) 1728 : (56 − x) = 36.
Решение
(x − 23) : 26 = 8
x − 23 = 8 * 26
x = 208 + 23
x = 231
Ответ: 2311728 : (56 − x) = 36
56 − x = 1728 : 36
x = 56 − 48
x = 8
Ответ: 8
Задание № 495. Отец с сыном посадили 108 кустов помидоров, причем отец посадил в 2 раза больше, чем сын. Сколько кустов помидоров посадил сын?
Решение
Пусть сын посадил x кустов, тогда 2x кустов посадил отец.
Составим уравнение:
2x + x = 108
3x = 108
x = 108 : 3
x = 36
Ответ: 36 кустов посадил сын.
Задание № 496. В два магазина завезли 268 кг шампиньонов, причем в первый магазин завезли шампиньонов в 3 раза меньше, чем во второй. Сколько килограммов шампиньонов завезли в каждый магазин?
Решение
Пусть x кг шампиньонов завезли во второй магазин, тогда 3x кг шампиньонов завезли в первый магазин.
Составим уравнение:
3x + x = 268
4x = 268
x = 268 : 4
x = 67
3x = 3 * 67 = 201
Ответ: 67 кг шампиньонов завезли во второй магазин, 201 кг шампиньонов завезли в первый магазин.
Задание № 497. В двух залах кинотеатра демонстрировались два кинофильма. В первом зале зрителей было в 7 раз больше, чем во втором. Сколько зрителей находилось во втором зале, если известно, что их было на 156 меньше, чем в первом?
Решение
Пусть x зрителей было во втором зале, тогда 7x зрителей было в первом зале.
Составим уравнение:
7x − x = 156
6x = 156
x = 156 : 6
x = 26
Ответ: 26 зрителей было во втором зале.
Задание № 498. Валентин подарил Виктории роза и орхидеи, причем орхидей было в 4 раза меньше, чем роз. Сколько роз подарил Валентин, если известно, что их было на 51 больше, чем орхидей?
Решение
Пусть орхидей было x штук, тогда 4x штук было роз.
Составим уравнение:
4x − x = 51
3x = 51
x = 51 : 3
x = 17
4x = 4 * 17 = 68
Ответ: 17 орхидей и 68 роз подарил Валентин Виктории..
Задание № 499. Из вершины прямого угла проведен луч так, что он делит прямой угол на два угла, один из которых больше второго на 20°. Найдите величину каждого из образовавшихся углов.
Решение
Пусть первый угол равен x градусов, тогда второй угол равен x + 20 градусов.
Составим уравнение:
x + x + 20 = 90
2x = 90 − 20
x = 70 : 2
x = 35
x + 20 = 35 + 20 = 55.
Ответ: 35° величина первого угла, 55° величина второго угла.
Задание № 500. Из вершины развернутого угла проведен луч так, что он делит развернутый угол на два угла, один из которых меньше второго на 50°. Найдите величину каждого из образовавшихся углов.
Решение
Пусть первый угол равен x градусов, тогда второй угол равен x + 50 градусов.
Составим уравнение:
x + x + 50 = 180
2x = 180 − 50
x = 130 : 2
x = 65
x + 50 = 65 + 50 = 115
Ответ: 65° величина первого угла, 115° величина второго угла.
Задание № 501. В три магазина завезли 264 кг яблок. В первый магазин завезли в 3 раза больше яблок, чем в третий, а во второй − в 2 раза больше, чем в третий. Сколько килограммов яблок завезли в каждый магазин?
Решение
Пусть в третий магазин завезли x кг яблок, тогда:
3x кг яблок завезли в первый магазин;
2x кг яблок завезли во второй магазин.
Составим уравнение:
x + 2x + 3x = 264
6x = 264
x = 264 : 6
x = 44 (кг)
2x = 2 * 44 = 88 (кг)
3x = 3 * 44 = 132 (кг)
Ответ: 44 кг яблок завезли в третий магазин, 88 кг яблок завезли во второй магазин, 132 кг яблок завезли в первый магазин.
129
Ответы к странице 129
Задание № 502. За четыре дня путешествия капитан Врунгель проплыл 546 миль. Во второй день он проплыл в 4 раза больше, чем в первый, в третий − в 3 раза больше, чем в первый, а в четвертый − в 5 раз больше, чем в первый. Сколько миль проплывал капитан Врунгель ежедневно?
Решение
Пусть в первый день капитан Врунгель проплыл x миль, тогда:
4x миль он проплыл во второй день;
3x миль он проплыл в третий день;
5x миль он проплыл в четвертый день.
Составим уравнение:
x + 4x + 3x + 5x = 546
13x = 546
x = 546 : 13
x = 42 (мили)
4x = 4 * 42 = 168 (миль)
3x = 3 * 42 = 126 (миль)
5x = 5 * 42 = 210 (миль)
Ответ: 42 мили проплыл капитан Врунгель в первый день, 168 миль во второй день, 126 миль в третий день, 210 миль в четвертый день.
Задание № 503. Егор, Саша и Алеша поймали 256 окуней. Егор поймал в 3 раза больше рыб, чем Саша, а Алеша − столько, сколько Егор и Саша вместе. Сколько окуней поймал лучший рыбак?
Решение
Пусть x окуней поймал Саша, тогда:
3x окуней поймал Егор;
x + 3x = 4x окуней поймал Алеша.
Составим уравнение:
x + 3x + 4x = 256
8x = 256
x = 256 : 8
x = 32 (ок.) поймал Саша;
3x = 3 * 32 = 96 (ок.) поймал Егор;
4x = 4 * 32 = 128 (ок.) поймал Алеша.
128 > 96 > 32
Ответ: лучший рыбак − Алеша, он поймал 128 окуней.
Задание № 504. Красная Шапочка, Мальвина, Золушка и Дюймовочка слепили 500 пельменей. Красная Шапочка слепила в 2 раза больше пельменей, чем Дюймовочка, Мальвина − столько, сколько Мальвина и Дюймовочка вместе, а Золушка − столько, сколько Мальвина и Дюймовочка вместе. Сколько пельменей слепила каждая девочка?
Решение
Пусть x пельменей слепила Дюймовочка, тогда:
2x пельменей слепила Красная шапочка;
x + 2x = 3x пельменей слепила Мальвина;
x + 3x = 4x пельменей слепила Золушка.
Составим уравнение:
x + 2x + 3x + 4x = 500
10x = 500
x = 500 : 10
x = 50 (п.) слепила Дюймовочка
2x = 2 * 50 = 100 (п.) слепила Красная шапочка
3x = 3 * 50 = 150 (п.) слепила Мальвина
4x = 4 * 50 = 200 (п.) слепила Золушка
Ответ: 50, 100, 150 и 200 пельменей.
Задание № 505. В трех вагонах электропоезда ехало 246 пассажиров. В первом вагоне было в 2 раза больше пассажиров, чем во втором, а в третьем − на 78 пассажиров больше, чем во втором. Сколько пассажиров ехало в каждом вагоне?
Решение
Пусть x пассажиров ехало во втором вагоне, тогда:
2x пассажиров ехало в первом вагоне;
x + 78 пассажиров ехало в третьем вагоне.
Составим уравнение:
x + 2x + x + 78 = 246
4x = 246 − 78
x = 168 : 4
x = 42 (п.) ехало во втором вагоне
2x = 2 * 42 = 84 (п.) ехало в первом вагоне
x + 78 = 42 + 78 = 120 (п.) ехало в третьем вагоне
Ответ: 42, 84 и 120 пассажиров.
Задание № 506. В три школы отправили 552 кг апельсинов, причем в одну школу отправили в 6 раз меньше апельсинов, чем во вторую, и на 136 кг меньше, чем в третью. Сколько килограммов апельсинов отправили в каждую школу?
Решение
Пусть x кг апельсинов отправили в первую школу, тогда:
6x кг апельсинов отправили во вторую школу;
x + 136 кг апельсинов отправили в третью школу.
Составим уравнение:
x + 6x + x + 136 = 552
8x = 552 − 136
x = 416 : 8
x = 52 (кг) апельсинов отправили в первую школу
6x = 6 * 52 = 312 (кг) апельсинов отправили во вторую школу
x + 136 = 52 + 136 = 188 (кг) апельсинов отправили в третью школу
Ответ: 52 кг апельсинов отправили в первую школу, 312 кг во вторую, 188 кг в третью.
Задание № 507. Одна из сторон треугольника в 5 раз меньше второй и на 25 см меньше третьей. Найдите стороны треугольника, если его периметр равен 74 см.
Решение
Пусть x см длина первой стороны треугольника, тогда:
5x см длина второй стороны треугольника;
x + 25 см длина третьей стороны треугольника.
Составим уравнение:
x + 5x + x + 25 = 74
7x = 74 − 25
x = 49 : 7
x = 7 (см) длина первой стороны треугольника
5x = 5 * 7 = 35 (см) длина второй стороны треугольника
x + 25 = 7 + 25 = 32 (см) длина третьей стороны треугольника
Ответ: 7 см, 35 см, 32 см.
Задание № 508. Одна из сторон треугольника в 2 раза больше второй стороны, вторая − на 7 дм меньше третьей. Найдите стороны треугольника, если его периметр равен 99 дм.
Решение
Пусть x дм длина второй стороны треугольника, тогда:
2x дм длина первой стороны треугольника;
x + 7 дм длина третьей стороны треугольника.
Составим уравнение:
x + 2x + x + 7 = 99
4x = 99 − 7
x = 92 : 4
x = 23 (дм) длина второй стороны треугольника
2x = 2 * 23 = 46 (дм) длина первой стороны треугольника
x + 7 = 23 + 7 = 30 (дм) длина третьей стороны треугольника
Ответ: 23 дм, 46 дм, 30 дм.
Задание № 509. 1) Верно ли, что если каждое слагаемое делится на некоторое число, то и сумма этих слагаемых делится на это число? Проиллюстрируйте свой ответ примерами.
2) Может ли сумма нескольких слагаемых делиться на некоторое число, если каждое слагаемое не делится на это число?
Ответы
1) 2 + 4 + 6 + 8 + 10 + 50 = 80 верно, так как каждое слагаемое делится на 2 и сумма также делится на 2;
4 + 8 + 12 + 16 + 20 + 100 = 160 верно, так как каждое слагаемое делится на 4 и сумма также делится на 4.2) Может, например:
3 + 5 + 7 + 9 = 24 делится и на 2, и на 4, и на 6, и на 8, но при этом не одно из слагаемых не делится на эти числа.
Задание № 510. Как изменится частное, если:
1) делимое увеличить в 7 раз; частное увеличится в 7 раз
2) делитель увеличить в 4 раза; частное уменьшится в 4 раза
3) делимое увеличить в 8 раз, а делитель − в 2 раза; частное увеличится в 4 раза
4) делимое уменьшить в 9 раз, а делитель − в 3 раза; частное уменьшится в 3 раза
5) делимое увеличить в 6 раз, а делитель уменьшить в 2 раза; частное увеличится в 12 раз
6) делимое уменьшить в 6 раз, а делитель увеличить в 2 раза? частное уменьшится в 12 раз
130
Ответы к странице 130
Задание № 511. Делимое увеличили в 3 раза. Как надо изменить делитель, чтобы частное:
1) увеличилось в 6 раз; уменьшить делитель в 2 раза
2) уменьшилось в 6 раз; увеличить делитель в 18 раз
3) не изменилось? увеличить делитель в 3 раза
Задание № 512. При каких значениях a верно равенство:
1) a : 1 = a при любом a
2) 0 : a = 0 при любом a
3) a : a = 1 при любом a, кроме 0.
4) a : 9 = 0 при a = 0
5) 16 : a = 0 ни при каком a
6) a : a = 0 ни при каком a
Задание № 513. Вычислите удобным способом:
(44 * 58) : 11 = (44 : 11) * 58 = 4 * 58 = 232
(69 * 60) : 30 = (60 : 30) * 69 = 2 * 69 = 138
(26 * 20) : 13 = (26 : 13) * 20 = 2 * 20 = 40
(63 * 88) : 21 = (63 : 21) * 88 = 3 * 88 = 264
(350 * 48) : 70 = (350 : 70) * 48 = 5 * 48 = 240
(47 * 200) : 50 = (200 : 50) * 47 = 4 * 47 = 188
(2 * 17 * 14) : 28 = (28 * 17) : 28 = (28 : 28) * 17 = 17
(21 * 18) : 14 = (3 * 7 * 2 * 9) : 14 = (27 * 14) : 14 = (14 : 14) * 27 = 27
(5 * 11 * 32) : 16 = 5 * 11 * (32 : 16) = 5 * 11 * 2 = 110
Задание № 514. Вычислите удобным способом:
(36 * 21) : 12 = (36 : 12) * 21 = 3 * 21 = 63
(40 * 420) : 60 = (420 : 60) * 40 = 7 * 40 = 280
(5 * 6 * 78) : 3 = (30 * 78) : 3 = (30 : 3) * 78 = 10 * 78 = 780
(45 * 63) : 81 = (5 * 9 * 7 * 9) : 81 = (35 * 81) : 81 = (81 : 81) * 35 = 1 * 35 = 35
Задание № 515. Расставьте в записи 7 * 9 + 12 : 3 − 2 скобки так, чтобы значение полученного выражения было равно: 1) 75; 2) 23.
Ответ
1) 7 * 9 + 12 : (3 − 2) = 63 + 12 = 75
2) (7 * 9 + 12) : 3 − 2 = 75 : 3 − 2 = 25 − 2 = 23
Задание № 516. Расставьте в записи 4 * 12 + 18 : 6 + 3 скобки так, чтобы значение полученного выражения было равно: 1) 50; 2) 72.
Ответ
1) 4 * 12 + 18 : (6 + 3) = 48 + 18 : 9 = 48 + 2 = 50
2) 4 * (12 + 18 : 6 + 3) = 4 * (12 + 3 + 3) = 4 * 18 = 72
Задание № 517. Составьте числовое выражение с использованием только знаков четырех арифметических действий и четырех цифр 2 так, чтобы значение полученного выражения было равно: 1) 1; 2) 2; 3) 3; 4) 4; 5) 5; 6) 6; 7) 8; 
Ответ
2 : 2 + (2 − 2) = 1
2 : 2 + 2 : 2 = 2
2 * 2 − 2 : 2 = 4 − 1 = 3
2 * (2 : 2) + 2 = 4
2 * 2 + 2 : 2 = 4 + 1 = 5
(2 : 2 + 2) * 2 = 3 * 2 = 6
2 + 2 + 2 + 2 + 2 = 10
2 * 2 * 2 + 2 = 10
Задание № 518. Периметр четырехугольника ABCD равен 34 см, AB = 6 см, сторона BC в 2 раза больше стороны AB, стороны CD и AD равны. Вычислите длину стороны AD.
1) BC = 2AB = 2 * 6 = 12 (см)
2) 6 + 12 = 18 (см) — сумма сторон AB и BC
3) 34 − 18 = 16 (см) — сумма сторон CD и AD
4) 16 : 2 = 8 (см) — длина стороны CD и AD
Ответ: 8 см.
Задание № 519. Купили розовые и зеленые конверты. Розовых среди них было 18 конвертов. С марками было 12 конвертов, из них 8 были розовыми. Сколько всего купили конвертов?
Решение
1) 12 − 8 = 4 ( к.) — зеленых с марками
2) 18 + 4 = 22 (к.) — всего купили
Ответ: 22 конверта.
Задание № 520. На столе расположено семь зубчатых колес так, что первое сцеплено со вторым, второе − с третьим и т.д., а седьмое сцеплено с первым. Могут ли все колеса вращаться одновременно?
Решение
Рассмотрим как будут вращаться колеса:
− первое по часовой стрелке;
− второе против часовой стрелки;
− третье по часовой стрелке, следовательно нечетные колеса будут вращаться по часовой;
− семь − нечетное число − крутится по часовой, значит колесо, зацепленное с ним должно вращаться против часовой стрелки, что противоречит пункту 1, значит колеса вращаться одновременно не могут.
133
Ответы к странице 133
Задание № 521. Выполните деление с остатком:
1) 42 : 5;
2) 592 : 24;
3) 428 : 37;
4) 684 : 30;
5) 1372 : 13;
6) 5721 : 28;
7) 3196 : 74;

9) 12387 : 185.
Решение
Задание № 522. Выполните деление с остатком:
1) 54 : 7;
2) 212 : 6;
3) 158 : 12;
4) 534 : 15;
5) 2964 : 18;
6) 4848 : 106.
Решение
Задание № 523. 1) Найдите остаток при делении на 10 числа: 31; 47; 53; 148; 1596; 67389; 240750.
2) Найдите остаток при делении на 5 числа: 14; 61; 86; 235; 2658; 54769; 687903.
1) Так как число нацело делится на 10, когда оно заканчивается на 0, то остатки будут:
1; 7; 3; 8; 6; 9; 0.2) Так как число нацело делится на 5, когда оно заканчивается на 0 ил на 5, то остатки будут:
4; 1; 1; 0; 3; 4; 3.
Задание № 524. Найдите остаток при делении на 100 числа: 106; 202; 421; 836; 2764; 100098; 672305; 1306579; 562400.
Так как число нацело делится на 100, когда оно заканчивается на 00, то остатки будут:
6; 2; 21; 36; 64; 98; 5; 79; 0.
Задание № 525. Запишите остатки, которые можно получить при делении на: 1) 7; 2) 13; 3) 24.
1) 1, 2, 3, 4, 5, 6.
2) 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11.
3) 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20, 21, 22, 23.
Задание № 526. Запишите остатки, которые можно получить при делении на: 1) 5; 2) 19.
1) 1, 2, 3, 4.
2) 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19.
Задание № 527. Блокнот стоит 130 р. Сколько блокнотов можно купить на 700 р.?
Решение
700 : 130 = 5 (остаток 50)
Ответ: 5 блокнотов можно купить на 700 р. и станется 50 р. сдачи
Задание № 528. На один грузовик можно нагрузить 5 т песка. Сколько требуется таких грузовиков, чтобы перевезти 42 т песка?
Решение
42 : 5 = 8 (остаток 2)
Ответ: потребуется 9 грузовиков, чтобы перевезти 42 т песка.
Задание № 529. В один ящик помещается 20 кг яблок. Сколько надо ящиков, чтобы разложить в них 176 кг яблок?
Решение
176 : 20 = 8 (остаток 16)
Ответ: 9 ящиков.
Задание № 530. Заполните таблицу.
134
Ответы к странице 134
Задание № 531. Найдите делимое, если делитель равен 12, неполное частное − 7, а остаток − 9.
Ответ
12 * 7 + 9 = 84 + 9 = 93
Задание № 532. Найдите делимое, если делитель равен 18, неполное частное − 4, а остаток − 11.
Ответ
18 * 4 + 11 = 72 + 11 = 83
Задание № 533. Выразите делимое через неполное частное, делитель и остаток в виде равенства a = bq + r, где a − делимое, b − делитель, q − неполное частное, r − остаток, если a = 82, b = 8.
Ответ
a = bq + r
82 = 8 * q + r
82 = 8 * 10 + 2
Задание № 534. Выразите делимое через неполное частное, делитель и остаток в виде равенства a = bq + r, где a − делимое, b − делитель, q − неполное частное, r − остаток, если a = 45, b = 7.
Решение
a = bq + r
45 = 7 * q + r
45 = 7 * 6 + 3
Задание № 535. При каком наименьшем натуральном a значение выражения:
1) 48 + a делится нацело на 6;
2) 65 − a делится нацело на 8;
3) 96 − a при делении на 9 дает остаток 4?
Решение
1) при a = 6,
48 + a = 48 + 6 = 54
54 : 6 = 92) при a = 1,
65 − a = 65 − 1 = 64
64 : 8 = 83) при a = 2,
96 − a = 96 − 2 = 94
94 : 9 = 9 * 10 + 4
Задание № 536. При каком наименьшем натуральном a значение выражения:
1) 53 + a делится нацело на 7;
2) a + 24 при делении на 5 дает остаток 2?
Решение 7 гуру
1) при a = 3,
53 + a = 53 + 3 = 56
56 : 7 = 82) при a = 3,
a + 24 = 3 + 24 = 27
27 : 5 = 5 (остаток 2)
Задание № 537. Катя разделила число 211 на некоторое число и получила в остатке 26. На какое число делила Катя?
Решение
211 − 26 = 185
Так как остаток равен 26, то делитель числа 185 должен быть больше 26.
185 = 5 * 37 = 1 * 185
то есть Катя могла поделить число 211 на 37 или на 185, чтобы получить в остатке 26.
Ответ: 37 или 185.
Задание № 538. Миша разделил число 111 на некоторое число и получил в остатке 7. На какое число делил Миша?
Решение
111 − 7 = 104
Так как остаток равен 7, то делитель числа 104 должен быть больше 7.
104 = 1 * 104 = 2 * 52 = 4 * 26 = 8 * 13
Ответ: Миша мог поделить число 111 на 104, 52, 26, 13 или 8.
Задание № 539. Павел разделил число 70 на некоторое число и получил в остатке 4. На какое число делил Павел?
Решение
70 − 4 = 66
Так как остаток равен 4, то делитель числа 70 должен быть больше 4.
66 = 1 * 66 = 2 * 33 = 3 * 22 = 6 * 11
Ответ: Павел мог поделить число 70 на 66, 33, 22, 11 или 6.
Задание № 540. Какое наибольшее количество понедельников может быть в году?
Решение
366 : 7 = 52 (ост. 2), значит понедельников 52 и в год может войти еще 1 понедельник.
Понедельников может быть 53 при условии, что год начинается с понедельника.
Задание № 541. В одном осеннем месяце суббот и понедельников оказалось больше, чем пятниц. Каким днем недели было девятнадцатое число этого месяца? Какой это был месяц?
Решение
В месяце полных 4 недели, в неделе 7 дней, то есть 4 * 7 = 28 дней.
По условию суббот и понедельников больше, чем пятниц, следовательно месяц начнется с субботы и закончится понедельником, то есть нужно еще прибавить субботу, воскресенье и понедельник, то есть еще 3 дня.
Получается, сто в искомом месяце 28 + 3 = 31 день и следовательно этот месяц октябрь, так как осенью только в октябре 31 день.
Если месяц начинается с субботы, то 2 * 7 = 14 число будет пятницей, 15 − субботой, 16 − воскресеньем,…, 19 − средой.
Задание № 542. Известно, что число a − делимое, число b − делитель, причем a < b. найдите неполное частное и остаток при делении a на число b.
Решение
Неполное частное = 0, остаток = a.
Задание № 543. Докажите, что последняя цифра числа a равна остатку при делении этого числа на 10.
Решение
Число нацело делится на 10 тогда, когда оно оканчивается на 0. Поэтому последняя цифра числа a будет равна остатку при делении на 10, так как 0 + последняя цифра числа a = последняя цифра числа a.
Задание № 544. Придумайте буквенное выражение, при подстановке в которое вместо буквы любого натурального числа получится числовое выражение, значение которого:
1) при делении на 3 даёт в остатке 1; 3b + 1
2) при делении на 8 даёт в остатке 3; 8b + 3
3) при делении на 11 даёт в остатке 7. 11b + 7
135
Ответы к странице 135
Задание № 545. Упростите выражение и найдите его значение:
1) 14a * 6b, если a = 2, b = 3;
2) 25m * 3n, если m = 8, n = 1;
3) 5x + 8x − 3x, если x = 17;
4) 16y − y + 5y, если y = 23.
Решение
14a * 6b = 84ab = 84 * 2 * 3 = 84 * 6 = 504
25m * 3n = 75mn = 75 * 8 * 1 = 75 * 8 = 600
5x + 8x − 3x = 10x = 10 * 17 = 170
16y − y + 5y = 20y = 20 * 23 = 460
Задание № 546. Периметр прямоугольника равен 54 см, а его ширина на 3 см меньше длины. Найдите стороны прямоугольника.
Решение
54 : 2 = 27 (см) — длина + ширина
27 − 3 = 24 (см) — две ширины
24 : 2 = 12 (см) — ширина прямоугольника
12 + 3 = 15 (см) — длина прямоугольника
Ответ: 12 см и 15 см.
Задание № 547. Известно, что веревка сгорает за 4 мин и горит при этом неравномерно.
Как с помощью:
1) одной веревки отмерить 2 мин;
2) двух таких веревок отмерить 3 мин?
Ответ
1) Поджечь веревку с двух концов, когда она сгорит полностью, то пройдет 2 минуты.
2) Первую веревку поджечь с двух концов и одновременно вторую с одной стороны.
Когда первая веревка сгорит поджечь вторую со второй стороны.
136-137
Ответы к странице 136-137
Параграф 20. Степень числа
Страница 136
Задание № 548. Назовите основание и показатель степени.
1) число 4 − основание степени, а число 8 − показатель степени.
2) число 13 − основание степени, а число 10 − показатель степени.
3) число a − основание степени, а число 9 − показатель степени.
4) число 6 − основание степени, а число m − показатель степени.
5) число 2 − основание степени, а число 39 − показатель степени.
6) число 93 − основание степени, а число 1 − показатель степени.
Страница 137
Задание № 549. Упростите выражение, заменив произведение одинаковых множителей степенью:
1) 9 * 9 * 9 * 9 * 9;
2) 10 * 10 * 10;
3) a * a * a * a;
4) x * x * x * x * x * x;
5) 3m * 3m * 3m * 3m * 3m;
6) 6*6*…*6 10-множителей
7) у*у*…*у 8-множителей

Ответ
Задание № 550. Найдите значение выражения:
1) 33;
2) 72;
3) 54;
4) 25;
5) 06;
6) 112.
Ответ
33 = 3 * 3 * 3 = 27
72 = 7 * 7 = 49
54 = 5 * 5 * 5 * 5 = 625
25 = 2 * 2 * 2 * 2 * 2 = 32
06 = 0
112 = 1
Задание № 551. Найдите значение выражения:
1) 93 ;
2) 122 ;
3) 24 ;
4) 1100 ;
5) 1001 ;
6) 103 .
Ответ
93 = 9 * 9 * 9 = 729
122 = 12 * 12 = 144
24 = 2 * 2 * 2 * 2 = 16
1100 = 1
1001 = 100
103 = 10 * 10 * 10 = 1000
Задание № 552. Вычислите:
102 − 72 = 100 − 49 = 51
53 − 52 = 125 − 25 = 100
422 : 14 − 42 * 6 = 1764 : 14 − 16 * 6 = 126 − 96 = 30
83 : 42 − 23 = 512 : 16 − 8 = 32 − 8 = 24
252 : ( 242 + 72 ) = 625 : ( 576 + 49 ) = 625 : 625 = 1
103 − 102 + 93 = 1000 − 100 + 729 = 900 + 729 = 1629
Задание № 553. Вычислите:
1) 32 + 42 = 9 + 16 = 25
2) 33 + 23 = 27 + 8 = 35
3) 262 − ( 122 * 3 + 175 ) = 676 − ( 144 * 3 + 175 ) = 676 − ( 432 + 175 ) = 676 − 607 = 69
4) 63 − 2 * 43 − 13 = 216 − 2 * 64 − 1 = 87
5) 152 : ( 132 − 124 ) = 225 : ( 169 − 124 ) = 225 : 45 = 5
6) 83 : ( 42 − 23 ) = 512 : ( 16 − 8 ) = 512 : 8 = 64
Задание № 554. Найдите значение выражения:
1) 16 − c3 , если c = 2;
2) x3 − x2 , если x = 10;
3) 15a2 , если a = 4;
4) a2 b3 , если a = 6, b = 10;
5) ( x2 − y2 ) : ( x − y ) , если x = 4, y = 2;
6) ( x2 − y2 ) : x − y , если x = 4, y = 2;
7) x2 − y2 : ( x − y ) , если x = 4, y = 2;

Ответ
1) 16 − c3 = 16 − 2 3 = 16 − 8 = 8
2) x3 − x2 = 103 − 102 = 1000 − 100 = 900
3) 15a2 = 15 * 42 = 15 * 16 = 240
4) a2 b3 = 62 * 103 = 36 * 1000 = 36000
5) ( x2 − y2 ) : ( x − y ) = ( 42 − 22 ) : ( 4 − 2 ) = ( 16 − 4 ) : 2 = 12 2 = 6
6) ( x2 − y2 ) : x − y = ( 42 − 22 ) : 4 − 2 = ( 16 − 4 ) : 4 − 2 = 12 : 4 − 2 = 3 − 2 = 1
7) x2 − y2 : ( x − y ) = 42 − 22 : ( 4 − 2 ) = 16 − 4 : 2 = 16 − 2 = 14
x2 − y2 : x − y = 42 − 22 : 4 − 2 = 16 − 4 : 4 − 2 = 16 − 1 − 2 = 13
Задание № 555. 1) x2 − 14 , если x = 5; 7; 18;
2) 2y2 + 13 , если y = 6; 8; 9; 100.
Ответ
1) при x = 5: x2 − 14 = 52 − 14 = 25 − 14 = 11 ;
при x = 7: x2 − 14 = 72 − 14 = 49 − 14 = 35 ;
при x = 18: x2 − 14 = 182 − 14 = 324 − 14 = 310 .2) при y = 6: 2y2 + 13 = 2 * 62 + 13 = 2 * 36 + 13 = 72 + 13 = 85 ;
при y = 8: 2y2 + 13 = 2 * 82 + 13 = 2 * 64 + 13 = 128 + 13 = 141 ;
при y = 9: 2y2 + 13 = 2 * 92 + 13 = 2 * 81 + 13 = 162 + 13 = 175 ;
при y = 100: 2y2 + 13 = 2 * 1002 + 13 = 2 * 10000 + 13 = 20000 + 13 = 20013 .
Задание № 556. Запишите в виде степени с основанием 3 число;
1) 9;
2) 27;
3) 243;
4) 81.
Ответ
9 = 32 27 = 33 243 = 35 81 = 34
Задание № 557. Запишите в виде степени с основанием 2 число;
1) 4;
2) 16;
3) 32;
4) 256.
Ответ
4 = 22 16 = 24 32 = 25 256 = 28
138
Ответы к странице 138
Задание № 558. Составьте числовое выражение и найдите его значение:
1) сумма куба числа 5 и квадрата числа 8;
2) разность квадратов чисел 6 и 2;
3) квадрат разности чисел 6 и 2;
4) разность куба числа 3 и квадрат числа 5.
Ответ
53 + 82 = 125 + 64 = 189
62 − 22 = 36 − 4 = 32
(6 − 2)2 = 42 = 16
33 − 52 = 27 − 25 = 2
Задание № 559. Составьте числовое выражение и найдите его значение:
1) куб разности чисел 9 и 8;
2) квадрат суммы чисел 8 и 7;
3) сумма квадратов чисел 8 и 7;
4) разность кубов чисел 4 и 1.
Ответ
(9 −
3 = 13 = 1
(8 + 7)2 = 152 = 225
82 + 72 = 64 + 49 =113
43 − 13 = 64 − 1 = 63
Задание № 560. Решите уравнение:
1) 7(x − 19) = 133;
2) 9(213 − 2x) = 927;
3) 1344 : (x + 26) = 32;
4) 384 : (51 − 5x) = 24.
Решение
7(x − 19) = 133
x − 19 = 133 : 7
x = 19 + 19
x = 38
Ответ: 389(213 − 2x) = 927
213 − 2x = 927 : 9
2x = 213 − 103
x = 110 : 2
x = 55
Ответ: 551344 : (x + 26) = 32
x + 26 = 1344 : 32
x = 42 − 26
x = 16
Ответ: 16384 : (51 − 5x) = 24
51 − 5x = 384 : 24
5x = 51 − 16
x = 35 : 5
x = 7
Ответ: 7
Задание № 561. Для приготовления десяти порций мороженого используют 200 г сахара. На сколько порций мороженого хватит 500 г сахара?
Решение
200 : 10 = 20 (г) — сахара используют на одну порцию мороженого
500 : 20 = 25 (п)
Ответ: на 25 порций мороженого.
Задание № 562. Вася задумал трёхзначное число, у которого с каждым из чисел 652, 153 и 673 совпадает один из разрядов, а два других не совпадают. Какое число задумал Вася?
Ответ: Вася задумал число 172.
Задание № 563. В очереди за билетами в цирк стояли Миша, Наташа, Петя, Дима и Маша. Маша купила билет раньше, чем Миша, но позже, чем Наташа. Петя и Наташа не стояли рядом, а Дима не был рядом ни с Наташей, ни с Машей, ни с Петей. Кто за кем стоял в очереди?
Решение
В очереди дети стояли следующем образом: Наташа, Маша, Петя, Миша, Дима.
142
Ответы к странице 142
Параграф 21. Площадь. Площадь прямоугольника
Задание № 564. 1) Сколько квадратных сантиметров содержит 1 дм2 ? 1 м2 ?
Ответ
1 дм2 = 10 см * 10 см = 100 см2
1 м2 = 100 см * 100 см = 10000 см2
2) Сколько квадратных сантиметров содержит 1 км2 ?
Ответ
1 км2 = 1000 м * 1000 м = 1000000 м2
Задание № 565. Вычислите площадь прямоугольника, соседние стороны которого равны 14 см и 8 см.
Решение
S = a * b = 14 * 8 = 112 (см2)
Задание № 566. Вычислите площадь квадрата со стороной 7 дм.
S = a2 = 72 = 7 * 7 = 49 (дм2)
Задание № 567. Одна сторона прямоугольника равна 16 см, а соседняя сторона − на 6 см длиннее. Вычислите площадь прямоугольника.
Решение
16 + 6 = 22 (см)
S = 16 * 22 = 352 (см2)
Ответ: площадь прямоугольника 352 см2 .
Задание № 568. Одна сторона прямоугольника равна 48 см, а соседняя сторона − в 8 раз меньше. Вычислите площадь прямоугольника.
Решение
48 : 8 = 6 (см) вторая сторона прямоугольника
S = 48 * 6 = 288 (см2) — площадь
Ответ: площадь прямоугольника 288 см2 .
Задание № 569. Периметр прямоугольника равен 162 дм, а одна из сторон − 47 дм. Найдите площадь прямоугольника.
Решение
1) 47 * 2 = 94 (дм) — сумма двух противоположных сторон прямоугольника
2) 162 − 94 = 68 (дм) — сумма двух других противоположны сторон прямоугольника
3) 68 : 2 = 34 (дм) — ширина прямоугольника
4) 47 * 34 = 1598 (дм2) — площадь прямоугольника.
Ответ: 1598 дм2.
Задание № 570. Периметр прямоугольника равен 96 м, и он в 8 раз больше одной из сторон прямоугольника. Найдите площадь прямоугольника.
Решение
1) 96 : 8 = 12 (м) — одна из сторон прямоугольника
2) 12 * 2 = 24 (м) — сумма двух противоположных сторон прямоугольника
3) 96 − 24 = 72 (м) — сумма двух других противоположных сторон прямоугольника
4) 72 : 2 = 36 (м) — длина прямоугольника
5) 12 * 36 = 432 (м2 ) — площадь прямоугольника
Ответ: 432 м2 .
Задание № 571. Найдите площадь квадрата, периметр которого равен 96 см.
Решение
1) 96 : 4 = 24 (см) — сторона квадрата
2) S = 242 = 24 * 24 = 576 (м2 ) — площадь квадрата
Ответ: 576 м2 .
Задание № 572. Периметр прямоугольника равен 4 м 8 дм, одна из его сторон в 5 раз больше соседней стороны. Найдите площадь прямоугольника.
Решение
4 м 8 дм = 480 см;
480 : 2 = 240 (см) — ширина + длина
пусть ширина равна x см, тогда длина 5x см.
Составим уравнение:
x + 5x = 240
6x = 240
x = 240 : 6
x = 40 (см) — ширина прямоугольника.
5x = 5 * 40 = 200 (см) — длина прямоугольника.
40 * 200 = 8000 (см2 ) — площадь прямоугольника
Ответ: 8000 см2 .
Задание № 573. Периметр прямоугольника равен 6 дм 8 см, одна из его сторон на 1 дм 6 см меньше соседней стороны. Найдите площадь прямоугольника.
Решение
6 дм 8 см = 68 см; 1 дм 6 см = 16 см.
68 : 2 = 34 (см) ширина + длина
Пусть ширина x см, а длина x + 16, тогда:
x + x + 16 = 34
2x = 34 − 16
x = 18 : 2
x = 9 (см) — ширина прямоугольника
x + 16 = 9 + 16 = 25 (см) — длина прямоугольника
9 * 25 = 225 (см2 ) площадь прямоугольника
Ответ: 225 см2
Задание № 574. Выразите:
1) в арах: 12 га; 45 га; 6 га 28 а; 14 га 68 а; 32400 м2 ; 123800 м2 ; 2 км2 14 га 5 а; 4 км2 72 га 16 a;
2) в квадратных метрах: 5 а; 17 а; 8 а; 63 га; 5 га 72 а; 14 га 43 а;
3) в гектарах и арах: 530 а; 1204 а; 16300 м2 ; 85200 м2 .
Ответы
1) 12 га = 12 * 100 = 1200а;
45 га = 45 * 100 = 4500а;
6 га 28 а = 6 * 100 + 28 = 628 а;
14 га 68 а = 14 * 100 + 68 = 1468 а;
32400 м2 = 32400 : 100 = 324 а;
123800 м2 = 123800 : 100 = 1238 а;
2 км2 14 га 5 а = 2 * 10000 + 14 * 100 + 5 = 20000 + 1400 + 5 = 21405 а;
4 км2 72 га 16 a = 4 * 10000 + 72 * 100 + 16 = 40000 + 7200 + 16 = 47216 а.2) 5 а = 5 * 100 = 500 м2 ;
17 а = 17 * 100 = 1700 м2 ;
8 а = 8 * 100 = 800 м2 ;
63 га = 63 * 10000 = 630000 м2 ;
5 га 72 а = 5 * 10000 + 72 * 100 = 50000 + 7200 = 57200 м2 ;
14 га 43 а = 14 * 10000 + 43 * 100 = 140000 + 4300 = 144300 м2 .3) 530 а = 5 га + 30 а;
1204 а = 12 га 4 а;
16300 м2 = 1 га 63 а;
85200 м2 = 8 га 52 а.
Задание № 575. Выразите:
1) в квадратных сантиметрах: 8 дм2 ; 16 дм2 ; 4 м2 ; 38 м2 ; 16 м2 19 дм2 ; 74 м2 3 дм2 ;
2) в гектарах: 340000 м2 ; 5830000 м2 ; 53 км2 ; 14 км2 ; 5 км2 18 га; 24 км2 6 га.
1) 8 дм2 = 8 * 100 = 800 см2 ;
16 дм2 = 16 * 100 = 1600 см2 ;
4 м2 = 4 * 10000 = 40000 см2 ;
38 м2 = 38 * 10000 = 380000 см2 ;
16 м2 19 дм2 = 16 * 10000 + 19 * 100 = 160000 + 1900 = 161900 см2 ;
74 м2 3 дм2 = 74 * 10000 + 3 * 100 = 740000 + 300 = 740300 см2 .2) 340000 м2 = 340000 : 10000 = 34 га;
5830000 м2 = 5830000 : 10000 = 583 га;
53 км2 = 53 * 100 = 5300 га;
14 км2 = 14 * 100 = 1400 га;
5 км2 18 га = 5 * 100 + 18 = 518 га;
24 км2 6 га = 24 * 100 + 6 = 2406 га.
Задание № 576. Поле прямоугольной формы имеет площадь 56 а, его длина − 80 м. Вычислите периметр поля.
Решение
56 a = 5600 м2
1) 5600 : 80 = 70 (м) — ширина поля
2) 2 * 70 + 2 * 80 = 140 + 160 = 300 (м) — периметр поля
Ответ: 300 м.
Задание № 577. Поле прямоугольной формы имеет площадь 48 а, его ширина − 150 м. Вычислите периметр поля.
Решение
48 a = 4800 м2
1) 4800 : 150 = 32 (м) — длина поля
2) 2 * 32 + 2 * 150 = 64 + 300 = 364 (м) периметр поля
Ответ: 364 м.
Задание № 578. Вычислите периметр и площадь фигуры, изображенной на рисунке 149 (размеры даны в сантиметрах).
Решение
а) P = 8 + 18 + 15 + 18 + 10 + 8 + 5 = 82 см
S 1 = 5 * 8 = 40 см2
S 2 = 15 * 18 = 270 см2
S = S 1 + S 2 = 40 + 270 = 310 см2б) P = 16 * 2 + 4 * 2 + 6 * 2 + 3 + 11 = 32 + 8 + 12 + 3 + 11 = 66 см
S 1 = 3 * 6 = 18 см2
S 2 = 11 * 16 = 176 см2
S = S 1 + S 2 = 18 + 176 = 194 см2
143
Ответы к странице 143
Задание № 579. Вычислите периметр и площадь фигуры, изображенной на рисунке 150 (размеры даны в сантиметрах).
Решение
P = 18 * 2 + (12 + 6 + 12) * 2 + 4 * 2 = 36 + 60 + 8 = 104 см
S 1 = 6 * 4 = 24 см2
S 2 = 18 * ( 12 + 12 + 6 ) = 18 * 30 = 540 см2
S = S 2 − S 1 = 540 − 24 = 516 см2
Ответ: 104 см и 516 см2.
Задание № 580. Хватит ли 5 т гороха, чтобы засеять им поле, имеющее форму прямоугольника со сторонами 500 м и 400 м, если на 1 га земли надо высеять 260 кг гороха?
Решение
500 * 400 = 200000 м2 = 20 га площадь поля;
260 * 20 = 5200 кг = 5 т 200 кг необходимо гороха, чтобы засеять все поле:
5 т 200 кг > 5 т
Ответ: 5 т гороха не хватит.
Задание № 581. Отец решил облицевать кафелем стену кухни, длина которой равна 4 м 50 см, а высота − 3 м. Хватит ли ему 20 ящиков кафеля, если одна плитка имеет форму квадрата со стороной 15 см, а в одном ящике находится 30 плиток?
Решение
450 * 300 = 135000 (см2 ) — площадь кухонной стены
15 * 15 = 225 (см2 ) — площадь одной плитки
20 * 30 = 600 (пл.) — было всего
135000 : 225 = 600 (пл.) — необходимо, чтобы облицевать стену
600 = 600
Ответ: 20 ящиков кафеля хватит.
Задание № 582. Фермер Петр Трудолюб посадил в теплице огурцы. Длина теплице равна 16 м 50 см, а ширина − 12 м. Сколько килограммов огурцов соберет фермер в своей теплице, если с 1 м2 собирает 30 кг огурцов?
Решение
16 м 50 см = 1650 см
12 м = 1200 см
1650 * 1200 = 1980000 (см2 )= 198 (м2 ) − площадь теплицы
198 * 30 = 5940 (кг) — огурцов соберет фермер в своей теплице
Ответ: 5940 (кг)
Задание № 583. Расход эмалевой краски на однослойное покрытие составляет 180 г на 1 м2 . Хватит ли 3 кг эмали, чтобы покрасить стену длиной 6 м и высотой 3 м?
Решение
6 * 3 = 18 (м2 ) — площадь стены
18 * 180 = 3240 (г) = 3 кг 240 г краски необходимо, чтобы покрасить стену
3 кг 240 г > 3 кг
Ответ: краски не хватит.
Задание № 584. Квадрат со стороной 12 см и прямоугольник, длина которого равна 18 см, являются равновеликими. Найдите периметр прямоугольника.
Решение
12 * 12 = 144 (см2 ) — площадь квадрата
144 : 18 = 8 (см) — ширина прямоугольника
2 * 8 + 2 * 18 = 16 + 36 = 52 (см) — периметр прямоугольника
Ответ: 52 см.
Задание № 585. Квадрат и прямоугольник имеют равные площади, соседние стороны прямоугольника равны 3 см и 12 см. Найдите периметр квадрата.
Решение
3 * 12 = 36 (см2 ) — площадь прямоугольника
6 * 6 = 36 (см2 ) — площадь квадрата
P = 4 * 6 = 24 (см) — периметр квадрата
Ответ: 24 см.
Задание № 586. Ширина прямоугольника равна 26 см. На сколько квадратных сантиметров увеличится площадь этого прямоугольника, если его длину увеличить на 4 см?
Решение
4 * 26 = 104 (см2 ), то есть на 104 квадратных сантиметров увеличится площадь этого прямоугольника, если его длину увеличить на 4 см.
Задание № 587. Во сколько раз увеличится периметр и площадь прямоугольника, если каждую его сторону увеличить в 4 раза?
Решение
Периметр прямоугольника равен 2a + 2b = 2(a + b).
Если каждую сторону увеличить в 4 раза, то периметр будет равен 2 * 4a + 2 * 4b = 8(a + b).
8(a + b) : 2(a + b) = 4, то есть периметр увеличится в 4 раза.
Площадь прямоугольника равна a * b.
Если каждую сторону увеличить в 4 раза, то площадь будет равна 4a * 4b = 16ab.
8(a + b) : 2(a + b) = 4, то есть периметр увеличится в 4 раза.
16ab : ab = 16, то есть площадь увеличится в 16 раз.
144
Ответы к странице 144
Страница 144
Задание № 588. Длина прямоугольника равна 32 см. На сколько квадратных сантиметров уменьшится площадь этого прямоугольника, если его ширину уменьшить на 5 см?
Решение
5 * 32 = 160 (см2 ), то есть на 160 квадратных сантиметров уменьшится площадь прямоугольника, если его ширину уменьшить на 5 см.
Задание № 589. Площадь квадрата ABCD равна 16 см2 (рис.151). Чему равна площадь прямоугольника ACFE?
Решение
S ACFE = S ADE + S ADC + S CDF
S ACD = S ADE + S CDF = S ABCD : 2 =16 : 2 = 8 (см2 )
S ACFE = 8 + 8 = 16 (см2 )
Задание № 590. Стороны прямоугольного листа бумаги имеют целочисленную длину (в сантиметрах), а площадь листа равна 12 см2 . Сколько квадратов площадью 4 с м 2 можно вырезать из этого прямоугольника?
Ответ
2 квадрата, если размеры листа 3 см Х 4 см;
3 квадрата, если размеры листа 2 см Х 6 см.
Задание № 591. Стороны прямоугольного листа бумаги имеют целочисленную длину (в сантиметрах), а площадь листа равна 18 см2 . Сколько квадратов со стороной 3 см можно вырезать из этого листа?
Ответ
2 квадрата, если размеры листа 3 см Х 6 см.
Задание № 592. Внутри прямоугольника ABCD (рис. 152) вырезали отверстие прямоугольной формы. Как одним прямолинейным разрезом разделить полученную фигуру на две фигуры с равными площадями?
Ответ
Задание № 593. Используя четыре из пяти изображенных на рисунке 153 фигур, составьте квадрат.
Задание № 594. Можно ли разрезать квадрат на несколько частей так, чтобы потом их них можно было составить два квадрата, длины сторон которых выражаются целым числом сантиметров, если сторона данного квадрата равна:
1) 5 см;
2) 6 см?
Ответы
1) 52 = 32 + 42 , поэтому если сторона квадрата равна 5 см, то его можно разрезать на квадраты со стороной 1 см, затем сложить два квадрата, длина сторон которых равны 3 см и 4 см.
2) Если стороны квадрата равны 6 см, то его невозможно разрезать на несколько частей так, чтобы потом из них можно было бы сложить два квадрата с целочисленными длинами, так как 62 = 36 нельзя записать как сумму квадратов двух чисел.
145
Ответы к странице 145
Задание № 595. Из вершины прямого угла ABC (рис. 154) провели лучи BD и BE так, что угол ABE оказался больше угла DBE на 34°, а угол CBD больше угла DBE на 23°. Какова градусная мера угла DBE?
Решение
∠ABD = ∠ABE − ∠DBE = 34°;
∠CBE = ∠CBD − ∠DBE = 23°;
∠DBE = 90° − 34° − 23° = 33°.
Задание № 596. Выполните действия:
1) 1008 * 604 − 105984 : 12 − 54321;
2) (57 * 34 + 812754 : 27) : 18.
Решение
Задание № 597. Расстояние между городами A и B равно 30 км. Из города A в город B выехал велосипедист и двигался со скоростью 15 км/ч. Одновременно из города B в направлении города A вылетела птица со скоростью 30 км/ч. Встретившись с велосипедистом, птица развернулась и полетела навстречу велосипедисту. Встретившись с ним, птица развернулась и полетела назад в город B и т.д. Сколько километров пролетела птица за то время, пока велосипедист ехал из города A в город B?
Решение
1) 30 : 15 = 2 (ч) — потратил велосипедист, чтобы доехать из города A в город B
2) 30 * 2 = 60 (км) — пролетела птица за то время, пока велосипедист ехал из города A в город
Ответ: 60 км.
150
Ответы к странице 150
Параграф 22. Прямоугольный параллелепипед. Пирамида
Устные задания
1.
1) 1300 2) 7800 3) 943000
2.
1) 48аb 2) 180mnk 3) 5600abcd
3.
1) 2a+2b 2) 15-5b 3) 42mn+48mp
4.
28 : 7 = 4 (см)
(7 + 4) * 2 = 22 (см2)
5.
6 ц = 600 кг
600 : 12 = 50 (ящ.)
6.
36 : 4 = 9 (раз)
Задание № 598. На рисунке 169 изображен прямоугольный параллелепипед ABCDMNKP. Назовите:
1) грани, которым принадлежит вершина C;
2) ребра, равные ребру BC;
3) верхнюю грань;
4) вершины, принадлежащие нижней грани;
5) грани, имеющие общее ребро AM;
6) грань, равную грани DPKC.
Ответы
1) ABCD; CDPK; CBNK.
2) AD; MP; NK.
3) MNKP
4) A; B; C; D.
5) AMPD; AMNB.
6) AMNB.
151
Ответы к странице 151
Задание № 599. Измерения прямоугольного параллелепипеда MNKPEFST (рис. 170) равны 9 см, 5 см и 6 см. Вычислите сумму длин всех его ребер и площадь его поверхности.
Ответы
9 * 4 + 5 * 4 + 6 * 4 = 36 + 20 + 24 = 80 (см) — сумма длин всех ребер прямоугольного параллелепипеда
6 * 9 * 2 + 6 * 5 * 2 + 9 * 5 * 2 = 108 + 60 + 90 = 258 (см2) — площадь прямоугольного параллелепипеда
Задание № 600. Найдите сумму длин всех ребер прямоугольного параллелепипеда, измерения которого равны 13 см, 16 см, 21 см.
Ответ
13 * 4 + 16 * 4 + 21 * 4 = 4 * (13 + 16 + 21) = 4 * 50 = 200 (см) сумма длин всех ребер прямоугольного параллелепипеда
Задание № 601. Найдите площадь поверхности прямоугольного параллелепипеда, измерения которого равны 9 м, 24 м, 11 м.
Ответ
S = 2 * 9 * 24 + 2 * 9 * 11 + 2 * 11 * 24 = 2 * 216 + 2 * 99 + 2 * 264 = 432 + 198 + 528 = 1158 (м2)
Задание № 602. Вычислите площадь поверхности и сумму длин всех ребер куба (рис. 171), ребро которого равно 5 см.
Ответ
5 * 12 = 60 (см) — сумма длин всех ребер
S = 5 * 5 * 6 = 150 (см2) — площадь поверхности
Задание № 603. Найдите сумму длин всех ребер и площадь поверхности куба, если его ребро равно 7 см.
Ответ
7 * 12 = 84 (см) сумма длин всех ребер
S = 7 * 7 * 6 = 294 (см2) площадь поверхности
Задание № 604. На рисунке 172 изображена пирамида MABC. Укажите:
1) основание пирамиды;
2) вершину пирамиды;
3) боковые грани пирамиды;
4) боковые ребра пирамиды;
5) ребра основания пирамиды.
Ответы
1) основание пирамиды: ABC.
2) вершина пирамиды: M.
3) боковые грани пирамиды: AMB; BMC; AMC.
4) боковые ребра пирамиды: MA; MB; MC.
5) ребра основания пирамиды: AB; BC; AC.
Задание № 605. На рисунке 173 изображена пирамида SABCD. Укажите:
1) основание пирамиды;
2) вершину пирамиды;
3) боковые грани пирамиды;
4) боковые ребра пирамиды;
5) ребра основания пирамиды.
Ответы
1) основание пирамиды: ABCD.
2) вершина пирамиды: S.
3) боковые грани пирамиды: SAB; SAD; SDC; SBC.
4) боковые ребра пирамиды: SA; SB; SC; SD.
5) ребра основания пирамиды: AB; BC; AD; DC.
152
Ответы к странице 152
Задание № 606. На рисунке 174 изображена развертка прямоугольного параллелепипеда.
1) Из скольких прямоугольников состоит развертка?
2) Сколько пар равных прямоугольников содержит развертка?
3) Какова площадь этой развертки, если измерения параллелепипеда равны 10 см, 7 см и 3 см?
Ответы
1) Развертка состоит из 6 прямоугольников.
2) 3 пары равных прямоугольников содержит развертка.
3) S = 2 * (10 * 7) + 2 * (10 * 3) + 2 * (7 * 3) = 2 * 70 + 2 * 30 + 2 * 21 = 140 + 60 + 42 = 242 (см2) — площадь развертки.
Задание № 607. Вычислите площадь поверхности прямоугольного параллелепипеда, развертка которого изображена на рисунке 175.
Ответ
S = 2 * (6 * 4) + 2 * (2 * 6) + 2 * (2 * 4) = 2 * 24 + 2 * 12 + 2 * 8 = 48 + 24 + 16 = 88 (см2) — площадь поверхности прямоугольного параллелепипеда.
Задание № 608. Высота прямоугольного параллелепипеда равна 20 см, что на 5 см больше его ширины и в 3 раза меньше его длины. Вычислите площадь поверхности параллелепипеда.
Ответ
20 − 5 = 5 (см) — ширина прямоугольного параллелепипеда
20 * 3 = 60 (см) — длина прямоугольного параллелепипеда
S = 2 * (15 * 20) + 2 * (15 * 60) + 2 * (20 * 60) = 2 * 300 + 2 * 900 + 2 * 1200 = 600 + 1800 + 2400 = 4800 (см2) площадь поверхности прямоугольного параллелепипеда.
4800 см2 = 48 дм2
Задание № 609. Высота длин всех ребер прямоугольного параллелепипеда равна 28 см. Найдите сумму длин трех его ребер, имеющих общую вершину.
Ответ
28 : 4 = 7 (см) — сумма длин трех ребер, имеющих общую вершину.
153
Ответы к странице 153
Задание № 610. Прямоугольный параллелепипед и куб имеют равные площади поверхностей. Длина параллелепипеда равна 18 м, что в 2 раза больше, чем его ширина, и на 8 м больше, чем его высота. Найдите ребро куба.
Решение
18 : 2 = 9 (м) ширина параллелепипеда
18 − 8 = 10 (м) высота параллелепипеда
S = 2 * (9 * 10) + 2 * (9 * 18) + 2 * (10 * 18) = 2 * 90 + 2 * 162 + 2 * 180 = 180 + 324 + 360 = 864 (м2)
площадь поверхности прямоугольного параллелепипеда, а значит и куба.
864 : 6 = 144 (м2) площадь грани куба,
а так 144 = 12 * 12, значит ребро куба равно 12 см.
Задание № 611. Брусок, имеющий форму прямоугольного параллелепипеда с измерениями 4 см, 5 см и 6 см, покрасили со всех сторон и разрезали на кубики с ребром 1 см. Сколько получилось кубиков, у которых окрашено:
1) три грани;
2) две грани;
3) одна грань?
Ответы
1) Кубиков у которых окрашено три грани 8 штук, так как они находятся в вершинах параллелепипеда, а количество вершин равно 8.
2) Кубики у которых окрашено две грани, это те кубики которые находятся вдоль ребер:
8 + 12 + 16 = 36 кубиков.
3) Кубиков у которых окрашено одна грань: 12 + 16 + 24 = 52 кубика.
Задание № 612
Скорость космического корабля «Восток», на которой Юрий Гагарин совершил свой полет, равна 8 км/с. 1) За сколько минут он пролетал 960 км? 2) Какое расстояние он пролетал за 1 ч?
Решение
960 : 8 = 120 с = 2 (мин.)
Ответ: за 2 минуты.8 * 60 * 60 = 28 800 (км)
Ответ: 28 800 км он пролетал за час.
Задание № 613. Из листа картона можно вырезать шесть одинаковых квадратов. Сколько листов картона надо для того, чтобы вырезать 50 таких квадратов.
Решение
50 : 6 = 8 (ост. 2) — значит нужно больше 8 листов, но меньше 9-ти. А так как мы считаем целыми листами, то нужно 9 листов.
Ответ: потребуется 9 листов.
Задание № 614. Поезд отправился со станции в 16 ч со скоростью 54 км/ч. В 19 ч с этой же станции в противоположном направлении отправился второй поезд. В 24 ч расстояние между ними было равно 642 км. С какой скоростью двигался второй поезд?
Решение
24 − 16 = 8 (ч) время движения первого поезда
24 − 19 = 5 (ч) время движения второго поезда
8 * 54 = 432 (км) проехал первый поезд
642 − 432 = 210 (км) проехал второй поезд
210 : 5 = 42 (км/ч) скорость второго поезда
Ответ: 42 км/ч.
Задание № 615. Решите уравнение:
1) 6x + 8x − 7x = 714;
2) 23x − 19x + 5x = 1827;
3) 11x − 6x + 17 = 2042;
4) 5x + 3x − 47 = 6401.
Решение
6x + 8x − 7x = 714
7x = 714
x = 714 : 7
x = 10223x − 19x + 5x = 1827
9x = 1827
x = 1827 : 9
x = 20311x − 6x + 17 = 2042
5x = 2042 − 17
x = 2025 : 5
x = 4055x + 3x − 47 = 6401
8x = 6401 + 47
x = 6448 : 8
x = 806
Задание № 616. Как с помощью линейки измерить диагональ кирпича, имея еще несколько таких кирпичей? (Диагональ параллелепипеда − это отрезок, соединяющий две его вершины, не принадлежащие одной грани.)
Ответ
156-157
Ответы к странице 156
Задание № 617. 1) Сколько сантиметров в одном дециметре? Квадратных сантиметров в одном квадратном дециметре? Кубических сантиметров в одном кубическом дециметре?
2) Сколько сантиметров в одном метре? Квадратных сантиметров в одном квадратном метре? Кубических сантиметров в одном кубическом метре?
Ответ
1) 1 дм = 10 см
1 дм2 = 10 * 10 = 100 см2
1 дм3 = 10 * 10 * 10 = 1000 см32) 1 м = 100 см
1 м2 = 100 * 100 = 10000 см2
1 м3 = 100 * 100 * 100 = 1000000 см3
Ответы к странице 157
Задание № 618. Фигуры, изображенные на рисунке 179, сложены из кубиков, ребра которых равны 1 см. Найдите объем каждой фигуры.
Ответ
V1= 5∗4∗3 = 60 (см3) объем прямоугольно параллелепипеда в который вложена первая фигура
4 * 2 + 3 * 2 + 2 * 2 = 8 + 6 + 4 = 18 (см3) объем первой фигуры
V2= 6∗4∗4 = 96 (см3) объем прямоугольно параллелепипеда в который вложена вторая фигура
4 * 5 + 3 * 5 = 20 + 15 = 35 (см3) объем второй фигуры.
Задание № 619. Вычислите объем прямоугольного параллелепипеда, измерения которого равны 12 м, 15 м и 6 м.
Ответ
V = abc = 12 * 15 * 6 = 12 * 90 = 1080 (м3 ) объем прямоугольного параллелепипеда.
Задание № 620. Чему равен объем куба, ребро которого равно 6 см?
Ответ
V= a3 = 63 = 6∗6∗6 = 216 (см3 )
Задание № 621. Чему равен объем прямоугольного параллелепипеда с измерениями 10 дм, 8 дм и 4 дм?
Ответ
V = abc = 10 * 8 * 4 = 10 * 32 = 320 (дм3) объем прямоугольного параллелепипеда.
Задание № 622. Выразите:
1) в кубических миллиметрах: 7 см3 ; 38 см3 ; 12 см3 243 мм3 ; 42 см3 68 мм3 ; 54 см3 4 мм3 ; 1 дм3 20 мм3 ; 18 дм3 172 см3 ; 35 дм3 67 см3 96 мм3 ;
2) в кубических дециметрах: 4 м3 ; 264 м3 ; 10 м3 857 дм3 ; 28 м3 2 дм3 ; 44000 см3 ; 5430000 см3 .
Решение
1) 7 см3 = 7 * 1000 = 7000 мм3
38 см3 = 38 * 1000 = 38000 мм3
12 см3 243 мм3 = 12 * 1000 + 243 = 12243 мм3
42 см3 68 мм3 = 42 * 1000 + 68 = 42068 мм3
54 см3 4 мм3 = 54 * 1000 + 4 = 54004 мм3
1 дм3 20 мм3 = 1 * 1000000 + 20 = 1000020 мм3
18 дм3 172 см3 = 18 * 1000000 + 172 * 1000 = 18172000 мм3
35 дм3 67 см3 96 мм3 = 35 * 1000000 + 67 * 1000 + 96 = 35067096 мм32) 4 м3 = 4 * 1000 = 4000 дм3
264 м3 = 264 * 1000 = 264000 дм3
10 м3 857 дм3 = 10 * 1000 + 857 = 10857 дм3
28 м3 2 дм3 = 28 * 1000 + 2 = 28002 дм3
44000 см3 = 44000 : 1000 = 44 дм3
5430000 см3 = 5430000 : 1000 = 5430 дм3
Задание № 623. Выразите в кубических сантиметрах: 8 дм3 ; 62 дм3 ; 378000 мм3 ; 520000 мм3 ; 78 дм3 325 см3 ; 56 дм3 14 см3 ; 8 м3 4 дм3 6 см3 .
Решение
8 дм3 = 8 * 1000 = 8000 см3
62 дм3 = 62 * 1000 = 62000 см3
378000 мм3 = 378000 : 1000 = 378 см3
520000 мм3 = 520000 : 1000 = 520 см3
78 дм3 325 см3 = 78 * 1000 + 325 = 78325 см3
56 дм3 14 см3 = 56 * 1000 + 14 = 56014 см3
8 м3 4 дм3 6 см3 = 8 * 1000000 + 4 * 1000 + 6 = 8004006 см3
Задание № 624. Ширина прямоугольного параллелепипеда равна 15 дм, длина − на 3 дм больше ширины, а высота − в 3 раза меньше длины. Найдите объем данного параллелепипеда.
15 + 3 = 18 (дм) длина прямоугольного параллелепипеда;
18 : 3 = 6 (дм) высота прямоугольного параллелепипеда;
15 * 6 * 18 = 90 * 18 = 1620 (дм3) объем прямоугольного параллелепипеда.
Задание № 625. Высота прямоугольного параллелепипеда равна 20 см, что на 4 см меньше его длины и в 5 раз больше его ширины. Вычислите объем данного параллелепипеда.
Решение
20 + 4 = 24 (cм) длина прямоугольного параллелепипеда
20 : 5 = 4 (cм) ширина прямоугольного параллелепипеда
20 * 4 * 24 = 80 * 24 = 1920 (см3 ) объем прямоугольного параллелепипеда
Задание № 626. Объем прямоугольного параллелепипеда равна 560 см3 , длина − 14 cм, ширина − 8 см. Найдите высоту данного параллелепипеда.
Решение
14 * 8 = 112 (см2) — площадь основания прямоугольного параллелепипеда
560 : 12 = 5 (см) — высота прямоугольного параллелепипеда
158
Ответы к странице 158
Задание № 627. Длина прямоугольного параллелепипеда равна 18 см, высота − 15 см, а объем − 3240 см3 . Найдите ширину данного параллелепипеда.
Решение
V = abc
b = V : (ac) = 3240 : (18 * 15) = 3240 : 270 = 12 (см) — ширина прямоугольного параллелепипеда.
Задание № 628. Объем комнаты, имеющей форму прямоугольного параллелепипеда, равен 144 м3 , а высота − 4 м. Найдите площадь пола комнаты.
Решение
V = S * h
S = V : h = 144 : 4 = 36 (м2) — площадь пола комнаты.
Задание № 629. Спортивный зал имеет форму прямоугольного параллелепипеда, его объем равен 960 м3 , а площадь пола равна 192 м 2 . Найдите высоту спортивного зала.
Решение
V = S * h
h = V : S = 960 : 192 = 5 (м) — высота зала
Задание № 630. Найдите объем фигуры, изображенной на рисунке 180 (размеры даны в сантиметрах).
Решение
30 * 20 * 25 = 15000 (см3 ) — объем большого прямоугольного параллелепипеда
15 * 20 * 5 = 1500 (см3 ) — объем выемки
15000 − 1500 = 13500 (см3 ) — объем фигуры
Задание № 631. Найдите объем фигуры, изображенной на рисунке 181 (размеры даны в сантиметрах).
Решение
14 * 12 * (8 +
= 168 * 16 = 2688 (см3 ) — объем левого прямоугольного параллелепипеда;
8 * 8 * (14 += 64 * 22 = 1408 (см3 ) — объем центрального прямоугольного параллелепипеда;
15 * 14 * (8 += 210 * 16 = 3360 (см3 ) — объем правого прямоугольного параллелепипеда;
2688 + 1408 + 3360 = 7456 (см3 ) — объем фигуры.
Задание № 632. Ребро куба, изготовленного из цинка, равно 4 см. Найдите массу куба, если масса 1 см3 цинка составляет 7 г.
Решение
V = a 3 = 4 3 = 4 ∗ 4 ∗ 4 = 64 (см3 ) — объем куба
7 * 64 = 448 (г) — масса куба
Задание № 633. Знайка сконструировал землеройную машину, которая за 8 ч может вырыть траншею, имеющую форму прямоугольного параллелепипеда, длиной 150 м, глубиной 80 см и шириной 60 см. Сколько кубометров земли выкапывает эта машина за 1 ч? Работа скольких коротышек выполняет эта машина, если за 8 ч один коротышка может выкопать 240 дм3 земли?
Решение
150 м = 15000 см
1) 15000 * 80 * 60 = 72000000 (см3 ) — выроет машина за 8 ч
2) 72000000 см3 = 72000 дм3 = 72 м3 — выкапывает машина за 8 ч
3) 72 : 8 = 9 (м3 ) — выкапывает машина за 1 ч работы
4) 72000 : 240 = 300 (к.) — заменяет землеройная машина
Ответ: 72 кубометра, 300 коротышек.
159
Ответы к странице 159
Задание № 634. Куб и прямоугольный параллелепипед имеют равные объемы. Найдите площадь поверхности куба, если длина прямоугольного параллелепипеда равна 12 см, что в 2 раза больше ширины и в 4 раза больше высота параллелепипеда.
Решение
12 : 2 = 6 (см) ширина прямоугольного параллелепипеда
12 : 4 = 3 (см) высота прямоугольного параллелепипеда
12 * 6 * 3 = 216 (см3 ) объем прямоугольного параллелепипеда, а значит и куба
216 = 6 * 6 * 6, значит ребро куба равно 6 см
У куба 6 сторон.
6 * (6 * 6) = 216 (см2) площадь поверхности куба
Ответ: 216 см2
Задание № 635. Ребро одного куба в 4 раза больше ребра второго. Во сколько раз:
1) площадь поверхности первого куба больше площади поверхности второго;
2) объем первого куба больше объема второго?
Решение
1) Пусть a − ребро малого куба, тогда 4a − ребро большого куба, тогда:
6 ∗ ( a ∗ a ) = 6 a2 площадь поверхности малого куба
6 ∗ ( 4 a ∗ 4 a ) = 96 a2 площадь поверхности большого куба
96 a2 : 6 a2 = 16 , то есть в 16 раз площадь поверхности большого куба больше площади поверхности малого2) Пусть a − ребро малого куба, тогда 4a − ребро большого куба, тогда:
a ∗ a ∗ a = a3 объем малого куба
4 a ∗ 4 a ∗ 4 a = 64 a3 объем большого куба
64 a3 : a3 = 64 , то есть в 64 раза объем большого куба больше объем малого.
Задание № 636. Как изменится объем прямоугольного параллелепипеда, если:
1) длину увеличить в 4 раза, ширину − в 2 раза, высоту − в 5 раз;
2) ширину уменьшить в 4 раза, высоту − в 2 раза, а длину увеличить в 16 раз?
Решение
1) V = 4a * 2b * 5c = 40abc, то есть объем прямоугольного параллелепипеда увеличится в 40 раз.
2) V = (a : 4) * (b : 2) * (с * 16) = (16 : 8)abc = 2abc, то есть объем прямоугольного параллелепипеда увеличится в 2 раза.
Задание № 637. Как изменится объем прямоугольного параллелепипеда, если:
1) каждое измерение увеличить в 2 раза;
2) длину уменьшить в 3 раза, высоту − в 5 раз, а ширину увеличить в 15 раз?
Решение
1) V = 2a * 2b * 2c = 8abc, то есть объем прямоугольного параллелепипеда увеличится в 8 раз.
2) V = (a : 3) * (b : 5) * (с * 15) = (15 : 15)abc = abc, то есть объем прямоугольного параллелепипеда останется прежним.
Задание № 638. В бассейн, площадь дна которого равна 1 га, налили 1000000 л воды. Можно ли в этом бассейне провести соревнования по плаванию?
Решение
1 га = 1000000 дм2 площадь дна бассейна
1000000 л = 1000000 дм3 объем налитой воды
V = S * h, значит h = V : S = 1000000 дм3 : 1000000 дм2 = 1 дм = 10 см глубина налитой воды, следовательно соревнования по плаванию в таком количестве воды провести невозможно.
Задание № 639. В кубе с ребром 3 см проделали три сквозных отверстия со стороной 1 см (рис. 182). Найдите объем оставшейся части.
Решение
3 * 3 * 3 = 27 (см3 ) — объем большого куба
1 * 1 * 1 = 1 (см3 ) — объем одного вырезанного кубики
Всего вырезали 7 кубиков
7 * 1 = 7 (см3 ) — объем вырезанной части
27 − 7 = 20 (см3 ) — объем оставшейся части
Задание № 640. Размеры куса мыла, имеющие форму прямоугольного параллелепипеда, равны 12 см, 6 см и 4 см. Каждый день используют одинаковую массу мыла. Через 14 дней все размеры куска мыла уменьшились в 2 раза. На сколько дней хватит оставшегося куска мыла?
Решение
1) 12 * 6 * 4 = 288 (см3 ) — объем нового куска мыла
2) 6 * 3 * 2 = 36 (см3 ) — объем куска мыла через 14 дней
3) 288 − 36 = 252 (см3 ) — объем истраченного мыла за 14 дней
4) 252 : 14 = 18 (см3 ) — мыла тратится в день
5) 36 : 18 = 2, то есть на два дня хватит оставшегося куска мыла.
Ответ: на 2 дня.
Задание № 641
В школьном коридоре, длина которого 30 м, ширина — 35 дм, надо заменить ленолеум. Какое наименьшее количество рулонов линолеума для этого нужно, если длина рулона линолеума равна 12 м, а ширина 160 см?
Решение
35 дм = 350 см
1) 350 : 160 = 2 (ост. 30) — 30 см не хватает, чтобы положить линолеум по все ширине. Чтобы покрыть коридор линолеумом в один ряд по ширине нужны 2 рулона материала и плюс полоска шириной в 30 см.2) 30 : 12 = 2 (ост. 6) — то есть 2 рулона и еще пол-рулона (6 м) нужно уложить по длине.
1 ряд по длине — 2 рулона + полоса 12 м х 30 см
2 ряд по длине — 2 рулона + полоса 12 м х 30 см
3 ряд по длине — (половина рулона + половина рулона) + полоса 6 м х 30 см.Половина рулона + половина рулона = 1 целый рулон.
3 полоски: 12 м на 30 см, 12 м на 30 см и 6 м на 30 см можно выкроить из 1 целого рулона.3) 2 + 2 + 1 + 1 = 6 (р.) — линолеума потребуется
Ответ: 6 рулонов нужно для замены линолеума в коридоре.
Задание № 641 из старого учебника. Из одного города одновременно в противоположных направлениях выехали автобус и грузовик. Через 4 ч после начала движения расстояние между ними составляло 528 км. Скорость движения автобуса 58 км/ч. С какой скоростью двигался грузовик?
Решение
1) 528 : 4 = 132 (км/ч) — общая скорость автобуса и грузовика
2) 132 − 58 = 74 (км/ч) — скорость грузовика
Ответ: 74 км/ч.
Задание № 642. Из двух населенных пунктов, расстояние между которыми равно 54 км, одновременно выехали навстречу друг другу два велосипедиста и встретились через 2 ч после начала движения. Скорость движения первого велосипедиста составляла 12 км/ч. С какой скоростью двигался второй велосипедист?
Решение
1) 12 * 2 = 24 (км) — проехал первый велосипедист
2) 54 − 24 = 30 (км) — проехал второй велосипедист
3) 30 : 2 = 15 (км/ч) — скорость второго велосипедиста
Ответ: 15 км/ч.
160
Ответы к странице 160
Задание № 643. Найдите значение выражения:
1) 7a + 7b, если a + b = 14;
2) m * 17 + n * 17, если m + n = 1000;
3) k * 9 + 9l, если k + l = 12;
4) 4c − 4d, если c − d = 125;
5) x * 23 − 23y, если x − y = 4;
6) 56p − r * 56, если p − r = 11.
Решение
1) 7a + 7b = 7 * (a + b) = 7 * 14 = 98
2) m * 17 + n * 17 = 17 * (m + n) = 17 * 1000 = 17000
3) k * 9 + 9 l = 9 * (k + l) = 9 * 12 = 108
4) 4c − 4d = 4 * (c − d) = 4 * 125 = 500
5) x * 23 − 23y = 23 * (x − y) = 23 * 4 = 92
6) 56p − r * 56 = 56 * (p − r) = 56 * 11 = 616
Задание № 644. В записи первого трехзначного числа используются только цифры 2 и 3, а в записи второго − только цифры 3 и 4. Может ли произведение этих чисел записываться только цифрами 2 и 4?
Ответ
Не может, потому что умножение 3 на 2 дает число 6, умножение 2 на 4 дает 8, а 3 на 3 дает 9.
163
Ответы к странице 163
Параграф 24. Комбинаторные задачи
Задание № 645. Запишите все двузначные числа, в записи которых используются только цифры 1, 2 и 3 (цифры могут повторяться).
Ответ
11; 12; 13; 21; 22; 23; 31; 32; 33.
Задание № 646. Запишите все двузначные числа, в записи которых используются только цифры 1, 2 и 0 (цифры могут повторяться).
Ответ
10; 11; 12; 20; 21; 22.
Задание № 647. У ослика Иа−Иа есть три надувных шарика: красный, зеленый и желтый. Он хочет подарить по одному шарику своим друзьям: Винни−Пуху, Пятачку и Кролику. Сколько у ослика Иа − Иа есть вариантов сделать подарки своим друзьям?
Решение
Записываем первую букву для Винни, вторую для Пятачка, третью для Кролика. Обозначим цвета шариков по первым буквам (К — красный, Ж — желтый, З — зеленый). Получится 6 вариантов из трех букв: КЗЖ, КЖЗ, ЗКЖ, ЗЖК, ЖЗК, ЖКЗ.
Задание № 648. Сколько двузначных чисел, все цифры которых различны, можно составить из цифр 0, 1 и 2?
Ответ
Четыре цифры: 10; 12; 20; 21.
Задание № 649. В футбольном турнире участвуют команды 5 «А» класса, 5 «Б» класса и 5 «В» класса. Сколько существует способов распределения первого и второго мест среди этих команд? Решение какой задачи из номеров 645 − 648 аналогично решению этой задачи?
Решение
Место
5А 1 2 — — 1 2
5Б 2 1 1 2 — —
5В — — 2 1 2 1Существует 6 способов распределения первого и второго мест среди команд.
Задача аналогична задаче 647.
164
Ответы к странице 164
Задание № 650. Запишите все трехзначные числа, для записи которых используются только цифры:
1) 3, 4 и 6;
2) 4, 7 и 0.
(Цифры не могут повторяться)
Ответ 7 гуру
1) 346; 364; 436; 463; 634; 643.
20 470; 407; 704; 740.
Задание № 651. Сколько различных трехзначных чисел можно составить из цифр:
1) 1 и 2;
2) 0 и 1?
(Цифры могут повторяться.)
Ответ
1) 111; 112; 121; 122; 211; 212; 221; 222.
2) 100; 101; 110; 111.
Задание № 652. Запишите все двузначные числа, в записи которых используются только цифры 2, 4, 9 и 0. (Цифры могут повторяться)
Решение
20; 22; 24; 29; 40; 42; 44; 49; 90; 92; 94; 99.
Задание № 653. Сколько двузначных чисел можно составить из цифр 6, 7, 8 и 9 так, чтобы цифры были записаны в порядке возрастания?
Ответ
Шесть чисел: 67; 68; 69; 78; 79; 89.
Задание № 654. Сколько двузначных чисел можно составить из цифр 6, 7, 8 и 9 так, чтобы цифры были записаны в порядке убывания?
Ответ
Шесть чисел: 98; 97; 96; 87; 86; 76.
Задание № 655. Сколько существует двузначных чисел, сумма цифр которых равна 5?
Ответ
Пять чисел: 14; 23; 32; 41; 50.
Задание № 656. Сколько двузначных чисел, сумма цифр которых равна четному числу, можно составить из цифр 1, 2, 3, 4 (цифры могут повторяться)?
Ответ
Восемь чисел: 11; 13; 22; 24; 31; 33; 42; 44.
Задание № 657. Сколько двузначных чисел, сумма цифр которых равна нечетному числу, можно составить из цифр 0, 1, 2, 3?
Ответ
Шесть чисел: 10; 12; 21; 23; 30; 32.
Задание № 658. Кот Базилио и лиса Алиса решили украсть золотой ключик, который хранится в каморке папы Карло. Чтобы туда проникнуть, нужно подобрать двузначный код. Им известно, что дверь в каморку закрывает Буратино, который знает пока что только четыре цифры: 0, 1, 2 и 3. Какое наибольшее количество вариантов придется перебрать коту и лисе, чтобы открыть дверь?
Ответ
16 вариантов:
00 10 20 30
01 11 12 13
02 12 22 32
03 13 23 33
165
Ответы к странице 165
Задание № 659. Сколько существует различных прямоугольников, периметры которых равны 24 см, а длины сторон выражены целым числом сантиметров?
Решение
P = 2 * (a + b) − периметр прямоугольника
a + b = P : 2 = 24 : 2 = 12 (см)
Существует 6 прямоугольников следующих размеров:
1 см Х 11 см;
2 см Х 10 см;
3 см Х 9 см;
4 см Х 8 см;
5 см Х 7 см;
6 см Х 6 см.
Задание № 660. У Ани есть 30 одинаковых кубиков. Сколько различных прямоугольных параллелепипедов она может из них составить, если для построения одного параллелепипеда надо использовать все имеющиеся 30 кубиков?
Решение
Пять различных прямоугольных параллелепипедов можно составить:
1 Х 1 Х 30;
2 Х 5 Х 3;
1 Х 3 Х 10;
1 Х 2 Х 15;
1 Х 5 Х 6.
Задание № 661. На прямой отметили четыре точки A,B, C и D. Сколько отрезков с концами в отмеченных точках можно провести? Какой из рисунков § 24 помогает решить эту задачу?
Решение
Можно провести 6 отрезков: AB; AC; AD; BC; BD; CD.
Рисунок 182 помогает решить эту задачу.
Задание № 662. Подножие горы и ее вершину связывают три тропы. Сколько существует маршрутов, ведущих от подножия к вершине и затем вниз к подножию?
Решение
Подножие горы и ее вершину связывают три тропы. Сколько существует маршрутов, ведущих от подножия к вершине и затем вниз к подножию.
3 * 3 = 9 маршрутов: AOA; AOB; AOC; BOA; BOB; BOC; COA; COB; COC.
Задание № 663. Спортивной команде предлагают футболки трех цветов − красного, зеленого и синего, а шорты двух цветов − белого и желтого. Сколько вариантов выбора формы есть у команды?
Решение
К каждым шортам можно подобрать по 3 футболки, значит
2 * 3 = 6
Ответ: 6 вариантов выбора — БК, БЗ, БС, ЖК, ЖЗ, ЖС
Задание № 664. У Тани есть четыре платья и две пары туфель. Сколько у Тани есть вариантов выбора наряда?
Решение
4 * 2 = 8 вариантов
Задание № 665. В отряде космонавтов есть три пилота и два инженера. Сколько существует способов составить экипаж, состоящий из одного пилота и одного инженера?
Решение
3 * 2 = 6 вариантов
Задание № 666. На рисунке 185 изображен план одного района города. Отрезками изображены улицы. Сколько существует маршрутов из точки А в точку В, если передвигаться разрешено по улицам, ведущим вверх или вправо?
Решение
Шесть маршрутов: AHDEB; AGCFB; AHOEB; AHOFB; AGOEB; AGOFB.
Задание № 667. В записи 1 * 2 * 3 * 4 вместо каждой звездочки можно поставить один из знаков «+» или «*». Чему равно наибольшее значение выражения, которое можно получить?
Ответ
1 + 2 * 3 * 4 = 25
Задание № 668. Расстояние между двумя селами равно 28 км. Из этих сел одновременно в одном направлении выехали мотоциклист и автобус. Автобус ехал впереди со скоростью 42 км/ч, а мотоциклист ехал со скоростью 56 км/ч. Через сколько часов после начала движения мотоциклист догонит автобус?
Решение
1) 56 − 42 = 14 (км) — скорость сближения мотоциклиста и автобуса;
2) 28 : 14 = 2 (ч) — потребуется мотоциклисту, чтобы догнать автобус.
Ответ: 2 часа.
166
Ответы к странице 166
Задание № 669
Решите уравнение:
1) 1376 : (34 − x) = 86;
2) 9680 : (x + 219) = 16;
3) (x − 57) : 29 = 205;
4) (x − 72) * 9 = 927.
Решение уравнений
1376 : (34 − x) = 86
34 − x = 1376 : 86
x = 34 − 16
x = 189680 : (x + 219) = 16
x + 219 = 9680 : 16
x = 605 − 219
x = 386(x − 57) : 29 = 205
x − 57 = 205 * 29
x = 5945 + 57
x = 6002(x − 72) * 9 = 927
x − 72 = 927 : 9
x = 103 + 72
x = 175
Задание № 670
1) Одно из слагаемых в 14 раз больше другого. Во сколько раз их сумма больше меньшего слагаемого?
Решение
Пусть x − меньшее слагаемое, тогда большее 14x.
14x + x = 15x − сумма слагаемых.
15x : x = 15, то есть в 15 раз сумма больше меньшего слагаемого.
2) Вычитаемое в 12 раз больше разности. Во сколько раз уменьшаемое больше разности?
Решение
Пусть разность равна x, тогда вычитаемое равно 12x.
a − x = 12x
a = 13x
13x : x = 13, то есть в 13 раз уменьшаемое больше разности.
Задание № 671
На ферме есть 156 коров, каждая из которых даёт в день 12 л молока. Молоко с фермы вывозят в бидонах ёмкостью 40 л. В некоторый день на ферме было в наличии 42 пустых бидона. Хватит ли бидонов, чтобы вывезти с фермы надоенное молоко?
Решение
(12 * 156) : 40 = 1872 : 40 = 46 (ост. 32) (б.)
_1872 |40
160 |46
_272
240
32
Значит, 47 бидонов нужно, чтобы вывезти молоко, надоенное за день (46 бидонов + 1 бидон для остатка)
Ответ: 42 бидона не хватит.
Задание № 672
Решите кроссворд:
По горизонтали: 2. Результат арифметического действия. 3. Единица измерения времени. 4. Единица измерения углов. 5. Компонент умножения. 6. Компонент сложения.
По вертикали: 1. «Царица наук».
1 математика
2 частное
3 секунда
4 градус
5 множитель
6 слагаемое
Задача от мудрой совы
Задание № 673. В классе 30 учащихся. Они сидят по двое за 15 партами так, что половина всех девочек сидит с мальчиками. Можно ли учеников класса пересадить так, чтобы половина всех мальчиков сидела с девочками?
Решение
Если половина девочек сидит с мальчиками, то вторая половина девочек сидит друг с другом, по две за партой. Значит, половина количества девочек − четное число.
Предположим, что учеников удалось пересадить так, что половина мальчиков сидит с девочками. Тогда, по аналогичному рассуждению, половина количества мальчиков тоже четное число.
Значит и половина всего класса будет четным числом, так как это сумма двух четных чисел: половина количества мальчиков + половина количества девочек.
Так как половина учеников класса равна 30 : 2 = 15 − нечетное число, то невозможно учеников класса пересадить так, чтобы половина всех мальчиков сидела с девочками.
167-168
Ответы к странице 167-168
1) В
2) А
3) А
4) Г
5) Б
6) Г
7) Б
Б
9) В
10) В
11) Б
12) А
173
Ответы к странице 173
Раздел 2. Дробные числа и действия над ними.
Глава 4. Обыкновенные дроби
Параграф 15. Понятие обыкновенной дроби
Задание № 674. Прочитайте дроби. Назовите числитель и знаменатель каждой дроби и поясните, что они означают.
Решение
1/5 − одна пятая; числитель равен 1; знаменатель равен 5;
7/9 − семь девятых; числитель равен 7; знаменатель равен 9;
8/11 − восемь одиннадцатых; числитель равен 8; знаменатель равен 11;
5/16 − пять шестнадцатых; числитель равен 5; знаменатель равен 16;
6/13 − шесть тринадцатых; числитель равен 6; знаменатель равен 13;
21/29 − двадцать одна двадцать девятая; числитель равен 21; знаменатель равен 29.
Знаменатель дроби показывает, на сколько равных частей разделили нечто целое, а числитель − сколько таких частей взяли.
Задание № 675. Запишите в виде дроби число:
1) две пятых;
2) семь тринадцатых;
3) двадцать две шестидесятых;
4) тридцать четыре сорок третьих;
5) тридцать девять сотых;
6) сто двадцать семь тысячных.
2 , 7 , 22 , 34 , 39 , 127
5 13 60 43 100 1000
Задание № 676. Запишите дробью, какая часть фигуры, изображенной на рисунке 190, закрашена.
а) 1
2
б) 3
8
в) 5
6
г) 1
8
174
Ответы к странице 174
Задание № 677. Перерисуйте фигуру, изображенную на рисунке 191, в тетрадь и закрасьте соответствующую часть фигуры.
Ответ
Задание № 678. Выразите:
1) в метрах: 1 см; 5 см; 24 см; 1 дм; 7 дм; 1 мм; 4 мм; 39 мм; 247 мм;
2) в часах: 1 мин; 7 мин; 19 мин; 39 мин; 1 с; 4 с; 58 с.
Решение
1) 1 см = 1 м
100
5 см = 5 м
100
24 см = 24 м
100
1 дм = 1 м
10
7 дм = 7 м
10
1 мм = 1 м
1000
4 мм = 4 м
1000
39 мм = 39 м
1000
247 мм = 247 м
10002) 1 мин = 1 ч
60
7 мин = 7 ч
60
19 мин = 19 ч
60
39 мин = 39 ч
60
1 с = 1 ч
3600
4 с = 4 ч
3600
58 с = 58 ч
3600
Задание № 679. Выразите в тоннах: 1 кг; 327 кг; 58 кг; 1 ц; 3 ц.
Решение
1 кг = 1 т
1000
327 кг = 327 т
1000
58 кг = 58 т
1000
1 ц = 1 т
10
3 ц = 3 т
10
Задание № 680. В саду росло 56 деревьев, из них 23 − яблони. Какую часть деревьев составляли яблони?
Ответ
23 составляли яблони
56
Задание № 681. В 5 классе учатся 32 ученика, из них 7 учеников получили за контрольную работу по математике оценку «5». Какая часть учеников класса получила за контрольную работу по математике оценку «5»?
Ответ
7 − учеников класса получила оценку «5».
32
Задание № 682. В книге напечатаны два рассказа. Один рассказ занимает 14 страниц, а второй − 19 страниц. Какую часть книги занимает каждый рассказ?
Решение
14 + 19 = 33 (стр.) — всего в книге
14 книги занимает первый рассказ
3319 книги занимает второй рассказ
33
Задание № 683. Маша испекла 24 пирожка с капустой и 28 пирожков с повидлом. Какую часть всех пирожков составляли пирожки с капустой и какую часть − пирожки с повидлом?
Решение
24 + 28 = 52 (п.) — было всего
24 всех пирожков составляли пирожки с капустой
5228 всех пирожков составляли пирожки с повидлом
52
175
Ответы к странице 175
Задание № 684
Найдите от числа 36:
1) 1/3 ;
2) 3/4 ;
3) 5/6 ;
4) 4/9 ;
5) 5/12 ;
6) 11/18 .
Ответы
36 : 3 * 1 = 12
36 : 6 * 5 = 30
36 : 12 * 5 = 15
36 : 4 * 3 = 27
36 : 12 * 5 = 15
36 : 18 * 11 = 22
Задание № 685
Найдите от числа 28:
1) 1/2 ;
2) 3/7 ;
3) 9/14 ;
4) 19/28 .
Ответы
28 : 2 * 1 = 14
28 : 7 * 3 = 12
28 : 14 * 9 = 18
28 : 28 * 19 = 19
Задание № 686
Андрей прочитал 4/9 книги, в которой 180 страниц. Сколько страниц прочитал Андрей?
Решение
180 : 9 * 4 = 80 (стр.)
Ответ: 80 страниц прочитал Андрей.
Задание № 687
Золушка сделала 72 вареника с творогом и с картошкой, причем вареники с творогом составляли 5/8 всех вареников. Сколько вареников с творогом сделала Золушка?
Решение
72 : 8 * 5 = 9 * 5 = 45 (в.)
Ответ: 45 вареников с творогом сделала Золушка.
Задание № 688
Во время Северной войны (1700 − 1721 гг.) между Россией и Швецией у деревни Лесная 28 сентября 1708 г. русская армия разбила шестнадцатитысячное шведское войско. Численность русской армии составляла 7/8 численности шведской. Какова была численность русской армии, сражавшейся у деревни Лесная?
Решение
16000 : 8 * 7 = 2000 * 7 = 14000 (ч.)
Ответ: 14000 человек — численность русской армии.
Задание № 689
Длина минутной стрелки курантов на Спасской башне Московского Кремля равна 328 см. Высота цифр на циферблате курантов составляет 9/41 длины минутной стрелки. Вычислите высоту цифр на циферблате.
Решение
328 : 41 * 9 = 72 (см)
Ответ: 72 см высота цифр на циферблате.
Задание № 690
Колокольня Ивана Великого на территории Московского Кремля стоит на небольшом фундаменте, сложенном из глыб белого камня в виде пирамиды, расширяющейся в глубину. Каменный фундамент колокольни для прочности опирается на свайное основание, образованное большим количеством вбитых в землю бревен. Глубина фундамента составляет 2/27 высоты колокольни, а длина бревен свайного основания − 2/3 глубины фундамента. Вычислите глубину фундамента колокольни (в метрах) и длину свай (в сантиметрах), если высота колокольни равна 81 м.
Решение
1) 81 : 27 * 2 = 6 (м) — глубина фундамента
6 м = 600 см
2) 600 : 3 * 2 = 400 (см) — длина свай
Ответ: 6 м, 400 см.
Задание № 691
Найдите число, если:
1) 1/2 ;
2) 1/5 ;
3) 2/3 ;
4) 3/7 ;
5) 7/11 ;
6) 21/23 его равняется 42.
Решение
42 : 1 * 2 = 84
42 : 1 * 5 = 210
42 : 2 * 3 = 63
42 : 3 * 7 = 98
42 : 7 * 11 = 66
42 : 21 * 23 = 46
176
Ответы к странице 176
Задание № 692
Найдите число, если:
1) 1/9 ;
2) 2/5 ;
3) 2/9 ;
4) 3/10 ;
5) 5/6 ;
6) 18/19 его равняется 90.
Решение
90 : 1 * 9 = 810
90 : 2 * 9 = 405
90 : 5 * 6 = 108
90 : 2 * 5 = 225
90 : 3 * 10 = 300
90 : 18 * 19 = 95
Задание № 693
Начертите координатный луч, единичный отрезок которого равен 9 см. Отметьте на нем точки: А(1/9) ; В(2/9) ; С(4/9) ; D(5/9) ; Е(8/9) .
Ответ
А В С D Е
Задание № 694
Начертите координатный луч, единичный отрезок которого равен 12 см. Отметьте на нем точки, соответствующие дробям: 1/12 ; 2/12 ; 5/12 ; 6/12 ; 8/12 ; 11/12 .
Ответ
Задание № 695
В саду росло 24 вишни, что составляло 2/9 всех деревьев сада. Сколько всего деревьев росло в саду?
Решение
24 : 2 * 9 = 108 (д.)
Ответ: 108 деревьев росло в саду.
Задание № 696
За контрольную работу по математике оценку «4» получили 12 учащихся, что составляло 4/11 учащихся класса. Сколько учащихся в этом классе?
Решение
12 : 4 * 11 = 33 (уч.)
Ответ: 33 учащихся в этом классе
Задание № 697
Какую часть площадь закрашенного треугольника (рис. 192) составляет от площади:
1) треугольника ABD;
2) четырехугольника ABCD;
3) четырехугольника ABCE.
Ответ
1) 1 2) 1 3) 1
4 8 12
Задание № 698
Сторона квадрата ABCD равна 8 см (рис. 193). Найдите общую площадь закрашенных частей квадрата.
Решение
а) 8 * 8 = 64 (см2) − площадь всего квадрата
2 фигуры занимает закрашенная часть
8
64 : 8 * 2 = 16 (см2) − площадь закрашенной частиб) 8 * 8 = 64 (см2) − площадь всего квадрата
6 фигуры занимает закрашенная часть
16
64 : 16 * 6 = 24 (см2) − площадь закрашенной части
Задание № 699
Сторона квадрата ABCD равна 4 см (рис. 194). Найдите общую площадь закрашенных частей квадрата.
Решение
а) 4 * 4 = 16 (см2) − площадь всего квадрата
3 фигуры занимает закрашенная часть
8
16 : 8 * 3 = 6 (см2) − площадь закрашенной частиб) 4 * 4 = 16 (см2) − площадь всего квадрата
4 фигуры занимает закрашенная часть
8
16 : 8 * 4 = 8 (см2) − площадь закрашенной части
177
Ответы к странице 177
Задание № 700
Сколько градусов составляют:
1) 2/15 величины прямого угла;
2) 11/20 величины развернутого угла?
Решение
1) 90° : 15 * 2 = 12°
2) 180° : 20 * 11 = 99°
Задание № 701
Сколько градусов составляют:
1) 7/18 величины прямого угла;
2) 5/12 величины развернутого угла?
Решение
1) 90° : 18 * 7 = 5 * 7 = 35°
2) 180° : 12 * 5 = 15 * 5 = 75°
Задание № 702
Три рыбака поймали 168 рыб. Щукин поймал 5/14 всех рыб, Окунев − 8/21 всех рыб, а Карасев − остальные. Сколько рыб поймал Карасев?
Решение
1) 168 : 14 * 5 = 12 * 5 = 60 (р.) — поймал Щукин;
2) 168 : 21 * 8 = 8 * 8 = 64 (р.) — поймал Окунев;
3) 60 + 64 = 124 (р.) — поймали Щукин и Окунев вместе;
4) 168 − 124 = 44 (р.) — поймал Карасев.
Ответ: 44 рыбы.
Задание № 703
За четыре дня яхта капитана Врунгеля «Беда» прошла 624 км. В первый день было пройдено 2/13 всего расстояния, во второй − 5/26 , в третий − 5/12 , а в четвертый − оставшееся расстояние. Сколько километров прошла яхта в четвертый день?
Решение
1) 624 : 13 * 2 = 48 * 2 = 96 (км) — прошла яхта в первый день
2) 624 : 26 * 5 = 24 * 5 = 120 (км) — прошла яхта во второй день
3) 624 : 12 * 5 = 52 * 5 = 260 (км) — прошла яхта в третий день
4) 96 + 120 + 260 = 476 (км) — прошла яхта за 3 дня
5) 624 − 476 = 148 (км) — прошла яхта в четвертый день
Ответ: 148 км.
Задание № 704
Мыши в знак примирения подарили коту Леопольду 9 кг 450 г корма «Мурзик». За первую неделю Леопольд съел 8/21 подарка, а за вторую неделю − 9/13 остатка. Сколько граммов корма «Мурзик» съел Леопольд за вторую неделю?
Решение
1) 9450 : 21 * 8 = 450 * 8 = 3600 (г) съел кот Леопольд за первую неделю
_9450 |21
84 |450
_105
105
0
×450
8
3600
2) 9450 − 3600 = 5850 (г) корма осталось после первой недели
3) 5850 : 13 * 9 = 450 * 9 = 4050 (г) корма съел Леопольд за вторую неделю
_5850 |13
52 |450
_65
65
0
×450
9
4050
Ответ: 4050 г.
Задание № 705
Илья Муромец заготовил для своего коня на зиму 4 т 9 ц овса. В декабре конь съел 3/7 всего запаса овса, а в январе − 9/14 остатка. Сколько центнеров овса конь съел в январе?
Решение
4 т 9 ц = 4900 кг овса.
700
1) 4900 : 7 * 3 = 2100 (кг) овса съел конь в декабре
2) 4900 − 2100 = 2800 (кг) овса осталось после декабря
3) 2800 : 14 * 9 = 200 * 9 = 1800 (кг) съел конь в январе
1800 кг = 18 ц
Ответ: 18 ц.
Задание № 706
Фермеры Иван, Петр и Семен вырастили вместе 612 т ячменя и поделили урожай между собой. Ивану досталось 5/17 всего урожая, Петру − 9/16 остатка. Сколько тонн ячменя получил Семен?
Решение
1) 612 : 17 * 5 = 36 * 5 = 180 (т) — ячменя досталось Ивану
2) 612 − 180 = 432 (т) — ячменя осталось
27
3) 432 : 16 * 9 = 243 (т) — ячменя досталось Петру
4) 180 + 243 = 423 (т) — ячменя досталось Ивану и Петру вместе
5) 612 − 423 = 189 (т) — ячменя досталось Семену
Ответ: 189 т.
Задание № 707
Чебурашка, крокодил и Шапокляк поехали в Астрахань на уборку арбузов. Вместе они заработали 10240 р. и разделили их в соответствии с тем, кто как работал. Чебурашка получил 11/32 заработанных денег, крокодил Гена − 5/8 остатка. Кто из этой компании самый работящий?
Решение
320
1) 10240 : 32 * 11 = 3520 (р.) — заработал Чебурашка
2) 10240 − 3520 = 6720 (р.) — осталось
840
3) 6720 : 8 * 5 = 4200 (р.) — заработал крокодил Гена
4) 3520 + 4200 = 7720 (р.) — заработали Чебурашка и крокодил вместе
5) 10240 − 7720 = 2520 (р.) — заработала Шапокляк
4200 > 3520 > 2520, следовательно больше всех заработал крокодил Гена.
Ответ: крокодил Гена самый работящий.
178
Ответы к странице 178
Задание № 708
В детский санаторий завезли бананы, апельсины и мандарины. Масса апельсинов составляет 12/35 массы бананов, а масса мандаринов − 7/12 массы апельсинов. Сколько килограммов апельсинов и мандаринов вместе завезли в санаторий, если бананов завезли 245 кг?
Решение
1) 245 : 35 * 12 = 7 * 12 = 84 (кг) — завезли апельсинов
2) 84 : 12 * 7 = 7 * 7 = 49 (кг) — завезли мандаринов
3) 84 + 49 = 133 (кг) — мандаринов и апельсинов вместе завезли в санаторий
Ответ: 133 кг.
Задание № 709
Путешествуя на катере по Волге, турист в первый день проплыл 72 км, во второй день − 7/8 того, что проплыл в первый день, а в третий − 8/9 того, что проплыл во второй. На сколько километров меньше проплыл турист в третий день, чем во второй?
Решение
1) 72 : 8 * 7 = 9 * 7 = 63 (км) — проплыл турист во второй день
2) 63 : 9 * 8 = 7 * 8 = 56 (км) — проплыл турист в третий день
3) 63 − 56 = 7 (км) — на столько меньше проплыл турист в третий день, чем во второй.
Ответ: на 7 км.
Задание № 710
Из двух портов, расстояние между которыми равно 576 миль, одновременно навстречу друг другу вышли яхта капитана Врунгеля и корабль юнги Солнышкина. Яхта капитана Врунгеля проходила за день 42 мили, что составляют 7/9 того, что проплывал за день корабль Солнышкина. Через сколько дней после начала движения встретятся мореплаватели?
Решение
1) 42 : 7 * 9 = 6 * 9 = 54 (мили) — проплывал за день корабль Солнышкина
2) 42 + 54 = 96 (мили) — в день проходили вместе яхта капитана Врунгеля и корабль Солнышкина
3) 576 : 96 = 6 (д.) — плыли до встречи яхта капитана Врунгеля и корабль Солнышкина
Ответ: 6 дней.
Задание № 711
Из Цветочного и Солнечного городов выехали одновременно навстречу друг другу Знайка и Незнайка. Знайка ехал со скоростью 56 км/ч, что составляло 8/11 скорости движения Незнайки. Через сколько часов после начала движения они встретятся, если расстояние между городами равно 532 км?
Решение
1) 56 : 8 * 11 = 7 * 11 = 77 (км/ч) — скорость Незнайки
2) 56 + 77 = 133 (км/ч) — скорость Знайки и Незнайки
3) 532 : 133 = 4 (ч) — пройдет до встречи Знайки и Незнайки
Ответ: через 4 часа.
Задание № 712
Найдите число, 2/3 которого равны 3/7 числа 210.
Решение
1) 210 : 7 * 3 = 30 * 3 = 90 − это 3 7 числа 210;
2) 90 : 2 * 3 = 45 * 3 = 135 — искомое число.
Ответ: 135.
Задание № 713
Найдите 5/8 числа, 5/12 которого равны 160.
Решение
1) 160 : 5 * 12 = 32 * 12 = 384 − число 5/12 которого равны 160;
2) 384 : 8 * 5 = 48 * 5 = 240 − искомое число.
Ответ: 240.
Задание № 714
Одно из слагаемых равно 324, и оно составляет 12/25 суммы. Найдите второе слагаемое.
Решение
1) 324 : 12 * 25 = 27 * 25 = 675 − сумма двух чисел
2) 675 − 324 = 351 − второе слагаемое
Ответ: 351.
Задание № 715
Найдите разность двух чисел, если вычитаемое равно 658 и оно составляет 7/15 уменьшаемого.
Решение
1) 658 : 7 * 15 = 94 * 15 = 1410 − уменьшаемое
2) 1410 − 658 = 752 − разность двух чисел
Ответ: 752.
Задание № 716
Решите уравнение:
1) 9x − 4x + 39 = 94; 2) 7y + 2y − 34 = 83.
Решение
9x − 4x + 39 = 94
5x = 94 − 39
5x = 55
x = 55 : 5
x = 117y + 2y − 34 = 83
9y = 83 + 34
9y = 117
y = 117 : 9
y = 13
Задание № 717
С двух яблонь садовник собрал 65 кг яблок, причем с одной яблони он собрал на 17 кг меньше, чем со второй. Сколько килограммов яблок он собрал с каждой яблони?
Решение
1) 65 — 17 = 48 (кг) — яблок собрал садовник без учета разницы в 17 кг, а значит с обеих яблонь одинаковое количество
2) 48 : 2 = 24 (кг) — яблок он собрал с первой яблони
3) 24 + 17 = 41 (кг) — яблок собрал со второй яблони
Ответ: 24 кг и 41 кг.
Решение через х:
Пусть x кг яблок собрал с первой яблони, тогда
x + 17 кг яблок собрал садовник со второй яблони.
Так как всего было собрано 65 кг яблок, то:
x + x + 17 = 65
2x = 65 − 17
x = 48 : 2
x = 24 кг собрал садовник с первой яблони
x + 17 = 24 + 17 = 41 кг яблок собрал садовник со второй яблони
Ответ: 24 кг и 41 кг.
179
Ответы к странице 179
Задание № 718. Задача от мудрой совы
К пяти разным замкам есть пять ключей, причем неизвестно, какой ключ к какому замку подходит. Барон Мюнхаузен утверждает, что можно не более чем за десять попыток подобрать ключ к каждому замку. Прав ли барон Мюнхаузен?
Решение
Берем первый ключ и поочередно пробуем им открыть замки. Если к первым четырем замкам ключ не подошел, то значит первый ключ подходит к пятому замку, следовательно первым ключом мы сделали 4 попытки.
Берем второй ключ и поочередно пробуем им открыть оставшиеся 4 замка. Если к первым трем замкам ключ не подошел, то значит второй ключ подходит к четвертому замку, следовательно вторым ключом мы сделали 3 попытки.
Берем третий ключ и поочередно пробуем им открыть оставшиеся 3 замка. Если к первым двум замкам ключ не подошел, то значит третий ключ подходит к третьему замку, следовательно третьим ключом мы сделали 2 попытки.
Берем четвертый ключ и поочередно пробуем им открыть оставшиеся 2 замка. Если к первому замку ключ не подошел, то значит четвертый ключ подходит ко второму замку, следовательно вторым ключом мы сделали 1 попытку.
Остается пятый ключ, который подходит к первому замку.
Получается:
1 ключ (4 попытки) + 2 ключ (3 попытки) + 3 ключ (2 попытки) + 4 ключ (1 попытка) + 5 ключ (0 попыток) = 4 + 3 + 2 + 1 = 10 попыток всего.
184
Ответы к странице 184
Параграф 26. Правильные и неправильные дроби
Задание № 719
Запишите все правильные дроби со знаменателем 8.
Решение
1 , 2 , 3 , 4 , 5 , 6 , 7
8 8 8 8 8 8 8
Задание № 720
Запишите все правильные дроби со знаменателем 11.
Решение
1 2 3 4 5 6 7 8 9 10
11 11 11 11 11 11 11 11 11 11
Задание № 721
Запишите все неправильные дроби с числителем 8.
Решение
8 8 8 8 8 8 8 8
1 2 3 4 5 6 7 8
Задание № 722
Запишите все неправильные дроби с числителем 11.
Решение
11 11 11 11 11 11 11 11 11 11 11
1 2 3 4 5 6 7 8 9 10 11
Задание № 723 с ответами
Сравните числа:
1) 5 < 7
13 13
2) 37 > 34
41 41
3) 9 > 4
25 25
4) 11 < 11
15 13
5) 29 > 29
5 6
6) 5 > 5
23 24
7) 7 < 1
12
16 > 1
15
9) 34 = 1
34
10) 3 = 19
3 19
11) 3 < 4
4 3
12) 32 < 5
37 4
Задание № 724 с ответами
Сравните числа:
1) 16 > 9
23 23
2) 29 < 31
58 58
3) 17 < 21
100 100
4) 17 > 17
40 45
5) 9 < 9
4 2
6) 3 < 3
98 94
7) 1 > 11
14
1 < 28
25
9) 1 = 68
68
10) 22 = 4
22 4
11) 27 < 28
28 27
12) 7 > 57
6 59
185
Ответы к странице 185
Задание № 725
Расположите дроби в порядке убывания: 4/27 ; 9/27 ; 8/27 ; 5/27 ; 24/27 ; 20/27 .
Решение
24 ; 20 ; 9 ; 8 ; 5 ; 4 .
27 27 27 27 27 27
Задание № 726
Расположите дроби в порядке возрастания: 3/20 ; 1/20 ; 7/20 ; 9/20 ; 17/20 ; 6/20 .
Решение
1 ; 3 ; 6 ; 7 ; 9 ; 17 .
20 20 20 20 20 20
Задание № 727
Масса осколка Царь-колокола равна 11 500 кг. Масса царь-колокола составляет 400/23 массы этого осколка. Найдите массу Царь-колокола.
Ответ
1) 11 500 : 23 • 400 = 500 • 400 = 200 000 (кг) — масса Царь-колокола.
Ответ: 200 000 кг.
Задание № 728
Порция пельменей в кафе «Пампушечка» состоит из 18 пельменей. Иван Гурманов съедает за обедом 20/9 порции. Сколько пельменей съедает за обедом Иван? На сколько пельменей больше одной порции он съедает?
Ответ
1) 18 : 9 • 20 = 2 • 20 = 40 (шт.) — пельменей съедает Иван Гурманов.
2) 40 — 18 = 22 (шт.) — пельменей съедает Иван Гурманов больше одной порции.
Ответ: 40 штук пельменей, на 22 штуки больше одной порции.
Задание № 729
Найдите все натуральные значения x, при которых дробь x/9 будет правильной.
Решение
x = {1, 2, 3, 4, 5, 6, 7, 8}
Задание № 730
Найдите все натуральные значения x, при которых дробь x/15 будет правильной.
Решение
x = {1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14}
Задание № 731
Найдите все натуральные значения x, при которых дробь 6/x будет неправильной.
Решение
x = {1, 2, 3, 4, 5, 6}
Задание № 732
Найдите все натуральные значения x, при которых дробь 13/x будет неправильной.
Решение
x = {1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13}
Задание № 733
Найдите все натуральное значение x, при которых выполняется неравенство:
1) x/14 < 9/14 ;
2) 9/16 < 9/x .
Решение
x < 9 верно при:
14 14
x = 1; 2; 3; 4; 5; 6; 7; 8.9 < 9 верно при:
16 х
x = 1; 2; 3; 4; 5; 6; 7; 8; 9; 10; 11; 12; 13; 14; 15.
Задание № 734
Найдите все натуральные значение x, при которых выполняется неравенство:
1) 7/17 > x/17 ;
2) 12/x > 12/11 .
Решение
7 > x верно при:
17 17
x = 1; 2; 3; 4; 5; 6.12 > 12 верно при:
x 11
x = 1; 2; 3; 4; 5; 6; 7; 8; 9; 10.
Задание № 735
Какие цифры можно поставить вместо звездочки, чтобы:
1) дробь 4 ∗ 6 была неправильной;
476
2) дробь 584 была правильной?
5 ∗ 6
Решение
1) цифра 7: 476
476
цифра 8: 486
476
цифра 9: 496
4762) цифра 8: 584
586
цифра 9: 584
596
Задание № 736
Найдите все натуральные значения b, при которых дробь (3 b + 2) / 16 будет правильной.
Решение
Дробь будет правильной, если числитель будет меньше знаменателя, тогда:
3b + 2 < 16
3b < 16 − 2
3b < 14
b < 14 : 3
b < 4 целых и 2 в остатке.
Тогда при b = 1; 2; 3; 4 данная дробь будет правильной.
186
Ответы к странице 186
Задание № 737
Найдите все натуральные значения b, при которых дробь 42 / (10 + 4 b) будет неправильной.
Решение
Дробь будет неправильной, если числитель будет равен или больше знаменателя, тогда:
10 + 4b ⩽ 42
4b ⩽ 42 − 10
4b ⩽ 32
b ⩽ 32 : 4
b ⩽ 8.
Тогда при b = 1; 2; 3; 4; 5; 6; 7; 8 данная дробь будет неправильной.
Задание № 738
Найдите все натуральные значения a, при которых:
1) обе дроби a/12 и 7/a будут правильными;
2) дробь 3/a будет правильной, а дробь 6/a − неправильной.
Решение
1) При 7 < a < 12, то есть при: a = {8, 9, 10, 11}
2) При 3 < a < 8, то есть при: a = {4, 5, 6}
Задание № 739
Найдите все натуральные значения a, при которых:
1) обе дроби a/8 и 9/a будут неправильными;
2) обе дроби a/10 и 15/a будут неправильными, а дробь a/13 − правильной.
1) При 7 < a < 10, то есть при: a = {8, 9}
2) При 9 < a < 13, то есть при: a = {10, 11, 12}
Задание № 740
Объем прямоугольного параллелепипеда равен 180 д м 3 , а два его измерения − 6 дм и 15 дм. Найдите сумму длин всех ребер параллелепипеда.
Решение
1) 180 : (6 * 15) = 180 : 90 = 2 (дм) — длина третьего измерения
2) 4 * 2 + 4 * 6 + 4 * 15 = 4 * (2 + 6 + 15) = 4 * 23 = 92 (дм) — сумма длин всех ребер
Ответ: 92 см.
Задание № 741
Из двух городов, расстояние между которыми равно 392 км, выехали одновременно навстречу друг другу два автомобиля. Скорость одного автомобиля равна 48 км/ч, что составляет 6/7 скорости второго. Какое расстояние будет между автомобилями через 5 ч после начала движения?
Решение
1) 48 : 6 * 7 = 56 (км/ч) — скорость второго автомобиля
2) 48 + 56 = 104 (км/ч) — суммарная скорость двух автомобилей
3) 104 * 5 = 520 (км) — проедут оба автомобиля за 5 часов
4) 520 − 392 = 128 (км) — будет между автомобилями через 5 ч после начала движения
Ответ: 128 км.
Задание № 742
Мартышка, Удав, Слоненок и Попугай съели вместе 70 бананов, причем каждый из них съел хотя бы один банан. Мартышка съела больше, чем кто−либо из них, Попугай и Слоненок съели вместе 45 бананов. Сколько бананов съел Удав?
Решение
1) 70 − 45 = 25 (б.) — съели Мартышка и Удав вместе
Так как Попугай и Слоненок съели вместе 45 бананов, то кто-то из них максимально мог съесть только 23 банана.
Так как Мартышка съела больше всех, то значит она съела 24 банана (так как это больше 23, а 25 она съесть не могла, так как Удаву бы бананов не досталось).
2) 25 − 24 = 1 (б.) — съел Удав.
Ответ: 1 банан.
189
Ответы к странице 189
Параграф 27. Сложение и вычитание дробей с одинаковыми знаменателями
Задание № 743 с ответами
Выполните действия:
1) 7 + 5 = 7 + 5 = 12
18 18 18 18
2) 11 + 8 = 11 + 8 = 19
24 24 24 24
3) 23 − 14 = 23 − 14 = 9
47 47 47 47
4) 31 − 16 = 31 − 16 = 15
58 58 58 58
5) 3 + 6 − 8 = 3 + 6 − 8 = 1
29 29 29 29 29
6) 29 − 14 − 9 = 29 − 14 − 9 = 6
64 64 64 64 64
Задание № 744 с ответами
Выполните действия:
1) 5 + 6 = 5 + 6 = 11
19 19 19 19
2) 7 − 4 = 7 − 4 = 3
13 13 13 13
3) 19 + 4 − 22 = 19 + 4 − 22 = 1
25 25 25 25 25
4) 34 − 15 − 8 = 34 − 15 − 8 = 11
39 39 39 39 39
Задание № 745
Решите уравнение:
1) 4/15 + x = 11/15
2) 16/21 − x = 9/21
3) x − 4/35 = 12/35
Решение
4 + x = 11
15 15
x = 11 − 4
15 15
x = 7
1516 − x = 9
21 21
x = 16 — 9
21 21
x = 7
21x − 4 = 12
35 35
x = 12 + 4
35 35
x = 16
35
Задание № 746
Решите уравнение:
1) 7/10 + x = 9/10 ;
2) 29/32 − x = 15/32 .
Решение
7 + x = 9
10 10
x = 9 − 7
10 10
x = 2
1029 − x = 15
32 32
x = 29 — 15
32 32
x = 14
32
Задание № 747
В первый день Миша прочитал 5/16 книги, а во второй день − 7/16 книги. Какую часть книги прочитал Миша за два дня?
Решение
5 + 7 = 12 книги прочитал Миша за два дня
16 16 16
Ответ: 12 16
Задание № 748
Для перевозки груза использовали несколько грузовиков. На один из них положили 6/19 груза, а на второй − 8/19 груза. Какую часть груза положили на эти два грузовика?
Решение
6 + 8 = 14 груза положили на эти два грузовика
19 19 19
Ответ: 14 19 груза.
Задание № 749
Кот Базилио съел за обедом 9/20 кг сосисок, а лиса Алиса − на 3/20 кг больше, чем Базилио. Сколько килограммов сосисок съели за обедом Базилио и Алиса вместе?
Решение
9 + 3 = 12 (кг) — съела лиса Алиса
20 20 20
9 + 12 = 21 (кг) — съели за обедом Базилио и Алиса вместе
20 20 20
Ответ: 21 кг.
20
190
Ответы к странице 190
Задание № 750
Отправившись на прогулку, черепаха Тортила за первый час проползла 23/50 км, что на 5/50 км больше, чем за второй час. Сколько километров проползла Тортила за два часа?
Решение
23 − 5 = 18 (км) — проползла черепаха за второй час
50 50 50
23 + 18 = 41 (км) — проползла Тортила за два часа
50 50 50
Ответ: 41 км.
50
Задание № 751
Решите уравнение:
1) 52/63 − x/63 = 25/63
2) x/38 + 14/38 = 23/38
3) ( 12/13 + x ) − 5/13 = 9/13
4) ( x − 21/31 ) + 14/31 = 25/31
Решение
52 − x = 25
63 63 63
x = 52 — 25
63 63 63
x = 27
63 63
x = 27x + 14 = 23
38 38 38
x = 23 − 14
38 38 38
x = 9
38 38
x = 9(12 + x ) − 5 = 9
13 13 13
12 + x = 5 + 9
13 13 13
x = 14 − 12
13 13
x = 2
13(x − 21 ) + 14 = 25
31 31 31
x − 21 = 25 — 14
31 31 31
x = 11 + 21
31 31
x = 32
31
Задание № 752
Решите уравнение:
1) x/72 − 13/72 = 29/72 ;
2) ( 29/42 − a ) − 13/42 = 11/42 ;
3) 15/17 − ( b − 3/17 ) = 6/17 ;
4) 29/43 − ( m + 13/43 ) = 5/43 .
Решение
x − 13 = 29
72 72 72
x = 29 + 13
72 72 72
x = 42
72 72
x = 42(29 − a ) − 13 = 11
42 42 42
29 − a = 11 + 13
42 42 42
29 − a = 24
42 42
a = 29 — 24
42 42
a = 5
4215 − ( b − 3 ) = 6
17 17 17
b − 3 = 15 − 6
17 17 17
b − 3 = 9
17 17
b = 9 + 3
17 17
b = 12
1729 − ( m + 13 ) = 5
43 43 43
m + 13 = 29 — 5
43 43 43
m + 13 = 24
43 43
m = 24 — 13
43 43
m = 11
43
Задание № 753
Овощной магазин реализовал 240 кг картофеля. В первый день было продано 3/16 картофеля, а во второй − 7/16 . Сколько килограммов картофеля магазин реализовал за два дня?
Решение
3 + 7 = 10 картофеля было продано за 2 дня
16 16 16
240 : 16 * 10 = 15 * 10 = 150 (кг) — картофеля магазин реализовал за два дня.
Ответ: 150 кг.
Задание № 754
Протяженность построенной дороги составляет 92 км. За первый месяц построили 6/23 дороги, а за второй месяц − 9/23 . Сколько километров дороги было построено за два месяца?
Решение
6 + 9 = 15 части дороги построили за 2 месяца
23 23 23
92 : 23 * 15 = 4 * 15 = 60 (км) дороги было построено за два месяца
Ответ: 60 км.
Задание № 755
Найдите числа, которых не хватает в цепочке вычислений:
1) n = 972 − 60 = 912
a = 60 : 12 = 5
b = 12 + 19 = 31
c = 155 : b = 155 : 31 = 5
d = 155 − 108 = 47
m = 972 : 108 = 92) x = 192 − 100 = 92
y = 192 : 16 = 12
z = 16 + 32 = 48
p = 384 : z = 384 : 48 = 8
m = 100 − 39 = 61
q = 384 − m = 384 − 61 = 323
191
Ответы к странице 191
Задание № 756
Найдите все натуральные числа, при делении которых на 7 неполное частное будет равно остатку.
Решение
Пусть n − искомое число, тогда:
n = 7x + x
x = 1, n = 7 * 1 + 1 = 7 + 1 = 8
x = 2, n = 7 * 2 + 2 = 14 + 2 = 16
x = 3, n = 7 * 3 + 3 = 21 + 3 = 24
x = 4, n = 7 * 4 + 4 = 28 + 4 = 32
x = 5, n = 7 * 5 + 5 = 35 + 5 = 40
x = 6, n = 7 * 6 + 6 = 42 + 6 = 48
Ответ: числа 8; 16; 24; 32; 40; 48.
Задание № 757
В коробке лежат 4 белых, 5 черных и 6 красных шаров. Какое наименьшее количество шаров надо вынуть из коробки, чтобы среди них обязательно оказались:
1) 3 шара одного цвета;
2) шары всех трех цветов?
Решение
1) Допустим, что за первые 6 попыток было вынуто 2 белых, 2 черных и 2 красных шара. Тогда при вынимании 7 шара обязательно окажется 3 шара одного цвета.
Ответ: 7 шаров.2) Допустим, что за первые 11 попыток было вынуто 6 красных и 5 черных шаров. Тогда при вынимании 12 шара обязательно окажутся 3 шары всех трех цветов, так как в коробке останутся только белые шары.
Ответ: 12 шаров.
193
Ответы к странице 193
Параграф 28. Дроби и деление натуральных чисел
Задание № 758
Запишите в виде дроби частное: 1) 4 : 12; 2) 6 : 25 3) 16 : 8; 4) 14 : 23; 5) 12 : 23; 6) 17 : 11.
Решение
4 6 16 14 12 17
12 25 8 23 23 11
Задание № 759
Запишите в виде дроби частное: 1) 5 : 7; 2) 19 : 4; 3) 1 : 6; 4) 30 : 4; 5) 6 : 1; 6) 12 : 39.
Решение
5 19 1 30 6 12
7 4 6 4 1 39
Задание № 760
Запишите дробь в виде частного: 1) 7/12 ; 2) 17/584 ; 3) 11/7 .
Решение
7 = 7 : 12
12
17 = 17 : 584
584
11 = 11 : 7
7
Задание № 761
Запишите дробь в виде частного: 1) 5/7 ; 2) 3/10 ; 3) 29/5 .
Решение
5 = 5 : 7
7
3 = 3 : 10
10
29 = 29 : 5
5
Задание № 762
Запишите число 6 в виде дроби со знаменателем: 1) 1; 2) 4; 3) 19.
Решение
6 = 6
1
6 = 24
4
6 = 114
19
Задание № 763
Запишите число 12 в виде дроби со знаменателем: 1) 1; 2) 5; 3) 23.
Решение
12 = 12
1
12 = 60
5
12 = 276
23
Задание № 764
Решите уравнение:
1) b/7 = 12 ;
2) 169/m = 13 ;
3) 126 = 21 .
8 − y
Решение
b = 12
7
b = 12 * 7
b = 84169 = 13
m
m = 169 : 13
m = 13126 = 21
8 − y
8 − y = 126 : 21
8 − y = 6
у = 8 — 2
y = 2
Задание № 765
Решите уравнение:
1) x/4 = 5 ;
2) 105/y = 7 ;
3) x + 12 = 14 .
6
Решение
x = 5
4
x = 5 * 4
x = 20105 = 7
y
y = 105 : 7
y = 15x + 12 = 14
6
x + 12 = 14 * 6
x + 12 = 84
x = 84 − 12
x = 72
Задание № 766
У фермера Петра Грушина есть участок земли прямоугольной формы. Длина участка равна 28 м, что составляет 7/4 его ширины. На площади, равной 30/56 всего участка, фермер разбил яблоневой сад. Найдите площадь сада.
Решение
1) 28 : 7 * 4 = 16 (м) — ширина участка
2) 28 * 16 = 448 (м2) — площадь участка
3) 448 : 56 * 30 = 8 * 30 = 240 (м2) — площадь сада
Ответ: 240 м2.
194
Ответы к странице 194
Задание № 767
На один грузовик можно погрузить 3 т груза. Сколько надо грузовиков, чтобы перевезти 28 т?
Решение
28 : 3 = 9 (ост. 1) при погрузке груза на 9 грузовиков останется еще одна тонна. Значит необходимо 10 грузовиков.
Ответ: 10 грузовиков.
Задание № 768
В 5 классе учатся 5 учеников. Сможет ли каждый ученик этого класса обменяться открытками с пятью своими одноклассниками?
Решение
Нельзя, так как ученик не сможет обменяться открыткой сам с собой, а одноклассников у каждого всего 4.
198
Ответы к странице 198
Параграф 29. Смешанные числа
Задание № 769 с ответами
Преобразуйте неправильную дробь в смешанное число
Задание № 770 с ответами
Преобразуйте неправильную дробь в смешанное число
Задание № 771 с ответами
Запишите частное в виде дроби и выделите из полученной дроби целую и дробную части
Задание № 772 с ответами
Запишите частное в виде дроби и выделите из полученной дроби целую и дробную части.
Задание № 773 с ответами
Запишите число в виде неправильной дроби
Задание № 774 с ответами
Запишите число в виде неправильной дроби
Задание № 775 с ответами
Выполните действия
Задание № 776 с ответами
Выполните действия
199
Ответы к странице 199
Задание № 777 с ответами
Вычислите
Задание № 778 с ответами
Вычислите
Задание № 779 с ответами
Решите уравнение
Задание № 780 с ответами
Решите уравнение
Задание № 781 с ответами
Решите уравнение
Задание № 782
Степан, Иван и Андрей съели арбуз. Степан съел 2/9 арбуза, Иван − 4/9. Какую часть арбуза съел Андрей?
Решение
1) 2 + 4 = 6 арбуза съели Степан и Иван вместе
9 9 9
2) 1− 6 = 9 — 6 = 3 арбуза съел Андрей
9 9 9 9
Ответ: 3 арбуза.
9
Задание № 783
Мария, Ирина, Елена и Ольга съели торт. Мария съела 3/16 торта, Ирина − 5/16, Елена − 2/16. Какую часть торта съела Ольга?
1) 3 + 5 + 2 = 10 торта съели Маша, Ирина и Лена вместе
16 16 16 16
2) 1 − 10 = 16 − 10 = 6 торта съела Ольга
16 16 16 16
Ответ: 6 торта.
16
200
Ответы к странице 200
Задание № 784
Три тракториста вспахали вместе поле. Бригадир записал, что один из них вспахал 5/13 поля, второй − 4/13 , а третий − 6/13 . Не ошибся ли бригадир?
Решение
Все поле равно 1, а вспахали:
$frac5{13}+frac4{13}+frac6{13}=frac{15}{13}=1frac2{13}$
Ответ: бригадир ошибся и записал больше, чем вспахали на самом деле.
Задание № 785
Фермер решил выделить под морковь 3/20 огорода, под свеклу − 4/20 , под лук − 6/20 , под горох − 2/20 , под картофель − 7/20 . Сможет ли он реализовать свой план?
Решение
Весь огород равен 1, фермер запланировал засадить:
$frac3{20}+frac4{20}+frac6{20}+frac2{20}+frac7{20}=frac{22}{20}=1frac2{20}$ часть огорода, а это больше, чем целый огород.Ответ: не сможет.
Задание № 786
1) Какое наибольшее натуральное число удовлетворяет неравенству: 1) n < 123/30 ; 2) 198/15 > n ?
Решение
n < 123
30
$frac{123}{30}=4frac3{20}$
4 < 123
30
Ответ: n = 4198 > n
15
$frac{198}{15}=13frac3{15}$
198 > 13
15
Ответ: n = 13
2) Какое наименьшее натуральное число удовлетворяет неравенству: 1) m > 13/5 ; 2) 275/10 < m ?
Решение
m > 13
5
$frac{13}5=2frac35$3 > 13
5
Ответ: m = 3275 < m
10
$frac{275}{10}=27frac5{10}$275 < 28
10
Ответ: m = 28
Задание № 787
1) Какое наибольшее натуральное число удовлетворяет неравенству: 1) n < 206/13 ; 2) 324/16 > n ?
Решение
n < 206
13
$frac{206}{13}=15frac{11}{13}$15 < 206
13
Ответ: n = 15324 > n
16
$frac{324}{16}=20frac4{16}$324 > 20
16
Ответ: n = 20
2) Какое наименьшее натуральное число удовлетворяет неравенству: 1) m > 34/6 ; 2) 421/16 < m ?
Решение
m > 34
6
34 = 5 4
6 6
6 > 34
6
Ответ: m = 6421 < m
16
421 = 26 5
16 16
421 < 27
16
Ответ: m = 27
Задание № 788
Найдите все натуральное значение x, при которых верно неравенство
Решение
2 1 < x < 3 2
3 3 3
7 < x < 11
3 3 3
x = {8, 9, 10}1 5 < 17 < 2 1
12 x 8
17 < 17 < 17
12 x 8
x = {9, 10, 11}
Задание № 789
Найдите все натуральное значение x, при которых верно неравенство:
Решение
3 11 < x < 4
15 15
56 < x < 60
15 15 15
x = {57, 58, 59}3 1 < 25 < 8 1
8 x 3
25 < 25 < 25
8 x 3
x = {4, 5, 6, 7}
Задание № 790
При каких натуральных значениях a является верным неравенство, левая часть которого − неправильная дробь: 1) 20/a < 2 ; 2) 4/a < a ?
Решение
20 < 2
a
20 < 20
a 10
a = {11, 12, 13, 14, 15, 16, 17, 18, 19, 20}4 > a
a
4 > a
a 1
a = 1, так как:
4 > 1
1 1
Задание № 791
При каких натуральных значениях a является верным неравенство 10/a > a , левая часть которого − неправильная дробь?
Решение
10 > a верно при a = {1, 2, 3}
a
Задание № 792
Одна из сторон треугольника в 2 раза меньше второй и на 7 см меньше третьей. Найдите стороны треугольника, если его периметр равен 39 см.
Решение:
Схема:
1 ________|
2 ________|________| } 39 см
3 ________|__7см_|Поскольку 1 из сторон треугольника в 2 раза меньше 2й и на 7 см меньше 3й, то 1ю примем за 1 часть, 2ю за 2 части, а 3ю за (1 часть + 7 см).
1) 39 — 7 = 32 (см) — приходится на 4 равные части
2) 32 : 4 = 8 (см) — 1 часть, то есть длина первой стороны
3) 8 * 2 = 16 (см) — длина второй стороны
4) 8 + 7 = 15 (см) — длина третьей стороны треугольника
Ответ: 8 см, 16 см, 15 см.
Решение через х
Пусть x см длина первой стороны, тогда:
2x см длина второй стороны;
x + 7 см длина третьей стороны треугольника.
Так как периметр треугольника равен сумме длин всех его сторон, то:
x + 2x + x + 7 = 39
4x = 39 − 7
x = 32 : 4
x = 8 (см) — длина первой стороны;
2x = 2 * 8 = 16 (см) — длина второй стороны;
x + 7 = 8 + 7 = 15 (см) — длина третьей стороны треугольника.
Ответ: 8 см, 16 см, 15 см.
201
Ответы к странице 201
Задание № 793
Общая площадь трех крупнейших волжских водохранилищ Куйбышевского, Рыбинского и Волгоградского составляет 14 197 км2 . Площадь Волгоградского водохранилища на 1 463 км2 меньше площади Рыбинского водохранилища и на 3 383 км2 меньше площади Куйбышевского водохранилища. Найдите площадь каждого водохранилища.
Решение
Пусть x км2 площадь Волгоградского водохранилища, тогда:
x + 1463 км2 — площадь Рыбинского водохранилища;
x + 3383 км2 — площадь Куйбышевского водохранилища.
Так как общая площадь всех водохранилищ равна 14197 км2 , то:
x + x + 1463 + x + 3383 = 14197
3x = 14197 − 3383 − 1463
x = 9351 : 3
x = 3117 (км2) — площадь Волгоградского водохранилища;
3117 + 1463 = 4580 (км2) — площадь Рыбинского водохранилища;
3117 + 3383 = 6500 (км2) — площадь Куйбышевского водохранилища.
Ответ: 3117 км2 ; 4580 км2 ; 6500 км2 .
Задание № 794
Пакет кефира стоит 68 р. У Кати есть 200 р. Какое наибольшее количество пакетов кефира она может купить? Сколько денег останется у Кати?
Решение
200 : 68 = 2 (ост. 64)
Ответ: 2 пакета кефира, 64 рубля останется.
Задание № 795
По дороге в одном направлении идут два пешехода. В 12 ч 54 мин расстояние между ними было 540 м. Скорость пешехода, который идет впереди, равна 25 м/мин, что составляет 5/8 скорости пешехода, который идет сзади. В котором часу второй пешеход догонит первого?
Решение:
1) 25 : 5/8 = 25 * 8/5 = 40 (м/мин) — скорость пешехода который догоняет
2) 40 — 25 = 15 (м/мин) — скорость пешехода который идет на сближение
3) 540 : 15 = 36 (мин) — через столько один догонит второго
4) 12 ч 54 мин + 36 мин = 13 ч 30 мин
Ответ: в 13 ч 30 мин.
Задание № 796
Ученики Федоров, Сидоров и Петров входили в сборную школы по шахматам. Имена этих учеников были Федор, Сидор и Петр. Известно, что фамилия Федора не Петров, волосы у Сидора рыжего цвета и учится он в 6 классе: Петров учится в 7 классе, а волосы у Федорова черного цвета. Укажите фамилию и имя каждого мальчика.
Решение
Петров не Федор, тогда:
Петров или Сидор или Петр;
Сидор учится в 6 классе, а Петров в 7, следовательно Петров Петр.
Сидор не может быть Федоровым, так как у Сидора волосы рыжие, а у Федорова черные, следовательно Сидор Сидоров, а Федор Федоров.
Ответ:
Петр Петров;
Сидор Сидоров;
Федор Федоров.
202-203
Ответы к странице 202-203
Задание №4 Проверьте себя в тестовой форме
1. А
2. Б
3. В
4. Г
5. А
6. Б
7. Б
8. Г
9. В
10. А
11. Б
12 . Б
207-208
Ответы к странице 207-208
Глава 5. Десятичные дроби
Параграф 30. Представление о десятичных дробях
Задание № 797 с ответами
Запишите в виде десятичной дроби:
Задание № 798 с ответами
Прочитайте десятичную дробь:
1,6 − одна целая шесть десятых
12,8 − двенадцать целых восемь десятых
5,24 − пять целых двадцать четыре десятых
6,325 − шесть целых триста двадцать пять тысячных
17,4192 − семнадцать целых четыре тысячи сто девяносто две десятитысячных
0,5 − ноль целых пять десятых
0,05 − ноль целых пять сотых
0,005 − ноль целых пять тысячных
3,04 − три целых четыре сотых
0,0304 − ноль целых триста четыре десятитысячных
12,098 − двенадцать целых девяносто восемь тысячных
0,01012 − ноль целых одна тысяч двенадцать стотысячных
Задание № 799 с ответами
Запишите в виде десятичной дроби:
Задание № 800 с ответами
Выделите целую и дробную части и запишите данное число в виде десятичной дроби:
Задание № 801 с ответами
Выделите целую и дробную части числа и запишите данное число в виде десятичной дроби:
Задание № 802 с ответами
Запишите число в виде обыкновенной дроби или смешанного числа:
Задание № 803 с ответами
Запишите число в виде обыкновенной дроби или смешанного числа:
Задание № 804
Запишите в виде десятичной дроби число, в котором:
1) три единицы, четыре десятых, пять сотых;
2) два десятка, восемь единиц, одна сотня, девять тысячных;
3) восемь сотен, девять единиц, семь десятых, шесть тысячных;
4) одна тысяча, одна десятитысячная.
Ответ
3,45
28,019
809,706
1000,0001
Задание № 805
Запишите в виде десятичной дроби число, в котором:
1) две единицы, семь десятых;
2) три десятка, две десятых, восемь сотых;
3) одна сотая, три тысячных.
Ответ
2,7
30,28
0,013
209
Ответы к странице 209
Задание № 806 с ответами
Выразите в дециметрах и запишите в виде десятичной дроби:
48 см = 4,8 дм
424 см = 42,4 дм
8 см 6 мм = 0,86 дм
64 см 5 мм = 6,45 дм
6 мм = 0,06 дм
3 см = 0,3 дм
Задание № 807 с ответами
Выразите в килограммах и запишите в виде десятичной дроби:
1 347 г = 1,347 кг
4 256 г = 4,256 кг
382 г = 0,382 кг
48 г = 0,048 кг
9 г = 0,009 кг
5 кг 24 г = 5,024 кг
10 кг 6 г = 10,006 кг
2 ц 358 г = 200,358 кг
Задание № 808 с ответами
Выразите в метрах и запишите в виде десятичной дроби:
125 см = 1,25 м
18 см = 0,18 м
4 дм 4 см = 0,44 м
58 дм 6 см = 5,86 м
2 см = 0,02 м
4 м 6 дм 5 см = 4,65 м
Задание № 809
Запишите в виде десятичной дроби частное:
1) 28 : 10;
2) 7 : 10;
3) 456 : 100;
4) 2648 : 100;
5) 8351 : 1000;
6) 3590 : 1000;
7) 674 : 1000;

9) 4 : 1000.
Ответ
Задание № 810 с ответами
Запишите в виде десятичной дроби частное:
Задание № 811
Какие числа на координатном луче соответствуют:
1) точкам A, B, C, D, F, E (рис.204);
2) точкам M, N, K, P, R, S (рис.205)?
Ответ запишите в виде десятичных дробей.
Ответ
1) A(0,4); B(0,8); C(1,1); D(1,7); F(1,9); E(2,2).
2) M(5,9); N(6,3); K(6,6); P(7,2); R(7,7); S(8,4).
Задание № 812
Начертите координатный луч, взяв за единичный такой отрезок, длина которого в десять раз больше стороны клетки тетради. Отметьте на луче точки, соответствующие числам 0,3; 0,7; 0,9; 1,1; 1,5; 2,1.
Решение
A(0,3); B(0,7); C(0,9); D(1,1); E(1,5); F(2,1).
Задание № 813
Начертите координатный луч, взяв за единичный такой отрезок, длина которого в десять раз больше стороны клетки тетради. Отметьте на луче точки, соответствующие числам 0,1; 0,6; 0,8; 1,4; 1,9; 2,2.
Решение
A(0,1); B(0,6); C(0,8); D(1,4); E(1,9); F(2,2).
210
Ответы к странице 210
Ответы к упражнениям для повторения
Задание № 814
Мама поручила сыну купить продукты. На хлеб он потратил 3/50 всех денег, на молоко − 13/50, на овощи − 11/50, а 19/50 всех денег − на фрукты. На какую покупку было потрачено наибольшее количество денег? Наименьшее количество денег? Остались ли деньги у мальчика после покупок?
Решение
19 13 11 3
50 > 50 > 50 > 50 , следовательно больше всего денег сын потратил на фрукты, а меньше всего на хлеб.
Все деньги равны 1, тогда:
19 13 11 3 46
50 + 50 + 50 + 50 = 50 всех денег израсходовал сын, а значит:
1 − 46 = 4
50 50 части всех денег осталось неизрасходованной.
Ответ: больше всего денег сын потратил на фрукты, а меньше всего на хлеб,
4
50 от всех денег осталось.
Задание № 815
Во сколько раз 5/6 мин меньше, чем 4 мин 10 с.
Решение
5 ∗ 60 = 50 (с)
6
4 мин 10 с = 4 * 60 + 10 = 240 + 10 = 250 (с)
250 : 50 = 5, то есть в пять раз 5/6 мин меньше, чем 4 мин 10 с.
Ответ: в 5 раз.
Задание № 816
Во сколько раз 5 ч 50 мин больше, чем 7/12 ч?
Решение
5 ч 50 мин = 5 * 60 + 50 = 300 + 50 = 350 (мин.)
7 ∗ 60 = 60 : 12 ∗ 7 = 5 ∗ 7 = 35 (мин.)
12
350 : 35 = 10, то есть в 10 раз 5 ч 50 мин больше, чем 7/12 ч.
Ответ: в 10 раз.
Задание № 817
Какие цифры можно поставить вместо звездочки, чтобы образовалось верное неравенство:
1) 346* < 3463;
2) 4*40 > 4735.
Решение
цифра 0: 3460 < 3463
цифра 1: 3461 < 3463
цифра 2: 3462 < 3463цифра 7: 4740 > 4735
цифра 8: 4840 > 4735
цифра 9: 4940 > 4735
Задание № 818
В числах стерли несколько цифр и вместо них поставили звездочки.
Сравните эти числа:
1) 35*** и 32**;
2) 52 и **98.
Решение
1) 35*** > 32***, так как 5 > 2.
2) 52* < **98, так как трехзначное число всегда меньше четырехзначного.
Задание № 819
Как поделить поровну 7 яблок между 12 друзьями, если каждое яблоко можно разрезать не более чем на 4 части?
Решение
Каждое из 4 яблок поделили на 3 равные части, получили 4 * 3 = 12 равных частей, затем каждое из оставшихся 3 яблок поделили на равные 4 части получили 3 * 4 = 12 равных частей.
Получается, что каждый из друзей получил две дольки: 1/3 часть яблока + 1/4 часть яблока.
213
Ответы к странице 213
Параграф 31. Сравнение десятичных дробей
Задание № 820
Запишите десятичную дробь:
1) с двумя цифрами после запятой, равную числу 0,4;
2) с четырьмя цифрами после запятой, равную числу 3,26;
3) с тремя цифрами после запятой, равную числу 42;
4) с двумя цифрами после запятой, равную числу 18,50000.
Ответ
0,4 = 0,40
3,26 = 3,2600
42 = 42,000
18,5000 = 18,50
Задание № 821
Запишите несколько десятичных дробей, равных данной:
1) 5,400;
2) 12,5080;
3) 0,980.
Ответ
5,400 = 5,4 = 5,40 = 5,4000
12,5080 = 12,508 = 12,50800 = 12,508000
0,980 = 0,98 = 0,9800 = 0,98000
Задание № 822
Уравняйте количество цифр после запятой в данных дробях:
1) 2,16; 18,5; 0,476; 1,4;
2) 8,1; 19,64; 5,345; 0,9872.
Ответ
1) 2,16 = 2,160
18,5 = 18,500
0,476 = 0,476
1,4 = 1,400
2) 8,1 = 8,1000
19,64 = 19,6400
5,345 = 5,3450
0,9872 = 0,9872
Задание № 823
Сравните числа:
1) 9,4 и 9,6;
2) 5,5 и 4,8;
3) 6,3 и 6,31;
4) 3,29 и 3,316;
5) 0,3 и 0,08;
6) 7,2 и 7,094.
Ответ
9,4 < 9,6
5,5 > 4,8
6,3 < 6,31
3,29 < 3,316
0,3 > 0,08
7,2 > 7,094
Задание № 824
Сравните числа:
1) 16,8 и 17,3;
2) 12,7 и 12,5;
3) 24,92 и 24,9;
4) 18,486 и 18,5;
5) 0,065 и 0,1;
6) 96,35 и 96,087.
Ответ
16,8 < 17,3
12,7 > 12,5
24,92 > 24,9
18,486 < 18,5
0,065 < 0,1
96,35 > 96,087
Задание № 825
Запишите числа в порядке убывания: 8,5; 8,16; 8,4; 8,49; 8,05; 8,61.
Ответ
8,61; 8,5; 8,49; 8,4; 8,16; 8,05.
Задание № 826
Запишите числа в порядке возрастания: 9,6; 9,8; 9,53; 9,02; 9,2; 9,613.
Ответ
9,02; 9,2; 9,53; 9,6; 9,613; 9,8.
Задание № 827
Найдите все натуральные значения x, при которых верно неравенство:
1) 4,45 < x < 7,002;
2) 9,8 < x < 13,4.
Решение
1) 4,45 < x < 7,002 неравенство верно при: x = 5; 6; 7.
2) 9,8 < x < 13,4 неравенство верно при: x = 10; 11; 12; 13.
214
Ответы к странице 214
Задание № 828
Найдите все натуральные значения x, при которых верно неравенство:
1) 7,4 < x < 8,2;
2) 12 < x < 19,65.
Решение
1) 7,4 < x < 8,2 неравенство верно при:
x = 8.
2) 12 < x < 19,65 неравенство верно при:
x = 13; 14; 15; 16; 17; 18; 19.
Задание № 829
Между какими соседними числами натурального ряда находится дробь:
1) 6,99;
2) 12,79;
3) 1,529;
4) 3,109?
Ответ запишите в виде двойного неравенства.
Решение
6 < 6,99 < 7
12 < 12,79 < 13
1 < 1,529 < 2
3 < 3,109 < 4
Задание № 830
Между какими соседними числами натурального ряда находится дробь:
1) 5,32;
2) 24,01?
Ответ запишите в виде двойного неравенства.
Решение
5 < 5,32 < 6
24 < 24,01 < 25
Задание № 831
Какие цифры можно поставить вместо звездочки, чтобы образовалось верное неравенство:
1) 6,38 < 6,3;
2) 8,1 > 8,9;
3) 16,25 < 1*,32?
Решение
1) цифра 9: 6,38 < 6,39
2) цифра 0: 8,1 > 8,09
3) цифра 6: 16,25 < 16,32;
цифра 7: 16,25 < 17,32;
цифра 8: 16,25 < 18,32;
цифра 9: 16,25 < 19,32.
Задание № 832
Какие цифры можно поставить вместо звездочки, чтобы образовалось верно неравенство:
1) 9,5 < 9,12;
2) 12,58 > 12,4;
3) 0,0*3 > 0,064?
Решение
1) цифра 0: 9,05 < 9,12
2) цифра 0: 12,58 > 12,04
цифра 1: 12,58 > 12,14
цифра 2: 12,58 > 12,24
цифра 3: 12,58 > 12,34
цифра 4: 12,58 > 12,44
цифра 5: 12,58 > 12,54
3) цифра 7: 0,073 > 0,064
цифра 8: 0,083 > 0,064
цифра 9: 0,093 > 0,064
Задание № 833
Запишите наибольшую десятичную дробь:
1) с двумя цифрами после запятой, меньшую, чем 1;
2) с одной цифрой после запятой, меньшую, чем 2;
3) с тремя цифрами после запятой, меньшую, чем 3;
4) с четырьмя цифрами после запятой, меньшую, чем 1.
Ответы
0,99
1,9
2,999
0,9999
Задание № 834
Запишите наименьшую десятичную дробь:
1) с одной цифрой после запятой, большую, чем 1;
2) с двумя цифрами после запятой, большую, чем 1;
3) с тремя цифрами после запятой, большую, чем 4;
4) с четырьмя цифрами после запятой, большую, чем 10.
Ответы
1,1
1,01
4,001
10,0001
Задание № 835
Напишите три числа, каждое из которых:
1) больше 3,4 и меньше 3,6;
2) больше 0,527 и меньше 0,528;
3) больше 2,003 и меньше 2,00301.
Ответы
1) 3,47; 3,5; 3,59.
2) 0,5271; 0,5275; 0,5279.
3) 2,003002; 2,003005; 2,003009.
Задание № 836
Напишите три числа, каждое из которых больше 10,53, но меньше 10,55.
Решение
10,53 < 10,537 < 10,55;
10,53 < 10,542 < 10,55;
10,53 < 10,549 < 10,55.
Задание № 837
Какие цифры можно поставить вместо звездочек, чтобы образовалось верное неравенство (в правой и левой частях неравенства звездочкой обозначена одна и та же цифра):
1) 0,*2 > 0,4*;
2) 2,5* < 2,*6;
3) 0,7*5 < 0,*69;
4) 0,6* > 0,7*;
5) 0,*6 < 0,6*;
6) 0,*6 > 0,6*?
Решение
1)
цифра 5: 0,52 > 0,45;
цифра 6: 0,62 > 0,46;
цифра 7: 0,72 > 0,47;
цифра 8: 0,82 > 0,48;
цифра 9: 0,92 > 0,49.
2)
цифра 5: 2,55 < 2,56;
цифра 6: 2,56 < 2,66;
цифра 7: 2,57 < 2,76;
цифра 8: 2,58 < 2,86;
цифра 9: 2,59 < 2,96.
3)
цифра 8: 0,785 < 0,869;
цифра 9: 0,795 < 0,969.
4)
0,6* > 0,7* нет таких значений
5)
цифра 0: 0,06 < 0,60;
цифра 1: 0,16 < 0,61;
цифра 2: 0,26 < 0,62;
цифра 3: 0,36 < 0,63;
цифра 4: 0,46 < 0,64;
цифра 5: 0,56 < 0,65.
6)
цифра 7: 0,76 > 0,67;
цифра 8: 0,86 > 0,68;
цифра 9: 0,96 > 0,69.
215
Ответы к странице 215
Ответы к упражнениям для повторения
Задание № 838
Вычислите:
1) ( 714 : 7 − 100 ) 6 ;
2) ( 963 : 9 − 618 : 6 ) 3 .
Решение
( 714 : 7 − 100 ) 6 = ( 102 − 100 ) 6 = 2 6 = 64
( 963 : 9 − 618 : 6 ) 3 = ( 107 − 103 ) 3 = 4 3 = 64
Задание № 839
Максим спешит в школу и идет со скоростью 6 км/ч. Успеет ли Максим дойти до школы за 20 мин, если его дом находится на расстоянии 1 км от нее?
Решение
6 км/ч = 6 * 1000 : 60 = 100 м/мин − скорость Максима в минутах
1) 100 * 20 = 2000 (м) — проходит Максим за 20 минут
2000 м = 2 км
2) 20 : 2 = 10 (мин.) — Максим идет 1 км
Ответ: успеет дойти за 10 минут.
Задание № 840
Картонный прямоугольник, площадь которого равна 3 д м 2 , а длины сторон выражаются целым числом сантиметров, разрезали на полоски шириной 1 см и сложили из них одну длинную полоску. Какой длины получилась полоска?
Ответ
3 дм2 = 300 см2
300 : 1 = 300 (см) = 3 (м)
Ответ: длина полоски 3 метра.
Задание № 841
Расположите в порядке убывания все трехзначные числа, которые можно записать с помощью цифр 2, 4 и 5 (цифры в записи числа не повторяются).
Ответ
542; 524; 452; 425; 254; 245.
Задание № 842
Расположите в порядке возрастания все трехзначные числа, которые можно записать с помощью цифр 1, 2 и 3 (цифры в записи числа не повторяются).
Ответ
123; 132; 213; 231; 312; 321.
Задание № 843
В пачке было 1000 конвертов. За какое наименьшее время почтальон сможет отложить 850 конвертов, если за 1 мин он отсчитывает 100 конвертов?
Решение
1) 1000 − 850 = 150 (к.) — необходимо убрать из пачки, чтобы там осталось 850 конвертов
100 конвертов отсчитывает почтальон за 1 минуту, тогда:
2) 100 : 2 = 50 (к.) — отсчитывает почтальон за 30 секунд, следовательно 150 конвертов почтальон отсчитает за 1 мин 30 секунд.
Ответ: 1 мин 30 секунд.
218-219
Ответы к странице 218-219
Параграф 32. Округление чисел. Прикидки
Задание № 844
Округлите:
1) до десятых: 9,374; 0,5298; 10,444; 54,06; 74,95;
2) до сотых: 13,405; 28,2018; 0,2375; 18,0025; 26,399;
3) до единиц: 18,25; 3,099; 9,73; 239,81;
4) до тысячных: 0,5261; 9,9999; 1,58762.
Решение
1) 9,374 ≈ 9,4;
0,5298 ≈ 0,5;
10,444 ≈ 10,4;
54,06 ≈ 54,1;
74,95 ≈ 75,0.2) 13,405 ≈ 13,41;
28,2018 ≈ 28,20;
0,2375 ≈ 0,24;
18,0025 ≈ 18,00;
26,399 ≈ 26,40.3) 18,25 ≈ 18;
3,099 ≈ 3;
9,73 ≈ 10;
239,81 ≈ 240.4) 0,5261 ≈ 0,526;
9,9999 ≈ 10,000;
1,58762 ≈ 1,588.
Задание № 845
Округлите:
1) до десятых: 16,88; 4,651; 1,29; 48,23; 36,96;
2) до сотых: 8,636; 2,7848; 0,9996; 104,9438;
3) до единиц: 25,54; 8,47; 55,64; 62,32;
4) до тысячных: 2,3984; 8,55555; 47,7853.
Решение
1)
16,88 ≈ 16,9;
4,651 ≈ 4,7;
1,29 ≈ 1,3;
48,23 ≈ 48,2;
36,96 ≈ 37,0.
2)
8,636 ≈ 8,64;
2,7848 ≈ 2,78;
0,9996 ≈ 1,00;
104,9438 ≈ 104,94.
3)
25,54 ≈ 26;
8,47 ≈ 8;
55,64 ≈ 56;
62,32 ≈ 62.
4)
2,3984 ≈ 2,398;
8,55555 ≈ 8,556;
47,7853 ≈ 47,785.
Задание № 846
Округлите:
1) до десятков: 459; 1623; 492685; 999;
2) до сотен: 6056; 7538; 55555; 7988;
3) до тысяч: 7345; 4956; 129808;
4) до миллионов: 42573468; 59676657;
5) до наивысшего разряда данного числа: 836; 32464; 7145962; 432560678.
Решение
1)
459 ≈ 460;
1623 ≈ 1620;
492685 ≈ 492690;
999 ≈ 1000.
2)
6056 ≈ 6100;
7538 ≈ 7500;
55555 ≈ 55600;
7988 ≈ 8000.
3)
7345 ≈ 7000;
4956 ≈ 5000;
129808 ≈ 130000.
4)
42573468 ≈ 43000000;
59676657 ≈ 60000000.
5)
836 ≈ 800;
32464 ≈ 30000;
7145962 ≈ 7000000;
432560678 ≈ 400000000.
Задание № 847
Округлите:
1) до десятков: 534; 18357; 4783386;
2) до сотен: 2223; 1374;
3) до тысяч: 312864; 67314;
4) до миллионов: 5032999; 9821893;
5) до наивысшего разряда данного числа: 4562; 583037; 28099897.
Решение
1)
534 ≈ 530;
18357 ≈ 18360;
4783386 ≈ 4783390.
2)
2223 ≈ 2200;
1374 ≈ 1400.
3)
312864 ≈ 313000;
67314 ≈ 67000.
4)
5032999 ≈ 5000000;
9821893 ≈ 10000000.
5)
4562 ≈ 5000;
583037 ≈ 600000;
28099897 ≈ 30000000.
Задание № 848
Округлите: 1) до тысяч; 2) до сотен; 3) до десятков; 4) до единиц; 5) до десятых; 6) до сотых; 7) до тысячных число:
а) 8 419,3576;
б) 6 745,2891;
в) 9 421,5307.
Ответы
а
1) 8 419,3576 ≈ 8000;
2) 8 419,3576 ≈ 8400;
3) 8 419,3576 ≈ 8420;
4) 8 419,3576 ≈ 8419;
5) 8 419,3576 ≈ 8419,4;
6) 8 419,3576 ≈ 8419,36;
7) 8 419,3576 ≈ 8419,358.
б
1) 6 745,2891 ≈ 7000;
2) 6 745,2891 ≈ 6700;
3) 6 745,2891 ≈ 6 750;
4) 6 745,2891 ≈ 6 745;
5) 6 745,2891 ≈ 6 745,3;
6) 6 745,2891 ≈ 6 745,29;
7) 6 745,2891 ≈ 6 745,289.
в
1) 9 421,5307 ≈ 9000;
2) 9 421,5307 ≈ 9400;
3) 9 421,5307 ≈ 9420;
4) 9 421,5307 ≈ 9422;
5) 9 421,5307 ≈ 9421,5;
6) 9 421,5307 ≈ 9421,53;
7) 9 421,5307 ≈ 9421,531.
Задание № 849
Округлите десятичные дроби, отбросив выделенные цифры, и укажите, до какого разряда выполнено округление:
1) 24,56;
2) 8,0358;
3) 0,007289;
4) 6,848641975.
Решение
24,56 ≈ 24,6 − до десятых
8,0358 ≈ 8,04 − до сотых
0,007289 ≈ 0,01 − до сотых
6,848641975 ≈ 6,848642 − до миллионных
Задание № 850
Округлите десятичные дроби, отбросив выделенные цифры, и укажите, до какого разряда выполнено округление:
1) 5,874;
2) 3,529;
3) 20,7846;
4) 2,33496.
Решение
5,874 ≈ 5,9 − до десятых
3,529 ≈ 3,53 − до сотых
20,7846 ≈ 20,78 − до сотых
2,33496 ≈ 2,335 − до тысячных
Задание № 851
Запишите в метрах, предварительно округлив до сотен сантиметров:
469 см; 3244 см; 5382 см; 20460 см; 50083 см; 312245 см.
469 см ≈ 500 см = 5 м;
3244 см ≈ 3200 см = 32 м;
5382 см ≈ 5400 см = 54 м;
20460 см ≈ 20500 см = 205 м;
50083 см ≈ 50100 см = 501 м;
312245 см ≈ 312200 см = 3122 м.
Задание № 852
Запишите в тоннах, предварительно округлив до тысяч килограммов: 3842 кг; 4506 кг; 8329 кг; 869 кг.
Ответы
3842 кг ≈ 4000 кг = 4 т;
4506 кг ≈ 5000 кг = 5 т;
8329 кг ≈ 8000 кг = 8 т;
869 кг ≈ 1000 кг = 1 т.
Задание № 853
Планета Земля движется вокруг Солнца со средней скоростью 107228 км/ч. Округлите это число:
1) до десятков километров в час;
2) до сотен километров в час;
3) до тысяч километров в час;
4) до десятков тысяч километров в час;
5) до сотен тысяч километров в час.
Решение
1) 107228 ≈ 107230
2) 107228 ≈ 107200
3) 107228 ≈ 107000
4) 107228 ≈ 110000
5) 107228 ≈ 100000
Задание № 854
Запишите в километрах, предварительно округлив до тысяч метров: 1469 м; 5424 м; 6823 м; 18096 м; 324711 м; 549628 м.
Ответы
1469 м ≈ 1000 м = 1 км;
5424 м ≈ 5000 м = 5 км;
6823 м ≈ 7000 м = 7 км;
18096 м ≈ 18000 м = 18 км;
324711 м ≈ 325000 м = 325 км;
549628 м ≈ 550000 м = 550 км.
220
Ответы к странице 220
Задание № 855
Какие цифры можно поставить вместо звездочки, чтобы округление было выполнено верно:
1) 4,9* ≈ 4,9;
2) 63,5 ≈ 64;
3) 13,299 ≈ 13,2?
Решение
1) цифры 0; 1; 2; 3; 4.
2) цифры 5; 6; 7; 8; 9.
3) цифры 0; 1; 2; 3; 4.
Задание № 856
Какие цифры можно поставить вместо звездочки, чтобы округление было выполнено верно:
1) 5,474 ≈ 5,47;
2) 231 ≈ 2400?
Решение
1) цифры 0; 1; 2; 3; 4.
2) цифры 5; 6; 7; 8; 9.
Задание № 857
У Вити есть 2500 р. На свой день рождения он хочет угостить каждого из 30 своих одноклассников шоколадкой. Одна шоколадка стоит 78 р. Узнав это, Витя сразу сообразил, что денег ему хватит. Как, по вашему мнению, он смог это быстро определить?
Решение
78 р. ≈ 80 р;
80 * 30 = 2400 (руб.)
То есть если денег хватает на 30 шоколадок по 80 рублей, то их тем более хватит на шоколадки по 78 рублей.
Ответ: денег хватит.
Задание № 857 из старого учебника
У Вити есть 500 р. На свой день рождения он хочет угостить каждого из 24 своих одноклассников шоколадкой. Одна шоколадка стоит 19 р. Узнав это, Витя сразу сообразил, что денег ему хватит. Как, по вашему мнению, он смог это быстро определить?
Решение
19 р. ≈ 20 р;
24 чел ≈ 25 чел;
25 * 20 = 500 (руб.)
То есть если денег хватает на 25 шоколадок по 20 рублей, то их тем более хватит на 24 шоколадки по 19 рублей.
Ответ: денег хватит.
Задание № 858
Требуется привезти 102 ящика массой 30,7 кг каждый. Водитель автомобиля, грузоподъемность которого составляет 3 т, быстро определил, что выполнить это задание, сделав один рейс, невозможно. Как, по вашему мнению, он смог это быстро определить?
Решение
30,7 кг ≈ 31 кг;
102 ящика ≈ 100 ящиков;
31 * 100 = 3100 кг = 3,1 т > 3 т.
То есть, если невозможно перевезти за 1 рейс 100 ящиков, то тем более нельзя перевезти 102 ящика.
Ответ: за один рейс груз перевезти нельзя.
Задание № 859
Кролик живет до 12 лет, что составляет:
1) 6/7 продолжительности жизни овцы;
2) 2/3 продолжительности жизни козы;
3) 3/5 продолжительности жизни фазана.
Найдите продолжительность жизни овцы, козы и фазана.
Решение
1) 12 : 6 * 7 = 2 * 7 = 14 (лет) — живет овца
2) 12 : 2 * 3 = 6 * 3 = 18 (лет) — живет коза
3) 12 : 3 * 5 = 4 * 5 = 20 (лет) — живет фазан
Ответ: 14 лет, 18 лет и 20 лет.
Задание № 860
1) При преобразовании неправильной дроби a/7 в смешанное число получили неполное частное 19 и остаток 5. Найдите значение a.
2) При преобразовании неправильной дроби m/12 в смешанное число получили неполное частное 20 и остаток 10. Найдите значение m.
Решение
1) a = 19 * 7 + 5 = 133 + 5 = 138, тогда:
a = 138 = 19 5
7 7 72) m = 20 * 12 + 10 = 240 + 10 = 250, тогда:
m = 250 = 20 10
12 12 12
Задание № 861
Масса торта составляет 4/5 кг и еще 4/5 его массы. Какова масса торта?
Решение
Пусть весь торт весит x кг, тогда:
4 x составляет 4/5 его массы.
5
1 кг = 1000 г, тогда:
4 кг = 1000 : 5 ∗ 4 = 200 ∗ 4 = 800 г .
5
Составим уравнение:
800 + 4 x = x
5
x − 4 x = 800
5
5 x − 4 x = 800
5 5
1 x = 800
5
x = 800 : 1 * 5 = 4000 (г)
4000 г = 4 кг
Ответ: 4 кг — масса торта.
Задание № 862
Вася рассказал друзьям, что позавчера ему еще было 10 лет, а в следующем году ему исполнится 13. Как такое может быть?
Ответ
Такое может быть если день рождения Васи 31 декабря, тогда получается:
разговор Васи с друзьями состоялся 1 января,
30 декабря прошлого года ему было еще 10 лет,
31 декабря прошлого года исполнилось 11 лет,
31 декабря настоящего года исполнится 12 лет,
31 декабря следующего года исполнится 13 лет.
223
Ответы к странице 223
Параграф 33. Сложение и вычитание десятичных дробей
Задание № 863
Вычислите:
1) 0,6 + 0,4;
2) 0,66 + 0,04;
3) 0,666 + 0,004;
4) 0,66 + 0,4;
5) 0,666 + 0,04;
6) 0,66 + 0,34.
Решение
0,6 + 0,4 = 1
+0.6
0.4
10,66 + 0,04 = 0,7
+0.66
0.04
0.70,666 + 0,004 = 0,67
+0.666
0.004
0.670,66 + 0,4 = 1,06
+0.66
0.4
1.060,666 + 0,04 = 0,706
+0.666
0.04
0.7060,66 + 0,34 = 1
+0.66
0.34
1
Задание № 864
Выполните сложение:
1) 12,5 + 23,9;
2) 18,74 + 3,3;
3) 6,6 + 14;
4) 13,72 + 24,318;
5) 4,18 + 7,52;
6) 43,523 + 36,477.
Решение
12,5 + 23,9 = 35,4
+12.5
23.9
36.418,74 + 3,3 = 22,04
+18.74
3.3
22.046,6 + 14 = 20,6
+6.6
14
20.613,72 + 24,318 = 38,038
+13.72
24.318
38.0384,18 + 7,52 = 11,7
+4.18
7.52
11.743,523 + 36,477 = 80,000
+43.523
36.477
80
Задание № 865
Выполните сложение:
1) 4,7 + 5,8;
2) 6,9 + 3,45;
3) 16 + 4,2;
4) 0,823 + 0,729;
5) 5,4 + 13,691;
6) 38,246 + 56,254.
Решение
4,7 + 5,8 = 10,5
+4.7
5.8
10.56,9 + 3,45 = 10,35
+6.9
3.45
10.3516 + 4,2 = 20,2
+16
4.2
20.20,823 + 0,729 = 1,552
+0.823
0.729
1.5525,4 + 13,691 = 19,091
+5.4
13.691
19.09138,246 + 56,254 = 94,500
+38.246
56.254
94.5
Задание № 866
Выполните вычитание:
1) 14,4 − 8,9;
2) 72,28 − 54,46;
3) 35,4 − 16,72;
4) 43 − 0,451;
5) 10,25 − 5,2974;
6) 52,302 − 25,59.
Решение
14,4 − 8,9 = 5,5
−14.4
8.9
5.572,28 − 54,46 = 17,82
−72.28
54.46
17.8235,4 − 16,72 = 18,68
−35.40
16.72
18.6843 − 0,451 = 42,549
−43.000
0.451
42.54910,25 − 5,2974 = 4,9526
−10.2500
5.2974
4.952652,302 − 25,59 = 26,712
−52.302
25.590
26.712
Задание № 867
Выполните вычитание:
1) 9,2 − 6,7;
2) 29,36 − 19,59;
3) 13,5 − 8,28;
4) 20 − 5,63;
5) 8,3 − 4,678;
6) 38,06 − 17,4.
Решение
9,2 − 6,7 = 2,5
−9.2
6.7
2.529,36 − 19,59 = 9,77
−29.36
19.59
9.7713,5 − 8,28 = 5,22
−13.50
8.28
5.2220 − 5,63 = 14,37
−20.00
5.63
14.378,3 − 4,678 = 3,622
−8.300
4.678
3.62238,06 − 17,4 = 20,66
−38.06
17.40
20.66
Задание № 868
Решите уравнение:
1) x + 4,83 = 9;
2) 43,78 − x = 5,384;
3) x − 14,852 = 15,148;
4) 2,395 + x = 10.
Решение
x + 4,83 = 9
x = 9 − 4,83
x = 4,1743,78 − x = 5,384
x = 43,78 − 5,384
x = 38,396x − 14,852 = 15,148
x = 15,148 + 14,852
x = 302,395 + x = 10
x = 10 − 2,395
x = 7,605
Задание № 869
Решите уравнение:
1) 15,62 + x = 20;
2) 9,54 − x = 7,268;
3) x − 36,76 = 19,24;
4) x + 0,24 = 8,1.
Решение
15,62 + x = 20
x = 20 − 15,62
x = 4,389,54 − x = 7,268
x = 9,54 − 7,268
x = 2,272x − 36,76 = 19,24
x = 19,24 + 36,76
x = 56x + 0,24 = 8,1
x = 8,1 − 0,24
x = 7,86
Задание № 870
В декабре фермер получил прибыль в размере 438,86 тысячи рублей, а в январе − на 16,4 тысячи рублей больше, чем в декабре. Сколько тысяч рублей составила прибыль фермера за декабрь и январь вместе?
Решение
1) 438,86 + 16,4 = 455,26 (тыс.руб.) — составила прибыль в январе
2) 438,86 + 455,26 = 894,12 (тыс.руб.) — составила прибыль за декабрь и январь вместе
Ответ: 894,12 тыс.руб.
Задание № 871
Баба−яга купила новую двухкомнатную избушку на курьих ножках. Площадь одной комнаты составляет 17,6 м2, что на 5,9 м2 меньше, чем площадь второй. Вычислите для Бабы−яги общую площадь двух ее комнат.
1) 17,6 + 5,9 = 23,5 (м2) — площадь второй комнаты
2) 17,6 + 23,5 = 41,1 (м2) — общая площадь.
Ответ: 41,1 м2.
Задание № 872
Собственная скорость теплохода равна 23,8 км/ч, скорость течения реки − 1,6 км/ч. Найдите скорость теплохода против течения и его скорость о течению реки.
1) 23,8 − 1,6 = 22,2 (км/ч) — скорость теплохода против течения
2) 23,8 + 1,6 = 25,4 (км/ч) — скорость теплохода по течению
Ответ: 22,2 км/ч и 25,4 км/ч.
Задание № 873
Собственная скорость моторной лодки равна 16,4 км/ч, скорость течения − 1,8 км/ч. Найдите скорость лодки по течению и ее скорость против течения реки.
1) 16,4 + 1,8 = 18,2 (км/ч) — скорость лодки по течению
2) 16,4 − 1,8 = 14,6 (км/ч) — скорость лодки против течения
Ответ: 18,2 км/ч и 14,6 км/ч.
Задание № 874
Скорость катера по течению реки равна 30,2 км/ч, а скорость течения − 2,2 км/ч. Найдите собственную скорость катера и его скорость против течения.
1) 30,2 − 2,2 = 28 (км/ч) — собственная скорость катера
2) 28 − 2,2 = 25,8 (км/ч) — скорость катера против течения
Ответ: 28 км/ч и 25,8 км/ч.
224
Ответы к странице 224
Задание № 875
Скорость катера на подводных крыльях против течения реки равна 68,5 км/ч, а скорость течения − 1,5 км/ч. Найдите собственную скорость катера и его скорость по течению.
Решение задачи
1) 68,5 + 1,5 = 70 (км/ч) — собственная скорость катера
2) 70 + 1,5 = 71,5 (км/ч) — скорость катера по течению
Ответ: 70 км/ч и 71,5 км/ч.
Задание № 876
Скорость лодки против течения реки равна 18,8 км/ч, а ее собственная скорость − 20,2 км/ч. Найдите скорость течения и скорость лодки по течению реки.
Решение задачи
1) 20,2 − 18,8 = 1,4 (км/ч) — скорость течения реки
2) 20,2 + 1,4 = 21,6 (км/ч) — скорость лодки по течению реки
Ответ: 1,4 км/ч и 21,6 км/ч.
Задание № 877
Скорость катера по течению реки равна 32,6 км/ч, а его собственная скорость − 30,4 км/ч. Найдите скорость течения и скорость катера против течения реки.
Решение задачи
1) 32,6 − 30,4 = 2,2 (км/ч) — скорость течения
2) 30,4 − 2,2 = 28,2 (км/ч) — скорость катера против течения
Ответ: 2,2 км/ч и 28,2 км/ч.
Задание № 878
Лена и Оля собрали вместе 3,2 кг грибов, причем Лена собрала 1,68 кг. Кто из девочек собрал больше грибов и на сколько килограммов?
Решение задачи
1) 3,2 − 1,68 = 1,52 (кг) — собрала Оля
2) 1,68 − 1,52 = на 0,16 (кг) — грибов Лена собрала больше, чем Оля
Ответ: на 0,16 кг.
Задание № 879
В первый день туристы прошли 6,3 км, что на 2,84 км меньше, чем во второй день. После двух дней похода им осталось пройти еще 14,35 км. Какова протяженность туристического маршрута?
Решение задачи
1) 6,3 + 2,84 = 9,14 (км) — прошли туристы во второй день
2) 6,3 + 9,14 = 15,44 (км) — прошли туристы за первые два дня
3) 15,44 + 14,35 = 29,79 (км) — протяженность маршрута
Ответ: 29,79 км.
Задание № 880
За первую неделю магазин продал 2,16 кг картофеля, а за вторую − на 0,976 т больше, чем за первую. После этого в магазине осталось 3,58 т картофеля. Сколько тонн картофеля было завезено в магазин?
Решение задачи
1) 2,16 + 0,976 = 3,136 (т) — картофеля продал магазин за вторую неделю
2) 2,16 + 3,136 = 5,296 (т) — картофеля продал магазин за две недели
3) 5,296 + 3,58 = 8,876 (т) — картофеля завезли в магазин
Ответ: 8,876 т.
Задание № 881
Найдите общую площадь пустынь на поверхности земного шара, если площадь пустынь в Австралии равна 0,4 млн.км2, в Америке − на 1,2 млн.км2 больше, чем в Австралии, в Азии − на 1,4 млн.км2 больше, чем в Америке, а в Африке − на 2,8 млн.км2 больше, чем в Америке.
Решение
1) 0,4 + 1,2 = 1,6 (млн.км2) — площадь пустынь в Америке
2) 1,6 + 1,4 = 3 (млн.км2) — площадь пустынь в Азии
3) 1,6 + 2,8 = 4,4 (млн.км2) — площадь пустынь в Африке
4) 0,4 + 1,6 + 3,0 + 4,4 = 9,4 (млн.км2) — общая площадь пустынь на поверхности земного шара
Ответ: 9,4 млн.км2 .
Задание № 882
Наибольшее озеро в мире − Каспийское море − имеет глубину 1,025 км. Озеро Байкал − самое глубокое в мире. Его глубина на 0,515 км больше глубины Каспийского моря. Глубина озера Танганьика (Африка) составляет 1,47 км. На сколько Байкал глубже Танганьики, а Танганьика глубже Каспийского моря?
Решение задачи
1) 1,025 + 0,515 = 1,54 (км) — глубина Байкала
2) 1,54 − 1,47 = 0,07 (км) — Байкал глубже Танганьики
0,07 км = 70 м
3) 1,47 − 1,025 = 0,445 (км) — Танганьика глубже Каспийского моря
0,445 км = 445 м
Ответ: на 70 м, на 445 м.
225
Ответы к странице 225
Задание № 883
Отправившись на ядре в путешествие на Луну, барон Мюнхаузен в первую минуту пролетел 234,7 км, что на 18,6 км меньше, чем во вторую минуту. В третью минуту он пролетел на 156,4 км меньше, чем в первую и вторую минуты вместе. Сколько километров пролетел Мюнхаузен за первые три минуты полета?
Решение задачи
1) 234,7 + 18,6 = 253,3 (км) — пролетел Мюнхаузен во вторую минуту
2) 234,7 + 253,3 = 488 (км) — пролетел Мюнхаузен за первые две минуты
3) 488 − 156,4 = 331,6 (км) — пролетел Мюнхаузен за третью минуту
4) 488 + 331,6 = 819,6 (км) — пролетел Мюнхаузен за первые три минуты
Ответ: 819,6 км.
Задание № 884
В понедельник в столовой израсходовали 12,4 кг сахара, что на 2,8 кг больше, чем во вторник. В среду сахара было израсходовано на 5,6 кг меньше, чем в понедельник и во вторник вместе. Сколько всего килограммов сахара израсходовали в понедельник, вторник и среду?
Решение задачи
1) 12,4 − 2,8 = 9,6 (кг) — сахара израсходовали во вторник
2) 12,4 + 9,6 = 22 (кг) — сахара израсходовали в понедельник и вторник вместе
3) 22 − 5,6 = 16,4 (кг) — сахара израсходовали в среду
4) 22 + 16,4 = 38,4 (кг) — сахара израсходовали всего за три дня
Ответ: 38,4 кг.
Задание № 885
За три дня на шахте добыли 2436,86 т угля. За первый день добыча составляла 827,48 т, а за второй − на 59,59 т меньше, чем за первый. Сколько тонн угля добыли за третий день?
Решение задачи
1) 827,48 − 59,59 = 767,89 (т) — угля добыли во второй день
2) 827,48 + 767,89 = 1595,37 (т) — угля добыли в первые два дня
3) 2436,86 − 1595,37 = 841,49 (т) — угля добыли в третий день
Ответ: 841,49 т.
Задание № 886
Фермер Василий Работящий взял в аренду три участка земли общей площадью 3428,32 га. Площадь одного из этих участков была равна 1506,46 га, что на 237,64 га меньше площади второго участка. Найдите площадь третьего участка.
Решение задачи
1) 1506,46 + 237,64 = 1744,1 (га) — площадь второго участка
2) 1506,46 + 1744,1 = 3250,56 (га) — площадь двух участков
3) 3428,32 − 3250,56 = 177,76 (га) — площадь третьего участка
Ответ: 177,76 га.
Задание № 887
Ломаная состоит из трех звеньев. Длина первого звена 9,2 см, что на 3,5 см больше длины второго звена и на 4,9 см меньше длины третьего. Найдите длину ломаной.
Решение задачи
1) 9,2 − 3,5 = 5,7 (см) — длина второго звена
2) 9,2 + 4,9 = 14,1 (см) — длина третьего звена
3) 9,2 + 5,7 + 14,1 = 29 (см) — длина ломаной
Ответ: 29 см.
Задание № 888
Одна из сторон треугольника равна 12,4 дм, что на 3,8 дм меньше второй стороны и на 2,6 дм больше третьей. Вычислите периметр треугольника.
Решение задачи
1) 12,4 + 3,8 = 16,2 (дм) — длина второй стороны
2) 12,4 − 2,6 = 9,8 (дм) — длина третьей стороны
3) 12,4 + 16,2 + 9,8 = 38,4 (дм) — периметр треугольника
Ответ: 38,4 дм.
Задание № 889
Найдите значение выражения:
1) 18,61 + 7,54 + 3,4;
2) 86,58 + 32,6 + 5,079;
3) 28,964 + 51,16 + 48,036;
4) 84,25 + 72,844 + 17,156 + 16,85;
5) 26,836 − 7,59 − 12,6 − 3,5801;
6) 489,2 − (164,4 + 92,16 − 138,254).
Решение
Задание № 890
Найдите значение выражения:
1) 5,68 + 13,27 + 4,9;
2) 18,35 + 1,4 + 38,016;
3) 16,528 + 42,5 + 13,472;
4) 76,1 + 38,83 + 24,9 + 52,17;
5) 14,02 − 10,379 + 5,004 − 7,3245;
6) 642,7 − (365,2 − 41,54 + 125,086).
Решение
Задание № 891
Решите уравнение:
1) (1,34 + x) − 58,3 = 4,26;
2) (94,2 − a) − 1,26 = 3,254;
3) 4,75 − (x − 0,67) = 3,025;
4) 40,3 − (63,4 − a) = 36,62.
Решение
(1,34 + x) − 58,3 = 4,26
1,34 + x = 4,26 + 58,3
1,34 + x = 62,56
x = 62,56 − 1,34
x = 61,22
Ответ: x = 61,22(94,2 − a) − 1,26 = 3,254
94,2 − a = 3,254 + 1,26
94,2 − a = 4,514
a = 94,2 − 4,514
a = 89,686
Ответ: a = 89,6864,75 − (x − 0,67) = 3,025
x − 0,67 = 4,75 − 3,025
x − 0,67 = 1,725
x = 1,725 + 0,67
x = 2,395
Ответ: x = 2,39540,3 − (63,4 − a) = 36,62
63,4 − a = 40,3 − 36,62
63,4 − a = 3,68
a = 63,4 − 3,68
a = 59,72
Ответ: a = 59,72
Задание № 892
Решите уравнение:
1) (x − 50,6) + 2,15 = 42,9;
2) 31,28 − (m + 4,2) = 15,093.
Решение уравнения
(x − 50,6) + 2,15 = 42,9
x − 50,6 = 42,9 − 2,15
x − 50,6 = 40,75
x = 40,75 + 50,6
x = 91,35
Ответ: x = 91,3531,28 − (m + 4,2) = 15,093
m + 4,2 = 31,28 − 15,093
m + 4,2 = 16,187
m = 16,187 − 4,2
m = 11,987
Ответ: m = 11,987
226
Ответы к странице 226
Задание № 893
Выполните сложение, выбирая удобный порядок вычислений:
1) (2,45 + 0,276) + 4,55;
2) (9,37 + 13,6) + 6,4;
3) 5,12 + 3,75 + 5,25 + 4,88;
4) 0,234 + 0,631 + 0,766 + 0,369.
Решение
1) (2,45 + 0,276) + 4,55 = (2,45 + 4,55) + 0,276 = 7 + 0,276 = 7,276
2) (9,37 + 13,6) + 6,4 = (13,6 + 6,4) + 9,37 = 20 + 9,37 = 29,37
3) 5,12 + 3,75 + 5,25 + 4,88 = (5,12 + 4,88) + (3,75 + 5,25) = 10 + 9 = 19
4) 0,234 + 0,631 + 0,766 + 0,369 = (0,234 + 0,766) + (0,631 + 0,369) = 1 + 1 = 2
Задание № 894
Выполните сложение, выбирая удобный порядок вычислений:
1) (12,82 + 8,394) + 5,18;
2) 2,53 + 15,1 + 4,47 + 14,9.
Решение
1) (12,82 + 8,394) + 5,18 = (12,82 + 5,18) + 8,394 = 18 + 8,394 = 26,394
2) 2,53 + 15,1 + 4,47 + 14,9 = (2,53 + 4,47) + (15,1 + 14,9) = 7 + 30 = 37
Задание № 895
Упросите выражение:
1) 2,46 + a + 81,139 + 14,8;
2) m + 0,47 + 5,062 + m + 43,295;
3) x + 0,3 + 0,9007 + 4,58 + 3x;
4) 7c + 236,7 + 2c + 0,82 + 4,325.
Решение
1) 2,46 + a + 81,139 + 14,8 = a + (2,46 + 81,139 + 14,8) = a + (83,599 + 14,8) = a + (83,599 + 14,8) = a + 98,399
2) m + 0,47 + 5,062 + m + 43,295 = (m + m) + (0,47 + 5,062 + 43,295) = 2m + (5,532 + 43,295) = 2m + 48,827
3) x + 0,3 + 0,9007 + 4,58 + 3x = (x + 3x) + (0,3 + 0,9007 + 4,58) = 4x + (1,2007 + 4,58) = 4x + 5,7807
4) 7c + 236,7 + 2c + 0,82 + 4,325 = (7c + 2c) + (236,7 + 0,82 + 4,325) = 9c + (237,52 + 4,325) = 9c + 241,845
Задание № 896
Найдите числа, которых не хватает в цепочке вычислений:
a = 14,36 + 18,54 = 32,9;
b = a − 27,032 = 32,9 − 27,032 = 5,868;
x = 10 − b = 10 − 5,868 = 4,132.
Ответ:
a = 32,9;
b = 5,868;
x = 4,132.
Задание № 897 с ответами
Найдите числа, которых не хватает в цепочке вычислений:
a = 39,8 − 14,48 = 25,32;
x = 74,123 − a = 74,123 − 25,32 = 48,803;
y = 74,123 − 40,2 = 33,923.
Ответ: a = 25,32; x = 48,803; y = 33,923.
Задание № 898 с ответами
Вместо звездочек поставьте цифры так, чтобы сложение (вычитание) было выполнено верно:
+17,64
87,59
105,232,536
+ 6,978
+20,527
30,041−72,28
39,59
32,69−99,705
64,864
34,841
Задание № 899
Как, изменится сумма, если:
1) одно из слагаемых увеличить на 6,8, а второе − на 4,25;
2) одно из слагаемых увеличить на 14,3, а второе уменьшить на 7,15;
3) одно из слагаемых увеличить на 3,2, а второе уменьшить на 3,2?
Решение
1) 6,8 + 4,25 = 11,05, то есть сумма увеличится на 11,05
2) 14,3 − 7,15 = 7,15, то есть сумма увеличится на 7,15
3) 3,2 − 3,2 = 0, то есть сумма не изменится
Задание № 900
Как изменится разность, если:
1) уменьшаемое увеличить на 9,25;
2) уменьшаемое уменьшить на 7,6;
3) вычитаемое увеличить на 12,2;
4) вычитаемое уменьшить на 17,96;
5) уменьшаемое увеличить на 2,3, а вычитаемое уменьшить на 1,7;
6) уменьшаемое уменьшить на 6,1, а вычитаемое увеличить на 3,4?
Решение
1) разность увеличится на 9,25
2) разность уменьшится на 7,6
3) разность уменьшится на 12,2
4) разность увеличится на 17,96
5) 2,3 + 1,7 = 4, то есть разность увеличится на 4
6) 6,1 + 3,4) = 9,5, то есть разность уменьшится на 9,5
Задание № 901
Выразите данные величины в дециметрах и выполните действия:
1) 2,34 дм − 18 см;
2) 9,6 дм + 4 см;
3) 49 дм − 324 см;
4) 5,63 м + 2345 см;
5) 9 м 8 дм 3 см − 25 см 8 мм;
6) 1 м 5 дм 6 см − 16 см 9 мм.
Решение
2,34 дм − 18 см = 2,34 дм − 1,8 дм = 0,54 дм
9,6 дм + 4 см = 9,6 дм + 0,4 дм = 10 дм
49 дм − 324 см = 49 дм − 32,4 дм = 16,6 дм
5,63 м + 2345 см = 56,3 дм + 234,5 дм = 290,8 дм
9 м 8 дм 3 см − 25 см 8 мм = 98,3 дм − 2,58 дм = 95,72 дм
1 м 5 дм 6 см − 16 см 9 мм = 15,6 дм − 1,69 дм = 13,91 дм
227
Ответы к странице 227
Задание № 902
Выразите данные величины в арах и выполните действия:
1) 3 а 82 м 2 + 8 а 9 м 2 ;
2) 28 а 7 м 2 + 14 а 26 м 2 ;
3) 57 а 22 м 2 − 48 а 4 м 2 ;
4) 41 а 5 м 2 − 36 а 19 м 2 ;
5) 9 га 6 а 8 м 2 + 18 а 10 м 2 ;
6) 24 га 8 а 4 м 2 − 24 а 20 м 2 .
Решение
3 а 82 м 2 + 8 а 9 м 2 = 3,82 а + 8,09 а = 11,91 а
28 а 7 м 2 + 14 а 26 м 2 = 28,07 а + 14,26 а = 42,33 а
57 а 22 м 2 − 48 а 4 м 2 = 57,22 а − 48,04 а = 9,18 а
41 а 5 м 2 − 36 а 19 м 2 = 41,05 а − 36,19 а = 4,86 а
9 га 6 а 8 м 2 + 18 а 10 м 2 = 906,08 а + 18,10 а = 924,18 а
24 га 8 а 4 м 2 − 24 а 20 м 2 = 2408,04 а − 24,2 а = 2383,84 а
Задание № 903
Выразите данные величины в центнерах и выполните действия:
1) 9 ц − 524 кг;
2) 8 ц 44 кг − 836 кг;
3) 42 ц 5 кг + 85 кг;
4) 2,92 т + 684 кг;
5) 7 т 6 ц 4 кг − 8 ц 18 кг;
6) 1 т 2 ц 3 кг − 1 т 15 кг.
Решение
1) 9 ц − 524 кг = 9 ц − 5,24 ц = 3,76 ц
2) 8 ц 44 кг − 836 кг = 8,44 ц − 8,36 ц = 0,08 ц
3) 42 ц 5 кг + 85 кг = 42,05 ц + 0,85 ц = 42,9 ц
4) 2,92 т + 684 кг = 29,2 ц + 6,84 ц = 36,04 ц
5) 7 т 6 ц 4 кг − 8 ц 18 кг = 76,04 ц − 8,18 ц = 67,86 ц
6) 1 т 2 ц 3 кг − 1 т 15 кг = 12,3 ц − 10,15 ц = 1,88 ц
Задание № 904
Найдите значение выражения, выбирая удобный порядок вычислений:
1) (4,12 + 0,116) − 1,12;
2) (5,93 + 67,5) − 27,5;
3) 0,844 − (0,244 + 0,018);
4) 7,29 − (3,961 + 2,29).
Решение
1) (4,12 + 0,116) − 1,12 = (4,12 − 1,12) + 0,116 = 3 + 0,116 = 3,116
2) (5,93 + 67,5) − 27,5 = (67,5 − 27,5) + 5,93 = 40 + 5,93 = 45,93
3) 0,844 − (0,244 + 0,018) = (0,844 − 0,244) − 0,018 = 0,6 − 0,018 = 0,582
4) 7,29 − (3,961 + 2,29) = (7,29 − 2,29) − 3,961 = 5 − 3,961 = 1,039
Задание № 905
От двух пристаней, расстояние между которыми равно 24 км, одновременно в одном направлении отчалили лодка и катер (лодка двигалась впереди катера). Скорость лодки равна 8 км/ч и составляет 4/5 скорости катера. Через сколько часов после начала движения катер догонит лодку?
Решение
1) 8 : 4 * 5 = 10 (км/ч) — скорость катера
2) 10 − 8 = 2 (км/ч) — разница скоростей катера и лодки
3) 24 : 2 = 12 (ч) — потребуется катеру, чтобы догнать лодку
Ответ: через 12 ч.
Задание № 906
Длина бассейна равна 12 м, ширина его составляет 3/4 длины, а глубина − 2/3 ширины. Водой было наполнено 11/18 объема бассейна. Сколько кубических метров воды налили в бассейн?
Решение
1) 12 : 4 * 3 = 9 (м) — ширина бассейна
2) 9 : 3 * 2 = 6 (м) — глубина бассейна
3) 12 * 9 * 6 = 648 (м3) — объем бассейна
4) 648 : 18 * 11 = 396 (м3) — воды налили в бассейн
Ответ: 396 м3.
Задание № 907
За шоколадку и четыре пирожных заплатили 414 р., а за такую же шоколадку и восемь таких пирожных − 750 р. Сколько рублей стоит шоколадка?
Решение
1 шоколадка 8 пирожных − 1 шоколадка 4 пирожных = 4 пирожных, тогда:
1) 750 − 414 = 336 (р.) — стоят 4 пирожных
2) 414 − 336 = 78 (р.) — стоит шоколадка
Ответ: 78 р.
Задание № 907 из старого учебника
За шоколадку и четыре пирожных заплатили 138 р., а за такую же шоколадку и восемь таких же пирожных − 250 р. Сколько рублей стоит шоколадка?
Решение
1 шоколадка 8 пирожных − 1 шоколадка 4 пирожных = 4 пирожных, тогда:
1) 250 − 138 = 112 (р.) — стоят 4 пирожных
2) 138 − 112 = 26 (р.) — стоит шоколадка
Ответ: 26 р.
Задание № 908
Хитрый Лисенок предложил Петру Скупердяйкину: «Каждый раз, когда ты перейдешь мост, который я заколдую, твои деньги удвоятся. За это ты будешь мне каждый раз отдавать 24 монеты». Сделал Скупердяйкин так три раза и остался совсем без денег. Сколько денег было у Петра до встречи с Хитрым Лисенком?
Решение
Пусть x монет было у Скупердяйкина до встречи с Хитрым Лисенком, тогда
(2x − 24) монет стало у Скупердяйкина после первого перехода моста.
2 * (2x − 24) − 24 = 4x − 48 − 24 = 4x − 72 (монеты) стало у Скупердяйкина после второго перехода моста;
2 * (4x − 72) − 24 = 8x − 144 − 24 = 8x − 168 (монет) стало у Скупердяйкина после трех переходов моста.
Так как после трех переходов у Скупердяйкина осталось ноль монет, то:
8x − 168 = 0
8x = 168
x = 168 : 8
x = 21 (монета) была у Скупердяйкина до встречи с Хитрым Лисенком.
Ответ: 21 монета.
228
Ответы к странице 228
Задание №5 Проверьте себя в тестовой форме
1-А
2-А
3-Б
4-В
5-В
6-Б
7-А
8-Г
9-Б
10-В
11-Г
12-Б
231
Ответы к странице 231
Параграф 34. Умножение десятичных дробей
Задание № 909
Сколько цифр записано справа от запятой в произведении чисел:
1) 4,2 и 8,14;
2) 9,36 и 19,426;
3) 0,018 и 0,001?
Решение
1) 1 цифра + 2 цифры = 3 цифры
2) 2 цифры + 3 цифры = 5 цифр
3) 3 цифры + 3 цифры = 6 цифр
Задание № 910
Найдите произведение:
1) 6,58 * 10;
2) 6,58 * 100;
3) 6,58 * 1000;
4) 6,58 * 10000.
Решение
6,58 * 10 = 65,8
6,58 * 100 = 658
6,58 * 1000 = 6580
6,58 * 10000 = 65800
Задание № 911
Выполните умножение:
1) 9,6 * 10;
2) 0,065 * 100;
3) 7,03 * 100;
4) 32,97 * 1000;
5) 8,1 * 10000;
6) 0,028 * 10000.
Решение
9,6 * 10 = 96
0,065 * 100 = 6,5
7,03 * 100 = 703
32,97 * 1000 = 32970
8,1 * 10000 = 81000
0,028 * 10000 = 280
Задание № 912
Выполните умножение:
1) 3,284 * 10;
2) 6,3 * 100;
3) 4,125 * 1000;
4) 924,587 * 100000.
Решение
3,284 * 10 = 32,84
6,3 * 100 = 630
4,125 * 1000 = 4125
924,587 * 100000 = 92458700
Задание № 913
Известно, что 428 * 76 = 32528. Поставьте в правой части равенства запятую так, чтобы умножение было выполнено правильно:
1) 4,28 * 76 = 32528;
2) 42,8 * 7,6 = 32528;
3) 4,28 * 7,6 = 32528;
4) 42,8 * 0,76 = 32528;
5) 0,428 * 7,6 = 32528;
6) 0,428 * 0,076 = 32528.
Решение
4,28 * 76 = 325,28
42,8 * 7,6 = 325,28
4,28 * 7,6 = 32,528
42,8 * 0,76 = 32,528
0,428 * 7,6 = 3,2528
0,428 * 0,076 = 0,032528
232
Ответы к странице 232
Задание № 914
Выполните умножение:
1) 2,4 * 3,6;
2) 2,7 * 5,3;
3) 4,5 * 8,4;
4) 2,8 * 5,14;
5) 9,16 * 5,5;
6) 0,37 * 1,9;
7) 42,25 * 6;

9) 6,132 * 5,2;
10) 0,018 * 0,65;
11) 2,376 * 0,42;
12) 1,35 * 9,214.
Решение
Задание № 915
Выполните умножение:
1) 7,2 * 4,8;
2) 8,1 * 6,5;
3) 5,8 * 2,5;
4) 3,02 * 7,3;
5) 8,35 * 1,8;
6) 4,8 * 0,64;
7) 8 * 90,45;

9) 8,4 * 18,454;
10) 0,85 * 0,032;
11) 0,76 * 5,098;
12) 0,275 * 1,64.
Решение
Задание № 916
Выполните умножение:
1) 4,6 * 0,1;
2) 35,1 * 0,01;
3) 436 * 0,001;
4) 729 * 0,0001;
5) 6,58 * 0,1;
6) 6,58 * 0,001.
Решение
4,6 * 0,1 = 0,46
35,1 * 0,01 = 0,351
436 * 0,001 = 0,436
729 * 0,0001 = 0,0729
6,58 * 0,1 = 0,658
6,58 * 0,001 = 0,00658
Задание № 917
Выполните умножение:
1) 57 * 0,1;
2) 2,7 * 0,01;
3) 38,1 * 0,001;
4) 0,8 * 0,00001.
Решение
57 * 0,1 = 5,7
2,7 * 0,01 = 0,027
38,1 * 0,001 = 0,0381
0,8 * 0,00001 = 0,000008
Задание № 918 с ответами
Вычислите:
0,4 2 = 0 , 4 ∗ 0 , 4 = 0 , 16
0,2 3 = 0 , 2 ∗ 0 , 2 ∗ 0 , 2 = 0 , 008
1,6 2 = 1 , 6 ∗ 1 , 6 = 2 , 56
0,1 5 = 0 , 1 ∗ 0 , 1 ∗ 0 , 1 ∗ 0 , 1 ∗ 0 , 1 = 0 , 00001
!Задание № 919 с ответами
Найдите значение выражения:
1) 12,3 * 0,8 − 5,4 * 1,6 = 9,84 − 8,64 = 1,2
2) (46 − 34,17) * 0,09 = 11,83 * 0,09 = 1,0647
3) (3,126 − 1,7) * (0,15 + 7,4) = 1,426 * 7,55 = 10,7663
!Задание № 920 с ответами
Найдите значение выражения:
1) 5,6 * 0,08 + 0,23 * 2,4 = 0,448 + 0,552 = 1
2) (72 − 42,56) * 0,08 = 29,44 * 0,08 = 2,3552
3) (9,38 + 5,12) * (8,4 − 3,24)= 14,5 * 5,16 = 74,82
Задание № 921
Вычислите площадь теннисного корта, длина и ширина которого равны 23,75 м и 10, 92 м. Округлите ответ до единиц.
S = a * b = 23,75 * 10,92 = 259,35 (м2)
×23.75
10.92
4750
21375
0
2375
259.3500Ответ: 259 м2.
Задание № 922
Площадь деревянного Кремля, построенного при Иване Калите, равнялась 19,9 га, что в 1,38 раза меньше площади современного Кремля. Сколько гектаров составляет площадь современного кремля? Ответ округлите до десятых.
Решение:
19,9 * 1,38 = 27,462 (га) ≈ 27,5 (га) — площадь современного Кремля
Ответ: 27,5 га.
Задание № 923
В первый день регаты яхта «Беда» двигалась 12,6 ч со скоростью 26,5 км/ч, а на следующий день − 10,5 ч со скоростью 28,4 км/ч. Какой путь преодолела яхта за два дня регаты?
Решение
1) 12,6 * 26,5 = 333,9 (км) − прошла яхта «Беда» в первый день.
×12.6
26.5
630
756
252
333.902) 10,5 * 28,4 = 298,2 (км) − прошла яхта «Беда» во второй день.
×10.5
28.4
420
840
210
298.203) 333,9 + 298,2 = 632,1 (км) — преодолела яхта за два дня регаты.
+333.9
298.2
632.1Ответ: 632,1 км.
Задание № 924
Фермер продал 12,8 кг вишен по 180 р. за килограмм и 26,5 кг слив по 80 р. за килограмм. За какие фрукты он выручил больше денег и на сколько рублей?
Решение
1) 12,8 * 180 = 2304 (р.) — выручил фермер за вишни.
×12.8
180
1024
128
2304.02) 26,5 * 80 = 2120 (р.) — выручил фермер за сливы.
×26.5
80
2120.03) 2304 − 2120 = 184 (р.) — разница вырученного за вишни и сливы.
Ответ: на 184 рубля больше выручил фермер за вишни, чем за сливы.
Задание № 924 из старого учебника
Фермер продал 15,8 кг вишен по 40 р. за килограмм и 20,5 кг слив по 32 р. за килограмм. За какие фрукты он выручил больше денег и на сколько рублей?
Решение
1) 15,8 * 40 = 632 (р.) — выручил фермер за вишни.
×15.8
40
632.02) 20,5 * 32 = 656 (р.) — выручил фермер за сливы.
×20.5
32
410
615
656.03) 656 − 632 = 24 (р.) — разница вырученного за вишни и сливы.
Ответ: на 24 рубля больше выручил фермер за сливы.
233
Ответы к странице 233
Задание № 925
В походе группа туристов 8,5 ч шла пешком со скоростью 4,2 км/ч и 9,2 ч плыла по реке на плоту со скоростью 3,5 км/ч. Какое из расстояний, преодоленных туристами, − по суше или по реке − больше и на сколько километров?
Решение
1) 8,5 * 4,2 = 35,7 (км) — прошли туристы пешком.
×8.5
4.2
170
340
35.702) 9,2 * 3,5 = 32,2 (км) — проплыли туристы на плоту.
×9.2
3.5
460
276
32.203) 35,7 − 32,2 = 3,5 (км) разница расстояний, преодоленных по суше и реке.
Ответ: на 3,5 км больше туристы прошли по суше, чем проплыли по реке.
Задание № 926 с ответами
Вычислите значение выражения наиболее удобным способом:
0,2 * 32,8 * 5 = (0,2 * 5) * 32,8 = 1 * 32,8 = 32,8
0,25 * 24,3 * 0,4 = (0,25 * 0,4) * 24,3 = 0,1 * 24,3 = 2,43
0,8 * 47,5 * 12,5 = (0,8 * 12,5) * 47,5 = 10 * 47,5 = 475
73 * 0,5 * 0,4 = (0,5 * 0,4) * 73 = 0,2 * 73 = 14,6
Задание № 927 с ответами
Вычислите значение выражения наиболее удобным способом:
0,4 * 17 * 2,5 = (0,4 * 2,5) * 17 = 1 * 17 = 17
0,125 * 4,3 * 80 = (0,125 * 80) * 4,3 = 10 * 4,3 = 43
0,05 * 6,73 * 0,2 = (0,05 * 0,2) * 6,73 = 0,01 * 6,73 = 0,0673
0,4 * 0,36 * 5 = (0,4 * 5) * 0,36 = 2 * 0,36 = 0,72
Задание № 928 с ответами
Упростите выражение:
1) 1,3 * 0,2a = 0,26a
2) 0,9b * 8 = 7,2b
3) 0,23 * 40b = 9,2b
4) 2,8 * y * 0,5 = 1,4y
5) 0,6a * 0,08b = 0,048ab
6) 1,1x * 1,4y = 1,54xy
7) 0,27m * 0,3n = 0,081mn
0,4a * 8 * b * 0,3c = 0,96abc
9) 1,2x * 0,3y * 5z = 1,8xyz
Задание № 929
Упростите выражение и найдите его значение:
1) 0,5a * 20b, если a = 4, b = 6,8;
2) 0,25x * 0,4y, если x = 1,2, y = 0,3;
3) 4m * 0,5n если m = 0,22, n = 100;
4) 0,8k * 12,5c, если k = 0,58, с = 0,1.
Решение
1) 0,5a * 20b = 10ab = 10 * 4 * 6,8 = 4 * 68 = 272
2) 0,25x * 0,4y = 0,1xy = 0,1 * 1,2 * 0,3 = 0,12 * 0,3 = 0,36
3) 4m * 0,5n = 2mn = 2 * 0,22 * 100 = 2 * 22 = 44
4) 0,8k * 12,5c = 10kc = 10 * 0,58 * 0,1 = 1 * 0,58 = 0,58
Задание № 930 с ответами
Вычислите значение выражения наиболее удобным способом:
1) 3,18 * 7,8 + 3,18 * 2,2 = 3,18 * (7,8 + 2,2) = 3,18 * 10 = 31,8
2) 59,8 * 4,9 − 59,7 * 4,9 = 4,9 * (59,8 − 59,7) = 4,9 * 0,1 = 0,49
3) 0,946 * 26,8 + 0,946 * 23,2 = 0,946 * (26,8 + 23,2) = 0,946 * 50 = 47,3
4) 7,54 * 3,24 − 7,54 * 3,14 = 7,54 * (3,24 − 3,14) = 7,54 * 0,1 = 0,754
Задание № 931 с ответами
Вычислите значение выражения наиболее удобным способом:
1) 0,47 * 6,32 + 6,32 * 0,53 = 6,32 * (0,47 + 0,53) = 6,32 * 1 = 6,32
2) 1,25 * 2,34 + 4,46 * 1,25 = 1,25 * (2,34 + 4,46) = 1,25 * 6,8 = 8,5
3) 85,6 * 9,2 − 85,3 * 9,2 = 9,2 * (85,6 − 85,3) = 9,2 * 0,3 = 2,76
4) 7,12 * 13,9 − 7,12 * 3,4 = 7,12 * (13,9 − 3,4) = 7,12 * 10,5 = 74,76
Задание № 932
Выразите величины в одинаковых единицах измерения и сравните их:
1) 1,36 кг и 589,6 г;
2) 2396,4 г и 2,278 кг;
3) 28,4 мм и 2,84 см;
4) 92,6 см и 9,24 дм;
5) 31,6 кг и 0,432 ц;
6) 85,1 ц и 8,09 т.
Решение
1360 г > 589,6 г
1,36 кг > 589,6 г2396,4 г > 2278 г
2396,4 г > 2,278 кг2,84 см = 2,84 см
28,4 мм = 2,84 см9,26 дм > 9,24 дм
92,6 см > 9,24 дм31,6 кг < 43,2 кг
31,6 кг < 0,432 ц85,1 ц > 80,9 ц
85,1 ц > 80,9 ц
Задание № 933
Выразите величины в одинаковых единицах измерения и сравните их:
1) 6,4 дм и 64,2 см;
2) 265,8 см и 2,663 м;
3) 4,2 ц и 416,5 кг;
4) 0,8 т и 7,36 ц.
Решение
6,4 дм < 6,42 дм
6,4 дм < 64,2 см265,8 см < 266,3 см
265,8 см < 2,663 м420 кг > 416,5 кг
4,2 ц > 416,5 кг8 ц > 7,36 ц
0,8 т > 7,36 ц
Задание № 934
При Петре I в России с развитием торговли и промышленности назрела необходимость приведения в определенную систему различных мер. Так, были утверждены такие единицы длины: верста, сажень, аршин, вершок. Верста была равна 500 саженям, сажень − 3 аршинам, аршин − 16 вершкам. Скольким километрам равна верста, если вершок равен 4,445 см?
Решение задачи
16 * 4,445 = 71,12 (см) — длина 1 аршина.
3 * 71,12 = 213,36 (см) = 2,1336 (м) — длина 1 сажени.
500 * 2,1336 = 1066,80 (м) = 1,0668 (км) — длина 1 версты.
Ответ: 1,0668 км.
234
Ответы к странице 234
Задание № 935
В старину в России пользовались такими мерами массы: пуд, фунт, золотник. Пуд был равен 40 фунтам, фунт − 96 золотникам. Скольким килограммам равен пуд, если золотник равен 4,266 г? Ответ округлите до сотых.
Решение
1) 96 * 4,266 = 409,536 (г) — равен 1 фунт.
2) 40 * 409,536 = 16381,44 (г) = 16,38144 (кг) ≈ 16,38 (кг) — равен 1 пуд.
Ответ: 16,38 кг.
Задание № 936
Из одного села в одном направлении одновременно выехали два велосипедиста. Один из них ехал со скоростью 11,4 км/ч, а второй − со скоростью 9,8 км/ч. Какое расстояние будет между ними через 6,5 ч после начала движения?
Решение
1) 11,4 * 6,5 = 74,1 (км) — проедет за 6,5 ч первый велосипедист.
2) 9,8 * 6,5 = 63,7 (км) — проедет за 6,5 ч второй велосипедист.
3) 74,1 − 63,7 = 10,4 (км) — разница пройденного расстояния первым и вторым велосипедистами.
Ответ: 10,4 км.
Задание № 937
Из одного порта в другой одновременно вышли теплоход и катер. Скорость теплохода равна 26,3 км/ч, а скорость катера − 30,8 км/ч. Какое расстояние будет между ними через 5,4 ч после начала движения?
Решение
1) 30,8 − 26,3 = 4,5 (км/ч) — разница скоростей теплохода и катера.
2) 4,5 * 5,4 = 24,3 (км) — будет между теплоходом и катером через 5,4 часа.
Ответ: 24,3 км.
Задание № 938
С одной станции в противоположных направлениях одновременно отправились два поезда. Один из них двигался со скоростью 63,4 км/ч, а второй − со скоростью 58,6 км/ч. Какое расстояние будет между ними через 9,3 ч после начала движения?
Решение
1) 63,4 + 58,6 = 122 (км/ч) — суммарная скорость двух поездов.
2) 122 * 9,3 = 1134,6 (км) — будет между поездами через 9,3 ч после начала движения.
Ответ: 1134,6 км.
Задание № 939
Из одного города в противоположных направлениях одновременно отправились два автомобиля. Скорость одного автомобиля равна 72,5 км/ч, что на 8,7 км/ч больше, чем скорость второго. Какое расстояние будет между ними через 7,6 ч после начала движения?
Решение
1) 72,5 − 8,7 = 63,8 (км/ч) — скорость второго автомобиля.
2) 72,5 + 63,8 = 136,3 (км/ч) — суммарная скорость двух автомобилей.
3) 136,3 * 7,6 = 1035,88 (км) — будет между автомобилями через 7,6 ч после начала движения.
Ответ: 1035,88 км.
Задание № 940
Из двух городов навстречу друг другу одновременно выехали велосипедист и легковой автомобиль. Велосипедист ехал со скоростью 13,8 км/ч, а автомобиль − в 6,3 раза быстрее. Найдите расстояние между городами, если велосипедист и автомобиль встретились через 4,5 ч после начала движения.
Решение
1) 13,8 * 6,3 = 86,94 (км/ч) — скорость автомобиля.
2) 13,8 + 86,94 = 100,74 (км/ч) — суммарная скорость автомобиля и велосипедиста.
3) 100,74 * 4,5 = 453,33 (км) — расстояние между городами.
Ответ: 453,33 км.
Задание № 941
Из двух сел навстречу друг другу одновременно начали движение велосипедист и пешеход. Пешеход шел со скоростью 3,2 км/ч, что в 4,2 раза меньше скорости велосипедиста. Найдите расстояние между селами, если велосипедист и пешеход встретились через 1,6 ч после начала движения.
Решение
1) 3,2 * 4,2 = 13,44 (км/ч) — скорость велосипедиста.
2) 3,2 + 13,44 = 16,64 (км/ч) — суммарная скорость или скорость сближения велосипедиста и пешехода.
3) 16,64 * 1,6 = 26,624 (км) — расстояние между селами.
Ответ: 26,624 км.
!Задание № 942 с ответами
Найдите значение выражения:
1) (8,2 * 0,45 + 14,71) * 3,8 − 49,436 = (3,69 + 14,71) * 3,8 − 49,436 = 18,4 * 3,8 − 49,436 = 69,92 − 49,436 = 20,484
2) (3,6 * 4,25 − 0,7) * 5,9 + 7,9 * 0,2 = (15,3 − 0,7) * 5,9 + 1,58 = 14,6 * 5,9 + 1,58 = 86,14 + 1,58 = 87,72
3) 0,7 * (34,1 − 18,4) + 0,5 * 18,6 − (9,8 + 1,6) * 1,4 = 0,7 * 15,7 + 9,3 − 11,4 * 1,4 = 10,99 + 9,3 − 15,96 = 20,29 − 15,96 = 4,33
Задание № 943 с ответами
Найдите значение выражения:
1) (2,35 * 6,8 − 6,793) * 0,4 + 1,3252 = (15,98 − 6,793) * 0,4 + 1,3252 = 9,187 * 0,4 + 1,3252 = 3,6748 + 1,3252 = 5
2) 3,4 * 6,5 − 0,25 * (17,6 * 1,5 + 3,28) = 22,1 − 0,25 * (26,4 + 3,28) = 22,1 − 0,25 * 29,68 = 22,1 − 7,42 = 14,68
3) (36,8 − 15,3) * 0,4 + 0,6 * 12,4 − (18,6 − 13,8) * 0,5 = 21,5 * 0,4 + 7,44 − 4,8 * 0,5 = 8,6 + 7,44 − 2,4 = 13,64
Задание № 944
На какое число надо умножить число 7,08, чтобы получить:
1) 70,8;
2) 7080;
3) 0,708;
4) 0,000708?
Ответ
1) 7,08 * 10 = 70,8
2) 7,08 * 1000 = 7080
3) 7,08 * 0,1 = 0,708
4) 7,08 * 0,0001 = 0,000708
235
Ответы к странице 235
Задание № 945
На какое число надо умножить число 0,47, чтобы получить:
1) 47;
2) 47000;
3) 0,047;
4) 0,000047?
Ответы
1) 0,47 * 100 = 47
2) 0,47 * 100000 = 47000
3) 0,47 * 0,1 = 0,047
4) 0,47 * 0,0001 = 0,000047
Задание № 946 с ответами
Вычислите значение выражения наиболее удобным способом:
1) 6,5 * 2,46 − 6,5 * 2,29 − 6,5 * 0,17 = 6,5 * (2,46 − 2,29 − 0,17) = 6,5 * 0 = 0
2) 12,36 * 1,39 + 1,11 * 12,36 − 2,5 * 4,36 = 12,36 * (1,39 + 1,11) − 2,5 * 4,36 = 12,36 * 2,5 − 2,5 * 4,36 = 2,5 * (12,36 − 4,36) = 2,5 * 8 = 20
Задание № 947 с ответами
Вычислите значение выражения наиболее удобным способом:
1) 0,37 * 4,6 − 1,8 * 0,37 + 0,37 * 7,2 = 0,37 * (4,6 − 1,8 + 7,2) = 0,37 * 10 = 3,7
2) 6,74 * 0,13 + 0,47 * 6,74 + 0,6 * 1,76 = 6,74 * (0,13 + 0,47) + 0,6 * 1,76 = 6,74 * 0,6 + 0,6 * 1,76 = 0,6 * (6,74 + 1,76) = 0,6 * 8,5 = 5,1
Задание № 948
Упростите выражение и найдите его значение:
1) 0,13p + 0,47p, если p = 0,14;
2) 0,072b − 0,043b, если b = 5,4;
3) 3,8x + 1,7x − 5,4x + 0,1x, если x = 0,678;
4) 8,6c − 3,5c − 0,1c + 0,296, если c = 0,58.
Решение
1) 0,13p + 0,47p = 0,6p = 0,6 * 0,14 = 0,084
2) 0,072b − 0,043b = 0,029b = 0,029 * 5,4 = 0,1566
3) 3,8x + 1,7x − 5,4x + 0,1x = (3,8 + 1,7 − 5,4 + 0,1)x = 0,2x = 0,2 * 0,678 = 0,1356
4) 8,6c − 3,5c − 0,1c + 0,296 = (8,6 − 3,5 − 0,1)c + 0,296 = 5c + 0,296 = 5 * 0,58 + 0,296 = 2,9 + 0,296 = 3,196
Задание № 949
Упростите выражение и найдите его значение:
1) 3,4x + 5,6x, если x = 0,08;
2) 5,4a − 3,9a, если a = 0,26;
3) 1,8m − 0,5m + 0,7m, если m = 3,94;
4) 0,19z − 0,12z + 0,33z − 1,92, если z = 8,2.
Решение
1) 3,4x + 5,6x = 9x = 9 * 0,08 = 0,72
2) 5,4a − 3,9a = 1,5a = 1,5 * 0,26 = 0,39
3) 1,8m − 0,5m + 0,7m = (1,8 − 0,5 + 0,7)m = 2m = 2 * 3,94 = 7,88
4) 0,19z − 0,12z + 0,33z − 1,92 = (0,19 − 0,12 + 0,33)z − 1,92 = 0,4z − 1,92 = 0,4 * 8,2 − 1,92 = 3,28 − 1,92 = 1,36
Задание № 950
Лодка плыла 1,8 ч по течению реки и 2,6 ч против течения. Какой путь проплыла лодка за все время движения, если скорость течения равна 2,4 км/ч, а собственная скорость лодки − 18,9 км/ч?
Решение
18,9 + 2,4 = 21,3 (км/ч) — скорость лодки по течению.
21,3 * 1,8 = 38,34 (км) — проплыла лодка по течению.
18,9 − 2,4 = 16,5 (км/ч) — скорость лодки против течения.
16,5 * 2,6 = 42,9 (км) — проплыла лодка против течения.
38,34 + 42,9 = 81,24 (км) — проплыла лодка всего.
Ответ: 81,24 км.
Задание № 951
Теплоход шел 4,5 ч против течения и 0,8 ч по течению реки. Какой путь прошел теплоход, если его скорость против течения равна 24,6 км/ч, а скорость течения − 1,8 км/ч?
Решение
24,6 * 4,5 = 110,7 (км) — прошел теплоход против течения.
24,6 + 2 * 1,8 = 24,6 + 3,6 = 28,2 (км/ч) — скорость лодки по течению.
28,2 * 0,8 = 22,56 (км) — прошел теплоход по течению.
110,7 + 22,56 = 133,26 (км) — всего прошел теплоход.
Ответ: 133,26 км.
Задание № 952
1) Одна из сторон прямоугольника равна 2,3 м, что на 3,4 м меньше соседней стороны. Вычислите площадь и периметр прямоугольника.
Решение
1) 2,3 + 3,4 = 5,7 (м) длина второй стороны прямоугольника.
2) 2,3 * 5,7 = 13,11 (м2) площадь прямоугольника.
3) 2 * (2,3 + 5,7) = 2 * 8 = 16 (м) периметр прямоугольника.
Ответ: 13,11 м2, 16 м.
2) Сторона квадрата равна 3,2 см. Вычислите его площадь и периметр.
Решение
1) 3,2 * 3,2 = 10,24 (см2) — площадь квадрата.
2) 4 * 3,2 = 12,8 (см) — периметр квадрата.
Ответ: 10,24 см2, 12,8 см.
Задание № 953
Одна из сторон прямоугольника равна 5,8 дм, что на 1,3 дм больше соседней стороны. Вычислите площадь и периметр прямоугольника.
Решение
5,8 − 1,3 = 4,5 (дм) — длина второй стороны прямоугольника.
5,8 * 4,5 = 26,1 (дм2) — площадь прямоугольника.
2 * (5,8 + 4,5) = 2 * 10,3 = 20,6 (дм) — периметр прямоугольника.
Ответ: 26,1 м2, 20,6 дм.
Задание № 954
Измерения прямоугольного параллелепипеда равны 4,6 см, 2,4 см и 3,6 см.
Найдите:
1) сумму длин всех его ребер;
2) площадь его поверхности;
3) его объем.
Решение
1) 4 * 4,6 + 4 * 2,4 + 4 * 3,6 = 4 * (4,6 + 2,4 + 3,6) = 4 * 10,6 = 42,4 см сумма длин всех ребер прямоугольного параллелепипеда;
2) 2 * (4,6 * 2,4) + 2 * (4,6 * 3,6) + 2 * (2,4 * 3,6) = 2 * 11,04 + 2 * 16,56 + 2 * 8,64 = 2 * (11,04 + 11,56 + 8,64) = 2 * 36,24 = 72,48 (см2) — площадь поверхности прямоугольного параллелепипеда;
3) 4,6 * 2,4 * 3,6 = 11,04 * 3,6 = 39,744 (см3) объем поверхности прямоугольного параллелепипеда.
Задание № 955
Ребро куба равно 0,6 дм.
Найдите:
1) сумму длин всех его ребер;
2) площадь его поверхности;
3) его объем.
1) 12 * 0,6 = 7,2 (дм) — сумма длин всех ребер куба.
2) 6 * (0,6 * 0,6) = 6 * 0,36 = 2,16 (дм2) — площадь поверхности куба.
3) 0,6 * 0,6 * 0,6 = 0,36 * 0,6 = 0,216 (дм3) — объем куба.
Задание № 956
Ширина прямоугольного параллелепипеда равна 4,5 см, что в 2 раза меньше его длины и на 0,9 см больше его высоты.
Найдите:
1) сумму длин всех его ребер;
2) площадь его поверхности;
3) его объем.
Решение
4,5 * 2 = 9 (см) — длина прямоугольного параллелепипеда.
4,5 − 0,9 = 3,6 (см) — высота прямоугольного параллелепипеда.
1) 4 * 4,5 + 4 * 9 + 4 * 3,6 = 4 * (4,5 + 9 + 3,6) = 4 * 17,1 = 68,4 (см) сумма длин всех ребер прямоугольного параллелепипеда.
2) 2 * (4,5 * 9) + 2 * (4,5 * 3,6) + 2 * (3,6 * 9) = 2 * 40,5 + 2 * 16,2 + 2 * 32,4 = 2 * (40,5 + 16,2 + 32,4) = 2 * 89,1 = 178,2 (см2) — площадь поверхности прямоугольного параллелепипеда.
3) 4,5 * 9 * 3,6 = 40,5 * 3,6 = 145,8 (см3 ) — объем прямоугольного параллелепипеда.
236-237
Ответы к странице 236-237
Задание № 957
Мама поручила Саше купить 1,5 кг печенья, 0,8 кг вафель и 0,5 кг конфет. Хватит ли Саше 1400 р., если 1 кг печенья стоит 450 р., 1 кг вафель − 440 р., а 1 кг конфет − 600 р.?
Решение задачи
1) 1,5 * 450 = 675 (р.) — стоит печенье.
2) 0,8 * 440 = 352 (р.) — стоят вафли.
3) 0,5 * 600 = 300 (р.) — стоят конфеты.
4) 675 + 352 + 300 = 1327 (р.) — стоимость всей покупки.
1400 р. > 1327 р., значит Саше хватит денег на покупку.
Ответ: денег хватит.
Задание № 957 из старого учебника
Мама поручила Саше купить 1,5 кг печенья, 0,8 кг вафель и 0,5 кг конфет. Хватит ли Саше 360 р., если 1 кг печенья стоит 72 р., 1 кг вафель − 90 р., а 1 кг конфет − 240 р.?
Решение задачи
1) 1,5 * 72 = 108 (р.) — стоит печенье.
2) 0,8 * 90 = 72 (р.) — стоят вафли.
3) 0,5 * 240 = 120 (р.) — стоят конфеты.
4) 108 + 72 + 120 = 180 + 120 = 300 (р.) — стоимость всей покупки.
360 р. > 300 р., значит Саше хватит денег на покупку.
Ответ: денег хватит.
Задание № 958
К своему дню рождения Буратино купил 12 кг шоколадных конфет по 3,4 сольдо за килограмм, 7,5 кг зефира по 2,6 сольдо и 14 бутылок лимонада по 1,5 сольдо за бутылку. Сколько денег осталось у Буратино, если сначала у него было 100 сольдо?
Решение задачи
1) 12 * 3,4 = 40,8 (с.) — стоят конфеты.
2) 7,5 * 2,6 = 19,5 (с.) — стоит зефир.
3) 14 * 1,5 = 21 (с.) — стоит лимонад.
4) 100 − (40,8 + 19,5 + 21) = 100 − 81,3 = 18,7 (с.) — осталось у Буратино.
Ответ: 18,7 сольдо.
Задание № 958 из старого учебника
На покупку ткани для нового платья портняжки получили 500 гульденов. Они приобрели 20,4 м шелка по 1,75 гульдена за метр, 18,5 м парчи по 2,38 гульдена, 12,5 м кружев по 2,16 гульдена, 32,8 м бархата по 2,05 гульдена и 44,4 м золотой пряжи по 3,45 гульдена. Сколько денег осталось у портняжек?
Решение задачи
1) 20,4 * 1,75 = 35,7 (г.) — потратили на шелк.
2) 18,5 * 2,38 = 44,03 (г.) — потратили на парчу.
3) 12,5 * 2,16 = 27 (г.) — потратили на кружево.
4) 32,8 * 2,05 = 67,24 (г.) — потратили на бархат.
5) 44,4 * 3,45 = 153,18 (г.) — потратили на пряжу.
6) 500 − (35,7 + 44,03 + 27 + 67,24 + 153,18) = 500 − 327,15 = 172,85 (г.) — осталось у портняжек.
Ответ: 172,85 гульденов.
Задание № 959
Ваня коллекционирует монеты и значки. Треть четверти всех монет составляет 12 монет, а четверть трети всех значков − 12 значков. Чего больше, монет или значков, у Вани в коллекции?
Решение задачи
1) 12 : 3 * 4 = 4 * 4 = 16 (м.) — было у Вани.
2) 12 : 4 * 3 = 3 * 3 = 9 (з.) — было у Вани.
3) 16 − 9 = 7, то есть на 7 монет было у Вани больше, чем значков.
Ответ: монет было больше.
Задание № 960
Длина прямоугольного листа бумаги равна 50 см, а ширина − 12 см. Сколько квадратов площадью 100 см2 можно вырезать из этого листа бумаги?
Решение задачи
1) 10 * 10 = 100, то есть длина стороны квадрата равна 10 см.
2) 50 : 10 = 5 (к.) — со стороной 10 см умещаются в прямоугольный лист по длине.
3) 12 : 10 = 1,2 (к.) — то есть 1 квадрат со стороной 10 см умещается в прямоугольный лист по ширине.
4) 5 * 1 = 5 (к.) — можно вырезать из данного листа бумаги, после чего останется от листа бумаги полоска длиной 50 см и шириной 2 см.
Ответ: 5 квадратов.
Задание № 961
Из плохо закрытого по небрежности водопроводного крана каждую секунду вытекает одна капля воды. 1) Сколько граммов воды вытечет за сутки, если масса 100 капель равна 7 г? Округлите ответ до тысячи граммов и выразите в килограммах.
2) Сколько тонн воды вытечет за сутки, если в городе 120000 квартир, в каждой из которых плохо закрыт кран?
3) Сколько дней можно было бы поливать вытекшей во всем городе водой огород площадью 10 а, на котором высажена капуста, если для полива 1 м2 огорода требуется 15 л воды в сутки?
Решение задачи
1) 1 сутки = 24 часа = 24 • 60 • 60 = 86 400 сек — значит за сутки из одного крана вытечет 86 400 капель воды.
86 400 : 100 • 7 = 6 048 (г) ≈ 6 000 (г) = 6 кг — воды вытечет из одного крана за сутки.
2) 6 • 120 000 = 720 000 (кг) = 720 тонн — воды вытечет за сутки из 120 000 квартир.
3) 10 ар = 1 000 м²
15 • 1 000 = 15 000 (л) — воды потребуется для полива 10 аров огорода в сутки.
720 000 : 15 000 = 48 (сут.) — можно поливать огород вытекшей в городе водой.Ответ: за сутки из одного крана вытекает примерно 6 кг воды; в городе из 120 000 квартир за сутки вытекает примерно 720 тонн воды; вытекшей в городе водой можно поливать огород в течении 48 суток.
241
Ответы к странице 241
Параграф 35.Деление десятичных дробей
Задание № 963 с ответами
Выполните деление:
1) 56,87 : 10 = 5,687
2) 7 : 10 = 0,7
3) 14,49 : 100 = 0,1449
4) 12 : 100 = 0,12
5) 0,04 : 100 = 0,0004
6) 28 : 1000 = 0,028
Задание № 964
Выполните деление:
1) 256 : 10;
2) 37,5 : 10;
3) 3 : 100;
4) 70,2 : 100;
5) 0,96 : 1000;
6) 125,7 : 1000.
Решение
1) 256 : 10 = 25,6
2) 37,5 : 10 = 3,75
3) 3 : 100 = 0,03
4) 70,2 : 100 = 0,702
5) 0,96 : 1000 = 0,00096
6) 125,7 : 1000 = 0,1257
!Задание № 965 с ответами
Найдите частное:
1) 2,4 : 8 = 0,3
2) 0,42 : 7 = 0,06
3) 5,5 : 5 = 1,1
4) 0,048 : 12 = 0,004
5) 7 : 2 = 3,5
6) 6,36 : 6 = 1,06
7) 0,5 : 2 = 0,25
19 : 2 = 9,5
9) 0,24 : 3 = 0,08
!Задание № 966 с ответами
Выполните деление:
1) 8,68 : 7 = 1,24
2) 169,2 : 8 = 21,15
3) 89,6 : 28 = 3,2
4) 33,28 : 52 = 0,64
5) 9,044 : 38 = 0,238
6) 144,96 : 48 = 3,02
7) 13 : 2 = 6,5
21 : 14 = 1,5
9) 6 : 12 = 0,5
10) 1 : 125 = 0,008
11) 7,982 : 26 = 0,307
12) 0,0432 : 36 = 0,0012
!Задание № 967 с ответами
Выполните деление:
1) 85,2 : 6 = 14,2
2) 13,8 : 4 = 3,45
3) 78,2 : 34 = 2,3
4) 11,34 : 42 = 0,27
5) 3,198 : 26 = 0,123
6) 453,2 : 22 = 20,6
7) 48,16 : 16 = 3,01
17 : 5 = 3,4
9) 2 : 8 = 0,25
10) 14 : 112 = 0,125
11) 45 : 6 = 7,5
12) 0,1242 : 69 = 0,0018
!Задание № 968
Вычислите:
1) 21,6 − 12,6 : 18 + 6;
2) (21,6 − 12,6) : 18 + 6;
3) (21,6 − 12,6) : (18 + 6);
4) 21,6 − 12,6 : (18 + 6).
Решение
1) 21,6 − 12,6 : 18 + 6 = 21,6 − 0,7 + 6 = 20,9 + 6 = 26,9
2) (21,6 − 12,6) : 18 + 6 = 9 : 18 + 6 = 0,5 + 6 = 6,5
3) (21,6 − 12,6) : (18 + 6) = 9 : 24 = 0,375
4) 21,6 − 12,6 : (18 + 6) = 21,6 − 12,6 : 24 = 21,6 − 0,525 = 21,075
!Задание № 969
Найдите значение выражения:
1) 3,6 : 9 + 0,18 * 5;
2) 70,28 : 14 − 32,8 : 10 + 10,58 : 23;
3) 47,04 − 47,04 : (46 + 38);
4) (140 − 12,32) : 42 + 3,15 * 16.
Решение
1) 3,6 : 9 + 0,18 * 5 = 0,4 + 0,9 = 1,3
2) 70,28 : 14 − 32,8 : 10 + 10,58 : 23 = 5,02 − 3,28 + 0,46 = 1,74 + 0,46 = 2,2
3) 47,04 − 47,04 : (46 + 38) = 47,04 − 47,04 : 84 = 47,04 − 0,56 = 46,48
4) (140 − 12,32) : 42 + 3,15 * 16 = 127,68 : 42 + 50,4 = 3,04 + 50,4 = 53,44
!Задание № 970
Выполните действия:
1) 3,8 * 1,7 − 36,24 : 12;
2) 53,4 : 15 + 224 : 100 − 36 : 8;
3) 22,08 − 22,08 : (74 − 26);
4) (134 − 15,97) : 29 + 4,24 * 35.
Решение
1) 3,8 * 1,7 − 36,24 : 12 = 6,46 − 3,02 = 3,44
2) 53,4 : 15 + 224 : 100 − 36 : 8 = 3,56 + 2,24 − 4,5 = 5,8 − 4,5 = 1,3
3) 22,08 − 22,08 : (74 − 26) = 22,08 − 22,08 : 48 = 22,08 − 0,46 = 21,62
4) (134 − 15,97) : 29 + 4,24 * 35 = 118,03 : 29 + 148,4 = 4,07 + 148,4 = 152,47
242
Ответы к странице 242
Задание № 971
Решите уравнение:
1) x * 13 = 132,6;
2) 64,6 : x = 17;
3) x : 14,5 = 4,6;
4) 9,728x + 7,272x = 4,08;
5) 38,6x − 16,6x = 14,74;
6) 1,2x + 4,6x − 2,8x = 0,15.
Решение
x * 13 = 132,6
x = 132,6 : 13
x = 10,2
_132,6 |13
13 |10,2
_26
26
064,6 : x = 17
x = 64,6 : 17
x = 3,8
_64,6 |17
51 |3,8
_136
136
0x : 14,5 = 4,6
x = 4,6 * 14,5
x = 66,70
×4.6
14.5
230
184
46
66.709,728x + 7,272x = 4,08
17x = 4,08
x = 4,08 : 17
x = 0,24
_4,08 |17
34 |0,24
_68
68
038,6x − 16,6x = 14,74
22x = 14,74
x = 14,74 : 22
x = 0,67
_14,74 |22
132 |0,67
_154
154
01,2x + 4,6x − 2,8x = 0,15
3x = 0,15
x = 0,15 : 3
x = 0,05_0,15 |3
15 |0,05
0
Задание № 972
Решите уравнение:
1) 12 * x = 112,8;
2) 178,5 : x = 21;
3) x : 3,2 = 10,5;
4) y + 27y = 0,952;
5) 33m − m = 102,4;
6) 2,7x − 1,3x + 3,6x = 2.
Решение
12 * x = 112,8
x = 112,8 : 12
x = 9,4
_112,8 |12
108 |9,4
_48
48
0178,5 : x = 21
x = 178,5 : 21
x = 8,5
_178,5 |21
168 | 8,5
_105
105
0x : 3,2 = 10,5
x = 10,5 * 3,2
x = 33,6
×10.5
3.2
210
315
33.60y + 27y = 0,952
28y = 0,952
y = 0,952 : 28
y = 0,034
_0,952 |28
84 |0,034
_112
112
033m − m = 102,4
32m = 102,4
m = 102,4 : 32
m = 3,2
_102,4 |32
96 |3,2
_64
64
02,7x − 1,3x + 3,6x = 2
5x = 2
x = 2 : 5
x = 0,4
_2 |5
0 |0,4
_20
20
0
!Задание № 973 с ответами
Преобразуйте в десятичную дробь:
1) 3/4 = 0,75
2) 9/20 = 0,45
3) 23/32 = 0,71875
4) 53/40 = 1,325
5) 263/125 = 2,104
!Задание № 974 с ответами
Преобразуйте в десятичную дробь:
1/2 = 0,5
5/8 = 0,625
19/25 = 0,76
19/8 = 2,375
47/200 = 0,235
Задание № 975 с ответами
Найдите частное:
1) 3,2 : 0,4 = 32 : 4 = 8
2) 0,36 : 0,9 = 3,6 : 9 = 0,4
3) 0,084 : 0,04 = 8,4 : 4 = 2,1
4) 0,012 : 0,6 = 0,12 : 6 = 0,02
5) 2,4 : 0,12 = 240 : 12 = 20
6) 0,3248 : 0,016 = 3248 : 160 = 20,3
!Задание № 976 с ответами
Выполните деление:
1) 45,6 : 2,4 = 456 : 24 = 19
2) 29,88 : 8,3 = 3,6
3) 60 : 1,25 = 48
4) 8,4 : 0,07 = 120
5) 9,246 : 0,23 = 40,2
6) 0,18564 : 0,78 = 0,238
7) 0,56 : 0,8 = 5,6 : 8 = 0,7
0,026 : 0,65 = 0,04
9) 3 : 0,016 = 187,5
10) 19,798 : 5,21 = 3,8
11) 0,2278 : 0,067 = 3,4
12) 24,1248 : 0,048 = 502,6
!Задание № 977 с ответами
Выполните деление:
1) 28,8 : 1,8 = 288 : 18 = 16
2) 12,88 : 4,6 = 128,8 : 46 = 2,8
3) 81 : 2,25 = 8100 : 225 = 36
4) 9,6 : 0,04 = 960 : 4 = 240
5) 4,928 : 0,16 = 492,8 : 16 = 30,8
6) 0,22274 : 0,43 = 22,274 : 43 = 0,518
7) 0,72 : 0,9 = 7,2 : 9 = 0,8
0,014 : 0,56 = 1,4 : 56 = 0,025
9) 1 : 0,025 = 1000 : 25 = 40
10) 7,488 : 3,12 = 748,8 : 312 = 2,4
11) 0,1218 : 0,058 = 121,8 : 58 = 2,1
12) 6,1244 : 0,061 = 6124,4 : 61 = 100,4
Задание № 978 с ответами
Выполните деление:
1) 93,42 : 0,1 = 934,2
2) 8 : 0,1 = 80
3) 12,7 : 0,01 = 1270
4) 4 : 0,001 = 4000
5) 79,35 : 0,001 = 79350
6) 4,87 : 0,00001 = 487000
Задание № 979 с ответами
Выполните деление:
1) 84,6 : 0,1 = 846
2) 54 : 0,1 = 540
3) 0,73 : 0,01 = 73
4) 5 : 0,01 = 500
5) 239,16 : 0,001 = 239160
6) 1,9 : 0,0001 = 19000
Задание № 980
Решите уравнение:
1) y * 4,9 = 2,94;
2) y * 0,7 = 0,0091;
3) y : 2,3 = 5,6;
4) 7,8a + 5,4a = 3,3;
5) 1,3x − 0,82x = 6;
6) x − 0,28x = 36.
Решение
y * 4,9 = 2,94
y = 2,94 : 4,9
y = 0,6
_29,4 |49
294 |0,6
0y * 0,7 = 0,0091
y = 0,0091 : 0,7
y = 0,013
_0,091 |7
7 |0,013
_21
21
0y : 2,3 = 5,6
y = 5,6 * 2,3
y = 12,88
×5.6
2.3
168
112
12.887,8a + 5,4a = 3,3
13,2a = 3,3
a = 3,3 : 13,2
a = 0,25
_33 |132
0 |0,25
_330
264
_660
660
01,3x − 0,82x = 6
0,48x = 6
x = 6 : 0,48
x = 12,5
_600 |48
48 |12,5
_120
96
_240
240
0x − 0,28x = 36
0,72x = 36
x = 36 : 0,72
x = 50
_3600 |72
360 |50
0
Задание № 981
Найдите корень уравнения:
1) 9,2 * y = 3,68;
2) 0,3y = 0,0162;
3) y : 1,2 = 10,2;
4) 3,8a + 4,6a = 13,44;
5) b − 0,872b = 32;
6) 4,9m − 0,1m = 3,84.
Решение
9,2 * y = 3,68
y = 3,68 : 9,2
y = 0,4
_36,8 |92
368 |0,4
00,3y = 0,0162
y = 0,0162 : 0,3
y = 0,054
_0,162 |3
15 |0,054
_12
12
0y : 1,2 = 10,2
y = 10,2 * 1,2
y = 12,24
×10.2
1.2
204
102
12.243,8a + 4,6a = 13,44
8,4a = 13,44
a = 13,44 : 8,4
a = 1,6
_134,4 |84
84 |1,6
_504
504
0b − 0,872b = 32
0,128b = 32
b = 32 : 0,128
b = 250
_32000 |128
256 |250
_640
640
04,9m − 0,1m = 3,84
4,8m = 3,84
m = 3,84 : 4,8
m = 0,8
_38,4 |48
384 |0,8
0
243
Ответы к странице 243
Задание № 982
Поезд проехал 135,8 км за 2,8 ч. Сколько километров он проедет за 6,2 ч с той же скоростью?
Решение задачи
1) 135,8 : 22,8 = 48,5 (км/ч) — скорость поезда.
_1358 |28
112 |48,5
_238
224
_140
140
02) 6,2 * 48,5 = 300,7 (км) — проедет поезд за 6,2 ч.
×6.2
48.5
310
496
248
300.70Ответ: 300,7 км.
Задание № 983
За 3,6 кг конфет Буратино заплатили 288 сольдо. Сколько сольдо надо заплатить за 6,5 кг таких конфет?
Решение
1) 288 : 3,6 = 80 (с.) — стоит 1 кг конфет.
_2880 |36
288 |80
02) 80 * 6,5 = 520 (с.) — надо заплатить за 6,5 кг таких конфет.
×80
6.5
4
48
520.0Ответ: 520 сольдо.
Задание № 984
Алладин купил для обезьянки Абу 6 кг бананов и 8 кг фиников, заплатив за все 136,4 драхмы. Сколько стоит 1 кг фиников, если 1 кг бананов стоит 10,2 драхмы?
Решение
1) 10,2 * 6 = 61,2 (д.) — заплатил Алладин за бананы.
×10.2
6
61.22) 136,4 − 61,2 = 75,2 (д.) — заплатил Алладин за финики.
−136.4
61.2
75.23) 75,2 : 8 = 9,4 (д.) — стоит 1 кг фиников.
_75,2 |8
72 |9,4
_32
32
0Ответ: 9,4 драхмы.
Задание № 985
Собрали 456,3 кг яблок и груш. Яблоки разложили в 9 ящиков по 23,5 кг в каждый, а груши − поровну в 12 корзинок. Сколько килограммов груш было в каждой корзине?
Решение
1) 23,5 * 9 = 211,5 (кг) — яблок собрали.
×23.5
9
211.52) 456,3 − 211,5 = 244,8 (кг) — груш собрали.
_456.3
211.5
244.83) 244,8 : 12 = 20,4 (кг) — груш было в каждой корзине.
_244,8 |12
24 |20,4
_48
48
0Ответ: 20,4 кг.
Задание № 986
От проволоки длиной 12 м отрезали кусок, длина которого составляла 0,1 длины всей проволоки. Сколько метров проволоки отрезали?
Решение
12 * 0,1 = 1,2 (м) — проволоки отрезали.
Ответ: 1,2 метра.
Задание № 987
Михаил Степанович собрал в своем саду 320 кг фруктов и ягод, причем виноград составлял 0,01 собранного урожая. Сколько килограммов винограда собрал Михаил Степанович?
Решение
320 * 0,01 = 3,2 (кг) — винограда собрал Михаил Степанович.
Ответ: 3,2 кг.
Задание № 988
Олег прочитал 0,6 книги, в которой 180 страниц. Сколько страниц прочитал Олег?
Решение
180 * 0,6 = 108 (с.) — прочитал Олег.
Ответ: 108 страниц.
Задание № 989
Катя слепила 120 вареников с вишней и с картошкой, причем вареники с вишней составляли 0,8 всех вареников. Сколько вареников с вишней слепила Катя?
Решение
120 * 0,8 = 96 (в.) — с вишней слепила Катя.
Ответ: 96 вареников.
Задание № 990
Турист прошел 2,7 км, что составляет 0,1 туристского маршрута. Сколько километров составляет туристский маршрут?
Решение
Пусть весь маршрут x км, тогда:
0,1x = 2,7
x = 2,7 : 0,1
x = 27 (км) составляет туристский маршрут.
Ответ: 27 км.
Задание № 991
Иван Иванович купил сыну шоколадку за 12,5 р., потратив на эту покупку 0,001 полученной премии. Сколько рублей составляет премия Ивана Ивановича?
Решение
Пусть x рублей составляет премия Ивана Ивановича, тогда:
0,001x = 12,5
x = 12,5 : 0,001
x = 12500 рублей составляет премия Ивана Ивановича.
Ответ: 12500 рублей.
Задание № 992
В парке растет 48 елей, что составляет 0,6 всех деревьев. Сколько деревьев растет в парке?
Решение
Пусть x всех деревьев, тогда:
0,6x = 48
x = 48 : 0,6
x = 80 (д.) — растет в парке.
Ответ: 80 деревьев.
Задание № 993
На птицеферме было 960 цыплят, что составляло 0,8 всех птиц. Сколько всего птиц было на ферме?
Решение
Пусть x всех птиц, тогда:
0,8x = 960
x = 960 : 0,8
x = 1200 (п.) — было на ферме.
Ответ: 1200 птиц.
!Задание № 994 с ответами
Найдите значение выражения:
1) 84 : 0,35 − 4,64 : 5,8 − 60 : 48 + 2,9 : 0,58 = 240 − 0,8 − 1,25 + 5 = 242,95
2) 40 − (2,0592 : 0,072 − 19,63) = 40 − (2,0592 : 0,072 − 19,63) = 40 − (28,6 − 19,63) = 40 − 8,97 = 31,03
3) 7,67 : 0,65 − (0,394 + 0,7688) : 0,57 = 11,8 − 1,1628 : 0,57 = 11,8 − 2,04 = 9,76
!Задание № 995 с ответами
Вычислите:
1) 2,46 : 4,1 + 15 : 0,25 − 4 : 25 − 14,4 : 0,32 = 0,6 + 60 − 0,16 − 45 = 15,44
2) 50 − (2,3256 : 0,068 + 9,38) = 50 − (34,2 + 9,38) = 50 − 43,58 = 6,42
3) 6,63 : 0,85 − (34 − 30,9248) : 0,62 = 7,8 − 3,0752 : 0,62 = 7,8 − 4,96 = 2,84
Задание № 996
Найдите объем куба, сумма длин всех ребер которого равна 30 дм.
Решение
1) 30 : 12 = 2,5 (дм) — длина одного ребра куба.
2) 2,5 * 2,5 * 2,5 = 15,625 (дм3) — объем куба.
Ответ: 15,625 дм3.
Задание № 997
Найдите площадь квадрата, периметр которого равен 12,8 см.
Решение
12,8 : 4 = 3,2 (см) — длина стороны квадрата.
3,2 * 3,2 = 10,24 (см2) — площадь квадрата.
Ответ: 10,24 см2.
244
Ответы к странице 244
!Задание № 998 с ответами
Выполните действия:
1) (39 − 5,8 * 1,2) : (42,4 − 38,4 : 16) = (39 − 6,96) : (42,4 − 2,4) = 32,04 : 40 = 0,801
2) (57,12 : 1,4 + 4,324 : 0,46) * 1,5 − 28,16 = (40,8 + 9,4) * 1,5 − 28,16 = 50,2 * 1,5 − 28,16 = 75,3 − 28,16 = 47,14
!Задание № 999 с ответами
Выполните действия:
(14,6 * 2,8 − 4,94) : (57,6 : 18 + 2,8) = (40,88 − 4,94) : (3,2 + 2,8) = 35,94 : 6 = 5,99
(55,08 : 1,8 − 4,056 : 0,52) * 6,5 − 93,78 = (30,6 − 7,8) * 6,5 − 93,78 = 22,8 * 6,5 − 93,78 = 148,2 − 93,78 = 54,42
Задание № 1000
Найдите корень уравнения:
1) (1,8 + x) * 21 = 71,4;
2) 16(4x − 3,4) = 6,08;
3) (x − 1,25) * 4,5 = 27;
4) (x + 19,64) * 0,18 = 144;
5) 17(1,6 − 5x) = 2,38;
6) 9,66 : (x + 0,17) = 23;
7) 5,6 : (x − 6) = 8;

9) 34,12 − x : 3,08 = 34,03;
10) x : 100 − 1,2367 = 2,9633;
11) 9,2(0,01y + 0,412) = 4,6;
12) 8,8(0,12y − 0,04) = 0,44.
Решение
(1,8 + x) * 21 = 71,4
1,8 + x = 71,4 : 21
1,8 + x = 3,4
x = 3,4 − 1,8
x = 1,616(4x − 3,4) = 6,08
4x − 3,4 = 6,08 : 16
4x = 0,38 + 3,4
x = 3,78 : 4
x = 0,945(x − 1,25) * 4,5 = 27
x − 1,25 = 27 : 4,5
x = 6 + 1,25
x = 7,25(x + 19,64) * 0,18 = 144
x + 19,64 = 144 : 0,18
x = 800 − 19,64
x = 780,3617(1,6 − 5x) = 2,38
1,6 − 5x = 2,38 : 17
1,6 − 5x = 0,14
5x = 1,6 − 0,14
x = 1,46 : 5
x = 0,2929,66 : (x + 0,17) = 23
x + 0,17 = 9,66 : 23
x = 0,42 − 0,17
x = 0,255,6 : (x − 6) = 8
x − 6 = 5,6 : 8
x = 0,7 + 6
x = 6,75,6 : x − 6 = 8
5,6 : x = 8 + 6
x = 5,6 : 14
x = 0,434,12 − x : 3,08 = 34,03
x : 3,08 = 34,12 − 34,03
x = 3,08 * 0,09
x = 0,2772x : 100 − 1,2367 = 2,9633
x : 100 = 2,9633 + 1,2367
x = 4,2 * 100
x = 4209,2(0,01y + 0,412) = 4,6
0,01y + 0,412 = 4,6 : 9,2
0,01y = 0,5 − 0,412
y = 0,088 : 0,01
y = 8,88,8(0,12y − 0,04) = 0,44
0,12y − 0,04 = 0,44 : 8,8
0,12y = 0,05 + 0,04
0,12y = 0,09
y = 0,09 : 0,12
y = 0,75
Задание № 1001
Решите уравнение:
1) 8(x − 1,4) = 0,56;
2) (4,6 − x) * 19 = 4,18;
3) (51,32 + x) * 0,12 = 72;
4) 17,28 : (56 − x) = 36.
Решение
8(x − 1,4) = 0,56
x − 1,4 = 0,56 : 8
x = 0,07 + 1,4
x = 1,47(4,6 − x) * 19 = 4,18
4,6 − x = 4,18 : 19
x = 4,6 − 0,22
x = 4,38(51,32 + x) * 0,12 = 72
51,32 + x = 72 : 0,12
x = 600 − 51,32
x = 548,6817,28 : (56 − x) = 36
56 − x = 17,28 : 36
x = 56 − 0,48
x = 55,52
Задание № 1002
Найдите корень уравнения:
1) 9b + 6b − 0,15 = 6,15;
2) 17x − x + 5x − 1,9 = 17;
3) 1,7x + 88,42 = 94,2;
4) 16,4 − 5,4x = 14,78;
5) 10,2x − 7,4x + 0,88 = 2;
6) 0,6y + 0,18y − 2,376 = 5,58.
Решение
9b + 6b − 0,15 = 6,15
15b = 6,15 + 0,15
b = 6,3 : 15
b = 0,4217x − x + 5x − 1,9 = 17
21x = 17 + 1,9
x = 18,9 : 21
x = 0,91,7x + 88,42 = 94,2
1,7x = 94,2 − 88,42
x = 5,78 : 1,7
x = 3,416,4 − 5,4x = 14,78
5,4x = 16,4 − 14,78
x = 1,62 : 5,4
x = 0,310,2x − 7,4x + 0,88 = 2
2,8x = 2 − 0,88
x = 1,12 : 2,8
x = 0,40,6y + 0,18y − 2,376 = 5,58
0,78y = 5,58 + 2,376
y = 7,956 : 0,78
y = 10,2
Задание № 1003
Решите уравнение:
1) 14,63x + 3,37x − 0,48 = 2,4;
2) 16a − 7a + 0,96 = 2,22;
3) 9,3 − 0,14x = 8,95;
4) 8,6x − 6,9x + 0,49 = 1.
Решение
14,63x + 3,37x − 0,48 = 2,4
18x = 2,4 + 0,48
x = 2,88 : 18
x = 0,1616a − 7a + 0,96 = 2,22
9a = 2,22 − 0,96
a = 1,26 : 9
a = 0,149,3 − 0,14x = 8,95
0,14x = 9,3 − 8,95
x = 0,35 : 0,14
x = 2,58,6x − 6,9x + 0,49 = 1
1,7x = 1 − 0,49
x = 0,51 : 1,7
x = 0,3
Задание № 1004
Расстояние между двумя островами равно 556,5 км. От этих островов навстречу друг другу одновременно отправились два корабля, которые встретились через 7 ч после отплытия. Один из кораблей шел со скоростью 36,8 км/ч. С какой скоростью двигался второй корабль?
Решение задачи
1) 556,5 : 7 = 79,5 (км/ч) — скорость сближения двух кораблей.
_556,5 |7
49 |79,5
_66
63
_35
35
02) 79,5 − 36,8 = 42,7 (км/ч) — скорость второго корабля.
−79.5
36.8
42.7Ответ: 42,7 км/ч.
Задание № 1005
Из своих жилищ навстречу друг другу одновременно вышли Братец Еж и Братец Кролик и встретились через 12 мин после начала движения. С какой скоростью двигался Братец Еж, если расстояние между их жилищами равно 136,8 м, а Братец Кролик шел со скоростью 9,6 м/мин?
Решение задачи
1) 136,8 : 12 = 11,4 (м/мин) — скорость сближения Братца Ежа и Братца Кролика.
_136,8 |12
12 | 11,4
_16
12
_48
48
02) 11,4 − 9,6 = 1,8 (м/мин) — скорость Братца Ежа.
−11.4
9.6
1.8Ответ: 1,8 м/мин.
Задание № 1006
От двух станций, расстояние между которыми равно 20,8 км, в одном направлении одновременно отправились два поезда. Впереди шел поезд со скоростью 54,6 км/ч. Через 5 ч после начала движения его догнал второй поезд. Найдите скорость второго поезда.
Решение задачи
1) 54,6 * 5 = 273 (км) — прошел первый поезд за 5 часов.
×54.6
5
273.02) 273 + 20,8 = 293,8 (км) — прошел второй поезд до встречи.
+273
20.8
293.83) 293,8 : 5 = 58,76 (км/ч) — скорость второго поезда.
_293,8 |5
25 |58,76
_43
40
_38
35
_30
30
0Ответ: 58,76 км/ч.
Задание № 1007
Расстояние между селами равно 12,2 км. Из этих сел в одном направлении одновременно выехали два всадника. Один всадник скакал со скоростью 10,2 км/ч и догнал второго через 2 ч после начала движения. Найдите скорость второго всадника.
Решение задачи
1) 10,2 * 2 = 20,4 (км) — проехал первый всадник за 2 часа.
2) 20,4 − 12,2 = 8,2 (км) — проехал до встречи второй всадник.
3) 8,2 : 2 = 4,1 (км/ч) — скорость второго всадника.
Ответ: 4,1 км/ч.
245
Ответы к странице 245
Задание № 1008
Из села Уютное со скоростью 9,4 км/ч выехал велосипедист. Когда он отъехал от Уютного на 1,26 км, следом выехал второй велосипедист со скоростью 11,2 км/ч. За какое время второй велосипедист догонит первого?
Решение
1) 11,2 − 9,4 = 1,8 (км/ч) скорость сближения велосипедистов.
2) 1,26 : 1,8 = 0,7 (ч) или
7 * 60 : 10 = 42 (мин) потребуется второму велосипедисту, чтобы догнать первого.
_12,6 |18
126 |0,7
0Ответ: 42 минуты.
Задание № 1009
Мыши увидели кота Леопольда на расстоянии 30,4 м и бросились в погоню. Через сколько минут мыши догонят кота, если Леопольд убегает со скоростью 298,8 м/мин, а мыши догоняют его со скоростью 302 м/мин?
Решение
1) 302 − 298,8 = 3,2 (м/мин) — скорость сближения кота Леопольда и мышей.
2) 30,4 : 3,2 = 9,5 (мин) или 9 мин 30 секунд потребуется мышам, чтобы догнать кота Леопольда.
_304 |32
288 |9,5
_160
160
0Ответ: через 9 мин 30 секунд.
Задание № 1010
Моторная лодка проплыла 28,64 км по течению реки и 52,16 км против течения. Сколько времени плыла лодка, если ее собственная скорость равна 34,2 км/ч, а скорость течения − 1,6 км/ч?
Решение
1) 34,2 + 1,6 = 35,8 (км/ч) — скорость лодки по течению.
2) 28,64 : 35,8 = 0,8 (ч) — плыла лодка по течению.
_286,4 |358
2864 |0,8
03) 34,2 − 1,6 = 32,6 (км/ч) — скорость лодки против течения.
4) 52,16 : 32,6 = 1,6 (ч) — плыла лодка против течения.
_521,6 |326
326 |1,6
_1956
1956
05) 0,8 + 1,6 = 2,4 (ч) — время лодки в пути.
Ответ: 2,4 часа.
Задание № 1011
Катер прошел 54,9 км по течению реки и 60,49 км против течения. На сколько минут дольше шел катер против течения, чем по течению, если скорость катера в стоячей воде равна 28,4 км/ч, а скорость течения − 2,1 км/ч?
Решение
1) 28,4 + 2,1 = 30,5 (км/ч) — скорость катера по течению.
2) 28,4 − 2,1 = 26,3 (км/ч) — скорость катера против течения.
3) 54,9 : 30,5 = 1,8 (ч) — шел катер по течению.
_549 |305
305 |1,8
_2440
2440
04) 60,49 : 26,3 = 2,3 (ч) — шел катер против течения.
_604,9 |263
526 |2,3
_789
789
05) 2,3 − 1,8 = 0,5 (ч) — на столько дольше шел катер против течения, чем по течению.
0,5 ч = 30 минОтвет: на 30 минут.
Задание № 1012
На три участка поля площадью 8,4 га, 6,8 га и 5,2 га было завезено удобрение: на первый − навоз, на второй − торф, а на третий − смесь навоза и торфа (в одинаковом количестве на 1 га). Урожай ржи с этих участков соответственно составил: 63 ц, 61,2 ц и 57,2 ц. Какой удобрение лучше влияет на урожайность ржи?
Решение
1) 63 : 8,4 = 7,5 (ц/га) — урожайность после внесения навоза.
_630 |84
588 |7,5
_420
420
02) 61,2 : 6,8 = 9 (ц/га) — урожайность после внесения торфа.
_612 |68
612 |9
03) 57,2 : 5,2 = 11 (ц/га) урожайность после внесения смеси навоза и торфа.
_572 |52
52 |11
_52
52
011 > 9 > 7,5, значит смесь навоза и торфа лучше влияет на урожайность.
Ответ: смесь навоза и торфа.
!Задание № 1013
На двух участках площадью по 5,4 га каждый вырастили 30,24 ц льна и 49,68 ц ячменя, не внося удобрений. На двух других участках площадью по 7,5 га каждый вырастили 39,75 ц льна и 170,25 ц ячменя, но уже с использованием удобрений. Сравните урожайность льна и ячменя, выращенных с удобрениями и без них.
Решение
1) 30,24 : 5,4 = 5,6 (ц/га) — урожайность льна до внесения удобрений.
2) 49,68 : 5,4 = 9,2 (ц/га) — урожайность ячменя до внесения удобрений.
3) 39,75 : 7,5 = 5,3 (ц/га) — урожайность льна с удобрениями.
4) 170,25 : 7,5 = 22,7 (ц/га) — урожайность ячменя с удобрениями.
5) 5,6 − 5,3 = 0,3 (ц/га) — снижение урожайности льна снизилась после внесения удобрения.
6) 22,7 − 9,2 = 13,5 (ц/га) — увеличение урожайности ячменя после внесения удобрений.
Ответ: после внесения удобрений урожайность льна снизилась на 0,3 ц/га, а урожайность ячменя увеличилась на 13,5 ц/га.
246
Ответы к странице 246
Задание № 1014
Площадь прямоугольника равна площади квадрата со стороной 2,1 см. Одна из сторон прямоугольника равна 0,9 см. Вычислите периметр прямоугольника.
Решение
1) 2,1 * 2,1 = 4,41 (см2) — площадь квадрата.
2) 4,41 : 0,9 = 4,9 (см) — вторая сторона прямоугольника.
3) 2 * (0,9 + 4,9) = 2 * 5,8 = 11,6 (см) — периметр прямоугольника.
Ответ: 11,6 см.
Задание № 1015
Площадь прямоугольника равна 5,76 м2, а одна из его сторон − 3,6 м. Вычислите периметр прямоугольника.
Решение задачи
1) 5,76 : 3,6 = 1,6 (м) — длина второй стороны прямоугольника.
2) 2 * (3,6 + 1,6) = 2 * 5,2 = 10,4 (см) — периметр прямоугольника.
Ответ: 10,4 см.
Задание № 1016
Пользуясь формулой объема прямоугольного параллелепипеда V = Sh, вычислите:
1) площадь S основания, если V = 9,12 см3, h = 0,6 см;
2) высоту h, если V = 76,65 см3, S = 10,5 см2.
Решение
V = Sh
S = V : h = 9,12 : 0,6 = 15,2 (см2)V = Sh
h = V : S = 76,65 : 10,5 = 7,3 (см)
Задание № 1017
Первый насос перекачивает 18,56 м3 воды за 3,2 ч, а второй − 22,32 м3 воды за 3,6 ч. У какого из насосов скорость перекачивания воды больше и на сколько кубических метров?
Решение задачи
1) 18,56 : 3,2 = 5,8 (м3/ч) — скорость перекачивания воды первого насоса.
2) 22,32 : 3,6 = 6,2 (м3/ч) — скорость перекачивания воды второго насоса.
3) 6,2 − 5,8 = 0,4 (м3/ч) — на столько больше скорость перекачивания воды второго насоса, чем скорость перекачивания воды первого насоса.
Ответ: скорость второго больше на 0,4 м3/ч.
Задание № 1018
Кролики Серенький и Беленький собирали капусту. Серенький собрал 65,34 кг за 5,4 ч, а Беленький − 76,32 кг за 7,2 ч. У кого из кроликов производительность труда (количество собранной капусты за 1 ч) выше и на сколько килограммов?
Решение задачи
1) 65,34 : 5,4 = 12,1 (кг/ч) — производительность труда Серенького.
2) 76,32 : 7,2 = 10,6 (кг/ч) — производительность труда Беленького.
3) 12,1 − 10,6 = 1,5 (кг/ч) — на столько производительность труда Серенького выше производительности труда Беленького.
Ответ: производительность труда Серенького на 1,5 кг/ч выше производительности труда Беленького.
Задание № 1019
За несколько месяцев школьная библиотека потратила 4936 р. на покупку книг. За первый месяц было потрачено 0,4 этой суммы, а за второй − 0,35 оставшейся суммы. Сколько денег было потрачено за второй месяц?
Решение задачи
1) 4936 * 0,4 = 1974,4 (р.) — было потрачено в первый месяц.
2) 4936 − 1974,4 = 2961,6 (р.) — осталось после первого месяца.
3) 2961,6 * 0,35 = 1036,56 (р.) — потратили во второй месяц.
Ответ: 1036,56 рубля.
Задание № 1020
Было отремонтировано 456,8 км дороги. За первую неделю отремонтировали 0,15 дороги, а за вторую − 0,3 остатка. Сколько километров дороги отремонтировали за вторую неделю работы?
Решение задачи
1) 456,8 * 0,15 = 68,52 (км) — дороги отремонтировали за первую неделю.
2) 456,8 − 68,52 = 388,28 (км) — дороги осталось отремонтировать после первой недели.
3) 388,28 * 0,3 = 116,484 (км) — дороги отремонтировали за вторую неделю.
Ответ: 116,484 км.
Задание № 1021
Одно из слагаемых равно 2,88, что составляет 0,36 суммы. Найдите второе слагаемое.
Решение задачи
1) 2,88 : 0,36 = 8 — сумма.
2) 8 − 2,88 = 5,12 — второе слагаемое.
Ответ: 5,12.
Задание № 1022
Найдите разность двух чисел, если вычитаемое равно 65,8 и оно составляет 0,28 уменьшаемого.
Решение задачи
1) 65,8 : 0,28 = 235 — уменьшаемое.
2) 235 − 65,8 = 169,2 — разность.
Ответ: 169,2.
Задание № 1023
Найдите число, 0,85 которого равно 0,68 от числа 50.
Решение
1) 0,68 : 0,85 = 0,8
2) 50 * 0,8 = 40
Ответ: 40.
Задание № 1024
Найдите 0,128 числа, 0,32 которого равны 80.
Решение
1) 80 : 0,32 = 250
2) 250 * 0,128 = 32
Ответ: 32.
Задание № 1025 с ответом
Вместо звездочек поставьте цифры так, чтобы деление было выполнено верно:
Задание № 1026
Когда мальчик прочитал 0,35 книги, а потом еще 0,1 книги, то оказалось, что он прочитал на 15 страниц меньше половины книги. Сколько страниц в книге?
Решение задачи через х
Пусть x страниц в книге, тогда:
0,35x + 0,1x = 0,45x (с.) — прочитал мальчик.
0,5x (с.) — половина книги.
Так как мальчик прочитал на 15 страниц меньше половину книги, то:
0,5x − 0,45x = 15
0,05x = 15
x = 15 : 0,05
x = 300 (с.) — в книге
Ответ: 300 страниц.
247
Ответы к странице 247
Задание № 1027
Если в некоторой десятичной дроби перенести запятую вправо через одну цифру, то она увеличится на 62,01. Найдите эту дробь.
Решение задачи через х
Пусть x искомая дробь, тогда:
10x дробь, после переноса запятой в право на 2 знака.
Так как дробь увеличилась на 62,01, то:
10x − x = 62,01
9x = 62,01
x = 62,01 : 9
x = 6,89 искомая дробь.
Ответ: 6,89.
Задание № 1028
Моторная лодка за 3,5 ч проплыла 43,4 км по течению реки и за 4,5 ч проплыла 39,6 км против течения. Найдите собственную скорость лодки и скорость течения.
Решение задачи
1) 43,4 : 3,5 = 12,4 (км/ч) — скорость лодки по течению.
2) 39,6 : 4,5 = 8,8 (км/ч) — скорость лодки против течения.
3) (12,4 − 8,8) : 2 = 3,6 : 2 = 1,8 (км/ч) — скорость течения.
4) 12,4 − 1,8 = 10,6 (км/ч) — собственная скорость лодки.
Ответ: 10,6 км/ч; 1,8 км/ч.
Задание № 1029
Луч OC делит развернутый угол AOB на два угла так, что угол AOC на 50° больше угла BOC. Найдите градусные меры углов AOC и BOC.
Решение
∠AOB − развернутый, значит ∠AOB = 180°.
Пусть ∠BOC = x°, тогда:
∠AOC = (x + 50)°.
Составим уравнение:
x + x + 50 = 180
2x = 180 − 50
x = 130 : 2
x = 65° следовательно ∠BOC = 65°.
∠AOC = x + 50 = 65 + 50 = 115°.
Ответ: ∠AOC = 115°; ∠BOC = 65°.
Задание № 1030
Луч OC делит прямой угол AOB на два угла так, что угол AOC в 4 раза меньше угла BOC. Найдите градусные меры углов AOC и BOC.
Решение
∠AOB прямой, следовательно ∠AOB = 90°.
Пусть ∠AOC = x°, тогда:
∠BOC = 4x°.
Составим уравнение:
4x + x = 90
5x = 90
x = 90 : 5
x = 18° следовательно ∠AOC = 18°.
∠BOC = 4 * 18 = 72°.
Ответ: ∠AOC = 18°; ∠BOC = 72°.
Задание № 1031
Составьте выражение для вычисления площади закрашенной фигуры, изображенной на рисунке 211.
а) S = ab − cd
б) S = b(d + a) − ac
Задание № 1032
Семь карандашей стоят дороже восьми тетрадей. Что дороже: восемь карандашей или девять тетрадей?
Решение задачи
7 карандашей дороже 8 тетрадей
7 + 1 карандашей дороже 8 + 1 тетрадей, следовательно:
8 карандашей дороже 9 тетрадей.
Ответ: 8 карандашей дороже 9 тетрадей.
249-250
Ответы к странице 249-250
Параграф 36. Среднее арифметическое
Задание № 1033
Найдите среднее арифметическое чисел:
1) 10,3 и 9,1;
2) 2,8; 16,9 и 22.
Решение
(10,3 + 9,1) : 2 = 19,4 : 2 = 9,7
(2,8 + 16,9 + 22) : 3 = 41,7 : 3 = 13,9
Задание № 1034
Найдите среднее арифметическое чисел:
1) 4,2 и 2,1;
2) 3,9; 6; 9,18 и 15,8.
Решение
(4,2 + 2,1) : 2 = 6,3 : 2 = 3,15
(3,9 + 6 + 9,18 + 15,8) : 4 = 34,88 : 4 = 8,72
Задание № 1035
В течении недели в 8 ч утра Саша измерял температуру воздуха. Он получил такие результаты: 20°С; 18°С; 16°С; 15°С; 14°С; 17°С; 19°С. Найдите среднее значение проведенных измерений.
Решение задачи
(20 + 18 + 16 + 15 + 14 + 17 + 19) : 7 = 119 : 7 = 17
Ответ: 17°С.
Задание № 1036
Найдите среднюю оценку учеников вашего класса по математике за II четверть. Ответ округлите до единиц.
Решение
Нужно сложить оценки по математике за II четверть всех учеников вашего класса и полученную сумму поделить на количество учеников в вашем классом.
Задание № 1037
1) Поезд ехал со скоростью 4 ч со скоростью 64 км/ч и 5 ч со скоростью 53,2 км/ч. Найдите среднюю скорость поезда на протяжении всего пути.
Решение задачи
1) 64 * 4 = 256 (км) — проехал поезд за первые 4 часа пути.
2) 53,2 * 5 = 266 (км) — проехал поезд за вторые 5 часов пути.
3) ) 256 + 266 = 522 (км) — длина всего пути.
4) 4 + 5 = 9 (ч) — поезд был в пути.
5) 522 : 9 = 58 (км/ч) — средняя скорость поезда на протяжении всего пути.
Ответ: 58 км/ч.
2) В автомастерской работает 10 человек. У двоих из них месячная зарплата составляет 22800 р., у четверых — 28000 р., у троих 31000 р., а у одного 32000 р. Какова средняя зарплата работников мастерской?
1) 2*22800 + 4*28000 + 3*31000 + 32000 = 282600 (р.) — получают все работники
2) 282600 : 10 = 28260 (р.) — средняя зарплата работников мастерской
Ответ: 28260 р.
Задание № 1038
1) Автомобиль ехал 3 ч со скоростью 56,4 км/ч и 4 ч со скоростью 62,7 км/ч. Найдите среднюю скорость автомобиля на всем пути.
Решение задачи
1) 56,4 * 3 = 169,2 (км) — проехал автомобиль за первые 3 часа пути.
2) 62,7 * 4 = 250,8 (км) — проехал автомобиль за вторые 4 часа пути.
3) 169,2 + 250,8 = 420 (км) — длина всего пути.
4) 3 + 4 = 7 (ч) — ехал автомобиль весь путь.
5) 420 : 7 = 60 (км/ч) — средняя скорость автомобиля на всем пути.
Ответ: 60 км/ч.
2) Фермер собрал с каждого гектара поля площадью 30 га по 30,2 ц пшеницы, а с каждого гектара поля площадью 20 га — по 32, 3 ц пшеницы. Какой средний урожай с одного гектара собрал фермер.
1) 30,2 * 30 = 906 (ц) — пшеницы собрал фермер с первого поля
2) 32,3 * 20 = 646 (ц) — пшеницы собрал фермер со второго поля
3) 906 + 646 = 1552 (ц) — пшеницы собрал фермер с обеих полей
4) 30 + 20 = 50 (га) — площадь двух полей
5) 1552 : 50 = 31,04 (ц) — средний урожай с одного гектара
Ответ: 31,04 ц пшеницы.
Задание № 1039
Среднее арифметическое чисел 7,8 и x равно 7,2. Найдите число x.
Решение
(7,8 + x) : 2 = 7,2
7,8 + x = 7,2 * 2
x = 14,4 − 7,8
x = 6,6
Ответ: 6,6
Задание № 1040
Среднее арифметическое чисел 6,4 и y равно 8,5. Найдите число y.
Решение
(6,4 + y) : 2 = 8,5
6,4 + y = 8,5 * 2
y = 17 − 6,4
y = 10,6
Ответ: 10,6
Задание № 1041
Среднее арифметическое двух чисел, одно из которых в 4 раза меньше второго, равно 10. Найдите эти числа.
Решение задачи через х
Пусть x − одно число, тогда:
4x − второе число.
Составим уравнение:
(x + 4x) : 2 = 10
5x = 10 * 2
x = 20 : 5
x = 4 − одно число;
4x = 4 * 4 = 16 − второе число.
Ответ: 4 и 16.
Задание № 1042
Среднее арифметическое двух чисел, одно из которых на 4,6 больше второго, равно 8,2. Найдите эти числа.
Решение
Пусть x − второе число, тогда:
x + 4,6 − первое число.
Составим уравнение:
(x + x + 4,6) : 2 = 8,2
2x + 4,6 = 8,2 * 2
2x = 16,4 − 4,6
x = 11,8 : 2
x = 5,9 − второе число;
x + 4,6 = 5,9 + 4,6 = 10,5 − первое число.
Ответ: 5,9 и 10,5.
Задание № 1043
Отметьте на координатном луче числа а и b и их среднее арифметическое, если: 1) а = 2, b = 6; 2) а = 4, b = 7. Как расположена точка, соответствующая среднему арифметическому чисел а и b, относительно точек, соответствующих числам а и b?
Решение
а b
.____.____.____.__
0 2 4 6
Точка расположена точно посередине отрезка ab на одинаковом расстоянии от этих точек.
Задание № 1044
Принимая участие в математической олимпиаде, Дима решил 10 задач. За каждую задачу он мог получить не более 12 баллов. За первые восемь задач мальчик получил среднюю оценку 7 баллов. Сколько баллов получил Дима за каждую из оставшихся двух задач, если среднее количество баллов за одну задачу составляло 8 баллов?
Решение задачи
1) 7 * 8 = 56 (б.) — набрал Дима за первые восемь задач.
2) 8 * 10 = 80 (б.) — набрал Дима за все 10 задач.
3) 80 − 56 = 24 (б.) — набрал Дима за последние две задачи.
4) 24 : 2 = 12 (б.) — набрал Дима за каждую из оставшихся двух задач.
Ответ: по 12 баллов.
Задание № 1045
Автомобиль ехал 3,4 ч по шоссе со скоростью 90 км/ч и 1,6 ч по грунтовой дороге. С какой скоростью ехал автомобиль по грунтовой дороге, если средняя скорость на протяжении всего пути составляла 75,6 км/ч?
Решение задачи
1) 90 * 3,4 = 306 (км) — проехал автомобиль по шоссе.
2) 3,4 + 1,6 = 5 (ч) — общее время в пути.
3) 75,6 * 5 = 378 (км) — длина всего пути.
4) 378 − 306 = 72 (км) — проехал автомобиль по грунтовой дороге.
5) 72 : 1,6 = 45 (км/ч) — скорость автомобиля по грунтовой дороге.
Ответ: 45 км/ч.
Задание № 1046?
Купили 2 кг конфет одного вида по 255 р. за килограмм, 4 кг конфет второго вида по 285 р. за килограмм и еще 3 кг конфет третьего вида. Средняя цена купленных конфет составляла 260 р. за килограмм. Сколько стоил килограмм конфет третьего вида?
Решение задачи
1) 255 * 2 = 510 (р.) — потратили на конфеты первого вида.
2) 285 * 4 = 1140 (р.) — потратили на конфеты второго вида.
3) 510 + 1140 = 1650 (р.) — потратили за конфеты первых двух видов.
4) 2 + 4 + 3 = 9 (кг) — конфет купили всего.
5) 260 * 9 = 2340 (р.) — потратили на конфеты всего.
6) 2340 − 1650 = 690 (р.) — потратили на конфеты третьего вида.
7) 690 : 3 = 230 (р.) — стоил килограмм конфет третьего вида.
Ответ: 230 рублей.
Задание № 1047
Среднее арифметическое четырех чисел равно 2,1, а среднее арифметическое трех других чисел − 2,8. Найдите среднее арифметическое этих семи чисел.
Решение задачи
1) 2,1 * 4 = 8,4 — сумма четырех чисел.
2) 2,8 * 3 = 8,4 — сумма трех чисел.
3) 8,4 + 8,4 = 16,8 — сумма всех семи чисел.
4) 16,8 : 7 = 2,4 — среднее арифметическое этих семи чисел.
Ответ: 2,4.
251-252
Ответы к странице 251-252
Задание № 1048
Среднее арифметическое семи чисел равно 10,2, а среднее арифметическое трех других чисел − 6,8. Найдите среднее арифметическое этих десяти чисел.
Решение задачи
1) 10,2 * 7 = 71,4 — сумма семи чисел.
2) 6,8 * 3 = 20,4 — сумма трех чисел.
3) 71,4 + 20,4 = 91,8 — сумма всех десяти чисел.
4) 91,8 : 10 = 9,18 — среднее арифметическое этих десяти чисел.
Ответ: 9,18.
Задание № 1049
Средний возраст одиннадцати футболистов команды равен 22 годам. Во время игры одного из футболистов удалили с поля, после чего средний возраст оставшихся игроков составил 21 год. Сколько лет было футболисту, который покинул поле?
Решение задачи
1) 11 * 22 = 242 (г.) — суммарный возраст одиннадцати футболистов.
2) 11 − 1 = 10 (иг.) — осталось на поле.
3) 10 * 21 = 210 (лет) — суммарный возраст десяти футболистов.
4) 242 − 210 = 32 (г.) — было футболисту, который покинул поле.
Ответ: 32 года.
Задание № 1050
На сколько среднее арифметическое всех четных чисел от 1 до 1000 включительно больше, чем среднее арифметическое всех нечетных чисел от 1 до 1000 включительно?
Решение
Всего чисел от 1 до 1000 равно 1000, из них:
500 − четных чисел;
500 − нечетных чисел.
Разобьем четные числа попарно:
2 и 1000; 4 и 998 и т.д.
Найдем среднее арифметическое пары:
(2 + 1000) : 2 = 1002 : 2 = 501;
(4 + 998) : 2 = 1002 : 2 = 501.
Так сумма каждой пары четных чисел равна 1002, то и среднее арифметическое каждой пары чисел будет равно 501, следовательно среднее арифметическое всех четных чисел равно 501.
Разобьем нечетные числа попарно:
1 и 999; 3 и 997 и т.д.
Найдем среднее арифметическое пары:
(1 + 999) : 2 = 1000 : 2 = 500;
(3 + 997) : 2 = 1000 : 2 = 500.
Так сумма каждой пары нечетных чисел равна 1000, то и среднее арифметическое каждой пары чисел будет равно 500, следовательно среднее арифметическое всех нечетных чисел равно 500.
501 − 500 = 1, значит среднее арифметическое всех четных чисел от 1 до 1000 включительно на 1 больше, чем среднее арифметическое всех нечетных чисел от 1 до 1000 включительно.
Ответ: на 1.
Задание № 1051
Семь гномов собрались вечером вокруг костра. Оказалось, что рост каждого гнома равен среднему арифметическому роста двух его соседей. Докажите, что все гномы были одного роста.
Решение
Допустим, что не все гномы были одного роста. Тогда самый высокий гном не может быть выше ни одного из двух своих соседей, так как тогда его рост не будет равен среднему арифметическому двух его соседей. Следовательно все гномы были одного роста.
Задание № 1052
Найдите числа, которых не хватает в цепочке вычислений:
1) 9,88 : a = 3,8
a = 9,88 : 3,8
a = 2,6;
3,8 − b = 1,74
b = 3,8 − 1,74
b = 2,06;
1,74 * c = 6,09
c = 6,09 : 1,74
c = 3,5.
Ответ: a = 2,6; b = 2,06; c = 3,5.2) 6,2 * x = 17,36
x = 17,36 : 6,2
x = 2,8;
17,36 + y = 20,1
y = 20,1 − 17,36
y = 2,74;
20,1 : z = 1,5
z = 20,1 : 1,5
z = 13,4.
Ответ: x = 2,8; y = 2,74; z = 13,4.
Задание № 1053
1) Периметр прямоугольника равен 36,8 см, а одна из его сторон − 13,8 см. Вычислите площадь прямоугольника.
Решение
1) 36,8 : 2 = 18,4 (см) — сумма длин двух соседних сторон прямоугольника.
2) 18,4 − 13,8 = 4,6 (см) — длина второй стороны прямоугольника.
3) 13,8 * 4,6 = 63,48 (см2) — площадь прямоугольника.
Ответ: 63,48 см2.
2) Ширина прямоугольного параллелепипеда равна 7,2 см, что составляет 0,8 его длины и 0,18 его высоты. Вычислите объем параллелепипеда.
Решение
1) 7,2 : 0,8 = 9 (см) — длина прямоугольного параллелепипеда.
2) 7,2 : 0,18 = 40 (см) — высота параллелепипеда.
3) 7,2 * 9 * 40 = 7,2 * 360 = 2592 (см3) — объем параллелепипеда.
Ответ: 2592 см3.
Задание № 1054
В 25 банок разлили поровну 32 кг меда. Сколько меда налили в каждую банку? Ответ округлите до десятых.
Решение
32 : 25 = 1,28 ≈ 1,3 кг меда разлили в каждую банку.
_32 |25
25 |1,28
_70
50
_200
200
0
Ответ: ≈ 1,3 кг.
Задание № 1055
Одновременно на сковороду можно положить двух карасей. Чтобы поджарить одного карася с одной стороны, нужна 1 мин. Можно ли за 3 мин поджарить с двух сторон трех карасей?
Решение
Действие 1:
Положим на сковороду двух карасей и зажарим им за одну минуту одну сторону.
Действие 2:
Убираем одного карася со сковороды, а второго переворачиваем и кладем на сковороду третьего карася, жарим еще одну минуту.
Действие 3:
Убираем со сковороды обжаренного с двух сторон карася, переворачиваем третьего карася и положим на сковороду убранного после первого действия карася, жарим еще одну минут.
После этого получается, что за три минуты у нас все три карася обжарены с двух сторон.
Ответ: можно.
254-255
Ответы к странице 254-255
Параграф 37. Проценты
Задание № 1056
Найдите:
1) 1% от числа 800;
2) 1% от числа 4;
3) 12% от числа 45;
4) 15% от числа 60;
5) 84% от числа 140;
6) 120% от числа 50.
Решение
1) 800 : 100 * 1 = 8 * 1 = 8
2) 4 : 100 * 1 = 0,04 * 1 = 0,04
3) 45 : 100 * 12 = 0,45 * 12 = 5,4
4) 60 : 100 * 15 = 0,6 * 15 = 9
5) 140 : 100 * 84 = 1,4 * 84 = 117,6
6) 50 : 100 * 120 = 0,5 * 120 = 60
Задание № 1057
Найдите:
1) 1% от числа 76;
2) 7% от числа 300;
3) 26% от числа 10;
4) 30% от числа 120;
5) 94% от числа 16,5;
6) 156% от числа 62.
Решение
1) 76 : 100 * 1 = 0,76 * 1 = 0,76
2) 300 : 100 * 7 = 3 * 7 = 21
3) 26 : 100 * 10 = 0,26 * 10 = 2,6
4) 30 : 100 * 120 = 0,3 * 120 = 36
5) 94 : 100 * 16,5 = 0,94 * 16,5 = 15,51
6) 156 : 100 * 62 = 1,56 * 62 = 96,72
Задание № 1058
Суша занимает 29% площади поверхности Земли, а остальную поверхность занимает Мировой океан. Сколько процентов площади поверхности Земли занимает Мировой океан?
Решение задачи
Площадь поверхности Земли равна 100, тогда:
100 − 29 = 71% − занимает Мировой океан.
Ответ: 71%.
Задание № 1059
Жители городов России составляют 73% всего населения России. Сколько процентов населения России составляет сельское население?
Решение
Все население России равно 100%, тогда:
100 − 73 = 27% составляет сельское население.
Ответ: 27%.
Задание № 1060
Сколько процентов площади квадрата, изображенного на рисунке 213, закрашено?
Решение
а)
10 * 10 = 100 (кл.) — общая площадь квадрата.
3 * 4 + 4 * 2 + 2 * 2 = 12 + 8 + 4 = 24 (кл.) — площадь закрашенной части.
24 : 100 * 100% = 24% площади квадрата закрашено.
Ответ: 24%.б)
10 * 10 = 100 (кл.) — общая площадь квадрата.
5 * 10 = 50 (кл.) — площадь закрашенной части.
50 : 100 * 100% = 50% площади квадрата закрашено.
Ответ: 50%.в)
10 * 10 = 100 (кл.) — общая площадь квадрата.
6 * 10 = 60 (кл.) — площадь закрашенной части.
60 : 100 * 100% = 60% площади квадрата закрашено.
Ответ: 60%.г)
10 * 10 = 100 (кл.) — общая площадь квадрата.
2 * 2 + 3 * 8 = 4 + 24 = 28 (кл.) — площадь закрашенной части.
28 : 100 * 100% = 28% площади квадрата закрашено.
Ответ: 28%.
256
Ответы к странице 256
Задание № 1061
Начертите квадрат, сторона которого в 10 раз больше стороны тетрадной клетки. Закрасьте часть квадрата, площадь которой от площади квадрата составляет:
1) 5%;
2) 10%;
3) 20%;
4) 42%;
5) 50%;
6) 67%;
7) 92%;

Ответ
Площадь квадрата составляет 10 * 10 = 100 (кл.), значит 1 клетка равна 1 % от площади квадрата.
Задание № 1062
Запишите в виде десятичной дроби:
1) 1%;
2) 8%;
3) 30%;
4) 140%;
5) 200%;
6) 4,5%.
Решение
1% = 1 : 100 = 0,01
8% = 8 : 100 = 0,08
30% = 30 : 100 = 0,3
140% = 140 : 100 = 1,4
200% = 200 : 100 = 2
4,5% = 4,5 : 100 = 0,045
Задание № 1063
Запишите в виде десятичной дроби:
1) 6%;
2) 14%;
3) 40%;
4) 84%;
5) 160%;
6) 600%.
Решение
6% = 6 : 100 = 0,06
14% = 14 : 100 = 0,14
40% = 40 : 100 = 0,4
84% = 84 : 100 = 0,84
160% = 160 : 100 = 1,6
Задание № 1064
Запишите в процентах:
1) 0,24;
2) 0,04;
3) 0,4;
4) 0,682;
5) 1,6;
6) 8.
Решение
0,24 = 0,24 * 100% = 24%
0,04 = 0,04 * 100% = 4%
0,4 = 0,4 * 100% = 40%
0,682 = 0,682 * 100% = 68,2%
1,6 = 1,6 * 100% = 160%
8 = 8 * 100% = 800%
Задание № 1065
Запишите в процентах:
1) 0,58;
2) 0,8;
3) 0,08;
4) 0,008;
5) 2,5;
6) 10.
Решение
0,58 = 0,58 * 100% = 58%
0,8 = 0,8 * 100% = 80%
0,08 = 0,08 * 100% = 8%
0,008 = 0,008 * 100% = 0,8%
2,5 = 2,5 * 100% = 250%
10 = 10 * 100% = 1000%
Задание № 1066
Запишите в виде обыкновенной дроби:
1) 50%;
2) 25%;
3) 10%;
4) 20%;
5) 80%;
6) 75%.
Решение
50% = 1
10025% = 25
10010% = 10
10020% = 20
10080% = 80
10075% = 75
100
Задание № 1067
Площадь поля равна 420 га. Рожью засеяли 15% поля. Сколько гектаров поля засеяли рожью?
Решение
Существует 3 способа решения задач такого типа. Выбирайте тот, которым учил вас ваш учитель математики (чаще всего это способ №3)
1 способ.
Всё поле примем за 100%
1) 420 : 100 = 4,2 (га) — составляют 1%
2) 4, 2 * 15 = 63 (га) — площадь поля, засеянная рожью.
Ответ: 63 га.х4,2
1 5
21 0
42
63,0
2 способ. Нахождение части от целого. Нужно перевести проценты в обыкновенную дробь.
15% = 15/100, то есть найдем долю 15/100 от 420
420 : 100 * 15 = 63 (га) — площадь поля, засеянная рожью.
Ответ: 63 га.
3 способ. Переводим проценты в десятичную дробь и умножаем на целое.
15% = 0,15
420 * 0,15 = 63 (га) — засеяли рожью.
×420
0.15
210
42
63.00Ответ: 63 га.
Задание № 1068
Участники авторалли должны были преодолеть 565 км. В первый день было пройдено 72% маршрута. Сколько километров было пройдено в первый день?
Решение
72% = 0,72
565 * 0,72 = 406,8 (км) — было пройдено в первый день.
×565
0.72
1130
3955
406.80Ответ: 406,8 км.
Задание № 1069
Сплав содержит 8% меди. Сколько килограммов меди содержится в 360 кг сплава?
Решение
8% = 0,08
360 * 0,08 = 28,8 (кг) меди содержится в 360 кг сплава.
×360
0.08
28.80Ответ: 28,8 кг.
Задание № 1070
В морской воде содержится 6% соли. Сколько соли содержится в 250 кг морской воды?
Решение
6% = 0,06
250 * 0,06 = 15 (кг) соли содержится в 250 кг морской воды
×250
0.06
15.00Ответ: 15 кг.
Задание № 1071
За два дня продали 125 кг яблок, причем в первый день продали 46% яблок. Сколько килограммов яблок продали во второй день?
Решение
46% = 0,46
1) 12,5 * 0,46 = 57,5 (кг) — яблок продали в первый день
2) 125 − 57,5 = 67,5 (кг) — яблок продали во второй день
Ответ: 67,5 кг.
Задание № 1072
Илья Муромец, победив Соловья−разбойника, нашел в его логове 80 пудов золота и серебра. Золото составляло 45% сокровищ. Сколько пудов серебра нашел Илья Муромец?
Решение
Все сокровище составляет 100%, тогда:
1) 100 − 45 = 55 (%) — составляло серебро.
55 % = 0,55
2) 80 * 0,55 = 44 (п.) — серебра нашел Илья Муромец.
Ответ: 44 пуда.
Или другим способом:
45% = 0,45
1) 80 * 0,45 = 36 (п) — составляло золото
2) 80 — 36 = 44 (п.) — серебра нашел Илья Муромец.
Ответ: 44 пуда.
257
Ответы к странице 257
Задание № 1073
Дед Устим собрал со своего огорода 1200 кг овощей. Из них 26% составляли огурцы, 48% − картофель, а остальное − капуста. Сколько килограммов капусты собрал дед Устим?
Решение
Все овощи составляют 100%, тогда:
1) 100 − (26 + 48) = 100 − 74 = 26 (%) — составляла капуста.
26 % = 0,26
2) 1200 * 0,26 = 312 (кг) — капусты собрал дед Устим.
Ответ: 312 кг.
Другой способ решения:
26 % = 0, 26
1200 * 0,26 = 312 (кг) — масса собранных огурцовх 1200
0,26
72
24
312,00 = 3122) 48 % = 0,48
1200 * 0,48 = 576 (кг) — масса картофеля, которую собрал дед Устимх 0,48
1200
96
48
576,00 = 5763) 1200 — (312 + 576) = 1200 — 888 = 312 (кг) — масса собранной капусты
Ответ: 312 кг.
Задание № 1074
В магазин поступило 200 банок варенья. 24% этого количество составляли банки с клубничным вареньем, 32% − с малиновым, а остальное − с вишневым. Сколько банок вишневого варенья поступило в магазин?
Решение
Все банки с вареньем составляют 100%, тогда:
1) 100 − (24 + 32) = 100 − 56 = 44 (%) — составляли банки с вишневым вареньем.
44 % = 0,44
2) 200 * 0,44 = 88 (б.) — вишневого варенья поступило в магазин.
Ответ: 88 банок.
Задание № 1075
В 2007 г. потребление мяса и мясопродуктов в Российской Федерации составляло 60 кг на душу населения. В 2013 г. потребление мяса и мясопродуктов на душу населения составило 125% по отношению к 2007 г. Сколько килограммов составило потребление мяса и мясопродуктов на душу населения в 2013 г.?
Решение
125% = 1,25
60 * 1,25 = 75 (кг) — составило потребление мяса и мясопродуктов на душу населения в 2013 г.
Ответ: 75 кг.
Задание № 1076
В 2005 г. потребление яиц в Российской Федерации составляло 250 штук на душу населения. В 2013 г. потребление яиц на душу населения составило 107,2% по отношению к 2005 г. Каким было потребление яиц на душу населения в 2013 г.?
Решение
107,2% = 1,072
250 * 1,072 = 268 (яиц) составляло потребление яиц на душу населения в 2013 г.
Ответ: 268 яиц.
Задание № 1077
Во время Русско−турецкой войны 1787−1791 гг. состоялось сражение при реке Рымник. 11 сентября 1789 г. объединенное русско−австрийское войско под командованием великого русского полководца А.В. Суворова разбило стотысячную турецкую армию. Численность войск под руководством Суворова составляла 25% численности турецкой армии, а численность русских полков составляла 28% численности русско−австрийского войска. Сколько русских воинов принимало участие в битве при Рымнике?
Решение
25% = 0,25
28% = 0,28
1) 100000 * 0,25 = 25000 (ч.) — численность войск под руководством Суворова
2) 25000 * 0,28 = 7000 (ч.) — численность численность русских полков
Ответ: 7000 человек.
Задание № 1078
В саду росло 1500 деревьев, из них 60% составляли фруктовые деревья. Вишневые деревья составляли 52% фруктовых деревьев. Сколько вишневых деревьев росло в саду?
Решение
60% = 0,6
52% = 0,52
1) 1500 * 0,6 = 900 (д.) — фруктовых.
2) 900 * 0,52 = 468 (д.) — вишневых.
Ответ: 468 вишневых деревьев.
Задание № 1079
Убытки акционерного общества «Лебедь, рак и щука» за три летних месяца составили 246000 р. В июне убытки составили 35% этой суммы, а финансовые потери за июль составили 110% июньских потерь. Сколько рублей составили потери акционерного общества в июле?
Решение
35% = 0,35
110% = 1,1
1) 246000 * 0,35 = 86100 (р.) — составили убытки в июне.
2) 86100 * 1,1 = 94710 (р.) — составили убытки в июле.
Ответ: 94710 рублей.
Задание № 1080
Длина прямоугольника равна 80 см, его ширина составляет 80% длины. Найдите периметр и площадь прямоугольника.
Решение
80% = 0,8
1) 80 * 0,8 = 64 (см) — ширина прямоугольника.
2) 2 * (80 + 64) = 2 * 144 = 288 (см) — периметр прямоугольника.
3) 80 * 64 = 5120 (см2) — площадь прямоугольника.
Ответ: 288 см, 5120 см2.
Задание № 1081
Длина прямоугольного параллелепипеда равна 60 см, его ширина составляет 70% длины, а высоты − 125% длины. Вычислите объем параллелепипеда.
Решение
70% = 0,7
1) 60 * 0,7 = 42 (см) — составляет ширина параллелепипеда.
2) 60 * 1,25 = 75 (см) — составляет высота параллелепипеда.
3) 60 * 75 * 42 = 4500 * 42 = 189000 (см3) — составляет объем параллелепипеда.
Ответ: 189000 см3.
Задание № 1082
Ширина прямоугольника равна 40 см, его длина составляет 135% ширины. Найдите периметр и площадь прямоугольника.
Решение
135% = 1,35
1) 40 * 1,35 = 54 (см) — составляет длина прямоугольника.
2) 2 * (40 + 54) = 2 * 94 = 188 (см) — периметр прямоугольника.
3) 40 * 54 = 2160 (см2) — площадь прямоугольника.
Ответ: 188 см и 2160 см2.
Задание № 1083
Сергей Иванович положил в банк 14000 р. под 10% годовых. Какая сумма будет на его счете через год? Через два года?
Решение
10% = 0,1
1) 14000 * 0,1 = 1400 (р.) — сумма процентов за первый год.
2) 14000 + 1400 = 15400 (р.) — стало на счете через год.
3) 15400 * 0,1 = 1540 (р.) — сумма процентов за второй год.
4) 15400 + 1540 = 16940 (р.) — стало на счете через два года.
Ответ: 15400 рублей, 16940 рублей.
258-259
Ответы к странице 258-259
Задание № 1084
Отправившись в морское путешествие, экипаж яхты взял с собой 2400 л пресной воды. Каждую неделю он тратил 15% того запаса воды, который у него был в начале этой недели. Сколько литров воды осталось через неделю путешествия? Через две недели?
Решение задачи
1) 2400 * 0,15 = 360 (л) — воды потратили за первую неделю.
2) 2400 − 360 = 2040 (л) — воды осталось через неделю.
3) 2040 * 0,15 = 306 (л) — воды потратили за вторую неделю.
4) 2040 − 306 = 1734 (л) — осталось через две недели.
Ответ: 2040 л; 1734 л.
Задание № 1085
За четыре дня яхта прошла 800 км. В первый день было пройдено 30% всего расстояния, во второй день − 5/8 того, что было пройдено в первый день, а в третий день − 128% того, что было пройдено во второй. Сколько километров прошла яхта в четвертый день?
Решение задачи
1) 800 * 0,3 = 240 (км) — прошла яхта в первый день.
2) 240 : 8 * 5 = 30 * 5 = 150 (км) — прошла яхта во второй день.
3) 150 * 1,28 = 192 (км) — прошла яхта в третий день.
4) 800 − (240 + 150 + 192) = 800 − 582 = 218 (км) — прошла яхта в четвертый день.
Ответ: 218 км.
Задание № 1086
Четыре предприятия перевели на счёт краеведческого музея 1 800 000 р. Первое предприятие перечислило 24 % этой суммы, второе — 125 % того, что перечислило первое предприятие, третье — 4/9 того, что перечислило второе предприятие, а остальную сумму — четвёртое предприятие. Сколько рублей перечислило четвёртое предприятие?
Решение задачи
1) 1 800 000 : 100 • 24 = 18 000 • 24 = 432 000 (р) — перечислило 1 предприятие.
2) 432 000 : 100 • 125 = 4 320 • 125 = 540 000 (р) — перечислило 2 предприятие.
3) 540 000 : 9 • 4 = 60 000 • 4 = 240 000 (р) — перечислило 3 предприятие.
4) 432 000 + 540 000 + 240 000 = 1 212 000 (р) — перечислили 1, 2 и 3 предприятие вместе.
5) 1 800 000 — 1 212 000 = 588 000 (р) — перечислило 4 предприятие.
Ответ: 588 000 р.
Задание № 1087
Инна испекла пирожки с повидлом и угостила ими своих друзей. Они съели 24 пирожка, после чего у Инны осталась 1/5 всех пирожков. Сколько всего пирожков испекла девочка?
Решение задачи
Пусть все пирожки равны 1, тогда:
1−1 = 4 (п.) было съедено
5 5
24 : 4 * 5 = 6 * 5 = 30 (п.) — испекла девочка.
Ответ: 30 пирожков.
Задание № 1088
Найдите числа, которых не хватает в цепочке вычислений:
1) m * 0,75 = 15
m = 15 : 0,75
m = 20;
15 − x = 2,56
x = 15 − 2,56
x = 12,44;
2,56 : n = 3,2
n = 2,56 : 3,2
n = 0,8.
Ответ: m = 20; x = 12,44; n = 0,8.2) a * 2,6 = 27,04
a = 27,04 : 2,6
a = 10,4;
27,04 + b = 30
b = 30 − 27,04
b = 2,96;
30 : c = 125
c = 30 : 125
c = 0,24.
Ответ: a = 10,4; b = 2,96; c = 0,24.
Задание № 1089
Иван Трудолюб собрал по 1200 ц кукурузы с одного гектара поля, площадь которого составляла 12,5 га. Для перевозки урожая он арендовал грузовики, каждый из которых перевозил по 2,5 т и сделал по 15 рейсов. Сколько грузовиков арендовал Иван Трудолюб?
Решение задачи
1) 1200 * 12,5 = 15000 ц = 1500 т было собрано кукурузы.
2) 1500 : 2,5 = 600 (р.) — было сделано.
3) 600 : 15 = 40 (г.) — арендовал Иван Трудолюб.
Ответ: 40 грузовиков.
Задание № 1090
Из двух пунктов, расстояние между которыми равно 260 км, навстречу друг другу одновременно выехали два автомобиля. Скорость одного автомобиля равна 70 км/ч, а скорость второго − 60 км/ч. Какое расстояние будет между автомобилями через 2,5 ч после начала движения?
Решение задачи
1) 70 + 60 = 130 (км/ч) — скорость сближения автомобилей.
2) 130 * 2,5 = 325 (км) — суммарное расстояние которое проедут автомобили за 2,5 ч.
3) 325 − 260 = 65 (км) — будет между автомобилями через 2,5 ч после начала движения.
Ответ: 65 км.
Задание № 1091
В 5 классе диктант по русскому языку писали 30 учеников. Петя Ленивцев сделал больше всех ошибок − 14. Покажите, что по крайней мере три ученика сделали одинаковое количество ошибок (в этом классе могли быть ученики, которые не сделали ни одной ошибки).
Решение
Так как Петя сделал больше всего ошибок, то каждый из оставшихся учеников мог сделать от 1 до 13 ошибок.
30 − 1 = 29 (уч.) — кроме Пети учились в классе.
29 : 13 = 2 (ост. 3) то есть по крайней мере три ученика сделали одинаковое количество ошибок.
260
Ответы к странице 260
Параграф 38. Нахождение числа по его процентам
Задание № 1092 с ответами
Заполните таблицу.
1% числа 6 3 4,2 7,68
Данное число 600 300 420 768
Задание № 1093
Найдите число, если:
1) 20% этого числа равны 40;
2) 54% этого числа равны 81;
3) 280% этого числа равны 70;
4) 320% этого числа равны 16.
Решение
1) 40 : 20% = 40 : 0,2 = 200
2) 81 : 54% = 81 : 0,54 = 150
3) 70 : 280% = 70 : 0,28 = 25
4) 16 : 320% = 16 : 0,32 = 5
Задание № 1094
Найдите число, если:
1) 1% этого числа равны 7;
2) 1% этого числа равны 0,36;
3) 12% этого числа равны 4,8;
4) 104% этого числа равны 260.
Решение
1) 7 : 1% = 7 : 0,01 = 700
2) 0,36 : 1% = 0,36 : 0,01 = 36
3) 4,8 : 12% = 4,8 : 0,12 = 40
4) 260 : 104% = 260 : 1,04 = 250
Задание № 1095
За первую неделю турист прошел 32 км, что составляет 40% туристского маршрута. Какова длина всего маршрута?
Решение задачи
32 км составляет 40%
40% = 0,4
32 : 0,4 = 320 : 4 = 80 (км) — длина всего маршрута.
Ответ: 80 км.
261
Ответы к странице 261
Задание № 1096
Михаил купил справочник по математике, потратив на него 45% имевшихся у него денег. Сколько денег было у Михаила, если справочник стоит 36 р.?
Решение задачи
36 р. составляют 45%
45% = 0,45
36 : 0,45 = 3600 : 45 = 80 (р.) — было у Михаила.
Ответ: 80 рублей.
Задание № 1097
Руда содержит 60% железа. Сколько тонн руды надо взять, чтобы получить 72 т железа?
Решение задачи
72 т составляют 60%
60% = 0,6
72 : 0,6 = 720 : 6 = 120 (т.) — руды надо взять, чтобы получить 72 т железа.
Ответ: 120 тонн.
Задание № 1098
Раствор содержит 14% соли. Сколько килограммов раствора надо взять, чтобы получить 49 кг соли?
Решение задачи
49 кг составляют 14%
14% = 0,14
49 : 0,14 = 4900 : 14 = 350 (кг) — раствора надо взять, чтобы получить 49 кг соли.
Ответ: 350 килограммов.
Задание № 1099
Банк выплачивает своим вкладчикам 8% годовых. Сколько денег надо вложить в банк, чтобы через год получить 600 р. прибыли?
Решение задачи
600 р. составляют 8%
8% = 0,08
600 : 0,08 = 60000 : 8 = 7500 (р.) — надо вложить в банк, чтобы через год получить 600 р. прибыли.
Ответ: 7500 рублей.
Задание № 1100
Масса сушеных слив составляет 15% массы свежих. Сколько надо взять свежих слив, чтобы получить 36 кг сушеных?
Решение задачи
36 кг составляют 15%
15% = 0,15
36 : 0,15 = 3600 : 15 = 240 (кг) — надо взять свежих слив, чтобы получить 36 кг сушеных.
Ответ: 240 кг.
Задание № 1101
За неделю бригада отремонтировала 138 м дороги, что составляет 115% плана. Сколько метров дороги планировали отремонтировать за неделю?
Решение задачи
138 м составляют 115%
115% = 1,15
138 : 1,15 = 13800 : 115 = 120 (м) — дороги планировали отремонтировать за неделю.
Ответ: 120 метров.
Задание № 1102
За обедом пончик съел 28,8 кг варенья, что составило 120% того, что он планировал съесть. Сколько варенья планировал съесть Пончик за обедом?
Решение задачи
28,8 кг составляют 120%
120% = 1,2
28,8 : 1,2 = 288 : 12 = 24 (кг) — варенья планировал съесть Пончик за обедом.
Ответ: 24 кг.
Задание № 1103
Во время сушки яблоки теряют 84% своей массы. Сколько килограммов свежих яблок надо взять, чтобы получить 24 кг сушеных?
Решение задачи
Масса свежих яблок составляет 100%, тогда:
1) 100 − 84 = 16 (%) — массы остается в сушеных яблоках.
24 кг составляют 16%
16% = 0,16
2) 24 : 0,16 = 2400 : 16 = 150 (кг) — свежих яблок надо взять, чтобы получить 24 кг сушеных.
Ответ: 150 кг.
Задание № 1104
При тушении мясо теряет 24% своей массы. Сколько килограммов сырого мяса надо взять, чтобы получить 19 кг тушеного?
Решение задачи
Масса сырого мяса составляет 100%, тогда:
1) 100 − 24 = 76 (%) — составляет масса тушеного мяса от сырого.
76 % составляют 19 кг
76 % = 0,76
2) 19 : 0,76 = 1900 : 76 = 25 (кг) — сырого мяса надо взять, чтобы получить 19 кг тушеного.
Ответ: 25 кг.
Задание № 1105
На обед в харчевне «Три пескаря» лиса Алиса и кот Базилио заказали салат «Оливье», жареного поросенка и торт−мороженое. Когда им принесли счет, оказалось, что за салат надо заплатить 28% суммы, за поросенка − 54%, а за торт − остальные 108 сольдо. Сколько сольдо стоил обед Алисы и Базилио?
Решение задачи
Стоимость всего обеда составляет 100%, тогда:
1) 100 − (28 + 54) = 100 − 82 = 18 (%) — составляет стоимость торта.
108 с. составляют 18%
18% = 0,18
2) 108 : 0,18 = 10800 : 18 = 600 (с.) — стоил обед Алисы и Базилио.
Ответ: 600 сольдо.
Задание № 1106
Трое друзей собирали грибы. Первый собрал 37% всех грибов, второй − 25%, а третий − остальные 152 гриба. Сколько всего грибов они собрали?
Решение задачи
Количество всех собранных грибов составляет 100%, тогда:
1) 100 − (37 + 25) = 100 − 62 = 38 (%) — собрал третий.
152 г. составляют 38%
38% = 0,38
2) 152 : 0,38 = 15200 : 38 = 400 (г.) — всего было собрано.
Ответ: 400 грибов.
Задание № 1107
Длина прямоугольного параллелепипеда равна 50 см, а ширина составляет 24% длины. Вычислите объем параллелепипеда, если ширина составляет 30% высоты.
Решение задачи
1) 50 * 0,24 = 12 (см) — ширина параллелепипеда.
2) 12 : 0,3 = 120 : 3 = 40 (см) — высота параллелепипеда.
3) 50 * 40 * 12 = 2000 * 12 = 24000 (см3) = 24 (дм3) — объем параллелепипеда.
Ответ: 24 дм3.
Задание № 1108
В первый день турист прошел 7,2 км, во второй день − 150% того, что в первый. Сколько километров прошел турист за три дня, если во второй день он прошел 90% того, что в третий?
Решение задачи
1) 7,2 * 1,5 = 10,8 (км) — прошел турист во второй день.
2) 10,8 : 0,9 = 108 : 9 = 12 (км) — прошел турист в третий день.
3) 7,2 + 10,8 + 12 = 18 + 12 = 30 (км) — прошел турист за 3 дня.
Ответ: 30 км.
Задание № 1109
В саду росли яблони и вишни, причем яблони составляли 41% всех деревьев. Вишневых деревьев было на 54 больше, чем яблонь. Сколько деревьев росло в саду? Сколько среди них было вишневых деревьев?
Решение задачи
Все деревья составляют 100%, тогда:
1) 100 − 41 = 59 (%) — всех деревьев составляют вишни.
2) 59 − 41 = на 18 (%) — от всех деревьев вишен в саду больше, чем яблонь.
54 д. составляют 18%
18% = 0,18
3) 54 : 0,18 = 300 (д.) — росло в саду всего.
59% = 0,59
4) 300 * 0,59 = 177 (д.) — вишен росло в саду.
Ответ: 300 деревьев всего, из них 177 вишен.
262
Ответы к странице 262
Задание № 1110
За два дня проложили кабель. В первый день проложили 68% кабеля, а во второй − на 115,2 м меньше, чем в первый. Сколько всего метров кабеля проложили за два дня? Сколько метров кабеля проложили в первый день?
Решение задачи
Вся длина проложенного кабеля составляет 100%, тогда:
1) 100 − 68 = 32 (%) — кабеля проложили во второй день.
2) 68 − 32 = на 36 (%) — от длины всего кабеля в первый день проложили больше, чем во второй.
115,2 м составляют 36%
36% = 0,36
3) 115,2 : 0,36 = 11520 : 36 = 320 (м) — длина всего кабеля.
68% = 0,68
4) 320 * 0,68 = 217,6 (м) — кабеля проложили в первый день.
Ответ: 320 м, 217,6 м.
Задание № 1111
В саду растут красные, розовые и белые розы. Красные розы составляют 40% всех роз, розовые − 58% остальных роз, а белых роз растет 126. Сколько всего роз растет в саду?
Решение задачи
Все количество роз составляет 100%, тогда:
1) 100 − 40 = 60 (%) — составляют розовые и белые розы.
2) 60 * 0,58 = 34,8 (%) — составляют розовые розы.
3) 40 + 34,8 = 74,8 (%) — составляют красные и розовые розы.
4) 100 − 74,8 = 25,2 (%) — составляют белые розы.
5) 126 : 0,252 = 126000 : 252 = 500 (роз) — всего растет в саду.
Ответ: 500 роз.
Задание № 1112
В первый день Саша прочитал 25% всей книги, во второй − 68% оставшихся страниц, а в третий − последние 96 страниц. Сколько всего страниц в книге?
Решение задачи
Всего страниц в книге 100%, тогда:
1) 100 − 25 = 75 (%) — страниц всей книги прочитал Саша в второй и третий дни.
2) 75 * 0,38 = 51 (%) — страниц всей книги прочитал Саша во второй день.
3) 75 − 51 = 24 (%) — страниц всей книги прочитал Саша в третий день.
4) 96 : 0,24 = 9600 : 24 = 400 (стр.) — было в книге всего.
Ответ: 400 страниц.
Задание № 1113
Сколько килограммов картофеля продал магазин за три дня, если в первый день продали 32% всего картофеля, во второй − 45% оставшегося, а в третий − 561 кг?
Решение задачи
Весь проданный картофель составляет 100%, тогда:
1) 100 − 32 = 68 (%) — всего картофеля продали во второй и в третий день.
2) 68 * 0,45 = 30,6 (%) — всего картофеля продали во второй день.
3) 68 − 30,6 = 37,4 (%) — всего картофеля продали в третий день.
4) 561 : 0,374 = 561000 : 374 = 1500 (кг) — картофеля продал магазин за три дня.
Ответ: 1500 кг.
Задание № 1114
На новогодний праздник в школу завезли три вида мороженого: шоколадное, клубничное и ванильное. Шоколадное составляло 52 % всего мороженого, клубничное − 25 % шоколадного, а ванильное − остальные 140 кг. Сколько килограммов мороженого завезли в школу?
Решение задачи
Все мороженое составляет 100%, тогда:
1) 100 − 52 = 48 (%) — составляет клубничное и ванильное мороженое.
25% = 0,25
2) 52 * 0,25 = 13 (%) — составляет клубничное мороженое.
3) 48 − 13 = 35 (%) — составляет ванильное мороженое.
140 кг составляют 35%
35% = 0,35
4) 140 : 0,35 = 14000 : 35 = 400 (кг) — мороженого завезли в школу.
Ответ: 400 кг.
Задание № 1115
В саду растут розы, гладиолусы и георгины. Розы составляют 60% всех цветов, гладиолусы − 40% количества роз, а георгинов растет 32. Сколько роз растет в саду?
Решение задачи
Все цветы составляют 100%, тогда:
1) 100% − 60% = 40 (%) — составляют гладиолусы и георгины.
40 % = 0,04
2) 60 * 0,4 = 24 (%) — составляют гладиолусы.
3) 40 − 24 = 16 (%) — составляют георгины.
32 ц. составляют 16 %
16 % = 0,16
4) 32 : 0,16 = 3200 : 16 = 200 (ц.) — было всего.
5) 200 * 0,6 = 120 (ц.) — роз растет в саду.
Ответ: 120 роз.
Задание № 1116
Заполните пропуски вычислений, если:
1) x = 2,6;
2) x = 8.
Решение
2,6 * 0,8 = 2,08
2,08 − 0,19 = 1,89
1,89 : 0,9 = 18,9 : 9 = 2,1
2,1 + 1,1 = 3,28 * 0,8 = 6,4
6,4 − 0,19 = 6,21
6,21 − 0,45 = 5,76
5,76 : 0,9 = 57,6 : 9 = 6,4
Задание № 1117
Решите уравнение:
1) 0,31x + 1,2 = 1,2124
2) 0,5x − 17 = 40,52
3) 4,6 − 0,03x = 1,3
4) 0,4x + 0,24x − 0,26 = 0,764
Решение
0,31x + 1,2 = 1,2124
0,31x = 1,2124 − 1,2
0,31x = 0,0124
x = 0,0124 : 0,31
x = 0,04
_1,24 |31
124 |0,04
00,5x − 17 = 40,52
0,5x = 40,52 + 17
0,5x = 57,52
x = 57,52 : 0,5
x = 115,04
_575,2 |5
5 |115,04
_7
5
_25
25
_20
20
04,6 − 0,03x = 1,3
0,03x = 4,6 − 1,3
0,03x = 3,3
x = 3,3 : 0,03
x = 110
_330 |3
3 |110
_3
3
00,4x + 0,24x − 0,26 = 0,764
0,64x = 0,764 + 0,26
0,64x = 1,024
x = 1,024 : 0,64
x = 1,6
_102,4 |64
64 |1,6
_384
384
0
Задание № 1118
Ширина Красной площади в Москве равна 130 м. Длина ее в 5,34 раза больше ширины. Сколько квадратных метров составляет ее площадь? Ответ округлите до тысяч.
Решение задачи
1) 130 * 5,34 = 694,2 (м) — длина Красной площади.
×130
5.34
52
39
65
694.202) 130 * 684,2 = 90246 (м2) ≈ 90000 (м2) — площадь Красной площади.
×130
684.2
26
52
104
78
88946.0Ответ: 90000 м2.
263
Ответы к странице 263
Задание № 1119
Часовая стрелка курантов на Спасской башне Московского Кремля на 0,31 м короче минутной. Когда часы показывают 18.00, то расстояние между концами стрелок равно 6,25 м. Вычислите длину каждой стрелки.
Решение задачи
1) (6,25 − 0,31) : 2 = 2,97 (м) — длина часовой стрелки.
2) 2,97 + 0,31 = 3,28 (м) — длина минутной стрелки.
Ответ: 2,97 м; 3,28 м.
Задание № 1120
От двух пристаней, расстояние между которыми равно 63 км, навстречу друг другу одновременно отплыли две моторные лодки. Скорость одной из них равна 16 км/ч. Лодки встретились через 2 ч 6 мин после начала движения. Найдите скорость второй лодки.
Решение задачи
2 ч 6 мин = 2,1 ч
1) 63 : 2,1 = 30 (км/ч) — скорость сближения лодок.
2) 30 − 16 = 14 (км/ч) — скорость второй лодки.
Ответ: 14 км/ч.
Задание № 1121
Сколько существует двузначных чисел, для записи которых используются только:
1) цифры 0, 2, 4, 6 и 8;
2) цифры 1, 3, 5, 7 и 9?
(Цифры могут повторяться.)
Решение
1) Первой цифрой в числе может стать любая цифра кроме нуля, значит для первой цифры есть 4 варианта.
Второй цифрой в числе может быть любая из данных цифр, значит для второй цифры есть 5 вариантов.
4 * 5 = 20 двузначных чисел можно записать, для записи которых используются только цифры 0, 2, 4, 6 и 8:
20, 40, 60, 80;
22, 42, 62, 82;
24, 44, 64, 84;
26, 46, 66, 86;
28, 48, 68, 88.
Ответ: 20 чисел.2) Первой цифрой в числе может быть любая из данных цифр, значит для второй цифры есть 5 вариантов.
Второй цифрой в числе может быть любая из данных цифр, значит для второй цифры есть 5 вариантов.
5 * 5 = 25 двузначных чисел можно записать, для записи которых используются только цифры 1, 3, 5, 7 и 9:
11, 13, 15, 17, 19;
31, 33, 35, 37, 39;
51, 53, 55, 57, 59;
71, 73, 75, 77, 79;
91, 93, 95, 97, 99.
Ответ: 25 чисел.
Задание № 1122
Для просмотра кинофильма в зрительном зале собрались ученики нескольких школ. Оказалось, что ученики одной из школ составляют 47% количества зрителей. Сколько всего зрителей было в зале, если в нем 280 мест и более половины мест было занято?
Решение задачи
280 : 2 = 140 мест составляют половину мест в зале;
Всего зрителей было 100% и больше 140 человек, тогда:
1% зрителей не может быть дробным числом, так как тогда 47% учеников одной из школ также будет числом дробным, что невозможно.
1% зрителей > 1 зрителя, так как при 1% = 1, в зале было бы 1 * 100 = 100 зрителей, что неверно по условию задачи.
1% зрителей < 3 зрителей, так как при 1% = 3, в зале было бы 3 * 100 = 300 зрителей, а мест всего 280.
Значит 1% зрителей = 2 зрителя, тогда 2 * 100 = 200 зрителей было в зале.
Ответ: 200 зрителей.
264
Ответы к странице 264
Задание №6 Проверьте себя в тестовой форме
1 В
2 Г
3 Б
4 А
5 А
6 Г
7 Б
8 Г
9 Б
10 В
11 Б
12 В
Решение заданий «Проверь себя»
1. Сколько цифр записано справа от запятой в произведении чисел 2,64 и 3,72?
Чтобы перемножить десятичные дроби, сначала перемножим их, как натуральные числа, а потом поставим запятую на столько знаков справа, сколько в обоих множителях. В 1-м множителе 2 знака, во 2-м тоже 2, значит в произведении будет 4.
2. Чему равна половина одной сотой?
_0,01 |2
0 |0,005
_0
0
_10
10
0
3. Упростите выражение 0,2а*1,5b.
Согласно переместительному свойству умножения можно записать
0,2а*1,5b = 0,2*1,5*а*b = 0,3аb
4. Чему равно значение выражения 48:(1,07 + 0,53) — 1,6?
48 : (1,07 + 0,53) — 1,6 = 48 : 1,6 — 1,6 = 480 : 16 — 1,6 = 30 — 1,6 = 28,4
5. Упростите выражение 2,1с — 0,6с + 3,9с.
2,1с — 0,6с + 3,9с = (2,1 — 0,6 + 3,9) * с = (1,5 + 3,9) * с = 5,4с
6. Чему равно значение выражения (36 — 1,8 * 2,7) : 0,9?
(36 — 1,8 * 2,7) : 0,9 = (36 — 4,86) : 0,9 = 31,14 : 0,9 = 34,6
7. В стаде было 200 животных, из них 34% составляли овцы. Сколько овец было в стаде?
34% = 0,34
200 * 0,34 = 68 (ов.) — было в стаде
Ответ: 68 овец.
8. Сплав содержит 28% меди. Какова масса сплава, если он содержит 56 т меди?
28% составляют 56 т
28% = 0,28
56 : 0,28 = 200 (т) — масса сплава
Ответ: 200 т.
9. Велосипедист проехал 20 км со скоростью 10 км/ч и 15 км со скоростью 5 км/ч. Найдите среднюю скорость движения велосипедиста.
1) 20 : 10 = 2 (ч) — ехал велосипедист со скоростью 10 км/ч
2) 15 : 5 = 3 (ч) — ехал велосипедист со скоростью 5 км/ч
3) 2 + 3 = 5 (ч) — всего ехал велосипедист
4) 20 + 15 = 35 (км) — проехал велосипедист всего
5) 35 : 5 = 7 (км/ч) — средняя скорость велосипедиста
Ответ: 7 км/ч.
10. Десять автобусных остановок расположены на прямой улице так, что расстояния между любыми соседними остановками одинаковы. Расстояние между первой и третьей остановками равно 1,2 км. Каково расстояние между первой и последней остановками?
1) 1,2 : 2 = 0,6 (км) — расстояние между соседними остановками
2) 0,6 * 9 = 5,4 (км) — расстояние между первой и последней остановками
Ответ: 5,4 км.
11. На какое наименьшее натуральное число надо умножить число 3,6, чтобы произведение было натуральным числом?
Нужно такое число, при умножении которого на 6 в конце будет 0, мы перенесем запятую на 1 знак и останется натуральное число. Наименьшим таким числом является число 5, потому что 6 * 5 = 30,
3,6 * 5 = 18.
12. В магазин завезли яблоки и груши, причем груши составляли 35% завезенных фруктов. Яблок было на 126 кг больше, чем груш. Сколько килограммов яблок и груш завезли в магазин?
100 — 35 = 65 (%) — завезли яблок
65 — 35 = 30 (%) — разница между яблоками и грушами
30% составляют 126 кг
30% = 0,3
126 : 0,3 = 420 (кг) — фруктов завезли в магазин
Ответ: 420 кг.
273
Ответы к странице 273
Ответы к упражнениям для повторения за курс 5 класса
!Задание № 1123
1) 154 * 78 + 3900 : 65 − 216 * 53 = 12012 + 60 − 11448 = 12072 − 11448 = 624
2) 16728 : 82 − 5580 : 45 + 726 * 29 = 204 − 124 + 21054 = 80 + 21054 = 21134
3) (21518 : 53 − 24332 : 79) * 267 = (406 − 308) * 267 = 98 * 267 = 26166
4) (53734 : 67 − 59925 : 85) * 436 = (802 − 705) * 436 = 97 * 436 = 42292
5) (327 * 84 + 207673) : 47 = (27468 + 207673) : 47 = 235141 : 47 = 5003
6) (924 * 93 + 30271) : 29 = (85932 + 30271) : 29 = 116203 : 29 = 4007
7) (216 * 28 − 463680 : 92) : (86 * 64 − 4496) = (6048 − 5040) : (5504 − 4496) = 1008 : 1008 = 1
(1004 * 19 − 75110 : 37) : (408 * 435 − 177479) = (19076 − 2030) : (177480 − 177479) = 17046 : 1 = 17046
9) 61 − (1428 : 136 + 4,3) * 3,4 = 61 − (10,5 + 4,3) * 3,4 = 61 − 14,8 * 3,4 = 61 − 14,8 * 3,4 = 61 − 50,32 = 10,68
10) 40 − (2550 : 204 − 6,9) * 6,7 = 40 − (12,5 − 6,9) * 6,7 = 40 − 5,6 * 6,7 = 40 − 37,52 = 2,48
11) 37,72 : 4,6 − (1,43 + 2,728) * 1,5 = 8,2 − 4,158 * 1,5 = 8,2 − 6,237 = 1,963
12) 7,2 * 3,8 + (3,24 − 2,1312) : 0,42 = 27,36 + 1,1088 : 0,42 = 27,36 + 2,64 = 30
13) 3,564 : 0,66 + 0,4992 : 0,052 − 83 * 0,107 = 5,4 + 9,6 − 8,881 = 15 − 8,881 = 6,119
14) 98 * 0,035 − 0,0288 : 0,36 − 3 : 16 = 3,43 − 0,08 − 0,1875 = 3,35 − 0,1875 = 3,1625
15) (0,084 * 4,8 − 0,2132 : 6,5 + 0,0296) : 0,625 = (0,4032 − 0,0328 + 0,0296) : 0,625 = (0,3704 + 0,0296) : 0,625 = 0,4 : 0,625 = 0,64
16) (0,056 * 7,4 + 4,2106 : 7,4 − 0,0834) : 0,375 = (0,4144 + 0,569 − 0,0834) : 0,375 = (0,9834 − 0,0834) : 0,375 = 0,9 : 0,375 = 2,4
17) (20,6 − 16,74) * 0,1 + (23,4 + 8,95) : 100 = 3,86 * 0,1 + 32,35 : 100 = 0,386 + 0,3235 = 0,7095
18) (0,326 + 3,724) * 100 − (0,19682 − 0,0987) : 0,001 = 4,05 * 100 − 0,09812 : 0,001 = 405 − 98,12 = 306,88
19) (2,04 − 1 1/4) : 1/20 = (2,04 − 1,25) : 0,05 = 0,79 : 0,05 =15,8
20) (3,42 − 2 5/8) :1/50 = (3,42 − 2,625) : 0,02 = 0,795 : 0,02 = 39,75
21) 23 : ( 6 5/17 + 1 12/17) − (4 2/5 − 2 3/5) : 5 = 23 : 8 − 1 4/5 : 5 = 2,875 − 1,8:5 = 2,875 − 0,36 = 2,515
22) (7 4/13 − 4 4/13) : 0,15 − 4 : (13 6/13 + 11 7/13) = 3 : 0,15 − 4 : 25 = 20 − 0,16 = 19,84
!Задание № 1124
Составьте числовое выражение и найдите его значение:
1) разность суммы 17,23 и 16,37 и разности чисел 9 и 6,328;
2) разность разности чисел 12 3/13 и 4 7/13 и суммы чисел 1 5/13 и 3 11/13;
3) произведение суммы чисел 16 5/11 и 5 6/11 и числа 3,245;
4) частное разности чисел 4,8 и 3,762 и числа 0,06;
5) произведение суммы чисел 3,47 и 3,46 и их разности;
6) частное разности чисел 6,3 и 4,2 и их суммы;
7) сумма произведения чисел 0,125 и 16 и частного чисел 28 и 0,56;

9) частное суммы чисел 86,9 и 667,6 и суммы чисел 37,1 и 13,2;
10) произведение суммы чисел 1,367 и 6,033 и разности чисел 12 и 11,15.
Решение
1) (17,23 + 16,37) − (9 − 6,328) = 33,6 − 2,672 = 30,928
2) (12 3/13 − 4 7/13) − (1 5/13 + 3 11/13) = 7 9/13 − 5 3/13 = 2 6/13
3) (16 5/11 + 5 6/11) ∗ 3,245 = 22 ∗ 3,245 = 71,39
4) (4,8 − 3,762) : 0,06 = 1,038 : 0,06 = 17,3
5) (3,47 + 3,46) * (3,47 − 3,46) = 6,93 * 0,01 = 0,0693
6) (6,3 − 4,2) : (6,3 + 4,2) = 2,1 : 10,5 = 0,2
7) (0,125 * 16) + (28 : 0,56) = 2 + 50 = 52
(0,128 : 0,4) − (0,126 : 0,6) = 0,32 − 0,21 = 0,11
9) (86,9 + 667,6) : (37,1 + 13,2) = 754,5 : 50,3 = 15
10) (1,367 + 6,033) * (12 − 11,15) = 7,4 * 0,85 = 6,29
274
Ответы к странице 274
!Задание № 1125
На сколько:
1) разность чисел 6,2 и 1,4 меньше их произведения;
2) разность чисел 11,88 и 2,64 больше их частного;
3) сумма чисел 7,8 и 6,5 больше их частного;
4) произведение чисел 7,6 и 0,8 меньше разности этих чисел;
5) произведение чисел 14,5 и 1,06 больше разности чисел 16,1 и 4,386;
6) частное чисел 2 и 250 больше произведения чисел 0,18 и 0,04?
Решение
1) 6,2 * 1,4 − (6,2 − 1,4) = 8,68 − 4,8 = 3,88
2) (11,88 − 2,64) − (11,88 : 2,64) = 9,24 − 4,5 = 4,74
3) (7,8 + 6,5) − (7,8 : 6,5) = 14,3 − 1,2 = 13,1
4) (7,6 − 0,8) − 7,6 * 0,8 = 6,8 − 6,08 = 0,72
5) (14,5 * 1,06) − (16,1 − 4,386) = 15,37 − 11,714 = 3,656
6) (2 : 250) − (0,18 * 0,04) = 0,008 − 0,0072 = 0,0008
Задание № 1126
1) Запишите четыре числа, первое из которых равно 3,24, а каждое последующее в 10 раз больше предыдущего.
2) Запишите пять чисел, первое из которых равно 430, а каждое последующее в 10 раз меньше предыдущего.
Решение
1) 3,24; 32,4; 324; 3240.
2) 430; 43; 4,3; 0,43; 0,043.
Задание № 1127
Найдите значение выражения:
1) 72 : (x − 17) − 4, если x = 35;
2) (x + 259) : (x − 205), если x = 321;
3) 61,32 − 61,32 : (a + b), если a = 3,6, b = 4,8;
4) 4,346 : x − y : 0,25, если x = 0,82, y = 0,4;
5) 2,04 : x + 5,19y, если x = 3,4, y = 0,4;
6) 1,4m − 0,3n, если m = 2,6, n = 5,09;
7) 1000x + 0,01y, если x = 0,2346, y = 26540;

9) x + y − z, если x= 9 2/21, y = 6 5/21, z = 7 13/21;
10) a − b − c + d, если a = 10 , b = 3 9/14, c = 4 13/14 , d = 2 8/14.
Решение
1) 72 : (x − 17) − 4 = 72 : (35 − 17) − 4 = 72 : 18 − 4 = 4 − 4 = 0
2) (x + 259) : (x − 205) = (321 + 259) : (321 − 205) = 580 : 116 = 5
3) 61,32 − 61,32 : (a + b) = 61,32 − 61,32 : (3,6 + 4,8) = 61,32 − 61,32 : 8,4 = 61,32 − 7,3 = 54,02
4) 4,346 : x − y : 0,25 = 4,346 : 0,82 − 0,4 : 0,25 = 5,3 − 1,6 = 3,7
5) 2,04 : x + 5,19y = 2,04 : 3,4 + 5,19 * 0,4 = 0,6 + 2,076 = 2,676
6) 1,4m − 0,3n = 1,4 * 2,6 − 0,3 * 5,09 = 3,64 − 1,527 = 2,113
7) 1000x + 0,01y = 1000 * 0,2346 + 0,01 * 26540 = 234,6 + 265,4 = 500
453x − 0,1827y = 453 * 0,1 − 0,1827 * 100 = 45,3 − 18,27 = 27,03
9) x + y − z = 9 2/21 + 6 5/21 − 7 13/21 = (8 + 6 − 7) + (23/21 + 5/21 − 13/21) = 7 15/21
10) a − b − c + d = 10 − 3 9/14 − 4 13/14 + 2 8/14 = (9 − 3 − 4 + 2) + (14/14 − 9/14 − 13/14 + 8/14) = 4
Задание № 1128 с ответами
Решите уравнение:
275
Ответы к странице 275
Задание № 1129
Решите уравнение:
1) 0,11x + 0,08x = 45,6;
2) 2,9x − 1,1x = 5,04;
3) x − 0,64x = 2,808;
4) 7x + 9x + 0,32 = 2,72;
5) 5y + 7y − 0,024 = 0,204;
6) 2,4x − 1,5x + 47 = 1919;
7) 0,8(x − 1,9) = 0,56;

9) 1,7(5x − 0,16) = 0,238;
10) 0,8(100 − 0,04x) = 8,64;
11) x : 1,15 = 0,16;
12) 0,408 : x = 1,7;
13) (x + 9,14) : 7,2 = 5;
14) 2,2 − x : 0,3 = 0,13;
15) 5,6 : (x + 1,6) = 0,08;
16) 5,6 : x + 0,16 = 0,3;
17) 4,13 − 1,7x = 4,028;
18) 64 : (2,4y + 19,04) = 3,2.
Решение
1)
0,11x + 0,08x = 45,6
0,19x = 45,6
x = 45,6 : 0,19
x = 240
_4560 |19
38 |240
_76
76
02)
2,9x − 1,1x = 5,04
1,8x = 5,04
x = 5,04 : 1,8
x = 2,8
_50,4 |18
36 |2,8
_144
144
03)
x − 0,64x = 2,808
0,36x = 2,808
x = 2,808 : 0,36
x = 7,8
_280,8 |36
252 |7,8
_288
288
04)
7x + 9x + 0,32 = 2,72
16x = 2,72 − 0,32
16x = 2,4
x = 2,4 : 16
x = 0,15
_2.72
0.32
2.40_2,4 |16
16 |0,15
_80
80
05)
5y + 7y − 0,024 = 0,204
12y = 0,204 + 0,024
y = 0,228 : 12
y = 0,019
+0.204
0.024
0.228_0,228 |12
12 |0,019
_108
108
06)
2,4x − 1,5x + 47 = 1919
0,9x = 1919 − 47
0,9x = 1872
x = 1872 : 0,9
x = 2080
_1919
47
1872_18720 |9
18 |2080
_72
72
07)
0,8(x − 1,9) = 0,56
x − 1,9 = 0,56 : 0,8
x = 0,7 + 1,9
x = 2,6
_5,6 |8
56 |0,7
0+0.7
1.9
2.6

0,32(x + 1,4) = 73,6
x + 1,4 = 73,6 : 0,32
x = 230 − 1,4
x = 228,6
_7360 |32
64 |230
_96
96
0_230.0
1.4
228.69)
1,7(5x − 0,16) = 0,238
5x − 0,16 = 0,238 : 1,7
5x = 0,14 + 0,16
x = 0,3 : 5
x = 0,06
_2,38 |17
17 |0,14
_68
68
0+0.14
0.16
0.3_0,3 |5
0 |0,06
_30
30
010)
0,8(100 − 0,04x) = 8,64
100 − 0,04x = 8,64 : 0,8
0,04x = 100 − 10,8
x = 89,2 : 0,04
x = 2230
_86,4 |8
8 |10,8
_64
64
0_100.7
10.8
89.2_8920 |4
8 |2230
_9
8
_12
12
011)
x : 1,15 = 0,16
x = 0,16 * 1,15
x = 0,184
×0.16
1.15
80
16
16
0.184012)
0,408 : x = 1,7
x = 0,408 : 1,7
x = 0,24
_4,08 |17
34 |0,24
_68
68
013)
(x + 9,14) : 7,2 = 5
x + 9,14 = 5 * 7,2
x = 36 − 9,14
x = 26,86
×7.2
5
36.0_36.00
9.14
26.8614)
2,2 − x : 0,3 = 0,13
x : 0,3 = 2,2 − 0,13
x = 2,07 * 0,3
x = 0,621
_2.20
0.13
2.07×2.07
0.3
0.62115)
5,6 : (x + 1,6) = 0,08
x + 1,6 = 5,6 : 0,08
x = 70 − 1,6
x = 68,4
_560 |8
56 |70
0_70.0
1.6
68.416)
5,6 : x + 0,16 = 0,3
5,6 : x = 0,3 − 0,16
5,6 : x = 0,14
x = 5,6 : 0,14
x = 40
_0.30
0.16
0.14_560 |14
56 |40
017)
4,13 − 1,7x = 4,028
1,7x = 4,13 − 4,028
x = 0,102 : 1,7
x = 0,06
_4.130
4.028
0.102_1,02 |17
102 |0,06
018)
64 : (2,4y + 19,04) = 3,2
2,4y + 19,04 = 64 : 3,2
2,4y = 20 − 19,04
y = 0,96 : 2,4
y = 0,4
_20.00
19.04
0.96_9,6 |24
96 |0,4
0
Задание № 1130
1) К какому числу надо прибавить 4,2, чтобы произведение полученной суммы и числа 0,6 было равным 19,2?
2) Из какого числа надо вычесть 9,4, чтобы произведение полученной разности и числа 0,5 было равным 0,12?
3) На какое число надо умножить 12,3, чтобы сумма полученного произведения и числа 7,9 была равна 12,82?
4) Какое удвоенное число надо вычесть из 20,04, чтобы получить 9,1?
5) Какое число надо умножить на 0,4, чтобы сумма полученного произведения и числа 3,8 была равна произведению чисел 20,5 и 4?
Решение
1)
(x + 4,2) * 0,6 = 19,2
x + 4,2 = 19,2 : 0,6
x = 32 − 4,2
x = 27,8
_192 |6
18 |32
_12
12
0_32.0
4.2
27.82)
(x − 9,4) * 0,5 = 0,12
x − 9,4 = 0,12 : 0,5
x = 0,24 + 9,4
x = 9,64
_1,2 |5
10 |0,24
_20
20
0+0.24
9.40
9.643)
12,3x + 7,9 = 12,82
12,3x = 12,82 − 7,9
x = 4,92 : 12,3
x = 0,4
_12.82
7.90
4.92_49,2 |123
492 |0,4
04)
20,04 − 2x = 9,1
2x = 20,04 − 9,1
x = 10,94 : 2
x = 5,47
_20.04
9.10
10.94_10,94 |2
10 |5,47
_9
8
_14
14
05)
0,4x + 3,8 = 20,5 * 4
0,4x + 3,8 = 82
0,4x = 82 − 3,8
x = 78,2 : 0,4
x = 195,5
×20.5
4
82.0_82.0
3.8
78.2_782 |4
4 |195,5
_38
36
_22
20
_20
20
0
Задание № 1131
Найдите числа, которых не хватает в цепочке вычислений:…
Решение
1)
2,8x = 7,28
x = 7,28 : 2,8
x = 2,6
_72,8 |28
56 |2,6
_168
168
07,28 + y = 9
y = 9 − 7,28
y = 1,72
_9.00
7.28
1.729 : z = 0,15
z = 9 : 0,15
z = 60
_900 |15
90 |60
02)
a : 1,4 = 2,15
a = 2,15 * 1,4
a = 3,01
×2.15
1.4
860
215
3.0103)
z = 1,2 * 4,5 = 5,4
×1.2
4.5
60
48
5.40y : 0,3 = 5,4
y = 5,4 * 0,3
y = 1,62
×5.4
0.3
1.621,2 + x = 1,62
x = 1,62 − 1,2
x = 0,42
_1.62
1.20
0.424)
a : 0,16 = 40
a = 40 * 0,16
a = 6,4
×0.16
40
6.400,32c = 40
c = 40 : 0,32
c = 125
_4000 |32
32 |125
_80
64
_160
160
06,4 : b = 0,32
b = 6,4 : 0,32
b = 20
_640 |32
64 |20
0
Задание № 1132
Не выполняя вычислений, сравните значения выражений:
1) 12 * 0,34 и (12 * 34) : 100;
2) 520 * 0,05 и (520 * 5) : 10;
3) 0,3 * 0,9 и (3 * 9) : 100;
4) 3,648 : 0,06 и 364,8 : 0,6.
Решение
1) (12 * 34) : 100 = 12 * 0,34, тогда:
12 * 0,34 = (12 * 34) : 100
2) (520 * 5) : 10 = 520 * 0,5, тогда:
520 * 0,05 < (520 * 5) : 10
3) (3 * 9) : 100 = 0,3 * 0,9, тогда:
0,3 * 0,9 = (3 * 9) : 100
4) 3,648 : 0,06 = 36,48 : 0,6, тогда:
3,648 : 0,06 < 364,8 : 0,6
Задание № 1133
Не выполняя вычислений, укажите корень уравнения:
1) x * 0,86 = (7 * 86) : 100;
2) 2,4y = (24 * 16) : 100;
3) (54 * z) : 10 = 5,4 * 6;
4) a : 0,35 = (7,16 * 100) : 35;
5) b : 6,5 = 130 : 65;
6) 46,2 : c = 0,462 : 0,0007.
Решение
1) x * 0,86 = (7 * 86) : 100
x * 0,86 = 7 * 0,86
x = 72) 2,4y = (24 * 16) : 100
2,4y = 2,4 * 1,6
y = 1,63) (54 * z) : 10 = 5,4 * 6
5,4 * z = 5,4 * 6
z = 64) a : 0,35 = (7,16 * 100) : 35
a : 0,35 = 7,16 : 0,35
a = 7,165) b : 6,5 = 130 : 65
b : 6,5 = 13 : 6,5
b = 136) 46,2 : c = 0,462 : 0,0007
46,2 : c = 46,2 : 0,07
c = 0,07
276
Ответы к странице 276
Задание № 1134
Найдите все натуральные значения x, при которых верно неравенство:
1) 2,4 < x < 6;
2) 3,2 < x < 8;
3) 7,5 < x < 11,1;
4) 9 < x < 14;
5) 11 < x < 13;
6) 1,2 < x < 1,9;
7) 0,72 < x < 3,07;

Решение
1) 2,4 < x < 6 верно при x = 3; 4; 5.
2) 3,2 < x < 8 верно при x = 4; 5; 6; 7.
3) 7,5 < x < 11,1 верно при x = 8; 9; 10; 11.
4) 9 < x < 14 верно при x = 10; 11; 12; 13.
5) 11 < x < 13 верно при x = 12.
6) 1,2 < x < 1,9 не верно ни при каких натуральных значениях x.
7) 0,72 < x < 3,07 верно при x = 1; 2; 3.
7 4/9 < x < 10,1 верно при x = 8; 9; 10.
Задание № 1135
Найдите наибольшее натуральное значение x, при котором будет верным неравенство:
1) 3x < 19,4;
2) 5x < 32,6;
Решение
1) 3x < 19,4
19,4 : 3 ≈ 6,5, значит наибольшее натуральное значение x, при котором будет верным неравенство равно 6.2) 5x < 32,6
32,6 : 5 = 6,52, значит наибольшее натуральное значение x, при котором будет верным неравенство равно 6.
Задание № 1136
Найдите наименьшее натуральное значение x, при котором будет верным неравенство:
1) 4x > 14;
2) 7x > 40 7/9.
Решение
1) 4x > 14
14 : 4 = 3,5, значит наименьшее натуральное значение x, при котором будет верным неравенство равно 4.2) 7x > 40 7/9
40 : 7 ≈ 5,7, значит наименьшее натуральное значение x, при котором будет верным неравенство равно 6.
Задание № 1137
Агрофирма «Сажай−собирай» вырастила на двух полях рожь. С одного поля собрали 392 ц ржи, а со второго − 896 ц. Площадь второго поля на 18 га больше, чем площадь первого. Найдите площадь каждого поля, если урожайность 1 га земли на этих полях одинакова.
Решение
1) 896 − 392 = 504 (ц) — разница собранного урожая со второго поля и с перового.
2) 504 : 18 = 28 (ц/га) — урожайность каждого поля.
3) 392 : 28 = 14 (га) — площадь первого поля.
4) 896 : 28 = 32 (га) — площадь второго поля.
Ответ: 14 га; 32 га.
Задание № 1138
Акционерное общество «Приятного аппетита» продало в субботу 46 коробок конфет, а в воскресенье − 62 такие коробки. В воскресенье было продано на 120 кг конфет больше, чем в субботу. Сколько килограммов конфет было продано в субботу и сколько − в воскресенье?
Решение
1) 62 − 46 = 16 (к.) — разница проданных конфет в воскресенье и субботу.
2) 120 : 16 = 7,5 (кг) — конфет содержится в одной коробке.
3) 46 * 7,5 = 345 (кг) — конфет продали в субботу.
4) 345 + 120 = 465 (кг) — конфет продали в воскресенье.
Ответ: 345 кг; 465 кг.
Задание № 1139
Коза−дереза собрала с поля площадью 2,3 га по 400 ц капусты с гектара. Сколько автомашин грузоподъемностью 3,5 т ей надо заказать для перевозки урожая?
Решение
1) 2,4 * 400 = 920 ц = 92 (т) — капусты собрали.
2) 92 : 3,5 ≈ 26,3 (ав.)
значит необходимо заказать 27 автомашин.
Ответ: 27 автомашин.
Задание № 1140
Фермер засеял поле прямоугольной формы пшеницей. Длина поля составляла 37,5 м, что в 1,5 раза больше его ширины. Сколько центнеров собрал фермер со всего поля, если с каждого ара он собрал 42,8 ц? Запишите полученный ответ в тоннах, центнерах и килограммах.
Решение
1) 37,5 : 1,5 = 25 (м) — ширина поля.
2) 37,5 * 2,5 = 937,5 (м2) — площадь поля.
937,5 м2 = 9,375 а
3) 0,375 * 42,8 = 401,25 (ц) — пшеницы собрал фермер со своего поля.
401,25 ц = 40 т 1 ц 25 кг
Ответ: 40 т 1 ц 25 кг.
Задание № 1141
Миша купил 6 пирожных и получил 28 крон сдачи. Для покупки 9 пирожных Мише не хватило 8 крон Сколько крон стоит одно пирожное?
Решение
1) 9 − 6 = 3 (п.) — дополнительно хотел купить Миша.
2) 28 + 8 = 36 (к.) — необходимо на покупку 3 пирожных.
3) 36 : 3 = 12 (к.) — стоит одно пирожное.
Ответ: 12 крон.
Задание № 1142
Первый штамповочный пресс изготавливает 36 деталей за 18 мин., а второй тоже количество таких деталей — за 9 мин. За сколько минут они изготовят 36 деталей, работая одновременно.
Решение
1) 36 : 18 = 2 (шт/мин) — производительность первого пресса.
2) 36 : 9 = 4 (шт/мин) — производительность второго пресса.
3) 2 + 4 = 6 (шт/мин) — производительность двух прессов вместе.
4) 36 : 6 = 6 (мин) — потребуется двум пресам для изготовления 36 деталей.
Ответ: 6 мин.
Задание № 1142 из старого учебника
Пончик может съесть 360 пирожных за 18 мин, а Сиропчик то же самое количество пирожных − за 12 мин. За сколько минут Пончик и Сиропчик смогут вместе съесть эти пирожные?
Решение
1) 360 : 18 = 20 (п.) — за 1 минуту съедает Пончик.
2) 360 : 12 = 30 (п.) — за 1 минуту съедает Сиропчик.
3) 20 + 30 = 50 (п.) — за 1 минуту съедают Пончик и Сиропчик вместе.
4) 360 : 50 = 7,2 (мин) — потребуется Пончику и Сиропчику, чтобы съесть совместно 360 пирожных.
Ответ: 7,2 минуты.
Задание № 1143
Через первую трубу в бассейн, объём которого равен 300 м³, можно наполнить водой за 3 ч, а через вторую трубу — за 6 ч. За сколько часов будет наполнен бассейн, если открыть одновременно обе трубы?
Решение
1) 300 : 3 = 100 (м³/ч) — производительность первой трубы.
2) 300 : 6 = 50 (м³/ч) — производительность второй трубы.
3) 100 + 50 = 150 (м³/ч) — производительность двух труб вместе.
4) 300 : 150 = 2 (часа) — потребуется для наполнения бассейна при работе двух труб одновременно.
Ответ: 2 часа.
Задание № 1143 из старого учебника
Работник Балда может нарубить 300 м3 дров за 3 мин, а черт то же самое количество дров − за 6 мин. За сколько минут они вместе могут нарубить такое количество дров?
Решение
1) 300 : 3 = 100 (м3) — дров в 1 минуту может наколоть Балда.
2) 300 : 6 = 50 (м3) — дров в 1 минуту может наколоть черт.
3) 100 + 50 = 150 (м3) — дров в 1 минуту могут наколоть Балда и черт вместе.
4) 300 : 150 = 2 (мин) — потребуется Балде и черту, чтобы совместно наколоть 300 м3 дров.
Ответ: 2 минуты.
277
Ответы к странице 277
Задание № 1144
Два насоса одновременно выкачивали воду из бассейна. Один насос за минуту выкачивал 200 л воды, а второй − 140 л. Сколько времени работали насосы и сколько воды выкачал каждый из них, если первый насос выкачал на 210 л больше, чем второй?
Решение задачи
1) 200 − 140 = 60 (л/мин) — разница производительности первого и второго насосов.
2) 210 : 60 = 3,5 (мин) — работали насосы.
3) 200 * 3,5 = 700 (л) — выкачал первый насос.
4) 140 * 3,5 = 490 (л) — выкачал второй насос.
Ответ: 3,5 мин, 700 л, 490 л.
Задание № 1145
Масса ведра с водой равна 12,5 кг. Когда из ведра вылили половину воды, то масса ведра с водой стала 7 кг. Какова масса пустого ведра?
Решение задачи
1) 12,5 − 7 = 5,5 (кг) — масса половины ведра воды.
2) 7 − 5,5 = 1,5 (кг) — масса пустого ведра.
Ответ: 1,5 кг.
Задание № 1146
У принцессы Моды было 30 платьев и 24 маскарадных костюма, на пошив которых пошло 163,5 м ткани. На каждое платье потратили на 0,5 м ткани больше, чем на каждый костюм. Сколько ткани пошло на одно платье и сколько − на один костюм?
Решение задачи через х
Пусть x м ткани потратили на пошив одного костюма, тогда:
x + 0,5 м ткани потратили на пошив оного платья;
24x м ткани потратили на пошив 24 костюмов;
30(x + 0,5) м ткани потратили на пошив 30 платьев.
Так как всего потратили 163,5 м ткани, то:
24x + 30(x + 0,5) = 163,5
24x + 30x + 15 = 163,5
54x = 163,5 − 15
x = 148,5 : 54
x = 2,75 (м) — ткани потратили на пошив одного костюма.
x + 0,5 = 2,75 + 0,5 = 3,25 (м) — ткани потратили на пошив оного платья.
Ответ: 3,25 м; 2,75 м.
Задание № 1147
В кладовой было 15 ящиков и 12 корзин, в которых хранилось 576 кг яблок, причем в каждом ящике было на 6 кг яблок больше, чем в каждой корзине. Сколько килограммов яблок было в каждом ящике и сколько в каждой корзине?
Решение через х
Пусть x кг яблок хранилось в каждой корзине, тогда:
(x + 6) яблок хранилось в каждом ящике;
12x кг яблок всего хранилось в корзинах;
15(x + 6) кг яблок всего хранилось в ящиках;
а всего было 576 кг яблок.
Составим уравнение:
12x + 15(x + 6) = 576
12x + 15x + 90 = 576
27x = 576 − 90
x = 486 : 27
x = 18 (кг) — яблок хранилось в каждой корзине.
x + 6 = 18 + 6 = 24 (кг) — яблок хранилось в каждом ящике.
Ответ: 24 кг, 18 кг.
Задание № 1148
За завтраком медведь Михайло Потапыч съел 7,5 кг меда, за обедом − в 1,2 раза больше, чем за завтраком, а за ужином − 0,8 того, что съел за обедом. Сколько килограммов меда съел Михайло Потапыч за день?
Решение
1) 7,5 * 1,2 = 9 (кг) — меда съел Михайло Потапыч за обедом.
2) 9 * 0,8 = 7,2 (кг) — меда съел Михайло Потапыч за ужином.
3) 7,5 + 9 + 7,2 = 23,7 (кг) — меда съел Михайло Потапыч за день.
Ответ: 23,7 кг.
Задание № 1149
1) Автомобиль преодолевает расстояние между двумя городами за 3,6 ч, если двигается со скоростью 62,5 км/ч. С какой скоростью он должен двигаться, чтобы преодолеть это расстояние за 3 ч?
2) Поезд проходит расстояние между двумя станциями за 4,2 ч, двигаясь со скоростью 54 км/ч. За какое время он пройдет это расстояние, если будет двигаться со скоростью 63 км/ч?
Решение
1) 3,6 * 6,25 = 225 (км) — длина всего пути.
2) 225 : 3 = 75 (км/ч) — необходимая скорость.
Ответ 75 км/ч.1) 4,2 * 54 = 226,8 (км) — длина всего пути.
2) 226,8 : 63 = 3,6 (ч) — потребуется поезду, чтобы пройти 54 км.
Ответ: 3,6 ч.
Задание № 1150
От двух станций навстречу друг другу одновременно отправились два поезда. Один поезд проходил 14,7 км за каждые 1/4 ч, а второй − 22,4 км за 1/3 ч. Через сколько часов после начала движения расстояние между поездами будет 37,8 км, если расстояние между станциями равно 138,6 км?
Решение
1) 14,7 : 1 * 4 = 58,8 (км/ч) — скорость первого поезда.
2) 22,4 : 1 * 3 = 67,2 (км/ч) — скорость второго поезда.
3) 58,8 + 67,2 = 126 (км/ч) — суммарная скорость двух поездов.1 вариант: поезда не доехали 37,8 км друг до друга, тогда:
4) 138,6 − 37,8 = 100,8 (км) — суммарное расстояние пройденное поездами;
5) 100,8 : 126 = 0,8 (ч) — ехали поезда до того того момента, пока расстояние между ними не стало 37,8 км.2 вариант: поезда встретились и разъехались на 37,8 км друг от друга, тогда:
4) 138,6 + 37,8 = 176,4 (км) — суммарное расстояние пройденное поездами;
5) 176,4 : 126 = 1,4 (ч) — ехали поезда до того того момента, пока расстояние между ними не стало 37,8 км.
Ответ: 0,8ч; 1,4ч.
Задание № 1151
Из одного пункта в одном направлении одновременно вышли два пешехода. Один идет со скоростью 5,2 км/ч, а второй − 4,3 км/ч. Какое расстояние будет между ними через 4 ч после начала движения?
Решение
1) 5,2 − 4,3 = 0,9 (км/ч) — разница скоростей двух пешеходов.
2) 0,9 * 4 = 3,6 (км) — будет между пешеходами через 4 ч после начала движения.
Ответ: 3,6 км.
Задание № 1152
Из одного пункта в одном направлении одновременно выехали автомобиль и автобус. Автомобиль двигался со скоростью 72 км/ч, а автобус − со скоростью 64 км/ч. Через сколько часов после начала движения расстояние между автомобилем и автобусом будет 52 км?
Решение
1) 72 − 64 = 8 (км/ч) — разница скоростей автомобиля и автобуса.
2) 52 : 8 = 6,5 (ч) — потребуется, чтобы расстояние между автомобилем и автобусом составило 52 км.
Ответ: 6,5 ч.
278
Ответы к странице 278
Задание № 1153
Из одного пункта в одном направлении одновременно выехали два всадника. Через 5 ч после начала движения расстояние между ними было 6 км. Скорость одного из всадников равна 8,4 км/ч. Найдите скорость второго всадника.
Решение
6 : 5 = 1,2 (км/ч) — скорость сближения всадников.
1 вариант: второй всадник отстал от первого на 6 км, тогда:
8,4 − 1,2 = 7,2 (км/ч) — скорость второго всадника.2 вариант: второй всадник обогнал первого на 6 км, тогда:
8,4 + 1,2 = 9,6 (км/ч) — скорость второго всадника.
Ответ: 7,2 км/ч или 9,6 км/ч.
Задание № 1154
Из одного пункта в противоположных направлениях одновременно выехали автомобиль и автобус. Скорость автомобиля равна 72 км/ч, а скорость автобуса − в 1,2 раза меньше скорости автомобиля. Каким будет расстояние между автомобилями и автобусом через 3 ч 15 мин после начала движения?
Решение
1) 72 : 1,2 = 60 (км/ч) — скорость автобуса.
2) 72 + 60 = 132 (км/ч) — суммарная скорость автомобиля и автобуса.
3 ч 15 мин = 3,25 ч
3) 132 * 3,25 = 429 (км) — будет расстояние между автомобилями и автобусом через 3 ч 15 мин после начала движения.
Ответ: 429 км.
Задание № 1155
Из одного пункта в противоположных направлениях одновременно вышли два пешехода. Скорость одного пешехода равна 4,2 км/ч, что составляет 7/6 скорости второго. Через сколько часов после начала движения расстояние между пешеходами будет 19,5 км?
Решение
1) 4,2 : 7 * 6 = 0,6 * 6 = 3,6 (км/ч) — скорость второго пешехода.
2) 4,2 + 3,6 = 7,8 (км/ч) — суммарная скорость пешеходов.
3) 19,5 : 7,8 = 2,5 (ч) — потребуется, чтобы расстояние между пешеходами стало 19,5 км.
Ответ: 2,5 ч.
Задание № 1156
От одной станции в противоположных направлениях одновременно отправились два поезда. Через 2 ч 45 мин после начала движения расстояние между поездами было 330 км. Скорость одного поезда равна 56 км/ч. Найдите скорость второго поезда.
Решение
2 ч 45 мин = 2,75 ч
1) 330 : 2,75 = 120 (км/ч) — суммарная скорость двух поездов.
2) 120 − 56 = 64 (км/ч) — скорость второго поезда.
Ответ: 64 км/ч.
Задание № 1157
Из двух пунктов, расстояние между которыми равно 84 км, в одном направлении одновременно выехали два автомобиля со скоростями 68,4 км/ч и 57,9 км/ч. Автомобиль с меньшей скоростью двигался впереди. Через сколько часов после начала движения один автомобиль догонит второй?
Решение
1) 68,4 − 57,9 = 10,5 (км/ч) — скорость сближения автомобилей.
2) 84 : 10,5 = 8 (ч) — потребуется одному автомобилю, чтобы догнать второй.
Ответ: через 8 ч.
Задание № 1158
Из двух пунктов в одном направлении одновременно вышли два пешехода. Пешеход, который двигался со скоростью 4,8 км/ч, догнал пешехода, который двигался со скоростью 4,2 км/ч, через 2,5 ч после начала движения. Найдите расстояние между пунктами, из которых вышли пешеходы.
Решение
1) 4,8 − 2,4 = 0,6 (км/ч) — скорость сближения пешеходов.
2) 0,6 * 2,5 = 1,5 (км) — расстояние между пунктами.
Ответ: 1,5 км.
Задание № 1159
Из двух пунктов в одном направлении одновременно выехали велосипедист и мотоциклист. Мотоциклист двигался со скоростью 76,2 км/ч и догнал велосипедиста, который двигался со скоростью 9,8 км/ч, через 3,5 ч после начала движения. Найдите, какое расстояние было между велосипедистом и мотоциклистом в начале движения.
Решение
1) 76,2 − 9,8 = 66,4 (км/ч) — скорость сближения велосипедиста и мотоциклиста.
2) 66,4 * 3,5 = 232,4 (км) — было между велосипедистом и мотоциклистом в начале движения.
Ответ: 232,4 км.
Задание № 1160
Из двух пунктов, расстояние между которыми равно 189 км, одновременно в одном направлении выехали грузовик и легковой автомобиль. Грузовик ехал со скоростью 48 км/ч, и через 7 ч после начала движения его догнал легковой автомобиль. С какой скоростью ехал легковой автомобиль?
Решение
1) 48 * 7 = 336 (км) — проехал грузовик за 7 часов.
2) 336 + 189 = 525 (км) — проехал легковой автомобиль.
3) 525 : 7 = 75 (км/ч) — скорость легкового автомобиля.
Ответ: 75 км/ч.
279
Ответы к странице 279
Задание № 1161
Из двух пунктов, расстояние между которыми равно 111 км, в одном направлении одновременно выехали мотоциклист и всадник. Мотоциклист ехал со скоростью 82 км/ч и догнал всадника через 1,5 ч после начала движения. Найдите скорость всадника.
Решение задачи
1) 111 : 1,5 = 74 (км/ч) — скорость сближения мотоциклиста и всадника.
2) 82 − 74 = 8 (км/ч) — скорость всадника.
Ответ: 8 км/ч.
Задание № 1162
В 10 ч из пункта A выехал грузовик со скоростью 42,4 км/ч, а в 13 ч 30 мин из этого пункта в том же направлении мотоциклист со скоростью 78,5 км/ч. Какое расстояние будет между ними в 15 ч 30 мин? В 18 ч?
Решение задачи
15 ч 30 мин − 10 ч = 5 ч 30 мин = 5,5 ч был в пути грузовик.
15 ч 30 мин − 13 ч 30 мин = 2 ч был в пути мотоциклист.
42,4 * 5,5 = 233,2 (км) — проехал грузовик до 15 ч 30 мин.
78,5 * 2 = 157 (км) — проехал мотоциклист до 15 ч 30 мин.
233,2 − 157 = 76,2 (км) — расстояние, которое было между грузовиком и мотоциклистом в 15 ч 30 мин.
18 ч − 10 ч = 8 ч — был в пути грузовик.
18 ч − 13 ч 30 мин = 4,5 ч — был в пути мотоциклист.
42,4 * 8 = 339,2 (км) — проехал грузовик до 18 ч.
78,5 * 4,5 = 353,25 (км) — проехал мотоциклист до 18 ч.
353,25 − 339,2 = 14,05 (км) — расстояние, которое было между грузовиком и мотоциклистом в 18 ч.
Ответ: 76,2 км; 14,05 км.
Задание № 1163
Теплоход прошел 237 км против течения реки за 6 ч. Какой путь он пройдет в стоячей воде за 8 ч, если скорость течения равна 1,5 км/ч?
Решение задачи
1) 237 : 6 = 39,5 (км/ч) — скорость теплохода против течения.
2) 39,5 + 1,5 = 41 (км/ч) — скорость теплохода в стоячей воде.
3) 41 * 8 = 328 (км) — пройдет теплоход за 8 ч в стоячей воде.
Ответ: 328 км.
Задание № 1164
Катер прошел по течению реки 119 км за 3,5 ч. Какое расстояние пройдет он против течения реки за 5 ч, если скорость катера в стоячей воде равна 32,8 км/ч?
Решение задачи
1) 119 : 3,5 = 34 (км/ч) — скорость катера по течению реки.
2) 34 − 32,8 = 1,2 (км/ч) — скорость течения.
3) 32,8 − 1,2 = 31,6 (км/ч) — скорость катера против течения реки.
4) 31,6 * 5 = 158 (км) — пройдет катер за 5 часов против течения реки.
Ответ: 158 км.
Задание № 1165
Скорость теплохода по течению реки равна 29,6 км/ч, а против течения − 27,8 км/ч. Найдите скорость течения и собственную скорость теплохода.
Решение задачи
1) (29,6 − 24,8) : 2 = 4,8 : 2 = 2,4 (км/ч) — скорость течения.
2) 29,6 − 2,4 = 27,2 (км/ч) — собственная скорость теплохода.
Ответ: 2,4 км/ч; 27,2 км/ч.
Задание № 1166
Собственная скорость катера равна 28 км/ч, а скорость течения − 1,8 км/ч. Сначала катер шел 1,4 ч против течения, а потом 0,8 ч по течению. Какой путь прошел катер за все это время?
Решение задачи
1) 28 + 1,8 = 29,8 (км/ч) — скорость катера по течению.
2) 28 − 1,8 = 26,2 (км/ч) — скорость катера против течения.
3) 26,2 * 1,4 = 36,68 (км) — прошел катер против течения.
4) 29,8 * 0,8 = 23,84 (км) — прошел катер по течению.
5) 36,68 + 23,84 = 60,52 (км) — весь путь, который прошел катер.
Ответ: 60,52 км.
Задание № 1167
От двух пристаней навстречу друг другу одновременно отчалили два катера. Через сколько часов после начала движения они встретятся, если собственная скорость каждого катера равна 24,5 км/ч, расстояние между пристанями − 171,5 км, а скорость течения − 1,6 км/ч? Есть ли в условии задачи лишние данные?
Решение
24,5 − 1,6 − скорость катера против течения.
24,5 + 1,6 − скорость катера по течению, тогда:
24,5 − 1,6 + 24,5 + 1,6 = (24,5 + 24,5) + (1,6 − 1,6) = 49 + 0 = 49 км/ч суммарная скорость катеров. Получается, для того чтобы найти суммарную скорость катеров нам не нужно знать скорость течения реки.
171,5 : 49 = 3,5 (ч) — будут плыть катера до встречи.
Ответ: 3,5 ч; скорость течения реки лишнее данное.
Задание № 1168
От двух пристаней навстречу друг другу одновременно отчалили лодка и теплоход. Лодка, собственная скорость которой равна 10,8 км/ч, двигалась по течению реки, а теплоход, собственная скорость которого − 30,2 км/ч, двигался против течения. Через сколько часов после начала движения они встретятся, если расстояние между пристанями равно 205 км?
Решение задачи
1) 10,8 + 30,2 = 41 (км/ч) — скорость сближения лодки и теплохода.
2) 205 : 41 = 5 (ч) — будут плыть лодка и теплоход до встречи.
Ответ: 5 ч.
Задание № 1169
Рыбак переправлялся через реку на лодке со скоростью 20 м/мин. На какое расстояние снесет лодку, если ширина реки 150 м, а скорость течения равна 0,2 м/с?
Решение задачи
1) 150 : 20 = 7,5 (мин) — потребуется лодке, чтобы переплыть реку.
2) 0,2 м/с = 0,2 * 60 = 12 (м/мин)
3) 7,5 * 12 = 90 м расстояние на которое снесет лодку.
Ответ: 90 м.
Задание № 1170
На спуск с горы турист тратит 0,75 времени, нужного ему для подъема на эту гору. С горы турист спускается за 1,2 ч, а поднимается со скоростью 7,5 м/мин. Какова высота горы, на которую поднимается турист?
Решение задачи
1,2 * 60 мин = 72 мин
1) 72 : 0,75 = 96 (мин) — турист поднимается на гору;
2) 96 * 7,5 = 720 (м) — высота горы.
Ответ: 720 м.
Задание № 1171
Машинист скорого поезда, движущегося со скоростью 56 км/ч, заметил, что встречный товарный поезд, который двигался со скоростью 34 км/ч, прошел мимо него за 15 с. Какова длина товарного поезда?
Решение задачи
15 с : 60 = 0,25 мин
1) 56 + 34 = 90 (км/ч) — скорость сближения поездов.
90 км/ч = 90 км/ч * 1000 м : 60 мин = 1500 м/мин
2) 1500 * 0,25 = 375 (м) — длина товарного поезда.
Ответ: 375 м.
280
Ответы к странице 280
Задание № 1172
Машинист товарного поезда, который двигался со скоростью 36 км/ч, заметил, что встречный пассажирский поезд, длина которого 180 м, прошел мимо него за 8 с. С какой скоростью двигался пассажирский поезд?
Решение задачи
1) 180 : 8 = 22,5 (м/с) — скорость сближения поездов.
22,5 м/с = 22,5 * 3600 : 1000 = 81 км/ч;
2) 81 − 36 = 45 (км/ч) скорость пассажирского поезда.
Ответ: 45 км/ч.
Задание № 1173
В 9 ч утра Незнайка вышел из Цветочного города в Солнечный со скоростью 3,6 км/ч. В 12 ч 30 мин следом за ним на вездеходе собственной конструкции выехали Винтик и Шпунтик. Вездеход двигался со скоростью 12 км/ч и прибыл в Солнечный город одновременно с Незнайкой. Сколько времени шел Незнайка? Каково расстояние между Цветочным и Солнечным городами?
Решение задачи
1) 12 ч 30 мин − 9 ч = 3,5 ч — шел Незнайка до 12 ч 30 мин.
2) 3,5 * 3,6 = 12,6 (км) — прошел Незнайка до 12 ч 30 мин.
3) 12 − 3,6 = 8,4 (км/ч) — скорость сближения Незнайки и вездехода.
4) 12,6 : 8,4 = 1,5 (ч) — ехал вездеход, пока не догнал Незнайку.
5) 12 * 1,5 = 18 (км) — расстояние между городами.
6) 12 ч 30 мин + 1 ч 30 мин = 14 ч время, в которое Незнайка и вездеход добрались до города.
7) 14 − 9 = 5 (ч) — шел Незнайка из одного города в другой.
Ответ: 5 ч; 18 км.
Задание № 1174
Кот Мурзик купил на базаре 18 кг сметаны, а кот Мурчик − 28 кг. За обедом Мурзик съел 0,65 купленной сметаны, а Мурчик − 3/7 своей сметаны. Кто из котов съел больше сметаны и на сколько килограммов?
Решение задачи
1) 18 * 0,65 = 11,7 (кг) — сметаны съел Мурзик.
2) 28 : 7 * 3 = 4 * 3 = 12 (кг) — сметаны съел Мурчик.
3) 12 − 11,7 = 0,3 (кг) — сметаны съел Мурчик больше Мурзика.
Ответ: на 0,3 кг сметаны съел Мурчик больше Мурзика.
Задание № 1175
Мальчик−с−пальчик в сапогах−скороходах за 3 ч преодолел 1590 км. За первый час он прошел 15/53 этого расстояния, за второй − 25/57 оставшегося пути. Сколько километров он преодолел за третий час?
Решение задачи
1) 1590 : 53 * 15 = 30 * 15 = 450 (км) — преодолел мальчик−с−пальчик за первый час.
2) 1590 − 450 = 1140 (км) — осталось пройти после первого часа пути.
3) 1140 : 57 * 25 = 20 * 25 = 500 (км) — преодолел мальчик−с−пальчик за второй час.
4) 1590 − (450 + 500) = 1590 − 950 = 640 (км) — преодолел мальчик−с−пальчик за третий час.
Ответ: 640 км.
Задание № 1176
Было собрано 240 кг семечек подсолнечника. Сколько подсолнечного масла можно изготовить из собранных семечек, если масса зерна составляет 0,7 массы семечек подсолнечника, а масса полученного масла − 0,4 массы зерна?
Решение задачи
1) 240 * 0,7 = 168 (кг) — весит зерно.
2) 168 * 0,4 = 67,2 (кг) — подсолнечного масла можно изготовить из собранных семечек.
Ответ: 67,2 кг.
Задание № 1177
Три великана ели на обед пельмени. Первый великан съел 1200 пельменей, второй − 8/15 того, что съел первый, а третий − 0,85 того, что съел второй. Сколько всего пельменей съели великаны?
Решение задачи
1) 1200 : 15 * 8 = 80 * 8 = 640 (п.) — съел второй великан.
2) 640 * 0,85 = 544 (п.) — съел третий великан.
3) 1200 + 640 + 544 = 2384 (п.) — всего съели три великаны.
Ответ: 2384 пельменя.
Задание № 1178
Периметр треугольника равен 48 см. Длина одной из сторон треугольника составляет 5/16периметра, а длина второй − 0,64 длины первой стороны. Найдите стороны треугольника.
Решение задачи
1) 48 : 16 * 5 = 3 * 5 = 15 (см) — длина первой стороны треугольника.
2) 15 * 0,64 = 9,6 (см) — длина второй стороны треугольника.
3) 48 − (15 + 9,6) = 48 − 24,6 = 23,4 (см) — длина третьей стороны треугольника.
Ответ: 15 см; 9,6 см; 23,4 см.
Задание № 1179
Основание равнобедренного треугольника равно 6,5 см, а длина боковой стороны составляет 0,8 длины основания. Вычислите периметр треугольника.
Решение задачи
1) 6,5 * 0,8 = 5,2 (см) — длина боковой стороны треугольника.
2) 6,5 + 2 * 5,2 = 6,5 + 10,4 = 16,9 (см) — периметр треугольника.
Ответ: 16,9 см.
Задание № 1180
Вычислите:
1) 0,1 от суммы чисел 34,56 и 7,94;
2) 5/6 от разности чисел 42,3 и 5,4;
3) 0,36 от произведения чисел 12,5 и 1,6;
4) 7/12 от частного чисел 14,4 и 0,01.
Решение
1) 0,1 * (34,56 + 7,94) = 0,1 * 42,5 = 4,25
2) (42,3 − 5,4) ∗ 5/6 = 36,9 : 6 ∗ 5 = 6,15 ∗ 5 = 30,75
3) 0,36 * (12,5 * 1,6) = 0,36 * 20 = 7,2
4) (14,4 : 0,01) ∗ 7/12 = 1440 : 12 ∗ 7 = 120 ∗ 7 = 840
281
Ответы к странице 281
Задание № 1181
Средняя продолжительность жизни белого медведя − 32 года, что составляет 2/3 средней продолжительности жизни носорога, 4/5 − льва и 4/25 − слона. Найдите среднюю продолжительность жизни носорога, льва и слона.
Решение задачи
1) 32 : 2 * 3 = 16 * 3 = 48 (лет) — средняя продолжительность жизни носорога.
2) 32 : 4 * 5 = 8 * 5 = 40 (лет) — средняя продолжительность жизни льва.
3) 32 : 4 * 25 = 8 * 25 = 200 (лет) — средняя продолжительность жизни слона.
Ответ: 48 лет; 40 лет; 200 лет.
Задание № 1182
Фермер собрал в своем саду урожай фруктов. Яблоки составляли 0,6 собранных фруктов. Яблок сорта белый налив было 35 кг, и они составляли 7/18 всех яблок. Сколько килограммов фруктов собрал фермер?
Решение задачи
1) 35 : 7 * 18 = 5 * 18 = 90 (кг) — яблок собрал фермер.
2) 90 : 0,6 = 150 (кг) — фруктов всего собрал фермер.
Ответ: 150 кг.
Задание № 1183
Когда автомобиль проехал 0,3, а потом еще 0,4 всего пути, то оказалось, что он проехал на 12 км больше половины пути, который нужно было проехать. Сколько километров должен был проехать автомобиль?
Решение через х
Пусть x км весь путь, тогда:
0,3x + 0,4x = 0,7x (км) — проехал автомобиль.
0,5x км — половина пути.
Так как автомобиль проехал на 12 км больше половины пути, то:
0,7x − 0,5x = 12
0,2x = 12
x = 12 : 0,2
x = 60 (км) — должен был проехать автомобиль.
Ответ: 60 км.
Задание № 1184
В двух ящиках лежали яблоки. В первом ящике было 22,4 кг яблок, что составляло 0,35 всех яблок. Сколько килограммов яблок лежало во втором ящике?
Решение задачи
1) 22,4 : 0,35 = 64 (кг) — яблок было всего.
2) 64 − 22,4 = 41,6 (кг) — яблок лежало во втором ящике.
Ответ: 41,6 кг.
Задание № 1185
За день продали 3,6 ц колбасы, что составляло 0,48 ее запасов. Сколько центнеров колбасы осталось?
Решение задачи
1) 3,6 : 0,48 = 7,5 (ц) — колбасы было всего.
2) 7,5 − 3,6 = 3,9 (ц) — колбасы осталось.
Ответ: 3,9 ц.
Задание № 1186
Звездолет «Серебряная молния» вылетел с космической станции STAR на станцию MOON. В первый час звездолет пролетел 48,72 млн.км, что составляло 0,56 того, что ему осталось пролететь. Найдите расстояние между станциями.
Решение задачи
1) 48,72 : 0,56 = 87 (млн.км) — оставалось пролететь звездолету.
2) 87 + 48,72 = 135,72 (млн.км) — расстояние между станциями.
Ответ: 135,72 млн.км.
Задание № 1187
Марья−искусница испекла пирожки с маком и с вишней. Пирожки с маком составляли 5/17 от общего количества. Сколько всего пирожков испекла Марья−искусница, если пирожков с вишней было на 28 больше, чем с маком?
Решение задачи через х
Пусть x пирожков испекли всего, тогда:
5/17x было пирожков с маком;
x − 5/17x = (17/17 − 5/17)х = 12/17x пирожков было с вишней.
Так как, пирожков с вишней было на 28 больше, чем с маком, то:
12/17x − 5/17x = 28
7/17x = 28
x = 28 : 7 * 17 = 4 * 17 = 68 (п.) всего испекла Марья−искусница.
Ответ: 68 пирожков.
Задание № 1188
Найдите число:
1) 0,8 которого составляет сумма чисел 19,4 и 20,64;
2) 4/15 которого составляет разность чисел 7 и 4,76;
3) 0,42 которого составляет произведение чисел 7,2 и 3,5;
4) 6/7 которого составляет частное чисел 0,54 и 0,9.
Решение
1) (19,4 + 20,64) : 0,8 = 40,04 : 0,8 = 50,05
2) (7 − 4,76) : 4/15 = 2,24 : 4 ∗ 15 = 0,56 ∗ 15 = 8,4
3) (7,2 * 3,5) : 0,42 = 25,2 : 0,42 = 60
4) (0,54 : 0,9) : 6/7 = 0,6 : 6 ∗ 7 = 0,1 ∗ 7 = 0,7
Задание № 1189
На рисунке 215 угол DOE − прямой. Какие из изображенных углов тупые? Сколько острых углов изображено на этом рисунке?
Решение
Тупые углы: ∠BOC, ∠BOE, ∠AOD.
Острые углы: ∠AOC, ∠AOE, ∠DOB.
282
Ответы к странице 282
Задание № 1190
Начертите тупой угол и проведите из его вершины луч так, чтобы образовался прямой угол. Сколько решений имеет задача?
Решение
1 вариант:
∠AOB − тупой, ∠AOC − прямой.
2 вариант:
∠AOB − тупой, ∠COB − прямой.
3 вариант:
∠AOB − тупой, ∠COB − прямой.
4 вариант:
∠AOB − тупой, ∠AOC − прямой.
Ответ: задача имеет 4 решения.
Задание № 1191
Найдите градусную меру угла BAE, если ∠BAD = 67°, ∠CAD = 34°, ∠CAE = 56°(рис.216).
Решение
∠DAE = ∠CAE − ∠CAD = 56° − 34° = 22°;
∠BAE = ∠BAD + ∠DAE = 67° + 22° = 89°.
Ответ: ∠BAE = 89°.
Задание № 1192
Угол MOK − развернутый, ∠MOA = 62°, луч OC − биссектриса угла AOK. Вычислите градусную меру угла COA.
Решение
∠AOK = ∠MOK − ∠MOA = 180° − 62° = 118°
∠COA = ∠COK = ∠AOK : 2 = 118° : 2 = 59°
Ответ: ∠COA = 59°.
Задание № 1193
Запишите все треугольники и прямоугольники, изображенные на рисунке 217.
Решение
Треугольники: ΔBCE; ΔADE; ΔBEM; ΔAME; ΔBEA.
Прямоугольники: ABCD; MBCE; AMED.
Задание № 1194
Периметр треугольника равен 30 см, одна из его сторон − 7,4 см, а две другие стороны равны между собой. Найдите длины равных сторон.
Решение
1) 30 − 7,4 = 22,6 (см) — суммарная длина двух других сторон.
2) 22,6 : 2 = 11,3 (см) — длина каждой из равных сторон.
Ответ: 11,3 см.
Задание № 1195
Начертите прямоугольник со сторонами 6 см и 2 см. Постройте квадрат, периметр которого равен периметру этого прямоугольника. Вычислите площади прямоугольника и квадрата.
Решение
P = 2 * (6 + 2) = 2 * 8 = 16 (см) — периметр прямоугольника;
16 : 4 = 4 см длина стороны квадрата.
SABCD = 6∗2 = 12 (см2)
SEFHG = 4∗4 = 16 (см2)
Ответ: 12 см2, 16 см2.
Задание № 1196
Квадрат со стороной 1 м разделили на четыре равные части и провели диагональ (рис.218). Чему равна площадь заштрихованной фигуры?
Решение
Разделим квадрат на 16 равных квадратов, тогда
получаем 4 целиком закрашенных квадратов и 4 закрашенных наполовину
4 + (4 : 2) = 4 + 2 = 6 (кв.) — закрашенных
6/16 = 0,375 (м2) — площадь закрашенной фигуры.
Ответ: 0,375 м2.
Задание № 1197
Периметр квадрата равен 11,2 см. Найдите периметр прямоугольника, площадь которого равна площади данного квадрата, а одна из сторон прямоугольника − 9,8 см?
Решение
1) 11,2 : 4 = 2,8 (см) — длина стороны квадрата.
2) 2,8 * 2,8 = 7,84 (см2) — площадь квадрата.
3) 7,84 : 9,8 = 0,8 (см) — длина второй стороны прямоугольника.
4) 2 * (9,8 + 0,8) = 2 * 10,6 = 21,2 (см) — периметр прямоугольника.
Ответ: 21,2 см.
Задание № 1198
Длина прямоугольника равна 45 см. На сколько уменьшится площадь этого прямоугольника, если его ширина уменьшится на 4 см?
Решение
Пусть x см ширина прямоугольника, тогда
45x (см2) — площадь прямоугольника.
x − 4 (см) — уменьшенная ширина прямоугольника.
45 * (x − 4) = 45x − 180 (см2) — уменьшенная площадь прямоугольника.
45x − (45x − 180) = 45x − 45x + 180 = 180 (см2)
Ответ: при уменьшении ширины прямоугольника на 4 см его площадь уменьшится на 180 см2.
Задание № 1199
Ребро одного куба в 3 раза больше ребра второго. Во сколько раз объем первого куба больше, чем объем второго?
Решение
Пусть ребро одного куба равно a, тогда
V1=a3
3a — ребро второго куба.
V2 = (3a)3 = 27a3
27a3 : a3 = 27.
Ответ: в 27 раз объем большего куба больше объема меньшего куба.
Задание № 1200
Объем прямоугольного параллелепипеда равен 320 см3. Каждое измерение этого параллелепипеда уменьшили в 2 раза. Найдите объем полученного параллелепипеда.
Решение
Пусть a, b и c измерения прямоугольного параллелепипеда, тогда:
V1 = abc = 320 (см3)
0,5a, 0,5b и 0,5c в 2 раза уменьшенные измерения прямоугольного параллелепипеда;
V2 = 0,5a ∗ 0,5b ∗ 0,5c = 0,125 abc = 0,125 ∗ 320 = 40 (см3) — объем уменьшенного прямоугольного параллелепипеда.
Ответ: 40 см3.
Задание № 1201
Длина прямоугольного параллелепипеда равна 12 см, ширина − 5 см, высота − 9 см. На сколько увеличится объем параллелепипеда, если каждое его измерение увеличить на 1 см?
Решение
V1 = 12 ∗ 5 ∗ 9 = 60 ∗ 9 = 540 (см3) − объем исходного параллелепипеда.
V1 = (12 + 1) ∗ (5 + 1) ∗ (9 + 1) = 13 ∗ 6 ∗ 10 = 78 ∗ 10 = 780 (см3) − объем увеличенного параллелепипеда.
780 − 540 = 240 (см3) — разность размеров двух параллелепипедов.
Ответ: 240 см3.
283
Ответы к странице 283
Задание № 1202
Длина прямоугольного параллелепипеда равна 36 см, ширина составляет 5/9 его длины. Найдите объем параллелепипеда, если его ширина составляет 5/4 высоты.
Решение
1) 36 : 9 * 5 = 20 (см) — ширина параллелепипеда.
2) 20 : 5 * 4 = 16 (см) — высота параллелепипеда.
3) 36 * 20 * 16 = 11520 (см3) — объем параллелепипеда.
Ответ: 11520 см3.
Задание № 1203
Ширина прямоугольного параллелепипеда равна 42 см, что составляет 7/15 его длины, а высота составляет 5/9 длины. Найдите объем параллелепипеда.
Решение
1) 42 : 7 * 15 = 90 (см) — длина параллелепипеда.
2) 90 : 9 * 5 = 50 (см) — высота параллелепипеда.
3) 42 * 90 * 50 = 189000 (см3) — объем параллелепипеда.
189000 см3 = 189 дм3
Ответ: 189 дм3.
Задание № 1204
Прямолинейный участок шоссе проходит через села Вишневое, Яблоневое и Грушевое. Расстояние между селами Вишневое и Яблоневое равно 3,2 км, что в 1,5 раза меньше расстояния между селами Яблоневое и Грушевое. Найдите расстояние между селами Вишневое и Грушевое. Сколько решений имеет задача?
Решение
1 вариант:
1) 3,2 * 1,5 = 4,8 (км) — расстояние между Яблоневым и Грушевым.
2) 3,2 + 4,8 = 8 (км) — расстояние между Вишневым и Грушевым.2 вариант:
1) 3,2 * 1,5 = 4,8 (км) — расстояние между Яблоневым и Грушевым.
2) 4,8 − 3,2 = 1,6 (км) — расстояние между Вишневым и Грушевым.
Ответ: 8 км или 1,6 км.
Задание № 1205
В бассейн, имеющий форму прямоугольного параллелепипеда, ежесекундно поступает 0,8 л воды и ежесекундно выливается 0,75 л воды. Длина бассейна равна 4,05 м, ширина − 120 см, глубина 75 см. За сколько часов наполнится бассейн?
Решение
4,05 м = 40,5 дм;
120 см = 12 дм;
75 см = 7,5 дм.
0,8 − 0,75 = 0,05 л = 0,05 дм3 — воды наполняется бассейн каждую секунду.
40,5 * 12 * 7,5 = 3645 дм3 — объем бассейна.
3645 : 0,05 = 72900 с = 20,25 ч потребуется, чтобы наполнить бассейн.
Ответ: 20,25 ч.
Задание № 1206
В двух мешках было 82,3 кг яблок, причем в одном мешке было на 7,9 кг больше, чем во втором. Сколько килограммов яблок было в каждом мешке?
Решение
Пусть x кг яблок было в одном мешке, тогда
x + 7,9 кг яблок было в другом мешке,
а всего было 82,3 кг яблок.
Составим уравнение:
x + x + 7,9 = 82,3
2x = 82,3 − 7,9
x = 74,4 : 2
x = 37,2 (кг) — яблок было в одном мешке.
x + 7,9 = 37,2 + 7,9 = 45,1 кг яблок было в другом мешке.
Ответ: 37,2 кг; 45,1 кг.
Задание № 1207
За 2 ч турист прошел 9,6 км, причем в первый час он прошел на 1,2 км меньше, чем во второй. Найдите, какое расстояние проходил турист за каждый час.
Решение
Пусть x км прошел турист за первый час, тогда
x + 1,2 км прошел турист за второй час,
а всего турист прошел 9,6 км.
Составим уравнение:
x + x + 1,2 = 9,6
2x = 9,6 − 1,2
x = 8,4 : 2
x = 4,2 (км) — прошел турист за первый час.
x + 1,2 = 4,2 + 1,2 = 5,4 км прошел турист за второй час.
Ответ: 4,2 км; 5,4 км.
Задание № 1208
Маша и Вера собрали 17,6 кг груш, причем Маша собрала на 2,7 кг груш больше, чем Вера. Сколько килограммов груш собрала каждая девочка?
Решение
Пусть x кг груш собрала Вера, тогда
(x + 2,7) кг груш собрала Маша,
а всего Маша и Вера собрали 17,6 кг груш.
Составим уравнение:
x + x + 2,7 = 17,6
2x = 17,6 − 2,7
x = 14,9 : 2
x = 7,45 (кг) — груш собрала Вера.
x + 2,7 = 7,45 + 2,7 = 10,15 (кг) — груш собрала Маша.
Ответ: 7,45 кг; 10,15 кг.
Задание № 1209
Крокодил Гена съел в 4 раза больше мороженого, чем Чебурашка. Сколько мороженого съел каждый из них, если Чебурашка съел на 2,4 кг меньше, чем крокодил Гена?
Решение
Пусть x кг мороженого съел Чебурашка, тогда
4x кг мороженого съел крокодил Гена,
а Чебурашка съел на 2,4 кг меньше, чем крокодил Гена.
Составим уравнение:
4x − x = 2,4
3x = 2,4
x = 2,4 : 3
x = 0,8 (кг) — мороженого съел Чебурашка.
4x = 4 * 0,8 = 3,2 кг мороженого съел крокодил Гена.
Ответ: 0,8 кг; 3,2 кг.
Задание № 1210
За два дня путешествия велотуристы преодолели 126 км, причем во второй день они проехали в 3,5 раза больше, чем в первый. Найдите, сколько километров они проезжали каждый день.
Решение
Пусть x км проехали велотуристы в первый день, тогда
3,5x км проехали велотуристы во второй день,
а за два дня путешествия велотуристы преодолели 126 км.
Составим уравнение:
x + 3,5x = 126
4,5x = 126
x = 126 : 4,5
x = 28 (км) — проехали велотуристы в первый день.
3,5x = 3,5 * 28 = 98 км проехали велотуристы во второй день.
Ответ: 28 км; 98 км.
Задание № 1211
Звездолет «Сириус» пролетает за 1 с на 650 км больше, чем звездолет «Арктур». Найдите скорость каждого звездолета (в километрах за секунду), если скорость «Арктура» в 2,3 раза меньше, чем скорость «Сириуса».
Решение
Пусть x км/с скорость «Арктура», тогда
2,3x км/с скорость «Сириуса»,
а звездолет «Сириус» пролетает за 1 с на 650 км больше, чем звездолет «Арктур».
Составим уравнение:
2,3x − x = 650
1,3x = 650
x = 650 : 1,3
x = 500 (км/с) — скорость «Арктура».
2,3x = 2,3 * 500 = 1150 (км/с) — скорость «Сириуса».
Ответ: 500 км/с; 1150 км/с.
Задание № 1212
Ниф−Ниф, Нуф−Нуф и Наф−Наф купили строительные материалы для ремонта своих домиков, потратив на их приобретение 7400 р. Найдите затраты каждого поросенка, если Ниф−Ниф заплатил на 643 р., а Нуф−Нуф − на 325 р. больше, чем Наф−Наф.
Решение
Пусть x рублей потратил Наф−Наф, тогда
x + 643 рублей потратил Ниф−Ниф;
x + 325 рублей потратил Нуф−Нуф.
Всего было потрачено 7400 р.
Составим уравнение:
x + x + 643 + x + 325 = 7400
3x = 7400 − 643 − 325
x = 6432 : 3
x = 2144 рублей потратил Наф−Наф;
x + 643 = 2144 + 643 = 2787 рублей потратил Ниф−Ниф;
x + 325 = 2144 + 325 = 2469 рублей потратил Нуф−Нуф.
Ответ: 2144 р.; 2787 р.; 2469 р.
Задачи 1206-1212 — на нахождение слагаемых по сумме и разности, их можно решать не через х, а по действиям через уравнивание частей. Алгоритм тут >>
284-285
Ответы к странице 284-285
Задание № 1213
За три дня продали 280 кг помидоров, причем в первый день продали в 2,8 раз меньше, чем во второй, и в 4,2 раза меньше, чем в третий. Сколько килограммов помидоров продавали каждый день?
Решение
Пусть x кг помидоров продали в первый день, тогда:
2,8x кг помидоров продали во второй день;
4,2x кг помидоров продали в третий день;
а всего продали 280 кг.
Составим уравнение:
x + 2,8x + 4,2x = 280
8x = 280
x = 280 : 8
x = 35 (кг) — помидоров продали в первый день, тогда:
2,8x = 2,8 * 35 = 98 (кг) — помидоров продали во второй день.
4,2x = 4,2 * 35 = 147 (кг) — помидоров продали в третий день.
Ответ: 35 кг; 98 кг; 147 кг.
Задание № 1214
Два автомобиля выехали навстречу друг другу из двух городов, расстояние между которыми равно 960 км. Через 6,5 после начала движения они еще не встретились и расстояние между ними было 115 км. Найдите скорость каждого автомобиля, если скорость одного из них на 10 км/ч больше скорости второго.
Решение
Пусть x км/ч скорость первого автомобиля, тогда:
x + 10 км/ч скорость второго автомобиля;
6,5x км проехал первый автомобиль;
6,5(x + 10) км проехал второй автомобиль;
6,5x + 6,5(x + 10) км суммарное расстояние которое проехали оба автомобиля;
а через 6,5 после начала движения они еще не встретились и расстояние между ними было 115 км.
Составим уравнение:
6,5x + 6,5(x + 10) = 960 − 115
6,5x + 6,5x + 65 = 845
13x = 845 − 65
x = 780 : 13
x = 60 (км/ч) — скорость первого автомобиля.
x + 10 = 60 + 10 = 70 (км/ч) — скорость второго автомобиля.
Ответ: 60 км/ч; 70 км/ч.
Задание № 1215
Из двух городов, расстояние между которыми равно 112 км, навстречу друг другу одновременно выехали мотоциклист и велосипедист. Найдите скорость каждого из них, если они встретились через 1,6 ч после выезда и скорость мотоциклиста в 4 раза больше скорости велосипедиста.
Решение
Пусть x км/ч скорость велосипедиста, тогда
4x км/ч скорость мотоциклиста;
1,6x км проехал до встречи велосипедист;
1,6 * 4x = 6,4x км проехал до встречи мотоциклист;
а суммарно они проехали расстояние, равное расстоянию между городами.
Составим уравнение:
1,6x + 6,4x = 112
8x = 112
x = 112 : 8
x = 14 (км/ч) — скорость велосипедиста.
4x = 4 * 14 = 56 (км/ч) — скорость мотоциклиста.
Ответ: 14 км/ч; 56 км/ч.
Задание № 1216
Собственная скорость лодки в 8 раз больше скорости течения реки. Найдите скорость течения и собственную скорость лодки, если:
1) за 5 часов движения против течения лодка прошла 42 км;
2) за 4 часа движения по течению реки лодка прошла 50,4 км.
Решение
1) Пусть x км/ч скорость течения реки, тогда
8x км/ч скорость лодки;
8x − x = 7x (км/ч) — скорость лодки против течения;
а за 5 часов движения против течения лодка прошла 42 км.
Составим уравнение:
7x = 42 : 5
7x = 8,4
x = 8,4 : 7
x = 1,2 (км/ч) — скорость течения реки.
8x = 8 * 1,2 = 9,6 (км/ч) — скорость лодки.
Ответ: 1,2 км/ч; 9,6 км/ч.2) Пусть x км/ч скорость течения реки, тогда:
8x км/ч скорость лодки;
8x + x = 9x км/ч скорость лодки по течению,
а за 4 часа движения по течению реки лодка прошла 50,4 км.
Составим уравнение:
9x = 50,4 : 4
9x = 12,6
x = 12,6 : 9
x = 1,4 (км/ч) — скорость течения реки.
8x = 8 * 1,4 = 11,2 (км/ч) — скорость лодки.
Ответ: 1,4 км/ч; 11,2 км/ч.
Задание № 1217
Сумма длины и ширины прямоугольника равна 12 дм, причем ширина на 3,2 дм меньше длины. Вычислите площадь прямоугольника.
Решение
Пусть x дм ширина прямоугольника, тогда
x + 3,2 дм длина прямоугольника,
а сумма длины и ширины прямоугольника равна 12 дм.
Составим уравнение:
x + x + 3,2 = 12
2x = 12 − 3,2
x = 8,8 : 2
x = 4,4 (дм) — ширина прямоугольника.
x + 3,2 = 4,4 + 3,2 = 7,6 дм длина прямоугольника.
S = 4,4 * 7,6 = 33,44 дм2 площадь прямоугольника.
Ответ: 33,44 дм2.
Задание № 1218
Ежик Остроколючкин собрал 49 кг грибов. Белых грибов оказалось в 8 раз больше, чем маслят, а маслят − в 5 раз меньше, чем опят. Ежик отнес грибы на рынок и продал их: белые грибы − по 125 р. за килограмм, маслята − по 100 р., а опята − по 68 р. Сколько денег заработал Остроколючкин?
Решение
Пусть x кг маслят собрал ежик, тогда
8x кг белых грибов собрал ежик;
5x кг опят собрал ежик;
а всего ежик собрал 49 кг грибов.
Составим уравнение:
x + 8x + 5x = 49
14x = 49
x = 49 : 14
x = 3,5 (кг) — маслят собрал ежик.
8x = 8 * 3,5 = 28 (кг) — белых грибов собрал ежик.
5x = 5 * 3,5 = 17,5 (кг) — опят собрал ежик.
3,5 * 100 = 350 (р.) — выручил ежик на продаже маслят.
28 * 125 = 3500 (р.) — выручил ежик на продаже белых грибов.
17,5 * 68 = 1190 (р.) — выручил ежик на продаже опят.
350 + 4200 + 1190 = 5040 (р.) — заработал Остроколючкин.
Ответ: 5040 рублей.
Задание № 1219
В двух мешках было 74,8 кг сахара. Если из одного мешка пересыпать во второй 6,3 кг, то в обоих мешках сахара станет поровну. Сколько килограммов сахара было в каждом мешке?
Решение
Пусть x кг сахара было в первом мешке, тогда
74,8 − x кг сахара было во втором мешке;
x − 6,3 кг сахара стало в первом мешке;
74,8 − x + 6,3 = 81,1 − x кг сахара стало во втором мешке;
а сахара в мешках стало поровну.
Составим уравнение:
x − 6,3 = 81,1 − x
x + x = 81,1 + 6,3
2x = 87,4
x = 43,7 (кг) — сахара было в первом мешке.
74,8 − x = 74,8 − 43,7 = 31,1 (кг) — сахара было во втором мешке.
Ответ: 43,7 кг; 31,1 кг.
Задание № 1220
Вася и Маша собрали вместе 26,2 кг клубники. Вася отдал Маше 3,5 кг своей клубники, после чего у него осталось на 2,4 кг клубники больше, чем стало у Маши. Сколько килограммов клубники собрала Маша?
Решение
Пусть x кг клубники собрала Маша, тогда
26,2 − x кг клубники собрал Вася;
x + 3,5 кг клубники стало у Маши;
26,2 − x − 3,5 = 22,7 − x (кг) клубники стало у Васи;
а у Васи осталось на 2,4 кг клубники больше, чем стало у Маши.
Составим уравнение:
22,7 − x − (x + 3,5) = 2,4
22,7 − x − x − 3,5 = 2,4
22,7 − 2x − 3,5 = 2,4
2x = 22,7 — 3,5 — 2,4
2x = 16,8
x = 16,8 : 2
x = 8,4 (кг) — клубники собрала Маша.
Ответ: 8,4 кг.
Задание № 1221
Если в некоторой десятичной дроби перенести запятую влево через две цифры, то она уменьшится на 158,4. Найдите эту дробь.
Решение
Пусть x − искомая дробь. Так как запятую перенесли влево через две цифры, значит эту дробь умножили на 0,01, тогда
0,01x стала новая дробь,
а новая дробь меньше исходной на 158,4.
Составим уравнение:
x − 0,01x = 158,4
0,99x = 158,4
x = 158,4 : 0,99
x = 160,0 − искомая дробь.
Ответ: 160,0.
Задание № 1222
Решите кроссворд:
По горизонтали:
3. Решение уравнения.
6. Вид многоугольника.
7. Прямоугольник у которого все стороны равны.
11. Число, определяющее положение точки на координатном луче.
12. 1/10 метра.
15. 1000 килограммов.
16. Вид четырехугольника.
17. Прибор для измерения углов.
19. Знак, разделяющий целую и дробную части десятичной дроби.
По вертикали:
1. Результат умножения.
2. Геометрическая фигура.
4. Третья степень числа.
5. Луч, делящий угол пополам.
8. Трехзначное число.
9. Результат вычитания.
10. 1/1000 килограмма.
13. Результат сложения.
14. Знак арифметического действия.
16. Сумма сторон многоугольника.
18. В равенстве 27 = 6 * 4 + 3 число 3 есть … при делении числа 27 на число 6.