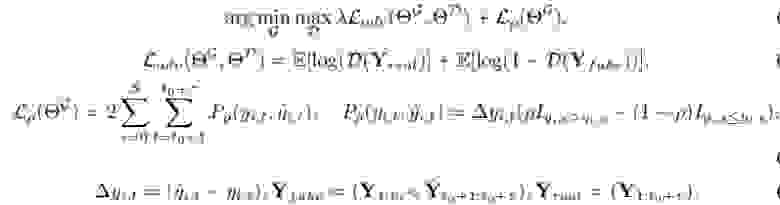Понятие временных рядов в бизнес аналитике - Контакты компаний и предприятий

Время на прочтение
9 мин

Количество просмотров 13K

Читая главы книг по статистическому анализу, я часто вижу анализ или прогнозирование временных рядов. В этой статье я опишу некоторые основные понятия в теории анализа временных рядов, классические статистические алгоритмы прогнозирования а так же рассмотрю применение моделей глубоких нейросетей для таких задач .

Поэтому, если Вы готовы погрузиться в одну из интереснейших тем статистики и Вы любитель машинного обучения, продолжайте читать).

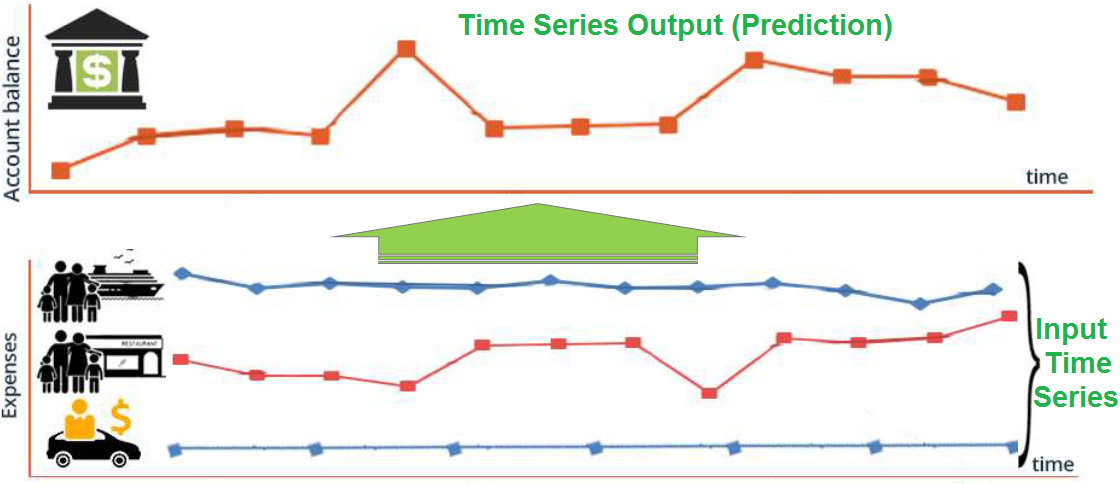
Временной ряд отличается от обычной последовательности тем, что каждое его значение взято на одинаково расположенных точках времени. На обложке статьи показан пример.

Стоит упомянуть, что мы можем найти очень большое количество литературы об алгоритмах анализа временных рядов, потому, что необходимость прогнозировать именно этот тип данных возникает задолго до машинного обучения. В промышленности многие специалисты по данным до сих пор используют простые авторегрессионные модели вместо глубокого обучения для предсказания временных рядов. Обычно основными причинами выбора этих методов остаются интерпретируемость, ограниченность данных, простота использования и стоимость обучения. Поэтому, первая часть статьи посвящена статистике: статистические понятия в анализе временных рядов и классические алгоритмы прогнозирования.

Компоненты и временного ряда и аналитические коэффициенты

Основные понятия в статистическом анализе временных рядов:

Тренд — компонента, описывающая долгосрочное изменение уровня ряда.

Сезонность — компонента, обозначаемая как Q, описывает циклические изменения уровня ряда.

Ошибка (random noise) — непрогнозируемая случайная компонента, описывает нерегулярные изменения в данных, необъяснимые другими компонентами.

Автокорреляция — статистическая взаимосвязь между последовательностями величин одного ряда. Это один из самых важных коэффициентов в анализе временного ряда. Чтобы посчитать автокорреляцию, используется корреляция между временным рядом и её сдвинутой копией от величины временного сдвига. Сдвиг ряда называется лагом.

Автокорреляционная функция— график автокорреляции при разных лагах

Компоненты ряда

К такому графику, можно добавить также визуализацию автокорреляционной функции.

Стационарный ряд — ряд, в котором свойства не зависят от времени. При таких компонентах ряда, как тренд или сезонность, ряд не является стационарным. Это интуитивное понятие. На практике есть два вида стационарности — строгая и слабая. В следующих алгоритмах, нам достаточно слабой. Она заключается в постоянной дисперсии (без гетероскедастичности) и в постоянности среднего значения ряда.

Гетероскедастичность — не равномерная дисперсия. То есть, не однородность наблюдений.

В python, например, реализованы библиотеки, через которые мы можем проверить ряд на стационарность, гетероскедастичность или построить автокорреляционную функцию.

Статистические модели предсказания

Перейдём к самому интересному — прогнозирование .

Авторегрессионная модель (Auto regression method (AR))

Это линейная модель, в которой прогнозированная величина является суммой прошлых значений, умноженных на числовой множитель.

$X_t = C + ϕ_1X_{t-1}+ϕ_2X_{t-2}...+ ϵ_t$

Скользящее среднее (Moving average method (MA))

Скользящее среднее-это расчет для анализа точек данных путем создания ряда средних значений различных подмножеств полного набора данных. Мне этот метод часто напоминает Тренд ряда. Скользящее среднее часто применяется для анализа временных рядов акций.

Метод скользящего среднего с авторегрессией и интегрированием (Auto regressive integrated moving average (ARIMA)

Существует также модель ARMA. Которая представляет собой сочетание моделей выше. Разница между моделями ARMA и ARIMA описана ниже.

Теорема Волда — утверждение математической статистики, согласно которому каждый временной ряд можно представить в виде скользящего среднего бесконечного порядка

Так как модель ARMA , согласно теореме о разложении Волда , теоретически достаточна для описания регулярного стационарного временного ряда, мы заинтересованы в стационарности ряда.

Почему стационарность так важна? Предполагается, что, если временной ряд ведет себя определенным образом, очень высока вероятность того, что он повторит те же паттерны в будущем.

Поэтому, нам стоит применить преобразование для нестационарного ряда. Здесь есть два подхода — удаление тренда и взятие разности. Почему тут интегрирование? В математике есть раздел — исчисление конечных разностей, в котором интегрированием называется взятие разности .

Вот такое скромное описание основных моделей прогнозирования, применяемых ещё до машинного обучения. Если вам интересна эта тема, советую почитать об ARIMA с сезонностью (Seasonal auto regressive integrated moving average (SARIMA)) или о моделях ARCH, GARCH

Нейронные сети для предсказания временных рядов

Давайте рассмотрим, с какими проблемами может столкнуться нейронный алгоритм в работе с временными рядами.

Далее, для понимания я буду напоминать основы моделей.

Первое, что приходит на ум — это, конечно, рекуррентные нейросети.

$h_t = σ(W_xx_t + W_hh_{t−1} + b_h) \ y_t = σ(W_yh_t + b_y)$

Одна из идей, сделавшая RNN неоправданно эффективными — «авторегрессия» (auto-regression), это значит, что созданная переменная добавляется в последовательность в качестве входных данных. В машинном обучении часто применяется эта техника, особенно в работе с временными рядами.

Хотя рекуррентная сеть и должна работать со всей последовательностью, к сожалению, присутствует проблема «затухающего градиента»(vanishing gradient problem). Что значит, что более старые входы не влияют на текущий выход. Такие модели, как LSTM пытаются решить эту проблему, добавляя дополнительные параметры (separate memory ).

Такие модели считывают ввод данных последовательно. Если Вам интересна это тема, советую узнать также об алгоритме Seq2Seq. Нам нужна архитектура, в которой обработка последовательности производится сразу, что практически не оставляло бы места для потери информации. Да, такая архитектура реализована в кодировщике модели Transformer. Эта характеристика позволяет модели изучать контекст переменной на основе всего его окружения. Кроме того, по сравнению с рекуррентными нейросетями, чаще всего они быстрее.

Алгоритм внимания и Transformer для временных рядов

Эта относительно новая идея слоя внимания очень интересна. Чаще всего такие модели применяются для обработки последовательностей текста. В этой статье я опишу некоторое количество разновидностей моделей со слоем внимания, но углубляться в модели, используемые только для текста(BERT, GPT-2 и XLNet), конечно, я не буду. Хотя, с их недавним успехом в НЛП можно было бы ожидать широкой адаптации к прогнозированию временных рядов.

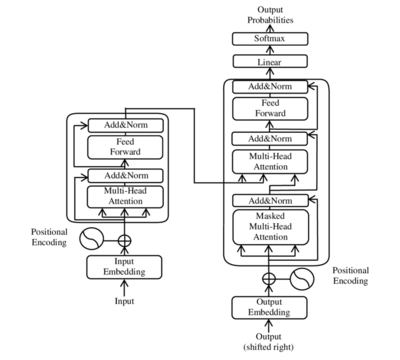
Оригинальная архитектура трансформера( Vanilla Transformer ) является авто-энкодером. Кодер получает на вход последовательность с позиционной информацией. Декодер получает на вход часть этой последовательности и выход кодировщика. Но архитектура некоторых моделей на основе трансформера состоит только из encoder. Например, BERT.

Как можно заметить, модель состоит из преобразования входных векторов, позиционного кодирования, нормализации, слоёв прямого распространения, линейного слоя и слоёв внимания.

В психологии внимание — это концентрация сознания на одних стимулах, исключая другие. Слой внимания в нейросетях — математические модели, позволяющие оценить взаимосвязь между значениями. _{Возможно я не одна заметила интуитивное сходство с автокорреляцией}

Вот пример визуализации результата простого слоя внимания для последовательности слов. Таким образом, трансформеры сохраняют прямые связи со всеми предыдущими временными значениями, позволяя информации распространяться по гораздо более длинным последовательностям. Весь механизм помещён в формулу с функцией softmax

Более подробное описание слоя внимания

Давайте рассмотрим слой внимания в трансформерах поближе. Для примера возьмём последовательность слов. Далее мы рассмотрим применение таких архитектур и для временных рядов.

Из того, что все элементы последовательности подаются сразу следует, что нам нужно добавить некоторую информацию, указывающую порядок элементов. Для этого мы вводим технику, называемую позиционным кодированием (pos.encoding). Здесь применяется функция синуса или косинуса. На изображении архитектуры сети её можно заметить.

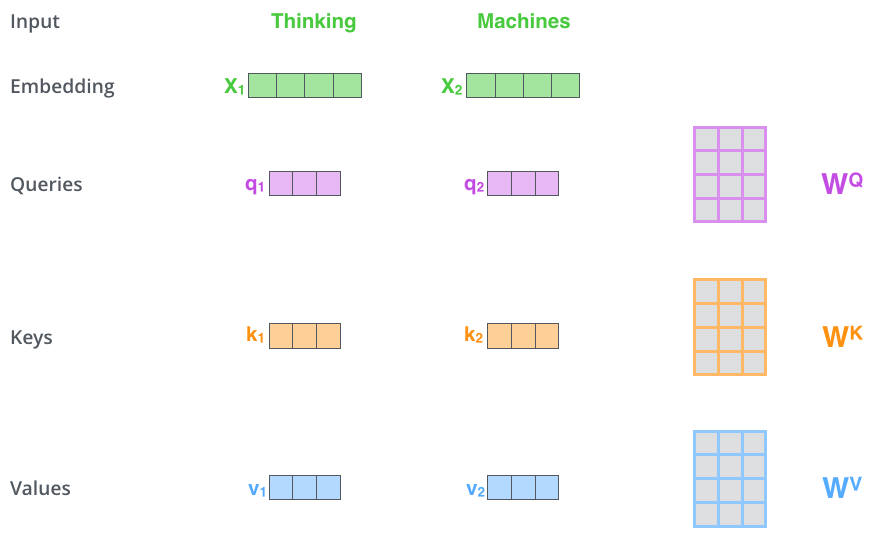
Обратите внимание на архитектуру трансформера выше. Можно заметить, что слой внимания принимает три значения. Это преобразованные входные вектора. Итак, для каждого слова мы создаем вектор запроса, вектор ключа и вектор значения (Query vector, a Key vector, and a Value vector ). Эти вектора создаются путем умножения вложения на три матрицы весов.

Далее рассчитывается оценка путём скалярного умножения вектора ключа на вектор запроса.

Нам нужно сопоставить каждое слово входного предложения с этим словом. Оценка определяет, сколько внимания нужно уделять другим частям входного предложения, когда мы кодируем слово в определенной позиции.

В целях нормализации, стоит разделить полученное значение на квадратный корень из размерности векторов ключа.

Полученное значение помещаем в функцию softmax. Softmax нормализует оценки, чтобы все они были положительными и в сумме давали 1 .

Такой вот коэффициент мы получили. Теперь, с помощью умножения на значение (V) можно получить обработанный вектор

Для вывода слоя(получения результирующего вектора) остаётся произвести суммирование

Результирующий вектор — это тот, который мы можем отправить в нейронную сеть с прямой связью.

Я попыталась интуитивно описать следующую формулу

Виды трансформеров и их результаты в задаче прогнозирования временных рядов электричества

Существуют работы, посвященные моделям для прогнозирования временных рядов на основе трансформера. Давайте рассмотрим некоторые из них.

Первая работа, которая мне очень понравилась — Deep Transformer Models for Time Series Forecasting: The Influenza Prevalence Case . Здесь на примере задачи прогнозирования гриппоподобных заболеваний автор сопоставил некоторые результаты различных моделей, работающих с временными рядами.

Архитектура очень похожа на оригинальный трансформер. В качестве оптимизатора в этой работе использовался Adam. Для регуляризации авторы добавили dropout и dropout rate — 0.2 для каждого слоя.

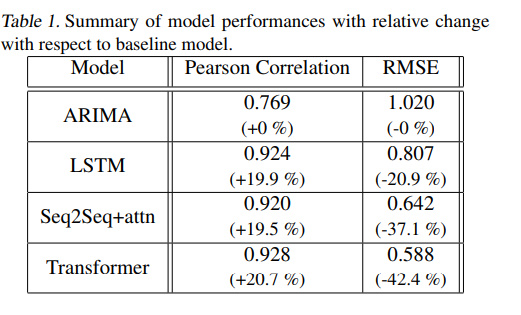
Посмотрим на результаты модели, оценка которой взята с RMSE и с коэффициентом корреляции

В следующей работе — Adversarial Sparse Transformer for Time Series Forecasting, нужно быть знакомым с генеративно-состязательными нейросетями, потому, что автор применил очень интересную идею создания генеративной модели для прогнозирования.

Применяется стохастический градиентный спуск

Оптимизация

где: ΘG — параметры генератора , ΘD — параметры дискриминатора .

Обучилась нейросеть на данных часового ряда потребления электроэнергии ( electricity ).

В результате, ошибка обычного трансформера примерно в 3 раза меньше, чем ARIMA ( 0.036 ), а ошибка модели описанной выше в 4 раза меньше, чем ARIMA ( 0.025 )

Вообще, большее количество типов данных сейчас предсказывается с использованием глубоких нейросетей. Некоторые архитектуры позволяют это сделать и для временных рядов.

Использованная литература

Источник

Все курсы > Вводный курс > Занятие 20

Понятие временного ряда

Временной ряд (time series) — это данные, последовательно собранные в регулярные промежутки времени.

К таким данным относятся, например, цены на акции, объемы продаж чего-либо, изменения температуры с течением времени и т.д. Посмотрим на изменение обычных данных и временных рядов.

Основное отличие: перекрестные данные предполагают независимость наблюдений, во временных рядах будущее зависит от прошлого.

Работа с временными рядами предполагает два аспекта:

Анализ временного ряда (time series analysis), т.е. понимание его структуры и закономерностей; и
Моделирование и построение прогноза на будущее (time series forecasting)

Договоримся о терминах:

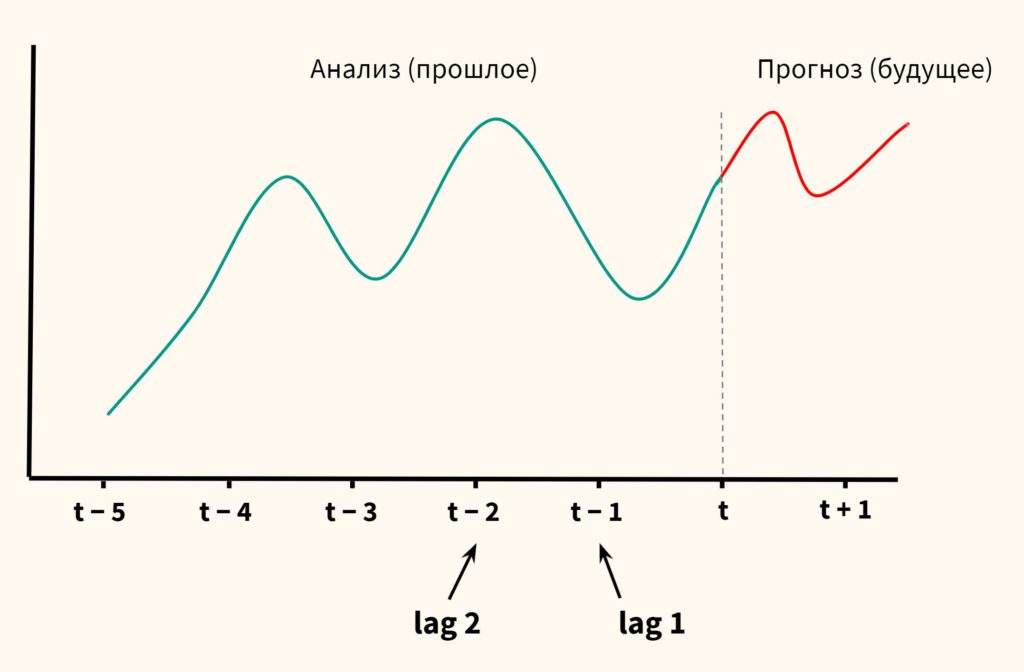
Во-первых, определим нотацию периодов. Временем t обозначим настоящее, t−1, t−2,… прошлое, t+1, t+2,… будущее.
Во-вторых, введем важное понятие временного лага (lag), т.е. запаздывания по сравнению с заданным периодом.

Датасеты

Мы будем использовать два популярных набора данных, а именно (1) ежемесячные данные о количестве пассажиров, перевезенных одной американской авиакомпанией с 1949 по 1960 годы и (2) ежедневные данные о родившихся в Калифорнии в 1959 году девочках.

Подгружать внешние данные в ноутбук Google Colab мы уже умеем. Можем переходить непосредственно к работе с кодом.

Откроем ноутбук к этому занятию⧉

Анализ временных рядов

# импортируем необходимые библиотеки

import pandas as pd

import numpy as np

import matplotlib.pyplot as plt

Импорт данных и работа в библиотеке Pandas

Для начала давайте импортируем данные. Пока что мы будем использовать только первый набор данных с информацией об авиаперевозках.

# импортируем файл с данными о пассажирах

passengers = pd.read_csv(«/content/passengers.csv»)

passengers.head()

Сделаем дату индексом.

# превратим дату в индекс и сделаем изменение постоянным

passengers.set_index(‘Month’, inplace = True)

passengers.head()

Питон воспринимает дату как число. Это не очень удобно, если мы хотим делать срезы и в целом изменять данные во времени. Дату можно преобразовать в специальный объект datetime.

# превратим дату (наш индекс) в объект datetime

passengers.index = pd.to_datetime(passengers.index)

# посмотрим на первые пять дат и на тип данных

passengers.index[:5]

DatetimeIndex([‘1949-01-01’, ‘1949-02-01’, ‘1949-03-01’, ‘1949-04-01’,

‘1949-05-01’],

dtype=’datetime64[ns]’, name=’Month’, freq=None)

Все эти операции также можно проделать в одну строчку.

passengers = pd.read_csv(‘/content/passengers.csv’, index_col = ‘Month’, parse_dates = True)

Теперь мы можем делать срезы за определенный период, например, с августа 1949 по март 1950 года.

passengers[‘1949-08’:‘1950-03’]

Обратите внимание, что в отличие от других перечней в Питоне (например, списков), во временном ряде мы получаем данные и по начальной, и по конечной дате среза (в частности, март 1950 года вошел в наш интервал).

Изменение шага временного ряда, сдвиг и скользящее среднее

Отдельно хотелось бы поговорить про возможность обобщения и изменения данных. Помимо прочего, мы можем изменить шаг (resample) нашего временного ряда, и посмотреть средние показатели перевозок, например, за год.

passengers.resample(rule = ‘AS’).mean().head()

Кроме того, мы можем сдвинуть (shift) наши данные на n периодов вперед или назад.

# произведем сдвиг на два периода (в данном случае месяца) вперед

passengers.shift(2, axis = 0).head()

Что логично, после сдвига первые два значения определяются как пропущенные (NaN или Not a number).

Мы также можем рассчитать скользящее среднее (moving average, rolling average) за n предыдущих периодов. Вначале посмотрим, что это такое.

Теперь давайте рассчитаем его для наших данных. Период, за который рассчитывается скользящее среднее, также называется окном (window).

# рассчитаем скользящее среднее для трех месяцев

passengers.rolling(window = 3).mean().head()

Опять же, так как в данном случае мы использовали три месяца для расчета скользящего среднего, этот показатель недоступен для первых двух значений. В целом, скользящее среднее сглаживает временные показатели (мы это увидим на графике в следующем разделе).

Построение графиков

Для того чтобы построить график временного ряда мы можем воспользоваться инструментами, которые уже содержатся в библиотеке Pandas. Например, простым методом .plot().

График можно усложнить.

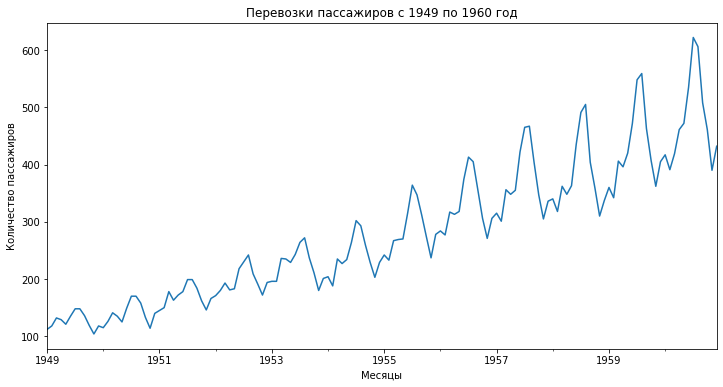
# изменим размер графика, уберем легенду и добавим подписи

ax = passengers.plot(figsize = (12,6), legend = None)

ax.set(title = ‘Перевозки пассажиров с 1949 по 1960 год’, xlabel = ‘Месяцы’, ylabel = ‘Количество пассажиров’)

Визуализацию можно также построить с помощью библиотеки Matplotlib. Давайте выведем на одном графике перевозки пассажиров и скользящее среднее.

# зададим размер графика

plt.figure(figsize = (15,8))

# поочередно зададим кривые (перевозки и скользящее среднее) с подписями и цветом

plt.plot(passengers, label = ‘Перевозки пассажиров по месяцам’, color = ‘steelblue’)

plt.plot(passengers.rolling(window = 12).mean(), label = ‘Скользящее среднее за 12 месяцев’, color = ‘orange’)

# добавим легенду, ее положение на графике и размер шрифта

plt.legend(title = », loc = ‘upper left’, fontsize = 14)

# добавим подписи к осям и заголовки

plt.xlabel(‘Месяцы’, fontsize = 14)

plt.ylabel(‘Количество пассажиров’, fontsize = 14)

plt.title(‘Перевозки пассажиров с 1949 по 1960 год’, fontsize = 16)

# выведем обе кривые на одном графике

plt.show()

Как вы видите, скользящее среднее сильно сглаживает показатели. Также обратите внимание, что так как в данном случае мы взяли окно равное двенадцати месяцам, то первое значение скользящего среднего мы получили только за декабрь 1949 года (самое начало желтой кривой на графике).

В целом не стоит недооценивать важность визуальной оценки ряда на графике. Многие особенности можно выявить именно так.

Разложение временного ряда на компоненты

Выявление компонентов временного ряда (time series decomposition) предполагает его разложение на тренд, сезонность и случайные колебания. Дадим несколько неформальных определений.

Тренд — долгосрочное изменение уровня ряда
Сезонность предполагает циклические изменения уровня ряда с постоянным периодом
Случайные колебания — непрогнозируемое случайное изменение ряда

В Питоне в модуле statsmodels есть функция seasonal_decompose(). Воспользуемся ей для визуализации компонентов ряда.

Перед этим импортируем второй датасет для последующего сравнения.

# для наглядности импортируем второй датасет

# сразу превратим дату в индекс и преобразуем ее в объект datetime

births = pd.read_csv(‘/content/births.csv’, index_col = ‘Date’, parse_dates = True)

births.head(3)

Теперь давайте разложим наш временной ряд по авиаперевозкам на компоненты.

# импортируем функцию seasonal_decompose из statsmodels

from statsmodels.tsa.seasonal import seasonal_decompose

# задаем размер графика

from pylab import rcParams

rcParams[‘figure.figsize’] = 11, 9

# применяем функцию к данным о перевозках

decompose = seasonal_decompose(passengers)

decompose.plot()

plt.show()

Сделаем то же самое с данными о рождаемости.

decompose = seasonal_decompose(births)

decompose.plot()

plt.show()

Как мы видим, графики совершенно разные. В следующем разделе мы изучим это различие более подробно.

Стационарность

Стационарность (stationarity) временного ряда как раз означает, что такие компоненты как тренд и сезонность отсутствуют. Говоря более точно, среднее значение и дисперсия не меняются со смещением во времени.

Понимание того, стационарные ли у нас данные или нестационарные важно для последующего моделирования.

Стационарность процесса можно оценить визуально. Датасет о перевозках демонстрирует очевидный тренд и сезонность, в то время как в наборе данных о рождаемости этого не видно (см. графики выше).

Для более точной оценки стационарности можно применить тест Дики-Фуллера (Dickey-Fuller test). О том, что такое статистический вывод мы с вами уже говорили.

В данном случае гипотезы звучат следующим образом.

Нулевая гипотеза предполагает, что процесс нестационарный
Альтернативная гипотеза соответственно говорит об обратном

Применим этот тест к обоим датасетам. Используем пороговое значение, равное 0,05 (5%).

# импортируем необходимую функцию

from statsmodels.tsa.stattools import adfuller

# передадим ей столбец с данными о перевозках и поместим результат в adf_test

adf_test = adfuller(passengers[‘#Passengers’])

# выведем p-value

print(‘p-value = ‘ + str(adf_test[1]))

p-value = 0.9918802434376409

Как мы видим, вероятность (p-value) для данных о перевозках существенно выше 0,05. Мы не можем отвергнуть нулевую гипотезу. Процесс нестанионарный. Проведем тест для второго набора данных.

# теперь посмотрим на данные о рождаемости

adf_test = adfuller(births[‘Births’])

# выведем p-value

print(‘p-value = ‘ +str(adf_test[1]))

p-value = 5.243412990149865e-05

Результат существенно меньше 5%. Временной ряд стационарен.

Надо сказать, что наша визуальная оценка полностью совпала с математическими вычислениями.

Автокорреляция

Изучая статистику, мы с вами уже познакомились с корреляцией. Корреляция показывает силу взаимосвязи двух переменных и позволяет строить модель.

Автокорреляция также показывает степень взаимосвязи в диапазоне от –1 до 1, но только не двух переменных, а одной и той же переменной в разные моменты времени.

Допустим, у нас есть временной ряд и этот же ряд, взятый с лагом 1, 2 и 3.

Мы можем посчитать автокорреляцию ряда с лагом 1.

# для начала возьмем искусственные данные

data = np.array([16, 21, 15, 24, 18, 17, 20])

# для сдвига на одно значение достаточно взять этот ряд, начиная со второго элемента

lag_1 = data[1:]

# посчитаем корреляцию для лага 1 (у исходных данных мы убрали последний элемент)

# так как мы получим корреляционную матрицу, возьмем первую строку и второй столбец [0, 1]

np.round(np.corrcoef(data[:—1], lag_1)[0,1], 2)

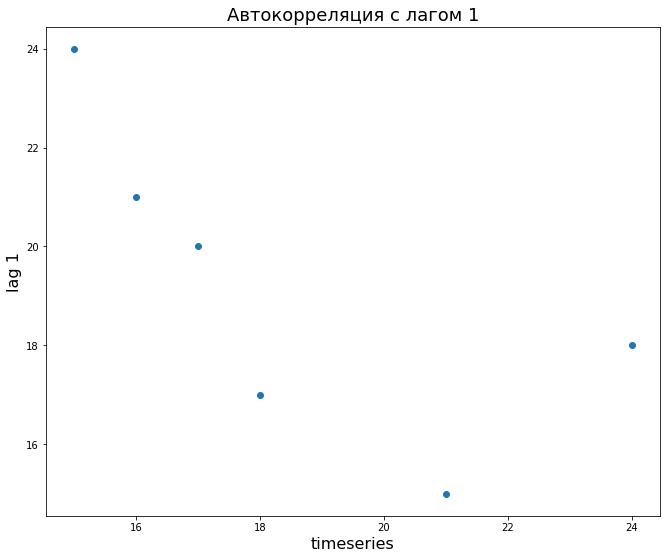
Визуально это будет выглядеть следующим образом (вспомните график обычной корреляции).

# построим точечную диаграмму

plt.scatter(data[:—1], lag_1)

# добавим подписи

plt.xlabel(‘timeseries’, fontsize = 16)

plt.ylabel(‘lag 1’, fontsize = 16)

plt.title(‘Автокорреляция с лагом 1’, fontsize = 18)

Аналогично мы можем посчитать корреляцию для лагов 2 и 3 и на самом деле любого другого лага. Такие измерения автокорреляции удобно вычислить и изобразить с помощью графика автокорреляционной функции (autocorrelation function, ACF).

# импортируем автокорреляционную функцию (ACF)

from statsmodels.graphics.tsaplots import plot_acf

# применим функцию к нашему набору данных

plot_acf(data, alpha = None)

plt.show()

В частности, мы видим, что автокорреляция ряда с самим собой (первый столбец) равна 1, что логично. Второй столбец (то есть лаг 1) как раз примерно равен – 0,71.

Разные значения, полученные через np.corrcoef() и plot_acf(), объясняются небольшим различием в заложенных в этих функциях формулах.

Теперь построим график ACF для наших данных о перевозках.

# импортируем функцию для построения автокорреляционной функции (ACF)

from statsmodels.graphics.tsaplots import plot_acf

# применим ее к данным о пассажирах

plot_acf(passengers)

plt.show()

Автокорреляция позволяет выявлять тренд и сезонность, а также используется при подборе параметров моделей. В частности, мы видим, что лаг 12 сильнее коррелирует с исходным рядом, чем соседние лаги 10 и 11. То же самое можно сказать и про лаг 24. Такая автокорреляция позволяет предположить наличие (ежегодных) сезонных колебаний.

То, что корреляция постоянно положительная говорит о наличии тренда. Все это согласуется с тем, что мы узнали о данных, когда раскладывали их на компоненты.

Также замечу, что синяя граница позволяет оценить статистическую значимость корреляции. Если столбец выходит за ее пределы, то автокорреляция достаточно сильна и ее можно использовать при построении модели.

Сравним полученный выше график с графиком автокорреляционной функции данных о рождаемости.

# построим аналогичный график для данных о рождаемости

plot_acf(births)

plt.show()

Во-первых, важно отметить, что автокорреляция в данном случае намного слабее. Во-вторых, мы не можем выявить четкой сезонности и тренда.

Моделирование и построение прогноза

На сегодняшнем занятии мы познакомимся с двумя типами моделей: экспоненциальное сглаживание и модель ARMA (и ее более продвинутые версии, ARIMA, SARIMA и SARIMAX).

Экспоненциальное сглаживание

Вновь обратимся к скользящему среднему (см. выше). В этой модели (1) всем предыдущим наблюдениям задавался одинаковый вес и (2) количество таких наблюдений было ограничено (мы называли это размером окна).

Однако логично предположить, что недавние наблюдения более важны для прогноза, чем более отдаленные. Кроме того, мы можем взять все, а не некоторые из имеющихся у нас наблюдений.

В модели экспоненциального сглаживания (exponential smoothing) или экспоненциального скользящего среднего мы как раз (1) берем все предыдущие значения и (2) задаем каждому из наблюдений определенный вес и (экспоненциально) уменьшаем этот вес по мере углубления в прошлое.

Приведем формулу.

$$ hat{y}_{t+1} = alpha cdot y_t + (1-alpha) cdot hat{y}_{t} $$

где ŷ_t+1 — это прогнозное значение, y_t — истинное значение в текущий период, ŷ_t — прогнозное значение в текущий период.

Как мы видим, прогнозное значение зависит как от истинного, так и от прогнозного значений. Важность этих значений определяется параметром альфа, который варьируется от 0 до 1. Чем альфа больше, тем больший вес у истинного наблюдения.

Формула рекурсивна, т.е. каждый раз мы умножаем (1 – α) на очередное прогнозное значение и так до конца временного ряда.

Практика

На Питоне эту модель не сложно прописать руками.

alpha = 0.2

# первое значение совпадает со значением временного ряда

exp_smoothing = [births[‘Births’][0]]

# в цикле for последовательно применяем формулу ко всем элементам ряда

for i in range(1, len(births[‘Births’])):

exp_smoothing.append(alpha * births[‘Births’][i] + (1 — alpha) * exp_smoothing[i — 1])

# выведем прогнозное значение для 366-го дня (1 января 1960 года)

exp_smoothing[—1]

Для временного ряда, состоящего из 365 наблюдений (весь 1959 год), мы получим 365 прогнозных значений (вплоть до 1 января 1960 года включительно).

len(births), len(exp_smoothing)

Теперь добавим эти данные в исходный датафрейм births.

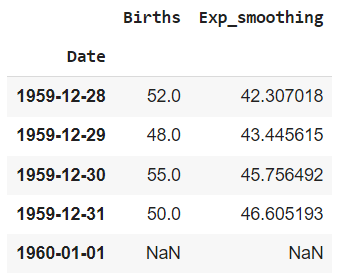
# добавим кривую сглаживаия в качестве столбца в датафрейм

births[‘Exp_smoothing’] = exp_smoothing

births.tail(3)

Единственный нюанс, так как фактические значения описывают период с 1 января по 31 декабря 1959 года, а прогнозные со 2 января 1959 года по 1 января 1960, мы не можем просто их соединить. Второй столбец нужно сдвинуть на один день вперед.

# для этого импортируем класс timedelta

from datetime import timedelta

# возьмём последний индекс (31 декабря 1959 года)

last_date = births.iloc[[—1]].index

# # «прибавим» один день

last_date = last_date + timedelta(days = 1)

last_date

# добавим его в датафрейм

births = births.append(pd.DataFrame(index = last_date))

# значения за этот день останутся пустыми

births.tail()

Сдвинем второй столбец.

births[‘Exp_smoothing’] = births[‘Exp_smoothing’].shift(1)

И посмотрим на начало и конец датафрейма.

# как и должно быть первое прогнозное значение совпадает с предыдущим фактическим

births.head()

# и у нас есть прогноз на один день вперед

births.tail()

Проверим правильность расчетов, найдя последнее прогнозное значение по формуле выше.

$$ hat{y}_{366} = 0,2 times y_{355} + 0,8 times hat{y}_{355} = 0,2 times 50 + 0,8 times 45.756492 = 46.6051936 $$

Результаты совпадают. Теперь выведем фактические и прогнозные значения на графике.

# зададим размер

plt.figure(figsize = (15,8))

# выведем данные о рождаемости и кривую экспоненциального сглаживания

plt.plot(births[‘Births’], label = ‘Данные о рождаемости’, color = ‘steelblue’)

plt.plot(births[‘Exp_smoothing’], label = ‘Экспоненциальное сглаживание’, color = ‘orange’)

# добавим легенду, ее положение на графике и размер шрифта

plt.legend(title = », loc = ‘upper left’, fontsize = 14)

# добавим подписи к осям и заголовки

plt.ylabel(‘Количество родившихся’, fontsize = 14)

plt.xlabel(‘Месяцы’, fontsize = 14)

plt.title(‘Рождаемость в 1959 году. Прогноз на 1 января 1960 года’, fontsize = 16)

plt.show()

Очень советую в качестве упражнения попробовать построить график с несколькими значениями альфа от 0 до 1.

Модель экспоненциального сглаживания можно усложнить и тогда она будет улавливать тренд и сезонность. Кроме того, усложненные модели способны предсказывать более одного значения (обратите внимание, здесь мы смогли сделать прогноз лишь на один день вперёд).

Работа над ошибками. На видео в формуле экспоненциального сглаживания есть ошибка.

alpha = 0.2

# первое значение совпадает со значением временного ряда

exp_smoothing = [births[‘Births’][0]]

# в цикле for последовательно применяем формулу ко всем элементам ряда

for i in range(0, len(births[‘Births’])):

exp_smoothing.append(alpha * births[‘Births’][i] + (1 — alpha) * exp_smoothing[i — 1])

Должно быть.

alpha = 0.2

# первое значение совпадает со значением временного ряда

exp_smoothing = [births[‘Births’][0]]

# в цикле for последовательно применяем формулу ко всем элементам ряда

for i in range(1, len(births[‘Births’])):

exp_smoothing.append(alpha * births[‘Births’][i] + (1 — alpha) * exp_smoothing[i — 1])

Как вы видите расчет прогнозного значения в цикле следовало начинать с наблюдения
[births[‘Births’][1], а не
[births[‘Births’][0]. Из-за этого последующие результаты оказались некорректными. В лекции и ноутбуке код исправлен.

Теперь поговорим про модели семейства ARMA.

Модель ARMA

Модель ARMA состоит из двух компонентов.

компоненты модели ARMA: авторегрессия и скользящее среднее

Авторегрессия (autoregressive model, AR) — это регрессия ряда на собственные значения в прошлом. Другими словами, наши признаки в модели обычной регрессии мы заменяем значениями той же переменной, но за предыдущие периоды.

Когда мы прогнозируем значение в период t с помощью данных за предыдущий период (AR(1)), уравнение будет выглядеть следующим образом.

$$ y_t = c + varphi cdot y_{t-1} $$

где c — это константа, $varphi$ — вес модели, y_t–1 — значение в период t – 1.

То, сколько предыдущих периодов использовать определяется параметром p. Обычно записывается как AR(p).

Модель скользящего среднего (moving average, MA) помогает учесть случайные колебания или отклонения (ошибки) истинного значения от прогнозного. Можно также сказать, что модель скользящего среднего — это авторегрессия на ошибку.

Обратите внимание, что скользящее среднее временного ряда, которое мы рассмотрели выше, и модель скользящего среднего — это разные понятия.

Если использовать ошибку только предыдущего наблюдения, то уравнение будет выглядеть следующим образом.

$$ y_t = mu + varphi cdot varepsilon_{t-1} $$

где μ — это среднее значение временного ряда, φ — вес модели, ε_t–1 — ошибка в период t – 1.

Такую модель принято называть моделью скользящего среднего с параметром q = 1 или MA(1). Разумеется, параметр q может принимать и другие значения (MA(q)).

Модель ARMA с параметрами (или как еще говорят порядками, orders) p и q или ARMA(p, q) позволяет описать любой стационарный временной ряд.

ARMA предполагает, что в данных отсутствует тренд и сезонность (данные стационарны). Если данные нестационарны, нужно использовать более сложные версии этих моделей:

ARIMA, здесь добавляется компонент Integrated (I), который отвечает за удаление тренда (сам процесс называется дифференцированием); и
SARIMA, эта модель учитывает сезонность (Seasonality, S)
SARIMAX включает еще и внешние или экзогенные факторы (eXogenous factors, отсюда и буква X в названии), которые напрямую не учитываются моделью, но влияют на нее.

Параметров у модели SARIMAX больше. Их полная версия выглядит как SARIMAX(p, d, q) x (P, D, Q, s). В данном случае, помимо известных параметров p и q, у нас появляется параметр d, отвечающий за тренд, а также набор параметров (P, D, Q, s), отвечающих за сезонность.

Теперь давайте воспользуемся моделью SARIMAX для прогнозирования авиаперевозок.

Практика

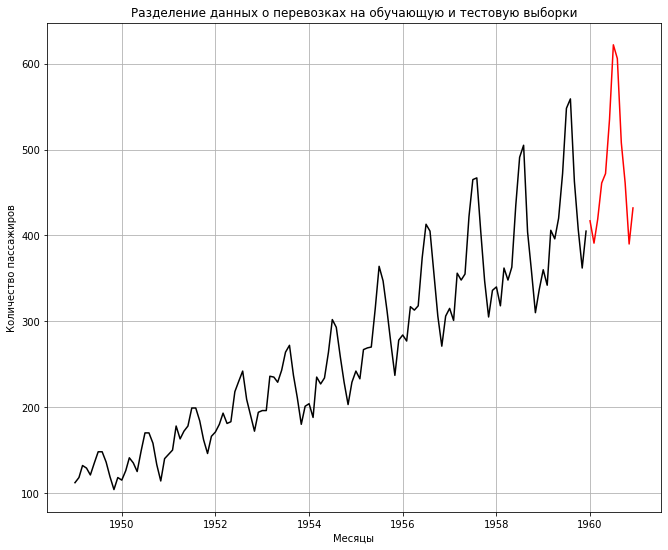
В первую очередь нужно разбить данные на обучающую и тестовую выборки. Как мы помним, у нас есть данные с января 1949 года по декабрь 1960 года.

# обучающая выборка будет включать данные до декабря 1959 года включительно

train = passengers[:‘1959-12’]

# тестовая выборка начнется с января 1960 года (по сути, один год)

test = passengers[‘1960-01’:]

Посмотрим на разделение на графике.

plt.plot(train, color = «black»)

plt.plot(test, color = «red»)

# заголовок и подписи к осям

plt.title(‘Разделение данных о перевозках на обучающую и тестовую выборки’)

plt.ylabel(‘Количество пассажиров’)

plt.xlabel(‘Месяцы’)

# добавим сетку

plt.grid()

plt.show()

Далее нам нужно обучить модель. При обучении модели SARIMAX, самое важное — правильно подобрать гиперпараметры, о которых говорилось выше. Процесс подбора гиперпараметров достаточно сложен, и сегодня мы воспользуемся уже готовыми значениями.

# принудительно отключим предупреждения системы

import warnings

warnings.simplefilter(action = ‘ignore’, category = Warning)

# обучим модель с соответствующими параметрами, SARIMAX(3, 0, 0)x(0, 1, 0, 12)

# импортируем класс модели

from statsmodels.tsa.statespace.sarimax import SARIMAX

# создадим объект этой модели

model = SARIMAX(train,

order = (3, 0, 0),

seasonal_order = (0, 1, 0, 12))

# применим метод fit

result = model.fit()

Теперь мы готовы делать прогноз. Вначале сделаем тестовый прогноз, соответствующий периоду тестовой выборки (1960 год), для того, чтобы оценить качество работы модели.

# тестовый прогнозный период начнется с конца обучающего периода

start = len(train)

# и закончится в конце тестового

end = len(train) + len(test) — 1

# применим метод predict

predictions = result.predict(start, end)

predictions

1960-01-01 422.703385

1960-02-01 404.947178

1960-03-01 466.293258

1960-04-01 454.781295

1960-05-01 476.848627

1960-06-01 527.162825

1960-07-01 601.449809

1960-08-01 610.821690

1960-09-01 513.229987

1960-10-01 455.692618

1960-11-01 409.200046

1960-12-01 450.754160

Freq: MS, Name: predicted_mean, dtype: float64

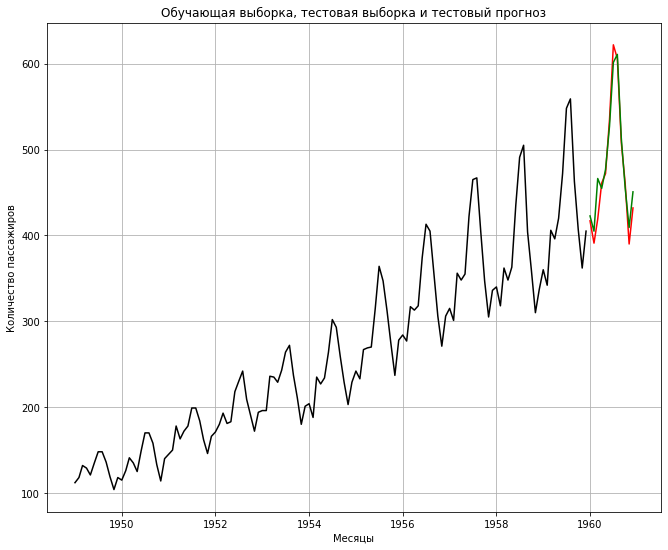
Построим соответствующий график.

# выведем три кривые (обучающая, тестовая выборка и тестовый прогноз)

plt.plot(train, color = «black»)

plt.plot(test, color = «red»)

plt.plot(predictions, color = «green»)

# заголовок и подписи к осям

plt.title(«Обучающая выборка, тестовая выборка и тестовый прогноз»)

plt.ylabel(‘Количество пассажиров’)

plt.xlabel(‘Месяцы’)

# добавим сетку

plt.grid()

plt.show()

В целом модель хорошо описывает временной ряд. Мы также можем использовать знакомые нам метрики среднеквадратической ошибки (MSE) и корня среднеквадратической ошибки (RMSE) для оценки качества.

# импортируем метрику

from sklearn.metrics import mean_squared_error

# рассчитаем MSE

print(mean_squared_error(test, predictions))

# и RMSE

print(np.sqrt(mean_squared_error(test, predictions)))

317.39564617023217

17.815601201481588

Теперь можно делать прогноз на будущее. Возьмём горизонт равный трем годам (1961, 1962 и 1963 год). Всего должно получиться 36 прогнозных значений.

# прогнозный период с конца имеющихся данных

start = len(passengers)

# и закончится 36 месяцев спустя

end = (len(passengers) — 1) + 3 * 12

# теперь построим прогноз на три года вперед

forecast = result.predict(start, end)

# посмотрим на весь 1963 год

forecast[—12:]

1963-01-01 518.603433

1963-02-01 497.908985

1963-03-01 556.406781

1963-04-01 542.133831

1963-05-01 561.524759

1963-06-01 609.244560

1963-07-01 681.016634

1963-08-01 687.950661

1963-09-01 587.995797

1963-10-01 528.167673

1963-11-01 479.454532

1963-12-01 518.856113

Freq: MS, Name: predicted_mean, dtype: float64

Посмотрим на прогнозные значения на графике.

# выведем две кривые (фактические данные и прогноз на будущее)

plt.plot(passengers, color = ‘black’)

plt.plot(forecast, color = ‘blue’)

# заголовок и подписи к осям

plt.title(‘Фактические данные и прогноз на будущее’)

plt.ylabel(‘Количество пассажиров’)

plt.xlabel(‘Месяцы’)

# добавим сетку

plt.grid()

plt.show()

Подведем итог

Занятие было насыщенным. Мы узнали, (1) чем временные ряды отличаются от структурных данных, (2) научились анализировать временные ряды с помощью Питона, а также (3) строить графики.

При прогнозировании временных рядов мы (4) использовали модель экспоненциального сглаживания и (5) познакомились с семейством моделей ARMA.

Вопросы для закрепления

Чем структурные/перекрестные данные отличаются от временных рядов?

Посмотреть правильный ответ

Ответ: во временных рядах значение наблюдаемой величины зависит от времени, в структурных данных — от других величин или переменных.

Что определяет параметр альфа в модели экспоненциального сглаживания?

Посмотреть правильный ответ

Ответ: значение параметра альфа близкое к единице повышает значимость текущего истинного наблюдения, если альфа близка к нулю — превалирует предыдущее прогнозное значение.

Из каких компонентов состоит модель ARMA?

Посмотреть правильный ответ

Ответ: модель ARMA состоит из компонента авторегрессии (AR), т.е. регрессии на собственные значения в прошлом, и модели скользящего среднего (MA), учитывающей отклонение от среднего значения или ошибку.

В рамках вводного курса осталась одна тема, основы нейронных сетей.

Ответы на вопросы

Вопрос. Вы не могли бы более детально рассказать, как подбираются параметры в модели SARIMAX. В частности, как были подобраны параметры (3, 0, 0)x(0, 1, 0, 12)?

Ответ. Параметры SARIMAX можно подобрать с помощью функции auto_arima. Выбор наиболее удачных параметров осуществляется на основе определенного критерия.

По умолчанию используется, так называемый, Akaike Information Criterion или AIC, который рассчитывается для каждой комбинации параметров. Чем ниже AIC модели, тем лучше.

Я привел код auto_arima в конце ноутбука⧉.

Вопрос. У меня уточнение: скажите, там, где мы считаем экспоненциальное сглаживание,

# в цикле for последовательно применяем формулу ко всем элементам ряда

for i in range(0, len(births[‘Births’])):

exp_smoothing.append(alpha * births[‘Births’][i] + (1 — alpha) * exp_smoothing[i — 1])

там, может быть, нужно в цикле
for i in range(0, len(births[‘Births’])): поставить начальное значение счетчика = 1:
for i in range(1, len(births[‘Births’]))?

Я проверял выкладки в Экселе — и, когда цикл стартует с нуля, получается ошибка. Возможно, это потому, что в начале списка получается задублированное значение первого элемента (мы сначала вручную вносим в список
[births[‘Births’][0]], а потом это же делаем на первой итерации, когда значение счетчика = 0)

Ответ. Да, действительно, первое прогнозное значение мы вносим вручную (оно совпадает с первым фактическим значением), поэтому должно быть

for i in range(1, len(births[‘Births’])):

Внес изменения в ноутбук и текст лекции.

Источник

Временной ряд — это упорядоченная последовательность значений какого-либо показателя за несколько периодов времени. Основная характеристика, которая отличает временной ряд от простой выборки данных, — указанное время измерения или номер изменения по порядку.

Пример временного ряда: биржевой курс.

Пример выборки данных: электронные почты клиентов магазина.

Временные ряды используются для аналитики и прогнозирования, когда важно определить, что будет происходить с показателями в ближайший час/день/месяц/год: например, сколько пользователей скачают за день мобильное приложение. Показатели для составления временных рядов могут быть не только техническими, но и экономическими, социальными и даже природными.

Они сыграли фундаментальную роль в обработке сигналов связи во время Второй мировой войны. После их начали использовать в анализе временных рядов в 1970 году.

ARMA (Autoregressive Moving Average) — авторегрессионная модель скользящей средней.

ARIMA (Autoregressive Integrated Moving Average) — авторегрессионная интегрированная модель скользящей средней.

AR → Авторегрессионная модель

В ней значения в будущем определяются как значения из прошлого, умноженные на коэффициенты.

I → Интегрированный

Это относится к различным методам вычисления различий между последовательными наблюдениями для получения стационарного процесса из нестационарного.

MA → Модель скользящей средней

Это регрессионная модель, которая использует прошлые ошибки прогноза для прогнозирования интересующей переменной.

Для работы с временными рядами с сезонными компонентами используется SARIMA (интегрированное скользящее среднее сезонной авторегрессии). Это расширение модели ARIMA, добавляющее в нее сезонные условия.

Prophet разработан командой Facebook Core Data Science и представляет собой инструмент с открытым исходным кодом для бизнес-прогнозирования. Модель Prophet основана на трех переменных:

g (t) — тренд. Логистическая функция позволяет моделировать рост с насыщением, когда при увеличении показателя снижается темп его роста.

s (t) — сезонность отвечает за моделирование периодических изменений, связанных с недельной и годовой сезонностью.

h (t) — праздники и события. Учитываются аномальные дни, которые не влияют на сезонность.

ε(t) — ошибка. Содержит информацию, которую модель не учитывает.

У Prophet существует больше инструментов для обработки и сортировки данных по сезонности, чем у SARIMA. Такое преимущество позволяет анализировать временные ряды с различной сезонностью — неделей, месяцем, кварталом или годом.

Преимущество этого метода — возможность сделать прогноз на длительный период. Математически экспоненциальное сглаживание выражается так:

a (alfa) — коэффициент сглаживания, который принимает значения от 0 до 1. Он определяет, насколько продолжительность изменит существующие значения в базе данных.

x — текущее значение временного ряда (например, объем продаж).

y — сглаженная величина на текущий период.

t — значение тренда за предыдущий период.

Пример экспоненциального сглаживания:

Источник

Голубая линия на графике — это исходные данные, темно-синяя линия представляет экспоненциальное сглаживание временного ряда с коэффициентом сглаживания 0,3, а оранжевая линия использует коэффициент сглаживания 0,05. Чем меньше коэффициент сглаживания, тем более плавным будет временной ряд.

Предполагается, что временные ряды генерируются регулярно, но на практике это не всегда так. В нерегулярных рядах измерения нельзя провести через одинаковые промежутки времени. Примером нерегулярного временного ряда является пополнение банковской карты.

Помимо регулярности, временные ряды делятся на детерминированные и недетерминированные.

Детерминированный временной ряд — ряд, в котором нет случайных аспектов или показателей: он может быть выражен формулой. Это значит, что мы можем проанализировать, как показатели вели себя в прошлом, и точно прогнозировать их поведение в будущем.

Недетерминированный временной ряд имеет случайный аспект и прогнозирование будущих действий становится сложнее. Природа таких показателей случайна.

Стационарные и нестационарные ряды

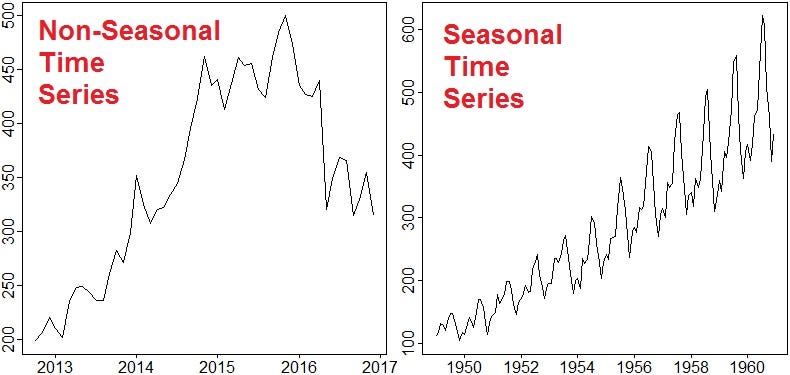
Пример визуализации стационарного и нестационарного ряда. Источник

На наблюдение за показателями и их систематизацией влияют тенденции и сезонные эффекты. От этих условий зависит сложность моделирования системы прогнозирования. Временные ряды можно разделить по наличию или отсутствию тенденций и сезонных эффектов на стационарные и нестационарные.

В стационарных временных рядах статистические свойства не зависят от времени, поэтому результат легко предсказать. Большинство статистических методов предполагают, что все временные ряды должны быть стационарными. Пример стационарных временных рядов — рождаемость в России. Конечно, она зависит от множества факторов, но ее спад или рост возможно предсказать: у рождаемости нет ярко выраженной сезонности.

В нестационарных временных рядах статистические свойства меняются со временем. Они показывают сезонные эффекты, тренды и другие структуры, которые зависят от временного показателя. Пример — международные перелеты авиакомпаний. Количество пассажиров на тех или иных направлениях меняется в зависимости от сезонности.

Для классических статистических методов удобнее создавать модели стационарных временных рядов. Если прослеживается четкая тенденция или сезонность во временных рядах, то следует смоделировать эти компоненты и удалить их из наблюдений.

Прогнозирование временных рядов — популярная аналитическая задача, которую используют в разных сферах жизни — бизнесе, науке, исследованиях общества и потребительского поведения. Прогнозы используются для предсказания, например, сколько серверов понадобится онлайн-магазину, когда спрос на товар вырастет.

Источник

Анализ временных рядов

На входе анализа – временной ряд, т.е. собранные с некоторой периодичностью (ежедневно, еженедельно, ежемесячно) данные по какому-либо показателю (например, объём продаж). Временные ряды часто бывают подвержены влиянию одного или нескольких следующих факторов.

Аналитика бизнеса
Методы анализа данных Data Mining
Анализ временных рядов

Анализ временных рядов

Анализ данных в динамике, построение прогнозов

Для чего нужен анализ временных рядов?

Краткое описание характерных особенностей ряда.
Подбор статистической модели (моделей), описывающей данный временной ряд.
Предсказание будущих значений на основе прошлых наблюдений.
Управление процессом, порождающим временной ряд.

Как это работает?

1) Тренд – плавно изменяющаяся, не циклическая компонента, описывающая чистое влияние долговременных факторов, эффект которых сказывается постепенно.

2) Сезонная компонента временного ряда описывает поведение, изменяющееся регулярно в течение заданного периода (года, месяца, недели, дня). Она состоит из последовательности почти повторяющихся циклов.

3) Циклическая компонента временного ряда описывает относительно длительные периоды подъема и спада. Она состоит из циклов, которые меняются по амплитуде и протяжённости.

4) Автокорреляция – корреляция временного ряда с самим собой. Возникает тогда, когда каждое соседнее значение связано с предыдущим (например, запоминаемость рекламы).

Задача анализа состоит в выявлении этих факторов, нейтрализации их эффекта и построении модели, наилучшим образом описывающей временной ряд. При моделировании используются такие методы, как удаление тренда, декомпозиция сезонности, экспоненциальное сглаживание, анализ автокорреляции, построение авторегрессии и скользящего среднего, и т.д.

Что получаем в итоге?

Модель «чистого» временного ряда, из которого удалены влияние тренда, сезонности, цикличности, автокорреляции и других процессов. Такая модель служит для построения прогнозов и доверительных интервалов к ним.

Каковы преимущества метода — анализ временных рядов?

Многие продукты и рынки подвержены влиянию сезонного фактора, имеют тенденции и циклы развития. Анализ временных рядов помогает отделить влияние общих факторов от мер, предпринятых маркетингом компании.

Почитать еще

Машинное обучение

Глубокое обучение – это продвинутая форма машинного обучения. Глубокое обучение относится к способности компьютерных систем, известных

Выборка. Типы выборок

Суммарная численность объектов наблюдения (люди, домохозяйства, предприятия, населенные пункты и т.д.), обладающих определенным набором признаков

Обзор основных видов сегментации

Загрузить программу ВІ Демонстрации решений Аналитика бизнеса Оглавление Сегментация бренда Сегментация помогает принимать более эффективные

Несколько видео о наших продуктах

Проиграть видео

Презентация аналитической платформы Tibco Spotfire

Проиграть видео

Отличительные особенности Tibco Spotfire 10X

Проиграть видео

Как аналитика данных помогает менеджерам компании

Источник

У нас будет серия из 3 постов о временных рядах для бизнеса:

Временные ряды для бизнеса: общее введение
Временные ряды для бизнеса: (ARIMA) для прогнозирования бюджета
Временные ряды для бизнеса: глубокое обучение (LSTM) и цена опциона на акции

Введение в временные ряды

Освоение бизнес-параметров во всех включенных областях — действительно серьезная задача, особенно для изучения эволюции ключевых показателей эффективности и показателей с течением времени. Методы временных рядов использовались для уточнения, мониторинга и прогнозирования некоторых причинно-следственных связей, они позволяют найти ответы на такие вопросы, как «как прошлое повлияло на будущее?».

Временной ряд — это последовательность упорядоченных во времени наблюдений (точек данных, собранных с постоянными интервалами времени) данного явления, которое изменяется с течением времени. Временной ряд анализ используется для определения временных закономерностей, существующих в данных, с целью определения хорошей модели, которая может использоваться для прогнозирования будущего поведения бизнес-показателей ( цена на фондовом рынке, бюджет, продажи, оборот,…).

Временные ряды позволяют понять своевременные закономерности / характеристики в данных и проанализировать тенденции в бизнес-показателях ниже некоторых типичных шаблонов временных рядов:

Случаи использования временных рядов и области приложений:

Есть несколько применений моделей временных рядов:

Бизнес: цепочка поставок, бронирование, веб-трафик и т. д.
Финансы: опционы на акции, биржа, эконометрика и т. д.
Наука: астрономия, погода, прогноз землетрясений и т. д.
Инженерное дело: датчики и управление Обработка сигналов,…
Здоровье: диагностика, биомедицинский мониторинг и т. д.

Типы временных рядов:

Стационарные и нестационарные данные:

Для статистических моделей временных рядов нестационарные данные (среднее значение и дисперсия непостоянны с зависящей от времени ковариацией) непредсказуемы и не могут быть смоделированы или спрогнозированы, например:

Случайное блуждание: Y (t) = α + Y (t-1) + ε (t)
Детерминированный тренд: Y (t) = α + β.t + ε (t)
Случайное блуждание с детерминированным трендом: Y (t) = α + Y (t-1) + β.t + ε (t)

где α представляют дрейф, а ε (t) — белый шум.

Нестационарные данные должны быть преобразованы в стационарные данные, чтобы они были последовательными и надежными. это преобразование обеспечивается операцией дифференцирования, при которой значения данных заменяются разницей между их значениями и предыдущими значениями (вычитая Y (t-1) из Y (t), беря разность Y (t) — Y (t-1) )). Иногда операцию дифференцирования необходимо повторять определенное количество раз, пока результирующая функция не станет стационарной.

Линейный против нелинейного:

Для линейного временного ряда точки данных X (t) a представлены как линейная комбинация прошлых значений:

X(t) = α1.X(t-1)+…+αn.X(t-1) + ε(t)

Из-за своей простоты линейные временные ряды иногда не могут уловить важные особенности.

Нелинейный временной ряд намного сложнее, он отображает особенности, которые нельзя смоделировать с помощью линейной функции: изменяющаяся во времени дисперсия, асимметричные циклы, структуры с более высоким моментом, пороги и разрывы.

Сезонный и несезонный:

Сезонность — это наличие изменений, которые происходят с определенными регулярными интервалами менее года, она представляет собой периодические, повторяющиеся и в целом регулярные и предсказуемые модели фиксированного и известного периода (день, неделя, месяц и т. д.) ).

Одномерный против многомерного:

Одномерные временные ряды зависят от одной переменной времени, в то время как набор данных многомерных временных рядов содержит несколько зависимых переменных времени, которые принимаются во внимание при прогнозировании будущих значений. в этом случае X (t) включает несколько временных рядов, которые могут способствовать прогнозированию Y (t + 1).

В приведенном ниже примере для одномерного временного ряда мы используем только исторические данные температуры для прогнозирования будущих значений. для многомерных временных рядов мы объединяем 5 временных рядов (температура, облачность, точка росы, влажность и ветер), чтобы сделать более точный прогноз, поскольку мы также улавливаем закономерности других переменных в дополнение к переменной температуры, которую мы изучение.

Другой пример многомерного временного ряда — это прогноз баланса счета с использованием в качестве входных данных всех видов расходов.

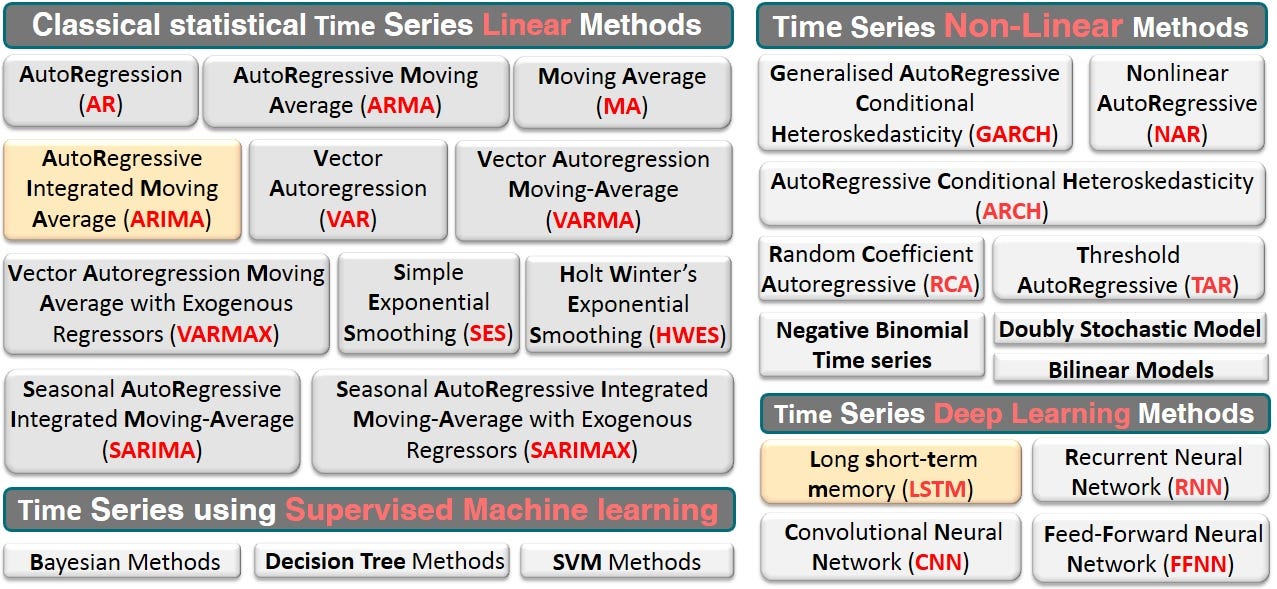
Наиболее известные методы временных рядов:

Белый ящик против черных алгоритмов

для временных рядов мы находим оба вида алгоритмов:

Белые ящики, как и все статистические методы, такие как AR, ARMA и ARIMA.
Черные ящики, такие как методы глубокого обучения (LSTM, RNN, CNN, FFNN) и некоторые методы контролируемого обучения, такие как SVM.

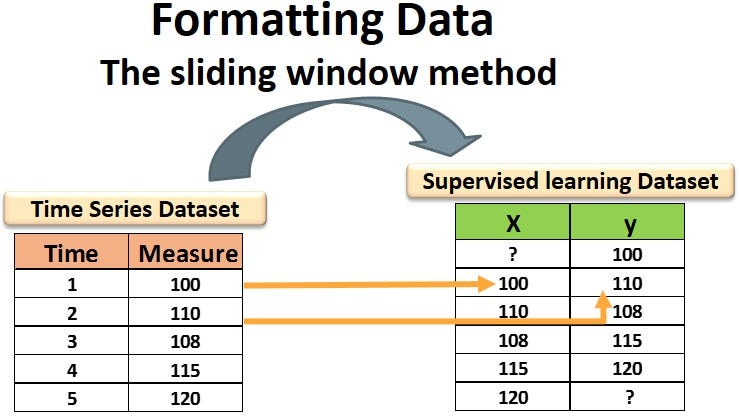
Временные ряды и контролируемое обучение

Контролируемое обучение можно использовать для решения проблемы временных рядов путем переформулирования данных временных рядов. Мы делаем это, используя метод скользящего окна, который форматирует набор данных и адаптирует его к контролируемому режиму обучения: предыдущие временные шаги используются в качестве входных переменных, а следующий временной шаг — в качестве выходной переменной (см. Рисунок ниже).

Заключение

В этом посте мы увидели обзор принципов и методов временных рядов, в следующих двух постах мы сосредоточимся на двух примерах, ARIMA и LSTM, и увидим, как их можно применить для прогнозирования соответственно бюджета и цены опциона на акции.

Источник

Time series analysis is mainly used to explain, describe, and predict changes via the time of chosen variables. Many companies use time series forecasting, and analysis to develop business strategies. These techniques help businesses in measuring, tracking, defining, and predicting business trends. Time series analysis provides you with an opportunity to know the impact of the past over the future.

What is meant by Time Series?

Time series is a sequence of data points spread over a specific duration of time, where time is the independent variable and other variables are not constant. The time-series data is analyzed over a regular temporal interval.

Time series data can be helpful in the following cases:

Tracking weather data on an hourly, daily, and weekly basis
Tracking the performance of websites
Predicting earthquakes

The time series has 4 variations like

Seasonal variations
Trend variations
Cyclical variations, and
Random variations

What is Time Series Analysis?

Time series analysis is the process of determining the basic patterns disposed by the data over a duration of time. This approach isn’t expensive and is used to forecast business-related metrics including sales, turnover, analysis of the stock market, and budgetary analysis.

Applications of Time Series Analysis

Time series in the financial domain: Most financial investments and decisions related to businesses are taken into account based on future changes in the financial domain. After analyzing financial data, an expert can easily predict necessary forecasts for financial applications in many areas including risk evolution, portfolio construction, and so on. Time series analysis has become part of financial analysis and is used to predict foreign currency risk, interest rates, etc. Financial forecasting analysis is used by business experts, and policymakers to make better decisions related to production, purchases, and allocation of resources.
Time series in the medical industry: Medicine has developed as a data-driven field and constantly contributing to time series analysis with advancements. In the medical sector, one shouldn’t forget to examine the change of behaviour overtime on absolute values.
Time series in astronomy domain: Several areas of astronomy and astrophysics needs the help of time series. However, the astronomy domain comprises arranging objects, faultless measurements, and trajectories, so astronomical experts use time series analysis to study objects as per their choices. Time series data had a remarkable impact on understanding, and measuring everything related to the universe.
Time series forecasting in business development: Businesses can make informed decisions with the help of time series forecasting, as the process includes analysis of past data patterns.

It is also helpful in forecasting upcoming potentials, and events in the below mentioned ways:

Reliability: Time series forecasting is reliable when the data displays a broad time period like huge numbers of observations for a longer period of time.
Trend evaluation: Time series techniques can be conducted to identify trends, for instance, these techniques check data observations to find out when measurements show an increase or decrease in a sale of a specific product.
Seasonal patterns: Variations of recorded data points reveal seasonal patterns and fluctuations that consider as a platform for data forecasting. The received details are important for markets whose products vary seasonally and help businesses in product development planning, and delivery requirements.
Growth: Time series technique is helpful in measuring endogenous, and financial growth.

Time series analysis and its applications are useful in controlling problems in businesses. As it involves the understanding of past behaviour to predict the future, which is very important for business planning. It also helps in the evaluation of present achievements.

Let’s look at the top 5-time series analysis tactics for business development:

Deep learning for Time series analysis: Time series forecasting isn’t simple when working with noisy data, many inputs and output variables, long sequences, and multi-step forecasts. The different time-series capabilities offered by deep learning methods include automatic learning, temporal dependence, and automatic handling of temporal structures.
Time-series data analysis: By gathering data at various points in time, it’s possible to do time-series data analysis. This is when compared to the cross-sectional data that notices businesses at a single point in time.
Autocorrelation and Seasonality: Autocorrelation defines the level of similarity between the provided time series, and its delayed type over a period of time. This time series indicates a set of values of an entity. It helps identify the relationship between the present values, and the past values of a variable/entity. Seasonality is one of the foremost characteristics of time series data. It takes place if the time series displays predictable, and continuous patterns at time periods that are no larger than a year. The perfect example of this is retail sales that are at a peak level between September to December and weak between January and February.
Time series analysis in R: Data miners and statisticians use an R programming language to develop data analysis. It consists of a series of libraries specially designed for data science. R offers remarkable features to communicate the discoveries with documentation tools that make it simpler to explain analysis to the whole team. It offers both qualities, and formal equations for time series models like white noise, autoregression, easy moving average, and random walk. You can find many types of R functions for time series data such as simulating, forecasting, and modelling trends. R is the perfect business forecasting tool and is best for doing time series analysis.
Time series regression: This statistical technique is used for guessing a future response by considering the old response history called autoregressive dynamic. Predictors use the time series regression method to guess the behaviour of dynamic systems from experimental data.

Three goals such as predicting, modelling, and characterization can be achieved with the help of regression analysis. The prime objective plays a vital role in achieving these three goals. At times, modelling is simple to predict better, and otherwise, it is enough to know and explain what’s happening. Most of the time, the repetitive method is used in predicting, and modelling.

What are the Benefits of Using Deep Learning to Analyze Time Series?

The use of deep learning for time series analysis involves the following benefits:

Trouble-free extract features: Deep neural networks reduce the necessity of the data scaling process and stationary data and feature engineering procedures which are necessary for time-series forecasting. These neural networks can learn by themselves, if proper training is provided, they can extract features from the raw input data without any difficulty.
Not difficult to predict from training data: Data can be represented at several points in time using many deep learning models including gradient booster regressor, random forest, and time-delay neural networks.

Advantages of Time Series Analysis:

The time-series data will lead to arduous, and complicated calculations because of its nature which in turn makes forecasting difficult. With the help of Python and R languages, analysts can create and tune perfect time series forecasts with minimal effort.
Time series models have fewer assumptions and are stable. It means in case a large and unpredicted event occurs; the model can provide valuable insight to solutions throughout the event.

Disadvantages:

The major disadvantage is that time series analysis is expensive because forecasts are derived from historical data patterns that are necessary to predict the upcoming market behaviour.

Источник

Временной ряд – совокупность Наблюдений (Observation), собранных за определенный временной интервал. Этот тип данных используется для поиска долгосрочного тренда, прогнозирования будущего и прочих видов анализа. В отличие от Датасетов (Dataset) без временных рядов в качестве Признаков (Feature), наборы с временными рядами не выполняют основное требование линейной регрессии о независимости наблюдений.

Временной ряд – стоимость акции компании LG на моменты открытия и закрытия биржи

Наряду с тенденцией увеличиваться или уменьшаться, большинство датасетов с временными рядами демонстрируют сезонные тенденции. Например, изучая сбыт пуховиков на протяжении пяти лет, мы увидим более высокий их уровень продаж в холодное время года каждый год.

Такие свойства временного ряда коренным образом меняют характер взаимодействия при создании Модели (Model) Машинного обучения (ML). Прежде чем использовать такие данные для обучения Нейронной сети (Neural Network), стоит добиться так называемой Стационарности (Stationarity).

Стационарность

Стационарность – это свойство временного ряда, постоянство его статистических свойств: Cреднего значения (Average) и Дисперсии (Variance). Это важно, поскольку большинство моделей работают, исходя из предположения о стационарности. Предполагается, что, если временной ряд ведет себя определенным образом, очень высока вероятность того, что он повторит те же паттерны в будущем. Стационарные ряды к тому же более просты в обработке.

Временные ряды и statsmodels

Поработаем с временным рядом – хронологией стоимости акции компании LG. Для начала протестируем данные на стационарность, то есть пригодность к использованию в качестве обучающих данных модели машинного обучения и предскажем стоимость акции с помощью Модели Бокса — Дженкинса (ARIMA). Для начала импортируем все необходимые библиотеки:

import matplotlib.pyplot as plt
from numpy import log
import pandas as pd

from sklearn.metrics import mean_squared_error

from statsmodels.tsa.stattools import adfuller
from statsmodels.tsa.arima_model import ARIMA

Помимо классических библиотек NumPy и Pandas нам понадобятся также классы Среднеквадратической ошибки (Mean Squared Error), теста Дики-Фуллера и непосредственно модели ARIMA. Теперь загрузим в ноутбук хронологию стоимости акции за текущий торговый год, то есть за период 01.01.2021 по 13.03.2021:

df = pd.read_csv('https://www.dropbox.com/s/j04e6thkqmk02z1/LPL.csv?dl=1')
df.head()

Мы получили такой игрушечный датасет с помощью сервиса Yahoo. Finance, и набор отображаемых признаков обусловлен политикой сервиса:

Отобразим с помощью Линейной диаграммы (Line Plot) цену акции на момент открытия биржи:

plt.plot(df['Open'])
plt.figure(figsize = (25, 10)) # Размер графика в дюймах
plt.show()

За два с небольшим месяца стоимость акции колебалась в пределах 8.5 – 11.5 долларов за штуку:

Именно с такими данными мы и будем создавать модель машинного обучения. Прежде чем приступить к построению модели, стоит выяснить, являются ли такие данные стационарными? В этом поможет тест Дики-Фуллера. Мы выберем целевой признак (Target Feature), значение которого впоследствии и будем предсказывать, – это цена открытия (Open) и сравним коэффициент такого теста с критическими значениями уровней Статистической значимости (Statistical Significance). Чтобы нейтрализовать восходящий тренд, мы логарифмизируем данные с помощью np.log, тем самым приведем более высокие поздние значения к масштабу более ранних:

Y = df['Open'].values # Выделим целевой признак 
Y = log(Y)
result = adfuller(Y)
print('Коэффициент расширенного теста Дики-Фуллера: %f' % result[0])
print('Критические значения: %f' % result[1])
for key, value in result[4].items():
	print('t%s: %.3f' % (key, value))

Итак, метрика теста равна 0,220931, и само по себе это значение не очень показательно. Оно работает в сравнении с критическими значениями Статистической значимости. Итак, Статистика (Statistics) теста равна 0.220931, и это значение больше всех трех значениями уровней статистической значимости, что означает стационарность.

Коэффициент расширенного теста Дики-Фуллера: -2.160400
Критические значения: 0.220931
	1%: -3.578
	5%: -2.925
	10%: -2.601

Настало время самой задорной части: предскажем стоимость акции. Для этого разделим датасет на Тренировочную (Train Data) и Тестовую части (Test Data) в пропорции 80 на 20. Для наглядности построим график, где эти части будут окрашены синим и красным соответственно:

train_data, test_data = df[0:int(len(df) * 0.8)], df[int(len(df) * 0.8):]
plt.figure(figsize = (25, 10))
plt.title('Стоимость акций LG') # Название графика
plt.xlabel('Даты') # Название оси X
plt.ylabel('Цены') # Название оси Y
plt.plot(df['Open'], 'blue', label = 'Тренировочные данные') # Левая синяя часть линейного графика
plt.plot(test_data['Open'], 'red', label = 'Тестовые данные') # Правая красная часть линейного графика
plt.legend()

Мы получили вот такое разделение:

Определим функцию smape_kun(), которая поможет в дальнейшем охарактеризовать эффективность предсказаний модели – Симметричная средняя абсолютная ошибка в процентах (SMAPE):

def smape_kun(y_true, y_pred):
    return np.mean((np.abs(y_pred - y_true) * 200/ (np.abs(y_pred) + np.abs(y_true))))

Создадим пустые списки predictions и history, которые будем пополнять предсказаниями, и запустим цикл длительностью в тестовую часть датасета:

train_ar = train_data['Open'].values
test_ar = test_data['Open'].values

history = [x for x in train_ar]
predictions = list()
for t in range(len(test_ar)):
    model = ARIMA(history, order = (5, 1, 0)) # Параметризуем модель
    model_fit = model.fit(disp = 0) # Передадим обучающие данные
    output = model_fit.forecast() # Сгенерируем предсказания
    yhat = output[0] # Сделаем первое предсказание отдельной переменной
    predictions.append(yhat) # Добавим в список предсказаний первое значение
    obs = test_ar[t] # Создадим служебную переменную obs (observation)
    history.append(obs) # Пополним служебной переменной список history 

# Определим эффективность модели    
error = mean_squared_error(test_ar, predictions)
print('Тестовая среднеквадратическая ошибка: %.3f' % error)
error2 = smape_kun(test_ar, predictions)
print('Симметричная средняя абсолютная ошибка в процентах: %.3f' % error2)

Данных было немного, однако ошибка небольшая (измеряется в процентах):

Тестовая среднеквадратическая ошибка: 0.030
Симметричная средняя абсолютная ошибка в процентах: 2.269

Изучим сгенерированный список предсказаний, вызвав наполненный список predictions:

predictions

Мир неидеален, потому наш список наполнился предсказаниями – массивами в один элемент, что может сгененировать новичку дополнительную работу в будущем. Но, к счастью, не в нашем случае:

[array([9.93664905]),
 array([10.25150669]),
 array([10.31789186]),
 array([10.13737506]),
 array([10.07325307]),
 array([9.96248479]),
 array([9.79555676]),
 array([9.83781138]),
 array([9.63763933]),
 array([9.89237211])]

Для пущей наглядности визуализируем тестовые (реальные) значения стоимости акции и предсказанные:

plt.figure(figsize = (25, 10))
plt.plot(df['Open'], 'green', color = 'blue', label = 'Тренировочные данные') # Обучающие данные
plt.plot(test_data.index, predictions, color = 'green', marker = 'o', 
         linestyle = 'dashed', label = 'Предказанная цена') # Предсказания модели
plt.plot(test_data.index, test_data['Open'], color = 'red', label = 'Реальная цена') # Реальные тестовые данные
plt.title('Предсказанные цены акции LG') 
plt.xlabel('Даты')
plt.ylabel('Цены')
plt.xticks(np.arange(0, 60, 10), df['Date'][0:60:10]) # Зададим даты как подписи оси X
plt.legend() # Отобразим легенду диаграммы

Сейчас гораздо лучше видно, что модель не очень точна, вероятно, из-за малого объема тренировочных данных, но сейчас это не главное. Мы научились готовить данные с временными рядами к загрузке в модель.

Ноутбук, не требующий дополнительной настройки на момент написания статьи, можно скачать здесь.

Фото: @diegojimenez

Источник