В
табл. 6.1 приведены основные
временные параметры сетевых графиков.
Таблица
6.1
|
Элемент cети, |
Наименование параметра |
Условное обозначение параметра |
|
Событие i |
Ранний |
tp(i) |
|
Поздний |
tn(i) |
|
|
Резерв |
R(i) |
|
|
Работа |
Продолжительность |
t(i,j) |
|
Ранний |
tрн(i |
|
|
Ранний |
tро(i, |
|
|
Поздний |
tпн(i, |
|
|
Поздний |
tпо(i, |
|
|
Полный |
RП(i, |
|
|
Частный |
R1(i, |
|
|
Частный |
Rс(i, |
|
|
Независимый |
RН(i, |
|
|
Путь L |
Продолжительность |
t(L) |
|
Продолжительность |
tкр |
|
|
Резерв |
R(L) |
Рассмотрим
содержание и расчет указанных параметров.
Начнем
с параметров
событий. Как
уже отмечалось, событие не может наступить
прежде, чем свершатся все предшествующие
работы. Поэтому ранний
(или ожидаемый) срок tp(i)
свершения i-го события определяется
продолжительностью максимального пути,
предшествующего этому событию:
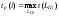
(6.1)
где
LПi
—
любой путь, предшествующий i-му
событию, т.е. путь от исходного до
i-го
события сети.
Если
событие
i
имеет несколько предшествующих путей,
а следовательно, несколько предшествующих
событий j,
то ранний срок свершения события i
удобно находить по формуле:

Задержка
свершения события i
по отношению к своему раннему сроку не
отразится на сроке свершения завершающего
события (а значит, и на сроке выполнения
комплекса работ) до тех пор, пока сумма
срока свершения этого события и
продолжительности (длины) максимального
из последующих за ним путей не превысит
длины критического пути.
Поэтому
поздний
(или предельный) срок tП(i)
свершения
i-го
события равен:
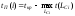
где
Lci
— любой
путь, следующий за i-м
событием,
т.е. путь от
i-го
до завершающего события сети.
Если
событие i
имеет
несколько последующих путей, а,
следовательно, несколько последующих
событий j,
то
поздний срок свершения события i
удобно находить по формуле:

Резерв
времени R(i)
i-го
события определяется как разность между
поздним и ранним сроками его свершения:
R(i)
=tП(i)
—tp(i). (6.5)
Резерв
времени события показывает, на какой
допустимый период времени можно задержать
наступление этого события, не вызывая
при этом увеличения срока выполнения
комплекса работ.
Критические
события резервов времени не имеют, так
как любая задержка в свершении события,
лежащего на критическом пути, вызовет
такую же задержку в свершении завершающего
события.
Из
этого следует, что для того чтобы
определить длину и топологию критического
пути, вовсе не обязательно перебирать
все полные пути сетевого графика и
определять их длины. Определив
ранний срок наступления завершающего
события сети, мы тем самым определяем
длину критического пути, а выявив события
с нулевыми резервами времени, определяем
его топологию.
Задача
1. Определить
временные параметры событий и критический
путь для сетевого графика, изображенного
на рис. 6.4.
Решение.
Найденные параметры сведем в табл. 6.2.
При
определении ранних сроков свершения
событий tp(i)
двигаемся
по сетевому графику слева направо и
используем формулы (6.1) и (6.2).
Для
i=0
(нулевого события) очевидно, что tР(0)
= 0.
Для i=1
tp(1)=tp(0)+t(0,1)
=
0+8 = 8 (суток), так как для события 1
существует только один предшествующий
путь Ln1:
0 →1. Для
i=
2 tp(2)
=
tp(1)+t(1,2)
= 8+9
= 17 (суток), так как для события 2
существует
только один предшествующий путь Ln2:
0 →1→2. Для
i
=
3 tp(3)
=
max{tp(0)+t(0,3);
tp(1)+t(1,3)}
= mах{0+13;
8+4} = mах{13;
12} = 13 (суток), так как для события 3
существуют
два предшествующих пути Ln3
0 →1→3 и
0→3
и
два предшествующих события –
0
и
1.
Таблица
6.2
|
Номер события |
Сроки свершения |
Резерв времени |
|
|
ранний tp(i) |
поздний tп(i) |
||
|
0 |
0 |
0 |
0 |
|
1 |
8 |
9 |
1 |
|
2 |
17 |
40 |
23 |
|
3 |
13 |
13 |
0 |
|
4 |
23 |
26 |
3 |
|
5 |
20 |
20 |
0 |
|
6 |
29 |
29 |
0 |
|
7 |
33 |
43 |
10 |
|
8 |
37 |
38 |
1 |
|
9 |
42 |
42 |
0 |
|
10 |
48 |
48 |
0 |
|
11 |
61 |
61 |
0 |
Аналогично:
tp(4)
=
max{tp(1)+t(1,4);
tp(3)+t(3,4)}
= mах{8+6;
13+10} = mах{14;
23} = 23(суткам),
tp(5)
=
max{tp(3)+t(3,5);
tp(0)+t(0,5)}
= mах{13+7;
0+9} = mах{20;
9} = 20(суткам),
tp(6)
=
max{tp(4)+t(3,4);
tp(3)+t(3,6);
tp(5)+t(5,6)}
= mах{23+3;
13+6; 20+9} = mах{26;
19; 29} = 29 (суткам) и т.д.
Длина
критического пути равна раннему сроку
свершения завершающего события 11
(см. табл.
6.2):
tкр=tр,(11)=61
(суткам).
При
определении поздних сроков свершения
событий tП(i)
двигаемся по сети в обратном направлении,
т.е. справа налево, и используем формулы
(6.3) и (6.4).
Для
i=11
(завершающего
события) поздний срок свершения события
должен равняться его раннему сроку
(иначе изменится длина критического
пути): tn(11)=tp(11)=61
(сутки).
Для
i=10
tП(10)=tp(11)-t(10,11)=61-13=48
(суток), так как для события 10
существует
только один последующий путь LС10:10→11.
Для
i=9
tП(9)
=
min{tП(10)-t(9,10);
tП(11)-t(9,10)}
= min{48-6;
61-17} = min{42;
44}=42 (суткам), так как для события 9
существуют два последующих пути
LC9:9→10→11
и
9→11
и
два последующих события –
10
и
11.
Аналогично:
tП(8)=tП(9)-t(8,9)=42-4=
38 (суткам);
tП(7)=tП(10)-t(7,10)=
48-5
= 43 (суткам);
tП(6)
=
min{tП(7)-t(6,7);
tП(10)-t(6,10);
tП(9)-t(6,
9); tП(8)-t(6,8);}
=min
(43-4;
48-5; 42-13; 38-8) = min
(39; 43; 29; 30)= 29 (суткам) и т.д.
По
формуле (6.5) определяем резервы времени
i-го
события:
R(0)
= 0; R(1)
= 9-8 = 1; R(2)=
40-17 = 23
и т.д.
Резерв
времени, например, события 2
— R(2)
= 23
–
означает, что время свершения события
2
может
быть задержано на 23 суток без увеличения
общего срока выполнения проекта.
Анализируя табл. 2, видим, что не имеют
резервов времени события 0,
3, 5, 6, 9, 11. Эти
события и образуют критический путь
(на рис. 5 он выделен жирным шрифтом)
Теперь
перейдем к параметрам
работ.
Отдельная работа
может начаться (и окончиться) в ранние,
поздние или другие промежуточные сроки.
В дальнейшем при оптимизации графика
возможно любое размещение работы в
заданном интервале.
Очевидно,
что ранний срок tрн(i,
j)
начала
работы
(i,
j)
совпадает
с ранним сроком наступления начального
(предшествующего) события i,
т.е.:
tрн(i,
j)
=
tp(i). (6.6)
Тогда
ранний срок tро(i,
j)
окончания
работы (i,j)
определяется
по формуле:
tрo(i,
j)
= ‘tp(i)+t(i,j).
(6.7)
Ни
одна работа не может окончиться позже
допустимого позднего срока своего
конечного события. Поэтому поздний срок
окончания работы (i,j)
определяется
соотношением:
tпо(i,
j)=tП(j),
(6.8)
а
поздний срок tnн(i,
j)
начала
этой работы — соотношением:

(6.9)
Таким
образом, в рамках сетевой модели моменты
начала и окончания работы тесно связаны
с соседними событиями ограничениями
(6.6)—(6.9).
Прежде
чем рассматривать резервы времени
работ, обратимся к резерву времени пути.
Такие резервы имеют все некритические
пути. Резерв
времени пути
R(L)
определяется как разность между длиной
критического и рассматриваемого пути:
R(L)=tкр
— t(L). (6.10)
Он
показывает, насколько в сумме могут
быть увеличены продолжительности всех
работ, принадлежащих этому пути. Если
затянуть выполнение работ, лежащих на
этом пути, на время большее чем R(L),
то
критический путь переместится на путь
L.
Отсюда
можно сделать вывод, что любая
из работ пути L
на его участке, не совпадающем с
критическим путем (замкнутым между
двумя событиями критического пути),
обладает резервом времени.
Среди
резервов времени работ выделяют четыре
разновидности.
Полный
резерв времени RП(i,
j)
работы (i,
j)
показывает, насколько можно увеличить
время выполнения данной работы при
условии, что срок выполнения комплекса
работ не изменится. Полный резерв RП(i,
j)
определяется по формуле:

Полный
резерв времени работы равен резерву
максимального из путей, проходящего
через данную работу. Этим резервом можно
располагать при выполнении данной
работы, если ее начальное событие
свершится в самый ранний срок, и можно
допустить свершение конечного события
в его самый поздний срок (рис. 6.6).
(6.11)
Важным
свойством полного резерва времени
работы является то, что он принадлежит
не только этой работе, но и всем полным
путям, проходящим через нее. При
использовании полного резерва времени
только для одной работы резервы времени
остальных работ, лежащих на максимальном
пути, проходящем через нее, будут
полностью исчерпаны. Резервы времени
работ, лежащих на других (не максимальных
по длительности) путях, проходящих через
эту работу, сократятся соответственно
на величину использованного резерва.
Остальные
резервы времени работы являются частями
ее полного резерва.
Частный
резерв времени первого вида ri
работы
(i,
j)
есть часть полного резерва времени, на
которую можно увеличить продолжительность
работы, не изменив при этом позднего
срока ее начального события. Этим
резервом можно располагать при выполнении
данной работы в предположении, что ее
начальное и конечное события свершаются
в свои самые поздние сроки (см. рис. 6.6).
R1
находится по формуле:
R1(i,j)=tn(j)-tp(i)-t(i,j), (6.12)
R1(i,
j)=RП(i,
j)-R(i). (6.13)
Частный
резерв времени второго вида, или
свободный
резерв времени Rc
работы
(i,
j)
представляет часть полного резерва
времени, на которую можно увеличить
продолжительность работы, не изменив
при этом раннего срока ее конечного
события. Этим
резервом можно располагать при выполнении
данной работы в предположении, что ее
начальное и конечное события свершатся
в свои самые ранние сроки.
Rc
находится по формуле:
Rc(i,
j)=tp(j)-tp(i)-t(i,
j),
(6.14)
R1(i,
j)=RП(i,
j)-R(j). (6.15)
Свободным
резервом времени можно пользоваться
для предотвращения случайностей, которые
могут возникнуть в ходе выполнения
работ. Если планировать выполнение
работ по ранним срокам их начала и
окончания, то всегда будет возможность
при необходимости перейти на поздние
сроки начала и окончания работ.
Независимый
резерв времени Rн,
работы (i,
j)
— часть полного резерва времени,
получаемая для случая, когда все
предшествующие работы заканчиваются
в поздние сроки, а все последующие работы
начинаются в ранние сроки.
Rн(i,
j)=tp(j)-tП(i)-t(i,
j), (6.16)
или
Rн(i,j)=RП(i,j)-r(i).
(6.17)
Использование
независимого резерва времени не влияет
на величину резервов времени других
работ. Независимые резервы стремятся
использовать тогда, когда окончание
предыдущей работы произошло в поздний
допустимый срок, а последующие работы
хотят выполнить в ранние сроки. Если
величина независимого резерва,
определяемая по формуле (6.16) или (6.17),
равна нулю или положительна, то такая
возможность есть. Если же величина Rн(i,
j)
отрицательна,
то этой возможности нет, так как предыдущая
работа еще не оканчивается, а последующая
уже должна начаться. Поэтому отрицательное
значение Rн(i,
j)
не имеет
реального смысла. А фактически независимый
резерв имеют лишь те работы, которые не
лежат на максимальных путях, проходящих
через их начальные и конечные события.
Следует
отметить, что резервы времени работы
(i,
j),
показанные на рис. 6.6, могут состоять из
двух временных отрезков, если интервал
продолжительности работы t(i,
j)
занимает
промежуточную позицию между двумя его
крайними положениями, изображенными
на графиках.
Таким
образом, если
частный резерв времени первого вида
может быть использован на увеличение
продолжительности данной и последующих
работ без затрат резерва времени
предшествующих работ, а свободный резерв
времени — на увеличение продолжительности
данной и предшествующих работ без
нарушения резерва времени последующих
работ, то независимый резерв времени
может быть использован для увеличения
продолжительности только данной работы.
Работы,
лежащие на критическом пути, так же как
и критические события, резервов времени
не имеют.
Если
на критическом пути лежит начальное
событие i,
то
Rп(i,
j)
=R1(i,
j).
(6.18)
Если
на критическом пути лежит конечное
событие j,
то
Rп(i,
j)
=Rс(i,
j).
(6.19)
Если
на критическом пути лежат начальное и
конечное события i
и j,
но
сама работа не принадлежит этому пути,
то
Rп(i,
j) =R1(i,
j)=Rс(i,
j) =Rн(i,
j). (6.20)
Соотношения
(6.18) — (6.20) можно использовать при проверке
правильности расчетов резервов времени
отдельных работ.
Задача
2.
Вычислить временные параметры работ
для сетевого графика, изображенного на
рис. 6.4.
Результаты
расчетов сведем в табл. 6.3.
Вычисление
временных параметров работы (i,
j)
покажем
на примере работы (1,
4):
ранний
срок начала работы (по формуле (6.16)):
tpн(1,4)=tр(1)=8(суток),
ранний
срок окончания работы (по формуле 6.17):
tpо(1,4)=tр(1)+t(1,4)=
=8+6=14
(суток);
поздний
срок начала работы (по формуле 6.19):
tпн(1,4)=tп(4)-t(1,4)=
26
—6 = 20 (суток), где tn(4)
= 26
(см. табл. 6.2);
поздний
срок окончания работы (по формуле 6.18):
tпо(1
4)=tп(4)=26(суток).
Таким
образом, работа (t,
4) должна
начаться в интервале [8; 28] (суток) и
окончиться в интервале [12; 26] (суток) от
начала выполнения проекта.
Полный
резерв работы (1,
4) (по формуле
6.11): Rn(1,4)=tп(4)-tp(1)-
—t(1,4)
= 26-8-6=12
(суток), т.е. срок выполнения данной
работы можно увеличить на 12 суток, при
этом срок выполнения комплекса работ
не изменится.
Таблица
6.3
|
№ п/п |
Работа (i,j) |
Продолжитель- ностьработы t(i,j) |
Сроки начала |
Резервы |
||||||
|
tрн(i,j) |
tрo(i,j) |
tпн(i,j) |
tпо(i,j) |
Rп(i,j) |
Rj(i,j) |
Rc(i,j) |
Rн(i,j) |
|||
|
1 |
(0,1) |
8 |
0 |
8 |
1 |
9 |
1 |
1 |
0 |
0 |
|
2 |
(0,3) |
13 |
0 |
13 |
0 |
13 |
0 |
0 |
0 |
0 |
|
3 |
(0,5) |
9 |
0 |
9 |
11 |
20 |
11 |
11 |
11 |
11 |
|
4 |
(1,2) |
9 |
8 |
17 |
31 |
40 |
23 |
22 |
0 |
|
|
5 |
(1,4) |
6 |
8 |
14 |
20 |
26 |
12 |
11 |
9 |
8 |
|
6 |
(1,3) |
4 |
8 |
12 |
9 |
13 |
1 |
0 |
1 |
0 |
|
7 |
(2,7) |
3 |
17 |
20 |
40 |
43 |
23 |
0 |
13 |
|
|
8 |
(3,4) |
10 |
13 |
23 |
16 |
26 |
3 |
3 |
0 |
0 |
|
9 |
(3,5) |
7 |
13 |
20 |
13 |
20 |
0 |
0 |
0 |
0 |
|
10 |
(3,6) |
б |
13 |
19 |
23 |
29 |
10 |
10 |
10 |
10 |
|
11 |
(4,7) |
8 |
23 |
31 |
35 |
43 |
12 |
9 |
2 |
— |
|
12 |
(4,6) |
3 |
23 |
26 |
26 |
29 |
3 |
0 |
3 |
0 |
|
13 |
(5,6) |
9 |
20 |
29 |
20 |
29 |
0 |
0 |
0 |
0 |
|
14 |
(5,8) |
10 |
20 |
30 |
28 |
38 |
8 |
8 |
7 |
7 |
|
15 |
(5,9) |
6 |
20 |
26 |
36 |
42 |
16 |
16 |
16 |
16 |
|
16 |
(6,7) |
4 |
29 |
33 |
39 |
43 |
10 |
10 |
0 |
0 |
|
17 |
(6,10) |
5 |
29 |
34 |
43 |
48 |
14 |
14 |
14 |
14 |
|
18 |
(6,9) |
13 |
29 |
42 |
29 |
42 |
0 |
0 |
0 |
0 |
|
19 |
(6,8) |
8 |
29 |
37 |
30 |
38 |
1 |
1 |
0 |
0 |
|
20 |
(7,10) |
5 |
33 |
38 |
43 |
48 |
10 |
0 |
10 |
0 |
|
21 |
(8,9) |
4 |
37 |
41 |
38 |
42 |
1 |
0 |
1 |
0 |
|
22 |
(9,10) |
6 |
42 |
48 |
42 |
48 |
0 |
0 |
0 |
0 |
|
23 |
(9,11) |
17 |
42 |
59 |
44 |
61 |
2 |
2 |
2 |
2 |
|
24 |
(10,11) |
13 |
48 |
61 |
48 |
61 |
0 |
0 |
0 |
0 |
Покажем
на примере работы (1,
4), что
полный резерв времени работы равен
продолжительности максимального из
путей, проходящих через данную работу.
Через
работу (1,
4)
проходят
семь полных путей (см. рис. 6.4):
|
Путь |
Продолжительность, |
|
|
L1 |
0→1→4→6→7→10→11 |
39 |
|
L2 |
0→1→4→6→8→9→10→11 |
48 |
|
L3 |
0→1→4→6→8→9→11 |
46 |
|
L4 |
0→1→4→6→9→10→11 |
49 |
|
L5 |
0→1→4→6→9→11 |
47 |
|
L6 |
0→1→4→6→10→11 |
35 |
|
L7 |
0→1→4→7→10→11 |
40 |
Отсюда
максимальным из путей, проходящих через
работу (1,
4),
является
путь L4
продолжительностью
49 (суток), резерв времени которого (по
формуле (6.10)) R(L4)
=61-49=12
(суток).
Как
видим, полный резерв времени работы (1,
4)
оказался
равным резерву пути L4
–
максимального из путей, проходящих
через эту работу. Если увеличить
продолжительность выполнения работы
t(1,
4) на
12 суток, т.е. с 6 до 18 суток, то полностью
будет исчерпан резерв времени пути L4
, т.е.
этот путь станет также критическим, а
резервы времени других путей уменьшатся
соответственно на 12 суток.
Частный
резерв времени работы (1, 4)
первого
вида определим по формуле (6.12) (или по
формуле 13): R1(1,
4) = tn(4)-tn(1)=t(1,
4)= 26-9-6=11
(суток) (или R1(1,
4)
=
Rn(1,
4)
– Rn(1,4)-R(1)
= 12
— 1 = 11 (суток), т.е. при сохранении общего
срока выполнения проекта на 11 суток
может быть задержано выполнение работы
(1, 4)
и
последующих работ (по любому из путей
L1,
l2,,
…,
L7)
без затрат резерва времени предшествующих
ей работ (в данном случае без затрат
резерва времени одной предшествующей
работы (0,1)).
Частный
резерв времени второго вида, или свободный
резерв времени, работы (1,
4) найдем
по формуле (6.14) (или 6.15)): Rc(1,
4)
= tp(4)-tp(1)
— —t(l,4)
= 23-8-6
= 9 (суток) (или Rc(1,
4)
= Rn(1,
4)-R(4)
= 12-3
= 9 (суток), т.е. при сохранении общего
срока выполнения проекта на 9 суток
может быть задержано выполнение работы
(1,
4) и
предшествующих ей работ (в данном случае
работы (0,
1)) без
нарушения резерва времени последующих
работ.
Независимый
резерв времени работы (1,
4)
определим
по формуле (6.16) (или (6.17)): RH(1,
4) = tp(4)-tn(1)-t(1,
4) =
23-9-6 = 8 (суток) (или Rн(1,4)
=
=Rn(1,4)-R(1)-R(4)
= 12-1-3
= 8 (суток), т.е. на 8 суток может быть
увеличена продолжительность работы
(1,
4)
без
изменения резервов времени всех остальных
работ.
Обратим
внимание на то, что независимые резервы
работ (1,
2),
(2, 7) и
(4,
7) отрицательны
(в табл. 6.3 они обозначены прочерком).
Например, Rн(2,
7) =tp(7)-tn(2)-t(2,
7)
= 33-40-3 = -10. Это означает, что работа (2,
7) продолжительностью
3 (суток) должна закончиться на 33-и сутки
после начала комплекса работ, а начаться
на 40-е сутки, что, естественно, невозможно.
Подчеркнем,
что резервы критических работ (0,
3), (3, 5), (5, 6), (6, 9), (9, 10), (10, 11), так
же как и резервы критических событий,
равны нулю.
Следует
отметить, что в случае достаточно простых
сетевых графиков результаты расчета
их временных параметров можно фиксировать
прямо на графике. Параметры событий
записываются в кружках, разделенных на
четыре части, а параметры работ –
над соответствующими стрелками (рис.
6.7). При этом отпадает необходимость
составления таблиц.
Анализ сетевой модели
Параметры сетевой
модели. Параметрами сетевой модели являются:
Наиболее раннее возможное время наступления 
определяется следующей рекуррентной формулой:
 |
( 14.1) |
где 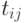
продолжительность 
работы; 

Вычисления по формуле (14.1) выполняются шаг за шагом, двигаясь в порядке
нумерации событий.
Самое позднее допустимое время наступления события
определяется с помощью аналогичной рекуррентной формулы, но обращаясь не
к предшествующим, а к последующим событиям.
 |
( 14.2) |
где 
множество событий, следующих за 
Для определения 
конечного события 
этом 
Резервом времени данного события называется
разность между 

 |
( 14.3) |
Полный резерв времени работы 
 |
( 14.4) |
Свободный резерв времени работы 
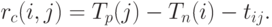 |
( 14.5) |
[c.75]
Так как критический путь, его продолжительность и резервы времени работ определяются на основании параметров сети, то прежде всего производится их расчет. При этом соблюдается такая последовательность в расчетах вначале определяем раннее начало и раннее окончание работ, потом позднее начало и позднее скончание работ, критический путь, полные и частные резервы.
[c.104]
RL — полный резерв времени пути KJ, и г i, — полным и частный резерв времени работы
[c.104]
Полный резерв времени работы / ,-/ — это время, на которое можно перенести начало работы или увеличить ее продолжительность без изменения общего срока окончания всего комплекса работ. Этот резерв определяется как разность между ранним и поздним началом работ или между их ранним и поздним окончанием [c.105]
Резервы времени. Продолжительность критического пути больше продолжительности любого другого пути, следовательно, у некритических путей и лежащих на них работ и событий имеются резервы времени. При расчете сетевых графиков определяют резервы времени событии, полных путей, полные и свободные резервы времени работ
[c.91]
Резерв времени любого полного пути P(/-i) равен разности между длиной критического пути п полного пути, для которого определяют резерв, т. е. /кр—l(L ). Этот резерв времени показывает, на сколько можно увеличить продолжительность выполнения работ, лежащих на некритических участках данного полного пути, не увеличивая сроки разработки комплекса в целом,
[c.91]
Свободный резерв времени работы показывает, какую часть полного резерва времени можно использовать для данной конкретной работы.
[c.92]
Полный резерв времени работ P,,(i /) находят, вычитая и.з данных графы 8 данные графы 6 или и.ч графы 7 графы 5.
[c.94]
Полный резерв времени работы ТРИ. Величина
[c.70]
Определение полного резерва времени работы дано в табл. 4.5. Величина Те» определяется вычитанием значения Т 9 из значения Tj1 последовательно в каждой строке.
[c.70]
Полный резерв времени работы определяется формулой
[c.384]
Работы и события сетевого графика имеют резервы времени. Работы имеют полные и свободные резервы времени.
[c.49]
Полный резерв времени работы Rn(i, /) равен разности между поздним сроком наступления следующего за ней события / и ранним сроком наступления предшествующего ей события / без продолжительности этой работы ((, /) [c.49]
Полный резерв времени работы — это время, на которое можно увеличить продолжительность работы или перенести сроки ее начала, чтобы продолжительность проходящего через нее максимального пути не превысила продолжительности критического пути. Если полный резерв (запас) времени будет исчерпан, то данная работа станет критической, соответственно критическим станет и путь, на котором она лежит.
[c.49]
Резервы времени работ на сетевых графиках изображаются дробью под стрелкой (работой) полный резерв — в числителе, свободный — в знаменателе.
[c.50]
Полный резерв времени работ [R(i—/) ] определяется как разность между данными граф 6 и 4 или граф 7 и 5 табл. 4.
[c.52]
Полный резерв времени работы равен разности между числовым значением правого сектора события, в которое данная работа входит, и числовым значением левого сектора события,
[c.53]
Резервы времени работ изображаются на сетевых графиках п од стрелками дробью полный резерв — в числителе, свобод- ный — в знаменателе.
[c.54]
Полный резерв времени работы Ru ц — это максимальное количество времени, на которое можно увеличить продолжительность данной работы, не изменяя при этом продолжительности критического пути [c.233]
Важным свойством полного резерва времени работы является то, что если его использовать частично или целиком для увеличения длительности какой-либо работы, то соответственно уменьшится резерв времени всех остальных работ, лежащих на этом пути.
[c.233]
Полный резерв времени работы показывает, на сколько можно увеличить продолжительность работы, чтобы проходящий через нее максимальный путь (при условии сохранения плановых сроков выполнения других работ, лежащих на этом пути) не превысил длины критического. Полный резерв времени любой работы рассчитывается как разность между поздним и ранним сроками свершения начального события.
[c.176]
Вдоль шкалы абсцисс на рис. 5.3 расположены в масштабе времени возможные сроки наступления события i и события j. Между этими событиями, показанными в кружках, выполняется работа ty. Время выполнения работы меньше, чем период между поздним сроком наступления предшествующего события Тц1 и ранним сроком наступления последующего события Tpj. Проведя вертикальные линии из точек возможного наступления событий и точек начала и окончания работы t(j, получим отрезки АВ, А1 В, D и F, с помощью которых легко представить себе величины полного и свободного резервов времени работ.
[c.41]
Резервы времени. К ним относятся резервы времени полного пути, полные и свободные резервы времени работ.
[c.332]
Полный резерв времени работы показывает, на сколько можно увеличить продолжительность данной работы, чтобы проходящий через нее максимальный путь не превысил длины критического пути. Полный резерв времени любой работы Р (, /> определяется по формуле
[c.332]
Свободный резерв времени работы показывает, какая часть полного резерва времени может быть использована для данной конкретной работы. Свободный резерв определяется выражением
[c.332]
Полный резерв времени работы Рп (/ -) находят вычитанием из данных графы 8 данных графы 6 или из графы 7 — графы 5.
[c.335]
Резервы времени. К ним относятся резервы времени полного пути, полные и свободные резервы времени работ, резерв времени события.
[c.378]
Резерв времени работы, определенный посредством резерва времени пути, на котором она. находится, называется полным резервом времени работы ij и обозначается через Rn .
[c.367]
Значения полных резервов времени работ также заносятся в табл. 134.
[c.368]
Полный резерв времени работы rn(i, j), вычисляемый по формуле [c.167]
Суть полного резерва времени работы заключается в том, что задержка в выполнении работы (i, j) на величину At > rn приводит к задержке в наступлении завершающего события на величину At-r(ij).
[c.167]
В качестве базовой методики вычисления главных показателей графика проекта используется хорошо зарекомендовавший себя метод критического пути — основа методов сетевого планирования и управления. Под методом критического пути понимают совокупность методик и формул сетевого планирования и управления, обеспечивающих автоматическое вычисление для всех работ графика моментов раннего и позднего начала, раннего и позднего окончания, а также полных и свободных резервов времени. Работы, имеющие отрицательный или нулевой резерв времени, считают находящимися на критическом пути. Часто в состав критического пути включают работы, имеющие достаточно малый резерв времени, не превосходящий некоторой заранее заданной малой положительной вели-
[c.28]
Полный резерв времени работы рассчитывают по формуле
[c.310]
Если из цифры, помещенной в правом секторе конечного события (/), вычесть показатель, проставленный в левом секторе начального (i) события и продолжительность самой работы tom(i—/), то получим полный резерв времени данной работы — Pn(i—/). Свободный резерв времени работ — P (i—/) находят как разность цифр левого сектора конечного события (/), правого сектора начального события (t) продолжительности работы.
[c.111]
Полный резерв времени работы Rn Tf-Tf-t,, Rail — полный резерв времени работы
[c.63]



