По бизнес-плану четырёхлетний проект предполагает начальное вложение — 20 млн рублей. По итогам каждого года планируется прирост вложенных средств на 16% по сравнению с началом года. Начисленные проценты остаются вложенными в проект. Кроме этого, сразу после начислений процентов нужны дополнительные вложения: целое число n млн рублей и в первый, и во второй годы, а также целое число m млн рублей и в третий, и в четвёртый годы. Найдите наименьшее значение n, при котором первоначальные вложения за два года как минимум удвоятся, и наименьшее значение m, для которого при найденном ранее значении n первоначальные вложения за четыре года как минимум утроятся.
Спрятать решение
Решение.
К началу 2-го года получится млн вложений, а к началу 3-го года —
По условию Наименьшее целое решение:
Тогда к началу 3-го года получится
млн.
К началу 4-го года имеем млн, а в конце проекта
По условию откуда
Получаем, что m = 2 — наименьшее целое решение.
Ответ: 7 и 2 млн руб.
Спрятать критерии
Критерии проверки:
| Критерии оценивания выполнения задания | Баллы |
|---|---|
| Обоснованно получен верный ответ | 2 |
| Верно построена математическая модель | 1 |
| Решение не соответствует ни одному из критериев, перечисленных выше | 0 |
| Максимальный балл | 2 |
ЕГЭ 2022 ФИПИ. Вариант 7. Задача 15.
Производство х тыс. единиц продукции в q=2x2+5x+10 млн рублей в год. При цене p тыс. рублей за единицу годовая прибыль от продажи этой продукции (в млн рублей) составляет px-q. При каком наименьшем значении p через 12 лет суммарная прибыль может составить не менее 744 млн рублей при некотором значении х?
Решение.
Так как при цене p тыс. рублей за единицу годовая прибыль от продажи этой продукции (в млн рублей) составляет px-q, то за 12 лет суммарная прибыль составит 12px-12q млн рублей, и по условию эта сумма должна быть не менее 744 млн рублей при некотором значении х.
Получаем неравенство: 12px-12q ≥ 744.
Подставим данное значение q=2x2+5x+10. Получим:
12px-12(2x2+5x+10) ≥ 744. Упростим, разделив обе части неравенства на 12.
px-(2x2+5x+10) ≥ 62;
px-2x2-5x-10 ≥ 62;
-2x2+px-5x-10 ≥ 62;
-2x2+(p-5)x-10-62 ≥ 0;
2x2-(p-5)x+72 ≤ 0.
Для того, чтобы это неравенство имело решения, дискриминант квадратного уравнения 2x2-(p-5)x+72 = 0 должен быть неотрицательным.
D=b2-4ac=(p-5)2-4∙2∙72=(p-5)2-576 ≥ 0;
(p-5)2-242 ≥ 0;
(p-5+24)(p-5-24) ≥ 0;
(p+19)(p-29) ≥ 0.
Последнее неравенство будет верным при p ≤ -19 или p ≥ 29. Но значение p не может быть отрицательным, значит, наименьшее значение p=29.
Мы ответили на вопрос задачи, но интересно знать значение х. Подставим значение p=29 в неравенство 2x2-(p-5)x+72 ≤ 0.
2х2-24х+72 ≤ 0;
х2-12х+36 ≤ 0;
(х-6)2 ≤ 0. Единственно возможное значение х=6.
Таким образом, при производстве 6 тысяч единиц продукции при цене 29 тысяч рублей за единицу через 12 лет прибыль составит не менее 744 млн рублей.
Ответ: 29.
Экономические задачи ЕГЭ Это страница с нужной вам задачей
ЕГЭ 2022 ФИПИ. Вариант 8. Задача 15.
Производство х тыс. единиц продукции в q=3x2+6x+13 млн рублей в год. При цене p тыс. рублей за единицу годовая прибыль от продажи этой продукции (в млн рублей) составляет px-q. При каком наименьшем значении p через пять лет суммарная прибыль может составить не менее 70 млн рублей при некотором значении х?
Решение.
Так как при цене p тыс. рублей за единицу годовая прибыль от продажи этой продукции (в млн рублей) составляет px-q, а за пять лет суммарная прибыль должна составить не менее 70 млн рублей при некотором значении х, то за год эта возможная прибыль будет не менее 70:5=14 млн. рублей.
Получаем неравенство: px-q ≥ 14.
Подставим данное значение q=3x2+6x+13. Получим:
px-3x2-6x-13 ≥ 14;
-3x2+px-6x-27 ≥ 0;
3x2-(p-6)x+27 ≤ 0.
Для того, чтобы это неравенство имело решения дискриминант квадратного уравнения 3x2-(p-6)x+27 = 0 должен быть неотрицательным.
D=b2-4ac=(p-6)2-4∙3∙27=(p-6)2-324 ≥ 0;
(p-6)2-182 ≥ 0;
(p-6+18)(p-6-18) ≥ 0;
(p+12)(p-24) ≥ 0.
Последнее неравенство будет верным при p ≤ -12 или p ≥ 24. Но значение p не может быть отрицательным, значит, наименьшее значение p=24.
Подставим найденное значение p=24 в неравенство 3x2-(p-6)x+27 ≤ 0.
3х2-18х+27 ≤ 0;
х2-6х+9 ≤ 0;
(х-3)2 ≤ 0. Единственно возможное значение х=3.
Таким образом, при производстве 3 тысяч единиц продукции при цене 24 тысячи рублей за единицу через пять лет прибыль составит не менее 70 млн рублей.
Ответ: 24.
ЕГЭ 2022 ФИПИ. Вариант 20. Задача 15.
Бригаду из 30 рабочих нужно распределить по двум объектам. Если на первом объекте работает p человек, то каждый из них получает в сутки 200p рублей. Если на втором объекте работает p человек, то каждый из них получает в сутки (50p+300) рублей. Как нужно распределить рабочих по объектам, чтобы их суммарная суточная зарплата оказалась наименьшей? Сколько рублей в этом случае придётся заплатить за сутки всем рабочим?
Решение.
Пусть в 1-й бригаде работает p человек, тогда во 2-й бригаде (30-p) человек. Тогда суммарная суточная зарплата составит:
200p∙p+(50(30-p)+300)(30-p). Упростим выражение.
200p2+(1500-50p+300)(30-p)=
=200p2+(1800-50p)(30-p)=
=200p2+54000-1500p-1800p+50p2=
250p2-3300p+54000.
Составим функцию F(p) – зависимости суточной зарплаты от количества рабочих p на 1-м объекте и исследуем её на минимум с помощью производной.
F(p)=250p2-3300+54000.
F’(p)=500p-3300.
F’(p)=0 при 500p=3300; p=6,6 – критическая точка.
Так как F’(p) < 0 при p < 6,6 и F’(p) > 0 при p > 6,6, то
p=6,6 – точка минимума функции F’(p).
Но так как p – целое число, то округлим значение 6,6 до 7.
p = 6,6 ≈ 7.
Итак, на 1-м объекте будут работать 7 человек,
а на 2-м объекте 30-7=23 человека.
Следовательно, суммарная суточная зарплата составит:
F(7)=250 ∙ 72 -3300 ∙ 7+54000 = 250∙49-23100+54000 =
= 12250+54000-23100 = 66250-23100 = 43150 (рублей).
Ответ: 1-й объект – 7 рабочих; 2-й объект – 23 рабочих; 43150 рублей – суммарная суточная зарплата.
ЕГЭ 2022 ФИПИ. Вариант 27. Задача 15.
По бизнес-плану четырёхлетний проект предполагает начальное вложение 25 млн рублей. По итогам каждого года планируется прирост вложенных средств на 20 % по сравнению с началом года. Начисленные проценты остаются вложенными в проект. Кроме этого, сразу после начислений процентов нужны дополнительные вложения: целое число n млн рублей и в первый, и во второй годы, а также целое число m млн рублей и в третий, и в четвёртый годы. Найдите наименьшее значение n, при котором первоначальные вложения за два года как минимум удвоятся, и наименьшее значение m, такое, что при найденном ранее значении n первоначальные вложения за четыре года вырастут как минимум в четыре раза.
Решение.
1 год. Итоги 1,2∙25=30 (здесь и далее все величины в млн рублей).
Вложение 30+n.
2 год. Итоги 1,2(30+n)=36+1,2n.
Вложение 36+1,2n +n=36+2,2n.
Так как за два года первоначальные вложения как минимум удвоятся, то
36+2,2n ≥ 2∙25;
2,2n ≥ 50-36;
2,2n ≥ 14;
n ≥ 140:22;
n ≥ 6,36… .
n = 7 – наименьшее целое.
3 год. Итоги 1,2(36+2,2∙7)=1,2(36+15,4)=1,2∙51,4=61,68.
Вложение 61,68+m.
4 год. Итоги 1,2(61,68+m)=74,016+1,2m.
Вложение. 74,016+2,2m.
Так как за четыре года первоначальные вложения вырастут как минимум в четыре раза, то
74,016+2,2m ≥ 4∙25;
2,2m ≥ 100-74,016;
2,2m ≥ 25,984;
m ≥ 259,84:22;
m ≥ 11,81… .
m = 12 – наименьшее целое.
Ответ: 7 млн рублей и 12 млн рублей.
ЕГЭ 2022 ФИПИ. Вариант 28. Задача 15.
По бизнес-плану четырёхлетний проект предполагает начальное вложение 20 млн рублей. По итогам каждого года планируется прирост вложенных средств на 15 % по сравнению с началом года. Начисленные проценты остаются вложенными в проект. Кроме этого, сразу после начислений процентов нужны дополнительные вложения: целое число n млн рублей и в первый, и во второй годы, а также целое число m млн рублей и в третий, и в четвёртый годы. Найдите наименьшее значение n, при котором первоначальные вложения за два года как минимум удвоятся, и наименьшее значение m, такое, что при найденном ранее значении n первоначальные вложения за четыре года как минимум утроятся.
Решение.
1 год. Итоги 1,15∙20=23 (здесь и далее все величины в млн рублей).
Вложение 23+n.
2 год. Итоги 1,15(23+n)=26,45+1,15n.
Вложение 26,45+1,15n+n=26,45+2,15n.
Так как за два года первоначальные вложения как минимум удвоятся, то
26,45+2,15n ≥ 2∙20;
2,15n ≥ 40-26,45;
2,15n ≥ 13,55;
n ≥ 1355:215;
n ≥ 6,30… .
n = 7 – наименьшее целое.
3 год. Итоги 1,15(26,45+2,15∙7)=1,15(26,46+15,05)=1,15∙41,5=47,725.
Вложение 47,725+m.
4 год. Итоги 1,15(47,725+m)=54,88375+1,15m.
Вложение. 54,88375+2,15m.
Так как за четыре года первоначальные вложения как минимум утроятся, то
54,88375+2,15m ≥ 3∙20;
2,15m ≥ 60-54,88375;
2,15m ≥ 5,11625;
m ≥ 511,625:215;
m ≥ 2,379… .
m = 3 – наименьшее целое.
Ответ: 7 млн рублей и 3 млн рублей.
ЕГЭ 2022 ФИПИ. Вариант 30. Задача 15.
По бизнес-плану четырёхлетний проект предполагает начальное вложение 10 млн рублей. По итогам каждого года планируется прирост вложенных средств на 12 % по сравнению с началом года. Начисленные проценты остаются вложенными в проект. Кроме этого, сразу после начислений процентов нужны дополнительные вложения: целое число n млн рублей и в первый, и во второй годы, а также целое число m млн рублей и в третий, и в четвёртый годы. Найдите наименьшее значение n, при котором первоначальные вложения за два года вырастут как минимум в полтора раза, и наименьшее значение m, такое, что при найденном ранее значении n первоначальные вложения за четыре года как минимум утроятся.
Решение.
1 год. Итоги 1,12∙10=11,2 (здесь и далее все величины в млн рублей).
Вложение 11,2+n.
2 год. Итоги 1,12(11,2+n)=12,544+1,12n.
Вложение 12,544+1,12n+n=12,544+2,12n.
Так как за два года первоначальные вложения вырастут как минимум в полтора раза, то
12,544+2,12n ≥ 1,5∙10;
2,12n ≥ 15-12,544;
2,12n ≥ 2,456;
n ≥ 245,6:212;
n ≥ 1,16… .
n = 2 – наименьшее целое.
Итак, в проекте 12,544 + 2,12∙2=16,784 млн рублей.
3 год. Итоги 1,12∙16,784=18,79808.
Вложение 18,79808+m.
4 год. Итоги 1,12(18,79808+m)=21,0538496+1,12m.
Вложение. 21,0538496+2,12m.
Так как за четыре года первоначальные вложения как минимум утроятся, то
21,0538496+2,12m ≥ 3∙10;
2,12m ≥ 30-21,0538496;
2,12m ≥ 8,9461504;
m ≥ 894,61504:212;
m ≥ 4,22… .
m = 5 – наименьшее целое.
Ответ: 2 млн рублей и 5 млн рублей.
Навигация
Задание 17. Вариант 7. ЕГЭ 2020 из 36 вариантов.
Задание 17. По бизнес-плану четырёхлетний проект предполагает начальное вложение — 25 млн рублей. По итогам каждого года планируется прирост вложенных средств на 20 % по сравнению с началом года. Начисленные проценты остаются вложенными в проект. Кроме этого, сразу после начислений процентов нужны дополнительные вложения: целое число n млн рублей и в первый, и во второй годы, а также целое число m млн рублей и в третий, и в четвёртый годы. Найдите наименьшее значение n, при котором первоначальные вложения за два года как минимум удвоятся, и наименьшее значение m, такое, что при найденном ранее значении n первоначальные вложения за четыре года вырастут как минимум в четыре раза.
Решение.
К началу 2-го года получится млн вложений, а к началу 3-го года –
По условию . Наименьшее целое решение n = 7. Тогда к началу 3-го года получится
36+15,4 = 51,4 млн.
К началу 4-го года имеем млн, а в конце проекта
По условию ,
откуда
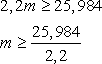
Получаем, что m = 12 – наименьшее целое решение.
Ответ: 7 и 12 млн. руб.
Экзаменационные задания по математике (профильный уровень) содержат задачу с экономическим содержанием под №17. Это задание повышенного уровня сложности, которое оценивается максимально в 3 балла. Для того, чтобы успешно решать подобные задачи, ученики должны не только владеть определенным математическим инструментарием, но и уметь строить простейшие математические модели по заданным условиям. При подготовке учащихся к решению данных задач возникает ряд вопросов, которые надо с ними предварительно обсудить.
1. Что нам дает решение экономических задач?
На самом деле при решении экономических задач формируются навыки, столь необходимые в реальности. Это:
- навык моделирования процесса по реальной ситуации;
- знакомство с кредитной системой изнутри;
- понимание основ расчета прибыли и затрат;
- навык анализа информации;
- навык решения практических задач;
- развитие алгоритмического мышления;
- умение структурировать информацию.
2. Какие типы экономических задач нам могут встретиться на экзамене?
В отличие от других экзаменационных заданий, «экономические» задачи не отличаются большим разнообразием и встречаются лишь нескольких типов. Это:
Задачи на кредиты и вклады:
- вклады;
- кредиты с различными схемами выплат.
Задачи на оптимальный выбор:
- экстремальные задачи;
- задачи на ограничение производственных возможностей.
Прежде, чем приступить, собственно, к решению задач, следует провести предварительную подготовку, которая заключается в следующем:
- Хорошо объяснить проценты и разобрать различные задачи на понимание процента;
- Простой и сложный процент;
- Понимание расчета выгоды и альтернативной стоимости;
- Вычисление производной, нахождение минимума и максимума;
- Моделирование процесса, описанного в задаче;
Перед началом объяснения экономической задачи полезно повторить темы:
- Задачи на проценты
- Арифметическая прогрессия
- Производная
Полезные задачи на проценты
1) На сколько процентов 5 больше, чем 4? На сколько процентов 4 меньше, чем 5?
Должно быть понимание того, что основа — это то, с чем сравниваем.
5:4=1,25, то есть 5 больше, чем 4 на 25%.
4:5=0,8, то есть 4 меньше, чем 5 на 20 %.
2) Сколько процентов от 20 составляет 25? Сколько процентов от 25 составляет 20?
25:20=1,25=125%
20:25=0.8=80%
3) Цена винограда в сентябре увеличилась на 10%, а в октябре снизилась на 10%. Как изменилась цена винограда по сравнению с первоначальной?
Можно пока показать в рублях: 100р → 110р → 99р.
Затем перейти решению задачи:
Пусть х — начальная цена, тогда цена в сентябре — 1,1х, а цена в октябре-
1,1х-1,1х*0,1=0,99х, то есть цена понизилась на 1%.
Полезные задачи на арифметическую прогрессию
1. В кинотеатре в каждом ряду на 2 сиденья больше, чем в предыдущем. В первом ряду 12 сидений, всего 30 рядов. Сколько мест в кинотеатре?
При изучении темы «Арифметическая прогрессия» решение подобных задач не вызывает затруднений у учащихся. Достаточно применить формулу для нахождения суммы n первых членов арифметической прогрессии.
а30 = 70, S30 = (12+70)*30/2=1230.
А после предложить задачу:
2. Первоначальный долг составлял 200 тыс. руб., и каждый месяц убывал на 20 тыс.руб. За сколько месяцев был выплачен этот долг?
Можно воспользоваться схемой:
200 тыс → 180 т ыс → 160 тыс → … → 0, за 10 месяцев
Полезные задачи на понимание процесса:
1) Доходы фирмы составили 200 тыс.руб., а расходы — 180 тыс.руб. Чему была равна прибыль компании?
Решение:
П(прибыль)= Д(доход)-Р(расходы)
П=200 тыс-180тыс
П=20 тыс. р.
Ответ: 20 000 рублей.
2) Доходы и расходы фирмы зависят от того, какое количество продукта она произвела. Фирма производит Q единиц продукции. Доходы считаются по формуле 150Q, а расходы Q2+10Q-3000. По какой формуле можно рассчитать прибыль фирмы? При каком значении Q прибыль будет максимальной? Найдите эту максимальную прибыль.
Решение:
П(прибыль)= Д(доход)-Р(расходы)
П=150Q-(Q2+10Q-3000)
П= -Q2+140Q+3000
(П)ꞌ= -2Q+140
-2Q+140=0
Q=70 — точка максимума.
Max П=П(70)=7900(р)
Ответ: 7900 рублей.
3) На заводе можно за день произвести 100 деталей первого типа либо 50 деталей второго типа, при этом оборудование и материалы будут использованы полностью. Прибыль от детали первого типа 700 рублей, а второго — 1000 рублей. Сегодня нужно изготовить 20 деталей первого типа, а остальные — второго. Какое наибольшее количество деталей второго типа можно произвести? Какую прибыль при этом можно получить?
Решение:
1. 20/100=20% мощности потратили
2. На 2 тип деталей осталось 80%
0,8*50=40(дет)
3. П= 20*700+40*1000=54000(р)
Ответ: 54000 рублей
И, после того, как была проведена соответствующая подготовка, можно приступать к решению задач. Разумеется, решение следует начинать с более простых задач, постепенно усложняя разбираемые ситуации.
Задачи, которые я буду рассматривать, взяты из сборника по подготовке к ЕГЭ под редакцией И.В.Ященко 2020 г.
Наибольшее количество задач, которые встречаются в этом сборнике (и не только) — это задачи на кредиты и вклады.
Математическая модель: вклады и кредиты
(Вариант 3)
«В июле планируется взять кредит в банке на некоторую сумму. Условия его возврата таковы:
- каждый январь долг возрастает на 15% по сравнению с концом предыдущего года;
- с февраля по июнь каждого года необходимо выплатить часть долга, равную 1,587 млн. рублей.
Сколько млн. рублей было взято в банке, если известно, что он был полностью погашен двумя равными платежами (то есть за 2 года)?»
Решение:
Пусть сумма кредита равна S, тогда
| n |
Долг до начисления % |
Долг после начисления % |
Выплаты |
|
1г |
S |
1,15 *S |
1,587 |
|
2г |
1,15 *S-1,587 |
1,15*(1,15 *S-1,587) |
1,587 |
|
3г |
0 |
Поскольку долг стал равен нулю после второй выплаты, то можно составить уравнение:
1,15*(1,15 *S-1,587) -1,587=0
1,152S- 1,15*1,587=1,587
S=2,58 (млн. р.)
Ответ: 2,58 млн. р.
(Вариант 16)
«31 декабря 2014 года Михаил взял в банке некоторую сумму в кредит под 10% годовых. Схема выплаты кредита следующая: 31 декабря каждого следующего года банк начисляет проценты на оставшуюся сумму долга (то есть увеличивает долг на10%), затем Михаил переводит в банк 2928200 рублей. Какую сумму взял Михаил в банке, если он выплатил долг четырьмя равными платежами (то есть за 4 года)?»
Решение:
Пусть Михаил взял в банке S млн. рублей, тогда:
| n |
Долг до начисления % |
Долг после начисления % |
Выплаты |
|
1г |
S |
1,1 *S |
2928200 |
|
2г |
1,1 *S-2928200 |
1,1*(1,1 *S-2928200) |
2928200 |
|
3г |
1,1*(1,1*S-2928200)—2928200 |
1,1*(1,1*(1,1 *S-2928200)-2928200) |
2928200 |
|
4г |
1,1*(1,1*(1,1*S-2928200)-2928200)-2928200 |
1,1*(1,1*(1,1*(1,1*S-2928200)-2928200)-2928200) |
2928200 |
|
5г |
0 |
Поскольку долг стал равен нулю после четвертой выплаты, то можно составить уравнение:
1,1*(1,1*(1,1*(1,1 *S-2928200)-2928200)-2928200)- 2928200=0
1,14S-1,13*2928200-1,12*2928200-1,1*2928200-2928200=0
S= 9282000 (р)
Ответ: 9282000 рублей.
(Вариант 7)
«По бизнес-плану четырехлетний проект предполагает начальное вложение — 25 млн. рублей. По итогам каждого года планируется прирост вложенных средств на 20% по сравнению с началом года. Начисленные проценты остаются вложенными в проект. Кроме того, сразу после начислений процентов нужны дополнительные вложения: целое число n млн. рублей и в первый, и во второй годы, а также целое число m млн. рублей и в третий, и в четвертый годы. Найдите наименьшее значение n, при котором первоначальные вложения за два года, как минимум удвоятся, и наименьшее значение m, такое, что при найденном ранее значении n первоначальные вложения за четыре года вырастут как минимум в четыре раза.»
Решение:
Итак, имеем:
| n |
Вклад до начисления % |
Вклад после начисления % |
Дополнительные вложения |
|
1 |
25 |
1,2*25=30 |
n |
|
2 |
30+n |
1,2*(30+n)=36+1,2n |
n |
|
3 |
36+2,2n |
1,2*(36+2,2n)=43,2+2,64n |
m |
|
4 |
43,2+2,64n+m |
1,2*(43,2+2,64n+m) |
m |
|
5 |
1,2*(43,2+2,64n+m)+m |
1) Поскольку за первые два года начальные вложения, как минимум, должны удвоиться, получаем неравенство:
36+2,2n ≥ 2*25
n ≥ 6,3
Но, по условию, n-целое число. Значит n=7.
2) За четыре года первоначальные вложения вырастут, как минимум, в четыре раза. Значит:
1,2*(43,2+2,64n+m)+m ≥ 4*25
Если n=7, то
1,2*(43,2+2,64*7+m)+m ≥ 4*25
m ≥ 11,8
По условию m-целое число. Значит m=12.
Ответ: n=7; m=12.
(Вариант 5)
«15-го декабря планируется взять кредит в банке на сумму 600 000 рублей на n+1 месяц. Условия возврата таковы:
- 1-го числа каждого месяца долг возрастает на 3% по сравнению с концом предыдущего месяца;
- со 2-го по 14-е число каждого месяца необходимо выплатить часть долга;
- 15-го числа каждого месяца с 1-го по n -й долг должен быть на одну и ту же сумму меньше долга на 15-е число предыдущего месяца;
- 15 числа n-го месяца долг составит 200 тыс. рублей;
- к 15-му числу (n+1)-го месяца кредит должен быть полностью погашен.
Найдите n, если известно, что общая сумма выплат после полного погашения кредита составит 852 000 рублей?»
Решение:
По условию задачи имеем:
Пусть S — сумма кредита (по условию задачи, 600 тыс. руб.), p = 3% — банковский процент. За первые n месяцев долг уменьшился на 600 − 200 = 400 (тыс. руб.), а так как по условию долг уменьшается равномерно (т.е. каждый месяц на одну и ту же величину), то за каждый месяц он уменьшался на величину x = 400/n (тыс. руб.). Кроме основного долга (600 тыс. руб.), клиент выплачивает банку ежемесячные проценты (начисляются 1 числа каждого месяца на оставшуюся на данный момент сумму долга), запишем суммы всех переплат банку в таблицу:
| n |
Долг до начисления % |
Начисленный % |
|
1 |
S |
S*0,03 |
|
2 |
S-x |
(S-x)*0,03 |
|
3 |
S-2x |
(S-2x)*0.03 |
|
… |
… |
… |
|
n |
S-(n-1)x |
(S-(n-1)x)*0.03 |
|
n+1 |
200 |
200*0.03 |
Сумму всех выплат можно выразить формулой Sв= Sк + S%. Значит, получаем уравнение:
600+0,03*(600+ … +200)= 852.
Но выражение, записанное в скобках, есть сумма (n+1) члена арифметической прогрессии, которую можно переписать в виде:
(600+200)*(n+1)/2 = 400*(n+1)
Тогда уравнение принимает вид:
600+0,03*400*(n+1)=852
n = 20.
Ответ: 20
(Вариант 13)
«15-го июня планируется взять кредит в банке на сумму 1300 тысяч рублей на 16 месяцев. Условия возврата таковы:
- 1-го числа каждого месяца долг возрастает на r% по сравнению с концом предыдущего месяца;
- со 2-го по 14-е число каждого месяца необходимо выплатить часть долга;
- 15-го числа каждого месяца с 1-го по 15-й долг должен быть на одну и ту же сумму меньше долга на 15-е число предыдущего месяца;
- 15 числа 15-го месяца долг составит 100 тыс. рублей;
- к 15-му числу 16-го месяца кредит должен быть полностью погашен.
Найдите r, если известно, что общая сумма выплат после полного погашения кредита составит 1636 тысяч рублей?»
Решение:
По условию задачи имеем:
Пусть S — сумма кредита (по условию задачи, 1300 тыс. руб.), p = r% — банковский процент. За первые 15 месяцев долг уменьшился на 1300 − 100 = 1200 (тыс. руб.), а так как по условию долг уменьшается равномерно (т.е. каждый месяц на одну и ту же величину), то за каждый месяц он уменьшался на величину 1200/15=80 (тыс. руб.). Кроме основного долга (1300 тыс. руб.), клиент выплачивает банку ежемесячные проценты (начисляются 1 числа каждого месяца на оставшуюся на данный момент сумму долга), запишем суммы всех переплат банку в таблицу:
| n |
Долг до начисления % |
Начисленный % |
|
1 |
S |
S*r/100 |
|
2 |
S-80 |
(S-80)* r/100 |
|
3 |
S-2*80 |
(S-2*80)* r/100 |
|
… |
… |
… |
|
15 |
S-14*80 |
(S-14*80)* r/100 |
|
16 |
100 |
100* r/100 |
Сумму всех выплат можно выразить формулой Sв= Sк + S%. Значит, получаем уравнение:
1300+ (1300*r/100 + … +100* r/100) =1636
1300+ r/100*(1300+ … +100) =1636
Но выражение, записанное в скобках, есть сумма 16 членов арифметической прогрессии, которую можно переписать в виде:
(1300+100)*16/2 =1400*8 =11200
Тогда уравнение принимает вид:
1300+ r/100*11200=1636
Откуда r = 3%
Ответ: 3%
См. продолжение статьи
По бизнес-плану четырёхлетний проект предполагает начальное вложение
36 вариантов ФИПИ Ященко 2022 Вариант 28 Задание 18 № задачи в базе 2734
По бизнес-плану четырёхлетний проект предполагает начальное вложение — 20 млн рублей. По итогам каждого года планируется прирост вложенных средств на 15 % по сравнению с началом года. Начисленные проценты остаются вложенными в проект. Кроме этого, сразу после начислений процентов нужны дополнительные вложения: целое число n млн рублей в первый и второй годы, а также целое число m млн рублей в третий и четвёртый годы. Найдите наименьшие значения n, при котором первоначальные вложения за два года как минимум удвоятся, и наименьшее значение m, такое, что при найденном ранее значении n первоначальные вложения за четыре года как минимум утроятся
Ответ: 7 и 3
ФИПИ 2023 🔥 …
Примечание: По бизнес-плану четырёхлетний проект предполагает начальное вложение ! 36 вариантов ФИПИ Ященко 2022 Вариант 28 Задание 18 # 36 вариантов ЕГЭ 2021 ФИПИ школе Ященко Вариант 18 Задание 17 # Задача-Аналог 1514
Рейтинг сложности задачи:
-
15-го января планируется взять кредит в банке на шесть месяцев в размере 1 млн рублей. Условия его возврата таковы:
— 1-го числа каждого месяца долг увеличивается на r процентов по сравнению с концом предыдущего месяца, где r — целое число;
— со 2-го по 14-е число каждого месяца необходимо выплатить часть долга;
— 15-го числа каждого месяца долг должен составлять некоторую сумму в соответствии со следующей таблицей.
Найдите наибольшее значение r , при котором общая сумма выплат будет меньше 1,2 млн рублей.
2. У фермера есть два поля, каждое площадью 20 гектаров. На каждом поле можно выращивать картофель и свёклу, поля можно делить между этими культурами в любой пропорции. Урожайность картофеля на первом поле составляет 230 ц/га, а на втором — 150 ц/га. Урожайность свёклы на первом поле составляет 250 ц/га, а на втором — 300 ц/га.
Фермер может продавать картофель по цене 1800 руб. за центнер, а свёклу — по цене 1600 руб. за центнер.
Какой наибольший доход может получить фермер?
3. 15 января планируется взять кредит в банке на 5 месяцев. Условия его возврата таковы:
– 1–го числа каждого месяца долг возрастает на 5% по сравнению с концом предыдущего месяца;
– со 2–го по 14–е число каждого месяца необходимо выплатить часть долга;
– 15–го числа каждого месяца долг должен быть на одну и ту же величину меньше долга на 15–е число предыдущего месяца.
Сколько процентов от суммы кредита составляет общая сумма денег, которую нужно выплатить банку за весь срок кредитования?
4. В июле Виктор планирует взять в кредит 2,5 млн рублей. Условия его возврата таковы:
— каждый январь долг возрастает на 20% по сравнению с кондом предыдущего года;
— с февраля по июнь каждого года Виктор должен выплатить некоторую часть долга.
На какое минимальное количество лет Виктор может взять кредит, чтобы ежегодные выплаты были не более 760 тысяч рублей?
5. 15–го января планируется взять кредит в банке на 18 месяцев. Условия его возврата таковы:
— 1–го числа каждого месяца долг возрастает на 2% по сравнению с концом предыдущего месяца;
— со 2–го по 14–е число каждого месяца необходимо выплатить часть долга;
— 15–го числа каждого месяца долг должен быть на одну и ту же величину меньше долга на 15–е число предыдущего месяца.
Известно, что за первые 9 месяцев нужно выплатить банку 1024 тыс. рублей. Какую сумму планируется взять в кредит?
6. По бизнес-плану четырёхлетний проект предполагает начальное вложение 12 млн рублей. По итогам каждого года планируется прирост вложенных средств на 15% по сравнению с началом года.
Начисленные проценты остаются вложенными в проект. Кроме этого, сразу после начислений процентов нужны дополнительные вложения: целое число n млн рублей в конце первого и второго года, а также целое число m млн рублей в конце третьего и четвёртого года.
Найдите наименьшее значение n, при котором первоначальные вложения за два года как минимум удвоятся, и наименьшее такое значение m, что при найденном ранее значении n первоначальные вложения за четыре года как минимум утроятся.
7. 31 декабря 2016 года Алексей взял в банке 2 184 000 рублей в кредит под 20% годовых. Схема выплат кредита следующая — 31 декабря каждого следующего года банк начисляет проценты на оставшуюся сумму долга (то есть увеличивает долг на 20%), затем Алексей переводит в банк x рублей. Какой должна быть сумма x, чтобы Алексей выплатил долг тремя равными платежами (то есть за три года)?
8. По вкладу « А» банк в конце каждого года планирует увеличивать на 10 % сумму, имеющуюся на вкладе в начале года, а по вкладу « Б» — увеличивать эту сумму на 8 % в первый год и на одинаковое целое число n процентов и за второй, и за третий годы.
Найдите наименьшее значение n , при котором за три года хранения вклад « Б» окажется выгоднее вклада « А» при одинаковых суммах первоначальных взносов.
9. Лев взял кредит в банке на срок 40 месяцев. По договору Лев должен вернуть кредит ежемесячными платежами. В конце каждого месяца к оставшейся сумме долга добавляется p% этой суммы, затем следует платеж Льва. Ежемесячные платежи подбираются таким образом, чтобы долг уменьшался равномерно.Известно, что наибольший платеж Льва был в 25 раз меньше первоначальной суммы долга. Найдите p.
10. На первый курс на специальность «Оборудование и машины» поступило 46 человек: 34 мальчика и 12 девочек. Их распределяют по двум группам численностью 22 и 24 человека, причем в каждой группе должна учиться по крайней мере одна девочка. Каким должно быть распределение по группам, чтобы сумма чисел, равных процентам девочек в первой и второй группах, была наибольшей?
11. В мае 2017 года планируется взять кредит в банке на шесть лет в размере S млн рублей.
Условия его возврата таковы:
— каждый декабрь каждого года долг возрастает на 10%;— с января по апрель каждого года необходимо выплатить часть долга;
— в мае 2018, 2019 и 2020 годов долг остается равным S млн рублей;
— выплаты в 2021, 2022 и 2023 годах равны между собой;— к маю 2023 года долг будет выплачен полностью.
Найдите наименьшее целое S, при котором общая сумма выплат не превысит 13 млн рублей.
12. По вкладу «Классика» банк в конце каждого года планирует начислять 12% годовых, а по вкладу «Бонус» — увеличивать сумму вклада на 7% в первый год и на одинаковое целое число n процентов в последующие годы.Найдите наименьшее значение n, при котором за 4 года хранения вклад «Бонус» окажется выгоднее вклада «Классика» при равных суммах первоначальных взносов.
13. По бизнес- плану предполагается вложить в четырёхлетний проект целое число миллионов рублей. По итогам каждого года планируется прирост средств вкладчика на 20 % по сравнению с началом года. Начисленные проценты остаются вложенными в проект.
Кроме этого, сразу после начислений процентов нужны дополнительные вложения: по 20 миллионов рублей в первый и второй годы, а также по 10 миллионов в третий и четвёртый годы. Найдите наименьший размер первоначальных вложений, при котором они за два года станут больше 100 миллионов, а за четыре года станут больше 170 миллионов рублей.
14. 15 января планируется взять кредит в банке на 24 месяца. Условия его возврата таковы:
– 1-го числа каждого месяца долг возрастает на 2% по сравнению с концом предыдущего месяца;
– со 2-го по 14-е число каждого месяца необходимо выплатить часть долга;
– 15-го числа каждого месяца долг должен быть на одну и ту же величину меньше долга на 15-е число предыдущего месяца.
Известно, что в течение второго года (последних 12 месяцев) кредитования нужно вернуть банку 1695 тыс. рублей. Какую сумму планируется взять в кредит?
15. 15 января планируется взять кредит в банке на 24 месяца. Условия его возврата таковы:
– 1-го числа каждого месяца долг возрастает на 3% по сравнению с концом предыдущего месяца;
– со 2-го по 14-е число каждого месяца необходимо выплатить часть долга;
– 15-го числа каждого месяца долг должен быть на одну и ту же величину меньше долга на 15-е число предыдущего месяца.
Известно, что в течение первого года (первых 12 месяцев) кредитования нужно вернуть банку 933 тыс. рублей. Какую сумму нужно вернуть банку в течение второго года (последних 12 месяцев) кредитования?
16. 15 января планируется взять кредит в банке на 9 месяцев. Условия его возврата таковы:
– 1-го числа каждого месяца долг возрастает на 2% по сравнению с концом предыдущего месяца;
– со 2-го по 14-е число каждого месяца необходимо выплатить часть долга;
– 15-го числа каждого месяца долг должен быть на одну и ту же величину меньше долга на 15-е число предыдущего месяца.
Известно, что на пятый месяц (с 2 по 14 июня) кредитования нужно вернуть банку 44 тыс. рублей. Какую сумму нужно выплатить банку в течении всего срока кредитования?
17. 15 января планируется взять кредит в банке на 15 месяцев. Условия его возврата таковы:
– 1-го числа каждого месяца долг возрастает на r% по сравнению с концом предыдущего месяца;
– со 2-го по 14-е число каждого месяца необходимо выплатить часть долга;
– 15-го числа каждого месяца долг должен быть на одну и ту же величину меньше долга на 15-е число предыдущего месяца.
Известно, что общая сумма денег, которую нужно выплатить банку за весь срок кредитования, на 24% больше, чем сумма, взятая в кредит. Найдите r.
18. В двух областях есть по 160 рабочих, каждый из которых готов трудиться по 5 часов в сутки на добыче алюминия или никеля.
В первой области один рабочий за час добывает 0,1 кг алюминия или 0,1 кг никеля. Во второй области для добычи x кг алюминия в день требуется x^2 человеко-часов труда, а для добычи у кг никеля в день требуется у^2 человеко-часов труда.
Для нужд промышленности можно использовать алюминий или никель, причем 1 кг алюминия можно заменить 1 кг никеля. Какую наибольшую массу металлов можно добыть суммарно в двух областях для нужд промышленности?
19. В двух областях есть по 90 рабочих, каждый из которых готов трудиться по 5 часов в сутки на добыче алюминия или никеля. В первой области один рабочий за час добывает 0,3 кг алюминия или 0,1 кг никеля. Во второй области для добычи x кг алюминия в день требуется x^2 человеко-часов труда, а для добычи y кг никеля в день требуется y^2 человеко-часов труда.
Для нужд промышленности можно использовать алюминий или никель, причем 1 кг алюминия можно заменить 1 кг никеля. Какую наибольшую массу металлов можно добыть суммарно в двух областях для нужд промышленности?
20. В двух областях есть по 20 рабочих, каждый из которых готов трудиться по 10 часов в сутки на добыче алюминия или никеля. В первой области один рабочий за час добывает 0,1 кг алюминия или 0,1 кг никеля.
Во второй области для добычи х кг алюминия в день требуется x^2 человеко-часов труда, а для добычи у кг никеля в день требуется y^2 человеко-часов труда.
Обе области поставляют добытый металл на завод, где для нужд промышленности производится сплав алюминия и никеля, в котором на 3 кг алюминия приходится 1 кг никеля.
При этом области договариваются между собой вести добычу металлов так, чтобы завод мог произвести наибольшее количество сплава. Сколько килограммов сплава при таких условиях ежедневно сможет произвести завод?
21. В двух шахтах добывают алюминий и никель.
В первой шахте имеется 60 рабочих, каждый из которых готов трудиться 5 часов в день. При этом один рабочий за час добывает 2 кг алюминия или 3 кг никеля.
Во второй шахте имеется 260 рабочих, каждый из которых готов трудиться 5 часов в день. При этом один рабочий за час добывает 3 кг алюминия или 2 кг никеля.
Обе шахты поставляют добытый металл на завод, где для нужд промышленности производится сплав алюминия и никеля, в котором на 2 кг алюминия приходится 1 кг никеля.
При этом шахты договариваются между собой вести добычу металлов так, чтобы завод мог произвести наибольшее количество сплава. Сколько килограммов сплава при таких условиях ежедневно сможет произвести завод?
22. На каждом из двух комбинатов изготавливают детали А и В.
На первом комбинате работают 40 человек, и один рабочий изготавливает за смену 15 деталей А или 5 деталей В.
На втором комбинате работает 160 человек, и один рабочий изготавливает за смену 5 деталей А или 15 деталей В.
Оба эти комбината поставляют детали на комбинат, из которых собирают изделие, для изготовления которого нужно 2 детали А и 1 деталь В. При этом комбинаты договариваются между собой изготавливать детали так, что бы можно было собрать наибольшее количество изделий.
Сколько изделий при таких условиях может собрать комбинат за смену?
23. В июле 2016 года планируется взять кредит в банке на три года в размере S млн рублей, где S — целое число. Условия его возврата таковы:
— каждый январь долг увеличивается на 15 % по сравнению с концом
предыдущего года;
— с февраля по июнь каждого года необходимо выплатить одним платежом часть долга;
— в июле каждого года долг должен составлять часть кредита в соответствии со следующей таблицей.
Найдите наибольшее значение S , при котором каждая из выплат будет меньше 4 млн рублей.
Найдите наибольшее значение S , при котором каждая из выплат будет меньше 4 млн рублей.
24. В июле 2020 года планируется взять кредит в банке на сумму 600 000 рублей. Условия его возврата таковы:
— каждый январь долг увеличивается на r % по сравнению с концом предыдущего года;
— с февраля по июнь каждого года необходимо выплатить одним платежом часть долга.
Найдите r, если известно, что кредит будет полностью погашен за два года, причём в первый год будет выплачено 360 000 рублей, а во второй год — 330 000 рублей.
25. В двух областях есть по 250 рабочих, каждый из которых готов трудиться по 5 часов в сутки на добыче алюминия или никеля.
В первой области один рабочий за час добывает 0,2 кг алюминия или 0,1 кг никеля.
Во второй области для добычи x кг алюминия в день требуется x^2 человеко-часов труда, а для добычи y кг никеля в день требуется y^2 человеко-часов труда.
Для нужд промышленности можно использовать алюминий или никель, причем 1 кг алюминия можно заменить 1 кг никеля.
Какую наибольшую массу металлов можно добыть суммарно в двух областях для нужд промышленности?
26. В двух областях есть по 50 рабочих, каждый из которых готов трудиться по 10 часов в сутки на добыче алюминия или никеля.
В первой области один рабочий за час добывает 0,2 кг алюминия или 0,1 кг никеля.
Во второй области для добычи х кг алюминия в день требуется x^2 человеко-часов труда, а для добычи у кг никеля в день требуется y^2 человеко-часов труда.
Обе области поставляют добытый металл на завод, где для нужд промышленности производится сплав алюминия и никеля, в котором на 1 кг алюминия приходится 2 кг никеля.
При этом области договариваются между собой вести добычу металлов так, чтобы завод мог произвести наибольшее количество сплава. Сколько килограммов сплава при таких условиях ежедневно сможет произвести завод?
27. Клиент банка планирует взять 15-го августа кредит на 17 месяцев. Условия возврата таковы:
1-го числа каждого месяца долг возрастает на r% по сравнению с концом предыдущего месяца;
со 2-го по 14-е число каждого месяца необходимо выплатить часть долга;
15-го числа каждого месяца долг должен быть на одну и ту же величину меньше долга на 15-е число предыдущего месяца.
Известно, что общая сумма денег, которую нужно выплатить банку за весь срок кредитования, на 15% больше, чем сумма взятая в кредит. Найдите r
28. 15 января планируется взять кредит в банке на 24 месяца. Условия его возврата таковы:
– 1-го числа каждого месяца долг возрастает на 2% по сравнению с концом предыдущего месяца;
– со 2-го по 14-е число каждого месяца необходимо выплатить часть долга;
– 15-го числа каждого месяца долг должен быть на одну и ту же величину меньше долга на 15-е число предыдущего месяца.
Известно, что в течение первого года (первых 12 месяцев) кредитования нужно вернуть банку 2466 тыс. рублей. Какую сумму нужно выплатить банку за последние 12 месяцев ?
29. 15 января планируется взять кредит в банке на некоторую сумму на 31 месяца. Условия его возврата таковы:
– 1-го числа каждого месяца долг увеличивается на 1% по сравнению с концом предыдущего месяца;
– со 2-го по 14-е число каждого месяца необходимо выплатить одним платежом часть долга;
– на 15-ое число каждого месяца с 1 -ого по 30-ый долг должен быть на 20 тыс. рублей меньше долга на 15-е число предыдущего месяца;
-к 15-му числу 31-ого месяца долг должен быть погашён полностью.
Сколько тысяч рублей составляет долг на 15 число 30-ого месяца, если банку всего было выплачено 1348 тыс. рублей?
30. 31 декабря 2014 года Василий взял в банке некоторую сумму в кредит под 11% годовых. Схема выплат кредита следующая — 31 декабря каждого следующего года банк начисляет проценты на оставшуюся сумму долга (то есть увеличивает долг на 11%), затем Василий переводит в банк 3 696 300 рублей. Какую сумму взял Василий в банке, если он выплатил долг двумя равными платежами (то есть за 2 года)?
Источник






































