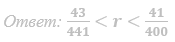По бизнес-плану четырёхлетний проект предполагает начальное вложение — 12 млн рублей. По итогам каждого года планируется прирост вложенных средств на 10% по сравнению с началом года. Начисленные проценты планируется оставлять вложенными в проект. Кроме этого, сразу после начислений процентов потребуются дополнительные вложения: целое число n млн рублей в первый и во второй годы, а также целое число m млн рублей в третий и в четвёртый годы. Найдите наименьшее значение n, при котором первоначальные вложения за два года как минимум удвоятся, и наименьшее такое значение m, что при найденном ранее значении n первоначальные вложения за четыре года как минимум утроятся.
Спрятать решение
Решение.
К началу 2-го года получится млн рублей вложений, а к началу 3-го года —
По условию откуда следует, что
Наименьшее целое значение n = 5 . Тогда к началу 3-го года получится
млн рублей.
К началу 4-года получим млн рублей, а к концу проекта —
По условию откуда следует, что
Наименьшее целое значение m = 3.
Ответ: n = 5 млн рублей и m = 3 млн рублей.
Спрятать критерии
Критерии проверки:
| Критерии оценивания выполнения задания | Баллы |
|---|---|
| Обоснованно получен верный ответ | 2 |
| Верно построена математическая модель | 1 |
| Решение не соответствует ни одному из критериев, перечисленных выше | 0 |
| Максимальный балл | 2 |
По бизнес-плану предполагается вложить в четырёхлетний проект 10 млн рублей. По итогам каждого года планируется прирост вложенных средств на 15 % по сравнению с началом года. Начисленные проценты остаются вложенными в проект. Кроме этого, сразу после начислений процентов нужны дополнительные вложения: целое число n млн рублей в первый и второй годы, а также целое число m млн рублей в третий и четвёртый годы.
Найдите наименьшие значения n и m, при которых первоначальные вложения за два года как минимум удвоятся, а за четыре года как минимум утроятся
РЕШЕНИЕ ОТ
iuv
✪ ЛУЧШЕЕ РЕШЕНИЕ
через год вложения составят 10*1,15 млн рублей
+ n млн рублей
итого (10*1,15+n) млн рублей
через два года вложения составят (10*1,15+n)*1,15 млн рублей + n млн рублей
итого ((10*1,15+n)*1,15+n) млн рублей
эта сумма должна быть больше чем 2*10 млн рублей
((10*1,15+n)*1,15+n) > 20
13,225+n*2,15 > 20
n*2,15 > 20 — 13,225
n > (20 — 13,225)/2,15
n > 3,151162791
n = 4
по итогам 2 лет получаем сумму
((10*1,15+n)*1,15+n)= ((10*1,15+4)*1,15+4)=21,825 млн рублей
через три года вложения составят 21,825 *1,15 млн рублей
+ m млн рублей
итого (21,825 *1,15+m) млн рублей
через четыре года вложения составят (21,825 *1,15+m) *1,15 млн рублей + m млн рублей
итого ((21,825 *1,15+m) *1,15 +m) млн рублей
эта сумма должна быть больше чем 3*10 млн рублей
((21,825 *1,15+m) *1,15 +m) > 30
28,86356 +m*2,15 > 30
m*2,15 > 30 — 28,86356
m > (30 — 28,86356)/2,15
m > 0,52858
m = 1
по итогам 4 лет получаем сумму
((21,825 *1,15+m)*1,15+m)= ((21,825 *1,15+1)*1,15+1)= 31,0136 млн рублей
ответ n=4; m=1
Вопрос к решению?
Нашли ошибку?
Добавил slava191, просмотры: ☺ 17899 ⌚ 04.03.2016. математика 10-11 класс
По бизнес-плану четырёхлетний проект предполагает начальное вложение
36 вариантов ФИПИ Ященко 2022 Вариант 28 Задание 18 № задачи в базе 2734
По бизнес-плану четырёхлетний проект предполагает начальное вложение — 20 млн рублей. По итогам каждого года планируется прирост вложенных средств на 15 % по сравнению с началом года. Начисленные проценты остаются вложенными в проект. Кроме этого, сразу после начислений процентов нужны дополнительные вложения: целое число n млн рублей в первый и второй годы, а также целое число m млн рублей в третий и четвёртый годы. Найдите наименьшие значения n, при котором первоначальные вложения за два года как минимум удвоятся, и наименьшее значение m, такое, что при найденном ранее значении n первоначальные вложения за четыре года как минимум утроятся
Ответ: 7 и 3
ФИПИ 2023 🔥 …
Примечание: По бизнес-плану четырёхлетний проект предполагает начальное вложение ! 36 вариантов ФИПИ Ященко 2022 Вариант 28 Задание 18 # 36 вариантов ЕГЭ 2021 ФИПИ школе Ященко Вариант 18 Задание 17 # Задача-Аналог 1514
Рейтинг сложности задачи:
Условие
По бизнес-плану четырехлетний проект предполагает начальное вложение 12 млн. рублей. По итогам года планируется прирост вложенных средств на 15 процентов по сравнению с началом года.Начисленные проценты остаются вложенными в проект.Кроме этого, сразу же после начислений процентов нужны дополнительные вложения.
предмет не задан
3184
О решение…
На нашем сайте такое бывает редко, но решение к данной задаче еще никто не написал.
Что Вы можете сделать?
- Выставите данный вопрос вновь. Перейдите на главную страницу.
- Найдите похожую задачу. Используйте поиск.
Написать комментарий
Задание 17. Вариант 7. ЕГЭ 2020 из 36 вариантов.
Задание 17. По бизнес-плану четырёхлетний проект предполагает начальное вложение — 25 млн рублей. По итогам каждого года планируется прирост вложенных средств на 20 % по сравнению с началом года. Начисленные проценты остаются вложенными в проект. Кроме этого, сразу после начислений процентов нужны дополнительные вложения: целое число n млн рублей и в первый, и во второй годы, а также целое число m млн рублей и в третий, и в четвёртый годы. Найдите наименьшее значение n, при котором первоначальные вложения за два года как минимум удвоятся, и наименьшее значение m, такое, что при найденном ранее значении n первоначальные вложения за четыре года вырастут как минимум в четыре раза.
Решение.
К началу 2-го года получится млн вложений, а к началу 3-го года –
По условию . Наименьшее целое решение n = 7. Тогда к началу 3-го года получится
36+15,4 = 51,4 млн.
К началу 4-го года имеем млн, а в конце проекта
По условию ,
откуда
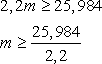
Получаем, что m = 12 – наименьшее целое решение.
Ответ: 7 и 12 млн. руб.
БАЗА ЗАДАНИЙ
Задание № 15. Финансовая математика.
39. Григорий является владельцем двух заводов в разных городах. На заводах производятся абсолютно одинаковые товары, но на заводе, расположенном во втором городе, используется более совершенное оборудование. В результате, если рабочие на заводе, расположенном в первом городе, трудятся суммарно t2 часов в неделю, то за эту неделю они производят 3t единиц товара; если рабочие на заводе, расположенном во втором городе, трудятся суммарно t2 часов в неделю, то за эту неделю они производят 5t единиц товара. За каждый час работы (на каждом из заводов) Григорий платит рабочему 500 рублей. Григорий готов выделять 6 800 000 рублей в неделю на оплату труда рабочих. Какое наибольшее количество единиц товара можно произвести за неделю на этих двух заводах?
Ответ: 680
40. Владимир является владельцем двух заводов в разных городах. На заводах производятся абсолютно одинаковые товары, но на заводе, расположенном во втором городе, используется более совершенное оборудование. В результате, если рабочие на заводе, расположенном в первом городе, трудятся суммарно t2 часов в неделю, то за эту неделю они производят 4 t единиц товара; если рабочие на заводе, расположенном во втором городе, трудятся суммарно t2 часов в неделю, то за эту неделю они производят 5t единиц товара. За каждый час работы (на каждом из заводов) Владимир платит рабочему 500 рублей. Владимиру нужно каждую неделю производить 410 единиц товара. Какую наименьшую сумму придётся тратить еженедельно на оплату труда рабочих?
Ответ: 2050000 р
41. Вадим является владельцем двух заводов в разных городах. На заводах производятся абсолютно одинаковые товары при использовании одинаковых технологий. Если рабочие на одном из заводов трудятся суммарно t2 часов в неделю, то за эту неделю они производят t единиц товара. За каждый час работы на заводе, расположенном в первом городе, Вадим платит рабочему 200 рублей, а на заводе, расположенном во втором городе, — 300 рублей. Вадим готов выделять 1 200 000 рублей в неделю на оплату труда рабочих. Какое наибольшее количество единиц товара можно произвести за неделю на этих двух заводах?
Ответ: 100
42. Строительство нового завода стоит 75 млн рублей. Затраты на производство х тыс. ед. продукции на таком заводе равны 0,5x2 + x + 7 млн рублей в год. Если продукцию завода продать по цене р тыс. рублей за единицу, то прибыль фирмы (в млн рублей) за один год составит px — (0,5x2 + x + 7). Когда завод будет построен, фирма будет выпускать продукцию в таком количестве, чтобы прибыль была наибольшей. При каком наименьшем значении р строительство завода окупится не более, чем за 3 года?
Ответ: 9000 р
43. Пенсионный фонд владеет ценными бумагами, которые стоят t2 тыс. рублей в конце года t ( t=1; 2; …). В конце любого года пенсионный фонд может продать ценные бумаги и положить деньги на счёт в банке, при этом в конце каждого следующего года сумма на счёте будет увеличиваться на 10%. В конце какого года пенсионному фонду следует продать ценные бумаги, чтобы в конце двадцать пятого года сумма на его счёте была наибольшей?
Ответ: 21 год
44. Пенсионный фонд владеет ценными бумагами, которые стоят t2 тыс. рублей в конце года t (t=1; 2; … ). В конце любого года пенсионный фонд может продать ценные бумаги и положить деньги на счёт в банке, при этом в конце каждого следующего года сумма на счёте будет увеличиваться в 1+r раз. Пенсионный фонд хочет продать ценные бумаги в конце такого года, чтобы в конце двадцать пятого года сумма на его счёте была наибольшей. Расчёты показали, что для этого ценные бумаги нужно продавать строго в конце двадцать первого года. При каких положительных значениях r это возможно?
45. Первичная информация разделяется по серверам №1 и №2 и обрабатывается на них. С сервера №1 при объёме t2 Гбайт входящей в него информации выходит 20t Гбайт, а с сервера №2 при объёме t2 Гбайт входящей в него информации выходит 21t Гбайт обработанной информации; 25 < t < 55. Каков наибольший общий объём выходящей информации при общем объёме входящей информации в 3364 Гбайт?
Ответ: 1682
46. Зависимость объема Q (в шт.) купленного у фирмы товара от цены Р (в руб. за шт.) выражается формулой Q = 15000 — P, (1000 ≤ P ≤ 15000). Доход от продажи товара составляет PQ рублей. Затраты на производство Q единиц товара составляют 3000Q + 5000000 рублей.Прибыль равна разности дохода от продажи товара и затрат на его производство.Стремясь привлечь внимание покупателей, фирма уменьшила цену продукции на 20%, однако ее прибыль не изменилась. На сколько процентов следует увеличить сниженную цену, чтобы добиться наибольшей прибыли?
Ответ: 12,5%
47. Зависимость количества Q (в шт. 0 ≤ Q ≤ 15000) купленного у фирмы товара от цены P (в руб. за шт.) выражается формулой Q = 15000 — P. Затраты на производство Q единиц товара составляют 3000Q + 10000000 рублей. Кроме затрат на производство, фирма должна платить налог t рублей (0 < t < 10000) с каждой произведённой единицы товара. Таким образом, прибыль фирмы составляет PQ — 3000Q — 10000000 — tQ рублей, а общая сумма налогов, собранных государством, равна tQ рублей. Фирма производит такое количество товара, при котором её прибыль максимальна. При каком значении t общая сумма налогов, собранных государством, будет максимальной?
Ответ: 6000
48. В двух областях есть по 160 рабочих, каждый из которых готов трудиться по 5 часов в сутки на добыче алюминия или никеля. В первой области один рабочий за час добывает 0,1 кг алюминия или 0,1 кг никеля. Во второй области для добычи x кг алюминия в день требуется x2 человеко-часов труда, а для добычи у кг никеля в день требуется y2 человеко-часов труда.
Для нужд промышленности можно использовать или алюминий, или никель, причём 1 кг алюминия можно заменить 1 кг никеля. Какую наибольшую массу металлов можно за сутки суммарно добыть в двух областях?
Ответ: 120 кг
49. Строительство нового завода стоит 220 млн рублей. Затраты на производство х тыс. ед. продукции на таком заводе равны 0,5х2 + x + 7 млн рублей в год. Если продукцию завода продать по цене р тыс. рублей за единицу, то прибыль фирмы (в млн рублей) за один год составит px — (0,5х2 + x + 7). Когда завод будет построен, фирма будет выпускать продукцию в таком количестве, чтобы прибыль была наибольшей. В первый год после постройки завода цена продукции p = 9 тыс. руб. за единицу, каждый следующий год цена продукции увеличивается на 1 тыс. руб. за единицу. За сколько лет окупится строительство завода?
Ответ: 5 лет
50. Производство x тыс. единиц продукции обходится в q = 0,5x2 + x + 7 млн рублей в год. При цене p тыс. рублей за единицу годовая прибыль от продажи этой продукции (в млн рублей) составляет px − q. При каком наименьшем значении p через три года суммарная прибыль составит не менее 75 млн рублей?
Ответ: 9
51. В регионе А среднемесячный доход на душу населения в 2014 году составлял 43740 рублей и ежегодно увеличивался на 25%. В регионе Б среднемесячный доход на душу населения в 2014 году составлял 60000 рублей. В течение трех лет суммарный доход жителей региона Б увеличивался на 17% ежегодно, а население увеличивалось на m% ежегодно. В 2017 году среднемесячный доход на душу населения в регионах А и Б стал одинаковым. Найдите m.
Ответ: 4
52. По бизнес-плану четырёхлетний проект предполагает начальное вложение 12 млн рублей. По итогам каждого года планируется прирост вложенных средств на 15 % по сравнению с началом года. Начисленные проценты остаются вложенными в проект. Кроме этого, сразу после начислений процентов нужны дополнительные вложения: целое число n млн рублей в конце первого и второго года, а также целое число m млн рублей в конце третьего и четвёртого года. Найдите наименьшее значение n, при котором первоначальные вложения за два года как минимум удвоятся, и наименьшее такое значение m, что при найденном ранее значении n первоначальные вложения за четыре года как минимум утроятся.
Ответ: 4 и 2 млн руб.
53. По вкладу «А» банк в конце каждого года планирует увеличивать на 10 % сумму, имеющуюся на вкладе в начале года, а по вкладу «Б» — увеличивать эту сумму на 8 % в первый год и на одинаковое целое число n процентов и за второй, и за третий годы. Найдите наименьшее значение n, при котором за три года хранения вклад «Б» окажется выгоднее вклада «А» при одинаковых суммах первоначальных взносов.
Ответ: 12
54. В начале года Алексей приобрел ценные бумаги на сумму 9 тыс. рублей. В середине каждого года стоимость ценных бумаг возрастает на 2 тыс. рублей. В любой момент Алексей может продать ценные бумаги и положить вырученные деньги на банковский счет. В середине каждого года сумма на счете будет увеличиваться на 9%. В начале какого года после покупки Алексей должен продать ценные бумаги, чтобы через двадцать лет после покупки ценных бумаг сумма на банковском счете была наибольшей?
Ответ: 8
55. 15-го января планируется взять кредит в банке на 11 месяцев. Условия его возврата таковы:
— 1-го числа каждого месяца долг возрастает на 4% по сравнению с концом предыдущего месяца;
— со 2-го по 14-е число каждого месяца необходимо выплатить часть долга;
—15-го числа каждого месяца долг должен быть на одну и ту же сумму меньше долга на 15-е число предыдущего месяца.
Известно, что на шестой месяц кредитования выплата составит 25 тыс. рублей. Какую суму нужно вернуть банку в течение всего срока кредитования?
Ответ: 275 000 рублей.
56. Евгений хочет купить пакет акций быстрорастущей компании. В начале года у Евгения было недостаточно денег, а пакет стоил 195 000 рублей. В середине каждого месяца Евгений откладывает на покупку пакета акций одну и ту же сумму, а в конце месяца пакет дорожает, но не более чем на 40%. Какую наименьшую сумму нужно откладывать Евгению каждый месяц, чтобы через некоторое время выкупить желаемый пакет акций?
Ответ: 127 400 рублей.
57. Василий взял кредит в банке на срок 14 месяцев. В конце каждого месяца общая сумма оставшегося долга увеличивается на 8 %, а затем уменьшается на сумму, уплаченную Василием. Суммы, выплачиваемые в конце каждого месяца, подбираются так, чтобы в результате сумма долга каждый месяц уменьшалась равномерно, то есть на одну и ту же величину. Сколько процентов от суммы кредита составила общая сумма, уплаченная Василием банку?
Ответ: 160%.
- В банк был положен вклад под 10% годовых. Через год, после начисления процентов, вкладчик снял со счета 2000 рублей, а еще через год (опять после начисления процентов) снова внес 2000 рублей. Вследствие этих действий через три года со времени открытия вклада вкладчик получил сумму меньше запланированной (если бы не было промежуточных операций со вкладом). На сколько рублей меньше запланированной суммы он получил?
- Миша и Маша положили в один и тот же банк одинаковые суммы под 10% годовых. Через год сразу после начисления процентов Миша снял со своего счета 5000 рублей, а еще через год снова внес 5000 рублей. Маша, наоборот, через год доложила на свой счет 5000 рублей, а еще через год сразу после начисления процентов сняла со счета 5000 рублей. Кто через три года со времени первоначального вложения получит большую сумму и на сколько рублей?
- Близнецы Саша и Паша положили в банк по 50 000 рублей на три года под 10% годовых Однако через год и Саша, и Паша сняли со своих счетов соответственно 10% и 20% имеющихся денег. Еще через год каждый из них снял со своего счета соответственно 20 000 рублей и 15 000 рублей. У кого из братьев к концу третьего года на счету окажется большая сумма денег? На сколько рублей?
- Василий кладет в банк 1 000 000 рублей под 10% годовых на 4 года (проценты начисляются один раз после истечения года) с правом докладывать три раза (в конце каждого года после начисления процентов) на счет фиксированную сумму 133 000 рублей. Какая максимальная сумма может быть на счете у Василия через 4 года?
- Саша положил некоторую сумму в банк на 4 года под 10% годовых. Одновременно с ним Паша такую же сумму положил на два года в другой банк под 15% годовых. Через два года Паша решил продлить срок вклада еще на 2 года. Однако к тому времени процентная ставка по вкладам в этом банке изменилась и составляла уже p% годовых. В итоге через четыре года на счету у Паши оказалась большая сумма, чем у Саши, причем эта разность составила менее 10% от суммы, вложенной каждым первоначально. Найдите наибольшее возможное целое значение процентной ставки.
- В начале года 5/6 некоторой суммы денег вложили в банк А, а то, что осталось — в банк Б. Если вклад находится в банке с начала года, то к концу года он возрастает на определённый процент, величина которого зависит от банка. Известно, что к концу первого года сумма вкладов стала равна 670 у. е., к концу следующего — 749 у. е. Если первоначально 5/6 суммы было бы вложено в банк Б, а оставшуюся вложили бы в банк А, то по истечении одного года сумма выросла бы до 710 у. е. Определите сумму вкладов по истечении второго года в этом случае.
- В банк помещена сумма 3900 тысяч рублей под 50% годовых. В конце каждого из первых четырех лет хранения после начисления процентов вкладчик дополнительно вносил на счет одну и ту же фиксированную сумму. К концу пятого года после начисления процентов оказалось, что размер вклада увеличился по сравнению с первоначальным на 725%. Какую сумму вкладчик ежегодно добавлял к вкладу?
- Баба Валя, накопив часть своей пенсии, решила улучшить свое материальное положение. Она узнала, что в Спёрбанке от пенсионеров принимают вклады под определенный процент годовых и на этих условиях внесла свои сбережения в ближайшее отделение Спёрбанка. Но через некоторое время соседка ей рассказала, что недалеко от той местности, где проживают пенсионеры, есть коммерческий банк, в котором процент годовых для пенсионеров-вкладчиков в 20 раз выше, чем в Спёрбанке. Баба Валя не доверяла коммерческим банкам, но стремление улучшить свое материальное положение взяло верх. После долгих колебаний и ровно через год после открытия счета в Спёрбанке Баба Валя сняла половину образовавшейся суммы от ее вклада, заявив: «Такой навар меня не устраивает!» и открыла счет в том коммерческом банке, о котором говорила ее соседка, не теряя надежды на значительное улучшение своего материального благосостояния. Надежды оправдались: через год сумма Бабы Вали в коммерческом банке превысила ее первоначальные кровные сбережения на 65%. Сожалела Баба Валя, что год назад в Спёрбанке сняла не всю сумму, а лишь половину, однако, подумала: «А где же мы не теряли?..» Гендиректор коммерческого банка оказался хорошим: не оставил Бабу Валю без денег. А каков в Спёрбанке процент годовых для пенсионеров?
- Банк под определенный процент принял некоторую сумму. Через год четверть накопленной суммы была снята со счета. Банк увеличил процент годовых на 40 процентных пунктов (то есть увеличил ставку а% до (а + 40)%). К концу следующего года накопленная сумма в 1,44 раза превысила первоначальный вклад. Каков процент новых годовых?
- Гражданин Петров по случаю рождения сына открыл 1 сентября 2008 года в банке счёт, на который он ежегодно кладет 1000 рублей. По условиям вклада банк ежегодно начисляет 20% на сумму, находящуюся на счёте. Через 6 лет у гражданина Петрова родилась дочь, и 1 сентября 2014 года он открыл в другом банке счёт, на который ежегодно кладёт по 2200 рублей, а банк начисляет 44% в год. В каком году после очередного пополнения суммы вкладов сравняются, если деньги со счетов не снимают?
- Известно, что вклад, находящийся в банке с начала года, возрастает к концу года на определенный процент, свой для каждого банка. В начале года Степан положил 60% некоторой суммы денег в первый банк, а оставшуюся часть суммы во второй банк. К концу года сумма этих вкладов стала равна 590 000 руб., а к концу следующего года 701 000 руб. Если бы Степан первоначально положил 60% своей суммы во второй банк, а оставшуюся часть в первый, то по истечении одного года сумма вкладов стала бы равной 610 000 руб. Какова была бы сумма вкладов в этом случае к концу второго года?
- По вкладу «А» банк в течение трёх лет в конце каждого года увеличивает на 10% сумму, имеющуюся на вкладе в начале года, а по вкладу «Б» — увеличивает на 11% в течение каждого из первых двух лет. Найдите наименьшее целое число процентов за третий год по вкладу «Б», при котором за все три года этот вклад всё ещё останется выгоднее вклада «А».
- По вкладу «А» банк в конце каждого года планирует увеличивать на 10% сумму, имеющуюся на вкладе в начале года, а по вкладу «Б» — увеличивать эту сумму на 5% в первый год и на одинаковое целое число n процентов и за второй, и за третий годы. Найдите наименьшее значение n, при котором за три года хранения вклад «Б» окажется выгоднее вклада «А» при одинаковых суммах первоначальных взносов.
- По бизнес-плану предполагается изначально вложить в четырёхлетний проект 10 млн рублей. По итогам каждого года планируется прирост вложенных средств на 15% по сравнению с началом года. Начисленные проценты остаются вложенными в проект. Кроме этого, сразу после начислений процентов нужны дополнительные вложения: по целому числу n млн рублей в первый и второй годы, а также по целому числу m млн рублей в третий и четвёртый годы. Найдите наименьшие значения n и m, при которых первоначальные вложения за два года как минимум удвоятся, а за четыре года как минимум утроятся.
- Вклад в размере 10 млн рублей планируется открыть на четыре года. В конце каждого года вклад увеличивается на 10% по сравнению с его размером в начале года, а, кроме этого, в начале третьего года и четвёртого годов вклад ежегодно пополняется на одну и ту же фиксированную сумму, равную целому числу миллионов рублей. Найдите наименьший возможный размер такой суммы, при котором через четыре года вклад станет не меньше 30 млн рублей.
- По бизнес-плану предполагается вложить в четырёхлетний проект целое число миллионов рублей. По итогам каждого года планируется прирост средств вкладчика на 20% по сравнению с началом года. Начисленные проценты остаются вложенными в проект. Кроме этого, сразу после начислений процентов нужны дополнительные вложения: по 20 миллионов рублей в первый и второй годы, а также по 10 миллионов в третий и четвёртый годы. Найдите наименьший размер первоначальных вложений, при котором общая сумма средств вкладчика за два года станет больше 125 миллионов, а за четыре года станет больше 200 миллионов рублей.
- 1 апреля 2017 г. Андрей Петрович положил 10 000 рублей на банковский вклад сроком на 1 год с ежемесячным начислением процентов и капитализацией под a% годовых. Это означает, что первого числа каждого месяца сумма вклада увеличивается на одно и то же количество процентов, рассчитанное таким образом, что за 12 месяцев она увеличится ровно на a%. Через 6 месяцев сумма вклада составила 10 500 рублей. Найдите a.
- 1 апреля 2019 г. Андрей Петрович положил 10 000 рублей на банковский вклад сроком на 1 год с ежемесячным начислением процентов и капитализацией под 21% годовых. Это означает, что первого числа каждого месяца сумма вклада увеличивается на одно и то же количество процентов, рассчитанное таким образом, что за 12 месяцев она увеличится ровно на 21%. Через сколько месяцев сумма вклада впервые превысит 11 000 рублей?
- Планируется открыть вклад на 4 года, положив на счет целое число миллионов рублей. В конце каждого года сумма, лежащая на вкладе, увеличивается на 10%, а в начале третьего и четвертого года вклад пополняется на 3 миллиона рублей. Найдите наименьший первоначальный вклад, при котором начисленные проценты за весь срок будут более 5 миллионов рублей.
- Вклад планируется открыть на четыре года. Первоначальный вклад составляет целое число миллионов рублей. В конце каждого года банк увеличивает вклад на 10% по сравнению с его размером в начале года. Кроме этого, в начале третьего и четвертого годов вкладчик ежегодно пополняет вклад на 10 млн рублей. Найдите наибольший размер первоначального вклада, при котором банк за четыре года начислит на вклад меньше 15 млн рублей.
- 5 января 2020 года Андрей планирует открыть вклад на сумму 3 миллиона рублей. Первые три года 2 января банк будет начислять 10% на сумму вклада, а в последующие годы банк будет начислять 5% на сумму вклада. 4 января каждого года Андрей будет делать дополнительный взнос на вклад так, чтобы после этого величина вклада на 5 января была больше величины вклада на 5 января прошлого года на одно и то же число. Определите общий размер начислений банка, если 3 января 2031 года на вкладе будет лежать 24,15 миллиона рублей.
- 3 января 2020 года Георгий планирует положить на депозит вклад размером 2 миллиона рублей. 1 января каждого года банк начисляет 10% на сумму вклада, 2 января каждого года Георгий делает дополнительный взнос на вклад так, чтобы после этого разности между величиной вклада на 3 января и величиной вклада на 3 января прошлого года образовывали арифметическую прогрессию с разностью 1 млн руб. Определите общий размер начислений банка, если 3 января 2027 года на вкладе будет лежать 30 млн руб.
- Егор положил в банк некоторую сумму денег. Через год, после начисления процентов, он добавил на свой счет сумму, составляющую 0,9 исходной, в результате чего остаток на счете стал равен 3,4 миллиона рублей. А еще через год, после начисления процентов, остаток на его счете увеличился 2,2 раза по сравнению с исходной суммой. Какую сумму (в млн руб.) Егор положил в банк первоначально, если в конце каждого года банк начислял один и тот же процент годовых?
- По вкладу «А» банк в конце каждого года увеличивает на 10% сумму, имеющуюся на вкладе в начале года, а по вкладу «Б» — увеличивает эту сумму на 11% в течение каждого из первых двух лет. Найдите наибольшее натуральное число процентов, начисленное за третий год по вкладу «Б», при котором за все три года этот вклад будет менее выгоден, чем вклад «А».
- Марина и Надежда открыли вклады одинакового размера в одном из банков на четыре года. Ежегодно в течение первых трёх лет банк увеличивал каждый вклад на 10%, а в конце четвёртого года на 12% по сравнению с его размером в начале года. Кроме этого, в начале третьего и четвёртого годов Марина ежегодно пополняла вклад на x рублей, где x — натуральное число. Надежда пополняла свой вклад только в начале третьего года, но на сумму 2x рублей. Найдите наименьшее значение x, при котором через четыре года на счету Надежды стало на целое число десятков рублей больше, чем у Марины.
- По вкладу «А» банк в конце каждого года планирует увеличивать на 10% сумму, имеющуюся на вкладе в начале года, а по вкладу «Б» — увеличивать эту сумму на 7% в первый год и на одинаковое целое число n процентов и за второй, и за третий годы. Найдите наименьшее значение n, при котором за три года хранения вклад «Б» окажется выгоднее вклада «А» при одинаковых суммах первоначальных взносов.
- Семен и Матвей открыли вклады одинакового размера в одном из банков на три года. Ежегодно в течение первых двух лет банк увеличивал каждый вклад на 10%, а в конце третьего года — на 5% по сравнению с его размером в начале года. Кроме этого, в начале второго и третьего годов Семен ежегодно пополнял вклад на х тысяч рублей, где х — натуральное число. Матвей пополнял свой вклад только в начале третьего года, но на сумму 2х тысяч рублей. Найдите наименьшее значение х, при котором через три года на счету Семена стало на четное число тысяч рублей больше, чем у Матвея.
- Трейдер потратил треть своих денег на приобретение акций одного акционерного общества (АО), а остальные деньги — на акции второго АО. Спустя три месяца цены акций обоих АО выросли на определенные для каждого АО проценты, а еще через три месяца цены акций выросли на столько же процентов, что и в предыдущий период. В результате за полгода общая стоимость акций трейдера выросла на 98%. Если бы после первых трех месяцев трейдер продал все акции первого АО по новой цене и на все полученные деньги приобрел бы акции второго АО, то общий прирост инвестиций за полгода составил бы 110%. Какой процент прибыли получит трейдер за полгода, вложив всю сумму в акции первого АО?
- В банк помещен вклад 64 000 рублей под 25% годовых. В конце каждого из первых трех лет после начисления процентов вкладчик дополнительно клал на счет одну и ту же фиксированную сумму. К концу четвертого года после начисления процентов оказалось, что вклад составляет 385 000 рублей. Какую сумму в рублях ежегодно добавлял вкладчик?
- По вкладу «А» банк в конце каждого года планирует увеличивать на 7% сумму, имеющуюся на вкладе в начале года, а по вкладу «Б» — увеличивать эту сумму на 6% в первый год и на целое число n процентов во второй год. Найдите наименьшее значение n, при котором за два года хранения вклад «Б» окажется выгоднее вклада «А» при одинаковых суммах первоначальных вкладов.
- По бизнес-плану четырёхлетний проект предполагает начальное вложение — 12 млн рублей. По итогам каждого года планируется прирост вложенных средств на 10% по сравнению с началом года. Начисленные проценты планируется оставлять вложенными в проект. Кроме этого, сразу после начислений процентов потребуются дополнительные вложения: целое число n млн рублей в первый и во второй годы, а также целое число m млн рублей в третий и в четвёртый годы. Найдите наименьшее значение n, при котором первоначальные вложения за два года как минимум удвоятся, и наименьшее такое значение m, что при найденном ранее значении n первоначальные вложения за четыре года как минимум утроятся.