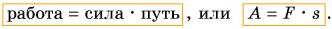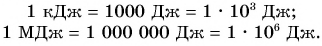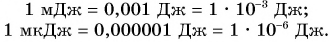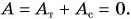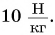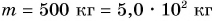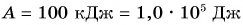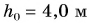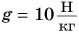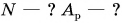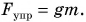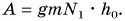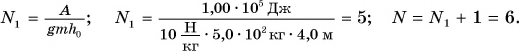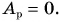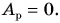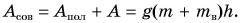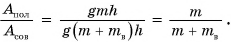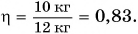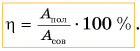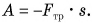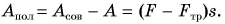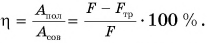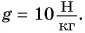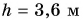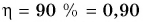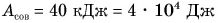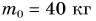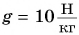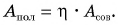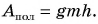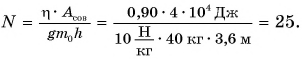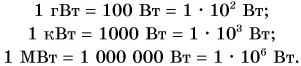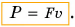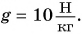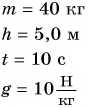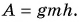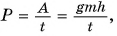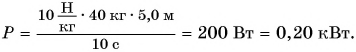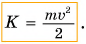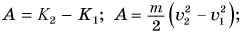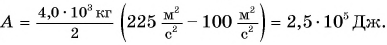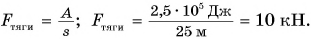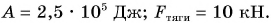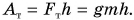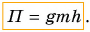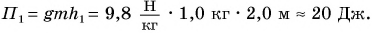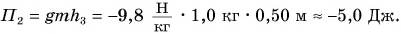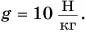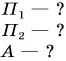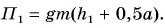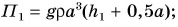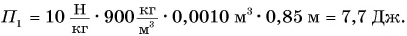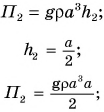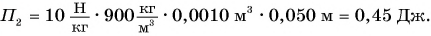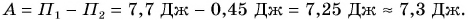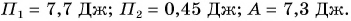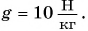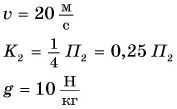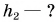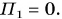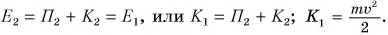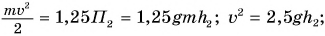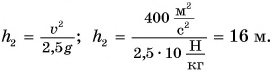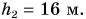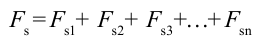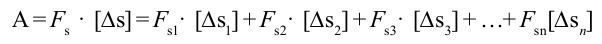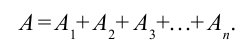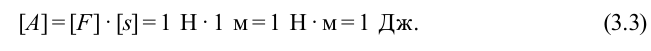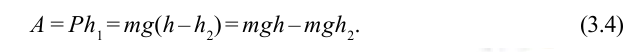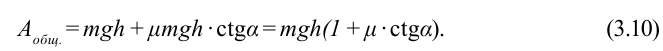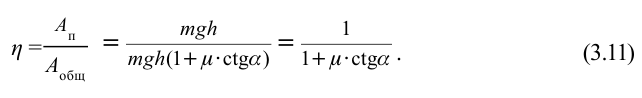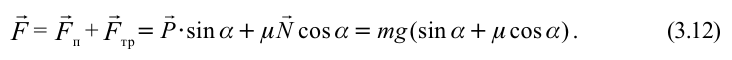Отношение работы к интервалу времени за который эта работа совершена т е это скорость совершения

Работа постоянной силы равна произведению модулей силы и перемещения точки приложения силы и косинуса угла между ними.

Мощность – отношение работы к интервалу времени, за который эта работа совершена, т. е. мощность характеризуется скоростью совершения работы.

Кинетическая энергия – энергия, которой обладает движущееся тело.

Кинетическая энергия материальной точки – величина равная половине произведения массы материальной точки на квадрат её скорости.

Теорема об изменении кинетической энергии: изменение кинетической энергии материальной точки при её перемещении равно работе, совершённой силой, действующей на точку при этом перемещении. Консервативными силами называют силы, работа которых не зависит от формы траектории точки приложения силы и по замкнутой траектории равна нулю.

Потенциальной энергией тела в поле силы тяжести называют величину, равную произведению массы тела на ускорение свободного падения и на высоту тела над поверхностью Земли.

Потенциальной энергией упруго деформированного тела называют величину, равную половине произведения коэффициента упругости тела на квадрат удлинения или сжатия.

Потенциальная энергия – энергия взаимодействия тел, обусловленная их взаимным расположением или взаимным расположением частей тела.

Полная механическая энергия равна сумме кинетической и потенциальной энергий тел, входящих в систему.

Закон сохранения энергии – энергия не создаётся и не уничтожается, а только превращается из одной формы в другую.

Механическая работа и мощность силы

Подробности

Обновлено 13.08.2018 12:29

Просмотров: 585

«Физика — 10 класс»

Закон сохранения энергии — фундаментальный закон природы, позволяющий описывать большинство происходящих явлений.

Описание движения тел также возможно с помощью таких понятий динамики, как работа и энергия.

Вспомните, что такое работа и мощность в физике.

Совпадают ли эти понятия с бытовыми представлениями о них?

Все наши ежедневные действия сводятся к тому, что мы с помощью мышц либо приводим в движение окружающие тела и поддерживаем это движение, либо же останавливаем движущиеся тела.

Этими телами являются орудия труда (молоток, ручка, пила), в играх — мячи, шайбы, шахматные фигуры. На производстве и в сельском хозяйстве люди также приводят в движение орудия труда.

Применение машин во много раз увеличивает производительность труда благодаря использованию в них двигателей.

Назначение любого двигателя в том, чтобы приводить тела в движение и поддерживать это движение, несмотря на торможение как обычным трением, так и «рабочим» сопротивлением (резец должен не просто скользить по металлу, а, врезаясь в него, снимать стружку; плуг должен взрыхлять землю и т. д.). При этом на движущееся тело должна действовать со стороны двигателя сила.

Работа совершается в природе всегда, когда на какое-либо тело в направлении его движения или против него действует сила (или несколько сил) со стороны другого тела (других тел).

Сила тяготения совершает работу при падении капель дождя или камня с обрыва. Одновременно совершает работу и сила сопротивления, действующая на падающие капли или на камень со стороны воздуха. Совершает работу и сила упругости, когда распрямляется согнутое ветром дерево.

Определение работы.

Второй закон Ньютона в импульсной форме Δ = Δt позволяет определить, как меняется скорость тела по модулю и направлению, если на него в течение времени Δt действует сила .

Воздействия на тела сил, приводящих к изменению модуля их скорости, характеризуются величиной, зависящей как от сил, так и от перемещений тел. Эту величину в механике и называют работой силы.

Изменение скорости по модулю возможно лишь в том случае, когда проекция силы F_r на направление перемещения тела отлична от нуля. Именно эта проекция определяет действие силы, изменяющей скорость тела по модулю. Она совершает работу. Поэтому работу можно рассматривать как произведение проекции силы F_r на модуль перемещения |Δ| (рис. 5.1):

А = F_r|Δ|.         (5.1)

Если угол между силой и перемещением обозначить через α, то F_r = Fcosα.

Следовательно, работа равна:

А = |Δ|cosα.         (5.2)

Наше бытовое представление о работе отличается от определения работы в физике. Вы держите тяжёлый чемодан, и вам кажется, что вы совершаете работу. Однако с точки зрения изики ваша работа равна нулю.

Работа постоянной силы равна произведению модулей силы и перемещения точки приложения силы и косинуса угла между ними.

В общем случае при движении твёрдого тела перемещения его разных точек различны, но при определении работы силы мы под Δ понимаем перемещение её точки приложения. При поступательном движении твёрдого тела перемещение всех его точек совпадает с перемещением точки приложения силы.

Работа, в отличие от силы и перемещения, является не векторной, а скалярной величиной. Она может быть положительной, отрицательной или равной нулю.

Знак работы определяется знаком косинуса угла между силой и перемещением. Если α < 90°, то А > 0, так как косинус острых углов положителен. При α > 90° работа отрицательна, так как косинус тупых углов отрицателен. При α = 90° (сила перпендикулярна перемещению) работа не совершается.

Если на тело действует несколько сил, то проекция равнодействующей силы на перемещение равна сумме проекций отдельных сил:

F_r = F_1r + F_2r + … .

Поэтому для работы равнодействующей силы получаем

А = F_1r|Δ| + F_2r|Δ| + … = А₁ + А₂ + … .         (5.3)

Если на тело действует несколько сил, то полная работа (алгебраическая сумма работ всех сил) равна работе равнодействующей силы.

Совершённую силой работу можно представить графически. Поясним это, изобразив на рисунке зависимость проекции силы от координаты тела при его движении по прямой.

Пусть тело движется вдоль оси ОХ (рис. 5.2), тогда

Fcosα = F_x, |Δ| = Δ_х.

Для работы силы получаем

А = F|Δ|cosα = F_xΔx.

Очевидно, что площадь прямоугольника, заштрихованного на рисунке (5.3, а), численно равна работе при перемещении тела из точки с координатой х1 в точку с координатой х2.

Формула (5.1) справедлива в том случае, когда проекция силы на перемещение постоянна. В случае криволинейной траектории, постоянной или переменной силы мы разделяем траекторию на малые отрезки, которые можно считать прямолинейными, а проекцию силы на малом перемещении Δ — постоянной.

Тогда, вычисляя работу на каждом перемещении Δ а затем суммируя эти работы, мы определяем работу силы на конечном перемещении (рис. 5.3, б).

Единица работы.

Единицу работы можно установить с помощью основной формулы (5.2). Если при перемещении тела на единицу длины на него действует сила, модуль которой равен единице, и направление силы совпадает с направлением перемещения её точки приложения (α = 0), то и работа будет равна единице. В Международной системе (СИ) единицей работы является джоуль (обозначается Дж):

1 Дж = 1 Н • 1 м = 1 Н • м.

Джоуль — это работа, совершаемая силой 1 Н на перемещении 1 если направления силы и перемещения совпадают.

Часто используют кратные единицы работы — килоджоуль и мега джоуль:

1 кДж = 1000 Дж,

1 МДж = 1000000 Дж.

Мощность.

Работа может быть совершена как за большой промежуток времени, так и за очень малый. На практике, однако, далеко не безразлично, быстро или медленно может быть совершена работа. Временем, в течение которого совершается работа, определяют производительность любого двигателя. Очень большую работу может совершить и крошечный электромоторчик, но для этого понадобится много времени. Потому наряду с работой вводят величину, характеризующую быстроту, с которой она производится, — мощность.

Мощность — это отношение работы А к интервалу времени Δt, за который эта работа совершена, т. е. мощность — это скорость совершения работы:

Подставляя в формулу (5.4) вместо работы А её выражение (5.2), получаем

Таким образом, если сила и скорость тела постоянны, то мощность равна произведению модуля вектора силы на модуль вектора скорости и на косинус угла между направлениями этих векторов. Если же эти величины переменные, то по формуле (5.4) можно определить среднюю мощность подобно определению средней скорости движения тела.

Понятие мощности вводится для оценки работы за единицу времени, совершаемой каким-либо механизмом (насосом, подъёмным краном, мотором машины и т. д.). Поэтому в формулах (5.4) и (5.5) под всегда подразумевается сила тяги.

В СИ мощность выражается в ваттах (Вт).

Мощность равна 1 Вт, если работа, равная 1 Дж, совершается за 1 с.

Наряду с ваттом используются более крупные (кратные) единицы мощности:

1 кВт (киловатт) = 1000 Вт,
1 МВт (мегаватт) = 1 000 000 Вт.

Источник: «Физика — 10 класс», 2014, учебник Мякишев, Буховцев, Сотский

Законы сохранения в механике — Физика, учебник для 10 класса — Класс!ная физика

Импульс материальной точки —
Закон сохранения импульса —
Реактивное движение. Успехи в освоении космоса —
Примеры решения задач по теме «Закон сохранения импульса» —
Механическая работа и мощность силы —
Энергия. Кинетическая энергия —
Примеры решения задач по теме «Кинетическая энергия и её изменение» —
Работа силы тяжести. Консервативные силы —
Работа силы упругости. Консервативные силы —
Потенциальная энергия —
Закон сохранения энергии в механике —
Работа силы тяготения. Потенциальная энергия в поле тяготения —
Примеры решения задач по теме «Закон сохранения механической энергии» —
Основное уравнение динамики вращательного движения —
Закон сохранения момента импульса. Кинетическая энергия абсолютно твёрдого тела, вращающегося относительно неподвижной оси —
Примеры решения задач по теме «Динамика вращательного движения абсолютно твёрдого тела»

08.11.21                                                                                                                 
 Группа: МЖКХ-9 (физика)

Урок № 35

Тема: Мощность.

Цель: дать
определения понятию мощность. Решение задач на тему мощность.

Тип
урока: урок изучения нового
материала.

Формы
работы: фронтальный опрос,
объяснение, решение задач.

Ход
урока:

1.
Организационный момент

Сегодня на уроке мы определим что такое мощность 
и научимся решать задачи по нахождению мощности.

2.
Повторение
материала.

1.
Дать
определение работа силы? (это воздействие на тело сил, приводящих к
изменению модуля их скорости, характеризуются величиной, зависящей как от сил,
так и от перемещений тел).

2. Чему равна работа (формула)? (А = F|Δ|cosα).

3. Единица измерения работы? (Джоуль — это работа, совершаемая силой 1 Н на перемещении 1
если направления силы и перемещения совпадают).

3.
Изучение
нового материала.

Определение. Работа может быть совершена как за большой промежуток
времени, так и за очень малый. На практике, однако, далеко не безразлично,
быстро или медленно может быть совершена работа. Временем, в течение которого
совершается работа, определяют производительность любого двигателя. Очень
большую работу может совершить и крошечный электромоторчик, но для этого
понадобится много времени. Потому наряду с работой вводят величину,
характеризующую быстроту, с которой она производится, — мощность.

Мощность — это отношение работы А к интервалу времени Δt, за который
эта работа совершена, т. е. мощность — это скорость совершения работы:

    (1)

Подставляя
в формулу (1) вместо работы А её выражение (), получаем:

     
(2)

Таким
образом, если сила и скорость тела постоянны, то мощность равна произведению
модуля вектора силы на модуль вектора скорости и на косинус угла между
направлениями этих векторов. Если же эти величины переменные, то по формуле (1) можно определить среднюю мощность подобно определению
средней скорости движения тела.

Понятие
мощности вводится для оценки работы за единицу времени, совершаемой каким-либо
механизмом (насосом, подъёмным краном, мотором машины и т. д.). Поэтому в
формулах (1) и (2) под  всегда подразумевается сила тяги.

В СИ
мощность выражается в ваттах (Вт).

Наряду с
ваттом используются более крупные (кратные) единицы мощности: 1 кВт (киловатт)
= 1000 Вт, 1 МВт (мегаватт) = 1 000 000 Вт.

4. Закрепление
изученного материала. Решение
задач.

Решение
задач. (Образцы
заданий ЕГЭ)

А1. На горизонтальной поверхности
находится тело, на которое действуют с силой 10 Н, направленной под углом 60° к
горизонту (см. Рис стр.134). Под действием этой силы тело перемещается по
поверхности на 5 м. Работа силы равна

1) 3000 Дж       2) 50 Дж
      3) 25 Дж       4) 0

Решение: по определению работы
постоянной силы . Подставляем значения: А= 10*5= 50* = 25 (Дж). Ответ: 3.

А2. Мальчик тянет санки за верёвку с
силой 50 Н. Пройдя с санками 100 м, он совершил работу 2500 Дж. Чему равен угол
между верёвкой и дорогой?

1) 90°       2) 45°  
    3) 60°       4) 30°

Решение: по определению работы постоянной силы . Подставляем значения:   Ответ: 3.

АЗ. С помощью динамометра,
расположенного под углом 30° к горизонтальной поверхности, равномерно
перемещают брусок массой 100 г на расстояние, равное 20 см. Работа
равнодействующей всех сил равна

1) 0       2) 0,01 Дж  
    3) 0,02 Дж       4) 0,03 Дж

Решение: т.к. перемещение бруска
равномерное, ускорение ɑ=0. Тогда по второму з.Ньютона равнодействующая всех
сил F=ma=0. Значит, по определению работы
постоянной силы: 0.

А4. Под действием силы тяги 1000 Н
автомобиль движется с постоянной скоростью 72 км/ч. Мощность двигателя равна

1) 10 кВт       2) 20 кВт
      3) 40 кВт       4) 72 кВт

Решение: При равномерном движении
перемещение: .По
определению работы: . Найдем
мощность по формуле:  . Подставляем
значения: Р=1000*20=20*10³ (Вт) = 20кВт.

А5. Какую мощность развивает двигатель
подъёмного механизма крана, если он равномерно поднимает плиту массой 600 кг на
высоту 4 м за 3 с?

1) 72 000 Вт       2) 8000
Вт       3) 7200 Вт       4) 800 Вт

Решение: т.к. перемещение плиты
равномерное, ускорение ɑ=0. Тогда по второму з.Ньютона равнодействующая всех
сил F=ma=0. Тогда:F_тяги=mg. Значит, по определению работы: , тогда работа подъёмного механизма: mg. Найдем мощность по формуле: ,подставляем значения:

5.Рефлексия. (2 мин.)

Что вы узнали нового на уроке?

6. Подведение итогов. Д/з. (5 мин.)

Параграф №44

В начале урока мы поставили цель дать
определение понятию мощность и научится решать задачи на тему мощность. Мы
добились результатов?

Озвучить оценки.

Содержание:

Работа, мощность и энергия:

Мы часто слышим от друзей: «Я сегодня выполнил большую работу: выучил наизусть стихотворение и решил пять задач по математике». Но с точки зрения физики никакой работы не совершено, даже если выучить наизусть целую поэму. Что же такое работа в физике?

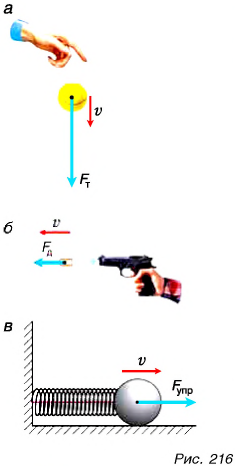
В физике работа оценивает то, что вызвала сила, действуя на движущееся тело. Покажем это на примерах. Рассмотрите внимательно рисунок 216. Что общего в результатах действия силы тяжести на мяч (рис. 216, а), силы давления газа на пулю в пистолете (рис. 216, б) и силы упругости сжатой пружины на шарик (рис. 216, в) после пережигания нити? Все перечисленные силы вызывают разгон тел (мяча, пули, шарика), т. е. увеличение скорости движения.

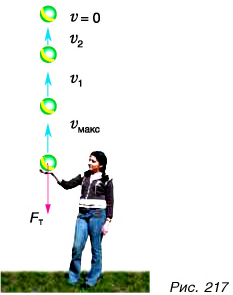
Л может ли сила, действующая на движущееся тело, уменьшать его скорость? Подбросьте мяч и наблюдайте за его движением вверх (рис. 217). Теперь сила тяжести уменьшает скорость его движения. Во всех случаях, когда сила изменяет скорость движения (увеличивает или уменьшает), говорят, что сила совершает механическую работу.

Механическая работа является физической величиной. Ее значение можно рассчитать. Рассмотрим самый простой случай: направление силы совпадает с направлением движения. Например, идет разгон спортивных саней (рис. 218). Изменение скорости саней, а значит, и работа по их разгону зависят от значения действующей силы (силы спортсменов, разгоняющих сани) и от пройденного санями пути. Чем больше сила и путь, тем большая совершается работа. Этот вывод справедлив для всех движущихся под действием силы тел.

Таким образом, механическая работа — физическая величина, пропорциональная действующей на тело силе и пройденному пути.

Обозначим работу буквой А. Тогда, если направление силы совпадает с направлением движения тела,

Единицей работы в СИ является 1 джоуль (1 Дж). Названа она в честь известного английского физика Дж. П. Джоуля. Один джоуль — это работа, совершаемая силой 1 Н на пути 1 м.

1 джоуль = 1 ньютон • 1 метр.

Для измерения большой работы используют кратные джоулю единицы:

В случае малой работы применяются дольные единицы:

Из формулы работы следует, что если есть силы, но нет движения, то нет и работы. Например, сила тяжести, действующая на лежащий на столе мяч (рис. 219, а), работы не совершает, а в случае падающего мяча (рис. 219, б) — совершает.

Сила не всегда увеличивает скорость движения тела. Так, при движении мяча вверх (см. рис. 217) сила тяжести замедляет его движение. Аналогично при скольжении шайбы по льду сила трения уменьшает скорость движения шайбы. Работу силы (тяжести, трения) в подобных случаях считают отрицательной.

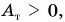
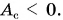
Но положительная и отрицательная работы могут совершаться одновременно и даже быть равными по абсолютной величине. В этом случае скорость движения постоянна. Например, электропоезд на данном участке пути движется равномерно. Это значит, что равнодействующая сил (тяги двигателя и сопротивления движению) равна нулю. По и сила тяги, и сила сопротивления совершают работу. Только работа силы тяги  а силы сопротивления Сумма же их равна 0, т. е.

Главные выводы:

1. Механическая работа характеризует результат действия силы на движущееся тело и пропорциональна действующей на тело силе и пройденному телом пути.
2. Силы, ускоряющие движение тела; совершают положительную работу.
3. Силы, замедляющие движение тела, совершают отрицательную работу.
4. Единица работы в СИ — 1 джоуль (1 Дж).

Пример решения задачи:

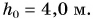
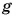
Подъемный кран равномерно поднимает с земли бетонную плиту массой m = 500 кг на один из этажей строящегося дома. Сила упругости троса при этом совершает работу А = 100 кДж. Определите, на какой этаж была поднята плита, если высота одного этажа Чему равна работа равнодействующей сил, приложенных к плите? Коэффициент  примите равным 

Дано:

Решение:

При равномерном подъеме сила упругости троса равна силе тяжести, действующей на плиту: 

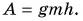
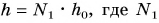
Работа силы упругости  Высота подъема  — число этажей. Тогда 

Отсюда  

Так как движение плиты равномерное, то равнодействующая сил, приложенных к ней, 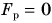 и работа 

Ответ: плита поднята на 6-й этаж; работа равнодействующей сил 

Полезная и совершённая работа

Оценивая работу машины, механизма и др., говорят об их коэффициенте полезного действия (КПД). Но что такое КПД? Что означают слова «полезного действия»? А что такое неполезное действие?

Рассмотрим ситуацию: идет уборка картофеля на поле. Фермер поднимает картофель в ведре в кузов автомашины (рис. 221), выгружает, а ведро опускает на землю. Механическую работу совершает мускульная сила фермера, поднявшего ведро массой, например, 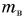 = 2,0 кг и картофель массой m = 10,0 кг на высоту h = 1,5 м. Какая работа здесь является полезной?

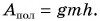
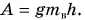
Цель фермера — погрузить в кузов картофель. Исходя из этого, полезной работой является работа по подъему картофеля: А вот работа но подъему самого ведра не является полезной: Вся же совершенная (полная работа) равна:

Какую долю составляет полезная работа от совершенной?

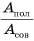
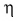
Обозначим отношение  буквой  (эта) и назовем коэффициентом полезного действия (КПД). Тогда

КПД, как правило, выражают в процентах. 

Таким образом, КПД (эффективность работы) в данном случае равен 83 %.

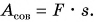
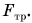
Рассмотрим еще один пример. Дети разгоняют санки, действуя силой F в направлении их движения (рис. 222). Совершенная (полная) работа здесь Цель детей — увеличить скорость движения санок. Но на санки действует еще сила трения скольжения  Она тормозит движение санок. Значит, работа детей по преодолению силы трения не является полезной:

Полезной же работой была

Тогда доля полезной работы (КПД)

Физическая величина, равная отношению полезной работы к совершенной (полной), называется коэффициентом полезного действия.

А могут ли механизм, машина, человек работать так, чтобы КПД = 100 %, т. е. чтобы вся совершенная работа была полезной?

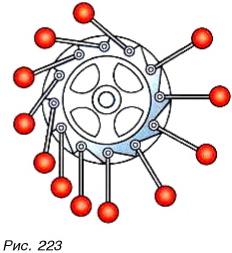
Ученые неоднократно пытались создать такую машину (рис. 223), но все попытки оказались безуспешными. (Самостоятельно познакомьтесь в Интернете или справочной литературе с информацией о вечном двигателе.) В работе любой машины, механизма всегда есть неполезная работа, идущая на преодоление трения, сопротивления. А значит, КПД всегда меньше 100 %. А вот сделать неполезную работу минимальной означает повысить КПД.

Главные выводы:

1. Совершенная (т. е. полная) механическая работа всегда больше полезной.
2. КПД показывает, какую долю составляет полезная работа от всей совершенной.
3. Чем больше полезная работа, тем выше КПД.
4. КПД всегда меньше 100 %.

Пример решения задачи:

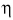
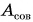
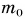
При подъеме картофеля из хранилища глубиной h = 3,6 м подъемным устройством с КПД  = 90 % совершена работа  = 40 кДж. Сколько мешков картофеля массой  = 40 кг каждый было поднято из хранилища? Примите

Дано:

Решение:

Зная совершенную работу и КПД, можно найти полезную работу по подъему мешков картофеля:

Полезная работа — это работа подъемного устройства по преодолению силы тяжести, действующей на картофель:

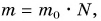
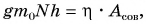
Масса  где N — число мешков картофеля. Тогда  откуда

Ответ: N = 25 мешков.

Мощность и единицы мощности

Приобретая автомобиль (рис. 226), газонокосилку, микроволновую печь (рис. 227) и др., человек интересуется их мощностью. Именно мощность является паспортной характеристикой машин и механизмов. Что же такое мощность? Почему так важно ее знать?

Рассмотрим пример. Человек лопатой копает яму для погреба в течение нескольких дней. Такую же яму экскаватор (рис. 228) выкопает за несколько минут. Работа выполняется одинаковая. Одинаковая масса грунта поднимается на одну и ту же высоту. Но быстрота совершения работы человеком и экскаватором разная. За единицу времени экскаватор выполняет во много раз большую работу, чем человек. Для описания быстроты совершения работы вводится мощность.

Физическая величина, равная отношению работы к промежутку времени, за который эта работа совершена, называется мощностью. Обозначается мощность буквой Р.

За единицу мощности в СИ принимается мощность, при которой действующая на тело сила за время t = 1 с совершает работу А = 1 Дж. Эта единица мощности называется ватт (Вт) в честь английского изобретателя Дж. Уатта. Для измерения больших мощностей используют кратные единицы: гектоватт (гВт), киловатт (кВт), мегаватт (МВт). Обратите внимание:

Для малых мощностей употребляются дольные единицы — милливатт (мВт), микроватт (мкВт): 

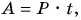
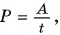
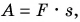
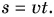
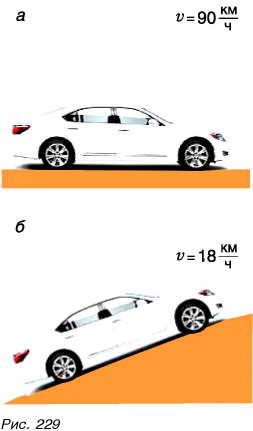
В быту часто необдуманно единицу мощности киловатт принимают за единицу работы. Но работа из чего следует, что единицей работы может быть только киловатт-час (кВт • ч), но не киловатт (кВт). Выразим мощность через другие единицы — силу и скорость. Мощность но работа путь Тогда

Мощность пропорциональна силе, совершающей работу, и скорости движения. Тогда при постоянной мощности чем меньше скорость, тем больше сила. Вот почему водитель, трогаясь с места или поднимаясь в гору (рис. 229), когда требуется большая сила, едет на малой скорости. Тем самым он увеличивает силу тяги двигателя автомобиля.

Главные выводы

1. Мощность — физическая величина, характеризующая быстроту совершения работы.
2. Единицей мощности в СИ является 1 ватт.
3. Одинаковую мощность можно получить либо при большой скорости и небольшой силе, либо при малой скорости и большой силе.

Для любознательных

В автомобилестроении по традиции используют старинную единицу мощности — лошадиную силу (л. с.). С помощью рисунка сформулируйте самостоятельно определение мощности в 1 лошадиную силу.

Запишем связь 1 л. с. и ватта: 1 л. с. = 736 Вт.

В этих внесистемных единицах мощность первого белорусского трактора МТЗ-2 (1953 г.) была равна 37 л. с. Освоенный в 2010 г. трактор «Беларус-3023» имеет двигатель мощностью 300 л. с. Переведите эти знамения мощности в единицы СИ самостоятельно и сравните их.

Пример решения задачи:

На уроке физкультуры мальчик массой m = 40 кг поднялся по канату на высоту h = 5,0 м за промежуток времени t = 10 с. Определите среднюю мощность, развиваемую мальчиком при подъеме. Коэффициент

Дано:

Решение:

При подъеме по канату работа мускульной силы рук идет на преодоление силы тяжести.

Тогда 

Ответ: P = 0, 20 кВт.

Кинетическая энергия

Энергия — одно из наиболее важных и сложных понятий. Причем не только в физике, но и в других науках. А что же такое кинетическая энергия?

Рассмотрим два примера. Шайба, попадая в сетку ворот (рис. 230), прогибает ее. Молот для забивания свай (рис. 231), падая на сваю, загоняет ее в землю на некоторую глубину. Чтобы сильнее прогнуть сетку или глубже забить сваю, шайба и молот должны иметь большую скорость. И шайба, и молот совершили работу. При этом скорость их движения изменилась (уменьшилась до нуля). Совершенные ими работы были разными, даже если предположить, что скорости движения были одинаковыми. Но массы молота и шайбы не равны.

Если тело способно совершить работу, то оно обладает энергией. В физике энергию движущегося тела называют кинетической (от греч. kinetikos — приводящий в движение). Кинетическая энергия обозначается буквой К (или 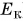) и измеряется в СИ в тех же единицах, что и работа, т. е. в джоулях.

Большая кинетическая энергия движущихся тел — камня, автомобиля, железнодорожного состава (рис. 232), метеорита и др. — означает, во-первых, что при разгоне их до данной скорости разгоняющей силой была совершена большая работа и, во-вторых, при их остановке тормозящей силой будет совершена такая же большая работа.

Из примеров следует, что кинетическая энергия зависит от массы тела и скорости его движения. Какой является эта зависимость?

Опыты показывают, что кинетическая энергия прямо пропорциональна массе тела и квадрату скорости его движения:

Увеличение скорости движения тела, например в 4 раза, приводит к возрастанию кинети- Обратите внимание! ческой энергии в 16 раз. Об этом должны всегда помнить водители и пешеходы.

Главные выводы:

1. Кинетическая энергия выражает способность движущихся тел совершать работу.
2. Кинетическая энергия, как и работа, измеряется в джоулях.
3. Кинетическая энергия тела зависит от его массы и скорости.
4. Изменить (увеличить или уменьшить) кинетическую энергию тела можно только путем совершения работы (положительной или отрицательной).

Пример решения задачи:

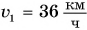
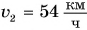
Скорость движения груженого автомобиля массой m = 4,0 т увеличилась от до  на пути s = 25 м. Определите силу тяги двигателя автомобиля и работу, которую совершила эта сила. Сопротивление движению не учитывать.

Дано:

Решение:

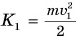
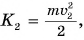
Чтобы увеличить кинетическую энергию от  до  сила тяги должна была совершить работу:

Но работа 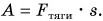 Отсюда 

Ответ: 

Потенциальная энергия

При разгоне любого тела (санок, автомобиля и др.) у него возникает способность совершить механическую работу — у движущегося тела появляется кинетическая энергия. А если тело неподвижно? Обладает ли оно способностью совершить работу?

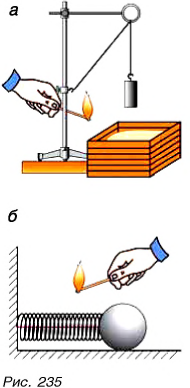
Проведем два опыта. В первом поднимем и укрепим на нити над ящиком с песком гирю (рис. 235, а). Во втором между упором и шариком поместим предварительно сжатую и связанную ниткой пружину (рис. 235, б). Оба тела (гиря и пружина) неподвижны 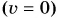 и не обладают кинетической энергией. Но и у гири, и у пружины есть возможность совершить работу. Для этого достаточно в обоих случаях пережечь нить. В физике говорят, что тела (поднятая гиря, взаимодействующая с Землей, и сжатая пружина) обладают потенциальной энергией (от лат. potentia — скрытая способность). Потенциальную энергию в СИ измеряют в тех же единицах, что и работу, — в джоулях.

Важно понимать, что потенциальная энергия не появляется сама по себе. В этих опытах гиря была поднята над столом, пружина была сжата какой-то силой. Значит, чтобы тело запасло потенциальную энергию, необходимо совершить работу. Чем сильнее будет сжата пружина, чем выше будет поднято тело, тем больше у них будет запас потенциальной энергии. Тела, представленные на рисунке 236, уже обладают потенциальной энергией. У трамплина она вызвана прогибом (деформацией) доски, у мышеловки — закручиванием пружины, у лука — изменением расположения древка и тетивы. Из этих и других примеров следует, что потенциальная энергия — это энергия, обусловленная взаимным расположением взаимодействующих тел или частей тела (гири и Земли, стрелы и тетивы, звеньев пружины). Обозначается потенциальная энергия буквой П (или ).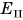

Именно благодаря потенциальной энергии сжатой (закрученной) пружины работают механические часы, реле времени микроволновых печей, стиральных машин, движутся некоторые детские игрушки. Потенциальная энергия поднятой с помощью плотины воды заставляет работать гидроэлектростанции (рис. 237).

Главные выводы:

1. Неподвижные взаимодействующие тела (система тел) могут обладать способностью совершать механическую работу, а значит, потенциальной энергией.
2. Значение потенциальной энергии зависит от взаимного расположения взаимодействующих тел (частей тела).
3. Потенциальная энергия изменяется только при совершении работы.

Расчет потенциальной энергии

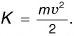
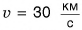
Кинетическая энергия тела, зависящая от его массы и скорости, выражается формулой Данная формула справедлива и для планеты Земля, мчащейся со скоростью по орбите вокруг Солнца, и для невидимого нашему глазу атома. Существует ли единая формула для расчета потенциальной энергии?

Рассмотрим отдельно два случая: потенциальную энергию притяжения поднятого над поверхностью Земли тела и потенциальную энергию деформированного тела.

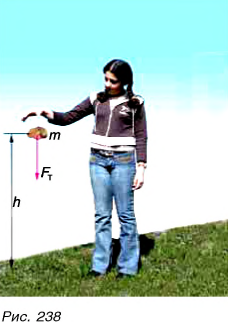
В первом случае формулу для расчета потенциальной энергии легко вывести. Если тело массой m поднято относительно поверхности Земли на высоту h (рис. 238), то при его падении сила тяжести 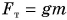может совершить работу:

Это и есть потенциальная энергия поднятого тела:

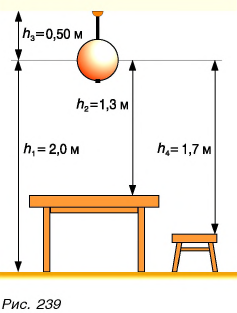
Значение потенциальной энергии относительно. Так, относительно пола потенциальная энергия светильника (рис. 239) массой m = 1,0 кг, центр тяжести которого расположен на высоте 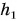 от пола, равна:

Относительно потолка 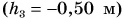 она равна:

Поэтому, приводя значение потенциальной энергии, необходимо указывать уровень, относительно которого она задана, — нулевой уровень потенциальной энергии (это может быть, к примеру, поверхность пола, потолка, стола и т. д.).

Гораздо сложнее дело обстоит с расчетом потенциальной энергии деформированного тела. Мы можем растянуть или сжать пружину, изогнуть или закрутить ее (рис. 240). Потенциальная энергия у пружины будет в каждом из этих случаев. И чем больше упругая деформация, тем больше потенциальная энергия пружины. В данном примере расчет потенциальной энергии придется вести по различным формулам. Более детально с этим вы будете знакомиться в 9-м классе.

Главные выводы:

1. Потенциальная энергия притяжения тела к Земле зависит от массы тела и высоты его подъема над нулевым уровнем энергии.
2. Значение потенциальной энергии тела зависит от выбора нулевого уровня энергии.
3. Потенциальная энергия деформированного тела зависит от величины деформации.

Пример решения задачи:

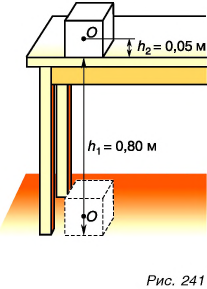
Парафиновый однородный кубик с длиной ребра а = 10 см лежит на столе на высоте 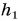 = 0,80 м от пола. Определите потенциальную энергию кубика относительно поверхностей: а) пола; б) стола. Какую работу нужно совершить, чтобы поднять кубик с пола на стол? Коэффициент 

Дано:

Решение:

Потенциальная энергия кубика относительно поверхности пола (рис. 241) определяется положением его центра (точки O):

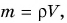
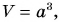
Масса кубика  объем  тогда:

Потенциальная энергия кубика относительно поверхности стола:

Работа по подъему кубика на высоту 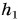 равна изменению его потенциальной энергии. Получаем:

Ответ: 

Закон сохранения механической энергии

Кинетическая и потенциальная энергии — это два вида механической энергии. Связаны ли они друг с другом? И если да, то в чем выражается эта связь?

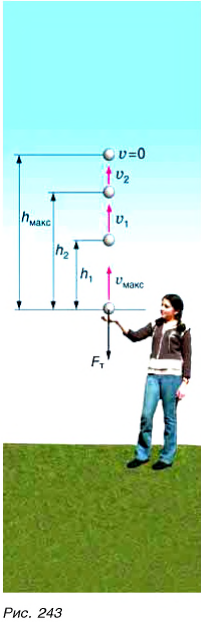
Проследим за движением брошенного вверх металлического шарика (рис. 243). В нижней точке траектории сила действия руки на шарик сообщает ему кинетическую энергию. Шарик движется вверх. Скорость его движения, а значит, и кинетическая энергия уменьшаются. Но исчезает ли кинетическая энергия бесследно? Поднимаясь выше, шарик приобретает все большую потенциальную энергию (вспомните: 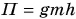). В верхней точке скорость и кинетическая энергия шарика равны нулю, а потенциальная максимальна. Значит, в рассмотренном примере происходит превращение энергии из одного вида (кинетической) в другой (потенциальную). При возвращении шарика обратно снова будет идти превращение энергии: с уменьшением высоты (и потенциальной энергии) увеличивается скорость движения шарика (и кинетическая энергия).

Если сопротивление воздуха мало (и им можно пренебречь), брошенный вверх шарик возвращается назад практически с такой же, как в момент бросания, скоростью и кинетической энергией.

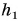
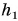
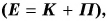
А каким будет значение механической энергии шарика в промежуточных точках? Например, на высоте  (рис. 243)? При подъеме шарика на высоту  его кинетическая энергия уменьшилась, но при этом появилась потенциальная энергия. А чему равна их сумма, т. е. полная механическая энергия? Данный и подобные опыты и расчеты показывают, что если сил сопротивления нет, то полная механическая энергия тела (системы тел), равная сумме кинетической и потенциальной энергий сохраняется. Данное утверждение о постоянстве механической энергии в физике называют законом сохранения механической энергии.

Если силами трения или сопротивления движению нельзя пренебречь, этот закон не выполняется. Заменим в опыте металлический шарик на пенопластовый брусок такой же массы (рис. 244). Мы увидим, что даже при большей, чем у металлического шарика, начальной скорости он не поднимется на такую же высоту и вернется назад с заметно меньшей скоростью. Убывает кинетическая энергия движущейся по горизонтальной поверхности льда шайбы, но потенциальная энергия взамен не появляется. За счет кинетической энергии шайбы совершается работа против сил трения.

В заключение заметим, что явление превращения энергии из одного вида в другой человек научился использовать в практических целях. Энергия падающей воды приводит в действие водяные мельницы и гидроэлектростанции. В Республике Беларусь успешно реализуется государственная программа использования энергии рек. Важная роль в ней отводится таким рекам, как Неман и Западная Двина. Па Немане работает Гродненская ГЭС мощностью 17 МВт. Установленная мощность Витебской ГЭС на Западной Двине — 40 МВт.

Кинетическую энергию ветра человек с давних времен начал использовать с помощью паруса (рис. 245), затем стал применять в ветряных мельницах. В последние годы в нашей стране начато сооружение ветроэлектростанций (рис. 246). Они уникальны тем, что не оказывают вредного воздействия на окружающую среду. Во многих странах успешно используют энергию приливов и отливов вод морей и океанов. Там созданы приливные электростанции.

Главные выводы:

1. Кинетическая и потенциальная энергии взаимо-превращаемы.
2. При отсутствии сил трения и сопротивления движению полная механическая энергия тела (системы тел) сохраняется.
3. Закон сохранения механической энергии не выполняется, если силами трения (сопротивления) нельзя пренебречь.

• Заказать решение задач по физике

Пример решения задачи:

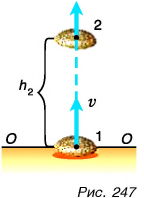
Камень бросили вертикально вверх со скоростью 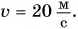На какой высоте от точки бросания кинетическая энергия камня будет в 4 раза меньше его потенциальной энергии? Сопротивлением движению камня пренебречь. Коэффициент

Дано:

Решение:

За нулевой уровень потенциальной энергии примем уровень O — O, проходящий через точку бросания камня (рис. 247). Значит, 

Полная механическая энергия камня в точке бросания 1:

 

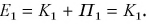
Полная механическая энергия камня в точке 2:

По условию 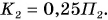Значит,

Ответ: 

Энергия и работа

Энергия – эта количественная мера различных форм движения и взаимодействия (по гречески слово «энергия» означает действие). Энергия в зависимости от вида движения в природе проявляется по-разному. Например, механическая, тепловая, электромагнитная, ядерная энергия и другие. В результате взаимодействия энергия одного вида превращается в энергию другого вида. Однако во всех этих процессах энергия, переданная от одного тела второму (независимо от ее вида), будет равна энергии, полученной вторым телом от первого.

Как известно из второго закона Ньютона, чтобы изменить механическое движение тела на него должны подействовать другие тела. Иначе говоря, среди этих тел происходит обмен энергиями. Для описания такого обмена энергии в механике введено понятие механическая работа, которую принято обозначать буквой .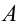

Механическая работа. Величина, равная скалярному произведению силы на перемещение в направлении действия силы, называется механической работой, т.е. 

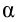
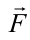
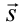
Здесь: – угол между силой  и перемещением s (рисунок 3.1). 
Если учитывать, что 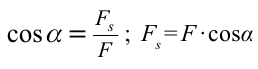, то уравнение (3.1) примет вид:

Здесь 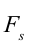– проекция силы в направлении смещения.
Основываясь на выражении (3.2), можно сделать следующий вывод:
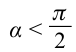
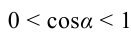
если , то – работа силы положительна, направление силы и смещение совпадают;
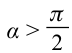
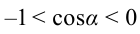
если , то – работа силы отрицательная, направления силы и смещения противоположны;
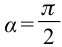
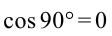
если , то – работа, выполненная силой, равна нулю, направление силы будет перпендикулярным к направлению смещения.
Работа считается аддитивной (аддитив – по-латински означает суммарный) величиной (в физике аддитивность величины означает, что величина, относящаяся к системе в целом, равна сумме величины, относящихся к ее составным частям).
Если на тело действует несколько сил, то будет:

тогда полная работа равна работе, выполненной равнодействующей сил.

или

Единица работы. Единица измерения работы в системе СИ – Джоуль (Дж):

В качестве единицы работы в СИ принята работа выполненная силой 1Н при смещении тела на 1 м.
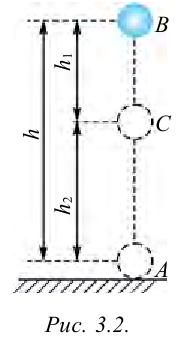
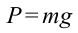
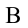
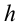
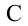
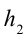
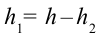
Работа силы тяжести. На поверхности Земли на тело действует сила тяжести со стороны Земли, равная . При перемещении тела из точки на высоте от поверхности Земли в точку на высоте от поверхности Земли, смещение тела равно: (рис. 3.2).

Здесь выполненная силой тяжести работа выражается следующей формулой:

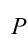
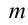
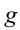
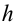
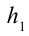
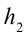
Здесь: – вес тела, – его масса, – ускорение свободного падения, – расстояние между уровнями и  по вертикали.
Работа, выполненная силой тяжести, не зависит от формы пути, зависит только от высоты спуска. Поэтому работа, выполненная под действием силы тяжести, зависит не от формы  траектории, а от начального и конечного состояний. Такая сила называются потенциальной или консервативной. Поле такой силы называется потенциальным полем.

При движении тела вниз из-за соответствия направления силы тяжести и смещения выполненная работа будет положительной, при движении вверх из-за противоположности направлений работа будет отрицательной. Поэтому в случае, когда тело под воздействием силы тяжести смещено и вернулось обратно, выполненная общая работа равняется нулю.

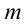
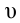
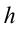
Полной механической энергией системы называется сумма кинетической и потенциальной энергии системы. Например, полная механическая энергия тела массой , двигающегося со скоростью  относительно Земли на высоте от поверхности Земли:

Полная механическая энергия системы остается неизменной с течением времени:
 

Возможны лишь превращения потенциальной энергии и кинетическую и обратно. Выражение (3.5) представляет собой закон сохранения механической энергии.

Проведенные многочисленные эксперименты, теоретические выводы подтвердили строгое соблюдение закона сохранения энергии. 
В природе постоянно происходят превращения одного вида энергии в другой (например, механическая энергия переходит в тепловую энергию). Поэтому этот закон также называют законом сохранения и превращения энергии. Этот закон является основным законом природы и действителен не только для макроскопических, но и микроскопических систем.

Энергия никогда не исчезает, ниоткуда не появляется, она может только преобразовываться из одного вида в другой. 

В закрытых системах полная энергия сохраняется.

Например, потенциальная энергия тела, падающего с высоты 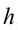, зависит от его веса и абсолютно не зависит от времени проведения экспериментов.
Коэффициент полезного действия. Введена величина, показывающая, какая часть израсходованной энергии машин и двигателей превращается в полезную работу.

Отношение полезной работы к полной работе называется коэффициентом полезного действия (КПД) и обозначается буквой .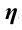 
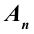
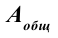
Если полезную работу обозначить , полную работу , тогда формулу КПД можно записать в виде:

КПД не может быть больше единицы (100%). В машинах и двигателях в результате работы силы трения часть полной энергии расходуется и поэтому КПД всегда меньше единицы.

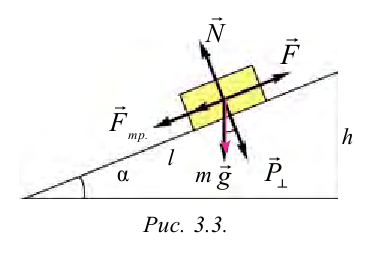
Рассмотрим наклонную плоскость и выполненную работу при подъеме тела вверх. По «золотому правилу» механики, во сколько раз выигрываем в силе, во столько раз проиграем в расстоянии. Но из-за увеличения расстояния смещения не меняется выполненная работа.

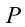
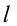
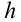
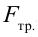
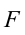
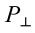
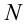
Рассмотрим груз с весом на наклонной плоскости длиной , высотой  (рис. 3.3). Здесь на тело действует сила трения , параллельная наклонной поверхности тянущая вверх сила , перпендикулярно направленная к наклонной плоскости и противоположно направленная перпендикулярно к поверхности сила (реактивная сила поверхности).
Если не учитывать силу трения, получим уравнение:

Однако с учетом силы трения,

Тогда 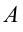пишется в следующем виде:

Коэффициент полезного действия:

Сила притяжения, действующая на груз, равна:
 

• Взрослым: Skillbox, Geekbrains, Хекслет, Eduson, XYZ, Яндекс.
• 8-11 класс: Умскул, Лектариум, Годограф, Знанио.
• До 7 класса: Алгоритмика, Кодланд, Реботика.
• Английский: Инглекс, Puzzle, Novakid.

Механическая работа и мощность силы

Описывать движение тела можно с помощью работы и энергии. Все наши бытовые явления, начинающиеся с подъема с кровати – это работа мышц, которая регулирует особенности нашего движения. Мы можем двигать окружающиеся нас объекты за счёт мышц или же, наоборот, останавливать их. На какие конкретно тела мы воздействуем? Да на какие угодно! Вбивая гвоздь в деревянную стену, мы прикладываем силу к молотку. Если мы играем в футбол во дворе, то объект нашей силы – это мяч.

Но, если мы говорим о масштабном производстве, то одними мышцами тут не справится. Применение машин во много раз увеличивает производительность труда за счёт использования двигателей.

Двигатель – это такое устройство, которое приводит тела в движение и поддерживает это движение, несмотря на воздействие внешних сил (трения, «рабочего сопротивления» и т.д.).

Запишем второй закон Ньютона в импульсной форме: Δp=FΔt. Он позволяет определить зависимость изменения скорости v тела по модулю и направлению от воздействия на него силы F за некоторое время Δt.

Работа

Воздействия на тела сил, приводящих к изменению модуля их скорости, характеризуются величиной, зависящей как от сил, так и от перемещений тел. Эта величина называется работой силы.

Скорость может измениться по модулю только в том случае, когда проекция силы F_r на направление перемещения тела не равна нулю. Именно такая проекция характеризует действие силы, изменяющей скорость тела по модулю. Собственно, поэтому работу можно рассматривать как произведение проекции силы F_r на модуль перемещения |Δr|: A=F_r|Δr|.

Теперь обозначим угол между силой и перемещением α. Получается, что сила будет равна: F_r=Fcosα. Подставляем и получаем: A= F|Δr|cosα.

Таким образом, работа постоянной силы – это произведение модулей силы, перемещения точки и косинуса угла между ними.

Когда твёрдое тело двигается, то все его точки перемещаются неодинаково. Однако при определении работы силы под Δr понимается перемещение её точки приложения (то есть места, куда прикладывается эта сила). В случае поступательного движения перемещение всех точек одинаково, поэтому достаточно учесть одну точку приложения силы.

Мы привыкли к векторным величинам, хотя работа, в отличии от перемещения и силы, является скалярной величиной. Она может быть и положительной, и отрицательной, и равной нулю.

Знак работы зависит от знака косинуса угла между перемещением и силой. В случае, когда α < 90°, то А > 0 (т.к. косинус острых углов положителен). При α > 90° работа, наоборот, отрицательна (т.к. угол тупой). В случае, когда α = 90° работа вовсе не совершается.

Допустим, что на тело действует несколько сил. Тогда проекция равнодействующей силы на перемещение равна сумме проекций отдельных сил: F_r = F_1r + F_2r + … .

В этом случае работа равнодействующей силы равна: А = F_1r|Δr| + F_2r|Δr| + … = А₁ + А₂ + … .

Полная работа при воздействии на тело нескольких сил равна работе равнодействующей силы.

Графическое представление работы

Рассмотрим движение тела вдоль оси ОX: Fcosα = F_x, |Δr| = Δ_х. Следовательно: А = F|Δr|cosα = F_xΔx.

Площадь прямоугольника, который заштрихован на рисунке ниже – это и есть работа при перемещении тела из начальной координаты x₁ в конечную – x₂.

Это мы рассмотрели случай прямолинейного движения. Однако, если тело движется по криволинейной траектории, то необходимо разделить её путь на небольшие отрезки, которые можно считать прямолинейными, а проекцию силы на малом перемещении Δr – постоянной. Далее нужно вычислить работу каждого участка и просуммировать их.

Единица работы

В Международной системе СИ единицей работы является джоуль [Дж]: 1 Дж = 1 Н • 1 м = 1 Н • м.

Джоуль представляет собой работу, которую совершает сила 1 Н при перемещении тела на 1 м, при условии, что направления силы и перемещения одинаковы.

Мощность

Работа может совершаться как быстро, так и медленно. В физике очень важно понимать быстроту процесса. Например, ключевым параметром двигателя является его мощность. То есть время, за которое он завершил работу.

Мощность – это отношение работы A к интервалу времени Δt, за который эта работа совершена. Другими словами, мощность – есть скорость совершения работы: N=A/Δt.

Значит, N=(F|Δr|/Δt)cosα=Fvcosα.

Понятие мощности необходимо для оценки работы за единицу времени. В системе СИ она выражается в ваттах [Вт]. В случае, когда мощность равна 1 Вт, идёт речь о работе, равной 1 Дж, которая совершается в течение 1 с.

Механическая работа, мощность и КПД механизма

1. Механическая работа (или работа силы над телом) – физическая величина, равная по модулю произведению силы на путь, пройденный телом вдоль направления этой силы. Если вектор силы перпендикулярен направлению движения тела, то совершаемая этой силой работа равна нулю; если вектор силы сонаправлен с направлением движения тела, то работу силы считают положительной; если вектор силы противоположен направлению движения тела, то работу силы считают отрицательной.

• В случае, когда точка приложения силы перемещается в направлении действия силы, механическая работа А равна произведению модуля F силы на путь s, пройденный точкой приложения силы: А = Fs.
• Единица работы в СИ 1 Джоуль (Дж) = 1 Нм.
• «Золотое правило» механики с использованием понятия работы: никакой простой механизм не дает выигрыша в работе.

Таблица «Механическая работа, мощность и КПД»

---

2. Коэффициент полезного действия (КПД) – физическая величина, равная отношению полезной работы к полной совершённой работе. КПД показывает долю полезной работы от полной и, как и все доли, всегда имеет положительный знак и не имеет «своей» единицы для измерения. Значение КПД обычно выражают в процентах, которое нужно переводить в десятичную дробь для дальнейших вычислений.

• Коэффициентом полезного действия (КПД) механизма называют отношение полезной работы А_пол к совершенной А_сов, выраженное в процентах: η = А_пол/А_сов · 100%.
• КПД любого реального механизма меньше 100 % (из-за трения и из-за того, что сами механизмы и их части имеют некоторую массу).

3. Мощность действия – физическая величина, равная отношению механической работы ко времени, за которое она была совершена. Мощность характеризует быстроту (скорость) совершения работы. Мощность принято вычислять только для тех действий, в которых механическая работа положительна.

• Мощностью N называют отношение совершенной работы А к промежутку времени t, за который эта работа совершена: N = A/t
• Единица мощности в СИ 1 ватт (Вт) = 1 Дж/с.
• Мощность можно выразить через силу и скорость с помощью формулы N = Fv.

---

Схема «Механическая работа. Мощность»

---

Конспект урока по физике в 7 класса «Механическая работа и энергия».

Смотреть задачи: 1) на механическую работу,  2) механическую мощность, 3) на КПД простых механизмов.

Следующая тема: «Простые механизмы. Блоки»

Популярное на сайте:

Как быстро выучить стихотворение наизусть? Запоминание стихов является стандартным заданием во многих школах. 

Как научится читать по диагонали? Скорость чтения зависит от скорости восприятия каждого отдельного слова в тексте. 

Как быстро и эффективно исправить почерк?  Люди часто предполагают, что каллиграфия и почерк являются синонимами, но это не так.

Как научится говорить грамотно и правильно? Общение на хорошем, уверенном и естественном русском языке является достижимой целью.