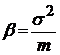В теории надежности наиболее часто используются
следующие законы распределения времени безотказной работы: экспоненциальный,
распределение Вейбулла, нормальный закон распределения или распределение
Гаусса, гамма-распределение.
Экспоненциальный закон
распределения.
Для экспоненциального закона распределения имеем
следующие зависимости:
Где λ – параметр экспоненциального распределения,
которым является интенсивность отказа объекта.
Дисперсия времени безотказной работы равна:
Если λt<<1, то
Важным свойством экспоненциального
распределения
является следующее: вероятность безотказной работы на интервале (t, t+τ) не
зависит от времени предшествующей работы t, а зависит только
от длины интервала τ.
Пусть дан интервал времени (0, t) и (0,
t+τ). Тогда где
– вероятность безотказной работы системы
или элемента за время ;
– вероятность безотказной работы системы
или элемента за время ;
– вероятность безотказной работы системы
или элемента за время , при условии, что объекты безотказно
проработали время t.
В случае экспоненциального закона . Но так как
вероятность безотказной работы объекта до момента времени t равна , то получим
.
Опыт эксплуатации современных устройств и систем показывает,
что во многих случаях их характеристики надежности подчиняются
экспоненциальному закону. Это объясняется тем, что современные системы, в том
числе и системы управления, состоят из высоконадежных первичных элементов.
Рисунок 1. Зависимости показателей надежности для
экспоненциального закона распределения времени безотказной работы.
Равенство среднеквадратического отклонения среднему
времени работы до отказа – характерный признак экспоненциального распределения.
Распределение Вейбулла.
Распределение Вейбулла является двухпараметрическим
распределением и используется часто для оценки показателей надежности при
постепенных отказах, вызываемых старением, износом, недостаточной прочностью и
т.д. изделий или объектов.
Для распределения Вейбулла имеем следующие
зависимости:
Где и
– параметры распределения
Вейбулла.
Где Г – гамма-функция, определяемая по таблицам.
Графики, характеризующие распределение Вейбулла для
различных значений α.
Рисунок 2. Зависимости интенсивновностей
отказов при распределении Вейбулла времени безотказной работы.
При m=1 распределение Вейбулла переходит в
эспоненциальное распределение, а при m=2 – в распределение Рэлея.
Нормальное распределение Гаусса.
Нормальное распределение случайной величины возникает
всякий раз, когда случайная величина зависит от большого числа однородных по
своему влиянию случайных факторов, причем влияние каждого из этих факторов по
сравнению с совокупностью всех остальных – незначительно.
В случае, если σ<<Т (практически, если Т≥3σ),
что соблюдается в большинстве случаев для элементов, используемых в САУ,
получим
Где Т и σ – параметры нормального
распределения, причем Т – математическое ожидание случайной величины – времени
безотказной работы объекта, σ – среднеквадратическое отклонение случайной
величины.
Для определения функции Q(t) часто
пользуются функцией Лапласа Ф(u), где – квантиль нормального распределения
(берется по таблице).
Q(t) связана
с функцией Ф(u) при
σ<<T
соотношением:
Рисунок 3. Зависимости показателей
надежности при нормальном законе распределения времени безотказной работы.
Наблюдения за
эксплуатацией большого количества
однотипных элементов в технических
объектах различного назначения,
работающих в примерно одинаковых
условиях и на схожих по интенсивности
нагрузках, показали, что количество
отказов этих элементов различно в
разные периоды наработки. Можно выделить
три периода наработки, которые заметно
отличаются количеством отказов и
интенсивностью их проявления. На
начальном этапе эксплуатации количество
отказов постепенно снижается (приработка),
затем следует период эксплуатации с
примерно постоянным количеством отказов
в одинаковые интервалы времени и при
дальнейшем увеличении наработки
происходит нарастание числа отказов
вследствие быстрого накопления
повреждений (например, вследствие
износа). Эти периоды эксплуатации
характеризуются определённым значением
интенсивности отказов (t),
показанной на рис.2.
Рис.2. Типичная
-
характеристика
Кривую на рис.2
принято называть -
характеристикой. Как показано на рис.2
первый участок -
характеристики отличается повышенным
уровнем интенсивности отказов. В этот
период (рис.2.,I) происходит приработка
составных элементов объекта, устранение
мелких дефектов изготовления и сборки,
выявление и устранение отступлений от
технической документации. Для данного
этапа эксплуатации объекта иногда
используют термин « этап выжигания
дефектов». При отработке конструкции
и технологии изготовления, а также при
совершенствовании выходного контроля
интенсивность отказов на начальном
этапе эксплуатации может быть снижена.
При нормальной
эксплуатации (рис.2.,II) интенсивность
отказов практически не меняется с
наработкой. Причинами отказов в этот
период бывают, как правило, воздействие
на объект неучтённых при проектировании
факторов или эксплуатация объектов в
условиях, действие которых трудно
предусмотреть заранее.
Третий период
эксплуатации (рис.2.,III) характеризуется
возрастанием интенсивности отказов.
Это обычно связано с предельным
накоплением повреждений в материалах
основных деталей, а также с износом или
старением конструкционных материалов.
Этот период обычно связан с повышенными
материальными затратами а поддержание
работоспособности объектов. Основные
из них идут на запасные части и на
восстановление изношенных деталей.
В практических
расчётах надёжности
— характеристики отдельных элементов
имеют большое значение. Часто модели
надёжности сложных технических систем
полностью создаются на использовании
подобных характеристик. Во многих
случаях решение вопросов обоснования
сроков технического обслуживания,
объёмов регламентных работ невозможно
без знания
— характеристик комплектующих элементов.
Эти характеристики в большинстве своём
получаются на основе статистической
обработки экспериментальных данных
или результатов эксплуатации объектов
– аналогов. Одним из важных моментов
такой обработки является выявление
теоретического закона распределения,
соответствующего реальной статистике
наработок между отказами объекта или
его элементов.
Анализ типовых
— характеристик показывает, что каждый
из этапов эксплуатации (рис.2) может
быть поставлен в соответствие определённому
теоретическому закону распределения.
Обычно период нормальной эксплуатации
соответствует экспоненциальному закону,
а этап старения и повышенного износа
может быть описан нормальным законом,
законом Вейбулла или некоторыми другими.
Приработка элементов может быть
представлена многими теоретическими
законами распределения и в том числе
законом Вейбулла. Таким образом, изучение
особенностей основных теоретических
законов распределения может способствовать
выявлению закономерностей изменения
показателей надёжности реальных
объектов.
Установление закона распределения времени безотказной работы системы по известным законам распределения элементов
КУРСОВОЙ
ПРОЕКТ
Установление
закона распределения времени безотказной работы системы по известным законам
распределения элементов
ЗАДАНИЕ НА КУРСОВУЮ РАБОТУ
Техническая система S состоит
из трех элементов схемы, соединения которых приведены в вариантах заданий на
курсовую работу. Времена безотказной работы Х1, Х2,
Х3 элементов системы являются непрерывными случайными величинами
с известными законами распределения вероятностей. Внешняя среда Е оказывает
воздействие на работу систем виде случайной величины V с известным
дискретным распределением вероятностей.
Требуется оценить надежность системы
S методом статистического моделирования на ЭВМ с последующей обработкой
результатов эксперимента.
СОДЕРЖАНИЕ
Введение
. Разработка алгоритма статистического моделирования
. Статистическая обработка данных
.1 Вычисление основных характеристик выборки
.2 Формирование статистического ряда и графическое представление
данных
.3 Подбор подходящего закона распределения вероятностей
. Определение характеристик надежности системы
Заключение
ВВЕДЕНИЕ
Разработка математических моделей и
методов, позволяющих определить время безотказной работы системы аналитически,
является сложной, а подчас и неразрешимой задачей. С этой целью часто
используется метод статистического моделирования с последующей обработкой
результатов эксперимента. Предметом статистического моделирования является
изучение сложных процессов и систем, подверженных, как правило, воздействию
случайных факторов, путем проведения экспериментов с их моделями.
Суть метода проста — имитируется
“жизнь” системы при многократном повторении испытаний. При этом моделируются и
регистрируются случайно меняющиеся внешние воздействия на систему. Для каждой
ситуации по сравнениям модели просчитываются системные показатели. Существующие
современные методы математической статистики позволяют ответить на вопрос,
можно ли и с каким доверием использовать данные моделирования. Если эти
показатели доверия для нас достаточны, мы можем использовать модель для изучения
данной системы.
Можно говорить об универсальности
статистического моделирования, поскольку оно является одним из наиболее
эффективных средств исследования и проектирования сложных систем по критериям
надежности и часто единственным практически реализуемым методом исследования
процесса их функционирования.
.
РАЗРАБОТКА АЛГОРИТМА СТАТИСТИЧЕСКОГО МОДЕЛИРОВАНИЯ
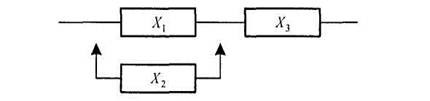
Проведем имитацию работы системы,
структурная схема которой изображена на рисунке 1.1. Согласно схеме, сначала
работают элементы 1 и 3, а элемент 2 находится в резерве. При отказе элемента
X3 наступает отказ системы. При отказе элемента X1 в работу включается элемент
X2, но это событие не является отказом системы. Система откажет, если после
этого произойдет отказ элемента X3 или X2.
Законы распределения времени
безотказной работы элементов и воздействия внешней среды сведены в таблицу 1.
Таблица 1.1 — Законы распределения
времени безотказной работы элементов и V
|
X1 |
X2 |
X3 |
V |
|
U(15;22) |
U(15;22) |
N(19; 2,2) |
П(0;5) |
В таблице 1 приняты следующие
обозначения законов распределения:
N — нормальное распределение;
U — равномерное распределение;
П — распределение Пуассона;
В скобках указаны параметры
распределений.
На листе Excel (таблица 2)
предусмотрим место для значений случайных величин. Колонки А и В —
вспомогательные, в них заносятся равномерно распределенные случайные числа
(РРСЧ) из промежутка [0; 1]. В колонки С, D, Е и F заносятся значения заданных
случайных величин Х1, Х2, Х3 и V соответственно,
полученные путем преобразования РРСЧ. Колонка G служит для значений случайной
величины Y, а колонка Н- для значений случайной величины Z.
Таблица 1.2 — Получение случайных
чисел
|
A |
B |
C |
D |
E |
F |
G |
H |
||||||||||
|
РРСЧ |
РРСЧ |
X1 |
X2 |
X3 |
V |
Y |
Z |
||||||||||
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
|||||||||
|
2 |
0.171 |
0.19231 |
16.1971 |
16.3461 |
22.9949 |
0 |
22.9949 |
22.99489 |
|||||||||
|
3 |
0.8873 |
0.2987 |
21.2108 |
17.0909 |
22.42 |
1 |
22.42 |
22.52002 |
|||||||||
|
4 |
0.3579 |
0.05191 |
17.5056 |
15.3634 |
24.3513 |
2 |
24.3513 |
24.55127 |
|||||||||
|
5 |
0.5222 |
0.14113 |
18.6552 |
15.9879 |
23.3536 |
1 |
23.3536 |
23.45365 |
|||||||||
|
6 |
0.0538 |
0.64018 |
15.3767 |
19.4812 |
21.0778 |
1 |
21.0778 |
21.17783 |
|||||||||
|
7 |
0.7393 |
0.08815 |
20.1754 |
15.617 |
23.8487 |
0 |
23.8487 |
23.84872 |
|||||||||
|
8 |
0.5923 |
0.73397 |
19.1462 |
20.1378 |
20.7303 |
0 |
20.7303 |
20.73028 |
|||||||||
|
9 |
0.6062 |
0.55668 |
19.2434 |
18.8968 |
21.3812 |
0 |
21.3812 |
21.38121 |
|||||||||
|
10 |
0.0735 |
0.19348 |
15.5143 |
16.3543 |
22.9875 |
0 |
22.9875 |
22.98753 |
|||||||||
|
11 |
0.7643 |
0.97502 |
20.3502 |
21.8251 |
19.4949 |
1 |
19.4949 |
19.5949 |
|||||||||
|
12 |
0.3379 |
0.19516 |
17.3655 |
16.3662 |
22.977 |
0 |
22.977 |
22.97697 |
|||||||||
|
13 |
0.5278 |
0.98716 |
18.6943 |
21.9101 |
19.3537 |
0 |
19.3537 |
19.35373 |
|||||||||
|
14 |
0.29 |
0.67286 |
17.0299 |
19.71 |
20.9584 |
1 |
20.9584 |
21.05841 |
|||||||||
|
15 |
0.5915 |
0.0468 |
19.1404 |
15.3276 |
24.4442 |
1 |
24.4442 |
24.54423 |
|||||||||
|
16 |
0.2785 |
0.48554 |
16.9495 |
18.3988 |
21.6446 |
0 |
21.6446 |
21.64457 |
|||||||||
|
17 |
0.3325 |
0.38124 |
17.3272 |
17.6687 |
22.0553 |
0 |
22.0553 |
22.05527 |
|||||||||
|
18 |
0.1347 |
0.29248 |
15.943 |
17.0474 |
22.4496 |
0 |
22.4496 |
22.44964 |
|||||||||
|
19 |
0.1228 |
0.08858 |
15.8596 |
15.6201 |
23.8438 |
0 |
23.8438 |
23.84384 |
|||||||||
|
20 |
0.2 |
0.18879 |
16.4001 |
16.3215 |
23.0172 |
1 |
23.0172 |
23.11719 |
|||||||||
|
21 |
0.183 |
0.64497 |
16.2812 |
19.5148 |
21.0604 |
0 |
21.0604 |
21.06039 |
|||||||||
|
22 |
0.2911 |
0.88163 |
17.0375 |
21.1714 |
20.1043 |
0 |
20.1043 |
20.10433 |
|||||||||
|
23 |
0.3324 |
0.24364 |
17.3271 |
16.7055 |
22.6971 |
1 |
22.6971 |
22.79714 |
|||||||||
|
24 |
0.9455 |
0.76149 |
21.6187 |
20.3304 |
20.6241 |
0 |
20.6241 |
20.62407 |
|||||||||
|
25 |
0.3737 |
0.75757 |
17.6162 |
20.303 |
20.6394 |
0 |
20.6394 |
20.63937 |
|||||||||
|
26 |
0.082 |
0.37502 |
15.5738 |
17.6252 |
22.0812 |
1 |
22.0812 |
22.1812 |
|||||||||
|
27 |
0.75 |
0.58438 |
20.2497 |
19.0907 |
21.2804 |
2 |
21.2804 |
21.48037 |
|||||||||
|
28 |
0.9783 |
0.19576 |
21.8478 |
16.3703 |
22.9733 |
0 |
22.9733 |
22.97325 |
|||||||||
|
29 |
0.2289 |
0.91018 |
16.6025 |
21.3713 |
19.9545 |
0 |
19.9545 |
19.95447 |
|||||||||
|
30 |
0.2389 |
0.18616 |
16.6726 |
16.3031 |
23.034 |
0 |
23.034 |
23.03403 |
|||||||||
|
31 |
0.2318 |
0.89009 |
16.6223 |
21.2307 |
20.0616 |
1 |
20.0616 |
20.16161 |
|||||||||
|
32 |
0.6252 |
0.46095 |
19.3764 |
18.2267 |
21.738 |
1 |
21.738 |
21.83803 |
|||||||||
|
33 |
0.4595 |
0.21629 |
18.2166 |
22.8499 |
0 |
22.8499 |
22.84985 |
||||||||||
|
34 |
0.9072 |
0.53285 |
21.3505 |
18.73 |
21.4685 |
1 |
21.4685 |
21.56854 |
|||||||||
|
35 |
0.5605 |
0.43412 |
18.9238 |
18.0389 |
21.842 |
0 |
21.842 |
21.84205 |
|||||||||
|
36 |
0.5025 |
0.1617 |
18.5174 |
16.1319 |
23.1997 |
0 |
23.1997 |
23.19968 |
|||||||||
|
37 |
0.9112 |
0.88768 |
21.3782 |
21.2138 |
20.0739 |
0 |
20.0739 |
20.07392 |
|||||||||
|
38 |
0.7037 |
0.80659 |
19.926 |
20.6461 |
20.4424 |
0 |
20.4424 |
20.44243 |
|||||||||
|
39 |
0.3227 |
0.76105 |
17.2586 |
20.3273 |
20.6258 |
2 |
20.6258 |
20.82579 |
|||||||||
|
40 |
0.3619 |
0.80267 |
17.5336 |
20.6187 |
20.4587 |
1 |
20.4587 |
20.55869 |
|||||||||
|
41 |
0.1935 |
0.18994 |
16.3547 |
16.3296 |
23.0098 |
1 |
23.0098 |
23.10985 |
|||||||||
|
42 |
0.1079 |
0.19205 |
15.7551 |
16.3443 |
22.9965 |
0 |
22.9965 |
22.9965 |
|||||||||
|
43 |
0.5064 |
0.63815 |
18.5447 |
19.467 |
21.0852 |
1 |
21.0852 |
21.18521 |
|||||||||
|
44 |
0.7882 |
0.91819 |
20.5176 |
21.4274 |
19.9089 |
1 |
19.9089 |
20.00893 |
|||||||||
|
45 |
0.7903 |
0.40227 |
20.5324 |
17.8159 |
21.969 |
1 |
21.969 |
22.06898 |
|||||||||
|
46 |
0.778 |
0.72986 |
20.4458 |
20.109 |
20.7459 |
1 |
20.7459 |
20.84592 |
|||||||||
|
47 |
0.4819 |
0.07686 |
18.373 |
15.538 |
23.9837 |
2 |
23.9837 |
24.18368 |
|||||||||
|
48 |
0.7193 |
0.09148 |
20.035 |
15.6404 |
23.8115 |
0 |
23.8115 |
23.81152 |
|||||||||
|
49 |
0.7091 |
0.48441 |
19.9636 |
18.3909 |
21.6488 |
0 |
21.6488 |
21.64882 |
|||||||||
|
50 |
0.3251 |
0.10511 |
17.2759 |
15.7358 |
23.6697 |
1 |
23.6697 |
23.76975 |
|||||||||
|
51 |
0.4855 |
0.51527 |
18.3987 |
18.6069 |
21.5335 |
1 |
21.5335 |
21.63346 |
|||||||||
|
52 |
0.5394 |
0.85791 |
18.7761 |
21.0054 |
20.218 |
0 |
20.218 |
20.21799 |
|||||||||
|
53 |
0.2186 |
0.35398 |
16.5303 |
17.4778 |
22.1706 |
0 |
22.1706 |
22.17064 |
|||||||||
|
54 |
0.3895 |
0.07278 |
17.7268 |
15.5095 |
24.0363 |
0 |
24.0363 |
24.0363 |
|||||||||
|
55 |
0.5179 |
0.9639 |
18.625 |
21.7473 |
19.5966 |
1 |
19.5966 |
19.69657 |
|||||||||
|
56 |
0.8626 |
0.79521 |
21.0382 |
20.5665 |
20.4894 |
0 |
20.4894 |
20.48935 |
|||||||||
|
57 |
0.7789 |
0.57993 |
20.4526 |
19.0595 |
21.2965 |
0 |
21.2965 |
21.29654 |
|||||||||
|
58 |
0.1587 |
0.21327 |
16.111 |
16.4929 |
22.8675 |
1 |
22.8675 |
22.96752 |
|||||||||
|
59 |
0.8317 |
0.77336 |
20.8219 |
20.4135 |
20.5773 |
0 |
20.5773 |
20.5773 |
|||||||||
|
60 |
0.721 |
0.1639 |
20.0467 |
16.1473 |
23.184 |
1 |
23.184 |
23.28404 |
|||||||||
|
61 |
0.5082 |
0.34413 |
18.5571 |
17.4089 |
22.2134 |
1 |
22.2134 |
22.31341 |
|||||||||
|
62 |
0.7356 |
0.23895 |
20.1492 |
16.6727 |
22.7225 |
0 |
22.7225 |
22.72246 |
|||||||||
|
63 |
0.365 |
0.86286 |
17.5548 |
21.04 |
20.1949 |
1 |
20.1949 |
20.29492 |
|||||||||
|
64 |
0.4651 |
0.1716 |
18.2555 |
16.2012 |
23.1306 |
0 |
23.1306 |
23.13058 |
|||||||||
|
65 |
0.7983 |
0.07606 |
20.5882 |
15.5324 |
23.9938 |
0 |
23.9938 |
23.99381 |
|||||||||
|
66 |
0.5702 |
0.23739 |
18.9911 |
16.6617 |
22.731 |
1 |
22.731 |
22.83101 |
|||||||||
|
67 |
0.6109 |
0.82403 |
19.2762 |
20.7682 |
20.3688 |
0 |
20.3688 |
20.36877 |
|||||||||
|
68 |
0.0041 |
0.2783 |
15.0285 |
16.9481 |
22.5187 |
0 |
22.5187 |
22.51872 |
|||||||||
|
69 |
0.785 |
0.9443 |
20.4949 |
21.6101 |
19.7449 |
1 |
19.7449 |
19.84486 |
|||||||||
|
70 |
0.8918 |
0.53466 |
21.2424 |
18.7426 |
21.4619 |
0 |
21.4619 |
21.4619 |
|||||||||
|
71 |
0.2876 |
0.93123 |
17.0131 |
21.5186 |
19.8305 |
1 |
19.8305 |
19.93049 |
|||||||||
|
72 |
0.7099 |
0.42221 |
19.9692 |
21.8891 |
1 |
21.8891 |
21.98905 |
||||||||||
|
73 |
0.4713 |
0.22849 |
18.2991 |
16.5994 |
22.7803 |
0 |
22.7803 |
22.78025 |
|||||||||
|
74 |
0.0006 |
0.52785 |
15.004 |
18.695 |
21.4869 |
0 |
21.4869 |
21.48695 |
|||||||||
|
75 |
0.0344 |
0.74589 |
15.241 |
20.2213 |
20.6846 |
0 |
20.6846 |
20.68461 |
|||||||||
|
76 |
0.2828 |
0.17089 |
16.9793 |
16.1963 |
23.1354 |
2 |
23.1354 |
23.33543 |
|||||||||
|
77 |
0.345 |
0.70212 |
17.4153 |
19.9148 |
20.8502 |
0 |
20.8502 |
20.85024 |
|||||||||
|
78 |
0.701 |
0.64212 |
19.9067 |
19.4948 |
21.0708 |
0 |
21.0708 |
21.07078 |
|||||||||
|
79 |
0.1174 |
0.87807 |
15.822 |
21.1465 |
20.1219 |
0 |
20.1219 |
20.12192 |
|||||||||
|
80 |
0.2169 |
0.4916 |
16.5182 |
18.4412 |
21.6218 |
0 |
21.6218 |
21.62176 |
|||||||||
|
81 |
0.5866 |
0.03539 |
19.1064 |
15.2477 |
24.6872 |
2 |
24.6872 |
24.88724 |
|||||||||
|
82 |
0.0043 |
0.12656 |
15.0301 |
15.8859 |
23.4732 |
0 |
23.4732 |
23.47316 |
|||||||||
|
83 |
0.8089 |
0.457 |
20.6624 |
18.199 |
21.7532 |
1 |
21.7532 |
21.85319 |
|||||||||
|
84 |
0.7906 |
0.85221 |
20.5345 |
20.9655 |
20.2442 |
1 |
20.2442 |
20.34419 |
|||||||||
|
85 |
0.8737 |
0.40368 |
21.1159 |
17.8258 |
21.9633 |
1 |
21.9633 |
22.06329 |
|||||||||
|
86 |
0.4599 |
0.18859 |
18.2193 |
16.3201 |
23.0185 |
1 |
23.0185 |
23.11848 |
|||||||||
|
87 |
0.5394 |
0.25531 |
18.7761 |
16.7871 |
22.6354 |
0 |
22.6354 |
22.63539 |
|||||||||
|
88 |
0.3042 |
0.54338 |
17.1297 |
18.8037 |
21.4299 |
2 |
21.4299 |
21.62985 |
|||||||||
|
89 |
0.3317 |
0.91946 |
17.3216 |
21.4363 |
19.9015 |
0 |
19.9015 |
19.90154 |
|||||||||
|
90 |
0.8826 |
0.82901 |
21.1779 |
20.8031 |
20.3473 |
1 |
20.3473 |
20.44729 |
|||||||||
|
91 |
0.184 |
0.56785 |
16.288 |
18.975 |
21.3405 |
0 |
21.3405 |
21.34049 |
|||||||||
|
92 |
0.7566 |
0.30612 |
20.2964 |
17.1428 |
22.3851 |
0 |
22.3851 |
22.38513 |
|||||||||
|
93 |
0.8152 |
0.53524 |
20.7063 |
18.7467 |
21.4598 |
0 |
21.4598 |
21.45975 |
|||||||||
|
94 |
0.5689 |
0.25779 |
18.9825 |
16.8045 |
22.6225 |
0 |
22.6225 |
22.62249 |
|||||||||
|
95 |
0.0808 |
0.00626 |
15.5656 |
15.0438 |
26.0083 |
1 |
26.0083 |
26.10827 |
|||||||||
|
96 |
0.3424 |
0.9551 |
17.3965 |
21.6857 |
19.6669 |
0 |
19.6669 |
19.66686 |
|||||||||
|
97 |
0.8418 |
0.38299 |
20.8929 |
17.6809 |
22.048 |
0 |
22.048 |
22.04801 |
|||||||||
|
98 |
0.9332 |
0.33859 |
21.5325 |
17.3701 |
22.2378 |
0 |
22.2378 |
22.23776 |
|||||||||
|
99 |
0.3413 |
0.16508 |
17.3889 |
16.1556 |
23.1757 |
0 |
23.1757 |
23.17575 |
|||||||||
|
100 |
0.8572 |
0.19002 |
21.0002 |
16.3301 |
23.0094 |
0 |
23.0094 |
23.00937 |
|||||||||
|
101 |
0.2131 |
0.14993 |
16.4914 |
16.0495 |
23.2859 |
1 |
23.2859 |
23.38588 |
|||||||||
В ячейки первой строки A1, B1,..,H1
помещаются заголовки таблицы. В ячейки A2 и В2 помещаются РРСЧ в соответствии с
формулами А2=СЛЧИС(), В2=СЛЧИС().
В ячейки C2, D2, E2 помещаются
значения случайных величин X1, X2, X3, первые
две которые имеют равномерное распределение, а третья — нормальное
распределение в соответствии с формулами разыгрывания:
=15+(22-15)*A2,=15+(22-15)*B2,=19+2.2*КОРЕНЬ(-2*LN(C3))*COS(2*ПИ()).
В ячейку F2 помещается значение
дискретной случайной величины V, подчиненной распределению Пуассона.
Рассмотрим структурную схему,
изображенную на рисунке 1. При отказе элемента X3 наступает отказ системы. При
отказе элемента X1 в работу включается элемент X2, но это событие не является
отказом системы. Система откажет, если после этого произойдет отказ элемента X3
или X2. Время до отказа этой системы равно наименьшему из времени совместной
работы элементов X1 и X2 или X3, т.е Y=МИН(X1+X2;X3).
По этому в ячейку G2 помещается
формула, расчет по которой даст значение случайной величины Y:
=МИН(С2+D2;E2),
В ячейку Н2 помещается формула для
расчета случайной величины Z:
= =G2/1+0.1*F2.
В результате этих действий будут
заполнены ячейки второй строки А2, В2,..,H2. По заданию необходимо получить 100
значений данных случайных величин. Поэтому содержимое ячеек А2, В2,..,H2
копируется в следующие строки, вплоть до 101 строки (таблица 1.2)
2. СТАТИСТИЧЕСКАЯ ОБРАБОТКА ДАННЫХ
.1 ВЫЧЕСЛЕНИЕ ОСНОВНЫХ ХАРАКТЕРИСТИК
ВЫБОРКИ
Основными числовыми характеристиками
выборочной совокупности являются: выборочное среднее, выборочная дисперсия,
выборочное среднее квадратическое (или стандартное) отклонение, наименьшее и
наибольшее значения, размах выборки, асимметрия, эксцесс.
Для расчета указанных характеристик
в Excel необходимо поставить курсор в ячейку, в которую будет записано значение
характеристики, вызвать соответствующую функцию и в качестве ее аргумента
указать блок ячеек со статистическими данными.
Для удобства следующих операций
значения случайной величины Z (статистические данные) перепишем на
другой лист в прямоугольный блок ячеек, например в ячейки Al: J10.
Значения вычисляемых характеристик
будем располагать в ячейках с G12 по G19, как показано в таблице 4.3.
Вычисление выборочных характеристик
осуществляется по формулам:
выборочное среднее: G12 = СРЗНАЧ
(А1: J10),
выборочная дисперсия: G13 = ДИСП
(Al: J10),
выборочное среднее квадратическое
отклонение:= СТАНДОТКЛОН(Al: J10) ИЛИ G14 = КОРЕНЬ(G13),
наименьшее значение: G15 = МИН(А1:
J10),
наибольшее значение: G16 = МАКС (Al:
J10),
размах выборки: G17 = G16 — G15,
асимметрия: G18 = СКОС (Al: J10),
эксцесс: G19 = ЭКСЦЕСС(Al: J10).
Таблица 2.1 — Расчет выборочных
характеристик
|
A |
B |
C |
D |
E |
F |
G |
H |
I |
J |
|
|
1 |
22.995 |
22.977 |
20.104 |
21.838 |
22.996 |
20.218 |
22.722 |
21.989 |
23.473 |
22.385 |
|
2 |
22.52 |
19.3537 |
22.797 |
22.85 |
21.185 |
22.171 |
20.295 |
22.78 |
21.853 |
21.46 |
|
3 |
24.551 |
21.0584 |
20.624 |
21.569 |
20.009 |
24.036 |
23.131 |
21.487 |
20.344 |
22.622 |
|
4 |
23.454 |
24.5442 |
20.639 |
21.842 |
22.069 |
19.697 |
23.994 |
20.685 |
22.063 |
26.108 |
|
5 |
21.178 |
21.6446 |
22.181 |
20.846 |
20.489 |
22.831 |
23.335 |
23.118 |
19.667 |
|
|
6 |
23.849 |
22.0553 |
21.48 |
20.074 |
24.184 |
21.297 |
20.369 |
20.85 |
22.635 |
22.048 |
|
7 |
20.73 |
22.4496 |
22.973 |
20.442 |
23.812 |
22.968 |
22.519 |
21.071 |
21.63 |
22.238 |
|
8 |
21.381 |
23.8438 |
19.954 |
20.826 |
21.649 |
20.577 |
19.845 |
20.122 |
19.902 |
23.176 |
|
9 |
22.988 |
23.1172 |
23.034 |
20.559 |
23.77 |
23.284 |
21.462 |
21.622 |
20.447 |
23.009 |
|
10 |
19.595 |
21.0604 |
20.162 |
23.11 |
21.633 |
22.313 |
19.93 |
24.887 |
21.34 |
23.386 |
|
11 |
||||||||||
|
12 |
Выборочное среднее |
21.936 |
||||||||
|
13 |
Выборочная дисперсия |
1.967 |
||||||||
|
14 |
Выборочное ср. квадратичное отклонение |
1.4025 |
||||||||
|
15 |
Наименьшее значение |
19.354 |
||||||||
|
16 |
Наибольшее значение |
26.108 |
||||||||
|
17 |
Размах выборки |
6.7545 |
||||||||
|
18 |
Асимметрия |
0.2381 |
||||||||
|
19 |
Эксцесс |
-0.449 |
.2 ФОРМИРОВАНИЕ СТАТИСТИЧЕСКОГО РЯДА
И ГРАФИЧЕСКОЕ ПРЕДСТАВЛЕНИЕ ДАННЫХ
Для наглядного представления
статистических данных используется группировка. Числовая ось разбивается на
интервалы, и для каждого интервала подсчитывается число элементов выборки,
которые в него попали. Группировка данных производится в следующей
последовательности:
наименьшее значение округляется в
меньшую сторону, а наибольшее — в большую сторону до «хороших» чисел хmin
и хmax;
— выбирается количество
групп k, удовлетворяющее неравенству 6 < k < 20; иногда оно
определяется по формуле .
Например, если объем выборки п=100, то к = 10;
находится шаг по формуле
,
где R = хтах
— хmin — длина промежутка, в котором содержатся статистические
данные;
определяются границы
частичных интервалов:
,
,
,…
;
(1)
в каждом интервале
вычисляются средние значения ;
для каждого интервала ,
i = 1, 2,…,k находятся:
а) частоты пi,
т. е. число выборочных значений, попавших в интервал;
б) относительные частоты
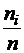
в) накопленные частоты ;
г) накопленные
относительные частоты 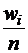
Для выборочной
совокупности (таблица 3.3) результаты группировки в Excel представлены в
таблице 3.4.
Сначала следует указать
объем выборки, максимальное и минимальное значения, размах выборки, количество
групп и шаг:
А23 = 100, В23 = 100,
С23 = 0, D23 = В23 — С23, Е23 = 10, F23 = D23 / Е23.
В ячейках А25: Н25
указываются заголовки таблицы. В этой таблице колонки В и С можно заполнить в
соответствии с формулами (1) или заполнить две строки и скопировать их в
последующие так, чтобы всего получилось k = 10 строк. Колонку D можно
заполнить, используя формулу:
D26 = (В26 + С26) / 2
надежность система
статистический моделирование
с последующим
копированием в ячейки D27: D35.
Таблица 2.2 —
Группировка статистических данных
|
A |
B |
C |
D |
E |
F |
G |
H |
|
|
22 |
n |
Xmax |
Xmin |
R |
k |
h |
||
|
23 |
100 |
29 |
19 |
10 |
10 |
1 |
||
|
24 |
||||||||
|
25 |
Группа |
Левая граница |
Правая граница |
Середина |
Частота |
Относ. Частота |
Накоп. Частота |
Накоп. Относит. Частота |
|
26 |
1 |
19 |
20 |
19.5 |
8 |
0.08 |
8 |
0.08 |
|
27 |
2 |
20 |
21 |
20.5 |
21 |
0.21 |
29 |
0.29 |
|
28 |
3 |
21 |
22 |
21.5 |
22 |
0.22 |
51 |
0.51 |
|
29 |
4 |
22 |
23 |
22.5 |
25 |
0.25 |
76 |
0.76 |
|
30 |
5 |
23 |
24 |
23.5 |
18 |
0.18 |
94 |
0.94 |
|
31 |
6 |
24 |
25 |
24.5 |
5 |
0.05 |
99 |
0.99 |
|
32 |
7 |
25 |
26 |
25.5 |
0 |
0 |
99 |
0.99 |
|
33 |
8 |
26 |
27 |
26.5 |
1 |
0.01 |
100 |
1 |
|
34 |
9 |
27 |
28 |
27.5 |
0 |
0 |
100 |
1 |
|
35 |
10 |
28 |
29 |
28.5 |
0 |
0 |
100 |
1 |
Для заполнения колонки Е следует
выделить ячейки Е26: Е35 и обратиться к функции ЧАСТОТА, указав массив
статистических данных и массив правых границ интервалов:
{= ЧАСТОТА (А1:J10; С26:С35)}.
Одновременное нажатие клавиш
<Ctrl>+<Shift>+<Enter> приведет к заполнению выделенных
ячеек.
Заполнение колонки F производится по
формуле:= Е26 / $А$23
с последующим копированием в ячейки
F27: F35.
Далее заполняются две ячейки колонки
G по формулам: = Е26, G27 = G26 + Е27
с последующим копированием G27 в
ячейки G28: G35.
Колонка Н заполняется по формуле:
Н26 = G26 / $А$23
с последующим копированием в ячейки
Н27: Н35.
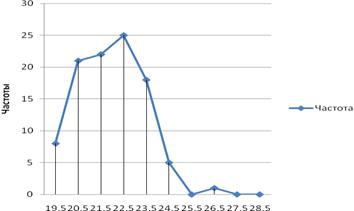
Середины
Рисунок 1 — Полигон частот
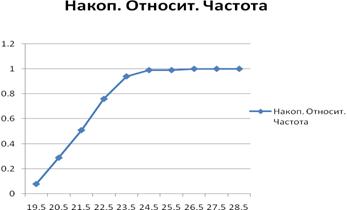
середины
Рисунок 2 — Кумулята частот
Данные, собранные в таблице 2.2,
нуждаются в наглядном представлении. Формами такого наглядного представления
являются:
полигоны частот — графическая
зависимость частот (относительных частот) от середин интервалов (рисунок 1);
кумуляты частот — графическая
зависимость накопленных частот (накопленных относительных частот) от середин
интервалов (рисунок 2).
.3 ПОДБОР ПОДХОДЯЩЕГО ЗАКОНА
РАСПРЕДЕЛЕНИЯ ВЕРОЯТНОСТЕЙ
При достаточно большом объеме
выборки статистические данные позволяют подобрать подходящее распределение
вероятностей. С этой целью можно рассмотреть некоторые известные распределения,
например равномерное, нормальное и гамма-распределение.
Предположим, что случайная величина X
имеет функцию распределения F(x). Будем называть это предположение
гипотезой о виде распределения случайной величины X. Чтобы иметь полную
информацию о распределении случайной величины, надо знать параметры этого
распределения или их некоторые оценки. Как правило, параметры распределений
берутся такими, чтобы математическое ожидание случайной величины X было
равно выборочной средней, а среднее квадратическое отклонение случайной
величины X — выборочному среднему квадратическому отклонению. Указанные
выборочные характеристики находятся в ячейках G12 и G14 соответственно.
Откроем новый лист Excel и поместим
эти значения в ячейки А2 и В2 соответственно (таблица 3.5). Определим параметры
равномерного, нормального и гамма-распределений в соответствии с формулами:
,
,
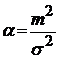
и запишем их в ячейки:=
А2 — В2·КОРЕНЬ(3),= А2 + В2·КОРЕНЬ(3),= А2,= В2,= (А2/В2)^2,= В2^2/А2.
Далее построим таблицу,
шапка которой располагается в ячейках А14: Е14.
В ячейках А15: А24
содержатся середины частичных интервалов, взятые из ячеек D26: D35 предыдущего
листа. В ячейках В15: В24 вычислены плотности относительных частот как частное
от деления относительных частот предыдущего листа (ячейки F26: F35) на
шаг (ячейка $F$23).
Таблица 2.3 — Значения
плотностей распределения
|
A |
B |
C |
D |
E |
||||||
|
1 |
Матем. Ожидание |
Сред. кв. отклонение |
||||||||
|
2 |
21.93637526 |
1.402484928 |
||||||||
|
3 |
||||||||||
|
4 |
Равн.расп |
|||||||||
|
5 |
a |
19.50720011 |
||||||||
|
6 |
b |
24.36555041 |
||||||||
|
7 |
Норм.распр. |
|||||||||
|
8 |
m |
21.93637526 |
||||||||
|
9 |
σ |
1.402484928 |
||||||||
|
10 |
Гамма-распр. |
|||||||||
|
11 |
α |
244.6433013 |
||||||||
|
12 |
β |
0.089666773 |
||||||||
|
14 |
Середина |
Плотность относит. частот |
Плотность равномерного распр. |
Плотность норм. распр. |
плотность Гамма-распр. |
|||||
|
15 |
19.5 |
0.08 |
0 |
0.062908 |
#ЧИСЛО! |
|||||
|
16 |
20.5 |
0.21 |
0.205831185 |
0.168362 |
#ЧИСЛО! |
|||||
|
17 |
21.5 |
0.22 |
0.205831185 |
0.271013 |
#ЧИСЛО! |
|||||
|
18 |
22.5 |
0.25 |
0.205831185 |
0.262387 |
#ЧИСЛО! |
|||||
|
19 |
23.5 |
0.18 |
0.205831185 |
0.152792 |
#ЧИСЛО! |
|||||
|
20 |
24.5 |
0.05 |
0 |
0.053513 |
#ЧИСЛО! |
|||||
|
21 |
25.5 |
0 |
0 |
0.011273 |
#ЧИСЛО! |
|||||
|
22 |
26.5 |
0.01 |
0 |
0.001428 |
#ЧИСЛО! |
|||||
|
23 |
27.5 |
0 |
0 |
0.000109 |
#ЧИСЛО! |
|||||
|
24 |
28.5 |
0 |
0 |
0.000005 |
#ЧИСЛО! |
Плотности равномерного, нормального
и гамма-распределения рассчитываются в соответствии с формулами:
,
,
,
затем они копируются в
блок ячеек С16:Е24.
Построим гистограмму
частот, совмещенную с плотностью каждого из указанных ранее распределений.
Гистограмма частот- это графическое изображение зависимости плотности
относительных частот ni / nh от соответствующего интервала
группировки. В этом случае площадь гистограммы равна единице, и гистограмма
может служить аналогом плотности распределения вероятностей случайной величины X.
Графическое изображение гистограммы и кривых различных распределений приведено
на рисунках 3 — 5. При этом используется нестандартная диаграмма типа
«График | гистограмма».
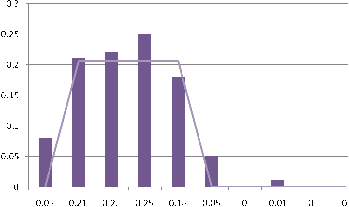
Рисунок 3 — Сглаживание
гистограммы плотностью равномерного распределения
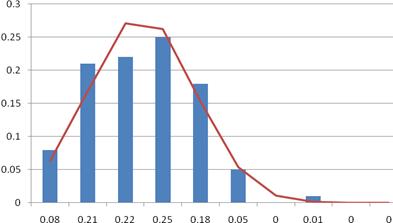
Рисунок 4 — Сглаживание
гистограммы плотностью нормаьного распределения
По внешнему виду этих
графиков вполне можно судить о соответствии кривой распределения данной
гистограмме, т. е. о том, какая кривая ближе к полученной гистограмме.
Используя критерий ,
надо установить, верна ли принятая нами гипотеза о распределении случайной
величины X, т. е. о соответствии функции распределения F(x) экспериментальным
данным, чтобы ошибка не превышала заданного уровня значимости (вероятность
того, что будет отвергнута правильная гипотеза).
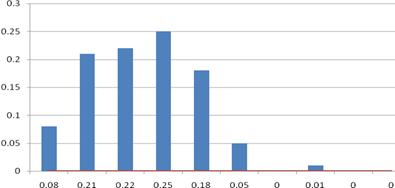
Рисунок 5 — Сглаживание
гистограммы плотностью гамма-распределения
Для применения критерия необходимо,
чтобы частоты пi, соответствующие каждому интервалу, были не
меньше 5. Если это не так, рядом стоящие интервалы объединяются, а их частоты
суммируются. В результате общее количество интервалов может уменьшиться до
значения .
Далее вычисляется следующая сумма:
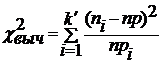
где рi —
теоретическая вероятность того, что случайная величина X примет значение
из интервала [ai-1, аi]. Мы предположили,
что случайная величина X имеет функцию распределения F(x), поэтому
pt =F(ai)-F(ai-1). Образец расчетов по
формуле (2) в Excel для трех распределений показан в таблице 6.
В колонке А содержатся
левые, а в колонке В — правые границы интервалов. В колонке С находятся
соответствующие частоты. Заметим, что интервалы с 5-го по 10-й объединены в
один, чтобы все частоты были не менее пяти. Количество интервалов вместо k =
10 стало равным k’ = 5. В колонке D рассчитываются теоретические
вероятности в зависимости от вида распределения. Как обычно, вычисляется одно
значение, которое копируется в другие ячейки:
для равномерного
распределения:
= ЕСЛИ(В45 < $В$5; 0;
ЕСЛИ(В45 <= $В$6,
(В45 — $В$5)/($В$6 —
$В$5); 1)) — ЕСЛИ(А45 < $В$5; 0,
ЕСЛИ(А45 <= $В$6;
(А45 — $В$5)/($В$6 — $В$5); 1)).
для нормального
распределения:
D52 = НОРМРАСП(В53;
$В$8; $В$9; ИСТИНА) — НОРМРАСП(А53; $В$8; $В$9; ИСТИНА).
для
гамма-распределения:=ГАММАРАСП(В61; $В$11; $В$12; ИСТИНА)- ГАММАРАСП(А61;
$В$11; $В$12; ИСТИНА).
Таблица 2.4 — Подбор
распределения на основе критерия χ2
|
A |
B |
C |
D |
E |
|
|
43 |
Левая граница |
Правая граница |
Частота |
Вероятности |
χ² |
|
44 |
Равномерное распределение |
||||
|
45 |
19 |
20 |
8 |
0.101433585 |
0.452905772 |
|
46 |
20 |
21 |
21 |
0.205831185 |
0.008443336 |
|
47 |
21 |
22 |
22 |
0.205831185 |
0.097533966 |
|
48 |
22 |
23 |
25 |
0.205831185 |
я |
|
49 |
23 |
24 |
18 |
0.205831185 |
0.324173482 |
|
50 |
24 |
29 |
6 |
0.075241675 |
0.308749983 |
|
51 |
Сумма |
1.191806539 |
|||
|
52 |
Нормальное распределение |
||||
|
53 |
19 |
20 |
8 |
0.06554593 |
0.318738516 |
|
54 |
20 |
21 |
21 |
0.168487582 |
1.022793981 |
|
55 |
21 |
22 |
22 |
0.265914992 |
0.792804683 |
|
56 |
22 |
23 |
25 |
0.257797892 |
0.02358713 |
|
57 |
23 |
24 |
18 |
0.153519334 |
0.456766991 |
|
58 |
24 |
29 |
6 |
0.070590439 |
0.158884685 |
|
59 |
Сумма |
2.773575986 |
|||
|
60 |
Гамма-распределение |
||||
|
61 |
19 |
20 |
8 |
0.065581985 |
0.316976029 |
|
62 |
20 |
21 |
21 |
0.175459958 |
0.679935488 |
|
63 |
21 |
22 |
22 |
0.270652617 |
0.947963351 |
|
64 |
22 |
23 |
25 |
0.252103096 |
0.001754447 |
|
65 |
23 |
24 |
18 |
0.147637418 |
0.709397903 |
|
66 |
24 |
29 |
6 |
0.073695366 |
0.254511305 |
|
67 |
Сумма |
2.910538523 |
|||
|
68 |
|||||
|
69 |
Критическое значение критерия |
5.991464547 |
В колонке Е рассчитываются слагаемые
соотношения (2) по формуле:
Е45 = (С45 — 100·D45)^2/(100·D45),
которая копируется в другие ячейки колонки Е.
Согласно (2) для каждого
рассмотренного распределения определяются итоговые суммы:
Е51 = СУММ(Е45:Е50),
Е59 = СУММ(Е53:Е58),
Е67 = СУММ(Е61:Е66),
которые равны соответственно 11,095,
10,945и 2,576.
Гипотеза о виде закона
распределения должна быть принята, если вычисленное значение достаточно
мало, а именно не превосходит критического значения которое
определяется по распределению в
зависимости от заданного уровня значимости и числа степеней
свободы .
Здесь s — число неизвестных параметров распределения, которые были
определены по выборке (для равномерного, нормального и гамма-распределения s
= 2). В данном примере r = k’—s-1 = 5-3 = 2. Полагая =
0,05, критическое значение критерия в
Excel рассчитывается по формуле:
Е66 = ХИ2ОБР(0,05;2)
Поскольку 2.77<
5,991, то принимается гипотеза о том, что статистические данные имеют
нормальное распределение с параметрам m=21.936 и σ
=1.402 соответственно.
3. ОПРЕДЕЛЕНИЕ
ХАРАКТЕРИСТИК НАДЕЖНОСТИ СИСТЕМЫ
В разделе 2.3 было
установлено, что случайная величина Z принадлежит множеству
Г(244.64;0.089) с плотностью распределения вероятностей:
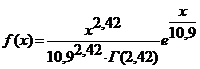
Основными
характеристиками надежности невосстанавливаемой системы являются среднее время
безотказной работы и вероятность безотказной работы в течение времени t.
Среднее время
безотказной работы системы T1 равно математическому ожиданию m,
т. е. T1 = 26,38 час.
Вероятность безотказной
работы вычисляется по формуле:
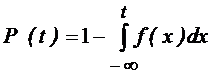
Построим график функции ,
используя Excel. В ячейках А71: А91 запишем значения аргумента t,
изменяющегося от 0 до 27 часов с шагом 1 час.
Так как случайная
величина Z имеет нормальное распределение, то в ячейку В71 записывается
формула:
В71 = 1 — НОРМРАСП(А71;
$В$8; $В$9; ИСТИНА),
которая затем копируется
в ячейки В72: В98 (таблица 3.7). При этом используется аргумент истина,
который, согласно равенству (3), соответствует интегральной функции
распределения (а не плотности распределения). В результате будет получена
таблица значений вероятности безотказной работы , график
которой представлен на рисунке 6.
Таблица 3 — Значения
вероятности безотказной работы системы
|
68 |
A |
B |
|
69 |
Вероятность безотказной работы |
|
|
70 |
t,час |
P(t) |
|
71 |
0 |
1 |
|
72 |
1 |
1 |
|
73 |
2 |
1 |
|
74 |
3 |
1 |
|
75 |
4 |
1 |
|
76 |
5 |
1 |
|
77 |
6 |
1 |
|
78 |
7 |
1 |
|
79 |
8 |
1 |
|
80 |
9 |
1 |
|
81 |
10 |
1 |
|
82 |
11 |
1 |
|
83 |
12 |
1 |
|
84 |
13 |
1 |
|
85 |
14 |
0.999999992 |
|
86 |
15 |
0.999999621 |
|
87 |
16 |
0.999988458 |
|
88 |
17 |
0.999784011 |
|
89 |
18 |
0.997497524 |
|
90 |
19 |
0.981856407 |
|
91 |
20 |
0.916310477 |
По таблице 3 и графику
функции (рисунок
6) можно определить вероятность того, что система безотказно проработает в
течение заданного времени.
Рисунок 6 — График
вероятности безотказной работы системы
ЗАКЛЮЧЕНИЕ
В данной курсовой работе
изучили методы статистического моделирования применительно к задачам нахождения
законов распределения времени безотказной работы и показателей надежности
технических систем с использованием прикладных программных средств.
Оценили надежность
системы S методом статистического моделирования на ЭВМ.
Разработали алгоритмы
разыгрывания случайных величин Х1,Х2,Х3 и V с использованием генераторов
случайных чисел, содержащихся в Microsoft Excel.
Определили время
безотказной работы системы Y в зависимости от времени безотказной работы
Х1,Х2,Х3 элементов на основе структурной схемы расчета надежности.
Определили время
безотказной работы системы с учетом влияния внешней среды Z.
Построили моделирующий
алгоритм, имитирующий работу системы S и учитывающий возможность отказа
элементов и случайные воздействия внешней среды E. Реализовали полученный
алгоритм на ЭВМ.
Сформировали
статистический ряд, содержащий границы и середины частичных интервалов, а также
соответствующие частоты; вычислили относительные, накопленные и накопленные
относительные частоты.
Для величины Z построили
полигон и кумуляту частот. Рассмотрели три непрерывных
распределения(равномерное, нормальное, гамма-), изобразили на гистограмме для Z
плотности этих распределений.
С помощью критерия выполнили
проверку справедливости гипотезы о соответствии статистических данных выбранным
распределениям, в данном случае статические данные имеют нормальное распределение.
Определили плотность
распределения, математическое ожидание, дисперсию и среднее квадратическое
отклонение времени безотказной работы Z системы. Определили основные
характеристики надежности системы.
ЛИТЕРАТУРА
1 Зорин В.А., Бочаров B.C. Надежность машин: Учебник. —
Орел: Изд. ОрелГТУ,2010. — 549с.
Шарыпов А.В., Осипов Г.В. Основы теории надежности
транспортных систем: Учебное пособие. — Курган: Изд-во Курганского гос. ун-та,
2006.- 128 с.
Половко А.М.,Гуров С.В. Основы теории надежности. — СПб.:
БХВ-Петербург, 2009. — 704 с.
Половко А.М.,Гуров С.В. Основы теории надежности.
Практикум. — СПб.: БХВ-Петербург, 2006. — 560 с.
Распределение — время — безотказная работа
Cтраница 1
Распределение времени безотказной работы представляет существенный интерес при решении ряда практических вопросов. Сюда относятся вопросы контроля качества продукции, расчета межоперационных запасов и ряд других. Поэтому необходимо изучить теоретические схемы возникновения неисправностей и соответствующие им распределения времени безотказной работы.
[1]
Распределение времени безотказной работы сложных систем в большом числе случаев можно аппроксимировать экспоненциальным распределением, поэтому рассмотрим случай показательного распределения. Предположим, что проверки производят через каждые х единиц времени.
[2]
Такое распределение времени безотказной работы называется экспоненциальным.
[4]
Отклонения распределения времени безотказной работы от экспоненциального происходят в основном по двум причинам: 1) преобладают ранние отказы из-за элементов со скрытыми дефектами, не обнаруженными во время выходного контроля производства и тренировки; 2) преобладают поздние отказы из-за постепенного износа деталей, накапливаемого разрушения, усталости и пр. На участке старения система имеет возрастающую со временем интенсивность отказов. Как показано в [21], при высокой однородности качества изделий модель с постоянной средней скоростью износа и накоплением разрушений приводит к гамма-распределению с целочисленным параметром &1. Именно такое распределение наблюдается в системе при последовательном соединении элементов, имеющих гамма-распределение времени безотказной работы, параметры которого несколько изменяются от элемента к элементу.
[5]
Закон распределения времени безотказной работы хроматографа — экспоненциальный.
[6]
Требуется исследовать распределение времени тк безотказной работы устройства.
[7]
Экспоненциальный закон распределения времени безотказной работы применим к механизмам, прошедшим предварительную приработку. Этот вид распределения используется также при анализе внезапных отказов.
[8]
Если закон распределения времени безотказной работы известен по предшествующей аппаратуре, то табл. 30 — 12 дает достаточную исходную информацию для определения показателей безотказности. Подобную же таблицу необходимо иметь и для определения показателей ремонтопригодности.
[9]
Если закон распределения времени безотказной работы данной аппаратуры — по опыту эксплуатации предшествующей аппаратуры не был определен, то табл. 5 — 10 дает достаточную исходную информацию, чтобы наряду с показателями безотказности аппаратуры найти и закон распределения. Подобную же таблицу необходимо иметь и для определения показателей ремонтопригодности.
[10]
Требуется выявить закон распределения времени безотказной работы.
[11]
Анализ кривых плотностей распределения времени безотказной работы насосов показал, что отказы насосов по причине износа рабочих колес, изготовленных из стали 20Х13Л, начинают появляться уже после IOOO-IIOO часов, в то время как для насосов с рабочими колесами из стали XI7H2I они появляются лишь после 2000 — 3000 часов работы насосов.
[12]
Для выявления закона распределения времени безотказной работы подшипникового узла, составим табл. 1 [35], в которой введены следующие обозначения: xt — вариационный ряд наработок между отказами; n — L — наблюдаемые числа появления наработок между отказами; Я, — суммы частот наработок; п — число опытов.
[13]
Выше указывалось, что распределение времени безотказной работы устройств обычно подчиняется экспоненциальному закону.
[14]
Экспоненциальный закон хорошо описывает распределение времени безотказной работы объектов при внезапных отказах, распределение времени между соседними отказами и времени восстановления. Для объектов, у которых явно выражены при эксплуатации явления износа и старения, применение1 экспоненциального закона недопустимо.
[15]
Страницы:
1
2
3
4